Bisymulacja, automaty czasowe
|
|
|
- Lidia Domańska
- 7 lat temu
- Przeglądów:
Transkrypt
1 Krzysztof Nozderko 13 grudzień 2005
2 Plan wykładu 1 Automaty czasowe 2 Regiony 3 Bisymulacja
3 Plan wykładu 1 Automaty czasowe 2 Regiony 3 Bisymulacja
4 Plan wykładu 1 Automaty czasowe 2 Regiony 3 Bisymulacja
5 Automaty czasowe Automat czasowy to model matematyczny do modelowania zachowań w systemach zależnych od czasu.
6 Automaty czasowe Automat czasowy to model matematyczny do modelowania zachowań w systemach zależnych od czasu. Automat czasowy = +
7 Automaty czasowe - przykład start Zwróćmy uwagę na: a x:=0, y:=0 miejsca/lokacje: start, loop, end zegary: x, y loop x<=10 c end y>=20 x:=0, y:=0 b x==10 x:=0 niezmiennik lokacji: x<=10 etykiety akcji: a, b, c warunki umożliwienia akcji: x==10, y>=20 resetowanie zegarów: x:=0, y:=0
8 Automaty czasowe - przykład start Zwróćmy uwagę na: a x:=0, y:=0 miejsca/lokacje: start, loop, end zegary: x, y loop x<=10 c end y>=20 x:=0, y:=0 b x==10 x:=0 niezmiennik lokacji: x<=10 etykiety akcji: a, b, c warunki umożliwienia akcji: x==10, y>=20 resetowanie zegarów: x:=0, y:=0
9 Automaty czasowe - przykład start Zwróćmy uwagę na: a x:=0, y:=0 miejsca/lokacje: start, loop, end zegary: x, y loop x<=10 c end y>=20 x:=0, y:=0 b x==10 x:=0 niezmiennik lokacji: x<=10 etykiety akcji: a, b, c warunki umożliwienia akcji: x==10, y>=20 resetowanie zegarów: x:=0, y:=0
10 Automaty czasowe - przykład start Zwróćmy uwagę na: a x:=0, y:=0 miejsca/lokacje: start, loop, end zegary: x, y loop x<=10 c end y>=20 x:=0, y:=0 b x==10 x:=0 niezmiennik lokacji: x<=10 etykiety akcji: a, b, c warunki umożliwienia akcji: x==10, y>=20 resetowanie zegarów: x:=0, y:=0
11 Automaty czasowe - przykład start Zwróćmy uwagę na: a x:=0, y:=0 miejsca/lokacje: start, loop, end zegary: x, y loop x<=10 c end y>=20 x:=0, y:=0 b x==10 x:=0 niezmiennik lokacji: x<=10 etykiety akcji: a, b, c warunki umożliwienia akcji: x==10, y>=20 resetowanie zegarów: x:=0, y:=0
12 Automaty czasowe - przykład start Zwróćmy uwagę na: a x:=0, y:=0 miejsca/lokacje: start, loop, end zegary: x, y loop x<=10 c end y>=20 x:=0, y:=0 b x==10 x:=0 niezmiennik lokacji: x<=10 etykiety akcji: a, b, c warunki umożliwienia akcji: x==10, y>=20 resetowanie zegarów: x:=0, y:=0
13 Automaty czasowe - zegary Zegary moga występować zegary - zmienne o wartościach z R + {0} Oznacza się je jako x, y, z,...
14 Przykład z życia podwójne kliknięcie start przyciskam Podwójne kliknięcie wcisnieta_mysz chcemy podwójnie kliknać (ang. doubleclick) w ikonę kursor myszki nieruchomo znajduje się nad ikona puszczam x:=0 zwolniona_mysz przyciskam x>1 przyciskam x<=1 aplikacja
15 Przykład z życia menadżer logowania Menadżer logowania uruchamiamy komputer dostępne: Linux i Windows domyślnie Linux wybór strzałkami i Enterem start x<=10 linux x==10 x<10 Enter Enter start_linuxa strzalka strzalka x<10 strzalka start_windowsa Enter windows
16 Automat czasowy - oznaczenia Wstęp do definicji C - skończony zbiór zegarów, np: {x, y,...} Σ - skończony alfabet, np: {a, b,...} oznaczajacy akcje B(C) - zbiór ograniczeń zegarów; koniunkcja ograniczeń (górnych i/lub dolnych) nakładanych na: poszczególne zegary, np: x > 4, 2 y < 3, z < 20,... różnicę dowolnych dwóch zegarów, np: x y < 3, 1 < y z 7
17 Automat czasowy - oznaczenia Wstęp do definicji C - skończony zbiór zegarów, np: {x, y,...} Σ - skończony alfabet, np: {a, b,...} oznaczajacy akcje B(C) - zbiór ograniczeń zegarów; koniunkcja ograniczeń (górnych i/lub dolnych) nakładanych na: poszczególne zegary, np: x > 4, 2 y < 3, z < 20,... różnicę dowolnych dwóch zegarów, np: x y < 3, 1 < y z 7
18 Automat czasowy - oznaczenia Wstęp do definicji C - skończony zbiór zegarów, np: {x, y,...} Σ - skończony alfabet, np: {a, b,...} oznaczajacy akcje B(C) - zbiór ograniczeń zegarów; koniunkcja ograniczeń (górnych i/lub dolnych) nakładanych na: poszczególne zegary, np: x > 4, 2 y < 3, z < 20,... różnicę dowolnych dwóch zegarów, np: x y < 3, 1 < y z 7
19 Automat czasowy - oznaczenia Wstęp do definicji C - skończony zbiór zegarów, np: {x, y,...} Σ - skończony alfabet, np: {a, b,...} oznaczajacy akcje B(C) - zbiór ograniczeń zegarów; koniunkcja ograniczeń (górnych i/lub dolnych) nakładanych na: poszczególne zegary, np: x > 4, 2 y < 3, z < 20,... różnicę dowolnych dwóch zegarów, np: x y < 3, 1 < y z 7
20 Automat czasowy - oznaczenia Wstęp do definicji C - skończony zbiór zegarów, np: {x, y,...} Σ - skończony alfabet, np: {a, b,...} oznaczajacy akcje B(C) - zbiór ograniczeń zegarów; koniunkcja ograniczeń (górnych i/lub dolnych) nakładanych na: poszczególne zegary, np: x > 4, 2 y < 3, z < 20,... różnicę dowolnych dwóch zegarów, np: x y < 3, 1 < y z 7
21 Interpretacja warunku x < 1 y 4 interpretacja warunku x < C = {x, y} x
22 Ograniczenia zegarów B(C) stałe użyte do ograniczania zegarów sa liczbami wymiernymi liczby wymierne występuja dostatecznie gęsto x>3/4 x>9/8 x<7/8 x<4/3 mnożymy wszystkie stałe przez wspólny mianownik ułamków - w efekcie wszystkie stałe sa naturalne x>18 x>27 x<21 x<32
23 Automat czasowy - definicja Definicja Automat czasowy A jest krotka <N, l 0, E, I>, gdzie: N to skończony zbiór lokacji l 0 N to lokacja poczatkowa E N B(C) Σ 2 C N, to zbiór krawędzi Piszemy l g,a,r l gdy (l,g,a,r,l ) E I : N B(C) przyporzadkowuje lokacjom ich niezmienniki;
24 Automat czasowy - semantyka System tranzykcyjny Najprostsza semantyka automatu czasowego jest tzw. system tranzakcyjny, oznaczany jako T (A)
25 Semantyka T (A) stany Stany Stan = (lokacja, wskazania zegarów)
26 Semantyka T (A) stany Stany Stan = (lokacja, wskazania zegarów) Przykłady stanów: a start x:=0, y:=0 (start, [x = 0, y = 0]), (start, [x = π, y = π]), (loop, [x = 3, y = 20+ 3]),... Ile jest stanów? loop x<=10 c end y>=20 x:=0, y:=0 b x==10 x:=0
27 Semantyka T (A) stany Stany Stan = (lokacja, wskazania zegarów) Przykłady stanów: a start x:=0, y:=0 (start, [x = 0, y = 0]), (start, [x = π, y = π]), (loop, [x = 3, y = 20+ 3]),... Ile jest stanów? loop x<=10 c end y>=20 x:=0, y:=0 b x==10 x:=0
28 Semantyka T (A) stany Stany Stan = (lokacja, wskazania zegarów) Przykłady stanów: a start x:=0, y:=0 (start, [x = 0, y = 0]), (start, [x = π, y = π]), (loop, [x = 3, y = 20+ 3]),... Ile jest stanów? loop x<=10 c end y>=20 x:=0, y:=0 b x==10 x:=0
29 Semantyka T (A) stany Stany Stan = (lokacja, wskazania zegarów) Przykłady stanów: a start x:=0, y:=0 (start, [x = 0, y = 0]), (start, [x = π, y = π]), (loop, [x = 3, y = 20+ 3]),... Ile jest stanów? loop x<=10 c end y>=20 x:=0, y:=0 b x==10 x:=0
30 Semantyka T (A) stany Stany Stan = (lokacja, wskazania zegarów) Przykłady stanów: a start x:=0, y:=0 (start, [x = 0, y = 0]), (start, [x = π, y = π]), (loop, [x = 3, y = 20+ 3]),... Ile jest stanów? loop x<=10 c end y>=20 x:=0, y:=0 b x==10 x:=0
31 Semantyka T (A) stany Stany Stan = (lokacja, wskazania zegarów) Przykłady stanów: a start x:=0, y:=0 (start, [x = 0, y = 0]), (start, [x = π, y = π]), (loop, [x = 3, y = 20+ 3]),... Ile jest stanów? continuum loop x<=10 c end y>=20 x:=0, y:=0 b x==10 x:=0
32 Semantyka T (A) zwykłe akcje Zwykłe akcje zwykłe akcje składaja się z l0 l1 a x<=7 y:=0 etykiety warunku umożliwienia - określa czy akcja może zaiść zbioru zegarów do zresetowania - zajście akcji ustawia te zegary na 0
33 Semantyka T (A) upływ czasu Upływ czasu to rodzaj akcji, których na rysunku się nie zaznacza upłynięcie t R + jednostek czasu oznacza zwiększenie wartości wszystkich zegarów o t zegary tykaja więc w tym samym tempie upływ czasu nie zmienia lokacji - czas płynie w miejscu
34 Semantyka T (A) upływ czasu Upływ czasu to rodzaj akcji, których na rysunku się nie zaznacza upłynięcie t R + jednostek czasu oznacza zwiększenie wartości wszystkich zegarów o t zegary tykaja więc w tym samym tempie upływ czasu nie zmienia lokacji - czas płynie w miejscu Ile jest takich akcji?
35 Semantyka T (A) upływ czasu Upływ czasu to rodzaj akcji, których na rysunku się nie zaznacza upłynięcie t R + jednostek czasu oznacza zwiększenie wartości wszystkich zegarów o t zegary tykaja więc w tym samym tempie upływ czasu nie zmienia lokacji - czas płynie w miejscu Ile jest takich akcji? continuum
36 Semantyka T (A) niezmienniki Niezmienniki lokacji to warunki, które musza być prawdziwe, gdy system znajduje się w danej lokacji
37 Semantyka T (A) niezmienniki Niezmienniki lokacji to warunki, które musza być prawdziwe, gdy system znajduje się w danej lokacji wymuszaja postęp, ograniczajac możliwość upływu czasu l0 x<=5 l1
38 Semantyka T (A) niezmienniki Niezmienniki lokacji to warunki, które musza być prawdziwe, gdy system znajduje się w danej lokacji wymuszaja postęp, ograniczajac możliwość upływu czasu ograniczaja też zwykłe akcje, akcja a nigdy nie zajdzie l0 x<=5 l0 a x>5 l1 l1 x<=5
39 Przykład z życia przejazd kolejowy Zautomatyzowany przejazd kolejowy automatycznie podnoszony i opuszczany szlaban automat produktowy, składajacy się z komponentów: Pociag, Szlaban, Kontroler wymóg bezpieczeństwa: gdy pociag przejeżdża przez przejazd, szlaban jest opuszczony
40 Przykład z życia przejazd kolejowy Pociag Szlaban s0 approach x:=0 s1 x<=5 t0 lower y:=0 t1 y<=1 exit in x>2 up y>=1 down out raise x<=5 s3 s2 x<=5 y<=2 t3 y:=0 t2 Kontroler exit approach u2 z:=0 u0 z:=0 u1 z<=1 raise lower z<=1 z=1 bezpieczeństwo: Pociag w s2 Szlaban w t2
41 Potrzeba abstrakcji Weryfikacja sprawdzenie, czy T (A) = ϕ? własności bezpieczeństwa sprowadzaja się do pytania o osiagalność czy osiagalny jest zły stan? EFźle T (A) jest ogromne (nieskończone) rozwiazanie: abstrakcja
42 Regiony Idea y utożsamiamy wartościowania nierozróżnialne ze względu na wykonalność dalszych przejść chcemy podzielić przestrzeń na skończona ilość klas abstrakcji region [1<x<2; 1<y<2; x>y] 2 1 punkt [x=1,5; y=1,25] x
43 Regiony wstęp do definicji Przekształćmy automat tak, by wszystkie stałe były naturalne. Oznaczenia k max := największa ze stałych w A lub w ϕ frac(r) część ułamkowa liczby r R
44 Regiony intuicje Intuicje wskazania zegarów k MAX można utożsamić wskazania zegarów maja część całkowita i ułamkowa część całkowita musimy ja znać dokładnie abstrahujemy od dokładnej warości części ułamkowej nt. części ułamkowej wystarczy, że wiemy czy jest zerowa w jakiej kolejności zegary wraz z upływem czasu będa przechodzić do kolejnych wartości całkowitych
45 Regiony intuicje Intuicje wskazania zegarów k MAX można utożsamić wskazania zegarów maja część całkowita i ułamkowa część całkowita musimy ja znać dokładnie abstrahujemy od dokładnej warości części ułamkowej nt. części ułamkowej wystarczy, że wiemy czy jest zerowa w jakiej kolejności zegary wraz z upływem czasu będa przechodzić do kolejnych wartości całkowitych
46 Regiony intuicje Intuicje wskazania zegarów k MAX można utożsamić wskazania zegarów maja część całkowita i ułamkowa część całkowita musimy ja znać dokładnie abstrahujemy od dokładnej warości części ułamkowej nt. części ułamkowej wystarczy, że wiemy czy jest zerowa w jakiej kolejności zegary wraz z upływem czasu będa przechodzić do kolejnych wartości całkowitych
47 Regiony intuicje Intuicje wskazania zegarów k MAX można utożsamić wskazania zegarów maja część całkowita i ułamkowa część całkowita musimy ja znać dokładnie abstrahujemy od dokładnej warości części ułamkowej nt. części ułamkowej wystarczy, że wiemy czy jest zerowa w jakiej kolejności zegary wraz z upływem czasu będa przechodzić do kolejnych wartości całkowitych
48 Regiony intuicje Intuicje wskazania zegarów k MAX można utożsamić wskazania zegarów maja część całkowita i ułamkowa część całkowita musimy ja znać dokładnie abstrahujemy od dokładnej warości części ułamkowej nt. części ułamkowej wystarczy, że wiemy czy jest zerowa w jakiej kolejności zegary wraz z upływem czasu będa przechodzić do kolejnych wartości całkowitych
49 Regiony def. dla automatu bezprzekatniowego Rownoważność wartościowań zegarów Niech v, v - wartościowania zegarów. Wartościowania sa równoważne (oznaczamy v v ) wtw, gdy x, y C 1 v(x) > k max v (x) > k max 2 jeżeli v(x) k max i v(y) k max, to a) v(x) = v (x) b) frac(v(x)) = 0 frac(v (x)) = 0 c) frac(v(x)) frac(v(y)) frac(v (x)) frac(v (y))
50 Automat bezprzekatniowy przykład regionów y 3 2 C = {x, y} k MAX = x
51 Automat przekatniowy przykład regionów y 3 2 C = {x, y} k MAX = x
52 Regiony klasy abstrakcji Ile jest regionów?
53 Regiony klasy abstrakcji Ile jest regionów? Skończenie wiele
54 Regiony klasy abstrakcji Ile jest regionów? Skończenie wiele A ile dokładniej?
55 Regiony klasy abstrakcji Ile jest regionów? Skończenie wiele A ile dokładniej? wykładniczo względem ilości zegarów można szacować O(k MAX C )
56 Automat regionów R(A) R(A) Automat regionów oznaczamy jako R(A). Stany Stan = (lokacja, region) Relacja przejścia upływ czasu (l, [u]) (l, [v]) jeśli t R +, t. że (l, u) t (l, v) w T (A) zwykłe akcje (l, [u]) a (l, [v]) jeśli akcja a, t. że (l, u) a (l, v) w T (A)
57 Przykład R(A) Automat A l x>=2 x:=0 Automat R(A) l x = 0
58 Przykład R(A) Automat A l x>=2 x:=0 Automat R(A) l l x = 0 0 < x < 1
59 Przykład R(A) Automat A l x>=2 x:=0 Automat R(A) l l x = 0 0 < x < 1 l x = 1
60 Przykład R(A) Automat A Automat R(A) l l x = 0 0 < x < 1 l x = 1 l x>=2 x:=0 l 1 < x < 2
61 Przykład R(A) Automat A Automat R(A) l l x = 0 0 < x < 1 l x = 1 l x>=2 x:=0 l x = 2 l 1 < x < 2
62 Przykład R(A) Automat A Automat R(A) l l x = 0 0 < x < 1 l x = 1 l x>=2 x:=0 l x > 2 l x = 2 l 1 < x < 2
63 Przykład R(A) Automat A Automat R(A) l l x = 0 0 < x < 1 l x = 1 l x>=2 x:=0 l x > 2 l x = 2 l 1 < x < 2
64 Poprawność abstrakcji R(A) ϕ formuła TCTL (TCTL = rozszerzenie CTL X ; operatory wzbogacone o przedziały czasowe) Poprawność abstrakcji R(A) T (A) = ϕ R(A) = ϕ
65 Bisymualcja jako gra Weżmy dwa modele. Żeby rozstrzygnać, czy sa one z punktu widzenia obserwatora nierozróżnialne, zagramy w pewna grę.
66 Bisymualcja jako gra Weżmy dwa modele. Żeby rozstrzygnać, czy sa one z punktu widzenia obserwatora nierozróżnialne, zagramy w pewna grę. Gra w bisymulację jest dwóch graczy gracz Odróżniajacy chce udowodnić różność modeli gracz Broniacy chce obronić tezę o równoważności modeli jeśli graczowi Odróżniajacemu uda się odróżnić modele w skończonej liczbie kroków wygrywa, modele nie sa w bisymulacji wpp. wygrywa gracz Broniacy modele sa w bisymulacji
67 Bisymualcja jako gra Weżmy dwa modele. Żeby rozstrzygnać, czy sa one z punktu widzenia obserwatora nierozróżnialne, zagramy w pewna grę. Gra w bisymulację jest dwóch graczy gracz Odróżniajacy chce udowodnić różność modeli gracz Broniacy chce obronić tezę o równoważności modeli jeśli graczowi Odróżniajacemu uda się odróżnić modele w skończonej liczbie kroków wygrywa, modele nie sa w bisymulacji wpp. wygrywa gracz Broniacy modele sa w bisymulacji
68 Bisymualcja jako gra Weżmy dwa modele. Żeby rozstrzygnać, czy sa one z punktu widzenia obserwatora nierozróżnialne, zagramy w pewna grę. Gra w bisymulację jest dwóch graczy gracz Odróżniajacy chce udowodnić różność modeli gracz Broniacy chce obronić tezę o równoważności modeli jeśli graczowi Odróżniajacemu uda się odróżnić modele w skończonej liczbie kroków wygrywa, modele nie sa w bisymulacji wpp. wygrywa gracz Broniacy modele sa w bisymulacji
69 Bisymualcja jako gra Weżmy dwa modele. Żeby rozstrzygnać, czy sa one z punktu widzenia obserwatora nierozróżnialne, zagramy w pewna grę. Gra w bisymulację jest dwóch graczy gracz Odróżniajacy chce udowodnić różność modeli gracz Broniacy chce obronić tezę o równoważności modeli jeśli graczowi Odróżniajacemu uda się odróżnić modele w skończonej liczbie kroków wygrywa, modele nie sa w bisymulacji wpp. wygrywa gracz Broniacy modele sa w bisymulacji
70 Bisymualcja jako gra Weżmy dwa modele. Żeby rozstrzygnać, czy sa one z punktu widzenia obserwatora nierozróżnialne, zagramy w pewna grę. Gra w bisymulację jest dwóch graczy gracz Odróżniajacy chce udowodnić różność modeli gracz Broniacy chce obronić tezę o równoważności modeli jeśli graczowi Odróżniajacemu uda się odróżnić modele w skończonej liczbie kroków wygrywa, modele nie sa w bisymulacji wpp. wygrywa gracz Broniacy modele sa w bisymulacji
71 Gra w bisymulację Zasady gry W pętli: gracz Odróżniajacy wybiera sobie 1 z modeli i wykonuje w nim jakaś akcję gracz Broniacy w drugim z modeli wykonuje akcję o takiej samej etykiecie jeśli nie potrafi to przegrywa
72 Gra w bisymulację Zasady gry W pętli: gracz Odróżniajacy wybiera sobie 1 z modeli i wykonuje w nim jakaś akcję gracz Broniacy w drugim z modeli wykonuje akcję o takiej samej etykiecie jeśli nie potrafi to przegrywa Uwaga: W kolejnych turach gracz Odróżniajacy może wybierać różne modele.
73 Bisymulacja przykład s1 w1 a a a s2 s3 w2 b b b b b s4 s5 s6 s7 w3
74 Bisymulacja przykład s1 w1 a a a s2 s3 w2 b b b b b s4 s5 s6 s7 Bisymulacja: {(s 1, w 1 ), (s 2, w 2 ), (s 3, w 2 ), (s 4, w 3 ), (s 5, w 3 ), (s 6, w 3 ), (s 7, w 3 )} w3
75 Bisymulacja przykład s1 w1 a a a s2 w2 w3 b c b c s3 s4 w4 w5
76 Bisymulacja przykład s1 w1 a a a s2 w2 w3 b c b c s3 s4 w4 w5 Nie ma bisymulacji.
77 Bisymulacja przykład s1 w1 a a a s2 b s3 b w2 b
78 Bisymulacja przykład s1 w1 a a a s2 b s3 b w2 b Bisymulacja: {(s 1, w 1 ), (s 2, w 2 ), (s 3, w 2 )}
79 Bisymulacja przykład s1 w1 a a a s2 b w2 b s3 b b s4 w3
80 Bisymulacja przykład s1 w1 a a a s2 b w2 b s3 b b s4 w3 Nie ma bisymulacji.
81 Bisymulacja trochę głębiej strategia wygrywajaca gracza Broniacego to relacja bisymulacji jeśli by zabronić graczowi Odróżniajacemu zmienianie stron, mielibyśmy symulację jeśli system A symuluje B oraz B symuluje A, to systemy sa symulacyjnie równoważne jeśli A i B sa symulacyjnie równoważne A symuluje B przy pomocy relacji R B symuluje A przy pomocy relacji R 1, to systemy sa w bisymulacji
82 Bisymulacja trochę głębiej strategia wygrywajaca gracza Broniacego to relacja bisymulacji jeśli by zabronić graczowi Odróżniajacemu zmienianie stron, mielibyśmy symulację jeśli system A symuluje B oraz B symuluje A, to systemy sa symulacyjnie równoważne jeśli A i B sa symulacyjnie równoważne A symuluje B przy pomocy relacji R B symuluje A przy pomocy relacji R 1, to systemy sa w bisymulacji
83 Bisymulacja trochę głębiej strategia wygrywajaca gracza Broniacego to relacja bisymulacji jeśli by zabronić graczowi Odróżniajacemu zmienianie stron, mielibyśmy symulację jeśli system A symuluje B oraz B symuluje A, to systemy sa symulacyjnie równoważne jeśli A i B sa symulacyjnie równoważne A symuluje B przy pomocy relacji R B symuluje A przy pomocy relacji R 1, to systemy sa w bisymulacji
84 Bisymulacja trochę głębiej strategia wygrywajaca gracza Broniacego to relacja bisymulacji jeśli by zabronić graczowi Odróżniajacemu zmienianie stron, mielibyśmy symulację jeśli system A symuluje B oraz B symuluje A, to systemy sa symulacyjnie równoważne jeśli A i B sa symulacyjnie równoważne A symuluje B przy pomocy relacji R B symuluje A przy pomocy relacji R 1, to systemy sa w bisymulacji
85 Bisymulacja w systemach zależnych od czasu Rodzaje tranzycji t = upływ t jednostek czasu a = zajście akcji a = = t t = a = t t a Przypomnienie w T (A) mamy do dyspozycji: t i a w R(A) mamy do dyspozycji: = i a
86 Bisymulacja w systemach zależnych od czasu Timed-bisimulation Relacja w T (A). Gra w bisymulacje, w której alfabetem akcji, który bisymulacja ma zachowywać jest Σ R + {0}. Trzeba dbać zarówno o przejścia a jak i t. Intuicja Dwa automaty sa timed-bisimilar wtw wykonuja takie same przejścia a w tym samym czasie.
87 Bisymulacja w systemach zależnych od czasu Untimed-bisimulation Relacja w T (A). Gra w bisymulacje, w której alfabetem akcji, który bisymulacja ma zachowywać jest Σ {τ}. τ to specjalna etykieta symbolizujaca upływ czasu Fakt Abstrakcja wykorzystywana do tworzenia regionów jest bisymulacja w T (A) względem tranzycji = a i = i a, ale nie t
88 Osiagalność w systemach zależnych od czasu Bisymulacja jest słaba Żeby testować osiagalność można używać silniejszych abstrakcji niż bisymulacja. Można użyć np. symulacji pseudo-bisymulacji pseudo-symulacji
Bisymulacja. Niezawodność systemów współbieżnych i obiektowych. Grzegorz Maj Grzegorz Maj Bisymulacja
 Niezawodność systemów współbieżnych i obiektowych 18.03.2009 Plan prezentacji Przypomnienie: Plan prezentacji Przypomnienie: Gra bisymulacyjna Plan prezentacji Przypomnienie: Gra bisymulacyjna Definicje
Niezawodność systemów współbieżnych i obiektowych 18.03.2009 Plan prezentacji Przypomnienie: Plan prezentacji Przypomnienie: Gra bisymulacyjna Plan prezentacji Przypomnienie: Gra bisymulacyjna Definicje
Bisymulacja. Niezawodność systemów współbieżnych i obiektowych. Grzegorz Maj Grzegorz Maj Bisymulacja
 Niezawodność systemów współbieżnych i obiektowych 11.03.2009 Czym będziemy się zajomwać? Plan prezentacji Silna bisymulacja i silna równoważność Plan prezentacji Silna bisymulacja i silna równoważność
Niezawodność systemów współbieżnych i obiektowych 11.03.2009 Czym będziemy się zajomwać? Plan prezentacji Silna bisymulacja i silna równoważność Plan prezentacji Silna bisymulacja i silna równoważność
Automaty czasowe. Sposoby weryfikacji UPPAAL. Narzędzie do weryfikacji automatów czasowych. Aleksander Zabłocki. 6 maja 2009
 Narzędzie do weryfikacji automatów czasowych 6 maja 2009 Plan 1 2 3 Modeluje układy (komunikujacych się) automatów czasowych Weryfikuje podane własności wyrażane w uproszczonym CTL Powstaje na uniwersytetach
Narzędzie do weryfikacji automatów czasowych 6 maja 2009 Plan 1 2 3 Modeluje układy (komunikujacych się) automatów czasowych Weryfikuje podane własności wyrażane w uproszczonym CTL Powstaje na uniwersytetach
Logika Stosowana. Wykład 1 - Logika zdaniowa. Marcin Szczuka. Instytut Informatyki UW. Wykład monograficzny, semestr letni 2016/2017
 Logika Stosowana Wykład 1 - Logika zdaniowa Marcin Szczuka Instytut Informatyki UW Wykład monograficzny, semestr letni 2016/2017 Marcin Szczuka (MIMUW) Logika Stosowana 2017 1 / 30 Plan wykładu 1 Język
Logika Stosowana Wykład 1 - Logika zdaniowa Marcin Szczuka Instytut Informatyki UW Wykład monograficzny, semestr letni 2016/2017 Marcin Szczuka (MIMUW) Logika Stosowana 2017 1 / 30 Plan wykładu 1 Język
Algorytmiczne aspekty teorii gier: Wykład 5
 Algorytmiczne aspekty teorii gier: Wykład 5 Wykład prowadził dr hab. Igor Walukiewicz Notatki przygotował Dymitr Pszenicyn 02-04-2003 1 Spis treści 1 Przypomnienie 3 1.1
Algorytmiczne aspekty teorii gier: Wykład 5 Wykład prowadził dr hab. Igor Walukiewicz Notatki przygotował Dymitr Pszenicyn 02-04-2003 1 Spis treści 1 Przypomnienie 3 1.1
LOGIKA Klasyczny Rachunek Zdań
 LOGIKA Klasyczny Rachunek Zdań Robert Trypuz trypuz@kul.pl 5 listopada 2013 Robert Trypuz (trypuz@kul.pl) Klasyczny Rachunek Zdań 5 listopada 2013 1 / 24 PLAN WYKŁADU 1 Alfabet i formuła KRZ 2 Zrozumieć
LOGIKA Klasyczny Rachunek Zdań Robert Trypuz trypuz@kul.pl 5 listopada 2013 Robert Trypuz (trypuz@kul.pl) Klasyczny Rachunek Zdań 5 listopada 2013 1 / 24 PLAN WYKŁADU 1 Alfabet i formuła KRZ 2 Zrozumieć
Algebrę L = (L, Neg, Alt, Kon, Imp) nazywamy algebrą języka logiki zdań. Jest to algebra o typie
 3. Wykłady 5 i 6: Semantyka klasycznego rachunku zdań. Dotychczas rozwinęliśmy klasyczny rachunek na gruncie czysto syntaktycznym, a więc badaliśmy metodę sprawdzania, czy dana formuła B jest dowodliwa
3. Wykłady 5 i 6: Semantyka klasycznego rachunku zdań. Dotychczas rozwinęliśmy klasyczny rachunek na gruncie czysto syntaktycznym, a więc badaliśmy metodę sprawdzania, czy dana formuła B jest dowodliwa
FINCH PONG. Realizator: Partner: Patronat:
 FINCH PONG Realizator: Partner: Patronat: Dzisiaj nauczymy robota Finch kontrolować ruchy paletki do finch ponga. Będziemy poruszać paletką w prawo i w lewo, żeby piłka odbijała się od niej. 6. Wprowadzamy
FINCH PONG Realizator: Partner: Patronat: Dzisiaj nauczymy robota Finch kontrolować ruchy paletki do finch ponga. Będziemy poruszać paletką w prawo i w lewo, żeby piłka odbijała się od niej. 6. Wprowadzamy
Logika Temporalna i Automaty Czasowe
 Modelowanie i Analiza Systemów Informatycznych Logika Temporalna i Automaty Czasowe (1) Wprowadzenie do logiki temporalnej Paweł Głuchowski, Politechnika Wrocławska wersja 2.2 Program wykładów 1. Wprowadzenie
Modelowanie i Analiza Systemów Informatycznych Logika Temporalna i Automaty Czasowe (1) Wprowadzenie do logiki temporalnej Paweł Głuchowski, Politechnika Wrocławska wersja 2.2 Program wykładów 1. Wprowadzenie
Rozwiązania około dwustu łatwych zadań z języków formalnych i złożoności obliczeniowej i być może jednego chyba trudnego (w trakcie tworzenia)
 Rozwiązania około dwustu łatwych zadań z języków formalnych i złożoności obliczeniowej i być może jednego chyba trudnego (w trakcie tworzenia) Kamil Matuszewski 20 lutego 2017 22 lutego 2017 Zadania, które
Rozwiązania około dwustu łatwych zadań z języków formalnych i złożoności obliczeniowej i być może jednego chyba trudnego (w trakcie tworzenia) Kamil Matuszewski 20 lutego 2017 22 lutego 2017 Zadania, które
Instrukcja korzystania z Systemu Telnom - Nominacje
 Instrukcja korzystania z Systemu Telnom - Nominacje Opis panelu użytkownika Pierwsze zalogowanie w systemie Procedura resetowania hasła Składanie nominacji krok po kroku System Telnom Nominacje znajduje
Instrukcja korzystania z Systemu Telnom - Nominacje Opis panelu użytkownika Pierwsze zalogowanie w systemie Procedura resetowania hasła Składanie nominacji krok po kroku System Telnom Nominacje znajduje
1 Zbiory. 1.1 Kiedy {a} = {b, c}? (tzn. podać warunki na a, b i c) 1.2 Udowodnić, że A {A} A =.
 1 Zbiory 1.1 Kiedy {a} = {b, c}? (tzn. podać warunki na a, b i c) 1.2 Udowodnić, że A {A} A =. 1.3 Pokazać, że jeśli A, B oraz (A B) (B A) = C C, to A = B = C. 1.4 Niech {X t } będzie rodziną niepustych
1 Zbiory 1.1 Kiedy {a} = {b, c}? (tzn. podać warunki na a, b i c) 1.2 Udowodnić, że A {A} A =. 1.3 Pokazać, że jeśli A, B oraz (A B) (B A) = C C, to A = B = C. 1.4 Niech {X t } będzie rodziną niepustych
Logika Temporalna i Automaty Czasowe
 Modelowanie i Analiza Systemów Informatycznych Logika Temporalna i Automaty Czasowe (7) Automaty czasowe NuSMV Paweł Głuchowski, Politechnika Wrocławska wersja 2.3 Treść wykładu NuSMV NuSMV symboliczny
Modelowanie i Analiza Systemów Informatycznych Logika Temporalna i Automaty Czasowe (7) Automaty czasowe NuSMV Paweł Głuchowski, Politechnika Wrocławska wersja 2.3 Treść wykładu NuSMV NuSMV symboliczny
Rozszerzenia sieci Petriego
 Rozszerzenia sieci Petriego Ograniczenia klasycznej sieci Petriego Trudność w modelowaniu specyficznych przepływów: testowania braku żetonów w danym miejscu, blokowania odpalania, itp. Brak determinizmu
Rozszerzenia sieci Petriego Ograniczenia klasycznej sieci Petriego Trudność w modelowaniu specyficznych przepływów: testowania braku żetonów w danym miejscu, blokowania odpalania, itp. Brak determinizmu
Rozszerzenia sieci Petriego
 Rozszerzenia sieci Petriego Ograniczenia klasycznej sieci Petriego Trudność w modelowaniu specyficznych przepływów: testowania braku żetonów w danym miejscu, blokowania odpalania, itp. Brak determinizmu
Rozszerzenia sieci Petriego Ograniczenia klasycznej sieci Petriego Trudność w modelowaniu specyficznych przepływów: testowania braku żetonów w danym miejscu, blokowania odpalania, itp. Brak determinizmu
Minimalizacja automatów niedeterministycznych na słowach skończonych i nieskończonych
 Szczepan Hummel Minimalizacja automatów niedeterministycznych na słowach skończonych i nieskończonych 24.11.2005 1. Minimalizacja automatów deterministycznych na słowach skończonych (DFA) [HU] relacja
Szczepan Hummel Minimalizacja automatów niedeterministycznych na słowach skończonych i nieskończonych 24.11.2005 1. Minimalizacja automatów deterministycznych na słowach skończonych (DFA) [HU] relacja
Przykład: Σ = {0, 1} Σ - zbiór wszystkich skończonych ciagów binarnych. L 1 = {0, 00, 000,...,1, 11, 111,... } L 2 = {01, 1010, 001, 11}
 Języki Ustalmy pewien skończony zbiór symboli Σ zwany alfabetem. Zbiór Σ zawiera wszystkie skończone ciagi symboli z Σ. Podzbiór L Σ nazywamy językiem a x L nazywamy słowem. Specjalne słowo puste oznaczamy
Języki Ustalmy pewien skończony zbiór symboli Σ zwany alfabetem. Zbiór Σ zawiera wszystkie skończone ciagi symboli z Σ. Podzbiór L Σ nazywamy językiem a x L nazywamy słowem. Specjalne słowo puste oznaczamy
02DRAP - Aksjomatyczna definicja prawdopodobieństwa, zasada w-w
 02DRAP - Aksjomatyczna definicja prawdopodobieństwa, zasada w-w A Zadania na ćwiczenia Zadanie A.1. Niech Ω = R oraz F będzie σ-ciałem generowanym przez rodzinę wszystkich przedziałów otwartych typu (,
02DRAP - Aksjomatyczna definicja prawdopodobieństwa, zasada w-w A Zadania na ćwiczenia Zadanie A.1. Niech Ω = R oraz F będzie σ-ciałem generowanym przez rodzinę wszystkich przedziałów otwartych typu (,
Konfiguracja Połączenia
 2012.07.17Aktualizacja: 2012.10.11, 12:50 Konfiguracjaja klienta PPPoE w Windows 7 1. Klikamy na ikonę połączeń sieciowych przy zegarze i otwieramy "Centrum sieci i udostępniania". Aby wyłączyć protokół
2012.07.17Aktualizacja: 2012.10.11, 12:50 Konfiguracjaja klienta PPPoE w Windows 7 1. Klikamy na ikonę połączeń sieciowych przy zegarze i otwieramy "Centrum sieci i udostępniania". Aby wyłączyć protokół
Poprawność semantyczna
 Poprawność składniowa Poprawność semantyczna Poprawność algorytmu Wypisywanie zdań z języka poprawnych składniowo Poprawne wartościowanie zdań języka, np. w języku programowania skutki wystąpienia wyróżnionych
Poprawność składniowa Poprawność semantyczna Poprawność algorytmu Wypisywanie zdań z języka poprawnych składniowo Poprawne wartościowanie zdań języka, np. w języku programowania skutki wystąpienia wyróżnionych
Spacery losowe generowanie realizacji procesu losowego
 Spacery losowe generowanie realizacji procesu losowego Michał Krzemiński Streszczenie Omówimy metodę generowania trajektorii spacerów losowych (błądzenia losowego), tj. szczególnych procesów Markowa z
Spacery losowe generowanie realizacji procesu losowego Michał Krzemiński Streszczenie Omówimy metodę generowania trajektorii spacerów losowych (błądzenia losowego), tj. szczególnych procesów Markowa z
Języki, automaty i obliczenia
 Języki, automaty i obliczenia Wykład 10: Maszyny Turinga Sławomir Lasota Uniwersytet Warszawski 29 kwietnia 2015 Plan Maszyny Turinga (Niedeterministyczna) maszyna Turinga M = (A, Q, q 0, F, T, B, δ) A
Języki, automaty i obliczenia Wykład 10: Maszyny Turinga Sławomir Lasota Uniwersytet Warszawski 29 kwietnia 2015 Plan Maszyny Turinga (Niedeterministyczna) maszyna Turinga M = (A, Q, q 0, F, T, B, δ) A
Logika Temporalna i Automaty Czasowe
 Modelowanie i Analiza Systemów Informatycznych Logika Temporalna i Automaty Czasowe (4) Modelowa weryfikacja systemu Paweł Głuchowski, Politechnika Wrocławska wersja 2.1 Treść wykładu Własności współbieżnych
Modelowanie i Analiza Systemów Informatycznych Logika Temporalna i Automaty Czasowe (4) Modelowa weryfikacja systemu Paweł Głuchowski, Politechnika Wrocławska wersja 2.1 Treść wykładu Własności współbieżnych
IMIĘ NAZWISKO... grupa C... sala Egzamin ELiTM I
 IMIĘ NAZWISKO............................ grupa C... sala 10... Egzamin ELiTM I 02.02.15 1. 2. 3. 4.. 1. (8 pkt.) Niech X a,b = {(x, y) R 2 : (x b) 2 + (y 1 b )2 a 2 } dla a, b R, a > 0, b 0. Wyznaczyć:
IMIĘ NAZWISKO............................ grupa C... sala 10... Egzamin ELiTM I 02.02.15 1. 2. 3. 4.. 1. (8 pkt.) Niech X a,b = {(x, y) R 2 : (x b) 2 + (y 1 b )2 a 2 } dla a, b R, a > 0, b 0. Wyznaczyć:
4. Postęp arytmetyczny i geometryczny. Wartość bezwzględna, potęgowanie i pierwiastkowanie liczb rzeczywistych.
 Jarosław Wróblewski Matematyka dla Myślących, 008/09. Postęp arytmetyczny i geometryczny. Wartość bezwzględna, potęgowanie i pierwiastkowanie liczb rzeczywistych. 15 listopada 008 r. Uwaga: Przyjmujemy,
Jarosław Wróblewski Matematyka dla Myślących, 008/09. Postęp arytmetyczny i geometryczny. Wartość bezwzględna, potęgowanie i pierwiastkowanie liczb rzeczywistych. 15 listopada 008 r. Uwaga: Przyjmujemy,
Elementy modelowania matematycznego
 Elementy modelowania matematycznego Łańcuchy Markowa: zagadnienia graniczne. Ukryte modele Markowa. Jakub Wróblewski jakubw@pjwstk.edu.pl http://zajecia.jakubw.pl/ KLASYFIKACJA STANÓW Stan i jest osiągalny
Elementy modelowania matematycznego Łańcuchy Markowa: zagadnienia graniczne. Ukryte modele Markowa. Jakub Wróblewski jakubw@pjwstk.edu.pl http://zajecia.jakubw.pl/ KLASYFIKACJA STANÓW Stan i jest osiągalny
Test z przedmiotu zajęcia komputerowe
 Test z przedmiotu zajęcia komputerowe 1. System operacyjny to: a) nowoczesna gra komputerowa, b) program niezbędny do pracy na komputerze, c) urządzenie w komputerze. d) przeglądarka internetowa 2.Angielskie
Test z przedmiotu zajęcia komputerowe 1. System operacyjny to: a) nowoczesna gra komputerowa, b) program niezbędny do pracy na komputerze, c) urządzenie w komputerze. d) przeglądarka internetowa 2.Angielskie
Kombinowanie o nieskończoności. 3. Jak policzyć nieskończone materiały do ćwiczeń
 Kombinowanie o nieskończoności. 3. Jak policzyć nieskończone materiały do ćwiczeń Projekt Matematyka dla ciekawych świata spisał: Michał Korch 22 marzec 2018 Szybkie przypomnienie z wykładu Prezentacja
Kombinowanie o nieskończoności. 3. Jak policzyć nieskończone materiały do ćwiczeń Projekt Matematyka dla ciekawych świata spisał: Michał Korch 22 marzec 2018 Szybkie przypomnienie z wykładu Prezentacja
Brain Game. Wstęp. Scratch
 Scratch 2 Brain Game Każdy Klub Kodowania musi być zarejestrowany. Zarejestrowane kluby można zobaczyć na mapie na stronie codeclubworld.org - jeżeli nie ma tam twojego klubu sprawdź na stronie jumpto.cc/18cplpy
Scratch 2 Brain Game Każdy Klub Kodowania musi być zarejestrowany. Zarejestrowane kluby można zobaczyć na mapie na stronie codeclubworld.org - jeżeli nie ma tam twojego klubu sprawdź na stronie jumpto.cc/18cplpy
1.Instalacja. Przechodzimy przez kolejne okna instalatora klikacjąć Dalej. wolek.zallegro.pl
 1.Instalacja Przechodzimy przez kolejne okna instalatora klikacjąć Dalej. 1 Dla instalacji jednostanowiskowej zaznaczamy aplikacje Serwera i Klienta. W przypadku, gdy pilot ma pracować z kilkoma komputerami
1.Instalacja Przechodzimy przez kolejne okna instalatora klikacjąć Dalej. 1 Dla instalacji jednostanowiskowej zaznaczamy aplikacje Serwera i Klienta. W przypadku, gdy pilot ma pracować z kilkoma komputerami
SimplySign logowanie i rejestracja na komputerze oraz dodanie certyfikatu do programu Płatnik
 SimplySign logowanie i rejestracja na komputerze oraz dodanie certyfikatu do programu Płatnik 1. INSTALACJA CERTYFIKATU SIMPLY SIGN W MAGAZYNIE SYSTEMOWYM. W celu użytkowania certyfikatu SimplySign na
SimplySign logowanie i rejestracja na komputerze oraz dodanie certyfikatu do programu Płatnik 1. INSTALACJA CERTYFIKATU SIMPLY SIGN W MAGAZYNIE SYSTEMOWYM. W celu użytkowania certyfikatu SimplySign na
Instrukcja instalacji certyfikatu kwalifikowanego w programie Płatnik. wersja 1.8
 Instrukcja instalacji certyfikatu kwalifikowanego w programie Płatnik wersja 1.8 Spis treści 1. INSTALACJA CERTYFIKATU Z KARTY KRYPTOGRAFICZNEJ W MAGAZYNIE SYSTEMOWYM... 3 Wczytanie danych z karty CryptoCERTUM...
Instrukcja instalacji certyfikatu kwalifikowanego w programie Płatnik wersja 1.8 Spis treści 1. INSTALACJA CERTYFIKATU Z KARTY KRYPTOGRAFICZNEJ W MAGAZYNIE SYSTEMOWYM... 3 Wczytanie danych z karty CryptoCERTUM...
Ekran tytułowy (menu główne)
 Wstęp Ten multimedialny program edukacyjny przeznaczony jest dla uczniów szkół podstawowych. Oferując ciekawe zadania tekstowe, służy przede wszystkim doskonaleniu umiejętności matematycznych. Program
Wstęp Ten multimedialny program edukacyjny przeznaczony jest dla uczniów szkół podstawowych. Oferując ciekawe zadania tekstowe, służy przede wszystkim doskonaleniu umiejętności matematycznych. Program
Andrzej Wiśniewski Logika I Materiały do wykładu dla studentów kognitywistyki. Wykład 9. Koniunkcyjne postacie normalne i rezolucja w KRZ
 Andrzej Wiśniewski Logika I Materiały do wykładu dla studentów kognitywistyki Wykład 9. Koniunkcyjne postacie normalne i rezolucja w KRZ 1 Inferencyjna równoważność formuł Definicja 9.1. Formuła A jest
Andrzej Wiśniewski Logika I Materiały do wykładu dla studentów kognitywistyki Wykład 9. Koniunkcyjne postacie normalne i rezolucja w KRZ 1 Inferencyjna równoważność formuł Definicja 9.1. Formuła A jest
Andrzej Wiśniewski Logika I Materiały do wykładu dla studentów kognitywistyki. Wykład 10. Twierdzenie o pełności systemu aksjomatycznego KRZ
 Andrzej Wiśniewski Logika I Materiały do wykładu dla studentów kognitywistyki Wykład 10. Twierdzenie o pełności systemu aksjomatycznego KRZ 1 Tezy KRZ Pewien system aksjomatyczny KRZ został przedstawiony
Andrzej Wiśniewski Logika I Materiały do wykładu dla studentów kognitywistyki Wykład 10. Twierdzenie o pełności systemu aksjomatycznego KRZ 1 Tezy KRZ Pewien system aksjomatyczny KRZ został przedstawiony
Rozdział 5. Administracja kontami użytkowników
 Rozdział 5. Administracja kontami użytkowników Ćwiczenia zawarte w tym rozdziale pozwolą przygotować oddzielne środowisko pracy dla każdego użytkownika komputera. Windows XP, w porównaniu do systemów Windows
Rozdział 5. Administracja kontami użytkowników Ćwiczenia zawarte w tym rozdziale pozwolą przygotować oddzielne środowisko pracy dla każdego użytkownika komputera. Windows XP, w porównaniu do systemów Windows
0.1. Logika podstawowe pojęcia: zdania i funktory, reguły wnioskowania, zmienne zdaniowe, rachunek zdań.
 Wykłady z Analizy rzeczywistej i zespolonej w Matematyce stosowanej Wykład ELEMENTY LOGIKI ALGEBRA BOOLE A Logika podstawowe pojęcia: zdania i funktory, reguły wnioskowania, zmienne zdaniowe, rachunek
Wykłady z Analizy rzeczywistej i zespolonej w Matematyce stosowanej Wykład ELEMENTY LOGIKI ALGEBRA BOOLE A Logika podstawowe pojęcia: zdania i funktory, reguły wnioskowania, zmienne zdaniowe, rachunek
Logika Temporalna i Automaty Czasowe
 Modelowanie i Analiza Systemów Informatycznych Logika Temporalna i Automaty Czasowe (7) Automaty czasowe NuSMV Paweł Głuchowski, Politechnika Wrocławska wersja 2.4 Treść wykładu NuSMV NuSMV symboliczny
Modelowanie i Analiza Systemów Informatycznych Logika Temporalna i Automaty Czasowe (7) Automaty czasowe NuSMV Paweł Głuchowski, Politechnika Wrocławska wersja 2.4 Treść wykładu NuSMV NuSMV symboliczny
Definicja: alfabetem. słowem długością słowa
 Definicja: Niech X będzie zbiorem niepustym. Zbiór ten będziemy nazywać alfabetem. Skończony ciąg elementów alfabetu X będziemy nazywać słowem a liczbę elementów tego ciągu nazywamy długością słowa. Na
Definicja: Niech X będzie zbiorem niepustym. Zbiór ten będziemy nazywać alfabetem. Skończony ciąg elementów alfabetu X będziemy nazywać słowem a liczbę elementów tego ciągu nazywamy długością słowa. Na
Imię, nazwisko, nr indeksu
 Imię, nazwisko, nr indeksu (kod) (9 punktów) Wybierz 9 z poniższych pytań i wybierz odpowiedź tak/nie (bez uzasadnienia). Za prawidłowe odpowiedzi dajemy +1 punkt, za złe -1 punkt. Punkty policzymy za
Imię, nazwisko, nr indeksu (kod) (9 punktów) Wybierz 9 z poniższych pytań i wybierz odpowiedź tak/nie (bez uzasadnienia). Za prawidłowe odpowiedzi dajemy +1 punkt, za złe -1 punkt. Punkty policzymy za
Modelowanie matematyczne a eksperyment
 Modelowanie matematyczne a eksperyment Budowanie modeli w środowisku Hildegard Urban-Woldron Ogólnopolska konferencja, 28.10. 2011, Warszawa Plan Budowanie modelu w środowisku Równania i wartości Uruchomienie
Modelowanie matematyczne a eksperyment Budowanie modeli w środowisku Hildegard Urban-Woldron Ogólnopolska konferencja, 28.10. 2011, Warszawa Plan Budowanie modelu w środowisku Równania i wartości Uruchomienie
1. Internet Explorer a) Uruchamiamy przeglądarkę Internet Explorer i przechodzimy do ustawień
 UWAGA! Instrukcja tylko dla informatyków! Wprowadzenie zmian na jej podstawie przez osobę nieuprawnioną może doprowadzić do utraty certyfikatów i konieczności pracy bez dostępu do systemu CEPiK 2.0 1.
UWAGA! Instrukcja tylko dla informatyków! Wprowadzenie zmian na jej podstawie przez osobę nieuprawnioną może doprowadzić do utraty certyfikatów i konieczności pracy bez dostępu do systemu CEPiK 2.0 1.
F t+ := s>t. F s = F t.
 M. Beśka, Całka Stochastyczna, wykład 1 1 1 Wiadomości wstępne 1.1 Przestrzeń probabilistyczna z filtracją Niech (Ω, F, P ) będzie ustaloną przestrzenią probabilistyczną i niech F = {F t } t 0 będzie rodziną
M. Beśka, Całka Stochastyczna, wykład 1 1 1 Wiadomości wstępne 1.1 Przestrzeń probabilistyczna z filtracją Niech (Ω, F, P ) będzie ustaloną przestrzenią probabilistyczną i niech F = {F t } t 0 będzie rodziną
Semantyka rachunku predykatów
 Relacje Interpretacja Wartość Spełnialność Logika obliczeniowa Instytut Informatyki Relacje Interpretacja Wartość Plan Plan Relacje O co chodzi? Znaczenie w logice Relacje 3 Interpretacja i wartościowanie
Relacje Interpretacja Wartość Spełnialność Logika obliczeniowa Instytut Informatyki Relacje Interpretacja Wartość Plan Plan Relacje O co chodzi? Znaczenie w logice Relacje 3 Interpretacja i wartościowanie
Podstawowe Pojęcia. Semantyczne KRZ
 Logika Matematyczna: Podstawowe Pojęcia Semantyczne KRZ I rok Językoznawstwa i Informacji Naukowej UAM 2006-2007 Jerzy Pogonowski Zakład Logiki Stosowanej UAM http://www.logic.amu.edu.pl Dodatek: ściąga
Logika Matematyczna: Podstawowe Pojęcia Semantyczne KRZ I rok Językoznawstwa i Informacji Naukowej UAM 2006-2007 Jerzy Pogonowski Zakład Logiki Stosowanej UAM http://www.logic.amu.edu.pl Dodatek: ściąga
Konstrukcja liczb rzeczywistych przy pomocy ciągów Cauchy ego liczb wymiernych
 Konstrukcja liczb rzeczywistych przy pomocy ciągów Cauchy ego liczb wymiernych Marcin Michalski 14.11.014 1 Wprowadzenie Jedną z intuicji na temat liczb rzeczywistych jest myślenie o nich jako liczbach,
Konstrukcja liczb rzeczywistych przy pomocy ciągów Cauchy ego liczb wymiernych Marcin Michalski 14.11.014 1 Wprowadzenie Jedną z intuicji na temat liczb rzeczywistych jest myślenie o nich jako liczbach,
Za pierwszy niebanalny algorytm uważa się algorytm Euklidesa wyszukiwanie NWD dwóch liczb (400 a 300 rok przed narodzeniem Chrystusa).
 Algorytmy definicja, cechy, złożoność. Algorytmy napotykamy wszędzie, gdziekolwiek się zwrócimy. Rządzą one wieloma codziennymi czynnościami, jak np. wymiana przedziurawionej dętki, montowanie szafy z
Algorytmy definicja, cechy, złożoność. Algorytmy napotykamy wszędzie, gdziekolwiek się zwrócimy. Rządzą one wieloma codziennymi czynnościami, jak np. wymiana przedziurawionej dętki, montowanie szafy z
Egzamin z logiki i teorii mnogości, rozwiązania zadań
 Egzamin z logiki i teorii mnogości, 08.02.2016 - rozwiązania zadań 1. Niech φ oraz ψ będą formami zdaniowymi. Czy formuła [( x : φ(x)) ( x : ψ(x))] [ x : (φ(x) ψ(x))] jest prawem rachunku kwantyfikatorów?
Egzamin z logiki i teorii mnogości, 08.02.2016 - rozwiązania zadań 1. Niech φ oraz ψ będą formami zdaniowymi. Czy formuła [( x : φ(x)) ( x : ψ(x))] [ x : (φ(x) ψ(x))] jest prawem rachunku kwantyfikatorów?
procesów Współbieżność i synchronizacja procesów Wykład prowadzą: Jerzy Brzeziński Dariusz Wawrzyniak
 Wykład prowadzą: Jerzy Brzeziński Dariusz Wawrzyniak Plan wykładu Abstrakcja programowania współbieżnego Instrukcje atomowe i ich przeplot Istota synchronizacji Kryteria poprawności programów współbieżnych
Wykład prowadzą: Jerzy Brzeziński Dariusz Wawrzyniak Plan wykładu Abstrakcja programowania współbieżnego Instrukcje atomowe i ich przeplot Istota synchronizacji Kryteria poprawności programów współbieżnych
7 Twierdzenie Fubiniego
 M. Beśka, Wstęp do teorii miary, wykład 7 19 7 Twierdzenie Fubiniego 7.1 Miary produktowe Niech i będą niepustymi zbiorami. Przez oznaczmy produkt kartezjański i tj. zbiór = { (x, y : x y }. Niech E oraz
M. Beśka, Wstęp do teorii miary, wykład 7 19 7 Twierdzenie Fubiniego 7.1 Miary produktowe Niech i będą niepustymi zbiorami. Przez oznaczmy produkt kartezjański i tj. zbiór = { (x, y : x y }. Niech E oraz
10. Wstęp do Teorii Gier
 10. Wstęp do Teorii Gier Definicja Gry Matematycznej Gra matematyczna spełnia następujące warunki: a) Jest co najmniej dwóch racjonalnych graczy. b) Zbiór możliwych dezycji każdego gracza zawiera co najmniej
10. Wstęp do Teorii Gier Definicja Gry Matematycznej Gra matematyczna spełnia następujące warunki: a) Jest co najmniej dwóch racjonalnych graczy. b) Zbiór możliwych dezycji każdego gracza zawiera co najmniej
Rys.1. Technika zestawiania części za pomocą polecenia WSTAWIAJĄCE (insert)
 Procesy i techniki produkcyjne Wydział Mechaniczny Ćwiczenie 3 (2) CAD/CAM Zasady budowy bibliotek parametrycznych Cel ćwiczenia: Celem tego zestawu ćwiczeń 3.1, 3.2 jest opanowanie techniki budowy i wykorzystania
Procesy i techniki produkcyjne Wydział Mechaniczny Ćwiczenie 3 (2) CAD/CAM Zasady budowy bibliotek parametrycznych Cel ćwiczenia: Celem tego zestawu ćwiczeń 3.1, 3.2 jest opanowanie techniki budowy i wykorzystania
Wykład 10. Stwierdzenie 1. X spełnia warunek Borela wtedy i tylko wtedy, gdy każda scentrowana rodzina zbiorów domkniętych ma niepusty przekrój.
 Wykład 10 Twierdzenie 1 (Borel-Lebesgue) Niech X będzie przestrzenią zwartą Z każdego pokrycia X zbiorami otwartymi można wybrać podpokrycie skończone Dowód Lemat 1 Dla każdego pokrycia U przestrzeni ośrodkowej
Wykład 10 Twierdzenie 1 (Borel-Lebesgue) Niech X będzie przestrzenią zwartą Z każdego pokrycia X zbiorami otwartymi można wybrać podpokrycie skończone Dowód Lemat 1 Dla każdego pokrycia U przestrzeni ośrodkowej
Próbny egzamin z matematyki dla uczniów klas II LO i III Technikum. w roku szkolnym 2012/2013
 Próbny egzamin z matematyki dla uczniów klas II LO i III Technikum w roku szkolnym 2012/2013 I. Zakres materiału do próbnego egzaminu maturalnego z matematyki: 1) liczby rzeczywiste 2) wyrażenia algebraiczne
Próbny egzamin z matematyki dla uczniów klas II LO i III Technikum w roku szkolnym 2012/2013 I. Zakres materiału do próbnego egzaminu maturalnego z matematyki: 1) liczby rzeczywiste 2) wyrażenia algebraiczne
Obliczenia iteracyjne
 Lekcja Strona z Obliczenia iteracyjne Zmienne iteracyjne (wyliczeniowe) Obliczenia iteracyjne wymagają zdefiniowania specjalnej zmiennej nazywanej iteracyjną lub wyliczeniową. Zmienną iteracyjną od zwykłej
Lekcja Strona z Obliczenia iteracyjne Zmienne iteracyjne (wyliczeniowe) Obliczenia iteracyjne wymagają zdefiniowania specjalnej zmiennej nazywanej iteracyjną lub wyliczeniową. Zmienną iteracyjną od zwykłej
Dokumentacja projektu Makao karciana gra sieciowa
 Dokumentacja projektu Makao karciana gra sieciowa 1 Spis treści Specyfikacja wymagań...3 Diagram przypadków użycia...4 Scenariusze...5 Diagramy sekwencji...6 Diagram modelu domeny...8 Projekt graficznego
Dokumentacja projektu Makao karciana gra sieciowa 1 Spis treści Specyfikacja wymagań...3 Diagram przypadków użycia...4 Scenariusze...5 Diagramy sekwencji...6 Diagram modelu domeny...8 Projekt graficznego
Algebra relacji. nazywamy każdy podzbiór iloczynu karteziańskiego D 1 D 2 D n.
 Algebra relacji Definicja 1 (Relacja matematyczna). Relacją R między elementami zbioru D 1 D 2 D n, gdzie przypomnijmy D 1 D 2 D n = {(d 1, d 2,..., d n ) : d i D i, i = 1, 2,..., n}, nazywamy każdy podzbiór
Algebra relacji Definicja 1 (Relacja matematyczna). Relacją R między elementami zbioru D 1 D 2 D n, gdzie przypomnijmy D 1 D 2 D n = {(d 1, d 2,..., d n ) : d i D i, i = 1, 2,..., n}, nazywamy każdy podzbiór
Arytmetyka. Działania na liczbach, potęga, pierwiastek, logarytm
 Arytmetyka Działania na liczbach, potęga, pierwiastek, logarytm Zbiory liczbowe Zbiór liczb naturalnych N = {1,2,3,4, }. Zbiór liczb całkowitych Z = {, 3, 2, 1,0,1,2,3, }. Zbiory liczbowe Zbiór liczb wymiernych
Arytmetyka Działania na liczbach, potęga, pierwiastek, logarytm Zbiory liczbowe Zbiór liczb naturalnych N = {1,2,3,4, }. Zbiór liczb całkowitych Z = {, 3, 2, 1,0,1,2,3, }. Zbiory liczbowe Zbiór liczb wymiernych
KRAJOWA MAPA ZAGROŻEŃ BEZPIECZEŃSTWA INSTRUKCJA OBSŁUGI
 KRAJOWA MAPA ZAGROŻEŃ BEZPIECZEŃSTWA INSTRUKCJA OBSŁUGI Aby skorzystać z możliwości zgłoszenia zagrożenia bezpieczeństwa publicznego na mapie należy wykonać następujące czynności 1. Po wpisaniu adresu
KRAJOWA MAPA ZAGROŻEŃ BEZPIECZEŃSTWA INSTRUKCJA OBSŁUGI Aby skorzystać z możliwości zgłoszenia zagrożenia bezpieczeństwa publicznego na mapie należy wykonać następujące czynności 1. Po wpisaniu adresu
Kształcenie w zakresie podstawowym. Klasa 1
 Kształcenie w zakresie podstawowym. Klasa 1 Poniżej podajemy umiejętności, jakie powinien zdobyć uczeń z każdego działu, aby uzyskać poszczególne stopnie. Na ocenę dopuszczającą uczeń powinien opanować
Kształcenie w zakresie podstawowym. Klasa 1 Poniżej podajemy umiejętności, jakie powinien zdobyć uczeń z każdego działu, aby uzyskać poszczególne stopnie. Na ocenę dopuszczającą uczeń powinien opanować
WYWIAD Plus 4.0. WYWIAD Plus 4.0 może współpracować z systemem POMOST Std w wersji co najmniej Rejestracja pracy socjalnej
 WYWIAD Plus 4.0 Wersja 4.0 jest pierwszą wersją WYWIAD Plus, wprowadzającą pakiet dodatkowych usług, rozszerzający możliwości oprogramowania ponad zakres przewidziany wymaganiami homologacyjnymi. W kolejnych
WYWIAD Plus 4.0 Wersja 4.0 jest pierwszą wersją WYWIAD Plus, wprowadzającą pakiet dodatkowych usług, rozszerzający możliwości oprogramowania ponad zakres przewidziany wymaganiami homologacyjnymi. W kolejnych
Kryteria oceniania z matematyki zakres podstawowy Klasa I
 Kryteria oceniania z matematyki zakres podstawowy Klasa I zakres Dopuszczający Dostateczny Dobry bardzo dobry Zdanie logiczne ( proste i złożone i forma zdaniowa oraz prawa logiczne dotyczące alternatywy,
Kryteria oceniania z matematyki zakres podstawowy Klasa I zakres Dopuszczający Dostateczny Dobry bardzo dobry Zdanie logiczne ( proste i złożone i forma zdaniowa oraz prawa logiczne dotyczące alternatywy,
5. Administracja kontami uŝytkowników
 5. Administracja kontami uŝytkowników Windows XP, w porównaniu do systemów Windows 9x, znacznie poprawia bezpieczeństwo oraz zwiększa moŝliwości konfiguracji uprawnień poszczególnych uŝytkowników. Natomiast
5. Administracja kontami uŝytkowników Windows XP, w porównaniu do systemów Windows 9x, znacznie poprawia bezpieczeństwo oraz zwiększa moŝliwości konfiguracji uprawnień poszczególnych uŝytkowników. Natomiast
Obliczenia inspirowane Naturą
 Obliczenia inspirowane Naturą Wykład 01 Modele obliczeń Jarosław Miszczak IITiS PAN Gliwice 05/10/2016 1 / 33 1 2 3 4 5 6 2 / 33 Co to znaczy obliczać? Co to znaczy obliczać? Deterministyczna maszyna Turinga
Obliczenia inspirowane Naturą Wykład 01 Modele obliczeń Jarosław Miszczak IITiS PAN Gliwice 05/10/2016 1 / 33 1 2 3 4 5 6 2 / 33 Co to znaczy obliczać? Co to znaczy obliczać? Deterministyczna maszyna Turinga
Logika Matematyczna (2,3)
 Logika Matematyczna (2,3) Jerzy Pogonowski Zakład Logiki Stosowanej UAM www.logic.amu.edu.pl pogon@amu.edu.pl 11, 18 X 2007 Jerzy Pogonowski (MEG) Logika Matematyczna (2,3) 11, 18 X 2007 1 / 34 Język KRZ
Logika Matematyczna (2,3) Jerzy Pogonowski Zakład Logiki Stosowanej UAM www.logic.amu.edu.pl pogon@amu.edu.pl 11, 18 X 2007 Jerzy Pogonowski (MEG) Logika Matematyczna (2,3) 11, 18 X 2007 1 / 34 Język KRZ
Przykładowa konfiguracja konta pocztowego w programie Thunderbird z wykorzystaniem MKS 2k7 (MS Windows Vista Busissnes)
 Przykładowa konfiguracja konta pocztowego w programie Thunderbird z wykorzystaniem MKS 2k7 (MS Windows Vista Busissnes) KROK NR 1: Uruchamiamy dowolną przeglądarkę internetową w celu pobrania najnowszej
Przykładowa konfiguracja konta pocztowego w programie Thunderbird z wykorzystaniem MKS 2k7 (MS Windows Vista Busissnes) KROK NR 1: Uruchamiamy dowolną przeglądarkę internetową w celu pobrania najnowszej
Multiprocessor Shared-Memory Information Exchange. Damian Klata, Adam Bułak
 Multiprocessor Shared-Memory Information Exchange Damian Klata, Adam Bułak Wstęp Zajmiemy się analizą protokołu opartego na komunikacji przez pamięć dzieloną opracowany przez firmę Westinghouse. Protokół
Multiprocessor Shared-Memory Information Exchange Damian Klata, Adam Bułak Wstęp Zajmiemy się analizą protokołu opartego na komunikacji przez pamięć dzieloną opracowany przez firmę Westinghouse. Protokół
Prognozowanie i Symulacje. Wykład I. Matematyczne metody prognozowania
 Prognozowanie i Symulacje. Wykład I. e-mail:e.kozlovski@pollub.pl Spis treści Szeregi czasowe 1 Szeregi czasowe 2 3 Szeregi czasowe Definicja 1 Szereg czasowy jest to proces stochastyczny z czasem dyskretnym
Prognozowanie i Symulacje. Wykład I. e-mail:e.kozlovski@pollub.pl Spis treści Szeregi czasowe 1 Szeregi czasowe 2 3 Szeregi czasowe Definicja 1 Szereg czasowy jest to proces stochastyczny z czasem dyskretnym
Instrukcja instalacji oprogramowania Flow!Works na komputerze z systemem Windows 7
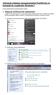 Instrukcja instalacji oprogramowania Flow!Works na komputerze z systemem Windows 7 W celu zainstalowania oprogramowania należy: 1. Wyłączyć kontrolę konta użytkownika: Uwaga! Pominięcie tego kroku spowoduje
Instrukcja instalacji oprogramowania Flow!Works na komputerze z systemem Windows 7 W celu zainstalowania oprogramowania należy: 1. Wyłączyć kontrolę konta użytkownika: Uwaga! Pominięcie tego kroku spowoduje
Wykład 21 Funkcje mierzalne. Kostrukcja i własności całki wzglȩdem miary przeliczalnie addytywnej
 Wykład 2 Funkcje mierzalne. Kostrukcja i własności całki wzglȩdem miary przeliczalnie addytywnej czȩść II (opracował: Piotr Nayar) Definicja 2.. Niech (E, E) bȩdzie przestrzenia mierzalna i niech λ : E
Wykład 2 Funkcje mierzalne. Kostrukcja i własności całki wzglȩdem miary przeliczalnie addytywnej czȩść II (opracował: Piotr Nayar) Definicja 2.. Niech (E, E) bȩdzie przestrzenia mierzalna i niech λ : E
Kultywator rolniczy - dobór parametrów sprężyny do zadanych warunków pracy
 Metody modelowania i symulacji kinematyki i dynamiki z wykorzystaniem CAD/CAE Laboratorium 6 Kultywator rolniczy - dobór parametrów sprężyny do zadanych warunków pracy Opis obiektu symulacji Przedmiotem
Metody modelowania i symulacji kinematyki i dynamiki z wykorzystaniem CAD/CAE Laboratorium 6 Kultywator rolniczy - dobór parametrów sprężyny do zadanych warunków pracy Opis obiektu symulacji Przedmiotem
Maszyna Turinga języki
 Maszyna Turinga języki Teoria automatów i języków formalnych Dr inż. Janusz Majewski Katedra Informatyki Maszyna Turinga (1) b b b A B C B D A B C b b Q Zależnie od symbolu obserwowanego przez głowicę
Maszyna Turinga języki Teoria automatów i języków formalnych Dr inż. Janusz Majewski Katedra Informatyki Maszyna Turinga (1) b b b A B C B D A B C b b Q Zależnie od symbolu obserwowanego przez głowicę
Elementy logiki matematycznej
 Elementy logiki matematycznej Przedmiotem logiki matematycznej jest badanie tzw. wyrażeń logicznych oraz metod rozumowania i sposobów dowodzenia używanych w matematyce, a także w innych dziedzinach, w
Elementy logiki matematycznej Przedmiotem logiki matematycznej jest badanie tzw. wyrażeń logicznych oraz metod rozumowania i sposobów dowodzenia używanych w matematyce, a także w innych dziedzinach, w
Unity 3D - pierwsze skrypty
 www.math.uni.lodz.pl/ radmat Cel ćwiczeń Celem bieżących ćwiczeń jest napisanie pierwszych, prostych skryptów, m.in wyświetlających upływający czas gry oraz jej stan. Wykorzystamy projekt z poprzednich
www.math.uni.lodz.pl/ radmat Cel ćwiczeń Celem bieżących ćwiczeń jest napisanie pierwszych, prostych skryptów, m.in wyświetlających upływający czas gry oraz jej stan. Wykorzystamy projekt z poprzednich
TWORZENIE POŁĄCZENIA INTERNETOWEGO PRZEZ TELEFON
 TWORZENIE POŁĄCZENIA INTERNETOWEGO PRZEZ TELEFON 1. W lewym górnym rogu kontrolera wybieramy Start -> Settings 2. U dołu ekrany wybieramy zakładkę Connections, a następnie ikonę o tej samej nazwie Connections.
TWORZENIE POŁĄCZENIA INTERNETOWEGO PRZEZ TELEFON 1. W lewym górnym rogu kontrolera wybieramy Start -> Settings 2. U dołu ekrany wybieramy zakładkę Connections, a następnie ikonę o tej samej nazwie Connections.
Teoria obliczeń i złożoność obliczeniowa
 Teoria obliczeń i złożoność obliczeniowa Kontakt: dr hab. inż. Adam Kasperski, prof. PWr. pokój 509 B4 adam.kasperski@pwr.wroc.pl materiały + informacje na stronie www. Zaliczenie: Egzamin Literatura Problemy
Teoria obliczeń i złożoność obliczeniowa Kontakt: dr hab. inż. Adam Kasperski, prof. PWr. pokój 509 B4 adam.kasperski@pwr.wroc.pl materiały + informacje na stronie www. Zaliczenie: Egzamin Literatura Problemy
Matematyka liczby zespolone. Wykład 1
 Matematyka liczby zespolone Wykład 1 Siedlce 5.10.015 Liczby rzeczywiste Zbiór N ={0,1,,3,4,5, } nazywamy zbiorem Liczb naturalnych, a zbiór N + ={1,,3,4, } nazywamy zbiorem liczb naturalnych dodatnich.
Matematyka liczby zespolone Wykład 1 Siedlce 5.10.015 Liczby rzeczywiste Zbiór N ={0,1,,3,4,5, } nazywamy zbiorem Liczb naturalnych, a zbiór N + ={1,,3,4, } nazywamy zbiorem liczb naturalnych dodatnich.
PIERWSZE URUCHOMIENIE PROGRAMU ITNC PROGRAMMING STATION
 PIERWSZE URUCHOMIENIE PROGRAMU ITNC PROGRAMMING STATION 1. Pobranie programu itnc 530 Programming station Program powinien być przygotowany w dostępnym w wersji edukacyjnej programu itnc 530 Programming
PIERWSZE URUCHOMIENIE PROGRAMU ITNC PROGRAMMING STATION 1. Pobranie programu itnc 530 Programming station Program powinien być przygotowany w dostępnym w wersji edukacyjnej programu itnc 530 Programming
INSTRUKCJA UŻYTKOWNIKA
 INSTRUKCJA UŻYTKOWNIKA INSTRUKCJA DLA KLIENTA Logowanie i resetowanie hasła Wersja 0.1 Marki, dn. 2018-02-21 Strona 2 z 7 Spis treści 1. CEL DOKUMENTU... 3 2. DEFINICJA NAZW I SKRÓTÓW... 3 3. SCENARIUSZ
INSTRUKCJA UŻYTKOWNIKA INSTRUKCJA DLA KLIENTA Logowanie i resetowanie hasła Wersja 0.1 Marki, dn. 2018-02-21 Strona 2 z 7 Spis treści 1. CEL DOKUMENTU... 3 2. DEFINICJA NAZW I SKRÓTÓW... 3 3. SCENARIUSZ
Przewodnik instalacji i rozpoczynania pracy. Dla DataPage+ 2013
 Przewodnik instalacji i rozpoczynania pracy Dla DataPage+ 2013 Ostatnia aktualizacja: 25 lipca 2013 Spis treści Instalowanie wymaganych wstępnie komponentów... 1 Przegląd... 1 Krok 1: Uruchamianie Setup.exe
Przewodnik instalacji i rozpoczynania pracy Dla DataPage+ 2013 Ostatnia aktualizacja: 25 lipca 2013 Spis treści Instalowanie wymaganych wstępnie komponentów... 1 Przegląd... 1 Krok 1: Uruchamianie Setup.exe
Metalogika (1) Jerzy Pogonowski. Uniwersytet Opolski. Zakład Logiki Stosowanej UAM
 Metalogika (1) Jerzy Pogonowski Zakład Logiki Stosowanej UAM www.logic.amu.edu.pl pogon@amu.edu.pl Uniwersytet Opolski Jerzy Pogonowski (MEG) Metalogika (1) Uniwersytet Opolski 1 / 21 Wstęp Cel: wprowadzenie
Metalogika (1) Jerzy Pogonowski Zakład Logiki Stosowanej UAM www.logic.amu.edu.pl pogon@amu.edu.pl Uniwersytet Opolski Jerzy Pogonowski (MEG) Metalogika (1) Uniwersytet Opolski 1 / 21 Wstęp Cel: wprowadzenie
Kultura logiczna Klasyczny rachunek zdań 2/2
 Kultura logiczna Klasyczny rachunek zdań 2/2 Bartosz Gostkowski bgostkowski@gmail.com Kraków 29 III 2 Plan wykładu: Wartościowanie w KRZ Tautologie KRZ Wartościowanie v, to funkcja, która posyła zbiór
Kultura logiczna Klasyczny rachunek zdań 2/2 Bartosz Gostkowski bgostkowski@gmail.com Kraków 29 III 2 Plan wykładu: Wartościowanie w KRZ Tautologie KRZ Wartościowanie v, to funkcja, która posyła zbiór
KONSTRUKCJA TRÓJKĄTA 1 KONSTRUKCJA TRÓJKĄTA 2 KONSTRUKCJA CZWOROKĄTA KONSTRUKCJA OKRĘGU KONSTRUKCJA STYCZNYCH
 Wstęp Ten multimedialny program edukacyjny zawiera zadania konstrukcyjne pozwalające na samodzielne ćwiczenie i sprawdzenie wiadomości w zakresie konstrukcji podstawowych figur geometrycznych. Jest przeznaczony
Wstęp Ten multimedialny program edukacyjny zawiera zadania konstrukcyjne pozwalające na samodzielne ćwiczenie i sprawdzenie wiadomości w zakresie konstrukcji podstawowych figur geometrycznych. Jest przeznaczony
Algorytmy sztucznej inteligencji
 www.math.uni.lodz.pl/ radmat Przeszukiwanie z ograniczeniami Zagadnienie przeszukiwania z ograniczeniami stanowi grupę problemów przeszukiwania w przestrzeni stanów, które składa się ze: 1 skończonego
www.math.uni.lodz.pl/ radmat Przeszukiwanie z ograniczeniami Zagadnienie przeszukiwania z ograniczeniami stanowi grupę problemów przeszukiwania w przestrzeni stanów, które składa się ze: 1 skończonego
Instrukcja instalacji programu serwisowego NTSN krok po kroku
 Instrukcja instalacji programu serwisowego NTSN krok po kroku 1. Pobieramy program serwisowy ze strony http://serwis.monument9.pl/program_serwisowy/ - bezpośredni link znajduje się w polu POBIERZ PROGRAM.
Instrukcja instalacji programu serwisowego NTSN krok po kroku 1. Pobieramy program serwisowy ze strony http://serwis.monument9.pl/program_serwisowy/ - bezpośredni link znajduje się w polu POBIERZ PROGRAM.
Indukcja matematyczna. Zasada minimum. Zastosowania.
 Indukcja matematyczna. Zasada minimum. Zastosowania. Arkadiusz Męcel Uwagi początkowe W trakcie zajęć przyjęte zostaną następujące oznaczenia: 1. Zbiory liczb: R - zbiór liczb rzeczywistych; Q - zbiór
Indukcja matematyczna. Zasada minimum. Zastosowania. Arkadiusz Męcel Uwagi początkowe W trakcie zajęć przyjęte zostaną następujące oznaczenia: 1. Zbiory liczb: R - zbiór liczb rzeczywistych; Q - zbiór
Praktyczne metody weryfikacji
 Praktyczne metody weryfikacji Sławomir Lasota Uniwersytet Warszawski semestr zimowy 06/07. p.1/?? I. Motywacja czyli po co?. p.2/?? czerwiec 1996. p.3/?? nieobsłużony wyjatek szacunkowy koszt: 600 mln
Praktyczne metody weryfikacji Sławomir Lasota Uniwersytet Warszawski semestr zimowy 06/07. p.1/?? I. Motywacja czyli po co?. p.2/?? czerwiec 1996. p.3/?? nieobsłużony wyjatek szacunkowy koszt: 600 mln
Podręcznik programu KNetWalk. Fela Winkelmolen Eugene Trounev Polskie tłumaczenie: Krzysztof Woźniak
 Fela Winkelmolen Eugene Trounev Polskie tłumaczenie: Krzysztof Woźniak 2 Spis treści 1 Wprowadzenie 6 2 Jak grać 7 3 Zasady gry, strategia gry i sztuczki 8 3.1 Zasady............................................
Fela Winkelmolen Eugene Trounev Polskie tłumaczenie: Krzysztof Woźniak 2 Spis treści 1 Wprowadzenie 6 2 Jak grać 7 3 Zasady gry, strategia gry i sztuczki 8 3.1 Zasady............................................
Andrzej Wiśniewski Logika II. Materiały do wykładu dla studentów kognitywistyki
 Andrzej Wiśniewski Logika II Materiały do wykładu dla studentów kognitywistyki Wykład 5. Wprowadzenie do semantyki teoriomodelowej cz.5. Wynikanie logiczne 1 Na poprzednim wykładzie udowodniliśmy m.in.:
Andrzej Wiśniewski Logika II Materiały do wykładu dla studentów kognitywistyki Wykład 5. Wprowadzenie do semantyki teoriomodelowej cz.5. Wynikanie logiczne 1 Na poprzednim wykładzie udowodniliśmy m.in.:
Praktyczne wykorzystanie arkusza kalkulacyjnego w pracy nauczyciela część 1
 Praktyczne wykorzystanie arkusza kalkulacyjnego w pracy nauczyciela część 1 Katarzyna Nawrot Spis treści: 1. Podstawowe pojęcia a. Arkusz kalkulacyjny b. Komórka c. Zakres komórek d. Formuła e. Pasek formuły
Praktyczne wykorzystanie arkusza kalkulacyjnego w pracy nauczyciela część 1 Katarzyna Nawrot Spis treści: 1. Podstawowe pojęcia a. Arkusz kalkulacyjny b. Komórka c. Zakres komórek d. Formuła e. Pasek formuły
OPERACJE NA PLIKACH I FOLDERACH
 OPERACJE NA PLIKACH I FOLDERACH Czym są pliki i foldery? krótkie przypomnienie Wszelkie operacje można przedstawić w postaci cyfrowej. Do tego celu wykorzystywane są bity - ciągi zer i jedynek. Zapisany
OPERACJE NA PLIKACH I FOLDERACH Czym są pliki i foldery? krótkie przypomnienie Wszelkie operacje można przedstawić w postaci cyfrowej. Do tego celu wykorzystywane są bity - ciągi zer i jedynek. Zapisany
Rozdział 4: PIERWSZE KROKI
 Rozdział 4: PIERWSZE KROKI 4. Pierwsze kroki 4.1. Uruchomienie programu Program najłatwiej uruchomić za pośrednictwem skrótu na pulpicie, choć równie dobrze możemy tego dokonać poprzez Menu Start systemu
Rozdział 4: PIERWSZE KROKI 4. Pierwsze kroki 4.1. Uruchomienie programu Program najłatwiej uruchomić za pośrednictwem skrótu na pulpicie, choć równie dobrze możemy tego dokonać poprzez Menu Start systemu
R o g e r A c c e s s C o n t r o l S y s t e m 5. Nota aplikacyjna nr 016 Wersja dokumentu: Rev. A. obecności w VISO
 R o g e r A c c e s s C o n t r o l S y s t e m 5 Nota aplikacyjna nr 016 Wersja dokumentu: Rev. A Rejestracja i monitorowanie obecności w VISO Uwaga: Niniejszy dokument dotyczy RACS v5.5 (VISO 1.5.2 lub
R o g e r A c c e s s C o n t r o l S y s t e m 5 Nota aplikacyjna nr 016 Wersja dokumentu: Rev. A Rejestracja i monitorowanie obecności w VISO Uwaga: Niniejszy dokument dotyczy RACS v5.5 (VISO 1.5.2 lub
Mathcad c.d. - Macierze, wykresy 3D, rozwiązywanie równań, pochodne i całki, animacje
 Mathcad c.d. - Macierze, wykresy 3D, rozwiązywanie równań, pochodne i całki, animacje Opracował: Zbigniew Rudnicki Powtórka z poprzedniego wykładu 2 1 Dokument, regiony, klawisze: Dokument Mathcada realizuje
Mathcad c.d. - Macierze, wykresy 3D, rozwiązywanie równań, pochodne i całki, animacje Opracował: Zbigniew Rudnicki Powtórka z poprzedniego wykładu 2 1 Dokument, regiony, klawisze: Dokument Mathcada realizuje
Logika Stosowana. Wykład 2 - Logika modalna Część 3. Marcin Szczuka. Instytut Informatyki UW. Wykład monograficzny, semestr letni 2017/2018
 Logika Stosowana Wykład 2 - Logika modalna Część 3 Marcin Szczuka Instytut Informatyki UW Wykład monograficzny, semestr letni 2017/2018 Marcin Szczuka (MIMUW) Logika Stosowana 2018 1 / 36 Plan wykładu
Logika Stosowana Wykład 2 - Logika modalna Część 3 Marcin Szczuka Instytut Informatyki UW Wykład monograficzny, semestr letni 2017/2018 Marcin Szczuka (MIMUW) Logika Stosowana 2018 1 / 36 Plan wykładu
Temat 1: Pojęcie gry, gry macierzowe: dominacje i punkty siodłowe
 Temat 1: Pojęcie gry, gry macierzowe: dominacje i punkty siodłowe Teorię gier można określić jako teorię podejmowania decyzji w szczególnych warunkach. Zajmuje się ona logiczną analizą sytuacji konfliktu
Temat 1: Pojęcie gry, gry macierzowe: dominacje i punkty siodłowe Teorię gier można określić jako teorię podejmowania decyzji w szczególnych warunkach. Zajmuje się ona logiczną analizą sytuacji konfliktu
Podstawy Informatyki. Algorytmy i ich poprawność
 Podstawy Informatyki Algorytmy i ich poprawność Błędy Błędy: językowe logiczne Błędy językowe Związane ze składnią języka Wykrywane automatycznie przez kompilator lub interpreter Prosty sposób usuwania
Podstawy Informatyki Algorytmy i ich poprawność Błędy Błędy: językowe logiczne Błędy językowe Związane ze składnią języka Wykrywane automatycznie przez kompilator lub interpreter Prosty sposób usuwania
NetDrive czyli jak w prosty sposób zarządzać zawartością FTP
 NetDrive czyli jak w prosty sposób zarządzać zawartością FTP W razie jakichkolwiek wątpliwości, pytań lub uwag odnośnie niniejszego dokumentu proszę o kontakt pod adresem info@lukaszpiec.pl. Można także
NetDrive czyli jak w prosty sposób zarządzać zawartością FTP W razie jakichkolwiek wątpliwości, pytań lub uwag odnośnie niniejszego dokumentu proszę o kontakt pod adresem info@lukaszpiec.pl. Można także
n := {n} n. Istnienie liczb naturalnych gwarantują: Aksjomat zbioru pustego, Aksjomat pary nieuporządkowanej oraz Aksjomat sumy.
 Konsekt wykładu ELiTM 6 Konstrukcje liczbowe Konstrukcja von Neumanna liczb naturalnych. Definicja 0 - liczba naturalna zero. Jeżeli n jest liczbą naturalną, to nastęną o niej jest liczba n {n} n. Istnienie
Konsekt wykładu ELiTM 6 Konstrukcje liczbowe Konstrukcja von Neumanna liczb naturalnych. Definicja 0 - liczba naturalna zero. Jeżeli n jest liczbą naturalną, to nastęną o niej jest liczba n {n} n. Istnienie
Teoria liczb. Wykład nr 9: Przybliżanie liczb rzeczywistych. Ułamki łańcuchowe (cz.1) Semestr letni 2018/2019
 Teoria liczb Wykład nr 9: Przybliżanie liczb rzeczywistych. Ułamki łańcuchowe (cz.1) Semestr letni 2018/2019 Trzy sposoby definiowania liczb rzeczywistych Dedekind Parę (A, B) podzbiorów zbioru Q nazywamy
Teoria liczb Wykład nr 9: Przybliżanie liczb rzeczywistych. Ułamki łańcuchowe (cz.1) Semestr letni 2018/2019 Trzy sposoby definiowania liczb rzeczywistych Dedekind Parę (A, B) podzbiorów zbioru Q nazywamy
