Krótka historia pomiaru czasu, czyli od zegara słonecznego do zegara atomowego 1
|
|
|
- Maksymilian Czajka
- 8 lat temu
- Przeglądów:
Transkrypt
1 4 FOTON 81, Lato 2003 Krótka historia pomiaru czasu, czyli od zegara słonecznego do zegara atomowego 1 Jarosław Koperski Instytut Fizyki UJ Streszczenie Przełom tysiącleci może skłaniać każdego z nas do refleksji nad upływającym czasem. Artykuł pokazuje inwencję rodzaju ludzkiego w dziedzinie mierzenia tej wielkości fizycznej. Począwszy od zegarów słonecznych, starożytnych zegarów wodnych, przez zegary mechaniczne, zegary kwarcowe, aż po zegary atomowe wszystkie przytaczane przykłady są efektem niezwykłej pasji człowieka w dążeniu do jak największej precyzji pomiaru.... czym zatem jest czas? Gdy nikt mnie o to nie pyta, wiem czym czas jest; gdy zaś chcę pytającemu wytłumaczyć gubię się... Św. Augustyn, ok. 400 r. n.e. Wprowadzenie Przełom tysiącleci daje fizykowi okazję do prześledzenia sposobów, jakich używał człowiek do mierzenia czasu. Do sposobów tych zaliczają się zarówno te najprostsze, wykorzystujące np. ruch Słońca po nieboskłonie, jak i te bardzo złożone, których zastosowanie wymagało rozwoju wiedzy, głębokiego poznania i wykorzystania zjawisk mikroświata. Pytanie, które pojawia się na wstępie: co to jest czas? 2, jest oczywiste. Czas możemy zdefiniować jako porządek wydarzeń lub jako jeden z elementów czterowymiarowej geometrii czasoprzestrzeni. Inna definicja określa czas jako wielkość mierzoną przez zegar 3. Bezsporne jest, że czas jest wielkością fizycz- 1 Na podstawie wykładu habilitacyjnego wygłoszonego pod tym samym tytułem dnia 7 marca 2002 roku. 2 Słownik języka polskiego pod redakcją M. Szymczaka (PWN, Warszawa 1978) podaje definicję: czas to nieprzerwany ciąg chwil, trwania; jest jedną z podstawowych (obok przestrzeni) form bytu materii. Pojęcie czasu absolutnego wprowadził Sir Isaac Newton, czasu względnego Albert Einstein, a czas urojony pojawił się w teorii Stephena Hawkinga. 3 Słowo zegar, określające miernik czasu, pojawiło się dopiero w XIV wieku n.e. Początkowo słowo to oznaczało dzwon, jako że pierwsze zegary mechaniczne instalowano w owym czasie na dzwonnicach kościołów.
2 FOTON 81, Lato ną, więc może być mierzony i, jak się okaże, może być mierzony z bardzo dużą dokładnością. Pomiar czasu t jest procesem bardzo prostym i sprowadza się do kilku podstawowych czynności. Zaczynamy mierzyć czas od pewnej chwili początkowej t 0. Następnie wielokrotnie mierzymy ustalony przez nas elementarny interwał czasowy Δt, sumujemy wyniki pomiarów wszystkich Δt i dodajemy do ustalonej wcześniej chwili początkowej t 0. Taki sposób pomiaru narzuca nam wymogi na miernik czasu, który musi posiadać niezbędne elementy. Podstawową sprawą jest dysponowanie powtarzalnym procesem zaznaczania równych przedziałów czasowych Δt. Kolejne elementy to: sposób liczenia przedziałów czasowych Δt oraz sposób pokazywania wyniku końcowego. Dzieje mierzenia czasu to trzy główne epoki: epoka przepływu ciągłego, trwająca do ok roku, kiedy to wynaleziono mechanizm wychwytowy, następnie epoka kontroli nierezonansowej, która zakończyła się w 1656 roku skonstruowaniem pierwszego zegara wahadłowego, oraz epoka kontroli rezonansowej, trwająca do dziś, a naznaczona w 1927 roku skonstruowaniem zegara kwarcowego oraz uruchomieniem zegara atomowego w roku Jednak wcześniej, długo przed epoką przepływu ciągłego, używano zegarów słonecznych. Zegary słoneczne Zegary słoneczne, zwane gnomonami, wykorzystywały cykliczny proces wędrówki Słońca po nieboskłonie ze wschodu na zachód, będący konsekwencją dobowego obrotu Ziemi dookoła własnej osi. Podczas gdy Słońce wędrowało po niebie, długość i pozycja cienia rzucanego przez wbity w ziemię pionowy słup wyznaczały porę dnia. Na półkuli północnej cień przesuwał się zgodnie ze znanym dziś ruchem wskazówek zegara z zachodu na wschód (patrz rys. 1). Na półkuli południowej cień przesuwał się w kierunku przeciwnym. (a) Rys. 1. (a) Przenośny zegar słoneczny. Pozycja i długość cienia oznaczały porę dnia. (b) Ilustracja działania zegara słonecznego na półkuli północnej
3 6 FOTON 81, Lato 2003 Niestety, zegary słoneczne pokazywały tylko słoneczny czas lokalny. Ich dokładność była bardzo ograniczona. Nie uwzględniały rocznej zmiany nachylenia osi obrotu Ziemi względem płaszczyzny orbity Ziemi wokół Słońca. Jednak ich podstawową wadą było to, że działały tylko w obecności Słońca. Pojawiło się pytanie: jak mierzyć czas w nocy? Epoka przepływu ciągłego Zapoczątkowało ją pojawienie się urządzeń, w których upływający czas wyznaczał stały i ciągły przepływ substancji ciekłej lub sypkiej. Jednymi z pierwszych urządzeń tego typu były wodne klepsydry 4. Początek ich używania był wielkim postępem, jako że stało się możliwe mierzenie czasu również pod nieobecność Słońca. W przypadku klepsydr wodnych procesem cyklicznym, potrzebnym do wyznaczenia interwałów Δt, było przelewanie się określonej ilości wody pomiędzy dwoma zbiornikami: górnym i dolnym. Naturalne było, i zauważyli to pierwsi użytkownicy, że w miarę ubywania wody, czyli w miarę zmniejszania się masy i wysokości słupa wody w górnym zbiorniku, malało ciśnienie słupa wody w miejscu, gdzie znajdował się otwór pomiędzy zbiornikami. Powodowało to nieregularności w pracy klepsydr. Rozwiązanie przedstawione na rys. 2 pokazuje jeden ze sposobów stosowanych w celu ominięcia tego problemu. Niestety, klepsydry wodne nie były miernikami dokładnymi. Ich główną wadą były niekontrolowane ubytki wody (powodujące ich przyśpieszanie ) oraz nieregularności sezonowe, takie jak zmiany temperatury, wilgotności itp. Jak nietrudno się domyślić, częściowym ominięciem tych problemów było zastosowanie klepsydr piaskowych 4. W zegarach tych materiałem sypkim był proszek cynowy, ołowiowy lub po prostu piasek. Proces odmierzania stałych przedziałów Δt pozostał podobny jak w klepsydrach wodnych. Zegary piaskowe nie były jednak dokładniejsze. Problemem powodującym ich złe działanie było tarcie działające pomiędzy przesypującymi się ziarenkami, powodujące zmniejszanie się ich średnicy i, w konsekwencji, szybsze przemieszczanie się materiału sypkiego przez otwór. Powodowało to przyspieszanie zegara. Szukano zatem innych rozwiązań. 4 Nazwa klepsydra pochodzi od dwóch greckich słów: kléptõ (kradnę) oraz hýdõr (woda) i jest nieściśle przypisywana tylko przepływowym zegarom piaskowym, które pojawiły się dopiero w średniowieczu.
4 FOTON 81, Lato D E F A C B Rys. 2. Zaawansowana konstrukcja klepsydry wodnej z III wieku p.n.e. Z naczynia górnego A w kształcie lejka do naczynia dolnego B wpływała woda ze stałą prędkością. Podnoszący się poziom wody w naczyniu B powodował wypychanie pływaka C połączonego z zębatką D, która unosząc się, powodowała obrót wskazówki godzinnej E. Nadmiar wody z lejka odprowadzany był na zewnątrz F, co zapewniało stałą wysokość słupa wody w naczyniu A Epoka kontroli nierezonansowej Przełomowym krokiem w rozwoju mierników czasu było zastąpienie wody lub materiału sypkiego bądź to odważnikiem o odpowiedniej masie (tu procesem cyklicznym było uwalnianie energii potencjalnej odważnika w polu grawitacyjnym), bądź też nawiniętą lub ściśniętą sprężyną (tu procesem cyklicznym było uwalnianie energii sprężystości sprężyny). Epokę przepływu ciągłego zakończyło wynalezienie mechanizmu pozwalającego na pełną kontrolę procesów uwalniania energii odważnika lub sprężyny. Miało to miejsce ok roku i było dziełem Henry de Vicka, pracującego dla króla Francji Karola V. Dało to początek epoce kontroli nierezonansowej.
5 8 FOTON 81, Lato 2003 Fakt konstrukcji i zastosowania tego mechanizmu, zwanego ZAPADKO- WYM MECHANIZMEM WYCHWYTOWYM był, niezwykle doniosły oto po raz pierwszy do kontroli miernika czasu użyty został ruch drgający! Mechanizm wychwytowy pozwalał na precyzyjną regulację prędkości uwalniania energii odważnika (patrz rys. 3). Osiągnięto wówczas cel: dokładność pracy zegara z zapadkowym mechanizmem wychwytowym była zdecydowanie większa od dokładności klepsydr wodnych czy klepsydr z materiałem sypkim. kolebnik zapadki m Rys. 3. Zapadkowy mechanizm wychwytowy. Składał się z koła koronowego, do osi którego przyczepiony był odważnik. Ruch koła koronowego regulowany był za pomocą dwóch zapadek umieszczonych na osi oscylującego kolebnika Epoka kontroli rezonansowej Zegary wahadłowe Epoka kontroli nierezonansowej trwała do końca XVI wieku. Wtedy to pojawiło się WAHADŁO stabilny oscylator mechaniczny. Przełom zapoczątkowały studia Galileusza nad grawitacyjnym wahadłem prostym. Około roku 1583 Galileusz odkrył, że okres wahadła prostego zależy tylko od jego długości i nie zależy od amplitudy (tzw. izochronizm) 5. Niestety, Galileusz nie wykorzystał wahadła jako elementu oscylującego w zegarze, podał jednak przepis, jak to zrobić. Z przepisu tego skorzystał Christiaan Huygens, duński astronom i matematyk, który w 1656 roku skonstruował pierwszy zegar wahadłowy. Wydarzenie to za- 5 Wniosek ten Galileusz wysnuł, obserwując wahania lampy wiszącej w katedrze w Pizie.
6 FOTON 81, Lato początkowało kolejną epokę w rozwoju mierników czasu epokę kontroli periodycznej, zwanej rezonansową 6. W konstrukcji zegara wahadłowego rolę kolebnika przejęło oscylujące wahadło, które zakończone było kotwicowym mechanizmem wychwytowym, uwalniającym, w rytm ruchów wahadła, pojedyncze zęby koła mechanizmu. Całość napędzana była energią potencjalną odważnika (patrz rys. 4). Dokładność zegarów wahadłowych zdecydowanie przewyższyła zegary z mechanizmem zapadkowym i kolebnikiem, a jedną z donioślejszych korzyści z zastosowania przekładni zębatych było wprowadzenie używanych do dziś wskazówek minutowej i sekundowej. m Rys. 4. Kotwicowy mechanizm wychwytowy Jest oczywiste, że dla precyzyjnego ustalenia okresu drgań wahadła T ( T 2 g ) konieczny był precyzyjny dobór jego długości l oraz stabilizacja podczas pracy. Czy wiecie, że nawet bardzo mała zmiana l, np. o 2 mm, spowodowana np. wzrostem temperatury otoczenia o 2 C, prowadziła do spowolnienia zegara o 1 sekundę na dobę? Na wiele lat problem stabilizacji l stał się wielkim wyzwaniem dla konstruktorów zegarów wahadłowych. Pod koniec XIX wieku zegary wahadłowe osiągnęły stabilność pracy ok. 0,01 sekundy na dobę i stały się wyposażeniem obserwatoriów astronomicznych. Były najdokładniejszymi miernikami czasu, aż do pierwszej połowy XX wieku. 6 Również zasługą Huygensa było skonstruowanie zegara, w którym zamiast wahadła zastosował koło balansowe ze spiralną sprężyną. Rozwiązanie to stosuje się do dnia dzisiejszego.
7 10 FOTON 81, Lato 2003 Chronometry A teraz słów kilka o chronometrach 7. W pierwszej połowie XVIII wieku zaistniała konieczność udoskonalenia metody pomiaru długości geograficznej. Pomyłki nawigacyjne podczas podróży morskich, powodowane błędami jej wyznaczania, prowadziły do wielu tragedii. Konkursy ogłaszane przez władców Hiszpanii, Portugalii i Królestwa Brytanii zachęcały wynalazców, którzy dążyli do skonstruowania chronometrów na tyle dokładnych, aby ich zastosowanie na morzu, w warunkach dużych zmian temperatury, ciśnienia i wilgotności, umożliwiało wyznaczanie długości geograficznej z pożądaną dokładnością 8. Jednym z tych, którzy stanęli do konkursu, był John Harrison, syn cieśli, zegarmistrz, rzemieślnik z Yorkshire w Anglii. Harrison zrezygnował z metod pozwalających na stabilizację l. Skupił się na konstrukcji elementu oscylującego zbudowanego z materiałów o małych współczynnikach rozszerzalności termicznej, niezawodnego mechanizmu wychwytowego oraz na udoskonaleniu łożysk, czyli minimalizacji sił tarcia. Zbudował cztery modele chronometrów. Dopiero ostatni model (patrz rys. 5(b)), powstały 26 lat po przystąpieniu do konkursu, charakteryzujący się zmienioną koncepcją (miniaturyzacja), posiadał żądaną dokładność i wytrzymałość na zmienne warunki podróży morskich. Pozwalał na wyznaczanie długości geograficznej z dokładnością do 0,5 stopnia! Przewyższało to narzucane konkursem wymagania. (a) (b) Rys. 5. Chronometry Harrisona: (a) ważący 33 kg model H.1. z 1735 roku oraz (b) model H.4. z 1761 roku mający średnicę 13 cm. Modelem H.4, który wyglądał jak duży zegarek kieszonkowy, Harrison wygrał konkurs i zdobył nagrodę w wysokości 10 tysięcy funtów (równoważną obecnie kilku milionom dolarów) 7 Nazwa pochodzi od greckich słów chrónos czas i metréõ mierzyć. Był to przenośny zegar o dużej dokładności, stosowany m.in. w nawigacji. 8 Zasada wyznaczania długości geograficznej z pomiaru czasu opiera się na porównaniu wskazania chronometru umieszczonego na płynącym statku z czasem, w którym statek opuścił port (1 godz.= 15 długości geogr.).
8 FOTON 81, Lato Zegary elektryczne Jak zauważyliśmy, okres wahadła zależy nie tylko od l, ale również od przyspieszenia ziemskiego g. Pod koniec XIX wieku stabilność zegarów wahadłowych (ok. 0,01 0,001 sekundy na dobę) zaczynała graniczyć z tą, dla której wpływ zmian g z kształtem Ziemi miał już znaczenie. Naturalnym dążeniem było zatem uniezależnienie się od wpływu g. Jednym ze sposobów było wykorzystanie drgań prądu zmiennego. Częstością podstawową była częstość 50 Hz ze źródła prądu zmiennego. Przez odpowiednią obróbkę w układach elektronicznych zapewniano generację częstości 1 Hz, będącej podstawą dla wskaźnika sekundowego. Później wskazówki zamieniono na wyświetlacze cyfrowe, ciekłokrystaliczne lub diody emitujące światło. Zegary kwarcowe Inną możliwość uniezależnienia się od wpływu g na element oscylujący otworzyła seria wynalazków związanych ze zjawiskiem piezoelektrycznym 9, odkrytym w roku 1880 przez braci Pierre a i Paul-Jacques a Curie. Dało to początek tzw. generatorom kwarcowym. Generator kwarcowy (patrz rys. 6(a)) został użyty do konstrukcji tzw. ZEGA- RA KWARCOWEGO. Jak łatwo się domyślić, teraz procesem odpowiedzialnym za odmierzanie równych przedziałów Δt stały się oscylacje kryształu. Zalet płynących z takiego rozwiązania było wiele: kwarc był piezoelektrykiem, miał własności niezależne od temperatury, był stabilny mechanicznie i chemicznie, był też powszechny w przyrodzie oraz łatwy do hodowania. Pierwszy zegar kwarcowy zbudowali w 1927 roku Warren Marrison i Joseph Horton. Należy zaznaczyć, że jako standardy czasu zegary kwarcowe natychmiast wyparły zegary wahadłowe i w latach czterdziestych XX wieku zamieniły je w większości obserwatoriów astronomicznych. Ich stabilność pracy przewyższyła o dwa rzędy wielkości stabilność pracy najprecyzyjniejszych zegarów wahadłowych. W roku 1970 pojawiły się pierwsze powszechnie dostępne zegarki kwarcowe na rękę. Użyto w nich kwarcowego generatora pokazanego na rys. 6(b). Niestety, oscylator kwarcowy nie był doskonały, zużywał się. Na skutek warunków zewnętrznych mógł zmieniać swoje własności i powodować nieregularności w pracy zegara kwarcowego. 9 Sprzężenie własności mechanicznych i elektrycznychi w odpowiednio wyciętym krysztale kwarcu. Na powierzchni kryształu kwarcu poddanego działaniu nacisku mechanicznego pojawia się ładunek elektryczny. Ten sam kryształ umieszczony w odpowiednim obwodzie elektrycznym wibruje i generuje sygnał elektryczny o stałej częstości.
9 12 FOTON 81, Lato 2003 (a) (b) Rys. 6. (a) Jeden z pierwszych generatorów z użyciem kryształu kwarcowego. (b) Kwarcowy generator stroikowy stosowany w zegarkach na rękę Zegary atomowe Obecnie obowiązujące wzorce czasu oparte są na ZEGARACH ATOMOWYCH. Są one wynikiem maksymalnego uniezależnienia się od własności oscylatora stosowanego do generacji interwałów Δt. Przejście pomiędzy dwoma poziomami energetycznymi w atomie oferuje taką niezależność. Jest ona oczywista: przejście energetyczne nie zużywa się, w każdych warunkach jest takie samo. W 1955 roku powstał pierwszy zegar atomowy pracujący z wykorzystaniem rezonansowego przejścia w atomach cezu. Nazywał się Caesium I i został zbudowany przez Louisa Essena i Jacka Parry ego z Narodowego Laboratorium Fizycznego w Anglii. Jednak zegar atomowy nie rezygnował z użycia rezonatora kwarcowego. Następowało w nim stałe sprawdzanie częstości oscylatora kwarcowego poprzez wykorzystanie precyzyjnych oscylacji atomowych pomiędzy dwoma poziomami energetycznymi. Bardzo ogólnie rzecz ujmując, nie wdając się w szczegóły, zasada działania Caesium I przedstawia się następująco. W źródle produkowana jest wiązka atomów cezu w stanie podstawowym. Atomy posiadają strukturę nadsubtelną: dwa poziomy o różnych energiach odległe o około 9,2 GHz (1 GHz = 10 9 Hz). Jest to tzw. przejście zegarowe 10. W obszarze poza źródłem, w obecności zewnętrznego pola magnetycznego B, następuje przestrzenna selekcja podpoziomów energetycznych zaangażowanych w 10 Obecnie obowiązującą jednostką czasu w układzie SI jest sekunda. Jej definicja została podana w 1967 roku na XIII Konferencji Wag i Miar. Jest czasem trwania okresów promieniowania, odpowiadającego przejściu pomiędzy dwoma poziomami struktury nadsubtelnej w stanie podstawowym cezu.
10 FOTON 81, Lato przejście zegarowe, a różniących się między sobą własnościami wynikającymi z oddziaływaniem z polem B. Podpoziomy o wyższej energii są eliminowane i tylko podpoziomy o niższej energii trafiają w obszar mikrofalowej wnęki rezonansowej 11, która może powodować przejścia do podpoziomu energii wyższej. Za wnęką następuje kolejna przestrzenna selekcja podpoziomów i mierzy się ilość tych o wyższej energii. Następnie, w pętli sprzężenia zwrotnego, wynik pomiaru służy do poprawienia częstości oscylatora kwarcowego, który zasila wnękę rezonansową. Licznik elektroniczny przetwarza częstość oscylacji kryształu na interwały Δt = 1 s. Burzliwy rozwój zegarów atomowych nastąpił w latach siedemdziesiątych XX wieku, kiedy to zastosowanie laserów spowodowało odejście od magnetycznych metod separacji atomów i zastosowanie metod pompowania optycznego (patrz Foton 75, 2001). Stabilność pracy zegarów atomowych jest bardzo duża (1 sekunda na 6 milionów lat!). Jako standardy czasu wyparły one zegary kwarcowe. W latach oficjalnym standardem czasu był zegar NIST-7, zbudowany w Narodowym Instytucie Standardów i Technologii (NIST) w USA. Niestety, i zegar atomowy nie jest miernikiem doskonałym. Jednym ze źródeł niedokładności zegara atomowego jest efekt Dopplera drugiego rzędu, którego wielkość jest proporcjonalna do kwadratu prędkości atomów. Wpływ tego efektu może być minimalizowany przez spowalnianie atomów np. przez tzw. chłodzenie laserowe (patrz Foton 75). Fontanny atomowe Do głównych czynników, jakie wpływają na dokładność D zegara atomowego, należą: Δν szerokość przejścia zegarowego (duża dla przejść dozwolonych, mała dla przejść wzbronionych), ν rez rezonansowa częstość tego przejścia, N ilość atomów oddziałujących z polem promieniowania wnęki oraz τ czas tego oddziaływania. Zależność ta wyraża się za pomocą formuły D 1, (1) rez N z której widać, że dokładność jest tym większa, im mniejsza jest Δν oraz im większe są ν rez, N oraz τ. Zatem, po pierwsze, należało zwiększyć czas τ. Wynikiem była kolejna generacja zegarów atomowych skonstruowanych z użyciem fontann atomowych. Przyjętym rozwiązaniem było połączenie pomysłu Jerrolda Zachariasa, który w roku 1953 zbudował pierwszą fontannę atomową, z techniką chłodzenia ato- 11 Przejścia pomiędzy podpoziomami oddalonymi od siebie o 9,2 GHz odbywają się w obszarze mikrofal.
11 14 FOTON 81, Lato 2003 mów. W metodzie tej obniża się początkową prędkość atomów (poprzez chłodzenie laserowe jak największej ilości atomów N w pułapce magnetooptycznej), wytwarza fontannę, oraz wykorzystuje fakt, że atomy z relatywnie małą prędkością w okolicy punktu zwrotnego w fontannie dwukrotnie przebywają obszar oddziaływania z wnęką rezonansową. Najdokładniejszy na świecie zegar z użyciem fontanny atomowej uruchomiono 1993 roku w Paryżu, w grupie André Clairona i Christopha Salomona. Stabilność pracy paryskiego zegara jest bezprecedensowa i wynosi 1 sekundę na 30 milionów lat! Od 1995 roku jest oficjalnym standardem czasu obok zegara na fontannie cezowej NIST F-1, działającego w NIST, w USA. Zegary jonowe Zgodnie z formułą (1), wzrost dokładności można też osiągnąć, zwiększając ν rez. W porównaniu z dotychczas omawianymi przejściami mikrofalowymi, wielce obiecujące jest zastosowanie przejść optycznych (częstości ~THz, 1 THz = Hz). Spowoduje to wzrost ν rez o 6 rzędów wielkości! Realizację z wykorzystaniem przejść optycznych przewiduje się dla zegarów jonowych (sposoby pułapkowania jonów są łatwiejsze od sposobów pułapkowania neutralnych atomów). Zakładana stabilność pracy jest absolutnie niewiarygodna: 1 s na 10 miliardów lat! D (sekundy / dobę), zegar mechaniczny, 1360, zegary wahadłowe, zegary kwarcowe, zegary atomowe, zegary atomowe (SO "Alfa"), zegary jonowe przewidywania } rok Rys. 7. Wielki postęp w dokładności pomiaru czasu: w 1360 roku stabilność pracy wynosiła 2 godziny na dobę, w roku sekundę na 30 mln lat (wzrost o 13 rzędów wielkości w ciągu 640 lat, w tym 6 rzędów wielkości przez ostatnie 45 lat). Przewidywania na najbliższe 5 lat (zegary atomowe na Stacji Orbitalnej Alfa i zegary jonowe na przejściach optycznych) są imponujące
12 FOTON 81, Lato Podsumowanie Dynamika rozwoju mierników czasu może być zilustrowana postępem w dokładności pomiaru czasu, który można wyrazić dopuszczalnym przez dany miernik błędem w sekundach na dobę (patrz rys. 7). Trudno jest wyrokować na temat przyszłości mierników czasu. Czy w najbliższych latach nastąpi jakiś znaczący przełom na miarę tych sprzed kilkudziesięciu lat? Czy raczej będą kontynuowane obecne sposoby? Czas pokaże. Zegar wahadłowy, szafkowy, wyk. Gobier, Paryż 1654 r. dla króla Jana Kazimierza obudowa przerobiona w XVIII w. Eksponat z Muzeum im. Przypkowskich w Jędrzejowie
Masatoshi Koshiba laureat Nagrody Nobla 2002 (po prawej) w czasach szkolnych z młodszym bratem
 Masatoshi Koshiba laureat Nagrody Nobla 2002 (po prawej) w czasach szkolnych z młodszym bratem Zdjęcie dzięki uprzejmości Biura Public Relations Uniwersytetu Tokio. Na okładce afisz uczennicy Katarzyny
Masatoshi Koshiba laureat Nagrody Nobla 2002 (po prawej) w czasach szkolnych z młodszym bratem Zdjęcie dzięki uprzejmości Biura Public Relations Uniwersytetu Tokio. Na okładce afisz uczennicy Katarzyny
Redefinicja jednostek układu SI
 CENTRUM NAUK BIOLOGICZNO-CHEMICZNYCH / WYDZIAŁ CHEMII UNIWERSYTETU WARSZAWSKIEGO Redefinicja jednostek układu SI Ewa Bulska MIERZALNE WYZWANIA ŚWIATA MIERZALNE WYZWANIA ŚWIATA MIERZALNE WYZWANIA ŚWIATA
CENTRUM NAUK BIOLOGICZNO-CHEMICZNYCH / WYDZIAŁ CHEMII UNIWERSYTETU WARSZAWSKIEGO Redefinicja jednostek układu SI Ewa Bulska MIERZALNE WYZWANIA ŚWIATA MIERZALNE WYZWANIA ŚWIATA MIERZALNE WYZWANIA ŚWIATA
SCHEMAT BLOKOWY MECHANIZMU ZEGAROWEEGO
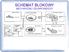 SCHEMAT BLOKOWY MECHANIZMU ZEGAROWEEGO DYSTRYBUCJA ENERGII WYCHWYT Jak widać ze schematu blokowego wychwyt jest połączony na zasadzie sprzężenia zwrotnego z przekładnią chodu z jednej strony i z regulatorem
SCHEMAT BLOKOWY MECHANIZMU ZEGAROWEEGO DYSTRYBUCJA ENERGII WYCHWYT Jak widać ze schematu blokowego wychwyt jest połączony na zasadzie sprzężenia zwrotnego z przekładnią chodu z jednej strony i z regulatorem
Wykład FIZYKA I. 5. Energia, praca, moc. http://www.if.pwr.wroc.pl/~wozniak/fizyka1.html. Dr hab. inż. Władysław Artur Woźniak
 Wykład FIZYKA I 5. Energia, praca, moc Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej http://www.if.pwr.wroc.pl/~wozniak/fizyka1.html ENERGIA, PRACA, MOC Siła to wielkość
Wykład FIZYKA I 5. Energia, praca, moc Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej http://www.if.pwr.wroc.pl/~wozniak/fizyka1.html ENERGIA, PRACA, MOC Siła to wielkość
Ćwiczenie M-2 Pomiar przyśpieszenia ziemskiego za pomocą wahadła rewersyjnego Cel ćwiczenia: II. Przyrządy: III. Literatura: IV. Wstęp. l Rys.
 Ćwiczenie M- Pomiar przyśpieszenia ziemskiego za pomocą wahadła rewersyjnego. Cel ćwiczenia: pomiar przyśpieszenia ziemskiego przy pomocy wahadła fizycznego.. Przyrządy: wahadło rewersyjne, elektroniczny
Ćwiczenie M- Pomiar przyśpieszenia ziemskiego za pomocą wahadła rewersyjnego. Cel ćwiczenia: pomiar przyśpieszenia ziemskiego przy pomocy wahadła fizycznego.. Przyrządy: wahadło rewersyjne, elektroniczny
1. Przeznaczenie testera.
 1. Przeznaczenie testera. Q- tester jest przeznaczony do badania kwarcowych analogowych i cyfrowych zegarków i zegarów. Q- tester służy do mierzenia odchyłki dobowej (s/d), odchyłki miesięcznej (s/m),
1. Przeznaczenie testera. Q- tester jest przeznaczony do badania kwarcowych analogowych i cyfrowych zegarków i zegarów. Q- tester służy do mierzenia odchyłki dobowej (s/d), odchyłki miesięcznej (s/m),
WYKŁAD 2 Podstawy spektroskopii wibracyjnej, model oscylatora harmonicznego i anharmonicznego. Częstość oscylacji a struktura molekuły Prof. dr hab.
 WYKŁAD 2 Podstawy spektroskopii wibracyjnej, model oscylatora harmonicznego i anharmonicznego. Częstość oscylacji a struktura molekuły Prof. dr hab. Halina Abramczyk POLITECHNIKA ŁÓDZKA Wydział Chemiczny
WYKŁAD 2 Podstawy spektroskopii wibracyjnej, model oscylatora harmonicznego i anharmonicznego. Częstość oscylacji a struktura molekuły Prof. dr hab. Halina Abramczyk POLITECHNIKA ŁÓDZKA Wydział Chemiczny
O 2 O 1. Temat: Wyznaczenie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego
 msg M 7-1 - Temat: Wyznaczenie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego Zagadnienia: prawa dynamiki Newtona, moment sił, moment bezwładności, dynamiczne równania ruchu wahadła fizycznego,
msg M 7-1 - Temat: Wyznaczenie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego Zagadnienia: prawa dynamiki Newtona, moment sił, moment bezwładności, dynamiczne równania ruchu wahadła fizycznego,
Wyznaczanie przyspieszenia ziemskiego za pomocą wahadła prostego
 Ćwiczenie M6 Wyznaczanie przyspieszenia ziemskiego za pomocą wahadła prostego M6.1. Cel ćwiczenia Celem ćwiczenia jest wyznaczenie przyspieszenia ziemskiego poprzez analizę ruchu wahadła prostego. M6..
Ćwiczenie M6 Wyznaczanie przyspieszenia ziemskiego za pomocą wahadła prostego M6.1. Cel ćwiczenia Celem ćwiczenia jest wyznaczenie przyspieszenia ziemskiego poprzez analizę ruchu wahadła prostego. M6..
Szczegółowy rozkład materiału z fizyki dla klasy II gimnazjum zgodny z nową podstawą programową.
 Szczegółowy rozkład materiału z fizyki dla klasy gimnazjum zgodny z nową podstawą programową. Lekcja organizacyjna. Omówienie programu nauczania i przypomnienie wymagań przedmiotowych Tytuł rozdziału w
Szczegółowy rozkład materiału z fizyki dla klasy gimnazjum zgodny z nową podstawą programową. Lekcja organizacyjna. Omówienie programu nauczania i przypomnienie wymagań przedmiotowych Tytuł rozdziału w
Fizyka Laserów wykład 14. Czesław Radzewicz
 Fizyka Laserów wykład 14 Czesław Radzewicz 1. Krótka historia zegarmistrzostwa 2. Współczesne standardy czasu i częstości 3. Optyczny zegar atomowy: wzorzec atomowy oscylator grzebień częstości 4. Po co?
Fizyka Laserów wykład 14 Czesław Radzewicz 1. Krótka historia zegarmistrzostwa 2. Współczesne standardy czasu i częstości 3. Optyczny zegar atomowy: wzorzec atomowy oscylator grzebień częstości 4. Po co?
Dr inż. Michał Marzantowicz,Wydział Fizyki P.W. p. 329, Mechatronika.
 Sprawy organizacyjne Dr inż. Michał Marzantowicz,Wydział Fizyki P.W. marzan@mech.pw.edu.pl p. 329, Mechatronika http://adam.mech.pw.edu.pl/~marzan/ http://www.if.pw.edu.pl/~wrobel Suma punktów: 38 2 sprawdziany
Sprawy organizacyjne Dr inż. Michał Marzantowicz,Wydział Fizyki P.W. marzan@mech.pw.edu.pl p. 329, Mechatronika http://adam.mech.pw.edu.pl/~marzan/ http://www.if.pw.edu.pl/~wrobel Suma punktów: 38 2 sprawdziany
Fizyka i wielkości fizyczne
 Fizyka i wielkości fizyczne Fizyka: - Stosuje opis matematyczny zjawisk - Formułuje prawa fizyczne na podstawie doświadczeń - Opiera się na prawach podstawowych (aksjomatach) Wielkością fizyczną jest każda
Fizyka i wielkości fizyczne Fizyka: - Stosuje opis matematyczny zjawisk - Formułuje prawa fizyczne na podstawie doświadczeń - Opiera się na prawach podstawowych (aksjomatach) Wielkością fizyczną jest każda
a, F Włodzimierz Wolczyński sin wychylenie cos cos prędkość sin sin przyspieszenie sin sin siła współczynnik sprężystości energia potencjalna
 Włodzimierz Wolczyński 3 RUCH DRGAJĄCY. CZĘŚĆ 1 wychylenie sin prędkość cos cos przyspieszenie sin sin siła współczynnik sprężystości sin sin 4 3 1 - x. v ; a ; F v -1,5T,5 T,75 T T 8t x -3-4 a, F energia
Włodzimierz Wolczyński 3 RUCH DRGAJĄCY. CZĘŚĆ 1 wychylenie sin prędkość cos cos przyspieszenie sin sin siła współczynnik sprężystości sin sin 4 3 1 - x. v ; a ; F v -1,5T,5 T,75 T T 8t x -3-4 a, F energia
PRACA Pracą mechaniczną nazywamy iloczyn wartości siły i wartości przemieszczenia, które nastąpiło zgodnie ze zwrotem działającej siły.
 PRACA Pracą mechaniczną nazywamy iloczyn wartości siły i wartości przemieszczenia, które nastąpiło zgodnie ze zwrotem działającej siły. Pracę oznaczamy literą W Pracę obliczamy ze wzoru: W = F s W praca;
PRACA Pracą mechaniczną nazywamy iloczyn wartości siły i wartości przemieszczenia, które nastąpiło zgodnie ze zwrotem działającej siły. Pracę oznaczamy literą W Pracę obliczamy ze wzoru: W = F s W praca;
Skale czasu. dr inż. Stefan Jankowski
 Skale czasu dr inż. Stefan Jankowski s.jankowski@am.szczecin.pl Definition of Time Co mierzą zegary (przyp. fizykom Albert Einstein, Donald Ivey, and others) Coś co zapobiega aby wszystko nie działo się
Skale czasu dr inż. Stefan Jankowski s.jankowski@am.szczecin.pl Definition of Time Co mierzą zegary (przyp. fizykom Albert Einstein, Donald Ivey, and others) Coś co zapobiega aby wszystko nie działo się
- wiązki pompująca & próbkująca oddziaływanie selektywne prędkościowo widma bezdopplerowskie. 0 k. z L 0 k. L 0 k
 Podsumowanie W1 Lasery w spektroskopii atomowej/molekularnej a) spektroskopia klasyczna b) spektroskopia bezdopplerowska 1. Spektroskopia nasyceniowa nasycenie selekcja prędkości - wiązki pompująca & próbkująca
Podsumowanie W1 Lasery w spektroskopii atomowej/molekularnej a) spektroskopia klasyczna b) spektroskopia bezdopplerowska 1. Spektroskopia nasyceniowa nasycenie selekcja prędkości - wiązki pompująca & próbkująca
Siła sprężystości - przypomnienie
 Siła sprężystości - przypomnienie Pomiary siły sprężystości wykonane kilka wykładów wcześniej (z uwzględnieniem kierunku siły). F = kx = 0.13x 0 F x cm mg Prawo Hooke a Ciało m na idealnie gładkiej powierzchni
Siła sprężystości - przypomnienie Pomiary siły sprężystości wykonane kilka wykładów wcześniej (z uwzględnieniem kierunku siły). F = kx = 0.13x 0 F x cm mg Prawo Hooke a Ciało m na idealnie gładkiej powierzchni
WYZNACZANIE PRZYSPIESZENIA ZIEMSKIEGO ZA POMOCĄ WAHADŁA MATEMATYCZNEGO
 Włodzimierz Nawrocki Pracownia Edukacji Matematycznej, Fizycznej i Chemicznej ŁCDNiKP WYZNACZANIE PRZYSPIESZENIA ZIEMSKIEGO ZA POMOCĄ WAHADŁA MATEMATYCZNEGO IV etap edukacji Pierwsza część zajęć ma charakter
Włodzimierz Nawrocki Pracownia Edukacji Matematycznej, Fizycznej i Chemicznej ŁCDNiKP WYZNACZANIE PRZYSPIESZENIA ZIEMSKIEGO ZA POMOCĄ WAHADŁA MATEMATYCZNEGO IV etap edukacji Pierwsza część zajęć ma charakter
Pomiar indukcji pola magnetycznego w szczelinie elektromagnesu
 Ćwiczenie E5 Pomiar indukcji pola magnetycznego w szczelinie elektromagnesu E5.1. Cel ćwiczenia Celem ćwiczenia jest pomiar siły elektrodynamicznej (przy pomocy wagi) działającej na odcinek przewodnika
Ćwiczenie E5 Pomiar indukcji pola magnetycznego w szczelinie elektromagnesu E5.1. Cel ćwiczenia Celem ćwiczenia jest pomiar siły elektrodynamicznej (przy pomocy wagi) działającej na odcinek przewodnika
Ćwiczenie nr X ANALIZA DRGAŃ SAMOWZBUDNYCH TYPU TARCIOWEGO
 Ćwiczenie nr X ANALIZA DRGAŃ SAMOWZBUDNYCH TYPU TARCIOWEGO Celem ćwiczenia jest zbadanie zachowania układu oscylatora harmonicznego na taśmociągu w programie napisanym w środowisku Matlab, dla następujących
Ćwiczenie nr X ANALIZA DRGAŃ SAMOWZBUDNYCH TYPU TARCIOWEGO Celem ćwiczenia jest zbadanie zachowania układu oscylatora harmonicznego na taśmociągu w programie napisanym w środowisku Matlab, dla następujących
Materiał do tematu: Piezoelektryczne czujniki ciśnienia. piezoelektryczny
 Materiał do tematu: Piezoelektryczne czujniki ciśnienia Efekt piezoelektryczny Cel zajęć: Celem zajęć jest zapoznanie się ze zjawiskiem piezoelektrycznym, zachodzącym w niektórych materiałach krystalicznych
Materiał do tematu: Piezoelektryczne czujniki ciśnienia Efekt piezoelektryczny Cel zajęć: Celem zajęć jest zapoznanie się ze zjawiskiem piezoelektrycznym, zachodzącym w niektórych materiałach krystalicznych
Metody badania kosmosu
 Metody badania kosmosu Zakres widzialny Fale radiowe i mikrofale Promieniowanie wysokoenergetyczne Detektory cząstek Pomiar sił grawitacyjnych Obserwacje prehistoryczne Obserwatorium słoneczne w Goseck
Metody badania kosmosu Zakres widzialny Fale radiowe i mikrofale Promieniowanie wysokoenergetyczne Detektory cząstek Pomiar sił grawitacyjnych Obserwacje prehistoryczne Obserwatorium słoneczne w Goseck
Kinematyka relatywistyczna
 Kinematyka relatywistyczna Fizyka I (B+C) Wykład VI: Prędkość światła historia pomiarów doświadczenie Michelsona-Morleya prędkość graniczna Teoria względności Einsteina Dylatacja czasu Prędkość światła
Kinematyka relatywistyczna Fizyka I (B+C) Wykład VI: Prędkość światła historia pomiarów doświadczenie Michelsona-Morleya prędkość graniczna Teoria względności Einsteina Dylatacja czasu Prędkość światła
DYNAMIKA dr Mikolaj Szopa
 dr Mikolaj Szopa 17.10.2015 Do 1600 r. uważano, że naturalną cechą materii jest pozostawanie w stanie spoczynku. Dopiero Galileusz zauważył, że to stan ruchu nie zmienia się, dopóki nie ingerujemy I prawo
dr Mikolaj Szopa 17.10.2015 Do 1600 r. uważano, że naturalną cechą materii jest pozostawanie w stanie spoczynku. Dopiero Galileusz zauważył, że to stan ruchu nie zmienia się, dopóki nie ingerujemy I prawo
Wyznaczanie sił działających na przewodnik z prądem w polu magnetycznym
 Ćwiczenie 11A Wyznaczanie sił działających na przewodnik z prądem w polu magnetycznym 11A.1. Zasada ćwiczenia W ćwiczeniu mierzy się przy pomocy wagi siłę elektrodynamiczną, działającą na odcinek przewodnika
Ćwiczenie 11A Wyznaczanie sił działających na przewodnik z prądem w polu magnetycznym 11A.1. Zasada ćwiczenia W ćwiczeniu mierzy się przy pomocy wagi siłę elektrodynamiczną, działającą na odcinek przewodnika
A) 14 km i 14 km. B) 2 km i 14 km. C) 14 km i 2 km. D) 1 km i 3 km.
 ŁÓDZKIE CENTRUM DOSKONALENIA NAUCZYCIELI I KSZTAŁCENIA PRAKTYCZNEGO Kod pracy Wypełnia Przewodniczący Wojewódzkiej Komisji Wojewódzkiego Konkursu Przedmiotowego z Fizyki Imię i nazwisko ucznia... Szkoła...
ŁÓDZKIE CENTRUM DOSKONALENIA NAUCZYCIELI I KSZTAŁCENIA PRAKTYCZNEGO Kod pracy Wypełnia Przewodniczący Wojewódzkiej Komisji Wojewódzkiego Konkursu Przedmiotowego z Fizyki Imię i nazwisko ucznia... Szkoła...
PL B1. Płonka Krzysztof,Bielsko-Biała,PL BUP 25/06. Rygiel Andrzej, Kancelaria Rzecznika Patentowego
 RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 204808 (13) B1 (21) Numer zgłoszenia: 375609 (51) Int.Cl. G04B 15/08 (2006.01) G04C 3/04 (2006.01) Urząd Patentowy Rzeczypospolitej Polskiej (22)
RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 204808 (13) B1 (21) Numer zgłoszenia: 375609 (51) Int.Cl. G04B 15/08 (2006.01) G04C 3/04 (2006.01) Urząd Patentowy Rzeczypospolitej Polskiej (22)
Laboratorium techniki laserowej Ćwiczenie 2. Badanie profilu wiązki laserowej
 Laboratorium techniki laserowej Ćwiczenie 2. Badanie profilu wiązki laserowej 1. Katedra Optoelektroniki i Systemów Elektronicznych, WETI, Politechnika Gdaoska Gdańsk 2006 1. Wstęp Pomiar profilu wiązki
Laboratorium techniki laserowej Ćwiczenie 2. Badanie profilu wiązki laserowej 1. Katedra Optoelektroniki i Systemów Elektronicznych, WETI, Politechnika Gdaoska Gdańsk 2006 1. Wstęp Pomiar profilu wiązki
Zadanie 18. Współczynnik sprężystości (4 pkt) Masz do dyspozycji statyw, sprężynę, linijkę oraz ciężarek o znanej masie z uchwytem.
 Przykładowy zestaw zadań z fizyki i astronomii Poziom podstawowy 11 Zadanie 18. Współczynnik sprężystości (4 pkt) Masz do dyspozycji statyw, sprężynę, linijkę oraz ciężarek o znanej masie z uchwytem. 18.1
Przykładowy zestaw zadań z fizyki i astronomii Poziom podstawowy 11 Zadanie 18. Współczynnik sprężystości (4 pkt) Masz do dyspozycji statyw, sprężynę, linijkę oraz ciężarek o znanej masie z uchwytem. 18.1
cz. 1. dr inż. Zbigniew Szklarski
 Wykład 14: Pole magnetyczne cz. 1. dr inż. Zbigniew Szklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Wektor indukcji pola magnetycznego, siła Lorentza v F L Jeżeli na dodatni ładunek
Wykład 14: Pole magnetyczne cz. 1. dr inż. Zbigniew Szklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Wektor indukcji pola magnetycznego, siła Lorentza v F L Jeżeli na dodatni ładunek
BADANIE DRGAŃ TŁUMIONYCH WAHADŁA FIZYCZNEGO
 ĆWICZENIE 36 BADANIE DRGAŃ TŁUMIONYCH WAHADŁA FIZYCZNEGO Cel ćwiczenia: Wyznaczenie podstawowych parametrów drgań tłumionych: okresu (T), częstotliwości (f), częstotliwości kołowej (ω), współczynnika tłumienia
ĆWICZENIE 36 BADANIE DRGAŃ TŁUMIONYCH WAHADŁA FIZYCZNEGO Cel ćwiczenia: Wyznaczenie podstawowych parametrów drgań tłumionych: okresu (T), częstotliwości (f), częstotliwości kołowej (ω), współczynnika tłumienia
ĆWICZENIE NR.6. Temat : Wyznaczanie drgań mechanicznych przekładni zębatych podczas badań odbiorczych
 ĆWICZENIE NR.6 Temat : Wyznaczanie drgań mechanicznych przekładni zębatych podczas badań odbiorczych 1. Wstęp W nowoczesnych przekładniach zębatych dąży się do uzyskania małych gabarytów w stosunku do
ĆWICZENIE NR.6 Temat : Wyznaczanie drgań mechanicznych przekładni zębatych podczas badań odbiorczych 1. Wstęp W nowoczesnych przekładniach zębatych dąży się do uzyskania małych gabarytów w stosunku do
Aplikacje Systemów. Nawigacja inercyjna. Gdańsk, 2016
 Aplikacje Systemów Wbudowanych Nawigacja inercyjna Gdańsk, 2016 Klasyfikacja systemów inercyjnych 2 Nawigacja inercyjna Podstawowymi blokami, wchodzącymi w skład systemów nawigacji inercyjnej (INS ang.
Aplikacje Systemów Wbudowanych Nawigacja inercyjna Gdańsk, 2016 Klasyfikacja systemów inercyjnych 2 Nawigacja inercyjna Podstawowymi blokami, wchodzącymi w skład systemów nawigacji inercyjnej (INS ang.
LIV OLIMPIADA FIZYCZNA 2004/2005 Zawody II stopnia
 LIV OLIMPIADA FIZYCZNA 004/005 Zawody II stopnia Zadanie doświadczalne Masz do dyspozycji: cienki drut z niemagnetycznego metalu, silny magnes stały, ciężarek o masie m=(100,0±0,5) g, statyw, pręty stalowe,
LIV OLIMPIADA FIZYCZNA 004/005 Zawody II stopnia Zadanie doświadczalne Masz do dyspozycji: cienki drut z niemagnetycznego metalu, silny magnes stały, ciężarek o masie m=(100,0±0,5) g, statyw, pręty stalowe,
Pomiar prędkości obrotowej
 2.3.2. Pomiar prędkości obrotowej Metody: Kontaktowe mechaniczne (prądniczki tachometryczne różnych typów), Bezkontaktowe: optyczne (światło widzialne, podczerwień, laser), elektromagnetyczne (indukcyjne,
2.3.2. Pomiar prędkości obrotowej Metody: Kontaktowe mechaniczne (prądniczki tachometryczne różnych typów), Bezkontaktowe: optyczne (światło widzialne, podczerwień, laser), elektromagnetyczne (indukcyjne,
Ćwiczenie 2a. Pomiar napięcia z izolacją galwaniczną Doświadczalne badania charakterystyk układów pomiarowych CZUJNIKI POMIAROWE I ELEMENTY WYKONAWCZE
 Politechnika Łódzka Katedra Mikroelektroniki i Technik Informatycznych 90-924 Łódź, ul. Wólczańska 221/223, bud. B18 tel. 42 631 26 28 faks 42 636 03 27 e-mail secretary@dmcs.p.lodz.pl http://www.dmcs.p.lodz.pl
Politechnika Łódzka Katedra Mikroelektroniki i Technik Informatycznych 90-924 Łódź, ul. Wólczańska 221/223, bud. B18 tel. 42 631 26 28 faks 42 636 03 27 e-mail secretary@dmcs.p.lodz.pl http://www.dmcs.p.lodz.pl
Fizyka. Program Wykładu. Program Wykładu c.d. Kontakt z prowadzącym zajęcia. Rok akademicki 2013/2014. Wydział Zarządzania i Ekonomii
 Fizyka Wydział Zarządzania i Ekonomii Kontakt z prowadzącym zajęcia dr Paweł Możejko 1e GG Konsultacje poniedziałek 9:00-10:00 paw@mif.pg.gda.pl Rok akademicki 2013/2014 Program Wykładu Mechanika Kinematyka
Fizyka Wydział Zarządzania i Ekonomii Kontakt z prowadzącym zajęcia dr Paweł Możejko 1e GG Konsultacje poniedziałek 9:00-10:00 paw@mif.pg.gda.pl Rok akademicki 2013/2014 Program Wykładu Mechanika Kinematyka
Imię i nazwisko: ... WOJEWÓDZKI KONKURS Z FIZYKI Z ASTRONOMIĄ DLA UCZNIÓW GIMNAZJUM ROK SZKOLNY 2012/2013 ETAP I SZKOLNY
 (pieczątka szkoły) Imię i nazwisko:.................................. Klasa.................................. Czas rozwiązywania zadań: 45 minut WOJEWÓDZKI KONKURS Z FIZYKI Z ASTRONOMIĄ DLA UCZNIÓW GIMNAZJUM
(pieczątka szkoły) Imię i nazwisko:.................................. Klasa.................................. Czas rozwiązywania zadań: 45 minut WOJEWÓDZKI KONKURS Z FIZYKI Z ASTRONOMIĄ DLA UCZNIÓW GIMNAZJUM
Tadeusz Lesiak. Dynamika punktu materialnego: Praca i energia; zasada zachowania energii
 Mechanika klasyczna Tadeusz Lesiak Wykład nr 4 Dynamika punktu materialnego: Praca i energia; zasada zachowania energii Energia i praca T. Lesiak Mechanika klasyczna 2 Praca Praca (W) wykonana przez stałą
Mechanika klasyczna Tadeusz Lesiak Wykład nr 4 Dynamika punktu materialnego: Praca i energia; zasada zachowania energii Energia i praca T. Lesiak Mechanika klasyczna 2 Praca Praca (W) wykonana przez stałą
- wiązki pompująca & próbkująca oddziaływanie selektywne prędkościowo widma bezdopplerowskie T. 0 k. z L 0 k. L 0 k
 Podsumowanie W1 Lasery w spektroskopii atomowej/molekularnej a) spektroskopia klasyczna b) spektroskopia bezdopplerowska 1. Spektroskopia nasyceniowa - wiązki pompująca & próbkująca oddziaływanie selektywne
Podsumowanie W1 Lasery w spektroskopii atomowej/molekularnej a) spektroskopia klasyczna b) spektroskopia bezdopplerowska 1. Spektroskopia nasyceniowa - wiązki pompująca & próbkująca oddziaływanie selektywne
Kinematyka relatywistyczna
 Kinematyka relatywistyczna Fizyka I (B+C) Wykład V: Prędkość światła historia pomiarów doświadczenie Michelsona-Morleya prędkość graniczna Teoria względności Einsteina Dylatacja czasu Prędkość światła
Kinematyka relatywistyczna Fizyka I (B+C) Wykład V: Prędkość światła historia pomiarów doświadczenie Michelsona-Morleya prędkość graniczna Teoria względności Einsteina Dylatacja czasu Prędkość światła
PL B1. UNIWERSYTET WARMIŃSKO-MAZURSKI W OLSZTYNIE, Olsztyn-Kortowo, PL BUP 10/10. ANDRZEJ LEMPASZEK, Słupy, PL
 PL 211929 B1 RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 211929 (13) B1 (21) Numer zgłoszenia: 386478 (51) Int.Cl. H02K 7/18 (2006.01) F03B 13/10 (2006.01) Urząd Patentowy Rzeczypospolitej Polskiej
PL 211929 B1 RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 211929 (13) B1 (21) Numer zgłoszenia: 386478 (51) Int.Cl. H02K 7/18 (2006.01) F03B 13/10 (2006.01) Urząd Patentowy Rzeczypospolitej Polskiej
Spis treści. Tom 1 Przedmowa do wydania polskiego 13. Przedmowa 15. Wstęp 19
 Spis treści Tom 1 Przedmowa do wydania polskiego 13 Przedmowa 15 1 Wstęp 19 1.1. Istota fizyki.......... 1 9 1.2. Jednostki........... 2 1 1.3. Analiza wymiarowa......... 2 3 1.4. Dokładność w fizyce.........
Spis treści Tom 1 Przedmowa do wydania polskiego 13 Przedmowa 15 1 Wstęp 19 1.1. Istota fizyki.......... 1 9 1.2. Jednostki........... 2 1 1.3. Analiza wymiarowa......... 2 3 1.4. Dokładność w fizyce.........
I. Przedmiot i metodologia fizyki
 I. Przedmiot i metodologia fizyki Rodowód fizyki współczesnej Świat zjawisk fizycznych: wielkości fizyczne, rzędy wielkości, uniwersalność praw Oddziaływania fundamentalne i poszukiwanie Teorii Ostatecznej
I. Przedmiot i metodologia fizyki Rodowód fizyki współczesnej Świat zjawisk fizycznych: wielkości fizyczne, rzędy wielkości, uniwersalność praw Oddziaływania fundamentalne i poszukiwanie Teorii Ostatecznej
Warunki uzyskania oceny wyższej niż przewidywana ocena końcowa.
 NAUCZYCIEL FIZYKI mgr Beata Wasiak KARTY INFORMACYJNE Z FIZYKI DLA POSZCZEGÓLNYCH KLAS GIMNAZJUM KLASA I semestr I DZIAŁ I: KINEMATYKA 1. Pomiary w fizyce. Umiejętność dokonywania pomiarów: długości, masy,
NAUCZYCIEL FIZYKI mgr Beata Wasiak KARTY INFORMACYJNE Z FIZYKI DLA POSZCZEGÓLNYCH KLAS GIMNAZJUM KLASA I semestr I DZIAŁ I: KINEMATYKA 1. Pomiary w fizyce. Umiejętność dokonywania pomiarów: długości, masy,
LASERY I ICH ZASTOSOWANIE
 LASERY I ICH ZASTOSOWANIE Laboratorium Instrukcja do ćwiczenia nr 3 Temat: Efekt magnetooptyczny 5.1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą modulowania zmiany polaryzacji światła oraz
LASERY I ICH ZASTOSOWANIE Laboratorium Instrukcja do ćwiczenia nr 3 Temat: Efekt magnetooptyczny 5.1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą modulowania zmiany polaryzacji światła oraz
Opis ćwiczenia. Cel ćwiczenia Poznanie budowy i zrozumienie istoty pomiaru przyspieszenia ziemskiego za pomocą wahadła rewersyjnego Henry ego Katera.
 ĆWICZENIE WYZNACZANIE PRZYSPIESZENIA ZIEMSKIEGO ZA POMOCĄ WAHADŁA REWERSYJNEGO Opis ćwiczenia Cel ćwiczenia Poznanie budowy i zrozumienie istoty pomiaru przyspieszenia ziemskiego za pomocą wahadła rewersyjnego
ĆWICZENIE WYZNACZANIE PRZYSPIESZENIA ZIEMSKIEGO ZA POMOCĄ WAHADŁA REWERSYJNEGO Opis ćwiczenia Cel ćwiczenia Poznanie budowy i zrozumienie istoty pomiaru przyspieszenia ziemskiego za pomocą wahadła rewersyjnego
KOOF Szczecin: www.of.szc.pl
 3OF_III_D KOOF Szczecin: www.of.szc.pl XXXII OLIMPIADA FIZYCZNA (198/1983). Stopień III, zadanie doświadczalne D Źródło: Nazwa zadania: Działy: Słowa kluczowe: Komitet Główny Olimpiady Fizycznej; Waldemar
3OF_III_D KOOF Szczecin: www.of.szc.pl XXXII OLIMPIADA FIZYCZNA (198/1983). Stopień III, zadanie doświadczalne D Źródło: Nazwa zadania: Działy: Słowa kluczowe: Komitet Główny Olimpiady Fizycznej; Waldemar
Literatura: A.Weintrit: Jednostki miar wczoraj i dziś. Przegląd systemów miar i wag na lądzie i na morzu
 Literatura: A.Weintrit: Jednostki miar wczoraj i dziś. Przegląd systemów miar i wag na lądzie i na morzu HISTORIA POMIARU CZASU Pierwszym przyrządem służącym do wyznaczania czasu był gnomon, wynaleziony
Literatura: A.Weintrit: Jednostki miar wczoraj i dziś. Przegląd systemów miar i wag na lądzie i na morzu HISTORIA POMIARU CZASU Pierwszym przyrządem służącym do wyznaczania czasu był gnomon, wynaleziony
DRGANIA SWOBODNE UKŁADU O DWÓCH STOPNIACH SWOBODY. Rys Model układu
 Ćwiczenie 7 DRGANIA SWOBODNE UKŁADU O DWÓCH STOPNIACH SWOBODY. Cel ćwiczenia Doświadczalne wyznaczenie częstości drgań własnych układu o dwóch stopniach swobody, pokazanie postaci drgań odpowiadających
Ćwiczenie 7 DRGANIA SWOBODNE UKŁADU O DWÓCH STOPNIACH SWOBODY. Cel ćwiczenia Doświadczalne wyznaczenie częstości drgań własnych układu o dwóch stopniach swobody, pokazanie postaci drgań odpowiadających
Ziemia jako planeta w Układzie Słonecznym
 Wykład udostępniam na licencji Creative Commons: Ziemia jako planeta w Układzie Słonecznym Data courtesy Marc Imhoff of NASA GSFC and Christopher Elvidge of NOAA NGDC. Image by Craig Mayhew and Robert
Wykład udostępniam na licencji Creative Commons: Ziemia jako planeta w Układzie Słonecznym Data courtesy Marc Imhoff of NASA GSFC and Christopher Elvidge of NOAA NGDC. Image by Craig Mayhew and Robert
Drgania. O. Harmoniczny
 Dobrej fazy! Drgania O. Harmoniczny Położenie równowagi, 5 lipca 218 r. 1 Zadanie Zegar Małgorzata Berajter, update: 217-9-6, id: pl-ciepło-5, diff: 2 Pewien zegar, posiadający wahadło ze srebra, odmierza
Dobrej fazy! Drgania O. Harmoniczny Położenie równowagi, 5 lipca 218 r. 1 Zadanie Zegar Małgorzata Berajter, update: 217-9-6, id: pl-ciepło-5, diff: 2 Pewien zegar, posiadający wahadło ze srebra, odmierza
Podstawowy problem mechaniki klasycznej punktu materialnego można sformułować w sposób następujący:
 Dynamika Podstawowy problem mechaniki klasycznej punktu materialnego można sformułować w sposób następujący: mamy ciało (zachowujące się jak punkt materialny) o znanych właściwościach (masa, ładunek itd.),
Dynamika Podstawowy problem mechaniki klasycznej punktu materialnego można sformułować w sposób następujący: mamy ciało (zachowujące się jak punkt materialny) o znanych właściwościach (masa, ładunek itd.),
Ćw. nr 31. Wahadło fizyczne o regulowanej płaszczyźnie drgań - w.2
 1 z 6 Zespół Dydaktyki Fizyki ITiE Politechniki Koszalińskiej Ćw. nr 3 Wahadło fizyczne o regulowanej płaszczyźnie drgań - w.2 Cel ćwiczenia Pomiar okresu wahań wahadła z wykorzystaniem bramki optycznej
1 z 6 Zespół Dydaktyki Fizyki ITiE Politechniki Koszalińskiej Ćw. nr 3 Wahadło fizyczne o regulowanej płaszczyźnie drgań - w.2 Cel ćwiczenia Pomiar okresu wahań wahadła z wykorzystaniem bramki optycznej
n n 1 2 = exp( ε ε ) 1 / kt = exp( hν / kt) (23) 2 to wzór (22) przejdzie w następującą równość: ρ (ν) = B B A / B 2 1 hν exp( ) 1 kt (24)
 n n 1 2 = exp( ε ε ) 1 / kt = exp( hν / kt) (23) 2 to wzór (22) przejdzie w następującą równość: ρ (ν) = B B A 1 2 / B hν exp( ) 1 kt (24) Powyższe równanie określające gęstość widmową energii promieniowania
n n 1 2 = exp( ε ε ) 1 / kt = exp( hν / kt) (23) 2 to wzór (22) przejdzie w następującą równość: ρ (ν) = B B A 1 2 / B hν exp( ) 1 kt (24) Powyższe równanie określające gęstość widmową energii promieniowania
Czym jest Fizyka? Podstawowa nauka przyrodnicza badanie fundamentalnych i uniwersalnych właściwości materii oraz zjawisk w przyrodzie gr. physis - prz
 FIZYKA 1 Czym jest fizyka jako nauka? Fizyka i technika Wielkości fizyczne skalarne, wektorowe, tensorowe operacje na wektorach Pomiar i jednostki fizyczne Prawa i zasady fizyki Czym jest Fizyka? Podstawowa
FIZYKA 1 Czym jest fizyka jako nauka? Fizyka i technika Wielkości fizyczne skalarne, wektorowe, tensorowe operacje na wektorach Pomiar i jednostki fizyczne Prawa i zasady fizyki Czym jest Fizyka? Podstawowa
Menu. Badające rozproszenie światła,
 Menu Badające rozproszenie światła, Instrumenty badające pole magnetyczne Ziemi Pole magnetyczne Ziemi mierzy się za pomocą magnetometrów. Instrumenty badające pole magnetyczne Ziemi Rodzaje magnetometrów:»
Menu Badające rozproszenie światła, Instrumenty badające pole magnetyczne Ziemi Pole magnetyczne Ziemi mierzy się za pomocą magnetometrów. Instrumenty badające pole magnetyczne Ziemi Rodzaje magnetometrów:»
Doświadczalne wyznaczanie współczynnika sztywności (sprężystości) sprężyny
 Doświadczalne wyznaczanie współczynnika sztywności (sprężystości) Wprowadzenie Wartość współczynnika sztywności użytej można wyznaczyć z dużą dokładnością metodą statyczną. W tym celu należy zawiesić pionowo
Doświadczalne wyznaczanie współczynnika sztywności (sprężystości) Wprowadzenie Wartość współczynnika sztywności użytej można wyznaczyć z dużą dokładnością metodą statyczną. W tym celu należy zawiesić pionowo
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podstawy Automatyki Badanie i synteza kaskadowego adaptacyjnego układu regulacji do sterowania obiektu o
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podstawy Automatyki Badanie i synteza kaskadowego adaptacyjnego układu regulacji do sterowania obiektu o
Zapisy podstawy programowej Uczeń: 2. 1) wyjaśnia cechy budowy i określa położenie różnych ciał niebieskich we Wszechświecie;
 Geografia listopad Liceum klasa I, poziom rozszerzony XI Ziemia we wszechświecie Zapisy podstawy programowej Uczeń: 2. 1) wyjaśnia cechy budowy i określa położenie różnych ciał niebieskich we Wszechświecie;
Geografia listopad Liceum klasa I, poziom rozszerzony XI Ziemia we wszechświecie Zapisy podstawy programowej Uczeń: 2. 1) wyjaśnia cechy budowy i określa położenie różnych ciał niebieskich we Wszechświecie;
Scenariusz lekcji fizyki
 Scenariusz lekcji fizyki Temat: BADAMY SIŁĘ CIĘZKOŚCI. JAK SIŁA ZALEŻY OD MASY CIAŁA. I klasa Gimnazjum Towarzystwa Salezjańskiego Studenci prowadzący lekcje: Agnieszka Gościniak i Anna Kimlińska Studenci
Scenariusz lekcji fizyki Temat: BADAMY SIŁĘ CIĘZKOŚCI. JAK SIŁA ZALEŻY OD MASY CIAŁA. I klasa Gimnazjum Towarzystwa Salezjańskiego Studenci prowadzący lekcje: Agnieszka Gościniak i Anna Kimlińska Studenci
Politechnika Białostocka INSTRUKCJA DO ĆWICZEŃ LABORATORYJNYCH
 Politechnika Białostocka Wydział Budownictwa i Inżynierii Środowiska INSTRUKCJA DO ĆWICZEŃ LABORATORYJNYCH Temat ćwiczenia: Próba skręcania pręta o przekroju okrągłym Numer ćwiczenia: 4 Laboratorium z
Politechnika Białostocka Wydział Budownictwa i Inżynierii Środowiska INSTRUKCJA DO ĆWICZEŃ LABORATORYJNYCH Temat ćwiczenia: Próba skręcania pręta o przekroju okrągłym Numer ćwiczenia: 4 Laboratorium z
Jak ciężka jest masa?
 "Masa jest nie tylko miarą bezwładności, posiada również ciężar". Co oznacza, że nie tylko wpływa na przyspieszenie pod wpływem siły, ale powoduje, że gdy znajduje się w polu grawitacyjnym Ziemi, doświadcza
"Masa jest nie tylko miarą bezwładności, posiada również ciężar". Co oznacza, że nie tylko wpływa na przyspieszenie pod wpływem siły, ale powoduje, że gdy znajduje się w polu grawitacyjnym Ziemi, doświadcza
Rozdział 1. Prędkość i przyspieszenie... 5 Rozdział 2. Składanie ruchów Rozdział 3. Modelowanie zjawisk fizycznych...43 Numeryczne całkowanie,
 Rozdział 1. Prędkość i przyspieszenie... 5 Rozdział. Składanie ruchów... 11 Rozdział 3. Modelowanie zjawisk fizycznych...43 Rozdział 4. Numeryczne całkowanie, czyli obliczanie pracy w polu grawitacyjnym
Rozdział 1. Prędkość i przyspieszenie... 5 Rozdział. Składanie ruchów... 11 Rozdział 3. Modelowanie zjawisk fizycznych...43 Rozdział 4. Numeryczne całkowanie, czyli obliczanie pracy w polu grawitacyjnym
lim Np. lim jest wyrażeniem typu /, a
 Wykład 3 Pochodna funkcji złożonej, pochodne wyższych rzędów, reguła de l Hospitala, różniczka funkcji i jej zastosowanie, pochodna jako prędkość zmian 3. Pochodna funkcji złożonej. Jeżeli funkcja złożona
Wykład 3 Pochodna funkcji złożonej, pochodne wyższych rzędów, reguła de l Hospitala, różniczka funkcji i jej zastosowanie, pochodna jako prędkość zmian 3. Pochodna funkcji złożonej. Jeżeli funkcja złożona
Wykład FIZYKA I. Dr hab. inż. Władysław Artur Woźniak. Katedra Optyki i Fotoniki Wydział Podstawowych Problemów Techniki Politechnika Wrocławska
 Wykład FIZYKA I 1. Ruch drgający tłumiony i wymuszony Katedra Optyki i Fotoniki Wydział Podstawowych Problemów Techniki Politechnika Wrocławska http://www.if.pwr.wroc.pl/~wozniak/fizyka1.html DRGANIA HARMONICZNE
Wykład FIZYKA I 1. Ruch drgający tłumiony i wymuszony Katedra Optyki i Fotoniki Wydział Podstawowych Problemów Techniki Politechnika Wrocławska http://www.if.pwr.wroc.pl/~wozniak/fizyka1.html DRGANIA HARMONICZNE
OPTYKA KWANTOWA Wykład dla 5. roku Fizyki
 OPTYKA KWANTOWA Wykład dla 5. roku Fizyki c Adam Bechler 2006 Instytut Fizyki Uniwersytetu Szczecińskiego Rezonansowe oddziaływanie układu atomowego z promieniowaniem "! "!! # $%&'()*+,-./-(01+'2'34'*5%.25%&+)*-(6
OPTYKA KWANTOWA Wykład dla 5. roku Fizyki c Adam Bechler 2006 Instytut Fizyki Uniwersytetu Szczecińskiego Rezonansowe oddziaływanie układu atomowego z promieniowaniem "! "!! # $%&'()*+,-./-(01+'2'34'*5%.25%&+)*-(6
Ruch drgający. Ruch harmoniczny prosty, tłumiony i wymuszony
 Ruch drgający Ruch harmoniczny prosty, tłumiony i wymuszony Ruchem drgającym nazywamy ruch ciała zachodzący wokół stałego położenia równowagi. Ruchy drgające dzielimy na ruchy: okresowe, nieokresowe. Ruch
Ruch drgający Ruch harmoniczny prosty, tłumiony i wymuszony Ruchem drgającym nazywamy ruch ciała zachodzący wokół stałego położenia równowagi. Ruchy drgające dzielimy na ruchy: okresowe, nieokresowe. Ruch
Wyznaczanie modułu Younga metodą strzałki ugięcia
 Ćwiczenie M12 Wyznaczanie modułu Younga metodą strzałki ugięcia M12.1. Cel ćwiczenia Celem ćwiczenia jest wyznaczenie wartości modułu Younga różnych materiałów poprzez badanie strzałki ugięcia wykonanych
Ćwiczenie M12 Wyznaczanie modułu Younga metodą strzałki ugięcia M12.1. Cel ćwiczenia Celem ćwiczenia jest wyznaczenie wartości modułu Younga różnych materiałów poprzez badanie strzałki ugięcia wykonanych
REDEFINICJA SI W ROLACH GŁÓWNYCH: STAŁE PODSTAWOWE
 KONFERENCJA POMIARY INNOWACJE AKREDYTACJE RZESZÓW, 1 WRZEŚNIA 2018 BIURO STRATEGII WYDZIAŁ STRATEGII I ROZWOJU dokładnie REDEFINICJA W ROLACH GŁÓWNYCH: STAŁE PODSTAWOWE Aleksandra Gadomska 1919-2019 METROLOGIA
KONFERENCJA POMIARY INNOWACJE AKREDYTACJE RZESZÓW, 1 WRZEŚNIA 2018 BIURO STRATEGII WYDZIAŁ STRATEGII I ROZWOJU dokładnie REDEFINICJA W ROLACH GŁÓWNYCH: STAŁE PODSTAWOWE Aleksandra Gadomska 1919-2019 METROLOGIA
PRACOWNIA FIZYCZNA DLA UCZNIÓW WAHADŁA SPRZĘŻONE
 PRACOWNA FZYCZNA DLA UCZNÓW WAHADŁA SPRZĘŻONE W ćwiczeniu badać będziemy drgania dwóch wahadeł sprzężonych za pomocą sprężyny. Wahadła są jednakowe (mają ten sam moment bezwładności, tę samą masę m i tę
PRACOWNA FZYCZNA DLA UCZNÓW WAHADŁA SPRZĘŻONE W ćwiczeniu badać będziemy drgania dwóch wahadeł sprzężonych za pomocą sprężyny. Wahadła są jednakowe (mają ten sam moment bezwładności, tę samą masę m i tę
SPEKTROSKOPIA IR I SPEKTROSKOPIA RAMANA JAKO METODY KOMPLEMENTARNE
 SPEKTROSKOPIA IR I SPEKTROSKOPIA RAMANA JAKO METODY KOMPLEMENTARNE Promieniowanie o długości fali 2-50 μm nazywamy promieniowaniem podczerwonym. Absorpcja lub emisja promieniowania z tego zakresu jest
SPEKTROSKOPIA IR I SPEKTROSKOPIA RAMANA JAKO METODY KOMPLEMENTARNE Promieniowanie o długości fali 2-50 μm nazywamy promieniowaniem podczerwonym. Absorpcja lub emisja promieniowania z tego zakresu jest
Zjawisko piezoelektryczne 1. Wstęp
 Zjawisko piezoelektryczne. Wstęp W roku 880 Piotr i Jakub Curie stwierdzili, że na powierzchni niektórych kryształów poddanych działaniu zewnętrznych naprężeń mechanicznych indukują się ładunki elektryczne,
Zjawisko piezoelektryczne. Wstęp W roku 880 Piotr i Jakub Curie stwierdzili, że na powierzchni niektórych kryształów poddanych działaniu zewnętrznych naprężeń mechanicznych indukują się ładunki elektryczne,
Treści nauczania (program rozszerzony)- 25 spotkań po 4 godziny lekcyjne
 (program rozszerzony)- 25 spotkań po 4 godziny lekcyjne 1, 2, 3- Kinematyka 1 Pomiary w fizyce i wzorce pomiarowe 12.1 2 Wstęp do analizy danych pomiarowych 12.6 3 Jak opisać położenie ciała 1.1 4 Opis
(program rozszerzony)- 25 spotkań po 4 godziny lekcyjne 1, 2, 3- Kinematyka 1 Pomiary w fizyce i wzorce pomiarowe 12.1 2 Wstęp do analizy danych pomiarowych 12.6 3 Jak opisać położenie ciała 1.1 4 Opis
S. Baran - Podstawy fizyki materii skondensowanej Fonony. Fonony
 Fonony Drgania płaszczyzn sieciowych podłużne poprzeczne źródło: Ch. Kittel Wstęp do fizyki..., rozdz. 4, rys. 2, 3, str. 118 Drgania płaszczyzn sieciowych Do opisu drgań sieci krystalicznej wystarczą
Fonony Drgania płaszczyzn sieciowych podłużne poprzeczne źródło: Ch. Kittel Wstęp do fizyki..., rozdz. 4, rys. 2, 3, str. 118 Drgania płaszczyzn sieciowych Do opisu drgań sieci krystalicznej wystarczą
Pomiary rezystancji izolacji
 Stan izolacji ma decydujący wpływ na bezpieczeństwo obsługi i prawidłowe funkcjonowanie instalacji oraz urządzeń elektrycznych. Dobra izolacja to obok innych środków ochrony również gwarancja ochrony przed
Stan izolacji ma decydujący wpływ na bezpieczeństwo obsługi i prawidłowe funkcjonowanie instalacji oraz urządzeń elektrycznych. Dobra izolacja to obok innych środków ochrony również gwarancja ochrony przed
ĆWICZENIE 15 BADANIE WZMACNIACZY MOCY MAŁEJ CZĘSTOTLIWOŚCI
 1 ĆWICZENIE 15 BADANIE WZMACNIACZY MOCY MAŁEJ CZĘSTOTLIWOŚCI 15.1. CEL ĆWICZENIA Celem ćwiczenia jest poznanie podstawowych właściwości wzmacniaczy mocy małej częstotliwości oraz przyswojenie umiejętności
1 ĆWICZENIE 15 BADANIE WZMACNIACZY MOCY MAŁEJ CZĘSTOTLIWOŚCI 15.1. CEL ĆWICZENIA Celem ćwiczenia jest poznanie podstawowych właściwości wzmacniaczy mocy małej częstotliwości oraz przyswojenie umiejętności
Drgania w obwodzie LC. Autorzy: Zbigniew Kąkol Kamil Kutorasiński
 Drgania w obwodzie L Autorzy: Zbigniew Kąkol Kamil Kutorasiński 016 Drgania w obwodzie L Autorzy: Zbigniew Kąkol, Kamil Kutorasiński Rozpatrzmy obwód złożony z szeregowo połączonych indukcyjności L (cewki)
Drgania w obwodzie L Autorzy: Zbigniew Kąkol Kamil Kutorasiński 016 Drgania w obwodzie L Autorzy: Zbigniew Kąkol, Kamil Kutorasiński Rozpatrzmy obwód złożony z szeregowo połączonych indukcyjności L (cewki)
Podstawy fizyki wykład 5
 Podstawy fizyki wykład 5 Dr Piotr Sitarek Instytut Fizyki, Politechnika Wrocławska Grawitacja Pole grawitacyjne Prawo powszechnego ciążenia Pole sił zachowawczych Prawa Keplera Prędkości kosmiczne Czarne
Podstawy fizyki wykład 5 Dr Piotr Sitarek Instytut Fizyki, Politechnika Wrocławska Grawitacja Pole grawitacyjne Prawo powszechnego ciążenia Pole sił zachowawczych Prawa Keplera Prędkości kosmiczne Czarne
Fizyka 1 Wróbel Wojciech. w poprzednim odcinku
 w poprzednim odcinku 1 Nauka - technika 2 Metodologia Problem Hipoteza EKSPERYMENT JAKO NARZĘDZIE WERYFIKACJI 3 Fizyka wielkości fizyczne opisują właściwości obiektów i pozwalają również ilościowo porównać
w poprzednim odcinku 1 Nauka - technika 2 Metodologia Problem Hipoteza EKSPERYMENT JAKO NARZĘDZIE WERYFIKACJI 3 Fizyka wielkości fizyczne opisują właściwości obiektów i pozwalają również ilościowo porównać
Wymagania edukacyjne- kl. I
 mgr Szczeklik Jerzy MOS Łysa Góra 2015/2016 Wymagania edukacyjne Wstęp: Wymagania edukacyjne- kl. I Nauka, metoda naukowa, nauki przyrodnicze, Mierzenie, jednostki miar, wzorce jednostek Ruch i siły: Tor
mgr Szczeklik Jerzy MOS Łysa Góra 2015/2016 Wymagania edukacyjne Wstęp: Wymagania edukacyjne- kl. I Nauka, metoda naukowa, nauki przyrodnicze, Mierzenie, jednostki miar, wzorce jednostek Ruch i siły: Tor
1. Nazwij zaznaczone na mapkach cywilizacje. Naucz się odnajdywać te cywilizacje na mapkach różnego typu (także współczesnych)
 ............ CYWILIZACJE STAROŻYTNEGO WSCHODU 1. Nazwij zaznaczone na mapkach cywilizacje. Naucz się odnajdywać te cywilizacje na mapkach różnego typu (także współczesnych) 2. Przeczytaj uważnie tekst,
............ CYWILIZACJE STAROŻYTNEGO WSCHODU 1. Nazwij zaznaczone na mapkach cywilizacje. Naucz się odnajdywać te cywilizacje na mapkach różnego typu (także współczesnych) 2. Przeczytaj uważnie tekst,
DYNAMIKA SIŁA I JEJ CECHY
 DYNAMIKA SIŁA I JEJ CECHY Wielkość wektorowa to wielkość fizyczna mająca cztery cechy: wartość liczbowa punkt przyłożenia (jest początkiem wektora, zaznaczamy na rysunku np. kropką) kierunek (to linia
DYNAMIKA SIŁA I JEJ CECHY Wielkość wektorowa to wielkość fizyczna mająca cztery cechy: wartość liczbowa punkt przyłożenia (jest początkiem wektora, zaznaczamy na rysunku np. kropką) kierunek (to linia
Ćwiczenie 402. Wyznaczanie siły wyporu i gęstości ciał. PROSTOPADŁOŚCIAN (wpisz nazwę ciała) WALEC (wpisz numer z wieczka)
 2012 Katedra Fizyki SGGW Nazwisko... Data... Nr na liście... Imię... Wydział... Dzień tyg.... Ćwiczenie 402 Godzina... Wyznaczanie siły wyporu i gęstości ciał WIELKOŚCI FIZYCZNE JEDNOSTKI WALEC (wpisz
2012 Katedra Fizyki SGGW Nazwisko... Data... Nr na liście... Imię... Wydział... Dzień tyg.... Ćwiczenie 402 Godzina... Wyznaczanie siły wyporu i gęstości ciał WIELKOŚCI FIZYCZNE JEDNOSTKI WALEC (wpisz
Temperatura i ciepło
 Temperatura i ciepło Zerowa zasada termodynamiki Ciepło: Sposób przekazu energii wewnętrznej w skutek różnicy temperatur Ciała są w kontakcie termalnym jeżeli ciepło może być przekazywane między nimi Kiedy
Temperatura i ciepło Zerowa zasada termodynamiki Ciepło: Sposób przekazu energii wewnętrznej w skutek różnicy temperatur Ciała są w kontakcie termalnym jeżeli ciepło może być przekazywane między nimi Kiedy
M2. WYZNACZANIE MOMENTU BEZWŁADNOŚCI WAHADŁA OBERBECKA
 M WYZNACZANE MOMENTU BEZWŁADNOŚC WAHADŁA OBERBECKA opracowała Bożena Janowska-Dmoch Do opisu ruchu obrotowego ciał stosujemy prawa dynamiki ruchu obrotowego, w których występują wielkości takie jak: prędkość
M WYZNACZANE MOMENTU BEZWŁADNOŚC WAHADŁA OBERBECKA opracowała Bożena Janowska-Dmoch Do opisu ruchu obrotowego ciał stosujemy prawa dynamiki ruchu obrotowego, w których występują wielkości takie jak: prędkość
Wstęp do Optyki i Fizyki Materii Skondensowanej
 Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 5 wykład: Piotr Fita pokazy: Jacek Szczytko ćwiczenia: Aneta Drabińska, Paweł Kowalczyk, Barbara Piętka, Michał Karpiński Wydział
Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 5 wykład: Piotr Fita pokazy: Jacek Szczytko ćwiczenia: Aneta Drabińska, Paweł Kowalczyk, Barbara Piętka, Michał Karpiński Wydział
Wyznaczanie przenikalności magnetycznej i krzywej histerezy
 Ćwiczenie 13 Wyznaczanie przenikalności magnetycznej i krzywej histerezy 13.1. Zasada ćwiczenia W uzwojeniu, umieszczonym na żelaznym lub stalowym rdzeniu, wywołuje się przepływ prądu o stopniowo zmienianej
Ćwiczenie 13 Wyznaczanie przenikalności magnetycznej i krzywej histerezy 13.1. Zasada ćwiczenia W uzwojeniu, umieszczonym na żelaznym lub stalowym rdzeniu, wywołuje się przepływ prądu o stopniowo zmienianej
KONKURS PRZEDMIOTOWY Z FIZYKI dla uczniów gimnazjów. Schemat punktowania zadań
 1 KONKURS PRZEDMIOTOWY Z FIZYKI dla uczniów gimnazjów 18 stycznia 018 r. zawody II stopnia (rejonowe) Schemat punktowania zadań Maksymalna liczba punktów 60. 85% 51pkt. Uwaga! 1. Za poprawne rozwiązanie
1 KONKURS PRZEDMIOTOWY Z FIZYKI dla uczniów gimnazjów 18 stycznia 018 r. zawody II stopnia (rejonowe) Schemat punktowania zadań Maksymalna liczba punktów 60. 85% 51pkt. Uwaga! 1. Za poprawne rozwiązanie
Wstęp do Optyki i Fizyki Materii Skondensowanej
 Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 5 wykład: Piotr Fita pokazy: Jacek Szczytko ćwiczenia: Aneta Drabińska, Paweł Kowalczyk, Barbara Piętka Wydział Fizyki Uniwersytet
Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 5 wykład: Piotr Fita pokazy: Jacek Szczytko ćwiczenia: Aneta Drabińska, Paweł Kowalczyk, Barbara Piętka Wydział Fizyki Uniwersytet
WOJEWÓDZKI KONKURS Z FIZYKI DLA UCZNIÓW GIMNAZJUM ROK SZKOLNY 2014/2015, ETAP REJONOWY
 WOJEWÓDZKI KONKURSZ FIZYKI DLA UCZNIÓW GIMNAZJÓW ROK SZKOLNY 2014/2015 IMIĘ I NAZWISKO UCZNIA wpisuje komisja konkursowa po rozkodowaniu pracy! KOD UCZNIA: ETAP II REJONOWY Informacje: 1. Czas rozwiązywania
WOJEWÓDZKI KONKURSZ FIZYKI DLA UCZNIÓW GIMNAZJÓW ROK SZKOLNY 2014/2015 IMIĘ I NAZWISKO UCZNIA wpisuje komisja konkursowa po rozkodowaniu pracy! KOD UCZNIA: ETAP II REJONOWY Informacje: 1. Czas rozwiązywania
Czy da się zastosować teorię względności do celów praktycznych?
 Czy da się zastosować teorię względności do celów praktycznych? Witold Chmielowiec Centrum Fizyki Teoretycznej PAN IX Festiwal Nauki 24 września 2005 Mapa Ogólna Teoria Względności Szczególna Teoria Względności
Czy da się zastosować teorię względności do celów praktycznych? Witold Chmielowiec Centrum Fizyki Teoretycznej PAN IX Festiwal Nauki 24 września 2005 Mapa Ogólna Teoria Względności Szczególna Teoria Względności
SPIS TREŚCI ««*» ( # * *»»
 ««*» ( # * *»» CZĘŚĆ I. POJĘCIA PODSTAWOWE 1. Co to jest fizyka? 11 2. Wielkości fizyczne 11 3. Prawa fizyki 17 4. Teorie fizyki 19 5. Układ jednostek SI 20 6. Stałe fizyczne 20 CZĘŚĆ II. MECHANIKA 7.
««*» ( # * *»» CZĘŚĆ I. POJĘCIA PODSTAWOWE 1. Co to jest fizyka? 11 2. Wielkości fizyczne 11 3. Prawa fizyki 17 4. Teorie fizyki 19 5. Układ jednostek SI 20 6. Stałe fizyczne 20 CZĘŚĆ II. MECHANIKA 7.
Zadanie 2. Oceń prawdziwość poniższych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F, jeśli zdanie jest fałszywe.
 Zadanie 1. W pewnej odległości od siebie umieszczono dwie identyczne kulki o metalizowanych powierzchniach. Ładunek elektryczny zgromadzony na pierwszej kulce wynosił +6q, a na drugiej -4q (gdzie q oznacza
Zadanie 1. W pewnej odległości od siebie umieszczono dwie identyczne kulki o metalizowanych powierzchniach. Ładunek elektryczny zgromadzony na pierwszej kulce wynosił +6q, a na drugiej -4q (gdzie q oznacza
GŁÓWNE CECHY ŚWIATŁA LASEROWEGO
 GŁÓWNE CECHY ŚWIATŁA LASEROWEGO Światło może być rozumiane jako: Strumień fotonów o energii E Fala elektromagnetyczna. = hν i pędzie p h = = hν c Najprostszym przypadkiem fali elektromagnetycznej jest
GŁÓWNE CECHY ŚWIATŁA LASEROWEGO Światło może być rozumiane jako: Strumień fotonów o energii E Fala elektromagnetyczna. = hν i pędzie p h = = hν c Najprostszym przypadkiem fali elektromagnetycznej jest
KOOF Szczecin: www.of.szc.pl
 Źródło: LI OLIMPIADA FIZYCZNA (1/2). Stopień III, zadanie doświadczalne - D Nazwa zadania: Działy: Słowa kluczowe: Komitet Główny Olimpiady Fizycznej; Andrzej Wysmołek, kierownik ds. zadań dośw. plik;
Źródło: LI OLIMPIADA FIZYCZNA (1/2). Stopień III, zadanie doświadczalne - D Nazwa zadania: Działy: Słowa kluczowe: Komitet Główny Olimpiady Fizycznej; Andrzej Wysmołek, kierownik ds. zadań dośw. plik;
I. PROMIENIOWANIE CIEPLNE
 I. PROMIENIOWANIE CIEPLNE - lata '90 XIX wieku WSTĘP Widmo promieniowania elektromagnetycznego zakres "pokrycia" różnymi rodzajami fal elektromagnetycznych promieniowania zawartego w danej wiązce. rys.i.1.
I. PROMIENIOWANIE CIEPLNE - lata '90 XIX wieku WSTĘP Widmo promieniowania elektromagnetycznego zakres "pokrycia" różnymi rodzajami fal elektromagnetycznych promieniowania zawartego w danej wiązce. rys.i.1.
E107. Bezpromieniste sprzężenie obwodów RLC
 E7. Bezpromieniste sprzężenie obwodów RLC Cel doświadczenia: Pomiar amplitudy sygnału w rezonatorze w zależności od wzajemnej odległości d cewek generatora i rezonatora. Badanie wpływu oporu na tłumienie
E7. Bezpromieniste sprzężenie obwodów RLC Cel doświadczenia: Pomiar amplitudy sygnału w rezonatorze w zależności od wzajemnej odległości d cewek generatora i rezonatora. Badanie wpływu oporu na tłumienie
OPTYKA KWANTOWA Wykład dla 5. roku Fizyki
 OPTYKA KWANTOWA Wykład dla 5. roku Fizyki c Adam Bechler 006 Instytut Fizyki Uniwersytetu Szczecińskiego Równania (3.7), pomimo swojej prostoty, nie posiadają poza nielicznymi przypadkami ścisłych rozwiązań,
OPTYKA KWANTOWA Wykład dla 5. roku Fizyki c Adam Bechler 006 Instytut Fizyki Uniwersytetu Szczecińskiego Równania (3.7), pomimo swojej prostoty, nie posiadają poza nielicznymi przypadkami ścisłych rozwiązań,
