analiza nieliniowa i równania różniczkowe patroni sesji: Jubileuszowy Zjazd Matematyków Polskich w stulecie Polskiego Towarzystwa Matematycznego
|
|
|
- Teodor Stasiak
- 5 lat temu
- Przeglądów:
Transkrypt
1 analiza nieliniowa i równania różniczkowe patroni sesji: Juliusz Paweł Schauder Stanisław Zaremba Jubileuszowy Zjazd Matematyków Polskich w stulecie Polskiego Towarzystwa Matematycznego Kraków 3-7 września 2019
2 Spis treści Analiza nieliniowa i równania różniczkowe 6 7 Piotr Bartłomiejczyk Homotopie gradientowe versus właściwe gradientowe 9 Bartosz Bieganowski, Jarosław Mederski Bound states for the Schrödinger equation with mixedtype nonlinearities 11 Piotr Biler Nonlinear nonlocal heat equations: global solutions vs blowup
3 12 Iwona Chlebicka (Skrzypczak), Youssef Ahmida, Piotr Gwiazda, Ahmed Youssfi, Anna Zatorska- Goldstein Renormalized solutions to parabolic problems with strongly nonstandard growth 14 Magdalena Chmara Rozwiązania okresowe anizotropowych układów Eulera- Lagrange a - istnienie i krotność TBA 16 Tomasz Cieślak 17 Aleksander Ćwiszewski, Piotr Kokocki Rozwiązania stacjonarne zagadnień eliptycznych na R N 19 Grzegorz Gabor Niezmienniczość i silna niezmienniczość w inkluzjach różniczkowych 20 Marek Galewski Some remarks on monotone and variational methods with applications to nonlinear equations 21 Anna Gołębiewska Bifurkacje z orbit rozwiązań układów eliptycznych
4 23 Grzegorz Graff Fixed point indices of iterates for a boundary fixed point 25 Joanna Janczewska Bifurkacje sprężystego pręta pod działaniem siły ściskającej na podłożu Winklera 27 Piotr Kalita, Piotr Zgliczyński Rigorous FEM for integration of dissipative PDEs in 1d 28 Grzegorz Karch Nieciągłe stany stacjonarne układów reakcji-dyfuzji 29 Joanna Kluczenko Bifurkacje z orbit rozwiązań eliptycznych równań różniczkowych z warunkiem Neumanna 32 Piotr Kokocki Niezmienniki homotopijne dla układów równań w rezonansie 34 Michał Kowalczyk, Angela Pistoia, Giusi Vaira Maximal solution of the Liouville equation in doubly connected domains
5 35 Jakub Maksymiuk, Sonia Acinas, Fernando Mazzone Dualność Clarke a dla układów Hamiltonowskich z niestandardowym wzrostem 37 Michał Miśkiewicz Minimalizujące przekształcenia harmoniczne wpływ przekształcenia brzegowego na osobliwości 39 Piotr B. Mucha Density patches in viscous fluid mechanics 40 Aleksandra Orpel Existence and asymptotics of positive solutions for semipositone problems 42 Lucjan Sapa, Bogusław Bożek, Marek Danielewski Mathematical models of interdiffusion 44 Jakub Siemianowski, Wojciech Kryszewski Układy równań eliptycznych na R N 45 Mikołaj Sierżęga On some generalisations of the rigidity result for the Giga-Kohn equation
6 46 Jakub Skrzeczkowski Modele populacyjne ze strukturą - optymalizacja rozwiązań miarowych 48 Maciej Starostka Klasy homotopii własciwych odwzorowań gradientowych 49 Andrzej Szulkin, Jarosław Mederski Stała typu Sobolewa dla operatora curl i stany podstawowe dla równania curl-curl 51 Agnieszka Świerczewska-Gwiazda, C. Bardos, E. Feireisl, P. Gwiazda, E. Titi, E. Wiedemann Onsager s Conjecture for General Conservation Laws 53 Anna Zatorska-Goldstein Nieliniowe zagadnienia eliptyczne o anizotropowej strukturze z danymi o niskiej regularności 54 Dariusz Pączka Adhesive contact problem for viscoplastic materials 56 Filip Pietrusiak On the solvability of the boundary value problems for discrete p ( )-Laplacian on finite graphs
7 Homotopie gradientowe versus właściwe gradientowe Piotr Bartłomiejczyk Politechnika Gdańska A. Parusiński ([1]) pokazał, że jeśli gradientowe pola wektorowe na dysku w R n nieznikające na brzegu mają ten sam stopień Brouwera, to są gradientowo homotopijne. Z kolei, M. Starostka ([2]) udowodnił, że podobna implikacja nie zachodzi w klasie właściwych pól gradientowych w R n o stopniu 1. Mianowicie, metodami teorii indeksu Conleya wykazał, że odwzorowania f(x) = x oraz g(x) = ( x 1, x 2, x 3,..., x n ) nie są właściwie gradientowo homotopijne, pomimo że deg f = deg g = 1. W referacie przedstawimy dwa twierdzenia stanowiące rozwinięcie i uzupełnienie wspomnianych wyżej wyników. Nasz pierwszy rezultat mówi, że jeżeli odrzucimy założenie właściwości, zachowując jednak założenie zwartości zbioru zer odwzorowań i homotopii, to implikacja typu Parusińskiego zachodzi w R n dla n 2. Natomiast drugi rezultat stwierdza, że zbiór klas właściwej gradientowej homotopii właściwych gradientowych odwzorowań o stopniu 1 na płaszczyźnie ma dokładnie dwa elementy. Jest to wspólna praca z Piotrem Nowakiem-Przygodzkim. Bibliografia [1] A. Parusiński, Gradient homotopies of gradient vector fields, Studia Math. 96: (1990).
8 [2] M. Starostka, Connected components of the space of proper gradient vector fields, arxiv: [math.ds].
9 Bound states for the Schrödinger equation with mixed-type nonlinearities Bartosz Bieganowski Uniwersytet Mikołaja Kopernika We investigate the existence and multiplicity of solutions for the Schrödinger equation of the form u + V (x)u = g(x, u), x R N, u H 1 (R N ). In nonlinear optics, this equation describes the propagation of a electromagnetic wave in a periodic waveguide, e.g. photonic crystals. The external potential V takes into account the linear properties of the material and as usual we assume that V is Z N -periodic and 0 lies in the spectral gap of the Schrödinger operator + V (x). The nonlinear function g is responsible for the polarization of the medium. For instance, in Kerr-like media one has g(x, u) = u 2 u and in the saturation effect g is asymptotically linear and is of the form g(x, u) = u 2 u. Recently it has been shown that materials 1+ u 2 with large range of prescribed properties can be created and our aim is to model a wide range of nonlinear phenomena that allow to consider a composite of materials with different nonlinear polarization. In our case g may be linear for some R N \ K (for sufficiently large u ) and nonlinear outside of it, where K is a given Z N -periodic set. In particular we may combine the Kerr-like nonlinearity with a saturation effect. Under our conditions the energy functional has the linking geometry and Cerami sequences are bounded. This allows to
10 use a variant of linking theorem to obtain the existence of solutions. However, the multiplicity of solutions seem to be difficult to obtain by standard methods. Hence we reduce the problem to an appropriate subspace of H 1 (R N ), where the quadratic form is positive-definite and use a Cerami-type condition, and a variant of Benci s pseudoindex to show the multiplicity of solutions. In fact we refine a recent critical point theory from [2] for strongly indefinite functionals which do not have to be globally super-quadratic. References [1] B. Bieganowski, J. Mederski: Bound states for the Schrödinger equation with mixed-type nonlinearities, arxiv: [2] J. Mederski, J. Schino, A. Szulkin, Multiple solutions to a nonlinear curl-curl problem in R N, arxiv:
11 Nonlinear nonlocal heat equations: global solutions vs blowup Piotr Biler Uniwersyte Wrocławski The existence of global-in-time solutions for a nonlinear heat equation with nonlocal diffusion, power nonlinearity and suitably small data (either compared in the pointwise sense to the singular solution or in the norm of a critical Morrey space) is discussed. Then, asymptotics of subcritical solutions is determined as in [2]. These results are compared with conditions on the initial data in [1] leading to a finite time blowup. References [1] P. Biler, Blowup of solutions for nonlinear nonlocal heat equation, hmonatsh. Math.: 1 14 (2019), [2] P. Biler and D. Pilarczyk, Around a singular solution of a nonlocal nonlinear heat equation, NoDEA, Nonlinear Differ. Equ. Appl. 26:5 (2019),
12 Renormalized solutions to parabolic problems with strongly nonstandard growth Iwona Chlebicka (Skrzypczak) Uniwersytet Warszawski We provide existence and uniqueness of renormalized solutions to a general nonlinear parabolic equation t u diva(t, x, u) = f L 1 (Ω T ), where the growth of A is governed by a fully anisotropic N- function inhomogeneous in time and in space. In turn, our studies cover (not studied so far) cases in variable exponent spaces t u div(b(x, t) u p(x,t) 2 u) = f L 1 (Ω T ), for log-hölder continuous exponent p : Ω T (1, ), as well as problems posed in fully anisotropic Orlicz spaces (under no growth conditions), weighted Sobolev spaces (with bouded weights), and double-phase spaces within the range of parameters sharp for density of smooth functions. References [1] I. Chlebicka, P. Gwiazda, A. Zatorska-Goldstein, Parabolic equation in time and space dependent anisotropic Musielak-Orlicz spaces in absence of Lavrentiev s phenomenon, Annales de l Institut Henri Poincaré. Analyse Non Lineairé (C), DOI: /j.anihpc
13 [2] I. Chlebicka, P. Gwiazda, A. Zatorska-Goldstein, Renormalized solutions to parabolic equation in time and space dependent anisotropic Musielak-Orlicz spaces in absence of Lavrentiev s phenomenon, J. Differ. Equations, 267 (2) (2019), [3] I. Chlebicka, A pocket guide to nonlinear differential equations in Musielak-Orlicz spaces, Nonlinear Analysis 175 (2018), [4] P. Gwiazda, I. Skrzypczak, A. Zatorska-Goldstein, Existence of renormalized solutions to elliptic equation in Musielak-Orlicz space, J. Differ. Equations 264 (1) (2018), [5] Y. Ahmida, I. Chlebicka, P. Gwiazda, A. Youssfi, Gossez s approximation theorems in Musielak-Orlicz-Sobolev spaces, J. Functional Analysis 275 (9) (2018), [6] I. Chlebicka, P. Gwiazda, and A. Zatorska-Goldstein. Well-posedness of parabolic equations in the non-reflexive and anisotropic Musielak-Orlicz spaces in the class of renormalized solutions, J. Differ. Equations 265 (11) (2018),
14 Rozwiązania okresowe anizotropowych układów Eulera-Lagrange a - istnienie i krotność Magdalena Chmara magdalena.chmara@pg.edu.pl Politechnika Gdańska Szukamy rozwiązań zagadnienia d dt L v(t, u(t), u(t)) = L x (t, u(t), u(t)) dla p.w. t [a, b] u(a) = u(b), gdzie L(t, x, v) = F(t, x, v) + V (t, x) + f(t)x, wzrost F C 1 (I R N R N, R) zadany jest za pomocą anizotropowej G-funkcji spełniającej warunki 2 i 2. Korzystając z twierdzenia o przełęczy górskiej oraz z wariacyjnej zasady Ekelanda uzyskujemy istnienie co najmniej dwóch nietrywialnych rozwiązań należących do anizotropowej przestrzeni Orlicza- Sobolewa. Otrzymane rezultaty są uogólnieniem znanych wyników dla przypadków gdy F jest p-tą potęgą bądź izotropową G-funkcją. Bibliografia [1] M. Chmara, J. Maksymiuk, Mountain pass type periodic solutions for Euler Lagrange equations in anisotropic Orlicz Sobolev space, J. Math. Anal. Appl., 470: , (2019). [2] Zhang, Ziheng and Yuan, Rong, Homoclinic solutions for p-laplacian Hamiltonian systems with combined nonlinearities, Qual. Theory Dyn. Syst., 16: , (2017).
15
16 TBA Tomasz Cieślak Polska Akademia Nauk
17 Rozwiązania stacjonarne zagadnień eliptycznych na R N Aleksander Ćwiszewski aleks@mat.umk.pl Uniwersytet Mikołaja Koperniak w Toruniu, Będziemy szukać rozwiązań zagadnień eliptycznych postaci u + V (x)u = λu + f(x, u), x R N, z potencjałem typu Kato-Rellicha V L (R N ) + L p (R N ), wykładnikiem p 2, ograniczoną funkcją Carathéodoriego f : R N R R i parametrem λ R. Rozważać będziemy zagadnieni w rezonansie, tj. gdy λ σ p ( +V ). Wykażemy, że jeśli f spałnia warunki typu Landesmana-Lasera lub tzw. warunki silnego rezonansu, to zagadnienie posiada nietrywialne rozwiązanie. Metody oparte są na badaniu półpotoku parabolicznego, wykorzystaniu jego odpowiedniej geometrii do obliczenia indeksów Conleya w wersji Ryabakowskiego oraz wykorzystaniu własności zbiorów nieredukowalnych. Referat przedstawia wyniki uzyskane wspólnie z Piotrem Kokockim. Bibliografia [1] K.P. Rybakowski, The homotopy index and partial differential equations, Universitext. Springer, Berlin (1987). [2] M. Prizzi, On admissibility of parabolic equations in R N, Fund. Math., 176, (2003). [3] P. Kokocki, Connecting orbits for nonlinear differential equations at resonance, J. Differ. Equ. 255 (7), 1554
18 1575 (2013). [4] A. Ćwiszewski and P. Kokocki, Stationary solutions and connecting orbits for resonant parabolic equations on R N, preprint [5] A. Ćwiszewski and W. Kryszewski, Bifurcation from infinity for elliptic problems on R N, Calc. Var. 58:13 (2019).
19 Niezmienniczość i silna niezmienniczość w inkluzjach różniczkowych Grzegorz Gabor ggabor@mat.umk.pl Uniwersytet Mikołaja Kopernika w Toruniu Dla przestrzeni Banacha X i domkniętego podzbioru K X rozważamy problem { x (t) F(x(t)) (lub x (t) Ax(t) + F(x(t))) dla p.w. t 0, x(0) = x 0 K, (1) gdzie A : D(A) X jest generatorem C 0 -półgrupy i F : Ω X (Ω K jest pewnym otwartym otoczeniem) jest odwzorowaniem o domkniętych, wypukłych i ograniczonych wartościach. Szukamy warunków dostatecznych dla niezmienniczości (i silnej niezmienniczości) zbioru K, oznaczającej, że każde absolutnie ciągłe (dla A 0 odpowiednio: łagodne) rozwiązanie problemu (1) pozostaje w zbiorze K dla każdego t 0 (lub, w przypadku silnej niezmienniczości, pozostaje w zbiorze intk dla każdego t > 0). Przedyskutujemy warunki słabsze niż różne rodzaje lipschitzowości spotykane w literaturze, co ma swoje uzasadnienie w zagadnieniach pochodzących od równań różniczkowych cząstkowych. Ponadto pokażemy konsekwencje silnej niezmienniczości w problemach impulsowych z impulsami zależnymi od stanu układu.
20 Some remarks on monotone and variational methods with applications to nonlinear equations Marek Galewski Uniwersytet Łódzki Using monotonicity methods and some variational argument we will consider nonlinear problems which involve monotone potential mappings satisfying condition (S) and their compact perturbations. We investigate when functional whose minimum is obtained by a direct method of the calculus of variations satisfies the Palais-Smale condition, then provide structure conditions on the derivative of the action functional under which bounded Palais-Smale sequences are convergent. Finally, we make some comment concerning the convergence of Palais-Smale sequence obtained in the mountain pass theorem due to Rabier. We end our considerations with a three critical point type result. Some examples will be given. References [1] H. Gajewski, K. Gröger, K. Zacharias, Nichtlineare Operatorgleichungen und Operatordifferentialgleichungen, Akademie-Verlag, Berlin, [2] D. G. Figueredo, Lectures on the Ekeland Variational Principle with Applications and Detours, Preliminary Lecture Notes, SISSA, 1988.
21 Bifurkacje z orbit rozwiązań układów eliptycznych Anna Gołębiewska aniar@mat.umk.pl Uniwersytet Mikołaja Kopernika w Toruniu Rozważmy układ równań eliptycznych z warunkiem brzegowym Neumanna: { A u = u F(u, λ) w U u ν = 0 na U, (2) gdzie U jest otwartym, ograniczonym zbiorem, A = diag(±1,..., ±1). Ponadto załóżmy, że układ ma dodatkowe symetrie - w szczególności można rozpatrywać sytuację, gdy zbiór U jest SO(N)-niezmienniczy lub potencjał F jest Γ-niezmienniczy, przy czym Γ jest zwartą grupą Liego. Przy takich założeniach rozwiązania trywialne układu nie muszą być izolowane, lecz mogą tworzyć orbity rozwiązań. Dlatego przedmiotem naszych badań jest bifurkacja z orbit. W tym celu definiujemy indeks orbity, wykorzystując stopień niezmienniczych funkcjonałów silnie nieokreślonych. Używając tego indeksu można sformułować symetryczną wersję globalnego twierdzenia bifurkacyjnego Rabinowitza. Twierdzenie to może być zastosowane do badania bifurkacji rozwiązań nietrywialnych z orbit rozwiązań trywialnych układu (2). Bibliografia [1] A. Gołębiewska, J. Kluczenko, Connected sets of solutions for a nonlinear Neumann problem, Diff. Int. Equ.
22 30(11-12) (2017). [2] A. Gołębiewska, J. Kluczenko, P. Stefaniak, Bifurcations from the orbit of solutions of the Neumann problem, Calc. Var. 57(1) (2018), [3] A. Gołębiewska, P. Stefaniak, Global bifurcation index of critical orbit of strongly indefinite functional, arxiv:
23 Fixed point indices of iterates for a boundary fixed point Grzegorz Graff grzegorz.graff@pg.edu.pl Politechnika Gdańska Let M be a manifold with non-empty boundary M. Consider f : (M, M) (M, M) and let f = f M : M M. The sequence of fixed point indices at an isolated fixed point x 0 M, (ind(f n, x 0 )) n, plays an important role in the study of dynamical properties of the map f near x 0. On the other hand, as x 0 is also an isolated fixed point of f, one may consider the sequence (ind( f, x 0 )) n. In this talk we describe the relations between the mentioned above sequences of indices for different classes of maps. The study of this problem is motivated by its potential applications in differential equations, periodic point theory and magnetohydrodynamics. We will refer to the results obtained in the collaboration with J. Jezierski, P. Nowak-Przygodzki and A. Myszkowski. Research supported by the National Science Centre, Poland, under the grant Sheng 1 no. 2018/30/Q/ST1/ References [1] H. Barge, K. Wójcik, Mayer-Vietoris property of the fixed point index, Topol. Methods Nonlinear Anal. 50 (2): (2017). [2] G. Graff, J. Jezierski, Minimal number of periodic points of smooth boundary-preserving self-maps of simplyconnected manifolds, Geom. Dedicata 187:
24 (2017).
25 Bifurkacje sprężystego pręta pod działaniem siły ściskającej na podłożu Winklera Joanna Janczewska Politechnika Gdańska Teoria bifurkacji dostarcza wielu metod do badania deformacji elastycznych konstrukcji, w szczególności prȩtów, płyt i powłok. Mój wykład oparty bȩdzie na artykule [1], w którym wykorzystujemy teoriȩ stopnia Brouwera do badania deformacji jednorodnego, sprȩżystego prȩta na podłożu Winklera. Zakładamy, że prȩt znajduje siȩ w położeniu poziomym i jest poddawany działaniu siły ściskaj acej. Lewy koniec prȩta jest wolny, a prawy swobodnie podparty. Pokazujemy, że zjawisko bifurkacji zachodzi wtedy i tylko wtedy, gdy problem zlinearyzowany posiada rozwi azania nietrywialne. Zastosowanie teorii stopnia daje dodatkow a informacjȩ, że punkty bifurkacji s a punktami rozgałȩzienia, czyli odchodz a od nich continuua rozwi azań. Bibliografia [1] M. Izydorek, J. Janczewska, N. Waterstraat, A. Zgorzelska, Bifurcation of equilibrium forms of an elastic rod on a two-parameter Winkler foundation, Nonlinear Anal. Real World Appl. 39: (2018). [2] J. Janczewska, Local properties of the solution set of the operator equation in Banach spaces in a neighbourhood of a bifurcation point, Cent. Eur. J. Math. 2:
26 (2004). [3] A. Borisovich, J. Dymkowska, Elementy Analizy Funkcjonalnej z Zastosowaniem w Mechanice Ciał Sprężystych, Politechnika Gdańska, Gdańsk, 2003.
27 Rigorous FEM for integration of dissipative PDEs in 1d Piotr Kalita Uniwersytet Jagielloński We describe a computer assisted algorithm for rigorous integration forward in time of dissipative PDEs. Contrary to the previous work, the algorithm is not based on the finite dimensional approximation in Fourier basis but in the Finite Element basis, making it more flexible. As an illustration of the algorithm we present the computer assisted and constructive proof of the existence of time periodic solution for the one dimensional Burgers equation with Dirichlet boundary conditions and non-autonomous periodic forcing. This is joint work with Piotr Zgliczyński.
28 Nieciągłe stany stacjonarne układów reakcjidyfuzji Grzegorz Karch Uniwersytet Wrocławski Na wykładzie omówione zostaną wyniki uzyskane w ostatnich latach wspólnie z Anną Marciniak-Czochrą i Kanako Suzuki, oraz ostatnio z Szymonem Cyganem, dotyczące układów równań reakcji- dyfuzji modelujących zjawiska z biologii i medycyny. W układach tych niektóre komponenty nie podlegają zjawisku dyfuzji co prowadzi tworzenia się stabilnych rozwiązań stacjonarnych ze skokami. Bibliografia [1] S. Cygan, A. Marciniak-Czochra, G. Karch, and K. Suzuki, Regular and discontinues stationary solutions of reaction-diffusion-ode systems, (2019), preprint. [2] A. Marciniak-Czochra, G. Karch, and K. Suzuki, Instability of Turing patterns in reaction-diffusion-ode systems, J. Math. Biol. 74 (3) (2017),
29 Bifurkacje z orbit rozwiązań eliptycznych równań różniczkowych z warunkiem Neumanna Joanna Kluczenko jgawrycka@matman.uwm.edu.pl Uniwersytet Warmińsko-Mazurski w Olsztynie Wyklad będzie prezentacją wyników zawartych we wspólnej pracy z Anią Gołębiewską oraz Piotrem Stefaniakiem. Celem prezentacji będzie badanie własności słabych, nietrywialnych rozwiązań nieliniowych układów równań eliptycznych z warunkiem brzegowym Neumanna, to znaczy układów postaci: { u = λ F(u) in B N u ν = 0 on S N 1 (3), gdzie B N oznacza kulę jednostkową w R N, S N 1 = B N oraz F : R m R spełnia pewne dodatkowe założenia. Aby uzyskać sytuację niezmienniczą będziemy zakładać, że na przestrzeni R m jest zdefiniowane działanie zwartej grupy Liego Γ oraz F jest odwzorowanniem Γ-niezmienniczym. Oznaczmy przez G grupę Γ SO(N), zaś przez H 1 (B N ) pierwszą przestrzeń Sobolewa na zbiorze B N. Rozważmy ponadto przestrzeń Hilberta H = m i=1 H1 (B N ), która jest ortogonalną G-reprezentacją z działaniem zadanym wzorem (γ, α)(u)(x) = γu(α 1 x) dla (γ, α) G, u H. Do badania słabych rozwiązań układu (3) zastosujemy metody wariacyjne, to znaczy stowarzyszymy z tym układem funkcjonał Φ: H R R, którego punkty krytyczne będą we wzajemnie jednoznacznej odpowiedniości ze słabymi rozwiązaniami układu (3). Z symetrii
30 układu (3) wynika, że gradient funkcjonału Φ jest operatorem G-współzmienniczym. Zauważmy, że jeżeli u 0 F 1 (0), to również γu 0 F 1 (0) dla wszystkich γ Γ. W tej sytuacji punkt krytyczny u 0 nie jest izolowany, dokładniej, mamy do czynienia z orbitą punktów krytycznych. Zatem dla u 0 F 1 (0) funkcja stała ũ 0 u 0 jest rozwiązaniem układu (3) dla wszystkich λ R oraz punkt (gũ 0, λ) jest punktem krytycznym funkcjonału Φ dla każdego g G. Rozważmy rodzinę rozwiązań trywialnych T = G(ũ 0 ) R H R. Na wykładzie zbadamy istnienie bifurkacji nietrywialnych rozwiązań z rodziny T, to znaczy zbadamy istniene takich λ 0 R, że G(ũ 0 ) {λ 0 )} {(v, λ) (H R)\T : v Φ(v, λ) = 0}. Ponadto, korzystając z teorii stopnia odwzorowań współzmienniczych zdefiniowanego w [2] lub stopnia silnie nieokreślonych funkcjonałów niezmienniczych z pracy [3], sformułujemy warunki dostateczne na istnienie lokalnej oraz globalnej bifurkacji, przy użyciu wartości własnych macierzy Hessego odwzorowania F oraz wartości i podprzestrzeni własnych operatora Laplace a. Na wykładzie scharakteryzujemy również orbity na których zachodzi zjawisko łamania symetrii rozwiązań układu (3). Bibliografia [1] A. Gołȩbiewska, J. Kluczenko, P. Stefaniak, Bifurcations from the orbit of solutions of the Neumann problem, Calc. Var. Partial Differential Equations 57, no 1, Art. 21,23 pp. [2] A. Gołȩbiewska, S. Rybicki, Global bifurcations of critical orbits of G-invariant strongly indefinite functionals,
31 Nonl.Anal.74(5), [3] S. Rybicki, Degree for equivariant gradient maps, Milan.J.Math. 73,
32 Niezmienniki homotopijne dla układów równań w rezonansie Piotr Kokocki pkokocki@mat.umk.pl Uniwersytet Mikołaja Kopernika w Toruniu Zajmujemy się badaniem maksymalnych ograniczonych zbiorów niezmienniczych dla parabolicznego układu m 1 równań postaci u k (t) = A k u k (t)+λ k u k (t)+f k (x, u(t), u(t)), 1 k m, gdzie λ 1,..., λ m R są parametrami, A k jest eliptycznym operatorem różniczkowym z warunkami Dirichleta na zbiorze Ω R n oraz f = (f 1,..., f m ) jest ograniczonym zaburzeniem. Interesuje nas sytuacja, gdy powyższy układ jest w rezonansie, czyli, dla dowolnego 1 k m parametr λ k jest wartością własną operatora A k. Wówczas, nietrudno wskazać przykłady zaburzeń f, dla których powyższy układ nie posiada rozwiązań ograniczonych. Naszym celem jest wprowadzenie rodziny, zależnych od parametru, warunków rezonansowych dla odwzorowania f, gwarantujących, że maksymalny ograniczony zbiór niezmienniczy K dla naszego układu jest niepusty i zwarty. Ponadto zależność tych rodzin od wspomnianego parametru pozwala na interpolację między klasycznymi warunkami Landesmana-Lazera oraz warunkami z silnym rezonansem. Stosowana przez nas metoda niezmienników homotopijnych polegać będzie na wyznaczeniu indeksu Rybakowskiego-Conley a zbioru K w zależności od wprowadzonych wcześniej warunków rezonansowych.
33 Bibliografia [1] P. Kokocki, Maximal bounded invariant sets for systems of evolution equations at resonance, w przygotowaniu
34 Maximal solution of the Liouville equation in doubly connected domains Michał Kowalczyk University of Chile, Santiago, Chile. Co-authors: Angela Pistoia Sapienza Universitá di Roma, via Antonio Scarpa 16, 00161, Roma, Italy. Giusi Vaira Universitá della Campania L. Vanvitelli", Caserta, Italy. In this talk I will discuss a new existence result for the widely studied Liouville problem u + λ 2 e u = 0 in a bounded, two dimensional, doubly connected domain with Dirichlet boundary conditions. I will show that for a sequence of λ n 0 this equation has solutions that blow-up in in the whole domain. Profiles of the blowing-up solutions are related to a free boundary problem which gives a solution to an optimal partition problem for the given domain. I will also describe the role of the free boundary problem in other classical equations such as the mean field model or the prescribed Gaussian curvature equation.
35 Dualność Clarke a dla układów Hamiltonowskich z niestandardowym wzrostem Jakub Maksymiuk jakub.maksymiuk@pg.edu.pl Politechnika Gdańska Rozważmy następujący układ Hamiltonowski: { u(t) = J H(t, u(t)) p.w. t [0, T ] u(0) = u(t ) (HS) gdzie H : [0, T ] R 2N R jest funkcją klasy C 1, wypukłą w zmiennej u, której wzrost jest wyznaczony przez G-funkcję G : R 2N [0, ). Z uwagi na strukturę równania (HS) wymagamy, aby G spełniała dodatkowo warunek symplektyczności G (Jz) = G(z). Typowym przykładem takiej funkcji jest G(x, y) = 1/p x p +1/q y q. Korzystając z dualności Clarke a otrzymujemy twierdzenie o istnieniu. Twierdzenie. Niech G będzie symplektyczną G-funkcją taką, że G 2. Załóżmy, że: [1] istnieje ξ L G takie, że dla p.w. t [0, T ] i u R 2N zachodzi H(t, u) ξ(t), u, [2] istnieje Λ > 0 spełniająca Λ 1 > T max{1, C G /2} oraz α L 1 takie, że dla p.w. t [0, T ] i u R 2N zachodzi [3] H(t, u) G(Λu) + α(t), T lim H(t, u) dt =. u 0
36 Wtedy układ (HS) posiada rozwiązanie w przestrzeni Orlicza-Sobolewa W 1 T LG ([0, T ], R 2N ). Powyższe twierdzenie jest uogólnieniem wcześniejszych wyników podanych w [1] dla hamiltonianów o wzroście podkwadratowym oraz w pracy [2] dla przypadku wzrostu z p-tą potęgą. Analogicznie jak w wymienionych pracach, korzystając z dualności Lagranga e dowodzimy także istnienie rozwiązań równania { d dt Φ( q) + V (t, q) = 0 q(0) = q(t ), q(0) = q(t ) p.w. t [0, T ] gdzie Φ: R N [0, ) jest G-funkcją spełniającą warunek 2 2. Bibliografia [1] J. Mawhin, M. Willem Critical point theory and Hamiltonian systems, Springer-Verlag, New York, 1989 [2] Y. Tian,W. Ge, Periodic solutions of non-autonomous second-order systems with a p-laplacian, Nonl. Anal., 66: , (2007) [3] S. Acinas, J. Maksymiuk, F. Mazzone, Clarke duality for Hamiltonian systems with nonstandard growth, Nonl. Anal. 188: 1-21 (2019)
37 Minimalizujące przekształcenia harmoniczne wpływ przekształcenia brzegowego na osobliwości Michał Miśkiewicz Uniwersytet Warszawski Minimalizujące przekształcenia harmoniczne uogólniają klasyczne funkcje harmoniczne; są to przekształcenia między rozmaitościami minimalizujące energię Dirichleta (całkę z kwadratu gradientu). W ogólności nie są jednak gładkie w całej dziedzinie posiadają tzw. zbiór osobliwy (czyli punkty nieciągłości) kowymiaru 3. Podczas referatu skupię się na przekształceniach w standardową sferę S 2 przyjmujących zadane wartości na brzegu obszaru. Oprócz oszacowań na rozmiar zbioru osobliwego w terminach energii przekształcenia brzegowego omówię też wpływ małych zaburzeń przekształcenia brzegowego na osobliwości wewnątrz obszaru. Przedstawię prosty wynik stabilnościowy, który pozwala na oszacowanie odległości Wassersteina zbiorów osobliwych dwóch przekształceń harmonicznych. Referat oparty jest na wynikach uzyskanych wspólnie z Katarzyną Mazowiecką i Arminem Schikorrą. Bibliografia [1] K. Mazowiecka, M. Miśkiewicz, A. Schikorra On the size of the singular set of minimizing harmonic maps into the sphere in dimension three,
38 arxiv preprint (2018). [2] K. Mazowiecka, M. Miśkiewicz, A. Schikorra On the size of the singular set of minimizing harmonic maps into the 2-sphere in dimension four and higher, arxiv preprint (2019).
39 Density patches in viscous fluid mechanics Piotr B. Mucha Uniwersytet Warszawski I would like to present the current results of the issue of density patches in the regime determined by the Navier- Stokes equations. In few words, the goal is to analyze the motion of the density given initially as a characteristic function of a set. The key element is the uniqueness of the evolution, connected with a need of relatively high regularity of the velocity. Here we need to introduce a new technique of the shift of regularity. The talk will mostly based on joint results with Raphael Danchin (Paris12).
40 References [1] R. Danchin, P.B. Mucha, The Incompressible Navier- Stokes Equations in Vacuum Comm. Pure Appl. Math. 72 (2019), no. 7, [2] R. Danchin, P.B. Mucha, Incompressible flows with piecewise constant density. Arch. Ration. Mech. Anal. 207 (2013), no. 3, 991?1023. [3] R. Danchin, P.B. Mucha, A Lagrangian approach for the incompressible Navier-Stokes equations with variable density. Comm. Pure Appl. Math. 65 (2012), no. 10, 1458?1480. Existence and asymptotics of positive solutions for semipositone problems Aleksandra Orpel aleksandra.orpel@wmii.uni.lodz.pl Unwersytet Łódzki We investigate the existence of a large number of positive evanescent solutions for the following semilinear elliptic equation u(x) + f(x, u(x)) + g(x)x u(x) = 0, x R n and x > R, where f(x, ) can be negative at the origin. Our results are based on a certain iteration schema, in which we apply the sub and supersolution method developed by Noussair and Swanson. We show that the solutions have the minimal growth and finite energy in a neighborhood of infinity. Our approach allows us to consider superlinear problems with g without radial symmetry. References
41 [1] E.S. Noussair and C.A. Swanson, Multiple finite energy solutions of critical semilinear field equations, J. Math. Anal. Appl. 195: (1995). [2] A. Orpel, Increasing sequences of positive evanescent solutions of nonlinear elliptic equations, J. Differential Equations 259: (2015). [3] L. Sankar, S. Sasi and R. Shivaji, Semipositone problems with falling zeros on exterior domains, J. Math. Anal. Appl. 401: (2013).
42 Mathematical models of interdiffusion Lucjan Sapa Akademia Górniczo-Hutnicza Co-authors: Bogusław Bożek Akademia Górniczo-Hutnicza Marek Danielewski Akademia Górniczo-Hutnicza We study the diffusional transport in an s-component solid solution. The local mass conservation law for fluxes with the Darken drift term and the Vegard rule lead to the parabolic-elliptic system of strongly coupled nonlinear differential equations t c i + div ( D i (c 1,..., c s ) c i + c i F ) = 0 on [0, T ] Ω, F = div ( s k=1 Ω ) kd k (c 1,..., c s ) c k on [0, T ] Ω, Fdx = 0 on [0, T ], Ω with the nonlinear coupled initial-boundary Robin type conditions. We will present theorems on well-posedness in the suitable Sobolev spaces. Moreover, finite implicit difference methods (FDM) and theorems concerned convergence and stability will be given.
43 References [1] B. Bożek, L. Sapa, M. Danielewski, Difference methods to one and multidimensional interdiffusion models with Vegard rule, Math. Model. Anal. 24: (2019). [2] L. Sapa, B. Bożek, M. Danielewski, Existence, uniqueness and properties of global weak solutions to interdiffusion with Vegard rule, Topol. Methods Nonlinear Anal. 52: (2018).
44 Układy równań eliptycznych na R N Jakub Siemianowski jsiem@mat.umk.pl Uniwersytet Mikołaja Kopernika w Toruniu Rozważamy układ M równań eliptycznych postaci L 1 u 1 = f 1 (x, u, Du), na R N. L M u M = f M (x, u, Du), ( ) gdzie u = (u 1,..., u M ) : R N R M, Du jest macierzą Jacobiego funkcji u, każdy L i jest eliptycznym liniowym operatorem różniczkowym drugiego rzędu oraz f = (f 1,..., f N ) : R N R M R MN R M nieliniowym zaburzeniem. Szukamy rozwiązań u w przestrzeni H 1 (R N, R M ). Układ ( ) uzupełniony jest geometrycznymi założeniami, dotyczącymi styczności f do pewnego zbioru ograniczeń, który jest jednocześnie niezmienniczy względem rezolwent operatora L 1... L M, oraz odpowiednim wzrostem f. Najpierw rozwiązujemy pomocnicze układy typu ( ) na dużych kulach B(0, n) przy użyciu indeksu punktów stałych. Następnie stosujemy tzw. oszacowania ogonowe (ang. tail estimate technique), aby wykazać zbieżność ciągu rozwiązań pomocniczych do wyjściowego problemu ( ).
45 On some generalisations of the rigidity result for the Giga-Kohn equation Mikołaj Sierżęga Uniwersytet Warszawski. What we refer to as the Giga-Kohn equation is a semilinear elliptic equation of Ornstein-Uhlenbeck type: u x 2 u αu+ u p 1 u = 0, on R n, p > 1. (4) In [1] it was shown that when α = 1 n+2 p 1 and p n 2, n 1, all bounded solutions are necessarily constant. In this talk I will discuss some generalisations of this result. Bibliografia [1] Giga, Y., Kohn, R.V., Asymptotically self-similar blowup of semilinear heat equations. Comm. Pure Appl. Math. 38 (1985), no. 3,
46 Modele populacyjne ze strukturą - optymalizacja rozwiązań miarowych Jakub Skrzeczkowski jakub.skrzeczkowski@student.uw.edu.pl Uniwersytet Warszawski Zajmujemy się równaniem transportu z warunkiem brzegowym: { t µ t + x (b(x, µ t )µ t ) = c(x, µ t )µ t R + [0, T ], b(0, µ t )D λ µ t (0) = R a(x, µ + t )dµ t (x) [0, T ], (5) oraz początkowym µ 0 = ν. Wiadomo, że (5) jest dobrze postawione w przestrzeni nieujemnych i ograniczonych miar Radona M + (R + ) z tzw. flat metric ρ F [1]. Rozważmy (5) z zaburzonymi funkcjami modelowymi postaci f h (x, µ) = f 0 (x, µ) + hf p (x, µ) dla f = a, b, c. Czy i w jakim sensie h µ t h jest różniczkowalne? Pokażemy, że nie jest w M(R + ) z metryką ρ F. Następnie, wykażemy Fréchetowską różniczkowalność w większej przestrzeni Z = M(R + ) (C 1+α ) [2,3]. Bibliografia [1] P. Gwiazda, T. Lorenz, A. Marciniak-Czochra A nonlinear structured population model: Lipschitz continuity of measure valued solutions with respect to model ingredients, J. Differential Equations, 248 (2010), [2] P. Gwiazda, S. C. Hille, K. Łyczek, A. Świerczewska- Gwiazda Differentiability in perturbation parameter of
47 measure solutions to perturbed transport equation, arxiv: [3] J. Skrzeczkowski, Measure solutions to perturbed structured population models - differentiability with respect to perturbation parameter, arxiv:
48 Klasy homotopii własciwych odwzorowań gradientowych Maciej Starostka Ruhr Universitat Bochum W [1] A. Parusinski pokazał, ze dwa odwzorowania gradientowe na dysku sa homotopijne wtedy i tylko wtedy, gdy maja ten sam stopien. Pokazemy, ze ta teza przestaje byc prawdziwa jezeli dysk zastapimy przestrzenia euklidesowa i bedziemy rozpatrywac odwzorowania własciwe. Bibliografia [1] A. Parusinski, Gradient Homotopies of Gradient Vector Fields, Studia Math. XCVI (1990), 73?80 [2] M. Starostka, Connected components of the space of proper gradient vector fields, 2018, arxiv:
49 Stała typu Sobolewa dla operatora curl i stany podstawowe dla równania curl-curl Andrzej Szulkin andrzejs@math.su.se Uniwersytet Sztokholmski, Szwecja Dla podzbioru otwartego Ω R 3 zdefiniujmy S(Ω) := inf{ u 2 2 / u 2 6 : u C 0 (Ω) \ {0}} (jak zwykle p oznacza normę w L p (Ω)). S(Ω) jest stałą Sobolewa ze względu na zanurzenie D 1,2 0 (Ω) L 6 (Ω). Wiadomo, że jest ona niezależna od Ω, infimum jest osiągane wtedy i tylko wtedy gdy Ω = R 3 i jest realizowane przez stan podstawowy równania u = u 4 u w przestrzeni D 1,2 (R 3 ). Naturalnym uogólnieniem dla operatora curl mogłaby się wydawać stała S(Ω) := inf{ u 2 2 / u 2 6 : u C 0 (Ω, R3 ) \ {0}}. Ponieważ jądro operatora curl jest nietrywialne ( u = 0 u = φ), stała ta zawsze byłaby równa 0. Na niniejszym odczycie zdefiniujemy inną stałą, S curl (Ω), jako pewne infimum. Ma ona następujące własności: S curl (Ω) > S(Ω); S curl (Ω) nie zależy od Ω; infimum jest osiągane gdy Ω = R 3 i realizowane przez stan podstawowy równania ( u) = u 4 u, które można wyprowadzić z układu równań Maxwella. Otwarty pozostaje problem (nie)istnienia minimum gdy Ω R 3.
50 Jeśli czas pozwoli, krótko przedyskutujemy również problem Brezisa i Nirenberga dla operatora curl-curl na zbiorach ograniczonych. Powyższy materiał pochodzi z pracy w przygotowaniu z Jarosławem Mederskim.
51 Onsager s Conjecture for General Conservation Laws Agnieszka Świerczewska-Gwiazda aswiercz@mimuw.edu.pl Uniwersytet Warszawski A common feature of systems of conservation laws of continuum physics is that they are endowed with natural companion laws which are in such case most often related to the second law of thermodynamics. This observation easily generalizes to any symmetrizable system of conservation laws. They are endowed with nontrivial companion conservation laws, which are immediately satisfied by classical solutions. Not surprisingly, weak solutions may fail to satisfy companion laws, which are then often relaxed from equality to inequality and overtake a role of a physical admissibility condition for weak solutions. We want to discuss what is a critical regularity of weak solutions to a general system of conservation laws to satisfy an associated companion law as an equality. An archetypal example of such result was derived for the incompressible Euler system by Constantin et al. ([1]) in the context of the seminal Onsager s conjecture. This general result can serve as a simple criterion to numerous systems of mathematical physics to prescribe the regularity of solutions needed for an appropriate companion law to be satisfied. The talk is based on the common results with C. Bardos, E. Feireisl, P. Gwiazda, E. S. Titi and E. Wiedemann ([2]-[5])
52 References [1] C. Bardos, P. Gwiazda, E. S. Titi, A. Świerczewska- Gwiazda and E. Wiedemann, On the Extension of Onsager s Conjecture for General Conservation Laws, J. Nonlinear Sci. 29: (2019). [2] P. Constantin, W. E, and E. S. Titi. Onsager s conjecture on the energy conservation for solutions of Euler s equation, Comm. Math. Phys., 165: (1994). [3] E. Feireisl, P. Gwiazda, A. Świerczewska-Gwiazda, E. Wiedemann, Regularity and Energy Conservation for the Compressible Euler Equations, Arch. Ration. Mech. Anal. 223: (2017). [4] P. Gwiazda, M. Michálek, A. Świerczewska-Gwiazda, A note on weak solutions of conservation laws and energy/entropy conservation, Arch. Ration. Mech. Anal. 229: (2018). [5] M. Omladič and P. Šemrl, Matrix spaces with bounded number of eigenvalues, Linear Algebra Appl. 249: (1996).
53 Nieliniowe zagadnienia eliptyczne o anizotropowej strukturze z danymi o niskiej regularności Anna Zatorska-Goldstein azator@mimuw.edu.pl Uniwersytet Warszawski W czasie swojego wystąpienia zaprezentuję wyniki uzyskane wraz z Angelą Alberico, Andreą Cianchi, oraz Iwoną Chlebicką. Badaliśmy problem istnienia i regularności rozwiązań zagadnień brzegowych dla operatorów różniczkowych w postaci dywergencyjnej, dla których warunki eliptyczności oraz wzrostu opisane są dość ogólną funkcją klasy Orlicza. Minimalistyczna lista założeń na tę funkcję (rośnie szybciej niż liniowa, ale nie musi być ani radialna, ani spełniać żadnych warunków podwajania) pozwala uwzględnić operatory o anizotropowej strukturze. W przypadku, gdy dane w równaniu są mało regularne, tak, że nie należą do przestrzeni dualnej do naturalnej przestrzeni słabych rozwiązań (w ogólności mogą być miarami), wykazaliśmy istnienie rozwiązań uogólnionych oraz regularność rozwiązania i jego gradientu w przestrzeniach typu Marcinkiewicza. Dla danych opisanych funkcją całkowalną wykazaliśmy także jednoznaczność rozwiązań uogólnionych. Bibliografia [1] A. Alberico, A. Cianchi, I. Chlebicka, and A. Zatorska- Goldstein. Fully anisotropic elliptic problems with minimally integrable data, arxiv: , 2019.
54 Postery Adhesive contact problem for viscoplastic materials Dariusz Pączka Uniwesytet Warszawski We examine a mathematical model that describes a quasistatic adhesive contact between a viscoplastic body and deformable foundation. The material s behaviour is described by the rate-type constitutive law which involves functions with a non-polynomial growth. The contact is modeled by the normal compliance condition with limited penetration and adhesion, a subdifferential friction condition also depending on adhesion, and the evolution of bonding field is governed by an ordinary differential equation. We present the variational formulation of this problem which is a system of an almost history-dependent variational-hemivariational inequality for the displacement field and an ordinary differential equation for the bonding field. The result on existence and uniqueness of solution to a variational-hemivariational inequality in the reflexive Orlicz Sobolev space is proved and applied to the adhesive contact problem. References [1] D. Pączka, Adhesive contact problem for viscoplastic materials, Nonlinear Anal. Real World Appl. 51 (2020)
55 [2] M. Sofonea and S. Migórski, Variational-hemivariational inequalities with applications, Monographs and Research Notes in Mathematics, Boca Raton, FL: CRC Press, 2018.
56 On the solvability of the boundary value problems for discrete p ( )-Laplacian on finite graphs Filip Pietrusiak filip.pietrusiak@edu.p.lodz.pl Uniwesytet Łódzki I use non-classical monotonicity methods in order to investigate existence of solutions to boundary value problems connected to the discrete p ( ) Laplacian on weighted finite graphs with nonlinearities given in a non-potential form. Positive solutions are also considered. In potential form sufficient condition for uniqueness is recived. Bibliografia [1] M. Galewski, R. Wieteska, Existence and multiplicity results for boundary value problems connected with the discrete p( )-Laplacian on weighted finite graphs, Applied Mathematics and Computation, 290, , [2] S. Migórski, A. Ochal, M.Sofonea, Nonlinear inclusions and hemivariational inequalities. Models and analysis of contact problems, Advances in Mechanics and Mathematics, Volume 26. New York: Springer, 2013.
Table of contents. Thursday 05 September Friday 06 September Saturday 07 September
 Table of contents Thursday 05 September 2019... 1 Friday 06 September 2019... 2 Saturday 07 September 2019... 4 i Thursday 05 September 2019 Jubileuszowy Zjazd Matematyków Polskich w stulecie PTM Thursday
Table of contents Thursday 05 September 2019... 1 Friday 06 September 2019... 2 Saturday 07 September 2019... 4 i Thursday 05 September 2019 Jubileuszowy Zjazd Matematyków Polskich w stulecie PTM Thursday
analiza nieliniowa i równania różniczkowe cząstkowe patroni sesji
 analiza nieliniowa i równania różniczkowe cząstkowe patroni sesji Juliusz Paweł Schauder Stanisław Zaremba Jubileuszowy Zjazd Matematyków Polskich w stulecie Polskiego Towarzystwa Matematycznego Kraków
analiza nieliniowa i równania różniczkowe cząstkowe patroni sesji Juliusz Paweł Schauder Stanisław Zaremba Jubileuszowy Zjazd Matematyków Polskich w stulecie Polskiego Towarzystwa Matematycznego Kraków
i równania różniczkowe cząstkowe analiza nieliniowa Jubileuszowy Zjazd Matematyków Polskich patroni sesji:
 analiza nieliniowa i równania różniczkowe cząstkowe patroni sesji: Juliusz Paweł Schauder Stanisław Zaremba Jubileuszowy Zjazd Matematyków Polskich w stulecie Polskiego Towarzystwa Matematycznego Kraków
analiza nieliniowa i równania różniczkowe cząstkowe patroni sesji: Juliusz Paweł Schauder Stanisław Zaremba Jubileuszowy Zjazd Matematyków Polskich w stulecie Polskiego Towarzystwa Matematycznego Kraków
O problemie sterowania aproksymacyjnego dla semiliniowych inkluzji różniczkowych w przestrzeniach Hilberta
 O problemie sterowania aproksymacyjnego dla semiliniowych inkluzji różniczkowych w przestrzeniach Hilberta Krzysztof RYKACZEWSKI Uniwersytet Mikołaja Kopernika w Toruniu SNA 2011 Toruń, 10 września 2011
O problemie sterowania aproksymacyjnego dla semiliniowych inkluzji różniczkowych w przestrzeniach Hilberta Krzysztof RYKACZEWSKI Uniwersytet Mikołaja Kopernika w Toruniu SNA 2011 Toruń, 10 września 2011
O pewnych klasach funkcji prawie okresowych (niekoniecznie ograniczonych)
 (niekoniecznie ograniczonych) Wydział Matematyki i Informatyki Uniwersytet im. Adama Mickiewicza, Poznań Będlewo, 25-30 maja 2015 Funkcje prawie okresowe w sensie Bohra Definicja Zbiór E R nazywamy względnie
(niekoniecznie ograniczonych) Wydział Matematyki i Informatyki Uniwersytet im. Adama Mickiewicza, Poznań Będlewo, 25-30 maja 2015 Funkcje prawie okresowe w sensie Bohra Definicja Zbiór E R nazywamy względnie
A sufficient condition of regularity for axially symmetric solutions to the Navier-Stokes equations
 A sufficient condition of regularity for axially symmetric solutions to the Navier-Stokes equations G. Seregin & W. Zajaczkowski A sufficient condition of regularity for axially symmetric solutions to
A sufficient condition of regularity for axially symmetric solutions to the Navier-Stokes equations G. Seregin & W. Zajaczkowski A sufficient condition of regularity for axially symmetric solutions to
STRESZCZENIE ROZPRAWY DOKTORSKIEJ PIOTRA NOWAKA-PRZYGODZKIEGO TYP HOMOTOPIJNY PRZESTRZENI ODWZOROWAŃ GRADIENTOWYCH
 Gdańsk 11.02.2013 STRESZCZENIE ROZPRAWY DOKTORSKIEJ PIOTRA NOWAKA-PRZYGODZKIEGO TYP HOMOTOPIJNY PRZESTRZENI ODWZOROWAŃ GRADIENTOWYCH 1. HISTORIA PROBLEMATYKI PORUSZANEJ W ROZPRAWIE W latach osiemdziesiątych
Gdańsk 11.02.2013 STRESZCZENIE ROZPRAWY DOKTORSKIEJ PIOTRA NOWAKA-PRZYGODZKIEGO TYP HOMOTOPIJNY PRZESTRZENI ODWZOROWAŃ GRADIENTOWYCH 1. HISTORIA PROBLEMATYKI PORUSZANEJ W ROZPRAWIE W latach osiemdziesiątych
Fale biegnące w równaniach reakcji-dyfuzji
 Fale biegnące w równaniach reakcji-dyfuzji Piotr Bartłomiejczyk Politechnika Gdańska Między teorią a zastosowaniami: Matematyka w działaniu Będlewo, 25 30 maja 2015 P. Bartłomiejczyk Fale biegnące 1 /
Fale biegnące w równaniach reakcji-dyfuzji Piotr Bartłomiejczyk Politechnika Gdańska Między teorią a zastosowaniami: Matematyka w działaniu Będlewo, 25 30 maja 2015 P. Bartłomiejczyk Fale biegnące 1 /
WYBUCHY ROZWIA ZAŃ NIELINIOWYCH RÓWNAŃ PARABOLICZNYCH: nieliniowe równanie ciep la, model Keller Segela chemotaksji
 WYBUCHY ROZWIA ZAŃ NIELINIOWYCH RÓWNAŃ PARABOLICZNYCH: nieliniowe równanie ciep la, model Keller Segela chemotaksji Piotr BILER Instytut Matematyczny, Uniwersytet Wroc lawski, pl. Grunwaldzki 2/4, 50 384
WYBUCHY ROZWIA ZAŃ NIELINIOWYCH RÓWNAŃ PARABOLICZNYCH: nieliniowe równanie ciep la, model Keller Segela chemotaksji Piotr BILER Instytut Matematyczny, Uniwersytet Wroc lawski, pl. Grunwaldzki 2/4, 50 384
Convolution semigroups with linear Jacobi parameters
 Convolution semigroups with linear Jacobi parameters Michael Anshelevich; Wojciech Młotkowski Texas A&M University; University of Wrocław February 14, 2011 Jacobi parameters. µ = measure with finite moments,
Convolution semigroups with linear Jacobi parameters Michael Anshelevich; Wojciech Młotkowski Texas A&M University; University of Wrocław February 14, 2011 Jacobi parameters. µ = measure with finite moments,
Aerodynamics I Compressible flow past an airfoil
 Aerodynamics I Compressible flow past an airfoil transonic flow past the RAE-8 airfoil (M = 0.73, Re = 6.5 10 6, α = 3.19 ) Potential equation in compressible flows Full potential theory Let us introduce
Aerodynamics I Compressible flow past an airfoil transonic flow past the RAE-8 airfoil (M = 0.73, Re = 6.5 10 6, α = 3.19 ) Potential equation in compressible flows Full potential theory Let us introduce
Towards Stability Analysis of Data Transport Mechanisms: a Fluid Model and an Application
 Towards Stability Analysis of Data Transport Mechanisms: a Fluid Model and an Application Gayane Vardoyan *, C. V. Hollot, Don Towsley* * College of Information and Computer Sciences, Department of Electrical
Towards Stability Analysis of Data Transport Mechanisms: a Fluid Model and an Application Gayane Vardoyan *, C. V. Hollot, Don Towsley* * College of Information and Computer Sciences, Department of Electrical
Proposal of thesis topic for mgr in. (MSE) programme in Telecommunications and Computer Science
 Proposal of thesis topic for mgr in (MSE) programme 1 Topic: Monte Carlo Method used for a prognosis of a selected technological process 2 Supervisor: Dr in Małgorzata Langer 3 Auxiliary supervisor: 4
Proposal of thesis topic for mgr in (MSE) programme 1 Topic: Monte Carlo Method used for a prognosis of a selected technological process 2 Supervisor: Dr in Małgorzata Langer 3 Auxiliary supervisor: 4
Elementy równań różniczkowych cząstkowych
 Elementy równań różniczkowych cząstkowych Magdalena Jakubek kwiecień 2016 1 Równania różniczkowe cząstkowe Problem brzegowy i problem początkowy Klasyfikacja równań Rodzaje warunków brzegowych Najważniejsze
Elementy równań różniczkowych cząstkowych Magdalena Jakubek kwiecień 2016 1 Równania różniczkowe cząstkowe Problem brzegowy i problem początkowy Klasyfikacja równań Rodzaje warunków brzegowych Najważniejsze
Hard-Margin Support Vector Machines
 Hard-Margin Support Vector Machines aaacaxicbzdlssnafiyn9vbjlepk3ay2gicupasvu4iblxuaw2hjmuwn7ddjjmxm1bkcg1/fjqsvt76fo9/gazqfvn8y+pjpozw5vx8zkpvtfxmlhcwl5zxyqrm2vrg5zw3vxmsoezi4ogkr6phieky5crvvjhriqvdom9l2xxftevuwcekj3lktmhghgniauiyutvrwxtvme34a77kbvg73gtygpjsrfati1+xc8c84bvraowbf+uwnipyehcvmkjrdx46vlykhkgykm3ujjdhcyzqkxy0chur6ax5cbg+1m4bbjptjcubuz4kuhvjoql93hkin5hxtav5x6yyqopnsyuneey5ni4keqrxbar5wqaxbik00icyo/iveiyqqvjo1u4fgzj/8f9x67bzmxnurjzmijtlybwfgcdjgfdtajwgcf2dwaj7ac3g1ho1n4814n7wwjgjmf/ys8fenfycuzq==
Hard-Margin Support Vector Machines aaacaxicbzdlssnafiyn9vbjlepk3ay2gicupasvu4iblxuaw2hjmuwn7ddjjmxm1bkcg1/fjqsvt76fo9/gazqfvn8y+pjpozw5vx8zkpvtfxmlhcwl5zxyqrm2vrg5zw3vxmsoezi4ogkr6phieky5crvvjhriqvdom9l2xxftevuwcekj3lktmhghgniauiyutvrwxtvme34a77kbvg73gtygpjsrfati1+xc8c84bvraowbf+uwnipyehcvmkjrdx46vlykhkgykm3ujjdhcyzqkxy0chur6ax5cbg+1m4bbjptjcubuz4kuhvjoql93hkin5hxtav5x6yyqopnsyuneey5ni4keqrxbar5wqaxbik00icyo/iveiyqqvjo1u4fgzj/8f9x67bzmxnurjzmijtlybwfgcdjgfdtajwgcf2dwaj7ac3g1ho1n4814n7wwjgjmf/ys8fenfycuzq==
Helena Boguta, klasa 8W, rok szkolny 2018/2019
 Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Składają się na
Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Składają się na
Machine Learning for Data Science (CS4786) Lecture 11. Spectral Embedding + Clustering
 Machine Learning for Data Science (CS4786) Lecture 11 Spectral Embedding + Clustering MOTIVATING EXAMPLE What can you say from this network? MOTIVATING EXAMPLE How about now? THOUGHT EXPERIMENT For each
Machine Learning for Data Science (CS4786) Lecture 11 Spectral Embedding + Clustering MOTIVATING EXAMPLE What can you say from this network? MOTIVATING EXAMPLE How about now? THOUGHT EXPERIMENT For each
Dystrybucje, wiadomości wstępne (I)
 Temat 8 Dystrybucje, wiadomości wstępne (I) Wielkości fizyczne opisujemy najczęściej przyporządkowując im funkcje (np. zależne od czasu). Inną drogą opisu tych wielkości jest przyporządkowanie im funkcjonałów
Temat 8 Dystrybucje, wiadomości wstępne (I) Wielkości fizyczne opisujemy najczęściej przyporządkowując im funkcje (np. zależne od czasu). Inną drogą opisu tych wielkości jest przyporządkowanie im funkcjonałów
Zastosowania metod analitycznej złożoności obliczeniowej do przetwarzania sygnałów cyfrowych oraz w metodach numerycznych teorii aproksymacji
 Zastosowania metod analitycznej złożoności obliczeniowej do przetwarzania sygnałów cyfrowych oraz w metodach numerycznych teorii aproksymacji Marek A. Kowalski Uniwersytet Kardynała Stefana Wyszyńskiego
Zastosowania metod analitycznej złożoności obliczeniowej do przetwarzania sygnałów cyfrowych oraz w metodach numerycznych teorii aproksymacji Marek A. Kowalski Uniwersytet Kardynała Stefana Wyszyńskiego
ANALIZA WŁAŚCIWOŚCI FILTRU PARAMETRYCZNEGO I RZĘDU
 POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 78 Electrical Engineering 2014 Seweryn MAZURKIEWICZ* Janusz WALCZAK* ANALIZA WŁAŚCIWOŚCI FILTRU PARAMETRYCZNEGO I RZĘDU W artykule rozpatrzono problem
POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 78 Electrical Engineering 2014 Seweryn MAZURKIEWICZ* Janusz WALCZAK* ANALIZA WŁAŚCIWOŚCI FILTRU PARAMETRYCZNEGO I RZĘDU W artykule rozpatrzono problem
ZASTOSOWANIE RACHUNKU OPERATORÓW MIKUS- IŃSKIEGO W PEWNYCH ZAGADNIENIACH DYNAMIKI KONSTRUKCJI
 Budownictwo 18 Mariusz Poński ZASTOSOWANIE RACHUNKU OPERATORÓW MIKUS- IŃSKIEGO W PEWNYCH ZAGADNIENIACH DYNAMIKI KONSTRUKCJI 1. Metody transformacji całkowych Najczęściej spotykaną metodą rozwiązywania
Budownictwo 18 Mariusz Poński ZASTOSOWANIE RACHUNKU OPERATORÓW MIKUS- IŃSKIEGO W PEWNYCH ZAGADNIENIACH DYNAMIKI KONSTRUKCJI 1. Metody transformacji całkowych Najczęściej spotykaną metodą rozwiązywania
13 Równanie struny drgającej. Równanie przewodnictwa ciepła.
 Równanie struny drgającej. Równanie przewodnictwa ciepła 13 1 13 Równanie struny drgającej. Równanie przewodnictwa ciepła. 13.1 Równanie struny drgającej Równanie różniczkowe liniowe drugiego rzędu typu
Równanie struny drgającej. Równanie przewodnictwa ciepła 13 1 13 Równanie struny drgającej. Równanie przewodnictwa ciepła. 13.1 Równanie struny drgającej Równanie różniczkowe liniowe drugiego rzędu typu
Metody Obliczeniowe w Nauce i Technice
 23. Rozwiązywanie równań różniczkowych cząstkowych Marian Bubak Department of Computer Science AGH University of Science and Technology Krakow, Poland bubak@agh.edu.pl dice.cyfronet.pl Contributors Magdalena
23. Rozwiązywanie równań różniczkowych cząstkowych Marian Bubak Department of Computer Science AGH University of Science and Technology Krakow, Poland bubak@agh.edu.pl dice.cyfronet.pl Contributors Magdalena
Title: On the curl of singular completely continous vector fields in Banach spaces
 Title: On the curl of singular completely continous vector fields in Banach spaces Author: Adam Bielecki, Tadeusz Dłotko Citation style: Bielecki Adam, Dłotko Tadeusz. (1973). On the curl of singular completely
Title: On the curl of singular completely continous vector fields in Banach spaces Author: Adam Bielecki, Tadeusz Dłotko Citation style: Bielecki Adam, Dłotko Tadeusz. (1973). On the curl of singular completely
Uniwersytet Rzeszowski
 Seminarium z Równań Różniczkowych 21 marca 2017 r., godz. 12:15, sala 270 (B2): mgr Grzegorz Głowa, mgr Jarosław Napora, wykorzystaniem języka R, cz.2 Analizy statystyczne z 7 marca 2017 r., godz. 12:15,
Seminarium z Równań Różniczkowych 21 marca 2017 r., godz. 12:15, sala 270 (B2): mgr Grzegorz Głowa, mgr Jarosław Napora, wykorzystaniem języka R, cz.2 Analizy statystyczne z 7 marca 2017 r., godz. 12:15,
deep learning for NLP (5 lectures)
 TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 6: Finish Transformers; Sequence- to- Sequence Modeling and AJenKon 1 Roadmap intro (1 lecture) deep learning for NLP (5
TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 6: Finish Transformers; Sequence- to- Sequence Modeling and AJenKon 1 Roadmap intro (1 lecture) deep learning for NLP (5
ϕ(t k ; p) dla pewnego cigu t k }.
 VI. Trajektorie okresowe i zbiory graniczne. 1. Zbiory graniczne. Rozważamy równanie (1.1) x = f(x) z funkcją f : R n R n określoną na całej przestrzeni R n. Będziemy zakładać, że funkcja f spełnia założenia,
VI. Trajektorie okresowe i zbiory graniczne. 1. Zbiory graniczne. Rozważamy równanie (1.1) x = f(x) z funkcją f : R n R n określoną na całej przestrzeni R n. Będziemy zakładać, że funkcja f spełnia założenia,
Wybrana bibliografia
 Z ŻAŁOBNEJ KARTY Studia Gdańskie, t. VI W Gdańsku 11 grudnia 2008 roku zmarł dr hab. Andrzej Borysowicz (ur. 11 lutego 1961 roku w Woroneżu), profesor nadzwyczajny GWSH, znakomity matematyk, znawca następujących
Z ŻAŁOBNEJ KARTY Studia Gdańskie, t. VI W Gdańsku 11 grudnia 2008 roku zmarł dr hab. Andrzej Borysowicz (ur. 11 lutego 1961 roku w Woroneżu), profesor nadzwyczajny GWSH, znakomity matematyk, znawca następujących
Linear Classification and Logistic Regression. Pascal Fua IC-CVLab
 Linear Classification and Logistic Regression Pascal Fua IC-CVLab 1 aaagcxicbdtdbtmwfafwdgxlhk8orha31ibqycvkdgpshdqxtwotng2pxtvqujmok1qlky5xllzrnobbediegwcap4votk2kqkf+/y/tnphdschtadu/giv3vtea99cfma8fpx7ytlxx7ckns4sylo3doom7jguhj1hxchmy/irhrlgh67lxb5x3blis8jjqynmedqujiu5zsqqagrx+yjcfpcrydusshmzeluzsg7tttiew5khhcuzm5rv0gn1unw6zl3gbzlpr3liwncyr6aaqinx4wnc/rpg6ix5szd86agoftuu0g/krjxdarph62enthdey3zn/+mi5zknou2ap+tclvhob9sxhwvhaqketnde7geqjp21zvjsfrcnkfhtejoz23vq97elxjlpbtmxpl6qxtl1sgfv1ptpy/yq9mgacrzkgje0hjj2rq7vtywnishnnkzsqekucnlblrarlh8x8szxolrrxkb8n6o4kmo/e7siisnozcfvsedlol60a/j8nmul/gby8mmssrfr2it8lkyxr9dirxxngzthtbaejv
Linear Classification and Logistic Regression Pascal Fua IC-CVLab 1 aaagcxicbdtdbtmwfafwdgxlhk8orha31ibqycvkdgpshdqxtwotng2pxtvqujmok1qlky5xllzrnobbediegwcap4votk2kqkf+/y/tnphdschtadu/giv3vtea99cfma8fpx7ytlxx7ckns4sylo3doom7jguhj1hxchmy/irhrlgh67lxb5x3blis8jjqynmedqujiu5zsqqagrx+yjcfpcrydusshmzeluzsg7tttiew5khhcuzm5rv0gn1unw6zl3gbzlpr3liwncyr6aaqinx4wnc/rpg6ix5szd86agoftuu0g/krjxdarph62enthdey3zn/+mi5zknou2ap+tclvhob9sxhwvhaqketnde7geqjp21zvjsfrcnkfhtejoz23vq97elxjlpbtmxpl6qxtl1sgfv1ptpy/yq9mgacrzkgje0hjj2rq7vtywnishnnkzsqekucnlblrarlh8x8szxolrrxkb8n6o4kmo/e7siisnozcfvsedlol60a/j8nmul/gby8mmssrfr2it8lkyxr9dirxxngzthtbaejv
RESONANCE OF TORSIONAL VIBRATION OF SHAFTS COUPLED BY MECHANISMS
 SCIENTIFIC BULLETIN OF LOZ TECHNICAL UNIVERSITY Nr 78, TEXTILES 55, 997 ZESZYTY NAUKOWE POLITECHNIKI ŁÓZKIEJ Nr 78, WŁÓKIENNICTWO z. 55, 997 Pages: 8- http://bhp-k4.p.loz.pl/ JERZY ZAJACZKOWSKI Loz Technical
SCIENTIFIC BULLETIN OF LOZ TECHNICAL UNIVERSITY Nr 78, TEXTILES 55, 997 ZESZYTY NAUKOWE POLITECHNIKI ŁÓZKIEJ Nr 78, WŁÓKIENNICTWO z. 55, 997 Pages: 8- http://bhp-k4.p.loz.pl/ JERZY ZAJACZKOWSKI Loz Technical
"Dynamical Systems and Applications II"
 The Institute of MathematicsTechnicalUniversity of Łódź, Łódź, Poland, The Institute of MathematicsUniversity of Białystok, Białystok, Poland, and Juliusz Schauder University Centre for Nonlinear Studies,
The Institute of MathematicsTechnicalUniversity of Łódź, Łódź, Poland, The Institute of MathematicsUniversity of Białystok, Białystok, Poland, and Juliusz Schauder University Centre for Nonlinear Studies,
tum.de/fall2018/ in2357
 https://piazza.com/ tum.de/fall2018/ in2357 Prof. Daniel Cremers From to Classification Categories of Learning (Rep.) Learning Unsupervised Learning clustering, density estimation Supervised Learning learning
https://piazza.com/ tum.de/fall2018/ in2357 Prof. Daniel Cremers From to Classification Categories of Learning (Rep.) Learning Unsupervised Learning clustering, density estimation Supervised Learning learning
Weronika Mysliwiec, klasa 8W, rok szkolny 2018/2019
 Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Tresci zadań rozwiązanych
Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Tresci zadań rozwiązanych
MACIERZE FIBONACCIEGO GENEROWANE PRZEZ OPERACJE RÓŻ NICOWE
 ZESZYTY NAUKOWE AKADEMII MARYNARKI WOJENNEJ ROK LII NR 3 (186) 2011 Hubert Wysocki Akademia Marynarki Wojennej MACIERZE FIBONACCIEGO GENEROWANE PRZEZ OPERACJE RÓŻ NICOWE STRESZCZENIE Na gruncie teorii
ZESZYTY NAUKOWE AKADEMII MARYNARKI WOJENNEJ ROK LII NR 3 (186) 2011 Hubert Wysocki Akademia Marynarki Wojennej MACIERZE FIBONACCIEGO GENEROWANE PRZEZ OPERACJE RÓŻ NICOWE STRESZCZENIE Na gruncie teorii
2. Definicja pochodnej w R n
 2. Definicja pochodnej w R n Niech będzie dana funkcja f : U R określona na zbiorze otwartym U R n. Pochodną kierunkową w punkcie a U w kierunku wektora u R n nazywamy granicę u f(a) = lim t 0 f(a + tu)
2. Definicja pochodnej w R n Niech będzie dana funkcja f : U R określona na zbiorze otwartym U R n. Pochodną kierunkową w punkcie a U w kierunku wektora u R n nazywamy granicę u f(a) = lim t 0 f(a + tu)
Zagadnienia stacjonarne
 Zagadnienia stacjonarne Karol Hajduk 19 grudnia 2012 Nierówność wariacyjna (u (t), v u(t)) + a(u, v u) + Ψ(v) Ψ(u) (f, v u), v V. Zagadnienie stacjonarne ma postać (u (t) = 0): a(u, v u) + Ψ(v) Ψ(u) (f,
Zagadnienia stacjonarne Karol Hajduk 19 grudnia 2012 Nierówność wariacyjna (u (t), v u(t)) + a(u, v u) + Ψ(v) Ψ(u) (f, v u), v V. Zagadnienie stacjonarne ma postać (u (t) = 0): a(u, v u) + Ψ(v) Ψ(u) (f,
OpenPoland.net API Documentation
 OpenPoland.net API Documentation Release 1.0 Michał Gryczka July 11, 2014 Contents 1 REST API tokens: 3 1.1 How to get a token............................................ 3 2 REST API : search for assets
OpenPoland.net API Documentation Release 1.0 Michał Gryczka July 11, 2014 Contents 1 REST API tokens: 3 1.1 How to get a token............................................ 3 2 REST API : search for assets
Zadania do wykładu Jakościowa Teoria Równań Różniczkowych Zwyczajnych
 Zadania do wykładu Jakościowa Teoria Równań Różniczkowych Zwyczajnych [ ] e Zadanie 1 Pokazać, że X(t) = 2t cos t sin t e 2t jest specjalną macierzą fundamentalną w sin t cos t [ 2 cos chwili τ = 0 układu
Zadania do wykładu Jakościowa Teoria Równań Różniczkowych Zwyczajnych [ ] e Zadanie 1 Pokazać, że X(t) = 2t cos t sin t e 2t jest specjalną macierzą fundamentalną w sin t cos t [ 2 cos chwili τ = 0 układu
Struktury Geometryczne Mechaniki
 Struktury Geometryczne Mechaniki Paweł Urbański u rb a n ski@fuw.ed u.p l Kat edra Met od Mat ematycznych Fizyki Uniwersyt et Warszawski Sympozjum IFT, 08.12.2007 p. 1/23 MOTYWACJE Dlaczego mechanika (analityczna)?
Struktury Geometryczne Mechaniki Paweł Urbański u rb a n ski@fuw.ed u.p l Kat edra Met od Mat ematycznych Fizyki Uniwersyt et Warszawski Sympozjum IFT, 08.12.2007 p. 1/23 MOTYWACJE Dlaczego mechanika (analityczna)?
The Lorenz System and Chaos in Nonlinear DEs
 The Lorenz System and Chaos in Nonlinear DEs April 30, 2019 Math 333 p. 71 in Chaos: Making a New Science by James Gleick Adding a dimension adds new possible layers of complexity in the phase space of
The Lorenz System and Chaos in Nonlinear DEs April 30, 2019 Math 333 p. 71 in Chaos: Making a New Science by James Gleick Adding a dimension adds new possible layers of complexity in the phase space of
R E P R E S E N T A T I O N S
 Z E S Z Y T Y N A U K O W E A K A D E M I I M A R Y N A R K I W O J E N N E J S C I E N T I F I C J O U R N A L O F P O L I S H N A V A L A C A D E M Y 2017 (LVIII) 4 (211) DOI: 10.5604/01.3001.0010.6752
Z E S Z Y T Y N A U K O W E A K A D E M I I M A R Y N A R K I W O J E N N E J S C I E N T I F I C J O U R N A L O F P O L I S H N A V A L A C A D E M Y 2017 (LVIII) 4 (211) DOI: 10.5604/01.3001.0010.6752
 aforementioned device she also has to estimate the time when the patients need the infusion to be replaced and/or disconnected. Meanwhile, however, she must cope with many other tasks. If the department
aforementioned device she also has to estimate the time when the patients need the infusion to be replaced and/or disconnected. Meanwhile, however, she must cope with many other tasks. If the department
Informacja o przestrzeniach Sobolewa
 Wykład 11 Informacja o przestrzeniach Sobolewa 11.1 Definicja przestrzeni Sobolewa Niech R n będzie zbiorem mierzalnym. Rozważmy przestrzeń Hilberta X = L 2 () z iloczynem skalarnym zdefiniowanym równością
Wykład 11 Informacja o przestrzeniach Sobolewa 11.1 Definicja przestrzeni Sobolewa Niech R n będzie zbiorem mierzalnym. Rozważmy przestrzeń Hilberta X = L 2 () z iloczynem skalarnym zdefiniowanym równością
Zestaw zadań z Równań różniczkowych cząstkowych I 18/19
 Zestaw zadań z Równań różniczkowych cząstkowych I 18/19 Zad 1. Znaleźć rozwiązania ogólne u = u(x, y) następujących równań u x = 1, u y = 2xy, u yy = 6y, u xy = 1, u x + y = 0, u xxyy = 0. Zad 2. Znaleźć
Zestaw zadań z Równań różniczkowych cząstkowych I 18/19 Zad 1. Znaleźć rozwiązania ogólne u = u(x, y) następujących równań u x = 1, u y = 2xy, u yy = 6y, u xy = 1, u x + y = 0, u xxyy = 0. Zad 2. Znaleźć
1 Relacje i odwzorowania
 Relacje i odwzorowania Relacje Jacek Kłopotowski Zadania z analizy matematycznej I Wykazać, że jeśli relacja ρ X X jest przeciwzwrotna i przechodnia, to jest przeciwsymetryczna Zbadać czy relacja ρ X X
Relacje i odwzorowania Relacje Jacek Kłopotowski Zadania z analizy matematycznej I Wykazać, że jeśli relacja ρ X X jest przeciwzwrotna i przechodnia, to jest przeciwsymetryczna Zbadać czy relacja ρ X X
Modern methods of statistical physics
 Modern methods of statistical physics František Slanina Institute of Physics, Academy of Sciences of the Czech Republic, Prague slanina@fzu.cz www.fzu.cz/ slanina Ising model Renormalisation group Modern
Modern methods of statistical physics František Slanina Institute of Physics, Academy of Sciences of the Czech Republic, Prague slanina@fzu.cz www.fzu.cz/ slanina Ising model Renormalisation group Modern
O przecinkach i nie tylko
 O przecinkach i nie tylko Jerzy Trzeciak Dział Wydawnictw IMPAN publ@impan.pl https://www.impan.pl/pl/wydawnictwa/dla-autorow 7 sierpnia 2018 Przecinek Sformułuję najpierw kilka zasad, którymi warto się
O przecinkach i nie tylko Jerzy Trzeciak Dział Wydawnictw IMPAN publ@impan.pl https://www.impan.pl/pl/wydawnictwa/dla-autorow 7 sierpnia 2018 Przecinek Sformułuję najpierw kilka zasad, którymi warto się
Z52: Algebra liniowa Zagadnienie: Zastosowania algebry liniowej Zadanie: Operatory różniczkowania, zagadnienie brzegowe.
 Z5: Algebra liniowa Zagadnienie: Zastosowania algebry liniowej Zadanie: Operatory różniczkowania zagadnienie brzegowe Dyskretne operatory różniczkowania Numeryczne obliczanie pochodnych oraz rozwiązywanie
Z5: Algebra liniowa Zagadnienie: Zastosowania algebry liniowej Zadanie: Operatory różniczkowania zagadnienie brzegowe Dyskretne operatory różniczkowania Numeryczne obliczanie pochodnych oraz rozwiązywanie
Jak trudne jest numeryczne całkowanie (O złożoności zadań ciągłych)
 Jak trudne jest numeryczne całkowanie (O złożoności zadań ciągłych) Uniwersytet Warszawski Wydział Matematyki, Informatyki i Mechaniki leszekp@mimuw.edu.pl Horyzonty 2014 17-03-2014 Będlewo Zadania numeryczne
Jak trudne jest numeryczne całkowanie (O złożoności zadań ciągłych) Uniwersytet Warszawski Wydział Matematyki, Informatyki i Mechaniki leszekp@mimuw.edu.pl Horyzonty 2014 17-03-2014 Będlewo Zadania numeryczne
II. Równania autonomiczne. 1. Podstawowe pojęcia.
 II. Równania autonomiczne. 1. Podstawowe pojęcia. Definicja 1.1. Niech Q R n, n 1, będzie danym zbiorem i niech f : Q R n będzie daną funkcją określoną na Q. Równanie różniczkowe postaci (1.1) x = f(x),
II. Równania autonomiczne. 1. Podstawowe pojęcia. Definicja 1.1. Niech Q R n, n 1, będzie danym zbiorem i niech f : Q R n będzie daną funkcją określoną na Q. Równanie różniczkowe postaci (1.1) x = f(x),
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa.
 VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
EXAMPLES OF CABRI GEOMETRE II APPLICATION IN GEOMETRIC SCIENTIFIC RESEARCH
 Anna BŁACH Centre of Geometry and Engineering Graphics Silesian University of Technology in Gliwice EXAMPLES OF CABRI GEOMETRE II APPLICATION IN GEOMETRIC SCIENTIFIC RESEARCH Introduction Computer techniques
Anna BŁACH Centre of Geometry and Engineering Graphics Silesian University of Technology in Gliwice EXAMPLES OF CABRI GEOMETRE II APPLICATION IN GEOMETRIC SCIENTIFIC RESEARCH Introduction Computer techniques
TTIC 31210: Advanced Natural Language Processing. Kevin Gimpel Spring Lecture 9: Inference in Structured Prediction
 TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 9: Inference in Structured Prediction 1 intro (1 lecture) Roadmap deep learning for NLP (5 lectures) structured prediction
TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 9: Inference in Structured Prediction 1 intro (1 lecture) Roadmap deep learning for NLP (5 lectures) structured prediction
STOCHASTYCZNY MODEL BEZPIECZEŃSTWA OBIEKTU W PROCESIE EKSPLOATACJI
 1-2011 PROBLEMY EKSPLOATACJI 89 Franciszek GRABSKI Akademia Marynarki Wojennej, Gdynia STOCHASTYCZNY MODEL BEZPIECZEŃSTWA OBIEKTU W PROCESIE EKSPLOATACJI Słowa kluczowe Bezpieczeństwo, procesy semimarkowskie,
1-2011 PROBLEMY EKSPLOATACJI 89 Franciszek GRABSKI Akademia Marynarki Wojennej, Gdynia STOCHASTYCZNY MODEL BEZPIECZEŃSTWA OBIEKTU W PROCESIE EKSPLOATACJI Słowa kluczowe Bezpieczeństwo, procesy semimarkowskie,
Few-fermion thermometry
 Few-fermion thermometry Phys. Rev. A 97, 063619 (2018) Tomasz Sowiński Institute of Physics of the Polish Academy of Sciences Co-authors: Marcin Płodzień Rafał Demkowicz-Dobrzański FEW-BODY PROBLEMS FewBody.ifpan.edu.pl
Few-fermion thermometry Phys. Rev. A 97, 063619 (2018) Tomasz Sowiński Institute of Physics of the Polish Academy of Sciences Co-authors: Marcin Płodzień Rafał Demkowicz-Dobrzański FEW-BODY PROBLEMS FewBody.ifpan.edu.pl
MODEL RACHUNKU OPERATORÓW DLA RÓŻ NICY WSTECZNEJ PRZY PODSTAWACH
 ZESZYTY NAUKOWE AKADEMII MARYNARKI WOJENNEJ ROK LIV NR 1 (192) 2013 Hubert Wysocki Akademia Marynarki Wojennej Wydział Mechaniczno-Elektryczny, Katedra Matematyki i Fizyki 81-103 Gdynia, ul. J. Śmidowicza
ZESZYTY NAUKOWE AKADEMII MARYNARKI WOJENNEJ ROK LIV NR 1 (192) 2013 Hubert Wysocki Akademia Marynarki Wojennej Wydział Mechaniczno-Elektryczny, Katedra Matematyki i Fizyki 81-103 Gdynia, ul. J. Śmidowicza
Lecture 18 Review for Exam 1
 Spring, 2019 ME 323 Mechanics of Materials Lecture 18 Review for Exam 1 Reading assignment: HW1-HW5 News: Ready for the exam? Instructor: Prof. Marcial Gonzalez Announcements Exam 1 - Wednesday February
Spring, 2019 ME 323 Mechanics of Materials Lecture 18 Review for Exam 1 Reading assignment: HW1-HW5 News: Ready for the exam? Instructor: Prof. Marcial Gonzalez Announcements Exam 1 - Wednesday February
Modele matematyczne drapieżnictwa
 Modele matematyczne drapieżnictwa Dariusz WRZOSEK Instytut Matematyki Stosowanej i Mechaniki Uniwersytet Warszawski BIOFIZMAT, Grudzień 2015 Rodzaje odziaływań miedzygatunkowych Podstawowe oddziaływania
Modele matematyczne drapieżnictwa Dariusz WRZOSEK Instytut Matematyki Stosowanej i Mechaniki Uniwersytet Warszawski BIOFIZMAT, Grudzień 2015 Rodzaje odziaływań miedzygatunkowych Podstawowe oddziaływania
Twierdzenie Hilberta o nieujemnie określonych formach ternarnych stopnia 4
 Twierdzenie Hilberta o nieujemnie określonych formach ternarnych stopnia 4 Strona 1 z 23 Andrzej Sładek, Instytut Matematyki UŚl sladek@math.us.edu.pl Letnia Szkoła Instytutu Matematyki 20-23 września
Twierdzenie Hilberta o nieujemnie określonych formach ternarnych stopnia 4 Strona 1 z 23 Andrzej Sładek, Instytut Matematyki UŚl sladek@math.us.edu.pl Letnia Szkoła Instytutu Matematyki 20-23 września
Przedmioty do wyboru oferowane na stacjonarnych studiach II stopnia (magisterskich) dla II roku w roku akademickim 2015/2016
 Przedmioty do wyboru oferowane na stacjonarnych studiach II stopnia (magisterskich) dla II roku w roku akademickim 2015/2016 Przedmioty do wyboru oferowane na semestr IV - letni (I rok) Prowadzący Przedmiot
Przedmioty do wyboru oferowane na stacjonarnych studiach II stopnia (magisterskich) dla II roku w roku akademickim 2015/2016 Przedmioty do wyboru oferowane na semestr IV - letni (I rok) Prowadzący Przedmiot
Z-ZIP Równania Różniczkowe. Differential Equations
 MODULE DESCRIPTION Module code Z-ZIP-1002 Module name Równania Różniczkowe Module name in English Differential Equations Valid from academic year 2016/2017 A. MODULE PLACEMENT IN THE SYLLABUS Field of
MODULE DESCRIPTION Module code Z-ZIP-1002 Module name Równania Różniczkowe Module name in English Differential Equations Valid from academic year 2016/2017 A. MODULE PLACEMENT IN THE SYLLABUS Field of
Dystrybucje. Marcin Orchel. 1 Wstęp Dystrybucje Pochodna dystrybucyjna Przestrzenie... 5
 Dystrybucje Marcin Orchel Spis treści 1 Wstęp 1 1.1 Dystrybucje................................... 1 1.2 Pochodna dystrybucyjna............................ 3 1.3 Przestrzenie...................................
Dystrybucje Marcin Orchel Spis treści 1 Wstęp 1 1.1 Dystrybucje................................... 1 1.2 Pochodna dystrybucyjna............................ 3 1.3 Przestrzenie...................................
WYKORZYSTANIE SYSTEMU Mathematica DO ROZWIĄZYWANIA ZAGADNIEŃ PRZEWODZENIA CIEPŁA
 39/19 ARCHIWUM ODLEWNICTWA Rok 006, Rocznik 6, Nr 19 Archives of Foundry Year 006, Volume 6, Book 19 PAN - Katowice PL ISSN 164-5308 WYKORZYSTANIE SYSTEMU Mathematica DO ROZWIĄZYWANIA ZAGADNIEŃ PRZEWODZENIA
39/19 ARCHIWUM ODLEWNICTWA Rok 006, Rocznik 6, Nr 19 Archives of Foundry Year 006, Volume 6, Book 19 PAN - Katowice PL ISSN 164-5308 WYKORZYSTANIE SYSTEMU Mathematica DO ROZWIĄZYWANIA ZAGADNIEŃ PRZEWODZENIA
Fig 5 Spectrograms of the original signal (top) extracted shaft-related GAD components (middle) and
 Fig 4 Measured vibration signal (top). Blue original signal. Red component related to periodic excitation of resonances and noise. Green component related. Rotational speed profile used for experiment
Fig 4 Measured vibration signal (top). Blue original signal. Red component related to periodic excitation of resonances and noise. Green component related. Rotational speed profile used for experiment
Zwyczajne równania różniczkowe (ZRR) Metody Runge go-ku/y
 Zwyczajne równania różniczkowe (ZRR) Metody Runge go-ku/y Metoda Runge go-ku/y (4) Embedded Runge-Kutta methods. Są to jawne metody z dwoma zbiorami współczynników, pozwalające oszacować błąd obliczeń.
Zwyczajne równania różniczkowe (ZRR) Metody Runge go-ku/y Metoda Runge go-ku/y (4) Embedded Runge-Kutta methods. Są to jawne metody z dwoma zbiorami współczynników, pozwalające oszacować błąd obliczeń.
O zbiorach małych w polskich grupach abelowych
 O zbiorach małych w polskich grupach abelowych Eliza Jabłońska Katedra Matematyki Politechniki Rzeszowskiej Warsztaty z Analizy Rzeczywistej, Konopnica 2016 E. Jabłońska (KM PRz) O zbiorach małych Konopnica
O zbiorach małych w polskich grupach abelowych Eliza Jabłońska Katedra Matematyki Politechniki Rzeszowskiej Warsztaty z Analizy Rzeczywistej, Konopnica 2016 E. Jabłońska (KM PRz) O zbiorach małych Konopnica
Wykład Matematyka A, I rok, egzamin ustny w sem. letnim r. ak. 2002/2003. Każdy zdający losuje jedno pytanie teoretyczne i jedno praktyczne.
 Wykład Matematyka A, I rok, egzamin ustny w sem. letnim r. ak. 2002/2003. Każdy zdający losuje jedno pytanie teoretyczne i jedno praktyczne. pytania teoretyczne:. Co to znaczy, że wektory v, v 2 i v 3
Wykład Matematyka A, I rok, egzamin ustny w sem. letnim r. ak. 2002/2003. Każdy zdający losuje jedno pytanie teoretyczne i jedno praktyczne. pytania teoretyczne:. Co to znaczy, że wektory v, v 2 i v 3
Wyk lad z Algebry Liniowej dla studentów WNE UW. Rok akademicki 2017/2018. Przyk lady zadań na ćwiczenia. 1. Które z cia
 Wyk lad z Algebry Liniowej dla studentów WNE UW. Rok akademicki 2017/2018. Przyk lady zadań na ćwiczenia. 1. Które z cia gów: ( 1, 1, 1, 1), (2, 3, 1, 4), (4, 3, 2, 1), (4, 0, 3, 1) sa rozwia 2 zaniami
Wyk lad z Algebry Liniowej dla studentów WNE UW. Rok akademicki 2017/2018. Przyk lady zadań na ćwiczenia. 1. Które z cia gów: ( 1, 1, 1, 1), (2, 3, 1, 4), (4, 3, 2, 1), (4, 0, 3, 1) sa rozwia 2 zaniami
Revenue Maximization. Sept. 25, 2018
 Revenue Maximization Sept. 25, 2018 Goal So Far: Ideal Auctions Dominant-Strategy Incentive Compatible (DSIC) b i = v i is a dominant strategy u i 0 x is welfare-maximizing x and p run in polynomial time
Revenue Maximization Sept. 25, 2018 Goal So Far: Ideal Auctions Dominant-Strategy Incentive Compatible (DSIC) b i = v i is a dominant strategy u i 0 x is welfare-maximizing x and p run in polynomial time
28 maja, Problem Dirichleta, proces Wienera. Procesy Stochastyczne, wykład 14, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1126
 Problem Dirichleta, proces Wienera Procesy Stochastyczne, wykład 14, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1126 28 maja, 2012 Funkcje harmoniczne Niech będzie operatorem Laplace a w
Problem Dirichleta, proces Wienera Procesy Stochastyczne, wykład 14, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1126 28 maja, 2012 Funkcje harmoniczne Niech będzie operatorem Laplace a w
Machine Learning for Data Science (CS4786) Lecture11. Random Projections & Canonical Correlation Analysis
 Machine Learning for Data Science (CS4786) Lecture11 5 Random Projections & Canonical Correlation Analysis The Tall, THE FAT AND THE UGLY n X d The Tall, THE FAT AND THE UGLY d X > n X d n = n d d The
Machine Learning for Data Science (CS4786) Lecture11 5 Random Projections & Canonical Correlation Analysis The Tall, THE FAT AND THE UGLY n X d The Tall, THE FAT AND THE UGLY d X > n X d n = n d d The
. α p S n 1u p (x) = up F (u(x), λ), gdzie (1) F C 2 (R p R, R), (2) u F (u, λ) = λu + u g(u, λ), gdzie g C 2 (R p R, R) i dla każdego λ R zachodzi
 PIOTR STEFANIAK 1. Preliminaria Oznaczmy przez S n 1 operator Laplace a-beltrami ego na sferze S n 1 R[1, 1] R[n 2, 0] oraz rozważmy następujący układ równań: α 1 S n 1u 1 x) = u1 F ux), λ) α 2 S n 1u
PIOTR STEFANIAK 1. Preliminaria Oznaczmy przez S n 1 operator Laplace a-beltrami ego na sferze S n 1 R[1, 1] R[n 2, 0] oraz rozważmy następujący układ równań: α 1 S n 1u 1 x) = u1 F ux), λ) α 2 S n 1u
ANALIZA MATEMATYCZNA Z ELEMENTAMI STATYSTYKI MATEMATYCZNEJ
 ANALIZA MATEMATYCZNA Z ELEMENTAMI STATYSTYKI MATEMATYCZNEJ FUNKCJE DWÓCH ZMIENNYCH RZECZYWISTYCH Definicja 1. Niech A będzie dowolnym niepustym zbiorem. Metryką w zbiorze A nazywamy funkcję rzeczywistą
ANALIZA MATEMATYCZNA Z ELEMENTAMI STATYSTYKI MATEMATYCZNEJ FUNKCJE DWÓCH ZMIENNYCH RZECZYWISTYCH Definicja 1. Niech A będzie dowolnym niepustym zbiorem. Metryką w zbiorze A nazywamy funkcję rzeczywistą
Matematyka Stosowana na Politechnice Wrocławskiej. Komitet Matematyki PAN, luty 2017 r.
 Matematyka Stosowana na Politechnice Wrocławskiej Komitet Matematyki PAN, luty 2017 r. Historia kierunku Matematyka Stosowana utworzona w 2012 r. na WPPT (zespół z Centrum im. Hugona Steinhausa) studia
Matematyka Stosowana na Politechnice Wrocławskiej Komitet Matematyki PAN, luty 2017 r. Historia kierunku Matematyka Stosowana utworzona w 2012 r. na WPPT (zespół z Centrum im. Hugona Steinhausa) studia
Sterowanie optymalne
 Sterowanie optymalne Sterowanie Procesami Ciągłymi 2017 Optymalizacja statyczna funkcji Funkcja celu/kryterialna/kosztów Ograniczenie Q(x) min x x = arg min Q(x) x x X, gdzie X zbiór rozwiązań dopuszczalnych
Sterowanie optymalne Sterowanie Procesami Ciągłymi 2017 Optymalizacja statyczna funkcji Funkcja celu/kryterialna/kosztów Ograniczenie Q(x) min x x = arg min Q(x) x x X, gdzie X zbiór rozwiązań dopuszczalnych
Dyskretna teoria Morse a
 Dyskretna teoria Morse a Toruńska Letnia Szkoła Matematyki 2011 Michał Kukieła Uniwersytet Mikołaja Kopernika w Toruniu θ R θ Klasyczna teoria Morse a M n - zwarta rozmaitość gładka bez brzegu, f : M n
Dyskretna teoria Morse a Toruńska Letnia Szkoła Matematyki 2011 Michał Kukieła Uniwersytet Mikołaja Kopernika w Toruniu θ R θ Klasyczna teoria Morse a M n - zwarta rozmaitość gładka bez brzegu, f : M n
Model Pasywnego Trasera w Lokalnie Ergodycznym Środowisku
 w Lokalnie Ergodycznym Środowisku Tymoteusz Chojecki UMCS, Lublin Tomasz Komorowski IMPAN, Warszawa Kościelisko, 10 września 2016, XLV Konferencja Zastosowań Matematyki T. Komorowski, T. Chojecki w Lokalnie
w Lokalnie Ergodycznym Środowisku Tymoteusz Chojecki UMCS, Lublin Tomasz Komorowski IMPAN, Warszawa Kościelisko, 10 września 2016, XLV Konferencja Zastosowań Matematyki T. Komorowski, T. Chojecki w Lokalnie
Zagadnienia brzegowe dla równań eliptycznych
 Temat 7 Zagadnienia brzegowe dla równań eliptycznych Rozważmy płaski obszar R 2 ograniczony krzywą. la równania Laplace a (Poissona) stawia się trzy podstawowe zagadnienia brzegowe. Zagadnienie irichleta
Temat 7 Zagadnienia brzegowe dla równań eliptycznych Rozważmy płaski obszar R 2 ograniczony krzywą. la równania Laplace a (Poissona) stawia się trzy podstawowe zagadnienia brzegowe. Zagadnienie irichleta
ZASTOSOWANIE RACHUNKU UŁAMKOWEGO RZĘDU DO MODELOWANIA PEWNEJ KLASY GENERATORÓW NIELINIOWYCH
 ELEKTRYKA 4 Zeszyt (9) Rok LX Andrzej ZAWADZKI, Maciej WŁODARCZYK Politechnika Świętokrzyska w Kielcach ZASTOSOWANIE RACHUNKU UŁAMKOWEGO RZĘDU DO MODELOWANIA PEWNEJ KLASY GENERATORÓW NIELINIOWYCH Streszczenie.
ELEKTRYKA 4 Zeszyt (9) Rok LX Andrzej ZAWADZKI, Maciej WŁODARCZYK Politechnika Świętokrzyska w Kielcach ZASTOSOWANIE RACHUNKU UŁAMKOWEGO RZĘDU DO MODELOWANIA PEWNEJ KLASY GENERATORÓW NIELINIOWYCH Streszczenie.
Operatorowe wersje twierdzenia Radona-Nikodyma
 Operatorowe wersje twierdzenia Radona-Nikodyma Zakład Równań Funkcyjnych Letnia Szkoła Instytutu Matematyki UŚ, 22-26 września 2014r. skalarne twierdzenie Radona-Nikodyma Załóżmy, że X = (X, A) jest przestrzenia
Operatorowe wersje twierdzenia Radona-Nikodyma Zakład Równań Funkcyjnych Letnia Szkoła Instytutu Matematyki UŚ, 22-26 września 2014r. skalarne twierdzenie Radona-Nikodyma Załóżmy, że X = (X, A) jest przestrzenia
harmonic functions and the chromatic polynomial
 harmonic functions and the chromatic polynomial R. Kenyon (Brown) based on joint work with A. Abrams, W. Lam The chromatic polynomial with n colors. G(n) of a graph G is the number of proper colorings
harmonic functions and the chromatic polynomial R. Kenyon (Brown) based on joint work with A. Abrams, W. Lam The chromatic polynomial with n colors. G(n) of a graph G is the number of proper colorings
Matematyka 3. Suma szeregu. Promień zbieżności szeregu. Przykład 1: Przykład 2: GenerateConditions
 Matematyka 3 Suma szeregu? Sum i max Sum[f, {i, i max }] evaluates the sum f. Sum[f, {i, i min, i max }] starts with i = i min. Sum[f, {i, i min, i max, di}] uses steps di. Sum[f, {i, {i 1, i 2, }}] uses
Matematyka 3 Suma szeregu? Sum i max Sum[f, {i, i max }] evaluates the sum f. Sum[f, {i, i min, i max }] starts with i = i min. Sum[f, {i, i min, i max, di}] uses steps di. Sum[f, {i, {i 1, i 2, }}] uses
Stability of Tikhonov Regularization Class 07, March 2003 Alex Rakhlin
 Stability of Tikhonov Regularization 9.520 Class 07, March 2003 Alex Rakhlin Plan Review of Stability Bounds Stability of Tikhonov Regularization Algorithms Uniform Stability Review notation: S = {z 1,...,
Stability of Tikhonov Regularization 9.520 Class 07, March 2003 Alex Rakhlin Plan Review of Stability Bounds Stability of Tikhonov Regularization Algorithms Uniform Stability Review notation: S = {z 1,...,
DOI: / /32/37
 . 2015. 4 (32) 1:18 DOI: 10.17223/1998863 /32/37 -,,. - -. :,,,,., -, -.,.-.,.,.,. -., -,.,,., -, 70 80. (.,.,. ),, -,.,, -,, (1886 1980).,.,, (.,.,..), -, -,,,, ; -, - 346, -,.. :, -, -,,,,,.,,, -,,,
. 2015. 4 (32) 1:18 DOI: 10.17223/1998863 /32/37 -,,. - -. :,,,,., -, -.,.-.,.,.,. -., -,.,,., -, 70 80. (.,.,. ),, -,.,, -,, (1886 1980).,.,, (.,.,..), -, -,,,, ; -, - 346, -,.. :, -, -,,,,,.,,, -,,,
Relaxation of the Cosmological Constant
 Relaxation of the Cosmological Constant with Peter Graham and David E. Kaplan The Born Again Universe + Work in preparation + Work in progress aaab7nicdvbns8nafhypx7v+vt16wsycp5kioseifw8ekthwaepzbf7apztn2n0ipfrhepggifd/jzf/jzs2brudwbhm5rhvtzakro3rfjqlpewv1bxyemvjc2t7p7q719zjphi2wcisdr9qjyjlbblubn6ncmkccoweo6vc7zyg0jyrd2acoh/tgeqrz9ryqdo7sdgq9qs1t37m5ibu3v2qqvekpqyfmv3qry9mwbajnexqrbuemxp/qpxhtoc00ss0ppsn6ac7lkoao/yns3wn5mgqiykszz80zkz+n5jqwotxhnhktm1q//zy8s+vm5nowp9wmwygjzt/fgwcmitkt5oqk2rgjc2hthg7k2fdqigztqgklwfxkfmfte/qnuw3p7xgzvfhgq7gei7bg3nowdu0oqumrvaiz/dipm6t8+q8zamlp5jzhx9w3r8agjmpzw==
Relaxation of the Cosmological Constant with Peter Graham and David E. Kaplan The Born Again Universe + Work in preparation + Work in progress aaab7nicdvbns8nafhypx7v+vt16wsycp5kioseifw8ekthwaepzbf7apztn2n0ipfrhepggifd/jzf/jzs2brudwbhm5rhvtzakro3rfjqlpewv1bxyemvjc2t7p7q719zjphi2wcisdr9qjyjlbblubn6ncmkccoweo6vc7zyg0jyrd2acoh/tgeqrz9ryqdo7sdgq9qs1t37m5ibu3v2qqvekpqyfmv3qry9mwbajnexqrbuemxp/qpxhtoc00ss0ppsn6ac7lkoao/yns3wn5mgqiykszz80zkz+n5jqwotxhnhktm1q//zy8s+vm5nowp9wmwygjzt/fgwcmitkt5oqk2rgjc2hthg7k2fdqigztqgklwfxkfmfte/qnuw3p7xgzvfhgq7gei7bg3nowdu0oqumrvaiz/dipm6t8+q8zamlp5jzhx9w3r8agjmpzw==
Primal Formulation. Find u h V h such that. A h (u h, v h )= fv h dx v h V h, where. u h v h dx. A h (u h, v h ) = DGFEM Primal Formulation.
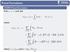 aaaftxicbvtnbtnaehzdsov5aqthlimaokskuviowkfs+vekehjfkbapg6znehmvwa9d7zqksvwipa1xeaeuvagnhni1nshou5ll8tcz33w7o+thyjlunc7vtcq16vr1jc0b9s1bt+9sbe/cpzfbhbhajwepok9dlclngvyvu5x+ciok/sgnp8pjs+m/ndjiskb8vbchhfh4lniieaw05oxu6j0mxkjfjgeicthxvbrimhigpkzsws1+7ngn7w1nha8jbyzioeiddyoymhzxhrmg8/myu4bgqyq5zx05wctq2f89glebdsku09n1gzoggftogizzcvkp9bivtytcghv4ydfkaokbqdmwvf2iabcyov4hgec5x8+wjyhgdr3u8qq+hjtqfz9mkn5ceqd7mjutwp0pt3jqttw1gxsfagjrhccytefbhiolawya5kogufle59x8ky6pwvsyq8nkrepyaf7omhnlclq5bbtr3es84varia+kt2l8swbyhpgymznwpc/sfbysspy2s73baxeybzenbmhswsu61po1hdyaxd4vinas5vm3e6pbgipfckepjwjjq0wmeezptcmwpvlbkk10cg814oiej/0ibrm6njfgx8olf6gjfaw8ueoz4fw+s1inng4sjsjyuuhyqqoygwraxa9wwusj4hfawcriwisqd0eykh2jsluei3skhawdjomihx4jszkkaxqlwhkor4nccss2wqjdqsjgjrkljt0rulqfxlj0pnlrsvtoyjoq0hxuwaw3olnxuk5mksialft5mant/usi6uv9aqs5xzwhctrestftsvvw/0xe6yiidnisbwd91gjifmhuj1b3dwaug/399rn29/3+7uglypy2rfvwa6thda0n1qh12jq2+hapfkt8r/yo/kz+qv6p/q3+y0mra0xopau01jf+ayoux6w=
aaaftxicbvtnbtnaehzdsov5aqthlimaokskuviowkfs+vekehjfkbapg6znehmvwa9d7zqksvwipa1xeaeuvagnhni1nshou5ll8tcz33w7o+thyjlunc7vtcq16vr1jc0b9s1bt+9sbe/cpzfbhbhajwepok9dlclngvyvu5x+ciok/sgnp8pjs+m/ndjiskb8vbchhfh4lniieaw05oxu6j0mxkjfjgeicthxvbrimhigpkzsws1+7ngn7w1nha8jbyzioeiddyoymhzxhrmg8/myu4bgqyq5zx05wctq2f89glebdsku09n1gzoggftogizzcvkp9bivtytcghv4ydfkaokbqdmwvf2iabcyov4hgec5x8+wjyhgdr3u8qq+hjtqfz9mkn5ceqd7mjutwp0pt3jqttw1gxsfagjrhccytefbhiolawya5kogufle59x8ky6pwvsyq8nkrepyaf7omhnlclq5bbtr3es84varia+kt2l8swbyhpgymznwpc/sfbysspy2s73baxeybzenbmhswsu61po1hdyaxd4vinas5vm3e6pbgipfckepjwjjq0wmeezptcmwpvlbkk10cg814oiej/0ibrm6njfgx8olf6gjfaw8ueoz4fw+s1inng4sjsjyuuhyqqoygwraxa9wwusj4hfawcriwisqd0eykh2jsluei3skhawdjomihx4jszkkaxqlwhkor4nccss2wqjdqsjgjrkljt0rulqfxlj0pnlrsvtoyjoq0hxuwaw3olnxuk5mksialft5mant/usi6uv9aqs5xzwhctrestftsvvw/0xe6yiidnisbwd91gjifmhuj1b3dwaug/399rn29/3+7uglypy2rfvwa6thda0n1qh12jq2+hapfkt8r/yo/kz+qv6p/q3+y0mra0xopau01jf+ayoux6w=
Rozpoznawanie twarzy metodą PCA Michał Bereta 1. Testowanie statystycznej istotności różnic między jakością klasyfikatorów
 Rozpoznawanie twarzy metodą PCA Michał Bereta www.michalbereta.pl 1. Testowanie statystycznej istotności różnic między jakością klasyfikatorów Wiemy, że możemy porównywad klasyfikatory np. za pomocą kroswalidacji.
Rozpoznawanie twarzy metodą PCA Michał Bereta www.michalbereta.pl 1. Testowanie statystycznej istotności różnic między jakością klasyfikatorów Wiemy, że możemy porównywad klasyfikatory np. za pomocą kroswalidacji.
SIMR 2016/2017, Analiza 2, wykład 1, Przestrzeń wektorowa
 SIMR 06/07, Analiza, wykład, 07-0- Przestrzeń wektorowa Przestrzeń wektorowa (liniowa) - przestrzeń (zbiór) w której określone są działania (funkcje) dodawania elementów i mnożenia elementów przez liczbę
SIMR 06/07, Analiza, wykład, 07-0- Przestrzeń wektorowa Przestrzeń wektorowa (liniowa) - przestrzeń (zbiór) w której określone są działania (funkcje) dodawania elementów i mnożenia elementów przez liczbę
Wstęp do układów statycznych
 Uniwersystet Warszawski 1 maja 2010 Wprowadzenie Standardowe układy dynamiczne - przestrzeń X wraz z przekształceniem f : X X zachowującym strukturę. Typowe przykłady: X - przestrzeń metryczna, f - przekształcenie
Uniwersystet Warszawski 1 maja 2010 Wprowadzenie Standardowe układy dynamiczne - przestrzeń X wraz z przekształceniem f : X X zachowującym strukturę. Typowe przykłady: X - przestrzeń metryczna, f - przekształcenie
ODWZOROWANIA JEDNO- I WIELOWARTOŚCIOWE. PODOBIEŃSTWA, RÓŻNICE I PROBLEMY Z TEGO WYNIKAJĄCE.
 Wydział Matematyki, Informatyki i Ekonometrii Uniwersytet Zielonogórski ODWZOROWANIA JEDNO- I WIELOWARTOŚCIOWE. PODOBIEŃSTWA, RÓŻNICE I PROBLEMY Z TEGO WYNIKAJĄCE. Joachim Syga III Konferencja Zastosowań
Wydział Matematyki, Informatyki i Ekonometrii Uniwersytet Zielonogórski ODWZOROWANIA JEDNO- I WIELOWARTOŚCIOWE. PODOBIEŃSTWA, RÓŻNICE I PROBLEMY Z TEGO WYNIKAJĄCE. Joachim Syga III Konferencja Zastosowań
System BCD z κ. Adam Slaski na podstawie wykładów, notatek i uwag Pawła Urzyczyna. Semestr letni 2009/10
 System BCD z κ Adam Slaski na podstawie wykładów, notatek i uwag Pawła Urzyczyna Semestr letni 2009/10 Rozważamy system BCD ze stałą typową κ i aksjomatami ω κ κ i κ ω κ. W pierwszej części tej notatki
System BCD z κ Adam Slaski na podstawie wykładów, notatek i uwag Pawła Urzyczyna Semestr letni 2009/10 Rozważamy system BCD ze stałą typową κ i aksjomatami ω κ κ i κ ω κ. W pierwszej części tej notatki
ZAGADNIENIA DO EGZAMINU MAGISTERSKIEGO
 ZAGADNIENIA DO EGZAMINU MAGISTERSKIEGO Na egzaminie magisterskim student powinien: 1) omówić wyniki zawarte w pracy magisterskiej posługując się swobodnie pojęciami i twierdzeniami zamieszczonymi w pracy
ZAGADNIENIA DO EGZAMINU MAGISTERSKIEGO Na egzaminie magisterskim student powinien: 1) omówić wyniki zawarte w pracy magisterskiej posługując się swobodnie pojęciami i twierdzeniami zamieszczonymi w pracy
1 Pochodne wyższych rzędów
 1 Pochodne wyższych rzędów Definicja 1.1 (Pochodne cząstkowe drugiego rzędu) Niech f będzie odwzorowaniem o wartościach w R m, określonym na zbiorze G R k. Załóżmy, że zbiór tych x G, dla których istnieje
1 Pochodne wyższych rzędów Definicja 1.1 (Pochodne cząstkowe drugiego rzędu) Niech f będzie odwzorowaniem o wartościach w R m, określonym na zbiorze G R k. Załóżmy, że zbiór tych x G, dla których istnieje
WYZNACZANIE RUCHU CIECZY LEPKIEJ METODĄ SZTUCZNEJ ŚCIŚLIWOŚCI NA SIATKACH NAKŁADAJĄCYCH SIĘ
 MODELOWANIE INŻYNIERSKIE ISNN 896-77X 3, s. 67-7, Gliwice 006 WYZNACZANIE RUCHU CIECZY LEPKIEJ METODĄ SZTUCZNEJ ŚCIŚLIWOŚCI NA SIATKACH NAKŁADAJĄCYCH SIĘ ZBIGNIEW KOSMA BOGDAN NOGA PRZEMYSŁAW MOTYL Instytut
MODELOWANIE INŻYNIERSKIE ISNN 896-77X 3, s. 67-7, Gliwice 006 WYZNACZANIE RUCHU CIECZY LEPKIEJ METODĄ SZTUCZNEJ ŚCIŚLIWOŚCI NA SIATKACH NAKŁADAJĄCYCH SIĘ ZBIGNIEW KOSMA BOGDAN NOGA PRZEMYSŁAW MOTYL Instytut
DUAL SIMILARITY OF VOLTAGE TO CURRENT AND CURRENT TO VOLTAGE TRANSFER FUNCTION OF HYBRID ACTIVE TWO- PORTS WITH CONVERSION
 ELEKTRYKA 0 Zeszyt (9) Rok LX Andrzej KUKIEŁKA Politechnika Śląska w Gliwicach DUAL SIMILARITY OF VOLTAGE TO CURRENT AND CURRENT TO VOLTAGE TRANSFER FUNCTION OF HYBRID ACTIVE TWO- PORTS WITH CONVERSION
ELEKTRYKA 0 Zeszyt (9) Rok LX Andrzej KUKIEŁKA Politechnika Śląska w Gliwicach DUAL SIMILARITY OF VOLTAGE TO CURRENT AND CURRENT TO VOLTAGE TRANSFER FUNCTION OF HYBRID ACTIVE TWO- PORTS WITH CONVERSION
Institutional Determinants of IncomeLevel Convergence in the European. Union: Are Institutions Responsible for Divergence Tendencies of Some
 Institutional Determinants of IncomeLevel Convergence in the European Union: Are Institutions Responsible for Divergence Tendencies of Some Countries? Dr Mariusz Próchniak Katedra Ekonomii II, Szkoła Główna
Institutional Determinants of IncomeLevel Convergence in the European Union: Are Institutions Responsible for Divergence Tendencies of Some Countries? Dr Mariusz Próchniak Katedra Ekonomii II, Szkoła Główna
UOGÓLNIONE LICZBY HORADAMA I RACHUNEK RÓŻ NIC WSTECZNYCH
 ZESZYTY NAUKOWE AKADEMII MARYNARKI WOJENNEJ ROK LII NR 1 (184) 2011 Hubert Wysocki Akademia Marynarki Wojennej UOGÓLNIONE LICZBY HORADAMA I RACHUNEK RÓŻ NIC WSTECZNYCH STRESZCZENIE W artykule wprowadzono
ZESZYTY NAUKOWE AKADEMII MARYNARKI WOJENNEJ ROK LII NR 1 (184) 2011 Hubert Wysocki Akademia Marynarki Wojennej UOGÓLNIONE LICZBY HORADAMA I RACHUNEK RÓŻ NIC WSTECZNYCH STRESZCZENIE W artykule wprowadzono
Analysis of Movie Profitability STAT 469 IN CLASS ANALYSIS #2
 Analysis of Movie Profitability STAT 469 IN CLASS ANALYSIS #2 aaaklnictzzjb9tgfmcnadpg7oy0lxa9edva9kkapdarhyk2k7gourinlwsweyzikuyiigvyleiv/cv767fpf/5crc1xt9va5mx7w3m/ecuqw1kuztpx/rl3/70h73/w4cog9dhhn3z62d6jzy+yzj766txpoir9nzszisjynetqr+rvlfvyoozu5xbybpsxb1wahul8phczdt2v4zgchb7uecwphlyigrgkjcyiflfyci0kxnmr4z6kw0jsokvot8isntpa3gbknlcufiv/h+hh+eur4fomd417rvtfjoit5pfju6yxiab2fmwk0y/feuybobqk+axnke8xzjjhfyd8kkpl9zdoddkazd5j6bzpemjb64smjb6vb4xmehysu08lsrszopxftlzee130jcb0zjxy7r5wa2f1s2off2+dyatrughnrtpkuprlcpu55zlxpss/yqe2eamjkcf0jye8w8yas0paf6t0t2i9stmcua+inbi2rt01tz22tubbqwidypvgz6piynkpobirkxgu54ibzoti4pkw2i5ow9lnuaoabhuxfxqhvnrj6w15tb3furnbm+scyxobjhr5pmj5j/w5ix9wsa2tlwx9alpshlunzjgnrwvqbpwzjl9wes+ptyn+ypy/jgskavtl8j0hz1djdhzwtpjbbvpr1zj7jpg6ve7zxfngj75zee0vmp9qm2uvgu/9zdofq6r+g8l4xctvo+v+xdrfr8oxiwutycu0qgyf8icuyvp/sixfi9zxe11vp6mrjjovpmxm6acrtbia+wjr9bevlgjwlz5xd3rfna9g06qytaoofk8olxbxc7xby2evqjmmk6pjvvzxmpbnct6+036xp5vdbrnbdqph8brlfn/n/khnfumhf6z1v7h/80yieukkd5j0un82t9mynxzmk0s/bzn4tacdziszdhwrl8x5ako8qp1n1zn0k6w2em0km9zj1i4yt1pt3xiprw85jmc2m1ut2geum6y6es2fwx6c+wlrpykblopbuj5nnr2byygfy5opllv4+jmm7s6u+tvhywbnb0kv2lt5th4xipmiij+y1toiyo7bo0d+vzvovjkp6aoejsubhj3qrp3fjd/m23pay8h218ibvx3nicofvd1xi86+kh6nb/b+hgsjp5+qwpurzlir15np66vmdehh6tyazdm1k/5ejtuvurgcqux6yc+qw/sbsaj7lkt4x9qmtp7euk6zbdedyuzu6ptsu2eeu3rxcz06uf6g8wyuveznhkbzynajbb7r7cbmla+jbtrst0ow2v6ntkwv8svnwqnu5pa3oxfeexf93739p93chq/fv+jr8r0d9brhpcxr2w88bvqbr41j6wvrb+u5dzjpvx+veoaxwptzp/8cen+xbg==
Analysis of Movie Profitability STAT 469 IN CLASS ANALYSIS #2 aaaklnictzzjb9tgfmcnadpg7oy0lxa9edva9kkapdarhyk2k7gourinlwsweyzikuyiigvyleiv/cv767fpf/5crc1xt9va5mx7w3m/ecuqw1kuztpx/rl3/70h73/w4cog9dhhn3z62d6jzy+yzj766txpoir9nzszisjynetqr+rvlfvyoozu5xbybpsxb1wahul8phczdt2v4zgchb7uecwphlyigrgkjcyiflfyci0kxnmr4z6kw0jsokvot8isntpa3gbknlcufiv/h+hh+eur4fomd417rvtfjoit5pfju6yxiab2fmwk0y/feuybobqk+axnke8xzjjhfyd8kkpl9zdoddkazd5j6bzpemjb64smjb6vb4xmehysu08lsrszopxftlzee130jcb0zjxy7r5wa2f1s2off2+dyatrughnrtpkuprlcpu55zlxpss/yqe2eamjkcf0jye8w8yas0paf6t0t2i9stmcua+inbi2rt01tz22tubbqwidypvgz6piynkpobirkxgu54ibzoti4pkw2i5ow9lnuaoabhuxfxqhvnrj6w15tb3furnbm+scyxobjhr5pmj5j/w5ix9wsa2tlwx9alpshlunzjgnrwvqbpwzjl9wes+ptyn+ypy/jgskavtl8j0hz1djdhzwtpjbbvpr1zj7jpg6ve7zxfngj75zee0vmp9qm2uvgu/9zdofq6r+g8l4xctvo+v+xdrfr8oxiwutycu0qgyf8icuyvp/sixfi9zxe11vp6mrjjovpmxm6acrtbia+wjr9bevlgjwlz5xd3rfna9g06qytaoofk8olxbxc7xby2evqjmmk6pjvvzxmpbnct6+036xp5vdbrnbdqph8brlfn/n/khnfumhf6z1v7h/80yieukkd5j0un82t9mynxzmk0s/bzn4tacdziszdhwrl8x5ako8qp1n1zn0k6w2em0km9zj1i4yt1pt3xiprw85jmc2m1ut2geum6y6es2fwx6c+wlrpykblopbuj5nnr2byygfy5opllv4+jmm7s6u+tvhywbnb0kv2lt5th4xipmiij+y1toiyo7bo0d+vzvovjkp6aoejsubhj3qrp3fjd/m23pay8h218ibvx3nicofvd1xi86+kh6nb/b+hgsjp5+qwpurzlir15np66vmdehh6tyazdm1k/5ejtuvurgcqux6yc+qw/sbsaj7lkt4x9qmtp7euk6zbdedyuzu6ptsu2eeu3rxcz06uf6g8wyuveznhkbzynajbb7r7cbmla+jbtrst0ow2v6ntkwv8svnwqnu5pa3oxfeexf93739p93chq/fv+jr8r0d9brhpcxr2w88bvqbr41j6wvrb+u5dzjpvx+veoaxwptzp/8cen+xbg==
IX. Rachunek różniczkowy funkcji wielu zmiennych. 1. Funkcja dwóch i trzech zmiennych - pojęcia podstawowe. - funkcja dwóch zmiennych,
 IX. Rachunek różniczkowy funkcji wielu zmiennych. 1. Funkcja dwóch i trzech zmiennych - pojęcia podstawowe. Definicja 1.1. Niech D będzie podzbiorem przestrzeni R n, n 2. Odwzorowanie f : D R nazywamy
IX. Rachunek różniczkowy funkcji wielu zmiennych. 1. Funkcja dwóch i trzech zmiennych - pojęcia podstawowe. Definicja 1.1. Niech D będzie podzbiorem przestrzeni R n, n 2. Odwzorowanie f : D R nazywamy
8 Całka stochastyczna względem semimartyngałów
 M. Beśka, Całka Stochastyczna, wykład 8 148 8 Całka stochastyczna względem semimartyngałów 8.1 Całka stochastyczna w M 2 Oznaczmy przez Ξ zbiór procesów postaci X t (ω) = ξ (ω)i {} (t) + n ξ i (ω)i (ti,
M. Beśka, Całka Stochastyczna, wykład 8 148 8 Całka stochastyczna względem semimartyngałów 8.1 Całka stochastyczna w M 2 Oznaczmy przez Ξ zbiór procesów postaci X t (ω) = ξ (ω)i {} (t) + n ξ i (ω)i (ti,
