Digraf o V wierzchołkach posiada V 2 krawędzi, zatem liczba różnych digrafów o V wierzchołkach wynosi 2 VxV
|
|
|
- Joanna Szczepańska
- 6 lat temu
- Przeglądów:
Transkrypt
1 Graf skierowany (digraf) zbiór wierzchołków i zbiór krawędzi skierowanych łączących (co najwyżej jeden raz) uporządkowane pary wierzchołków. Mówimy wtedy, że krawędź łączy pierwszy wierzchołek z drugim (albo, że prowadzi od pierwszego wierzchołka do drugiego). Nie dopuszczamy krawędzi wielokrotnych, ale przyjmujemy, że każdy wierzchołek ma jedną pętlę Digraf o V wierzchołkach posiada V 2 krawędzi, zatem liczba różnych digrafów o V wierzchołkach wynosi 2 VxV
2 Ścieżka skierowana ciąg wierzchołków, w którym każdy jest połączony krawędzią ze swoim następnikiem. Mówimy, że wierzchołek t jest osiągalny z s, jeśli istnieje ścieżka skierowana z s do t.
3 Przykład grafu skierowanego Lista wierzchołków i krawędzi
4 Reprezentacja dla digrafów jest taka sama jak dla grafów nieskierowanych Macierz sąsiedztwa
5 Lista sąsiedztwa
6 Jeśli każdy wierzchołek digrafu posiada pętlę oraz każdej krawędzie skierowanej odpowiada krawędź w przeciwną stronę, nie ma różnicy pomiędzy reprezentacjami grafów skierowanych i nieskierowanych.
7 Stopień wejściowy (indegree) wierzchołka, to liczba krawędzi wychodzących z tego wierzchołka, a stopień wyjściowy (outdegree) wierzchołka, to liczba krawędzi wychodzących z tego wierzchołka. Żaden wierzchołek nie jest osiągany z wierzchołka o stopniu wejściowym 0, zwanego ujściem. Wierzchołek o stopniu wejściowym 0, zwany źródłem, nie jest osiągany z żadnego innego wierzchołka.
8 Stopień wejściowy (indegree) wierzchołka, to liczba krawędzi wychodzących z tego wierzchołka, a stopień wyjściowy (outdegree) wierzchołka, to liczba krawędzi wychodzących z tego wierzchołka. Żaden wierzchołek nie jest osiągany z wierzchołka o stopniu wejściowym 0, zwanego ujściem. Wierzchołek o stopniu wejściowym 0, zwany źródłem, nie jest osiągany z żadnego innego wierzchołka. n, m ilość wierzchołków i krawędzi
9
10 Odwrotnością digrafu nazywamy digraf otrzymany przez odwrócenie kierunków wszystkich krawędzi. Odwrotności używamy wtedy, kiedy chcemy wiedzieć, skąd krawędzie przychodzą.
11 Reprezentacja macierzowa a odwrotność digrafu Tworzymy kopię macierzy i transponujemy ją (czyli zamieniamy wiersze z kolumnami) Albo Jeżeli wiemy, że graf nie będzie modyfikowany zamieniamy miejscami końce krawędzi przy odwołaniach do nich, np. krawędź s-t jest oznaczona 1 w adj[s][t], a w odwrotności grafu 1 byłaby w adj[t][s]. Zatem, jeśli wywołujemy edge(s, t), to w odwrotności wystarczy wywołać edge(t,s ). Albo Utrzymujemy dwie reprezentacje każdej krawędzi skierowanej, ale z dodatkowym bitem informacji określającym kierunek
12 template <class ingraph, class outgraph> void reverse(const ingraph &G, outgraph &R) { for(int v = 0; v < G.V(); v++) { typename ingraph::adjiterator A(G,v); for (int w = A.beg();!A.end(); w = A.nxt()) R.insert(Edge(w, v)); } } Odwracanie digrafu funkcja dodaje odwrócone krawędzie digrafu wskazanego przez pierwszy argument do digrafu z drugiego argumentu.
13 Dag skierowany graf acykliczny, czyli digraf bez cykli skierowanych.
14 Digraf jest silnie spójny, jeśli każdy jego wierzchołek jest osiągalny z dowolnego innego. Dwa wierzchołki w digrafie s i t są silnie połączone, jeśli istnieje ścieżka skierowana z s do t i z t do s. Własność 1. Digraf, który nie jest silnie spójny, składa się ze zbioru silnie spójnych składowych (silnych składowych), będących maksymalnymi podgrafami silnie spójnymi oraz ze zbioru krawędzi pomiędzy silnymi składowymi.
15 Definicja. Dla danego digrafu D, określamy digraf K(D) o własnościach: każdy wierzchołek odpowiada jednej silnej składowej w D, każda krawędź odpowiada zbiorowi krawędzi w D, łączących wierzchołki pomiędzy właściwymi składowymi (odpowiadającymi obu końcom krawędzi z K(D)). Wówczas K(D) jest dagiem, który nazywamy jądrem digrafu D składowe Ten digraf ma 4 silne składowe Jądro digrafu
16 Jakie problemy mogą pojawiać się w digrafach? Wykrywanie cykli skierowanych czy digraf posiada cykle skierowane (czy jest dagiem)? Własność Digraf jest dagiem wtedy i tylko wtedy, gdy - podczas sprawdzania go algorytmem przeszukiwania w głąb nie napotkamy krawędzi powrotnych Osiągalność z pojedynczego źródła jakie wierzchołki są osiągane z danego wierzchołka początkowego s, ile jest takich wierzchołków? Własność. Problem osiągalności z pojedynczego źródła s można rozwiązać za pomocą algorytmu przeszukiwania w głąb rozpoczętego w wierzchołku s w czasie proporcjonalnym do liczby krawędzi podgrafu indukowanego przez wierzchołki osiągalne z s.
17 Pozostaje rozważyć algorytm przeszukiwania w głąb DFS, czyli Depth- First-Search (jest również algorytm przeszukiwania wszerz BSF) grafu. Zaczniemy od grafu nieskierowanego. Idea jest podobna do przechodzenia przez drzewo w kolejności pre-order (najpierw rodzic, a potem rekursywnie - dzieci)
18 Pozostaje rozważyć algorytm przeszukiwania w głąb DFS, czyli Depth- First-Search (jest również algorytm przeszukiwania wszerz BSF) grafu. Zaczniemy od grafu nieskierowanego. Idea jest podobna do przechodzenia przez drzewo w kolejności pre-order (najpierw rodzic, a potem rekursywnie - dzieci) Algorytm odwiedza sąsiadów korzystając z rekurencji. Wędrując z u do v, rekurencyjnie odwiedzamy wszystkich sąsiadów v do tej pory nieodwiedzonych, potem wracamy do u. Możliwe jest, że w2 nie był odwiedzany, kiedy rekurencyjnie odwiedzaliśmy w1, ale zostanie odwiedzony w czasie, gdy powrócimy z wywołania rekurencyjnego.
19 Fragment algorytmu zapisany w pseudokodzie.
20 Jak to działa? Co było poprzednikiem?
21
22
23
24
25
26
27 RDS(7) kończy, bo już nie ma nieodwiedzonych sąsiadów.
28 Jak tym algorytmem znajdywać ścieżkę?
29 Otrzymujemy w ten sposób drzewo ścieżek DFS
30 Złożoność czasowa DFS z zastosowaniem list sąsiedztwa: Nigdy nie odwiedzamy wierzchołka więcej niż raz. Sprawdzamy zatem wszystkie wierzchołki grafu (wiemy, że suma stopni wszystkich wierzchołków jest równa 2E. Dla każdego wierzchołka zabiera to czas proporcjonalny do stopnia wierzchołka +1. Stąd czas wykonania DFS jest proporcjonalny do sumy ilości wierzchołków i krawędzi, czyli O(V+E).
31 Złożoność czasowa DFS z zastosowaniem macierzy sąsiedztwa: Czas wykonania DFS jest proporcjonalny do kwadratu ilości wierzchołków, czyli O(V 2 ). Wniosek: Czas działania algorytmu DFS jest liniowy względem rozmiaru struktury danych użytej do reprezentowania grafu.
32 Możemy wzbogacić rysunek drzewa dla algorytmu DFS, aby uzyskać więcej informacji. Dwie reprezentacja każdej przetwarzanej krawędzi ( w obu kierunkach) Algorytm bada wszystkie krawędzie Jedna reprezentacja każdej przetwarzanej krawędzi Drzewo DFS jest innym sposobem przedstawienia grafu
33 Krawędź do jeszcze nie odwiedzonego wierzchołka Prowadzą do wierzchołków, dla których DFS jest w trakcie wywołania rekurencyjnego DFS napotkał krawędź prowadzącą do wierzchołka już odwiedzonego Obejście drzewa w porządku prefiksowym jest takie samo jak kolejność badania krawędzi grafu przez DFS
34 Jeśli w grafie po lewej usuniemy szare wierzchołki (środkowy rysunek) i zastąpimy wierzchołki zewnętrzne krawędziami, to otrzymamy na powrót wyjściowy graf (prawy rysunek) Krawędź do jeszcze nie odwiedzonego wierzchołka Prowadzą do wierzchołków, dla których DFS jest w trakcie wywołania rekurencyjnego DFS napotkał krawędź prowadzącą do wierzchołka już odwiedzonego Obejście drzewa w porządku prefiksowym jest takie samo jak kolejność badania krawędzi grafu przez DFS
35 Krawędzie Drzewowe reprezentują wywołania rekurencyjne Powrotne łączą wierzchołki z ich przodkami nie będącymi ich ojcami w drzewie DFS Gałąź drzewowa krawędź z wierzchołka v do w, jeśli w jest nienaznaczony Gałąź do ojca krawędź z wierzchołka v do w, jeśli wskaźnik na ojca w jest równy v Gałąź powrotna krawędź z wierzchołka v do w, jeśli numer w porządku prefiksowym w jest mniejszy niż numer w porządku prefiksowym v Gałąź zstępująca krawędź z wierzchołka v do w, jeśli numer w porządku prefiksowym w jest większy niż numer w porządku prefiksowym v
36 Jeśli graf nie jest spójny, to dynamikę przeszukiwania DFS można opisać za pomocą lasu DFS, zawierającym po jednym drzewie dla każdej składowej spójnej. Używając reprezentacji grafu w postaci list sąsiedztwa odwiedzamy krawędzie w innej kolejności, niż wtedy, gdy użyjemy reprezentacji grafu w postaci macierzy sąsiedztwa.
37 Las DFS odpowiada przeszukiwaniu w głąb grafu reprezentowanego w postaci macierzy sąsiedztwa. Graf posiada 3 składowe spójne, więc las zawiera 3 drzewa. Do okrągłych wierzchołków prowadzą krawędzie drzewa, do kwadratowych krawędzie powrotne. Szary kolor wskazuje, że krawędzie do tych wierzchołków zostały już wcześniej napotkane w odwrotnej orientacji.
38 Las DFS odpowiada przeszukiwaniu w głąb grafu reprezentowanego w postaci listy sąsiedztwa. Graf posiada 3 składowe spójne, więc las zawiera 3 drzewa. Do okrągłych wierzchołków prowadzą krawędzie drzewa, do kwadratowych krawędzie powrotne. Szary kolor wskazuje, że krawędzie do tych wierzchołków zostały już wcześniej napotkane w odwrotnej orientacji.
39 Klasyfikacja krawędzi dla digrafów: Krawędzie drzewowe krawędzie reprezentujące wywołania rekurencyjne Krawędzie powrotne krawędzie prowadzące do przodka danego wierzchołka w drzewie DFS Krawędzie zstępujące krawędzie do potomka danego wierzchołka w drzewie DFS Krawędzie poprzeczne pozostałe krawędzie (nie prowadzą ani do potomka, ani do przodka w drzewie DFS)
40 Las DFS dla digrafu reprezentowanego za pomocą list sąsiedztwa Zewnętrzne węzły reprezentują wierzchołki już odwiedzone, pozostała część lasu jest digrafem o wszystkich krawędziach biegnących w dół.
41 Las DFS dla digrafu reprezentowanego za pomocą list sąsiedztwa Krawędź poprzeczna Zewnętrzne węzły reprezentują wierzchołki już odwiedzone, pozostała część lasu jest digrafem o wszystkich krawędziach biegnących w dół. Krawędź drzewowa do węzła wewnętrznego Krawędź zstępująca Krawędź powrotna
42 Własność. W lesie DFS dla digrafu krawędź do odwiedzanego węzła jest krawędzią powrotną, jeśli prowadzi do węzła o wyższym numerze postfiksowym krawędzią poprzeczną, jeśli prowadzi do węzła o niższym numerze prefiksowym krawędzią zstępującą, jeśli prowadzi do węzła o wyższym numerze prefiksowym
43 Lasy DFS dla tego samego digrafu mogą się znacznie różnić np. liczba drzew lasu DFS zależy od wyboru wierzchołka początkowego.
44 Czy digraf posiada cykle skierowane (czy digraf jest dagiem)? W grafach nieskierowanych każda krawędź do odwiedzanego wierzchołka wskazuje na istnienie cyklu, w digrafach trzeba rozważać krawędzie powrotne. Własność. Digraf jest dagiem wtedy i tylko wtedy, gdy podczas badania za pomocą DFS każdej krawędzi nie napotkamy krawędzi powrotnych.
45 Dowód. Każda krawędź powrotna należy do cyklu skierowanego zawierającego samą krawędź oraz ścieżkę w drzewie łączącą oba węzły, nie znajdziemy więc krawędzi powrotnych, przeszukując dag za pomocą DFS. W drugą stronę: wystarczy pokazać, że jeśli digraf posiada cykl, to DFS napotka krawędź powrotną. Jeśli v jest pierwszym wierzchołkiem cyklu odwiedzonym przez DFS, to wierzchołek ten ma najniższy numer prefiksowy spośród wszystkich krawędzi cyklu. Krawędź cyklu prowadząca do tego wierzchołka będzie więc krawędzią powrtoną: zostanie ona napotkana podczas wywołania rekurencyjnego z vi będzie prowadzić od pewnego węzła cyklu do węzła o niższym numerze prefiksowym.
46 Głównym celem DFS jest systematyczne odwiedzenie wszystkich wierzchołków i krawędzi Jakie wierzchołki są osiągane z danego wierzchołka początkowego s? Ile jest takich wierzchołków? Problem osiągalności z pojedynczego źródła
47 Głównym celem DFS jest systematyczne odwiedzenie wszystkich wierzchołków i krawędzi Jakie wierzchołki są osiągane z danego wierzchołka początkowego s? Ile jest takich wierzchołków? Problem osiągalności z pojedynczego źródła Własność Problem osiągalności z pojedynczego źródła s można rozwiązać za pomocą DFS rozpoczętego w wierzchołku s w czasie proporcjonalnym do liczby krawędzi podgrafu indukowanego przez wierzchołki osiągane z s.
48 Dowód. Własność ta jest prawdziwa dla grafu z jednym wierzchołkiem bez krawędzi. Dla dowolnego digrafu przeprowadzamy dowód indukcyjnie. Zakładamy, że własność zachodzi dla wszystkich digrafów o mniejszej liczbie wierzchołków. Wtedy pierwsza wzięta pod uwagę krawędź s dzieli digraf na podgrafy indukowane przez dwa zbiory wierzchołków: a) Wierzchołki możliwe do osiągnięcia po ścieżkach skierowanych niezawierających s i rozpoczynających się tą krawędzią b) Wierzchołki, do których nie da się dojść po ścieżkach skierowanych niezawierających s i rozpoczynających się tą krawędzią. Do tych podgrafów stosujemy założenie indukcyjne nie ma krawędzi z wierzchołków pierwszego podgrafu do innych niż s wierzchołków drugiego podgrafu. Krawędzie do s zostaną zignorowane, ponieważ wierzchołek s ma najniższy numer prefiksowy oraz wszystkie wierzchołki pierwszego podgrafu mają niższy numer prefiksowy niż dowolny wierzchołek drugiego podgrafu. Zatem wszystkie krawędzie z wierzchołków drugiego podgrafu wierzchołków pierwszego podgrafu zostaną pominięte.
49 Definicja Domknięciem przechodnim digrafu nazywamy digraf o tym samym zbiorze wierzchołków, dla którego krawędź z wierzchołka s do t istnieje wtedy i tylko wtedy, gdy w digrafie wyjściowym istnieje ścieżka skierowana z s do t. W domknięciu przechodnim z każdego wierzchołka wychodzą krawędzie do wszystkich osiągalnych z niego wierzchołków
50 Definicja Domknięciem przechodnim digrafu nazywamy digraf o tym samym zbiorze wierzchołków, dla którego krawędź z wierzchołka s do t istnieje wtedy i tylko wtedy, gdy w digrafie wyjściowym istnieje ścieżka skierowana z s do t. W domknięciu przechodnim z każdego wierzchołka wychodzą krawędzie do wszystkich osiągalnych z niego wierzchołków Własność Domknięcie przechodnie digrafu można wyznaczyć, konstruując dla niego macierz sąsiedztwa A, dodając pętlę dla każdego wierzchołka, a następnie obliczając A V
51 A V =A*A*A* *A mnożenie boolowskie macierzy boolowskiej przez siebie V razy. for(s = 0; s < V; s++) for(t = 0; t < V; t++) for(i = 0; C[s][t] = 0; i < V; i++) C[s][t] += A[s][i]*B[i][t]; C=A*B for(s = 0; s < V; s++) for(t = 0; t < V; t++) for(i = 0; C[s][t] = 0; i < V; i++) if(a[s][i] && B[i][t]) C[s][t]= 1; + or * and mnożenie macierzy boolowskich
52 A V =A*A*A* *A mnożenie boolowskie macierzy boolowskiej przez siebie V razy. for(s = 0; s < V; s++) for(t = 0; t < V; t++) for(i = 0; C[s][t] = 0; i < V; i++) C[s][t] += A[s][i]*B[i][t]; C=A*B for(s = 0; s < V; s++) for(t = 0; t < V; t++) for(i = 0; C[s][t] = 0; i < V; i++) if(a[s][i] && B[i][t]) C[s][t]= 1; + or * and mnożenie macierzy boolowskich C=A*A=A 2 dla każdej pary wierzchołków s i t, w C znajduje się krawędź z s do t wtedy i tylko wtedy, gdy mażna wskazać wierzchołek i, dla którego w A istnieją krawędzie z s do i oraz z i do t. Krawędzie w A 2 odpowiadają ścieżkom skierowanym o długości 2 w A. Jeśli do każdego wierzchołka dołączymy pętlę, to A 2 zawiera także wszystkie krawędzie z A.
53 Własność Domknięcie przechodnie digrafu można wyznaczyć, konstruując dla niego macierz sąsiedztwa A, dodając pętlę dla każdego wierzchołka, a następnie obliczając A V Dowód. Opierając się na poprzednim rozumowaniu, pokazuje się, że A 3 zawiera krawędzie odpowiadające ścieżkom o długości nie większej niż 3, A 4 o długości nie większej niż 4, itd. Ścieżki o długości większej niż V można pominąć, bo z zasady szufladkowej Dirichleta wynika, że na takiej ścieżce przynajmniej jeden wierzchołek musi wystąpić dwukrotnie (mamy ich tylko V). Taka ścieżka nie wnosi nic nowego do domknięcia przechodniego, ponieważ istnieje krótsze połączenie pomiędzy jej dwoma końcami
54 Złożoność czasowa: Mamy: V mnożeń macierzy, każde o czasie wykonania rzędu V 3, zatem wychodzi nam V 4. Dla mnożeń boolowskich mamy lg V operacji mnożenia macierzy, bo liczymy kolejno A 2, A 4, A 8,, aż wykładnik będzie większy bądź równy V. Stąd mamy V 3 lg V=A V.
55 Jeszcze prościej: Algorytm Warshalla wyznacza domknięcie przechodnie digrafu w czasie rzędu V 3. Algorytm dla gęstych digrafów: For(i = 0; i < V; i++) for(s = 0; s < V; s++) for(t = 0; t < V; t++) if(a[s][i] && A[i][t]) A[s][t]= 1; Różnica tkwi w kolejności pętli for
56 Czy da się jeszcze poprawić algorytm Warshalla? For(i = 0; i < V; i++) for(s = 0; s < V; s++) for(t = 0; t < V; t++) if(a[s][i] && A[i][t]) A[s][t]= 1; TAK Można skrócić czas wykonania algorytmu przesuwając sprawdzenie A[s][i] poza wewnętrzna pętlę (nie zależy od t). Unikamy t-krotnego wykonywania wewnętrznej pętli, gdy A[s][i]=0.
57 Czy da się jeszcze poprawić algorytm Warshalla? For(i = 0; i < V; i++) for(s = 0; s < V; s++) for(t = 0; t < V; t++) if(a[s][i] && A[i][t]) A[s][t]= 1; TAK Można skrócić czas wykonania algorytmu przesuwając sprawdzenie A[s][i] poza wewnętrzna pętlę (nie zależy od t). Unikamy t-krotnego wykonywania wewnętrznej pętli, gdy A[s][i]=0. Dla wielkich grafów rzadkich koszt wykonywania algorytmu jest wciąż duży!
58 Jak to poprawić? Nie jest potrzebna cała macierz, by wyznaczyć domknięcie przechodnie. Wystarczy sprawdzić istnienie jedynie niewielkiej liczby krawędzi, więc można wstępnie przetworzyć dany digraf, tzn. posługując się abstrakcyjnym typem danych, który udostępnia operację sprawdzania osiągalności posługujemy się wtedy terminem abstrakcyjnego domknięcia przechodniego.
59 Jak to poprawić? Nie jest potrzebna cała macierz, by wyznaczyć domknięcie przechodnie. Wystarczy sprawdzić istnienie jedynie niewielkiej liczby krawędzi, więc można wstępnie przetworzyć dany digraf, tzn. posługując się abstrakcyjnym typem danych, który udostępnia operację sprawdzania osiągalności posługujemy się wtedy terminem abstrakcyjnego domknięcia przechodniego. Własność. Sprawdzanie w stałym czasie osiągalności (abstrakcyjne domknięcie przechodnie) dla digrafu może być zrealizowane po wykonaniu operacji wstępnych w czasie rzędu V 3, przy wykorzystaniu pamięci rzędu V 2. Własność. Z wykorzystaniem DFS można uzyskać stały czas dla sprawdzania osiągalności dla abstrakcyjnego domknięcia przechodniego digrafu, wykonując operacje wstępne (wyznaczanie domknięcia przechodniego) w czasie rzędu V(V+E) i przy wykorzystaniu pamięci rzędu V 2
60 Dowód. DFS wyznacza wszystkie wierzchołki osiągalne z wierzchołka początkowego w czasie rzędu E, dla reprezentacji w postaci listy sąsiedztwa. Jeśli uruchomimy DFS V razy, jednokrotnie z każdego wierzchołka, to otrzymamy zbiory wierzchołków osiągalnych z każdego z wierzchołków (czyli domknięcie przechodnie) w czasie rzędu V(V+E).
Przykłady grafów. Graf prosty, to graf bez pętli i bez krawędzi wielokrotnych.
 Grafy Graf Graf (ang. graph) to zbiór wierzchołków (ang. vertices), które mogą być połączone krawędziami (ang. edges) w taki sposób, że każda krawędź kończy się i zaczyna w którymś z wierzchołków. Graf
Grafy Graf Graf (ang. graph) to zbiór wierzchołków (ang. vertices), które mogą być połączone krawędziami (ang. edges) w taki sposób, że każda krawędź kończy się i zaczyna w którymś z wierzchołków. Graf
Struktury danych i złożoność obliczeniowa Wykład 5. Prof. dr hab. inż. Jan Magott
 Struktury danych i złożoność obliczeniowa Wykład. Prof. dr hab. inż. Jan Magott Algorytmy grafowe: podstawowe pojęcia, reprezentacja grafów, metody przeszukiwania, minimalne drzewa rozpinające, problemy
Struktury danych i złożoność obliczeniowa Wykład. Prof. dr hab. inż. Jan Magott Algorytmy grafowe: podstawowe pojęcia, reprezentacja grafów, metody przeszukiwania, minimalne drzewa rozpinające, problemy
Porównanie algorytmów wyszukiwania najkrótszych ścieżek międz. grafu. Daniel Golubiewski. 22 listopada Instytut Informatyki
 Porównanie algorytmów wyszukiwania najkrótszych ścieżek między wierzchołkami grafu. Instytut Informatyki 22 listopada 2015 Algorytm DFS w głąb Algorytm przejścia/przeszukiwania w głąb (ang. Depth First
Porównanie algorytmów wyszukiwania najkrótszych ścieżek między wierzchołkami grafu. Instytut Informatyki 22 listopada 2015 Algorytm DFS w głąb Algorytm przejścia/przeszukiwania w głąb (ang. Depth First
a) 7 b) 19 c) 21 d) 34
 Zadanie 1. Pytania testowe dotyczące podstawowych własności grafów. Zadanie 2. Przy każdym z zadań może się pojawić polecenie krótkiej charakterystyki algorytmu. Zadanie 3. W zadanym grafie sprawdzenie
Zadanie 1. Pytania testowe dotyczące podstawowych własności grafów. Zadanie 2. Przy każdym z zadań może się pojawić polecenie krótkiej charakterystyki algorytmu. Zadanie 3. W zadanym grafie sprawdzenie
Reprezentacje grafów nieskierowanych Reprezentacje grafów skierowanych. Wykład 2. Reprezentacja komputerowa grafów
 Wykład 2. Reprezentacja komputerowa grafów 1 / 69 Macierz incydencji Niech graf G będzie grafem nieskierowanym bez pętli o n wierzchołkach (x 1, x 2,..., x n) i m krawędziach (e 1, e 2,..., e m). 2 / 69
Wykład 2. Reprezentacja komputerowa grafów 1 / 69 Macierz incydencji Niech graf G będzie grafem nieskierowanym bez pętli o n wierzchołkach (x 1, x 2,..., x n) i m krawędziach (e 1, e 2,..., e m). 2 / 69
Ogólne wiadomości o grafach
 Ogólne wiadomości o grafach Algorytmy i struktury danych Wykład 5. Rok akademicki: / Pojęcie grafu Graf zbiór wierzchołków połączonych za pomocą krawędzi. Podstawowe rodzaje grafów: grafy nieskierowane,
Ogólne wiadomości o grafach Algorytmy i struktury danych Wykład 5. Rok akademicki: / Pojęcie grafu Graf zbiór wierzchołków połączonych za pomocą krawędzi. Podstawowe rodzaje grafów: grafy nieskierowane,
Grafem nazywamy strukturę G = (V, E): V zbiór węzłów lub wierzchołków, Grafy dzielimy na grafy skierowane i nieskierowane:
 Wykład 4 grafy Grafem nazywamy strukturę G = (V, E): V zbiór węzłów lub wierzchołków, E zbiór krawędzi, Grafy dzielimy na grafy skierowane i nieskierowane: Formalnie, w grafach skierowanych E jest podzbiorem
Wykład 4 grafy Grafem nazywamy strukturę G = (V, E): V zbiór węzłów lub wierzchołków, E zbiór krawędzi, Grafy dzielimy na grafy skierowane i nieskierowane: Formalnie, w grafach skierowanych E jest podzbiorem
Sortowanie topologiczne skierowanych grafów acyklicznych
 Sortowanie topologiczne skierowanych grafów acyklicznych Metody boolowskie w informatyce Robert Sulkowski http://robert.brainusers.net 23 stycznia 2010 1 Definicja 1 (Cykl skierowany). Niech C = (V, A)
Sortowanie topologiczne skierowanych grafów acyklicznych Metody boolowskie w informatyce Robert Sulkowski http://robert.brainusers.net 23 stycznia 2010 1 Definicja 1 (Cykl skierowany). Niech C = (V, A)
Matematyka dyskretna
 Matematyka dyskretna Wykład 13: Teoria Grafów Gniewomir Sarbicki Literatura R.J. Wilson Wprowadzenie do teorii grafów Definicja: Grafem (skończonym, nieskierowanym) G nazywamy parę zbiorów (V (G), E(G)),
Matematyka dyskretna Wykład 13: Teoria Grafów Gniewomir Sarbicki Literatura R.J. Wilson Wprowadzenie do teorii grafów Definicja: Grafem (skończonym, nieskierowanym) G nazywamy parę zbiorów (V (G), E(G)),
Wykład 7. Algorytmy grafowe
 Wykład Algorytmy grafowe Algorytmy grafowe i podstawowe algorytmy przeszukiwania Problem Definicje i własności Reprezentacja Przeszukiwanie wszerz (Breadthirst Search) Przeszukiwanie w głąb (Depthirst
Wykład Algorytmy grafowe Algorytmy grafowe i podstawowe algorytmy przeszukiwania Problem Definicje i własności Reprezentacja Przeszukiwanie wszerz (Breadthirst Search) Przeszukiwanie w głąb (Depthirst
Zofia Kruczkiewicz, Algorytmu i struktury danych, Wykład 14, 1
 Wykład Algorytmy grafowe metoda zachłanna. Właściwości algorytmu zachłannego:. W przeciwieństwie do metody programowania dynamicznego nie występuje etap dzielenia na mniejsze realizacje z wykorzystaniem
Wykład Algorytmy grafowe metoda zachłanna. Właściwości algorytmu zachłannego:. W przeciwieństwie do metody programowania dynamicznego nie występuje etap dzielenia na mniejsze realizacje z wykorzystaniem
MATEMATYKA DYSKRETNA - MATERIAŁY DO WYKŁADU GRAFY
 ERIAŁY DO WYKŁADU GRAFY Graf nieskierowany Grafem nieskierowanym nazywamy parę G = (V, E), gdzie V jest pewnym zbiorem skończonym (zwanym zbiorem wierzchołków grafu G), natomiast E jest zbiorem nieuporządkowanych
ERIAŁY DO WYKŁADU GRAFY Graf nieskierowany Grafem nieskierowanym nazywamy parę G = (V, E), gdzie V jest pewnym zbiorem skończonym (zwanym zbiorem wierzchołków grafu G), natomiast E jest zbiorem nieuporządkowanych
Teoria grafów podstawy. Materiały pomocnicze do wykładu. wykładowca: dr Magdalena Kacprzak
 Teoria grafów podstawy Materiały pomocnicze do wykładu wykładowca: dr Magdalena Kacprzak Grafy zorientowane i niezorientowane Przykład 1 Dwa pociągi i jeden most problem wzajemnego wykluczania się Dwa
Teoria grafów podstawy Materiały pomocnicze do wykładu wykładowca: dr Magdalena Kacprzak Grafy zorientowane i niezorientowane Przykład 1 Dwa pociągi i jeden most problem wzajemnego wykluczania się Dwa
WYŻSZA SZKOŁA INFORMATYKI STOSOWANEJ I ZARZĄDZANIA
 DROGI i CYKLE w grafach Dla grafu (nieskierowanego) G = ( V, E ) drogą z wierzchołka v 0 V do v t V nazywamy ciąg (naprzemienny) wierzchołków i krawędzi grafu: ( v 0, e, v, e,..., v t, e t, v t ), spełniający
DROGI i CYKLE w grafach Dla grafu (nieskierowanego) G = ( V, E ) drogą z wierzchołka v 0 V do v t V nazywamy ciąg (naprzemienny) wierzchołków i krawędzi grafu: ( v 0, e, v, e,..., v t, e t, v t ), spełniający
E: Rekonstrukcja ewolucji. Algorytmy filogenetyczne
 E: Rekonstrukcja ewolucji. Algorytmy filogenetyczne Przypominajka: 152 drzewo filogenetyczne to drzewo, którego liśćmi są istniejące gatunki, a węzły wewnętrzne mają stopień większy niż jeden i reprezentują
E: Rekonstrukcja ewolucji. Algorytmy filogenetyczne Przypominajka: 152 drzewo filogenetyczne to drzewo, którego liśćmi są istniejące gatunki, a węzły wewnętrzne mają stopień większy niż jeden i reprezentują
Grafy (3): drzewa. Wykłady z matematyki dyskretnej dla informatyków i teleinformatyków. UTP Bydgoszcz
 Grafy (3): drzewa Wykłady z matematyki dyskretnej dla informatyków i teleinformatyków UTP Bydgoszcz 13 (Wykłady z matematyki dyskretnej) Grafy (3): drzewa 13 1 / 107 Drzewo Definicja. Drzewo to graf acykliczny
Grafy (3): drzewa Wykłady z matematyki dyskretnej dla informatyków i teleinformatyków UTP Bydgoszcz 13 (Wykłady z matematyki dyskretnej) Grafy (3): drzewa 13 1 / 107 Drzewo Definicja. Drzewo to graf acykliczny
Digraf. 13 maja 2017
 Digraf 13 maja 2017 Graf skierowany, digraf, digraf prosty Definicja 1 Digraf prosty G to (V, E), gdzie V jest zbiorem wierzchołków, E jest rodziną zorientowanych krawędzi, między różnymi wierzchołkami,
Digraf 13 maja 2017 Graf skierowany, digraf, digraf prosty Definicja 1 Digraf prosty G to (V, E), gdzie V jest zbiorem wierzchołków, E jest rodziną zorientowanych krawędzi, między różnymi wierzchołkami,
Algorytmy grafowe. Wykład 2 Przeszukiwanie grafów. Tomasz Tyksiński CDV
 Algorytmy grafowe Wykład 2 Przeszukiwanie grafów Tomasz Tyksiński CDV Rozkład materiału 1. Podstawowe pojęcia teorii grafów, reprezentacje komputerowe grafów 2. Przeszukiwanie grafów 3. Spójność grafu,
Algorytmy grafowe Wykład 2 Przeszukiwanie grafów Tomasz Tyksiński CDV Rozkład materiału 1. Podstawowe pojęcia teorii grafów, reprezentacje komputerowe grafów 2. Przeszukiwanie grafów 3. Spójność grafu,
Grafy i Zastosowania. 9: Digrafy (grafy skierowane) c Marcin Sydow
 9: Digrafy (grafy skierowane) Spis zagadnień Digrafy Porządki częściowe Turnieje Przykłady: głosowanie większościowe, ścieżka krytyczna Digraf (graf skierowany) Digraf to równoważny termin z terminem graf
9: Digrafy (grafy skierowane) Spis zagadnień Digrafy Porządki częściowe Turnieje Przykłady: głosowanie większościowe, ścieżka krytyczna Digraf (graf skierowany) Digraf to równoważny termin z terminem graf
Graf. Definicja marca / 1
 Graf 25 marca 2018 Graf Definicja 1 Graf ogólny to para G = (V, E), gdzie V jest zbiorem wierzchołków (węzłów, punktów grafu), E jest rodziną krawędzi, które mogą być wielokrotne, dokładniej jednoelementowych
Graf 25 marca 2018 Graf Definicja 1 Graf ogólny to para G = (V, E), gdzie V jest zbiorem wierzchołków (węzłów, punktów grafu), E jest rodziną krawędzi, które mogą być wielokrotne, dokładniej jednoelementowych
Algorytmiczna teoria grafów
 Przedmiot fakultatywny 20h wykładu + 20h ćwiczeń 21 lutego 2014 Zasady zaliczenia 1 ćwiczenia (ocena): kolokwium, zadania programistyczne (implementacje algorytmów), praca na ćwiczeniach. 2 Wykład (egzamin)
Przedmiot fakultatywny 20h wykładu + 20h ćwiczeń 21 lutego 2014 Zasady zaliczenia 1 ćwiczenia (ocena): kolokwium, zadania programistyczne (implementacje algorytmów), praca na ćwiczeniach. 2 Wykład (egzamin)
Złożoność obliczeniowa klasycznych problemów grafowych
 Złożoność obliczeniowa klasycznych problemów grafowych Oznaczenia: G graf, V liczba wierzchołków, E liczba krawędzi 1. Spójność grafu Graf jest spójny jeżeli istnieje ścieżka łącząca każdą parę jego wierzchołków.
Złożoność obliczeniowa klasycznych problemów grafowych Oznaczenia: G graf, V liczba wierzchołków, E liczba krawędzi 1. Spójność grafu Graf jest spójny jeżeli istnieje ścieżka łącząca każdą parę jego wierzchołków.
Podstawowe pojęcia dotyczące drzew Podstawowe pojęcia dotyczące grafów Przykłady drzew i grafów
 Podstawowe pojęcia dotyczące drzew Podstawowe pojęcia dotyczące grafów Przykłady drzew i grafów Drzewa: Drzewo (ang. tree) jest strukturą danych zbudowaną z elementów, które nazywamy węzłami (ang. node).
Podstawowe pojęcia dotyczące drzew Podstawowe pojęcia dotyczące grafów Przykłady drzew i grafów Drzewa: Drzewo (ang. tree) jest strukturą danych zbudowaną z elementów, które nazywamy węzłami (ang. node).
Matematyka dyskretna. Andrzej Łachwa, UJ, /14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 13/14 Grafy podstawowe definicje Graf to para G=(V, E), gdzie V to niepusty i skończony zbiór, którego elementy nazywamy wierzchołkami
Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 13/14 Grafy podstawowe definicje Graf to para G=(V, E), gdzie V to niepusty i skończony zbiór, którego elementy nazywamy wierzchołkami
1. Algorytmy przeszukiwania. Przeszukiwanie wszerz i w głąb.
 1. Algorytmy przeszukiwania. Przeszukiwanie wszerz i w głąb. Algorytmy przeszukiwania w głąb i wszerz są najczęściej stosowanymi algorytmami przeszukiwania. Wykorzystuje się je do zbadania istnienia połączenie
1. Algorytmy przeszukiwania. Przeszukiwanie wszerz i w głąb. Algorytmy przeszukiwania w głąb i wszerz są najczęściej stosowanymi algorytmami przeszukiwania. Wykorzystuje się je do zbadania istnienia połączenie
Matematyczne Podstawy Informatyki
 Matematyczne Podstawy Informatyki dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska Rok akademicki 2013/2014 Informacje podstawowe 1. Konsultacje: pokój
Matematyczne Podstawy Informatyki dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska Rok akademicki 2013/2014 Informacje podstawowe 1. Konsultacje: pokój
Wykład 10 Grafy, algorytmy grafowe
 . Typy złożoności obliczeniowej Wykład Grafy, algorytmy grafowe Typ złożoności oznaczenie n Jedna operacja trwa µs 5 logarytmiczna lgn. s. s.7 s liniowa n. s.5 s. s Logarytmicznoliniowa nlgn. s.8 s.4 s
. Typy złożoności obliczeniowej Wykład Grafy, algorytmy grafowe Typ złożoności oznaczenie n Jedna operacja trwa µs 5 logarytmiczna lgn. s. s.7 s liniowa n. s.5 s. s Logarytmicznoliniowa nlgn. s.8 s.4 s
Drzewa spinające MST dla grafów ważonych Maksymalne drzewo spinające Drzewo Steinera. Wykład 6. Drzewa cz. II
 Wykład 6. Drzewa cz. II 1 / 65 drzewa spinające Drzewa spinające Zliczanie drzew spinających Drzewo T nazywamy drzewem rozpinającym (spinającym) (lub dendrytem) spójnego grafu G, jeżeli jest podgrafem
Wykład 6. Drzewa cz. II 1 / 65 drzewa spinające Drzewa spinające Zliczanie drzew spinających Drzewo T nazywamy drzewem rozpinającym (spinającym) (lub dendrytem) spójnego grafu G, jeżeli jest podgrafem
TEORETYCZNE PODSTAWY INFORMATYKI
 1 TEORETYCZNE PODSTAWY INFORMATYKI WFAiS UJ, Informatyka Stosowana I rok studiów, I stopień Wykład 14c 2 Definicje indukcyjne Twierdzenia dowodzone przez indukcje Definicje indukcyjne Definicja drzewa
1 TEORETYCZNE PODSTAWY INFORMATYKI WFAiS UJ, Informatyka Stosowana I rok studiów, I stopień Wykład 14c 2 Definicje indukcyjne Twierdzenia dowodzone przez indukcje Definicje indukcyjne Definicja drzewa
SPÓJNOŚĆ. ,...v k. }, E={v 1. v k. i v k. ,...,v k-1. }. Wierzchołki v 1. v 2. to końce ścieżki.
 SPÓJNOŚĆ Graf jest spójny, gdy dla każdego podziału V na dwa rozłączne podzbiory A i B istnieje krawędź z A do B. Definicja równoważna: Graf jest spójny, gdy każde dwa wierzchołki są połączone ścieżką
SPÓJNOŚĆ Graf jest spójny, gdy dla każdego podziału V na dwa rozłączne podzbiory A i B istnieje krawędź z A do B. Definicja równoważna: Graf jest spójny, gdy każde dwa wierzchołki są połączone ścieżką
Algorytm Dijkstry znajdowania najkrótszej ścieżki w grafie
 Algorytm Dijkstry znajdowania najkrótszej ścieżki w grafie Używane struktury danych: V - zbiór wierzchołków grafu, V = {1,2,3...,n} E - zbiór krawędzi grafu, E = {(i,j),...}, gdzie i, j Î V i istnieje
Algorytm Dijkstry znajdowania najkrótszej ścieżki w grafie Używane struktury danych: V - zbiór wierzchołków grafu, V = {1,2,3...,n} E - zbiór krawędzi grafu, E = {(i,j),...}, gdzie i, j Î V i istnieje
Czy istnieje zamknięta droga spaceru przechodząca przez wszystkie mosty w Królewcu dokładnie jeden raz?
 DROGI i CYKLE EULERA w grafach Czy istnieje zamknięta droga spaceru przechodząca przez wszystkie mosty w Królewcu dokładnie jeden raz? Czy można narysować podaną figurę nie odrywając ołówka od papieru
DROGI i CYKLE EULERA w grafach Czy istnieje zamknięta droga spaceru przechodząca przez wszystkie mosty w Królewcu dokładnie jeden raz? Czy można narysować podaną figurę nie odrywając ołówka od papieru
Lista 0. Kamil Matuszewski 1 marca 2016
 Lista 0 Kamil Matuszewski marca 206 2 3 4 5 6 7 8 0 0 Zadanie 4 Udowodnić poprawność mnożenia po rosyjsku Zastanówmy się co robi nasz algorytm Mamy podane liczby n i m W każdym kroku liczbę n dzielimy
Lista 0 Kamil Matuszewski marca 206 2 3 4 5 6 7 8 0 0 Zadanie 4 Udowodnić poprawność mnożenia po rosyjsku Zastanówmy się co robi nasz algorytm Mamy podane liczby n i m W każdym kroku liczbę n dzielimy
Algorytmy i str ruktury danych. Metody algorytmiczne. Bartman Jacek
 Algorytmy i str ruktury danych Metody algorytmiczne Bartman Jacek jbartman@univ.rzeszow.pl Metody algorytmiczne - wprowadzenia Znamy strukturę algorytmów Trudność tkwi natomiast w podaniu metod służących
Algorytmy i str ruktury danych Metody algorytmiczne Bartman Jacek jbartman@univ.rzeszow.pl Metody algorytmiczne - wprowadzenia Znamy strukturę algorytmów Trudność tkwi natomiast w podaniu metod służących
Matematyka dyskretna. Andrzej Łachwa, UJ, /14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2012 andrzej.lachwa@uj.edu.pl 13/14 Grafy podstawowe definicje Graf to para G=(V, E), gdzie V to niepusty i skończony zbiór, którego elementy nazywamy wierzchołkami
Matematyka dyskretna Andrzej Łachwa, UJ, 2012 andrzej.lachwa@uj.edu.pl 13/14 Grafy podstawowe definicje Graf to para G=(V, E), gdzie V to niepusty i skończony zbiór, którego elementy nazywamy wierzchołkami
Wstęp do programowania. Drzewa. Piotr Chrząstowski-Wachtel
 Wstęp do programowania Drzewa Piotr Chrząstowski-Wachtel Drzewa Drzewa definiują matematycy, jako spójne nieskierowane grafy bez cykli. Równoważne określenia: Spójne grafy o n wierzchołkach i n-1 krawędziach
Wstęp do programowania Drzewa Piotr Chrząstowski-Wachtel Drzewa Drzewa definiują matematycy, jako spójne nieskierowane grafy bez cykli. Równoważne określenia: Spójne grafy o n wierzchołkach i n-1 krawędziach
Matematyka dyskretna. Andrzej Łachwa, UJ, /15
 Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl 14/15 Grafy podstawowe definicje Graf to para G=(V, E), gdzie V to niepusty i skończony zbiór, którego elementy nazywamy wierzchołkami
Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl 14/15 Grafy podstawowe definicje Graf to para G=(V, E), gdzie V to niepusty i skończony zbiór, którego elementy nazywamy wierzchołkami
Matematyka dyskretna - 7.Drzewa
 Matematyka dyskretna - 7.Drzewa W tym rozdziale zajmiemy się drzewami: specjalnym przypadkiem grafów. Są one szczególnie przydatne do przechowywania informacji, umożliwiającego szybki dostęp do nich. Definicja
Matematyka dyskretna - 7.Drzewa W tym rozdziale zajmiemy się drzewami: specjalnym przypadkiem grafów. Są one szczególnie przydatne do przechowywania informacji, umożliwiającego szybki dostęp do nich. Definicja
Segmentacja obrazów cyfrowych z zastosowaniem teorii grafów - wstęp. autor: Łukasz Chlebda
 Segmentacja obrazów cyfrowych Segmentacja obrazów cyfrowych z zastosowaniem teorii grafów - wstęp autor: Łukasz Chlebda 1 Segmentacja obrazów cyfrowych - temat pracy Temat pracy: Aplikacja do segmentacji
Segmentacja obrazów cyfrowych Segmentacja obrazów cyfrowych z zastosowaniem teorii grafów - wstęp autor: Łukasz Chlebda 1 Segmentacja obrazów cyfrowych - temat pracy Temat pracy: Aplikacja do segmentacji
Egzamin, AISDI, I termin, 18 czerwca 2015 r.
 Egzamin, AISDI, I termin, 18 czerwca 2015 r. 1 W czasie niezależnym do danych wejściowych działają algorytmy A. sortowanie bąbelkowego i Shella B. sortowanie szybkiego i przez prosty wybór C. przez podział
Egzamin, AISDI, I termin, 18 czerwca 2015 r. 1 W czasie niezależnym do danych wejściowych działają algorytmy A. sortowanie bąbelkowego i Shella B. sortowanie szybkiego i przez prosty wybór C. przez podział
TEORIA GRAFÓW I SIECI
 TEORIA GRAFÓW I SIECI Temat nr : Grafy Berge a dr hab. inż. Zbigniew TARAPATA, prof. WAT e-mail: zbigniew.tarapata@wat.edu.pl http://tarapata.edu.pl tel.: 6-83-95-0, p.5/00 Zakład Badań Operacyjnych i
TEORIA GRAFÓW I SIECI Temat nr : Grafy Berge a dr hab. inż. Zbigniew TARAPATA, prof. WAT e-mail: zbigniew.tarapata@wat.edu.pl http://tarapata.edu.pl tel.: 6-83-95-0, p.5/00 Zakład Badań Operacyjnych i
Algorytmy grafowe. Wykład 1 Podstawy teorii grafów Reprezentacje grafów. Tomasz Tyksiński CDV
 Algorytmy grafowe Wykład 1 Podstawy teorii grafów Reprezentacje grafów Tomasz Tyksiński CDV Rozkład materiału 1. Podstawowe pojęcia teorii grafów, reprezentacje komputerowe grafów 2. Przeszukiwanie grafów
Algorytmy grafowe Wykład 1 Podstawy teorii grafów Reprezentacje grafów Tomasz Tyksiński CDV Rozkład materiału 1. Podstawowe pojęcia teorii grafów, reprezentacje komputerowe grafów 2. Przeszukiwanie grafów
Wykład 2. Drzewa zbalansowane AVL i 2-3-4
 Wykład Drzewa zbalansowane AVL i -3-4 Drzewa AVL Wprowadzenie Drzewa AVL Definicja drzewa AVL Operacje wstawiania i usuwania Złożoność obliczeniowa Drzewa -3-4 Definicja drzewa -3-4 Operacje wstawiania
Wykład Drzewa zbalansowane AVL i -3-4 Drzewa AVL Wprowadzenie Drzewa AVL Definicja drzewa AVL Operacje wstawiania i usuwania Złożoność obliczeniowa Drzewa -3-4 Definicja drzewa -3-4 Operacje wstawiania
G. Wybrane elementy teorii grafów
 Dorota Miszczyńska, Marek Miszczyński KBO UŁ Wybrane elementy teorii grafów 1 G. Wybrane elementy teorii grafów Grafy są stosowane współcześnie w różnych działach nauki i techniki. Za pomocą grafów znakomicie
Dorota Miszczyńska, Marek Miszczyński KBO UŁ Wybrane elementy teorii grafów 1 G. Wybrane elementy teorii grafów Grafy są stosowane współcześnie w różnych działach nauki i techniki. Za pomocą grafów znakomicie
Programowanie obiektowe
 Programowanie obiektowe Sieci powiązań Paweł Daniluk Wydział Fizyki Jesień 2015 P. Daniluk (Wydział Fizyki) PO w. IX Jesień 2015 1 / 21 Sieci powiązań Można (bardzo zgrubnie) wyróżnić dwa rodzaje powiązań
Programowanie obiektowe Sieci powiązań Paweł Daniluk Wydział Fizyki Jesień 2015 P. Daniluk (Wydział Fizyki) PO w. IX Jesień 2015 1 / 21 Sieci powiązań Można (bardzo zgrubnie) wyróżnić dwa rodzaje powiązań
Algebrą nazywamy strukturę A = (A, {F i : i I }), gdzie A jest zbiorem zwanym uniwersum algebry, zaś F i : A F i
 Algebrą nazywamy strukturę A = (A, {F i : i I }), gdzie A jest zbiorem zwanym uniwersum algebry, zaś F i : A F i A (symbol F i oznacza ilość argumentów funkcji F i ). W rozważanych przez nas algebrach
Algebrą nazywamy strukturę A = (A, {F i : i I }), gdzie A jest zbiorem zwanym uniwersum algebry, zaś F i : A F i A (symbol F i oznacza ilość argumentów funkcji F i ). W rozważanych przez nas algebrach
Algorytmy z powracaniem
 Algorytmy z powracaniem Materiały Grafem nazywamy zbiór G = (V, E), gdzie: V jest zbiorem wierzchołków (ang. vertex) E jest zbiorem krawędzi (E można też określić jako podzbiór zbioru nieuporządkowanych
Algorytmy z powracaniem Materiały Grafem nazywamy zbiór G = (V, E), gdzie: V jest zbiorem wierzchołków (ang. vertex) E jest zbiorem krawędzi (E można też określić jako podzbiór zbioru nieuporządkowanych
Ścieżki w grafach. Grafy acykliczne i spójne
 TEORIA GRAFÓW I SIECI - ROZDZIAL II Ścieżki w grafach. Grafy acykliczne i spójne Ścieżka lub droga w grafie [digrafie] G nazywamy dowolny ciag d = (a 0, k 1, a 1,..., k n, a n ), gdzie n N {0}, a i V G,
TEORIA GRAFÓW I SIECI - ROZDZIAL II Ścieżki w grafach. Grafy acykliczne i spójne Ścieżka lub droga w grafie [digrafie] G nazywamy dowolny ciag d = (a 0, k 1, a 1,..., k n, a n ), gdzie n N {0}, a i V G,
Wstęp do Programowania potok funkcyjny
 Wstęp do Programowania potok funkcyjny Marcin Kubica 2010/2011 Outline 1 Podstawowe pojęcia Definition Graf = wierzchołki + krawędzie. Krawędzie muszą mieć różne końce. Między dwoma wierzchołkami może
Wstęp do Programowania potok funkcyjny Marcin Kubica 2010/2011 Outline 1 Podstawowe pojęcia Definition Graf = wierzchołki + krawędzie. Krawędzie muszą mieć różne końce. Między dwoma wierzchołkami może
Podstawy programowania 2. Temat: Drzewa binarne. Przygotował: mgr inż. Tomasz Michno
 Instrukcja laboratoryjna 5 Podstawy programowania 2 Temat: Drzewa binarne Przygotował: mgr inż. Tomasz Michno 1 Wstęp teoretyczny Drzewa są jedną z częściej wykorzystywanych struktur danych. Reprezentują
Instrukcja laboratoryjna 5 Podstawy programowania 2 Temat: Drzewa binarne Przygotował: mgr inż. Tomasz Michno 1 Wstęp teoretyczny Drzewa są jedną z częściej wykorzystywanych struktur danych. Reprezentują
TEORIA GRAFÓW I SIECI
 TEORIA GRAFÓW I SIECI Temat nr 1: Definicja grafu. Rodzaje i części grafów dr hab. inż. Zbigniew TARAPATA, prof. WAT e-mail: zbigniew.tarapata@wat.edu.pl http://tarapata.edu.pl tel.: 261-83-95-04, p.225/100
TEORIA GRAFÓW I SIECI Temat nr 1: Definicja grafu. Rodzaje i części grafów dr hab. inż. Zbigniew TARAPATA, prof. WAT e-mail: zbigniew.tarapata@wat.edu.pl http://tarapata.edu.pl tel.: 261-83-95-04, p.225/100
Programowanie obiektowe
 Programowanie obiektowe Sieci powiązań Paweł Daniluk Wydział Fizyki Jesień 2014 P. Daniluk (Wydział Fizyki) PO w. IX Jesień 2014 1 / 24 Sieci powiązań Można (bardzo zgrubnie) wyróżnić dwa rodzaje powiązań
Programowanie obiektowe Sieci powiązań Paweł Daniluk Wydział Fizyki Jesień 2014 P. Daniluk (Wydział Fizyki) PO w. IX Jesień 2014 1 / 24 Sieci powiązań Można (bardzo zgrubnie) wyróżnić dwa rodzaje powiązań
. Podstawy Programowania 2. Grafy i ich reprezentacje. Arkadiusz Chrobot. 9 czerwca 2016
 Podstawy Programowania 2 Grafy i ich reprezentacje Arkadiusz Chrobot Zakład Informatyki 9 czerwca 2016 1 42 Plan 1 Wstęp 2 Teoria grafów 3 Grafy jako struktury danych 4 Zastosowania grafów 2 42 Wstęp Wstęp
Podstawy Programowania 2 Grafy i ich reprezentacje Arkadiusz Chrobot Zakład Informatyki 9 czerwca 2016 1 42 Plan 1 Wstęp 2 Teoria grafów 3 Grafy jako struktury danych 4 Zastosowania grafów 2 42 Wstęp Wstęp
Matematyczne Podstawy Informatyki
 Matematyczne Podstawy Informatyki dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska Rok akademicki 03/0 Przeszukiwanie w głąb i wszerz I Przeszukiwanie metodą
Matematyczne Podstawy Informatyki dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska Rok akademicki 03/0 Przeszukiwanie w głąb i wszerz I Przeszukiwanie metodą
Wykład 3. Złożoność i realizowalność algorytmów Elementarne struktury danych: stosy, kolejki, listy
 Wykład 3 Złożoność i realizowalność algorytmów Elementarne struktury danych: stosy, kolejki, listy Dynamiczne struktury danych Lista jest to liniowo uporządkowany zbiór elementów, z których dowolny element
Wykład 3 Złożoność i realizowalność algorytmów Elementarne struktury danych: stosy, kolejki, listy Dynamiczne struktury danych Lista jest to liniowo uporządkowany zbiór elementów, z których dowolny element
Suma dwóch grafów. Zespolenie dwóch grafów
 Suma dwóch grafów G 1 = ((G 1 ), E(G 1 )) G 2 = ((G 2 ), E(G 2 )) (G 1 ) i (G 2 ) rozłączne Suma G 1 G 2 graf ze zbiorem wierzchołków (G 1 ) (G 2 ) i rodziną krawędzi E(G 1 ) E(G 2 ) G 1 G 2 G 1 G 2 Zespolenie
Suma dwóch grafów G 1 = ((G 1 ), E(G 1 )) G 2 = ((G 2 ), E(G 2 )) (G 1 ) i (G 2 ) rozłączne Suma G 1 G 2 graf ze zbiorem wierzchołków (G 1 ) (G 2 ) i rodziną krawędzi E(G 1 ) E(G 2 ) G 1 G 2 G 1 G 2 Zespolenie
ZASADY PROGRAMOWANIA KOMPUTERÓW ZAP zima 2014/2015. Drzewa BST c.d., równoważenie drzew, kopce.
 POLITECHNIKA WARSZAWSKA Instytut Automatyki i Robotyki ZASADY PROGRAMOWANIA KOMPUTERÓW ZAP zima 204/205 Język programowania: Środowisko programistyczne: C/C++ Qt Wykład 2 : Drzewa BST c.d., równoważenie
POLITECHNIKA WARSZAWSKA Instytut Automatyki i Robotyki ZASADY PROGRAMOWANIA KOMPUTERÓW ZAP zima 204/205 Język programowania: Środowisko programistyczne: C/C++ Qt Wykład 2 : Drzewa BST c.d., równoważenie
Wstęp do Programowania potok funkcyjny
 Wstęp do Programowania potok funkcyjny Marcin Kubica 2010/2011 Outline 1 BFS DFS Algorytm Dijkstry Algorytm Floyda-Warshalla Podstawowe pojęcia Definition Graf = wierzchołki + krawędzie. Krawędzie muszą
Wstęp do Programowania potok funkcyjny Marcin Kubica 2010/2011 Outline 1 BFS DFS Algorytm Dijkstry Algorytm Floyda-Warshalla Podstawowe pojęcia Definition Graf = wierzchołki + krawędzie. Krawędzie muszą
Przypomnij sobie krótki wstęp do teorii grafów przedstawiony na początku semestru.
 Spis treści 1 Drzewa 1.1 Drzewa binarne 1.1.1 Zadanie 1.1.2 Drzewo BST (Binary Search Tree) 1.1.2.1 Zadanie 1 1.1.2.2 Zadanie 2 1.1.2.3 Zadanie 3 1.1.2.4 Usuwanie węzła w drzewie BST 1.1.2.5 Zadanie 4
Spis treści 1 Drzewa 1.1 Drzewa binarne 1.1.1 Zadanie 1.1.2 Drzewo BST (Binary Search Tree) 1.1.2.1 Zadanie 1 1.1.2.2 Zadanie 2 1.1.2.3 Zadanie 3 1.1.2.4 Usuwanie węzła w drzewie BST 1.1.2.5 Zadanie 4
Programowanie dynamiczne cz. 2
 Programowanie dynamiczne cz. 2 Wykład 7 16 kwietnia 2019 (Wykład 7) Programowanie dynamiczne cz. 2 16 kwietnia 2019 1 / 19 Outline 1 Mnożenie ciągu macierzy Konstruowanie optymalnego rozwiązania 2 Podstawy
Programowanie dynamiczne cz. 2 Wykład 7 16 kwietnia 2019 (Wykład 7) Programowanie dynamiczne cz. 2 16 kwietnia 2019 1 / 19 Outline 1 Mnożenie ciągu macierzy Konstruowanie optymalnego rozwiązania 2 Podstawy
Rozwiązywanie problemów metodą przeszukiwania
 Rozwiązywanie problemów metodą przeszukiwania Dariusz Banasiak Katedra Informatyki Technicznej W4/K9 Politechnika Wrocławska Reprezentacja problemu w przestrzeni stanów Jedną z ważniejszych metod sztucznej
Rozwiązywanie problemów metodą przeszukiwania Dariusz Banasiak Katedra Informatyki Technicznej W4/K9 Politechnika Wrocławska Reprezentacja problemu w przestrzeni stanów Jedną z ważniejszych metod sztucznej
Matematyka dyskretna. Andrzej Łachwa, UJ, B/14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl 1B/14 Drogi w grafach Marszruta (trasa) w grafie G z wierzchołka w do wierzchołka u to skończony ciąg krawędzi w postaci. W skrócie
Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl 1B/14 Drogi w grafach Marszruta (trasa) w grafie G z wierzchołka w do wierzchołka u to skończony ciąg krawędzi w postaci. W skrócie
prowadzący dr ADRIAN HORZYK /~horzyk e-mail: horzyk@agh tel.: 012-617 Konsultacje paw. D-13/325
 PODSTAWY INFORMATYKI WYKŁAD 8. prowadzący dr ADRIAN HORZYK http://home home.agh.edu.pl/~ /~horzyk e-mail: horzyk@agh agh.edu.pl tel.: 012-617 617-4319 Konsultacje paw. D-13/325 DRZEWA Drzewa to rodzaj
PODSTAWY INFORMATYKI WYKŁAD 8. prowadzący dr ADRIAN HORZYK http://home home.agh.edu.pl/~ /~horzyk e-mail: horzyk@agh agh.edu.pl tel.: 012-617 617-4319 Konsultacje paw. D-13/325 DRZEWA Drzewa to rodzaj
Zad. 1 Zad. 2 Zad. 3 Zad. 4 Zad. 5 SUMA
 Zad. 1 Zad. 2 Zad. 3 Zad. 4 Zad. 5 SUMA Zad. 1 (12p.)Niech n 3k > 0. Zbadać jaka jest najmniejsza możliwa liczba krawędzi w grafie, który ma dokładnie n wierzchołków oraz dokładnie k składowych, z których
Zad. 1 Zad. 2 Zad. 3 Zad. 4 Zad. 5 SUMA Zad. 1 (12p.)Niech n 3k > 0. Zbadać jaka jest najmniejsza możliwa liczba krawędzi w grafie, który ma dokładnie n wierzchołków oraz dokładnie k składowych, z których
Podstawowe własności grafów. Wykład 3. Własności grafów
 Wykład 3. Własności grafów 1 / 87 Suma grafów Niech będą dane grafy proste G 1 = (V 1, E 1) oraz G 2 = (V 2, E 2). 2 / 87 Suma grafów Niech będą dane grafy proste G 1 = (V 1, E 1) oraz G 2 = (V 2, E 2).
Wykład 3. Własności grafów 1 / 87 Suma grafów Niech będą dane grafy proste G 1 = (V 1, E 1) oraz G 2 = (V 2, E 2). 2 / 87 Suma grafów Niech będą dane grafy proste G 1 = (V 1, E 1) oraz G 2 = (V 2, E 2).
Algorytmy i Struktury Danych.
 Algorytmy i Struktury Danych. Grafy dr hab. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 9 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 9 1 / 20
Algorytmy i Struktury Danych. Grafy dr hab. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 9 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 9 1 / 20
Matematyczne Podstawy Informatyki
 Matematyczne Podstawy Informatyki dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska Rok akademicki 2013/2014 Twierdzenie 2.1 Niech G będzie grafem prostym
Matematyczne Podstawy Informatyki dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska Rok akademicki 2013/2014 Twierdzenie 2.1 Niech G będzie grafem prostym
TEORIA GRAFÓW I SIECI
 TEORIA GRAFÓW I SIECI Temat nr 3: Marszruty, łańcuchy, drogi w grafach dr hab. inż. Zbigniew TARAPATA, prof. WAT e-mail: zbigniew.tarapata@wat.edu.pl http://tarapata.edu.pl tel.: 261-83-95-04, p.225/100
TEORIA GRAFÓW I SIECI Temat nr 3: Marszruty, łańcuchy, drogi w grafach dr hab. inż. Zbigniew TARAPATA, prof. WAT e-mail: zbigniew.tarapata@wat.edu.pl http://tarapata.edu.pl tel.: 261-83-95-04, p.225/100
EGZAMIN - Wersja A. ALGORYTMY I STRUKTURY DANYCH Lisek89 opracowanie kartki od Pani dr E. Koszelew
 1. ( pkt) Dany jest algorytm, który dla dowolnej liczby naturalnej n, powinien wyznaczyd sumę kolejnych liczb naturalnych mniejszych od n. Wynik algorytmu jest zapisany w zmiennej suma. Algorytm i=1; suma=0;
1. ( pkt) Dany jest algorytm, który dla dowolnej liczby naturalnej n, powinien wyznaczyd sumę kolejnych liczb naturalnych mniejszych od n. Wynik algorytmu jest zapisany w zmiennej suma. Algorytm i=1; suma=0;
Wstęp do sieci neuronowych, wykład 11 Łańcuchy Markova
 Wstęp do sieci neuronowych, wykład 11 Łańcuchy Markova M. Czoków, J. Piersa 2010-12-21 1 Definicja Własności Losowanie z rozkładu dyskretnego 2 3 Łańcuch Markova Definicja Własności Losowanie z rozkładu
Wstęp do sieci neuronowych, wykład 11 Łańcuchy Markova M. Czoków, J. Piersa 2010-12-21 1 Definicja Własności Losowanie z rozkładu dyskretnego 2 3 Łańcuch Markova Definicja Własności Losowanie z rozkładu
WSTĘP DO INFORMATYKI. Drzewa i struktury drzewiaste
 Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej WSTĘP DO INFORMATYKI Adrian Horzyk Drzewa i struktury drzewiaste www.agh.edu.pl DEFINICJA DRZEWA Drzewo
Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej WSTĘP DO INFORMATYKI Adrian Horzyk Drzewa i struktury drzewiaste www.agh.edu.pl DEFINICJA DRZEWA Drzewo
Elementy teorii grafów Elementy teorii grafów
 Spis tresci 1 Spis tresci 1 Często w zagadnieniach praktycznych rozważa się pewien zbiór obiektów wraz z zależnościami jakie łączą te obiekty. Dla przykładu można badać pewną grupę ludzi oraz strukturę
Spis tresci 1 Spis tresci 1 Często w zagadnieniach praktycznych rozważa się pewien zbiór obiektów wraz z zależnościami jakie łączą te obiekty. Dla przykładu można badać pewną grupę ludzi oraz strukturę
Wstęp do sieci neuronowych, wykład 12 Łańcuchy Markowa
 Wstęp do sieci neuronowych, wykład 12 Łańcuchy Markowa M. Czoków, J. Piersa 2012-01-10 1 Łańcucha Markowa 2 Istnienie Szukanie stanu stacjonarnego 3 1 Łańcucha Markowa 2 Istnienie Szukanie stanu stacjonarnego
Wstęp do sieci neuronowych, wykład 12 Łańcuchy Markowa M. Czoków, J. Piersa 2012-01-10 1 Łańcucha Markowa 2 Istnienie Szukanie stanu stacjonarnego 3 1 Łańcucha Markowa 2 Istnienie Szukanie stanu stacjonarnego
Algorytmy i Struktury Danych.
 Algorytmy i Struktury Danych. Grafy dr hab. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 9 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 9 1 / 53
Algorytmy i Struktury Danych. Grafy dr hab. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 9 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 9 1 / 53
. Podstawy Programowania 2. Algorytmy dfs i bfs. Arkadiusz Chrobot. 2 czerwca 2019
 Podstawy Programowania Algorytmy dfs i bfs Arkadiusz Chrobot Zakład Informatyki czerwca 09 / 70 Plan Wstęp Algorytm BFS Podsumowanie / 70 Wstęp Wstęp Istnieje wiele algorytmów związanych z grafami, które
Podstawy Programowania Algorytmy dfs i bfs Arkadiusz Chrobot Zakład Informatyki czerwca 09 / 70 Plan Wstęp Algorytm BFS Podsumowanie / 70 Wstęp Wstęp Istnieje wiele algorytmów związanych z grafami, które
Metody uporządkowania
 Metody uporządkowania W trakcie faktoryzacji macierzy rzadkiej ilość zapełnień istotnie zależy od sposobu numeracji równań. Powstaje problem odnalezienia takiej numeracji, przy której ilość zapełnień będzie
Metody uporządkowania W trakcie faktoryzacji macierzy rzadkiej ilość zapełnień istotnie zależy od sposobu numeracji równań. Powstaje problem odnalezienia takiej numeracji, przy której ilość zapełnień będzie
Algorytmy i Struktury Danych
 Algorytmy i Struktury Danych Kopce Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 11 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych Wykład 11 1 / 69 Plan wykładu
Algorytmy i Struktury Danych Kopce Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 11 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych Wykład 11 1 / 69 Plan wykładu
Metody Kompilacji Wykład 3
 Metody Kompilacji Wykład 3 odbywa się poprzez dołączenie zasad(reguł) lub fragmentów kodu do produkcji w gramatyce. Włodzimierz Bielecki WI ZUT 2 Na przykład, dla produkcji expr -> expr 1 + term możemy
Metody Kompilacji Wykład 3 odbywa się poprzez dołączenie zasad(reguł) lub fragmentów kodu do produkcji w gramatyce. Włodzimierz Bielecki WI ZUT 2 Na przykład, dla produkcji expr -> expr 1 + term możemy
Dynamiczne drzewa. Marian M. Kędzierski. 26 listopada Wstęp Euler-Tour Trees Dynamiczna spójność Algorytm Dinica Link-Cut Trees
 Dynamiczne drzewa Marian M. Kędzierski 26 listopada 2009 Plan prezentacji Wstęp 1 Wstęp Zagadnienie dynamicznych drzew SPLITiJOINnadrzewachBST 2 Euler-TourTrees Operacje na ET-drzewach Rozszerzenia 3 Dynamicznaspójność
Dynamiczne drzewa Marian M. Kędzierski 26 listopada 2009 Plan prezentacji Wstęp 1 Wstęp Zagadnienie dynamicznych drzew SPLITiJOINnadrzewachBST 2 Euler-TourTrees Operacje na ET-drzewach Rozszerzenia 3 Dynamicznaspójność
WYŻSZA SZKOŁA INFORMATYKI STOSOWANEJ I ZARZĄDZANIA
 DRZEWA i LASY Drzewem nazywamy graf spójny nie zawierający cykli elementarnych. Lasem nazywamy graf nie zawierający cykli elementarnych. Przykłady drzew i lasów takie krawędzie są wykluczone drzewo las
DRZEWA i LASY Drzewem nazywamy graf spójny nie zawierający cykli elementarnych. Lasem nazywamy graf nie zawierający cykli elementarnych. Przykłady drzew i lasów takie krawędzie są wykluczone drzewo las
Metody uporządkowania
 Metody uporządkowania W trakcie faktoryzacji macierzy rzadkiej ilość zapełnień istotnie zależy od sposobu numeracji równań. Powstaje problem odnalezienia takiej numeracji, przy której: o ilość zapełnień
Metody uporządkowania W trakcie faktoryzacji macierzy rzadkiej ilość zapełnień istotnie zależy od sposobu numeracji równań. Powstaje problem odnalezienia takiej numeracji, przy której: o ilość zapełnień
Kolorowanie wierzchołków Kolorowanie krawędzi Kolorowanie regionów i map. Wykład 8. Kolorowanie
 Wykład 8. Kolorowanie 1 / 62 Kolorowanie wierzchołków - definicja Zbiory niezależne Niech G będzie grafem bez pętli. Definicja Mówimy, że G jest grafem k kolorowalnym, jeśli każdemu wierzchołkowi możemy
Wykład 8. Kolorowanie 1 / 62 Kolorowanie wierzchołków - definicja Zbiory niezależne Niech G będzie grafem bez pętli. Definicja Mówimy, że G jest grafem k kolorowalnym, jeśli każdemu wierzchołkowi możemy
Marek Miszczyński KBO UŁ. Wybrane elementy teorii grafów 1
 Marek Miszczyński KBO UŁ. Wybrane elementy teorii grafów 1 G. Wybrane elementy teorii grafów W matematyce teorię grafów klasyfikuje się jako gałąź topologii. Jest ona jednak ściśle związana z algebrą i
Marek Miszczyński KBO UŁ. Wybrane elementy teorii grafów 1 G. Wybrane elementy teorii grafów W matematyce teorię grafów klasyfikuje się jako gałąź topologii. Jest ona jednak ściśle związana z algebrą i
Indukowane Reguły Decyzyjne I. Wykład 3
 Indukowane Reguły Decyzyjne I Wykład 3 IRD Wykład 3 Plan Powtórka Grafy Drzewa klasyfikacyjne Testy wstęp Klasyfikacja obiektów z wykorzystaniem drzewa Reguły decyzyjne generowane przez drzewo 2 Powtórzenie
Indukowane Reguły Decyzyjne I Wykład 3 IRD Wykład 3 Plan Powtórka Grafy Drzewa klasyfikacyjne Testy wstęp Klasyfikacja obiektów z wykorzystaniem drzewa Reguły decyzyjne generowane przez drzewo 2 Powtórzenie
KURS MATEMATYKA DYSKRETNA
 KURS MATEMATYKA DYSKRETNA LEKCJA 28 Grafy hamiltonowskie ZADANIE DOMOWE www.akademia.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowiedź (tylko jedna jest prawdziwa). Pytanie 1 Drogę nazywamy
KURS MATEMATYKA DYSKRETNA LEKCJA 28 Grafy hamiltonowskie ZADANIE DOMOWE www.akademia.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowiedź (tylko jedna jest prawdziwa). Pytanie 1 Drogę nazywamy
Drzewa. Jeżeli graf G jest lasem, który ma n wierzchołków i k składowych, to G ma n k krawędzi. Własności drzew
 Drzewa Las - graf, który nie zawiera cykli Drzewo - las spójny Jeżeli graf G jest lasem, który ma n wierzchołków i k składowych, to G ma n k krawędzi. Własności drzew Niech T graf o n wierzchołkach będący
Drzewa Las - graf, który nie zawiera cykli Drzewo - las spójny Jeżeli graf G jest lasem, który ma n wierzchołków i k składowych, to G ma n k krawędzi. Własności drzew Niech T graf o n wierzchołkach będący
Algorytm DFS Wprowadzenie teoretyczne. Algorytm DFS Wprowadzenie teoretyczne. Algorytm DFS Animacja. Algorytm DFS Animacja. Notatki. Notatki.
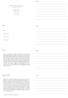 Podstawy Programowania Algorytmy dfs i bfs Arkadiusz Chrobot Zakład Informatyki czerwca 09 / 70 Plan Wstęp Podsumowanie / 70 Wstęp Istnieje wiele algorytmów związanych z grafami, które w skrócie nazywane
Podstawy Programowania Algorytmy dfs i bfs Arkadiusz Chrobot Zakład Informatyki czerwca 09 / 70 Plan Wstęp Podsumowanie / 70 Wstęp Istnieje wiele algorytmów związanych z grafami, które w skrócie nazywane
(4) x (y z) = (x y) (x z), x (y z) = (x y) (x z), (3) x (x y) = x, x (x y) = x, (2) x 0 = x, x 1 = x
 2. Wykład 2: algebry Boole a, kraty i drzewa. 2.1. Algebra Boole a. 1 Ważnym dla nas przykładem algebr są algebry Boole a, czyli algebry B = (B,,,, 0, 1) typu (2, 2, 1, 0, 0) spełniające własności: (1)
2. Wykład 2: algebry Boole a, kraty i drzewa. 2.1. Algebra Boole a. 1 Ważnym dla nas przykładem algebr są algebry Boole a, czyli algebry B = (B,,,, 0, 1) typu (2, 2, 1, 0, 0) spełniające własności: (1)
AiSD zadanie trzecie
 AiSD zadanie trzecie Gliwiński Jarosław Marek Kruczyński Konrad Marek Grupa dziekańska I5 5 czerwca 2008 1 Wstęp Celem postawionym przez zadanie trzecie było tzw. sortowanie topologiczne. Jest to typ sortowania
AiSD zadanie trzecie Gliwiński Jarosław Marek Kruczyński Konrad Marek Grupa dziekańska I5 5 czerwca 2008 1 Wstęp Celem postawionym przez zadanie trzecie było tzw. sortowanie topologiczne. Jest to typ sortowania
Wysokość drzewa Głębokość węzła
 Drzewa Drzewa Drzewo (ang. tree) zbiór węzłów powiązanych wskaźnikami, spójny i bez cykli. Drzewo posiada wyróżniony węzeł początkowy nazywany korzeniem (ang. root). Drzewo ukorzenione jest strukturą hierarchiczną.
Drzewa Drzewa Drzewo (ang. tree) zbiór węzłów powiązanych wskaźnikami, spójny i bez cykli. Drzewo posiada wyróżniony węzeł początkowy nazywany korzeniem (ang. root). Drzewo ukorzenione jest strukturą hierarchiczną.
Badania operacyjne: Wykład Zastosowanie kolorowania grafów w planowaniu produkcji typu no-idle
 Badania operacyjne: Wykład Zastosowanie kolorowania grafów w planowaniu produkcji typu no-idle Paweł Szołtysek 12 czerwca 2008 Streszczenie Planowanie produkcji jest jednym z problemów optymalizacji dyskretnej,
Badania operacyjne: Wykład Zastosowanie kolorowania grafów w planowaniu produkcji typu no-idle Paweł Szołtysek 12 czerwca 2008 Streszczenie Planowanie produkcji jest jednym z problemów optymalizacji dyskretnej,
ĆWICZENIE 1: Przeszukiwanie grafów cz. 1 strategie ślepe
 Instytut Mechaniki i Inżynierii Obliczeniowej Wydział Mechaniczny Technologiczny, Politechnika Śląska www.imio.polsl.pl METODY HEURYSTYCZNE ĆWICZENIE 1: Przeszukiwanie grafów cz. 1 strategie ślepe opracował:
Instytut Mechaniki i Inżynierii Obliczeniowej Wydział Mechaniczny Technologiczny, Politechnika Śląska www.imio.polsl.pl METODY HEURYSTYCZNE ĆWICZENIE 1: Przeszukiwanie grafów cz. 1 strategie ślepe opracował:
Wstęp do programowania. Zastosowania stosów i kolejek. Piotr Chrząstowski-Wachtel
 Wstęp do programowania Zastosowania stosów i kolejek Piotr Chrząstowski-Wachtel FIFO - LIFO Kolejki i stosy służą do przechowywania wartości zbiorów dynamicznych, czyli takich, które powstają przez dodawanie
Wstęp do programowania Zastosowania stosów i kolejek Piotr Chrząstowski-Wachtel FIFO - LIFO Kolejki i stosy służą do przechowywania wartości zbiorów dynamicznych, czyli takich, które powstają przez dodawanie
Zadanie 1: Piętnastka
 Informatyka, studia dzienne, inż. I st. semestr VI Sztuczna Inteligencja i Systemy Ekspertowe 2010/2011 Prowadzący: mgr Michał Pryczek piątek, 12:00 Data oddania: Ocena: Grzegorz Graczyk 150875 Marek Rogalski
Informatyka, studia dzienne, inż. I st. semestr VI Sztuczna Inteligencja i Systemy Ekspertowe 2010/2011 Prowadzący: mgr Michał Pryczek piątek, 12:00 Data oddania: Ocena: Grzegorz Graczyk 150875 Marek Rogalski
dodatkowe operacje dla kopca binarnego: typu min oraz typu max:
 ASD - ćwiczenia IX Kopce binarne własność porządku kopca gdzie dla każdej trójki wierzchołków kopca (X, Y, Z) porządek etykiet elem jest następujący X.elem Y.elem oraz Z.elem Y.elem w przypadku kopca typu
ASD - ćwiczenia IX Kopce binarne własność porządku kopca gdzie dla każdej trójki wierzchołków kopca (X, Y, Z) porządek etykiet elem jest następujący X.elem Y.elem oraz Z.elem Y.elem w przypadku kopca typu
Nierówność Krafta-McMillana, Kodowanie Huffmana
 Nierówność Krafta-McMillana, Kodowanie Huffmana Kodowanie i kompresja informacji - Wykład 2 1 marca 2010 Test na jednoznaczna dekodowalność Kod a jest prefiksem kodu b jeśli b jest postaci ax. x nazywamy
Nierówność Krafta-McMillana, Kodowanie Huffmana Kodowanie i kompresja informacji - Wykład 2 1 marca 2010 Test na jednoznaczna dekodowalność Kod a jest prefiksem kodu b jeśli b jest postaci ax. x nazywamy
Algorytmy Równoległe i Rozproszone Część V - Model PRAM II
 Algorytmy Równoległe i Rozproszone Część V - Model PRAM II Łukasz Kuszner pokój 209, WETI http://www.sphere.pl/ kuszner/ kuszner@sphere.pl Oficjalna strona wykładu http://www.sphere.pl/ kuszner/arir/ 2005/06
Algorytmy Równoległe i Rozproszone Część V - Model PRAM II Łukasz Kuszner pokój 209, WETI http://www.sphere.pl/ kuszner/ kuszner@sphere.pl Oficjalna strona wykładu http://www.sphere.pl/ kuszner/arir/ 2005/06
Sieć (graf skierowany)
 Sieci Sieć (graf skierowany) Siecia (grafem skierowanym) G = (V, A) nazywamy zbiór wierzchołków V oraz zbiór łuków A V V. V = {A, B, C, D, E, F}, A = {(A, B), (A, D), (A, C), (B, C),..., } Ścieżki i cykle
Sieci Sieć (graf skierowany) Siecia (grafem skierowanym) G = (V, A) nazywamy zbiór wierzchołków V oraz zbiór łuków A V V. V = {A, B, C, D, E, F}, A = {(A, B), (A, D), (A, C), (B, C),..., } Ścieżki i cykle
