Algorytmy i Struktury Danych.
|
|
|
- Helena Bielecka
- 6 lat temu
- Przeglądów:
Transkrypt
1 Algorytmy i Struktury Danych. Grafy dr hab. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 9 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 9 1 / 20
2 Plan wykładu Wyszukiwanie spójnych składowych grafu (ang. Connected components) Sortowanie topologiczne (ang. Topological sort) Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 9 2 / 20
3 Spójne składowe Definicja Każda spójna składowa grafu G = (V, E) jest maksymalnym podzbiorem wierzchołków U zbioru V takim, że dla dowolnych dwóch wierzchołków z U istnieje łacz aca je ścieżka w G. Jeżeli graf składa się z jednej spójnej składowej to mówimy, że jest spójny (ang. connected). Każdy graf nieskierowany można podzielić na jedna lub większa liczbę spójnych składowych (ang. connected components). Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 9 3 / 20
4 Spójne składowe Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 9 4 / 20
5 Spójne podgrafy Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 9 5 / 20
6 Spójne składowe - algorytm Wejście: G = (V, E) Wyjście: Spójne składowe grafu G 1 J. Hopcroft, R. Tarjan. Efficient algorithms for graph manipulation Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 9 6 / 20
7 Spójne składowe - algorytm Wejście: G = (V, E) Wyjście: Spójne składowe grafu G Algorytmy DFS oraz BFS wyznaczaja spójne składowe grafu G 1. 1 J. Hopcroft, R. Tarjan. Efficient algorithms for graph manipulation Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 9 6 / 20
8 Spójne składowe - algorytm Wejście: G = (V, E) Wyjście: Spójne składowe grafu G Algorytmy DFS oraz BFS wyznaczaja spójne składowe grafu G 1. Złożoność: O((m + n). 1 J. Hopcroft, R. Tarjan. Efficient algorithms for graph manipulation Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 9 6 / 20
9 Spójne składowe - algorytm DFS Require: Graf (V, E), tablica visited o rozmiarze V = n Algorytm DFS: 1: for all i := 1 to n do 2: visited[i] := 0; 3: end for 4: for all i := 1 to n do 5: if visited[i] = 0 then 6: visit(i, visited); 7: end if 8: end for Require: Graf (V, E), tablica visited o rozmiarze V = n Algorytm visit(i,visited): 1: print(i); 2: visited[i] := 1; 3: for each neighbor j of i do 4: if visited[j] = 0 then 5: visit(j); 6: end if 7: end for Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 9 7 / 20
10 Implementacja void Graph::dfs_rek(int a) { bool* visited = new (nothrow) bool[this->n]; for (int k = 0; k < this->n; ++k) visited[k] = false; for (int k = a; k < this->n; ++k) { if (visited[k] == false) this->visit(k,visited); delete[] visited; void Graph::visit(int a, bool* visited) { displayvertex(a); visited[a] = true; int c = this->getunvisitedvertex(a, visited); while (c!= -1){ if (visited [c] == false) visit(c,visited); c = this->getunvisitedvertex(a, visited); Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 9 8 / 20
11 Wykonanie Krawedzie grafu: A-B A-C B-A B-D C-A C-D D-B D-C DFS - odwiedzone wierzcholki: ABDC DFS rekurencyjny - odwiedzone wierzcholki: ABDC BFS - odwiedzone wierzcholki: ABCD Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 9 9 / 20
12 Spójne składowe Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 9 10 / 20
13 Sortowanie Topologiczne - sformułowanie problemu Wejście: Acykliczny graf skierowany G = (V, E). Wyjście: Liniowy porzadek wierzchołków z V taki, że jeśli graf G zawiera krawędź (u, v), to w tym porzadku wierzchołek u występuje przed wierzchołkiem v. Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 9 11 / 20
14 Sortowanie topologicznie - przykład Wierzchołki w każdym grafie acyklicznym skierowanym można posortować topologicznie na jeden lub więcej sposobów 7,5,3,11,8,2,9,10 7,5,11,2,3,10,8,9 3,7,8,5,11,10,9,2 5,7,11,2,3,8,9, Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 9 12 / 20
15 Sortowanie Topologiczne - algorytm bazujacy na DFS Wykonaj TopologicalDFS na wejściowym acyklicznym grafie skierowanym G = (V, E). Wypisz wierzchołki w porzadku malejacym ze względu na ich czas końcowy - umieszczony w tablicy final. Złożoność: O( V + E ) Wejście: Graf G, tablice visited oraz final o rozmiarze V = n Algorytm TopologicalDFS: 1: t := 0 2: for all i := 1 to n do 3: visited[i] := 0; final[i] := 0 4: end for 5: for all i := 1 to n do 6: if visited[i] = 0 then 7: visit(i, t, visited, final); 8: end if 9: end for Algorytm visit(i,t,visited,final): 1: visited[i] := 1; 2: for each outgoing edge j of i do 3: if visited[j] = 0 then 4: visit(j, t, visited, final); 5: end if 6: end for 7: t = t + 1; 8: final[i] = t; Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 9 13 / 20
16 Sortowanie Topologiczne - przykład Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 9 14 / 20
17 Implementacja Aby na postawie implementacji z poprzedniego wykładu wykonać implementację grafu skierowanego, wystarczy zmienić metodę addedge na następujac a void Graph::addEdge(int a, int b) { if (a >= 0 && a < this->n && b >= 0 && b < this->n) this->adj[a][b] = true; else { cout << "Niepoprawne dane\n\n"; Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 9 15 / 20
18 Implementacja void Graph::topological_visit(int a, int & t, bool* visited, int* fin) { visited[a] = true; int c = this->getunvisitedvertex(a, visited); while (c!= -1){ if (visited [c] == false) topological_visit(c,t,visited,fin); c = this->getunvisitedvertex(a, visited); t++; fin[a] = t; Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 9 16 / 20
19 Implementacja void Graph::topological_dfs() { bool* visited = new (nothrow) bool[this->n]; int* fin = new (nothrow) int[this->n]; int t = 0; for (int k = 0; k < this->n; ++k) { visited[k] = false; fin[k] = 0; for (int k = 0; k < this->n; ++k) { if (visited[k] == false) this->topological_visit(k,t,visited,fin); delete[] visited; for (int k = 0; k < this->n; ++k){ int idx = max(fin,this->n); displayvertex(idx); fin[idx] = -1; delete[] fin; Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 9 17 / 20
20 Sortowanie topologiczne - Algorytm 2 Metoda usuwania wierzchołków o stopniu wejściowym równym zero Wykorzystywana własność: jeśli graf jest acyklicznym grafem skierowanym, to posiada przynajmniej jeden wierzchołek o stopniu wejściowym równym zero. Idea: Dopóki graf posiada wierzchołki o stopniu wejściowym zero, znajdujemy taki wierzchołek, usuwamy go z grafu wraz ze wszystkimi wychodzacymi z niego krawędziami i umieszczamy go na liście wierzchołków posortowanych topologicznie. Jeśli w grafie pozostana jakieś wierzchołki, to graf posiada cykle i sortowania topologicznego nie można wykonać. Złożoność: O( V + E ) Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 9 18 / 20
21 Sortowanie topologiczne - Algorytm 2 Algorytm: G = (V, E) 1: Q - Zbiór wszystkich wierzchoków bez krawędzi wchodzacych; 2: while Q! = do 3: Usuń wierzchołek n z Q. 4: Wypisz n. 5: for all m V takiego, że (n, m) E do 6: E = E \ (n, m) 7: if m nie ma już więcej krawędzi wchodzacych then 8: Wstaw m do Q. 9: end if 10: end for 11: end while 12: if E! = then 13: Graf G ma cykl. 14: end if Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 9 19 / 20
22 Sortowanie topologiczne - Algorytm 2, przykład Usuwamy Usuwamy Usuwamy 3 5 Usuwamy 4 5 Usuwamy 5 Sortowanie topologiczne: 1, 2, 3, 4, 5 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 9 20 / 20
Algorytmy i Struktury Danych.
 Algorytmy i Struktury Danych. Grafy Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 8 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 8 1 / 39 Plan wykładu
Algorytmy i Struktury Danych. Grafy Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 8 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 8 1 / 39 Plan wykładu
Algorytmy i Struktury Danych.
 Algorytmy i Struktury Danych. Grafy dr hab. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 8 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 8 1 / 42
Algorytmy i Struktury Danych. Grafy dr hab. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 8 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 8 1 / 42
Algorytmy i Struktury Danych.
 Algorytmy i Struktury Danych. Grafy Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 7 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 7 1 / 43 Grafy -
Algorytmy i Struktury Danych. Grafy Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 7 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 7 1 / 43 Grafy -
Algorytmy i Struktury Danych
 Algorytmy i Struktury Danych Drzewa poszukiwań binarnych dr hab. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 12 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych
Algorytmy i Struktury Danych Drzewa poszukiwań binarnych dr hab. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 12 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych
Podstawowe algorytmy i ich implementacje w C. Wykład 9
 Wstęp do programowania 1 Podstawowe algorytmy i ich implementacje w C Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 9 Element minimalny i maksymalny zbioru Element minimalny
Wstęp do programowania 1 Podstawowe algorytmy i ich implementacje w C Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 9 Element minimalny i maksymalny zbioru Element minimalny
Grafem nazywamy strukturę G = (V, E): V zbiór węzłów lub wierzchołków, Grafy dzielimy na grafy skierowane i nieskierowane:
 Wykład 4 grafy Grafem nazywamy strukturę G = (V, E): V zbiór węzłów lub wierzchołków, E zbiór krawędzi, Grafy dzielimy na grafy skierowane i nieskierowane: Formalnie, w grafach skierowanych E jest podzbiorem
Wykład 4 grafy Grafem nazywamy strukturę G = (V, E): V zbiór węzłów lub wierzchołków, E zbiór krawędzi, Grafy dzielimy na grafy skierowane i nieskierowane: Formalnie, w grafach skierowanych E jest podzbiorem
Algorytmy i Struktury Danych.
 Algorytmy i Struktury Danych. Liniowe struktury danych - Lista Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 5 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych.
Algorytmy i Struktury Danych. Liniowe struktury danych - Lista Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 5 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych.
Algorytmy grafowe. Wykład 2 Przeszukiwanie grafów. Tomasz Tyksiński CDV
 Algorytmy grafowe Wykład 2 Przeszukiwanie grafów Tomasz Tyksiński CDV Rozkład materiału 1. Podstawowe pojęcia teorii grafów, reprezentacje komputerowe grafów 2. Przeszukiwanie grafów 3. Spójność grafu,
Algorytmy grafowe Wykład 2 Przeszukiwanie grafów Tomasz Tyksiński CDV Rozkład materiału 1. Podstawowe pojęcia teorii grafów, reprezentacje komputerowe grafów 2. Przeszukiwanie grafów 3. Spójność grafu,
Struktury danych i złożoność obliczeniowa Wykład 5. Prof. dr hab. inż. Jan Magott
 Struktury danych i złożoność obliczeniowa Wykład. Prof. dr hab. inż. Jan Magott Algorytmy grafowe: podstawowe pojęcia, reprezentacja grafów, metody przeszukiwania, minimalne drzewa rozpinające, problemy
Struktury danych i złożoność obliczeniowa Wykład. Prof. dr hab. inż. Jan Magott Algorytmy grafowe: podstawowe pojęcia, reprezentacja grafów, metody przeszukiwania, minimalne drzewa rozpinające, problemy
Algorytmy i Struktury Danych
 Algorytmy i Struktury Danych Kopce Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 11 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych Wykład 11 1 / 69 Plan wykładu
Algorytmy i Struktury Danych Kopce Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 11 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych Wykład 11 1 / 69 Plan wykładu
Algorytmy i Struktury Danych.
 Algorytmy i Struktury Danych. Drzewa poszukiwań binarnych. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 10 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych.
Algorytmy i Struktury Danych. Drzewa poszukiwań binarnych. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 10 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych.
Algorytmy Grafowe. dr hab. Bożena Woźna-Szcześniak, prof. UJD. Wykład 5 i 6. Uniwersytet Humanistyczno-Przyrodniczy im. Jana Długosza w Częstochowie
 Algorytmy Grafowe dr hab. Bożena Woźna-Szcześniak, prof. UJD Uniwersytet Humanistyczno-Przyrodniczy im. Jana Długosza w Częstochowie b.wozna@ujd.edu.pl Wykład 5 i 6 B. Woźna-Szcześniak (UJD) Algorytmy
Algorytmy Grafowe dr hab. Bożena Woźna-Szcześniak, prof. UJD Uniwersytet Humanistyczno-Przyrodniczy im. Jana Długosza w Częstochowie b.wozna@ujd.edu.pl Wykład 5 i 6 B. Woźna-Szcześniak (UJD) Algorytmy
Algorytmy i Struktury Danych.
 Algorytmy i Struktury Danych. Metoda Dziel i zwyciężaj. Problem Sortowania, cd. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 2 Bożena Woźna-Szcześniak (AJD) Algorytmy
Algorytmy i Struktury Danych. Metoda Dziel i zwyciężaj. Problem Sortowania, cd. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 2 Bożena Woźna-Szcześniak (AJD) Algorytmy
Algorytmy i Struktury Danych.
 Algorytmy i Struktury Danych. Organizacja wykładu. Problem Sortowania. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 1 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury
Algorytmy i Struktury Danych. Organizacja wykładu. Problem Sortowania. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 1 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury
Algorytmy i Struktury Danych.
 Algorytmy i Struktury Danych. Liniowe struktury danych - Lista uporzadkowana. Wartownicy. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 6 Bożena Woźna-Szcześniak (AJD)
Algorytmy i Struktury Danych. Liniowe struktury danych - Lista uporzadkowana. Wartownicy. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 6 Bożena Woźna-Szcześniak (AJD)
Algorytmy i Struktury Danych
 Algorytmy i Struktury Danych Drzewa poszukiwań binarnych dr hab. Bożena Woźna-Szcześniak Jan Długosz University, Poland Wykład 8 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych Wykład 8 1 /
Algorytmy i Struktury Danych Drzewa poszukiwań binarnych dr hab. Bożena Woźna-Szcześniak Jan Długosz University, Poland Wykład 8 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych Wykład 8 1 /
Wstęp do Programowania potok funkcyjny
 Wstęp do Programowania potok funkcyjny Marcin Kubica 2010/2011 Outline 1 Podstawowe pojęcia Definition Graf = wierzchołki + krawędzie. Krawędzie muszą mieć różne końce. Między dwoma wierzchołkami może
Wstęp do Programowania potok funkcyjny Marcin Kubica 2010/2011 Outline 1 Podstawowe pojęcia Definition Graf = wierzchołki + krawędzie. Krawędzie muszą mieć różne końce. Między dwoma wierzchołkami może
Programowanie Proceduralne
 Programowanie Proceduralne Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 1 Bożena Woźna-Szcześniak (AJD) Programowanie Proceduralne Wykład 1 1 / 59 Cel wykładów z programowania
Programowanie Proceduralne Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 1 Bożena Woźna-Szcześniak (AJD) Programowanie Proceduralne Wykład 1 1 / 59 Cel wykładów z programowania
Algorytmy Grafowe. dr hab. Bożena Woźna-Szcześniak, prof. UJD. Wykład 1,2,3. Uniwersytet Humanistyczno-Przyrodniczy im. Jana Długosza w Częstochowie
 Algorytmy Grafowe dr hab. Bożena Woźna-Szcześniak, prof. UJD Uniwersytet Humanistyczno-Przyrodniczy im. Jana Długosza w Częstochowie b.wozna@ujd.edu.pl Wykład 1,2,3 B. Woźna-Szcześniak (UJD) Algorytmy
Algorytmy Grafowe dr hab. Bożena Woźna-Szcześniak, prof. UJD Uniwersytet Humanistyczno-Przyrodniczy im. Jana Długosza w Częstochowie b.wozna@ujd.edu.pl Wykład 1,2,3 B. Woźna-Szcześniak (UJD) Algorytmy
Sortowanie topologiczne skierowanych grafów acyklicznych
 Sortowanie topologiczne skierowanych grafów acyklicznych Metody boolowskie w informatyce Robert Sulkowski http://robert.brainusers.net 23 stycznia 2010 1 Definicja 1 (Cykl skierowany). Niech C = (V, A)
Sortowanie topologiczne skierowanych grafów acyklicznych Metody boolowskie w informatyce Robert Sulkowski http://robert.brainusers.net 23 stycznia 2010 1 Definicja 1 (Cykl skierowany). Niech C = (V, A)
Algorytmy i Struktury Danych.
 Algorytmy i Struktury Danych. Grafy dr hab. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 9 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 9 1 / 53
Algorytmy i Struktury Danych. Grafy dr hab. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 9 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 9 1 / 53
Wstęp do Programowania potok funkcyjny
 Wstęp do Programowania potok funkcyjny Marcin Kubica 2010/2011 Outline 1 BFS DFS Algorytm Dijkstry Algorytm Floyda-Warshalla Podstawowe pojęcia Definition Graf = wierzchołki + krawędzie. Krawędzie muszą
Wstęp do Programowania potok funkcyjny Marcin Kubica 2010/2011 Outline 1 BFS DFS Algorytm Dijkstry Algorytm Floyda-Warshalla Podstawowe pojęcia Definition Graf = wierzchołki + krawędzie. Krawędzie muszą
Przykłady grafów. Graf prosty, to graf bez pętli i bez krawędzi wielokrotnych.
 Grafy Graf Graf (ang. graph) to zbiór wierzchołków (ang. vertices), które mogą być połączone krawędziami (ang. edges) w taki sposób, że każda krawędź kończy się i zaczyna w którymś z wierzchołków. Graf
Grafy Graf Graf (ang. graph) to zbiór wierzchołków (ang. vertices), które mogą być połączone krawędziami (ang. edges) w taki sposób, że każda krawędź kończy się i zaczyna w którymś z wierzchołków. Graf
Ogólne wiadomości o grafach
 Ogólne wiadomości o grafach Algorytmy i struktury danych Wykład 5. Rok akademicki: / Pojęcie grafu Graf zbiór wierzchołków połączonych za pomocą krawędzi. Podstawowe rodzaje grafów: grafy nieskierowane,
Ogólne wiadomości o grafach Algorytmy i struktury danych Wykład 5. Rok akademicki: / Pojęcie grafu Graf zbiór wierzchołków połączonych za pomocą krawędzi. Podstawowe rodzaje grafów: grafy nieskierowane,
Matematyczne Podstawy Informatyki
 Matematyczne Podstawy Informatyki dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska Rok akademicki 03/0 Przeszukiwanie w głąb i wszerz I Przeszukiwanie metodą
Matematyczne Podstawy Informatyki dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska Rok akademicki 03/0 Przeszukiwanie w głąb i wszerz I Przeszukiwanie metodą
MATEMATYKA DYSKRETNA - MATERIAŁY DO WYKŁADU GRAFY
 ERIAŁY DO WYKŁADU GRAFY Graf nieskierowany Grafem nieskierowanym nazywamy parę G = (V, E), gdzie V jest pewnym zbiorem skończonym (zwanym zbiorem wierzchołków grafu G), natomiast E jest zbiorem nieuporządkowanych
ERIAŁY DO WYKŁADU GRAFY Graf nieskierowany Grafem nieskierowanym nazywamy parę G = (V, E), gdzie V jest pewnym zbiorem skończonym (zwanym zbiorem wierzchołków grafu G), natomiast E jest zbiorem nieuporządkowanych
Podstawowe własności grafów. Wykład 3. Własności grafów
 Wykład 3. Własności grafów 1 / 87 Suma grafów Niech będą dane grafy proste G 1 = (V 1, E 1) oraz G 2 = (V 2, E 2). 2 / 87 Suma grafów Niech będą dane grafy proste G 1 = (V 1, E 1) oraz G 2 = (V 2, E 2).
Wykład 3. Własności grafów 1 / 87 Suma grafów Niech będą dane grafy proste G 1 = (V 1, E 1) oraz G 2 = (V 2, E 2). 2 / 87 Suma grafów Niech będą dane grafy proste G 1 = (V 1, E 1) oraz G 2 = (V 2, E 2).
Wstęp do programowania. Drzewa. Piotr Chrząstowski-Wachtel
 Wstęp do programowania Drzewa Piotr Chrząstowski-Wachtel Drzewa Drzewa definiują matematycy, jako spójne nieskierowane grafy bez cykli. Równoważne określenia: Spójne grafy o n wierzchołkach i n-1 krawędziach
Wstęp do programowania Drzewa Piotr Chrząstowski-Wachtel Drzewa Drzewa definiują matematycy, jako spójne nieskierowane grafy bez cykli. Równoważne określenia: Spójne grafy o n wierzchołkach i n-1 krawędziach
Zofia Kruczkiewicz, Algorytmu i struktury danych, Wykład 14, 1
 Wykład Algorytmy grafowe metoda zachłanna. Właściwości algorytmu zachłannego:. W przeciwieństwie do metody programowania dynamicznego nie występuje etap dzielenia na mniejsze realizacje z wykorzystaniem
Wykład Algorytmy grafowe metoda zachłanna. Właściwości algorytmu zachłannego:. W przeciwieństwie do metody programowania dynamicznego nie występuje etap dzielenia na mniejsze realizacje z wykorzystaniem
Algorytmy z powracaniem
 Algorytmy z powracaniem Materiały Grafem nazywamy zbiór G = (V, E), gdzie: V jest zbiorem wierzchołków (ang. vertex) E jest zbiorem krawędzi (E można też określić jako podzbiór zbioru nieuporządkowanych
Algorytmy z powracaniem Materiały Grafem nazywamy zbiór G = (V, E), gdzie: V jest zbiorem wierzchołków (ang. vertex) E jest zbiorem krawędzi (E można też określić jako podzbiór zbioru nieuporządkowanych
Algorytmy Grafowe. dr hab. Bożena Woźna-Szcześniak, prof. UJD. Wykład 7,8,9. Uniwersytet Humanistyczno-Przyrodniczy im. Jana Długosza w Częstochowie
 Algorytmy Grafowe dr hab. Bożena Woźna-Szcześniak, prof. UJD Uniwersytet Humanistyczno-Przyrodniczy im. Jana Długosza w Częstochowie b.wozna@ujd.edu.pl Wykład 7,8,9 B. Woźna-Szcześniak (UJD) Algorytmy
Algorytmy Grafowe dr hab. Bożena Woźna-Szcześniak, prof. UJD Uniwersytet Humanistyczno-Przyrodniczy im. Jana Długosza w Częstochowie b.wozna@ujd.edu.pl Wykład 7,8,9 B. Woźna-Szcześniak (UJD) Algorytmy
Algorytmy i Struktury Danych.
 Algorytmy i Struktury Danych. Treści programowe. Złożoność obliczeniowa algorytmu na przykładach. dr hab. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 1 Bożena Woźna-Szcześniak
Algorytmy i Struktury Danych. Treści programowe. Złożoność obliczeniowa algorytmu na przykładach. dr hab. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 1 Bożena Woźna-Szcześniak
Spis treści. Przykład. Przykład 1 Przykład 2. Twórcy Informacje wstępne Pseudokod Przykład. 1 Grafy skierowane z wagami - przypomnienie
 Algorytmy Grafowe dr hab. Bożena Woźna-Szcześniak, prof. UJD Uniwersytet Humanistyczno-Przyrodniczy im. Jana Długosza w Częstochowie b.wozna@ujd.edu.pl Wykład 1,11,1 B. Woźna-Szcześniak (UJD) Algorytmy
Algorytmy Grafowe dr hab. Bożena Woźna-Szcześniak, prof. UJD Uniwersytet Humanistyczno-Przyrodniczy im. Jana Długosza w Częstochowie b.wozna@ujd.edu.pl Wykład 1,11,1 B. Woźna-Szcześniak (UJD) Algorytmy
Wstęp do Informatyki
 Wstęp do Informatyki dr hab. Bożena Woźna-Szcześniak, prof. AJD bwozna@gmail.com Jan Długosz University, Poland Wykład 8 Bożena Woźna-Szcześniak (AJD) Wstęp do Informatyki Wykład 8 1 / 32 Instrukcje iteracyjne
Wstęp do Informatyki dr hab. Bożena Woźna-Szcześniak, prof. AJD bwozna@gmail.com Jan Długosz University, Poland Wykład 8 Bożena Woźna-Szcześniak (AJD) Wstęp do Informatyki Wykład 8 1 / 32 Instrukcje iteracyjne
Algorytmy i struktury danych. Drzewa: BST, kopce. Letnie Warsztaty Matematyczno-Informatyczne
 Algorytmy i struktury danych Drzewa: BST, kopce Letnie Warsztaty Matematyczno-Informatyczne Drzewa: BST, kopce Definicja drzewa Drzewo (ang. tree) to nieskierowany, acykliczny, spójny graf. Drzewo może
Algorytmy i struktury danych Drzewa: BST, kopce Letnie Warsztaty Matematyczno-Informatyczne Drzewa: BST, kopce Definicja drzewa Drzewo (ang. tree) to nieskierowany, acykliczny, spójny graf. Drzewo może
Wstęp do Programowania 2
 Wstęp do Programowania 2 dr Bożena Woźna-Szcześniak bwozna@gmail.com Akademia im. Jana Długosza Wykład 5 W programowaniu obiektowym programista koncentruje się na obiektach. Zadaje sobie pytania typu:
Wstęp do Programowania 2 dr Bożena Woźna-Szcześniak bwozna@gmail.com Akademia im. Jana Długosza Wykład 5 W programowaniu obiektowym programista koncentruje się na obiektach. Zadaje sobie pytania typu:
Algorytmy i Struktury Danych.
 Algorytmy i Struktury Danych. Podstawowe struktury danych, cd. Wykład na podstawie ksiażki Roberta Sedgewicka i Kevina Wayne: Algorithms. Furth Edition. Princeton University dr hab. Bożena Woźna-Szcześniak
Algorytmy i Struktury Danych. Podstawowe struktury danych, cd. Wykład na podstawie ksiażki Roberta Sedgewicka i Kevina Wayne: Algorithms. Furth Edition. Princeton University dr hab. Bożena Woźna-Szcześniak
Algorytmy Równoległe i Rozproszone Część V - Model PRAM II
 Algorytmy Równoległe i Rozproszone Część V - Model PRAM II Łukasz Kuszner pokój 209, WETI http://www.sphere.pl/ kuszner/ kuszner@sphere.pl Oficjalna strona wykładu http://www.sphere.pl/ kuszner/arir/ 2005/06
Algorytmy Równoległe i Rozproszone Część V - Model PRAM II Łukasz Kuszner pokój 209, WETI http://www.sphere.pl/ kuszner/ kuszner@sphere.pl Oficjalna strona wykładu http://www.sphere.pl/ kuszner/arir/ 2005/06
Wykład 7. Algorytmy grafowe
 Wykład Algorytmy grafowe Algorytmy grafowe i podstawowe algorytmy przeszukiwania Problem Definicje i własności Reprezentacja Przeszukiwanie wszerz (Breadthirst Search) Przeszukiwanie w głąb (Depthirst
Wykład Algorytmy grafowe Algorytmy grafowe i podstawowe algorytmy przeszukiwania Problem Definicje i własności Reprezentacja Przeszukiwanie wszerz (Breadthirst Search) Przeszukiwanie w głąb (Depthirst
a) 7 b) 19 c) 21 d) 34
 Zadanie 1. Pytania testowe dotyczące podstawowych własności grafów. Zadanie 2. Przy każdym z zadań może się pojawić polecenie krótkiej charakterystyki algorytmu. Zadanie 3. W zadanym grafie sprawdzenie
Zadanie 1. Pytania testowe dotyczące podstawowych własności grafów. Zadanie 2. Przy każdym z zadań może się pojawić polecenie krótkiej charakterystyki algorytmu. Zadanie 3. W zadanym grafie sprawdzenie
Minimalne drzewa rozpinające
 KNM UŚ 26-28 listopada 2010 Ostrzeżenie Wprowadzenie Motywacja Definicje Niektóre pojęcia pojawiające się podczas tego referatu są naszymi autorskimi tłumaczeniami z języka angielskiego. Nie udało nam
KNM UŚ 26-28 listopada 2010 Ostrzeżenie Wprowadzenie Motywacja Definicje Niektóre pojęcia pojawiające się podczas tego referatu są naszymi autorskimi tłumaczeniami z języka angielskiego. Nie udało nam
Wykład 8. Drzewo rozpinające (minimum spanning tree)
 Wykład 8 Drzewo rozpinające (minimum spanning tree) 1 Minimalne drzewo rozpinające - przegląd Definicja problemu Własności minimalnych drzew rozpinających Algorytm Kruskala Algorytm Prima Literatura Cormen,
Wykład 8 Drzewo rozpinające (minimum spanning tree) 1 Minimalne drzewo rozpinające - przegląd Definicja problemu Własności minimalnych drzew rozpinających Algorytm Kruskala Algorytm Prima Literatura Cormen,
Wstęp do sieci neuronowych, wykład 11 Łańcuchy Markova
 Wstęp do sieci neuronowych, wykład 11 Łańcuchy Markova M. Czoków, J. Piersa 2010-12-21 1 Definicja Własności Losowanie z rozkładu dyskretnego 2 3 Łańcuch Markova Definicja Własności Losowanie z rozkładu
Wstęp do sieci neuronowych, wykład 11 Łańcuchy Markova M. Czoków, J. Piersa 2010-12-21 1 Definicja Własności Losowanie z rozkładu dyskretnego 2 3 Łańcuch Markova Definicja Własności Losowanie z rozkładu
Porównanie algorytmów wyszukiwania najkrótszych ścieżek międz. grafu. Daniel Golubiewski. 22 listopada Instytut Informatyki
 Porównanie algorytmów wyszukiwania najkrótszych ścieżek między wierzchołkami grafu. Instytut Informatyki 22 listopada 2015 Algorytm DFS w głąb Algorytm przejścia/przeszukiwania w głąb (ang. Depth First
Porównanie algorytmów wyszukiwania najkrótszych ścieżek między wierzchołkami grafu. Instytut Informatyki 22 listopada 2015 Algorytm DFS w głąb Algorytm przejścia/przeszukiwania w głąb (ang. Depth First
Wykład 10 Grafy, algorytmy grafowe
 . Typy złożoności obliczeniowej Wykład Grafy, algorytmy grafowe Typ złożoności oznaczenie n Jedna operacja trwa µs 5 logarytmiczna lgn. s. s.7 s liniowa n. s.5 s. s Logarytmicznoliniowa nlgn. s.8 s.4 s
. Typy złożoności obliczeniowej Wykład Grafy, algorytmy grafowe Typ złożoności oznaczenie n Jedna operacja trwa µs 5 logarytmiczna lgn. s. s.7 s liniowa n. s.5 s. s Logarytmicznoliniowa nlgn. s.8 s.4 s
Wstęp do sieci neuronowych, wykład 12 Łańcuchy Markowa
 Wstęp do sieci neuronowych, wykład 12 Łańcuchy Markowa M. Czoków, J. Piersa 2012-01-10 1 Łańcucha Markowa 2 Istnienie Szukanie stanu stacjonarnego 3 1 Łańcucha Markowa 2 Istnienie Szukanie stanu stacjonarnego
Wstęp do sieci neuronowych, wykład 12 Łańcuchy Markowa M. Czoków, J. Piersa 2012-01-10 1 Łańcucha Markowa 2 Istnienie Szukanie stanu stacjonarnego 3 1 Łańcucha Markowa 2 Istnienie Szukanie stanu stacjonarnego
Algorytmy i Struktury Danych.
 Algorytmy i Struktury Danych. Problem Sortowania, cd. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 3 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład
Algorytmy i Struktury Danych. Problem Sortowania, cd. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 3 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład
Języki programowania, wtorek , 12:15-13:45 Zadanie 11 - ostatnie
 Języki programowania, wtorek 10.01.2017, 12:15-13:45 Zadanie 11 - ostatnie Dzisiaj wykorzystamy kolejną bardzo ważną rzecz języka C++ - szablony funkcji i szablony klas. Wstęp co to są klasy i funkcje
Języki programowania, wtorek 10.01.2017, 12:15-13:45 Zadanie 11 - ostatnie Dzisiaj wykorzystamy kolejną bardzo ważną rzecz języka C++ - szablony funkcji i szablony klas. Wstęp co to są klasy i funkcje
Kurs programowania. Wykład 9. Wojciech Macyna. 28 kwiecień 2016
 Wykład 9 28 kwiecień 2016 Java Collections Framework (w C++ Standard Template Library) Kolekcja (kontener) Obiekt grupujacy/przechowuj acy jakieś elementy (obiekty lub wartości). Przykładami kolekcji sa
Wykład 9 28 kwiecień 2016 Java Collections Framework (w C++ Standard Template Library) Kolekcja (kontener) Obiekt grupujacy/przechowuj acy jakieś elementy (obiekty lub wartości). Przykładami kolekcji sa
Reprezentacje grafów nieskierowanych Reprezentacje grafów skierowanych. Wykład 2. Reprezentacja komputerowa grafów
 Wykład 2. Reprezentacja komputerowa grafów 1 / 69 Macierz incydencji Niech graf G będzie grafem nieskierowanym bez pętli o n wierzchołkach (x 1, x 2,..., x n) i m krawędziach (e 1, e 2,..., e m). 2 / 69
Wykład 2. Reprezentacja komputerowa grafów 1 / 69 Macierz incydencji Niech graf G będzie grafem nieskierowanym bez pętli o n wierzchołkach (x 1, x 2,..., x n) i m krawędziach (e 1, e 2,..., e m). 2 / 69
ZASADY PROGRAMOWANIA KOMPUTERÓW ZAP zima 2014/2015. Drzewa BST c.d., równoważenie drzew, kopce.
 POLITECHNIKA WARSZAWSKA Instytut Automatyki i Robotyki ZASADY PROGRAMOWANIA KOMPUTERÓW ZAP zima 204/205 Język programowania: Środowisko programistyczne: C/C++ Qt Wykład 2 : Drzewa BST c.d., równoważenie
POLITECHNIKA WARSZAWSKA Instytut Automatyki i Robotyki ZASADY PROGRAMOWANIA KOMPUTERÓW ZAP zima 204/205 Język programowania: Środowisko programistyczne: C/C++ Qt Wykład 2 : Drzewa BST c.d., równoważenie
Programowanie Procedurale
 Programowanie Procedurale Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 6 Bożena Woźna-Szcześniak (AJD) Programowanie Procedurale Wykład 6 1 / 27 Zbiór ctime zawiera deklarcję
Programowanie Procedurale Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 6 Bożena Woźna-Szcześniak (AJD) Programowanie Procedurale Wykład 6 1 / 27 Zbiór ctime zawiera deklarcję
Złożoność obliczeniowa klasycznych problemów grafowych
 Złożoność obliczeniowa klasycznych problemów grafowych Oznaczenia: G graf, V liczba wierzchołków, E liczba krawędzi 1. Spójność grafu Graf jest spójny jeżeli istnieje ścieżka łącząca każdą parę jego wierzchołków.
Złożoność obliczeniowa klasycznych problemów grafowych Oznaczenia: G graf, V liczba wierzchołków, E liczba krawędzi 1. Spójność grafu Graf jest spójny jeżeli istnieje ścieżka łącząca każdą parę jego wierzchołków.
Strategia "dziel i zwyciężaj"
 Strategia "dziel i zwyciężaj" W tej metodzie problem dzielony jest na kilka mniejszych podproblemów podobnych do początkowego problemu. Problemy te rozwiązywane są rekurencyjnie, a następnie rozwiązania
Strategia "dziel i zwyciężaj" W tej metodzie problem dzielony jest na kilka mniejszych podproblemów podobnych do początkowego problemu. Problemy te rozwiązywane są rekurencyjnie, a następnie rozwiązania
Sieć (graf skierowany)
 Sieci Sieć (graf skierowany) Siecia (grafem skierowanym) G = (V, A) nazywamy zbiór wierzchołków V oraz zbiór łuków A V V. V = {A, B, C, D, E, F}, A = {(A, B), (A, D), (A, C), (B, C),..., } Ścieżki i cykle
Sieci Sieć (graf skierowany) Siecia (grafem skierowanym) G = (V, A) nazywamy zbiór wierzchołków V oraz zbiór łuków A V V. V = {A, B, C, D, E, F}, A = {(A, B), (A, D), (A, C), (B, C),..., } Ścieżki i cykle
Egzaminy i inne zadania. Semestr II.
 Egzaminy i inne zadania. Semestr II. Poniższe zadania są wyborem zadań ze Wstępu do Informatyki z egzaminów jakie przeprowadziłem w ciągu ostatnich lat. Ponadto dołączyłem szereg zadań, które pojawiały
Egzaminy i inne zadania. Semestr II. Poniższe zadania są wyborem zadań ze Wstępu do Informatyki z egzaminów jakie przeprowadziłem w ciągu ostatnich lat. Ponadto dołączyłem szereg zadań, które pojawiały
Algorytmy i Struktury Danych.
 Algorytmy i Struktury Danych. Problem Sortowania. Metoda Dziel i zwyciężaj. dr hab. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 4 Bożena Woźna-Szcześniak (AJD) Algorytmy
Algorytmy i Struktury Danych. Problem Sortowania. Metoda Dziel i zwyciężaj. dr hab. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 4 Bożena Woźna-Szcześniak (AJD) Algorytmy
Digraf. 13 maja 2017
 Digraf 13 maja 2017 Graf skierowany, digraf, digraf prosty Definicja 1 Digraf prosty G to (V, E), gdzie V jest zbiorem wierzchołków, E jest rodziną zorientowanych krawędzi, między różnymi wierzchołkami,
Digraf 13 maja 2017 Graf skierowany, digraf, digraf prosty Definicja 1 Digraf prosty G to (V, E), gdzie V jest zbiorem wierzchołków, E jest rodziną zorientowanych krawędzi, między różnymi wierzchołkami,
Teoria obliczeń i złożoność obliczeniowa
 Teoria obliczeń i złożoność obliczeniowa Kontakt: dr hab. inż. Adam Kasperski, prof. PWr. pokój 509 B4 adam.kasperski@pwr.wroc.pl materiały + informacje na stronie www. Zaliczenie: Egzamin Literatura Problemy
Teoria obliczeń i złożoność obliczeniowa Kontakt: dr hab. inż. Adam Kasperski, prof. PWr. pokój 509 B4 adam.kasperski@pwr.wroc.pl materiały + informacje na stronie www. Zaliczenie: Egzamin Literatura Problemy
Algorytmy i Struktury Danych.
 Algorytmy i Struktury Danych. Podstawowe struktury danych dr hab. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 6 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych.
Algorytmy i Struktury Danych. Podstawowe struktury danych dr hab. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 6 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych.
Algorytmy i Struktury Danych.
 Algorytmy i Struktury Danych. Abstrakcyjne struktury danych dr hab. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 5 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury
Algorytmy i Struktury Danych. Abstrakcyjne struktury danych dr hab. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 5 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury
Znajdowanie skojarzeń na maszynie równoległej
 11 grudnia 2008 Spis treści 1 Skojarzenia w różnych klasach grafów Drzewa Grafy gęste Grafy regularne dwudzielne Claw-free graphs 2 Drzewa Skojarzenia w drzewach Fakt Wybierajac krawędź do skojarzenia
11 grudnia 2008 Spis treści 1 Skojarzenia w różnych klasach grafów Drzewa Grafy gęste Grafy regularne dwudzielne Claw-free graphs 2 Drzewa Skojarzenia w drzewach Fakt Wybierajac krawędź do skojarzenia
RKI Zajęcia 14 Przeszukiwanie grafu w głąb
 RKI Zajęcia 14 Przeszukiwanie grafu w głąb Piersa Jarosław 2010-05-09 1 Wprowadzenie Natenczas Wojski chwycił na taśmie przypięty Swój róg bawoli, długi, cętkowany, kręty Jak wąż boa, oburącz do ust go
RKI Zajęcia 14 Przeszukiwanie grafu w głąb Piersa Jarosław 2010-05-09 1 Wprowadzenie Natenczas Wojski chwycił na taśmie przypięty Swój róg bawoli, długi, cętkowany, kręty Jak wąż boa, oburącz do ust go
Wykład 6_1 Abstrakcyjne typy danych stos Realizacja tablicowa i za pomocą rekurencyjnych typów danych
 Wykład 6_ Abstrakcyjne typy danych stos Realizacja tablicowa i za pomocą rekurencyjnych typów danych Abstrakcyjny typ danych Klient korzystający z abstrakcyjnego typu danych: o ma do dyspozycji jedynie
Wykład 6_ Abstrakcyjne typy danych stos Realizacja tablicowa i za pomocą rekurencyjnych typów danych Abstrakcyjny typ danych Klient korzystający z abstrakcyjnego typu danych: o ma do dyspozycji jedynie
Programowanie dynamiczne i algorytmy zachłanne
 Programowanie dynamiczne i algorytmy zachłanne Tomasz Głowacki tglowacki@cs.put.poznan.pl Zajęcia finansowane z projektu "Rozwój i doskonalenie kształcenia na Politechnice Poznańskiej w zakresie technologii
Programowanie dynamiczne i algorytmy zachłanne Tomasz Głowacki tglowacki@cs.put.poznan.pl Zajęcia finansowane z projektu "Rozwój i doskonalenie kształcenia na Politechnice Poznańskiej w zakresie technologii
Wykład X. Programowanie. dr inż. Janusz Słupik. Gliwice, Wydział Matematyki Stosowanej Politechniki Śląskiej. c Copyright 2016 Janusz Słupik
 Wykład X Wydział Matematyki Stosowanej Politechniki Śląskiej Gliwice, 2016 c Copyright 2016 Janusz Słupik Drzewa binarne Drzewa binarne Drzewo binarne - to drzewo (graf spójny bez cykli) z korzeniem (wyróżnionym
Wykład X Wydział Matematyki Stosowanej Politechniki Śląskiej Gliwice, 2016 c Copyright 2016 Janusz Słupik Drzewa binarne Drzewa binarne Drzewo binarne - to drzewo (graf spójny bez cykli) z korzeniem (wyróżnionym
Algorytm Dijkstry znajdowania najkrótszej ścieżki w grafie
 Algorytm Dijkstry znajdowania najkrótszej ścieżki w grafie Używane struktury danych: V - zbiór wierzchołków grafu, V = {1,2,3...,n} E - zbiór krawędzi grafu, E = {(i,j),...}, gdzie i, j Î V i istnieje
Algorytm Dijkstry znajdowania najkrótszej ścieżki w grafie Używane struktury danych: V - zbiór wierzchołków grafu, V = {1,2,3...,n} E - zbiór krawędzi grafu, E = {(i,j),...}, gdzie i, j Î V i istnieje
Algorytmy i Struktury Danych.
 Algorytmy i Struktury Danych. Liniowe struktury danych. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 4 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład
Algorytmy i Struktury Danych. Liniowe struktury danych. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 4 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład
Struktury danych i złożoność obliczeniowa Wykład 2. Prof. dr hab. inż. Jan Magott
 Struktury danych i złożoność obliczeniowa Wykład 2. Prof. dr hab. inż. Jan Magott Metody konstrukcji algorytmów: Siłowa (ang. brute force), Dziel i zwyciężaj (ang. divide-and-conquer), Zachłanna (ang.
Struktury danych i złożoność obliczeniowa Wykład 2. Prof. dr hab. inż. Jan Magott Metody konstrukcji algorytmów: Siłowa (ang. brute force), Dziel i zwyciężaj (ang. divide-and-conquer), Zachłanna (ang.
Temat: Struktury danych do reprezentacji grafów. Wybrane algorytmy grafowe.
 Temat: Struktury danych do reprezentacji grafów. Wybrane algorytmy grafowe. Oznaczenia G = V, E - graf bez wag, gdzie V - zbiór wierzchołków, E- zbiór krawdzi V = n - liczba wierzchołków grafu G E = m
Temat: Struktury danych do reprezentacji grafów. Wybrane algorytmy grafowe. Oznaczenia G = V, E - graf bez wag, gdzie V - zbiór wierzchołków, E- zbiór krawdzi V = n - liczba wierzchołków grafu G E = m
Informatyka II. Laboratorium.
 Informatyka II. Laboratorium. Ćwiczenie 13. Reprezentacja grafów w Java. Wyszukiwanie najkrótszej ścieżki w grafie. I. Wstęp. Grafy [1] są podstawową strukturą danych dla wielu algorytmów stosowanych w
Informatyka II. Laboratorium. Ćwiczenie 13. Reprezentacja grafów w Java. Wyszukiwanie najkrótszej ścieżki w grafie. I. Wstęp. Grafy [1] są podstawową strukturą danych dla wielu algorytmów stosowanych w
Algorytmiczna teoria grafów
 Przedmiot fakultatywny 20h wykładu + 20h ćwiczeń 21 lutego 2014 Zasady zaliczenia 1 ćwiczenia (ocena): kolokwium, zadania programistyczne (implementacje algorytmów), praca na ćwiczeniach. 2 Wykład (egzamin)
Przedmiot fakultatywny 20h wykładu + 20h ćwiczeń 21 lutego 2014 Zasady zaliczenia 1 ćwiczenia (ocena): kolokwium, zadania programistyczne (implementacje algorytmów), praca na ćwiczeniach. 2 Wykład (egzamin)
Siedem cudów informatyki czyli o algorytmach zdumiewajacych
 Siedem cudów informatyki czyli o algorytmach zdumiewajacych Łukasz Kowalik kowalik@mimuw.edu.pl Instytut Informatyki Uniwersytet Warszawski Łukasz Kowalik, Siedem cudów informatyki p. 1/25 Problem 1: mnożenie
Siedem cudów informatyki czyli o algorytmach zdumiewajacych Łukasz Kowalik kowalik@mimuw.edu.pl Instytut Informatyki Uniwersytet Warszawski Łukasz Kowalik, Siedem cudów informatyki p. 1/25 Problem 1: mnożenie
Algorytmy i struktury danych. Co dziś? Tytułem przypomnienia metoda dziel i zwyciężaj. Wykład VIII Elementarne techniki algorytmiczne
 Algorytmy i struktury danych Wykład VIII Elementarne techniki algorytmiczne Co dziś? Algorytmy zachłanne (greedyalgorithms) 2 Tytułem przypomnienia metoda dziel i zwyciężaj. Problem można podzielić na
Algorytmy i struktury danych Wykład VIII Elementarne techniki algorytmiczne Co dziś? Algorytmy zachłanne (greedyalgorithms) 2 Tytułem przypomnienia metoda dziel i zwyciężaj. Problem można podzielić na
WYŻSZA SZKOŁA INFORMATYKI STOSOWANEJ I ZARZĄDZANIA
 DROGI i CYKLE w grafach Dla grafu (nieskierowanego) G = ( V, E ) drogą z wierzchołka v 0 V do v t V nazywamy ciąg (naprzemienny) wierzchołków i krawędzi grafu: ( v 0, e, v, e,..., v t, e t, v t ), spełniający
DROGI i CYKLE w grafach Dla grafu (nieskierowanego) G = ( V, E ) drogą z wierzchołka v 0 V do v t V nazywamy ciąg (naprzemienny) wierzchołków i krawędzi grafu: ( v 0, e, v, e,..., v t, e t, v t ), spełniający
Struktury danych i złozoność obliczeniowa. Prof. dr hab. inż. Jan Magott
 Struktury danych i złozoność obliczeniowa Prof. dr hab. inż. Jan Magott Formy zajęć: Wykład 1 godz., Ćwiczenia 1 godz., Projekt 2 godz.. Adres strony z materiałami do wykładu: http://www.zio.iiar.pwr.wroc.pl/sdizo.html
Struktury danych i złozoność obliczeniowa Prof. dr hab. inż. Jan Magott Formy zajęć: Wykład 1 godz., Ćwiczenia 1 godz., Projekt 2 godz.. Adres strony z materiałami do wykładu: http://www.zio.iiar.pwr.wroc.pl/sdizo.html
Podstawy algorytmiki i programowania - wykład 6 Sortowanie- algorytmy
 1 Podstawy algorytmiki i programowania - wykład 6 Sortowanie- algorytmy Treści prezentowane w wykładzie zostały oparte o: S. Prata, Język C++. Szkoła programowania. Wydanie VI, Helion, 2012 www.cplusplus.com
1 Podstawy algorytmiki i programowania - wykład 6 Sortowanie- algorytmy Treści prezentowane w wykładzie zostały oparte o: S. Prata, Język C++. Szkoła programowania. Wydanie VI, Helion, 2012 www.cplusplus.com
prowadzący dr ADRIAN HORZYK /~horzyk e-mail: horzyk@agh tel.: 012-617 Konsultacje paw. D-13/325
 PODSTAWY INFORMATYKI WYKŁAD 8. prowadzący dr ADRIAN HORZYK http://home home.agh.edu.pl/~ /~horzyk e-mail: horzyk@agh agh.edu.pl tel.: 012-617 617-4319 Konsultacje paw. D-13/325 DRZEWA Drzewa to rodzaj
PODSTAWY INFORMATYKI WYKŁAD 8. prowadzący dr ADRIAN HORZYK http://home home.agh.edu.pl/~ /~horzyk e-mail: horzyk@agh agh.edu.pl tel.: 012-617 617-4319 Konsultacje paw. D-13/325 DRZEWA Drzewa to rodzaj
Algorytm selekcji Hoare a. Łukasz Miemus
 Algorytm selekcji Hoare a Łukasz Miemus 1 lutego 2006 Rozdział 1 O algorytmie 1.1 Problem Mamy tablicę A[N] różnych elementów i zmienną int K, takie że 1 K N. Oczekiwane rozwiązanie to określenie K-tego
Algorytm selekcji Hoare a Łukasz Miemus 1 lutego 2006 Rozdział 1 O algorytmie 1.1 Problem Mamy tablicę A[N] różnych elementów i zmienną int K, takie że 1 K N. Oczekiwane rozwiązanie to określenie K-tego
Algorytmy i struktury danych
 Algorytmy i struktury danych Wykład 11 - Grafy i podstawowe algorytmy grafowe (ciąg dalszy) Janusz Szwabiński Plan wykładu: Przeszukiwanie w głąb Studium przypadku - zagadnienie skoczka szachowego (ang.
Algorytmy i struktury danych Wykład 11 - Grafy i podstawowe algorytmy grafowe (ciąg dalszy) Janusz Szwabiński Plan wykładu: Przeszukiwanie w głąb Studium przypadku - zagadnienie skoczka szachowego (ang.
. Podstawy Programowania 2. Algorytmy dfs i bfs. Arkadiusz Chrobot. 2 czerwca 2019
 Podstawy Programowania Algorytmy dfs i bfs Arkadiusz Chrobot Zakład Informatyki czerwca 09 / 70 Plan Wstęp Algorytm BFS Podsumowanie / 70 Wstęp Wstęp Istnieje wiele algorytmów związanych z grafami, które
Podstawy Programowania Algorytmy dfs i bfs Arkadiusz Chrobot Zakład Informatyki czerwca 09 / 70 Plan Wstęp Algorytm BFS Podsumowanie / 70 Wstęp Wstęp Istnieje wiele algorytmów związanych z grafami, które
RKI Zajęcia 13 Przeszukiwanie grafu wszerz
 RKI Zajęcia 13 Przeszukiwanie grafu wszerz Piersa Jarosław 2010-04-25 1 Wprowadzenie Biega, krzyczy pan Hilary: Gdzie są moje okulary? Szuka w spodniach i w surducie, W prawym bucie, w lewym bucie. Julian
RKI Zajęcia 13 Przeszukiwanie grafu wszerz Piersa Jarosław 2010-04-25 1 Wprowadzenie Biega, krzyczy pan Hilary: Gdzie są moje okulary? Szuka w spodniach i w surducie, W prawym bucie, w lewym bucie. Julian
Programowanie w VB Proste algorytmy sortowania
 Programowanie w VB Proste algorytmy sortowania Sortowanie bąbelkowe Algorytm sortowania bąbelkowego polega na porównywaniu par elementów leżących obok siebie i, jeśli jest to potrzebne, zmienianiu ich
Programowanie w VB Proste algorytmy sortowania Sortowanie bąbelkowe Algorytm sortowania bąbelkowego polega na porównywaniu par elementów leżących obok siebie i, jeśli jest to potrzebne, zmienianiu ich
Digraf o V wierzchołkach posiada V 2 krawędzi, zatem liczba różnych digrafów o V wierzchołkach wynosi 2 VxV
 Graf skierowany (digraf) zbiór wierzchołków i zbiór krawędzi skierowanych łączących (co najwyżej jeden raz) uporządkowane pary wierzchołków. Mówimy wtedy, że krawędź łączy pierwszy wierzchołek z drugim
Graf skierowany (digraf) zbiór wierzchołków i zbiór krawędzi skierowanych łączących (co najwyżej jeden raz) uporządkowane pary wierzchołków. Mówimy wtedy, że krawędź łączy pierwszy wierzchołek z drugim
Algorytm DFS Wprowadzenie teoretyczne. Algorytm DFS Wprowadzenie teoretyczne. Algorytm DFS Animacja. Algorytm DFS Animacja. Notatki. Notatki.
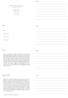 Podstawy Programowania Algorytmy dfs i bfs Arkadiusz Chrobot Zakład Informatyki czerwca 09 / 70 Plan Wstęp Podsumowanie / 70 Wstęp Istnieje wiele algorytmów związanych z grafami, które w skrócie nazywane
Podstawy Programowania Algorytmy dfs i bfs Arkadiusz Chrobot Zakład Informatyki czerwca 09 / 70 Plan Wstęp Podsumowanie / 70 Wstęp Istnieje wiele algorytmów związanych z grafami, które w skrócie nazywane
Programowanie dynamiczne
 Programowanie dynamiczne Programowanie rekurencyjne: ZALETY: - prostota - naturalność sformułowania WADY: - trudność w oszacowaniu zasobów (czasu i pamięci) potrzebnych do realizacji Czy jest możliwe wykorzystanie
Programowanie dynamiczne Programowanie rekurencyjne: ZALETY: - prostota - naturalność sformułowania WADY: - trudność w oszacowaniu zasobów (czasu i pamięci) potrzebnych do realizacji Czy jest możliwe wykorzystanie
Grafy i Zastosowania. 5: Drzewa Rozpinające. c Marcin Sydow. Drzewa rozpinające. Cykle i rozcięcia fundamentalne. Zastosowania
 Grafy i Grafy i 5: Rozpinające Spis zagadnień Grafy i i lasy cykle fundamentalne i własności cykli i rozcięć przestrzenie cykli i rozcięć* : zastosowanie w sieciach elektrycznych minimalne * algorytm Kruskala*
Grafy i Grafy i 5: Rozpinające Spis zagadnień Grafy i i lasy cykle fundamentalne i własności cykli i rozcięć przestrzenie cykli i rozcięć* : zastosowanie w sieciach elektrycznych minimalne * algorytm Kruskala*
Wstęp do programowania. Listy. Piotr Chrząstowski-Wachtel
 Wstęp do programowania Listy Piotr Chrząstowski-Wachtel Do czego stosujemy listy? Listy stosuje się wszędzie tam, gdzie występuje duży rozrzut w możliwym rozmiarze danych, np. w reprezentacji grafów jeśli
Wstęp do programowania Listy Piotr Chrząstowski-Wachtel Do czego stosujemy listy? Listy stosuje się wszędzie tam, gdzie występuje duży rozrzut w możliwym rozmiarze danych, np. w reprezentacji grafów jeśli
Struktury danych i złożoność obliczeniowa Wykład 7. Prof. dr hab. inż. Jan Magott
 Struktury danych i złożoność obliczeniowa Wykład 7 Prof. dr hab. inż. Jan Magott Problemy NP-zupełne Transformacją wielomianową problemu π 2 do problemu π 1 (π 2 π 1 ) jest funkcja f: D π2 D π1 spełniająca
Struktury danych i złożoność obliczeniowa Wykład 7 Prof. dr hab. inż. Jan Magott Problemy NP-zupełne Transformacją wielomianową problemu π 2 do problemu π 1 (π 2 π 1 ) jest funkcja f: D π2 D π1 spełniająca
Rozwiązywanie problemów metodą przeszukiwania
 Rozwiązywanie problemów metodą przeszukiwania Dariusz Banasiak Katedra Informatyki Technicznej W4/K9 Politechnika Wrocławska Reprezentacja problemu w przestrzeni stanów Jedną z ważniejszych metod sztucznej
Rozwiązywanie problemów metodą przeszukiwania Dariusz Banasiak Katedra Informatyki Technicznej W4/K9 Politechnika Wrocławska Reprezentacja problemu w przestrzeni stanów Jedną z ważniejszych metod sztucznej
Drzewa poszukiwań binarnych
 1 Drzewa poszukiwań binarnych Kacper Pawłowski Streszczenie W tej pracy przedstawię zagadnienia związane z drzewami poszukiwań binarnych. Przytoczę poszczególne operacje na tej strukturze danych oraz ich
1 Drzewa poszukiwań binarnych Kacper Pawłowski Streszczenie W tej pracy przedstawię zagadnienia związane z drzewami poszukiwań binarnych. Przytoczę poszczególne operacje na tej strukturze danych oraz ich
Wstęp do programowania. Zastosowania stosów i kolejek. Piotr Chrząstowski-Wachtel
 Wstęp do programowania Zastosowania stosów i kolejek Piotr Chrząstowski-Wachtel FIFO - LIFO Kolejki i stosy służą do przechowywania wartości zbiorów dynamicznych, czyli takich, które powstają przez dodawanie
Wstęp do programowania Zastosowania stosów i kolejek Piotr Chrząstowski-Wachtel FIFO - LIFO Kolejki i stosy służą do przechowywania wartości zbiorów dynamicznych, czyli takich, które powstają przez dodawanie
Podejście zachłanne, a programowanie dynamiczne
 Podejście zachłanne, a programowanie dynamiczne Algorytm zachłanny pobiera po kolei elementy danych, za każdym razem wybierając taki, który wydaje się najlepszy w zakresie spełniania pewnych kryteriów
Podejście zachłanne, a programowanie dynamiczne Algorytm zachłanny pobiera po kolei elementy danych, za każdym razem wybierając taki, który wydaje się najlepszy w zakresie spełniania pewnych kryteriów
Indukowane Reguły Decyzyjne I. Wykład 3
 Indukowane Reguły Decyzyjne I Wykład 3 IRD Wykład 3 Plan Powtórka Grafy Drzewa klasyfikacyjne Testy wstęp Klasyfikacja obiektów z wykorzystaniem drzewa Reguły decyzyjne generowane przez drzewo 2 Powtórzenie
Indukowane Reguły Decyzyjne I Wykład 3 IRD Wykład 3 Plan Powtórka Grafy Drzewa klasyfikacyjne Testy wstęp Klasyfikacja obiektów z wykorzystaniem drzewa Reguły decyzyjne generowane przez drzewo 2 Powtórzenie
Programowanie i struktury danych
 Programowanie i struktury danych 1 / 30 STL Standard Template Library, STL (ang. = Standardowa Biblioteka Wzorców) biblioteka C++ zawierająca szablony (wzorce), które umożliwiają wielokrotne użycie. Główne
Programowanie i struktury danych 1 / 30 STL Standard Template Library, STL (ang. = Standardowa Biblioteka Wzorców) biblioteka C++ zawierająca szablony (wzorce), które umożliwiają wielokrotne użycie. Główne
Problem 1 prec f max. Algorytm Lawlera dla problemu 1 prec f max. 1 procesor. n zadań T 1,..., T n (ich zbiór oznaczamy przez T )
 Joanna Berlińska Algorytmika w projektowaniu systemów - ćwiczenia 1 1 Problem 1 prec f max 1 procesor (ich zbiór oznaczamy przez T ) czas wykonania zadania T j wynosi p j z zadaniem T j związana jest niemalejąca
Joanna Berlińska Algorytmika w projektowaniu systemów - ćwiczenia 1 1 Problem 1 prec f max 1 procesor (ich zbiór oznaczamy przez T ) czas wykonania zadania T j wynosi p j z zadaniem T j związana jest niemalejąca
TEORIA GRAFÓW I SIECI
 TEORIA GRAFÓW I SIECI Temat nr : Grafy Berge a dr hab. inż. Zbigniew TARAPATA, prof. WAT e-mail: zbigniew.tarapata@wat.edu.pl http://tarapata.edu.pl tel.: 6-83-95-0, p.5/00 Zakład Badań Operacyjnych i
TEORIA GRAFÓW I SIECI Temat nr : Grafy Berge a dr hab. inż. Zbigniew TARAPATA, prof. WAT e-mail: zbigniew.tarapata@wat.edu.pl http://tarapata.edu.pl tel.: 6-83-95-0, p.5/00 Zakład Badań Operacyjnych i
Grafy (3): drzewa. Wykłady z matematyki dyskretnej dla informatyków i teleinformatyków. UTP Bydgoszcz
 Grafy (3): drzewa Wykłady z matematyki dyskretnej dla informatyków i teleinformatyków UTP Bydgoszcz 13 (Wykłady z matematyki dyskretnej) Grafy (3): drzewa 13 1 / 107 Drzewo Definicja. Drzewo to graf acykliczny
Grafy (3): drzewa Wykłady z matematyki dyskretnej dla informatyków i teleinformatyków UTP Bydgoszcz 13 (Wykłady z matematyki dyskretnej) Grafy (3): drzewa 13 1 / 107 Drzewo Definicja. Drzewo to graf acykliczny
