Stany wysokospinowe w teorii sprzężonych klasterów w połączeniu z metodą równań ruchu dla układów podwójnie zjonizowanych
|
|
|
- Bogusław Gajewski
- 4 lat temu
- Przeglądów:
Transkrypt
1 Wszczęcie przewodu doktorskiego Proponowany temat pracy: Stany wysokospinowe w teorii sprzężonych klasterów w połączeniu z metodą równań ruchu dla układów podwójnie zjonizowanych Łukasz Lupa Opiekun naukowy: dr hab. Monika Musiał, prof. UŚ Uniwersytet Śląski Instytut Chemii Zakład Chemii Teoretycznej Katowice, 2013
2 Spis treści 1 Wstęp 3 2 Metoda sprzężonych klasterów Wyrażenienaenergięwmetodziesprzężonychklasterów Równaniametodysprzężonychklasterów Elektronowe stany wzbudzone i zjonizowane w oparciu o metodę sprzężonych klasterów Metodarównańruchu Metoda równań ruchu w połączeniu z metodą sprzężonych klasterów WariantymetodDIP-EOM-CCiDEA-EOM-CC Cel badań wchodzących w zakres pracy doktorskiej RównaniaDIP-EOM-CCiDEA-EOM-CC Przykładcząsteczki1,2-diazyny Przykładdimerusodu Podsumowanie 22 Bibliografia 23 2
3 1 Wstęp Poszukiwanie wydajnych i skutecznych metod obliczeniowych przeznaczonych do badania struktury materii stanowi w świetle niebywałego rozwoju techniki komputerowej jeden z ważniejszych tematów badawczych współczesnej nauki, w szczególności współczesnej chemii. Jeżeli główne kierunki rozwoju nowoczesnej chemii opisać słowami kluczowymi bio eko info to rozwijanie metod obliczeniowych lokuje się, oczywiście, w części info. Szczególną rolę odgrywają te metody, które pozwalają opisywać strukturę materii na poziomie molekularnym. Należą do nich metody obliczeniowe chemii kwantowej. Niniejsza praca odnosi się do teorii opartych na funkcji falowej, zalicza się więc do kategorii WFT(Wave Function Theory) a nie DFT(Density Functional Theory) i dotyczy metod wywodzących się z pierwszej zasady, umożliwiających rozwiązanie równania Schrödingera z dużą dokładnością. W tej kategorii metod szczególne miejsce zajmują metody oparte na eksponencjalnej parametryzacji funkcji falowej, inaczej mówiąc oparte na teorii sprzężonych klasterów(coupled Cluster CC)[1 10]. Teoria CC można rzec zdominowała metody obliczeniowe pozwalające na osiąganie wysokich dokładności opisu struktury elektronowej molekuł, a równocześnie wchodzi na te obszary badawcze, które coraz bardziej stanowią przedmiot zainteresowania chemików. Głównym celem niniejszej pracy jest opracowanie nowych metod obliczeniowych chemii kwantowej opartych na obliczeniach podwójnego potencjału jonizacji(double Ionization Potential DIP) i podwójnego powinowactwa elektronowego(double Electron Affinity DEA) w celu teoretycznego wyznaczania energii wzbudzeń (Excitation Energy EE) stanów wysokospinowych przy użyciu metody sprzężonych klasterów, opartej na funkcji referencyjnej RHF(Restricted Hartree-Fock), która pozwala na wyznaczanie stanów czystych spinowo(bez kontaminacji). Obliczenia DIP i DEA mogą być wykorzystane z powodzeniem do wyznaczania poprawnych krzywych energii potencjalnej opisujących dysocjację wiązania. Cel szczegółowy pracy jest więc związany z opracowaniem i wdrożeniem nowych metod obliczeniowych sformułowanych w ramach teorii CC w oparciu o metodę równań ruchu(equation-of-motion EOM) ukierunkowanych na wyznaczanie DIP i DEA. Metody te zostały zastosowane do generowania krzywych energii potencjalnej dla molekuł, których dwudodatnie lub dwuujemne jony dysocjują na fragmenty zamkniętopowłokowe. 3
4 Prowadząc obliczenia typu DIP dla cząsteczki A uzyskujemy informację o stanachelektronowychjonua 2.JeżelizastosujemyschematDIPdojonuA 2 towrzeczywistości uzyskujemy opis neutralnej cząsteczki A. Podobnie prowadząc obliczenia typudeadlajonua 2 uzyskujemywyniki(np.opisstanówelektronowych)dlacząsteczki A. Co przez to zyskujemy? Otóż główna przyczyna trudności wygenerowania poprawnej krzywej energii potencjalnej w całym zakresie długości wiązań w oparciu o jednowyznacznikową funkcję referencyjną związana jest z niewłaściwym opisem dysocjacji właśnie na poziomie funkcji jednoreferencyjnej. Jeżeli natomiast np. jon A 2 dysocjujenafragmentyzamkniętopowłokowe,tooczywiściesytuacjatakabędzie poprawnie opisana przez funkcję typu RHF. 4
5 2 Metoda sprzężonych klasterów Punktem wyjściowym do obliczeń metodą sprzężonych klasterów[1 11] jest funkcjareferencyjnaφ 0,wyznaczananajczęściejmetodąHartree-Focka.Funkcjafalowa Ψ 0,opisującastanpodstawowy,danajestprzeznastępującewyrażenie: zaś operator wzbudzeń T definiujemy jako: Ψ 0 =e T Φ 0 (1) T=T 1 T 2 T 3...T N (2) gdzienjestliczbąelektronówwukładzie,natomiastt n jestoperatoremwzbudzeń n-krotnych, który w formalizmie drugiej kwantyzacji przyjmuje postać: T n = 1 (n!) 2 ij...ab... t ab... ij...a b...ji (3) Zakładany,żewspółczynnikit ab... ij...(nazywane amplitudami) są antysymetryzowane. Oznacza to, że zamiana miejscami dowolnych dwóch sąsiednich indeksów zmienia znak.symbolea,b,...(i,j,...)oznaczająoperatorykreacji(anihilacji)elektronów napoziomacha,b,...(i,j,...). PoddziałaniemoperatorówT n nafunkcjęreferencyjnąφ 0 powstajekombinacjaliniowakonfiguracjiwzbudzonych,wktórejamplitudyt ab... ij... są współczynnikami kombinacjiliniowej.rozwijającoperatore T wszeregotrzymujemy: zatem: e T = n 1 n! Tn =1T 1 2 T2 1 6 T3... (4) Ψ 0 =(1T 1 T T2 1 T 1T T T3 1...)Φ 0 (5) OperatoryT n zesobąkomutują,gdyżzbudowanesązparoperatorówkreacjiwsensie cząstkowo-dziurowym. Otrzymane rozwinięcie klasterowe jest rozwinięciem funkcji Ψ 0 nakonfiguracjewzbudzonewzględemφ 0. Jeśli długość rozwinięcia operatora klasterowego jest równa liczbie elektronów w rozważanym układzie mamy do czynienia z wariantem nazywanym pełną metodą sprzężonych klasterów(fcc Full CC). Metoda taka daje dokładną wartość energii korelacji(identyczną z wartością energii uzyskaną za pomocą metody pełnego mieszania konfiguracji, tj. Full Configuration Interaction FCI) w danej bazie funkcyjnej. 5
6 Jednak uwzględnienie w rozwinięciu operatora klasterowego T wzbudzeń o wysokiej krotności sprawia, że zaprogramowanie takich wariantów jest wyjątkowo trudne i pracochłonne. Kosztowne jest również wykonywanie obliczeń takim programem, charakteryzuje je bowiem wysoka zależność czasu obliczeń od rozmiaru bazy funkcyjnej. Tak więc w praktyce zmuszeni jesteśmy do wprowadzania ograniczenia na sumę po operatorach klasterowych i wówczas mówimy o modelach przybliżonych, w których operator klasterowy T definiujemy: T = T 1 T 2 T 3...T n n<n (6) czyli ograniczamy ten operator do wzbudzeń określonego typu. W związku z tym mamyprzykładowomodelccd[12,13]wktórymt =T 2,CCSD[14 18]gdzie T =T 1 T 2,CCSDT[19 21]zT =T 1 T 2 T 3,CCSDTQ[22,23]wktórym T=T 1 T 2 T 3 T 4,czyteżCCSDTQP[24]zT=T 1 T2T 3 T 4 T 5. Znane są również przybliżone warianty iteracyjne, w których konstruuje się i rozwiązuje równania na wszystkie amplitudy klasterowe wynikające z rozważanego modelu, przy czym w odniesieniu do operatora klasterowego odnoszącego się do wzbudzeń o najwyższej krotności, rozważa się tylko część wyrazów wynikających z rozwinięcia eksponencjalnego. Kryterium wyboru stanowi albo rząd rachunku perturbacyjnego albo też rząd procedury obliczeniowej. Znanych jest szereg tego typu metod,któreogólnieoznaczasięjakocct 1 T n m (gdziem=1,2,3),czyliprzykładowo CCSDT 1[25], CCSDT 2[26], CCSDT 3[26], CCSDTQ 1[27], CCSDTQ 2, CCSDTQ 3. Ich nieiteracyjne warianty to CCSD(T)[28] czy też CCSD[T][29, 30], atakżeanalogiczneprzybliżeniadlaoperatorat 4 [31]czyteżT 5 [32],wktórychto rozwiązujemyrównaniacct 1 T n 1 anastępnienabazieuzbieżnionychamplitud T 1...T n 1 konstruujemy(wjednejiteracji)operatort n iuzyskujemypoprawkido energiiwpołączeniuzenergiąuzyskanązmodelucct 1 T n 1. Oddzielna linia tematyczna to rozwijanie niestandardowych wariantów metody CC, jak np. związanych z włączaniem czynnika renormalizacyjnego do poprawek nieiteracyjnych[33 36], albo też opartych na połączeniu prawie liniowej metody CC(AL-CC)[37] z zewnętrznie korygowanymi modelami CC(externally corrected)[38 49], czy też związanych ze sfaktoryzowaną postacią operatorów wyższego rzędu,oznaczanychakronimami:ccsdt(q f )[50,51]iCCSDTQ(P f )[52]orazwiele innych. 6
7 2.1 Wyrażenie na energię w metodzie sprzężonych klasterów Wprowadzając rozwinięcie klasterowe do równania Schrödingera otrzymujemy: H N e T Φ 0 = E 0 e T Φ 0 (7) gdzieh N =H E HF tohamiltonianwporządkunormalnym,zaś E 0 =E 0 E HF to energia korelacji elektronowej. DokonującrzutowaniarównaniaSchrödingeranawektorΦ 0 otrzymujemy: HN Φ0 e T Φ0 = E0 (8) Φ0 H 0 N e T Φ0 Φ VN 0 e T Φ0 = E0 }{{} (9) 0 gdziev N =V Φ 0 V Φ0 jestoperatoremzaburzeniawporządkunormalnym. Jak wspomniano wcześniej punktem wyjścia do obliczeń metodą sprzężonych klasterów jest zwykle metoda Hartree-Focka. W takim przypadku, podstawiając postaćoperatorav N : V N = 1 4 tu rs N(r s ut) (10) rstu gdzie indeksy r, s, t, u odnoszą się do orbitali molekularnych. Wyrażenie na energię korelacji przyjmie ostatecznie postać: E 0 = ( 1 ab ij t ab abij 4 ij 2 1 ab ) ij t a i t b j (11) 2.2 Równania metody sprzężonych klasterów Równania na amplitudy klasterowe otrzymujemy poprzez rzutowanie równania SchrödingeranawektorykonfiguracjiwzbudzonychΦ ab... ij... : Φ ab... ij... e T H N e T Φ0 = 0 (12) Charakterystyczną cechą metody sprzężonych klasterów jest to, że amplitudy wzbudzeń n-krotnych zależą także od amplitud wyższych i niższych wzbudzeń. Dzięki temu przykładowo ograniczając obliczenia do amplitud wzbudzeń 3-krotnych uwzględniamy częściowo wpływ wzbudzeń 5-krotnych. Zastosowanie formalizmu diagramatycznego znacznie upraszcza wyprowadzanie równań na poszczególne amplitudy. 7
8 3 Elektronowe stany wzbudzone i zjonizowane w oparciu o metodę sprzężonych klasterów Metoda sprzężonych klasterów pozwala uzyskać poprawkę korelacyjną do energii stanu podstawowego oraz eksponencjalną parametryzację funkcji tego stanu. Aby uzyskać energie stanów wzbudzonych, energie jonizacji czy też powinowactwo elektronowe można skorzystać z metody równań ruchu[11, 53 62]. 3.1 Metoda równań ruchu FunkcjafalowaΨ k stanówwzbudzonych(zjonizowanych,podwójniezjonizowanych) w metodzie równań ruchu jest parametryzowana przez działanie liniowego operatora R na funkcję stanu podstawowego: Ψ0 Ψ k =R(k) k=1,2,... (13) R(k)=r 0 (k)r 1 (k)r 2 (k)r 3 (k)... (14) gdzier 0 jeststałąwprzypadkuenergiiwzbudzeńlubzeremdlaenergiijonizacji i powinowactw elektronowych. Operator R można dla poszczególnych przypadków zdefiniować za pomocą operatorów kreacji-anihilacji: energie wzbudzeń(excitation Energies EE[55 57, 61, 63 65]) R EE (k) = r 0 (k) ri a (k)a i 1 a i 4 ab ij 1 36abc ijl potencjał jonizacji(ionization Potential IP[8, 66]) r ab ij (k)a b ji r abc ijl(k)a b c lji... (15) R IP (k) = r i (k)i 1 r i 2 ij(k)a a ji a ij 1 rijl ab 12 (k)a b lji... (16) ab ijl powinowactwo elektronowe(electron Affinity EA[58, 67]) R EA (k) = a 1 12 r a (k)a 1 2 abc ij ri(k)a ab b i ab i rij abc (k)a b c ji... (17) 8
9 podwójny potencjał jonizacji(double Ionization Potential DIP[68]) R DIP (k) = 1 r ij (k)ji 1 rijl a 2 ij 6 (k)a lji... (18) a ijl podwójne powinowactwo elektronowe(double Electron Affinity DEA[69]) R DEA (k) = 1 r ab (k)a b 1 ri abc (k)a b c i... (19) 2 ab 6abc i R EE R EE 1 R EE 2 R EE 3 R IP R IP 1 R IP 2 R IP 3 R EA R EA 1 R EA 2 R EA 3 R DIP R DIP 2 R DIP 3 R DEA R DEA 2 R DEA 3 Rysunek 1: Diagramatyczna reprezentacja amplitud operatora R. Wstawiając funkcję falową Ψ k dorównaniaschrödingeraotrzymujemy: H N R(k) Ψ0 = Ek R(k) Ψ0 (20) 9
10 natomiast mnożąc lewostronnie równanie Schrödingera przez R(k): Ψ0 R(k)H N = E0 R(k) Ψ 0 Odejmując dwa powyższe równania otrzymujemy: [ HN,R(k) ] Ψ0 =ωk R(k) Ψ 0 (21) (22) gdzieω k = E k E 0 =E k E 0 jestefektemenergetycznymrozważanegoprocesu. 3.2 Metoda równań ruchu w połączeniu z metodą sprzężonych klasterów Standardem w tego typu obliczeniach jest wariant odpowiadający metodzie EE- EOM-CCSD[55, 57, 58, 70, 71], polegający na uwzględnieniu w definicji operatorówrittylkowzbudzeńpojedynczych(t 1,R 1 )ipodwójnych(t 2,R 2 ).Istnieje także grupa metod przybliżonych(iteracyjnych jak i nieiteracyjnych), włączających wsposóbniekompletnyspójnewzbudzeniapotrójne,czylioperatory:t 3 ir 3,m.in. metody: EE-EOM-CCSDT-1, EE-EOM-CCSDT-3, EE-EOM-CCSD(T), EE-EOM- CCSD( T)orazEE-EOM-CCSD(T )[72 75].PonadtoistniejemetodaEE-EOM- CCSDT włączająca wzbudzenia potrójne w sposób kompletny[63 65]. Zakładając, że funkcja falowa stanu podstawowego zdefiniowana jest poprzez rozwinięcieklasterowe Ψ0 =e T Φ0 możnazapisać: [ HN,R(k) ] e T Φ0 =ωk R(k)e T Φ0 (23) Mnożącpowyższerównanielewostronnieprzeze T otrzymujemy: e T[ H N,R(k) ] e T Φ0 =ωk e T R(k)e T Φ0 Operatory T oraz R komutują, zatem: [ HN,R(k) ] Φ0 =ωk R(k) Φ 0 (24) (25) gdzie: H N =e T H N e T = ( HN e T) c (26) jest hamiltonianem transformowanym przez podobieństwo, którego n-ciałowe elementyoznaczamyjakoi n k.jakoże H N zawieratakżediagramyzamknięte(= E 0 ), 10
11 które są eliminowane przez komutator, można pozbyć się komutatora poprzez wprowadzenieoznaczenia H N,o dladiagramówotwartych: Zapisując w formie macierzowej: H N,o R(k) Φ 0 =ωk R(k) Φ 0 (27) HR=ωR (28) gdzie Hreprezentujemacierzoperatora H N,o wpodprzestrzenikonfiguracyjnej w przypadku modelu CCSDT wzbudzeń pojedynczych, podwójnych i potrójnych: S H S S H D S H T H= D H S D H D D H T,S=Φa i,d=φab ij,t=φabc ijl (29) T H S T H D T H T Dla przypadku modelu CCSD zostają jedynie wzbudzenia pojedyncze i podwójne: H= S H S S H D D H S D H D,S=Φ a i,d=φab ij, (30) WprzypadkuobliczeńDIPlubDEAwmodeluCCSDTmacierz Hprzyjmujepostać: H= D H D D H T T H D T H T (31) natomiast w modelu CCSD: gdzie dla DIP: H= [ D H D ] (32) D=Φ ij,t=φ a ijl (33) natomiast dla DEA: D=Φ ab,t=φ abc i (34) Jakożemacierz Hniejesthermitowskaposiadaonaróżnelewe(L)iprawe(R) wektory własne odpowiadające tym samym wartościom własnym. Oba wektory potrzebne są do konstrukcji macierzy gęstości, nie są jednak konieczne do wyznaczenia energii wzbudzeń czy jonizacji. 11
12 3.3 Warianty metod DIP-EOM-CC i DEA-EOM-CC Standardowe warianty metod DIP-EOM-CC i DEA-EOM-CC polegają na obliczaniu stanu podstawowego metodą CC, a następnie odpowiednio zjonizowanych stanów wzbudzonych metodą EOM. Podczas tych obliczeń w rozwinięciach operatorów T oraz R uwzględnia się wzbudzenia do danego poziomu, identycznego dla T i R. Oznacza to, że w przypadku DIP-EOM-CCSD oraz DEA-EOM-CCSD operatoryograniczonesądot=t 1 T 2 ir=r 2,natomiastdlaDIP-EOM-CCSDToraz DEA-EOM-CCSDTdoT=T 1 T 2 T 3 ir=r 2 R 3.Najwolniejszymetapemtych obliczeń są obliczenia stanu podstawowego metodą CC, dla których rząd procedury obliczeniowejwynosin 6 dlaccsdorazn 8 dlaccsdt,podczasgdyskalowalność obliczeńeomwynosiodpowiednion 4 in 6. W metodach hybrydowych, oznaczanych akronimami DIP-EOM-CCSDT oraz DEA-EOM-CCSDT, stosuje się nieco inne podejście. Podczas obliczeń stanu podstawowego metodą CC uwzględnia się wzbudzenia niższego rzędu niż podczas późniejszychobliczeńmetodąeom(t=t 1 T 2,R=R 2 R 3 ).Zabiegtenpozwala uzyskać wyniki o jakości zbliżonej do pełnych metod DIP-EOM-CCSDT i DEA- EOM-CCSDT,jednakżeoznacznielepszejskalowalności(n 6 zarównodlaobliczeń stanu podstawowego jak i dla obliczeń stanów zjonizowanych dodatnio lub ujemnie, a w konsekwencji energii wzbudzeń). Lepsza skalowalność przekłada się bezpośrednio na skrócenie czasu obliczeń. 12
13 4 Cel badań wchodzących w zakres pracy doktorskiej Celem badań, wchodzących w zakres pracy doktorskiej, jest opracowanie, zaprogramowanie i zastosowanie w obliczeniach nowych wariantów metody EOM-CC do opisu stanów wysokospinowych dla wybranych klas molekuł, a w szczególności generowanie poprawnych krzywych energii potencjalnej. Główny nurt pracy związany jest z wyznaczaniem podwójnego powinowactwa elektronowego oraz podwójnego potencjału jonizacji przy użyciu metody EOM-CC, a następnie wykorzystaniem tych danych do opisu stanów wzbudzonych w sytuacjach kiedy liczenie energii wzbudzeń metodą EE-EOM-CC jest utrudnione lub wręcz niemożliwe. Rozwijane metody są szczególnie przydatne do badania stanów wysokospinowych(np. trypletów, kwintetów). 4.1 Równania DIP-EOM-CC i DEA-EOM-CC Najdogodniejszym sposobem wyprowadzania równań EOM-CC jest posłużenie się techniką diagramatyczną[10, 76]. Wszystkie równania zamieszczone w niniejszej pracy zostały wyprowadzone właśnie przy jej użyciu, a ściślej rzecz ujmując przy użyciu formalizmu diagramów Goldstone a. Nie będę wchodził w szczegóły odnośnie konstrukcji diagramów, jej opis można znaleźć w pracach[10, 76], zaznaczę tylko, że elementy hamiltonianu transformowanego( H)naRys.2-7oznaczonesąliniąfalistą,natomiastwystępującenatych rysunkach amplitudy R zdefiniowane są na Rys. 1. Równania wyprowadzone przy użyciu tego formalizmu zostały bezpośrednio przełożone na kod programu komputerowego, bez konieczności posługiwania się równaniami zapisanymi przy użyciu formalizmu algebraicznego. Nowatorskość zaimplementowanych metod polega na sformułowaniu metod DIP- EOM-CC i DEA-EOM-CC w ujęciu Goldstone a dla stanów wysokospinowych opartych na funkcji RHF. O ile standardowa metoda EOM-CC dostarcza wyniki odnoszące się do stanów singletowych przy użyciu funkcji RHF, to jej rozszerzenie na stany trypletowe czy też kwintetowe otrzymuje się wykorzystując obliczenia dla funkcji referencyjnej typu UHF(Unrestricted Hartree-Fock, HF bez ograniczeń spinowych) a nie RHF(nawet dla układów zamkniętopowłokowych). Powoduje to znaczne 13
14 wydłużenie czasu obliczeń, a przede wszystkim problemy z łamaniem symetrii spinowej(niekiedy także przestrzennej). W ramach tej pracy zaproponowano nowatorski sposób obliczania stanów wysokospinowych, np. trypletów(rys. 3, 6) i kwintetów (Rys. 4, 7), przy użyciu funkcji RHF dla układów zamkniętopowłokowych. Dzięki takiemu podejściu jesteśmy w stanie obejść trudności związanie np. z generowaniem krzywych energii potencjalnej opartych na funkcji UHF. Przykłady takich obliczeń zamieszczono w następnych podrozdziałach. = α β = α β Rysunek2:RównaniametodyDIP-EOM-CCSDT dlas Z =0wformalizmiediagramów Goldstone a. 14
15 = α α = α α Rysunek3:RównaniametodyDIP-EOM-CCSDT dlas Z =1wformalizmiediagramów Goldstone a. = α α α β α α α β α α α β α α α β α α α β Rysunek4:RównaniametodyDIP-EOM-CCSDT dlas Z =2wformalizmiediagramów Goldstone a. 15
16 Największy zysk z nowego podejścia do równań EOM-CC uzyskano dla przypadkus Z =2.LiczbadiagramówwporównaniuzmodelemdlaS Z =0drastycznie malejez21wkładów(rys.2,5)dozaledwie4(rys.4,7). = α β = α β Rysunek5:RównaniametodyDEA-EOM-CCSDT dlas Z =0wformalizmiediagramów Goldstone a. 16
17 = α α = α α Rysunek6:RównaniametodyDEA-EOM-CCSDT dlas Z =1wformalizmiediagramów Goldstone a. = α α α β α α α β α α α β α α α β α α α β Rysunek7:RównaniametodyDEA-EOM-CCSDT dlas Z =2wformalizmiediagramów Goldstone a. 17
18 4.2 Przykład cząsteczki 1,2-diazyny Cząsteczka1,2-diazyny(N 2 H 2 ),izoelektronowazcząsteczkąetylenu,jestprzedmiotem wielu badań, zarówno teoretycznych jak i eksperymentalnych. Występuje ona w postaci dwóch izomerów, cis i trans, o dominujących konfiguracjach odpowiednio1a 2 1b 2 2a 2 2b 2 3a 2 4a 2 3b 2 4b 2 oraz1a 2 1b 2 2a 2 2b 2 3a 2 3b 2 4a 2 5a 2.Dowyznaczenia energii stanu podstawowego i stanów wzbudzonych obu izomerów dobrze nadaje się jednoreferencyjna metoda CC w połączeniu z EOM, jednakże do opisu procesu izomeryzacji metody te w klasycznym ujęciu są niewystarczające. Podczas izomeryzacji trzeba wziąć pod uwagę konfiguracje obu izomerów cis i trans, dlatego też dobre wyniku uzyskuje się przy pomocy wieloreferencyjnej metody CC(MultireferenceCoupledCluster MRCC)[68,77]. Obliczenia metodami wieloreferencyjnymi są z natury dużo bardziej kosztowne i czasochłonne, dlatego też możliwość opisu procesu izomeryzacji 1,2-diazyny przy użyciu metod jednoreferencyjnych była by dużym osiągnięciem. Taki opis jest możliwyprzyużyciumetodydip-eom-cc[78].dwuujemnyjonn 2 H 2 2 posiada dominującąkonfigurację1a 2 1b 2 2a 2 2b 2 3a 2 3b 2 4a 2 5a 2 4b 2 zarównowformiecisjakitrans. Konfiguracja ta dominuje także dla pośrednich geometrii cząsteczki, dzięki czemu opis procesu jej izomeryzacji nie wymaga zastosowania metod wieloreferencyjnych. WykonującobliczeniametodąCCdlajonuN 2 H 2 2, a następnie stosując metodę DIP-EOM, uzyskujemy ostatecznie opis cząsteczki obojętnej. Rysunki 8 i 9 przedstawiają opis procesu izomeryzacji cząsteczki 1,2-diazyny uzyskany przy pomocy metod RHF, CCSD oraz DIP-EOM-CCSDT. Metody RHF oraz CCSD dają poważny błąd w okolicy połowy procesu, podczas gdy opis uzyskany metodą DIP-EOM-CCSDT jest poprawny w całym zakresie kątów. Użycie do opisu większej bazy funkcyjnej(rys. 9) dodatkowo pogłębia błąd metod RHF i CCSD. Próby opisania stanów wzbudzonych podczas procesu izomeryzacji za pomocą metody EE-EOM-CCSD(Rys. 10) dają ten sam błąd, co opis stanu podstawowego metodami RHF i CCSD. Metoda DIP-EOM-CCSDT pozawala uzyskać poprawny opis stanu podstawowego i stanów wzbudzonych(rys. 11) relatywnie małym nakładem czasu i mocy obliczeniowej w porównaniu z metodami wieloreferencyjnymi. 18
19 N 2 H 2 (GS: cc-pvdz basis set) RHF CCSD DIP-EOM-CCSDT E(Hartrees) Angle( o ) Rysunek 8: Krzywe energii potencjalnej dla stanu podstawowego uzyskane metodami RHF, CCSD oraz DIP-EOM-CCSDT dla stanu podstawowego cząsteczki 1,2- diazyny w bazie cc-pvdz N 2 H 2 (GS: cc-pvtz basis set) RHF CCSD DIP-EOM-CCSDT E(Hartrees) Angle( o ) Rysunek 9: Krzywe energii potencjalnej dla stanu podstawowego uzyskane metodami RHF, CCSD oraz DIP-EOM-CCSDT dla stanu podstawowego cząsteczki 1,2- diazyny w bazie cc-pvtz. 19
20 N 2 H 2 (cc-pvdz basis set) GS CCSD 1 1 A EE-EOM-CCSD B EE-EOM-CCSD 3 3 A EE-EOM-CCSD B EE-EOM-CCSD E(Hartrees) Angle( o ) Rysunek 10: Krzywe energii potencjalnej uzyskane metodą EE-EOM-CCSD dla stanu podstawowego oraz dwóch najniższych stanów wzbudzonych(singletowego i trypletowego) cząsteczki 1,2-diazyny w bazie cc-pvdz N 2 H 2 (cc-pvdz basis set) GS DIP-EOM-CCSDT 1 A DIP-EOM-CCSDT 1 B DIP-EOM-CCSDT 3 A DIP-EOM-CCSDT 3 B DIP-EOM-CCSDT E(Hartrees) Angle( o ) Rysunek 11: Krzywe energii potencjalnej uzyskane metodą DIP-EOM-CCSDT dla stanu podstawowego oraz dwóch najniższych stanów wzbudzonych(singletowego i trypletowego) cząsteczki 1,2-diazyny w bazie cc-pvdz. 20
21 4.3 Przykład dimeru sodu Dimersodu(Na 2 ),jakoprzykładowydimermetalualkalicznego,jestprzedmiotem wielu badań zarówno doświadczalnych jak i teoretycznych. Dotychczasowe prace eksperymentalne i obliczenia teoretyczne pozwoliły uzyskać informacje na temat jego stanu podstawowego oraz singletowych i trypletowych stanów wzbudzonych. Brak jest jednak w literaturze danych na temat stanów kwintetowych. Metoda DEA- EOM-CCSDT,zastosowanadlajonuNa 2 2,dajemożliwośćopisutychstanówwpełnym zakresie odległości międzyatomowych podczas procesu dysocjacji cząsteczki. Krzywe energii potencjalnej przedstawione na Rys. 12 uzyskano za pomocą nowo opracowanego programu przystosowanego specjalnie do uzyskiwania stanów kwintetowych. Ograniczenie równań jedynie do stanów kwintetowych pozwoliło na redukcję wkładów diagramatycznych z 21 do zaledwie 4, co znacząco poprawiło czas obliczeń i otworzyło drogę do dalszych obliczeń dla układów bardziej złożonych Na 2 (6-31G* basis set; valence electrons correlated) 1 5 Σ g DEA-EOM-CCSDT 1 5 Σ u DEA-EOM-CCSDT 1 5 Π u DEA-EOM-CCSDT 1 5 Π g DEA-EOM-CCSDT E (Hartrees) R (Angstroms) Rysunek 12: Krzywe energii potencjalnej uzyskane metodą DEA-EOM-CCSDT dla kwintetowychstanówwzbudzonychcząsteczkina 2 wbazie6-31g*. 21
22 5 Podsumowanie W ramach niniejszej pracy rozwijane są nowe metody obliczeniowe chemii kwantowej oparte na teorii sprzężonych klasterów, które w połączeniu z metodą równań ruchu pozwalają na wyznaczenie energii i charakterystykę stanów wzbudzonych i zjonizowanych układów wysokospinowych. Główną zaletą opracowanych metod jest to, że oparte są one na funkcji RHF a nie UHF, w wyniku czego omijane są standardowe problemy sformułowania UHF. Wymagało to zdefiniowania i rozwiązania innych równań, ale podejście to obniża dość znacznie koszt obliczeń. Schematy DIP i DEA oferują efektywne narzędzia do wyznaczania energii stanu podstawowego oraz energii wzbudzeń dla tych klas molekuł, dysocjują na fragmenty zamkniętopowłokowe po dołączeniu lub usunięciu elektronów. 22
23 Literatura [1]F.Coester,Nucl.Phys.,7,421(1958) [2]F.Coester,H.Kümmel,Nucl.Phys.,17,477(1960) [3]J.Čizek,J.Chem.Phys.,45,4256(1966) [4]J.Čizek,Adv.Chem.Phys.,14,15(1969) [5]J.Paldus,J.ČizekandI.Shavitt,Phys.Rev.,A5,50(1974) [6]R.J.Bartlett,J.Phys.Chem.,93,1697(1989) [7]R.J.Bartlett,inModernElectronicStructureTheory,Part2,editedbyD.R. Yarkony,(World Scientific Publishing, New York, 1995), p [8] R. J. Bartlett and J. F. Stanton, in Reviews in Computational Chemistry, edited byk.b.lipkowitzandd.b.boyd(vchpublishers,newyork,1994),vol. 5,p.65 [9]J.PaldusandX.Li,Adv.Chem.Phys.110,1(1999) [10]R.J.Bartlett,M.Musiał,Rev.Mod.Phys.,79,291(2007) [11] M. Jaworska, M. Musiał, T. Pluta, Wybrane zagadnienia chemii kwantowej, Uniwersytet Śląski(2009) [12]R.J.Bartlett,G.D.Purvis,Int.J.Quantum.Chem.,14,561(1978) [13]J.A.Pople,R.Krishnan,H.B.Schlegel,J.S.Binkley,Int.J.Quantum.Chem. Symp., 14, 545(1978) [14]G.D.Purvis,R.J.Bartlett,J.Chem.Phys.,76,1910(1982) [15]G.E.Scuseria,A.C.Scheiner,T.J.Lee,J.E.Rice,H.F.Schaefer,J.Chem. Phys., 86, 2881(1987) [16]G.E.Scuseria,C.L.Janssen,H.F.Schaefer,J.Chem.Phys.,89,7382(1988) [17]T.J.Lee,J.E.Rice,Chem.Phys.Lett.,150,406(1988) 23
24 [18] M. Urban, I. Cernusak, V. Kello, J. Noga, in Electron Correlation in Atoms and Molecules, Vol. 1 of Methods in Computational Chemistry, S. Wilson, Ed. Plenum, New York, pp (1987) [19]J.Noga,R.J.Bartlett,J.Chem.Phys.,86,7041(1987),errata:89,3401(1988) [20]G.E.Scuseria,H.F.Schaefer,Chem.Phys.Lett.,152,382(1988) [21]J.D.Watts,R.J.Bartlett,J.Chem.Phys.,93,6104(1989). [22]S.A.Kucharski,R.J.Bartlett,Theor.Chim.Acta.,80,387(1991) [23]S.A.Kucharski,R.J.Bartlett,J.Chem.Phys.,97,4282(1992) [24]M.Musiał,R.J.Bartlett,J.Chem.Phys.,116,4382(2002) [25]Y.S.Lee,S.A.Kucharski,R.J.Bartlett,J.Chem.Phys.,81,5906(1984) [26]J.Noga,R.J.Bartlett,M.Urban,Chem.Phys.Lett.,134,126(1987) [27]S.A.Kucharski,R.J.Bartlett,Chem.Phys.Lett.,158,550(1989) [28] K. Raghavachari, G. W. Trucks, J. A. Pople, M. Head-Gordon, Chem. Phys. Lett., 157, 479(1989) [29]M.Urban,J.Noga,S.J.Cole,R.J.Bartlett,J.Chem.Phys.,83,4041(1985) [30]S.J.Cole,R.J.Bartlett,J.Chem.Phys.,86,873(1987) [31]S.A.Kucharski,R.J.Bartlett,J.Chem.Phys.,108,5243(1998) [32]M.Musiał,S.A.Kucharski,R.J.Bartlett,Chem.Phys.Lett.,320,542(2000) [33]K.Kowalski,P.Piecuch,J.Chem.Phys.,113,18(2000) [34] K. Kowalski, P. Piecuch, J. Chem. Phys., 113, 5644(2000) [35] P. Piecuch, S. A. Kucharski, K. Kowalski, Chem. Phys. Lett., 344, 176(2001) [36] P. Piecuch, S. A. Kucharski, K. Kowalski, M. Musiał, Comp. Phys., Com., 149, 71(2002) [37] K. Jankowski, I. Grabowski, K. Kowalski, J. Chem. Phys., 109, 6255(1998) 24
25 [38] P. Piecuch, J. Paldus, Theoret. Chim. Acta, 83, 69(1992) [39] P. Piecuch, R. Toboła, J. Paldus, Phys.Rev., A54, 1210(1996) [40] J. Paldus, J. Čižek, M. Takahashi, Phys.Rev., A30, 2193(1984) [41] J. Paldus, J. Planelles, Theor. Chim. Acta, 89, 13(1994) [42]J.Planelles,J.Paldus,X.Li,Theor.Chim.Acta,89,33(1994) [43]J.Planelles,J.Paldus,X.Li,Theor.Chim.Acta,89,59(1994) [44] L. Stolarczyk, Chem. Phys. Lett., 217, 1(1994) [45] G. Peris, J. Planelles, J. Paldus Int.J.Quantum Chem., 62, 137(1997) [46]G.Peris,J.Planelles,F.Rajadall,J.Paldus,J.Chem.Phys.,107,90(1997) [47]X.Li,J.Paldus,J.Chem.Phys.,107,6257(1997) [48]X.Li,J.Paldus,J.Chem.Phys.,108,637(1998) [49]X.Li,J.Paldus,Chem.Phys.Lett.,286,145(1998) [50]S.A.Kucharski,R.J.Bartlett,J.Chem.Phys.,110,8223(1999) [51]S.A.Kucharski,M.Kolaski,R.J.Bartlett,J.Chem.Phys.,114,692(2001) [52] M. Musiał, S. A. Kucharski, R. J. Bartlett, J. Mol. Struct.(THEOCHEM), 547 (2001) [53]D.J.Rowe,Rev.Mod.Phys.,40,153(1968) [54] K. Emrich, Nucl. Phys., 351, 397(1981) [55]J.Geertsen,M.Rittby,andR.J.Bartlett,Chem.Phys.Lett.,164,57(1989) [56]J.F.StantonandR.J.Bartlett,J.Chem.Phys.,98,7029(1993) [57]D.C.ComeauandR.J.Bartlett,Chem.Phys.Lett.,207,414(1993) [58]M.Nooijen,R.J.Bartlett,J.Chem.Phys.,102,3629(1995) 25
26 [59] H. J. Monkhorst, Int. J. Quantum Chem., Quantum Chem. Symposium, 11, 421(1977) [60] M. Takahashi, J. Paldus, J. Chem. Phys., 85, 1486(1986) [61] H. Sekino, R. J. Bartlett, Int. J. Quantum Chem., Quantum Chem. Symp., 18, 255(1984) [62]H.Koch,H.J.A.Jensen,T.Helgaker,andP.Jörgensen,Mol.Phys,93,3345 (1990) [63]S.A.Kucharski,M.Włoch,M.Musiał,R.J.Bartlett,J.Chem.Phys.,115, 8263(2001) [64] K. Kowalski, P. Piecuch, J. Chem. Phys., 115, 643(2001) [65]S.Hirata,J.Chem.Phys.,121,51(2004) [66]M.Musiał,S.A.Kucharski,R.J.Bartlett,J.Chem.Phys.,118,1128(2003) [67]M.Musiał,R.J.Bartlett,J.Chem.Phys.,119,1901(2003) [68]M.Musiał,A.Perera,R.J.Bartlett,J.Chem.Phys.,134,114108(2011) [69]M.Musiał,S.A.Kucharski,R.J.Bartlett,J.Chem.TheoryComput.,7,3088 (2011) [70]J.F.Stanton,R.J.Bartlett,J.Chem.Phys.,98,7029(1993) [71]J.F.Stanton,J.Gauss,J.Chem.Phys.,101,8938(1994) [72]J.D.Watts,R.J.Bartlett,J.Chem.Phys.,101,3073(1994) [73]J.D.Watts,R.J.Bartlett,Chem.Phys.Lett.,233,81(1995) [74]J.D.Watts,R.J.Bartlett,Chem.Phys.Lett.,258,581(1996) [75]J.F.Stanton,J.Gauss,J.Chem.Phys.,111,8785(1999) [76] S. A. Kucharski, R. J. Bartlett, Adv. Quantum. Chem., 18, 281(1986) [77]M.Musiał,R.J.Bartlett,J.Chem.Phys.,135,044121(2011) [78]M.Musiał,Ł.Lupa,K.Szopa,S.A.Kucharski,Struct.Chem.,23,1377(2012) 26
27 Dorobek naukowy Publikacje: Monika Musiał, Łukasz Lupa, Katarzyna Szopa, Stanisław A. Kucharski, Potential energy curves via double ionization potential calculations: example of 1,2-diazene molecule, Structural Chemistry, 23, 1377(2012) Postery: Monika Musiał, Łukasz Lupa, Equation-of-motion coupled cluster method for hight spin double electron attachment calculations, 53th Sanibel Symposium, St. Simons Island, Georgia, USA(luty 2013) Łukasz Lupa, Katarzyna Kowalska-Szojda, Monika Musiał, Stanisław A. Kucharski, Krzywe energii potencjalnej z obliczeń powinowactwa elektronowego naprzykładziemolekułyna 2,55ZjazdPTChemiSITPChem,Białystok (wrzesień 2012) Monika Musiał, Katarzyna Kowalska-Szojda, Łukasz Lupa, Katarzyna Szopa, Stanisław A. Kucharski, Potential energy curves via double ionization potential calculations: example of 1,2-diazene molecule, 10th Central European Symposium on Theoretical Chemistry, Toruń, Polska(wrzesień 2011) Łukasz Lupa, Monika Musiał, Katarzyna Szopa, Stanisław A. Kucharski, Double ionization potential equation-of-motion coupled cluster method for potential energy curve production: example of the 1,2-diazene molecule, 54 Zjazd PTChem i SITPChem, Lublin(wrzesień 2011)
Grupa Moniki Musiał. Uniwersytet Śląski Instytut Chemii Zakład Chemii Teoretycznej
 Wieloreferencyjna metoda sprzężonych klasterów w dwuwalencyjnych sektorach przestrzeni Focka oraz metoda równań ruchu w zastosowaniu do opisu stanów wzbudzonych Grupa Moniki Musiał Uniwersytet Śląski Instytut
Wieloreferencyjna metoda sprzężonych klasterów w dwuwalencyjnych sektorach przestrzeni Focka oraz metoda równań ruchu w zastosowaniu do opisu stanów wzbudzonych Grupa Moniki Musiał Uniwersytet Śląski Instytut
Rozwój i zastosowanie wieloreferencyjnych metod sprzężonych klasterów w opisie stanów podstawowych i wzbudzonych układów atomowych i molekularnych
 Rozwój i zastosowanie wieloreferencyjnych metod sprzężonych klasterów w opisie stanów podstawowych i wzbudzonych układów atomowych i molekularnych Justyna Cembrzyńska Zakład Mechaniki Kwantowej Uniwersytet
Rozwój i zastosowanie wieloreferencyjnych metod sprzężonych klasterów w opisie stanów podstawowych i wzbudzonych układów atomowych i molekularnych Justyna Cembrzyńska Zakład Mechaniki Kwantowej Uniwersytet
Uniwersytet Śląski w Katowicach str. 1 Wydział Matematyki, Fizyki i Chemii
 Uniwersytet Śląski w Katowicach str. 1 Kierunek i poziom studiów: Chemia, drugi Sylabus modułu: Chemia teoretyczna (023) 1. Informacje ogólne koordynator modułu dr hab. Monika Musiał, prof. UŚ rok akademicki
Uniwersytet Śląski w Katowicach str. 1 Kierunek i poziom studiów: Chemia, drugi Sylabus modułu: Chemia teoretyczna (023) 1. Informacje ogólne koordynator modułu dr hab. Monika Musiał, prof. UŚ rok akademicki
Monika Musia l. METODA MIESZANIA KONFIGURACJI Configuration Interaction (CI) (ujȩcie wyznacznikowe)
 Monika Musia l METODA MIESZANIA KONFIGURACJI Configuration Interaction (CI) (ujȩcie wyznacznikowe) ĤΨ i = E i Ψ i W metodzie mieszania konfiguracji wariacyjna funkcja falowa, jest liniow a kombinacj a
Monika Musia l METODA MIESZANIA KONFIGURACJI Configuration Interaction (CI) (ujȩcie wyznacznikowe) ĤΨ i = E i Ψ i W metodzie mieszania konfiguracji wariacyjna funkcja falowa, jest liniow a kombinacj a
Metoda oddzia lywania konfiguracji (CI)
 Metoda oddzia lywania konfiguracji (CI) Spinorbitale: obsadzone φ a i wirtualne φ r : ɛ a ɛ HOMO, ɛ r ɛ LUMO ê r a wykonuje podstawienie φ a φ r, np. ê 7 2 φ 1 φ 2 φ 3... φ N = φ 1 φ 7 φ 3... φ N Operator
Metoda oddzia lywania konfiguracji (CI) Spinorbitale: obsadzone φ a i wirtualne φ r : ɛ a ɛ HOMO, ɛ r ɛ LUMO ê r a wykonuje podstawienie φ a φ r, np. ê 7 2 φ 1 φ 2 φ 3... φ N = φ 1 φ 7 φ 3... φ N Operator
RACHUNEK ZABURZEŃ. Monika Musiał
 RACHUNEK ZABURZEŃ Monika Musiał Rachunek zaburzeń jest podstawową obok metody wariacyjnej techniką obliczeniową stosowaną do rozwiązywania równania Schrödingera. Idea metody zaburzeniowej sprowadza się
RACHUNEK ZABURZEŃ Monika Musiał Rachunek zaburzeń jest podstawową obok metody wariacyjnej techniką obliczeniową stosowaną do rozwiązywania równania Schrödingera. Idea metody zaburzeniowej sprowadza się
METODY POSTHARTREE-FOCKOWSKIE MONIKA MUSIA L
 METODY POSTHARTREE-FOCKOWSKIE MONIKA MUSIA L Jednym z ważniejszych zadań chemii kwantowej jest opracowywanie nowych metod obliczeniowych umożliwiaj acych bardzo dok ladne wyznaczanie e- nergii korelacji
METODY POSTHARTREE-FOCKOWSKIE MONIKA MUSIA L Jednym z ważniejszych zadań chemii kwantowej jest opracowywanie nowych metod obliczeniowych umożliwiaj acych bardzo dok ladne wyznaczanie e- nergii korelacji
Teoria Orbitali Molekularnych. tworzenie wiązań chemicznych
 Teoria Orbitali Molekularnych tworzenie wiązań chemicznych Zbliżanie się atomów aż do momentu nałożenia się ich orbitali H a +H b H a H b Wykres obrazujący zależność energii od odległości atomów długość
Teoria Orbitali Molekularnych tworzenie wiązań chemicznych Zbliżanie się atomów aż do momentu nałożenia się ich orbitali H a +H b H a H b Wykres obrazujący zależność energii od odległości atomów długość
Ćwiczenie 3. Spektroskopia elektronowa. Etylen. Trypletowe przejścia elektronowe *
 Ćwiczenie 3 Spektroskopia elektronowa. Etylen. Trypletowe przejścia elektronowe * 1 Ćwiczenie 3 Spektroskopia elektronowa. Etylen. Trypletowe przejścia elektronowe * I. Narysuj etylen a) Wybierz Default
Ćwiczenie 3 Spektroskopia elektronowa. Etylen. Trypletowe przejścia elektronowe * 1 Ćwiczenie 3 Spektroskopia elektronowa. Etylen. Trypletowe przejścia elektronowe * I. Narysuj etylen a) Wybierz Default
Nowe modele obliczeniowe wieloreferencyjnej metody sprzężonych klasterów sformułowanej w przestrzeni Hilberta.
 Uniwersytet Śląski Wydział Matematyki, Fizyki i Chemii Zamknięcie przewodu doktorskiego Katarzyna Szopa Nowe modele obliczeniowe wieloreferencyjnej metody sprzężonych klasterów sformułowanej w przestrzeni
Uniwersytet Śląski Wydział Matematyki, Fizyki i Chemii Zamknięcie przewodu doktorskiego Katarzyna Szopa Nowe modele obliczeniowe wieloreferencyjnej metody sprzężonych klasterów sformułowanej w przestrzeni
Prof. dr hab. Leszek Meissner Toruń, 24 września 2018 r. Instytut Fizyki Uniwersytet Mikołaja Kopernika Toruń
 Prof. dr hab. Leszek Meissner Toruń, 24 września 2018 r. Instytut Fizyki Uniwersytet Mikołaja Kopernika 87-100 Toruń Ocena rozprawy doktorskiej magister Aleksandry Tucholskiej zatytułowanej Momenty przejścia
Prof. dr hab. Leszek Meissner Toruń, 24 września 2018 r. Instytut Fizyki Uniwersytet Mikołaja Kopernika 87-100 Toruń Ocena rozprawy doktorskiej magister Aleksandry Tucholskiej zatytułowanej Momenty przejścia
Uwzględnienie energii korelacji w metodach ab initio - przykłady
 Uwzględnienie energii korelacji w metodach ab initio - przykłady Funkcje falowe (i funkcje bazy) jawnie skorelowane - zależa jawnie od odległości międzyelektronowych r ij = r i r j Funkcje falowe w postaci
Uwzględnienie energii korelacji w metodach ab initio - przykłady Funkcje falowe (i funkcje bazy) jawnie skorelowane - zależa jawnie od odległości międzyelektronowych r ij = r i r j Funkcje falowe w postaci
że w wyniku pomiaru zmiennej dynamicznej A, której odpowiada operator αˆ otrzymana zostanie wartość 2.41?
 TEST. Ortogonalne i znormalizowane funkcje f i f są funkcjami własnymi operatora αˆ, przy czym: α ˆ f =. 05 f i α ˆ f =. 4f. Stan pewnej cząstki opisuje 3 znormalizowana funkcja falowa Ψ = f + f. Jakie
TEST. Ortogonalne i znormalizowane funkcje f i f są funkcjami własnymi operatora αˆ, przy czym: α ˆ f =. 05 f i α ˆ f =. 4f. Stan pewnej cząstki opisuje 3 znormalizowana funkcja falowa Ψ = f + f. Jakie
Zakład Chemii Teoretycznej Obrony prac licencjackich, r., godzina 9.00, sala 149 ul. Bankowa czerwca 2012
 Zakład Chemii Teoretycznej Obrony prac licencjackich, 15.06.2012 r., godzina 9.00, sala 149 ul. Bankowa 12. 5 czerwca 2012 1. Mieszczak Magdalena Wyznaczanie podwójnego potencjału jonizacji dla cząsteczki
Zakład Chemii Teoretycznej Obrony prac licencjackich, 15.06.2012 r., godzina 9.00, sala 149 ul. Bankowa 12. 5 czerwca 2012 1. Mieszczak Magdalena Wyznaczanie podwójnego potencjału jonizacji dla cząsteczki
WYKŁAD NR 3 OPIS DRGAŃ NORMALNYCH UJĘCIE KLASYCZNE I KWANTOWE.
 1 WYKŁAD NR 3 OPIS DRGAŃ NORMALNYCH UJĘCIE KLASYCZNE I KWANTOWE. Współrzędne wewnętrzne 2 F=-fq q ξ i F i =-f ij x j U = 1 2 fq2 U = 1 2 ij f ij ξ i ξ j 3 Najczęściej stosowaną metodą obliczania drgań
1 WYKŁAD NR 3 OPIS DRGAŃ NORMALNYCH UJĘCIE KLASYCZNE I KWANTOWE. Współrzędne wewnętrzne 2 F=-fq q ξ i F i =-f ij x j U = 1 2 fq2 U = 1 2 ij f ij ξ i ξ j 3 Najczęściej stosowaną metodą obliczania drgań
Title: Analityczne pierwsze pochodne energii w układach podwójnie zjonizowanych na podstawie metody równań ruchu teorii sprzężonych klasterów
 Title: Analityczne pierwsze pochodne energii w układach podwójnie zjonizowanych na podstawie metody równań ruchu teorii sprzężonych klasterów Author: Katarzyna Kowalska-Szojda Citation style: Kowalska-Szojda
Title: Analityczne pierwsze pochodne energii w układach podwójnie zjonizowanych na podstawie metody równań ruchu teorii sprzężonych klasterów Author: Katarzyna Kowalska-Szojda Citation style: Kowalska-Szojda
Struktura elektronowa σ-kompleksu benzenu z centrum aktywnym Fe IV O cytochromu P450
 Struktura elektronowa σ-kompleksu benzenu z centrum aktywnym Fe IV O cytochromu P450 Modelowanie metodami DFT, CASSCF i CASPT2 Andrzej Niedziela 1 1 Wydział Chemii Uniwersytet Jagielloński 14.01.2009 /Seminarium
Struktura elektronowa σ-kompleksu benzenu z centrum aktywnym Fe IV O cytochromu P450 Modelowanie metodami DFT, CASSCF i CASPT2 Andrzej Niedziela 1 1 Wydział Chemii Uniwersytet Jagielloński 14.01.2009 /Seminarium
METODA SPRZȨŻONYCH KLASTERÓW METODA MIESZANIA KONFIGURACJI. Monika Musia l
 METODA SPRZȨŻONYCH KLASTERÓW METODA MIESZANIA KONFIGURACJI Monika Musia l Jednym z ważniejszych zadań chemii kwantowej jest opracowywanie nowych metod obliczeniowych umożliwiaj acych bardzo dok ladne wyznaczanie
METODA SPRZȨŻONYCH KLASTERÓW METODA MIESZANIA KONFIGURACJI Monika Musia l Jednym z ważniejszych zadań chemii kwantowej jest opracowywanie nowych metod obliczeniowych umożliwiaj acych bardzo dok ladne wyznaczanie
Rozdział 22 METODA FUNKCJONAŁÓW GĘSTOŚCI Wstęp. Janusz Adamowski METODY OBLICZENIOWE FIZYKI 1
 Janusz Adamowski METODY OBLICZENIOWE FIZYKI 1 Rozdział 22 METODA FUNKCJONAŁÓW GĘSTOŚCI 22.1 Wstęp Definiujemy dla gazu elektronowego operatory anihilacji ψ σ (r) i kreacji ψ σ(r) pola fermionowego ψ σ
Janusz Adamowski METODY OBLICZENIOWE FIZYKI 1 Rozdział 22 METODA FUNKCJONAŁÓW GĘSTOŚCI 22.1 Wstęp Definiujemy dla gazu elektronowego operatory anihilacji ψ σ (r) i kreacji ψ σ(r) pola fermionowego ψ σ
Metody obliczeniowe chemii kwantowej
 Uniwersytet Śląski Metody obliczeniowe chemii kwantowej Monika Musiał Spis treści 1 Metody obliczeniowe chemii kwantowej uwzględniające korelację elektronową 3 1.1 Wstęp... 4 1.2 Rachunekzaburzeń... 6
Uniwersytet Śląski Metody obliczeniowe chemii kwantowej Monika Musiał Spis treści 1 Metody obliczeniowe chemii kwantowej uwzględniające korelację elektronową 3 1.1 Wstęp... 4 1.2 Rachunekzaburzeń... 6
Graficzna reprezentacja orbitali atomowych s, p i d. Graficzny obraz schematu EA w obliczeniach energii termów atomowych dla atomu sodu.
 Wizualizacja Graficzna reprezentacja orbitali atomowych s, p i d. Graficzny obraz schematu EA w obliczeniach energii termów atomowych dla atomu sodu. Graficzny obraz schematu DEA w obliczeniach energii
Wizualizacja Graficzna reprezentacja orbitali atomowych s, p i d. Graficzny obraz schematu EA w obliczeniach energii termów atomowych dla atomu sodu. Graficzny obraz schematu DEA w obliczeniach energii
13.1 Układy helopodobne (trójcząstkowe układy dwuelektronowe)
 Janusz Adamowski METODY OBLICZENIOWE FIZYKI 1 Rozdział 13 UKŁADY KILKU CZĄSTEK W MECHANICE KWANTOWEJ 13.1 Układy helopodobne (trójcząstkowe układy dwuelektronowe) Zajmiemy się kwantowym opisem atomu He
Janusz Adamowski METODY OBLICZENIOWE FIZYKI 1 Rozdział 13 UKŁADY KILKU CZĄSTEK W MECHANICE KWANTOWEJ 13.1 Układy helopodobne (trójcząstkowe układy dwuelektronowe) Zajmiemy się kwantowym opisem atomu He
Podstawy chemii obliczeniowej
 Podstawy chemii obliczeniowej Anna Kaczmarek Kędziera Katedra Chemii Materiałów, Adsorpcji i Katalizy Wydział Chemii UMK, Toruń Elementy chemii obliczeniowej i bioinformatyki 2015 Plan wykładu 15 godzin
Podstawy chemii obliczeniowej Anna Kaczmarek Kędziera Katedra Chemii Materiałów, Adsorpcji i Katalizy Wydział Chemii UMK, Toruń Elementy chemii obliczeniowej i bioinformatyki 2015 Plan wykładu 15 godzin
Metody rozwiązania równania Schrödingera
 Metody rozwiązania równania Schrödingera Równanie Schrödingera jako algebraiczne zagadnienie własne Rozwiązanie analityczne dla skończonej i nieskończonej studni potencjału Problem rozwiązania równania
Metody rozwiązania równania Schrödingera Równanie Schrödingera jako algebraiczne zagadnienie własne Rozwiązanie analityczne dla skończonej i nieskończonej studni potencjału Problem rozwiązania równania
METODA MIESZANIA KONFIGURACJI Configuration Interaction (CI)
 METODA MIESZANIA KONFIGURACJI Configuration Interaction (CI) lub ĤΨ i = E i Ψ i Ψ i = K r=0 c riφ r ĤΨ = EΨ Ψ = c o Φ o + ia ca i Φ a i + ijab cab ij Φ ab ij + ijkabc cabc ijk Φ abc ijk + Funkcje Φ r (Φij..
METODA MIESZANIA KONFIGURACJI Configuration Interaction (CI) lub ĤΨ i = E i Ψ i Ψ i = K r=0 c riφ r ĤΨ = EΨ Ψ = c o Φ o + ia ca i Φ a i + ijab cab ij Φ ab ij + ijkabc cabc ijk Φ abc ijk + Funkcje Φ r (Φij..
Budowa atomów. Atomy wieloelektronowe Układ okresowy pierwiastków
 Budowa atomów Atomy wieloelektronowe Układ okresowy pierwiastków Model atomu Bohra atom zjonizowany (ciągłe wartości energii) stany wzbudzone jądro Energia (ev) elektron orbita stan podstawowy Poziomy
Budowa atomów Atomy wieloelektronowe Układ okresowy pierwiastków Model atomu Bohra atom zjonizowany (ciągłe wartości energii) stany wzbudzone jądro Energia (ev) elektron orbita stan podstawowy Poziomy
Rzędy wiązań chemicznych
 Seminarium Magisterskie Rzędy wiązań chemicznych w ujęciu Teorii Komunikacji Opracowanie Dariusz Szczepanik Promotor Dr hab. Janusz Mrozek Rzędy wiązań chemicznych w ujęciu Teorii Komunikacji Plan prezentacji
Seminarium Magisterskie Rzędy wiązań chemicznych w ujęciu Teorii Komunikacji Opracowanie Dariusz Szczepanik Promotor Dr hab. Janusz Mrozek Rzędy wiązań chemicznych w ujęciu Teorii Komunikacji Plan prezentacji
5. Rozwiązywanie układów równań liniowych
 5. Rozwiązywanie układów równań liniowych Wprowadzenie (5.1) Układ n równań z n niewiadomymi: a 11 +a 12 x 2 +...+a 1n x n =a 10, a 21 +a 22 x 2 +...+a 2n x n =a 20,..., a n1 +a n2 x 2 +...+a nn x n =a
5. Rozwiązywanie układów równań liniowych Wprowadzenie (5.1) Układ n równań z n niewiadomymi: a 11 +a 12 x 2 +...+a 1n x n =a 10, a 21 +a 22 x 2 +...+a 2n x n =a 20,..., a n1 +a n2 x 2 +...+a nn x n =a
c) prawdopodobieństwo znalezienia cząstki między x=1.0 a x=1.5 jest równe
 TEST 1. Ortogonalne i znormalizowane funkcje f 1 i f są funkcjami własnymi operatora, przy czym: f 1 =1.05 f 1 i f =.41 f. Stan pewnej cząstki opisuje znormalizowana funkcja 1 3 falowa = f1 f. Jakie jest
TEST 1. Ortogonalne i znormalizowane funkcje f 1 i f są funkcjami własnymi operatora, przy czym: f 1 =1.05 f 1 i f =.41 f. Stan pewnej cząstki opisuje znormalizowana funkcja 1 3 falowa = f1 f. Jakie jest
Wyznaczanie krzywych energii potencjalnej dla wybranych cząsteczek dwuatomowych
 Wyznaczanie krzywych energii potencjalnej dla wybranych cząsteczek dwuatomowych Wstęp Krzywa energii potencjalnej 1 to wykres zależności energii potencjalnej cząsteczek od długości wiązania (czyli od wzajemnej
Wyznaczanie krzywych energii potencjalnej dla wybranych cząsteczek dwuatomowych Wstęp Krzywa energii potencjalnej 1 to wykres zależności energii potencjalnej cząsteczek od długości wiązania (czyli od wzajemnej
Spójne wzbudzenia trzykrotne w metodzie sprzężonych klasterów w zastosowaniu do opisu stanów wzbudzonych w układach otwartop owłokowy ch
 Uniwersytet Śląski W ydział M atem atyki, Fizyki i Chemii Tomasz Kuś Spójne wzbudzenia trzykrotne w metodzie sprzężonych klasterów w zastosowaniu do opisu stanów wzbudzonych w układach otwartop owłokowy
Uniwersytet Śląski W ydział M atem atyki, Fizyki i Chemii Tomasz Kuś Spójne wzbudzenia trzykrotne w metodzie sprzężonych klasterów w zastosowaniu do opisu stanów wzbudzonych w układach otwartop owłokowy
Modelowanie molekularne
 Modelowanie molekularne metodami chemii kwantowej Dr hab. Artur Michalak Zakład Chemii Teoretycznej Wydział Chemii UJ Wykład 4 http://www.chemia.uj.edu.pl/~michalak/mmod2007/ Podstawowe idee i metody chemii
Modelowanie molekularne metodami chemii kwantowej Dr hab. Artur Michalak Zakład Chemii Teoretycznej Wydział Chemii UJ Wykład 4 http://www.chemia.uj.edu.pl/~michalak/mmod2007/ Podstawowe idee i metody chemii
Oddzia lywania miedzycz. jony molekularne lub atomy. edzy A i B:
 Notatki do wyk ladu XIII Oddzia lywania miedzycz asteczkowe A i B zamknietopow lokowe czasteczki, jony molekularne lub atomy. Energia oddzia lywania E oddz mi edzy A i B: E oddz = E AB (E A + E B ) ()
Notatki do wyk ladu XIII Oddzia lywania miedzycz asteczkowe A i B zamknietopow lokowe czasteczki, jony molekularne lub atomy. Energia oddzia lywania E oddz mi edzy A i B: E oddz = E AB (E A + E B ) ()
IX. MECHANIKA (FIZYKA) KWANTOWA
 IX. MECHANIKA (FIZYKA) KWANTOWA IX.1. OPERACJE OBSERWACJI. a) klasycznie nie ważna kolejność, w jakiej wykonujemy pomiary. AB = BA A pomiar wielkości A B pomiar wielkości B b) kwantowo wartość obserwacji
IX. MECHANIKA (FIZYKA) KWANTOWA IX.1. OPERACJE OBSERWACJI. a) klasycznie nie ważna kolejność, w jakiej wykonujemy pomiary. AB = BA A pomiar wielkości A B pomiar wielkości B b) kwantowo wartość obserwacji
Hierarchia baz gaussowskich (5)
 Hierarchia baz gaussowskich (5) Bazy split-valence czyli VDZ, VTZ, etc. (np. bazy Pople a 6-31G, 6-311G, etc) Bazy split-valence spolaryzowane VDZP, VTZP, etc. Bazy bazy Dunninga (konsystentne korelacyjnie)
Hierarchia baz gaussowskich (5) Bazy split-valence czyli VDZ, VTZ, etc. (np. bazy Pople a 6-31G, 6-311G, etc) Bazy split-valence spolaryzowane VDZP, VTZP, etc. Bazy bazy Dunninga (konsystentne korelacyjnie)
Metody numeryczne Wykład 4
 Metody numeryczne Wykład 4 Dr inż. Michał Łanczont Instytut Elektrotechniki i Elektrotechnologii E419, tel. 4293, m.lanczont@pollub.pl, http://m.lanczont.pollub.pl Zakres wykładu Metody skończone rozwiązywania
Metody numeryczne Wykład 4 Dr inż. Michał Łanczont Instytut Elektrotechniki i Elektrotechnologii E419, tel. 4293, m.lanczont@pollub.pl, http://m.lanczont.pollub.pl Zakres wykładu Metody skończone rozwiązywania
OPTYKA KWANTOWA Wykład dla 5. roku Fizyki
 OPTYKA KWANTOWA Wykład dla 5. roku Fizyki c Adam Bechler 2006 Instytut Fizyki Uniwersytetu Szczecińskiego Rezonansowe oddziaływanie układu atomowego z promieniowaniem "! "!! # $%&'()*+,-./-(01+'2'34'*5%.25%&+)*-(6
OPTYKA KWANTOWA Wykład dla 5. roku Fizyki c Adam Bechler 2006 Instytut Fizyki Uniwersytetu Szczecińskiego Rezonansowe oddziaływanie układu atomowego z promieniowaniem "! "!! # $%&'()*+,-./-(01+'2'34'*5%.25%&+)*-(6
Analityczne pierwsze pochodne energii w układach podwójnie zjonizowanych na podstawie metody równań ruchu teorii sprzężonych klasterów
 UNIWERSYTET ŚLĄSKI Wydział Matematyki, Fizyki i Chemii Zamknięcie przewodu doktorskiego Katarzyna Kowalska-Szojda Analityczne pierwsze pochodne energii w układach podwójnie zjonizowanych na podstawie metody
UNIWERSYTET ŚLĄSKI Wydział Matematyki, Fizyki i Chemii Zamknięcie przewodu doktorskiego Katarzyna Kowalska-Szojda Analityczne pierwsze pochodne energii w układach podwójnie zjonizowanych na podstawie metody
Cząsteczki. 1.Dlaczego atomy łącz. 2.Jak atomy łącz. 3.Co to jest wiązanie chemiczne? Jakie sąs. typy wiąza
 Cząsteczki 1.Dlaczego atomy łącz czą się w cząsteczki?.jak atomy łącz czą się w cząsteczki? 3.Co to jest wiązanie chemiczne? Co to jest rząd d wiązania? Jakie sąs typy wiąza zań? Dlaczego atomy łącz czą
Cząsteczki 1.Dlaczego atomy łącz czą się w cząsteczki?.jak atomy łącz czą się w cząsteczki? 3.Co to jest wiązanie chemiczne? Co to jest rząd d wiązania? Jakie sąs typy wiąza zań? Dlaczego atomy łącz czą
Metody obliczeniowe chemii teoretycznej
 Metody obliczeniowe chemii teoretycznej mechanika kwantowa mechanika klasyczna ւ ց WFT DFT MM FFM metody bazuj ace na metody bazuj ace na Mechanika Molekularna funkcji falowej gȩstości elektronowej Wave
Metody obliczeniowe chemii teoretycznej mechanika kwantowa mechanika klasyczna ւ ց WFT DFT MM FFM metody bazuj ace na metody bazuj ace na Mechanika Molekularna funkcji falowej gȩstości elektronowej Wave
Wykład 5: Cząsteczki dwuatomowe
 Wykład 5: Cząsteczki dwuatomowe Wiązania jonowe i kowalencyjne Ograniczenia teorii Lewisa Orbitale cząsteczkowe Kombinacja liniowa orbitali atomowych Orbitale dwucentrowe Schematy nakładania orbitali Diagramy
Wykład 5: Cząsteczki dwuatomowe Wiązania jonowe i kowalencyjne Ograniczenia teorii Lewisa Orbitale cząsteczkowe Kombinacja liniowa orbitali atomowych Orbitale dwucentrowe Schematy nakładania orbitali Diagramy
UKŁADY ALGEBRAICZNYCH RÓWNAŃ LINIOWYCH
 Transport, studia I stopnia rok akademicki 2011/2012 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Adam Wosatko Uwagi wstępne Układ liniowych równań algebraicznych można
Transport, studia I stopnia rok akademicki 2011/2012 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Adam Wosatko Uwagi wstępne Układ liniowych równań algebraicznych można
Uniwersytet Śląski w Katowicach str. 1 Wydział Matematyki, Fizyki i Chemii
 Uniwersytet Śląski w Katowicach str. 1 Kierunek i poziom studiów: Chemia, pierwszy poziom Sylabus modułu: Chemia kwantowa 021 Nazwa wariantu modułu (opcjonalnie): 1. Informacje ogólne koordynator modułu
Uniwersytet Śląski w Katowicach str. 1 Kierunek i poziom studiów: Chemia, pierwszy poziom Sylabus modułu: Chemia kwantowa 021 Nazwa wariantu modułu (opcjonalnie): 1. Informacje ogólne koordynator modułu
Modelowanie molekularne
 Modelowanie molekularne metodami chemii kwantowej Dr hab. Artur Michalak Zakład Chemii Teoretycznej Wydział Chemii UJ Wykład 4 http://www.chemia.uj.edu.pl/~michalak/mmod2007/ Podstawowe idee i metody chemii
Modelowanie molekularne metodami chemii kwantowej Dr hab. Artur Michalak Zakład Chemii Teoretycznej Wydział Chemii UJ Wykład 4 http://www.chemia.uj.edu.pl/~michalak/mmod2007/ Podstawowe idee i metody chemii
Modelowanie molekularne
 Ck08 Modelowanie molekularne metodami chemii kwantowej Dr hab. Artur Michalak Zakład Chemii Teoretycznej Wydział Chemii UJ Wykład 10 http://www.chemia.uj.edu.pl/~michalak/mmod2007/ Podstawowe idee i metody
Ck08 Modelowanie molekularne metodami chemii kwantowej Dr hab. Artur Michalak Zakład Chemii Teoretycznej Wydział Chemii UJ Wykład 10 http://www.chemia.uj.edu.pl/~michalak/mmod2007/ Podstawowe idee i metody
Postulaty mechaniki kwantowej
 3.10.2004 11. Postulaty mechaniki kwantowej 120 Rozdział 11 Postulaty mechaniki kwantowej Mechanika kwantowa, jak zresztą każda teoria fizyczna, bazuje na kilku postulatach, które przyjmujemy "na wiarę".
3.10.2004 11. Postulaty mechaniki kwantowej 120 Rozdział 11 Postulaty mechaniki kwantowej Mechanika kwantowa, jak zresztą każda teoria fizyczna, bazuje na kilku postulatach, które przyjmujemy "na wiarę".
II. POSTULATY MECHANIKI KWANTOWEJ W JĘZYKU WEKTORÓW STANU. Janusz Adamowski
 II. POSTULATY MECHANIKI KWANTOWEJ W JĘZYKU WEKTORÓW STANU Janusz Adamowski 1 1 Przestrzeń Hilberta Do opisu stanów kwantowych używamy przestrzeni Hilberta. Przestrzenią Hilberta H nazywamy przestrzeń wektorową
II. POSTULATY MECHANIKI KWANTOWEJ W JĘZYKU WEKTORÓW STANU Janusz Adamowski 1 1 Przestrzeń Hilberta Do opisu stanów kwantowych używamy przestrzeni Hilberta. Przestrzenią Hilberta H nazywamy przestrzeń wektorową
WYKŁAD 3 CZĄSTECZKI WIELOATOMOWE ZWIĄZKI WĘGLA
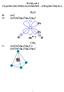 WYKŁAD 3 ZĄSTEZKI WIELOATOMOWE ZWIĄZKI WĘGLA O : (s) O: (s) (s) (p z ) (p x ) (p y ) px py s 90 o? s 4 : (s) (s) (p x ) (p y ) (s) (s) (p x ) (p y ) (p z ) s pz px py s so : (s) s s.orbital MOLEKULARNY
WYKŁAD 3 ZĄSTEZKI WIELOATOMOWE ZWIĄZKI WĘGLA O : (s) O: (s) (s) (p z ) (p x ) (p y ) px py s 90 o? s 4 : (s) (s) (p x ) (p y ) (s) (s) (p x ) (p y ) (p z ) s pz px py s so : (s) s s.orbital MOLEKULARNY
KARTA PRZEDMIOTU. Informacje ogólne WYDZIAŁ MATEMATYCZNO-PRZYRODNICZY. SZKOŁA NAUK ŚCISŁYCH UNIWERSYTET KARDYNAŁA STEFANA WYSZYŃSKIEGO W WARSZAWIE
 1 2 4 5 6 7 8 8.0 Kod przedmiotu Nazwa przedmiotu Jednostka Punkty ECTS Język wykładowy polski Poziom przedmiotu podstawowy K_W01 2 wiedza Symbole efektów kształcenia K_U01 2 umiejętności K_K01 11 kompetencje
1 2 4 5 6 7 8 8.0 Kod przedmiotu Nazwa przedmiotu Jednostka Punkty ECTS Język wykładowy polski Poziom przedmiotu podstawowy K_W01 2 wiedza Symbole efektów kształcenia K_U01 2 umiejętności K_K01 11 kompetencje
Modele kp Studnia kwantowa
 Modele kp Studnia kwantowa Przegląd modeli pozwalających obliczyć strukturę pasmową materiałów półprzewodnikowych. Metoda Fal płaskich Transformata Fouriera Przykładowe wyniki Model Kaine Hamiltonian z
Modele kp Studnia kwantowa Przegląd modeli pozwalających obliczyć strukturę pasmową materiałów półprzewodnikowych. Metoda Fal płaskich Transformata Fouriera Przykładowe wyniki Model Kaine Hamiltonian z
Rozdział 23 KWANTOWA DYNAMIKA MOLEKULARNA Wstęp. Janusz Adamowski METODY OBLICZENIOWE FIZYKI 1
 Janusz Adamowski METODY OBLICZENIOWE FIZYKI 1 Rozdział 3 KWANTOWA DYNAMIKA MOLEKULARNA 3.1 Wstęp Metoda ta umożliwia opis układu złożonego z wielu jonów i elektronów w stanie podstawowym. Hamiltonian układu
Janusz Adamowski METODY OBLICZENIOWE FIZYKI 1 Rozdział 3 KWANTOWA DYNAMIKA MOLEKULARNA 3.1 Wstęp Metoda ta umożliwia opis układu złożonego z wielu jonów i elektronów w stanie podstawowym. Hamiltonian układu
Wstęp do Modelu Standardowego
 Wstęp do Modelu Standardowego Plan (Uzupełnienie matematyczne II) Abstrakcyjna przestrzeń stanów Podstawowe własności Iloczyn skalarny amplitudy prawdopodobieństwa Operatory i ich hermitowskość Wektory
Wstęp do Modelu Standardowego Plan (Uzupełnienie matematyczne II) Abstrakcyjna przestrzeń stanów Podstawowe własności Iloczyn skalarny amplitudy prawdopodobieństwa Operatory i ich hermitowskość Wektory
obrotów. Funkcje falowe cząstki ze spinem - spinory. Wykład II.3 29 Pierwsza konwencja Condona-Shortley a
 Wykład II.1 25 Obroty układu kwantowego Interpretacja aktywna i pasywna. Macierz obrotu w trzech wymiarach a operator obrotu w przestrzeni stanów. Reprezentacja obrotu w przestrzeni funkcji falowych. Transformacje
Wykład II.1 25 Obroty układu kwantowego Interpretacja aktywna i pasywna. Macierz obrotu w trzech wymiarach a operator obrotu w przestrzeni stanów. Reprezentacja obrotu w przestrzeni funkcji falowych. Transformacje
Wstęp do Optyki i Fizyki Materii Skondensowanej
 Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 9 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2014/15
Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 9 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2014/15
Wiązania. w świetle teorii kwantów fenomenologicznie
 Wiązania w świetle teorii kwantów fenomenologicznie Wiązania Teoria kwantowa: zwiększenie gęstości prawdopodobieństwa znalezienia elektronów w przestrzeni pomiędzy atomami c a a c b b Liniowa kombinacja
Wiązania w świetle teorii kwantów fenomenologicznie Wiązania Teoria kwantowa: zwiększenie gęstości prawdopodobieństwa znalezienia elektronów w przestrzeni pomiędzy atomami c a a c b b Liniowa kombinacja
Komputerowa Analiza Danych Doświadczalnych
 Komputerowa Analiza Danych Doświadczalnych dr inż. Adam Kisiel kisiel@if.pw.edu.pl pokój 117b (12b) 1 Materiały do wykładu Transparencje do wykładów: http://www.if.pw.edu.pl/~kisiel/kadd/kadd.html Literatura
Komputerowa Analiza Danych Doświadczalnych dr inż. Adam Kisiel kisiel@if.pw.edu.pl pokój 117b (12b) 1 Materiały do wykładu Transparencje do wykładów: http://www.if.pw.edu.pl/~kisiel/kadd/kadd.html Literatura
Zad. 3: Układ równań liniowych
 1 Cel ćwiczenia Zad. 3: Układ równań liniowych Wykształcenie umiejętności modelowania kluczowych dla danego problemu pojęć. Definiowanie właściwego interfejsu klasy. Zwrócenie uwagi na dobór odpowiednich
1 Cel ćwiczenia Zad. 3: Układ równań liniowych Wykształcenie umiejętności modelowania kluczowych dla danego problemu pojęć. Definiowanie właściwego interfejsu klasy. Zwrócenie uwagi na dobór odpowiednich
TEORIA ORBITALI MOLEKULARNYCH (MO) dr Henryk Myszka - Uniwersytet Gdański - Wydział Chemii
 TERIA RBITALI MLEKULARNYCH (M) Metoda (teoria) orbitali molekularnych (M) podstawy metody M - F. Hund, R.S. Mulliken Teoria M zakłada, że zachowanie się elektronu w cząsteczce opisuje orbital molekularny
TERIA RBITALI MLEKULARNYCH (M) Metoda (teoria) orbitali molekularnych (M) podstawy metody M - F. Hund, R.S. Mulliken Teoria M zakłada, że zachowanie się elektronu w cząsteczce opisuje orbital molekularny
Teoria funkcjonału gęstości
 Teoria funkcjonału gęstości Łukasz Rajchel Interdyscyplinarne Centrum Modelowania Matematycznego i Komputerowego Uniwersytet Warszawski lrajchel1981@gmail.com Wykład dostępny w sieci: http://tiger.chem.uw.edu.pl/staff/lrajchel/
Teoria funkcjonału gęstości Łukasz Rajchel Interdyscyplinarne Centrum Modelowania Matematycznego i Komputerowego Uniwersytet Warszawski lrajchel1981@gmail.com Wykład dostępny w sieci: http://tiger.chem.uw.edu.pl/staff/lrajchel/
O MACIERZACH I UKŁADACH RÓWNAŃ
 O MACIERZACH I UKŁADACH RÓWNAŃ Problem Jak rozwiązać podany układ równań? 2x + 5y 8z = 8 4x + 3y z = 2x + 3y 5z = 7 x + 8y 7z = Definicja Równanie postaci a x + a 2 x 2 + + a n x n = b gdzie a, a 2, a
O MACIERZACH I UKŁADACH RÓWNAŃ Problem Jak rozwiązać podany układ równań? 2x + 5y 8z = 8 4x + 3y z = 2x + 3y 5z = 7 x + 8y 7z = Definicja Równanie postaci a x + a 2 x 2 + + a n x n = b gdzie a, a 2, a
Wstęp do Modelu Standardowego
 Wstęp do Modelu Standardowego Plan Wstęp do QFT (tym razem trochę równań ) Funkcje falowe a pola Lagranżjan revisited Kilka przykładów Podsumowanie Tomasz Szumlak AGH-UST Wydział Fizyki i Informatyki Stosowanej
Wstęp do Modelu Standardowego Plan Wstęp do QFT (tym razem trochę równań ) Funkcje falowe a pola Lagranżjan revisited Kilka przykładów Podsumowanie Tomasz Szumlak AGH-UST Wydział Fizyki i Informatyki Stosowanej
Atomy wieloelektronowe
 Wiązania atomowe Atomy wieloelektronowe, obsadzanie stanów elektronowych, układ poziomów energii. Przykładowe konfiguracje elektronów, gazy szlachetne, litowce, chlorowce, układ okresowy pierwiastków,
Wiązania atomowe Atomy wieloelektronowe, obsadzanie stanów elektronowych, układ poziomów energii. Przykładowe konfiguracje elektronów, gazy szlachetne, litowce, chlorowce, układ okresowy pierwiastków,
Ważne rozkłady i twierdzenia c.d.
 Ważne rozkłady i twierdzenia c.d. Funkcja charakterystyczna rozkładu Wielowymiarowy rozkład normalny Elipsa kowariacji Sploty rozkładów Rozkłady jednostajne Sploty z rozkładem normalnym Pobieranie próby
Ważne rozkłady i twierdzenia c.d. Funkcja charakterystyczna rozkładu Wielowymiarowy rozkład normalny Elipsa kowariacji Sploty rozkładów Rozkłady jednostajne Sploty z rozkładem normalnym Pobieranie próby
Rozwiązywanie układów równań liniowych
 Rozwiązywanie układów równań liniowych Marcin Orchel 1 Wstęp Jeśli znamy macierz odwrotną A 1, to możęmy znaleźć rozwiązanie układu Ax = b w wyniku mnożenia x = A 1 b (1) 1.1 Metoda eliminacji Gaussa Pierwszy
Rozwiązywanie układów równań liniowych Marcin Orchel 1 Wstęp Jeśli znamy macierz odwrotną A 1, to możęmy znaleźć rozwiązanie układu Ax = b w wyniku mnożenia x = A 1 b (1) 1.1 Metoda eliminacji Gaussa Pierwszy
Algebra. macierzy brzegowych z zastosowaniami. Micha Kolupa Zbigniew Âleszyƒski
 Algebra macierzy brzegowych z zastosowaniami Micha Kolupa Zbigniew Âleszyƒski Algebra macierzy brzegowych z zastosowaniami Algebra macierzy brzegowych z zastosowaniami Micha Kolupa Zbigniew Âleszyƒski
Algebra macierzy brzegowych z zastosowaniami Micha Kolupa Zbigniew Âleszyƒski Algebra macierzy brzegowych z zastosowaniami Algebra macierzy brzegowych z zastosowaniami Micha Kolupa Zbigniew Âleszyƒski
INTERPOLACJA I APROKSYMACJA FUNKCJI
 Transport, studia niestacjonarne I stopnia, semestr I Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Adam Wosatko Wprowadzenie Na czym polega interpolacja? Interpolacja polega
Transport, studia niestacjonarne I stopnia, semestr I Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Adam Wosatko Wprowadzenie Na czym polega interpolacja? Interpolacja polega
OPTYKA KWANTOWA Wykład dla 5. roku Fizyki
 OPTYKA KWANTOWA Wykład dla 5. roku Fizyki c Adam Bechler 2006 Instytut Fizyki Uniwersytetu Szczecińskiego Równania optyki półklasycznej Posłużymy się teraz równaniem (2.4), i Ψ t = ĤΨ ażeby wyprowadzić
OPTYKA KWANTOWA Wykład dla 5. roku Fizyki c Adam Bechler 2006 Instytut Fizyki Uniwersytetu Szczecińskiego Równania optyki półklasycznej Posłużymy się teraz równaniem (2.4), i Ψ t = ĤΨ ażeby wyprowadzić
SPEKTROMETRIA IRMS. (Isotope Ratio Mass Spectrometry) Pomiar stosunków izotopowych (R) pierwiastków lekkich (H, C, O, N, S)
 SPEKTROMETRIA IRMS (Isotope Ratio Mass Spectrometry) Pomiar stosunków izotopowych (R) pierwiastków lekkich (H, C, O, N, S) R = 2 H/ 1 H; 13 C/ 12 C; 15 N/ 14 N; 18 O/ 16 O ( 17 O/ 16 O), 34 S/ 32 S Konstrukcja
SPEKTROMETRIA IRMS (Isotope Ratio Mass Spectrometry) Pomiar stosunków izotopowych (R) pierwiastków lekkich (H, C, O, N, S) R = 2 H/ 1 H; 13 C/ 12 C; 15 N/ 14 N; 18 O/ 16 O ( 17 O/ 16 O), 34 S/ 32 S Konstrukcja
II.3 Atom helu i zakaz Pauliego. Atomy wieloelektronowe. Układ okresowy
 II.3 Atom helu i zakaz Pauliego. Atomy wieloelektronowe. Układ okresowy 1. Atom helu: struktura poziomów, reguły wyboru, 2. Zakaz Pauliego, 3. Moment pędu w atomach wieloelektronowych: sprzężenie LS i
II.3 Atom helu i zakaz Pauliego. Atomy wieloelektronowe. Układ okresowy 1. Atom helu: struktura poziomów, reguły wyboru, 2. Zakaz Pauliego, 3. Moment pędu w atomach wieloelektronowych: sprzężenie LS i
21 Symetrie Grupy symetrii Grupa translacji
 21 Symetrie 21.1 Grupy symetrii Spróbujmy odpowiedzieć sobie na pytanie, jak zmienia się stan układu kwantowego pod wpływem transformacji układu współrzędnych. Najprostszą taką transformacją jest np. przesunięcie
21 Symetrie 21.1 Grupy symetrii Spróbujmy odpowiedzieć sobie na pytanie, jak zmienia się stan układu kwantowego pod wpływem transformacji układu współrzędnych. Najprostszą taką transformacją jest np. przesunięcie
1.1 Przegląd wybranych równań i modeli fizycznych. , u x1 x 2
 Temat 1 Pojęcia podstawowe 1.1 Przegląd wybranych równań i modeli fizycznych Równaniem różniczkowym cząstkowym rzędu drugiego o n zmiennych niezależnych nazywamy równanie postaci gdzie u = u (x 1, x,...,
Temat 1 Pojęcia podstawowe 1.1 Przegląd wybranych równań i modeli fizycznych Równaniem różniczkowym cząstkowym rzędu drugiego o n zmiennych niezależnych nazywamy równanie postaci gdzie u = u (x 1, x,...,
III.1 Atom helu i zakaz Pauliego. Atomy wieloelektronowe. Układ okresowy
 III.1 Atom helu i zakaz Pauliego. Atomy wieloelektronowe. Układ okresowy r. akad. 2004/2005 1. Atom helu: struktura poziomów, reguły wyboru, 2. Zakaz Pauliego, 3. Moment pędu w atomach wieloelektronowych:
III.1 Atom helu i zakaz Pauliego. Atomy wieloelektronowe. Układ okresowy r. akad. 2004/2005 1. Atom helu: struktura poziomów, reguły wyboru, 2. Zakaz Pauliego, 3. Moment pędu w atomach wieloelektronowych:
Temat Ocena dopuszczająca Ocena dostateczna Ocena dobra Ocena bardzo dobra Ocena celująca. Uczeń:
 Chemia - klasa I (część 2) Wymagania edukacyjne Temat Ocena dopuszczająca Ocena dostateczna Ocena dobra Ocena bardzo dobra Ocena celująca Dział 1. Chemia nieorganiczna Lekcja organizacyjna. Zapoznanie
Chemia - klasa I (część 2) Wymagania edukacyjne Temat Ocena dopuszczająca Ocena dostateczna Ocena dobra Ocena bardzo dobra Ocena celująca Dział 1. Chemia nieorganiczna Lekcja organizacyjna. Zapoznanie
WEKTORY I WARTOŚCI WŁASNE MACIERZY. = λ c (*) problem przybliżonego rozwiązania zagadnienia własnego dla operatorów w mechanice kwantowej
 WEKTORY I WARTOŚCI WŁASNE MACIERZY Ac λ c (*) ( A λi) c nietrywialne rozwiązanie gdy det A λi problem przybliżonego rozwiązania zagadnienia własnego dla operatorów w mechanice kwantowej A - macierzowa
WEKTORY I WARTOŚCI WŁASNE MACIERZY Ac λ c (*) ( A λi) c nietrywialne rozwiązanie gdy det A λi problem przybliżonego rozwiązania zagadnienia własnego dla operatorów w mechanice kwantowej A - macierzowa
TEORIA PASMOWA CIAŁ STAŁYCH
 TEORIA PASMOWA CIAŁ STAŁYCH Skolektywizowane elektrony w metalu Weźmy pod uwagę pewną ilość atomów jakiegoś metalu, np. sodu. Pojedynczy atom sodu zawiera 11 elektronów o konfiguracji 1s 2 2s 2 2p 6 3s
TEORIA PASMOWA CIAŁ STAŁYCH Skolektywizowane elektrony w metalu Weźmy pod uwagę pewną ilość atomów jakiegoś metalu, np. sodu. Pojedynczy atom sodu zawiera 11 elektronów o konfiguracji 1s 2 2s 2 2p 6 3s
Atom wodoru. Model klasyczny: nieruchome jądro +p i poruszający się wokół niego elektron e w odległości r; energia potencjalna elektronu:
 ATOM WODORU Atom wodoru Model klasyczny: nieruchome jądro +p i poruszający się wokół niego elektron e w odległości r; energia potencjalna elektronu: U = 4πε Opis kwantowy: wykorzystując zasadę odpowiedniości
ATOM WODORU Atom wodoru Model klasyczny: nieruchome jądro +p i poruszający się wokół niego elektron e w odległości r; energia potencjalna elektronu: U = 4πε Opis kwantowy: wykorzystując zasadę odpowiedniości
Modyfikacja schematu SCPF obliczeń energii polaryzacji
 Modyfikacja schematu SCPF obliczeń energii polaryzacji Zakład Metod Obliczeniowych Chemii 11 kwietnia 2006 roku 1 Po co? Jak? 2 Algorytm Analiza zbieżności 3 dla układów symetrycznych 4 Fulleren 5 Po co?
Modyfikacja schematu SCPF obliczeń energii polaryzacji Zakład Metod Obliczeniowych Chemii 11 kwietnia 2006 roku 1 Po co? Jak? 2 Algorytm Analiza zbieżności 3 dla układów symetrycznych 4 Fulleren 5 Po co?
METODA MACIERZOWA OBLICZANIA OBWODÓW PRĄDU PRZEMIENNEGO
 POZNAN UNIVERSITY OF TECHNOLOGY ACADEMIC JOURNALS No 93 Electrical Engineering 2018 DOI 10.21008/j.1897-0737.2018.93.0026 Piotr FRĄCZAK METODA MACIERZOWA OBLICZANIA OBWODÓW PRĄDU PRZEMIENNEGO W pracy przedstawiono
POZNAN UNIVERSITY OF TECHNOLOGY ACADEMIC JOURNALS No 93 Electrical Engineering 2018 DOI 10.21008/j.1897-0737.2018.93.0026 Piotr FRĄCZAK METODA MACIERZOWA OBLICZANIA OBWODÓW PRĄDU PRZEMIENNEGO W pracy przedstawiono
POSTULATY MECHANIKI KWANTOWEJ cd i formalizm matematyczny
 POSTULATY MECHANIKI KWANTOWEJ cd i formalizm matematyczny Funkcja Falowa Postulat 1 Dla każdego układu istnieje funkcja falowa (funkcja współrzędnych i czasu), która jest ciągła, całkowalna w kwadracie,
POSTULATY MECHANIKI KWANTOWEJ cd i formalizm matematyczny Funkcja Falowa Postulat 1 Dla każdego układu istnieje funkcja falowa (funkcja współrzędnych i czasu), która jest ciągła, całkowalna w kwadracie,
Postać Jordana macierzy
 Rozdział 8 Postać Jordana macierzy Niech F = R lub F = C Macierz J r λ) F r r postaci λ 1 0 0 0 λ 1 J r λ) = 0 λ 1 0 0 λ gdzie λ F nazywamy klatką Jordana stopnia r Oczywiście J 1 λ) = [λ Definicja 81
Rozdział 8 Postać Jordana macierzy Niech F = R lub F = C Macierz J r λ) F r r postaci λ 1 0 0 0 λ 1 J r λ) = 0 λ 1 0 0 λ gdzie λ F nazywamy klatką Jordana stopnia r Oczywiście J 1 λ) = [λ Definicja 81
Mechanika kwantowa. Jak opisać atom wodoru? Jak opisać inne cząsteczki?
 Mechanika kwantowa Jak opisać atom wodoru? Jak opisać inne cząsteczki? Mechanika kwantowa Elektron fala stojąca wokół jądra Mechanika kwantowa Równanie Schrödingera Ĥ E ψ H ˆψ = Eψ operator różniczkowy
Mechanika kwantowa Jak opisać atom wodoru? Jak opisać inne cząsteczki? Mechanika kwantowa Elektron fala stojąca wokół jądra Mechanika kwantowa Równanie Schrödingera Ĥ E ψ H ˆψ = Eψ operator różniczkowy
3. Cząsteczki i wiązania
 3. Cząsteczki i wiązania Elektrony walencyjne Wiązania jonowe i kowalencyjne Wiązanie typu σ i π Hybrydyzacja Przewidywanie kształtu cząsteczek AX n Orbitale zdelokalizowane Cząsteczki związków organicznych
3. Cząsteczki i wiązania Elektrony walencyjne Wiązania jonowe i kowalencyjne Wiązanie typu σ i π Hybrydyzacja Przewidywanie kształtu cząsteczek AX n Orbitale zdelokalizowane Cząsteczki związków organicznych
składa się z m + 1 uporządkowanych niemalejąco liczb nieujemnych. Pomiędzy p, n i m zachodzi następująca zależność:
 TEMATYKA: Krzywe typu Splajn (Krzywe B sklejane) Ćwiczenia nr 8 Krzywe Bezier a mają istotne ograniczenie. Aby uzyskać kształt zawierający wiele punktów przegięcia niezbędna jest krzywa wysokiego stopnia.
TEMATYKA: Krzywe typu Splajn (Krzywe B sklejane) Ćwiczenia nr 8 Krzywe Bezier a mają istotne ograniczenie. Aby uzyskać kształt zawierający wiele punktów przegięcia niezbędna jest krzywa wysokiego stopnia.
Rys Wykres kosztów skrócenia pojedynczej czynności. k 2. Δk 2. k 1 pp. Δk 1 T M T B T A
 Ostatnim elementem przykładu jest określenie związku pomiędzy czasem trwania robót na planowanym obiekcie a kosztem jego wykonania. Związek ten określa wzrost kosztów wykonania realizacji całego przedsięwzięcia
Ostatnim elementem przykładu jest określenie związku pomiędzy czasem trwania robót na planowanym obiekcie a kosztem jego wykonania. Związek ten określa wzrost kosztów wykonania realizacji całego przedsięwzięcia
Geometria cząsteczek wieloatomowych. Hybrydyzacja orbitali atomowych.
 Geometria cząsteczek wieloatomowych. Hybrydyzacja orbitali atomowych. Geometria cząsteczek Geometria cząsteczek decyduje zarówno o ich właściwościach fizycznych jak i chemicznych, np. temperaturze wrzenia,
Geometria cząsteczek wieloatomowych. Hybrydyzacja orbitali atomowych. Geometria cząsteczek Geometria cząsteczek decyduje zarówno o ich właściwościach fizycznych jak i chemicznych, np. temperaturze wrzenia,
RÓWNANIE SCHRÖDINGERA NIEZALEŻNE OD CZASU
 X. RÓWNANIE SCHRÖDINGERA NIEZALEŻNE OD CZASU Równanie Schrődingera niezależne od czasu to równanie postaci: ħ 2 2m d 2 x dx 2 V xx = E x (X.1) Warunki regularności na x i a) skończone b) ciągłe c) jednoznaczne
X. RÓWNANIE SCHRÖDINGERA NIEZALEŻNE OD CZASU Równanie Schrődingera niezależne od czasu to równanie postaci: ħ 2 2m d 2 x dx 2 V xx = E x (X.1) Warunki regularności na x i a) skończone b) ciągłe c) jednoznaczne
Układy równań liniowych. Krzysztof Patan
 Układy równań liniowych Krzysztof Patan Motywacje Zagadnienie kluczowe dla przetwarzania numerycznego Wiele innych zadań redukuje się do problemu rozwiązania układu równań liniowych, często o bardzo dużych
Układy równań liniowych Krzysztof Patan Motywacje Zagadnienie kluczowe dla przetwarzania numerycznego Wiele innych zadań redukuje się do problemu rozwiązania układu równań liniowych, często o bardzo dużych
Definicje i przykłady
 Rozdział 1 Definicje i przykłady 1.1 Definicja równania różniczkowego 1.1 DEFINICJA. Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie F (t, x, ẋ, ẍ,..., x (n) ) = 0. (1.1) W równaniu tym t jest
Rozdział 1 Definicje i przykłady 1.1 Definicja równania różniczkowego 1.1 DEFINICJA. Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie F (t, x, ẋ, ẍ,..., x (n) ) = 0. (1.1) W równaniu tym t jest
Dotyczy to zarówno istniejących już związków, jak i związków, których jeszcze dotąd nie otrzymano.
 Chemia teoretyczna to dział chemii zaliczany do chemii fizycznej, zajmujący się zagadnieniami związanymi z wiedzą chemiczną od strony teoretycznej, tj. bez wykonywania eksperymentów na stole laboratoryjnym.
Chemia teoretyczna to dział chemii zaliczany do chemii fizycznej, zajmujący się zagadnieniami związanymi z wiedzą chemiczną od strony teoretycznej, tj. bez wykonywania eksperymentów na stole laboratoryjnym.
Opis korelacji elektronowej w dużych układach molekularnych. Implementacja metodologii LT-AO-MP2
 Opis korelacji elektronowej w dużych układach molekularnych. metodologii Jakub Sumera Krzysztof Kowalczyk 7 stycznia 2009 roku Spis treści Wstęp 1 Wstęp 2 3 4 Plan pracy Wstęp implementacja AO MP2 kwadratowo
Opis korelacji elektronowej w dużych układach molekularnych. metodologii Jakub Sumera Krzysztof Kowalczyk 7 stycznia 2009 roku Spis treści Wstęp 1 Wstęp 2 3 4 Plan pracy Wstęp implementacja AO MP2 kwadratowo
WIĄZANIA. Co sprawia, że ciała stałe istnieją i są stabilne? PRZYCIĄGANIE ODPYCHANIE
 WIĄZANIA Co sprawia, że ciała stałe istnieją i są stabilne? PRZYCIĄGANIE ODPYCHANIE Przyciąganie Wynika z elektrostatycznego oddziaływania między elektronami a dodatnimi jądrami atomowymi. Może to być
WIĄZANIA Co sprawia, że ciała stałe istnieją i są stabilne? PRZYCIĄGANIE ODPYCHANIE Przyciąganie Wynika z elektrostatycznego oddziaływania między elektronami a dodatnimi jądrami atomowymi. Może to być
Programowanie celowe #1
 Programowanie celowe #1 Problem programowania celowego (PC) jest przykładem problemu programowania matematycznego nieliniowego, który można skutecznie zlinearyzować, tzn. zapisać (i rozwiązać) jako problem
Programowanie celowe #1 Problem programowania celowego (PC) jest przykładem problemu programowania matematycznego nieliniowego, który można skutecznie zlinearyzować, tzn. zapisać (i rozwiązać) jako problem
Obliczenia iteracyjne
 Lekcja Strona z Obliczenia iteracyjne Zmienne iteracyjne (wyliczeniowe) Obliczenia iteracyjne wymagają zdefiniowania specjalnej zmiennej nazywanej iteracyjną lub wyliczeniową. Zmienną iteracyjną od zwykłej
Lekcja Strona z Obliczenia iteracyjne Zmienne iteracyjne (wyliczeniowe) Obliczenia iteracyjne wymagają zdefiniowania specjalnej zmiennej nazywanej iteracyjną lub wyliczeniową. Zmienną iteracyjną od zwykłej
Wykład Budowa atomu 3
 Wykład 14. 12.2016 Budowa atomu 3 Model atomu według mechaniki kwantowej Równanie Schrödingera dla atomu wodoru i jego rozwiązania Liczby kwantowe n, l, m l : - Kwantowanie energii i liczba kwantowa n
Wykład 14. 12.2016 Budowa atomu 3 Model atomu według mechaniki kwantowej Równanie Schrödingera dla atomu wodoru i jego rozwiązania Liczby kwantowe n, l, m l : - Kwantowanie energii i liczba kwantowa n
Z52: Algebra liniowa Zagadnienie: Zastosowania algebry liniowej Zadanie: Operatory różniczkowania, zagadnienie brzegowe.
 Z5: Algebra liniowa Zagadnienie: Zastosowania algebry liniowej Zadanie: Operatory różniczkowania zagadnienie brzegowe Dyskretne operatory różniczkowania Numeryczne obliczanie pochodnych oraz rozwiązywanie
Z5: Algebra liniowa Zagadnienie: Zastosowania algebry liniowej Zadanie: Operatory różniczkowania zagadnienie brzegowe Dyskretne operatory różniczkowania Numeryczne obliczanie pochodnych oraz rozwiązywanie
Liczby zmiennoprzecinkowe i błędy
 i błędy Elementy metod numerycznych i błędy Kontakt pokój B3-10 tel.: 829 53 62 http://golinski.faculty.wmi.amu.edu.pl/ golinski@amu.edu.pl i błędy Plan wykładu 1 i błędy Plan wykładu 1 2 i błędy Plan
i błędy Elementy metod numerycznych i błędy Kontakt pokój B3-10 tel.: 829 53 62 http://golinski.faculty.wmi.amu.edu.pl/ golinski@amu.edu.pl i błędy Plan wykładu 1 i błędy Plan wykładu 1 2 i błędy Plan
METODY NUMERYCZNE. wykład. konsultacje: wtorek 10:00-11:30 środa 10:00-11:30. dr inż. Grażyna Kałuża pokój
 METODY NUMERYCZNE wykład dr inż. Grażyna Kałuża pokój 103 konsultacje: wtorek 10:00-11:30 środa 10:00-11:30 www.kwmimkm.polsl.pl Program przedmiotu wykład: 15 godzin w semestrze laboratorium: 30 godzin
METODY NUMERYCZNE wykład dr inż. Grażyna Kałuża pokój 103 konsultacje: wtorek 10:00-11:30 środa 10:00-11:30 www.kwmimkm.polsl.pl Program przedmiotu wykład: 15 godzin w semestrze laboratorium: 30 godzin
Algorytm Grovera. Kwantowe przeszukiwanie zbiorów. Robert Nowotniak
 Wydział Fizyki Technicznej, Informatyki i Matematyki Stosowanej Politechnika Łódzka 13 listopada 2007 Plan wystapienia 1 Informatyka Kwantowa podstawy 2 Opis problemu (przeszukiwanie zbioru) 3 Intuicyjna
Wydział Fizyki Technicznej, Informatyki i Matematyki Stosowanej Politechnika Łódzka 13 listopada 2007 Plan wystapienia 1 Informatyka Kwantowa podstawy 2 Opis problemu (przeszukiwanie zbioru) 3 Intuicyjna
ROZWIĄZYWANIE RÓWNAŃ NIELINIOWYCH
 Transport, studia I stopnia Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Adam Wosatko Postać ogólna równania nieliniowego Często występującym, ważnym problemem obliczeniowym
Transport, studia I stopnia Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Adam Wosatko Postać ogólna równania nieliniowego Często występującym, ważnym problemem obliczeniowym
