Program Data Visualizer w badaniu przebiegów chaotycznych
|
|
|
- Elżbieta Kuczyńska
- 7 lat temu
- Przeglądów:
Transkrypt
1 ZESZYTY NAUKOWE MA OPOLSKIEJ WY SZEJ SZKO Y EKONOMICZNEJ W TARNOWIE Z. 1(10)/2007 PAWE WO OSZYN* Program Data Visualizer w badaniu przebiegów chaotycznych S ³ o w a k l u c z o w e: chaotyczne szeregi czasowe, analiza danych komputerowych, wizualizacja danych komputerowych S t r e s z c z e n i e: Dynamika systemów chaotycznych czêsto badana jest przy wykorzystaniu metod symulacji komputerowej. Program Data Visualizer zosta³ przez autora zaprojektowany i zaimplementowany z myœl¹ o dostarczeniu wygodnego narzêdzia do analizy i wizualizacji zachowania chaotycznych systemów dynamicznych. Dane w postaci szeregów czasowych mog¹ zostaæ poddane edycji, a nastêpnie s¹ wyœwietlane w odrêbnych oknach w formie wykresów czasowych lub obrazów fazowych. Obrazy fazowe mog¹ byæ uzupe³nione przez wyœwietlenie wektorów kierunkowych wskazuj¹cych nastêpny punkt obrazu na p³aszczyÿnie fazowej. Analiza w³asnoœci chaotycznych szeregów czasowych, w tym równie badanie ich obrazów fazowych, mo e znaleÿæ zastosowanie w klasyfikacji systemów chaotycznych. 1. Wprowadzenie W badaniu w³asnoœci systemów dynamicznych generuj¹cych przebiegi chaotyczne szeroko stosowane s¹ metody eksperymentalne. Metody symulacji komputerowej pozwalaj¹ wzglêdnie ³atwo otrzymywaæ d³ugie ci¹gi obserwacji modelu systemu chaotycznego. Równie wybranym programem komputerowym mo e prowadziæ analizê otrzymanych w procesie symulacji rezultatów. W tym celu wykorzystuje siê dostêpne programy ogólnego przeznaczenia (najczêœciej arkusze obliczeniowe, np. MS Excel) lub specjalnie zaprojektowane i zaimplementowane programy analizy i wizualizacji danych. Jednym z takich programów jest omawiany ni ej Data Visualizer. * Dr Pawe³ Wo³oszyn jest pracownikiem Akademii Górniczo-Hutniczej im. S. Staszica w Krakowie. Kontakt: pawel.woloszyn@agh.edu.pl.
2 202 Pawe³ Wo³oszyn Zachowanie chaotyczne obserwowane w systemach dynamicznych jest ca³kowicie zdeterminowane i pozbawione zupe³nie elementów losowoœci. Przebiegi chaotyczne s¹ jednak bardzo nieregularne i w praktyce uniemo liwiaj¹ przewidywanie ich przysz³ych wartoœci (Baker, 1998; Ott, 1997; Schuster, 1995). Dotyczy to zw³aszcza przewidywania w d³u szym horyzoncie czasowym. W krótkich przedzia³ach czasu zachowanie systemu chaotycznego jest z regu³y w znacznym stopniu przewidywalne. 2. Chaos w prostych modelach nieliniowych Warunkiem pojawienia siê przebiegów chaotycznych w deterministycznym modelu s¹ nieliniowe zale noœci opisuj¹ce badany system. Jednym z najprostszych przyk³adów modelu systemu chaotycznego jest odwzorowanie kwadratowe (Stewart, 1996) opisywane zale noœci¹: x t +1 =2x 2 t 1 (1) Warunek nieliniowoœci modelu jest spe³niony w efekcie wystêpowania w równaniu (1) funkcji kwadratowej. Równanie to bezpoœrednio pozwala na generowanie dowolnej d³ugoœci szeregów czasowych. Nale y w tym celu przyj¹æ pewn¹ wartoœæ liczbow¹ z przedzia³u ( 1; 1) traktowan¹ jako wartoœæ startowa x 0 dla pocz¹tkowej chwili czasu t = 0. Stosuj¹c zale noœæ (1) wyznaczana jest wartoœæ generowanego szeregu czasowego dla momentu czasu t = 1. Systematycznie powtarzaj¹c obliczenia dla kolejnych momentów czasu t = 2, t = 3,... otrzymujemy szereg czasowy opisuj¹cy zachowanie systemu w dyskretnych momentach symulowanego czasu. Wygodnym narzêdziem przeprowadzenia procedury generowania szeregu czasowego jest elektroniczny arkusz obliczeniowy. W przeprowadzonych eksperymentach symulacyjnych wykorzystano program MS Excel. Dla wartoœci pocz¹tkowej x 0 = 0, formu³y wpisane w kolumnie B arkusza obliczeniowego wyznaczaj¹ kolejne wartoœci szeregu (rys. 1). Obliczone wartoœci mo na przedstawiæ graficznie na wykresie liniowym (rys. 2). Analizuj¹c rysunek 2 dostrzegamy wystêpuj¹ce w badanym modelu (1) zachowanie chaotyczne przejawiaj¹ce siê zdecydowanie nieregularnym przebiegiem zmiennej x t. Poprzez wykorzystanie wizualizacji szeregu chaotycznego w postaci wykresu jego wartoœci mo na dostrzec znacznie wiêcej cech i w³asnoœci badanego zjawiska ni w przypadku przegl¹dania wartoœci badanego szeregu w formie stabelaryzowanej przedstawionej na rysunku 1. Dobieraj¹c bardziej specyficzne metody wizualizacji znacznie zwiêkszaj¹ siê mo liwoœci percepcji charakterystycznych w³asnoœci szeregu czasowego. Jedn¹ z metod wizualizacji chaotycznego szeregu czasowego jest sporz¹dzenie jego obrazu fazowego nazywanego równie wykresem fazowym. W tym celu przy generowaniu wartoœci szeregu czasowego obliczane by³y równie jego pierwsze ró nice oznaczone przez Äx w kolumnie B arkusza obliczeniowego przedstawionego na rysunku 1.
3 Program Data Visualizer w badaniu przebiegów chaotycznych 203 Rys. 1. Generowanie chaotycznego szeregu czasowego w programie MS Excel Rys. 2. Wykres wartoœci zmiennej xt wygenerowanych w programie MS Excel przy wykorzystaniuodwzorowania x t + 1 =2x t 2 1 dla wartoœci pocz¹tkowej x 0 = , iteracje Wykresy fazowe szeregów czasowych W przedstawionych wy ej rozwa aniach badaliœmy zachowanie modelu systemu dynamicznego poprzez bezpoœredni¹ analizê wartoœci szeregów czasowych reprezentuj¹cych zmienn¹ obserwowan¹ w systemie. W przypadku systemów ekonomicznych czêsto stosowana jest taka metoda badawcza. Inn¹ metod¹ badania dynamiki systemu jest przedstawienie w przestrzeni stanów tego systemu trajek-
4 204 Pawe³ Wo³oszyn torii opisuj¹cej jego zachowanie w czasie, a nastêpnie analizowanie w³asnoœci skonstruowanej trajektorii. Uporz¹dkowany zbiór wartoœci wybranych zmiennych systemu opisuje stan tego systemu w pewnej chwili czasu. Równoczeœnie wspomniany zbiór wartoœci (nazywanych ogólnie zbiorem wartoœci zmiennych stanu) wyznacza jeden punkt w przestrzeni stanów systemu. Z natury rzeczy w ogólnym przypadku stan systemu dynamicznego wyznaczany jest w wielowymiarowej przestrzeni. Je eli system opisywany jest jedynie przez dwie zmienne, jego przestrzeñ stanów redukuje siê do dwóch wymiarów tworz¹c p³aszczyznê fazow¹. Obrazem fazowym (wykresem fazowym) systemu dynamicznego w przestrzeni jego stanów jest zbiór punktów tej przestrzeni odpowiadaj¹cy poszczególnym momentom czasu, w których nastêpuje rejestrowanie wartoœci obserwowanych zmiennych systemu. Obraz fazowy nazywaæ bêdziemy równie trajektori¹ systemu dynamicznego. Trajektoria systemu w sposób syntetyczny wizualizuje jego dynamikê, staj¹c siê pewnego rodzaju portretem fazowym tego systemu (czêsto u ywa siê tego terminu w znaczeniu obrazu fazowego). Sporz¹dzanie obrazu fazowego systemu dynamicznego, a nastêpnie badanie tego obrazu pozwala niejednokrotnie dostrzec zale noœci, które mog¹ byæ trudne do zauwa enia przy bezpoœredniej analizie uszeregowanych w czasie wartoœci szeregów czasowych. W prostym, dwuwymiarowym przypadku, p³aszczyzna fazowa systemu dynamicznego jest wyznaczona przez pewn¹ zmienn¹ systemu oraz jej pochodn¹ wzglêdem czasu. Zarówno wybrana zmienna systemu, jak i jej pochodna s¹ reprezentowane przez odpowiednie szeregi czasowe. Na wykres fazowy systemu sk³adaj¹ siê punkty, których wspó³rzêdne na p³aszczyÿnie fazowej wyznaczone s¹ przez pary odpowiadaj¹cych sobie wartoœci obydwu szeregów odnosz¹ce siê do tej samej chwili czasu. Zbiór uzyskanych w opisany sposób punktów stanowi trajektoriê badanego systemu. W praktyce badania dynamiki wybranego systemu czêsto zdarza siê, e dysponujemy tylko jednym szeregiem czasowym przedstawiaj¹cym wartoœci pewnej zmiennej i nie znamy odpowiadaj¹cego mu szeregu reprezentuj¹cego pochodn¹ tej zmiennej. Brakuj¹cy szereg czasowy odpowiadaj¹cy pochodnej zwykle konstruowany jest na podstawie posiadanego oryginalnego szeregu poprzez operacjê wyznaczania jego pierwszych ró nic. Jest to wygodna metoda ze wzglêdu na jej prostotê obliczeniow¹. Poszczególne wartoœci szeregu odpowiadaj¹cego pochodnej równe s¹ ró nicom kolejnych s¹siaduj¹cych ze sob¹ wartoœci podstawowego szeregu czasowego. WeŸmy pod uwagê model systemu dynamicznego opisanego odwzorowaniem (1). Na podstawie wspomnianego odwzorowania generujemy szereg czasowy zmiennej x. Nastêpnie, obliczaj¹c ró nice kolejnych par wartoœci otrzymanego szeregu, tworzymy nowy szereg czasowy x' zgodnie z zale noœci¹: x t x x t 1 t (2)
5 Program Data Visualizer w badaniu przebiegów chaotycznych 205 Fragment otrzymanego szeregu pochodnej przedstawiony zosta³ na rysunku 3, który koresponduje z wykresem pokazanym na rysunku 2. Przy okazji ³atwo zauwa yæ i wykazaæ prawid³owoœæ dotycz¹c¹ zakresu wartoœci tego szeregu. Wszystkie jego wartoœci mieszcz¹ siê w przedziale [ 1,125; 2]. Rys. 3. Wykres wartoœci pochodnej xt xt 1 xt zmiennej x generowanej w programie MS Excel 2 przez odwzorowanie xt 1 2xt 1 dla wartoœci pocz¹tkowej x 0 = 0, , iteracje ród³o: opracowanie w³asne Rys. 4. Obraz fazowy odwzorowania x t +1 =2x 2 t 1, oœ pozioma zmienna x, oœ pionowa pochodna x' zast¹piona ró nic¹ x' t = x t + 1 x t, 300 iteracji ród³o: opracowanie w³asne
6 206 Pawe³ Wo³oszyn Dysponuj¹c obydwoma szeregami czasowymi x oraz x' mo emy zbudowaæ obraz fazowy odwzorowania kwadratowego (1), który przedstawiony zosta³ na rysunku 4. Oœ pozioma reprezentuje wartoœci zmiennej x, a oœ pionowa wartoœci pochodnej x'. W prosty sposób analitycznie mo na okreœliæ równanie krzywej przedstawiaj¹cej obraz fazowy tego odwzorowania: y =2x 2 x 1 (3) 3. Oprogramowanie wspomagaj¹ce badanie chaotycznych szeregów czasowych Jak stwierdzono we wstêpie do niniejszej pracy, jej zasadniczym celem jest prezentacja oprogramowania zaprojektowanego i wykonanego przez autora w celu wspomagania badania szeregów czasowych przy wykorzystaniu obrazów fazowych dotycz¹cych zwi¹zanych z nimi przekszta³ceñ. Omawiany program nosz¹cy nazwê Data Visualizer wersja 1.5 zosta³ napisany w jêzyku C++ przy wykorzystaniu kompilatora Microsoft Visual C i jest przeznaczony do uruchamiania pod kontrol¹ systemu operacyjnego MS Windows. Przedstawiana wersja programu Data Visualizer ma charakter prototypowy i mo e byæ poddawana modyfikowaniu w miarê formu³owania nowych wymagañ w trakcie u ytkowania programu. W celu przedstawienia mo liwoœci programu Data Visualizer rozwa my inne przekszta³cenie generuj¹ce chaotyczne szeregi czasowe: x t+1 =x t + (n x t )(ax + k) (4) Na podstawie odwzorowania (4), po przyjêciu (w du ej mierze arbitralnie) pewnych wartoœci dla wystêpuj¹cych w tym odwzorowaniu parametrów n = 460, a = 0,7, k = 0,0046 oraz zak³adaj¹c wartoœæ pocz¹tkow¹ x 0 = 571, wygenerowany zosta³ szereg czasowy o d³ugoœci 5000 wartoœci. Wykorzystuj¹c ten sam model systemu dynamicznego okreœlony odwzorowaniem (4) generujemy drugi szereg czasowy przy zachowaniu poprzednich wartoœci parametrów n, a oraz k. Jedyn¹ ró nic¹ w stosunku do pierwszego wygenerowanego szeregu czasowego jest niewielka zmiana wartoœci pocz¹tkowej x 0 = 567. Dysponuj¹c dwoma szeregami czasowymi x (1) oraz x (2) o jednakowej d³ugoœci, wygenerowanymi przez odwzorowanie (4) mo emy utworzyæ ich sumê daj¹c¹ w wyniku nowy szereg czasowy: x t =x (1) t +x (2) t (5) Otrzymany na podstawie zale noœci (5) chaotyczny szereg czasowy w postaci numerycznej zosta³ wprowadzony do programu Data Visualizer. Wykorzystuj¹c
7 Program Data Visualizer w badaniu przebiegów chaotycznych 207 Obszar menu Obszar skalowania Paski narzêdzi Obszar prezentacyjny Rys. 5. Ogólny widok i struktura funkcjonalna g³ównego okna programu Data Visualizer przyk³ad tego szeregu czasowego omówimy krótko mo liwoœci obliczeniowe i prezentacyjne programu Data Visualizer. Na rysunku 5 przedstawiony zosta³ ogólny widok g³ównego okna omawianego programu przy rozwiniêtej jednej z pozycji wielopoziomowego systemu menu. Ogólna struktura g³ównego okna programu Data Visualizer, które stanowi zarazem podstawowy interfejs komunikacyjny u ytkownika programu, obejmuje cztery zasadnicze obszary funkcjonalne. Obszary te u³o one jeden nad drugim (zaznaczone zosta³y one tak e symbolicznie na rysunku 5) to: Obszar menu Obszar skalowania Paski narzêdzi Obszar prezentacyjny Obszar menu programu Data Visualizer odpowiada typowemu wielopoziomowemu menu w wielodokumentowych aplikacjach pracuj¹cych pod kontrol¹ systemu operacyjnego MS Windows. Menu pierwszego poziomu zawiera pozycje: File Wczytywanie danych Ÿród³owych, zapisywanie danych, tworzenie nowych plików z danymi, wyjœcie z programu.
8 208 Pawe³ Wo³oszyn Skalowanie osi poziomej Skalowanie osi pionowej Przesuwanie œrodka uk³adu wspó³rzêdnych w poziomie Przesuwanie œrodka uk³adu wspó³rzêdnych w pionie Wybór rozmiaru znacznika Wybór rozmiaru wektora Rys. 6. Obszar skalowania w g³ównym oknie programu Data Visualizer podzielony na grupy steruj¹ce formatem wyœwietlania danych View Data Window Help Sterowanie wszystkimi elementami wyœwietlanymi w g³ównym oknie programu, wybór trybu wyœwietlania wykresów i obrazów fazowych w oknach prezentacyjnych. Importowanie danych, edycja wprowadzonych danych. Tworzenie nowych okien prezentacyjnych, sterowanie rozmiarami i rozmieszczanie otwartych okien. Podstawowe informacje o programie. Obszar skalowania, pokazany i opisany odnoœnikami na rysunku 6, s³u y do ustalania skali osi poziomej i pionowej tworzonych obrazów fazowych oraz wykresów czasowych. W obszarze tym mo na równie dokonywaæ przesuniêcia ca³ego wykresu w dowolnym kierunku na p³aszczyÿnie rysowania. Kolejn¹ mo liwoœci¹ jest wybór rozmiaru znaczników poszczególnych punktów obrazu fazowego, a tak e rozmiaru wektorów kierunkowych. Paski narzêdzi, jak w wiêkszoœci innych programów uruchamianych w systemie MS Windows, s³u ¹ do szybkiego dostêpu do najczêœciej wykorzystywanych funkcji programu. Niektóre przyciski paska narzêdziowego umo liwiaj¹ wykonanie operacji niedostêpnej dla u ytkownika w inny sposób. Narzêdzia dostêpne w programie Data Visualizer przedstawione zosta³y na rysunku 7. Do programu Data Visualizer, jak wynika z opisu wejœciowego pliku tekstowego, s¹ faktycznie wprowadzane równolegle trzy szeregi czasowe. Pierwszy i drugi szereg s³u ¹ do konstruowania obrazu fazowego. Trzeci szereg mo e byæ w specjalny sposób reprezentowany na tworzonych przez program wykresach (mo e przyk³adowo reprezentowaæ czas wyra any numerem iteracji zwi¹zanej z kolejn¹ wartoœci¹ podstawowego szeregu). Rysunek 8 pokazuje okno edycyjne programu
9 Program Data Visualizer w badaniu przebiegów chaotycznych 209 Nowy plik Otwieranie pliku Zapisywanie pliku Wy³¹czanie wykresu Wykres czasowy Obraz fazowy Znaczniki kolorowe Pikselizacja Linie ³¹cz¹ce Znaczniki punktów Wektory kierunkowe Skala 1.0 Skala 0.5 Skala 2.0 Œrodek symetryczny Pierwsza æwiartka Druga æwiartka Trzecia æwiartka Czwarta æwiartka Rys. 7. Paski narzêdzi programu Data Visualizer Rys. 8. Okno edycyjne danych wprowadzanych do programu Data Visualizer
10 210 Pawe³ Wo³oszyn Rys. 9. Skalowanie wykresów w oknach prezentacyjnych Data Visualizer, w którym mo na przegl¹daæ i dokonywaæ edycji wprowadzonych do programu danych. Wyœwietlane w oknach program Data Visualizer wykresy mog¹ podlegaæ procesowi skalowania w celu uzyskania specyficznego sposobu wizualizowania danych. Wspomniane mo liwoœci ilustruje rysunek 9. Program pozwala równie na inne przekszta³cenia prezentacyjne, takie jak mapowanie cech oraz pikselizacja wykresu. Dodatkowo do obrazu fazowego szeregu czasowego mo e byæ dodana uzupe³niaj¹ca informacja zakodowana w postaci kolorowej mapy na³o onej na wykres. 5. Wektory kierunkowe Obrazy fazowe konstruowane w oknach prezentacyjnych programu Data Visualizer mog¹ byæ uzupe³nione przez wyœwietlenie wektorów kierunkowych zaznaczaj¹cych na p³aszczyÿnie fazowej kierunek odpowiadaj¹cy nastêpnemu punktowi obrazu fazowego zgodnie z kolejnoœci¹ wystêpowania wartoœci w badanym szeregu czasowym.
11 Program Data Visualizer w badaniu przebiegów chaotycznych 211 Rys. 10. Obraz fazowy szeregu czasowego (7), m = 0,399, x (1) 0 = 0,9, x (2)0 = 0,7, 6000 iteracji Pokrewnym w stosunku do odwzorowania (4) jest odwzorowanie logistyczne definiowane zale noœci¹: x t+1 =mx t (1 x t ) (6) gdzie m jest sta³ym parametrem, który w du ej mierze decyduje o dynamice odwzorowania. Wykorzystuj¹c odwzorowanie (6) generujemy dwa jednakowej d³ugoœci szeregi czasowe x (1) oraz x (2), które nastêpnie s³u ¹ wyznaczeniu szeregu czasowego bêd¹cego œredni¹ arytmetyczn¹ obydwu szeregów sk³adowych: y t = (x (1) t +x (2) t)/2 (7) Na rysunku 10 przedstawiony zosta³ obraz fazowy utworzonego szeregu czasowego uzupe³niony o wektory kierunkowe wskazuj¹ce na p³aszczyÿnie fazowej kierunek, w którym w stosunku do pewnego punktu znajduje siê nastêpny punkt obrazu fazowego. Kolejnoœæ punktów obrazu fazowego odpowiada kolejnoœci wystêpowania poszczególnych wartoœci w szeregu czasowym. Ka dy wektor na rysunku 10 ma d³ugoœæ proporcjonaln¹ do geometrycznej odleg³oœci pomiêdzy odpowiednimi dwoma nastêpuj¹cymi po sobie punktami obrazu fazowego.
12 212 Pawe³ Wo³oszyn Rys. 11. Powiêkszony fragment obrazu fazowego z rysunku 10 z zaznaczonymi punktami i wektorami kierunkowymi Wraz ze zwiêkszeniem w programie Data Visualizer rozmiarów rysowanych wektorów kierunkowych widaæ wyraÿnie wystêpuj¹cy na obrazie fazowym prawoskrêtny wir. Jego charakterystyczny kszta³t w powiêkszeniu pokazuje rysunek 11, na którym dodatkowo zaznaczone zosta³y poszczególne punkty obrazu fazowego. 6. Zakoñczenie Prezentowane w niniejszej pracy rozwa ania dotyczy³y zagadnieñ zwi¹zanych z chaosem obserwowanym w szeregach czasowych generowanych przez proste modele matematyczne systemów dynamicznych. G³ówne podejœcie badawcze obejmowa³o szerokie wykorzystanie metod eksperymentalnych maj¹cych formê komputerowych symulacji zachowania siê matematycznego modelu systemu dynamicznego. Analiza dotycz¹ca konstruowanych obrazów fazowych chaotycznych szeregów czasowych wymaga³a opracowania specjalizowanego oprogramowania Data Visualizer. Za pomoc¹ tego programu mo na by³o w prosty sposób wizualizowaæ badane szeregi czasowe przy wykorzystaniu grupy ró norodnych przekszta³ceñ graficznych. Analiza w³asnoœci chaotycznych szeregów czasowych, w tym równie badanie ich obrazów fazowych, mo e znaleÿæ zastosowanie w klasyfikacji systemów chaotycznych.
13 Program Data Visualizer w badaniu przebiegów chaotycznych 213 Bibliografia Baker G. L., Gollub J. P Wstêp do dynamiki uk³adów chaotycznych. Warszawa: Wydawnictwo Naukowe PWN. ISBN O t t E. 1997: Chaos w uk³adach dynamicznych. Warszawa: WNT. ISBN S c h u s t e r H. G. 1995: Chaos deterministyczny. Wprowadzenie. Warszawa: Wydawnictwo Naukowe PWN. ISBN S t e w a r t I. 1996: Czy Bóg gra w koœci? Nowa matematyka chaos. Warszawa: Wydawnictwo Naukowe PWN. ISBN Data Visualizer Programme Applied in Analysis of Chaotic Series Summary: The dynamics of chaotic systems is often examined with help of computer simulation methods. The results of computer experiments are analysed with methods offered by available computer programmes of common use or with especially built software. Data Visualizer programme was designed and implemented by the author in order to provide a comfortable tool to analyse and visualize data which constitute the observations of chaotic dynamic systems. The data in the form of chaotic time series, being implemented into Data Visualizer programme can be subject to edition and subsequently displayed in separate windows in the form of time charts or phase images. All charts are subject to calibration in order to achieve a specific method of visualizing data. The programme also allows different presentation transformations, such as mapping features and pixellation of the chart. Phase image, built in presentation windows of Data Visualizer programme can be completed by displaying direction vectors which indicate the next point of the image on the phase plane. By means of Data Visualizer programme it is possible to visualize the time sequences being analysed in a simple way, using a group of varied graphic transformations. The analysis of chaotic qualities of time series, including the examination of their phase images can be applied into the classification of chaotic systems. K e y w o r d s: chaotic time sequences, computer data analysis, computer data visualization
Z³o one chaotyczne szeregi czasowe
 JACEK WO OSZYN, PAWE WO OSZYN* Z³o one chaotyczne szeregi czasowe 1. Wprowadzenie Zjawiska zachowania chaotycznego obserwowane w œwiecie rzeczywistym i jego modelach matematycznych zwi¹zane s¹ z charakterem
JACEK WO OSZYN, PAWE WO OSZYN* Z³o one chaotyczne szeregi czasowe 1. Wprowadzenie Zjawiska zachowania chaotycznego obserwowane w œwiecie rzeczywistym i jego modelach matematycznych zwi¹zane s¹ z charakterem
Symulacyjne badanie stabilnoœci numerycznej odcinkami liniowych modeli systemów chaotycznych
 JACEK WO OSZYN Symulacyjne badanie stabilnoœci numerycznej odcinkami liniowych modeli systemów chaotycznych Wstêp W otaczaj¹cej nas rzeczywistoœci wiele systemów cechuje dynamika, w której obserwowaæ mo
JACEK WO OSZYN Symulacyjne badanie stabilnoœci numerycznej odcinkami liniowych modeli systemów chaotycznych Wstêp W otaczaj¹cej nas rzeczywistoœci wiele systemów cechuje dynamika, w której obserwowaæ mo
Rys Mo liwe postacie funkcji w metodzie regula falsi
 5.3. Regula falsi i metoda siecznych 73 Rys. 5.1. Mo liwe postacie funkcji w metodzie regula falsi Rys. 5.2. Przypadek f (x), f (x) > w metodzie regula falsi 74 V. Równania nieliniowe i uk³ady równañ liniowych
5.3. Regula falsi i metoda siecznych 73 Rys. 5.1. Mo liwe postacie funkcji w metodzie regula falsi Rys. 5.2. Przypadek f (x), f (x) > w metodzie regula falsi 74 V. Równania nieliniowe i uk³ady równañ liniowych
gdy wielomian p(x) jest podzielny bez reszty przez trójmian kwadratowy x rx q. W takim przypadku (5.10)
 5.5. Wyznaczanie zer wielomianów 79 gdy wielomian p(x) jest podzielny bez reszty przez trójmian kwadratowy x rx q. W takim przypadku (5.10) gdzie stopieñ wielomianu p 1(x) jest mniejszy lub równy n, przy
5.5. Wyznaczanie zer wielomianów 79 gdy wielomian p(x) jest podzielny bez reszty przez trójmian kwadratowy x rx q. W takim przypadku (5.10) gdzie stopieñ wielomianu p 1(x) jest mniejszy lub równy n, przy
PREZENTACJA INFORMACJI FINANSOWEJ w analizach i modelowaniu finansowym. - dane z rynków finansowych DANE RÓD OWE
 DANE RÓD OWE PREZENTACJA INFORMACJI FINANSOWEJ - dane z rynków finansowych - w formie baz danych - w formie tabel na stronach internetowych - w formie plików tekstowych o uk³adzie kolumnowym - w formie
DANE RÓD OWE PREZENTACJA INFORMACJI FINANSOWEJ - dane z rynków finansowych - w formie baz danych - w formie tabel na stronach internetowych - w formie plików tekstowych o uk³adzie kolumnowym - w formie
POMIAR STRUMIENIA PRZEP YWU METOD ZWÊ KOW - KRYZA.
 POMIAR STRUMIENIA PRZEP YWU METOD ZWÊ KOW - KRYZA. Do pomiaru strumienia przep³ywu w rurach metod¹ zwê kow¹ u ywa siê trzech typów zwê ek pomiarowych. S¹ to kryzy, dysze oraz zwê ki Venturiego. (rysunek
POMIAR STRUMIENIA PRZEP YWU METOD ZWÊ KOW - KRYZA. Do pomiaru strumienia przep³ywu w rurach metod¹ zwê kow¹ u ywa siê trzech typów zwê ek pomiarowych. S¹ to kryzy, dysze oraz zwê ki Venturiego. (rysunek
PRAWA ZACHOWANIA. Podstawowe terminy. Cia a tworz ce uk ad mechaniczny oddzia ywuj mi dzy sob i z cia ami nie nale cymi do uk adu za pomoc
 PRAWA ZACHOWANIA Podstawowe terminy Cia a tworz ce uk ad mechaniczny oddzia ywuj mi dzy sob i z cia ami nie nale cymi do uk adu za pomoc a) si wewn trznych - si dzia aj cych na dane cia o ze strony innych
PRAWA ZACHOWANIA Podstawowe terminy Cia a tworz ce uk ad mechaniczny oddzia ywuj mi dzy sob i z cia ami nie nale cymi do uk adu za pomoc a) si wewn trznych - si dzia aj cych na dane cia o ze strony innych
MATEMATYKA 4 INSTYTUT MEDICUS FUNKCJA KWADRATOWA. Kurs przygotowawczy na studia medyczne. Rok szkolny 2010/2011. tel. 0501 38 39 55 www.medicus.edu.
 INSTYTUT MEDICUS Kurs przygotowawczy na studia medyczne Rok szkolny 00/0 tel. 050 38 39 55 www.medicus.edu.pl MATEMATYKA 4 FUNKCJA KWADRATOWA Funkcją kwadratową lub trójmianem kwadratowym nazywamy funkcję
INSTYTUT MEDICUS Kurs przygotowawczy na studia medyczne Rok szkolny 00/0 tel. 050 38 39 55 www.medicus.edu.pl MATEMATYKA 4 FUNKCJA KWADRATOWA Funkcją kwadratową lub trójmianem kwadratowym nazywamy funkcję
7. OPRACOWYWANIE DANYCH I PROWADZENIE OBLICZEŃ powtórka
 7. OPRACOWYWANIE DANYCH I PROWADZENIE OBLICZEŃ powtórka Oczekiwane przygotowanie informatyczne absolwenta gimnazjum Zbieranie i opracowywanie danych za pomocą arkusza kalkulacyjnego Uczeń: wypełnia komórki
7. OPRACOWYWANIE DANYCH I PROWADZENIE OBLICZEŃ powtórka Oczekiwane przygotowanie informatyczne absolwenta gimnazjum Zbieranie i opracowywanie danych za pomocą arkusza kalkulacyjnego Uczeń: wypełnia komórki
3.2 Warunki meteorologiczne
 Fundacja ARMAAG Raport 1999 3.2 Warunki meteorologiczne Pomiary podstawowych elementów meteorologicznych prowadzono we wszystkich stacjach lokalnych sieci ARMAAG, równolegle z pomiarami stê eñ substancji
Fundacja ARMAAG Raport 1999 3.2 Warunki meteorologiczne Pomiary podstawowych elementów meteorologicznych prowadzono we wszystkich stacjach lokalnych sieci ARMAAG, równolegle z pomiarami stê eñ substancji
Informacje o omawianym programie. Założenia programu omawianego w przykładzie
 1 Komunikacja człowiek - komputer Przedmiot: Komunikacja człowiek - komputer Ćwiczenie: 3 Temat dwiczenia: Projektowanie interfejsu programu typu bazodanowego dr Artur Bartoszewski CZĘŚD I analiza przykładowego
1 Komunikacja człowiek - komputer Przedmiot: Komunikacja człowiek - komputer Ćwiczenie: 3 Temat dwiczenia: Projektowanie interfejsu programu typu bazodanowego dr Artur Bartoszewski CZĘŚD I analiza przykładowego
SYMULACJA STOCHASTYCZNA W ZASTOSOWANIU DO IDENTYFIKACJI FUNKCJI GÊSTOŒCI PRAWDOPODOBIEÑSTWA WYDOBYCIA
 Górnictwo i Geoin ynieria Rok 29 Zeszyt 4 2005 Ryszard Snopkowski* SYMULACJA STOCHASTYCZNA W ZASTOSOWANIU DO IDENTYFIKACJI FUNKCJI GÊSTOŒCI PRAWDOPODOBIEÑSTWA WYDOBYCIA 1. Wprowadzenie W monografii autora
Górnictwo i Geoin ynieria Rok 29 Zeszyt 4 2005 Ryszard Snopkowski* SYMULACJA STOCHASTYCZNA W ZASTOSOWANIU DO IDENTYFIKACJI FUNKCJI GÊSTOŒCI PRAWDOPODOBIEÑSTWA WYDOBYCIA 1. Wprowadzenie W monografii autora
(0) (1) (0) Teoretycznie wystarczy wzi¹æ dowoln¹ macierz M tak¹, by (M) < 1, a nastêpnie obliczyæ wektor (4.17)
 4.6. Metody iteracyjne 65 Z definicji tej wynika, e istnieje skalar, taki e Av = v. Liczbê nazywamy wartoœci¹ w³asn¹ macierzy A. Wartoœci w³asne macierzy A s¹ pierwiastkami wielomianu charakterystycznego
4.6. Metody iteracyjne 65 Z definicji tej wynika, e istnieje skalar, taki e Av = v. Liczbê nazywamy wartoœci¹ w³asn¹ macierzy A. Wartoœci w³asne macierzy A s¹ pierwiastkami wielomianu charakterystycznego
III. INTERPOLACJA Ogólne zadanie interpolacji. Niech oznacza funkcjê zmiennej x zale n¹ od n + 1 parametrów tj.
 III. INTERPOLACJA 3.1. Ogólne zadanie interpolacji Niech oznacza funkcjê zmiennej x zale n¹ od n + 1 parametrów tj. Definicja 3.1. Zadanie interpolacji polega na okreœleniu parametrów tak, eby dla n +
III. INTERPOLACJA 3.1. Ogólne zadanie interpolacji Niech oznacza funkcjê zmiennej x zale n¹ od n + 1 parametrów tj. Definicja 3.1. Zadanie interpolacji polega na okreœleniu parametrów tak, eby dla n +
IV. UK ADY RÓWNAÑ LINIOWYCH
 IV. UK ADY RÓWNAÑ LINIOWYCH 4.1. Wprowadzenie Uk³ad równañ liniowych gdzie A oznacza dan¹ macierz o wymiarze n n, a b dany n-elementowy wektor, mo e byæ rozwi¹zany w skoñczonej liczbie kroków za pomoc¹
IV. UK ADY RÓWNAÑ LINIOWYCH 4.1. Wprowadzenie Uk³ad równañ liniowych gdzie A oznacza dan¹ macierz o wymiarze n n, a b dany n-elementowy wektor, mo e byæ rozwi¹zany w skoñczonej liczbie kroków za pomoc¹
Innym wnioskiem z twierdzenia 3.10 jest
 38 Innym wnioskiem z twierdzenia 3.10 jest Wniosek 3.2. Jeœli funkcja f ma ci¹g³¹ pochodn¹ rzêdu n + 1 na odcinku [a, b] zawieraj¹cym wêz³y rzeczywiste x i (i = 0, 1,..., k) i punkt x, to istnieje wartoœæ
38 Innym wnioskiem z twierdzenia 3.10 jest Wniosek 3.2. Jeœli funkcja f ma ci¹g³¹ pochodn¹ rzêdu n + 1 na odcinku [a, b] zawieraj¹cym wêz³y rzeczywiste x i (i = 0, 1,..., k) i punkt x, to istnieje wartoœæ
DWP. NOWOή: Dysza wentylacji po arowej
 NOWOŒÆ: Dysza wentylacji po arowej DWP Aprobata Techniczna AT-15-550/2007 SMAY Sp. z o.o. / ul. Ciep³ownicza 29 / 1-587 Kraków tel. +48 12 78 18 80 / fax. +48 12 78 18 88 / e-mail: info@smay.eu Przeznaczenie
NOWOŒÆ: Dysza wentylacji po arowej DWP Aprobata Techniczna AT-15-550/2007 SMAY Sp. z o.o. / ul. Ciep³ownicza 29 / 1-587 Kraków tel. +48 12 78 18 80 / fax. +48 12 78 18 88 / e-mail: info@smay.eu Przeznaczenie
Projektowanie procesów logistycznych w systemach wytwarzania
 GABRIELA MAZUR ZYGMUNT MAZUR MAREK DUDEK Projektowanie procesów logistycznych w systemach wytwarzania 1. Wprowadzenie Badania struktury kosztów logistycznych w wielu krajach wykaza³y, e podstawowym ich
GABRIELA MAZUR ZYGMUNT MAZUR MAREK DUDEK Projektowanie procesów logistycznych w systemach wytwarzania 1. Wprowadzenie Badania struktury kosztów logistycznych w wielu krajach wykaza³y, e podstawowym ich
Przedmowa Czêœæ pierwsza. Podstawy frontalnych automatów komórkowych... 11
 Spis treœci Przedmowa... 9 Czêœæ pierwsza. Podstawy frontalnych automatów komórkowych... 11 1. Wstêp... 13 1.1. Rys historyczny... 14 1.2. Klasyfikacja automatów... 18 1.3. Automaty komórkowe a modelowanie
Spis treœci Przedmowa... 9 Czêœæ pierwsza. Podstawy frontalnych automatów komórkowych... 11 1. Wstêp... 13 1.1. Rys historyczny... 14 1.2. Klasyfikacja automatów... 18 1.3. Automaty komórkowe a modelowanie
Uniwersytet Rzeszowski
 Uniwersytet Rzeszowski Interdyscyplinarne Centrum Modelowania Komputerowego Inżynieria oprogramowania Część 1: Tworzenie dokumentacji projektowej Opracował: dr inż. Przemysław Pardel v2.01 2014 1. Dokumentacja
Uniwersytet Rzeszowski Interdyscyplinarne Centrum Modelowania Komputerowego Inżynieria oprogramowania Część 1: Tworzenie dokumentacji projektowej Opracował: dr inż. Przemysław Pardel v2.01 2014 1. Dokumentacja
VRRK. Regulatory przep³ywu CAV
 Regulatory przep³ywu CAV VRRK SMAY Sp. z o.o. / ul. Ciep³ownicza 29 / 1-587 Kraków tel. +48 12 680 20 80 / fax. +48 12 680 20 89 / e-mail: info@smay.eu Przeznaczenie Regulator sta³ego przep³ywu powietrza
Regulatory przep³ywu CAV VRRK SMAY Sp. z o.o. / ul. Ciep³ownicza 29 / 1-587 Kraków tel. +48 12 680 20 80 / fax. +48 12 680 20 89 / e-mail: info@smay.eu Przeznaczenie Regulator sta³ego przep³ywu powietrza
Przyk³adowe zdania. Wydawnictwo Szkolne OMEGA. Zadanie 1. Zadanie 2. Zadanie 3. Zadanie 4. Zadanie 5. Zadanie 6. Zadanie 7. Zadanie 8. Zadanie 9.
 Zadanie. Przyk³adowe zdania Napisz równanie prostej przechodz¹cej przez punkty A (, ) i B (, 4 ). Zadanie. Napisz równanie prostej, której wspó³czynnik kierunkowy równy jest, wiedz¹c, e przechodzi ona
Zadanie. Przyk³adowe zdania Napisz równanie prostej przechodz¹cej przez punkty A (, ) i B (, 4 ). Zadanie. Napisz równanie prostej, której wspó³czynnik kierunkowy równy jest, wiedz¹c, e przechodzi ona
GEO-SYSTEM Sp. z o.o. GEO-RCiWN Rejestr Cen i Wartości Nieruchomości Podręcznik dla uŝytkowników modułu wyszukiwania danych Warszawa 2007
 GEO-SYSTEM Sp. z o.o. 02-732 Warszawa, ul. Podbipięty 34 m. 7, tel./fax 847-35-80, 853-31-15 http:\\www.geo-system.com.pl e-mail:geo-system@geo-system.com.pl GEO-RCiWN Rejestr Cen i Wartości Nieruchomości
GEO-SYSTEM Sp. z o.o. 02-732 Warszawa, ul. Podbipięty 34 m. 7, tel./fax 847-35-80, 853-31-15 http:\\www.geo-system.com.pl e-mail:geo-system@geo-system.com.pl GEO-RCiWN Rejestr Cen i Wartości Nieruchomości
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI
 WPISUJE ZDAJ CY KOD PESEL PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY PRZED MATUR MAJ 2012 1. SprawdŸ, czy arkusz egzaminacyjny zawiera 16 stron (zadania 1 11). Ewentualny brak zg³oœ przewodnicz¹cemu
WPISUJE ZDAJ CY KOD PESEL PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY PRZED MATUR MAJ 2012 1. SprawdŸ, czy arkusz egzaminacyjny zawiera 16 stron (zadania 1 11). Ewentualny brak zg³oœ przewodnicz¹cemu
Zadanie 21. Stok narciarski
 Numer zadania Zadanie. Stok narciarski KLUCZ DO ZADA ARKUSZA II Je eli zdaj cy rozwi e zadanie inn, merytorycznie poprawn metod otrzymuje maksymaln liczb punktów Numer polecenia i poprawna odpowied. sporz
Numer zadania Zadanie. Stok narciarski KLUCZ DO ZADA ARKUSZA II Je eli zdaj cy rozwi e zadanie inn, merytorycznie poprawn metod otrzymuje maksymaln liczb punktów Numer polecenia i poprawna odpowied. sporz
Witold Bednarek. Konkurs matematyczny w gimnazjum Przygotuj siê sam!
 Witold Bednarek Konkurs matematyczny w gimnazjum Przygotuj siê sam! OPOLE Wydawnictwo NOWIK Sp.j. 2012 Spis treœci Od autora......................................... 4 Rozgrzewka.......................................
Witold Bednarek Konkurs matematyczny w gimnazjum Przygotuj siê sam! OPOLE Wydawnictwo NOWIK Sp.j. 2012 Spis treœci Od autora......................................... 4 Rozgrzewka.......................................
Tytu : GRAPHER Podr cznik u ytkownika ISBN: 978-83-920531-7-0 Autor: Zbigniew Galon Rok wydania: 2009 Stron: 408 Wydawca: Gambit COiS Sp. z o.o.
 Tytu : GRAPHER Podr cznik u ytkownika ISBN: 978-83-920531-7-0 Autor: Zbigniew Galon Rok wydania: 2009 Stron: 408 Wydawca: Spis tre ci: 1 CO ZAWIERA TEN PODR CZNIK? 9 1.1 CZ STO U YWANE POJ CIA 10 2 DO
Tytu : GRAPHER Podr cznik u ytkownika ISBN: 978-83-920531-7-0 Autor: Zbigniew Galon Rok wydania: 2009 Stron: 408 Wydawca: Spis tre ci: 1 CO ZAWIERA TEN PODR CZNIK? 9 1.1 CZ STO U YWANE POJ CIA 10 2 DO
PROGRAM NAUCZANIA INFORMATYKA
 PROGRAM NAUCZANIA INFORMATYKA KLASA VI Program nauczania: DKOS 5002 38/05 Podręcznik: Informatyka Europejczyjka. Wydawnictwo HELION Lp. Temat lekcji podstawowe Wymagania programowe ponadpodstawowe 1 Lekcja
PROGRAM NAUCZANIA INFORMATYKA KLASA VI Program nauczania: DKOS 5002 38/05 Podręcznik: Informatyka Europejczyjka. Wydawnictwo HELION Lp. Temat lekcji podstawowe Wymagania programowe ponadpodstawowe 1 Lekcja
INSTRUKCJA WebPTB 1.0
 INSTRUKCJA WebPTB 1.0 Program WebPTB wspomaga zarządzaniem budynkami w kontekście ich bezpieczeństwa fizycznego. Zawiera zestawienie budynków wraz z ich cechami fizycznymi, które mają wpływ na bezpieczeństwo
INSTRUKCJA WebPTB 1.0 Program WebPTB wspomaga zarządzaniem budynkami w kontekście ich bezpieczeństwa fizycznego. Zawiera zestawienie budynków wraz z ich cechami fizycznymi, które mają wpływ na bezpieczeństwo
EGZAMIN MATURALNY Z INFORMATYKI
 Miejsce na naklejkê z kodem (Wpisuje zdaj¹cy przed rozpoczêciem pracy) KOD ZDAJ CEGO MIN-W2A1P-021 EGZAMIN MATURALNY Z INFORMATYKI Instrukcja dla zdaj¹cego Czas pracy 120 minut 1. Proszê sprawdziæ, czy
Miejsce na naklejkê z kodem (Wpisuje zdaj¹cy przed rozpoczêciem pracy) KOD ZDAJ CEGO MIN-W2A1P-021 EGZAMIN MATURALNY Z INFORMATYKI Instrukcja dla zdaj¹cego Czas pracy 120 minut 1. Proszê sprawdziæ, czy
Wytyczne Województwa Wielkopolskiego
 5. Wytyczne Województwa Wielkopolskiego Projekt wspó³finansowany przez Uniê Europejsk¹ z Europejskiego Funduszu Rozwoju Regionalnego oraz Bud etu Pañstwa w ramach Wielkopolskiego Regionalnego Programu
5. Wytyczne Województwa Wielkopolskiego Projekt wspó³finansowany przez Uniê Europejsk¹ z Europejskiego Funduszu Rozwoju Regionalnego oraz Bud etu Pañstwa w ramach Wielkopolskiego Regionalnego Programu
K P K P R K P R D K P R D W
 KLASA III TECHNIKUM POZIOM PODSTAWOWY I ROZSZERZONY PROPOZYCJA POZIOMÓW WYMAGAŃ Wyróżnione zostały następujące wymagania programowe: konieczne (K), podstawowe (P), rozszerzające (R), dopełniające (D) i
KLASA III TECHNIKUM POZIOM PODSTAWOWY I ROZSZERZONY PROPOZYCJA POZIOMÓW WYMAGAŃ Wyróżnione zostały następujące wymagania programowe: konieczne (K), podstawowe (P), rozszerzające (R), dopełniające (D) i
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI
 PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY Czas pracy 80 minut Instrukcja dla zdaj¹cego. SprawdŸ, czy arkusz egzaminacyjny zawiera stron (zadania 0). Ewentualny brak zg³oœ przewodnicz¹cemu
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY Czas pracy 80 minut Instrukcja dla zdaj¹cego. SprawdŸ, czy arkusz egzaminacyjny zawiera stron (zadania 0). Ewentualny brak zg³oœ przewodnicz¹cemu
L A K M A R. Rega³y DE LAKMAR
 Rega³y DE LAKMAR Strona 2 I. KONSTRUKCJA REGA ÓW 7 1 2 8 3 4 1 5 6 Rys. 1. Rega³ przyœcienny: 1 noga, 2 ty³, 3 wspornik pó³ki, 4pó³ka, 5 stopka, 6 os³ona dolna, 7 zaœlepka, 8 os³ona górna 1 2 3 4 9 8 1
Rega³y DE LAKMAR Strona 2 I. KONSTRUKCJA REGA ÓW 7 1 2 8 3 4 1 5 6 Rys. 1. Rega³ przyœcienny: 1 noga, 2 ty³, 3 wspornik pó³ki, 4pó³ka, 5 stopka, 6 os³ona dolna, 7 zaœlepka, 8 os³ona górna 1 2 3 4 9 8 1
S Z R - 2 8 1 A p l i k a c j a
 GWARANCJA GWARANCJA ul. Konstantynowska 79/81 95-200 Pabianice tel/fax 42-2152383, 2270971 e-mail: fif@fif.com.pl SAMOCZYNNY ZA CZNIK REZERWY S Z R - 2 8 1 A p l i k a c j a g o o d i d e a s g o o d s
GWARANCJA GWARANCJA ul. Konstantynowska 79/81 95-200 Pabianice tel/fax 42-2152383, 2270971 e-mail: fif@fif.com.pl SAMOCZYNNY ZA CZNIK REZERWY S Z R - 2 8 1 A p l i k a c j a g o o d i d e a s g o o d s
Krótka informacja o instytucjonalnej obs³udze rynku pracy
 Agnieszka Miler Departament Rynku Pracy Ministerstwo Gospodarki, Pracy i Polityki Spo³ecznej Krótka informacja o instytucjonalnej obs³udze rynku pracy W 2000 roku, zosta³o wprowadzone rozporz¹dzeniem Prezesa
Agnieszka Miler Departament Rynku Pracy Ministerstwo Gospodarki, Pracy i Polityki Spo³ecznej Krótka informacja o instytucjonalnej obs³udze rynku pracy W 2000 roku, zosta³o wprowadzone rozporz¹dzeniem Prezesa
PRZETWORNIK PROGRAMOWALNY NAPIÊCIA I PR DU STA EGO TYPU P20H
 PRZETWORNIK PROGRAMOWALNY NAPIÊCIA I PR DU STA EGO TYPU P20H Instrukcja konfiguracji przetwornika P20H za pomoc¹ programu LPCon 1 2 Spis treœci 1. Konfiguracja przetwornika za pomoc¹ programu LPCon...
PRZETWORNIK PROGRAMOWALNY NAPIÊCIA I PR DU STA EGO TYPU P20H Instrukcja konfiguracji przetwornika P20H za pomoc¹ programu LPCon 1 2 Spis treœci 1. Konfiguracja przetwornika za pomoc¹ programu LPCon...
Temat: Funkcje. Własności ogólne. A n n a R a j f u r a, M a t e m a t y k a s e m e s t r 1, W S Z i M w S o c h a c z e w i e 1
 Temat: Funkcje. Własności ogólne A n n a R a j f u r a, M a t e m a t y k a s e m e s t r 1, W S Z i M w S o c h a c z e w i e 1 Kody kolorów: pojęcie zwraca uwagę * materiał nieobowiązkowy A n n a R a
Temat: Funkcje. Własności ogólne A n n a R a j f u r a, M a t e m a t y k a s e m e s t r 1, W S Z i M w S o c h a c z e w i e 1 Kody kolorów: pojęcie zwraca uwagę * materiał nieobowiązkowy A n n a R a
WYKŁAD 8. Postacie obrazów na różnych etapach procesu przetwarzania
 WYKŁAD 8 Reprezentacja obrazu Elementy edycji (tworzenia) obrazu Postacie obrazów na różnych etapach procesu przetwarzania Klasy obrazów Klasa 1: Obrazy o pełnej skali stopni jasności, typowe parametry:
WYKŁAD 8 Reprezentacja obrazu Elementy edycji (tworzenia) obrazu Postacie obrazów na różnych etapach procesu przetwarzania Klasy obrazów Klasa 1: Obrazy o pełnej skali stopni jasności, typowe parametry:
tel/fax 018 443 82 13 lub 018 443 74 19 NIP 7343246017 Regon 120493751
 Zespół Placówek Kształcenia Zawodowego 33-300 Nowy Sącz ul. Zamenhoffa 1 tel/fax 018 443 82 13 lub 018 443 74 19 http://zpkz.nowysacz.pl e-mail biuro@ckp-ns.edu.pl NIP 7343246017 Regon 120493751 Wskazówki
Zespół Placówek Kształcenia Zawodowego 33-300 Nowy Sącz ul. Zamenhoffa 1 tel/fax 018 443 82 13 lub 018 443 74 19 http://zpkz.nowysacz.pl e-mail biuro@ckp-ns.edu.pl NIP 7343246017 Regon 120493751 Wskazówki
7. REZONANS W OBWODACH ELEKTRYCZNYCH
 OBWODY SYGNAŁY 7. EZONANS W OBWODAH EEKTYZNYH 7.. ZJAWSKO EZONANS Obwody elektryczne, w których występuje zjawisko rezonansu nazywane są obwodami rezonansowymi lub drgającymi. ozpatrując bezźródłowy obwód
OBWODY SYGNAŁY 7. EZONANS W OBWODAH EEKTYZNYH 7.. ZJAWSKO EZONANS Obwody elektryczne, w których występuje zjawisko rezonansu nazywane są obwodami rezonansowymi lub drgającymi. ozpatrując bezźródłowy obwód
JADWIGA SKIMINA PUBLIKACJA NA TEMAT: NAUKA MS. WORD 2000 W KLASIE IV
 JADWIGA SKIMINA PUBLIKACJA NA TEMAT: NAUKA MS. WORD 2000 W KLASIE IV Uczniowie klas czwartych dopiero zaczynają naukę o komputerach. Niektórzy z nich dopiero na lekcjach informatyki zetknęli się po raz
JADWIGA SKIMINA PUBLIKACJA NA TEMAT: NAUKA MS. WORD 2000 W KLASIE IV Uczniowie klas czwartych dopiero zaczynają naukę o komputerach. Niektórzy z nich dopiero na lekcjach informatyki zetknęli się po raz
ECDL Advanced Moduł AM3 Przetwarzanie tekstu Syllabus, wersja 2.0
 ECDL Advanced Moduł AM3 Przetwarzanie tekstu Syllabus, wersja 2.0 Copyright 2010, Polskie Towarzystwo Informatyczne Zastrzeżenie Dokument ten został opracowany na podstawie materiałów źródłowych pochodzących
ECDL Advanced Moduł AM3 Przetwarzanie tekstu Syllabus, wersja 2.0 Copyright 2010, Polskie Towarzystwo Informatyczne Zastrzeżenie Dokument ten został opracowany na podstawie materiałów źródłowych pochodzących
G PROGRAMMING. Part #4
 G PROGRAMMING Part #4 Tablice, wykresy, klastry Tablice Zbiór elementów danych tego samego typu Zastosowanie gromadzenie danych z powtarzalnych operacji odczytu, obliczeń (magazynowanie danych przebiegów
G PROGRAMMING Part #4 Tablice, wykresy, klastry Tablice Zbiór elementów danych tego samego typu Zastosowanie gromadzenie danych z powtarzalnych operacji odczytu, obliczeń (magazynowanie danych przebiegów
Modelowanie œrodowiska 3D z danych pomiarowych**
 AUTOMATYKA 2005 Tom 9 Zeszyt 3 Jacek Nowakowski *, Daniel Kaczorowski * Modelowanie œrodowiska 3D z danych pomiarowych** 1. Wprowadzenie Jednym z obszarów mo liwego wykorzystania symulacji komputerowej
AUTOMATYKA 2005 Tom 9 Zeszyt 3 Jacek Nowakowski *, Daniel Kaczorowski * Modelowanie œrodowiska 3D z danych pomiarowych** 1. Wprowadzenie Jednym z obszarów mo liwego wykorzystania symulacji komputerowej
Jerzy Stopa*, Stanis³aw Rychlicki*, Pawe³ Wojnarowski* ZASTOSOWANIE ODWIERTÓW MULTILATERALNYCH NA Z O ACH ROPY NAFTOWEJ W PÓ NEJ FAZIE EKSPLOATACJI
 WIERTNICTWO NAFTA GAZ TOM 24 ZESZYT 1 2007 Jerzy Stopa*, Stanis³aw Rychlicki*, Pawe³ Wojnarowski* ZASTOSOWANIE ODWIERTÓW MULTILATERALNYCH NA Z O ACH ROPY NAFTOWEJ W PÓ NEJ FAZIE EKSPLOATACJI 1. WPROWADZENIE
WIERTNICTWO NAFTA GAZ TOM 24 ZESZYT 1 2007 Jerzy Stopa*, Stanis³aw Rychlicki*, Pawe³ Wojnarowski* ZASTOSOWANIE ODWIERTÓW MULTILATERALNYCH NA Z O ACH ROPY NAFTOWEJ W PÓ NEJ FAZIE EKSPLOATACJI 1. WPROWADZENIE
ZA CZNIK C: FUNKCJE KLAWISZY I SPOSOBY WPROWADZANIA PARAMETRÓW
 ZA CZNIKI ZA CZNIK C: FUNKCJE KLAWISZY I SPOSOBY WPROWADZANIA PARAMETRÓW Pola, do których wprowadzamy dane, mog¹ byæ: znakowe, numeryczne, typu daty oraz typu memo (pola tekstowe). Istniej¹ ró nice w wykorzystaniu
ZA CZNIKI ZA CZNIK C: FUNKCJE KLAWISZY I SPOSOBY WPROWADZANIA PARAMETRÓW Pola, do których wprowadzamy dane, mog¹ byæ: znakowe, numeryczne, typu daty oraz typu memo (pola tekstowe). Istniej¹ ró nice w wykorzystaniu
Wyznaczanie współczynnika sprężystości sprężyn i ich układów
 Ćwiczenie 63 Wyznaczanie współczynnika sprężystości sprężyn i ich układów 63.1. Zasada ćwiczenia W ćwiczeniu określa się współczynnik sprężystości pojedynczych sprężyn i ich układów, mierząc wydłużenie
Ćwiczenie 63 Wyznaczanie współczynnika sprężystości sprężyn i ich układów 63.1. Zasada ćwiczenia W ćwiczeniu określa się współczynnik sprężystości pojedynczych sprężyn i ich układów, mierząc wydłużenie
14.Rozwiązywanie zadań tekstowych wykorzystujących równania i nierówności kwadratowe.
 Matematyka 4/ 4.Rozwiązywanie zadań tekstowych wykorzystujących równania i nierówności kwadratowe. I. Przypomnij sobie:. Wiadomości z poprzedniej lekcji... Że przy rozwiązywaniu zadań tekstowych wykorzystujących
Matematyka 4/ 4.Rozwiązywanie zadań tekstowych wykorzystujących równania i nierówności kwadratowe. I. Przypomnij sobie:. Wiadomości z poprzedniej lekcji... Że przy rozwiązywaniu zadań tekstowych wykorzystujących
Fabian Stasiak. Zbiór wicze Autodesk Inventor 2018 KURS ZAAWANSOWANY. ExpertBooks
 Fabian Stasiak PRZYK ADOWE WICZENIE Z PODR CZNIKA Zbiór wicze Autodesk Inventor 2018 KURS ZAAWANSOWANY ExpertBooks 60 wiczenie 1.15 Podstawy pracy z cz ciami wielobry owymi. Zawias W tym wiczeniu poznamy
Fabian Stasiak PRZYK ADOWE WICZENIE Z PODR CZNIKA Zbiór wicze Autodesk Inventor 2018 KURS ZAAWANSOWANY ExpertBooks 60 wiczenie 1.15 Podstawy pracy z cz ciami wielobry owymi. Zawias W tym wiczeniu poznamy
System zwieñczeñ nasad¹ wentylacyjn¹
 System zwieñczeñ nasad¹ wentylacyjn¹ Z e f i r - 1 5 0 System zwieñczeñ nasad¹ wentylacyjn¹ ZeFir-150 dla wielorodzinnego budownictwa mieszkaniowego Wywietrzniki grawitacyjne ZeFir Urz¹dzenia ca³kowicie
System zwieñczeñ nasad¹ wentylacyjn¹ Z e f i r - 1 5 0 System zwieñczeñ nasad¹ wentylacyjn¹ ZeFir-150 dla wielorodzinnego budownictwa mieszkaniowego Wywietrzniki grawitacyjne ZeFir Urz¹dzenia ca³kowicie
Ćwiczenie: "Ruch harmoniczny i fale"
 Ćwiczenie: "Ruch harmoniczny i fale" Opracowane w ramach projektu: "Wirtualne Laboratoria Fizyczne nowoczesną metodą nauczania realizowanego przez Warszawską Wyższą Szkołę Informatyki. Zakres ćwiczenia:
Ćwiczenie: "Ruch harmoniczny i fale" Opracowane w ramach projektu: "Wirtualne Laboratoria Fizyczne nowoczesną metodą nauczania realizowanego przez Warszawską Wyższą Szkołę Informatyki. Zakres ćwiczenia:
revati.pl Drukarnia internetowa Szybki kontakt z klientem Obs³uga zapytañ ofertowych rozwi¹zania dla poligrafii Na 100% procent wiêcej klientów
 revati.pl rozwi¹zania dla poligrafii Systemy do sprzeda y us³ug poligraficznych w internecie Drukarnia Szybki kontakt z klientem Obs³uga zapytañ ofertowych Na 100% procent wiêcej klientów drukarnia drukarnia
revati.pl rozwi¹zania dla poligrafii Systemy do sprzeda y us³ug poligraficznych w internecie Drukarnia Szybki kontakt z klientem Obs³uga zapytañ ofertowych Na 100% procent wiêcej klientów drukarnia drukarnia
Powszechność nauczania języków obcych w roku szkolnym
 Z PRAC INSTYTUTÓW Jadwiga Zarębska Warszawa, CODN Powszechność nauczania języków obcych w roku szkolnym 2000 2001 Ö I. Powszechność nauczania języków obcych w różnych typach szkół Dane przedstawione w
Z PRAC INSTYTUTÓW Jadwiga Zarębska Warszawa, CODN Powszechność nauczania języków obcych w roku szkolnym 2000 2001 Ö I. Powszechność nauczania języków obcych w różnych typach szkół Dane przedstawione w
Moduł. Rama 2D suplement do wersji Konstruktora 4.6
 Moduł Rama 2D suplement do wersji Konstruktora 4.6 110-1 Spis treści 110. RAMA 2D - SUPLEMENT...3 110.1 OPIS ZMIAN...3 110.1.1 Nowy tryb wymiarowania...3 110.1.2 Moduł dynamicznego przeglądania wyników...5
Moduł Rama 2D suplement do wersji Konstruktora 4.6 110-1 Spis treści 110. RAMA 2D - SUPLEMENT...3 110.1 OPIS ZMIAN...3 110.1.1 Nowy tryb wymiarowania...3 110.1.2 Moduł dynamicznego przeglądania wyników...5
Zasady racjonalnego dokumentowania systemu zarządzania
 Jerzy Kowalczyk Zasady racjonalnego dokumentowania systemu zarządzania Zasady doskonalenia systemu zarządzania oraz podstawowe procedury wspomagające Zarządzanie jakością VERLAG DASHÖFER Wydawnictwo VERLAG
Jerzy Kowalczyk Zasady racjonalnego dokumentowania systemu zarządzania Zasady doskonalenia systemu zarządzania oraz podstawowe procedury wspomagające Zarządzanie jakością VERLAG DASHÖFER Wydawnictwo VERLAG
WYPRAWKA SZKOLNA 2015
 WYPRAWKA SZKOLNA 2015 Pion Edukacji i Usług Społecznych Urzędu Miejskiego w Śremie informuje, że w ramach Rządowego programu pomocy uczniom w 2015r. Wyprawka szkolna można skorzystać z pomocy na dofinansowanie:
WYPRAWKA SZKOLNA 2015 Pion Edukacji i Usług Społecznych Urzędu Miejskiego w Śremie informuje, że w ramach Rządowego programu pomocy uczniom w 2015r. Wyprawka szkolna można skorzystać z pomocy na dofinansowanie:
X. M A N A G E R. q Przeznaczenie modu³u q Wykaz funkcji q Codzienna eksploatacja
 X. M A N A G E R q Przeznaczenie modu³u q Wykaz funkcji q Codzienna eksploatacja Schemat funkcjonalny modu³u MANAGER SPIS TREŒCI X.1. PRZEZNACZENIE MODU U...X-3 X.2. WYKAZ FUNKCJI...X-4 X.3. CODZIENNA
X. M A N A G E R q Przeznaczenie modu³u q Wykaz funkcji q Codzienna eksploatacja Schemat funkcjonalny modu³u MANAGER SPIS TREŒCI X.1. PRZEZNACZENIE MODU U...X-3 X.2. WYKAZ FUNKCJI...X-4 X.3. CODZIENNA
Nowe funkcjonalności
 Nowe funkcjonalności 1 I. Aplikacja supermakler 1. Nowe notowania Dotychczasowe notowania koszykowe, z racji ograniczonej możliwości personalizacji, zostały zastąpione nowymi tabelami z notowaniami bieżącymi.
Nowe funkcjonalności 1 I. Aplikacja supermakler 1. Nowe notowania Dotychczasowe notowania koszykowe, z racji ograniczonej możliwości personalizacji, zostały zastąpione nowymi tabelami z notowaniami bieżącymi.
Mathematica - podstawy
 Mathematica - podstawy Artur Kalinowski Semestr letni 2011/2012 Artur Kalinowski Mathematica - podstawy 1 / 27 Spis tre±ci Program Mathematica 1 Program Mathematica 2 3 4 5 Artur Kalinowski Mathematica
Mathematica - podstawy Artur Kalinowski Semestr letni 2011/2012 Artur Kalinowski Mathematica - podstawy 1 / 27 Spis tre±ci Program Mathematica 1 Program Mathematica 2 3 4 5 Artur Kalinowski Mathematica
REGULAMIN X GMINNEGO KONKURSU INFORMATYCZNEGO
 REGULAMIN X GMINNEGO KONKURSU INFORMATYCZNEGO 1. Postanowienia ogólne 1. Organizatorem konkursu jest Zespół Szkół w Podolu-Górowej. 2. Konkurs przeznaczony jest dla uczniów szkół podstawowych i gimnazjów
REGULAMIN X GMINNEGO KONKURSU INFORMATYCZNEGO 1. Postanowienia ogólne 1. Organizatorem konkursu jest Zespół Szkół w Podolu-Górowej. 2. Konkurs przeznaczony jest dla uczniów szkół podstawowych i gimnazjów
ZADANIA OTWARTE KRÓTKIEJ ODPOWIEDZI
 Zadanie 51. ( pkt) Rozwi równanie 3 x 1. 1 x Zadanie 5. ( pkt) x 3y 5 Rozwi uk ad równa. x y 3 Zadanie 53. ( pkt) Rozwi nierówno x 6x 7 0. ZADANIA OTWARTE KRÓTKIEJ ODPOWIEDZI Zadanie 54. ( pkt) 3 Rozwi
Zadanie 51. ( pkt) Rozwi równanie 3 x 1. 1 x Zadanie 5. ( pkt) x 3y 5 Rozwi uk ad równa. x y 3 Zadanie 53. ( pkt) Rozwi nierówno x 6x 7 0. ZADANIA OTWARTE KRÓTKIEJ ODPOWIEDZI Zadanie 54. ( pkt) 3 Rozwi
ZAŁĄCZNIK NR 1. Zakres wiedzy i umiejętności oraz wykaz proponowanej bibliografii
 ZAŁĄCZNIK NR 1 Zakres wiedzy i umiejętności oraz wykaz proponowanej bibliografii I. Obszary umiejętności sprawdzane na kaŝdym etapie Konkursu 1. Wykorzystanie i tworzenie informacji. Uczeń: 1) interpretuje
ZAŁĄCZNIK NR 1 Zakres wiedzy i umiejętności oraz wykaz proponowanej bibliografii I. Obszary umiejętności sprawdzane na kaŝdym etapie Konkursu 1. Wykorzystanie i tworzenie informacji. Uczeń: 1) interpretuje
biegle i poprawnie posługuje się terminologią informatyczną,
 INFORMATYKA KLASA 1 1. Wymagania na poszczególne oceny: 1) ocenę celującą otrzymuje uczeń, który: samodzielnie wykonuje na komputerze wszystkie zadania z lekcji, wykazuje inicjatywę rozwiązywania konkretnych
INFORMATYKA KLASA 1 1. Wymagania na poszczególne oceny: 1) ocenę celującą otrzymuje uczeń, który: samodzielnie wykonuje na komputerze wszystkie zadania z lekcji, wykazuje inicjatywę rozwiązywania konkretnych
Krótka instrukcja opracowania danych w programie SciDAVis v. 1-D013-win
 Krótka instrukcja opracowania danych w programie SciDAVis v. 1-D013-win 1 Instalacja programu SciDAVis Microsoft Windows Informacje na temat projektu SciDAVis dostępne są na stronie http://scidavis.sourceforge.net/.
Krótka instrukcja opracowania danych w programie SciDAVis v. 1-D013-win 1 Instalacja programu SciDAVis Microsoft Windows Informacje na temat projektu SciDAVis dostępne są na stronie http://scidavis.sourceforge.net/.
Komentarz do prac egzaminacyjnych w zawodzie technik administracji 343[01] ETAP PRAKTYCZNY EGZAMINU POTWIERDZAJĄCEGO KWALIFIKACJE ZAWODOWE
![Komentarz do prac egzaminacyjnych w zawodzie technik administracji 343[01] ETAP PRAKTYCZNY EGZAMINU POTWIERDZAJĄCEGO KWALIFIKACJE ZAWODOWE Komentarz do prac egzaminacyjnych w zawodzie technik administracji 343[01] ETAP PRAKTYCZNY EGZAMINU POTWIERDZAJĄCEGO KWALIFIKACJE ZAWODOWE](/thumbs/39/18551291.jpg) Komentarz do prac egzaminacyjnych w zawodzie technik administracji 343[01] ETAP PRAKTYCZNY EGZAMINU POTWIERDZAJĄCEGO KWALIFIKACJE ZAWODOWE OKE Kraków 2012 Zadanie egzaminacyjne zostało opracowane
Komentarz do prac egzaminacyjnych w zawodzie technik administracji 343[01] ETAP PRAKTYCZNY EGZAMINU POTWIERDZAJĄCEGO KWALIFIKACJE ZAWODOWE OKE Kraków 2012 Zadanie egzaminacyjne zostało opracowane
Chmura obliczeniowa. do przechowywania plików online. Anna Walkowiak CEN Koszalin 2015-10-16
 Chmura obliczeniowa do przechowywania plików online Anna Walkowiak CEN Koszalin 2015-10-16 1 Chmura, czyli co? Chmura obliczeniowa (cloud computing) to usługa przechowywania i wykorzystywania danych, do
Chmura obliczeniowa do przechowywania plików online Anna Walkowiak CEN Koszalin 2015-10-16 1 Chmura, czyli co? Chmura obliczeniowa (cloud computing) to usługa przechowywania i wykorzystywania danych, do
Narzêdzia wspomagaj¹ce zarz¹dzanie bezpieczeñstwem pracy w przedsiêbiorstwie komputerowy program doboru œrodków ochrony indywidualnej DOBÓR
 mgr in. ADAM POŒCIK mgr in. ANDRZEJ BIERNACKI Centralny Instytut Ochrony Pracy Narzêdzia wspomagaj¹ce zarz¹dzanie bezpieczeñstwem pracy w przedsiêbiorstwie komputerowy program doboru œrodków ochrony indywidualnej
mgr in. ADAM POŒCIK mgr in. ANDRZEJ BIERNACKI Centralny Instytut Ochrony Pracy Narzêdzia wspomagaj¹ce zarz¹dzanie bezpieczeñstwem pracy w przedsiêbiorstwie komputerowy program doboru œrodków ochrony indywidualnej
(wymiar macierzy trójk¹tnej jest równy liczbie elementów na g³ównej przek¹tnej). Z twierdzen 1 > 0. Zatem dla zale noœci
 56 Za³ó my, e twierdzenie jest prawdziwe dla macierzy dodatnio okreœlonej stopnia n 1. Macierz A dodatnio okreœlon¹ stopnia n mo na zapisaæ w postaci n 1 gdzie A n 1 oznacza macierz dodatnio okreœlon¹
56 Za³ó my, e twierdzenie jest prawdziwe dla macierzy dodatnio okreœlonej stopnia n 1. Macierz A dodatnio okreœlon¹ stopnia n mo na zapisaæ w postaci n 1 gdzie A n 1 oznacza macierz dodatnio okreœlon¹
Kreowanie i analizowanie eksperymentów pełnoczynnikowych w programie Minitab. Osoba kontaktowa: Katarzyna Kornicka Telefon:
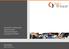 Kreowanie i analizowanie eksperymentów pełnoczynnikowych w programie Minitab Osoba kontaktowa: Katarzyna Kornicka Telefon: +48 785 9 353 Rozpoczęcie pracy z programem Minitab ver 5 Session Window, tutaj
Kreowanie i analizowanie eksperymentów pełnoczynnikowych w programie Minitab Osoba kontaktowa: Katarzyna Kornicka Telefon: +48 785 9 353 Rozpoczęcie pracy z programem Minitab ver 5 Session Window, tutaj
Opis zmian funkcjonalności platformy E-GIODO wprowadzonych w związku z wprowadzeniem możliwości wysyłania wniosków bez podpisu elektronicznego
 Opis zmian funkcjonalności platformy E-GIODO wprowadzonych w związku z wprowadzeniem możliwości wysyłania wniosków bez podpisu elektronicznego Wstęp. Dodanie funkcjonalności wysyłania wniosków bez podpisów
Opis zmian funkcjonalności platformy E-GIODO wprowadzonych w związku z wprowadzeniem możliwości wysyłania wniosków bez podpisu elektronicznego Wstęp. Dodanie funkcjonalności wysyłania wniosków bez podpisów
Monitoring oraz rozliczenie zu ycia. energii i mediów. Systemy pomiarowe, monitorowanie, archiwizacja i wizualizacja
 Monitoring oraz rozliczenie zu ycia energii i mediów Systemy pomiarowe, monitorowanie, archiwizacja i wizualizacja Zacznij mierzyæ i zobacz swój zysk O firmie Metronic Systems jest nowoczesn¹ firm¹ in
Monitoring oraz rozliczenie zu ycia energii i mediów Systemy pomiarowe, monitorowanie, archiwizacja i wizualizacja Zacznij mierzyæ i zobacz swój zysk O firmie Metronic Systems jest nowoczesn¹ firm¹ in
Czy przedsiêbiorstwo, którym zarz¹dzasz, intensywnie siê rozwija, ma wiele oddzia³ów lub kolejne lokalizacje w planach?
 Czy przedsiêbiorstwo, którym zarz¹dzasz, intensywnie siê rozwija, ma wiele oddzia³ów lub kolejne lokalizacje w planach? Czy masz niedosyt informacji niezbêdnych do tego, by mieæ pe³en komfort w podejmowaniu
Czy przedsiêbiorstwo, którym zarz¹dzasz, intensywnie siê rozwija, ma wiele oddzia³ów lub kolejne lokalizacje w planach? Czy masz niedosyt informacji niezbêdnych do tego, by mieæ pe³en komfort w podejmowaniu
Gra yna Œwiderska BIOZ. w budownictwie. poradnik
 Gra yna Œwiderska BIOZ w budownictwie poradnik Warszawa 2008 Copyright by Gra yna Œwiderska i Oficyna Wydawnicza POLCEN Sp. z o.o. Warszawa 2008 Autorzy Gra yna Œwiderska autor g³ówny W³adys³aw Korzeniewski
Gra yna Œwiderska BIOZ w budownictwie poradnik Warszawa 2008 Copyright by Gra yna Œwiderska i Oficyna Wydawnicza POLCEN Sp. z o.o. Warszawa 2008 Autorzy Gra yna Œwiderska autor g³ówny W³adys³aw Korzeniewski
Wyk³ad INTERPOLACJA.
 Wyk³ad 1. 3.10.2003 INTERPOLACJA. G³ównym zadaniem interpolacji jest wyznaczenie mo liwie szybki sposób wartoœci funkcji f(x) dla zmiennej niezale nej x, która nie nale y do tablicy danych (x i,y i ).
Wyk³ad 1. 3.10.2003 INTERPOLACJA. G³ównym zadaniem interpolacji jest wyznaczenie mo liwie szybki sposób wartoœci funkcji f(x) dla zmiennej niezale nej x, która nie nale y do tablicy danych (x i,y i ).
Centralna Komisja Egzaminacyjna Arkusz zawiera informacje prawnie chronione do momentu rozpocz cia egzaminu. PESEL
 Centralna Komisja Egzaminacyjna Arkusz zawiera informacje prawnie chronione do momentu rozpocz cia egzaminu. Uk ad graficzny CKE 0 KOD UCZNIA UZUPE NIA ZESPÓ NADZORUJ CY PESEL miejsce na naklejk z kodem
Centralna Komisja Egzaminacyjna Arkusz zawiera informacje prawnie chronione do momentu rozpocz cia egzaminu. Uk ad graficzny CKE 0 KOD UCZNIA UZUPE NIA ZESPÓ NADZORUJ CY PESEL miejsce na naklejk z kodem
EGZAMIN MATURALNY Z MATEMATYKI
 ARKUSZ ZAWIERA INFORMACJE PRAWNIE CHRONIONE DO MOMENTU ROZPOCZ CIA EGZAMINU! Miejsce na naklejk MMA-P1_1P-092 EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY MAJ ROK 2009 Czas pracy 120 minut Instrukcja
ARKUSZ ZAWIERA INFORMACJE PRAWNIE CHRONIONE DO MOMENTU ROZPOCZ CIA EGZAMINU! Miejsce na naklejk MMA-P1_1P-092 EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY MAJ ROK 2009 Czas pracy 120 minut Instrukcja
2 kwh/1000h. Rozporz¹dzenie 874/2012/EU Pobieranie etykiet energetycznych
 1679 2 kwh/1000h Rozporz¹dzenie 874/2012/EU Pobieranie etykiet energetycznych Na stronie internetowej Rábalux proszê wybraæ podkreœlony lub normalny 1odnoœnik. 4 5 6 3 7 1 2 8 2Program tworzenia etykiet
1679 2 kwh/1000h Rozporz¹dzenie 874/2012/EU Pobieranie etykiet energetycznych Na stronie internetowej Rábalux proszê wybraæ podkreœlony lub normalny 1odnoœnik. 4 5 6 3 7 1 2 8 2Program tworzenia etykiet
elektroniczna Platforma Usług Administracji Publicznej
 elektroniczna Platforma Usług Administracji Publicznej A Instrukcja użytkownika Instalacja usług wersja 1.1 Ministerstwo Spraw Wewnętrznych i Administracji ul. Batorego 5, 02-591 Warszawa www.epuap.gov.pl
elektroniczna Platforma Usług Administracji Publicznej A Instrukcja użytkownika Instalacja usług wersja 1.1 Ministerstwo Spraw Wewnętrznych i Administracji ul. Batorego 5, 02-591 Warszawa www.epuap.gov.pl
1. Rozwiązać układ równań { x 2 = 2y 1
 Dzień Dziecka z Matematyką Tomasz Szymczyk Piotrków Trybunalski, 4 czerwca 013 r. Układy równań szkice rozwiązań 1. Rozwiązać układ równań { x = y 1 y = x 1. Wyznaczając z pierwszego równania zmienną y,
Dzień Dziecka z Matematyką Tomasz Szymczyk Piotrków Trybunalski, 4 czerwca 013 r. Układy równań szkice rozwiązań 1. Rozwiązać układ równań { x = y 1 y = x 1. Wyznaczając z pierwszego równania zmienną y,
Pomiar prędkości dźwięku w metalach
 Pomiar prędkości dźwięku w metalach Ćwiczenie studenckie dla I Pracowni Fizycznej Barbara Pukowska Andrzej Kaczmarski Krzysztof Sokalski Instytut Fizyki UJ Eksperymenty z dziedziny akustyki są ciekawe,
Pomiar prędkości dźwięku w metalach Ćwiczenie studenckie dla I Pracowni Fizycznej Barbara Pukowska Andrzej Kaczmarski Krzysztof Sokalski Instytut Fizyki UJ Eksperymenty z dziedziny akustyki są ciekawe,
CZY JEDNYM POSUNIÊCIEM DA SIÊ ROZWI ZAÆ WSZYSTKIE UK ADY DWÓCH RÓWNAÑ LINIOWYCH?
 47. CZY JEDNYM POSUNIÊCIEM DA SIÊ ROZI ZAÆ SZYSTKIE UK ADY DÓCH RÓNAÑ LINIOYCH? 1. Realizowane treœci podstawy programowej Przedmiot Matematyka Informatyka Realizowana treœæ podstawy programowej 7. Równania.
47. CZY JEDNYM POSUNIÊCIEM DA SIÊ ROZI ZAÆ SZYSTKIE UK ADY DÓCH RÓNAÑ LINIOYCH? 1. Realizowane treœci podstawy programowej Przedmiot Matematyka Informatyka Realizowana treœæ podstawy programowej 7. Równania.
EGZAMIN MATURALNY Z MATEMATYKI
 pobrano z www.sqlmedia.pl ARKUSZ ZAWIERA INFORMACJE PRAWNIE CHRONIONE DO MOMENTU ROZPOCZ CIA EGZAMINU! Miejsce na naklejk MMA-P1_1P-092 EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY MAJ ROK 2009 Czas
pobrano z www.sqlmedia.pl ARKUSZ ZAWIERA INFORMACJE PRAWNIE CHRONIONE DO MOMENTU ROZPOCZ CIA EGZAMINU! Miejsce na naklejk MMA-P1_1P-092 EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY MAJ ROK 2009 Czas
INSTRUKCJA OBS UGI KARI WY CZNIK P YWAKOWY
 INSTRUKCJA OBS UGI KARI WY CZNIK P YWAKOWY Wydanie paÿdziernik 2004 r PRZEDSIÊBIORSTWO AUTOMATYZACJI I POMIARÓW INTROL Sp. z o.o. ul. Koœciuszki 112, 40-519 Katowice tel. 032/ 78 90 000, fax 032/ 78 90
INSTRUKCJA OBS UGI KARI WY CZNIK P YWAKOWY Wydanie paÿdziernik 2004 r PRZEDSIÊBIORSTWO AUTOMATYZACJI I POMIARÓW INTROL Sp. z o.o. ul. Koœciuszki 112, 40-519 Katowice tel. 032/ 78 90 000, fax 032/ 78 90
Promocja i identyfikacja wizualna projektów współfinansowanych ze środków Europejskiego Funduszu Społecznego
 Promocja i identyfikacja wizualna projektów współfinansowanych ze środków Europejskiego Funduszu Społecznego Białystok, 19 grudzień 2012 r. Seminarium współfinansowane ze środków Unii Europejskiej w ramach
Promocja i identyfikacja wizualna projektów współfinansowanych ze środków Europejskiego Funduszu Społecznego Białystok, 19 grudzień 2012 r. Seminarium współfinansowane ze środków Unii Europejskiej w ramach
Szczegółowy opis zamówienia
 ZFE-II.042.2. 24.2015 Szczegółowy opis zamówienia I. Zasady przeprowadzenia procedury zamówienia 1. Zamówienie realizowane jest na podstawie art.70 1 i 70 3 70 5 Kodeksu Cywilnego ( Dz. U. z 2014 r. poz.
ZFE-II.042.2. 24.2015 Szczegółowy opis zamówienia I. Zasady przeprowadzenia procedury zamówienia 1. Zamówienie realizowane jest na podstawie art.70 1 i 70 3 70 5 Kodeksu Cywilnego ( Dz. U. z 2014 r. poz.
STRATEGIA ROZWOJU WYDZIA U GOSPODARKI REGIONALNEJ I TURYSTYKI W JELENIEJ GÓRZE UNIWERSYTETU EKONOMICZNEGO WE WROC AWIU
 Uniwersytet Ekonomiczny we Wroc³awiu STRATEGIA ROZWOJU WYDZIA U GOSPODARKI REGIONALNEJ I TURYSTYKI W JELENIEJ GÓRZE UNIWERSYTETU EKONOMICZNEGO WE WROC AWIU Strategiê zatwierdzono Uchwa³¹ Rady Wydzia³u
Uniwersytet Ekonomiczny we Wroc³awiu STRATEGIA ROZWOJU WYDZIA U GOSPODARKI REGIONALNEJ I TURYSTYKI W JELENIEJ GÓRZE UNIWERSYTETU EKONOMICZNEGO WE WROC AWIU Strategiê zatwierdzono Uchwa³¹ Rady Wydzia³u
Badanie bezszczotkowego silnika prądu stałego z magnesami trwałymi (BLDCM)
 Badanie bezszczotkowego silnika prądu stałego z magnesami trwałymi (BLDCM) Celem ćwiczenia jest zapoznanie się z budową, zasadą działania oraz sterowaniem bezszczotkowego silnika prądu stałego z magnesami
Badanie bezszczotkowego silnika prądu stałego z magnesami trwałymi (BLDCM) Celem ćwiczenia jest zapoznanie się z budową, zasadą działania oraz sterowaniem bezszczotkowego silnika prądu stałego z magnesami
PLANY WYNIKOWE W ZAKRESIE III KLASY GIMNAZJUM. opracowane na podstawie materia³ów katechetycznych Jezus prowadzi i zbawia z serii W DRODZE DO EMAUS
 PLANY WYNIKOWE W ZAKRESIE III KLASY GIMNAZJUM opracowane na podstawie materia³ów katechetycznych Jezus prowadzi i zbawia z serii W DRODZE DO EMAUS Dzia³anie nauczyciela, w tym równie katechety, jest œciœle
PLANY WYNIKOWE W ZAKRESIE III KLASY GIMNAZJUM opracowane na podstawie materia³ów katechetycznych Jezus prowadzi i zbawia z serii W DRODZE DO EMAUS Dzia³anie nauczyciela, w tym równie katechety, jest œciœle
Pawe Karpi ski. Zdj cie Ratusza
 Pawe Karpi ski Zdj cie Ratusza Pawe Karpi ski Zdj cie wn trza ratusza Dzielnicy Warszawa Bemowo Jacek Kwa niewski Obróbka techniczna i eksperymenty z perspektyw Grudzie 2007 Zdj cie wykonano technik sklejania
Pawe Karpi ski Zdj cie Ratusza Pawe Karpi ski Zdj cie wn trza ratusza Dzielnicy Warszawa Bemowo Jacek Kwa niewski Obróbka techniczna i eksperymenty z perspektyw Grudzie 2007 Zdj cie wykonano technik sklejania
Opis modułu analitycznego do śledzenia rotacji towaru oraz planowania dostaw dla programu WF-Mag dla Windows.
 Opis modułu analitycznego do śledzenia rotacji towaru oraz planowania dostaw dla programu WF-Mag dla Windows. Zadaniem modułu jest wspomaganie zarządzania magazynem wg. algorytmu just in time, czyli planowanie
Opis modułu analitycznego do śledzenia rotacji towaru oraz planowania dostaw dla programu WF-Mag dla Windows. Zadaniem modułu jest wspomaganie zarządzania magazynem wg. algorytmu just in time, czyli planowanie
Gramatyka i słownictwo
 WYMAGANIA PROGRAMOWE Z JĘZYKA ANGIELSKIEGO KL. 4 a/b SP4 Gramatyka i słownictwo uczeń potrafi poprawnie operować niedużą ilością struktur prostych (czasownik to be - w formie pełnej i skróconej, zaimki
WYMAGANIA PROGRAMOWE Z JĘZYKA ANGIELSKIEGO KL. 4 a/b SP4 Gramatyka i słownictwo uczeń potrafi poprawnie operować niedużą ilością struktur prostych (czasownik to be - w formie pełnej i skróconej, zaimki
Technologie Informacyjne
 Technologie Informacyjne Szkoła Główna Służby Pożarniczej Zakład Informatyki i Łączności April 11, 2016 Technologie Informacyjne Wprowadzenie : wizualizacja obrazów poprzez wykorzystywanie technik komputerowych.
Technologie Informacyjne Szkoła Główna Służby Pożarniczej Zakład Informatyki i Łączności April 11, 2016 Technologie Informacyjne Wprowadzenie : wizualizacja obrazów poprzez wykorzystywanie technik komputerowych.
Filtracja obrazów w dziedzinie Fouriera
 Filtracja obrazów w dziedzinie Fouriera Filtracj mo na zinterpretowa jako mno enie punktowe dwóch F-obrazów - jednego pochodz cego od filtrowanego obrazu i drugiego b d cego filtrem. Wykres amplitudy F-
Filtracja obrazów w dziedzinie Fouriera Filtracj mo na zinterpretowa jako mno enie punktowe dwóch F-obrazów - jednego pochodz cego od filtrowanego obrazu i drugiego b d cego filtrem. Wykres amplitudy F-
Podstawowe działania w rachunku macierzowym
 Podstawowe działania w rachunku macierzowym Marcin Detka Katedra Informatyki Stosowanej Kielce, Wrzesień 2004 1 MACIERZE 1 1 Macierze Macierz prostokątną A o wymiarach m n (m wierszy w n kolumnach) definiujemy:
Podstawowe działania w rachunku macierzowym Marcin Detka Katedra Informatyki Stosowanej Kielce, Wrzesień 2004 1 MACIERZE 1 1 Macierze Macierz prostokątną A o wymiarach m n (m wierszy w n kolumnach) definiujemy:
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI
 Miejsce na naklejkê z kodem szko³y dysleksja PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY Przed matur¹ MAJ 2011 r. Czas pracy 180 minut Instrukcja dla zdaj¹cego 1. SprawdŸ, czy arkusz egzaminacyjny
Miejsce na naklejkê z kodem szko³y dysleksja PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY Przed matur¹ MAJ 2011 r. Czas pracy 180 minut Instrukcja dla zdaj¹cego 1. SprawdŸ, czy arkusz egzaminacyjny
 EKONOMETRIA dr inż.. ALEKSANDRA ŁUCZAK Uniwersytet Przyrodniczy w Poznaniu Katedra Finansów w i Rachunkowości ci Zakład Metod Ilościowych Collegium Maximum,, pokój j 617 Tel. (61) 8466091 luczak@up.poznan.pl
EKONOMETRIA dr inż.. ALEKSANDRA ŁUCZAK Uniwersytet Przyrodniczy w Poznaniu Katedra Finansów w i Rachunkowości ci Zakład Metod Ilościowych Collegium Maximum,, pokój j 617 Tel. (61) 8466091 luczak@up.poznan.pl
Fabian Stasiak. Przyk adowe wiczenie z podr cznika: Zbiór wicze. Autodesk Inventor Kurs podstawowy.
 Fabian Stasiak Przyk adowe wiczenie z podr cznika: Zbiór wicze. Autodesk Inventor 2017. Kurs podstawowy ExpertBooks 614 Rozdzia 8. Tworzenie dokumentacji rysunkowej 2D wiczenie 8.8 Wymiarowanie w widoku
Fabian Stasiak Przyk adowe wiczenie z podr cznika: Zbiór wicze. Autodesk Inventor 2017. Kurs podstawowy ExpertBooks 614 Rozdzia 8. Tworzenie dokumentacji rysunkowej 2D wiczenie 8.8 Wymiarowanie w widoku
PAKIET MathCad - Część III
 Opracowanie: Anna Kluźniak / Jadwiga Matla Ćw3.mcd 1/12 Katedra Informatyki Stosowanej - Studium Podstaw Informatyki PAKIET MathCad - Część III RÓWNANIA I UKŁADY RÓWNAŃ 1. Równania z jedną niewiadomą MathCad
Opracowanie: Anna Kluźniak / Jadwiga Matla Ćw3.mcd 1/12 Katedra Informatyki Stosowanej - Studium Podstaw Informatyki PAKIET MathCad - Część III RÓWNANIA I UKŁADY RÓWNAŃ 1. Równania z jedną niewiadomą MathCad
