Systemy ekspertowe. Wykład 2 Reprezentacja wiedzy Rachunek zdań. Joanna Kołodziejczyk. Joanna Kołodziejczyk Systemy ekspertowe / 41
|
|
|
- Roman Stefaniak
- 6 lat temu
- Przeglądów:
Transkrypt
1 Systemy ekspertowe Wykład 2 Reprezentacja wiedzy Joanna Kołodziejczyk 2016 Joanna Kołodziejczyk Systemy ekspertowe / 41
2 Reprezentowanie wiedzy Plan wykładu 1 Reprezentowanie wiedzy 2 Logika a reprezentacji wiedzy 3 4 Literatura Joanna Kołodziejczyk Systemy ekspertowe / 41
3 Reprezentowanie wiedzy Kodowanie wiedzy Kodowanie wiedzy oznacza formalny sposób zapisu wiedzy (w postaci symboli), która ma być zgromadzona w systemie. Do form reprezentacji można zaliczyć: postać regułowa (IF - THEN) drzewa decyzyjne tablice decyzyjne sieci semantyczne Joanna Kołodziejczyk Systemy ekspertowe / 41
4 Reprezentowanie wiedzy Wiedza jak pokazać w systemie Baza wiedzy (KB) zbiór zdań w języku formalnym lub inaczej w języku reprezentacji wiedzy. Joanna Kołodziejczyk Systemy ekspertowe / 41
5 Reprezentowanie wiedzy Programowanie deklaratywne Podejście deklaratywne podejście ma zapewnić wykonywanie następujących zadań: TELL możliwość poinformowania systemu o nowej wiedzy (wprowadzanie nowych zdań). ASK odpytywanie systemu co jest mu wiadome (odpowiedź powinna wynikać z bazy wiedzy). ASK i TELL mogą wymagać wnioskowania czyli wyprowadzania nowych zdań na podstawie wcześniej zadanych. Joanna Kołodziejczyk Systemy ekspertowe / 41
6 Reprezentowanie wiedzy Zależność pomiędzy reprezentacją i rzeczywistością Representation formalna reprezentacja wiedzy World rzeczywistość Semnatics znaczenie Sentences zdania reprezentujące wiedzę w jakimś języku formalnym Facts rzeczywiste zdarzenia, fakty Follows następstwo Entails konsekwencja Joanna Kołodziejczyk Systemy ekspertowe / 41
7 Logika a reprezentacji wiedzy Plan wykładu 1 Reprezentowanie wiedzy 2 Logika a reprezentacji wiedzy 3 4 Literatura Joanna Kołodziejczyk Systemy ekspertowe / 41
8 Logika a reprezentacji wiedzy Logika podstawy Logika Jest formalnym językiem reprezentowania wiedzy o obiektach, z której można wyciągać wnioski (konkluzje) o właściwościach tych obiektów. Logika elementy: Składnia określa budowę zdań w danym języku formalny. Wnioskowanie musi uwzględniać manipulowanie i generowanie symbolami zdań w określonej składni. Semantyka określa znaczenie wyrażenia. W logice semantyka definiuje prawdziwość (TRUE) każdego zdania w odniesieniu do rozpatrywanej rzeczywistości. System wnioskowania. Joanna Kołodziejczyk Systemy ekspertowe / 41
9 Logika a reprezentacji wiedzy Po co stosować język logiki? Jako system wnioskowania (proof system): Dany jest zbiór faktów (aksjomatów) i zbiór reguł wnioskowania. Celem jest ustalenie, które fakty wynikają z aksjomatów i reguł wnioskowania. W takim spojrzeniu na logikę wykonuje się czysto mechaniczne operacje na symbolach i nie patrzy się na znaczenie zdań, którymi się manipuluje. Nie oznacza to, że dowód nie wymaga kreatywności, ale znaczenie zdania jest w takim wypadku nieistotne. Jako teoria modeli (model theory): Zdania uzyskują znaczenie, co nazywa się interpretacją. W tym wypadku język logiki jest używany do sformalizowania właściwości struktur i określenia, kiedy zdanie jest prawdziwe. Teoria modeli zmusza do precyzyjnego definiowania pojęcia prawdy. W zależności od interpretacji prawda może mieć zupełnie inne znaczenie. Joanna Kołodziejczyk Systemy ekspertowe / 41
10 Logika a reprezentacji wiedzy Poprawność systemu wnioskowania Cechy systemu wnioskowania Niepodważalność (sound) każda dowiedziona w nim formuła jest ważna i poprawna. Zupełność (complete) jeżeli każda ważna i poprawna formuła może być w nim dowiedziona. Systemy zupełne: rachunek zdań, logika predykatów pierwszego rzędu. Systemy niezupełne: logika predykatów drugiego rzędu. Joanna Kołodziejczyk Systemy ekspertowe / 41
11 Logika a reprezentacji wiedzy Przykład składni i semantyki Arytmetyka to język formalny do reprezentowania zależności i operacji na liczbach. Składnia: x + 2 y jest poprawnym wyrażeniem a x2 + y > nie jest poprawnym wyrażeniem Semantyka: x + 2 y jest prawdą witw, gdy liczba x + 2 jest nie mniejsza niż liczba y x + 2 y jest prawdziwe w takiej rzeczywistości, gdzie x = 7 i y = 1 x + 2 y jest fałszywe w takiej rzeczywistości, gdzie x = 0 i y = 6 Joanna Kołodziejczyk Systemy ekspertowe / 41
12 Logika a reprezentacji wiedzy Logiki Język reprezentacji Co opisuje? Jakie może być przekonanie o faktach? fakty true/ false/ nieznany Rachunek predykatów fakty, obiekty, rela- true/ false/ nieznany pierwszego cje rzędu Logika temporalna fakty, obiekty, relacje, true/ false/ nieznany czas Teoria prawdopodobieństwa fakty, reguły przekonanie w skali [0,1] Logika rozmyta fakty, reguły przekonanie w skali [0,1] Joanna Kołodziejczyk Systemy ekspertowe / 41
13 Logika a reprezentacji wiedzy Przykład wnioskowania Logiczny system wnioskowania: Monty Python A witch Joanna Kołodziejczyk Systemy ekspertowe / 41
14 Plan wykładu 1 Reprezentowanie wiedzy 2 Logika a reprezentacji wiedzy 3 4 Literatura Joanna Kołodziejczyk Systemy ekspertowe / 41
15 Składnia rachunku zdań jest najprostszym składniowo systemem logicznym. Pewne założenia przenoszą się jednak na rachunek predykatów pierwszego rzędu. Alfabet rachunku zdań 1 stałe: True i False 2 symbole oznaczające zdania (formuły, atomy): P, Q1 3 nawiasy okrągłe wokół zdania: (P Q) 4 zdania złożone przez kombinację symboli, stałych z pięcioma symbolami operacji. Joanna Kołodziejczyk Systemy ekspertowe / 41
16 Operatory rachunku zdań 1 Negacja S. Jeżeli S (positive literal) jest formułą, to S (negative literal) jest formułą. 2 Koniunkcja. Jeżeli S 1 i S 2 to formuły, to S 1 S 2 jest formułą. 3 Dysjunkcja. Jeżeli S 1 i S 2 to formuły, to S 1 S 2 jest formułą. 4 Implikacja (warunek). Jeżeli S 1 i S 2 to formuły, to S 1 S 2 jest formułą. Implikacja znana jest też jako reguła czyli zdania typu IF-THEN 5 Równoważność. Jeżeli S 1 i S 2 to formuły, to S 1 S 2 jest formułą. Czytane: wtedy i tylko wtedy. Joanna Kołodziejczyk Systemy ekspertowe / 41
17 Semantyka rachunku zdań Specyfikuje interpretację każdego symbolu i stałych i określa znaczenie zależności logicznych. Znaczenie symboli (ich interpretacja) jest dowolna. np. P może znaczyć Paryż jest stolicą Francji, czy też Piotr ma niebieskie oczy P może stać się True, jeżeli fakt, o którym mówi zaistniał. Zdania złożone mają takie znacznie, które wynika z ich składowych. Można zdania złożone traktować jak funkcje. Gdy podane są wartości wejściowe, to można obliczyć wartość wynikową. Joanna Kołodziejczyk Systemy ekspertowe / 41
18 Tablica prawdy P Q P P Q P Q P Q P Q false false true false false true true false true true false true true false true false false false true false false true true false true true true true Joanna Kołodziejczyk Systemy ekspertowe / 41
19 Interpretacja implikacji Przykład Ojciec obiecuje Jasiowi: Jeśli p q {}}{{}}{ jutro będzie ładna pogoda, to pójdziemy na grzyby. Obietnica jest implikacją p q. Ojciec nie dotrzyma słowa tylko w jednym przypadku: jeżeli jutro będzie ładna pogoda (tzn. p = 1), a nie pójdą z Jasiem na grzyby (tzn. q = 0). Dlatego przyjmujemy, że implikacja p q jest fałszywa tylko wtedy, gdy p = 1 i q = 0. Joanna Kołodziejczyk Systemy ekspertowe / 41
20 Walidacja przez tablicę prawdy Zwalidować zdanie: ((P H) H) P P H P H (P H) H ((P H) H) P false false false false true false true true false true true false true true true true true true false true Joanna Kołodziejczyk Systemy ekspertowe / 41
21 Zadania Zapisać w składni rachunku zdań i zwalidować. 1 Jeżeli pan Kowalski sprzedał wrotki i pan Kowalski kupił rower, to nie jest prawdą, że pan Kowalski nie sprzedał wrotek lub nie pan Kowalski nie kupił roweru. 2 Jeżeli Jan Kowalski studiuje, to jest to równoważne, że nie jest prawdą, że Jan Kowalski nie studiuje. 3 Jeżeli Jan Kowalski ma dom i Anna Kowalska ma dom, to wynika z tego, że nie jest prawdą, że Jan Kowalski ma dom lub Anna Kowalska nie ma domu. 4 Jeżeli Nowak był poetą i Kowalski nie był poetą to jest równoważne, że nie jest prawdą, że obaj byli poetami. Joanna Kołodziejczyk Systemy ekspertowe / 41
22 Tautologie (α β) (β α) przemiennosc (α β) (β α) przemiennosc ((α β) γ) (α (β γ)) lacznosc ((α β) γ) (α (β γ)) lacznosc ( α) α eliminacja podwojnej negacji (α β) ( β α) (α β) ( α β) eliminacja implikacji (α β) ((α β) (β α)) eliminacja rownowaznosci (α β) ( α β) De Morgan (α β) ( α β) De Morgan (α (β γ)) ((α β) (α γ)) rozdzielnosc wzgledem (α (β γ)) ((α β) (α γ)) rozdzielnosc wzgledem Joanna Kołodziejczyk Systemy ekspertowe / 41
23 Schematy wnioskowania Modus ponendo ponens (Modus Ponens) Zapisujemy: P Q P Q lub jako tautologię: (P (P Q)) Q) Nazywana regułą dedukcji. Jeżeli prawdziwa jest reguła/implikacja (IF THEN) i część przesłankowa reguły P, to możemy wnioskować Q, czyli konsekwencję reguły. W sztucznej inteligencji nazywany wnioskowaniem w przód. Jeżeli dziś jest niedziela, to jutro jest poniedziałek. np. Dziś jest niedziela. Jutro jest poniedziałek. Joanna Kołodziejczyk Systemy ekspertowe / 41
24 Schematy wnioskowania Modus ponendo tollens (P Q) Zapisujemy: P Q lub jako tautologię: (P (P Q)) Q) Czytamy jako: Albo... albo Nie mogę pójść do kina i oglądać telewizji. Albo pójdę do kina, albo obejrzę telewizję. np. Pójdę do kina. Nie obejrzę telewizji. Joanna Kołodziejczyk Systemy ekspertowe / 41
25 Schematy wnioskowania Modus tollendo tollens Zapisujemy: P Q Q P Nazywany zaprzeczeniem konsekwencji. Nie jest możliwe, by przesłanka była prawdziwa i konsekwencja była fałszywa. Jeżeli pies wyczuje obcego, będzie warczał np. Pies nie warczał. Zatem pies nie wyczuł nikogo obcego. Joanna Kołodziejczyk Systemy ekspertowe / 41
26 Schematy wnioskowania Modus tollendo ponens (sylogizm dysjunkcyjny/elimienacja dysjunkcji) Zapisujemy: P Q P Q Wiemy, że przynajmniej jedno ze stwierdzeń jest prawdziwe i wiemy, że inne nie jest prawdziwe, zatem wnioskujemy o prawdziwości drugiego. Pójdę do kina lub obejrzę telewizję np. Nie pójdę do kina. Obejrzę telewizję Joanna Kołodziejczyk Systemy ekspertowe / 41
27 Schematy wnioskowania Sylogizm warunkowy Zapisujemy: P Q Q R P R np. Jeżeli nie wstanę, to nie pójdę do pracy. Jeżeli nie pójdę do pracy, nie zarobię. Jeżeli nie wstanę, to nie zarobię. Przykład prowadzący do absurdalnych wniosków Jeżeli Cezar pozostanie w domu, to nie zostanie zabity. Jeżeli Cezar nie zostanie zabity, to wygłosi przemówienie w senacie. Jeżeli Cezar pozostanie w domu, to wygłosi przemówienie w senacie. Błąd wnioskowania wynika z tego, że nie bierze się pod uwagę kontekstowego połączenia przesłanek i konkluzji. Joanna Kołodziejczyk Systemy ekspertowe / 41
28 Schematy wnioskowania Eliminacja koniunkcji Zapisujemy: A B B lub A B A z iloczynu można wnioskować każdy czynnik Bob lubi jabłka i pomarańcze. np. Bob lubi jabłka. Joanna Kołodziejczyk Systemy ekspertowe / 41
29 Schematy wnioskowania Rezolucja Zapisujemy: A B A C B C z MP A B A B otrzymujemy A B A B Jeżeli A jest prawdziwe, to aby prawdziwa była druga przesłanka, to C musi być prawdziwe. Natomiast jeżeli A jest fałszywe, to aby pierwsza przesłanka była prawdziwa, B musi być prawdziwe. Jeżeli ktoś jest Grekiem to jest europejczykiem. np. Homer jest Grekiem. Homer jest europejczykiem Joanna Kołodziejczyk Systemy ekspertowe / 41
30 Koniunkcyjna postać normalna CNF Regułę rezolucji stosuje się tylko dla dysjunkcji literałów (zdań). Zatem konieczne będzie posiadanie bazy wiedzy w postaci takich właśnie sum logicznych. Każde zdanie w rachunku zdań jest logicznym równoważnikiem koniunkcji dysjunkcji literałów, to znaczy, że dowolne zdanie można na taką formę koniunkcyjną przekształcić. Koniunkcyjna forma/postać normalna (Conjunctive Normal Form lub CNF) Jest to koniunkcja dysjunkcji literałów czyli iloczyn sum logicznych np., klauzula1 klauzula2 {}}{{}}{ (A B) (B C D) Klauzula Jest to suma literałów. Powyższy przykład zawiera dwie klauzule. Joanna Kołodziejczyk Systemy ekspertowe / 41
31 Wumpus by Michael Genesereth Joanna Kołodziejczyk Systemy ekspertowe / 41
32 Wumpus - opis Miara osiągów użycie strzały złoto +1000; śmierć -1000; -1 za każdy ruch; -10 za Środowisko Tablica 4 4 pomieszczeń. Agent zaczyna w polu [1, 1] twarzą skierowaną w prawo. Położenie wumpusa i złota wybierane jest losowo z pominięciem pola startowego. Każde z pól z prawdopodobieństwem 0.2 może być dołkiem Aktualizatory Skręć w lewo, skręć w prawo, idź, chwytaj, upuść, strzelaj (do końca wiersza lub kolumny, lub wumpusa), umiera Czujniki Pola przylegające do wumpusa cuchną (stench). W polach przylegających do dołka czuć powiew (breeze). Blask jest w polu gdzie znajduje się złoto (glitter). Jeżeli uderzy się w ścianę to jest to sygnalizowane. Zabicie wumpusa jest oznajmiane jego krzykiem. [Stench, Breez, None, None, None] Joanna Kołodziejczyk Systemy ekspertowe / 41
33 Wumpus World w rachunku zdań Plansza 4x4. Zasady "fizyka"gry: (B x,y (P x 1,y P x+1,y P x,y 1 P x,y+1 ) (S x,y (W x 1,y W x+1,y W x,y 1 W x,y+1 ) Przynajmniej jeden Wumpus na planszy W 1,1 W 1,2 W 1,3 W 4,4 Co najwyżej jeden Wumpus na planszy (dla każdych dwóch sąsiednich pól) n(n 1) 2 reguł W 1,1 W 1,2 Nie można umrzeć na starcie P 1,1 W 1,1 W sumie 155 zdań zawierających 64 symbole. Joanna Kołodziejczyk Systemy ekspertowe / 41
34 Algorytm konwersji do koniunkcyjnej postaci normalnej Zdanie do przekształcenia: B 1,1 (P 1,2 P 2,1 ) 1 Eliminacja, zamień A B na (A B) (B A). (B 1,1 (P 1,2 P 2,1 )) ((P 1,2 P 2,1 ) B 1,1 ) 2 Eliminacja, zamień A B na A B. ( B 1,1 P 1,2 P 2,1 ) ( (P 1,2 P 2,1 ) B 1,1 ) 3 Przesunięcie do nawiasów stosując prawa de Morgana i podwójną negacje: ( B 1,1 P 1,2 P 2,1 ) (( P 1,2 P 2,1 ) B 1,1 ) 4 Zastosowanie prawa rozdzielności względem : ( B 1,1 P 1,2 P 2,1 ) ( P 1,2 B 1,1 ) ( P 2,1 B 1,1 ) Joanna Kołodziejczyk Systemy ekspertowe / 41
35 Algorytm rezolucji Algorytm rezolucji Nazywany dowodzenia przez sprzeczność (reducio ad absurdum). Aby wykazać, iż A jest spełnione (wynika) z bazy wiedzy KB wykazane zostanie, że KB A jest niespełnialne, czyli prowadzi do zadnia pustego. Uzyskanie sprzeczności potwierdza postawione założenie. Baza wiedzy musi zostać uprzednio przekształcona do postaci CNF. Jeżeli dowodzi się złożone zdanie logiczne, to też musi zostać przekształcone na postać CNF. Joanna Kołodziejczyk Systemy ekspertowe / 41
36 Algorytm rezolucji 1 Zamiana wszystkich zdań w bazie wiedzy i zdania do udowodnienia na postać CNF i utwórzenie z nich jedenego zbiór klauzul roboczych. 2 Zastosuj regułę rezolucji do wszystkich możliwych par klauzul, które zawierają literały komplementarne. W wyniku zastosowania reguły rezolucji powstaną rezolwenty (klauzule bez literałów komplementanych). 3 Jeżeli rezolwenty nie istnieją w zbiorze klauzul roboczych dodaj je do niego. 4 Idź do kroku 2 lub zakończ, gdy uzyskasz zdanie puste (udowodniono hipotezę) lub nie tworzą się żadne nowe klauzule (nie można dowieźć hipotezy z bazy wiedzy). Joanna Kołodziejczyk Systemy ekspertowe / 41
37 Przykład dowodzenia z użyciem rezolucji KB = (B 1,1 (P 1,2 P 2,1 )) B 1,1 Dowodzimy: α = P 1,2 Po konwersji KB α na CNF otrzymujemy pierwszy wiersz na schemacie. Drugi wiersz powstaje jako rezolwenty z połączeń wszystkich klauzul z pierwszego wiersza. Ostatecznie dwie klauzule zostają połączone prowadząc do klauzuli pustej (sprzeczności) oznaczonej jako mały kwadrat. Zatem dowiedliśmy, że α. Joanna Kołodziejczyk Systemy ekspertowe / 41
38 : wady i zalety jest deklaratywny. dopuszcza częściową/alternatywnę/zanegowaną informacje (w przeciwieństwie do wiekszosci struktur danych i baz danych). jest zależny od składni: znaczenie B 1,1 P 1,2 wynika ze znaczenia B 1,1 i P 1,2. Składnia w rachunku zdań jest niezależna od kontekstu (w przeciwieństwie do języka naturalnego). ma bardzo ograniczoną moc wyrażania (w przeciwieństwie do języka naturalnego), np. nie da się wyrazić zdania pułapki powodują wiatr w sąsiednich polach inaczej niż przez napisanie oddzielnego zdania dla każdego pola. Joanna Kołodziejczyk Systemy ekspertowe / 41
39 Przydatny aplet Ciekawa baza Joanna Kołodziejczyk Systemy ekspertowe / 41
40 Literatura Plan wykładu 1 Reprezentowanie wiedzy 2 Logika a reprezentacji wiedzy 3 4 Literatura Joanna Kołodziejczyk Systemy ekspertowe / 41
41 Literatura Wykorzystana literatura (do samodzielnego studiowania) Jean Gallier Propositional Logic. http: // www. cis. upenn. edu/ ~cis510/ tcl/ chap3. pdf S.J. Russel, P. Norvig Artificial Intelligence. A modern approach. Pearson Education wyd. 2, p Joanna Kołodziejczyk Systemy ekspertowe / 41
Reprezentowanie wiedzy Logika a reprezentacji wiedzy Rachunek zdań Literatura. Systemy ekspertowe. Wykład 2 Reprezentacja wiedzy Rachunek zdań
 Systemy ekspertowe Wykład 2 Reprezentacja wiedzy Rachunek zdań Joanna Kołodziejczyk 18 marca 2014 Plan wykładu 1 Reprezentowanie wiedzy 2 Logika a reprezentacji wiedzy 3 Rachunek zdań 4 Literatura Kodowanie
Systemy ekspertowe Wykład 2 Reprezentacja wiedzy Rachunek zdań Joanna Kołodziejczyk 18 marca 2014 Plan wykładu 1 Reprezentowanie wiedzy 2 Logika a reprezentacji wiedzy 3 Rachunek zdań 4 Literatura Kodowanie
Tautologia (wyrażenie uniwersalnie prawdziwe - prawo logiczne)
 Tautologia (wyrażenie uniwersalnie prawdziwe - prawo logiczne) Definicja 1: Tautologia jest to takie wyrażenie, którego wartość logiczna jest prawdą przy wszystkich możliwych wartościowaniach zmiennych
Tautologia (wyrażenie uniwersalnie prawdziwe - prawo logiczne) Definicja 1: Tautologia jest to takie wyrażenie, którego wartość logiczna jest prawdą przy wszystkich możliwych wartościowaniach zmiennych
Elementy logiki. Wojciech Buszkowski Wydział Matematyki i Informatyki UAM Zakład Teorii Obliczeń
 Elementy logiki Wojciech Buszkowski Wydział Matematyki i Informatyki UAM Zakład Teorii Obliczeń 1 Klasyczny Rachunek Zdań 1.1 Spójniki logiczne Zdaniem w sensie logicznym nazywamy wyrażenie, które jest
Elementy logiki Wojciech Buszkowski Wydział Matematyki i Informatyki UAM Zakład Teorii Obliczeń 1 Klasyczny Rachunek Zdań 1.1 Spójniki logiczne Zdaniem w sensie logicznym nazywamy wyrażenie, które jest
Podstawy Sztucznej Inteligencji (PSZT)
 Podstawy Sztucznej Inteligencji (PSZT) Paweł Wawrzyński Wnioskowanie logiczne i systemy eksperckie Systemy posługujące się logiką predykatów: część 3/3 Dzisiaj Uogólnienie Poprawność i pełność wnioskowania
Podstawy Sztucznej Inteligencji (PSZT) Paweł Wawrzyński Wnioskowanie logiczne i systemy eksperckie Systemy posługujące się logiką predykatów: część 3/3 Dzisiaj Uogólnienie Poprawność i pełność wnioskowania
Rachunek zdań i predykatów
 Rachunek zdań i predykatów Agnieszka Nowak 14 czerwca 2008 1 Rachunek zdań Do nauczenia :! 1. ((p q) p) q - reguła odrywania RO 2. reguła modus tollens MT: ((p q) q) p ((p q) q) p (( p q) q) p (( p q)
Rachunek zdań i predykatów Agnieszka Nowak 14 czerwca 2008 1 Rachunek zdań Do nauczenia :! 1. ((p q) p) q - reguła odrywania RO 2. reguła modus tollens MT: ((p q) q) p ((p q) q) p (( p q) q) p (( p q)
Metoda tabel semantycznych. Dedukcja drogi Watsonie, dedukcja... Definicja logicznej konsekwencji. Logika obliczeniowa.
 Plan Procedura decyzyjna Reguły α i β - algorytm Plan Procedura decyzyjna Reguły α i β - algorytm Logika obliczeniowa Instytut Informatyki 1 Procedura decyzyjna Logiczna konsekwencja Teoria aksjomatyzowalna
Plan Procedura decyzyjna Reguły α i β - algorytm Plan Procedura decyzyjna Reguły α i β - algorytm Logika obliczeniowa Instytut Informatyki 1 Procedura decyzyjna Logiczna konsekwencja Teoria aksjomatyzowalna
Ziemia obraca się wokół Księżyca, bo posiadając odpowiednią wiedzę można stwierdzić, czy są prawdziwe, czy fałszywe. Zdaniami nie są wypowiedzi:
 1 Elementy logiki W logice zdaniem nazywamy wypowiedź oznajmującą, która (w ramach danej nauki) jest albo prawdziwa, albo fałszywa. Tak więc zdanie może mieć jedną z dwóch wartości logicznych. Prawdziwość
1 Elementy logiki W logice zdaniem nazywamy wypowiedź oznajmującą, która (w ramach danej nauki) jest albo prawdziwa, albo fałszywa. Tak więc zdanie może mieć jedną z dwóch wartości logicznych. Prawdziwość
Programowanie deklaratywne i logika obliczeniowa
 Programowanie deklaratywne i logika obliczeniowa Programowanie deklaratywne i logika obliczeniowa Wykład logika 12 godzin Dr hab. inż. Joanna Józefowska, prof. PP dyżur: poniedziałek 9.30-11.00 p. 10,
Programowanie deklaratywne i logika obliczeniowa Programowanie deklaratywne i logika obliczeniowa Wykład logika 12 godzin Dr hab. inż. Joanna Józefowska, prof. PP dyżur: poniedziałek 9.30-11.00 p. 10,
wykład 6 Agent wnioskujący oparty o logikę dr inż. Joanna Kołodziejczyk Zakład Sztucznej Inteligencji ISZiMM
 gent wnioskujący oparty o logikę wykład 6 dr inż Joanna Kołodziejczyk jkolodziejczyk@wipspl Zakład Sztucznej Inteligencji ISZiMM ESI - wykład 6 p Plan wykładu gent zawierajacy wiedzę Świat wumpusów hunt
gent wnioskujący oparty o logikę wykład 6 dr inż Joanna Kołodziejczyk jkolodziejczyk@wipspl Zakład Sztucznej Inteligencji ISZiMM ESI - wykład 6 p Plan wykładu gent zawierajacy wiedzę Świat wumpusów hunt
Myślenie w celu zdobycia wiedzy = poznawanie. Myślenie z udziałem rozumu = myślenie racjonalne. Myślenie racjonalne logiczne statystyczne
 Literatura: podstawowa: C. Radhakrishna Rao, Statystyka i prawda, 1994. G. Wieczorkowska-Wierzbińska, J. Wierzbiński, Statystyka. Od teorii do praktyki, 2013. A. Aczel, Statystyka w zarządzaniu, 2002.
Literatura: podstawowa: C. Radhakrishna Rao, Statystyka i prawda, 1994. G. Wieczorkowska-Wierzbińska, J. Wierzbiński, Statystyka. Od teorii do praktyki, 2013. A. Aczel, Statystyka w zarządzaniu, 2002.
Dalszy ciąg rachunku zdań
 Dalszy ciąg rachunku zdań Wszystkie możliwe funktory jednoargumentowe p f 1 f 2 f 3 f 4 0 0 0 1 1 1 0 1 0 1 Wszystkie możliwe funktory dwuargumentowe p q f 1 f 2 f 3 f 4 f 5 f 6 f 7 f 8 f 9 f 10 f 11 f
Dalszy ciąg rachunku zdań Wszystkie możliwe funktory jednoargumentowe p f 1 f 2 f 3 f 4 0 0 0 1 1 1 0 1 0 1 Wszystkie możliwe funktory dwuargumentowe p q f 1 f 2 f 3 f 4 f 5 f 6 f 7 f 8 f 9 f 10 f 11 f
Logika Stosowana. Wykład 2 - Logika modalna Część 2. Marcin Szczuka. Instytut Informatyki UW. Wykład monograficzny, semestr letni 2016/2017
 Logika Stosowana Wykład 2 - Logika modalna Część 2 Marcin Szczuka Instytut Informatyki UW Wykład monograficzny, semestr letni 2016/2017 Marcin Szczuka (MIMUW) Logika Stosowana 2017 1 / 27 Plan wykładu
Logika Stosowana Wykład 2 - Logika modalna Część 2 Marcin Szczuka Instytut Informatyki UW Wykład monograficzny, semestr letni 2016/2017 Marcin Szczuka (MIMUW) Logika Stosowana 2017 1 / 27 Plan wykładu
Metoda Tablic Semantycznych
 Procedura Plan Reguły Algorytm Logika obliczeniowa Instytut Informatyki Plan Procedura Reguły 1 Procedura decyzyjna Logiczna równoważność formuł Logiczna konsekwencja Procedura decyzyjna 2 Reguły α, β,
Procedura Plan Reguły Algorytm Logika obliczeniowa Instytut Informatyki Plan Procedura Reguły 1 Procedura decyzyjna Logiczna równoważność formuł Logiczna konsekwencja Procedura decyzyjna 2 Reguły α, β,
Uwagi wprowadzajace do reguł wnioskowania w systemie tabel analitycznych logiki pierwszego rzędu
 Witold Marciszewski: Wykład Logiki, 17 luty 2005, Collegium Civitas, Warszawa Uwagi wprowadzajace do reguł wnioskowania w systemie tabel analitycznych logiki pierwszego rzędu 1. Poniższe wyjaśnienie (akapit
Witold Marciszewski: Wykład Logiki, 17 luty 2005, Collegium Civitas, Warszawa Uwagi wprowadzajace do reguł wnioskowania w systemie tabel analitycznych logiki pierwszego rzędu 1. Poniższe wyjaśnienie (akapit
Wykład 10 i 11. Logiczni agenci. w oparciu o: S. Russel, P. Norvig. Artificial Intelligence. A Modern Approach. Logiczni agenci (4g)
 Wykład 0 i w oparciu o: S. Russel, P. Norvig. Artificial Intelligence. A Modern Approach P. Kobylański Wprowadzenie do Sztucznej Inteligencji 26 / 302 agenci oparci na wiedzy rachunek zdań dowodzenie w
Wykład 0 i w oparciu o: S. Russel, P. Norvig. Artificial Intelligence. A Modern Approach P. Kobylański Wprowadzenie do Sztucznej Inteligencji 26 / 302 agenci oparci na wiedzy rachunek zdań dowodzenie w
Np. Olsztyn leży nad Łyną - zdanie prawdziwe, wartość logiczna 1 4 jest większe od 5 - zdanie fałszywe, wartość logiczna 0
 ĆWICZENIE 1 Klasyczny Rachunek Zdań (KRZ): zdania w sensie logicznym, wartości logiczne, spójniki logiczne, zmienne zdaniowe, tabele prawdziwościowe dla spójników logicznych, formuły, wartościowanie zbioru
ĆWICZENIE 1 Klasyczny Rachunek Zdań (KRZ): zdania w sensie logicznym, wartości logiczne, spójniki logiczne, zmienne zdaniowe, tabele prawdziwościowe dla spójników logicznych, formuły, wartościowanie zbioru
Logika pragmatyczna dla inżynierów
 Logika pragmatyczna Logika pragmatyczna dla inżynierów Kontakt: dr hab. inż. Adam Kasperski pokój 509 B4 adam.kasperski@pwr.edu.pl materiały + literatura + informacje na stronie www. Zaliczenie: Test pisemny
Logika pragmatyczna Logika pragmatyczna dla inżynierów Kontakt: dr hab. inż. Adam Kasperski pokój 509 B4 adam.kasperski@pwr.edu.pl materiały + literatura + informacje na stronie www. Zaliczenie: Test pisemny
Rachunek zdań. Materiały pomocnicze do wykładu. wykładowca: dr Magdalena Kacprzak
 Rachunek zdań Materiały pomocnicze do wykładu wykładowca: dr Magdalena Kacprzak RACHUNEK ZDAŃ Zdania Definicja Zdanie jest to stwierdzenie w języku naturalnym, któremu można przypisać wartość prawdy lub
Rachunek zdań Materiały pomocnicze do wykładu wykładowca: dr Magdalena Kacprzak RACHUNEK ZDAŃ Zdania Definicja Zdanie jest to stwierdzenie w języku naturalnym, któremu można przypisać wartość prawdy lub
SID Wykład 5 Wnioskowanie w rachunku zdań
 SID Wykład 5 Wnioskowanie w rachunku zdań Wydział Matematyki, Informatyki i Mechaniki UW slezak@mimuw.edu.pl Bazy wiedzy Inference engines Knowledge base domain-independent algorithms domain-specific content
SID Wykład 5 Wnioskowanie w rachunku zdań Wydział Matematyki, Informatyki i Mechaniki UW slezak@mimuw.edu.pl Bazy wiedzy Inference engines Knowledge base domain-independent algorithms domain-specific content
Reguły gry zaliczenie przedmiotu wymaga zdania dwóch testów, z logiki (za ok. 5 tygodni) i z filozofii (w sesji); warunkiem koniecznym podejścia do
 Reguły gry zaliczenie przedmiotu wymaga zdania dwóch testów, z logiki (za ok. 5 tygodni) i z filozofii (w sesji); warunkiem koniecznym podejścia do testu z filozofii jest zaliczenie testu z logiki i zaliczenie
Reguły gry zaliczenie przedmiotu wymaga zdania dwóch testów, z logiki (za ok. 5 tygodni) i z filozofii (w sesji); warunkiem koniecznym podejścia do testu z filozofii jest zaliczenie testu z logiki i zaliczenie
MATEMATYKA DYSKRETNA, PODSTAWY LOGIKI I TEORII MNOGOŚCI
 MATEMATYKA DYSKRETNA, PODSTAWY LOGIKI I TEORII MNOGOŚCI Program wykładów: dr inż. Barbara GŁUT Wstęp do logiki klasycznej: rachunek zdań, rachunek predykatów. Elementy semantyki. Podstawy teorii mnogości
MATEMATYKA DYSKRETNA, PODSTAWY LOGIKI I TEORII MNOGOŚCI Program wykładów: dr inż. Barbara GŁUT Wstęp do logiki klasycznej: rachunek zdań, rachunek predykatów. Elementy semantyki. Podstawy teorii mnogości
LOGIKA I TEORIA ZBIORÓW
 LOGIKA I TEORIA ZBIORÓW Logika Logika jest nauką zajmującą się zdaniami Z punktu widzenia logiki istotne jest, czy dane zdanie jest prawdziwe, czy nie Nie jest natomiast istotne o czym to zdanie mówi Definicja
LOGIKA I TEORIA ZBIORÓW Logika Logika jest nauką zajmującą się zdaniami Z punktu widzenia logiki istotne jest, czy dane zdanie jest prawdziwe, czy nie Nie jest natomiast istotne o czym to zdanie mówi Definicja
SZTUCZNA INTELIGENCJA
 SZTUCZNA INTELIGENCJA WYKŁAD 10. WNIOSKOWANIE W LOGICE ROZMYTEJ Częstochowa 2014 Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska WNIOSKOWANIE W LOGICE DWUWARTOŚCIOWEJ W logice
SZTUCZNA INTELIGENCJA WYKŁAD 10. WNIOSKOWANIE W LOGICE ROZMYTEJ Częstochowa 2014 Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska WNIOSKOWANIE W LOGICE DWUWARTOŚCIOWEJ W logice
Wprowadzenie do Sztucznej Inteligencji
 Wprowadzenie do Sztucznej Inteligencji Wykład 2 Informatyka Studia Inżynierskie Automatyczne dowodzenie twierdzeń O teoriach formalnie na przykładzie rachunku zdań Zastosowanie dedukcji: system Logic Theorist
Wprowadzenie do Sztucznej Inteligencji Wykład 2 Informatyka Studia Inżynierskie Automatyczne dowodzenie twierdzeń O teoriach formalnie na przykładzie rachunku zdań Zastosowanie dedukcji: system Logic Theorist
Logika Stosowana. Wykład 1 - Logika zdaniowa. Marcin Szczuka. Instytut Informatyki UW. Wykład monograficzny, semestr letni 2016/2017
 Logika Stosowana Wykład 1 - Logika zdaniowa Marcin Szczuka Instytut Informatyki UW Wykład monograficzny, semestr letni 2016/2017 Marcin Szczuka (MIMUW) Logika Stosowana 2017 1 / 30 Plan wykładu 1 Język
Logika Stosowana Wykład 1 - Logika zdaniowa Marcin Szczuka Instytut Informatyki UW Wykład monograficzny, semestr letni 2016/2017 Marcin Szczuka (MIMUW) Logika Stosowana 2017 1 / 30 Plan wykładu 1 Język
Logika pragmatyczna. Logika pragmatyczna. Kontakt: Zaliczenie:
 Logika pragmatyczna Logika pragmatyczna Kontakt: dr hab. inż. Adam Kasperski pokój 509 B4 adam.kasperski@pwr.wroc.pl materiały + literatura + informacje na stronie www. Zaliczenie: Kolokwium pisemne na
Logika pragmatyczna Logika pragmatyczna Kontakt: dr hab. inż. Adam Kasperski pokój 509 B4 adam.kasperski@pwr.wroc.pl materiały + literatura + informacje na stronie www. Zaliczenie: Kolokwium pisemne na
Logika formalna wprowadzenie. Ponieważ punkty 10.i 12. nie były omawiane na zajęciach, dlatego można je przeczytać fakultatywnie.
 Logika formalna wprowadzenie Ponieważ punkty 10.i 12. nie były omawiane na zajęciach, dlatego można je przeczytać fakultatywnie. 1. Zdanie logicznie prawdziwe (Prawda logiczna) Zdanie, którego analityczność
Logika formalna wprowadzenie Ponieważ punkty 10.i 12. nie były omawiane na zajęciach, dlatego można je przeczytać fakultatywnie. 1. Zdanie logicznie prawdziwe (Prawda logiczna) Zdanie, którego analityczność
Konsekwencja logiczna
 Konsekwencja logiczna Niech Φ 1, Φ 2,..., Φ n będa formułami logicznymi. Formuła Ψ wynika logicznie z Φ 1, Φ 2,..., Φ n jeżeli (Φ 1 Φ 2 Φ n ) Ψ jest tautologia. Formuły Φ 1, Φ 2,..., Φ n nazywamy założeniami
Konsekwencja logiczna Niech Φ 1, Φ 2,..., Φ n będa formułami logicznymi. Formuła Ψ wynika logicznie z Φ 1, Φ 2,..., Φ n jeżeli (Φ 1 Φ 2 Φ n ) Ψ jest tautologia. Formuły Φ 1, Φ 2,..., Φ n nazywamy założeniami
Rachunek zdao i logika matematyczna
 Rachunek zdao i logika matematyczna Pojęcia Logika - Zajmuje się badaniem ogólnych praw, według których przebiegają wszelkie poprawne rozumowania, w szczególności wnioskowania. Rachunek zdao - dział logiki
Rachunek zdao i logika matematyczna Pojęcia Logika - Zajmuje się badaniem ogólnych praw, według których przebiegają wszelkie poprawne rozumowania, w szczególności wnioskowania. Rachunek zdao - dział logiki
LOGIKA Dedukcja Naturalna
 LOGIKA Dedukcja Naturalna Robert Trypuz Katedra Logiki KUL 7 stycznia 2014 Robert Trypuz (Katedra Logiki) Założeniowy system klasycznego rachunku zdań 7 stycznia 2014 1 / 42 PLAN WYKŁADU 1 Przykład dowodów
LOGIKA Dedukcja Naturalna Robert Trypuz Katedra Logiki KUL 7 stycznia 2014 Robert Trypuz (Katedra Logiki) Założeniowy system klasycznego rachunku zdań 7 stycznia 2014 1 / 42 PLAN WYKŁADU 1 Przykład dowodów
Adam Meissner.
 Instytut Automatyki i Inżynierii Informatycznej Politechniki Poznańskiej Adam Meissner Adam.Meissner@put.poznan.pl http://www.man.poznan.pl/~ameis SZTUCZNA INTELIGENCJA Podstawy logiki pierwszego rzędu
Instytut Automatyki i Inżynierii Informatycznej Politechniki Poznańskiej Adam Meissner Adam.Meissner@put.poznan.pl http://www.man.poznan.pl/~ameis SZTUCZNA INTELIGENCJA Podstawy logiki pierwszego rzędu
Lista 1 (elementy logiki)
 Podstawy nauczania matematyki 1. Zdanie Lista 1 (elementy logiki) EE I rok W logice zdaniem logicznym nazywamy wyrażenie oznajmujące o którym można powiedzieć że jest prawdziwe lub fałszywe. Zdania z reguły
Podstawy nauczania matematyki 1. Zdanie Lista 1 (elementy logiki) EE I rok W logice zdaniem logicznym nazywamy wyrażenie oznajmujące o którym można powiedzieć że jest prawdziwe lub fałszywe. Zdania z reguły
1. Wstęp do logiki. Matematyka jest nauką dedukcyjną. Nowe pojęcia definiujemy za pomocą pojęć pierwotnych lub pojęć uprzednio wprowadzonych.
 Elementy logiki i teorii zbiorów. 1. Wstęp do logiki. Matematyka jest nauką dedukcyjną. Nowe pojęcia definiujemy za pomocą pojęć pierwotnych lub pojęć uprzednio wprowadzonych. Pojęcia pierwotne to najprostsze
Elementy logiki i teorii zbiorów. 1. Wstęp do logiki. Matematyka jest nauką dedukcyjną. Nowe pojęcia definiujemy za pomocą pojęć pierwotnych lub pojęć uprzednio wprowadzonych. Pojęcia pierwotne to najprostsze
Drzewa Semantyczne w KRZ
 Drzewa Semantyczne w KRZ Jerzy Pogonowski Zakład Logiki Stosowanej UAM www.logic.amu.edu.pl pogon@amu.edu.pl 7 XII 2006, 13:30 15:00 Jerzy Pogonowski (MEG) Drzewa Semantyczne w KRZ 7 XII 2006, 13:30 15:00
Drzewa Semantyczne w KRZ Jerzy Pogonowski Zakład Logiki Stosowanej UAM www.logic.amu.edu.pl pogon@amu.edu.pl 7 XII 2006, 13:30 15:00 Jerzy Pogonowski (MEG) Drzewa Semantyczne w KRZ 7 XII 2006, 13:30 15:00
Logika rachunek zdań
 Wprowadzenie do Wykładu 1 Logika Logika rachunek zdań Materiały pomocnicze do wykładu dla Studentów Informatyki Stosowanej Wydział EAIiIB AGH Antoni Ligęza Materiały pomocnicze: http://home.agh.edu.pl/~ligeza
Wprowadzenie do Wykładu 1 Logika Logika rachunek zdań Materiały pomocnicze do wykładu dla Studentów Informatyki Stosowanej Wydział EAIiIB AGH Antoni Ligęza Materiały pomocnicze: http://home.agh.edu.pl/~ligeza
METODY DOWODZENIA TWIERDZEŃ I AUTOMATYZACJA ROZUMOWAŃ
 METODY DOWODZENIA TWIERDZEŃ I AUTOMATYZACJA ROZUMOWAŃ KONWERSATORIUM 6: REZOLUCJA V rok kognitywistyki UAM 1 Kilka uwag terminologicznych Słuchacze zapewne pamiętają z zajęć dotyczących PROLOGu poniższą
METODY DOWODZENIA TWIERDZEŃ I AUTOMATYZACJA ROZUMOWAŃ KONWERSATORIUM 6: REZOLUCJA V rok kognitywistyki UAM 1 Kilka uwag terminologicznych Słuchacze zapewne pamiętają z zajęć dotyczących PROLOGu poniższą
Wstęp do logiki. Klasyczny Rachunek Zdań III
 Wstęp do logiki Klasyczny Rachunek Zdań III Przypomnijmy: Logika: = Teoria form (schematów, reguł) poprawnych wnioskowań. Wnioskowaniem nazywamy jakąkolwiek skończoną co najmniej dwuwyrazową sekwencję
Wstęp do logiki Klasyczny Rachunek Zdań III Przypomnijmy: Logika: = Teoria form (schematów, reguł) poprawnych wnioskowań. Wnioskowaniem nazywamy jakąkolwiek skończoną co najmniej dwuwyrazową sekwencję
Logika. Michał Lipnicki. 15 stycznia Zakład Logiki Stosowanej UAM. Michał Lipnicki () Logika 15 stycznia / 37
 Logika Michał Lipnicki Zakład Logiki Stosowanej UAM 15 stycznia 2011 Michał Lipnicki () Logika 15 stycznia 2011 1 / 37 Wstęp Materiały na dzisiejsze zajęcia zostały opracowane na podstawie pomocy naukowych
Logika Michał Lipnicki Zakład Logiki Stosowanej UAM 15 stycznia 2011 Michał Lipnicki () Logika 15 stycznia 2011 1 / 37 Wstęp Materiały na dzisiejsze zajęcia zostały opracowane na podstawie pomocy naukowych
Wstęp do logiki. Klasyczny Rachunek Zdań II
 Wstęp do logiki Klasyczny Rachunek Zdań II DEF. 1 (Słownik). Następujące znaki tworzą słownik języka KRZ: p 1, p 2, p 3, (zmienne zdaniowe) ~,,,, (spójniki) ), ( (nawiasy). DEF. 2 (Wyrażenie). Wyrażeniem
Wstęp do logiki Klasyczny Rachunek Zdań II DEF. 1 (Słownik). Następujące znaki tworzą słownik języka KRZ: p 1, p 2, p 3, (zmienne zdaniowe) ~,,,, (spójniki) ), ( (nawiasy). DEF. 2 (Wyrażenie). Wyrażeniem
Klasyczny rachunek zdań 1/2
 Klasyczny rachunek zdań /2 Elementy logiki i metodologii nauk spotkanie VI Bartosz Gostkowski Poznań, 7 XI 9 Plan wykładu: Zdanie w sensie logicznym Klasyczny rachunek zdań reguły słownikowe reguły składniowe
Klasyczny rachunek zdań /2 Elementy logiki i metodologii nauk spotkanie VI Bartosz Gostkowski Poznań, 7 XI 9 Plan wykładu: Zdanie w sensie logicznym Klasyczny rachunek zdań reguły słownikowe reguły składniowe
Logika rachunek zdań
 Wprowadzenie do Wykładu 1 Logika Logika rachunek zdań Materiały pomocnicze do wykładu dla Studentów Informatyki Wydział EAIiIB AGH Antoni Ligęza Materiały pomocnicze: http://home.agh.edu.pl/~ligeza Wprowadzenie
Wprowadzenie do Wykładu 1 Logika Logika rachunek zdań Materiały pomocnicze do wykładu dla Studentów Informatyki Wydział EAIiIB AGH Antoni Ligęza Materiały pomocnicze: http://home.agh.edu.pl/~ligeza Wprowadzenie
Logika predykatów pierwszego rzędu PROLOG. Zarządzanie wiedzą. Wykład Reprezentacja wiedzy logika predykatów. Joanna Kołodziejczyk.
 Wykład Reprezentacja wiedzy logika predykatów maj 2010 Logika predykatów pierwszego rzędu Plan wykładu Logika predykatów pierwszego rzędu Porównanie z rachunkiem zdań Rachunek zdań ograniczona ekspresja
Wykład Reprezentacja wiedzy logika predykatów maj 2010 Logika predykatów pierwszego rzędu Plan wykładu Logika predykatów pierwszego rzędu Porównanie z rachunkiem zdań Rachunek zdań ograniczona ekspresja
4 Klasyczny rachunek zdań
 4 Klasyczny rachunek zdań Elementy Logiki i Teorii Mnogości 2015/2016 Spis najważniejszych tautologii: (a) p p prawo wyłączonego środka (b) ( p) p prawo podwójnej negacji (c) p q q p (d) p q q p prawo
4 Klasyczny rachunek zdań Elementy Logiki i Teorii Mnogości 2015/2016 Spis najważniejszych tautologii: (a) p p prawo wyłączonego środka (b) ( p) p prawo podwójnej negacji (c) p q q p (d) p q q p prawo
Kultura logiczna Klasyczny rachunek zdań 1/2
 Kultura logiczna Klasyczny rachunek zdań /2 Bartosz Gostkowski bgostkowski@gmail.com Kraków 22 III 2 Plan wykładu: Zdanie w sensie logicznym Klasyczny rachunek zdań reguły słownikowe reguły składniowe
Kultura logiczna Klasyczny rachunek zdań /2 Bartosz Gostkowski bgostkowski@gmail.com Kraków 22 III 2 Plan wykładu: Zdanie w sensie logicznym Klasyczny rachunek zdań reguły słownikowe reguły składniowe
Przykładowe dowody formuł rachunku kwantyfikatorów w systemie tabel semantycznych
 Przykładowe dowody formuł rachunku kwantyfikatorów w systemie tabel semantycznych Zapoznaj z poniŝszym tekstem reprezentującym wiedzę logiczną o wartościach logicznych będących interpretacjami formuł złoŝonych
Przykładowe dowody formuł rachunku kwantyfikatorów w systemie tabel semantycznych Zapoznaj z poniŝszym tekstem reprezentującym wiedzę logiczną o wartościach logicznych będących interpretacjami formuł złoŝonych
Elementy logiki i teorii mnogości
 Elementy logiki i teorii mnogości Zdanie logiczne Zdanie logiczne jest to zdanie oznajmujące, któremu można przypisać określoną wartość logiczną. W logice klasycznej zdania dzielimy na: prawdziwe (przypisujemy
Elementy logiki i teorii mnogości Zdanie logiczne Zdanie logiczne jest to zdanie oznajmujące, któremu można przypisać określoną wartość logiczną. W logice klasycznej zdania dzielimy na: prawdziwe (przypisujemy
Lekcja 3: Elementy logiki - Rachunek zdań
 Lekcja 3: Elementy logiki - Rachunek zdań S. Hoa Nguyen 1 Materiał a) Zdanie proste, złożone b) Spójniki logiczne (funktory zdaniotwórcze):,,,,, (alternatywa wykluczająca - XOR). c) Tautologia, zdanie
Lekcja 3: Elementy logiki - Rachunek zdań S. Hoa Nguyen 1 Materiał a) Zdanie proste, złożone b) Spójniki logiczne (funktory zdaniotwórcze):,,,,, (alternatywa wykluczająca - XOR). c) Tautologia, zdanie
Metody Sztucznej Inteligencji (studia inżynierskie)
 Politechnika Warszawska Ośrodek Kształcenia Na Odległość Metody Sztucznej Inteligencji (studia inżynierskie) Autor: Włodzimierz Kasprzak Opracowanie multimedialne: Warszawa, wrzesień 2014 Metody Sztucznej
Politechnika Warszawska Ośrodek Kształcenia Na Odległość Metody Sztucznej Inteligencji (studia inżynierskie) Autor: Włodzimierz Kasprzak Opracowanie multimedialne: Warszawa, wrzesień 2014 Metody Sztucznej
Andrzej Wiśniewski Logika I Materiały do wykładu dla studentów kognitywistyki. Wykład 9. Koniunkcyjne postacie normalne i rezolucja w KRZ
 Andrzej Wiśniewski Logika I Materiały do wykładu dla studentów kognitywistyki Wykład 9. Koniunkcyjne postacie normalne i rezolucja w KRZ 1 Inferencyjna równoważność formuł Definicja 9.1. Formuła A jest
Andrzej Wiśniewski Logika I Materiały do wykładu dla studentów kognitywistyki Wykład 9. Koniunkcyjne postacie normalne i rezolucja w KRZ 1 Inferencyjna równoważność formuł Definicja 9.1. Formuła A jest
Logika rachunek zdań
 Wprowadzenie do Wykładu 1 Logika Logika rachunek zdań Materiały pomocnicze do wykładu dla Studentów Informatyki Stosowanej Wydział EAIiIB AGH Antoni Ligęza Materiały pomocnicze: http://home.agh.edu.pl/~ligeza
Wprowadzenie do Wykładu 1 Logika Logika rachunek zdań Materiały pomocnicze do wykładu dla Studentów Informatyki Stosowanej Wydział EAIiIB AGH Antoni Ligęza Materiały pomocnicze: http://home.agh.edu.pl/~ligeza
15. DOWODZENIE VI WTÓRNE REGUŁY WNIOSKOWANIA I REGUŁY PODSTAWIANIA
 15. DOWODZENIE VI WTÓRNE REGUŁY WNIOSKOWANIA I REGUŁY PODSTAWIANIA W systemie SD dla każdego spójnika istnieje reguła wprowadzania i reguła eliminacji tegoż spójnika. Niemniej jednak dowodzenie za pomocą
15. DOWODZENIE VI WTÓRNE REGUŁY WNIOSKOWANIA I REGUŁY PODSTAWIANIA W systemie SD dla każdego spójnika istnieje reguła wprowadzania i reguła eliminacji tegoż spójnika. Niemniej jednak dowodzenie za pomocą
LOGIKA Klasyczny Rachunek Zdań
 LOGIKA Klasyczny Rachunek Zdań Robert Trypuz trypuz@kul.pl 5 listopada 2013 Robert Trypuz (trypuz@kul.pl) Klasyczny Rachunek Zdań 5 listopada 2013 1 / 24 PLAN WYKŁADU 1 Alfabet i formuła KRZ 2 Zrozumieć
LOGIKA Klasyczny Rachunek Zdań Robert Trypuz trypuz@kul.pl 5 listopada 2013 Robert Trypuz (trypuz@kul.pl) Klasyczny Rachunek Zdań 5 listopada 2013 1 / 24 PLAN WYKŁADU 1 Alfabet i formuła KRZ 2 Zrozumieć
III rok kognitywistyki UAM,
 METODY DOWODZENIA TWIERDZEŃ I AUTOMATYZACJA ROZUMOWAŃ WYKŁAD 14: POWTÓRKA III rok kognitywistyki UAM, 2016 2017 Dzisiejszy wykład w całości poświęcony będzie omówieniu przykładowych zadań, podobnych do
METODY DOWODZENIA TWIERDZEŃ I AUTOMATYZACJA ROZUMOWAŃ WYKŁAD 14: POWTÓRKA III rok kognitywistyki UAM, 2016 2017 Dzisiejszy wykład w całości poświęcony będzie omówieniu przykładowych zadań, podobnych do
Wybierz cztery z poniższych pięciu zadań. Poprawne rozwiazanie dwóch zadań oznacza zdany egzamin.
 Logika, II rok Etnolingwistyki UAM, 20 VI 2008. Imię i Nazwisko:.............................. GRUPA: I Wybierz cztery z poniższych pięciu zadań. Poprawne rozwiazanie dwóch zadań oznacza zdany egzamin.
Logika, II rok Etnolingwistyki UAM, 20 VI 2008. Imię i Nazwisko:.............................. GRUPA: I Wybierz cztery z poniższych pięciu zadań. Poprawne rozwiazanie dwóch zadań oznacza zdany egzamin.
Logika Stosowana. Wykład 7 - Zbiory i logiki rozmyte Część 3 Prawdziwościowa logika rozmyta. Marcin Szczuka. Instytut Informatyki UW
 Logika Stosowana Wykład 7 - Zbiory i logiki rozmyte Część 3 Prawdziwościowa logika rozmyta Marcin Szczuka Instytut Informatyki UW Wykład monograficzny, semestr letni 2016/2017 Marcin Szczuka (MIMUW) Logika
Logika Stosowana Wykład 7 - Zbiory i logiki rozmyte Część 3 Prawdziwościowa logika rozmyta Marcin Szczuka Instytut Informatyki UW Wykład monograficzny, semestr letni 2016/2017 Marcin Szczuka (MIMUW) Logika
Wstęp do Techniki Cyfrowej... Algebra Boole a
 Wstęp do Techniki Cyfrowej... Algebra Boole a Po co AB? Świetne narzędzie do analitycznego opisu układów logicznych. 1854r. George Boole opisuje swój system dedukcyjny. Ukoronowanie zapoczątkowanych w
Wstęp do Techniki Cyfrowej... Algebra Boole a Po co AB? Świetne narzędzie do analitycznego opisu układów logicznych. 1854r. George Boole opisuje swój system dedukcyjny. Ukoronowanie zapoczątkowanych w
Ćwiczenia do rozdziału 2, zestaw A: z książki Alfreda Tarskiego Wprowadzenie do logiki
 0 1 Ćwiczenia do rozdziału 2, zestaw A: z książki Alfreda Tarskiego Wprowadzenie do logiki 2. W następujących dwóch prawach wyróżnić wyrażenia specyficznie matematyczne i wyrażenia z zakresu logiki (do
0 1 Ćwiczenia do rozdziału 2, zestaw A: z książki Alfreda Tarskiego Wprowadzenie do logiki 2. W następujących dwóch prawach wyróżnić wyrażenia specyficznie matematyczne i wyrażenia z zakresu logiki (do
STANDARDOWE FUNKCJE PRZYNALEŻNOŚCI. METODY HEURYSTYCZNE wykład 6. (alternatywa dla s) (zdef. poprzez klasę s) GAUSSOWSKA F.
 METODY HEURYSTYCZNE wykład 6 STANDARDOWE FUNKCJE PRZYNALEŻNOŚCI 2 GAUSSOWSKA F. PRZYNALEŻNOŚCI F. PRZYNALEŻNOŚCI KLASY s środek; a określa szerokość krzywej 3 4 F. PRZYNALEŻNOŚCI KLASY π F. PRZYNALEŻNOŚCI
METODY HEURYSTYCZNE wykład 6 STANDARDOWE FUNKCJE PRZYNALEŻNOŚCI 2 GAUSSOWSKA F. PRZYNALEŻNOŚCI F. PRZYNALEŻNOŚCI KLASY s środek; a określa szerokość krzywej 3 4 F. PRZYNALEŻNOŚCI KLASY π F. PRZYNALEŻNOŚCI
Elementy logiki i teorii mnogości Wyk lad 1: Rachunek zdań
 Elementy logiki i teorii mnogości Wyk lad 1: Rachunek zdań Micha l Ziembowski m.ziembowski@mini.pw.edu.pl www.mini.pw.edu.pl/ ziembowskim/ October 2, 2016 M. Ziembowski (WUoT) Elementy logiki i teorii
Elementy logiki i teorii mnogości Wyk lad 1: Rachunek zdań Micha l Ziembowski m.ziembowski@mini.pw.edu.pl www.mini.pw.edu.pl/ ziembowskim/ October 2, 2016 M. Ziembowski (WUoT) Elementy logiki i teorii
Elementy logiki. Algebra Boole a. Analiza i synteza układów logicznych
 Elementy logiki: Algebra Boole a i układy logiczne 1 Elementy logiki dla informatyków Wykład III Elementy logiki. Algebra Boole a. Analiza i synteza układów logicznych Elementy logiki: Algebra Boole a
Elementy logiki: Algebra Boole a i układy logiczne 1 Elementy logiki dla informatyków Wykład III Elementy logiki. Algebra Boole a. Analiza i synteza układów logicznych Elementy logiki: Algebra Boole a
Elementy logiki. Zdania proste i złożone
 Elementy logiki Zdania proste i złożone. Jaka jest wartość logiczna następujących zdań: (a) jest dzielnikiem 7 lub suma kątów wewnętrznych w trójkącie jest równa 80. (b) Jeśli sin 0 =, to 5 < 5. (c) Równanie
Elementy logiki Zdania proste i złożone. Jaka jest wartość logiczna następujących zdań: (a) jest dzielnikiem 7 lub suma kątów wewnętrznych w trójkącie jest równa 80. (b) Jeśli sin 0 =, to 5 < 5. (c) Równanie
Przykłady zdań w matematyce. Jeśli a 2 + b 2 = c 2, to trójkąt o bokach długości a, b, c jest prostokątny (a, b, c oznaczają dane liczby dodatnie),
 Elementy logiki 1 Przykłady zdań w matematyce Zdania prawdziwe: 1 3 + 1 6 = 1 2, 3 6, 2 Q, Jeśli x = 1, to x 2 = 1 (x oznacza daną liczbę rzeczywistą), Jeśli a 2 + b 2 = c 2, to trójkąt o bokach długości
Elementy logiki 1 Przykłady zdań w matematyce Zdania prawdziwe: 1 3 + 1 6 = 1 2, 3 6, 2 Q, Jeśli x = 1, to x 2 = 1 (x oznacza daną liczbę rzeczywistą), Jeśli a 2 + b 2 = c 2, to trójkąt o bokach długości
Logika Matematyczna (10)
 Logika Matematyczna (10) Jerzy Pogonowski Zakład Logiki Stosowanej UAM www.logic.amu.edu.pl pogon@amu.edu.pl Rezolucja w KRZ Jerzy Pogonowski (MEG) Logika Matematyczna (10) Rezolucja w KRZ 1 / 39 Plan
Logika Matematyczna (10) Jerzy Pogonowski Zakład Logiki Stosowanej UAM www.logic.amu.edu.pl pogon@amu.edu.pl Rezolucja w KRZ Jerzy Pogonowski (MEG) Logika Matematyczna (10) Rezolucja w KRZ 1 / 39 Plan
Systemy ekspertowe. Wnioskowanie w systemach regułowych. Część piąta. Autor Roman Simiński.
 Część piąta Autor Roman Simiński Kontakt siminski@us.edu.pl www.us.edu.pl/~siminski Niniejsze opracowanie zawiera skrót treści wykładu, lektura tych materiałów nie zastąpi uważnego w nim uczestnictwa.
Część piąta Autor Roman Simiński Kontakt siminski@us.edu.pl www.us.edu.pl/~siminski Niniejsze opracowanie zawiera skrót treści wykładu, lektura tych materiałów nie zastąpi uważnego w nim uczestnictwa.
0.1. Logika podstawowe pojęcia: zdania i funktory, reguły wnioskowania, zmienne zdaniowe, rachunek zdań.
 Wykłady z Analizy rzeczywistej i zespolonej w Matematyce stosowanej Wykład ELEMENTY LOGIKI ALGEBRA BOOLE A Logika podstawowe pojęcia: zdania i funktory, reguły wnioskowania, zmienne zdaniowe, rachunek
Wykłady z Analizy rzeczywistej i zespolonej w Matematyce stosowanej Wykład ELEMENTY LOGIKI ALGEBRA BOOLE A Logika podstawowe pojęcia: zdania i funktory, reguły wnioskowania, zmienne zdaniowe, rachunek
Kultura logiczna Wnioskowania dedukcyjne
 Kultura logiczna Wnioskowania dedukcyjne Bartosz Gostkowski bgostkowski@gmail.com Kraków 25 IV 2010 Plan wykładu: Intuicje dotyczące poprawności wnioskowania Wnioskowanie dedukcyjne Reguły niezawodne a
Kultura logiczna Wnioskowania dedukcyjne Bartosz Gostkowski bgostkowski@gmail.com Kraków 25 IV 2010 Plan wykładu: Intuicje dotyczące poprawności wnioskowania Wnioskowanie dedukcyjne Reguły niezawodne a
Rachunek logiczny. 1. Język rachunku logicznego.
 Rachunek logiczny. Podstawową własnością rozumowania poprawnego jest zachowanie prawdy: rozumowanie poprawne musi się kończyć prawdziwą konkluzją, o ile wszystkie przesłanki leżące u jego podstaw były
Rachunek logiczny. Podstawową własnością rozumowania poprawnego jest zachowanie prawdy: rozumowanie poprawne musi się kończyć prawdziwą konkluzją, o ile wszystkie przesłanki leżące u jego podstaw były
Notacja. - operator implikacji, - operator koniunkcji v operator alternatywy - operator równoważności ~ operator negacji Duża litera (np.
 Systemy ekspertowe Notacja - operator implikacji, - operator koniunkcji v operator alternatywy - operator równoważności ~ operator negacji Duża litera (np. A) - fakt Klauzula Horna Klauzula Horna mówi,
Systemy ekspertowe Notacja - operator implikacji, - operator koniunkcji v operator alternatywy - operator równoważności ~ operator negacji Duża litera (np. A) - fakt Klauzula Horna Klauzula Horna mówi,
Jest to zasadniczo powtórka ze szkoły średniej, być może z niektórymi rzeczami nowymi.
 Logika Jest to zasadniczo powtórka ze szkoły średniej, być może z niektórymi rzeczami nowymi. Często słowu "logika" nadaje się szersze znaczenie niż temu o czym będzie poniżej: np. mówi się "logiczne myślenie"
Logika Jest to zasadniczo powtórka ze szkoły średniej, być może z niektórymi rzeczami nowymi. Często słowu "logika" nadaje się szersze znaczenie niż temu o czym będzie poniżej: np. mówi się "logiczne myślenie"
Zasada rozszerzania. A U A jest zbiorem rozmytym, B jest obrazem zbioru A Przeniesienie rozmytości A w odwzorowaniu f na zbiór B. sup.
 Zasada rozszerzania f U V U jest zbiorem rozmytym V = f( ), jest obrazem zbioru Przeniesienie rozmytości w odwzorowaniu f na zbiór v) = ( v)? ( f ( ) = sup ( u) gdy ( v) 0 1 = 1 u f ( v) f( ) ( v) 1 0
Zasada rozszerzania f U V U jest zbiorem rozmytym V = f( ), jest obrazem zbioru Przeniesienie rozmytości w odwzorowaniu f na zbiór v) = ( v)? ( f ( ) = sup ( u) gdy ( v) 0 1 = 1 u f ( v) f( ) ( v) 1 0
RACHUNEK ZDAŃ 7. Dla każdej tautologii w formie implikacji, której poprzednik również jest tautologią, następnik także jest tautologią.
 Semantyczne twierdzenie o podstawianiu Jeżeli dana formuła rachunku zdań jest tautologią i wszystkie wystąpienia pewnej zmiennej zdaniowej w tej tautologii zastąpimy pewną ustaloną formułą, to otrzymana
Semantyczne twierdzenie o podstawianiu Jeżeli dana formuła rachunku zdań jest tautologią i wszystkie wystąpienia pewnej zmiennej zdaniowej w tej tautologii zastąpimy pewną ustaloną formułą, to otrzymana
Składnia rachunku predykatów pierwszego rzędu
 Początek Gramatyka Kwantyfikatory Poprawność Logika obliczeniowa Instytut Informatyki Początek Gramatyka Kwantyfikatory Poprawność Plan wykładu 1 Na (dobry) początek Zrozumieć słowa Oswoić znaki 2 Gramatyka
Początek Gramatyka Kwantyfikatory Poprawność Logika obliczeniowa Instytut Informatyki Początek Gramatyka Kwantyfikatory Poprawność Plan wykładu 1 Na (dobry) początek Zrozumieć słowa Oswoić znaki 2 Gramatyka
1. Składnia. Logika obliczeniowa - zadania 1 SKŁADNIA Teoria
 Logika obliczeniowa - zadania 1 SKŁADNIA 1. Składnia 1.1. Teoria 1. Składnia oznacza reguły tworzenia... z.... 2. Rachunek predykatów pierwszego rzędu (w skrócie: rachunek predykatów) wyróżnia cztery zbiory
Logika obliczeniowa - zadania 1 SKŁADNIA 1. Składnia 1.1. Teoria 1. Składnia oznacza reguły tworzenia... z.... 2. Rachunek predykatów pierwszego rzędu (w skrócie: rachunek predykatów) wyróżnia cztery zbiory
Andrzej Wiśniewski Logika I Materiały do wykładu dla studentów kognitywistyki. Wykłady 7 i 8. Aksjomatyczne ujęcie Klasycznego Rachunku Zdań
 Andrzej Wiśniewski Logika I Materiały do wykładu dla studentów kognitywistyki Wykłady 7 i 8. Aksjomatyczne ujęcie Klasycznego Rachunku Zdań 1 Istnieje wiele systemów aksjomatycznych Klasycznego Rachunku
Andrzej Wiśniewski Logika I Materiały do wykładu dla studentów kognitywistyki Wykłady 7 i 8. Aksjomatyczne ujęcie Klasycznego Rachunku Zdań 1 Istnieje wiele systemów aksjomatycznych Klasycznego Rachunku
Imię i nazwisko:... OBROŃCY PRAWDY
 Egzamin: Logika Matematyczna, I rok JiNoI, 30 czerwca 2014 Imię i nazwisko:........................................... OBROŃCY PRAWDY Wybierz dokładnie cztery z poniższych pięciu zadań i spróbuj je rozwiazać.
Egzamin: Logika Matematyczna, I rok JiNoI, 30 czerwca 2014 Imię i nazwisko:........................................... OBROŃCY PRAWDY Wybierz dokładnie cztery z poniższych pięciu zadań i spróbuj je rozwiazać.
Logika. Michał Lipnicki. 18 listopada Zakład Logiki Stosowanej UAM. Michał Lipnicki Logika 18 listopada / 1
 Logika Michał Lipnicki Zakład Logiki Stosowanej UAM 18 listopada 2012 Michał Lipnicki Logika 18 listopada 2012 1 / 1 Wstęp Materiały na dzisiejsze zajęcia zostały opracowane na podstawie pomocy naukowych
Logika Michał Lipnicki Zakład Logiki Stosowanej UAM 18 listopada 2012 Michał Lipnicki Logika 18 listopada 2012 1 / 1 Wstęp Materiały na dzisiejsze zajęcia zostały opracowane na podstawie pomocy naukowych
Reprezentacja wiedzy i wnioskowanie
 i wnioskowanie Dariusz Banasiak Katedra Informatyki Technicznej Wydział Elektroniki Wiedza AI to nauka o komputerowych modelach wiedzy umożliwiających rozumienie, wnioskowanie i działanie. Inteligentne
i wnioskowanie Dariusz Banasiak Katedra Informatyki Technicznej Wydział Elektroniki Wiedza AI to nauka o komputerowych modelach wiedzy umożliwiających rozumienie, wnioskowanie i działanie. Inteligentne
Logika Matematyczna (1)
 Logika Matematyczna (1) Jerzy Pogonowski Zakład Logiki Stosowanej UAM www.logic.amu.edu.pl pogon@amu.edu.pl Wprowadzenie Jerzy Pogonowski (MEG) Logika Matematyczna (1) Wprowadzenie 1 / 20 Plan konwersatorium
Logika Matematyczna (1) Jerzy Pogonowski Zakład Logiki Stosowanej UAM www.logic.amu.edu.pl pogon@amu.edu.pl Wprowadzenie Jerzy Pogonowski (MEG) Logika Matematyczna (1) Wprowadzenie 1 / 20 Plan konwersatorium
reguły ogólne, charakteryzujące operator konsekwencji ; reguły szczegółowe dotyczące spójników logicznych: wprowadzanie, eliminacja.
 System naturalnej dedukcji Gentzena Sąd postaci: Γ f (f formuła,γ zbiórformuł) czytamy: konsekwencją założeń Γ jest wniosek f Reguły systemu: reguły ogólne, charakteryzujące operator konsekwencji ; reguły
System naturalnej dedukcji Gentzena Sąd postaci: Γ f (f formuła,γ zbiórformuł) czytamy: konsekwencją założeń Γ jest wniosek f Reguły systemu: reguły ogólne, charakteryzujące operator konsekwencji ; reguły
(g) (p q) [(p q) p]; (h) p [( p q) ( p q)]; (i) [p ( p q)]; (j) p [( q q) r]; (k) [(p q) (q p)] (p q); (l) [(p q) (r s)] [(p s) (q r)];
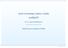
![(g) (p q) [(p q) p]; (h) p [( p q) ( p q)]; (i) [p ( p q)]; (j) p [( q q) r]; (k) [(p q) (q p)] (p q); (l) [(p q) (r s)] [(p s) (q r)]; (g) (p q) [(p q) p]; (h) p [( p q) ( p q)]; (i) [p ( p q)]; (j) p [( q q) r]; (k) [(p q) (q p)] (p q); (l) [(p q) (r s)] [(p s) (q r)];](/thumbs/58/42277365.jpg) Logika 1. Czy następujące sformułowania są zdaniami: (a) Wszystkie koty w Polsce są czarne. (b) Jak to udowodnić? (c) x + y = 7. (d) Jeśli x 2 = y 2, to x = y. (e) Jeśli x = y, to x 2 = y 2. (f) 2 n +
Logika 1. Czy następujące sformułowania są zdaniami: (a) Wszystkie koty w Polsce są czarne. (b) Jak to udowodnić? (c) x + y = 7. (d) Jeśli x 2 = y 2, to x = y. (e) Jeśli x = y, to x 2 = y 2. (f) 2 n +
Alfred N. Whitehead
 Plan wykładu Automatyczne dowodzenie twierdzeń Dowodzenie twierdzeń matematycznych Dedukcja Logic Theorist Means-endsends Analysis Rezolucja Programowanie w logice PROLOG Logic Theorist - 1956 Automatyczne
Plan wykładu Automatyczne dowodzenie twierdzeń Dowodzenie twierdzeń matematycznych Dedukcja Logic Theorist Means-endsends Analysis Rezolucja Programowanie w logice PROLOG Logic Theorist - 1956 Automatyczne
Matematyka ETId Elementy logiki
 Matematyka ETId Izolda Gorgol pokój 131A e-mail: I.Gorgol@pollub.pl tel. 081 5384 563 http://antenor.pol.lublin.pl/users/gorgol Zdania w sensie logicznym DEFINICJA Zdanie w sensie logicznym - zdanie oznajmujace,
Matematyka ETId Izolda Gorgol pokój 131A e-mail: I.Gorgol@pollub.pl tel. 081 5384 563 http://antenor.pol.lublin.pl/users/gorgol Zdania w sensie logicznym DEFINICJA Zdanie w sensie logicznym - zdanie oznajmujace,
RBD Relacyjne Bazy Danych
 Wykład 7 RBD Relacyjne Bazy Danych Bazy Danych - A. Dawid 2011 1 Selekcja σ C (R) W wyniku zastosowania operatora selekcji do relacji R powstaje nowa relacja T do której należy pewien podzbiór krotek relacji
Wykład 7 RBD Relacyjne Bazy Danych Bazy Danych - A. Dawid 2011 1 Selekcja σ C (R) W wyniku zastosowania operatora selekcji do relacji R powstaje nowa relacja T do której należy pewien podzbiór krotek relacji
Inżynieria wiedzy Wnioskowanie oparte na wiedzy niepewnej Opracowane na podstawie materiałów dra Michała Berety
 mgr Adam Marszałek Zakład Inteligencji Obliczeniowej Instytut Informatyki PK Inżynieria wiedzy Wnioskowanie oparte na wiedzy niepewnej Opracowane na podstawie materiałów dra Michała Berety Wstępnie na
mgr Adam Marszałek Zakład Inteligencji Obliczeniowej Instytut Informatyki PK Inżynieria wiedzy Wnioskowanie oparte na wiedzy niepewnej Opracowane na podstawie materiałów dra Michała Berety Wstępnie na
Jak wnioskują maszyny?
 Jak wnioskują maszyny? Andrzej Szałas informatyka + 1 Plan wykładu Plan wykładu Modelowanie wnioskowania Wyszukiwanie, a wnioskowanie Klasyczny rachunek zdań Diagramy Venna Wprowadzenie do automatycznego
Jak wnioskują maszyny? Andrzej Szałas informatyka + 1 Plan wykładu Plan wykładu Modelowanie wnioskowania Wyszukiwanie, a wnioskowanie Klasyczny rachunek zdań Diagramy Venna Wprowadzenie do automatycznego
JEZYKOZNAWSTWO. I NAUKI O INFORMACJI, ROK I Logika Matematyczna: egzamin pisemny 18 czerwca Imię i Nazwisko:... I
 JEZYKOZNAWSTWO I NAUKI O INFORMACJI, ROK I Logika Matematyczna: egzamin pisemny 18 czerwca 2013 Imię i Nazwisko:.................................................................................. I Wybierz
JEZYKOZNAWSTWO I NAUKI O INFORMACJI, ROK I Logika Matematyczna: egzamin pisemny 18 czerwca 2013 Imię i Nazwisko:.................................................................................. I Wybierz
Część 2. Funkcje logiczne układy kombinacyjne
 Część 2 Funkcje logiczne układy kombinacyjne Zapis funkcji logicznych układ funkcjonalnie pełny Arytmetyka Bool a najważniejsze aksjomaty i tożsamości Minimalizacja funkcji logicznych Układy kombinacyjne
Część 2 Funkcje logiczne układy kombinacyjne Zapis funkcji logicznych układ funkcjonalnie pełny Arytmetyka Bool a najważniejsze aksjomaty i tożsamości Minimalizacja funkcji logicznych Układy kombinacyjne
Elementy logiki Klasyczny rachunek zdań. Wojciech Buszkowski Zakład Teorii Obliczeń Wydział Matematyki i Informatyki Uniwersytet im.
 Elementy logiki. Klasyczny rachunek zdań. Elementy logiki Klasyczny rachunek zdań Wojciech Buszkowski Zakład Teorii Obliczeń Wydział Matematyki i Informatyki Uniwersytet im. Adama Mickiewicza 1 Spójniki
Elementy logiki. Klasyczny rachunek zdań. Elementy logiki Klasyczny rachunek zdań Wojciech Buszkowski Zakład Teorii Obliczeń Wydział Matematyki i Informatyki Uniwersytet im. Adama Mickiewicza 1 Spójniki
Andrzej Wiśniewski Logika II. Materiały do wykładu dla studentów kognitywistyki
 Andrzej Wiśniewski Logika II Materiały do wykładu dla studentów kognitywistyki Wykład 5. Wprowadzenie do semantyki teoriomodelowej cz.5. Wynikanie logiczne 1 Na poprzednim wykładzie udowodniliśmy m.in.:
Andrzej Wiśniewski Logika II Materiały do wykładu dla studentów kognitywistyki Wykład 5. Wprowadzenie do semantyki teoriomodelowej cz.5. Wynikanie logiczne 1 Na poprzednim wykładzie udowodniliśmy m.in.:
Zagadnienia podstawowe dotyczące metod formalnych w informatyce
 Zagadnienia podstawowe dotyczące metod formalnych w informatyce! Logika Analiza języka i czynności badawczych (np. rozumowanie, definiowanie, klasyfikowanie) w celu poznania takich reguł posługiwania się
Zagadnienia podstawowe dotyczące metod formalnych w informatyce! Logika Analiza języka i czynności badawczych (np. rozumowanie, definiowanie, klasyfikowanie) w celu poznania takich reguł posługiwania się
Logika Rachunek zdań
 Wprowadzenie do Wykładu 1 Logika Rachunek zdań Materiały pomocnicze do wykładu dla Studentek i Studentów Informatyki Wydziału EAIiIB AGH Antoni Ligęza : 2016 Materiały pomocnicze: http://home.agh.edu.pl/~ligeza
Wprowadzenie do Wykładu 1 Logika Rachunek zdań Materiały pomocnicze do wykładu dla Studentek i Studentów Informatyki Wydziału EAIiIB AGH Antoni Ligęza : 2016 Materiały pomocnicze: http://home.agh.edu.pl/~ligeza
Paradygmaty dowodzenia
 Paradygmaty dowodzenia Sprawdzenie, czy dana formuła rachunku zdań jest tautologią polega zwykle na obliczeniu jej wartości dla 2 n różnych wartościowań, gdzie n jest liczbą zmiennych zdaniowych tej formuły.
Paradygmaty dowodzenia Sprawdzenie, czy dana formuła rachunku zdań jest tautologią polega zwykle na obliczeniu jej wartości dla 2 n różnych wartościowań, gdzie n jest liczbą zmiennych zdaniowych tej formuły.
Logika Matematyczna (1)
 Logika Matematyczna (1) Jerzy Pogonowski Zakład Logiki Stosowanej UAM www.logic.amu.edu.pl pogon@amu.edu.pl 4 X 2007 Jerzy Pogonowski (MEG) Logika Matematyczna (1) 4 X 2007 1 / 18 Plan konwersatorium Dzisiaj:
Logika Matematyczna (1) Jerzy Pogonowski Zakład Logiki Stosowanej UAM www.logic.amu.edu.pl pogon@amu.edu.pl 4 X 2007 Jerzy Pogonowski (MEG) Logika Matematyczna (1) 4 X 2007 1 / 18 Plan konwersatorium Dzisiaj:
Rachunek predykatów. Formuły rachunku predykatów. Plan wykładu. Relacje i predykaty - przykłady. Relacje i predykaty
 Rachunek predykatów Wykład 4 Plan wykładu Relacje i predykaty Formuły rachunku predykatów Interpretacje Logiczna równoważność Metoda tabel Modele skończone i nieskończone Rozstrzygalność Relacje i predykaty
Rachunek predykatów Wykład 4 Plan wykładu Relacje i predykaty Formuły rachunku predykatów Interpretacje Logiczna równoważność Metoda tabel Modele skończone i nieskończone Rozstrzygalność Relacje i predykaty
PODSTAWY SZTUCZNEJ INTELIGENCJI
 Katedra Informatyki Stosowanej Politechnika Łódzka PODSTAWY SZTUCZNEJ INTELIGENCJI Laboratorium PROGRAMOWANIE SYSTEMÓW EKSPERTOWYCH Opracowanie: Dr hab. inŝ. Jacek Kucharski Dr inŝ. Piotr Urbanek Cel ćwiczenia
Katedra Informatyki Stosowanej Politechnika Łódzka PODSTAWY SZTUCZNEJ INTELIGENCJI Laboratorium PROGRAMOWANIE SYSTEMÓW EKSPERTOWYCH Opracowanie: Dr hab. inŝ. Jacek Kucharski Dr inŝ. Piotr Urbanek Cel ćwiczenia
1 Podstawowe oznaczenia
 Poniżej mogą Państwo znaleźć skondensowane wiadomości z wykładu. Należy je traktować jako przegląd pojęć, które pojawiły się na wykładzie. Materiały te nie są w pełni tożsame z tym co pojawia się na wykładzie.
Poniżej mogą Państwo znaleźć skondensowane wiadomości z wykładu. Należy je traktować jako przegląd pojęć, które pojawiły się na wykładzie. Materiały te nie są w pełni tożsame z tym co pojawia się na wykładzie.
Maciej Grzesiak Instytut Matematyki Politechniki Poznańskiej. Elementy logiki
 Maciej Grzesiak Instytut Matematyki Politechniki Poznańskiej Elementy logiki 1. Elementy logiki W logice zdaniem nazywamy wypowiedź oznajmującą, która (w ramach danej nauki) jest albo prawdziwa, albo fałszywa.
Maciej Grzesiak Instytut Matematyki Politechniki Poznańskiej Elementy logiki 1. Elementy logiki W logice zdaniem nazywamy wypowiedź oznajmującą, która (w ramach danej nauki) jest albo prawdziwa, albo fałszywa.
Andrzej Wiśniewski Logika II. Materiały do wykładu dla studentów kognitywistyki. Wykład 14. Wprowadzenie do logiki intuicjonistycznej
 Andrzej Wiśniewski Logika II Materiały do wykładu dla studentów kognitywistyki Wykład 14. Wprowadzenie do logiki intuicjonistycznej 1 Przedstawione na poprzednich wykładach logiki modalne możemy uznać
Andrzej Wiśniewski Logika II Materiały do wykładu dla studentów kognitywistyki Wykład 14. Wprowadzenie do logiki intuicjonistycznej 1 Przedstawione na poprzednich wykładach logiki modalne możemy uznać
Rachunek zdań 1 zastaw zadań
 Rachunek zdań 1 zastaw zadań Zadanie 1 ([1]) Wyraź w języku KRZ następujące zdania języka naturalnego: (a) Jeśli Jan jest ateistą to Jan nie jest katolikiem. (b) Jeśli Jan jest ateistą to nieprawda, że
Rachunek zdań 1 zastaw zadań Zadanie 1 ([1]) Wyraź w języku KRZ następujące zdania języka naturalnego: (a) Jeśli Jan jest ateistą to Jan nie jest katolikiem. (b) Jeśli Jan jest ateistą to nieprawda, że
Internet Semantyczny i Logika I
 Internet Semantyczny i Logika I Warstwy Internetu Semantycznego Dowód Zaufanie Logika OWL, Ontologie Podpis cyfrowy RDF, schematy RDF XML, schematy XML przestrzenie nazw URI Po co nam logika? Potrzebujemy
Internet Semantyczny i Logika I Warstwy Internetu Semantycznego Dowód Zaufanie Logika OWL, Ontologie Podpis cyfrowy RDF, schematy RDF XML, schematy XML przestrzenie nazw URI Po co nam logika? Potrzebujemy
