Ciągi Podzbiory Symbol Newtona Zasada szufladkowa Dirichleta Zasada włączania i wyłączania. Ilość najkrótszych dróg. Kombinatoryka. Magdalena Lemańska
|
|
|
- Mateusz Kurek
- 6 lat temu
- Przeglądów:
Transkrypt
1 Kombinatoryka Magdalena Lemańska
2 Literatura Matematyka Dyskretna Andrzej Szepietowski Discrete Mathematics Seymour Lipschutz, Marc Lipson Aspekty kombinatoryki Victor Bryant Combinatorics V.K. Balakrishnan
3 Ciągi długości k Ile ciągów długości k można utworzyć z elementów zbioru zawierającego n symboli?
4 Ciągi długości k Ile ciągów długości k można utworzyć z elementów zbioru zawierającego n symboli? 1 Jeśli zbiór symboli zawiera dwa elementy a, b, to można utworzyć dwa ciągi długości jeden: i cztery ciągi długości dwa: (a); (b) (a, a); (a, b); (b, a); (b, b).
5 Ciągi długości k Ile ciągów długości k można utworzyć z elementów zbioru zawierającego n symboli? 1 Jeśli zbiór symboli zawiera dwa elementy a, b, to można utworzyć dwa ciągi długości jeden: i cztery ciągi długości dwa: (a); (b) (a, a); (a, b); (b, a); (b, b). 2 Aby uzyskać ciągi długości trzy, postępujemy w następujący sposób: bierzemy cztery ciągi długości dwa i najpierw do każdego z nich dopisujemy na początku a. Otrzymujemy w ten sposób komplet (a, a, a); (a, a, b); (a, b, a); (a.b, b).
6 Ciągi długości k Ile ciągów długości k można utworzyć z elementów zbioru zawierającego n symboli? 1 Jeśli zbiór symboli zawiera dwa elementy a, b, to można utworzyć dwa ciągi długości jeden: i cztery ciągi długości dwa: (a); (b) (a, a); (a, b); (b, a); (b, b). 2 Aby uzyskać ciągi długości trzy, postępujemy w następujący sposób: bierzemy cztery ciągi długości dwa i najpierw do każdego z nich dopisujemy na początku a. Otrzymujemy w ten sposób komplet (a, a, a); (a, a, b); (a, b, a); (a.b, b). 3 Potem do tych samych czterech ciągów długości dwa dopisujemy na początku symbol b i otrzymujemy komplet: (b, a, a); (b, a, b); (b, b, a); (b, b, b).
7 Ciągi długości k Ile ciągów długości k można utworzyć z elementów zbioru zawierającego n symboli? 1 Jeśli zbiór symboli zawiera dwa elementy a, b, to można utworzyć dwa ciągi długości jeden: i cztery ciągi długości dwa: (a); (b) (a, a); (a, b); (b, a); (b, b). 2 Aby uzyskać ciągi długości trzy, postępujemy w następujący sposób: bierzemy cztery ciągi długości dwa i najpierw do każdego z nich dopisujemy na początku a. Otrzymujemy w ten sposób komplet (a, a, a); (a, a, b); (a, b, a); (a.b, b). 3 Potem do tych samych czterech ciągów długości dwa dopisujemy na początku symbol b i otrzymujemy komplet: (b, a, a); (b, a, b); (b, b, a); (b, b, b). 4 Komplety te są rozłączne i oba zawierają różne ciągi. Razem tworzą zbiór wszystkich ciągów długości trzy.
8 Ciągi długości k Ile ciągów długości k można utworzyć z elementów zbioru zawierającego n symboli? 1 Jeśli zbiór symboli zawiera dwa elementy a, b, to można utworzyć dwa ciągi długości jeden: i cztery ciągi długości dwa: (a); (b) (a, a); (a, b); (b, a); (b, b). 2 Aby uzyskać ciągi długości trzy, postępujemy w następujący sposób: bierzemy cztery ciągi długości dwa i najpierw do każdego z nich dopisujemy na początku a. Otrzymujemy w ten sposób komplet (a, a, a); (a, a, b); (a, b, a); (a.b, b). 3 Potem do tych samych czterech ciągów długości dwa dopisujemy na początku symbol b i otrzymujemy komplet: (b, a, a); (b, a, b); (b, b, a); (b, b, b). 4 Komplety te są rozłączne i oba zawierają różne ciągi. Razem tworzą zbiór wszystkich ciągów długości trzy. Twierdzenie Liczba ciągów długości k o elementach ze zbioru {a, b} wynosi 2 k.
9 Uogólnienie Jeśli zbiór symboli zawiera n elementów, to powtarzając powyższe rozumowanie możemy sią przekonać, że istnieje n ciągów długości jeden, n 2 ciągów długości dwa i ogólnie ciągów długości k + 1 jest n razy więcej niż ciągów długości k. Zachodzi zatem twierdzenie.
10 Uogólnienie Jeśli zbiór symboli zawiera n elementów, to powtarzając powyższe rozumowanie możemy sią przekonać, że istnieje n ciągów długości jeden, n 2 ciągów długości dwa i ogólnie ciągów długości k + 1 jest n razy więcej niż ciągów długości k. Zachodzi zatem twierdzenie. Twierdzenie Liczba ciągów długości k o elementach ze zbioru n-elementowego wynosi n k.
11 Uogólnienie Jeśli zbiór symboli zawiera n elementów, to powtarzając powyższe rozumowanie możemy sią przekonać, że istnieje n ciągów długości jeden, n 2 ciągów długości dwa i ogólnie ciągów długości k + 1 jest n razy więcej niż ciągów długości k. Zachodzi zatem twierdzenie. Twierdzenie Liczba ciągów długości k o elementach ze zbioru n-elementowego wynosi n k. Funkcje Policzymy teraz, ile jest funkcji ze zbioru k-elementowego A w zbiór n-elementowy B.
12 Uogólnienie Jeśli zbiór symboli zawiera n elementów, to powtarzając powyższe rozumowanie możemy sią przekonać, że istnieje n ciągów długości jeden, n 2 ciągów długości dwa i ogólnie ciągów długości k + 1 jest n razy więcej niż ciągów długości k. Zachodzi zatem twierdzenie. Twierdzenie Liczba ciągów długości k o elementach ze zbioru n-elementowego wynosi n k. Funkcje Policzymy teraz, ile jest funkcji ze zbioru k-elementowego A w zbiór n-elementowy B. Funkcja jako ciąg Każdą funkcję f : A B można przedstawić jako ciąg (f (1), f (2),..., f (k)).
13 Uogólnienie Jeśli zbiór symboli zawiera n elementów, to powtarzając powyższe rozumowanie możemy sią przekonać, że istnieje n ciągów długości jeden, n 2 ciągów długości dwa i ogólnie ciągów długości k + 1 jest n razy więcej niż ciągów długości k. Zachodzi zatem twierdzenie. Twierdzenie Liczba ciągów długości k o elementach ze zbioru n-elementowego wynosi n k. Funkcje Policzymy teraz, ile jest funkcji ze zbioru k-elementowego A w zbiór n-elementowy B. Funkcja jako ciąg Każdą funkcję f : A B można przedstawić jako ciąg (f (1), f (2),..., f (k)). Ciąg ten jest długości k, a jego elementy są wzięte ze zbioru B.
14 Zauważmy, że każdej funkcji odpowiada jeden ciąg i na odwrót, każdy ciąg (b 1,..., b k ) opisuje jedną funkcję: taką, która dla każdego 1 i k przypisuje wartość f (i) = b i.
15 Zauważmy, że każdej funkcji odpowiada jeden ciąg i na odwrót, każdy ciąg (b 1,..., b k ) opisuje jedną funkcję: taką, która dla każdego 1 i k przypisuje wartość f (i) = b i. W takim razie funkcji ze zbioru A w zbiór B jest tyle samo, co ciągów długości k = A z elementami ze zbioru B. Udowodniliśmy więc poniższe twierdzenie.
16 Zauważmy, że każdej funkcji odpowiada jeden ciąg i na odwrót, każdy ciąg (b 1,..., b k ) opisuje jedną funkcję: taką, która dla każdego 1 i k przypisuje wartość f (i) = b i. W takim razie funkcji ze zbioru A w zbiór B jest tyle samo, co ciągów długości k = A z elementami ze zbioru B. Udowodniliśmy więc poniższe twierdzenie. Twierdzenie Jeśli zbiór A zawiera k elementów, a zbiór B zawiera n elementów, to liczba funkcji ze zbioru A w zbiór B wynosi n k.
17 Zauważmy, że każdej funkcji odpowiada jeden ciąg i na odwrót, każdy ciąg (b 1,..., b k ) opisuje jedną funkcję: taką, która dla każdego 1 i k przypisuje wartość f (i) = b i. W takim razie funkcji ze zbioru A w zbiór B jest tyle samo, co ciągów długości k = A z elementami ze zbioru B. Udowodniliśmy więc poniższe twierdzenie. Twierdzenie Jeśli zbiór A zawiera k elementów, a zbiór B zawiera n elementów, to liczba funkcji ze zbioru A w zbiór B wynosi n k. Zadanie Wypisz wszystkie funkcje F : X Y, gdzie: X = {1, 2, 3}, Y = {a, b} X = {a, b}, Y = {1, 2, 3}. Zrobić to samo z dodatkowym warunkiem, że funkcje są różnowartościowe.
18 Zauważmy, że każdej funkcji odpowiada jeden ciąg i na odwrót, każdy ciąg (b 1,..., b k ) opisuje jedną funkcję: taką, która dla każdego 1 i k przypisuje wartość f (i) = b i. W takim razie funkcji ze zbioru A w zbiór B jest tyle samo, co ciągów długości k = A z elementami ze zbioru B. Udowodniliśmy więc poniższe twierdzenie. Twierdzenie Jeśli zbiór A zawiera k elementów, a zbiór B zawiera n elementów, to liczba funkcji ze zbioru A w zbiór B wynosi n k. Zadanie Wypisz wszystkie funkcje F : X Y, gdzie: X = {1, 2, 3}, Y = {a, b} X = {a, b}, Y = {1, 2, 3}. Zrobić to samo z dodatkowym warunkiem, że funkcje są różnowartościowe. Zadanie Ile jest funkcji f ze zbioru {1,..., n} w zbiór {a, b, c}? Ile spośród nich spełnia warunek f (1) = a? Ile spełnia warunek f (1) f (2)?
19 Ciągi bez powtórzeń Policzmy teraz, ile jest ciągów bez powtórzeń, czyli ciągów rȯżnowartościowych. Jeśli elementy bierzemy ze zbioru trzyelementowego {1, 2, 3}, to możemy utworzyć: trzy ciągi jednoelementowe: sześć ciągów dwuoelementowych: oraz sześć ciągów trójelementowych: (1), (2), (3) (1, 2), (1, 3), (2, 1), (2, 3), (3, 1), (3, 2) (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1)
20 Ciągi bez powtórzeń Policzmy teraz, ile jest ciągów bez powtórzeń, czyli ciągów rȯżnowartościowych. Jeśli elementy bierzemy ze zbioru trzyelementowego {1, 2, 3}, to możemy utworzyć: trzy ciągi jednoelementowe: sześć ciągów dwuoelementowych: oraz sześć ciągów trójelementowych: (1), (2), (3) (1, 2), (1, 3), (2, 1), (2, 3), (3, 1), (3, 2) (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1) Przykład Ile różnowartościowych ciągów długości cztery można stworzyć dla zbioru siedmioelementowego?
21 Twierdzenie Jeśli elementy wybieramy ze zbioru n-elementowego A, to liczba ciągów k-elementowych bez powtórzeń, które można wybrać z tego zbioru, wynosi n(n 1)... (n k + 1).
22 Twierdzenie Jeśli elementy wybieramy ze zbioru n-elementowego A, to liczba ciągów k-elementowych bez powtórzeń, które można wybrać z tego zbioru, wynosi n(n 1)... (n k + 1). Zadanie Ile jest liczb trzycyfrowych w systemach dziesiętnym, trójkowym i dwójkowym?
23 Twierdzenie Jeśli elementy wybieramy ze zbioru n-elementowego A, to liczba ciągów k-elementowych bez powtórzeń, które można wybrać z tego zbioru, wynosi n(n 1)... (n k + 1). Zadanie Ile jest liczb trzycyfrowych w systemach dziesiętnym, trójkowym i dwójkowym? Zadanie Ile istnieje liczb naturalnych pięciocyfrowych, w których zapisie nie występuje cyfra zero? Ile istnieje liczb naturalnych pięciocyfrowych takich, w których cyfra setek jest 5?
24 Permutacje Permutacje to ciągi bez powtórzeń długości n, wybierane ze zbioru n-elementowego.
25 Permutacje Permutacje to ciągi bez powtórzeń długości n, wybierane ze zbioru n-elementowego. Przykład Na przykład, mamy dwie permutacje dwuelementowe: (2, 1), (1, 2) oraz sześć permutacji trzyelementowych: (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1).
26 Permutacje Permutacje to ciągi bez powtórzeń długości n, wybierane ze zbioru n-elementowego. Przykład Na przykład, mamy dwie permutacje dwuelementowe: (2, 1), (1, 2) oraz sześć permutacji trzyelementowych: (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1). Ilość permutacji Zgodnie z poprzednim twierdzeniem, ilość permutacji w zbiorze n-elementowym wynosi n(n 1)... 1, czyli jest równa n!.
27 Permutacje Permutacje to ciągi bez powtórzeń długości n, wybierane ze zbioru n-elementowego. Przykład Na przykład, mamy dwie permutacje dwuelementowe: (2, 1), (1, 2) oraz sześć permutacji trzyelementowych: (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1). Ilość permutacji Zgodnie z poprzednim twierdzeniem, ilość permutacji w zbiorze n-elementowym wynosi n(n 1)... 1, czyli jest równa n!. Zadanie Rodzina sześcioosobowa (rodzice i czworo dzieci) ustawia się w szeregu do zdjęcia. Ile różnych fotografii można otrzymać, jeśli: a) każdy może stać obok każdego; b) rodzice stoją na dwóch końcach szeregu?
28 Permutacje Permutacje to ciągi bez powtórzeń długości n, wybierane ze zbioru n-elementowego. Przykład Na przykład, mamy dwie permutacje dwuelementowe: (2, 1), (1, 2) oraz sześć permutacji trzyelementowych: (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1). Ilość permutacji Zgodnie z poprzednim twierdzeniem, ilość permutacji w zbiorze n-elementowym wynosi n(n 1)... 1, czyli jest równa n!. Zadanie Rodzina sześcioosobowa (rodzice i czworo dzieci) ustawia się w szeregu do zdjęcia. Ile różnych fotografii można otrzymać, jeśli: a) każdy może stać obok każdego; b) rodzice stoją na dwóch końcach szeregu? Zadanie Na egzaminie posadzono w sposób losowy w jednym rzędzie dziesięciu zdających, w tym dwóch z jednej szkoły. Na ile sposobów można rozsadzić zdających tak, by: a) znajomi z jednej szkoły nie siedzieli obok siebie; b) siedzieli na przeciwnych końcach rzędu; c) między nimi siedziały dokładnie trzy inne osoby?
29 Inna definicja permutacji Czasami używa się innej definicji permutacji. Mianowicie, permutacja n-elementowa to dowolna funkcja różnowartościowa ze zbioru {1, 2,..., n} na ten sam zbiór.
30 Inna definicja permutacji Czasami używa się innej definicji permutacji. Mianowicie, permutacja n-elementowa to dowolna funkcja różnowartościowa ze zbioru {1, 2,..., n} na ten sam zbiór. Oznaczenia Na oznaczenie permutacji używa się zapisu: ( 1...n ) π(1)...π(n)
31 Inna definicja permutacji Czasami używa się innej definicji permutacji. Mianowicie, permutacja n-elementowa to dowolna funkcja różnowartościowa ze zbioru {1, 2,..., n} na ten sam zbiór. Oznaczenia Na oznaczenie permutacji używa się zapisu: ( 1...n ) π(1)...π(n) Składanie permutacji Dwie permutacje n-elementowe można składać tak, jak składa się funkcje. Złożenie permutacji określone jest wzorem: π 1 π 2 (x) = π 1 (π 2 (x)).
32 Inna definicja permutacji Czasami używa się innej definicji permutacji. Mianowicie, permutacja n-elementowa to dowolna funkcja różnowartościowa ze zbioru {1, 2,..., n} na ten sam zbiór. Oznaczenia Na oznaczenie permutacji używa się zapisu: ( 1...n ) π(1)...π(n) Składanie permutacji Dwie permutacje n-elementowe można składać tak, jak składa się funkcje. Złożenie permutacji określone jest wzorem: π 1 π 2 (x) = π 1 (π 2 (x)). Własności permutacji Zbiór wszystkich permutacji na zbiorze {1, 2,..., n} z działaniem złożenia ma następujące własności:
33 Własności permutacji
34 Własności permutacji Złożenie permutacji jest łączne, tzn. dla każdych trzech permutacji π, σ, ρ : jest π (σ ρ) = (π σ) ρ.
35 Własności permutacji Złożenie permutacji jest łączne, tzn. dla każdych trzech permutacji π, σ, ρ : jest π (σ ρ) = (π σ) ρ. Wśród permutacji istnieje identyczność id, czyli permutacja, która każdemu x z dziedziny przypisuje wartość id(x) = x. Identyczność jest elementem neutralnym składania permutacji, ponieważ dla każdej permutacji π, id π = π id = π.
36 Własności permutacji Złożenie permutacji jest łączne, tzn. dla każdych trzech permutacji π, σ, ρ : jest π (σ ρ) = (π σ) ρ. Wśród permutacji istnieje identyczność id, czyli permutacja, która każdemu x z dziedziny przypisuje wartość id(x) = x. Identyczność jest elementem neutralnym składania permutacji, ponieważ dla każdej permutacji π, id π = π id = π. Dla każdej permutacji π istnieje permutacja odwrotna π 1, spełniająca warunek π π 1 = π 1 π = id.
37 Własności permutacji Złożenie permutacji jest łączne, tzn. dla każdych trzech permutacji π, σ, ρ : jest π (σ ρ) = (π σ) ρ. Wśród permutacji istnieje identyczność id, czyli permutacja, która każdemu x z dziedziny przypisuje wartość id(x) = x. Identyczność jest elementem neutralnym składania permutacji, ponieważ dla każdej permutacji π, id π = π id = π. Dla każdej permutacji π istnieje permutacja odwrotna π 1, spełniająca warunek π π 1 = π 1 π = id. Zadanie Obliczyć π 1 π 2, π 2 π 1, π 1 1, π 1 2, jeśli π 1 = ( 12345) 25431, π1 = ( ).
38 Podzbiory Policzmy teraz, ile podzbiorów ma skończony zbiór n-elementowy. Jeśli zbiór składa się z trzech elementów: {a, b, c}, to możemy łatwo wypisać wszystkie jego podzbiory:, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}.
39 Podzbiory Policzmy teraz, ile podzbiorów ma skończony zbiór n-elementowy. Jeśli zbiór składa się z trzech elementów: {a, b, c}, to możemy łatwo wypisać wszystkie jego podzbiory:, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}. Rozważmy teraz ogólnie podzbiory zbioru {1, 2,..., n}. Z każdym zbiorem A {1, 2,..., n} związana jest jego funkcja charakterystyczna, określona wzorem: χ A (i) = 1, i A, χ A (i) = 0, i / A.
40 Podzbiory Policzmy teraz, ile podzbiorów ma skończony zbiór n-elementowy. Jeśli zbiór składa się z trzech elementów: {a, b, c}, to możemy łatwo wypisać wszystkie jego podzbiory:, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}. Rozważmy teraz ogólnie podzbiory zbioru {1, 2,..., n}. Z każdym zbiorem A {1, 2,..., n} związana jest jego funkcja charakterystyczna, określona wzorem: χ A (i) = 1, i A, χ A (i) = 0, i / A. Dziedziną funkcji jest zbiór {1, 2,..., n}, a przeciwdziedziną zbiór {0, 1}. Zauważmy, że każdemu podzbiorowi odpowiada jedna funkcja charakterystyczna i na odwrót, jeśli weźmiemy dowolną funkcę χ : {1, 2,..., n} {0, 1}, to wyznacza ona zbiór A = {i : χ(i) = 1}.
41 Z powyższych rozważań wynika, że liczba podzbiorów zbioru n-elementowego jest równa liczbie funkcji ze zbioru {1, 2,..., n} w zbiór {0, 1}. Czyli na podstawie wcześniejszego twierdzenia o funkcjach mamy:
42 Z powyższych rozważań wynika, że liczba podzbiorów zbioru n-elementowego jest równa liczbie funkcji ze zbioru {1, 2,..., n} w zbiór {0, 1}. Czyli na podstawie wcześniejszego twierdzenia o funkcjach mamy: Twierdzenie Każdy zbiór n-elementowy ma 2 n podzbiorów.
43 Podzbiory k-elementowe Zastanowimy się teraz nad podzbiorami określonej mocy.
44 Podzbiory k-elementowe Zastanowimy się teraz nad podzbiorami określonej mocy. Dla zbioru czteroelementowego {1, 2, 3, 4} mamy jeden podzbiór pusty (zeroelementowy), cztery podzbiory jednoelementowe {1}, {2}, {3}, {4}; sześć podzbiorów dwuelementowych: {1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}; cztery podzbiory trzyelementowe: {1, 2, 3}, {1, 2, 4}, {1, 3, 4}, {2, 3, 4} i jeden podzbiór czteroelementowy: {1, 2, 3, 4}.
45 Podzbiory k-elementowe Zastanowimy się teraz nad podzbiorami określonej mocy. Dla zbioru czteroelementowego {1, 2, 3, 4} mamy jeden podzbiór pusty (zeroelementowy), cztery podzbiory jednoelementowe {1}, {2}, {3}, {4}; sześć podzbiorów dwuelementowych: {1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}; cztery podzbiory trzyelementowe: {1, 2, 3}, {1, 2, 4}, {1, 3, 4}, {2, 3, 4} i jeden podzbiór czteroelementowy: {1, 2, 3, 4}. Liczbę podzbiorów k-elementowych zbioru n-elementowego oznacza się przez ( n k).
46 Podzbiory k-elementowe Zastanowimy się teraz nad podzbiorami określonej mocy. Dla zbioru czteroelementowego {1, 2, 3, 4} mamy jeden podzbiór pusty (zeroelementowy), cztery podzbiory jednoelementowe {1}, {2}, {3}, {4}; sześć podzbiorów dwuelementowych: {1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}; cztery podzbiory trzyelementowe: {1, 2, 3}, {1, 2, 4}, {1, 3, 4}, {2, 3, 4} i jeden podzbiór czteroelementowy: {1, 2, 3, 4}. Liczbę podzbiorów k-elementowych zbioru n-elementowego oznacza się przez ( n k). Właśnie pokazaliśmy, że ( 4 ( 4 ( 4 ( 4 ( 4 = 1, = 4, = 6, = 4, = 1. 0) 1) 2) 3) 4)
47 Twierdzenie Dla 0 < k n mamy: ( n k) = ( n 1 ) + k 1 ( n 1 ). k
48 Twierdzenie Dla 0 < k n mamy: ( n k) = ( n 1 ) + k 1 ( n 1 ). k Jeśli 0 k n, to symbol Newtona można obliczyć ze wzoru: ( n n! = k) k!(n k)!.
49 Twierdzenie Dla 0 < k n mamy: ( n k) = ( n 1 ) + k 1 ( n 1 ). k Jeśli 0 k n, to symbol Newtona można obliczyć ze wzoru: ( n n! = k) k!(n k)!. Twierdzenie Dla każdej liczby rzeczywistej t oraz liczby całkowitej n 0 zachodzi wzór (1 + t) n = n k=0 ( n k) t k.
50 Twierdzenie Dla 0 < k n mamy: ( n k) = ( n 1 ) + k 1 ( n 1 ). k Jeśli 0 k n, to symbol Newtona można obliczyć ze wzoru: ( n n! = k) k!(n k)!. Twierdzenie Dla każdej liczby rzeczywistej t oraz liczby całkowitej n 0 zachodzi wzór (1 + t) n = n k=0 ( n k) t k. Wniosek Dla dowolnych liczb rzeczywistych a, b oraz liczby całkowitej n 0 zachodzi wzór (a + b) n = n k=0 ( n k) a n k b k.
51 Twierdzenie Dla 0 < k n mamy: ( n k) = ( n 1 ) + k 1 ( n 1 ). k Jeśli 0 k n, to symbol Newtona można obliczyć ze wzoru: ( n n! = k) k!(n k)!. Twierdzenie Dla każdej liczby rzeczywistej t oraz liczby całkowitej n 0 zachodzi wzór (1 + t) n = n k=0 ( n k) t k. Wniosek Dla dowolnych liczb rzeczywistych a, b oraz liczby całkowitej n 0 zachodzi wzór (a + b) n = n k=0 ( n k) a n k b k. Jeśli podstawimy t = 1 do wzoru z twierdzenia, to otrzymamy 2 n = n k=0 ( n k), co potwierdza jeszcze raz, że wszystkich podzbiorów zbioru n-elementowego jest 2 n.
52 Zasada szufladkowa Dirichleta Zasada szufladkowa Dirichleta Jeżeli n obiektów jest rozmieszczonych w m szufladach i n > m, to istnieje co najmniej jedna szuflada z przynajmniej dwoma obiektami.
53 Zasada szufladkowa Dirichleta Zasada szufladkowa Dirichleta Jeżeli n obiektów jest rozmieszczonych w m szufladach i n > m, to istnieje co najmniej jedna szuflada z przynajmniej dwoma obiektami. Przykład Na sali znajduje się 47 osób. Pokazać, że na sali znajdzie się siedem osób urodzonych tego samego dnia tygodnia.
54 Zasada szufladkowa Dirichleta Zasada szufladkowa Dirichleta Jeżeli n obiektów jest rozmieszczonych w m szufladach i n > m, to istnieje co najmniej jedna szuflada z przynajmniej dwoma obiektami. Przykład Na sali znajduje się 47 osób. Pokazać, że na sali znajdzie się siedem osób urodzonych tego samego dnia tygodnia. Przykład Spośród liczb {1, 2,..., 9} wylosowano sześć. Udowodnić, że spośród wybranych liczb można wybrać dwie, które sumują się do 10.
55 Zasada szufladkowa Dirichleta Zasada szufladkowa Dirichleta Jeżeli n obiektów jest rozmieszczonych w m szufladach i n > m, to istnieje co najmniej jedna szuflada z przynajmniej dwoma obiektami. Przykład Na sali znajduje się 47 osób. Pokazać, że na sali znajdzie się siedem osób urodzonych tego samego dnia tygodnia. Przykład Spośród liczb {1, 2,..., 9} wylosowano sześć. Udowodnić, że spośród wybranych liczb można wybrać dwie, które sumują się do 10. Przykład Pewna grupa osób wita się, podając sobie ręce. Nikt nie wita się z samym sobą i żadna para osób nie wita się podwójnie. Czy muszą być dwie osoby, które witały tą samą liczbę osób?
56 Zasada włączania i wyłączania.
57 Zasada włączania i wyłączania. Zadanie W klasie liczącej 33 osoby, 17 uczniów uczy się włoskiego, 17 hiszpańskiego i 15 portugalskiego. Wśród nich 7 uczniów uczy się hiszpańskiego i włoskiego, 9 włoskiego i portugalskiego, 6 hiszpańskiego i portugalskiego. Dwóch uczniów uczy się wszystkich trzech języków. Ilu uczniów nie uczy się żadnego języka?
58 Zasada włączania i wyłączania. Zadanie W klasie liczącej 33 osoby, 17 uczniów uczy się włoskiego, 17 hiszpańskiego i 15 portugalskiego. Wśród nich 7 uczniów uczy się hiszpańskiego i włoskiego, 9 włoskiego i portugalskiego, 6 hiszpańskiego i portugalskiego. Dwóch uczniów uczy się wszystkich trzech języków. Ilu uczniów nie uczy się żadnego języka? Zadanie Do pracy zgłosiło się 16 tłumaczy znających rosyjski, hiszpański lub angielski. 12 znało rosyjski, 15 hiszpański, a angielski tylu samo, co rosyjski i hiszpański jednocześnie. Ilu znało hiszpański i angielski, ale nie znało rosyjskiego, jeśli wiadomo, że 8 znało rosyjski i angielski?
59 Zasada włączania i wyłączania. Zadanie W klasie liczącej 33 osoby, 17 uczniów uczy się włoskiego, 17 hiszpańskiego i 15 portugalskiego. Wśród nich 7 uczniów uczy się hiszpańskiego i włoskiego, 9 włoskiego i portugalskiego, 6 hiszpańskiego i portugalskiego. Dwóch uczniów uczy się wszystkich trzech języków. Ilu uczniów nie uczy się żadnego języka? Zadanie Do pracy zgłosiło się 16 tłumaczy znających rosyjski, hiszpański lub angielski. 12 znało rosyjski, 15 hiszpański, a angielski tylu samo, co rosyjski i hiszpański jednocześnie. Ilu znało hiszpański i angielski, ale nie znało rosyjskiego, jeśli wiadomo, że 8 znało rosyjski i angielski? Zasada włączania i wyłączania Dla zbiorów A 1,..., A n, skończonych i parami rozłącznych: A 1 A 2... A n = A 1 + A A n.
60 Zasada włączania i wyłączania Zasada włączania i wyłączania Dla zbiorów skończonych A 1,..., A n zachodzi: A 1 A 2... A n = A 1 + A A n 2 + A n 1 + A n A 1 A 2 A 1 A 3... A n 2 A n A n 1 A n + A 1 A 2 A A n 2 A n 1 A n ( 1) n+1 A 1 A 2... A n.
61 Ilość najkrótszych dróg Ile jest najkrótszych dróg z A do B?
62 Mamy 9 skrzyżowań, wybieramy 6 z których idziemy na wschód lub 3, na których idziemy na północ. Mamy więc ( 9 3) = ( 9 6) = 94.
63 Mamy 9 skrzyżowań, wybieramy 6 z których idziemy na wschód lub 3, na których idziemy na północ. Mamy więc ( 9 3) = ( 9 6) = 94. Ogólnie, ( dla kratki m n rysujemy m + n odcinków, a więc ilość najkrótszych dróg to m+n ) ( m = m+n ) n.
64 Mamy 9 skrzyżowań, wybieramy 6 z których idziemy na wschód lub 3, na których idziemy na północ. Mamy więc ( 9 3) = ( 9 6) = 94. Ogólnie, ( dla kratki m n rysujemy m + n odcinków, a więc ilość najkrótszych dróg to m+n ) ( m = m+n ) n. Przykład Ile rozwiązań ma ma równanie x 1 + x 2 + x 3 + x 4 = 7, gdzie x i są liczbami całkowitymi?
Podzbiory Symbol Newtona Zasada szuadkowa Dirichleta Zasada wª czania i wyª czania. Ilo± najkrótszych dróg. Kombinatoryka. Magdalena Lema«ska
 Kombinatoryka Magdalena Lema«ska Zasady zaliczenia przedmiotu Zasady zaliczenia przedmiotu Maksymalna ilo± punktów to 100 punktów = 100 procent. Zasady zaliczenia przedmiotu Maksymalna ilo± punktów to
Kombinatoryka Magdalena Lema«ska Zasady zaliczenia przedmiotu Zasady zaliczenia przedmiotu Maksymalna ilo± punktów to 100 punktów = 100 procent. Zasady zaliczenia przedmiotu Maksymalna ilo± punktów to
Funkcja. x X! y Y : x, y f. f : X Y f x = y f : x y. Funkcja o dziedzinie X i przeciwdziedzinie Y to dowolna relacja f XxY taka, że: Notacje:
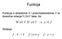 Funkcja Funkcja o dziedzinie X i przeciwdziedzinie Y to dowolna relacja f XxY taka, że: Notacje: x X! y Y : x, y f f : X Y f x = y f : x y Przykłady f: N N, f(n) = 2n f: N R, f(n) = n/2 f: N {13}, f(n)
Funkcja Funkcja o dziedzinie X i przeciwdziedzinie Y to dowolna relacja f XxY taka, że: Notacje: x X! y Y : x, y f f : X Y f x = y f : x y Przykłady f: N N, f(n) = 2n f: N R, f(n) = n/2 f: N {13}, f(n)
KOMBINATORYKA. Problem przydziału prac
 KOMBINATORYKA Dział matematyki zajmujący się badaniem różnych możliwych zestawień i ugrupowań, jakie można tworzyć z dowolnego zbioru skończonego. Zbiory skończone, najczęściej wraz z pewną relacją obiekty
KOMBINATORYKA Dział matematyki zajmujący się badaniem różnych możliwych zestawień i ugrupowań, jakie można tworzyć z dowolnego zbioru skończonego. Zbiory skończone, najczęściej wraz z pewną relacją obiekty
Matematyka dyskretna. Andrzej Łachwa, UJ, /10
 Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 6/10 Zasada Dirichleta 1 ZASADA SZUFLADKOWA DIRICHLETA (1ZSD) Jeśli n obiektów jest rozmieszczonych w m szufladach i n > m > 0, to
Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 6/10 Zasada Dirichleta 1 ZASADA SZUFLADKOWA DIRICHLETA (1ZSD) Jeśli n obiektów jest rozmieszczonych w m szufladach i n > m > 0, to
Matematyka dyskretna. Andrzej Łachwa, UJ, A/10
 Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 8A/10 Zbiory przeliczalne Przyjmujemy, że Zn = {0, 1, 2, 3, n-1} dla n>0 oraz Zn = przy n=0. Zbiór skończony to zbiór bijektywny z
Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 8A/10 Zbiory przeliczalne Przyjmujemy, że Zn = {0, 1, 2, 3, n-1} dla n>0 oraz Zn = przy n=0. Zbiór skończony to zbiór bijektywny z
Matematyka dyskretna. Andrzej Łachwa, UJ, /15
 Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl 8/15 Zbiory przeliczalne Przyjmujemy, że = {0, 1, 2, 3, n 1} dla n>0 oraz = przy n=0. Zbiór skończony to zbiór bijektywny z pewnym
Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl 8/15 Zbiory przeliczalne Przyjmujemy, że = {0, 1, 2, 3, n 1} dla n>0 oraz = przy n=0. Zbiór skończony to zbiór bijektywny z pewnym
Matematyka dyskretna. Andrzej Łachwa, UJ, a/14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 8a/14 Zbiory przeliczalne Przyjmujemy, że = {0, 1, 2, 3, n-1} dla n>0 oraz = przy n=0. Zbiór skończony to zbiór bijektywny z pewnym
Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 8a/14 Zbiory przeliczalne Przyjmujemy, że = {0, 1, 2, 3, n-1} dla n>0 oraz = przy n=0. Zbiór skończony to zbiór bijektywny z pewnym
Kombinatoryka. Jerzy Rutkowski. Teoria. P n = n!. (1) Zadania obowiązkowe
 Kombinatoryka Jerzy Rutkowski 2. Elementy kombinatoryki 2.1. Permutacje Definicja 1. Niech n N. Permutacją n-elementowego zbioru A nazywamy dowolną funkcję różnowartościową f : {1,..., n} A. Innymi słowy:
Kombinatoryka Jerzy Rutkowski 2. Elementy kombinatoryki 2.1. Permutacje Definicja 1. Niech n N. Permutacją n-elementowego zbioru A nazywamy dowolną funkcję różnowartościową f : {1,..., n} A. Innymi słowy:
Matematyka Dyskretna. Andrzej Szepietowski. 25 czerwca 2002 roku
 Matematyka Dyskretna Andrzej Szepietowski 25 czerwca 2002 roku Rozdział 1 Kombinatoryka 11 Ci agi Zastanówmy siȩ, ile ci agów długości można utworzyć z elementów zbioru zawieraj acego symboli Jeżeli zbiór
Matematyka Dyskretna Andrzej Szepietowski 25 czerwca 2002 roku Rozdział 1 Kombinatoryka 11 Ci agi Zastanówmy siȩ, ile ci agów długości można utworzyć z elementów zbioru zawieraj acego symboli Jeżeli zbiór
Matematyka dyskretna. Andrzej Łachwa, UJ, /10
 Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 10/10 Podziały i liczby Stirlinga Liczba Stirlinga dla cykli (często nazywana liczbą Stirlinga pierwszego rodzaju) to liczba permutacji
Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 10/10 Podziały i liczby Stirlinga Liczba Stirlinga dla cykli (często nazywana liczbą Stirlinga pierwszego rodzaju) to liczba permutacji
Rachunek prawdopodobieństwa
 Rachunek prawdopodobieństwa Sebastian Rymarczyk srymarczyk@afm.edu.pl Tematyka zajęć 1. Elementy kombinatoryki. 2. Definicje prawdopodobieństwa. 3. Własności prawdopodobieństwa. 4. Zmienne losowe, parametry
Rachunek prawdopodobieństwa Sebastian Rymarczyk srymarczyk@afm.edu.pl Tematyka zajęć 1. Elementy kombinatoryki. 2. Definicje prawdopodobieństwa. 3. Własności prawdopodobieństwa. 4. Zmienne losowe, parametry
Matematyka dyskretna. Andrzej Łachwa, UJ, /14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2017 andrzej.lachwa@uj.edu.pl 9/14 Zasada Dirichleta 1 ZASADA SZUFLADKOWA DIRICHLETA (1ZSD) Jeśli n obiektów jest rozmieszczonych w m szufladach i n > m > 0, to
Matematyka dyskretna Andrzej Łachwa, UJ, 2017 andrzej.lachwa@uj.edu.pl 9/14 Zasada Dirichleta 1 ZASADA SZUFLADKOWA DIRICHLETA (1ZSD) Jeśli n obiektów jest rozmieszczonych w m szufladach i n > m > 0, to
Zasada indukcji matematycznej
 Zasada indukcji matematycznej Twierdzenie 1 (Zasada indukcji matematycznej). Niech ϕ(n) będzie formą zdaniową zmiennej n N 0. Załóżmy, że istnieje n 0 N 0 takie, że 1. ϕ(n 0 ) jest zdaniem prawdziwym,.
Zasada indukcji matematycznej Twierdzenie 1 (Zasada indukcji matematycznej). Niech ϕ(n) będzie formą zdaniową zmiennej n N 0. Załóżmy, że istnieje n 0 N 0 takie, że 1. ϕ(n 0 ) jest zdaniem prawdziwym,.
SPRAWDZIAN KOMBINATORYKA
 www.zadania.info NAJWIEKSZY INTERNETOWY ZBIÓR ZADAŃ Z MATEMATYKI SPRAWDZIAN KOMBINATORYKA 12 GRUDNIA 2011 CZAS PRACY: 45 MIN. ZADANIE 1 Spośród liczb {1, 2, 3,..., 1000} losujemy jednocześnie dwie, które
www.zadania.info NAJWIEKSZY INTERNETOWY ZBIÓR ZADAŃ Z MATEMATYKI SPRAWDZIAN KOMBINATORYKA 12 GRUDNIA 2011 CZAS PRACY: 45 MIN. ZADANIE 1 Spośród liczb {1, 2, 3,..., 1000} losujemy jednocześnie dwie, które
Moneta 1 Moneta 2 Kostka O, R O,R 1,2,3,4,5, Moneta 1 Moneta 2 Kostka O O ( )
 Nowa matura kombinatoryka i rachunek prawdopodobieństwa Zadania zamknięte (0 1 pkt) 1. Doświadczenie losowe polega na rzucie dwiema symetrycznymi monetami i sześcienną kostką do gry. Prawdopodobieństwo
Nowa matura kombinatoryka i rachunek prawdopodobieństwa Zadania zamknięte (0 1 pkt) 1. Doświadczenie losowe polega na rzucie dwiema symetrycznymi monetami i sześcienną kostką do gry. Prawdopodobieństwo
Matematyka dyskretna. Andrzej Łachwa, UJ, /14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2012 andrzej.lachwa@uj.edu.pl 11/14 Współczynniki multimianowe (wielomianowe) Współczynniki dwumianowe pojawiały się przy rozwinięciu dwumianu. Odpowiadały one
Matematyka dyskretna Andrzej Łachwa, UJ, 2012 andrzej.lachwa@uj.edu.pl 11/14 Współczynniki multimianowe (wielomianowe) Współczynniki dwumianowe pojawiały się przy rozwinięciu dwumianu. Odpowiadały one
Logarytmy. Funkcje logarytmiczna i wykładnicza. Równania i nierówności wykładnicze i logarytmiczne.
 Logarytmy. Funkcje logarytmiczna i wykładnicza. Równania i nierówności wykładnicze i logarytmiczne. Definicja. Niech a i b będą dodatnimi liczbami rzeczywistymi i niech a. Logarytmem liczby b przy podstawie
Logarytmy. Funkcje logarytmiczna i wykładnicza. Równania i nierówności wykładnicze i logarytmiczne. Definicja. Niech a i b będą dodatnimi liczbami rzeczywistymi i niech a. Logarytmem liczby b przy podstawie
Matematyka dyskretna. Andrzej Łachwa, UJ, A/14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl 9A/14 Zasada Dirichleta 1 ZASADA SZUFLADKOWA DIRICHLETA (1ZSD) Jeśli n obiektów jest rozmieszczonych w m szufladach i n > m > 0, to
Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl 9A/14 Zasada Dirichleta 1 ZASADA SZUFLADKOWA DIRICHLETA (1ZSD) Jeśli n obiektów jest rozmieszczonych w m szufladach i n > m > 0, to
zdarzenie losowe - zdarzenie którego przebiegu czy wyniku nie da się przewidzieć na pewno.
 Rachunek prawdopodobieństwa Podstawowym celem rachunku prawdopodobieństwa jest określanie szans zajścia pewnych zdarzeń. Pojęcie podstawowe rachunku prawdopodobieństwa to: zdarzenie losowe - zdarzenie
Rachunek prawdopodobieństwa Podstawowym celem rachunku prawdopodobieństwa jest określanie szans zajścia pewnych zdarzeń. Pojęcie podstawowe rachunku prawdopodobieństwa to: zdarzenie losowe - zdarzenie
Ćwiczenia z metodyki nauczania rachunku prawdopodobieństwa
 Ćwiczenia z metodyki nauczania rachunku prawdopodobieństwa 25 marca 209 Zadanie. W urnie jest b kul białych i c kul czarnych. Losujemy n kul bez zwracania. Jakie jest prawdopodobieństwo, że pierwsza kula
Ćwiczenia z metodyki nauczania rachunku prawdopodobieństwa 25 marca 209 Zadanie. W urnie jest b kul białych i c kul czarnych. Losujemy n kul bez zwracania. Jakie jest prawdopodobieństwo, że pierwsza kula
Rachunek prawdopodobieństwa (Elektronika, studia niestacjonarne) Wykład 1
 Rachunek prawdopodobieństwa (Elektronika, studia niestacjonarne) Wykład 1 Przygotowując wykład korzystam głównie z książki Jakubowski, Sztencel Wstęp do teorii prawdopodobieństwa. Jakubowski, Sztencel:
Rachunek prawdopodobieństwa (Elektronika, studia niestacjonarne) Wykład 1 Przygotowując wykład korzystam głównie z książki Jakubowski, Sztencel Wstęp do teorii prawdopodobieństwa. Jakubowski, Sztencel:
Teoria liczb. Magdalena Lemańska. Magdalena Lemańska,
 Teoria liczb Magdalena Lemańska Literatura Matematyka Dyskretna Andrzej Szepietowski http://wazniak.mimuw.edu.pl/ Discrete Mathematics Seymour Lipschutz, Marc Lipson Wstęp Teoria liczb jest dziedziną matematyki,
Teoria liczb Magdalena Lemańska Literatura Matematyka Dyskretna Andrzej Szepietowski http://wazniak.mimuw.edu.pl/ Discrete Mathematics Seymour Lipschutz, Marc Lipson Wstęp Teoria liczb jest dziedziną matematyki,
Grupy. Permutacje 1. (G2) istnieje element jednostkowy (lub neutralny), tzn. taki element e G, że dla dowolnego a G zachodzi.
 Grupy. Permutacje 1 1 Definicja grupy Niech G będzie zbiorem. Działaniem na zbiorze G nazywamy odwzorowanie (oznaczane, jak mnożenie, przez ) przyporządkowujące każdej parze uporządkowanej (a, b) G G element
Grupy. Permutacje 1 1 Definicja grupy Niech G będzie zbiorem. Działaniem na zbiorze G nazywamy odwzorowanie (oznaczane, jak mnożenie, przez ) przyporządkowujące każdej parze uporządkowanej (a, b) G G element
KOMBINATORYKA OBIEKTY KOMBINATORYCZNE MATEMATYKA DYSKRETNA (2014/2015)
 MATEMATYKA DYSKRETNA (2014/2015) dr hab. inż. Małgorzata Sterna malgorzata.sterna@cs.put.poznan.pl www.cs.put.poznan.pl/msterna/ KOMBINATORYKA OBIEKTY KOMBINATORYCZNE TEORIA ZLICZANIA Teoria zliczania
MATEMATYKA DYSKRETNA (2014/2015) dr hab. inż. Małgorzata Sterna malgorzata.sterna@cs.put.poznan.pl www.cs.put.poznan.pl/msterna/ KOMBINATORYKA OBIEKTY KOMBINATORYCZNE TEORIA ZLICZANIA Teoria zliczania
Matematyka dyskretna dla informatyków
 Matematyka dyskretna dla informatyków Część I: Elementy kombinatoryki Jerzy Jaworski Zbigniew Palka Jerzy Szymański Uniwersytet im. Adama Mickiewicza Poznań 2007 4 Zależności rekurencyjne Wiele zależności
Matematyka dyskretna dla informatyków Część I: Elementy kombinatoryki Jerzy Jaworski Zbigniew Palka Jerzy Szymański Uniwersytet im. Adama Mickiewicza Poznań 2007 4 Zależności rekurencyjne Wiele zależności
Jak odróżnić wariację z powtórzeniami od wariacji bez powtórzeń, kombinacji?
 Jak odróżnić wariację z powtórzeniami od wariacji bez powtórzeń, kombinacji? Porada niniejsza traktuje o tzw. elementach kombinatoryki. Często zdarza się, że rozwiązujący zadania z tej dziedziny mają problemy
Jak odróżnić wariację z powtórzeniami od wariacji bez powtórzeń, kombinacji? Porada niniejsza traktuje o tzw. elementach kombinatoryki. Często zdarza się, że rozwiązujący zadania z tej dziedziny mają problemy
Matematyka dyskretna. Andrzej Łachwa, UJ, B/14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl 12B/14 Permutacje bez punktów stałych Nieporządek na zbiorze X to permutacja taka, że dla dowolnego, czyli permutacja "bez punktów
Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl 12B/14 Permutacje bez punktów stałych Nieporządek na zbiorze X to permutacja taka, że dla dowolnego, czyli permutacja "bez punktów
Podstawy metod probabilistycznych. dr Adam Kiersztyn
 Podstawy metod probabilistycznych dr Adam Kiersztyn Przestrzeń zdarzeń elementarnych i zdarzenia losowe. Zjawiskiem lub doświadczeniem losowym nazywamy taki proces, którego przebiegu i ostatecznego wyniku
Podstawy metod probabilistycznych dr Adam Kiersztyn Przestrzeń zdarzeń elementarnych i zdarzenia losowe. Zjawiskiem lub doświadczeniem losowym nazywamy taki proces, którego przebiegu i ostatecznego wyniku
Podstawowe struktury algebraiczne
 Rozdział 1 Podstawowe struktury algebraiczne 1.1. Działania wewnętrzne Niech X będzie zbiorem niepustym. Dowolną funkcję h : X X X nazywamy działaniem wewnętrznym w zbiorze X. Działanie wewnętrzne, jak
Rozdział 1 Podstawowe struktury algebraiczne 1.1. Działania wewnętrzne Niech X będzie zbiorem niepustym. Dowolną funkcję h : X X X nazywamy działaniem wewnętrznym w zbiorze X. Działanie wewnętrzne, jak
Matematyka dyskretna zestaw II ( )
 Matematyka dyskretna zestaw II (17-18.10.2016) Uwaga: Część z zadań z tego zestawu opiera się na zasadzie szufladkowej Dirichleta. Zadanie 1. Na ile sposobów można umieścić w 7 szufladach 3 koszule tak,
Matematyka dyskretna zestaw II (17-18.10.2016) Uwaga: Część z zadań z tego zestawu opiera się na zasadzie szufladkowej Dirichleta. Zadanie 1. Na ile sposobów można umieścić w 7 szufladach 3 koszule tak,
Zbiory, relacje i funkcje
 Zbiory, relacje i funkcje Zbiory będziemy zazwyczaj oznaczać dużymi literami A, B, C, X, Y, Z, natomiast elementy zbiorów zazwyczaj małymi. Podstawą zależność między elementem zbioru a zbiorem, czyli relację
Zbiory, relacje i funkcje Zbiory będziemy zazwyczaj oznaczać dużymi literami A, B, C, X, Y, Z, natomiast elementy zbiorów zazwyczaj małymi. Podstawą zależność między elementem zbioru a zbiorem, czyli relację
I Powiatowy Konkurs Matematyczny dla uczniów klas pierwszych szkół ponadgimnazjalnych 28 kwietnia 2003
 I Powiatowy Konkurs Matematyczny dla uczniów klas pierwszych szkół ponadgimnazjalnych 8 kwietnia 003 W tym konkursie nie ma przegranych. To, że tu jesteś, jest już Twoim sukcesem. Więc Jeśli zadanie wydaje
I Powiatowy Konkurs Matematyczny dla uczniów klas pierwszych szkół ponadgimnazjalnych 8 kwietnia 003 W tym konkursie nie ma przegranych. To, że tu jesteś, jest już Twoim sukcesem. Więc Jeśli zadanie wydaje
Spotkanie olimpijskie nr lutego 2013 Kombinatoryka i rachunek prawdopodobieństwa
 Spotkanie olimpijskie nr 5 16 lutego 2013 Kombinatoryka i rachunek prawdopodobieństwa Kombinatoryka Jadwiga Słowik Reguła mnożenia Jeśli wybór polega na podjęciu k decyzji, przy czym pierwszą decyzję możemy
Spotkanie olimpijskie nr 5 16 lutego 2013 Kombinatoryka i rachunek prawdopodobieństwa Kombinatoryka Jadwiga Słowik Reguła mnożenia Jeśli wybór polega na podjęciu k decyzji, przy czym pierwszą decyzję możemy
Wykład 10. Stwierdzenie 1. X spełnia warunek Borela wtedy i tylko wtedy, gdy każda scentrowana rodzina zbiorów domkniętych ma niepusty przekrój.
 Wykład 10 Twierdzenie 1 (Borel-Lebesgue) Niech X będzie przestrzenią zwartą Z każdego pokrycia X zbiorami otwartymi można wybrać podpokrycie skończone Dowód Lemat 1 Dla każdego pokrycia U przestrzeni ośrodkowej
Wykład 10 Twierdzenie 1 (Borel-Lebesgue) Niech X będzie przestrzenią zwartą Z każdego pokrycia X zbiorami otwartymi można wybrać podpokrycie skończone Dowód Lemat 1 Dla każdego pokrycia U przestrzeni ośrodkowej
Prawdopodobieństwo. Prawdopodobieństwo. Jacek Kłopotowski. Katedra Matematyki i Ekonomii Matematycznej SGH. 16 października 2018
 Katedra Matematyki i Ekonomii Matematycznej SGH 16 października 2018 Definicja σ-algebry Definicja Niech Ω oznacza zbiór niepusty. Rodzinę M podzbiorów zbioru Ω nazywamy σ-algebrą (lub σ-ciałem) wtedy
Katedra Matematyki i Ekonomii Matematycznej SGH 16 października 2018 Definicja σ-algebry Definicja Niech Ω oznacza zbiór niepusty. Rodzinę M podzbiorów zbioru Ω nazywamy σ-algebrą (lub σ-ciałem) wtedy
Matematyka dyskretna. Andrzej Łachwa, UJ, /14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl 3/14 Funkcje Funkcja o dziedzinie X i przeciwdziedzinie Y to dowolna relacja f X Y taka, że x X!y Y: (x,y) f. Dziedzinę i przeciwdziedzinę
Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl 3/14 Funkcje Funkcja o dziedzinie X i przeciwdziedzinie Y to dowolna relacja f X Y taka, że x X!y Y: (x,y) f. Dziedzinę i przeciwdziedzinę
Funkcje. Oznaczenia i pojęcia wstępne. Elementy Logiki i Teorii Mnogości 2015/2016
 Funkcje Elementy Logiki i Teorii Mnogości 2015/2016 Oznaczenia i pojęcia wstępne Niech f X Y będzie relacją. Relację f nazywamy funkcją, o ile dla dowolnego x X istnieje y Y taki, że (x, y) f oraz dla
Funkcje Elementy Logiki i Teorii Mnogości 2015/2016 Oznaczenia i pojęcia wstępne Niech f X Y będzie relacją. Relację f nazywamy funkcją, o ile dla dowolnego x X istnieje y Y taki, że (x, y) f oraz dla
0.1 Kombinatoryka. n! = (n 1) n. Przyjmujemy umownie że 0! = 1 Wypiszmy silnie kolejnych liczb naturalnych
 1 0.1 Kombinatoryka Kombinatoryka obejmuje takie pojȩcia jak silnia liczby naturalnej n, permutacje, wariacje bez powtȯrzeṅ i wariacje z powtȯrzeniami oraz kombinacje. Niżej podajemy opis tych pojȩċ z
1 0.1 Kombinatoryka Kombinatoryka obejmuje takie pojȩcia jak silnia liczby naturalnej n, permutacje, wariacje bez powtȯrzeṅ i wariacje z powtȯrzeniami oraz kombinacje. Niżej podajemy opis tych pojȩċ z
Z4. Ankieta złożona ma być z trzech pytań: A, B i C. Na ile sposobów można ją ułożyć zmieniając tylko kolejność pytań? ODP. Jest 6 możliwych sposobów.
 PERMUTACJE Z1. Oblicz: Z2. Doprowadź do najprostszej postaci wyrażenia: Z3. Sprawdź czy prawdziwa jest równość: Dana równość jest prawdziwa. Z4. Ankieta złożona ma być z trzech pytań: A, B i C. Na ile
PERMUTACJE Z1. Oblicz: Z2. Doprowadź do najprostszej postaci wyrażenia: Z3. Sprawdź czy prawdziwa jest równość: Dana równość jest prawdziwa. Z4. Ankieta złożona ma być z trzech pytań: A, B i C. Na ile
RACHUNEK PRAWDOPODOBIEŃSTWA WYKŁAD 1. L. Kowalski, Statystyka, 2005
 RACHUNEK PRAWDOPODOBIEŃSTWA WYKŁAD 1. Literatura: Marek Cieciura, Janusz Zacharski, Metody probabilistyczne w ujęciu praktycznym, L. Kowalski, Statystyka, 2005 R.Leitner, J.Zacharski, "Zarys matematyki
RACHUNEK PRAWDOPODOBIEŃSTWA WYKŁAD 1. Literatura: Marek Cieciura, Janusz Zacharski, Metody probabilistyczne w ujęciu praktycznym, L. Kowalski, Statystyka, 2005 R.Leitner, J.Zacharski, "Zarys matematyki
Doświadczenie i zdarzenie losowe
 Doświadczenie i zdarzenie losowe Doświadczenie losowe jest to takie doświadczenie, które jest powtarzalne w takich samych warunkach lub zbliżonych, a którego wyniku nie można przewidzieć jednoznacznie.
Doświadczenie i zdarzenie losowe Doświadczenie losowe jest to takie doświadczenie, które jest powtarzalne w takich samych warunkach lub zbliżonych, a którego wyniku nie można przewidzieć jednoznacznie.
Matematyka dyskretna. Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl. Przykłady zadań egzaminacyjnych (do liczenia lub dowodzenia)
 Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl Przykłady zadań egzaminacyjnych (do liczenia lub dowodzenia) 1. Ile układów kart w pokerze to Dwie pary? Dwie pary to układ 5 kart
Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl Przykłady zadań egzaminacyjnych (do liczenia lub dowodzenia) 1. Ile układów kart w pokerze to Dwie pary? Dwie pary to układ 5 kart
2 Rodziny zbiorów. 2.1 Algebry i σ - algebry zbiorów. M. Beśka, Wstęp do teorii miary, rozdz. 2 11
 M. Beśka, Wstęp do teorii miary, rozdz. 2 11 2 Rodziny zbiorów 2.1 Algebry i σ - algebry zbiorów Niech X będzie niepustym zbiorem. Rodzinę indeksowaną zbiorów {A i } i I 2 X nazywamy rozbiciem zbioru X
M. Beśka, Wstęp do teorii miary, rozdz. 2 11 2 Rodziny zbiorów 2.1 Algebry i σ - algebry zbiorów Niech X będzie niepustym zbiorem. Rodzinę indeksowaną zbiorów {A i } i I 2 X nazywamy rozbiciem zbioru X
Matematyka dyskretna. Andrzej Łachwa, UJ, A/14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 9A/14 Permutacje Permutacja zbioru skończonego X to bijekcja z X w X. Zbiór permutacji zbioru oznaczamy przez, a permutacje małymi
Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 9A/14 Permutacje Permutacja zbioru skończonego X to bijekcja z X w X. Zbiór permutacji zbioru oznaczamy przez, a permutacje małymi
02DRAP - Aksjomatyczna definicja prawdopodobieństwa, zasada w-w
 02DRAP - Aksjomatyczna definicja prawdopodobieństwa, zasada w-w A Zadania na ćwiczenia Zadanie A.1. Niech Ω = R oraz F będzie σ-ciałem generowanym przez rodzinę wszystkich przedziałów otwartych typu (,
02DRAP - Aksjomatyczna definicja prawdopodobieństwa, zasada w-w A Zadania na ćwiczenia Zadanie A.1. Niech Ω = R oraz F będzie σ-ciałem generowanym przez rodzinę wszystkich przedziałów otwartych typu (,
Macierze. Rozdział Działania na macierzach
 Rozdział 5 Macierze Funkcję, która każdej parze liczb naturalnych (i, j) (i 1,..., n; j 1,..., m) przyporządkowuje dokładnie jedną liczbę a ij F, gdzie F R lub F C, nazywamy macierzą (rzeczywistą, gdy
Rozdział 5 Macierze Funkcję, która każdej parze liczb naturalnych (i, j) (i 1,..., n; j 1,..., m) przyporządkowuje dokładnie jedną liczbę a ij F, gdzie F R lub F C, nazywamy macierzą (rzeczywistą, gdy
Zajęcia nr. 3 notatki
 Zajęcia nr. 3 notatki 22 kwietnia 2005 1 Funkcje liczbowe wprowadzenie Istnieje nieskończenie wiele funkcji w matematyce. W dodaktu nie wszystkie są liczbowe. Rozpatruje się funkcje które pobierają argumenty
Zajęcia nr. 3 notatki 22 kwietnia 2005 1 Funkcje liczbowe wprowadzenie Istnieje nieskończenie wiele funkcji w matematyce. W dodaktu nie wszystkie są liczbowe. Rozpatruje się funkcje które pobierają argumenty
Wykłady z Matematyki Dyskretnej
 Wykłady z Matematyki Dyskretnej dla kierunku Informatyka dr Instytut Informatyki Politechnika Krakowska Wykłady na bazie materiałów: dra hab. Andrzeja Karafiata dr hab. Joanny Kołodziej, prof. PK Informacje
Wykłady z Matematyki Dyskretnej dla kierunku Informatyka dr Instytut Informatyki Politechnika Krakowska Wykłady na bazie materiałów: dra hab. Andrzeja Karafiata dr hab. Joanny Kołodziej, prof. PK Informacje
Elementy kombinatoryki
 Elementy kombinatoryki Wykłady z matematyki dyskretnej dla informatyków i teleinformatyków UTP Bydgoszcz 04 (Wykłady z matematyki dyskretnej) Elementy kombinatoryki 04 1 / 59 Permutacje Definicja. Permutacja
Elementy kombinatoryki Wykłady z matematyki dyskretnej dla informatyków i teleinformatyków UTP Bydgoszcz 04 (Wykłady z matematyki dyskretnej) Elementy kombinatoryki 04 1 / 59 Permutacje Definicja. Permutacja
Zadanie 2. Obliczyć rangę dowolnego elementu zbioru uporządkowanego N 0 N 0, gdy porządek jest zdefiniowany następująco: (a, b) (c, d) (a c b d)
 Matemaryka dyskretna - zadania Zadanie 1. Opisać zbiór wszystkich elementów rangi k zbioru uporządkowanego X dla każdej liczby naturalnej k, gdy X jest rodziną podzbiorów zbioru skończonego Y. Elementem
Matemaryka dyskretna - zadania Zadanie 1. Opisać zbiór wszystkich elementów rangi k zbioru uporządkowanego X dla każdej liczby naturalnej k, gdy X jest rodziną podzbiorów zbioru skończonego Y. Elementem
Rodzinę F złożoną z podzbiorów zbioru X będziemy nazywali ciałem zbiorów, gdy spełnione są dwa następujące warunki.
 3. Funkcje borelowskie. Rodzinę F złożoną z podzbiorów zbioru X będziemy nazywali ciałem zbiorów, gdy spełnione są dwa następujące warunki. (1): Jeśli zbiór Y należy do rodziny F, to jego dopełnienie X
3. Funkcje borelowskie. Rodzinę F złożoną z podzbiorów zbioru X będziemy nazywali ciałem zbiorów, gdy spełnione są dwa następujące warunki. (1): Jeśli zbiór Y należy do rodziny F, to jego dopełnienie X
Matematyka dyskretna. Andrzej Łachwa, UJ, /15
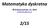 Matematyka dyskretna Andrzej Łachwa, UJ, 2014 andrzej.lachwa@uj.edu.pl 2/15 Funkcje Funkcja o dziedzinie X i przeciwdziedzinie Y to dowolna relacja f XG Y taka, że: Dziedzinę i przeciwdziedzinę funkcji
Matematyka dyskretna Andrzej Łachwa, UJ, 2014 andrzej.lachwa@uj.edu.pl 2/15 Funkcje Funkcja o dziedzinie X i przeciwdziedzinie Y to dowolna relacja f XG Y taka, że: Dziedzinę i przeciwdziedzinę funkcji
Matematyka dyskretna. Andrzej Łachwa, UJ, /10
 Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 2/10 funkcje Funkcja o dziedzinie X i przeciwdziedzinie Y to dowolna relacja f X Y taka, że x X!y Y: (x,y) f. Dziedzinę i przeciwdziedzinę
Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 2/10 funkcje Funkcja o dziedzinie X i przeciwdziedzinie Y to dowolna relacja f X Y taka, że x X!y Y: (x,y) f. Dziedzinę i przeciwdziedzinę
LOGIKA I TEORIA ZBIORÓW
 LOGIKA I TEORIA ZBIORÓW Logika Logika jest nauką zajmującą się zdaniami Z punktu widzenia logiki istotne jest, czy dane zdanie jest prawdziwe, czy nie Nie jest natomiast istotne o czym to zdanie mówi Definicja
LOGIKA I TEORIA ZBIORÓW Logika Logika jest nauką zajmującą się zdaniami Z punktu widzenia logiki istotne jest, czy dane zdanie jest prawdziwe, czy nie Nie jest natomiast istotne o czym to zdanie mówi Definicja
WYKŁAD 1. Witold Bednorz, Paweł Wolff. Rachunek Prawdopodobieństwa, WNE, Instytut Matematyki Uniwersytet Warszawski
 WYKŁAD 1 Witold Bednorz, Paweł Wolff Instytut Matematyki Uniwersytet Warszawski Rachunek Prawdopodobieństwa, WNE, 2010-2011 Wprowadzenie Gry hazardowe Wprowadzenie Gry hazardowe Klasyczna definicja prawdopodobieństwa.
WYKŁAD 1 Witold Bednorz, Paweł Wolff Instytut Matematyki Uniwersytet Warszawski Rachunek Prawdopodobieństwa, WNE, 2010-2011 Wprowadzenie Gry hazardowe Wprowadzenie Gry hazardowe Klasyczna definicja prawdopodobieństwa.
Obóz Naukowy Olimpiady Matematycznej Gimnazjalistów
 Obóz Naukowy Olimpiady Matematycznej Gimnazjalistów Liga zadaniowa 0/03 Seria IV październik 0 rozwiązania zadań 6. Dla danej liczby naturalnej n rozważamy wszystkie sumy postaci a b a b 3 a 3 b 3 a b...n
Obóz Naukowy Olimpiady Matematycznej Gimnazjalistów Liga zadaniowa 0/03 Seria IV październik 0 rozwiązania zadań 6. Dla danej liczby naturalnej n rozważamy wszystkie sumy postaci a b a b 3 a 3 b 3 a b...n
STATYSTYKA. Rafał Kucharski. Uniwersytet Ekonomiczny w Katowicach 2015/16 ROND, Finanse i Rachunkowość, rok 2
 STATYSTYKA Rafał Kucharski Uniwersytet Ekonomiczny w Katowicach 2015/16 ROND, Finanse i Rachunkowość, rok 2 Wybrane litery alfabetu greckiego α alfa β beta Γ γ gamma δ delta ɛ, ε epsilon η eta Θ θ theta
STATYSTYKA Rafał Kucharski Uniwersytet Ekonomiczny w Katowicach 2015/16 ROND, Finanse i Rachunkowość, rok 2 Wybrane litery alfabetu greckiego α alfa β beta Γ γ gamma δ delta ɛ, ε epsilon η eta Θ θ theta
Matematyka dyskretna. Andrzej Łachwa, UJ, /14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2012 andrzej.lachwa@uj.edu.pl 2/14 Funkcji podłogi z logarytmu można użyć do wyliczenia liczby cyfr liczby naturalnej k (k>0): w układzie dziesiętnym log 10 (k)
Matematyka dyskretna Andrzej Łachwa, UJ, 2012 andrzej.lachwa@uj.edu.pl 2/14 Funkcji podłogi z logarytmu można użyć do wyliczenia liczby cyfr liczby naturalnej k (k>0): w układzie dziesiętnym log 10 (k)
FUNKCJE. (odwzorowania) Funkcje 1
 FUNKCJE (odwzorowania) Funkcje 1 W matematyce funkcja ze zbioru X w zbiór Y nazywa się odwzorowanie (przyporządkowanie), które każdemu elementowi zbioru X przypisuje jeden, i tylko jeden element zbioru
FUNKCJE (odwzorowania) Funkcje 1 W matematyce funkcja ze zbioru X w zbiór Y nazywa się odwzorowanie (przyporządkowanie), które każdemu elementowi zbioru X przypisuje jeden, i tylko jeden element zbioru
Matematyka dyskretna. Andrzej Łachwa, UJ, /15
 Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl 7/15 Rachunek różnicowy Dobrym narzędziem do obliczania skończonych sum jest rachunek różnicowy. W rachunku tym odpowiednikiem operatora
Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl 7/15 Rachunek różnicowy Dobrym narzędziem do obliczania skończonych sum jest rachunek różnicowy. W rachunku tym odpowiednikiem operatora
ELEMENTY KOMBINATORYKI
 ELEMENTY KOMBINATORYKI Kombinatoryka to dział matematyki, który zajmuje się zliczaniem, na ile sposobów może zajść jakieś zjawisko. Powstała dzięki grom hazardowym a dopiero później rozwinęła się w gałąź
ELEMENTY KOMBINATORYKI Kombinatoryka to dział matematyki, który zajmuje się zliczaniem, na ile sposobów może zajść jakieś zjawisko. Powstała dzięki grom hazardowym a dopiero później rozwinęła się w gałąź
Metody probabilistyczne
 Metody probabilistyczne 2. Aksjomatyczna definicja prawdopodobieństwa Wojciech Kotłowski Instytut Informatyki PP http://www.cs.put.poznan.pl/wkotlowski/ 10.10.2017 1 / 33 Klasyczna definicja prawdopodobieństwa
Metody probabilistyczne 2. Aksjomatyczna definicja prawdopodobieństwa Wojciech Kotłowski Instytut Informatyki PP http://www.cs.put.poznan.pl/wkotlowski/ 10.10.2017 1 / 33 Klasyczna definicja prawdopodobieństwa
Wykład 2. Prawdopodobieństwo i elementy kombinatoryki
 Wstęp do probabilistyki i statystyki Wykład 2. Prawdopodobieństwo i elementy kombinatoryki dr hab.inż. Katarzyna Zakrzewska, prof.agh Katedra Elektroniki, AGH e-mail: zak@agh.edu.pl http://home.agh.edu.pl/~zak
Wstęp do probabilistyki i statystyki Wykład 2. Prawdopodobieństwo i elementy kombinatoryki dr hab.inż. Katarzyna Zakrzewska, prof.agh Katedra Elektroniki, AGH e-mail: zak@agh.edu.pl http://home.agh.edu.pl/~zak
Statystyka matematyczna
 Statystyka matematyczna Wykład 2 Magdalena Alama-Bućko 5 marca 2018 Magdalena Alama-Bućko Statystyka matematyczna 5 marca 2018 1 / 14 Prawdopodobieństwo klasyczne Ω - zbiór wszystkich zdarzeń elementarnych
Statystyka matematyczna Wykład 2 Magdalena Alama-Bućko 5 marca 2018 Magdalena Alama-Bućko Statystyka matematyczna 5 marca 2018 1 / 14 Prawdopodobieństwo klasyczne Ω - zbiór wszystkich zdarzeń elementarnych
Lista zadań - Relacje
 MATEMATYKA DYSKRETNA Lista zadań - Relacje Zadania obliczeniowe Zad. 1. Która z poniższych relacji jest funkcją? a) Relacja składająca się ze wszystkich par uporządkowanych, których poprzednikami są studenci,
MATEMATYKA DYSKRETNA Lista zadań - Relacje Zadania obliczeniowe Zad. 1. Która z poniższych relacji jest funkcją? a) Relacja składająca się ze wszystkich par uporządkowanych, których poprzednikami są studenci,
Elementy logiki matematycznej
 Elementy logiki matematycznej Przedmiotem logiki matematycznej jest badanie tzw. wyrażeń logicznych oraz metod rozumowania i sposobów dowodzenia używanych w matematyce, a także w innych dziedzinach, w
Elementy logiki matematycznej Przedmiotem logiki matematycznej jest badanie tzw. wyrażeń logicznych oraz metod rozumowania i sposobów dowodzenia używanych w matematyce, a także w innych dziedzinach, w
Funkcje liniowe i wieloliniowe w praktyce szkolnej. Opracowanie : mgr inż. Renata Rzepińska
 Funkcje liniowe i wieloliniowe w praktyce szkolnej Opracowanie : mgr inż. Renata Rzepińska . Wprowadzenie pojęcia funkcji liniowej w nauczaniu matematyki w gimnazjum. W programie nauczania matematyki w
Funkcje liniowe i wieloliniowe w praktyce szkolnej Opracowanie : mgr inż. Renata Rzepińska . Wprowadzenie pojęcia funkcji liniowej w nauczaniu matematyki w gimnazjum. W programie nauczania matematyki w
Matematyka dyskretna. Andrzej Łachwa, UJ, A/15
 Matematyka dyskretna Andrzej Łachwa, UJ, 2015 andrzej.lachwa@uj.edu.pl 10A/15 Permutacje Permutacja zbioru skończonego X to bijekcja z X w X. Zbiór permutacji zbioru oznaczamy przez, a permutacje małymi
Matematyka dyskretna Andrzej Łachwa, UJ, 2015 andrzej.lachwa@uj.edu.pl 10A/15 Permutacje Permutacja zbioru skończonego X to bijekcja z X w X. Zbiór permutacji zbioru oznaczamy przez, a permutacje małymi
WYŻSZA SZKOŁA INFORMATYKI STOSOWANEJ I ZARZĄDZANIA
 ZBIORY Z POWTÓRZENIAMI W zbiorze z powtórzeniami ten sam element może występować kilkakrotnie. Liczbę wystąpień nazywamy krotnością tego elementu w zbiorze X = { x,..., x n } - zbiór k,..., k n - krotności
ZBIORY Z POWTÓRZENIAMI W zbiorze z powtórzeniami ten sam element może występować kilkakrotnie. Liczbę wystąpień nazywamy krotnością tego elementu w zbiorze X = { x,..., x n } - zbiór k,..., k n - krotności
zaznaczymy na osi liczbowej w ten sposób:
 1. Zagadnienia teoretyczne. 1.1. Przedział domknięty Przykład 1. Pisząc mamy na myśli wszystkie liczby rzeczywiste od -4 do 7, razem z -4 i 7. Jeśli napiszemy, będziemy mówić o zbiorze wszystkich liczb
1. Zagadnienia teoretyczne. 1.1. Przedział domknięty Przykład 1. Pisząc mamy na myśli wszystkie liczby rzeczywiste od -4 do 7, razem z -4 i 7. Jeśli napiszemy, będziemy mówić o zbiorze wszystkich liczb
Rozdział 5. Macierze. a 11 a a 1m a 21 a a 2m... a n1 a n2... a nm
 Rozdział 5 Macierze Funkcję, która każdej parze liczb naturalnych (i,j) (i = 1,,n;j = 1,,m) przyporządkowuje dokładnie jedną liczbę a ij F, gdzie F = R lub F = C, nazywamy macierzą (rzeczywistą, gdy F
Rozdział 5 Macierze Funkcję, która każdej parze liczb naturalnych (i,j) (i = 1,,n;j = 1,,m) przyporządkowuje dokładnie jedną liczbę a ij F, gdzie F = R lub F = C, nazywamy macierzą (rzeczywistą, gdy F
Wykład 1: Przestrzeń probabilistyczna. Prawdopodobieństwo klasyczne. Prawdopodobieństwo geometryczne.
 Rachunek prawdopodobieństwa MAP1151 Wydział Elektroniki, rok akad. 2011/12, sem. letni Wykładowca: dr hab. A. Jurlewicz Wykład 1: Przestrzeń probabilistyczna. Prawdopodobieństwo klasyczne. Prawdopodobieństwo
Rachunek prawdopodobieństwa MAP1151 Wydział Elektroniki, rok akad. 2011/12, sem. letni Wykładowca: dr hab. A. Jurlewicz Wykład 1: Przestrzeń probabilistyczna. Prawdopodobieństwo klasyczne. Prawdopodobieństwo
KONSPEKT FUNKCJE cz. 1.
 KONSPEKT FUNKCJE cz. 1. DEFINICJA FUNKCJI Funkcją nazywamy przyporządkowanie, w którym każdemu elementowi zbioru X odpowiada dokładnie jeden element zbioru Y Zbiór X nazywamy dziedziną, a jego elementy
KONSPEKT FUNKCJE cz. 1. DEFINICJA FUNKCJI Funkcją nazywamy przyporządkowanie, w którym każdemu elementowi zbioru X odpowiada dokładnie jeden element zbioru Y Zbiór X nazywamy dziedziną, a jego elementy
Matematyka dyskretna. Andrzej Łachwa, UJ, /14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 6/14 Sumy Oto dwie konwencje zapisu skończonych sum wyrazów: (notacja Sigma, Fourier, 1820) Czasami stosowana jest ogólniejsza notacja,
Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 6/14 Sumy Oto dwie konwencje zapisu skończonych sum wyrazów: (notacja Sigma, Fourier, 1820) Czasami stosowana jest ogólniejsza notacja,
Elementy rachunku prawdopodobieństwa (M. Skośkiewicz, A. Siejka, K. Walczak, A. Szpakowska)
 Elementy rachunku prawdopodobieństwa (M. Skośkiewicz, A. Siejka, K. Walczak, A. Szpakowska) Twierdzenie (o mnożeniu) Podstawowe pojęcia i wzory kombinatoryczne. Niech,, będą zbiorami mającymi odpowiednio,,
Elementy rachunku prawdopodobieństwa (M. Skośkiewicz, A. Siejka, K. Walczak, A. Szpakowska) Twierdzenie (o mnożeniu) Podstawowe pojęcia i wzory kombinatoryczne. Niech,, będą zbiorami mającymi odpowiednio,,
2. FUNKCJE. jeden i tylko jeden element y ze zbioru, to takie przyporządkowanie nazwiemy FUNKCJĄ, lub
 WYKŁAD 2 1 2. FUNKCJE. 2.1.PODSTAWOWE DEFINICJE. Niech będą dane zbiory i. Jeżeli każdemu elementowi x ze zbioru,, przyporządkujemy jeden i tylko jeden element y ze zbioru, to takie przyporządkowanie nazwiemy
WYKŁAD 2 1 2. FUNKCJE. 2.1.PODSTAWOWE DEFINICJE. Niech będą dane zbiory i. Jeżeli każdemu elementowi x ze zbioru,, przyporządkujemy jeden i tylko jeden element y ze zbioru, to takie przyporządkowanie nazwiemy
Matematyka dyskretna. Andrzej Łachwa, UJ, 2019 Zadania 1-100
 Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl Zadania 1-100 Udowodnij, że A (B C) = (A B) (A C) za pomocą diagramów Venna. Udowodnij formalnie, że (A B i A C) A B C oraz że (A
Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl Zadania 1-100 Udowodnij, że A (B C) = (A B) (A C) za pomocą diagramów Venna. Udowodnij formalnie, że (A B i A C) A B C oraz że (A
Kombinatoryka i rachunek prawdopodobieństwa
 Kombinatoryka i rachunek prawdopodobieństwa Jerzy Rutkowski Kombinatoryka i rachunek prawdopodobieństwa 2. Elementy kombinatoryki 2.1. Permutacje Definicja 1. Niech n N. Permutacją n-elementowego zbioru
Kombinatoryka i rachunek prawdopodobieństwa Jerzy Rutkowski Kombinatoryka i rachunek prawdopodobieństwa 2. Elementy kombinatoryki 2.1. Permutacje Definicja 1. Niech n N. Permutacją n-elementowego zbioru
Przykładowe zadania na kółko matematyczne dla uczniów gimnazjum
 1 Przykładowe zadania na kółko matematyczne dla uczniów gimnazjum Zagadnienia, które uczeń powinien znać przy rozwiązywaniu opisanych zadań: zastosowanie równań w zadaniach tekstowych, funkcje i ich monotoniczność,
1 Przykładowe zadania na kółko matematyczne dla uczniów gimnazjum Zagadnienia, które uczeń powinien znać przy rozwiązywaniu opisanych zadań: zastosowanie równań w zadaniach tekstowych, funkcje i ich monotoniczność,
0.1. Logika podstawowe pojęcia: zdania i funktory, reguły wnioskowania, zmienne zdaniowe, rachunek zdań.
 Wykłady z Analizy rzeczywistej i zespolonej w Matematyce stosowanej Wykład ELEMENTY LOGIKI ALGEBRA BOOLE A Logika podstawowe pojęcia: zdania i funktory, reguły wnioskowania, zmienne zdaniowe, rachunek
Wykłady z Analizy rzeczywistej i zespolonej w Matematyce stosowanej Wykład ELEMENTY LOGIKI ALGEBRA BOOLE A Logika podstawowe pojęcia: zdania i funktory, reguły wnioskowania, zmienne zdaniowe, rachunek
5. Algebra działania, grupy, grupy permutacji, pierścienie, ciała, pierścień wielomianów.
 5. Algebra działania, grupy, grupy permutacji, pierścienie, ciała, pierścień wielomianów. Algebra jest jednym z najstarszych działów matematyki dotyczącym początkowo tworzenia metod rozwiązywania równań
5. Algebra działania, grupy, grupy permutacji, pierścienie, ciała, pierścień wielomianów. Algebra jest jednym z najstarszych działów matematyki dotyczącym początkowo tworzenia metod rozwiązywania równań
W. Guzicki Zadanie 41 z Informatora Maturalnego poziom podstawowy 1
 W. Guzicki Zadanie 41 z Informatora Maturalnego poziom podstawowy 1 W tym tekście zobaczymy rozwiązanie zadania 41 z Informatora o egzaminie maturalnym z matematyki od roku szkolnego 014/015 oraz rozwiązania
W. Guzicki Zadanie 41 z Informatora Maturalnego poziom podstawowy 1 W tym tekście zobaczymy rozwiązanie zadania 41 z Informatora o egzaminie maturalnym z matematyki od roku szkolnego 014/015 oraz rozwiązania
Teoria miary. WPPT/Matematyka, rok II. Wykład 5
 Teoria miary WPPT/Matematyka, rok II Wykład 5 Funkcje mierzalne Niech (X, F) będzie przestrzenią mierzalną i niech f : X R. Twierdzenie 1. NWSR 1. {x X : f(x) > a} F dla każdego a R 2. {x X : f(x) a} F
Teoria miary WPPT/Matematyka, rok II Wykład 5 Funkcje mierzalne Niech (X, F) będzie przestrzenią mierzalną i niech f : X R. Twierdzenie 1. NWSR 1. {x X : f(x) > a} F dla każdego a R 2. {x X : f(x) a} F
1 Elementy kombinatoryki i teorii prawdopodobieństwa
 1 Elementy kombinatoryki i teorii prawdopodobieństwa 1.1 Elementy kombinatoryki W rozwiązywaniu pewnych problemów związanych z obliczaniem prawdopodobieństwa o skończonej liczbie zdażeń elementarnych bardzo
1 Elementy kombinatoryki i teorii prawdopodobieństwa 1.1 Elementy kombinatoryki W rozwiązywaniu pewnych problemów związanych z obliczaniem prawdopodobieństwa o skończonej liczbie zdażeń elementarnych bardzo
Matematyka dyskretna
 Matematyka dyskretna Zbiór zadań kolekcjonowanych w ciągu semestralnego kursu Matematyka dyskretna prof. dr hab. M. Morayne dla studentów informatyki magisterskiej WPPT PWr wiosna-lato 2005 UWAGA: Zadania
Matematyka dyskretna Zbiór zadań kolekcjonowanych w ciągu semestralnego kursu Matematyka dyskretna prof. dr hab. M. Morayne dla studentów informatyki magisterskiej WPPT PWr wiosna-lato 2005 UWAGA: Zadania
0 + 0 = 0, = 1, = 1, = 0.
 5 Kody liniowe Jak już wiemy, w celu przesłania zakodowanego tekstu dzielimy go na bloki i do każdego z bloków dodajemy tak zwane bity sprawdzające. Bity te są w ścisłej zależności z bitami informacyjnymi,
5 Kody liniowe Jak już wiemy, w celu przesłania zakodowanego tekstu dzielimy go na bloki i do każdego z bloków dodajemy tak zwane bity sprawdzające. Bity te są w ścisłej zależności z bitami informacyjnymi,
Matematyka dyskretna. Andrzej Łachwa, UJ, /14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2017 andrzej.lachwa@uj.edu.pl 14/14 TWIERDZENIE HALLA Twierdzenie o kojarzeniu małżeństw rozważa dwie grupy - dziewcząt i chłopców, oraz podgrupy dziewczyn i podgrupy
Matematyka dyskretna Andrzej Łachwa, UJ, 2017 andrzej.lachwa@uj.edu.pl 14/14 TWIERDZENIE HALLA Twierdzenie o kojarzeniu małżeństw rozważa dwie grupy - dziewcząt i chłopców, oraz podgrupy dziewczyn i podgrupy
Wokół Problemu Steinhausa z teorii liczb
 Wokół Problemu Steinhausa z teorii liczb Konferencja MathPAD 0 Piotr Jędrzejewicz Wydział Matematyki i Informatyki Uniwersytetu Mikołaja Kopernika w Toruniu Celem referatu jest przedstawienie sposobu wykorzystania
Wokół Problemu Steinhausa z teorii liczb Konferencja MathPAD 0 Piotr Jędrzejewicz Wydział Matematyki i Informatyki Uniwersytetu Mikołaja Kopernika w Toruniu Celem referatu jest przedstawienie sposobu wykorzystania
Matematyka dyskretna. Wykład 2: Kombinatoryka. Gniewomir Sarbicki
 Matematya dysretna Wyład 2: Kombinatorya Gniewomir Sarbici Kombinatorya Definicja Kombinatorya zajmuje się oreślaniem mocy zbiorów sończonych, w szczególności mocy zbiorów odwzorowań jednego zbioru w drugi
Matematya dysretna Wyład 2: Kombinatorya Gniewomir Sarbici Kombinatorya Definicja Kombinatorya zajmuje się oreślaniem mocy zbiorów sończonych, w szczególności mocy zbiorów odwzorowań jednego zbioru w drugi
Arytmetyka. Arytmetyka. Magdalena Lemańska. Magdalena Lemańska,
 Arytmetyka Magdalena Lemańska System dziesiętny System dziesiętny Weźmy liczbę 178. Składa się ona z jednej setki, siedmiu dziesiątek i ośmiu jedności. System dziesiętny System dziesiętny Weźmy liczbę
Arytmetyka Magdalena Lemańska System dziesiętny System dziesiętny Weźmy liczbę 178. Składa się ona z jednej setki, siedmiu dziesiątek i ośmiu jedności. System dziesiętny System dziesiętny Weźmy liczbę
W. Guzicki Próbna matura, grudzień 2014 r. poziom rozszerzony 1
 W. Guzicki Próbna matura, grudzień 20 r. poziom rozszerzony Próbna matura rozszerzona (jesień 20 r.) Zadanie kilka innych rozwiązań Wojciech Guzicki Zadanie. Oblicz prawdopodobieństwo warunkowe, że w trzykrotnym
W. Guzicki Próbna matura, grudzień 20 r. poziom rozszerzony Próbna matura rozszerzona (jesień 20 r.) Zadanie kilka innych rozwiązań Wojciech Guzicki Zadanie. Oblicz prawdopodobieństwo warunkowe, że w trzykrotnym
Złożoność informacyjna Kołmogorowa. Paweł Parys
 Złożoność informacyjna Kołmogorowa Paweł Parys Serock 2012 niektóre liczby łatwiej zapamiętać niż inne... (to zależy nie tylko od wielkości liczby) 100...0 100 100... 100 100 100 25839496603316858921 31415926535897932384
Złożoność informacyjna Kołmogorowa Paweł Parys Serock 2012 niektóre liczby łatwiej zapamiętać niż inne... (to zależy nie tylko od wielkości liczby) 100...0 100 100... 100 100 100 25839496603316858921 31415926535897932384
Matematyka dyskretna. Andrzej Łachwa, UJ, /15
 Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl 6/15 Sumy Oto dwie konwencje zapisu skończonych sum wyrazów: (notacja Sigma, Fourier, 1820) Czasami stosowana jest ogólniejsza notacja,
Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl 6/15 Sumy Oto dwie konwencje zapisu skończonych sum wyrazów: (notacja Sigma, Fourier, 1820) Czasami stosowana jest ogólniejsza notacja,
1. Elementy kombinatoryki - zadania do wyboru
 . Elementy kombinatoryki - zadania do wyboru Bernadeta Tomasz Zadania dodatkowe Zadanie.. Mamy do wyboru mieszkania i auta. Na ile sposobów można dokonać wyboru, jeśli. mamy wybrać mieszkanie i samochód,.
. Elementy kombinatoryki - zadania do wyboru Bernadeta Tomasz Zadania dodatkowe Zadanie.. Mamy do wyboru mieszkania i auta. Na ile sposobów można dokonać wyboru, jeśli. mamy wybrać mieszkanie i samochód,.
Algebra abstrakcyjna
 Algebra abstrakcyjna Przykłady 1. Sama liczba 0 tworzy grupę (rzędu 1) ze względu na zwykłe dodawanie, również liczba 1 tworzy grupę (rzędu 1) ze względu na zwykłe mnożenie.. Liczby 1 i 1 stanowią grupą
Algebra abstrakcyjna Przykłady 1. Sama liczba 0 tworzy grupę (rzędu 1) ze względu na zwykłe dodawanie, również liczba 1 tworzy grupę (rzędu 1) ze względu na zwykłe mnożenie.. Liczby 1 i 1 stanowią grupą
1 Działania na zbiorach
 M. Beśka, Wstęp do teorii miary, rozdz. 1 1 1 Działania na zbiorach W rozdziale tym przypomnimy podstawowe działania na zbiorach koncentrując się na własnościach tych działań, które będą przydatne w dalszej
M. Beśka, Wstęp do teorii miary, rozdz. 1 1 1 Działania na zbiorach W rozdziale tym przypomnimy podstawowe działania na zbiorach koncentrując się na własnościach tych działań, które będą przydatne w dalszej
Zestaw zadań dotyczących liczb całkowitych
 V Zestaw zadań dotyczących liczb całkowitych Opracowanie Monika Fabijańczyk ROZDZIAŁ 1 Cechy podzielności Poniższe zadania zostały wybrane z różnych zbiorów zadań, opracowań, konkursów matematycznych.
V Zestaw zadań dotyczących liczb całkowitych Opracowanie Monika Fabijańczyk ROZDZIAŁ 1 Cechy podzielności Poniższe zadania zostały wybrane z różnych zbiorów zadań, opracowań, konkursów matematycznych.
W. Guzicki Próbna matura, grudzień 2014 r. poziom rozszerzony 1
 W. Guzicki Próbna matura, grudzień 01 r. poziom rozszerzony 1 Próbna matura rozszerzona (jesień 01 r.) Zadanie 18 kilka innych rozwiązań Wojciech Guzicki Zadanie 18. Okno na poddaszu ma mieć kształt trapezu
W. Guzicki Próbna matura, grudzień 01 r. poziom rozszerzony 1 Próbna matura rozszerzona (jesień 01 r.) Zadanie 18 kilka innych rozwiązań Wojciech Guzicki Zadanie 18. Okno na poddaszu ma mieć kształt trapezu
Zadanie 1. Na diagramie Venna dla 3 zbiorów zaznacz:
 Zadanie 1 Na diagramie Venna dla 3 zbiorów zaznacz: A B C Zadanie 1 Na diagramie Venna dla 3 zbiorów zaznacz: A B C A B C Zadanie 1 Na diagramie Venna dla 3 zbiorów zaznacz: A B C A B C A B C Zadanie 1
Zadanie 1 Na diagramie Venna dla 3 zbiorów zaznacz: A B C Zadanie 1 Na diagramie Venna dla 3 zbiorów zaznacz: A B C A B C Zadanie 1 Na diagramie Venna dla 3 zbiorów zaznacz: A B C A B C A B C Zadanie 1
Wykład z równań różnicowych
 Wykład z równań różnicowych 1 Wiadomości wstępne Umówmy się, że na czas tego wykładu zrezygnujemy z oznaczania n-tego wyrazu ciągu symbolem typu x n, y n itp. Zamiast tego pisać będziemy x (n), y (n) itp.
Wykład z równań różnicowych 1 Wiadomości wstępne Umówmy się, że na czas tego wykładu zrezygnujemy z oznaczania n-tego wyrazu ciągu symbolem typu x n, y n itp. Zamiast tego pisać będziemy x (n), y (n) itp.
