KOMBINATORYKA OBIEKTY KOMBINATORYCZNE MATEMATYKA DYSKRETNA (2014/2015)
|
|
|
- Krystian Julian Sadowski
- 8 lat temu
- Przeglądów:
Transkrypt
1 MATEMATYKA DYSKRETNA (2014/2015) dr hab. inż. Małgorzata Sterna KOMBINATORYKA OBIEKTY KOMBINATORYCZNE
2 TEORIA ZLICZANIA Teoria zliczania poszukiwanie odpowiedzi na pytanie ile? bez faktycznego zliczania. Kombinatoryka analiza problemów kombinatorycznych, dotyczących zbiorów skończonych. Zliczaniu podlegają m.in. obiekty kombinatoryczne tj. : wariacje z/bez powtórzeń, permutacje z/bez powtórzeń, kombinacje z/bez powtórzeń. Podstawowe prawa teorii zliczania: prawo sumy i iloczynu, zasada włączania i wyłączania, zasada szufladkowa Dirichleta, zasada dwoistości. 2
3 PRAWO SUMY Liczba sposobów na jakie można wybrać element należący do jednego z dwóch rozłącznych zbiorów jest równa sumie mocy tych zbiorów. Dla zbiorów skończonych rozłącznych A i B (AB=): AB = A + B. Dla dowolnych zbiorów skończonych A i B: AB = A + B - AB. Uogólnienie prawa sumy dla wielu zbiorów, to zasada włączania/wyłączania: n i1 A i? 3
4 PRAWO SUMY - PRZYKŁAD 1 A= B= AB= grupa agentów składa się z 2 kobiet i 4 mężczyzn na ile sposobów można wybrać agenta do realizacji zadania specjalnego? AB = A + B = = 6 4
5 PRAWO SUMY - PRZYKŁAD 2 Ile jest liczb podzielnych przez 2 lub 3 w zbiorze {1, 2,..., 100}? A - zbiór liczb podzielnych przez 2 A = 100 / 2 =50 B zbiór liczb podzielnych przez 3 B = 100 / 3 =33 AB zbiór liczb podzielnych przez 2 lub 3 AB AB zbiór liczb podzielnych przez 2 i 3 AB = 100 / 6 =16 AB = A + B - AB = = 67 5
6 PRAWO ILOCZYNU Liczba sposobów na jakie można wybrać uporządkowaną parę elementów jest równa liczbie możliwości na jakie można wybrać pierwszy element przemnożonej przez liczbę możliwości na jakie można wybrać drugi element. Dla pary zbiorów skończonych A i B: AB = A B. Dla dowolnych zbiorów skończonych A 1,..., A n : A 1... A n = A 1... A n = A i. n i1 6
7 PRAWO ILOCZYNU- PRZYKŁAD A= B= grupa agentów składa się z 2 kobiet i 4 mężczyzn na ile sposobów można wybrać zespół agentów, który ma udawać parę małżeńską? AB = A B = 4 2 = 8, mężczyzna kobieta 7
8 WARIACJA Z POWTÓRZENIAMI k-wyrazową wariacją z powtórzeniami z n-elementowego zbioru A nazywamy każdy k-wyrazowy ciąg mogących się powtarzać elementów tego zbioru (kn lub k>n). liczba wszystkich k-wyrazowych wariacji z powtórzeniami ze zbioru n-elementowego wynosi: V(n,k) k n liczba wariacji z powtórzeniami, to liczba możliwych rozmieszczeń k rozróżnialnych elementów w n rozróżnialnych pudełkach 8
9 WARIACJA Z POWTÓRZENIAMI - PRZYKŁAD n=6 k=4 grupa agentów składa się z 6 osób raz do roku organizowane są zawody dla agentów w 4 różnych dyscyplinach, w których liczy się tylko zwycięstwo ile jest możliwych rozstrzygnięć zawodów? kolejność osób ma znaczenie - oznacza dyscyplinę (ciąg) jeden agent może wygrać w kilku dyscyplinach (powtórzenia) wariacja z powtórzeniami V(n,k) k n V(6,4)
10 WARIACJA Z POWTÓRZENIAMI - PRZYKŁAD n=6 k=4 ciąg k elementów wybranych z n elementów k=4 rozróżnialnych elementów wrzucanych w dowolny sposób do pudełek n=6 rozróżnialnych pudełek 10
11 WARIACJA BEZ POWTÓRZEŃ k-wyrazową wariacją bez powtórzeń z n-elementowego zbioru A nazywamy każdy k-wyrazowy ciąg różnych elementów tego zbioru (kn). liczba wszystkich k-wyrazowych wariacji bez powtórzeń ze zbioru n-elementowego wynosi: V(n, k) = n (n-1) (n-2)... (n-k+1), dla kn czyli V(n,k) n!, (n k)! dla k n 11
12 WARIACJA BEZ POWTÓRZEŃ- PRZYKŁAD n= k=3 grupa agentów składa się z 6 osób pod koniec roku przydzielane są trzy nagrody dla najlepszych agentów ile jest możliwych rozstrzygnięć konkursu? kolejność osób ma znaczenie - oznacza zajęte miejsce (ciąg) jeden agent może uzyskać tylko jedną nagrodę (brak powtórzeń) wariacja bez powtórzeniami V(n,k) n! 6! 6! V(6,3) 120 (n k)! (6 3)! 3! 12
13 PERMUTACJA BEZ POWTÓRZEŃ permutacją bez powtórzeń nazywamy liniowe uporządkowanie k rozróżnialnych elementów zbioru n-elementowego (kn) czyli k-elementową wariację bez powtórzeń zbioru n-elementowego liczba wszystkich k-wyrazowych permutacji bez powtórzeń zbioru n-elementowego wynosi: n! P(n,k) V(n,k), dla k n (n k)! n! istnieje jedna permutacja pusta (k=0) P(n,0) 1 n! istnieje n! permutacji elementów zbioru (n=k) n! n! P(n,n) n! (n n)! 0! 13
14 PERMUTACJA BEZ POWTÓRZEŃ - PRZYKŁAD Ile istnieje anagramów słowa KOMPUTER? każdy anagram to liniowe uporządkowanie 8 różnych liter słowa KOMPUTER np. PUMTERKO, ERTUMPKO,... n = k = 8 P(8,8) = V(8,8) = 8! =
15 GENEROWANIE PERMUTACJI porządek leksykograficzny x1...xn y1...yn ( xl yl xk k1 lk y k )
16 GENEROWANIE PERMUTACJI porządek antyleksykograficzny x1...xn ' y1...yn (xk yk xl kn lk y ) l
17 GENEROWANIE PERMUTACJI porządek o minimalnej liczbie transpozcji kolejne permutacje otrzymywane są w wyniku zamiany pary elementów
18 PERMUTACJA Z POWTÓRZENIAMI permutacją n-elementową z powtórzeniami zbioru A={a 1,a 2,...,a k }, w której element a 1 powtarza się n 1 razy,..., element a k powtarza się n k razy, n n k = n, nazywamy każdy ciąg n-wyrazowy, w którym poszczególne elementy zbioru A powtarzają się wskazaną liczbę razy (kn lub k>n) liczba takich n-elementowych permutacji z powtórzeniami wynosi: n! P(n,n 1,n2,...,nk ), dla n n1 n2... nk n 1!n 2!...n k! n można ją zapisać jako współczynnik wielomianowy n1,n 2,..., nk 18
19 PERMUTACJA Z POWTÓRZENIAMI - PRZYKŁAD Ile jest różnych anagramów słowa NONSENS? każdy anagram to ciąg elementów ze zbioru A={N, O, S, E} np. OSNENNS, SNENNOS,... elementy powtarzają się: n N =3, n O =1, n S =2, n E =1 razy n =n N +n O +n S +n E =7 P(n,n P(n,n N N,n,n O O,n,n S S,n,n E E 7! ) P(7,3,1,2,1) 420 3! 1! 2! 1! 7 ) 3,1, 2,1 7! 420 3! 1! 2! 1! 19
20 PERMUTACJA Z POWTÓRZENIAMI P(n, n 1, n 2,..., n k ) to liczba: n-elementowych permutacji z powtórzeniami elementów k typów, rozmieszczeń n rozróżnialnych obiektów w k rozróżnialnych pudełkach, takich że w i-tym pudełku znajduje się n i obiektów, podziałów uporządkowanych zbioru. 20
21 PERMUTACJA Z POWTÓRZENIAMI A ROZMIESZENIE ELEMENTÓW W PUDEŁKACH permutacja z powtórzeniami słowa NONSENS o długości 7 liter to przydzielenie do 4 pudełek odpowiadających literom {N, O, S, E} pozycji w permutacji, czyli numerów ze zbioru {1,..., 7} liczba przydzielonych danej literze pozycji musi być równa liczbie liter danego rodzaju w analizowanym słowie O S N E N N S N O S E P(n,n N,n O,n S,n E ) P(7,3,1,2,1) 7! 3! 1! 2! 1!
22 PODZIAŁY ZBIORU Podziałem zbioru niepustego S nazywamy rodzinę niepustych rozłącznych podzbiorów S, których suma wynosi S. (liczbę podziałów zbioru opisują liczby Stirlinga drugiego rodzaju) Podziałem uporządkowanym zbioru niepustego S nazywamy ciąg (A 1, A 2,...,A k ), którego elementy A 1, A 2,...,A k tworzą podział zbioru S. Jeżeli zbiór S ma n elementów i jeśli n n k =n, to liczba podziałów uporządkowanych (A 1, A 2,..., A k ) tego zbioru, takich że A i =n i, dla i=1,...,k wynosi: P(n,n n! 1,n2,...,nk ), dla n n1 n2... nk n 1!n 2!...n k! 22
23 PODZIAŁY ZBIORU - PRZYKŁAD S={1,2,3,4,5,6,7,8} podziały zbioru S, np.: {1,4,3}, {2,5,6,7,8} {1,5}, {2,4,7}, {3,6,8} podziały uporządkowane zbioru S, np: ({1,4,3}, {2,5,6,7,8}) ({2,5,6,7,8}, {1,4,3}) ({1,5}, {2,4,7}, {3,6,8}) ({1,5}, {3,6,8}, {2,4,7}) ({2,4,7}, {1,5}, {3,6,8}) 23
24 PRZYKŁAD n=6 k=3 n 1 =2 n 2 =1 n 3 =3 w celu wykonania zadania specjalnego agenci muszą dojechać na miejsce akcji trzema pojazdami, w których powinny jechać odpowiednio 2, 1 i 3 osoby na ile sposobów agenci mogą dojechać na miejsce akcji? grupa agentów (zbiór) zostaje podzielona na podzbiory (samochody) samochody są rozróżnialne (uporządkowane) uporządkowany podział zbioru 24
25 PRZYKŁAD n=6 k=3 uporządkowany podział zbioru n 1 =2 n 2 =1 n 3 =3,, A 1 A 2 A 3 n 1 =2 n 2 =1 n 3 =3 n 1, n 2, n...,..., n k n! n!n!...n 1 2 k! 6! 2!1!3! 60 25
26 PRZYKŁAD n=6 k=3 uporządkowany podział zbioru n 1 =2 n 2 =1 n 3 =3,, rozmieszczenie n=6 elementów w k=3 pudełkach taki, że w poszczególnych pudełkach znajduje się określona liczba elementów (n 1 =2, n 2 =1, n 3 =3) 26
27 PRZYKŁAD n=6 k=3 n 1 =2 n 2 =1 n 3 =3 poszczególni agenci to pozycje permutacji n-elementowej informacja którym samochodem jadą, to element permutacji permutacja z powtórzeniami n=6 elementów k=3 typów powtarzających się określoną liczbę razy 27
28 GENEROWANIE WSZYSTKICH PODZIAŁÓW ZBIORU z podziału A 1,...,A k zbioru {1,..., n-1} można uzyskać podział A 1,..., A k zbioru {1,...,n} w następujący sposób: A 1 {n}, A 2,..., A k A 1, A 2 {n},..., A k A 1, A 2,..., A k {n} A 1, A 2,..., A k, {n} 28
29 GENEROWANIE PODZIAŁÓW ZBIORU - PRZYKŁAD istnieje 15 podziałów zbioru {1,2,3,4} {1} liczba podziałów jest określona przez liczby Bella {1,2} {1}{2} {1,2,3} {1,2}{3} {1,3}{2} {1}{2,3} {1}{2}{3} {1,2,3,4} {1,2,4}{3} {1,3,4}{2} {1,4}{2,3} {1,4}{2}{3} {1,2,3}{4} {1,2}{3,4} {1,3}{2,4} {1}{2,3,4} {1}{2,4}{3} {1,2}{3}{4} {1,3}{2}{4} {1}{2,3}{4} {1}{2}{3,4} {1}{2}{3}{4} 29
30 KOMBINACJA BEZ POWTÓRZEŃ kombinacją k-elementową bez powtórzeń n-elementowego zbioru A nazywamy każdy k-elementowy podzbiór zbioru A (kn) liczba wszystkich k-elementowych kombinacji bez powtórzeń zbioru n-elementowego wynosi: n! n C(n,k), dla k n (n k)! k! k C(n,k) 1 P(n,k) k! 1 k! n! (n k)! 30
31 KOMBINACJA BEZ POWTÓRZEŃ - PRZYKŁAD n=6 k=3 zadanie specjalne powinno wykonać 3 agentów na ile sposobów można wybrać zespół do wykonania zadania? kolejność osób nie ma znaczenia liczy się przynależność do zespołu (podzbiór) agent może być wybrany tylko jednokrotnie (brak powtórzeń) kombinacja bez powtórzeń n 6 6! C(n,k) C(6,3) 20 k 3 (6 3)!3! 31
32 GENEROWANIE WSZYSTKICH PODZBIORÓW ZBIORU każdemu podzbiorowi Y n-elementowego zbioru X={x 1,..., x n }, YX, można przyporządkować liczbę binarną b 1...b n o wartości z zakresu od 0 do 2 n -1, gdzie b i 0, jesli 1, jesli x x i i Y Y generując wszystkie liczby binarne r, 0r2 n -1, można wyznaczyć wszystkie podzbiory zbioru n-elementowego X 32
33 GENEROWANIE WSZYSTKICH PODZBIORÓW ZBIORU - PRZYKŁAD istnieje 2 3 =8 podzbiorów zbioru {a,b,c} generacja podzbiorów przez generowanie liczb binarnych =7 a b c {a} {b} {a, b} {c} {a, c} {b, c} {a, b, c} w oparciu o kod Grey a kolejne podzbiory powstają przez dodanie/odjęcie pojedynczego elementu: a b c {a} {a, b} {b} {b, c} {a, b, c} {a, c} {c} 33
34 GENEROWANIE PODZBIORÓW K-ELEMENTOWYCH podzbiorowi k-elementowemu zbioru A={1, 2,..., n} odpowiada pewien ciąg (i 1,..., i r,..., i k ), gdzie i r A, 1rk. w celu wygenerowania podzbiorów k-elementowych należy wyznaczyć wszystkie ciągi o długości k spośród n symboli w porządku leksykograficznym 34
35 GENEROWANIE PODZBIORÓW K-ELEMENTOWYCH - PRZYKŁAD liczba podzbiorów 4-elementowych zbioru 6-elementowego A={1,2,3,4,5,6}: 6 6! ! 2! generacja podzbiorów przez generacje permutacji 4-elementowych ze zbioru 6 elementowego w porządku leksykograficznym i 1 i 2 i 3 i i 1 i 2 i 3 i i 1 i 2 i 3 i
36 KOMBINACJA Z POWTÓRZENIAMI zestaw k-elementów, z których każdy należy do jednego z n-rodzajów elementów, nazywamy k-elementową kombinacja z powtórzeniami ze zbioru n-elementowego (kn lub k>n) liczba wszystkich k-elementowych kombinacji z powtórzeniami ze zbioru n-elementowego wynosi: n k -1 C(n,k) k (n k 1)! k!(n -1)! 36
37 KOMBINACJA Z POWTÓRZENIAMI liczba C(n,k) określa liczbę: k-elementowych kombinacji z powtórzeniami ze zbioru n-elementowego, rozmieszczeń k identycznych elementów w n rozróżnialnych pudełkach całkowitoliczbowych rozwiązań równania postaci: x 1 +x x n =k, x i 0 dla 1 i n, 37
38 KOMBINACJA Z POWTÓRZENIAMI - PRZYKŁAD 1$ 1$ 1$ 1$ n=6 k=4 w zawodach na najlepszego agenta rozgrywane są 4 konkursy, w których zwycięzca otrzymuje nagrodę 1$ na ile sposobów może być rozdzielona pula nagród? kolejność osób nie ma znaczenie ponieważ nagroda jest taka sama w każdym konkursie jeden agent może wygrać w kilku konkursach (powtórzenia) kombinacja z powtórzeniami n k C(n,k) C(6,4) 126 k
39 uporządkowanie elementów jest istotne powtórzenia elementów są dopuszczalne obiekt kombinatoryczny liczba obiektów kombinatorycznych + - wariacja (permutacja) bez powtórzeń V(n,k) P(n,k) 0 k n n! (n k)! + + wariacja z powtórzeniami V(n,k) n,k 0 n k kombinacja bez powtórzeń kombinacja z powtórzeniami n C(n,k) k 0 k n n k C(n,k) k n,k
40 k elementów n pudełek obiekt kombinatoryczny liczba obiektów kombinatorycznych identyczne rozróżnialne kombinacja z powtórzeniami n k C(n,k) k n,k 0 1 rozróżnialne rozróżnialne wariacja z powtórzeniami V(n,k) n,k 0 n k rozróżnialne identyczne liczby Stirlinga 2- giego rodzaju? identyczne identyczne podziały liczb całkowitych? 40
41 ZLICZANIE A RACHUNEK PRAWDOPODOBIEŃSTWA Zliczanie obiektów kombinatorycznych (wariacji, permutacji, kombinacji,...) umożliwia określanie prawdopodobieństwa zdarzeń. Każdy obiekt kombinatoryczny można interpretować jako zdarzenie elementarne -. Zbiór wszystkich zdarzeń elementarnych (obiektów kombinatorycznych danego typu) tworzy przestrzeń zdarzeń elementarnych -. Zdarzenie E, to podzbiór zbioru, E. 41
42 ZLICZANIE A RACHUNEK PRAWDOPODOBIEŃSTWA w klasycznym rachunku prawdopodobieństwa zakłada się, że: zdarzenia elementarne są rozłączne, i równie prawdopodobne, 1 P( ) oraz P( ) P({ }) 1 P(E) E wówczas prawdopodobieństwo zdarzenia E, P(E), wynosi: zliczając: wszystkie zdarzenia elementarne i zdarzenia elementarne wspierające dane zdarzenie E możemy wyznaczyć prawdopodobieństwo zdarzenia E - P(E). 42
43 ZLICZANIE A RACHUNEK PRAWDOPODOBIEŃSTWA - PRZYKŁAD Jakie jest prawdopodobieństwo otrzymania fulla w pierwszym rozdaniu? pojedyncze rozdanie, to wybór 5 kart z talii 52 kart 10 2 A 5 A wszystkie możliwe rozdania tworzą przestrzeń liczba możliwych rozdań, to liczba podzbiorów 5-elementowych ze zbioru 52 elementowego kombinacji bez powtórzeń ! 5! 47!
44 ZLICZANIE A RACHUNEK PRAWDOPODOBIEŃSTWA - PRZYKŁAD aby określić prawdopodobieństwo wystąpienia fulla należy zliczyć liczbę rozdań będących fullami E full jest zbiorem kart 2 typów (po 2 i 3 karty) A A A liczba fulli wynika z liczby typów fulli par typów kart pokolorowań kart pokolorowań kart danego typu 44
45 ZLICZANIE A RACHUNEK PRAWDOPODOBIEŃSTWA - PRZYKŁAD A A A liczba typów fulli parę kart 2 typów (10, A) wybieramy spośród 13 typów kart {A,K,D,J,10,9,8,7,6,5,4,3,2} wybór jest ciągiem dwóch różnych elementów czyli wariacją bez powtórzeń 10 A n=13 k=2 (n k)! n! 13! (13 2)! 13! ! 45
46 ZLICZANIE A RACHUNEK PRAWDOPODOBIEŃSTWA - PRZYKŁAD 10 każdy z 156 typów fulli należy pokolorować liczba pokolorowań dla każdego typu fulla kolorując kartę dokonujemy wyboru 2 lub 3 kolorów spośród 4 {,,,} 10 wybór jest podzbiorem 2 lub 3 różnych elementów czyli kombinacją bez powtórzeń 10 A n=4 k=2 A n 4 4! n 4 4! 6 4 k 2 2!2! k 3 3!1! z prawa iloczynu liczbę pokolorowań należy wymnożyć liczba pokolorowań wynosi 6 4 =24 A A n=4 k=3 46
47 ZLICZANIE A RACHUNEK PRAWDOPODOBIEŃSTWA - PRZYKŁAD E A A A 13! (13 2)! = A 5 A 52 5 = prawdopodobieństwo otrzymania fulla wynosi P(E) E ,
Matematyka dyskretna. Andrzej Łachwa, UJ, A/14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 9A/14 Permutacje Permutacja zbioru skończonego X to bijekcja z X w X. Zbiór permutacji zbioru oznaczamy przez, a permutacje małymi
Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 9A/14 Permutacje Permutacja zbioru skończonego X to bijekcja z X w X. Zbiór permutacji zbioru oznaczamy przez, a permutacje małymi
Matematyka dyskretna. Andrzej Łachwa, UJ, A/15
 Matematyka dyskretna Andrzej Łachwa, UJ, 2015 andrzej.lachwa@uj.edu.pl 10A/15 Permutacje Permutacja zbioru skończonego X to bijekcja z X w X. Zbiór permutacji zbioru oznaczamy przez, a permutacje małymi
Matematyka dyskretna Andrzej Łachwa, UJ, 2015 andrzej.lachwa@uj.edu.pl 10A/15 Permutacje Permutacja zbioru skończonego X to bijekcja z X w X. Zbiór permutacji zbioru oznaczamy przez, a permutacje małymi
Matematyka dyskretna. Andrzej Łachwa, UJ, /10
 Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 7/10 Generowanie podzbiorów Weźmy n-elementowy zbiór X={x 1, x 2 x n }. Każdemu podzbiorowi YX przyporządkujemy ciąg binarny b 0 b
Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 7/10 Generowanie podzbiorów Weźmy n-elementowy zbiór X={x 1, x 2 x n }. Każdemu podzbiorowi YX przyporządkujemy ciąg binarny b 0 b
WYŻSZA SZKOŁA INFORMATYKI STOSOWANEJ I ZARZĄDZANIA
 ZBIORY Z POWTÓRZENIAMI W zbiorze z powtórzeniami ten sam element może występować kilkakrotnie. Liczbę wystąpień nazywamy krotnością tego elementu w zbiorze X = { x,..., x n } - zbiór k,..., k n - krotności
ZBIORY Z POWTÓRZENIAMI W zbiorze z powtórzeniami ten sam element może występować kilkakrotnie. Liczbę wystąpień nazywamy krotnością tego elementu w zbiorze X = { x,..., x n } - zbiór k,..., k n - krotności
KOMBINATORYKA. Problem przydziału prac
 KOMBINATORYKA Dział matematyki zajmujący się badaniem różnych możliwych zestawień i ugrupowań, jakie można tworzyć z dowolnego zbioru skończonego. Zbiory skończone, najczęściej wraz z pewną relacją obiekty
KOMBINATORYKA Dział matematyki zajmujący się badaniem różnych możliwych zestawień i ugrupowań, jakie można tworzyć z dowolnego zbioru skończonego. Zbiory skończone, najczęściej wraz z pewną relacją obiekty
Kombinatoryka. Reguła dodawania. Reguła dodawania
 Kombinatoryka Dział matematyki, który zajmuje się obliczaniem liczebności zbiorów bądź długości ciągów, które łączą w określony sposób elementy należące do skończonego zbioru (teoria zliczania). W jakich
Kombinatoryka Dział matematyki, który zajmuje się obliczaniem liczebności zbiorów bądź długości ciągów, które łączą w określony sposób elementy należące do skończonego zbioru (teoria zliczania). W jakich
RACHUNEK PRAWDOPODOBIEŃSTWA WYKŁAD 1. L. Kowalski, Statystyka, 2005
 RACHUNEK PRAWDOPODOBIEŃSTWA WYKŁAD 1. Literatura: Marek Cieciura, Janusz Zacharski, Metody probabilistyczne w ujęciu praktycznym, L. Kowalski, Statystyka, 2005 R.Leitner, J.Zacharski, "Zarys matematyki
RACHUNEK PRAWDOPODOBIEŃSTWA WYKŁAD 1. Literatura: Marek Cieciura, Janusz Zacharski, Metody probabilistyczne w ujęciu praktycznym, L. Kowalski, Statystyka, 2005 R.Leitner, J.Zacharski, "Zarys matematyki
Wykłady z Matematyki Dyskretnej
 Wykłady z Matematyki Dyskretnej dla kierunku Informatyka dr Instytut Informatyki Politechnika Krakowska Wykłady na bazie materiałów: dra hab. Andrzeja Karafiata dr hab. Joanny Kołodziej, prof. PK Informacje
Wykłady z Matematyki Dyskretnej dla kierunku Informatyka dr Instytut Informatyki Politechnika Krakowska Wykłady na bazie materiałów: dra hab. Andrzeja Karafiata dr hab. Joanny Kołodziej, prof. PK Informacje
Metody probabilistyczne
 Metody probabilistyczne 1. Prawdopodobieństwo klasyczne Wojciech Kotłowski Instytut Informatyki PP http://www.cs.put.poznan.pl/wkotlowski/ 03.10.2017 1 / 19 Rys historyczny Francja, XVII w.: gry hazardowe
Metody probabilistyczne 1. Prawdopodobieństwo klasyczne Wojciech Kotłowski Instytut Informatyki PP http://www.cs.put.poznan.pl/wkotlowski/ 03.10.2017 1 / 19 Rys historyczny Francja, XVII w.: gry hazardowe
Spotkanie olimpijskie nr lutego 2013 Kombinatoryka i rachunek prawdopodobieństwa
 Spotkanie olimpijskie nr 5 16 lutego 2013 Kombinatoryka i rachunek prawdopodobieństwa Kombinatoryka Jadwiga Słowik Reguła mnożenia Jeśli wybór polega na podjęciu k decyzji, przy czym pierwszą decyzję możemy
Spotkanie olimpijskie nr 5 16 lutego 2013 Kombinatoryka i rachunek prawdopodobieństwa Kombinatoryka Jadwiga Słowik Reguła mnożenia Jeśli wybór polega na podjęciu k decyzji, przy czym pierwszą decyzję możemy
Wykład 1: Przestrzeń probabilistyczna. Prawdopodobieństwo klasyczne. Prawdopodobieństwo geometryczne.
 Rachunek prawdopodobieństwa MAP1151 Wydział Elektroniki, rok akad. 2011/12, sem. letni Wykładowca: dr hab. A. Jurlewicz Wykład 1: Przestrzeń probabilistyczna. Prawdopodobieństwo klasyczne. Prawdopodobieństwo
Rachunek prawdopodobieństwa MAP1151 Wydział Elektroniki, rok akad. 2011/12, sem. letni Wykładowca: dr hab. A. Jurlewicz Wykład 1: Przestrzeń probabilistyczna. Prawdopodobieństwo klasyczne. Prawdopodobieństwo
Rachunek prawdopodobieństwa
 Rachunek prawdopodobieństwa Sebastian Rymarczyk srymarczyk@afm.edu.pl Tematyka zajęć 1. Elementy kombinatoryki. 2. Definicje prawdopodobieństwa. 3. Własności prawdopodobieństwa. 4. Zmienne losowe, parametry
Rachunek prawdopodobieństwa Sebastian Rymarczyk srymarczyk@afm.edu.pl Tematyka zajęć 1. Elementy kombinatoryki. 2. Definicje prawdopodobieństwa. 3. Własności prawdopodobieństwa. 4. Zmienne losowe, parametry
Podstawy metod probabilistycznych. dr Adam Kiersztyn
 Podstawy metod probabilistycznych dr Adam Kiersztyn Przestrzeń zdarzeń elementarnych i zdarzenia losowe. Zjawiskiem lub doświadczeniem losowym nazywamy taki proces, którego przebiegu i ostatecznego wyniku
Podstawy metod probabilistycznych dr Adam Kiersztyn Przestrzeń zdarzeń elementarnych i zdarzenia losowe. Zjawiskiem lub doświadczeniem losowym nazywamy taki proces, którego przebiegu i ostatecznego wyniku
Matematyka dyskretna. Andrzej Łachwa, UJ, /14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2017 andrzej.lachwa@uj.edu.pl 14/14 TWIERDZENIE HALLA Twierdzenie o kojarzeniu małżeństw rozważa dwie grupy - dziewcząt i chłopców, oraz podgrupy dziewczyn i podgrupy
Matematyka dyskretna Andrzej Łachwa, UJ, 2017 andrzej.lachwa@uj.edu.pl 14/14 TWIERDZENIE HALLA Twierdzenie o kojarzeniu małżeństw rozważa dwie grupy - dziewcząt i chłopców, oraz podgrupy dziewczyn i podgrupy
Matematyka dyskretna. Andrzej Łachwa, UJ, /10
 Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 10/10 Podziały i liczby Stirlinga Liczba Stirlinga dla cykli (często nazywana liczbą Stirlinga pierwszego rodzaju) to liczba permutacji
Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 10/10 Podziały i liczby Stirlinga Liczba Stirlinga dla cykli (często nazywana liczbą Stirlinga pierwszego rodzaju) to liczba permutacji
STATYSTYKA. Rafał Kucharski. Uniwersytet Ekonomiczny w Katowicach 2015/16 ROND, Finanse i Rachunkowość, rok 2
 STATYSTYKA Rafał Kucharski Uniwersytet Ekonomiczny w Katowicach 2015/16 ROND, Finanse i Rachunkowość, rok 2 Wybrane litery alfabetu greckiego α alfa β beta Γ γ gamma δ delta ɛ, ε epsilon η eta Θ θ theta
STATYSTYKA Rafał Kucharski Uniwersytet Ekonomiczny w Katowicach 2015/16 ROND, Finanse i Rachunkowość, rok 2 Wybrane litery alfabetu greckiego α alfa β beta Γ γ gamma δ delta ɛ, ε epsilon η eta Θ θ theta
WYDZIAŁ PODSTAWOWYCH PROBLEMÓW TECHNIKI KARTA PRZEDMIOTU
 Zał. nr do ZW WYDZIAŁ PODSTAWOWYCH PROBLEMÓW TECHNIKI KARTA PRZEDMIOTU Nazwa w języku polskim MATEMATYKA DYSKRETNA Nazwa w języku angielskim DISCRETE MATHEMATICS Kierunek studiów (jeśli dotyczy): Matematyka
Zał. nr do ZW WYDZIAŁ PODSTAWOWYCH PROBLEMÓW TECHNIKI KARTA PRZEDMIOTU Nazwa w języku polskim MATEMATYKA DYSKRETNA Nazwa w języku angielskim DISCRETE MATHEMATICS Kierunek studiów (jeśli dotyczy): Matematyka
Matematyka dyskretna - wykład - część Podstawowe algorytmy kombinatoryczne
 A. Permutacja losowa Matematyka dyskretna - wykład - część 2 9. Podstawowe algorytmy kombinatoryczne Załóżmy, że mamy tablice p złożoną z n liczb (ponumerowanych od 0 do n 1). Aby wygenerować losową permutację
A. Permutacja losowa Matematyka dyskretna - wykład - część 2 9. Podstawowe algorytmy kombinatoryczne Załóżmy, że mamy tablice p złożoną z n liczb (ponumerowanych od 0 do n 1). Aby wygenerować losową permutację
TEORETYCZNE PODSTAWY INFORMATYKI
 1 TEORETYCZNE PODSTAWY INFORMATYKI WFAiS UJ, Informatyka Stosowana I rok studiów, I stopień Wykład 4 część I 2 Kombinatoryka Wariacje z powtórzeniami Permutacje Wariacje bez powtórzeń Kombinacje Łączenie
1 TEORETYCZNE PODSTAWY INFORMATYKI WFAiS UJ, Informatyka Stosowana I rok studiów, I stopień Wykład 4 część I 2 Kombinatoryka Wariacje z powtórzeniami Permutacje Wariacje bez powtórzeń Kombinacje Łączenie
Matematyczne Podstawy Kognitywistyki
 Matematyczne Podstawy Kognitywistyki Dorota Leszczyńska-Jasion Kombinatoryka, ci agi liczbowe, skończone przestrzenie probabilistyczne Przykłady zagadnień kombinatorycznych Rozważmy układ n miast o bardzo
Matematyczne Podstawy Kognitywistyki Dorota Leszczyńska-Jasion Kombinatoryka, ci agi liczbowe, skończone przestrzenie probabilistyczne Przykłady zagadnień kombinatorycznych Rozważmy układ n miast o bardzo
Teoretyczne podstawy informatyki
 Teoretyczne podstawy informatyki Wykład 3b Kombinatoryka i prawdopodobieństwo Kombinatoryka i prawdopodobieństwo Często spotykamy się z problemem obliczenia wartości wyrażającej prawdopodobieństwo zajścia
Teoretyczne podstawy informatyki Wykład 3b Kombinatoryka i prawdopodobieństwo Kombinatoryka i prawdopodobieństwo Często spotykamy się z problemem obliczenia wartości wyrażającej prawdopodobieństwo zajścia
Kombinatoryka. Jerzy Rutkowski. Teoria. P n = n!. (1) Zadania obowiązkowe
 Kombinatoryka Jerzy Rutkowski 2. Elementy kombinatoryki 2.1. Permutacje Definicja 1. Niech n N. Permutacją n-elementowego zbioru A nazywamy dowolną funkcję różnowartościową f : {1,..., n} A. Innymi słowy:
Kombinatoryka Jerzy Rutkowski 2. Elementy kombinatoryki 2.1. Permutacje Definicja 1. Niech n N. Permutacją n-elementowego zbioru A nazywamy dowolną funkcję różnowartościową f : {1,..., n} A. Innymi słowy:
Wstęp do rachunku prawdopodobieństwa
 wykład : Wstęp do rachunku prawdopodobieństwa STTYSTYK OPISOW Wanda Olech Katedra Genetyki i Ochrony Zwierząt Statystyka zajmuje się Zjawiskami losowymi - które bada przez doświadczenie U podstaw współczesnej
wykład : Wstęp do rachunku prawdopodobieństwa STTYSTYK OPISOW Wanda Olech Katedra Genetyki i Ochrony Zwierząt Statystyka zajmuje się Zjawiskami losowymi - które bada przez doświadczenie U podstaw współczesnej
Elementy kombinatoryki
 Elementy kombinatoryki Wykłady z matematyki dyskretnej dla informatyków i teleinformatyków UTP Bydgoszcz 04 (Wykłady z matematyki dyskretnej) Elementy kombinatoryki 04 1 / 59 Permutacje Definicja. Permutacja
Elementy kombinatoryki Wykłady z matematyki dyskretnej dla informatyków i teleinformatyków UTP Bydgoszcz 04 (Wykłady z matematyki dyskretnej) Elementy kombinatoryki 04 1 / 59 Permutacje Definicja. Permutacja
Wstęp. Kurs w skrócie
 Mariola Zalewska Zakład Metod Matematycznych i Statystycznych Zarządzania Wydział Zarządzania Uniwersystet Warszawski I rok DSM Rachunek Prawdopodobieństwa Wstęp Kombinatoryka Niezależność zdarzeń, Twierdzenie
Mariola Zalewska Zakład Metod Matematycznych i Statystycznych Zarządzania Wydział Zarządzania Uniwersystet Warszawski I rok DSM Rachunek Prawdopodobieństwa Wstęp Kombinatoryka Niezależność zdarzeń, Twierdzenie
ĆWICZENIA nr 1 - KOMBINATORYKA - czyli sztuka liczenia autor: mgr inż. Agnieszka Herczak
 ĆWCZENA nr 1 - KOMBNATORYKA - czyli sztuka liczenia autor: mgr inż. Agnieszka Herczak. Reguła mnożenia Jeżeli pewien wybór zależy od skończenie wielu decyzji, przy czym podejmując pierwszą mamy k 1 możliwości
ĆWCZENA nr 1 - KOMBNATORYKA - czyli sztuka liczenia autor: mgr inż. Agnieszka Herczak. Reguła mnożenia Jeżeli pewien wybór zależy od skończenie wielu decyzji, przy czym podejmując pierwszą mamy k 1 możliwości
Wykład 2. Prawdopodobieństwo i elementy kombinatoryki
 Wstęp do probabilistyki i statystyki Wykład 2. Prawdopodobieństwo i elementy kombinatoryki dr hab.inż. Katarzyna Zakrzewska, prof.agh Katedra Elektroniki, AGH e-mail: zak@agh.edu.pl http://home.agh.edu.pl/~zak
Wstęp do probabilistyki i statystyki Wykład 2. Prawdopodobieństwo i elementy kombinatoryki dr hab.inż. Katarzyna Zakrzewska, prof.agh Katedra Elektroniki, AGH e-mail: zak@agh.edu.pl http://home.agh.edu.pl/~zak
Matematyka dyskretna dla informatyków
 Matematyka dyskretna dla informatyków Część I: Elementy kombinatoryki Jerzy Jaworski Zbigniew Palka Jerzy Szymański Uniwersytet im. Adama Mickiewicza Poznań 2007 4 Zależności rekurencyjne Wiele zależności
Matematyka dyskretna dla informatyków Część I: Elementy kombinatoryki Jerzy Jaworski Zbigniew Palka Jerzy Szymański Uniwersytet im. Adama Mickiewicza Poznań 2007 4 Zależności rekurencyjne Wiele zależności
Ciągi Podzbiory Symbol Newtona Zasada szufladkowa Dirichleta Zasada włączania i wyłączania. Ilość najkrótszych dróg. Kombinatoryka. Magdalena Lemańska
 Kombinatoryka Magdalena Lemańska Literatura Matematyka Dyskretna Andrzej Szepietowski http://wazniak.mimuw.edu.pl/ Discrete Mathematics Seymour Lipschutz, Marc Lipson Aspekty kombinatoryki Victor Bryant
Kombinatoryka Magdalena Lemańska Literatura Matematyka Dyskretna Andrzej Szepietowski http://wazniak.mimuw.edu.pl/ Discrete Mathematics Seymour Lipschutz, Marc Lipson Aspekty kombinatoryki Victor Bryant
Rachunek prawdopodobieństwa (Elektronika, studia niestacjonarne) Wykład 1
 Rachunek prawdopodobieństwa (Elektronika, studia niestacjonarne) Wykład 1 Przygotowując wykład korzystam głównie z książki Jakubowski, Sztencel Wstęp do teorii prawdopodobieństwa. Jakubowski, Sztencel:
Rachunek prawdopodobieństwa (Elektronika, studia niestacjonarne) Wykład 1 Przygotowując wykład korzystam głównie z książki Jakubowski, Sztencel Wstęp do teorii prawdopodobieństwa. Jakubowski, Sztencel:
ELEMENTY KOMBINATORYKI
 ELEMENTY KOMBINATORYKI Kombinatoryka to dział matematyki, który zajmuje się zliczaniem, na ile sposobów może zajść jakieś zjawisko. Powstała dzięki grom hazardowym a dopiero później rozwinęła się w gałąź
ELEMENTY KOMBINATORYKI Kombinatoryka to dział matematyki, który zajmuje się zliczaniem, na ile sposobów może zajść jakieś zjawisko. Powstała dzięki grom hazardowym a dopiero później rozwinęła się w gałąź
RACHUNEK PRAWDOPODOBIEŃSTWA I KOMBINATORYKA
 RACHUNEK PRAWDOPODOBIEŃSTWA I KOMBINATORYKA Doświadczenia losowe Rachunek prawdopodobieństwa zajmuje się zdarzeniami jakie zachodzą, gdy przeprowadzamy doświadczenia losowe. Mówimy, że doświadczenie jest
RACHUNEK PRAWDOPODOBIEŃSTWA I KOMBINATORYKA Doświadczenia losowe Rachunek prawdopodobieństwa zajmuje się zdarzeniami jakie zachodzą, gdy przeprowadzamy doświadczenia losowe. Mówimy, że doświadczenie jest
01DRAP - klasyczna definicja prawdopodobieństwa
 01DRAP - klasyczna definicja prawdopodobieństwa Ω zbiór zdarzeń elementarnych. Gdy Ω < oraz P({ω} = 1 Ω, dla każdego ω Ω (tzn. każde zdarzenie elementarne jest równo prawdopodobne, to P (A = A Ω Przydatne
01DRAP - klasyczna definicja prawdopodobieństwa Ω zbiór zdarzeń elementarnych. Gdy Ω < oraz P({ω} = 1 Ω, dla każdego ω Ω (tzn. każde zdarzenie elementarne jest równo prawdopodobne, to P (A = A Ω Przydatne
Matematyka dyskretna. Andrzej Łachwa, UJ, /15
 Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl 10/15 WARIACJE Liczba wariacji, czyli różnych ciągów k-elementowych o wyrazach ze zbioru n-elementowego, wynosi n k. Ciąg k-elementowy,
Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl 10/15 WARIACJE Liczba wariacji, czyli różnych ciągów k-elementowych o wyrazach ze zbioru n-elementowego, wynosi n k. Ciąg k-elementowy,
Matematyka dyskretna zestaw II ( )
 Matematyka dyskretna zestaw II (17-18.10.2016) Uwaga: Część z zadań z tego zestawu opiera się na zasadzie szufladkowej Dirichleta. Zadanie 1. Na ile sposobów można umieścić w 7 szufladach 3 koszule tak,
Matematyka dyskretna zestaw II (17-18.10.2016) Uwaga: Część z zadań z tego zestawu opiera się na zasadzie szufladkowej Dirichleta. Zadanie 1. Na ile sposobów można umieścić w 7 szufladach 3 koszule tak,
01DRAP - klasyczna definicja prawdopodobieństwa
 01DRAP - klasyczna definicja prawdopodobieństwa Ω zbiór zdarzeń elementarnych. Gdy Ω < oraz P({ω} = 1 Ω, dla każdego ω Ω (tzn. każde zdarzenie elementarne jest równo prawdopodobne, to P (A = A Ω Przydatne
01DRAP - klasyczna definicja prawdopodobieństwa Ω zbiór zdarzeń elementarnych. Gdy Ω < oraz P({ω} = 1 Ω, dla każdego ω Ω (tzn. każde zdarzenie elementarne jest równo prawdopodobne, to P (A = A Ω Przydatne
Rachunek prawdopodobieństwa i statystyka matematyczna. Leszek Adamczyk Wykłady dla kierunku Fizyka Medyczna w semestrze letnim 2016/2017
 Rachunek prawdopodobieństwa i statystyka matematyczna Leszek Adamczyk Wykłady dla kierunku Fizyka Medyczna w semestrze letnim 2016/2017 1 1 Wstęp Rachunek prawdopodobieństwa i statystyka to: działy matematyki
Rachunek prawdopodobieństwa i statystyka matematyczna Leszek Adamczyk Wykłady dla kierunku Fizyka Medyczna w semestrze letnim 2016/2017 1 1 Wstęp Rachunek prawdopodobieństwa i statystyka to: działy matematyki
1 Ćwiczenia: Funkcje całkowitoliczbowe
 1 Ćwiczenia: Funkcje całkowitoliczbowe 1.1 Funkcje podłoga i sufit (Floor and ceiling functions) podłoga (część całkowita) x = największa liczba całkowita mniejsza lub równa x sufit x = najmniejsza liczba
1 Ćwiczenia: Funkcje całkowitoliczbowe 1.1 Funkcje podłoga i sufit (Floor and ceiling functions) podłoga (część całkowita) x = największa liczba całkowita mniejsza lub równa x sufit x = najmniejsza liczba
Matematyka dyskretna. Wykład 2: Kombinatoryka. Gniewomir Sarbicki
 Matematya dysretna Wyład 2: Kombinatorya Gniewomir Sarbici Kombinatorya Definicja Kombinatorya zajmuje się oreślaniem mocy zbiorów sończonych, w szczególności mocy zbiorów odwzorowań jednego zbioru w drugi
Matematya dysretna Wyład 2: Kombinatorya Gniewomir Sarbici Kombinatorya Definicja Kombinatorya zajmuje się oreślaniem mocy zbiorów sończonych, w szczególności mocy zbiorów odwzorowań jednego zbioru w drugi
MATEMATYKA DYSKRETNA (2014/2015) dr hab. inż. Małgorzata Sterna PROSTOKĄTY ŁACIŃSKIE
 MATEMATYKA DYSKRETNA (0/0) dr hab. inż. Małgorzata Sterna malgorzata.sterna@cs.put.poznan.pl www.cs.put.poznan.pl/msterna/ PROSTOKĄTY ŁACIŃSKIE PROSTOKĄTY ŁACIŃSKIE Prostokąt łaciński o wymiarze pq o elementach
MATEMATYKA DYSKRETNA (0/0) dr hab. inż. Małgorzata Sterna malgorzata.sterna@cs.put.poznan.pl www.cs.put.poznan.pl/msterna/ PROSTOKĄTY ŁACIŃSKIE PROSTOKĄTY ŁACIŃSKIE Prostokąt łaciński o wymiarze pq o elementach
Rachunek prawdopodobieństwa i kombinatoryka. Rachunek prawdopodobieństwa. Podstawowe pojęcia rachunku prawdopodobieństwa
 Rachunek prawdopodobieństwa i kombinatoryka Spis treści Rachunek prawdopodobieństwa Podstawowe pojęcia rachunku prawdopodobieństwa Liczba wyników doświadczenia losowego. Reguła mnożenia i reguła dodawania
Rachunek prawdopodobieństwa i kombinatoryka Spis treści Rachunek prawdopodobieństwa Podstawowe pojęcia rachunku prawdopodobieństwa Liczba wyników doświadczenia losowego. Reguła mnożenia i reguła dodawania
Matematyka Dyskretna Rozgrzewka I test semestr letni 2012/2013
 Matematyka Dyskretna Rozgrzewka I test semestr letni 2012/2013 Zadanie 1. Dla n naturalnego mamy zdanie: Jeżeli n jest liczbą pierwszą, to n jest równa 2 lub jest liczbą nieparzystą. Możemy je zapisać
Matematyka Dyskretna Rozgrzewka I test semestr letni 2012/2013 Zadanie 1. Dla n naturalnego mamy zdanie: Jeżeli n jest liczbą pierwszą, to n jest równa 2 lub jest liczbą nieparzystą. Możemy je zapisać
01DRAP - klasyczna definicja prawdopodobieństwa
 01DRAP - klasyczna definicja prawdopodobieństwa Ω zbiór zdarzeń elementarnych. Gdy Ω < oraz P({ω} = 1 Ω, dla każdego ω Ω (tzn. każde zdarzenie elementarne jest równo prawdopodobne, to P (A = A Ω Przydatne
01DRAP - klasyczna definicja prawdopodobieństwa Ω zbiór zdarzeń elementarnych. Gdy Ω < oraz P({ω} = 1 Ω, dla każdego ω Ω (tzn. każde zdarzenie elementarne jest równo prawdopodobne, to P (A = A Ω Przydatne
Matematyka dyskretna Literatura Podstawowa: 1. K.A. Ross, C.R.B. Wright: Matematyka Dyskretna, PWN, 1996 (2006) 2. J. Jaworski, Z. Palka, J.
 Matematyka dyskretna Literatura Podstawowa: 1. K.A. Ross, C.R.B. Wright: Matematyka Dyskretna, PWN, 1996 (2006) 2. J. Jaworski, Z. Palka, J. Szmański: Matematyka dyskretna dla informatyków, UAM, 2008 Uzupełniająca:
Matematyka dyskretna Literatura Podstawowa: 1. K.A. Ross, C.R.B. Wright: Matematyka Dyskretna, PWN, 1996 (2006) 2. J. Jaworski, Z. Palka, J. Szmański: Matematyka dyskretna dla informatyków, UAM, 2008 Uzupełniająca:
STATYSTYKA wykład 1. Wanda Olech. Katedra Genetyki i Ogólnej Hodowli Zwierząt
 STTYSTYK wykład 1 Wanda Olech Katedra Genetyki i Ogólnej Hodowli Zwierząt Statystyka Pierwotnie oznaczała stan rzeczy (od status) i do XVIII wieku używana dla określenia zbioru wiadomości o państwie Statystyka
STTYSTYK wykład 1 Wanda Olech Katedra Genetyki i Ogólnej Hodowli Zwierząt Statystyka Pierwotnie oznaczała stan rzeczy (od status) i do XVIII wieku używana dla określenia zbioru wiadomości o państwie Statystyka
Statystyka matematyczna
 Statystyka matematyczna Wykład 1 Magdalena Alama-Bućko 25 lutego 2019 Magdalena Alama-Bućko Statystyka matematyczna 25 lutego 2019 1 / 18 Wykład : 10h (przez 10 tygodni po 45 minut) Ćwiczenia : 15h (45
Statystyka matematyczna Wykład 1 Magdalena Alama-Bućko 25 lutego 2019 Magdalena Alama-Bućko Statystyka matematyczna 25 lutego 2019 1 / 18 Wykład : 10h (przez 10 tygodni po 45 minut) Ćwiczenia : 15h (45
Kombinatoryka i rachunek prawdopodobieństwa
 Kombinatoryka i rachunek prawdopodobieństwa Jerzy Rutkowski Kombinatoryka i rachunek prawdopodobieństwa 2. Elementy kombinatoryki 2.1. Permutacje Definicja 1. Niech n N. Permutacją n-elementowego zbioru
Kombinatoryka i rachunek prawdopodobieństwa Jerzy Rutkowski Kombinatoryka i rachunek prawdopodobieństwa 2. Elementy kombinatoryki 2.1. Permutacje Definicja 1. Niech n N. Permutacją n-elementowego zbioru
Zdarzenia losowe i prawdopodobieństwo
 Rozdział 1 Zdarzenia losowe i prawdopodobieństwo 1.1 Klasyfikacja zdarzeń Zdarzenie elementarne pojęcie aprioryczne, które nie może być zdefiniowane. Odpowiednik pojęcia punkt w geometrii. Zdarzenie elementarne
Rozdział 1 Zdarzenia losowe i prawdopodobieństwo 1.1 Klasyfikacja zdarzeń Zdarzenie elementarne pojęcie aprioryczne, które nie może być zdefiniowane. Odpowiednik pojęcia punkt w geometrii. Zdarzenie elementarne
Statystyka w analizie i planowaniu eksperymentu
 5 marca 2011 Zasady 10 wyk ladów; egzamin pisemny; Literatura 1 A. Lomnicki Wprowadzenie do statystyki dla przyrodników PWN 1999. 2 W. Krysicki, J. Bartos, W. Dyczka, K. Królikowska, M. Wasilewski Rachunek
5 marca 2011 Zasady 10 wyk ladów; egzamin pisemny; Literatura 1 A. Lomnicki Wprowadzenie do statystyki dla przyrodników PWN 1999. 2 W. Krysicki, J. Bartos, W. Dyczka, K. Królikowska, M. Wasilewski Rachunek
WYKŁAD 1. Witold Bednorz, Paweł Wolff. Rachunek Prawdopodobieństwa, WNE, Instytut Matematyki Uniwersytet Warszawski
 WYKŁAD 1 Witold Bednorz, Paweł Wolff Instytut Matematyki Uniwersytet Warszawski Rachunek Prawdopodobieństwa, WNE, 2010-2011 Wprowadzenie Gry hazardowe Wprowadzenie Gry hazardowe Klasyczna definicja prawdopodobieństwa.
WYKŁAD 1 Witold Bednorz, Paweł Wolff Instytut Matematyki Uniwersytet Warszawski Rachunek Prawdopodobieństwa, WNE, 2010-2011 Wprowadzenie Gry hazardowe Wprowadzenie Gry hazardowe Klasyczna definicja prawdopodobieństwa.
Statystyka matematyczna
 Statystyka matematyczna Wykład 1 Magdalena Alama-Bućko 20 lutego 2017 Magdalena Alama-Bućko Statystyka matematyczna 20 lutego 2017 1 / 21 Wykład : 10h (przez 10 tygodni po 45 minut) Ćwiczenia : 15h (45
Statystyka matematyczna Wykład 1 Magdalena Alama-Bućko 20 lutego 2017 Magdalena Alama-Bućko Statystyka matematyczna 20 lutego 2017 1 / 21 Wykład : 10h (przez 10 tygodni po 45 minut) Ćwiczenia : 15h (45
Kombinatoryka i rachunek prawdopodobieństwa
 Kombinatoryka i rachunek prawdopodobieństwa Kombinatoryka i rachunek prawdopodobieństwa Jerzy Rutkowski 2. Elementy kombinatoryki 2.. Permutacje Teoria Definicja. Niech n N. Permutacją n-elementowego zbioru
Kombinatoryka i rachunek prawdopodobieństwa Kombinatoryka i rachunek prawdopodobieństwa Jerzy Rutkowski 2. Elementy kombinatoryki 2.. Permutacje Teoria Definicja. Niech n N. Permutacją n-elementowego zbioru
Rachunek prawdopodobieństwa
 Rachunek prawdopodobieństwa Tomasz Górecki Wydział Matematyki i Informatyki Uniwersytet im. Adama Mickiewicza Wciągu ćwiczeń zostaną przeprowadzone 2 kolokwia. Na każdym z nichbędziedozdobycia25punktów(5zadańpo5punktówkażde).
Rachunek prawdopodobieństwa Tomasz Górecki Wydział Matematyki i Informatyki Uniwersytet im. Adama Mickiewicza Wciągu ćwiczeń zostaną przeprowadzone 2 kolokwia. Na każdym z nichbędziedozdobycia25punktów(5zadańpo5punktówkażde).
Rachunek prawdopodobieństwa Rozdział 1. Wstęp
 Rachunek prawdopodobieństwa Rozdział 1. Wstęp 1.1. Prawdopodobieństwo klasyczne Katarzyna Rybarczyk-Krzywdzińska Definicja Zadaliśmy pytanie. Bolek, Lolek i Tola wstąpili do kasyna. Dla każdego z nich
Rachunek prawdopodobieństwa Rozdział 1. Wstęp 1.1. Prawdopodobieństwo klasyczne Katarzyna Rybarczyk-Krzywdzińska Definicja Zadaliśmy pytanie. Bolek, Lolek i Tola wstąpili do kasyna. Dla każdego z nich
( ) ( ) Przykład: Z trzech danych elementów: a, b, c, można utworzyć trzy następujące 2-elementowe kombinacje: ( ) ( ) ( ).
 KOMBINATORYKA Kombinatoryka zajmuje się wyznaczaniem liczby elementów zbiorów skończonych utworzonych zgodnie z określonymi zasadami. Do podstawowych pojęć kombinatorycznych należą: PERMUTACJE Silnia.
KOMBINATORYKA Kombinatoryka zajmuje się wyznaczaniem liczby elementów zbiorów skończonych utworzonych zgodnie z określonymi zasadami. Do podstawowych pojęć kombinatorycznych należą: PERMUTACJE Silnia.
Matematyka dyskretna. Andrzej Łachwa, UJ, 2019 Zadania
 Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl Zadania 101-170 101. Oblicz postać zwartą symbolu { n 4}. 102. Udowodnij, że n k =1 ( 1) k ( n k) =1 103. Ile może być 4-cyfrowych
Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl Zadania 101-170 101. Oblicz postać zwartą symbolu { n 4}. 102. Udowodnij, że n k =1 ( 1) k ( n k) =1 103. Ile może być 4-cyfrowych
Wymagania egzaminacyjne z matematyki. Klasa 3C. MATeMATyka. Nowa Era. Klasa 3
 Wymagania egzaminacyjne z matematyki. lasa 3C. MATeMATyka. Nowa Era. y są ze sobą ściśle powiązane ( + P + R + D + W), stanowiąc ocenę szkolną, i tak: ocenę dopuszczającą (2) otrzymuje uczeń, który spełnił
Wymagania egzaminacyjne z matematyki. lasa 3C. MATeMATyka. Nowa Era. y są ze sobą ściśle powiązane ( + P + R + D + W), stanowiąc ocenę szkolną, i tak: ocenę dopuszczającą (2) otrzymuje uczeń, który spełnił
STATYSTYKA wykład 1. Wanda Olech. Katedra Genetyki i Ogólnej Hodowli Zwierząt
 STTYSTYK wykład 1 Wanda Olech Katedra Genetyki i Ogólnej Hodowli Zwierząt Plan wykładów Data WYKŁDY 1.X rachunek prawdopodobieństwa; 8.X zmienna losowa jednowymiarowa, funkcja rozkładu, dystrybuanta 15.X
STTYSTYK wykład 1 Wanda Olech Katedra Genetyki i Ogólnej Hodowli Zwierząt Plan wykładów Data WYKŁDY 1.X rachunek prawdopodobieństwa; 8.X zmienna losowa jednowymiarowa, funkcja rozkładu, dystrybuanta 15.X
Do rozwiązania większości zadań często wystarcza reguła mnożenia i wzór na kombinację.
 Kombinatoryka Spis treści Kombinatoryka a prawdopodobieństwo Reguła mnożenia Prezentacja wyników za pomocą drzewa Elementy kombinatoryki Kombinatoryka Silnia Permutacja Wariacja bez powtórzeń Wariacja
Kombinatoryka Spis treści Kombinatoryka a prawdopodobieństwo Reguła mnożenia Prezentacja wyników za pomocą drzewa Elementy kombinatoryki Kombinatoryka Silnia Permutacja Wariacja bez powtórzeń Wariacja
Rachunek prawdopodobieństwa- wykład 2
 Rachunek prawdopodobieństwa- wykład 2 Pojęcie dyskretnej przestrzeni probabilistycznej i określenie prawdopodobieństwa w tej przestrzeni dr Marcin Ziółkowski Instytut Matematyki i Informatyki Uniwersytet
Rachunek prawdopodobieństwa- wykład 2 Pojęcie dyskretnej przestrzeni probabilistycznej i określenie prawdopodobieństwa w tej przestrzeni dr Marcin Ziółkowski Instytut Matematyki i Informatyki Uniwersytet
Matematyka dyskretna. Andrzej Łachwa, UJ, /10
 Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 6/10 Zasada Dirichleta 1 ZASADA SZUFLADKOWA DIRICHLETA (1ZSD) Jeśli n obiektów jest rozmieszczonych w m szufladach i n > m > 0, to
Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 6/10 Zasada Dirichleta 1 ZASADA SZUFLADKOWA DIRICHLETA (1ZSD) Jeśli n obiektów jest rozmieszczonych w m szufladach i n > m > 0, to
1 Działania na zbiorach
 M. Beśka, Wstęp do teorii miary, rozdz. 1 1 1 Działania na zbiorach W rozdziale tym przypomnimy podstawowe działania na zbiorach koncentrując się na własnościach tych działań, które będą przydatne w dalszej
M. Beśka, Wstęp do teorii miary, rozdz. 1 1 1 Działania na zbiorach W rozdziale tym przypomnimy podstawowe działania na zbiorach koncentrując się na własnościach tych działań, które będą przydatne w dalszej
Zadanie 2. Obliczyć rangę dowolnego elementu zbioru uporządkowanego N 0 N 0, gdy porządek jest zdefiniowany następująco: (a, b) (c, d) (a c b d)
 Matemaryka dyskretna - zadania Zadanie 1. Opisać zbiór wszystkich elementów rangi k zbioru uporządkowanego X dla każdej liczby naturalnej k, gdy X jest rodziną podzbiorów zbioru skończonego Y. Elementem
Matemaryka dyskretna - zadania Zadanie 1. Opisać zbiór wszystkich elementów rangi k zbioru uporządkowanego X dla każdej liczby naturalnej k, gdy X jest rodziną podzbiorów zbioru skończonego Y. Elementem
Statystyka z elementami rachunku prawdopodobieństwa
 Statystyka z elementami rachunku prawdopodobieństwa dr hab. Tomasz Górecki tomasz.gorecki@amu.edu.pl Zakład Rachunku Prawdopodobieństwa i Statystyki Matematycznej Wydział Matematyki i Informatyki Uniwersytet
Statystyka z elementami rachunku prawdopodobieństwa dr hab. Tomasz Górecki tomasz.gorecki@amu.edu.pl Zakład Rachunku Prawdopodobieństwa i Statystyki Matematycznej Wydział Matematyki i Informatyki Uniwersytet
Symbol, alfabet, łańcuch
 Łańcuchy i zbiory łańcuchów Teoria automatów i języków formalnych Dr inŝ. Janusz Majewski Katedra Informatyki Symbol, alfabet, łańcuch Symbol Symbol jest to pojęcie niedefiniowane (synonimy: znak, litera)
Łańcuchy i zbiory łańcuchów Teoria automatów i języków formalnych Dr inŝ. Janusz Majewski Katedra Informatyki Symbol, alfabet, łańcuch Symbol Symbol jest to pojęcie niedefiniowane (synonimy: znak, litera)
Matematyka dyskretna. Andrzej Łachwa, UJ, A/10
 Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 8A/10 Zbiory przeliczalne Przyjmujemy, że Zn = {0, 1, 2, 3, n-1} dla n>0 oraz Zn = przy n=0. Zbiór skończony to zbiór bijektywny z
Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 8A/10 Zbiory przeliczalne Przyjmujemy, że Zn = {0, 1, 2, 3, n-1} dla n>0 oraz Zn = przy n=0. Zbiór skończony to zbiór bijektywny z
Matematyka dyskretna. Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl. Przykłady zadań egzaminacyjnych (do liczenia lub dowodzenia)
 Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl Przykłady zadań egzaminacyjnych (do liczenia lub dowodzenia) 1. Ile układów kart w pokerze to Dwie pary? Dwie pary to układ 5 kart
Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl Przykłady zadań egzaminacyjnych (do liczenia lub dowodzenia) 1. Ile układów kart w pokerze to Dwie pary? Dwie pary to układ 5 kart
Ćw,1. Wypisz wszystkie k-wyrazowe wariacje bez powtórzeń zbioru A = {1, 2,3 }, gdy: a) k = l, b) k = 2, c) k = 3. Wariacje 1 z 6
 Wariacje bez powtórzeń Jeśli w doświadczeniu losowym ze zbioru n-elementowego wybieramy k elementów w ten sposób, że: wybrane elementy nie mogą się powtarzać kolejność wybranych elementów jest istotna
Wariacje bez powtórzeń Jeśli w doświadczeniu losowym ze zbioru n-elementowego wybieramy k elementów w ten sposób, że: wybrane elementy nie mogą się powtarzać kolejność wybranych elementów jest istotna
Teoretyczne podstawy informatyki
 Teoretyczne podstawy informatyki Wykład 12a: Prawdopodobieństwo i algorytmy probabilistyczne http://hibiscus.if.uj.edu.pl/~erichter/dydaktyka2010/tpi-2010 Prof. dr hab. Elżbieta Richter-Wąs 1 Teoria prawdopodobieństwa
Teoretyczne podstawy informatyki Wykład 12a: Prawdopodobieństwo i algorytmy probabilistyczne http://hibiscus.if.uj.edu.pl/~erichter/dydaktyka2010/tpi-2010 Prof. dr hab. Elżbieta Richter-Wąs 1 Teoria prawdopodobieństwa
Zbiory. Specjalnym zbiorem jest zbiór pusty nie zawierajacy żadnych elementów. Oznaczamy go symbolem.
 Zbiory Pojęcie zbioru jest w matematyce pojęciem pierwotnym, którego nie definiujemy. Gdy a jest elementem należacym do zbioru A to piszemy a A. Stosujemy również oznaczenie a / A jeżeli (a A). Będziemy
Zbiory Pojęcie zbioru jest w matematyce pojęciem pierwotnym, którego nie definiujemy. Gdy a jest elementem należacym do zbioru A to piszemy a A. Stosujemy również oznaczenie a / A jeżeli (a A). Będziemy
Matematyka dyskretna. Andrzej Łachwa, UJ, a/14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 8a/14 Zbiory przeliczalne Przyjmujemy, że = {0, 1, 2, 3, n-1} dla n>0 oraz = przy n=0. Zbiór skończony to zbiór bijektywny z pewnym
Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 8a/14 Zbiory przeliczalne Przyjmujemy, że = {0, 1, 2, 3, n-1} dla n>0 oraz = przy n=0. Zbiór skończony to zbiór bijektywny z pewnym
1. Elementy kombinatoryki - zadania do wyboru
 . Elementy kombinatoryki - zadania do wyboru Bernadeta Tomasz Zadania dodatkowe Zadanie.. Mamy do wyboru mieszkania i auta. Na ile sposobów można dokonać wyboru, jeśli. mamy wybrać mieszkanie i samochód,.
. Elementy kombinatoryki - zadania do wyboru Bernadeta Tomasz Zadania dodatkowe Zadanie.. Mamy do wyboru mieszkania i auta. Na ile sposobów można dokonać wyboru, jeśli. mamy wybrać mieszkanie i samochód,.
Wykład 2. Prawdopodobieństwo i elementy kombinatoryki
 Wstęp do probabilistyki i statystyki Wykład 2. Prawdopodobieństwo i elementy kombinatoryki dr inż. Krystyna Schneider, Katedra Elektroniki, AGH e-mail: kryschna@agh.edu.pl http://home.agh.edu.pl/~kryschna
Wstęp do probabilistyki i statystyki Wykład 2. Prawdopodobieństwo i elementy kombinatoryki dr inż. Krystyna Schneider, Katedra Elektroniki, AGH e-mail: kryschna@agh.edu.pl http://home.agh.edu.pl/~kryschna
Wprowadzenie do kombinatoryki
 Wprowadzenie do kombinatoryki http://www.matemaks.pl/kombinatoryka.html Kombinatoryka jest działem matematyki, który pomaga odpowiedzieć na pytania typu: "ile jest możliwych wyników w rzucie monetą?",
Wprowadzenie do kombinatoryki http://www.matemaks.pl/kombinatoryka.html Kombinatoryka jest działem matematyki, który pomaga odpowiedzieć na pytania typu: "ile jest możliwych wyników w rzucie monetą?",
Elementy rachunku prawdopodobieństwa (M. Skośkiewicz, A. Siejka, K. Walczak, A. Szpakowska)
 Elementy rachunku prawdopodobieństwa (M. Skośkiewicz, A. Siejka, K. Walczak, A. Szpakowska) Twierdzenie (o mnożeniu) Podstawowe pojęcia i wzory kombinatoryczne. Niech,, będą zbiorami mającymi odpowiednio,,
Elementy rachunku prawdopodobieństwa (M. Skośkiewicz, A. Siejka, K. Walczak, A. Szpakowska) Twierdzenie (o mnożeniu) Podstawowe pojęcia i wzory kombinatoryczne. Niech,, będą zbiorami mającymi odpowiednio,,
Funkcja. x X! y Y : x, y f. f : X Y f x = y f : x y. Funkcja o dziedzinie X i przeciwdziedzinie Y to dowolna relacja f XxY taka, że: Notacje:
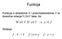 Funkcja Funkcja o dziedzinie X i przeciwdziedzinie Y to dowolna relacja f XxY taka, że: Notacje: x X! y Y : x, y f f : X Y f x = y f : x y Przykłady f: N N, f(n) = 2n f: N R, f(n) = n/2 f: N {13}, f(n)
Funkcja Funkcja o dziedzinie X i przeciwdziedzinie Y to dowolna relacja f XxY taka, że: Notacje: x X! y Y : x, y f f : X Y f x = y f : x y Przykłady f: N N, f(n) = 2n f: N R, f(n) = n/2 f: N {13}, f(n)
MATEMATYKA DYSKRETNA. doc. dr hab. inż. Marek Libura
 Marek Libura MATEMATYKA DYSKRETNA 1 MATEMATYKA DYSKRETNA doc. dr hab. inż. Marek Libura Instytut Badań Systemowych PAN 01-447 Warszawa, Newelska 6, pok. 324 Marek.Libura@ibspan.waw.pl tel.(48)(22)8373578
Marek Libura MATEMATYKA DYSKRETNA 1 MATEMATYKA DYSKRETNA doc. dr hab. inż. Marek Libura Instytut Badań Systemowych PAN 01-447 Warszawa, Newelska 6, pok. 324 Marek.Libura@ibspan.waw.pl tel.(48)(22)8373578
FUNKCJE. (odwzorowania) Funkcje 1
 FUNKCJE (odwzorowania) Funkcje 1 W matematyce funkcja ze zbioru X w zbiór Y nazywa się odwzorowanie (przyporządkowanie), które każdemu elementowi zbioru X przypisuje jeden, i tylko jeden element zbioru
FUNKCJE (odwzorowania) Funkcje 1 W matematyce funkcja ze zbioru X w zbiór Y nazywa się odwzorowanie (przyporządkowanie), które każdemu elementowi zbioru X przypisuje jeden, i tylko jeden element zbioru
5. Algebra działania, grupy, grupy permutacji, pierścienie, ciała, pierścień wielomianów.
 5. Algebra działania, grupy, grupy permutacji, pierścienie, ciała, pierścień wielomianów. Algebra jest jednym z najstarszych działów matematyki dotyczącym początkowo tworzenia metod rozwiązywania równań
5. Algebra działania, grupy, grupy permutacji, pierścienie, ciała, pierścień wielomianów. Algebra jest jednym z najstarszych działów matematyki dotyczącym początkowo tworzenia metod rozwiązywania równań
1.1 Definicja. 1.2 Przykład. 1.3 Definicja. Niech G oznacza dowolny, niepusty zbiór.
 20. Definicje i przykłady podstawowych struktur algebraicznych (grupy, pierścienie, ciała, przestrzenie liniowe). Pojęcia dotyczące przestrzeni liniowych (liniowa zależność i niezależność układu wektorów,
20. Definicje i przykłady podstawowych struktur algebraicznych (grupy, pierścienie, ciała, przestrzenie liniowe). Pojęcia dotyczące przestrzeni liniowych (liniowa zależność i niezależność układu wektorów,
Uzupełnienia dotyczące zbiorów uporządkowanych (3 lutego 2011).
 Uzupełnienia dotyczące zbiorów uporządkowanych (3 lutego 2011). Poprzedniczka tej notatki zawierała błędy! Ta pewnie zresztą też ; ). Ćwiczenie 3 zostało zmienione, bo żądałem, byście dowodzili czegoś,
Uzupełnienia dotyczące zbiorów uporządkowanych (3 lutego 2011). Poprzedniczka tej notatki zawierała błędy! Ta pewnie zresztą też ; ). Ćwiczenie 3 zostało zmienione, bo żądałem, byście dowodzili czegoś,
Moneta 1 Moneta 2 Kostka O, R O,R 1,2,3,4,5, Moneta 1 Moneta 2 Kostka O O ( )
 Nowa matura kombinatoryka i rachunek prawdopodobieństwa Zadania zamknięte (0 1 pkt) 1. Doświadczenie losowe polega na rzucie dwiema symetrycznymi monetami i sześcienną kostką do gry. Prawdopodobieństwo
Nowa matura kombinatoryka i rachunek prawdopodobieństwa Zadania zamknięte (0 1 pkt) 1. Doświadczenie losowe polega na rzucie dwiema symetrycznymi monetami i sześcienną kostką do gry. Prawdopodobieństwo
Typy zadań kombinatorycznych:
 Typy zadań kombinatorycznych: I. Ustawianie wszystkich elementów zbioru w pewnej kolejności Przestawieniem nazywamy ustawienie elementów danego zbioru w pewnej kolejności. Liczba przestawień określa na
Typy zadań kombinatorycznych: I. Ustawianie wszystkich elementów zbioru w pewnej kolejności Przestawieniem nazywamy ustawienie elementów danego zbioru w pewnej kolejności. Liczba przestawień określa na
Matematyka podstawowa X. Rachunek prawdopodobieństwa
 Matematyka podstawowa X Rachunek prawdopodobieństwa Zadania wprowadzające: 1. Rzucasz trzy razy monetą a) Napisz zbiór wszystkich wyników tego doświadczenia losowego. Ile ich jest? Wyrzuciłeś większą liczbę
Matematyka podstawowa X Rachunek prawdopodobieństwa Zadania wprowadzające: 1. Rzucasz trzy razy monetą a) Napisz zbiór wszystkich wyników tego doświadczenia losowego. Ile ich jest? Wyrzuciłeś większą liczbę
Statystyka matematyczna
 Statystyka matematyczna Wykład 1 Magdalena Alama-Bućko 26 lutego 2018 Magdalena Alama-Bućko Statystyka matematyczna 26 lutego 2018 1 / 16 Wykład : 10h (przez 10 tygodni po 45 minut) zaliczenie wykładu
Statystyka matematyczna Wykład 1 Magdalena Alama-Bućko 26 lutego 2018 Magdalena Alama-Bućko Statystyka matematyczna 26 lutego 2018 1 / 16 Wykład : 10h (przez 10 tygodni po 45 minut) zaliczenie wykładu
Lista zadań - Relacje
 MATEMATYKA DYSKRETNA Lista zadań - Relacje Zadania obliczeniowe Zad. 1. Która z poniższych relacji jest funkcją? a) Relacja składająca się ze wszystkich par uporządkowanych, których poprzednikami są studenci,
MATEMATYKA DYSKRETNA Lista zadań - Relacje Zadania obliczeniowe Zad. 1. Która z poniższych relacji jest funkcją? a) Relacja składająca się ze wszystkich par uporządkowanych, których poprzednikami są studenci,
Plan wynikowy. Klasa III Technik pojazdów samochodowych/ Technik urządzeń i systemów energetyki odnawialnej. Kształcenie ogólne w zakresie podstawowym
 Oznaczenia: wymagania konieczne, P wymagania podstawowe, R wymagania rozszerzające, D wymagania dopełniające, W wymagania wykraczające. Plan wynikowy lasa III Technik pojazdów samochodowych/ Technik urządzeń
Oznaczenia: wymagania konieczne, P wymagania podstawowe, R wymagania rozszerzające, D wymagania dopełniające, W wymagania wykraczające. Plan wynikowy lasa III Technik pojazdów samochodowych/ Technik urządzeń
Rachunek prawdopodobieństwa - ćwiczenia pierwsze Kombinatoryka. kierunek: informatyka i ekonometria I
 Rachunek prawdopodobieństwa - ćwiczenia pierwsze Kombinatoryka. kierunek: informatyka i ekonometria I dr Jarosław Kotowicz 07.10.2011 Spis treści 1 Kombinatoryka 1 1 Kombinatoryka permutacja bez powtórzeń
Rachunek prawdopodobieństwa - ćwiczenia pierwsze Kombinatoryka. kierunek: informatyka i ekonometria I dr Jarosław Kotowicz 07.10.2011 Spis treści 1 Kombinatoryka 1 1 Kombinatoryka permutacja bez powtórzeń
WYŻSZA SZKOŁA INFORMATYKI STOSOWANEJ I ZARZĄDZANIA Pod auspicjami Polskiej Akademii Nauk Warszawa, ul. Newelska 6, tel.
 WYŻSZA SZKOŁA INFORMATYKI STOSOWANEJ I ZARZĄDZANIA Pod auspicjami Polskiej Akademii Nauk 01-447 Warszawa, ul. Newelska 6, tel. 22 3486544 Wydział Informatyki Kierunek studiów Profil Stopień studiów Forma
WYŻSZA SZKOŁA INFORMATYKI STOSOWANEJ I ZARZĄDZANIA Pod auspicjami Polskiej Akademii Nauk 01-447 Warszawa, ul. Newelska 6, tel. 22 3486544 Wydział Informatyki Kierunek studiów Profil Stopień studiów Forma
Statystyka Astronomiczna
 Statystyka Astronomiczna czyli zastosowania statystyki w astronomii historycznie astronomowie mieli wkład w rozwój dyscypliny Rachunek prawdopodobieństwa - gałąź matematyki Statystyka - metoda oceny właściwości
Statystyka Astronomiczna czyli zastosowania statystyki w astronomii historycznie astronomowie mieli wkład w rozwój dyscypliny Rachunek prawdopodobieństwa - gałąź matematyki Statystyka - metoda oceny właściwości
a. zbiór wszystkich potasowań talii kart (w którym S dostaje 13 pierwszych kart, W - 13 kolejnych itd.);
 03DRAP - Przykłady przestrzeni probabilistycznych Definicja 1 Przestrzeń probabilistyczna to trójka (Ω, F, P), gdzie Ω zbiór zdarzeń elementarnych, F σ ciało zdarzeń (podzbiorów Ω), P funkcja prawdopodobieństwa/miara
03DRAP - Przykłady przestrzeni probabilistycznych Definicja 1 Przestrzeń probabilistyczna to trójka (Ω, F, P), gdzie Ω zbiór zdarzeń elementarnych, F σ ciało zdarzeń (podzbiorów Ω), P funkcja prawdopodobieństwa/miara
Rachunek prawdopodobieństwa dla informatyków
 Rachunek prawdopodobieństwa dla informatyków Adam Roman Instytut Informatyki UJ Wykład 1 rys historyczny zdarzenia i ich prawdopodobieństwa aksjomaty i reguły prawdopodobieństwa prawdopodobieństwo warunkowe
Rachunek prawdopodobieństwa dla informatyków Adam Roman Instytut Informatyki UJ Wykład 1 rys historyczny zdarzenia i ich prawdopodobieństwa aksjomaty i reguły prawdopodobieństwa prawdopodobieństwo warunkowe
Matematyka dyskretna
 Matematyka dyskretna Wykład 6: Ciała skończone i kongruencje Gniewomir Sarbicki 24 lutego 2015 Relacja przystawania Definicja: Mówimy, że liczby a, b Z przystają modulo m (co oznaczamy jako a = b (mod
Matematyka dyskretna Wykład 6: Ciała skończone i kongruencje Gniewomir Sarbicki 24 lutego 2015 Relacja przystawania Definicja: Mówimy, że liczby a, b Z przystają modulo m (co oznaczamy jako a = b (mod
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: Kierunek: Informatyka Rodzaj przedmiotu: MATEMATYKA DYSKRETNA Discrete mathematics Forma studiów: Stacjonarne Poziom kwalifikacji: Kod przedmiotu: A_06 Rok: I obowiązkowy w ramach treści
Nazwa przedmiotu: Kierunek: Informatyka Rodzaj przedmiotu: MATEMATYKA DYSKRETNA Discrete mathematics Forma studiów: Stacjonarne Poziom kwalifikacji: Kod przedmiotu: A_06 Rok: I obowiązkowy w ramach treści
= 10 9 = Ile jest wszystkich dwucyfrowych liczb naturalnych podzielnych przez 3? A. 12 B. 24 C. 29 D. 30. Sposób I = 30.
 Kombinatoryka i rachunek prawdopodobieństwa Zadania zamknięte (0 1 pkt) 1. Flagę, taką jak pokazano na rysunku, należy zszyć z trzech jednakowej szerokości pasów kolorowej tkaniny. Oba pasy zewnętrzne
Kombinatoryka i rachunek prawdopodobieństwa Zadania zamknięte (0 1 pkt) 1. Flagę, taką jak pokazano na rysunku, należy zszyć z trzech jednakowej szerokości pasów kolorowej tkaniny. Oba pasy zewnętrzne
a. zbiór wszystkich potasowań talii kart (w którym S dostaje 13 pierwszych kart, W - 13 kolejnych itd.);
 03DRAP - Przykłady przestrzeni probabilistycznych A Zadania na ćwiczenia Zadanie A1 (wskazówka: pierwsze ćwicznia i rozdział 23 przykł 1 i 2) Zbuduj model przestrzeni klasycznej (czyli takiej, w której
03DRAP - Przykłady przestrzeni probabilistycznych A Zadania na ćwiczenia Zadanie A1 (wskazówka: pierwsze ćwicznia i rozdział 23 przykł 1 i 2) Zbuduj model przestrzeni klasycznej (czyli takiej, w której
STATYSTYKA MATEMATYCZNA
 STATYSTYKA MATEMATYCZNA 1. Wykład wstępny. Teoria prawdopodobieństwa i elementy kombinatoryki 2. Zmienne losowe i ich rozkłady 3. opulacje i próby danych, estymacja parametrów 4. Testowanie hipotez 5.
STATYSTYKA MATEMATYCZNA 1. Wykład wstępny. Teoria prawdopodobieństwa i elementy kombinatoryki 2. Zmienne losowe i ich rozkłady 3. opulacje i próby danych, estymacja parametrów 4. Testowanie hipotez 5.
WYKŁAD 4: KOMBINATORYKA. CIAGI LICZBOWE. SKOŃCZONE PRZESTRZENIE PROBABILISTYCZNE.
 MATEMATYCZNE PODSTAWY KOGNITYWISTYKI WYKŁAD 4: KOMBINATORYKA. CIAGI LICZBOWE. SKOŃCZONE PRZESTRZENIE PROBABILISTYCZNE. KOGNITYWISTYKA UAM, 016 017 JERZY POGONOWSKI Zakład Logiki i Kognitywistyki UAM pogon@amu.edu.pl
MATEMATYCZNE PODSTAWY KOGNITYWISTYKI WYKŁAD 4: KOMBINATORYKA. CIAGI LICZBOWE. SKOŃCZONE PRZESTRZENIE PROBABILISTYCZNE. KOGNITYWISTYKA UAM, 016 017 JERZY POGONOWSKI Zakład Logiki i Kognitywistyki UAM pogon@amu.edu.pl
Matematyka dyskretna
 Matematyka dyskretna Zbiór zadań kolekcjonowanych w ciągu semestralnego kursu Matematyka dyskretna prof. dr hab. M. Morayne dla studentów informatyki magisterskiej WPPT PWr wiosna-lato 2005 UWAGA: Zadania
Matematyka dyskretna Zbiór zadań kolekcjonowanych w ciągu semestralnego kursu Matematyka dyskretna prof. dr hab. M. Morayne dla studentów informatyki magisterskiej WPPT PWr wiosna-lato 2005 UWAGA: Zadania
Matematyka dyskretna. Andrzej Łachwa, UJ, /14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2017 andrzej.lachwa@uj.edu.pl 9/14 Zasada Dirichleta 1 ZASADA SZUFLADKOWA DIRICHLETA (1ZSD) Jeśli n obiektów jest rozmieszczonych w m szufladach i n > m > 0, to
Matematyka dyskretna Andrzej Łachwa, UJ, 2017 andrzej.lachwa@uj.edu.pl 9/14 Zasada Dirichleta 1 ZASADA SZUFLADKOWA DIRICHLETA (1ZSD) Jeśli n obiektów jest rozmieszczonych w m szufladach i n > m > 0, to
