Matematyka dyskretna zestaw II ( )
|
|
|
- Błażej Matusiak
- 6 lat temu
- Przeglądów:
Transkrypt
1 Matematyka dyskretna zestaw II ( ) Uwaga: Część z zadań z tego zestawu opiera się na zasadzie szufladkowej Dirichleta. Zadanie 1. Na ile sposobów można umieścić w 7 szufladach 3 koszule tak, aby każda była w innej szufladzie? Zadanie 2. Oblicz sumę wszystkich liczb trzycyfrowych zapisanych za pomocą cyfr {0,1,2,3}. Zadanie 3. Ile jest liczb naturalnych trzycyfrowych, w których cyfra dziesiątek jest o 2 większa od cyfry jedności? Zadanie 4. W Dużym Lotku jest losowanych numerów spośród 49. Ile różnych wyników można otrzymać w tym losowaniu? Zadanie 5. Na ile sposobów można posadzić 7 osób na 7-miu numerowanych miejscach? Zadanie 6. W turnieju szachowym, rozgrywanym systemem każdy z każdym, bez rewanżu, miało brać udział 8 zawodników. Jeden z nich zrezygnował. O ile zmniejszyła się liczba zaplanowanych rozgrywek? Zadanie 7. Na wyspie jest 2012 czerwonych, 2013 zielonych i 2014 niebieskich kameleonów. Jeśli spotkają się dwa kameleony różnych kolorów, każdy z nich zmienia swój kolor na trzeci kolor. Czy może dojść do sytuacji, w której na wyspie wszystkie kameleony będą miały ten sam kolor? 1
2 Zadanie 8. Udowodnij, że w dowolnej grupie osób zawsze znajdą się dwie takie, które mają tyle samo znajomych (przyjmujemy, że jeśli osoba math zna osobę math to także osoba math zna osobę math ). Zadanie 9. W zestawie zadań jest 15 zadań łatwych i 5 trudnych. Na ile sposobów można z tego zestawu wybrać 10 zadań tak aby wśród nich było 7 zadań łatwych i 3 trudne? Zadanie 10. Z tali 52 karty wybieramy 4 losowo karty. jakie jest prawdopodobieństwo tego że wśród wybranych kart nie bedzie ani jednego kiera? jakie jest prawdopodobieństwo tego że wśród wybranych kart bedzie co najmniej jeden as? Zadanie 11. Odtwórzmy w sposób przypadkowy 3 utwory z płyty zawierającej 12 utworów(utwory moga się powtarzać). Ile jest różnych możliwych zestawów? Zadanie 12. W przedziale kolejowym jest 8 miejsc. Na ile różnych sposobów może w nim zająć miejsca 8 pasażerów? Zadanie 13. Na ile sposobów można wybrać trzy gałki lodów o różnych smakach spośród 10 rodzajów lodów? Zadanie 14. Na obozie młodzieżowym jest 30 osób. Na ile róznych sposobów można wybrać spośród uczestników 3 osoby dyżurujące w kuchni? Zadanie 15. Wśród 10 mężczyzn jest 2 brunetów, 5 szatynów, a pozostali są łysi. Na ile sposobów można wybrać 5 osobwy zespół, w którym będzie 1 brunet, 2 szatynów i 2 łysych? 2
3 Zadanie 16. Ze wsi A do wsi B prowadzi 5 ścieżek przez las. Na ile sposobów można odbyć spacer A-B-A tak, aby spacer ze wsi B do wsi A odbyć inną ścieżką niż ze wsi A do wsi B? Zadanie 17. Ile jest wszystkich liczb naturalnych trzycyfrowych podzielnych przez 5? Zadanie 18. Dane są dwa pojemniki. W pierwszym z nich znajduje się 9 kul: 4 białe, 3 czarne i 2 zielone. W drugim pojemniku jest 6 kul: 2 białe, 3 czarne i 1 zielona. Z każdego pojemnika losujemy po jednej kuli. Oblicz prawdopodobieństwo wylosowania dwóch kul różnych kolorów. Zadanie 19. Udowodnij, że w grupie 2012 osób przynajmniej 2 osoby mają taką samą liczbę znajomych (osoba A zna osobę B wtedy i tylko wtedy, gdy osoba B zna osobę A). Zadanie 20. Udowodnij, że w gronie 6 osób albo pewne 3 osoby się znają, albo pewne 3 osoby się nie znają. Zadanie 21. Udowodnij, że wśród dowolnych 7 różnych liczb całkowitych musza być takie 2, których suma lub różnica dzieli się przez 10. Zadanie 22. Spośród liczb 1,2,3,...,9 wybrano sześć.udowodnij, że spośród wybranych liczb można wybrać dwie których suma wynosi 10. Zadanie 23. Dany jest pewien zbiór 2015 liczb naturalnych. Wykaż, że można z tego zbioru wybrać takie trzy liczby x, y, z, aby liczba (x?y)z była podzielna przez Zadanie 24. W sześciokącie foremnym o boku długości 1 umieszczono 7 punktów. Udowodnij, że istnieją 2 punkty, których odległość jest mniejsza lub równa 1. 3
4 Zadanie 25. W sześcianie o boku 1 umieszczono 217 punktów. Wykaż, że istnieją 2 punkty odległe o co najwyżej. Zadanie 26. Przy okrągłym stole ma usiąść n osób. Na stole postawiono karteczki z ich imionami (każdy ma inaczej na imię). Usiedli przy stole w taki sposób że żaden nie siedział na miejscu przy odpowiednim imieniu. Wykaz że można tak obrócić stół, aby przynajmniej dwoje ludzi siedziało na odpowiednim miejscu. Zadanie 27. Przy Okrągłym Stole siedzi 12 Rycerzy. W czasie obrad każdych dwóch siedzących obok siebie pokłóciło się. Król Artur musi posłać w misję 5 Rycerzy. Na ile sposobów może to zrobić jeśli nie chce, aby wśród wysłanych byli jacyś kłócący się Rycerze? Zadanie 28. Mnich benedyktyn wpisuje na oprawie każdej z ksiąg znajdujących się w bibliotece klasztornej kolejny numer. Ile razy napisze cyfrę 9, jeśli wiadomo, że księgozbiór liczy sobie woluminów, zaś mnich rozpoczyna numerowanie od 1? Zadanie 29. Towarzystwo złożone z 8 par małżeńskich dzieli się na 4 grupy po 4 osoby dla odbycia spaceru łódką. Na ile sposobów można to zrobić tak, aby w każdej łódce znalazły się 2 panie i 2 panów? W ilu przypadkach danych mężczyzna znajdzie się w łódce ze swoją żoną? Łódki nie są numerowane. Zadanie 30. W ilu permutacjach liczb 1,...,5 żadna z liczb nie stoi na swoim miejscu? Zadanie 31. Proszę wypisać wszystkie funkcje ze zbioru {1,2,3} na zbiór {a,b}. Proszę wskazać funkcje iniekcje oraz suriekcje. Zadania a j należy wykonać korzystając z odpowiednich wzorów na permutacje, kombinacje, itd. tłumacząc za każdym razem możliwość ich użycia. 4
5 Zadanie 32. Na ile sposobów k różnych tabliczek czekolady można rozdzielić pomiędzy n osób (każda z osób może otrzymać więcej niż jedną tabliczkę)? Zadanie 33. Na ile sposobów k różnych tabliczek czekolady można rozdzielić pomiędzy n osób (każda z osób może otrzymać najwyżej jedną tabliczkę)? Zadanie 34. Na ile sposobów k identycznych tabliczek czekolady można rozdzielić pomiędzy n osób (każda z osób może otrzymać więcej niż jedną tabliczkę)? Zadanie 35. Na ile sposobów k różnych tabliczek czekolady można rozdzielić pomiędzy n osób (każda z osób może otrzymać najwyżej jedną tabliczkę)? Zadanie 36. Jaka jest ilość funkcji różnowartościowych f z {1,2,...,k} do {1,2,...,n}? Zadanie 37. Jaka jest ilość funkcji f z {1,2,...,k} do {1,2,...,n}? Zadanie 38. Na ile sposobów można wybrać k-elementowy podzbiór ze zbioru n-elementowego? Zadanie 39. Na ile sposobów k-najwyższych rangą urzędników w Polsce może zostać wybranych z pośród n-osób? (Ma to być uporządkowana lista, a nie zbiór.) Zadanie 40. Na ile sposobów k cukierków (niekoniecznie tego samego rodzaju) może zostać wybranych z pośród n rodzajów? Zadanie 41. Na ile sposobów k dzieci może wybrać jeden cukierek (każdy o innym smaku) z pośród n różnych smaków cukierków? 5
6 Zadanie 42. Na ile sposobów można ustawić litery a, b, c, d, e, f w takiej kolejności, by litery a i b sąsiadowały z sobą? Zadanie 43. Na ile sposobów można ustawić litery a, b, c, d, e, f w takiej kolejności, by litery a i b nie sąsiadowały z sobą? Zadanie 44. Na ile sposobów można ustawić litery a, b, c, d, e, f w takiej kolejności, by litery a i b sąsiadowały z sobą, ale litery a i c nie? Zadanie 45. Na ile sposobów można rozmieścić 14 przedmiotów (jednego rodzaju) w 3 pudełkach tak, by w jednym z pudełek znalazło się co najmniej 8 przedmiotów? Zadanie 46. Na ile sposobów można rozmieścić 14 przedmiotów w 3 pudełkach tak, by w żadnym z pudełek nie znalazło się więcej niż 7 przedmiotów? Zadanie 47. Ile jest liczb między 0 a 999, których suma cyfr jest równa 20? Wskazówka: każda z cyfr musi być równa co najmniej 2; można zastosować część ( b ). 6
Lista zadania nr 2 Metody probabilistyczne i statystyka studia I stopnia informatyka (rok 2) Wydziału Ekonomiczno-Informatycznego Filia UwB w Wilnie
 Lista zadania nr 2 Metody probabilistyczne i statystyka studia I stopnia informatyka (rok 2) Wydziału Ekonomiczno-Informatycznego Filia UwB w Wilnie Jarosław Kotowicz Instytut Matematyki Uniwersytet w
Lista zadania nr 2 Metody probabilistyczne i statystyka studia I stopnia informatyka (rok 2) Wydziału Ekonomiczno-Informatycznego Filia UwB w Wilnie Jarosław Kotowicz Instytut Matematyki Uniwersytet w
Matematyka podstawowa X. Rachunek prawdopodobieństwa
 Matematyka podstawowa X Rachunek prawdopodobieństwa Zadania wprowadzające: 1. Rzucasz trzy razy monetą a) Napisz zbiór wszystkich wyników tego doświadczenia losowego. Ile ich jest? Wyrzuciłeś większą liczbę
Matematyka podstawowa X Rachunek prawdopodobieństwa Zadania wprowadzające: 1. Rzucasz trzy razy monetą a) Napisz zbiór wszystkich wyników tego doświadczenia losowego. Ile ich jest? Wyrzuciłeś większą liczbę
Z4. Ankieta złożona ma być z trzech pytań: A, B i C. Na ile sposobów można ją ułożyć zmieniając tylko kolejność pytań? ODP. Jest 6 możliwych sposobów.
 PERMUTACJE Z1. Oblicz: Z2. Doprowadź do najprostszej postaci wyrażenia: Z3. Sprawdź czy prawdziwa jest równość: Dana równość jest prawdziwa. Z4. Ankieta złożona ma być z trzech pytań: A, B i C. Na ile
PERMUTACJE Z1. Oblicz: Z2. Doprowadź do najprostszej postaci wyrażenia: Z3. Sprawdź czy prawdziwa jest równość: Dana równość jest prawdziwa. Z4. Ankieta złożona ma być z trzech pytań: A, B i C. Na ile
Prawdopodobieństwo
 Prawdopodobieństwo http://www.matemaks.pl/ Wstęp do rachunku prawdopodobieństwa http://www.matemaks.pl/wstep-do-rachunku-prawdopodobienstwa.html Rachunek prawdopodobieństwa pomaga obliczyć szansę zaistnienia
Prawdopodobieństwo http://www.matemaks.pl/ Wstęp do rachunku prawdopodobieństwa http://www.matemaks.pl/wstep-do-rachunku-prawdopodobienstwa.html Rachunek prawdopodobieństwa pomaga obliczyć szansę zaistnienia
SPRAWDZIAN KOMBINATORYKA
 www.zadania.info NAJWIEKSZY INTERNETOWY ZBIÓR ZADAŃ Z MATEMATYKI SPRAWDZIAN KOMBINATORYKA 12 GRUDNIA 2011 CZAS PRACY: 45 MIN. ZADANIE 1 Spośród liczb {1, 2, 3,..., 1000} losujemy jednocześnie dwie, które
www.zadania.info NAJWIEKSZY INTERNETOWY ZBIÓR ZADAŃ Z MATEMATYKI SPRAWDZIAN KOMBINATORYKA 12 GRUDNIA 2011 CZAS PRACY: 45 MIN. ZADANIE 1 Spośród liczb {1, 2, 3,..., 1000} losujemy jednocześnie dwie, które
Elementy statystyki opisowej, teoria prawdopodobieństwa i kombinatoryka
 Wymagania egzaminacyjne: a) oblicza średnią arytmetyczną, średnią ważoną, medianę i odchylenie standardowe danych; interpretuje te parametry dla danych empirycznych, b) zlicza obiekty w prostych sytuacjach
Wymagania egzaminacyjne: a) oblicza średnią arytmetyczną, średnią ważoną, medianę i odchylenie standardowe danych; interpretuje te parametry dla danych empirycznych, b) zlicza obiekty w prostych sytuacjach
Kombinatoryka i rachunek prawdopodobieństwa (rozszerzenie)
 Kombinatoryka i rachunek prawdopodobieństwa (rozszerzenie) (1) Ile liczb czterocyfrowych można utworzyć używając jedynie cyfr 1,2,3,4,5,6,7,8? (2) Ile liczb czterocyfrowych o różnych cyfrach można utworzyć
Kombinatoryka i rachunek prawdopodobieństwa (rozszerzenie) (1) Ile liczb czterocyfrowych można utworzyć używając jedynie cyfr 1,2,3,4,5,6,7,8? (2) Ile liczb czterocyfrowych o różnych cyfrach można utworzyć
Moneta 1 Moneta 2 Kostka O, R O,R 1,2,3,4,5, Moneta 1 Moneta 2 Kostka O O ( )
 Nowa matura kombinatoryka i rachunek prawdopodobieństwa Zadania zamknięte (0 1 pkt) 1. Doświadczenie losowe polega na rzucie dwiema symetrycznymi monetami i sześcienną kostką do gry. Prawdopodobieństwo
Nowa matura kombinatoryka i rachunek prawdopodobieństwa Zadania zamknięte (0 1 pkt) 1. Doświadczenie losowe polega na rzucie dwiema symetrycznymi monetami i sześcienną kostką do gry. Prawdopodobieństwo
PRAWDOPODOBIEŃSTWO I KOMBINATORYKA
 PRAWDOPODOBIEŃSTWO I KOMBINATORYKA ZADANIE ( PKT) Z urny zawierajacej kule w dwóch kolorach wybieramy losowo dwie. Prawdopodobieństwo wylosowania co najmniej jednej kuli białej jest równe 8, a prawdopodobieństwo
PRAWDOPODOBIEŃSTWO I KOMBINATORYKA ZADANIE ( PKT) Z urny zawierajacej kule w dwóch kolorach wybieramy losowo dwie. Prawdopodobieństwo wylosowania co najmniej jednej kuli białej jest równe 8, a prawdopodobieństwo
NAJWIEKSZY INTERNETOWY ZBIÓR ZADAŃ Z MATEMATYKI ZADANIE 1 oczka. ZADANIE 2 iloczynu oczek równego 12.
 IMIE I NAZWISKO ZADANIE 1 Rzucamy sześcienna kostka do gry. Jakie jest prawdopodobieństwo, że wypadna co najmniej dwa oczka. ZADANIE 2 Rzucamy trzy razy symetryczna sześcienna kostka do gry. Oblicz prawdopodobieństwo
IMIE I NAZWISKO ZADANIE 1 Rzucamy sześcienna kostka do gry. Jakie jest prawdopodobieństwo, że wypadna co najmniej dwa oczka. ZADANIE 2 Rzucamy trzy razy symetryczna sześcienna kostka do gry. Oblicz prawdopodobieństwo
ZADANIE 1 ZADANIE 2. NAJWIEKSZY INTERNETOWY ZBIÓR ZADAŃ Z MATEMATYKI A) 5,5 B) 8 C) 5,75 D) 4. nie wygramy nagrody jest równe A)
 ZADANIE 1 Średnia arytmetyczna licz 5,5,7,3,9,9,4,4 jest liczba A) 5,5 B) 8 C) 5,75 D) 4 ZADANIE 2 Na loterii jest 10 losów, z których 4 sa wygrywajace. Kupujemy jeden los. Prawdopodobieństwo zdarzenia,
ZADANIE 1 Średnia arytmetyczna licz 5,5,7,3,9,9,4,4 jest liczba A) 5,5 B) 8 C) 5,75 D) 4 ZADANIE 2 Na loterii jest 10 losów, z których 4 sa wygrywajace. Kupujemy jeden los. Prawdopodobieństwo zdarzenia,
liczb naturalnych czterocyfrowych. Mamy do dyspozycji następujące cyfry: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. g) Ile jest liczb czterocyfrowych parzystych?
 KOMBINATORYKA ZADANIA Z ROZWIĄZANIAMI 1. Udziel odpowiedzi na poniższe pytania: a) Ile jest możliwych wyników w rzucie jedną kostką? W rzucie jedną kostką możemy otrzymać jeden spośród następujących wyników:
KOMBINATORYKA ZADANIA Z ROZWIĄZANIAMI 1. Udziel odpowiedzi na poniższe pytania: a) Ile jest możliwych wyników w rzucie jedną kostką? W rzucie jedną kostką możemy otrzymać jeden spośród następujących wyników:
WITAMY SERDECZNIE NA MIĘDZYSZKOLNYCH WARSZTATACH MATEMATYCZNYCH 12
 Dobry matematyk potrafi dostrzegać fakty, matematyk wybitny analogie między faktami, zaś matematyk genialny analogie między analogiami. Stefan Banach WITAMY SERDECZNIE NA MIĘDZYSZKOLNYCH WARSZTATACH MATEMATYCZNYCH
Dobry matematyk potrafi dostrzegać fakty, matematyk wybitny analogie między faktami, zaś matematyk genialny analogie między analogiami. Stefan Banach WITAMY SERDECZNIE NA MIĘDZYSZKOLNYCH WARSZTATACH MATEMATYCZNYCH
c) Zaszły oba zdarzenia A i B; d) Zaszło zdarzenie A i nie zaszło zdarzenie B;
 Rachunek prawdopodobieństwa rozwiązywanie zadań 1. Rzucamy dwa razy symetryczną sześcienną kostką do gry. Zapisujemy liczbę oczek, jakie wypadły w obu rzutach. Wypisz zdarzenia elementarne tego doświadczenia.
Rachunek prawdopodobieństwa rozwiązywanie zadań 1. Rzucamy dwa razy symetryczną sześcienną kostką do gry. Zapisujemy liczbę oczek, jakie wypadły w obu rzutach. Wypisz zdarzenia elementarne tego doświadczenia.
Zadanie 1. Na diagramie Venna dla 3 zbiorów zaznacz:
 Zadanie 1 Na diagramie Venna dla 3 zbiorów zaznacz: A B C Zadanie 1 Na diagramie Venna dla 3 zbiorów zaznacz: A B C A B C Zadanie 1 Na diagramie Venna dla 3 zbiorów zaznacz: A B C A B C A B C Zadanie 1
Zadanie 1 Na diagramie Venna dla 3 zbiorów zaznacz: A B C Zadanie 1 Na diagramie Venna dla 3 zbiorów zaznacz: A B C A B C Zadanie 1 Na diagramie Venna dla 3 zbiorów zaznacz: A B C A B C A B C Zadanie 1
Kombinatoryka. Jerzy Rutkowski. Teoria. P n = n!. (1) Zadania obowiązkowe
 Kombinatoryka Jerzy Rutkowski 2. Elementy kombinatoryki 2.1. Permutacje Definicja 1. Niech n N. Permutacją n-elementowego zbioru A nazywamy dowolną funkcję różnowartościową f : {1,..., n} A. Innymi słowy:
Kombinatoryka Jerzy Rutkowski 2. Elementy kombinatoryki 2.1. Permutacje Definicja 1. Niech n N. Permutacją n-elementowego zbioru A nazywamy dowolną funkcję różnowartościową f : {1,..., n} A. Innymi słowy:
Kombinatoryka i rachunek prawdopodobieństwa
 Kombinatoryka i rachunek prawdopodobieństwa Jerzy Rutkowski Kombinatoryka i rachunek prawdopodobieństwa 2. Elementy kombinatoryki 2.1. Permutacje Definicja 1. Niech n N. Permutacją n-elementowego zbioru
Kombinatoryka i rachunek prawdopodobieństwa Jerzy Rutkowski Kombinatoryka i rachunek prawdopodobieństwa 2. Elementy kombinatoryki 2.1. Permutacje Definicja 1. Niech n N. Permutacją n-elementowego zbioru
Typy zadań kombinatorycznych:
 Typy zadań kombinatorycznych: I. Ustawianie wszystkich elementów zbioru w pewnej kolejności Przestawieniem nazywamy ustawienie elementów danego zbioru w pewnej kolejności. Liczba przestawień określa na
Typy zadań kombinatorycznych: I. Ustawianie wszystkich elementów zbioru w pewnej kolejności Przestawieniem nazywamy ustawienie elementów danego zbioru w pewnej kolejności. Liczba przestawień określa na
Kurs ZDAJ MATURĘ Z MATEMATYKI MODUŁ 14 Zadania statystyka, prawdopodobieństwo i kombinatoryka
 1 TEST WSTĘPNY 1. (1p) Zestaw danych 3, 5, x, 7, 10, 12 jest uporządkowany niemalejąco. Mediana tego zestawu jest równa 6, więc liczba x jest równa A. 7 B. 6 C. 5 D. 4 2. (2p) Średnia arytmetyczna liczb:
1 TEST WSTĘPNY 1. (1p) Zestaw danych 3, 5, x, 7, 10, 12 jest uporządkowany niemalejąco. Mediana tego zestawu jest równa 6, więc liczba x jest równa A. 7 B. 6 C. 5 D. 4 2. (2p) Średnia arytmetyczna liczb:
L.Kowalski zadania z rachunku prawdopodobieństwa-zestaw 1 ZADANIA - ZESTAW 1. (odp. a) B A C, b) A, c) A B, d) Ω)
 ZADANIA - ZESTAW 1 Zadanie 1.1 Rzucamy trzy razy monetą. A i - zdarzenie polegające na tym, że otrzymamy orła w i - tym rzucie. Określić zbiór zdarzeń elementarnych. Wypisać zdarzenia elementarne sprzyjające
ZADANIA - ZESTAW 1 Zadanie 1.1 Rzucamy trzy razy monetą. A i - zdarzenie polegające na tym, że otrzymamy orła w i - tym rzucie. Określić zbiór zdarzeń elementarnych. Wypisać zdarzenia elementarne sprzyjające
Rachunek prawdopodobieństwa - ćwiczenia pierwsze Kombinatoryka. kierunek: informatyka i ekonometria I
 Rachunek prawdopodobieństwa - ćwiczenia pierwsze Kombinatoryka. kierunek: informatyka i ekonometria I dr Jarosław Kotowicz 07.10.2011 Spis treści 1 Kombinatoryka 1 1 Kombinatoryka permutacja bez powtórzeń
Rachunek prawdopodobieństwa - ćwiczenia pierwsze Kombinatoryka. kierunek: informatyka i ekonometria I dr Jarosław Kotowicz 07.10.2011 Spis treści 1 Kombinatoryka 1 1 Kombinatoryka permutacja bez powtórzeń
Matematyka dyskretna. Andrzej Łachwa, UJ, /14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2017 andrzej.lachwa@uj.edu.pl 9/14 Zasada Dirichleta 1 ZASADA SZUFLADKOWA DIRICHLETA (1ZSD) Jeśli n obiektów jest rozmieszczonych w m szufladach i n > m > 0, to
Matematyka dyskretna Andrzej Łachwa, UJ, 2017 andrzej.lachwa@uj.edu.pl 9/14 Zasada Dirichleta 1 ZASADA SZUFLADKOWA DIRICHLETA (1ZSD) Jeśli n obiektów jest rozmieszczonych w m szufladach i n > m > 0, to
1. Elementy kombinatoryki - zadania do wyboru
 . Elementy kombinatoryki - zadania do wyboru Bernadeta Tomasz Zadania dodatkowe Zadanie.. Mamy do wyboru mieszkania i auta. Na ile sposobów można dokonać wyboru, jeśli. mamy wybrać mieszkanie i samochód,.
. Elementy kombinatoryki - zadania do wyboru Bernadeta Tomasz Zadania dodatkowe Zadanie.. Mamy do wyboru mieszkania i auta. Na ile sposobów można dokonać wyboru, jeśli. mamy wybrać mieszkanie i samochód,.
KURS PRAWDOPODOBIEŃSTWO
 KURS PRAWDOPODOBIEŃSTWO Lekcja 2 Klasyczna definicja prawdopodobieństwa ZADANIE DOMOWE www.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowiedź (tylko jedna jest prawdziwa). Pytanie 1 Według klasycznej
KURS PRAWDOPODOBIEŃSTWO Lekcja 2 Klasyczna definicja prawdopodobieństwa ZADANIE DOMOWE www.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowiedź (tylko jedna jest prawdziwa). Pytanie 1 Według klasycznej
Lista zadania nr 1 Metody probabilistyczne i statystyka studia I stopnia informatyka (rok 2) Wydziału Ekonomiczno-Informatycznego Filia UwB w Wilnie
 Lista zadania nr 1 Metody probabilistyczne i statystyka studia I stopnia informatyka (rok 2 Wydziału Ekonomiczno-Informatycznego Filia UwB w Wilnie Jarosław Kotowicz Instytut Matematyki Uniwersytet w Białymstoku
Lista zadania nr 1 Metody probabilistyczne i statystyka studia I stopnia informatyka (rok 2 Wydziału Ekonomiczno-Informatycznego Filia UwB w Wilnie Jarosław Kotowicz Instytut Matematyki Uniwersytet w Białymstoku
KURS WSPOMAGAJĄCY PRZYGOTOWANIA DO MATURY Z MATEMATYKI ZDAJ MATMĘ NA MAKSA. przyjmuje wartości większe od funkcji dokładnie w przedziale
 Zestaw nr 1 Poziom Rozszerzony Zad.1. (1p) Liczby oraz, są jednocześnie ujemne wtedy i tylko wtedy, gdy A. B. C. D. Zad.2. (1p) Funkcja przyjmuje wartości większe od funkcji dokładnie w przedziale. Wtedy
Zestaw nr 1 Poziom Rozszerzony Zad.1. (1p) Liczby oraz, są jednocześnie ujemne wtedy i tylko wtedy, gdy A. B. C. D. Zad.2. (1p) Funkcja przyjmuje wartości większe od funkcji dokładnie w przedziale. Wtedy
Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
 Zadanie PP RP 1. Z pojemnika, w którym znajdują się cztery losy z numerami 112, 121, 211, 212 losujemy trzy razy po jednym losie, po każdym losowaniu zwracając wylosowany los do pojemnika. Oblicz prawdopodobieństwo,
Zadanie PP RP 1. Z pojemnika, w którym znajdują się cztery losy z numerami 112, 121, 211, 212 losujemy trzy razy po jednym losie, po każdym losowaniu zwracając wylosowany los do pojemnika. Oblicz prawdopodobieństwo,
Matematyka dyskretna. Andrzej Łachwa, UJ, /10
 Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 6/10 Zasada Dirichleta 1 ZASADA SZUFLADKOWA DIRICHLETA (1ZSD) Jeśli n obiektów jest rozmieszczonych w m szufladach i n > m > 0, to
Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 6/10 Zasada Dirichleta 1 ZASADA SZUFLADKOWA DIRICHLETA (1ZSD) Jeśli n obiektów jest rozmieszczonych w m szufladach i n > m > 0, to
Rachunek prawdopodobieństwa
 Rachunek prawdopodobieństwa Sebastian Rymarczyk srymarczyk@afm.edu.pl Tematyka zajęć 1. Elementy kombinatoryki. 2. Definicje prawdopodobieństwa. 3. Własności prawdopodobieństwa. 4. Zmienne losowe, parametry
Rachunek prawdopodobieństwa Sebastian Rymarczyk srymarczyk@afm.edu.pl Tematyka zajęć 1. Elementy kombinatoryki. 2. Definicje prawdopodobieństwa. 3. Własności prawdopodobieństwa. 4. Zmienne losowe, parametry
Skrypt 30. Prawdopodobieństwo
 Projekt Innowacyjny program nauczania matematyki dla liceów ogólnokształcących współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 30 Prawdopodobieństwo 5.
Projekt Innowacyjny program nauczania matematyki dla liceów ogólnokształcących współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 30 Prawdopodobieństwo 5.
PRZYKŁADOWY ARKUSZ EGZAMINACYJNY Z MATEMATYKI
 PRZYKŁADOWY ARKUSZ EGZAMINACYJNY Z MATEMATYKI Zestaw P1 POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla piszącego 1. Sprawdź, czy arkusz zawiera 16 stron.. W zadaniach od 1. do 5. są podane 4 odpowiedzi:
PRZYKŁADOWY ARKUSZ EGZAMINACYJNY Z MATEMATYKI Zestaw P1 POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla piszącego 1. Sprawdź, czy arkusz zawiera 16 stron.. W zadaniach od 1. do 5. są podane 4 odpowiedzi:
01DRAP - klasyczna definicja prawdopodobieństwa
 01DRAP - klasyczna definicja prawdopodobieństwa Ω zbiór zdarzeń elementarnych. Gdy Ω < oraz P({ω} = 1 Ω, dla każdego ω Ω (tzn. każde zdarzenie elementarne jest równo prawdopodobne, to P (A = A Ω Przydatne
01DRAP - klasyczna definicja prawdopodobieństwa Ω zbiór zdarzeń elementarnych. Gdy Ω < oraz P({ω} = 1 Ω, dla każdego ω Ω (tzn. każde zdarzenie elementarne jest równo prawdopodobne, to P (A = A Ω Przydatne
Matematyka dyskretna. Andrzej Łachwa, UJ, A/14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl 9A/14 Zasada Dirichleta 1 ZASADA SZUFLADKOWA DIRICHLETA (1ZSD) Jeśli n obiektów jest rozmieszczonych w m szufladach i n > m > 0, to
Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl 9A/14 Zasada Dirichleta 1 ZASADA SZUFLADKOWA DIRICHLETA (1ZSD) Jeśli n obiektów jest rozmieszczonych w m szufladach i n > m > 0, to
Zadanie 1. Oblicz prawdopodobieństwo, że rzucając dwiema kostkami do gry otrzymamy:
 Zadanie 1. Oblicz prawdopodobieństwo, że rzucając dwiema kostkami do gry otrzymamy: a) sumę oczek równą 6, b) iloczyn oczek równy 6, c) sumę oczek mniejszą niż 11, d) iloczyn oczek będący liczbą parzystą,
Zadanie 1. Oblicz prawdopodobieństwo, że rzucając dwiema kostkami do gry otrzymamy: a) sumę oczek równą 6, b) iloczyn oczek równy 6, c) sumę oczek mniejszą niż 11, d) iloczyn oczek będący liczbą parzystą,
PRÓBNY EGZAMIN GIMNAZJALNY
 PRÓBNY EGZAMIN GIMNAZJALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO 24 MARCA 2012 CZAS PRACY: 90 MINUT 1 ZADANIE 1 (1 PKT.) Która równość jest fałszywa? Wybierz odpowiedź spośród
PRÓBNY EGZAMIN GIMNAZJALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO 24 MARCA 2012 CZAS PRACY: 90 MINUT 1 ZADANIE 1 (1 PKT.) Która równość jest fałszywa? Wybierz odpowiedź spośród
Ciągi Podzbiory Symbol Newtona Zasada szufladkowa Dirichleta Zasada włączania i wyłączania. Ilość najkrótszych dróg. Kombinatoryka. Magdalena Lemańska
 Kombinatoryka Magdalena Lemańska Literatura Matematyka Dyskretna Andrzej Szepietowski http://wazniak.mimuw.edu.pl/ Discrete Mathematics Seymour Lipschutz, Marc Lipson Aspekty kombinatoryki Victor Bryant
Kombinatoryka Magdalena Lemańska Literatura Matematyka Dyskretna Andrzej Szepietowski http://wazniak.mimuw.edu.pl/ Discrete Mathematics Seymour Lipschutz, Marc Lipson Aspekty kombinatoryki Victor Bryant
KOMBINATORYKA OBIEKTY KOMBINATORYCZNE MATEMATYKA DYSKRETNA (2014/2015)
 MATEMATYKA DYSKRETNA (2014/2015) dr hab. inż. Małgorzata Sterna malgorzata.sterna@cs.put.poznan.pl www.cs.put.poznan.pl/msterna/ KOMBINATORYKA OBIEKTY KOMBINATORYCZNE TEORIA ZLICZANIA Teoria zliczania
MATEMATYKA DYSKRETNA (2014/2015) dr hab. inż. Małgorzata Sterna malgorzata.sterna@cs.put.poznan.pl www.cs.put.poznan.pl/msterna/ KOMBINATORYKA OBIEKTY KOMBINATORYCZNE TEORIA ZLICZANIA Teoria zliczania
01DRAP - klasyczna definicja prawdopodobieństwa
 01DRAP - klasyczna definicja prawdopodobieństwa Ω zbiór zdarzeń elementarnych. Gdy Ω < oraz P({ω} = 1 Ω, dla każdego ω Ω (tzn. każde zdarzenie elementarne jest równo prawdopodobne, to P (A = A Ω Przydatne
01DRAP - klasyczna definicja prawdopodobieństwa Ω zbiór zdarzeń elementarnych. Gdy Ω < oraz P({ω} = 1 Ω, dla każdego ω Ω (tzn. każde zdarzenie elementarne jest równo prawdopodobne, to P (A = A Ω Przydatne
RACHUNEK PRAWDOPODOBIEŃSTWA ZADANIA Z ROZWIĄZANIAMI. Uwaga! Dla określenia liczebności zbioru (mocy zbioru) użyto zamiennie symboli: Ω lub
 RACHUNEK PRAWDOPODOBIEŃSTWA ZADANIA Z ROZWIĄZANIAMI Uwaga! Dla określenia liczebności zbioru (mocy zbioru) użyto zamiennie symboli: Ω lub 1. W grupie jest 15 kobiet i 18 mężczyzn. Losujemy jedną osobę
RACHUNEK PRAWDOPODOBIEŃSTWA ZADANIA Z ROZWIĄZANIAMI Uwaga! Dla określenia liczebności zbioru (mocy zbioru) użyto zamiennie symboli: Ω lub 1. W grupie jest 15 kobiet i 18 mężczyzn. Losujemy jedną osobę
R_PRACA KLASOWA 1 Statystyka i prawdopodobieństwo.
 R_PRACA KLASOWA 1 Statystyka i prawdopodobieństwo. Zadanie 1. Wyznacz średnią arytmetyczną, dominantę i medianę zestawu danych: 1, 5, 3, 2, 2, 4, 4, 6, 7, 1, 1, 4, 5, 5, 3. Zadanie 2. W zestawie danych
R_PRACA KLASOWA 1 Statystyka i prawdopodobieństwo. Zadanie 1. Wyznacz średnią arytmetyczną, dominantę i medianę zestawu danych: 1, 5, 3, 2, 2, 4, 4, 6, 7, 1, 1, 4, 5, 5, 3. Zadanie 2. W zestawie danych
Próbny Egzamin Gimnazjalny z Matematyki Zestaw przygotowany przez serwis 24 marca 2012 Czas pracy: 90 minut
 Strona 1 /Gimnazjum/Egzamin gimnazjalny Próbny Egzamin Gimnazjalny z Matematyki Zestaw przygotowany przez serwis www.zadania.info 24 marca 2012 Czas pracy: 90 minut Zadanie 1 (1 pkt.) Która równość jest
Strona 1 /Gimnazjum/Egzamin gimnazjalny Próbny Egzamin Gimnazjalny z Matematyki Zestaw przygotowany przez serwis www.zadania.info 24 marca 2012 Czas pracy: 90 minut Zadanie 1 (1 pkt.) Która równość jest
Liczby rzeczywiste, wyrażenia algebraiczne, równania i nierówności, statystyka, prawdopodobieństwo.
 Liczby rzeczywiste, wyrażenia algebraiczne, równania i nierówności, statystyka, prawdopodobieństwo. Zagadnienia szczegółowe: obliczanie wartości wyrażeń arytmetycznych; działania na pierwiastkach i potęgach;
Liczby rzeczywiste, wyrażenia algebraiczne, równania i nierówności, statystyka, prawdopodobieństwo. Zagadnienia szczegółowe: obliczanie wartości wyrażeń arytmetycznych; działania na pierwiastkach i potęgach;
Matematyka dyskretna. Andrzej Łachwa, UJ, A/14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 9A/14 Permutacje Permutacja zbioru skończonego X to bijekcja z X w X. Zbiór permutacji zbioru oznaczamy przez, a permutacje małymi
Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 9A/14 Permutacje Permutacja zbioru skończonego X to bijekcja z X w X. Zbiór permutacji zbioru oznaczamy przez, a permutacje małymi
Matematyka dyskretna. Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl. Przykłady zadań egzaminacyjnych (do liczenia lub dowodzenia)
 Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl Przykłady zadań egzaminacyjnych (do liczenia lub dowodzenia) 1. Ile układów kart w pokerze to Dwie pary? Dwie pary to układ 5 kart
Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl Przykłady zadań egzaminacyjnych (do liczenia lub dowodzenia) 1. Ile układów kart w pokerze to Dwie pary? Dwie pary to układ 5 kart
WOJEWÓDZKI KONKURS MATEMATYCZNY
 Kod ucznia Liczba punktów WOJEWÓDZKI KONKURS MATEMATYCZNY DLA UCZNIÓW GIMNAZJÓW W ROKU SZKOLNYM 016/017 0.0.017 1. Test konkursowy zawiera zadania. Są to zadania zamknięte i otwarte. Na ich rozwiązanie
Kod ucznia Liczba punktów WOJEWÓDZKI KONKURS MATEMATYCZNY DLA UCZNIÓW GIMNAZJÓW W ROKU SZKOLNYM 016/017 0.0.017 1. Test konkursowy zawiera zadania. Są to zadania zamknięte i otwarte. Na ich rozwiązanie
KOMBINATORYKA. Problem przydziału prac
 KOMBINATORYKA Dział matematyki zajmujący się badaniem różnych możliwych zestawień i ugrupowań, jakie można tworzyć z dowolnego zbioru skończonego. Zbiory skończone, najczęściej wraz z pewną relacją obiekty
KOMBINATORYKA Dział matematyki zajmujący się badaniem różnych możliwych zestawień i ugrupowań, jakie można tworzyć z dowolnego zbioru skończonego. Zbiory skończone, najczęściej wraz z pewną relacją obiekty
Doświadczenie i zdarzenie losowe
 Doświadczenie i zdarzenie losowe Doświadczenie losowe jest to takie doświadczenie, które jest powtarzalne w takich samych warunkach lub zbliżonych, a którego wyniku nie można przewidzieć jednoznacznie.
Doświadczenie i zdarzenie losowe Doświadczenie losowe jest to takie doświadczenie, które jest powtarzalne w takich samych warunkach lub zbliżonych, a którego wyniku nie można przewidzieć jednoznacznie.
EGZAMIN MATURALNY Z MATEMATYKI SIERPIEŃ 2011 POZIOM PODSTAWOWY. Czas pracy: 170 minut. Liczba punktów do uzyskania: 50 WPISUJE ZDAJĄCY
 entralna Komisja Egzaminacyjna rkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. Układ graficzny KE 2010 KO WPISUJE ZJĄY PESEL Miejsce na naklejkę z kodem EGZMIN MTURLNY Z MTEMTYKI
entralna Komisja Egzaminacyjna rkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. Układ graficzny KE 2010 KO WPISUJE ZJĄY PESEL Miejsce na naklejkę z kodem EGZMIN MTURLNY Z MTEMTYKI
PRÓBNY EGZAMIN MATURALNY
 PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO POZIOM PODSTAWOWY 17 KWIETNIA 2010 CZAS PRACY: 170 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT.) Jeżeli liczba 3b
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO POZIOM PODSTAWOWY 17 KWIETNIA 2010 CZAS PRACY: 170 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT.) Jeżeli liczba 3b
PRÓBNY EGZAMIN MATURALNY
 PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO POZIOM PODSTAWOWY 17 KWIETNIA 2010 CZAS PRACY: 170 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT.) Jeżeli liczba 3b
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO POZIOM PODSTAWOWY 17 KWIETNIA 2010 CZAS PRACY: 170 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT.) Jeżeli liczba 3b
LICZBY POWTÓRKA I (0, 2) 10 II (2, 5) 5 III 25 IV Liczba (0, 4) 5 jest równa liczbom A) I i III B) II i IV C) II i III D) I i II E) III i IV
 LICZBY POWTÓRKA ZADANIE (3 PKT) W tabeli zapisano cztery liczby. I (0, 2) 0 II (2, 5) 5 ( III 25 ) 2 ( 25 ) 3 IV 2 5 5 Liczba (0, 4) 5 jest równa liczbom A) I i III B) II i IV C) II i III D) I i II E)
LICZBY POWTÓRKA ZADANIE (3 PKT) W tabeli zapisano cztery liczby. I (0, 2) 0 II (2, 5) 5 ( III 25 ) 2 ( 25 ) 3 IV 2 5 5 Liczba (0, 4) 5 jest równa liczbom A) I i III B) II i IV C) II i III D) I i II E)
Funkcja. x X! y Y : x, y f. f : X Y f x = y f : x y. Funkcja o dziedzinie X i przeciwdziedzinie Y to dowolna relacja f XxY taka, że: Notacje:
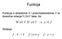 Funkcja Funkcja o dziedzinie X i przeciwdziedzinie Y to dowolna relacja f XxY taka, że: Notacje: x X! y Y : x, y f f : X Y f x = y f : x y Przykłady f: N N, f(n) = 2n f: N R, f(n) = n/2 f: N {13}, f(n)
Funkcja Funkcja o dziedzinie X i przeciwdziedzinie Y to dowolna relacja f XxY taka, że: Notacje: x X! y Y : x, y f f : X Y f x = y f : x y Przykłady f: N N, f(n) = 2n f: N R, f(n) = n/2 f: N {13}, f(n)
02DRAP - Aksjomatyczna definicja prawdopodobieństwa, zasada w-w
 02DRAP - Aksjomatyczna definicja prawdopodobieństwa, zasada w-w A Zadania na ćwiczenia Zadanie A.1. Niech Ω = R oraz F będzie σ-ciałem generowanym przez rodzinę wszystkich przedziałów otwartych typu (,
02DRAP - Aksjomatyczna definicja prawdopodobieństwa, zasada w-w A Zadania na ćwiczenia Zadanie A.1. Niech Ω = R oraz F będzie σ-ciałem generowanym przez rodzinę wszystkich przedziałów otwartych typu (,
01DRAP - klasyczna definicja prawdopodobieństwa
 01DRAP - klasyczna definicja prawdopodobieństwa Ω zbiór zdarzeń elementarnych. Gdy Ω < oraz P({ω} = 1 Ω, dla każdego ω Ω (tzn. każde zdarzenie elementarne jest równo prawdopodobne, to P (A = A Ω Przydatne
01DRAP - klasyczna definicja prawdopodobieństwa Ω zbiór zdarzeń elementarnych. Gdy Ω < oraz P({ω} = 1 Ω, dla każdego ω Ω (tzn. każde zdarzenie elementarne jest równo prawdopodobne, to P (A = A Ω Przydatne
ZAGADNIENIA NA EGZAMIN POPRAWKOWY Z MATEMATYKI W KLASIE III TECHNIKUM.
 ZAGADNIENIA NA EGZAMIN POPRAWKOWY Z MATEMATYKI W KLASIE III TECHNIKUM. I Geometria analityczna 1. Równanie prostej w postaci ogólnej i kierunkowej powtórzenie 2. Wzajemne położenie dwóch prostych powtórzenie
ZAGADNIENIA NA EGZAMIN POPRAWKOWY Z MATEMATYKI W KLASIE III TECHNIKUM. I Geometria analityczna 1. Równanie prostej w postaci ogólnej i kierunkowej powtórzenie 2. Wzajemne położenie dwóch prostych powtórzenie
= 10 9 = Ile jest wszystkich dwucyfrowych liczb naturalnych podzielnych przez 3? A. 12 B. 24 C. 29 D. 30. Sposób I = 30.
 Kombinatoryka i rachunek prawdopodobieństwa Zadania zamknięte (0 1 pkt) 1. Flagę, taką jak pokazano na rysunku, należy zszyć z trzech jednakowej szerokości pasów kolorowej tkaniny. Oba pasy zewnętrzne
Kombinatoryka i rachunek prawdopodobieństwa Zadania zamknięte (0 1 pkt) 1. Flagę, taką jak pokazano na rysunku, należy zszyć z trzech jednakowej szerokości pasów kolorowej tkaniny. Oba pasy zewnętrzne
Zdarzenie losowe (zdarzenie)
 Zdarzenie losowe (zdarzenie) Ćw. 1. Ze zbioru cyfr (l, 2,3,..., 9} losowo wybieramy jedną. a) Wypisz zdarzenia elementarne, sprzyjające: zdarzeniu A, że wybrano liczbę parzystą zdarzeniu B, że wybrano
Zdarzenie losowe (zdarzenie) Ćw. 1. Ze zbioru cyfr (l, 2,3,..., 9} losowo wybieramy jedną. a) Wypisz zdarzenia elementarne, sprzyjające: zdarzeniu A, że wybrano liczbę parzystą zdarzeniu B, że wybrano
P r a w d o p o d o b i eństwo Lekcja 1 Temat: Lekcja organizacyjna. Program. Kontrakt.
 P r a w d o p o d o b i eństwo Lekcja 1 Temat: Lekcja organizacyjna. Program. Kontrakt. Lekcja 2 Temat: Podstawowe pojęcia związane z prawdopodobieństwem. Str. 10-21 1. Doświadczenie losowe jest to doświadczenie,
P r a w d o p o d o b i eństwo Lekcja 1 Temat: Lekcja organizacyjna. Program. Kontrakt. Lekcja 2 Temat: Podstawowe pojęcia związane z prawdopodobieństwem. Str. 10-21 1. Doświadczenie losowe jest to doświadczenie,
ZAGADANIENIA NA EGZAMIN USTNY Z MATEMATYKI
 ZAGADANIENIA NA EGZAMIN USTNY Z MATEMATYKI SEMESTR I ZESTAW. Podaj liczbę przeciwną i odwrotną do liczby 2 2. Jak zmieniła się cena wyrobu po podwyżce o 20%, a następnie po obniżeniu otrzymanej ceny o
ZAGADANIENIA NA EGZAMIN USTNY Z MATEMATYKI SEMESTR I ZESTAW. Podaj liczbę przeciwną i odwrotną do liczby 2 2. Jak zmieniła się cena wyrobu po podwyżce o 20%, a następnie po obniżeniu otrzymanej ceny o
Prawdopodobieństwo Warunkowe Prawdopodobieństwo Całkowite Niezależność Stochastyczna Zdarzeń
 Prawdopodobieństwo Warunkowe Prawdopodobieństwo Całkowite Niezależność Stochastyczna Zdarzeń Zadanie 1 Po potasowaniu sześciu kart: asa, dwójki, trójki, czwórki, piątki i szóstki wyłożono na stół w rzędzie
Prawdopodobieństwo Warunkowe Prawdopodobieństwo Całkowite Niezależność Stochastyczna Zdarzeń Zadanie 1 Po potasowaniu sześciu kart: asa, dwójki, trójki, czwórki, piątki i szóstki wyłożono na stół w rzędzie
Prawdopodobieństwo zadania na sprawdzian
 Prawdopodobieństwo zadania na sprawdzian Zad. 1. Zdarzenia A, B, C oznaczają, że wzięto co najmniej po jednej książce odpowiednio z pierwszych, drugich i trzecich dzieł zebranych. Każde z dzieł zebranych
Prawdopodobieństwo zadania na sprawdzian Zad. 1. Zdarzenia A, B, C oznaczają, że wzięto co najmniej po jednej książce odpowiednio z pierwszych, drugich i trzecich dzieł zebranych. Każde z dzieł zebranych
Zadania należy samodzielnie rozwiązać, a następnie sprawdzić poprawność wyniku!
 Zadania testowe kombinatoryka (opracowanie: Mirosława Gałdyś na bazie http://www.zadania.info/) Zadania należy samodzielnie rozwiązać, a następnie sprawdzić poprawność wyniku! 1. Ze zbioru cyfr * + losujemy
Zadania testowe kombinatoryka (opracowanie: Mirosława Gałdyś na bazie http://www.zadania.info/) Zadania należy samodzielnie rozwiązać, a następnie sprawdzić poprawność wyniku! 1. Ze zbioru cyfr * + losujemy
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) PRAWDOPODOBIEŃSTWO ZAJŚCIA ZDARZENIA A POD WARUNKIEM, ŻE ZASZŁO ZDARZENIE B
 KLASYCZ NA DEFINICJA PRAW DOPOD OBIEŃSTWA ( ) PRAWDOPOD OBIEŃSTW O W A RUNKOWE PRAWDOPODOBIEŃSTWO ZAJŚCIA ZDARZENIA A POD WARUNKIEM, ŻE ZASZŁO ZDARZENIE B ( ) WIĘC CO OZNACZA, ŻE ZDARZENIE B NIE MA WPŁYWU
KLASYCZ NA DEFINICJA PRAW DOPOD OBIEŃSTWA ( ) PRAWDOPOD OBIEŃSTW O W A RUNKOWE PRAWDOPODOBIEŃSTWO ZAJŚCIA ZDARZENIA A POD WARUNKIEM, ŻE ZASZŁO ZDARZENIE B ( ) WIĘC CO OZNACZA, ŻE ZDARZENIE B NIE MA WPŁYWU
Matematyka dyskretna. Andrzej Łachwa, UJ, /14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2017 andrzej.lachwa@uj.edu.pl 14/14 TWIERDZENIE HALLA Twierdzenie o kojarzeniu małżeństw rozważa dwie grupy - dziewcząt i chłopców, oraz podgrupy dziewczyn i podgrupy
Matematyka dyskretna Andrzej Łachwa, UJ, 2017 andrzej.lachwa@uj.edu.pl 14/14 TWIERDZENIE HALLA Twierdzenie o kojarzeniu małżeństw rozważa dwie grupy - dziewcząt i chłopców, oraz podgrupy dziewczyn i podgrupy
Matematyka dyskretna. Andrzej Łachwa, UJ, A/15
 Matematyka dyskretna Andrzej Łachwa, UJ, 2015 andrzej.lachwa@uj.edu.pl 10A/15 Permutacje Permutacja zbioru skończonego X to bijekcja z X w X. Zbiór permutacji zbioru oznaczamy przez, a permutacje małymi
Matematyka dyskretna Andrzej Łachwa, UJ, 2015 andrzej.lachwa@uj.edu.pl 10A/15 Permutacje Permutacja zbioru skończonego X to bijekcja z X w X. Zbiór permutacji zbioru oznaczamy przez, a permutacje małymi
ZASADA SZUFLADKOWA DIRICHLETA
 ZASADA SZUFLADKOWA DIRICHLETA Andrzej FRYSZKOWSKI SZCZECIN, 27 MARCA 2014 Andrzej FRYSZKOWSKI () ZASADA SZUFLADKOWA DIRICHLETA SZCZECIN, 27 MARCA 2014 1 / 25 BROSZURA OMG I (2005/2006) (opracowanie: Joanna
ZASADA SZUFLADKOWA DIRICHLETA Andrzej FRYSZKOWSKI SZCZECIN, 27 MARCA 2014 Andrzej FRYSZKOWSKI () ZASADA SZUFLADKOWA DIRICHLETA SZCZECIN, 27 MARCA 2014 1 / 25 BROSZURA OMG I (2005/2006) (opracowanie: Joanna
RACHUNEK PRAWDOPODOBIEŃSTWA
 Umiejętności opracowanie: Maria Lampert LISTA MOICH OSIĄGNIĘĆ RACHUNEK PRAWDOPODOBIEŃSTWA Co powinienem umieć Umiejętności znam pojęcie zdarzenia elementarnego znam pojęcie doświadczenia losowego i potrafię
Umiejętności opracowanie: Maria Lampert LISTA MOICH OSIĄGNIĘĆ RACHUNEK PRAWDOPODOBIEŃSTWA Co powinienem umieć Umiejętności znam pojęcie zdarzenia elementarnego znam pojęcie doświadczenia losowego i potrafię
Statystyka podstawowe wzory i definicje
 1 Statystyka podstawowe wzory i definicje Średnia arytmetyczna to suma wszystkich liczb (a 1, a 2,, a n) podzielona przez ich ilość (n) Przykład 1 Dany jest zbiór liczb {6, 8, 11, 2, 5, 3}. Oblicz średnią
1 Statystyka podstawowe wzory i definicje Średnia arytmetyczna to suma wszystkich liczb (a 1, a 2,, a n) podzielona przez ich ilość (n) Przykład 1 Dany jest zbiór liczb {6, 8, 11, 2, 5, 3}. Oblicz średnią
PRÓBNY EGZAMIN MATURALNY
 PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO POZIOM PODSTAWOWY 2 MARCA 2019 CZAS PRACY: 170 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT) Cena towaru bez podatku
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO POZIOM PODSTAWOWY 2 MARCA 2019 CZAS PRACY: 170 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT) Cena towaru bez podatku
PRÓBNY EGZAMIN GIMNAZJALNY
 PRÓBNY EGZAMIN GIMNAZJALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO 2 KWIETNIA 2016 CZAS PRACY: 90 MINUT 1 Informacja do zadań 1 i 2 Pomiędzy dworcem kolejowym i lotniskiem kursuja
PRÓBNY EGZAMIN GIMNAZJALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO 2 KWIETNIA 2016 CZAS PRACY: 90 MINUT 1 Informacja do zadań 1 i 2 Pomiędzy dworcem kolejowym i lotniskiem kursuja
KONKURS Z MATEMATYKI DLA UCZNIÓW SZKÓŁ PODSTAWOWYCH
 pieczątka WKK Kod ucznia - - Dzień Miesiąc Rok DATA URODZENIA UCZNIA KONKURS Z MATEMATYKI DLA UCZNIÓW SZKÓŁ PODSTAWOWYCH ETAP WOJEWÓDZKI Drogi Uczniu, witaj na III etapie konkursu matematycznego. Przeczytaj
pieczątka WKK Kod ucznia - - Dzień Miesiąc Rok DATA URODZENIA UCZNIA KONKURS Z MATEMATYKI DLA UCZNIÓW SZKÓŁ PODSTAWOWYCH ETAP WOJEWÓDZKI Drogi Uczniu, witaj na III etapie konkursu matematycznego. Przeczytaj
ARKUSZ PRÓBNEJ MATURY Z OPERONEM MATEMATYKA
 Miejsce na identyfikację szkoły ARKUSZ PRÓBNEJ MATURY Z OPERONEM MATEMATYKA Instrukcja dla zdającego POZIOM ROZSZERZONY Czas pracy: 180 minut 1. Sprawdź, czy arkusz egzaminacyjny zawiera 16 stron (zadania
Miejsce na identyfikację szkoły ARKUSZ PRÓBNEJ MATURY Z OPERONEM MATEMATYKA Instrukcja dla zdającego POZIOM ROZSZERZONY Czas pracy: 180 minut 1. Sprawdź, czy arkusz egzaminacyjny zawiera 16 stron (zadania
Statystyka matematyczna
 Statystyka matematyczna Wykład 2 Magdalena Alama-Bućko 5 marca 2018 Magdalena Alama-Bućko Statystyka matematyczna 5 marca 2018 1 / 14 Prawdopodobieństwo klasyczne Ω - zbiór wszystkich zdarzeń elementarnych
Statystyka matematyczna Wykład 2 Magdalena Alama-Bućko 5 marca 2018 Magdalena Alama-Bućko Statystyka matematyczna 5 marca 2018 1 / 14 Prawdopodobieństwo klasyczne Ω - zbiór wszystkich zdarzeń elementarnych
KONKURS Z MATEMATYKI DLA UCZNIÓW SZKÓŁ PODSTAWOWYCH
 Kod ucznia - - Dzień Miesiąc Rok pieczątka WKK DATA URODZENIA UCZNIA KONKURS Z MATEMATYKI DLA UCZNIÓW SZKÓŁ PODSTAWOWYCH ETAP REJONOWY Drogi Uczniu, witaj na II etapie konkursu matematycznego. Przeczytaj
Kod ucznia - - Dzień Miesiąc Rok pieczątka WKK DATA URODZENIA UCZNIA KONKURS Z MATEMATYKI DLA UCZNIÓW SZKÓŁ PODSTAWOWYCH ETAP REJONOWY Drogi Uczniu, witaj na II etapie konkursu matematycznego. Przeczytaj
Wprowadzenie do kombinatoryki
 Wprowadzenie do kombinatoryki http://www.matemaks.pl/kombinatoryka.html Kombinatoryka jest działem matematyki, który pomaga odpowiedzieć na pytania typu: "ile jest możliwych wyników w rzucie monetą?",
Wprowadzenie do kombinatoryki http://www.matemaks.pl/kombinatoryka.html Kombinatoryka jest działem matematyki, który pomaga odpowiedzieć na pytania typu: "ile jest możliwych wyników w rzucie monetą?",
Matematyka. Zadanie 1. Zadanie 2. Oblicz. Zadanie 3. Zadanie 4. Wykaż, że liczba. 2 2 jest podzielna przez 5. Zadanie 5.
 Matematyka Zadanie 1. Oblicz liczby Zadanie. Oblicz Zadanie 3. Wykaż, że liczba jest podzielna przez Zadanie 4. Wykaż, że liczba 30 0 jest podzielna przez 5. Zadanie 5. n 1 Uzasadnij, że prawdziwa jest
Matematyka Zadanie 1. Oblicz liczby Zadanie. Oblicz Zadanie 3. Wykaż, że liczba jest podzielna przez Zadanie 4. Wykaż, że liczba 30 0 jest podzielna przez 5. Zadanie 5. n 1 Uzasadnij, że prawdziwa jest
ELEMENTY KOMBINATORYKI
 ELEMENTY KOMBINATORYKI Kombinatoryka to dział matematyki, który zajmuje się zliczaniem, na ile sposobów może zajść jakieś zjawisko. Powstała dzięki grom hazardowym a dopiero później rozwinęła się w gałąź
ELEMENTY KOMBINATORYKI Kombinatoryka to dział matematyki, który zajmuje się zliczaniem, na ile sposobów może zajść jakieś zjawisko. Powstała dzięki grom hazardowym a dopiero później rozwinęła się w gałąź
MAŁOPOLSKI KONKURS MATEMATYCZNY dla uczniów dotychczasowych gimnazjów i klas dotychczasowych gimnazjów prowadzonych w szkołach innego typu
 MAŁOPOLSKI KONKURS MATEMATYCZNY dla uczniów dotychczasowych gimnazjów i klas dotychczasowych gimnazjów prowadzonych w szkołach innego typu województwa małopolskiego Rok szkolny 2018/2019 ETAP REJONOWY
MAŁOPOLSKI KONKURS MATEMATYCZNY dla uczniów dotychczasowych gimnazjów i klas dotychczasowych gimnazjów prowadzonych w szkołach innego typu województwa małopolskiego Rok szkolny 2018/2019 ETAP REJONOWY
Kombinatoryka i rachunek prawdopodobieństwa
 Kombinatoryka i rachunek prawdopodobieństwa Kombinatoryka i rachunek prawdopodobieństwa Jerzy Rutkowski 2. Elementy kombinatoryki 2.. Permutacje Teoria Definicja. Niech n N. Permutacją n-elementowego zbioru
Kombinatoryka i rachunek prawdopodobieństwa Kombinatoryka i rachunek prawdopodobieństwa Jerzy Rutkowski 2. Elementy kombinatoryki 2.. Permutacje Teoria Definicja. Niech n N. Permutacją n-elementowego zbioru
1. W tubie, w kształcie walca, o wysokości 6 cm umieszczono pionowo trzy piłeczki, które ściśle przylegały do ścianek i do siebie nawzajem.
 Warto rozwiązać: 1. W tubie, w kształcie walca, o wysokości 6 cm umieszczono pionowo trzy piłeczki, które ściśle przylegały do ścianek i do siebie nawzajem. Oceń prawdziwość podanych zdań. Wybierz, jeśli
Warto rozwiązać: 1. W tubie, w kształcie walca, o wysokości 6 cm umieszczono pionowo trzy piłeczki, które ściśle przylegały do ścianek i do siebie nawzajem. Oceń prawdziwość podanych zdań. Wybierz, jeśli
Propozycje rozwiązań zadań otwartych z próbnej matury rozszerzonej przygotowanej przez OPERON.
 Propozycje rozwiązań zadań otwartych z próbnej matury rozszerzonej przygotowanej przez OPERON. Zadanie 6. Dane są punkty A=(5; 2); B=(1; -3); C=(-2; -8). Oblicz odległość punktu A od prostej l przechodzącej
Propozycje rozwiązań zadań otwartych z próbnej matury rozszerzonej przygotowanej przez OPERON. Zadanie 6. Dane są punkty A=(5; 2); B=(1; -3); C=(-2; -8). Oblicz odległość punktu A od prostej l przechodzącej
ZADANIA OTWARTE KRÓTKIEJ ODPOWIEDZI
 Zadanie 51. ( pkt) Rozwiąż równanie 3 x = 1. 1 x Zadanie 5. ( pkt) x+ 3y = 5 Rozwiąż układ równań. x y = 3 Zadanie 53. ( pkt) Rozwiąż nierówność x + 6x 7 0. ZNI OTWRTE KRÓTKIEJ OPOWIEZI Zadanie 54. ( pkt)
Zadanie 51. ( pkt) Rozwiąż równanie 3 x = 1. 1 x Zadanie 5. ( pkt) x+ 3y = 5 Rozwiąż układ równań. x y = 3 Zadanie 53. ( pkt) Rozwiąż nierówność x + 6x 7 0. ZNI OTWRTE KRÓTKIEJ OPOWIEZI Zadanie 54. ( pkt)
KONKURS PRZEDMIOTOWY Z MATEMATYKI Finał 12 marca 2009 r.
 KOD Nr zad. 1 2 3 4 5 6 7 8 9 10 11 12 Razem Max liczba pkt. 3 3 3 3 3 3 3 3 4 3 3 6 40 Liczba pkt. Kuratorium Oświaty w Katowicach KONKURS PRZEDMIOTOWY Z MATEMATYKI Finał 12 marca 2009 r. Przeczytaj uważnie
KOD Nr zad. 1 2 3 4 5 6 7 8 9 10 11 12 Razem Max liczba pkt. 3 3 3 3 3 3 3 3 4 3 3 6 40 Liczba pkt. Kuratorium Oświaty w Katowicach KONKURS PRZEDMIOTOWY Z MATEMATYKI Finał 12 marca 2009 r. Przeczytaj uważnie
ZAGADNIENIA NA EGZAMIN POPRAWKOWY Z MATEMATYKI W KLASIE III TECHNIKUM.
 ZAGADNIENIA NA EGZAMIN POPRAWKOWY Z MATEMATYKI W KLASIE III TECHNIKUM. I GEOMETRIA ANALITYCZNA 1. Równanie prostej w postaci ogólnej i kierunkowej powtórzenie 2. Wzajemne położenie dwóch prostych powtórzenie
ZAGADNIENIA NA EGZAMIN POPRAWKOWY Z MATEMATYKI W KLASIE III TECHNIKUM. I GEOMETRIA ANALITYCZNA 1. Równanie prostej w postaci ogólnej i kierunkowej powtórzenie 2. Wzajemne położenie dwóch prostych powtórzenie
DODATKOWA PULA ZADAŃ DO EGZAMINU. Rozważmy ciąg zdefiniowany tak: s 0 = a. s n+1 = 2s n +b (dla n=0,1,2 ) Pokaż, że s n = 2 n a +(2 n =1)b
 DODATKOWA PULA ZADAŃ DO EGZAMINU Rozważmy ciąg zdefiniowany tak: s 0 = a s n+1 = 2s n +b (dla n=0,1,2 ) Pokaż, że s n = 2 n a +(2 n =1)b Udowodnij, że liczba postaci 5 n+1 +2 3 n +1 jest podzielna przez
DODATKOWA PULA ZADAŃ DO EGZAMINU Rozważmy ciąg zdefiniowany tak: s 0 = a s n+1 = 2s n +b (dla n=0,1,2 ) Pokaż, że s n = 2 n a +(2 n =1)b Udowodnij, że liczba postaci 5 n+1 +2 3 n +1 jest podzielna przez
RACHUNEK PRAWDOPODOBIEŃSTWA I KOMBINATORYKA
 RACHUNEK PRAWDOPODOBIEŃSTWA I KOMBINATORYKA Doświadczenia losowe Rachunek prawdopodobieństwa zajmuje się zdarzeniami jakie zachodzą, gdy przeprowadzamy doświadczenia losowe. Mówimy, że doświadczenie jest
RACHUNEK PRAWDOPODOBIEŃSTWA I KOMBINATORYKA Doświadczenia losowe Rachunek prawdopodobieństwa zajmuje się zdarzeniami jakie zachodzą, gdy przeprowadzamy doświadczenia losowe. Mówimy, że doświadczenie jest
BAZA ZADAŃ KLASA 3 Ha 2014/2015
 BAZA ZADAŃ KLASA 3 Ha 2014/2015 GEOMETRIA 1 W trójkącie prostokątnym wysokość poprowadzona na przeciwprostokątną ma długość 10 cm, a promień okręgu opisanego ma długość 19 cm Oblicz pole tego trójkąta
BAZA ZADAŃ KLASA 3 Ha 2014/2015 GEOMETRIA 1 W trójkącie prostokątnym wysokość poprowadzona na przeciwprostokątną ma długość 10 cm, a promień okręgu opisanego ma długość 19 cm Oblicz pole tego trójkąta
Matematyka dyskretna. Andrzej Łachwa, UJ, 2019 Zadania
 Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl Zadania 101-170 101. Oblicz postać zwartą symbolu { n 4}. 102. Udowodnij, że n k =1 ( 1) k ( n k) =1 103. Ile może być 4-cyfrowych
Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl Zadania 101-170 101. Oblicz postać zwartą symbolu { n 4}. 102. Udowodnij, że n k =1 ( 1) k ( n k) =1 103. Ile może być 4-cyfrowych
a. zbiór wszystkich potasowań talii kart (w którym S dostaje 13 pierwszych kart, W - 13 kolejnych itd.);
 03DRAP - Przykłady przestrzeni probabilistycznych A Zadania na ćwiczenia Zadanie A1 (wskazówka: pierwsze ćwicznia i rozdział 23 przykł 1 i 2) Zbuduj model przestrzeni klasycznej (czyli takiej, w której
03DRAP - Przykłady przestrzeni probabilistycznych A Zadania na ćwiczenia Zadanie A1 (wskazówka: pierwsze ćwicznia i rozdział 23 przykł 1 i 2) Zbuduj model przestrzeni klasycznej (czyli takiej, w której
XV Olimpiada Matematyczna Juniorów
 XV Olimpiada Matematyczna Juniorów Zawody stopnia pierwszego część testowa (26 września 209 r.) Rozwiązania zadań testowych. odatnia liczba a jest mniejsza od. Wynika z tego, że a) a 2 > a; b) a > a; c)
XV Olimpiada Matematyczna Juniorów Zawody stopnia pierwszego część testowa (26 września 209 r.) Rozwiązania zadań testowych. odatnia liczba a jest mniejsza od. Wynika z tego, że a) a 2 > a; b) a > a; c)
EGZAMIN MATURALNY Z MATEMATYKI
 Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 015 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę dysleksja EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY DATA: 5 sierpnia
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 015 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę dysleksja EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY DATA: 5 sierpnia
PRÓBNY EGZAMIN GIMNAZJALNY
 PRÓBNY EGZAMIN GIMNAZJALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO 16 MARCA 2019 CZAS PRACY: 90 MINUT 1 Informacja do zadań 1 i 2 Poniższa tabela przedstawia temperaturę odczytywana
PRÓBNY EGZAMIN GIMNAZJALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO 16 MARCA 2019 CZAS PRACY: 90 MINUT 1 Informacja do zadań 1 i 2 Poniższa tabela przedstawia temperaturę odczytywana
Jak odróżnić wariację z powtórzeniami od wariacji bez powtórzeń, kombinacji?
 Jak odróżnić wariację z powtórzeniami od wariacji bez powtórzeń, kombinacji? Porada niniejsza traktuje o tzw. elementach kombinatoryki. Często zdarza się, że rozwiązujący zadania z tej dziedziny mają problemy
Jak odróżnić wariację z powtórzeniami od wariacji bez powtórzeń, kombinacji? Porada niniejsza traktuje o tzw. elementach kombinatoryki. Często zdarza się, że rozwiązujący zadania z tej dziedziny mają problemy
c) ( 13 (1) (2) Zadanie 2. Losując bez zwracania kolejne litery ze zbioru AAAEKMMTTY, jakie jest prawdopodobieństwo Odp.
 Zadania na kolokwium nr Zadanie. Spośród kart w tali wylosowano. Jakie jest prawdopodobieństwo: pików, kierów, trefli i karo otrzymania wszystkich kolorów otrzymania dokładnie pików a ( b ( ( c ( ( ( (
Zadania na kolokwium nr Zadanie. Spośród kart w tali wylosowano. Jakie jest prawdopodobieństwo: pików, kierów, trefli i karo otrzymania wszystkich kolorów otrzymania dokładnie pików a ( b ( ( c ( ( ( (
PRÓBNY EGZAMIN MATURALNY
 PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW NR 1949 WYGENEROWANY AUTOMATYCZNIE W SERWISIE ZADANIA.INFO POZIOM PODSTAWOWY CZAS PRACY: 170 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT) Trzecia część liczby
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW NR 1949 WYGENEROWANY AUTOMATYCZNIE W SERWISIE ZADANIA.INFO POZIOM PODSTAWOWY CZAS PRACY: 170 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT) Trzecia część liczby
Wstęp do rachunku prawdopodobieństwa
 wykład : Wstęp do rachunku prawdopodobieństwa STTYSTYK OPISOW Wanda Olech Katedra Genetyki i Ochrony Zwierząt Statystyka zajmuje się Zjawiskami losowymi - które bada przez doświadczenie U podstaw współczesnej
wykład : Wstęp do rachunku prawdopodobieństwa STTYSTYK OPISOW Wanda Olech Katedra Genetyki i Ochrony Zwierząt Statystyka zajmuje się Zjawiskami losowymi - które bada przez doświadczenie U podstaw współczesnej
EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY 2 CZERWCA 2015. Godzina rozpoczęcia: 9:00. Czas pracy: 170 minut. Liczba punktów do uzyskania: 50
 Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. Układ graficzny CKE 013 KOD UZUPEŁNIA ZDAJĄCY PESEL Miejsce na naklejkę z kodem dysleksja EGZAMIN MATURALNY Z MATEMATYKI POZIOM
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. Układ graficzny CKE 013 KOD UZUPEŁNIA ZDAJĄCY PESEL Miejsce na naklejkę z kodem dysleksja EGZAMIN MATURALNY Z MATEMATYKI POZIOM
KURS PRAWDOPODOBIEŃSTWO
 KURS PRAWDOPODOBIEŃSTWO Lekcja 1 Elementy kombinatoryki ZADANIE DOMOWE www.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowiedź (tylko jedna jest prawdziwa). Pytanie 1 Kombinatorykę można określić
KURS PRAWDOPODOBIEŃSTWO Lekcja 1 Elementy kombinatoryki ZADANIE DOMOWE www.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowiedź (tylko jedna jest prawdziwa). Pytanie 1 Kombinatorykę można określić
Test kwalifikacyjny na I Warsztaty Matematyczne
 Test kwalifikacyjny na I Warsztaty Matematyczne Na pytania odpowiada się tak lub nie poprzez wpisanie odpowiednio T bądź N w pole obok pytania. W danym trzypytaniowym zestawie możliwa jest dowolna kombinacja
Test kwalifikacyjny na I Warsztaty Matematyczne Na pytania odpowiada się tak lub nie poprzez wpisanie odpowiednio T bądź N w pole obok pytania. W danym trzypytaniowym zestawie możliwa jest dowolna kombinacja
