Łukasz Kowalik, ASD 2003: Algorytmy grafowe 1

Transkrypt

1 Łukaz Kowalik, ASD 2003: Algorytmy grafowe Algorytmy grafowe Przypomnienie. Graf możemy reprezentować w pamięci na dwa pooby: macierz ąiedztwa lity ąiedztwa W algorytmach nie będziemy jawnie odwoływać ię do tych truktur danych. Będziemy dopuzczać wyrażenia typu oraz kontrukcje for all, na oznaczenie pętli, która wykonuje ię razy, za każdym razem zmienna oznacza inny wierzchołek ze zbioru. Podcza całego wykładu przez będziemy oznaczać liczbę wierzchołków grafu, przez liczbę jego krawędzi. Przykład problemu grafowego. Dla danego grafu niekierowanego obliczyć liczbę pójnych kładowych i każdemu wierzchołkowi przypiać numer jego pójnej kładowej. Przezukiwanie grafu Częto przy rozwiązywaniu problemów grafowych konieczne jet zebranie informacji o trukturze grafu. W tym celu najczęściej przezukujemy graf, tzn. wędrujemy po grafie przechodząc wzdłuż krawędzi i odwiedzając kolejne wierzchołki. Podcza przezukiwania grafu wierzchołki będą odwiedzane w kolejności charakterytycznej dla wybranego algorytmu przezukiwania. Nie jet obojętne, jaki algorytm wybierzemy dobieramy najwłaściwzy algorytm do problemu. Poznamy dwie najważniejze metody przezukiwania grafu: Przezukiwanie w głąb (DFS, Depth Firt Search) Przezukiwanie wzerz (BFS, Breadth Firt Search). Przezukiwanie w głab Idea przezukiwania w głąb polega na tym, że od pewnego wierzchołka idziemy ścieżką po wierzchołkach jezcze nieodwiedzonych tak głęboko jak ię da. Gdy nie możemy już przedłużyć ścieżki wycofujemy ię do poprzedniego wierzchołka i próbujemy z niego wyruzyć dalej po wierzchołkach nieodwiedzonych. Spójrzmy na algorytm. Za każdym razem, gdy wykonuje ię obrót pętli for all "!, prawdzana jet jedna krawędź grafu (od do ). Jeśli wierzchołek nie jet jezcze odwiedzony, przechodzimy od do. Algorytm prawdza każdą krawędź grafu co najwyżej dwa razy. Dlatego złożoność czaowa algorytmu jet #%$&(')+*. Zatoowanie: pójne kładowe Algorytmy przezukiwania ą częto zkieletami innych algorytmów rozwiązujących konkretne problemy. Rozważmy np. problem pójnych kładowych. Algorytm 2 pokazuje, jak rozzerzyć DFS aby znajdować pójne kładowe.

2 Łukaz Kowalik, ASD 2003: Algorytmy grafowe 2 Algorithm DFS : for all do 2: "! 3: for all do 4: if not! then 5: OdwiedźDFS( ) procedure OdwiedźDFS( ) : "! 2: for all "! do 3: if not "! then 4: OdwiedźDFS( )! Algorithm 2 Zatoowanie DFS: znajdowanie pójnych kładowych. : for all do 2: "! 3: + {zmienna globalna} 4: for all do 5: if not then 6: + ' 7: OdwiedźDFS( ) procedure OdwiedźDFS( ) : "! 2: "! + 3: for all "! do 4: if not "! then 5: OdwiedźDFS( ) Po zakończeniu Algorytmu 2 zmienna + zawiera liczbę pójnych kładowych grafu. Dla każdego wierzchołka grafu, w komórce tablicy! znajduje ię numer pójnej kładowej, do której należy. Przezukiwanie wzerz Podcza przezukiwania wzerz nie zawze odwiedzane ą wzytkie wierzchołki grafu. Odwiedzamy jedynie wierzchołki oiagalne z pewnego utalonego wierzchołka, tzn. takie wierzchołki, do których itnieje ścieżka z wierzchołka. W przypadku grafu niekierowanego oznacza to po protu, że odwiedzamy wzytkie wierzchołki w pójnej kładowej zawierającej. Idea algorytmu: najpierw odwiedzamy wierzchołki odległe o od, potem odległe o 2, 3, 4, itd... Natychmiatowe zatoowanie przezukiwania wzerz: Dla każdego wierzchołka w grafie

3 Łukaz Kowalik, ASD 2003: Algorytmy grafowe 3 znajdziemy odległość od do ; jej wartość zapizemy w tablicy "!. W tablicy "! zapizemy numer wierzchołka, z którego wezliśmy do. Algorithm 3 BFS : for all do 2:! 3:! ' 4:! 5:! 6:! 7:! :.Utwórz {tworzy putą kolejkę FIFO } 9:.Dodaj( ) 0: while not.puta do :.Uuń 2: for all "! do 3: if not "! then 4: "! 5: "! "!' 6: "! 7:.Dodaj( ) Lemat. Niech będzie wierzchołkiem na poczatku kolejki w dowolnym momencie wykonania algorytmu BFS. Za wierzchołkiem w kolejce pojawia ię pewna liczba wierzchołków "!, a w dalzej kolejności aż do końca kolejki natępują wierzchołki takie że takich że!! "!'. Uzaadnienie. Pokażemy, że warunek opiany w lemacie jet niezmiennikiem pętli while. Na początku warunek jet pełniony: w kolejce jet tylko jeden wierzchołek. Załóżmy teraz, że właśnie rozpoczyna ię kolejny obrót pętli while i niezmiennik jet pełniony. Pokażemy, że po kolejnym obrocie pętli niezmiennik pozotanie pełniony. Jet jane, że warunek pozotaje pełniony po uunięciu z kolejki na początku pętli while. Jeśli jet otatnim wierzchołkiem w kolejce to! "! lub! "! '. Zobaczmy co ię dzieje, gdy wtawiany jet do kolejki wierzchołek, nieodwiedzony jezcze ąiad. Wtedy "! "!"'. A więc po wtawieniu (i wzytkich innych nieodwiedzonych ąiadów ) niezmiennik pozotanie pełniony. Wnioek. Wartości w tablicy! dla kolejnych wierzchołków wtawianych do kolejki nie maleja. Twierdzenie. Algorytm BFS dla każdego wierzchołka poprawnie oblicza odległość z do i zapamiętuje ja w tablicy "!.

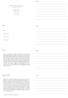
4 Łukaz Kowalik, ASD 2003: Algorytmy grafowe 4 Uzaadnienie. Jet jane, że algorytm poprawnie oblicza odległość z do (równą 0). Załóżmy teraz, że algorytm poprawnie oblicza odległość z do wierzchołków odległych o od. Pokażemy, że dla wierzchołków odległych o ' obliczenia także ą poprawne. Niech będzie dowolnym wierzchołkiem odległym od o %'. Rozważmy, moment, w którym jet wtawiany do kolejki. Niech będzie dowolnym wierzchołkiem odległym od o. Założyliśmy, że dla odległość jet poprawnie obliczana, a więc po wtawieniu do kolejki "!. Z drugiej trony łatwo zobaczyć, że! ' (inaczej itnieje ścieżka od do krótza niż ' ). Ponieważ wartości tablicy nie maleją (wnioek ), muiał być wtawiony do kolejki przed. A więc wzytkie wierzchołki odległe o od zotały wtawione przed. Niech będzie wierzchołkiem bezpośrednio przed na najkrótzej ścieżce od do. Jeśli takich najkrótzych ścieżek jet wiele wybieramy tą, dla której zotał najwcześniej tawiony $ * ' ' $ * do kolejki. Oczywiście!. Gdy wierzchołek był uuwany z kolejki, nie mógł być odwiedzony (mógł być odwiedzony tylko z wierzchołka odległego o od, a jet pierwzym takim wierzchołkiem w kolejce). W takim razie po uunięciu wierzchołek będzie wtawiony do kolejki i!!, czyli odległość do też jet poprawnie obliczana. Wnioek 2. Niech będzie najkrótzą ścieżka od do (, ). Wtedy!,!,... itd, tzn.!, czyli można ja odtworzyć w czaie #%$ *. Drzewo najkrótzych ścieżek. Na ryunku przedtawiono graf po przetworzeniu przez algorytm BFS. Strzałki odpowiadają zawartości tablicy. Widzimy, że tworzą one drzewo o korzeniu w. Nazywamy je drzewem najkrótzych ścieżek. Z takiego drzewa morzemy łatwo odczytać najkrótze ścieżki od do innych wierzchołków. r t u v w x y r 0 t 2 u v w x y Ryunek : Drzewo najkrótzych ścieżek Analiza złożoności czaowej. Jak zwykle oznaczamy przez liczbę wierzchołków, przez liczbę krawędzi. Operacje na kolejce zajmują cza $& *, bo każdy wierzchołek może być tylko Innymi łowy dowód jet przez indukcję po odległóci od do!#"%$ oznacza odległość od do ".

5 Łukaz Kowalik, ASD 2003: Algorytmy grafowe 5 raz wtawiony do kolejki i raz z niej uunięty. Zauważmy też, że litę ąiedztwa dowolnego wierzchołka przeglądamy co najwyżej raz, po uunięciu z kolejki. Liczba wzytkich elementów na litach ąiedztwa wynoi a więc przeglądanie lit ąiedztwa zajmuje natomiat cza $ +*. Złożoność czaowa algorytmu przezukiwania wzerz wynoi więc $&%')+*. Problem najkrótzej ście żki Dane: $ * graf niekierowany, funkcja *, tzn. dla każdej krawędzi mamy jej długość, czyli nieujemną liczbę rzeczywitą $ *, wyróżniony wierzchołek. W takim grafie za długość ścieżki przyjmiemy umę długości jej krawędzi. Zmienia wtedy wój en także pojęcie odległości dwóch wierzchołków (długości najkrótzej ścieżki łączacej wierzchołki). Taką nową odległość będziemy oznaczać przez $& *. Problem: Dla każdego enie odległości ). Patrz ry. 2. Najkrótza ścieżka od do (złożona z pogru- Przykład: najkrótza ścieżka. bionych krawędzi) ma długość 7. obliczyć $ *. Obliczyć drzewo najkrótzych ścieżek (w r u 2 x 3 y 7 w v 2 t Ryunek 2: Graf z wagami na krawędziach i najkrótza ścieżka od do. Algorytm Dijktry, zaada działania (ry. 3). W każdym momencie zbiór podzielony jet na dwa zbiory rozłączne:. wierzchołki, dla których już znamy odległość od pozotałe wierzchołki. Dodatkowo wierzchołki leżą bliżej niż wierzchołki z, tzn. jeśli i to $ &* $ *. Co więcej, dla każdego wierzchołka z najkrótza ścieżka z przechodzi tylko po wierzchołkach z. Na początku,. Algorytm w każdym kroku przenoi jeden wierzchołek z do.

6 Łukaz Kowalik, ASD 2003: Algorytmy grafowe 6 W tablicy! będziemy dla każdego wierzchołka przechowywać długość najkrótzej ścieżki z do przechodzacej tylko po wierzchołkach, lub ' jeśli takiej drogi nie ma. Zauważmy, że wartości tablica będzie zawierać liczby rzeczywite dla wierzchołków z (będzie to prawdziwa odległość od ) oraz dla tych wierzchołków z, które mają choć jednego ąiada w. Dla pozotałych wierzchołków będzie zawierała '. (0) L 9 2 (3) r (2) u 2 x () 5 3 (9) v 7 w (+ ) y (9) t (+ ) Ryunek 3: Działanie algorytmu Dijktry. Pogrubiono najlepze znalezione dotąd ścieżki z. W nawiaach wartości. Lemat 2. Niech zbiory, i tablica maja właności takie, jak opiano powyżej. Niech będzie takim wierzchołkiem, że "! jet najmniejze, tzn. dla każdego! "!. Wtedy "! $ * i można przenieść do. L v u Ryunek 4: Lemat 2. Ścieżka zaznaczona linią przerywana ma długość "!. Uzaadnienie. Zobaczmy, co by było, gdyby "! $ *, tzn. itniałaby ścieżka od do, przechodząca przez wierzchołek poza, krótza niż "!. Niech będzie pierwzym wierzchołkiem poza na tej ścieżce (patrz ry. 4). Ten fragment ścieżki, od do, jet równocześnie najkrótzą ścieżką od do i przechodzi tylko przez wierzchołki z. W takim razie ma długość!. Ale! "! czyli naza ścieżka nie może być krótza niż "!.

7 Łukaz Kowalik, ASD 2003: Algorytmy grafowe 7 Uwaga. Po przenieieniu z do muimy być może odświeżyć niektóre wartości w tablicy. Zmienić mogły ię tylko wartości dla ąiadów. Dla każdego takiego ąiada prawdzamy, czy nowa ścieżka od do przedłużona o krawędź jet krótza niż najkrótza dotąd znaleziona ścieżka do. Jeśli tak jet zapamiętujemy długość nowej ścieżki w "! (patrz ry 5). x (5) x () L 5 u(0) 7 y(+ ) z(+ ) L 5 u(0) 7 y(5) z (7) Ryunek 5: Odświeżanie wartości tablicy podano wartości w tablicy. po przenieieniu wierzchołka u. W nawiaach Algorithm 4 Algorytm Dijktry. : ; 2:!! 3: for all do 4: if then 5:! $ * 6: "! 7: ele :! ' 9: "! 0: for to do 2: : wierzchołek z t.ż. "! jet najmniejze 3: 4: for all "! do 5: if and "!' $ * "! then 6: "! "!' $ * 7: "! Analiza złożoności. Złożoność algorytmu Dijktry zależy w itotny poób od użytych truktur danych. Potrzebna jet truktura przechowująca elementy zbioru i udotępniająca natępujące operacje: Znalezienie w wierzchołka o najmniejzej wartości,

8 Łukaz Kowalik, ASD 2003: Algorytmy grafowe Uunięcie takiego wierzchołka, Zmniejzenie wartości. Taka pecyfikacja odpowiada dokładnie kolejce priorytetowej dla zbioru, w którym kluczami elementów ą wartości z tablicy. Dwie pierwze operacje to min oraz UuńMin. Więkzość kolejek priorytetowych udotępnia także trzecią operację, operację zmniejzenia klucza. Na przykład żeby zmniejzyć klucz elementu! w kopcu binarnym zapamiętanym w tablicy, wytarczy wpiać w! nową wartość klucza i wywołać procedurę DoGóry (A, k). Wnioek 3. Algorytm Dijktry, w którym do implementacji kolejki priorytetowej użyto kopców binarnych ma złożoność $ $ ') * *. Dowód. Za operacje dominujące możemy przyjąć opracje na kolejce priorytetowej. Wzytkie operacje na kopcu binarnym zawierającym nie więcej niż elementów wykonują ię w czaie $ *. Każdy wierzchołek jet raz wtawiany i raz uuwany z kopca, a więc wzytkie wtawienia i uunięcia zajmują cza $& *. Wartość klucza jet zmniejzana tylko raz dla każdej krawędzi, a więc w umie te operacje zajmują cza $ *. Uwaga. Algorytm Dijktry pozotaje nie zmieniony, jeśli dany graf jet kierowany (tzn. wierzchołki ą połączne trzałkami z wagami). Problemy najkrótzych ścieżek tanowią jeden z najintenywniej badanych obzarów algorytmicznej teorii grafów. Przez pewien cza algorytm Dijktry był główną motywacją badań nad kolejkami priorytetowymi. Użycie zaawanowanych kolejek priorytetowych (kopców Fibonacciego) zmniejza złożoność algorytmu Dijktry do $& (' +*.