1. Algorytmy przeszukiwania. Przeszukiwanie wszerz i w głąb.
|
|
|
- Bożena Kowalska
- 8 lat temu
- Przeglądów:
Transkrypt
1 1. Algorytmy przeszukiwania. Przeszukiwanie wszerz i w głąb. Algorytmy przeszukiwania w głąb i wszerz są najczęściej stosowanymi algorytmami przeszukiwania. Wykorzystuje się je do zbadania istnienia połączenie między dwoma wierzchołkami w grafie. Aby zbadać istnienie połączenia w grafie podajemy dwa wierzchołki: pierwszy - zwany stanem początkowym, oraz drugi - zwany stanem końcowym. W przypadku przeszukiwania grafów skończonych omawiane algorytmy są równoważne, tzn zbieżność algorytmu przeszukiwania w głąb pociąga za sobą zbieżność algorytmu przeszukiwania wszerz i odwrotnie. Jeżeli przeszukujemy graf nieskończony, algorytm przeszukiwania wszerz jest zbieżny, natomiast algorytm przeszukiwania w głąb nie. Brak zbieżności ma miejsce wówczas, gdy przeszukujemy krawiędź nieskończoną, która nie prowadzi do wierzchołka końcowego. Omawiając algorytm posłużymi się przykładem. Zadamy konkretny graf oraz stany: początkowy i końcowy i opiszemy przebieg działania algorytmu. Niech dany będzie graf: Rysunek 1: Graf do przeszukiwania. Dowolny graf można opisać w postaci listy połączeń. Lista zawiera n linii, gdzie n oznacza liczbę wierzchołków grafu. W i tej linii są umiszczone numery wierzchołków, z którymi i ty wierzchołek jest połączony. Lista połączeń dla rozważanego grafu wygląda następująco: 1. 2, 6, , , , , 8, , 7 1
2 7. 6, , , , , 10 Przeszukiwanie wszerz Przeszukiwanie grafu wszerz polega na odwiedzaniu wszystkich wierzchołków grafu sąsiadujących z wierzchołkiem początkowym, następnie wierzchołków w odległośi 2 od wierzchołka początkowego i tak kolejno. Przy każdym odwiedzeniu należy sprawidzić, czy stan, w którym się znajdujemy jest stanem końcowym. Odwiedzając kolejne wierzchołki należy pamiętać, żeby nie odwiedzać wierzchołków wcześniej odwiedzonych, tzn. każdy wierzchołek możemy odwiedzić dokładnie raz. W przypadku, gdy odwiedzimy wszystkie możliwe wierzchołki i nie znajdziemy stanu końcowego, nie istnieje droga miedzy szukanymi wierzchołkami. Zaletą algorytmu przeszukiwania wszerz jest to, że na pewno nie pominiemy żadnego wierzchołka, zwykle jednak odwiedzamy za dużo wierzchołków, co jest wadą algorytmu. Przeszukiwanie wszerz odbywa się przy użyciu kolejki FIFO (first in first out). Algorytm przebiega następująco: 1. Utwórz kolejkę FIFO 2. Zapisz do kolejki stan początkowy 3. Pobierz z kolejki stan i nazwij go S 4. Jesli (a) S jest poszukiwanym stanem końcowym zwróć SUKCES i zakończ algorytm (b) S=NULL (lista jest pusta) zwróć BRAK ROZWIAZANIA i zakończ algorytm (c) S nie jest poszukiwanym stanem końcowym to generuj wszystkie możliwe stany następujące po S (które można wyprowadzić z S zgodnie z wcześniej ustalonymi regułami a które nie były już rozważane) i zapisz je do kolejki 5. Idz do 3 Zadanie polega na stwierdzeniu, czy w wyżej podanym grafie wierzchołki 1 i 5 są połączone. Wykorzystywane funkcje: make fifo() - funkcja tworzy listę typu FIFO put fifo(x) - funkcja dodaje element x do listy get fifo() - funkcja pobiera elemet z listy Oto przebieg wykonywania algorytmu: 2
3 Numer Krok Wykonywana Stan Odwiedzone etapu algorytmu operacja kolejki wierzchołki 1 1 make fifo() NULL NULL 2 2 put fifo(1) S:=get fifo() (S=1) NULL put fifo(2), put fifo(6), put fifo(9) 5 5 Powrót do S:=get fifo() (S=2) put fifo(3) 8 5 Powrót do S:=get fifo() (S=6) put fifo(7) 11 5 Powrót do S:=get fifo() (S=9) put fifo(10) 14 5 Powrót do S:=get fifo() (S=3) put fifo(4) 17 5 Powrót do S:=get fifo() (S=7) put fifo(8) 20 5 Powrót do S:=get fifo() (S=10) put fifo(11) 23 5 Powrót do S:=get fifo() (S=4) put fifo(5) 26 5 Powrót do S:=get fifo() (S=8) nic 29 5 Powrót do S:=get fifo() (S=11) nic 32 5 Powrót do S:=get fifo() (S=5) NULL NULL return(sukces) 3
4 Przeszukiwanie w głąb Przeszukiwanie grafu w głąb polega na przeszukiwaniu poszczególnych krawędzi grafu. Przechodzimy krawędz najdalej ja się da, jeżeli dana ścieżka nie doprowadziła nas do wierzchołka końcowego wówczas cofamy sie do momentu, z którego możemy pójść inną scieżką. Podobnie jak w przypadku przeszukiwania wszerz, przeszukując graf metodą w głąb pojedynczy wierzchołek może być odwiedziny dokładnie jeden raz. Przy każdym odwiedzeniu należy sprawidzić, czy nie znajdujemy się w stanie końcowym. W przypadku, gdy odwiedzimy wszystkie możliwe wierzchołki i nie znajdziemy stanu końcowego, nie istnieje droga miedzy szukanymi wierzchołkami. Zaletą algorytmu przeszukiwania w głąb jest to, że nie przeszukujemy wszystkich wierzchołków grafu, dodatkowo przeszukując ścieżką prowadzącą bezpośrednio do wierzchołka końcowego możemy odwiedzić minimalną ilość wierzchołków łączących stan początkowy z końcowym. Wadą jest to, że zwykle przszukiwanie odbywa się niewłaściwą scieżką co prowadzi do zabrnięcia w ślepą uliczkę, z której należy się wycofać do wierzchołka, z którego istnieje możliwość pójścia dalej. Przeszukiwanie w głąb odbywa się przy użyciu kolejki LIFO (last in first out) zwanej inaczej STOS. Algorytm przebiega następująco: 1. Utwórz STOS 2. Zapisz na stos stan początkowy 3. Pobierz ze stosu stan i nazwij go S 4. Jesli (a) S jest poszukiwanym stanem końcowym zwróć SUKCES i zakończ algorytm (b) S=NULL (lista jest pusta) zwróć BRAK ROZWIAZANIA i zakończ algorytm (c) S nie jest poszukiwanym stanem końcowym to generuj wszystkie możliwe stany następujące po S (które można wyprowadzić z S zgodnie z wcześniej ustalonymi regułami a które nie były już rozważane) i zapisz je do kolejki 5. Idz do 3 Zadanie polega na stwierdzeniu, czy w wyżej podanym grafie wierzchołki 1 i 5 są połączone. Wykorzystywane funkcje: make stos() - funkcja tworzy STOS put stos(x) - funkcja dodaje element x na stos get stos() - funkcja pobiera elemet ze stosu Oto przebieg wykonywania algorytmu: 4
5 Numer Krok Wykonywana Stan Odwiedzone etapu algorytmu operacja kolejki wierzchołki 1 1 make stos() NULL NULL 2 2 put stos(1) S:=get stos() (S=1) NULL put stos(2), put stos(6), put stos(9) 5 5 Powrót do S:=get stos() (S=9) put stos(10) Powrót do S:=get stos() (S=10) put stos(11) Powrót do S:=get stos() (S=11) put stos(5) Powrót do S:=get stos() (S=5) Wykonywanie punktu (a) return(sukces) W tak realizowanym algorytmie poruszamy się wzdłuż jednej krawędzi ale dla danego wierzchołka odwiedzamy wszystkich jego sąsiadów. Możemy skonstruować algorytm tak, aby z danego wierzchołka generować tylko jeden (wybrany) stan następującey po nim. Wówczas algorytm będzie przebiegał następująco: 1. Utwórz STOS 2. Przyjmij S stan początkowy i zapisz na stos 3. Jesli (a) S jest poszukiwanym stanem końcowym zwróć SUKCES i zakończ algorytm (b) S=NULL (lista jest pusta) zwróć BRAK ROZWIAZANIA i zakończ algorytm (c) S nie jest poszukiwanym stanem końcowym to: 4. Idz do 3 i. jeśli istnieje możliwy stan następujący po S to S przyjmij ten stan i zapisz na stos ii. w przeciwnym przypadku zdejmij element ze stosu, następnie S przyjmij stan ze stosu (nie zdejmując elementu ze stosu) 5
6 Zadanie polega na swierdzeniu, czy wierzchołki 1 i 11 są połączone. Oto przebieg wykonywania algorytmu: Numer Krok Wykonywana Stan Odwiedzone etapu algorytmu operacja stosu wierzchołki 1 1 make stos() NULL NULL 2 2 S=1; put stos(s) Wykonywanie punktu i S=2; put stos(s) 4 4 Powrót do Wykonywanie punktu i S=3; put stos(s) 6 4 Powrót do Wykonywanie punktu i S=4; put stos(s) 8 4 Powrót do Wykonywanie punktu i S=5; put stos(s) 10 4 Powrót do Wykonywanie punktu i S=8; put stos(s) 12 4 Powrót do Wykonywanie punktu i S=7; put stos(s) 14 4 Powrót do Wykonywanie punktu i S=6; put stos(s) 16 4 Powrót do Wykonywanie punktu ii S=get stos() put stos(s) (S=7) 18 4 Powrót do Wykonywanie punktu ii S=get stos() put stos(s) (S=8) 20 4 Powrót do Wykonywanie punktu ii S=get stos(); put stos(s) (S=5) 22 4 Powrót do Wykonywanie punktu i S=11; put stos(s) 24 4 Powrót do Wykonywanie punktu a return(sukces) Taki przebieg algorytmu oprócz odpowiedzi na pytanie czy dwa wierzchołki są ze sobą połączone, generuje drogę prowadzacą od wierzchołka początkowego do wierzchołka końcowego (zwykle nie jest to optymalna droga). Jest to stan stosu w momencie zakończenia działania algorytmu. 6
7 Zadania Zadanie będą polegały na zastosowaniu powyższych algorytmów do sprawdzenia, czy dwa wierzchołki w grafie są ze sobą połączone. Zadanie 1 Napisać program, w oparciu o padane algorytmy, sprawdzającey, czy dwa wierzchołki w grafie są połączone. Zakładamy, ze program wczytuje graf z pliku o podanej w linii poleceń nazwie. Następnie pyta o numery wierzchołków do sprawdzenia. Wierzchołki numerujemy liczbami naturalnymi z przedziału [1, 100]. W pliku pierwsza linia zawiera liczbę wierzchołków, kolejne są listowym opisem grafu. Tak więc linia 2 zawiera sopis wierzchołków, z którymi łączy się wierzchołek 1, linia 3 - spis wierzchołków, z którymi łączy się wierzchołek 2, itd. Kolejne wierzchołki w linii rozdzielone są spacją. Każda linia na końcu zawiera liczbę 0, która oznacza koniec listy wierzchołków sąsiadujących z danym wierzchołkiem. Oto przykładowy plik z danymi dla rozważanego w przykładach grafu: Zadanie 2 Napisać program, w oparciu o podany algorytm, sprawdzający czy możliwe jest przejście w labiryncie od jednego miejsca do drugiego. Zakładamy że program wczytuje labirynt z pliku o podanej w linii poleceń nazwie. Następnie pyta się o współrzędne pola startowego i końcowego. Maksymalny rozmiar planszy to 100 wierszy i 100 kolumn. Każde pole na planszy ma numer z przedziału [0, 15]. Numer ten oznacza jekiego typu jest pole, to znaczy gdzie możemy się z niego przemieścić. Oto dostępne pola (lewe górne ma numer 0, prawe dolne - 15, numeracja wierszami): Rysunek 2: Pola labryntu. W pliku pierwsza linia zawiera liczbę wierszy, druga - liczbę kolumn, kolejne natomiast to opis pól w danym wierszu. Tak więc linia 3 zawiera opis pól wiersza 7
8 1, linia 4 - opis pól wiersza drugiego, itd. Kolejne pola w wierszu rozdzielone są spacjami. Oto przykładowy wygląd labiryntu i odpowiadającego mu pliku z danymi: Rysunek 3: Plansza labiryntu Ilustrowany na ekranie - na przykład pola odwiedzone niech mają inny kolor. W realizacji tekstowej program powinien wyświetlać (lub zapisywać do pliku) współrzędne odwiedzanych pól. Uwaga Jak łatwo zauważyć labirynt można utożsamiać z grafem. Poszczególne pola labiryntu są wierzchołkami, a rodzaj pola jednoznacznie definiuje listę wieszchołków sąsiadujących z rozważanym. Dla powyższego labiryntu plik opisujący go jako graf wygląda następująco:
Algorytmiczna teoria grafów
 Przedmiot fakultatywny 20h wykładu + 20h ćwiczeń 21 lutego 2014 Zasady zaliczenia 1 ćwiczenia (ocena): kolokwium, zadania programistyczne (implementacje algorytmów), praca na ćwiczeniach. 2 Wykład (egzamin)
Przedmiot fakultatywny 20h wykładu + 20h ćwiczeń 21 lutego 2014 Zasady zaliczenia 1 ćwiczenia (ocena): kolokwium, zadania programistyczne (implementacje algorytmów), praca na ćwiczeniach. 2 Wykład (egzamin)
Znajdowanie wyjścia z labiryntu
 Znajdowanie wyjścia z labiryntu Zadanie to wraz z problemem pakowania najcenniejszego plecaka należy do problemów optymalizacji, które dotyczą znajdowania najlepszego rozwiązania wśród wielu możliwych
Znajdowanie wyjścia z labiryntu Zadanie to wraz z problemem pakowania najcenniejszego plecaka należy do problemów optymalizacji, które dotyczą znajdowania najlepszego rozwiązania wśród wielu możliwych
a) 7 b) 19 c) 21 d) 34
 Zadanie 1. Pytania testowe dotyczące podstawowych własności grafów. Zadanie 2. Przy każdym z zadań może się pojawić polecenie krótkiej charakterystyki algorytmu. Zadanie 3. W zadanym grafie sprawdzenie
Zadanie 1. Pytania testowe dotyczące podstawowych własności grafów. Zadanie 2. Przy każdym z zadań może się pojawić polecenie krótkiej charakterystyki algorytmu. Zadanie 3. W zadanym grafie sprawdzenie
Algorytmy grafowe. Wykład 2 Przeszukiwanie grafów. Tomasz Tyksiński CDV
 Algorytmy grafowe Wykład 2 Przeszukiwanie grafów Tomasz Tyksiński CDV Rozkład materiału 1. Podstawowe pojęcia teorii grafów, reprezentacje komputerowe grafów 2. Przeszukiwanie grafów 3. Spójność grafu,
Algorytmy grafowe Wykład 2 Przeszukiwanie grafów Tomasz Tyksiński CDV Rozkład materiału 1. Podstawowe pojęcia teorii grafów, reprezentacje komputerowe grafów 2. Przeszukiwanie grafów 3. Spójność grafu,
SZTUCZNA INTELIGENCJA
 SZTUCZNA INTELIGENCJA WYKŁAD 12. PRZESZUKIWANIE Częstochowa 2014 Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska ROZWIĄZYWANIE PROBLEMÓW JAKO PRZESZUKIWANIE Istotną rolę podczas
SZTUCZNA INTELIGENCJA WYKŁAD 12. PRZESZUKIWANIE Częstochowa 2014 Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska ROZWIĄZYWANIE PROBLEMÓW JAKO PRZESZUKIWANIE Istotną rolę podczas
Instrukcje dla zawodników
 Instrukcje dla zawodników Nie otwieraj arkusza z zadaniami dopóki nie zostaniesz o to poproszony. Instrukcje poniżej zostaną ci odczytane i wyjaśnione. 1. Arkusz składa się z 3 zadań. 2. Każde zadanie
Instrukcje dla zawodników Nie otwieraj arkusza z zadaniami dopóki nie zostaniesz o to poproszony. Instrukcje poniżej zostaną ci odczytane i wyjaśnione. 1. Arkusz składa się z 3 zadań. 2. Każde zadanie
Rozwiązywanie problemów metodą przeszukiwania
 Rozwiązywanie problemów metodą przeszukiwania Dariusz Banasiak Katedra Informatyki Technicznej W4/K9 Politechnika Wrocławska Reprezentacja problemu w przestrzeni stanów Jedną z ważniejszych metod sztucznej
Rozwiązywanie problemów metodą przeszukiwania Dariusz Banasiak Katedra Informatyki Technicznej W4/K9 Politechnika Wrocławska Reprezentacja problemu w przestrzeni stanów Jedną z ważniejszych metod sztucznej
Ogólne wiadomości o grafach
 Ogólne wiadomości o grafach Algorytmy i struktury danych Wykład 5. Rok akademicki: / Pojęcie grafu Graf zbiór wierzchołków połączonych za pomocą krawędzi. Podstawowe rodzaje grafów: grafy nieskierowane,
Ogólne wiadomości o grafach Algorytmy i struktury danych Wykład 5. Rok akademicki: / Pojęcie grafu Graf zbiór wierzchołków połączonych za pomocą krawędzi. Podstawowe rodzaje grafów: grafy nieskierowane,
Ćwiczenie 1 Planowanie trasy robota mobilnego w siatce kwadratów pól - Algorytm A
 Ćwiczenie 1 Planowanie trasy robota mobilnego w siatce kwadratów pól - Algorytm A Zadanie do wykonania 1) Utwórz na pulpicie katalog w formacie Imię nazwisko, w którym umieść wszystkie pliki związane z
Ćwiczenie 1 Planowanie trasy robota mobilnego w siatce kwadratów pól - Algorytm A Zadanie do wykonania 1) Utwórz na pulpicie katalog w formacie Imię nazwisko, w którym umieść wszystkie pliki związane z
Wydział Matematyki I Informatyki ul. Słoneczna Olsztyn
 Klucz Napisać program sprawdzający czy dany klucz pasuje do danego zamka. Dziurka w zamku reprezentowana jest w postaci tablicy zero-jedynkowej i jest spójna. Klucz zakodowany jest jako ciąg par liczb
Klucz Napisać program sprawdzający czy dany klucz pasuje do danego zamka. Dziurka w zamku reprezentowana jest w postaci tablicy zero-jedynkowej i jest spójna. Klucz zakodowany jest jako ciąg par liczb
Algorytm Dijkstry znajdowania najkrótszej ścieżki w grafie
 Algorytm Dijkstry znajdowania najkrótszej ścieżki w grafie Używane struktury danych: V - zbiór wierzchołków grafu, V = {1,2,3...,n} E - zbiór krawędzi grafu, E = {(i,j),...}, gdzie i, j Î V i istnieje
Algorytm Dijkstry znajdowania najkrótszej ścieżki w grafie Używane struktury danych: V - zbiór wierzchołków grafu, V = {1,2,3...,n} E - zbiór krawędzi grafu, E = {(i,j),...}, gdzie i, j Î V i istnieje
Pomorski Czarodziej 2016 Zadania. Kategoria C
 Pomorski Czarodziej 2016 Zadania. Kategoria C Poniżej znajduje się 5 zadań. Za poprawne rozwiązanie każdego z nich możesz otrzymać 10 punktów. Jeżeli otrzymasz za zadanie maksymalną liczbę punktów, możesz
Pomorski Czarodziej 2016 Zadania. Kategoria C Poniżej znajduje się 5 zadań. Za poprawne rozwiązanie każdego z nich możesz otrzymać 10 punktów. Jeżeli otrzymasz za zadanie maksymalną liczbę punktów, możesz
Porównanie algorytmów wyszukiwania najkrótszych ścieżek międz. grafu. Daniel Golubiewski. 22 listopada Instytut Informatyki
 Porównanie algorytmów wyszukiwania najkrótszych ścieżek między wierzchołkami grafu. Instytut Informatyki 22 listopada 2015 Algorytm DFS w głąb Algorytm przejścia/przeszukiwania w głąb (ang. Depth First
Porównanie algorytmów wyszukiwania najkrótszych ścieżek między wierzchołkami grafu. Instytut Informatyki 22 listopada 2015 Algorytm DFS w głąb Algorytm przejścia/przeszukiwania w głąb (ang. Depth First
Projekty zaliczeniowe Podstawy Programowania 2012/2013
 Projekty zaliczeniowe Podstawy Programowania 2012/2013 0. Zasady ogólne W skład projektu wchodzą następujące elementy: dokładny opis rozwiązywanego problemu opis słowny rozwiązania problemu wraz z pseudokodami
Projekty zaliczeniowe Podstawy Programowania 2012/2013 0. Zasady ogólne W skład projektu wchodzą następujące elementy: dokładny opis rozwiązywanego problemu opis słowny rozwiązania problemu wraz z pseudokodami
Pole wielokąta. Wejście. Wyjście. Przykład
 Pole wielokąta Liczba punktów: 60 Limit czasu: 1-3s Limit pamięci: 26MB Oblicz pole wielokąta wypukłego. Wielokąt wypukły jest to wielokąt, który dla dowolnych jego dwóch punktów zawiera również odcinek
Pole wielokąta Liczba punktów: 60 Limit czasu: 1-3s Limit pamięci: 26MB Oblicz pole wielokąta wypukłego. Wielokąt wypukły jest to wielokąt, który dla dowolnych jego dwóch punktów zawiera również odcinek
Matematyczne Podstawy Informatyki
 Matematyczne Podstawy Informatyki dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska Rok akademicki 03/0 Przeszukiwanie w głąb i wszerz I Przeszukiwanie metodą
Matematyczne Podstawy Informatyki dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska Rok akademicki 03/0 Przeszukiwanie w głąb i wszerz I Przeszukiwanie metodą
ANALIZA ALGORYTMÓW. Analiza algorytmów polega między innymi na odpowiedzi na pytania:
 ANALIZA ALGORYTMÓW Analiza algorytmów polega między innymi na odpowiedzi na pytania: 1) Czy problem może być rozwiązany na komputerze w dostępnym czasie i pamięci? 2) Który ze znanych algorytmów należy
ANALIZA ALGORYTMÓW Analiza algorytmów polega między innymi na odpowiedzi na pytania: 1) Czy problem może być rozwiązany na komputerze w dostępnym czasie i pamięci? 2) Który ze znanych algorytmów należy
Działanie algorytmu oparte jest na minimalizacji funkcji celu jako suma funkcji kosztu ( ) oraz funkcji heurystycznej ( ).
 Algorytm A* Opracowanie: Joanna Raczyńska 1.Wstęp Algorytm A* jest heurystycznym algorytmem służącym do znajdowania najkrótszej ścieżki w grafie. Jest to algorytm zupełny i optymalny, co oznacza, że zawsze
Algorytm A* Opracowanie: Joanna Raczyńska 1.Wstęp Algorytm A* jest heurystycznym algorytmem służącym do znajdowania najkrótszej ścieżki w grafie. Jest to algorytm zupełny i optymalny, co oznacza, że zawsze
Heurystyczne metody przeszukiwania
 Heurystyczne metody przeszukiwania Dariusz Banasiak Katedra Informatyki Technicznej W4/K9 Politechnika Wrocławska Pojęcie heurystyki Metody heurystyczne są jednym z ważniejszych narzędzi sztucznej inteligencji.
Heurystyczne metody przeszukiwania Dariusz Banasiak Katedra Informatyki Technicznej W4/K9 Politechnika Wrocławska Pojęcie heurystyki Metody heurystyczne są jednym z ważniejszych narzędzi sztucznej inteligencji.
ĆWICZENIE 1: Przeszukiwanie grafów cz. 1 strategie ślepe
 Instytut Mechaniki i Inżynierii Obliczeniowej Wydział Mechaniczny Technologiczny, Politechnika Śląska www.imio.polsl.pl METODY HEURYSTYCZNE ĆWICZENIE 1: Przeszukiwanie grafów cz. 1 strategie ślepe opracował:
Instytut Mechaniki i Inżynierii Obliczeniowej Wydział Mechaniczny Technologiczny, Politechnika Śląska www.imio.polsl.pl METODY HEURYSTYCZNE ĆWICZENIE 1: Przeszukiwanie grafów cz. 1 strategie ślepe opracował:
Zadanie 1: Piętnastka
 Informatyka, studia dzienne, inż. I st. semestr VI Sztuczna Inteligencja i Systemy Ekspertowe 2010/2011 Prowadzący: mgr Michał Pryczek piątek, 12:00 Data oddania: Ocena: Grzegorz Graczyk 150875 Marek Rogalski
Informatyka, studia dzienne, inż. I st. semestr VI Sztuczna Inteligencja i Systemy Ekspertowe 2010/2011 Prowadzący: mgr Michał Pryczek piątek, 12:00 Data oddania: Ocena: Grzegorz Graczyk 150875 Marek Rogalski
Heurystyki. Strategie poszukiwań
 Sztuczna inteligencja Heurystyki. Strategie poszukiwań Jacek Bartman Zakład Elektrotechniki i Informatyki Instytut Techniki Uniwersytet Rzeszowski DLACZEGO METODY PRZESZUKIWANIA? Sztuczna Inteligencja
Sztuczna inteligencja Heurystyki. Strategie poszukiwań Jacek Bartman Zakład Elektrotechniki i Informatyki Instytut Techniki Uniwersytet Rzeszowski DLACZEGO METODY PRZESZUKIWANIA? Sztuczna Inteligencja
5c. Sieci i przepływy
 5c. Sieci i przepływy Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie zima 2016/2017 rzegorz Kosiorowski (Uniwersytet Ekonomiczny w Krakowie) 5c. Sieci i przepływy zima 2016/2017 1 / 40 1 Definicje
5c. Sieci i przepływy Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie zima 2016/2017 rzegorz Kosiorowski (Uniwersytet Ekonomiczny w Krakowie) 5c. Sieci i przepływy zima 2016/2017 1 / 40 1 Definicje
Grafem nazywamy strukturę G = (V, E): V zbiór węzłów lub wierzchołków, Grafy dzielimy na grafy skierowane i nieskierowane:
 Wykład 4 grafy Grafem nazywamy strukturę G = (V, E): V zbiór węzłów lub wierzchołków, E zbiór krawędzi, Grafy dzielimy na grafy skierowane i nieskierowane: Formalnie, w grafach skierowanych E jest podzbiorem
Wykład 4 grafy Grafem nazywamy strukturę G = (V, E): V zbiór węzłów lub wierzchołków, E zbiór krawędzi, Grafy dzielimy na grafy skierowane i nieskierowane: Formalnie, w grafach skierowanych E jest podzbiorem
1 Automaty niedeterministyczne
 Szymon Toruńczyk 1 Automaty niedeterministyczne Automat niedeterministyczny A jest wyznaczony przez następujące składniki: Alfabet skończony A Zbiór stanów Q Zbiór stanów początkowych Q I Zbiór stanów
Szymon Toruńczyk 1 Automaty niedeterministyczne Automat niedeterministyczny A jest wyznaczony przez następujące składniki: Alfabet skończony A Zbiór stanów Q Zbiór stanów początkowych Q I Zbiór stanów
3. Macierze i Układy Równań Liniowych
 3. Macierze i Układy Równań Liniowych Rozważamy równanie macierzowe z końcówki ostatniego wykładu ( ) 3 1 X = 4 1 ( ) 2 5 Podstawiając X = ( ) x y i wymnażając, otrzymujemy układ 2 równań liniowych 3x
3. Macierze i Układy Równań Liniowych Rozważamy równanie macierzowe z końcówki ostatniego wykładu ( ) 3 1 X = 4 1 ( ) 2 5 Podstawiając X = ( ) x y i wymnażając, otrzymujemy układ 2 równań liniowych 3x
Spacery losowe generowanie realizacji procesu losowego
 Spacery losowe generowanie realizacji procesu losowego Michał Krzemiński Streszczenie Omówimy metodę generowania trajektorii spacerów losowych (błądzenia losowego), tj. szczególnych procesów Markowa z
Spacery losowe generowanie realizacji procesu losowego Michał Krzemiński Streszczenie Omówimy metodę generowania trajektorii spacerów losowych (błądzenia losowego), tj. szczególnych procesów Markowa z
Przykłady grafów. Graf prosty, to graf bez pętli i bez krawędzi wielokrotnych.
 Grafy Graf Graf (ang. graph) to zbiór wierzchołków (ang. vertices), które mogą być połączone krawędziami (ang. edges) w taki sposób, że każda krawędź kończy się i zaczyna w którymś z wierzchołków. Graf
Grafy Graf Graf (ang. graph) to zbiór wierzchołków (ang. vertices), które mogą być połączone krawędziami (ang. edges) w taki sposób, że każda krawędź kończy się i zaczyna w którymś z wierzchołków. Graf
Badania operacyjne: Wykład Zastosowanie kolorowania grafów w planowaniu produkcji typu no-idle
 Badania operacyjne: Wykład Zastosowanie kolorowania grafów w planowaniu produkcji typu no-idle Paweł Szołtysek 12 czerwca 2008 Streszczenie Planowanie produkcji jest jednym z problemów optymalizacji dyskretnej,
Badania operacyjne: Wykład Zastosowanie kolorowania grafów w planowaniu produkcji typu no-idle Paweł Szołtysek 12 czerwca 2008 Streszczenie Planowanie produkcji jest jednym z problemów optymalizacji dyskretnej,
Programowanie obiektowe
 Laboratorium z przedmiotu Programowanie obiektowe - zestaw 04 Cel zajęć. Celem zajęć jest zapoznanie się ze sposobem działania popularnych. Wprowadzenie teoretyczne. Rozważana w ramach niniejszych zajęć
Laboratorium z przedmiotu Programowanie obiektowe - zestaw 04 Cel zajęć. Celem zajęć jest zapoznanie się ze sposobem działania popularnych. Wprowadzenie teoretyczne. Rozważana w ramach niniejszych zajęć
Podstawy programowania, Poniedziałek , 8-10 Projekt, część 1
 Podstawy programowania, Poniedziałek 30.05.2016, 8-10 Projekt, część 1 1. Zadanie Projekt polega na stworzeniu logicznej gry komputerowej działającej w trybie tekstowym o nazwie Minefield. 2. Cele Celem
Podstawy programowania, Poniedziałek 30.05.2016, 8-10 Projekt, część 1 1. Zadanie Projekt polega na stworzeniu logicznej gry komputerowej działającej w trybie tekstowym o nazwie Minefield. 2. Cele Celem
Uniwersytet Zielonogórski Wydział Elektrotechniki, Informatyki i Telekomunikacji Instytut Sterowania i Systemów Informatycznych
 Uniwersytet Zielonogórski Wydział Elektrotechniki, Informatyki i Telekomunikacji Instytut Sterowania i Systemów Informatycznych ELEMENTY SZTUCZNEJ INTELIGENCJI Laboratorium nr 9 PRZESZUKIWANIE GRAFÓW Z
Uniwersytet Zielonogórski Wydział Elektrotechniki, Informatyki i Telekomunikacji Instytut Sterowania i Systemów Informatycznych ELEMENTY SZTUCZNEJ INTELIGENCJI Laboratorium nr 9 PRZESZUKIWANIE GRAFÓW Z
Algorytmy sztucznej inteligencji
 www.math.uni.lodz.pl/ radmat Przeszukiwanie z ograniczeniami Zagadnienie przeszukiwania z ograniczeniami stanowi grupę problemów przeszukiwania w przestrzeni stanów, które składa się ze: 1 skończonego
www.math.uni.lodz.pl/ radmat Przeszukiwanie z ograniczeniami Zagadnienie przeszukiwania z ograniczeniami stanowi grupę problemów przeszukiwania w przestrzeni stanów, które składa się ze: 1 skończonego
Algorytmy i struktury danych
 POLITECHNIKA KRAKOWSKA - WIEiK KATEDRA AUTOMATYKI i TECHNIK INFORMACYJNYCH Algorytmy i struktury danych www.pk.edu.pl/~zk/aisd_hp.html Wykładowca: dr inż. Zbigniew Kokosiński zk@pk.edu.pl Wykład 5: Algorytmy
POLITECHNIKA KRAKOWSKA - WIEiK KATEDRA AUTOMATYKI i TECHNIK INFORMACYJNYCH Algorytmy i struktury danych www.pk.edu.pl/~zk/aisd_hp.html Wykładowca: dr inż. Zbigniew Kokosiński zk@pk.edu.pl Wykład 5: Algorytmy
Podstawy programowania, Poniedziałek , 8-10 Projekt, część 3
 Podstawy programowania, Poniedziałek 13.05.2015, 8-10 Projekt, część 3 1. Zadanie Projekt polega na stworzeniu logicznej gry komputerowej działającej w trybie tekstowym o nazwie Minefield. 2. Cele Celem
Podstawy programowania, Poniedziałek 13.05.2015, 8-10 Projekt, część 3 1. Zadanie Projekt polega na stworzeniu logicznej gry komputerowej działającej w trybie tekstowym o nazwie Minefield. 2. Cele Celem
Struktury danych i złożoność obliczeniowa Wykład 7. Prof. dr hab. inż. Jan Magott
 Struktury danych i złożoność obliczeniowa Wykład 7 Prof. dr hab. inż. Jan Magott Problemy NP-zupełne Transformacją wielomianową problemu π 2 do problemu π 1 (π 2 π 1 ) jest funkcja f: D π2 D π1 spełniająca
Struktury danych i złożoność obliczeniowa Wykład 7 Prof. dr hab. inż. Jan Magott Problemy NP-zupełne Transformacją wielomianową problemu π 2 do problemu π 1 (π 2 π 1 ) jest funkcja f: D π2 D π1 spełniająca
Struktury danych: stos, kolejka, lista, drzewo
 Struktury danych: stos, kolejka, lista, drzewo Wykład: dane w strukturze, funkcje i rodzaje struktur, LIFO, last in first out, kolejka FIFO, first in first out, push, pop, size, empty, głowa, ogon, implementacja
Struktury danych: stos, kolejka, lista, drzewo Wykład: dane w strukturze, funkcje i rodzaje struktur, LIFO, last in first out, kolejka FIFO, first in first out, push, pop, size, empty, głowa, ogon, implementacja
5.4. Tworzymy formularze
 5.4. Tworzymy formularze Zastosowanie formularzy Formularz to obiekt bazy danych, który daje możliwość tworzenia i modyfikacji danych w tabeli lub kwerendzie. Jego wielką zaletą jest umiejętność zautomatyzowania
5.4. Tworzymy formularze Zastosowanie formularzy Formularz to obiekt bazy danych, który daje możliwość tworzenia i modyfikacji danych w tabeli lub kwerendzie. Jego wielką zaletą jest umiejętność zautomatyzowania
LOGIKA I TEORIA ZBIORÓW
 LOGIKA I TEORIA ZBIORÓW Logika Logika jest nauką zajmującą się zdaniami Z punktu widzenia logiki istotne jest, czy dane zdanie jest prawdziwe, czy nie Nie jest natomiast istotne o czym to zdanie mówi Definicja
LOGIKA I TEORIA ZBIORÓW Logika Logika jest nauką zajmującą się zdaniami Z punktu widzenia logiki istotne jest, czy dane zdanie jest prawdziwe, czy nie Nie jest natomiast istotne o czym to zdanie mówi Definicja
etrader Pekao Podręcznik użytkownika Strumieniowanie Excel
 etrader Pekao Podręcznik użytkownika Strumieniowanie Excel Spis treści 1. Opis okna... 3 2. Otwieranie okna... 3 3. Zawartość okna... 4 3.1. Definiowanie listy instrumentów... 4 3.2. Modyfikacja lub usunięcie
etrader Pekao Podręcznik użytkownika Strumieniowanie Excel Spis treści 1. Opis okna... 3 2. Otwieranie okna... 3 3. Zawartość okna... 4 3.1. Definiowanie listy instrumentów... 4 3.2. Modyfikacja lub usunięcie
Algorytmy mrówkowe. H. Bednarz. Wydział Informatyki Zachodniopomorski Uniwersytet Technologiczny w Szczecinie Inteligentne systemy informatyczne
 Algorytmy mrówkowe H. Bednarz Wydział Informatyki Zachodniopomorski Uniwersytet Technologiczny w Szczecinie Inteligentne systemy informatyczne 13 kwietnia 2015 1 2 3 4 Przestrzeń poszukiwań Ograniczenia
Algorytmy mrówkowe H. Bednarz Wydział Informatyki Zachodniopomorski Uniwersytet Technologiczny w Szczecinie Inteligentne systemy informatyczne 13 kwietnia 2015 1 2 3 4 Przestrzeń poszukiwań Ograniczenia
Dokumentacja Użytkownika: Panel administracyjny PayBM
 Blue Media Dokumentacja Użytkownika: Panel administracyjny PayBM Dokumentacja dla Partnerów Blue Media S.A. str.1 Spis treści 1. Logowanie do panelu administracyjnego PayBM... 3 2. Lista transakcji...
Blue Media Dokumentacja Użytkownika: Panel administracyjny PayBM Dokumentacja dla Partnerów Blue Media S.A. str.1 Spis treści 1. Logowanie do panelu administracyjnego PayBM... 3 2. Lista transakcji...
Algorytmy przeszukiwania
 Algorytmy przeszukiwania Przeszukiwanie liniowe Algorytm stosowany do poszukiwania elementu w zbiorze, o którym nic nie wiemy. Aby mieć pewność, że nie pominęliśmy żadnego elementu zbioru przeszukujemy
Algorytmy przeszukiwania Przeszukiwanie liniowe Algorytm stosowany do poszukiwania elementu w zbiorze, o którym nic nie wiemy. Aby mieć pewność, że nie pominęliśmy żadnego elementu zbioru przeszukujemy
Program EWIDENCJA ODZIEŻY ROBOCZEJ INSTRUKCJA UŻYTKOWNIKA Przejdź do strony producenta programu
 Program EWIDENCJA ODZIEŻY ROBOCZEJ INSTRUKCJA UŻYTKOWNIKA Przejdź do strony producenta programu http://www.jarsoft.poznan.pl/ 1. STRUKTURA PROGRAMU Program EWIDENCJA ODZIEŻY ROBOCZEJ jest aplikacją wspierającą
Program EWIDENCJA ODZIEŻY ROBOCZEJ INSTRUKCJA UŻYTKOWNIKA Przejdź do strony producenta programu http://www.jarsoft.poznan.pl/ 1. STRUKTURA PROGRAMU Program EWIDENCJA ODZIEŻY ROBOCZEJ jest aplikacją wspierającą
Algorytm Stentz a D. Przemysław Klęsk Katedra Metod Sztucznej Inteligencji i Matematyki Stosowanej
 Algorytm tentz a D Przemysław Klęsk pklesk@wi.zut.edu.pl Katedra Metod ztucznej Inteligencji i Matematyki tosowanej Zadanie W nieznanym terenie (lub znanym tylko częściowo) należy dojść do celu o podanych
Algorytm tentz a D Przemysław Klęsk pklesk@wi.zut.edu.pl Katedra Metod ztucznej Inteligencji i Matematyki tosowanej Zadanie W nieznanym terenie (lub znanym tylko częściowo) należy dojść do celu o podanych
Reprezentacje grafów nieskierowanych Reprezentacje grafów skierowanych. Wykład 2. Reprezentacja komputerowa grafów
 Wykład 2. Reprezentacja komputerowa grafów 1 / 69 Macierz incydencji Niech graf G będzie grafem nieskierowanym bez pętli o n wierzchołkach (x 1, x 2,..., x n) i m krawędziach (e 1, e 2,..., e m). 2 / 69
Wykład 2. Reprezentacja komputerowa grafów 1 / 69 Macierz incydencji Niech graf G będzie grafem nieskierowanym bez pętli o n wierzchołkach (x 1, x 2,..., x n) i m krawędziach (e 1, e 2,..., e m). 2 / 69
Wstęp do programowania. Zastosowania stosów i kolejek. Piotr Chrząstowski-Wachtel
 Wstęp do programowania Zastosowania stosów i kolejek Piotr Chrząstowski-Wachtel FIFO - LIFO Kolejki i stosy służą do przechowywania wartości zbiorów dynamicznych, czyli takich, które powstają przez dodawanie
Wstęp do programowania Zastosowania stosów i kolejek Piotr Chrząstowski-Wachtel FIFO - LIFO Kolejki i stosy służą do przechowywania wartości zbiorów dynamicznych, czyli takich, które powstają przez dodawanie
Sztuczna Inteligencja i Systemy Doradcze
 Sztuczna Inteligencja i Systemy Doradcze Przeszukiwanie przestrzeni stanów algorytmy ślepe Przeszukiwanie przestrzeni stanów algorytmy ślepe 1 Strategie slepe Strategie ślepe korzystają z informacji dostępnej
Sztuczna Inteligencja i Systemy Doradcze Przeszukiwanie przestrzeni stanów algorytmy ślepe Przeszukiwanie przestrzeni stanów algorytmy ślepe 1 Strategie slepe Strategie ślepe korzystają z informacji dostępnej
Metody iteracyjne rozwiązywania układów równań liniowych (5.3) Normy wektorów i macierzy (5.3.1) Niech. x i. i =1
 Normy wektorów i macierzy (5.3.1) Niech 1 X =[x x Y y =[y1 x n], oznaczają wektory przestrzeni R n, a yn] niech oznacza liczbę rzeczywistą. Wyrażenie x i p 5.3.1.a X p = p n i =1 nosi nazwę p-tej normy
Normy wektorów i macierzy (5.3.1) Niech 1 X =[x x Y y =[y1 x n], oznaczają wektory przestrzeni R n, a yn] niech oznacza liczbę rzeczywistą. Wyrażenie x i p 5.3.1.a X p = p n i =1 nosi nazwę p-tej normy
Algorytmy mrówkowe (optymalizacja kolonii mrówek, Ant Colony optimisation)
 Algorytmy mrówkowe (optymalizacja kolonii mrówek, Ant Colony optimisation) Jest to technika probabilistyczna rozwiązywania problemów obliczeniowych, które mogą zostać sprowadzone do problemu znalezienie
Algorytmy mrówkowe (optymalizacja kolonii mrówek, Ant Colony optimisation) Jest to technika probabilistyczna rozwiązywania problemów obliczeniowych, które mogą zostać sprowadzone do problemu znalezienie
1. Kalkulator czterech działań. 2. Konwersja ciągu znaków do tablicy.
 1. Kalkulator czterech działań. Kalkulator czterech działań: +, -, *, \ (bez nawiasów). Wejście: łańcuch znakowy, np. 1+2*3\4-5\2=, -2+4e-1= Liczby mogą być w formacie, np. +1.45, -2, 1e-10. 2. Konwersja
1. Kalkulator czterech działań. Kalkulator czterech działań: +, -, *, \ (bez nawiasów). Wejście: łańcuch znakowy, np. 1+2*3\4-5\2=, -2+4e-1= Liczby mogą być w formacie, np. +1.45, -2, 1e-10. 2. Konwersja
. Podstawy Programowania 2. Algorytmy dfs i bfs. Arkadiusz Chrobot. 2 czerwca 2019
 Podstawy Programowania Algorytmy dfs i bfs Arkadiusz Chrobot Zakład Informatyki czerwca 09 / 70 Plan Wstęp Algorytm BFS Podsumowanie / 70 Wstęp Wstęp Istnieje wiele algorytmów związanych z grafami, które
Podstawy Programowania Algorytmy dfs i bfs Arkadiusz Chrobot Zakład Informatyki czerwca 09 / 70 Plan Wstęp Algorytm BFS Podsumowanie / 70 Wstęp Wstęp Istnieje wiele algorytmów związanych z grafami, które
Wykaz stali z projektu.
 Wykaz stali z projektu. Program służy do wykonywania wykazu stali z wielu rysunków. Może być również wykorzystywany do sprawdzania poprawności opisu stali na wykonywanym rysunku. Aby korzystać z programu
Wykaz stali z projektu. Program służy do wykonywania wykazu stali z wielu rysunków. Może być również wykorzystywany do sprawdzania poprawności opisu stali na wykonywanym rysunku. Aby korzystać z programu
Notacja RPN. 28 kwietnia wyliczanie i transformacja wyrażeń. Opis został przygotowany przez: Bogdana Kreczmera.
 1 wyliczanie i transformacja wyrażeń (wersja skrócona) Opis został przygotowany przez: Bogdana Kreczmera 28 kwietnia 2002 Strona 1 z 68 Zakład Podstaw Cybernetyki i Robotyki - trochę historii...............
1 wyliczanie i transformacja wyrażeń (wersja skrócona) Opis został przygotowany przez: Bogdana Kreczmera 28 kwietnia 2002 Strona 1 z 68 Zakład Podstaw Cybernetyki i Robotyki - trochę historii...............
Przychodnia 0. Stwórz projekt aplikacja konsolowa lub WPF (przemyśl wybór, bo zmiana może być czasochłonna). 1. Stwórz abstrakcyjną klasę Osoba.
 Przychodnia 0. Stwórz projekt aplikacja konsolowa lub WPF (przemyśl wybór, bo zmiana może być czasochłonna). 1. Stwórz abstrakcyjną klasę Osoba. W tej klasie wykonaj następujące czynności: a) dodaj pole
Przychodnia 0. Stwórz projekt aplikacja konsolowa lub WPF (przemyśl wybór, bo zmiana może być czasochłonna). 1. Stwórz abstrakcyjną klasę Osoba. W tej klasie wykonaj następujące czynności: a) dodaj pole
Listy, kolejki, stosy
 Listy, kolejki, stosy abc Lista O Struktura danych składa się z węzłów, gdzie mamy informacje (dane) i wskaźniki do następnych węzłów. Zajmuje tyle miejsca w pamięci ile mamy węzłów O Gdzie można wykorzystać:
Listy, kolejki, stosy abc Lista O Struktura danych składa się z węzłów, gdzie mamy informacje (dane) i wskaźniki do następnych węzłów. Zajmuje tyle miejsca w pamięci ile mamy węzłów O Gdzie można wykorzystać:
Programowanie aplikacji mobilnych
 Katedra Inżynierii Wiedzy laborki 3 Rysunek: Tworzymy projekt Rysunek: Tworzymy projekt Tworzenie GUI szybki sposób - ustawiamy kontrolki tak, aby łącznie uzyskać 9 przycisków typu ToggleButton oraz 3
Katedra Inżynierii Wiedzy laborki 3 Rysunek: Tworzymy projekt Rysunek: Tworzymy projekt Tworzenie GUI szybki sposób - ustawiamy kontrolki tak, aby łącznie uzyskać 9 przycisków typu ToggleButton oraz 3
Języki formalne i automaty Ćwiczenia 9
 Języki formalne i automaty Ćwiczenia 9 Autor: Marcin Orchel Spis treści Spis treści... 1 Wstęp teoretyczny... 2 Maszyna Mealy'ego... 2 Maszyna Moore'a... 2 Automat ze stosem... 3 Konwersja gramatyki bezkontekstowej
Języki formalne i automaty Ćwiczenia 9 Autor: Marcin Orchel Spis treści Spis treści... 1 Wstęp teoretyczny... 2 Maszyna Mealy'ego... 2 Maszyna Moore'a... 2 Automat ze stosem... 3 Konwersja gramatyki bezkontekstowej
Opis programu Konwersja MPF Spis treści
 Opis programu Konwersja MPF Spis treści Ogólne informacje o programie...2 Co to jest KonwersjaMPF...2 Okno programu...2 Podstawowe operacje...3 Wczytywanie danych...3 Przegląd wyników...3 Dodawanie widm
Opis programu Konwersja MPF Spis treści Ogólne informacje o programie...2 Co to jest KonwersjaMPF...2 Okno programu...2 Podstawowe operacje...3 Wczytywanie danych...3 Przegląd wyników...3 Dodawanie widm
Zadania domowe. Ćwiczenie 2. Rysowanie obiektów 2-D przy pomocy tworów pierwotnych biblioteki graficznej OpenGL
 Zadania domowe Ćwiczenie 2 Rysowanie obiektów 2-D przy pomocy tworów pierwotnych biblioteki graficznej OpenGL Zadanie 2.1 Fraktal plazmowy (Plasma fractal) Kwadrat należy pokryć prostokątną siatką 2 n
Zadania domowe Ćwiczenie 2 Rysowanie obiektów 2-D przy pomocy tworów pierwotnych biblioteki graficznej OpenGL Zadanie 2.1 Fraktal plazmowy (Plasma fractal) Kwadrat należy pokryć prostokątną siatką 2 n
Algorytmy i str ruktury danych. Metody algorytmiczne. Bartman Jacek
 Algorytmy i str ruktury danych Metody algorytmiczne Bartman Jacek jbartman@univ.rzeszow.pl Metody algorytmiczne - wprowadzenia Znamy strukturę algorytmów Trudność tkwi natomiast w podaniu metod służących
Algorytmy i str ruktury danych Metody algorytmiczne Bartman Jacek jbartman@univ.rzeszow.pl Metody algorytmiczne - wprowadzenia Znamy strukturę algorytmów Trudność tkwi natomiast w podaniu metod służących
Program EWIDENCJA ODZIEŻY ROBOCZEJ INSTRUKCJA UŻYTKOWNIKA Przejdź do strony producenta programu
 Program EWIDENCJA ODZIEŻY ROBOCZEJ INSTRUKCJA UŻYTKOWNIKA Przejdź do strony producenta programu http://www.jarsoft.poznan.pl/ 1. STRUKTURA PROGRAMU Program EWIDENCJA ODZIEŻY ROBOCZEJ jest aplikacją pracującą
Program EWIDENCJA ODZIEŻY ROBOCZEJ INSTRUKCJA UŻYTKOWNIKA Przejdź do strony producenta programu http://www.jarsoft.poznan.pl/ 1. STRUKTURA PROGRAMU Program EWIDENCJA ODZIEŻY ROBOCZEJ jest aplikacją pracującą
1. SFC W PAKIECIE ISAGRAF 2. EDYCJA PROGRAMU W JĘZYKU SFC. ISaGRAF WERSJE 3.4 LUB 3.5 1
 ISaGRAF WERSJE 3.4 LUB 3.5 1 1. SFC W PAKIECIE ISAGRAF 1.1. Kroki W pakiecie ISaGRAF użytkownik nie ma możliwości definiowania własnych nazw dla kroków. Z każdym krokiem jest związany tzw. numer odniesienia
ISaGRAF WERSJE 3.4 LUB 3.5 1 1. SFC W PAKIECIE ISAGRAF 1.1. Kroki W pakiecie ISaGRAF użytkownik nie ma możliwości definiowania własnych nazw dla kroków. Z każdym krokiem jest związany tzw. numer odniesienia
Algorytm DFS Wprowadzenie teoretyczne. Algorytm DFS Wprowadzenie teoretyczne. Algorytm DFS Animacja. Algorytm DFS Animacja. Notatki. Notatki.
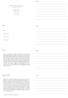 Podstawy Programowania Algorytmy dfs i bfs Arkadiusz Chrobot Zakład Informatyki czerwca 09 / 70 Plan Wstęp Podsumowanie / 70 Wstęp Istnieje wiele algorytmów związanych z grafami, które w skrócie nazywane
Podstawy Programowania Algorytmy dfs i bfs Arkadiusz Chrobot Zakład Informatyki czerwca 09 / 70 Plan Wstęp Podsumowanie / 70 Wstęp Istnieje wiele algorytmów związanych z grafami, które w skrócie nazywane
Wykłady z Matematyki Dyskretnej
 Wykłady z Matematyki Dyskretnej dla kierunku Informatyka dr Instytut Informatyki Politechnika Krakowska Wykłady na bazie materiałów: dra hab. Andrzeja Karafiata dr hab. Joanny Kołodziej, prof. PK Grafy
Wykłady z Matematyki Dyskretnej dla kierunku Informatyka dr Instytut Informatyki Politechnika Krakowska Wykłady na bazie materiałów: dra hab. Andrzeja Karafiata dr hab. Joanny Kołodziej, prof. PK Grafy
Zad. 1 Zad. 2 Zad. 3 Zad. 4 Zad. 5 SUMA
 Zad. 1 Zad. 2 Zad. 3 Zad. 4 Zad. 5 SUMA Zad. 1 (12p.)Niech n 3k > 0. Zbadać jaka jest najmniejsza możliwa liczba krawędzi w grafie, który ma dokładnie n wierzchołków oraz dokładnie k składowych, z których
Zad. 1 Zad. 2 Zad. 3 Zad. 4 Zad. 5 SUMA Zad. 1 (12p.)Niech n 3k > 0. Zbadać jaka jest najmniejsza możliwa liczba krawędzi w grafie, który ma dokładnie n wierzchołków oraz dokładnie k składowych, z których
Prezentacja multimedialna MS PowerPoint 2010 (podstawy)
 Prezentacja multimedialna MS PowerPoint 2010 (podstawy) Cz. 1. Tworzenie slajdów MS PowerPoint 2010 to najnowsza wersja popularnego programu do tworzenia prezentacji multimedialnych. Wygląd programu w
Prezentacja multimedialna MS PowerPoint 2010 (podstawy) Cz. 1. Tworzenie slajdów MS PowerPoint 2010 to najnowsza wersja popularnego programu do tworzenia prezentacji multimedialnych. Wygląd programu w
Turing i jego maszyny
 Turing Magdalena Lewandowska Politechnika Śląska, wydział MS, semestr VI 20 kwietnia 2016 1 Kim był Alan Turing? Biografia 2 3 Mrówka Langtona Bomba Turinga 4 Biografia Kim był Alan Turing? Biografia Alan
Turing Magdalena Lewandowska Politechnika Śląska, wydział MS, semestr VI 20 kwietnia 2016 1 Kim był Alan Turing? Biografia 2 3 Mrówka Langtona Bomba Turinga 4 Biografia Kim był Alan Turing? Biografia Alan
Matematyka dyskretna. Andrzej Łachwa, UJ, B/14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl 1B/14 Drogi w grafach Marszruta (trasa) w grafie G z wierzchołka w do wierzchołka u to skończony ciąg krawędzi w postaci. W skrócie
Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl 1B/14 Drogi w grafach Marszruta (trasa) w grafie G z wierzchołka w do wierzchołka u to skończony ciąg krawędzi w postaci. W skrócie
Matematyka dyskretna - 7.Drzewa
 Matematyka dyskretna - 7.Drzewa W tym rozdziale zajmiemy się drzewami: specjalnym przypadkiem grafów. Są one szczególnie przydatne do przechowywania informacji, umożliwiającego szybki dostęp do nich. Definicja
Matematyka dyskretna - 7.Drzewa W tym rozdziale zajmiemy się drzewami: specjalnym przypadkiem grafów. Są one szczególnie przydatne do przechowywania informacji, umożliwiającego szybki dostęp do nich. Definicja
Instrukcja użytkownika aplikacji modernizowanego Systemu Informacji Oświatowej
 Instrukcja użytkownika aplikacji modernizowanego Systemu Informacji Oświatowej WPROWADZANIE DANYCH DO SYSTEMU INFORMACJI OŚWIATOWEJ Nauczyciel Wersja kwiecień 2013 2 Spis treści ZBIÓR DANYCH O NAUCZYCIELACH...
Instrukcja użytkownika aplikacji modernizowanego Systemu Informacji Oświatowej WPROWADZANIE DANYCH DO SYSTEMU INFORMACJI OŚWIATOWEJ Nauczyciel Wersja kwiecień 2013 2 Spis treści ZBIÓR DANYCH O NAUCZYCIELACH...
INSTRUKCJA. SIMPLE.HCM Proces obsługi Kartoteki Pracownika, Kartoteki Przełożonego oraz Raportów kadrowo-płacowych
 INSTRUKCJA SIMPLE.HCM Proces obsługi Kartoteki Pracownika, Kartoteki Przełożonego oraz Raportów kadrowo-płacowych SPIS TREŚCI 1. KARTOTEKA PRACOWNIKA... 2 2. KARTOTEKA PRZEŁOŻONEGO... 3 3. LISTA RAPORTÓW
INSTRUKCJA SIMPLE.HCM Proces obsługi Kartoteki Pracownika, Kartoteki Przełożonego oraz Raportów kadrowo-płacowych SPIS TREŚCI 1. KARTOTEKA PRACOWNIKA... 2 2. KARTOTEKA PRZEŁOŻONEGO... 3 3. LISTA RAPORTÓW
System Obsługi Zleceń
 System Obsługi Zleceń Podręcznik Administratora Atinea Sp. z o.o., ul. Chmielna 5/7, 00-021 Warszawa NIP 521-35-01-160, REGON 141568323, KRS 0000315398 Kapitał zakładowy: 51.000,00zł www.atinea.pl wersja
System Obsługi Zleceń Podręcznik Administratora Atinea Sp. z o.o., ul. Chmielna 5/7, 00-021 Warszawa NIP 521-35-01-160, REGON 141568323, KRS 0000315398 Kapitał zakładowy: 51.000,00zł www.atinea.pl wersja
Grafy (3): drzewa. Wykłady z matematyki dyskretnej dla informatyków i teleinformatyków. UTP Bydgoszcz
 Grafy (3): drzewa Wykłady z matematyki dyskretnej dla informatyków i teleinformatyków UTP Bydgoszcz 13 (Wykłady z matematyki dyskretnej) Grafy (3): drzewa 13 1 / 107 Drzewo Definicja. Drzewo to graf acykliczny
Grafy (3): drzewa Wykłady z matematyki dyskretnej dla informatyków i teleinformatyków UTP Bydgoszcz 13 (Wykłady z matematyki dyskretnej) Grafy (3): drzewa 13 1 / 107 Drzewo Definicja. Drzewo to graf acykliczny
Zakład Podstaw Cybernetyki i Robotyki Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska
 1 Przykład wyliczania wyrażeń arytmetycznych Bogdan Kreczmer bogdan.kreczmer@pwr.wroc.pl Zakład Podstaw Cybernetyki i Robotyki Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Copyright
1 Przykład wyliczania wyrażeń arytmetycznych Bogdan Kreczmer bogdan.kreczmer@pwr.wroc.pl Zakład Podstaw Cybernetyki i Robotyki Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Copyright
1. Przypisy, indeks i spisy.
 1. Przypisy, indeks i spisy. (Wstaw Odwołanie Przypis dolny - ) (Wstaw Odwołanie Indeks i spisy - ) Przypisy dolne i końcowe w drukowanych dokumentach umożliwiają umieszczanie w dokumencie objaśnień, komentarzy
1. Przypisy, indeks i spisy. (Wstaw Odwołanie Przypis dolny - ) (Wstaw Odwołanie Indeks i spisy - ) Przypisy dolne i końcowe w drukowanych dokumentach umożliwiają umieszczanie w dokumencie objaśnień, komentarzy
Wstęp do Programowania potok funkcyjny
 Wstęp do Programowania potok funkcyjny Marcin Kubica 2010/2011 Outline 1 Podstawowe pojęcia Definition Graf = wierzchołki + krawędzie. Krawędzie muszą mieć różne końce. Między dwoma wierzchołkami może
Wstęp do Programowania potok funkcyjny Marcin Kubica 2010/2011 Outline 1 Podstawowe pojęcia Definition Graf = wierzchołki + krawędzie. Krawędzie muszą mieć różne końce. Między dwoma wierzchołkami może
Dokumentacja Systemu INSEMIK II Podręcznik użytkownika część V Badania buhaja INSEMIK II. Podręcznik użytkownika Moduł: Badania buhaja
 INSEMIK II Podręcznik użytkownika Moduł: Badania buhaja ZETO OLSZTYN Sp. z o.o. czerwiec 2009 1 1. Badania buhaja... 3 1.1. Filtr... 3 1.2. Szukaj... 6 1.3. Wydruk... 6 1.4. Karta buhaja... 8 2. Badania...
INSEMIK II Podręcznik użytkownika Moduł: Badania buhaja ZETO OLSZTYN Sp. z o.o. czerwiec 2009 1 1. Badania buhaja... 3 1.1. Filtr... 3 1.2. Szukaj... 6 1.3. Wydruk... 6 1.4. Karta buhaja... 8 2. Badania...
Dodawanie i modyfikacja atrybutów zbioru
 Dodawanie i modyfikacja atrybutów zbioru Program Moje kolekcje wyposażony został w narzędzia pozwalające na dodawanie, edycję oraz usuwanie atrybutów przypisanych do zbioru kolekcji. Dzięki takiemu rozwiązaniu
Dodawanie i modyfikacja atrybutów zbioru Program Moje kolekcje wyposażony został w narzędzia pozwalające na dodawanie, edycję oraz usuwanie atrybutów przypisanych do zbioru kolekcji. Dzięki takiemu rozwiązaniu
UONET+ moduł Dziennik
 UONET+ moduł Dziennik Sporządzanie ocen opisowych i diagnostycznych uczniów z wykorzystaniem schematów oceniania Przewodnik System UONET+ umożliwia sporządzanie ocen opisowych uczniów w oparciu o przygotowany
UONET+ moduł Dziennik Sporządzanie ocen opisowych i diagnostycznych uczniów z wykorzystaniem schematów oceniania Przewodnik System UONET+ umożliwia sporządzanie ocen opisowych uczniów w oparciu o przygotowany
dr inż. Jarosław Forenc
 Informatyka 2 Politechnika Białostocka - Wydział Elektryczny Elektrotechnika, semestr III, studia stacjonarne I stopnia Rok akademicki 2010/2011 Wykład nr 7 (24.01.2011) dr inż. Jarosław Forenc Rok akademicki
Informatyka 2 Politechnika Białostocka - Wydział Elektryczny Elektrotechnika, semestr III, studia stacjonarne I stopnia Rok akademicki 2010/2011 Wykład nr 7 (24.01.2011) dr inż. Jarosław Forenc Rok akademicki
Na poniższym rysunku widać fragment planszy. Pozycja pionka jest oznaczona przez. Pola, na które może dojść (w jednym ruchu), oznaczone są.
 Dwuwymiarowy Nim VII OIG zawody indywidualne, etap I. 8 XI 0-7 I 0 Dostępna pamięć: 6 MB. Jaś i Małgosia grają w nietypową grę. Odbywa się ona na planszy ograniczonej z dołu i z lewej, a nieskończonej
Dwuwymiarowy Nim VII OIG zawody indywidualne, etap I. 8 XI 0-7 I 0 Dostępna pamięć: 6 MB. Jaś i Małgosia grają w nietypową grę. Odbywa się ona na planszy ograniczonej z dołu i z lewej, a nieskończonej
Instrukcja użytkownika aplikacji modernizowanego Systemu Informacji Oświatowej
 Instrukcja użytkownika aplikacji modernizowanego Systemu Informacji Oświatowej WPROWADZANIE DANYCH DO SYSTEMU INFORMACJI OŚWIATOWEJ dla szkół i placówek oświatowych Moduł: DANE ZBIORCZE czerwiec 2013 2
Instrukcja użytkownika aplikacji modernizowanego Systemu Informacji Oświatowej WPROWADZANIE DANYCH DO SYSTEMU INFORMACJI OŚWIATOWEJ dla szkół i placówek oświatowych Moduł: DANE ZBIORCZE czerwiec 2013 2
Algorytmiczna teoria grafów Przepływy w sieciach.
 Algorytmiczna teoria grafów Sieć przepływowa Siecią przepływową S = (V, E, c) nazywamy graf zorientowany G = (V,E), w którym każdy łuk (u, v) E ma określoną przepustowość c(u, v) 0. Wyróżniamy dwa wierzchołki:
Algorytmiczna teoria grafów Sieć przepływowa Siecią przepływową S = (V, E, c) nazywamy graf zorientowany G = (V,E), w którym każdy łuk (u, v) E ma określoną przepustowość c(u, v) 0. Wyróżniamy dwa wierzchołki:
Laboratorium z przedmiotu Programowanie obiektowe - zestaw 04
 Laboratorium z przedmiotu Programowanie obiektowe - zestaw 04 Cel zajęć. Celem zajęć jest zapoznanie się ze sposobem działania popularnych kolekcji. Wprowadzenie teoretyczne. Rozważana w ramach niniejszych
Laboratorium z przedmiotu Programowanie obiektowe - zestaw 04 Cel zajęć. Celem zajęć jest zapoznanie się ze sposobem działania popularnych kolekcji. Wprowadzenie teoretyczne. Rozważana w ramach niniejszych
Bazy danych TERMINOLOGIA
 Bazy danych TERMINOLOGIA Dane Dane są wartościami przechowywanymi w bazie danych. Dane są statyczne w tym sensie, że zachowują swój stan aż do zmodyfikowania ich ręcznie lub przez jakiś automatyczny proces.
Bazy danych TERMINOLOGIA Dane Dane są wartościami przechowywanymi w bazie danych. Dane są statyczne w tym sensie, że zachowują swój stan aż do zmodyfikowania ich ręcznie lub przez jakiś automatyczny proces.
Literatura. 1) Pojęcia: złożoność czasowa, rząd funkcji. Aby wyznaczyć pesymistyczną złożoność czasową algorytmu należy:
 Temat: Powtórzenie wiadomości z PODSTAW INFORMATYKI I: Pojęcia: złożoność czasowa algorytmu, rząd funkcji kosztu. Algorytmy. Metody programistyczne. Struktury danych. Literatura. A. V. Aho, J.E. Hopcroft,
Temat: Powtórzenie wiadomości z PODSTAW INFORMATYKI I: Pojęcia: złożoność czasowa algorytmu, rząd funkcji kosztu. Algorytmy. Metody programistyczne. Struktury danych. Literatura. A. V. Aho, J.E. Hopcroft,
Architektura systemów komputerowych Laboratorium 7 Symulator SMS32 Stos, Tablice, Procedury
 Marcin Stępniak Architektura systemów komputerowych Laboratorium 7 Symulator SMS32 Stos, Tablice, Procedury 1. Informacje 1.1. Stos Stos jest strukturą danych, w której dane dokładane są na wierzch stosu
Marcin Stępniak Architektura systemów komputerowych Laboratorium 7 Symulator SMS32 Stos, Tablice, Procedury 1. Informacje 1.1. Stos Stos jest strukturą danych, w której dane dokładane są na wierzch stosu
Rozwiązywanie równań różniczkowych cząstkowych metodą elementów skończonych - wprowadzenie
 Rozwiązywanie równań różniczkowych cząstkowych metodą elementów skończonych - wprowadzenie Wprowadzenie Metoda Elementów Skończonych (MES) należy do numerycznych metod otrzymywania przybliżonych rozwiązań
Rozwiązywanie równań różniczkowych cząstkowych metodą elementów skończonych - wprowadzenie Wprowadzenie Metoda Elementów Skończonych (MES) należy do numerycznych metod otrzymywania przybliżonych rozwiązań
Ocenianie opisowe Optivum. Jak przygotować i wydrukować świadectwa lub arkusze ocen?
 Ocenianie opisowe Optivum Jak przygotować i wydrukować świadectwa lub arkusze ocen? W programie Ocenianie opisowe Optivum można przygotowywać raporty w oparciu o wcześniej sporządzony szablon dokumentu,
Ocenianie opisowe Optivum Jak przygotować i wydrukować świadectwa lub arkusze ocen? W programie Ocenianie opisowe Optivum można przygotowywać raporty w oparciu o wcześniej sporządzony szablon dokumentu,
Zawartość. Wstęp. Moduł Rozbiórki. Wstęp Instalacja Konfiguracja Uruchomienie i praca z raportem... 6
 Zawartość Wstęp... 1 Instalacja... 2 Konfiguracja... 2 Uruchomienie i praca z raportem... 6 Wstęp Rozwiązanie przygotowane z myślą o użytkownikach którzy potrzebują narzędzie do podziału, rozkładu, rozbiórki
Zawartość Wstęp... 1 Instalacja... 2 Konfiguracja... 2 Uruchomienie i praca z raportem... 6 Wstęp Rozwiązanie przygotowane z myślą o użytkownikach którzy potrzebują narzędzie do podziału, rozkładu, rozbiórki
MIO - LABORATORIUM. Imię i nazwisko Rok ak. Gr. Sem. Komputer Data ... 20 / EC3 VIII LAB...
 MIO - LABORATORIUM Temat ćwiczenia: TSP - Problem komiwojażera Imię i nazwisko Rok ak. Gr. Sem. Komputer Data Podpis prowadzącego... 20 / EC3 VIII LAB...... Zadanie Zapoznać się z problemem komiwojażera
MIO - LABORATORIUM Temat ćwiczenia: TSP - Problem komiwojażera Imię i nazwisko Rok ak. Gr. Sem. Komputer Data Podpis prowadzącego... 20 / EC3 VIII LAB...... Zadanie Zapoznać się z problemem komiwojażera
Wstęp do programowania
 Wstęp do programowania Stosy, kolejki, drzewa Paweł Daniluk Wydział Fizyki Jesień 2013 P. Daniluk(Wydział Fizyki) WP w. VII Jesień 2013 1 / 25 Listy Lista jest uporządkowanym zbiorem elementów. W Pythonie
Wstęp do programowania Stosy, kolejki, drzewa Paweł Daniluk Wydział Fizyki Jesień 2013 P. Daniluk(Wydział Fizyki) WP w. VII Jesień 2013 1 / 25 Listy Lista jest uporządkowanym zbiorem elementów. W Pythonie
System Gokart Timing
 System Gokart Timing 1 Spis treści System Gokart Timing... 1 Wstęp... 3 Słownik pojęć:... 3 Ogólny opis systemu... 3 Wymagania... 3 Aplikacja pomiarowa... 4 Interfejs... 4 Opis funkcji... 5 Aplikacja do
System Gokart Timing 1 Spis treści System Gokart Timing... 1 Wstęp... 3 Słownik pojęć:... 3 Ogólny opis systemu... 3 Wymagania... 3 Aplikacja pomiarowa... 4 Interfejs... 4 Opis funkcji... 5 Aplikacja do
MATERIAŁY DYDAKTYCZNE. Streszczenie: Z G Łukasz Próchnicki NIP w ramach projektu nr RPMA /15
 MATERIAŁY DYDAKTYCZNE w ramach projektu nr RPMA.10.01.01-14-3849/15 Streszczenie: Administracja witryny e-learning NIP 799-174-10-88 Spis treści 1. Ustawienia strony głównej... 2 2. Jak powinna wyglądać
MATERIAŁY DYDAKTYCZNE w ramach projektu nr RPMA.10.01.01-14-3849/15 Streszczenie: Administracja witryny e-learning NIP 799-174-10-88 Spis treści 1. Ustawienia strony głównej... 2 2. Jak powinna wyglądać
Ćwiczenie 1: Pierwsze kroki
 Ćwiczenie 1: Pierwsze kroki z programem AutoCAD 2010 1 Przeznaczone dla: nowych użytkowników programu AutoCAD Wymagania wstępne: brak Czas wymagany do wykonania: 15 minut W tym ćwiczeniu Lekcje zawarte
Ćwiczenie 1: Pierwsze kroki z programem AutoCAD 2010 1 Przeznaczone dla: nowych użytkowników programu AutoCAD Wymagania wstępne: brak Czas wymagany do wykonania: 15 minut W tym ćwiczeniu Lekcje zawarte
Spis treści. I. Logowanie się do aplikacji tos 3 II. Zmiana hasła 4 III. Panel główny 6 IV. Kontrahenci 8 V. Wystawienie pro formy 11
 1 Spis treści. I. Logowanie się do aplikacji tos 3 II. Zmiana hasła 4 III. Panel główny 6 IV. Kontrahenci 8 V. Wystawienie pro formy 11 2 I. Logowanie się do aplikacji tos. O fakcie udostępnienia tobie
1 Spis treści. I. Logowanie się do aplikacji tos 3 II. Zmiana hasła 4 III. Panel główny 6 IV. Kontrahenci 8 V. Wystawienie pro formy 11 2 I. Logowanie się do aplikacji tos. O fakcie udostępnienia tobie
Wstęp do Sztucznej Inteligencji
 Wstęp do Sztucznej Inteligencji Rozwiązywanie problemów-i Joanna Kołodziej Politechnika Krakowska Wydział Fizyki, Matematyki i Informatyki Rozwiązywanie problemów Podstawowe fazy: Sformułowanie celu -
Wstęp do Sztucznej Inteligencji Rozwiązywanie problemów-i Joanna Kołodziej Politechnika Krakowska Wydział Fizyki, Matematyki i Informatyki Rozwiązywanie problemów Podstawowe fazy: Sformułowanie celu -
UKŁADY ALGEBRAICZNYCH RÓWNAŃ LINIOWYCH
 Transport, studia I stopnia rok akademicki 2011/2012 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Adam Wosatko Uwagi wstępne Układ liniowych równań algebraicznych można
Transport, studia I stopnia rok akademicki 2011/2012 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Adam Wosatko Uwagi wstępne Układ liniowych równań algebraicznych można
