Symetria i asymetria zwierciadlana
|
|
|
- Urszula Kruk
- 8 lat temu
- Przeglądów:
Transkrypt
1 4 Symetria i asymetria zwierciadlana Antonina Kowalska Instytut Fizyki Uniwersytetu Jagiellońskiego Opracowanie na podstawie referatu wygłoszonego na seminarium w Castel Gandolfo w 1997 roku. Wstęp Herman Weyl w swojej pięknej książce zatytułowanej Symetria [1] mówi: Symetria jest ideą, za pomocą której człowiek stara się od niepamiętnych czasów ogarnąć myślą i tworzyć porządek, piękno i doskonałość. Z drugiej strony, jak obserwujemy, umysł człowieka ma wrodzoną tendencję do akceptowania symetrii obiektów (bardzo różnych obiektów) jako swojego rodzaju doskonałości. Tak było od najdawniejszych czasów. Dla starożytnych Greków: symetryczny znaczy mający właściwe proporcje; symetria to zgodność części składowych, dzięki której jednoczą się one w całość. Słowo symetria wywodzi się od greckiego słowa συµµετρεοµαι, co oznacza mierzyć, rachować. W szczególności dla Pitagorejczyków (VI IV wiek p.n.e.) [2, 3]: symetria to źródło porządku bytów; symetria zawiera w sobie liczbę; cały kosmos jest harmonią i liczbą (jak bliskie jest to współczesnym dociekaniom, szukającym u podstaw naszej rzeczywistości ukrytych symetrii opisywalnych jedynie strukturami matematycznymi!). Synonimami symetrii były dla Pitagorejczyków harmonia i przyjaźń. Podobno, gdy zapytano Pitagorasa, kto jest jego przyjacielem, odpowiedział: Ja i mój przyjaciel to tak, jak liczby przyjacielskie, np. 220 i 284. W liczbach przyjacielskich suma podzielników właściwych jednej liczby jest równa drugiej, i na odwrót: 220 = (l, 2, 4, 71, 142 są podzielnikami liczby 284) 284 = l (składniki te to podzielniki liczby 220) Są więc te liczby niejako wzajemnym odbiciem. Takich par znamy dzisiaj wiele, ale co ciekawe mają one związek z pewnymi grupami, a więc symetriami, występującymi w języku matematycznym fizyki, mianowicie z tzw. grupami Liego. Mówiąc o symetrii, bierzemy pod uwagę dwa elementy: przekształcenie i obiekt, który się przy tym przekształceniu nie zmienia, czyli jest względem tego przekształcenia symetryczny. Przykładami przekształceń mogą być obroty, prze-
2 5 sunięcia, odbicia zwierciadlane, symetryczne względem nich obiekty to na przykład: koło, pas nieskończony, trójkąt równoramienny. Człowiek od najdawniejszych czasów zajmował się obiektami symetrycznymi względem wymienionych przekształceń. Przykładem są tzw. bryły platońskie, niezmiennicze względem specyficznych obrotów, a także ornamenty płaskie, symetryczne względem pewnych połączeń trzech wymienionych wyżej przekształceń. Na przykład w starożytnym Egipcie odkryto w sposób praktyczny 17 typów takich ornamentów, ale dopiero na przełomie XIX i XX wieku wykazano, że są to wszystkie możliwe typy. W referacie tym prześledzimy dziwną historię symetrii zwierciadlanej i jej naruszenia, czyli asymetrii, tak jak ją postrzegano i badano od czasów najdawniejszych do chwili obecnej. Odbicia zwierciadlane Definicja odbicia Obierzmy (zob. rys. 1) dowolną prostą p prostopadłą do płaszczyzny E (na rys. 1 zaznaczono tylko ślad tej płaszczyzny) oraz dowolny punkt P na prostej p. Istnieje jeden i tylko jeden punkt P na p, który leży w tej samej odległości od E co punkt P, ale po innej jej stronie. P pokrywa się z P wtedy i tylko wtedy, gdy P leży na E. Rys. 1 Odbicie zwierciadlane w E jest to przekształcenie przestrzeni w nią samą: P P, które przenosi dowolny punkt P na miejsce jego obrazu zwierciadlanego P. O obiekcie, który się przy tym nie zmienia, mówimy, że ma symetrię zwierciadlaną względem E. Symetria zwierciadlana a psychika człowieka Można zapytać, dlaczego pozytywne odczucie symetrii zwierciadlanej było i jest tak głęboko zakorzenione w psychice ludzkiej. Niewątpliwie miała na to i ma wpływ obserwacja symetrii zewnętrznej ciała człowieka i otaczających go stworzeń [4, 5]. Najprostszy porządek, zestawienie dwóch elementów, obrazu i odbicia zwierciadlanego, tworzących razem figurę zwierciadlanie symetryczną, w jakiś sposób odpowiada psychice człowieka. Przejawia się to na przykład w radości dzieci z tzw. kleksowych malowideł [6]. Powstają one z kropli atramentu, umieszczonej wewnątrz złożonej kartki papieru, po jej rozłożeniu (rys. 2).
3 6 Rys. 2 Rys. 3. Odstępstwo od idealnej symetrii w naszym godle państwowym Może to pozytywne odczucie symetrii jest zakodowane w mechanizmie widzenia porządkującym sygnały z otaczającego nas świata (M. Zlat [5]) lub być może jest związane z procesem odkrywania praw symetrii, jakiejkolwiek symetrii (A.V. Shubnikov et al. [6]). Od najdawniejszych czasów obserwujemy w sztuce, że wszędzie tam, gdzie sens dzieła wymaga wyrażenia ładu i równowagi, tam kompozycję określa symetria zwierciadlana. Szczególnie jest to widoczne we wzorach heraldycznych, zdobnictwie posadzkowym, budowlach sakralnych, itp. Bardzo często jednak w dziełach tych obserwujemy mniejsze lub większe odstępstwa od tej symetrii, które w odczuciu twórców mają wnieść do dzieła elementy ruchu, życia [l, 5]. Tak naprawdę, jak zobaczymy dalej, symetria zwierciadlana jest naruszona, i to aż do bardzo głębokich obszarów naszego świata. Postawię więc tu pytanie retoryczne typu egzystencjalnego: czy tylko obserwacje zewnętrznego świata warunkują powszechne odczucie satysfakcji z symetrii, czy też może przyczyna tkwi przede wszystkim głębiej, w naszej łączności z jakąś ukrytą symetrią wszechświata? W dalszym ciągu będziemy się zajmować symetrią i asymetrią zwierciadlaną obiektów fizycznych, jak też oddziaływań między nimi. Na razie, aby lepiej zrozumieć naturę przekształcenia zwierciadlanego, rozważmy je kolejno w jedno-, dwu- oraz trójwymiarowej przestrzeni. Odbicia w jednym wymiarze Ś w i a t l i n i i. Wyobraźmy sobie (zob. M. Gardner [7]), że linię tę zamieszkują istoty zwane liniakami, dorośli: oraz dzieci:. Umieśćmy prostopadle do linii ich świata lustro E. Z ich punktu widzenia będzie to tylko punkt zwierciadła znajdujący się na tej linii. Dziecko będzie wyglądało tak samo, jak jego odbicie zwierciadlane, dziecko jest nakładalne na jego obraz zwierciadlany
4 7 przez przesunięcie bez wychodzenia poza jeden wymiar. Inaczej dorosły liniak ; on nie pokryje swojego obrazu zwierciadlanego bez wyjścia poza jeden wymiar. Powiemy, że dziecko jest tworem symetrycznym (czyli ma płaszczyznę symetrii, która redukuje się w tym przypadku do środkowego punktu odcinka), a dorosły liniak tworem asymetrycznym (pozbawionym jakiejkolwiek płaszczyzny symetrii ). Rys. 4 Odbicia w dwóch wymiarach Ś w i a t p ł a s k i. Wyobraźmy sobie, że płaszczyznę zamieszkują istoty zwane płaszczakami [7]. Umieśćmy zwierciadło prostopadle do ich świata (płaszczyzny), dla nich będzie to prosta. Na rysunku widzimy płaszczaka i jego obraz zwierciadlany. Rys. 5. Obraz 1 oraz obraz 2 są nakładalne,,płaszczak nie jest nakładalny na swój obraz poprzez przesunięcie lub obrót w jego płaszczyźnie. Można go tylko wyjąć do przestrzeni trójwymiarowej, obrócić i nałożyć na obraz. Tak jest, ponieważ płaszczak nie ma jakiejkolwiek płaszczyzny symetrii, czyli w tym przypadku linii symetrii. Powiemy, że płaszczak jest asymetryczny. Zauważmy, że umieszczenie luster w dowolnej pozycji daje obrazy nakładalne na siebie (po przesunięciu lub obróceniu).
5 8 W świecie linii symetryczna figura ma punkt zwany środkiem symetrii, który dzieli ją na zwierciadlane połowy. W świecie figur płaskich analogiem jest oś symetrii. Przykłady Rys. 6 Odbicia w trzech wymiarach W przestrzeni trójwymiarowej figura nakładalna na jej obraz zwierciadlany (po ewentualnym przesunięciu lub obrocie) ma przynajmniej jedną płaszczyznę symetrii ewentualnie połączoną z obrotem. Nazwiemy taką figurę krótko symetryczną. Zatem przez figurę asymetryczną będziemy tu rozumieć taką, która nie posiada ani jednej tego rodzaju płaszczyzny (może jednak być symetryczna względem obrotów właściwych). Niezależnie od liczby wymiarów: figura jest symetryczna (achiralna), jeżeli jest nakładalna (przez przesunięcie lub obrót) na jej obraz zwierciadlany; figura jest asymetryczna (chiralna), jeżeli nie jest nakładalna na jej obraz zwierciadlany bez przechodzenia w przestrzeń o większej liczbie wymiarów. Słowo chiralny pochodzi od greckiego słowa cheir = ręka. Figurę chiralną i jej obraz zwierciadlany nazywamy parą figur enancjomorficznych. Przykładami takich par w przestrzeni trójwymiarowej są: para rąk, para butów, śruby prawo- i lewoskrętna. Ciekawym przykładem figur enancjomorficznych są dwie połówki jabłka otrzymane w tzw. królewskim podziale jabłka [8]. Mówi się czasem, że obraz zwierciadlany obiektu chiralnego jest z nim identyczny, tylko zachodzi inaczej. Rys. 7. Przykłady par figur enancjomorficznych
6 9 Rys. 8. Królewski podział jabłka (patrz też str. 70) Odbicia kierunków 1. Strzałka obrazująca tzw. wektor polarny, na przykład wektor prędkości, jest nakładalna na swój obraz zwierciadlany, przy czym strzałka taka nie zmienia się przy odbiciu w płaszczyźnie równoległej do strzałki, a kierunek jej zmienia się na przeciwny przy odbiciu w płaszczyźnie prostopadłej do strzałki (zob. rys. 9a, b). Rys. 9a Rys. 9b 2. Kierunek może też być wyznaczony przez obracający się walec. Kierunek obrazuje się wtedy często także strzałką, umownie skierowaną tak, że jej koniec wskazuje na ten koniec walca, który widzimy obracający się przeciwnie do ruchu wskazówek zegara. Rys. 10
7 10 Taka strzałka zachowuje się przy odbiciu zwierciadlanym inaczej niż strzałka pierwsza (zob. rys. 11a, b). Wektor, który tak zachowuje się przy odbiciu, nosi nazwę wektora aksjalnego (przykładami są: kręt orbitalny (moment pędu), spinowy, pole magnetyczne, moment magnetyczny). Dla odróżnienia strzałki drugiej od pierwszej H. Genz [9] wprowadził dla wektora aksjalnego symbol:. W dalszym ciągu będziemy się posługiwać tym oznaczeniem. Rys. 11a Rys. 11b Jedna i druga strzałka są obiektami symetrycznymi (nakładalnymi na obraz zwierciadlany). 3. Asymetrycznym obiektem (chiralnym) jest dopiero śruba, czyli połączenie w tym samym obiekcie zwykłej strzałki i krążenia Rys. 12a Rys. 12b Asymetria istot żywych, kryształów i molekuł Człowiek i większość zwierząt mają tylko jedną płaszczyznę symetrii. Jest to symetria przybliżona (u człowieka: serce po lewej stronie, wyrostek po prawej, przewaga praworęczności nad leworęcznością itd.). Ta przybliżona symetria wykształcona została w dużym stopniu przez ewolucję. Na przykład u ryb: ruch pre-
8 11 ferował symetrię osiową, grawitacja podobnie tylko w innym kierunku, co w rezultacie dało płaszczyznę symetrii, przy czym na ogół żaden czynnik zewnętrzny nie wyróżnia strony prawej od lewej. Rośliny mają przeważnie przybliżoną symetrię stożkową: pion od siły grawitacji, brak poziomej płaszczyzny symetrii, nieskończona liczba pionowych płaszczyzn symetrii. Owoce mają często nieskończenie wiele płaszczyzn symetrii (ale banan tylko jedną). Rys. 13. Przykłady symetrii w przyrodzie Jeżeli jakieś istoty żywe występują w formie chiralnej, to ich enancjomorficzni partnerzy także pojawiają się w przyrodzie, choć raczej rzadko. Na przykład wśród ludzi istnieje leworęczna mniejszość; serce po prawej stronie występuje, lecz bardzo rzadko. Wśród roślin pojawiają się struktury spiralne. Większość pnących się roślin, które rosnąc, owijają się wokół innych, tworzy śrubę prawoskrętną, ale jest też wiele lewoskrętnych. Podobnie większość muszli ślimaków jest prawoskrętna, ale też wiele jest lewoskrętnych. Chiralność występuje także wśród bakterii [10]. Kryształy często mają płaszczyzny symetrii, ale istnieją kryształy nienakładalne na swój obraz zwierciadlany, które mają odmianę lewoskrętną i prawoskrętną. Rozważmy tu przykładowo: a) kwarc dwutlenek krzemu, w którym mamy śrubowe ułożenie atomów, a śruba może być zarówno lewa, jak i prawa. Obserwuje się występowanie obu form wzajemnie enancjomorficznych;
9 12 b) kwas winowy C 4 H 6 O 6 jest także chiralny i występuje w dwóch odmianach wzajemnie enancjomorficznych. Rys. 14a. Kryształ górski Rys. 14b. Kryształ kwasu winowego Molekuły. Nasuwa się pytanie, czy cząsteczki, z których zbudowany jest kryształ, rozważane jako indywidualne składniki (o danym składzie atomowym), są zawsze symetryczne? Jeżeli tak, to zawsze będą mieć te same własności, czy to występując w przyrodzie, czy otrzymane syntetycznie w laboratorium. Jeżeli jednak molekuła jest chiralna, wówczas można czy to znaleźć w przyrodzie, czy też zsyntetyzować dwie zupełnie inne formy tego samego związku chemicznego. Jedna forma będzie zawierała wyłącznie molekuły prawoskrętne, druga ich obrazy zwierciadlane molekuły lewoskrętne. Takie asymetryczne cząsteczki istnieją i nazywa się je stereoizomerami. Historia ich odkrycia jest bardzo ciekawa. Rozpoczęła się na początku XIX wieku. Fizyk i chemik francuski Jean Baptiste Biot odkrył, że wyżej wspomniane kryształy kwarcu mają zdolność obracania płaszczyzny polaryzacji światła (substancja optycznie czynna). Dwie formy enancjomorficzne obracają tę płaszczyznę w przeciwnych kierunkach. Stwierdził on ponadto, że gdy kryształy zostają rozpuszczone, to roztwór przestaje być czynny optycznie. Stąd wniosek: zdolność obracania płaszczyzny polaryzacji nie pochodzi z asymetrii cząsteczek kwarcu, lecz z asymetrii struktury krystalicznej, w której kwarc krystalizuje. Innym odkryciem Biota było to, że otrzymany z organizmów żywych roztwór kwasu winowego jest też optycznie czynny. Należało przypuszczać (roztwór!), że obiektami optycznie czynnymi są tu molekuły tej substancji. Louis Pasteur, młody fizyk francuski kontynuował tę tematykę. Wiadomo było wówczas, że oprócz kwasu winowego (substancja organiczna) istnieje kwas gronowy, prawie niczym się nieróżniący od winowego, a jedyna różnica polega na tym, że jest optycznie nieczynny. Pasteur wykrystalizował kwas gronowy i stwierdził pod mikroskopem, że zawiera on dwie odmiany enancjomorficzne kwasu winowego. Mozolnie oddzielił jedne kryształki od drugich i przygotował dwa roztwory. Stwierdził, że oba są czynne optycznie, ale płaszczyznę polaryzacji skręcają jeden w prawo, drugi w lewo.
10 13 Innym bardzo ważnym odkryciem Pasteura było stwierdzenie, że pewnego rodzaju pleśń zanurzona w roztworze kwasu gronowego czyni ten roztwór optycznie czynnym. Wywnioskował stąd, że asymetryczny żywy organizm żywi się potrzebną mu formą enancjomorficzną i w ten sposób dokonuje selekcji. Doszedł więc do przekonania, że tylko w tworach organicznych mogą się znajdować substancje asymetryczne złożone wyłącznie z jednego rodzaju asymetrycznych cząstek. A oto jego wypowiedź (rok 1850): Nieożywione symetryczne siły, działając na atomy czy cząsteczki symetryczne, nie mogą wytworzyć struktur asymetrycznych. Wytworzenie dwóch przeciwstawnych asymetrycznych połówek jest równoważne wytworzeniu symetrycznej całości, czy to w przypadku, gdy dwie asymetryczne połówki tworzą rzeczywiście jedną molekułę (mezoforma), czy to w przypadku, gdy istnieją jako dwie oddzielne molekuły, lewe i prawe składniki kwasu gronowego. Dopiero w roku 1874 odkryto strukturę cząsteczek kwasu winowego tłumaczącą ich asymetrię [7]. Inaczej ujmując powyższe, można powiedzieć, co następuje: jeżeli kiedykolwiek odkrywamy w przyrodzie związek chemiczny złożony z cząsteczek asymetrycznych, który nie jest wynikiem zachodzenia procesów fizjologicznych (w organizmach żywych), zawsze odkrywa się go w formie racemicznej (lub mezoformie), tzn. jest on mieszaniną równej ilości cząsteczek lewych i prawych. Łatwo zrozumieć, dlaczego tak się dzieje, gdy siły działające w przyrodzie są siłami zwierciadlanie symetrycznymi. Gdy tworzy się jakiś związek chemiczny, wówczas prawa przypadku nakazują, aby wytworzyły się w równych ilościach cząsteczki prawe i lewe. Nawet w laboratorium, jeżeli syntetyzuje się stereoizomery bez wprowadzania określonej asymetrii w warunkach ich syntezy, uzyskuje się racemiczną, symetryczną mieszaninę, która nie obraca płaszczyzny polaryzacji światła. Natomiast, jak wiemy dziś, wszystkie organizmy żywe w swojej najistotniejszej strukturze zawierają asymetrię, między innymi w postaci podwójnej prawoskrętnej spirali DNA (czyli kwasu dezoksyrybonukleinowego). Różne są hipotezy pochodzenia asymetrii organizmów żywych. Pasteur twierdził, że przy powstaniu życia musiała działać jakaś asymetria wszechświata. W związku z powyższym nasuwa się pytanie: czy rzeczywiście oddziaływania między obiektami fizycznymi są symetryczne, inaczej: czy prawa fizyki są symetryczne, czy asymetryczne zwierciadlanie?
11 14 W następnym zeszycie zajmiemy się symetrią i asymetrią oddziaływań. LITERATURA [1] Weyl H.: Symetria, PWN [2] Gajda J.: Pitagorejczycy, Wiedza Powszechna, Warszawa [3] Mozrzymas J.: Ewolucja idei symetrii. Wydawnictwo Uniwersytetu Wrocławskiego [4] Reichholf-Riehm H.: Motyle, Geo-Center, Warszawa [5] Zlat M.: Symetria w sztuce [w:] Symetrie w sztuce i naukach humanistycznych, pod red. J. Gajdy-Krynickiej, Leopoldinum, Wrocław [6] Shubnikov A.V., Koptsik V.A.: Symmetry in Science and Art, Plenum Press, N.Y [7] Gardner M.: Zwierciadlany wszechświat, PWN, [8] Hargittai I., Hargittai M.: Symmetry through the Eyes o f a Chemist, VCH, N.Y [9] Genz. H.: Symmetrie Buaplan der Natur, Piper, [10] Hegstrom R.A. Kondepudi D.K.: Scientific American, No. 1, 1990, 108. Przypominamy, że o symetriach można przeczytać w artykule Katarzyny Cieślar Symetria w przyrodzie, Foton 87, zima Zachęcamy również do zajrzenia na stronę: Jan Paweł II obserwuje demonstrowany przez Antoninę Kowalską królewski podział jabłka
7-9. Stereoizomeria. izomery. konstytucyjne różne szkielety węglowe, różne grupy funkcyjne różne położenia gr. funkcyjnych
 7-9. Stereoizomeria izomery konstytucyjne różne szkielety węglowe, różne grupy funkcyjne różne położenia gr. funkcyjnych stereoizomery zbudowane z takich samych atomów atomy połączone w takiej samej sekwencji
7-9. Stereoizomeria izomery konstytucyjne różne szkielety węglowe, różne grupy funkcyjne różne położenia gr. funkcyjnych stereoizomery zbudowane z takich samych atomów atomy połączone w takiej samej sekwencji
4. Stereoizomeria. izomery. konstytucyjne różne szkielety węglowe, różne grupy funkcyjne różne położenia gr. funkcyjnych
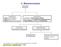 4. Stereoizomeria izomery konstytucyjne różne szkielety węglowe, różne grupy funkcyjne różne położenia gr. funkcyjnych stereoizomery zbudowane z takich samych atomów atomy połączone w takiej samej sekwencji
4. Stereoizomeria izomery konstytucyjne różne szkielety węglowe, różne grupy funkcyjne różne położenia gr. funkcyjnych stereoizomery zbudowane z takich samych atomów atomy połączone w takiej samej sekwencji
Symetria w fizyce materii
 Symetria w fizyce materii - Przekształcenia symetrii w dwóch i trzech wymiarach - Wprowadzenie w teorię grup; grupy symetrii - Wprowadzenie w teorię reprezentacji grup - Teoria grup a mechanika kwantowa
Symetria w fizyce materii - Przekształcenia symetrii w dwóch i trzech wymiarach - Wprowadzenie w teorię grup; grupy symetrii - Wprowadzenie w teorię reprezentacji grup - Teoria grup a mechanika kwantowa
Pawełek Malecki obecnie student fizyki UJ na rękach swego ojca, fizyka Piotra Maleckiego, z wizytą u Ojca Świętego
 Pawełek Malecki obecnie student fizyki UJ na rękach swego ojca, fizyka Piotra Maleckiego, z wizytą u Ojca Świętego FOTON 89, Lato 2005 1 Wiara i rozum Wiara i rozum (fides et ratio) są jak dwa skrzydła,
Pawełek Malecki obecnie student fizyki UJ na rękach swego ojca, fizyka Piotra Maleckiego, z wizytą u Ojca Świętego FOTON 89, Lato 2005 1 Wiara i rozum Wiara i rozum (fides et ratio) są jak dwa skrzydła,
PLANIMETRIA CZYLI GEOMETRIA PŁASZCZYZNY CZ. 1
 PLANIMETRIA CZYLI GEOMETRIA PŁASZCZYZNY CZ. 1 Planimetria to dział geometrii, w którym przedmiotem badań są własności figur geometrycznych leżących na płaszczyźnie (patrz określenie płaszczyzny). Pojęcia
PLANIMETRIA CZYLI GEOMETRIA PŁASZCZYZNY CZ. 1 Planimetria to dział geometrii, w którym przedmiotem badań są własności figur geometrycznych leżących na płaszczyźnie (patrz określenie płaszczyzny). Pojęcia
Geometria. Rozwiązania niektórych zadań z listy 2
 Geometria. Rozwiązania niektórych zadań z listy 2 Inne rozwiązanie zadania 2. (Wyznaczyć równanie stycznej do elipsy x 2 a 2 + y2 b 2 = 1 w dowolnym jej punkcie (x 0, y 0 ). ) Przypuśćmy, że krzywa na
Geometria. Rozwiązania niektórych zadań z listy 2 Inne rozwiązanie zadania 2. (Wyznaczyć równanie stycznej do elipsy x 2 a 2 + y2 b 2 = 1 w dowolnym jej punkcie (x 0, y 0 ). ) Przypuśćmy, że krzywa na
Kształtowanie w uczniach umiejętności identyfikowania zależności i analogii matematycznych w otaczającym świecie.
 Tytuł Mity, magia i matematyka Autor Sławomir Dziugieł Dział Figury płaskie - symetrie i inne przekształcenia geometryczne Innowacyjne cele edukacyjne Kształtowanie w uczniach umiejętności identyfikowania
Tytuł Mity, magia i matematyka Autor Sławomir Dziugieł Dział Figury płaskie - symetrie i inne przekształcenia geometryczne Innowacyjne cele edukacyjne Kształtowanie w uczniach umiejętności identyfikowania
Chemia organiczna. Stereochemia. Zakład Chemii Medycznej Pomorskiego Uniwersytetu Medycznego
 Chemia organiczna Stereochemia Zakład Chemii Medycznej Pomorskiego Uniwersytetu Medycznego Chemia organiczna jest nauką, która zajmuje się poszukiwaniem zależności pomiędzy budową cząsteczki a właściwościami
Chemia organiczna Stereochemia Zakład Chemii Medycznej Pomorskiego Uniwersytetu Medycznego Chemia organiczna jest nauką, która zajmuje się poszukiwaniem zależności pomiędzy budową cząsteczki a właściwościami
Krzywa uniwersalna Sierpińskiego
 Krzywa uniwersalna Sierpińskiego Małgorzata Blaszke Karol Grzyb Streszczenie W niniejszej pracy omówimy krzywą uniwersalną Sierpińskiego, zwaną również dywanem Sierpińskiego. Pokażemy klasyczną metodę
Krzywa uniwersalna Sierpińskiego Małgorzata Blaszke Karol Grzyb Streszczenie W niniejszej pracy omówimy krzywą uniwersalną Sierpińskiego, zwaną również dywanem Sierpińskiego. Pokażemy klasyczną metodę
1. Elementy (abstrakcyjnej) teorii grup
 1. Elementy (abstrakcyjnej) teorii grup Grupy symetrii def. Grupy Zbiór (skończony lub nieskończony) elementów {g} tworzy grupę gdy: - zdefiniowana operacja mnożenia (złożenia) g 1 g 2 = g 3 є G - (g 1
1. Elementy (abstrakcyjnej) teorii grup Grupy symetrii def. Grupy Zbiór (skończony lub nieskończony) elementów {g} tworzy grupę gdy: - zdefiniowana operacja mnożenia (złożenia) g 1 g 2 = g 3 є G - (g 1
Co należy zauważyć Rzuty punktu leżą na jednej prostej do osi rzutów x 12, którą nazywamy prostą odnoszącą Wysokość punktu jest odległością rzutu
 Oznaczenia A, B, 1, 2, I, II, punkty a, b, proste α, β, płaszczyzny π 1, π 2, rzutnie k kierunek rzutowania d(a,m) odległość punktu od prostej m(a,b) prosta przechodząca przez punkty A i B α(1,2,3) płaszczyzna
Oznaczenia A, B, 1, 2, I, II, punkty a, b, proste α, β, płaszczyzny π 1, π 2, rzutnie k kierunek rzutowania d(a,m) odległość punktu od prostej m(a,b) prosta przechodząca przez punkty A i B α(1,2,3) płaszczyzna
Definicja obrotu: Definicja elementów obrotu:
 5. Obroty i kłady Definicja obrotu: Obrotem punktu A dookoła prostej l nazywamy ruch punktu A po okręgu k zawartym w płaszczyźnie prostopadłej do prostej l w kierunku zgodnym lub przeciwnym do ruchu wskazówek
5. Obroty i kłady Definicja obrotu: Obrotem punktu A dookoła prostej l nazywamy ruch punktu A po okręgu k zawartym w płaszczyźnie prostopadłej do prostej l w kierunku zgodnym lub przeciwnym do ruchu wskazówek
Wstęp. Krystalografia geometryczna
 Wstęp Przedmiot badań krystalografii. Wprowadzenie do opisu struktury kryształów. Definicja sieci Bravais go i bazy atomowej, komórki prymitywnej i elementarnej. Podstawowe typy komórek elementarnych.
Wstęp Przedmiot badań krystalografii. Wprowadzenie do opisu struktury kryształów. Definicja sieci Bravais go i bazy atomowej, komórki prymitywnej i elementarnej. Podstawowe typy komórek elementarnych.
Projekt ROZWÓJ PRZEZ KOMPETENCJE jest współfinansowany przez Unię Europejską w ramach środków Europejskiego Funduszu Społecznego
 Projekt ROZWÓJ PRZEZ KOMPETENCJE jest współfinansowany przez Unię Europejską w ramach środków Europejskiego Funduszu Społecznego Program Operacyjny Kapitał Ludzki 2007-2013 CZŁOWIEK NAJLEPSZA INWESTYCJA
Projekt ROZWÓJ PRZEZ KOMPETENCJE jest współfinansowany przez Unię Europejską w ramach środków Europejskiego Funduszu Społecznego Program Operacyjny Kapitał Ludzki 2007-2013 CZŁOWIEK NAJLEPSZA INWESTYCJA
Stereochemia Jak przedstawiamy cząsteczkę z węglem tetraedrycznym:
 Stereochemia Jak przedstawiamy cząsteczkę z węglem tetraedrycznym: 2 wiązania leżą w płaszczyźnie kartki ( linia prosta ) 1 wiązanie wychodzi do przodu, przed kartkę ( linia pogrubiona ) 1 wiązanie wychodzi
Stereochemia Jak przedstawiamy cząsteczkę z węglem tetraedrycznym: 2 wiązania leżą w płaszczyźnie kartki ( linia prosta ) 1 wiązanie wychodzi do przodu, przed kartkę ( linia pogrubiona ) 1 wiązanie wychodzi
Weronika Łabaj. Geometria Bolyaia-Łobaczewskiego
 Weronika Łabaj Geometria Bolyaia-Łobaczewskiego Tematem mojej pracy jest geometria hiperboliczna, od nazwisk jej twórców nazywana też geometrią Bolyaia-Łobaczewskiego. Mimo, że odkryto ją dopiero w XIX
Weronika Łabaj Geometria Bolyaia-Łobaczewskiego Tematem mojej pracy jest geometria hiperboliczna, od nazwisk jej twórców nazywana też geometrią Bolyaia-Łobaczewskiego. Mimo, że odkryto ją dopiero w XIX
WYZNACZANIE WSPÓŁCZYNNIKA ZAŁAMANIA ŚWIATŁA METODĄ SZPILEK I ZA POMOCĄ MIKROSKOPU
 WYZNACZANIE WSPÓŁCZYNNIKA ZAŁAMANIA ŚWIATŁA METODĄ SZPILEK I ZA POMOCĄ MIKROSKOPU Cel ćwiczenia: 1. Zapoznanie z budową i zasadą działania mikroskopu optycznego. 2. Wyznaczenie współczynnika załamania
WYZNACZANIE WSPÓŁCZYNNIKA ZAŁAMANIA ŚWIATŁA METODĄ SZPILEK I ZA POMOCĄ MIKROSKOPU Cel ćwiczenia: 1. Zapoznanie z budową i zasadą działania mikroskopu optycznego. 2. Wyznaczenie współczynnika załamania
Podsumowanie wiadomości o przekształceniach izometrycznych na płaszczyźnie
 Podsumowanie wiadomości o przekształceniach izometrycznych na płaszczyźnie 1. Cele lekcji a) Wiadomości 1. Utrwalenie wiadomości o przekształceniach izometrycznych. b) Umiejętności 1. Uczeń potrafi zastąpić
Podsumowanie wiadomości o przekształceniach izometrycznych na płaszczyźnie 1. Cele lekcji a) Wiadomości 1. Utrwalenie wiadomości o przekształceniach izometrycznych. b) Umiejętności 1. Uczeń potrafi zastąpić
RJC # Alk l a k ny n Ster St eoi er zom eoi er zom y er Slides 1 to 30
 Alkany Stereoizomery Slides 1 to 30 Centrum asymetryczne (stereogeniczne) Atom węgla o hybrydyzacji sp 3 połączony z czterema róŝnymi podstawnikami tworzy centrum asymetryczne (stereogeniczne). Chiralność
Alkany Stereoizomery Slides 1 to 30 Centrum asymetryczne (stereogeniczne) Atom węgla o hybrydyzacji sp 3 połączony z czterema róŝnymi podstawnikami tworzy centrum asymetryczne (stereogeniczne). Chiralność
LOGIKA I TEORIA ZBIORÓW
 LOGIKA I TEORIA ZBIORÓW Logika Logika jest nauką zajmującą się zdaniami Z punktu widzenia logiki istotne jest, czy dane zdanie jest prawdziwe, czy nie Nie jest natomiast istotne o czym to zdanie mówi Definicja
LOGIKA I TEORIA ZBIORÓW Logika Logika jest nauką zajmującą się zdaniami Z punktu widzenia logiki istotne jest, czy dane zdanie jest prawdziwe, czy nie Nie jest natomiast istotne o czym to zdanie mówi Definicja
Wykład 1. Symetria Budowy Kryształów
 Wykład Symetria Budowy Kryształów Ciała krystaliczne i amorficzne Każda substancja ciekła (z wyjątkiem helu) podczas oziębiania traci swoje własności ciekłe i przechodzi w ciało stałe. Jednakże proces
Wykład Symetria Budowy Kryształów Ciała krystaliczne i amorficzne Każda substancja ciekła (z wyjątkiem helu) podczas oziębiania traci swoje własności ciekłe i przechodzi w ciało stałe. Jednakże proces
LASERY I ICH ZASTOSOWANIE
 LASERY I ICH ZASTOSOWANIE Laboratorium Instrukcja do ćwiczenia nr 3 Temat: Efekt magnetooptyczny 5.1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą modulowania zmiany polaryzacji światła oraz
LASERY I ICH ZASTOSOWANIE Laboratorium Instrukcja do ćwiczenia nr 3 Temat: Efekt magnetooptyczny 5.1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą modulowania zmiany polaryzacji światła oraz
Nowoczesna teoria atomistyczna
 Nowoczesna teoria atomistyczna Joseph Louis Proust Prawo stosunków stałych (1797) (1754-1826) John Dalton, Prawo stosunków wielokrotnych (1804) Louis Joseph Gay-Lussac Prawo stosunków objętościowych (1808)
Nowoczesna teoria atomistyczna Joseph Louis Proust Prawo stosunków stałych (1797) (1754-1826) John Dalton, Prawo stosunków wielokrotnych (1804) Louis Joseph Gay-Lussac Prawo stosunków objętościowych (1808)
Wykład 5. Komórka elementarna. Sieci Bravais go
 Wykład 5 Komórka elementarna Sieci Bravais go Doskonały kryształ składa się z atomów jonów, cząsteczek) uporządkowanych w sieci krystalicznej opisanej przez trzy podstawowe wektory translacji a, b, c,
Wykład 5 Komórka elementarna Sieci Bravais go Doskonały kryształ składa się z atomów jonów, cząsteczek) uporządkowanych w sieci krystalicznej opisanej przez trzy podstawowe wektory translacji a, b, c,
STEREOMETRIA CZYLI GEOMETRIA W 3 WYMIARACH
 STEREOMETRIA CZYLI GEOMETRIA W 3 WYMIARACH Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI 2 proste
STEREOMETRIA CZYLI GEOMETRIA W 3 WYMIARACH Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI 2 proste
Podstawy fizyki wykład 8
 Podstawy fizyki wykład 8 Dr Piotr Sitarek Instytut Fizyki, Politechnika Wrocławska Ładunek elektryczny Grecy ok. 600 r p.n.e. odkryli, że bursztyn potarty o wełnę przyciąga inne (drobne) przedmioty. słowo
Podstawy fizyki wykład 8 Dr Piotr Sitarek Instytut Fizyki, Politechnika Wrocławska Ładunek elektryczny Grecy ok. 600 r p.n.e. odkryli, że bursztyn potarty o wełnę przyciąga inne (drobne) przedmioty. słowo
RZUTOWANIE PROSTOKĄTNE
 RZUTOWANIE PROSTOKĄTNE WPROWADZENIE Wykonywanie rysunku technicznego - zastosowanie Rysunek techniczny przedmiotu jest najczęściej podstawą jego wykonania, dlatego odwzorowywany przedmiot nie powinien
RZUTOWANIE PROSTOKĄTNE WPROWADZENIE Wykonywanie rysunku technicznego - zastosowanie Rysunek techniczny przedmiotu jest najczęściej podstawą jego wykonania, dlatego odwzorowywany przedmiot nie powinien
Chiralność w fizyce jądrowej. na przykładzie Cs
 Chiralność w fizyce jądrowej 124 na przykładzie Cs Tomasz Marchlewski Uniwersytet Warszawski Seminarium Fizyki Jądra Atomowego 6 kwietnia 2017 1 Słowo chiralność Chiralne obiekty: Obiekty będące swoimi
Chiralność w fizyce jądrowej 124 na przykładzie Cs Tomasz Marchlewski Uniwersytet Warszawski Seminarium Fizyki Jądra Atomowego 6 kwietnia 2017 1 Słowo chiralność Chiralne obiekty: Obiekty będące swoimi
MATERIA. = m i liczby całkowite. ciała stałe. - kryształy - ciała bezpostaciowe (amorficzne) - ciecze KRYSZTAŁY. Periodyczność
 MATERIA ciała stałe - kryształy - ciała bezpostaciowe (amorficzne) - ciecze - gazy KRYSZTAŁY Periodyczność Kryształ (idealny) struktura zbudowana z powtarzających się w przestrzeni periodycznie identycznych
MATERIA ciała stałe - kryształy - ciała bezpostaciowe (amorficzne) - ciecze - gazy KRYSZTAŁY Periodyczność Kryształ (idealny) struktura zbudowana z powtarzających się w przestrzeni periodycznie identycznych
STRUKTURA CIAŁA STAŁEGO
 STRUKTURA CIAŁA STAŁEGO Podział ciał stałych Ciała - bezpostaciowe (amorficzne) Szkła, żywice, tłuszcze, niektóre proszki. Nie wykazują żadnych regularnych płaszczyzn ograniczających, nie można w nich
STRUKTURA CIAŁA STAŁEGO Podział ciał stałych Ciała - bezpostaciowe (amorficzne) Szkła, żywice, tłuszcze, niektóre proszki. Nie wykazują żadnych regularnych płaszczyzn ograniczających, nie można w nich
WIELOKĄTY FOREMNE I ICH PRZEKĄTNE
 WIELOKĄTY FOREMNE I ICH PRZEKĄTNE Krzysztof Lisiecki Kl. V a SP nr 6 im. Unii Europejskiej w Kłodzku Praca pod kierunkiem: mgr Moniki Chosińskiej Spis treści Lp. Tytuł Str. 1. Wstęp. 2 2. Pojęcia używane
WIELOKĄTY FOREMNE I ICH PRZEKĄTNE Krzysztof Lisiecki Kl. V a SP nr 6 im. Unii Europejskiej w Kłodzku Praca pod kierunkiem: mgr Moniki Chosińskiej Spis treści Lp. Tytuł Str. 1. Wstęp. 2 2. Pojęcia używane
(ok p.n.e.)
 (ok. 572-497 p.n.e.) Pitagoras pochodził z wyspy Samos. Znany jest głównie z słynnego twierdzenia o trójkącie prostokątnym, powszechnie zwanego jako twierdzenie Pitagorasa. Twierdzenie Pitagorasa ilustracja
(ok. 572-497 p.n.e.) Pitagoras pochodził z wyspy Samos. Znany jest głównie z słynnego twierdzenia o trójkącie prostokątnym, powszechnie zwanego jako twierdzenie Pitagorasa. Twierdzenie Pitagorasa ilustracja
WYKŁAD 5 Zastosowanie teorii grup w analizie widm oscylacyjnych
 WYKŁAD 5 Zastosowanie teorii grup w analizie widm oscylacyjnych Prof. dr hab. Halina Abramczyk Dr inż. Beata Brożek-Płuska POLITECHNIKA ŁÓDZKA Wydział Chemiczny, Instytut Techniki Radiacyjnej Laboratorium
WYKŁAD 5 Zastosowanie teorii grup w analizie widm oscylacyjnych Prof. dr hab. Halina Abramczyk Dr inż. Beata Brożek-Płuska POLITECHNIKA ŁÓDZKA Wydział Chemiczny, Instytut Techniki Radiacyjnej Laboratorium
Stożkiem nazywamy bryłę obrotową, która powstała przez obrót trójkąta prostokątnego wokół jednej z jego przyprostokątnych.
 1.4. Stożek W tym temacie dowiesz się: jak obliczać pole powierzchni bocznej i pole powierzchni całkowitej stożka, jak obliczać objętość stożka, jak wykorzystywać własności stożków w zadaniach praktycznych.
1.4. Stożek W tym temacie dowiesz się: jak obliczać pole powierzchni bocznej i pole powierzchni całkowitej stożka, jak obliczać objętość stożka, jak wykorzystywać własności stożków w zadaniach praktycznych.
( F ) I. Zagadnienia. II. Zadania
 ( F ) I. Zagadnienia 1. Rozchodzenie się fal akustycznych w układach biologicznych. 2. Wytwarzanie i detekcja fal akustycznych w ultrasonografii. 3. Budowa aparatu ultrasonograficznego metody obrazowania.
( F ) I. Zagadnienia 1. Rozchodzenie się fal akustycznych w układach biologicznych. 2. Wytwarzanie i detekcja fal akustycznych w ultrasonografii. 3. Budowa aparatu ultrasonograficznego metody obrazowania.
Opis ruchu obrotowego
 Opis ruchu obrotowego Oprócz ruchu translacyjnego ciała obserwujemy w przyrodzie inną jego odmianę: ruch obrotowy Ruch obrotowy jest zawsze względem osi obrotu W ruchu obrotowym wszystkie punkty zakreślają
Opis ruchu obrotowego Oprócz ruchu translacyjnego ciała obserwujemy w przyrodzie inną jego odmianę: ruch obrotowy Ruch obrotowy jest zawsze względem osi obrotu W ruchu obrotowym wszystkie punkty zakreślają
Zad.3. Jakub Trojgo i Jakub Wieczorek. 14 grudnia 2013
 Zad.3 Jakub Trojgo i Jakub Wieczorek 14 grudnia 2013 W pierwszej części naszej pracy będziemy chcieli zbadać ciągłość funkcji f(x, y) w przypadku gdy płaszczyzna wyposażona jest w jedną z topologii: a)
Zad.3 Jakub Trojgo i Jakub Wieczorek 14 grudnia 2013 W pierwszej części naszej pracy będziemy chcieli zbadać ciągłość funkcji f(x, y) w przypadku gdy płaszczyzna wyposażona jest w jedną z topologii: a)
Przekształcanie wykresów.
 Sławomir Jemielity Przekształcanie wykresów. Pokażemy tu, jak zmiana we wzorze funkcji wpływa na wygląd jej wykresu. A. Mamy wykres funkcji f(). Jak będzie wyglądał wykres f ( ) + a, a stała? ( ) f ( )
Sławomir Jemielity Przekształcanie wykresów. Pokażemy tu, jak zmiana we wzorze funkcji wpływa na wygląd jej wykresu. A. Mamy wykres funkcji f(). Jak będzie wyglądał wykres f ( ) + a, a stała? ( ) f ( )
Polarymetr. Ćwiczenie 74. Cel ćwiczenia Pomiar kąta skręcenia płaszczyzny polaryzacji w roztworach cukru. Wprowadzenie
 Ćwiczenie 74 Polarymetr Cel ćwiczenia Pomiar kąta skręcenia płaszczyzny polaryzacji w roztworach cukru. Wprowadzenie Światło liniowo spolaryzowane* rozchodzi się bez zmiany płaszczyzny polaryzacji w próŝni
Ćwiczenie 74 Polarymetr Cel ćwiczenia Pomiar kąta skręcenia płaszczyzny polaryzacji w roztworach cukru. Wprowadzenie Światło liniowo spolaryzowane* rozchodzi się bez zmiany płaszczyzny polaryzacji w próŝni
Pytania do spr / Własności figur (płaskich i przestrzennych) (waga: 0,5 lub 0,3)
 Pytania zamknięte / TEST : Wybierz 1 odp prawidłową. 1. Punkt: A) jest aksjomatem in. pewnikiem; B) nie jest aksjomatem, bo można go zdefiniować. 2. Prosta: A) to zbiór punktów; B) to zbiór punktów współliniowych.
Pytania zamknięte / TEST : Wybierz 1 odp prawidłową. 1. Punkt: A) jest aksjomatem in. pewnikiem; B) nie jest aksjomatem, bo można go zdefiniować. 2. Prosta: A) to zbiór punktów; B) to zbiór punktów współliniowych.
Elementy symetrii makroskopowej.
 Uniwersytet Śląski Instytut Chemii Zakład Krystalografii Laboratorium z Krystalografii Elementy symetrii makroskopowej. 2 godz. Cel ćwiczenia: zapoznanie się z działaniem elementów symetrii makroskopowej
Uniwersytet Śląski Instytut Chemii Zakład Krystalografii Laboratorium z Krystalografii Elementy symetrii makroskopowej. 2 godz. Cel ćwiczenia: zapoznanie się z działaniem elementów symetrii makroskopowej
Rachunek wektorowy - wprowadzenie. dr inż. Romuald Kędzierski
 Rachunek wektorowy - wprowadzenie dr inż. Romuald Kędzierski Graficzne przedstawianie wielkości wektorowych Długość wektora jest miarą jego wartości Linia prosta wyznaczająca kierunek działania wektora
Rachunek wektorowy - wprowadzenie dr inż. Romuald Kędzierski Graficzne przedstawianie wielkości wektorowych Długość wektora jest miarą jego wartości Linia prosta wyznaczająca kierunek działania wektora
Jarosław Wróblewski Matematyka dla Myślących, 2008/09
 9. Funkcje trygonometryczne. Elementy geometrii: twierdzenie Pitagorasa i twierdzenie cosinusów, twierdzenie o kącie wpisanym i środkowym, okrąg wpisany i opisany na wielokącie, wielokąty foremne (dokończenie).
9. Funkcje trygonometryczne. Elementy geometrii: twierdzenie Pitagorasa i twierdzenie cosinusów, twierdzenie o kącie wpisanym i środkowym, okrąg wpisany i opisany na wielokącie, wielokąty foremne (dokończenie).
PLANIMETRIA CZYLI GEOMETRIA PŁASZCZYZNY CZ. 3
 DEFINICJE PLANIMETRIA CZYLI GEOMETRIA PŁASZCZYZNY CZ. 3 Czworokąt to wielokąt o 4 bokach i 4 kątach. Przekątną czworokąta nazywamy odcinek łączący przeciwległe wierzchołki. Wysokością czworokąta nazywamy
DEFINICJE PLANIMETRIA CZYLI GEOMETRIA PŁASZCZYZNY CZ. 3 Czworokąt to wielokąt o 4 bokach i 4 kątach. Przekątną czworokąta nazywamy odcinek łączący przeciwległe wierzchołki. Wysokością czworokąta nazywamy
Atomowa budowa materii
 Atomowa budowa materii Wszystkie obiekty materialne zbudowane są z tych samych elementów cząstek elementarnych Cząstki elementarne oddziałują tylko kilkoma sposobami oddziaływania wymieniając kwanty pól
Atomowa budowa materii Wszystkie obiekty materialne zbudowane są z tych samych elementów cząstek elementarnych Cząstki elementarne oddziałują tylko kilkoma sposobami oddziaływania wymieniając kwanty pól
Łożysko z pochyleniami
 Łożysko z pochyleniami Wykonamy model części jak na rys. 1 Rys. 1 Część ta ma płaszczyznę symetrii (pokazaną na rys. 1). Płaszczyzna ta może być płaszczyzną podziału formy odlewniczej. Aby model można
Łożysko z pochyleniami Wykonamy model części jak na rys. 1 Rys. 1 Część ta ma płaszczyznę symetrii (pokazaną na rys. 1). Płaszczyzna ta może być płaszczyzną podziału formy odlewniczej. Aby model można
4.1. Modelowanie matematyczne
 4.1. Modelowanie matematyczne Model matematyczny Model matematyczny opisuje daną konstrukcję budowlaną za pomocą zmiennych. Wartości zmiennych będą należały to zbioru liczb rzeczywistych i będą one reprezentować
4.1. Modelowanie matematyczne Model matematyczny Model matematyczny opisuje daną konstrukcję budowlaną za pomocą zmiennych. Wartości zmiennych będą należały to zbioru liczb rzeczywistych i będą one reprezentować
Matematyka A kolokwium 26 kwietnia 2017 r., godz. 18:05 20:00. i = = i. +i sin ) = 1024(cos 5π+i sin 5π) =
 Matematyka A kolokwium 6 kwietnia 7 r., godz. 8:5 : Starałem się nie popełniać błędów, ale jeśli są, będę wdzięczny za wieści o nich Mam też nadzieję, że niektórzy studenci zechcą zrozumieć poniższy tekst,
Matematyka A kolokwium 6 kwietnia 7 r., godz. 8:5 : Starałem się nie popełniać błędów, ale jeśli są, będę wdzięczny za wieści o nich Mam też nadzieję, że niektórzy studenci zechcą zrozumieć poniższy tekst,
Geometria. Hiperbola
 Geometria. Hiperbola Definicja 1 Dano dwa punkty na płaszczyźnie: F 1 i F 2 oraz taką liczbę d, że F 1 F 2 > d > 0. Zbiór punktów płaszczyzny będących rozwiązaniami równania: XF 1 XF 2 = ±d. nazywamy hiperbolą.
Geometria. Hiperbola Definicja 1 Dano dwa punkty na płaszczyźnie: F 1 i F 2 oraz taką liczbę d, że F 1 F 2 > d > 0. Zbiór punktów płaszczyzny będących rozwiązaniami równania: XF 1 XF 2 = ±d. nazywamy hiperbolą.
domykanie relacji, relacja równoważności, rozkłady zbiorów
 1 of 8 2012-03-28 17:45 Logika i teoria mnogości/wykład 5: Para uporządkowana iloczyn kartezjański relacje domykanie relacji relacja równoważności rozkłady zbiorów From Studia Informatyczne < Logika i
1 of 8 2012-03-28 17:45 Logika i teoria mnogości/wykład 5: Para uporządkowana iloczyn kartezjański relacje domykanie relacji relacja równoważności rozkłady zbiorów From Studia Informatyczne < Logika i
p l s i k Czy świat jest symetryczny? No, ale po kolei! GAZETKA MATEMATYCZNA KWIECIEŃ 2018 Całkiem podobnie (tylko inaczej ) jest z SYMETRIĄ OSIOWĄ:
 p l s i k No, ale po kolei! GAZETKA MATEMATYCZNA KWIECIEŃ 2018 Powiedz mi, a zapomnę. Pokaż mi, a zapamiętam. Cześć Pozwól mi zrobić, a zrozumiem. Całkiem podobnie (tylko inaczej ) jest z SYMETRIĄ OSIOWĄ:
p l s i k No, ale po kolei! GAZETKA MATEMATYCZNA KWIECIEŃ 2018 Powiedz mi, a zapomnę. Pokaż mi, a zapamiętam. Cześć Pozwól mi zrobić, a zrozumiem. Całkiem podobnie (tylko inaczej ) jest z SYMETRIĄ OSIOWĄ:
Co ma piekarz do matematyki?
 Instytut Matematyki i Informatyki Politechnika Wrocławska Dolnośląski Festiwal Nauki Wrzesień 2009 x x (x 1, x 2 ) x (x 1, x 2 ) (x 1, x 2, x 3 ) x (x 1, x 2 ) (x 1, x 2, x 3 ) (x 1, x 2, x 3, x 4 ). x
Instytut Matematyki i Informatyki Politechnika Wrocławska Dolnośląski Festiwal Nauki Wrzesień 2009 x x (x 1, x 2 ) x (x 1, x 2 ) (x 1, x 2, x 3 ) x (x 1, x 2 ) (x 1, x 2, x 3 ) (x 1, x 2, x 3, x 4 ). x
Funkcje liniowe i wieloliniowe w praktyce szkolnej. Opracowanie : mgr inż. Renata Rzepińska
 Funkcje liniowe i wieloliniowe w praktyce szkolnej Opracowanie : mgr inż. Renata Rzepińska . Wprowadzenie pojęcia funkcji liniowej w nauczaniu matematyki w gimnazjum. W programie nauczania matematyki w
Funkcje liniowe i wieloliniowe w praktyce szkolnej Opracowanie : mgr inż. Renata Rzepińska . Wprowadzenie pojęcia funkcji liniowej w nauczaniu matematyki w gimnazjum. W programie nauczania matematyki w
Statyka Cieczy i Gazów. Temat : Podstawy teorii kinetyczno-molekularnej budowy ciał
 Statyka Cieczy i Gazów Temat : Podstawy teorii kinetyczno-molekularnej budowy ciał 1. Podstawowe założenia teorii kinetyczno-molekularnej budowy ciał: Ciała zbudowane są z cząsteczek. Pomiędzy cząsteczkami
Statyka Cieczy i Gazów Temat : Podstawy teorii kinetyczno-molekularnej budowy ciał 1. Podstawowe założenia teorii kinetyczno-molekularnej budowy ciał: Ciała zbudowane są z cząsteczek. Pomiędzy cząsteczkami
Algebra liniowa z geometrią
 Algebra liniowa z geometrią Maciej Czarnecki 15 stycznia 2013 Spis treści 1 Geometria płaszczyzny 2 1.1 Wektory i skalary........................... 2 1.2 Macierze, wyznaczniki, układy równań liniowych.........
Algebra liniowa z geometrią Maciej Czarnecki 15 stycznia 2013 Spis treści 1 Geometria płaszczyzny 2 1.1 Wektory i skalary........................... 2 1.2 Macierze, wyznaczniki, układy równań liniowych.........
FIGURY I PRZEKSZTAŁCENIA GEOMETRYCZNE
 Umiejętności opracowanie: Maria Lampert LISTA MOICH OSIĄGNIĘĆ FIGURY I PRZEKSZTAŁCENIA GEOMETRYCZNE Co powinienem umieć Umiejętności znam podstawowe przekształcenia geometryczne: symetria osiowa i środkowa,
Umiejętności opracowanie: Maria Lampert LISTA MOICH OSIĄGNIĘĆ FIGURY I PRZEKSZTAŁCENIA GEOMETRYCZNE Co powinienem umieć Umiejętności znam podstawowe przekształcenia geometryczne: symetria osiowa i środkowa,
Oto przykłady przedmiotów, które są bryłami obrotowymi.
 1.3. Bryły obrotowe. Walec W tym temacie dowiesz się: co to są bryły obrotowe, jak rozpoznawać walce wśród innych brył, jak obliczać pole powierzchni bocznej i pole powierzchni całkowitej walca, jak obliczać
1.3. Bryły obrotowe. Walec W tym temacie dowiesz się: co to są bryły obrotowe, jak rozpoznawać walce wśród innych brył, jak obliczać pole powierzchni bocznej i pole powierzchni całkowitej walca, jak obliczać
IX Olimpiada Matematyczna Gimnazjalistów
 IX Olimpiada Matematyczna Gimnazjalistów Zawody stopnia pierwszego część testowa www.omg.edu.pl (3 października 2013 r.) Rozwiązania zadań testowych 1. Liczba 3 9 3 27 jest a) niewymierna; b) równa 3 27;
IX Olimpiada Matematyczna Gimnazjalistów Zawody stopnia pierwszego część testowa www.omg.edu.pl (3 października 2013 r.) Rozwiązania zadań testowych 1. Liczba 3 9 3 27 jest a) niewymierna; b) równa 3 27;
Wielokąty foremne. (Konstrukcje platońskie)
 Wielokąty foremne (Konstrukcje platońskie) 1 Definicja 1. Wielokąt wypukły nazywa się foremny, jeżeli ma wszystkie kąty równe i wszystkie boki równe. Przykładami wielokątów foremnych są trójkąt równoboczny,
Wielokąty foremne (Konstrukcje platońskie) 1 Definicja 1. Wielokąt wypukły nazywa się foremny, jeżeli ma wszystkie kąty równe i wszystkie boki równe. Przykładami wielokątów foremnych są trójkąt równoboczny,
Rzutowanie z 4D na 3D
 Politechnika Wrocławska Instytut Informatyki Automatyki i Robotyki Wizualizacja danych sensorycznych Rzutowanie z 4D na 3D Autor: Daniel Piłat Opiekun projektu: dr inż. Bogdan Kreczmer 15 czerwca 2010
Politechnika Wrocławska Instytut Informatyki Automatyki i Robotyki Wizualizacja danych sensorycznych Rzutowanie z 4D na 3D Autor: Daniel Piłat Opiekun projektu: dr inż. Bogdan Kreczmer 15 czerwca 2010
Zasady rzutowania prostokątnego. metodą europejską. Opracował: Robert Urbanik Zespół Szkół Mechanicznych w Opolu. Zasady rzutowania prostokątnego
 Zasady rzutowania prostokątnego metodą europejską Opracował: Robert Urbanik Zespół Szkół Mechanicznych w Opolu Wiadomości ogólne Rzutem nazywamy rysunkowe odwzorowanie przedmiotu lub bryły geometrycznej
Zasady rzutowania prostokątnego metodą europejską Opracował: Robert Urbanik Zespół Szkół Mechanicznych w Opolu Wiadomości ogólne Rzutem nazywamy rysunkowe odwzorowanie przedmiotu lub bryły geometrycznej
Notacja Denavita-Hartenberga
 Notacja DenavitaHartenberga Materiały do ćwiczeń z Podstaw Robotyki Artur Gmerek Umiejętność rozwiązywania prostego zagadnienia kinematycznego jest najbardziej bazową umiejętność zakresu Robotyki. Wyznaczyć
Notacja DenavitaHartenberga Materiały do ćwiczeń z Podstaw Robotyki Artur Gmerek Umiejętność rozwiązywania prostego zagadnienia kinematycznego jest najbardziej bazową umiejętność zakresu Robotyki. Wyznaczyć
Własności jąder w stanie podstawowym
 Własności jąder w stanie podstawowym Najważniejsze liczby kwantowe charakteryzujące jądro: A liczba masowa = liczbie nukleonów (l. barionów) Z liczba atomowa = liczbie protonów (ładunek) N liczba neutronów
Własności jąder w stanie podstawowym Najważniejsze liczby kwantowe charakteryzujące jądro: A liczba masowa = liczbie nukleonów (l. barionów) Z liczba atomowa = liczbie protonów (ładunek) N liczba neutronów
LXVII OLIMPIADA FIZYCZNA ZAWODY II STOPNIA
 LXVII OLIMPIADA FIZYCZNA ZAWODY II STOPNIA CZĘŚĆ TEORETYCZNA Za każde zadanie można otrzymać maksymalnie 0 punktów. Zadanie 1. przedmiot. Gdzie znajduje się obraz i jakie jest jego powiększenie? Dla jakich
LXVII OLIMPIADA FIZYCZNA ZAWODY II STOPNIA CZĘŚĆ TEORETYCZNA Za każde zadanie można otrzymać maksymalnie 0 punktów. Zadanie 1. przedmiot. Gdzie znajduje się obraz i jakie jest jego powiększenie? Dla jakich
CorelDraw - podstawowe operacje na obiektach graficznych
 CorelDraw - podstawowe operacje na obiektach graficznych Przesuwanie obiektu Wymaż obszar roboczy programu CorelDraw (klawisze Ctrl+A i Delete). U góry kartki narysuj dowolnego bazgrołka po czym naciśnij
CorelDraw - podstawowe operacje na obiektach graficznych Przesuwanie obiektu Wymaż obszar roboczy programu CorelDraw (klawisze Ctrl+A i Delete). U góry kartki narysuj dowolnego bazgrołka po czym naciśnij
2. Charakterystyki geometryczne przekroju
 . CHRKTERYSTYKI GEOMETRYCZNE PRZEKROJU 1.. Charakterystyki geometryczne przekroju.1 Podstawowe definicje Z przekrojem pręta związane są trzy wielkości fizyczne nazywane charakterystykami geometrycznymi
. CHRKTERYSTYKI GEOMETRYCZNE PRZEKROJU 1.. Charakterystyki geometryczne przekroju.1 Podstawowe definicje Z przekrojem pręta związane są trzy wielkości fizyczne nazywane charakterystykami geometrycznymi
Pracę wykonali: -Bryjak Mateusz -Chudziak Paweł -Palacz Angelika -Skorwider Dariusz
 Pracę wykonali: -Bryjak Mateusz -Chudziak Paweł -Palacz Angelika -Skorwider Dariusz Symetria osiowa- przekształcenie płaszczyzny względem pewnej prostej, jest ona osią symetrii. Każdemu punktowi A przyporządkowujemy
Pracę wykonali: -Bryjak Mateusz -Chudziak Paweł -Palacz Angelika -Skorwider Dariusz Symetria osiowa- przekształcenie płaszczyzny względem pewnej prostej, jest ona osią symetrii. Każdemu punktowi A przyporządkowujemy
TWIERDZENIE TALESA W PRZESTRZENI
 TWIERDZENIE TALESA W PRZESTRZENI PRACA BADAWCZA autor Agnieszka Duszeńko Uniwersytet Wrocławski Wydział Matematyki i Informatyki 2005 Na płaszczyźnie: Najpopularniejsza, powszechnie znana wersja twierdzenia
TWIERDZENIE TALESA W PRZESTRZENI PRACA BADAWCZA autor Agnieszka Duszeńko Uniwersytet Wrocławski Wydział Matematyki i Informatyki 2005 Na płaszczyźnie: Najpopularniejsza, powszechnie znana wersja twierdzenia
POMIARY OPTYCZNE 1. Wykład 1. Dr hab. inż. Władysław Artur Woźniak
 POMIARY OPTYCZNE Wykład Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej Pokój 8/ bud. A- http://www.if.pwr.wroc.pl/~wozniak/ OPTYKA GEOMETRYCZNA Codzienne obserwacje: światło
POMIARY OPTYCZNE Wykład Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej Pokój 8/ bud. A- http://www.if.pwr.wroc.pl/~wozniak/ OPTYKA GEOMETRYCZNA Codzienne obserwacje: światło
TEORIA WĘZŁÓW. Natalia Grzechnik 10B2
 TEORIA WĘZŁÓW Natalia Grzechnik 10B2 Słowem wstępu zastosowanie teorii węzłów Biologiczna rola węzłów w białkach Wyznaczanie topologii białek Kryptografia Biofizyka Opis struktur DNA, RNA, białek DNA a
TEORIA WĘZŁÓW Natalia Grzechnik 10B2 Słowem wstępu zastosowanie teorii węzłów Biologiczna rola węzłów w białkach Wyznaczanie topologii białek Kryptografia Biofizyka Opis struktur DNA, RNA, białek DNA a
Kolorowanie płaszczyzny, prostych i okręgów
 Kolorowanie płaszczyzny, prostych i okręgów Jadwiga Czyżewska Pisane pod kierunkiem W.Guzickiego W 2013 roku na II etapie VIII edycji Olimpiady Matematycznej Gimnazjalistów pojawiło się zadanie o następującej
Kolorowanie płaszczyzny, prostych i okręgów Jadwiga Czyżewska Pisane pod kierunkiem W.Guzickiego W 2013 roku na II etapie VIII edycji Olimpiady Matematycznej Gimnazjalistów pojawiło się zadanie o następującej
3. KINEMATYKA Kinematyka jest częścią mechaniki, która zajmuje się opisem ruchu ciał bez wnikania w jego przyczyny. Oznacza to, że nie interesuje nas
 3. KINEMATYKA Kinematyka jest częścią mechaniki, która zajmuje się opisem ruchu ciał bez wnikania w jego przyczyny. Oznacza to, że nie interesuje nas oddziaływanie między ciałami, ani też rola, jaką to
3. KINEMATYKA Kinematyka jest częścią mechaniki, która zajmuje się opisem ruchu ciał bez wnikania w jego przyczyny. Oznacza to, że nie interesuje nas oddziaływanie między ciałami, ani też rola, jaką to
Karta pracy M+ do multipodręcznika dla klasy 8 szkoły podstawowej
 Karta pracy M+ do multipodręcznika dla klasy 8 szkoły podstawowej Geometria w starożytnym świecie Część A. Sprawdź, czy rozumiesz film. 1. Skreśl w tekście niewłaściwe słowa i sformułowania. Bryły platońskie
Karta pracy M+ do multipodręcznika dla klasy 8 szkoły podstawowej Geometria w starożytnym świecie Część A. Sprawdź, czy rozumiesz film. 1. Skreśl w tekście niewłaściwe słowa i sformułowania. Bryły platońskie
RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ
 RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ Wykład 6 2016/2017, zima 1 MOMENT PĘDU I ENERGIA KINETYCZNA W RUCHU PUNKTU MATERIALNEGO PO OKRĘGU Definicja momentu pędu L=mrv=mr 2 ω L=Iω I= mr 2 p L r ω Moment
RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ Wykład 6 2016/2017, zima 1 MOMENT PĘDU I ENERGIA KINETYCZNA W RUCHU PUNKTU MATERIALNEGO PO OKRĘGU Definicja momentu pędu L=mrv=mr 2 ω L=Iω I= mr 2 p L r ω Moment
MECHANIKA 2. Wykład Nr 3 KINEMATYKA. Temat RUCH PŁASKI BRYŁY MATERIALNEJ. Prowadzący: dr Krzysztof Polko
 MECHANIKA 2 Wykład Nr 3 KINEMATYKA Temat RUCH PŁASKI BRYŁY MATERIALNEJ Prowadzący: dr Krzysztof Polko Pojęcie Ruchu Płaskiego Rys.1 Ruchem płaskim ciała sztywnego nazywamy taki ruch, w którym wszystkie
MECHANIKA 2 Wykład Nr 3 KINEMATYKA Temat RUCH PŁASKI BRYŁY MATERIALNEJ Prowadzący: dr Krzysztof Polko Pojęcie Ruchu Płaskiego Rys.1 Ruchem płaskim ciała sztywnego nazywamy taki ruch, w którym wszystkie
Laboratorium techniki laserowej. Ćwiczenie 5. Modulator PLZT
 Laboratorium techniki laserowej Katedra Optoelektroniki i Systemów Elektronicznych, WETI, Politechnika Gdaoska Gdańsk 006 1.Wstęp Rozwój techniki optoelektronicznej spowodował poszukiwania nowych materiałów
Laboratorium techniki laserowej Katedra Optoelektroniki i Systemów Elektronicznych, WETI, Politechnika Gdaoska Gdańsk 006 1.Wstęp Rozwój techniki optoelektronicznej spowodował poszukiwania nowych materiałów
Opis ćwiczenia. Cel ćwiczenia Poznanie budowy i zrozumienie istoty pomiaru przyspieszenia ziemskiego za pomocą wahadła rewersyjnego Henry ego Katera.
 ĆWICZENIE WYZNACZANIE PRZYSPIESZENIA ZIEMSKIEGO ZA POMOCĄ WAHADŁA REWERSYJNEGO Opis ćwiczenia Cel ćwiczenia Poznanie budowy i zrozumienie istoty pomiaru przyspieszenia ziemskiego za pomocą wahadła rewersyjnego
ĆWICZENIE WYZNACZANIE PRZYSPIESZENIA ZIEMSKIEGO ZA POMOCĄ WAHADŁA REWERSYJNEGO Opis ćwiczenia Cel ćwiczenia Poznanie budowy i zrozumienie istoty pomiaru przyspieszenia ziemskiego za pomocą wahadła rewersyjnego
Symetria i asymetria zwierciadlana (cz. II)
 4 FOTON 90, Jesień 2005 Symetria i asymetria zwierciadlana (cz. II) Antonina Kowalska Instytut Fizyki Uniwersytetu Jagiellońskiego Symetria i asymetria oddziaływań Pierwsza część artykułu zakończyła się
4 FOTON 90, Jesień 2005 Symetria i asymetria zwierciadlana (cz. II) Antonina Kowalska Instytut Fizyki Uniwersytetu Jagiellońskiego Symetria i asymetria oddziaływań Pierwsza część artykułu zakończyła się
TRYGONOMETRIA FUNKCJE TRYGONOMETRYCZNE KĄTA SKIEROWANEGO
 TRYGONOMETRIA Trygonometria to dział matematyki, którego przedmiotem badań są związki między bokami i kątami trójkątów oraz tzw. funkcje trygonometryczne. Trygonometria powstała i rozwinęła się głównie
TRYGONOMETRIA Trygonometria to dział matematyki, którego przedmiotem badań są związki między bokami i kątami trójkątów oraz tzw. funkcje trygonometryczne. Trygonometria powstała i rozwinęła się głównie
GEOPLAN Z SIATKĄ TRÓJKĄTNĄ
 TEMAT NUMERU 9 GEOPLAN Z SIATKĄ TRÓJKĄTNĄ Marzenna Grochowalska W Matematyce w Szkole wiele miejsca poświęcono geoplanom z siatką kwadratową oraz ich zaletom 1. Równie ciekawą pomocą dydaktyczną jest geoplan
TEMAT NUMERU 9 GEOPLAN Z SIATKĄ TRÓJKĄTNĄ Marzenna Grochowalska W Matematyce w Szkole wiele miejsca poświęcono geoplanom z siatką kwadratową oraz ich zaletom 1. Równie ciekawą pomocą dydaktyczną jest geoplan
MECHANIKA 2 RUCH POSTĘPOWY I OBROTOWY CIAŁA SZTYWNEGO. Wykład Nr 2. Prowadzący: dr Krzysztof Polko
 MECHANIKA 2 Wykład Nr 2 RUCH POSTĘPOWY I OBROTOWY CIAŁA SZTYWNEGO Prowadzący: dr Krzysztof Polko WSTĘP z r C C(x C,y C,z C ) r C -r B B(x B,y B,z B ) r C -r A r B r B -r A A(x A,y A,z A ) Ciało sztywne
MECHANIKA 2 Wykład Nr 2 RUCH POSTĘPOWY I OBROTOWY CIAŁA SZTYWNEGO Prowadzący: dr Krzysztof Polko WSTĘP z r C C(x C,y C,z C ) r C -r B B(x B,y B,z B ) r C -r A r B r B -r A A(x A,y A,z A ) Ciało sztywne
Elementy astronomii w nauczaniu przyrody. dr Krzysztof Rochowicz Zakład Dydaktyki Fizyki UMK 2011
 Elementy astronomii w nauczaniu przyrody dr Krzysztof Rochowicz Zakład Dydaktyki Fizyki UMK 2011 Szkic referatu Krótki przegląd wątków tematycznych przedmiotu Przyroda w podstawie MEN Astronomiczne zasoby
Elementy astronomii w nauczaniu przyrody dr Krzysztof Rochowicz Zakład Dydaktyki Fizyki UMK 2011 Szkic referatu Krótki przegląd wątków tematycznych przedmiotu Przyroda w podstawie MEN Astronomiczne zasoby
Spin spina fizykę i... SPiN. prof. Mariusz P. Dąbrowski
 Spin spina fizykę i... SPiN prof. Mariusz P. Dąbrowski Co łączy ze sobą rowerzystę, łyżwiarkę i tancerza hip-hopu... Ziemię, gwiazdę... czarną dziurę w kosmosie... z cząstkami w Wielkim Zderzaczu Hadronów?
Spin spina fizykę i... SPiN prof. Mariusz P. Dąbrowski Co łączy ze sobą rowerzystę, łyżwiarkę i tancerza hip-hopu... Ziemię, gwiazdę... czarną dziurę w kosmosie... z cząstkami w Wielkim Zderzaczu Hadronów?
METODA RZUTÓW MONGE A (II CZ.)
 RZUT PUNKTU NA TRZECIĄ RZUTNIĘ METODA RZUTÓW MONGE A (II CZ.) Dodanie trzeciej rzutni pozwala na dostrzeżenie ważnej, ogólnej zależności. Jeżeli trzecia rzutnia została postawiona na drugiej - pionowej,
RZUT PUNKTU NA TRZECIĄ RZUTNIĘ METODA RZUTÓW MONGE A (II CZ.) Dodanie trzeciej rzutni pozwala na dostrzeżenie ważnej, ogólnej zależności. Jeżeli trzecia rzutnia została postawiona na drugiej - pionowej,
Badanie właściwości optycznych roztworów.
 ĆWICZENIE 4 (2018), STRONA 1/6 Badanie właściwości optycznych roztworów. Cel ćwiczenia - wyznaczenie skręcalności właściwej sacharozy w roztworach wodnych oraz badanie współczynnika załamania światła Teoria
ĆWICZENIE 4 (2018), STRONA 1/6 Badanie właściwości optycznych roztworów. Cel ćwiczenia - wyznaczenie skręcalności właściwej sacharozy w roztworach wodnych oraz badanie współczynnika załamania światła Teoria
Kąty Ustawienia Kół. WERTHER International POLSKA Sp. z o.o. dr inż. Marek Jankowski 2007-01-19
 WERTHER International POLSKA Sp. z o.o. dr inż. Marek Jankowski 2007-01-19 Kąty Ustawienia Kół Technologie stosowane w pomiarach zmieniają się, powstają coraz to nowe urządzenia ułatwiające zarówno regulowanie
WERTHER International POLSKA Sp. z o.o. dr inż. Marek Jankowski 2007-01-19 Kąty Ustawienia Kół Technologie stosowane w pomiarach zmieniają się, powstają coraz to nowe urządzenia ułatwiające zarówno regulowanie
Wykład FIZYKA II. 5. Magnetyzm. Dr hab. inż. Władysław Artur Woźniak
 Wykład FIZYKA II 5. Magnetyzm Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej http://www.if.pwr.wroc.pl/~wozniak/fizyka2.html MAGNESY Pierwszymi poznanym magnesem był magnetyt
Wykład FIZYKA II 5. Magnetyzm Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej http://www.if.pwr.wroc.pl/~wozniak/fizyka2.html MAGNESY Pierwszymi poznanym magnesem był magnetyt
Mechanika teoretyczna
 Wypadkowa -metoda analityczna Mechanika teoretyczna Wykład nr 2 Wypadkowa dowolnego układu sił. Równowaga. Rodzaje sił i obciążeń. Rodzaje ustrojów prętowych. Składowe poszczególnych sił układu: Składowe
Wypadkowa -metoda analityczna Mechanika teoretyczna Wykład nr 2 Wypadkowa dowolnego układu sił. Równowaga. Rodzaje sił i obciążeń. Rodzaje ustrojów prętowych. Składowe poszczególnych sił układu: Składowe
STATYCZNA PRÓBA SKRĘCANIA
 Mechanika i wytrzymałość materiałów - instrukcja do ćwiczenia laboratoryjnego: Wprowadzenie STATYCZNA PRÓBA SKRĘCANIA Opracowała: mgr inż. Magdalena Bartkowiak-Jowsa Skręcanie pręta występuje w przypadku
Mechanika i wytrzymałość materiałów - instrukcja do ćwiczenia laboratoryjnego: Wprowadzenie STATYCZNA PRÓBA SKRĘCANIA Opracowała: mgr inż. Magdalena Bartkowiak-Jowsa Skręcanie pręta występuje w przypadku
3. FUNKCJA LINIOWA. gdzie ; ół,.
 1 WYKŁAD 3 3. FUNKCJA LINIOWA FUNKCJĄ LINIOWĄ nazywamy funkcję typu : dla, gdzie ; ół,. Załóżmy na początek, że wyraz wolny. Wtedy mamy do czynienia z funkcją typu :.. Wykresem tej funkcji jest prosta
1 WYKŁAD 3 3. FUNKCJA LINIOWA FUNKCJĄ LINIOWĄ nazywamy funkcję typu : dla, gdzie ; ół,. Załóżmy na początek, że wyraz wolny. Wtedy mamy do czynienia z funkcją typu :.. Wykresem tej funkcji jest prosta
Stereochemia Ułożenie atomów w przestrzeni
 Slajd 1 Stereochemia Ułożenie atomów w przestrzeni Slajd 2 Izomery Izomery to różne związki posiadające ten sam wzór sumaryczny izomery izomery konstytucyjne stereoizomery izomery cis-trans izomery zawierające
Slajd 1 Stereochemia Ułożenie atomów w przestrzeni Slajd 2 Izomery Izomery to różne związki posiadające ten sam wzór sumaryczny izomery izomery konstytucyjne stereoizomery izomery cis-trans izomery zawierające
INFORMATYKA a FILOZOFIA
 INFORMATYKA a FILOZOFIA (Pytania i odpowiedzi) Pytanie 1: Czy potrafisz wymienić pięciu filozofów, którzy zajmowali się także matematyką, logiką lub informatyką? Ewentualnie na odwrót: Matematyków, logików
INFORMATYKA a FILOZOFIA (Pytania i odpowiedzi) Pytanie 1: Czy potrafisz wymienić pięciu filozofów, którzy zajmowali się także matematyką, logiką lub informatyką? Ewentualnie na odwrót: Matematyków, logików
Własności walca, stożka i kuli.
 Własności walca, stożka i kuli. 1. Cele lekcji a) Wiadomości Uczeń: - zna pojęcie bryły obrotowej, - zna definicje: walca, stożka, kuli, - zna budowę brył obrotowych, - zna pojęcia związane z symetrią
Własności walca, stożka i kuli. 1. Cele lekcji a) Wiadomości Uczeń: - zna pojęcie bryły obrotowej, - zna definicje: walca, stożka, kuli, - zna budowę brył obrotowych, - zna pojęcia związane z symetrią
Aby opisać strukturę krystaliczną, konieczne jest określenie jej części składowych: sieci przestrzennej oraz bazy atomowej.
 2. Podstawy krystalografii Podczas naszych zajęć skupimy się przede wszystkim na strukturach krystalicznych. Kryształem nazywamy (def. strukturalna) substancję stałą zbudowaną z atomów, jonów lub cząsteczek
2. Podstawy krystalografii Podczas naszych zajęć skupimy się przede wszystkim na strukturach krystalicznych. Kryształem nazywamy (def. strukturalna) substancję stałą zbudowaną z atomów, jonów lub cząsteczek
Spektroskopia magnetycznego rezonansu jądrowego - wprowadzenie
 Spektroskopia magnetycznego rezonansu jądrowego - wprowadzenie Streszczenie Spektroskopia magnetycznego rezonansu jądrowego jest jedną z technik spektroskopii absorpcyjnej mającej zastosowanie w chemii,
Spektroskopia magnetycznego rezonansu jądrowego - wprowadzenie Streszczenie Spektroskopia magnetycznego rezonansu jądrowego jest jedną z technik spektroskopii absorpcyjnej mającej zastosowanie w chemii,
Opis matematyczny odbicia światła od zwierciadła kulistego i przejścia światła przez soczewki.
 Opis matematyczny odbicia światła od zwierciadła kulistego i przejścia światła przez soczewki. 1. Równanie soczewki i zwierciadła kulistego. Z podobieństwa trójkątów ABF i LFD (patrz rysunek powyżej) wynika,
Opis matematyczny odbicia światła od zwierciadła kulistego i przejścia światła przez soczewki. 1. Równanie soczewki i zwierciadła kulistego. Z podobieństwa trójkątów ABF i LFD (patrz rysunek powyżej) wynika,
PODSTAWY > Figury płaskie (1) KĄTY. Kąt składa się z ramion i wierzchołka. Jego wielkość jest mierzona w stopniach:
 PODSTAWY > Figury płaskie (1) KĄTY Kąt składa się z ramion i wierzchołka. Jego wielkość jest mierzona w stopniach: Kąt możemy opisać wpisując w łuk jego miarę (gdy jest znana). Gdy nie znamy miary kąta,
PODSTAWY > Figury płaskie (1) KĄTY Kąt składa się z ramion i wierzchołka. Jego wielkość jest mierzona w stopniach: Kąt możemy opisać wpisując w łuk jego miarę (gdy jest znana). Gdy nie znamy miary kąta,
KONKURS MATEMATYCZNY DLA UCZNIÓW SZKÓŁ GIMNAZJALNYCH
 ...... kod pracy ucznia pieczątka nagłówkowa szkoły KONKURS MATEMATYCZNY DLA UCZNIÓW SZKÓŁ GIMNAZJALNYCH ETAP SZKOLNY Drogi Uczniu, witaj na I etapie konkursu matematycznego. Przeczytaj uważnie instrukcję
...... kod pracy ucznia pieczątka nagłówkowa szkoły KONKURS MATEMATYCZNY DLA UCZNIÓW SZKÓŁ GIMNAZJALNYCH ETAP SZKOLNY Drogi Uczniu, witaj na I etapie konkursu matematycznego. Przeczytaj uważnie instrukcję
Symetryczne eksperymenty
 Maciej Frączek Dominik Trąbka uczniowie klasy 2b Gimnazjum nr 37 z Oddziałami Integracyjnymi Im. Maksymiliana Marii Kolbe w Krakowie Os. Złotego Wieku 36 Symetryczne eksperymenty Opiekun mgr Teresa Sklepek
Maciej Frączek Dominik Trąbka uczniowie klasy 2b Gimnazjum nr 37 z Oddziałami Integracyjnymi Im. Maksymiliana Marii Kolbe w Krakowie Os. Złotego Wieku 36 Symetryczne eksperymenty Opiekun mgr Teresa Sklepek
Teoria. a, jeśli a < 0.
 Teoria Definicja 1 Wartością bezwzględną liczby a R nazywamy liczbę a określoną wzorem a, jeśli a 0, a = a, jeśli a < 0 Zgodnie z powyższym określeniem liczba a jest równa odległości liczby a od liczby
Teoria Definicja 1 Wartością bezwzględną liczby a R nazywamy liczbę a określoną wzorem a, jeśli a 0, a = a, jeśli a < 0 Zgodnie z powyższym określeniem liczba a jest równa odległości liczby a od liczby
