A B. Modelowanie reakcji chemicznych: numeryczne rozwiązywanie równań na szybkość reakcji chemicznych B: 1. da dt. A v. v t
|
|
|
- Nina Krzemińska
- 9 lat temu
- Przeglądów:
Transkrypt
1 B: 1 Modelowanie reakcji chemicznych: numeryczne rozwiązywanie równań na szybkość reakcji chemicznych 1. ZałóŜmy, Ŝe zmienna A oznacza stęŝenie substratu, a zmienna B stęŝenie produktu reakcji chemicznej opisanej równaniem A B. 2. Szybkość reakcji chemicznej, v, jest wielkością wskazującą jak szybko z A powstaje B. 3. Na szybkość reakcji mają wpływ róŝne czynniki, co moŝna stwierdzić wykonując odpowiednie eksperymenty. Z pewnością, szybkość reakcji jest proporcjonalna do stęŝenia substratu A. 4. Zatem, dla tej reakcji chemicznej, v = k A, gdzie k jest współczynnikiem proporcjonalności. Równanie to nazwę się równania kinetycznego reakcji chemicznej. 5. Szybkość reakcji chemicznej w danej chwili jest pochodną stęŝenia substratu A po czasie, v = da/dt. PrzybliŜoną wartość szybkości zmian stęŝenia moŝna obliczyć stosując małe przyrosty czasu, t: v = da dt A B delta_t (parametr t) k (parametr k) A0 (wartość stęŝenia substancji A dla t=0) B0 (wartość stęŝenia substancji B dla t=0) A v t A( t + t) A( t) v t 6. Rozwiązanie powyŝszego równania polega na obliczeniu nowej wartości A w chwili t + t. Znając poprzednią wartość A w chwili t, A(t), oraz szybkość zmian, v, otrzymujemy: v t A( t + t) A( t) A( t) + v t A( t + t) A( t + t) A( t) + v t 7. Wartość v otrzymana w kolejnych iteracjach (powtórzeniach) jest coraz bliŝsza prawidłowego rozwiązania, poniewaŝ t staje się za kaŝdym razem mniejsze. (przybliŝenie jest tym lepsze im przyrost czasu jest mniejszy...) 8. PoniewaŜ stęŝenie A zmniejsza się podczas reakcji, szybkość reakcji zdefiniowana jako v=da/dt ma wartość ujemną. A celu uniknięcia stosowania ujemnej wartości szybkości reakcji, chwilowa szybkość zmian stęŝenia A jest zwykle zapisywana jako v=-da/dt. W tej sytuacji ostatnie równanie iteracji przyjmuje postać A(t + t) A(t) + (-v t). B: 1
2 B: 2 Modelowanie reakcji chemicznych: numeryczne rozwiązywanie równań na szybkość reakcji chemicznej w programie Excel i w programie Modellus 1. Excel (rysunek po lewej stronie): numeryczne rozwiązanie modelu matematycznego modelu szybkości reakcji A B. Zmiana stęŝenia A, w kolejnych wierszach, wynosi ( v t). Podstawą tego modelu jest równanie iteracyjne nowa wartość= stara wartość + szybkość zmian * przyrost czasu. 2. Modellus (rysunek po prawej stronie): szybkość reakcji chemicznej w postaci funkcji (v = k A) a szybkość zmian stęŝenia w postaci równania róŝniczkowego da/dt= -v... A B Wartości otrzymane w programie Modellus są bardziej dokładne. W programie Excel moŝemy uzyskać lepsze przybliŝenie przypisując delta_t mniejszą wartość. Sprawdźcie to dla delta_ t= 0.01 (będziesz potrzebować 10 razy więcej komórek...). Chwilowa szybkość zmian stęŝenia A jest ujemna, Równanie kinetyczne... poniewaŝ A maleje z szybkością -v Opcje... Max =3 Krok = 0.1 Miejsc dz.=3 B: 2
3 B: 3 B: 10 Modelowanie w Modellusie nieodwracalnych reakcji chemicznych 1. Wprowadźmy niewielką zmianę w modelu dla reakcji chemicznej A B... A B 2. Równanie kinetyczne reakcji dla tej reakcji jest następujące: v 1 = k 1 A StęŜenie substratu A zmniejsza się z szybkością v a stęŝenie produktu B zwiększa się z tę samą szybkością, v Zakładamy, Ŝe na początku reakcji (t=0) stęŝenie A=1 (wpisujemy 1 w oknie wartości początkowych) a stęŝenie B=0. Podczas reakcji substrat A zostanie całkowicie przekształcony w produkt B. 6. Jeśli na początku obecna jest niewielka ilość produktu B, związek A zostanie równieŝ całkowicie przekształcony w B. 7. Co się będzie działo, jeśli na początku reakcji (t=0) stęŝenia A i B są równe (na przykład A=B=1)? Czy moŝesz naszkicować wykres stęŝenia A i B w funkcji czasu? 8. Sprawdź wnioski wykorzystując model. B: 3
4 B: 4 Modelowanie w Modellusie odwracalnych reakcji chemicznych 1. RozwaŜymy teraz model najprostszej reakcji odwracalnej: A B, reakcji w której reagent A jest przekształcany w B, i w tym samym czasie reagent B jest przekształcany w A. A B 2. Reakcja A B opisana jest równaniem kinetycznym v 1 = k 1 A... a reakcja odwrotna B A równaniem v 2=k 2 B Zakładamy, Ŝe na początku reakcji stęŝenie A jest 1, natomiast reagent B jeszcze nie utworzył się (B=0). Reagent A przekształca się w B i jednocześnie powstający reagent B przekształca się w A do momentu ustalenia się ich stęŝeń na stałym poziomie. Równowaga zostaje osiągnięta po określonym czasie, który zaleŝy od wartości stałych szybkości, k 1 i k 2. Zmieniając wartości stałych k 1 i k 2 sprawdź jak wpływają one na czas potrzebny do osiągnięcia równowagi Czy zajdzie reakcja chemiczna, jeśli w chwili t=0 jest obecny tylko związek B? Co będzie się działo ze stęŝeniem związku A? 5. Co się stanie jeśli dla t=0 stęŝenia A i B są równe (np. A=B=1) ale stałe szybkości róŝne? Naszkicuj wykresy stęŝeń A i B w funkcji czasu. Porównaj swoje przewidywania z modelem. 6. Co się będzie działo gdy stałe szybkości są równe? Sprawdź i przedyskutuj... B: 4
5 B: 5 Równowaga chemiczna i zmiana stęŝeń w stanie równowagi 1. Spójrzmy znowu na model najprostszej reakcji odwracalnej A B. 2. Modellus pozwala zmieniać interaktywnie wartości zmiennych lub niezaleŝnych parametrów w oknie animacji. Na przykład uŝytkownik moŝe zmienić wartość stęŝenia A w trakcie działania modelu za pomocą interaktywnego kontrolera poziomu tej zmiennej. 3. Po osiągnięciu przez układ stanu równowagi w trakcie działania modelu, naciśnij przycisk pauza. 4. Za pomocą myszki zwiększ aktualną wartość stęŝenia reagenta A Naciśnij ponownie przycisk pauza Jak zareagował układ reakcji na to zaburzenie równowagi? A B 7. Jaka będzie reakcja układu jeśli zwiększymy stęŝenie reagenta B zamiast A? 8. Przeanalizuj wykresy szybkości badanej reakcji i reakcji do niej odwrotnej. Czy przebieg tych wykresów odpowiada zakłóceniu równowagi? Wyjaśnij tok rozumowania. 9. Więcej informacji na temat zakłócania równowagi reakcji moŝesz znaleźć np. na stronie internetowej: B: 5
6 B: 6 Modelowanie w Modellusie reakcji odwracalnych z dwoma substratami i jednym produktem 1. Model przedstawiony po prawej stronie dotyczy reakcji substratów A i B, której produktem jest związek C. W tym samym czasie związek C rozkłada się na A i B. A + B C 2. Reakcja A + B C opisana jest równaniem kinetycznym v1 = k1 A B, a reakcja do niej odwrotna C A +B równaniem v2 = k2 C 3. Zakładamy, Ŝe na początku reakcji mamy jedynie reagenty A i B: A i B reagują ze sobą tworząc C, reagent C rozkłada się na A i B...w końcu wszystkie stęŝenia osiągają stałą wartość. Równowaga jest osiągana po określonym czasie, który zaleŝy od wartości stałych szybkości reakcji, k1 i k2. Sprawdź, jak wartość tych stałych wpływa na czas potrzebny do osiągnięcia stanu równowagi Czy zajdzie reakcja, jeśli w chwili t=0 jest tylko związek C? Co się będzie działo ze stęŝeniem reagentów A i B? 5. Co się stanie, jeśli w chwili t = 0 stęŝenia A, B i C są równe. (np. A=B=C=1) ale stałe szybkości róŝne? Spróbuj naszkicować wykres zaleŝności stęŝeń A, B i C w funkcji czasu. Sprawdź swoje przewidywania za pomocą modelu. 6. Co się będzie działo, gdy stałe szybkości mają taką samą wartość? Sprawdź i przedyskutuj... B: 6
7 B: 7 Modelowanie w Modellusie reakcji odwracalnych z jednym substratem i dwoma produktami 1. Model przedstawiony po prawej stronie dotyczy reakcji, w której związek A rozkłada się na B i C, a w tym samym czasie B reaguje z C dając znowu związek A. A B + C 2. Reakcja A B + C opisana jest równaniem kinetycznym v 1 = k 1 A, a reakcja do niej odwrotna B + C A równaniem v 2 = k 2 B C 3. Zakładamy, Ŝe na początku reakcji mamy jedynie związek A, A rozkłada się na B i C, w tym samym czasie B i C przekształcają się w A...w końcu wszystkie stęŝenia osiągają stałą wartość. Równowaga jest osiągana po określonym czasie, który zaleŝy od wartości stałych szybkości reakcji, k 1 i k 2. Sprawdź, jak wartość tych stałych wpływa na czas potrzebny do osiągnięcia stanu równowagi Czy zajdzie reakcja, jeśli w chwili t=0 jest tylko związek A? Co się będzie działo ze stęŝeniem reagentów B i C 5. Co się stanie, jeśli w chwili t=0 stęŝenia A, B i C są równe. (np. A=B=C=1) ale stałe szybkości róŝne? Spróbuj naszkicować wykres zaleŝności stęŝeń A, B i C w funkcji czasu. Sprawdź swoje przewidywania za pomocą modelu. 6. Co się będzie działo, gdy stałe szybkości mają taką samą wartość? Sprawdź i przedyskutuj... B: 7
8 B: 8 Modelowanie w Modellusie dwóch reakcji chemicznych następujących po sobie, pierwsza i druga nieodwracalna 1. Model przedstawiony po prawej stronie dotyczy dwóch reakcji następujących po sobie: reagent A przekształca się w reagent B, a reagent B w reagent C. A B C 2. Pierwsza reakcja A B przebiega według równania kinetycznego v 1 = k 1 A, a druga reakcja B C według równania v 2 = k 2 B. 3. StęŜenie związku A maleje z szybkością v a stęŝenie związku B wzrasta z szybkością v 1 i jednocześnie maleje z szybkością v a stęŝenie związku C wzrasta z szybkością v Zakładając, Ŝe na początku reakcji (t=0) mamy jedynie związek A, A zostanie całkowicie przekształcony w związek B, a związek B w związek C Co się stanie, jeśli w chwili t=0 mamy pewną ilość związku A i związku B, ale nie ma związku C? Przedyskutuj, uzasadnij i sprawdź swoje przewidywania. 8. Co się stanie, jeśli w chwili t=0 mamy pewną ilość związku B, ale nie ma związku A i C? Przedyskutuj, uzasadnij i sprawdź swoje przewidywania. 9. Co się stanie, jeśli na początku (t=0) mamy tylko związek A, a szybkość reakcji 1 jest duŝa, a reakcji 2 mała? Przedyskutuj, uzasadnij i sprawdź swoje przewidywania. B: 8
9 B: 9 Modelowanie w Modellusie dwóch reakcji chemicznych następujących po sobie: pierwsza odwracalna, druga nieodwracalna Model przedstawiony po prawej stronie dotyczy dwóch reakcji następujących po sobie: reagent A przekształca się w sposób odwracalny w reagent B, a reagent B w reagent C w reakcji nieodwracalnej. A B C 2. StęŜenie związku A maleje z szybkością v 1 (reakcja A B) i wzrasta z szybkością v 2 (reakcja B A) a stęŝenie związku B wzrasta z szybkością v1 (B powstaje z A) i maleje z szybkością v 2 (B przekształca się w A), ale takŝe maleje z szybkością v 3 (B przekształca się w C, reakcja B C) a stęŝenie związku C wzrasta z szybkością v 3 (powstaje z B w reakcji B C). 5. Co się stanie, jeśli na początku reakcji (t = 0) mamy jedynie związki A i B, a nie ma związku C? Przedyskutuj, uzasadnij i sprawdź swoje przewidywania. 6. Co się stanie, jeśli w chwili t=0 jest pewna ilość związku B, ale nie ma związków A i C? Przedyskutuj, uzasadnij i sprawdź swoje przewidywania. 7. Co się stanie, jeśli w chwili t=0 mamy pewną ilość związku C, ale nie ma związku A i B? Przedyskutuj, uzasadnij i sprawdź swoje przewidywania. B: 9
10 B: 10 Modelowanie w Modellusie dwóch reakcji chemicznych następujących po sobie: pierwsza nieodwracalna, druga odwracalna Model przedstawiony po prawej stronie dotyczy dwóch reakcji następujących po sobie: reagent A przekształca się w sposób nieodwracalny w reagent B, a reagent B w reagent C w reakcji odwracalnej. A B C 2. StęŜenie związku A maleje z szybkością v 1 (reakcja A B) a stęŝenie związku B wzrasta z szybkością v1 (B powstaje z A) i maleje z szybkością v 2 (B przekształca się w C, reakcja B C), ale takŝe wzrasta z szybkością v 3 (C przekształca się w B, reakcja C B) a stęŝenie związku C wzrasta z szybkością v 2 (powstaje z B w reakcji B C) i zimniejsza się z szybkością v 3 (C przekształca się w B, reakcja C B). 5. Co się stanie, jeśli na początku reakcji (t = 0) mamy jedynie związki A i B, a nie ma związku C? Przedyskutuj, uzasadnij i sprawdź swoje przewidywania. 6. Co się stanie, jeśli w chwili t =0 jest pewna ilość związku B, ale nie ma związków A i C? Przedyskutuj, uzasadnij i sprawdź swoje przewidywania. 7. Co się stanie, jeśli w chwili t = 0 mamy pewną ilość związku C, ale nie ma związku A i B? Przedyskutuj, uzasadnij i sprawdź swoje przewidywania. B: 10
Modelowanie reakcji chemicznych
 Modelowanie reakcji chemicznych Przykładowe ćwiczenia w Excelu i Modellusie 2007 IT for US Projekt jest finansowany przy wsparciu Komisji Europejskiej, nr grantu 119001-CP-1-2004-1-PL-COMENIUS-C21. Materiały
Modelowanie reakcji chemicznych Przykładowe ćwiczenia w Excelu i Modellusie 2007 IT for US Projekt jest finansowany przy wsparciu Komisji Europejskiej, nr grantu 119001-CP-1-2004-1-PL-COMENIUS-C21. Materiały
Badanie zależności położenia cząstki od czasu w ruchu wzdłuż osi Ox
 A: 1 OK Muszę to powtórzyć... Potrzebuję pomocy Badanie zależności położenia cząstki od czasu w ruchu wzdłuż osi Ox 1. Uruchom program Modellus. 2. Wpisz x do okna modelu. 3. Naciśnij przycisk Interpretuj
A: 1 OK Muszę to powtórzyć... Potrzebuję pomocy Badanie zależności położenia cząstki od czasu w ruchu wzdłuż osi Ox 1. Uruchom program Modellus. 2. Wpisz x do okna modelu. 3. Naciśnij przycisk Interpretuj
Dokąd on zmierza? Przemieszczenie i prędkość jako wektory
 A: 1 OK Muszę to powtórzyć... Potrzebuję pomocy Dokąd on zmierza? Przemieszczenie i prędkość jako wektory Łódź żegluje po morzu... Płynie z szybkością 10 węzłów (węzeł to 1 mila morska na godzinę czyli
A: 1 OK Muszę to powtórzyć... Potrzebuję pomocy Dokąd on zmierza? Przemieszczenie i prędkość jako wektory Łódź żegluje po morzu... Płynie z szybkością 10 węzłów (węzeł to 1 mila morska na godzinę czyli
1. Zaproponuj doświadczenie pozwalające oszacować szybkość reakcji hydrolizy octanu etylu w środowisku obojętnym
 1. Zaproponuj doświadczenie pozwalające oszacować szybkość reakcji hydrolizy octanu etylu w środowisku obojętnym 2. W pewnej chwili szybkość powstawania produktu C w reakcji: 2A + B 4C wynosiła 6 [mol/dm
1. Zaproponuj doświadczenie pozwalające oszacować szybkość reakcji hydrolizy octanu etylu w środowisku obojętnym 2. W pewnej chwili szybkość powstawania produktu C w reakcji: 2A + B 4C wynosiła 6 [mol/dm
Ćwiczenie 14. Maria Bełtowska-Brzezinska KINETYKA REAKCJI ENZYMATYCZNYCH
 Ćwiczenie 14 aria Bełtowska-Brzezinska KINETYKA REAKCJI ENZYATYCZNYCH Zagadnienia: Podstawowe pojęcia kinetyki chemicznej (szybkość reakcji, reakcje elementarne, rząd reakcji). Równania kinetyczne prostych
Ćwiczenie 14 aria Bełtowska-Brzezinska KINETYKA REAKCJI ENZYATYCZNYCH Zagadnienia: Podstawowe pojęcia kinetyki chemicznej (szybkość reakcji, reakcje elementarne, rząd reakcji). Równania kinetyczne prostych
1 Kinetyka reakcji chemicznych
 Podstawy obliczeń chemicznych 1 1 Kinetyka reakcji chemicznych Szybkość reakcji chemicznej definiuje się jako ubytek stężenia substratu lub wzrost stężenia produktu w jednostce czasu. ν = c [ ] 2 c 1 mol
Podstawy obliczeń chemicznych 1 1 Kinetyka reakcji chemicznych Szybkość reakcji chemicznej definiuje się jako ubytek stężenia substratu lub wzrost stężenia produktu w jednostce czasu. ν = c [ ] 2 c 1 mol
Wyznaczanie stałej szybkości reakcji wymiany jonowej
 Wyznaczanie stałej szybkości reakcji wymiany jonowej Ćwiczenie laboratoryjne nr 4 Elementy termodynamiki i kinetyki procesowej Anna Ptaszek Elementy kinetyki chemicznej Pojęcie szybkości reakcji Pojęcie
Wyznaczanie stałej szybkości reakcji wymiany jonowej Ćwiczenie laboratoryjne nr 4 Elementy termodynamiki i kinetyki procesowej Anna Ptaszek Elementy kinetyki chemicznej Pojęcie szybkości reakcji Pojęcie
a) 1 mol b) 0,5 mola c) 1,7 mola d) potrzebna jest znajomość objętości zbiornika, aby można było przeprowadzić obliczenia
 1. Oblicz wartość stałej równowagi reakcji: 2HI H 2 + I 2 w temperaturze 600K, jeśli wiesz, że stężenia reagentów w stanie równowagi wynosiły: [HI]=0,2 mol/dm 3 ; [H 2 ]=0,02 mol/dm 3 ; [I 2 ]=0,024 mol/dm
1. Oblicz wartość stałej równowagi reakcji: 2HI H 2 + I 2 w temperaturze 600K, jeśli wiesz, że stężenia reagentów w stanie równowagi wynosiły: [HI]=0,2 mol/dm 3 ; [H 2 ]=0,02 mol/dm 3 ; [I 2 ]=0,024 mol/dm
ZADANIA DO ĆWICZEŃ. 1.4 Gospodarka wytwarza trzy produkty A, B, C. W roku 1980 i 1990 zarejestrowano następujące ilości produkcji i ceny:
 ZADANIA DO ĆWICZEŃ Y produkt krajowy brutto, C konsumpcja, I inwestycje, Y d dochody osobiste do dyspozycji, G wydatki rządowe na zakup towarów i usług, T podatki, Tr płatności transferowe, S oszczędności,
ZADANIA DO ĆWICZEŃ Y produkt krajowy brutto, C konsumpcja, I inwestycje, Y d dochody osobiste do dyspozycji, G wydatki rządowe na zakup towarów i usług, T podatki, Tr płatności transferowe, S oszczędności,
Wykład 4. Anna Ptaszek. 27 października Katedra Inżynierii i Aparatury Przemysłu Spożywczego. Chemia fizyczna - wykład 4. Anna Ptaszek 1 / 31
 Wykład 4 Katedra Inżynierii i Aparatury Przemysłu Spożywczego 27 października 2015 1 / 31 Podstawy kinetyki chemicznej pochodna funkcji i jej interpretacja, pojęcie szybkości i prędkości, stechiometria
Wykład 4 Katedra Inżynierii i Aparatury Przemysłu Spożywczego 27 października 2015 1 / 31 Podstawy kinetyki chemicznej pochodna funkcji i jej interpretacja, pojęcie szybkości i prędkości, stechiometria
Układy równań liniowych. Ax = b (1)
 Układy równań liniowych Dany jest układ m równań z n niewiadomymi. Liczba równań m nie musi być równa liczbie niewiadomych n, tj. mn. a a... a b n n a a... a b n n... a a... a b m m mn n m
Układy równań liniowych Dany jest układ m równań z n niewiadomymi. Liczba równań m nie musi być równa liczbie niewiadomych n, tj. mn. a a... a b n n a a... a b n n... a a... a b m m mn n m
Przedmiot: Chemia budowlana Zakład Materiałoznawstwa i Technologii Betonu
 Przedmiot: Chemia budowlana Zakład Materiałoznawstwa i Technologii Betonu Ćw. 4 Kinetyka reakcji chemicznych Zagadnienia do przygotowania: Szybkość reakcji chemicznej, zależność szybkości reakcji chemicznej
Przedmiot: Chemia budowlana Zakład Materiałoznawstwa i Technologii Betonu Ćw. 4 Kinetyka reakcji chemicznych Zagadnienia do przygotowania: Szybkość reakcji chemicznej, zależność szybkości reakcji chemicznej
Wykład z Chemii Ogólnej i Nieorganicznej
 Wykład z Chemii Ogólnej i Nieorganicznej Część 5 ELEMENTY STATYKI CHEMICZNEJ Katedra i Zakład Chemii Fizycznej Collegium Medicum w Bydgoszczy Uniwersytet Mikołaja Kopernika w Toruniu Prof. dr hab. n.chem.
Wykład z Chemii Ogólnej i Nieorganicznej Część 5 ELEMENTY STATYKI CHEMICZNEJ Katedra i Zakład Chemii Fizycznej Collegium Medicum w Bydgoszczy Uniwersytet Mikołaja Kopernika w Toruniu Prof. dr hab. n.chem.
Wykresy i własności funkcji
 Wykresy i własności funkcji Zad : (profil matematyczno-fizyczny) a) Wykres funkcji f(x) = x 6x + bx + c przechodzi przez punkt P = (, ), a współczynnik kierunkowy stycznej do wykresu tej funkcji w punkcie
Wykresy i własności funkcji Zad : (profil matematyczno-fizyczny) a) Wykres funkcji f(x) = x 6x + bx + c przechodzi przez punkt P = (, ), a współczynnik kierunkowy stycznej do wykresu tej funkcji w punkcie
Inżynieria Biomedyczna
 1.Obliczyć przy jakim stężeniu kwasu octowego stopień dysocjacji osiągnie wartość 3.%, jeżeli wiadomo, że stopień dysocjacji 15.%-wego roztworu (d=1.2 g/cm 3 ) w 2. Do 1 cm 3 2% (d=1.2 g/cm 3 ) roztworu
1.Obliczyć przy jakim stężeniu kwasu octowego stopień dysocjacji osiągnie wartość 3.%, jeżeli wiadomo, że stopień dysocjacji 15.%-wego roztworu (d=1.2 g/cm 3 ) w 2. Do 1 cm 3 2% (d=1.2 g/cm 3 ) roztworu
Chemia - laboratorium
 Chemia - laboratorium Wydział Geologii, Geofizyki i Ochrony Środowiska Studia stacjonarne, Rok I, Semestr zimowy 013/14 Dr hab. inż. Tomasz Brylewski e-mail: brylew@agh.edu.pl tel. 1-617-59 Katedra Fizykochemii
Chemia - laboratorium Wydział Geologii, Geofizyki i Ochrony Środowiska Studia stacjonarne, Rok I, Semestr zimowy 013/14 Dr hab. inż. Tomasz Brylewski e-mail: brylew@agh.edu.pl tel. 1-617-59 Katedra Fizykochemii
Szukanie rozwiązań funkcji uwikłanych (równań nieliniowych)
 Szukanie rozwiązań funkcji uwikłanych (równań nieliniowych) Funkcja uwikłana (równanie nieliniowe) jest to funkcja, która nie jest przedstawiona jawnym przepisem, wzorem wyrażającym zależność wartości
Szukanie rozwiązań funkcji uwikłanych (równań nieliniowych) Funkcja uwikłana (równanie nieliniowe) jest to funkcja, która nie jest przedstawiona jawnym przepisem, wzorem wyrażającym zależność wartości
Enzymologia I. Kinetyka - program Gepasi. Uniwersytet Warszawski Wydział Biologii Zakład Regulacji Metabolizmu
 Enzymologia I Kinetyka - program Gepasi Uniwersytet Warszawski Wydział Biologii Zakład Regulacji Metabolizmu I zasada + II zasada termodynamiki zmiana entalpii i entropii może zostać wyrażona ilościowo
Enzymologia I Kinetyka - program Gepasi Uniwersytet Warszawski Wydział Biologii Zakład Regulacji Metabolizmu I zasada + II zasada termodynamiki zmiana entalpii i entropii może zostać wyrażona ilościowo
Odwracalność przemiany chemicznej
 Odwracalność przemiany chemicznej Na ogół wszystkie reakcje chemiczne są odwracalne, tzn. z danych substratów tworzą się produkty, a jednocześnie produkty reakcji ulegają rozkładowi na substraty. Fakt
Odwracalność przemiany chemicznej Na ogół wszystkie reakcje chemiczne są odwracalne, tzn. z danych substratów tworzą się produkty, a jednocześnie produkty reakcji ulegają rozkładowi na substraty. Fakt
Drgania. W Y K Ł A D X Ruch harmoniczny prosty. k m
 Wykład z fizyki Piotr Posmykiewicz 119 W Y K Ł A D X Drgania. Drgania pojawiają się wtedy, gdy układ zostanie wytrącony ze stanu równowagi stabilnej. MoŜna przytoczyć szereg znanych przykładów: kołysząca
Wykład z fizyki Piotr Posmykiewicz 119 W Y K Ł A D X Drgania. Drgania pojawiają się wtedy, gdy układ zostanie wytrącony ze stanu równowagi stabilnej. MoŜna przytoczyć szereg znanych przykładów: kołysząca
Czytanie wykresów to ważna umiejętność, jeden wykres zawiera więcej informacji, niż strona tekstu. Dlatego musisz umieć to robić.
 Analiza i czytanie wykresów Czytanie wykresów to ważna umiejętność, jeden wykres zawiera więcej informacji, niż strona tekstu. Dlatego musisz umieć to robić. Aby dobrze odczytać wykres zaczynamy od opisu
Analiza i czytanie wykresów Czytanie wykresów to ważna umiejętność, jeden wykres zawiera więcej informacji, niż strona tekstu. Dlatego musisz umieć to robić. Aby dobrze odczytać wykres zaczynamy od opisu
Bezwładność - Zrywanie nici nad i pod cięŝarkiem (rozszerzenie klasycznego ćwiczenia pokazowego)
 6COACH 6 Bezwładność - Zrywanie nici nad i pod cięŝarkiem (rozszerzenie klasycznego ćwiczenia pokazowego) Program: Coach 6 Projekt: na ZMN060c CMA Coach Projects\PTSN Coach 6\Zrywanienici\Zestaw.cma Przykład
6COACH 6 Bezwładność - Zrywanie nici nad i pod cięŝarkiem (rozszerzenie klasycznego ćwiczenia pokazowego) Program: Coach 6 Projekt: na ZMN060c CMA Coach Projects\PTSN Coach 6\Zrywanienici\Zestaw.cma Przykład
Politechnika Warszawska. Wydział Budownictwa Mechaniki i Petrochemii w Płocku Laboratorium Chemii Budowlanej
 Politechnika Warszawska Wydział Budownictwa Mechaniki i Petrochemii w Płocku Laboratorium Chemii Budowlanej Instrukcja do ćwiczenia: SZYBKOŚĆ PRZEMIAN CHEMICZNYCH Opracowała: dr inŝ. Maria Bukowska Płock,
Politechnika Warszawska Wydział Budownictwa Mechaniki i Petrochemii w Płocku Laboratorium Chemii Budowlanej Instrukcja do ćwiczenia: SZYBKOŚĆ PRZEMIAN CHEMICZNYCH Opracowała: dr inŝ. Maria Bukowska Płock,
Materiał powtórzeniowy do sprawdzianu - reakcje egzoenergetyczne i endoenergetyczne, szybkość reakcji chemicznych
 Materiał powtórzeniowy do sprawdzianu - reakcje egzoenergetyczne i endoenergetyczne, szybkość reakcji chemicznych I. Reakcje egzoenergetyczne i endoenergetyczne 1. Układ i otoczenie Układ - ogół substancji
Materiał powtórzeniowy do sprawdzianu - reakcje egzoenergetyczne i endoenergetyczne, szybkość reakcji chemicznych I. Reakcje egzoenergetyczne i endoenergetyczne 1. Układ i otoczenie Układ - ogół substancji
Kinetyka chemiczna jest działem fizykochemii zajmującym się szybkością i mechanizmem reakcji chemicznych w różnych warunkach. a RT.
 Ćwiczenie 12, 13. Kinetyka chemiczna. Kinetyka chemiczna jest działem fizykochemii zajmującym się szybkością i mechanizmem reakcji chemicznych w różnych warunkach. Szybkość reakcji chemicznej jest związana
Ćwiczenie 12, 13. Kinetyka chemiczna. Kinetyka chemiczna jest działem fizykochemii zajmującym się szybkością i mechanizmem reakcji chemicznych w różnych warunkach. Szybkość reakcji chemicznej jest związana
a) jeżeli przedstawiona reakcja jest reakcją egzotermiczną, to jej prawidłowy przebieg jest przedstawiony na wykresie za pomocą linii...
 1. Spośród podanych reakcji wybierz reakcję egzoenergetyczną: a) Redukcja tlenku miedzi (II) wodorem b) Otrzymywanie tlenu przez rozkład chloranu (V) potasu c) Otrzymywanie wapna palonego w procesie prażenia
1. Spośród podanych reakcji wybierz reakcję egzoenergetyczną: a) Redukcja tlenku miedzi (II) wodorem b) Otrzymywanie tlenu przez rozkład chloranu (V) potasu c) Otrzymywanie wapna palonego w procesie prażenia
Tworzenie i modyfikowanie wykresów
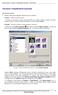 Tworzenie i modyfikowanie wykresów Aby utworzyć wykres: Zaznacz dane, które mają być zilustrowane na wykresie: I sposób szybkie tworzenie wykresu Naciśnij na klawiaturze klawisz funkcyjny F11 (na osobnym
Tworzenie i modyfikowanie wykresów Aby utworzyć wykres: Zaznacz dane, które mają być zilustrowane na wykresie: I sposób szybkie tworzenie wykresu Naciśnij na klawiaturze klawisz funkcyjny F11 (na osobnym
ĆWICZENIE 3. Farmakokinetyka nieliniowa i jej konsekwencje terapeutyczne na podstawie zmian stężenia fenytoiny w osoczu krwi
 ĆWICZENIE 3 Farmakokinetyka nieliniowa i jej konsekwencje terapeutyczne na podstawie zmian stężenia fenytoiny w osoczu krwi Celem ćwiczenia jest wyznaczenie podstawowych parametrów charakteryzujących kinetykę
ĆWICZENIE 3 Farmakokinetyka nieliniowa i jej konsekwencje terapeutyczne na podstawie zmian stężenia fenytoiny w osoczu krwi Celem ćwiczenia jest wyznaczenie podstawowych parametrów charakteryzujących kinetykę
WYKŁADY. Matematyka. dla studentów I roku Farmacji WUM. dr Justyna Kurkowiak
 WYKŁADY Matematyka dla studentów I roku Farmacji WUM dr Justyna Kurkowiak 209-0-0 WARUNKI ZALICZENIA Matematyka (I semestr) W semestrze można zdobyć 00 punktów. PUNKTACJA Kolokwium I Kolokwium II Kartkówki
WYKŁADY Matematyka dla studentów I roku Farmacji WUM dr Justyna Kurkowiak 209-0-0 WARUNKI ZALICZENIA Matematyka (I semestr) W semestrze można zdobyć 00 punktów. PUNKTACJA Kolokwium I Kolokwium II Kartkówki
Funkcje IV. Wymagania egzaminacyjne:
 Wymagania egzaminacyjne: a) określa funkcję za pomocą wzoru, tabeli, wykresu, opisu słownego, b) odczytuje z wykresu funkcji: dziedzinę i zbiór wartości, miejsca zerowe, maksymalne przedziały, w których
Wymagania egzaminacyjne: a) określa funkcję za pomocą wzoru, tabeli, wykresu, opisu słownego, b) odczytuje z wykresu funkcji: dziedzinę i zbiór wartości, miejsca zerowe, maksymalne przedziały, w których
Próbny egzamin z matematyki dla uczniów klas II LO i III Technikum. w roku szkolnym 2012/2013
 Próbny egzamin z matematyki dla uczniów klas II LO i III Technikum w roku szkolnym 2012/2013 I. Zakres materiału do próbnego egzaminu maturalnego z matematyki: 1) liczby rzeczywiste 2) wyrażenia algebraiczne
Próbny egzamin z matematyki dla uczniów klas II LO i III Technikum w roku szkolnym 2012/2013 I. Zakres materiału do próbnego egzaminu maturalnego z matematyki: 1) liczby rzeczywiste 2) wyrażenia algebraiczne
Podstawy termodynamiki
 Podstawy termodynamiki Organizm żywy z punktu widzenia termodynamiki Parametry stanu Funkcje stanu: U, H, F, G, S I zasada termodynamiki i prawo Hessa II zasada termodynamiki Kierunek przemian w warunkach
Podstawy termodynamiki Organizm żywy z punktu widzenia termodynamiki Parametry stanu Funkcje stanu: U, H, F, G, S I zasada termodynamiki i prawo Hessa II zasada termodynamiki Kierunek przemian w warunkach
Wykład 4. Anna Ptaszek. 9 października Katedra Inżynierii i Aparatury Przemysłu Spożywczego. Chemia fizyczna - wykład 4. Anna Ptaszek 1 / 29
 Wykład 4 Katedra Inżynierii i Aparatury Przemysłu Spożywczego 9 października 2015 1 / 29 Podstawy kinetyki chemicznej pochodna funkcji i jej interpretacja, pojęcie szybkości i prędkości, stechiometria
Wykład 4 Katedra Inżynierii i Aparatury Przemysłu Spożywczego 9 października 2015 1 / 29 Podstawy kinetyki chemicznej pochodna funkcji i jej interpretacja, pojęcie szybkości i prędkości, stechiometria
Definicja pochodnej cząstkowej
 1 z 8 gdzie punkt wewnętrzny Definicja pochodnej cząstkowej JeŜeli iloraz ma granicę dla to granicę tę nazywamy pochodną cząstkową funkcji względem w punkcie. Oznaczenia: Pochodną cząstkową funkcji względem
1 z 8 gdzie punkt wewnętrzny Definicja pochodnej cząstkowej JeŜeli iloraz ma granicę dla to granicę tę nazywamy pochodną cząstkową funkcji względem w punkcie. Oznaczenia: Pochodną cząstkową funkcji względem
KONDUKTOMETRIA. Konduktometria. Przewodnictwo elektrolityczne. Przewodnictwo elektrolityczne zaleŝy od:
 KONDUKTOMETRIA Konduktometria Metoda elektroanalityczna oparta na pomiarze przewodnictwa elektrolitycznego, którego wartość ulega zmianie wraz ze zmianą stęŝenia jonów zawartych w roztworze. Przewodnictwo
KONDUKTOMETRIA Konduktometria Metoda elektroanalityczna oparta na pomiarze przewodnictwa elektrolitycznego, którego wartość ulega zmianie wraz ze zmianą stęŝenia jonów zawartych w roztworze. Przewodnictwo
1) 2) 3) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) 21) 22) 23) 24) 25)
 1) Wykresem funkcji kwadratowej f jest parabola o wierzchołku w początku układu współrzędnych i przechodząca przez punkt. Wobec tego funkcja f określona wzorem 2) Punkt należy do paraboli o równaniu. Wobec
1) Wykresem funkcji kwadratowej f jest parabola o wierzchołku w początku układu współrzędnych i przechodząca przez punkt. Wobec tego funkcja f określona wzorem 2) Punkt należy do paraboli o równaniu. Wobec
Zadanie ChemCad - Batch Reaktor
 Zadanie ChemCad - Batch Reaktor Opracowanie: dr inŝ. E.Wolak Treść zadania: Octan sodu powstaje w wyniku reakcji: NaOH + C2 H5COOCH3 C2H5OH + CH3COONa Wodorotlenek sodu i octan etylu zasilają reaktor okresowy
Zadanie ChemCad - Batch Reaktor Opracowanie: dr inŝ. E.Wolak Treść zadania: Octan sodu powstaje w wyniku reakcji: NaOH + C2 H5COOCH3 C2H5OH + CH3COONa Wodorotlenek sodu i octan etylu zasilają reaktor okresowy
Obliczenia iteracyjne
 Lekcja Strona z Obliczenia iteracyjne Zmienne iteracyjne (wyliczeniowe) Obliczenia iteracyjne wymagają zdefiniowania specjalnej zmiennej nazywanej iteracyjną lub wyliczeniową. Zmienną iteracyjną od zwykłej
Lekcja Strona z Obliczenia iteracyjne Zmienne iteracyjne (wyliczeniowe) Obliczenia iteracyjne wymagają zdefiniowania specjalnej zmiennej nazywanej iteracyjną lub wyliczeniową. Zmienną iteracyjną od zwykłej
EXCEL Prowadzący: dr hab. inż. Marek Jaszczur Poziom: początkujący
 EXCEL Prowadzący: dr hab. inż. Marek Jaszczur Poziom: początkujący Laboratorium 3: Macierze i wykresy Cel: wykonywanie obliczeń na wektorach i macierzach, wykonywanie wykresów Czas wprowadzenia 25 minut,
EXCEL Prowadzący: dr hab. inż. Marek Jaszczur Poziom: początkujący Laboratorium 3: Macierze i wykresy Cel: wykonywanie obliczeń na wektorach i macierzach, wykonywanie wykresów Czas wprowadzenia 25 minut,
EGZAMIN MATURALNY Z MATEMATYKI
 Miejsce na naklejkę z kodem (Wpisuje zdający przed rozpoczęciem pracy) KOD ZDAJĄCEGO MMA-R2G1P-021 EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY Czas pracy 10 minut ARKUSZ II MAJ ROK 200 Instrukcja
Miejsce na naklejkę z kodem (Wpisuje zdający przed rozpoczęciem pracy) KOD ZDAJĄCEGO MMA-R2G1P-021 EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY Czas pracy 10 minut ARKUSZ II MAJ ROK 200 Instrukcja
Excel - użycie dodatku Solver
 PWSZ w Głogowie Excel - użycie dodatku Solver Dodatek Solver jest narzędziem używanym do numerycznej optymalizacji nieliniowej (szukanie minimum funkcji) oraz rozwiązywania równań nieliniowych. Przed pierwszym
PWSZ w Głogowie Excel - użycie dodatku Solver Dodatek Solver jest narzędziem używanym do numerycznej optymalizacji nieliniowej (szukanie minimum funkcji) oraz rozwiązywania równań nieliniowych. Przed pierwszym
EXCEL. Diagramy i wykresy w arkuszu lekcja numer 6. Instrukcja. dla Gimnazjum 36 - Ryszard Rogacz Strona 20
 Diagramy i wykresy w arkuszu lekcja numer 6 Tworzenie diagramów w arkuszu Excel nie jest sprawą skomplikowaną. Najbardziej czasochłonne jest przygotowanie danych. Utworzymy następujący diagram (wszystko
Diagramy i wykresy w arkuszu lekcja numer 6 Tworzenie diagramów w arkuszu Excel nie jest sprawą skomplikowaną. Najbardziej czasochłonne jest przygotowanie danych. Utworzymy następujący diagram (wszystko
Rys. 1. Zestawienie rocznych kosztów ogrzewania domów
 :: Trik 1. Wykres, w którym oś pozioma jest skalą wartości :: Trik 2. Automatyczne uzupełnianie pominiętych komórek :: Trik 3. Niestandardowe sortowanie wg 2 kluczy :: Trik 4. Przeliczanie miar za pomocą
:: Trik 1. Wykres, w którym oś pozioma jest skalą wartości :: Trik 2. Automatyczne uzupełnianie pominiętych komórek :: Trik 3. Niestandardowe sortowanie wg 2 kluczy :: Trik 4. Przeliczanie miar za pomocą
Notatki do tematu Metody poszukiwania rozwiązań jednokryterialnych problemów decyzyjnych metody dla zagadnień liniowego programowania matematycznego
 Notatki do tematu Metody poszukiwania rozwiązań jednokryterialnych problemów decyzyjnych metody dla zagadnień liniowego programowania matematycznego część III Analiza rozwiązania uzyskanego metodą simpleksową
Notatki do tematu Metody poszukiwania rozwiązań jednokryterialnych problemów decyzyjnych metody dla zagadnień liniowego programowania matematycznego część III Analiza rozwiązania uzyskanego metodą simpleksową
Skrypt 23. Geometria analityczna. Opracowanie L7
 Projekt Innowacyjny program nauczania matematyki dla liceów ogólnokształcących współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 2 Geometria analityczna 1.
Projekt Innowacyjny program nauczania matematyki dla liceów ogólnokształcących współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 2 Geometria analityczna 1.
Ćwiczenie IX KATALITYCZNY ROZKŁAD WODY UTLENIONEJ
 Wprowadzenie Ćwiczenie IX KATALITYCZNY ROZKŁAD WODY UTLENIONEJ opracowanie: Barbara Stypuła Celem ćwiczenia jest poznanie roli katalizatora w procesach chemicznych oraz prostego sposobu wyznaczenia wpływu
Wprowadzenie Ćwiczenie IX KATALITYCZNY ROZKŁAD WODY UTLENIONEJ opracowanie: Barbara Stypuła Celem ćwiczenia jest poznanie roli katalizatora w procesach chemicznych oraz prostego sposobu wyznaczenia wpływu
Wprowadzenie wideo do Modellusa
 Wprowadzenie wideo do Modellusa Przykładowe ćwiczenia ITforUS (Technologia informacyjna dla zrozumienia przedmiotów przyrodniczych) 2007 IT for US Projekt jest finansowany przy wsparciu Komisji Europejskiej,
Wprowadzenie wideo do Modellusa Przykładowe ćwiczenia ITforUS (Technologia informacyjna dla zrozumienia przedmiotów przyrodniczych) 2007 IT for US Projekt jest finansowany przy wsparciu Komisji Europejskiej,
ĆWICZENIE 1. Farmakokinetyka podania dożylnego i pozanaczyniowego leku w modelu jednokompartmentowym
 ĆWICZENIE 1 Farmakokinetyka podania dożylnego i pozanaczyniowego leku w modelu jednokompartmentowym Celem ćwiczenia jest wyznaczenie parametrów farmakokinetycznych leków podanych w jednorazowych dawkach:
ĆWICZENIE 1 Farmakokinetyka podania dożylnego i pozanaczyniowego leku w modelu jednokompartmentowym Celem ćwiczenia jest wyznaczenie parametrów farmakokinetycznych leków podanych w jednorazowych dawkach:
Inżynieria Biomedyczna
 1.Obliczyć przy jakim stężeniu kwasu octowego stopień dysocjacji osiągnie wartość 3.%, jeżeli wiadomo, że stopień dysocjacji 15.%-wego roztworu (d=1.2 g/cm 3 ) w 2. Do 1 cm 3 2% (d=1.2 g/cm 3 ) roztworu
1.Obliczyć przy jakim stężeniu kwasu octowego stopień dysocjacji osiągnie wartość 3.%, jeżeli wiadomo, że stopień dysocjacji 15.%-wego roztworu (d=1.2 g/cm 3 ) w 2. Do 1 cm 3 2% (d=1.2 g/cm 3 ) roztworu
Kinetyka. Kinetyka. Stawia dwa pytania: 1)Jak szybko biegną reakcje? 2) W jaki sposób przebiegają reakcje? energia swobodna, G. postęp reakcji.
 Kinetyka energia swobodna, G termodynamika stan 1 kinetyka termodynamika stan 2 postęp reakcji 1 Kinetyka Stawia dwa pytania: 1)Jak szybko biegną reakcje? 2) W jaki sposób przebiegają reakcje? 2 Jak szybko
Kinetyka energia swobodna, G termodynamika stan 1 kinetyka termodynamika stan 2 postęp reakcji 1 Kinetyka Stawia dwa pytania: 1)Jak szybko biegną reakcje? 2) W jaki sposób przebiegają reakcje? 2 Jak szybko
3. Badanie kinetyki enzymów
 3. Badanie kinetyki enzymów Przy stałym stężeniu enzymu, a przy zmieniającym się początkowym stężeniu substratu, zmiany szybkości reakcji katalizy, wyrażonej jako liczba moli substratu przetworzonego w
3. Badanie kinetyki enzymów Przy stałym stężeniu enzymu, a przy zmieniającym się początkowym stężeniu substratu, zmiany szybkości reakcji katalizy, wyrażonej jako liczba moli substratu przetworzonego w
Mathcad c.d. - Macierze, wykresy 3D, rozwiązywanie równań, pochodne i całki, animacje
 Mathcad c.d. - Macierze, wykresy 3D, rozwiązywanie równań, pochodne i całki, animacje Opracował: Zbigniew Rudnicki Powtórka z poprzedniego wykładu 2 1 Dokument, regiony, klawisze: Dokument Mathcada realizuje
Mathcad c.d. - Macierze, wykresy 3D, rozwiązywanie równań, pochodne i całki, animacje Opracował: Zbigniew Rudnicki Powtórka z poprzedniego wykładu 2 1 Dokument, regiony, klawisze: Dokument Mathcada realizuje
Modelowanie matematyczne a eksperyment
 Modelowanie matematyczne a eksperyment Budowanie modeli w środowisku Hildegard Urban-Woldron Ogólnopolska konferencja, 28.10. 2011, Warszawa Plan Budowanie modelu w środowisku Równania i wartości Uruchomienie
Modelowanie matematyczne a eksperyment Budowanie modeli w środowisku Hildegard Urban-Woldron Ogólnopolska konferencja, 28.10. 2011, Warszawa Plan Budowanie modelu w środowisku Równania i wartości Uruchomienie
WYMAGANIA EDUKACYJNE Z MATEMATYKI KLASA III ZAKRES ROZSZERZONY (90 godz.) , x
 WYMAGANIA EDUACYJNE Z MATEMATYI LASA III ZARES ROZSZERZONY (90 godz.) Oznaczenia: wymagania konieczne (dopuszczający); P wymagania podstawowe (dostateczny); R wymagania rozszerzające (dobry); D wymagania
WYMAGANIA EDUACYJNE Z MATEMATYI LASA III ZARES ROZSZERZONY (90 godz.) Oznaczenia: wymagania konieczne (dopuszczający); P wymagania podstawowe (dostateczny); R wymagania rozszerzające (dobry); D wymagania
Kinetyka. energia swobodna, G. postęp reakcji. stan 1 stan 2. kinetyka
 Kinetyka postęp reakcji energia swobodna, G termodynamika kinetyka termodynamika stan 1 stan 2 Kinetyka Stawia dwa pytania: 1) Jak szybko biegną reakcje? 2) W jaki sposób przebiegają reakcje? 1) Jak szybko
Kinetyka postęp reakcji energia swobodna, G termodynamika kinetyka termodynamika stan 1 stan 2 Kinetyka Stawia dwa pytania: 1) Jak szybko biegną reakcje? 2) W jaki sposób przebiegają reakcje? 1) Jak szybko
Rys 1 Schemat modelu masa- sprężyna- tłumik
 Rys 1 Schemat modelu masa- sprężyna- tłumik gdzie: m-masa bloczka [kg], ẏ prędkośćbloczka [ m s ]. 3. W kolejnym energię potencjalną: gdzie: y- przemieszczenie bloczka [m], k- stała sprężystości, [N/m].
Rys 1 Schemat modelu masa- sprężyna- tłumik gdzie: m-masa bloczka [kg], ẏ prędkośćbloczka [ m s ]. 3. W kolejnym energię potencjalną: gdzie: y- przemieszczenie bloczka [m], k- stała sprężystości, [N/m].
Rozwiązywanie równań nieliniowych
 Rozwiązywanie równań nieliniowych Marcin Orchel 1 Wstęp Przykłady wyznaczania miejsc zerowych funkcji f : f(ξ) = 0. Wyszukiwanie miejsc zerowych wielomianu n-tego stopnia. Wymiar tej przestrzeni wektorowej
Rozwiązywanie równań nieliniowych Marcin Orchel 1 Wstęp Przykłady wyznaczania miejsc zerowych funkcji f : f(ξ) = 0. Wyszukiwanie miejsc zerowych wielomianu n-tego stopnia. Wymiar tej przestrzeni wektorowej
Microsoft EXCEL SOLVER
 Microsoft EXCEL SOLVER 1. Programowanie liniowe z wykorzystaniem dodatku Microsoft Excel Solver Cele Po ukończeniu tego laboratorium słuchacze potrafią korzystając z dodatku Solver: formułować funkcję
Microsoft EXCEL SOLVER 1. Programowanie liniowe z wykorzystaniem dodatku Microsoft Excel Solver Cele Po ukończeniu tego laboratorium słuchacze potrafią korzystając z dodatku Solver: formułować funkcję
Y t=0. x(t)=v t. R(t) y(t)=d. Przelatujący supersamolot. R(t ) = D 2 + V 2 t 2. T = t + Δt = t + R(t) = t + D2 + V 2 t 2 T = R2 D 2 V. + R V d.
 Przelatujący supersamolot Y t= R(t) D x(t)=v t y(t)=d Superszybki samolot o prędkości V przelatuje po linii prostej przechodzącej w odległości D od obserwatora (dla ułatwienia przyjąć X=Vt). Na skutek
Przelatujący supersamolot Y t= R(t) D x(t)=v t y(t)=d Superszybki samolot o prędkości V przelatuje po linii prostej przechodzącej w odległości D od obserwatora (dla ułatwienia przyjąć X=Vt). Na skutek
1. Znajdowanie miejsca zerowego funkcji metodą bisekcji.
 1. Znajdowanie miejsca zerowego funkcji metodą bisekcji. Matematyczna funkcja f ma być określona w programie w oddzielnej funkcji języka C (tak, aby moŝna było łatwo ją zmieniać). Przykładowa funkcja to:
1. Znajdowanie miejsca zerowego funkcji metodą bisekcji. Matematyczna funkcja f ma być określona w programie w oddzielnej funkcji języka C (tak, aby moŝna było łatwo ją zmieniać). Przykładowa funkcja to:
POLITECHNIKA POZNAŃSKA ZAKŁAD CHEMII FIZYCZNEJ ĆWICZENIA PRACOWNI CHEMII FIZYCZNEJ
 ZALEŻNOŚĆ STAŁEJ SZYBKOŚCI REAKCJI OD TEMPERATURY WSTĘP Szybkość reakcji drugiego rzędu: A + B C (1) zależy od stężenia substratów A oraz B v = k [A][B] (2) Gdy jednym z reagentów jest rozpuszczalnik (np.
ZALEŻNOŚĆ STAŁEJ SZYBKOŚCI REAKCJI OD TEMPERATURY WSTĘP Szybkość reakcji drugiego rzędu: A + B C (1) zależy od stężenia substratów A oraz B v = k [A][B] (2) Gdy jednym z reagentów jest rozpuszczalnik (np.
10 zadań związanych z granicą i pochodną funkcji.
 0 zadań związanych z granicą i pochodną funkcji Znajdź przedziały monotoniczności funkcji f() 4, określonej dla (0,) W przedziale ( 0,) wyrażenie 4 przyjmuje wartości ujemne, dlatego dla (0,) funkcja f()
0 zadań związanych z granicą i pochodną funkcji Znajdź przedziały monotoniczności funkcji f() 4, określonej dla (0,) W przedziale ( 0,) wyrażenie 4 przyjmuje wartości ujemne, dlatego dla (0,) funkcja f()
Kształcenie w zakresie podstawowym. Klasa 2
 Kształcenie w zakresie podstawowym. Klasa 2 Poniżej podajemy umiejętności, jakie powinien zdobyć uczeń z każdego działu, aby uzyskać poszczególne stopnie. Na ocenę dopuszczającą uczeń powinien opanować
Kształcenie w zakresie podstawowym. Klasa 2 Poniżej podajemy umiejętności, jakie powinien zdobyć uczeń z każdego działu, aby uzyskać poszczególne stopnie. Na ocenę dopuszczającą uczeń powinien opanować
ZAJĘCIA 25. Wartość bezwzględna. Interpretacja geometryczna wartości bezwzględnej.
 ZAJĘCIA 25. Wartość bezwzględna. Interpretacja geometryczna wartości bezwzględnej. 1. Wartość bezwzględną liczby jest określona wzorem: x, dla _ x 0 x =, x, dla _ x < 0 Wartość bezwzględna liczby nazywana
ZAJĘCIA 25. Wartość bezwzględna. Interpretacja geometryczna wartości bezwzględnej. 1. Wartość bezwzględną liczby jest określona wzorem: x, dla _ x 0 x =, x, dla _ x < 0 Wartość bezwzględna liczby nazywana
Termodynamika techniczna i chemiczna, 2015/16, zadania do kol. 1, zadanie nr 1 1
 Termodynamika techniczna i chemiczna, 2015/16, zadania do kol. 1, zadanie nr 1 1 [Imię, nazwisko, grupa] prowadzący 1. Obliczyć zmianę entalpii dla izobarycznej (p = 1 bar) reakcji chemicznej zapoczątkowanej
Termodynamika techniczna i chemiczna, 2015/16, zadania do kol. 1, zadanie nr 1 1 [Imię, nazwisko, grupa] prowadzący 1. Obliczyć zmianę entalpii dla izobarycznej (p = 1 bar) reakcji chemicznej zapoczątkowanej
Zagadnienia do pracy klasowej: Kinetyka, równowaga, termochemia, chemia roztworów wodnych
 Zagadnienia do pracy klasowej: Kinetyka, równowaga, termochemia, chemia roztworów wodnych 1. Równanie kinetyczne, szybkość reakcji, rząd i cząsteczkowość reakcji. Zmiana szybkości reakcji na skutek zmiany
Zagadnienia do pracy klasowej: Kinetyka, równowaga, termochemia, chemia roztworów wodnych 1. Równanie kinetyczne, szybkość reakcji, rząd i cząsteczkowość reakcji. Zmiana szybkości reakcji na skutek zmiany
Laboratorium Inżynierii Bioreaktorów
 Laboratorium Inżynierii Bioreaktorów Ćwiczenie nr 1 Reaktor chemiczny: Wyznaczanie równania kinetycznego oraz charakterystyka reaktorów o działaniu ciągłym Cele ćwiczenia: 1 Wyznaczenie równania kinetycznego
Laboratorium Inżynierii Bioreaktorów Ćwiczenie nr 1 Reaktor chemiczny: Wyznaczanie równania kinetycznego oraz charakterystyka reaktorów o działaniu ciągłym Cele ćwiczenia: 1 Wyznaczenie równania kinetycznego
OPRACOWANIE MONIKA KASIELSKA
 KONSPEKT LEKCJI MATEMATYKI DIAGNOZA UMIEJĘTNOŚCI ZGODNYCH ZE STANDARDAMI WYMAGAŃ MATURALNYCH PRZEDMIOT : Matematyka KLASA: III TEMAT: Rozwiązywanie problemów poprzez stosowanie algorytmów. STANDARDY WYMAGAŃ
KONSPEKT LEKCJI MATEMATYKI DIAGNOZA UMIEJĘTNOŚCI ZGODNYCH ZE STANDARDAMI WYMAGAŃ MATURALNYCH PRZEDMIOT : Matematyka KLASA: III TEMAT: Rozwiązywanie problemów poprzez stosowanie algorytmów. STANDARDY WYMAGAŃ
Wyznaczanie krzywej ładowania kondensatora
 Ćwiczenie E10 Wyznaczanie krzywej ładowania kondensatora E10.1. Cel ćwiczenia Celem ćwiczenia jest zbadanie przebiegu procesu ładowania kondensatora oraz wyznaczenie stałej czasowej szeregowego układu.
Ćwiczenie E10 Wyznaczanie krzywej ładowania kondensatora E10.1. Cel ćwiczenia Celem ćwiczenia jest zbadanie przebiegu procesu ładowania kondensatora oraz wyznaczenie stałej czasowej szeregowego układu.
Konrad Słodowicz sk30792 AR22 Zadanie domowe satelita
 Konrad Słodowicz sk3079 AR Zadanie domowe satelita Współrzędne kartezjańskie Do opisu ruchu satelity potrzebujemy 4 zmiennych stanu współrzędnych położenia i prędkości x =r x =r x 3 = r 3, x 4 = r 4 gdzie
Konrad Słodowicz sk3079 AR Zadanie domowe satelita Współrzędne kartezjańskie Do opisu ruchu satelity potrzebujemy 4 zmiennych stanu współrzędnych położenia i prędkości x =r x =r x 3 = r 3, x 4 = r 4 gdzie
WYKORZYSTANIE NARZĘDZIA Solver DO ROZWIĄZYWANIA ZAGADNIENIA Problem przydziału
 WYKORZYSTANIE NARZĘDZIA Solver DO ROZWIĄZYWANIA ZAGADNIENIA Problem przydziału Problem przydziału Przykład Firma KARMA zamierza w okresie letnim przeprowadzić konserwację swoich urządzeń; mieszalników,
WYKORZYSTANIE NARZĘDZIA Solver DO ROZWIĄZYWANIA ZAGADNIENIA Problem przydziału Problem przydziału Przykład Firma KARMA zamierza w okresie letnim przeprowadzić konserwację swoich urządzeń; mieszalników,
Rodzaje zadań w nauczaniu fizyki
 Jan Tomczak Rodzaje zadań w nauczaniu fizyki Typologia zadań pisemnych wg. prof. B. Niemierki obejmuje 2 rodzaje, 6 form oraz 15 typów zadań. Rodzaj: Forma: Typ: Otwarte Rozszerzonej odpowiedzi - czynności
Jan Tomczak Rodzaje zadań w nauczaniu fizyki Typologia zadań pisemnych wg. prof. B. Niemierki obejmuje 2 rodzaje, 6 form oraz 15 typów zadań. Rodzaj: Forma: Typ: Otwarte Rozszerzonej odpowiedzi - czynności
FLAC Fast Lagrangian Analysis of Continua
 FLAC Fast Lagrangian Analysis of Continua Program FLAC jest oparty o metodę róŝnic skończonych. Metoda RóŜnic Skończonych (MRS) jest chyba najstarszą metodą numeryczną. W metodzie tej kaŝda pochodna w
FLAC Fast Lagrangian Analysis of Continua Program FLAC jest oparty o metodę róŝnic skończonych. Metoda RóŜnic Skończonych (MRS) jest chyba najstarszą metodą numeryczną. W metodzie tej kaŝda pochodna w
Badanie funkcji. Zad. 1: 2 3 Funkcja f jest określona wzorem f( x) = +
 Badanie funkcji Zad : Funkcja f jest określona wzorem f( ) = + a) RozwiąŜ równanie f() = 5 b) Znajdź przedziały monotoniczności funkcji f c) Oblicz największą i najmniejszą wartość funkcji f w przedziale
Badanie funkcji Zad : Funkcja f jest określona wzorem f( ) = + a) RozwiąŜ równanie f() = 5 b) Znajdź przedziały monotoniczności funkcji f c) Oblicz największą i najmniejszą wartość funkcji f w przedziale
Skrypt 7. Funkcje. Opracowanie: L1
 Projekt Innowacyjny program nauczania matematyki dla liceów ogólnokształcących współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 7 Funkcje 8. Miejsce zerowe
Projekt Innowacyjny program nauczania matematyki dla liceów ogólnokształcących współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 7 Funkcje 8. Miejsce zerowe
Otrzymaliśmy w ten sposób ograniczenie na wartości parametru m.
 Dla jakich wartości parametru m dziedziną funkcji f ( x) = x + mx + m 1 jest zbiór liczb rzeczywistych? We wzorze funkcji f(x) pojawia się funkcja kwadratowa, jednak znajduje się ona pod pierwiastkiem.
Dla jakich wartości parametru m dziedziną funkcji f ( x) = x + mx + m 1 jest zbiór liczb rzeczywistych? We wzorze funkcji f(x) pojawia się funkcja kwadratowa, jednak znajduje się ona pod pierwiastkiem.
Kultywator rolniczy - dobór parametrów sprężyny do zadanych warunków pracy
 Metody modelowania i symulacji kinematyki i dynamiki z wykorzystaniem CAD/CAE Laboratorium 6 Kultywator rolniczy - dobór parametrów sprężyny do zadanych warunków pracy Opis obiektu symulacji Przedmiotem
Metody modelowania i symulacji kinematyki i dynamiki z wykorzystaniem CAD/CAE Laboratorium 6 Kultywator rolniczy - dobór parametrów sprężyny do zadanych warunków pracy Opis obiektu symulacji Przedmiotem
3. FUNKCJA LINIOWA. gdzie ; ół,.
 1 WYKŁAD 3 3. FUNKCJA LINIOWA FUNKCJĄ LINIOWĄ nazywamy funkcję typu : dla, gdzie ; ół,. Załóżmy na początek, że wyraz wolny. Wtedy mamy do czynienia z funkcją typu :.. Wykresem tej funkcji jest prosta
1 WYKŁAD 3 3. FUNKCJA LINIOWA FUNKCJĄ LINIOWĄ nazywamy funkcję typu : dla, gdzie ; ół,. Załóżmy na początek, że wyraz wolny. Wtedy mamy do czynienia z funkcją typu :.. Wykresem tej funkcji jest prosta
KOŚć i przyspieszenie. O PRĘDKOŚCI. Aby ZROZumIEć to POjĘCIE,
 2 Siła i ruch Prędkość i przyspieszenie Ruch JEDNOSTAJNY ZaNIm będziemy mogli zrozumieć ZASADY ruchu, musimy WIEDZIEć, czym są pręd- KOŚć i przyspieszenie. NajPIERw pomówmy O PRĘDKOŚCI. Aby ZROZumIEć to
2 Siła i ruch Prędkość i przyspieszenie Ruch JEDNOSTAJNY ZaNIm będziemy mogli zrozumieć ZASADY ruchu, musimy WIEDZIEć, czym są pręd- KOŚć i przyspieszenie. NajPIERw pomówmy O PRĘDKOŚCI. Aby ZROZumIEć to
Bogdan Walkowiak. Zakład Biofizyki
 Bogdan Walkowiak Zakład Biofizyki Politechnika Łódzka Potencjał termodynamiczny - jest to taka funkcja termodynamiczna, której zmiana w procesie odwracalnym jest równa różnicy całkowitej pracy wykonanej
Bogdan Walkowiak Zakład Biofizyki Politechnika Łódzka Potencjał termodynamiczny - jest to taka funkcja termodynamiczna, której zmiana w procesie odwracalnym jest równa różnicy całkowitej pracy wykonanej
SZYBKOŚĆ REAKCJI CHEMICZNYCH. RÓWNOWAGA CHEMICZNA
 SZYBKOŚĆ REAKCJI CHEMICZNYCH. RÓWNOWAGA CHEMICZNA Zadania dla studentów ze skryptu,,obliczenia z chemii ogólnej Wydawnictwa Uniwersytetu Gdańskiego 1. Reakcja między substancjami A i B zachodzi według
SZYBKOŚĆ REAKCJI CHEMICZNYCH. RÓWNOWAGA CHEMICZNA Zadania dla studentów ze skryptu,,obliczenia z chemii ogólnej Wydawnictwa Uniwersytetu Gdańskiego 1. Reakcja między substancjami A i B zachodzi według
TYPY REAKCJI CHEMICZNYCH
 CHEMIA SPALANIA TYPY REAKCJI CHEMICZNYCH Jednocząsteczkowe (I rzędu): A C+D (np. C 2 H 6 CH 3 + CH 3 ) Dwucząsteczkowe (II- rzędu) (np. H + O 2 OH + O) A + B C + D Trójcząsteczkowe (III rzędu) A + B +
CHEMIA SPALANIA TYPY REAKCJI CHEMICZNYCH Jednocząsteczkowe (I rzędu): A C+D (np. C 2 H 6 CH 3 + CH 3 ) Dwucząsteczkowe (II- rzędu) (np. H + O 2 OH + O) A + B C + D Trójcząsteczkowe (III rzędu) A + B +
Małopolski Konkurs Chemiczny dla Gimnazjalistów
 ... kod ucznia Małopolski Konkurs Chemiczny dla Gimnazjalistów Etap II (rejonowy) 21 stycznia 2009 roku Wypełnia rejonowa komisja konkursowa 1. Zadanie 1. 2. 3. 4. 5. Suma 2. PoniŜej podano treść pięciu
... kod ucznia Małopolski Konkurs Chemiczny dla Gimnazjalistów Etap II (rejonowy) 21 stycznia 2009 roku Wypełnia rejonowa komisja konkursowa 1. Zadanie 1. 2. 3. 4. 5. Suma 2. PoniŜej podano treść pięciu
R L. Badanie układu RLC COACH 07. Program: Coach 6 Projekt: CMA Coach Projects\ PTSN Coach 6\ Elektronika\RLC.cma Przykłady: RLC.cmr, RLC1.
 OAH 07 Badanie układu L Program: oach 6 Projekt: MA oach Projects\ PTSN oach 6\ Elektronika\L.cma Przykłady: L.cmr, L1.cmr, V L Model L, Model L, Model L3 A el ćwiczenia: I. Obserwacja zmian napięcia na
OAH 07 Badanie układu L Program: oach 6 Projekt: MA oach Projects\ PTSN oach 6\ Elektronika\L.cma Przykłady: L.cmr, L1.cmr, V L Model L, Model L, Model L3 A el ćwiczenia: I. Obserwacja zmian napięcia na
Rozwiązywanie układów równań liniowych
 Rozwiązywanie układów równań liniowych Marcin Orchel 1 Wstęp Jeśli znamy macierz odwrotną A 1, to możęmy znaleźć rozwiązanie układu Ax = b w wyniku mnożenia x = A 1 b (1) 1.1 Metoda eliminacji Gaussa Pierwszy
Rozwiązywanie układów równań liniowych Marcin Orchel 1 Wstęp Jeśli znamy macierz odwrotną A 1, to możęmy znaleźć rozwiązanie układu Ax = b w wyniku mnożenia x = A 1 b (1) 1.1 Metoda eliminacji Gaussa Pierwszy
Numeryczne rozwiązywanie równań i układów równań
 Lekcja Strona z 2 Numeryczne rozwiązywanie równań i układów równań Rozwiązywanie pojedynczego równania - funkcja root Do rozwiązywania jednego równania z jedną niewiadomą służy funkcja root(f(z), z), gdzie:
Lekcja Strona z 2 Numeryczne rozwiązywanie równań i układów równań Rozwiązywanie pojedynczego równania - funkcja root Do rozwiązywania jednego równania z jedną niewiadomą służy funkcja root(f(z), z), gdzie:
Zadania rachunkowe z termokinetyki w programie Maxima
 Zadania rachunkowe z termokinetyki w programie Maxima pliku, polecenia do wpisywania w programie Maxima zapisane są czcionką typu: zmienna_w_maximie: 10; inny przykład f(x):=x+2*x+5; Problem 1 komorze
Zadania rachunkowe z termokinetyki w programie Maxima pliku, polecenia do wpisywania w programie Maxima zapisane są czcionką typu: zmienna_w_maximie: 10; inny przykład f(x):=x+2*x+5; Problem 1 komorze
Jak korzystać z Excela?
 1 Jak korzystać z Excela? 1. Dane liczbowe, wprowadzone (zaimportowane) do arkusza kalkulacyjnego w Excelu mogą przyjmować różne kategorie, np. ogólne, liczbowe, walutowe, księgowe, naukowe, itd. Jeśli
1 Jak korzystać z Excela? 1. Dane liczbowe, wprowadzone (zaimportowane) do arkusza kalkulacyjnego w Excelu mogą przyjmować różne kategorie, np. ogólne, liczbowe, walutowe, księgowe, naukowe, itd. Jeśli
Kinetyka reakcji chemicznych. Dr Mariola Samsonowicz
 Kinetyka reakcji chemicznych Dr Mariola Samsonowicz 1 Czym zajmuje się kinetyka chemiczna? Badaniem szybkości reakcji chemicznych poprzez analizę eksperymentalną i teoretyczną. Zdefiniowanie równania kinetycznego
Kinetyka reakcji chemicznych Dr Mariola Samsonowicz 1 Czym zajmuje się kinetyka chemiczna? Badaniem szybkości reakcji chemicznych poprzez analizę eksperymentalną i teoretyczną. Zdefiniowanie równania kinetycznego
ROZWIĄZYWANIE UKŁADÓW RÓWNAŃ NIELINIOWYCH PRZY POMOCY DODATKU SOLVER PROGRAMU MICROSOFT EXCEL. sin x2 (1)
 ROZWIĄZYWANIE UKŁADÓW RÓWNAŃ NIELINIOWYCH PRZY POMOCY DODATKU SOLVER PROGRAMU MICROSOFT EXCEL 1. Problem Rozważmy układ dwóch równań z dwiema niewiadomymi (x 1, x 2 ): 1 x1 sin x2 x2 cos x1 (1) Nie jest
ROZWIĄZYWANIE UKŁADÓW RÓWNAŃ NIELINIOWYCH PRZY POMOCY DODATKU SOLVER PROGRAMU MICROSOFT EXCEL 1. Problem Rozważmy układ dwóch równań z dwiema niewiadomymi (x 1, x 2 ): 1 x1 sin x2 x2 cos x1 (1) Nie jest
13. Równania różniczkowe - portrety fazowe
 13. Równania różniczkowe - portrety fazowe Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie rzegorz Kosiorowski (Uniwersytet Ekonomiczny 13. wrównania Krakowie) różniczkowe - portrety fazowe 1 /
13. Równania różniczkowe - portrety fazowe Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie rzegorz Kosiorowski (Uniwersytet Ekonomiczny 13. wrównania Krakowie) różniczkowe - portrety fazowe 1 /
5. Administracja kontami uŝytkowników
 5. Administracja kontami uŝytkowników Windows XP, w porównaniu do systemów Windows 9x, znacznie poprawia bezpieczeństwo oraz zwiększa moŝliwości konfiguracji uprawnień poszczególnych uŝytkowników. Natomiast
5. Administracja kontami uŝytkowników Windows XP, w porównaniu do systemów Windows 9x, znacznie poprawia bezpieczeństwo oraz zwiększa moŝliwości konfiguracji uprawnień poszczególnych uŝytkowników. Natomiast
Lista zadań. Babilońska wiedza matematyczna
 Lista zadań Babilońska wiedza matematyczna Zad. 1 Babilończycy korzystali z tablicy dodawania - utwórz w arkuszu kalkulacyjnym EXCEL tablicę dodawania liczb w układzie sześćdziesiątkowym, dla liczb ze
Lista zadań Babilońska wiedza matematyczna Zad. 1 Babilończycy korzystali z tablicy dodawania - utwórz w arkuszu kalkulacyjnym EXCEL tablicę dodawania liczb w układzie sześćdziesiątkowym, dla liczb ze
MATEMATYKA Wymagania edukacyjne i zakres materiału dla klasy drugiej poziom podstawowy w roku szkolnym 2013/2014 ZAKRES MATERIAŁU, TREŚCI NAUCZANIA
 MATEMATYKA Wymagania edukacyjne i zakres materiału dla klasy drugiej poziom podstawowy w roku szkolnym 2013/2014 ZAKRES MATERIAŁU, TREŚCI NAUCZANIA 1. Funkcje i ich własności. odróżnić przyporządkowanie,
MATEMATYKA Wymagania edukacyjne i zakres materiału dla klasy drugiej poziom podstawowy w roku szkolnym 2013/2014 ZAKRES MATERIAŁU, TREŚCI NAUCZANIA 1. Funkcje i ich własności. odróżnić przyporządkowanie,
Chemia fizyczna/ termodynamika, 2015/16, zadania do kol. 1, zadanie nr 1 1
 Chemia fizyczna/ termodynamika, 2015/16, zadania do kol. 1, zadanie nr 1 1 [Imię, nazwisko, grupa] prowadzący Uwaga! Proszę stosować się do następującego sposobu wprowadzania tekstu w ramkach : pola szare
Chemia fizyczna/ termodynamika, 2015/16, zadania do kol. 1, zadanie nr 1 1 [Imię, nazwisko, grupa] prowadzący Uwaga! Proszę stosować się do następującego sposobu wprowadzania tekstu w ramkach : pola szare
WYDZIAŁ ELEKTRYCZNY POLITECHNIKI WARSZAWSKIEJ INSTYTUT ELEKTROENERGETYKI ZAKŁAD ELEKTROWNI I GOSPODARKI ELEKTROENERGETYCZNEJ
 WYDZIAŁ ELEKTRYCZNY POLITECHNIKI WARSZAWSKIEJ INSTYTUT ELEKTROENERGETYKI ZAKŁAD ELEKTROWNI I GOSPODARKI ELEKTROENERGETYCZNEJ LABORATORIUM EKONOMIKA W ELEKTROTECHNICE INSTRUKCJA DO ĆWICZENIA 6 Analiza decyzji
WYDZIAŁ ELEKTRYCZNY POLITECHNIKI WARSZAWSKIEJ INSTYTUT ELEKTROENERGETYKI ZAKŁAD ELEKTROWNI I GOSPODARKI ELEKTROENERGETYCZNEJ LABORATORIUM EKONOMIKA W ELEKTROTECHNICE INSTRUKCJA DO ĆWICZENIA 6 Analiza decyzji
Zakres materiału obowiązujący do egzaminu poprawkowego z matematyki klasa 1 d LO
 Zakres materiału obowiązujący do egzaminu poprawkowego z matematyki klasa 1 d LO Dział programowy. Zakres realizacji 1. Liczby, działania i procenty Liczby wymierne i liczby niewymierne-działania, kolejność
Zakres materiału obowiązujący do egzaminu poprawkowego z matematyki klasa 1 d LO Dział programowy. Zakres realizacji 1. Liczby, działania i procenty Liczby wymierne i liczby niewymierne-działania, kolejność
Instrukcja obsługi programu Do-Exp
 Instrukcja obsługi programu Do-Exp Autor: Wojciech Stark. Program został utworzony w ramach pracy dyplomowej na Wydziale Chemicznym Politechniki Warszawskiej. Instrukcja dotyczy programu Do-Exp w wersji
Instrukcja obsługi programu Do-Exp Autor: Wojciech Stark. Program został utworzony w ramach pracy dyplomowej na Wydziale Chemicznym Politechniki Warszawskiej. Instrukcja dotyczy programu Do-Exp w wersji
7. WYZNACZANIE SIŁ WEWNĘTRZNYCH W BELKACH
 7. WYZNCZNIE SIŁ WEWNĘTRZNYCH W ELKCH Zadanie 7.1 Dla belki jak na rysunku 7.1.1 ułożyć równania sił wewnętrznych i sporządzić ich wykresy. Dane: q, a, M =. Rys.7.1.1 Rys.7.1. W zależności od rodzaju podpór
7. WYZNCZNIE SIŁ WEWNĘTRZNYCH W ELKCH Zadanie 7.1 Dla belki jak na rysunku 7.1.1 ułożyć równania sił wewnętrznych i sporządzić ich wykresy. Dane: q, a, M =. Rys.7.1.1 Rys.7.1. W zależności od rodzaju podpór
ĆWICZENIE 2. Farmakokinetyka wlewu dożylnego
 ĆWICZENIE 2 Farmakokinetyka wlewu dożylnego Celem ćwiczenia jest wyznaczenie parametrów farmakokinetycznych leku podanego drogą wlewu dożylnego w modelu 1-kompartmentowym z wykorzystaniem programu TopFit
ĆWICZENIE 2 Farmakokinetyka wlewu dożylnego Celem ćwiczenia jest wyznaczenie parametrów farmakokinetycznych leku podanego drogą wlewu dożylnego w modelu 1-kompartmentowym z wykorzystaniem programu TopFit
