Sztuczna Inteligencja i Systemy Doradcze
|
|
|
- Amelia Władysława Rybak
- 9 lat temu
- Przeglądów:
Transkrypt
1 Sztuczna Inteligencja i Systemy Doradcze Przeszukiwanie przestrzeni stanów gry Przeszukiwanie przestrzeni stanów gry 1
2 Gry a problemy przeszukiwania Nieprzewidywalny przeciwnik rozwiązanie jest strategią specyfikującą posunięcie dla każdej możliwej odpowiedzi przeciwnika Ograniczenia czasowe Mało prawdopodobne znalezienie celu, trzeba aproksymować Historia: Komputer rozważa różne scenariusze rozgrywki (Babbage, 1846) Algorytmy dla gier z pełną inform. (Zermelo, 1912; Von Neumann, 1944) Skończony horyzont, aproksymacyjna ocena stanu gry (Zuse, 1945; Wiener, 1948; Shannon, 1950) Pierwszy program grający w szachy (Turing, 1951) Zastosowanie uczenia maszynowego do poprawy trafności oceny stanu gry (Samuel, ) Odcięcia umożliwiające głębsze przeszukiwanie (McCarthy, 1956) Przeszukiwanie przestrzeni stanów gry 2
3 Rodzaje gier deterministyczne niedeterministyczne Pełna szachy, warcaby, backgammon, informacja go, otello monopoly Niepełna bridge, poker, scrabble, informacja nuclear war Przeszukiwanie przestrzeni stanów gry 3
4 Gracze: MAX i MIN Gra deterministyczna: 2 graczy Stan początkowy: stan planszy i wskazanie gracza rozpoczynającego (MAX) Funkcja następnika: zbiór par (posunięcie,stan) opisujących wszystkie dopuszczalne posunięcia z bieżącego stanu Test końca gry: sprawdza, czy stan gry jest końcowy Funkcja użyteczności (wypłaty): numeryczna wartość dla stanów końcowych np. wypłaty dla wygranej, porażki i remisu mogą być odpowiednio +1, -1 i 0. Przeszukiwanie przestrzeni stanów gry 4
5 Drzewo gry deterministycznej: 2 graczy MAX (X) MIN (O) X X X X X X X X X MAX (X) X O X O X O... MIN (O) X O X X O X X O X TERMINAL Utility X O X X O X X O X O X O O X X O X X O X O O Przeszukiwanie przestrzeni stanów gry 5
6 Strategia minimax: algorytm Dla gier deterministycznych z pełną informacją Pomysł: wybiera ruch zapewniający największą wypłatę tzn. największą wartość minimax (funkcja Minimax-Value) przy założeniu, źe przeciwnik gra optymalnie function Minimax-Decision(state, game) returns an action action, state the a, s in Successors(state) such that Minimax-Value(s,game) is maximized return action function Minimax-Value(state,game) returns a utility value if Terminal-Test(state) then return Utility(state) else if max is to move in state then return the highest Minimax-Value of Successors(state) else return the lowest Minimax-Value of Successors(state) Przeszukiwanie przestrzeni stanów gry 6
7 Strategia minimax: przyklad Gracz MAX maksymalizuje funkcję wypłaty (węzły ) wybiera ruch w lewą gałąź drzewa Gracz MIN minimalizuje funkcję wypłaty (węzły ) wybiera ruch do lewego liścia poddrzewa MAX 3 A 1 A 2 A 3 MIN A 11 A 13 A 21 A 22 A 23 A 32 A 33 A 12 A Przeszukiwanie przestrzeni stanów gry 7
8 Strategia minimax: wlasnosci Użyteczność?? Przeszukiwanie przestrzeni stanów gry 8
9 Strategia minimax: wlasnosci Użyteczność?? Gry determinist. z pełną informacją z dowolną liczbą graczy Pełność?? Przeszukiwanie przestrzeni stanów gry 9
10 Strategia minimax: wlasnosci Użyteczność?? Gry determinist. z pełną informacją z dowolną liczbą graczy Pełność?? Tak, jeśli drzewo przeszukiwań jest skończone Gry z nieskończonym drzewem przesz. mogą mieć strategie skończone! Optymalność?? Przeszukiwanie przestrzeni stanów gry 10
11 Strategia minimax: wlasnosci Użyteczność?? Gry determinist. z pełną informacją z dowolną liczbą graczy Pełność?? Tak, jeśli drzewo przeszukiwań jest skończone Gry z nieskończonym drzewem przesz. mogą mieć strategie skończone! Optymalność?? Tak, jeśli przeciwnik gra optymalnie W ogólności nieoptymalne Złożoność czasowa?? Przeszukiwanie przestrzeni stanów gry 11
12 Strategia minimax: wlasnosci Użyteczność?? Gry determinist. z pełną informacją z dowolną liczbą graczy Pełność?? Tak, jeśli drzewo przeszukiwań jest skończone Gry z nieskończonym drzewem przesz. mogą mieć strategie skończone! Optymalność?? Tak, jeśli przeciwnik gra optymalnie W ogólności nieoptymalne Złożoność czasowa?? O(b m ) Złożoność pamięciowa?? Przeszukiwanie przestrzeni stanów gry 12
13 Strategia minimax: wlasnosci Użyteczność?? Gry determinist. z pełną informacją z dowolną liczbą graczy Pełność?? Tak, jeśli drzewo przeszukiwań jest skończone Gry z nieskończonym drzewem przesz. mogą mieć strategie skończone! Optymalność?? Tak, jeśli przeciwnik gra optymalnie W ogólności nieoptymalne Złożoność czasowa?? O(b m ) Złożoność pamięciowa?? O(bm) (przezzukiwanie wgłąb) Przeszukiwanie przestrzeni stanów gry 13
14 Strategia minimax: wlasnosci Użyteczność?? Gry determinist. z pełną informacją z dowolną liczbą graczy Pełność?? Tak, jeśli drzewo przeszukiwań jest skończone Gry z nieskończonym drzewem przesz. mogą mieć strategie skończone! Optymalność?? Tak, jeśli przeciwnik gra optymalnie W ogólności nieoptymalne Złożoność czasowa?? O(b m ) Złożoność pamięciowa?? O(bm) (przezzukiwanie wgłąb) Dla szachów, b 35, m 100 dla sensownych rozgrywek dokładne rozwiązanie zupełnie nieosiągalne Przeszukiwanie przestrzeni stanów gry 14
15 Strategia minimax z odcieciem Problem: brak czasu na pełne przeszukanie przestrzeni stanów np. 100 sekund na posunięcie, szybkość 10 4 węzłów/sek 10 6 węzłów na ruch Rozwiązanie: przeszukiwanie z odcięciem ograniczającym głębokość przeszukiwania Przeszukiwanie przestrzeni stanów gry 15
16 Strategia minimax z odcieciem: algorytm function Minimax-Decision(state, game) returns an action action, state the a, s in Successors(state) such that Minimax-Cutoff(s,game) is maximized return action function Minimax-Cutoff(state,game) returns a utility value if Cutoff-Test(state) then return Eval(state) else if max is to move in state then return the highest Minimax-Value of Successors(state) else return the lowest Minimax-Value of Successors(state) Funkcja oceny Eval szacuje wypłatę dla danego stanu gry = rzeczywistej wypłacie dla stanów końcowych Przeszukiwanie przestrzeni stanów gry 16
17 Funkcja oceny: przyklad Black to move White slightly better White to move Black winning Dla szachów, przeważnie liniowa ważona suma cech Eval(s) = w 1 f 1 (s) + w 2 f 2 (s) w n f n (s) np. w 1 = 9 z f 1 (s) = (liczba białych hetmanów) (liczba czarnych hetmanów), itd. Przeszukiwanie przestrzeni stanów gry 17
18 Strategia minimax z odcieciem: wlasnosci Funkcja oceny wypłaty Eval w grach deterministycznych ma znaczenie wyłącznie porządkujące zachowuje działanie przy dowolnym przekształceniu monotonicznym funkcji Eval MAX MIN Przeszukiwanie przestrzeni stanów gry 18
19 Strategia minimax z odcieciem: skutecznosc W praktyce dla szachów b m = 10 6, b = 35 m = 4 4-warstwowe przeszukiwanie nowicjusz Potrzeba lepiej: 8-warstwowe przeszukiwanie typowy PC, mistrz 12-warstwowe przeszukiwanie Deep Blue, Kasparov Przeszukiwanie przestrzeni stanów gry 19
20 Przeszukiwanie stabilne Problem: Stany mają taką samą wartość oceny (na korzyść czarnych), ale stan z prawej niestabilny : kolejny ruch daje dużą zmianę oceny stanu gry (na korzyść białych) (a) White to move (b) White to move Przeszukiwanie przestrzeni stanów gry 20
21 Przeszukiwanie stabilne Problem: Stany mają taką samą wartość oceny (na korzyść czarnych), ale stan z prawej niestabilny : kolejny ruch daje dużą zmianę oceny stanu gry (na korzyść białych) (a) White to move (b) White to move Rozwiązanie: przeszukiwanie stabilne stany niestabilne są rozwijane do momentu osiągnięcia stanu stabilnego Przeszukiwanie przestrzeni stanów gry 21
22 Przeszukiwanie z pojedynczym rozwinieciem Efekt horyzontu: gracz wykonuje ruchy odsuwając nieuniknione posunięcie na korzyść przeciwnika poza horyzont przeszukiwania np. czarna wieża powtarza szachowanie białego króla Black to move Przeszukiwanie przestrzeni stanów gry 22
23 Przeszukiwanie z pojedynczym rozwinieciem Efekt horyzontu: gracz wykonuje ruchy odsuwając nieuniknione posunięcie na korzyść przeciwnika poza horyzont przeszukiwania np. czarna wieża powtarza szachowanie białego króla Black to move Rozwiązanie: przeszukiwanie z pojedynczym rozwinięciem algorytm wykonuje pogłębione przeszukiwanie dla wybranych posunięć wyraźnie lepszych od pozostałych Przeszukiwanie przestrzeni stanów gry 23
24 Strategia minimax z odcieciem α β MAX MIN MAX MIN V α jest najlepszą wartością dla max poza bieżącą ścieżką przeszukiwania Jeśli V jest gorsze niż α, max nigdy nie wejdzie do tej gałęzi gałąź z V można odciąć β jest definiowane analogicznie dla min Przeszukiwanie przestrzeni stanów gry 24
25 Strategia minimax z odcieciem α β: algorytm function Alpha-Beta-Search(state, game) returns an action action, state the a, s in Successors[game](state) such that Min-Value(s,game,,+ ) is maximized return action function Max-Value(state,game,α,β) returns the minimax value of state if Cutoff-Test(state) then return Eval(state) for each s in Successors(state) do α max(α,min-value(s,game,α,β)) if α β then return β return α function Min-Value(state,game,α,β) returns the minimax value of state if Cutoff-Test(state) then return Eval(state) for each s in Successors(state) do β min(β,max-value(s,game,α,β)) if β α then return α return β Przeszukiwanie przestrzeni stanów gry 25
26 Strategia minimax z odcieciem α β: przyklad MAX 3 MIN Przeszukiwanie przestrzeni stanów gry 26
27 Strategia minimax z odcieciem α β: przyklad MAX 3 MIN X X Przeszukiwanie przestrzeni stanów gry 27
28 Strategia minimax z odcieciem α β: przyklad MAX 3 MIN X X 14 Przeszukiwanie przestrzeni stanów gry 28
29 Strategia minimax z odcieciem α β: przyklad MAX 3 MIN X X 14 5 Przeszukiwanie przestrzeni stanów gry 29
30 Strategia minimax z odcieciem α β: przyklad MAX 3 3 MIN X X Przeszukiwanie przestrzeni stanów gry 30
31 Strategia minimax z odcieciem α β: wlasnosci Odcinanie jest czyste : nie ma wpływu na optymalność i wynik przeszukiwania Własciwe uporządkowanie posunięć poprawia efektywność odcinania Dla perfekcyjnego uporządkowania posunięć złożoność czasowa = O(b m/2 ) podwaja głębokość przeszukiwania może łatwo zejść do 8-ego poziomu i grać dobre szachy Przeszukiwanie przestrzeni stanów gry 31
32 Gry deterministyczne: osiagniecia Warcaby: Chinook zakończył 40-letnie panowanie mistrza świata Mariona Tinsley w Użył biblioteki wszystkich zakończeń dla 8 lub mniej pionków na planszy, w sumie 443,748,401,247 pozycji. Szachy: Deep Blue pokonał mistrza świata Gary Kasparowa w meczu z 6-ioma partiami w Deep Blue przeszukiwał 200 milionów pozycji na sekundę, używając bardzo wyszukanej funkcji oceny, i nieznanych metod rozszerzających niektóre ścieżki przeszukiwania do głębokości 40. Otello: mistrz świata odmówił rozgrywki z komputerami, które są zbyt silne. Go: mistrz świata odmówił rozgrywki z komputerami, które są zbyt słabe. W go, b > 300, więc większość programów używa bazy wiedzy z wzorcami do wyboru dopuszczalnych ruchów. Przeszukiwanie przestrzeni stanów gry 32
33 Gry niedeterministyczne Źródło niedeterminizmu: rzut kostką, tasowanie kart Przykład z rzucaniem monetą: MAX CHANCE MIN Przeszukiwanie przestrzeni stanów gry 33
34 Gry niedeterministyczne: backgammon Przeszukiwanie przestrzeni stanów gry 34
35 Strategia usrednionego minimax Uogólnienie strategii minimax dla gier niedeterministycznych function ExpectiMinimax-Decision(state, game) returns an action action, state the a, s in Successors(state) such that ExpectiMinimax-Value(s,game) is maximized return action function ExpectiMinimax-Value(state,game) returns a utility value if Terminal-Test(state) then return Utility(state) else if state is a Max node then return the highest ExpectiMinimax-Value of Successors(state) else if state is a Min node then return the lowest ExpectiMinimax-Value of Successors(state) else if state is a chance node then return average of ExpectiMinimax-Value of Successors(state) Przeszukiwanie przestrzeni stanów gry 35
36 Strategia usrednionego minimax: wlasnosci MAX DICE MIN Działanie funkcji oceny Eval jest zachowane tylko dla dodatnich liniowych przekształceń tej funkcji Stąd Eval powinna być propocjonalna do wartości oczekiwanej wypłaty Przeszukiwanie przestrzeni stanów gry 36
37 Strategia usrednionego minimax z odcieciem α-β [, + ] [, + ] [, + ] [, + ] [, + ] [, + ] Przeszukiwanie przestrzeni stanów gry 37
38 Strategia usrednionego minimax z odcieciem α-β [, + ] [, + ] [, 2 ] [, + ] [, + ] [, + ] 2 Przeszukiwanie przestrzeni stanów gry 38
39 Strategia usrednionego minimax z odcieciem α-β [, + ] [, + ] [ 2, 2 ] [, + ] [, + ] [, + ] 2 2 Przeszukiwanie przestrzeni stanów gry 39
40 Strategia usrednionego minimax z odcieciem α-β [, 2 ] [, + ] [ 2, 2 ] [, 2 ] [, + ] [, + ] Przeszukiwanie przestrzeni stanów gry 40
41 Strategia usrednionego minimax z odcieciem α-β [ 1.5, 1.5 ] [, + ] [ 2, 2 ] [ 1, 1 ] [, + ] [, + ] Przeszukiwanie przestrzeni stanów gry 41
42 Strategia usrednionego minimax z odcieciem α-β [ 1.5, 1.5 ] [, + ] [ 2, 2 ] [ 1, 1 ] [, 0 ] [, + ] Przeszukiwanie przestrzeni stanów gry 42
43 Strategia usrednionego minimax z odcieciem α-β [ 1.5, 1.5 ] [, + ] [ 2, 2 ] [ 1, 1 ] [ 0, 0 ] [, + ] Przeszukiwanie przestrzeni stanów gry 43
44 Strategia usrednionego minimax z odcieciem α-β [ 1.5, 1.5 ] [, 0.5 ] [ 2, 2 ] [ 1, 1 ] [ 0, 0 ] [, 1 ] Przeszukiwanie przestrzeni stanów gry 44
45 Strategia usrednionego minimax z odcieciem α-β Bardziej efektywna, jeśli wartość wypłaty ograniczona [ 2, 2 ] [ 2, 2 ] [ 2, 2 ] [ 2, 2 ] [ 2, 2 ] [ 2, 2 ] Przeszukiwanie przestrzeni stanów gry 45
46 Strategia usrednionego minimax z odcieciem α-β Bardziej efektywna, jeśli wartość wypłaty ograniczona [ 2, 2 ] [ 2, 2 ] [ 2, 2 ] [ 2, 2 ] [ 2, 2 ] [ 2, 2 ] 2 Przeszukiwanie przestrzeni stanów gry 46
47 Strategia usrednionego minimax z odcieciem α-β Bardziej efektywna, jeśli wartość wypłaty ograniczona [ 0, 2 ] [ 2, 2 ] [ 2, 2 ] [ 2, 2 ] [ 2, 2 ] [ 2, 2 ] 2 2 Przeszukiwanie przestrzeni stanów gry 47
48 Strategia usrednionego minimax z odcieciem α-β Bardziej efektywna, jeśli wartość wypłaty ograniczona [ 0, 2 ] [ 2, 2 ] [ 2, 2 ] [ 2, 2 ] [ 2, 2 ] [ 2, 2 ] Przeszukiwanie przestrzeni stanów gry 48
49 Strategia usrednionego minimax z odcieciem α-β Bardziej efektywna, jeśli wartość wypłaty ograniczona [ 1.5, 1.5 ] [ 2, 2 ] [ 2, 2 ] [ 1, 1 ] [ 2, 2 ] [ 2, 2 ] Przeszukiwanie przestrzeni stanów gry 49
50 Strategia usrednionego minimax z odcieciem α-β Bardziej efektywna, jeśli wartość wypłaty ograniczona [ 1.5, 1.5 ] [ 2, 1 ] [ 2, 2 ] [ 1, 1 ] [ 2, 0 ] [ 2, 2 ] Przeszukiwanie przestrzeni stanów gry 50
51 Gry niedeterministyczne: wlasnosci Rzuty kostką zwiększają b: 21 możliwych rzutów dla 2 kostek Backgammon 20 dopuszczalnych posunięć glebokość 4 = 20 (21 20) Jak głębokość wzrasta, prawdopodobieństwo osiągnięcia danego węzła maleje wartość sprawdzania wprzód jest nikła Odcinanie α β jest dużo mniej efektywne Program TDGammon: przeszukiwanie na głębokość 2 + bardzo dobra funkcja oceny stanu Eval poziom mistrza świata Przeszukiwanie przestrzeni stanów gry 51
52 Gry z niepelna informacja Np. gry karciane, w których początkowy zestaw kart przeciwnika jest nieznany Można policzyć prawdopodobieństwo każdego rozdania wygląda jak jeden duży rzut kostką na początku gry Pomysł: algorytm oblicza wartość minimax dla każdej akcji w każdym możliwym rozdaniu i wybiera akcje z największą wartością uśrednioną po wszystkich rozdaniach GIB, najlepszy program do brydża, przybliża tą ideę 1) generuje 100 rozdań zgodnych z informacją z licytacji 2) wybiera akcję, która zbiera średnio najwięcej lew Przeszukiwanie przestrzeni stanów gry 52
53 Gry z niepelna informacja: przyklad Gra w otwarte karty, Max gra pierwszy Przeszukiwanie przestrzeni stanów gry 53
54 Gry z niepelna informacja: przyklad Gra w otwarte karty, Max gra pierwszy MAX MIN MAX MIN Przeszukiwanie przestrzeni stanów gry 54
55 Gry z niepelna informacja: przyklad Gra w otwarte karty, Max gra pierwszy MAX MIN MAX MIN MAX MIN Przeszukiwanie przestrzeni stanów gry 55
56 Gry z niepelna informacja: przyklad Gra w otwarte karty, Max gra pierwszy MAX MIN MAX MIN MAX MIN Jeśli Max rozpocząlby z 6 lub 6, miałby gwarantowany remis Przeszukiwanie przestrzeni stanów gry 56
57 Gry z niepelna informacja: przyklad MAX MIN MAX MIN MAX MIN Jeśli Max rozpocząlby z 6 lub 6, miałby gwarantowany remis uśrednienie nie jest optymalne! ważne, która informacja będzie dostępna w którym momencie gry Przeszukiwanie przestrzeni stanów gry 57
SID Wykład 4 Gry Wydział Matematyki, Informatyki i Mechaniki UW
 SID Wykład 4 Gry Wydział Matematyki, Informatyki i Mechaniki UW slezak@mimuw.edu.pl Gry a problemy przeszukiwania Nieprzewidywalny przeciwnik rozwiazanie jest strategia specyfikujac a posunięcie dla każdej
SID Wykład 4 Gry Wydział Matematyki, Informatyki i Mechaniki UW slezak@mimuw.edu.pl Gry a problemy przeszukiwania Nieprzewidywalny przeciwnik rozwiazanie jest strategia specyfikujac a posunięcie dla każdej
WPROWADZENIE DO SZTUCZNEJ INTELIGENCJI
 POLITECHNIKA WARSZAWSKA WYDZIAŁ MECHANICZNY ENERGETYKI I LOTNICTWA MEL WPROWADZENIE DO SZTUCZNEJ INTELIGENCJI NS 586 Dr inż. Franciszek Dul 6. GRY POSZUKIWANIA W OBECNOŚCI PRZECIWNIKA Gry Pokażemy, w jaki
POLITECHNIKA WARSZAWSKA WYDZIAŁ MECHANICZNY ENERGETYKI I LOTNICTWA MEL WPROWADZENIE DO SZTUCZNEJ INTELIGENCJI NS 586 Dr inż. Franciszek Dul 6. GRY POSZUKIWANIA W OBECNOŚCI PRZECIWNIKA Gry Pokażemy, w jaki
Sztuczna Inteligencja i Systemy Doradcze
 Sztuczna Inteligencja i Systemy Doradcze Przeszukiwanie przestrzeni stanów algorytmy ślepe Przeszukiwanie przestrzeni stanów algorytmy ślepe 1 Strategie slepe Strategie ślepe korzystają z informacji dostępnej
Sztuczna Inteligencja i Systemy Doradcze Przeszukiwanie przestrzeni stanów algorytmy ślepe Przeszukiwanie przestrzeni stanów algorytmy ślepe 1 Strategie slepe Strategie ślepe korzystają z informacji dostępnej
Algorytmy dla gier dwuosobowych
 Algorytmy dla gier dwuosobowych Wojciech Dudek Seminarium Nowości Komputerowe 5 czerwca 2008 Plan prezentacji Pojęcia wstępne (gry dwuosobowe, stan gry, drzewo gry) Algorytm MiniMax Funkcje oceniające
Algorytmy dla gier dwuosobowych Wojciech Dudek Seminarium Nowości Komputerowe 5 czerwca 2008 Plan prezentacji Pojęcia wstępne (gry dwuosobowe, stan gry, drzewo gry) Algorytm MiniMax Funkcje oceniające
Gry. wykład 5. dr inż. Joanna Kołodziejczyk. Zakład Sztucznej Inteligencji ISZiMM. ESI - wykład 5 p. 1
 Gry wykład 5 dr inż. Joanna Kołodziejczyk jkolodziejczyk@wi.ps.pl Zakład Sztucznej Inteligencji ISZiMM ESI - wykład 5 p. 1 Plan wykładu Adversarial search jak postępować, gdy inni agenci sa naszymi przeciwnikami,
Gry wykład 5 dr inż. Joanna Kołodziejczyk jkolodziejczyk@wi.ps.pl Zakład Sztucznej Inteligencji ISZiMM ESI - wykład 5 p. 1 Plan wykładu Adversarial search jak postępować, gdy inni agenci sa naszymi przeciwnikami,
Wykład 7 i 8. Przeszukiwanie z adwersarzem. w oparciu o: S. Russel, P. Norvig. Artificial Intelligence. A Modern Approach
 (4g) Wykład 7 i 8 w oparciu o: S. Russel, P. Norvig. Artificial Intelligence. A Modern Approach P. Kobylański Wprowadzenie do Sztucznej Inteligencji 177 / 226 (4g) gry optymalne decyzje w grach algorytm
(4g) Wykład 7 i 8 w oparciu o: S. Russel, P. Norvig. Artificial Intelligence. A Modern Approach P. Kobylański Wprowadzenie do Sztucznej Inteligencji 177 / 226 (4g) gry optymalne decyzje w grach algorytm
Wyznaczanie strategii w grach
 Wyznaczanie strategii w grach Dariusz Banasiak Katedra Informatyki Technicznej W4/K9 Politechnika Wrocławska Definicja gry Teoria gier i konstruowane na jej podstawie programy stanowią jeden z głównych
Wyznaczanie strategii w grach Dariusz Banasiak Katedra Informatyki Technicznej W4/K9 Politechnika Wrocławska Definicja gry Teoria gier i konstruowane na jej podstawie programy stanowią jeden z głównych
Podstawy sztucznej inteligencji
 wykład II Problem solving 03 październik 2012 Jakie problemy możemy rozwiązywać? Cel: Zbudować inteligentnego agenta planującego, rozwiązującego problem. Szachy Kostka rubika Krzyżówka Labirynt Wybór trasy
wykład II Problem solving 03 październik 2012 Jakie problemy możemy rozwiązywać? Cel: Zbudować inteligentnego agenta planującego, rozwiązującego problem. Szachy Kostka rubika Krzyżówka Labirynt Wybór trasy
Marcel Stankowski Wrocław, 23 czerwca 2009 INFORMATYKA SYSTEMÓW AUTONOMICZNYCH
 Marcel Stankowski Wrocław, 23 czerwca 2009 INFORMATYKA SYSTEMÓW AUTONOMICZNYCH Przeszukiwanie przestrzeni rozwiązań, szukanie na ślepo, wszerz, w głąb. Spis treści: 1. Wprowadzenie 3. str. 1.1 Krótki Wstęp
Marcel Stankowski Wrocław, 23 czerwca 2009 INFORMATYKA SYSTEMÓW AUTONOMICZNYCH Przeszukiwanie przestrzeni rozwiązań, szukanie na ślepo, wszerz, w głąb. Spis treści: 1. Wprowadzenie 3. str. 1.1 Krótki Wstęp
Tworzenie gier na urządzenia mobilne
 Katedra Inżynierii Wiedzy Teoria podejmowania decyzji w grze Gry w postaci ekstensywnej Inaczej gry w postaci drzewiastej, gry w postaci rozwiniętej; formalny opis wszystkich możliwych przebiegów gry z
Katedra Inżynierii Wiedzy Teoria podejmowania decyzji w grze Gry w postaci ekstensywnej Inaczej gry w postaci drzewiastej, gry w postaci rozwiniętej; formalny opis wszystkich możliwych przebiegów gry z
Heurystyki. Strategie poszukiwań
 Sztuczna inteligencja Heurystyki. Strategie poszukiwań Jacek Bartman Zakład Elektrotechniki i Informatyki Instytut Techniki Uniwersytet Rzeszowski DLACZEGO METODY PRZESZUKIWANIA? Sztuczna Inteligencja
Sztuczna inteligencja Heurystyki. Strategie poszukiwań Jacek Bartman Zakład Elektrotechniki i Informatyki Instytut Techniki Uniwersytet Rzeszowski DLACZEGO METODY PRZESZUKIWANIA? Sztuczna Inteligencja
Sztuczna Inteligencja i Systemy Doradcze
 ztuczna Inteligencja i ystemy Doradcze Przeszukiwanie przestrzeni stanów Przeszukiwanie przestrzeni stanów 1 Postawienie problemu eprezentacja problemu: stany: reprezentują opisy różnych stanów świata
ztuczna Inteligencja i ystemy Doradcze Przeszukiwanie przestrzeni stanów Przeszukiwanie przestrzeni stanów 1 Postawienie problemu eprezentacja problemu: stany: reprezentują opisy różnych stanów świata
Teoria gier. Wykład7,31III2010,str.1. Gry dzielimy
 Wykład7,31III2010,str.1 Gry dzielimy Wykład7,31III2010,str.1 Gry dzielimy ze względu na: liczbę graczy: 1-osobowe, bez przeciwników(np. pasjanse, 15-tka, gra w życie, itp.), Wykład7,31III2010,str.1 Gry
Wykład7,31III2010,str.1 Gry dzielimy Wykład7,31III2010,str.1 Gry dzielimy ze względu na: liczbę graczy: 1-osobowe, bez przeciwników(np. pasjanse, 15-tka, gra w życie, itp.), Wykład7,31III2010,str.1 Gry
Teoria gier. Teoria gier. Odróżniać losowość od wiedzy graczy o stanie!
 Gry dzielimy ze względu na: liczbę graczy: 1-osobowe, bez przeciwników(np. pasjanse, 15-tka, gra w życie, itp.), 2-osobowe(np. szachy, warcaby, go, itp.), wieloosobowe(np. brydż, giełda, itp.); wygraną/przegraną:
Gry dzielimy ze względu na: liczbę graczy: 1-osobowe, bez przeciwników(np. pasjanse, 15-tka, gra w życie, itp.), 2-osobowe(np. szachy, warcaby, go, itp.), wieloosobowe(np. brydż, giełda, itp.); wygraną/przegraną:
Wstęp do Sztucznej Inteligencji
 Wstęp do Sztucznej Inteligencji Rozwiązywanie problemów-i Joanna Kołodziej Politechnika Krakowska Wydział Fizyki, Matematyki i Informatyki Rozwiązywanie problemów Podstawowe fazy: Sformułowanie celu -
Wstęp do Sztucznej Inteligencji Rozwiązywanie problemów-i Joanna Kołodziej Politechnika Krakowska Wydział Fizyki, Matematyki i Informatyki Rozwiązywanie problemów Podstawowe fazy: Sformułowanie celu -
Partition Search i gry z niezupełną informacją
 MIMUW 21 stycznia 2010 1 Co to jest gra? Proste algorytmy 2 Pomysł Algorytm Przykład użycia 3 Monte Carlo Inne spojrzenie Definicja Co to jest gra? Proste algorytmy Grą o wartościach w przedziale [0, 1]
MIMUW 21 stycznia 2010 1 Co to jest gra? Proste algorytmy 2 Pomysł Algorytm Przykład użycia 3 Monte Carlo Inne spojrzenie Definicja Co to jest gra? Proste algorytmy Grą o wartościach w przedziale [0, 1]
Algorytmy z powrotami. Algorytm minimax
 Algorytmy z powrotami. Algorytm minimax Algorytmy i struktury danych. Wykład 7. Rok akademicki: 2010/2011 Algorytm z powrotami rozwiązanie problemu budowane jest w kolejnych krokach, po stwierdzeniu (w
Algorytmy z powrotami. Algorytm minimax Algorytmy i struktury danych. Wykład 7. Rok akademicki: 2010/2011 Algorytm z powrotami rozwiązanie problemu budowane jest w kolejnych krokach, po stwierdzeniu (w
Algorytmy i struktury danych. Co dziś? Tytułem przypomnienia metoda dziel i zwyciężaj. Wykład VIII Elementarne techniki algorytmiczne
 Algorytmy i struktury danych Wykład VIII Elementarne techniki algorytmiczne Co dziś? Algorytmy zachłanne (greedyalgorithms) 2 Tytułem przypomnienia metoda dziel i zwyciężaj. Problem można podzielić na
Algorytmy i struktury danych Wykład VIII Elementarne techniki algorytmiczne Co dziś? Algorytmy zachłanne (greedyalgorithms) 2 Tytułem przypomnienia metoda dziel i zwyciężaj. Problem można podzielić na
Metody teorii gier. ALP520 - Wykład z Algorytmów Probabilistycznych p.2
 Metody teorii gier ALP520 - Wykład z Algorytmów Probabilistycznych p.2 Metody teorii gier Cel: Wyprowadzenie oszacowania dolnego na oczekiwany czas działania dowolnego algorytmu losowego dla danego problemu.
Metody teorii gier ALP520 - Wykład z Algorytmów Probabilistycznych p.2 Metody teorii gier Cel: Wyprowadzenie oszacowania dolnego na oczekiwany czas działania dowolnego algorytmu losowego dla danego problemu.
3. MINIMAX. Rysunek 1: Drzewo obrazujące przebieg gry.
 3. MINIMAX. Bardzo wygodną strukturą danych pozwalającą reprezentować stan i przebieg gry (szczególnie gier dwuosobowych) jest drzewo. Węzły drzewa reprezentują stan gry po wykonaniu ruchu przez jednego
3. MINIMAX. Bardzo wygodną strukturą danych pozwalającą reprezentować stan i przebieg gry (szczególnie gier dwuosobowych) jest drzewo. Węzły drzewa reprezentują stan gry po wykonaniu ruchu przez jednego
Kolejka priorytetowa. Często rozważa się kolejki priorytetowe, w których poszukuje się elementu minimalnego zamiast maksymalnego.
 Kolejki Kolejka priorytetowa Kolejka priorytetowa (ang. priority queue) to struktura danych pozwalająca efektywnie realizować następujące operacje na zbiorze dynamicznym, którego elementy pochodzą z określonego
Kolejki Kolejka priorytetowa Kolejka priorytetowa (ang. priority queue) to struktura danych pozwalająca efektywnie realizować następujące operacje na zbiorze dynamicznym, którego elementy pochodzą z określonego
Metody przeszukiwania
 Metody przeszukiwania Co to jest przeszukiwanie Przeszukiwanie polega na odnajdywaniu rozwiązania w dyskretnej przestrzeni rozwiązao. Zwykle przeszukiwanie polega na znalezieniu określonego rozwiązania
Metody przeszukiwania Co to jest przeszukiwanie Przeszukiwanie polega na odnajdywaniu rozwiązania w dyskretnej przestrzeni rozwiązao. Zwykle przeszukiwanie polega na znalezieniu określonego rozwiązania
MODELOWANIE RZECZYWISTOŚCI
 MODELOWANIE RZECZYWISTOŚCI Daniel Wójcik Instytut Biologii Doświadczalnej PAN Szkoła Wyższa Psychologii Społecznej d.wojcik@nencki.gov.pl dwojcik@swps.edu.pl tel. 022 5892 424 http://www.neuroinf.pl/members/danek/swps/
MODELOWANIE RZECZYWISTOŚCI Daniel Wójcik Instytut Biologii Doświadczalnej PAN Szkoła Wyższa Psychologii Społecznej d.wojcik@nencki.gov.pl dwojcik@swps.edu.pl tel. 022 5892 424 http://www.neuroinf.pl/members/danek/swps/
Porządek symetryczny: right(x)
 Porządek symetryczny: x lef t(x) right(x) Własność drzewa BST: W drzewach BST mamy porządek symetryczny. Dla każdego węzła x spełniony jest warunek: jeżeli węzeł y leży w lewym poddrzewie x, to key(y)
Porządek symetryczny: x lef t(x) right(x) Własność drzewa BST: W drzewach BST mamy porządek symetryczny. Dla każdego węzła x spełniony jest warunek: jeżeli węzeł y leży w lewym poddrzewie x, to key(y)
10. Wstęp do Teorii Gier
 10. Wstęp do Teorii Gier Definicja Gry Matematycznej Gra matematyczna spełnia następujące warunki: a) Jest co najmniej dwóch racjonalnych graczy. b) Zbiór możliwych dezycji każdego gracza zawiera co najmniej
10. Wstęp do Teorii Gier Definicja Gry Matematycznej Gra matematyczna spełnia następujące warunki: a) Jest co najmniej dwóch racjonalnych graczy. b) Zbiór możliwych dezycji każdego gracza zawiera co najmniej
TEORIA GIER DEFINICJA (VON NEUMANN, MORGENSTERN) GRA. jednostek (graczy) znajdujących się w sytuacji konfliktowej (konflikt interesów),w
 TEORIA GIER GRA DEFINICJA (VON NEUMANN, MORGENSTERN) Gra składa się z zestawu reguł określających możliwości wyboru postępowania jednostek (graczy) znajdujących się w sytuacji konfliktowej (konflikt interesów),w
TEORIA GIER GRA DEFINICJA (VON NEUMANN, MORGENSTERN) Gra składa się z zestawu reguł określających możliwości wyboru postępowania jednostek (graczy) znajdujących się w sytuacji konfliktowej (konflikt interesów),w
WPROWADZENIE DO SZTUCZNEJ INTELIGENCJI
 POLITECHNIKA WARSZAWSKA WYDZIAŁ MECHANICZNY ENERGETYKI I LOTNICTWA MEL WPROWADZENIE DO SZTUCZNEJ INTELIGENCJI NS 586 Dr inż. Franciszek Dul Poziomy sztucznej inteligencji Sztuczna świadomość? Uczenie się
POLITECHNIKA WARSZAWSKA WYDZIAŁ MECHANICZNY ENERGETYKI I LOTNICTWA MEL WPROWADZENIE DO SZTUCZNEJ INTELIGENCJI NS 586 Dr inż. Franciszek Dul Poziomy sztucznej inteligencji Sztuczna świadomość? Uczenie się
MODELOWANIE RZECZYWISTOŚCI
 MODELOWANIE RZECZYWISTOŚCI Daniel Wójcik Instytut Biologii Doświadczalnej PAN d.wojcik@nencki.gov.pl tel. 022 5892 424 http://www.neuroinf.pl/members/danek/swps/ Podręcznik Iwo Białynicki-Birula Iwona
MODELOWANIE RZECZYWISTOŚCI Daniel Wójcik Instytut Biologii Doświadczalnej PAN d.wojcik@nencki.gov.pl tel. 022 5892 424 http://www.neuroinf.pl/members/danek/swps/ Podręcznik Iwo Białynicki-Birula Iwona
CZYM JEST SZTUCZNA INTELIGENCJA? REPREZENTACJA WIEDZY SZTUCZNA INTELIGENCJA PROJEKTOWANIE ALGORYTMÓW I METODY SZTUCZNEJ INTELIGENCJI
 PROJEKTOWANIE ALGORYTMÓW I METODY SZTUCZNEJ INTELIGENCJI CZYM JEST SZTUCZNA INTELIGENCJA? Jak działa ludzki mózg? SZTUCZNA INTELIGENCJA Jak zasymulować ludzki mózg? Co to kogo obchodzi zróbmy coś pożytecznego
PROJEKTOWANIE ALGORYTMÓW I METODY SZTUCZNEJ INTELIGENCJI CZYM JEST SZTUCZNA INTELIGENCJA? Jak działa ludzki mózg? SZTUCZNA INTELIGENCJA Jak zasymulować ludzki mózg? Co to kogo obchodzi zróbmy coś pożytecznego
Zadanie 1 Przygotuj algorytm programu - sortowanie przez wstawianie.
 Sortowanie Dane wejściowe: ciąg n-liczb (kluczy) (a 1, a 2, a 3,..., a n 1, a n ) Dane wyjściowe: permutacja ciągu wejściowego (a 1, a 2, a 3,..., a n 1, a n) taka, że a 1 a 2 a 3... a n 1 a n. Będziemy
Sortowanie Dane wejściowe: ciąg n-liczb (kluczy) (a 1, a 2, a 3,..., a n 1, a n ) Dane wyjściowe: permutacja ciągu wejściowego (a 1, a 2, a 3,..., a n 1, a n) taka, że a 1 a 2 a 3... a n 1 a n. Będziemy
Adam Meissner. SZTUCZNA INTELIGENCJA Gry dwuosobowe
 Instytut Automatyki i Inżynierii Informatycznej Politechniki Poznańskiej Adam Meissner Adam.Meissner@put.poznan.pl http://www.man.poznan.pl/~ameis SZTUCZNA INTELIGENCJA Gry dwuosobowe Literatura [1] Sterling
Instytut Automatyki i Inżynierii Informatycznej Politechniki Poznańskiej Adam Meissner Adam.Meissner@put.poznan.pl http://www.man.poznan.pl/~ameis SZTUCZNA INTELIGENCJA Gry dwuosobowe Literatura [1] Sterling
ZASADY PROGRAMOWANIA KOMPUTERÓW ZAP zima 2014/2015. Drzewa BST c.d., równoważenie drzew, kopce.
 POLITECHNIKA WARSZAWSKA Instytut Automatyki i Robotyki ZASADY PROGRAMOWANIA KOMPUTERÓW ZAP zima 204/205 Język programowania: Środowisko programistyczne: C/C++ Qt Wykład 2 : Drzewa BST c.d., równoważenie
POLITECHNIKA WARSZAWSKA Instytut Automatyki i Robotyki ZASADY PROGRAMOWANIA KOMPUTERÓW ZAP zima 204/205 Język programowania: Środowisko programistyczne: C/C++ Qt Wykład 2 : Drzewa BST c.d., równoważenie
Wykład2,24II2010,str.1 Przeszukiwanie przestrzeni stanów powtórka
 Wykład2,24II2010,str.1 Przeszukiwanie przestrzeni stanów powtórka DEFINICJA: System produkcji M zbiórst.zw.stanów wyróżnionys 0 St.zw.stanpoczątkowy podzbiórg St.zw.stanówdocelowych zbiórot.zw.operacji:
Wykład2,24II2010,str.1 Przeszukiwanie przestrzeni stanów powtórka DEFINICJA: System produkcji M zbiórst.zw.stanów wyróżnionys 0 St.zw.stanpoczątkowy podzbiórg St.zw.stanówdocelowych zbiórot.zw.operacji:
Wysokość drzewa Głębokość węzła
 Drzewa Drzewa Drzewo (ang. tree) zbiór węzłów powiązanych wskaźnikami, spójny i bez cykli. Drzewo posiada wyróżniony węzeł początkowy nazywany korzeniem (ang. root). Drzewo ukorzenione jest strukturą hierarchiczną.
Drzewa Drzewa Drzewo (ang. tree) zbiór węzłów powiązanych wskaźnikami, spójny i bez cykli. Drzewo posiada wyróżniony węzeł początkowy nazywany korzeniem (ang. root). Drzewo ukorzenione jest strukturą hierarchiczną.
Teoria gier. wstęp. 2011-12-07 Teoria gier Zdzisław Dzedzej 1
 Teoria gier wstęp 2011-12-07 Teoria gier Zdzisław Dzedzej 1 Teoria gier zajmuje się logiczną analizą sytuacji, gdzie występują konflikty interesów, a także istnieje możliwość kooperacji. Zakładamy zwykle,
Teoria gier wstęp 2011-12-07 Teoria gier Zdzisław Dzedzej 1 Teoria gier zajmuje się logiczną analizą sytuacji, gdzie występują konflikty interesów, a także istnieje możliwość kooperacji. Zakładamy zwykle,
Rozwiązywanie problemów metodą przeszukiwania
 Rozwiązywanie problemów metodą przeszukiwania Dariusz Banasiak Katedra Informatyki Technicznej W4/K9 Politechnika Wrocławska Reprezentacja problemu w przestrzeni stanów Jedną z ważniejszych metod sztucznej
Rozwiązywanie problemów metodą przeszukiwania Dariusz Banasiak Katedra Informatyki Technicznej W4/K9 Politechnika Wrocławska Reprezentacja problemu w przestrzeni stanów Jedną z ważniejszych metod sztucznej
Rachunek prawdopodobieństwa w grach losowych.
 Rachunek prawdopodobieństwa w grach losowych. Lista zawiera kilkadziesiąt zadań dotyczących różnych gier z użyciem kart i kości, w tym tych najbardziej popularnych jak brydż, tysiąc itp. Kolejne zadania
Rachunek prawdopodobieństwa w grach losowych. Lista zawiera kilkadziesiąt zadań dotyczących różnych gier z użyciem kart i kości, w tym tych najbardziej popularnych jak brydż, tysiąc itp. Kolejne zadania
Elementy Modelowania Matematycznego
 Elementy Modelowania Matematycznego Wykład 12 Teoria gier II Spis treści Wstęp Oligopol, cła oraz zbrodnia i kara Strategie mieszane Analiza zachowań w warunkach dynamicznych Indukcja wsteczna Gry powtarzane
Elementy Modelowania Matematycznego Wykład 12 Teoria gier II Spis treści Wstęp Oligopol, cła oraz zbrodnia i kara Strategie mieszane Analiza zachowań w warunkach dynamicznych Indukcja wsteczna Gry powtarzane
Teoria Gier - wojna, rybołówstwo i sprawiedliwość w polityce.
 Liceum Ogólnokształcące nr XIV we Wrocławiu 5 maja 2009 1 2 Podobieństwa i różnice do gier o sumie zerowej Równowaga Nasha I co teraz zrobimy? 3 Idee 1 Grać będą dwie osoby. U nas nazywają się: pan Wiersz
Liceum Ogólnokształcące nr XIV we Wrocławiu 5 maja 2009 1 2 Podobieństwa i różnice do gier o sumie zerowej Równowaga Nasha I co teraz zrobimy? 3 Idee 1 Grać będą dwie osoby. U nas nazywają się: pan Wiersz
Uniwersytet Zielonogórski Wydział Elektrotechniki, Informatyki i Telekomunikacji Instytut Sterowania i Systemów Informatycznych
 Uniwersytet Zielonogórski Wydział Elektrotechniki, Informatyki i Telekomunikacji Instytut Sterowania i Systemów Informatycznych ELEMENTY SZTUCZNEJ INTELIGENCJI Laboratorium nr 9 PRZESZUKIWANIE GRAFÓW Z
Uniwersytet Zielonogórski Wydział Elektrotechniki, Informatyki i Telekomunikacji Instytut Sterowania i Systemów Informatycznych ELEMENTY SZTUCZNEJ INTELIGENCJI Laboratorium nr 9 PRZESZUKIWANIE GRAFÓW Z
Elementy kognitywistyki II: Sztuczna inteligencja. WYKŁAD III: Problemy agenta
 Elementy kognitywistyki II: Sztuczna inteligencja WYKŁAD III: Problemy agenta To już było: AI to dziedzina zajmująca się projektowaniem agentów Określenie agenta i agenta racjonalnego Charakterystyka PAGE
Elementy kognitywistyki II: Sztuczna inteligencja WYKŁAD III: Problemy agenta To już było: AI to dziedzina zajmująca się projektowaniem agentów Określenie agenta i agenta racjonalnego Charakterystyka PAGE
ALGORYTMY I STRUKTURY DANYCH
 LGORTM I STRUKTUR DNH Temat 6: Drzewa ST, VL Wykładowca: dr inż. bigniew TRPT e-mail: bigniew.tarapata@isi.wat.edu.pl http://www.tarapata.strefa.pl/p_algorytmy_i_struktury_danych/ Współautorami wykładu
LGORTM I STRUKTUR DNH Temat 6: Drzewa ST, VL Wykładowca: dr inż. bigniew TRPT e-mail: bigniew.tarapata@isi.wat.edu.pl http://www.tarapata.strefa.pl/p_algorytmy_i_struktury_danych/ Współautorami wykładu
Algorytmy i Struktury Danych, 2. ćwiczenia
 Algorytmy i Struktury Danych, 2. ćwiczenia 2015-10-09 Spis treści 1 Szybkie potęgowanie 1 2 Liczby Fibonacciego 2 3 Dowód, że n 1 porównań jest potrzebne do znajdowania minimum 2 4 Optymalny algorytm do
Algorytmy i Struktury Danych, 2. ćwiczenia 2015-10-09 Spis treści 1 Szybkie potęgowanie 1 2 Liczby Fibonacciego 2 3 Dowód, że n 1 porównań jest potrzebne do znajdowania minimum 2 4 Optymalny algorytm do
Archipelag Sztucznej Inteligencji
 Archipelag Sztucznej Inteligencji Istniejące metody sztucznej inteligencji mają ze sobą zwykle niewiele wspólnego, więc można je sobie wyobrażać jako archipelag wysp, a nie jako fragment stałego lądu.
Archipelag Sztucznej Inteligencji Istniejące metody sztucznej inteligencji mają ze sobą zwykle niewiele wspólnego, więc można je sobie wyobrażać jako archipelag wysp, a nie jako fragment stałego lądu.
Podstawy sztucznej inteligencji
 wykład 2 Strategie przeszukiwania - ślepe i heurystyczne 27 październik 2011 Plan wykładu 1 Strategie czyli jak znaleźć rozwiązanie problemu Jak wykonać przeszukiwanie Przeszukiwanie przestrzeni stanów
wykład 2 Strategie przeszukiwania - ślepe i heurystyczne 27 październik 2011 Plan wykładu 1 Strategie czyli jak znaleźć rozwiązanie problemu Jak wykonać przeszukiwanie Przeszukiwanie przestrzeni stanów
Informatyka Systemów Autonomicznych
 Grzegorz Bartoszek 148326 Informatyka Systemów Autonomicznych Systemy informatyczne działające w świecie statycznym, quasi-statycznym i dynamicznym Prowadzący: dr inż. Marek Piasecki 1.Wstęp Systemy komputerowe
Grzegorz Bartoszek 148326 Informatyka Systemów Autonomicznych Systemy informatyczne działające w świecie statycznym, quasi-statycznym i dynamicznym Prowadzący: dr inż. Marek Piasecki 1.Wstęp Systemy komputerowe
TEORIA GIER W EKONOMII WYKŁAD 5: GRY DWUOSOBOWE KOOPERACYJNE O SUMIE NIESTAŁEJ
 TEORI GIER W EKONOMII WYKŁD 5: GRY DWUOSOOWE KOOPERCYJNE O SUMIE NIESTŁEJ dr Robert Kowalczyk Katedra nalizy Nieliniowej Wydział Matematyki i Informatyki UŁ Gry dwumacierzowe Skończoną grę dwuosobową o
TEORI GIER W EKONOMII WYKŁD 5: GRY DWUOSOOWE KOOPERCYJNE O SUMIE NIESTŁEJ dr Robert Kowalczyk Katedra nalizy Nieliniowej Wydział Matematyki i Informatyki UŁ Gry dwumacierzowe Skończoną grę dwuosobową o
W którym rozważamy problemy pojawiające się, gdy próbujemy planować z góry w świecie zawierającym wrogiego agenta.
 Rozdział 5 Gry W którym rozważamy problemy pojawiające się, gdy próbujemy planować z góry w świecie zawierającym wrogiego agenta. 5.1 Wprowadzenie: gry jako problemy szukania Gry angażowały zdolności intelektualne
Rozdział 5 Gry W którym rozważamy problemy pojawiające się, gdy próbujemy planować z góry w świecie zawierającym wrogiego agenta. 5.1 Wprowadzenie: gry jako problemy szukania Gry angażowały zdolności intelektualne
Działanie algorytmu oparte jest na minimalizacji funkcji celu jako suma funkcji kosztu ( ) oraz funkcji heurystycznej ( ).
 Algorytm A* Opracowanie: Joanna Raczyńska 1.Wstęp Algorytm A* jest heurystycznym algorytmem służącym do znajdowania najkrótszej ścieżki w grafie. Jest to algorytm zupełny i optymalny, co oznacza, że zawsze
Algorytm A* Opracowanie: Joanna Raczyńska 1.Wstęp Algorytm A* jest heurystycznym algorytmem służącym do znajdowania najkrótszej ścieżki w grafie. Jest to algorytm zupełny i optymalny, co oznacza, że zawsze
Rachunek prawdopodobieństwa- wykład 2
 Rachunek prawdopodobieństwa- wykład 2 Pojęcie dyskretnej przestrzeni probabilistycznej i określenie prawdopodobieństwa w tej przestrzeni dr Marcin Ziółkowski Instytut Matematyki i Informatyki Uniwersytet
Rachunek prawdopodobieństwa- wykład 2 Pojęcie dyskretnej przestrzeni probabilistycznej i określenie prawdopodobieństwa w tej przestrzeni dr Marcin Ziółkowski Instytut Matematyki i Informatyki Uniwersytet
Teoria gier. prof. UŚ dr hab. Mariusz Boryczka. Wykład 4 - Gry o sumie zero. Instytut Informatyki Uniwersytetu Śląskiego
 Instytut Informatyki Uniwersytetu Śląskiego Wykład 4 - Gry o sumie zero Gry o sumie zero Dwuosobowe gry o sumie zero (ogólniej: o sumie stałej) były pierwszym typem gier dla których podjęto próby ich rozwiązania.
Instytut Informatyki Uniwersytetu Śląskiego Wykład 4 - Gry o sumie zero Gry o sumie zero Dwuosobowe gry o sumie zero (ogólniej: o sumie stałej) były pierwszym typem gier dla których podjęto próby ich rozwiązania.
Podstawy Sztucznej Inteligencji (PSZT)
 Podstawy Sztucznej Inteligencji (PSZT) Paweł Wawrzyński Przeszukiwanie Przeszukiwanie przestrzeni stanów Motywacja Rozwiązywanie problemów: poszukiwanie sekwencji operacji prowadzącej do celu poszukiwanie
Podstawy Sztucznej Inteligencji (PSZT) Paweł Wawrzyński Przeszukiwanie Przeszukiwanie przestrzeni stanów Motywacja Rozwiązywanie problemów: poszukiwanie sekwencji operacji prowadzącej do celu poszukiwanie
Alfa-beta Ulepszenie minimax Liczba wierzchołk ow w drzewie gry. maksymalnie wd. minimalnie wbd/2c + wdd/2e Algorytmy przeszukiwania drzewa gry 5
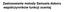 Zastosowanie metody Samuela doboru współczynników funkcji oceniajacej w programie grajacym w anty-warcaby Daniel Osman promotor: dr hab. inż. Jacek Mańdziuk 1 Spis treści Algorytmy przeszukiwania drzewa
Zastosowanie metody Samuela doboru współczynników funkcji oceniajacej w programie grajacym w anty-warcaby Daniel Osman promotor: dr hab. inż. Jacek Mańdziuk 1 Spis treści Algorytmy przeszukiwania drzewa
Sztuczna inteligencja w programowaniu gier
 ztuczna inteligencja w programowaniu gier Algorytmy przeszukiwania przestrzeni rozwiązań Krzysztof Ślot Wprowadzenie Ogólna charakterystyka zagadnienia Cel przeszukiwania: znaleźć element będący rozwiązaniem
ztuczna inteligencja w programowaniu gier Algorytmy przeszukiwania przestrzeni rozwiązań Krzysztof Ślot Wprowadzenie Ogólna charakterystyka zagadnienia Cel przeszukiwania: znaleźć element będący rozwiązaniem
Przeszukiwanie przestrzeni rozwiązań, szukanie na ślepo, wszerz, wgłąb
 POLITECHNIKA WROCŁAWSKA WYDZIAŁ ELEKTRONIKI INFORMATYKA SYSTEMÓW AUTONOMICZNYCH Przeszukiwanie przestrzeni rozwiązań, szukanie na ślepo, wszerz, wgłąb AUTOR: Krzysztof Górski Indeks: 133247 e-mail: 133247@student.pwr.wroc.pl
POLITECHNIKA WROCŁAWSKA WYDZIAŁ ELEKTRONIKI INFORMATYKA SYSTEMÓW AUTONOMICZNYCH Przeszukiwanie przestrzeni rozwiązań, szukanie na ślepo, wszerz, wgłąb AUTOR: Krzysztof Górski Indeks: 133247 e-mail: 133247@student.pwr.wroc.pl
Heurystyczne metody przeszukiwania
 Heurystyczne metody przeszukiwania Dariusz Banasiak Katedra Informatyki Technicznej W4/K9 Politechnika Wrocławska Pojęcie heurystyki Metody heurystyczne są jednym z ważniejszych narzędzi sztucznej inteligencji.
Heurystyczne metody przeszukiwania Dariusz Banasiak Katedra Informatyki Technicznej W4/K9 Politechnika Wrocławska Pojęcie heurystyki Metody heurystyczne są jednym z ważniejszych narzędzi sztucznej inteligencji.
Internetowe Ko³o M a t e m a t yc z n e
 Internetowe Ko³o M a t e m a t yc z n e Stowarzyszenie na rzecz Edukacji Matematycznej Zestaw 3 szkice rozwiązań zadań 1. Plansza do gry składa się z 15 ustawionych w rzędzie kwadratów. Pierwszy z graczy
Internetowe Ko³o M a t e m a t yc z n e Stowarzyszenie na rzecz Edukacji Matematycznej Zestaw 3 szkice rozwiązań zadań 1. Plansza do gry składa się z 15 ustawionych w rzędzie kwadratów. Pierwszy z graczy
11. Gry Macierzowe - Strategie Czyste i Mieszane
 11. Gry Macierzowe - Strategie Czyste i Mieszane W grze z doskonałą informacją, gracz nie powinien wybrać akcję w sposób losowy (o ile wypłaty z różnych decyzji nie są sobie równe). Z drugiej strony, gdy
11. Gry Macierzowe - Strategie Czyste i Mieszane W grze z doskonałą informacją, gracz nie powinien wybrać akcję w sposób losowy (o ile wypłaty z różnych decyzji nie są sobie równe). Z drugiej strony, gdy
Jak oceniać, gdy nic nie wiemy?
 Jak oceniać, gdy nic nie wiemy? Jasiek Marcinkowski II UWr 25 października 2012 Jasiek Marcinkowski (II UWr) Jak oceniać, gdy nic nie wiemy? 25 października 2012 1 / 10 Jak się gra w gry, o których dużo
Jak oceniać, gdy nic nie wiemy? Jasiek Marcinkowski II UWr 25 października 2012 Jasiek Marcinkowski (II UWr) Jak oceniać, gdy nic nie wiemy? 25 października 2012 1 / 10 Jak się gra w gry, o których dużo
Szachy INSTRUKCJA. rekwizyty: 1) Bierki - 32 szt. 2) plansza - 1 szt.
 INSTRUKCJA Szachy rekwizyty: 1) Bierki - 32 szt. 2) plansza - 1 szt. Partia szachowa jest rozgrywana między dwoma przeciwnikami, którzy wykonują posunięcia bierkami na kwadratowej tablicy, zwanej szachownicą.
INSTRUKCJA Szachy rekwizyty: 1) Bierki - 32 szt. 2) plansza - 1 szt. Partia szachowa jest rozgrywana między dwoma przeciwnikami, którzy wykonują posunięcia bierkami na kwadratowej tablicy, zwanej szachownicą.
Drzewa binarne. Drzewo binarne to dowolny obiekt powstały zgodnie z regułami: jest drzewem binarnym Jeśli T 0. jest drzewem binarnym Np.
 Drzewa binarne Drzewo binarne to dowolny obiekt powstały zgodnie z regułami: jest drzewem binarnym Jeśli T 0 i T 1 są drzewami binarnymi to T 0 T 1 jest drzewem binarnym Np. ( ) ( ( )) Wielkość drzewa
Drzewa binarne Drzewo binarne to dowolny obiekt powstały zgodnie z regułami: jest drzewem binarnym Jeśli T 0 i T 1 są drzewami binarnymi to T 0 T 1 jest drzewem binarnym Np. ( ) ( ( )) Wielkość drzewa
Programowanie dynamiczne
 Programowanie dynamiczne Patryk Żywica 5 maja 2008 1 Spis treści 1 Problem wydawania reszty 3 1.1 Sformułowanie problemu...................... 3 1.2 Algorytm.............................. 3 1.2.1 Prosty
Programowanie dynamiczne Patryk Żywica 5 maja 2008 1 Spis treści 1 Problem wydawania reszty 3 1.1 Sformułowanie problemu...................... 3 1.2 Algorytm.............................. 3 1.2.1 Prosty
SZACHY mini INSTRUKCJA. rekwizyty: 1) Bierki - 32 szt. 2) plansza - 1 szt.
 INSTRUKCJA SZACHY mini rekwizyty: 1) Bierki - 32 szt. 2) plansza - 1 szt. Partia szachowa jest rozgrywana między dwoma przeciwnikami, którzy wykonują posunięcia bierkami na kwadratowej tablicy, zwanej
INSTRUKCJA SZACHY mini rekwizyty: 1) Bierki - 32 szt. 2) plansza - 1 szt. Partia szachowa jest rozgrywana między dwoma przeciwnikami, którzy wykonują posunięcia bierkami na kwadratowej tablicy, zwanej
Algorytmy i struktury danych. Drzewa: BST, kopce. Letnie Warsztaty Matematyczno-Informatyczne
 Algorytmy i struktury danych Drzewa: BST, kopce Letnie Warsztaty Matematyczno-Informatyczne Drzewa: BST, kopce Definicja drzewa Drzewo (ang. tree) to nieskierowany, acykliczny, spójny graf. Drzewo może
Algorytmy i struktury danych Drzewa: BST, kopce Letnie Warsztaty Matematyczno-Informatyczne Drzewa: BST, kopce Definicja drzewa Drzewo (ang. tree) to nieskierowany, acykliczny, spójny graf. Drzewo może
SZTUCZNA INTELIGENCJA
 Instytut Automatyki, Robotyki i Informatyki Politechniki Poznańskiej Adam Meissner Adam.Meissner@put.poznan.pl http://www.man.poznan.pl/~ameis Literatura SZTUCZNA INTELIGENCJA Modelowanie problemów za
Instytut Automatyki, Robotyki i Informatyki Politechniki Poznańskiej Adam Meissner Adam.Meissner@put.poznan.pl http://www.man.poznan.pl/~ameis Literatura SZTUCZNA INTELIGENCJA Modelowanie problemów za
Gry o sumie niezerowej
 Gry o sumie niezerowej Równowagi Nasha 2011-12-06 Zdzisław Dzedzej 1 Pytanie Czy profile równowagi Nasha są dobrym rozwiązaniem gry o dowolnej sumie? Zaleta: zawsze istnieją (w grach dwumacierzowych, a
Gry o sumie niezerowej Równowagi Nasha 2011-12-06 Zdzisław Dzedzej 1 Pytanie Czy profile równowagi Nasha są dobrym rozwiązaniem gry o dowolnej sumie? Zaleta: zawsze istnieją (w grach dwumacierzowych, a
Teoria gier. dr Przemysław Juszczuk. Wykład 2 - Gry o sumie zero. Instytut Informatyki Uniwersytetu Śląskiego
 Instytut Informatyki Uniwersytetu Śląskiego Wykład 2 - Gry o sumie zero Gry o sumie zero Dwuosobowe gry o sumie zero (ogólniej: o sumie stałej) były pierwszym typem gier dla których podjęto próby ich rozwiązania.
Instytut Informatyki Uniwersytetu Śląskiego Wykład 2 - Gry o sumie zero Gry o sumie zero Dwuosobowe gry o sumie zero (ogólniej: o sumie stałej) były pierwszym typem gier dla których podjęto próby ich rozwiązania.
Hyper-resolution. Śmieciarki w Manncheim
 Hyper-resolution Hyper-resolution Algorytm repeat NGi NGi NGj NGi nowe Nogoods, które da się wywieść z NGi if NGi then NGi NGi NGi roześlij NGi do wszystkich sąsiadów if NGi then stop end until NGi nie
Hyper-resolution Hyper-resolution Algorytm repeat NGi NGi NGj NGi nowe Nogoods, które da się wywieść z NGi if NGi then NGi NGi NGi roześlij NGi do wszystkich sąsiadów if NGi then stop end until NGi nie
Każdy węzeł w drzewie posiada 3 pola: klucz, adres prawego potomka i adres lewego potomka. Pola zawierające adresy mogą być puste.
 Drzewa binarne Każdy węzeł w drzewie posiada pola: klucz, adres prawego potomka i adres lewego potomka. Pola zawierające adresy mogą być puste. Uporządkowanie. Zakładamy, że klucze są różne. Klucze leżące
Drzewa binarne Każdy węzeł w drzewie posiada pola: klucz, adres prawego potomka i adres lewego potomka. Pola zawierające adresy mogą być puste. Uporządkowanie. Zakładamy, że klucze są różne. Klucze leżące
Drzewa czerwono-czarne.
 Binboy at Sphere http://binboy.sphere.p l Drzewa czerwono-czarne. Autor: Jacek Zacharek Wstęp. Pojęcie drzewa czerwono-czarnego (red-black tree) zapoczątkował Rudolf Bayer w książce z 1972 r. pt. Symmetric
Binboy at Sphere http://binboy.sphere.p l Drzewa czerwono-czarne. Autor: Jacek Zacharek Wstęp. Pojęcie drzewa czerwono-czarnego (red-black tree) zapoczątkował Rudolf Bayer w książce z 1972 r. pt. Symmetric
Tworzenie gier na urządzenia mobilne
 Katedra Inżynierii Wiedzy Wykład 11 O czym dzisiaj? labirynty, dużo labiryntów; automaty komórkowe; algorytmy do budowy labiryntów; algorytmy do szukania wyjścia z labiryntów; Blueprints i drzewa zachowań
Katedra Inżynierii Wiedzy Wykład 11 O czym dzisiaj? labirynty, dużo labiryntów; automaty komórkowe; algorytmy do budowy labiryntów; algorytmy do szukania wyjścia z labiryntów; Blueprints i drzewa zachowań
33. NIE TYLKO WORECZKI CZYLI O ROZUMIENIU SYSTEMU DZIESIĘTNEGO, CZ. I
 150 Mirosław Dąbrowski 33. NIE TYLKO WORECZKI CZYLI O ROZUMIENIU SYSTEMU DZIESIĘTNEGO, CZ. I Cele ogólne w szkole podstawowej: zdobycie przez uczniów umiejętności wykorzystywania posiadanych wiadomości
150 Mirosław Dąbrowski 33. NIE TYLKO WORECZKI CZYLI O ROZUMIENIU SYSTEMU DZIESIĘTNEGO, CZ. I Cele ogólne w szkole podstawowej: zdobycie przez uczniów umiejętności wykorzystywania posiadanych wiadomości
Tworzenie gier na urządzenia mobilne
 Katedra Inżynierii Wiedzy Wykład 8 Przekształcenia wiedzy generalizacja/specjalizacja; abstrakcja/konkretyzacja; podobieństwo/kontrastowanie; wyjaśnianie/predykcja. Przetwarzanie danych Przetwarzanie wstępne
Katedra Inżynierii Wiedzy Wykład 8 Przekształcenia wiedzy generalizacja/specjalizacja; abstrakcja/konkretyzacja; podobieństwo/kontrastowanie; wyjaśnianie/predykcja. Przetwarzanie danych Przetwarzanie wstępne
Elementy kognitywistyki II:
 Elementy kognitywistyki II: Sztuczna inteligencja WYKŁAD IV: Agent szuka rozwiązania (na ślepo) Poprzednio: etapy rozwiązywania problemu sformułowanie celu sformułowanie problemu stan początkowy (initial
Elementy kognitywistyki II: Sztuczna inteligencja WYKŁAD IV: Agent szuka rozwiązania (na ślepo) Poprzednio: etapy rozwiązywania problemu sformułowanie celu sformułowanie problemu stan początkowy (initial
METODY SZTUCZNEJ INTELIGENCJI 2 Opis projektu
 Kamil Figura Krzysztof Kaliński Bartek Kutera METODY SZTUCZNEJ INTELIGENCJI 2 Opis projektu Porównanie metod uczenia z rodziny TD z algorytmem Layered Learning na przykładzie gry w warcaby i gry w anty-warcaby
Kamil Figura Krzysztof Kaliński Bartek Kutera METODY SZTUCZNEJ INTELIGENCJI 2 Opis projektu Porównanie metod uczenia z rodziny TD z algorytmem Layered Learning na przykładzie gry w warcaby i gry w anty-warcaby
Narzędzia AI. Jakub Wróblewski jakubw@pjwstk.edu.pl Pokój 312. http://zajecia.jakubw.pl SZTUCZNA INTELIGENCJA (ARTIFICIAL INTELLIGENCE)
 Narzędzia AI Jakub Wróblewski jakubw@pjwstk.edu.pl Pokój 312 http://zajecia.jakubw.pl SZTUCZNA INTELIGENCJA (ARTIFICIAL INTELLIGENCE) Nauka o maszynach realizujących zadania, które wymagają inteligencji
Narzędzia AI Jakub Wróblewski jakubw@pjwstk.edu.pl Pokój 312 http://zajecia.jakubw.pl SZTUCZNA INTELIGENCJA (ARTIFICIAL INTELLIGENCE) Nauka o maszynach realizujących zadania, które wymagają inteligencji
Mixed-UCT: Zastosowanie metod symulacyjnych do poszukiwania równowagi Stackelberga w grach wielokrokowych
 Mixed-UCT: Zastosowanie metod symulacyjnych do poszukiwania równowagi Stackelberga w grach wielokrokowych Jan Karwowski Zakład Sztucznej Inteligencji i Metod Obliczeniowych Wydział Matematyki i Nauk Informacyjnych
Mixed-UCT: Zastosowanie metod symulacyjnych do poszukiwania równowagi Stackelberga w grach wielokrokowych Jan Karwowski Zakład Sztucznej Inteligencji i Metod Obliczeniowych Wydział Matematyki i Nauk Informacyjnych
Uniwersytet Warszawski Teoria gier dr Olga Kiuila LEKCJA 3
 LEKCJA 3 Wybór strategii mieszanej nie jest wyborem określonych decyzji, lecz pozornie sztuczną procedurą która wymaga losowych lub innych wyborów. Gracze mieszają nie dlatego że jest im obojętna strategia,
LEKCJA 3 Wybór strategii mieszanej nie jest wyborem określonych decyzji, lecz pozornie sztuczną procedurą która wymaga losowych lub innych wyborów. Gracze mieszają nie dlatego że jest im obojętna strategia,
Załącznik nr 1 do Regulaminu turnieju Tysiąca Studnia 2018
 Załącznik nr 1 do Regulaminu turnieju Tysiąca Studnia 2018 Zasady gry Tysiąc Gra karciana na 3 bądź 4 osób. Zwycięzcą zostaje gracz, który dzięki sumie punktów zdobytych w poszczególnych rozdaniach jako
Załącznik nr 1 do Regulaminu turnieju Tysiąca Studnia 2018 Zasady gry Tysiąc Gra karciana na 3 bądź 4 osób. Zwycięzcą zostaje gracz, który dzięki sumie punktów zdobytych w poszczególnych rozdaniach jako
 Szachowisko Żywe Szachy (zapraszamy do znajomych) www.szachowisko.wordpress.com Szachowisko co to takiego? Szachowisko żywe szachy w Lublinie to projekt realizowany przez młodzież przy wsparciu Fundacji
Szachowisko Żywe Szachy (zapraszamy do znajomych) www.szachowisko.wordpress.com Szachowisko co to takiego? Szachowisko żywe szachy w Lublinie to projekt realizowany przez młodzież przy wsparciu Fundacji
Drzewo. Drzewo uporządkowane ma ponumerowanych (oznaczonych) następników. Drzewo uporządkowane składa się z węzłów, które zawierają następujące pola:
 Drzewa Drzewa Drzewo (ang. tree) zbiór węzłów powiązanych wskaźnikami, spójny i bez cykli. Drzewo posiada wyróżniony węzeł początkowy nazywany korzeniem (ang. root). Drzewo ukorzenione jest strukturą hierarchiczną.
Drzewa Drzewa Drzewo (ang. tree) zbiór węzłów powiązanych wskaźnikami, spójny i bez cykli. Drzewo posiada wyróżniony węzeł początkowy nazywany korzeniem (ang. root). Drzewo ukorzenione jest strukturą hierarchiczną.
2010 W. W. Norton & Company, Inc. Oligopol
 2010 W. W. Norton & Company, Inc. Oligopol Oligopol Monopol jedna firma na rynku. Duopol dwie firmy na rynku. Oligopol kilka firm na rynku. W szczególności decyzje każdej firmy co do ceny lub ilości produktu
2010 W. W. Norton & Company, Inc. Oligopol Oligopol Monopol jedna firma na rynku. Duopol dwie firmy na rynku. Oligopol kilka firm na rynku. W szczególności decyzje każdej firmy co do ceny lub ilości produktu
34. NIE TYLKO WORECZKI CZYLI O ROZUMIENIU SYSTEMU DZIESIĘTNEGO, CZ. II
 157 Mirosław Dąbrowski 34. NIE TYLKO WORECZKI CZYLI O ROZUMIENIU SYSTEMU DZIESIĘTNEGO, CZ. II Cele ogólne w szkole podstawowej: zdobycie przez uczniów umiejętności wykorzystywania posiadanych wiadomości
157 Mirosław Dąbrowski 34. NIE TYLKO WORECZKI CZYLI O ROZUMIENIU SYSTEMU DZIESIĘTNEGO, CZ. II Cele ogólne w szkole podstawowej: zdobycie przez uczniów umiejętności wykorzystywania posiadanych wiadomości
prowadzący dr ADRIAN HORZYK /~horzyk e-mail: horzyk@agh tel.: 012-617 Konsultacje paw. D-13/325
 PODSTAWY INFORMATYKI WYKŁAD 8. prowadzący dr ADRIAN HORZYK http://home home.agh.edu.pl/~ /~horzyk e-mail: horzyk@agh agh.edu.pl tel.: 012-617 617-4319 Konsultacje paw. D-13/325 DRZEWA Drzewa to rodzaj
PODSTAWY INFORMATYKI WYKŁAD 8. prowadzący dr ADRIAN HORZYK http://home home.agh.edu.pl/~ /~horzyk e-mail: horzyk@agh agh.edu.pl tel.: 012-617 617-4319 Konsultacje paw. D-13/325 DRZEWA Drzewa to rodzaj
Skowrońska-Szmer. Instytut Organizacji i Zarządzania Politechniki Wrocławskiej Zakład Zarządzania Jakością. 04.01.2012r.
 mgr inż. Anna Skowrońska-Szmer Instytut Organizacji i Zarządzania Politechniki Wrocławskiej Zakład Zarządzania Jakością 04.01.2012r. 1. Cel prezentacji 2. Biznesplan podstawowe pojęcia 3. Teoria gier w
mgr inż. Anna Skowrońska-Szmer Instytut Organizacji i Zarządzania Politechniki Wrocławskiej Zakład Zarządzania Jakością 04.01.2012r. 1. Cel prezentacji 2. Biznesplan podstawowe pojęcia 3. Teoria gier w
ĆWICZENIE 1: Przeszukiwanie grafów cz. 1 strategie ślepe
 Instytut Mechaniki i Inżynierii Obliczeniowej Wydział Mechaniczny Technologiczny, Politechnika Śląska www.imio.polsl.pl METODY HEURYSTYCZNE ĆWICZENIE 1: Przeszukiwanie grafów cz. 1 strategie ślepe opracował:
Instytut Mechaniki i Inżynierii Obliczeniowej Wydział Mechaniczny Technologiczny, Politechnika Śląska www.imio.polsl.pl METODY HEURYSTYCZNE ĆWICZENIE 1: Przeszukiwanie grafów cz. 1 strategie ślepe opracował:
Wprowadzenie do Sztucznej Inteligencji
 Wprowadzenie do Sztucznej Inteligencji Wykład Informatyka Studia InŜynierskie Przeszukiwanie przestrzeni stanów Przestrzeń stanów jest to czwórka uporządkowana [N,[, S, GD], gdzie: N jest zbiorem wierzchołków
Wprowadzenie do Sztucznej Inteligencji Wykład Informatyka Studia InŜynierskie Przeszukiwanie przestrzeni stanów Przestrzeń stanów jest to czwórka uporządkowana [N,[, S, GD], gdzie: N jest zbiorem wierzchołków
25. NIE TYLKO WORECZKI CZYLI O ROZUMIENIU SYSTEMU DZIESIĘTNEGO, CZ. I
 124 25. NIE TYLKO WORECZKI CZYLI O ROZUMIENIU SYSTEMU DZIESIĘTNEGO, CZ. I Mirosław Dąbrowski 25. NIE TYLKO WORECZKI CZYLI O ROZUMIENIU SYSTEMU DZIESIĘTNEGO, CZ. I Cele ogólne w szkole podstawowej: zdobycie
124 25. NIE TYLKO WORECZKI CZYLI O ROZUMIENIU SYSTEMU DZIESIĘTNEGO, CZ. I Mirosław Dąbrowski 25. NIE TYLKO WORECZKI CZYLI O ROZUMIENIU SYSTEMU DZIESIĘTNEGO, CZ. I Cele ogólne w szkole podstawowej: zdobycie
Wykład 2. Drzewa zbalansowane AVL i 2-3-4
 Wykład Drzewa zbalansowane AVL i -3-4 Drzewa AVL Wprowadzenie Drzewa AVL Definicja drzewa AVL Operacje wstawiania i usuwania Złożoność obliczeniowa Drzewa -3-4 Definicja drzewa -3-4 Operacje wstawiania
Wykład Drzewa zbalansowane AVL i -3-4 Drzewa AVL Wprowadzenie Drzewa AVL Definicja drzewa AVL Operacje wstawiania i usuwania Złożoność obliczeniowa Drzewa -3-4 Definicja drzewa -3-4 Operacje wstawiania
Szachy, backgammon (tryktrak) i warcaby
 Szachy, backgammon (tryktrak) i warcaby pl Zasady gry Tchibo GmbH D-22290 Hamburg 92630AB6X6VII 2017-07 Drodzy Klienci! Trzy klasyczne gry w praktycznym, ozdobnym pudełku z drewna. Już od wieków gry te
Szachy, backgammon (tryktrak) i warcaby pl Zasady gry Tchibo GmbH D-22290 Hamburg 92630AB6X6VII 2017-07 Drodzy Klienci! Trzy klasyczne gry w praktycznym, ozdobnym pudełku z drewna. Już od wieków gry te
Programowanie w VB Proste algorytmy sortowania
 Programowanie w VB Proste algorytmy sortowania Sortowanie bąbelkowe Algorytm sortowania bąbelkowego polega na porównywaniu par elementów leżących obok siebie i, jeśli jest to potrzebne, zmienianiu ich
Programowanie w VB Proste algorytmy sortowania Sortowanie bąbelkowe Algorytm sortowania bąbelkowego polega na porównywaniu par elementów leżących obok siebie i, jeśli jest to potrzebne, zmienianiu ich
Problemy Decyzyjne Markowa
 Problemy Decyzyjne Markowa na podstawie AIMA ch17 i slajdów S. Russel a Wojciech Jaśkowski Instytut Informatyki, Politechnika Poznańska 18 kwietnia 2013 Sekwencyjne problemy decyzyjne Cechy sekwencyjnego
Problemy Decyzyjne Markowa na podstawie AIMA ch17 i slajdów S. Russel a Wojciech Jaśkowski Instytut Informatyki, Politechnika Poznańska 18 kwietnia 2013 Sekwencyjne problemy decyzyjne Cechy sekwencyjnego
TEORIA GIER W EKONOMII WYKŁAD 2: GRY DWUOSOBOWE O SUMIE ZEROWEJ. dr Robert Kowalczyk Katedra Analizy Nieliniowej Wydział Matematyki i Informatyki UŁ
 TEORIA GIER W EKONOMII WYKŁAD 2: GRY DWUOSOBOWE O SUMIE ZEROWEJ dr Robert Kowalczyk Katedra Analizy Nieliniowej Wydział Matematyki i Informatyki UŁ Definicja gry o sumie zerowej Powiemy, że jest grą o
TEORIA GIER W EKONOMII WYKŁAD 2: GRY DWUOSOBOWE O SUMIE ZEROWEJ dr Robert Kowalczyk Katedra Analizy Nieliniowej Wydział Matematyki i Informatyki UŁ Definicja gry o sumie zerowej Powiemy, że jest grą o
WYKŁAD 11 Uczenie maszynowe drzewa decyzyjne
 WYKŁAD 11 Uczenie maszynowe drzewa decyzyjne Reprezentacja wiedzy w postaci drzew decyzyjnych entropia, przyrost informacji algorytmy ID3, C4.5 problem przeuczenia wyznaczanie reguł rzykładowe drzewo decyzyjne
WYKŁAD 11 Uczenie maszynowe drzewa decyzyjne Reprezentacja wiedzy w postaci drzew decyzyjnych entropia, przyrost informacji algorytmy ID3, C4.5 problem przeuczenia wyznaczanie reguł rzykładowe drzewo decyzyjne
Niech x 1,..., x n będzie ciągiem zdarzeń. ---
 Matematyczne podstawy kryptografii, Ćw2 TEMAT 7: Teoria Shannona. Kody Huffmana, entropia. BIBLIOGRAFIA: [] Cz. Bagiński, cez.wipb.pl, [2] T. H. Cormen, C. E. Leiserson, R. L Rivest, Wprowadzenie do algorytmów,
Matematyczne podstawy kryptografii, Ćw2 TEMAT 7: Teoria Shannona. Kody Huffmana, entropia. BIBLIOGRAFIA: [] Cz. Bagiński, cez.wipb.pl, [2] T. H. Cormen, C. E. Leiserson, R. L Rivest, Wprowadzenie do algorytmów,
Wykład 3. Złożoność i realizowalność algorytmów Elementarne struktury danych: stosy, kolejki, listy
 Wykład 3 Złożoność i realizowalność algorytmów Elementarne struktury danych: stosy, kolejki, listy Dynamiczne struktury danych Lista jest to liniowo uporządkowany zbiór elementów, z których dowolny element
Wykład 3 Złożoność i realizowalność algorytmów Elementarne struktury danych: stosy, kolejki, listy Dynamiczne struktury danych Lista jest to liniowo uporządkowany zbiór elementów, z których dowolny element
ATOLL. Wykonali: Aleksandra Kuchta, Łukasz Wójcik, Sztuczna Inteligencja, Semestr trzeci, Kierunek Informatyka, Wydział Informatyki i Zarządzania,
 Sztuczna Inteligencja, Semestr trzeci, Kierunek Informatyka, Wydział Informatyki i Zarządzania, Politechnika Poznańska ATOLL Wykonali: Aleksandra Kuchta, WFT, PP, nr 76690, rok IV Łukasz Wójcik, WIiZ,
Sztuczna Inteligencja, Semestr trzeci, Kierunek Informatyka, Wydział Informatyki i Zarządzania, Politechnika Poznańska ATOLL Wykonali: Aleksandra Kuchta, WFT, PP, nr 76690, rok IV Łukasz Wójcik, WIiZ,
Prognozowanie rozgrywki grą planszową
 Prognozowanie rozgrywki grą planszową - Cześć Anka! Co ty tam gryzmolisz? - Witaj dowcipasku. A ja po prostu projektuję grę planszową dla uczniów podstawówki. Nawet nie masz pojęcia Marku, jak są ciekawe
Prognozowanie rozgrywki grą planszową - Cześć Anka! Co ty tam gryzmolisz? - Witaj dowcipasku. A ja po prostu projektuję grę planszową dla uczniów podstawówki. Nawet nie masz pojęcia Marku, jak są ciekawe
Wykład 6. Wyszukiwanie wzorca w tekście
 Wykład 6 Wyszukiwanie wzorca w tekście 1 Wyszukiwanie wzorca (przegląd) Porównywanie łańcuchów Algorytm podstawowy siłowy (naive algorithm) Jak go zrealizować? Algorytm Rabina-Karpa Inteligentne wykorzystanie
Wykład 6 Wyszukiwanie wzorca w tekście 1 Wyszukiwanie wzorca (przegląd) Porównywanie łańcuchów Algorytm podstawowy siłowy (naive algorithm) Jak go zrealizować? Algorytm Rabina-Karpa Inteligentne wykorzystanie
Ćwiczenia: Ukryte procesy Markowa lista 1 kierunek: matematyka, specjalność: analiza danych i modelowanie, studia II
 Ćwiczenia: Ukryte procesy Markowa lista kierunek: matematyka, specjalność: analiza danych i modelowanie, studia II dr Jarosław Kotowicz Zadanie. Dany jest łańcuch Markowa, który może przyjmować wartości,,...,
Ćwiczenia: Ukryte procesy Markowa lista kierunek: matematyka, specjalność: analiza danych i modelowanie, studia II dr Jarosław Kotowicz Zadanie. Dany jest łańcuch Markowa, który może przyjmować wartości,,...,
