Ciekawostki matematyczne i nie tylko!!! Nieskończoność i googol
|
|
|
- Stanisława Mróz
- 8 lat temu
- Przeglądów:
Transkrypt
1 Ciekawostki matematyczne i nie tylko!!! Nieskończoność i googol "Istnieje liczba największa, ale dosięgnąć jej nie zdoła człowiek. Tylko bogowie mają tę moc i oni jedni potrafią policzyć gwiazdy na niebie" Od początku historii ludzie borykali się z problemami nieskończoności. Próby opanowania pojęcia nieskończoności zaczęły się już w starożytnej Grecji, w szkole pitagorejskiej, w której słusznie przyjmowano, że nieskończoność to jest coś, czemu nie można przypisać żadnej wielkości. W czasach Platona, problem ten zapoczątkował teorię przestrzeni, czasu i nieskończoności. Później pojęcie nieskończoności w matematyce uzyskało sens precyzyjny i nie wydaje się już nieprzejrzyste. Ma ono nawet swój symbol: rodzaj położonej ósemki, zwanej także lemniskatą. Istnienie nieskończoności nie może być przedmiotem dowodu matematycznego, gdyż nieskończoność zbioru liczb, czyli niemożność ich przeliczenia, jest jednym z podstawowych aksjomatów, na których opiera się cała dzisiejsza matematyka. Googol nie odpowiada więc żadnej rzeczywistej ilości. Niczego aż tyle nie ma. Liczba nie przedstawia nic wyobrażalnego, przekracza ona wszystko, co można policzyć lub zmierzyć na świecie. Google to najpopularniejsza wyszukiwarka internetowa na świecie. Ta nazwa miała odzwierciedlać ogrom stron WWW, przeszukiwanych każdorazowo przez wyszukiwarkę.
2 SP1 W SWARZĘDZU Gazetka matematyczno-informatyczna Ważne tematy: Wszystkie drogi prowadzą z Grecji Dzień Dziecka w SP1 Szkoła myślenia Co to jest pi? Tajemnica Pitagorasa Rebusy Ciekawostki Zespół redakcyjny: uczestnicy koła matematycznego i informatycznego pod opieką Elżbiety Brodowskiej-Dukiewicz Rozalii Dziekan oraz Katarzyny Waśko
3 Grupa nauczycieli naszej szkoły przystąpiła do ogólnopolskiego programu Szkoła Myślenia. Program "Szkoła Myślenia" jest częścią akcji "Szkoła z klasą", która jest prowadzona przez Fundację Centrum Edukacji Obywatelskiej oraz Agorę S.A, wydawcę "Gazety Wyborczej". Akcję wspomaga Polsko-Amerykańska Fundacja Wolności. Celem programu jest kształtowanie umiejętności: rozumowania i wnioskowania naukowego, zadawania pytań badawczych, twórczego myślenia i rozwiązywania problemów, stosowania wiedzy w praktyce Zadaniem zespołu realizującego program jest przygotowanie projektu na dowolny temat. Tematy projektów w naszej szkole związane były z tematyką grecką oto ich tytuły: Jaka była tajemnica Pitagorasa? Co to jest pi? Jaki wpływ mieli myśliciele greccy na rozwój matematyki? Wycieczka do Grecji
4 Jeśli chcesz się o tym dowiedzieć to weź aktywny udział w festiwalu twórczych aktywności Wszystkie drogi wiodą z Grecji. Nauczyciele matematyki włączając się do projektu przygotowali wiele ciekawostek o sławnych matematykach żyjących w starożytnych czasach na terenie Grecji. Uczniowie klas VIc i VId przygotowali przedstawienie Żywot Pitagorasa. Oglądając je znajdziecie odpowiedź na postawione pytanie. PITAGORAS Wybitny grecki matematyk i filozof, który w dużym stopniu przyczynił się do rozwoju matematyki i astronomii, urodził się w 572 roku na wyspie Samos, zmarł w roku 497 p.n.e. W wieku 40 lat opuścił Jonię, dużo podróżował (Indie), aż wreszcie osiadł w Krotonie, gdzie założył szkołę i związek pitagorejski. Zapoczątkował on teorię liczb, podał dowód o kwadracie zbudowanym na przeciwprostokątnej w trójkącie prostokątnym (nazywany twierdzeniem Pitagorasa), opracował matematyczne podstawy zasady harmonii w muzyce. Około 530 roku p.n.e. w Krotonie w Italii założył tzw. Szkołę Pitagorejską. Motto pitagorejczyków brzmiało Wszystko jest liczbą. Znakiem rozpoznawczym był pentagram inaczej gwiazda pitagorejska. Jest to pięciokąt foremny, którego boki przedłużone w obie strony tworzą pięciokąt gwiaździsty. Tym znakiem pitagorejczycy pozdrawiali się i wzajemnie rozpoznawali, kreśląc go między innymi na piasku. Jest to ciekawa figura. Suma kątów wewnętrznych równa się dwóm kątom prostym, przypomina więc nam o trójkącie, którego suma kątów wewnętrznych także się równa kątowi półpełnemu.
5 Odkrycie istnienia liczb niewymiernych było wstrząsające. Fakt ten skrzętnie ukrywano, ponieważ było to niezgodne z dotychczasową filozofią, niezgodne z harmonią świata. Załamała się wiara w to, że wszystkie zjawiska we wszechświecie można ująć za pomocą liczb naturalnych. Oto ułożona przez pitagorejczyków symbolika liczb: 1 - oznaczała punkt, 2 - linia, 3 - figura geometryczna, 4 - ciało geometryczne (figura w przestrzeni), 5 - własności ciał fizycznych, 6 - życie, 7 - duch, 8 - miłość, 9 - roztropność, sprawiedliwość, 10 - doskonałość wszechświata
6 Rusz głową!!! Zad. 1 Ile lat minęło od roku urodzenia Pitagorasa do tej pory? ( = 2580) W którym wieku, w której połowie urodził się i zmarł? (572rok p.n.e. to I połowa VI wieku) Zad.2 Zagadka Pitagoras zapytany o liczbę swoich uczniów,odpowiedział: Połowa moich uczniów uczy się matematyki, czwarta część przyrody, siódma część milczenia, resztę stanowią trzy kobiety. Ilu uczniów miał Pitagoras? Zad.4 Ułóż jak najwięcej wyrazów ze słowa PITAGORAS. (np. agora, toga, pit, rasa, gitara ) Zapraszam także na wystawę prac uczniowskich Wzory matematyczne na wesoło wykonane przez uczniów klas piątych i szóstych. Tales z Miletu: Jak ty rodzicom, tak dzieci tobie. Kropla drąży skałę. Najtrudniej poznać samego siebie. Największą mądrością jest czas, wszystko ujawni. Nie mów nikomu co się dzieje w domu. Pitagoras: Liczba jest istotą wszystkich rzeczy. Musisz sam sobie zaufać, aby zaufali ci inni. Muzyka budzi w sercu pragnienie dobrych czynów. Najkrótsze wyrazy "tak" i "nie" wymagają najdłuższego zastanowienia. U przyjaciół wszystko jest wspólne.
7 Już w czasach zamierzchłych starożytni rachmistrze zauważyli, że wszystkie koła mają ze sobą coś wspólnego, że ich średnica i obwód pozostają wobec siebie w takim samym stosunku, a liczba ta bliska jest 3. W Starym Testamencie obwód koła był właśnie trzykrotnością średnicy, a w jednym z najstarszych tekstów matematycznych - papirusie Rhinda (XVII w. p. n. e.) wartość ta była przedstawiana jako 3, Liczba π to stosunek długości okręgu do długości jego średnicy, jest wielkością stałą i wynosi w przybliżeniu 3, Liczba π nazywana bywa często ludolfiną Ale dlaczego w przybliżeniu? Dziś jesteśmy w stanie obliczyć wartość pi do milionów miejsc po przecinku. Poniżej podane jest rozwinięcie dziesiętne liczby л z dokładnością 50 cyfr po przecinku: π=3, Uczeni szukając kontaktu z cywilizacjami pozaziemskimi, wysłali w kosmos drogą radiową informację o wartości liczby π. Wierzą, że inteligentne istoty spoza Ziemi znają tę liczbę i rozpoznają nasz komunikat. Liczba π weszła także do języka potocznego: "pi razy oko". Ciekawostka Dlaczego pociąg jak jedzie to stuka? Elementem poruszającym się po torze jest koło. A obręcz koła to nic innego jak okrąg. Należy przeanalizować wzór na długość okręgu: O = 2πr, 2 = to stała, r = określony promień, a π = trzy z...hakiem. I ten hak stuka!
8 Rebusy + a + ó=o y=as rz = s ion m = t + z Wykreśl z tabelki imiona 9 myślicieli greckich, a z pozostałych liter utwórz hasło- złotą myśl jednego z ukrytych myślicieli. A r c h i m e d e s S T a l e s P r z y o j a P l a t o n c k i e l C h i l o n r P i t a g o r a s a j e s t j a k d r t u g E p i k u r I e j D e m o k r y t s H e r a k l i t a Hasło: to motto.
(ok p.n.e.)
 (ok. 572-497 p.n.e.) Pitagoras pochodził z wyspy Samos. Znany jest głównie z słynnego twierdzenia o trójkącie prostokątnym, powszechnie zwanego jako twierdzenie Pitagorasa. Twierdzenie Pitagorasa ilustracja
(ok. 572-497 p.n.e.) Pitagoras pochodził z wyspy Samos. Znany jest głównie z słynnego twierdzenia o trójkącie prostokątnym, powszechnie zwanego jako twierdzenie Pitagorasa. Twierdzenie Pitagorasa ilustracja
Są to liczby najpowszechniej używane w życiu codziennym.
 NR1 LICZBY RZECZYWISTE ZASTOSOWANIE: Są to liczby najpowszechniej używane w życiu codziennym. Określanie ilości lat, Określanie ilości osób znajdujących się w pokoju i tym podobne, Określanie wzrostu,
NR1 LICZBY RZECZYWISTE ZASTOSOWANIE: Są to liczby najpowszechniej używane w życiu codziennym. Określanie ilości lat, Określanie ilości osób znajdujących się w pokoju i tym podobne, Określanie wzrostu,
Grecki matematyk, filozof, mistyk PITAGORAS
 Grecki matematyk, filozof, mistyk PITAGORAS FAKTY I MITY Dotarcie do prawdy związanej z życiem Pitagorasa jest bardzo trudne, ponieważ nie zostawił on po sobie żadnego pisma. Wywarł jednak ogromny wpływ
Grecki matematyk, filozof, mistyk PITAGORAS FAKTY I MITY Dotarcie do prawdy związanej z życiem Pitagorasa jest bardzo trudne, ponieważ nie zostawił on po sobie żadnego pisma. Wywarł jednak ogromny wpływ
Historia π (czyt. Pi)
 Historia liczby π Historia π (czyt. Pi) Już w czasach zamierzchłych starożytni rachmistrze zauważyli, że wszystkie koła mają ze sobą coś wspólnego, że ich średnica i obwód pozostają wobec siebie w takim
Historia liczby π Historia π (czyt. Pi) Już w czasach zamierzchłych starożytni rachmistrze zauważyli, że wszystkie koła mają ze sobą coś wspólnego, że ich średnica i obwód pozostają wobec siebie w takim
GSP077 Pakiet. KArty pracy. MateMatyka. Ekstraklasa 6klasisty matematyka kpracy 6 pak 1.indd 1
 GSP077 klasa Pakiet 6 KArty pracy MateMatyka Ekstraklasa 6klasisty matematyka kpracy 6 pak.indd 9/24/3 2:2 PM Instrukcja matematyka Uważnie czytaj teksty zadań i polecenia. Rozwiązania zapisz długopisem
GSP077 klasa Pakiet 6 KArty pracy MateMatyka Ekstraklasa 6klasisty matematyka kpracy 6 pak.indd 9/24/3 2:2 PM Instrukcja matematyka Uważnie czytaj teksty zadań i polecenia. Rozwiązania zapisz długopisem
Jego pitagorejska szkołą stała się kolebką, z której wywodzi się Numerologia współczesna.
 Naucz się wróżb numerologii Od wieków liczby fascynowały ludzi. Babilończycy, Hebrajczycy czy Fenicjanie wierzyli w wielką siłę. Pitagoras, grecki matematyk i astrolog żyjący około 580-500 roku p.n.e.
Naucz się wróżb numerologii Od wieków liczby fascynowały ludzi. Babilończycy, Hebrajczycy czy Fenicjanie wierzyli w wielką siłę. Pitagoras, grecki matematyk i astrolog żyjący około 580-500 roku p.n.e.
O liczbach niewymiernych
 O liczbach niewymiernych Agnieszka Bier Spotkania z matematyką jakiej nie znacie ;) 8 stycznia 0 Liczby wymierne i niewymierne Definicja Liczbę a nazywamy wymierną, jeżeli istnieją takie liczby całkowite
O liczbach niewymiernych Agnieszka Bier Spotkania z matematyką jakiej nie znacie ;) 8 stycznia 0 Liczby wymierne i niewymierne Definicja Liczbę a nazywamy wymierną, jeżeli istnieją takie liczby całkowite
Czym jest liczba π? O liczbie π. Paweł Zwoleński. Studenckie Koło Naukowe Matematyków Wydział Matematyczno-Fizyczny Politechnika Śląska
 Studenckie Koło Naukowe Matematyków Wydział Matematyczno-Fizyczny Politechnika Śląska 200.03.4 Motywacja wprowadzenia π Kluczowym momentem w historii liczby π było zauważenie przez starożytnych Babilończyków
Studenckie Koło Naukowe Matematyków Wydział Matematyczno-Fizyczny Politechnika Śląska 200.03.4 Motywacja wprowadzenia π Kluczowym momentem w historii liczby π było zauważenie przez starożytnych Babilończyków
Cud grecki. Cud grecki. Wrocław, 2 marca 2016
 Wrocław, 2 marca 2016 Wykształcenie podstawowe Spośród wielu twierdzeń i faktów pochodzących ze starożytnej Grecji w szkole na lekcjach matematyki pojawiają się: Twierdzenie Talesa Wykształcenie podstawowe
Wrocław, 2 marca 2016 Wykształcenie podstawowe Spośród wielu twierdzeń i faktów pochodzących ze starożytnej Grecji w szkole na lekcjach matematyki pojawiają się: Twierdzenie Talesa Wykształcenie podstawowe
Dlaczego liczba Π ma swoje święto?
 Dlaczego liczba Π ma swoje święto? 14 marca 2016 Szkolne Święto Matematyki w Gimnazjum nr 2 w Skawinie Liczba Pi jest wykorzystywana prawie w każdej sytuacji, w której musimy dokonać pomiarów przy pomocy
Dlaczego liczba Π ma swoje święto? 14 marca 2016 Szkolne Święto Matematyki w Gimnazjum nr 2 w Skawinie Liczba Pi jest wykorzystywana prawie w każdej sytuacji, w której musimy dokonać pomiarów przy pomocy
Z HISTORII MATEMATYKI. Willebrord Snell
 Z HISTORII MATEMATYKI Willebrord Snell (1580-1626) Najbardziej znany z prawa które stworzył (prawa Snella) które mówi, że kąty padania promieni światła i ich załamania: spełniają zależność: Jak widać jest
Z HISTORII MATEMATYKI Willebrord Snell (1580-1626) Najbardziej znany z prawa które stworzył (prawa Snella) które mówi, że kąty padania promieni światła i ich załamania: spełniają zależność: Jak widać jest
Twierdzenie Pitagorasa. Autor. Wstęp. Pitagoras. Dariusz Kulma
 Twierdzenie Pitagorasa Autor Dariusz Kulma Wstęp Myli się ten kto myśli, że najbardziej znane twierdzenie na świecie dotyczące geometrii czyli twierdzenie Pitagorasa zawdzięczamy tylko samemu Pitagorasowi.
Twierdzenie Pitagorasa Autor Dariusz Kulma Wstęp Myli się ten kto myśli, że najbardziej znane twierdzenie na świecie dotyczące geometrii czyli twierdzenie Pitagorasa zawdzięczamy tylko samemu Pitagorasowi.
KRZYŻÓWKA 2. 11. Może być np. równoboczny lub rozwartokątny. Jego pole to a b HASŁO:
 KRZYŻÓWKA.Wyznaczają ją dwa punkty.. Jego pole to π r² 3. Jego pole to a a 4.Figura przestrzenna, której podstawą jest dowolny wielokąt, a ściany boczne są trójkątami o wspólnym wierzchołku. 5.Prosta mająca
KRZYŻÓWKA.Wyznaczają ją dwa punkty.. Jego pole to π r² 3. Jego pole to a a 4.Figura przestrzenna, której podstawą jest dowolny wielokąt, a ściany boczne są trójkątami o wspólnym wierzchołku. 5.Prosta mająca
Krzywe stożkowe Lekcja II: Okrąg i jego opis w różnych układach współrzędnych
 Krzywe stożkowe Lekcja II: Okrąg i jego opis w różnych układach współrzędnych Wydział Matematyki Politechniki Wrocławskiej Okrąg Okrąg jest szczególną krzywą stożkową. Wyznacza nam koło, które jest podstawą
Krzywe stożkowe Lekcja II: Okrąg i jego opis w różnych układach współrzędnych Wydział Matematyki Politechniki Wrocławskiej Okrąg Okrąg jest szczególną krzywą stożkową. Wyznacza nam koło, które jest podstawą
Temat lekcji: Twierdzenia Pitagorasa zastosowanie do rozwiązywania zadań. Prowadząca zajęcia Joanna Sadkowska
 Temat lekcji: Twierdzenia Pitagorasa zastosowanie do rozwiązywania zadań. Prowadząca zajęcia Joanna Sadkowska Ogólne cele nauczania: przypomnienie i utrwalenie wiadomości dotyczących twierdzeń Pitagorasa,
Temat lekcji: Twierdzenia Pitagorasa zastosowanie do rozwiązywania zadań. Prowadząca zajęcia Joanna Sadkowska Ogólne cele nauczania: przypomnienie i utrwalenie wiadomości dotyczących twierdzeń Pitagorasa,
Troszkę Geometrii. Kinga Kolczyńska - Przybycień
 Spis tresci O Geometrii 1 O Geometrii 2 3 4 5 6 7 Spis tresci O Geometrii 1 O Geometrii 2 3 4 5 6 7 Kilka słów o mierzeniu Otóż jak sama nazwa Geometria (z gr geo-ziemia, metria-miara) ma ona coś wspólnego
Spis tresci O Geometrii 1 O Geometrii 2 3 4 5 6 7 Spis tresci O Geometrii 1 O Geometrii 2 3 4 5 6 7 Kilka słów o mierzeniu Otóż jak sama nazwa Geometria (z gr geo-ziemia, metria-miara) ma ona coś wspólnego
Tytuł. Autor. Dział. Innowacyjne cele edukacyjne. Czas. Przebieg. Etap 1 - Wprowadzenie z rysem historycznym i dyskusją
 Tytuł Kto nie zna geometrii, niech tu nie wchodzi czyli geometria brył platońskich Autor Dariusz Kulma Dział Bryły Innowacyjne cele edukacyjne Uczeń zapoznaje się z kolejnymi wielościanami foremnymi. Czas
Tytuł Kto nie zna geometrii, niech tu nie wchodzi czyli geometria brył platońskich Autor Dariusz Kulma Dział Bryły Innowacyjne cele edukacyjne Uczeń zapoznaje się z kolejnymi wielościanami foremnymi. Czas
SCENARIUSZ LEKCJI MATEMATYKI W KLASIE IV
 SCENARIUSZ LEKCJI MATEMATYKI W KLASIE IV Opracowała: Hanna Nowakowska Szkoła Podstawowa im. Jana Pawła II w Żydowie TEMAT : ŻEGNAMY FIGURY PŁASKIE Cel ogólny: Utrwalenie wiadomości o figurach płaskich
SCENARIUSZ LEKCJI MATEMATYKI W KLASIE IV Opracowała: Hanna Nowakowska Szkoła Podstawowa im. Jana Pawła II w Żydowie TEMAT : ŻEGNAMY FIGURY PŁASKIE Cel ogólny: Utrwalenie wiadomości o figurach płaskich
3. Liczba Pi. 1. Cele lekcji. a. 2. Metoda i forma pracy. b. 3. Środki dydaktyczne
 1. 2. 3. Liczba Pi 1. Cele lekcji Cel ogólny lekcji: Poznanie zależności pomiędzy długością okręgu a jego średnicą. Poznanie liczby niewymiernej π. a) Wiadomości Uczeń Zna liczbę niewymierną π. b) Umiejętności
1. 2. 3. Liczba Pi 1. Cele lekcji Cel ogólny lekcji: Poznanie zależności pomiędzy długością okręgu a jego średnicą. Poznanie liczby niewymiernej π. a) Wiadomości Uczeń Zna liczbę niewymierną π. b) Umiejętności
WYMAGANIA EDUKACYJNE NA POSZCZEGÓLNE OCENY MATEMATYKA KLASA 8 DZIAŁ 1. LICZBY I DZIAŁANIA
 WYMAGANIA EDUKACYJNE NA POSZCZEGÓLNE OCENY MATEMATYKA KLASA 8 DZIAŁ 1. LICZBY I DZIAŁANIA zna znaki używane do zapisu liczb w systemie rzymskim; zna zasady zapisu liczb w systemie rzymskim; umie zapisać
WYMAGANIA EDUKACYJNE NA POSZCZEGÓLNE OCENY MATEMATYKA KLASA 8 DZIAŁ 1. LICZBY I DZIAŁANIA zna znaki używane do zapisu liczb w systemie rzymskim; zna zasady zapisu liczb w systemie rzymskim; umie zapisać
Temat: Koło i okrąg. Pojęcia związane z okręgiem promień, średnica, styczna, sieczna.
 Spotkanie 2 Temat: Koło i okrąg. Pojęcia związane z okręgiem promień, średnica, styczna, sieczna. Zajęcia rozpoczynamy od pytania, co oznacza nazwa projektu, w którym uczniowie biorą udział: Pi i sigma.
Spotkanie 2 Temat: Koło i okrąg. Pojęcia związane z okręgiem promień, średnica, styczna, sieczna. Zajęcia rozpoczynamy od pytania, co oznacza nazwa projektu, w którym uczniowie biorą udział: Pi i sigma.
Klasa III technikum Egzamin poprawkowy z matematyki sierpień I. CIĄGI LICZBOWE 1. Pojęcie ciągu liczbowego. b) a n =
 /9 Narysuj wykres ciągu (a n ) o wyrazie ogólnym: I. CIĄGI LICZBOWE. Pojęcie ciągu liczbowego. a) a n =5n dla n
/9 Narysuj wykres ciągu (a n ) o wyrazie ogólnym: I. CIĄGI LICZBOWE. Pojęcie ciągu liczbowego. a) a n =5n dla n
Uczę się kopiować, wycinać i wklejać określone fragmenty tekstu
 EDYTOR TEKSTU WORD FORMATOWANIE TEKSTU Ćwiczenie 1 Napisz poniższy tekst, a następnie skopiuj go i zmień kolejność wierszy. Sformatuj kolejne dwa akapity w wybrany przez siebie sposób (inaczej niż pierwszy
EDYTOR TEKSTU WORD FORMATOWANIE TEKSTU Ćwiczenie 1 Napisz poniższy tekst, a następnie skopiuj go i zmień kolejność wierszy. Sformatuj kolejne dwa akapity w wybrany przez siebie sposób (inaczej niż pierwszy
WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE VIII
 WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE VIII Uczeń na ocenę dopuszczającą: - zna znaki używane do zapisu liczb w systemie rzymskim, - umie zapisać i odczytać liczby naturalne dodatnie w systemie rzymskim
WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE VIII Uczeń na ocenę dopuszczającą: - zna znaki używane do zapisu liczb w systemie rzymskim, - umie zapisać i odczytać liczby naturalne dodatnie w systemie rzymskim
Liczbę Pi określamy jako stosunek długości okręgu do jego średnicy. Jest to wielkość stała i wynosi w przybliżeniu: π
 Liczbę Pi określamy jako stosunek długości okręgu do jego średnicy. Jest to wielkość stała i wynosi w przybliżeniu: π 3,141592653589793238462643383279502884 Używany dzisiaj symbol π wprowadzony został
Liczbę Pi określamy jako stosunek długości okręgu do jego średnicy. Jest to wielkość stała i wynosi w przybliżeniu: π 3,141592653589793238462643383279502884 Używany dzisiaj symbol π wprowadzony został
Wymagania na egzamin poprawkowy z matematyki dla klasy I C LO (Rok szkolny 2015/16) Wykaz zakładanych osiągnięć ucznia klasy I liceum
 Wymagania na egzamin poprawkowy z matematyki dla klasy I C LO (Rok szkolny 05/6) Wykaz zakładanych osiągnięć ucznia klasy I liceum (osiągnięcia ucznia w zakresie podstawowym) I. Liczby rzeczywiste. Język
Wymagania na egzamin poprawkowy z matematyki dla klasy I C LO (Rok szkolny 05/6) Wykaz zakładanych osiągnięć ucznia klasy I liceum (osiągnięcia ucznia w zakresie podstawowym) I. Liczby rzeczywiste. Język
Kółka matematycznego?
 Lucyna Adamczyk Jak można wykorzystać komputer na zajęciach Kółka matematycznego? Matematyka ma to do siebie, że kto raz znalazł się pod jej urokiem, wracać będzie do niej zawsze, a to znacznie ułatwi
Lucyna Adamczyk Jak można wykorzystać komputer na zajęciach Kółka matematycznego? Matematyka ma to do siebie, że kto raz znalazł się pod jej urokiem, wracać będzie do niej zawsze, a to znacznie ułatwi
PYTANIA TEORETYCZNE Z MATEMATYKI
 Zbiory liczbowe: 1. Wymień znane Ci zbiory liczbowe. 2. Co to są liczby rzeczywiste? 3. Co to są liczby naturalne? 4. Co to są liczby całkowite? 5. Co to są liczby wymierne? 6. Co to są liczby niewymierne?
Zbiory liczbowe: 1. Wymień znane Ci zbiory liczbowe. 2. Co to są liczby rzeczywiste? 3. Co to są liczby naturalne? 4. Co to są liczby całkowite? 5. Co to są liczby wymierne? 6. Co to są liczby niewymierne?
SZKOŁA PODSTAWOWA NR 1 IM. ŚW. JANA KANTEGO W ŻOŁYNI. Wymagania na poszczególne oceny klasa VIII Matematyka z kluczem
 SZKOŁA PODSTAWOWA NR 1 IM. ŚW. JANA KANTEGO W ŻOŁYNI Wymagania na poszczególne oceny klasa VIII Matematyka z kluczem I. Wymagania konieczne (na ocenę dopuszczającą) obejmują wiadomości i umiejętności umożliwiające
SZKOŁA PODSTAWOWA NR 1 IM. ŚW. JANA KANTEGO W ŻOŁYNI Wymagania na poszczególne oceny klasa VIII Matematyka z kluczem I. Wymagania konieczne (na ocenę dopuszczającą) obejmują wiadomości i umiejętności umożliwiające
Matematyka dyskretna. Andrzej Łachwa, UJ, /14
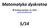 Matematyka dyskretna Andrzej Łachwa, UJ, 2012 andrzej.lachwa@uj.edu.pl 5/14 Rekurencja Weźmy dla przykładu wzór (przepis) na liczenie silni: n! to iloczyn kolejnych liczb naturalnych od 1 do n oraz 0!=1.
Matematyka dyskretna Andrzej Łachwa, UJ, 2012 andrzej.lachwa@uj.edu.pl 5/14 Rekurencja Weźmy dla przykładu wzór (przepis) na liczenie silni: n! to iloczyn kolejnych liczb naturalnych od 1 do n oraz 0!=1.
Scenariusz lekcji matematyki w kl. V.
 Scenariusz lekcji matematyki w kl. V. T em a t : Powtórzenie wiadomości o czworokątach. C z a s z a jęć: 1 jednostka lekcyjna (45 minut). C e l e o g ó l n e : utrwalenie wiadomości o figurach geometrycznych
Scenariusz lekcji matematyki w kl. V. T em a t : Powtórzenie wiadomości o czworokątach. C z a s z a jęć: 1 jednostka lekcyjna (45 minut). C e l e o g ó l n e : utrwalenie wiadomości o figurach geometrycznych
Szkice rozwiązań zadań z arkuszy maturalnych zamieszczonych w 47. numerze Świata Matematyki, który można nabyć w sklepie na
 Szkice rozwiązań zadań z arkuszy maturalnych zamieszczonych w 47. numerze Świata Matematyki, który można nabyć w sklepie na www.swiatmatematyki.pl 1. Wypiszmy początkowe potęgi liczby Zestaw podstawowy
Szkice rozwiązań zadań z arkuszy maturalnych zamieszczonych w 47. numerze Świata Matematyki, który można nabyć w sklepie na www.swiatmatematyki.pl 1. Wypiszmy początkowe potęgi liczby Zestaw podstawowy
Geometria. Rodzaje i własności figur geometrycznych:
 Geometria Jest jednym z działów matematyki, którego przedmiotem jest badanie figur geometrycznych i zależności między nimi. Figury geometryczne na płaszczyźnie noszą nazwę figur płaskich, w przestrzeni
Geometria Jest jednym z działów matematyki, którego przedmiotem jest badanie figur geometrycznych i zależności między nimi. Figury geometryczne na płaszczyźnie noszą nazwę figur płaskich, w przestrzeni
PLANIMETRIA CZYLI GEOMETRIA PŁASZCZYZNY CZ. 1
 PLANIMETRIA CZYLI GEOMETRIA PŁASZCZYZNY CZ. 1 Planimetria to dział geometrii, w którym przedmiotem badań są własności figur geometrycznych leżących na płaszczyźnie (patrz określenie płaszczyzny). Pojęcia
PLANIMETRIA CZYLI GEOMETRIA PŁASZCZYZNY CZ. 1 Planimetria to dział geometrii, w którym przedmiotem badań są własności figur geometrycznych leżących na płaszczyźnie (patrz określenie płaszczyzny). Pojęcia
WYMAGANIA EDUKACYJNE NIEZBĘDNE DO UZYSKANIA ŚRÓDROCZNYCH I ROCZNYCH OCEN KLASYFIKACYJNYCH Z MATEMATYKI W KLASIE II GIMNAZJUM
 WYMAGANIA EDUKACYJNE NIEZBĘDNE DO UZYSKANIA ŚRÓDROCZNYCH I ROCZNYCH OCEN KLASYFIKACYJNYCH Z MATEMATYKI W KLASIE II GIMNAZJUM OCENA ŚRÓDROCZNA: NIEDOSTATECZNY ocenę niedostateczny otrzymuje uczeń, który
WYMAGANIA EDUKACYJNE NIEZBĘDNE DO UZYSKANIA ŚRÓDROCZNYCH I ROCZNYCH OCEN KLASYFIKACYJNYCH Z MATEMATYKI W KLASIE II GIMNAZJUM OCENA ŚRÓDROCZNA: NIEDOSTATECZNY ocenę niedostateczny otrzymuje uczeń, który
Końcoworoczne kryteria oceniania dla klasy II z matematyki przygotowały mgr Magdalena Murawska i mgr Iwona Śliczner
 Końcoworoczne kryteria oceniania dla klasy II z matematyki przygotowały mgr Magdalena Murawska i mgr Iwona Śliczner Semestr I Rozdział: Potęgi i pierwiastki zapisuje w postaci potęgi iloczyn tych samych
Końcoworoczne kryteria oceniania dla klasy II z matematyki przygotowały mgr Magdalena Murawska i mgr Iwona Śliczner Semestr I Rozdział: Potęgi i pierwiastki zapisuje w postaci potęgi iloczyn tych samych
Zagadnienia z matematyki dla klasy II oraz przykładowe zadania
 Zagadnienia z matematyki dla klasy II oraz przykładowe zadania FUNKCJA KWADRATOWA Wykres funkcji f () = a Przesunięcie wykresu funkcji f() = a o wektor Postać kanoniczna i postać ogólna funkcji kwadratowej
Zagadnienia z matematyki dla klasy II oraz przykładowe zadania FUNKCJA KWADRATOWA Wykres funkcji f () = a Przesunięcie wykresu funkcji f() = a o wektor Postać kanoniczna i postać ogólna funkcji kwadratowej
WYMAGANIA EDUKACYJNE
 GIMNAZJUM NR 2 W RYCZOWIE WYMAGANIA EDUKACYJNE niezbędne do uzyskania poszczególnych śródrocznych i rocznych ocen klasyfikacyjnych z MATEMATYKI w klasie II gimnazjum str. 1 Wymagania edukacyjne niezbędne
GIMNAZJUM NR 2 W RYCZOWIE WYMAGANIA EDUKACYJNE niezbędne do uzyskania poszczególnych śródrocznych i rocznych ocen klasyfikacyjnych z MATEMATYKI w klasie II gimnazjum str. 1 Wymagania edukacyjne niezbędne
Wymagania edukacyjne niezbędne do uzyskania poszczególnych śródrocznych ocen klasyfikacyjnych z matematyki klasa 2 (oddział gimnazjalny)
 edukacyjne niezbędne do uzyskania poszczególnych śródrocznych ocen klasyfikacyjnych z matematyki klasa 2 (oddział gimnazjalny) Stopień Rozdział 1. Potęgi i pierwiastki zapisuje w postaci potęgi iloczyn
edukacyjne niezbędne do uzyskania poszczególnych śródrocznych ocen klasyfikacyjnych z matematyki klasa 2 (oddział gimnazjalny) Stopień Rozdział 1. Potęgi i pierwiastki zapisuje w postaci potęgi iloczyn
Wymagania edukacyjne niezbędne do otrzymania poszczególnych śródrocznych i rocznych ocen klasyfikacyjnych z matematyki dla klasy VIII
 Wymagania edukacyjne niezbędne do otrzymania poszczególnych śródrocznych i rocznych ocen klasyfikacyjnych z matematyki dla klasy VIII Temat 1. System rzymski. 2. Własności liczb naturalnych. 3. Porównywanie
Wymagania edukacyjne niezbędne do otrzymania poszczególnych śródrocznych i rocznych ocen klasyfikacyjnych z matematyki dla klasy VIII Temat 1. System rzymski. 2. Własności liczb naturalnych. 3. Porównywanie
Katalog wymagań programowych na poszczególne stopnie szkolne
 rozpoznaje figury podobne zna własności figur podobnych rozpoznaje trójkąty prostokątne podobne Rozdział 6. Figury podobne zna cechy podobieństwa trójkątów prostokątnych podobnych podaje skalę podobieństwa
rozpoznaje figury podobne zna własności figur podobnych rozpoznaje trójkąty prostokątne podobne Rozdział 6. Figury podobne zna cechy podobieństwa trójkątów prostokątnych podobnych podaje skalę podobieństwa
Geometria. Zadanie 1. Liczba przekątnych pięciokąta foremnego jest równa A. 4 B. 5 C. 6 D. 7
 Geometria Zadanie 1. Liczba przekątnych pięciokąta foremnego jest równa A. 4 B. 5 C. 6 D. 7 W tym przypadku możemy wykonać szkic pięciokąta i policzyć przekątne: Zadanie. Promień okręgu opisanego na kwadracie
Geometria Zadanie 1. Liczba przekątnych pięciokąta foremnego jest równa A. 4 B. 5 C. 6 D. 7 W tym przypadku możemy wykonać szkic pięciokąta i policzyć przekątne: Zadanie. Promień okręgu opisanego na kwadracie
Przypomnienie wiadomości dla trzecioklasisty C z y p a m i ę t a s z?
 Przypomnienie wiadomości dla trzecioklasisty C z y p a m i ę t a s z? Liczby naturalne porządkowe, (0 nie jest sztywno związane z N). Przykłady: 1, 2, 6, 148, Liczby całkowite to liczby naturalne, przeciwne
Przypomnienie wiadomości dla trzecioklasisty C z y p a m i ę t a s z? Liczby naturalne porządkowe, (0 nie jest sztywno związane z N). Przykłady: 1, 2, 6, 148, Liczby całkowite to liczby naturalne, przeciwne
Matematyk Roku gminny konkurs matematyczny. FINAŁ 20 maja 2016 KLASA TRZECIA
 Twój kod:.. "Matematyka nie taka straszna jak ją malują Matematyk Roku 06 - gminny konkurs matematyczny FINAŁ 0 maja 06 KLASA TRZECIA. Przed Tobą zestaw 0 zadań konkursowych. Zanim rozpoczniesz pracę nad
Twój kod:.. "Matematyka nie taka straszna jak ją malują Matematyk Roku 06 - gminny konkurs matematyczny FINAŁ 0 maja 06 KLASA TRZECIA. Przed Tobą zestaw 0 zadań konkursowych. Zanim rozpoczniesz pracę nad
Scenariusz lekcji matematyki, klasa 1 LO.
 Scenariusz lekcji matematyki, klasa 1 LO. Temat lekcji: Czworokąty: rodzaje, własności, pola czworokątów. Cele: po lekcji uczeń: - rozpoznaje czworokąty, - zna własności czworokątów, - potrafi wskazać
Scenariusz lekcji matematyki, klasa 1 LO. Temat lekcji: Czworokąty: rodzaje, własności, pola czworokątów. Cele: po lekcji uczeń: - rozpoznaje czworokąty, - zna własności czworokątów, - potrafi wskazać
Katalog wymagań programowych na poszczególne stopnie szkolne
 rozpoznaje figury podobne zna własności figur podobnych rozpoznaje trójkąty prostokątne podobne Rozdział 6. Figury podobne zna cechy podobieństwa trójkątów prostokątnych podobnych podaje skalę podobieństwa
rozpoznaje figury podobne zna własności figur podobnych rozpoznaje trójkąty prostokątne podobne Rozdział 6. Figury podobne zna cechy podobieństwa trójkątów prostokątnych podobnych podaje skalę podobieństwa
Wojewódzki Konkurs Matematyczny dla uczniów gimnazjów. Etap Wojewódzki 16 lutego 2018 Czas 90 minut Rozwiązania i punktacja
 Wojewódzki Konkurs Matematyczny dla uczniów gimnazjów. Etap Wojewódzki 6 lutego 208 Czas 90 minut Rozwiązania i punktacja ZADANIA ZAMKNIĘTE Zadanie. ( punkt) Odległość między miastami A i B na mapie wynosi
Wojewódzki Konkurs Matematyczny dla uczniów gimnazjów. Etap Wojewódzki 6 lutego 208 Czas 90 minut Rozwiązania i punktacja ZADANIA ZAMKNIĘTE Zadanie. ( punkt) Odległość między miastami A i B na mapie wynosi
PODSTAWY > Figury płaskie (1) KĄTY. Kąt składa się z ramion i wierzchołka. Jego wielkość jest mierzona w stopniach:
 PODSTAWY > Figury płaskie (1) KĄTY Kąt składa się z ramion i wierzchołka. Jego wielkość jest mierzona w stopniach: Kąt możemy opisać wpisując w łuk jego miarę (gdy jest znana). Gdy nie znamy miary kąta,
PODSTAWY > Figury płaskie (1) KĄTY Kąt składa się z ramion i wierzchołka. Jego wielkość jest mierzona w stopniach: Kąt możemy opisać wpisując w łuk jego miarę (gdy jest znana). Gdy nie znamy miary kąta,
Przedmiotowy system oceniania Wymagania na poszczególne oceny,,liczy się matematyka
 Przedmiotowy system oceniania Wymagania na poszczególne oceny,,liczy się matematyka I. Potęgi i pierwiastki. Klasa II 1. Zapisuje w postaci potęgi iloczyn tych samych czynników i odwrotnie. 2. Oblicza
Przedmiotowy system oceniania Wymagania na poszczególne oceny,,liczy się matematyka I. Potęgi i pierwiastki. Klasa II 1. Zapisuje w postaci potęgi iloczyn tych samych czynników i odwrotnie. 2. Oblicza
GEOPLAN Z SIATKĄ TRÓJKĄTNĄ
 TEMAT NUMERU 9 GEOPLAN Z SIATKĄ TRÓJKĄTNĄ Marzenna Grochowalska W Matematyce w Szkole wiele miejsca poświęcono geoplanom z siatką kwadratową oraz ich zaletom 1. Równie ciekawą pomocą dydaktyczną jest geoplan
TEMAT NUMERU 9 GEOPLAN Z SIATKĄ TRÓJKĄTNĄ Marzenna Grochowalska W Matematyce w Szkole wiele miejsca poświęcono geoplanom z siatką kwadratową oraz ich zaletom 1. Równie ciekawą pomocą dydaktyczną jest geoplan
wymagania programowe z matematyki kl. II gimnazjum
 wymagania programowe z matematyki kl. II gimnazjum Umie obliczyć potęgę liczby wymiernej o wykładniku naturalnym. 1. Arytmetyka występują potęgi o wykładniku naturalnym. Umie zapisać i porównać duże liczby
wymagania programowe z matematyki kl. II gimnazjum Umie obliczyć potęgę liczby wymiernej o wykładniku naturalnym. 1. Arytmetyka występują potęgi o wykładniku naturalnym. Umie zapisać i porównać duże liczby
WYMAGANIA EDUKACYJN KRYTERIA OCENY Z MATEMATYKI W KLASIE II GIMNAZJUM
 Na ocenę dopuszczającą uczeń umie : WYMAGANIA EDUKACYJN KRYTERIA OCENY Z MATEMATYKI W KLASIE II GIMNAZJUM stosować cztery podstawowe działania na liczbach wymiernych, zna kolejność wykonywania działań
Na ocenę dopuszczającą uczeń umie : WYMAGANIA EDUKACYJN KRYTERIA OCENY Z MATEMATYKI W KLASIE II GIMNAZJUM stosować cztery podstawowe działania na liczbach wymiernych, zna kolejność wykonywania działań
Mini tablice matematyczne. Figury geometryczne
 Mini tablice matematyczne Figury geometryczne Spis treści Własności kwadratu Ciekawostka:Kwadrat magiczny Prostokąt Własności prostokąta Trapez Własności trapezu Równoległobok Własności równoległoboku
Mini tablice matematyczne Figury geometryczne Spis treści Własności kwadratu Ciekawostka:Kwadrat magiczny Prostokąt Własności prostokąta Trapez Własności trapezu Równoległobok Własności równoległoboku
KONSPEKT DO LEKCJI. Cele lekcji: ogólne:
 KONSPEKT DO LEKCJI Przedmiot: matematyka Temat: Rozwiązywanie zadań tekstowych z zastosowaniem równań. Klasa: III gimnazjum Prowadząca: mgr Julita Otok Obserwator: nauczyciele zespołu matematyczno - przyrodniczego
KONSPEKT DO LEKCJI Przedmiot: matematyka Temat: Rozwiązywanie zadań tekstowych z zastosowaniem równań. Klasa: III gimnazjum Prowadząca: mgr Julita Otok Obserwator: nauczyciele zespołu matematyczno - przyrodniczego
WOJEWÓDZKI KONKURS MATEMATYCZNY
 Kod ucznia Liczba punktów WOJEWÓDZKI KONKURS MATEMATYCZNY DLA UCZNIÓW GIMNAZJÓW W ROKU SZKOLNYM 018/019 17.1.018 1. Test konkursowy zawiera zadania. Są to zadania zamknięte i otwarte. Na ich rozwiązanie
Kod ucznia Liczba punktów WOJEWÓDZKI KONKURS MATEMATYCZNY DLA UCZNIÓW GIMNAZJÓW W ROKU SZKOLNYM 018/019 17.1.018 1. Test konkursowy zawiera zadania. Są to zadania zamknięte i otwarte. Na ich rozwiązanie
WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE II W PUBLICZNYM GIMNAZJUM NR 2 W ZESPOLE SZKÓŁ W RUDKACH
 WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE II W PUBLICZNYM GIMNAZJUM NR 2 W ZESPOLE SZKÓŁ W RUDKACH Marzena Zbrożyna DOPUSZCZAJĄCY: Uczeń potrafi: odczytać informacje z tabeli odczytać informacje z diagramu
WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE II W PUBLICZNYM GIMNAZJUM NR 2 W ZESPOLE SZKÓŁ W RUDKACH Marzena Zbrożyna DOPUSZCZAJĄCY: Uczeń potrafi: odczytać informacje z tabeli odczytać informacje z diagramu
Zaproszenie do udziału w Festiwalu Liczba π na dwóch brzegach Brdy.
 Zaproszenie do udziału w Festiwalu Liczba π na dwóch brzegach Brdy. 1. Festiwal jest organizowany przez Gimnazjum nr 9, Liceum nr 9 oraz Gimnazjum Integracyjne nr 38 w ramach Festiwalu liczby na dwóch
Zaproszenie do udziału w Festiwalu Liczba π na dwóch brzegach Brdy. 1. Festiwal jest organizowany przez Gimnazjum nr 9, Liceum nr 9 oraz Gimnazjum Integracyjne nr 38 w ramach Festiwalu liczby na dwóch
Matematyka dyskretna. Andrzej Łachwa, UJ, A/15
 Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 4A/15 Liczby Fibonacciego Spośród ciągów zdefiniowanych rekurencyjnie, jednym z najsłynniejszych jest ciąg Fibonacciego (z roku 1202)
Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 4A/15 Liczby Fibonacciego Spośród ciągów zdefiniowanych rekurencyjnie, jednym z najsłynniejszych jest ciąg Fibonacciego (z roku 1202)
WOJEWÓDZKI KONKURS MATEMATYCZNY
 WOJEWÓDZKI KONKURS MATEMATYCZNY DLA UCZNIÓW GIMNAZJUM W ROKU SZKOLNYM 2018/2019 Schemat punktowania zadania zamknięte Za każdą poprawną odpowiedź uczeń otrzymuje 1 punkt. Numer zadania Poprawna odpowiedź
WOJEWÓDZKI KONKURS MATEMATYCZNY DLA UCZNIÓW GIMNAZJUM W ROKU SZKOLNYM 2018/2019 Schemat punktowania zadania zamknięte Za każdą poprawną odpowiedź uczeń otrzymuje 1 punkt. Numer zadania Poprawna odpowiedź
Krzyżówka oraz hasła do krzyżówki. Kalina R., Przewodnik po matematyce dla klas VII-VIII, część IV, SENS, Poznań 1997, s.20-22.
 Omnibus matematyczny 1. Cele lekcji a) Wiadomości Uczeń: zna pojęcia matematyczne z zakresu szkoły podstawowej i gimnazjum. b) Umiejętności Uczeń: potrafi podać odpowiednie pojęcie matematyczne na podstawie
Omnibus matematyczny 1. Cele lekcji a) Wiadomości Uczeń: zna pojęcia matematyczne z zakresu szkoły podstawowej i gimnazjum. b) Umiejętności Uczeń: potrafi podać odpowiednie pojęcie matematyczne na podstawie
COMENIUS PROJEKT ROZWOJU SZKOŁY. Sezamie, otwórz się! - rozwijanie zdolności uczenia i myślenia uczniów.
 COMENIUS PROJEKT ROZWOJU SZKOŁY Sezamie, otwórz się! - rozwijanie zdolności uczenia i myślenia uczniów. GIMNAZJUM 20 GDAŃSK POLSKA Maj 2006 SCENARIUSZ LEKCJI MATEMATYKI Z WYKORZYSTANIEM METODY STACJI UCZENIA
COMENIUS PROJEKT ROZWOJU SZKOŁY Sezamie, otwórz się! - rozwijanie zdolności uczenia i myślenia uczniów. GIMNAZJUM 20 GDAŃSK POLSKA Maj 2006 SCENARIUSZ LEKCJI MATEMATYKI Z WYKORZYSTANIEM METODY STACJI UCZENIA
KONKURS MATEMATYCZNY
 PAŃSTWOWA WYŻSZA SZKOŁA ZAWODOWA W CHEŁMIE INSTYTUT MATEMATYKI i INFORMATYKI 22-100 Chełm, ul. Pocztowa 54 tel./fax. (082) 562 11 24 KONKURS MATEMATYCZNY im. Samuela Chróścikowskiego 10 kwiecień 2015r.
PAŃSTWOWA WYŻSZA SZKOŁA ZAWODOWA W CHEŁMIE INSTYTUT MATEMATYKI i INFORMATYKI 22-100 Chełm, ul. Pocztowa 54 tel./fax. (082) 562 11 24 KONKURS MATEMATYCZNY im. Samuela Chróścikowskiego 10 kwiecień 2015r.
1. FUNKCJE DZIAŁ Z PODRĘCZNIKA L.P. NaCoBeZu kryteria sukcesu w języku ucznia
 L.P. DZIAŁ Z PODRĘCZNIKA 1. FUNKCJE 2. POTĘGI I PIERWIASTKI NaCoBeZu kryteria sukcesu w języku ucznia 1. Wiem, co to jest układ współrzędnych, potrafię nazwać osie układu. 2. Rysuję układ współrzędnych
L.P. DZIAŁ Z PODRĘCZNIKA 1. FUNKCJE 2. POTĘGI I PIERWIASTKI NaCoBeZu kryteria sukcesu w języku ucznia 1. Wiem, co to jest układ współrzędnych, potrafię nazwać osie układu. 2. Rysuję układ współrzędnych
3.1. Obliczanie obwodu koła.
 #3. Należy wykonać zestaw komponentów pozwalających na wyliczenia: obwodu, pola powierzchni dla figur geometrycznych: koło, kwadrat, prostokąt, trójkąt równoramiennego. 3.1. Obliczanie obwodu koła. Jako
#3. Należy wykonać zestaw komponentów pozwalających na wyliczenia: obwodu, pola powierzchni dla figur geometrycznych: koło, kwadrat, prostokąt, trójkąt równoramiennego. 3.1. Obliczanie obwodu koła. Jako
WOJEWÓDZKI KONKURS MATEMATYCZNY
 Kod ucznia Liczba punktów WOJEWÓDZKI KONKURS MATEMATYCZNY DLA UCZNIÓW SZKÓŁ PODSTAWOWYCH W ROKU SZKOLNYM 2018/2019 28.02.2019 R. 1. Test konkursowy zawiera 24 zadania. Są to zadania zamknięte i otwarte.
Kod ucznia Liczba punktów WOJEWÓDZKI KONKURS MATEMATYCZNY DLA UCZNIÓW SZKÓŁ PODSTAWOWYCH W ROKU SZKOLNYM 2018/2019 28.02.2019 R. 1. Test konkursowy zawiera 24 zadania. Są to zadania zamknięte i otwarte.
Krzywe stożkowe Lekcja III: Okrąg i liczba π
 Krzywe stożkowe Lekcja III: Okrąg i liczba π Wydział Matematyki Politechniki Wrocławskiej Wzajemne położenie prostej i okręgu Istnieją trzy możliwe wzajemne położenia prostej o równaniu y = ax + b względem
Krzywe stożkowe Lekcja III: Okrąg i liczba π Wydział Matematyki Politechniki Wrocławskiej Wzajemne położenie prostej i okręgu Istnieją trzy możliwe wzajemne położenia prostej o równaniu y = ax + b względem
KONKURS PRZEDMIOTOWY Z MATEMATYKI DLA UCZNIÓW GIMNAZJUM
 pieczątka WKK Kod ucznia - - Dzień Miesiąc Rok DATA URODZENIA UCZNIA KONKURS PRZEDMIOTOWY Z MATEMATYKI DLA UCZNIÓW GIMNAZJUM ETAP WOJEWÓDZKI Drogi Uczniu Witaj na II etapie konkursu matematycznego. Przeczytaj
pieczątka WKK Kod ucznia - - Dzień Miesiąc Rok DATA URODZENIA UCZNIA KONKURS PRZEDMIOTOWY Z MATEMATYKI DLA UCZNIÓW GIMNAZJUM ETAP WOJEWÓDZKI Drogi Uczniu Witaj na II etapie konkursu matematycznego. Przeczytaj
Wymagania edukacyjne z matematyki do programu pracy z podręcznikiem Matematyka wokół nas
 Wymagania edukacyjne z matematyki do programu pracy z podręcznikiem Matematyka wokół nas klasa I 1)Działania na liczbach: dopuszczający: uczeń potrafi poprawnie wykonać cztery podstawowe działania na ułamkach
Wymagania edukacyjne z matematyki do programu pracy z podręcznikiem Matematyka wokół nas klasa I 1)Działania na liczbach: dopuszczający: uczeń potrafi poprawnie wykonać cztery podstawowe działania na ułamkach
WYMAGANIA EDUKACYJNE NA POSZCZEGÓLNE OCENY Z MATEMATYKI W KLASIE 8 SZKOŁY PODSTAWOWEJ
 WYMAGANIA EDUKACYJNE NA POSZCZEGÓLNE OCENY Z MATEMATYKI W KLASIE 8 SZKOŁY PODSTAWOWEJ 1) ocenę celującą otrzymuje uczeń, który spełnił wymagania na ocenę bardzo dobrą oraz: - umie zapisać i odczytać w
WYMAGANIA EDUKACYJNE NA POSZCZEGÓLNE OCENY Z MATEMATYKI W KLASIE 8 SZKOŁY PODSTAWOWEJ 1) ocenę celującą otrzymuje uczeń, który spełnił wymagania na ocenę bardzo dobrą oraz: - umie zapisać i odczytać w
Zadanie 2 Średnia arytmetyczna liczb: ; A) 9 B) ; x jest równa 3. Zatem x wynosi: C) 3 D) 8
 Zadanie Całkowity dochód pewnej rodziny wynosił 200zł miesięcznie. Diagram kołowy przedstawia procentowy udział poszczególnych wydatków w budżecie rodziny. Korzystając z diagramu wskaż zdanie prawdziwe
Zadanie Całkowity dochód pewnej rodziny wynosił 200zł miesięcznie. Diagram kołowy przedstawia procentowy udział poszczególnych wydatków w budżecie rodziny. Korzystając z diagramu wskaż zdanie prawdziwe
SCENARIUSZ LEKCJI. Temat: Powtórzenie wiadomości z działu: Wyrażenia algebraiczne
 Scenariusz lekcji matematyki : Wyrażenia algebraiczne kl. I gimnazjum Autor: mgr Beata Senka Nauczycielka matematyki w Zespole Szkół nr 1 w Pile SCENARIUSZ LEKCJI Temat: Powtórzenie wiadomości z działu:
Scenariusz lekcji matematyki : Wyrażenia algebraiczne kl. I gimnazjum Autor: mgr Beata Senka Nauczycielka matematyki w Zespole Szkół nr 1 w Pile SCENARIUSZ LEKCJI Temat: Powtórzenie wiadomości z działu:
wymagania programowe z matematyki kl. III gimnazjum
 wymagania programowe z matematyki kl. III gimnazjum 1. Liczby i wyrażenia algebraiczne Zna pojęcie notacji wykładniczej. Umie zapisać liczbę w notacji wykładniczej. Umie porównywać liczy zapisane w różny
wymagania programowe z matematyki kl. III gimnazjum 1. Liczby i wyrażenia algebraiczne Zna pojęcie notacji wykładniczej. Umie zapisać liczbę w notacji wykładniczej. Umie porównywać liczy zapisane w różny
MISTRZ MATEMATYKI. Test sprawdzający wiadomości uczniów pierwszej klasy gimnazjum w ramach realizacji programu Matematyka 2001.
 MISTRZ MATEMATYKI Test sprawdzający wiadomości uczniów pierwszej klasy gimnazjum w ramach realizacji programu Matematyka 00. Zakres materiału: DZIAŁANIA NA ZBIORACH LICZB RZECZYWISTYCH Wykonała: mgr Krystyna
MISTRZ MATEMATYKI Test sprawdzający wiadomości uczniów pierwszej klasy gimnazjum w ramach realizacji programu Matematyka 00. Zakres materiału: DZIAŁANIA NA ZBIORACH LICZB RZECZYWISTYCH Wykonała: mgr Krystyna
Matematyka podstawowa VII Planimetria Teoria
 Matematyka podstawowa VII Planimetria Teoria 1. Rodzaje kątów: a) Kąty wierzchołkowe; tworzą je dwie przecinające się proste, mają takie same miary. b) Kąty przyległe; mają wspólne jedno ramię, ich suma
Matematyka podstawowa VII Planimetria Teoria 1. Rodzaje kątów: a) Kąty wierzchołkowe; tworzą je dwie przecinające się proste, mają takie same miary. b) Kąty przyległe; mają wspólne jedno ramię, ich suma
TABELA ODPOWIEDZI. kod ucznia
 MAŁOPOLSKI KONKURS MATEMATYCZNY dla uczniów dotychczasowych gimnazjów i klas dotychczasowych gimnazjów prowadzonych w szkołach innego typu województwa małopolskiego Rok szkolny 018/019 ETAP SZKOLNY 5 października
MAŁOPOLSKI KONKURS MATEMATYCZNY dla uczniów dotychczasowych gimnazjów i klas dotychczasowych gimnazjów prowadzonych w szkołach innego typu województwa małopolskiego Rok szkolny 018/019 ETAP SZKOLNY 5 października
ZESTAWY PYTAŃ NA USTNY EGZAMIN SEMESTRALNY Z MATEMATYKI SEMESTR I
 ZESTAWY PYTAŃ NA USTNY EGZAMIN SEMESTRALNY Z MATEMATYKI SEMESTR I I 1. Co to jest ułamek? Jakie znasz rodzaje ułamków? 2. Kiedy dwa odcinki są do siebie równoległe? 3. Kiedy dwie figury nazywamy przystającymi?
ZESTAWY PYTAŃ NA USTNY EGZAMIN SEMESTRALNY Z MATEMATYKI SEMESTR I I 1. Co to jest ułamek? Jakie znasz rodzaje ułamków? 2. Kiedy dwa odcinki są do siebie równoległe? 3. Kiedy dwie figury nazywamy przystającymi?
ZAGADNIENIA NA EGZAMIN POPRAWKOWY Z MATEMATYKI W KLASIE III TECHNIKUM.
 ZAGADNIENIA NA EGZAMIN POPRAWKOWY Z MATEMATYKI W KLASIE III TECHNIKUM. I. Trygonometria. 1. Definicje funkcji trygonometrycznych kąta ostrego w trójkącie prostokątnym. 2. Rozwiązywanie trójkątów prostokątnych
ZAGADNIENIA NA EGZAMIN POPRAWKOWY Z MATEMATYKI W KLASIE III TECHNIKUM. I. Trygonometria. 1. Definicje funkcji trygonometrycznych kąta ostrego w trójkącie prostokątnym. 2. Rozwiązywanie trójkątów prostokątnych
OKREŚLENIE WYMAGAŃ NA POSZCZEGÓLNE OCENY Z MATEMATYKI DLA UCZNIÓW GIMNAZJUM
 OKREŚLENIE WYMAGAŃ NA POSZCZEGÓLNE OCENY Z MATEMATYKI DLA UCZNIÓW GIMNAZJUM (założone osiągnięcia ucznia w klasach I III gimnazjum zgodnie z programem nauczania Matematyka z plusem (DPN-5002-17/08) realizującym
OKREŚLENIE WYMAGAŃ NA POSZCZEGÓLNE OCENY Z MATEMATYKI DLA UCZNIÓW GIMNAZJUM (założone osiągnięcia ucznia w klasach I III gimnazjum zgodnie z programem nauczania Matematyka z plusem (DPN-5002-17/08) realizującym
WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLAS IA I IB NA ROK SZKOLNY 2014/2015
 WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLAS IA I IB NA ROK SZKOLNY 2014/2015 UŁAMKI ZWYKŁE I DZIESIĘTNE Rozpoznaje ułamki właściwe i niewłaściwe Rozszerza ułamek zwykły Skraca ułamek zwykły Zapisuje ułamek
WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLAS IA I IB NA ROK SZKOLNY 2014/2015 UŁAMKI ZWYKŁE I DZIESIĘTNE Rozpoznaje ułamki właściwe i niewłaściwe Rozszerza ułamek zwykły Skraca ułamek zwykły Zapisuje ułamek
Pomiar pól wielokątów nieregularnych w terenie.
 Pomiar pól wielokątów nieregularnych w terenie. Czas trwania zajęć: 45 minut Kontekst w jakim wprowadzono doświadczenie: Pierwsza część zajęć odbywa się w terenie (boisko szkolne lub inny teren o nieutwardzonej
Pomiar pól wielokątów nieregularnych w terenie. Czas trwania zajęć: 45 minut Kontekst w jakim wprowadzono doświadczenie: Pierwsza część zajęć odbywa się w terenie (boisko szkolne lub inny teren o nieutwardzonej
Dydaktyka matematyki (II etap edukacyjny) II rok matematyki Semestr letni 2016/2017 Ćwiczenia nr 9
 Dydaktyka matematyki (II etap edukacyjny) II rok matematyki Semestr letni 2016/2017 Ćwiczenia nr 9 Karta pracy: podzielność przez 9 Niektóre są dobre, z drobnymi usterkami. Największy błąd: nie ma sformułowanej
Dydaktyka matematyki (II etap edukacyjny) II rok matematyki Semestr letni 2016/2017 Ćwiczenia nr 9 Karta pracy: podzielność przez 9 Niektóre są dobre, z drobnymi usterkami. Największy błąd: nie ma sformułowanej
Blok V: Ciągi. Różniczkowanie i całkowanie. c) c n = 1 ( 1)n n. d) a n = 1 3, a n+1 = 3 n a n. e) a 1 = 1, a n+1 = a n + ( 1) n
 V. Napisz 4 początkowe wyrazy ciągu: Blok V: Ciągi. Różniczkowanie i całkowanie a) a n = n b) a n = n + 3 n! c) a n = n! n(n + ) V. Oblicz (lub zapisz) c, c 3, c k, c n k dla: a) c n = 3 n b) c n = 3n
V. Napisz 4 początkowe wyrazy ciągu: Blok V: Ciągi. Różniczkowanie i całkowanie a) a n = n b) a n = n + 3 n! c) a n = n! n(n + ) V. Oblicz (lub zapisz) c, c 3, c k, c n k dla: a) c n = 3 n b) c n = 3n
KONKURS MATEMATYCZNY
 PAŃSTWOWA WYŻSZA SZKOŁA ZAWODOWA W CHEŁMIE INSTYTUT MATEMATYKI i INFORMATYKI 22-100 Chełm, ul. Pocztowa 54 tel./fax. (082) 562 11 24 KONKURS MATEMATYCZNY im. Samuela Chróścikowskiego 30 marzec 2017r. godz.
PAŃSTWOWA WYŻSZA SZKOŁA ZAWODOWA W CHEŁMIE INSTYTUT MATEMATYKI i INFORMATYKI 22-100 Chełm, ul. Pocztowa 54 tel./fax. (082) 562 11 24 KONKURS MATEMATYCZNY im. Samuela Chróścikowskiego 30 marzec 2017r. godz.
WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE DRUGIEJ GIMNAZJUM w roku szkolnym 2015/2016
 WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE DRUGIEJ GIMNAZJUM w roku szkolnym 2015/2016 Dział Na ocenę dopuszczającą Na ocenę dostateczną Na ocenę dobrą POTĘGI PIERWIASTKI Uczeń: zna i rozumie pojęcie o
WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE DRUGIEJ GIMNAZJUM w roku szkolnym 2015/2016 Dział Na ocenę dopuszczającą Na ocenę dostateczną Na ocenę dobrą POTĘGI PIERWIASTKI Uczeń: zna i rozumie pojęcie o
Maria Romanowska UDOWODNIJ, ŻE... PRZYKŁADOWE ZADANIA MATURALNE Z MATEMATYKI
 Maria Romanowska UDOWODNIJ, ŻE... PRZYKŁADOWE ZADANIA MATURALNE Z MATEMATYKI Matematyka dla liceum ogólnokształcącego i technikum w zakresie podstawowym i rozszerzonym Z E S Z Y T M E T O D Y C Z N Y Miejski
Maria Romanowska UDOWODNIJ, ŻE... PRZYKŁADOWE ZADANIA MATURALNE Z MATEMATYKI Matematyka dla liceum ogólnokształcącego i technikum w zakresie podstawowym i rozszerzonym Z E S Z Y T M E T O D Y C Z N Y Miejski
MATURA Przygotowanie do matury z matematyki
 MATURA 2012 Przygotowanie do matury z matematyki Część VII: Planimetria ROZWIĄZANIA Powtórka jest organizowana przez redaktorów portalu MatmaNa6.pl we współpracy z dziennikarzami Gazety Lubuskiej. Witaj,
MATURA 2012 Przygotowanie do matury z matematyki Część VII: Planimetria ROZWIĄZANIA Powtórka jest organizowana przez redaktorów portalu MatmaNa6.pl we współpracy z dziennikarzami Gazety Lubuskiej. Witaj,
Wymagania edukacyjne z matematyki w klasie IV
 Wymagania edukacyjne z matematyki w klasie IV Na ocenę dopuszczającą uczeń potrafi: Dodawać i odejmować w pamięci liczby dwucyfrowe. Obliczyć wartości wyrażeń arytmetycznych z zachowaniem kolejności wykonywania
Wymagania edukacyjne z matematyki w klasie IV Na ocenę dopuszczającą uczeń potrafi: Dodawać i odejmować w pamięci liczby dwucyfrowe. Obliczyć wartości wyrażeń arytmetycznych z zachowaniem kolejności wykonywania
KONKURS PRZEDMIOTOWY Z MATEMATYKI DLA UCZNIÓW GIMNAZJUM
 KONKURS PRZEDMIOTOWY Z MATEMATYKI DLA UCZNIÓW GIMNAZJUM Klucz odpowiedzi do ETAPU WOJEWÓDZKIEGO Zadania zamknięte: Nr zadania 3 4 5 6 7 8 9 0 Poprawna odpowiedź D C B A C C B D C A Zadania otwarte:. Zadania
KONKURS PRZEDMIOTOWY Z MATEMATYKI DLA UCZNIÓW GIMNAZJUM Klucz odpowiedzi do ETAPU WOJEWÓDZKIEGO Zadania zamknięte: Nr zadania 3 4 5 6 7 8 9 0 Poprawna odpowiedź D C B A C C B D C A Zadania otwarte:. Zadania
MMC TALES Konkurs Matematyczny MERIDIAN
 A MMC TALES Konkurs Matematyczny MERIDIAN Sobota, 26 stycznia 2008 Czas pracy: 75 minut Maksymalna liczba punktów do uzyskania: 120 W czasie testu nie wolno używać kalkulatorów ani innych pomocy naukowych.
A MMC TALES Konkurs Matematyczny MERIDIAN Sobota, 26 stycznia 2008 Czas pracy: 75 minut Maksymalna liczba punktów do uzyskania: 120 W czasie testu nie wolno używać kalkulatorów ani innych pomocy naukowych.
Rozwijanie uzdolnień matematycznych uczniów. semestr letni, 2018/2019 wykład nr 4
 Rozwijanie uzdolnień matematycznych uczniów semestr letni, 2018/2019 wykład nr 4 Przekształcenia zadań Dwa wyróżnienia: D.T. (za księżyce Hipokratesa), B.S. (za ładne zadanie patrz zadanie domowe). Bardzo
Rozwijanie uzdolnień matematycznych uczniów semestr letni, 2018/2019 wykład nr 4 Przekształcenia zadań Dwa wyróżnienia: D.T. (za księżyce Hipokratesa), B.S. (za ładne zadanie patrz zadanie domowe). Bardzo
nazwa zadania/ nr grupy realizowanych w Publicznym Gimnazjum w Janowcu Wielkopolskim nazwa i adres szkoły
 88-430 Janowiec Wielkopolski, pokój nr, tel. 5 30 3 034 wew. 4 PROGRAM TEMATYCZNY ZAJĘĆ ZAJĘCIA ROZWIJAJĄCE Z MATEMATYKI/GRUPA nazwa zadania/ nr grupy realizowanych w Publicznym Gimnazjum w Janowcu Wielkopolskim
88-430 Janowiec Wielkopolski, pokój nr, tel. 5 30 3 034 wew. 4 PROGRAM TEMATYCZNY ZAJĘĆ ZAJĘCIA ROZWIJAJĄCE Z MATEMATYKI/GRUPA nazwa zadania/ nr grupy realizowanych w Publicznym Gimnazjum w Janowcu Wielkopolskim
GIMNAZJUM Wymagania edukacyjne z matematyki na poszczególne oceny półroczne i roczne w roku szkolnym
 GIMNAZJUM Wymagania edukacyjne z matematyki na poszczególne oceny półroczne i roczne w roku szkolnym 2013-2014 Ocenę celującą otrzymuje uczeń, który: wykorzystuje na lekcjach matematyki wiadomości z innych
GIMNAZJUM Wymagania edukacyjne z matematyki na poszczególne oceny półroczne i roczne w roku szkolnym 2013-2014 Ocenę celującą otrzymuje uczeń, który: wykorzystuje na lekcjach matematyki wiadomości z innych
SEMESTRALNE BADANIE WYNIKÓW NAUCZANIA MATEMATYKI W KLASACH III. Kartoteka testu. Nr zad Czynność ucznia Kategoria celów
 SEMESTRALNE BADANIE WYNIKÓW NAUCZANIA MATEMATYKI W KLASACH III Kartoteka testu Nr zad Czynność ucznia Kategoria celów Poziom wymagań Porównuje liczby wymierne i wskazuje prawidłową odpowiedź B P Oblicza
SEMESTRALNE BADANIE WYNIKÓW NAUCZANIA MATEMATYKI W KLASACH III Kartoteka testu Nr zad Czynność ucznia Kategoria celów Poziom wymagań Porównuje liczby wymierne i wskazuje prawidłową odpowiedź B P Oblicza
KONKURS MATEMATYCZNY DLA UCZNIÓW GIMNAZJUM ETAP WOJEWÓDZKI
 Kod ucznia - - Dzień Miesiąc Rok pieczątka WKK DATA URODZENIA UCZNIA KONKURS MATEMATYCZNY DLA UCZNIÓW GIMNAZJUM ETAP WOJEWÓDZKI Drogi Uczniu Witaj na III etapie konkursu matematycznego. Przeczytaj uważnie
Kod ucznia - - Dzień Miesiąc Rok pieczątka WKK DATA URODZENIA UCZNIA KONKURS MATEMATYCZNY DLA UCZNIÓW GIMNAZJUM ETAP WOJEWÓDZKI Drogi Uczniu Witaj na III etapie konkursu matematycznego. Przeczytaj uważnie
WOJEWÓDZKI KONKURS MATEMATYCZNY dla uczniów gimnazjów i oddziałów gimnazjalnych województwa pomorskiego w roku szkolnym 2018/2019 etap wojewódzki
 WOJEWÓDZKI KONKURS MATEMATYCZNY dla uczniów gimnazjów i oddziałów gimnazjalnych województwa pomorskiego w roku szkolnym 2018/2019 etap wojewódzki Zad.1. (0-3) PRZYKŁADOWE ROZWIĄZANIA I KRYTERIA OCENIANIA
WOJEWÓDZKI KONKURS MATEMATYCZNY dla uczniów gimnazjów i oddziałów gimnazjalnych województwa pomorskiego w roku szkolnym 2018/2019 etap wojewódzki Zad.1. (0-3) PRZYKŁADOWE ROZWIĄZANIA I KRYTERIA OCENIANIA
KRYTERIA OCEN Z MATEMATYKI DLA UCZNIÓW KL. II GIMNAZJUM
 KRYTERIA OCEN Z MATEMATYKI DLA UCZNIÓW KL. II GIMNAZJUM POTĘGI I PIERWIASTKI - pojęcie potęgi o wykładniku naturalnym; - wzór na mnożenie i dzielenie potęg o tych samych podstawach; - wzór na potęgowanie
KRYTERIA OCEN Z MATEMATYKI DLA UCZNIÓW KL. II GIMNAZJUM POTĘGI I PIERWIASTKI - pojęcie potęgi o wykładniku naturalnym; - wzór na mnożenie i dzielenie potęg o tych samych podstawach; - wzór na potęgowanie
WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE DRUGIEJ GIMNAZJUM. rok szkolny 2016/2017
 WYMAGANIA EDUKACYJNE Z MAYKI W KLASIE DRUGIEJ GIMNAZJUM rok szkolny 2016/2017 POZIOMY WYMAGAŃ EDUKACYJNYCH: K konieczny - ocena dopuszczająca (2) P podstawowy - ocena dostateczna (3) R rozszerzający -
WYMAGANIA EDUKACYJNE Z MAYKI W KLASIE DRUGIEJ GIMNAZJUM rok szkolny 2016/2017 POZIOMY WYMAGAŃ EDUKACYJNYCH: K konieczny - ocena dopuszczająca (2) P podstawowy - ocena dostateczna (3) R rozszerzający -
Twierdzenie Pitagorasa
 Imię Nazwisko: Paweł Rogaliński Nr indeksu: 123456 Grupa: wtorek 7:30 Data: 10-10-2012 Twierdzenie Pitagorasa Tekst artykułu jest skrótem artykułu Twierdzenie Pitagorasa zamieszczonego w polskiej edycji
Imię Nazwisko: Paweł Rogaliński Nr indeksu: 123456 Grupa: wtorek 7:30 Data: 10-10-2012 Twierdzenie Pitagorasa Tekst artykułu jest skrótem artykułu Twierdzenie Pitagorasa zamieszczonego w polskiej edycji
Osiągnięcia ponadprzedmiotowe
 W rezultacie kształcenia matematycznego uczeń potrafi: Osiągnięcia ponadprzedmiotowe Umiejętności konieczne i podstawowe czytać teksty w stylu matematycznym wykorzystywać słownictwo wprowadzane przy okazji
W rezultacie kształcenia matematycznego uczeń potrafi: Osiągnięcia ponadprzedmiotowe Umiejętności konieczne i podstawowe czytać teksty w stylu matematycznym wykorzystywać słownictwo wprowadzane przy okazji
