Matematyczne aspekty rozszyfrowania Enigmy
|
|
|
- Seweryna Górecka
- 6 lat temu
- Przeglądów:
Transkrypt
1 Uniwersytet Jagielloński Wydział Matematyki i Informatyki Instytut Matematyki Kraków, 2003 Matematyczne aspekty rozszyfrowania Enigmy Zbigniew Błocki
2 Marian Rejewski ( )
3 15 VII armia niemiecka wprowadza Enigmy do użytku 1928/29 - kurs kryptologii w Instytucie Matematyki Uniwersytetu Poznańskiego zorganizowany przez Biuro Szyfrów Oddziału II Sztabu Głównego 1 IX Biuro Szyfrów w Warszawie zatrudnia Mariana Rejewskiego, Jerzego Różyckiego i Henryka Zygalskiego; początek prac nad złamaniem kodu Enigmy
4
5 Grupa permutacji I n = {1, 2,..., n} (n = 26, I n = {a, b,..., x, y, z}) S n = {A : I n I n - bijekcja} - grupa nieprzemienna (z działaniem AB = A B). Każdy element A S n posiada element odwrotny A 1 AA 1 = A 1 A = id, (AB) 1 = B 1 A 1. Jeżeli a 1,..., a k I n, a i a j dla i j, to przez (a 1 a 2... a k ) oznaczamy cykl długości k a 1 a 2... a k a 1. Każdą permutację można przedstawić jako złożenie cykli rozłącznych A = (a 1... a k )(b 1... b l )...
6 Konstrukcja i działanie Enigmy S Klawiatura I II III R = R Lampki 1 S 1 I 1 II 1 III 1 S = (a 1 b 1 )... (a 6 b 6 ) = S 1 - połączenia wtyczkowe Zakładając, że obraca się tylko pierwszy wirnik (25 na 26 razy), mamy I =P α+1 NP α 1, II =P β MP β, III =P γ LP γ, gdzie α, β, γ {1, 2,..., 26} - ustawienie wirników, P = (1, ) - obrót o 1/26 pełnego kąta, N, M, L, R - połączenia wewnętrzne wirników (identyczne we wszystkich Enigmach danej sieci).
7 N, M, L 26! R 26! !213 α, β, γ 3! S 26! 6!14!
8 Sposób szyfrowania depesz (1932 r.) S, α, β, γ - klucz dzienny (wg. księgi szyfrów) α, β, γ - klucz depeszy (wybierany przez szyfranta) Początek każdej depeszy miał postać A 1 (α), A 2 (β), A 3 (γ), A 4 (α), A 5 (β), A 6 (γ), przy czym permutacje A 1,..., A 6 były stałe danego dnia (A 1 i = A i, tzn. A i składają się z transpozycji rozłącznych). Posiadając odp. ilość zaszyfrowanych depesz z danego dnia (ok. 80) można odtworzyć permutacje A i+3 A 1 i = A i+3 A i, i = 1, 2, 3.
9 Odtworzenie kluczy depesz (jesień 1932) Permutacje A i+3 A i miały zawsze następującą własność cykle danej długości występują ( ) w liczbie parzystej Twierdzenie. X S 2m spełnia ( ) wtedy i tylko wtedy, gdy istnieją A, B S 2m takie, że A = A 1, B = B 1 oraz X = AB.
10 Algorytm znajdowania A, B (zakładając, że znamy iloczyn AB spełniający ( )): - Cykle danej długości grupujemy w pary; - Dla danej pary cykli długości k mamy dokł. k możliwości: (a 1... a k )(b 1... b k ) =(a k b l )(a k 1 b l 1 )... (a 1 b l+1 ) (a k b l 1 )(a k 1 b l 2 )... (a 1 b l ) - Do wyboru właściwych permutacji A i z ok. kilku tysięcy możliwych rozwiązań wykorzystywano nawyki szyfrantów (np. wybieranie trzech takich samych liter jako kluczy depesz).
11 Konstrukcja i działanie Enigmy S Klawiatura I II III R = R Lampki 1 S 1 I 1 II 1 III 1 S = (a 1 b 1 )... (a 6 b 6 ) = S 1 - połączenia wtyczkowe Zakładając, że obraca się tylko pierwszy wirnik (25 na 26 razy), mamy I =P α+1 NP α 1, II =P β MP β, III =P γ LP γ, gdzie α, β, γ {1, 2,..., 26} - ustawienie wirników, P = (1, ) - obrót o 1/26 pełnego kąta, N, M, L, R - połączenia wewnętrzne wirników (identyczne we wszystkich Enigmach danej sieci).
12 Odtworzenie połączeń wewnętrznych Zakładając, że obraca się tylko pierwszy wirnik (20 na 26 razy), mamy gdzie A i = S 1 P α+i N 1 P α i QP α+i NP α i S, i = 1,..., 6, Q = P β M 1 P β+γ L 1 P γ RP γ LP γ+β MP β. Mamy zatem układ 6 równań z 4 niewiadomymi S, N, Q, α. Przełom: 9 XII 1932 Rejewski otrzymuje przekazane przez wywiad francuski (Gustave Bertrand) klucze dzienne za wrzesień i październik 1932 r.
13 U i = N 1 P α i QP α+i N, i = 1,..., 6 U i+1 U i+2 = (N 1 P N)U i U i+1 (N 1 P N) 1, i = 1,..., 4. Obserwacja. Jeżeli ( ) A= =(a A(1)... A(26) 1... a k )(b 1... b l )..., to XAX 1 = ( ) X(1)... X(26) X(A(1))... X(A(26)) = (X(a 1 )... X(a k ))(X(b 1 )... X(b l ))...
14 Wniosek. Równanie XAX 1 = B ma rozwiązanie X wtedy i tylko wtedy, gdy permutacje A i B są podobne (tzn. zbiór długości cykli rozłącznych jest taki sam).
15 H Klawiatura S I II III R = R Lampki 1 H 1 S 1 I 1 II 1 III 1 H = H = ( q v e r t z )... a b c d e f... ( a b c d e f )... a b c d e f... (w Enigmie handl.) (w Enigmie wojsk.)!
16 Odczytywanie depesz ( ) - wykonanie replik Enigmy przez warszawską firmę AVA; - metoda rusztu (wykorzystująca fakt, że permutacja S nie zmienia 14 z 26 znaków); - skatalogowanie długości cykli permutacji A i+3 A i w zależności od α, β, γ przy pomocy specjalnie skonstruowanego urządzenia zwanego cyklometrem (permutacje te są postaci S 1... S, zatem długości ich cykli nie zależą od S).
17 styczeń kod Enigmy złamany! liczne zmiany w Enigmach: zwiększenie liczby wirników oraz liczby połączeń wtyczkowych, częstsze zmiany kodów, itd. początek Polacy odczytują 75% depesz niemieckich 15 IX zasadnicza zmiana sposobu szyfrowania konstrukcja bomby kryptologicznej (ang. bombe) oraz płacht Zygalskiego VII spotkanie z Brytyjczykami i Francuzami w Warszawie Amerykanie łamią japoński kod Purple Brytyjczycy konstruują maszynę Colossus książka F.Winterbothama The Ultra Secret??? - Anglicy przyznają, że to nie oni złamali Enigmę
18
19
Temat: Marian Adam Rejewski Człowiek, który rozszyfrował Enigmę.
 Temat: Marian Adam Rejewski Człowiek, który rozszyfrował Enigmę. Paca zaliczeniowa na kolokwium z przedmiotu Informatyka. Źródło informacji: http://pl.wikipedia.org/wiki/marian_rejewski Łódź, 17-11-2013
Temat: Marian Adam Rejewski Człowiek, który rozszyfrował Enigmę. Paca zaliczeniowa na kolokwium z przedmiotu Informatyka. Źródło informacji: http://pl.wikipedia.org/wiki/marian_rejewski Łódź, 17-11-2013
Polacy którzy złamali enigmę
 Polacy którzy złamali enigmę Czym jest Enigma? P o c h o d z e n i e i z a s a d a d z i a ł a n i a Człowiek a maszyna Pod koniec I wojny światowej kryptolodzy znali i potrafili skutecznie złamać wszystkie
Polacy którzy złamali enigmę Czym jest Enigma? P o c h o d z e n i e i z a s a d a d z i a ł a n i a Człowiek a maszyna Pod koniec I wojny światowej kryptolodzy znali i potrafili skutecznie złamać wszystkie
Matematyczna podróż w głąb Enigmy
 Matematyczna podróż w głąb Enigmy Przemysław Biecek 1 Teresa Jurlewicz 2 1 IM PAN, BioTech UWr, 2 IMiI PWr 22 lutego 2008 Szyfr Skytale Skytale to jedna z najstarszych metod szyfrowania. Używana w starożytnej
Matematyczna podróż w głąb Enigmy Przemysław Biecek 1 Teresa Jurlewicz 2 1 IM PAN, BioTech UWr, 2 IMiI PWr 22 lutego 2008 Szyfr Skytale Skytale to jedna z najstarszych metod szyfrowania. Używana w starożytnej
Tajna wiadomość. Scenariusz lekcji
 1 scenariusz 1 CELE OGÓLNE poznanie metod szyfrowania wiadomości zrozumienie algorytmu szyfru Cezara Tajna wiadomość Scenariusz lekcji CELE SZCZEGÓŁOWE Uczeń: Zapamiętanie wiadomości (A): wymienia podstawowe
1 scenariusz 1 CELE OGÓLNE poznanie metod szyfrowania wiadomości zrozumienie algorytmu szyfru Cezara Tajna wiadomość Scenariusz lekcji CELE SZCZEGÓŁOWE Uczeń: Zapamiętanie wiadomości (A): wymienia podstawowe
Enigma. Odszyfrować Zwycięstwo Specyfikacja techniczna wystawy
 Specyfikacja techniczna wystawy Tablice Tablice 23 tablice wykonane z komatexu o grubości 4mm, wydruk grafiki wykonany bezpośrednio na komatexie. Każda tablica ma wymiary 1405x2000mm. Wersja anglojęzyczna.
Specyfikacja techniczna wystawy Tablice Tablice 23 tablice wykonane z komatexu o grubości 4mm, wydruk grafiki wykonany bezpośrednio na komatexie. Każda tablica ma wymiary 1405x2000mm. Wersja anglojęzyczna.
Szymon Dąbrowski. Kurs kryptologii - scenariusz zajęć dodatkowych. Przedział wiekowy uczestników: lat Zakładany czas: 45 minut
 Kurs kryptologii - scenariusz zajęć dodatkowych Szymon Dąbrowski Przedział wiekowy uczestników: 14-18 lat Zakładany czas: 45 minut Temat: Śladami pogromców Enigmy 1. Główne zagadnienia zajęć: 2. Cele zajęć
Kurs kryptologii - scenariusz zajęć dodatkowych Szymon Dąbrowski Przedział wiekowy uczestników: 14-18 lat Zakładany czas: 45 minut Temat: Śladami pogromców Enigmy 1. Główne zagadnienia zajęć: 2. Cele zajęć
Jak polscy matematycy złamali Enigmę
 Jak polscy matematycy złamali Enigmę Adam Doliwa doliwa@matman.uwm.edu.pl WYDZIAŁ MATEMATYKI I INFORMATYKI UWM Olsztyn, 8 lutego 2013 r. Adam Doliwa (UWM) Rejewski 8-II-2013 1 / 22 Podczas XXVI Sesji Rady
Jak polscy matematycy złamali Enigmę Adam Doliwa doliwa@matman.uwm.edu.pl WYDZIAŁ MATEMATYKI I INFORMATYKI UWM Olsztyn, 8 lutego 2013 r. Adam Doliwa (UWM) Rejewski 8-II-2013 1 / 22 Podczas XXVI Sesji Rady
Gratulujemy udziału w etapie rejonowym Wojewódzkiego Interdyscyplinarnego Konkursu o Wielkich Polakach pod hasłem: Bohater Polski Niepodległej
 Gratulujemy udziału w etapie rejonowym Wojewódzkiego Interdyscyplinarnego Konkursu o Wielkich Polakach pod hasłem: Bohater Polski Niepodległej Marian Rejewski życie, dzieło i pamięć na tle historii Polski
Gratulujemy udziału w etapie rejonowym Wojewódzkiego Interdyscyplinarnego Konkursu o Wielkich Polakach pod hasłem: Bohater Polski Niepodległej Marian Rejewski życie, dzieło i pamięć na tle historii Polski
Złamanie szyfru Enigmy przy użyciu teorii permutacji
 Instytut Matematyki Wydział Matematyki i Informatyki Uniwersytet Jagielloński Złamanie szyfru Enigmy przy użyciu teorii permutacji Joanna Wąsik Praca magisterska pod kierunkiem prof. dr. hab. Zbigniewa
Instytut Matematyki Wydział Matematyki i Informatyki Uniwersytet Jagielloński Złamanie szyfru Enigmy przy użyciu teorii permutacji Joanna Wąsik Praca magisterska pod kierunkiem prof. dr. hab. Zbigniewa
Od złamania Enigmy do współczesnej kryptologii
 Od złamania Enigmy do współczesnej kryptologii Jerzy Gawinecki Instytut Matematyki i Kryptologii, Wydział Cybernetyki Wojskowa Akademia Techniczna jgawinecki@wat.edu.pl < 154 > Informatyka + Wszechnica
Od złamania Enigmy do współczesnej kryptologii Jerzy Gawinecki Instytut Matematyki i Kryptologii, Wydział Cybernetyki Wojskowa Akademia Techniczna jgawinecki@wat.edu.pl < 154 > Informatyka + Wszechnica
UCHWAŁA NR XV/250/11 SEJMIKU WOJEWÓDZTWA KUJAWSKO-POMORSKIEGO z dnia 28 listopada 2011 r.
 UCHWAŁA NR XV/250/11 SEJMIKU WOJEWÓDZTWA KUJAWSKO-POMORSKIEGO z dnia 28 listopada 2011 r. w sprawie nadania imienia Pedagogicznej Bibliotece Wojewódzkiej w Bydgoszczy Na podstawie art. 18 pkt 20 ustawy
UCHWAŁA NR XV/250/11 SEJMIKU WOJEWÓDZTWA KUJAWSKO-POMORSKIEGO z dnia 28 listopada 2011 r. w sprawie nadania imienia Pedagogicznej Bibliotece Wojewódzkiej w Bydgoszczy Na podstawie art. 18 pkt 20 ustawy
Wszechnica Popołudniowa: Tendencje w rozwoju informatyki i jej zastosowań Od złamania Enigmy do współczesnej kryptologii.
 Wszechnica Popołudniowa: Tendencje w rozwoju informatyki i jej zastosowań Od złamania Enigmy do współczesnej kryptologii Jerzy Gawinecki Od złamania Enigmy do współczesnej kryptologii Rodzaj zajęć: Wszechnica
Wszechnica Popołudniowa: Tendencje w rozwoju informatyki i jej zastosowań Od złamania Enigmy do współczesnej kryptologii Jerzy Gawinecki Od złamania Enigmy do współczesnej kryptologii Rodzaj zajęć: Wszechnica
Macierze - obliczanie wyznacznika macierzy z użyciem permutacji
 Macierze - obliczanie wyznacznika macierzy z użyciem permutacji I LO im. F. Ceynowy w Świeciu Radosław Rudnicki joix@mat.uni.torun.pl 17.03.2009 r. Typeset by FoilTEX Streszczenie Celem wykładu jest wprowadzenie
Macierze - obliczanie wyznacznika macierzy z użyciem permutacji I LO im. F. Ceynowy w Świeciu Radosław Rudnicki joix@mat.uni.torun.pl 17.03.2009 r. Typeset by FoilTEX Streszczenie Celem wykładu jest wprowadzenie
TAJEMNICE ENIGMY" STANISŁAW PORTALSKI. i w końcu w lotnictwie (1933 r.). W ten sposób Niemcy wprowadzili maszynę szyfrową, której szyfr był
 STANISŁAW PORTALSKI Prof. dr inż. Stanisław PortaIski urodził się w Starej Białej koło Płocka w 1920 r. Przed wybuchem II wojny światowej w 1939 r. ukończył z wyróżnieniem Gimnazjum i Liceum im. Władysława
STANISŁAW PORTALSKI Prof. dr inż. Stanisław PortaIski urodził się w Starej Białej koło Płocka w 1920 r. Przed wybuchem II wojny światowej w 1939 r. ukończył z wyróżnieniem Gimnazjum i Liceum im. Władysława
Grupy. Permutacje 1. (G2) istnieje element jednostkowy (lub neutralny), tzn. taki element e G, że dla dowolnego a G zachodzi.
 Grupy. Permutacje 1 1 Definicja grupy Niech G będzie zbiorem. Działaniem na zbiorze G nazywamy odwzorowanie (oznaczane, jak mnożenie, przez ) przyporządkowujące każdej parze uporządkowanej (a, b) G G element
Grupy. Permutacje 1 1 Definicja grupy Niech G będzie zbiorem. Działaniem na zbiorze G nazywamy odwzorowanie (oznaczane, jak mnożenie, przez ) przyporządkowujące każdej parze uporządkowanej (a, b) G G element
Zastosowanie teorii liczb w kryptografii na przykładzie szyfru RSA
 Zastosowanie teorii liczb w kryptografii na przykładzie szyfru RSA Grzegorz Bobiński Uniwersytet Mikołaja Kopernika Toruń, 22.05.2010 Kodowanie a szyfrowanie kodowanie sposoby przesyłania danych tak, aby
Zastosowanie teorii liczb w kryptografii na przykładzie szyfru RSA Grzegorz Bobiński Uniwersytet Mikołaja Kopernika Toruń, 22.05.2010 Kodowanie a szyfrowanie kodowanie sposoby przesyłania danych tak, aby
Sprawozdanie w ramach projektu: Informatyka mój sposób na poznanie i opisanie świata na temat przetwarzania rozproszonego projekt BOINC: Enigma@home
 Sprawozdanie w ramach projektu: Informatyka mój sposób na poznanie i opisanie świata na temat przetwarzania rozproszonego projekt BOINC: Enigma@home Projekt współfinansowany przez Unię Europejską w ramach
Sprawozdanie w ramach projektu: Informatyka mój sposób na poznanie i opisanie świata na temat przetwarzania rozproszonego projekt BOINC: Enigma@home Projekt współfinansowany przez Unię Europejską w ramach
Macierze. Rozdział Działania na macierzach
 Rozdział 5 Macierze Funkcję, która każdej parze liczb naturalnych (i, j) (i 1,..., n; j 1,..., m) przyporządkowuje dokładnie jedną liczbę a ij F, gdzie F R lub F C, nazywamy macierzą (rzeczywistą, gdy
Rozdział 5 Macierze Funkcję, która każdej parze liczb naturalnych (i, j) (i 1,..., n; j 1,..., m) przyporządkowuje dokładnie jedną liczbę a ij F, gdzie F R lub F C, nazywamy macierzą (rzeczywistą, gdy
Zarys algorytmów kryptograficznych
 Zarys algorytmów kryptograficznych Laboratorium: Algorytmy i struktury danych Spis treści 1 Wstęp 1 2 Szyfry 2 2.1 Algorytmy i szyfry........................ 2 2.2 Prosty algorytm XOR......................
Zarys algorytmów kryptograficznych Laboratorium: Algorytmy i struktury danych Spis treści 1 Wstęp 1 2 Szyfry 2 2.1 Algorytmy i szyfry........................ 2 2.2 Prosty algorytm XOR......................
KALENDARIUM ŻYCIA I DZIAŁALNOŚCI MARIANA REJEWSKIEGO NA TLE WYDARZEŃ ZWIĄZANYCH Z HISTORIĄ MASZYNY SZYFRUJĄCEJ ENIGMA
 Jerzy Lelwic * KALENDARIUM ŻYCIA I DZIAŁALNOŚCI MARIANA REJEWSKIEGO NA TLE WYDARZEŃ ZWIĄZANYCH Z HISTORIĄ MASZYNY SZYFRUJĄCEJ ENIGMA 1905 1923 okres bydgoski 16.08.1905 narodziny Mariana Adama Rejewskiego,
Jerzy Lelwic * KALENDARIUM ŻYCIA I DZIAŁALNOŚCI MARIANA REJEWSKIEGO NA TLE WYDARZEŃ ZWIĄZANYCH Z HISTORIĄ MASZYNY SZYFRUJĄCEJ ENIGMA 1905 1923 okres bydgoski 16.08.1905 narodziny Mariana Adama Rejewskiego,
Matematyczna podróż w głąb Enigmy
 Barbara Roszkowska Lech Matematyczna podróż w głąb Enigmy MATEMATYKA LA CIEKAWYCH ŚWIATA Kryptologia Steganografia (steganos- zakryty) zajmuje się ukrywaniem istnienia wiadomości Kryptografia (kryptos)
Barbara Roszkowska Lech Matematyczna podróż w głąb Enigmy MATEMATYKA LA CIEKAWYCH ŚWIATA Kryptologia Steganografia (steganos- zakryty) zajmuje się ukrywaniem istnienia wiadomości Kryptografia (kryptos)
Teoria liczb. Magdalena Lemańska. Magdalena Lemańska,
 Teoria liczb Magdalena Lemańska Literatura Matematyka Dyskretna Andrzej Szepietowski http://wazniak.mimuw.edu.pl/ Discrete Mathematics Seymour Lipschutz, Marc Lipson Wstęp Teoria liczb jest dziedziną matematyki,
Teoria liczb Magdalena Lemańska Literatura Matematyka Dyskretna Andrzej Szepietowski http://wazniak.mimuw.edu.pl/ Discrete Mathematics Seymour Lipschutz, Marc Lipson Wstęp Teoria liczb jest dziedziną matematyki,
Wstęp...str.3. Szyfry przesuwające...str.4. Szyfry monoalfabetyczne...str.5. Szyfr Cezara...str.6. Szyfr Cezara z użyciem cyfr...str.
 Wstęp...str.3 Szyfry przesuwające...str.4 Szyfry monoalfabetyczne...str.5 Szyfr Cezara...str.6 Szyfr Cezara z użyciem cyfr...str.7 Tablica Thritemiusa...str.8 Tablica Blaisa de Vignère a...str.9 Szyfr
Wstęp...str.3 Szyfry przesuwające...str.4 Szyfry monoalfabetyczne...str.5 Szyfr Cezara...str.6 Szyfr Cezara z użyciem cyfr...str.7 Tablica Thritemiusa...str.8 Tablica Blaisa de Vignère a...str.9 Szyfr
Enigma. Odszyfrować Zwycięstwo Specyfikacja techniczna wystawy
 Specyfikacja techniczna wystawy Tablice Tablice 23 tablice wykonane z komatexu o grubości 4mm, wydruk grafiki wykonany bezpośrednio na komatexie. Każda tablica ma wymiary 1405x2000mm. Wersja anglojęzyczna.
Specyfikacja techniczna wystawy Tablice Tablice 23 tablice wykonane z komatexu o grubości 4mm, wydruk grafiki wykonany bezpośrednio na komatexie. Każda tablica ma wymiary 1405x2000mm. Wersja anglojęzyczna.
DROGI ŁAMANIA ENIGMY
 Andrzej Czesław Żak DROGI ŁAMANIA ENIGMY My most secret source Winston Churchill o Enigmie Rewolucyjną zmianę w przekazie tajnych informacji przyniósł wynalazek radia i zastosowanie na szeroką skalę łączności
Andrzej Czesław Żak DROGI ŁAMANIA ENIGMY My most secret source Winston Churchill o Enigmie Rewolucyjną zmianę w przekazie tajnych informacji przyniósł wynalazek radia i zastosowanie na szeroką skalę łączności
KALENDARIUM. z życia i działalności Mariana REJEWSKIEGO na tle wydarzeń związanych z historią maszyny szyfrującej ENIGMA okres bydgoski
 Jerzy Lelwic, kustosz Muzeum Wojsk Lądowych KALENDARIUM z życia i działalności Mariana REJEWSKIEGO na tle wydarzeń związanych z historią maszyny szyfrującej ENIGMA 1905-1923 okres bydgoski 16.08.1905 narodziny
Jerzy Lelwic, kustosz Muzeum Wojsk Lądowych KALENDARIUM z życia i działalności Mariana REJEWSKIEGO na tle wydarzeń związanych z historią maszyny szyfrującej ENIGMA 1905-1923 okres bydgoski 16.08.1905 narodziny
Szyfrowanie RSA (Podróż do krainy kryptografii)
 Szyfrowanie RSA (Podróż do krainy kryptografii) Nie bójmy się programować z wykorzystaniem filmów Academy Khana i innych dostępnych źródeł oprac. Piotr Maciej Jóźwik Wprowadzenie metodyczne Realizacja
Szyfrowanie RSA (Podróż do krainy kryptografii) Nie bójmy się programować z wykorzystaniem filmów Academy Khana i innych dostępnych źródeł oprac. Piotr Maciej Jóźwik Wprowadzenie metodyczne Realizacja
Kodowanie i szyfrowanie na lekcjach matematyki. Częstochowa, r.
 Kodowanie i szyfrowanie na lekcjach matematyki Agnieszka Perczak perczak@womczest.edu.pl Częstochowa, 25.04.2019 r. Podstawowe kierunki realizacji polityki oświatowej państwa w roku szkolnym 2018/2019
Kodowanie i szyfrowanie na lekcjach matematyki Agnieszka Perczak perczak@womczest.edu.pl Częstochowa, 25.04.2019 r. Podstawowe kierunki realizacji polityki oświatowej państwa w roku szkolnym 2018/2019
Jak m atem atycy polscy rozszyfrowali Enigm ę
 ROCZNIKI POLSKIEGO TOWARZYSTWA MATEMATYCZNEGO Seria II: WIADOMOŚCI MATEMATYCZNE XXIII (1980) M arian R ejewski Jak m atem atycy polscy rozszyfrowali Enigm ę Od Redakcji. Rozpowszechnione przekonanie, że
ROCZNIKI POLSKIEGO TOWARZYSTWA MATEMATYCZNEGO Seria II: WIADOMOŚCI MATEMATYCZNE XXIII (1980) M arian R ejewski Jak m atem atycy polscy rozszyfrowali Enigm ę Od Redakcji. Rozpowszechnione przekonanie, że
Funkcja. x X! y Y : x, y f. f : X Y f x = y f : x y. Funkcja o dziedzinie X i przeciwdziedzinie Y to dowolna relacja f XxY taka, że: Notacje:
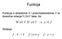 Funkcja Funkcja o dziedzinie X i przeciwdziedzinie Y to dowolna relacja f XxY taka, że: Notacje: x X! y Y : x, y f f : X Y f x = y f : x y Przykłady f: N N, f(n) = 2n f: N R, f(n) = n/2 f: N {13}, f(n)
Funkcja Funkcja o dziedzinie X i przeciwdziedzinie Y to dowolna relacja f XxY taka, że: Notacje: x X! y Y : x, y f f : X Y f x = y f : x y Przykłady f: N N, f(n) = 2n f: N R, f(n) = n/2 f: N {13}, f(n)
Matematyka dyskretna
 Matematyka dyskretna Wykład 12: Krzywe eliptyczne Gniewomir Sarbicki Rozważać będziemy przestrzeń K n Definicja: x y λ K x = λy. Relację nazywamy różnieniem się o skalar Przykład: [4, 10, 6, 14] [6, 15,
Matematyka dyskretna Wykład 12: Krzywe eliptyczne Gniewomir Sarbicki Rozważać będziemy przestrzeń K n Definicja: x y λ K x = λy. Relację nazywamy różnieniem się o skalar Przykład: [4, 10, 6, 14] [6, 15,
Algorytmy i Struktury Danych, 9. ćwiczenia
 Algorytmy i Struktury Danych, 9. ćwiczenia 206-2-09 Plan zajęć usuwanie z B-drzew join i split na 2-3-4 drzewach drzepce adresowanie otwarte w haszowaniu z analizą 2 B-drzewa definicja każdy węzeł ma następujące
Algorytmy i Struktury Danych, 9. ćwiczenia 206-2-09 Plan zajęć usuwanie z B-drzew join i split na 2-3-4 drzewach drzepce adresowanie otwarte w haszowaniu z analizą 2 B-drzewa definicja każdy węzeł ma następujące
RSA. R.L.Rivest A. Shamir L. Adleman. Twórcy algorytmu RSA
 RSA Symetryczny system szyfrowania to taki, w którym klucz szyfrujący pozwala zarówno szyfrować dane, jak również odszyfrowywać je. Opisane w poprzednich rozdziałach systemy były systemami symetrycznymi.
RSA Symetryczny system szyfrowania to taki, w którym klucz szyfrujący pozwala zarówno szyfrować dane, jak również odszyfrowywać je. Opisane w poprzednich rozdziałach systemy były systemami symetrycznymi.
Złamanie szyfru Enigmy a losy II wojny światowej
 08.01.2014 Złamanie szyfru Enigmy a losy II wojny światowej Autor: Wieczorna Image not found http://wieczorna.pl/index.php/uploads/photos/middle_ Rozszyfrowanie Enigmy to coś, czym Polacy się szczycą.
08.01.2014 Złamanie szyfru Enigmy a losy II wojny światowej Autor: Wieczorna Image not found http://wieczorna.pl/index.php/uploads/photos/middle_ Rozszyfrowanie Enigmy to coś, czym Polacy się szczycą.
Kongruencje twierdzenie Wilsona
 Kongruencje Wykład 5 Twierdzenie Wilsona... pojawia się po raz pierwszy bez dowodu w Meditationes Algebraicae Edwarda Waringa (1770), profesora (Lucasian Professor) matematyki w Cambridge, znanego głównie
Kongruencje Wykład 5 Twierdzenie Wilsona... pojawia się po raz pierwszy bez dowodu w Meditationes Algebraicae Edwarda Waringa (1770), profesora (Lucasian Professor) matematyki w Cambridge, znanego głównie
Bezpieczeństwo danych, zabezpieczanie safety, security
 Bezpieczeństwo danych, zabezpieczanie safety, security Kryptologia Kryptologia, jako nauka ścisła, bazuje na zdobyczach matematyki, a w szczególności teorii liczb i matematyki dyskretnej. Kryptologia(zgr.κρυπτός
Bezpieczeństwo danych, zabezpieczanie safety, security Kryptologia Kryptologia, jako nauka ścisła, bazuje na zdobyczach matematyki, a w szczególności teorii liczb i matematyki dyskretnej. Kryptologia(zgr.κρυπτός
MASZYNY SZYFRUJĄCE II WOJNY ŚWIATOWEJ
 Iwona Banaszek MASZYNY SZYFRUJĄCE II WOJNY ŚWIATOWEJ Enigma - niemiecka przenośna maszyna szyfrująca opracowana przez Hugo Kocha, który sprzedał patent rozwiązań wykorzystanych przy jej budowie inżynierowi
Iwona Banaszek MASZYNY SZYFRUJĄCE II WOJNY ŚWIATOWEJ Enigma - niemiecka przenośna maszyna szyfrująca opracowana przez Hugo Kocha, który sprzedał patent rozwiązań wykorzystanych przy jej budowie inżynierowi
Algorytmy asymetryczne
 Algorytmy asymetryczne Klucze występują w parach jeden do szyfrowania, drugi do deszyfrowania (niekiedy klucze mogą pracować zamiennie ) Opublikowanie jednego z kluczy nie zdradza drugiego, nawet gdy można
Algorytmy asymetryczne Klucze występują w parach jeden do szyfrowania, drugi do deszyfrowania (niekiedy klucze mogą pracować zamiennie ) Opublikowanie jednego z kluczy nie zdradza drugiego, nawet gdy można
a) Zapisz wynik działania powyższego algorytmu dla słów ARKA i MOTOR...
 2 Egzamin maturalny z informatyki Zadanie 1. Szyfrowanie (8 pkt) Poniższy algorytm szyfruje słowo s przy pomocy pewnego szyfru przestawieniowego. Zaszyfrowane słowo zostaje zapisane w zmiennej w. Algorytm
2 Egzamin maturalny z informatyki Zadanie 1. Szyfrowanie (8 pkt) Poniższy algorytm szyfruje słowo s przy pomocy pewnego szyfru przestawieniowego. Zaszyfrowane słowo zostaje zapisane w zmiennej w. Algorytm
INŻYNIERIA BEZPIECZEŃSTWA LABORATORIUM NR 2 ALGORYTM XOR ŁAMANIE ALGORYTMU XOR
 INŻYNIERIA BEZPIECZEŃSTWA LABORATORIUM NR 2 ALGORYTM XOR ŁAMANIE ALGORYTMU XOR 1. Algorytm XOR Operacja XOR to inaczej alternatywa wykluczająca, oznaczona symbolem ^ w języku C i symbolem w matematyce.
INŻYNIERIA BEZPIECZEŃSTWA LABORATORIUM NR 2 ALGORYTM XOR ŁAMANIE ALGORYTMU XOR 1. Algorytm XOR Operacja XOR to inaczej alternatywa wykluczająca, oznaczona symbolem ^ w języku C i symbolem w matematyce.
UNIWERSYTET IM. ADAMA MICKIEWICZA W POZNANIU
 UNIWERSYTET IM. ADAMA MICKIEWICZA W POZNANIU Wydział Matematyki i Informatyki PASJA TO SZUKANIE NOWYCH ROZWIĄZAŃ. STUDIUJ Z NAMI I UCZYŃ Z NIEJ SPOSÓB NA ŻYCIE. O WYDZIALE 30.01.1919 r. utworzono Wydział
UNIWERSYTET IM. ADAMA MICKIEWICZA W POZNANIU Wydział Matematyki i Informatyki PASJA TO SZUKANIE NOWYCH ROZWIĄZAŃ. STUDIUJ Z NAMI I UCZYŃ Z NIEJ SPOSÓB NA ŻYCIE. O WYDZIALE 30.01.1919 r. utworzono Wydział
Szyfrowanie wiadomości
 Szyfrowanie wiadomości I etap edukacyjny / II etap edukacyjny Już w starożytności ludzie używali szyfrów do przesyłania tajnych wiadomości. Początkowo były one proste, jednak z biegiem czasu wprowadzano
Szyfrowanie wiadomości I etap edukacyjny / II etap edukacyjny Już w starożytności ludzie używali szyfrów do przesyłania tajnych wiadomości. Początkowo były one proste, jednak z biegiem czasu wprowadzano
Przykładowe zadania z teorii liczb
 Przykładowe zadania z teorii liczb I. Podzielność liczb całkowitych. Liczba a = 346 przy dzieleniu przez pewną liczbę dodatnią całkowitą b daje iloraz k = 85 i resztę r. Znaleźć dzielnik b oraz resztę
Przykładowe zadania z teorii liczb I. Podzielność liczb całkowitych. Liczba a = 346 przy dzieleniu przez pewną liczbę dodatnią całkowitą b daje iloraz k = 85 i resztę r. Znaleźć dzielnik b oraz resztę
Ciągi Podzbiory Symbol Newtona Zasada szufladkowa Dirichleta Zasada włączania i wyłączania. Ilość najkrótszych dróg. Kombinatoryka. Magdalena Lemańska
 Kombinatoryka Magdalena Lemańska Literatura Matematyka Dyskretna Andrzej Szepietowski http://wazniak.mimuw.edu.pl/ Discrete Mathematics Seymour Lipschutz, Marc Lipson Aspekty kombinatoryki Victor Bryant
Kombinatoryka Magdalena Lemańska Literatura Matematyka Dyskretna Andrzej Szepietowski http://wazniak.mimuw.edu.pl/ Discrete Mathematics Seymour Lipschutz, Marc Lipson Aspekty kombinatoryki Victor Bryant
Analiza matematyczna i algebra liniowa Macierze
 Analiza matematyczna i algebra liniowa Macierze Wojciech Kotłowski Instytut Informatyki Politechniki Poznańskiej email: imię.nazwisko@cs.put.poznan.pl pok. 2 (CW) tel. (61)665-2936 konsultacje: poniedziałek
Analiza matematyczna i algebra liniowa Macierze Wojciech Kotłowski Instytut Informatyki Politechniki Poznańskiej email: imię.nazwisko@cs.put.poznan.pl pok. 2 (CW) tel. (61)665-2936 konsultacje: poniedziałek
ŁAMACZE SZYFRÓW kurs kryptologii WYKŁAD 2, str. 1
 ŁAMACZE SZYFRÓW kurs kryptologii WYKŁAD 2, str. 1 Wykład 2, ŚCIŚLE TAJNE w którym poznamy szyfr Ottendorfa, którego teoretycznie nie można złamać bez znajomości klucza. Poznamy też historię, która dowiodła,
ŁAMACZE SZYFRÓW kurs kryptologii WYKŁAD 2, str. 1 Wykład 2, ŚCIŚLE TAJNE w którym poznamy szyfr Ottendorfa, którego teoretycznie nie można złamać bez znajomości klucza. Poznamy też historię, która dowiodła,
LICZBY PIERWSZE. 14 marzec 2007. Jeśli matematyka jest królową nauk, to królową matematyki jest teoria liczb. C.F.
 Jeśli matematyka jest królową nauk, to królową matematyki jest teoria liczb. C.F. Gauss (1777-1855) 14 marzec 2007 Zasadnicze twierdzenie teorii liczb Zasadnicze twierdzenie teorii liczb Ile jest liczb
Jeśli matematyka jest królową nauk, to królową matematyki jest teoria liczb. C.F. Gauss (1777-1855) 14 marzec 2007 Zasadnicze twierdzenie teorii liczb Zasadnicze twierdzenie teorii liczb Ile jest liczb
2 Kryptografia: algorytmy symetryczne
 1 Kryptografia: wstęp Wyróżniamy algorytmy: Kodowanie i kompresja Streszczenie Wieczorowe Studia Licencjackie Wykład 14, 12.06.2007 symetryczne: ten sam klucz jest stosowany do szyfrowania i deszyfrowania;
1 Kryptografia: wstęp Wyróżniamy algorytmy: Kodowanie i kompresja Streszczenie Wieczorowe Studia Licencjackie Wykład 14, 12.06.2007 symetryczne: ten sam klucz jest stosowany do szyfrowania i deszyfrowania;
1. Maszyny rotorowe Enigma
 Połączenie podstawowych metod szyfrowania, czyli pojedynczych podstawień lub przestawień, daje szyfr złoŝony nazywany szyfrem kaskadowym lub produktowym (ang. product cipher). Szyfry takie są połączeniem
Połączenie podstawowych metod szyfrowania, czyli pojedynczych podstawień lub przestawień, daje szyfr złoŝony nazywany szyfrem kaskadowym lub produktowym (ang. product cipher). Szyfry takie są połączeniem
HISTORIA KOMPUTERÓW 2015/16. Bartosz Klin.
 HISTORIA KOMPUTERÓW 2015/16 Bartosz Klin klin@mimuw.edu.pl http://www.mimuw.edu.pl/~klin/ Oś czasu Turing Shannon Zuse Atanasoff Stibitz Aiken 1930 1935 1940 1945 Z3 ABC Z1 Bell Labs Mark I Harvard Mark
HISTORIA KOMPUTERÓW 2015/16 Bartosz Klin klin@mimuw.edu.pl http://www.mimuw.edu.pl/~klin/ Oś czasu Turing Shannon Zuse Atanasoff Stibitz Aiken 1930 1935 1940 1945 Z3 ABC Z1 Bell Labs Mark I Harvard Mark
Rozdział 5. Macierze. a 11 a a 1m a 21 a a 2m... a n1 a n2... a nm
 Rozdział 5 Macierze Funkcję, która każdej parze liczb naturalnych (i,j) (i = 1,,n;j = 1,,m) przyporządkowuje dokładnie jedną liczbę a ij F, gdzie F = R lub F = C, nazywamy macierzą (rzeczywistą, gdy F
Rozdział 5 Macierze Funkcję, która każdej parze liczb naturalnych (i,j) (i = 1,,n;j = 1,,m) przyporządkowuje dokładnie jedną liczbę a ij F, gdzie F = R lub F = C, nazywamy macierzą (rzeczywistą, gdy F
Matematyka dyskretna dla informatyków
 Matematyka dyskretna dla informatyków Część I: Elementy kombinatoryki Jerzy Jaworski Zbigniew Palka Jerzy Szymański Uniwersytet im. Adama Mickiewicza Poznań 2007 4 Zależności rekurencyjne Wiele zależności
Matematyka dyskretna dla informatyków Część I: Elementy kombinatoryki Jerzy Jaworski Zbigniew Palka Jerzy Szymański Uniwersytet im. Adama Mickiewicza Poznań 2007 4 Zależności rekurencyjne Wiele zależności
Marian Rejewski ( )
 Marian Rejewski (1905 1980) Marian Rejewski w wieku 5 lat Fot. ze zbiorów Janiny Sylwestrzak M Młodość Marian Adam Rejewski urodził się 16 sierpnia 1905 r. w Bydgoszczy. Jego matka, Matylda z domu Thoms,
Marian Rejewski (1905 1980) Marian Rejewski w wieku 5 lat Fot. ze zbiorów Janiny Sylwestrzak M Młodość Marian Adam Rejewski urodził się 16 sierpnia 1905 r. w Bydgoszczy. Jego matka, Matylda z domu Thoms,
Równania różniczkowe liniowe rzędu pierwszego
 Katedra Matematyki i Ekonomii Matematycznej SGH 21 kwietnia 2016 Wstęp Definicja Równanie różniczkowe + p (x) y = q (x) (1) nazywamy równaniem różniczkowym liniowym pierwszego rzędu. Jeśli q (x) 0, to
Katedra Matematyki i Ekonomii Matematycznej SGH 21 kwietnia 2016 Wstęp Definicja Równanie różniczkowe + p (x) y = q (x) (1) nazywamy równaniem różniczkowym liniowym pierwszego rzędu. Jeśli q (x) 0, to
a 11 a a 1n a 21 a a 2n... a m1 a m2... a mn x 1 x 2... x m ...
 Wykład 15 Układy równań liniowych Niech K będzie ciałem i niech α 1, α 2,, α n, β K. Równanie: α 1 x 1 + α 2 x 2 + + α n x n = β z niewiadomymi x 1, x 2,, x n nazywamy równaniem liniowym. Układ: a 21 x
Wykład 15 Układy równań liniowych Niech K będzie ciałem i niech α 1, α 2,, α n, β K. Równanie: α 1 x 1 + α 2 x 2 + + α n x n = β z niewiadomymi x 1, x 2,, x n nazywamy równaniem liniowym. Układ: a 21 x
Marian Rejewski Klasy I-III
 Marian Rejewski Klasy I-III Organizator: Patronat medialny: Patronat honorowy: TABELKA AKTYWNOŚCI IMIĘ I NAZWISKO UCZNIA LEKCJA I LEKCJA II LEKCJA III LEKCJA IV CZY WIESZ ŻE... Marian Rejewski urodził
Marian Rejewski Klasy I-III Organizator: Patronat medialny: Patronat honorowy: TABELKA AKTYWNOŚCI IMIĘ I NAZWISKO UCZNIA LEKCJA I LEKCJA II LEKCJA III LEKCJA IV CZY WIESZ ŻE... Marian Rejewski urodził
Łamanie szyfrów. Kryptografia w szkole podstawowej
 REFLEKSJE Łamanie szyfrów Kryptografia w szkole podstawowej Jerzy Kołodziejczyk, dyrektor Szkoły Podstawowej nr 4 w Gryficach 42 Uczniowie klas IV VI Szkoły Podstawowej nr 4 w Gryficach wykazujący zainteresowanie
REFLEKSJE Łamanie szyfrów Kryptografia w szkole podstawowej Jerzy Kołodziejczyk, dyrektor Szkoły Podstawowej nr 4 w Gryficach 42 Uczniowie klas IV VI Szkoły Podstawowej nr 4 w Gryficach wykazujący zainteresowanie
Kryptografia szyfrowanie i zabezpieczanie danych
 Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej WSTĘP DO INFORMATYKI Adrian Horzyk Kryptografia szyfrowanie i zabezpieczanie danych www.agh.edu.pl
Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej WSTĘP DO INFORMATYKI Adrian Horzyk Kryptografia szyfrowanie i zabezpieczanie danych www.agh.edu.pl
Matematyka dyskretna
 Matematyka dyskretna Wykład 4: Podzielność liczb całkowitych Gniewomir Sarbicki Dzielenie całkowitoliczbowe Twierdzenie: Dla każdej pary liczb całkowitych (a, b) istnieje dokładnie jedna para liczb całkowitych
Matematyka dyskretna Wykład 4: Podzielność liczb całkowitych Gniewomir Sarbicki Dzielenie całkowitoliczbowe Twierdzenie: Dla każdej pary liczb całkowitych (a, b) istnieje dokładnie jedna para liczb całkowitych
Matematyka dyskretna
 Matematyka dyskretna Wykład 6: Ciała skończone i kongruencje Gniewomir Sarbicki 2 marca 2017 Relacja przystawania Definicja: Mówimy, że liczby a, b Z przystają modulo m (co oznaczamy jako a = b (mod m)),
Matematyka dyskretna Wykład 6: Ciała skończone i kongruencje Gniewomir Sarbicki 2 marca 2017 Relacja przystawania Definicja: Mówimy, że liczby a, b Z przystają modulo m (co oznaczamy jako a = b (mod m)),
Projekt AS KOMPETENCJI jest współfinansowany przez Unię Europejską w ramach środków Europejskiego Funduszu Społecznego
 Projekt AS KOMPETENCJI jest współfinansowany przez Unię Europejską w ramach środków Europejskiego Funduszu Społecznego Program Operacyjny Kapitał Ludzki 2007-2013 CZŁOWIEK NAJLEPSZA INWESTYCJA Publikacja
Projekt AS KOMPETENCJI jest współfinansowany przez Unię Europejską w ramach środków Europejskiego Funduszu Społecznego Program Operacyjny Kapitał Ludzki 2007-2013 CZŁOWIEK NAJLEPSZA INWESTYCJA Publikacja
To bez wątpienia jeden z największych astronomów w historii, nie tylko Polski, ale i całego świata. Zmienił całkowicie światopogląd ludzkości na
 To bez wątpienia jeden z największych astronomów w historii, nie tylko Polski, ale i całego świata. Zmienił całkowicie światopogląd ludzkości na sprawy świata, jego postrzegania, otworzył ludziom horyzonty,
To bez wątpienia jeden z największych astronomów w historii, nie tylko Polski, ale i całego świata. Zmienił całkowicie światopogląd ludzkości na sprawy świata, jego postrzegania, otworzył ludziom horyzonty,
Teoria grafów - Teoria rewersali - Teoria śladów
 17 maja 2012 1 Planarność Wzór Eulera Kryterium Kuratowskiego Algorytmy testujące planarność 2 Genom i jego przekształcenia Grafy złamań Sortowanie przez odwrócenia Inne rodzaje sortowania Algorytmy sortujące
17 maja 2012 1 Planarność Wzór Eulera Kryterium Kuratowskiego Algorytmy testujące planarność 2 Genom i jego przekształcenia Grafy złamań Sortowanie przez odwrócenia Inne rodzaje sortowania Algorytmy sortujące
UWAGI O CIĄGU SKOKÓW LICZB MILNORA. 1. Wstęp Rozważać będziemy izolowaną osobliwość niezdegenerowaną dwóch zmiennych (1) f = a αβ x α y β
 UWAGI O CIĄGU SKOKÓW LICZB MILNORA MARIA MICHALSKA I JUSTYNA WALEWSKA 1. Wstęp Rozważać będziemy izolowaną osobliwość niezdegenerowaną dwóch zmiennych (1) f = a αβ x α y β mα+lβ lm taką, że a l0 a 0m 0
UWAGI O CIĄGU SKOKÓW LICZB MILNORA MARIA MICHALSKA I JUSTYNA WALEWSKA 1. Wstęp Rozważać będziemy izolowaną osobliwość niezdegenerowaną dwóch zmiennych (1) f = a αβ x α y β mα+lβ lm taką, że a l0 a 0m 0
100-lecie Polskiej Szkoły Matematycznej... filatelistycznie
 100-lecie Polskiej Szkoły Matematycznej... filatelistycznie Jan SWADŹBA, Katowice... niestety, niedostrzeżone przez Pocztę Polską. W planie wydawnictw Poczty w 2018 roku widzimy 100-lecie Niepodległości,
100-lecie Polskiej Szkoły Matematycznej... filatelistycznie Jan SWADŹBA, Katowice... niestety, niedostrzeżone przez Pocztę Polską. W planie wydawnictw Poczty w 2018 roku widzimy 100-lecie Niepodległości,
Podstawowe pojęcia. Co w matematyce możemy nazwać. węzłem, a co. splotem?
 Magdalena Czarna Podstawowe pojęcia Co w matematyce możemy nazwać węzłem, a co splotem? Podstawowe pojęcia Węzeł to krzywa zamknięta (splątany okrąg) w przestrzeni 3-wymiarowej. W związku z tym węzłem
Magdalena Czarna Podstawowe pojęcia Co w matematyce możemy nazwać węzłem, a co splotem? Podstawowe pojęcia Węzeł to krzywa zamknięta (splątany okrąg) w przestrzeni 3-wymiarowej. W związku z tym węzłem
Zaawansowane metody numeryczne
 Wykład 6 Własności wielomianów ortogonalnych Wszystkie znane rodziny wielomianów ortogonalnych dzielą pewne wspólne cechy: 1) definicja za pomocą wzoru różniczkowego, jawnej sumy lub funkcji tworzącej;
Wykład 6 Własności wielomianów ortogonalnych Wszystkie znane rodziny wielomianów ortogonalnych dzielą pewne wspólne cechy: 1) definicja za pomocą wzoru różniczkowego, jawnej sumy lub funkcji tworzącej;
DB Algebra liniowa semestr zimowy 2018
 DB Algebra liniowa semestr zimowy 2018 SPIS TREŚCI Teoria oraz większość zadań w niniejszym skrypcie zostały opracowane na podstawie książek: 1 G Banaszak, W Gajda, Elementy algebry liniowej cz I, Wydawnictwo
DB Algebra liniowa semestr zimowy 2018 SPIS TREŚCI Teoria oraz większość zadań w niniejszym skrypcie zostały opracowane na podstawie książek: 1 G Banaszak, W Gajda, Elementy algebry liniowej cz I, Wydawnictwo
Tę wiedzę, wraz z kopiami
 96 Zanim było Bletchley Park Katarzyna Dzierzbicka Według historyków, złamanie kodu Enigmy niemieckiej maszyny szyfrującej przyczyniło się do ocalenia ok. 30 mln ludzi. Pierwsi dokonali tego Polacy a nie,
96 Zanim było Bletchley Park Katarzyna Dzierzbicka Według historyków, złamanie kodu Enigmy niemieckiej maszyny szyfrującej przyczyniło się do ocalenia ok. 30 mln ludzi. Pierwsi dokonali tego Polacy a nie,
1. ODPOWIEDZI DO ZADAŃ TESTOWYCH
 R O Z W I A Z A N I A 1. ODPOWIEDZI DO ZADAŃ TESTOWYCH 1. Dla dowolnych zbiorów A, B, C zachodzi równość (A B) (B C) (C A) = (A B C) (A B C), A (B C) = (A B) (A C), A (B C) = (A B) (A C). 2. Wyrażenie
R O Z W I A Z A N I A 1. ODPOWIEDZI DO ZADAŃ TESTOWYCH 1. Dla dowolnych zbiorów A, B, C zachodzi równość (A B) (B C) (C A) = (A B C) (A B C), A (B C) = (A B) (A C), A (B C) = (A B) (A C). 2. Wyrażenie
Matematyczne Podstawy Informatyki
 Matematyczne Podstawy Informatyki dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska Rok akademicki 2013/2014 Automat ze stosem Automat ze stosem to szóstka
Matematyczne Podstawy Informatyki dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska Rok akademicki 2013/2014 Automat ze stosem Automat ze stosem to szóstka
Funkcje charakterystyczne zmiennych losowych, linie regresji 1-go i 2-go rodzaju
 Funkcje charakterystyczne zmiennych losowych, linie regresji -go i 2-go rodzaju Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych Wydział Informatyki Politechniki
Funkcje charakterystyczne zmiennych losowych, linie regresji -go i 2-go rodzaju Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych Wydział Informatyki Politechniki
Materiały Oddziału II Sztabu Głównego dotyczące przygotowań wojennych Niemiec
 Centralne Archiwum Wojskowe Materiały Oddziału II Sztabu Głównego dotyczące przygotowań wojennych Niemiec Od połowy lat dwudziestych w wojsku niemieckim używano maszyny do szyfrowania depesz, uważając
Centralne Archiwum Wojskowe Materiały Oddziału II Sztabu Głównego dotyczące przygotowań wojennych Niemiec Od połowy lat dwudziestych w wojsku niemieckim używano maszyny do szyfrowania depesz, uważając
Matematyka dyskretna. Andrzej Łachwa, UJ, /10
 Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 10/10 Podziały i liczby Stirlinga Liczba Stirlinga dla cykli (często nazywana liczbą Stirlinga pierwszego rodzaju) to liczba permutacji
Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 10/10 Podziały i liczby Stirlinga Liczba Stirlinga dla cykli (często nazywana liczbą Stirlinga pierwszego rodzaju) to liczba permutacji
Pochodna funkcji. Niech f : A R, a A i załóżmy, że istnieje α > 0 taka, że
 Niec f : A R, a A i załóżmy, że istnieje α > 0 taka, że (a α, a + α) A. Niec f : A R, a A i załóżmy, że istnieje α > 0 taka, że (a α, a + α) A. Definicja Ilorazem różnicowym funkcji f w punkcie a nazywamy
Niec f : A R, a A i załóżmy, że istnieje α > 0 taka, że (a α, a + α) A. Niec f : A R, a A i załóżmy, że istnieje α > 0 taka, że (a α, a + α) A. Definicja Ilorazem różnicowym funkcji f w punkcie a nazywamy
Matematyka dyskretna
 Matematyka dyskretna Wykład 6: Ciała skończone i kongruencje Gniewomir Sarbicki 24 lutego 2015 Relacja przystawania Definicja: Mówimy, że liczby a, b Z przystają modulo m (co oznaczamy jako a = b (mod
Matematyka dyskretna Wykład 6: Ciała skończone i kongruencje Gniewomir Sarbicki 24 lutego 2015 Relacja przystawania Definicja: Mówimy, że liczby a, b Z przystają modulo m (co oznaczamy jako a = b (mod
VI. Równania różniczkowe liniowe wyższych rzędów
 VI. 1. Równanie różniczkowe liniowe n-tego rzędu o zmiennych współczynnikach Niech podobnie jak w poprzednim paragrafie K = C lub K = R. Podobnie jak w dziedzinie rzeczywistej wprowadzamy pochodne wyższych
VI. 1. Równanie różniczkowe liniowe n-tego rzędu o zmiennych współczynnikach Niech podobnie jak w poprzednim paragrafie K = C lub K = R. Podobnie jak w dziedzinie rzeczywistej wprowadzamy pochodne wyższych
0 --> 5, 1 --> 7, 2 --> 9, 3 -->1, 4 --> 3, 5 --> 5, 6 --> 7, 7 --> 9, 8 --> 1, 9 --> 3.
 (Aktualizacja z dnia 3 kwietnia 2013) MATEMATYKA DYSKRETNA - informatyka semestr 2 (lato 2012/2013) Zadania do omówienia na zajęciach w dniach 21 i 28 kwietnia 2013 ZESTAW NR 3/7 (przykłady zadań z rozwiązaniami)
(Aktualizacja z dnia 3 kwietnia 2013) MATEMATYKA DYSKRETNA - informatyka semestr 2 (lato 2012/2013) Zadania do omówienia na zajęciach w dniach 21 i 28 kwietnia 2013 ZESTAW NR 3/7 (przykłady zadań z rozwiązaniami)
Podstawowe struktury algebraiczne
 Rozdział 1 Podstawowe struktury algebraiczne 1.1. Działania wewnętrzne Niech X będzie zbiorem niepustym. Dowolną funkcję h : X X X nazywamy działaniem wewnętrznym w zbiorze X. Działanie wewnętrzne, jak
Rozdział 1 Podstawowe struktury algebraiczne 1.1. Działania wewnętrzne Niech X będzie zbiorem niepustym. Dowolną funkcję h : X X X nazywamy działaniem wewnętrznym w zbiorze X. Działanie wewnętrzne, jak
PLAN STUDIÓW STACJONARNYCH PIERWSZEGO STOPNIA MATEMATYKA. od roku akademickiego 2015/2016
 PLAN STUDIÓ STACJONARNYCH PIRSZGO STOPNIA MATMATYKA od roku akademickiego 20/2016 Semestr 1 stęp do logiki i teorii mnogości 45 75 1 7 Analiza matematyczna 1 1) 60 90 8 Algebra liniowa 1 60 90 7 Geometria
PLAN STUDIÓ STACJONARNYCH PIRSZGO STOPNIA MATMATYKA od roku akademickiego 20/2016 Semestr 1 stęp do logiki i teorii mnogości 45 75 1 7 Analiza matematyczna 1 1) 60 90 8 Algebra liniowa 1 60 90 7 Geometria
PODSTAWY RACHUNKU WEKTOROWEGO
 Transport, studia niestacjonarne I stopnia, semestr I Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Adam Wosatko Ewa Pabisek Skalar Definicja Skalar wielkość fizyczna (lub geometryczna)
Transport, studia niestacjonarne I stopnia, semestr I Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Adam Wosatko Ewa Pabisek Skalar Definicja Skalar wielkość fizyczna (lub geometryczna)
Kodowanie i kompresja Streszczenie Studia Licencjackie Wykład 14, Kryptografia: algorytmy asymetryczne (RSA)
 Kodowanie i kompresja Streszczenie Studia Licencjackie Wykład 14, 7.06.2005 1 Kryptografia: algorytmy asymetryczne (RSA) Niech E K (x) oznacza szyfrowanie wiadomości x kluczem K (E od encrypt, D K (x)
Kodowanie i kompresja Streszczenie Studia Licencjackie Wykład 14, 7.06.2005 1 Kryptografia: algorytmy asymetryczne (RSA) Niech E K (x) oznacza szyfrowanie wiadomości x kluczem K (E od encrypt, D K (x)
Podstawy systemów kryptograficznych z kluczem jawnym RSA
 Podstawy systemów kryptograficznych z kluczem jawnym RSA RSA nazwa pochodząca od nazwisk twórców systemu (Rivest, Shamir, Adleman) Systemów z kluczem jawnym można używać do szyfrowania operacji przesyłanych
Podstawy systemów kryptograficznych z kluczem jawnym RSA RSA nazwa pochodząca od nazwisk twórców systemu (Rivest, Shamir, Adleman) Systemów z kluczem jawnym można używać do szyfrowania operacji przesyłanych
Zestaw zadań dotyczących liczb całkowitych
 V Zestaw zadań dotyczących liczb całkowitych Opracowanie Monika Fabijańczyk ROZDZIAŁ 1 Cechy podzielności Poniższe zadania zostały wybrane z różnych zbiorów zadań, opracowań, konkursów matematycznych.
V Zestaw zadań dotyczących liczb całkowitych Opracowanie Monika Fabijańczyk ROZDZIAŁ 1 Cechy podzielności Poniższe zadania zostały wybrane z różnych zbiorów zadań, opracowań, konkursów matematycznych.
Kryptografia systemy z kluczem tajnym. Kryptografia systemy z kluczem tajnym
 Krótkie vademecum (słabego) szyfranta Podstawowe pojęcia: tekst jawny (otwarty) = tekst zaszyfrowany (kryptogram) alfabet obu tekstów (zwykle różny) jednostki tekstu: na przykład pojedyncza litera, digram,
Krótkie vademecum (słabego) szyfranta Podstawowe pojęcia: tekst jawny (otwarty) = tekst zaszyfrowany (kryptogram) alfabet obu tekstów (zwykle różny) jednostki tekstu: na przykład pojedyncza litera, digram,
Bezpieczeństwo w Internecie
 Elektroniczne Przetwarzanie Informacji Konsultacje: czw. 14.00-15.30, pokój 3.211 Plan prezentacji Szyfrowanie Cechy bezpiecznej komunikacji Infrastruktura klucza publicznego Plan prezentacji Szyfrowanie
Elektroniczne Przetwarzanie Informacji Konsultacje: czw. 14.00-15.30, pokój 3.211 Plan prezentacji Szyfrowanie Cechy bezpiecznej komunikacji Infrastruktura klucza publicznego Plan prezentacji Szyfrowanie
Wykład VIII. Systemy kryptograficzne Kierunek Matematyka - semestr IV. dr inż. Janusz Słupik. Wydział Matematyki Stosowanej Politechniki Śląskiej
 Wykład VIII Kierunek Matematyka - semestr IV Wydział Matematyki Stosowanej Politechniki Śląskiej Gliwice, 2014 c Copyright 2014 Janusz Słupik Egzotyczne algorytmy z kluczem publicznym Przypomnienie Algorytm
Wykład VIII Kierunek Matematyka - semestr IV Wydział Matematyki Stosowanej Politechniki Śląskiej Gliwice, 2014 c Copyright 2014 Janusz Słupik Egzotyczne algorytmy z kluczem publicznym Przypomnienie Algorytm
Teoria węzłów matematycznych - warkocze. Karolina Krzysztoń 10B2
 Teoria węzłów matematycznych - warkocze Karolina Krzysztoń 10B2 Pojęcie węzła W matematyce węzły to zamknięte pętle umieszczone w przestrzeni trójwymiarowej, czyli zaplątane sznurki z połączonymi końcami.
Teoria węzłów matematycznych - warkocze Karolina Krzysztoń 10B2 Pojęcie węzła W matematyce węzły to zamknięte pętle umieszczone w przestrzeni trójwymiarowej, czyli zaplątane sznurki z połączonymi końcami.
Wykład 14. Elementy algebry macierzy
 Wykład 14 Elementy algebry macierzy dr Mariusz Grządziel 26 stycznia 2009 Układ równań z dwoma niewiadomymi Rozważmy układ równań z dwoma niewiadomymi: a 11 x + a 12 y = h 1 a 21 x + a 22 y = h 2 a 11,
Wykład 14 Elementy algebry macierzy dr Mariusz Grządziel 26 stycznia 2009 Układ równań z dwoma niewiadomymi Rozważmy układ równań z dwoma niewiadomymi: a 11 x + a 12 y = h 1 a 21 x + a 22 y = h 2 a 11,
Przestrzenie liniowe
 Przestrzenie liniowe Mirosław Sobolewski Wydział Matematyki, Informatyki i Mechaniki UW 2 wykład z algebry liniowej Warszawa, październik 2015 Mirosław Sobolewski (UW) Warszawa, wrzesień 2015 1 / 10 Przestrzenie
Przestrzenie liniowe Mirosław Sobolewski Wydział Matematyki, Informatyki i Mechaniki UW 2 wykład z algebry liniowej Warszawa, październik 2015 Mirosław Sobolewski (UW) Warszawa, wrzesień 2015 1 / 10 Przestrzenie
ODSZYFROWAĆ ZWYCIĘSTWO DZIAŁANIA SAMORZĄDU WOJEWÓDZTWA WIELKOPOLSKIEGO ZWIĄZANE Z PROMOWANIEM WIEDZY O BOHATERACH SUKCESU KRYPTOLOGICZNEGO
 ODSZYFROWAĆ ZWYCIĘSTWO DZIAŁANIA SAMORZĄDU WOJEWÓDZTWA WIELKOPOLSKIEGO ZWIĄZANE Z PROMOWANIEM WIEDZY O BOHATERACH SUKCESU KRYPTOLOGICZNEGO DZIAŁANIA SAMORZĄDU WOJEWÓDZTWA WIELKOPOLSKIEGO ZWIĄZANE Z PROMOWANIEM
ODSZYFROWAĆ ZWYCIĘSTWO DZIAŁANIA SAMORZĄDU WOJEWÓDZTWA WIELKOPOLSKIEGO ZWIĄZANE Z PROMOWANIEM WIEDZY O BOHATERACH SUKCESU KRYPTOLOGICZNEGO DZIAŁANIA SAMORZĄDU WOJEWÓDZTWA WIELKOPOLSKIEGO ZWIĄZANE Z PROMOWANIEM
Treści programowe. Matematyka. Efekty kształcenia. Literatura. Terminy wykładów i ćwiczeń. Warunki zaliczenia. tnij.org/ktrabka
 Treści programowe Matematyka Katarzyna Trąbka-Więcław Elementy algebry liniowej. Macierze i wyznaczniki. Ciągi liczbowe, granica ciągu i granica funkcji, rachunek granic, wyrażenia nieoznaczone, ciągłość
Treści programowe Matematyka Katarzyna Trąbka-Więcław Elementy algebry liniowej. Macierze i wyznaczniki. Ciągi liczbowe, granica ciągu i granica funkcji, rachunek granic, wyrażenia nieoznaczone, ciągłość
Przypomnienie: typ permutacji mówi ile jest cykli każdej długości, np.: ( 12345
 Zadania z ćwiczeń #6 (pt 17 marca) Matematyka Dyskretna Enigma była maszyną do szyfrowania, używaną od 1920 m.in. w Niemczech. Podstawowa wersja ma: 26 klawiszy, 26 lampek, 3 walcowate rotory na osi zakończonej
Zadania z ćwiczeń #6 (pt 17 marca) Matematyka Dyskretna Enigma była maszyną do szyfrowania, używaną od 1920 m.in. w Niemczech. Podstawowa wersja ma: 26 klawiszy, 26 lampek, 3 walcowate rotory na osi zakończonej
Kodowanie i kompresja Streszczenie Studia Licencjackie Wykład 15, Kryptografia: algorytmy asymetryczne (RSA)
 Kodowanie i kompresja Streszczenie Studia Licencjackie Wykład 15, 19.06.2005 1 Kryptografia: algorytmy asymetryczne (RSA) Niech E K (x) oznacza szyfrowanie wiadomości x kluczem K (E od encrypt, D K (x)
Kodowanie i kompresja Streszczenie Studia Licencjackie Wykład 15, 19.06.2005 1 Kryptografia: algorytmy asymetryczne (RSA) Niech E K (x) oznacza szyfrowanie wiadomości x kluczem K (E od encrypt, D K (x)
kryptografię (z gr. κρυπτός oraz γράφω gráfo pisać ), czyli gałąź wiedzy o utajnianiu wiadomości;
 Już w starożytności ludzie używali szyfrów do przesyłania tajnych wiadomości. Początkowo były one proste, jednak z biegiem czasu wprowadzano coraz bardziej skomplikowane metody szyfrowania. Wraz z rozwojem
Już w starożytności ludzie używali szyfrów do przesyłania tajnych wiadomości. Początkowo były one proste, jednak z biegiem czasu wprowadzano coraz bardziej skomplikowane metody szyfrowania. Wraz z rozwojem
PROBLEMATYKA BEZPIECZEŃSTWA SIECI RADIOWYCH Algorytm szyfrowania AES. Zygmunt Kubiak Instytut Informatyki Politechnika Poznańska
 PROBLEMATYKA BEZPIECZEŃSTWA SIECI RADIOWYCH Algorytm szyfrowania AES Zygmunt Kubiak Instytut Informatyki Politechnika Poznańska Wprowadzenie Problemy bezpieczeństwa transmisji Rozwiązania stosowane dla
PROBLEMATYKA BEZPIECZEŃSTWA SIECI RADIOWYCH Algorytm szyfrowania AES Zygmunt Kubiak Instytut Informatyki Politechnika Poznańska Wprowadzenie Problemy bezpieczeństwa transmisji Rozwiązania stosowane dla
Algebra liniowa z geometria. - zadania Rok akademicki 2010/2011
 1 GEOMETRIA ANALITYCZNA 1 Wydział Fizyki Algebra liniowa z geometria - zadania Rok akademicki 2010/2011 Agata Pilitowska i Zbigniew Dudek 1 Geometria analityczna 1.1 Punkty i wektory 1. Sprawdzić, czy
1 GEOMETRIA ANALITYCZNA 1 Wydział Fizyki Algebra liniowa z geometria - zadania Rok akademicki 2010/2011 Agata Pilitowska i Zbigniew Dudek 1 Geometria analityczna 1.1 Punkty i wektory 1. Sprawdzić, czy
ŁAMIEMY SZYFR CEZARA. 1. Wstęp. 2. Szyfr Cezara w szkole. Informatyka w Edukacji, XV UMK Toruń, 2018
 Informatyka w Edukacji, XV UMK Toruń, 2018 ŁAMIEMY SZYFR CEZARA Ośrodek Edukacji Informatycznej i Zastosowań Komputerów 02-026 Warszawa, ul. Raszyńska 8/10 {maciej.borowiecki, krzysztof.chechlacz}@oeiizk.waw.pl
Informatyka w Edukacji, XV UMK Toruń, 2018 ŁAMIEMY SZYFR CEZARA Ośrodek Edukacji Informatycznej i Zastosowań Komputerów 02-026 Warszawa, ul. Raszyńska 8/10 {maciej.borowiecki, krzysztof.chechlacz}@oeiizk.waw.pl
Matematyka Dyskretna Zestaw 2
 Materiały dydaktyczne Matematyka Dyskretna (Zestaw ) Matematyka Dyskretna Zestaw 1. Wykazać, że nie istnieje liczba naturalna, która przy dzieleniu przez 18 daje resztę 13, a przy dzieleniu przez 1 daje
Materiały dydaktyczne Matematyka Dyskretna (Zestaw ) Matematyka Dyskretna Zestaw 1. Wykazać, że nie istnieje liczba naturalna, która przy dzieleniu przez 18 daje resztę 13, a przy dzieleniu przez 1 daje
