Karta pracy M+ do multipodręcznika dla klasy 1 gimnazjum
|
|
|
- Daria Sokołowska
- 7 lat temu
- Przeglądów:
Transkrypt
1 Karta pracy M+ do multipodręcznika dla klasy 1 gimnazjum Bezkresne pola pomidorowe Część A. Sprawdź, czy rozumiesz film. 1. Uzupełnij poniższy tekst brakującymi słowami. Uprawa pomidorów w Kalifornii Stany Zjednoczone... Północnej są największym... żywności na świecie. Stanem, w którym produkuje się jej najwięcej, jest.... Najbardziej intensywne uprawy rolne są zlokalizowane na terenach, które jeszcze kilkadziesiąt lat temu były.... Nie dziwi więc, że najcenniejsza jest tu.... Trzeba ją transportować z odległych terenów systemem akweduktów i.... Szacuje się, że uprawy wymagają 14 miliardów... wody rocznie. Dlatego farmerzy często rezygnują z upraw roślin wymagających więcej wody na rzecz tych, które wymagają jej mniej. Z tego powodu hodowla drzew... często jest zastępowana uprawą.... Liczba ludności Kalifornii szybko.... W ciągu ostatnich 80 lat wzrosła do... Wody potrzeba więc coraz więcej. W uprawianiu obszarów nawodnionej pustyni pomagają ludziom zdobycze nauki i techniki. Olbrzymie... zaopatrzone w... ścinają krzewy, zrywają z nich pomidory i sortują je, oddzielając dojrzałe owoce od.... Potrzeby rolnictwa zmuszają do poszukiwania lepszych sposobów wykorzystywania ziemi, wody i pracy. Liczne organizacje i pracownicy naukowi rozwiązują technologiczne problemy amerykańskiego rolnictwa. Pytanie, które nurtuje ich najbardziej, brzmi: jak wyprodukować więcej..., zużywając przy tym mniejszą niż do tej pory ilość....
2 2. Wykorzystując tekst oraz wiadomości z filmu, ustal, które zdania są prawdziwe, a które ywe. Zaznacz odpowiednie pola. Najwięcej pomidorów w USA uprawia się w stanie Oregon. Aby móc uprawiać warzywa na obszarach pustynnych, trzeba te obszary najpierw nawodnić. Migdałowce potrzebują dwa razy mniej wody niż krzewy pomidorowe. Liczba ludności Kalifornii potroiła się w ciągu ostatnich 80 lat. W rolnictwie dąży się do tego, by przy jak największym udziale zasobów, uzyskiwać jak najmniejszy efekt. USA to największy eksporter żywności. 3. Dopasuj podpis do odpowiedniego kadru. Wpisz w okienkach właściwe numery. 1. Kombajn zbierający pomidory 4. Praca w polu trwa przez cały dzień 2. Ziemia bez wody staje się pustynią 5. Kombajn i przyczepy pełne pomidorów 3. System nawadniający pustynne gleby 2 6. Maszyna do niszczenia gałęzi
3 Część B. Rozwiąż poniższe zadania. Tabelka przedstawia dane dotyczące uprawy pomidorów w Kalifornii. Skorzystaj z poniższych informacji podczas rozwiązywania kolejnych dwóch zadań. Rok Powierzchnia (akry) Wydajność (tona/akr) Ilość zebranych pomidorów (tony) Cena za 1 tonę ($) Uzyskany dochód (tys. $) , , , , , , , , , , ,83 65, , , , , , , , , , , oraz data dostępu: r. Zadanie 1. Uzupełnij luki w tabeli. Wpisz brakujące informacje. Zadanie 2. Wykorzystując dane z tabeli, wskaż zdania prawdziwe. Najdroższe pomidory były w roku Między rokiem 2000 a 2012 powierzchnia upraw pomidorów zmalała o akrów. Największy dochód z upraw pomidorów uzyskano w roku Najmniej pomidorów z jednego akra zebrano w roku Różnica między największą a najmniejszą powierzchnią upraw pomidorów w podanych latach wynosi akrów. Zadanie 3. Akr to obszar, który można było zaorać pługiem ciągniętym przez woły w ciągu jednego dnia. Przyjmuje się, że akr to około 40,47 ara. Ile hektarów mogłyby zaorać 4 zaprzęgi wołów w ciągu sześciu dni?
4 Zadanie 4. Ile średnio hektarów ziemi przeznaczono na uprawę pomidorów w Kalifornii w latach ? Zadanie 5. W USA jeden bilion oznacza nasz miliard i liczy tysiąc milionów. Jeden galon amerykański to 3,79 litra, natomiast jeden galon angielski to 4,55 litra. Wyraź w hektolitrach dane na temat ilości wody potrzebnej do rocznej uprawy pomidorów w Kalifornii (14 bilionów galonów). W filmie nie podano, czy zużycie wody liczono w galonach angielskich czy amerykańskich. Posłuż się obiema jednostkami objętości i porównaj wyniki. Czy różnią się znacznie? Jak zmieni się ta różnica, gdy weźmiemy pod uwagę uprawę drzew migdałowych? Zadanie 6. Według danych statystycznych w Polsce uprawia się pomidory w około gospodarstw. Uprawy te zajmują łącznie około 6000 ha. Jak duże jest średnio pole obsadzone krzewami pomidorów w naszym kraju? Wyraź tę wielkość w arach. Zadanie 7. Powierzchnia stanu Kalifornia wynosi km 2. Oszacuj, jaki procent powierzchni tego stanu przeznacza się na uprawę pomidorów (skorzystaj z wyliczeń z zadania 4.). Oszacuj również, jaki procent powierzchni naszego kraju ( km 2 ) przeznacza się na uprawę tego warzywa. Porównaj obie liczby i sformułuj wniosek. Zadanie 8. Największymi producentami pomidorów na świecie są: Chiny, USA, Indie, Turcja, Egipt, Włochy, Iran i Hiszpania. Polska produkuje ok. 700 tys. ton pomidorów rocznie. Chiny i USA produkują łącznie 10 razy tyle pomidorów co Włochy. Indie produkują 2 razy tyle pomidorów co Włochy. Iran zaś produkuje o 1 milion ton pomidorów mniej niż Włochy oraz 2 razy mniej niż Turcja, która produkuje o 6 milionów ton pomidorów więcej niż Hiszpania. Hiszpania wytwarza ich 4 miliony ton. Oblicz, ile ton pomidorów produkują wymienione kraje. Dane dla USA (są zbliżone do produkcji w Kalifornii w roku 2012) weź z tabelki do zadania 1. Jak myślisz, które miejsce zajmuje nasz kraj? 4
5 Pomidor uprawny Wartości odżywcze na 100 g produktu woda 94,5 g witamina A 0,38 mg magnez 10 mg błonnik 1,4 g witamina B 1 0,06 mg fosfor 24 mg białko 0,9 g witamina B 2 0,04 mg żelazo 0,4 mg tłuszcze 0,2 g witamina B 6 0,11 mg sód 1,2 mg węglowodany 2,8 g witamina C 15 mg wapń 10 mg witamina PP 0,7 mg potas 280 mg Zadanie 9. Na podstawie powyższej tabeli odpowiedz na pytania. a) Jaki procent wartości odżywczych stanowią w pomidorze tłuszcze, a jaki węglowodany? b) Czy w pomidorach jest więcej witamin, czy potasu? O ile procent? Zadanie 10. Pomidory zajmują pierwsze miejsce na liście warzyw spożywanych w Polsce najchętniej około 16% wszystkich zjadanych warzyw. W roku 2012 zjedliśmy w sumie tony pomidorów. Ile kilogramów pomidorów zjadł statystyczny Polak? Ile ton warzyw zjedliśmy w 2012 roku? Przyjmij, że liczba ludności Polski to 38,5 mln. Odp.... 5
6 Część C. Zagadka. Rozwiąż krzyżówkę. W jednej z kolumn odczytasz rozwiązanie Ten czworokąt ma co najmniej jedną parę boków równoległych. 2. Jego brzeg to okrąg. 3. Część każdego kąta. 4. Długość, szerokość, wysokość. 5. Jego dwie przekątne przecinają się pod kątem prostym. 6. Odcinek w trójkącie poprowadzony z wierzchołka i prostopadły do podstawy. 7. Część płaszczyzny ograniczona łamaną zwyczajną zamkniętą złożoną z czterech odcinków. Część D. O co warto zapytać, o czym warto porozmawiać? Żaden z poniższych tematów nie wymaga wcześniejszego przygotowania. Jeżeli pojawią się trudne pytania, odpowiedzi na nie można poszukać w ramach zadania domowego. Zawsze warto porozmawiać o własnych doświadczeniach związanych z treścią filmu. 1. Pomidory uprawiane są od około 8 tysięcy lat. Przywieziono je do Europy z Ameryki Południowej na początku XVI wieku. Dlaczego należy jeść pomidory? Jakie mają wartości odżywcze? 2. Przecier, ketchup, suszone pomidory jakie jeszcze znasz przetwory z pomidorów? Który ze sposobów przechowywania pomidorów jest najlepszy? 3. Tomatina to święto pomidora obchodzone w hiszpań~ w ostatnią środę sierpnia. Tego skiej miejscowości Bunol dnia świętujący obrzucają się na ulicach pomidorami. Podoba się nam takie święto? 4. Nowoczesne metody upraw roślin. Jak w Polsce technika pomaga rolnikom przy jak najmniejszym wkładzie pracy i środków uzyskiwać jak największe plony? 5. Zasada najwięcej efektów jak najmniejszym kosztem jest ważna nie tylko w rolnictwie. W jakich jeszcze obszarach działalności człowieka jest pożądana, a jakich niewskazana? 6
7 Część E. Propozycje projektów i prac badawczych. Każda z propozycji zamieszczonych poniżej to pomysł na projekt angażujący uczniów w przedsięwzięcie o długim terminie realizacji. Uczniowie zbierają informacje, stawiają nurtujące ich pytania i odpowiadają na nie, gromadzą przedmioty, eksperymentują i prowadzą obserwacje. Wszystkie swoje czynności dokumentują, a następnie prezentują innym w formie plakatu, albumu czy prezentacji na ekranie. Każdy znajdzie w tych propozycjach coś dla siebie. 1. Warto spróbować wyhodować krzew lub krzewy pomidora. Można kupić i zasiać nasiona pomidorów rosnących w doniczkach. Ich owoce są małe, ale bardzo smaczne. Są różne sposoby uprawy doniczkowej. Jednym z nich jest uprawy do góry korzeniami. Ma ona liczne zalety. Przede wszystkim nie wymaga dużo miejsca i na plony nie musimy czekać do wiosny. Informacji o tej metodzie można szukać w internecie pod hasłem: Uprawy roślin do góry nogami. 2. Warto zrobić własne pomidorowe przetwory na zimę. Przedsięwzięcie wymaga planowania i kalkulacji kosztów. Można porównać koszty własnych przetworów z cenami analogicznych produktów dostępnych w sklepach. Zimą warto sięgnąć po zapasy i zaprezentować ich jakość w klasie. Można na przykład zrobić przecier pomidorowy lub wysuszyć pomidory (wysuszone mrozi się w zamrażarce lub przechowuje w słojach z oliwą i ziołami). 3. W Polsce nie uprawia się pomidorów na tak dużą skalę jak w USA. Jakie są tego przyczyny? Jak dużo pomidorów Polska importuje każdego roku? 4. Ważnym składnikiem pomidora jest potas. Wiemy, że jest to miękki i łatwopalny metal. Czy w takiej postaci występuje w pomidorze? Dlaczego nasz organizm potrzebuje potasu? Czy to, że wspomaga uczenie się? O potasie warto dowiedzieć się jak najwięcej. 7
Karta pracy M+ do multipodręcznika dla klasy siódmej
 Karta pracy M+ do multipodręcznika dla klasy siódmej Bezkresne pola pomidorowe Część A. Sprawdź, czy rozumiesz film. 1. Uzupełnij poniższy tekst brakującymi słowami. Uprawa pomidorów w Kalifornii Stany
Karta pracy M+ do multipodręcznika dla klasy siódmej Bezkresne pola pomidorowe Część A. Sprawdź, czy rozumiesz film. 1. Uzupełnij poniższy tekst brakującymi słowami. Uprawa pomidorów w Kalifornii Stany
Karta pracy M+ Do multipodręcznika dla klasy siódmej
 Karta pracy M+ Do multipodręcznika dla klasy siódmej Hawana miasto ogródków Część A. Sprawdź, czy zrozumiałeś film. A1. Uzupełnij poniższy tekst o brakujące słowa. Hawana miasto ogródków Hawana to stolica...,
Karta pracy M+ Do multipodręcznika dla klasy siódmej Hawana miasto ogródków Część A. Sprawdź, czy zrozumiałeś film. A1. Uzupełnij poniższy tekst o brakujące słowa. Hawana miasto ogródków Hawana to stolica...,
Karta pracy M+ do multipodręcznika dla klasy 8 szkoły podstawowej
 Karta pracy M+ do multipodręcznika dla klasy 8 szkoły podstawowej Matematyka miast Część A. Sprawdź, czy rozumiesz film. 1. Skreśl w tekście niewłaściwe słowa i sformułowania. Niesamowite odkrycie profesora
Karta pracy M+ do multipodręcznika dla klasy 8 szkoły podstawowej Matematyka miast Część A. Sprawdź, czy rozumiesz film. 1. Skreśl w tekście niewłaściwe słowa i sformułowania. Niesamowite odkrycie profesora
WYPEŁNIA KOMISJA KONKURSOWA
 WOJEWÓDZKI KONKURS PRZEDMIOTOWY DLA UCZNIÓW GIMNAZJÓW WOJEWÓDZTWA ŚLĄSKIEGO W ROKU SZKOLNYM 2015/2016 MATEMATYKA Informacje dla ucznia 1. Na stronie tytułowej arkusza w wyznaczonym miejscu wpisz swój kod
WOJEWÓDZKI KONKURS PRZEDMIOTOWY DLA UCZNIÓW GIMNAZJÓW WOJEWÓDZTWA ŚLĄSKIEGO W ROKU SZKOLNYM 2015/2016 MATEMATYKA Informacje dla ucznia 1. Na stronie tytułowej arkusza w wyznaczonym miejscu wpisz swój kod
Żywność. zapewnia prawidłowe funkcjonowanie. poprawia samopoczucie
 Warsztaty żywieniowe Żywność buduje i regeneruje dostarcza energii zapewnia prawidłowe funkcjonowanie poprawia samopoczucie Żaden pojedynczy produkt nie dostarczy Ci wszystkiego, czego potrzebujesz dlatego
Warsztaty żywieniowe Żywność buduje i regeneruje dostarcza energii zapewnia prawidłowe funkcjonowanie poprawia samopoczucie Żaden pojedynczy produkt nie dostarczy Ci wszystkiego, czego potrzebujesz dlatego
XV WOJEWÓDZKI KONKURS Z MATEMATYKI
 XV WOJEWÓDZKI KONKURS Z MATEMATYKI DLA UCZNIÓW DOTYCHCZASOWYCH GIMNAZJÓW ORAZ KLAS DOTYCHCZASOWYCH GIMNAZJÓW PROWADZONYCH W SZKOŁACH INNEGO TYPU WOJEWÓDZTWA ŚWIĘTOKRZYSKIEGO W ROKU SZKOLNYM 2017/2018 ETAP
XV WOJEWÓDZKI KONKURS Z MATEMATYKI DLA UCZNIÓW DOTYCHCZASOWYCH GIMNAZJÓW ORAZ KLAS DOTYCHCZASOWYCH GIMNAZJÓW PROWADZONYCH W SZKOŁACH INNEGO TYPU WOJEWÓDZTWA ŚWIĘTOKRZYSKIEGO W ROKU SZKOLNYM 2017/2018 ETAP
Biologia scenariusz 2
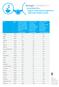 Załącznik nr 1. Zużycie wody przez mieszkańców wybranych krajów świata Kraj Rok Całkowite zużycie wody w przeliczeniu na mieszkańca (sektor rolnictwa, przemysłu i gospodarstw domowych łącznie) m 3 /osoba/rok
Załącznik nr 1. Zużycie wody przez mieszkańców wybranych krajów świata Kraj Rok Całkowite zużycie wody w przeliczeniu na mieszkańca (sektor rolnictwa, przemysłu i gospodarstw domowych łącznie) m 3 /osoba/rok
ZMNIEJSZ DYSTANS JEDZ LOKALNE! scenariusze zajęć
 ZMNIEJSZ DYSTANS JEDZ LOKALNE! scenariusze zajęć CZYM SĄ ŻYWNOŚCIOKILOMETRY? Żywnościokilometry to dystans, jaki żywność pokonuje z miejsca produkcji na nasz talerz. Emisje gazów cieplarnianych z transportu
ZMNIEJSZ DYSTANS JEDZ LOKALNE! scenariusze zajęć CZYM SĄ ŻYWNOŚCIOKILOMETRY? Żywnościokilometry to dystans, jaki żywność pokonuje z miejsca produkcji na nasz talerz. Emisje gazów cieplarnianych z transportu
Temat: Graniastosłupy- obliczanie pola powierzchni i objętości graniastosłupa.
 Scenariusz lekcji z matematyki dla klasy I Gimnazjum Temat: Graniastosłupy- obliczanie pola powierzchni i objętości graniastosłupa. Cel ogólny: rozróżniać rodzaje graniastosłupów oraz obliczać pole powierzchni
Scenariusz lekcji z matematyki dla klasy I Gimnazjum Temat: Graniastosłupy- obliczanie pola powierzchni i objętości graniastosłupa. Cel ogólny: rozróżniać rodzaje graniastosłupów oraz obliczać pole powierzchni
Skrypt 28. Przygotowanie do egzaminu Podstawowe figury geometryczne. 1. Przypomnienie i utrwalenie wiadomości dotyczących rodzajów i własności kątów
 Projekt Innowacyjny program nauczania matematyki dla gimnazjów współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 28 Przygotowanie do egzaminu Podstawowe figury
Projekt Innowacyjny program nauczania matematyki dla gimnazjów współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 28 Przygotowanie do egzaminu Podstawowe figury
Wojewódzki Konkurs Przedmiotowy z Matematyki dla uczniów szkół podstawowych województwa śląskiego w roku szkolnym 2014/2015
 Wojewódzki Konkurs Przedmiotowy z Matematyki dla uczniów szkół podstawowych województwa śląskiego w roku szkolnym 2014/2015 KOD UCZNIA Etap: Data: Czas pracy: rejonowy 13 stycznia 2015 r. 90 minut Informacje
Wojewódzki Konkurs Przedmiotowy z Matematyki dla uczniów szkół podstawowych województwa śląskiego w roku szkolnym 2014/2015 KOD UCZNIA Etap: Data: Czas pracy: rejonowy 13 stycznia 2015 r. 90 minut Informacje
Dydaktyka matematyki (II etap edukacyjny) II rok matematyki Semestr letni 2016/2017 Ćwiczenia nr 9
 Dydaktyka matematyki (II etap edukacyjny) II rok matematyki Semestr letni 2016/2017 Ćwiczenia nr 9 Karta pracy: podzielność przez 9 Niektóre są dobre, z drobnymi usterkami. Największy błąd: nie ma sformułowanej
Dydaktyka matematyki (II etap edukacyjny) II rok matematyki Semestr letni 2016/2017 Ćwiczenia nr 9 Karta pracy: podzielność przez 9 Niektóre są dobre, z drobnymi usterkami. Największy błąd: nie ma sformułowanej
W jaki sposób powinien odżywiać się młody człowiek?
 W jaki sposób powinien odżywiać się młody człowiek? Prawidłowe odżywianie się to dostarczanie organizmowi niezbędnych składników odżywczych, a tym samym energii i substratów potrzebnych do utrzymania zdrowia
W jaki sposób powinien odżywiać się młody człowiek? Prawidłowe odżywianie się to dostarczanie organizmowi niezbędnych składników odżywczych, a tym samym energii i substratów potrzebnych do utrzymania zdrowia
Prawidłowe odżywianie. Czy marnujemy szansę na zdrowe żywienie?
 Katedra Żywienia Człowieka Uniwersytet Warmińsko-Mazurski w Olsztynie Polskie Towarzystwo Nauk Żywieniowych Prawidłowe odżywianie. Czy marnujemy szansę na zdrowe żywienie? prof. dr hab. Lidia Wądołowska
Katedra Żywienia Człowieka Uniwersytet Warmińsko-Mazurski w Olsztynie Polskie Towarzystwo Nauk Żywieniowych Prawidłowe odżywianie. Czy marnujemy szansę na zdrowe żywienie? prof. dr hab. Lidia Wądołowska
Konkurs przedmiotowy z matematyki dla uczniów gimnazjów 13 marca 2015 r. zawody III stopnia (wojewódzkie)
 Kod ucznia:... Konkurs przedmiotowy z matematyki dla uczniów gimnazjów 13 marca 2015 r. zawody III stopnia (wojewódzkie) Witamy Cię na trzecim etapie Konkursu przedmiotowego z matematyki. Przed przystąpieniem
Kod ucznia:... Konkurs przedmiotowy z matematyki dla uczniów gimnazjów 13 marca 2015 r. zawody III stopnia (wojewódzkie) Witamy Cię na trzecim etapie Konkursu przedmiotowego z matematyki. Przed przystąpieniem
WYPEŁNIA KOMISJA KONKURSOWA
 WOJEWÓDZKI KONKURS PRZEDMIOTOWY DLA UCZNIÓW GIMNAZJÓW WOJEWÓDZTWA ŚLĄSKIEGO W ROKU SZKOLNYM 2016/2017 MATEMATYKA Informacje dla ucznia 1. Na stronie tytułowej arkusza w wyznaczonym miejscu wpisz swój kod
WOJEWÓDZKI KONKURS PRZEDMIOTOWY DLA UCZNIÓW GIMNAZJÓW WOJEWÓDZTWA ŚLĄSKIEGO W ROKU SZKOLNYM 2016/2017 MATEMATYKA Informacje dla ucznia 1. Na stronie tytułowej arkusza w wyznaczonym miejscu wpisz swój kod
Karta pracy M+ do multipodręcznika dla klasy 4 szkoły podstawowej
 Karta pracy M+ do multipodręcznika dla klasy 4 szkoły podstawowej Jak powstają świece Część A. Sprawdź, czy rozumiesz film. 1. Uzupełnij poniższy tekst brakującymi słowami. Od plastrów w pszczelich ulach
Karta pracy M+ do multipodręcznika dla klasy 4 szkoły podstawowej Jak powstają świece Część A. Sprawdź, czy rozumiesz film. 1. Uzupełnij poniższy tekst brakującymi słowami. Od plastrów w pszczelich ulach
Wybieram zdrowie i zdrowe odżywianie
 Wybieram zdrowie i zdrowe odżywianie Doktorze Zdrówko, co to znaczy być zdrowym? Być zdrowym, to nie tylko nie chorować, ale też czuć się dobrze, być radosnym i sprawnym fizycznie. Czy wiesz, co pomaga
Wybieram zdrowie i zdrowe odżywianie Doktorze Zdrówko, co to znaczy być zdrowym? Być zdrowym, to nie tylko nie chorować, ale też czuć się dobrze, być radosnym i sprawnym fizycznie. Czy wiesz, co pomaga
Zawartość składników pokarmowych w roślinach
 Zawartość składników pokarmowych w roślinach Poszczególne rośliny różnią się zawartością składników pokarmowych zarówno w organach wegetatywnych, jak i generatywnych. Wynika to z różnych funkcji, jakie
Zawartość składników pokarmowych w roślinach Poszczególne rośliny różnią się zawartością składników pokarmowych zarówno w organach wegetatywnych, jak i generatywnych. Wynika to z różnych funkcji, jakie
Karta pracy M+ Do multipodręcznika dla klasy 1 gimnazjum
 Karta pracy M+ Do multipodręcznika dla klasy 1 gimnazjum Hawana miasto ogródków Część A. Sprawdź, czy zrozumiałeś film. A1. Uzupełnij poniższy tekst o brakujące słowa. Hawana miasto ogródków Hawana to
Karta pracy M+ Do multipodręcznika dla klasy 1 gimnazjum Hawana miasto ogródków Część A. Sprawdź, czy zrozumiałeś film. A1. Uzupełnij poniższy tekst o brakujące słowa. Hawana miasto ogródków Hawana to
7. PLANIMETRIA.GEOMETRIA ANALITYCZNA
 7. PLANIMETRIA.GEOMETRIA ANALITYCZNA ZADANIA ZAMKNIĘTE 1. Okrąg o równaniu : A) nie przecina osi, B) nie przecina osi, C) przechodzi przez początek układu współrzędnych, D) przechodzi przez punkt. 2. Stosunek
7. PLANIMETRIA.GEOMETRIA ANALITYCZNA ZADANIA ZAMKNIĘTE 1. Okrąg o równaniu : A) nie przecina osi, B) nie przecina osi, C) przechodzi przez początek układu współrzędnych, D) przechodzi przez punkt. 2. Stosunek
Ocena sytuacji rynku sprzedaży zbóż
 - 1 - AgriNet24 Internetowe sondaże Ocena sytuacji rynku sprzedaży zbóż lipiec 2014, Wrocław - 2 - Informacje o badaniu Grupa docelowa Technika wywiadów Internauci, Użytkownicy Agrofoto.pl CAPI Liczebność
- 1 - AgriNet24 Internetowe sondaże Ocena sytuacji rynku sprzedaży zbóż lipiec 2014, Wrocław - 2 - Informacje o badaniu Grupa docelowa Technika wywiadów Internauci, Użytkownicy Agrofoto.pl CAPI Liczebność
Jak obracać trójkąt, by otrzymać bryłę o największej. objętości?
 Jak obracać trójkąt, by otrzymać bryłę o największej objętości? Czas trwania zajęć: 40 minut Kontekst w jakim wprowadzono doświadczenie: Trójkąt o bokach długości: cm, 4 cm, 5 cm obrócono o kąt 60 o w
Jak obracać trójkąt, by otrzymać bryłę o największej objętości? Czas trwania zajęć: 40 minut Kontekst w jakim wprowadzono doświadczenie: Trójkąt o bokach długości: cm, 4 cm, 5 cm obrócono o kąt 60 o w
WOJEWÓDZKI KONKURS MATEMATYCZNY dla uczniów gimnazjów i oddziałów gimnazjalnych województwa pomorskiego w roku szkolnym 2018/2019 etap wojewódzki
 WOJEWÓDZKI KONKURS MATEMATYCZNY dla uczniów gimnazjów i oddziałów gimnazjalnych województwa pomorskiego w roku szkolnym 2018/2019 etap wojewódzki Zad.1. (0-3) PRZYKŁADOWE ROZWIĄZANIA I KRYTERIA OCENIANIA
WOJEWÓDZKI KONKURS MATEMATYCZNY dla uczniów gimnazjów i oddziałów gimnazjalnych województwa pomorskiego w roku szkolnym 2018/2019 etap wojewódzki Zad.1. (0-3) PRZYKŁADOWE ROZWIĄZANIA I KRYTERIA OCENIANIA
Karta pracy M+ do multipodręcznika dla klasy 1 gimnazjum. Skarby ziemi
 Karta pracy M+ do multipodręcznika dla klasy 1 gimnazjum Skarby ziemi Część A. Sprawdź, czy rozumiesz film. 1. Uzupełnij poniższy tekst brakującymi słowami. Źródła energii Dwa najważniejsze źródła energii,
Karta pracy M+ do multipodręcznika dla klasy 1 gimnazjum Skarby ziemi Część A. Sprawdź, czy rozumiesz film. 1. Uzupełnij poniższy tekst brakującymi słowami. Źródła energii Dwa najważniejsze źródła energii,
Scenariusz lekcji matematyki, klasa 1 LO.
 Scenariusz lekcji matematyki, klasa 1 LO. Temat lekcji: Czworokąty: rodzaje, własności, pola czworokątów. Cele: po lekcji uczeń: - rozpoznaje czworokąty, - zna własności czworokątów, - potrafi wskazać
Scenariusz lekcji matematyki, klasa 1 LO. Temat lekcji: Czworokąty: rodzaje, własności, pola czworokątów. Cele: po lekcji uczeń: - rozpoznaje czworokąty, - zna własności czworokątów, - potrafi wskazać
Kąty, trójkąty i czworokąty.
 Kąty, trójkąty i czworokąty. str. 1/5...... imię i nazwisko lp. w dzienniku...... klasa data 1. Do kartonu wstawiono 3 garnki (zobacz rysunek), których dna mają promienie:13 cm, 15 cm i 11 cm. Podaj długość
Kąty, trójkąty i czworokąty. str. 1/5...... imię i nazwisko lp. w dzienniku...... klasa data 1. Do kartonu wstawiono 3 garnki (zobacz rysunek), których dna mają promienie:13 cm, 15 cm i 11 cm. Podaj długość
Skrypt 17. Podobieństwo figur. 1. Figury podobne skala podobieństwa. Obliczanie wymiarów wielokątów powiększonych bądź pomniejszonych.
 Projekt Innowacyjny program nauczania matematyki dla gimnazjów współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 17 Podobieństwo figur 1. Figury podobne skala
Projekt Innowacyjny program nauczania matematyki dla gimnazjów współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 17 Podobieństwo figur 1. Figury podobne skala
Warzywa i owoce powinny wchodzić w skład codziennej diety, gdyż są źródłem cennych witamin, zwłaszcza witaminy C oraz B - karotenu.
 Warzywa i owoce powinny wchodzić w skład codziennej diety, gdyż są źródłem cennych witamin, zwłaszcza witaminy C oraz B - karotenu. Dostarczają także kwasu foliowego. Zawierają znaczne ilości składników
Warzywa i owoce powinny wchodzić w skład codziennej diety, gdyż są źródłem cennych witamin, zwłaszcza witaminy C oraz B - karotenu. Dostarczają także kwasu foliowego. Zawierają znaczne ilości składników
ARKUSZ HOSPITACJI DIAGNOZUJĄCEJ
 ARKUSZ HOSPITACJI DIAGNOZUJĄCEJ Nauczyciel: Małgorzata Drejka Gimnazjum nr 4 w Legionowie, klasa I F, zajęcia edukacyjne: matematyka Data: 12.06.2006. Cel główny: Obserwacja osiągniętego poziomu sprawności
ARKUSZ HOSPITACJI DIAGNOZUJĄCEJ Nauczyciel: Małgorzata Drejka Gimnazjum nr 4 w Legionowie, klasa I F, zajęcia edukacyjne: matematyka Data: 12.06.2006. Cel główny: Obserwacja osiągniętego poziomu sprawności
Klasa III technikum Egzamin poprawkowy z matematyki sierpień I. CIĄGI LICZBOWE 1. Pojęcie ciągu liczbowego. b) a n =
 /9 Narysuj wykres ciągu (a n ) o wyrazie ogólnym: I. CIĄGI LICZBOWE. Pojęcie ciągu liczbowego. a) a n =5n dla n
/9 Narysuj wykres ciągu (a n ) o wyrazie ogólnym: I. CIĄGI LICZBOWE. Pojęcie ciągu liczbowego. a) a n =5n dla n
MAŁOPOLSKI KONKURS MATEMATYCZNY dla uczniów dotychczasowych gimnazjów i klas dotychczasowych gimnazjów prowadzonych w szkołach innego typu
 MAŁOPOLSKI KONKURS MATEMATYCZNY dla uczniów dotychczasowych gimnazjów i klas dotychczasowych gimnazjów prowadzonych w szkołach innego typu województwa małopolskiego Rok szkolny 2017/2018 ETAP REJONOWY
MAŁOPOLSKI KONKURS MATEMATYCZNY dla uczniów dotychczasowych gimnazjów i klas dotychczasowych gimnazjów prowadzonych w szkołach innego typu województwa małopolskiego Rok szkolny 2017/2018 ETAP REJONOWY
Klasówka gr. A str. 1/3
 Klasówka gr. A str. 1/3 1. Boki trójkąta ABC mają długości 9 cm, 7cm, 8 cm. Boki trójkąta podobnego A B C w skali 1 2 mają długości: A. 18 cm, 14 cm, 16 cm B. 4 1 2 cm, 3 1 2 cm, 4 cm C. 4 1 2 cm, 7 cm,
Klasówka gr. A str. 1/3 1. Boki trójkąta ABC mają długości 9 cm, 7cm, 8 cm. Boki trójkąta podobnego A B C w skali 1 2 mają długości: A. 18 cm, 14 cm, 16 cm B. 4 1 2 cm, 3 1 2 cm, 4 cm C. 4 1 2 cm, 7 cm,
ZAPRAWIANIE NASION NIBY DROBIAZG, A TO PODSTAWA NOWOCZESNEJ OCHRONY ROŚLIN
 ZAPRAWIANIE NASION NIBY DROBIAZG, A TO PODSTAWA NOWOCZESNEJ OCHRONY ROŚLIN Polskie i zagraniczne firmy nasienne zrzeszone w PIN domagają się jak najszybszego finalnego uregulowania ustaw i przepisów wykonawczych
ZAPRAWIANIE NASION NIBY DROBIAZG, A TO PODSTAWA NOWOCZESNEJ OCHRONY ROŚLIN Polskie i zagraniczne firmy nasienne zrzeszone w PIN domagają się jak najszybszego finalnego uregulowania ustaw i przepisów wykonawczych
Ilość wody potrzebnej do wytworzenia produktu
 SCENARIUSZ Imię i nazwisko autorki/autora: Justyna Smuda Nazwa szkoły: Gimnazjum nr 16 w Zabrzu Temat: Odczytywanie danych statystycznych (przedmiot: matematyka). Czas trwania: 45 minut Poziom edukacyjny:
SCENARIUSZ Imię i nazwisko autorki/autora: Justyna Smuda Nazwa szkoły: Gimnazjum nr 16 w Zabrzu Temat: Odczytywanie danych statystycznych (przedmiot: matematyka). Czas trwania: 45 minut Poziom edukacyjny:
Wojewódzki Konkurs Przedmiotowy z Matematyki dla uczniów szkół podstawowych województwa śląskiego w roku szkolnym 2014/2015
 Wojewódzki Konkurs Przedmiotowy z Matematyki dla uczniów szkół podstawowych województwa śląskiego w roku szkolnym 20/205 KOD UCZNIA Etap: Data: Czas pracy: szkolny 7 listopada 20 r. 90 minut Informacje
Wojewódzki Konkurs Przedmiotowy z Matematyki dla uczniów szkół podstawowych województwa śląskiego w roku szkolnym 20/205 KOD UCZNIA Etap: Data: Czas pracy: szkolny 7 listopada 20 r. 90 minut Informacje
MATEMATYKA WYMAGANIA EDUKACYJNE DLA KLASY V
 MATEMATYKA WYMAGANIA EDUKACYJNE DLA KLASY V Na ocenę wyższą uczeń powinien opanować wiedzę i umiejętności na ocenę (oceny) niższą. Dział programowy: LICZBY NATURALNE podać przykład liczby naturalnej czytać
MATEMATYKA WYMAGANIA EDUKACYJNE DLA KLASY V Na ocenę wyższą uczeń powinien opanować wiedzę i umiejętności na ocenę (oceny) niższą. Dział programowy: LICZBY NATURALNE podać przykład liczby naturalnej czytać
WYMAGANIA EGZAMINACYJNE DLA KLASY V
 TEMAT WYMAGANIA EGZAMINACYJNE DLA KLASY V WYMAGANIA SZCZEGÓŁOWE 1.LICZBY I DZIAŁANIA 1. Zapisywanie i I. Liczby naturalne w dziesiątkowym układzie pozycyjnym. porównywanie liczb. Uczeń: 1) zapisuje i odczytuje
TEMAT WYMAGANIA EGZAMINACYJNE DLA KLASY V WYMAGANIA SZCZEGÓŁOWE 1.LICZBY I DZIAŁANIA 1. Zapisywanie i I. Liczby naturalne w dziesiątkowym układzie pozycyjnym. porównywanie liczb. Uczeń: 1) zapisuje i odczytuje
WYPEŁNIA KOMISJA KONKURSOWA
 WOJEWÓDZKI KONKURS PRZEDMIOTOWY DLA UCZNIÓW GIMNAZJÓW WOJEWÓDZTWA ŚLĄSKIEGO W ROKU SZKOLNYM 016/017 MATEMATYKA Informacje dla ucznia 1. Na stronie tytułowej arkusza w wyznaczonym miejscu wpisz swój kod
WOJEWÓDZKI KONKURS PRZEDMIOTOWY DLA UCZNIÓW GIMNAZJÓW WOJEWÓDZTWA ŚLĄSKIEGO W ROKU SZKOLNYM 016/017 MATEMATYKA Informacje dla ucznia 1. Na stronie tytułowej arkusza w wyznaczonym miejscu wpisz swój kod
KL. I. ZAD. 2 Zapytano rybaka, ile waży złowiona przez niego rybka. Rybak odpowiedział:
 KL. I ZAD. 1 2 3 0,5 x 3 5 Oblicz x : 1, 2 7 3 1 1,4 : 2 20 4 ZAD. 2 Zapytano rybaka, ile waży złowiona przez niego rybka. Rybak odpowiedział: 2 2 kg i jeszcze 2 razy po swojej masy. Ile waży złowiona
KL. I ZAD. 1 2 3 0,5 x 3 5 Oblicz x : 1, 2 7 3 1 1,4 : 2 20 4 ZAD. 2 Zapytano rybaka, ile waży złowiona przez niego rybka. Rybak odpowiedział: 2 2 kg i jeszcze 2 razy po swojej masy. Ile waży złowiona
WYPEŁNIA KOMISJA KONKURSOWA. Nr zadania Razem Liczba punktów możliwych do zdobycia
 WOJEWÓDZKI KONKURS PRZEDMIOTOWY DLA UCZNIÓW GIMNAZJÓW WOJEWÓDZTWA ŚLĄSKIEGO W ROKU SZKOLNYM 2015/2016 MATEMATYKA Informacje dla ucznia 1. Na stronie tytułowej arkusza w wyznaczonym miejscu wpisz swój kod
WOJEWÓDZKI KONKURS PRZEDMIOTOWY DLA UCZNIÓW GIMNAZJÓW WOJEWÓDZTWA ŚLĄSKIEGO W ROKU SZKOLNYM 2015/2016 MATEMATYKA Informacje dla ucznia 1. Na stronie tytułowej arkusza w wyznaczonym miejscu wpisz swój kod
Jedzmy zdrowo na kolorowo!
 Jedzmy zdrowo na kolorowo! Dlaczego powinniśmy jeść warzywa? Ponieważ są źródłem: -witamin: głównie: beta-karoten, witamina C, kwas foliowy oraz witaminy K, niacyna oraz witaminy E -składników mineralnych:
Jedzmy zdrowo na kolorowo! Dlaczego powinniśmy jeść warzywa? Ponieważ są źródłem: -witamin: głównie: beta-karoten, witamina C, kwas foliowy oraz witaminy K, niacyna oraz witaminy E -składników mineralnych:
PRAWIDŁOWE ODŻYWIANIE NASTOLATKÓW
 PRAWIDŁOWE ODŻYWIANIE NASTOLATKÓW Młody organizm, aby mógł prawidłowo się rozwijać potrzebuje wielu różnorodnych składników odżywczych, które powinny być nieodłączną częścią diety każdego dojrzewającego
PRAWIDŁOWE ODŻYWIANIE NASTOLATKÓW Młody organizm, aby mógł prawidłowo się rozwijać potrzebuje wielu różnorodnych składników odżywczych, które powinny być nieodłączną częścią diety każdego dojrzewającego
XII. GEOMETRIA PRZESTRZENNA GRANIASTOSŁUPY
 pitagoras.d2.pl XII. GEOMETRIA PRZESTRZENNA GRANIASTOSŁUPY Graniastosłup to wielościan posiadający dwie identyczne i równoległe podstawy oraz ściany boczne będące równoległobokami. Jeśli podstawy graniastosłupa
pitagoras.d2.pl XII. GEOMETRIA PRZESTRZENNA GRANIASTOSŁUPY Graniastosłup to wielościan posiadający dwie identyczne i równoległe podstawy oraz ściany boczne będące równoległobokami. Jeśli podstawy graniastosłupa
1 Pole figury. P 1. Oblicz pole prostokąta o podanych bokach. a) 7 cm i 5 cm b) cm i cm c) 15 cm i 5,2 dm
 68 Pola figur 6 Pola figur Pole figury P. Oblicz pole prostokąta o podanych bokach. a) 7 cm i 5 cm b) 3 2 cm i 2 7 cm c) 5 cm i 5,2 dm P 2. Oblicz pole prostokąta o podanych bokach. a) 8 cm i 6 cm b) 4
68 Pola figur 6 Pola figur Pole figury P. Oblicz pole prostokąta o podanych bokach. a) 7 cm i 5 cm b) 3 2 cm i 2 7 cm c) 5 cm i 5,2 dm P 2. Oblicz pole prostokąta o podanych bokach. a) 8 cm i 6 cm b) 4
Konspekt lekcji diagnozującej z biologii dla kl. II gimnazjum. Temat: Budowa i funkcjonowanie układu pokarmowego człowieka.
 Konspekt lekcji diagnozującej z biologii dla kl. II gimnazjum Temat: Budowa i funkcjonowanie układu pokarmowego człowieka. Hasło programowe: Budowa i funkcjonowanie organizmu człowieka. Cele lekcji: w
Konspekt lekcji diagnozującej z biologii dla kl. II gimnazjum Temat: Budowa i funkcjonowanie układu pokarmowego człowieka. Hasło programowe: Budowa i funkcjonowanie organizmu człowieka. Cele lekcji: w
Wojewódzki Konkurs Przedmiotowy z Matematyki dla uczniów gimnazjów województwa śląskiego w roku szkolnym 2013/2014
 Wojewódzki Konkurs Przedmiotowy z Matematyki dla uczniów gimnazjów województwa śląskiego w roku szkolnym 2013/2014 KOD UCZNI Etap: Data: Czas pracy: szkolny 13 listopada 2013 r. 120 minut Informacje dla
Wojewódzki Konkurs Przedmiotowy z Matematyki dla uczniów gimnazjów województwa śląskiego w roku szkolnym 2013/2014 KOD UCZNI Etap: Data: Czas pracy: szkolny 13 listopada 2013 r. 120 minut Informacje dla
EGZAMIN ÓSMOKLASISTY od roku szkolnego 2018/2019
 EGZAMIN ÓSMOKLASISTY od roku szkolnego 2018/2019 MATEMATYKA Przykładowy arkusz egzaminacyjny (EO_7) Czas pracy: do 150 minut GRUDZIEŃ 2017 Centralna Komisja Egzaminacyjna Warszawa Zadanie 1. (0 1) Z okazji
EGZAMIN ÓSMOKLASISTY od roku szkolnego 2018/2019 MATEMATYKA Przykładowy arkusz egzaminacyjny (EO_7) Czas pracy: do 150 minut GRUDZIEŃ 2017 Centralna Komisja Egzaminacyjna Warszawa Zadanie 1. (0 1) Z okazji
wymagania programowe z matematyki kl. II gimnazjum
 wymagania programowe z matematyki kl. II gimnazjum Umie obliczyć potęgę liczby wymiernej o wykładniku naturalnym. 1. Arytmetyka występują potęgi o wykładniku naturalnym. Umie zapisać i porównać duże liczby
wymagania programowe z matematyki kl. II gimnazjum Umie obliczyć potęgę liczby wymiernej o wykładniku naturalnym. 1. Arytmetyka występują potęgi o wykładniku naturalnym. Umie zapisać i porównać duże liczby
Konkurs matematyczny dla uczniów szkół podstawowych rok szkolny 2014/2015 III stopień - wojewódzki Kryteria oceniania
 Gimnazjum nr 26 w Gdańsku im. Jana III Sobieskiego ul. R. Traugutta 92 sekretariat@gim26.gda.pl 80-226 Gdańsk www.gim26.gda.pl tel. 58-341-02-33 fax 58-344-05-02 Zad.1. (0 1) Konkurs matematyczny dla uczniów
Gimnazjum nr 26 w Gdańsku im. Jana III Sobieskiego ul. R. Traugutta 92 sekretariat@gim26.gda.pl 80-226 Gdańsk www.gim26.gda.pl tel. 58-341-02-33 fax 58-344-05-02 Zad.1. (0 1) Konkurs matematyczny dla uczniów
Karta pracy M+ do multipodręcznika dla klasy 8 szkoły podstawowej
 Karta pracy M+ do multipodręcznika dla klasy 8 szkoły podstawowej Geometria w starożytnym świecie Część A. Sprawdź, czy rozumiesz film. 1. Skreśl w tekście niewłaściwe słowa i sformułowania. Bryły platońskie
Karta pracy M+ do multipodręcznika dla klasy 8 szkoły podstawowej Geometria w starożytnym świecie Część A. Sprawdź, czy rozumiesz film. 1. Skreśl w tekście niewłaściwe słowa i sformułowania. Bryły platońskie
WOJEWÓDZKI KONKURS PRZEDMIOTOWY DLA UCZNIÓW GIMNAZJÓW WOJEWÓDZTWA ŚLĄSKIEGO W ROKU SZKOLNYM 2015/2016 MATEMATYKA. Czas pracy: 120 minut
 WOJEWÓDZKI KONKURS PRZEDMIOTOWY DLA UCZNIÓW GIMNAZJÓW WOJEWÓDZTWA ŚLĄSKIEGO W ROKU SZKOLNYM 2015/2016 MATEMATYKA Informacje dla ucznia 1. Na stronie tytułowej arkusza w wyznaczonym miejscu wpisz swój kod
WOJEWÓDZKI KONKURS PRZEDMIOTOWY DLA UCZNIÓW GIMNAZJÓW WOJEWÓDZTWA ŚLĄSKIEGO W ROKU SZKOLNYM 2015/2016 MATEMATYKA Informacje dla ucznia 1. Na stronie tytułowej arkusza w wyznaczonym miejscu wpisz swój kod
WYMAGANIA EDUKACYJN KRYTERIA OCENY Z MATEMATYKI W KLASIE II GIMNAZJUM
 Na ocenę dopuszczającą uczeń umie : WYMAGANIA EDUKACYJN KRYTERIA OCENY Z MATEMATYKI W KLASIE II GIMNAZJUM stosować cztery podstawowe działania na liczbach wymiernych, zna kolejność wykonywania działań
Na ocenę dopuszczającą uczeń umie : WYMAGANIA EDUKACYJN KRYTERIA OCENY Z MATEMATYKI W KLASIE II GIMNAZJUM stosować cztery podstawowe działania na liczbach wymiernych, zna kolejność wykonywania działań
SPRAWDZIAN PRÓBNY W SZÓSTEJ KLASIE SZKOŁY PODSTAWOWEJ
 UZUPEŁNIA ZESPÓŁ NADZORUJĄCY KOD UCZNIA DATA URODZENIA UCZNIA miejsce na naklejkę z kodem dzień miesiąc rok SPRAWDZIAN PRÓBNY W SZÓSTEJ KLASIE SZKOŁY PODSTAWOWEJ Warzywa, owoce Czas pracy: 60 minut (można
UZUPEŁNIA ZESPÓŁ NADZORUJĄCY KOD UCZNIA DATA URODZENIA UCZNIA miejsce na naklejkę z kodem dzień miesiąc rok SPRAWDZIAN PRÓBNY W SZÓSTEJ KLASIE SZKOŁY PODSTAWOWEJ Warzywa, owoce Czas pracy: 60 minut (można
KONKURENCYJNOŚĆ PRODUKCJI SEKTORA ROLNEGO UKRAINY. Profesor dr hab. Tatjana Mostenska Państwowy Uniwersytet Przetwórstwa Żywności Ukrainy
 KONKURENCYJNOŚĆ PRODUKCJI SEKTORA ROLNEGO UKRAINY Profesor dr hab. Tatjana Mostenska Państwowy Uniwersytet Przetwórstwa Żywności Ukrainy Konkurencyjność produkcji wyznaczają wskaźniki: jakości, właściwości
KONKURENCYJNOŚĆ PRODUKCJI SEKTORA ROLNEGO UKRAINY Profesor dr hab. Tatjana Mostenska Państwowy Uniwersytet Przetwórstwa Żywności Ukrainy Konkurencyjność produkcji wyznaczają wskaźniki: jakości, właściwości
Wymagania na poszczególne oceny szkolne z. matematyki. dla uczniów klasy IIIa i IIIb. Gimnazjum im. Jana Pawła II w Mętowie. w roku szkolnym 2015/2016
 Wymagania na poszczególne oceny szkolne z matematyki dla uczniów klasy IIIa i IIIb Gimnazjum im. Jana Pawła II w Mętowie w roku szkolnym 2015/2016 DZIAŁ 1. FUNKCJE (11h) Uczeń: poda definicję funkcji (2)
Wymagania na poszczególne oceny szkolne z matematyki dla uczniów klasy IIIa i IIIb Gimnazjum im. Jana Pawła II w Mętowie w roku szkolnym 2015/2016 DZIAŁ 1. FUNKCJE (11h) Uczeń: poda definicję funkcji (2)
Program sfinansowany ze środków Funduszu Promocji Owoców i Warzyw. Organizator Stowarzyszenie Krajowa Unia Producentów Soków.
 Program sfinansowany ze środków Funduszu Promocji Owoców i Warzyw. Organizator Stowarzyszenie Krajowa Unia Producentów Soków. www.kups.org.pl І www.wszkole.5porcji.pl PRAWIDŁOWE ŻYWIENIE Prawidłowe żywienie
Program sfinansowany ze środków Funduszu Promocji Owoców i Warzyw. Organizator Stowarzyszenie Krajowa Unia Producentów Soków. www.kups.org.pl І www.wszkole.5porcji.pl PRAWIDŁOWE ŻYWIENIE Prawidłowe żywienie
Wojewódzki Konkurs Przedmiotowy z Matematyki dla uczniów gimnazjów województwa śląskiego w roku szkolnym 2011/2012
 Wojewódzki Konkurs Przedmiotowy z Matematyki dla uczniów gimnazjów województwa śląskiego w roku szkolnym 011/01 KOD UCZNIA Etap: Data: Czas pracy: wojewódzki lutego 01 r. 90 minut Informacje dla ucznia:
Wojewódzki Konkurs Przedmiotowy z Matematyki dla uczniów gimnazjów województwa śląskiego w roku szkolnym 011/01 KOD UCZNIA Etap: Data: Czas pracy: wojewódzki lutego 01 r. 90 minut Informacje dla ucznia:
WYMAGANIA EDUKACYJNE NIEZBĘDNE DO UZYSKANIA ŚRÓDROCZNYCH I ROCZNYCH OCEN KLASYFIKACYJNYCH Z MATEMATYKI W KLASIE V
 WYMAGANIA EDUKACYJNE NIEZBĘDNE DO UZYSKANIA ŚRÓDROCZNYCH I ROCZNYCH OCEN KLASYFIKACYJNYCH Z MATEMATYKI W KLASIE V OCENA ŚRÓDROCZNA: DOPUSZCZAJĄCY uczeń potrafi: zapisywać i odczytywać liczby w dziesiątkowym
WYMAGANIA EDUKACYJNE NIEZBĘDNE DO UZYSKANIA ŚRÓDROCZNYCH I ROCZNYCH OCEN KLASYFIKACYJNYCH Z MATEMATYKI W KLASIE V OCENA ŚRÓDROCZNA: DOPUSZCZAJĄCY uczeń potrafi: zapisywać i odczytywać liczby w dziesiątkowym
WYPEŁNIA KOMISJA KONKURSOWA
 WOJEWÓDZKI KONKURS PRZEDMIOTOWY DLA UCZNIÓW GIMNAZJÓW WOJEWÓDZTWA ŚLĄSKIEGO W ROKU SZKOLNYM 206/207 MATEMATYKA Informacje dla ucznia. Na stronie tytułowej arkusza w wyznaczonym miejscu wpisz swój kod ustalony
WOJEWÓDZKI KONKURS PRZEDMIOTOWY DLA UCZNIÓW GIMNAZJÓW WOJEWÓDZTWA ŚLĄSKIEGO W ROKU SZKOLNYM 206/207 MATEMATYKA Informacje dla ucznia. Na stronie tytułowej arkusza w wyznaczonym miejscu wpisz swój kod ustalony
Przedmiotowy system oceniania
 Przedmiotowy system oceniania gimnazjum - matematyka Opracowała mgr Katarzyna Kukuła 1 MATEMATYKA KRYTERIA OCEN Kryteria oceniania zostały określone przez podanie listy umiejętności, którymi uczeń musi
Przedmiotowy system oceniania gimnazjum - matematyka Opracowała mgr Katarzyna Kukuła 1 MATEMATYKA KRYTERIA OCEN Kryteria oceniania zostały określone przez podanie listy umiejętności, którymi uczeń musi
Bukiety matematyczne dla szkoły podstawowej http://www.mat.uni.torun.pl/~kolka/
 Bukiety matematyczne dla szkoły podstawowej http://www.mat.uni.torun.pl/~kolka/ 12 IX rok 2003/2004 Bukiet 1 O pewnych liczbach A, B i C wiadomo, że: A + B = 32, B + C = 40, C + A = 26. 1. Ile wynosi A
Bukiety matematyczne dla szkoły podstawowej http://www.mat.uni.torun.pl/~kolka/ 12 IX rok 2003/2004 Bukiet 1 O pewnych liczbach A, B i C wiadomo, że: A + B = 32, B + C = 40, C + A = 26. 1. Ile wynosi A
ZALECENIA ŻYWIENIOWE DLA DZIECI I MŁODZIEŻY. Gimnazjum nr 1 w Piastowie Lidia Kaczor, 2011r
 ZALECENIA ŻYWIENIOWE DLA DZIECI I MŁODZIEŻY Gimnazjum nr 1 w Piastowie Lidia Kaczor, 2011r PRAWIDŁOWE ODŻYWIANIE - definicja Prawidłowe odżywianie to nie tylko dostarczenie organizmowi energii, ale także
ZALECENIA ŻYWIENIOWE DLA DZIECI I MŁODZIEŻY Gimnazjum nr 1 w Piastowie Lidia Kaczor, 2011r PRAWIDŁOWE ODŻYWIANIE - definicja Prawidłowe odżywianie to nie tylko dostarczenie organizmowi energii, ale także
II. Działania na liczbach naturalnych. Uczeń:
 TEMAT 1. Zapisywanie i porównywanie liczb. 2. Rachunki pamięciowe. 3. Kolejność działań. 4. Sprytne rachunki. WYMAGANIA SZCZEGÓŁOWE Z PODSTAWY PROGRAMOWEJ Z 14. II. 2017. I. Liczby naturalne w dziesiątkowym
TEMAT 1. Zapisywanie i porównywanie liczb. 2. Rachunki pamięciowe. 3. Kolejność działań. 4. Sprytne rachunki. WYMAGANIA SZCZEGÓŁOWE Z PODSTAWY PROGRAMOWEJ Z 14. II. 2017. I. Liczby naturalne w dziesiątkowym
COMENIUS PROJEKT ROZWOJU SZKOŁY. Sezamie, otwórz się! - rozwijanie zdolności uczenia i myślenia uczniów.
 COMENIUS PROJEKT ROZWOJU SZKOŁY Sezamie, otwórz się! - rozwijanie zdolności uczenia i myślenia uczniów. GIMNAZJUM 20 GDAŃSK POLSKA Maj 2006 SCENARIUSZ LEKCJI GEOGRAFII Z WYKORZYSTANIEM METODY STACJI UCZENIA
COMENIUS PROJEKT ROZWOJU SZKOŁY Sezamie, otwórz się! - rozwijanie zdolności uczenia i myślenia uczniów. GIMNAZJUM 20 GDAŃSK POLSKA Maj 2006 SCENARIUSZ LEKCJI GEOGRAFII Z WYKORZYSTANIEM METODY STACJI UCZENIA
Dydaktyka matematyki (III etap edukacyjny) IV rok matematyki Semestr letni 2017/2018 Ćwiczenia nr 6
 Dydaktyka matematyki (III etap edukacyjny) IV rok matematyki Semestr letni 2017/2018 Ćwiczenia nr 6 Lang: Długość okręgu. pole pierścienia będę chciał znaleźć inne wyrażenie na pole pierścienia. oszacowanie
Dydaktyka matematyki (III etap edukacyjny) IV rok matematyki Semestr letni 2017/2018 Ćwiczenia nr 6 Lang: Długość okręgu. pole pierścienia będę chciał znaleźć inne wyrażenie na pole pierścienia. oszacowanie
ETAP SZKOLNY V Wojewódzki Konkurs Matematyczny dla uczniów szkół podstawowych województwa wielkopolskiego
 Informacje do zadań 1 3 Mieszkający w Poznaniu państwo Pyrkowscy bardzo lubią spędzać weekendy poza miastem. Pierwszego stycznia podjęli noworoczne postanowienie, że zakupią działkę rekreacyjną, żeby więcej
Informacje do zadań 1 3 Mieszkający w Poznaniu państwo Pyrkowscy bardzo lubią spędzać weekendy poza miastem. Pierwszego stycznia podjęli noworoczne postanowienie, że zakupią działkę rekreacyjną, żeby więcej
WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE V
 WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE V Uczeń na ocenę dopuszczającą potrafi: - Oszacować wyniki obliczeń na liczbach dziesiętnych w kontekście zakupów. - Korzystać z gotowego planu. - Narysować prostokąt
WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE V Uczeń na ocenę dopuszczającą potrafi: - Oszacować wyniki obliczeń na liczbach dziesiętnych w kontekście zakupów. - Korzystać z gotowego planu. - Narysować prostokąt
SPOŁECZEŃSTWO OD KUCHNI Integracja międzypokoleniowa mieszkańców Śliwkowego Szlaku
 SPOŁECZEŃSTWO OD KUCHNI Integracja międzypokoleniowa mieszkańców Śliwkowego Szlaku NASZE KULINARNE TRADYCJE NASZE KULINARNE TRADYCJE Co składa się na nie? Bez jakich produktów i potraw nie wyobrażamy sobie
SPOŁECZEŃSTWO OD KUCHNI Integracja międzypokoleniowa mieszkańców Śliwkowego Szlaku NASZE KULINARNE TRADYCJE NASZE KULINARNE TRADYCJE Co składa się na nie? Bez jakich produktów i potraw nie wyobrażamy sobie
KONKURS Z MATEMATYKI DLA UCZNIÓW SZKÓŁ PODSTAWOWYCH 2012/2013
 .... pieczątka WKK Kod ucznia Dzień Miesiąc Rok DATA URODZENIA UCZNIA KONKURS Z MATEMATYKI DLA UCZNIÓW SZKÓŁ PODSTAWOWYCH 2012/2013 ETAP WOJEWÓDZKI Drogi Uczniu! Witaj na etapie wojewódzkim konkursu matematycznego.
.... pieczątka WKK Kod ucznia Dzień Miesiąc Rok DATA URODZENIA UCZNIA KONKURS Z MATEMATYKI DLA UCZNIÓW SZKÓŁ PODSTAWOWYCH 2012/2013 ETAP WOJEWÓDZKI Drogi Uczniu! Witaj na etapie wojewódzkim konkursu matematycznego.
I POLA FIGUR zadania łatwe i średnie
 I POLA FIGUR zadania łatwe i średnie EWA MOLL- RYDZEWSKA IMIĘ I NAZWISKO: KLASA: GRUPA A 1. W trójkącie boki mają długości a = 9 cm i b = 6 cm. Wysokość poprowadzona na bok a ma długość 4 cm. Jaką długość
I POLA FIGUR zadania łatwe i średnie EWA MOLL- RYDZEWSKA IMIĘ I NAZWISKO: KLASA: GRUPA A 1. W trójkącie boki mają długości a = 9 cm i b = 6 cm. Wysokość poprowadzona na bok a ma długość 4 cm. Jaką długość
Wojewódzki Konkurs Przedmiotowy z Matematyki dla uczniów gimnazjów województwa śląskiego w roku szkolnym 2014/2015
 Wojewódzki Konkurs Przedmiotowy z Matematyki dla uczniów gimnazjów województwa śląskiego w roku szkolnym 204/205 KOD UCZNIA Etap: Data: Czas pracy: rejonowy 5 stycznia 205 r. 20 minut Informacje dla ucznia.
Wojewódzki Konkurs Przedmiotowy z Matematyki dla uczniów gimnazjów województwa śląskiego w roku szkolnym 204/205 KOD UCZNIA Etap: Data: Czas pracy: rejonowy 5 stycznia 205 r. 20 minut Informacje dla ucznia.
Wojewódzki Konkurs Przedmiotowy z Matematyki dla uczniów gimnazjów województwa śląskiego w roku szkolnym 2014/2015
 Wojewódzki Konkurs Przedmiotowy z Matematyki dla uczniów gimnazjów województwa śląskiego w roku szkolnym 2014/2015 KOD UCZNIA Etap: Data: Czas pracy: wojewódzki 4 marca 2015 r. 120 minut Informacje dla
Wojewódzki Konkurs Przedmiotowy z Matematyki dla uczniów gimnazjów województwa śląskiego w roku szkolnym 2014/2015 KOD UCZNIA Etap: Data: Czas pracy: wojewódzki 4 marca 2015 r. 120 minut Informacje dla
TEST DO KLASY MATEMATYCZNO FIZYCZNEJ VI 2013 Kod ucznia:
 TEST DO KLASY MATEMATYCZNO FIZYCZNEJ VI 2013 Kod ucznia: W zadaniach od 1 do 10 tylko jedna odpowiedź jest prawidłowa. Za poprawną odpowiedź otrzymasz 1 punkt; za brak odpowiedzi lub złą odpowiedź 0 punktów;
TEST DO KLASY MATEMATYCZNO FIZYCZNEJ VI 2013 Kod ucznia: W zadaniach od 1 do 10 tylko jedna odpowiedź jest prawidłowa. Za poprawną odpowiedź otrzymasz 1 punkt; za brak odpowiedzi lub złą odpowiedź 0 punktów;
WYMAGANIA SZCZEGÓŁOWE Z PODSTAWY PROGRAMOWEJ TEMAT 1.LICZBY I DZIAŁANIA
 TEMAT.LICZBY I DZIAŁANIA LICZBA GODZ. LEKCYJN YCH. Zapisywanie i porównywanie liczb.. Rachunki pamięciowe. 3. Kolejność działań. 4. Sprytne rachunki. WYMAGANIA SZCZEGÓŁOWE Z PODSTAWY PROGRAMOWEJ I. Liczby
TEMAT.LICZBY I DZIAŁANIA LICZBA GODZ. LEKCYJN YCH. Zapisywanie i porównywanie liczb.. Rachunki pamięciowe. 3. Kolejność działań. 4. Sprytne rachunki. WYMAGANIA SZCZEGÓŁOWE Z PODSTAWY PROGRAMOWEJ I. Liczby
1. Zapisywanie i porównywanie liczb. 2. Rachunki pamięciowe Kolejność działań Sprytne rachunki. 1 1.
 TEMAT.LICZBY I DZIAŁANIA LICZBA GODZIN LEKCYJNYCH WYMAGANIA SZCZEGÓŁOWE Z PODSTAWY PROGRAMOWEJ Z 4. II. 07.. Zapisywanie i porównywanie liczb.. Rachunki pamięciowe. 3. Kolejność działań. 4. Sprytne rachunki.
TEMAT.LICZBY I DZIAŁANIA LICZBA GODZIN LEKCYJNYCH WYMAGANIA SZCZEGÓŁOWE Z PODSTAWY PROGRAMOWEJ Z 4. II. 07.. Zapisywanie i porównywanie liczb.. Rachunki pamięciowe. 3. Kolejność działań. 4. Sprytne rachunki.
Gazetka dla rodziców na miesiąc październik 2016
 Gazetka dla rodziców na miesiąc październik 2016 22 września rozpoczęliśmy astronomiczną jesień. Ranki w tym miesiącu zwykle bywają chłodne, zaś w południe cieszymy się jeszcze ciepłym słonkiem. Jak zatem
Gazetka dla rodziców na miesiąc październik 2016 22 września rozpoczęliśmy astronomiczną jesień. Ranki w tym miesiącu zwykle bywają chłodne, zaś w południe cieszymy się jeszcze ciepłym słonkiem. Jak zatem
Arkusz Znów przyszła jesień
 ZADANIA ZAMKNIĘTE Arkusz Znów przyszła jesień Zadanie 1. (1 pkt) Korzystając z tabeli oblicz, jaka jest różnica czasu pomiędzy długością dnia słonecznego w pierwszym i ostatnim dniu jesieni. Data Wschód
ZADANIA ZAMKNIĘTE Arkusz Znów przyszła jesień Zadanie 1. (1 pkt) Korzystając z tabeli oblicz, jaka jest różnica czasu pomiędzy długością dnia słonecznego w pierwszym i ostatnim dniu jesieni. Data Wschód
WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLASY VI DZIAŁ I : LICZBY NATURALNE I UŁAMKI
 WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLASY VI NA OCENĘ DOPUSZCZAJĄCĄ : UCZEŃ zna nazwy działań (K) DZIAŁ I : LICZBY NATURALNE I UŁAMKI zna algorytm mnożenia i dzielenia ułamków dziesiętnych przez 10,
WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLASY VI NA OCENĘ DOPUSZCZAJĄCĄ : UCZEŃ zna nazwy działań (K) DZIAŁ I : LICZBY NATURALNE I UŁAMKI zna algorytm mnożenia i dzielenia ułamków dziesiętnych przez 10,
Wymagania szczegółowe z matematyki klasa 7
 Wymagania szczegółowe z matematyki klasa 7 Dział Szczegółowe wymagania Liczby całkowite (liczby dodatnie, ujemne i zero) - wyróżnia wśród liczb wymiernych liczby naturalne i całkowite oraz liczby pierwsze,
Wymagania szczegółowe z matematyki klasa 7 Dział Szczegółowe wymagania Liczby całkowite (liczby dodatnie, ujemne i zero) - wyróżnia wśród liczb wymiernych liczby naturalne i całkowite oraz liczby pierwsze,
Wyzwanie na Odchudzanie
 Gratulacje! Dzisiejszy temat: Idziemy na zakupy W yzwa nie na Odchudzanie Trzeba wiedzieć: W interesie dostawców i sprzedawców leży, aby sprzedać nam więcej żywności, niż naprawdę potrzebujemy. Służy temu
Gratulacje! Dzisiejszy temat: Idziemy na zakupy W yzwa nie na Odchudzanie Trzeba wiedzieć: W interesie dostawców i sprzedawców leży, aby sprzedać nam więcej żywności, niż naprawdę potrzebujemy. Służy temu
Jarosław Wróblewski Matematyka dla Myślących, 2008/09
 9. Funkcje trygonometryczne. Elementy geometrii: twierdzenie Pitagorasa i twierdzenie cosinusów, twierdzenie o kącie wpisanym i środkowym, okrąg wpisany i opisany na wielokącie, wielokąty foremne (dokończenie).
9. Funkcje trygonometryczne. Elementy geometrii: twierdzenie Pitagorasa i twierdzenie cosinusów, twierdzenie o kącie wpisanym i środkowym, okrąg wpisany i opisany na wielokącie, wielokąty foremne (dokończenie).
ZADANIA MATEMATYCZNE DLA UCZNIÓW KLAS VI zestaw drugi.
 ZADANIA MATEMATYCZNE DLA UCZNIÓW KLAS VI zestaw drugi. 21. Za bilety wstępu do pijalni wód mineralnych dla 4 osób dorosłych i 40 dzieci zapłacono 106 zł. Bilet dla osoby dorosłej kosztował 3,50 zł. Ile
ZADANIA MATEMATYCZNE DLA UCZNIÓW KLAS VI zestaw drugi. 21. Za bilety wstępu do pijalni wód mineralnych dla 4 osób dorosłych i 40 dzieci zapłacono 106 zł. Bilet dla osoby dorosłej kosztował 3,50 zł. Ile
Timac Agro Polska stawia na edukację i rozwój
 https://www. Timac Agro Polska stawia na edukację i rozwój Autor: Piotr Czyszkowski Data: 11 kwietnia 2016 Aktywne odżywianie roślin i gleby pod takim hasłem Timac Agro Polska rozpoczął wielką akcję edukacyjną.
https://www. Timac Agro Polska stawia na edukację i rozwój Autor: Piotr Czyszkowski Data: 11 kwietnia 2016 Aktywne odżywianie roślin i gleby pod takim hasłem Timac Agro Polska rozpoczął wielką akcję edukacyjną.
WOJEWÓDZKI KONKURS MATEMATYCZNY
 Kod ucznia Suma punktów Numer zadania 1-20 21 22 23 Liczba punktów WOJEWÓDZKI KONKURS MATEMATYCZNY DLA UCZNIÓW GIMNAZJÓW W ROKU SZKOLNYM 2014/2015 13 STYCZNIA 2015R. 1. Test konkursowy zawiera 23 zadania.
Kod ucznia Suma punktów Numer zadania 1-20 21 22 23 Liczba punktów WOJEWÓDZKI KONKURS MATEMATYCZNY DLA UCZNIÓW GIMNAZJÓW W ROKU SZKOLNYM 2014/2015 13 STYCZNIA 2015R. 1. Test konkursowy zawiera 23 zadania.
Międzyszkolne Zawody Matematyczne Klasa I LO i I Technikum - zakres podstawowy Etap wojewódzki 02.04.2005 rok Czas rozwiązywania zadań 150 minut
 Klasa I - zakres podstawowy Etap wojewódzki 17.04.004 rok Zad 1 ( 6 pkt) Znajdź wszystkie liczby czterocyfrowe podzielne przez 15, w których cyfrą tysięcy jest jeden, a cyfrą dziesiątek dwa. Odpowiedź
Klasa I - zakres podstawowy Etap wojewódzki 17.04.004 rok Zad 1 ( 6 pkt) Znajdź wszystkie liczby czterocyfrowe podzielne przez 15, w których cyfrą tysięcy jest jeden, a cyfrą dziesiątek dwa. Odpowiedź
Karta pracy M+ Do multipodręcznika dla klasy 4 szkoły podstawowej. Bochenek chleba
 Karta pracy M+ Do multipodręcznika dla klasy 4 szkoły podstawowej Bochenek chleba Część A. Sprawdź, czy zrozumiałeś film. A1. Uzupełnij poniższy tekst o brakujące słowa. Od pola pszenicy do mojej kanapki
Karta pracy M+ Do multipodręcznika dla klasy 4 szkoły podstawowej Bochenek chleba Część A. Sprawdź, czy zrozumiałeś film. A1. Uzupełnij poniższy tekst o brakujące słowa. Od pola pszenicy do mojej kanapki
Przykładowe rozwiązania
 Przykładowe rozwiązania (E. Ludwikowska, M. Zygora, M. Walkowiak) Klucz odpowiedzi do zadań zamkniętych Zadanie 1 2 3 4 5 6 7 8 9 10 11 12 13 Odpowiedź D C B A C B C C D C C D A Zadanie 14 15 16 17 18
Przykładowe rozwiązania (E. Ludwikowska, M. Zygora, M. Walkowiak) Klucz odpowiedzi do zadań zamkniętych Zadanie 1 2 3 4 5 6 7 8 9 10 11 12 13 Odpowiedź D C B A C B C C D C C D A Zadanie 14 15 16 17 18
11. Znajdż równanie prostej prostopadłej do prostej k i przechodzącej przez punkt A = (2;2).
 1. Narysuj poniższe figury: a), b), c) 2. Punkty A = (0;1) oraz B = (-1;0) należą do okręgu którego środek należy do prostej o równaniu x-2 = 0. Podaj równanie okręgu. 3. Znaleźć równanie okręgu przechodzącego
1. Narysuj poniższe figury: a), b), c) 2. Punkty A = (0;1) oraz B = (-1;0) należą do okręgu którego środek należy do prostej o równaniu x-2 = 0. Podaj równanie okręgu. 3. Znaleźć równanie okręgu przechodzącego
7 3 D. 15. ZADANIE 9. Przekątne są prostopadłe i dzielą się na połowę w punkcie przecięcia w: A. trójkącie B. trapezie C. rombie D.
 ZADANIE. Wynikiem działania + 5 : 5 4 jest liczba: A. B. 3 C. D. 3 ZADANIE. Wynikiem działania 3 : 0, + 0, 4 jest liczba: 3 3 A., 4 B. 3 C. 3 ZADANIE 3. Wynikiem działania 3 : 0, jest liczba: 3 5 7 3 D.
ZADANIE. Wynikiem działania + 5 : 5 4 jest liczba: A. B. 3 C. D. 3 ZADANIE. Wynikiem działania 3 : 0, + 0, 4 jest liczba: 3 3 A., 4 B. 3 C. 3 ZADANIE 3. Wynikiem działania 3 : 0, jest liczba: 3 5 7 3 D.
Skrypt 12. Figury płaskie Podstawowe figury geometryczne. 7. Rozwiązywanie zadao tekstowych związanych z obliczeniem pól i obwodów czworokątów
 Projekt Innowacyjny program nauczania matematyki dla gimnazjów współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 12 Figury płaskie Podstawowe figury geometryczne
Projekt Innowacyjny program nauczania matematyki dla gimnazjów współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 12 Figury płaskie Podstawowe figury geometryczne
Rozwiązania zadań. Arkusz maturalny z matematyki nr 1 POZIOM PODSTAWOWY
 Rozwiązania zadań Arkusz maturalny z matematyki nr POZIOM PODSTAWOWY Zadanie (pkt) Sposób I Skoro liczba jest środkiem przedziału, więc odległość punktu x od zapisujemy przy pomocy wartości bezwzględnej.
Rozwiązania zadań Arkusz maturalny z matematyki nr POZIOM PODSTAWOWY Zadanie (pkt) Sposób I Skoro liczba jest środkiem przedziału, więc odległość punktu x od zapisujemy przy pomocy wartości bezwzględnej.
Konspekt lekcji powtórzeniowej z matematyki w klasie V
 Maria Kożuch Konspekt lekcji powtórzeniowej z matematyki w klasie V Temat: Klasyfikacja czworokątów. Cele: Uczeń: - umierozróżniać czworokąty - potrafi nazwać czworokąty - umie wskazać na rysunku poszczególne
Maria Kożuch Konspekt lekcji powtórzeniowej z matematyki w klasie V Temat: Klasyfikacja czworokątów. Cele: Uczeń: - umierozróżniać czworokąty - potrafi nazwać czworokąty - umie wskazać na rysunku poszczególne
Temat: Odczytywanie danych statystycznych
 Temat: Odczytywanie danych statystycznych Autorka: Justyna Smuda Nazwa szkoły: Gimnazjum nr 16 w Zabrzu Czas trwania: 45 minut Poziom edukacyjny: III etap edukacyjny Związek z podstawą programową: Matematyka
Temat: Odczytywanie danych statystycznych Autorka: Justyna Smuda Nazwa szkoły: Gimnazjum nr 16 w Zabrzu Czas trwania: 45 minut Poziom edukacyjny: III etap edukacyjny Związek z podstawą programową: Matematyka
KRYTERIA OCEN Z MATEMATYKI DLA KLASY VII
 KRYTERIA OCEN Z MATEMATYKI DLA KLASY VII Na ocenę dopuszczającą uczeń powinien : Na ocenę dostateczną uczeń powinien: Na ocenę dobrą uczeń powinie: Na ocenę bardzo dobrą uczeń powinien: Na ocenę celującą
KRYTERIA OCEN Z MATEMATYKI DLA KLASY VII Na ocenę dopuszczającą uczeń powinien : Na ocenę dostateczną uczeń powinien: Na ocenę dobrą uczeń powinie: Na ocenę bardzo dobrą uczeń powinien: Na ocenę celującą
III POWIATOWY KONKURS MATEMATYCZNY DLA KLAS CZWARTYCH CO DWIE GŁOWY TO NIE JEDNA 2013 R.
 III POWIATOWY KONKURS MATEMATYCZNY DLA KLAS CZWARTYCH CO DWIE GŁOWY TO NIE JEDNA 2013 R. CZĘŚĆ I 7 KONKURENCJI ( CZAS 45 MINUT) DO ZDOBYCIA 25 PUNKTÓW KWADRAT MAGICZNY (3 pkt) INTRUZ (4 pkt) PIRAMIDA (3
III POWIATOWY KONKURS MATEMATYCZNY DLA KLAS CZWARTYCH CO DWIE GŁOWY TO NIE JEDNA 2013 R. CZĘŚĆ I 7 KONKURENCJI ( CZAS 45 MINUT) DO ZDOBYCIA 25 PUNKTÓW KWADRAT MAGICZNY (3 pkt) INTRUZ (4 pkt) PIRAMIDA (3
Autor scenariusza: Krystyna Jakubowska. Blok tematyczny: Prace w polu. Scenariusz nr 5
 Autor scenariusza: Krystyna Jakubowska Blok tematyczny: Prace w polu Scenariusz nr 5 I. Tytuł scenariusza: Wykorzystanie roślin okopowych. II. Czas realizacji: 2 jednostki lekcyjne. III. Edukacje (3 wiodące)
Autor scenariusza: Krystyna Jakubowska Blok tematyczny: Prace w polu Scenariusz nr 5 I. Tytuł scenariusza: Wykorzystanie roślin okopowych. II. Czas realizacji: 2 jednostki lekcyjne. III. Edukacje (3 wiodące)
WYMAGANIE EDUKACYJNE Z MATEMATYKI W KLASIE II GIMNAZJUM. dopuszczającą dostateczną dobrą bardzo dobrą celującą
 1. Statystyka odczytać informacje z tabeli odczytać informacje z diagramu 2. Mnożenie i dzielenie potęg o tych samych podstawach 3. Mnożenie i dzielenie potęg o tych samych wykładnikach 4. Potęga o wykładniku
1. Statystyka odczytać informacje z tabeli odczytać informacje z diagramu 2. Mnożenie i dzielenie potęg o tych samych podstawach 3. Mnożenie i dzielenie potęg o tych samych wykładnikach 4. Potęga o wykładniku
EGZAMIN ÓSMOKLASISTY MATEMATYKA
 www.galileusz.com.pl EGZAMIN ÓSMOKLASISTY MATEMATYKA ARKUSZ 100 minut 30 Zadanie 1. (0-1) Dane są liczby:,,,. Suma trzech spośród nich wynosi. Którą liczbę należy odrzucić, aby suma pozostałych trzech
www.galileusz.com.pl EGZAMIN ÓSMOKLASISTY MATEMATYKA ARKUSZ 100 minut 30 Zadanie 1. (0-1) Dane są liczby:,,,. Suma trzech spośród nich wynosi. Którą liczbę należy odrzucić, aby suma pozostałych trzech
KONKURS MATEMATYCZNY DLA UCZNIÓW GIMNAZJUM ETAP SZKOLNY
 ...................................... pieczątka nagłówkowa szkoły kod pracy ucznia KONKURS MATEMATYCZNY DLA UCZNIÓW GIMNAZJUM ETAP SZKOLNY Drogi Uczniu Witaj na I etapie konkursu matematycznego. Przeczytaj
...................................... pieczątka nagłówkowa szkoły kod pracy ucznia KONKURS MATEMATYCZNY DLA UCZNIÓW GIMNAZJUM ETAP SZKOLNY Drogi Uczniu Witaj na I etapie konkursu matematycznego. Przeczytaj
