Ogólny model liniowy
|
|
|
- Zuzanna Leszczyńska
- 7 lat temu
- Przeglądów:
Transkrypt
1 Ogólny model liniowy
2 Twórcy Autor statystyki testowej Wyprowadził wzór na gęstość rozkładu statystyki testowej Ronald Aylmer Fisher ( ) angielski genetyk George W. Snedecor ( ) amerykański matematyk
3 Ogólny model liniowy GLM jest zbiorem testów, w których zakłada się: 1. dane pochodzą z rozkładów normalnych o takiej samej wariancji przesunięte co najwyżej względem siebie 2. Dla pary zmiennych ciągłych to w obrębie jednej grupy danych ich przesunięcie względem siebie jest liniowe. 3. Statystyka testowa polega na porównywaniu sum kwadratów odchyleń średnich grupowych od wielkości wyliczanej poprzez równanie modelu do sum kwadratów odchyleń danych od średnich grupowych.
4 Statystyka testowa jednoczynnikowej analizy wariancji Programy pokazujące działanie testu gdy nie jest spełniona i gdy jest spełniona hipoteza zerowa
5 Regresja i korelacja Po odpowiednich przekształceniach (n 2) R 2 F 2 1 R Najczęściej stosowany test na sprawdzenie czy zależność Y od X istotnie różni się od 0.
6 Niepokojąco mocne założenia 1. Normalność rozkładu - Można się odwoływać do mocnego prawa wielkich liczb. - Można się odwoływać do prawa Lindenberga-Levy ego. 2. Jednakowość (jednorodność) wariancji - W przyrodzie częściej obserwuje się zjawisko wzrostu wariancji przy wzroście wartości oczekiwanej. 3. Liniowość współzależności - Nie ma żadnego modelu pokazującego, że liniowość jest lepsza od jakiejś innej krzywej. - Można stosować tu filozoficzne kryteria prostoty.
7 Błędy popełniane przy użyciu testów W połowie XX wieku pojawił się pomysł testowania testów stosowanych do analizy tego samego zagadnienia Zdefiniowano: Błąd I rodzaju wykazywanie istotności tam gdzie nie powinna być wykazywana Błąd II rodzaju nie wykazywanie istotności tam gdzie ona występuje Jerzy Spława- Neyman Uznano, że ten test jest lepszy, który minimalizuje te oba błędy. Wykazano, że testy GLM są bardzo odporne na: nienormalność rozkładu (byle nie bardziej skośnych od rozkładu wykładniczego), różnice wariancji (nawet gdy wykazujemy istotne różnice między wariancjami), nieliniowość zależnościach (byle kierunkowych) Częstość popełniania błędów I i II rodzaju po zmianach założeń nie odbiega od częstości popełniania takich błędów gdy dane spełniają założenia testów ANOVA
8 Założenie normalności Obowiązująca zasada sprawdź czy twoje dane maja rozkład normalny (najlepiej za pomocą testu Shapiro Wilka) i w każdej populacji/grupie osobno jeżeli wynik testu jest nieistotny (p>0.05) stosuj testy parametryczne, (np. GLM,Studenta) jeżeli wynik testu jest istotny (p 0.05) stosuj testy nieparametryczne (np. Wilkoxona) Matematyczna reguła przy małej próbie rzadziej uzyskujemy istotny (p<0.05) wynik w teście Shapiro- Wilka, ale częściej się mylimy się wykonując test parametryczny niż test nieparametryczny przy dużej próbie częściej uzyskujemy istotny (p<0.05) wynik w teście Shapiro- Wilka, ale rzadziej się mylimy się wykonując test parametryczny niż test nieparametryczny Obowiązująca zasada nie ma uzasadnienia matematycznego i prowadzi do błędów
9 Popularność Najpopularniejsze testy wykonywane do tej pory w biologii
10 Model statystyczny Model statystyczny jest eksperymentem fizycznym (obecnie komputerowym) polegającym na losowaniu próby z rozkładu w różnych układach. Model nie jest hipotezą zerową. W przypadku jednoczynnikowej analizy wariancji jest to ogół eksperymentów polegających na losowaniu prób (o dowolnej liczności) z rozkładów normalnych dowolnie przesuniętych względem siebie. Model można utożsamić z algorytmem jakiegoś programu (funkcji w R) losującego liczby z rozkładu. modelanova=function(k, n, mi, sig) { x=null for (i in 1:k){ for (j in 1:n[i]) x=c(x,rnorm(1,mi[i],sig)) } x }
11 Model statystyczny W przypadku analizy regresji jest to ogół eksperymentów polegających na losowaniu próby złożonej z par liczb (x,y) gdzie x jest losowane z rozkładu normalnego N(, 1 ) a y jest losowane z rozkładu normalnego N(ax+b, 1 ). modelregr=function(n, mi, sig1, sig2, a, b) { z=null x=rnorm(n,mi,sig1) y=null for (i in 1:n){y=c(y,rnorm(1,a*x[i]+b,sig2))} matrix(cbind(x,y),,2) }
12 Model - nomenklatura N zmienna losowa o rozkładzie normalnym standaryzowanym Jeżeli będą losowane liczby z rozkładu normalnego standaryzowanego, mnożone przez stałą s i do wyniku dodawane m, to otrzymane liczby pochodzić będą z rozkładu normalnego o wartości oczekiwanej m o odchyleniu standardowym s. U oznacza zmienna losowa o rozkładzie normalnym standaryzowanym N(0,1) Zapis X= + U oznacza zmienną X o rozkładzie normalnym N(, ) Ogólny zapis modelu dla jednoczynnikowej analizy wariancji X i U dla i=1,2,,k Ogólny zapis modelu dla regresji X 1 U Y ax b 2 U
13 Hipoteza zerowa i hipotezy alternatywne W jednoczynnikowej analizie wariancji prawie zawsze hipoteza zerowa brzmi: 1 = 2 =. = k Możliwe hipotezy alternatywne: Nieprawda, że 1 = 2 =. = k 1 2 = 3 =. = k 1 = 2 3 =. = k 1 2 lub 1 3 lub. lub 1 k KONTRASTY Zaprzeczenie logiczne każdej hipotezy alternatywnej formułuje hipotezę zerową
14 Wykonanie jednoczynnikowej Anovy w R Porównujemy następujące średnie: > lm(y~as.factor(x)) Call: lm(formula = y ~ as.factor(x)) Coefficients: (Intercept) as.factor(x)1 as.factor(x) > lm(y~as.factor(x)) Call: aov(formula = y ~ as.factor(x)) Terms: as.factor(x) Residuals Sum of Squares Deg. of Freedom 2 47 Residual standard error: Estimated effects may be unbalanced
15 Wykonanie jednoczynnikowej Anovy w R Porównujemy następujące średnie: > anova(lm(y~as.factor(x))) Analysis of Variance Table Response: y Df Sum Sq Mean Sq F value Pr(>F) as.factor(x) e-05 *** Residuals Signif. codes: 0 *** ** 0.01 * > anova(aov(y~as.factor(x))) Analysis of Variance Table Response: y Df Sum Sq Mean Sq F value Pr(>F) as.factor(x) e-05 *** Residuals Signif. codes: 0 *** ** 0.01 *
16 Wykonanie jednoczynnikowej Anovy w R > summary(lm(y~as.factor(x))) Call: lm(formula = y ~ as.factor(x), data = zz) Residuals: Min 1Q Median 3Q Max Coefficients: Estimate Std. Error t value Pr(> t ) (Intercept) as.factor(x) * as.factor(x) e-06 *** --- Signif. codes: 0 *** ** 0.01 * Residual standard error: on 47 degrees of freedom Multiple R-squared: , Adjusted R-squared: F-statistic: on 2 and 47 DF, p-value: 4.87e-05 > summary(aov(y~as.factor(x))) Df Sum Sq Mean Sq F value Pr(>F) as.factor(x) e-05 *** Residuals Signif. codes: 0 *** ** 0.01 *
17 Dwuczynnikowa analiza wariancji
18 Ocena pierwszej zmiennej ciągłej 1 zmienna dyskretna A B 2 zmienna dyskretna a b c Możliwe do wykonania testy: 1. Połączenie danych A z B i sprawdzenie czy jest istotna różnica między średnimi w grupach a, b i c 2. Połączenie danych a, b i c i sprawdzenie czy jest istotna różnica między średnimi w grupach A, B. Błąd pseudoreplikacji dane w każdej grupie połączonych danych nie są całkowicie niezależne od siebie
19 Ocena pierwszej zmiennej ciągłej 1 zmienna dyskretna A B 2 zmienna dyskretna a b c Możliwe do wykonania testy: 1. Sprawdzenie czy jest istotna różnica między średnimi w grupach a, b i c w grupie A i w grupie B. 2. Sprawdzenie czy jest istotna różnica między średnimi w grupach A, B w grupach a, b i c osobno. 5 testów wykonanych na tych samych danych możliwość uzyskania przypadkowej istotności.
20 Ocena pierwszej zmiennej ciągłej 1 zmienna dyskretna A B 2 zmienna dyskretna a b c Możliwe do wykonania testy: 1. Sprawdzenie jednym testem czy są różnice między aa, ab, ba, bb, ca, cb i zastosowanie testów post-choć albo kontrastów Porównywanie wielkości osobnika w grupach Ab z Bc, Aa z Bb itd. nie ma merytorycznego sensu. Uzyskanie dużej istotnej różnicy zupełnie nie moglibyśmy zinterpretować. Potrzebne nam są czyste odpowiedzi: Czy wielkość osobnika zależy od 1 zmiennej dyskretnej? Czy wielkość osobnika zależy od 2 zmiennej dyskretnej?
21 Pomysł Ronalda Fishera 1. Dane należące do zmiennej ciągłej X zależą od zmiennych dyskretnych płeć =(A, B) i sezon =(a, b, c) 2. Gdy pytamy się czy X zależy od sezonu : Wyliczamy najpierw średnią X 1* dla płci = A i X 2* dla płci = B Dla każdej wartości x zmiennej X wyliczamy x- X 1* (dla x o płci = A) albo x- X 2* (dla x o płci = B) Zapisujemy te dane pod nazwą X el_płeć. Wykonujemy jednoczynnikową analizę wariancji sprawdzającą czy X eld zależy od sezonu. 3. Gdy pytamy się czy X zależy od płci : Wyliczamy najpierw średnią X *1 dla sezonu = a, X *2 dla sezonu = b i X *3 dla sezonu = c Dla każdej wartości x zmiennej X wyliczamy x- X *1 (gdy x jest z sezonu = a) albo x- X *2 (gdy x z sezonu = b) albo x- X *3 (gdy x jest sezonu = c) Zapisujemy te dane pod nazwą X el_sezon. Wykonujemy jednoczynnikową analizę wariancji sprawdzającą czy X ele zależy od płci.
22 Pomysł Ronalda Fishera A B sezon = a A B sezon = b A B sezon = c 0
23 Pomysł Ronalda Fishera A B sezon = a A B Wpływ sezonu wyeliminowany sezon = b A B Wykonanie jednoczynnikowej analizy wariancji sezon = c 0
24 Pomysł Ronalda Fishera sezon = a lub b lub c A B Wpływ sezonu wyeliminowany Wykonanie jednoczynnikowej analizy wariancji 0 Połączenie danych i wykonanie dla nich jednoczynnikowej analizy wariancji
25 Model Model dwuczynnikowej analizy wariancji bez interakcji X i,* *, j U Wielkość generalna Poprawka związana z działaniem na X zmiennej D i,* 0 Poprawka związana z działaniem na X zmiennej D i *, j 0 j Model dwuczynnikowej analizy wariancji (z interakcją) X i, * *,j i, j U i i,j 0 j i,j 0 dla każdego j dla każdego i Poprawka na nieaddytywne oddziaływania na X zmiennych D i C
26 Model 2-Anova bez interakcji model2anova=function(k1, k2, n, mi, mi1, mi2, sig) { x=null for (i1 in 1:k1){ for (i2 in 1:k2){ for (j in 1:n[i1,i2]) x=c(x,rnorm(1,mi+mi1[i1]+mi2[i2],sig)) }} x }
27 Model 2-Anova z interakcją model2anovaint=function(k1, k2, n, mi, mi1, mi2, mi12, sig) { x=null for (i2 in 1:k2){ for (i1 in 1:k1){ for (j in 1:n[i1,i2]) x=c(x,rnorm(1,mi+mi1[i1]+mi2[i2]+mi12[i1,i2],sig)) } } x }
28 Dwuczynnikowa analiza wariancji - interakcje całkowity brak interakcji interakcja
29 Obowiązująca zasada Problem z istotną interakcją Istotna interakcja powoduje, że wyniki uzyskane dla efektów głównych są nieinterpretowalne sprawdź czy interakcja jest istotna (p-wartość<0.05) jeżeli jest istotna podziel dane na grupy wyróżnione przez jedną ze zmiennych i wykonaj test jednoczynnikowej ANOVA dla drugiej zmiennej. jeżeli jest nieistotna zacytuj w pracy wyniki efektów głównych Matematyczna reguła przy małej próbie rzadziej istotne interakcje, ale cytując wyniki dla efektów głównych popełniamy mniej błędów niż cytując wyniki wielu testów wynikających z podziału materiału najczęściej nieistotnych przy dużej próbie częściej uzyskujemy istotną interakcję, ale też wtedy najczęściej uzyskujemy istotne wyniki w testach zrobionych dla podzielonego materiału i w dodatku różnić się będą one interpretacją Obowiązująca zasada ma uzasadnienie matematyczne
30 Hipotezy zerowe 1. 1,* = 2,* = = k1,* =0 2. *,1 = *,2 = = *,k2 =0 3. Wszystkie i,j =0 dla i=1,2,,k 1, j=1,2,,k 2 Testowane równolegle do siebie. Oceniane jest prawdopodobieństwo zachodzenia hipotez alternatywnych dla każdej hipotezy osobno. Mnogość hipotez alternatywnych. KONTRASTY Dla biologów najważniejszy jest test GLM bez kontrastów.
31 Problem z wyliczaniem sum kwadratów odchyleń w układzie niezbalansowanym
32 Układ zbalansowany Czynnik 1 A B Z a... n n n b... Czynnik 2 n n n z n n... n Układ zbalansowany układ w którym liczby pomiarów obiektów dla każdej wartości 1 i 2 zmiennej dyskretnej są takie same
33 Tabela dwuczynnikowej analizy wariancji z interakcją
34 Problemy matematyczne W układzie zbalansowanym mamy: SS m,1 SS m,2 SS int SS w SS c Jest spełniony warunek, że po odjęciu średnich odpowiednich dla 1 zmiennej dyskretnej można robić jednoczynnikową analizę wariancji względem drugiej zmiennej dyskretnej i tylko p odczytywać z innego rozkładu F. W układzie niezbalansowanym mamy: SS m,1 SS m,2 SS int SS w SS c Przeszacowywanie wartości F? Ale którego?
35 Poprawianie testu dwuczynnikowej ANOVA Szukanie takiej reguły rozdzielania sum kwadratów między znane źródła zmienności aby po dodaniu czynników lub ich redukcji obowiązywała ta sama reguła rozdzielania sum kwadratów. Uogólnienie zjawiska obowiązującego dla układu zbalansowanego, że sumy kwadratów dla dodanego czynnika wylicza się tak jakby odjęto od danych średnie wynikłe z grupowania przez inne czynniki i wykonano na różnicach test jednoczynnikowej analizy wariancji. Pojawił się test GLM reguły zapisane w rachunku macierzowym Sprawdzenie doświadczalne, że błędy I rodzaju (uzyskiwanie istotności przy braku różnic między średnimi) oraz błędy II rodzaju (nie uzyskiwanie istotności gdy jest różnica między średnimi) są najmniejsze gdy stosowany jest test GLM
36 Problem z nadmiarem testów Nie istnieje jeden test GLM. Prawidłowe rozdzielanie sum kwadratów odchyleń między różne hipotezy (model uproszczony vs. model) można robić na wiele sposobów. I typ wyliczania sum kwadratów II typ wyliczania sum kwadratów III typ wyliczania sum kwadratów Drobne różnice w postawieniu hipotezy zerowej versus hipoteza alternatywna i niuanse interpretacyjne implikują koniecznością stosowania różnych testów. Biolodzy szukają testu odpowiadającego sposobowi rozumowania zaproponowanego prze Fishera: - III typ wyliczania sum kwadratów odchyleń. - Na ogół bez kontrastów (testy z kontrastami są opisywane post-hoc )
37 GLM GLM GLM ANOVA Problem z nadmiarem testów GLM Źródło St. sw. ANOVA Suma kw. Średnia kwadratów Wartość F Pr. > F SEZON PLEC SEZON*PLEC Źródło St. sw. Typ I Suma kw. Średnia kwadratów Wartość F Pr. > F SEZON PLEC SEZON*PLEC Źródło St. sw. Typ II Suma kw. Średnia kwadratów Wartość F Pr. > F SEZON PLEC SEZON*PLEC Źródło St. sw. Typ III Suma kw. Średnia kwadratów Wartość F Pr. > F SEZON PLEC SEZON*PLEC
38 GLM GLM GLM ANOVA Problem z nadmiarem testów GLM Źródło St. sw. ANOVA Suma kw. Średnia kwadratów Wartość F Pr. > F PLEC SEZON SEZON*PLEC Źródło St. sw. Typ I Suma kw. Średnia kwadratów Wartość F Pr. > F PLEC SEZON SEZON*PLEC Źródło St. sw. Typ II Suma kw. Średnia kwadratów Wartość F Pr. > F PLEC SEZON SEZON*PLEC Źródło St. sw. Typ III Suma kw. Średnia kwadratów Wartość F Pr. > F PLEC SEZON SEZON*PLEC
39 Problem z nadmiarem testów GLM > anova(aov(ciezar~sezon*plec,skunks)) Analysis of Variance Table Response: CIEZAR Df Sum Sq Mean Sq F value Pr(>F) SEZON PLEC SEZON:PLEC Residuals Signif. codes: 0 *** ** 0.01 * > > anova(aov(ciezar~plec*sezon,skunks)) Analysis of Variance Table Response: CIEZAR Df Sum Sq Mean Sq F value Pr(>F) PLEC SEZON PLEC:SEZON Residuals I typ wyliczania sum kwadratów
40 Problem z nadmiarem testów GLM > drop1(aov(ciezar ~ SEZON*PLEC,skunks),.~., test="f") Single term deletions Model: CIEZAR ~ SEZON * PLEC Df Sum of Sq RSS AIC F value Pr(>F) <none> SEZON PLEC SEZON:PLEC > drop1(aov(ciezar ~ PLEC*SEZON,skunks),.~., test="f") Single term deletions Model: CIEZAR ~ PLEC * SEZON Df Sum of Sq RSS AIC F value Pr(>F) <none> PLEC SEZON PLEC:SEZON > III typ wyliczania sum kwadratów z kontrastem prostym (treatment)
41 Problem z nadmiarem testów GLM > options(contrasts = c("contr.sum","contr.poly")) > drop1(aov(ciezar ~ PLEC*SEZON,skunks),.~.,test="F") Single term deletions Model: CIEZAR ~ PLEC * SEZON Df Sum of Sq RSS AIC F value Pr(>F) <none> PLEC SEZON PLEC:SEZON Signif. codes: 0 *** ** 0.01 * > drop1(aov(ciezar ~ SEZON*PLEC,skunks),.~.,test="F") Single term deletions Model: CIEZAR ~ SEZON * PLEC Df Sum of Sq RSS AIC F value Pr(>F) <none> SEZON PLEC SEZON:PLEC Signif. codes: 0 *** ** 0.01 * III typ wyliczania sum kwadratów bez kontrastów
42 Dwuczynnikowa analiza kowariancji
43 Ocena drugiej zmiennej ciągłej A 1 zmienna dyskretna B 2 zmienna dyskretna a b c (x1,1,1,y1,1,1 ),...,(x 1,1,n,y1,1, ) (x1,2,1,y1,2,1),...,(x 1,2,n,y1,2, ) 1,1 n1,1 1,2 n1,2 (x2,1,1,y2,1,1 ),...,(x 2,1,n,y2,1, ) (x2,2,1,y1,2,1),...,(x 2,2,n,y2,2, ) 2,1 n2,1 2,2 n2,2 (x3,1,1,y3,1,1 ),...,(x 3,1,n,y3,1, ) (x3,2,1,y3,2,1),...,(x 3,2,n,y3,2, ) 3,1 n3,1 3,2 n3,2 Założymy, że zmienne ciągłe są od siebie zależne tak samo w każdej grupie. Wyeliminujemy wpływ pierwszej zmiennej ciągłej. Zastosujemy dwuczynnikową analizę wariancji.
44 Ocena drugiej zmiennej ciągłej Co to znaczy, że zmienne ciągłe są tak samo zależne od siebie w różnych grupach? Y Dla bardzo dużych prób mają tak samo nachylone regresje tylko przesunięte względem siebie. Regresja wspólna aggregation regresssion X
45 Regresja wspólna Zespół k 1 k 2 prostych mających jednakowe nachylenie do osi 0X y i,j = ax i,j +b i,j takich, że suma sum kwadratów odchyleń danych dla i-tej wartości pierwszej zmiennej dyskretnej i j-tej wartości drugiej zmiennej od prostej y i,j = ax i,j +b i,j ma wartość minimalną. k1 k2 ni, j i 1 j 1 L 1 2 ( y i,j,l ax i,j,l bi,j) ma wartość minimalną. Warunek ten pozwala na wyprowadzenie wzorów dla a i wszystkich b i,j.
46 Likwidowanie wpływu X na Y Y X
47 Likwidowanie wpływu X na Y Y X
48 Likwidowanie wpływu X na Y Y X
49 Likwidowanie wpływu X na Y Y X
50 Likwidowanie wpływu X na Y Y Wykonujemy dwuczynnikową analizę wariancji dla zmiennej Y X
51 Model Model dwuczynnikowej analizy kowariancji X Y i,* ax b b i,* *,j b *,j i,j b i,j x U y U i,* 0 i *, j 0 j i j b b i,* *, j 0 0 i i,j 0 j i,j 0 dla każdego j dla każdego i i j b b i,j i,j 0 0 dla każdego j dla każdego i
52 Model 2-Ancova model2ancova=function(k1, k2, n, mi, mi1, m2, m12, a, b, b1, b2, b12, sigx, sigy) { x=null y=null for (i2 in 1:k2){ for (i1 in 1:k1){ for (j in 1:n[i1,i2]) x=c(x,rnorm(1,mi+mi1[i1]+mi2[i2]+mi12[i1,i2],sigx)) y=c(y,rnorm(1,b+b1[i1]+b2[i2]+b12[i1,i2],sigy)) } } cbind(x,y) }
53 GLM Problem z nadmiarem testów GLM Źródło St. sw. Typ III Suma kw. Średnia kwadratów Wartość F Pr. > F CIEZAR PLEC <.0001 SEZON <.0001 SEZON*PLEC > options(contrasts = c("contr.sum","contr.poly")) > drop1(aov(fluor~ciezar+plec*sezon,skunks),.~., test="f") > > drop1(aov(fluor~ciezar+plec*sezon,skunks), anova(aov(fluor~ciezar+plec*sezon,skunks)).~., test="f") Single term deletions Single Analysis term of deletions Variance Table Model: Model: Response: FLUOR FLUOR ~ CIEZAR + PLEC * SEZON FLUOR ~ CIEZAR Df + Sum PLEC Sq * Mean SEZON Sq F value Pr(>F) Df Sum of Sq RSS AIC F value Pr(>F) CIEZAR Df1 Sum 3483 of Sq 3483 RSS AIC F value ** Pr(>F) <none> <none> PLEC e-12 *** CIEZAR CIEZAR SEZON e *** PLEC e-07 *** PLEC:SEZON e-14 *** SEZON e-06 *** SEZON Residuals e-12 *** PLEC:SEZON PLEC:SEZON Signif. codes: 0 *** ** 0.01 * Signif. codes: 0 *** ** 0.01 * Signif. 1 codes: 0 *** ** 0.01 *
54 Wykonywanie GLM w R R nie pokazuje jaki typ wyliczania sum kwadratów został zaprogramowany. R nie pokazuje, że standardowo stosuje test z kontrastami prostymi, w którym porównuje się średnie z kolejnych grup do grupy pierwszej. Gdy wykonuje się próbne testy dla układu zbalansowanego, nie widać błędów. W wielu podręcznikach do R polecane jest wykonanie testu za pomocą funkcji anova(aov( )). Wydaje się, że autorzy tych podręczników nie zdają sobie z tego sprawy, że jest to test z I typem wyliczania sum kwadratów i kontrastem prostym. Pisząc w metodach pracy, że posługiwano się programem R przy wykonywaniu obliczeń statystycznych, w tym testu GLM, należy opisywać zastosowany model (z III typem wyliczania sum kwadratów i w układzie bez kontrastów), co nie jest konieczne gdy używamy programów SAS, Statistica, SPSS i wielu innych.
55 Koniec
KORELACJA 1. Wykres rozrzutu ocena związku między zmiennymi X i Y. 2. Współczynnik korelacji Pearsona
 KORELACJA 1. Wykres rozrzutu ocena związku między zmiennymi X i Y 2. Współczynnik korelacji Pearsona 3. Siła i kierunek związku między zmiennymi 4. Korelacja ma sens, tylko wtedy, gdy związek między zmiennymi
KORELACJA 1. Wykres rozrzutu ocena związku między zmiennymi X i Y 2. Współczynnik korelacji Pearsona 3. Siła i kierunek związku między zmiennymi 4. Korelacja ma sens, tylko wtedy, gdy związek między zmiennymi
Analiza wariancji i kowariancji
 Analiza wariancji i kowariancji Historia Analiza wariancji jest metodą zaproponowaną przez Ronalda A. Fishera. Po zakończeniu pierwszej wojny światowej był on pracownikiem laboratorium statystycznego w
Analiza wariancji i kowariancji Historia Analiza wariancji jest metodą zaproponowaną przez Ronalda A. Fishera. Po zakończeniu pierwszej wojny światowej był on pracownikiem laboratorium statystycznego w
Elementy statystyki STA - Wykład 5
 STA - Wykład 5 Wydział Matematyki i Informatyki Uniwersytet im. Adama Mickiewicza 1 ANOVA 2 Model jednoczynnikowej analizy wariancji Na model jednoczynnikowej analizy wariancji możemy traktować jako uogólnienie
STA - Wykład 5 Wydział Matematyki i Informatyki Uniwersytet im. Adama Mickiewicza 1 ANOVA 2 Model jednoczynnikowej analizy wariancji Na model jednoczynnikowej analizy wariancji możemy traktować jako uogólnienie
Analiza zależności cech ilościowych regresja liniowa (Wykład 13)
 Analiza zależności cech ilościowych regresja liniowa (Wykład 13) dr Mariusz Grządziel semestr letni 2012 Przykład wprowadzajacy W zbiorze danych homedata (z pakietu R-owskiego UsingR) można znaleźć ceny
Analiza zależności cech ilościowych regresja liniowa (Wykład 13) dr Mariusz Grządziel semestr letni 2012 Przykład wprowadzajacy W zbiorze danych homedata (z pakietu R-owskiego UsingR) można znaleźć ceny
Jednoczynnikowa analiza wariancji
 Jednoczynnikowa analiza wariancji Zmienna zależna ilościowa, numeryczna Zmienna niezależna grupująca (dzieli próbę na więcej niż dwie grupy), nominalna zmienną wyrażoną tekstem należy w SPSS przerekodować
Jednoczynnikowa analiza wariancji Zmienna zależna ilościowa, numeryczna Zmienna niezależna grupująca (dzieli próbę na więcej niż dwie grupy), nominalna zmienną wyrażoną tekstem należy w SPSS przerekodować
Testowanie hipotez dla dwóch zmiennych zależnych. Moc testu. Minimalna liczność próby; Regresja prosta; Korelacja Pearsona;
 LABORATORIUM 4 Testowanie hipotez dla dwóch zmiennych zależnych. Moc testu. Minimalna liczność próby; Regresja prosta; Korelacja Pearsona; dwie zmienne zależne mierzalne małe próby duże próby rozkład normalny
LABORATORIUM 4 Testowanie hipotez dla dwóch zmiennych zależnych. Moc testu. Minimalna liczność próby; Regresja prosta; Korelacja Pearsona; dwie zmienne zależne mierzalne małe próby duże próby rozkład normalny
Jak sprawdzić normalność rozkładu w teście dla prób zależnych?
 Jak sprawdzić normalność rozkładu w teście dla prób zależnych? W pliku zalezne_10.sta znajdują się dwie zmienne: czasu biegu przed rozpoczęciem cyklu treningowego (zmienna 1) oraz czasu biegu po zakończeniu
Jak sprawdzić normalność rozkładu w teście dla prób zależnych? W pliku zalezne_10.sta znajdują się dwie zmienne: czasu biegu przed rozpoczęciem cyklu treningowego (zmienna 1) oraz czasu biegu po zakończeniu
Regresja liniowa w R Piotr J. Sobczyk
 Regresja liniowa w R Piotr J. Sobczyk Uwaga Poniższe notatki mają charakter roboczy. Mogą zawierać błędy. Za przesłanie mi informacji zwrotnej o zauważonych usterkach serdecznie dziękuję. Weźmy dane dotyczące
Regresja liniowa w R Piotr J. Sobczyk Uwaga Poniższe notatki mają charakter roboczy. Mogą zawierać błędy. Za przesłanie mi informacji zwrotnej o zauważonych usterkach serdecznie dziękuję. Weźmy dane dotyczące
Statystyka i Analiza Danych
 Warsztaty Statystyka i Analiza Danych Gdańsk, 20-22 lutego 2014 Zastosowania analizy wariancji w opracowywaniu wyników badań empirycznych Janusz Wątroba StatSoft Polska Centrum Zastosowań Matematyki -
Warsztaty Statystyka i Analiza Danych Gdańsk, 20-22 lutego 2014 Zastosowania analizy wariancji w opracowywaniu wyników badań empirycznych Janusz Wątroba StatSoft Polska Centrum Zastosowań Matematyki -
Analiza wariancji - ANOVA
 Analiza wariancji - ANOVA Analiza wariancji jest metodą pozwalającą na podział zmienności zaobserwowanej wśród wyników eksperymentalnych na oddzielne części. Każdą z tych części możemy przypisać oddzielnemu
Analiza wariancji - ANOVA Analiza wariancji jest metodą pozwalającą na podział zmienności zaobserwowanej wśród wyników eksperymentalnych na oddzielne części. Każdą z tych części możemy przypisać oddzielnemu
Model regresji wielokrotnej Wykład 14 ( ) Przykład ceny domów w Chicago
 Model regresji wielokrotnej Wykład 14 (4.06.2007) Przykład ceny domów w Chicago Poniżej są przedstawione dane dotyczące cen domów w Chicago (źródło: Sen, A., Srivastava, M., Regression Analysis, Springer,
Model regresji wielokrotnej Wykład 14 (4.06.2007) Przykład ceny domów w Chicago Poniżej są przedstawione dane dotyczące cen domów w Chicago (źródło: Sen, A., Srivastava, M., Regression Analysis, Springer,
Statystyczna analiza danych w programie STATISTICA (wykład 2) Dariusz Gozdowski
 Statystyczna analiza danych w programie STATISTICA (wykład ) Dariusz Gozdowski Katedra Doświadczalnictwa i Bioinformatyki Wydział Rolnictwa i Biologii SGGW Weryfikacja (testowanie) hipotez statystycznych
Statystyczna analiza danych w programie STATISTICA (wykład ) Dariusz Gozdowski Katedra Doświadczalnictwa i Bioinformatyki Wydział Rolnictwa i Biologii SGGW Weryfikacja (testowanie) hipotez statystycznych
Analiza wariancji - ANOVA
 Analiza wariancji - ANOVA Analizę wariancji, często określaną skrótem ANOVA (Analysis of Variance), zawdzięczamy angielskiemu biologowi Ronaldowi A. Fisherowi, który opracował ją w 1925 roku dla rozwiązywania
Analiza wariancji - ANOVA Analizę wariancji, często określaną skrótem ANOVA (Analysis of Variance), zawdzięczamy angielskiemu biologowi Ronaldowi A. Fisherowi, który opracował ją w 1925 roku dla rozwiązywania
Przedmowa Wykaz symboli Litery alfabetu greckiego wykorzystywane w podręczniku Symbole wykorzystywane w zagadnieniach teorii
 SPIS TREŚCI Przedmowa... 11 Wykaz symboli... 15 Litery alfabetu greckiego wykorzystywane w podręczniku... 15 Symbole wykorzystywane w zagadnieniach teorii mnogości (rachunku zbiorów)... 16 Symbole stosowane
SPIS TREŚCI Przedmowa... 11 Wykaz symboli... 15 Litery alfabetu greckiego wykorzystywane w podręczniku... 15 Symbole wykorzystywane w zagadnieniach teorii mnogości (rachunku zbiorów)... 16 Symbole stosowane
Analiza wariancji. dr Janusz Górczyński
 Analiza wariancji dr Janusz Górczyński Wprowadzenie Powiedzmy, że badamy pewną populację π, w której cecha Y ma rozkład N o średniej m i odchyleniu standardowym σ. Powiedzmy dalej, że istnieje pewien czynnik
Analiza wariancji dr Janusz Górczyński Wprowadzenie Powiedzmy, że badamy pewną populację π, w której cecha Y ma rozkład N o średniej m i odchyleniu standardowym σ. Powiedzmy dalej, że istnieje pewien czynnik
Regresja liniowa wprowadzenie
 Regresja liniowa wprowadzenie a) Model regresji liniowej ma postać: gdzie jest zmienną objaśnianą (zależną); są zmiennymi objaśniającymi (niezależnymi); natomiast są parametrami modelu. jest składnikiem
Regresja liniowa wprowadzenie a) Model regresji liniowej ma postać: gdzie jest zmienną objaśnianą (zależną); są zmiennymi objaśniającymi (niezależnymi); natomiast są parametrami modelu. jest składnikiem
Importowanie danych do SPSS Eksportowanie rezultatów do formatu MS Word... 22
 Spis treści Przedmowa do wydania pierwszego.... 11 Przedmowa do wydania drugiego.... 15 Wykaz symboli.... 17 Litery alfabetu greckiego wykorzystywane w podręczniku.... 17 Symbole wykorzystywane w zagadnieniach
Spis treści Przedmowa do wydania pierwszego.... 11 Przedmowa do wydania drugiego.... 15 Wykaz symboli.... 17 Litery alfabetu greckiego wykorzystywane w podręczniku.... 17 Symbole wykorzystywane w zagadnieniach
LABORATORIUM 3. Jeśli p α, to hipotezę zerową odrzucamy Jeśli p > α, to nie mamy podstaw do odrzucenia hipotezy zerowej
 LABORATORIUM 3 Przygotowanie pliku (nazwy zmiennych, export plików.xlsx, selekcja przypadków); Graficzna prezentacja danych: Histogramy (skategoryzowane) i 3-wymiarowe; Wykresy ramka wąsy; Wykresy powierzchniowe;
LABORATORIUM 3 Przygotowanie pliku (nazwy zmiennych, export plików.xlsx, selekcja przypadków); Graficzna prezentacja danych: Histogramy (skategoryzowane) i 3-wymiarowe; Wykresy ramka wąsy; Wykresy powierzchniowe;
1. Jednoczynnikowa analiza wariancji 2. Porównania szczegółowe
 Zjazd 7. SGGW, dn. 28.11.10 r. Matematyka i statystyka matematyczna Tematy 1. Jednoczynnikowa analiza wariancji 2. Porównania szczegółowe nna Rajfura 1 Zagadnienia Przykład porównania wielu obiektów w
Zjazd 7. SGGW, dn. 28.11.10 r. Matematyka i statystyka matematyczna Tematy 1. Jednoczynnikowa analiza wariancji 2. Porównania szczegółowe nna Rajfura 1 Zagadnienia Przykład porównania wielu obiektów w
Testowanie hipotez statystycznych. Wnioskowanie statystyczne
 Testowanie hipotez statystycznych Wnioskowanie statystyczne Hipoteza statystyczna to dowolne przypuszczenie co do rozkładu populacji generalnej (jego postaci funkcyjnej lub wartości parametrów). Hipotezy
Testowanie hipotez statystycznych Wnioskowanie statystyczne Hipoteza statystyczna to dowolne przypuszczenie co do rozkładu populacji generalnej (jego postaci funkcyjnej lub wartości parametrów). Hipotezy
Tablica Wzorów Rachunek Prawdopodobieństwa i Statystyki
 Tablica Wzorów Rachunek Prawdopodobieństwa i Statystyki Spis treści I. Wzory ogólne... 2 1. Średnia arytmetyczna:... 2 2. Rozstęp:... 2 3. Kwantyle:... 2 4. Wariancja:... 2 5. Odchylenie standardowe:...
Tablica Wzorów Rachunek Prawdopodobieństwa i Statystyki Spis treści I. Wzory ogólne... 2 1. Średnia arytmetyczna:... 2 2. Rozstęp:... 2 3. Kwantyle:... 2 4. Wariancja:... 2 5. Odchylenie standardowe:...
Testowanie hipotez. Marcin Zajenkowski. Marcin Zajenkowski () Testowanie hipotez 1 / 25
 Testowanie hipotez Marcin Zajenkowski Marcin Zajenkowski () Testowanie hipotez 1 / 25 Testowanie hipotez Aby porównać ze sobą dwie statystyki z próby stosuje się testy istotności. Mówią one o tym czy uzyskane
Testowanie hipotez Marcin Zajenkowski Marcin Zajenkowski () Testowanie hipotez 1 / 25 Testowanie hipotez Aby porównać ze sobą dwie statystyki z próby stosuje się testy istotności. Mówią one o tym czy uzyskane
( x) Równanie regresji liniowej ma postać. By obliczyć współczynniki a i b należy posłużyć się następującymi wzorami 1 : Gdzie:
 ma postać y = ax + b Równanie regresji liniowej By obliczyć współczynniki a i b należy posłużyć się następującymi wzorami 1 : xy b = a = b lub x Gdzie: xy = też a = x = ( b ) i to dane empiryczne, a ilość
ma postać y = ax + b Równanie regresji liniowej By obliczyć współczynniki a i b należy posłużyć się następującymi wzorami 1 : xy b = a = b lub x Gdzie: xy = też a = x = ( b ) i to dane empiryczne, a ilość
Matematyka i statystyka matematyczna dla rolników w SGGW
 Było: Testowanie hipotez (ogólnie): stawiamy hipotezę, wybieramy funkcję testową f (test statystyczny), przyjmujemy poziom istotności α; tym samym wyznaczamy obszar krytyczny testu (wartość krytyczną funkcji
Było: Testowanie hipotez (ogólnie): stawiamy hipotezę, wybieramy funkcję testową f (test statystyczny), przyjmujemy poziom istotności α; tym samym wyznaczamy obszar krytyczny testu (wartość krytyczną funkcji
Testy nieparametryczne
 Testy nieparametryczne Testy nieparametryczne możemy stosować, gdy nie są spełnione założenia wymagane dla testów parametrycznych. Stosujemy je również, gdy dane można uporządkować według określonych kryteriów
Testy nieparametryczne Testy nieparametryczne możemy stosować, gdy nie są spełnione założenia wymagane dla testów parametrycznych. Stosujemy je również, gdy dane można uporządkować według określonych kryteriów
Testy post-hoc. Wrocław, 6 czerwca 2016
 Testy post-hoc Wrocław, 6 czerwca 2016 Testy post-hoc 1 metoda LSD 2 metoda Duncana 3 metoda Dunneta 4 metoda kontrastów 5 matoda Newman-Keuls 6 metoda Tukeya Metoda LSD Metoda Least Significant Difference
Testy post-hoc Wrocław, 6 czerwca 2016 Testy post-hoc 1 metoda LSD 2 metoda Duncana 3 metoda Dunneta 4 metoda kontrastów 5 matoda Newman-Keuls 6 metoda Tukeya Metoda LSD Metoda Least Significant Difference
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 6
 STATYSTYKA I DOŚWIADCZALNICTWO Wykład 6 Metody sprawdzania założeń w analizie wariancji: -Sprawdzanie równości (jednorodności) wariancji testy: - Cochrana - Hartleya - Bartletta -Sprawdzanie zgodności
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 6 Metody sprawdzania założeń w analizie wariancji: -Sprawdzanie równości (jednorodności) wariancji testy: - Cochrana - Hartleya - Bartletta -Sprawdzanie zgodności
Efekt główny Efekt interakcyjny efekt jednego czynnika zależy od poziomu drugiego czynnika Efekt prosty
 ANOVA DWUCZYNNIKOWA testuje różnice między średnimi w grupach wyznaczonych przez dwa czynniki i ich kombinacje. Analiza pozwala ustalić wpływ dwóch czynników na wartości zmiennej zależnej (ilościowej!)
ANOVA DWUCZYNNIKOWA testuje różnice między średnimi w grupach wyznaczonych przez dwa czynniki i ich kombinacje. Analiza pozwala ustalić wpływ dwóch czynników na wartości zmiennej zależnej (ilościowej!)
Analizy wariancji ANOVA (analysis of variance)
 ANOVA Analizy wariancji ANOVA (analysis of variance) jest to metoda równoczesnego badania istotności różnic między wieloma średnimi z prób pochodzących z wielu populacji (grup). Model jednoczynnikowy analiza
ANOVA Analizy wariancji ANOVA (analysis of variance) jest to metoda równoczesnego badania istotności różnic między wieloma średnimi z prób pochodzących z wielu populacji (grup). Model jednoczynnikowy analiza
Przykład 1. (A. Łomnicki)
 Plan wykładu: 1. Wariancje wewnątrz grup i między grupami do czego prowadzi ich ocena 2. Rozkład F 3. Analiza wariancji jako metoda badań założenia, etapy postępowania 4. Dwie klasyfikacje a dwa modele
Plan wykładu: 1. Wariancje wewnątrz grup i między grupami do czego prowadzi ich ocena 2. Rozkład F 3. Analiza wariancji jako metoda badań założenia, etapy postępowania 4. Dwie klasyfikacje a dwa modele
STATYSTYKA MATEMATYCZNA
 STATYSTYKA MATEMATYCZNA 1. Wykład wstępny. Teoria prawdopodobieństwa i elementy kombinatoryki. Zmienne losowe i ich rozkłady 3. Populacje i próby danych, estymacja parametrów 4. Testowanie hipotez statystycznych
STATYSTYKA MATEMATYCZNA 1. Wykład wstępny. Teoria prawdopodobieństwa i elementy kombinatoryki. Zmienne losowe i ich rozkłady 3. Populacje i próby danych, estymacja parametrów 4. Testowanie hipotez statystycznych
Weryfikacja hipotez statystycznych
 Weryfikacja hipotez statystycznych Hipoteza Test statystyczny Poziom istotności Testy jednostronne i dwustronne Testowanie równości wariancji test F-Fishera Testowanie równości wartości średnich test t-studenta
Weryfikacja hipotez statystycznych Hipoteza Test statystyczny Poziom istotności Testy jednostronne i dwustronne Testowanie równości wariancji test F-Fishera Testowanie równości wartości średnich test t-studenta
Statystyka matematyczna dla leśników
 Statystyka matematyczna dla leśników Wydział Leśny Kierunek leśnictwo Studia Stacjonarne I Stopnia Rok akademicki 03/04 Wykład 5 Testy statystyczne Ogólne zasady testowania hipotez statystycznych, rodzaje
Statystyka matematyczna dla leśników Wydział Leśny Kierunek leśnictwo Studia Stacjonarne I Stopnia Rok akademicki 03/04 Wykład 5 Testy statystyczne Ogólne zasady testowania hipotez statystycznych, rodzaje
Analiza wariancji Piotr J. Sobczyk 19 November 2016
 Analiza wariancji Piotr J. Sobczyk 19 November 2016 Zacznijmy zajęcia od klasycznego przykładu czyli testu Studenta dla dwóch prób. x 1,i N(µ 1, σ 2 ), i = 1,..., n 1 x 2,i N(µ 2, σ 2 ), i = 1,..., n 2
Analiza wariancji Piotr J. Sobczyk 19 November 2016 Zacznijmy zajęcia od klasycznego przykładu czyli testu Studenta dla dwóch prób. x 1,i N(µ 1, σ 2 ), i = 1,..., n 1 x 2,i N(µ 2, σ 2 ), i = 1,..., n 2
Spis treści. Przedmowa... XI. Rozdział 1. Pomiar: jednostki miar... 1. Rozdział 2. Pomiar: liczby i obliczenia liczbowe... 16
 Spis treści Przedmowa.......................... XI Rozdział 1. Pomiar: jednostki miar................. 1 1.1. Wielkości fizyczne i pozafizyczne.................. 1 1.2. Spójne układy miar. Układ SI i jego
Spis treści Przedmowa.......................... XI Rozdział 1. Pomiar: jednostki miar................. 1 1.1. Wielkości fizyczne i pozafizyczne.................. 1 1.2. Spójne układy miar. Układ SI i jego
weryfikacja hipotez dotyczących parametrów populacji (średnia, wariancja)
 PODSTAWY STATYSTYKI. Teoria prawdopodobieństwa i elementy kombinatoryki. Zmienne losowe i ich rozkłady 3. Populacje i próby danych, estymacja parametrów 4. Testowanie hipotez 5. Testy parametryczne (na
PODSTAWY STATYSTYKI. Teoria prawdopodobieństwa i elementy kombinatoryki. Zmienne losowe i ich rozkłady 3. Populacje i próby danych, estymacja parametrów 4. Testowanie hipotez 5. Testy parametryczne (na
Wprowadzenie do analizy korelacji i regresji
 Statystyka dla jakości produktów i usług Six sigma i inne strategie Wprowadzenie do analizy korelacji i regresji StatSoft Polska Wybrane zagadnienia analizy korelacji Przy analizie zjawisk i procesów stanowiących
Statystyka dla jakości produktów i usług Six sigma i inne strategie Wprowadzenie do analizy korelacji i regresji StatSoft Polska Wybrane zagadnienia analizy korelacji Przy analizie zjawisk i procesów stanowiących
Statystyka w analizie i planowaniu eksperymentu
 28 marca 2012 Analiza wariancji klasyfikacja jednokierunkowa - wst ep Przypuśćmy, że chcemy porównać wieksz a (niż dwie) liczbe grup. Aby porównać średnie w kilku grupach, można przeprowadzić analize wariancji.
28 marca 2012 Analiza wariancji klasyfikacja jednokierunkowa - wst ep Przypuśćmy, że chcemy porównać wieksz a (niż dwie) liczbe grup. Aby porównać średnie w kilku grupach, można przeprowadzić analize wariancji.
KORELACJE I REGRESJA LINIOWA
 KORELACJE I REGRESJA LINIOWA Korelacje i regresja liniowa Analiza korelacji: Badanie, czy pomiędzy dwoma zmiennymi istnieje zależność Obie analizy się wzajemnie przeplatają Analiza regresji: Opisanie modelem
KORELACJE I REGRESJA LINIOWA Korelacje i regresja liniowa Analiza korelacji: Badanie, czy pomiędzy dwoma zmiennymi istnieje zależność Obie analizy się wzajemnie przeplatają Analiza regresji: Opisanie modelem
Nowa oferta edukacyjna Uniwersytetu Wrocławskiego odpowiedzią na współczesne potrzeby rynku pracy i gospodarki opartej na wiedzy
 Projekt Nowa oferta edukacyjna Uniwersytetu Wrocławskiego odpowiedzią na współczesne potrzeby rynku pracy i gospodarki opartej na wiedzy Dane: 2000 największych spółek światowych z 2004 (Forbes Magazine)
Projekt Nowa oferta edukacyjna Uniwersytetu Wrocławskiego odpowiedzią na współczesne potrzeby rynku pracy i gospodarki opartej na wiedzy Dane: 2000 największych spółek światowych z 2004 (Forbes Magazine)
Statystyka. Rozkład prawdopodobieństwa Testowanie hipotez. Wykład III ( )
 Statystyka Rozkład prawdopodobieństwa Testowanie hipotez Wykład III (04.01.2016) Rozkład t-studenta Rozkład T jest rozkładem pomocniczym we wnioskowaniu statystycznym; stosuje się go wyznaczenia przedziału
Statystyka Rozkład prawdopodobieństwa Testowanie hipotez Wykład III (04.01.2016) Rozkład t-studenta Rozkład T jest rozkładem pomocniczym we wnioskowaniu statystycznym; stosuje się go wyznaczenia przedziału
weryfikacja hipotez dotyczących parametrów populacji (średnia, wariancja) założenie: znany rozkład populacji (wykorzystuje się dystrybuantę)
 PODSTAWY STATYSTYKI 1. Teoria prawdopodobieństwa i elementy kombinatoryki. Zmienne losowe i ich rozkłady 3. Populacje i próby danych, estymacja parametrów 4. Testowanie hipotez 5. Testy parametryczne (na
PODSTAWY STATYSTYKI 1. Teoria prawdopodobieństwa i elementy kombinatoryki. Zmienne losowe i ich rozkłady 3. Populacje i próby danych, estymacja parametrów 4. Testowanie hipotez 5. Testy parametryczne (na
Księgarnia PWN: George A. Ferguson, Yoshio Takane - Analiza statystyczna w psychologii i pedagogice
 Księgarnia PWN: George A. Ferguson, Yoshio Takane - Analiza statystyczna w psychologii i pedagogice Przedmowa do wydania polskiego Przedmowa CZĘŚĆ I. PODSTAWY STATYSTYKI Rozdział 1 Podstawowe pojęcia statystyki
Księgarnia PWN: George A. Ferguson, Yoshio Takane - Analiza statystyczna w psychologii i pedagogice Przedmowa do wydania polskiego Przedmowa CZĘŚĆ I. PODSTAWY STATYSTYKI Rozdział 1 Podstawowe pojęcia statystyki
Żródło:
 Testy t-studenta są testami różnic pomiędzy średnimi czyli służą do porównania ze sobą dwóch średnich Zmienne muszą być zmiennymi ilościowym (liczymy i porównujemy średnie!) Są to testy parametryczne Test
Testy t-studenta są testami różnic pomiędzy średnimi czyli służą do porównania ze sobą dwóch średnich Zmienne muszą być zmiennymi ilościowym (liczymy i porównujemy średnie!) Są to testy parametryczne Test
Podstawy statystyki dla psychologów. Podręcznik akademicki. Wydanie drugie poprawione. Wiesław Szymczak
 Podstawy statystyki dla psychologów. Podręcznik akademicki. Wydanie drugie poprawione. Wiesław Szymczak Autor prezentuje spójny obraz najczęściej stosowanych metod statystycznych, dodatkowo omawiając takie
Podstawy statystyki dla psychologów. Podręcznik akademicki. Wydanie drugie poprawione. Wiesław Szymczak Autor prezentuje spójny obraz najczęściej stosowanych metod statystycznych, dodatkowo omawiając takie
STATYSTYKA MATEMATYCZNA
 STATYSTYKA MATEMATYCZNA 1. Wykład wstępny. Teoria prawdopodobieństwa i elementy kombinatoryki 2. Zmienne losowe i ich rozkłady 3. Populacje i próby danych, estymacja parametrów 4. Testowanie hipotez 5.
STATYSTYKA MATEMATYCZNA 1. Wykład wstępny. Teoria prawdopodobieństwa i elementy kombinatoryki 2. Zmienne losowe i ich rozkłady 3. Populacje i próby danych, estymacja parametrów 4. Testowanie hipotez 5.
Statystyczna analiza danych w programie STATISTICA 7.1 PL (wykład 3) Dariusz Gozdowski
 Statystyczna analiza danych w programie STATISTICA 7.1 PL (wykład 3) Dariusz Gozdowski Katedra Doświadczalnictwa i Bioinformatyki Wydział Rolnictwa i Biologii SGGW Dwuczynnikowa analiza wariancji (2-way
Statystyczna analiza danych w programie STATISTICA 7.1 PL (wykład 3) Dariusz Gozdowski Katedra Doświadczalnictwa i Bioinformatyki Wydział Rolnictwa i Biologii SGGW Dwuczynnikowa analiza wariancji (2-way
Przykład 2. Na podstawie książki J. Kowal: Metody statystyczne w badaniach sondażowych rynku
 Przykład 2 Na podstawie książki J. Kowal: Metody statystyczne w badaniach sondażowych rynku Sondaż sieciowy analiza wyników badania sondażowego dotyczącego motywacji w drodze do sukcesu Cel badania: uzyskanie
Przykład 2 Na podstawie książki J. Kowal: Metody statystyczne w badaniach sondażowych rynku Sondaż sieciowy analiza wyników badania sondażowego dotyczącego motywacji w drodze do sukcesu Cel badania: uzyskanie
Permutacyjna metoda oceny istotności regresji
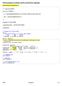 Permutacyjna metoda oceny istotności regresji (bez założenia normalności) f
Permutacyjna metoda oceny istotności regresji (bez założenia normalności) f
ANALIZA WARIANCJI - KLASYFIKACJA JEDNOCZYNNIKOWA
 ANALIZA WARIANCJI - KLASYFIKACJA JEDNOCZYNNIKOWA Na poprzednich zajęciach omawialiśmy testy dla weryfikacji hipotez, że dwie populacje o rozkładach normalnych mają jednakowe wartości średnie. Co jednak
ANALIZA WARIANCJI - KLASYFIKACJA JEDNOCZYNNIKOWA Na poprzednich zajęciach omawialiśmy testy dla weryfikacji hipotez, że dwie populacje o rozkładach normalnych mają jednakowe wartości średnie. Co jednak
X Y 4,0 3,3 8,0 6,8 12,0 11,0 16,0 15,2 20,0 18,9
 Zadanie W celu sprawdzenia, czy pipeta jest obarczona błędem systematycznym stałym lub zmiennym wykonano szereg pomiarów przy różnych ustawieniach pipety. Wyznacz równanie regresji liniowej, które pozwoli
Zadanie W celu sprawdzenia, czy pipeta jest obarczona błędem systematycznym stałym lub zmiennym wykonano szereg pomiarów przy różnych ustawieniach pipety. Wyznacz równanie regresji liniowej, które pozwoli
W2. Zmienne losowe i ich rozkłady. Wnioskowanie statystyczne.
 W2. Zmienne losowe i ich rozkłady. Wnioskowanie statystyczne. dr hab. Jerzy Nakielski Katedra Biofizyki i Morfogenezy Roślin Plan wykładu: 1. Etapy wnioskowania statystycznego 2. Hipotezy statystyczne,
W2. Zmienne losowe i ich rozkłady. Wnioskowanie statystyczne. dr hab. Jerzy Nakielski Katedra Biofizyki i Morfogenezy Roślin Plan wykładu: 1. Etapy wnioskowania statystycznego 2. Hipotezy statystyczne,
Katedra Genetyki i Podstaw Hodowli Zwierząt Wydział Hodowli i Biologii Zwierząt, UTP w Bydgoszczy
 Ćwiczenie: Analiza zmienności prosta Przykład w MS EXCEL Sprawdź czy genotyp jagniąt wpływa statystycznie na cechy użytkowości rzeźnej? Obliczenia wykonaj za pomocą modułu Analizy danych (jaganova.xls).
Ćwiczenie: Analiza zmienności prosta Przykład w MS EXCEL Sprawdź czy genotyp jagniąt wpływa statystycznie na cechy użytkowości rzeźnej? Obliczenia wykonaj za pomocą modułu Analizy danych (jaganova.xls).
dr hab. Dariusz Piwczyński, prof. nadzw. UTP
 dr hab. Dariusz Piwczyński, prof. nadzw. UTP Porównanie większej niż 2 liczby grup (k>2) Zmienna zależna skala przedziałowa Zmienna niezależna skala nominalna lub porządkowa 2 Istota teorii analizy wariancji
dr hab. Dariusz Piwczyński, prof. nadzw. UTP Porównanie większej niż 2 liczby grup (k>2) Zmienna zależna skala przedziałowa Zmienna niezależna skala nominalna lub porządkowa 2 Istota teorii analizy wariancji
Regresja ważona. Co, gdy nie ma stałej wariancji? Tu prawdziwe σ 2 =1 (dużo powtórzeń, więc wariancje są dobrze oszacowane) PAR Wykład 5 1/8
 Dobry chrześcijanin powinien wystrzegać się matematyków i tych wszystkich, którzy tworzą puste proroctwa. Istnieje niebezpieczeństwo, że matematycy zawarli przymierze z diabłem, aby zgubić duszę człowieka
Dobry chrześcijanin powinien wystrzegać się matematyków i tych wszystkich, którzy tworzą puste proroctwa. Istnieje niebezpieczeństwo, że matematycy zawarli przymierze z diabłem, aby zgubić duszę człowieka
Stanisław Cichocki. Natalia Nehrebecka. Wykład 9
 Stanisław Cichocki Natalia Nehrebecka Wykład 9 1 1. Dodatkowe założenie KMRL 2. Testowanie hipotez prostych Rozkład estymatora b Testowanie hipotez prostych przy użyciu statystyki t 3. Przedziały ufności
Stanisław Cichocki Natalia Nehrebecka Wykład 9 1 1. Dodatkowe założenie KMRL 2. Testowanie hipotez prostych Rozkład estymatora b Testowanie hipotez prostych przy użyciu statystyki t 3. Przedziały ufności
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 4
 STATYSTYKA I DOŚWIADCZALNICTWO Wykład 4 Inne układy doświadczalne 1) Układ losowanych bloków Stosujemy, gdy podejrzewamy, że może występować systematyczna zmienność między powtórzeniami np. - zmienność
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 4 Inne układy doświadczalne 1) Układ losowanych bloków Stosujemy, gdy podejrzewamy, że może występować systematyczna zmienność między powtórzeniami np. - zmienność
WNIOSKOWANIE STATYSTYCZNE
 STATYSTYKA WNIOSKOWANIE STATYSTYCZNE ESTYMACJA oszacowanie z pewną dokładnością wartości opisującej rozkład badanej cechy statystycznej. WERYFIKACJA HIPOTEZ sprawdzanie słuszności przypuszczeń dotyczących
STATYSTYKA WNIOSKOWANIE STATYSTYCZNE ESTYMACJA oszacowanie z pewną dokładnością wartości opisującej rozkład badanej cechy statystycznej. WERYFIKACJA HIPOTEZ sprawdzanie słuszności przypuszczeń dotyczących
Projekt Nowa oferta edukacyjna Uniwersytetu Wrocławskiego odpowiedzią na współczesne potrzeby rynku pracy i gospodarki opartej na wiedzy
 Projekt Nowa oferta edukacyjna Uniwersytetu Wrocławskiego odpowiedzią na współczesne potrzeby rynku pracy i gospodarki opartej na wiedzy Dane: Eksploracja (mining) Problemy: Jedna zmienna 2000 najwi ększych
Projekt Nowa oferta edukacyjna Uniwersytetu Wrocławskiego odpowiedzią na współczesne potrzeby rynku pracy i gospodarki opartej na wiedzy Dane: Eksploracja (mining) Problemy: Jedna zmienna 2000 najwi ększych
Liczba godzin Punkty ECTS Sposób zaliczenia. ćwiczenia 16 zaliczenie z oceną
 Wydział: Zarządzanie i Finanse Nazwa kierunku kształcenia: Finanse i Rachunkowość Rodzaj przedmiotu: podstawowy Opiekun: prof. nadzw. dr hab. Tomasz Kuszewski Poziom studiów (I lub II stopnia): II stopnia
Wydział: Zarządzanie i Finanse Nazwa kierunku kształcenia: Finanse i Rachunkowość Rodzaj przedmiotu: podstawowy Opiekun: prof. nadzw. dr hab. Tomasz Kuszewski Poziom studiów (I lub II stopnia): II stopnia
JEDNOCZYNNIKOWA ANALIZA WARIANCJI, ANOVA 1
 Powtórzenie: ANOVA 1 JEDNOCZYNNIKOWA ANALIZA WARIANCJI, ANOVA 1 Obserwowana (badana) cecha Y Czynnik wpływający na Y (badany) A A i i ty poziom czynnika A (i=1..a), n i liczba powtórzeń w i tej populacji
Powtórzenie: ANOVA 1 JEDNOCZYNNIKOWA ANALIZA WARIANCJI, ANOVA 1 Obserwowana (badana) cecha Y Czynnik wpływający na Y (badany) A A i i ty poziom czynnika A (i=1..a), n i liczba powtórzeń w i tej populacji
ZMIENNE LOSOWE. Zmienna losowa (ZL) X( ) jest funkcją przekształcającą przestrzeń zdarzeń elementarnych w zbiór liczb rzeczywistych R 1 tzn. X: R 1.
 Opracowała: Joanna Kisielińska ZMIENNE LOSOWE Zmienna losowa (ZL) X( ) jest funkcją przekształcającą przestrzeń zdarzeń elementarnych w zbiór liczb rzeczywistych R tzn. X: R. Realizacją zmiennej losowej
Opracowała: Joanna Kisielińska ZMIENNE LOSOWE Zmienna losowa (ZL) X( ) jest funkcją przekształcającą przestrzeń zdarzeń elementarnych w zbiór liczb rzeczywistych R tzn. X: R. Realizacją zmiennej losowej
Zadania ze statystyki cz. 8 I rok socjologii. Zadanie 1.
 Zadania ze statystyki cz. 8 I rok socjologii Zadanie 1. W potocznej opinii pokutuje przekonanie, że lepsi z matematyki są chłopcy niż dziewczęta. Chcąc zweryfikować tę opinię, przeprowadzono badanie w
Zadania ze statystyki cz. 8 I rok socjologii Zadanie 1. W potocznej opinii pokutuje przekonanie, że lepsi z matematyki są chłopcy niż dziewczęta. Chcąc zweryfikować tę opinię, przeprowadzono badanie w
Testowanie hipotez statystycznych
 Agenda Instytut Matematyki Politechniki Łódzkiej 2 stycznia 2012 Agenda Agenda 1 Wprowadzenie Agenda 2 Hipoteza oraz błędy I i II rodzaju Hipoteza alternatywna Statystyka testowa Zbiór krytyczny Poziom
Agenda Instytut Matematyki Politechniki Łódzkiej 2 stycznia 2012 Agenda Agenda 1 Wprowadzenie Agenda 2 Hipoteza oraz błędy I i II rodzaju Hipoteza alternatywna Statystyka testowa Zbiór krytyczny Poziom
Z poprzedniego wykładu
 PODSTAWY STATYSTYKI 1. Teoria prawdopodobieństwa i elementy kombinatoryki 2. Zmienne losowe i ich rozkłady 3. Populacje i próby danych, estymacja parametrów 4. Testowanie hipotez 5. Testy parametryczne
PODSTAWY STATYSTYKI 1. Teoria prawdopodobieństwa i elementy kombinatoryki 2. Zmienne losowe i ich rozkłady 3. Populacje i próby danych, estymacja parametrów 4. Testowanie hipotez 5. Testy parametryczne
TABELKA ANOVA (jednoczynnikowa)
 TABELKA ANOVA (jednoczynnikowa) Jednoczynnikowa ANOVA nazwa zmiennej zależnej Między grupami Suma kwadratów df Średni kwadrat F Istotność k 1 SSMG / dfmg MSMG / MSWG brane z tablic Wewnątrz grup 2 z 3
TABELKA ANOVA (jednoczynnikowa) Jednoczynnikowa ANOVA nazwa zmiennej zależnej Między grupami Suma kwadratów df Średni kwadrat F Istotność k 1 SSMG / dfmg MSMG / MSWG brane z tablic Wewnątrz grup 2 z 3
Stanisław Cichocki Natalia Nehrebecka. Zajęcia 8
 Stanisław Cichocki Natalia Nehrebecka Zajęcia 8 1. Testy diagnostyczne 2. Testowanie prawidłowości formy funkcyjnej modelu 3. Testowanie normalności składników losowych 4. Testowanie stabilności parametrów
Stanisław Cichocki Natalia Nehrebecka Zajęcia 8 1. Testy diagnostyczne 2. Testowanie prawidłowości formy funkcyjnej modelu 3. Testowanie normalności składników losowych 4. Testowanie stabilności parametrów
Statystyka i Analiza Danych
 Warsztaty Statystyka i Analiza Danych Gdańsk, 20-22 lutego 2014 Zastosowania wybranych technik regresyjnych do modelowania współzależności zjawisk Janusz Wątroba StatSoft Polska Centrum Zastosowań Matematyki
Warsztaty Statystyka i Analiza Danych Gdańsk, 20-22 lutego 2014 Zastosowania wybranych technik regresyjnych do modelowania współzależności zjawisk Janusz Wątroba StatSoft Polska Centrum Zastosowań Matematyki
WIELKA SGH-OWA POWTÓRKA ZE STATYSTYKI. Test zgodności i analiza wariancji Analiza wariancji
 WIELKA SGH-OWA POWTÓRKA ZE STATYSTYKI Test zgodności i analiza wariancji Analiza wariancji Test zgodności Chi-kwadrat Sprawdza się za jego pomocą ZGODNOŚĆ ROZKŁADU EMPIRYCZNEGO Z PRÓBY Z ROZKŁADEM HIPOTETYCZNYM
WIELKA SGH-OWA POWTÓRKA ZE STATYSTYKI Test zgodności i analiza wariancji Analiza wariancji Test zgodności Chi-kwadrat Sprawdza się za jego pomocą ZGODNOŚĆ ROZKŁADU EMPIRYCZNEGO Z PRÓBY Z ROZKŁADEM HIPOTETYCZNYM
Jednoczynnikowa analiza wariancji. Wnioskowanie dla jednoczynnikowej ANOV-y. Porównywanie poszczególnych średnich
 (Wykład 13) Jednoczynnikowa analiza wariancji Wnioskowanie dla jednoczynnikowej ANOV-y Format danych Hipotezy i model ANOVA Tabela ANOVA i test F Porównywanie poszczególnych średnich Jednoczynnikowa ANOVA
(Wykład 13) Jednoczynnikowa analiza wariancji Wnioskowanie dla jednoczynnikowej ANOV-y Format danych Hipotezy i model ANOVA Tabela ANOVA i test F Porównywanie poszczególnych średnich Jednoczynnikowa ANOVA
Spis treści. Księgarnia PWN: Bruce M. King, Edward W. Minium - Statystyka dla psychologów i pedagogów. Wstęp Wprowadzenie...
 Księgarnia PWN: Bruce M. King, Edward W. Minium - Statystyka dla psychologów i pedagogów Wstęp... 13 1. Wprowadzenie... 19 1.1. Statystyka opisowa.................................. 21 1.2. Wnioskowanie
Księgarnia PWN: Bruce M. King, Edward W. Minium - Statystyka dla psychologów i pedagogów Wstęp... 13 1. Wprowadzenie... 19 1.1. Statystyka opisowa.................................. 21 1.2. Wnioskowanie
Dwuczynnikowa ANOVA dla prób niezależnych w schemacie 2x2
 Dwuczynnikowa ANOVA dla prób niezależnych w schemacie 2x2 Poniżej prezentujemy przykładowe pytania z rozwiązaniami dotyczącymi dwuczynnikowej analizy wariancji w schemacie 2x2. Wszystkie rozwiązania są
Dwuczynnikowa ANOVA dla prób niezależnych w schemacie 2x2 Poniżej prezentujemy przykładowe pytania z rozwiązaniami dotyczącymi dwuczynnikowej analizy wariancji w schemacie 2x2. Wszystkie rozwiązania są
Szkice rozwiązań z R:
 Szkice rozwiązań z R: Zadanie 1. Założono doświadczenie farmakologiczne. Obserwowano przyrost wagi ciała (przyrost [gram]) przy zadanych dawkach trzech preparatów (dawka.a, dawka.b, dawka.c). Obiektami
Szkice rozwiązań z R: Zadanie 1. Założono doświadczenie farmakologiczne. Obserwowano przyrost wagi ciała (przyrost [gram]) przy zadanych dawkach trzech preparatów (dawka.a, dawka.b, dawka.c). Obiektami
Spis treści. Laboratorium III: Testy statystyczne. Inżynieria biomedyczna, I rok, semestr letni 2013/2014 Analiza danych pomiarowych
 1 Laboratorium III: Testy statystyczne Spis treści Laboratorium III: Testy statystyczne... 1 Wiadomości ogólne... 2 1. Krótkie przypomnienie wiadomości na temat testów statystycznych... 2 1.1. Weryfikacja
1 Laboratorium III: Testy statystyczne Spis treści Laboratorium III: Testy statystyczne... 1 Wiadomości ogólne... 2 1. Krótkie przypomnienie wiadomości na temat testów statystycznych... 2 1.1. Weryfikacja
STATYSTYKA I DOŚWIADCZALNICTWO. Wykład 2
 STATYSTYKA I DOŚWIADCZALNICTWO Wykład Parametry przedziałowe rozkładów ciągłych określane na podstawie próby (przedziały ufności) Przedział ufności dla średniej s X t( α;n 1),X + t( α;n 1) n s n t (α;
STATYSTYKA I DOŚWIADCZALNICTWO Wykład Parametry przedziałowe rozkładów ciągłych określane na podstawie próby (przedziały ufności) Przedział ufności dla średniej s X t( α;n 1),X + t( α;n 1) n s n t (α;
KARTA KURSU. Kod Punktacja ECTS* 1
 KARTA KURSU Nazwa Nazwa w j. ang. Wprowadzenie do statystyki Introduction to statistics Kod Punktacja ECTS* 1 Koordynator Prof. dr hab. Jerzy Wołek Zespół dydaktyczny Prof. dr hab. Jerzy Wołek doktoranci
KARTA KURSU Nazwa Nazwa w j. ang. Wprowadzenie do statystyki Introduction to statistics Kod Punktacja ECTS* 1 Koordynator Prof. dr hab. Jerzy Wołek Zespół dydaktyczny Prof. dr hab. Jerzy Wołek doktoranci
Analiza wariancji, część 2
 Analiza wariancji, część 2 1 / 74 Analiza kontrastów a priori Testy post hoc porównują wszystkie możliwe pary średnich i wykonuje się je dopiero po stwierdzeniu za pomocą testu F istotności danego czynnika.
Analiza wariancji, część 2 1 / 74 Analiza kontrastów a priori Testy post hoc porównują wszystkie możliwe pary średnich i wykonuje się je dopiero po stwierdzeniu za pomocą testu F istotności danego czynnika.
Testowanie hipotez statystycznych
 9 października 2008 ...czyli definicje na rozgrzewkę n-elementowa próba losowa - wektor n zmiennych losowych (X 1,..., X n ); intuicyjnie: wynik n eksperymentów realizacja próby (X 1,..., X n ) w ω Ω :
9 października 2008 ...czyli definicje na rozgrzewkę n-elementowa próba losowa - wektor n zmiennych losowych (X 1,..., X n ); intuicyjnie: wynik n eksperymentów realizacja próby (X 1,..., X n ) w ω Ω :
Błędy przy testowaniu hipotez statystycznych. Decyzja H 0 jest prawdziwa H 0 jest faszywa
 Weryfikacja hipotez statystycznych Hipotezą statystyczną nazywamy każde przypuszczenie dotyczące nieznanego rozkładu badanej cechy populacji, o prawdziwości lub fałszywości którego wnioskuje się na podstawie
Weryfikacja hipotez statystycznych Hipotezą statystyczną nazywamy każde przypuszczenie dotyczące nieznanego rozkładu badanej cechy populacji, o prawdziwości lub fałszywości którego wnioskuje się na podstawie
Metody statystyczne w socjologii SYLABUS A. Informacje ogólne Opis
 Elementy składowe sylabusu Nazwa jednostki prowadzącej kierunek Nazwa kierunku studiów Poziom kształcenia Profil studiów Forma studiów Kod przedmiotu Język przedmiotu Rodzaj przedmiotu Dziedzina i dyscyplina
Elementy składowe sylabusu Nazwa jednostki prowadzącej kierunek Nazwa kierunku studiów Poziom kształcenia Profil studiów Forma studiów Kod przedmiotu Język przedmiotu Rodzaj przedmiotu Dziedzina i dyscyplina
STATYSTYKA MATEMATYCZNA
 STATYSTYKA MATEMATYCZNA 1. Wykład wstępny. Teoria prawdopodobieństwa i elementy kombinatoryki 3. Zmienne losowe 4. Populacje i próby danych 5. Testowanie hipotez i estymacja parametrów 6. Test t 7. Test
STATYSTYKA MATEMATYCZNA 1. Wykład wstępny. Teoria prawdopodobieństwa i elementy kombinatoryki 3. Zmienne losowe 4. Populacje i próby danych 5. Testowanie hipotez i estymacja parametrów 6. Test t 7. Test
Zadania ze statystyki cz.8. Zadanie 1.
 Zadania ze statystyki cz.8. Zadanie 1. Wykonano pewien eksperyment skuteczności działania pewnej reklamy na zmianę postawy. Wylosowano 10 osobową próbę studentów, których poproszono o ocenę pewnego produktu,
Zadania ze statystyki cz.8. Zadanie 1. Wykonano pewien eksperyment skuteczności działania pewnej reklamy na zmianę postawy. Wylosowano 10 osobową próbę studentów, których poproszono o ocenę pewnego produktu,
Modele i wnioskowanie statystyczne (MWS), sprawozdanie z laboratorium 4
 Modele i wnioskowanie statystyczne (MWS), sprawozdanie z laboratorium 4 Konrad Miziński, nr albumu 233703 31 maja 2015 Zadanie 1 Wartości oczekiwane µ 1 i µ 2 oszacowano wg wzorów: { µ1 = 0.43925 µ = X
Modele i wnioskowanie statystyczne (MWS), sprawozdanie z laboratorium 4 Konrad Miziński, nr albumu 233703 31 maja 2015 Zadanie 1 Wartości oczekiwane µ 1 i µ 2 oszacowano wg wzorów: { µ1 = 0.43925 µ = X
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 5
 STATYSTYKA I DOŚWIADCZALNICTWO Wykład 5 Jednoczynnikowa analiza wariancji i porównania wielokrotne (układ losowanych bloków randomized block design RBD) Układ losowanych bloków Stosujemy, gdy podejrzewamy,
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 5 Jednoczynnikowa analiza wariancji i porównania wielokrotne (układ losowanych bloków randomized block design RBD) Układ losowanych bloków Stosujemy, gdy podejrzewamy,
Rozkłady statystyk z próby
 Rozkłady statystyk z próby Rozkłady statystyk z próby Przypuśćmy, że wykonujemy serię doświadczeń polegających na 4 krotnym rzucie symetryczną kostką do gry, obserwując liczbę wyrzuconych oczek Nr kolejny
Rozkłady statystyk z próby Rozkłady statystyk z próby Przypuśćmy, że wykonujemy serię doświadczeń polegających na 4 krotnym rzucie symetryczną kostką do gry, obserwując liczbę wyrzuconych oczek Nr kolejny
Weryfikacja hipotez statystycznych za pomocą testów statystycznych
 Weryfikacja hipotez statystycznych za pomocą testów statystycznych Weryfikacja hipotez statystycznych za pomocą testów stat. Hipoteza statystyczna Dowolne przypuszczenie co do rozkładu populacji generalnej
Weryfikacja hipotez statystycznych za pomocą testów statystycznych Weryfikacja hipotez statystycznych za pomocą testów stat. Hipoteza statystyczna Dowolne przypuszczenie co do rozkładu populacji generalnej
STATYSTYKA MATEMATYCZNA
 STATYSTYKA MATEMATYCZNA 1. Wykład wstępny. Teoria prawdopodobieństwa i elementy kombinatoryki 2. Zmienne losowe i ich rozkłady 3. Populacje i próby danych, estymacja parametrów 4. Testowanie hipotez 5.
STATYSTYKA MATEMATYCZNA 1. Wykład wstępny. Teoria prawdopodobieństwa i elementy kombinatoryki 2. Zmienne losowe i ich rozkłady 3. Populacje i próby danych, estymacja parametrów 4. Testowanie hipotez 5.
STATYSTYKA MATEMATYCZNA
 STATYSTYKA MATEMATYCZNA 1. Wykład wstępny. Teoria prawdopodobieństwa i elementy kombinatoryki 2. Zmienne losowe i ich rozkłady 3. Populacje i próby danych, estymacja parametrów 4. Testowanie hipotez 5.
STATYSTYKA MATEMATYCZNA 1. Wykład wstępny. Teoria prawdopodobieństwa i elementy kombinatoryki 2. Zmienne losowe i ich rozkłady 3. Populacje i próby danych, estymacja parametrów 4. Testowanie hipotez 5.
Statystyka i opracowanie danych- W 8 Wnioskowanie statystyczne. Testy statystyczne. Weryfikacja hipotez statystycznych.
 Statystyka i opracowanie danych- W 8 Wnioskowanie statystyczne. Testy statystyczne. Weryfikacja hipotez statystycznych. Dr Anna ADRIAN Paw B5, pok407 adan@agh.edu.pl Hipotezy i Testy statystyczne Każde
Statystyka i opracowanie danych- W 8 Wnioskowanie statystyczne. Testy statystyczne. Weryfikacja hipotez statystycznych. Dr Anna ADRIAN Paw B5, pok407 adan@agh.edu.pl Hipotezy i Testy statystyczne Każde
Zadanie 1 Zakładając liniową relację między wydatkami na obuwie a dochodem oszacować MNK parametry modelu: y t. X 1 t. Tabela 1.
 tel. 44 683 1 55 tel. kom. 64 566 811 e-mail: biuro@wszechwiedza.pl Zadanie 1 Zakładając liniową relację między wydatkami na obuwie a dochodem oszacować MNK parametry modelu: gdzie: y t X t y t = 1 X 1
tel. 44 683 1 55 tel. kom. 64 566 811 e-mail: biuro@wszechwiedza.pl Zadanie 1 Zakładając liniową relację między wydatkami na obuwie a dochodem oszacować MNK parametry modelu: gdzie: y t X t y t = 1 X 1
TESTOWANIE HIPOTEZ STATYSTYCZNYCH
 TETOWANIE HIPOTEZ TATYTYCZNYCH HIPOTEZA TATYTYCZNA przypuszczenie co do rozkładu populacji generalnej (jego postaci funkcyjnej lub wartości parametrów). Prawdziwość tego przypuszczenia jest oceniana na
TETOWANIE HIPOTEZ TATYTYCZNYCH HIPOTEZA TATYTYCZNA przypuszczenie co do rozkładu populacji generalnej (jego postaci funkcyjnej lub wartości parametrów). Prawdziwość tego przypuszczenia jest oceniana na
Statystyka od podstaw Janina Jóźwiak, Jarosław Podgórski
 Statystyka od podstaw Janina Jóźwiak, Jarosław Podgórski Książka jest nowoczesnym podręcznikiem przeznaczonym dla studentów uczelni i wydziałów ekonomicznych. Wykład podzielono na cztery części. W pierwszej
Statystyka od podstaw Janina Jóźwiak, Jarosław Podgórski Książka jest nowoczesnym podręcznikiem przeznaczonym dla studentów uczelni i wydziałów ekonomicznych. Wykład podzielono na cztery części. W pierwszej
Statystyka w pracy badawczej nauczyciela Wykład 4: Analiza współzależności. dr inż. Walery Susłow walery.suslow@ie.tu.koszalin.pl
 Statystyka w pracy badawczej nauczyciela Wykład 4: Analiza współzależności dr inż. Walery Susłow walery.suslow@ie.tu.koszalin.pl Statystyczna teoria korelacji i regresji (1) Jest to dział statystyki zajmujący
Statystyka w pracy badawczej nauczyciela Wykład 4: Analiza współzależności dr inż. Walery Susłow walery.suslow@ie.tu.koszalin.pl Statystyczna teoria korelacji i regresji (1) Jest to dział statystyki zajmujący
Copyright by Wydawnictwo Naukowe Scholar, Warszawa 2000, 2008
 Redaktor: Alicja Zagrodzka Korekta: Krystyna Chludzińska Projekt okładki: Katarzyna Juras Copyright by Wydawnictwo Naukowe Scholar, Warszawa 2000, 2008 ISBN 978-83-7383-296-1 Wydawnictwo Naukowe Scholar
Redaktor: Alicja Zagrodzka Korekta: Krystyna Chludzińska Projekt okładki: Katarzyna Juras Copyright by Wydawnictwo Naukowe Scholar, Warszawa 2000, 2008 ISBN 978-83-7383-296-1 Wydawnictwo Naukowe Scholar
Elementy Modelowania Matematycznego Wykład 4 Regresja i dyskryminacja liniowa
 Spis treści Elementy Modelowania Matematycznego Wykład 4 Regresja i dyskryminacja liniowa Romuald Kotowski Katedra Informatyki Stosowanej PJWSTK 2009 Spis treści Spis treści 1 Wstęp Bardzo często interesujący
Spis treści Elementy Modelowania Matematycznego Wykład 4 Regresja i dyskryminacja liniowa Romuald Kotowski Katedra Informatyki Stosowanej PJWSTK 2009 Spis treści Spis treści 1 Wstęp Bardzo często interesujący
Założenia do analizy wariancji. dr Anna Rajfura Kat. Doświadczalnictwa i Bioinformatyki SGGW
 Założenia do analizy wariancji dr Anna Rajfura Kat. Doświadczalnictwa i Bioinformatyki SGGW anna_rajfura@sggw.pl Zagadnienia 1. Normalność rozkładu cechy Testy: chi-kwadrat zgodności, Shapiro-Wilka, Kołmogorowa-Smirnowa
Założenia do analizy wariancji dr Anna Rajfura Kat. Doświadczalnictwa i Bioinformatyki SGGW anna_rajfura@sggw.pl Zagadnienia 1. Normalność rozkładu cechy Testy: chi-kwadrat zgodności, Shapiro-Wilka, Kołmogorowa-Smirnowa
Wnioskowanie statystyczne Weryfikacja hipotez. Statystyka
 Wnioskowanie statystyczne Weryfikacja hipotez Statystyka Co nazywamy hipotezą Każde stwierdzenie o parametrach rozkładu lub rozkładzie zmiennej losowej w populacji nazywać będziemy hipotezą statystyczną
Wnioskowanie statystyczne Weryfikacja hipotez Statystyka Co nazywamy hipotezą Każde stwierdzenie o parametrach rozkładu lub rozkładzie zmiennej losowej w populacji nazywać będziemy hipotezą statystyczną
Regresja wielokrotna. PDF created with FinePrint pdffactory Pro trial version http://www.fineprint.com
 Regresja wielokrotna Model dla zależności liniowej: Y=a+b 1 X 1 +b 2 X 2 +...+b n X n Cząstkowe współczynniki regresji wielokrotnej: b 1,..., b n Zmienne niezależne (przyczynowe): X 1,..., X n Zmienna
Regresja wielokrotna Model dla zależności liniowej: Y=a+b 1 X 1 +b 2 X 2 +...+b n X n Cząstkowe współczynniki regresji wielokrotnej: b 1,..., b n Zmienne niezależne (przyczynowe): X 1,..., X n Zmienna
Wprowadzenie do teorii ekonometrii. Wykład 1 Warunkowa wartość oczekiwana i odwzorowanie liniowe
 Wprowadzenie do teorii ekonometrii Wykład 1 Warunkowa wartość oczekiwana i odwzorowanie liniowe Zajęcia Wykład Laboratorium komputerowe 2 Zaliczenie EGZAMIN (50%) Na egzaminie obowiązują wszystkie informacje
Wprowadzenie do teorii ekonometrii Wykład 1 Warunkowa wartość oczekiwana i odwzorowanie liniowe Zajęcia Wykład Laboratorium komputerowe 2 Zaliczenie EGZAMIN (50%) Na egzaminie obowiązują wszystkie informacje
SIGMA KWADRAT. Weryfikacja hipotez statystycznych. Statystyka i demografia CZWARTY LUBELSKI KONKURS STATYSTYCZNO-DEMOGRAFICZNY
 SIGMA KWADRAT CZWARTY LUBELSKI KONKURS STATYSTYCZNO-DEMOGRAFICZNY Weryfikacja hipotez statystycznych Statystyka i demografia PROJEKT DOFINANSOWANY ZE ŚRODKÓW NARODOWEGO BANKU POLSKIEGO URZĄD STATYSTYCZNY
SIGMA KWADRAT CZWARTY LUBELSKI KONKURS STATYSTYCZNO-DEMOGRAFICZNY Weryfikacja hipotez statystycznych Statystyka i demografia PROJEKT DOFINANSOWANY ZE ŚRODKÓW NARODOWEGO BANKU POLSKIEGO URZĄD STATYSTYCZNY
