ALICJA BUDNIK Zakład Ekologii Ewolucyjnej Człowieka, Instytut Antropologii Wydział Biologii, Uniwersytet im. Adama Mickiewicza w Poznaniu
|
|
|
- Antoni Król
- 7 lat temu
- Przeglądów:
Transkrypt
1 XVII Warsztaty Antropologiczne im. Profesora Janusza Charzewskiego Łódź ALICJA BUDNIK Zakład Ekologii Ewolucyjnej Człowieka, Instytut Antropologii Wydział Biologii, Uniwersytet im. Adama Mickiewicza w Poznaniu MOŻLIWOŚCI ODTWARZANIA STRUKTURY GENETYCZNEJ POPULACJI NA PODSTAWIE ŹRÓDEŁ HISTORYCZNYCH Trudno przeceniać wagę badań nad genetyczną strukturą populacji ludzkich. Mają one wymiar zarówno praktyczny, jak teoretyczny. Można dzięki nim empirycznie weryfikować wyprowadzone wcześniej teoretycznie modelowe równania z zakresu genetyki populacyjnej. Można ponadto rekonstruować i wyjaśniać różnorakie aspekty z zakresu historii i ekologii lokalnych grup ludzkich. Badania te służą zatem odtwarzaniu mikroewolucji człowieka (Budnik 2000). Współcześnie, w dobie dynamicznego rozwoju metod i technik z zakresu biologii molekularnej, do rekonstrukcji struktury genetycznej grup ludzkich zaprzęga się coraz częściej badania DNA. Badania te, jakkolwiek ciekawe i ważne z poznawczego punktu widzenia, są jednak skomplikowane i kosztowne. Strukturę genetyczną populacji próbuje się jednak odczytywać także w bardziej tradycyjny sposób, ze źródeł historycznych, demograficznych, archiwalnych. Przyjrzyjmy się, w jaki sposób można powiązać oba rodzaje danych, jak przetłumaczyć wzajemnie na siebie dane genetyczne i demograficzne. Różnice genetyczne w zakresie danego locus między lineażami w obrębie tej samej populacji można wyrazić za pomocą wariancji częstości danego allelu ustandaryzowanej na kombinację średniej częstości tego allelu we wszystkich lineażach i jego alternatywnego wariantu. Wariancja jest tu matematyczną miarą zmienności genetycznej. W terminach genetyki populacyjnej określamy ją jako tzw. wariancję Wahlunda (Cavalli-Sforza i Bodmer 1971; Henneberg 1978). Ta standaryzowana wariancja genetyczna stanowi równocześnie współczynnik wsobności (inbredu) w populacji:
2 62 ALICJA BUDNIK f 2 pq 1 1 4Nm gdzie: f współczynnik wsobności, p, q średnie częstości alternatywnych alleli danego locus, jeśli w locus znajdują się tylko dwa allele, wtedy q 1 p, σ 2 wariancja genetyczna częstości danego allelu, N efektywna wielkość populacji, m współczynnik migracji. Jak wynika z podanych wyżej formuł, wariancja genetyczna zależna jest od rozmiarów populacji, a dokładniej od tzw. efektywnej wielkości populacji N (w uproszczeniu możemy tu przyjąć, że jest to liczba osób zdolnych do kojarzeń małżeńskich i reprodukcji) oraz od tego, ile alleli będzie napływało do badanej populacji za sprawą migracji (od współczynnika migracji m) (Cavalli-Sforza i Bodmer 1971). Już tu zatem pojawia się przełożenie danych genetycznych na kulturowe, demograficzne. Współczynnik wsobności oznacza prawdopodobieństwo, że losowo wybrany z populacji osobnik posiada w danym locus dwa allele identyczne ze względu na pochodzenie od tego samego przodka. Współczynnik wsobności mierzy zatem stopień homozygotyczności populacji. Pod pewnymi względami przypomina on współczynnik tzw. wewnątrzgrupowego spokrewnienia. Współczynnik spokrewnienia wewnątrzgrupowego to prawdopodobieństwo, że u dwóch losowo kojarzących się w populacji osób w danym locus występuje taki sam allel i że ta identyczność wynika z pochodzenia od tego samego przodka. Gdy kojarzenie małżeństw w grupie ludzkiej odbywa się losowo, nie ma w niej migracji oraz nie zachodzą mutacje, oba współczynniki są tożsame (Cavalli-Sforza i Bodmer 1971). Zauważmy, że współczynnik spokrewnienia wewnątrzgrupowego dotyczy pokolenia rodziców, współczynnik wsobności pokolenia potomstwa. Największe prawdopodobieństwo szybkiej i zauważalnej przebudowy puli genowej zaznacza się w małych, izolowanych populacjach. Zwrócił na to uwagę już w czterdziestych latach ubiegłego wieku jeden z twórców genetyki populacyjnej, Sewall Wright. Podane wcześniej równanie na współczynnik inbredu f stanowi uproszczoną postać wzoru dla tzw. wyspowego modelu międzygrupowej wymiany genów, jaki stworzył ten autor (Cavalli-Sforza i Bodmer 1971; Jorde 1980). Model ten dotyczy bardzo nielicznych przypadków populacji, które położone są w dużym oddaleniu od innych (jak wyspy) i wymieniają z nimi w bardzo niewielkim stopniu, z małym natężeniem migracji, osobniki a wraz z nimi geny. W rzeczywistości ta wymiana partnerów (i genów) odbywa się na ogół inaczej, bo różne jest rozmieszczenie populacji w przestrzeni i różne są systemy kojarzeń małżeńskich. W sytuacjach najczęściej spotykanych u człowieka trudno znaleźć wyraźne i bezwzględne bariery izolacyjne. Ze względu na niepełność lub brak takich barier trudno jest też wydzielić zbiory osób posiadających odrębne pule genów. Z drugiej strony, nie sposób też traktować
3 Możliwości odtwarzania struktury genetycznej populacji na podstawie źródeł 63 populacje ludzkie jako grupy nieograniczonego kojarzenia się, całkowicie panmiktyczne. Pamiętajmy, że nawet przy braku barier izolacyjnych, prawdopodobieństwo zawarcia małżeństwa zależne jest od odległości geograficznej. Mówimy wówczas o izolacji przez odległość (isolation by distance) (Cavalli- Sforza i Bodmer 1971; Henneberg 1976; 1979; Jorde 1980). Zaproponowano wiele modeli oceny stopnia tej izolacji. Wymiana genów w przestrzeni zamieszkałej przez ludzi może odbywać się na różne sposoby. O modelu wyspowym Wrighta już wspominaliśmy. W szczególnej sytuacji, gdy osiedla ludzkie położone są na przykład wzdłuż rzeki czy w kotlinie górskiej, geny napływają do badanej miejscowości z dwu stron, z osiedli położonych wzdłuż jednej linii. Opisują to modele jednowymiarowe nieciągłe ( schodkowe ), gdy geny przepływają skokowo z miejscowości 3 do 2, z 2 do 1 i z 1 do badanej (B) oraz ciągłe, gdy napływ genów odbywa się także bezpośrednio z dalej położonych osiedli (ryc. 1). O wiele częściej wymiana partnerów a wraz z nimi genów, które wnoszą do puli genowej, odbywa się w przestrzeni dwuwymiarowej. Modele dwuwymiarowe (podobnie jak poprzednio nieciągłe, schodkowe oraz bliższe rzeczywistości ciągłe) opisują napływ genów do badanej miejscowości z czterech stron (ryc. 2) (Cavalli-Sforza i Bodmer 1971; Henneberg 1979; Malinowski i Strzałko 1985). Prawdopodobieństwa kojarzenia się małżonków pochodzących z różnych odległości w pary ujmowano w postaci szeregu matematycznych zależności funkcyjnych a tworzone na ich podstawie teoretyczne rozkłady tych prawdopodobieństw próbowano dopasowywać do rzeczywistych za pomocą rozmaitych, empirycznie znajdowanych współczynników (np. Cavalli-Sforza i Bodmer 1971; Erikson i in. 1973; Jorde 1980; Morton 1982; Sujoldžić 1988; Sujoldžić i in. 1989; Smith i Sherren 1989; Rudan i in. 1998). Okazywało się to niezwykle trudne zarówno ze względu na stopień komplikacji proponowanych metod, jak i brak jednoznaczności w ocenie płynących z nich wyników. Pamiętajmy też, że zmienną, którą w tych modelach oceniano najczęściej były geograficzne odległości pomiędzy miejscami urodzenia współmałżonków, tymczasem pewien Ryc. 1. Jednowymiarowy model wymiany genów. B oznacza badaną miejscowość, numery 1, 2, 3 miejscowości położone po jej obu stronach wzdłuż jednej linii, m natężenie migracji. Strzałki skazują kierunek przepływu genów. Dalsze objaśnienia w tekście. Źródło: opracowanie własne na podstawie Cavalli-Sforza i Bodimer 1971; Henneberg 1979; Malinowski i Strzałko 1985
4 64 ALICJA BUDNIK stopień izolacji w kontaktach międzyludzkich może wynikać z innych przyczyn, niż bariery czy odległości geograficzne mogą mieć one charakter różnych zmiennych kulturowych. Henneberg (1976) zwraca tu uwagę, między innymi, na nakłady energetyczne, jakie trzeba ponieść na pokonanie odległości między osadami, by mieć szansę na poznanie potencjalnego życiowego partnera. Dla określenia i analizy takich specyficznych kontaktów Boyce wprowadził koncepcję tzw. znajomości sąsiedzkiej (neighbourhood knowledge). Chodzi tu także o ponoszone koszty ekonomiczne wynikające z sieci dróg, dostępności środków transportu itp. Nie mniej ważne są ludzkie wierzenia i bariery wyznaniowe a także preferowany na danym terenie i w danej grupie ludzkiej system kojarzeń małżeńskich (Henneberg 1976). System kojarzeń małżeńskich jest przejawem działalności kulturowej o decydującym znaczeniu dla wewnątrzi międzygrupowej wymiany genów. Jego analiza pozwala wnioskować o stanie i zachodzących w czasie przemianach pul genowych populacji. Jednymi z elementów systemu kojarzeń małżeńskich są endo- i egzogamia. Współczynniki endo- i egzogamii dostarczają informacji o przestrzennej strukturze zawierania małżeństw. Przypomnijmy, że pojęcie endogamii oznacza, najogólniej rzecz ujmując, kojarzenie się w obrębie tej samej grupy, egzogamii zawieranie małżeństw pomiędzy członkami różnych grup. Współczynniki endo- i egzogamii pozwalają na ocenę stopnia izolacji genetycznej grup ludzkich a jako elementy składowe współczynników wsobności i spokrewnienia wewnątrzgrupowego stanowią zarówno źródło informacji kulturowej, jak i genetycznej (Budnik 2005a). Ryc. 2. Dwuwymiarowy model wymiany genów. B badana miejscowość, 1,2 miejscowości, z których napływają geny, m natężenie migracji. Strzałki wskazują kierunek przepływu genów. Dalsze objaśnienia w tekście. Źródło: opracowanie własne na podstawie Cavalli-Sforza i Bodimer 1971; Henneberg 1979; Malinowski i Strzałko 1985
5 Możliwości odtwarzania struktury genetycznej populacji na podstawie źródeł 65 Dobre modele określające sposób wymiany genów wynikający z systemu kojarzeń małżeńskich zaproponował M. Henneberg (1976, 1977, 1979). Określają one prawdopodobieństwo zawarcia związku małżeńskiego pomiędzy osobą z danego osiedla z partnerem z innego osiedla, łączą w sobie przy tym informacje zarówno o odległościach geograficznych, jak i kulturowych. Prawdopodobieństwo to zależy od natężenia egzogamii (m), sposobu rozmieszczenia osiedli w przestrzeni (N c ) oraz od tzw. rzędu sąsiedztwa (ON). Rząd sąsiedztwa jest miarą sposobności do kontaktów między mieszkańcami różnych osiedli. W najprostszej sytuacji, przy braku barier izolacyjnych, jedynymi czynnikami określającymi wielkość rzędu sąsiedztwa ON będą odległość geograficzna i rozmieszczenie osiedli. Dla grup ludności zamieszkujących miejscowości położone bezpośrednio obok siebie, rząd sąsiedztwa równy będzie jedności, gdy rozdziela je jedna miejscowość, ON = 2 itd. Rozkład prawdopodobieństw zawierania małżeństw przez osoby pochodzące z różnych odległości ON odbija wtedy rozkład odległości geograficznych. Pojawienie się jakichkolwiek barier geograficznych lub kulturowych zaburza ten obraz mogą pojawić się utrudnienia w kontaktach nawet między osobami z miejscowości położonych bardzo blisko siebie. W takiej sytuacji odległość między nimi można określić jako rząd sąsiedztwa dalszy, niżby to wynikało z prostej odległości geograficznej. Możliwa jest oczywiście także sytuacja odwrotna. Rząd sąsiedztwa jest czymś więcej, niż odległość geograficzna jest odległością ekologiczno-kulturową. Podstawowa, wyjściowa wersja modelu Henneberga (1979) ma postać następującą: P ON ON 2 ON exp 1 Ncm 1 2 ON exp N m c Wyrażenie P ON w tym równaniu oznacza prawdopodobieństwo zawarcia małżeństwa z partnerem z odległości ON, ON to rząd sąsiedztwa, N c oznacza liczbę osiedli w odległości ON, m jest współczynnikiem egzogamii, natomiast α to rząd sąsiedztwa, w którym sumowane wyrażenie równa się praktycznie zeru. Ten wyjściowy model można modyfikować przystosowując go do różnych sytuacji badawczych. Gdy migracja odbywa się równomiernie we wszystkich kierunkach na płaszczyźnie, gdzie osiedla ludzkie rozmieszczone są mniej więcej w równej odległości, mówimy o izotropii dwuwymiarowej (2DIM). Powyższe równanie przybierze wówczas poniższą postać (Henneberg 1979): P ON ON ON exp 1 2m 1 ON exp 2m
6 66 ALICJA BUDNIK Jest to sytuacja, która występuje najczęściej. Może się jednak zdarzyć, że z jednej strony pojawi się znaczna bariera izolująca, która sprawi, że partnerzy będą napływać do badanej miejscowości z obszaru pomiędzy ramionami kąta 180 z półpłaszczyzny. Mówimy o izotropii 1,5-wymiarowej (1,5 DIM). Taka sytuacja wystąpiła, przykładowo, w miejscowościach Półwyspu Helskiego, gdzie od północy barierę stanowiło Morze Bałtyckie. Prawdopodobieństwo zawarcia małżeństwa przez osoby pochodzące z danej odległości ON obliczyć można wtedy ze wzoru (Henneberg 1979): P ON ON ON exp 1 m 1 ON exp m Wreszcie, w przypadku izotropii jednowymiarowej (1 DIM), gdy osiedla położone są w jednej linii, na przykład wzdłuż kotliny górskiej, koryta rzeki itp., równanie to uzyska jeszcze bardziej uproszczoną formę (Henneberg 1979): P ON ON1 2 ON exp 2m 1 ON exp 2m 2 Zauważmy, że w każdej z trzech omówionych powyżej sytuacji równania mają tylko jeden parametr wartość współczynnika egzogamii m. Zalety modeli zaproponowanych przez Henneberga pokażemy na przykładzie historycznych populacji kaszubskich z Jastarni i Kuźnicy na Półwyspie Hel. Niezbędne informacje o małżeństwach, w tym o miejscach urodzenia współmałżonków, pozyskano z urzędowych, prowadzonych w gotyku niemieckim, ksiąg małżeństw za lata , zdeponowanych w Urzędzie Stanu Cywilnego w Jastarni oraz w Państwowym Archiwum w Gdańsku. Badaniami objęto 401 małżeństw. Były to wszystkie małżeństwa zawarte we wspomnianym wyżej okresie (Budnik 2005a, 2005b). Ze względu na specyfikę grup kaszubskich oraz położenie Półwyspu Helskiego bardzo trudno było dopasować rzeczywisty rozkład odległości małżeńskich do jakiejkolwiek sytuacji modelowej. Ponieważ od północy Bałtyk stanowił barierę izolacyjną dla osad półwyspu, zastosowano dla nich model kojarzenia pomiędzy ramionami kąta 180. Gdy w równaniu Henneberga jednostki ON potraktowano wyłącznie jako jednostki odległości geograficznych między miejscami urodzenia współmałżonków, teoretyczne i empiryczne rozkłady prawdopodobieństw zawarcia małżeństwa między osobami z tak potraktowanych odległości ON różniły się zasadniczo (χ 2 = 58,04; p < 0,001; ryc. 3; Budnik 2005a). Okazało się, że ani Półwysep Helski, ani inne tereny, z którymi Kaszubi wymieniali partnerów nie tylko nie wykazywały homogeniczności geograficznej, ale brakowało tam także homogeniczności kulturowej. Osiedla rozrzucone
7 Możliwości odtwarzania struktury genetycznej populacji na podstawie źródeł 67 Ryc. 3. Rozkład odległości małżeńskich w populacjach kaszubskich z Jastarni i Kuźnicy w latach dla izotropii 1,5-wymiarowej; odległości geograficzne (χ 2 = 58,04; p < 0,001). Źródło: Budnik 2005a były w terenie nierównomiernie, różniły się także wielkością, składem narodowościowym i etnicznym mieszkańców, używanym przez nich językiem, nazwiskami i wyznawaną religią a ponadto częstością kontaktów. Dochodziła do tego dwojaka rola wody w Zatoce Puckiej, która z jednej strony stanowiła czynnik izolujący, z drugiej jednak stawała się stosunkowo łatwą drogą transportu. Zwłaszcza latem przepływano Zatokę bardzo często w drodze do Gdańska, zimą te wyprawy były z oczywistych powodów rzadsze, ale i tak odbywały się przynajmniej co dwa tygodnie. Na początku XX wieku podróże te znacznie ułatwiła komunikacja parowcowa (Gołębiewski 1975; Budnik 2005a). Dopiero uwzględnienie wszystkich tych czynników i potraktowanie jednostek odległości ON szerzej, jako odległości ekologiczno-kulturowych pozwoliło znaleźć model napływu genów do badanych miejscowości. Uzyskano doskonałą zgodność stworzonego w ten sposób rozkładu ekologiczno-kulturowych odległości małżeńskich z modelowym rozkładem dla izotropii 1,5-wymiarowej (ryc. 4; Budnik 2005a). Typ rozkładu odległości pomiędzy miejscami urodzenia współmałżonków decyduje o sposobie przepływu genów w przestrzeni i o stanie puli genowej w badanych populacjach. W zależności od natężenia i przestrzennego rozkładu migracji małżeńskich różną formę będą przybierały wewnątrzgrupowe współczynniki spokrewnienia f. Współczynniki te można oceniać za pomocą
8 68 ALICJA BUDNIK Ryc. 4. Rozkład odległości małżeńskich w populacjach kaszubskich z Jastarni i Kuźnicy w latach dla izotropii 1,5-wymiarowej; odległości ekologiczno-kulturowe (χ 2 = 3,23). Źródło: Budnik 2005a klasycznych równań Malécot a (Cavalli-Sforza i Bodmer 1971) oraz wyprowadzonych z nich równań Henneberga (1978; 1979). Według Malécot a (Cavalli-Sforza i Bodmer 1971) mają one następującą postać: (1) Dla migracji 2-wymiarowej f = [1 + 8πδσ 2 ( 1/ln2b)] 1, gdzie δ to gęstość zaludnienia osobami zdolnymi do rozrodu, 2σ 2 tzw. średni kwadrat odległości małżeńskich, zaś b oznacza poprawkę na działanie liniowych nacisków stabilizujących pulę genów, co w praktyce sprowadza się do natężenia mutacji stwierdzanych u człowieka (przyjęto b = ). (2) Dla migracji 1,5-wymiarowej równanie Malécot a trzeba było przekształcić do postaci przedstawionej poniżej (Budnik i Przybyszewska 1991) f = [1 + 2πδσ 2 ( 1/ln2b)] 1, oznaczenia jak wyżej. (3) Dla migracji 1-wymiarowej (Cavalli-Sforza i Bodmer 1971) f = [1 + 4δσ 2 b ] 1.
9 Możliwości odtwarzania struktury genetycznej populacji na podstawie źródeł 69 Według Henneberga (1979) odpowiednie formuły są następujące: (1) Dla migracji 2-wymiarowej (2) Dla migracji 1,5-wymiarowej (3) Dla migracji 1-wymiarowej f = [1 + 32π 3 m 3 N b ( 1/ln2b)] 1. f = [1 + 8π 3 m 3 N b ( 1/ln2b)] 1. f = [1 + 4mN b 2 b ] 1. Wyrażenie N b w równaniach oznacza tzw. efektywną wielkość populacji, czyli w uproszczeniu liczbę osób zdolnych do kojarzeń i uczestniczenia w rozrodzie; m to współczynnik egzogamii; pozostałe wyrażenia są takie same, jak w równaniach Malécot a. Dla omawianych już wcześniej populacji kaszubskich z Półwyspu Helskiego obliczono wartości współczynników wewnątrzgrupowego spokrewnienia f dla migracji 1,5-wymiarowej, pomiędzy ramionami kąta 180. Wartości f oszacowane metodą Malécot a przedstawia tabela 1 (Budnik 2005a). Tabela 1. Współczynniki spokrewnienia wewnątrzgrupowego f oszacowane metodą Malécot a dla historycznych populacji kaszubskich z przeciętnej osady Półwyspu Helskiego Okres 2σ 2 f a 0, b 0, a 0, b 0,0004 Współcześnie , a Wszystkie pary b Bez kilku par z bardzo dużych odległości (głównie z USA) Źródło: Budnik 2005a Jak widać, szacunki współczynnika f, zwłaszcza dla populacji historycznych, są tu nieprawdopodobnie niskie, znacznie niższe niż dla grup współczesnych. Jedną ze składowych równania Malécot a jest wariancja odległości pomiędzy miejscami urodzenia małżonków, określana jako średni kwadrat odległości. Obecność nawet niewielkiej liczby par pochodzących z dużych odległości natychmiast bardzo mocno podnosi tę wariancję, czego konsekwencją jest
10 70 ALICJA BUDNIK wydatne obniżenie wartości f. Właśnie taka sytuacja miała miejsce wśród Kaszubów helskich. Spadek wartości współczynnika spokrewnienia wewnątrzgrupowego spowodowało tam zaledwie kilka par, w których jedno ze współmałżonków urodziło się w USA. Ów spadek pozornie tylko świadczy o zmniejszeniu się spokrewnienia wewnątrzgrupowego, w rzeczywistości bowiem pary te miały kaszubskie pochodzenie, na kontynencie amerykańskim kojarzyły się we własnym, hermetycznym kręgu i w końcu na Półwysep Helski wróciły (Budnik 2005a). Usunięcie tych par z materiału spowodowało gwałtowne zmniejszenie się wariancji odległości małżeńskich i kilkutysięczny (!) wzrost wartości f (tabela1). Współczynniki f oszacowane metodą Henneberga wolne są od tych niedogodności i dały o wiele wyższe wartości (tabela 2). Bardzo niskie wartości współczynników egzogamii m, które wchodzą w zakres tych formuł, także wskazują na kojarzenie się w bardzo wąskim kręgu. Popierają one wartości f Henneberga a kłócą się z wartościami f uzyskanymi z równania Malécot a. Tabela 2. Współczynniki spokrewnienia wewnątrzgrupowego f oszacowane metodą Henneberga dla historycznych populacji kaszubskich z przeciętnej osady Półwyspu Helskiego Źródło: Budnik 2005a Okres N b m f ,24 0, ,313 0,007 Współcześnie 830 0,621 0,0005 Równania Henneberga mają inną trudność jest nią konieczność oszacowania efektywnej wielkości populacji (N b ). Oszacowania N b są zawsze trudne. Opierają się one na założeniach idealizacyjnych praktycznie niemożliwych do spełnienia u człowieka, jak niezachodzenie na siebie kolejnych pokoleń, niezmienność liczby osób tworzących te pokolenia, czy wydawanie na świat przez każdą osobę z populacji tej samej liczby potomstwa (Cavalli-Sforza i Bodmer 1971; Henneberg 1978; Jorde 1980). Jest wiele sposobów szacowania efektywnej wielkości populacji (przegląd np. w pracy A. Budnik 2005a). Tu odtworzono ją jako 1/3 średniej harmonicznej liczb ludności. Ryciny 5 i 6 pokazują inne przykłady populacji, dla których obliczono wartości współczynnika egzogamii i współczynnika spokrewnienia wewnątrzgrupowego metodą Henneberga. Tym razem spełnione były wymogi dla izotropii dwuwymiarowej i takich równań użyto. Jak widać, ludność XIX -wiecznej rzymsko-katolickiej parafii Dziekanowice z mikroregionu Ostrowa Lednickiego już przed wprowadzeniem reformy uwłaszczenia chłopów charakteryzowała się najwyższą wartością współczynnika egzogamii i najniższą
11 Możliwości odtwarzania struktury genetycznej populacji na podstawie źródeł 71 współczynnika spokrewnienia wewnątrzgrupowego. Była to nowoczesna, otwarta populacja o ciekawej, sięgającej czasów średniowiecza historii, w której izolacja złamana została bardzo dawno temu (Budnik i in. 2004). Inna wielkopolska parafia, Szczepanowo (Henneberg 1977), miała współczynniki egzogamii niemal dwukrotnie niższe a współczynniki f wyższe niż Dziekanowice. Najmniej korzystnie przedstawiała się uboga galicyjska parafia Wielkie Drogi z zaboru austriackiego (Puch 1993), gdzie egzogamia była ponad dwukrotnie niższa a spokrewnienie wewnątrzgrupowe ponad sześciokrotnie wyższe niż w parafii Dziekanowice. Po reformie uwłaszczeniowej wszystkie wartości m wydatnie Ryc. 5. Wartości współczynnika egzogamii m w wybranych parafiach wiejskich z XIX wieku. Źródło: Budnik i in (1); Henneberg 1977 (2); Puch 1993 (3) Ryc. 6. Wartości współczynnika spokrewnienia wewnątrzgrupowego f w wybranych parafiach wiejskich z XIX wieku. Źródło: Budnik i in (1); Henneberg 1977 (2); Puch 1993 (3)
12 72 ALICJA BUDNIK wzrosły a f zmalały, choć różnice między parafiami utrzymywały się nadal (ryc. 5 i 6). Widać więc, jak ważne wydarzenia o charakterze gospodarczym i społecznym odbijały się w omawianych miernikach. Wszystkie powyższe przykłady pokazują, że strukturę genetyczną populacji z powodzeniem odtwarzać można na podstawie macierzy migracji małżeńskich i odległości między miejscami urodzeń współmałżonków. Można do tego celu wykorzystać również częstości nazwisk wśród małżonków, uwzględniając częstość par izonimicznych, czyli takich gdzie małżonkowie już przed ślubem nosili to samo nazwisko. Idea użycia danych o małżeństwach pomiędzy osobami nazywającymi się przed ślubem tak samo, jako źródła informacji genetycznej nie jest nowa i sięga 1875 roku, kiedy to G. H. Darwin, syn słynnego Karola Darwina, opublikował w Dziennikach Towarzystwa Statystycznego artykuł o konsekwencjach zawierania małżeństw pomiędzy kuzynami I stopnia w Anglii. Jednak dopiero 90 lat później Crow i Mange (1965), a po nich i inni, sformułowali zasady szacowania współczynników wsobności w oparciu o analizę izonimii. W literaturze przedmiotu często podkreśla się, że w naszym kręgu cywilizacyjnym, gdzie dziedziczenie nazwisk jest patrylinearne, nazwiska zachowują się jak geny sprzężone z chromosomem Y (np. Jobling 2001; Graf i in. 2010; Boattini i in. 2011). Metoda izonomii doczekała się też uwag krytycznych (np. Rogers 1991; Mielke i Swedlund 1993). Mimo to nadal stanowi ona jeden z najwygodniejszych sposobów estymacji inbredu. Crow i Mange (1965) wyróżnili dwa komponenty składające się na wartość współczynnika wsobności F szacowanego z nazwisk część wynikającą z losowego kojarzenia się małżeństw (F r ) oraz część wynikającą z kojarzenia nielosowego (F n ). Klasyczne równania przedstawiają się następująco: F = F n + (1 F n )F r, F n = (P Σp i q i )/4(1 Σp i q i ), Fr = Σp i q i /4, gdzie: F oznacza współczynnik wsobności całkowitej; F n współczynnik wsobności wynikający z nielosowego kojarzenia się małżeństw; F r współczynnik wsobności wynikający z losowego kojarzenia się małżeństw; p i częstość danego nazwiska u żon; q i częstość danego nazwiska u mężów oraz P częstość par izonimicznych. W przypadku braku istotnych różnic w częstościach nazwisk żon i mężów wyrażenie Σp i q i można zastąpić przez Σx i gdzie x i oznacza częstość danego nazwiska w obu grupach małżonków łącznie. Najczęściej powtarzające się nazwiska w historycznych populacjach kaszubskich w Jastarni i Kuźnicy przedstawiono w tabeli 3. W Jastarni 6 nazwisk
13 Możliwości odtwarzania struktury genetycznej populacji na podstawie źródeł 73 wyczerpuje ponad 50% całkowitej zmienności, 15 nazwisk 75%. W Kuźnicy ponad połowę zmienności wyczerpują tylko dwa nazwiska a ¾ zmienności zaledwie 6 nazwisk. Tabela 3. Najczęściej spotykane nazwiska w osadach kaszubskich z Półwyspu Helskiego w latach Jastarnia Kuźnica Nazwisko % Nazwisko % Konkel 20 Budzisz 34,6 Kohnke 9,7 Konkel 19,1 Muża 7,3 Muża 8,4 Herrmann 6,8 Dettlaff 7,5 Selin 4,8 Nimoth 4,4 Barlasch 3,5 Struck 4 Źródło: opracowanie własne Tabela 4 zawiera wartości współczynników wsobności F i frakcje małżeństw izonimicznych P w populacjach z Jastarni i Kuźnicy oraz innych wybranych populacji polskich. Tabela 4. Wartości współczynników wsobności F i frakcje małżeństw izonimicznych P w wybranych populacjach polskich Populacja XIX i początki XX wieku Współcześnie F P F P Jastarnia 0,016 0,064 0,009 0,035 Kuźnica 0,044 0,17 0,04 0,156 Kartuskie 0,003 0,012 0,005 0,019 Tatarzy 0,017 0,063 Wielkopolska 0,001 0,004 0,0005 0,002 Źródło: opracowanie własne Jak widać, w populacjach kaszubskich z Półwyspu Helskiego a także we współczesnych grupach Tatarów polskich wartości współczynnika f są podwyższone w porównaniu z innymi populacjami. Szczególnie duże wartości inbredu oraz częstości par izonimicznych wystąpiły w Kuźnicy i ta sytuacja nie zmieniła się do dziś. Populacja kuźnicka prezentuje ponadto podwyższony poziom współczynnika F n. Wynika on najprawdopodobniej z wybiórczego, pozytywnego kojarzenia się par małżeńskich ze względu na rozpoznawalny społecznie stopień pokrewieństwa, jaki odzwierciedla tu wspólne nazwisko (ryc. 7 i 8).
14 74 ALICJA BUDNIK Ryc. 7. Wartości współczynników wsobności F oszacowane metodą izonimii małżeńskiej w historycznych populacjach kaszubskich i w Wielkopolsce. Źródło: opracowanie własne Ryc. 8. Wartości współczynników wsobności F oszacowane metodą izonimii małżeńskiej we współczesnych populacjach kaszubskich i w Wielkopolsce. Źródło: opracowanie własne BIBLIOGRAFIA Malinowski A., Strzałko J. (red.) Antropologia. Warszawa-Poznań: Państwowe Wydawnictwo Naukowe. Boattini A., Luiselli D., Sazzini M., Useli A., Tagarelli G., Petlener D Linking Italy and the Balkans. A Y-chromosome perspective from the Arbereshe of Calabria. Annals of Human Biology, 38(1):
15 Możliwości odtwarzania struktury genetycznej populacji na podstawie źródeł 75 Budnik A Genetic structure of historical and contemporary Kashubian Populations in Poland. [in:] Susanne C.H., Bodzsár E.B. (red.) Human Population Genetics in Europe. Budapest: Eőtvős University Press, pp Budnik A. 2005a. Uwarunkowania stanu i dynamiki biologicznej populacji kaszubskich w Polsce. Studium antropologiczne. Poznań: Wydawnictwo Naukowe UAM. Budnik A. 2005b. System kojarzeń małżeńskich w historycznych i współczesnych populacjach kaszubskich z Jastarni i Kuźnicy. Ocena stopnia izolacji genetycznej. Słupskie Prace Biologiczne, 1: Budnik A., Przybyszewska M Genetic description of the population of Wielkie Drogi village a specific case of mating distances distribution. Variability and Evolution, 1: Budnik A., Liczbińska G., Gumna I Demographic Trends and Biological Status of Historic Populations from Central Poland: The Ostrów Lednicki Microregion. American Journal of Physical Anthropology, 125: Cavalli-Sforza L.L., Bodmer W.F The Genetics of Human Populations. San Francisco: W.H. Freeman. Crow J.F., Mange A.P Measurement of inbreeding from the frequency of marriages between persons of the same surname. Eugenics Quarterly, 12: Darwin G. H., 1875, Marriages between first cousins in England and their effects. Journal of the Statistical Society of London, 38: Eriksson A.W., Fellman J. O, Workman P. L., Lalouel J. M Population studies on the Åland Islands. I. Prediction of kinship from migration and isolation by distance. Human Heredity, 23: Gołębiewski H Obrazki rybackie. Drugie wydanie na podstawie pierwodruku z 1888 roku. Gdańsk: Zrzeszenie Kaszubsko-Pomorskie, Oddział Miejski w Gdańsku. Graf O.M., Zlojutro M., Rubicz R., Crawford M Surname Distributions and Their Association with Y-Chromosome Markers in the Aleutian Islands. Human Biology, 82, 5 6: Henneberg M Izolacja grup ludzkich przez odległość. Model rozkładu odległości małżeńskich. [w:] Badania populacji ludzkich na materiałach współczesnych i historycznych. Poznań: Wydawnictwo Naukowe UAM, s Henneberg M Ocena dynamiki biologicznej wielkopolskiej dziewiętnastowiecznej populacji wiejskiej. II. System kojarzeń i płodność. Przegląd Antropologiczny, 43(2): Henneberg M Ocena dynamiki biologicznej wielkopolskiej dziewiętnastowiecznej populacji wiejskiej. III. Opis stanu puli genów na podstawie danych demograficznych. Przegląd Antropologiczny, 44(1): Henneberg M Breeding isolation between populations; theoretical model of mating distances distribution. Studies in Physical Anthropology, 5: Jobling M.A In the name of the father: Surnames and genetics. Trends in Genetics, 17(6): Jorde L.B The genetic structure of subdivided human populations. [in:] Mielke J.H, Crawford M.H. (eds.) Current Developments in Anthropological Genetics, vol. I, Theory and Methods, 1: Mielke J.H., Swedlund A.C Historical demography and population structure. [in:] Lasker G.W., Mascie-Taylor C.G.N. (eds.) Research strategies in human biology: field and survey studies. Cambridge: Cambridge University Press, pp Morton M.E Estimation of Demographic Parameters from Isolation by Distance. Human Heredity, 32:
16 76 ALICJA BUDNIK Puch E.A Dynamika biologiczna polskich społeczności wiejskich z różnych systemów ekologiczno-kulturowych w XVIII i XIX wieku. Przegląd Antropologiczny, 56(1 2): Rogers A.R Doubts about Isonymy. Human Biology, 63(5): Rudan I., Rudan P., Chaventre A., Janiájević B., Miličić J., Smolej-Narančić N., Sujoldžić A Model-bound and model-free approach in the holistic analysis of population structure: Example from the island of Pag. Croatia. Homo Journal of Comparative Human Biology, 49(2): Smith M. T., Sherren S. J The one-dimensional stepping-stone model of migration: An application to British coastal populations. Collegium Anthropologicum, 13(1): Sujoldžić A The Population Structure of the Island of Brač A Demographic and Migrational Analysis. Collegium Anthropologicum, 12(2): Sujoldžić A., Jovanović V., Angel J. L., Bennett L. A., Roberts D. F., Rudan P Migration within the island of Korcula, Yugoslavia. Annals of Human Biology, 16(6):
SYSTEM KOJARZEŃ MAŁŻEŃSKICH W HISTORYCZNYCH I WSPÓŁCZESNYCH POPULACJACH KASZUBSKICH Z JASTARNI I KUŹNICY. OCENA STOPNIA IZOLACJI GENETYCZNEJ
 S ł u p s k i e P r a c e B i o l o g i c z n e 1 2005 Alicja Budnik Uniwersytet im. Adama Mickiewicza, Poznań SYSTEM KOJARZEŃ MAŁŻEŃSKICH W HISTORYCZNYCH I WSPÓŁCZESNYCH POPULACJACH KASZUBSKICH Z JASTARNI
S ł u p s k i e P r a c e B i o l o g i c z n e 1 2005 Alicja Budnik Uniwersytet im. Adama Mickiewicza, Poznań SYSTEM KOJARZEŃ MAŁŻEŃSKICH W HISTORYCZNYCH I WSPÓŁCZESNYCH POPULACJACH KASZUBSKICH Z JASTARNI
PORÓWNYWANIE POPULACJI POD WZGLĘDEM STRUKTURY
 PORÓWNYWANIE POPULACJI POD WZGLĘDEM STRUKTURY obliczanie dystansu dzielącego grupy (subpopulacje) wyrażonego za pomocą indeksu F Wrighta (fixation index) w modelu jednego locus 1 Ćwiczenia III Mgr Kaczmarek-Okrój
PORÓWNYWANIE POPULACJI POD WZGLĘDEM STRUKTURY obliczanie dystansu dzielącego grupy (subpopulacje) wyrażonego za pomocą indeksu F Wrighta (fixation index) w modelu jednego locus 1 Ćwiczenia III Mgr Kaczmarek-Okrój
GENETYKA POPULACJI. Ćwiczenia 3 Biologia I MGR
 GENETYKA POPULACJI Ćwiczenia 3 Biologia I MGR Heterozygotyczność Rozpatrując różnorodność genetyczną w populacjach o układzie hierarchicznym zauważamy, że najwyższy poziom heterozygotyczności zawsze występuje
GENETYKA POPULACJI Ćwiczenia 3 Biologia I MGR Heterozygotyczność Rozpatrując różnorodność genetyczną w populacjach o układzie hierarchicznym zauważamy, że najwyższy poziom heterozygotyczności zawsze występuje
Genetyka populacji. Ćwiczenia 7
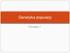 Genetyka populacji Ćwiczenia 7 Rodowody wraz z wynikami kontroli użytkowości stanowią podstawową informację potrzebną do doskonalenia zwierząt C F X S D C F C F S D strzałka oznacza przepływ genów między
Genetyka populacji Ćwiczenia 7 Rodowody wraz z wynikami kontroli użytkowości stanowią podstawową informację potrzebną do doskonalenia zwierząt C F X S D C F C F S D strzałka oznacza przepływ genów między
GENETYKA POPULACJI. Ćwiczenia 1 Biologia I MGR /
 GENETYKA POPULACJI Ćwiczenia 1 Biologia I MGR 1 ZAGADNIENIA struktura genetyczna populacji obliczanie frekwencji genotypów obliczanie frekwencji alleli przewidywanie struktury następnego pokolenia przy
GENETYKA POPULACJI Ćwiczenia 1 Biologia I MGR 1 ZAGADNIENIA struktura genetyczna populacji obliczanie frekwencji genotypów obliczanie frekwencji alleli przewidywanie struktury następnego pokolenia przy
ZARZĄDZANIE POPULACJAMI ZWIERZĄT
 ZARZĄDZANIE POPULACJAMI ZWIERZĄT Ćwiczenia 1 mgr Magda Kaczmarek-Okrój magda_kaczmarek_okroj@sggw.pl 1 ZAGADNIENIA struktura genetyczna populacji obliczanie frekwencji genotypów obliczanie frekwencji alleli
ZARZĄDZANIE POPULACJAMI ZWIERZĄT Ćwiczenia 1 mgr Magda Kaczmarek-Okrój magda_kaczmarek_okroj@sggw.pl 1 ZAGADNIENIA struktura genetyczna populacji obliczanie frekwencji genotypów obliczanie frekwencji alleli
ZARZĄDZANIE POPULACJAMI ZWIERZĄT SPOKREWNIENIE INBRED
 ZARZĄDZANIE POPULACJAMI ZWIERZĄT SPOKREWNIENIE INBRED Rodowody wraz z wynikami kontroli użytkowości stanowią podstawową informację potrzebną do doskonalenia zwierząt X S D C F C F C S D F strzałka oznacza
ZARZĄDZANIE POPULACJAMI ZWIERZĄT SPOKREWNIENIE INBRED Rodowody wraz z wynikami kontroli użytkowości stanowią podstawową informację potrzebną do doskonalenia zwierząt X S D C F C F C S D F strzałka oznacza
Spokrewnienie prawdopodobieństwo, że dwa losowe geny od dwóch osobników są genami IBD. IBD = identical by descent, geny identycznego pochodzenia
 prawdopodobieństwo, że dwa losowe geny od dwóch osobników są genami ID. Relationship Relatedness Kinship Fraternity ID = identical by descent, geny identycznego pochodzenia jest miarą względną. Przyjmuje
prawdopodobieństwo, że dwa losowe geny od dwóch osobników są genami ID. Relationship Relatedness Kinship Fraternity ID = identical by descent, geny identycznego pochodzenia jest miarą względną. Przyjmuje
Ekologia molekularna. wykład 4
 Ekologia molekularna wykład 4 Zróżnicowanie między populacjami Przyczyny odchyleń od HWE Czynniki demograficzne nielosowe kojarzenie wsobność (inbred) struktura genetyczna populacji (subpopulacje) migracje
Ekologia molekularna wykład 4 Zróżnicowanie między populacjami Przyczyny odchyleń od HWE Czynniki demograficzne nielosowe kojarzenie wsobność (inbred) struktura genetyczna populacji (subpopulacje) migracje
Selekcja, dobór hodowlany. ESPZiWP
 Selekcja, dobór hodowlany ESPZiWP Celem pracy hodowlanej jest genetyczne doskonalenie zwierząt w wyznaczonym kierunku. Trudno jest doskonalić zwierzęta już urodzone, ale można doskonalić populację w ten
Selekcja, dobór hodowlany ESPZiWP Celem pracy hodowlanej jest genetyczne doskonalenie zwierząt w wyznaczonym kierunku. Trudno jest doskonalić zwierzęta już urodzone, ale można doskonalić populację w ten
Ewolucjonizm NEODARWINIZM. Dr Jacek Francikowski Uniwersyteckie Towarzystwo Naukowe Uniwersytet Śląski w Katowicach
 Ewolucjonizm NEODARWINIZM Dr Jacek Francikowski Uniwersyteckie Towarzystwo Naukowe Uniwersytet Śląski w Katowicach Główne paradygmaty biologii Wspólne początki życia Komórka jako podstawowo jednostka funkcjonalna
Ewolucjonizm NEODARWINIZM Dr Jacek Francikowski Uniwersyteckie Towarzystwo Naukowe Uniwersytet Śląski w Katowicach Główne paradygmaty biologii Wspólne początki życia Komórka jako podstawowo jednostka funkcjonalna
2. CZYNNIKI ZABURZAJĄCE RÓWNOWAGĘ GENETYCZNĄ
 ZARZĄDZANIE POPULACJAMI ZWIERZĄT 2. CZYNNIKI ZABURZAJĄCE RÓWNOWAGĘ GENETYCZNĄ POPULACJI Fot. W. Wołkow Prowadzący: dr Wioleta Drobik Katedra Genetyki i Ogólnej Hodowli Zwierząt MIGRACJE Zmiana frekwencji
ZARZĄDZANIE POPULACJAMI ZWIERZĄT 2. CZYNNIKI ZABURZAJĄCE RÓWNOWAGĘ GENETYCZNĄ POPULACJI Fot. W. Wołkow Prowadzący: dr Wioleta Drobik Katedra Genetyki i Ogólnej Hodowli Zwierząt MIGRACJE Zmiana frekwencji
ZARZĄDZANIE POPULACJAMI ZWIERZĄT 1. RÓWNOWAGA GENETYCZNA POPULACJI. Prowadzący: dr Wioleta Drobik Katedra Genetyki i Ogólnej Hodowli Zwierząt
 ZARZĄDZANIE POPULACJAMI ZWIERZĄT 1. RÓWNOWAGA GENETYCZNA POPULACJI Fot. W. Wołkow Prowadzący: dr Wioleta Drobik Katedra Genetyki i Ogólnej Hodowli Zwierząt POPULACJA Zbiór organizmów żywych, które łączy
ZARZĄDZANIE POPULACJAMI ZWIERZĄT 1. RÓWNOWAGA GENETYCZNA POPULACJI Fot. W. Wołkow Prowadzący: dr Wioleta Drobik Katedra Genetyki i Ogólnej Hodowli Zwierząt POPULACJA Zbiór organizmów żywych, które łączy
ZARZĄDZANIE POPULACJAMI ZWIERZĄT DRYF GENETYCZNY EFEKTYWNA WIELKOŚĆ POPULACJI PRZYROST INBREDU
 ZARZĄDZANIE POPULACJAMI ZWIERZĄT DRYF GENETYCZNY EFEKTYWNA WIELKOŚĆ POPULACJI PRZYROST INBREDU DRYF GENETYCZNY ) Każdy żywy organizm wytwarza więcej gamet, niż zdolne jest przetrwać (Darwin). 2) Przypadek
ZARZĄDZANIE POPULACJAMI ZWIERZĄT DRYF GENETYCZNY EFEKTYWNA WIELKOŚĆ POPULACJI PRZYROST INBREDU DRYF GENETYCZNY ) Każdy żywy organizm wytwarza więcej gamet, niż zdolne jest przetrwać (Darwin). 2) Przypadek
Statystyka w pracy badawczej nauczyciela Wykład 4: Analiza współzależności. dr inż. Walery Susłow walery.suslow@ie.tu.koszalin.pl
 Statystyka w pracy badawczej nauczyciela Wykład 4: Analiza współzależności dr inż. Walery Susłow walery.suslow@ie.tu.koszalin.pl Statystyczna teoria korelacji i regresji (1) Jest to dział statystyki zajmujący
Statystyka w pracy badawczej nauczyciela Wykład 4: Analiza współzależności dr inż. Walery Susłow walery.suslow@ie.tu.koszalin.pl Statystyczna teoria korelacji i regresji (1) Jest to dział statystyki zajmujący
Pokrewieństwo, rodowód, chów wsobny
 Pokrewieństwo, rodowód, chów wsobny Pokrewieństwo Pokrewieństwo, z punktu widzenia genetyki, jest podobieństwem genetycznym. Im osobniki są bliżej spokrewnione, tym bardziej są podobne pod względem genetycznym.
Pokrewieństwo, rodowód, chów wsobny Pokrewieństwo Pokrewieństwo, z punktu widzenia genetyki, jest podobieństwem genetycznym. Im osobniki są bliżej spokrewnione, tym bardziej są podobne pod względem genetycznym.
Wprowadzenie do analizy korelacji i regresji
 Statystyka dla jakości produktów i usług Six sigma i inne strategie Wprowadzenie do analizy korelacji i regresji StatSoft Polska Wybrane zagadnienia analizy korelacji Przy analizie zjawisk i procesów stanowiących
Statystyka dla jakości produktów i usług Six sigma i inne strategie Wprowadzenie do analizy korelacji i regresji StatSoft Polska Wybrane zagadnienia analizy korelacji Przy analizie zjawisk i procesów stanowiących
Statystyka matematyczna dla leśników
 Statystyka matematyczna dla leśników Wydział Leśny Kierunek leśnictwo Studia Stacjonarne I Stopnia Rok akademicki 03/04 Wykład 5 Testy statystyczne Ogólne zasady testowania hipotez statystycznych, rodzaje
Statystyka matematyczna dla leśników Wydział Leśny Kierunek leśnictwo Studia Stacjonarne I Stopnia Rok akademicki 03/04 Wykład 5 Testy statystyczne Ogólne zasady testowania hipotez statystycznych, rodzaje
Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć)
 Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć) 1. Populacja generalna a losowa próba, parametr rozkładu cechy a jego ocena z losowej próby, miary opisu statystycznego
Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć) 1. Populacja generalna a losowa próba, parametr rozkładu cechy a jego ocena z losowej próby, miary opisu statystycznego
GENETYKA POPULACJI. Ćwiczenia 4 Biologia I MGR
 GEETYKA POPULACJI Ćwiczenia 4 Biologia I MGR Ad. Ćwiczenia Liczba możliwych genotypów w locus wieloallelicznym Geny sprzężone z płcią Prawo Hardy ego-weinberga p +pq+q = p+q= m( m ) p P Q Q P p AA Aa wszystkich_
GEETYKA POPULACJI Ćwiczenia 4 Biologia I MGR Ad. Ćwiczenia Liczba możliwych genotypów w locus wieloallelicznym Geny sprzężone z płcią Prawo Hardy ego-weinberga p +pq+q = p+q= m( m ) p P Q Q P p AA Aa wszystkich_
Opis wykonanych badań naukowych oraz uzyskanych wyników
 Opis wykonanych badań naukowych oraz uzyskanych wyników 1. Analiza danych (krok 2 = uwzględnienie epistazy w modelu): detekcja QTL przy wykorzystaniu modeli dwuwymiarowych z uwzględnieniem różnych modeli
Opis wykonanych badań naukowych oraz uzyskanych wyników 1. Analiza danych (krok 2 = uwzględnienie epistazy w modelu): detekcja QTL przy wykorzystaniu modeli dwuwymiarowych z uwzględnieniem różnych modeli
Analiza regresji - weryfikacja założeń
 Medycyna Praktyczna - portal dla lekarzy Analiza regresji - weryfikacja założeń mgr Andrzej Stanisz z Zakładu Biostatystyki i Informatyki Medycznej Collegium Medicum UJ w Krakowie (Kierownik Zakładu: prof.
Medycyna Praktyczna - portal dla lekarzy Analiza regresji - weryfikacja założeń mgr Andrzej Stanisz z Zakładu Biostatystyki i Informatyki Medycznej Collegium Medicum UJ w Krakowie (Kierownik Zakładu: prof.
1 Genetykapopulacyjna
 1 Genetykapopulacyjna Genetyka populacyjna zajmuje się badaniem częstości występowania poszczególnych alleli oraz genotypów w populacji. Bada także zmiany tych częstości spowodowane doborem naturalnym
1 Genetykapopulacyjna Genetyka populacyjna zajmuje się badaniem częstości występowania poszczególnych alleli oraz genotypów w populacji. Bada także zmiany tych częstości spowodowane doborem naturalnym
Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć)
 Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć) 1. Populacja generalna a losowa próba, parametr rozkładu cechy a jego ocena z losowej próby, miary opisu statystycznego
Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć) 1. Populacja generalna a losowa próba, parametr rozkładu cechy a jego ocena z losowej próby, miary opisu statystycznego
Zmienne zależne i niezależne
 Analiza kanoniczna Motywacja (1) 2 Często w badaniach spotykamy problemy badawcze, w których szukamy zakresu i kierunku zależności pomiędzy zbiorami zmiennych: { X i Jak oceniać takie 1, X 2,..., X p }
Analiza kanoniczna Motywacja (1) 2 Często w badaniach spotykamy problemy badawcze, w których szukamy zakresu i kierunku zależności pomiędzy zbiorami zmiennych: { X i Jak oceniać takie 1, X 2,..., X p }
Zmienność. środa, 23 listopada 11
 Zmienność http://ggoralski.com Zmienność Zmienność - rodzaje Zmienność obserwuje się zarówno między poszczególnymi osobnikami jak i między populacjami. Różnice te mogą mieć jednak różne podłoże. Mogą one
Zmienność http://ggoralski.com Zmienność Zmienność - rodzaje Zmienność obserwuje się zarówno między poszczególnymi osobnikami jak i między populacjami. Różnice te mogą mieć jednak różne podłoże. Mogą one
Analiza współzależności zjawisk
 Analiza współzależności zjawisk Informacje ogólne Jednostki tworzące zbiorowość statystyczną charakteryzowane są zazwyczaj za pomocą wielu cech zmiennych, które nierzadko pozostają ze sobą w pewnym związku.
Analiza współzależności zjawisk Informacje ogólne Jednostki tworzące zbiorowość statystyczną charakteryzowane są zazwyczaj za pomocą wielu cech zmiennych, które nierzadko pozostają ze sobą w pewnym związku.
Zadania ze statystyki, cz.6
 Zadania ze statystyki, cz.6 Zad.1 Proszę wskazać, jaką część pola pod krzywą normalną wyznaczają wartości Z rozkładu dystrybuanty rozkładu normalnego: - Z > 1,25 - Z > 2,23 - Z < -1,23 - Z > -1,16 - Z
Zadania ze statystyki, cz.6 Zad.1 Proszę wskazać, jaką część pola pod krzywą normalną wyznaczają wartości Z rozkładu dystrybuanty rozkładu normalnego: - Z > 1,25 - Z > 2,23 - Z < -1,23 - Z > -1,16 - Z
Wykład Centralne twierdzenie graniczne. Statystyka matematyczna: Estymacja parametrów rozkładu
 Wykład 11-12 Centralne twierdzenie graniczne Statystyka matematyczna: Estymacja parametrów rozkładu Centralne twierdzenie graniczne (CTG) (Central Limit Theorem - CLT) Centralne twierdzenie graniczne (Lindenberga-Levy'ego)
Wykład 11-12 Centralne twierdzenie graniczne Statystyka matematyczna: Estymacja parametrów rozkładu Centralne twierdzenie graniczne (CTG) (Central Limit Theorem - CLT) Centralne twierdzenie graniczne (Lindenberga-Levy'ego)
Rozwody w Polsce w ujęciu regionalnym
 Demografia i Gerontologia Społeczna Biuletyn Informacyjny 2013, Nr 4 Piotr Szukalski Instytut Socjologii Uniwersytet Łódzki pies@uni.lodz.pl Rozwody w Polsce w ujęciu regionalnym Fakt, iż ostatnie lata
Demografia i Gerontologia Społeczna Biuletyn Informacyjny 2013, Nr 4 Piotr Szukalski Instytut Socjologii Uniwersytet Łódzki pies@uni.lodz.pl Rozwody w Polsce w ujęciu regionalnym Fakt, iż ostatnie lata
Bliskie Spotkanie z Biologią. Genetyka populacji
 Bliskie Spotkanie z Biologią Genetyka populacji Plan wykładu 1) Częstości alleli i genotypów w populacji 2) Prawo Hardy ego-weinberga 3) Dryf genetyczny 4) Efekt założyciela i efekt wąskiego gardła 5)
Bliskie Spotkanie z Biologią Genetyka populacji Plan wykładu 1) Częstości alleli i genotypów w populacji 2) Prawo Hardy ego-weinberga 3) Dryf genetyczny 4) Efekt założyciela i efekt wąskiego gardła 5)
METODY STATYSTYCZNE W BIOLOGII
 METODY STATYSTYCZNE W BIOLOGII 1. Wykład wstępny 2. Populacje i próby danych 3. Testowanie hipotez i estymacja parametrów 4. Planowanie eksperymentów biologicznych 5. Najczęściej wykorzystywane testy statystyczne
METODY STATYSTYCZNE W BIOLOGII 1. Wykład wstępny 2. Populacje i próby danych 3. Testowanie hipotez i estymacja parametrów 4. Planowanie eksperymentów biologicznych 5. Najczęściej wykorzystywane testy statystyczne
Prognoza terminu sadzenia rozsady sałaty w uprawach szklarniowych. Janusz Górczyński, Jolanta Kobryń, Wojciech Zieliński
 Prognoza terminu sadzenia rozsady sałaty w uprawach szklarniowych Janusz Górczyński, Jolanta Kobryń, Wojciech Zieliński Streszczenie. W uprawach szklarniowych sałaty pojawia się następujący problem: kiedy
Prognoza terminu sadzenia rozsady sałaty w uprawach szklarniowych Janusz Górczyński, Jolanta Kobryń, Wojciech Zieliński Streszczenie. W uprawach szklarniowych sałaty pojawia się następujący problem: kiedy
Algorytmy genetyczne w optymalizacji
 Algorytmy genetyczne w optymalizacji Literatura 1. David E. Goldberg, Algorytmy genetyczne i ich zastosowania, WNT, Warszawa 1998; 2. Zbigniew Michalewicz, Algorytmy genetyczne + struktury danych = programy
Algorytmy genetyczne w optymalizacji Literatura 1. David E. Goldberg, Algorytmy genetyczne i ich zastosowania, WNT, Warszawa 1998; 2. Zbigniew Michalewicz, Algorytmy genetyczne + struktury danych = programy
Analiza korespondencji
 Analiza korespondencji Kiedy stosujemy? 2 W wielu badaniach mamy do czynienia ze zmiennymi jakościowymi (nominalne i porządkowe) typu np.: płeć, wykształcenie, status palenia. Punktem wyjścia do analizy
Analiza korespondencji Kiedy stosujemy? 2 W wielu badaniach mamy do czynienia ze zmiennymi jakościowymi (nominalne i porządkowe) typu np.: płeć, wykształcenie, status palenia. Punktem wyjścia do analizy
1 Podstawowe pojęcia z zakresu genetyki. 2 Podstawowy model dziedziczenia
 Rachunek Prawdopodobieństwa MAP8 Wydział Matematyki, Matematyka Stosowana Projekt - zastosowania rachunku prawdopodobieństwa w genetyce Opracowanie: Antonina Urbaniak Podstawowe pojęcia z zakresu genetyki
Rachunek Prawdopodobieństwa MAP8 Wydział Matematyki, Matematyka Stosowana Projekt - zastosowania rachunku prawdopodobieństwa w genetyce Opracowanie: Antonina Urbaniak Podstawowe pojęcia z zakresu genetyki
Wnioskowanie bayesowskie
 Wnioskowanie bayesowskie W podejściu klasycznym wnioskowanie statystyczne oparte jest wyłącznie na podstawie pobranej próby losowej. Możemy np. estymować punktowo lub przedziałowo nieznane parametry rozkładów,
Wnioskowanie bayesowskie W podejściu klasycznym wnioskowanie statystyczne oparte jest wyłącznie na podstawie pobranej próby losowej. Możemy np. estymować punktowo lub przedziałowo nieznane parametry rozkładów,
6.4 Podstawowe metody statystyczne
 156 Wstęp do statystyki matematycznej 6.4 Podstawowe metody statystyczne Spóbujemy teraz w dopuszczalnym uproszczeniu przedstawić istotę analizy statystycznej. W szczególności udzielimy odpowiedzi na postawione
156 Wstęp do statystyki matematycznej 6.4 Podstawowe metody statystyczne Spóbujemy teraz w dopuszczalnym uproszczeniu przedstawić istotę analizy statystycznej. W szczególności udzielimy odpowiedzi na postawione
Załóżmy, że obserwujemy nie jedną lecz dwie cechy, które oznaczymy symbolami X i Y. Wyniki obserwacji obu cech w i-tym obiekcie oznaczymy parą liczb
 Współzależność Załóżmy, że obserwujemy nie jedną lecz dwie cechy, które oznaczymy symbolami X i Y. Wyniki obserwacji obu cech w i-tym obiekcie oznaczymy parą liczb (x i, y i ). Geometrycznie taką parę
Współzależność Załóżmy, że obserwujemy nie jedną lecz dwie cechy, które oznaczymy symbolami X i Y. Wyniki obserwacji obu cech w i-tym obiekcie oznaczymy parą liczb (x i, y i ). Geometrycznie taką parę
PDF created with FinePrint pdffactory Pro trial version http://www.fineprint.com
 Analiza korelacji i regresji KORELACJA zależność liniowa Obserwujemy parę cech ilościowych (X,Y). Doświadczenie jest tak pomyślane, aby obserwowane pary cech X i Y (tzn i ta para x i i y i dla różnych
Analiza korelacji i regresji KORELACJA zależność liniowa Obserwujemy parę cech ilościowych (X,Y). Doświadczenie jest tak pomyślane, aby obserwowane pary cech X i Y (tzn i ta para x i i y i dla różnych
STATYSTYKA MATEMATYCZNA
 STATYSTYKA MATEMATYCZNA 1. Wykład wstępny. Teoria prawdopodobieństwa i elementy kombinatoryki 2. Zmienne losowe i ich rozkłady 3. Populacje i próby danych, estymacja parametrów 4. Testowanie hipotez 5.
STATYSTYKA MATEMATYCZNA 1. Wykład wstępny. Teoria prawdopodobieństwa i elementy kombinatoryki 2. Zmienne losowe i ich rozkłady 3. Populacje i próby danych, estymacja parametrów 4. Testowanie hipotez 5.
Ekologia molekularna. wykład 3
 Ekologia molekularna wykład 3 Dziedziczenie mendlowskie Grzegorz Mendel 1822-1884 Darwin + Mendel = Ronald Fisher 1890-1962 wykład 3/2 Prawo Hardy'ego-Weinberga A A gamety możliwe genotypy potomstwa genotyp
Ekologia molekularna wykład 3 Dziedziczenie mendlowskie Grzegorz Mendel 1822-1884 Darwin + Mendel = Ronald Fisher 1890-1962 wykład 3/2 Prawo Hardy'ego-Weinberga A A gamety możliwe genotypy potomstwa genotyp
6. Klasyczny algorytm genetyczny. 1
 6. Klasyczny algorytm genetyczny. 1 Idea algorytmu genetycznego została zaczerpnięta z nauk przyrodniczych opisujących zjawiska doboru naturalnego i dziedziczenia. Mechanizmy te polegają na przetrwaniu
6. Klasyczny algorytm genetyczny. 1 Idea algorytmu genetycznego została zaczerpnięta z nauk przyrodniczych opisujących zjawiska doboru naturalnego i dziedziczenia. Mechanizmy te polegają na przetrwaniu
W. Guzicki Próbna matura, grudzień 2014 r. poziom rozszerzony 1
 W. Guzicki Próbna matura, grudzień 01 r. poziom rozszerzony 1 Próbna matura rozszerzona (jesień 01 r.) Zadanie 18 kilka innych rozwiązań Wojciech Guzicki Zadanie 18. Okno na poddaszu ma mieć kształt trapezu
W. Guzicki Próbna matura, grudzień 01 r. poziom rozszerzony 1 Próbna matura rozszerzona (jesień 01 r.) Zadanie 18 kilka innych rozwiązań Wojciech Guzicki Zadanie 18. Okno na poddaszu ma mieć kształt trapezu
Genetyka ekologiczna i populacyjna W8
 Genetyka ekologiczna i populacyjna W8 Genetyka populacji: Treść wykładów Zmienność genetyczna i środowiskowa Mutacje i rekombinacje Kojarzenie krewniacze Częstość genów i genotypów w populacji i prawdopodobieństwo
Genetyka ekologiczna i populacyjna W8 Genetyka populacji: Treść wykładów Zmienność genetyczna i środowiskowa Mutacje i rekombinacje Kojarzenie krewniacze Częstość genów i genotypów w populacji i prawdopodobieństwo
Algorytm Genetyczny. zastosowanie do procesów rozmieszczenia stacji raportujących w sieciach komórkowych
 Algorytm Genetyczny zastosowanie do procesów rozmieszczenia stacji raportujących w sieciach komórkowych Dlaczego Algorytmy Inspirowane Naturą? Rozwój nowych technologii: złożone problemy obliczeniowe w
Algorytm Genetyczny zastosowanie do procesów rozmieszczenia stacji raportujących w sieciach komórkowych Dlaczego Algorytmy Inspirowane Naturą? Rozwój nowych technologii: złożone problemy obliczeniowe w
Rozdział 8. Regresja. Definiowanie modelu
 Rozdział 8 Regresja Definiowanie modelu Analizę korelacji można traktować jako wstęp do analizy regresji. Jeżeli wykresy rozrzutu oraz wartości współczynników korelacji wskazują na istniejąca współzmienność
Rozdział 8 Regresja Definiowanie modelu Analizę korelacji można traktować jako wstęp do analizy regresji. Jeżeli wykresy rozrzutu oraz wartości współczynników korelacji wskazują na istniejąca współzmienność
Prawdopodobieństwo i statystyka
 Wykład XIII: Prognoza. 26 stycznia 2015 Wykład XIII: Prognoza. Prognoza (predykcja) Przypuśćmy, że mamy dany ciąg liczb x 1, x 2,..., x n, stanowiących wyniki pomiaru pewnej zmiennej w czasie wielkości
Wykład XIII: Prognoza. 26 stycznia 2015 Wykład XIII: Prognoza. Prognoza (predykcja) Przypuśćmy, że mamy dany ciąg liczb x 1, x 2,..., x n, stanowiących wyniki pomiaru pewnej zmiennej w czasie wielkości
Instytut Politechniczny Państwowa Wyższa Szkoła Zawodowa. Diagnostyka i niezawodność robotów
 Instytut Politechniczny Państwowa Wyższa Szkoła Zawodowa Diagnostyka i niezawodność robotów Laboratorium nr 6 Model matematyczny elementu naprawialnego Prowadzący: mgr inż. Marcel Luzar Cele ćwiczenia:
Instytut Politechniczny Państwowa Wyższa Szkoła Zawodowa Diagnostyka i niezawodność robotów Laboratorium nr 6 Model matematyczny elementu naprawialnego Prowadzący: mgr inż. Marcel Luzar Cele ćwiczenia:
Statystyka matematyczna dla leśników
 Statystyka matematyczna dla leśników Wydział Leśny Kierunek leśnictwo Studia Stacjonarne I Stopnia Rok akademicki 2013/2014 Wykład 3 Zmienna losowa i jej rozkłady Zdarzenia losowe Pojęcie prawdopodobieństwa
Statystyka matematyczna dla leśników Wydział Leśny Kierunek leśnictwo Studia Stacjonarne I Stopnia Rok akademicki 2013/2014 Wykład 3 Zmienna losowa i jej rozkłady Zdarzenia losowe Pojęcie prawdopodobieństwa
Przestrzenie wektorowe
 Rozdział 4 Przestrzenie wektorowe Rozważania dotyczące przestrzeni wektorowych rozpoczniemy od kilku prostych przykładów. Przykład 4.1. W przestrzeni R 3 = {(x, y, z) : x, y, z R} wprowadzamy dwa działania:
Rozdział 4 Przestrzenie wektorowe Rozważania dotyczące przestrzeni wektorowych rozpoczniemy od kilku prostych przykładów. Przykład 4.1. W przestrzeni R 3 = {(x, y, z) : x, y, z R} wprowadzamy dwa działania:
Algorytm genetyczny (genetic algorithm)-
 Optymalizacja W praktyce inżynierskiej często zachodzi potrzeba znalezienia parametrów, dla których system/urządzenie będzie działać w sposób optymalny. Klasyczne podejście do optymalizacji: sformułowanie
Optymalizacja W praktyce inżynierskiej często zachodzi potrzeba znalezienia parametrów, dla których system/urządzenie będzie działać w sposób optymalny. Klasyczne podejście do optymalizacji: sformułowanie
KORELACJE I REGRESJA LINIOWA
 KORELACJE I REGRESJA LINIOWA Korelacje i regresja liniowa Analiza korelacji: Badanie, czy pomiędzy dwoma zmiennymi istnieje zależność Obie analizy się wzajemnie przeplatają Analiza regresji: Opisanie modelem
KORELACJE I REGRESJA LINIOWA Korelacje i regresja liniowa Analiza korelacji: Badanie, czy pomiędzy dwoma zmiennymi istnieje zależność Obie analizy się wzajemnie przeplatają Analiza regresji: Opisanie modelem
K wartość kapitału zaangażowanego w proces produkcji, w tys. jp.
 Sprawdzian 2. Zadanie 1. Za pomocą KMNK oszacowano następującą funkcję produkcji: Gdzie: P wartość produkcji, w tys. jp (jednostek pieniężnych) K wartość kapitału zaangażowanego w proces produkcji, w tys.
Sprawdzian 2. Zadanie 1. Za pomocą KMNK oszacowano następującą funkcję produkcji: Gdzie: P wartość produkcji, w tys. jp (jednostek pieniężnych) K wartość kapitału zaangażowanego w proces produkcji, w tys.
GENETYKA POPULACJI. Fot. W. Wołkow
 GENETYKA POPULACJI Fot. W. Wołkow GENETYKA POPULACJI Nauka która respektując zasady dziedziczenia z zakresu genetyki klasycznej bada mechanizmy dziedziczenia w odniesieniu do populacji Struktura genetyczna:
GENETYKA POPULACJI Fot. W. Wołkow GENETYKA POPULACJI Nauka która respektując zasady dziedziczenia z zakresu genetyki klasycznej bada mechanizmy dziedziczenia w odniesieniu do populacji Struktura genetyczna:
Statystyka. Wykład 8. Magdalena Alama-Bućko. 10 kwietnia Magdalena Alama-Bućko Statystyka 10 kwietnia / 31
 Statystyka Wykład 8 Magdalena Alama-Bućko 10 kwietnia 2017 Magdalena Alama-Bućko Statystyka 10 kwietnia 2017 1 / 31 Tematyka zajęć: Wprowadzenie do statystyki. Analiza struktury zbiorowości miary położenia
Statystyka Wykład 8 Magdalena Alama-Bućko 10 kwietnia 2017 Magdalena Alama-Bućko Statystyka 10 kwietnia 2017 1 / 31 Tematyka zajęć: Wprowadzenie do statystyki. Analiza struktury zbiorowości miary położenia
istocie dziedzina zajmująca się poszukiwaniem zależności na podstawie prowadzenia doświadczeń jest o wiele starsza: tak na przykład matematycy
 MODEL REGRESJI LINIOWEJ. METODA NAJMNIEJSZYCH KWADRATÓW Analiza regresji zajmuje się badaniem zależności pomiędzy interesującymi nas wielkościami (zmiennymi), mające na celu konstrukcję modelu, który dobrze
MODEL REGRESJI LINIOWEJ. METODA NAJMNIEJSZYCH KWADRATÓW Analiza regresji zajmuje się badaniem zależności pomiędzy interesującymi nas wielkościami (zmiennymi), mające na celu konstrukcję modelu, który dobrze
Komputerowa Analiza Danych Doświadczalnych
 Komputerowa Analiza Danych Doświadczalnych Prowadząca: dr inż. Hanna Zbroszczyk e-mail: gos@if.pw.edu.pl tel: +48 22 234 58 51 konsultacje: poniedziałek, 10-11, środa: 11-12 www: http://www.if.pw.edu.pl/~gos/students/kadd
Komputerowa Analiza Danych Doświadczalnych Prowadząca: dr inż. Hanna Zbroszczyk e-mail: gos@if.pw.edu.pl tel: +48 22 234 58 51 konsultacje: poniedziałek, 10-11, środa: 11-12 www: http://www.if.pw.edu.pl/~gos/students/kadd
Inteligentna analiza danych
 Numer indeksu 150946 Michał Moroz Imię i nazwisko Numer indeksu 150875 Grzegorz Graczyk Imię i nazwisko kierunek: Informatyka rok akademicki: 2010/2011 Inteligentna analiza danych Ćwiczenie I Wskaźniki
Numer indeksu 150946 Michał Moroz Imię i nazwisko Numer indeksu 150875 Grzegorz Graczyk Imię i nazwisko kierunek: Informatyka rok akademicki: 2010/2011 Inteligentna analiza danych Ćwiczenie I Wskaźniki
Statystyka opisowa. Wykład V. Regresja liniowa wieloraka
 Statystyka opisowa. Wykład V. e-mail:e.kozlovski@pollub.pl Spis treści 1 Prosta regresji cechy Y względem cech X 1,..., X k. 2 3 Wyznaczamy zależność cechy Y od cech X 1, X 2,..., X k postaci Y = α 0 +
Statystyka opisowa. Wykład V. e-mail:e.kozlovski@pollub.pl Spis treści 1 Prosta regresji cechy Y względem cech X 1,..., X k. 2 3 Wyznaczamy zależność cechy Y od cech X 1, X 2,..., X k postaci Y = α 0 +
Grażyna Liczbińska Księgi parafialne jako źródło informacji o populacjach historycznych. Przegląd Historyczny 102/2,
 Grażyna Liczbińska Księgi parafialne jako źródło informacji o populacjach historycznych Przegląd Historyczny 102/2, 267-282 2011 P R Z E G L Ą D Y B A D A Ń GRAŻYNA LICZBIŃSKA Uniwersytet im Adama Mickiewicza
Grażyna Liczbińska Księgi parafialne jako źródło informacji o populacjach historycznych Przegląd Historyczny 102/2, 267-282 2011 P R Z E G L Ą D Y B A D A Ń GRAŻYNA LICZBIŃSKA Uniwersytet im Adama Mickiewicza
Dryf genetyczny i jego wpływ na rozkłady próbek z populacji - modele matematyczne. Adam Bobrowski, IM PAN Katowice
 Dryf genetyczny i jego wpływ na rozkłady próbek z populacji - modele matematyczne Adam Bobrowski, IM PAN Katowice 1 Tematyka cyklu referatów Dryf genetyczny Matematyczne modele równowagi między mutacja
Dryf genetyczny i jego wpływ na rozkłady próbek z populacji - modele matematyczne Adam Bobrowski, IM PAN Katowice 1 Tematyka cyklu referatów Dryf genetyczny Matematyczne modele równowagi między mutacja
WYKŁAD 8 ANALIZA REGRESJI
 WYKŁAD 8 ANALIZA REGRESJI Regresja 1. Metoda najmniejszych kwadratów-regresja prostoliniowa 2. Regresja krzywoliniowa 3. Estymacja liniowej funkcji regresji 4. Testy istotności współczynnika regresji liniowej
WYKŁAD 8 ANALIZA REGRESJI Regresja 1. Metoda najmniejszych kwadratów-regresja prostoliniowa 2. Regresja krzywoliniowa 3. Estymacja liniowej funkcji regresji 4. Testy istotności współczynnika regresji liniowej
Estymacja punktowa i przedziałowa
 Temat: Estymacja punktowa i przedziałowa Kody znaków: żółte wyróżnienie nowe pojęcie czerwony uwaga kursywa komentarz 1 Zagadnienia 1. Statystyczny opis próby. Idea estymacji punktowej pojęcie estymatora
Temat: Estymacja punktowa i przedziałowa Kody znaków: żółte wyróżnienie nowe pojęcie czerwony uwaga kursywa komentarz 1 Zagadnienia 1. Statystyczny opis próby. Idea estymacji punktowej pojęcie estymatora
Elementy statystyki opisowej, podstawowe pojęcia statystyki matematycznej
 Elementy statystyki opisowej, podstawowe pojęcia statystyki matematycznej Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych Wydział Informatyki Politechniki
Elementy statystyki opisowej, podstawowe pojęcia statystyki matematycznej Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych Wydział Informatyki Politechniki
Anna Szewczyk. Wydział Geodezji Górniczej i InŜynierii środowiska AGH
 Anna Szewczyk Wydział Geodezji Górniczej i InŜynierii środowiska AGH Zastosowania biblioteki Genetics programu R The genetics Package Tytuł: Populacja genetyczna Wersja:1.2.0 Data utworzenia: 2005-11-09
Anna Szewczyk Wydział Geodezji Górniczej i InŜynierii środowiska AGH Zastosowania biblioteki Genetics programu R The genetics Package Tytuł: Populacja genetyczna Wersja:1.2.0 Data utworzenia: 2005-11-09
STATYSTYKA - PRZYKŁADOWE ZADANIA EGZAMINACYJNE
 STATYSTYKA - PRZYKŁADOWE ZADANIA EGZAMINACYJNE 1 W trakcie badania obliczono wartości średniej (15,4), mediany (13,6) oraz dominanty (10,0). Określ typ asymetrii rozkładu. 2 Wymień 3 cechy rozkładu Gauss
STATYSTYKA - PRZYKŁADOWE ZADANIA EGZAMINACYJNE 1 W trakcie badania obliczono wartości średniej (15,4), mediany (13,6) oraz dominanty (10,0). Określ typ asymetrii rozkładu. 2 Wymień 3 cechy rozkładu Gauss
Zadania ze statystyki cz. 8 I rok socjologii. Zadanie 1.
 Zadania ze statystyki cz. 8 I rok socjologii Zadanie 1. W potocznej opinii pokutuje przekonanie, że lepsi z matematyki są chłopcy niż dziewczęta. Chcąc zweryfikować tę opinię, przeprowadzono badanie w
Zadania ze statystyki cz. 8 I rok socjologii Zadanie 1. W potocznej opinii pokutuje przekonanie, że lepsi z matematyki są chłopcy niż dziewczęta. Chcąc zweryfikować tę opinię, przeprowadzono badanie w
Zadanie 1 Zakładając liniową relację między wydatkami na obuwie a dochodem oszacować MNK parametry modelu: y t. X 1 t. Tabela 1.
 tel. 44 683 1 55 tel. kom. 64 566 811 e-mail: biuro@wszechwiedza.pl Zadanie 1 Zakładając liniową relację między wydatkami na obuwie a dochodem oszacować MNK parametry modelu: gdzie: y t X t y t = 1 X 1
tel. 44 683 1 55 tel. kom. 64 566 811 e-mail: biuro@wszechwiedza.pl Zadanie 1 Zakładając liniową relację między wydatkami na obuwie a dochodem oszacować MNK parametry modelu: gdzie: y t X t y t = 1 X 1
Elementy Modelowania Matematycznego Wykład 4 Regresja i dyskryminacja liniowa
 Spis treści Elementy Modelowania Matematycznego Wykład 4 Regresja i dyskryminacja liniowa Romuald Kotowski Katedra Informatyki Stosowanej PJWSTK 2009 Spis treści Spis treści 1 Wstęp Bardzo często interesujący
Spis treści Elementy Modelowania Matematycznego Wykład 4 Regresja i dyskryminacja liniowa Romuald Kotowski Katedra Informatyki Stosowanej PJWSTK 2009 Spis treści Spis treści 1 Wstęp Bardzo często interesujący
Zadania ze statystyki, cz.7 - hipotezy statystyczne, błąd standardowy, testowanie hipotez statystycznych
 Zadania ze statystyki, cz.7 - hipotezy statystyczne, błąd standardowy, testowanie hipotez statystycznych Zad. 1 Średnia ocen z semestru letniego w populacji studentów socjologii w roku akademickim 2011/2012
Zadania ze statystyki, cz.7 - hipotezy statystyczne, błąd standardowy, testowanie hipotez statystycznych Zad. 1 Średnia ocen z semestru letniego w populacji studentów socjologii w roku akademickim 2011/2012
Zadania maturalne z biologii - 7
 Koło Biologiczne Liceum Ogólnokształcące nr II w Gliwicach 2015-2016 Zadania maturalne z biologii - 7 Zadania: Zad.1 (Jesika Stępień, Natalia Świetlak, Daniela Schwedka 3D) Przeczytaj tekst i na jego podstawie
Koło Biologiczne Liceum Ogólnokształcące nr II w Gliwicach 2015-2016 Zadania maturalne z biologii - 7 Zadania: Zad.1 (Jesika Stępień, Natalia Świetlak, Daniela Schwedka 3D) Przeczytaj tekst i na jego podstawie
 prof. dr hab. Irena E. Kotowska dr Katarzyna Kocot-Górecka, dr Magdalena Muszyńska mgr Wojciech Łątkowski Wykład: czwartek, godz.11.40-13.20, aula IV Zajęcia w laboratorium komputerowym budynek S: grupa
prof. dr hab. Irena E. Kotowska dr Katarzyna Kocot-Górecka, dr Magdalena Muszyńska mgr Wojciech Łątkowski Wykład: czwartek, godz.11.40-13.20, aula IV Zajęcia w laboratorium komputerowym budynek S: grupa
Model MULTIPOLES - narzędzie do prognozowania, projekcji i symulacji stanu i struktury ludności
 Model MULTIPOLES - narzędzie do prognozowania, projekcji i symulacji stanu i struktury ludności Dorota Kupiszewska i Marek Kupiszewski Konferencja Perspektywy demograficzne Europy Instytut Statystyki i
Model MULTIPOLES - narzędzie do prognozowania, projekcji i symulacji stanu i struktury ludności Dorota Kupiszewska i Marek Kupiszewski Konferencja Perspektywy demograficzne Europy Instytut Statystyki i
W1. Wprowadzenie. Statystyka opisowa
 W1. Wprowadzenie. Statystyka opisowa dr hab. Jerzy Nakielski Zakład Biofizyki i Morfogenezy Roślin Plan wykładu: 1. O co chodzi w statystyce 2. Etapy badania statystycznego 3. Zmienna losowa, rozkład
W1. Wprowadzenie. Statystyka opisowa dr hab. Jerzy Nakielski Zakład Biofizyki i Morfogenezy Roślin Plan wykładu: 1. O co chodzi w statystyce 2. Etapy badania statystycznego 3. Zmienna losowa, rozkład
Szacowanie wartości hodowlanej. Zarządzanie populacjami
 Szacowanie wartości hodowlanej Zarządzanie populacjami wartość hodowlana = wartość cechy? Tak! Przy h 2 =1 ? wybitny ojciec = wybitne dzieci Tak, gdy cecha wysokoodziedziczalna. Wartość hodowlana genetycznie
Szacowanie wartości hodowlanej Zarządzanie populacjami wartość hodowlana = wartość cechy? Tak! Przy h 2 =1 ? wybitny ojciec = wybitne dzieci Tak, gdy cecha wysokoodziedziczalna. Wartość hodowlana genetycznie
x 2 = a RÓWNANIA KWADRATOWE 1. Wprowadzenie do równań kwadratowych 2. Proste równania kwadratowe Równanie kwadratowe typu:
 RÓWNANIA KWADRATOWE 1. Wprowadzenie do równań kwadratowych Przed rozpoczęciem nauki o równaniach kwadratowych, warto dobrze opanować rozwiązywanie zwykłych równań liniowych. W równaniach liniowych niewiadoma
RÓWNANIA KWADRATOWE 1. Wprowadzenie do równań kwadratowych Przed rozpoczęciem nauki o równaniach kwadratowych, warto dobrze opanować rozwiązywanie zwykłych równań liniowych. W równaniach liniowych niewiadoma
Etapy modelowania ekonometrycznego
 Etapy modelowania ekonometrycznego jest podstawowym narzędziem badawczym, jakim posługuje się ekonometria. Stanowi on matematyczno-statystyczną formę zapisu prawidłowości statystycznej w zakresie rozkładu,
Etapy modelowania ekonometrycznego jest podstawowym narzędziem badawczym, jakim posługuje się ekonometria. Stanowi on matematyczno-statystyczną formę zapisu prawidłowości statystycznej w zakresie rozkładu,
GENETYCZNE PODSTAWY ZMIENNOŚCI ORGANIZMÓW ZASADY DZIEDZICZENIA CECH PODSTAWY GENETYKI POPULACYJNEJ
 GENETYCZNE PODSTAWY ZMIENNOŚCI ORGANIZMÓW ZASADY DZIEDZICZENIA CECH PODSTAWY GENETYKI POPULACYJNEJ ZMIENNOŚĆ - występowanie dziedzicznych i niedziedzicznych różnic między osobnikami należącymi do tej samej
GENETYCZNE PODSTAWY ZMIENNOŚCI ORGANIZMÓW ZASADY DZIEDZICZENIA CECH PODSTAWY GENETYKI POPULACYJNEJ ZMIENNOŚĆ - występowanie dziedzicznych i niedziedzicznych różnic między osobnikami należącymi do tej samej
Prognoza demograficzna dla gmin województwa dolnośląskiego do 2035 roku
 Prognoza demograficzna dla gmin województwa dolnośląskiego do 2035 roku Stanisława Górecka Robert Szmytkie Samorządowa Jednostka Organizacyjna Województwa Dolnośląskiego 1 UWAGI WSTĘPNE Prognoza została
Prognoza demograficzna dla gmin województwa dolnośląskiego do 2035 roku Stanisława Górecka Robert Szmytkie Samorządowa Jednostka Organizacyjna Województwa Dolnośląskiego 1 UWAGI WSTĘPNE Prognoza została
Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Elektroniki
 Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Elektroniki Przetwarzanie Sygnałów Studia Podyplomowe, Automatyka i Robotyka. Wstęp teoretyczny Zmienne losowe Zmienne losowe
Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Elektroniki Przetwarzanie Sygnałów Studia Podyplomowe, Automatyka i Robotyka. Wstęp teoretyczny Zmienne losowe Zmienne losowe
Ekonometria. Zajęcia
 Ekonometria Zajęcia 16.05.2018 Wstęp hipoteza itp. Model gęstości zaludnienia ( model gradientu gęstości ) zakłada, że gęstość zaludnienia zależy od odległości od okręgu centralnego: y t = Ae βx t (1)
Ekonometria Zajęcia 16.05.2018 Wstęp hipoteza itp. Model gęstości zaludnienia ( model gradientu gęstości ) zakłada, że gęstość zaludnienia zależy od odległości od okręgu centralnego: y t = Ae βx t (1)
TESTOWANIE HIPOTEZ STATYSTYCZNYCH
 TETOWANIE HIPOTEZ TATYTYCZNYCH HIPOTEZA TATYTYCZNA przypuszczenie co do rozkładu populacji generalnej (jego postaci funkcyjnej lub wartości parametrów). Prawdziwość tego przypuszczenia jest oceniana na
TETOWANIE HIPOTEZ TATYTYCZNYCH HIPOTEZA TATYTYCZNA przypuszczenie co do rozkładu populacji generalnej (jego postaci funkcyjnej lub wartości parametrów). Prawdziwość tego przypuszczenia jest oceniana na
Metody Ilościowe w Socjologii
 Metody Ilościowe w Socjologii wykład 2 i 3 EKONOMETRIA dr inż. Maciej Wolny AGENDA I. Ekonometria podstawowe definicje II. Etapy budowy modelu ekonometrycznego III. Wybrane metody doboru zmiennych do modelu
Metody Ilościowe w Socjologii wykład 2 i 3 EKONOMETRIA dr inż. Maciej Wolny AGENDA I. Ekonometria podstawowe definicje II. Etapy budowy modelu ekonometrycznego III. Wybrane metody doboru zmiennych do modelu
STATYSTYKA MATEMATYCZNA ZESTAW 0 (POWT. RACH. PRAWDOPODOBIEŃSTWA) ZADANIA
 STATYSTYKA MATEMATYCZNA ZESTAW 0 (POWT. RACH. PRAWDOPODOBIEŃSTWA) ZADANIA Zadanie 0.1 Zmienna losowa X ma rozkład określony funkcją prawdopodobieństwa: x k 0 4 p k 1/3 1/6 1/ obliczyć EX, D X. (odp. 4/3;
STATYSTYKA MATEMATYCZNA ZESTAW 0 (POWT. RACH. PRAWDOPODOBIEŃSTWA) ZADANIA Zadanie 0.1 Zmienna losowa X ma rozkład określony funkcją prawdopodobieństwa: x k 0 4 p k 1/3 1/6 1/ obliczyć EX, D X. (odp. 4/3;
FORECASTING THE DISTRIBUTION OF AMOUNT OF UNEMPLOYED BY THE REGIONS
 FOLIA UNIVERSITATIS AGRICULTURAE STETINENSIS Folia Univ. Agric. Stetin. 007, Oeconomica 54 (47), 73 80 Mateusz GOC PROGNOZOWANIE ROZKŁADÓW LICZBY BEZROBOTNYCH WEDŁUG MIAST I POWIATÓW FORECASTING THE DISTRIBUTION
FOLIA UNIVERSITATIS AGRICULTURAE STETINENSIS Folia Univ. Agric. Stetin. 007, Oeconomica 54 (47), 73 80 Mateusz GOC PROGNOZOWANIE ROZKŁADÓW LICZBY BEZROBOTNYCH WEDŁUG MIAST I POWIATÓW FORECASTING THE DISTRIBUTION
Rozdział 2: Metoda największej wiarygodności i nieliniowa metoda najmniejszych kwadratów
 Rozdział : Metoda największej wiarygodności i nieliniowa metoda najmniejszych kwadratów W tym rozdziale omówione zostaną dwie najpopularniejsze metody estymacji parametrów w ekonometrycznych modelach nieliniowych,
Rozdział : Metoda największej wiarygodności i nieliniowa metoda najmniejszych kwadratów W tym rozdziale omówione zostaną dwie najpopularniejsze metody estymacji parametrów w ekonometrycznych modelach nieliniowych,
 prof. dr hab. Irena E. Kotowska dr Katarzyna Kocot-Górecka dr Magdalena Muszyńska mgr Wojciech Łątkowski Wykład: poniedziałki, godz.15.20-17.00, sala 211, budynek A Zajęcia w laboratorium komputerowym:
prof. dr hab. Irena E. Kotowska dr Katarzyna Kocot-Górecka dr Magdalena Muszyńska mgr Wojciech Łątkowski Wykład: poniedziałki, godz.15.20-17.00, sala 211, budynek A Zajęcia w laboratorium komputerowym:
STATYSTYKA MATEMATYCZNA. rachunek prawdopodobieństwa
 STATYSTYKA MATEMATYCZNA rachunek prawdopodobieństwa treść Zdarzenia losowe pojęcie prawdopodobieństwa prawo wielkich liczb zmienne losowe rozkłady teoretyczne zmiennych losowych Zanim zajmiemy się wnioskowaniem
STATYSTYKA MATEMATYCZNA rachunek prawdopodobieństwa treść Zdarzenia losowe pojęcie prawdopodobieństwa prawo wielkich liczb zmienne losowe rozkłady teoretyczne zmiennych losowych Zanim zajmiemy się wnioskowaniem
Algorytmy genetyczne
 Algorytmy genetyczne Motto: Zamiast pracowicie poszukiwać najlepszego rozwiązania problemu informatycznego lepiej pozwolić, żeby komputer sam sobie to rozwiązanie wyhodował! Algorytmy genetyczne służą
Algorytmy genetyczne Motto: Zamiast pracowicie poszukiwać najlepszego rozwiązania problemu informatycznego lepiej pozwolić, żeby komputer sam sobie to rozwiązanie wyhodował! Algorytmy genetyczne służą
2. DZIAŁANIA NA WIELOMIANACH
 WIELOMIANY 1. Stopieo wielomianu. Działania na wielomianach 2. Równość wielomianów. 3. Pierwiastek wielomianu. Rozkład wielomianu na czynniki 4. Równania wielomianowe. 1.STOPIEŃ WIELOMIANU Wielomian to
WIELOMIANY 1. Stopieo wielomianu. Działania na wielomianach 2. Równość wielomianów. 3. Pierwiastek wielomianu. Rozkład wielomianu na czynniki 4. Równania wielomianowe. 1.STOPIEŃ WIELOMIANU Wielomian to
Algorytmy genetyczne
 9 listopada 2010 y ewolucyjne - zbiór metod optymalizacji inspirowanych analogiami biologicznymi (ewolucja naturalna). Pojęcia odwzorowujące naturalne zjawiska: Osobnik Populacja Genotyp Fenotyp Gen Chromosom
9 listopada 2010 y ewolucyjne - zbiór metod optymalizacji inspirowanych analogiami biologicznymi (ewolucja naturalna). Pojęcia odwzorowujące naturalne zjawiska: Osobnik Populacja Genotyp Fenotyp Gen Chromosom
Badanie naukowe: CZY MĄDROŚĆ TŁUMU RZECZYWIŚCIE ISTNIEJE?
 Badanie naukowe: CZY MĄDROŚĆ TŁUMU RZECZYWIŚCIE ISTNIEJE? Scientific research: IS CROWDSOURCING ACTUALLY REAL? Cele: - Sprawdzenie, czy zjawisko Mądrości Tłumu rzeczywiście działa w 3 różnych sytuacjach;
Badanie naukowe: CZY MĄDROŚĆ TŁUMU RZECZYWIŚCIE ISTNIEJE? Scientific research: IS CROWDSOURCING ACTUALLY REAL? Cele: - Sprawdzenie, czy zjawisko Mądrości Tłumu rzeczywiście działa w 3 różnych sytuacjach;
Statystyka i Analiza Danych
 Warsztaty Statystyka i Analiza Danych Gdańsk, 20-22 lutego 2014 Zastosowania analizy wariancji w opracowywaniu wyników badań empirycznych Janusz Wątroba StatSoft Polska Centrum Zastosowań Matematyki -
Warsztaty Statystyka i Analiza Danych Gdańsk, 20-22 lutego 2014 Zastosowania analizy wariancji w opracowywaniu wyników badań empirycznych Janusz Wątroba StatSoft Polska Centrum Zastosowań Matematyki -
Statystyka. Podstawowe pojęcia: populacja (zbiorowość statystyczna), jednostka statystyczna, próba. Cechy: ilościowe (mierzalne),
 Statystyka zbiór przetworzonych i zsyntetyzowanych danych liczbowych, nauka o ilościowych metodach badania zjawisk masowych, zmienna losowa będąca funkcją próby. Podstawowe pojęcia: populacja (zbiorowość
Statystyka zbiór przetworzonych i zsyntetyzowanych danych liczbowych, nauka o ilościowych metodach badania zjawisk masowych, zmienna losowa będąca funkcją próby. Podstawowe pojęcia: populacja (zbiorowość
SCHEMAT ROZWIĄZANIA ZADANIA OPTYMALIZACJI PRZY POMOCY ALGORYTMU GENETYCZNEGO
 SCHEMAT ROZWIĄZANIA ZADANIA OPTYMALIZACJI PRZY POMOCY ALGORYTMU GENETYCZNEGO. Rzeczywistość (istniejąca lub projektowana).. Model fizyczny. 3. Model matematyczny (optymalizacyjny): a. Zmienne projektowania
SCHEMAT ROZWIĄZANIA ZADANIA OPTYMALIZACJI PRZY POMOCY ALGORYTMU GENETYCZNEGO. Rzeczywistość (istniejąca lub projektowana).. Model fizyczny. 3. Model matematyczny (optymalizacyjny): a. Zmienne projektowania
Testowanie hipotez statystycznych
 Agenda Instytut Matematyki Politechniki Łódzkiej 2 stycznia 2012 Agenda Agenda 1 Wprowadzenie Agenda 2 Hipoteza oraz błędy I i II rodzaju Hipoteza alternatywna Statystyka testowa Zbiór krytyczny Poziom
Agenda Instytut Matematyki Politechniki Łódzkiej 2 stycznia 2012 Agenda Agenda 1 Wprowadzenie Agenda 2 Hipoteza oraz błędy I i II rodzaju Hipoteza alternatywna Statystyka testowa Zbiór krytyczny Poziom
Stanisław Cichocki Natalia Nehrebecka. Zajęcia 11-12
 Stanisław Cichocki Natalia Nehrebecka Zajęcia 11-12 1. Zmienne pominięte 2. Zmienne nieistotne 3. Obserwacje nietypowe i błędne 4. Współliniowość - Mamy 2 modele: y X u 1 1 (1) y X X 1 1 2 2 (2) - Potencjalnie
Stanisław Cichocki Natalia Nehrebecka Zajęcia 11-12 1. Zmienne pominięte 2. Zmienne nieistotne 3. Obserwacje nietypowe i błędne 4. Współliniowość - Mamy 2 modele: y X u 1 1 (1) y X X 1 1 2 2 (2) - Potencjalnie
Zawartość. Zawartość
 Opr. dr inż. Grzegorz Biesok. Wer. 2.05 2011 Zawartość Zawartość 1. Rozkład normalny... 3 2. Rozkład normalny standardowy... 5 3. Obliczanie prawdopodobieństw dla zmiennych o rozkładzie norm. z parametrami
Opr. dr inż. Grzegorz Biesok. Wer. 2.05 2011 Zawartość Zawartość 1. Rozkład normalny... 3 2. Rozkład normalny standardowy... 5 3. Obliczanie prawdopodobieństw dla zmiennych o rozkładzie norm. z parametrami
Urbanizacja obszarów wiejskich w Polsce na przełomie XX i XXI wieku
 Uniwersytet Mikołaja Kopernika w Toruniu Wydział Biologii i Nauk o Ziemi Instytut Geografii Jadwiga Biegańska Urbanizacja obszarów wiejskich w Polsce na przełomie XX i XXI wieku Praca doktorska wykonana
Uniwersytet Mikołaja Kopernika w Toruniu Wydział Biologii i Nauk o Ziemi Instytut Geografii Jadwiga Biegańska Urbanizacja obszarów wiejskich w Polsce na przełomie XX i XXI wieku Praca doktorska wykonana
