Podstawy graki 3D. Ostrosªup widzenia. Piotr Fulma«ski. 11 czerwca 2014
|
|
|
- Jan Marciniak
- 8 lat temu
- Przeglądów:
Transkrypt
1 Podstawy graki 3D Ostrosªup widzenia Piotr Fulma«ski Instytut Nauk Ekonomicznych i Informatyki, Pa«stwowa Wy»sza Szkoªa Zawodowa w Pªocku, Polska 11 czerwca 2014
2 1 3D projection Spis tre±ci
3 3D projection Types Podstawowym przeksztaªceniem w grace trójwymiarowej jest rzutowanie, gdy» komputerowa wizualizacja jakiegokolwiek obiektu przestrzennego wymaga odwzorowania go na pªaski ekran monitora. Metody rzutowania mo»emy podzieli na dwie grupy rzuty perspektywicze (realistyczna wizualizacja obiektów, wra»enie gª bi), rzuty równolegªe (rysunek techniczny; zachowuje równolegªo± prostych, stosunek dªugo±ci odcinków równolegªych itd).
4 3D projection Comments Przy rzutowaniu na pªaszczyzn Π obrazem punktu p jest punkt p przeci cia si tej pªaszczyzny z prost (nazywan promieniem rzutowania) przechodz c przez p. Oczywi±cie takich prostych jest niesko«czenie wiele, ale w przypadku rzutu perspektywicznego ustalamy,»e wszystkie proste (promienie rzutowania) maj wspólny punkt e (odlegªo± tego punktu od rzutni Π decyduje o deformacji rysunku); rzutu równolegªego ustalamy,»e wszystkie proste maj ten sam kierunek rzutowania d (je±li jest on prostopadªy do rzutni, to rzut nazywamy ortogonalnym).
5 3D projection In practice simple case In practice znalezienie wspórz dnych rzutu p punktu p sprowadza si do rozwi zania zadania wyznaczenia przeciecia pªaszczyzny Π i prostej (promienia rzutowania) okre±lonej punktem p i kierunkiem d przy rzucie równolegªym lub punktem p i ±rodkiem rzutowania e w przypadku rzutu perspektywicznego. Zauwa»my przy tym,»e milcz co zaªo»yli±my, i» poªo»enie wszelkich obiektów wyra»one jest w jednym i tym samym ukªadzie wspóªrz dnych: w ukªadzie, w którym zostaª opisany rysowany obiekt (ukªad danych, world-space coordinates); rys : wspolnyukladdlawszystkiego wszystkie obiekty umiejscowione s na scenie w taki sposób aby±my nie musieli przejmowa si ich widzialno±ci (tzn. zakªadamy,»e wszystkie obiekty daj si narysowa ).
6 3D projection In practice real case Unfortunately real life is not so simple. Jak ju» zauwa»yli±my, stosuj c uprzednio opisane podej±cie otrzymujemy wspóªrz dne punktu p w ukªadzie trójwymiarowym, w którym zostaª opisany rysowany obiekt (world-space coordinates). My natomiast potrzebujemy wspóªrz dnych w ukªadzie dwuwymiarowym okre±lonym na pªaszczy¹nie rzutowania Π. Metod wyznaczenia takich wspóªrz dnych jest wiele w dalszej cz ±ci omówimy: intuitive approach (screen space = view space), ostrosªup widzenia (view frustum). Dodatkow trudno±ci jest to,»e zwykle musimy pracowa z wi cej ni» dwoma ukªadami wspóªrz dnych (zwykle przynajmniej dwa, gdy» mamy ukªad danych oraz ukªad zwi zany z punktami pªaszczyzny Π). rys : wieleukladow
7 3D projection In practice: intuitive approach (screen space = view space): rzut równolegªy Najbardziej intuicyjnym rozwi zaniem jest przyj cie, i» rzutnia Π pokrywa si z pªaszczyzn z = 0 ukªadu obserwatora. Zalety takiego wyboru ukªadu najlepiej wida przy rzucie ortogonalnym, kiedy rzutem punktu p = (x, y, z) jest punkt p = (x, y, 0). Uogólniaj c rzut ortogonalny na dowolny rzut równolegªy w którym kierunek rzutu równolegªego tworzy z rzutni Π kat α otrzymujemy nast pujace wspóªrz dne x i y rzutu punktu p = (x, y, z) x = x + r cos ϕ y = y + r sin ϕ gdzie r = x ctg α a ϕ jest k tem nachylenia prostej przechodz cej przez (x, y, 0) i (x, y, 0) do osi x. Uzyskanie warto±ci dla α i ϕ nie jest trudne, gdy» zwykle kierunek d wyra»a si wªa±nie przez podanie tych k tów a nie odpowiednich skªadowych tworz cych wektor d. rys : ogolnyrzutrownolegly
8 3D projection In practice: intuitive approach (screen space = view space): rzut perspektywiczny Uto»samiamy obserwatora ze ±rodkiem rzutowania e, który znajduje si na ujemnej cz ±ci ukªadu w punkcie (0, 0, e z ) (a wi c korzystamy z lewoskr tnego ukªadu wspóªrz dnych, left-handed coordinate system). Korzystaj c jedynie z wªasno±ci podobie«stwa trójk tów bez kªopotu znajdujemy zale»no±ci pomi dzy p i p x = xs, y = ys, gdzie s jest skal podobie«stwa wynosz c e z z+e z (patrz rysunek) rys : rzutsrodkowy
9 3D projection View frustum In 3D computer graphics, the viewing frustum or view frustum is the region of space in the modeled world that may appear on the screen; it is the eld of view of the notional camera. The exact shape of this region varies depending on what kind of camera lens is being simulated, but typically it is a frustum of a rectangular pyramid (hence the name). The planes that cut the frustum perpendicular to the viewing direction are called the near plane and the far plane. Objects closer to the camera than the near plane or beyond the far plane are not drawn. Often, the far plane is placed innitely far away from the camera so all objects within the frustum are drawn regardless of their distance from the camera.
10 3D projection View frustum W tym podej±ciu ±rodek rzutowania e pokrywa si z wierzchoªkiem ostrosªupa widzenia a w konsekwencji screen space (czyli rzutnia Π) nie jest tym samym co ukªad obserwatora (view space). Zadania stawiane przed nami w tym podej±ciu to: wyznaczenie wierzchoªków lub pªaszczyzn ograniczaj cych ostrosªu widzenia; rozstrzyaganie czy punkt p le»y wewn trz ostrosªupa widzenia (w szczególno±ci interesuje nas wspóªrz dna z jej znajomo± pozwoli nam wyznacza obiekty zasªaniane o której nie mieli±my»adnej informacji w poprzednim podej±ciu); poszukiwanie wspóªrz dnych rzutu perspektywicznego p punktu p w ukªadzie ekranu (screen space) a wi c na rzutni Π.
11 View frustum parameters Before we start calculation notice that the view frustum is dened by two sets of parameters Set of view parameters : the camera position, the look and up vector. The up vector determines the tilt of the scene. These parameters determine the general direction and orientation for the view frustum. Set of projection parameters : these parameters determine the shape for the view frustum. The eld of view (fov) parameter determines how much of the scene will be visible, the near plane and far plane parameters are distances that dene clipping planes. The aspect ratio parameter denes the ratio between the width and height of the view volume (width is dened in the direction of the right vector, height is dened in the direction of the up vector). rys : viewfrustumparams
12 Height of view frustum Assume that view space is dened by unit vectors e 1 = (1, 0, 0), e 2 = (0, 1, 0) and e 3 = (0, 0, 1) coresponding to right, up and look vector respectively. Then it is very easy to calculate the centres of the near and far clip plane img : sideview n c = e + ne 3, f c = e + fe 3, where e corresponds to frustum top typicaly e = (0, 0, 0), n is a distance to near clipping plane, f is a far clipping plane and e 3 is a look vector.
13 Height of view frustum We can now use centre points as base points to calculate the corners of the near and far clip plane. The half height of the near and far plane are given by h n = n tg(ϕ), h f = f tg(ϕ), where ϕ is a half the eld of view in radians.
14 Width of view frustum For the width of the near and far plane we need to take the aspect ratio into account img : topview w n = h n a, w f = h f a, where a is a given aspect ration (which sholud full the following equation a = w n h n = w f ). h f
15 Coordinates of the 8 points that dene the view frustum volume p nrb = n c h n e 2 + w n e 1, p nrt = n c + h n e 2 + w n e 1, p nlt = n c + h n e 2 w n e 1, p nlb = n c h n e 2 w n e 1, p frb = f c h f e 2 + w f e 1, p frt = f c + h f e 2 + w f e 1, p t = f c + h f e 2 w f e 1, p b = f c h f e 2 w f e 1.
16 Homogeneous clip space. Transformation of x and y Now we are going to transform a vertex in the view frustum to a homogeneous coordinate in the unit cube. Assume that the view frustum is dened as a pyramid starting at point e = (0, 0, 0) and left-handed coordinate system is used. We start with the formula for the x and y value. The projected x and y coordinates can be found by projecting the x and y values of the vertices on the near plane and dividing by half the near plane width and height (see gure and compare with previous part of this lecture) img : projectionofyonthenearplane As we have seen before, the formula for the y coordinate is easy to derive by application of congruent triangles y n = y z, where n is the length of n c vector. In consequence y = yn z.
17 Homogeneous clip space. Transformation of x and y Now have a y value in the range [ h n, +h n ] for vertices inside the view frustum. For a correct DirectX or OpenGL projection transform we need to calculate a y value in the range of [ 1, +1]. To do this, we just need to divide the y value with half of the near height. Because the half height of the near plane, previously calculated, is given by h n = n tg(ϕ), then and nally y = y = yn zn tg(ϕ), y z tg(ϕ) The nal y coordinate is inside the [ 1, +1] range for vertices inside the view frustum.
18 Homogeneous clip space. Transformation of x and y The x coordinate is calculated in exactly the same way as y, but we need to take the aspect ratio of the view frustum into account x n = x z, where n is the length of n c vector. In consequence x = xn z. Again, for vertices inside the view frustum, x is in the range [ w n, +w n ] and this range needs to be converted to the range [ 1, +1]. The aspect ratio for a perspective transform which denes the width of the near plane relative to the height of the near plane is equal to so we have a = w n h n. w n = ah n, w n = an tg(ϕ).
19 Homogeneous clip space. Transformation of x and y In consequence we have x = xn zan tg(ϕ), and nally In consequence we have x = x za tg(ϕ). Again for vertices inside the view frustum, x is inside the range [ 1, +1].
20 Matrix form for the transformation As always we want to apply the formulas via a 4x4 matrix. The following matrix is only valid for the transformation of the x and y coordinates (matrix is in row major order) 1 a tg(ϕ) [x, y, z, 1] 0 tg(ϕ) [ [x, y, z, w ] = x a tg(ϕ), ] y tg(ϕ), z, z.
21 Matrix form for the transformation If we divide this homogeneous coordinate by the w coordinate to convert to a normal 3D coordinate, we get the following result ] [ [ x w, y w, z w [ x w, y w, z w = ] [ = x aw tg(ϕ), x az tg(ϕ), y w tg(ϕ), w w ] y z tg(ϕ), 1. The x and y coordinate are correct, however the z coordinate is messed up, it is always one. So we have to change something in the perspective matrix to create a valid z value. ].
22 Transformation z coordinate: shift and scale The DirectX and OpenGL pipeline requires that the z value after the perspective transform is in the range [0,1] (or [-1,1] for OpenGL). The z value before previously discussed transform is in the range [near, far]. We start with a simple range conversion that will transform the [n, f ] range to the range [0, 1]. Because the shift z n transform the [n, f ] range to the range [0, f n], so z n f n transform the [n, f ] range to the range [0, 1]. To t this conversion into the transformation matrix we have to split it into 2 terms, a factor to scale z with and a factor to shift z f + n n f. n
23 Transformation z coordinate: shift and scale Taking both factors, our matrix takes the form 1 a tg(ϕ) [x, y, z, 1] tg(ϕ) f n n 0 0 [ [x, y, z, w ] = x a tg(ϕ), f n 0 y tg(ϕ), z n f, n z Unfortunately, this is still not correct. When we convert the homogeneous coordinate back to a normal 3D coordinate we get ] [ [ x w, y w, z w = x az tg(ϕ), y z tg(ϕ), z n ]. (f n)z ].
24 Transformation z coordinate: shift and scale Notice, that the homogeneous conversion which results the form [ ] [ ] x w, y w, z x w = az tg(ϕ), y z tg(ϕ), z n (f n)z reintroduces undesirable term ( 1 ) into the transformed z coordinated, z which breaks our conversion. Fortunately there is a quick x to restore the range for the z values: it is enough multiply the shift factor with the f value (because division by z introduced range [0, 1]) f 1 a tg(ϕ) [x, y, z, 1] tg(ϕ) f n nf 0 0 f n 0
25 Final matrix 1 a tg(ϕ) [x, y, z, 1] tg(ϕ) f n nf f n [ ] [x, y, z, w x ] = a tg(ϕ), y (z n)f, tg(ϕ) f, n z ] [ ] w, y w, z x w = az tg(ϕ), y (z n)f, z tg(ϕ) (f n)z [ x
26 Final world Unfortunately the division by z introduces the non linearity of the z buer. This non linearity is usually sold as benecial for the precision of the z buer close to the camera, however it dramatically reduces the resolution of the z buer a bit further from the camera. For example, if the near plane is set to 1 and the far plane is set to 100 than when z is 40 the resulting transformed z is allready at 0.98, leaving only a small amount of resolution to the following 60% of the scene.
27 Convert to screen space coordinates Because our transformatio transforms the vertices to the range of [ 1, 1] we need to convert the range [ 1, 1] to the range [0, window width] for the x coordinate and to the range [0, window height] for the y coordinate. The window width and window height are expressed in pixel units. The formula for this conversion is x = xw 2 + w 2, y = yh 2 + h 2. The same expressed as a matrix [x, y, z, 1] w h w h
Teoria i praktyka programowania gier komputerowych
 Teoria i praktyka programowania gier komputerowych 3D projection Piotr Fulma«ski Wydziaª Matematyki i Informatyki, Uniwersytet Šódzki, Polska 8 grudnia 2014 Spis tre±ci 1 View (Camera) Space 2 3D projection
Teoria i praktyka programowania gier komputerowych 3D projection Piotr Fulma«ski Wydziaª Matematyki i Informatyki, Uniwersytet Šódzki, Polska 8 grudnia 2014 Spis tre±ci 1 View (Camera) Space 2 3D projection
Stereometria (geometria przestrzenna)
 Stereometria (geometria przestrzenna) Wzajemne poªo»enie prostych w przestrzeni Stereometria jest dziaªem geometrii, którego przedmiotem bada«s bryªy przestrzenne oraz ich wªa±ciwo±ci. Na pocz tek omówimy
Stereometria (geometria przestrzenna) Wzajemne poªo»enie prostych w przestrzeni Stereometria jest dziaªem geometrii, którego przedmiotem bada«s bryªy przestrzenne oraz ich wªa±ciwo±ci. Na pocz tek omówimy
Zadania z z matematyki dla studentów gospodarki przestrzennej UŠ. Marek Majewski Aktualizacja: 31 pa¹dziernika 2006
 Zadania z z matematyki dla studentów gospodarki przestrzennej UŠ Marek Majewski Aktualizacja: 1 pa¹dziernika 006 Spis tre±ci 1 Macierze dziaªania na macierzach. Wyznaczniki 1 Macierz odwrotna. Rz d macierzy
Zadania z z matematyki dla studentów gospodarki przestrzennej UŠ Marek Majewski Aktualizacja: 1 pa¹dziernika 006 Spis tre±ci 1 Macierze dziaªania na macierzach. Wyznaczniki 1 Macierz odwrotna. Rz d macierzy
Arkusz 4. Elementy geometrii analitycznej w przestrzeni
 Arkusz 4. Elementy geometrii analitycznej w przestrzeni Zadanie 4.1. Obliczy dªugo±ci podanych wektorów a) a = [, 4, 12] b) b = [, 5, 2 2 ] c) c = [ρ cos φ, ρ sin φ, h], ρ 0, φ, h R c) d = [ρ cos φ cos
Arkusz 4. Elementy geometrii analitycznej w przestrzeni Zadanie 4.1. Obliczy dªugo±ci podanych wektorów a) a = [, 4, 12] b) b = [, 5, 2 2 ] c) c = [ρ cos φ, ρ sin φ, h], ρ 0, φ, h R c) d = [ρ cos φ cos
Helena Boguta, klasa 8W, rok szkolny 2018/2019
 Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Składają się na
Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Składają się na
Elementy geometrii w przestrzeni R 3
 Elementy geometrii w przestrzeni R 3 Z.Šagodowski Politechnika Lubelska 29 maja 2016 Podstawowe denicje Wektorem nazywamy uporz dkowan par punktów (A,B) z których pierwszy nazywa si pocz tkiem a drugi
Elementy geometrii w przestrzeni R 3 Z.Šagodowski Politechnika Lubelska 29 maja 2016 Podstawowe denicje Wektorem nazywamy uporz dkowan par punktów (A,B) z których pierwszy nazywa si pocz tkiem a drugi
Graka komputerowa Wykªad 3 Geometria pªaszczyzny
 Graka komputerowa Wykªad 3 Geometria pªaszczyzny Instytut Informatyki i Automatyki Pa«stwowa Wy»sza Szkoªa Informatyki i Przedsi biorczo±ci w Šom»y 2 0 0 9 Spis tre±ci Spis tre±ci 1 Przeksztaªcenia pªaszczyzny
Graka komputerowa Wykªad 3 Geometria pªaszczyzny Instytut Informatyki i Automatyki Pa«stwowa Wy»sza Szkoªa Informatyki i Przedsi biorczo±ci w Šom»y 2 0 0 9 Spis tre±ci Spis tre±ci 1 Przeksztaªcenia pªaszczyzny
r = x x2 2 + x2 3.
 Przestrze«aniczna Def. 1. Przestrzeni aniczn zwi zan z przestrzeni liniow V nazywamy dowolny niepusty zbiór P z dziaªaniem ω : P P V (które dowolnej parze elementów zbioru P przyporz dkowuje wektor z przestrzeni
Przestrze«aniczna Def. 1. Przestrzeni aniczn zwi zan z przestrzeni liniow V nazywamy dowolny niepusty zbiór P z dziaªaniem ω : P P V (które dowolnej parze elementów zbioru P przyporz dkowuje wektor z przestrzeni
Elementy geometrii analitycznej w przestrzeni
 Wykªad 3 Elementy geometrii analitycznej w przestrzeni W wykªadzie tym wi kszy nacisk zostaª poªo»ony raczej na intuicyjne rozumienie deniowanych poj, ni» ±cisªe ich zdeniowanie. Dlatego niniejszy wykªad
Wykªad 3 Elementy geometrii analitycznej w przestrzeni W wykªadzie tym wi kszy nacisk zostaª poªo»ony raczej na intuicyjne rozumienie deniowanych poj, ni» ±cisªe ich zdeniowanie. Dlatego niniejszy wykªad
Tychy, plan miasta: Skala 1: (Polish Edition)
 Tychy, plan miasta: Skala 1:20 000 (Polish Edition) Poland) Przedsiebiorstwo Geodezyjno-Kartograficzne (Katowice Click here if your download doesn"t start automatically Tychy, plan miasta: Skala 1:20 000
Tychy, plan miasta: Skala 1:20 000 (Polish Edition) Poland) Przedsiebiorstwo Geodezyjno-Kartograficzne (Katowice Click here if your download doesn"t start automatically Tychy, plan miasta: Skala 1:20 000
Machine Learning for Data Science (CS4786) Lecture11. Random Projections & Canonical Correlation Analysis
 Machine Learning for Data Science (CS4786) Lecture11 5 Random Projections & Canonical Correlation Analysis The Tall, THE FAT AND THE UGLY n X d The Tall, THE FAT AND THE UGLY d X > n X d n = n d d The
Machine Learning for Data Science (CS4786) Lecture11 5 Random Projections & Canonical Correlation Analysis The Tall, THE FAT AND THE UGLY n X d The Tall, THE FAT AND THE UGLY d X > n X d n = n d d The
Teoria i praktyka programowania gier komputerowych
 Teoria i praktyka programowania gier komputerowych Piotr Fulma«ski Wydziaª Matematyki i Informatyki, Uniwersytet Šódzki, Polska 2 grudnia 2015 Spis tre±ci 1 Aim of this lecture 2 M view viewport transformation
Teoria i praktyka programowania gier komputerowych Piotr Fulma«ski Wydziaª Matematyki i Informatyki, Uniwersytet Šódzki, Polska 2 grudnia 2015 Spis tre±ci 1 Aim of this lecture 2 M view viewport transformation
Camspot 4.4 Camspot 4.5
 User manual (addition) Dodatek do instrukcji obsługi Camspot 4.4 Camspot 4.5 1. WiFi configuration 2. Configuration of sending pictures to e-mail/ftp after motion detection 1. Konfiguracja WiFi 2. Konfiguracja
User manual (addition) Dodatek do instrukcji obsługi Camspot 4.4 Camspot 4.5 1. WiFi configuration 2. Configuration of sending pictures to e-mail/ftp after motion detection 1. Konfiguracja WiFi 2. Konfiguracja
Wektory w przestrzeni
 Wektory w przestrzeni Informacje pomocnicze Denicja 1. Wektorem nazywamy uporz dkowan par punktów. Pierwszy z tych punktów nazywamy pocz tkiem wektora albo punktem zaczepienia wektora, a drugi - ko«cem
Wektory w przestrzeni Informacje pomocnicze Denicja 1. Wektorem nazywamy uporz dkowan par punktów. Pierwszy z tych punktów nazywamy pocz tkiem wektora albo punktem zaczepienia wektora, a drugi - ko«cem
Machine Learning for Data Science (CS4786) Lecture 11. Spectral Embedding + Clustering
 Machine Learning for Data Science (CS4786) Lecture 11 Spectral Embedding + Clustering MOTIVATING EXAMPLE What can you say from this network? MOTIVATING EXAMPLE How about now? THOUGHT EXPERIMENT For each
Machine Learning for Data Science (CS4786) Lecture 11 Spectral Embedding + Clustering MOTIVATING EXAMPLE What can you say from this network? MOTIVATING EXAMPLE How about now? THOUGHT EXPERIMENT For each
Weronika Mysliwiec, klasa 8W, rok szkolny 2018/2019
 Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Tresci zadań rozwiązanych
Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Tresci zadań rozwiązanych
Hard-Margin Support Vector Machines
 Hard-Margin Support Vector Machines aaacaxicbzdlssnafiyn9vbjlepk3ay2gicupasvu4iblxuaw2hjmuwn7ddjjmxm1bkcg1/fjqsvt76fo9/gazqfvn8y+pjpozw5vx8zkpvtfxmlhcwl5zxyqrm2vrg5zw3vxmsoezi4ogkr6phieky5crvvjhriqvdom9l2xxftevuwcekj3lktmhghgniauiyutvrwxtvme34a77kbvg73gtygpjsrfati1+xc8c84bvraowbf+uwnipyehcvmkjrdx46vlykhkgykm3ujjdhcyzqkxy0chur6ax5cbg+1m4bbjptjcubuz4kuhvjoql93hkin5hxtav5x6yyqopnsyuneey5ni4keqrxbar5wqaxbik00icyo/iveiyqqvjo1u4fgzj/8f9x67bzmxnurjzmijtlybwfgcdjgfdtajwgcf2dwaj7ac3g1ho1n4814n7wwjgjmf/ys8fenfycuzq==
Hard-Margin Support Vector Machines aaacaxicbzdlssnafiyn9vbjlepk3ay2gicupasvu4iblxuaw2hjmuwn7ddjjmxm1bkcg1/fjqsvt76fo9/gazqfvn8y+pjpozw5vx8zkpvtfxmlhcwl5zxyqrm2vrg5zw3vxmsoezi4ogkr6phieky5crvvjhriqvdom9l2xxftevuwcekj3lktmhghgniauiyutvrwxtvme34a77kbvg73gtygpjsrfati1+xc8c84bvraowbf+uwnipyehcvmkjrdx46vlykhkgykm3ujjdhcyzqkxy0chur6ax5cbg+1m4bbjptjcubuz4kuhvjoql93hkin5hxtav5x6yyqopnsyuneey5ni4keqrxbar5wqaxbik00icyo/iveiyqqvjo1u4fgzj/8f9x67bzmxnurjzmijtlybwfgcdjgfdtajwgcf2dwaj7ac3g1ho1n4814n7wwjgjmf/ys8fenfycuzq==
Lecture 20. Fraunhofer Diffraction - Transforms
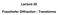 Lecture 20 Fraunhofer Diffraction - Transforms Fraunhofer Diffraction U P ' &iku 0 2 zz ) e ik PS m A exp ' &iku 0 2 zz ) e ik PS exp ik 2z a [x 2 m % y 2 m ]. m A exp ik 2z a & x m ) 2 % (y 0 & y m )
Lecture 20 Fraunhofer Diffraction - Transforms Fraunhofer Diffraction U P ' &iku 0 2 zz ) e ik PS m A exp ' &iku 0 2 zz ) e ik PS exp ik 2z a [x 2 m % y 2 m ]. m A exp ik 2z a & x m ) 2 % (y 0 & y m )
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition)
 Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Zakopane, plan miasta: Skala ok. 1: = City map (Polish Edition)
 Zakopane, plan miasta: Skala ok. 1:15 000 = City map (Polish Edition) Click here if your download doesn"t start automatically Zakopane, plan miasta: Skala ok. 1:15 000 = City map (Polish Edition) Zakopane,
Zakopane, plan miasta: Skala ok. 1:15 000 = City map (Polish Edition) Click here if your download doesn"t start automatically Zakopane, plan miasta: Skala ok. 1:15 000 = City map (Polish Edition) Zakopane,
Stargard Szczecinski i okolice (Polish Edition)
 Stargard Szczecinski i okolice (Polish Edition) Janusz Leszek Jurkiewicz Click here if your download doesn"t start automatically Stargard Szczecinski i okolice (Polish Edition) Janusz Leszek Jurkiewicz
Stargard Szczecinski i okolice (Polish Edition) Janusz Leszek Jurkiewicz Click here if your download doesn"t start automatically Stargard Szczecinski i okolice (Polish Edition) Janusz Leszek Jurkiewicz
Installation of EuroCert software for qualified electronic signature
 Installation of EuroCert software for qualified electronic signature for Microsoft Windows systems Warsaw 28.08.2019 Content 1. Downloading and running the software for the e-signature... 3 a) Installer
Installation of EuroCert software for qualified electronic signature for Microsoft Windows systems Warsaw 28.08.2019 Content 1. Downloading and running the software for the e-signature... 3 a) Installer
Revenue Maximization. Sept. 25, 2018
 Revenue Maximization Sept. 25, 2018 Goal So Far: Ideal Auctions Dominant-Strategy Incentive Compatible (DSIC) b i = v i is a dominant strategy u i 0 x is welfare-maximizing x and p run in polynomial time
Revenue Maximization Sept. 25, 2018 Goal So Far: Ideal Auctions Dominant-Strategy Incentive Compatible (DSIC) b i = v i is a dominant strategy u i 0 x is welfare-maximizing x and p run in polynomial time
Standardized Test Practice
 Standardized Test Practice 1. Which of the following is the length of a three-dimensional diagonal of the figure shown? a. 4.69 units b. 13.27 units c. 13.93 units 3 d. 16.25 units 8 2. Which of the following
Standardized Test Practice 1. Which of the following is the length of a three-dimensional diagonal of the figure shown? a. 4.69 units b. 13.27 units c. 13.93 units 3 d. 16.25 units 8 2. Which of the following
Wprowadzenie do programu RapidMiner, część 2 Michał Bereta 1. Wykorzystanie wykresu ROC do porównania modeli klasyfikatorów
 Wprowadzenie do programu RapidMiner, część 2 Michał Bereta www.michalbereta.pl 1. Wykorzystanie wykresu ROC do porównania modeli klasyfikatorów Zaimportuj dane pima-indians-diabetes.csv. (Baza danych poświęcona
Wprowadzenie do programu RapidMiner, część 2 Michał Bereta www.michalbereta.pl 1. Wykorzystanie wykresu ROC do porównania modeli klasyfikatorów Zaimportuj dane pima-indians-diabetes.csv. (Baza danych poświęcona
Katowice, plan miasta: Skala 1: = City map = Stadtplan (Polish Edition)
 Katowice, plan miasta: Skala 1:20 000 = City map = Stadtplan (Polish Edition) Polskie Przedsiebiorstwo Wydawnictw Kartograficznych im. Eugeniusza Romera Click here if your download doesn"t start automatically
Katowice, plan miasta: Skala 1:20 000 = City map = Stadtplan (Polish Edition) Polskie Przedsiebiorstwo Wydawnictw Kartograficznych im. Eugeniusza Romera Click here if your download doesn"t start automatically
Rachunek caªkowy funkcji wielu zmiennych
 Rachunek caªkowy funkcji wielu zmiennych I. Malinowska, Z. Šagodowski Politechnika Lubelska 8 czerwca 2015 Caªka iterowana podwójna Denicja Je»eli funkcja f jest ci gªa na prostok cie P = {(x, y) : a x
Rachunek caªkowy funkcji wielu zmiennych I. Malinowska, Z. Šagodowski Politechnika Lubelska 8 czerwca 2015 Caªka iterowana podwójna Denicja Je»eli funkcja f jest ci gªa na prostok cie P = {(x, y) : a x
SSW1.1, HFW Fry #20, Zeno #25 Benchmark: Qtr.1. Fry #65, Zeno #67. like
 SSW1.1, HFW Fry #20, Zeno #25 Benchmark: Qtr.1 I SSW1.1, HFW Fry #65, Zeno #67 Benchmark: Qtr.1 like SSW1.2, HFW Fry #47, Zeno #59 Benchmark: Qtr.1 do SSW1.2, HFW Fry #5, Zeno #4 Benchmark: Qtr.1 to SSW1.2,
SSW1.1, HFW Fry #20, Zeno #25 Benchmark: Qtr.1 I SSW1.1, HFW Fry #65, Zeno #67 Benchmark: Qtr.1 like SSW1.2, HFW Fry #47, Zeno #59 Benchmark: Qtr.1 do SSW1.2, HFW Fry #5, Zeno #4 Benchmark: Qtr.1 to SSW1.2,
WBiA Architektura i Urbanistyka. 1. Wykonaj dziaªania na macierzach: Które z iloczynów: A 2 B, AB 2, BA 2, B 2 3, B = 1 2 0
 WBiA Architektura i Urbanistyka Matematyka wiczenia 1. Wykonaj dziaªania na macierzach: 1) 2A + C 2) A C T ) B A 4) B C T 5) A 2 B T 1 0 2 dla A = 1 2 1 1 0 B = ( 1 2 1 0 1 ) C = 1 2 1 0 2 1 0 1 2. Które
WBiA Architektura i Urbanistyka Matematyka wiczenia 1. Wykonaj dziaªania na macierzach: 1) 2A + C 2) A C T ) B A 4) B C T 5) A 2 B T 1 0 2 dla A = 1 2 1 1 0 B = ( 1 2 1 0 1 ) C = 1 2 1 0 2 1 0 1 2. Które
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition)
 Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Krzywe i powierzchnie stopnia drugiego
 Krzywe i powierzchnie stopnia drugiego Iwona Malinowska, Zbigniew Šagodowski 25 maja 2015 I. Malinowska, Z. Lagodowski Geometria 25 maja 2015 1 / 30 Rozwa»my dwie proste przecinaj ce si pod k tem α, 0
Krzywe i powierzchnie stopnia drugiego Iwona Malinowska, Zbigniew Šagodowski 25 maja 2015 I. Malinowska, Z. Lagodowski Geometria 25 maja 2015 1 / 30 Rozwa»my dwie proste przecinaj ce si pod k tem α, 0
Some Linear Algebra. Vectors operations = =(,, ) =( 1 + 2, 1 + 2, ) λ =(λ,λ,λ ) Addition. Scalar multiplication.
 Basic Geometry Vectors operations Some Linear Algebra Addition + 2 =( 1 + 2, 1 + 2, 1 + 2 ) =(,, ) + Scalar multiplication λ =(λ,λ,λ ) Norm = 2 + 2 + 2 2 Scalar Product Commutative Linear Orthogonally
Basic Geometry Vectors operations Some Linear Algebra Addition + 2 =( 1 + 2, 1 + 2, 1 + 2 ) =(,, ) + Scalar multiplication λ =(λ,λ,λ ) Norm = 2 + 2 + 2 2 Scalar Product Commutative Linear Orthogonally
MaPlan Sp. z O.O. Click here if your download doesn"t start automatically
 Mierzeja Wislana, mapa turystyczna 1:50 000: Mikoszewo, Jantar, Stegna, Sztutowo, Katy Rybackie, Przebrno, Krynica Morska, Piaski, Frombork =... = Carte touristique (Polish Edition) MaPlan Sp. z O.O Click
Mierzeja Wislana, mapa turystyczna 1:50 000: Mikoszewo, Jantar, Stegna, Sztutowo, Katy Rybackie, Przebrno, Krynica Morska, Piaski, Frombork =... = Carte touristique (Polish Edition) MaPlan Sp. z O.O Click
SubVersion. Piotr Mikulski. SubVersion. P. Mikulski. Co to jest subversion? Zalety SubVersion. Wady SubVersion. Inne różnice SubVersion i CVS
 Piotr Mikulski 2006 Subversion is a free/open-source version control system. That is, Subversion manages files and directories over time. A tree of files is placed into a central repository. The repository
Piotr Mikulski 2006 Subversion is a free/open-source version control system. That is, Subversion manages files and directories over time. A tree of files is placed into a central repository. The repository
DUAL SIMILARITY OF VOLTAGE TO CURRENT AND CURRENT TO VOLTAGE TRANSFER FUNCTION OF HYBRID ACTIVE TWO- PORTS WITH CONVERSION
 ELEKTRYKA 0 Zeszyt (9) Rok LX Andrzej KUKIEŁKA Politechnika Śląska w Gliwicach DUAL SIMILARITY OF VOLTAGE TO CURRENT AND CURRENT TO VOLTAGE TRANSFER FUNCTION OF HYBRID ACTIVE TWO- PORTS WITH CONVERSION
ELEKTRYKA 0 Zeszyt (9) Rok LX Andrzej KUKIEŁKA Politechnika Śląska w Gliwicach DUAL SIMILARITY OF VOLTAGE TO CURRENT AND CURRENT TO VOLTAGE TRANSFER FUNCTION OF HYBRID ACTIVE TWO- PORTS WITH CONVERSION
Geometria. Šukasz Dawidowski. 25 kwietnia 2016r. Powtórki maturalne
 Geometria Šukasz Dawidowski Powtórki maturalne 25 kwietnia 2016r. Dane s równania postych, w których zawarte s boki trójk ta ABC : 3x 4y + 36 = 0 x y = 0 4x + 3y + 23 = 0 1. Obliczy wspóªrz dne wierzchoªków
Geometria Šukasz Dawidowski Powtórki maturalne 25 kwietnia 2016r. Dane s równania postych, w których zawarte s boki trójk ta ABC : 3x 4y + 36 = 0 x y = 0 4x + 3y + 23 = 0 1. Obliczy wspóªrz dne wierzchoªków
Rozpoznawanie twarzy metodą PCA Michał Bereta 1. Testowanie statystycznej istotności różnic między jakością klasyfikatorów
 Rozpoznawanie twarzy metodą PCA Michał Bereta www.michalbereta.pl 1. Testowanie statystycznej istotności różnic między jakością klasyfikatorów Wiemy, że możemy porównywad klasyfikatory np. za pomocą kroswalidacji.
Rozpoznawanie twarzy metodą PCA Michał Bereta www.michalbereta.pl 1. Testowanie statystycznej istotności różnic między jakością klasyfikatorów Wiemy, że możemy porównywad klasyfikatory np. za pomocą kroswalidacji.
EXAMPLES OF CABRI GEOMETRE II APPLICATION IN GEOMETRIC SCIENTIFIC RESEARCH
 Anna BŁACH Centre of Geometry and Engineering Graphics Silesian University of Technology in Gliwice EXAMPLES OF CABRI GEOMETRE II APPLICATION IN GEOMETRIC SCIENTIFIC RESEARCH Introduction Computer techniques
Anna BŁACH Centre of Geometry and Engineering Graphics Silesian University of Technology in Gliwice EXAMPLES OF CABRI GEOMETRE II APPLICATION IN GEOMETRIC SCIENTIFIC RESEARCH Introduction Computer techniques
Analysis of Movie Profitability STAT 469 IN CLASS ANALYSIS #2
 Analysis of Movie Profitability STAT 469 IN CLASS ANALYSIS #2 aaaklnictzzjb9tgfmcnadpg7oy0lxa9edva9kkapdarhyk2k7gourinlwsweyzikuyiigvyleiv/cv767fpf/5crc1xt9va5mx7w3m/ecuqw1kuztpx/rl3/70h73/w4cog9dhhn3z62d6jzy+yzj766txpoir9nzszisjynetqr+rvlfvyoozu5xbybpsxb1wahul8phczdt2v4zgchb7uecwphlyigrgkjcyiflfyci0kxnmr4z6kw0jsokvot8isntpa3gbknlcufiv/h+hh+eur4fomd417rvtfjoit5pfju6yxiab2fmwk0y/feuybobqk+axnke8xzjjhfyd8kkpl9zdoddkazd5j6bzpemjb64smjb6vb4xmehysu08lsrszopxftlzee130jcb0zjxy7r5wa2f1s2off2+dyatrughnrtpkuprlcpu55zlxpss/yqe2eamjkcf0jye8w8yas0paf6t0t2i9stmcua+inbi2rt01tz22tubbqwidypvgz6piynkpobirkxgu54ibzoti4pkw2i5ow9lnuaoabhuxfxqhvnrj6w15tb3furnbm+scyxobjhr5pmj5j/w5ix9wsa2tlwx9alpshlunzjgnrwvqbpwzjl9wes+ptyn+ypy/jgskavtl8j0hz1djdhzwtpjbbvpr1zj7jpg6ve7zxfngj75zee0vmp9qm2uvgu/9zdofq6r+g8l4xctvo+v+xdrfr8oxiwutycu0qgyf8icuyvp/sixfi9zxe11vp6mrjjovpmxm6acrtbia+wjr9bevlgjwlz5xd3rfna9g06qytaoofk8olxbxc7xby2evqjmmk6pjvvzxmpbnct6+036xp5vdbrnbdqph8brlfn/n/khnfumhf6z1v7h/80yieukkd5j0un82t9mynxzmk0s/bzn4tacdziszdhwrl8x5ako8qp1n1zn0k6w2em0km9zj1i4yt1pt3xiprw85jmc2m1ut2geum6y6es2fwx6c+wlrpykblopbuj5nnr2byygfy5opllv4+jmm7s6u+tvhywbnb0kv2lt5th4xipmiij+y1toiyo7bo0d+vzvovjkp6aoejsubhj3qrp3fjd/m23pay8h218ibvx3nicofvd1xi86+kh6nb/b+hgsjp5+qwpurzlir15np66vmdehh6tyazdm1k/5ejtuvurgcqux6yc+qw/sbsaj7lkt4x9qmtp7euk6zbdedyuzu6ptsu2eeu3rxcz06uf6g8wyuveznhkbzynajbb7r7cbmla+jbtrst0ow2v6ntkwv8svnwqnu5pa3oxfeexf93739p93chq/fv+jr8r0d9brhpcxr2w88bvqbr41j6wvrb+u5dzjpvx+veoaxwptzp/8cen+xbg==
Analysis of Movie Profitability STAT 469 IN CLASS ANALYSIS #2 aaaklnictzzjb9tgfmcnadpg7oy0lxa9edva9kkapdarhyk2k7gourinlwsweyzikuyiigvyleiv/cv767fpf/5crc1xt9va5mx7w3m/ecuqw1kuztpx/rl3/70h73/w4cog9dhhn3z62d6jzy+yzj766txpoir9nzszisjynetqr+rvlfvyoozu5xbybpsxb1wahul8phczdt2v4zgchb7uecwphlyigrgkjcyiflfyci0kxnmr4z6kw0jsokvot8isntpa3gbknlcufiv/h+hh+eur4fomd417rvtfjoit5pfju6yxiab2fmwk0y/feuybobqk+axnke8xzjjhfyd8kkpl9zdoddkazd5j6bzpemjb64smjb6vb4xmehysu08lsrszopxftlzee130jcb0zjxy7r5wa2f1s2off2+dyatrughnrtpkuprlcpu55zlxpss/yqe2eamjkcf0jye8w8yas0paf6t0t2i9stmcua+inbi2rt01tz22tubbqwidypvgz6piynkpobirkxgu54ibzoti4pkw2i5ow9lnuaoabhuxfxqhvnrj6w15tb3furnbm+scyxobjhr5pmj5j/w5ix9wsa2tlwx9alpshlunzjgnrwvqbpwzjl9wes+ptyn+ypy/jgskavtl8j0hz1djdhzwtpjbbvpr1zj7jpg6ve7zxfngj75zee0vmp9qm2uvgu/9zdofq6r+g8l4xctvo+v+xdrfr8oxiwutycu0qgyf8icuyvp/sixfi9zxe11vp6mrjjovpmxm6acrtbia+wjr9bevlgjwlz5xd3rfna9g06qytaoofk8olxbxc7xby2evqjmmk6pjvvzxmpbnct6+036xp5vdbrnbdqph8brlfn/n/khnfumhf6z1v7h/80yieukkd5j0un82t9mynxzmk0s/bzn4tacdziszdhwrl8x5ako8qp1n1zn0k6w2em0km9zj1i4yt1pt3xiprw85jmc2m1ut2geum6y6es2fwx6c+wlrpykblopbuj5nnr2byygfy5opllv4+jmm7s6u+tvhywbnb0kv2lt5th4xipmiij+y1toiyo7bo0d+vzvovjkp6aoejsubhj3qrp3fjd/m23pay8h218ibvx3nicofvd1xi86+kh6nb/b+hgsjp5+qwpurzlir15np66vmdehh6tyazdm1k/5ejtuvurgcqux6yc+qw/sbsaj7lkt4x9qmtp7euk6zbdedyuzu6ptsu2eeu3rxcz06uf6g8wyuveznhkbzynajbb7r7cbmla+jbtrst0ow2v6ntkwv8svnwqnu5pa3oxfeexf93739p93chq/fv+jr8r0d9brhpcxr2w88bvqbr41j6wvrb+u5dzjpvx+veoaxwptzp/8cen+xbg==
DODATKOWE ĆWICZENIA EGZAMINACYJNE
 I.1. X Have a nice day! Y a) Good idea b) See you soon c) The same to you I.2. X: This is my new computer. Y: Wow! Can I have a look at the Internet? X: a) Thank you b) Go ahead c) Let me try I.3. X: What
I.1. X Have a nice day! Y a) Good idea b) See you soon c) The same to you I.2. X: This is my new computer. Y: Wow! Can I have a look at the Internet? X: a) Thank you b) Go ahead c) Let me try I.3. X: What
Grafika komputerowa Wykład 4 Geometria przestrzenna
 Grafika komputerowa Wykład 4 Geometria przestrzenna Instytut Informatyki i Automatyki Państwowa Wyższa Szkoła Informatyki i Przedsiębiorczości w Łomży 2 0 0 9 Spis treści Spis treści 1 Geometria 3D - podstawowe
Grafika komputerowa Wykład 4 Geometria przestrzenna Instytut Informatyki i Automatyki Państwowa Wyższa Szkoła Informatyki i Przedsiębiorczości w Łomży 2 0 0 9 Spis treści Spis treści 1 Geometria 3D - podstawowe
Knovel Math: Jakość produktu
 Knovel Math: Jakość produktu Knovel jest agregatorem materiałów pełnotekstowych dostępnych w formacie PDF i interaktywnym. Narzędzia interaktywne Knovel nie są stworzone wokół specjalnych algorytmów wymagających
Knovel Math: Jakość produktu Knovel jest agregatorem materiałów pełnotekstowych dostępnych w formacie PDF i interaktywnym. Narzędzia interaktywne Knovel nie są stworzone wokół specjalnych algorytmów wymagających
Financial support for start-uppres. Where to get money? - Equity. - Credit. - Local Labor Office - Six times the national average wage (22000 zł)
 Financial support for start-uppres Where to get money? - Equity - Credit - Local Labor Office - Six times the national average wage (22000 zł) - only for unymployed people - the company must operate minimum
Financial support for start-uppres Where to get money? - Equity - Credit - Local Labor Office - Six times the national average wage (22000 zł) - only for unymployed people - the company must operate minimum
Wektor. Uporz dkowany ukªad liczb (najcz ±ciej: dwóch - na pªaszczy¹nie, trzech - w przestrzeni 3D).
 Wektor Uporz dkowany ukªad liczb (najcz ±ciej: dwóch - na pªaszczy¹nie, trzech - w przestrzeni 3D). Adam Szmagli«ski (IF PK) Wykªad z Fizyki dla I roku WIL Kraków, 10.10.2015 1 / 13 Wektor Uporz dkowany
Wektor Uporz dkowany ukªad liczb (najcz ±ciej: dwóch - na pªaszczy¹nie, trzech - w przestrzeni 3D). Adam Szmagli«ski (IF PK) Wykªad z Fizyki dla I roku WIL Kraków, 10.10.2015 1 / 13 Wektor Uporz dkowany
DO MONTAŻU POTRZEBNE SĄ DWIE OSOBY! INSTALLATION REQUIRES TWO PEOPLE!
 1 HAPPY ANIMALS B09 INSTRUKCJA MONTAŻU ASSEMBLY INSTRUCTIONS Akcesoria / Fittings K1 M M1 ZM1 Z T G1 17 szt. / pcs 13 szt. / pcs B1 13 szt. / pcs W4 13 szt. / pcs W6 14 szt. / pcs U1 1 szt. / pcs U N1
1 HAPPY ANIMALS B09 INSTRUKCJA MONTAŻU ASSEMBLY INSTRUCTIONS Akcesoria / Fittings K1 M M1 ZM1 Z T G1 17 szt. / pcs 13 szt. / pcs B1 13 szt. / pcs W4 13 szt. / pcs W6 14 szt. / pcs U1 1 szt. / pcs U N1
Jak zasada Pareto może pomóc Ci w nauce języków obcych?
 Jak zasada Pareto może pomóc Ci w nauce języków obcych? Artykuł pobrano ze strony eioba.pl Pokazuje, jak zastosowanie zasady Pareto może usprawnić Twoją naukę angielskiego. Słynna zasada Pareto mówi o
Jak zasada Pareto może pomóc Ci w nauce języków obcych? Artykuł pobrano ze strony eioba.pl Pokazuje, jak zastosowanie zasady Pareto może usprawnić Twoją naukę angielskiego. Słynna zasada Pareto mówi o
OpenPoland.net API Documentation
 OpenPoland.net API Documentation Release 1.0 Michał Gryczka July 11, 2014 Contents 1 REST API tokens: 3 1.1 How to get a token............................................ 3 2 REST API : search for assets
OpenPoland.net API Documentation Release 1.0 Michał Gryczka July 11, 2014 Contents 1 REST API tokens: 3 1.1 How to get a token............................................ 3 2 REST API : search for assets
HAPPY ANIMALS L01 HAPPY ANIMALS L03 HAPPY ANIMALS L05 HAPPY ANIMALS L07
 HAPPY ANIMALS L0 HAPPY ANIMALS L0 HAPPY ANIMALS L0 HAPPY ANIMALS L07 INSTRUKCJA MONTAŻU ASSEMBLY INSTRUCTIONS Akcesoria / Fittings K ZW W8 W7 Ø x 6 szt. / pcs Ø7 x 70 Narzędzia / Tools DO MONTAŻU POTRZEBNE
HAPPY ANIMALS L0 HAPPY ANIMALS L0 HAPPY ANIMALS L0 HAPPY ANIMALS L07 INSTRUKCJA MONTAŻU ASSEMBLY INSTRUCTIONS Akcesoria / Fittings K ZW W8 W7 Ø x 6 szt. / pcs Ø7 x 70 Narzędzia / Tools DO MONTAŻU POTRZEBNE
HAPPY ANIMALS L02 HAPPY ANIMALS L04 HAPPY ANIMALS L06 HAPPY ANIMALS L08
 HAPPY ANIMALS L02 HAPPY ANIMALS L04 HAPPY ANIMALS L06 HAPPY ANIMALS L08 INSTRUKCJA MONTAŻU ASSEMBLY INSTRUCTIONS Akcesoria / Fittings K O G ZW W8 W4 20 szt. / pcs 4 szt. / pcs 4 szt. / pcs 4 szt. / pcs
HAPPY ANIMALS L02 HAPPY ANIMALS L04 HAPPY ANIMALS L06 HAPPY ANIMALS L08 INSTRUKCJA MONTAŻU ASSEMBLY INSTRUCTIONS Akcesoria / Fittings K O G ZW W8 W4 20 szt. / pcs 4 szt. / pcs 4 szt. / pcs 4 szt. / pcs
Convolution semigroups with linear Jacobi parameters
 Convolution semigroups with linear Jacobi parameters Michael Anshelevich; Wojciech Młotkowski Texas A&M University; University of Wrocław February 14, 2011 Jacobi parameters. µ = measure with finite moments,
Convolution semigroups with linear Jacobi parameters Michael Anshelevich; Wojciech Młotkowski Texas A&M University; University of Wrocław February 14, 2011 Jacobi parameters. µ = measure with finite moments,
GRK 2. dr Wojciech Palubicki
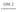 GRK dr Wojciech Palubicki Macierz wektor produkt jako Transformacja T: R n R m T Ԧx = A Ԧx Przemieszczanie wierzchołków - Transformacje Skalowanie Rotacja Translacja -y -y Macierz rotacji M wobec punktu
GRK dr Wojciech Palubicki Macierz wektor produkt jako Transformacja T: R n R m T Ԧx = A Ԧx Przemieszczanie wierzchołków - Transformacje Skalowanie Rotacja Translacja -y -y Macierz rotacji M wobec punktu
Machine Learning for Data Science (CS4786) Lecture 24. Differential Privacy and Re-useable Holdout
 Machine Learning for Data Science (CS4786) Lecture 24 Differential Privacy and Re-useable Holdout Defining Privacy Defining Privacy Dataset + Defining Privacy Dataset + Learning Algorithm Distribution
Machine Learning for Data Science (CS4786) Lecture 24 Differential Privacy and Re-useable Holdout Defining Privacy Defining Privacy Dataset + Defining Privacy Dataset + Learning Algorithm Distribution
Arkusz maturalny. Šukasz Dawidowski. 25 kwietnia 2016r. Powtórki maturalne
 Arkusz maturalny Šukasz Dawidowski Powtórki maturalne 25 kwietnia 2016r. Odwrotno±ci liczby rzeczywistej 1. 9 8 2. 0, (1) 3. 8 9 4. 0, (8) 3 4 4 4 1 jest liczba Odwrotno±ci liczby rzeczywistej 3 4 4 4
Arkusz maturalny Šukasz Dawidowski Powtórki maturalne 25 kwietnia 2016r. Odwrotno±ci liczby rzeczywistej 1. 9 8 2. 0, (1) 3. 8 9 4. 0, (8) 3 4 4 4 1 jest liczba Odwrotno±ci liczby rzeczywistej 3 4 4 4
y = The Chain Rule Show all work. No calculator unless otherwise stated. If asked to Explain your answer, write in complete sentences.
 The Chain Rule Show all work. No calculator unless otherwise stated. If asked to Eplain your answer, write in complete sentences. 1. Find the derivative of the functions y 7 (b) (a) ( ) y t 1 + t 1 (c)
The Chain Rule Show all work. No calculator unless otherwise stated. If asked to Eplain your answer, write in complete sentences. 1. Find the derivative of the functions y 7 (b) (a) ( ) y t 1 + t 1 (c)
Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition)
 Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition) J Krupski Click here if your download doesn"t start automatically Karpacz, plan miasta 1:10 000: Panorama
Karpacz, plan miasta 1:10 000: Panorama Karkonoszy, mapa szlakow turystycznych (Polish Edition) J Krupski Click here if your download doesn"t start automatically Karpacz, plan miasta 1:10 000: Panorama
OSTC GLOBAL TRADING CHALLENGE MANUAL
 OSTC GLOBAL TRADING CHALLENGE MANUAL Wrzesień 2014 www.ostc.com/game Po zarejestrowaniu się w grze OSTC Global Trading Challenge, zaakceptowaniu oraz uzyskaniu dostępu to produktów, użytkownik gry będzie
OSTC GLOBAL TRADING CHALLENGE MANUAL Wrzesień 2014 www.ostc.com/game Po zarejestrowaniu się w grze OSTC Global Trading Challenge, zaakceptowaniu oraz uzyskaniu dostępu to produktów, użytkownik gry będzie
ERASMUS + : Trail of extinct and active volcanoes, earthquakes through Europe. SURVEY TO STUDENTS.
 ERASMUS + : Trail of extinct and active volcanoes, earthquakes through Europe. SURVEY TO STUDENTS. Strona 1 1. Please give one answer. I am: Students involved in project 69% 18 Student not involved in
ERASMUS + : Trail of extinct and active volcanoes, earthquakes through Europe. SURVEY TO STUDENTS. Strona 1 1. Please give one answer. I am: Students involved in project 69% 18 Student not involved in
Instrukcja konfiguracji usługi Wirtualnej Sieci Prywatnej w systemie Mac OSX
 UNIWERSYTETU BIBLIOTEKA IEGO UNIWERSYTETU IEGO Instrukcja konfiguracji usługi Wirtualnej Sieci Prywatnej w systemie Mac OSX 1. Make a new connection Open the System Preferences by going to the Apple menu
UNIWERSYTETU BIBLIOTEKA IEGO UNIWERSYTETU IEGO Instrukcja konfiguracji usługi Wirtualnej Sieci Prywatnej w systemie Mac OSX 1. Make a new connection Open the System Preferences by going to the Apple menu
1. Przedstaw w postaci algebraicznej liczby zespolone: 2. Narysuj zbiory punktów na pªaszczy¹nie:
 ZADANIA Z MATEMATYKI Zestaw. Przedstaw w postaci algebraicznej liczby zespolone: (3 + j)(5 j) 3 j +j (5 + j) (3 + j) 3. Narysuj zbiory punktów na pªaszczy¹nie: +j +j 3 Re z = Im z = 5 z ( j) = z j z +
ZADANIA Z MATEMATYKI Zestaw. Przedstaw w postaci algebraicznej liczby zespolone: (3 + j)(5 j) 3 j +j (5 + j) (3 + j) 3. Narysuj zbiory punktów na pªaszczy¹nie: +j +j 3 Re z = Im z = 5 z ( j) = z j z +
JĘZYK ANGIELSKI POZIOM PODSTAWOWY
 EGZAMIN MATURALNY W ROKU SZKOLNYM 2013/2014 JĘZYK ANGIELSKI POZIOM PODSTAWOWY ROZWIĄZANIA ZADAŃ I SCHEMAT PUNKTOWANIA MAJ 2014 ZADANIA ZAMKNIĘTE Zadanie 1. Obszar standardów Rozumienie ze słuchu 1.1. 1.2.
EGZAMIN MATURALNY W ROKU SZKOLNYM 2013/2014 JĘZYK ANGIELSKI POZIOM PODSTAWOWY ROZWIĄZANIA ZADAŃ I SCHEMAT PUNKTOWANIA MAJ 2014 ZADANIA ZAMKNIĘTE Zadanie 1. Obszar standardów Rozumienie ze słuchu 1.1. 1.2.
Previously on CSCI 4622
 More Naïve Bayes aaace3icbvfba9rafj7ew423vr998obg2gpzkojyh4rcx3ys4lafzbjmjifdototmhoilml+hf/mn3+kl+jkdwtr64gbj+8yl2/ywklhsfircg/dvnp33s796mhdr4+fdj4+o3fvywvorkuqe5zzh0oanjakhwe1ra5zhaf5xvgvn35f62rlvtcyxpnm50awundy1hzwi46jbmgprbtrrvidrg4jre4g07kak+picee6xfgiwvfaltorirucni64eeigkqhpegbwaxglabftpyq4gjbls/hw2ci7tr2xj5ddfmfzwtazj6ubmyddgchbzpf88dmrktfonct6vazputos5zakunhfweow5ukcn+puq8m1ulm7kq+d154pokysx4zgxw4nwq6dw+rcozwnhbuu9et/tgld5cgslazuci1yh1q2ynca/u9ais0kukspulds3xxegvtyfycu8iwk1598e0z2xx/g6ef94ehbpo0d9ok9yiowsvfskh1ix2zcbpsdvaxgww7wj4zdn+he2hogm8xz9s+e7/4cuf/ata==
More Naïve Bayes aaace3icbvfba9rafj7ew423vr998obg2gpzkojyh4rcx3ys4lafzbjmjifdototmhoilml+hf/mn3+kl+jkdwtr64gbj+8yl2/ywklhsfircg/dvnp33s796mhdr4+fdj4+o3fvywvorkuqe5zzh0oanjakhwe1ra5zhaf5xvgvn35f62rlvtcyxpnm50awundy1hzwi46jbmgprbtrrvidrg4jre4g07kak+picee6xfgiwvfaltorirucni64eeigkqhpegbwaxglabftpyq4gjbls/hw2ci7tr2xj5ddfmfzwtazj6ubmyddgchbzpf88dmrktfonct6vazputos5zakunhfweow5ukcn+puq8m1ulm7kq+d154pokysx4zgxw4nwq6dw+rcozwnhbuu9et/tgld5cgslazuci1yh1q2ynca/u9ais0kukspulds3xxegvtyfycu8iwk1598e0z2xx/g6ef94ehbpo0d9ok9yiowsvfskh1ix2zcbpsdvaxgww7wj4zdn+he2hogm8xz9s+e7/4cuf/ata==
tum.de/fall2018/ in2357
 https://piazza.com/ tum.de/fall2018/ in2357 Prof. Daniel Cremers From to Classification Categories of Learning (Rep.) Learning Unsupervised Learning clustering, density estimation Supervised Learning learning
https://piazza.com/ tum.de/fall2018/ in2357 Prof. Daniel Cremers From to Classification Categories of Learning (Rep.) Learning Unsupervised Learning clustering, density estimation Supervised Learning learning
Instrukcja obsługi User s manual
 Instrukcja obsługi User s manual Konfigurator Lanberg Lanberg Configurator E-mail: support@lanberg.pl support@lanberg.eu www.lanberg.pl www.lanberg.eu Lanberg 2015-2018 WERSJA VERSION: 2018/11 Instrukcja
Instrukcja obsługi User s manual Konfigurator Lanberg Lanberg Configurator E-mail: support@lanberg.pl support@lanberg.eu www.lanberg.pl www.lanberg.eu Lanberg 2015-2018 WERSJA VERSION: 2018/11 Instrukcja
Dolny Slask 1: , mapa turystycznosamochodowa: Plan Wroclawia (Polish Edition)
 Dolny Slask 1:300 000, mapa turystycznosamochodowa: Plan Wroclawia (Polish Edition) Click here if your download doesn"t start automatically Dolny Slask 1:300 000, mapa turystyczno-samochodowa: Plan Wroclawia
Dolny Slask 1:300 000, mapa turystycznosamochodowa: Plan Wroclawia (Polish Edition) Click here if your download doesn"t start automatically Dolny Slask 1:300 000, mapa turystyczno-samochodowa: Plan Wroclawia
& portable system. Keep the frame, change the graphics, change position. Create a new stand!
 -EASY FRAMESmodular & portable system -EASY FRAMESmodular & portable system by Keep the frame, change the graphics, change position. Create a new stand! koncepcja the concept EASY FRAMES to system, który
-EASY FRAMESmodular & portable system -EASY FRAMESmodular & portable system by Keep the frame, change the graphics, change position. Create a new stand! koncepcja the concept EASY FRAMES to system, który
deep learning for NLP (5 lectures)
 TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 6: Finish Transformers; Sequence- to- Sequence Modeling and AJenKon 1 Roadmap intro (1 lecture) deep learning for NLP (5
TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 6: Finish Transformers; Sequence- to- Sequence Modeling and AJenKon 1 Roadmap intro (1 lecture) deep learning for NLP (5
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition)
 Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Realizacja systemów wbudowanych (embeded systems) w strukturach PSoC (Programmable System on Chip)
 Realizacja systemów wbudowanych (embeded systems) w strukturach PSoC (Programmable System on Chip) Embeded systems Architektura układów PSoC (Cypress) Możliwości bloków cyfrowych i analogowych Narzędzia
Realizacja systemów wbudowanych (embeded systems) w strukturach PSoC (Programmable System on Chip) Embeded systems Architektura układów PSoC (Cypress) Możliwości bloków cyfrowych i analogowych Narzędzia
Pielgrzymka do Ojczyzny: Przemowienia i homilie Ojca Swietego Jana Pawla II (Jan Pawel II-- pierwszy Polak na Stolicy Piotrowej) (Polish Edition)
 Pielgrzymka do Ojczyzny: Przemowienia i homilie Ojca Swietego Jana Pawla II (Jan Pawel II-- pierwszy Polak na Stolicy Piotrowej) (Polish Edition) Click here if your download doesn"t start automatically
Pielgrzymka do Ojczyzny: Przemowienia i homilie Ojca Swietego Jana Pawla II (Jan Pawel II-- pierwszy Polak na Stolicy Piotrowej) (Polish Edition) Click here if your download doesn"t start automatically
TTIC 31210: Advanced Natural Language Processing. Kevin Gimpel Spring Lecture 9: Inference in Structured Prediction
 TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 9: Inference in Structured Prediction 1 intro (1 lecture) Roadmap deep learning for NLP (5 lectures) structured prediction
TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 9: Inference in Structured Prediction 1 intro (1 lecture) Roadmap deep learning for NLP (5 lectures) structured prediction
USB firmware changing guide. Zmiana oprogramowania za przy użyciu połączenia USB. Changelog / Lista Zmian
 1 / 12 Content list / Spis Treści 1. Hardware and software requirements, preparing device to upgrade Wymagania sprzętowe i programowe, przygotowanie urządzenia do aktualizacji 2. Installing drivers needed
1 / 12 Content list / Spis Treści 1. Hardware and software requirements, preparing device to upgrade Wymagania sprzętowe i programowe, przygotowanie urządzenia do aktualizacji 2. Installing drivers needed
Patients price acceptance SELECTED FINDINGS
 Patients price acceptance SELECTED FINDINGS October 2015 Summary With growing economy and Poles benefiting from this growth, perception of prices changes - this is also true for pharmaceuticals It may
Patients price acceptance SELECTED FINDINGS October 2015 Summary With growing economy and Poles benefiting from this growth, perception of prices changes - this is also true for pharmaceuticals It may
Zdecyduj: Czy to jest rzeczywiście prześladowanie? Czasem coś WYDAJE SIĘ złośliwe, ale wcale takie nie jest.
 Zdecyduj: Czy to jest rzeczywiście prześladowanie? Czasem coś WYDAJE SIĘ złośliwe, ale wcale takie nie jest. Miłe przezwiska? Nie wszystkie przezwiska są obraźliwe. Wiele przezwisk świadczy o tym, że osoba,
Zdecyduj: Czy to jest rzeczywiście prześladowanie? Czasem coś WYDAJE SIĘ złośliwe, ale wcale takie nie jest. Miłe przezwiska? Nie wszystkie przezwiska są obraźliwe. Wiele przezwisk świadczy o tym, że osoba,
1 Przypomnienie wiadomo±ci ze szkoªy ±redniej. Rozwi zywanie prostych równa«i nierówno±ci
 Zebraª do celów edukacyjnych od wykªadowców PK, z ró»nych podr czników Maciej Zakarczemny 1 Przypomnienie wiadomo±ci ze szkoªy ±redniej Rozwi zywanie prostych równa«i nierówno±ci dotycz cych funkcji elementarnych,
Zebraª do celów edukacyjnych od wykªadowców PK, z ró»nych podr czników Maciej Zakarczemny 1 Przypomnienie wiadomo±ci ze szkoªy ±redniej Rozwi zywanie prostych równa«i nierówno±ci dotycz cych funkcji elementarnych,
17-18 września 2016 Spółka Limited w UK. Jako Wehikuł Inwestycyjny. Marek Niedźwiedź. InvestCamp 2016 PL
 17-18 września 2016 Spółka Limited w UK Jako Wehikuł Inwestycyjny InvestCamp 2016 PL Marek Niedźwiedź A G E N D A Dlaczego Spółka Ltd? Stabilność Bezpieczeństwo Narzędzia 1. Stabilność brytyjskiego systemu
17-18 września 2016 Spółka Limited w UK Jako Wehikuł Inwestycyjny InvestCamp 2016 PL Marek Niedźwiedź A G E N D A Dlaczego Spółka Ltd? Stabilność Bezpieczeństwo Narzędzia 1. Stabilność brytyjskiego systemu
Domy inaczej pomyślane A different type of housing CEZARY SANKOWSKI
 Domy inaczej pomyślane A different type of housing CEZARY SANKOWSKI O tym, dlaczego warto budować pasywnie, komu budownictwo pasywne się opłaca, a kto się go boi, z architektem, Cezarym Sankowskim, rozmawia
Domy inaczej pomyślane A different type of housing CEZARY SANKOWSKI O tym, dlaczego warto budować pasywnie, komu budownictwo pasywne się opłaca, a kto się go boi, z architektem, Cezarym Sankowskim, rozmawia
2017 R. Robert Gajewski: Mathcad Prime 4. Solution of examples Rozwiązania przykładów
 07 R. Robert Gajewski: Mathcad Prime 4 0. Calculate numerically and present results in different formats and precision. 0. Oblicz numerycznie i przedstaw wyniki w różnych formatach i z różną precyzją.
07 R. Robert Gajewski: Mathcad Prime 4 0. Calculate numerically and present results in different formats and precision. 0. Oblicz numerycznie i przedstaw wyniki w różnych formatach i z różną precyzją.
Zmiany techniczne wprowadzone w wersji Comarch ERP Altum
 Zmiany techniczne wprowadzone w wersji 2018.2 Copyright 2016 COMARCH SA Wszelkie prawa zastrzeżone Nieautoryzowane rozpowszechnianie całości lub fragmentu niniejszej publikacji w jakiejkolwiek postaci
Zmiany techniczne wprowadzone w wersji 2018.2 Copyright 2016 COMARCH SA Wszelkie prawa zastrzeżone Nieautoryzowane rozpowszechnianie całości lub fragmentu niniejszej publikacji w jakiejkolwiek postaci
1 Trochoidalny selektor elektronów
 1 Trochoidalny selektor elektronów W trochoidalnym selektorze elektronów TEM (Trochoidal Electron Monochromator) stosuje si skrzy»owane i jednorodne pola: elektryczne i magnetyczne. Jako pierwsi taki ukªad
1 Trochoidalny selektor elektronów W trochoidalnym selektorze elektronów TEM (Trochoidal Electron Monochromator) stosuje si skrzy»owane i jednorodne pola: elektryczne i magnetyczne. Jako pierwsi taki ukªad
Egzamin maturalny z języka angielskiego na poziomie dwujęzycznym Rozmowa wstępna (wyłącznie dla egzaminującego)
 112 Informator o egzaminie maturalnym z języka angielskiego od roku szkolnego 2014/2015 2.6.4. Część ustna. Przykładowe zestawy zadań Przykładowe pytania do rozmowy wstępnej Rozmowa wstępna (wyłącznie
112 Informator o egzaminie maturalnym z języka angielskiego od roku szkolnego 2014/2015 2.6.4. Część ustna. Przykładowe zestawy zadań Przykładowe pytania do rozmowy wstępnej Rozmowa wstępna (wyłącznie
XVII Warmi«sko-Mazurskie Zawody Matematyczne
 1 XVII Warmi«sko-Mazurskie Zawody Matematyczne Kategoria: klasa VIII szkoªy podstawowej i III gimnazjum Olsztyn, 16 maja 2019r. Zad. 1. Udowodnij,»e dla dowolnych liczb rzeczywistych x, y, z speªniaj cych
1 XVII Warmi«sko-Mazurskie Zawody Matematyczne Kategoria: klasa VIII szkoªy podstawowej i III gimnazjum Olsztyn, 16 maja 2019r. Zad. 1. Udowodnij,»e dla dowolnych liczb rzeczywistych x, y, z speªniaj cych
Leba, Rowy, Ustka, Slowinski Park Narodowy, plany miast, mapa turystyczna =: Tourist map = Touristenkarte (Polish Edition)
 Leba, Rowy, Ustka, Slowinski Park Narodowy, plany miast, mapa turystyczna =: Tourist map = Touristenkarte (Polish Edition) FotKart s.c Click here if your download doesn"t start automatically Leba, Rowy,
Leba, Rowy, Ustka, Slowinski Park Narodowy, plany miast, mapa turystyczna =: Tourist map = Touristenkarte (Polish Edition) FotKart s.c Click here if your download doesn"t start automatically Leba, Rowy,
Poniżej moje uwagi po zapoznaniu się z prezentowanymi zasadami:
 Witam wszystkich nawigatorów. Ostatnio zostały opublikowane nowe zasady CEC (opracowane przez Węgrów) dla zawodników i organizatorów CEC 2011, które obowiązują od tego sezonu. Choć w większości pokrywają
Witam wszystkich nawigatorów. Ostatnio zostały opublikowane nowe zasady CEC (opracowane przez Węgrów) dla zawodników i organizatorów CEC 2011, które obowiązują od tego sezonu. Choć w większości pokrywają
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition)
 Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Wojewodztwo Koszalinskie: Obiekty i walory krajoznawcze (Inwentaryzacja krajoznawcza Polski) (Polish Edition) Robert Respondowski Click here if your download doesn"t start automatically Wojewodztwo Koszalinskie:
Transformacje obiektów 3D
 Synteza i obróbka obrazu Transformacje obiektów 3D Opracowanie: dr inż. Grzegorz Szwoch Politechnika Gdańska Katedra Systemów Multimedialnych Lokalny układ współrzędnych Tworząc model obiektu, zapisujemy
Synteza i obróbka obrazu Transformacje obiektów 3D Opracowanie: dr inż. Grzegorz Szwoch Politechnika Gdańska Katedra Systemów Multimedialnych Lokalny układ współrzędnych Tworząc model obiektu, zapisujemy
Ankiety Nowe funkcje! Pomoc magda.szewczyk@slo-wroc.pl. magda.szewczyk@slo-wroc.pl. Twoje konto Wyloguj. BIODIVERSITY OF RIVERS: Survey to teachers
 1 z 7 2015-05-14 18:32 Ankiety Nowe funkcje! Pomoc magda.szewczyk@slo-wroc.pl Back Twoje konto Wyloguj magda.szewczyk@slo-wroc.pl BIODIVERSITY OF RIVERS: Survey to teachers Tworzenie ankiety Udostępnianie
1 z 7 2015-05-14 18:32 Ankiety Nowe funkcje! Pomoc magda.szewczyk@slo-wroc.pl Back Twoje konto Wyloguj magda.szewczyk@slo-wroc.pl BIODIVERSITY OF RIVERS: Survey to teachers Tworzenie ankiety Udostępnianie
ZASTOSOWANIE RÓWNANIA BOUSSINESQUE A DO OKREŚLANIA NAPRĘŻEŃ W GLEBIE WYWOŁANYCH ODDZIAŁYWANIEM ZESTAWÓW MASZYN
 Inżynieria Rolnicza 4(10)/008 ZASTOSOWANIE RÓWNANIA BOUSSINESQUE A DO OKREŚLANIA NAPRĘŻEŃ W GLEBIE WYWOŁANYCH ODDZIAŁYWANIEM ZESTAWÓW MASZYN Yuri Chigarev, Rafał Nowowiejski, Jan B. Dawidowski Instytut
Inżynieria Rolnicza 4(10)/008 ZASTOSOWANIE RÓWNANIA BOUSSINESQUE A DO OKREŚLANIA NAPRĘŻEŃ W GLEBIE WYWOŁANYCH ODDZIAŁYWANIEM ZESTAWÓW MASZYN Yuri Chigarev, Rafał Nowowiejski, Jan B. Dawidowski Instytut
Miedzy legenda a historia: Szlakiem piastowskim z Poznania do Gniezna (Biblioteka Kroniki Wielkopolski) (Polish Edition)
 Miedzy legenda a historia: Szlakiem piastowskim z Poznania do Gniezna (Biblioteka Kroniki Wielkopolski) (Polish Edition) Piotr Maluskiewicz Click here if your download doesn"t start automatically Miedzy
Miedzy legenda a historia: Szlakiem piastowskim z Poznania do Gniezna (Biblioteka Kroniki Wielkopolski) (Polish Edition) Piotr Maluskiewicz Click here if your download doesn"t start automatically Miedzy
Linear Classification and Logistic Regression. Pascal Fua IC-CVLab
 Linear Classification and Logistic Regression Pascal Fua IC-CVLab 1 aaagcxicbdtdbtmwfafwdgxlhk8orha31ibqycvkdgpshdqxtwotng2pxtvqujmok1qlky5xllzrnobbediegwcap4votk2kqkf+/y/tnphdschtadu/giv3vtea99cfma8fpx7ytlxx7ckns4sylo3doom7jguhj1hxchmy/irhrlgh67lxb5x3blis8jjqynmedqujiu5zsqqagrx+yjcfpcrydusshmzeluzsg7tttiew5khhcuzm5rv0gn1unw6zl3gbzlpr3liwncyr6aaqinx4wnc/rpg6ix5szd86agoftuu0g/krjxdarph62enthdey3zn/+mi5zknou2ap+tclvhob9sxhwvhaqketnde7geqjp21zvjsfrcnkfhtejoz23vq97elxjlpbtmxpl6qxtl1sgfv1ptpy/yq9mgacrzkgje0hjj2rq7vtywnishnnkzsqekucnlblrarlh8x8szxolrrxkb8n6o4kmo/e7siisnozcfvsedlol60a/j8nmul/gby8mmssrfr2it8lkyxr9dirxxngzthtbaejv
Linear Classification and Logistic Regression Pascal Fua IC-CVLab 1 aaagcxicbdtdbtmwfafwdgxlhk8orha31ibqycvkdgpshdqxtwotng2pxtvqujmok1qlky5xllzrnobbediegwcap4votk2kqkf+/y/tnphdschtadu/giv3vtea99cfma8fpx7ytlxx7ckns4sylo3doom7jguhj1hxchmy/irhrlgh67lxb5x3blis8jjqynmedqujiu5zsqqagrx+yjcfpcrydusshmzeluzsg7tttiew5khhcuzm5rv0gn1unw6zl3gbzlpr3liwncyr6aaqinx4wnc/rpg6ix5szd86agoftuu0g/krjxdarph62enthdey3zn/+mi5zknou2ap+tclvhob9sxhwvhaqketnde7geqjp21zvjsfrcnkfhtejoz23vq97elxjlpbtmxpl6qxtl1sgfv1ptpy/yq9mgacrzkgje0hjj2rq7vtywnishnnkzsqekucnlblrarlh8x8szxolrrxkb8n6o4kmo/e7siisnozcfvsedlol60a/j8nmul/gby8mmssrfr2it8lkyxr9dirxxngzthtbaejv
II wariant dwie skale ocen II alternative two grading scales
 Kryteria przeliczania uzyskanych przez kandydata ocen na punkty do listy rankingowej University Criteria for converting candidates grades into the points for the Ranking List Wymagane przedmioty : fizyka,
Kryteria przeliczania uzyskanych przez kandydata ocen na punkty do listy rankingowej University Criteria for converting candidates grades into the points for the Ranking List Wymagane przedmioty : fizyka,
Miedzy legenda a historia: Szlakiem piastowskim z Poznania do Gniezna (Biblioteka Kroniki Wielkopolski) (Polish Edition)
 Miedzy legenda a historia: Szlakiem piastowskim z Poznania do Gniezna (Biblioteka Kroniki Wielkopolski) (Polish Edition) Piotr Maluskiewicz Click here if your download doesn"t start automatically Miedzy
Miedzy legenda a historia: Szlakiem piastowskim z Poznania do Gniezna (Biblioteka Kroniki Wielkopolski) (Polish Edition) Piotr Maluskiewicz Click here if your download doesn"t start automatically Miedzy
MoA-Net: Self-supervised Motion Segmentation. Pia Bideau, Rakesh R Menon, Erik Learned-Miller
 MoA-Net: Self-supervised Motion Segmentation Pia Bideau, Rakesh R Menon, Erik Learned-Miller University of Massachusetts Amherst College of Information and Computer Science Motion Segmentation P Bideau,
MoA-Net: Self-supervised Motion Segmentation Pia Bideau, Rakesh R Menon, Erik Learned-Miller University of Massachusetts Amherst College of Information and Computer Science Motion Segmentation P Bideau,
Ankiety Nowe funkcje! Pomoc magda.szewczyk@slo-wroc.pl. magda.szewczyk@slo-wroc.pl. Twoje konto Wyloguj. BIODIVERSITY OF RIVERS: Survey to students
 Ankiety Nowe funkcje! Pomoc magda.szewczyk@slo-wroc.pl Back Twoje konto Wyloguj magda.szewczyk@slo-wroc.pl BIODIVERSITY OF RIVERS: Survey to students Tworzenie ankiety Udostępnianie Analiza (55) Wyniki
Ankiety Nowe funkcje! Pomoc magda.szewczyk@slo-wroc.pl Back Twoje konto Wyloguj magda.szewczyk@slo-wroc.pl BIODIVERSITY OF RIVERS: Survey to students Tworzenie ankiety Udostępnianie Analiza (55) Wyniki
EGZAMIN MATURALNY Z JĘZYKA ANGIELSKIEGO
 ARKUSZ ZAWIERA INFORMACJE PRAWNIE CHRONIONE DO MOMENTU ROZPOCZĘCIA EGZAMINU! Miejsce na naklejkę dysleksja MJA-R1_1P-082 EGZAMIN MATURALNY Z JĘZYKA ANGIELSKIEGO MAJ ROK 2008 POZIOM ROZSZERZONY CZĘŚĆ I
ARKUSZ ZAWIERA INFORMACJE PRAWNIE CHRONIONE DO MOMENTU ROZPOCZĘCIA EGZAMINU! Miejsce na naklejkę dysleksja MJA-R1_1P-082 EGZAMIN MATURALNY Z JĘZYKA ANGIELSKIEGO MAJ ROK 2008 POZIOM ROZSZERZONY CZĘŚĆ I
DO MONTAŻU POTRZEBNE SĄ DWIE OSOBY! INSTALLATION REQUIRES TWO PEOPLE!
 HAPPY ANIMALS RW08 INSTRUKCJA MONTAŻU ASSEMBLY INSTRUCTIONS Akcesoria / Fittings K M M ZM ZW G 0 szt. / pcs W szt. / pcs B szt. / pcs szt. / pcs W U 8 szt. / pcs 4 szt. / pcs U N szt. / pcs Ø3 x szt. /
HAPPY ANIMALS RW08 INSTRUKCJA MONTAŻU ASSEMBLY INSTRUCTIONS Akcesoria / Fittings K M M ZM ZW G 0 szt. / pcs W szt. / pcs B szt. / pcs szt. / pcs W U 8 szt. / pcs 4 szt. / pcs U N szt. / pcs Ø3 x szt. /
TTIC 31210: Advanced Natural Language Processing. Kevin Gimpel Spring Lecture 8: Structured PredicCon 2
 TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 8: Structured PredicCon 2 1 Roadmap intro (1 lecture) deep learning for NLP (5 lectures) structured predic+on (4 lectures)
TTIC 31210: Advanced Natural Language Processing Kevin Gimpel Spring 2019 Lecture 8: Structured PredicCon 2 1 Roadmap intro (1 lecture) deep learning for NLP (5 lectures) structured predic+on (4 lectures)
DO MONTAŻU POTRZEBNE SĄ DWIE OSOBY! INSTALLATION REQUIRES TWO PEOPLE!
 1 HAPPY ANIMALS SZ11 A INSTRUKCJA MONTAŻU ASSEMBLY INSTRUCTIONS Akcesoria / Fittings K1 M M1 ZM1 Z G1 szt. / pcs 0 szt. / pcs B1 6 szt. / pcs 6 szt. / pcs W6 0 szt. / pcs U1 19 szt. / pcs U 50 szt. / pcs
1 HAPPY ANIMALS SZ11 A INSTRUKCJA MONTAŻU ASSEMBLY INSTRUCTIONS Akcesoria / Fittings K1 M M1 ZM1 Z G1 szt. / pcs 0 szt. / pcs B1 6 szt. / pcs 6 szt. / pcs W6 0 szt. / pcs U1 19 szt. / pcs U 50 szt. / pcs
HAPPY K04 INSTRUKCJA MONTAŻU ASSEMBLY INSTRUCTIONS DO MONTAŻU POTRZEBNE SĄ DWIE OSOBY! INSTALLATION REQUIRES TWO PEOPLE! W5 W6 G1 T2 U1 U2 TZ1
 HAPPY K0 INSTRUKCJA MONTAŻU ASSEMBLY INSTRUCTIONS W Akcesoria / Fittings W W G K szt. / pcs M Ø Ø 0 Ø, Ø Ø. 0 ø8 M 8 szt. / pcs 0 szt. / pcs szt. / pcs T U U szt. / pcs szt. / pcs szt. / pcs S TZ szt.
HAPPY K0 INSTRUKCJA MONTAŻU ASSEMBLY INSTRUCTIONS W Akcesoria / Fittings W W G K szt. / pcs M Ø Ø 0 Ø, Ø Ø. 0 ø8 M 8 szt. / pcs 0 szt. / pcs szt. / pcs T U U szt. / pcs szt. / pcs szt. / pcs S TZ szt.
Assignment 3.1 (SA and LA)
 AW 11 Name u J2T0v1V9g XKru_ttaF NS^oQfOtXwUagr\eu GLHLOC^.F C XAqldlO FrEiIg\hXtHsO xrcewsqeprtvheed`. Assignment 3.1 (SA and LA) Find the area of each. 1) 11 m 2) 6.5 m 5 km 2.9 km 3) 4) 4.3 ft 6.2 km
AW 11 Name u J2T0v1V9g XKru_ttaF NS^oQfOtXwUagr\eu GLHLOC^.F C XAqldlO FrEiIg\hXtHsO xrcewsqeprtvheed`. Assignment 3.1 (SA and LA) Find the area of each. 1) 11 m 2) 6.5 m 5 km 2.9 km 3) 4) 4.3 ft 6.2 km
Sargent Opens Sonairte Farmers' Market
 Sargent Opens Sonairte Farmers' Market 31 March, 2008 1V8VIZSV7EVKIRX8(1MRMWXIVSJ7XEXIEXXLI(ITEVXQIRXSJ%KVMGYPXYVI *MWLIVMIWERH*SSHTIVJSVQIHXLISJJMGMEPSTIRMRKSJXLI7SREMVXI*EVQIVW 1EVOIXMR0E]XS[R'S1IEXL
Sargent Opens Sonairte Farmers' Market 31 March, 2008 1V8VIZSV7EVKIRX8(1MRMWXIVSJ7XEXIEXXLI(ITEVXQIRXSJ%KVMGYPXYVI *MWLIVMIWERH*SSHTIVJSVQIHXLISJJMGMEPSTIRMRKSJXLI7SREMVXI*EVQIVW 1EVOIXMR0E]XS[R'S1IEXL
