PORÓWNANIE METOD STATYSTYCZNYCH ZASTOSOWANYCH DO ZBADANIA WPŁYWU NAWOŻENIA AZOTEM NA CECHY WYTRZYMAŁOŚCIOWE ZIARNA ŻYTA
|
|
|
- Maksymilian Lewandowski
- 5 lat temu
- Przeglądów:
Transkrypt
1 Inżynieria Rolnicza (26)/2 PORÓWNNIE METOD STTYSTYCZNYCH ZSTOSOWNYCH DO ZBDNI WPŁYWU NWOŻENI ZOTEM N CECHY WYTRZYMŁOŚCIOWE ZIRN ŻYT Zofia Hanusz, Joanna Olejnik Katedra Zastosowań Matematyki i Informatyki, Uniwersytet Przyrodniczy w Lublinie Janusz Laskowski, dam Zdybel Katedra Eksploatacji Maszyn Przemysłu Spożywczego, Uniwersytet Przyrodniczy w Lublinie Streszczenie. W pracy zostaną przedstawione dwie różne metody statystyczne do oceny wpływu różnych dawek nawożenia azotem na wybrane cechy wytrzymałościowe ziarna żyta. Pierwsza metoda jest tradycyjną metodą analizy wariancji, natomiast druga jest niestandardową metodą, którą stosuje się do oceny mocy preparatu testowego względem preparatu standardowego. Porównania tych metod dokonamy dla cech fizycznych ziarna żyta odmiany milo i Esprit. Słowa kluczowe: analiza wariancji, względna moc preparatów, nawożenie azotowe, cechy fizyczne ziarna Wstęp W inżynierii rolniczej, w celu potwierdzenia przypuszczeń badacza, przeprowadza się eksperymenty, w wyniku których uzyskuje się wyniki liczbowe. W dalszym etapie badań bardzo istotne jest zastosowanie właściwej metody statystycznej, która pozwoli zweryfikować te przypuszczenia. Do tego celu najczęściej wykorzystywane są znane i powszechnie stosowane metody dostępne w pakietach statystycznych. Istnieją także inne metody, niezaimplementowane do pakietów statystycznych, które również można zastosować do analizy wyników. W pracy przedstawimy wyniki zastosowania dwóch metod statystycznych do analizy tych samych danych eksperymentalnych. Pierwsza z nich jest dobrze znaną analizą wariancji, natomiast druga polega na oszacowaniu względnej efektywności preparatów zastosowanych w doświadczeniu w kilku dawkach. Cel pracy Głównym celem pracy jest porównanie dwóch różnych metod statystycznych wykorzystanych do zbadania efektywności działania nawożenia azotowego na wybrane właściwości wytrzymałościowe ziarna dwóch odmian żyta: populacyjnej milo i mieszańcowej Esprit. 69
2 Zofia Hanusz, Janusz Laskowski, Joanna Olejnik, dam Zdybel Porównania tych metod dokonamy w oparciu o częściowe wyniki uzyskane w doświadczeniu przeprowadzonym w Katedrze Eksploatacji Maszyn Przemysłu Spożywczego, Uniwersytetu Przyrodniczego w Lublinie. Metodyka badań Rozważania tej pracy dotyczą analizy statystycznej wyników doświadczenia, przeprowadzonego w celu zbadania wpływu azotu na właściwości ziarna żyta. Ograniczymy się w nich do jednego sposobu nawożenia azotem, stosowanego przedsiewnie w dawkach: 3, 6 i 9 kg ha oraz czterech badanych cech ziarna: h odkształcenia do progu wytrzymałości doraźnej [mm], h 2 odkształcenia do progu zgniecenia ziarna [mm], f siły dla progu wytrzymałości doraźnej [N] oraz f 2 siły dla progu zgniecenia ziarna [N]. naliza statystyczna dotyczy jedynie małego fragmentu wyników eksperymentalnych, które w szerszym zakresie analizowane były w pracach Laskowski i Zdybel [23] oraz Zdybel [26]. W pracy zastosujemy dwie metody statystyczne i dokonamy porównania wniosków wypływających z ich zastosowania. Metoda. Zastosowanie analizy wariancji W tej części przedstawimy wyniki uzyskane dla dwukierunkowej analizy wariancji z interakcją, przeprowadzonej w pakiecie statystycznym SS. Pierwszy czynnik stanowią odmiany, natomiast drugi czynnik nawożenie. Liczba replikacji dla każdej dawki nawożenia wynosiła 2 ziaren. naliza wariancji została przeprowadzona dla każdej cechy oddzielnie. Uzyskane wyniki przedstawiono w tabelach 4, natomiast istotności różnic pomiędzy średnimi dla porównywanych odmian i dawek nawożeń, obliczone przy wykorzystaniu jednoczesnych przedziałów ufności Tukeya, zestawiono w tabelach 5 i 6. Ponadto, na wykresach zawartych na rysunku przedstawiono zachowanie się przeciętnych wartości badanych cech ziarna dla odmiany milo i Esprit. Tabela. naliza wariancji odkształcenia do progu wytrzymałości doraźnej ziarna Table. Variance analysis for deformation to grain immediate strength threshold Źródło zmienności Stopnie swobody Suma kwadratów Średnie kwadraty F krytyczny Odmiana,488,488 8,8 <, Nawożenie 2,275,38 39,98 <, Odmiana*Nawożenie 2,45,22,86,4263 Błąd 4,2959,26 Całość 9,5567 7
3 Porównanie metod statystycznych... Tabela 2. naliza wariancji odkształcenia do progu zgniecenia ziarna Table 2. Variance analysis for deformation to grain collapse threshold Źródło zmienności Stopnie swobody Suma kwadratów Średnie kwadraty F krytyczny Odmiana,, 2,9,97 Nawożenie 2,9,45,2,359 Odmiana*Nawożenie 2,,5,3,8763 Błąd 4,4324,38 Całość 9,4535 Tabela 3. naliza wariancji siły dla progu wytrzymałości doraźnej Table 3. Force variance analysis for immediate strength threshold Źródło zmienności Stopnie swobody Suma kwadratów Średnie kwadraty F krytyczny Odmiana 832,87 832,87 6,3 <, Nawożenie 2 962,8 48,4 9,4,2 Odmiana*Nawożenie 2 368,83 84,4 3,6,32 Błąd ,95 5, Całość ,72 Tabela 4. naliza wariancji siły dla progu zgniecenia ziarna Table 4. Force variance analysis for grain collapse threshold Źródło zmienności Stopnie swobody Suma kwadratów Średnie kwadraty F krytyczny Odmiana 3,38 3,38,4,849 Nawożenie , ,72 2,2,374 Odmiana*Nawożenie 2 9,54 59,77,4,8683 Błąd 4 446,9 365,67 Całość ,27 Tabela 5. Wartości średnie cech odmiany milo i Esprit (różne litery przy średnich oznaczają różnice istotne) Table 5. Mean values of milo and Esprit variety characteristics (different letters at mean values indicate significant differences) Odmiana h h 2 f f 2 milo,44 2,84 66,79 9,2 Esprit,4 B 2,3 6,52 B 899, 7
4 Zofia Hanusz, Janusz Laskowski, Joanna Olejnik, dam Zdybel Tabela 6. Wartości średnie cech dla zastosowanych dawek nawożenia azotem (różne litery przy średnich oznaczają różnice istotne) Table 6. Mean values of characteristics for applied nitrogen fertilisation doses (different letters at mean values indicate significant differences) Nawożenie h h 2 f f 2 3,479 2,365 67,2 888,74 6,395 B 2, ,4 896,67 9,388 B 2,8265 6,3 B 888,74 Rys.. Fig.. Wpływ dawek nawożenia azotem na wartości badanych cech ziarna żyta odmiany milo i Esprit: h odkształcenie do progu wytrzymałości doraźnej [mm], h 2 odkształcenie do progu zgniecenia ziarna [mm], f siła dla progu wytrzymałości doraźnej [N] oraz f 2 siła dla progu zgniecenia ziarna [N] The impact of nitrogen fertilisation doses on the values of studied grain characteristics for milo and Esprit variety rye: h deformation to immediate strength threshold [mm], deformation to grain collapse threshold [mm], f force for immediate strength threshold [N] and force for grain collapse threshold [N] 72
5 Porównanie metod statystycznych... Tabele -4 pokazują, że na poziomie istotności α =, 5 stwierdzono istotne zróżnicowanie odkształcenia do progu wytrzymałości doraźnej oraz siły dla progu wytrzymałości doraźnej odmiany milo i Esprit oraz zastosowanych dawek nawożeń. Nie stwierdzono natomiast istotnego wpływu nawożenia oraz odmian na zróżnicowanie odkształcenia do progu zgniecenia ziarna oraz siły dla progu zgniecenia ziarna. Tabele 5 i 6 pokazują, że odkształcenie do progu wytrzymałości doraźnej ziarna odmiany populacyjnej milo było istotnie wyższe niż dla odmiany Esprit oraz, że było ono istotnie wyższe dla dawki 3 kg ha - niż dla dawki 6 kg ha - oraz 9 kg ha -. Podobne wnioski uzyskano dla siły dla progu wytrzymałości doraźnej. Siła ta była istotnie wyższa dla ziarna odmiany milo, przy czym była istotnie wyższa dla dawek 3 kg ha - i 6 kg ha - niż dla dawki 9 kg ha -. Wpływ zastosowanych dawek nawożenia azotem dla poszczególnych cech zobrazowano na rysunku. Można zauważyć podobne oddziaływanie nawożenia na badane cechy wytrzymałościowe ziarna odmiany milo i Esprit. Metoda 2. Zastosowanie metody względnej mocy preparatów W tej metodzie ocenimy efektywność działania nawożenia azotowego na odmianę mieszańcową Esprit względem odmiany populacyjnej milo. Do oceny tej efektywności wykorzystamy względną moc preparatów, które stanowią nawożenia azotem [por. Hanusz 999; Olejnik 2]). W tej metodzie wykorzystuje się zależność funkcyjną cech ziarna od zastosowanych dawek nawożenia azotem. Z literatury wiadomo [por. Finney 952], że w praktyce badane cechy najczęściej liniowo zależą od logarytmów stosowanych dawek. Jeśli stosowane dawki nawożenia azotem podobnie działają na badane cechy dwóch odmian, wówczas współczynniki kierunkowe w zależnościach liniowych dla poszczególnych cech powinny być identyczne. Można zatem powiedzieć, że jeśli nawożenie podobnie działa na badane dwie odmiany żyta to dla każdej cechy proste regresji powinny być równoległe. Jeśli ponadto dla każdej cechy proste regresji są równoległe to możemy przyjąć, że czterowymiarowa obserwacja (h, h 2, f, f 2 ) da się opisać zależnościami: ( u ) e, h ( u ) + e, ( u ) e, f ( u ) e y, h α +, h h log y, h α + 2, h log 2 y = =, y, f α +, f f log y, f α + 2, f log 2, ( ue ) ee, h ( u ) E + ee, ( u E ) ee, f ( u ) e ye, h α + E, h h log ye, h α + 2 E, h log 2 y = =, E ye, f α + E, f f log ye, f α + 2 E, f log 2 E E, 73
6 Zofia Hanusz, Janusz Laskowski, Joanna Olejnik, dam Zdybel gdzie: oznacza odmianę milo, E Esprit, α i, j wyraz wolny w zależności regresyjnej, j współczynnik kierunkowy, u, u E oznaczają odpowiednio dawki azotu zastosowane dla odmiany milo i Esprit, - e błąd eksperymentalny ( i,j i =, E; j = h,, f, f 2 ). Logarytm względnej efektywności nawożenia azotem odmiany Esprit względem milo zdefiniujemy jako: α μ = log( ρ) = α α α α α, h E, h, E,, f E, f, E, = = = h h 2 f α α. () Powyższe równanie pokazuje, że logarytm względnej efektywności dla wszystkich cech łącznie, oznaczany w literaturze przez μ, możemy oszacować tylko wtedy, gdy dla każdej cechy ilorazy różnic wyrazów wolnych przez współczynniki kierunkowe są takie same. Warunek równoległości oraz warunek na równość ilorazów w (), sformułujemy jako dwie hipotezy, które zostaną w dalszej części zweryfikowane. Mianowicie, niech H : = (2) E oraz H : α α μ =, (3) μ E gdzie = [ ; ; ; ] i,h,,f, f = [ ; ; ; ] oznaczają wektory regresyjne dla 2 E E,h E, E, f E, f 2 odmiany milo i Esprit, α = [ α, α, α, α ], α = [ α, α, α, α ],h,, f, f 2 E E,h E, E, f E, f 2 wektory wyrazów wolnych dla tych odmian, natomiast = [,,, ] niech oznacza wspólny dla dwóch odmian wektor współczynników regresyjnych. Logarytm względ- h f f 2 nej efektywności μ we wzorze (3) jest wspólny dla wszystkich cech. Oszacowanie logarytmu względnej efektywności pozwoli na oszacowanie względnej efektywności, oznaczanej w literaturze przez ρ, która jest ilorazem dawek preparatów wywołujących te ue same wartości badanych cech, tzn. ρ =. Znajomość tej efektywności pozwoli nam ocenić dawkę nawożenia azotem pod odmianę Esprit, która będzie oddziaływała tak jak usta- u lona dawka tego nawożenia pod odmianę milo. Do weryfikacji zarówno hipotezy H w (2) jak i H w (3) wykorzystano funkcje μ testowe lambda Wilksa [por Hanusz 999] uzyskując wyniki zamieszczone w tabeli 7. 74
7 Porównanie metod statystycznych... Tabela 7. Wartości funkcji testowych, poziomy krytyczne oraz oceny efektywności Table 7. Values of test functions, critical levels, and efficiency assessments Hipoteza funkcji testowej H 4,5657,3348 H μ,356,9999 Ocena krytyczny Log(efektywności) Efektywność,23,547 Łatwo zauważyć, że na poziomie istotności α =, 5 obydwie hipotezy nie zostały odrzucone. Możemy zatem wnioskować, że hipoteza H o podobnym działaniu nawożenia azotem na cechy wytrzymałościowe odmiany milo i Esprit nie została odrzucona. Wniosek ten potwierdza nasze przypuszczenia wynikające z rysunku. nalogicznie też możemy stwierdzić, że na poziomie istotności α =, 5 hipoteza H nie została odrzucona. μ Istniały zatem przesłanki do tego, by oszacować efektywność nawożenia azotem odmiany milo i Esprit na cechy wytrzymałościowe ziarna. Efektywność ta wyniosła około,5, u czyli ρ ˆ = E, 5. W celu uzyskania takich samych wartości cech wytrzymałościowych, u dawka nawożenia azotem dla odmiany Esprit powinna wynosić ue, 5 u, czyli powinna być około 5% wyższa niż dawka stosowana dla odmiany milo. Z praktycznego punktu widzenia taka różnica może być zaniedbana. Możemy więc stwierdzić, że działanie nawożenia azotem na badane cechy wytrzymałościowe ziarna żyta odmiany milo i Esprit jest jednakowo efektywne. Podsumowanie. Wykorzystując analizę wariancji można badać zróżnicowanie wyników badanych cech pomiędzy odmianami, różnymi dawkami nawożenia azotem oraz dodatkowo zmienność w podklasach dla poszczególnych odmian i nawożeń (interakcje). W analizie wariancji nie uwzględnia się jednak wielkości zastosowanych dawek nawożenia. Stąd też moglibyśmy wyznaczać zależności regresyjne poszczególnych cech od stosowanych dawek i je analizować oddzielnie dla każdej odmiany i każdej cechy. by tego uniknąć zaproponowaliśmy drugą metodę, która dla wszystkich cech łącznie pozwoliła zbadać czy efektywność działania nawożenia azotem na badane cechy ziarna dla odmiany mieszańcowej Esprit jest taka sama jak dla odmiany populacyjnej milo. 2. Zastosowana metoda szacowania efektywności stosowanego azotu na wybrane cechy wytrzymałościowe ziarna żyta dla dwóch badanych odmian pozwoliła potwierdzić podobne działanie azotu na badane cechy odmiany milo i Esprit. Ponadto stwierdzono, że efektywność nawożenia dla tych dwóch odmian jest prawie identyczna, gdyż oszacowana względna moc niewiele różni się od jedności. 75
8 Zofia Hanusz, Janusz Laskowski, Joanna Olejnik, dam Zdybel Bibliografia Hanusz Z Szacowanie względnej mocy preparatów stosowanych w doświadczeniach rolniczych z wielowymiarowymi obserwacjami. Fragmenta gronomica. Nr 4 (64). s Finney D.J Statistical methods in Biological ssay. Hafner Publishing Company. New York. Laskowski J., Zdybel. 23. Wpływ nawożenia azotowego na właściwości wytrzymałościowe ziarna żyta odmiany milo. Inżynieria Rolnicza. Nr 9 (5). s Olejnik J. 2. Zastosowanie względnej efektywności preparatów do analizy danych eksperymentalnych w inżynierii rolniczej. Rozprawa doktorska. UP. Lublin. Maszynopis. Zdybel. 26. Wpływ nawożenia azotowego na właściwości wytrzymałościowe i technologiczne ziarna żyta. Rozprawa doktorska. R. Lublin. Maszynopis. COMPRISON OF STTISTICL METHODS EMPLOYED TO EXMINE THE IMPCT OF NITROGEN FERTILISTION ON STRENGTH CHRCTERISTICS OF RYE GRIN bstract. The paper will present two different statistical methods used to assess the impact of different nitrogen fertilisation doses on selected strength characteristics of rye grain. The first method is a conventional variance analysis method, while the other is a non-standard method used to evaluate the power of test preparation compared to standard preparation. Comparison of these methods will be carried out for physical properties of wheat grain (milo and Esprit varieties). Key words: variance analysis, relative power of preparations, nitrogen fertilisation, physical properties of grain utor do korespondencji: Zofia Hanusz; zofia.hanusz@up.lublin.pl Katedra Zastosowań Matematyki i Informatyki Uniwersytet Przyrodniczy w Lublinie kademicka Lublin 76
Elementy statystyki STA - Wykład 5
 STA - Wykład 5 Wydział Matematyki i Informatyki Uniwersytet im. Adama Mickiewicza 1 ANOVA 2 Model jednoczynnikowej analizy wariancji Na model jednoczynnikowej analizy wariancji możemy traktować jako uogólnienie
STA - Wykład 5 Wydział Matematyki i Informatyki Uniwersytet im. Adama Mickiewicza 1 ANOVA 2 Model jednoczynnikowej analizy wariancji Na model jednoczynnikowej analizy wariancji możemy traktować jako uogólnienie
1. Jednoczynnikowa analiza wariancji 2. Porównania szczegółowe
 Zjazd 7. SGGW, dn. 28.11.10 r. Matematyka i statystyka matematyczna Tematy 1. Jednoczynnikowa analiza wariancji 2. Porównania szczegółowe nna Rajfura 1 Zagadnienia Przykład porównania wielu obiektów w
Zjazd 7. SGGW, dn. 28.11.10 r. Matematyka i statystyka matematyczna Tematy 1. Jednoczynnikowa analiza wariancji 2. Porównania szczegółowe nna Rajfura 1 Zagadnienia Przykład porównania wielu obiektów w
Matematyka i statystyka matematyczna dla rolników w SGGW
 Było: Testowanie hipotez (ogólnie): stawiamy hipotezę, wybieramy funkcję testową f (test statystyczny), przyjmujemy poziom istotności α; tym samym wyznaczamy obszar krytyczny testu (wartość krytyczną funkcji
Było: Testowanie hipotez (ogólnie): stawiamy hipotezę, wybieramy funkcję testową f (test statystyczny), przyjmujemy poziom istotności α; tym samym wyznaczamy obszar krytyczny testu (wartość krytyczną funkcji
Porównanie dwóch rozkładów normalnych
 Porównanie dwóch rozkładów normalnych Założenia: 1. X 1 N(µ 1, σ 2 1), X 2 N(µ 2, σ 2 2) 2. X 1, X 2 są niezależne Ocena µ 1 µ 2 oraz σ 2 1/σ 2 2. Próby: X 11,..., X 1n1 ; X 21,..., X 2n2 X 1, varx 1,
Porównanie dwóch rozkładów normalnych Założenia: 1. X 1 N(µ 1, σ 2 1), X 2 N(µ 2, σ 2 2) 2. X 1, X 2 są niezależne Ocena µ 1 µ 2 oraz σ 2 1/σ 2 2. Próby: X 11,..., X 1n1 ; X 21,..., X 2n2 X 1, varx 1,
Matematyka i statystyka matematyczna dla rolników w SGGW WYKŁAD 11 DOŚWIADCZENIE JEDNOCZYNNIKOWE W UKŁADZIE CAŁKOWICIE LOSOWYM PORÓWNANIA SZCZEGÓŁOWE
 WYKŁAD 11 DOŚWIADCZENIE JEDNOCZYNNIKOWE W UKŁADZIE CAŁKOWICIE LOSOWYM PORÓWNANIA SZCZEGÓŁOWE Było: Przykład. W doświadczeniu polowym załoŝonym w układzie całkowicie losowym w czterech powtórzeniach porównano
WYKŁAD 11 DOŚWIADCZENIE JEDNOCZYNNIKOWE W UKŁADZIE CAŁKOWICIE LOSOWYM PORÓWNANIA SZCZEGÓŁOWE Było: Przykład. W doświadczeniu polowym załoŝonym w układzie całkowicie losowym w czterech powtórzeniach porównano
Współczynnik korelacji. Współczynnik korelacji jest miernikiem zależności między dwiema cechami Oznaczenie: ϱ
 Współczynnik korelacji Współczynnik korelacji jest miernikiem zależności między dwiema cechami Oznaczenie: ϱ Własności współczynnika korelacji 1. Współczynnik korelacji jest liczbą niemianowaną 2. ϱ 1,
Współczynnik korelacji Współczynnik korelacji jest miernikiem zależności między dwiema cechami Oznaczenie: ϱ Własności współczynnika korelacji 1. Współczynnik korelacji jest liczbą niemianowaną 2. ϱ 1,
Testy post-hoc. Wrocław, 6 czerwca 2016
 Testy post-hoc Wrocław, 6 czerwca 2016 Testy post-hoc 1 metoda LSD 2 metoda Duncana 3 metoda Dunneta 4 metoda kontrastów 5 matoda Newman-Keuls 6 metoda Tukeya Metoda LSD Metoda Least Significant Difference
Testy post-hoc Wrocław, 6 czerwca 2016 Testy post-hoc 1 metoda LSD 2 metoda Duncana 3 metoda Dunneta 4 metoda kontrastów 5 matoda Newman-Keuls 6 metoda Tukeya Metoda LSD Metoda Least Significant Difference
STATYSTYKA MATEMATYCZNA WYKŁAD 4. Testowanie hipotez Estymacja parametrów
 STATYSTYKA MATEMATYCZNA WYKŁAD 4 Testowanie hipotez Estymacja parametrów WSTĘP 1. Testowanie hipotez Błędy związane z testowaniem hipotez Etapy testowana hipotez Testowanie wielokrotne 2. Estymacja parametrów
STATYSTYKA MATEMATYCZNA WYKŁAD 4 Testowanie hipotez Estymacja parametrów WSTĘP 1. Testowanie hipotez Błędy związane z testowaniem hipotez Etapy testowana hipotez Testowanie wielokrotne 2. Estymacja parametrów
Analiza wariancji. dr Janusz Górczyński
 Analiza wariancji dr Janusz Górczyński Wprowadzenie Powiedzmy, że badamy pewną populację π, w której cecha Y ma rozkład N o średniej m i odchyleniu standardowym σ. Powiedzmy dalej, że istnieje pewien czynnik
Analiza wariancji dr Janusz Górczyński Wprowadzenie Powiedzmy, że badamy pewną populację π, w której cecha Y ma rozkład N o średniej m i odchyleniu standardowym σ. Powiedzmy dalej, że istnieje pewien czynnik
ANALIZA METROLOGICZNA WYNIKÓW BADAŃ NA PRZYKŁADZIE ŁOŻYSK ŚLIZGOWYCH
 PROBLEMY NIEKONWENCJONALNYCH UKŁADÓW ŁOŻYSKOWYCH Łódź 09-10 maja 1995 roku Jadwiga Janowska(Politechnika Warszawska) ANALIZA METROLOGICZNA WYNIKÓW BADAŃ NA PRZYKŁADZIE ŁOŻYSK ŚLIZGOWYCH SŁOWA KLUCZOWE
PROBLEMY NIEKONWENCJONALNYCH UKŁADÓW ŁOŻYSKOWYCH Łódź 09-10 maja 1995 roku Jadwiga Janowska(Politechnika Warszawska) ANALIZA METROLOGICZNA WYNIKÓW BADAŃ NA PRZYKŁADZIE ŁOŻYSK ŚLIZGOWYCH SŁOWA KLUCZOWE
Rozdział 8. Regresja. Definiowanie modelu
 Rozdział 8 Regresja Definiowanie modelu Analizę korelacji można traktować jako wstęp do analizy regresji. Jeżeli wykresy rozrzutu oraz wartości współczynników korelacji wskazują na istniejąca współzmienność
Rozdział 8 Regresja Definiowanie modelu Analizę korelacji można traktować jako wstęp do analizy regresji. Jeżeli wykresy rozrzutu oraz wartości współczynników korelacji wskazują na istniejąca współzmienność
Statystyka matematyczna. Wykład V. Parametryczne testy istotności
 Statystyka matematyczna. Wykład V. e-mail:e.kozlovski@pollub.pl Spis treści 1 Weryfikacja hipotezy o równości wartości średnich w dwóch populacjach 2 3 Weryfikacja hipotezy o równości wartości średnich
Statystyka matematyczna. Wykład V. e-mail:e.kozlovski@pollub.pl Spis treści 1 Weryfikacja hipotezy o równości wartości średnich w dwóch populacjach 2 3 Weryfikacja hipotezy o równości wartości średnich
WPŁYW TECHNICZNEGO UZBROJENIA PROCESU PRACY NA NADWYŻKĘ BEZPOŚREDNIĄ W GOSPODARSTWACH RODZINNYCH
 Inżynieria Rolnicza 4(102)/2008 WPŁYW TECHNICZNEGO UZBROJENIA PROCESU PRACY NA NADWYŻKĘ BEZPOŚREDNIĄ W GOSPODARSTWACH RODZINNYCH Sławomir Kocira Katedra Eksploatacji Maszyn i Zarządzania w Inżynierii Rolniczej,
Inżynieria Rolnicza 4(102)/2008 WPŁYW TECHNICZNEGO UZBROJENIA PROCESU PRACY NA NADWYŻKĘ BEZPOŚREDNIĄ W GOSPODARSTWACH RODZINNYCH Sławomir Kocira Katedra Eksploatacji Maszyn i Zarządzania w Inżynierii Rolniczej,
RÓWNOWAŻNOŚĆ METOD BADAWCZYCH
 RÓWNOWAŻNOŚĆ METOD BADAWCZYCH Piotr Konieczka Katedra Chemii Analitycznej Wydział Chemiczny Politechnika Gdańska Równoważność metod??? 2 Zgodność wyników analitycznych otrzymanych z wykorzystaniem porównywanych
RÓWNOWAŻNOŚĆ METOD BADAWCZYCH Piotr Konieczka Katedra Chemii Analitycznej Wydział Chemiczny Politechnika Gdańska Równoważność metod??? 2 Zgodność wyników analitycznych otrzymanych z wykorzystaniem porównywanych
ZWIĄZKI MIĘDZY CECHAMI ELEKTRYCZNYMI A AKTYWNOŚCIĄ WODY ŚRUTY PSZENICZNEJ
 Inżynieria Rolnicza 6(115)/2009 ZWIĄZKI MIĘDZY CECHAMI ELEKTRYCZNYMI A AKTYWNOŚCIĄ WODY ŚRUTY PSZENICZNEJ Deta Łuczycka Instytut Inżynierii Rolniczej, Uniwersytet Przyrodniczy we Wrocławiu Streszczenie.
Inżynieria Rolnicza 6(115)/2009 ZWIĄZKI MIĘDZY CECHAMI ELEKTRYCZNYMI A AKTYWNOŚCIĄ WODY ŚRUTY PSZENICZNEJ Deta Łuczycka Instytut Inżynierii Rolniczej, Uniwersytet Przyrodniczy we Wrocławiu Streszczenie.
Tab.1 Powierzchnia i liczba ankietowanych pól
 Monitoring wpływu stosowania kwalifikowanego materiału siewnego roślin zbożowych i okopowych na produkcję roślinną metodyka i wyniki. Materiał Materiał źródłowy stanowią wyniki badań ankietowych gospodarstw
Monitoring wpływu stosowania kwalifikowanego materiału siewnego roślin zbożowych i okopowych na produkcję roślinną metodyka i wyniki. Materiał Materiał źródłowy stanowią wyniki badań ankietowych gospodarstw
JEDNOCZYNNIKOWA ANALIZA WARIANCJI, ANOVA
 JEDNOCZYNNIKOWA ANALIZA WARIANCJI, ANOVA 1 Obserwowana (badana) cecha Y Czynnik wpływający na Y (badany) A A i i ty poziom czynnika A a liczba poziomów (j=1..a), n i liczba powtórzeń w i tej populacji
JEDNOCZYNNIKOWA ANALIZA WARIANCJI, ANOVA 1 Obserwowana (badana) cecha Y Czynnik wpływający na Y (badany) A A i i ty poziom czynnika A a liczba poziomów (j=1..a), n i liczba powtórzeń w i tej populacji
Porównanie wielu rozkładów normalnych
 Porównanie wielu rozkładów normalnych Założenia:. X i N(µ i, σi 2 ), i =,..., k 2. X,..., X k są niezależne Czy µ = = µ k? Czy σ 2 = = σ 2 k? Próby: X i,..., X ini, i =,..., k X i, varx i, s 2 i = varx
Porównanie wielu rozkładów normalnych Założenia:. X i N(µ i, σi 2 ), i =,..., k 2. X,..., X k są niezależne Czy µ = = µ k? Czy σ 2 = = σ 2 k? Próby: X i,..., X ini, i =,..., k X i, varx i, s 2 i = varx
Szkice rozwiązań z R:
 Szkice rozwiązań z R: Zadanie 1. Założono doświadczenie farmakologiczne. Obserwowano przyrost wagi ciała (przyrost [gram]) przy zadanych dawkach trzech preparatów (dawka.a, dawka.b, dawka.c). Obiektami
Szkice rozwiązań z R: Zadanie 1. Założono doświadczenie farmakologiczne. Obserwowano przyrost wagi ciała (przyrost [gram]) przy zadanych dawkach trzech preparatów (dawka.a, dawka.b, dawka.c). Obiektami
Statystyka. #6 Analiza wariancji. Aneta Dzik-Walczak Małgorzata Kalbarczyk-Stęclik. rok akademicki 2015/ / 14
 Statystyka #6 Analiza wariancji Aneta Dzik-Walczak Małgorzata Kalbarczyk-Stęclik rok akademicki 2015/2016 1 / 14 Analiza wariancji 2 / 14 Analiza wariancji Analiza wariancji jest techniką badania wyników,
Statystyka #6 Analiza wariancji Aneta Dzik-Walczak Małgorzata Kalbarczyk-Stęclik rok akademicki 2015/2016 1 / 14 Analiza wariancji 2 / 14 Analiza wariancji Analiza wariancji jest techniką badania wyników,
Wykład 3 Testowanie hipotez statystycznych o wartości średniej. średniej i wariancji z populacji o rozkładzie normalnym
 Wykład 3 Testowanie hipotez statystycznych o wartości średniej i wariancji z populacji o rozkładzie normalnym Wrocław, 08.03.2017r Model 1 Testowanie hipotez dla średniej w rozkładzie normalnym ze znaną
Wykład 3 Testowanie hipotez statystycznych o wartości średniej i wariancji z populacji o rozkładzie normalnym Wrocław, 08.03.2017r Model 1 Testowanie hipotez dla średniej w rozkładzie normalnym ze znaną
Analiza zależności cech ilościowych regresja liniowa (Wykład 13)
 Analiza zależności cech ilościowych regresja liniowa (Wykład 13) dr Mariusz Grządziel semestr letni 2012 Przykład wprowadzajacy W zbiorze danych homedata (z pakietu R-owskiego UsingR) można znaleźć ceny
Analiza zależności cech ilościowych regresja liniowa (Wykład 13) dr Mariusz Grządziel semestr letni 2012 Przykład wprowadzajacy W zbiorze danych homedata (z pakietu R-owskiego UsingR) można znaleźć ceny
Inżynieria Rolnicza 7(105)/2008
 Inżynieria Rolnicza 7(105)/2008 BADANIE ZALEŻNOŚCI POMIĘDZY KOSZTAMI EKSPLOATACJI CIĄGNIKÓW, MASZYN I URZĄDZEŃ ROLNICZYCH A CZASEM ICH ROCZNEGO WYKORZYSTANIA NA PRZYKŁADZIE WOZÓW ASENIZACYJNYCH Zbigniew
Inżynieria Rolnicza 7(105)/2008 BADANIE ZALEŻNOŚCI POMIĘDZY KOSZTAMI EKSPLOATACJI CIĄGNIKÓW, MASZYN I URZĄDZEŃ ROLNICZYCH A CZASEM ICH ROCZNEGO WYKORZYSTANIA NA PRZYKŁADZIE WOZÓW ASENIZACYJNYCH Zbigniew
Analiza wariancji i kowariancji
 Analiza wariancji i kowariancji Historia Analiza wariancji jest metodą zaproponowaną przez Ronalda A. Fishera. Po zakończeniu pierwszej wojny światowej był on pracownikiem laboratorium statystycznego w
Analiza wariancji i kowariancji Historia Analiza wariancji jest metodą zaproponowaną przez Ronalda A. Fishera. Po zakończeniu pierwszej wojny światowej był on pracownikiem laboratorium statystycznego w
ZASTOSOWANIE REGRESJI LOGISTYCZNEJ DO WYZNACZENIA CECH O NAJWIĘKSZEJ SILE DYSKRYMINACJI WIELKOŚCI WSKAŹNIKÓW POSTĘPU NAUKOWO-TECHNICZNEGO
 Inżynieria Rolnicza 8(96)/2007 ZASTOSOWANIE REGRESJI LOGISTYCZNEJ DO WYZNACZENIA CECH O NAJWIĘKSZEJ SILE DYSKRYMINACJI WIELKOŚCI WSKAŹNIKÓW POSTĘPU NAUKOWO-TECHNICZNEGO Agnieszka Prusak, Stanisława Roczkowska-Chmaj
Inżynieria Rolnicza 8(96)/2007 ZASTOSOWANIE REGRESJI LOGISTYCZNEJ DO WYZNACZENIA CECH O NAJWIĘKSZEJ SILE DYSKRYMINACJI WIELKOŚCI WSKAŹNIKÓW POSTĘPU NAUKOWO-TECHNICZNEGO Agnieszka Prusak, Stanisława Roczkowska-Chmaj
Testowanie hipotez statystycznych.
 Statystyka Wykład 10 Wrocław, 22 grudnia 2011 Testowanie hipotez statystycznych Definicja. Hipotezą statystyczną nazywamy stwierdzenie dotyczące parametrów populacji. Definicja. Dwie komplementarne w problemie
Statystyka Wykład 10 Wrocław, 22 grudnia 2011 Testowanie hipotez statystycznych Definicja. Hipotezą statystyczną nazywamy stwierdzenie dotyczące parametrów populacji. Definicja. Dwie komplementarne w problemie
Weryfikacja hipotez statystycznych
 Weryfikacja hipotez statystycznych Hipoteza Test statystyczny Poziom istotności Testy jednostronne i dwustronne Testowanie równości wariancji test F-Fishera Testowanie równości wartości średnich test t-studenta
Weryfikacja hipotez statystycznych Hipoteza Test statystyczny Poziom istotności Testy jednostronne i dwustronne Testowanie równości wariancji test F-Fishera Testowanie równości wartości średnich test t-studenta
WIELKA SGH-OWA POWTÓRKA ZE STATYSTYKI REGRESJA LINIOWA
 WIELKA SGH-OWA POWTÓRKA ZE STATYSTYKI REGRESJA LINIOWA Powtórka Powtórki Kowiariancja cov xy lub c xy - kierunek zależności Współczynnik korelacji liniowej Pearsona r siła liniowej zależności Istotność
WIELKA SGH-OWA POWTÓRKA ZE STATYSTYKI REGRESJA LINIOWA Powtórka Powtórki Kowiariancja cov xy lub c xy - kierunek zależności Współczynnik korelacji liniowej Pearsona r siła liniowej zależności Istotność
ZJAZD 4. gdzie E(x) jest wartością oczekiwaną x
 ZJAZD 4 KORELACJA, BADANIE NIEZALEŻNOŚCI, ANALIZA REGRESJI Analiza korelacji i regresji jest działem statystyki zajmującym się badaniem zależności i związków pomiędzy rozkładami dwu lub więcej badanych
ZJAZD 4 KORELACJA, BADANIE NIEZALEŻNOŚCI, ANALIZA REGRESJI Analiza korelacji i regresji jest działem statystyki zajmującym się badaniem zależności i związków pomiędzy rozkładami dwu lub więcej badanych
Testowanie hipotez statystycznych. Wnioskowanie statystyczne
 Testowanie hipotez statystycznych Wnioskowanie statystyczne Hipoteza statystyczna to dowolne przypuszczenie co do rozkładu populacji generalnej (jego postaci funkcyjnej lub wartości parametrów). Hipotezy
Testowanie hipotez statystycznych Wnioskowanie statystyczne Hipoteza statystyczna to dowolne przypuszczenie co do rozkładu populacji generalnej (jego postaci funkcyjnej lub wartości parametrów). Hipotezy
O testach wielowymiarowej normalności opartych na statystyce Shapiro-Wilka
 O testach wielowymiarowej normalności opartych na statystyce Shapiro-Wilka Katedra Zastosowań Matematyki i Informatyki Uniwersytet Przyrodniczy w Lublinie Wisła 2012, 7.12.2012 Plan prezentacji 1 Wprowadzenie
O testach wielowymiarowej normalności opartych na statystyce Shapiro-Wilka Katedra Zastosowań Matematyki i Informatyki Uniwersytet Przyrodniczy w Lublinie Wisła 2012, 7.12.2012 Plan prezentacji 1 Wprowadzenie
Tablica Wzorów Rachunek Prawdopodobieństwa i Statystyki
 Tablica Wzorów Rachunek Prawdopodobieństwa i Statystyki Spis treści I. Wzory ogólne... 2 1. Średnia arytmetyczna:... 2 2. Rozstęp:... 2 3. Kwantyle:... 2 4. Wariancja:... 2 5. Odchylenie standardowe:...
Tablica Wzorów Rachunek Prawdopodobieństwa i Statystyki Spis treści I. Wzory ogólne... 2 1. Średnia arytmetyczna:... 2 2. Rozstęp:... 2 3. Kwantyle:... 2 4. Wariancja:... 2 5. Odchylenie standardowe:...
WERYFIKACJA HIPOTEZ STATYSTYCZNYCH
 WERYFIKACJA HIPOTEZ STATYSTYCZNYCH I. TESTY PARAMETRYCZNE II. III. WERYFIKACJA HIPOTEZ O WARTOŚCIACH ŚREDNICH DWÓCH POPULACJI TESTY ZGODNOŚCI Rozwiązania zadań wykonywanych w Statistice przedstaw w pliku
WERYFIKACJA HIPOTEZ STATYSTYCZNYCH I. TESTY PARAMETRYCZNE II. III. WERYFIKACJA HIPOTEZ O WARTOŚCIACH ŚREDNICH DWÓCH POPULACJI TESTY ZGODNOŚCI Rozwiązania zadań wykonywanych w Statistice przedstaw w pliku
Analiza wariancji - ANOVA
 Analiza wariancji - ANOVA Analiza wariancji jest metodą pozwalającą na podział zmienności zaobserwowanej wśród wyników eksperymentalnych na oddzielne części. Każdą z tych części możemy przypisać oddzielnemu
Analiza wariancji - ANOVA Analiza wariancji jest metodą pozwalającą na podział zmienności zaobserwowanej wśród wyników eksperymentalnych na oddzielne części. Każdą z tych części możemy przypisać oddzielnemu
WPŁYW WILGOTNOŚCI NA WYBRANE WŁAŚCIWOŚCI MECHANICZNE ZIARNA PSZENICY
 Inżynieria Rolnicza 5(93)/2007 WPŁYW WILGOTNOŚCI NA WYBRANE WŁAŚCIWOŚCI MECHANICZNE ZIARNA PSZENICY Małgorzata Goździewska, Dariusz Piekarski, Dariusz Andrejko Katedra Inżynierii i Maszyn Spożywczych,
Inżynieria Rolnicza 5(93)/2007 WPŁYW WILGOTNOŚCI NA WYBRANE WŁAŚCIWOŚCI MECHANICZNE ZIARNA PSZENICY Małgorzata Goździewska, Dariusz Piekarski, Dariusz Andrejko Katedra Inżynierii i Maszyn Spożywczych,
Założenia do analizy wariancji. dr Anna Rajfura Kat. Doświadczalnictwa i Bioinformatyki SGGW
 Założenia do analizy wariancji dr Anna Rajfura Kat. Doświadczalnictwa i Bioinformatyki SGGW anna_rajfura@sggw.pl Zagadnienia 1. Normalność rozkładu cechy Testy: chi-kwadrat zgodności, Shapiro-Wilka, Kołmogorowa-Smirnowa
Założenia do analizy wariancji dr Anna Rajfura Kat. Doświadczalnictwa i Bioinformatyki SGGW anna_rajfura@sggw.pl Zagadnienia 1. Normalność rozkładu cechy Testy: chi-kwadrat zgodności, Shapiro-Wilka, Kołmogorowa-Smirnowa
Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć)
 Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć) 1. Populacja generalna a losowa próba, parametr rozkładu cechy a jego ocena z losowej próby, miary opisu statystycznego
Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć) 1. Populacja generalna a losowa próba, parametr rozkładu cechy a jego ocena z losowej próby, miary opisu statystycznego
ZASTOSOWANIE MODELU GOMPERTZ A W INŻYNIERII ROLNICZEJ
 Inżynieria Rolnicza 7(105)/2008 ZASTOSOWANIE MODELU GOMPERTZ A W INŻYNIERII ROLNICZEJ Zofia Hanusz Katedra Zastosowań Matematyki, Uniwersytet Przyrodniczy w Lublinie Zbigniew Siarkowski, Krzysztof Ostrowski
Inżynieria Rolnicza 7(105)/2008 ZASTOSOWANIE MODELU GOMPERTZ A W INŻYNIERII ROLNICZEJ Zofia Hanusz Katedra Zastosowań Matematyki, Uniwersytet Przyrodniczy w Lublinie Zbigniew Siarkowski, Krzysztof Ostrowski
b) Niech: - wśród trzech wylosowanych opakowań jest co najwyżej jedno o dawce 15 mg. Wówczas:
 ROZWIĄZANIA I ODPOWIEDZI Zadanie A1. Można założyć, że przy losowaniu trzech kul jednocześnie kolejność ich wylosowania nie jest istotna. A więc: Ω = 20 3. a) Niech: - wśród trzech wylosowanych opakowań
ROZWIĄZANIA I ODPOWIEDZI Zadanie A1. Można założyć, że przy losowaniu trzech kul jednocześnie kolejność ich wylosowania nie jest istotna. A więc: Ω = 20 3. a) Niech: - wśród trzech wylosowanych opakowań
Zad. 4 Należy określić rodzaj testu (jedno czy dwustronny) oraz wartości krytyczne z lub t dla określonych hipotez i ich poziomów istotności:
 Zadania ze statystyki cz. 7. Zad.1 Z populacji wyłoniono próbę wielkości 64 jednostek. Średnia arytmetyczna wartość cechy wyniosła 110, zaś odchylenie standardowe 16. Należy wyznaczyć przedział ufności
Zadania ze statystyki cz. 7. Zad.1 Z populacji wyłoniono próbę wielkości 64 jednostek. Średnia arytmetyczna wartość cechy wyniosła 110, zaś odchylenie standardowe 16. Należy wyznaczyć przedział ufności
WPŁYW SZYBKOŚCI STYGNIĘCIA NA WŁASNOŚCI TERMOFIZYCZNE STALIWA W STANIE STAŁYM
 2/1 Archives of Foundry, Year 200, Volume, 1 Archiwum Odlewnictwa, Rok 200, Rocznik, Nr 1 PAN Katowice PL ISSN 1642-308 WPŁYW SZYBKOŚCI STYGNIĘCIA NA WŁASNOŚCI TERMOFIZYCZNE STALIWA W STANIE STAŁYM D.
2/1 Archives of Foundry, Year 200, Volume, 1 Archiwum Odlewnictwa, Rok 200, Rocznik, Nr 1 PAN Katowice PL ISSN 1642-308 WPŁYW SZYBKOŚCI STYGNIĘCIA NA WŁASNOŚCI TERMOFIZYCZNE STALIWA W STANIE STAŁYM D.
CECHY TECHNICZNO-UŻYTKOWE A WARTOŚĆ WYBRANYCH TECHNICZNYCH ŚRODKÓW PRODUKCJI W ROLNICTWIE
 Inżynieria Rolnicza 9(107)/2008 CECHY TECHNICZNO-UŻYTKOWE A WARTOŚĆ WYBRANYCH TECHNICZNYCH ŚRODKÓW PRODUKCJI W ROLNICTWIE Zbigniew Kowalczyk Katedra Inżynierii Rolniczej i Informatyki, Uniwersytet Rolniczy
Inżynieria Rolnicza 9(107)/2008 CECHY TECHNICZNO-UŻYTKOWE A WARTOŚĆ WYBRANYCH TECHNICZNYCH ŚRODKÓW PRODUKCJI W ROLNICTWIE Zbigniew Kowalczyk Katedra Inżynierii Rolniczej i Informatyki, Uniwersytet Rolniczy
Estymacja parametrów modeli liniowych oraz ocena jakości dopasowania modeli do danych empirycznych
 Estymacja parametrów modeli liniowych oraz ocena jakości dopasowania modeli do danych empirycznych 3.1. Estymacja parametrów i ocena dopasowania modeli z jedną zmienną 23. Właściciel komisu w celu zbadania
Estymacja parametrów modeli liniowych oraz ocena jakości dopasowania modeli do danych empirycznych 3.1. Estymacja parametrów i ocena dopasowania modeli z jedną zmienną 23. Właściciel komisu w celu zbadania
Analizy wariancji ANOVA (analysis of variance)
 ANOVA Analizy wariancji ANOVA (analysis of variance) jest to metoda równoczesnego badania istotności różnic między wieloma średnimi z prób pochodzących z wielu populacji (grup). Model jednoczynnikowy analiza
ANOVA Analizy wariancji ANOVA (analysis of variance) jest to metoda równoczesnego badania istotności różnic między wieloma średnimi z prób pochodzących z wielu populacji (grup). Model jednoczynnikowy analiza
Zadania ze statystyki, cz.7 - hipotezy statystyczne, błąd standardowy, testowanie hipotez statystycznych
 Zadania ze statystyki, cz.7 - hipotezy statystyczne, błąd standardowy, testowanie hipotez statystycznych Zad. 1 Średnia ocen z semestru letniego w populacji studentów socjologii w roku akademickim 2011/2012
Zadania ze statystyki, cz.7 - hipotezy statystyczne, błąd standardowy, testowanie hipotez statystycznych Zad. 1 Średnia ocen z semestru letniego w populacji studentów socjologii w roku akademickim 2011/2012
Testowanie hipotez dla dwóch zmiennych zależnych. Moc testu. Minimalna liczność próby; Regresja prosta; Korelacja Pearsona;
 LABORATORIUM 4 Testowanie hipotez dla dwóch zmiennych zależnych. Moc testu. Minimalna liczność próby; Regresja prosta; Korelacja Pearsona; dwie zmienne zależne mierzalne małe próby duże próby rozkład normalny
LABORATORIUM 4 Testowanie hipotez dla dwóch zmiennych zależnych. Moc testu. Minimalna liczność próby; Regresja prosta; Korelacja Pearsona; dwie zmienne zależne mierzalne małe próby duże próby rozkład normalny
Statystyka w analizie i planowaniu eksperymentu
 28 marca 2012 Analiza wariancji klasyfikacja jednokierunkowa - wst ep Przypuśćmy, że chcemy porównać wieksz a (niż dwie) liczbe grup. Aby porównać średnie w kilku grupach, można przeprowadzić analize wariancji.
28 marca 2012 Analiza wariancji klasyfikacja jednokierunkowa - wst ep Przypuśćmy, że chcemy porównać wieksz a (niż dwie) liczbe grup. Aby porównać średnie w kilku grupach, można przeprowadzić analize wariancji.
Matematyka z el. statystyki, # 6 /Geodezja i kartografia II/
 Matematyka z el. statystyki, # 6 /Geodezja i kartografia II/ Uniwersytet Przyrodniczy w Lublinie Katedra Zastosowań Matematyki i Informatyki ul. Głęboka 28, bud. CIW, p. 221 e-mail: zdzislaw.otachel@up.lublin.pl
Matematyka z el. statystyki, # 6 /Geodezja i kartografia II/ Uniwersytet Przyrodniczy w Lublinie Katedra Zastosowań Matematyki i Informatyki ul. Głęboka 28, bud. CIW, p. 221 e-mail: zdzislaw.otachel@up.lublin.pl
Korelacja krzywoliniowa i współzależność cech niemierzalnych
 Korelacja krzywoliniowa i współzależność cech niemierzalnych Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych Wydział Informatyki Politechniki Szczecińskiej
Korelacja krzywoliniowa i współzależność cech niemierzalnych Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych Wydział Informatyki Politechniki Szczecińskiej
Wykorzystanie testu Levene a i testu Browna-Forsythe a w badaniach jednorodności wariancji
 Wydawnictwo UR 2016 ISSN 2080-9069 ISSN 2450-9221 online Edukacja Technika Informatyka nr 4/18/2016 www.eti.rzeszow.pl DOI: 10.15584/eti.2016.4.48 WIESŁAWA MALSKA Wykorzystanie testu Levene a i testu Browna-Forsythe
Wydawnictwo UR 2016 ISSN 2080-9069 ISSN 2450-9221 online Edukacja Technika Informatyka nr 4/18/2016 www.eti.rzeszow.pl DOI: 10.15584/eti.2016.4.48 WIESŁAWA MALSKA Wykorzystanie testu Levene a i testu Browna-Forsythe
Wprowadzenie do analizy korelacji i regresji
 Statystyka dla jakości produktów i usług Six sigma i inne strategie Wprowadzenie do analizy korelacji i regresji StatSoft Polska Wybrane zagadnienia analizy korelacji Przy analizie zjawisk i procesów stanowiących
Statystyka dla jakości produktów i usług Six sigma i inne strategie Wprowadzenie do analizy korelacji i regresji StatSoft Polska Wybrane zagadnienia analizy korelacji Przy analizie zjawisk i procesów stanowiących
Wpływ niektórych czynników na skład chemiczny ziarna pszenicy jarej
 NR 218/219 BIULETYN INSTYTUTU HODOWLI I AKLIMATYZACJI ROŚLIN 21 SZYMON DZIAMBA IZABELLA JACKOWSKA 1 Katedra Szczegółowej Uprawy Roślin 1 Katedra Chemii Akademia Rolnicza w Lublinie Wpływ niektórych czynników
NR 218/219 BIULETYN INSTYTUTU HODOWLI I AKLIMATYZACJI ROŚLIN 21 SZYMON DZIAMBA IZABELLA JACKOWSKA 1 Katedra Szczegółowej Uprawy Roślin 1 Katedra Chemii Akademia Rolnicza w Lublinie Wpływ niektórych czynników
Zadanie 1 Zakładając liniową relację między wydatkami na obuwie a dochodem oszacować MNK parametry modelu: y t. X 1 t. Tabela 1.
 tel. 44 683 1 55 tel. kom. 64 566 811 e-mail: biuro@wszechwiedza.pl Zadanie 1 Zakładając liniową relację między wydatkami na obuwie a dochodem oszacować MNK parametry modelu: gdzie: y t X t y t = 1 X 1
tel. 44 683 1 55 tel. kom. 64 566 811 e-mail: biuro@wszechwiedza.pl Zadanie 1 Zakładając liniową relację między wydatkami na obuwie a dochodem oszacować MNK parametry modelu: gdzie: y t X t y t = 1 X 1
Statystyka matematyczna Testowanie hipotez i estymacja parametrów. Wrocław, r
 Statystyka matematyczna Testowanie hipotez i estymacja parametrów Wrocław, 18.03.2016r Plan wykładu: 1. Testowanie hipotez 2. Etapy testowania hipotez 3. Błędy 4. Testowanie wielokrotne 5. Estymacja parametrów
Statystyka matematyczna Testowanie hipotez i estymacja parametrów Wrocław, 18.03.2016r Plan wykładu: 1. Testowanie hipotez 2. Etapy testowania hipotez 3. Błędy 4. Testowanie wielokrotne 5. Estymacja parametrów
Weryfikacja hipotez statystycznych, parametryczne testy istotności w populacji
 Weryfikacja hipotez statystycznych, parametryczne testy istotności w populacji Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych Wydział Informatyki Politechniki
Weryfikacja hipotez statystycznych, parametryczne testy istotności w populacji Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych Wydział Informatyki Politechniki
Wykład 5 Teoria eksperymentu
 Wykład 5 Teoria eksperymentu Wrocław, 22.03.2017r Co to jest teoria eksperymentu? eksperyment - badanie jakiegoś zjawiska polegające na celowym wywołaniu tego zjawiska lub jego zmian oraz obserwacji i
Wykład 5 Teoria eksperymentu Wrocław, 22.03.2017r Co to jest teoria eksperymentu? eksperyment - badanie jakiegoś zjawiska polegające na celowym wywołaniu tego zjawiska lub jego zmian oraz obserwacji i
WPŁYW WYBRANYCH CZYNNIKÓW NA RÓWNOMIERNOŚĆ DOZOWANIA I WYSIEWU NASION PSZENICY KOŁECZKOWYM ZESPOŁEM WYSIEWAJĄCYM
 Inżynieria Rolnicza 5(103)/2008 WPŁYW WYBRANYCH CZYNNIKÓW NA RÓWNOMIERNOŚĆ DOZOWANIA I WYSIEWU NASION PSZENICY KOŁECZKOWYM ZESPOŁEM WYSIEWAJĄCYM Piotr Markowski, Tadeusz Rawa, Adam Lipiński Katedra Maszyn
Inżynieria Rolnicza 5(103)/2008 WPŁYW WYBRANYCH CZYNNIKÓW NA RÓWNOMIERNOŚĆ DOZOWANIA I WYSIEWU NASION PSZENICY KOŁECZKOWYM ZESPOŁEM WYSIEWAJĄCYM Piotr Markowski, Tadeusz Rawa, Adam Lipiński Katedra Maszyn
ĆWICZENIE 11 ANALIZA KORELACJI I REGRESJI
 ĆWICZENIE 11 ANALIZA KORELACJI I REGRESJI Korelacja 1. Współczynnik korelacji 2. Współczynnik korelacji liniowej definicja 3. Estymacja współczynnika korelacji 4. Testy istotności współczynnika korelacji
ĆWICZENIE 11 ANALIZA KORELACJI I REGRESJI Korelacja 1. Współczynnik korelacji 2. Współczynnik korelacji liniowej definicja 3. Estymacja współczynnika korelacji 4. Testy istotności współczynnika korelacji
Rachunek prawdopodobieństwa i statystyka - W 9 Testy statystyczne testy zgodności. Dr Anna ADRIAN Paw B5, pok407
 Rachunek prawdopodobieństwa i statystyka - W 9 Testy statystyczne testy zgodności Dr Anna ADRIAN Paw B5, pok407 adan@agh.edu.pl Weryfikacja hipotez dotyczących postaci nieznanego rozkładu -Testy zgodności.
Rachunek prawdopodobieństwa i statystyka - W 9 Testy statystyczne testy zgodności Dr Anna ADRIAN Paw B5, pok407 adan@agh.edu.pl Weryfikacja hipotez dotyczących postaci nieznanego rozkładu -Testy zgodności.
METODA WARTOŚCIOWANIA PARAMETRÓW PROCESU PLANOWEGO OBSŁUGIWANIA TECHNICZNEGO MASZYN ROLNICZYCH
 Inżynieria Rolnicza 7(125)/2010 METODA WARTOŚCIOWANIA PARAMETRÓW PROCESU PLANOWEGO OBSŁUGIWANIA TECHNICZNEGO MASZYN ROLNICZYCH Zenon Grześ Instytut Inżynierii Rolniczej, Uniwersytet Przyrodniczy w Poznaniu
Inżynieria Rolnicza 7(125)/2010 METODA WARTOŚCIOWANIA PARAMETRÓW PROCESU PLANOWEGO OBSŁUGIWANIA TECHNICZNEGO MASZYN ROLNICZYCH Zenon Grześ Instytut Inżynierii Rolniczej, Uniwersytet Przyrodniczy w Poznaniu
Statystyka Opisowa z Demografią oraz Biostatystyka. Aleksander Denisiuk. denisjuk@euh-e.edu.pl
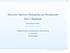 Statystyka Opisowa z Demografią oraz Biostatystyka TesttStudenta Aleksander Denisiuk denisjuk@euh-e.edu.pl Elblaska Uczelnia Humanistyczno-Ekonomiczna ul. Lotnicza 2 82-300 Elblag oraz Biostatystyka p.
Statystyka Opisowa z Demografią oraz Biostatystyka TesttStudenta Aleksander Denisiuk denisjuk@euh-e.edu.pl Elblaska Uczelnia Humanistyczno-Ekonomiczna ul. Lotnicza 2 82-300 Elblag oraz Biostatystyka p.
PDF created with FinePrint pdffactory Pro trial version http://www.fineprint.com
 Analiza korelacji i regresji KORELACJA zależność liniowa Obserwujemy parę cech ilościowych (X,Y). Doświadczenie jest tak pomyślane, aby obserwowane pary cech X i Y (tzn i ta para x i i y i dla różnych
Analiza korelacji i regresji KORELACJA zależność liniowa Obserwujemy parę cech ilościowych (X,Y). Doświadczenie jest tak pomyślane, aby obserwowane pary cech X i Y (tzn i ta para x i i y i dla różnych
Wykład 3 Hipotezy statystyczne
 Wykład 3 Hipotezy statystyczne Hipotezą statystyczną nazywamy każde przypuszczenie dotyczące nieznanego rozkładu obserwowanej zmiennej losowej (cechy populacji generalnej) Hipoteza zerowa (H 0 ) jest hipoteza
Wykład 3 Hipotezy statystyczne Hipotezą statystyczną nazywamy każde przypuszczenie dotyczące nieznanego rozkładu obserwowanej zmiennej losowej (cechy populacji generalnej) Hipoteza zerowa (H 0 ) jest hipoteza
Statystyka matematyczna Testowanie hipotez dla średnich w rozkładzie normalnym. Wrocław, r
 Statystyka matematyczna Testowanie hipotez dla średnich w rozkładzie normalnym Wrocław, 18.03.2016r Testowanie hipotez dla średniej w rozkładzie normalnym dla jednej próby Model 1 Testowanie hipotez dla
Statystyka matematyczna Testowanie hipotez dla średnich w rozkładzie normalnym Wrocław, 18.03.2016r Testowanie hipotez dla średniej w rozkładzie normalnym dla jednej próby Model 1 Testowanie hipotez dla
X WYKŁAD STATYSTYKA. 14/05/2014 B8 sala 0.10B Godz. 15:15
 X WYKŁAD STATYSTYKA 14/05/2014 B8 sala 0.10B Godz. 15:15 WYKŁAD 10 ANALIZA KORELACJI Korelacja 1. Współczynnik korelacji 2. Kowariancja 3. Współczynnik korelacji liniowej definicja 4. Estymacja współczynnika
X WYKŁAD STATYSTYKA 14/05/2014 B8 sala 0.10B Godz. 15:15 WYKŁAD 10 ANALIZA KORELACJI Korelacja 1. Współczynnik korelacji 2. Kowariancja 3. Współczynnik korelacji liniowej definicja 4. Estymacja współczynnika
Katedra Biotechnologii i Genetyki Zwierząt, Wydział Hodowli i Biologii Zwierząt, UTP w Bydgoszczy
 Temat: Weryfikacja hipotez statystycznych dla jednej i dwóch średnich. MS EXCEL Do weryfikacji różnic między dwiema grupami jednostek doświadczalnych w MS Excelu wykorzystujemy funkcję o nazwie T.TEST.
Temat: Weryfikacja hipotez statystycznych dla jednej i dwóch średnich. MS EXCEL Do weryfikacji różnic między dwiema grupami jednostek doświadczalnych w MS Excelu wykorzystujemy funkcję o nazwie T.TEST.
STATYSTYKA I DOŚWIADCZALNICTWO. Wykład 2
 STATYSTYKA I DOŚWIADCZALNICTWO Wykład Parametry przedziałowe rozkładów ciągłych określane na podstawie próby (przedziały ufności) Przedział ufności dla średniej s X t( α;n 1),X + t( α;n 1) n s n t (α;
STATYSTYKA I DOŚWIADCZALNICTWO Wykład Parametry przedziałowe rozkładów ciągłych określane na podstawie próby (przedziały ufności) Przedział ufności dla średniej s X t( α;n 1),X + t( α;n 1) n s n t (α;
ANALIZA WŁAŚCIWOŚCI TRAKCYJNYCH DARNI W ZMIENNYCH WARUNKACH GRUNTOWYCH
 Inżynieria Rolnicza 5(123)/21 ANALIZA WŁAŚCIWOŚCI TRAKCYJNYCH DARNI W ZMIENNYCH WARUNKACH GRUNTOWYCH Instytut Inżynierii Rolniczej, Uniwersytet Przyrodniczy we Wrocławiu Streszczenie. W pracy przedstawiono
Inżynieria Rolnicza 5(123)/21 ANALIZA WŁAŚCIWOŚCI TRAKCYJNYCH DARNI W ZMIENNYCH WARUNKACH GRUNTOWYCH Instytut Inżynierii Rolniczej, Uniwersytet Przyrodniczy we Wrocławiu Streszczenie. W pracy przedstawiono
Wnioskowanie statystyczne. Statystyka w 5
 Wnioskowanie statystyczne tatystyka w 5 Rozkłady statystyk z próby Próba losowa pobrana z populacji stanowi realizacje zmiennej losowej jak ciąg zmiennych losowych (X, X,... X ) niezależnych i mających
Wnioskowanie statystyczne tatystyka w 5 Rozkłady statystyk z próby Próba losowa pobrana z populacji stanowi realizacje zmiennej losowej jak ciąg zmiennych losowych (X, X,... X ) niezależnych i mających
Modele i wnioskowanie statystyczne (MWS), sprawozdanie z laboratorium 4
 Modele i wnioskowanie statystyczne (MWS), sprawozdanie z laboratorium 4 Konrad Miziński, nr albumu 233703 31 maja 2015 Zadanie 1 Wartości oczekiwane µ 1 i µ 2 oszacowano wg wzorów: { µ1 = 0.43925 µ = X
Modele i wnioskowanie statystyczne (MWS), sprawozdanie z laboratorium 4 Konrad Miziński, nr albumu 233703 31 maja 2015 Zadanie 1 Wartości oczekiwane µ 1 i µ 2 oszacowano wg wzorów: { µ1 = 0.43925 µ = X
Stanisław Cichocki. Natalia Nehrebecka. Wykład 9
 Stanisław Cichocki Natalia Nehrebecka Wykład 9 1 1. Dodatkowe założenie KMRL 2. Testowanie hipotez prostych Rozkład estymatora b Testowanie hipotez prostych przy użyciu statystyki t 3. Przedziały ufności
Stanisław Cichocki Natalia Nehrebecka Wykład 9 1 1. Dodatkowe założenie KMRL 2. Testowanie hipotez prostych Rozkład estymatora b Testowanie hipotez prostych przy użyciu statystyki t 3. Przedziały ufności
Zmienna bazowa. 100(1 α)% przedział ufności dla µ: 100(α)% test hipotezy dla µ = µ 0; odrzucić, jeżeli Ȳ nie jest w przedziale
 Wprowadzenie Wprowadzenie Wnioskowanie podsumowanie Zdefiniuj populację, która będzie przedmiotem badań Zbierz parametry, które będą przedmiotem wnioskowania Wybierz losową próbę z populacji Przeprowadź
Wprowadzenie Wprowadzenie Wnioskowanie podsumowanie Zdefiniuj populację, która będzie przedmiotem badań Zbierz parametry, które będą przedmiotem wnioskowania Wybierz losową próbę z populacji Przeprowadź
Wykład 9 Wnioskowanie o średnich
 Wykład 9 Wnioskowanie o średnich Rozkład t (Studenta) Wnioskowanie dla jednej populacji: Test i przedziały ufności dla jednej próby Test i przedziały ufności dla par Porównanie dwóch populacji: Test i
Wykład 9 Wnioskowanie o średnich Rozkład t (Studenta) Wnioskowanie dla jednej populacji: Test i przedziały ufności dla jednej próby Test i przedziały ufności dla par Porównanie dwóch populacji: Test i
VII WYKŁAD STATYSTYKA. 30/04/2014 B8 sala 0.10B Godz. 15:15
 VII WYKŁAD STATYSTYKA 30/04/2014 B8 sala 0.10B Godz. 15:15 WYKŁAD 7 (c.d) WERYFIKACJA HIPOTEZ STATYSTYCZNYCH PARAMETRYCZNE TESTY ISTOTNOŚCI Weryfikacja hipotez ( błędy I i II rodzaju, poziom istotności,
VII WYKŁAD STATYSTYKA 30/04/2014 B8 sala 0.10B Godz. 15:15 WYKŁAD 7 (c.d) WERYFIKACJA HIPOTEZ STATYSTYCZNYCH PARAMETRYCZNE TESTY ISTOTNOŚCI Weryfikacja hipotez ( błędy I i II rodzaju, poziom istotności,
Wykład 12 Testowanie hipotez dla współczynnika korelacji
 Wykład 12 Testowanie hipotez dla współczynnika korelacji Wrocław, 23 maja 2018 Współczynnik korelacji Niech będą dane dwie próby danych X = (X 1, X 2,..., X n ) oraz Y = (Y 1, Y 2,..., Y n ). Współczynnikiem
Wykład 12 Testowanie hipotez dla współczynnika korelacji Wrocław, 23 maja 2018 Współczynnik korelacji Niech będą dane dwie próby danych X = (X 1, X 2,..., X n ) oraz Y = (Y 1, Y 2,..., Y n ). Współczynnikiem
ANNALES UNIVERSITATIS MARIAE CURIE-SKŁ ODOWSKA LUBLIN POLONIA
 ANNALES UNIVERSITATIS MARIAE CURIE-SKŁ ODOWSKA LUBLIN POLONIA VOL. LVII SECTIO E 2002 1 Katedra Szczegółowej Uprawy Roślin, Akademia Rolnicza w Lublinie, ul. Akademicka 15, 20-950 Lublin 1, Poland 2 Instytut
ANNALES UNIVERSITATIS MARIAE CURIE-SKŁ ODOWSKA LUBLIN POLONIA VOL. LVII SECTIO E 2002 1 Katedra Szczegółowej Uprawy Roślin, Akademia Rolnicza w Lublinie, ul. Akademicka 15, 20-950 Lublin 1, Poland 2 Instytut
Wykład 12 Testowanie hipotez dla współczynnika korelacji
 Wykład 12 Testowanie hipotez dla współczynnika korelacji Wrocław, 24 maja 2017 Współczynnik korelacji Niech będą dane dwie próby danych X = (X 1, X 2,..., X n ) oraz Y = (Y 1, Y 2,..., Y n ). Współczynnikiem
Wykład 12 Testowanie hipotez dla współczynnika korelacji Wrocław, 24 maja 2017 Współczynnik korelacji Niech będą dane dwie próby danych X = (X 1, X 2,..., X n ) oraz Y = (Y 1, Y 2,..., Y n ). Współczynnikiem
Ćwiczenie: Weryfikacja hipotez statystycznych dla jednej i dwóch średnich.
 Ćwiczenie: Weryfikacja hipotez statystycznych dla jednej i dwóch średnich. EXCEL Do weryfikacji różnic między dwiema grupami jednostek doświadczalnych w Excelu wykorzystujemy funkcję o nazwie T.TEST. Zastosowana
Ćwiczenie: Weryfikacja hipotez statystycznych dla jednej i dwóch średnich. EXCEL Do weryfikacji różnic między dwiema grupami jednostek doświadczalnych w Excelu wykorzystujemy funkcję o nazwie T.TEST. Zastosowana
Estymacja punktowa i przedziałowa
 Temat: Estymacja punktowa i przedziałowa Kody znaków: żółte wyróżnienie nowe pojęcie czerwony uwaga kursywa komentarz 1 Zagadnienia 1. Statystyczny opis próby. Idea estymacji punktowej pojęcie estymatora
Temat: Estymacja punktowa i przedziałowa Kody znaków: żółte wyróżnienie nowe pojęcie czerwony uwaga kursywa komentarz 1 Zagadnienia 1. Statystyczny opis próby. Idea estymacji punktowej pojęcie estymatora
WPŁYW SYSTEMU UPRAWY, NAWADNIANIA I NAWOŻENIA MINERALNEGO NA BIOMETRYKĘ SAMOKOŃCZĄCEGO I TRADYCYJNEGO MORFOTYPU BOBIKU
 Inżynieria Rolnicza 5(103)/2008 WPŁYW SYSTEMU UPRAWY, NAWADNIANIA I NAWOŻENIA MINERALNEGO NA BIOMETRYKĘ SAMOKOŃCZĄCEGO I TRADYCYJNEGO MORFOTYPU BOBIKU Instytut Inżynierii Rolniczej, Akademia Rolnicza w
Inżynieria Rolnicza 5(103)/2008 WPŁYW SYSTEMU UPRAWY, NAWADNIANIA I NAWOŻENIA MINERALNEGO NA BIOMETRYKĘ SAMOKOŃCZĄCEGO I TRADYCYJNEGO MORFOTYPU BOBIKU Instytut Inżynierii Rolniczej, Akademia Rolnicza w
Porównanie generatorów liczb losowych wykorzystywanych w arkuszach kalkulacyjnych
 dr Piotr Sulewski POMORSKA AKADEMIA PEDAGOGICZNA W SŁUPSKU KATEDRA INFORMATYKI I STATYSTYKI Porównanie generatorów liczb losowych wykorzystywanych w arkuszach kalkulacyjnych Wprowadzenie Obecnie bardzo
dr Piotr Sulewski POMORSKA AKADEMIA PEDAGOGICZNA W SŁUPSKU KATEDRA INFORMATYKI I STATYSTYKI Porównanie generatorów liczb losowych wykorzystywanych w arkuszach kalkulacyjnych Wprowadzenie Obecnie bardzo
Statystyka i opracowanie danych Podstawy wnioskowania statystycznego. Prawo wielkich liczb. Centralne twierdzenie graniczne. Estymacja i estymatory
 Statystyka i opracowanie danych Podstawy wnioskowania statystycznego. Prawo wielkich liczb. Centralne twierdzenie graniczne. Estymacja i estymatory Dr Anna ADRIAN Paw B5, pok 407 adrian@tempus.metal.agh.edu.pl
Statystyka i opracowanie danych Podstawy wnioskowania statystycznego. Prawo wielkich liczb. Centralne twierdzenie graniczne. Estymacja i estymatory Dr Anna ADRIAN Paw B5, pok 407 adrian@tempus.metal.agh.edu.pl
Zawartość. Zawartość
 Opr. dr inż. Grzegorz Biesok. Wer. 2.05 2011 Zawartość Zawartość 1. Rozkład normalny... 3 2. Rozkład normalny standardowy... 5 3. Obliczanie prawdopodobieństw dla zmiennych o rozkładzie norm. z parametrami
Opr. dr inż. Grzegorz Biesok. Wer. 2.05 2011 Zawartość Zawartość 1. Rozkład normalny... 3 2. Rozkład normalny standardowy... 5 3. Obliczanie prawdopodobieństw dla zmiennych o rozkładzie norm. z parametrami
Analiza Danych Sprawozdanie regresja Marek Lewandowski Inf 59817
 Analiza Danych Sprawozdanie regresja Marek Lewandowski Inf 59817 Zadanie 1: wiek 7 8 9 1 11 11,5 12 13 14 14 15 16 17 18 18,5 19 wzrost 12 122 125 131 135 14 142 145 15 1 154 159 162 164 168 17 Wykres
Analiza Danych Sprawozdanie regresja Marek Lewandowski Inf 59817 Zadanie 1: wiek 7 8 9 1 11 11,5 12 13 14 14 15 16 17 18 18,5 19 wzrost 12 122 125 131 135 14 142 145 15 1 154 159 162 164 168 17 Wykres
Statystyka matematyczna dla leśników
 Statystyka matematyczna dla leśników Wydział Leśny Kierunek leśnictwo Studia Stacjonarne I Stopnia Rok akademicki 03/04 Wykład 5 Testy statystyczne Ogólne zasady testowania hipotez statystycznych, rodzaje
Statystyka matematyczna dla leśników Wydział Leśny Kierunek leśnictwo Studia Stacjonarne I Stopnia Rok akademicki 03/04 Wykład 5 Testy statystyczne Ogólne zasady testowania hipotez statystycznych, rodzaje
MASA WŁAŚCIWA NASION ZBÓś W FUNKCJI WILGOTNOŚCI. Wstęp. Materiał i metody
 InŜynieria Rolnicza 3/2006 Bronisława Barbara Kram Instytut InŜynierii Rolniczej Akademia Rolnicza we Wrocławiu MASA WŁAŚCIWA NASION ZBÓś W FUNKCJI WILGOTNOŚCI Wstęp Streszczenie Określono wpływ wilgotności
InŜynieria Rolnicza 3/2006 Bronisława Barbara Kram Instytut InŜynierii Rolniczej Akademia Rolnicza we Wrocławiu MASA WŁAŚCIWA NASION ZBÓś W FUNKCJI WILGOTNOŚCI Wstęp Streszczenie Określono wpływ wilgotności
Statystyka opisowa. Wykład V. Regresja liniowa wieloraka
 Statystyka opisowa. Wykład V. e-mail:e.kozlovski@pollub.pl Spis treści 1 Prosta regresji cechy Y względem cech X 1,..., X k. 2 3 Wyznaczamy zależność cechy Y od cech X 1, X 2,..., X k postaci Y = α 0 +
Statystyka opisowa. Wykład V. e-mail:e.kozlovski@pollub.pl Spis treści 1 Prosta regresji cechy Y względem cech X 1,..., X k. 2 3 Wyznaczamy zależność cechy Y od cech X 1, X 2,..., X k postaci Y = α 0 +
Temat: BADANIE ZGODNOŚCI ROZKŁADU CECHY (EMPIRYCZNEGO) Z ROZKŁADEM TEORETYCZNYM TEST CHI-KWADRAT. Anna Rajfura 1
 Temat: BADANIE ZGODNOŚCI ROZKŁADU CECHY (EMPIRYCZNEGO) Z ROZKŁADEM TEORETYCZNYM TEST CHI-KWADRAT Anna Rajfura 1 Przykład wprowadzający Wiadomo, Ŝe 40% owoców ulega uszkodzeniu podczas pakowania automatycznego.
Temat: BADANIE ZGODNOŚCI ROZKŁADU CECHY (EMPIRYCZNEGO) Z ROZKŁADEM TEORETYCZNYM TEST CHI-KWADRAT Anna Rajfura 1 Przykład wprowadzający Wiadomo, Ŝe 40% owoców ulega uszkodzeniu podczas pakowania automatycznego.
WIELKA SGH-OWA POWTÓRKA ZE STATYSTYKI. Test zgodności i analiza wariancji Analiza wariancji
 WIELKA SGH-OWA POWTÓRKA ZE STATYSTYKI Test zgodności i analiza wariancji Analiza wariancji Test zgodności Chi-kwadrat Sprawdza się za jego pomocą ZGODNOŚĆ ROZKŁADU EMPIRYCZNEGO Z PRÓBY Z ROZKŁADEM HIPOTETYCZNYM
WIELKA SGH-OWA POWTÓRKA ZE STATYSTYKI Test zgodności i analiza wariancji Analiza wariancji Test zgodności Chi-kwadrat Sprawdza się za jego pomocą ZGODNOŚĆ ROZKŁADU EMPIRYCZNEGO Z PRÓBY Z ROZKŁADEM HIPOTETYCZNYM
Temat: BADANIE ZGODNOŚCI ROZKŁADU CECHY (EMPIRYCZNEGO) Z ROZKŁADEM TEORETYCZNYM TEST CHI-KWADRAT. Anna Rajfura 1
 Temat: BADANIE ZGODNOŚCI ROZKŁADU CECHY (EMPIRYCZNEGO) Z ROZKŁADEM TEORETYCZNYM TEST CHI-KWADRAT Anna Rajfura 1 Przykład wprowadzający Wiadomo, że 40% owoców ulega uszkodzeniu podczas pakowania automatycznego.
Temat: BADANIE ZGODNOŚCI ROZKŁADU CECHY (EMPIRYCZNEGO) Z ROZKŁADEM TEORETYCZNYM TEST CHI-KWADRAT Anna Rajfura 1 Przykład wprowadzający Wiadomo, że 40% owoców ulega uszkodzeniu podczas pakowania automatycznego.
Statystyka i opracowanie danych- W 8 Wnioskowanie statystyczne. Testy statystyczne. Weryfikacja hipotez statystycznych.
 Statystyka i opracowanie danych- W 8 Wnioskowanie statystyczne. Testy statystyczne. Weryfikacja hipotez statystycznych. Dr Anna ADRIAN Paw B5, pok407 adan@agh.edu.pl Hipotezy i Testy statystyczne Każde
Statystyka i opracowanie danych- W 8 Wnioskowanie statystyczne. Testy statystyczne. Weryfikacja hipotez statystycznych. Dr Anna ADRIAN Paw B5, pok407 adan@agh.edu.pl Hipotezy i Testy statystyczne Każde
Idea. θ = θ 0, Hipoteza statystyczna Obszary krytyczne Błąd pierwszego i drugiego rodzaju p-wartość
 Idea Niech θ oznacza parametr modelu statystycznego. Dotychczasowe rozważania dotyczyły metod estymacji tego parametru. Teraz zamiast szacować nieznaną wartość parametru będziemy weryfikowali hipotezę
Idea Niech θ oznacza parametr modelu statystycznego. Dotychczasowe rozważania dotyczyły metod estymacji tego parametru. Teraz zamiast szacować nieznaną wartość parametru będziemy weryfikowali hipotezę
hipotez statystycznych
 Weryfikacja hipotez statystycznych Przykład. Producent pewnych detali twierdzi, że wadliwość jego produkcji nie przekracza 2%. Odbiorca pewnej partii tego produktu chce sprawdzić, czy może wierzyć producentowi.
Weryfikacja hipotez statystycznych Przykład. Producent pewnych detali twierdzi, że wadliwość jego produkcji nie przekracza 2%. Odbiorca pewnej partii tego produktu chce sprawdzić, czy może wierzyć producentowi.
Wykład 12 ( ): Testy dla dwóch prób w rodzinie rozkładów normalnych
 Wykład 12 (21.05.07): Testy dla dwóch prób w rodzinie rozkładów normalnych Przykład Rozważamy dane wygenerowane losowo; ( podobne do danych z przykładu 7.2 z książki A. Łomnickiego) n 1 = 9 poletek w dąbrowie,
Wykład 12 (21.05.07): Testy dla dwóch prób w rodzinie rozkładów normalnych Przykład Rozważamy dane wygenerowane losowo; ( podobne do danych z przykładu 7.2 z książki A. Łomnickiego) n 1 = 9 poletek w dąbrowie,
weryfikacja hipotez dotyczących parametrów populacji (średnia, wariancja)
 PODSTAWY STATYSTYKI. Teoria prawdopodobieństwa i elementy kombinatoryki. Zmienne losowe i ich rozkłady 3. Populacje i próby danych, estymacja parametrów 4. Testowanie hipotez 5. Testy parametryczne (na
PODSTAWY STATYSTYKI. Teoria prawdopodobieństwa i elementy kombinatoryki. Zmienne losowe i ich rozkłady 3. Populacje i próby danych, estymacja parametrów 4. Testowanie hipotez 5. Testy parametryczne (na
METODY STATYSTYCZNE W BIOLOGII
 METODY STATYSTYCZNE W BIOLOGII 1. Wykład wstępny 2. Populacje i próby danych 3. Testowanie hipotez i estymacja parametrów 4. Planowanie eksperymentów biologicznych 5. Najczęściej wykorzystywane testy statystyczne
METODY STATYSTYCZNE W BIOLOGII 1. Wykład wstępny 2. Populacje i próby danych 3. Testowanie hipotez i estymacja parametrów 4. Planowanie eksperymentów biologicznych 5. Najczęściej wykorzystywane testy statystyczne
LABORATORIUM 8 WERYFIKACJA HIPOTEZ STATYSTYCZNYCH PARAMETRYCZNE TESTY ISTOTNOŚCI
 LABORATORIUM 8 WERYFIKACJA HIPOTEZ STATYSTYCZNYCH PARAMETRYCZNE TESTY ISTOTNOŚCI WERYFIKACJA HIPOTEZ Hipoteza statystyczna jakiekolwiek przypuszczenie dotyczące populacji generalnej- jej poszczególnych
LABORATORIUM 8 WERYFIKACJA HIPOTEZ STATYSTYCZNYCH PARAMETRYCZNE TESTY ISTOTNOŚCI WERYFIKACJA HIPOTEZ Hipoteza statystyczna jakiekolwiek przypuszczenie dotyczące populacji generalnej- jej poszczególnych
KOSZTY UŻYTKOWANIA MASZYN W STRUKTURZE KOSZTÓW PRODUKCJI ROŚLINNEJ W WYBRANYM PRZEDSIĘBIORSTWIE ROLNICZYM
 Inżynieria Rolnicza 13/2006 Zenon Grześ, Ireneusz Kowalik Instytut Inżynierii Rolniczej Akademia Rolnicza w Poznaniu KOSZTY UŻYTKOWANIA MASZYN W STRUKTURZE KOSZTÓW PRODUKCJI ROŚLINNEJ W WYBRANYM PRZEDSIĘBIORSTWIE
Inżynieria Rolnicza 13/2006 Zenon Grześ, Ireneusz Kowalik Instytut Inżynierii Rolniczej Akademia Rolnicza w Poznaniu KOSZTY UŻYTKOWANIA MASZYN W STRUKTURZE KOSZTÓW PRODUKCJI ROŚLINNEJ W WYBRANYM PRZEDSIĘBIORSTWIE
Testowanie hipotez. Marcin Zajenkowski. Marcin Zajenkowski () Testowanie hipotez 1 / 25
 Testowanie hipotez Marcin Zajenkowski Marcin Zajenkowski () Testowanie hipotez 1 / 25 Testowanie hipotez Aby porównać ze sobą dwie statystyki z próby stosuje się testy istotności. Mówią one o tym czy uzyskane
Testowanie hipotez Marcin Zajenkowski Marcin Zajenkowski () Testowanie hipotez 1 / 25 Testowanie hipotez Aby porównać ze sobą dwie statystyki z próby stosuje się testy istotności. Mówią one o tym czy uzyskane
LABORATORIUM Populacja Generalna (PG) 2. Próba (P n ) 3. Kryterium 3σ 4. Błąd Średniej Arytmetycznej 5. Estymatory 6. Teoria Estymacji (cz.
 LABORATORIUM 4 1. Populacja Generalna (PG) 2. Próba (P n ) 3. Kryterium 3σ 4. Błąd Średniej Arytmetycznej 5. Estymatory 6. Teoria Estymacji (cz. I) WNIOSKOWANIE STATYSTYCZNE (STATISTICAL INFERENCE) Populacja
LABORATORIUM 4 1. Populacja Generalna (PG) 2. Próba (P n ) 3. Kryterium 3σ 4. Błąd Średniej Arytmetycznej 5. Estymatory 6. Teoria Estymacji (cz. I) WNIOSKOWANIE STATYSTYCZNE (STATISTICAL INFERENCE) Populacja
