MATERIAŁ UZUPEŁNIAJĄCY DO WYKŁADU - MATERIAŁOZNAWSTWO WBiIŚ, sem. 02
|
|
|
- Martyna Rudnicka
- 9 lat temu
- Przeglądów:
Transkrypt
1 2. Struktura materiałów 2.1. Budowa atomu MATERIAŁ UZUPEŁNIAJĄCY DO WYKŁADU - MATERIAŁOZNAWSTWO WBiIŚ, sem. 02 Każdy przedmiot, zarówno wytworzony przez przyrodę, jak i będący dziełem pracy ludzkiej, utworzony jest z materii, która za pomocą procesów chemicznych lub fizycznych można rozłożyć na proste składniki, zwane pierwiastkami. Składniki te nie ulegają zmianie w żadnych reakcjach chemicznych. Najmniejsza cząstka pierwiastka jest atom, będący skupieniem jeszcze drobniejszych cząstek materii, zwanych elementarnymi. Cząstkami tymi są elektrony, protony i neutrony. Teorię budowy pojedynczego izolowanego atomu opracowano z wykorzystaniem mechaniki falowej. Mechanika falowa umożliwia opisanie zachowania się elektronów w atomach i kryształach. Każdy atom składa się z części wewnętrznej, tj. tzw. jądra i części zewnętrznej - powłok elektronowych. Średnice wszystkich atomów są bardzo małe i zawierają się w granicach od 0,106 nm dla azotu do 0,58 nm dla fransu. Znacznie mniejsze rozmiary maja jądra atomów zbudowane z protonów i neutronów (średnice rzędu 0,0001 nm), a najmniejsze są średnice elektronów, które zawsze wynoszą 0, nm, czyli 2, mm. Podstawowa cecha atomu jest jego masa atomowa (ciężar atomowy), wyrażona jednostką względna w stosunku do 1/16 masy atomu tlenu (umownie przyjęto masę jednego atomu tlenu na 16 jednostek). Praktycznie za masę atomu przyjmuje się masę jego jądra (tj. protonów i neutronów) gdyż masa elektronów jest bardzo mała i wynosi 9, g, tzn. 0,00055 część masy atomu wodoru. Masa protonów wynosi 1, g, tzn. jest równa masie atomu wodoru (w jednostkach względnych ma masę równa 1), masa neutronów jest zbliżona do masy protonów. Elektrony krążą dookoła jądra z bardzo duża prędkością po ściśle określonych eliptycznych orbitach (torach) i zawierają w sobie jeden elementarny ładunek elektryczności ujemnej, równoważąc w ten sposób dodatnio naładowane jądro o ładunku równym sumie ładunków wszystkich elektronów, tak że atom jako całość jest elektrycznie obojętny. Trzeba jednak podkreślić, że elementarne ładunki dodatnie, równe co do wielkości elementarnym ładunkom ujemnym zawartym w elektronach, mają tylko protony, toteż ich liczba w atomie zawsze odpowiada liczbie elektronów. Natomiast liczba neutronów nie zawierających ładunku elektrycznego jest różna. Obecnie znanych jest 105 różnych pierwiastków chemicznych, przy czym ostatnich trzynaście zostało wytworzonych sztucznie. Wszystkie te pierwiastki można uszeregować w tzw. układ okresowy 1 wg wzrastających (z małymi wyjątkami) ciężarów atomowych, od najlżejszego wodoru do pierwiastków najcięższych. Każdy z nich ma swoją kolejną liczbę porządkową określającą zarówno wielkość ładunku elektrycznego jądra, a więc liczbę protonów, jak i miejsce w układzie okresowym, co jednocześnie ustala własności chemiczne pierwiastka i większość własności fizycznych (temperaturę topnienia, przewodnictwo elektryczne, budowę wewnętrzną, własności magnetyczne itd.). Okresowy układ pierwiastków w postaci obecnie najczęściej stosowanej przedstawiono na rys Jak widać, w niektórych przypadkach pierwiastek następny ma niższą masę atomową od poprzedniego (np. potas i argon, nikiel i kobalt itd.). Dzieje się tak dlatego, że większość pierwiastków jest mieszaniną swych izotopów 2 o różnych masach atomowych równych liczbom całkowitym. Występujący np. w potasie w największej ilości izotop ma masę atomową 39, odpowiedni izotop argonu - 40, w wyniku czego mieszanina izotopów argonu ma większą masę atomową, niż mieszanina izotopów potasu. Z tego samego powodu masa atomowa pierwiastków mających izotopy wyraża się przeważnie liczbą ułamkową (izotopy występują w różnych stosunkach). Układ okresowy w pionowych kolumnach grupuje pierwiastki o podobnych własnościach. W wierszach poziomych, zwanych okresami, umieszczone są z lewej metale, z prawej niemetale; do metali zalicza się wszystkie pierwiastki znajdujące się w układzie okresowym na lewo od galu, indu i talu, do niemetali pierwiastki znajdujące się na prawo od arsenu, antymonu i bizmutu. 1 Pierwszy zauważył to chemik rosyjski Dymitr Mendelejew ( ). 2 Izotopy odmiany tego samego pierwiastka, rożniące się tylko ilością neutronów w jądrze, np. nikiel ma 5 izotopów o masach atomowych równych 58, 60, 61, 62 i 64, tzn. zawierających po 28 protonów i odpowiednio 30, 32, 33, 34 i 36 neutronów.
2 Rysunek 2.1 Układ okresowy pierwiastków Natomiast pierwiastki znajdujące się w kolumnach IIIb, IVb i Vb zajmują miejsce pośrednie, gdyż bez zastrzeżeń nie można ich zaliczyć ani do jednej, ani do drugiej grupy. Jak wspomniano, elektrony poruszają się wokół jądra atomu po określonych torach, tworząc tzw. powłoki i podpowłoki elektronowe. Pierwiastki pierwszego okresu (H, Hę) mają tylko jedną powłokę elektronową, która nie może zawierać więcej niż 2 elektrony (podpowłoka s). Pierwiastki drugiego okresu (Li, Be, B itd.) mają dwie powłoki elektronowe; pierwsza zawiera 2 elektrony, druga 1-8 (1-2 na podpowłoce s i 0-6 na podpowłoce p). Pierwiastki trzeciego okresu (Na, Mg, Al itd.) pierwszą i drugą powłokę mają taką samą, jak ostatni pierwiastek drugiego okresu neon, ale poza tym mają jeszcze trzecią powłokę elektronową, złożoną z dwóch podpowłok: s, na której znajduje się 1-2 elektronów, i p, na której znajduje się 0-6 elektronów, przy czym maksymalną ilość elektronów zawiera atom ostatniego pierwiastka tego okresu - argonu, którego liczba atomowa wynosi 18. Strukturę elektronową atomów omówionych pierwiastków zapisuje się następująco: 1. H- 1s 1 2. He - 1s 2 3. Li 1s 2 2s 1 7. N - 1s 2 2s 2 2p Ne - 1s 2 2s 2 2p Na 1s 2 2s 2 2p 6 3s Ar - 1s 2 2s 2 2p 6 3s 2 3p 6, gdzie: l, 2, 3... są głównymi liczbami kwantowymi, określającymi poszczególne powłoki elektronowe K, L, M,...; s, p,... poboczne liczby kwantowe określające podpowłoki elektronowe; indeksy górne oznaczają liczbę elektronów w danej pod-powłoce elektronowej. Rozbudowa zewnętrznych powłok elektronowych atomów pierwiastków czwartego okresu przebiega nieco inaczej.
3 Rozpoczynający ten okres potas ma zewnętrzny elektron umieszczony w podpowłoce 4s zamiast 3d: 19. K - 1s 2 2s 2 2p 6 3s 2 3p 6 4s 1 podobnie 20. Ca- 1s 2 2s 2 2p 6 3s 2 3p 6 4s 2 Dopiero poczynając od skandu następuje rozbudowa podpowłoki 3d (mieszczącej maksymalnie 10 elektronów), poprzedzona całkowitym lub częściowym (chrom) zapełnieniem podpowłoki 4s: 21. Sc - 1s 2 2s 2 2p 6 3s 2 3p 6 3d 1 4s Ti - 1s 2 2s 2 2p 6 3s 2 3p 6 3d 2 4s Fe - 1s 2 2s 2 2p 6 3s 2 3p 6 3d 6 4s Co - 1s 2 2s 2 2p 6 3s 2 3p 6 3d 7 4s Ni - 1s 2 2s 2 2p 6 3s 2 3p 6 3d 8 4s Cu - 1s 2 2s 2 2p 6 3s 2 3p 6 3d 10 4s 1 Pierwiastki o rozbudowującej się podpowłoce d nazywają się pierwiastkami przejściowymi lub metalami przejściowymi. Pozostałe pierwiastki tego okresu po wypełnieniu podpowłok 3d i 4s rozbudowują podpowłokę 4p, osiągając dla kryptonu konfigurację 4s 2 4p 6, charakterystyczną dla gazu szlachetnego. Struktury elektronowe atomów pierwiastków piątego okresu rozbudowują się tak jak czwartego, tzn. w kolejności 5s, 4d i 5p. Okres szósty zawiera 32 pierwiastki. Cez, bar i lantan mają elektrony zewnętrzne rozmieszczone kolejno w podpowłokach 6s i 5d: 57. La - 1s 2 2s 2 2p 6 3s 2 3p 6 3d 10 4s 2 4p 6 4d 10 5s 2 5p 6 5d 1 6s 2 Kolejne jednak pierwiastki rozbudowują podpowłokę 4f, mieszczącą 14 elektronów. Te pierwiastki (od ceru do lutetu) nazywa się lantanowcami lub pierwiastkami ziem rzadkich. Dopiero po wypełnieniu podpowłoki 4f następuje uzupełnienie podpowłoki 5d, a później 6p. Ostatni pierwiastek tego okresu radon jest gazem szlachetnym, gdyż ma konfigurację elektronów zewnętrznych 6s 2 6p 6. W okresie siódmym trzy pierwsze pierwiastki frans, rad i aktyn mają zewnętrzne elektrony rozmieszczone kolejno w podpowłokach 7s i 6d. Począwszy od toru następuje rozbudowa podpowłoki 5f. Pierwiastki zawierające tę podpowłokę nazywają się aktynowcami, Od struktury elektronowej, a zwłaszcza od konfiguracji elektronów powłoki zewnętrznej zależą własności chemiczne pierwiastków. Atomy z powłoką zewnętrzną całkowicie wypełnioną elektronami mają kulistą chmurę elektronów, są chemicznie obojętne i w przyrodzie występują jako jednoatomowe. Atomy z powłoką zewnętrzną niecałkowicie wypełnioną elektronami mają mniej symetryczną powłokę elektronową i są skłonne do łączenia się w cząsteczki (np. wodór). Elektrony krążące w zewnętrznej powłoce nazywa się elektronami walencyjnymi lub wartościowości. Od nich zależą wiązania atomowe. Atom z niecałkowicie wypełnioną zewnętrzną powłoką, dążąc do uzyskania struktury elektronowej zbliżonej do struktury gazu szlachetnego, oddaje swoje lub przyłącza elektrony walencyjne innego atomu. Pierwiastki oddające swe elektrony walencyjne nazywa się elektrododatnimi, przyłączające elektrony -elektroujemnymi. Metale mają l lub 2 elektrony w zewnętrznej powłoce elektronowej i są zawsze pierwiastkami elektrododatnimi. Najbardziej typowe metale, jak sód, potas, miedź, srebro i złoto, mają tylko jeden elektron walencyjny. Do metali zalicza się także pierwiastki przejściowe i pierwiastki ziem rzadkich. Szczególna struktura elektronowa pierwiastków przejściowych wyjaśnia m.in. ich wysoką temperaturę topnienia oraz zdolność tworzenia trwałych związków z węglem i azotem. Pierwiastki mające trzy, cztery lub pięć elektronów walencyjnych (np. aluminium, cyna, bizmut) mają własności amfoteryczne i mogą zarówno oddawać, jak i przyłączać elektrony walencyjne. Pierwiastki o sześciu lub siedmiu elektronach walencyjnych są typowymi niemetalami.
4 2.2. Siły spójności MATERIAŁ UZUPEŁNIAJĄCY DO WYKŁADU - MATERIAŁOZNAWSTWO WBiIŚ, sem. 02 W zbiorach atomów tworzących większe skupienia materii występują określone siły przyciągania i odpychania. Bardzo trafną hipotezę co do natury tych połączeń postawił jeszcze Newton (1704 r.), który napisał: ja raczej wnoszę ze spójności tych ciał, że cząstki przyciągają, się wzajemnie pewną silą, która jest niezwykle duża, gdy cząstki się stykają przy małych odległościach... Są więc w przyrodzie czynniki, które powodują, ze cząstki zlepiają się wskutek bardzo silnego przyciągania". Twierdzenie to w ciągu 300 lat nie straciło swojej aktualności. Cząsteczki podlegające wiązaniu mogą być atomami określonego pierwiastka np. (H, N, 0) lub związku (np. CO). Każdy pierwiastek zależnie od temperatury i ciśnienia może istnieć w trzech stanach skupienia, tj. gazowym, ciekłym i stałym. W stanie gazowym odległości między atomami są duże rzędu dziesiątków średnic atomowych, w stanach ciekłych i stałym atomy znajdują się blisko siebie. Dlatego te oba stany nazywają się stanami skondensowanymi. Zawsze w przypadku połączenia się atomów ze sobą muszą między nimi działać określone siły, które zależą przede wszystkim od typu wiązania. Siły te mają zarówno charakter odpychający, jak i przyciągający, ale przy braku działania sił zewnętrznych równoważą się ze sobą, w wyniku czego ustala się między atomami równowagowa odległość, przy której siła wzajemnego oddziaływania jest równa zeru. Jeśli jednak na taki układ działa siła zewnętrzna, usiłująca zbliżyć lub oddalić atomy, powstają siły międzyatomowe przeciwdziałające temu działaniu nazywane siłami spójności. Wielkość tych sił decyduje o wytrzymałości mechanicznej ciał stałych. Rozważania teoretyczne wykazały, że siła przyciągania Fp występująca między atomami przy ich łączeniu, jest określona następującym wzorem ogólnym: natomiast siła odpychająca F F p O b r = m+1 a r = n+1 gdzie: a, b, m, n - stałe zależne od rodzaju kryształu, r - odległość między atomami (znak - oznacza przyciąganie, a +" odpychanie) Rysunek 2.2. Siły F(r) i energia potencjalna U(r) wzajemnego oddziaływania między atomami w funkcji odległości międzyatomowej r
5 Ponieważ przy zmniejszaniu odległości r siły odpychania zwiększają się szybciej niż siły przyciągania przy oddalaniu, wykładnik potęgowy m < n Siła wypadkowa F a r = FO + FP = n+ 1 m+1 Jeżeli wzrasta r o dr, to siła F wykonuje pracę Fdr kosztem zmniejszenia energii potencjalnej wzajemnego oddziaływania U. Możemy napisać zależność Fdr = du, czyli F = (du/dr). Stąd energia potencjalna w funkcji odległości międzyatomowej dwuatomowego układu będzie równa gdzie: A = a/n, B = b/n U = A n r Na rysunku przedstawiono zależność zmiany siły wypadkowej F i energii potencjalnej wzajemnego oddziaływania U w funkcji r. Z wykresu tego wynikają następujące wnioski: 1. Gdy r jest bardzo duże, wówczas zarówno siła wzajemnego oddziaływania, jak i energia U są równe zeru 2. Zmniejszanie r powoduje powstanie siły przyciągającej, która początkowo zwiększa się, a po przekroczeniu wartości r1 maleje, osiągając wartość zero przy odległości równowagowej r o Jednocześnie energia U maleje, osiągając minimum przy r = r o 3. Dalsze zmniejszanie r (poniżej r o ) powoduje powstanie siły odpychającej i zwiększenie energii U r B m r b
6 2.3. Rodzaje wiązań Wiązanie jonowe Wiązanie jonowe jest typowe dla kryształów jonowych, które z reguły są przeźroczyste, a ich przewodnictwo elektryczne jest bardzo małe. Cechuje je dość duża wytrzymałość mechaniczna i twardość oraz wysoka temperatura topnienia, a także mają one tendencję do łupliwości wzdłuż określonych płaszczyzn krystalograficznych, co świadczy o kierunkowym charakterze wiązania. Wiązanie jonowe jest spowodowane dążeniem różnych atomów do tworzenia trwałych 8-elektronowych konfiguracji gazów szlachetnych przez uwspólnienie elektronów. Tak na przykład w przypadku tworzenia cząsteczki NaCl atom sodu, mający na zewnętrznej orbicie l elektron, oddaje go atomowi chloru, stając się jonem dodatnim, a atom chloru, mający na ostatniej orbicie 7 elektronów, po dołączeniu dodatkowego elektronu staje się jonem ujemnym. Możemy to zapisać symbolicznie Na + Cl Na + + Cl - Wiązanie to oparte jest naprzyciąganiu kulombowskim, jakie powstaje między dwoma przeciwnymi ładunkami. Utworzona cząsteczka związku NaCl jest elektrycznie obojętna, ale ma zaznaczone bieguny elektryczne (czyli jest dipolem), co umożliwia jej łączenie się z innymi cząsteczkami i tworzenie kryształu. Na rysunku 2.3 pokazano schemat utworzenia jonów Na + i Cl - oraz kryształu NaCl. Do kryształów jonowych zaliczamy halogenki metali alkalicznych (sole) oraz wiele materiałów ceramicznych stosowanych w technice Wiązania atomowe Rysunek 2.3. Schemat powstawania wiązania jonowego w NaCI: a) przejście elektronu z atomu Na do Cl, b) utworzone jony, c) kryształ NaCI Wiązanie atomowe (zwane także kowalentnym lub homopolarnym) występuje w cząsteczkach gazów dwuatomowych (H 2, Cl 2, O 2, N 2 ), niektórych pierwiastkach stałych (C - diament, Ge, Si, Sn-a) i związkach (SiC), a także w polimerach. Jest to wiązanie silne i kierunkowe. Energia wiązania w diamencie wynosi 710 kj/mol, a w SiC 1,18 MJ/mol. Wiązanie tworzy się zgodnie z teorią Levisa-Kossela, na skutek dążenia atomów do tworzenia trwałych 2- lub 8-elektronowych konfiguracji gazów szlachetnych, dzięki powstawaniu par wiążących, których liczba zależy od grupy układu okresowego N (reguła 8-N). Elektrony przechodzą od jednego do drugiego atomu, zamieniając je w jony dodatnie, które są przyciągane przez elektrony znajdujące się między nimi. Wiązanie to można przedstawić schematycznie następująco H. + H = H : H :Cr + C1: =Cl :Cl
7 Rysunek 2.4. Wiązanie atomowe w krzemie (brak elektronu w parze stanowi dziurę, dodatkowy elektron jest elektronem przewodnictwa) W tlenie występują dwie pary wiążące, w azocie - trzy, w węglu, krzemie i germanie po cztery (rys. 2.4). Wiązanie atomowe może być zinterpretowane przy użyciu zasad mechaniki falowej (obliczenia wykonali Heitler i London 1927 r.). Zgodnie z zakazem Pauliego elektrony w parach mają takie same trzy liczby kwantowe i różnią się spinem. Przy antyrównoległych spinach energia układu zmniejsza się, osiągając minimum przy równowagowej odległości atomów w cząsteczce. W niektórych przypadkach (np. w diamencie) wiązanie atomowe powstaje w wyniku hybrydyzacji (zmieszania) stanów elektronowych 2s i 2p. Dzięki temu powstaje konfiguracja 1s 2 2s 1 2p 3 zamiast konfiguracji 1s 2 2s 2 2p 2 co umożliwi utworzenie czterech równorzędnych wiązań z sąsiednimi atomami o antyrównoległych spinach elektronów 2s i 2p. W przypadku gdy łączą się różne atomy za pomocą par elektronowych mamy do czynienia z wiązaniem atomowym spolaryzowanym. Na skutek różnego oddziaływania elektronów z rdzeniami atomów powstają dipole i wiązanie ma wtedy charakter pośredni między atomowym i jonowym. Nie jest to jednak regułą. W niektórych przypadkach (np. w metanie CH 4 ) symetryczny rozkład wiązań powoduje, że wypadkowy moment dipolowy jest równy zeru. Istnieją związki (np. NH 4 ), w których obydwa elektrony tworzące parę pochodzą od tego samego atomu. W tym przypadku atom azotu może za pomocą wolnej pary elektronowej przyłączyć dodatkowy jon H +. Takie wiązanie nazywa się koordynacyjnym Wiązanie van der Waalsa Wiązanie van der Vaalsa jest bardzo słabe (energia wiązań wynosi J/mol) i bezkierunkowe. Siły van der Waalsa działają w skroplonych gazach szlachetnych i między łańcuchami polimerów. Przyczyną powstawania tych sił jest nierównomierny rozkład ładunków w chmurach elektronowych. Pewna polaryzacja jest w tym przypadku wynikiem wzajemnego oddziaływania atomów. Chwilowe dipole indukują dipole w sąsiednich atomach. Wiązania van der Waalsa występują wraz z innymi w kryształach molekularnych, które składają się z cząsteczek o wiązaniach kowalentnych zespolonych ze sobą siłami van der Waalsa. Przykładem mogą być zestalone gazy (H, F, Cl, N) oraz kryształy jodu, siarki, selenu i telluru Wiązanie metaliczne Wiązanie metaliczne występuje między atomami metali w skondensowanych stanach skupienia. Istota tego wiązania wynika z teorii swobodnego elektronu (Drudego-Lorentza). Dzięki niskiemu potencjałowi jonizacyjnemu elektronów, po zbliżeniu się atomów do siebie, następuje oderwanie się elektronów wartościowości od rdzeni atomowych i utworzenie gazu elektronowego, w którym zachowują się jako cząstki swobodne. Poruszają się one między jonami i wiążą je na zasadzie elektrostatycznego przyciągania. Wiązanie metaliczne należy do wiązań silnych (energia wiązania jest pośrednia miedzy jonowym a atomowym) i jest bezkierunkowe. Poza tym typowymi własnościami metali są: dobre przewodnictwo elektryczne i cieplne, ciągliwość i metaliczny połysk. Z własnościami gazu elektronowego jest także związane charakterystyczne dla metali zwiększenie oporności ze wzrostem temperatury. Dotychczas brak jest uniwersalnej teorii wyjaśniającej związek między budową elektronową a strukturą oraz własnościami określonych metali.
8 Wielu badaczy przyjmuje, że wiązanie metaliczne jest podobne do wiązania kowalentnego (Ormont, Pauling). Na przykład w sodzie atomy po zbliżeniu mogą utworzyć wiązanie za pomocą pary elektronów 3s o różnych spinach. Następne elektrony mogą przejść na poziom 3p, gdyż na skutek hybrydyzacji ich energie są zbliżone. Muszą one jednak ulegać ciągłej wymianie z sąsiednimi atomami. Można więc powiedzieć, że istota wiązania jest atomowa, chociaż jest utrzymana, zakładana w teorii swobodnych elektronów, możliwość ich ruchu od atomu do atomu. Stąd wiązanie metaliczne bywa traktowane jako nienasycone wiązanie atomowe (z niedoborem elektronów), w którym duża liczba atomów jest połączona przez uwspólnienie elektronów wartościowości. Są także znane inne teorie; np. Wignera i Seitza, umożliwiająca wyliczenie wartości energii wiązań w metalach alkalicznych, nie sprawdza się jednak ona w przypadku innych metali).
9 2.4. Struktury krystaliczne metali Elementy krystalografii Materiały krystaliczne w pewnych warunkach przyjmują kształt charakterystycznych, regularnych brył geometrycznych kryształów. Budową kryształów zajmuje się krystalografia, traktująca materię jako zbiorowisko atomów o kształcie sztywnych kul, rozmieszczonych statycznie (nieruchomo) w przestrzeni. Odwzorowaniem przestrzennego rozmieszczenia atomów jest sieć przestrzenna, utworzona przez powtórzenie w trzech kierunkach podstawowego elementu, zwanego komórką zasadniczą albo sieciową. Jednoznaczne określenie komórki zasadniczej umożliwia więc odwzorowanie sieci przestrzennej. Przekształcenie geometryczne polegające na przesunięciu w określonym kierunku dowolnego tworu geometrycznego o stały wektor, nazywa się translacją. Translacje - a i + a punktu -A 000 prowadzą do utworzenia prostej sieciowej (rys. 2.5a). Translacje - b i + b prostej w kierunku nierównoległym do niej tworzą płaszczyznę sieciową (rys. 2.5b). Wreszcie translacje - c i + c płaszczyzny w kierunku nierównoległym do niej tworzą sieć przestrzenną (rys. 2.5c), której punkty A uvw translacyjnie identyczne z punktem wyjściowym /A 000 stanowią węzły sieci. Rysunek Konstrukcja sieci przestrzennej. Translacje: a) punktu, b) prostej, c) płaszczyzny Do jednoznacznego zdefiniowania komórki zasadniczej (sieci przestrzennej) w ogólnym przypadku konieczna jest znajomość trzech wektorów translacji: a, b, c, zwanych stałymi (parametrami) sieciowymi oraz trzech kątów sieciowych: α, β, γ. Przyjęty w krystalografii do opisu komórki zasadniczej układ współrzędnych przedstawiono na rys Istotną cechą sieci przestrzennej (układu węzłów, prostych i płaszczyzn sieciowych) jest symetria. Rysunek 2.6. Krystalograficzny układ współrzędnych
10 Wyróżnia się trzy podstawowe elementy symetrii: płaszczyznę, oś i środek. Płaszczyzna symetrii dzieli kryształ na dwie części, stanowiące wzajemne lustrzane odbicie. Oś symetrii jest osią obrotu, dookoła której obracając kryształ o pewien kąt otrzymuje się identyczne położenie wszystkich elementów kryształu jak przed obrotem. Zależnie od wartości kąta obrotu mogą być osie symetrii dwukrotne (180 ), czterokrotne (90 ) itp. Oś o największej krotności jest główną osią symetrii jej kierunek wyznacza orientację kryształu w przestrzeni. Wreszcie środek symetrii jest punktem, względem którego wszystkie elementy kryształu po obrocie o 180 zajmują położenia identyczne jak przed obrotem. Wszystkie płaszczyzny i osie symetrii kryształu przecinają się w środku jego symetrii. Z tego powodu symetrię wynikającą z opisanych elementów nazwano punktową. Możliwe są różnorodne kombinacje podstawowych elementów tworzące złożone elementy symetrii. Symetria sieci jest cechą znacznie ważniejszą od geometrycznego kształtu komórki zasadniczej, ponieważ bryły o różnym kształcie, np. sześcian i ośmiościan, mają identyczne elementy symetrii. Na podstawie symetrii punktowej możliwe sieci przestrzenne zalicza się do jednego z siedmiu układów krystalograficznych, których charakterystykę podano w tabl. 1. W określonym układzie krystalograficznym komórka zasadnicza może mieć różny kształt (przy stałej objętości), jak to przedstawiono poglądowo na rys. 2.5 b TABLICA 1. Charakterystyka układów krystalograficznych Parametry komórki zasadnicze Krotność elementów Układ krystalograficzny stale sieciowe kąty sieciowe parametry charakterystyczne osie płaszczyzny - prostopadłe do osi 2-kr. 3-kr. 4-kr. 6-kr. 2-kr. 4-kr. 6-kr. Środek trojskośny a b c α β γ a, b, c α, β, γ jednoskośny a b c α = γ = 90, β a, b, c, β rombowy a b c α β γ = 90 a, b, c romboedryczny a= b= c a = β = γ a, α tetragonalny a= b, c a = β = γ = 90 a, c/a heksagonalny a = b, c a = β = 90, γ = 120 a, c/a regularny a = b = c a = β = γ = 90 a W określonym układzie krystalograficznym, zależnie od pozycji obsadzonych atomami, wyróżnia się typy komórki zasadniczej, oznaczane symbolami: prostą (P) o obsadzonych atomami tylko narożach komórki, centrowanej podstawie (C) o dodatkowo obsadzonych atomami środkach podstaw, płaskocentryczną (F) o dodatkowo obsadzonych atomami środkach wszystkich ścian, przestrzenniecentryczną (I) o dodatkowo obsadzonym atomem środku komórki, złożoną o dodatkowo obsadzonym atomami wnętrzu komórki. Bravais (1848 r.) drogą translacji prostych komórek zasadniczych poszczególnych układów krystalograficznych wyprowadził 14 typów sieci, tzw. translacyjnych (rys. 2.7). Systematyka Bravais'ego wskazuje, który z wymienionych typów komórek zasadniczych możliwy jest w określonym układzie krystalograficznym.
11 Rysunek 2.7. Sieci translacyjne Bravais'ego Niezależnie od układu krystalograficznego i typu komórki zasadniczej sieć przestrzenną charakteryzują następujące wielkości: Liczba koordynacyjna ( l.k..). Jest to liczba najbliższych i równoodległych atomów od dowolnego atomu sieci. Odpowiada ona liczbie wiązań atomu, czyli stanowi energetyczną miarę trwałości struktury krystalicznej. Liczba atomów (l.a.) przypadająca na komórkę zasadniczą. Jest to wielkość charakteryzująca w pewien sposób wielkość komórki zasadniczej. Wypełnienie komórki zasadniczej (w.). Jest to stosunek objętości atomów (kul) do objętości komórki zasadniczej (bryły), charakteryzujący gęstość atomową struktury krystalicznej. Opis położenia płaszczyzn i kierunków krystalograficznych umożliwiają wskaźniki Millera. Płaszczyzna sieciowa odcina na osiach współrzędnych odcinki stanowiące ułamki lub wielokrotności stałych sieciowych (rys.2.8). Wskaźniki Millera płaszczyzny (hkl) są odwrotnościami tych odcinków, z uwzględnieniem znaku odpowiadającego zwrotowi osi, wyrażonymi w liczbach całkowitych. Jeżeli płaszczyzna jest równoległa do osi, to punkt jej przebicia przez tę oś leży w nieskończoności, której odwrotność jest zerem. Jeżeli odwrotności odcinków są liczbami ułamkowymi, to sprowadza się je do liczb całkowitych, mnożąc przez wspólną najmniejszą wielokrotną. Sposób wyznaczania wskaźników Millera płaszczyzny wyjaśnia przykład (rys.2.7). Płaszczyzna P odcina na osiach współrzędnych x, y, z odcinki odpowiednio 3, - 2, 4. Odwrotności odcinków 1/3, -1/2, 1/4 po pomnożeniu przez wspólną najmniej szą wielokrotną 12 prowadzą do wskaźników Millera płaszczyzny P (4-63). W szczególnym przypadku układu heksagonalnego często stosuje się układ współrzędnych x 1, x 2, x 3, z. Wskaźniki Millera-Bravais'ego płaszczyzny (hkil) wyznacza się analogicznie, pamiętając, że w układzie heksagonalnym równoważne osie x spełniają zależność wektorową x 1 + x 2 = -x 3, z której wynika równoważność wskaźników h + k = - i. Należy pamiętać, że wskaźniki, np. (111), opisują wszystkie płaszczyzny sieciowe równoległe. Grupę płaszczyzn równoważnych krystalograficznie, np. płaszczyzny sześcianu w sieci regularnej (100), (010), (001), (-100), (0-l0), (00-1) opisuje się wskaźnikami jednej z nich w nawiasach klamrowych, np. {100}.
12 Rysunek 2.8. Wyznaczanie wskaźników Millera płaszczyzny sieciowej. Na rysunku 2.9 pokazano oznaczenia typowych płaszczyzn sieciowych układów regularnego i heksagonalnego. Rysunek 2.9. Wskaźniki ważniejszych płaszczyzn: a) Millera układu regularnego, b) Millera-Bravais'ego układu heksagonalnego Prosta sieciowa przechodzi przez dwa węzły sieci. Wskaźniki Millera prostej [uvw] są współrzędnymi węzła sieci położonego najbliżej początku układu współrzędnych, przez który przechodzi prosta po takim przesunięciu równoległym, że przechodzi również przez początek układu. Współrzędne węzła wskaźniki Millera prostej przedstawia się z uwzględnieniem znaku odpowiadającego zwrotowi osi jako całkowite wielokrotności stałych sieciowych. Równoważny krystalograficznie zespół prostych sieciowych opisuje się wskaźnikami jednej z nich w nawiasach ostrych, np. <111>. Na rysunku 2.10 pokazano oznaczenie kilku prostych sieciowych w układach regularnym i heksagonalnym. W szczególnym przypadku sieci regularnej proste sieciowe prostopadłe do płaszczyzn sieciowych i odwrotnie mają jednakowe wskaźniki Millera. Tak na przykład kierunek [100] jest prostopadły do płaszczyzny (100), a np. płaszczyzna (111) jest prostopadła do kierunku [111].
13 Rys Wskaźniki ważniejszych kierunków: a) Millera układu regularnego, b) Millera-Bravais'ego układu heksagonalnego Struktury metaliczne W strukturach metalicznych węzły sieci obsadzone są rdzeniami atomowymi. Rdzeniem atomowym jest atom pozbawiony pewnej liczby elektronów wartościowości, czyli kation. W przypadku metali jednowartościowych rdzeń atomowy jest jednowartościowym kationem, natomiast w przypadku metali o większej wartościowości rdzeń atomowy zazwyczaj różni się swoim ładunkiem od wartościowości kationu w roztworze wodnym. Uwolnione elektrony, tzw. gaz elektronowy, poruszają się w określonych obszarach ruchem bezładnym (analogicznie jak cząsteczki gazu doskonałego), przenosząc się z powłoki jednego na powłokę drugiego rdzenia atomowego. Między dodatnimi ładunkami rdzeni atomowych i ujemnymi ładunkami elektronów swobodnych działają silne przyciągające siły elektrostatyczne bezkierunkowe wiązanie metaliczne, zapewniające spójność materiału. Znaczna energia wiązania metalicznego ( kj/mol) zapewnia dużą trwałość materiału, tj. przeważnie wysoką temperaturę topnienia i wrzenia, dużą wytrzymałość i twardość, a m. in. dzięki bezkierunkowości dobrą plastyczność. Obecność elektronów swobodnych zapewnia elektronowy charakter przewodnictwa, a więc dobre przewodnictwo elektryczne, o ujemnym współczynniku temperaturowym (przewodność elektryczna zmniejsza się ze wzrostem temperatury) oraz dobre przewodnictwo cieplne i stosunkowo dużą rozszerzalność cieplną. Wymienione cechy materiałów metalicznych są wyraźne w stanie stałym, znacznie słabsze w stanie ciekłym, a zanikają całkowicie w stanie gazowym. Ponadto pewne pierwiastki w odpowiednich warunkach przyjmują modyfikacje odznaczające się lub pozbawione wiązania metalicznego. Z tego powodu wiązanie metaliczne i wywołane nim właściwości traktuje się jako stan metaliczny, w którym materiał może się znajdować w odpowiednich warunkach zewnętrznych (temperatura, ciśnienie) Metale Przeważająca większość metali odznacza się jedną z trzech struktur: Al. -płaskocentryczną układu regularnego, A2 - przestrzenniecentryczna układu regularnego albo A3 - zwarta (złożoną) układu heksagonalnego. Struktura Al, oznaczana również symbolem RCS (rys. 2.11a), jest najgęściej wypełniona (74,04%) o liczbie atomów La. = 8 1/ /2 = 4 i 1.k. = 12. Dowolny atom " w sieci otoczony jest dwunastoma sąsiadami w najmniejszej, jednakowej odległości a 2/2 = 0,707a (rys. 2.11b). W strukturze najgęściej wypełnione atomami są cztery płaszczyzny ośmiościanu {111}, a w każdej z nich trzy kierunki <110>, w których atomy są do siebie styczne (rys c). Puste przestrzenie między atomami tworzą tzw. luki. Luki oktaedryczne (większe) zlokalizowane w środku komórki i na środkach jej krawędzi są otoczone sześcioma atomami, tworzącymi ośmiościan foremny (rys d). Luki tetraedryczne (mniejsze) zlokalizowane na przekątnych komórki w odległościach a 3/4 = 0,433a od naroży, otoczone są czterema atomami tworzącymi czworościan foremny (rys. 2.11e).
14 Rysunek Struktura Al: a) komórka zasadnicza, b) koordynacja sieci, c) płaszczyzny i kierunki gęsto wypełnione, d) luki oktaedryczne, e) luki tetraedryczne Ponieważ z warunku styczności wynika promień atomu R = a/2 2 = 0,353a, w lukach oktaedrycznych może się pomieścić kula (atom) o promieniu r =0,414R, a w tetraedrycznych o promieniu r = 0,225R. Struktura A2, oznaczana również symbolem RCP (rys.2.12a), ma mniejsze wypełnienie (68,02%) przy liczbie atomów l.a. = 8 1/8 +1 = 2 i Lk. = 8. Dowolny atom sieci otoczony jest ośmioma sąsiadami, w najmniejszej, jednakowej odległości a 3/2 = 0,866a (rys. 2.12b). Najgęściej obsadzonych atomami, ale o odmiennym rozkładzie w porównaniu ze strukturą Al, jest sześć płaszczyzn przekątnych komórki zasadniczej {ll0}, a w każdej są dwa kierunki <111> gęstego ułożenia stycznych do siebie atomów (rys. 2.12c). Struktura A2 ma analogiczne jak struktura Al rodzaje luk, lecz mniejszych, pomimo mniejszego wypełnienia sieci. Z warunku styczności wynika promień atomu R = a 3/4 = 0,433a. Luki oktaedryczne zlokalizowane na środkach ścian i na środkach krawędzi komórki zasadniczej (rys. 2.12d) mieszczą atomy o promieniu zaledwie r = 0,l54R. Luki tetraedryczne zlokalizowane na każdej ścianie komórki w połowie odległości między środkiem krawędzi i środkiem ściany (rys. 2.12e) mieszczą atomy o promieniu r = 0,291R. Rysunek Struktura A2: a) komórka zasadnicza, b) koordynacja sieci, c) płaszczyzny i kierunki gęsto wypełnione, d) luki oktaedryczne, e) luki tetraedryczne
15 Rysunek Struktura A3: a) komórka zasadnicza, b) koordynacja sieci, c) płaszczyzny i kierunki gęsto wypełnione, d) luki oktaedryczne, e) luki tetraedryczne Struktura A3 albo HZ (rys. 2.13a) o identycznym wypełnieniu jak Al (74,04%) ma l.a. = 12 1/ /2 + 3 = 6 i l.k. = 12. Dowolny atom sieci otoczony jest dwunastoma sąsiadami w jednakowej, najmniejszej odległości a (rys. 2.13b). Najgęściej obsadzona atomami jest płaszczyzna podstawy (0001), w której są trzy kierunki gęstego ułożenia stycznych atomów <1120> (rys. 2.13c). Promień atomowy dla tej struktury wynosi R = 0,5a. Luki oktaedryczne (rys. 2.13d) i tetraedryczne (rys. 2.13e) mieszczą atomy o identycznych średnicach jak w strukturze Al, odpowiednio r = 0,414R i r = 0,225R. Opisana idealna struktura A3, charakteryzująca się stycznością atomów w trzech kolejnych płaszczyznach (0001) jest możliwa tylko przy stosunku stałych sieciowych c/a = 8/3 = 1,633. Spośród metali o tej strukturze większość w przybliżeniu spełnia ten warunek (c/a = 1,56 = 1,63). Wyjątki stanowią cynk i kadm o wartościach stosunku c/a odpowiednio 1,86 i 1,89. Anomalie te są spowodowane elipsoidalnym zniekształceniem w kierunku osi c powłok elektronowych atomów oraz działaniem między płaszczyznami (0001) dodatkowego wiązania kowalencyjnego. Dla obu tych struktur liczbę koordynacyjną poprawnie) jest zapisywać w postaci 6 + 6, bowiem, od dowolnego atomu sieci w jednakowej najmniejszej odległości a jest sześć atomów, natomiast sześć pozostałych jest w jednakowej, nieco większej odległości a 2 /3+c 2 /4. Rysunek Układ płaszczyzn gęstego ułożenia: a) płaszczyzna heksagonalna, b) struktura A3, c) struktura Al
16 Struktury Al i A3 są do siebie podobne. Mianowicie, w obu występują płaszczyzny (o różnej orientacji krystalograficznej) z jednakowym gęstym ułożeniem atomów, o heksagonalnej symetrii (rys. 2.14a). Aby warunek najgęstszego ułożenia atomów był spełniony, druga płaszczyzna heksagonalna musi mieć środki atomów przesunięte w stosunku do pierwszej, natomiast trzecia może mieć środki atomów pokrywające się z pierwszą (rys. 2.14b) albo jeszcze bardziej przesunięte (rys. 2.14c).Kolejność płaszczyzn heksagonalnych w strukturze A3 (0001) odpowiada pierwszemu wariantowi, co można przedstawić symbolicznie zapisem AB AB AB..., a w strukturze A1 (111) - drugiemu wariantowi co przedstawia zapis ABC ABC ABC...Stosunkowo nieliczne metale mają odmienne struktury. Złożone struktury układu regularnego mają odmiany alotropowe (por. punkt 3.4) manganu: Mnα o l.a. = 58 atomów (typ A12) i Mnβ o l.a. = 20 atomów (typ A13). Cyna β (biała) i ind mają złożone struktury układu tetragonalnego (typ A5). Rtęć w stanie stałym (poniżej -38,8 C) ma strukturę układu romboedrycznego, o prostej komórce zasadniczej (typ A 10). Pierwiastki o słabiej zaznaczonych cechach metalicznych, jak As, Sb, Bi, Se, Te, mają różne struktury układu heksagonalnego, w których obok wiązania metalicznego współistnieje również wiązanie kowalencyjne. Wśród struktur metalicznych obserwuje się wyraźną prawidłowość: im większe są symetria, liczba koordynacyjna i wypełnienie sieci, tym wyraźniejsze są cechy metaliczne materiału. Sieć regularna płasko-centryczna występuje w większości metali (m.in. w żelazie γ, aluminium, niklu, miedzi, srebrze, złocie, platynie, palladzie, ołowiu i berylu). Metale te wykazują szczególnie dobrą plastyczność na gorąco, a niektóre także na zimno, i są bardzo dobrymi przewodnikami ciepła i prądu elektrycznego. Sieć regularna przestrzennie centryczna występuje w takich metalach, jak żelazo a, chrom, wolfram, molibden, wanad, tantal, niob, sód, potas itd. Metale tej grupy są mniej ciągliwe niż metale grupy pierwszej i nadają się przeważnie tylko do obróbki plastycznej na gorąco. Sieć heksagonalna przestrzennie centryczna występuje m.in. w magnezie, tytanie a, cyrkonie a, kobalcie a, cynku, kadmie i rtęci. Metale o sieci heksagonalnej mają znacznie gorsze własności plastyczne niż metale o sieci regularnej i tylko niektóre z nich mogą być obrabiane plastycznie na gorąco i na zimno. Sieć tetragonalna występuje w białej cynie, galu i indzie. Metale o sieci tetragonalnej cechuje niska twardość i niska temperatura topnienia. Trzeba podkreślić, że w omówionych typach sieci krystalizuje większość metali. Budowa wewnętrzna ma bardzo duży wpływ na własności metalu, zarówno chemiczne, jak fizyczne (tabl. 2.2) i mechaniczne. Z chemicznych własności uzależniona jest od niej przede wszystkim odporność metalu na korozję, z fizycznych przewodność cieplna i elektryczna, z mechanicznych wytrzymałość, plastyczność twardość. Niektóre własności fizyczne ważniejszych metali Tablica 2.2 Pierwiastek Typ sieci Parametr sieci, nm Tempera tura topnienia C Gęstość w 20 C g/cm Uwagi w temp. C a c Żelazo α A2 20 2, ,87 do 910 i pow C Żelazo γ A , C Aluminium A1 25 4, ,70 Magnez A3 25 3,2030 5, ,74 Miedź A1 18 3, ,96 Nikiel A1 20 3, ,90 Kobalt α A3 20 2,507 4,081-8,9 do 400 C Kobalt β A1 3, pow. 400 C Tytan α A3 20 2,9503 4,6831-4,54 do 882 C Tytan β A , pow. 882 C
17 Pojedyncze kryształy metali mają zazwyczaj bardzo małe wymiary, toteż każdy przedmiot składa się z dużej liczby kryształów. Budowa taka nosi nazwę wielokrystalicznej lub polikrystdlicznej. Z różnych przyczyn, o których będzie mowa dalej, poszczególne kryształy nie mogą w zgrupowaniu wielokrystalicznym przybierać prawidłowego kształtu, lecz są mniej lub więcej zdeformowane. Takie kryształy o nieprawidłowym kształcie nazywa się ziarnami lub krystalitami. Różnice między poszczególnymi ziarnami metali polegają na różnej orientacji przestrzennej ich sieci krystalicznych. Orientacja ta jest na ogół przypadkowa i z jednakowym prawdopodobieństwem może mieć w przestrzeni dowolny kierunek. Wskutek obróbki plastycznej na zimno (np. walcowania) można jednak uzyskać jednokierunkową orientację ziarn (tzw. teksturę walcowania). Oczywiście własności mechaniczne metalu w obu przypadkach będą zupełnie różne, przy czym przy jednokierunkowej orientacji ziarn będą się zmieniać zależnie od kierunku badania. Jest to spowodowane faktem, że różne płaszczyzny i kierunki sieci krystalicznej są obsadzone atomami niejednakowo. Na przykład w elementarnej komórce sieci regularnej przestrzennie centrycznej o parametrze a, każda ścianka o powierzchni a 2 obsadzona jest przez l atom (atomy leżące w wierzchołkach należą jednoczesne do 4 komórek elementarnych, więc (4 1/4 = 1), natomiast w płaszczyźnie przekątnej komórki o powierzchni a 2 2 znajdują się 2 atomy (4 1/4 + 1 atom środkowy). Mimo różnicy w wielkościach powierzchni, wyraźnie widać, że drugi płaszczyzna jest gęściej obsadzona atomami. Ilustruje to rys Rysunek Płaszczyzny krystalograficzne w elementarnej komórce sieci regularnej przestrzennie centrycznej: a) obsadzona jednym atomem, b) obsadzona dwoma atomami Podobnie dzieje się w przypadku innych sieci krystalicznych, tak że własność wszystkich pojedynczych kryształów metali zmieniają się zależnie od kierunki badania. Zjawisko to nazywa się anizotropią. W przypadku budowy wielkokrystalicznej anizotropia występuje szczególnie wyraźnie, gdy ziarna mają jednakową orientację. Nie występuje natomiast w przypadku różnej orientacji poszczególnych ziarn i wtedy mówi się, że metal jest izotropowy. Na przykład monokryształ żelaza α o sieci regularnej przestrzennie centrycznej charakteryzuje wartość współczynnika sprężystości wzdłużnej E = MPa, zależnie od kierunku badania. To samo żelazo o budowie wielkokrystalicznej wykazuje wartość E = MPa.
18
2.Prawo zachowania masy
 2.Prawo zachowania masy Zdefiniujmy najpierw pewne podstawowe pojęcia: Układ - obszar przestrzeni o określonych granicach Ośrodek ciągły - obszar przestrzeni którego rozmiary charakterystyczne są wystarczająco
2.Prawo zachowania masy Zdefiniujmy najpierw pewne podstawowe pojęcia: Układ - obszar przestrzeni o określonych granicach Ośrodek ciągły - obszar przestrzeni którego rozmiary charakterystyczne są wystarczająco
+ + Struktura cia³a sta³ego. Kryszta³y jonowe. Kryszta³y atomowe. struktura krystaliczna. struktura amorficzna
 Struktura cia³a sta³ego struktura krystaliczna struktura amorficzna odleg³oœci miêdzy atomami maj¹ tê sam¹ wartoœæ; dany atom ma wszêdzie takie samo otoczenie najbli szych s¹siadów odleg³oœci miêdzy atomami
Struktura cia³a sta³ego struktura krystaliczna struktura amorficzna odleg³oœci miêdzy atomami maj¹ tê sam¹ wartoœæ; dany atom ma wszêdzie takie samo otoczenie najbli szych s¹siadów odleg³oœci miêdzy atomami
PRAWA ZACHOWANIA. Podstawowe terminy. Cia a tworz ce uk ad mechaniczny oddzia ywuj mi dzy sob i z cia ami nie nale cymi do uk adu za pomoc
 PRAWA ZACHOWANIA Podstawowe terminy Cia a tworz ce uk ad mechaniczny oddzia ywuj mi dzy sob i z cia ami nie nale cymi do uk adu za pomoc a) si wewn trznych - si dzia aj cych na dane cia o ze strony innych
PRAWA ZACHOWANIA Podstawowe terminy Cia a tworz ce uk ad mechaniczny oddzia ywuj mi dzy sob i z cia ami nie nale cymi do uk adu za pomoc a) si wewn trznych - si dzia aj cych na dane cia o ze strony innych
Wyznaczanie współczynnika sprężystości sprężyn i ich układów
 Ćwiczenie 63 Wyznaczanie współczynnika sprężystości sprężyn i ich układów 63.1. Zasada ćwiczenia W ćwiczeniu określa się współczynnik sprężystości pojedynczych sprężyn i ich układów, mierząc wydłużenie
Ćwiczenie 63 Wyznaczanie współczynnika sprężystości sprężyn i ich układów 63.1. Zasada ćwiczenia W ćwiczeniu określa się współczynnik sprężystości pojedynczych sprężyn i ich układów, mierząc wydłużenie
'()(*+,-./01(23/*4*567/8/23/*98:)2(!."/+)012+3$%-4#"4"$5012#-4#"4-6017%*,4.!"#$!"#%&"!!!"#$%&"#'()%*+,-+
 '()(*+,-./01(23/*4*567/8/23/*98:)2(!."/+)012+3$%-4#"4"$5012#-4#"4-6017%*,4.!"#$!"#%&"!!!"#$%&"#'()%*+,-+ Ucze interpretuje i tworzy teksty o charakterze matematycznym, u ywa j zyka matematycznego do opisu
'()(*+,-./01(23/*4*567/8/23/*98:)2(!."/+)012+3$%-4#"4"$5012#-4#"4-6017%*,4.!"#$!"#%&"!!!"#$%&"#'()%*+,-+ Ucze interpretuje i tworzy teksty o charakterze matematycznym, u ywa j zyka matematycznego do opisu
Atom poziom podstawowy
 Atom poziom podstawowy Zadanie 1. (1 pkt) Źródło: CKE 2010 (PP), zad. 1. Atomy pewnego pierwiastka w stanie podstawowym maj nast puj c konfiguracj elektronów walencyjnych: 2s 2 2p 3 (L 5 ) Okre l po o
Atom poziom podstawowy Zadanie 1. (1 pkt) Źródło: CKE 2010 (PP), zad. 1. Atomy pewnego pierwiastka w stanie podstawowym maj nast puj c konfiguracj elektronów walencyjnych: 2s 2 2p 3 (L 5 ) Okre l po o
Atom poziom rozszerzony
 Atom poziom rozszerzony Zadanie 1. (1 pkt) Źródło: CKE 010 (PR), zad. 1. Atomy pierwiastka X tworz jony X 3+, których konfiguracj elektronow mo na zapisa : 1s s p 6 3s 3p 6 3d 10 Uzupe nij poni sz tabel,
Atom poziom rozszerzony Zadanie 1. (1 pkt) Źródło: CKE 010 (PR), zad. 1. Atomy pierwiastka X tworz jony X 3+, których konfiguracj elektronow mo na zapisa : 1s s p 6 3s 3p 6 3d 10 Uzupe nij poni sz tabel,
Od redakcji. Symbolem oznaczono zadania wykraczające poza zakres materiału omówionego w podręczniku Fizyka z plusem cz. 2.
 Od redakcji Niniejszy zbiór zadań powstał z myślą o tych wszystkich, dla których rozwiązanie zadania z fizyki nie polega wyłącznie na mechanicznym przekształceniu wzorów i podstawieniu do nich danych.
Od redakcji Niniejszy zbiór zadań powstał z myślą o tych wszystkich, dla których rozwiązanie zadania z fizyki nie polega wyłącznie na mechanicznym przekształceniu wzorów i podstawieniu do nich danych.
SPRAWDZIANY Z MATEMATYKI
 SPRAWDZIANY Z MATEMATYKI dla klasy III gimnazjum dostosowane do programu Matematyka z Plusem opracowała mgr Marzena Mazur LICZBY I WYRAŻENIA ALGEBRAICZNE Grupa I Zad.1. Zapisz w jak najprostszej postaci
SPRAWDZIANY Z MATEMATYKI dla klasy III gimnazjum dostosowane do programu Matematyka z Plusem opracowała mgr Marzena Mazur LICZBY I WYRAŻENIA ALGEBRAICZNE Grupa I Zad.1. Zapisz w jak najprostszej postaci
Proste struktury krystaliczne
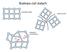 Budowa ciał stałych Proste struktury krystaliczne sc (simple cubic) bcc (body centered cubic) fcc (face centered cubic) np. Piryt FeSe 2 np. Żelazo, Wolfram np. Miedź, Aluminium Struktury krystaliczne
Budowa ciał stałych Proste struktury krystaliczne sc (simple cubic) bcc (body centered cubic) fcc (face centered cubic) np. Piryt FeSe 2 np. Żelazo, Wolfram np. Miedź, Aluminium Struktury krystaliczne
40. Międzynarodowa Olimpiada Fizyczna Meksyk, 12-19 lipca 2009 r. ZADANIE TEORETYCZNE 2 CHŁODZENIE LASEROWE I MELASA OPTYCZNA
 ZADANIE TEORETYCZNE 2 CHŁODZENIE LASEROWE I MELASA OPTYCZNA Celem tego zadania jest podanie prostej teorii, która tłumaczy tak zwane chłodzenie laserowe i zjawisko melasy optycznej. Chodzi tu o chłodzenia
ZADANIE TEORETYCZNE 2 CHŁODZENIE LASEROWE I MELASA OPTYCZNA Celem tego zadania jest podanie prostej teorii, która tłumaczy tak zwane chłodzenie laserowe i zjawisko melasy optycznej. Chodzi tu o chłodzenia
WOJEWÓDZKI KONKURS FIZYCZNY
 KOD UCZNIA Liczba uzyskanych punktów (maks. 40): Młody Fizyku! WOJEWÓDZKI KONKURS FIZYCZNY Etap rejonowy Masz do rozwiązania 20 zadań (w tym 3 otwarte). Całkowity czas na rozwiązanie wynosi 90 minut. W
KOD UCZNIA Liczba uzyskanych punktów (maks. 40): Młody Fizyku! WOJEWÓDZKI KONKURS FIZYCZNY Etap rejonowy Masz do rozwiązania 20 zadań (w tym 3 otwarte). Całkowity czas na rozwiązanie wynosi 90 minut. W
KLASA 3 GIMNAZJUM. 1. LICZBY I WYRAŻENIA ALGEBRAICZNE (26 h) 1. Lekcja organizacyjna 1. 2. System dziesiątkowy 2-4. 3. System rzymski 5-6
 KLASA 3 GIMNAZJUM TEMAT LICZBA GODZIN LEKCYJNYCH 1. LICZBY I WYRAŻENIA ALGEBRAICZNE (26 h) 1. Lekcja organizacyjna 1 2. System dziesiątkowy 2-4 WYMAGANIA SZCZEGÓŁOWE Z PODSTAWY PROGRAMOWEJ Z XII 2008 R.
KLASA 3 GIMNAZJUM TEMAT LICZBA GODZIN LEKCYJNYCH 1. LICZBY I WYRAŻENIA ALGEBRAICZNE (26 h) 1. Lekcja organizacyjna 1 2. System dziesiątkowy 2-4 WYMAGANIA SZCZEGÓŁOWE Z PODSTAWY PROGRAMOWEJ Z XII 2008 R.
Ćwiczenie: "Ruch harmoniczny i fale"
 Ćwiczenie: "Ruch harmoniczny i fale" Opracowane w ramach projektu: "Wirtualne Laboratoria Fizyczne nowoczesną metodą nauczania realizowanego przez Warszawską Wyższą Szkołę Informatyki. Zakres ćwiczenia:
Ćwiczenie: "Ruch harmoniczny i fale" Opracowane w ramach projektu: "Wirtualne Laboratoria Fizyczne nowoczesną metodą nauczania realizowanego przez Warszawską Wyższą Szkołę Informatyki. Zakres ćwiczenia:
Opis programu do wizualizacji algorytmów z zakresu arytmetyki komputerowej
 Opis programu do wizualizacji algorytmów z zakresu arytmetyki komputerowej 3.1 Informacje ogólne Program WAAK 1.0 służy do wizualizacji algorytmów arytmetyki komputerowej. Oczywiście istnieje wiele narzędzi
Opis programu do wizualizacji algorytmów z zakresu arytmetyki komputerowej 3.1 Informacje ogólne Program WAAK 1.0 służy do wizualizacji algorytmów arytmetyki komputerowej. Oczywiście istnieje wiele narzędzi
Wymagania na poszczególne oceny klasa 4
 Wymagania na poszczególne oceny klasa 4 a) Wymagania konieczne (na ocenę dopuszczającą) obejmują wiadomości i umiejętności umożliwiające uczniowi dalszą naukę, bez których uczeń nie jest w stanie zrozumieć
Wymagania na poszczególne oceny klasa 4 a) Wymagania konieczne (na ocenę dopuszczającą) obejmują wiadomości i umiejętności umożliwiające uczniowi dalszą naukę, bez których uczeń nie jest w stanie zrozumieć
Matematyka z plusemdla szkoły ponadgimnazjalnej WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE TRZECIEJ LICEUM. KATEGORIA B Uczeń rozumie:
 WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE TRZECIEJ LICEUM POZIOMY WYMAGAŃ EDUKACYJNYCH: K - konieczny ocena dopuszczająca P - podstawowy ocena dostateczna (dst.) R - rozszerzający ocena dobra (db.) D
WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE TRZECIEJ LICEUM POZIOMY WYMAGAŃ EDUKACYJNYCH: K - konieczny ocena dopuszczająca P - podstawowy ocena dostateczna (dst.) R - rozszerzający ocena dobra (db.) D
Strategia rozwoju kariery zawodowej - Twój scenariusz (program nagrania).
 Strategia rozwoju kariery zawodowej - Twój scenariusz (program nagrania). W momencie gdy jesteś studentem lub świeżym absolwentem to znajdujesz się w dobrym momencie, aby rozpocząć planowanie swojej ścieżki
Strategia rozwoju kariery zawodowej - Twój scenariusz (program nagrania). W momencie gdy jesteś studentem lub świeżym absolwentem to znajdujesz się w dobrym momencie, aby rozpocząć planowanie swojej ścieżki
4. STRUKTURA KRYSZTAŁÓW PÓŁPRZEWODNIKOWYCH. Irena Zubel Wydział Elektroniki Mikrosystemów i Fotoniki Politechnika Wrocławska (na prawach rękopisu)
 4. STRUKTURA KRYSZTAŁÓW PÓŁPRZEWODNIKOWYCH Irena Zubel Wydział Elektroniki Mikrosystemów i Fotoniki Politechnika Wrocławska (na prawach rękopisu) Krzem, podstawowe parametry 1. Konfiguracja elektronowa:
4. STRUKTURA KRYSZTAŁÓW PÓŁPRZEWODNIKOWYCH Irena Zubel Wydział Elektroniki Mikrosystemów i Fotoniki Politechnika Wrocławska (na prawach rękopisu) Krzem, podstawowe parametry 1. Konfiguracja elektronowa:
Podstawowe oddziaływania w Naturze
 Podstawowe oddziaływania w Naturze Wszystkie w zjawiska w Naturze są określone przez cztery podstawowe oddziaływania Silne Grawitacja Newton Elektromagnetyczne Słabe n = p + e - + ν neutron = proton +
Podstawowe oddziaływania w Naturze Wszystkie w zjawiska w Naturze są określone przez cztery podstawowe oddziaływania Silne Grawitacja Newton Elektromagnetyczne Słabe n = p + e - + ν neutron = proton +
7. REZONANS W OBWODACH ELEKTRYCZNYCH
 OBWODY SYGNAŁY 7. EZONANS W OBWODAH EEKTYZNYH 7.. ZJAWSKO EZONANS Obwody elektryczne, w których występuje zjawisko rezonansu nazywane są obwodami rezonansowymi lub drgającymi. ozpatrując bezźródłowy obwód
OBWODY SYGNAŁY 7. EZONANS W OBWODAH EEKTYZNYH 7.. ZJAWSKO EZONANS Obwody elektryczne, w których występuje zjawisko rezonansu nazywane są obwodami rezonansowymi lub drgającymi. ozpatrując bezźródłowy obwód
Harmonogramowanie projektów Zarządzanie czasem
 Harmonogramowanie projektów Zarządzanie czasem Zarządzanie czasem TOMASZ ŁUKASZEWSKI INSTYTUT INFORMATYKI W ZARZĄDZANIU Zarządzanie czasem w projekcie /49 Czas w zarządzaniu projektami 1. Pojęcie zarządzania
Harmonogramowanie projektów Zarządzanie czasem Zarządzanie czasem TOMASZ ŁUKASZEWSKI INSTYTUT INFORMATYKI W ZARZĄDZANIU Zarządzanie czasem w projekcie /49 Czas w zarządzaniu projektami 1. Pojęcie zarządzania
Podstawowe pojęcia: Populacja. Populacja skończona zawiera skończoną liczbę jednostek statystycznych
 Podstawowe pojęcia: Badanie statystyczne - zespół czynności zmierzających do uzyskania za pomocą metod statystycznych informacji charakteryzujących interesującą nas zbiorowość (populację generalną) Populacja
Podstawowe pojęcia: Badanie statystyczne - zespół czynności zmierzających do uzyskania za pomocą metod statystycznych informacji charakteryzujących interesującą nas zbiorowość (populację generalną) Populacja
Podstawowe działania w rachunku macierzowym
 Podstawowe działania w rachunku macierzowym Marcin Detka Katedra Informatyki Stosowanej Kielce, Wrzesień 2004 1 MACIERZE 1 1 Macierze Macierz prostokątną A o wymiarach m n (m wierszy w n kolumnach) definiujemy:
Podstawowe działania w rachunku macierzowym Marcin Detka Katedra Informatyki Stosowanej Kielce, Wrzesień 2004 1 MACIERZE 1 1 Macierze Macierz prostokątną A o wymiarach m n (m wierszy w n kolumnach) definiujemy:
Temat: Funkcje. Własności ogólne. A n n a R a j f u r a, M a t e m a t y k a s e m e s t r 1, W S Z i M w S o c h a c z e w i e 1
 Temat: Funkcje. Własności ogólne A n n a R a j f u r a, M a t e m a t y k a s e m e s t r 1, W S Z i M w S o c h a c z e w i e 1 Kody kolorów: pojęcie zwraca uwagę * materiał nieobowiązkowy A n n a R a
Temat: Funkcje. Własności ogólne A n n a R a j f u r a, M a t e m a t y k a s e m e s t r 1, W S Z i M w S o c h a c z e w i e 1 Kody kolorów: pojęcie zwraca uwagę * materiał nieobowiązkowy A n n a R a
1. Rozwiązać układ równań { x 2 = 2y 1
 Dzień Dziecka z Matematyką Tomasz Szymczyk Piotrków Trybunalski, 4 czerwca 013 r. Układy równań szkice rozwiązań 1. Rozwiązać układ równań { x = y 1 y = x 1. Wyznaczając z pierwszego równania zmienną y,
Dzień Dziecka z Matematyką Tomasz Szymczyk Piotrków Trybunalski, 4 czerwca 013 r. Układy równań szkice rozwiązań 1. Rozwiązać układ równań { x = y 1 y = x 1. Wyznaczając z pierwszego równania zmienną y,
Energia wiązania [ev] Wiązanie. Właściwości ciał stałych
![Energia wiązania [ev] Wiązanie. Właściwości ciał stałych Energia wiązania [ev] Wiązanie. Właściwości ciał stałych](/thumbs/42/23077809.jpg) Wiązanie Energia wiązania [ev] kowalencyjne 7-12 jonowe 7-10 metaliczne 1-4 wodorowe 0.2 0.4 Van der Waalsa 0.1 0.2 Właściwości ciał stałych - wysoka temperatura topnienia - twarde lub średniotwarde -
Wiązanie Energia wiązania [ev] kowalencyjne 7-12 jonowe 7-10 metaliczne 1-4 wodorowe 0.2 0.4 Van der Waalsa 0.1 0.2 Właściwości ciał stałych - wysoka temperatura topnienia - twarde lub średniotwarde -
NUMER IDENTYFIKATORA:
 Społeczne Liceum Ogólnokształcące z Maturą Międzynarodową im. Ingmara Bergmana IB WORLD SCHOOL 53 ul. Raszyńska, 0-06 Warszawa, tel./fax 668 54 5 www.ib.bednarska.edu.pl / e-mail: liceum.ib@rasz.edu.pl
Społeczne Liceum Ogólnokształcące z Maturą Międzynarodową im. Ingmara Bergmana IB WORLD SCHOOL 53 ul. Raszyńska, 0-06 Warszawa, tel./fax 668 54 5 www.ib.bednarska.edu.pl / e-mail: liceum.ib@rasz.edu.pl
MATEMATYKA 4 INSTYTUT MEDICUS FUNKCJA KWADRATOWA. Kurs przygotowawczy na studia medyczne. Rok szkolny 2010/2011. tel. 0501 38 39 55 www.medicus.edu.
 INSTYTUT MEDICUS Kurs przygotowawczy na studia medyczne Rok szkolny 00/0 tel. 050 38 39 55 www.medicus.edu.pl MATEMATYKA 4 FUNKCJA KWADRATOWA Funkcją kwadratową lub trójmianem kwadratowym nazywamy funkcję
INSTYTUT MEDICUS Kurs przygotowawczy na studia medyczne Rok szkolny 00/0 tel. 050 38 39 55 www.medicus.edu.pl MATEMATYKA 4 FUNKCJA KWADRATOWA Funkcją kwadratową lub trójmianem kwadratowym nazywamy funkcję
Zadania. SiOD Cwiczenie 1 ;
 1. Niech A będzie zbiorem liczb naturalnych podzielnych przez 6 B zbiorem liczb naturalnych podzielnych przez 2 C będzie zbiorem liczb naturalnych podzielnych przez 5 Wyznaczyć zbiory A B, A C, C B, A
1. Niech A będzie zbiorem liczb naturalnych podzielnych przez 6 B zbiorem liczb naturalnych podzielnych przez 2 C będzie zbiorem liczb naturalnych podzielnych przez 5 Wyznaczyć zbiory A B, A C, C B, A
Badanie silnika asynchronicznego jednofazowego
 Badanie silnika asynchronicznego jednofazowego Cel ćwiczenia Celem ćwiczenia jest poznanie budowy i zasady funkcjonowania silnika jednofazowego. W ramach ćwiczenia badane są zmiany wartości prądu rozruchowego
Badanie silnika asynchronicznego jednofazowego Cel ćwiczenia Celem ćwiczenia jest poznanie budowy i zasady funkcjonowania silnika jednofazowego. W ramach ćwiczenia badane są zmiany wartości prądu rozruchowego
Stechiometria równań reakcji chemicznych, objętość gazów w warunkach odmiennych od warunków normalnych (0 o C 273K, 273hPa)
 Karta pracy I/2a Stechiometria równań reakcji chemicznych, objętość gazów w warunkach odmiennych od warunków normalnych (0 o C 273K, 273hPa) I. Stechiometria równań reakcji chemicznych interpretacja równań
Karta pracy I/2a Stechiometria równań reakcji chemicznych, objętość gazów w warunkach odmiennych od warunków normalnych (0 o C 273K, 273hPa) I. Stechiometria równań reakcji chemicznych interpretacja równań
Kurs wyrównawczy dla kandydatów i studentów UTP
 Kurs wyrównawczy dla kandydatów i studentów UTP Część III Funkcja wymierna, potęgowa, logarytmiczna i wykładnicza Magdalena Alama-Bućko Ewa Fabińska Alfred Witkowski Grażyna Zachwieja Uniwersytet Technologiczno
Kurs wyrównawczy dla kandydatów i studentów UTP Część III Funkcja wymierna, potęgowa, logarytmiczna i wykładnicza Magdalena Alama-Bućko Ewa Fabińska Alfred Witkowski Grażyna Zachwieja Uniwersytet Technologiczno
Arkusz maturalny treningowy nr 7. W zadaniach 1. do 20. wybierz i zaznacz na karcie odpowiedzi poprawną odpowiedź.
 Czas pracy: 170 minut Liczba punktów do uzyskania: 50 Arkusz maturalny treningowy nr 7 W zadaniach 1. do 20. wybierz i zaznacz na karcie odpowiedzi poprawną odpowiedź. Zadanie 1. (0-1) Wyrażenie (-8x 3
Czas pracy: 170 minut Liczba punktów do uzyskania: 50 Arkusz maturalny treningowy nr 7 W zadaniach 1. do 20. wybierz i zaznacz na karcie odpowiedzi poprawną odpowiedź. Zadanie 1. (0-1) Wyrażenie (-8x 3
EGZAMIN MATURALNY Z MATEMATYKI
 Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 016 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę dysleksja EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY DATA: 9
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 016 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę dysleksja EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY DATA: 9
Informacje uzyskiwane dzięki spektrometrii mas
 Slajd 1 Spektrometria mas i sektroskopia w podczerwieni Slajd 2 Informacje uzyskiwane dzięki spektrometrii mas Masa cząsteczkowa Wzór związku Niektóre informacje dotyczące wzoru strukturalnego związku
Slajd 1 Spektrometria mas i sektroskopia w podczerwieni Slajd 2 Informacje uzyskiwane dzięki spektrometrii mas Masa cząsteczkowa Wzór związku Niektóre informacje dotyczące wzoru strukturalnego związku
Czas pracy 170 minut
 ORGANIZATOR WSPÓŁORGANIZATOR PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI MARZEC ROK 013 POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla piszącego 1. Sprawdź, czy arkusz zawiera 16 stron.. W zadaniach od
ORGANIZATOR WSPÓŁORGANIZATOR PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI MARZEC ROK 013 POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla piszącego 1. Sprawdź, czy arkusz zawiera 16 stron.. W zadaniach od
XXXV OLIMPIADA FIZYCZNA ETAP WSTĘPNY Zadanie teoretyczne
 XXXV OLIMPIADA FIZYCZNA ETAP WSTĘPNY Zadanie teoretyczne Wybierz lub podaj prawidłowa odpowiedź (wraz z krótkim uzasadnieniem) na dowolnie wybrane przez siebie siedem z pośród poniższych dziesięciu punktów:
XXXV OLIMPIADA FIZYCZNA ETAP WSTĘPNY Zadanie teoretyczne Wybierz lub podaj prawidłowa odpowiedź (wraz z krótkim uzasadnieniem) na dowolnie wybrane przez siebie siedem z pośród poniższych dziesięciu punktów:
STRUKTURA MATERIAŁÓW
 STRUKTURA MATERIAŁÓW ELEMENTY STRUKTURY MATERIAŁÓW 1. Wiązania miedzy atomami 2. Układ atomów w przestrzeni 3. Mikrostruktura 4. Makrostruktura 1. WIĄZANIA MIĘDZY ATOMAMI Siły oddziaływania między atomami
STRUKTURA MATERIAŁÓW ELEMENTY STRUKTURY MATERIAŁÓW 1. Wiązania miedzy atomami 2. Układ atomów w przestrzeni 3. Mikrostruktura 4. Makrostruktura 1. WIĄZANIA MIĘDZY ATOMAMI Siły oddziaływania między atomami
Projekt MES. Wykonali: Lidia Orkowska Mateusz Wróbel Adam Wysocki WBMIZ, MIBM, IMe
 Projekt MES Wykonali: Lidia Orkowska Mateusz Wróbel Adam Wysocki WBMIZ, MIBM, IMe 1. Ugięcie wieszaka pod wpływem przyłożonego obciążenia 1.1. Wstęp Analizie poddane zostało ugięcie wieszaka na ubrania
Projekt MES Wykonali: Lidia Orkowska Mateusz Wróbel Adam Wysocki WBMIZ, MIBM, IMe 1. Ugięcie wieszaka pod wpływem przyłożonego obciążenia 1.1. Wstęp Analizie poddane zostało ugięcie wieszaka na ubrania
Objaśnienia wartości, przyjętych do Projektu Wieloletniej Prognozy Finansowej Gminy Golina na lata 2012-2015
 Załącznik Nr 2 do Uchwały Nr XIX/75/2011 Rady Miejskiej w Golinie z dnia 29 grudnia 2011 r. Objaśnienia wartości, przyjętych do Projektu Wieloletniej Prognozy Finansowej Gminy Golina na lata 2012-2015
Załącznik Nr 2 do Uchwały Nr XIX/75/2011 Rady Miejskiej w Golinie z dnia 29 grudnia 2011 r. Objaśnienia wartości, przyjętych do Projektu Wieloletniej Prognozy Finansowej Gminy Golina na lata 2012-2015
UKŁAD ROZRUCHU SILNIKÓW SPALINOWYCH
 UKŁAD ROZRUCHU SILNIKÓW SPALINOWYCH We współczesnych samochodach osobowych są stosowane wyłącznie rozruszniki elektryczne składające się z trzech zasadniczych podzespołów: silnika elektrycznego; mechanizmu
UKŁAD ROZRUCHU SILNIKÓW SPALINOWYCH We współczesnych samochodach osobowych są stosowane wyłącznie rozruszniki elektryczne składające się z trzech zasadniczych podzespołów: silnika elektrycznego; mechanizmu
14P2 POWTÓRKA FIKCYJNY EGZAMIN MATURALNYZ FIZYKI I ASTRONOMII - II POZIOM PODSTAWOWY
 14P2 POWTÓRKA FIKCYJNY EGZAMIN MATURALNYZ FIZYKI I ASTRONOMII - II POZIOM PODSTAWOWY Ruch jednostajny po okręgu Pole grawitacyjne Rozwiązania zadań należy zapisać w wyznaczonych miejscach pod treścią zadania
14P2 POWTÓRKA FIKCYJNY EGZAMIN MATURALNYZ FIZYKI I ASTRONOMII - II POZIOM PODSTAWOWY Ruch jednostajny po okręgu Pole grawitacyjne Rozwiązania zadań należy zapisać w wyznaczonych miejscach pod treścią zadania
K P K P R K P R D K P R D W
 KLASA III TECHNIKUM POZIOM PODSTAWOWY I ROZSZERZONY PROPOZYCJA POZIOMÓW WYMAGAŃ Wyróżnione zostały następujące wymagania programowe: konieczne (K), podstawowe (P), rozszerzające (R), dopełniające (D) i
KLASA III TECHNIKUM POZIOM PODSTAWOWY I ROZSZERZONY PROPOZYCJA POZIOMÓW WYMAGAŃ Wyróżnione zostały następujące wymagania programowe: konieczne (K), podstawowe (P), rozszerzające (R), dopełniające (D) i
WZORU UŻYTKOWEGO EGZEMPLARZ ARCHIWALNY. d2)opis OCHRONNY. (19) PL (n)62894. Centralny Instytut Ochrony Pracy, Warszawa, PL
 RZECZPOSPOLITA POLSKA Urząd Patentowy Rzeczypospolitej Polskiej d2)opis OCHRONNY WZORU UŻYTKOWEGO (21) Numer zgłoszenia: 112772 (22) Data zgłoszenia: 29.11.2001 EGZEMPLARZ ARCHIWALNY (19) PL (n)62894 (13)
RZECZPOSPOLITA POLSKA Urząd Patentowy Rzeczypospolitej Polskiej d2)opis OCHRONNY WZORU UŻYTKOWEGO (21) Numer zgłoszenia: 112772 (22) Data zgłoszenia: 29.11.2001 EGZEMPLARZ ARCHIWALNY (19) PL (n)62894 (13)
Zarządzanie projektami. wykład 1 dr inż. Agata Klaus-Rosińska
 Zarządzanie projektami wykład 1 dr inż. Agata Klaus-Rosińska 1 DEFINICJA PROJEKTU Zbiór działań podejmowanych dla zrealizowania określonego celu i uzyskania konkretnego, wymiernego rezultatu produkt projektu
Zarządzanie projektami wykład 1 dr inż. Agata Klaus-Rosińska 1 DEFINICJA PROJEKTU Zbiór działań podejmowanych dla zrealizowania określonego celu i uzyskania konkretnego, wymiernego rezultatu produkt projektu
Klasyfikacja stali i przykłady oznaczeń
 Klasyfikacja stali i przykłady oznaczeń Definicja stali Stal jest to plastycznie (i ewentualnie cieplnie) obrobiony stop żelaza z węglem i innymi pierwiastkami, otrzymywanym w procesach stalowniczych ze
Klasyfikacja stali i przykłady oznaczeń Definicja stali Stal jest to plastycznie (i ewentualnie cieplnie) obrobiony stop żelaza z węglem i innymi pierwiastkami, otrzymywanym w procesach stalowniczych ze
CZ STECZKA. Do opisu wi za chemicznych stosuje si najcz ciej jedn z dwóch metod (teorii): metoda wi za walencyjnych (VB)
 CZ STECZKA Stanislao Cannizzaro (1826-1910) cz stki - elementy mikro wiata, termin obejmuj cy zarówno cz stki elementarne, jak i atomy, jony proste i zło one, cz steczki, rodniki, cz stki koloidowe; cz
CZ STECZKA Stanislao Cannizzaro (1826-1910) cz stki - elementy mikro wiata, termin obejmuj cy zarówno cz stki elementarne, jak i atomy, jony proste i zło one, cz steczki, rodniki, cz stki koloidowe; cz
KLASYFIKACJI I BUDOWY STATKÓW MORSKICH
 PRZEPISY KLASYFIKACJI I BUDOWY STATKÓW MORSKICH ZMIANY NR 3/2012 do CZĘŚCI II KADŁUB 2011 GDAŃSK Zmiany Nr 3/2012 do Części II Kadłub 2011, Przepisów klasyfikacji i budowy statków morskich, zostały zatwierdzone
PRZEPISY KLASYFIKACJI I BUDOWY STATKÓW MORSKICH ZMIANY NR 3/2012 do CZĘŚCI II KADŁUB 2011 GDAŃSK Zmiany Nr 3/2012 do Części II Kadłub 2011, Przepisów klasyfikacji i budowy statków morskich, zostały zatwierdzone
(12) OPIS PATENTOWY (19) PL
 RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 172279 (13) B1 (21) Numer zgłoszenia: 300123 Urząd Patentowy ( 2 2 ) Data zgłoszenia: 16.08.1993 Rzeczypospolitej Polskiej (51) IntCl6: E04B 5/19
RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 172279 (13) B1 (21) Numer zgłoszenia: 300123 Urząd Patentowy ( 2 2 ) Data zgłoszenia: 16.08.1993 Rzeczypospolitej Polskiej (51) IntCl6: E04B 5/19
DE-WZP.261.11.2015.JJ.3 Warszawa, 2015-06-15
 DE-WZP.261.11.2015.JJ.3 Warszawa, 2015-06-15 Wykonawcy ubiegający się o udzielenie zamówienia Dotyczy: postępowania prowadzonego w trybie przetargu nieograniczonego na Usługę druku książek, nr postępowania
DE-WZP.261.11.2015.JJ.3 Warszawa, 2015-06-15 Wykonawcy ubiegający się o udzielenie zamówienia Dotyczy: postępowania prowadzonego w trybie przetargu nieograniczonego na Usługę druku książek, nr postępowania
Temat: Czy świetlówki energooszczędne są oszczędne i sprzyjają ochronie środowiska? Imię i nazwisko
 Temat: Czy świetlówki energooszczędne są oszczędne i sprzyjają ochronie środowiska? Karta pracy III.. Imię i nazwisko klasa Celem nauki jest stawianie hipotez, a następnie ich weryfikacja, która w efekcie
Temat: Czy świetlówki energooszczędne są oszczędne i sprzyjają ochronie środowiska? Karta pracy III.. Imię i nazwisko klasa Celem nauki jest stawianie hipotez, a następnie ich weryfikacja, która w efekcie
Wyznaczanie statycznego i kinetycznego współczynnika tarcia przy pomocy równi pochyłej
 Wyznaczanie statycznego i kinetycznego współczynnika tarcia przy pomocy równi pochyłej Równia pochyła jest przykładem maszyny prostej. Jej konstrukcja składa się z płaskiej powierzchni nachylonej pod kątem
Wyznaczanie statycznego i kinetycznego współczynnika tarcia przy pomocy równi pochyłej Równia pochyła jest przykładem maszyny prostej. Jej konstrukcja składa się z płaskiej powierzchni nachylonej pod kątem
Lekcja 173, 174. Temat: Silniki indukcyjne i pierścieniowe.
 Lekcja 173, 174 Temat: Silniki indukcyjne i pierścieniowe. Silnik elektryczny asynchroniczny jest maszyną elektryczną zmieniającą energię elektryczną w energię mechaniczną, w której wirnik obraca się z
Lekcja 173, 174 Temat: Silniki indukcyjne i pierścieniowe. Silnik elektryczny asynchroniczny jest maszyną elektryczną zmieniającą energię elektryczną w energię mechaniczną, w której wirnik obraca się z
XIII KONKURS MATEMATYCZNY
 XIII KONKURS MTMTYZNY L UZNIÓW SZKÓŁ POSTWOWYH organizowany przez XIII Liceum Ogólnokształcace w Szczecinie FINŁ - 19 lutego 2013 Test poniższy zawiera 25 zadań. Za poprawne rozwiązanie każdego zadania
XIII KONKURS MTMTYZNY L UZNIÓW SZKÓŁ POSTWOWYH organizowany przez XIII Liceum Ogólnokształcace w Szczecinie FINŁ - 19 lutego 2013 Test poniższy zawiera 25 zadań. Za poprawne rozwiązanie każdego zadania
Warszawska Giełda Towarowa S.A.
 KONTRAKT FUTURES Poprzez kontrakt futures rozumiemy umowę zawartą pomiędzy dwoma stronami transakcji. Jedna z nich zobowiązuje się do kupna, a przeciwna do sprzedaży, w ściśle określonym terminie w przyszłości
KONTRAKT FUTURES Poprzez kontrakt futures rozumiemy umowę zawartą pomiędzy dwoma stronami transakcji. Jedna z nich zobowiązuje się do kupna, a przeciwna do sprzedaży, w ściśle określonym terminie w przyszłości
Klasyfikacja i oznakowanie substancji chemicznych i ich mieszanin. Dominika Sowa
 Klasyfikacja i oznakowanie substancji chemicznych i ich mieszanin Dominika Sowa Szczecin, 8 maj 2014 Program prezentacji: 1. Definicja substancji i mieszanin chemicznych wg Ustawy o substancjach chemicznych
Klasyfikacja i oznakowanie substancji chemicznych i ich mieszanin Dominika Sowa Szczecin, 8 maj 2014 Program prezentacji: 1. Definicja substancji i mieszanin chemicznych wg Ustawy o substancjach chemicznych
HiTiN Sp. z o. o. Przekaźnik kontroli temperatury RTT 4/2 DTR. 40 432 Katowice, ul. Szopienicka 62 C tel/fax.: + 48 (32) 353 41 31. www.hitin.
 HiTiN Sp. z o. o. 40 432 Katowice, ul. Szopienicka 62 C tel/fax.: + 48 (32) 353 41 31 www.hitin.pl Przekaźnik kontroli temperatury RTT 4/2 DTR Katowice, 1999 r. 1 1. Wstęp. Przekaźnik elektroniczny RTT-4/2
HiTiN Sp. z o. o. 40 432 Katowice, ul. Szopienicka 62 C tel/fax.: + 48 (32) 353 41 31 www.hitin.pl Przekaźnik kontroli temperatury RTT 4/2 DTR Katowice, 1999 r. 1 1. Wstęp. Przekaźnik elektroniczny RTT-4/2
Postrzeganie reklamy zewnętrznej - badania
 Według opublikowanych na początku tej dekady badań Demoskopu, zdecydowana większość respondentów (74%) przyznaje, że w miejscowości, w której mieszkają znajdują się nośniki reklamy zewnętrznej (specjalne,
Według opublikowanych na początku tej dekady badań Demoskopu, zdecydowana większość respondentów (74%) przyznaje, że w miejscowości, w której mieszkają znajdują się nośniki reklamy zewnętrznej (specjalne,
INSTRUKCJA BHP PRZY RECZNYCH PRACACH TRANSPORTOWYCH DLA PRACOWNIKÓW KUCHENKI ODDZIAŁOWEJ.
 INSTRUKCJA BHP PRZY RECZNYCH PRACACH TRANSPORTOWYCH DLA PRACOWNIKÓW KUCHENKI ODDZIAŁOWEJ. I. UWAGI OGÓLNE. 1. Dostarczanie posiłków, ich przechowywanie i dystrybucja musza odbywać się w warunkach zapewniających
INSTRUKCJA BHP PRZY RECZNYCH PRACACH TRANSPORTOWYCH DLA PRACOWNIKÓW KUCHENKI ODDZIAŁOWEJ. I. UWAGI OGÓLNE. 1. Dostarczanie posiłków, ich przechowywanie i dystrybucja musza odbywać się w warunkach zapewniających
Techniczne nauki М.М.Zheplinska, A.S.Bessarab Narodowy uniwersytet spożywczych technologii, Кijow STOSOWANIE PARY WODNEJ SKRAPLANIA KAWITACJI
 Techniczne nauki М.М.Zheplinska, A.S.Bessarab Narodowy uniwersytet spożywczych technologii, Кijow STOSOWANIE PARY WODNEJ SKRAPLANIA KAWITACJI SKLAROWANEGO SOKU JABŁKOWEGO Skutecznym sposobem leczenia soku
Techniczne nauki М.М.Zheplinska, A.S.Bessarab Narodowy uniwersytet spożywczych technologii, Кijow STOSOWANIE PARY WODNEJ SKRAPLANIA KAWITACJI SKLAROWANEGO SOKU JABŁKOWEGO Skutecznym sposobem leczenia soku
Kuratorium Oświaty w Lublinie
 Kuratorium Oświaty w Lublinie ZESTAW ZADAŃ KONKURSOWYCH Z CHEMII DLA UCZNIÓW GIMNAZJÓW ROK SZKOLNY 2014/2015 KOD UCZNIA ETAP OKRĘGOWY Instrukcja dla ucznia 1. Zestaw konkursowy zawiera 12 zadań. 2. Przed
Kuratorium Oświaty w Lublinie ZESTAW ZADAŃ KONKURSOWYCH Z CHEMII DLA UCZNIÓW GIMNAZJÓW ROK SZKOLNY 2014/2015 KOD UCZNIA ETAP OKRĘGOWY Instrukcja dla ucznia 1. Zestaw konkursowy zawiera 12 zadań. 2. Przed
Sprawdzian wiadomości z przyrody w klasie VI WNIKAMY W GŁĄB MATERII
 Sprawdzian wiadomości z przyrody w klasie VI WNIKAMY W GŁĄB MATERII Objaśnienia do sprawdzianu Litera oznacza poziom wymagań: K-konieczny, P-podstawowy, R-rozszerzony, D- dopełniający. Cyfra oznacza numer
Sprawdzian wiadomości z przyrody w klasie VI WNIKAMY W GŁĄB MATERII Objaśnienia do sprawdzianu Litera oznacza poziom wymagań: K-konieczny, P-podstawowy, R-rozszerzony, D- dopełniający. Cyfra oznacza numer
18 TERMODYNAMIKA. PODSUMOWANIE
 Włodzimierz Wolczyński 18 TERMODYNAMIKA. PODSUMOWANIE Zadanie 1 Oto cykl pracy pewnego silnika termodynamicznego w układzie p(v). p [ 10 5 Pa] 5 A 4 3 2 1 0 C B 5 10 15 20 25 30 35 40 V [ dm 3 ] Sprawność
Włodzimierz Wolczyński 18 TERMODYNAMIKA. PODSUMOWANIE Zadanie 1 Oto cykl pracy pewnego silnika termodynamicznego w układzie p(v). p [ 10 5 Pa] 5 A 4 3 2 1 0 C B 5 10 15 20 25 30 35 40 V [ dm 3 ] Sprawność
OGÓLNODOSTĘPNE IFORMACJE O WYNIKACH EGZAMINÓW I EFEKTYWNOŚCI NAUCZANIA W GIMNAZJACH przykłady ich wykorzystania i interpretowania
 Teresa Kutajczyk, WBiA OKE w Gdańsku Okręgowa Komisja Egzaminacyjna w Gdańsku OGÓLNODOSTĘPNE IFORMACJE O WYNIKACH EGZAMINÓW I EFEKTYWNOŚCI NAUCZANIA W GIMNAZJACH przykłady ich wykorzystania i interpretowania
Teresa Kutajczyk, WBiA OKE w Gdańsku Okręgowa Komisja Egzaminacyjna w Gdańsku OGÓLNODOSTĘPNE IFORMACJE O WYNIKACH EGZAMINÓW I EFEKTYWNOŚCI NAUCZANIA W GIMNAZJACH przykłady ich wykorzystania i interpretowania
Rozbudowa domu przedpogrzebowego na cmentarzu komunalnym w Bierutowie. Specyfikacja techniczna wykonania i odbioru robót budowlanych - Okna i drzwi
 SPECYFIKACJA TECHNICZNA WYKONANIA I ODBIORU ROBÓT BUDOWLANYCH * * * OKNA I DRZWI 1 1. POSTANOWIENIA OGÓLNE 1.1. Przedmiot ST Przedmiotem niniejszej części specyfikacji technicznej (ST) są wymagania dotyczące
SPECYFIKACJA TECHNICZNA WYKONANIA I ODBIORU ROBÓT BUDOWLANYCH * * * OKNA I DRZWI 1 1. POSTANOWIENIA OGÓLNE 1.1. Przedmiot ST Przedmiotem niniejszej części specyfikacji technicznej (ST) są wymagania dotyczące
PODSTAWY METROLOGII ĆWICZENIE 4 PRZETWORNIKI AC/CA Międzywydziałowa Szkoła Inżynierii Biomedycznej 2009/2010 SEMESTR 3
 PODSTAWY METROLOGII ĆWICZENIE 4 PRZETWORNIKI AC/CA Międzywydziałowa Szkoła Inżynierii Biomedycznej 29/2 SEMESTR 3 Rozwiązania zadań nie były w żaden sposób konsultowane z żadnym wiarygodnym źródłem informacji!!!
PODSTAWY METROLOGII ĆWICZENIE 4 PRZETWORNIKI AC/CA Międzywydziałowa Szkoła Inżynierii Biomedycznej 29/2 SEMESTR 3 Rozwiązania zadań nie były w żaden sposób konsultowane z żadnym wiarygodnym źródłem informacji!!!
Wydział Elektrotechniki, Elektroniki, Informatyki i Automatyki Katedra Przyrządów Półprzewodnikowych i Optoelektronicznych.
 Politechnika Łódzka Wydział Elektrotechniki, Elektroniki, Informatyki i Automatyki Katedra Przyrządów Półprzewodnikowych i Optoelektronicznych Niekonwencjonalne źródła energii Laboratorium Ćwiczenie 4
Politechnika Łódzka Wydział Elektrotechniki, Elektroniki, Informatyki i Automatyki Katedra Przyrządów Półprzewodnikowych i Optoelektronicznych Niekonwencjonalne źródła energii Laboratorium Ćwiczenie 4
SPECYFIKACJA ISTOTNYCH WARUNKÓW ZAMÓWIENIA
 SPECYFIKACJA ISTOTNYCH WARUNKÓW ZAMÓWIENIA Wójt Gminy Sońsk, 06-430 Sońsk ul.ciechanowska 20 tel. (0-23) 6713811 fax. (0-23) 6713818 zwany dalej zamawiającym zaprasza do składania ofert w trybie przetargu
SPECYFIKACJA ISTOTNYCH WARUNKÓW ZAMÓWIENIA Wójt Gminy Sońsk, 06-430 Sońsk ul.ciechanowska 20 tel. (0-23) 6713811 fax. (0-23) 6713818 zwany dalej zamawiającym zaprasza do składania ofert w trybie przetargu
art. 488 i n. ustawy z dnia 23 kwietnia 1964 r. Kodeks cywilny (Dz. U. Nr 16, poz. 93 ze zm.),
 Istota umów wzajemnych Podstawa prawna: Księga trzecia. Zobowiązania. Dział III Wykonanie i skutki niewykonania zobowiązań z umów wzajemnych. art. 488 i n. ustawy z dnia 23 kwietnia 1964 r. Kodeks cywilny
Istota umów wzajemnych Podstawa prawna: Księga trzecia. Zobowiązania. Dział III Wykonanie i skutki niewykonania zobowiązań z umów wzajemnych. art. 488 i n. ustawy z dnia 23 kwietnia 1964 r. Kodeks cywilny
SCENARIUSZ LEKCJI Liceum
 Proponowany scenariusz jest przykładem postępowania dydaktycznego wyprowadzonego z zasad konstruktywizmu edukacyjnego: SCENARIUSZ LEKCJI Liceum Temat lekcji: Czy huśtawka jest oscylatorem harmonicznym?
Proponowany scenariusz jest przykładem postępowania dydaktycznego wyprowadzonego z zasad konstruktywizmu edukacyjnego: SCENARIUSZ LEKCJI Liceum Temat lekcji: Czy huśtawka jest oscylatorem harmonicznym?
Wprowadzam : REGULAMIN REKRUTACJI DZIECI DO PRZEDSZKOLA NR 14
 ZARZĄDZENIE Nr 2/2016 z dnia 16 lutego 2016r DYREKTORA PRZEDSZKOLA Nr 14 W K O N I N I E W sprawie wprowadzenia REGULAMINU REKRUTACJI DZIECI DO PRZEDSZKOLA NR 14 IM KRASNALA HAŁABAŁY W KONINIE Podstawa
ZARZĄDZENIE Nr 2/2016 z dnia 16 lutego 2016r DYREKTORA PRZEDSZKOLA Nr 14 W K O N I N I E W sprawie wprowadzenia REGULAMINU REKRUTACJI DZIECI DO PRZEDSZKOLA NR 14 IM KRASNALA HAŁABAŁY W KONINIE Podstawa
TEORIE KWASÓW I ZASAD.
 TERIE KWASÓW I ZASAD. Teoria Arrheniusa (nagroda Nobla 1903 r). Kwas kaŝda substancja, która dostarcza jony + do roztworu. A + + A Zasada kaŝda substancja, która dostarcza jony do roztworu. M M + + Reakcja
TERIE KWASÓW I ZASAD. Teoria Arrheniusa (nagroda Nobla 1903 r). Kwas kaŝda substancja, która dostarcza jony + do roztworu. A + + A Zasada kaŝda substancja, która dostarcza jony do roztworu. M M + + Reakcja
Olej rzepakowy, jako paliwo do silników z zapłonem samoczynnym
 Coraz częściej jako paliwo stosuje się biokomponenty powstałe z roślin oleistych. Nie mniej jednak właściwości fizykochemiczne oleju napędowego i oleju powstałego z roślin znacząco różnią się miedzy sobą.
Coraz częściej jako paliwo stosuje się biokomponenty powstałe z roślin oleistych. Nie mniej jednak właściwości fizykochemiczne oleju napędowego i oleju powstałego z roślin znacząco różnią się miedzy sobą.
EGZAMIN MATURALNY Z MATEMATYKI
 Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 016 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę dyskalkulia dysleksja EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 016 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę dyskalkulia dysleksja EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY
tel/fax 018 443 82 13 lub 018 443 74 19 NIP 7343246017 Regon 120493751
 Zespół Placówek Kształcenia Zawodowego 33-300 Nowy Sącz ul. Zamenhoffa 1 tel/fax 018 443 82 13 lub 018 443 74 19 http://zpkz.nowysacz.pl e-mail biuro@ckp-ns.edu.pl NIP 7343246017 Regon 120493751 Wskazówki
Zespół Placówek Kształcenia Zawodowego 33-300 Nowy Sącz ul. Zamenhoffa 1 tel/fax 018 443 82 13 lub 018 443 74 19 http://zpkz.nowysacz.pl e-mail biuro@ckp-ns.edu.pl NIP 7343246017 Regon 120493751 Wskazówki
Kratownice Wieża Eiffel a
 Kratownice Wieża Eiffel a Kratownica jest to konstrukcja nośna, składająca się z prętów połączonch ze sobą w węzłach. Kratownica może bć: 1) płaska, gd wszstkie pręt leżą w jednej płaszczźnie, 2) przestrzenna,
Kratownice Wieża Eiffel a Kratownica jest to konstrukcja nośna, składająca się z prętów połączonch ze sobą w węzłach. Kratownica może bć: 1) płaska, gd wszstkie pręt leżą w jednej płaszczźnie, 2) przestrzenna,
Standardowe tolerancje wymiarowe WWW.ALBATROS-ALUMINIUM.COM
 Standardowe tolerancje wymiarowe WWW.ALBATROSALUMINIUM.COM Tolerancje standardowe gwarantowane przez Albatros Aluminium obowiązują dla wymiarów co do których nie dokonano innych uzgodnień podczas potwierdzania
Standardowe tolerancje wymiarowe WWW.ALBATROSALUMINIUM.COM Tolerancje standardowe gwarantowane przez Albatros Aluminium obowiązują dla wymiarów co do których nie dokonano innych uzgodnień podczas potwierdzania
RZECZPOSPOLITA POLSKA. Prezydent Miasta na Prawach Powiatu Zarząd Powiatu. wszystkie
 RZECZPOSPOLITA POLSKA Warszawa, dnia 11 lutego 2011 r. MINISTER FINANSÓW ST4-4820/109/2011 Prezydent Miasta na Prawach Powiatu Zarząd Powiatu wszystkie Zgodnie z art. 33 ust. 1 pkt 2 ustawy z dnia 13 listopada
RZECZPOSPOLITA POLSKA Warszawa, dnia 11 lutego 2011 r. MINISTER FINANSÓW ST4-4820/109/2011 Prezydent Miasta na Prawach Powiatu Zarząd Powiatu wszystkie Zgodnie z art. 33 ust. 1 pkt 2 ustawy z dnia 13 listopada
CZĄSTECZKI, WIĄZANIA CHEMICZNE
 1. ATOMY, CZĄSTECZKI, WIĄZANIA CHEMICZNE Iwona śak STRUKTURA ATOMOWA I WIĄZANIA CHEMICZNE Atomy składają się z dodatnio naładowanego jądra atomowego oraz z otaczających go ujemnie naładowanych elektronów.
1. ATOMY, CZĄSTECZKI, WIĄZANIA CHEMICZNE Iwona śak STRUKTURA ATOMOWA I WIĄZANIA CHEMICZNE Atomy składają się z dodatnio naładowanego jądra atomowego oraz z otaczających go ujemnie naładowanych elektronów.
LABORATORIUM NAUKI O MATERIAŁACH
 Politechnika Łódzka Wydział Mechaniczny Instytut Inżynierii Materiałowej LABORATORIUM NAUKI O MATERIAŁACH Ćwiczenie nr 4 Temat: Kształtowanie właściwości metodami technologicznymi. Łódź 2010 Cel ćwiczenia
Politechnika Łódzka Wydział Mechaniczny Instytut Inżynierii Materiałowej LABORATORIUM NAUKI O MATERIAŁACH Ćwiczenie nr 4 Temat: Kształtowanie właściwości metodami technologicznymi. Łódź 2010 Cel ćwiczenia
Chemia i technologia materiałów barwnych BADANIE WŁAŚCIWOŚCI ZWIĄZKÓW BARWNYCH WYKORZYSTANIEM SPEKTROFOTOMETRII UV-VIS.
 Chemia i technologia materiałów barwnych Ćwiczenia laboratoryjne BADANIE WŁAŚCIWOŚCI ZWIĄZKÓW BARWNYCH WYKORZYSTANIEM SPEKTROFOTOMETRII UV-VIS. Z Opracowanie: dr inŝ. Ewa Wagner-Wysiecka Politechnika Gdańska
Chemia i technologia materiałów barwnych Ćwiczenia laboratoryjne BADANIE WŁAŚCIWOŚCI ZWIĄZKÓW BARWNYCH WYKORZYSTANIEM SPEKTROFOTOMETRII UV-VIS. Z Opracowanie: dr inŝ. Ewa Wagner-Wysiecka Politechnika Gdańska
Edycja geometrii w Solid Edge ST
 Edycja geometrii w Solid Edge ST Artykuł pt.: " Czym jest Technologia Synchroniczna a czym nie jest?" zwracał kilkukrotnie uwagę na fakt, że nie należy mylić pojęć modelowania bezpośredniego i edycji bezpośredniej.
Edycja geometrii w Solid Edge ST Artykuł pt.: " Czym jest Technologia Synchroniczna a czym nie jest?" zwracał kilkukrotnie uwagę na fakt, że nie należy mylić pojęć modelowania bezpośredniego i edycji bezpośredniej.
ZASADY PRZYZNAWANIA ŚRODKÓW Z KRAJOWEGO FUNDUSZU SZKOLENIOWEGO PRZEZ POWIATOWY URZĄD PRACY W ŁASKU
 ZASADY PRZYZNAWANIA ŚRODKÓW Z KRAJOWEGO FUNDUSZU SZKOLENIOWEGO PRZEZ POWIATOWY URZĄD PRACY W ŁASKU I. INFORMACJE OGÓLNE 1. Na podstawie art. 69 a i 69 b ustawy o promocji zatrudnienia i instytucjach rynku
ZASADY PRZYZNAWANIA ŚRODKÓW Z KRAJOWEGO FUNDUSZU SZKOLENIOWEGO PRZEZ POWIATOWY URZĄD PRACY W ŁASKU I. INFORMACJE OGÓLNE 1. Na podstawie art. 69 a i 69 b ustawy o promocji zatrudnienia i instytucjach rynku
Instrukcja sporządzania skonsolidowanego bilansu Miasta Konina
 Załącznik Nr 1 Do zarządzenia Nr 92/2012 Prezydenta Miasta Konina z dnia 18.10.2012 r. Instrukcja sporządzania skonsolidowanego bilansu Miasta Konina Jednostką dominującą jest Miasto Konin (Gmina Miejska
Załącznik Nr 1 Do zarządzenia Nr 92/2012 Prezydenta Miasta Konina z dnia 18.10.2012 r. Instrukcja sporządzania skonsolidowanego bilansu Miasta Konina Jednostką dominującą jest Miasto Konin (Gmina Miejska
SPORZĄDZANIE ROZTWORÓW
 1. SPORZĄDZANIE ROZTWORÓW 1. Sporządzanie roztworu CuSO 4 o stęŝeniu procentowym StęŜeniem roztworu określa się ilość substancji (wyraŝoną w jednostkach masy lub objętości) zawartą w określonej jednostce
1. SPORZĄDZANIE ROZTWORÓW 1. Sporządzanie roztworu CuSO 4 o stęŝeniu procentowym StęŜeniem roztworu określa się ilość substancji (wyraŝoną w jednostkach masy lub objętości) zawartą w określonej jednostce
ANALOGOWE UKŁADY SCALONE
 ANALOGOWE UKŁADY SCALONE Ćwiczenie to ma na celu zapoznanie z przedstawicielami najważniejszych typów analogowych układów scalonych. Będą to: wzmacniacz operacyjny µa 741, obecnie chyba najbardziej rozpowszechniony
ANALOGOWE UKŁADY SCALONE Ćwiczenie to ma na celu zapoznanie z przedstawicielami najważniejszych typów analogowych układów scalonych. Będą to: wzmacniacz operacyjny µa 741, obecnie chyba najbardziej rozpowszechniony
Lekcja 15. Temat: Prąd elektryczny w róŝnych środowiskach.
 Lekcja 15 Temat: Prąd elektryczny w róŝnych środowiskach. Pod wpływem pola elektrycznego (przyłoŝonego napięcia) w materiałach, w których istnieją ruchliwe nośniki ładunku dochodzi do zjawiska przewodzenia
Lekcja 15 Temat: Prąd elektryczny w róŝnych środowiskach. Pod wpływem pola elektrycznego (przyłoŝonego napięcia) w materiałach, w których istnieją ruchliwe nośniki ładunku dochodzi do zjawiska przewodzenia
Wojewódzki Konkurs Przedmiotowy z Matematyki dla uczniów gimnazjów województwa śląskiego w roku szkolnym 2012/2013
 Wojewódzki Konkurs Przedmiotowy z Matematyki dla uczniów gimnazjów województwa śląskiego w roku szkolnym 2012/2013 KOD UCZNIA Etap: Data: Czas pracy: wojewódzki 4 marca 2013 r. 120 minut Informacje dla
Wojewódzki Konkurs Przedmiotowy z Matematyki dla uczniów gimnazjów województwa śląskiego w roku szkolnym 2012/2013 KOD UCZNIA Etap: Data: Czas pracy: wojewódzki 4 marca 2013 r. 120 minut Informacje dla
Metoda LBL (ang. Layer by Layer, pol. Warstwa Po Warstwie). Jest ona metodą najprostszą.
 Metoda LBL (ang. Layer by Layer, pol. Warstwa Po Warstwie). Jest ona metodą najprostszą. Po pierwsze - notacja - trzymasz swoją kostkę w rękach? Widzisz ścianki, którymi można ruszać? Notacja to oznaczenie
Metoda LBL (ang. Layer by Layer, pol. Warstwa Po Warstwie). Jest ona metodą najprostszą. Po pierwsze - notacja - trzymasz swoją kostkę w rękach? Widzisz ścianki, którymi można ruszać? Notacja to oznaczenie
Bazy danych. Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl www.uj.edu.pl/web/zpgk/materialy 9/15
 Bazy danych Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl www.uj.edu.pl/web/zpgk/materialy 9/15 Przechowywanie danych Wykorzystanie systemu plików, dostępu do plików za pośrednictwem systemu operacyjnego
Bazy danych Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl www.uj.edu.pl/web/zpgk/materialy 9/15 Przechowywanie danych Wykorzystanie systemu plików, dostępu do plików za pośrednictwem systemu operacyjnego
Jak usprawnić procesy controllingowe w Firmie? Jak nadać im szerszy kontekst? Nowe zastosowania naszych rozwiązań na przykładach.
 Jak usprawnić procesy controllingowe w Firmie? Jak nadać im szerszy kontekst? Nowe zastosowania naszych rozwiązań na przykładach. 1 PROJEKTY KOSZTOWE 2 PROJEKTY PRZYCHODOWE 3 PODZIAŁ PROJEKTÓW ZE WZGLĘDU
Jak usprawnić procesy controllingowe w Firmie? Jak nadać im szerszy kontekst? Nowe zastosowania naszych rozwiązań na przykładach. 1 PROJEKTY KOSZTOWE 2 PROJEKTY PRZYCHODOWE 3 PODZIAŁ PROJEKTÓW ZE WZGLĘDU
Waldemar Szuchta Naczelnik Urzędu Skarbowego Wrocław Fabryczna we Wrocławiu
 1 P/08/139 LWR 41022-1/2008 Pan Wrocław, dnia 5 5 września 2008r. Waldemar Szuchta Naczelnik Urzędu Skarbowego Wrocław Fabryczna we Wrocławiu WYSTĄPIENIE POKONTROLNE Na podstawie art. 2 ust. 1 ustawy z
1 P/08/139 LWR 41022-1/2008 Pan Wrocław, dnia 5 5 września 2008r. Waldemar Szuchta Naczelnik Urzędu Skarbowego Wrocław Fabryczna we Wrocławiu WYSTĄPIENIE POKONTROLNE Na podstawie art. 2 ust. 1 ustawy z
SPEKTROSKOPIA LASEROWA
 SPEKTROSKOPIA LASEROWA Spektroskopia laserowa dostarcza wiedzy o naturze zjawisk zachodz cych na poziomie atomów i cz steczek oraz oddzia ywaniu promieniowania z materi i nale y do jednej z najwa niejszych
SPEKTROSKOPIA LASEROWA Spektroskopia laserowa dostarcza wiedzy o naturze zjawisk zachodz cych na poziomie atomów i cz steczek oraz oddzia ywaniu promieniowania z materi i nale y do jednej z najwa niejszych
NACZYNIE WZBIORCZE INSTRUKCJA OBSŁUGI INSTRUKCJA INSTALOWANIA
 NACZYNIE WZBIORCZE INSTRUKCJA OBSŁUGI INSTRUKCJA INSTALOWANIA Kraków 31.01.2014 Dział Techniczny: ul. Pasternik 76, 31-354 Kraków tel. +48 12 379 37 90~91 fax +48 12 378 94 78 tel. kom. +48 665 001 613
NACZYNIE WZBIORCZE INSTRUKCJA OBSŁUGI INSTRUKCJA INSTALOWANIA Kraków 31.01.2014 Dział Techniczny: ul. Pasternik 76, 31-354 Kraków tel. +48 12 379 37 90~91 fax +48 12 378 94 78 tel. kom. +48 665 001 613
Techniki korekcyjne wykorzystywane w metodzie kinesiotapingu
 Techniki korekcyjne wykorzystywane w metodzie kinesiotapingu Jak ju wspomniano, kinesiotaping mo e byç stosowany jako osobna metoda terapeutyczna, jak równie mo e stanowiç uzupe nienie innych metod fizjoterapeutycznych.
Techniki korekcyjne wykorzystywane w metodzie kinesiotapingu Jak ju wspomniano, kinesiotaping mo e byç stosowany jako osobna metoda terapeutyczna, jak równie mo e stanowiç uzupe nienie innych metod fizjoterapeutycznych.
PRÓBNY EGZAMIN MATURALNY Z FIZYKI I ASTRONOMII
 dysleksja PRÓBNY EGZAMIN MATURALNY Z FIZYKI I ASTRONOMII Instrukcja dla zdaj cego (poziom rozszerzony) Czas pracy 120 minut 1. Prosz sprawdzi, czy arkusz egzaminacyjny zawiera 8 stron. Ewentualny brak
dysleksja PRÓBNY EGZAMIN MATURALNY Z FIZYKI I ASTRONOMII Instrukcja dla zdaj cego (poziom rozszerzony) Czas pracy 120 minut 1. Prosz sprawdzi, czy arkusz egzaminacyjny zawiera 8 stron. Ewentualny brak
dyfuzja w płynie nieruchomym (lub w ruchu laminarnym) prowadzi do wzrostu chmury zanieczyszczenia
 6. Dyspersja i adwekcja w przepływie urbulennym podsumowanie własności laminarnej (molekularnej) dyfuzji: ciągły ruch molekuł (molekularne wymuszenie) prowadzi do losowego błądzenia cząsek zanieczyszczeń
6. Dyspersja i adwekcja w przepływie urbulennym podsumowanie własności laminarnej (molekularnej) dyfuzji: ciągły ruch molekuł (molekularne wymuszenie) prowadzi do losowego błądzenia cząsek zanieczyszczeń
Gaz i jego parametry
 W1 30 Gaz doskonały Parametry gazu Równanie Clapeyrona Mieszaniny gazów Warunki normalne 1 Gazem doskonałym nazywamy gaz spełniaj niający następuj pujące warunki: - cząstki gazu zachowują się jako doskonale
W1 30 Gaz doskonały Parametry gazu Równanie Clapeyrona Mieszaniny gazów Warunki normalne 1 Gazem doskonałym nazywamy gaz spełniaj niający następuj pujące warunki: - cząstki gazu zachowują się jako doskonale
