PLAN WYKŁADU. Opis powietrza zawierającego parę wodną w stanie nasyconym oraz wodę. Entalpia Energia wewnętrzna Entropia 1 /23
|
|
|
- Tomasz Orłowski
- 6 lat temu
- Przeglądów:
Transkrypt
1 PAN WYKŁADU Ois owietza zawieająego aę woną w stanie nasyony oaz woę Entaia Enegia wewnętzna Entoia 1 /23
2 Poęzniki Saby, Cate 5 C&W, Cate 4 R&Y, Cate 2 2 /23
3 Paa wona w atosfeze Da teeatu i iśnień sotykany w atosfeze, iśnienie ay nasyonej zako zekaza watość 60 Pa, a stosunek zieszania 30 g kg -1, zyi Paa wona wystęuje w atosfeze tyko w iośia śaowy. Zgonie z ównanie Causiusa-Caeyona iśnienie ay nasyonej ośnie eksotenjanie z teeatuą. Paa wona jest oukowana w toika, gzie wysoka teeatua owiezni oza (SS sea sufae teeatue) oowiaa najwyższej watośi iśnienia ay nasyonej, a zate najwyższeu stosunkowi zieszania. Watość ta aeje w kieunku biegunów. 3 /23
4 Iość ay wonej zniejsza się w wyniku konensaji i wyaania w ostai oau skutek aiabatyznego ołazania w wyniku ozężania (u o góy) i zniejszania watośi iśnienia ay nasyonej. Konensaja zaozi ównież w wyższy szeokośia geogafizny na skutek ołazania aiayjnego. Poukja ay wonej na owiezni oza nastęuje tyko, jeśi zostanie zaabsobowana ewna iość ieła, ażeby ogła zajść zeiana fazowa. Cieło jest absobowane abo z oza abo bezośenio z oieniowania kótkofaowego. Kiey aa wona konensuje, ieło zeiany fazowej jest uwaniane o otozenia i ozostaje w atosfeze o wyanięiu oau. Obieg ay wonej w atosfeze nie owouje wyiany asy, ae tansfe ieła z oeanu o atosfey. 4 /23
5 NASA Wate Vao Pojet (NVAP) ota Coun Wate Vao 1992 e ean istibution of eiitabe wate, o tota atosei wate ao aboe te Eat's sufae, fo is eition inues ata fo bot sateite an aiosone obseations. (Iage outesy of oas Vone aa an Dai Rane, Cooao State Uniesity, Fot Coins.) 5 /23
6 Poesy owaząe o owstania ub ozau u Założyy, że uy twozą się w atosfeze, kiey wigotność wzgęna osiąga watość f100% (w zezywistośi ta watość jest niewiee większa o 100%). f s (, ) Wzost wigotnośi wzgęnej oże nastąić na skutek: wzostu zawatośi ay wonej w owietzu (wzost ); aowanie woy z owiezni ziei ub aowanie eszzu saająego w nienasyony owietzu i/ub ołozenia owietza (zniejszenie s (,)); izobayzne ołazanie (n. wyłazanie aiayjne), aiabatyzne ołazanie wznosząego się owietza. ieszania wó nienasyony as owietza 6 /23
7 Równania I i II zasay teoynaiki a owietza zawieająego aę wona oaz woę zastosujey o oisu nastęująy oesów: ołazanie izobayzne aiabatyzny i izobayzny oes aowania woy aiabatyzne i izobayzne ieszanie ozężanie aiabatyzne 7 /23
8 ENAPIA ZAMKNIĘEGO UKŁADU: POWIERZE, PARA WODNA I WODA 8 /23
9 9 /23 Zaiszey entaię jako funkję (,,,, ),,, Jeśi ukła jest zaknięty, to 0 oaz - ( ) Poizyy: oaz
10 10 /23 Zaiszey entaię jako suę wkłaów o: suego owietza (), ay wonej () oaz woy () Da woy óżnia oięzy iełe właśiwy zy stały iśnieniu i zy stałej objętośi jest bazo ała i atego i nie ozóżniać i zaisywać jako
11 11 /23 Da fazy gazowej (sue owietze i aa wona ) entaia jest funkją wyłąznie teeatuy: (, ): 0 Da fazy iekłej: ( ) 1 1 α α jest ałe a fazy skonensowanej, atego Można okazać, że wkła złonu związanego ze zianą iśnienia jest ały w oównaniu z złone wynikająy ze ziany teeatuy. 1 α Izobayzny wsółzynnik ozszezanośi s s s 0
12 0 ( ) Cieło właśiwe a niejenoonego ukłau stosunek zieszania entaia właśiwa Entaia właśiwa onosi się o asy suego owietza. 12 /23
13 Inteetaja entaii W zaeżnośi o tego jak zefiniujey ukła teoynaizny, złon w ównaniu oże być uważany za zęść entaii ub za zewnętzne źóło ieła. Da zakniętego ukłau ożna naisać: δq δq Da oesu aiabatyznego: 0 Rozważy teaz ukła, któy skłaa się z wigotnego owietza, z zewnętzny źółe ieła związany z aowanie ze zbionika woy (n. wigotne owietze na jezioe). δq δq Dwa owyższe ównania są ateatyznie takie sae, jenak w iewszy złon jest zęśią entaii, a w ugi zewnętzny źółe ieła. 13 /23
14 ENERGIA WEWNĘRZNA ZAMKNIĘEGO UKŁADU: POWIERZE, PARA WODNA I WODA 14 /23
15 Zaiszey enegię wewnętzną jako funkję UU(,,,, ). Postęujey oobnie jak w zyaku wyowazenia ównania na entaię. U U U U U U ( u u ) R u u e R ( zą wiekośi ~10 5 / J/kg) jest wiekośią bazo ałą w oównaniu z (2, J/kg). R stanowi ok. 5% watośi. U Poizyy: U U 15 /23
16 16 /23 0 u u u u u U Da fazy gazowej: sue owietze i aa wona (u, u ): U s u s u ( ) 1 u 1 u α s Ze związku Maxwea: 1 α Izooyzny wsółzynnik ozężiwośi:
17 U ( ) u Da fazy iekłej złon związany ze zianą objętośi ożna zaniebać: R R ~ ,03 JK 1 kg JK 1 kg 1 u 17 /23
18 ENROPIA ZAMKNIĘEGO UKŁADU: POWIERZE, PARA WODNA I WODA 18 /23
19 ( ) S V µ µ µ 0 S V µ µ µ / S ( ) V µ µ e V R ev R V V R R e ( e) e R n R ne Zaniebujey aę związaną z ozężiwośią woy A µ -µ jest nazwane affinity fo aoization. Jeśi aa wona i woa są w ównowaze, to µ µ i A /23
20 S ( ) V µ µ A µ -µ jest nazwane affinity fo aoization. Jeśi aa wona i woa są w ównowaze, to µ µ i A 0. Potenjał eizny jest zianą funkji Gibbsa związaną ze zianą iośi oi anego skłanika ub fazy (µg). Da izoteiznego oesu w któy uzestnizy jeen o ay wonej (abo asa M ): g s µ in i i µ g e R n e µ µ µ s o µ µ R n o e e 0 e R n e s 0 µ µ A A R A n e 2 R n e s R n e R s n e R n e e R n e s 2 R 20 /23
21 S ( ) V A V Rn R A 2 R ne ne V R n 2 A S ( ) Rn 2 A A / s A ( ) Rn 2 21 /23
22 22 / n n n n n t ( ) t ( ) A Rn s 2 ( ) A n R n s t ( ) A n R n s t
23 Anaogiznie ożna wowazić złon związany z oe: s ( ) t n R n A ii A i i 23 /23
Plan wykładu 6. Hanna Pawłowska Elementy termodynamiki atmosfery i fizyki chmur Wykład 6
 Plan wykłau 6 emoynamika związana z uhem ionowym Poe euo-aiabatyzny emeatua ekwiwalentna, temeatua ekwiwalentno-otenjalna, liqui wate otential temeatue Gaient wilgotno-aiabatyzny Hanna Pawłowka Elementy
Plan wykłau 6 emoynamika związana z uhem ionowym Poe euo-aiabatyzny emeatua ekwiwalentna, temeatua ekwiwalentno-otenjalna, liqui wate otential temeatue Gaient wilgotno-aiabatyzny Hanna Pawłowka Elementy
PLAN WYKŁADU. Opis pary wodnej w atmosferze Opis wilgotnego, nienasyconego powietrza 1 /22
 PLAN WYKŁADU Oi ay wonj w atofz Oi wilgotngo, ninayongo owitza /22 Poęzniki Salby, Chat 4 C&W, Chat 4 &Y, Chat 2 2 /22 OPIS PAY WODNEJ W AOSFEZE 3 /22 aua.naa.go 4 /22 Dla tatu i iśniń otykanyh w atofz,
PLAN WYKŁADU Oi ay wonj w atofz Oi wilgotngo, ninayongo owitza /22 Poęzniki Salby, Chat 4 C&W, Chat 4 &Y, Chat 2 2 /22 OPIS PAY WODNEJ W AOSFEZE 3 /22 aua.naa.go 4 /22 Dla tatu i iśniń otykanyh w atofz,
czyli politropa jest w tym przypadku przemianą przy stałym ciśnieniu nazywaną izobarą. Równanie przemiany izobarycznej ma postać (2.
 remiany_gau_dosk Charakterystyne remiany gau doskonałego. Premiana oitroowa Premianą oitroową naywamy remianę o równaniu idem (. ub V idem (. gdie V / m. W równaniah (. i (. jest wykładnikiem oitroy. Podstawowe
remiany_gau_dosk Charakterystyne remiany gau doskonałego. Premiana oitroowa Premianą oitroową naywamy remianę o równaniu idem (. ub V idem (. gdie V / m. W równaniah (. i (. jest wykładnikiem oitroy. Podstawowe
Fizykochemiczne podstawy inżynierii procesowej. Wykład IV Proste przemiany cd: Przemiana adiabatyczna Przemiana politropowa
 Fizykoheizne odstawy inżynierii roesowej Wykład IV Proste rzeiany d: Przeiana adiabatyzna Przeiana olitroowa Przeiana adiabatyzna (izentroowa) Przeiana adiabatyzna odbywa się w układzie adiabatyzny tzn.
Fizykoheizne odstawy inżynierii roesowej Wykład IV Proste rzeiany d: Przeiana adiabatyzna Przeiana olitroowa Przeiana adiabatyzna (izentroowa) Przeiana adiabatyzna odbywa się w układzie adiabatyzny tzn.
Fizyka Pogody i Klimatu
 Fizyka Pogoy i Kliatu Hanna Pawłowska Instytut Gofizyki Uniwsytt Waszawski hanna.awlowska awlowska@igf.fuw.u.l Fizyka Pogoy i Kliatu Hanna Pawłowska Wykła oynaika atosfy wilgotn owitz Fizyka Pogoy i Kliatu
Fizyka Pogoy i Kliatu Hanna Pawłowska Instytut Gofizyki Uniwsytt Waszawski hanna.awlowska awlowska@igf.fuw.u.l Fizyka Pogoy i Kliatu Hanna Pawłowska Wykła oynaika atosfy wilgotn owitz Fizyka Pogoy i Kliatu
 Ę ĘŃ ć Ą Ś ć ć ć ć ć ć Ń Ł ć Ń Ą ć ć Ę ć Ń ć Ń ć ź Ę Ń ć Ę ć ć ć ć ź ć ć ć ć ć ĄĄ Ę Ą ź ć Ą ć ć ź ź Ń Ą Ą Ę Ę Ę ć źć Ń Ą Ń ć Ł ź ź ć ć Ł ć Ę ć Ń Ń ź Ę ź ć Ę Ś Ń ć Ą Ń Ń Ń Ą Ą ź Ą Ę Ł ć Ń Ń ć ź Ń Ą Ę Ę
Ę ĘŃ ć Ą Ś ć ć ć ć ć ć Ń Ł ć Ń Ą ć ć Ę ć Ń ć Ń ć ź Ę Ń ć Ę ć ć ć ć ź ć ć ć ć ć ĄĄ Ę Ą ź ć Ą ć ć ź ź Ń Ą Ą Ę Ę Ę ć źć Ń Ą Ń ć Ł ź ź ć ć Ł ć Ę ć Ń Ń ź Ę ź ć Ę Ś Ń ć Ą Ń Ń Ń Ą Ą ź Ą Ę Ł ć Ń Ń ć ź Ń Ą Ę Ę
Krystyna Gronostaj Maria Nowotny-Różańska Katedra Chemii i Fizyki, FIZYKA Uniwersytet Rolniczy do użytku wewnętrznego ĆWICZENIE 4
 Kystyna Gonostaj Maia Nowotny-Różańska Katea Cheii i Fizyki, FIZYKA Uniwesytet Rolniczy o użytku wewnętznego ĆWICZENIE 4 WYZNACZANIE GĘSTOŚCI CIAŁ STAŁYCH I CIECZY PRZY POMOCY PIKNOMETRU Kaków, 2004-2012
Kystyna Gonostaj Maia Nowotny-Różańska Katea Cheii i Fizyki, FIZYKA Uniwesytet Rolniczy o użytku wewnętznego ĆWICZENIE 4 WYZNACZANIE GĘSTOŚCI CIAŁ STAŁYCH I CIECZY PRZY POMOCY PIKNOMETRU Kaków, 2004-2012
u (1.2) T Pierwsza zasada termodynamiki w formie różniczkowej ma postać (1.3)
 obl_en_wew_enal-2.do Oblizanie energii wewnęrznej i enalii 1. Energia wewnęrzna subsanji rosej Właśiwa energia wewnęrzna, u[j/kg] jes funkją sanu. Sąd dla subsanji rosej jes ona funkją dwóh niezależnyh
obl_en_wew_enal-2.do Oblizanie energii wewnęrznej i enalii 1. Energia wewnęrzna subsanji rosej Właśiwa energia wewnęrzna, u[j/kg] jes funkją sanu. Sąd dla subsanji rosej jes ona funkją dwóh niezależnyh
MECHANIKA BUDOWLI 12
 Olga Koacz, Kzysztof Kawczyk, Ada Łodygowski, Michał Płotkowiak, Agnieszka Świtek, Kzysztof Tye Konsultace naukowe: of. d hab. JERZY RAKOWSKI Poznań /3 MECHANIKA BUDOWLI. DRGANIA WYMUSZONE, NIETŁUMIONE
Olga Koacz, Kzysztof Kawczyk, Ada Łodygowski, Michał Płotkowiak, Agnieszka Świtek, Kzysztof Tye Konsultace naukowe: of. d hab. JERZY RAKOWSKI Poznań /3 MECHANIKA BUDOWLI. DRGANIA WYMUSZONE, NIETŁUMIONE
 ź ą ą ź ć ź ą ć ź ź ń ą ą ń ą ą ą Żą Żą ć ź ą ą ą ą ą ą ć ć ź ą ąą ą ą ą ąą ą ą ć ą ć ź ć ć ć ą ć ć ą ć ć ć ć ą ć ą ą ć ć ć ą ć ź ć ć ź ć ą ć ą ą ć ć Ę Ł Ż ć ą ą ć ć ą ć ć ć ą ą ń Ż ą ą ą ą ą ć ć ą ć ą
ź ą ą ź ć ź ą ć ź ź ń ą ą ń ą ą ą Żą Żą ć ź ą ą ą ą ą ą ć ć ź ą ąą ą ą ą ąą ą ą ć ą ć ź ć ć ć ą ć ć ą ć ć ć ć ą ć ą ą ć ć ć ą ć ź ć ć ź ć ą ć ą ą ć ć Ę Ł Ż ć ą ą ć ć ą ć ć ć ą ą ń Ż ą ą ą ą ą ć ć ą ć ą
Układ jednostek miar SI
 Układ jednostek iar SI Wiekośi i jednostki odstawowe Wiekość fizyzna Sybo Jednostka Długość [] etr Czas t [s] sekunda Masa,M [kg] kiogra eeratura terodynaizna (teeratura bezwzgędna) [K] kewin Natężenie
Układ jednostek iar SI Wiekośi i jednostki odstawowe Wiekość fizyzna Sybo Jednostka Długość [] etr Czas t [s] sekunda Masa,M [kg] kiogra eeratura terodynaizna (teeratura bezwzgędna) [K] kewin Natężenie
Aerotriangulacja metodą niezaleŝnych wiązek
 KP FC - aeo 27 Dwa zasanize etap pomiaow pomia wkonuje się na autogaie owm lub analitznm wkonuje się oientaję wewnętzną la kaŝego zjęia miez się współzęne tłowe otopunktów i punktów wiąŝąh oblizeniow blizenie
KP FC - aeo 27 Dwa zasanize etap pomiaow pomia wkonuje się na autogaie owm lub analitznm wkonuje się oientaję wewnętzną la kaŝego zjęia miez się współzęne tłowe otopunktów i punktów wiąŝąh oblizeniow blizenie
Uwagi do rozwiązań zadań domowych - archiwalne
 Uwagi do rozwiązań zadań doowyh - arhiwalne ROK AKADEMICKI 07/08 Zad. nr 8 [08.0.8] Przeiana nie była izohorą. Wykładnik oliroy ożna było oblizyć z równania z z Zad. nr 6 [07..9] Końową eeraurę rzeiany
Uwagi do rozwiązań zadań doowyh - arhiwalne ROK AKADEMICKI 07/08 Zad. nr 8 [08.0.8] Przeiana nie była izohorą. Wykładnik oliroy ożna było oblizyć z równania z z Zad. nr 6 [07..9] Końową eeraurę rzeiany
PLAN WYKŁADU. Sposoby dochodzenia do stanu nasycenia. Procesy związane z ruchem pionowym 1 /25
 PAN WYKŁADU Sooby ohoznia o tanu naynia Poy związan z uhm ionowym 1 /5 Poęzniki Saby, Chat 5 C&W, Chat 4 &Y, Chat /5 EMODYNAMIKA ZWIĄZANA Z UCHEM PIONOWYM Położni unktu konnaji C (iftin onnation ) Zminność
PAN WYKŁADU Sooby ohoznia o tanu naynia Poy związan z uhm ionowym 1 /5 Poęzniki Saby, Chat 5 C&W, Chat 4 &Y, Chat /5 EMODYNAMIKA ZWIĄZANA Z UCHEM PIONOWYM Położni unktu konnaji C (iftin onnation ) Zminność
Przejmowanie ciepła przy konwekcji swobodnej w przestrzeni ograniczonej (szczeliny)
 inż. Michał Stzeszewski 0-006 Pzejowanie ciepła pzy konwekcji swobonej w pzestzeni oganiczonej (szczeliny) Zaania o saozielnego ozwiązania v. 0.. powazenie celu uposzczenia achunkowego ozwiązania zjawiska
inż. Michał Stzeszewski 0-006 Pzejowanie ciepła pzy konwekcji swobonej w pzestzeni oganiczonej (szczeliny) Zaania o saozielnego ozwiązania v. 0.. powazenie celu uposzczenia achunkowego ozwiązania zjawiska
 ż Ą Ź Ą Ż ź ż ć Ą ż ź ć ź Ś ż ź ć ż ĄĄ ż ż ź ż ć ć Ę ć ż ć Ś ć ć ź ż ż ć ż ć Ę ć Ę Ę ż ż Ę ć Ś ż ć ż ć ż Ą ź ż źć ż ż ż ż ź ź ż ć ć ż ć ż ć ć ż Ę ć ź ć ć ż ć ć ż ć ć ć ć ż Źć ź ż ć ć Ę Ą Ę ć ź Ę Ę ż Ę
ż Ą Ź Ą Ż ź ż ć Ą ż ź ć ź Ś ż ź ć ż ĄĄ ż ż ź ż ć ć Ę ć ż ć Ś ć ć ź ż ż ć ż ć Ę ć Ę Ę ż ż Ę ć Ś ż ć ż ć ż Ą ź ż źć ż ż ż ż ź ź ż ć ć ż ć ż ć ć ż Ę ć ź ć ć ż ć ć ż ć ć ć ć ż Źć ź ż ć ć Ę Ą Ę ć ź Ę Ę ż Ę
powierzchnia rozdziału - dwie fazy ciekłe - jedna faza gazowa - dwa składniki
 Przejścia fazowe. powierzchnia rozdziału - skokowa zmiana niektórych parametrów na granicy faz. kropeki wody w atmosferze - dwie fazy ciekłe - jedna faza gazowa - dwa składniki Przykłady przejść fazowych:
Przejścia fazowe. powierzchnia rozdziału - skokowa zmiana niektórych parametrów na granicy faz. kropeki wody w atmosferze - dwie fazy ciekłe - jedna faza gazowa - dwa składniki Przykłady przejść fazowych:
 Ó Ó ą ć ą ą ą Ź ą ą Ż Ż Ę Ó Ż ą ć ć ź Ó Ź ź ź ą Ó Ś ą ą ć ć Ż ą Ż ą Ó ą ć ą Ż Ó ć ć ć Ę ą Ó Ł Ó Ź Ę ą ć ć ź Ó Ź Ó Ź ć ć ą Ż ą ź Ż Ź ć ć ć Ż Ę Ą ą ą Ź Ż Ź Ź ź ź Ź ć ą ą ź ź Ż Ż Ą ź Ę ą ć ą ą Ó Ź ć Ę ź ź
Ó Ó ą ć ą ą ą Ź ą ą Ż Ż Ę Ó Ż ą ć ć ź Ó Ź ź ź ą Ó Ś ą ą ć ć Ż ą Ż ą Ó ą ć ą Ż Ó ć ć ć Ę ą Ó Ł Ó Ź Ę ą ć ć ź Ó Ź Ó Ź ć ć ą Ż ą ź Ż Ź ć ć ć Ż Ę Ą ą ą Ź Ż Ź Ź ź ź Ź ć ą ą ź ź Ż Ż Ą ź Ę ą ć ą ą Ó Ź ć Ę ź ź
PLAN WYKŁADU. Ciepło właściwe Proces adiabatyczny Temperatura potencjalna II zasada termodynamiki. Procesy odwracalne i nieodwracalne 1 /35
 PLAN WYKŁADU Cieło właśiwe Proes adiabatyzny emeratura otenjalna II zasada termodynamiki Proesy odwraalne i nieodwraalne 1 /35 Podręzniki Salby, Chater 2, Chater 3 C&W, Chater 2 2 /35 CIEPŁO WŁAŚCIWE 3
PLAN WYKŁADU Cieło właśiwe Proes adiabatyzny emeratura otenjalna II zasada termodynamiki Proesy odwraalne i nieodwraalne 1 /35 Podręzniki Salby, Chater 2, Chater 3 C&W, Chater 2 2 /35 CIEPŁO WŁAŚCIWE 3
WYKŁAD 1. W przypadku zbiornika zawierającego gaz, stan układu jako całości jest opisany przez: temperaturę, ciśnienie i objętość.
 WYKŁAD 1 Pzedmiot badań temodynamiki. Jeśli chcemy opisać układ złożony z N cząstek, to możemy w amach mechaniki nieelatywistycznej dla każdej cząstki napisać ównanie uchu: 2 d i mi = Fi, z + Fi, j, i,
WYKŁAD 1 Pzedmiot badań temodynamiki. Jeśli chcemy opisać układ złożony z N cząstek, to możemy w amach mechaniki nieelatywistycznej dla każdej cząstki napisać ównanie uchu: 2 d i mi = Fi, z + Fi, j, i,
Laboratorium z Badania Maszyn
 Politechnika Wocłaska Instytut Techniki Cielnej i Mechaniki Płynó Zakła Mienicta i Eksloatacji Maszyn i Uzązeń Enegetycznych Laboatoiu z Baania Maszyn Ćiczenie n 5. Poia bilansoy ukłau ciełoniczego Poazący:
Politechnika Wocłaska Instytut Techniki Cielnej i Mechaniki Płynó Zakła Mienicta i Eksloatacji Maszyn i Uzązeń Enegetycznych Laboatoiu z Baania Maszyn Ćiczenie n 5. Poia bilansoy ukłau ciełoniczego Poazący:
MOBILNE ROBOTY KOŁOWE WYKŁAD 04 DYNAMIKA Maggie dr inż. Tomasz Buratowski. Wydział Inżynierii Mechanicznej i Robotyki Katedra Robotyki i Mechatroniki
 MOBILNE ROBOY KOŁOWE WYKŁD DYNMIK Maggie d inż. oasz Buatowski Wydział Inżynieii Mechanicznej i Robotyki Kateda Robotyki i Mechatoniki Modeowanie dynaiki dwu-kołowego obota obinego W odeowaniu dynaiki
MOBILNE ROBOY KOŁOWE WYKŁD DYNMIK Maggie d inż. oasz Buatowski Wydział Inżynieii Mechanicznej i Robotyki Kateda Robotyki i Mechatoniki Modeowanie dynaiki dwu-kołowego obota obinego W odeowaniu dynaiki
Fizyka 1- Mechanika. Wykład 5 2.XI Zygmunt Szefliński Środowiskowe Laboratorium Ciężkich Jonów
 izyka 1- Mechanika Wykład 5.XI.017 Zygunt Szefliński Śodowiskowe Laboatoiu Ciężkich Jonów szef@fuw.edu.pl http://www.fuw.edu.pl/~szef/ Ruch po okęgu - bezwładność Aby ciało pozostawało w uchu po okęgu
izyka 1- Mechanika Wykład 5.XI.017 Zygunt Szefliński Śodowiskowe Laboatoiu Ciężkich Jonów szef@fuw.edu.pl http://www.fuw.edu.pl/~szef/ Ruch po okęgu - bezwładność Aby ciało pozostawało w uchu po okęgu
Obieg pary wodnej w atmosferze nie powoduje wymiany masy, ale transfer ciepła z oceanu do atmosfery.
 Dla tatu i ciśniń otykanych w atofz, ciśnini ay nayconj zako zkacza watość 60 hpa, a tounk zizania 30 g kg -, czyli 0.03. Paa wona wytęuj w atofz tylko w ilościach ślaowych. Zgoni z ównani Clauiua-Clayona
Dla tatu i ciśniń otykanych w atofz, ciśnini ay nayconj zako zkacza watość 60 hpa, a tounk zizania 30 g kg -, czyli 0.03. Paa wona wytęuj w atofz tylko w ilościach ślaowych. Zgoni z ównani Clauiua-Clayona
Siła. Zasady dynamiki
 Siła. Zasady dynaiki Siła jest wielkością wektoową. Posiada okeśloną watość, kieunek i zwot. Jednostką siły jest niuton (N). 1N=1 k s 2 Pzedstawienie aficzne A Siła pzyłożona jest do ciała w punkcie A,
Siła. Zasady dynaiki Siła jest wielkością wektoową. Posiada okeśloną watość, kieunek i zwot. Jednostką siły jest niuton (N). 1N=1 k s 2 Pzedstawienie aficzne A Siła pzyłożona jest do ciała w punkcie A,
Sprężyny naciągowe z drutu o przekroju okrągłym
 Sprężyny naciągowe z o przekroju okrągłym Stal sprężynowa, zgodnie z normą PN-71/M80057 (EN 10270:1-SH oraz DIN 17223, C; nr mat. 1.1200) Stal sprężynowa nierdzewna, zgodnie z normą PN-71/M80057 (EN 10270:3-NS
Sprężyny naciągowe z o przekroju okrągłym Stal sprężynowa, zgodnie z normą PN-71/M80057 (EN 10270:1-SH oraz DIN 17223, C; nr mat. 1.1200) Stal sprężynowa nierdzewna, zgodnie z normą PN-71/M80057 (EN 10270:3-NS
ó ę ą ż ż ś ść Ó Ś ż Ó Ś ę ą żć ó ż Ó ż Ó ó ó ż Ó ż ó ą ą Ą ś ą ż ó ó ż ę Ć ż ż ż Ó ó ó ó ę ż ę Ó ż ę ż Ó Ę Ó ó Óś Ś ść ę ć Ś ę ąć śó ą ę ęż ó ó ż Ś ż
 Ó śó ą ę Ę śćś ść ę ą ś ó ą ó Ł Ó ż Ś ą ś Ó ą ć ó ż ść śó ą Óść ó ż ż ą Ś Ś ż Ó ą Ó ą Ć Ś ż ó ż ę ąś ó ć Ś Ó ó ś ś ś ó Ó ś Ź ż ą ó ą żą śó Ś Ó Ś ó Ś Ś ąś Ó ó ę ą ż ż ś ść Ó Ś ż Ó Ś ę ą żć ó ż Ó ż Ó ó ó
Ó śó ą ę Ę śćś ść ę ą ś ó ą ó Ł Ó ż Ś ą ś Ó ą ć ó ż ść śó ą Óść ó ż ż ą Ś Ś ż Ó ą Ó ą Ć Ś ż ó ż ę ąś ó ć Ś Ó ó ś ś ś ó Ó ś Ź ż ą ó ą żą śó Ś Ó Ś ó Ś Ś ąś Ó ó ę ą ż ż ś ść Ó Ś ż Ó Ś ę ą żć ó ż Ó ż Ó ó ó
V OGÓLNOPOLSKI KONKURS Z FIZYKI Fizyka się liczy I Etap ZADANIA 27 lutego 2013r.
 V OGÓLNOPOLSKI KONKURS Z FIZYKI Fizka się licz I Etap ZDNI 7 lutego 3r.. Dwa pociski wstrzeloo jeocześie w tę saą stroę z wóch puktów oległch o o. Pierwsz pocisk wstrzeloo z prękością o po kąte α. Z jaką
V OGÓLNOPOLSKI KONKURS Z FIZYKI Fizka się licz I Etap ZDNI 7 lutego 3r.. Dwa pociski wstrzeloo jeocześie w tę saą stroę z wóch puktów oległch o o. Pierwsz pocisk wstrzeloo z prękością o po kąte α. Z jaką
OŚRODKI WIELOSKŁADNIKOWE
 OŚOKI WIEOSKŁANIKOWE 9. KONENSACJA PAY WONEJ W WASTWIE zważmy warstwę materiału rwateg grubśi l, w której knensuje ara wna. ys. 9.1. Strefa knensaji Knensaja ta wuje: zmniejszenie ilśi ary wnej, zwiększenie
OŚOKI WIEOSKŁANIKOWE 9. KONENSACJA PAY WONEJ W WASTWIE zważmy warstwę materiału rwateg grubśi l, w której knensuje ara wna. ys. 9.1. Strefa knensaji Knensaja ta wuje: zmniejszenie ilśi ary wnej, zwiększenie
 Ł ś ą ś ż ą Ż ż ż ó ó ó ó ś ą ą Ś ą ą ó ą ś Ż ą ż ż ż ą ą Ś ą ą ą ż ś ą ó ą Ę ą ą ś ą ą ó ś ą ś Ą ż ż ą ą Ś ą Ż ą ż Ł ó ą ś ą ó ó Ę ą ą Ś ą ą ó ą ą ż ś ą ą Ę ż Ąą ą ś ą ą ą ą ś Ż ó ą ą ż ż ą ą Ś ą Ę ó
Ł ś ą ś ż ą Ż ż ż ó ó ó ó ś ą ą Ś ą ą ó ą ś Ż ą ż ż ż ą ą Ś ą ą ą ż ś ą ó ą Ę ą ą ś ą ą ó ś ą ś Ą ż ż ą ą Ś ą Ż ą ż Ł ó ą ś ą ó ó Ę ą ą Ś ą ą ó ą ą ż ś ą ą Ę ż Ąą ą ś ą ą ą ą ś Ż ó ą ą ż ż ą ą Ś ą Ę ó
9 6 6 0, 4 m 2 ), S t r o n a 1 z 1 1
 O p i s p r z e d m i o t u z a m ó w i e n i a - z a k r e s c z y n n o c i f U s ł u g i s p r z» t a n i a o b i e k t ó w G d y s k i e g o O r o d k a S p o r t u i R e ks r e a c j i I S t a d i
O p i s p r z e d m i o t u z a m ó w i e n i a - z a k r e s c z y n n o c i f U s ł u g i s p r z» t a n i a o b i e k t ó w G d y s k i e g o O r o d k a S p o r t u i R e ks r e a c j i I S t a d i
Pędu Momentu pędu Ładunku Liczby barionowej. Przedmiot: Fizyka. Przedmiot: Fizyka. Wydział EAIiE Kierunek: Elektrotechnika.
 ZASADY ZACHOWANIA W FIZYCE ZASADY ZACHOWANIA: Enegii Pęd Moent pęd Ładnk Liczby baionowej ZASADA ZACHOWANIA ENERGII W = E calk Paca siły zewnętznej Jeżeli W=0 to E calk =0 Ziana enegii całkowitej Ziana
ZASADY ZACHOWANIA W FIZYCE ZASADY ZACHOWANIA: Enegii Pęd Moent pęd Ładnk Liczby baionowej ZASADA ZACHOWANIA ENERGII W = E calk Paca siły zewnętznej Jeżeli W=0 to E calk =0 Ziana enegii całkowitej Ziana
PLAN WYKŁADU. Równowaga układu niejednorodnego Przemiany fazowe 1 /32
 PLAN WYKŁADU Rówowaa ukłau iejeoroeo Przemiay fazowe /32 Poręziki Salby, hater 4 &W, hater 4 R&Y, hater 2 2 /32 RÓWNOWAGA UKŁADU NIEJEDNORODNEGO 3 /32 Waruek rówowai la ukłau jeoroeo: rówowaa termiza (temeratura)
PLAN WYKŁADU Rówowaa ukłau iejeoroeo Przemiay fazowe /32 Poręziki Salby, hater 4 &W, hater 4 R&Y, hater 2 2 /32 RÓWNOWAGA UKŁADU NIEJEDNORODNEGO 3 /32 Waruek rówowai la ukłau jeoroeo: rówowaa termiza (temeratura)
 ć ć Ą Ą Ę ć ń ć Ę ć ć Ę Ń Ą ćń ć ć Ą ź ń ć ć ć ć ć Ę ń ńć ć ć Ń ń ć ć ć ć ć ć ć ń ć ź ń ć ć ć ć ć ć ć ć ń ń ń ń ć Ę Ń ÓŁ ź ń ń ź ń Ś ć Ą Ę Ą ń Ń ń Ń Ń ź Ę ć Ń Ą Ą ŚĆ ń ź ń Ą ć ń ć Ą ń Ę ń ń ć ń Ą ź ć Ę
ć ć Ą Ą Ę ć ń ć Ę ć ć Ę Ń Ą ćń ć ć Ą ź ń ć ć ć ć ć Ę ń ńć ć ć Ń ń ć ć ć ć ć ć ć ń ć ź ń ć ć ć ć ć ć ć ć ń ń ń ń ć Ę Ń ÓŁ ź ń ń ź ń Ś ć Ą Ę Ą ń Ń ń Ń Ń ź Ę ć Ń Ą Ą ŚĆ ń ź ń Ą ć ń ć Ą ń Ę ń ń ć ń Ą ź ć Ę
Rozważymy nieskończony strumień płatności i obliczymy jego wartość teraźniejszą.
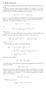 Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili to ówiy o encie
Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili to ówiy o encie
SK-7 Wprowadzenie do metody wektorów przestrzennych SK-8 Wektorowy model silnika indukcyjnego, klatkowego
 Ćwiczenia: SK-7 Wpowadzenie do metody wektoów pzetzennych SK-8 Wektoowy model ilnika indukcyjnego, klatkowego Wpowadzenie teoetyczne Wekto pzetzenny definicja i poawowe zależności. Dowolne wielkości kalane,
Ćwiczenia: SK-7 Wpowadzenie do metody wektoów pzetzennych SK-8 Wektoowy model ilnika indukcyjnego, klatkowego Wpowadzenie teoetyczne Wekto pzetzenny definicja i poawowe zależności. Dowolne wielkości kalane,
Rozważymy nieskończony strumień płatności i obliczymy jego wartość teraźniejszą.
 Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili, to ówiy o encie
Renty wieczyste Rozważyy nieskończony stuień płatności i obliczyy jego watość teaźniejszą Najpiew ozważy entę wieczystą polegającą na wypłacie jp co ok Jeśli piewsza płatność jest w chwili, to ówiy o encie
 2 7k 0 5k 2 0 1 5 S 1 0 0 P a s t w a c z ł o n k o w s k i e - Z a m ó w i e n i e p u b l i c z n e n a u s ł u g- i O g ł o s z e n i e o z a m ó w i e n i u - P r o c e d u r a o t w a r t a P o l
2 7k 0 5k 2 0 1 5 S 1 0 0 P a s t w a c z ł o n k o w s k i e - Z a m ó w i e n i e p u b l i c z n e n a u s ł u g- i O g ł o s z e n i e o z a m ó w i e n i u - P r o c e d u r a o t w a r t a P o l
FIZYKA 2. Janusz Andrzejewski
 FIZYKA 2 wykład 4 Janusz Andzejewski Pole magnetyczne Janusz Andzejewski 2 Pole gawitacyjne γ Pole elektyczne E Definicja wektoa B = γ E = Indukcja magnetyczna pola B: F B F G m 0 F E q 0 qv B = siła Loentza
FIZYKA 2 wykład 4 Janusz Andzejewski Pole magnetyczne Janusz Andzejewski 2 Pole gawitacyjne γ Pole elektyczne E Definicja wektoa B = γ E = Indukcja magnetyczna pola B: F B F G m 0 F E q 0 qv B = siła Loentza
Moment pędu w geometrii Schwarzshilda
 Moent pędu w geoetii Schwazshilda Zasada aksyalnego stazenia się : Doga po jakiej pousza się cząstka swobodna poiędzy dwoa zdazeniai w czasopzestzeni jest taka aby czas ziezony w układzie cząstki był aksyalny.
Moent pędu w geoetii Schwazshilda Zasada aksyalnego stazenia się : Doga po jakiej pousza się cząstka swobodna poiędzy dwoa zdazeniai w czasopzestzeni jest taka aby czas ziezony w układzie cząstki był aksyalny.
TERMODYNAMIKA PROCESOWA
 ERMODYNAMIKA PROCESOWA Wykład IV Charakterystyka ośrodków termodynamiznyh Prof. Antoni Kozioł, Wydział Chemizny Politehniki Wroławskiej Charakterystyka ośrodków termodynamiznyh właśiwośi termodynamizne
ERMODYNAMIKA PROCESOWA Wykład IV Charakterystyka ośrodków termodynamiznyh Prof. Antoni Kozioł, Wydział Chemizny Politehniki Wroławskiej Charakterystyka ośrodków termodynamiznyh właśiwośi termodynamizne
2 0 0 M P a o r a z = 0, 4.
 M O D E L O W A N I E I N Y N I E R S K I E n r 4 7, I S S N 1 8 9 6-7 7 1 X A N A L I Z A W Y T R Z Y M A O C I O W A S Y S T E M U U N I L O C K 2, 4 S T O S O W A N E G O W C H I R U R G I I S Z C Z
M O D E L O W A N I E I N Y N I E R S K I E n r 4 7, I S S N 1 8 9 6-7 7 1 X A N A L I Z A W Y T R Z Y M A O C I O W A S Y S T E M U U N I L O C K 2, 4 S T O S O W A N E G O W C H I R U R G I I S Z C Z
8. N i e u W y w a ć u r z ą d z e n i a, g d y j e s t w i l g o t n e l ug b d y j e s t n a r a W o n e n a b e z p o 6 r e d n i e d z i a ł a n i
 M G 4 0 1 v 4 G R I L L E L E K T R Y C Z N Y M G 4 0 1 I N S T R U K C J A M O N T A V U I B E Z P I E C Z N E G O U V Y T K O W A N I A S z a n o w n i P a s t w o, d z i ę k u j e m y z a z a k u p
M G 4 0 1 v 4 G R I L L E L E K T R Y C Z N Y M G 4 0 1 I N S T R U K C J A M O N T A V U I B E Z P I E C Z N E G O U V Y T K O W A N I A S z a n o w n i P a s t w o, d z i ę k u j e m y z a z a k u p
v! są zupełnie niezależne.
 Zasada ekwiartyji energii 7-7. Zasada ekwiartyji energii ównowaga termizna układów Zerowa zasada termodynamiki Jeżeli układy A i B oraz A i są arami w równowadze termiznej, to również układy B i są w równowadze
Zasada ekwiartyji energii 7-7. Zasada ekwiartyji energii ównowaga termizna układów Zerowa zasada termodynamiki Jeżeli układy A i B oraz A i są arami w równowadze termiznej, to również układy B i są w równowadze
Sprężyny naciskowe z drutu o przekroju okrągłym
 Sprężyny owe z o przekroju okrągłym Stal sprężynowa, zgodnie z normą PN-71/M80057 (EN 10270:1-SH oraz DIN 17223, C; nr mat. 1.1200) Stal sprężynowa nierdzewna, zgodnie z normą PN-71/M80057 (EN 10270:3-NS
Sprężyny owe z o przekroju okrągłym Stal sprężynowa, zgodnie z normą PN-71/M80057 (EN 10270:1-SH oraz DIN 17223, C; nr mat. 1.1200) Stal sprężynowa nierdzewna, zgodnie z normą PN-71/M80057 (EN 10270:3-NS
PRZENIKANIE PRZEZ ŚCIANKĘ PŁASKĄ JEDNOWARSTWOWĄ. 3. wnikanie ciepła od ścianki do ośrodka ogrzewanego
 PRZENIKANIE W pzemyśle uch ciepła zachodzi ównocześnie dwoma lub tzema sposobami, najczęściej odbywa się pzez pzewodzenie i konwekcję. Mechanizm tanspotu ciepła łączący wymienione sposoby uchu ciepła nazywa
PRZENIKANIE W pzemyśle uch ciepła zachodzi ównocześnie dwoma lub tzema sposobami, najczęściej odbywa się pzez pzewodzenie i konwekcję. Mechanizm tanspotu ciepła łączący wymienione sposoby uchu ciepła nazywa
 Í í Í Á ń ý ý Ż í í ď Í Ĺ ń Í ń Ę ń ý Ż Ż ź ń ń Ę ń ý ý í ŕ Ĺ Ĺ Í Á í Ż Í É Í Ü ö ä Ż Ż Ż Ę ń ć Ę Ż ń Ę Ż ć ń Ł Ą ń Ę í Ę Ż Ż ý Ż Ż Ą Í É đ í Ł Ę Ł ć ő ť Ę ń í ć Í Ę Ę Ł Ą Ł ć ď ć Ę Ę ń Ó Ü ü Ĺ ý Ę ä í
Í í Í Á ń ý ý Ż í í ď Í Ĺ ń Í ń Ę ń ý Ż Ż ź ń ń Ę ń ý ý í ŕ Ĺ Ĺ Í Á í Ż Í É Í Ü ö ä Ż Ż Ż Ę ń ć Ę Ż ń Ę Ż ć ń Ł Ą ń Ę í Ę Ż Ż ý Ż Ż Ą Í É đ í Ł Ę Ł ć ő ť Ę ń í ć Í Ę Ę Ł Ą Ł ć ď ć Ę Ę ń Ó Ü ü Ĺ ý Ę ä í
 Ł ą Ł Ł ż Ł Ł Ź ą ę ą ą ę ż ę Ę ą ą ź Ą ąą ś ę ą ą ę ś ę ś ść ę ż ę ś ę ś ś ę ę ą ę ś Ł ą Ł ę ę ś ę ę ś ę ś ą ą ę ś ę ś ę ę ś ę ę ś ę ą ę ś ę ą ę ę ś ż ę ś ę ę ą ęć Ś Ś ę ść ą ą Ó ę ś ę ę ęć ą ę ś ę ę
Ł ą Ł Ł ż Ł Ł Ź ą ę ą ą ę ż ę Ę ą ą ź Ą ąą ś ę ą ą ę ś ę ś ść ę ż ę ś ę ś ś ę ę ą ę ś Ł ą Ł ę ę ś ę ę ś ę ś ą ą ę ś ę ś ę ę ś ę ę ś ę ą ę ś ę ą ę ę ś ż ę ś ę ę ą ęć Ś Ś ę ść ą ą Ó ę ś ę ę ęć ą ę ś ę ę
PRZEMIANA ENERGII ELEKTRYCZNEJ W CIELE STAŁYM
 PRZEMIANA ENERGII ELEKTRYCZNE W CIELE STAŁYM Anaizowane są skutki pzepływu pądu pzemiennego o natężeniu I pzez pzewodnik okągły o pomieniu. Pzyęto wstępne założenia upaszcząace: - kształt pądu est sinusoidany,
PRZEMIANA ENERGII ELEKTRYCZNE W CIELE STAŁYM Anaizowane są skutki pzepływu pądu pzemiennego o natężeniu I pzez pzewodnik okągły o pomieniu. Pzyęto wstępne założenia upaszcząace: - kształt pądu est sinusoidany,
Kinematyka odwrotna:
 Kinematka owotna: ozwiązanie zaania kinematki owotnej owaza ię o wznazenia maiez zekztałenia H otai H E Wznazenie tej maiez olega na znalezieni jenego bąź wztkih ozwiązań ównania: T T n n q... q gzie q...
Kinematka owotna: ozwiązanie zaania kinematki owotnej owaza ię o wznazenia maiez zekztałenia H otai H E Wznazenie tej maiez olega na znalezieni jenego bąź wztkih ozwiązań ównania: T T n n q... q gzie q...
Hydrostatyka. Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
 Hydostatyka Pojekt współfinansowany pzez Unię Euopejską w aach Euopejskiego Funduszu Społecznego Hydostatyka Hydostatyka zajuje się opise echaniki płynów w stanie spoczynku. Płynai będziey nazywać tu zaówno
Hydostatyka Pojekt współfinansowany pzez Unię Euopejską w aach Euopejskiego Funduszu Społecznego Hydostatyka Hydostatyka zajuje się opise echaniki płynów w stanie spoczynku. Płynai będziey nazywać tu zaówno
Siły centralne, grawitacja (I)
 Pojęcia Gawitacja postawowe (I) i histoia Siły centalne, gawitacja (I) Enegia potencjalna E p B A E p ( ) E p A W ( ) F W ( A B) B A F Pawo gawitacji (siła gawitacji) - Newton 665 M N k F G G 6.6700 F,
Pojęcia Gawitacja postawowe (I) i histoia Siły centalne, gawitacja (I) Enegia potencjalna E p B A E p ( ) E p A W ( ) F W ( A B) B A F Pawo gawitacji (siła gawitacji) - Newton 665 M N k F G G 6.6700 F,
Katedra Silników Spalinowych i Pojazdów ATH ZAKŁAD TERMODYNAMIKI. Wyznaczanie stosunku c p /c v metodą Clementa-Desormesa.
 Katedra Siników Sainowyc i Pojazdów ATH ZAKŁAD TERMODYNAMIKI Wyznaczanie stosunku c /c v etodą Ceenta-Desoresa. Wrowadzenie teoretyczne Stosunek cieła właściwego rzy stały ciśnieniu do cieła właściwego
Katedra Siników Sainowyc i Pojazdów ATH ZAKŁAD TERMODYNAMIKI Wyznaczanie stosunku c /c v etodą Ceenta-Desoresa. Wrowadzenie teoretyczne Stosunek cieła właściwego rzy stały ciśnieniu do cieła właściwego
 Ą ń ń ć Ę Ę ć ć ń ń Ż ń ń Ą Ą ń Ż Ń Ż ć Ą ń ŚĆ ć Ę Ę Ą ń Ś ń ć Ę Ą ń Ę ń ń ń ń ć ń ń Ś Ź ń ć ć ń ć ń Ś Ż Ę Ń ń ń ń ń ń ć Ń Ę Ę Ę Ę Ę ńń ź ĄĘ Ę ź ń Ąń Ę Ę Ę Ź Ę Ę Ą Ś Ę Ę ć Ś Ą Ń ć ń ń ć Ś ć Ń Ó ń ń ć
Ą ń ń ć Ę Ę ć ć ń ń Ż ń ń Ą Ą ń Ż Ń Ż ć Ą ń ŚĆ ć Ę Ę Ą ń Ś ń ć Ę Ą ń Ę ń ń ń ń ć ń ń Ś Ź ń ć ć ń ć ń Ś Ż Ę Ń ń ń ń ń ń ć Ń Ę Ę Ę Ę Ę ńń ź ĄĘ Ę ź ń Ąń Ę Ę Ę Ź Ę Ę Ą Ś Ę Ę ć Ś Ą Ń ć ń ń ć Ś ć Ń Ó ń ń ć
Podstawy termodynamiki
 Podstawy termodynamiki Wykład Wroław University of ehnology 8-0-0 Podstawy termodynamiki 0 ermodynamika klasyzna Ois układu N ząstek na grunie mehaniki klasyznej wymaga rozwiązania N równań ruhu. d dt
Podstawy termodynamiki Wykład Wroław University of ehnology 8-0-0 Podstawy termodynamiki 0 ermodynamika klasyzna Ois układu N ząstek na grunie mehaniki klasyznej wymaga rozwiązania N równań ruhu. d dt
Rozwiązanie zadania 1.
 ozwiązaie zadaia. Zagadieie będziemy ozatywali w układzie, w któym stożek jest ieuhomy. a Poieważ zdezeie jest doskoale sężyste, a owiezhia stożka ieuhoma, atom gazu o zdezeiu będzie miał ędkość v skieowaą
ozwiązaie zadaia. Zagadieie będziemy ozatywali w układzie, w któym stożek jest ieuhomy. a Poieważ zdezeie jest doskoale sężyste, a owiezhia stożka ieuhoma, atom gazu o zdezeiu będzie miał ędkość v skieowaą
Nierelatywistyczne równania ruchu = zasady dynamiki Newtona
 DYNAMIKA: siły ównania uchu uch Nieelatywistyczne ównania uchu zasady dynaiki Newtona Pojęcia podstawowe dla punktu ateialnego Masa - iaa bezwładności Pęd iaa ilości uchu v v p v p v v v Siła wywołuje
DYNAMIKA: siły ównania uchu uch Nieelatywistyczne ównania uchu zasady dynaiki Newtona Pojęcia podstawowe dla punktu ateialnego Masa - iaa bezwładności Pęd iaa ilości uchu v v p v p v v v Siła wywołuje
1 3. N i e u W y w a ć w o d y d o d o g a s z a n i a g r i l l a! R e k o m e n d o w a n y j e s t p i a s e k Z a w s z e u p e w n i ć s i
 M G 4 2 7 v.1 2 0 1 6 G R I L L P R O S T O K Ą T N Y R U C H O M Y 5 2 x 6 0 c m z p o k r y w ą M G 4 2 7 I N S T R U K C J A M O N T A 7 U I B E Z P I E C Z N E G O U 7 Y T K O W A N I A S z a n o w
M G 4 2 7 v.1 2 0 1 6 G R I L L P R O S T O K Ą T N Y R U C H O M Y 5 2 x 6 0 c m z p o k r y w ą M G 4 2 7 I N S T R U K C J A M O N T A 7 U I B E Z P I E C Z N E G O U 7 Y T K O W A N I A S z a n o w
 ś Ę ś Ę ź ś Ó ś ś Ś ć ś ź Ź ść ć ś Ż ś ś Ż Ż Ż ś Ż ź ś ś ć Ż ś ś Ż ś ś ś ś Ó ś Ż ź ś ź ś ć ź ś ś ś ć ć Ń ś ś ś ź ś ś ś ś Ń ś Ż ś ś ś Ź Ó ć Ę ś ś ś Ń Ż Ś Ż ś ś ź ź ć Ó Ó ś ś ź Ś ć Ż Ń ś ź Ą ś ś Ż ć ć ść
ś Ę ś Ę ź ś Ó ś ś Ś ć ś ź Ź ść ć ś Ż ś ś Ż Ż Ż ś Ż ź ś ś ć Ż ś ś Ż ś ś ś ś Ó ś Ż ź ś ź ś ć ź ś ś ś ć ć Ń ś ś ś ź ś ś ś ś Ń ś Ż ś ś ś Ź Ó ć Ę ś ś ś Ń Ż Ś Ż ś ś ź ź ć Ó Ó ś ś ź Ś ć Ż Ń ś ź Ą ś ś Ż ć ć ść
Ę ę ę Łó-ź ----
 -Ę- - - - - - -ę- ę- - Łó-ź -ś - - ó -ą-ę- - -ł - -ą-ę - Ń - - -Ł - - - - - -óż - - - - - - - - - - -ż - - - - - -ś - - - - ł - - - -ą-ę- - - - - - - - - - -ę - - - - - - - - - - - - - ł - - Ł -ń ł - -
-Ę- - - - - - -ę- ę- - Łó-ź -ś - - ó -ą-ę- - -ł - -ą-ę - Ń - - -Ł - - - - - -óż - - - - - - - - - - -ż - - - - - -ś - - - - ł - - - -ą-ę- - - - - - - - - - -ę - - - - - - - - - - - - - ł - - Ł -ń ł - -
1.5. ZWIĄZKI KONSTYTUTYWNE STRONA FIZYCZNA
 .5. ZWIĄZKI KONSTYTUTYWN STRONA FIZYCZNA.5.. Wprowazenie Wyprowazone w rozziałach.3 (strona statyczna i.4 (strona geoetryczna równania (.3.36 i (.4. są niezależne o rozaju ciała aterialnego, które oże
.5. ZWIĄZKI KONSTYTUTYWN STRONA FIZYCZNA.5.. Wprowazenie Wyprowazone w rozziałach.3 (strona statyczna i.4 (strona geoetryczna równania (.3.36 i (.4. są niezależne o rozaju ciała aterialnego, które oże
I 3 + d l a : B E, C H, C Y, C Z, ES, F R, G B, G R, I E, I T, L T, L U V, P T, S K, S I
 M G 6 6 5 v 1. 2 0 1 5 G R I L L G A Z O W Y T R Ó J P A L N I K O W Y M G 6 6 5 I N S T R U K C J A U 7 Y T K O W A N I A I B E Z P I E C Z E Ń S T W A S z a n o w n i P a s t w o, D z i ę k u j e m y
M G 6 6 5 v 1. 2 0 1 5 G R I L L G A Z O W Y T R Ó J P A L N I K O W Y M G 6 6 5 I N S T R U K C J A U 7 Y T K O W A N I A I B E Z P I E C Z E Ń S T W A S z a n o w n i P a s t w o, D z i ę k u j e m y
Rozdział 1. Nazwa i adres Zamawiającego Gdyńskie Centrum Sportu jednostka budżetowa Rozdział 2. Informacja o trybie i stosowaniu przepisów
 Z n a k s p r a w y G C S D Z P I 2 7 1 0 4 52 0 1 5 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A W y k o n a n i e p o m i a r ó w i n s t a l a c j i e l e k t r y c
Z n a k s p r a w y G C S D Z P I 2 7 1 0 4 52 0 1 5 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A W y k o n a n i e p o m i a r ó w i n s t a l a c j i e l e k t r y c
 Ś Ę Ś Ą Ł Ę Ę Ę Ą ć Ę Ę ź ź Ń Ń Ę Ń Ń ź ź Ą ć Ą ć Ę Ą Ń Ń Ą Ę Ę ć Ą Ę ź Ą ć ć Ęć ć Ń ć ć ć ć ć Ś ć Ą ć ć ć Ń Ę Ś Ę Ę Ę ć Ę ć ć Ł ć Ń Ń Ęć Ę ź ć Ą Ę ź ć Ę Ę ź Ę Ą Ę Ą ć ź ź Ę ź Ę Ń ć ź ć ź Ę Ń Ę Ł Ę Ę ć
Ś Ę Ś Ą Ł Ę Ę Ę Ą ć Ę Ę ź ź Ń Ń Ę Ń Ń ź ź Ą ć Ą ć Ę Ą Ń Ń Ą Ę Ę ć Ą Ę ź Ą ć ć Ęć ć Ń ć ć ć ć ć Ś ć Ą ć ć ć Ń Ę Ś Ę Ę Ę ć Ę ć ć Ł ć Ń Ń Ęć Ę ź ć Ą Ę ź ć Ę Ę ź Ę Ą Ę Ą ć ź ź Ę ź Ę Ń ć ź ć ź Ę Ń Ę Ł Ę Ę ć
Siła tarcia. Tarcie jest zawsze przeciwnie skierowane do kierunku ruchu (do prędkości). R. D. Knight, Physics for scientists and engineers
 Siła tacia Tacie jest zawsze pzeciwnie skieowane do kieunku uchu (do pędkości). P. G. Hewitt, Fizyka wokół nas, PWN R. D. Knight, Physics fo scientists and enginees Symulacja molekulanego modelu tacia
Siła tacia Tacie jest zawsze pzeciwnie skieowane do kieunku uchu (do pędkości). P. G. Hewitt, Fizyka wokół nas, PWN R. D. Knight, Physics fo scientists and enginees Symulacja molekulanego modelu tacia
SPECYFIKACJA ISTOTNYCH WARUNKÓW ZAMÓWIENIA
 Z n a k s p r a w y G C S D Z P I 2 7 1 0 2 02 0 1 5 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A U s ł u g a d r u k o w a n i a d l a p o t r z e b G d y s k i e g o
Z n a k s p r a w y G C S D Z P I 2 7 1 0 2 02 0 1 5 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A U s ł u g a d r u k o w a n i a d l a p o t r z e b G d y s k i e g o
Novosibirsk, Russia, September 2002
 Noobk, ua, Septebe 00 W-5 (Jaoewc) 4 lajdów Dyaka były tywej Cało tywe jego uch uch potępowy cała tywego uch obotowy cała tywego wględe tałej o obotu. oet bewładośc Dyaka cała tywego uch łożoy cała tywego
Noobk, ua, Septebe 00 W-5 (Jaoewc) 4 lajdów Dyaka były tywej Cało tywe jego uch uch potępowy cała tywego uch obotowy cała tywego wględe tałej o obotu. oet bewładośc Dyaka cała tywego uch łożoy cała tywego
 Ó Ł ć ź Ą ź Ń Ł ź Ę Ł Ń ż ż ż Ź Ł ć ć Ą ź Ę ż Ć ć Ł ż ć ć ć ż ć ć ż ć ć ż Ę Ź Ę ć Ś Ę ć ź ż ź ż Ę ż Ł ż ż ż ż ź Ń ć ż ż Ó Ś Ś ż Ą Ś Ą Ź ź ż ż Ę Ź Ź ż ź ż Ź Ź ć ć ć ź ć ż ż Ź żć ć ć Ź ż ż ć ć ż ć ż ż ż
Ó Ł ć ź Ą ź Ń Ł ź Ę Ł Ń ż ż ż Ź Ł ć ć Ą ź Ę ż Ć ć Ł ż ć ć ć ż ć ć ż ć ć ż Ę Ź Ę ć Ś Ę ć ź ż ź ż Ę ż Ł ż ż ż ż ź Ń ć ż ż Ó Ś Ś ż Ą Ś Ą Ź ź ż ż Ę Ź Ź ż ź ż Ź Ź ć ć ć ź ć ż ż Ź żć ć ć Ź ż ż ć ć ż ć ż ż ż
PRZYCZYNY I SKUTKI ZMIENNOŚCI PARAMETRÓW MASZYN INDUKCYJNYCH
 LV SESJA STUENCKICH KÓŁ NAUKOWYCH PRZYCZYNY I SKUTKI ZMIENNOŚCI PARAMETRÓW MASZYN INUKCYJNYCH Wykonali: Michał Góki, V ok Elektotechnika Maciej Boba, V ok Elektotechnika Oiekun naukowy efeatu: d hab. inż.
LV SESJA STUENCKICH KÓŁ NAUKOWYCH PRZYCZYNY I SKUTKI ZMIENNOŚCI PARAMETRÓW MASZYN INUKCYJNYCH Wykonali: Michał Góki, V ok Elektotechnika Maciej Boba, V ok Elektotechnika Oiekun naukowy efeatu: d hab. inż.
 Ó Ć Ó Ż Ó Ó Ó Ó Ż Ó Ę Ę Ę Ó Ź Ź Ę Ź Ź Ó Ź Ż Ó Ó Ę Ó Ń Ą Ó Ą Ź Ź Ó Ę Ź Ó Ż Ń Ź Ż Ż Ź Ę Ż Ł Ó Ź Ó Ń Ż Ę Ó Ź Ó Ż Ó Ć Ę Ó Ó Ó Ć Ż Ę Ę Ó ÓĘ Ż Ź Ż Ę Ó Ź Ź Ą Ó Ę Ź Ó Ź Ł Ń Ę Ę Ń Ó Ó Ę Ó Ó Ź Ż Ó Ó Ź Ź Ó Ó Ż Ó
Ó Ć Ó Ż Ó Ó Ó Ó Ż Ó Ę Ę Ę Ó Ź Ź Ę Ź Ź Ó Ź Ż Ó Ó Ę Ó Ń Ą Ó Ą Ź Ź Ó Ę Ź Ó Ż Ń Ź Ż Ż Ź Ę Ż Ł Ó Ź Ó Ń Ż Ę Ó Ź Ó Ż Ó Ć Ę Ó Ó Ó Ć Ż Ę Ę Ó ÓĘ Ż Ź Ż Ę Ó Ź Ź Ą Ó Ę Ź Ó Ź Ł Ń Ę Ę Ń Ó Ó Ę Ó Ó Ź Ż Ó Ó Ź Ź Ó Ó Ż Ó
 Ę Ą Ę Ł Ł Ę ż Ł ż Ą ż ż ż ć ż ć Ł ż Ę Ą Ę Ł ż Ó ć ŚĆ Ś Ś Ń ż ż Ż Ć Ń Ę Ę ÓĘ ć ż ż Ó Ę Ó ć ć ż ż ż ż ż Ą ć Ł ż Ó ć ć Ł Ś ć Ż Ź Ś ć ć ż Ę ż ć ć ż ć Ą ż Ś Ł Ł ż ć ż ć Ą ż ć Ś ż ż ż ć ć ć ć Ć ż ć ż ć ż ż ż
Ę Ą Ę Ł Ł Ę ż Ł ż Ą ż ż ż ć ż ć Ł ż Ę Ą Ę Ł ż Ó ć ŚĆ Ś Ś Ń ż ż Ż Ć Ń Ę Ę ÓĘ ć ż ż Ó Ę Ó ć ć ż ż ż ż ż Ą ć Ł ż Ó ć ć Ł Ś ć Ż Ź Ś ć ć ż Ę ż ć ć ż ć Ą ż Ś Ł Ł ż ć ż ć Ą ż ć Ś ż ż ż ć ć ć ć Ć ż ć ż ć ż ż ż
 Ż Ź Ą Ó Ś Ó Ś Ó Ś Ż Ó Ś Ó ć Ź ć ć ń ć ć Ż Ż ĄĄ ć Ź ć Ó ć ń ń ń ń ń Ś ń Ź Ś ń ń Ó Ó ć Ó Ź ć Ż ć Ó Ż Ó Ż Ó ć Ź Ś Ś Ą Ć ń ć Ż ń Ó ć Ś Ś Ć Ś Ź ć ń ć ń Ż ń Ś Ż ń ń Ó Ó Ś Ś Ąń ń ń Ż Ż Ś ń Ą Ą Ś ć ń Ś Ó ć Ó Ż
Ż Ź Ą Ó Ś Ó Ś Ó Ś Ż Ó Ś Ó ć Ź ć ć ń ć ć Ż Ż ĄĄ ć Ź ć Ó ć ń ń ń ń ń Ś ń Ź Ś ń ń Ó Ó ć Ó Ź ć Ż ć Ó Ż Ó Ż Ó ć Ź Ś Ś Ą Ć ń ć Ż ń Ó ć Ś Ś Ć Ś Ź ć ń ć ń Ż ń Ś Ż ń ń Ó Ó Ś Ś Ąń ń ń Ż Ż Ś ń Ą Ą Ś ć ń Ś Ó ć Ó Ż
Opis i zakres czynności sprzątania obiektów Gdyńskiego Centrum Sportu
 O p i s i z a k r e s c z y n n o c is p r z» t a n i a o b i e k t ó w G d y s k i e g o C e n t r u m S p o r t u I S t a d i o n p i ł k a r s k i w G d y n i I A S p r z» t a n i e p r z e d m e c
O p i s i z a k r e s c z y n n o c is p r z» t a n i a o b i e k t ó w G d y s k i e g o C e n t r u m S p o r t u I S t a d i o n p i ł k a r s k i w G d y n i I A S p r z» t a n i e p r z e d m e c
Obiegi teoretyczne silników spalinowych
 Obiegi eeyzne ilniów alinwyh /9 8. OBIEGI EOREYCZNE SINIKÓW SPAINOWYCH Obiegi eeyzne łaająe ię z zemian gazów nałyh, ą wane w ehnie ja wzwe la zezywiyh zebiegów ieln-enegeyznyh. Objaśniają eeyznie zawany
Obiegi eeyzne ilniów alinwyh /9 8. OBIEGI EOREYCZNE SINIKÓW SPAINOWYCH Obiegi eeyzne łaająe ię z zemian gazów nałyh, ą wane w ehnie ja wzwe la zezywiyh zebiegów ieln-enegeyznyh. Objaśniają eeyznie zawany
 Ł Ą ż ż Ę ż Ó Ł ź ż ż Ś ż Ę Ę Ś Ą ć ż Ź Ś Ę Ś ĄÓ Ę Ź ż Ń ć ć ć ć ż ć ć Ę Ś ż ż ć ć ć Ę ć ż Ć Ś ć ć Ś ć ć ż ż ż Ź Ś ż ć ć ć ć ć ć Ś ć Ę ż Ę ć Ó ć ć ć ć Ę ć ć ć Ę Ś ż ć Ę Ź ć Ę Ć Ź ż ż Ś Ę ź ć Ź ż ć Ą ć
Ł Ą ż ż Ę ż Ó Ł ź ż ż Ś ż Ę Ę Ś Ą ć ż Ź Ś Ę Ś ĄÓ Ę Ź ż Ń ć ć ć ć ż ć ć Ę Ś ż ż ć ć ć Ę ć ż Ć Ś ć ć Ś ć ć ż ż ż Ź Ś ż ć ć ć ć ć ć Ś ć Ę ż Ę ć Ó ć ć ć ć Ę ć ć ć Ę Ś ż ć Ę Ź ć Ę Ć Ź ż ż Ś Ę ź ć Ź ż ć Ą ć
 Ę Ę Ę Ó Ę Ę Ó Ź ć Ł Ś Ó Ó Ł Ł Ż ć ć Ż Ą Ż ć Ę Ę ź ć ź Ą Ę Ż ć Ł Ę ć Ż Ę Ę ć ć Ż Ż Ę Ż Ż ć Ó Ę Ę ć Ę ć Ę Ę Ż Ż Ż Ż ź Ż Ę Ę ź Ę ź Ę Ż ć ć Ą Ę Ę ć Ę ć ć Ź Ą Ę ć Ę Ą Ę Ę Ę ć ć ć ć Ć Ą Ą ć Ę ć Ż ć Ę ć ć ć Ą
Ę Ę Ę Ó Ę Ę Ó Ź ć Ł Ś Ó Ó Ł Ł Ż ć ć Ż Ą Ż ć Ę Ę ź ć ź Ą Ę Ż ć Ł Ę ć Ż Ę Ę ć ć Ż Ż Ę Ż Ż ć Ó Ę Ę ć Ę ć Ę Ę Ż Ż Ż Ż ź Ż Ę Ę ź Ę ź Ę Ż ć ć Ą Ę Ę ć Ę ć ć Ź Ą Ę ć Ę Ą Ę Ę Ę ć ć ć ć Ć Ą Ą ć Ę ć Ż ć Ę ć ć ć Ą
 Ę Ł ć Ą ż Ł Ł Ą Ó ż Ł Ś Ę Ś Ó Ł Ń Ą Ą Ł Ą ĄĄ ż ć Ś Ź ć ć Ł ć ć ć Ś Ó Ś Ś ć ć ć ć Ó ć ć ć Ś ż Ł Ą ż Ś ż Ł ć ć Ó ć ć Ą ć Ś ć ż ć ć Ś ć Ł Ń ć ć Ę ć ć ć Ó ć ć ć ć ć ć ź ć ć Ó ć ć ć ć ć ż ć ć ć ć Ł ć ć ć ć
Ę Ł ć Ą ż Ł Ł Ą Ó ż Ł Ś Ę Ś Ó Ł Ń Ą Ą Ł Ą ĄĄ ż ć Ś Ź ć ć Ł ć ć ć Ś Ó Ś Ś ć ć ć ć Ó ć ć ć Ś ż Ł Ą ż Ś ż Ł ć ć Ó ć ć Ą ć Ś ć ż ć ć Ś ć Ł Ń ć ć Ę ć ć ć Ó ć ć ć ć ć ć ź ć ć Ó ć ć ć ć ć ż ć ć ć ć Ł ć ć ć ć
 Ż ź ź ź ź ź ć ć Ą Ą ć Ą ź ź ć Ż Ś ź ć ć Ę ć ź ź ć ź Ą ĄĄ Ń Ą Ń ć ć ć ć Ę ć Ń ć ć ć ć Ą ć ć ć ć ć Ń Ń ć ć ź ź ć Ę Ę ć Ą ć ć ć ć ć Ń Ę ć ć ć ć ć ć ć ć ć ź ć ź Ą ć ć ć Ń ć ć ć ć ź ć ć ć Ń Ń ć ź ź ć ź ź ć
Ż ź ź ź ź ź ć ć Ą Ą ć Ą ź ź ć Ż Ś ź ć ć Ę ć ź ź ć ź Ą ĄĄ Ń Ą Ń ć ć ć ć Ę ć Ń ć ć ć ć Ą ć ć ć ć ć Ń Ń ć ć ź ź ć Ę Ę ć Ą ć ć ć ć ć Ń Ę ć ć ć ć ć ć ć ć ć ź ć ź Ą ć ć ć Ń ć ć ć ć ź ć ć ć Ń Ń ć ź ź ć ź ź ć
 Ł Ą Ś Ą Ą ź ć ź Ł Ą ć ć ć ć ź Ś ć ć ć Ą Ł ć ź ć ć ć ć Ł ć ć ć ć ć Ł Ą ć Ś Ś Ż ć ź Ą ź ź ź ć ź ć ć ć ć ź ź ć ź ź ź Ś ź ź ć ć ć ć Ś ć ź ź ć ć Ą ź ź ź ź ź ć ć ć ć Ś ć ć ć Ś ć Ż Ł Ś Ł Ł Ł Ł Ż Ł Ś Ś ź ć Ą
Ł Ą Ś Ą Ą ź ć ź Ł Ą ć ć ć ć ź Ś ć ć ć Ą Ł ć ź ć ć ć ć Ł ć ć ć ć ć Ł Ą ć Ś Ś Ż ć ź Ą ź ź ź ć ź ć ć ć ć ź ź ć ź ź ź Ś ź ź ć ć ć ć Ś ć ź ź ć ć Ą ź ź ź ź ź ć ć ć ć Ś ć ć ć Ś ć Ż Ł Ś Ł Ł Ł Ł Ż Ł Ś Ś ź ć Ą
 ż ż ć ż Ż ż ż ć Ł ń ń ź ć ń Ś ż Ł ć ż Ź ż ń ż Ż Ś ć ź ż ć Ś ń ń ź ż ź ń Ś ń Ś ż ń ń ż ć ż ż Ą ć ń ń ń ć ż ć Ś ż Ć ć ż Ś Ś ć Ż ż Ś ć Ż Ż Ż Ą ń ń ć ń Ż ć ń ż Ż ń ż Ś ń Ś Ś ć Ż Ż Ć Ó Ż Ść ż Ż ż ż ń Ż Ż ć
ż ż ć ż Ż ż ż ć Ł ń ń ź ć ń Ś ż Ł ć ż Ź ż ń ż Ż Ś ć ź ż ć Ś ń ń ź ż ź ń Ś ń Ś ż ń ń ż ć ż ż Ą ć ń ń ń ć ż ć Ś ż Ć ć ż Ś Ś ć Ż ż Ś ć Ż Ż Ż Ą ń ń ć ń Ż ć ń ż Ż ń ż Ś ń Ś Ś ć Ż Ż Ć Ó Ż Ść ż Ż ż ż ń Ż Ż ć
 ń ń ź ź ć ń ń Ą Ź ń Ą ĄĄ Ą ń ź Ł Ł ń ć Ó Ą Ą ń ń ć ń ć ź ć ć Ó ć Ó ć Ś ć Ó ń ć ć ć ź ć Ą Ó Ź Ź Ź Ą ź Ó Ą ń ń Ź Ó Ź Ń ć Ń ć ź ń ń ń ń ń ń Ń ń Ź ń Ź Ź Ź ń ń ń Ą Ź Ó ĄĄ ń Ą ń ń Ó Ń Ó Ó ń Ą Ó ź ń ź Ą Ó Ą ź
ń ń ź ź ć ń ń Ą Ź ń Ą ĄĄ Ą ń ź Ł Ł ń ć Ó Ą Ą ń ń ć ń ć ź ć ć Ó ć Ó ć Ś ć Ó ń ć ć ć ź ć Ą Ó Ź Ź Ź Ą ź Ó Ą ń ń Ź Ó Ź Ń ć Ń ć ź ń ń ń ń ń ń Ń ń Ź ń Ź Ź Ź ń ń ń Ą Ź Ó ĄĄ ń Ą ń ń Ó Ń Ó Ó ń Ą Ó ź ń ź Ą Ó Ą ź
 Ą Ą Ś Ż Ą ć Ź ć Ó Ś Ż Ź Ó ć Ś Ż ć Ś Ź Ó ć Ż Ż Ź Ż Ó Ź Ó Ż Ż Ż Ż Ż Ś Ź Ś ć ć ć Ź ć ć Ó Ó Ó Ś Ą ć ć Ź Ż Ż Ż Ż ź Ż ź Ó Ś Ą Ź Ż Ż ć Ź Ó Ż Ó Ś Ą Ś Ś Ź Ż Ś Ż Ż Ź Ó ć Ś Ś Ść Ś Ż Ź Ó Ś Ó Ź Ó Ż Ź Ó Ś Ś Ż Ź Ż Ś
Ą Ą Ś Ż Ą ć Ź ć Ó Ś Ż Ź Ó ć Ś Ż ć Ś Ź Ó ć Ż Ż Ź Ż Ó Ź Ó Ż Ż Ż Ż Ż Ś Ź Ś ć ć ć Ź ć ć Ó Ó Ó Ś Ą ć ć Ź Ż Ż Ż Ż ź Ż ź Ó Ś Ą Ź Ż Ż ć Ź Ó Ż Ó Ś Ą Ś Ś Ź Ż Ś Ż Ż Ź Ó ć Ś Ś Ść Ś Ż Ź Ó Ś Ó Ź Ó Ż Ź Ó Ś Ś Ż Ź Ż Ś
 Ą Ł Ą Ą ś ś ż Ż ś ś ś ść ś ś Ą ś Ż ś ć ż ś ś ż ś ż Ć Ł Ż ż Ź ć ĄĄ Ż Ą Ż Ą Ź Ż Ł Ł Ę ś ś ś ż Ą ś Ą ś Ą Ż Ą Ż Ą Ć Ż Ż ś Ż Ą Ć Ł Ł Ę ś ż Ż ć ś ś ś ś Ż Ć ż ż ś ś ż ś ś Ż Ż ś ś ś ś ś Ż ż Ż ś ś Ż Ę ż ś ż Ź Ę
Ą Ł Ą Ą ś ś ż Ż ś ś ś ść ś ś Ą ś Ż ś ć ż ś ś ż ś ż Ć Ł Ż ż Ź ć ĄĄ Ż Ą Ż Ą Ź Ż Ł Ł Ę ś ś ś ż Ą ś Ą ś Ą Ż Ą Ż Ą Ć Ż Ż ś Ż Ą Ć Ł Ł Ę ś ż Ż ć ś ś ś ś Ż Ć ż ż ś ś ż ś ś Ż Ż ś ś ś ś ś Ż ż Ż ś ś Ż Ę ż ś ż Ź Ę
 Ę Ę Ę Ę Ę Ź Ą Ę Ą Ę Ą Ą Ę ć Ś ć Ę Ą ź Ą Ź ć Ę Ź Ę ć Ą Ę Ś Ę Ę Ź Ą Ę ć ź Ą Ź Ę ź Ę Ą Ś Ł Ą Ź Ę Ę Ę Ę ć Ę Ą Ę Ę Ą Ś Ą Ę ź ć Ę Ę Ę ź Ź ź Ą Ź Ę Ź ź Ź ć ć Ę Ę Ę Ą Ą Ą Ę ć Ę Ę ć Ę Ę Ą Ę Ą Ę Ę Ę Ą Ę Ś ć Ą ć ć
Ę Ę Ę Ę Ę Ź Ą Ę Ą Ę Ą Ą Ę ć Ś ć Ę Ą ź Ą Ź ć Ę Ź Ę ć Ą Ę Ś Ę Ę Ź Ą Ę ć ź Ą Ź Ę ź Ę Ą Ś Ł Ą Ź Ę Ę Ę Ę ć Ę Ą Ę Ę Ą Ś Ą Ę ź ć Ę Ę Ę ź Ź ź Ą Ź Ę Ź ź Ź ć ć Ę Ę Ę Ą Ą Ą Ę ć Ę Ę ć Ę Ę Ą Ę Ą Ę Ę Ę Ą Ę Ś ć Ą ć ć
















