Katarzyna Jesionek Zastosowanie symulacji dynamiki cieczy oraz ośrodków sprężystych w symulatorach operacji chirurgicznych.
|
|
|
- Urszula Milewska
- 9 lat temu
- Przeglądów:
Transkrypt
1 Katarzyna Jesionek Zastosowanie symulacji dynamiki cieczy oraz ośrodków sprężystych w symulatorach operacji chirurgicznych. Jedną z metod symulacji dynamiki cieczy jest zastosowanie metody siatkowej Boltzmanna. Metoda ta opiera się na wykorzystaniu równania Boltzmanna. Możemy bowiem przejść z przestrzeni fazowej, w której znajdują się wszystkie cząstki (atomy) reprezentujące badany układ, do przestrzeni konfiguracyjnej położeń i pędów jednej cząstki. Wprowadza się w tym celu pojęcie funkcji rozkładu. Funkcja rozkładu jest zdefiniowana jako liczba cząsteczek w skończonym elemencie przestrzeni prędkości i położeń f(r, v) [1, 2, 3, 4]. Można pokazać, że z dokładnością drugiego rzędu równanie Boltzmanna można zdyskretyzować. W tym celu wprowadzane są dyskretne wektory prędkości i dyskretną funkcję rozkładu. Równanie to nazywane jest siatkowym równaniem Boltzmanna: Cała przestrzeń pokrywana jest jednorodną, kartezjańską siecią. Ogranicza się też dozwolone kierunki wektora prędkości. Co ciekawe ilość tych kierunków jest zwykle dosyć mała (od kilku do kilkunastu). Dla modelu 2D wymagane jest co najmniej 9 wektorów prędkości, a dla modelu 3D: 13. Siatka D2Q9 i dyskretyzacja funkcji rozkładu oraz prędkości pokazana jest na rys. 1 [1, 2, 3, 4]. 1
2 Rys. 1. Siatka D2Q9 i dyskretyzacja funkcji rozkładu oraz prędkości [3, 4]. Znajomość funkcji rozkładu w każdym punkcie badanego układu umożliwia wyznaczenie hydrodynamicznych wielkości makroskopowych takich, jak gęstość i prędkość. Wielkości opisujące hydrodynamikę badanego układu wyrazić można przez kolejne momenty funkcji rozkładu. Korzystając z jej dyskretnej postaci, wielkości makroskopowe takie jak gęstość oraz prędkość lokalną możemy wyznaczyć w następujący sposób: gdzie: f i jest dyskretną funkcją rozkładu, e i są dozwolonymi kierunkami wektora prędkości, a zakresy sumowania w powyższych wzorach zależą od ilości dozwolonych wektorów prędkości. Główny algorytm metody LBM można przedstawić w dwóch krokach: relaksacja i propagacja. W kroku relaksacji obliczane są funkcje f*: f eq jest funkcją równowagową. Krok ten przedstawiony jest na rys. 2. Na podstawie funkcji rozkładu oznaczonych na rysunku przez czarne strzałki i kropkę obliczane są funkcje f* oznaczone czerwonym kolorem. Jak widać w tym kroku nie są potrzebne informacje o stanie sąsiednich węzłów i ten krok obliczany jest lokalnie w każdym węźle [1, 2, 3, 4]. 2
3 Rys. 2. Krok relaksacji [1] W kroku propagacji natomiast obliczone poprzednio funkcje f* są przekazywane do odpowiednich sąsiadów. W tym kroku następuje jedynie komunikacja między węzłami i nie wykonywane są obliczenia. Rys. 3. Krok propagacji [1]. Główną zaletą LBM jest więc możliwość przydzielenia każdemu węzłowi osobnego wątku, w którym wykonywane są obliczenia i między którymi odbywa się komunikacja. Jest to możliwe dzięki zastosowaniu nowoczesnych kart graficznych, które posiadają kilka tysięcy rdzeni i technologii CUDA. Oprogramowanie Sailfish wykorzystuje tą technologię. Porównanie wyników z wartościami teoretycznymi i obliczonymi inną metodą pozwala walidować otrzymane wyniki i poprawność skalowania jednostek. Porównanie takie pokazane jest na rys. 4. Porównanie to przeprowadzono dla trójwymiarowego cylindra. Na rysunku pokazany jest profil prędkości w połowie wysokości cylindra. Symulacja napędzana była różnicą ciśnień o wartości 6.5 Pa. W obecnym semestrze trwały prace nad walidacją symulacji dla geometrii U-rurki. Symulacja napędzana była różnicą ciśnień o wartości 27 Pa. Wyniki porównywane są z wynikami uzyskanymi metodą FVM. 3
4 Rys. 4. Profil prędkości [m/s] w połowie wysokości cylindra wyniki symulacji (LBM) i teoretyczny rozkład prędkości Poiseulle a. 4
5 Rys. 5. Profil prędkości [m/s] w środkowej części u-rurki dla przepływu wywołanego różnicą ciśnień 27 Pa. Metoda LBM pozwala generować przepływy zależne od czasu. W tym przypadku skoncentrowałam się nad przepływem pulsacyjnym przez U-rurkę napędzanym okresową różnicą ciśnień o przebiegu sinusoidalnym o amplitudzie 27Pa dla różnych konfiguracji symulacji. Celem tych symulacji było znalezienie zakresu parametrów dla których wyniki będą poprawne i zgodne. Ponadto nowe warunki brzegowe, które zapewniłyby swobodny wypływ, zostały ostatecznie wprowadzone do programu Sailfish. Bibliografia: 5
6 [1] S. Succi, The Lattice Boltzmann Equation for Fluid Dynamics and Beyond (Numerical Mathematics and Scientific Computation) [2] M. C. Sukop, D. T. Thorne, Lattice Boltzmann modeling: an introduction for geoscientists and engineers [3] M. Matyka, Symulacje komputerowe cieczy LBM w CUDA [4] M. Matyka, Modelowanie numeryczne transportu płynów przez ośrodki porowate 6
Od wielkoskalowych obliczeń równoległych do innowacyjnej diagnostyki w kardiologii.
 Od wielkoskalowych obliczeń równoległych do innowacyjnej diagnostyki w kardiologii. Opiekun naukowy: dr hab. prof. UŚ Marcin Kostur Celem tych badań jest zastosowanie symulacji układu krwionośnego do diagnostyki
Od wielkoskalowych obliczeń równoległych do innowacyjnej diagnostyki w kardiologii. Opiekun naukowy: dr hab. prof. UŚ Marcin Kostur Celem tych badań jest zastosowanie symulacji układu krwionośnego do diagnostyki
Numeryczna symulacja rozpływu płynu w węźle
 231 Prace Instytutu Mechaniki Górotworu PAN Tom 7, nr 3-4, (2005), s. 231-236 Instytut Mechaniki Górotworu PAN Numeryczna symulacja rozpływu płynu w węźle JERZY CYGAN Instytut Mechaniki Górotworu PAN,
231 Prace Instytutu Mechaniki Górotworu PAN Tom 7, nr 3-4, (2005), s. 231-236 Instytut Mechaniki Górotworu PAN Numeryczna symulacja rozpływu płynu w węźle JERZY CYGAN Instytut Mechaniki Górotworu PAN,
Programowanie Równoległe wykład 13. Symulacje komputerowe cieczy LBM w CUDA. Maciej Matyka Instytut Fizyki Teoretycznej
 Programowanie Równoległe wykład 13 Symulacje komputerowe cieczy LBM w CUDA Maciej Matyka Instytut Fizyki Teoretycznej Transport cieczy i gazów W wielu dziedzinach trzeba rozwiązać zagadnienie transportu
Programowanie Równoległe wykład 13 Symulacje komputerowe cieczy LBM w CUDA Maciej Matyka Instytut Fizyki Teoretycznej Transport cieczy i gazów W wielu dziedzinach trzeba rozwiązać zagadnienie transportu
Wielkoskalowe obliczenia komputerowej dynamiki płynów na procesorach graficznych -- pakiet Sailfish
 Michał Januszewski Materialy do broszury końcowej TWING. Wielkoskalowe obliczenia komputerowej dynamiki płynów na procesorach graficznych -- pakiet Sailfish Od około 5 lat procesory graficzne (GPU) znajdują
Michał Januszewski Materialy do broszury końcowej TWING. Wielkoskalowe obliczenia komputerowej dynamiki płynów na procesorach graficznych -- pakiet Sailfish Od około 5 lat procesory graficzne (GPU) znajdują
METODA ELEMENTÓW SKOŃCZONYCH.
 METODA ELEMENTÓW SKOŃCZONYCH. W programie COMSOL multiphisics 3.4 Wykonali: Łatas Szymon Łakomy Piotr Wydzał, Kierunek, Specjalizacja, Semestr, Rok BMiZ, MiBM, TPM, VII, 2011 / 2012 Prowadzący: Dr hab.inż.
METODA ELEMENTÓW SKOŃCZONYCH. W programie COMSOL multiphisics 3.4 Wykonali: Łatas Szymon Łakomy Piotr Wydzał, Kierunek, Specjalizacja, Semestr, Rok BMiZ, MiBM, TPM, VII, 2011 / 2012 Prowadzący: Dr hab.inż.
Modelowanie i Animacja
 Maciej Matyka Uniwersytet Wrocławski Maciej Matyka Plan wykładu Dlaczego animujemy używając komputera? Dlaczego animujemy używając komputera? Wyciąg z minimum programowego fizyki w liceum... Kinematyka
Maciej Matyka Uniwersytet Wrocławski Maciej Matyka Plan wykładu Dlaczego animujemy używając komputera? Dlaczego animujemy używając komputera? Wyciąg z minimum programowego fizyki w liceum... Kinematyka
Modelowanie komputerowe dynamiki płynów Maciej Matyka Instytut Fizyki Teoretycznej
 Modelowanie komputerowe dynamiki płynów 2011-12-05 Maciej Matyka Instytut Fizyki Teoretycznej Hydrodynamika http://www.realflow.com/ Konkursy na wydziale fizyki Lata 1999-2011 Oprogramowanie popularyzujące
Modelowanie komputerowe dynamiki płynów 2011-12-05 Maciej Matyka Instytut Fizyki Teoretycznej Hydrodynamika http://www.realflow.com/ Konkursy na wydziale fizyki Lata 1999-2011 Oprogramowanie popularyzujące
17.1 Podstawy metod symulacji komputerowych dla klasycznych układów wielu cząstek
 Janusz Adamowski METODY OBLICZENIOWE FIZYKI 1 Rozdział 17 KLASYCZNA DYNAMIKA MOLEKULARNA 17.1 Podstawy metod symulacji komputerowych dla klasycznych układów wielu cząstek Rozważamy układ N punktowych cząstek
Janusz Adamowski METODY OBLICZENIOWE FIZYKI 1 Rozdział 17 KLASYCZNA DYNAMIKA MOLEKULARNA 17.1 Podstawy metod symulacji komputerowych dla klasycznych układów wielu cząstek Rozważamy układ N punktowych cząstek
OPIS PRZEDMIOTU/MODUŁU KSZTAŁCENIA (SYLABUS)
 Załącznik nr 2 do zarządzenia Nr 33/2012 z dnia 25 kwietnia 2012 r. OPIS PRZEDMIOTU/MODUŁU KSZTAŁCENIA (SYLABUS) 1. Nazwa przedmiotu/modułu w języku polskim Symulacje komputerowe dynamiki płynów 2. Nazwa
Załącznik nr 2 do zarządzenia Nr 33/2012 z dnia 25 kwietnia 2012 r. OPIS PRZEDMIOTU/MODUŁU KSZTAŁCENIA (SYLABUS) 1. Nazwa przedmiotu/modułu w języku polskim Symulacje komputerowe dynamiki płynów 2. Nazwa
Implementacja modelu FHP w technologii NVIDIA CUDA
 Uniwersytet Wrocławski Wydział Fizyki i Astronomii Instytut Fizyki Teoretycznej Sebastian Szkoda Implementacja modelu FHP w technologii NVIDIA CUDA Opiekun: dr hab. Zbigniew Koza, prof. UWr. 1 Model 1.1
Uniwersytet Wrocławski Wydział Fizyki i Astronomii Instytut Fizyki Teoretycznej Sebastian Szkoda Implementacja modelu FHP w technologii NVIDIA CUDA Opiekun: dr hab. Zbigniew Koza, prof. UWr. 1 Model 1.1
Metoda Elementów Skończonych. Projekt: COMSOL Multiphysics 3.4.
 Politechnika Poznańska Metoda Elementów Skończonych Projekt: COMSOL Multiphysics 3.4. Prowadzący: dr hab. Tomasz Stręk Wykonali: Widerowski Karol Wysocki Jacek Wydział: Budowa Maszyn i Zarządzania Kierunek:
Politechnika Poznańska Metoda Elementów Skończonych Projekt: COMSOL Multiphysics 3.4. Prowadzący: dr hab. Tomasz Stręk Wykonali: Widerowski Karol Wysocki Jacek Wydział: Budowa Maszyn i Zarządzania Kierunek:
Politechnika Poznańska
 Politechnika Poznańska Wydział Budowy Maszyn i Zarządzania Mechanika i Budowa Maszyn Projekt: Metoda elementów skończonych Prowadzący: dr hab. Tomasz STRĘK prof. nadzw. Autorzy: Krystian Machalski Andrzej
Politechnika Poznańska Wydział Budowy Maszyn i Zarządzania Mechanika i Budowa Maszyn Projekt: Metoda elementów skończonych Prowadzący: dr hab. Tomasz STRĘK prof. nadzw. Autorzy: Krystian Machalski Andrzej
Materiały do laboratorium Przygotowanie Nowego Wyrobu dotyczące metody elementów skończonych (MES) Opracowała: dr inŝ.
 Materiały do laboratorium Przygotowanie Nowego Wyrobu dotyczące metody elementów skończonych (MES) Opracowała: dr inŝ. Jolanta Zimmerman 1. Wprowadzenie do metody elementów skończonych Działanie rzeczywistych
Materiały do laboratorium Przygotowanie Nowego Wyrobu dotyczące metody elementów skończonych (MES) Opracowała: dr inŝ. Jolanta Zimmerman 1. Wprowadzenie do metody elementów skończonych Działanie rzeczywistych
Metoda elementów skończonych-projekt
 Metoda elementów skończonych-projekt Ziarniak Marcin Nawrocki Maciej Mrówczyński Jakub M6/MiBM 1. Analiza odkształcenia kierownicy pod wpływem obciążenia W pierwszym zadaniu przedmiotem naszych badań będzie
Metoda elementów skończonych-projekt Ziarniak Marcin Nawrocki Maciej Mrówczyński Jakub M6/MiBM 1. Analiza odkształcenia kierownicy pod wpływem obciążenia W pierwszym zadaniu przedmiotem naszych badań będzie
Studentom zostaną dostarczone wzory lub materiały opisujące. Zachęcamy do wykonania projektów programistycznych w postaci apletów.
 W niniejszym dokumencie znajdują się propozycje projektów na rok 2008. Tematy sformułowane są ogólnie, po wyborze tematu i skontaktowaniu z prowadzącym zostaną określone szczegółowe wymagania co do projektu.
W niniejszym dokumencie znajdują się propozycje projektów na rok 2008. Tematy sformułowane są ogólnie, po wyborze tematu i skontaktowaniu z prowadzącym zostaną określone szczegółowe wymagania co do projektu.
METODA ELEMENTÓW SKOŃOCZNYCH Projekt
 METODA ELEMENTÓW SKOŃOCZNYCH Projekt Wykonali: Maciej Sobkowiak Tomasz Pilarski Profil: Technologia przetwarzania materiałów Semestr 7, rok IV Prowadzący: Dr hab. Tomasz STRĘK 1. Analiza przepływu ciepła.
METODA ELEMENTÓW SKOŃOCZNYCH Projekt Wykonali: Maciej Sobkowiak Tomasz Pilarski Profil: Technologia przetwarzania materiałów Semestr 7, rok IV Prowadzący: Dr hab. Tomasz STRĘK 1. Analiza przepływu ciepła.
Ćwiczenie 2 Numeryczna symulacja swobodnego spadku ciała w ośrodku lepkim (Instrukcja obsługi interfejsu użytkownika)
 Ćwiczenie 2 Numeryczna symulacja swobodnego spadku ciała w ośrodku lepkim (Instrukcja obsługi interfejsu użytkownika) 1 1 Cel ćwiczenia Celem ćwiczenia jest rozwiązanie równań ruchu ciała (kuli) w ośrodku
Ćwiczenie 2 Numeryczna symulacja swobodnego spadku ciała w ośrodku lepkim (Instrukcja obsługi interfejsu użytkownika) 1 1 Cel ćwiczenia Celem ćwiczenia jest rozwiązanie równań ruchu ciała (kuli) w ośrodku
Modelowanie jako sposób opisu rzeczywistości. Katedra Mikroelektroniki i Technik Informatycznych Politechnika Łódzka
 Modelowanie jako sposób opisu rzeczywistości Katedra Mikroelektroniki i Technik Informatycznych Politechnika Łódzka 2015 Wprowadzenie: Modelowanie i symulacja PROBLEM: Podstawowy problem z opisem otaczającej
Modelowanie jako sposób opisu rzeczywistości Katedra Mikroelektroniki i Technik Informatycznych Politechnika Łódzka 2015 Wprowadzenie: Modelowanie i symulacja PROBLEM: Podstawowy problem z opisem otaczającej
Numeryczna symulacja opływu wokół płata o zmodyfikowanej krawędzi natarcia. Michał Durka
 Numeryczna symulacja opływu wokół płata o zmodyfikowanej krawędzi natarcia Michał Durka Politechnika Poznańska Inspiracja Inspiracją mojej pracy był artykuł w Świecie Nauki opisujący znakomite charakterystyki
Numeryczna symulacja opływu wokół płata o zmodyfikowanej krawędzi natarcia Michał Durka Politechnika Poznańska Inspiracja Inspiracją mojej pracy był artykuł w Świecie Nauki opisujący znakomite charakterystyki
WYKORZYSTANIE OBLICZEŃ CFD W ENERGETYCE...1
 ...1 WOJCIECH MOKROSZ JOANNA BIGDA MATEUSZ NIERODA Mokrosz Sp z o.o. Rudy Streszczenie: W referacie zaprezentowano możliwości wykorzystania narzędzi CAD/CAM w procesach powiększania skali oraz optymalizacji
...1 WOJCIECH MOKROSZ JOANNA BIGDA MATEUSZ NIERODA Mokrosz Sp z o.o. Rudy Streszczenie: W referacie zaprezentowano możliwości wykorzystania narzędzi CAD/CAM w procesach powiększania skali oraz optymalizacji
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: MODELOWANIE PROCESÓW ENERGETYCZNYCH Kierunek: ENERGETYKA Rodzaj przedmiotu: specjalności obieralny Rodzaj zajęć: wykład, laboratorium I KARTA PRZEDMIOTU CEL PRZEDMIOTU PRZEWODNIK PO PRZEDMIOCIE
Nazwa przedmiotu: MODELOWANIE PROCESÓW ENERGETYCZNYCH Kierunek: ENERGETYKA Rodzaj przedmiotu: specjalności obieralny Rodzaj zajęć: wykład, laboratorium I KARTA PRZEDMIOTU CEL PRZEDMIOTU PRZEWODNIK PO PRZEDMIOCIE
Podczas wykonywania analizy w programie COMSOL, wykorzystywane jest poniższe równanie: 1.2. Dane wejściowe.
 Politechnika Poznańska Wydział Budowy Maszyn i Zarządzania Mechanika i Budowa Maszyn Grupa M3 Metoda Elementów Skończonych Prowadzący: dr hab. Tomasz Stręk, prof. nadzw. Wykonali: Marcin Rybiński Grzegorz
Politechnika Poznańska Wydział Budowy Maszyn i Zarządzania Mechanika i Budowa Maszyn Grupa M3 Metoda Elementów Skończonych Prowadzący: dr hab. Tomasz Stręk, prof. nadzw. Wykonali: Marcin Rybiński Grzegorz
WYZNACZANIE PARAMETRÓW PRZEPŁYWU CIECZY W PŁASZCZU CHŁODZĄCYM ZBIORNIKA CIŚNIENIOWEGO
 Inżynieria Rolnicza 2(90)/2007 WYZNACZANIE PARAMETRÓW PRZEPŁYWU CIECZY W PŁASZCZU CHŁODZĄCYM ZBIORNIKA CIŚNIENIOWEGO Jerzy Domański Katedra Mechaniki i Podstaw Konstrukcji Maszyn, Uniwersytet Warmińsko-Mazurski
Inżynieria Rolnicza 2(90)/2007 WYZNACZANIE PARAMETRÓW PRZEPŁYWU CIECZY W PŁASZCZU CHŁODZĄCYM ZBIORNIKA CIŚNIENIOWEGO Jerzy Domański Katedra Mechaniki i Podstaw Konstrukcji Maszyn, Uniwersytet Warmińsko-Mazurski
Mgr inż. Wojciech Chajec Pracownia Kompozytów, CNT Mgr inż. Adam Dziubiński Pracownia Aerodynamiki Numerycznej i Mechaniki Lotu, CNT SMIL
 Mgr inż. Wojciech Chajec Pracownia Kompozytów, CNT Mgr inż. Adam Dziubiński Pracownia Aerodynamiki Numerycznej i Mechaniki Lotu, CNT SMIL We wstępnej analizie przyjęto następujące założenia: Dwuwymiarowość
Mgr inż. Wojciech Chajec Pracownia Kompozytów, CNT Mgr inż. Adam Dziubiński Pracownia Aerodynamiki Numerycznej i Mechaniki Lotu, CNT SMIL We wstępnej analizie przyjęto następujące założenia: Dwuwymiarowość
MODELOWANIE NUMERYCZNE POLA PRZEPŁYWU WOKÓŁ BUDYNKÓW
 1. WSTĘP MODELOWANIE NUMERYCZNE POLA PRZEPŁYWU WOKÓŁ BUDYNKÓW mgr inż. Michał FOLUSIAK Instytut Lotnictwa W artykule przedstawiono wyniki dwu- i trójwymiarowych symulacji numerycznych opływu budynków wykonanych
1. WSTĘP MODELOWANIE NUMERYCZNE POLA PRZEPŁYWU WOKÓŁ BUDYNKÓW mgr inż. Michał FOLUSIAK Instytut Lotnictwa W artykule przedstawiono wyniki dwu- i trójwymiarowych symulacji numerycznych opływu budynków wykonanych
Numeryczne modelowanie mikrozwężkowego czujnika przepływu
 Numeryczne modelowanie mikrozwężkowego czujnika przepływu Antoni Gondek Tadeusz Filiciak Przedstawiono wybrane wyniki modelowania numerycznego podwójnej mikrozwężki stosowanej jako czujnik przepływu, dla
Numeryczne modelowanie mikrozwężkowego czujnika przepływu Antoni Gondek Tadeusz Filiciak Przedstawiono wybrane wyniki modelowania numerycznego podwójnej mikrozwężki stosowanej jako czujnik przepływu, dla
Wstęp do sieci neuronowych, wykład 12 Łańcuchy Markowa
 Wstęp do sieci neuronowych, wykład 12 Łańcuchy Markowa M. Czoków, J. Piersa 2012-01-10 1 Łańcucha Markowa 2 Istnienie Szukanie stanu stacjonarnego 3 1 Łańcucha Markowa 2 Istnienie Szukanie stanu stacjonarnego
Wstęp do sieci neuronowych, wykład 12 Łańcuchy Markowa M. Czoków, J. Piersa 2012-01-10 1 Łańcucha Markowa 2 Istnienie Szukanie stanu stacjonarnego 3 1 Łańcucha Markowa 2 Istnienie Szukanie stanu stacjonarnego
LABORATORIUM METODA ELEMENTÓW SKOŃCZONYCH
 LABORATORIUM METODA ELEMENTÓW SKOŃCZONYCH Projekt z wykorzystaniem programu COMSOL Multiphysics Prowadzący: dr hab. Tomasz Stręk, prof. PP Wykonali: Aleksandra Oźminkowska, Marta Woźniak Wydział: Elektryczny
LABORATORIUM METODA ELEMENTÓW SKOŃCZONYCH Projekt z wykorzystaniem programu COMSOL Multiphysics Prowadzący: dr hab. Tomasz Stręk, prof. PP Wykonali: Aleksandra Oźminkowska, Marta Woźniak Wydział: Elektryczny
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: Wprowadzenie do numerycznej mechaniki płynów Kierunek: Mechanika i Budowa Maszyn Rodzaj przedmiotu: obowiązkowy na specjalności: Inżynieria cieplna i samochodowa Rodzaj zajęć: wykład,
Nazwa przedmiotu: Wprowadzenie do numerycznej mechaniki płynów Kierunek: Mechanika i Budowa Maszyn Rodzaj przedmiotu: obowiązkowy na specjalności: Inżynieria cieplna i samochodowa Rodzaj zajęć: wykład,
INSTRUKCJA DO ĆWICZENIA NR 4
 KATEDRA MECHANIKI STOSOWANEJ Wydział Mechaniczny POLITECHNIKA LUBELSKA INSTRUKCJA DO ĆWICZENIA NR 4 PRZEDMIOT TEMAT Wybrane zagadnienia z optymalizacji elementów konstrukcji Zastosowanie optymalizacji
KATEDRA MECHANIKI STOSOWANEJ Wydział Mechaniczny POLITECHNIKA LUBELSKA INSTRUKCJA DO ĆWICZENIA NR 4 PRZEDMIOT TEMAT Wybrane zagadnienia z optymalizacji elementów konstrukcji Zastosowanie optymalizacji
Politechnika Poznańska Wydział Budowy Maszyn i Zarządzania. Projekt: Metoda Elementów Skończonych Program: COMSOL Multiphysics 3.4
 Politechnika Poznańska Wydział Budowy Maszyn i Zarządzania Projekt: Metoda Elementów Skończonych Program: COMSOL Multiphysics 3.4 Prowadzący: prof. nadzw. Tomasz Stręk Spis treści: 1.Analiza przepływu
Politechnika Poznańska Wydział Budowy Maszyn i Zarządzania Projekt: Metoda Elementów Skończonych Program: COMSOL Multiphysics 3.4 Prowadzący: prof. nadzw. Tomasz Stręk Spis treści: 1.Analiza przepływu
Informatyka I Lab 06, r.a. 2011/2012 prow. Sławomir Czarnecki. Zadania na laboratorium nr. 6
 Informatyka I Lab 6, r.a. / prow. Sławomir Czarnecki Zadania na laboratorium nr. 6 Po utworzeniu nowego projektu, dołącz bibliotekę bibs.h.. Największy wspólny dzielnik liczb naturalnych a, b oznaczamy
Informatyka I Lab 6, r.a. / prow. Sławomir Czarnecki Zadania na laboratorium nr. 6 Po utworzeniu nowego projektu, dołącz bibliotekę bibs.h.. Największy wspólny dzielnik liczb naturalnych a, b oznaczamy
PODSTAWY ELEKTOTECHNIKI LABORATORIUM
 PODSTAWY ELEKTOTECHNIKI LABORATORIUM AKADEMIA MORSKA Katedra Telekomunikacji Morskiej ĆWICZENIE 8 OBWODY PRĄDU STAŁEGO -PODSTAWOWE PRAWA 1. Cel ćwiczenia Doświadczalne zbadanie podstawowych praw teorii
PODSTAWY ELEKTOTECHNIKI LABORATORIUM AKADEMIA MORSKA Katedra Telekomunikacji Morskiej ĆWICZENIE 8 OBWODY PRĄDU STAŁEGO -PODSTAWOWE PRAWA 1. Cel ćwiczenia Doświadczalne zbadanie podstawowych praw teorii
NOWOCZESNE TECHNOLOGIE ENERGETYCZNE Rola modelowania fizycznego i numerycznego
 Politechnika Częstochowska Katedra Inżynierii Energii NOWOCZESNE TECHNOLOGIE ENERGETYCZNE Rola modelowania fizycznego i numerycznego dr hab. inż. Zbigniew BIS, prof P.Cz. dr inż. Robert ZARZYCKI Wstęp
Politechnika Częstochowska Katedra Inżynierii Energii NOWOCZESNE TECHNOLOGIE ENERGETYCZNE Rola modelowania fizycznego i numerycznego dr hab. inż. Zbigniew BIS, prof P.Cz. dr inż. Robert ZARZYCKI Wstęp
Nasyp przyrost osiadania w czasie (konsolidacja)
 Nasyp przyrost osiadania w czasie (konsolidacja) Poradnik Inżyniera Nr 37 Aktualizacja: 10/2017 Program: Plik powiązany: MES Konsolidacja Demo_manual_37.gmk Wprowadzenie Niniejszy przykład ilustruje zastosowanie
Nasyp przyrost osiadania w czasie (konsolidacja) Poradnik Inżyniera Nr 37 Aktualizacja: 10/2017 Program: Plik powiązany: MES Konsolidacja Demo_manual_37.gmk Wprowadzenie Niniejszy przykład ilustruje zastosowanie
Projekt 9: Dyfuzja ciepła - metoda Cranck-Nicloson.
 Projekt 9: Dyfuzja ciepła - metoda Cranck-Nicoson. Tomasz Chwiej stycznia 9 Wstęp n y ρ j= i= n x Rysunek : Siatka węzłów użyta w obiczeniach z zaznaczonymi warunkami brzegowymi: Diricheta (czerwony) i
Projekt 9: Dyfuzja ciepła - metoda Cranck-Nicoson. Tomasz Chwiej stycznia 9 Wstęp n y ρ j= i= n x Rysunek : Siatka węzłów użyta w obiczeniach z zaznaczonymi warunkami brzegowymi: Diricheta (czerwony) i
POLITECHNIKA LUBELSKA
 Badania opływu turbiny wiatrowej typu VAWT (Vertical Axis Wind Turbine) Międzyuczelniane Inżynierskie Warsztaty Lotnicze Cel prezentacji Celem prezentacji jest opis przeprowadzonych badań CFD oraz tunelowych
Badania opływu turbiny wiatrowej typu VAWT (Vertical Axis Wind Turbine) Międzyuczelniane Inżynierskie Warsztaty Lotnicze Cel prezentacji Celem prezentacji jest opis przeprowadzonych badań CFD oraz tunelowych
POLITECHNIKA ŚLĄSKA W GLIWICACH Wydział Mechaniczny Technologiczny PRACA DYPLOMOWA MAGISTERSKA
 POLITECHNIKA ŚLĄSKA W GLIWICACH Wydział Mechaniczny Technologiczny PRACA DYPLOMOWA MAGISTERSKA Wykorzystanie pakietu MARC/MENTAT do modelowania naprężeń cieplnych Spis treści Pole temperatury Przykład
POLITECHNIKA ŚLĄSKA W GLIWICACH Wydział Mechaniczny Technologiczny PRACA DYPLOMOWA MAGISTERSKA Wykorzystanie pakietu MARC/MENTAT do modelowania naprężeń cieplnych Spis treści Pole temperatury Przykład
Politechnika Poznańska
 Politechnika Poznańska Wydział Budowy Maszyn i Zarządzania Mechanika i Budowa Maszyn Grupa M2 Semestr V Metoda Elementów Skończonych prowadzący: dr hab. T. Stręk, prof. nadzw. wykonawcy: Grzegorz Geisler
Politechnika Poznańska Wydział Budowy Maszyn i Zarządzania Mechanika i Budowa Maszyn Grupa M2 Semestr V Metoda Elementów Skończonych prowadzący: dr hab. T. Stręk, prof. nadzw. wykonawcy: Grzegorz Geisler
Laboratorium komputerowe z wybranych zagadnień mechaniki płynów
 FORMOWANIE SIĘ PROFILU PRĘDKOŚCI W NIEŚCIŚLIWYM, LEPKIM PRZEPŁYWIE PRZEZ PRZEWÓD ZAMKNIĘTY Cel ćwiczenia Celem ćwiczenia będzie analiza formowanie się profilu prędkości w trakcie przepływu płynu przez
FORMOWANIE SIĘ PROFILU PRĘDKOŚCI W NIEŚCIŚLIWYM, LEPKIM PRZEPŁYWIE PRZEZ PRZEWÓD ZAMKNIĘTY Cel ćwiczenia Celem ćwiczenia będzie analiza formowanie się profilu prędkości w trakcie przepływu płynu przez
Modelowanie komputerowe w zagadnieniach środowiska. Strona:
 Modelowanie komputerowe w zagadnieniach środowiska Wykład 30 godzin + Laboratorium 30 godzin Strona: http://www.icm.edu.pl/~aniat/modele/wdw1 Literatura Modelowanie Urszula Foryś, Matematyka w biologii,
Modelowanie komputerowe w zagadnieniach środowiska Wykład 30 godzin + Laboratorium 30 godzin Strona: http://www.icm.edu.pl/~aniat/modele/wdw1 Literatura Modelowanie Urszula Foryś, Matematyka w biologii,
Politechnika Poznańska
 Poznań, 19.01.2013 Politechnika Poznańska Wydział Budowy Maszyn i Zarządzania Mechanika i Budowa Maszyn Technologia Przetwarzania Materiałów Semestr 7 METODA ELEMENTÓW SKOŃCZONYCH PROJEKT Prowadzący: dr
Poznań, 19.01.2013 Politechnika Poznańska Wydział Budowy Maszyn i Zarządzania Mechanika i Budowa Maszyn Technologia Przetwarzania Materiałów Semestr 7 METODA ELEMENTÓW SKOŃCZONYCH PROJEKT Prowadzący: dr
Modelowanie absorbcji cząsteczek LDL w ściankach naczyń krwionośnych
 Modelowanie absorbcji cząsteczek LDL w ściankach naczyń krwionośnych Plan prezentacji Co to jest LDL? 1 Budowa naczynia krwionośnego 2 Przykładowe wyniki 3 Mechanizmy wnikania blaszki miażdżycowej w ścianki
Modelowanie absorbcji cząsteczek LDL w ściankach naczyń krwionośnych Plan prezentacji Co to jest LDL? 1 Budowa naczynia krwionośnego 2 Przykładowe wyniki 3 Mechanizmy wnikania blaszki miażdżycowej w ścianki
MODELOWANIE ROZKŁADU TEMPERATUR W PRZEGRODACH ZEWNĘTRZNYCH WYKONANYCH Z UŻYCIEM LEKKICH KONSTRUKCJI SZKIELETOWYCH
 Budownictwo o Zoptymalizowanym Potencjale Energetycznym 2(18) 2016, s. 55-60 DOI: 10.17512/bozpe.2016.2.08 Maciej MAJOR, Mariusz KOSIŃ Politechnika Częstochowska MODELOWANIE ROZKŁADU TEMPERATUR W PRZEGRODACH
Budownictwo o Zoptymalizowanym Potencjale Energetycznym 2(18) 2016, s. 55-60 DOI: 10.17512/bozpe.2016.2.08 Maciej MAJOR, Mariusz KOSIŃ Politechnika Częstochowska MODELOWANIE ROZKŁADU TEMPERATUR W PRZEGRODACH
METODA ELEMENTÓW SKOŃCZONYCH
 INŻYNIERIA MECHANICZNA MECHANIKA I BUDOWA MASZYN WYDZIAŁ BUDOWY MASZYN I ZARZĄDZANIA POLITECHNIKA POZNAŃSKA METODA ELEMENTÓW SKOŃCZONYCH Projekt Wykonawca: Jakub Spychała Nr indeksu 96052 Prowadzący: prof.
INŻYNIERIA MECHANICZNA MECHANIKA I BUDOWA MASZYN WYDZIAŁ BUDOWY MASZYN I ZARZĄDZANIA POLITECHNIKA POZNAŃSKA METODA ELEMENTÓW SKOŃCZONYCH Projekt Wykonawca: Jakub Spychała Nr indeksu 96052 Prowadzący: prof.
Zadanie Cyfryzacja grida i analiza geometrii stropu pułapki w kontekście geologicznym
 Zadanie 1 1. Cyfryzacja grida i analiza geometrii stropu pułapki w kontekście geologicznym Pierwszym etapem wykonania zadania było przycięcie danego obrazu tak aby pozostał tylko obszar grida. Obrobiony
Zadanie 1 1. Cyfryzacja grida i analiza geometrii stropu pułapki w kontekście geologicznym Pierwszym etapem wykonania zadania było przycięcie danego obrazu tak aby pozostał tylko obszar grida. Obrobiony
FEM, generacja siatki, ciepło
 FEM, generacja siatki, ciepło Sposoby generacji siatki, błędy w metodzie FEM, modelowanie ciepła 05.06.2017 M. Rad Plan wykładu Teoria FEM Generacja siatki Błędy obliczeń Ciepło Realizacja obliczeń w FEMm
FEM, generacja siatki, ciepło Sposoby generacji siatki, błędy w metodzie FEM, modelowanie ciepła 05.06.2017 M. Rad Plan wykładu Teoria FEM Generacja siatki Błędy obliczeń Ciepło Realizacja obliczeń w FEMm
Kierunek: Matematyka Poziom studiów: Studia II stopnia Forma i tryb studiów: Stacjonarne
 Wydział: Matematyki Stosowanej Kierunek: Matematyka Poziom studiów: Studia II stopnia Forma i tryb studiów: Stacjonarne Specjalność: Matematyka ubezpieczeniowa Rocznik: 2016/2017 Język wykładowy: Polski
Wydział: Matematyki Stosowanej Kierunek: Matematyka Poziom studiów: Studia II stopnia Forma i tryb studiów: Stacjonarne Specjalność: Matematyka ubezpieczeniowa Rocznik: 2016/2017 Język wykładowy: Polski
WYZNACZANIE NIEPEWNOŚCI POMIARU METODAMI SYMULACYJNYMI
 WYZNACZANIE NIEPEWNOŚCI POMIARU METODAMI SYMULACYJNYMI Stefan WÓJTOWICZ, Katarzyna BIERNAT ZAKŁAD METROLOGII I BADAŃ NIENISZCZĄCYCH INSTYTUT ELEKTROTECHNIKI ul. Pożaryskiego 8, 04-703 Warszawa tel. (0)
WYZNACZANIE NIEPEWNOŚCI POMIARU METODAMI SYMULACYJNYMI Stefan WÓJTOWICZ, Katarzyna BIERNAT ZAKŁAD METROLOGII I BADAŃ NIENISZCZĄCYCH INSTYTUT ELEKTROTECHNIKI ul. Pożaryskiego 8, 04-703 Warszawa tel. (0)
POLITECHNIKA ŁÓDZKA INSTYTUT OBRABIAREK I TECHNOLOGII BUDOWY MASZYN. Ćwiczenie D - 4. Zastosowanie teoretycznej analizy modalnej w dynamice maszyn
 POLITECHNIKA ŁÓDZKA INSTYTUT OBRABIAREK I TECHNOLOGII BUDOWY MASZYN Ćwiczenie D - 4 Temat: Zastosowanie teoretycznej analizy modalnej w dynamice maszyn Opracowanie: mgr inż. Sebastian Bojanowski Zatwierdził:
POLITECHNIKA ŁÓDZKA INSTYTUT OBRABIAREK I TECHNOLOGII BUDOWY MASZYN Ćwiczenie D - 4 Temat: Zastosowanie teoretycznej analizy modalnej w dynamice maszyn Opracowanie: mgr inż. Sebastian Bojanowski Zatwierdził:
Numeryczne rozwiązanie równania Schrodingera
 Numeryczne rozwiązanie równania Schrodingera Równanie ruchu dla cząstki o masie m (elektron- cząstka elementarna o masie ~9.1 10-31 kg) Mechanika klasyczna - mechanika kwantowa 1. Druga zasada dynamiki
Numeryczne rozwiązanie równania Schrodingera Równanie ruchu dla cząstki o masie m (elektron- cząstka elementarna o masie ~9.1 10-31 kg) Mechanika klasyczna - mechanika kwantowa 1. Druga zasada dynamiki
dr inż. Cezary Żrodowski Wizualizacja Informacji WETI PG, sem. V, 2015/16 b) Operacja wyciągnięcia obrotowego z dodaniem materiału - uchwyt (1pkt)
 Zadanie 5 - Jacht 1. Budowa geometrii koła sterowego a) Szkic (1pkt) b) Operacja wyciągnięcia obrotowego z dodaniem materiału - uchwyt (1pkt) 1 c) Operacja wyciagnięcia liniowego z dodaniem materiału obręcze
Zadanie 5 - Jacht 1. Budowa geometrii koła sterowego a) Szkic (1pkt) b) Operacja wyciągnięcia obrotowego z dodaniem materiału - uchwyt (1pkt) 1 c) Operacja wyciagnięcia liniowego z dodaniem materiału obręcze
Transformata Fouriera
 Transformata Fouriera Program wykładu 1. Wprowadzenie teoretyczne 2. Algorytm FFT 3. Zastosowanie analizy Fouriera 4. Przykłady programów Wprowadzenie teoretyczne Zespolona transformata Fouriera Jeżeli
Transformata Fouriera Program wykładu 1. Wprowadzenie teoretyczne 2. Algorytm FFT 3. Zastosowanie analizy Fouriera 4. Przykłady programów Wprowadzenie teoretyczne Zespolona transformata Fouriera Jeżeli
Maciej Matyka. Modelowanie numeryczne transportu. płynów przez ośrodki porowate. Rozprawa doktorska. Promotor: dr hab.
 Rozprawa doktorska Modelowanie numeryczne transportu płynów przez ośrodki porowate Maciej Matyka Promotor: dr hab. Zbigniew Koza Uniwersytet Wrocławski Wydział Fizyki i Astronomii Wrocław, 2008 Spis treści
Rozprawa doktorska Modelowanie numeryczne transportu płynów przez ośrodki porowate Maciej Matyka Promotor: dr hab. Zbigniew Koza Uniwersytet Wrocławski Wydział Fizyki i Astronomii Wrocław, 2008 Spis treści
Politechnika Poznańska. Metoda Elementów Skończonych
 Politechnika Poznańska PROJEKT: Metoda Elementów Skończonych Prowadzący: Dr hab. Tomasz Stręk Autorzy: Rafał Wesoły Daniel Trojanowicz Wydział: WBMiZ Kierunek: MiBM Specjalność: IMe Spis treści: 1. Zagadnienie
Politechnika Poznańska PROJEKT: Metoda Elementów Skończonych Prowadzący: Dr hab. Tomasz Stręk Autorzy: Rafał Wesoły Daniel Trojanowicz Wydział: WBMiZ Kierunek: MiBM Specjalność: IMe Spis treści: 1. Zagadnienie
METODA ELEMENTÓW SKOŃCZONYCH
 METODA ELEMENTÓW SKOŃCZONYCH Projekt: COMSOLMultiphysics Prowadzący: dr hab. T. Stręk Wykonały: Barbara Drozdek Agnieszka Grabowska Grupa: IM Kierunek: MiBM Wydział: BMiZ Spis treści 1. ANALIZA PRZEPŁYWU
METODA ELEMENTÓW SKOŃCZONYCH Projekt: COMSOLMultiphysics Prowadzący: dr hab. T. Stręk Wykonały: Barbara Drozdek Agnieszka Grabowska Grupa: IM Kierunek: MiBM Wydział: BMiZ Spis treści 1. ANALIZA PRZEPŁYWU
Ćwiczenie 3: Wyznaczanie gęstości pozornej i porowatości złoża, przepływ gazu przez złoże suche, opory przepływu.
 1. Część teoretyczna Przepływ jednofazowy przez złoże nieruchome i ruchome Przepływ płynu przez warstwę luźno usypanego złoża występuje w wielu aparatach, np. w kolumnie absorpcyjnej, rektyfikacyjnej,
1. Część teoretyczna Przepływ jednofazowy przez złoże nieruchome i ruchome Przepływ płynu przez warstwę luźno usypanego złoża występuje w wielu aparatach, np. w kolumnie absorpcyjnej, rektyfikacyjnej,
Symulacja przepływu ciepła dla wybranych warunków badanego układu
 Symulacja przepływu ciepła dla wybranych warunków badanego układu I. Część teoretyczna Ciepło jest formą przekazywana energii, która jest spowodowana różnicą temperatur (inną formą przekazywania energii
Symulacja przepływu ciepła dla wybranych warunków badanego układu I. Część teoretyczna Ciepło jest formą przekazywana energii, która jest spowodowana różnicą temperatur (inną formą przekazywania energii
1. Przepływ ciepła - 3 - Rysunek 1.1 Projekt tarczy hamulcowej z programu SOLIDWORKS
 POLITECHNIKA POZNAŃSKA WYDZIAŁ BUDOWY MASZYN I ZARZĄDZANIA METODY ELEMENTÓW SKOŃCZONYCH PROJEKT PROWADZĄCY: PROF. NADZW. TOMASZ STRĘK WYKONALI: TOMASZ IZYDORCZYK, MICHAŁ DYMEK GRUPA: TPM2 SEMESTR: VII
POLITECHNIKA POZNAŃSKA WYDZIAŁ BUDOWY MASZYN I ZARZĄDZANIA METODY ELEMENTÓW SKOŃCZONYCH PROJEKT PROWADZĄCY: PROF. NADZW. TOMASZ STRĘK WYKONALI: TOMASZ IZYDORCZYK, MICHAŁ DYMEK GRUPA: TPM2 SEMESTR: VII
Modelowanie i symulacja zagadnień biomedycznych PROJEKT BARTŁOMIEJ GRZEBYTA, JAKUB OTWOROWSKI
 Modelowanie i symulacja zagadnień biomedycznych PROJEKT BARTŁOMIEJ GRZEBYTA, JAKUB OTWOROWSKI Spis treści Wstęp... 2 Opis problemu... 3 Metoda... 3 Opis modelu... 4 Warunki brzegowe... 5 Wyniki symulacji...
Modelowanie i symulacja zagadnień biomedycznych PROJEKT BARTŁOMIEJ GRZEBYTA, JAKUB OTWOROWSKI Spis treści Wstęp... 2 Opis problemu... 3 Metoda... 3 Opis modelu... 4 Warunki brzegowe... 5 Wyniki symulacji...
Obciążenia, warunki środowiskowe. Modele, pomiary. Tomasz Marcinkowski
 Obciążenia, warunki środowiskowe. Modele, pomiary. Tomasz Marcinkowski 1. Obciążenia środowiskowe (wiatr, falowanie morskie, prądy morskie, poziomy zwierciadła wody, oddziaływanie lodu) 2. Poziomy obciążeń
Obciążenia, warunki środowiskowe. Modele, pomiary. Tomasz Marcinkowski 1. Obciążenia środowiskowe (wiatr, falowanie morskie, prądy morskie, poziomy zwierciadła wody, oddziaływanie lodu) 2. Poziomy obciążeń
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: PODSTAWY MODELOWANIA PROCESÓW WYTWARZANIA Fundamentals of manufacturing processes modeling Kierunek: Mechanika i Budowa Maszyn Rodzaj przedmiotu: obowiązkowy na specjalności APWiR Rodzaj
Nazwa przedmiotu: PODSTAWY MODELOWANIA PROCESÓW WYTWARZANIA Fundamentals of manufacturing processes modeling Kierunek: Mechanika i Budowa Maszyn Rodzaj przedmiotu: obowiązkowy na specjalności APWiR Rodzaj
WYKORZYSTANIE MES DO WYZNACZANIA WPŁYWU PĘKNIĘCIA W STOPIE ZĘBA KOŁA NA ZMIANĘ SZTYWNOŚCI ZAZĘBIENIA
 ZESZYTY NAUKOWE POLITECHNIKI ŚLĄSKIEJ 2009 Seria: TRANSPORT z. 65 Nr kol. 1807 Tomasz FIGLUS, Piotr FOLĘGA, Piotr CZECH, Grzegorz WOJNAR WYKORZYSTANIE MES DO WYZNACZANIA WPŁYWU PĘKNIĘCIA W STOPIE ZĘBA
ZESZYTY NAUKOWE POLITECHNIKI ŚLĄSKIEJ 2009 Seria: TRANSPORT z. 65 Nr kol. 1807 Tomasz FIGLUS, Piotr FOLĘGA, Piotr CZECH, Grzegorz WOJNAR WYKORZYSTANIE MES DO WYZNACZANIA WPŁYWU PĘKNIĘCIA W STOPIE ZĘBA
Projekt Metoda Elementów Skończonych. COMSOL Multiphysics 3.4
 Projekt Metoda Elementów Skończonych w programie COMSOL Multiphysics 3.4 Wykonali: Dawid Trawiński Wojciech Sochalski Wydział: BMiZ Kierunek: MiBM Semestr: V Rok: 2015/2016 Prowadzący: dr hab. inż. Tomasz
Projekt Metoda Elementów Skończonych w programie COMSOL Multiphysics 3.4 Wykonali: Dawid Trawiński Wojciech Sochalski Wydział: BMiZ Kierunek: MiBM Semestr: V Rok: 2015/2016 Prowadzący: dr hab. inż. Tomasz
Politechnika Poznańska. Projekt Metoda Elementów Skończonych
 Politechnika Poznańska Projekt Metoda Elementów Skończonych Prowadzący: Dr hab. T. Stręk, prof. nadzw. Wykonali: Piotr Czajka Piotr Jabłoński Mechanika i Budowa Maszyn Profil dypl. : IiRW 2 Spis treści
Politechnika Poznańska Projekt Metoda Elementów Skończonych Prowadzący: Dr hab. T. Stręk, prof. nadzw. Wykonali: Piotr Czajka Piotr Jabłoński Mechanika i Budowa Maszyn Profil dypl. : IiRW 2 Spis treści
Sprawozdanie. z ćwiczeń laboratoryjnych z przedmiotu: Współczesne Materiały Inżynierskie. Temat ćwiczenia
 Sprawozdanie z ćwiczeń laboratoryjnych z przedmiotu: Współczesne Materiały Inżynierskie Temat ćwiczenia Badanie właściwości reologicznych cieczy magnetycznych Prowadzący: mgr inż. Marcin Szczęch Wykonawcy
Sprawozdanie z ćwiczeń laboratoryjnych z przedmiotu: Współczesne Materiały Inżynierskie Temat ćwiczenia Badanie właściwości reologicznych cieczy magnetycznych Prowadzący: mgr inż. Marcin Szczęch Wykonawcy
1. Część teoretyczna. Przepływ jednofazowy przez złoże nieruchome i ruchome
 1. Część teoretyczna Przepływ jednofazowy przez złoże nieruchome i ruchome Przepływ płynu przez warstwę luźno usypanego złoża występuje w wielu aparatach, np. w kolumnie absorpcyjnej, rektyfikacyjnej,
1. Część teoretyczna Przepływ jednofazowy przez złoże nieruchome i ruchome Przepływ płynu przez warstwę luźno usypanego złoża występuje w wielu aparatach, np. w kolumnie absorpcyjnej, rektyfikacyjnej,
KOMPUTEROWE MODELOWANIE I OBLICZENIA WYTRZYMAŁOŚCIOWE ZBIORNIKÓW NA GAZ PŁYNNY LPG
 Leon KUKIEŁKA, Krzysztof KUKIEŁKA, Katarzyna GELETA, Łukasz CĄKAŁA KOMPUTEROWE MODELOWANIE I OBLICZENIA WYTRZYMAŁOŚCIOWE ZBIORNIKÓW NA GAZ PŁYNNY LPG Streszczenie W artykule przedstawiono komputerowe modelowanie
Leon KUKIEŁKA, Krzysztof KUKIEŁKA, Katarzyna GELETA, Łukasz CĄKAŁA KOMPUTEROWE MODELOWANIE I OBLICZENIA WYTRZYMAŁOŚCIOWE ZBIORNIKÓW NA GAZ PŁYNNY LPG Streszczenie W artykule przedstawiono komputerowe modelowanie
= sin. = 2Rsin. R = E m. = sin
 Natężenie światła w obrazie dyfrakcyjnym Autorzy: Zbigniew Kąkol, Piotr Morawski Chcemy teraz znaleźć wyrażenie na rozkład natężenia w całym ekranie w funkcji kąta θ. Szczelinę dzielimy na N odcinków i
Natężenie światła w obrazie dyfrakcyjnym Autorzy: Zbigniew Kąkol, Piotr Morawski Chcemy teraz znaleźć wyrażenie na rozkład natężenia w całym ekranie w funkcji kąta θ. Szczelinę dzielimy na N odcinków i
MODELOWANIE ZA POMOCĄ MES Analiza statyczna ustrojów powierzchniowych
 MODELOWANIE ZA POMOCĄ MES Analiza statyczna ustrojów powierzchniowych PODSTAWY KOMPUTEROWEGO MODELOWANIA USTROJÓW POWIERZCHNIOWYCH Budownictwo, studia I stopnia, semestr VI przedmiot fakultatywny rok akademicki
MODELOWANIE ZA POMOCĄ MES Analiza statyczna ustrojów powierzchniowych PODSTAWY KOMPUTEROWEGO MODELOWANIA USTROJÓW POWIERZCHNIOWYCH Budownictwo, studia I stopnia, semestr VI przedmiot fakultatywny rok akademicki
PROJEKT MES COMSOL MULTIPHYSICS 3.4
 POLITECHNIKA POZNAŃSKA WYDZIAŁ BUDOWY MASZYN I ZARZĄDZANIA PROJEKT MES COMSOL MULTIPHYSICS 3.4 Prowadzący: dr hab. Tomasz Stręk, prof. nadz. Wykonali: Dawid Weremiuk Dawid Prusiewicz Kierunek: Mechanika
POLITECHNIKA POZNAŃSKA WYDZIAŁ BUDOWY MASZYN I ZARZĄDZANIA PROJEKT MES COMSOL MULTIPHYSICS 3.4 Prowadzący: dr hab. Tomasz Stręk, prof. nadz. Wykonali: Dawid Weremiuk Dawid Prusiewicz Kierunek: Mechanika
Metoda elementów skończonych
 Metoda elementów skończonych Wraz z rozwojem elektronicznych maszyn obliczeniowych jakimi są komputery zaczęły pojawiać się różne numeryczne metody do obliczeń wytrzymałości różnych konstrukcji. Jedną
Metoda elementów skończonych Wraz z rozwojem elektronicznych maszyn obliczeniowych jakimi są komputery zaczęły pojawiać się różne numeryczne metody do obliczeń wytrzymałości różnych konstrukcji. Jedną
W naukach technicznych większość rozpatrywanych wielkości możemy zapisać w jednej z trzech postaci: skalara, wektora oraz tensora.
 1. Podstawy matematyki 1.1. Geometria analityczna W naukach technicznych większość rozpatrywanych wielkości możemy zapisać w jednej z trzech postaci: skalara, wektora oraz tensora. Skalarem w fizyce nazywamy
1. Podstawy matematyki 1.1. Geometria analityczna W naukach technicznych większość rozpatrywanych wielkości możemy zapisać w jednej z trzech postaci: skalara, wektora oraz tensora. Skalarem w fizyce nazywamy
Zwój nad przewodzącą płytą
 Zwój nad przewodzącą płytą Z potencjału A można też wyznaczyć napięcie u0 jakie będzie się indukować w pojedynczym zwoju cewki odbiorczej: gdzie: Φ strumień magnetyczny przenikający powierzchnię, której
Zwój nad przewodzącą płytą Z potencjału A można też wyznaczyć napięcie u0 jakie będzie się indukować w pojedynczym zwoju cewki odbiorczej: gdzie: Φ strumień magnetyczny przenikający powierzchnię, której
Wykład FIZYKA I. 11. Fale mechaniczne. Dr hab. inż. Władysław Artur Woźniak
 Wykład FIZYKA I 11. Fale mechaniczne Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej http://www.if.pwr.wroc.pl/~wozniak/fizyka1.html FALA Falą nazywamy każde rozprzestrzeniające
Wykład FIZYKA I 11. Fale mechaniczne Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej http://www.if.pwr.wroc.pl/~wozniak/fizyka1.html FALA Falą nazywamy każde rozprzestrzeniające
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw udowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 2016/2017
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw udowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 2016/2017
OPTYMALIZACJA ZBIORNIKA NA GAZ PŁYNNY LPG
 Leon KUKIEŁKA, Krzysztof KUKIEŁKA, Katarzyna GELETA, Łukasz CĄKAŁA OPTYMALIZACJA ZBIORNIKA NA GAZ PŁYNNY LPG Streszczenie Praca dotyczy optymalizacji kształtu zbiornika toroidalnego na gaz LPG. Kryterium
Leon KUKIEŁKA, Krzysztof KUKIEŁKA, Katarzyna GELETA, Łukasz CĄKAŁA OPTYMALIZACJA ZBIORNIKA NA GAZ PŁYNNY LPG Streszczenie Praca dotyczy optymalizacji kształtu zbiornika toroidalnego na gaz LPG. Kryterium
Proces wykonywania modeli z nowej generacji mas modelowych stosowanych w metodzie wytapianych modeli analiza symulacyjna
 A R C H I V E S of F O U N D R Y E N G I N E E R I N G Published quarterly as the organ of the Foundry Commission of the Polish Academy of Sciences ISSN (1897-331) Volume 12 Special Issue 2/212 1 14 2/2
A R C H I V E S of F O U N D R Y E N G I N E E R I N G Published quarterly as the organ of the Foundry Commission of the Polish Academy of Sciences ISSN (1897-331) Volume 12 Special Issue 2/212 1 14 2/2
Metody Obliczeniowe Mikrooptyki i Fotoniki. Metoda propagacji wiązki BPM Modelowanie propagacji
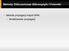 Metody Obliczeniowe Mikrooptyki i Fotoniki Metoda propagacji wiązki BPM Modelowanie propagacji Równanie BPM Równanie Helmholtza: n k 0 =0 Rozwiązanie zapisujemy jako: r =A r exp i k z Fala nośna k =n k
Metody Obliczeniowe Mikrooptyki i Fotoniki Metoda propagacji wiązki BPM Modelowanie propagacji Równanie BPM Równanie Helmholtza: n k 0 =0 Rozwiązanie zapisujemy jako: r =A r exp i k z Fala nośna k =n k
Politechnika Poznańska
 Politechnika Poznańska Metoda Elementów Skończonych Mechanika i Budowa Maszyn Prowadzący: dr hab. Tomasz Stręk, prof. nadzw. Wykonali: Maria Kubacka Paweł Jakim Patryk Mójta 1 Spis treści: 1. Symulacja
Politechnika Poznańska Metoda Elementów Skończonych Mechanika i Budowa Maszyn Prowadzący: dr hab. Tomasz Stręk, prof. nadzw. Wykonali: Maria Kubacka Paweł Jakim Patryk Mójta 1 Spis treści: 1. Symulacja
Załącznik nr 1 do Zapytania ofertowego: Opis przedmiotu zamówienia
 Załącznik nr 1 do Zapytania ofertowego: Opis przedmiotu zamówienia Postępowanie na świadczenie usług badawczo-rozwojowych referencyjny Zamawiającego: ZO CERTA 1/2017 Celem Projektu jest opracowanie wielokryterialnych
Załącznik nr 1 do Zapytania ofertowego: Opis przedmiotu zamówienia Postępowanie na świadczenie usług badawczo-rozwojowych referencyjny Zamawiającego: ZO CERTA 1/2017 Celem Projektu jest opracowanie wielokryterialnych
7.1. Modelowanie fizyczne 7.2. Modelowanie matematyczne 7.3. Kategorie modelowania matematycznego 7.4. Kategorie modelowania matematycznego 7.5.
 7.. Modelowanie fizyczne 7.2. Modelowanie matematyczne 7.3. Kategorie modelowania matematycznego 7.4. Kategorie modelowania matematycznego 7.5. Kategorie modelowania matematycznego 7.6. Symulatory niestacjonarne
7.. Modelowanie fizyczne 7.2. Modelowanie matematyczne 7.3. Kategorie modelowania matematycznego 7.4. Kategorie modelowania matematycznego 7.5. Kategorie modelowania matematycznego 7.6. Symulatory niestacjonarne
Symulacja statyczna sieci gazowej miasta Chełmna
 Andrzej J. Osiadacz Maciej Chaczykowski Łukasz Kotyński Teresa Zwiewka Symulacja statyczna sieci gazowej miasta Chełmna Andrzej J. Osiadacz, Maciej Chaczykowski, Łukasz Kotyński, Fluid Systems Sp z o.o.,
Andrzej J. Osiadacz Maciej Chaczykowski Łukasz Kotyński Teresa Zwiewka Symulacja statyczna sieci gazowej miasta Chełmna Andrzej J. Osiadacz, Maciej Chaczykowski, Łukasz Kotyński, Fluid Systems Sp z o.o.,
Nieskończona jednowymiarowa studnia potencjału
 Nieskończona jednowymiarowa studnia potencjału Zagadnienie dane jest następująco: znaleźć funkcje własne i wartości własne operatora energii dla cząstki umieszczonej w nieskończonej studni potencjału,
Nieskończona jednowymiarowa studnia potencjału Zagadnienie dane jest następująco: znaleźć funkcje własne i wartości własne operatora energii dla cząstki umieszczonej w nieskończonej studni potencjału,
Wykaz oznaczeń Przedmowa... 9
 Spis treści Wykaz oznaczeń... 6 Przedmowa... 9 1 WPROWADZENIE... 11 1.1 Mechanika newtonowska... 14 1.2 Mechanika lagranżowska... 19 1.3 Mechanika hamiltonowska... 20 2 WIĘZY I ICH KLASYFIKACJA... 23 2.1
Spis treści Wykaz oznaczeń... 6 Przedmowa... 9 1 WPROWADZENIE... 11 1.1 Mechanika newtonowska... 14 1.2 Mechanika lagranżowska... 19 1.3 Mechanika hamiltonowska... 20 2 WIĘZY I ICH KLASYFIKACJA... 23 2.1
Całkowanie numeryczne
 Całkowanie numeryczne Poniżej omówione zostanie kilka metod przybliżania operacji całkowania i różniczkowania w szczególności uzależnieniu pochodnej od jej różnic skończonych gdy równanie różniczkowe mamy
Całkowanie numeryczne Poniżej omówione zostanie kilka metod przybliżania operacji całkowania i różniczkowania w szczególności uzależnieniu pochodnej od jej różnic skończonych gdy równanie różniczkowe mamy
Krzysztof Łapsa Wyznaczenie prędkości fal ultradźwiękowych metodami interferencyjnymi
 Krzysztof Łapsa Wyznaczenie prędkości fal ultradźwiękowych metodami interferencyjnymi Cele ćwiczenia Praktyczne zapoznanie się ze zjawiskiem interferencji fal akustycznych Wyznaczenie prędkości fal ultradźwiękowych
Krzysztof Łapsa Wyznaczenie prędkości fal ultradźwiękowych metodami interferencyjnymi Cele ćwiczenia Praktyczne zapoznanie się ze zjawiskiem interferencji fal akustycznych Wyznaczenie prędkości fal ultradźwiękowych
Ćwiczenie 12/13. Komputerowy hologram Fouriera. Wprowadzenie teoretyczne
 Ćwiczenie 12/13 Komputerowy hologram Fouriera. Wprowadzenie teoretyczne W klasycznej holografii w wyniku interferencji dwóch wiązek: wiązki światła zmodyfikowanej przez pewien przedmiot i spójnej z nią
Ćwiczenie 12/13 Komputerowy hologram Fouriera. Wprowadzenie teoretyczne W klasycznej holografii w wyniku interferencji dwóch wiązek: wiązki światła zmodyfikowanej przez pewien przedmiot i spójnej z nią
Projekt 6: Równanie Poissona - rozwiązanie metodą algebraiczną.
 Projekt 6: Równanie Poissona - rozwiązanie metodą algebraiczną. Tomasz Chwiej 9 sierpnia 18 1 Wstęp 1.1 Dyskretyzacja n y V V 1 V 3 1 j= i= 1 V 4 n x Rysunek 1: Geometria układu i schemat siatki obliczeniowej
Projekt 6: Równanie Poissona - rozwiązanie metodą algebraiczną. Tomasz Chwiej 9 sierpnia 18 1 Wstęp 1.1 Dyskretyzacja n y V V 1 V 3 1 j= i= 1 V 4 n x Rysunek 1: Geometria układu i schemat siatki obliczeniowej
Projekt badawczy N N209 374139 Badania doświadczalne i numeryczne przepływu płynów lepkosprężystych
 Tworzenie siatek numerycznych na przykładzie układu cylinder cylinder przepływ Couette Układ, dla którego przedstawiono w ramach niniejszego rozdziału sposób generowania siatek numerycznych, stanowiły
Tworzenie siatek numerycznych na przykładzie układu cylinder cylinder przepływ Couette Układ, dla którego przedstawiono w ramach niniejszego rozdziału sposób generowania siatek numerycznych, stanowiły
Metoda Elementów skończonych PROJEKT. COMSOL Multiphysics 3.4
 POLITECHNIKA POZNAŃSKA WYDZIAŁ BUDOWY MASZYN I ZARZĄDZANIA MECHANIKA I BUDOWA MASZYN KONSTRUCJA MASZYN I URZĄDZEŃ Rok akademicki 2013/14, sem VII Metoda Elementów skończonych PROJEKT COMSOL Multiphysics
POLITECHNIKA POZNAŃSKA WYDZIAŁ BUDOWY MASZYN I ZARZĄDZANIA MECHANIKA I BUDOWA MASZYN KONSTRUCJA MASZYN I URZĄDZEŃ Rok akademicki 2013/14, sem VII Metoda Elementów skończonych PROJEKT COMSOL Multiphysics
METODY KOMPUTEROWE W MECHANICE
 METODY KOMPUTEROWE W MECHANICE wykład dr inż. Paweł Stąpór laboratorium 15 g, projekt 15 g. dr inż. Paweł Stąpór dr inż. Sławomir Koczubiej Politechnika Świętokrzyska Wydział Zarządzania i Modelowania
METODY KOMPUTEROWE W MECHANICE wykład dr inż. Paweł Stąpór laboratorium 15 g, projekt 15 g. dr inż. Paweł Stąpór dr inż. Sławomir Koczubiej Politechnika Świętokrzyska Wydział Zarządzania i Modelowania
BŁĘDY OBLICZEŃ NUMERYCZNYCH
 BŁĘDY OBLICZEŃ NUMERYCZNYCH błędy zaokrągleń skończona liczba cyfr (bitów) w reprezentacji numerycznej błędy obcięcia rozwinięcia w szeregi i procesy iteracyjne - w praktyce muszą być skończone błędy metody
BŁĘDY OBLICZEŃ NUMERYCZNYCH błędy zaokrągleń skończona liczba cyfr (bitów) w reprezentacji numerycznej błędy obcięcia rozwinięcia w szeregi i procesy iteracyjne - w praktyce muszą być skończone błędy metody
Nowoczesne narzędzia obliczeniowe do projektowania i optymalizacji kotłów
 Nowoczesne narzędzia obliczeniowe do projektowania i optymalizacji kotłów Mateusz Szubel, Mariusz Filipowicz Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie AGH University of Science and
Nowoczesne narzędzia obliczeniowe do projektowania i optymalizacji kotłów Mateusz Szubel, Mariusz Filipowicz Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie AGH University of Science and
METODA ELEMENTÓW SKOŃCZONYCH
 METODA ELEMENTÓW SKOŃCZONYCH Krzysztof Bochna Michał Sobolewski M-2 WBMiZ MiBM 2013/2014 1 SPIS TREŚCI 1. Analiza opływu wody wokół okrętu podwodnego USS Minnesota...3 1.1 Opis obiektu...3 1.2 Przebieg
METODA ELEMENTÓW SKOŃCZONYCH Krzysztof Bochna Michał Sobolewski M-2 WBMiZ MiBM 2013/2014 1 SPIS TREŚCI 1. Analiza opływu wody wokół okrętu podwodnego USS Minnesota...3 1.1 Opis obiektu...3 1.2 Przebieg
Automatyka i pomiary wielkości fizykochemicznych. Instrukcja do ćwiczenia III. Pomiar natężenia przepływu za pomocą sondy poboru ciśnienia
 Automatyka i pomiary wielkości fizykochemicznych Instrukcja do ćwiczenia III Pomiar natężenia przepływu za pomocą sondy poboru ciśnienia Sonda poboru ciśnienia Sonda poboru ciśnienia (Rys. ) jest to urządzenie
Automatyka i pomiary wielkości fizykochemicznych Instrukcja do ćwiczenia III Pomiar natężenia przepływu za pomocą sondy poboru ciśnienia Sonda poboru ciśnienia Sonda poboru ciśnienia (Rys. ) jest to urządzenie
Rozwiązywanie równań różniczkowych cząstkowych metodą elementów skończonych - wprowadzenie
 Rozwiązywanie równań różniczkowych cząstkowych metodą elementów skończonych - wprowadzenie Wprowadzenie Metoda Elementów Skończonych (MES) należy do numerycznych metod otrzymywania przybliżonych rozwiązań
Rozwiązywanie równań różniczkowych cząstkowych metodą elementów skończonych - wprowadzenie Wprowadzenie Metoda Elementów Skończonych (MES) należy do numerycznych metod otrzymywania przybliżonych rozwiązań
Modelowanie, sterowanie i symulacja manipulatora o odkształcalnych ramionach. Krzysztof Żurek Gdańsk,
 Modelowanie, sterowanie i symulacja manipulatora o odkształcalnych ramionach Krzysztof Żurek Gdańsk, 2015-06-10 Plan Prezentacji 1. Manipulatory. 2. Wprowadzenie do Metody Elementów Skończonych (MES).
Modelowanie, sterowanie i symulacja manipulatora o odkształcalnych ramionach Krzysztof Żurek Gdańsk, 2015-06-10 Plan Prezentacji 1. Manipulatory. 2. Wprowadzenie do Metody Elementów Skończonych (MES).
Prognozowanie i Symulacje. Wykład I. Matematyczne metody prognozowania
 Prognozowanie i Symulacje. Wykład I. e-mail:e.kozlovski@pollub.pl Spis treści Szeregi czasowe 1 Szeregi czasowe 2 3 Szeregi czasowe Definicja 1 Szereg czasowy jest to proces stochastyczny z czasem dyskretnym
Prognozowanie i Symulacje. Wykład I. e-mail:e.kozlovski@pollub.pl Spis treści Szeregi czasowe 1 Szeregi czasowe 2 3 Szeregi czasowe Definicja 1 Szereg czasowy jest to proces stochastyczny z czasem dyskretnym
Metody rozwiązania równania Schrödingera
 Metody rozwiązania równania Schrödingera Równanie Schrödingera jako algebraiczne zagadnienie własne Rozwiązanie analityczne dla skończonej i nieskończonej studni potencjału Problem rozwiązania równania
Metody rozwiązania równania Schrödingera Równanie Schrödingera jako algebraiczne zagadnienie własne Rozwiązanie analityczne dla skończonej i nieskończonej studni potencjału Problem rozwiązania równania
