POJEMNIK. Politechnika Warszawska. Teoria optymalizacji. Wydziaª Elektryczny ZADANIE PROBLEMOWE
|
|
|
- Włodzimierz Cieślik
- 6 lat temu
- Przeglądów:
Transkrypt
1 Politechnika Warszawska Wydziaª Elektryczny Teoria optymalizacji POJEMNIK ZADANIE PROBLEMOWE Laboratorium metod optymalizacji Temat wiczenia: Zadanie problemowe - pojemnik Prowadz cy: doc. dr in». Krzysztof Amborski Wykonawca: Paweª No»ykowski,
2 Spis tre±ci 1 Tre± zadania 2 2 Analiza zadania 2 3 Wykonanie zadania 3 4 Wnioski 4 1
3 1 Tre± zadania Blaszane pojemniki bez pokrywy w ksztaªcie prostopadªo±cianów o obj to±ci 0,25 m 3 maj by produkowane z dwóch rodzajów blachy. Dno pojemnika powinno by wykonane z blachy o grubo±ci 4 mm, ±ciany boczne za± z blachy o grubo±ci 2 mm. Blacha cienka pochodzi z odpadków i na jeden pojemnik nie wolno zu»y wi cej ni» 2,66 m 2. Odbiorca pojemników wymaga, aby ich szeroko± nie przekraczaªa 60 cm, wysoko± natomiast zawieraªa si w przedziale od 50 do 75 cm. Zakªadaj c,»e ci»ar 1 m 2 blachy jest proporcjonalny do jej grubo±ci, sformuªowa zadanie zaprojektowania pojemnika o minimalnym ci»arze. 2 Analiza zadania ±ciany y dno pojemnika z x 4mm 2mm Na podstawie tre±ci zadania mo»emy uªo»y nast puj ce ograniczenia: 1. Blaszane pojemniki bez pokrywy w ksztaªcie prostopadªo±cianów o obj to±ci 0,25 m 3 x y z = (1) 2. Blacha cienka pochodzi z odpadków i na jeden pojemnik nie wolno zu»y wi cej ni» 2,66 m 2. 2 x y + 2 y z 2, 66 (2) 3. Odbiorca pojemników wymaga, aby ich szeroko± nie przekraczaªa 60 cm x 0, 6 4. wysoko± natomiast zawieraªa si w przedziale od 50 do 75 cm. y 0, 5 y 0, Dodatkowo musimy wprowadzi ograniczenia wynikaj ce z praw zyki: x > 0 z > 0 2
4 Funkcja celu, któr b dziemy minimalizowa wynika z ostaniego zdania: Zakªadaj c,»e ci»ar 1 m 2 blachy jest proporcjonalny do jej grubo±ci, sformuªowa zadanie zaprojektowania pojemnika o minimalnym ci»arze. f(x, y, z) = 0, 004 x z + 0, 002 (2 x y + 2 y z) (3) Przeksztaªcaj c równanie (1) do postaci: z = x y i wstawiaj c do funkcji celu (3) otrzymujemy now posta funkcji celu: f(x, y) = 0, 004 y + 0, 002 (2 x y + 2 x ) upraszczaj c: f(x, y) = 0, 001 (4 x y + 1 x + 1 y ) Poniewa» staªa 0, 001 przed nawiasem nie wpªynie na wynik optymalizacji mo»emy ja pomina i ostatecznie: f(x, y) = 4 x y + 1 x + 1 y Ograniczenie (2) przyjmie posta : 2 x y + 1 2, 66 2 x 3 Wykonanie zadania Zadanie zostaªo wykonane z u»yciem ±rodowiska Matlab i pakietu Optimalization Toolbox. ródªo 1 myfun.m f u n c t i o n [ f ] = myfun ( x ) f = 4 * x ( 1 ) * x ( 2 ) + 1/x ( 1 ) + 1/x ( 2 ) ; ródªo 2 mycon.m f u n c t i o n [ c, ceq ] = mycon ( x ) c = 2 * x ( 1 ) * x ( 2 ) * (1/ x ( 1 ) ) ; ceq = [ ] ; ródªo 3 opt_zad.m f u n c t i o n opt_zad c l c ; o p t i o n s = optimset ( ' MaxIter ', 500, ' Display ', ' iter ', ' tolfun ', 1e 10, ' tolcon ', 1e 10, ' MaxFunEvals ', 500, ' TolX ', 1e 10); x0 = [ ] l b = [ ] ub = [ ] [ x, f v a l ] = fmincon ( ' myfun ', x0, [ ], [ ], [ ], [ ], lb, ub, ' mycon ', o p t i o n s ) ; disp ( 'x = ' ) ; disp ( x ) ; disp ( 'f(x) = ' ) ; disp ( f v a l ) ; 3
5 Uzyskany wynik przedstawia poni»szy listing: Listing 1 Wynik oblicze«x0 = l b = ub = Max Line s e a r c h D i r e c t i o n a l F i r s t o r d e r I t e r F count f ( x ) c o n s t r a i n t s t e p l e n g t h d e r i v a t i v e o p t i m a l i t y e e e e 08 Optimization terminated : f i r s t o r d e r o p t i m a l i t y measure l e s s than o p t i o n s. TolFun and maximum c o n s t r a i n t v i o l a t i o n i s l e s s than o p t i o n s. TolCon. Active i n e q u a l i t i e s ( to w i t h i n o p t i o n s. TolCon = 1e 10): lower upper i n e q l i n i n e q n o n l i n 1 x = f ( x ) = Optymalnym rozwi zaniem jest zatem: x = 0, 600 y = 0, 645 z = 0, 646 f(x, y, z) = 4, 765 Wszystkie zmienne mieszcz si w przyj tych ograniczeniach. 4 Wnioski Udaªo si zaprojektowa pojemnik o minimalnym ci»arze. rodowisko Matlab okazaªo si bardzo przydatne i przyjazne. 4
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Struktury i Algorytmy Wspomagania Decyzji Zapoznanie z narzędziami optymalizacyjnymi w środowisku MATLAB
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Struktury i Algorytmy Wspomagania Decyzji Zapoznanie z narzędziami optymalizacyjnymi w środowisku MATLAB
Temat: Co to jest optymalizacja? Maksymalizacja objętości naczynia prostopadłościennego za pomocą arkusza kalkulacyjngo.
 Konspekt lekcji Przedmiot: Informatyka Typ szkoły: Gimnazjum Klasa: II Nr programu nauczania: DKW-4014-87/99 Czas trwania zajęć: 90min Temat: Co to jest optymalizacja? Maksymalizacja objętości naczynia
Konspekt lekcji Przedmiot: Informatyka Typ szkoły: Gimnazjum Klasa: II Nr programu nauczania: DKW-4014-87/99 Czas trwania zajęć: 90min Temat: Co to jest optymalizacja? Maksymalizacja objętości naczynia
d) Definiowanie macierzy z wykorzystaniem funkcji systemu Matlak
 OPTYMALIZACJA W ŚRODOWISKU MATLAB. Cel ćwiczeń Celem ćwiczeń jest zaznajomienie studentów z podstawową obsługą środowiska obliczeń inżynierskich Matlab oraz zapoznanie się z możliwościami przeprowadzenia
OPTYMALIZACJA W ŚRODOWISKU MATLAB. Cel ćwiczeń Celem ćwiczeń jest zaznajomienie studentów z podstawową obsługą środowiska obliczeń inżynierskich Matlab oraz zapoznanie się z możliwościami przeprowadzenia
Spis treści. Koszalin 2006 [BADANIA OPERACYJNE PROGRAMOWANIE LINIOWE]
![Spis treści. Koszalin 2006 [BADANIA OPERACYJNE PROGRAMOWANIE LINIOWE] Spis treści. Koszalin 2006 [BADANIA OPERACYJNE PROGRAMOWANIE LINIOWE]](/thumbs/24/2378181.jpg) Spis treści 1 Zastosowanie Matlab a... 2 1.1 Wstęp... 2 1.2 Zagadnienie standardowe... 3 1.3 Zagadnienie transportowe... 5 1 Zastosowanie Matlab a Anna Tomkowska [BADANIA OPERACYJNE PROGRAMOWANIE LINIOWE]
Spis treści 1 Zastosowanie Matlab a... 2 1.1 Wstęp... 2 1.2 Zagadnienie standardowe... 3 1.3 Zagadnienie transportowe... 5 1 Zastosowanie Matlab a Anna Tomkowska [BADANIA OPERACYJNE PROGRAMOWANIE LINIOWE]
Rachunek ró»niczkowy funkcji jednej zmiennej
 Lista Nr 5 Rachunek ró»niczkowy funkcji jednej zmiennej 5.0. Obliczanie pochodnej funkcji Pochodne funkcji podstawowych. f() = α f () = α α. f() = log a f () = ln a '. f() = ln f () = 3. f() = a f () =
Lista Nr 5 Rachunek ró»niczkowy funkcji jednej zmiennej 5.0. Obliczanie pochodnej funkcji Pochodne funkcji podstawowych. f() = α f () = α α. f() = log a f () = ln a '. f() = ln f () = 3. f() = a f () =
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Metody optymalizacji Narzędzia optymalizacji w środowisku MATLAB Materiały pomocnicze do ćwiczeń laboratoryjnych
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Metody optymalizacji Narzędzia optymalizacji w środowisku MATLAB Materiały pomocnicze do ćwiczeń laboratoryjnych
Zasady rekrutacji 2016/2017 do liceum, technikum i szkoły zawodowej. Spis treści
 Zasady rekrutacji na rok szkolny 2016/2017 do III Liceum Ogólnokształcącego, Technikum Nr 3 i Zasadniczej Szkoły Zawodowej w Zespole Szkół RCKU w Piasecznie Spis treści 1. Etapy rekrutacji... 2 2. Warunki
Zasady rekrutacji na rok szkolny 2016/2017 do III Liceum Ogólnokształcącego, Technikum Nr 3 i Zasadniczej Szkoły Zawodowej w Zespole Szkół RCKU w Piasecznie Spis treści 1. Etapy rekrutacji... 2 2. Warunki
ARYTMETYKA MODULARNA. Grzegorz Szkibiel. Wiosna 2014/15
 ARYTMETYKA MODULARNA Grzegorz Szkibiel Wiosna 2014/15 Spis tre±ci 1 Denicja kongruencji i jej podstawowe wªasno±ci 3 2 Systemy pozycyjne 8 3 Elementy odwrotne 12 4 Pewne zastosowania elementów odwrotnych
ARYTMETYKA MODULARNA Grzegorz Szkibiel Wiosna 2014/15 Spis tre±ci 1 Denicja kongruencji i jej podstawowe wªasno±ci 3 2 Systemy pozycyjne 8 3 Elementy odwrotne 12 4 Pewne zastosowania elementów odwrotnych
Liniowe równania ró»niczkowe n tego rz du o staªych wspóªczynnikach
 Liniowe równania ró»niczkowe n tego rz du o staªych wspóªczynnikach Teoria obowi zuje z wykªadu, dlatego te» zostan tutaj przedstawione tylko podstawowe denicje, twierdzenia i wzory. Denicja 1. Równanie
Liniowe równania ró»niczkowe n tego rz du o staªych wspóªczynnikach Teoria obowi zuje z wykªadu, dlatego te» zostan tutaj przedstawione tylko podstawowe denicje, twierdzenia i wzory. Denicja 1. Równanie
Elementy geometrii w przestrzeni R 3
 Elementy geometrii w przestrzeni R 3 Z.Šagodowski Politechnika Lubelska 29 maja 2016 Podstawowe denicje Wektorem nazywamy uporz dkowan par punktów (A,B) z których pierwszy nazywa si pocz tkiem a drugi
Elementy geometrii w przestrzeni R 3 Z.Šagodowski Politechnika Lubelska 29 maja 2016 Podstawowe denicje Wektorem nazywamy uporz dkowan par punktów (A,B) z których pierwszy nazywa si pocz tkiem a drugi
Cz. X. MAKRONIWELACJA TERENU. Spis zawarto ci
 Cz. X. MAKRONIWELACJA TERENU A. Cz opisowa B. Cz graficzna Spis zawarto ci Spis rysunków: Skala: Rys. M-01 Plan sytuacyjny oznaczenie przekrojów 1: 1000 Przekroje podłu ne wzdłu kierunku: zachód (W)-wschód
Cz. X. MAKRONIWELACJA TERENU A. Cz opisowa B. Cz graficzna Spis zawarto ci Spis rysunków: Skala: Rys. M-01 Plan sytuacyjny oznaczenie przekrojów 1: 1000 Przekroje podłu ne wzdłu kierunku: zachód (W)-wschód
Załącznik Nr 1 do Uchwały Nr 147 Rady Miasta Konina z dnia 29 czerwca 2011 r.
 Załącznik Nr 1 do Uchwały Nr 147 Rady Miasta Konina z dnia 29 czerwca 2011 r. Regulamin udzielenia dotacji celowej na dofinansowanie kosztów inwestycji z zakresu ochrony środowiska i gospodarki wodnej
Załącznik Nr 1 do Uchwały Nr 147 Rady Miasta Konina z dnia 29 czerwca 2011 r. Regulamin udzielenia dotacji celowej na dofinansowanie kosztów inwestycji z zakresu ochrony środowiska i gospodarki wodnej
OBLICZENIA OPTYMALIZACYJNE W MATLABIE. WEiTI PW
 OBLICZENIA OPTYMALIZACYJNE W MATLABIE Definicje pojęć, na przykładzie projektowania iteracyjnego w oparciu o przebieg charakterystyki T(f) T f Definicje pojęć FUNKCJA CELU (objective function) (funkcjonał)
OBLICZENIA OPTYMALIZACYJNE W MATLABIE Definicje pojęć, na przykładzie projektowania iteracyjnego w oparciu o przebieg charakterystyki T(f) T f Definicje pojęć FUNKCJA CELU (objective function) (funkcjonał)
1 Metody iteracyjne rozwi zywania równania f(x)=0
 1 Metody iteracyjne rozwi zywania równania f()=0 1.1 Metoda bisekcji Zaªó»my,»e funkcja f jest ci gªa w [a 0, b 0 ]. Pierwiastek jest w przedziale [a 0, b 0 ] gdy f(a 0 )f(b 0 ) < 0. (1) Ustalmy f(a 0
1 Metody iteracyjne rozwi zywania równania f()=0 1.1 Metoda bisekcji Zaªó»my,»e funkcja f jest ci gªa w [a 0, b 0 ]. Pierwiastek jest w przedziale [a 0, b 0 ] gdy f(a 0 )f(b 0 ) < 0. (1) Ustalmy f(a 0
Elementarna statystyka Dwie próby: porównanie dwóch proporcji (Two-sample problem: comparing two proportions)
 Elementarna statystyka Dwie próby: porównanie dwóch proporcji (Two-sample problem: comparing two proportions) Alexander Bendikov Uniwersytet Wrocªawski 25 maja 2016 Elementarna statystyka Dwie próby: porównanie
Elementarna statystyka Dwie próby: porównanie dwóch proporcji (Two-sample problem: comparing two proportions) Alexander Bendikov Uniwersytet Wrocªawski 25 maja 2016 Elementarna statystyka Dwie próby: porównanie
Aproksymacja funkcji metod najmniejszych kwadratów
 Aproksymacja funkcji metod najmniejszych kwadratów Teoria Interpolacja polega na znajdowaniu krzywej przechodz cej przez wszystkie w zªy. Zdarzaj si jednak sytuacje, w których dane te mog by obarczone
Aproksymacja funkcji metod najmniejszych kwadratów Teoria Interpolacja polega na znajdowaniu krzywej przechodz cej przez wszystkie w zªy. Zdarzaj si jednak sytuacje, w których dane te mog by obarczone
Twierdzenie Wainera. Marek Czarnecki. Warszawa, 3 lipca Wydziaª Filozoi i Socjologii Uniwersytet Warszawski
 Twierdzenie Wainera Marek Czarnecki Wydziaª Filozoi i Socjologii Uniwersytet Warszawski Wydziaª Matematyki, Informatyki i Mechaniki Uniwersytet Warszawski Warszawa, 3 lipca 2009 Motywacje Dla dowolnej
Twierdzenie Wainera Marek Czarnecki Wydziaª Filozoi i Socjologii Uniwersytet Warszawski Wydziaª Matematyki, Informatyki i Mechaniki Uniwersytet Warszawski Warszawa, 3 lipca 2009 Motywacje Dla dowolnej
Rozwi zanie równania ró»niczkowego metod operatorow (zastosowanie transformaty Laplace'a).
 Rozwi zania zada«z egzaminu podstawowego z Analizy matematycznej 2.3A (24/5). Rozwi zanie równania ró»niczkowego metod operatorow (zastosowanie transformaty Laplace'a). Zadanie P/4. Metod operatorow rozwi
Rozwi zania zada«z egzaminu podstawowego z Analizy matematycznej 2.3A (24/5). Rozwi zanie równania ró»niczkowego metod operatorow (zastosowanie transformaty Laplace'a). Zadanie P/4. Metod operatorow rozwi
Funkcje wielu zmiennych
 dr Krzysztof yjewski Informatyka I rok I 0 in» 12 stycznia 2016 Funkcje wielu zmiennych Informacje pomocnicze Denicja 1 Niech funkcja f(x y) b dzie okre±lona przynajmniej na otoczeniu punktu (x 0 y 0 )
dr Krzysztof yjewski Informatyka I rok I 0 in» 12 stycznia 2016 Funkcje wielu zmiennych Informacje pomocnicze Denicja 1 Niech funkcja f(x y) b dzie okre±lona przynajmniej na otoczeniu punktu (x 0 y 0 )
Krzysztof Trajkowski. Przegląd pakietów do optymalizacji liniowej
 Krzysztof Trajkowski Przegląd pakietów do optymalizacji liniowej 1. Wprowadzenie Niniejsze opracowanie dotyczy opisu funkcji solvelp(linprog) i lp(lpsolve) za pomocą których możemy rozwiązywać zadania
Krzysztof Trajkowski Przegląd pakietów do optymalizacji liniowej 1. Wprowadzenie Niniejsze opracowanie dotyczy opisu funkcji solvelp(linprog) i lp(lpsolve) za pomocą których możemy rozwiązywać zadania
REMONT OGRODZENIA SZKOŁY PODSTAWOWEJ NR 162
 PW IKAR IWONA KARACZKO ul. Pomorska 290/292,92-113 ŁÓDŹ TEMAT OPRACOWANIA:: OPIS PRZEDMIOTU ZAMÓWIENIA REMONT OGRODZENIA SZKOŁY PODSTAWOWEJ NR 162 INWESTOR : SZKOŁA PODSTAWOWA NR 162 93-321 Łódź ul. Powszechna
PW IKAR IWONA KARACZKO ul. Pomorska 290/292,92-113 ŁÓDŹ TEMAT OPRACOWANIA:: OPIS PRZEDMIOTU ZAMÓWIENIA REMONT OGRODZENIA SZKOŁY PODSTAWOWEJ NR 162 INWESTOR : SZKOŁA PODSTAWOWA NR 162 93-321 Łódź ul. Powszechna
Funkcje, wielomiany. Informacje pomocnicze
 Funkcje, wielomiany Informacje pomocnicze Przydatne wzory: (a + b) 2 = a 2 + 2ab + b 2 (a b) 2 = a 2 2ab + b 2 (a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3 (a b) 3 = a 3 3a 2 b + 3ab 2 b 3 a 2 b 2 = (a + b)(a
Funkcje, wielomiany Informacje pomocnicze Przydatne wzory: (a + b) 2 = a 2 + 2ab + b 2 (a b) 2 = a 2 2ab + b 2 (a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3 (a b) 3 = a 3 3a 2 b + 3ab 2 b 3 a 2 b 2 = (a + b)(a
Zadbaj o to aby wszyscy pracownicy w Twojej firmie zostali odpowiednio przeszkoleni pod kątem BHP
 Zadbaj o to aby wszyscy pracownicy w Twojej firmie zostali odpowiednio przeszkoleni pod kątem BHP, gdyż zgodnie z Rozporządzeniem Ministra Gospodarki i Pracy z dnia 27 lipca 2004r w sprawie szkolenia w
Zadbaj o to aby wszyscy pracownicy w Twojej firmie zostali odpowiednio przeszkoleni pod kątem BHP, gdyż zgodnie z Rozporządzeniem Ministra Gospodarki i Pracy z dnia 27 lipca 2004r w sprawie szkolenia w
Obowiązki przedsiębiorców prowadzących stacje demontażu Art. 21. Przedsiębiorca prowadzący stację demontażu powinien zapewniać bezpieczne dla
 Obowiązki przedsiębiorców prowadzących stacje demontażu Art. 21. Przedsiębiorca prowadzący stację demontażu powinien zapewniać bezpieczne dla środowiska i zdrowia ludzi przetwarzanie pojazdów wycofanych
Obowiązki przedsiębiorców prowadzących stacje demontażu Art. 21. Przedsiębiorca prowadzący stację demontażu powinien zapewniać bezpieczne dla środowiska i zdrowia ludzi przetwarzanie pojazdów wycofanych
przewidywania zapotrzebowania na moc elektryczn
 do Wykorzystanie do na moc elektryczn Instytut Techniki Cieplnej Politechnika Warszawska Slide 1 of 20 do Coraz bardziej popularne staj si zagadnienia zwi zane z prac ¹ródªa energii elektrycznej (i cieplnej)
do Wykorzystanie do na moc elektryczn Instytut Techniki Cieplnej Politechnika Warszawska Slide 1 of 20 do Coraz bardziej popularne staj si zagadnienia zwi zane z prac ¹ródªa energii elektrycznej (i cieplnej)
ARYTMETYKA MODULARNA. Grzegorz Szkibiel. Wiosna 2014/15
 ARYTMETYKA MODULARNA Grzegorz Szkibiel Wiosna 2014/15 Spis tre±ci 1 Denicja kongruencji i jej podstawowe wªasno±ci 3 2 Systemy pozycyjne 8 3 Elementy odwrotne 12 4 Pewne zastosowania elementów odwrotnych
ARYTMETYKA MODULARNA Grzegorz Szkibiel Wiosna 2014/15 Spis tre±ci 1 Denicja kongruencji i jej podstawowe wªasno±ci 3 2 Systemy pozycyjne 8 3 Elementy odwrotne 12 4 Pewne zastosowania elementów odwrotnych
MODEL HAHNFELDTA I IN. ANGIOGENEZY NOWOTWOROWEJ Z UWZGL DNIENIEM LEKOOPORNO CI KOMÓREK NOWOTWOROWYCH
 MODEL HAHNFELDTA I IN. ANGIOGENEZY NOWOTWOROWEJ Z UWZGL DNIENIEM LEKOOPORNO CI KOMÓREK NOWOTWOROWYCH Urszula Fory± Zakªad Biomatematyki i Teorii Gier, Instytut Matematyki Stosowanej i Mechaniki, Wydziaª
MODEL HAHNFELDTA I IN. ANGIOGENEZY NOWOTWOROWEJ Z UWZGL DNIENIEM LEKOOPORNO CI KOMÓREK NOWOTWOROWYCH Urszula Fory± Zakªad Biomatematyki i Teorii Gier, Instytut Matematyki Stosowanej i Mechaniki, Wydziaª
ARYTMETYKA MODULARNA. Grzegorz Szkibiel. Wiosna 2014/15
 ARYTMETYKA MODULARNA Grzegorz Szkibiel Wiosna 2014/15 Spis tre±ci 1 Denicja kongruencji i jej podstawowe wªasno±ci 3 2 Systemy pozycyjne 8 3 Elementy odwrotne 12 4 Pewne zastosowania elementów odwrotnych
ARYTMETYKA MODULARNA Grzegorz Szkibiel Wiosna 2014/15 Spis tre±ci 1 Denicja kongruencji i jej podstawowe wªasno±ci 3 2 Systemy pozycyjne 8 3 Elementy odwrotne 12 4 Pewne zastosowania elementów odwrotnych
WZORU UŻYTKOWEGO EGZEMPLARZ ARCHIWALNY. d2)opis OCHRONNY. (19) PL (n)62894. Centralny Instytut Ochrony Pracy, Warszawa, PL
 RZECZPOSPOLITA POLSKA Urząd Patentowy Rzeczypospolitej Polskiej d2)opis OCHRONNY WZORU UŻYTKOWEGO (21) Numer zgłoszenia: 112772 (22) Data zgłoszenia: 29.11.2001 EGZEMPLARZ ARCHIWALNY (19) PL (n)62894 (13)
RZECZPOSPOLITA POLSKA Urząd Patentowy Rzeczypospolitej Polskiej d2)opis OCHRONNY WZORU UŻYTKOWEGO (21) Numer zgłoszenia: 112772 (22) Data zgłoszenia: 29.11.2001 EGZEMPLARZ ARCHIWALNY (19) PL (n)62894 (13)
Informacje pomocnicze
 Funkcje wymierne. Równania i nierówno±ci wymierne Denicja. (uªamki proste) Wyra»enia postaci Informacje pomocnicze A gdzie A d e R n N (dx e) n nazywamy uªamkami prostymi pierwszego rodzaju. Wyra»enia
Funkcje wymierne. Równania i nierówno±ci wymierne Denicja. (uªamki proste) Wyra»enia postaci Informacje pomocnicze A gdzie A d e R n N (dx e) n nazywamy uªamkami prostymi pierwszego rodzaju. Wyra»enia
Kolokwium Zadanie 1. Dla jakich warto±ci parametrów a i b funkcja sklejona
 Kolokwium 3 0.0. Zadanie. Dla jakich warto±ci parametrów a i b funkcja sklejona a : π, f() = cos() : π < π, a + b : π < jest ci gªa? Rozwi zanie: Funkcja jest ci gªa we wszystkich punktach poza, by mo»e,
Kolokwium 3 0.0. Zadanie. Dla jakich warto±ci parametrów a i b funkcja sklejona a : π, f() = cos() : π < π, a + b : π < jest ci gªa? Rozwi zanie: Funkcja jest ci gªa we wszystkich punktach poza, by mo»e,
K P K P R K P R D K P R D W
 KLASA III TECHNIKUM POZIOM PODSTAWOWY I ROZSZERZONY PROPOZYCJA POZIOMÓW WYMAGAŃ Wyróżnione zostały następujące wymagania programowe: konieczne (K), podstawowe (P), rozszerzające (R), dopełniające (D) i
KLASA III TECHNIKUM POZIOM PODSTAWOWY I ROZSZERZONY PROPOZYCJA POZIOMÓW WYMAGAŃ Wyróżnione zostały następujące wymagania programowe: konieczne (K), podstawowe (P), rozszerzające (R), dopełniające (D) i
ARKUSZ EGZAMINACYJNY ETAP PRAKTYCZNY EGZAMINU POTWIERDZAJ CEGO KWALIFIKACJE ZAWODOWE CZERWIEC 2012
 Zawód: technik in ynierii rodowiska i melioracji Symbol cyfrowy zawodu: 311[19] Numer zadania: 1 Arkusz zawiera informacje prawnie chronione do momentu rozpocz cia egzaminu 311[19]-01-122 Czas trwania
Zawód: technik in ynierii rodowiska i melioracji Symbol cyfrowy zawodu: 311[19] Numer zadania: 1 Arkusz zawiera informacje prawnie chronione do momentu rozpocz cia egzaminu 311[19]-01-122 Czas trwania
OBLICZENIA IZOLACYJNOŚCI AKUSTYCZNEJ PRZEGRÓD BUDOWLANYCH
 Nazwa opracowania: OBLICZENIA IZOLACYJNOŚCI AKUSTYCZNEJ PRZEGRÓD BUDOWLANYCH Inwestor: Wojskowa Agencja Mieszkaniowa Oddział Regionalny w Gdyni ul. M. Skłodowskiej Curie 19 81-231 Gdynia Inwestycja: Wielorodzinny
Nazwa opracowania: OBLICZENIA IZOLACYJNOŚCI AKUSTYCZNEJ PRZEGRÓD BUDOWLANYCH Inwestor: Wojskowa Agencja Mieszkaniowa Oddział Regionalny w Gdyni ul. M. Skłodowskiej Curie 19 81-231 Gdynia Inwestycja: Wielorodzinny
sektora oświaty objętych programem zwolnień
 Wsparcie pracowników instytucji sektora oświaty objętych programem zwolnień Zakres możliwej interwencji Osoby zwolnione w okresie do 6 miesięcy przed przystąpieniem do projektu, osoby zagrożone zwolnieniem
Wsparcie pracowników instytucji sektora oświaty objętych programem zwolnień Zakres możliwej interwencji Osoby zwolnione w okresie do 6 miesięcy przed przystąpieniem do projektu, osoby zagrożone zwolnieniem
Centrum Konsultingowo-Wdrożeniowe INTER-EKO Sp. z o.o.
 ul. Budziszyńska 2, 31-619 Kraków Tel.:+48126410002 E-mail: office@inter-eko.net.pl Internet: www.inter-eko.net.pl Opracowanie pt. Wytyczne dotyczące adaptacji akustycznej sali nr 127 w Pracowni Technik
ul. Budziszyńska 2, 31-619 Kraków Tel.:+48126410002 E-mail: office@inter-eko.net.pl Internet: www.inter-eko.net.pl Opracowanie pt. Wytyczne dotyczące adaptacji akustycznej sali nr 127 w Pracowni Technik
SPECYFIKACJA TECHNICZNA WYKONANIA I ODBIORU ROBÓT BUDOWLANYCH 45421000-4 ROBOTY W ZAKRESIE STOLARKI BUDOWLANEJ
 SPECYFIKACJA TECHNICZNA WYKONANIA I ODBIORU ROBÓT BUDOWLANYCH 45421000-4 ROBOTY W ZAKRESIE STOLARKI BUDOWLANEJ 1 SPIS TREŚCI 1. WSTĘP str. 3 2. MATERIAŁY str. 3 3. SPRZĘT str. 4 4.TRANSPORT str. 4 5. WYKONANIE
SPECYFIKACJA TECHNICZNA WYKONANIA I ODBIORU ROBÓT BUDOWLANYCH 45421000-4 ROBOTY W ZAKRESIE STOLARKI BUDOWLANEJ 1 SPIS TREŚCI 1. WSTĘP str. 3 2. MATERIAŁY str. 3 3. SPRZĘT str. 4 4.TRANSPORT str. 4 5. WYKONANIE
PROJEKT BUDOWLANY. Projekt posadowienia maszyny wytrzymałociowej
 PROJEKT BUDOWLANY Tytuł: Projekt posadowienia maszyny wytrzymałociowej Adres inwestycji: Uniwersytet Przyrodniczy we Wrocławiu Wydział Inynierii Kształtowania rodowiska i Geodezji Laboratorium Materiałów
PROJEKT BUDOWLANY Tytuł: Projekt posadowienia maszyny wytrzymałociowej Adres inwestycji: Uniwersytet Przyrodniczy we Wrocławiu Wydział Inynierii Kształtowania rodowiska i Geodezji Laboratorium Materiałów
ZGM/DZ/99/2014/ADM Bielsko-Biała, dnia 30. 12. 2014r.
 Z a k ł a d G o s p o d a r k i M i e s z k a n i o w e j 4 3 3 0 0 B i e l s k o B i a ł a u l. L i p n i c k a 2 6 Tel. (33) 499-06-02, Fax (33) 499-06-02, www.bip.zgm.eu ZGM/DZ/99/2014/ADM Bielsko-Biała,
Z a k ł a d G o s p o d a r k i M i e s z k a n i o w e j 4 3 3 0 0 B i e l s k o B i a ł a u l. L i p n i c k a 2 6 Tel. (33) 499-06-02, Fax (33) 499-06-02, www.bip.zgm.eu ZGM/DZ/99/2014/ADM Bielsko-Biała,
Metody numeryczne i statystyka dla in»ynierów
 Kierunek: Automatyka i Robotyka, II rok Wprowadzenie PWSZ Gªogów, 2009 Plan wykªadów Wprowadzenie, podanie zagadnie«, poj cie metody numerycznej i algorytmu numerycznego, obszar zainteresowa«i stosowalno±ci
Kierunek: Automatyka i Robotyka, II rok Wprowadzenie PWSZ Gªogów, 2009 Plan wykªadów Wprowadzenie, podanie zagadnie«, poj cie metody numerycznej i algorytmu numerycznego, obszar zainteresowa«i stosowalno±ci
PL-LS.054.24.2015 Pani Małgorzata Kidawa Błońska Marszałek Sejmu RP
 Warszawa, dnia 04 września 2015 r. RZECZPOSPOLITA POLSKA MINISTER FINANSÓW PL-LS.054.24.2015 Pani Małgorzata Kidawa Błońska Marszałek Sejmu RP W związku z interpelacją nr 34158 posła Jana Warzechy i posła
Warszawa, dnia 04 września 2015 r. RZECZPOSPOLITA POLSKA MINISTER FINANSÓW PL-LS.054.24.2015 Pani Małgorzata Kidawa Błońska Marszałek Sejmu RP W związku z interpelacją nr 34158 posła Jana Warzechy i posła
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: Podstawy i specjalne systemy wodociągowo-kanalizacyjne The basics of operation and special water supply and sewerage systems Kierunek: inżynieria środowiska Rodzaj przedmiotu: Poziom
Nazwa przedmiotu: Podstawy i specjalne systemy wodociągowo-kanalizacyjne The basics of operation and special water supply and sewerage systems Kierunek: inżynieria środowiska Rodzaj przedmiotu: Poziom
Ustawienie wózka w pojeździe komunikacji miejskiej - badania. Prawidłowe ustawienie
 Ustawienie wózka w pojeździe komunikacji miejskiej - badania Przodem do kierunku jazdy? Bokiem? Tyłem? Jak ustawić wózek, aby w razie awaryjnego hamowania dziecko było jak najbardziej bezpieczne? Na te
Ustawienie wózka w pojeździe komunikacji miejskiej - badania Przodem do kierunku jazdy? Bokiem? Tyłem? Jak ustawić wózek, aby w razie awaryjnego hamowania dziecko było jak najbardziej bezpieczne? Na te
CAŠKOWANIE METODAMI MONTE CARLO Janusz Adamowski
 III. CAŠKOWAIE METODAMI MOTE CARLO Janusz Adamowski 1 1 azwa metody Podstawowym zastosowaniem w zyce metody Monte Carlo (MC) jest opis zªo-»onych ukªadów zycznych o du»ej liczbie stopni swobody. Opis zªo»onych
III. CAŠKOWAIE METODAMI MOTE CARLO Janusz Adamowski 1 1 azwa metody Podstawowym zastosowaniem w zyce metody Monte Carlo (MC) jest opis zªo-»onych ukªadów zycznych o du»ej liczbie stopni swobody. Opis zªo»onych
EGZAMIN MATURALNY 2013 MATEMATYKA
 entralna Komisja Egzaminacyjna EGZMIN MTURLNY 0 MTEMTYK POZIOM PODSTWOWY Kryteria oceniania odpowiedzi MJ 0 Egzamin maturalny z matematyki Zadanie (0 ) Obszar standardów Zadanie (0 ) Opis wymagań pojęcia
entralna Komisja Egzaminacyjna EGZMIN MTURLNY 0 MTEMTYK POZIOM PODSTWOWY Kryteria oceniania odpowiedzi MJ 0 Egzamin maturalny z matematyki Zadanie (0 ) Obszar standardów Zadanie (0 ) Opis wymagań pojęcia
WYPOSAŻENIE WNĘTRZ W MEBLE ARCHIWUM ZAKŁADOWE
 WYPOSAŻENIE WNĘTRZ W MEBLE ARCHIWUM ZAKŁADOWE NAZWA I ADRES OBIEKTU BUDOWLANEGO INWESTOR ZAKRES OPRACOWANIA BUDYNEK URZĘDU MIASTA W STALOWEJ WOLI ul. Wolności 7, 37-450 Stalowa Wola URZĄD MIASTA W STALOWEJ
WYPOSAŻENIE WNĘTRZ W MEBLE ARCHIWUM ZAKŁADOWE NAZWA I ADRES OBIEKTU BUDOWLANEGO INWESTOR ZAKRES OPRACOWANIA BUDYNEK URZĘDU MIASTA W STALOWEJ WOLI ul. Wolności 7, 37-450 Stalowa Wola URZĄD MIASTA W STALOWEJ
GEO-SYSTEM Sp. z o.o. GEO-RCiWN Rejestr Cen i Wartości Nieruchomości Podręcznik dla uŝytkowników modułu wyszukiwania danych Warszawa 2007
 GEO-SYSTEM Sp. z o.o. 02-732 Warszawa, ul. Podbipięty 34 m. 7, tel./fax 847-35-80, 853-31-15 http:\\www.geo-system.com.pl e-mail:geo-system@geo-system.com.pl GEO-RCiWN Rejestr Cen i Wartości Nieruchomości
GEO-SYSTEM Sp. z o.o. 02-732 Warszawa, ul. Podbipięty 34 m. 7, tel./fax 847-35-80, 853-31-15 http:\\www.geo-system.com.pl e-mail:geo-system@geo-system.com.pl GEO-RCiWN Rejestr Cen i Wartości Nieruchomości
Wojewódzki Konkurs Matematyczny
 Wojewódzki Konkurs Matematyczny dla uczniów gimnazjów ETAP SZKOLNY 16 listopada 2012 Czas 90 minut Instrukcja dla Ucznia 1. Otrzymujesz do rozwi zania 10 zada«zamkni tych oraz 5 zada«otwartych. 2. Obok
Wojewódzki Konkurs Matematyczny dla uczniów gimnazjów ETAP SZKOLNY 16 listopada 2012 Czas 90 minut Instrukcja dla Ucznia 1. Otrzymujesz do rozwi zania 10 zada«zamkni tych oraz 5 zada«otwartych. 2. Obok
ODPOWIEDZI I SCHEMAT PUNKTOWANIA ZESTAW NR 2 POZIOM ROZSZERZONY. S x 3x y. 1.5 Podanie odpowiedzi: Poszukiwane liczby to : 2, 6, 5.
 Nr zadania Nr czynno ci... ODPOWIEDZI I SCHEMAT PUNKTOWANIA ZESTAW NR POZIOM ROZSZERZONY Etapy rozwi zania zadania Wprowadzenie oznacze : x, x, y poszukiwane liczby i zapisanie równania: x y lub: zapisanie
Nr zadania Nr czynno ci... ODPOWIEDZI I SCHEMAT PUNKTOWANIA ZESTAW NR POZIOM ROZSZERZONY Etapy rozwi zania zadania Wprowadzenie oznacze : x, x, y poszukiwane liczby i zapisanie równania: x y lub: zapisanie
2.Prawo zachowania masy
 2.Prawo zachowania masy Zdefiniujmy najpierw pewne podstawowe pojęcia: Układ - obszar przestrzeni o określonych granicach Ośrodek ciągły - obszar przestrzeni którego rozmiary charakterystyczne są wystarczająco
2.Prawo zachowania masy Zdefiniujmy najpierw pewne podstawowe pojęcia: Układ - obszar przestrzeni o określonych granicach Ośrodek ciągły - obszar przestrzeni którego rozmiary charakterystyczne są wystarczająco
Komentarz do prac egzaminacyjnych w zawodzie technik administracji 343[01] ETAP PRAKTYCZNY EGZAMINU POTWIERDZAJĄCEGO KWALIFIKACJE ZAWODOWE
![Komentarz do prac egzaminacyjnych w zawodzie technik administracji 343[01] ETAP PRAKTYCZNY EGZAMINU POTWIERDZAJĄCEGO KWALIFIKACJE ZAWODOWE Komentarz do prac egzaminacyjnych w zawodzie technik administracji 343[01] ETAP PRAKTYCZNY EGZAMINU POTWIERDZAJĄCEGO KWALIFIKACJE ZAWODOWE](/thumbs/39/18551291.jpg) Komentarz do prac egzaminacyjnych w zawodzie technik administracji 343[01] ETAP PRAKTYCZNY EGZAMINU POTWIERDZAJĄCEGO KWALIFIKACJE ZAWODOWE OKE Kraków 2012 Zadanie egzaminacyjne zostało opracowane
Komentarz do prac egzaminacyjnych w zawodzie technik administracji 343[01] ETAP PRAKTYCZNY EGZAMINU POTWIERDZAJĄCEGO KWALIFIKACJE ZAWODOWE OKE Kraków 2012 Zadanie egzaminacyjne zostało opracowane
g. Zamiast wiersza drugiego Język obcy wprowadzono pięć rozdzielnych wierszy następującej treści: Język obcy I, Język obcy
 ZAŁĄCZNIK 1c Zmiany w planach studiów na kierunku Elektrotechnika: Zmiany w grupie A. Przedmioty ogólne: a. Na studiach stacjonarnych, dla wszystkich specjalności zmieniono w wierszu pierwszym Wychowanie
ZAŁĄCZNIK 1c Zmiany w planach studiów na kierunku Elektrotechnika: Zmiany w grupie A. Przedmioty ogólne: a. Na studiach stacjonarnych, dla wszystkich specjalności zmieniono w wierszu pierwszym Wychowanie
Zarządzenie Nr 0151/18/2006 Wójta Gminy Kornowac z dnia 12 czerwca 2006r.
 Zarządzenie Nr 0151/18/2006 Wójta Gminy Kornowac z dnia 12 czerwca 2006r. w sprawie: ogłoszenia otwartego konkursu ofert na zadanie publiczne Gminy Kornowac w sprawie realizacji programu zdrowotnego: Ty
Zarządzenie Nr 0151/18/2006 Wójta Gminy Kornowac z dnia 12 czerwca 2006r. w sprawie: ogłoszenia otwartego konkursu ofert na zadanie publiczne Gminy Kornowac w sprawie realizacji programu zdrowotnego: Ty
1 Granice funkcji wielu zmiennych.
 AM WNE 008/009. Odpowiedzi do zada«przygotowawczych do czwartego kolokwium. Granice funkcji wielu zmiennych. Zadanie. Zadanie. Pochodne. (a) 0, Granica nie istnieje, (c) Granica nie istnieje, (d) Granica
AM WNE 008/009. Odpowiedzi do zada«przygotowawczych do czwartego kolokwium. Granice funkcji wielu zmiennych. Zadanie. Zadanie. Pochodne. (a) 0, Granica nie istnieje, (c) Granica nie istnieje, (d) Granica
X WARMI SKO-MAZURSKIE ZAWODY MATEMATYCZNE 18 maja 2012 (szkoªy ponadgimnazjalne)
 X WARMI SKO-MAZURSKIE ZAWODY MATEMATYCZNE 18 maja 2012 (szkoªy ponadgimnazjalne) Zadanie 1 Obecnie u»ywane tablice rejestracyjne wydawane s od 1 maja 2000r. Numery rejestracyjne aut s tworzone ze zbioru
X WARMI SKO-MAZURSKIE ZAWODY MATEMATYCZNE 18 maja 2012 (szkoªy ponadgimnazjalne) Zadanie 1 Obecnie u»ywane tablice rejestracyjne wydawane s od 1 maja 2000r. Numery rejestracyjne aut s tworzone ze zbioru
Czas pracy 170 minut
 ORGANIZATOR WSPÓŁORGANIZATOR PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI MARZEC ROK 013 POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla piszącego 1. Sprawdź, czy arkusz zawiera 16 stron.. W zadaniach od
ORGANIZATOR WSPÓŁORGANIZATOR PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI MARZEC ROK 013 POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla piszącego 1. Sprawdź, czy arkusz zawiera 16 stron.. W zadaniach od
XVII Warmi«sko-Mazurskie Zawody Matematyczne
 1 XVII Warmi«sko-Mazurskie Zawody Matematyczne Kategoria: klasa VIII szkoªy podstawowej i III gimnazjum Olsztyn, 16 maja 2019r. Zad. 1. Udowodnij,»e dla dowolnych liczb rzeczywistych x, y, z speªniaj cych
1 XVII Warmi«sko-Mazurskie Zawody Matematyczne Kategoria: klasa VIII szkoªy podstawowej i III gimnazjum Olsztyn, 16 maja 2019r. Zad. 1. Udowodnij,»e dla dowolnych liczb rzeczywistych x, y, z speªniaj cych
1. NAUCZANIE JĘZYKÓW NOWOŻYTNYCH (OBOWIĄZKOWYCH) W RAMACH PROGRAMU STUDIÓW STACJONARNYCH (CYKL A I B) I NIESTACJONARNYCH
 1 Szczegółowe przepisy wykonawcze na rok akadem. 2010/11 wprowadzające w życie Zarządzenie Rektora PWT we Wrocławiu w sprawie nauczania języków obcych na PWT we Wrocławiu z dnia 29 września 2009 r. 1.
1 Szczegółowe przepisy wykonawcze na rok akadem. 2010/11 wprowadzające w życie Zarządzenie Rektora PWT we Wrocławiu w sprawie nauczania języków obcych na PWT we Wrocławiu z dnia 29 września 2009 r. 1.
Raport z realizacji projektu szkoleń w ramach programu Komputer dla ucznia w roku 2008. Uczestnicy projektu oraz ewaluacja szkoleń
 Raport z realizacji projektu szkoleń w ramach programu Komputer dla ucznia w roku 2008 Uczestnicy projektu oraz ewaluacja szkoleń 1 Wprowadzenie Omawiane w raporcie szkolenia były realizowane przez OFEK
Raport z realizacji projektu szkoleń w ramach programu Komputer dla ucznia w roku 2008 Uczestnicy projektu oraz ewaluacja szkoleń 1 Wprowadzenie Omawiane w raporcie szkolenia były realizowane przez OFEK
ARKUSZ PRÓBNEJ MATURY Z OPERONEM MATEMATYKA
 Miejsce na identyfikację szkoły ARKUSZ PRÓBNEJ MATURY Z OPERONEM MATEMATYKA POZIOM PODSTAWOWY LISTOPAD 014 Czas pracy: 170 minut Instrukcja dla zdającego 1. Sprawdź, czy arkusz egzaminacyjny zawiera 1
Miejsce na identyfikację szkoły ARKUSZ PRÓBNEJ MATURY Z OPERONEM MATEMATYKA POZIOM PODSTAWOWY LISTOPAD 014 Czas pracy: 170 minut Instrukcja dla zdającego 1. Sprawdź, czy arkusz egzaminacyjny zawiera 1
Zadania z analizy matematycznej - sem. II Ekstrema funkcji wielu zmiennych, twierdzenia o funkcji odwrotnej i funkcji uwikªanej
 Zadania z analizy matematycznej - sem. II Ekstrema funkcji wielu zmiennych, twierdzenia o funkcji odwrotnej i funkcji uwikªanej Denicja 1. Niech X = R n b dzie przestrzeni unormowan oraz d(x, y) = x y.
Zadania z analizy matematycznej - sem. II Ekstrema funkcji wielu zmiennych, twierdzenia o funkcji odwrotnej i funkcji uwikªanej Denicja 1. Niech X = R n b dzie przestrzeni unormowan oraz d(x, y) = x y.
D- 10.03.01 TYMCZASOWE NAWIERZCHNIE Z ELEMENTÓW PREFABRYKOWANYCH
 D- 10.03.01 TYMCZASOWE NAWIERZCHNIE Z ELEMENTÓW PREFABRYKOWANYCH SPIS TREŚCI. 1. WSTĘP 2. MATERIAŁY 3. SPRZĘT 4. TRANSPORT 5. WYKONANIE ROBÓT 6. KONTROLA JAKOŚCI ROBÓT 7. OBMIAR ROBÓT 8. ODBIÓR ROBÓT 9.
D- 10.03.01 TYMCZASOWE NAWIERZCHNIE Z ELEMENTÓW PREFABRYKOWANYCH SPIS TREŚCI. 1. WSTĘP 2. MATERIAŁY 3. SPRZĘT 4. TRANSPORT 5. WYKONANIE ROBÓT 6. KONTROLA JAKOŚCI ROBÓT 7. OBMIAR ROBÓT 8. ODBIÓR ROBÓT 9.
EGZAMIN MATURALNY Z MATEMATYKI
 ARKUSZ ZAWIERA INFORMACJE PRAWNIE CHRONIONE DO MOMENTU ROZPOCZ CIA EGZAMINU! Miejsce na naklejk MMA-P1_1P-082 EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY MAJ ROK 2008 Czas pracy 120 minut Instrukcja
ARKUSZ ZAWIERA INFORMACJE PRAWNIE CHRONIONE DO MOMENTU ROZPOCZ CIA EGZAMINU! Miejsce na naklejk MMA-P1_1P-082 EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY MAJ ROK 2008 Czas pracy 120 minut Instrukcja
EGZAMIN MATURALNY Z MATEMATYKI
 ARKUSZ ZAWIERA INFORMACJE PRAWNIE CHRONIONE DO MOMENTU ROZPOCZ CIA EGZAMINU! Miejsce na naklejk MMA-P1_1P-082 EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY MAJ ROK 2008 Czas pracy 120 minut Instrukcja
ARKUSZ ZAWIERA INFORMACJE PRAWNIE CHRONIONE DO MOMENTU ROZPOCZ CIA EGZAMINU! Miejsce na naklejk MMA-P1_1P-082 EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY MAJ ROK 2008 Czas pracy 120 minut Instrukcja
Zarządzenie Nr 35/2008 BURMISTRZA ZBĄSZYNIA z dnia 25 marca 2008 r.
 35/2008 Plan dofinansowania form doskonalenia zawodowego nauczycieli w 2008 roku oraz ustalenie regulaminu przyznawania dofinansowania na doskonalenie zawodowe nauczycieli w Gminie Zbąszyń. Zarządzenie
35/2008 Plan dofinansowania form doskonalenia zawodowego nauczycieli w 2008 roku oraz ustalenie regulaminu przyznawania dofinansowania na doskonalenie zawodowe nauczycieli w Gminie Zbąszyń. Zarządzenie
PLAN POŁĄCZENIA SPÓŁEK PRZEZ PRZEJĘCIE. uzgodniony pomiędzy. CALL CENTER TOOLS spółką akcyjną. oraz. IPOM spółką z ograniczoną odpowiedzialnością
 PLAN POŁĄCZENIA SPÓŁEK PRZEZ PRZEJĘCIE uzgodniony pomiędzy CALL CENTER TOOLS spółką akcyjną IPOM spółką z ograniczoną odpowiedzialnością Warszawa, 29 stycznia 2015 roku Niniejszy plan połączenia przez
PLAN POŁĄCZENIA SPÓŁEK PRZEZ PRZEJĘCIE uzgodniony pomiędzy CALL CENTER TOOLS spółką akcyjną IPOM spółką z ograniczoną odpowiedzialnością Warszawa, 29 stycznia 2015 roku Niniejszy plan połączenia przez
Informacja o wyniku kontroli doraźnej w zakresie legalności wyboru trybu zamówienia z wolnej ręki
 Warszawa, 2015 r. UZP/DKD/WKZ/421/52( KNZ/25/15 )/15/GK Informacja o wyniku kontroli doraźnej w zakresie legalności wyboru trybu zamówienia z wolnej ręki Określenie postępowania o udzielenie zamówienia
Warszawa, 2015 r. UZP/DKD/WKZ/421/52( KNZ/25/15 )/15/GK Informacja o wyniku kontroli doraźnej w zakresie legalności wyboru trybu zamówienia z wolnej ręki Określenie postępowania o udzielenie zamówienia
1. CHARAKTERYSTYKA STUDIÓW 2. SYLWETKA ABSOLWENTA
 Dwuletnie studia indywidualne II stopnia na kierunku fizyka, specjalność Fizyka jądrowa i cząstek elementarnych, specjalizacje: Fizyka jądra atomowego, Struktura jąder atomowych i Fizyka cząstek i oddziaływań
Dwuletnie studia indywidualne II stopnia na kierunku fizyka, specjalność Fizyka jądrowa i cząstek elementarnych, specjalizacje: Fizyka jądra atomowego, Struktura jąder atomowych i Fizyka cząstek i oddziaływań
1. Oprocentowanie LOKATY TERMINOWE L.P. Nazwa Lokaty Okres umowny Oprocentowanie w skali roku. 9 miesięcy 2,30%
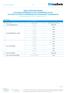 Duma Przedsiębiorcy 1/5 TABELA OPROCENTOWANIA AKTUALNIE OFEROWANYCH LOKAT BANKOWYCH W PLN DLA OSÓB FICZYCZNYCH PROWADZĄCYCH DZIAŁALNOŚĆ GOSPODARCZĄ (Zaktualizowana w dniu 27 kwietnia 2015 r.) 1. Oprocentowanie
Duma Przedsiębiorcy 1/5 TABELA OPROCENTOWANIA AKTUALNIE OFEROWANYCH LOKAT BANKOWYCH W PLN DLA OSÓB FICZYCZNYCH PROWADZĄCYCH DZIAŁALNOŚĆ GOSPODARCZĄ (Zaktualizowana w dniu 27 kwietnia 2015 r.) 1. Oprocentowanie
RZECZPOSPOLITA OPIS PATENTOWY 153 870
 RZECZPOSPOLITA OPIS PATENTOWY 153 870 POLSKA Patent dodatkowy do patentunr Zgłoszono: 89 04 19 (P. 278970) Pierwszeństwo Int. Cl.5 F26B 11/06 '"'TElHIA H L li A URZĄD PATENTOWY Zgłoszenie ogłoszono: 89
RZECZPOSPOLITA OPIS PATENTOWY 153 870 POLSKA Patent dodatkowy do patentunr Zgłoszono: 89 04 19 (P. 278970) Pierwszeństwo Int. Cl.5 F26B 11/06 '"'TElHIA H L li A URZĄD PATENTOWY Zgłoszenie ogłoszono: 89
Statystyka matematyczna - ZSTA LMO
 Statystyka matematyczna - ZSTA LMO Šukasz Smaga Wydziaª Matematyki i Informatyki Uniwersytet im. Adama Mickiewicza w Poznaniu Wykªad 4 Šukasz Smaga (WMI UAM) ZSTA LMO Wykªad 4 1 / 18 Wykªad 4 - zagadnienia
Statystyka matematyczna - ZSTA LMO Šukasz Smaga Wydziaª Matematyki i Informatyki Uniwersytet im. Adama Mickiewicza w Poznaniu Wykªad 4 Šukasz Smaga (WMI UAM) ZSTA LMO Wykªad 4 1 / 18 Wykªad 4 - zagadnienia
dr inż. Robert Geryło Seminarium Wyroby budowlane na rynku europejskim wymagania i kierunki zmian, Warszawa 16.3.2010
 Nowy zakres wymagań stawianych wyrobom budowlanym związanych z efektywnościąenergetyczną budownictwa dr inż. Robert Geryło Seminarium Wyroby budowlane na rynku europejskim wymagania i kierunki zmian, Warszawa
Nowy zakres wymagań stawianych wyrobom budowlanym związanych z efektywnościąenergetyczną budownictwa dr inż. Robert Geryło Seminarium Wyroby budowlane na rynku europejskim wymagania i kierunki zmian, Warszawa
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI
 Miejsce na naklejk z kodem szko y dysleksja PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY Czas pracy 120 minut Instrukcja dla zdaj cego 1. Sprawd, czy arkusz egzaminacyjny zawiera 15 stron (zadania
Miejsce na naklejk z kodem szko y dysleksja PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY Czas pracy 120 minut Instrukcja dla zdaj cego 1. Sprawd, czy arkusz egzaminacyjny zawiera 15 stron (zadania
Projekt konceptualny z Baz Danych "Centralny system zarz dzania salami na AGH"
 Projekt konceptualny z Baz Danych "Centralny system zarz dzania salami na AGH" Autorzy: Adrian Stanula Grzegorz Stopa Mariusz Sasko Data: 14 XI 2008 rok Spis tre±ci 1 Sformuªowanie zadania projektowego.
Projekt konceptualny z Baz Danych "Centralny system zarz dzania salami na AGH" Autorzy: Adrian Stanula Grzegorz Stopa Mariusz Sasko Data: 14 XI 2008 rok Spis tre±ci 1 Sformuªowanie zadania projektowego.
Surowiec Zużycie surowca Zapas A B C D S 1 0,5 0,4 0,4 0,2 2000 S 2 0,4 0,2 0 0,5 2800 Ceny 10 14 8 11 x
 Przykład: Przedsiębiorstwo może produkować cztery wyroby A, B, C, i D. Ograniczeniami są zasoby dwóch surowców S 1 oraz S 2. Zużycie surowca na jednostkę produkcji każdego z wyrobów (w kg), zapas surowca
Przykład: Przedsiębiorstwo może produkować cztery wyroby A, B, C, i D. Ograniczeniami są zasoby dwóch surowców S 1 oraz S 2. Zużycie surowca na jednostkę produkcji każdego z wyrobów (w kg), zapas surowca
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: OPTYMALIZACJA TERMOEKONOMICZNA W ENERGETYCE Termoeconomic Analysis of Thermal Systems in Power Engineering Kierunek: ENERGETYKA Rodzaj przedmiotu: specjalności obieralny Rodzaj zajęć:
Nazwa przedmiotu: OPTYMALIZACJA TERMOEKONOMICZNA W ENERGETYCE Termoeconomic Analysis of Thermal Systems in Power Engineering Kierunek: ENERGETYKA Rodzaj przedmiotu: specjalności obieralny Rodzaj zajęć:
Pan Waldemar Pawlak Wicepremier Minister Gospodarki
 PKPP/555/DK/2008 Dotyczy: nieuzasadnione podwy ki cen energii w wyniku realizacji Ustawy o KDT Warszawa, 28 pa dziernika 2008 Pan Waldemar Pawlak Wicepremier Minister Gospodarki Szanowny Panie Premierze,
PKPP/555/DK/2008 Dotyczy: nieuzasadnione podwy ki cen energii w wyniku realizacji Ustawy o KDT Warszawa, 28 pa dziernika 2008 Pan Waldemar Pawlak Wicepremier Minister Gospodarki Szanowny Panie Premierze,
Warszawa, dnia 6 listopada 2015 r. Poz. 1821 ROZPORZĄDZENIE MINISTRA ROLNICTWA I ROZWOJU WSI 1) z dnia 23 października 2015 r.
 DZIENNIK USTAW RZECZYPOSPOLITEJ POLSKIEJ Warszawa, dnia 6 listopada 2015 r. Poz. 1821 ROZPORZĄDZENIE MINISTRA ROLNICTWA I ROZWOJU WSI 1) z dnia 23 października 2015 r. w sprawie szczegółowych warunków
DZIENNIK USTAW RZECZYPOSPOLITEJ POLSKIEJ Warszawa, dnia 6 listopada 2015 r. Poz. 1821 ROZPORZĄDZENIE MINISTRA ROLNICTWA I ROZWOJU WSI 1) z dnia 23 października 2015 r. w sprawie szczegółowych warunków
PRZYK ADOWY ARKUSZ EGZAMINACYJNY Z MATEMATYKI
 PRZYK ADOWY ARKUSZ EGZAMINACYJNY Z MATEMATYKI Zestaw P POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla pisz cego 1. Sprawd, czy arkusz zawiera 17 stron.. W zadaniach od 1. do 0. s podane 4 odpowiedzi:
PRZYK ADOWY ARKUSZ EGZAMINACYJNY Z MATEMATYKI Zestaw P POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla pisz cego 1. Sprawd, czy arkusz zawiera 17 stron.. W zadaniach od 1. do 0. s podane 4 odpowiedzi:
W przypadku kandydatów do klasy o ukierunkowaniu politechnicznym brane będą pod uwagę oceny z następujących przedmiotów: a) matematyka b) fizyka
 Szczegółowe warunki rekrutacji Liceum Ogólnokształcącego z Oddziałami Dwujęzycznymi im. Władysława Broniewskiego w Strzelcach Opolskich w roku szkolnym 2016/2017 opracowany na podstawie: Ustawy z dnia
Szczegółowe warunki rekrutacji Liceum Ogólnokształcącego z Oddziałami Dwujęzycznymi im. Władysława Broniewskiego w Strzelcach Opolskich w roku szkolnym 2016/2017 opracowany na podstawie: Ustawy z dnia
Uchwały podjęte przez Nadzwyczajne Walne Zgromadzenie Zakładów Lentex S.A. z dnia 11 lutego 2014 roku
 Uchwały podjęte przez Nadzwyczajne Walne Zgromadzenie Zakładów Lentex S.A. z dnia 11 lutego 2014 roku Uchwała Nr 1 z dnia 11 lutego 2014 roku w sprawie wyboru przewodniczącego Nadzwyczajnego Walnego Zgromadzenia.
Uchwały podjęte przez Nadzwyczajne Walne Zgromadzenie Zakładów Lentex S.A. z dnia 11 lutego 2014 roku Uchwała Nr 1 z dnia 11 lutego 2014 roku w sprawie wyboru przewodniczącego Nadzwyczajnego Walnego Zgromadzenia.
JĘZYK ROSYJSKI POZIOM ROZSZERZONY
 EGZAMIN MATURALNY W ROKU SZKOLNYM 2013/2014 JĘZYK ROSYJSKI POZIOM ROZSZERZONY ROZWIĄZANIA ZAAŃ I SCHEMAT PUNKTOWANIA MAJ 2014 ZAANIA OTWARTE Zadanie 1. Przetwarzanie tekstu (0,5 pkt) 1.1. туристов 1.2.
EGZAMIN MATURALNY W ROKU SZKOLNYM 2013/2014 JĘZYK ROSYJSKI POZIOM ROZSZERZONY ROZWIĄZANIA ZAAŃ I SCHEMAT PUNKTOWANIA MAJ 2014 ZAANIA OTWARTE Zadanie 1. Przetwarzanie tekstu (0,5 pkt) 1.1. туристов 1.2.
PRZEDMIOTOWY SYSTEM OCENIANIA z przedmiotu matematyka
 PRZEDMIOTOWY SYSTEM OCENIANIA z przedmiotu matematyka 1. Wymagania edukacyjne treści i umiejętności podlegające ocenie. Ocena celująca Ocenę tę otrzymuje uczeń, którego wiedza wykracza poza obowiązujący
PRZEDMIOTOWY SYSTEM OCENIANIA z przedmiotu matematyka 1. Wymagania edukacyjne treści i umiejętności podlegające ocenie. Ocena celująca Ocenę tę otrzymuje uczeń, którego wiedza wykracza poza obowiązujący
MATEMATYKA POZIOM ROZSZERZONY PRZYK ADOWY ZESTAW ZADA NR 2. Miejsce na naklejk z kodem szko y CKE MARZEC ROK Czas pracy 150 minut
 Miejsce na naklejk z kodem szko y CKE MATEMATYKA POZIOM ROZSZERZONY MARZEC ROK 2008 PRZYK ADOWY ZESTAW ZADA NR 2 Czas pracy 150 minut Instrukcja dla zdaj cego 1. Sprawd, czy arkusz egzaminacyjny zawiera
Miejsce na naklejk z kodem szko y CKE MATEMATYKA POZIOM ROZSZERZONY MARZEC ROK 2008 PRZYK ADOWY ZESTAW ZADA NR 2 Czas pracy 150 minut Instrukcja dla zdaj cego 1. Sprawd, czy arkusz egzaminacyjny zawiera
Katalog. Nakładów Rzeczowych. nr K-49. Nowe technologie. Roboty budowlane w systemie Porotherm. Ściany w systemach Porotherm Profi i Porotherm DRYFIX
 Katalog nr K-49 Nakładów Rzeczowych Nowe technologie Roboty budowlane w systemie Porotherm. Ściany w systemach Porotherm Profi i Porotherm DRYFIX Wydawca: Katalog nr K-49 Nakładów Rzeczowych Nowe technologie
Katalog nr K-49 Nakładów Rzeczowych Nowe technologie Roboty budowlane w systemie Porotherm. Ściany w systemach Porotherm Profi i Porotherm DRYFIX Wydawca: Katalog nr K-49 Nakładów Rzeczowych Nowe technologie
TABELA OPROCENTOWANIA PRODUKTÓW BANKOWYCH BANKU SPÓŁDZIELCZEGO W DĄBROWIE TARNOWSKIEJ DLA KLIENTÓW INDYWIDUALNYCH
 Załącznik do uchwały Zarzadu z dnia 29-01-2016 roku TABELA OPROCENTOWANIA PRODUKTÓW BANKOWYCH BANKU SPÓŁDZIELCZEGO W DĄBROWIE TARNOWSKIEJ DLA KLIENTÓW INDYWIDUALNYCH Dąbrowa Tarnowska 2016 1 Spis treści:
Załącznik do uchwały Zarzadu z dnia 29-01-2016 roku TABELA OPROCENTOWANIA PRODUKTÓW BANKOWYCH BANKU SPÓŁDZIELCZEGO W DĄBROWIE TARNOWSKIEJ DLA KLIENTÓW INDYWIDUALNYCH Dąbrowa Tarnowska 2016 1 Spis treści:
Oprocentowanie środków pieniężnych dla klientów instytucjonalnych z Segmentu Klientów Biznesowych (Mikroprzedsiębiorstw) Banku BGŻ BNP Paribas S.A.
 Oprocentowanie środków pieniężnych dla klientów instytucjonalnych z Segmentu Klientów Biznesowych (Mikroprzedsiębiorstw) Banku BGŻ BNP Paribas S.A. z dnia 15 lutego 2016 r. Bank BGŻ BNP Paribas Spółka
Oprocentowanie środków pieniężnych dla klientów instytucjonalnych z Segmentu Klientów Biznesowych (Mikroprzedsiębiorstw) Banku BGŻ BNP Paribas S.A. z dnia 15 lutego 2016 r. Bank BGŻ BNP Paribas Spółka
PRZEDMIOTOWY SYSTEM OCENIANIA Z MATEMATYKI I LICEUM OGÓLNOKSZTAŁCĄCE IM. MIKOŁAJA KOPERNIKA W KROŚNIE
 PRZEDMIOTOWY SYSTEM OCENIANIA Z MATEMATYKI I LICEUM OGÓLNOKSZTAŁCĄCE IM. MIKOŁAJA KOPERNIKA W KROŚNIE Przedmiotowy system oceniania z matematyki jest zgodny z Rozporządzeniem Ministra Edukacji Narodowej
PRZEDMIOTOWY SYSTEM OCENIANIA Z MATEMATYKI I LICEUM OGÓLNOKSZTAŁCĄCE IM. MIKOŁAJA KOPERNIKA W KROŚNIE Przedmiotowy system oceniania z matematyki jest zgodny z Rozporządzeniem Ministra Edukacji Narodowej
Wykªad 7. Ekstrema lokalne funkcji dwóch zmiennych.
 Wykªad jest prowadzony w oparciu o podr cznik Analiza matematyczna 2. Denicje, twierdzenia, wzory M. Gewerta i Z. Skoczylasa. Wykªad 7. Ekstrema lokalne funkcji dwóch zmiennych. Denicja Mówimy,»e funkcja
Wykªad jest prowadzony w oparciu o podr cznik Analiza matematyczna 2. Denicje, twierdzenia, wzory M. Gewerta i Z. Skoczylasa. Wykªad 7. Ekstrema lokalne funkcji dwóch zmiennych. Denicja Mówimy,»e funkcja
PRZYK ADOWY ARKUSZ EGZAMINACYJNY Z MATEMATYKI
 PRZYK ADOWY ARKUSZ EGZAMINACYJNY Z MATEMATYKI Zestaw P POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla pisz cego 1. Sprawd, czy arkusz zawiera 17 stron.. W zadaniach od 1. do 0. s podane 4 odpowiedzi:
PRZYK ADOWY ARKUSZ EGZAMINACYJNY Z MATEMATYKI Zestaw P POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla pisz cego 1. Sprawd, czy arkusz zawiera 17 stron.. W zadaniach od 1. do 0. s podane 4 odpowiedzi:
Regulamin promocji Płaci się łatwo kartą MasterCard
 Regulamin promocji Płaci się łatwo kartą MasterCard Poznań, październik 2015 r. SPIS TREŚCI Rozdział 1 Postanowienia ogólne... 2 Rozdział 2 Nagrody i sposób ich przyznania... 3 Rozdział 3 Reklamacje...
Regulamin promocji Płaci się łatwo kartą MasterCard Poznań, październik 2015 r. SPIS TREŚCI Rozdział 1 Postanowienia ogólne... 2 Rozdział 2 Nagrody i sposób ich przyznania... 3 Rozdział 3 Reklamacje...
 Ż Ł ć ć ź ź Ś Ó ćę Ę Ą Ę ć Ę ć Ń Ż ć ć Ż ć ć ć ć ć ć ć ć ć Ź ć ć Ę ć ć ć Ą ć Ż ć Ł Ż ć Ę ć ć ć ć ć ć ć ć Ż ć Ż ć ć ć ć ć Ż ć Ą Ź ć Ą ź Ż ć ć ć ć ć Ź ź Ź ć Ż Ź Ż Ź Ź ć Ż ć Ę Ł Ż ć ź Ż ć ć ź ć ć ć ź Ż Ę
Ż Ł ć ć ź ź Ś Ó ćę Ę Ą Ę ć Ę ć Ń Ż ć ć Ż ć ć ć ć ć ć ć ć ć Ź ć ć Ę ć ć ć Ą ć Ż ć Ł Ż ć Ę ć ć ć ć ć ć ć ć Ż ć Ż ć ć ć ć ć Ż ć Ą Ź ć Ą ź Ż ć ć ć ć ć Ź ź Ź ć Ż Ź Ż Ź Ź ć Ż ć Ę Ł Ż ć ź Ż ć ć ź ć ć ć ź Ż Ę
 ć ŚĆ Ś Ż Ś ć ć ŚĆ ć ć ć Ś ź ź Ł Ń Ź ź ć Ś ć Ę Ś ź ć Ó ć ć Ś Ś Ś Ł Ś ć ć Ł ć ŚĆ Ś ź Ś Ś Ś Ś ć ć Ł ć Ę Ę ć Ś Ś ć Ś Ę ć Ę Ś Ś Ś Ś Ś Ś ć ć Ś Ż ć ć ć ć ć ć ć ć ć Ę Ż ć ć Ś Ś ź Ś Ś Ę Ł Ń ć Ę ć Ś ć Ż ć Ę Ę Ę
ć ŚĆ Ś Ż Ś ć ć ŚĆ ć ć ć Ś ź ź Ł Ń Ź ź ć Ś ć Ę Ś ź ć Ó ć ć Ś Ś Ś Ł Ś ć ć Ł ć ŚĆ Ś ź Ś Ś Ś Ś ć ć Ł ć Ę Ę ć Ś Ś ć Ś Ę ć Ę Ś Ś Ś Ś Ś Ś ć ć Ś Ż ć ć ć ć ć ć ć ć ć Ę Ż ć ć Ś Ś ź Ś Ś Ę Ł Ń ć Ę ć Ś ć Ż ć Ę Ę Ę
 ż Ść Ś Ś Ś Ś Ę Ą Ę ź Ę Ę ć ć Ź Ć Ó Ę Ę Ń Ś Ą ć Ę ć ć ćę ż ż ć Ó ż Ę Ń Ą Ą Ż Ę Ę Ść ć ż Ż ż Ż ć Ż ź Ę Ść Ż Ę Ść Ś ż Ń Ą ż Ę ż ż Ś ż ż Ó Ś Ę Ó ź ż ż ć ż Ś ż Ś ć ż ż Ś Ś ć Ż Ż Ó ż Ż Ż Ś Ś Ś ć Ź ż Ś Ś ć Ą
ż Ść Ś Ś Ś Ś Ę Ą Ę ź Ę Ę ć ć Ź Ć Ó Ę Ę Ń Ś Ą ć Ę ć ć ćę ż ż ć Ó ż Ę Ń Ą Ą Ż Ę Ę Ść ć ż Ż ż Ż ć Ż ź Ę Ść Ż Ę Ść Ś ż Ń Ą ż Ę ż ż Ś ż ż Ó Ś Ę Ó ź ż ż ć ż Ś ż Ś ć ż ż Ś Ś ć Ż Ż Ó ż Ż Ż Ś Ś Ś ć Ź ż Ś Ś ć Ą
WST P DO TEORII INFORMACJI I KODOWANIA. Grzegorz Szkibiel. Wiosna 2013/14
 WST P DO TEORII INFORMACJI I KODOWANIA Grzegorz Szkibiel Wiosna 2013/14 Spis tre±ci 1 Kodowanie i dekodowanie 4 1.1 Kodowanie a szyfrowanie..................... 4 1.2 Podstawowe poj cia........................
WST P DO TEORII INFORMACJI I KODOWANIA Grzegorz Szkibiel Wiosna 2013/14 Spis tre±ci 1 Kodowanie i dekodowanie 4 1.1 Kodowanie a szyfrowanie..................... 4 1.2 Podstawowe poj cia........................
Wyniki ogólnopolskiej analizy wyboru metody i wysoko ci przyj tych stawek w gminach wiejskich i miejskowiejskich
 Wyniki ogólnopolskiej analizy wyboru metody i wysoko ci przyj tych stawek w gminach wiejskich i miejskowiejskich Pawe Tomczak Dyrektor biura Zwi zku Gmin Wiejskich RP 2013-03-05 Zebrane dane z ponad 1200
Wyniki ogólnopolskiej analizy wyboru metody i wysoko ci przyj tych stawek w gminach wiejskich i miejskowiejskich Pawe Tomczak Dyrektor biura Zwi zku Gmin Wiejskich RP 2013-03-05 Zebrane dane z ponad 1200
Stereometria. Zimowe Powtórki Maturalne. 22 lutego 2016 r.
 Stereometria Zimowe Powtórki Maturalne 22 lutego 2016 r. 1. Przek tna sze±cianu o boku 1 ma dªugo± : 1. Przek tna sze±cianu o boku 1 ma dªugo± : 1 1. Przek tna sze±cianu o boku 1 ma dªugo± : 1 2 1. Przek
Stereometria Zimowe Powtórki Maturalne 22 lutego 2016 r. 1. Przek tna sze±cianu o boku 1 ma dªugo± : 1. Przek tna sze±cianu o boku 1 ma dªugo± : 1 1. Przek tna sze±cianu o boku 1 ma dªugo± : 1 2 1. Przek
Regulamin korzystania z serwisu http://www.monitorceidg.pl
 Regulamin korzystania z serwisu http://www.monitorceidg.pl 1 [POSTANOWIENIA OGÓLNE] 1. Niniejszy regulamin (dalej: Regulamin ) określa zasady korzystania z serwisu internetowego http://www.monitorceidg.pl
Regulamin korzystania z serwisu http://www.monitorceidg.pl 1 [POSTANOWIENIA OGÓLNE] 1. Niniejszy regulamin (dalej: Regulamin ) określa zasady korzystania z serwisu internetowego http://www.monitorceidg.pl


