Homogeneous hypersurfaces
|
|
|
- Elżbieta Murawska
- 5 lat temu
- Przeglądów:
Transkrypt
1 Differential Geometry Seminar, ANU p. 1/14 Homogeneous hypersurfaces Michael Eastwood [based on joint work with Vladimir Ezhov] Australian National University
2 Differential Geometry Seminar, ANU p. 2/14 A classification problem Σ G/H where G/H = your favourite homogeneous space Examples of G/H R n =(SO(n) R n )/SO(n)= Euclidean space R n =(GL(n,R) R n )/GL(n,R)= affine space RP n = SL(n+1,R)/P= real projective space S n = SO(n+1,1)/P= conformal space C n =(GL(n,C) C n )/GL(n,C)= complex affine space Today: real or complex (equi-)affine space
3 Differential Geometry Seminar, ANU p. 3/14 Curves in the real affine plane straight line circle (or ellipse) parabola Y= X α r=e αθ (spira mirabilis (Jacob Bernoulli)) Y= e X Y= X logx Normal forms y= 0 y= x 2 y= x 2 ± x 4 + bx 5 + Y= X logx y= x 2 + x x5 + Y= e X y= x 2 x x5 + b 2 = invariant
4 Differential Geometry Seminar, ANU p. 4/14 Non-degenerate equi-affine surfaces in C 3 Z= XY Z 2 = XY+ 1 XY Z= 1 X 2 (Z+ Y 2 ) 3 = 1 Z= XY+ X 3 (Cayley surface) Z= XY+ logx Nomizu & Sasaki 1991 Guggenheimer 1963 Equi-affine symmetries of the Cayley surface X X Y Y+ t Z Z+ tx X X+ s Y Y 3sX 3 2 s2 Z Z+ sy 3 2 s2 X 1 2 s3 (Abelian)
5 Infinitesimal symmetries Cayley surface z= xy+ x 3 x x y y+ t z z+ tx x z + y x x+s y y 3sx 3 2 s2 z z+ sy 3 2 s2 x 1 2 s3 3x y + y z + x z= xy+ =F(x,y) [ F x, F y, 1] M x y F(x,y) + β = 0 symmetry algebra g Differential Geometry Seminar, ANU p. 5/14
6 Differential Geometry Seminar, ANU p. 6/14 Normal forms Non-degenerate z= x 2 + y 2 + or z= xy+ Blaschke normal (Leichtweiß1989) z= g ij x i x j + a ijk x i x j x k + x i x i + r i z a j jk a j jk+ 2(n+2) 3 r k a ijk trace-free Pick invariant a ijk a ijk e.g. z= xy+ ax 3 + by 3 + ab z= xy+ x 3 + y 3 + or z= xy+ x 3 +
7 Differential Geometry Seminar, ANU p. 7/14 Affine homogeneous surfaces in C 3 N1 z= xy+ x 3 + y 3 + ax 4 2bx 3 y 2axy 3 + by 4 + O(5) N2 z= xy+ x 3 + y 3 +bx 4 (4b+9)x 3 y 1 9 (2b+9)(8b+9)x2 y 2 (4b+9)xy 3 +by 4 +O(5) N3 z= xy+ x 3 + y 3 +bx 4 +(4b 9)x 3 y+(6b 9)x 2 y 2 +(4b 9)xy 3 + by 4 + O(5) N4 N5 z= xy+ x 3 + y bx x2 y (1/b)y4 + O(5) where b/= 0 z= xy+ x 3 + x 4 + bx 3 y+ O(5) where b/= 0 N6 z= xy+ x 3 + x 4 + bx 5 + O(6) N7 z= xy+ x 3 + x 3 y+ O(5) (the Archimedean screw) N8 z= xy+ x 3 + O(5)=xy+ x 3 (the Cayley surface) N9 z= xy+ x 2 y 2 + O(5)=(1 1 4xy)/2 (hyperboloid) N10 z= xy+ O(5)=xy D1 z= x 2 + x 2 y+ x 3 y+ x 2 y 2 + x 5 + 3x 3 y 2 + x 2 y 3 + O(6) ( twisted cubic) D2 z= x 2 + x 4 + ax 5 + O(6)=afunction of x alone (cylinder) D3 z= x 2 +x 2 y+x 2 y 2 +x 5 +x 2 y 3 +4x 5 y+x 2 y 4 +ax 7 +10x 5 y 2 +x 2 y 5 +O(8) (cone) D4 z= x 2 + x 2 y+ x 2 y 2 + x 2 y 3 + O(6)=x 2 /(1 y) (cone) D5 z= x 2 + O(5)=x 2 (cylinder) F z= O(3)=0
8 Non-degenerate with non-vanishing Pick invariant z = xy + x 3 + y 3 + c 4,0 x 4 + c 3,1 x 3 y + c 2,2 x 2 y 2 + c 1,3 xy 3 + c 0,4 y 4 +O(5) c 4,0 c 3,1 = c 1,3 c 0,4 and c 2,2 =(2c 4,0 + c 1,3 )(4c 0,4 c 3,1 )/9 c 4,0 0 c 4,0 =0andc 0,4 =0 c 4,0 =0andc 1,3 =0 c 3,1 3 c 1,3 3 =0 c 3,1 = c 1,3 WLG 2c 0,4 + c 3,1 =0 (c 1,3 +9) 2 c 1,3 =0 c 1,3 = 9 c 1,3 =0 (2c 4,0 + c 1,3 )(c 4,0 3 c 0,4 3 )c 1,3 =0 c 1,3 = 2c 4,0 c 0,4 = c 4,0 WLG c 1,3 =0 16c 4,0 c 0,4 =81 N4 (2c 4,0 + c 1,3 )(4c 4,0 +9+c 1,3 )(4c 4,0 9 c 1,3 )=0 c 1,3 = 2c 4,0 c 1,3 = 4c 4,0 9 c 1,3 =4c 4,0 9 N1 N2 N3 47
9 Non-degenerate with vanishing Pick invariant z = xy + x 3 +O(4) z = xy +O(4) z = xy + x 3 + c 4,0 x 4 + c 3,1 x 3 y + c 2,2 x 2 y 2 + c 1,3 xy 3 + c 0,4 y 4 +O(5) c 0,4 = c 1,3 =0 q 3,3 c 2,2 =0 q 3,3 =0 c 2,2 =0 c 3,1 (3p 1,1 +4c 4,0 )c 2,2 =0 z = xy + c 4,0 x 4 + c 3,1 x 3 y + c 2,2 x 2 y 2 + c 1,3 xy 3 + c 0,4 y 4 +O(5) c 0,4 = c 1,3 = c 3,1 = c 4,0 =0 z = xy + x 2 y 2 +O(5) WLG p 3,3 = q 3,3 =0 no c 2,2 =0? yes c 3,1 =0 p 1,1 = 4c 4,0 /3 c 2,2 =0 c 2,2 =0 N9 no c z = xy + x 3 + x 4 + c 3,1 x 3 4,0 =0? y +O(5)WLG yes N10 no c 3,1 =0? no c 3,1 =0? yes yes q 3,3 = c 3,1 z = xy + x 3 + x 3 y +O(5)WLG p 1,1 = 2 p 1,1 = q 1,1 =0 z = xy + x 3 +O(5) N5 N7 N8 z = xy + x 3 + x 4 + c 5,0 x 5 + c 4,1 x 4 y + c 3,2 x 3 y 2 + c 2,3 x 2 y 3 + c 1,4 xy 4 + c 0,5 y 5 +O(6) N6 c 0,5 = c 1,4 = c 2,3 = c 3,2 = c 4,1 =0 48
10 Degenerate z = x 2 + c 2,1 x 2 y + c 1,2 xy 2 + c 0,3 y 3 +O(4) c 0,3 = c 1,2 =0 c 2,1 =1WLG no c Add Quartic Terms 2,1 =0? c 4,0 =0WLG Add Quartic Terms yes c 0,4 = c 1,3 =0 c 2,2 =1 c 0,4 = c 1,3 = c 2,2 = c 3,1 =0 c 3,1 =0? yes no c 3,1 =1WLG Add Quintic Terms Add Quintic Terms c 4,0 =1WLG Add Quintic Terms no c 4,0 =0? yes c 0,5 = c 1,4 = c 2,3 = c 3,2 = c 4,1 =0 c 0,6 = c 1,5 = c 3,3 = c 4,2 = c 6,0 =0 c 2,4 =1 c 5,1 =4 Add Quintic Terms c 0,5 = c 1,4 = c 2,3 = c 3,2 = c 4,1 = c 5,0 =0 D2 c 0,5 = c 1,4 = c 3,2 = c 4,1 =0 c 2,3 =1 D5 c 0,5 = c 1,4 =0 c 2,3 =1 c 3,2 =3 c 5,0 =1WLG no c 5,0 =0? yes Add Sextic Terms c 4,1 =0WLG D4 q 1,3 =3/2 c 5,0 =1 p 1,3 = 5 c 6,0 =0WLG D1 D3 Add Septic Terms c 0,7 = c 1,6 = c 3,4 = c 4,3 = c 6,1 =0 c 2,5 =1 c 5,2 =10 49
11 Differential Geometry Seminar, ANU p. 11/14 Non-degenerate equi-affine hypersurfaces in C 4 Equation Basepoint I1 W= XY+ Z 2 (0,0,0,0) I2 W 2 = XY+ Z (1,0,0,0) I3 W= XY+ Z 2 + X 3 (0,0,0,0) I4 W= XY+ Z 2 + logx (0,1,0,0) I5 W(XY+ Z) 2 = 1 (1,0,0,1) I6 W 2 (XY+ Z 2 ) 3 = 1 (1,0,0,1) A1 WXY Z= 1 (1,1,1,1) A2 WZ+ WY 2 + X 2 Z+ X 2 Y 2 = 1 (1,0,0,1) A3 6WXY Z 4X 3 Z 3X 2 Y 2 + W 2 Z 2 + 4WY 3 = 1 (1,0,0,1) A4 W= XY+ Z 2 + X 2 Z+ αx 4 (0,0,0,0)
12 Differential Geometry Seminar, ANU p. 12/14 Non-degenerate equi-affine hypersurfaces in C 4 Equation Basepoint B1 WZ 2 = Z+ X 3 + XY Z (1,0,0,1) B2 (W+ XY+ X 3 ) 2 Z= 1 (1,0,0,1) B3 (WZ+ Y 2 + X 2 Z) 4 = Z (1,0,0,1) B4 (W 2 + X 2 ) 2 (Z+ Y 2 ) 3 = 1 (1,0,0,1) B5 (W+ X 2 Z+ XY) 2 Z= 1 (1,0,0,1) B6 (W+ XY) 2 (Z+ X 2 )=1 (1,0,0,1) B7 WZ 2 = Z+ X 2 + XY Z (1,0,0,1) B8 (W+ Y Z+ X 2 Z) 5 = Z (1,0,0,1) B9 (WZ+ X 2 + Y Z 2 ) 5 = Z 4 (1,0,0,1) B10 W= XY+ Z 2 + XZ 2 (0,0,0,0) B11 W 2 = XY+ X 2 Y+ X 2 Z (1,1,0,1)
13 Invariants Pick invariant= a ijk a ijk a ijk a ijl a mnl a mnk Differential Geometry Seminar, ANU p. 13/14
14 Differential Geometry Seminar, ANU p. 14/14 THE END THANK YOU
(Arithmetic Invariant Theory) 1 (Geometric Invariant Theory, GIT) GIT
( 1 2) Gauss ( 3) 1 (Arithmetic Invariant Theory) 1 (Geometric Invariant Theory, GIT) GIT 2 2 V = Sym 2 C 2 := { f(x, y) = ax 2 + bxy + cy 2 a, b, c C } G = GL 2 (C) ( ) g = ( p r ) q G, s f(x, y) = ax
Counting quadrant walks via Tutte s invariant method
Counting quadrant walks via Tutte s invariant method Olivier Bernardi - Brandeis University Mireille Bousquet-Mélou - CNRS, Université de Bordeaux Kilian Raschel - CNRS, Université de Tours Vancouver,
Dupin cyclides osculating surfaces
Paweł Walczak, Uniwersytet Łódzki, Dijon, 25 stycznia 2012 Colaborators: Remi Langevin (UdeB), Adam Bartoszek, Szymon Walczak (UŁ) What is extrinsic conformal geometry? Conformal transformations = transformations
STATYSTYKA MATEMATYCZNA WYKŁAD listopada 2009
STATYSTYKA MATEMATYCZNA WYKŁAD 7 23 listopada 2009 Wykład 6 (16.XI.2009) zakończył się zdefiniowaniem współczynnika korelacji: E X µ x σ x Y µ y σ y = T WSPÓŁCZYNNIK KORELACJI ρ X,Y = ρ Y,X (!) WSPÓŁCZYNNIK
Wykład 14. Elementy algebry macierzy
Wykład 14 Elementy algebry macierzy dr Mariusz Grządziel 26 stycznia 2009 Układ równań z dwoma niewiadomymi Rozważmy układ równań z dwoma niewiadomymi: a 11 x + a 12 y = h 1 a 21 x + a 22 y = h 2 a 11,
WSKAZANIE OBSZARÓW OBJĘTYCH OCHRONĄ ŚCISŁĄ, CZYNNĄ I KRAJOBRAZOWĄ
43 Załącznik nr 4 WSKAZANIE OBSZARÓW OBJĘTYCH OCHRONĄ ŚCISŁĄ, CZYNNĄ I KRAJOBRAZOWĄ Lp. Rodzaj ochrony Lokalizacja 1) Powierzchnia ogółem w ha 1 Ochrona ścisła Oddziały 1b, 1c, 1d, 1f, 1g, 1h, 1i, 1j,
()*+,-. 01 ( 2 / / (:58; A B0((1C - D E D B FGHIJK % L?BMNO<=E)* I; P Q M RSC- 0,,,0 + 0 ( + TUVWXY X ; 4567 M Z[8"\)* M T U P Q ] ^_
![()*+,-. 01 ( 2 / / (:58; A B0((1C - D E D B FGHIJK % L?BMNO<=E)* I; P Q M RSC- 0,,,0 + 0 ( + TUVWXY X ; 4567 M Z[8\)* M T U P Q ] ^_](/thumbs/99/141555539.jpg "()*+,-. 01 ( 2 / / (:58; A B0((1C - D E D B FGHIJK % L?BMNO<=E)* I; P Q M RSC- 0,,,0 + 0 ( + TUVWXY X ; 4567 M Z[8\)* M T U P Q ] ^_")
()*+,-. 01 ( 2 / /03456789(:58; 8)? @ A B0((1C - D E D B FGHIJK % L?BMNO
General Certificate of Education Ordinary Level ADDITIONAL MATHEMATICS 4037/12
UNIVERSITY OF CAMBRIDGE INTERNATIONAL EXAMINATIONS General Certificate of Education Ordinary Level www.xtremepapers.com *6378719168* ADDITIONAL MATHEMATICS 4037/12 Paper 1 May/June 2013 2 hours Candidates
Zadania egzaminacyjne
Rozdział 13 Zadania egzaminacyjne Egzamin z algebry liniowej AiR termin I 03022011 Zadanie 1 Wyznacz sumę rozwiązań równania: (8z + 1 i 2 2 7 iz 4 = 0 Zadanie 2 Niech u 0 = (1, 2, 1 Rozważmy odwzorowanie
Analiza Matematyczna Praca domowa
Analiza Matematyczna Praca domowa J. de Lucas Zadanie 1. Pokazać, że dla wszystkich n naturalnych ( n ) exp kx k dx 1 dx n = 1 n (e k 1). (0,1) n k=1 n! k=1 Zadanie. Obliczyć dla dowolnego n. (0,1) n (x
Zadania nadobowiązkowe KRZYWE STOŻKOWE OKRĄG
OKRĄG Przykład 1. W układzie współrzędnych XOY narysujmy okrąg o środku w punkcie (0,0) i promieniu 1: Współrzędne dowolnego punktu P(x,y) leżącego na okręgu spełniają równanie + y =1, natomiast współrzędne
Factor each completely.
Math 2 Final Exam Packet Part I Name ID: 1 Date Block Factor each completely. 1) p 2 + p 28 A) ( p + 7)( p + 4) B) Not factorable C) ( p + 7)( p 4) D) ( p + 2)( p 14) 2) r 2 14r + 45 A) (r 5)(r + 9) B)
Lecture 18 Review for Exam 1
Spring, 2019 ME 323 Mechanics of Materials Lecture 18 Review for Exam 1 Reading assignment: HW1-HW5 News: Ready for the exam? Instructor: Prof. Marcial Gonzalez Announcements Exam 1 - Wednesday February
FUNKCJA LINIOWA, OKRĘGI
FUNKCJA LINIOWA, OKRĘGI. Napisz równanie prostej przechodzącej przez początek układu i prostopadłej do prostej 3x-y+=0.. Oblicz pole trójkąta ograniczonego osiami układy i prostą x+y-6=0. 3. Odcinek o
1 + x 1 x 1 + x + 1 x. dla x 0.. Korzystając z otrzymanego wykresu wyznaczyć funkcję g(m) wyrażającą liczbę pierwiastków równania.
10 1 Wykazać, że liczba 008 008 10 + + jest większa od Nie używając kalkulatora, porównać liczby a = log 5 log 0 + log oraz b = 6 5 Rozwiązać równanie x + 4y + x y + 1 = 4xy 4 W prostokątnym układzie współrzędnych
Stochastyczne równania różniczkowe, studia II stopnia
Stochastyczne równania różniczkowe, studia II stopnia Niech W t (ewentualnie W, W (t)), t oznacza proces Wienera oraz niech W = Niech W = (W, W 2,, W n ) oznacza n-wymiarowy proces Wienera Pokazać, że
CMYK!"#$ %& ' ()*+,-./ / 6789: ;.+ 7 <"= >? DE :.+,- 7 FGHIJIK1L M NO!PQRSTU VNO+,-WXY M IJIK1LV G"+,- Z [O"\] ^ _`!abc^ VNO +,- 0
![CMYK!#$ %& ' ()*+,-./ / 6789: ;.+ 7 <= >? DE :.+,- 7 FGHIJIK1L M NO!PQRSTU VNO+,-WXY M IJIK1LV G+,- Z [O\] ^ _`!abc^ VNO +,- 0](/thumbs/94/121022846.jpg "CMYK!#$ %& ' ()*+,-./ / 6789: ;.+ 7 <= >? DE :.+,- 7 FGHIJIK1L M NO!PQRSTU VNO+,-WXY M IJIK1LV G+,- Z [O\] ^ _`!abc^ VNO +,- 0")
!"#$ %& ' ()*+,-./0 1 0 1 23045/ 6789: ;.+ 7
! "#$% &'!& & ( )*)* +,&, -! &./ * * -!"#$%&' 0 0!"#$% &' 1 (% )*+,'-./01 ) 2340,5 ( 67 1* 89:; 9?FG HIJK LMHIJK1NO K LME O K L M < = > P Q
! "#$% &'!& & ( )*)* +,&, -! &./ * * -!"#$%&' 0 0!"#$% &' 1 (% )*+,'-./01 ) 2340,5 ( 67 1* 89:; ?@ABCDE 9?FG HIJK LMHIJK1NO K LME O K L M < = > P Q A BR S T. U V W? @ XY=> E 9 Z [\] ^ _`a`@bc 9 M
Algebra linowa w pigułce
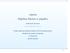Algebra Algebra linowa w pigułce Aleksander Denisiuk denisjuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych Wydział Informatyki w Gdańsku ul. Brzegi 55 80-045 Gdańsk Algebra p. 1 Algebra
! "#$ %! & '"$!!"# $%&'!"#$%&' $ ()*+,-./01 ( :6; * < = ; C D A # E F7GH IJ;KLMNAO% ) 7 J PQRSLTNAUVAW%X *+,- YS LMN
!"#$%!&'"$!!"#$%&'!"#$%&' $ )*+,-./01 23456789:6; *4?@*AB34@*AB>4? * < = 3 4 7 ; C D A # E F7GH IJ;KLMNAO% ) 7JPQRSLTNAUVAW%X *+,- YS LMNAUVAW%X +,- JZ[\!]/0&'+^_ *+,-`ab; c=c=f7gh "#$%&';IE./0,1/1!
Modelowanie zależności. Matematyczne podstawy teorii ryzyka i ich zastosowanie R. Łochowski
Modelowanie zależności pomiędzy zmiennymi losowymi Matematyczne podstawy teorii ryzyka i ich zastosowanie R. Łochowski P Zmienne losowe niezależne - przypomnienie Dwie rzeczywiste zmienne losowe X i Y
Zestaw nr 6 Pochodna funkcji jednej zmiennej. Styczna do krzywej. Elastyczność funkcji. Regu la de l Hospitala
Zestaw nr 6 Pochodna funkcji jednej zmiennej. Styczna do krzywej. Elastyczność funkcji. Regu la de l Hospitala November 12, 2009 Przyk ladowe zadania z rozwi azaniami Zadanie 1. Oblicz pochodne nastȩpuj
CMYK!"#$%&'! ( )*+,-./01! )*789 :;' " ABCDE0 6 )*+,- FGH 6 )*+,-I J KL M6NO > PQ!RS?TU )*+,-VW RSXGY P 6 )*+, P Z[\?TU]^_ `Rab`6 $ $ )*
![CMYK!#$%&'! ( )*+,-./01! )*789 :;' ABCDE0 6 )*+,- FGH 6 )*+,-I J KL M6NO > PQ!RS?TU )*+,-VW RSXGY P 6 )*+, P Z[\?TU]^_ `Rab`6 $ $ )*](/thumbs/97/131899428.jpg "CMYK!#$%&'! ( )*+,-./01! )*789 :;' ABCDE0 6 )*+,- FGH 6 )*+,-I J KL M6NO > PQ!RS?TU )*+,-VW RSXGY P 6 )*+, P Z[\?TU]^_ `Rab`6 $ $ )*")
!"#$%&'! ( )*+,-./01! 23 4 56 )*789 :;' ? @ " ABCDE0 6 )*+,- FGH 6 )*+,-I J KL M6NO > PQ!RS?TU )*+,-VW RSXGY P 6 )*+, P Z[\?TU]^_ `Rab`6 $ $ )*+,c!k Q6?TU )*+,I1 > )*+,-,,!"#$% &'! ( )*)+,&' -.! /0
n [2, 11] 1.5 ( G. Pick 1899).
![n [2, 11] 1.5 ( G. Pick 1899).](/thumbs/98/135090138.jpg "n [2, 11] 1.5 ( G. Pick 1899).")
1. / / 2. R 4k 3. 4. 5. 6. / 7. /n 8. n 1 / / Z d ( R d ) d P Z d R d R d? n > 0 n 1.1. R 2 6 n 5 n [Scherrer 1946] d 3 R 3 6 1.2 (Schoenberg 1937). d 3 R d n n = 3, 4, 6 1.1. d 3 R d 1.3. θ θ/π 1.4. 0
dr Mariusz Grządziel 15,29 kwietnia 2014 Przestrzeń R k R k = R R... R k razy Elementy R k wektory;
Wykłady 8 i 9 Pojęcia przestrzeni wektorowej i macierzy Układy równań liniowych Elementy algebry macierzy dodawanie, odejmowanie, mnożenie macierzy; macierz odwrotna dr Mariusz Grządziel 15,29 kwietnia
Porównanie modeli regresji. klasycznymi modelami regresji liniowej i logistycznej
Porównanie modeli logicznej regresji z klasycznymi modelami regresji liniowej i logistycznej Instytut Matematyczny, Uniwersytet Wrocławski Małgorzata Bogdan Instytut Matematyki i Informatyki, Politechnika
Równania różniczkowe liniowe wyższych rzędów o stałych współcz
Równania różniczkowe liniowe wyższych rzędów o stałych współczynnikach Katedra Matematyki i Ekonomii Matematycznej SGH 12 maja 2016 Równanie liniowe n-tego rzędu Definicja Równaniem różniczkowym liniowym
Olimpiada Matematyczna kilka zadań
Olimpiada Matematyczna kilka zadań 1. Wykazać, że dla dowolnych liczb a, b, c zachodzi nierówność a 2 + b 2 + c 2 ab + bc + ca. Uwaga Zadanie pojawiło si e w I Olimpiadzie Matematycznej (1949 r.) na poziomie
Prace Koła Matematyków Uniwersytetu Pedagogicznego w Krakowie (2017)
Prace Koła Mat. Uniw. Ped. w Krak. 4 (2017), 1 11 edagogicznego w Krakowie PKoło Matematyków Uniwersytetu Prace Koła Matematyków Uniwersytetu Pedagogicznego w Krakowie (2017) Magdalena Gwóźdź 1 Afiniczna
Przekształcenia liniowe
Przekształcenia liniowe Zadania Które z następujących przekształceń są liniowe? (a) T : R 2 R 2, T (x, x 2 ) = (2x, x x 2 ), (b) T : R 2 R 2, T (x, x 2 ) = (x + 3x 2, x 2 ), (c) T : R 2 R, T (x, x 2 )
() () *+, )# -"#),." ) / ()0)1,+0. ),." "./+0" ("0+ 0"/ 1. * )1,+0.) "0."1",0"#! "# $% &' $ && # %!"#$%&' ' ' ()* +,-./ :; 5 <9:; = $A$
() () *+, )# -"#),." ) / ()0)1,+0. ),." "./+0" ("0+ 0"/ 1. * )1,+0.) "0."1",0"#! "# $% &'$ && # %!"#$%&' ' '()* +,-./01 23456789:; 5 ?2@ $A$BCDE FG H IJ>#KLMN=OPQRS:;TU: ; TUV -. %.#! " #! $% &'
3. Funkcje wielu zmiennych
3 Funkcje wielu zmiennych 31 Ciagłość Zanim podamy definicję ciagłości dla funkcji wielu zmiennych wprowadzimy bardzo ogólne i abstrakcyjne pojęcie przestrzeni metrycznej Przestrzeń metryczna Metryka w
!" #! $%&' $ &!!$ :;!"# $ %& ' ( )* %+,-./0 1 +( :; :, ( BC+=D E -./0% : > / F-.FG91"# H F IH F+J K L M N O + F+PQ"# RS*T"U VW6
!" #! $%&' $ &!!$ :;!"# $ %& ' ( )* %+,-./0 1 +( 234 56 2789 :; :, ,?@6A ( BC+=D E -./0% : > / F-.FG91"# H F IH F+J K L M N O + F+PQ"# RS*T"U VW6 &+ F XY * ZL[ \ 6]M^ F _,`ab bc :&+ FX FY F c = ] F
!"#$ <'! '!! "#$% "!& ' '! : #! K LKMNO N+ K.& 0 4 ; )*7,7 78 O8 0% N 6 ( Z! K 0 5 Z D O " #\b$ %0 T& ' S4<G 0 M Z P Z ' 0'1 E'7 K6 %;() X * Z+, 0 G #
!"#$
Effective Governance of Education at the Local Level
Effective Governance of Education at the Local Level Opening presentation at joint Polish Ministry OECD conference April 16, 2012, Warsaw Mirosław Sielatycki Ministry of National Education Doskonalenie
!"#$%&'!"#$%&' ($!(#)*+,-$!./)0 1 $!.) $!23) 45$!"#6!"#789% & 8:; ); );<= );>? BCDE F GHIJK LMN O. ) )PQRS6 T U!"# V WX Y V 789 G7 WZ[ Y \E]^_ 7
![!#$%&'!#$%&' ($!(#)*+,-$!./)0 1 $!.) $!23) 45$!#6!#789% & 8:; ); );<= );>? BCDE F GHIJK LMN O. ) )PQRS6 T U!# V WX Y V 789 G7 WZ[ Y \E]^_ 7](/thumbs/98/138236014.jpg "!#$%&'!#$%&' ($!(#)*+,-$!./)0 1 $!.) $!23) 45$!#6!#789% & 8:; ); );<= );>? BCDE F GHIJK LMN O. ) )PQRS6 T U!# V WX Y V 789 G7 WZ[ Y \E]^_ 7")
!"#$%&'!"#$%&'($!(#)*+,-$!./)0 1 $!.) $!23) 45$!"#6!"#789% & 8:; ); );? );@A BCDE F GHIJK LMN O. ) )PQRS6 T U!"# V WX Y V 789 G7 WZ[ Y \E]^_ 7 `$ Wa b Y c _ U W Y B W 7 W #6!(# 8 %& WX! " #!"#$%&'()*
5 Równania różniczkowe zwyczajne rzędu drugiego
5 Równania różniczkowe zwyczajne rzędu drugiego Definicja 5.1. Równaniem różniczkowym zwyczajnym rzędu drugiego nazywamy równanie postaci F ( x, y, y, y ) = 0, (12) w którym niewiadomą jest funkcja y =
Some Linear Algebra. Vectors operations = =(,, ) =( 1 + 2, 1 + 2, ) λ =(λ,λ,λ ) Addition. Scalar multiplication.
Basic Geometry Vectors operations Some Linear Algebra Addition + 2 =( 1 + 2, 1 + 2, 1 + 2 ) =(,, ) + Scalar multiplication λ =(λ,λ,λ ) Norm = 2 + 2 + 2 2 Scalar Product Commutative Linear Orthogonally
[assumption]theorem [assumption]corollary [assumption]lemma [assumption]definition. Andrzej Sitarz
![[assumption]theorem [assumption]corollary [assumption]lemma [assumption]definition. Andrzej Sitarz](/thumbs/101/148499235.jpg "[assumption]theorem [assumption]corollary [assumption]lemma [assumption]definition. Andrzej Sitarz")
[assumption]theorem [assumption]corollary [assumption]lemma [assumption]definition κ-minkowski STAR PRODUCT AND ITS SYMMETRIES Andrzej Sitarz Jagiellonian University, Kraków 8.9.2010, Kɛρκυρα Joint work
Regresja form kwadratowych i algebry Jordana
Regresja form kwadratowych i algebry Jordana Jacek Wesołowski Wydział Matematyki i Nauk Informacyjnych Politechnika Warszawska, Warszawa Konferencja Statystyki Matematycznej Wisła 2009 współautor: G. Letac
CS 6170: Computational Topology, Spring 2019 Lecture 09
CS 6170: Computtionl Topology, Spring 2019 Lecture 09 Topologicl Dt Anlysis for Dt Scientists Dr. Bei Wng School of Computing Scientific Computing nd Imging Institute (SCI) University of Uth www.sci.uth.edu/~beiwng
)& J, + 2? - (4 2 =1 )& 216 6)6!"#$%& '!"#$%& ' & '!"#$%&' '%% # ()*(+,-' %./01,#23 % ( :./0 :; 78 F G2H
)& 6 6 6 J, + 2? (5@2 - (4 2(@ 2 +7?%@ =1 )& 216 6)6!"#$%& '!"#$%& ' & '!"#$%&' '%% # ()*(+,-' %./01,#23 % ( 45 16789:./0 :; 78 ?@=A,BCDE F ) @ G2HIJKL MNO # 78 P # MBQ R8 PS 78TU G2 HVWXNO Y "1 78
1 Działania na zbiorach
Algebra liniowa z geometrią /4 Działania na zbiorach Zadanie Czy działanie : R R R określone wzorem (x x ) (y y ) := (x y x y x y + x y ) jest przemienne? Zadanie W dowolnym zbiorze X określamy działanie
VI. Równania różniczkowe liniowe wyższych rzędów
VI. 1. Równanie różniczkowe liniowe n-tego rzędu o zmiennych współczynnikach Niech podobnie jak w poprzednim paragrafie K = C lub K = R. Podobnie jak w dziedzinie rzeczywistej wprowadzamy pochodne wyższych
Elementy geometrii analitycznej w R 3
Rozdział 12 Elementy geometrii analitycznej w R 3 Elementy trójwymiarowej przestrzeni rzeczywistej R 3 = {(x,y,z) : x,y,z R} możemy interpretować co najmniej na trzy sposoby, tzn. jako: zbiór punktów (x,
1 Równanie różniczkowe pierwszego rzędu
1 Równanie różniczkowe pierwszego rzędu Wiele zagadnień geometrycznych, fizycznych, ekonomicznych i innych prowadzi do zależności, w których pojawiają się pochodne. Przykład 1. Znaleźć krzywą dla której
5 ; / ;, /1 E #5 5!"#$%& ( :; )*+ 5.,-+ ( J KL /,01 1 / MNO )*+ 5 PCQRSTUV C KL,-+ QWXY )*+ C ZT[ \]^
![5 ; / ;, /1 E #5 5!#$%& ( :; )*+ 5.,-+ ( J KL /,01 1 / MNO )*+ 5 PCQRSTUV C KL,-+ QWXY )*+ C ZT[ \]^](/thumbs/103/160921057.jpg "5 ; / ;, /1 E #5 5!#$%& ( :; )*+ 5.,-+ ( J KL /,01 1 / MNO )*+ 5 PCQRSTUV C KL,-+ QWXY )*+ C ZT[ \]^")
5 ;/ 8+49 +0 +4 ;,/1 E#5 5!"#$%& ( 23456789:;?@AB?CDE )*+ 5.,-+ ( FGH@AIB,-+.)*+ JKL /,011/ MNO )*+ 5PCQRSTUV CKL,-+ QWXY )*+ CZT[ \]^. + 12 _`Oa )*+ Mbc,-+ CJ2C %V3BA,-+.)*+ 5C MaCVC BA3,-+ 3 3-2C@
Zależność. przyczynowo-skutkowa, symptomatyczna, pozorna (iluzoryczna),
Zależność przyczynowo-skutkowa, symptomatyczna, pozorna (iluzoryczna), funkcyjna stochastyczna Korelacja brak korelacji korelacja krzywoliniowa korelacja dodatnia korelacja ujemna Szereg korelacyjny numer
Algebra z geometrią Lista 1 - Liczby zespolone
Algebra z geometrią Lista 1 - Liczby zespolone 1. Oblicz a) (1 + i)(2 i); b) (3 + 2i) 2 ; c) (2 + i)(2 i); d) (3 i)/(1 + i); e) (1 + i 3)/(2 + i 3); f) (2 + i) 3 ; g) ( 3 i) 3 ; h) ( 2 + i 3) 2 2. Korzystając
DEGENERATE SINGULARITIES AND THEIR MILNOR NUMBERS
UNIVERSITATIS IAGELLONICAE ACTA MATHEMATICA doi: 10.4467/20843828AM.12.002.0454 FASCICULUS XLIX, 2011 DEGENERATE SINGULARITIES AND THEIR MILNOR NUMBERS by Szymon Brzostowski Abstract. We give an example
3. Znaleźć długość krzywej l = {y = x, 0 x 1}. 4. Obliczyć objętość bryły powstałej w wyniku obrotu dookoła osi OX krzywej
eria. Obliczyć całki (A) 2 x 2 dx (z definicji); 2 xe x dx; e 2xe x2 dx. 2. Obliczyć pole obszaru (A) {(x, y) : < x < 3, < y < x 2 +}; {(x, y) : 6x x 2 < y < x 2 6x+}. 3. Znaleźć długość krzywej l = {y
x = 1 t2 1 + t 2 y = 2t
Zadania o krzywych eliptycznych wykład DAKE 410 Zima 2012 prof. W.Gajda Zadanie 1. Niech E będzie krzywą zadaną równaniem y 2 = f(x), gdzie f Z[x] jest wielomianem unormowanym stopnia 3, który ma różne
! " # $%& $& ' % 7 8, 9:;1, ' < ABCDE F GHIJK LM 2 NO 5 P, 3 QR 4DE NWXQRYT.P NW&( 5 Z NW 5, 4DE LM X1 Z 2
!"# $%& $& '% 78,9:;1, '< =>?@ABCDE FGHIJKLM 2 NO5P, 3QR STUV>?@ 4DENWXQRYT.PNW&(5Z NW5, >?@X[\]^_`a@b c@b 4c@b&>?@ 4DELMX1 Z 2 YT&. 3 QRY8 *$%% 6 +% 3a *7% 6 >?@ 4DENWC 3 ]^ 8 3 XQR 9& " 6 6 6 ", 6 :
5 9; STU ()* +,-. /0#1 cp :Y ; :PQ ; $< + =>? AB)* + C 2D +,6E ; FFGHI)* + Y * JK L# M )* N ;O 7 )* +] P<Q)* +R STUV6 #)* +,- ] W
![5 9; STU ()* +,-. /0#1 cp :Y ; :PQ ; $< + =>? AB)* + C 2D +,6E ; FFGHI)* + Y * JK L# M )* N ;O 7 )* +] P<Q)* +R STUV6 #)* +,- ] W](/thumbs/96/128964612.jpg "5 9; STU ()* +,-. /0#1 cp :Y ; :PQ ; $< + =>? AB)* + C 2D +,6E ; FFGHI)* + Y * JK L# M )* N ;O 7 )* +] P<Q)* +R STUV6 #)* +,- ] W")
5 9; STU ()* +,-. /0#1 cp 2 3 3 4567 8 + 9:Y ; :PQ ; $< + =>? : @ AB)* + C 2D +,6E ; FFGHI)* + Y * JK L# M )* N ;O 7 )* +] P 2 )* +. Z[\,- X ]^_` :,- a ^ bc, #,
STATYSTYKA. Rafał Kucharski. Uniwersytet Ekonomiczny w Katowicach 2015/16 ROND, Finanse i Rachunkowość, rok 2
STATYSTYKA Rafał Kucharski Uniwersytet Ekonomiczny w Katowicach 2015/16 ROND, Finanse i Rachunkowość, rok 2 Zależność przyczynowo-skutkowa, symptomatyczna, pozorna (iluzoryczna), funkcyjna stochastyczna
Blok III: Funkcje elementarne. e) y = 1 3 x. f) y = x. g) y = 2x. h) y = 3x. c) y = 3x + 2. d) y = x 3. c) y = x. d) y = x.
Blok III: Funkcje elementarne III. Narysuj wykres funkcji: a) y = x y = x y = x y = x III. Narysuj wykres funkcji: a) y = x + y = 4 x III. Znajdź miejsca zerowe funkcji: a) y = 6 x y = x e) y = x f) y
Standardized Test Practice
Standardized Test Practice 1. Which of the following is the length of a three-dimensional diagonal of the figure shown? a. 4.69 units b. 13.27 units c. 13.93 units 3 d. 16.25 units 8 2. Which of the following
POPRAWIANIE JAKOŚCI OBRAZU W DZIEDZINIE PRZESTRZENNEJ (spatial image enhancement)
POPRAWIANIE JAKOŚCI OBRAZU W DZIEDZINIE PRZESTRZENNEJ (spatial image enhancement) Przetwarzanie obrazów cyfrowych w celu wydobycia / uwydatnienia specyficznych cech obrazu dla określonych zastosowań. Brak
Analiza płyt i powłok MES
Analiza płyt i powłok MES Jerzy Pamin e-mails: JPamin@L5.pk.edu.pl Podziękowania: M. Radwańska, A. Wosatko ANSYS, Inc. http://www.ansys.com Tematyka zajęć Klasyfikacja modeli i elementów skończonych Elementy
Funkcje charakterystyczne zmiennych losowych, linie regresji 1-go i 2-go rodzaju
Funkcje charakterystyczne zmiennych losowych, linie regresji -go i 2-go rodzaju Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych Wydział Informatyki Politechniki
Układy równań liniowych, macierze, Google
Układ równań linowych { x+2y = 6, 3x y = 4 (0) Spotkania z Matematyka Układy równań liniowych, macierze, Google Aleksander Denisiuk denisjuk@matman.uwm.edu.pl Uniwersytet Warmińsko-Mazurski w Olsztynie
2 Criminal records. Vocabulary. burglary. Crimes. Criminals
FR 2 C Vy G P P Vy C C P fi Sk R A W C C 1 Zjź z zę żzy yzy. Z y łóż zy ó łjąy zę (1 8). 1 k 2 4 y j y y z q y k q 5 6 7 8 4 Uzłj z (1 7) yz z ćzń 1, 2 j. y j. FR 1 T 2 T k M S. A k k. 4 I y k. 5 Ty k.
vf(c) =, vf(ft 1... t n )=vf(t 1 )... vf(t n ).
6. Wykład 6: Rachunek predykatów. Język pierwszego rzędu składa się z: symboli relacyjnych P i, i I, gdzie (P i ) oznaczać będzie ilość argumentów symbolu P i, symboli funkcyjnych f j, j J, gdzie (f j
XVII-wieczne metody w optymalizacji XXI wieku
XVII-wieczne metody w optymalizacji XXI wieku cykl wykładów Okno na podwórze Maria Michalska 19 stycznia 2012 Zarys 1 Wstęp 2 SOS optymalizacja 3 Wielomiany ograniczone 4 XXI wiek - SDP 5 XVII wiek - Newton
Matematyka dyskretna
Matematyka dyskretna Wykład 12: Krzywe eliptyczne Gniewomir Sarbicki Rozważać będziemy przestrzeń K n Definicja: x y λ K x = λy. Relację nazywamy różnieniem się o skalar Przykład: [4, 10, 6, 14] [6, 15,
Weronika Mysliwiec, klasa 8W, rok szkolny 2018/2019
Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Tresci zadań rozwiązanych
Gamma3. Notations. Primary definition. Specific values. General characteristics. Traditional name. Traditional notation
Gmm3 Nottios Trditiol me Geerlized icomplete gmm fuctio Trditiol ottio, z, z Mthemtic StdrdForm ottio Gmm, z, z Primry defiitio 06.07.0.000.0, z, z z z t t t Specific vlues Specilized vlues 06.07.03.000.0,
); );+ ) +994-,9+ 4)- &&5 6 E PQ 5 ' 65 ` c G%C c b NO F PQ 4 2<= 5& ]^ * 0, 945 `T 8 3 E - O6 4- ; `T ^E NV =&U Z I `T * 4 C G HG H
![); );+ ) +994-,9+ 4)- &&5 6 E PQ 5 ' 65 ` c G%C c b NO F PQ 4 2<= 5& ]^ * 0, 945 `T 8 3 E - O6 4- ; `T ^E NV =&U Z I `T * 4 C G HG H](/thumbs/102/153514188.jpg "); );+ ) +994-,9+ 4)- &&5 6 E PQ 5 ' 65 ` c G%C c b NO F PQ 4 2<= 5& ]^ * 0, 945 `T 8 3 E - O6 4- ; `T ^E NV =&U Z I `T * 4 C G HG H")
23 4 5 + );+494-4 + );+ ) +994-,9+ 4)- &&5 6 E PQ 5 ' 65 ` c G%C c b NO F PQ 4 2
Rynek, opcje i równania SDE
Rynek, opcje i równania SDE Adam Majewski Uniwersytet Gdański kwiecień 2009 Adam Majewski (Uniwersytet Gdański) Rynek, opcje i równania SDE kwiecień 2009 1 / 16 1 Rynek, portfel inwestycyjny, arbitraż
Helena Boguta, klasa 8W, rok szkolny 2018/2019
Poniższy zbiór zadań został wykonany w ramach projektu Mazowiecki program stypendialny dla uczniów szczególnie uzdolnionych - najlepsza inwestycja w człowieka w roku szkolnym 2018/2019. Składają się na
Modelowanie i wizualizowanie 3W-grafiki. Transformacje. Aleksander Denisiuk. denisjuk@matman.uwm.edu.pl
Modelowanie i wizualizowanie 3W-grafiki Transformacje Aleksander Denisiuk denisjuk@matman.uwm.edu.pl Uniwersytet Warmińsko-Mazurski w Olsztynie Wydział Matematyki i Informatyki ul. Słoneczna 54 10-561
Baza w jądrze i baza obrazu ( )
Przykład Baza w jądrze i baza obrazu (839) Znajdź bazy jądra i obrazu odwzorowania α : R 4 R 3, gdzie α(x, y, z, t) = (x + 2z + t, 2x + y 3z 5t, x y + z + 4t) () zór ten oznacza, że α jest odwzorowaniem
x y = 2z. + 2y, z 2y df
. Funkcje wielu zmiennych i funkcje uwikłane Zadanie.. Obliczyć przybliżoną wartość wyrażenia (, ) (,). Korzystamy z przybliżenia f, y) f, y ) + x x, y ) + y y, y ), gdzie x = x x a y = y y. Przybliżenie
New method for the conformal bootstrap with OPE truncations
New method for the conformal bootstrap with OPE truncations Wenliang LI Kyung Hee University, Seoul, South Korea Symposium: "Bootstrap Approach to Conformal Field Theories and Applications, OIST, March19-23,
RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE. Wiele obiektywnych prawidłowości przyrodniczych udaje się zapisać w postaci równości formalnej
RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE Wiele obiektywnych prawidłowości przyrodniczych udaje się zapisać w postaci równości formalnej F (x, y(x), y (1) (x), y () (x),..., y (n) (x)) = 0, gdzie y (k) (x) to k ta
& + >?! F:? ^K ) G^ : X +G $3 J I, 6 CA D J = Q =, G > =< b :! " 6 [ _ $ ) I 6 " $ [ ) " "3 ] <B, =b Q, 4 <a B F,[ < [ Z < 6-7 J :, ^ I$ b Z 3W&$c \,
![& + >?! F:? ^K ) G^ : X +G $3 J I, 6 CA D J = Q =, G > =< b :! 6 [ _ $ ) I 6 $ [ ) 3 ] <B, =b Q, 4 <a B F,[ < [ Z < 6-7 J :, ^ I$ b Z 3W&$c \,](/thumbs/98/137424798.jpg "& + >?! F:? ^K ) G^ : X +G $3 J I, 6 CA D J = Q =, G > =< b :! 6 [ _ $ ) I 6 $ [ ) 3 ] <B, =b Q, 4 <a B F,[ < [ Z < 6-7 J :, ^ I$ b Z 3W&$c \,")
& + >?! F:? ^K ) G^ : X +G $3 J I, 6 CA D J = Q =, G > =< b :! " 6 [ _ $ ) I 6 " $ [ ) " "3 ]
. α p S n 1u p (x) = up F (u(x), λ), gdzie (1) F C 2 (R p R, R), (2) u F (u, λ) = λu + u g(u, λ), gdzie g C 2 (R p R, R) i dla każdego λ R zachodzi
PIOTR STEFANIAK 1. Preliminaria Oznaczmy przez S n 1 operator Laplace a-beltrami ego na sferze S n 1 R[1, 1] R[n 2, 0] oraz rozważmy następujący układ równań: α 1 S n 1u 1 x) = u1 F ux), λ) α 2 S n 1u
Network Services for Spatial Data in European Geo-Portals and their Compliance with ISO and OGC Standards
INSPIRE Conference 2010 INSPIRE as a Framework for Cooperation Network Services for Spatial Data in European Geo-Portals and their Compliance with ISO and OGC Standards Elżbieta Bielecka Agnieszka Zwirowicz
Maszyna Turinga. Algorytm. czy program???? Problem Hilberta: Przykłady algorytmów. Cechy algorytmu: Pojęcie algorytmu
Problem Hilberta: 9 Czy istnieje ogólna mechaniczna procedura, która w zasadzie pozwoliłaby nam po kolei rozwiązać wszystkie matematyczne problemy (należące do odpowiednio zdefiniowanej klasy)? 2 Przykłady
I. Równania różniczkowe pierwszego rzędu
I. Równania różniczkowe pierwszego rzędu 1. Równanie różniczkowe pierwszego rzędu w postaci normalnej W rozdziale tym rozważamy równania różniczkowe zwyczajne pierwszego rzędu. Na początek zajmiemy się
Liczby zespolone. Zadanie 1. Oblicz: a) ( 3+i)( 1 3i) b) (3+i)2 (4i+1) i
Zadanie. Oblicz: a) ( 3+i)( 3i) +i b) (3+i)2 (4i+) i (2+i) 3 Liczby zespolone Zadanie 2. Zaznacz na płaszczyźnie Gaussa zbiór: a) {z : z > 3} b) {z : z i } c) {z : 4 z + + i < 9} Zadanie 3. Wykaż, że suma
Granica i ciągłość funkcji. 1 Granica funkcji rzeczywistej jednej zmiennej rzeczywistej
Wydział Matematyki Stosowanej Zestaw zadań nr 3 Akademia Górniczo-Hutnicza w Krakowie WEiP, energetyka, I rok Elżbieta Adamus 3 listopada 06r. Granica i ciągłość funkcji Granica funkcji rzeczywistej jednej
APROKSYMACJA SKOŃCZONEGO UKŁADU PUNKTÓW PŁASZCZYZNY FIGURĄ BĘDĄCĄ SUMĄ PUNKTU I PROSTEJ
B A D A N I A O P E R A C Y J N E I D E C Y Z J E Nr Agata KORCZAK* APROKSYMACJA SKOŃCZONEGO UKŁADU PUNKTÓW PŁASZCZYZNY FIGURĄ BĘDĄCĄ SUMĄ PUNKTU I PROSTEJ Przedstawiono nową metodę aproksymacji skończonego
Dualities and 5-brane webs for 5d rank 2 SCFTs
Dualities and 5-brane webs for 5d rank 2 SCFTs Sung-Soo Kim (UESTC) 2018-11-08 Hirotaka Hayashi (Tokai univ.), Kimyeong Lee (KIAS), Futoshi Yagi (SWJTU) arxiv: 1801.03916, 1806.10569 In this talk, we focus
! "# $ % "&' & ' ( "#$ 9: ; 9 < E(,= F1 GHI $!"#$%&' ()*+,-./01 23 $ & # '/2 45+,-/01 # '/2 4 $ & 67+' 8 9 : ; & < = & B + C < =
! "#$ % "&'& ' ( "#$ 9: ; 9 ?-@A,-B=C-D
- Wydział Fizyki Zestaw nr 2. Krzywe stożkowe
1 Algebra Liniowa z Geometria - Wydział Fizyki Zestaw nr 2 Krzywe stożkowe 1 Znaleźć współrze dne środka i promień okre gu x 2 8x + y 2 + 6y + 20 = 0 2 Znaleźć zbiór punktów płaszczyzny R 2, których odległość
Rachunek całkowy funkcji wielu zmiennych
Rachunek całkowy funkcji wielu zmiennych Całki potrójne wykład z MATEMATYKI Budownictwo studia niestacjonarne sem. II, rok ak. 2008/2009 Katedra Matematyki Wydział Informatyki olitechnika Białostocka 1
TEMAT: PRZEKSZTAŁCENIA WYKRESÓW FUNKCJI PRZESUNIĘCIE O WEKTOR
TEMAT: PRZEKSZTAŁCENIA WYKRESÓW FUNKCJI PRZESUNIĘCIE O WEKTOR W układzie współrzędnych zaznaczmy dowolny punkt A = (x, y) oraz wektor u r = [p, q]. Po przesunięciu punktu A o wektor u r otrzymamy punkt
Geometria Analityczna w Przestrzeni
Algebra p. 1/25 Algebra Geometria Analityczna w Przestrzeni Aleksander Denisiuk denisjuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych Wydział Informatyki w Gdańsku ul. Brzegi 55 80-045
Zadania z Algebry liniowej 3 semestr zimowy 2008/2009
Zadania z Algebry liniowej 3 semestr zimowy 2008/2009 1. Niech V będzie przestrzenią wektorową nad ciałem K i niech 0 K oraz θ V będą elementem zerowym ciała K i wektorem zerowym przestrzeni V. Posługując
Re(x 2 y 2 ) Im(x 2 + y 2 ) 2Re(xy) Im(x 2 y 2 ) Re(x 2 + y 2 ) 2Im(xy)
Zadania domowe z Metod Matematycznych Fizyki (2012/2013 Zad. 1 Wypisa tabel dziaªania grupy obrotów czworo±cianu A 4. Zad. 2 Znale¹ podgrupy grupy kwaternionów Q. Z jakimi grupami s izomorczne? Sprawdzi,»e
()!"#$% $% & '! " "#! &! '
()!"#$% $% & '! " "#! &! ' !" #$!"%&' (!" )*$!"%&' +,-".!" )*$!"%&' /01!" )*$!"%&' +,!" )*$!" 2%&' 3456 789!" )*$!"%&' 89:;1!" )*$!"%&' :;1 1 ?@5#AB 1
< > Sprawdzić prawdziwość poniższych zdań logicznych (odpowiedź uzasadnić) oraz podać ich zaprzeczenia:
Zadania na zajęcia z przedmiotu Repetytorium z matematyki elementarnej, GiK, 06/7 Zdania logiczne Funkcje zdaniowe i kwantyfikatory Ocenić wartość logiczną zdania (odpowiedź uzasadnić): < Nieprawda, że
WYRAŻENIA ALGEBRAICZNE GRUPA A. l. Wyrazy sumy algebraicznej 6x - 4a2 + 9ax to: 2. Po uporządkowaniu jednomianu 4a (- 6b) a otrzymamy:
WYRAŻENIA ALGEBRAICZNE GRUPA A l. Wyrazy sumy algebraicznej 6x - 4a2 + 9ax to: A. 6x, 4a2, 9ax B. -6x, -4a2, -9ax C. 6x, -4a2, 9ax. -6x, 4a2, -9ax 2. Po uporządkowaniu jednomianu 4a (- 6b) a otrzymamy:
Algebra liniowa. 1. Macierze.
Algebra liniowa 1 Macierze Niech m oraz n będą liczbami naturalnymi Przestrzeń M(m n F) = F n F n będącą iloczynem kartezjańskim m egzemplarzy przestrzeni F n z naturalnie określonymi działaniami nazywamy
Twierdzenie Hilberta o nieujemnie określonych formach ternarnych stopnia 4
Twierdzenie Hilberta o nieujemnie określonych formach ternarnych stopnia 4 Strona 1 z 23 Andrzej Sładek, Instytut Matematyki UŚl sladek@math.us.edu.pl Letnia Szkoła Instytutu Matematyki 20-23 września
Przykład 1 Dany jest płaski układ czterech sił leżących w płaszczyźnie Oxy. Obliczyć wektor główny i moment główny tego układu sił.
Przykład 1 Dany jest płaski układ czterech sił leżących w płaszczyźnie Oxy Obliczyć wektor główny i moment główny tego układu sił. Wektor główny układu sił jest równy Moment główny układu wynosi Przykład
DODATKOWE ĆWICZENIA EGZAMINACYJNE
I.1. X Have a nice day! Y a) Good idea b) See you soon c) The same to you I.2. X: This is my new computer. Y: Wow! Can I have a look at the Internet? X: a) Thank you b) Go ahead c) Let me try I.3. X: What
Układy równań i równania wyższych rzędów
Rozdział Układy równań i równania wyższych rzędów Układy równań różniczkowych zwyczajnych Wprowadzenie W poprzednich paragrafach zajmowaliśmy się równaniami różniczkowymi y = f(x, y), których rozwiązaniem