Zwykle układ scalony jest zamknięty w hermetycznej obudowie metalowej, ceramicznej lub wykonanej z tworzywa sztucznego.
|
|
|
- Bronisław Tomaszewski
- 7 lat temu
- Przeglądów:
Transkrypt
1 Techniki wykonania cyfrowych układów scalonych Cyfrowe układy scalone dzielimy ze względu na liczbę bramek elementarnych tworzących dany układ na: małej skali integracji SSI do 10 bramek, średniej skali integracji MSI od 10 do 100 bramek, dużej skali integracji LSI od 100 do bramek. wielkiej skali integracji (VLSI very large scale of integration) ultra wielkiej skali integracji (ULSI ultra large scale of integration) Ze względu na sposób wytwarzania dzielimy je na: TTL najpopularniejsze obecnie, jest to zmodyfikowana technika DTL, gdzie elementy diodowe zastąpiono bipolarnymi tranzystorami wieloemiterowymi, MOS wykorzystujące tranzystory unipolarne z kanałem typu P (PMOS) i z kanałem typu N (NMOS). W technice PMOS i NMOS wykonuje się układy MSI i LSI zawierające całe bloki funkcyjne, CMOS wykorzystujące unipolarne tranzystory komplementarne, są obecnie równie popularne jak TTL, ECL najszybsze układy wykorzystujące tranzystory bipolarne, I 2 L wykorzystujące tranzystory bipolarne, charakteryzują się dużą gęstością upakowania w strukturze scalonej, CTD oparte na technologii MOS, wykorzystują zjawisko magazynowania i transportu ładunku, reprezentującego informację, stosowane do budowy pamięci półprzewodnikowych. Zwykle układ scalony jest zamknięty w hermetycznej obudowie metalowej, ceramicznej lub wykonanej z tworzywa sztucznego.
2 Dlaczego scalamy układy??? Zalety scalania: duże upakowanie elementów funkcjonalnych w objętości (miniaturyzacja) duża niezawodność niska cena niskie czasy propagacji sygnału (duża częstotliwość pracy) małe zużycie energii Zadania układu scalonego Przetwornik A/C, licznik, sumator, konwerter systemu liczbowego, wzmacniacz sygnału, Układy scalone mogą realizować określone funkcje zgodne a algebrą Bool a Zamiennik: NAND (Funktory) Zamiennik: NOR
3 Korzystając wyłącznie z bramek NAND narysuj schematy realizujący funkcje: Przykłady: Realizacja układowa to (gdzie jest tutaj błąd?): Realizacja funkcji logicznych Jak wiesz, każda bramka wykonuje jakąś małą, prostą funkcję logiczną. Grupa kilku bramek może realizować bardziej skomplikowane funkcje. Oto przykładowa funkcja i jej fizyczny realizator.
4 Y = (A-B) * [(NIE C) +D]
5
6
7
8
9
10 Upraszczanie algebraiczne polega na stosowaniu tożsamości praw algebry Boole a poznanych juz na zajęciach. Wracając do r-a A-1, upraszczając je możemy otrzymać następujące postacie:
11 lub Realizacja układowa to: Realizacja funkcji logicznych Jak wiesz, każda bramka wykonuje jakąś małą, prostą funkcję logiczną. Grupa kilku bramek może realizować bardziej skomplikowane funkcje. Oto przykładowa funkcja i jej fizyczny realizator. Zauważ, że w funkcji najpierw jest dodawanie (alternatywa, czyli OR), potem mnożenie (koniunkcja, czyli AND), a mimo to pierwsza jest bramka AND. Dlaczego? Kolejność działań obowiązuje również na liczbach dwójkowych. To jest tylko schemat, a w realu pojedyncze bramki z trzema nóżkami nie istnieją (przynajmniej na zajęciach) ;). Są uwięzione w układach scalonych po kilka sztuk każdy. Spróbujmy zbudować realizator tej funkcji na prawdziwych układach scalonych. Potrzebujemy kości zawierające bramki NOT, AND i OR. Ich numery to kolejno 7404, 7408, Teraz wystarczy podpiąć układy do zasilania i poukładać przewody tak, jak na poprzednim schemacie. Do rzeczy.
12 Użyliśmy trzech kości, nieużyte pozostają cztery bramki NOT i po trzy bramki AND i OR. Trochę to mało ekonomiczne. Na szczęście istnieją Prawa De Morgana. Znasz je z teorii mnogości (zbiory), oraz z logiki. Teraz poznasz Prawa De Morgana dla UTK. :) Logika Prawa De Morgana ~(p q) (~p) (~q) Negacja alternatywy jest równoważna koniunkcji negacji. ~(p q) (~p) (~q) Negacja koniunkcji jest równoważna alternatywie negacji. Teoria mnogości (zbiory) (A B)' = A' B' Dopełnienie sumy zbiorów jest równoważne ilorazowi dopełnień. (A B)' = A' B' Dopełnienie ilorazu zbiorów jest równoważne sumie dopełnień. Algebra Boole'a a + b = a * b Negacja sumy jest równoważna ilorazowi negacji. a * b = a + b Negacja ilorazu jest równoważna sumie negacji. Jeśli dobrze się przyglądniesz to zauważysz, że to wszystko, to jest to samo, tylko znaki inne. Nawet, jeśli nie chwytasz, o co chodzi, to nie ważne. Istotne jest to abyś pamiętał, że każdą bramkę można zastąpić, używając bramek NAND lub NOR. Wynika to z Praw de Morgana. Zamienniki dla XOR i XNOR
13 Zamienniki NAND i NOR dla XOR i XNOR są ponadprogramowe. Spróbujmy zatem zamienić wszystkie bramki naszej funkcji...
14 ...na odpowiadające im konfiguracje bramek NAND. Przyjrzyj się teraz zaznaczonym bramkom. Czy ma to jakiś sens, kiedy jeden NAND jest po drugim? To tak, jakby ustawić dwa NOT obok siebie. Co to oznacza? Można je pominąć! W ostateczności, nasz układ wygląda tak. Przenieśmy teraz schemat na prawdziwy scalak.
15 Tym sposobem, zamiast trzech chipów jest jeden, używamy o jedną bramkę mniej, niż w normalnej budowie funkcji i nieużyta pozostaje tylko jedna bramka, zamiast dziesięciu! W masowej produkcji urządzeń cyfrowych taka oszczędność jest bardzo znacząca, zwłaszcza, że bramki NAND są najtańsze. Być może gorzej się czyta takową funkcję i jest to nieporęczne, ale dla maszyny nie ma to żadnego znaczenia.
16
Układy scalone. wstęp układy hybrydowe
 Układy scalone wstęp układy hybrydowe Ryszard J. Barczyński, 2012 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Publikacja współfinansowana
Układy scalone wstęp układy hybrydowe Ryszard J. Barczyński, 2012 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Publikacja współfinansowana
Cyfrowe układy scalone
 Cyfrowe układy scalone Ryszard J. Barczyński, 2010 2015 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Cyfrowe układy scalone Układy cyfrowe
Cyfrowe układy scalone Ryszard J. Barczyński, 2010 2015 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Cyfrowe układy scalone Układy cyfrowe
Cyfrowe układy scalone
 Cyfrowe układy scalone Ryszard J. Barczyński, 2012 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Publikacja współfinansowana ze środków
Cyfrowe układy scalone Ryszard J. Barczyński, 2012 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Publikacja współfinansowana ze środków
Bramki logiczne. 2. Cele ćwiczenia Badanie charakterystyk przejściowych inwertera. tranzystorowego, bramki 7400 i bramki 74132.
 Bramki logiczne 1. Czas trwania: 3h 2. Cele ćwiczenia Badanie charakterystyk przejściowych inwertera. tranzystorowego, bramki 7400 i bramki 74132. 3. Wymagana znajomość pojęć stany logiczne Hi, Lo, stan
Bramki logiczne 1. Czas trwania: 3h 2. Cele ćwiczenia Badanie charakterystyk przejściowych inwertera. tranzystorowego, bramki 7400 i bramki 74132. 3. Wymagana znajomość pojęć stany logiczne Hi, Lo, stan
Ćw. 8 Bramki logiczne
 Ćw. 8 Bramki logiczne 1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z podstawowymi bramkami logicznymi, poznanie ich rodzajów oraz najwaŝniejszych parametrów opisujących ich własności elektryczne.
Ćw. 8 Bramki logiczne 1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z podstawowymi bramkami logicznymi, poznanie ich rodzajów oraz najwaŝniejszych parametrów opisujących ich własności elektryczne.
Zbudować 2wejściową bramkę (narysować schemat): a) NANDCMOS, b) NORCMOS, napisać jej tabelkę prawdy i wyjaśnić działanie przy pomocy charakterystyk
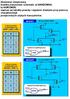 Zbudować 2wejściową bramkę (narysować schemat): a) NANDCMOS, b) NORCMOS, napisać jej tabelkę prawdy i wyjaśnić działanie przy pomocy charakterystyk przejściowych użytych tranzystorów. NOR CMOS Skale integracji
Zbudować 2wejściową bramkę (narysować schemat): a) NANDCMOS, b) NORCMOS, napisać jej tabelkę prawdy i wyjaśnić działanie przy pomocy charakterystyk przejściowych użytych tranzystorów. NOR CMOS Skale integracji
WSTĘP. Budowa bramki NAND TTL, ch-ka przełączania, schemat wewnętrzny, działanie 2
 WSTĘP O liczbie elementów użytych do budowy jakiegoś urządzenia elektronicznego, a więc i o możliwości obniżenia jego ceny, decyduje dzisiaj liczba zastosowanych w nim układów scalonych. Najstarszą rodziną
WSTĘP O liczbie elementów użytych do budowy jakiegoś urządzenia elektronicznego, a więc i o możliwości obniżenia jego ceny, decyduje dzisiaj liczba zastosowanych w nim układów scalonych. Najstarszą rodziną
Podstawy Automatyki. Wykład 13 - Układy bramkowe. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 13 - Układy bramkowe Instytut Automatyki i Robotyki Warszawa, 2015 Układy z elementów logicznych Bramki logiczne Elementami logicznymi (bramkami logicznymi) są urządzenia o dwustanowym sygnale wyjściowym
Wykład 13 - Układy bramkowe Instytut Automatyki i Robotyki Warszawa, 2015 Układy z elementów logicznych Bramki logiczne Elementami logicznymi (bramkami logicznymi) są urządzenia o dwustanowym sygnale wyjściowym
Bramki logiczne Podstawowe składniki wszystkich układów logicznych
 Układy logiczne Bramki logiczne A B A B AND NAND A B A B OR NOR A NOT A B A B XOR NXOR A NOT A B AND NAND A B OR NOR A B XOR NXOR Podstawowe składniki wszystkich układów logicznych 2 Podstawowe tożsamości
Układy logiczne Bramki logiczne A B A B AND NAND A B A B OR NOR A NOT A B A B XOR NXOR A NOT A B AND NAND A B OR NOR A B XOR NXOR Podstawowe składniki wszystkich układów logicznych 2 Podstawowe tożsamości
Automatyzacja Ćwicz. 2 Teoria mnogości i algebra logiki Akademia Morska w Szczecinie - Wydział Inżynieryjno-Ekonomiczny Transportu
 Automatyzacja Ćwicz. 2 Teoria mnogości i algebra logiki Historia teorii mnogości Teoria mnogości to inaczej nauka o zbiorach i ich własnościach; Zapoczątkowana przez greckich matematyków i filozofów w
Automatyzacja Ćwicz. 2 Teoria mnogości i algebra logiki Historia teorii mnogości Teoria mnogości to inaczej nauka o zbiorach i ich własnościach; Zapoczątkowana przez greckich matematyków i filozofów w
Automatyka Lab 1 Teoria mnogości i algebra logiki. Akademia Morska w Szczecinie - Wydział Inżynieryjno-Ekonomiczny Transportu
 Automatyka Lab 1 Teoria mnogości i algebra logiki Harmonogram zajęć Układy przełączające: 1. Algebra logiki - Wprowadzenie 2. Funkcje logiczne - minimalizacja funkcji 3. Bramki logiczne - rysowanie układów
Automatyka Lab 1 Teoria mnogości i algebra logiki Harmonogram zajęć Układy przełączające: 1. Algebra logiki - Wprowadzenie 2. Funkcje logiczne - minimalizacja funkcji 3. Bramki logiczne - rysowanie układów
Cyfrowe układy scalone
 Ryszard J. Barczyński, 2 25 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Układy cyfrowe stosowane są do przetwarzania informacji zakodowanej
Ryszard J. Barczyński, 2 25 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Układy cyfrowe stosowane są do przetwarzania informacji zakodowanej
Układy scalone. wstęp
 Układy scalone wstęp Ryszard J. Barczyński, 2016 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Układy scalone Układ scalony (ang. intergrated
Układy scalone wstęp Ryszard J. Barczyński, 2016 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Układy scalone Układ scalony (ang. intergrated
Architektura komputerów ćwiczenia Bramki logiczne. Układy kombinacyjne. Kanoniczna postać dysjunkcyjna i koniunkcyjna.
 Architektura komputerów ćwiczenia Zbiór zadań IV Bramki logiczne. Układy kombinacyjne. Kanoniczna postać dysjunkcyjna i koniunkcyjna. Wprowadzenie 1 1 fragmenty książki "Organizacja i architektura systemu
Architektura komputerów ćwiczenia Zbiór zadań IV Bramki logiczne. Układy kombinacyjne. Kanoniczna postać dysjunkcyjna i koniunkcyjna. Wprowadzenie 1 1 fragmenty książki "Organizacja i architektura systemu
Układy cyfrowe. Najczęściej układy cyfrowe służą do przetwarzania sygnałów o dwóch poziomach napięć:
 Układy cyfrowe W układach cyfrowych sygnały napięciowe (lub prądowe) przyjmują tylko określoną liczbę poziomów, którym przyporządkowywane są wartości liczbowe. Najczęściej układy cyfrowe służą do przetwarzania
Układy cyfrowe W układach cyfrowych sygnały napięciowe (lub prądowe) przyjmują tylko określoną liczbę poziomów, którym przyporządkowywane są wartości liczbowe. Najczęściej układy cyfrowe służą do przetwarzania
Tranzystor JFET i MOSFET zas. działania
 Tranzystor JFET i MOSFET zas. działania brak kanału v GS =v t (cutoff ) kanał otwarty brak kanału kanał otwarty kanał zamknięty w.2, p. kanał zamknięty Co było na ostatnim wykładzie? Układy cyfrowe Najczęściej
Tranzystor JFET i MOSFET zas. działania brak kanału v GS =v t (cutoff ) kanał otwarty brak kanału kanał otwarty kanał zamknięty w.2, p. kanał zamknięty Co było na ostatnim wykładzie? Układy cyfrowe Najczęściej
Arytmetyka liczb binarnych
 Wartość dwójkowej liczby stałoprzecinkowej Wartość dziesiętna stałoprzecinkowej liczby binarnej Arytmetyka liczb binarnych b n-1...b 1 b 0,b -1 b -2...b -m = b n-1 2 n-1 +... + b 1 2 1 + b 0 2 0 + b -1
Wartość dwójkowej liczby stałoprzecinkowej Wartość dziesiętna stałoprzecinkowej liczby binarnej Arytmetyka liczb binarnych b n-1...b 1 b 0,b -1 b -2...b -m = b n-1 2 n-1 +... + b 1 2 1 + b 0 2 0 + b -1
Podstawowe układy cyfrowe
 ELEKTRONIKA CYFROWA SPRAWOZDANIE NR 4 Podstawowe układy cyfrowe Grupa 6 Prowadzący: Roman Płaneta Aleksandra Gierut CEL ĆWICZENIA Celem ćwiczenia jest zapoznanie się z podstawowymi bramkami logicznymi,
ELEKTRONIKA CYFROWA SPRAWOZDANIE NR 4 Podstawowe układy cyfrowe Grupa 6 Prowadzący: Roman Płaneta Aleksandra Gierut CEL ĆWICZENIA Celem ćwiczenia jest zapoznanie się z podstawowymi bramkami logicznymi,
Elektronika cyfrowa i mikroprocesory. Dr inż. Aleksander Cianciara
 Elektronika cyfrowa i mikroprocesory Dr inż. Aleksander Cianciara Sprawy organizacyjne Warunki zaliczenia Lista obecności Kolokwium końcowe Ocena końcowa Konsultacje Poniedziałek 6:-7: Kontakt Budynek
Elektronika cyfrowa i mikroprocesory Dr inż. Aleksander Cianciara Sprawy organizacyjne Warunki zaliczenia Lista obecności Kolokwium końcowe Ocena końcowa Konsultacje Poniedziałek 6:-7: Kontakt Budynek
Zadania do wykładu 1, Zapisz liczby binarne w kodzie dziesiętnym: ( ) 2 =( ) 10, ( ) 2 =( ) 10, (101001, 10110) 2 =( ) 10
 Zadania do wykładu 1,. 1. Zapisz liczby binarne w kodzie dziesiętnym: (1011011) =( ) 10, (11001100) =( ) 10, (101001, 10110) =( ) 10. Zapisz liczby dziesiętne w naturalnym kodzie binarnym: (5) 10 =( ),
Zadania do wykładu 1,. 1. Zapisz liczby binarne w kodzie dziesiętnym: (1011011) =( ) 10, (11001100) =( ) 10, (101001, 10110) =( ) 10. Zapisz liczby dziesiętne w naturalnym kodzie binarnym: (5) 10 =( ),
Technologia wytwarzania układów scalonych (US) WYK. 17 SMK
 Technologia wytwarzania układów scalonych (US) WYK. 17 SMK Na podstawie: W. Marciniak, Przyrządy półprzewodnikowe i układy scalone, WNT, 1987 1. Historia US J. Kilby, Texas Instruments, 1958 przerzutnik
Technologia wytwarzania układów scalonych (US) WYK. 17 SMK Na podstawie: W. Marciniak, Przyrządy półprzewodnikowe i układy scalone, WNT, 1987 1. Historia US J. Kilby, Texas Instruments, 1958 przerzutnik
Podstawy Automatyki. Wykład 13 - Układy bramkowe. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 13 - Układy bramkowe Instytut Automatyki i Robotyki Warszawa, 2015 Układy z elementów logicznych Bramki logiczne Elementami logicznymi (bramkami logicznymi) są urządzenia o dwustanowym sygnale wyjściowym
Wykład 13 - Układy bramkowe Instytut Automatyki i Robotyki Warszawa, 2015 Układy z elementów logicznych Bramki logiczne Elementami logicznymi (bramkami logicznymi) są urządzenia o dwustanowym sygnale wyjściowym
I. Podstawowe zagadnienia z teorii układów cyfrowych
 I. Podstawowe zagadnienia z teorii układów cyfrowych. Wstęp Muzyka na płytach fonograficznych jest zapisana w formie kanaliku o zmiennym urzeźbieniu. Ruch igły prowadzonej przez kanalik odbywa się w sposób
I. Podstawowe zagadnienia z teorii układów cyfrowych. Wstęp Muzyka na płytach fonograficznych jest zapisana w formie kanaliku o zmiennym urzeźbieniu. Ruch igły prowadzonej przez kanalik odbywa się w sposób
Inwerter logiczny. Ilustracja 1: Układ do symulacji inwertera (Inverter.sch)
 DSCH2 to program do edycji i symulacji układów logicznych. DSCH2 jest wykorzystywany do sprawdzenia architektury układu logicznego przed rozpoczęciem projektowania fizycznego. DSCH2 zapewnia ergonomiczne
DSCH2 to program do edycji i symulacji układów logicznych. DSCH2 jest wykorzystywany do sprawdzenia architektury układu logicznego przed rozpoczęciem projektowania fizycznego. DSCH2 zapewnia ergonomiczne
Podstawy elektroniki cyfrowej dla Inżynierii Nanostruktur. Piotr Fita
 Podstawy elektroniki cyfrowej dla Inżynierii Nanostruktur Piotr Fita Elektronika cyfrowa i analogowa Układy analogowe - przetwarzanie sygnałów, których wartości zmieniają się w sposób ciągły w pewnym zakresie
Podstawy elektroniki cyfrowej dla Inżynierii Nanostruktur Piotr Fita Elektronika cyfrowa i analogowa Układy analogowe - przetwarzanie sygnałów, których wartości zmieniają się w sposób ciągły w pewnym zakresie
Katedra Przyrządów Półprzewodnikowych i Optoelektronicznych Laboratorium Przyrządów Półprzewodnikowych. Ćwiczenie 4
 Ćwiczenie 4 Cel ćwiczenia Celem ćwiczenia jest poznanie charakterystyk statycznych układów scalonych CMOS oraz ich własności dynamicznych podczas procesu przełączania. Wiadomości podstawowe. Budowa i działanie
Ćwiczenie 4 Cel ćwiczenia Celem ćwiczenia jest poznanie charakterystyk statycznych układów scalonych CMOS oraz ich własności dynamicznych podczas procesu przełączania. Wiadomości podstawowe. Budowa i działanie
dr inż. Rafał Klaus Zajęcia finansowane z projektu "Rozwój i doskonalenie kształcenia i ich zastosowań w przemyśle" POKL
 Technika cyfrowa w architekturze komputerów materiał do wykładu 2/3 dr inż. Rafał Klaus Zajęcia finansowane z projektu "Rozwój i doskonalenie kształcenia na Politechnice Poznańskiej w zakresie technologii
Technika cyfrowa w architekturze komputerów materiał do wykładu 2/3 dr inż. Rafał Klaus Zajęcia finansowane z projektu "Rozwój i doskonalenie kształcenia na Politechnice Poznańskiej w zakresie technologii
Ćwiczenie 26. Temat: Układ z bramkami NAND i bramki AOI..
 Temat: Układ z bramkami NAND i bramki AOI.. Ćwiczenie 26 Cel ćwiczenia Zapoznanie się ze sposobami konstruowania z bramek NAND różnych bramek logicznych. Konstruowanie bramek NOT, AND i OR z bramek NAND.
Temat: Układ z bramkami NAND i bramki AOI.. Ćwiczenie 26 Cel ćwiczenia Zapoznanie się ze sposobami konstruowania z bramek NAND różnych bramek logicznych. Konstruowanie bramek NOT, AND i OR z bramek NAND.
Synteza układów kombinacyjnych
 Sławomir Kulesza Technika cyfrowa Synteza układów kombinacyjnych Wykład dla studentów III roku Informatyki Wersja 4.0, 23/10/2014 Bramki logiczne Bramki logiczne to podstawowe elementy logiczne realizujące
Sławomir Kulesza Technika cyfrowa Synteza układów kombinacyjnych Wykład dla studentów III roku Informatyki Wersja 4.0, 23/10/2014 Bramki logiczne Bramki logiczne to podstawowe elementy logiczne realizujące
Ćwiczenie 24 Temat: Układy bramek logicznych pomiar napięcia i prądu. Cel ćwiczenia
 Ćwiczenie 24 Temat: Układy bramek logicznych pomiar napięcia i prądu. Cel ćwiczenia Poznanie własności i zasad działania różnych bramek logicznych. Zmierzenie napięcia wejściowego i wyjściowego bramek
Ćwiczenie 24 Temat: Układy bramek logicznych pomiar napięcia i prądu. Cel ćwiczenia Poznanie własności i zasad działania różnych bramek logicznych. Zmierzenie napięcia wejściowego i wyjściowego bramek
Automatyzacja i robotyzacja procesów produkcyjnych
 Automatyzacja i robotyzacja procesów produkcyjnych Instrukcja laboratoryjna Technika cyfrowa Opracował: mgr inż. Krzysztof Bodzek Cel ćwiczenia. Celem ćwiczenia jest zapoznanie studenta z zapisem liczb
Automatyzacja i robotyzacja procesów produkcyjnych Instrukcja laboratoryjna Technika cyfrowa Opracował: mgr inż. Krzysztof Bodzek Cel ćwiczenia. Celem ćwiczenia jest zapoznanie studenta z zapisem liczb
Algebra Boole a i jej zastosowania
 lgebra oole a i jej zastosowania Wprowadzenie Niech dany będzie zbiór dwuelementowy, którego elementy oznaczymy symbolami 0 oraz 1, tj. {0, 1}. W zbiorze tym określamy działania sumy :, iloczynu : _ oraz
lgebra oole a i jej zastosowania Wprowadzenie Niech dany będzie zbiór dwuelementowy, którego elementy oznaczymy symbolami 0 oraz 1, tj. {0, 1}. W zbiorze tym określamy działania sumy :, iloczynu : _ oraz
Podstawowe operacje arytmetyczne i logiczne dla liczb binarnych
 1 Podstawowe operacje arytmetyczne i logiczne dla liczb binarnych 1. Podstawowe operacje logiczne dla cyfr binarnych Jeśli cyfry 0 i 1 potraktujemy tak, jak wartości logiczne fałsz i prawda, to działanie
1 Podstawowe operacje arytmetyczne i logiczne dla liczb binarnych 1. Podstawowe operacje logiczne dla cyfr binarnych Jeśli cyfry 0 i 1 potraktujemy tak, jak wartości logiczne fałsz i prawda, to działanie
Wykład 2. Informatyka Stosowana. 8 października 2018, M. A-B. Informatyka Stosowana Wykład 2 8 października 2018, M. A-B 1 / 41
 Wykład 2 Informatyka Stosowana 8 października 2018, M. A-B Informatyka Stosowana Wykład 2 8 października 2018, M. A-B 1 / 41 Elementy logiki matematycznej Informatyka Stosowana Wykład 2 8 października
Wykład 2 Informatyka Stosowana 8 października 2018, M. A-B Informatyka Stosowana Wykład 2 8 października 2018, M. A-B 1 / 41 Elementy logiki matematycznej Informatyka Stosowana Wykład 2 8 października
Cyfrowe Elementy Automatyki. Bramki logiczne, przerzutniki, liczniki, sterowanie wyświetlaczem
 Cyfrowe Elementy Automatyki Bramki logiczne, przerzutniki, liczniki, sterowanie wyświetlaczem Układy cyfrowe W układach cyfrowych sygnały napięciowe (lub prądowe) przyjmują tylko określoną liczbę poziomów,
Cyfrowe Elementy Automatyki Bramki logiczne, przerzutniki, liczniki, sterowanie wyświetlaczem Układy cyfrowe W układach cyfrowych sygnały napięciowe (lub prądowe) przyjmują tylko określoną liczbę poziomów,
Układy kombinacyjne 1
 Układy kombinacyjne 1 Układy kombinacyjne są to układy cyfrowe, których stany wyjść są zawsze jednoznacznie określone przez stany wejść. Oznacza to, że doprowadzając na wejścia tych układów określoną kombinację
Układy kombinacyjne 1 Układy kombinacyjne są to układy cyfrowe, których stany wyjść są zawsze jednoznacznie określone przez stany wejść. Oznacza to, że doprowadzając na wejścia tych układów określoną kombinację
Technika Cyfrowa 2 wykład 4: FPGA odsłona druga technologie i rodziny układów logicznych
 Technika Cyfrowa 2 wykład 4: FPGA odsłona druga technologie i rodziny układów logicznych Dr inż. Jacek Mazurkiewicz Katedra Informatyki Technicznej e-mail: Jacek.Mazurkiewicz@pwr.edu.pl Elementy poważniejsze
Technika Cyfrowa 2 wykład 4: FPGA odsłona druga technologie i rodziny układów logicznych Dr inż. Jacek Mazurkiewicz Katedra Informatyki Technicznej e-mail: Jacek.Mazurkiewicz@pwr.edu.pl Elementy poważniejsze
Cyfrowe układy scalone c.d. funkcje
 Cyfrowe układy scalone c.d. funkcje Ryszard J. Barczyński, 206 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Kombinacyjne układy cyfrowe
Cyfrowe układy scalone c.d. funkcje Ryszard J. Barczyński, 206 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Kombinacyjne układy cyfrowe
Państwowa Wyższa Szkoła Zawodowa
 Państwowa Wyższa Szkoła Zawodowa w Legnicy Laboratorium Podstaw Elektroniki i Miernictwa Ćwiczenie nr 4 BADANIE BRAMEK LOGICZNYCH A. Cel ćwiczenia. - Poznanie zasad logiki binarnej. Prawa algebry Boole
Państwowa Wyższa Szkoła Zawodowa w Legnicy Laboratorium Podstaw Elektroniki i Miernictwa Ćwiczenie nr 4 BADANIE BRAMEK LOGICZNYCH A. Cel ćwiczenia. - Poznanie zasad logiki binarnej. Prawa algebry Boole
Elementy cyfrowe i układy logiczne
 Elementy cyfrowe i układy logiczne Wykład 4 Legenda Podział układów logicznych Układy cyfrowe, układy scalone Synteza logiczna Układy TTL, CMOS 2 1 Podział układów Układy logiczne kombinacyjne sekwencyjne
Elementy cyfrowe i układy logiczne Wykład 4 Legenda Podział układów logicznych Układy cyfrowe, układy scalone Synteza logiczna Układy TTL, CMOS 2 1 Podział układów Układy logiczne kombinacyjne sekwencyjne
Ćwiczenie 23. Temat: Własności podstawowych bramek logicznych. Cel ćwiczenia
 Temat: Własności podstawowych bramek logicznych. Cel ćwiczenia Ćwiczenie 23 Poznanie symboli własności. Zmierzenie parametrów podstawowych bramek logicznych TTL i CMOS. Czytanie schematów elektronicznych,
Temat: Własności podstawowych bramek logicznych. Cel ćwiczenia Ćwiczenie 23 Poznanie symboli własności. Zmierzenie parametrów podstawowych bramek logicznych TTL i CMOS. Czytanie schematów elektronicznych,
LABORATORIUM PROJEKTOWANIA UKŁADÓW VLSI
 Wydział EAIiE LABORATORIUM PROJEKTOWANIA UKŁADÓW VLSI Temat projektu OŚMIOWEJŚCIOWA KOMÓRKA UKŁADU PAL Z ZASTOSOWANIEM NA PRZYKŁADZIE MULTIPLEKSERA Autorzy Tomasz Radziszewski Zdzisław Rapacz Rok akademicki
Wydział EAIiE LABORATORIUM PROJEKTOWANIA UKŁADÓW VLSI Temat projektu OŚMIOWEJŚCIOWA KOMÓRKA UKŁADU PAL Z ZASTOSOWANIEM NA PRZYKŁADZIE MULTIPLEKSERA Autorzy Tomasz Radziszewski Zdzisław Rapacz Rok akademicki
Technika cyfrowa Synteza układów kombinacyjnych
 Sławomir Kulesza Technika cyfrowa Synteza układów kombinacyjnych Wykład dla studentów III roku Informatyki Wersja 2.0, 05/10/2011 Podział układów logicznych Opis funkcjonalny układów logicznych x 1 y 1
Sławomir Kulesza Technika cyfrowa Synteza układów kombinacyjnych Wykład dla studentów III roku Informatyki Wersja 2.0, 05/10/2011 Podział układów logicznych Opis funkcjonalny układów logicznych x 1 y 1
Logika binarna. Prawo łączności mówimy, że operator binarny * na zbiorze S jest łączny gdy (x * y) * z = x * (y * z) dla każdego x, y, z S.
 Logika binarna Logika binarna zajmuje się zmiennymi mogącymi przyjmować dwie wartości dyskretne oraz operacjami mającymi znaczenie logiczne. Dwie wartości jakie mogą te zmienne przyjmować noszą przy tym
Logika binarna Logika binarna zajmuje się zmiennymi mogącymi przyjmować dwie wartości dyskretne oraz operacjami mającymi znaczenie logiczne. Dwie wartości jakie mogą te zmienne przyjmować noszą przy tym
Logiczne układy bistabilne przerzutniki.
 Przerzutniki spełniają rolę elementów pamięciowych: -przy pewnej kombinacji stanów na pewnych wejściach, niezależnie od stanów innych wejść, stany wyjściowe oraz nie ulegają zmianie; -przy innej określonej
Przerzutniki spełniają rolę elementów pamięciowych: -przy pewnej kombinacji stanów na pewnych wejściach, niezależnie od stanów innych wejść, stany wyjściowe oraz nie ulegają zmianie; -przy innej określonej
TEST KONKURSOWY CZAS TESTU 40 MIN ILOŚĆ MAKSYMALNA PUNKTÓW 20 INSTRUKCJA:
 CZAS TESTU 40 MIN ILOŚĆ MAKSYMALNA PUNKTÓW 20 INSTRUKCJA: TEST KONKURSOWY 1. Do arkusza testu dołączona jest KARTA ODPOWIEDZI, na której wpisz swoje imię i nazwisko, nazwę szkoły i miasto. 2. Test zawiera
CZAS TESTU 40 MIN ILOŚĆ MAKSYMALNA PUNKTÓW 20 INSTRUKCJA: TEST KONKURSOWY 1. Do arkusza testu dołączona jest KARTA ODPOWIEDZI, na której wpisz swoje imię i nazwisko, nazwę szkoły i miasto. 2. Test zawiera
Podstawy układów mikroelektronicznych
 Podstawy układów mikroelektronicznych wykład dla kierunku Technologie Kosmiczne i Satelitarne Część 2. Podstawy działania układów cyfrowych. dr inż. Waldemar Jendernalik Katedra Systemów Mikroelektronicznych,
Podstawy układów mikroelektronicznych wykład dla kierunku Technologie Kosmiczne i Satelitarne Część 2. Podstawy działania układów cyfrowych. dr inż. Waldemar Jendernalik Katedra Systemów Mikroelektronicznych,
Wykład nr 1 Techniki Mikroprocesorowe. dr inż. Artur Cichowski
 Wykład nr 1 Techniki Mikroprocesorowe dr inż. Artur Cichowski ix jy i j {0,1} {0,1} Dla układów kombinacyjnych stan dowolnego wyjścia y i w danej chwili czasu zależy wyłącznie od aktualnej kombinacji stanów
Wykład nr 1 Techniki Mikroprocesorowe dr inż. Artur Cichowski ix jy i j {0,1} {0,1} Dla układów kombinacyjnych stan dowolnego wyjścia y i w danej chwili czasu zależy wyłącznie od aktualnej kombinacji stanów
Podstawy Automatyki. Wykład 12 - synteza i minimalizacja funkcji logicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 12 - synteza i minimalizacja funkcji logicznych Instytut Automatyki i Robotyki Warszawa, 2017 Synteza funkcji logicznych Terminy - na bazie funkcji trójargumenowej y = (x 1, x 2, x 3 ) (1) Elementarny
Wykład 12 - synteza i minimalizacja funkcji logicznych Instytut Automatyki i Robotyki Warszawa, 2017 Synteza funkcji logicznych Terminy - na bazie funkcji trójargumenowej y = (x 1, x 2, x 3 ) (1) Elementarny
Wykład 1. Informatyka Stosowana. 3 października Informatyka Stosowana Wykład 1 3 października / 26
 Wykład 1 Informatyka Stosowana 3 października 2016 Informatyka Stosowana Wykład 1 3 października 2016 1 / 26 Wykłady : 45h (w semestrze zimowym) ( Egzamin) 30h (w semetrze letnim ) ( Egzamin) Zajęcia praktyczne:
Wykład 1 Informatyka Stosowana 3 października 2016 Informatyka Stosowana Wykład 1 3 października 2016 1 / 26 Wykłady : 45h (w semestrze zimowym) ( Egzamin) 30h (w semetrze letnim ) ( Egzamin) Zajęcia praktyczne:
UTK Mirosław Rucioski
 Temat 11: Elektryczna implementacja systemu binarnego. UTK Mirosław Rucioski Cela kształcenia: Zna symbole graficzne i działania logiczne bramek: Bramka OR; Bramka AND; Bramka NOT - inwerter Bramki; NAND
Temat 11: Elektryczna implementacja systemu binarnego. UTK Mirosław Rucioski Cela kształcenia: Zna symbole graficzne i działania logiczne bramek: Bramka OR; Bramka AND; Bramka NOT - inwerter Bramki; NAND
Zapoznanie się z podstawowymi strukturami funktorów logicznych realizowanymi w technice RTL (Resistor Transistor Logic) oraz zasadą ich działania.
 adanie funktorów logicznych RTL - Ćwiczenie. Cel ćwiczenia Zapoznanie się z podstawowymi strukturami funktorów logicznych realizowanymi w technice RTL (Resistor Transistor Logic) oraz zasadą ich działania..
adanie funktorów logicznych RTL - Ćwiczenie. Cel ćwiczenia Zapoznanie się z podstawowymi strukturami funktorów logicznych realizowanymi w technice RTL (Resistor Transistor Logic) oraz zasadą ich działania..
BADANIE UKŁADÓW CYFROWYCH. CEL: Celem ćwiczenia jest poznanie właściwości statycznych układów cyfrowych serii TTL. PRZEBIEG ĆWICZENIA
 BADANIE UKŁADÓW CYFROWYCH CEL: Celem ćwiczenia jest poznanie właściwości statycznych układów cyfrowych serii TTL. PRZEBIEG ĆWICZENIA 1. OGLĘDZINY Dokonać oględzin badanego układu cyfrowego określając jego:
BADANIE UKŁADÓW CYFROWYCH CEL: Celem ćwiczenia jest poznanie właściwości statycznych układów cyfrowych serii TTL. PRZEBIEG ĆWICZENIA 1. OGLĘDZINY Dokonać oględzin badanego układu cyfrowego określając jego:
Automatyka Treść wykładów: Literatura. Wstęp. Sygnał analogowy a cyfrowy. Bieżące wiadomości:
 Treść wykładów: Automatyka dr inż. Szymon Surma szymon.surma@polsl.pl pok. 202, tel. +48 32 603 4136 1. Podstawy automatyki 1. Wstęp, 2. Różnice między sygnałem analogowym a cyfrowym, 3. Podstawowe elementy
Treść wykładów: Automatyka dr inż. Szymon Surma szymon.surma@polsl.pl pok. 202, tel. +48 32 603 4136 1. Podstawy automatyki 1. Wstęp, 2. Różnice między sygnałem analogowym a cyfrowym, 3. Podstawowe elementy
2019/09/16 07:46 1/2 Laboratorium AITUC
 2019/09/16 07:46 1/2 Laboratorium AITUC Table of Contents Laboratorium AITUC... 1 Uwagi praktyczne przed rozpoczęciem zajęć... 1 Lab 1: Układy kombinacyjne małej i średniej skali integracji... 1 Lab 2:
2019/09/16 07:46 1/2 Laboratorium AITUC Table of Contents Laboratorium AITUC... 1 Uwagi praktyczne przed rozpoczęciem zajęć... 1 Lab 1: Układy kombinacyjne małej i średniej skali integracji... 1 Lab 2:
Funkcje logiczne X = A B AND. K.M.Gawrylczyk /55
 Układy cyfrowe Funkcje logiczne AND A B X = A B... 2/55 Funkcje logiczne OR A B X = A + B NOT A A... 3/55 Twierdzenia algebry Boole a A + B = B + A A B = B A A + B + C = A + (B+C( B+C) ) = (A+B( A+B) )
Układy cyfrowe Funkcje logiczne AND A B X = A B... 2/55 Funkcje logiczne OR A B X = A + B NOT A A... 3/55 Twierdzenia algebry Boole a A + B = B + A A B = B A A + B + C = A + (B+C( B+C) ) = (A+B( A+B) )
Elementy logiki. Algebra Boole a. Analiza i synteza układów logicznych
 Elementy logiki: Algebra Boole a i układy logiczne 1 Elementy logiki dla informatyków Wykład III Elementy logiki. Algebra Boole a. Analiza i synteza układów logicznych Elementy logiki: Algebra Boole a
Elementy logiki: Algebra Boole a i układy logiczne 1 Elementy logiki dla informatyków Wykład III Elementy logiki. Algebra Boole a. Analiza i synteza układów logicznych Elementy logiki: Algebra Boole a
Ćwiczenie 1 Program Electronics Workbench
 Systemy teleinformatyczne Ćwiczenie Program Electronics Workbench Symulacja układów logicznych Program Electronics Workbench służy do symulacji działania prostych i bardziej złożonych układów elektrycznych
Systemy teleinformatyczne Ćwiczenie Program Electronics Workbench Symulacja układów logicznych Program Electronics Workbench służy do symulacji działania prostych i bardziej złożonych układów elektrycznych
Ćwiczenie D1 Bramki. Wydział Fizyki UW
 Wydział Fizyki UW Pracownia fizyczna i elektroniczna (w tym komputerowa) dla Inżynierii Nanostruktur (1100-1INZ7) oraz Energetyki i Chemii Jądrowej (1100-1ENPRFIZELEK) Ćwiczenie D1 Bramki Streszczenie
Wydział Fizyki UW Pracownia fizyczna i elektroniczna (w tym komputerowa) dla Inżynierii Nanostruktur (1100-1INZ7) oraz Energetyki i Chemii Jądrowej (1100-1ENPRFIZELEK) Ćwiczenie D1 Bramki Streszczenie
Komputerowa symulacja bramek w technice TTL i CMOS
 ZESPÓŁ LABORATORIÓW TELEMATYKI TRANSPORTU ZAKŁAD TELEKOMUNIKACJI W TRANSPORCIE WYDZIAŁ TRANSPORTU POLITECHNIKI WARSZAWSKIEJ LABORATORIUM ELEKTRONIKI INSTRUKCJA DO ĆWICZENIA NR 27 Komputerowa symulacja
ZESPÓŁ LABORATORIÓW TELEMATYKI TRANSPORTU ZAKŁAD TELEKOMUNIKACJI W TRANSPORCIE WYDZIAŁ TRANSPORTU POLITECHNIKI WARSZAWSKIEJ LABORATORIUM ELEKTRONIKI INSTRUKCJA DO ĆWICZENIA NR 27 Komputerowa symulacja
Część 2. Funkcje logiczne układy kombinacyjne
 Część 2 Funkcje logiczne układy kombinacyjne Zapis funkcji logicznych układ funkcjonalnie pełny Arytmetyka Bool a najważniejsze aksjomaty i tożsamości Minimalizacja funkcji logicznych Układy kombinacyjne
Część 2 Funkcje logiczne układy kombinacyjne Zapis funkcji logicznych układ funkcjonalnie pełny Arytmetyka Bool a najważniejsze aksjomaty i tożsamości Minimalizacja funkcji logicznych Układy kombinacyjne
Tranzystor bipolarny wzmacniacz OE
 Tranzystor bipolarny wzmacniacz OE projektowanie poradnikowe u 1 (t) C 1 U B0 I 1 R 1 R 2 I 2 T I B0 R E I E0 I C0 V CC R C C 2 U C0 U E0 C E u 2 (t) Zadania elementów: T tranzystor- sterowane źródło prądu
Tranzystor bipolarny wzmacniacz OE projektowanie poradnikowe u 1 (t) C 1 U B0 I 1 R 1 R 2 I 2 T I B0 R E I E0 I C0 V CC R C C 2 U C0 U E0 C E u 2 (t) Zadania elementów: T tranzystor- sterowane źródło prądu
Spis elementów aplikacji i przyrządów pomiarowych:
 CEL ĆWICZENIA: Celem ćwiczenia jest zbudowanie generatora przebiegów dowolnych WSTĘP: Generatory możemy podzielić na wiele rodzajów: poróżnić je między sobą ze względu na jakość otrzymanego przebiegu,
CEL ĆWICZENIA: Celem ćwiczenia jest zbudowanie generatora przebiegów dowolnych WSTĘP: Generatory możemy podzielić na wiele rodzajów: poróżnić je między sobą ze względu na jakość otrzymanego przebiegu,
Cyfrowe układy kombinacyjne. 5 grudnia 2013 Wojciech Kucewicz 2
 Cyfrowe układy kombinacyjne 5 grudnia 2013 Wojciech Kucewicz 2 Cyfrowe układy kombinacyjne X1 X2 X3 Xn Y1 Y2 Y3 Yn Układy kombinacyjne charakteryzuje funkcja, która każdemu stanowi wejściowemu X i X jednoznacznie
Cyfrowe układy kombinacyjne 5 grudnia 2013 Wojciech Kucewicz 2 Cyfrowe układy kombinacyjne X1 X2 X3 Xn Y1 Y2 Y3 Yn Układy kombinacyjne charakteryzuje funkcja, która każdemu stanowi wejściowemu X i X jednoznacznie
Układy TTL i CMOS. Trochę logiki
 Układy TTL i CMOS O liczbie elementów użytych do budowy jakiegoś urządzenia elektronicznego, a więc i o możliwości obniżenia jego ceny, decyduje dzisiaj liczba zastosowanych w nim układów scalonych. Najstarszą
Układy TTL i CMOS O liczbie elementów użytych do budowy jakiegoś urządzenia elektronicznego, a więc i o możliwości obniżenia jego ceny, decyduje dzisiaj liczba zastosowanych w nim układów scalonych. Najstarszą
ćwiczenie 202 Temat: Układy kombinacyjne 1. Cel ćwiczenia
 Opracował: dr inż. Jarosław Mierzwa KTER INFORMTKI TEHNIZNEJ Ćwiczenia laboratoryjne z Logiki Układów yfrowych ćwiczenie 202 Temat: Układy kombinacyjne 1. el ćwiczenia Ćwiczenie ma na celu praktyczne zapoznanie
Opracował: dr inż. Jarosław Mierzwa KTER INFORMTKI TEHNIZNEJ Ćwiczenia laboratoryjne z Logiki Układów yfrowych ćwiczenie 202 Temat: Układy kombinacyjne 1. el ćwiczenia Ćwiczenie ma na celu praktyczne zapoznanie
Wstęp do Techniki Cyfrowej... Algebra Boole a
 Wstęp do Techniki Cyfrowej... Algebra Boole a Po co AB? Świetne narzędzie do analitycznego opisu układów logicznych. 1854r. George Boole opisuje swój system dedukcyjny. Ukoronowanie zapoczątkowanych w
Wstęp do Techniki Cyfrowej... Algebra Boole a Po co AB? Świetne narzędzie do analitycznego opisu układów logicznych. 1854r. George Boole opisuje swój system dedukcyjny. Ukoronowanie zapoczątkowanych w
Temat: Pamięci. Programowalne struktury logiczne.
 Temat: Pamięci. Programowalne struktury logiczne. 1. Pamięci są układami służącymi do przechowywania informacji w postaci ciągu słów bitowych. Wykonuje się jako układy o bardzo dużym stopniu scalenia w
Temat: Pamięci. Programowalne struktury logiczne. 1. Pamięci są układami służącymi do przechowywania informacji w postaci ciągu słów bitowych. Wykonuje się jako układy o bardzo dużym stopniu scalenia w
Technika cyfrowa Synteza układów kombinacyjnych (I)
 Sławomir Kulesza Technika cyfrowa Synteza układów kombinacyjnych (I) Wykład dla studentów III roku Informatyki Wersja 2.0, 05/10/2011 Podział układów logicznych Opis funkcjonalny układów logicznych x 1
Sławomir Kulesza Technika cyfrowa Synteza układów kombinacyjnych (I) Wykład dla studentów III roku Informatyki Wersja 2.0, 05/10/2011 Podział układów logicznych Opis funkcjonalny układów logicznych x 1
Sprawdzenie poprawności podstawowych bramek logicznych: NOT, NAND, NOR
 Laboratorium Podstaw Techniki Cyfrowej dr Marek Siłuszyk mgr Arkadiusz Wysokiński Ćwiczenie 01 PTC Sprawdzenie poprawności podstawowych bramek logicznych: NOT, NAND, NOR opr. tech. Mirosław Maś Uniwersytet
Laboratorium Podstaw Techniki Cyfrowej dr Marek Siłuszyk mgr Arkadiusz Wysokiński Ćwiczenie 01 PTC Sprawdzenie poprawności podstawowych bramek logicznych: NOT, NAND, NOR opr. tech. Mirosław Maś Uniwersytet
TEST KONKURSOWY CZAS TESTU 40 MIN ILOŚĆ MAKSYMALNA PUNKTÓW 20 INSTRUKCJA:
 CZAS TESTU 40 MIN ILOŚĆ MAKSYMALNA PUNKTÓW 20 INSTRUKCJA: TEST KONKURSOWY 1. Do arkusza testu dołączona jest KARTA ODPOWIEDZI, na której wpisz swoje imię i nazwisko, nazwę szkoły i miasto. 2. Test zawiera
CZAS TESTU 40 MIN ILOŚĆ MAKSYMALNA PUNKTÓW 20 INSTRUKCJA: TEST KONKURSOWY 1. Do arkusza testu dołączona jest KARTA ODPOWIEDZI, na której wpisz swoje imię i nazwisko, nazwę szkoły i miasto. 2. Test zawiera
Technika Cyfrowa. dr inż. Marek Izdebski Kontakt: Instytut Fizyki PŁ, ul. Wólczańska 219, pok. 111, tel ,
 Technika Cyfrowa dr inż. Marek Izdebski Kontakt: Instytut Fizyki PŁ, ul. Wólczańska 29, pok., tel. 42 633667, e-mail: izdebski@p.lodz.pl Strona internetowa (materiały do wykładu i lab.): fizyka.p.lodz.pl/pl/dla-studentow/tc/
Technika Cyfrowa dr inż. Marek Izdebski Kontakt: Instytut Fizyki PŁ, ul. Wólczańska 29, pok., tel. 42 633667, e-mail: izdebski@p.lodz.pl Strona internetowa (materiały do wykładu i lab.): fizyka.p.lodz.pl/pl/dla-studentow/tc/
Podstawy Automatyki. Wykład 9 - Podstawy matematyczne automatyki procesów dyskretnych. dr inż. Jakub Możaryn. Instytut Automatyki i Robotyki
 Wykład 9 - Podstawy matematyczne automatyki procesów dyskretnych Instytut Automatyki i Robotyki Warszawa, 2015 Kody liczb całkowitych nieujemnych Kody liczbowe dzielimy na analityczne nieanalityczne (symboliczne)
Wykład 9 - Podstawy matematyczne automatyki procesów dyskretnych Instytut Automatyki i Robotyki Warszawa, 2015 Kody liczb całkowitych nieujemnych Kody liczbowe dzielimy na analityczne nieanalityczne (symboliczne)
LABORATORIUM. Technika Cyfrowa. Badanie Bramek Logicznych
 WYDZIAŁ ELEKTRYCZNY Katedra Inżynierii Systemów, Sygnałów i Elektroniki LABORATORIUM Technika Cyfrowa Badanie Bramek Logicznych Opracował: mgr inż. Andrzej Biedka 1 BADANIE FUNKCJI LOGICZNYCH 1.1 Korzystając
WYDZIAŁ ELEKTRYCZNY Katedra Inżynierii Systemów, Sygnałów i Elektroniki LABORATORIUM Technika Cyfrowa Badanie Bramek Logicznych Opracował: mgr inż. Andrzej Biedka 1 BADANIE FUNKCJI LOGICZNYCH 1.1 Korzystając
Spis treści Przełączanie złożonych układów liniowych z pojedynczym elementem reaktancyjnym 28
 Spis treści CZE ŚĆ ANALOGOWA 1. Wstęp do układów elektronicznych............................. 10 1.1. Filtr dolnoprzepustowy RC.............................. 13 1.2. Filtr górnoprzepustowy RC..............................
Spis treści CZE ŚĆ ANALOGOWA 1. Wstęp do układów elektronicznych............................. 10 1.1. Filtr dolnoprzepustowy RC.............................. 13 1.2. Filtr górnoprzepustowy RC..............................
Układy nieliniowe tranzystor bipolarny (n p n, p n p)
 Układy nieliniowe tranzystor bipolarny (n p n, p n p) Złącze emiterowe: polaryzacja przewodzenia IB B E Złącze kolektorowe: polaryzacja zaporowa C IE IC IE IB1 IB2 rekombinacja Silne domieszkowanie emitera:
Układy nieliniowe tranzystor bipolarny (n p n, p n p) Złącze emiterowe: polaryzacja przewodzenia IB B E Złącze kolektorowe: polaryzacja zaporowa C IE IC IE IB1 IB2 rekombinacja Silne domieszkowanie emitera:
Wykład 1. Informatyka Stosowana. 2 października Informatyka Stosowana Wykład 1 2 października / 33
 Wykład 1 Informatyka Stosowana 2 października 2017 Informatyka Stosowana Wykład 1 2 października 2017 1 / 33 Wykłady : 45h (w semestrze zimowym) (Egzamin) 30h (w semetrze letnim) (Egzamin) 3h lekcyjne
Wykład 1 Informatyka Stosowana 2 października 2017 Informatyka Stosowana Wykład 1 2 października 2017 1 / 33 Wykłady : 45h (w semestrze zimowym) (Egzamin) 30h (w semetrze letnim) (Egzamin) 3h lekcyjne
Komputerowa symulacja bramek w technice TTL i CMOS
 ZESPÓŁ LABORATORIÓW TELEMATYKI TRANSPORTU ZAKŁAD TELEKOMUNIKACJI W TRANSPORCIE WYDZIAŁ TRANSPORTU POLITECHNIKI WARSZAWSKIEJ LABORATORIUM ELEKTRONIKI INSTRUKCJA DO ĆWICZENIA NR 27 Komputerowa symulacja
ZESPÓŁ LABORATORIÓW TELEMATYKI TRANSPORTU ZAKŁAD TELEKOMUNIKACJI W TRANSPORCIE WYDZIAŁ TRANSPORTU POLITECHNIKI WARSZAWSKIEJ LABORATORIUM ELEKTRONIKI INSTRUKCJA DO ĆWICZENIA NR 27 Komputerowa symulacja
Podstawy techniki cyfrowej
 Podstawy techniki cyfrowej Wykład 1: Wstęp Dr hab. inż. Marek Mika Państwowa Wyższa Szkoła Zawodowa im. Jana Amosa Komeńskiego W Lesznie Plan Informacje o przedmiocie Wprowadzenie Podstawy matematyczne:
Podstawy techniki cyfrowej Wykład 1: Wstęp Dr hab. inż. Marek Mika Państwowa Wyższa Szkoła Zawodowa im. Jana Amosa Komeńskiego W Lesznie Plan Informacje o przedmiocie Wprowadzenie Podstawy matematyczne:
Laboratorium podstaw elektroniki
 150875 Grzegorz Graczyk numer indeksu imie i nazwisko 150889 Anna Janicka numer indeksu imie i nazwisko Grupa: 2 Grupa: 5 kierunek Informatyka semestr 2 rok akademicki 2008/09 Laboratorium podstaw elektroniki
150875 Grzegorz Graczyk numer indeksu imie i nazwisko 150889 Anna Janicka numer indeksu imie i nazwisko Grupa: 2 Grupa: 5 kierunek Informatyka semestr 2 rok akademicki 2008/09 Laboratorium podstaw elektroniki
0.1. Logika podstawowe pojęcia: zdania i funktory, reguły wnioskowania, zmienne zdaniowe, rachunek zdań.
 Wykłady z Analizy rzeczywistej i zespolonej w Matematyce stosowanej Wykład ELEMENTY LOGIKI ALGEBRA BOOLE A Logika podstawowe pojęcia: zdania i funktory, reguły wnioskowania, zmienne zdaniowe, rachunek
Wykłady z Analizy rzeczywistej i zespolonej w Matematyce stosowanej Wykład ELEMENTY LOGIKI ALGEBRA BOOLE A Logika podstawowe pojęcia: zdania i funktory, reguły wnioskowania, zmienne zdaniowe, rachunek
CYFROWE UKŁADY SCALONE STOSOWANE W AUTOMATYCE
 Pracownia Automatyki Katedry Tworzyw Drzewnych Ćwiczenie 5 str. 1/16 ĆWICZENIE 5 CYFROWE UKŁADY SCALONE STOSOWANE W AUTOMATYCE 1.CEL ĆWICZENIA: zapoznanie się z podstawowymi elementami cyfrowymi oraz z
Pracownia Automatyki Katedry Tworzyw Drzewnych Ćwiczenie 5 str. 1/16 ĆWICZENIE 5 CYFROWE UKŁADY SCALONE STOSOWANE W AUTOMATYCE 1.CEL ĆWICZENIA: zapoznanie się z podstawowymi elementami cyfrowymi oraz z
Ćwiczenie ZINTEGROWANE SYSTEMY CYFROWE. Pakiet edukacyjny DefSim Personal. Analiza prądowa IDDQ
 Ćwiczenie 2 ZINTEGROWANE SYSTEMY CYFROWE Pakiet edukacyjny DefSim Personal Analiza prądowa IDDQ K A T E D R A M I K R O E L E K T R O N I K I I T E C H N I K I N F O R M A T Y C Z N Y C H Politechnika
Ćwiczenie 2 ZINTEGROWANE SYSTEMY CYFROWE Pakiet edukacyjny DefSim Personal Analiza prądowa IDDQ K A T E D R A M I K R O E L E K T R O N I K I I T E C H N I K I N F O R M A T Y C Z N Y C H Politechnika
Elektryczna implementacja systemu binarnego.
 Elektryczna implementacja systemu binarnego. Cela kształcenia: Zna symbole graficzne i działania logiczne bramek: Bramka OR; Bramka AND; Bramka NOT - inwerter Bramki; NAND i NOR; Bramka XOR - ExclusixeOR.
Elektryczna implementacja systemu binarnego. Cela kształcenia: Zna symbole graficzne i działania logiczne bramek: Bramka OR; Bramka AND; Bramka NOT - inwerter Bramki; NAND i NOR; Bramka XOR - ExclusixeOR.
Wzmacniacze napięciowe z tranzystorami komplementarnymi CMOS
 Wzmacniacze napięciowe z tranzystorami komplementarnymi CMOS Cel ćwiczenia: Praktyczne wykorzystanie wiadomości do projektowania wzmacniacza z tranzystorami CMOS Badanie wpływu parametrów geometrycznych
Wzmacniacze napięciowe z tranzystorami komplementarnymi CMOS Cel ćwiczenia: Praktyczne wykorzystanie wiadomości do projektowania wzmacniacza z tranzystorami CMOS Badanie wpływu parametrów geometrycznych
Podstawowe bramki logiczne
 Temat i plan wykładu Podstawowe bramki logiczne 1. Elementarne funkcje logiczne, symbole 2. Struktura bramek bipolarnych, CMOS i BiCMOS 3. Parametry bramek 4. Rodziny układów cyfrowych 5. Elastyczność
Temat i plan wykładu Podstawowe bramki logiczne 1. Elementarne funkcje logiczne, symbole 2. Struktura bramek bipolarnych, CMOS i BiCMOS 3. Parametry bramek 4. Rodziny układów cyfrowych 5. Elastyczność
INSTYTUT CYBERNETYKI TECHNICZNEJ POLITECHNIKI WROCŁAWSKIEJ ZAKŁAD SZTUCZNEJ INTELIGENCJI I AUTOMATÓW
 INSTYTUT YERNETYKI TEHNIZNEJ POLITEHNIKI WROŁWSKIEJ ZKŁD SZTUZNEJ INTELIGENJI I UTOMTÓW Ćwiczenia laboratoryjne z Logiki Układów yfrowych ćwiczenie 22 temat: UKŁDY KOMINYJNE. EL ĆWIZENI Ćwiczenie ma na
INSTYTUT YERNETYKI TEHNIZNEJ POLITEHNIKI WROŁWSKIEJ ZKŁD SZTUZNEJ INTELIGENJI I UTOMTÓW Ćwiczenia laboratoryjne z Logiki Układów yfrowych ćwiczenie 22 temat: UKŁDY KOMINYJNE. EL ĆWIZENI Ćwiczenie ma na
Wstęp do sieci neuronowych, wykład 02 Perceptrony c.d. Maszyna liniowa.
 Wstęp do sieci neuronowych, wykład 02 Perceptrony c.d. Maszyna liniowa. Maja Czoków, Jarosław Piersa, Andrzej Rutkowski Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2018-10-15 Projekt
Wstęp do sieci neuronowych, wykład 02 Perceptrony c.d. Maszyna liniowa. Maja Czoków, Jarosław Piersa, Andrzej Rutkowski Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2018-10-15 Projekt
Lista tematów na kolokwium z wykładu z Techniki Cyfrowej w roku ak. 2013/2014
 Lista tematów na kolokwium z wykładu z Techniki Cyfrowej w roku ak. 2013/2014 Temat 1. Algebra Boole a i bramki 1). Podać przykład dowolnego prawa lub tożsamości, które jest spełnione w algebrze Boole
Lista tematów na kolokwium z wykładu z Techniki Cyfrowej w roku ak. 2013/2014 Temat 1. Algebra Boole a i bramki 1). Podać przykład dowolnego prawa lub tożsamości, które jest spełnione w algebrze Boole
AiR_UCiM_3/5 Układy Cyfrowe i Mikroprocesorowe Digital Circuits and Microprocessors
 Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2013/2014
Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2013/2014
KARTA PRZEDMIOTU. Nr Opis efektu kształcenia Metoda sprawdzenia efektu kształcenia. Forma prowadzenia zajęć
 Z1-PU7 WYDANIE N1 Strona 1 z 1 (pieczęć wydziału) KARTA PRZEDMIOTU 1. Nazwa przedmiotu: PROJEKTOWANIE URZĄDZEŃ CYFROWYCH I i II 2. Kod przedmiotu: PUC 3. Karta przedmiotu ważna od roku akademickiego: 2012/2013
Z1-PU7 WYDANIE N1 Strona 1 z 1 (pieczęć wydziału) KARTA PRZEDMIOTU 1. Nazwa przedmiotu: PROJEKTOWANIE URZĄDZEŃ CYFROWYCH I i II 2. Kod przedmiotu: PUC 3. Karta przedmiotu ważna od roku akademickiego: 2012/2013
Architektura komputerów Wykład 2
 Architektura komputerów Wykład 2 Jan Kazimirski 1 Elementy techniki cyfrowej 2 Plan wykładu Algebra Boole'a Podstawowe układy cyfrowe bramki Układy kombinacyjne Układy sekwencyjne 3 Algebra Boole'a Stosowana
Architektura komputerów Wykład 2 Jan Kazimirski 1 Elementy techniki cyfrowej 2 Plan wykładu Algebra Boole'a Podstawowe układy cyfrowe bramki Układy kombinacyjne Układy sekwencyjne 3 Algebra Boole'a Stosowana
Projekt Układów Logicznych
 Politechnika Opolska Wydział Elektrotechniki i Automatyki Kierunek: Informatyka Opole, dn. 21 maja 2005 Projekt Układów Logicznych Temat: Bramki logiczne CMOS Autor: Dawid Najgiebauer Informatyka, sem.
Politechnika Opolska Wydział Elektrotechniki i Automatyki Kierunek: Informatyka Opole, dn. 21 maja 2005 Projekt Układów Logicznych Temat: Bramki logiczne CMOS Autor: Dawid Najgiebauer Informatyka, sem.
O systemach liczbowych
 O systemach liczbowych 1. Systemy liczbowe Literatura:Turski,Propedeutyka...;Skomorowski,... 1.1. Dwójkowy system pozycyjny W dziesiętnym systemie pozycyjnym ciąg cyfr 321.23 oznacza liczbę 3 10 2 +2 10
O systemach liczbowych 1. Systemy liczbowe Literatura:Turski,Propedeutyka...;Skomorowski,... 1.1. Dwójkowy system pozycyjny W dziesiętnym systemie pozycyjnym ciąg cyfr 321.23 oznacza liczbę 3 10 2 +2 10
Układy cyfrowe w technologii CMOS
 Projektowanie układów VLSI Układy cyfrowe w technologii MOS ramki bramki podstawowe bramki złożone rysowanie topografii bramka transmisyjna Przerzutniki z bramkami transmisyjnymi z bramkami zwykłymi dr
Projektowanie układów VLSI Układy cyfrowe w technologii MOS ramki bramki podstawowe bramki złożone rysowanie topografii bramka transmisyjna Przerzutniki z bramkami transmisyjnymi z bramkami zwykłymi dr
TEST KONKURSOWY CZAS TESTU 40 MIN ILOŚĆ MAKSYMALNA PUNKTÓW 20 INSTRUKCJA:
 CZAS TESTU 40 MIN ILOŚĆ MAKSYMALNA PUNKTÓW 20 INSTRUKCJA: TEST KONKURSOWY 1. Do arkusza testu dołączona jest KARTA ODPOWIEDZI, na której wpisz swoje imię i nazwisko, nazwę szkoły i miasto. 2. Test zawiera
CZAS TESTU 40 MIN ILOŚĆ MAKSYMALNA PUNKTÓW 20 INSTRUKCJA: TEST KONKURSOWY 1. Do arkusza testu dołączona jest KARTA ODPOWIEDZI, na której wpisz swoje imię i nazwisko, nazwę szkoły i miasto. 2. Test zawiera
Dr inż. Jan Chudzikiewicz Pokój 117/65 Tel Materiały:
 Dr inż Jan Chudzikiewicz Pokój 7/65 Tel 683-77-67 E-mail: jchudzikiewicz@watedupl Materiały: http://wwwitawatedupl/~jchudzikiewicz/ Warunki zaliczenie: Otrzymanie pozytywnej oceny z kolokwium zaliczeniowego
Dr inż Jan Chudzikiewicz Pokój 7/65 Tel 683-77-67 E-mail: jchudzikiewicz@watedupl Materiały: http://wwwitawatedupl/~jchudzikiewicz/ Warunki zaliczenie: Otrzymanie pozytywnej oceny z kolokwium zaliczeniowego
Wprowadzenie do architektury komputerów systemy liczbowe, operacje arytmetyczne i logiczne
 Wprowadzenie do architektury komputerów systemy liczbowe, operacje arytmetyczne i logiczne 1. Bit Pozycja rejestru lub komórki pamięci służąca do przedstawiania (pamiętania) cyfry w systemie (liczbowym)
Wprowadzenie do architektury komputerów systemy liczbowe, operacje arytmetyczne i logiczne 1. Bit Pozycja rejestru lub komórki pamięci służąca do przedstawiania (pamiętania) cyfry w systemie (liczbowym)
Podstawy techniki cyfrowej cz.2 zima Rafał Walkowiak
 Podstawy techniki cyfrowej cz.2 zima 2015 Rafał Walkowiak 3.12.2015 Układy cyfrowe Ogólna struktura logiczna: Wej ster Dane układ sterowania bloki funkcjonalne dla realizacji określonych funkcji przetwarzania
Podstawy techniki cyfrowej cz.2 zima 2015 Rafał Walkowiak 3.12.2015 Układy cyfrowe Ogólna struktura logiczna: Wej ster Dane układ sterowania bloki funkcjonalne dla realizacji określonych funkcji przetwarzania
LABORATORIUM PRZYRZĄDÓW PÓŁPRZEWODNIKOWYCH
 Wydział Elektroniki Mikrosystemów i Fotoniki Politechniki Wrocławskiej STUDIA DZIENNE LABORATORIUM PRZYRZĄDÓW PÓŁPRZEWODNIKOWYCH Ćwiczenie nr 8 BADANIE WŁAŚCIWOŚCI UKŁADÓW CYFROWYCH CMOS I. Zagadnienia
Wydział Elektroniki Mikrosystemów i Fotoniki Politechniki Wrocławskiej STUDIA DZIENNE LABORATORIUM PRZYRZĄDÓW PÓŁPRZEWODNIKOWYCH Ćwiczenie nr 8 BADANIE WŁAŚCIWOŚCI UKŁADÓW CYFROWYCH CMOS I. Zagadnienia
