Heurystyczne przeszukiwanie grafów w gier dwuosobowych
|
|
|
- Jarosław Król
- 6 lat temu
- Przeglądów:
Transkrypt
1 Heurystyczne przeszukiwanie grafów w gier dwuosobowych Wykład Informatyka Studia InŜynierskie Teoria gier w dziedzinie SI Liczba graczy jednoosobowe, dwuosobowe oraz wieloosobowe Suma wypłat gry o sumie zerowej (zyski i straty uczestników bilansują się) gry o sumie niezerowej (wygrane i przegrane nie muszą się bilansować) Dostępna wiedza gry z pełną informacją (precyzyjna wiedza o sytuacji i celach przeciwnika) gry z niepełną informacją (brak wiedzy na temat przeciwnika, czynnik losowy źródłem niepewności) 1
2 Gry dwuosobowe - przeszukiwanie heurystyczne Dwóch przeciwników w posiadających pełną informację o stanie gry i wszystkich moŝliwych ruchach Jeden gracz nosi nazwę Max,, bo: maksymalizuje rezultat końcowy kaŝdy wzrost wartości oznacza poprawę dla tego gracza i równowar wnowaŝną stratę dla przeciwnika Drugi gracz nosi nazwę Min,, bo: imalizuje rezultat końcowy kaŝdy spadek wartości oznacza poprawę dla tego gracza i równowar wnowaŝną stratę dla przeciwnika Zasada
3 Min- wynik! Algorytm - wywołanie: result = MinMax(s,, MAXDEPTH, MAX) int MinMax(state s, int depth, int type) { if( is_teral_node(s) ) depth==0 ) return(eval(s)); if( type == MAX ){ best = - ; for(child=1; child<=numofsucc(s); child++) { val = MinMax(Succ(s,child), depth-1, MIN); if( val > best ) best = val; } //endfor } else { // type == MIN best = ; for(child=1; child<=numofsucc(s); child++) { val = MinMax(Succ(s,child), depth-1, MAX); if( val < best ) best = val; } //endfor } return best; } 3
4 Przykład - - gra NIM - korzeń MAX MAX MIN MAX Ocena: mniejsza wartość bo wygrał wygrana MIN MIN większa wartość bo wygrał wygrana MAX MAX MIN MAX MIN Przykład - - gra NIM - korzeń MIN 1 7 MIN MAX MIN Ocena: mniejsza wartość bo wygrał wygrana MIN MAX większa wartość bo wygrał wygrana MAX MIN MAX MIN MAX 4
5 Zasada nega (y) y = - = (x) x = - (z) z Algorytm neg- wywołanie: result = NegMax(s,, MAXDEPTH) int NegMax(state s, int depth) { if( is_teral_node(s) ) depth==0 ) return(eval(s,depth Eval(s,depth)); ); best = - ; for(child=1; child<=numofsucc(s); child++) { val = -NegMax(Succ(s,child), depth-1); if( val > best ) best = val; } //endfor return best; } Funkcja heurystycznej oceny stanu musi uwzględnia dniać,, kto wykonywałby ruch w ocenianym stanie. JeŜeli eli gracz MAX to ocena jest w postaci prostej, jeśli gracz MIN - w postaci zanegowanej. 5
6 Przykład nega- - gra NIM - ruch MIN 7-1 -MIN MAX -MIN Ocena: MIN wartość zanegowana MAX wartość prosta przegrał MIN wartość zaneg. przegrał MAX wartość prosta MAX -MIN MAX Przykład nega- - gra NIM - ruch MAX 7-1 MAX MIN MAX Ocena: MIN wartość zanegowana MAX wartość prosta przegrał MAX wartość prosta przegrał MIN wartość zanegowana -MIN MAX -MIN 6
7 Kółko i krzyŝyk yk - heurystyka Funkcja oceny heurystycznej stanu gry - róŝnica liczby moŝliwych wygranych gracza X i gracza O Gracz X ma 6 moŝliwych wygranych Gracz O ma 5 moŝliwych wygranych E(n) = 6-5 = 1 Gracz X ma 4 moŝliwych wygranych Gracz O ma 6 moŝliwych wygranych E(n) = 4-6 = -2 Gracz X ma 5 moŝliwych wygranych Gracz O ma 4 moŝliwych wygranych E(n) = 5-4 = 1 Kółko i krzyŝyk yk - przykład gry(1) -1 1 Ruch MAXa =1 5-5=05=0 6-5=1 5-5=05=0 4-5= 5=-1 5-4=1 6-4=2. głęg łębokość=2 5-6= 6=-1 5-5=05=0 5-6= 6=-1 6-6=06=0 4-6= 6=-2 7
8 . głęg łębokość=2 Kółko i krzyŝyk yk - przykład gry(2) =2 3-2=1 5-2=3 3-2=1 4-2=2 3-2=1 0 Ruch MAXa 4-3=1 3-3=03=0 5-3=2 3-3=03=0 4-3=1 4-3= =2 4-2=2 5-2=3 3-2=1 4-2=2 4-2=2 4-3=1 4-3=1 3-3=03=0 Kółko i krzyŝyk yk - przykład gry(3) Ruch MAXa 2-1=1 3-1=2 2-1=1 3-1=2-2-1=1 2-1=1 2-1= =1 2-2=02=0 3-2=1-2-1=1 3-1=2 3-1=2. głęg łębokość=2-2-2=02=0 2-2=02=0 3-2=1
9 Algorytm - (lub nega) Przyjmując c określony branching factor (b)) oraz stałą głębokość przeszukiwania (d)( ZłoŜoność pamięciowa O(bd) ZłoŜoność czasowa O(b d ) Czy moŝna ten wynik poprawić? Tak! Branch&bound Ograniczenie dolne - odcięcieα odcięcie cie α... Analiza lewego poddrzewa pokazała, a, Ŝe e MAX ma ruch o wartości 5. Po sprawdzeniu lewego liścia środkowego poddrzewa widać, Ŝe e wartość drugiego ruchu będzie b mniejsza lub równa r 3 (w stanie tym decyduje MIN!). Analiza pozostałych ruchów MINa nie ma zatem sensu, gdyŝ decyzja MAXa w korzeniu grafu nie moŝe e juŝ ulec zmianie niezaleŝnie od ich wartości. 9
10 Ograniczenie górne g - odcięcieβ odcięcie cie β Analiza lewego poddrzewa pokazała, a, Ŝe e MIN ma ruch o wartości 6. Po sprawdzeniu lewego liścia środkowego poddrzewa widać, Ŝe e wartość drugiego ruchu MINa będzie większa lub równa r 9 (w stanie tym decyduje MAX!). Analiza pozostałych ruchów MAXa nie ma zatem sensu, gdyŝ decyzja MINa w korzeniu grafu nie moŝe e juŝ ulec zmianie niezaleŝnie od ich wartości. : : przykład
11
12
13 9 9 β β
14 9 9 β β
15 β β
16 β 5 α β 5 5 α
17 β 5 5 α β 5 5 α
18 5 5 α β α β
19 5 5 α β α α β α
20 5 5 α β α α β α
21 Mechanizm odcięć alfa-beta Dwa ograniczenia: α dolne ograniczenie dla wierzchołków Max (najwyŝsza wartość jaką dotychczas osiągn gnął gracz Max) β górne ograniczenie dla wierzchołków Min (najniŝsza wartość jaką dotychczas osiągn gnął gracz Min) Wartość ograniczenia α ustalana jest w wierzchołku Max,, a wartość ograniczenia β - w wierzchołku Min Odcięcie cie α wykonywane jest w wierzchołku Min, a odcięcie cie β - w wierzchołku Max Kiedy tylko zachodzi warunek α β, nie ma potrzeby analizowania dalszych następnik pników w danego stanu Algorytm AlfaBeta (zapis -) ) wywołanie: result = AlphaBeta(s, MAXDEPTH, -,, MAX) int AlphaBeta(state s,int depth,int alpha,int beta,int type) { if( is_teral_node(s) depth == 0 ) return(eval(s)); if( type == MAX){ for(child=1; child<=numofsucc(s); child++) { val = AlphaBeta(Succ(s,child),depth-1, 1,alpha,beta,,beta,MIN); alpha = (val val,, alpha); if( alpha >= beta ) return beta; //cutoff } //endfor return alpha; } else { // type == MIN for(child=1; child<=numofsucc(s); child++) { val = AlphaBeta(Succ(s,child),depth-1,alpha, 1,alpha,beta,MAX); beta = (val val,, beta); if( alpha >= beta ) return alpha; //cutoff } //endfor return beta; } } 21
22 C 3 3 = 3 2 = = 3 0 A 3 D 0 E 0 α 2 5 = 0 = 2 B β 2 2 α A ma próg β = 3 (A nie będzie b większe niŝ 3) B odcięcie cie dla β,, bo 5 > 3 C ma próg α = 3 (C nie będzie b mniejsze niŝ 3) D odcięcie cie dla α,, bo 0 < 3 E odcięcie cie dla α,, bo 2 < 3 C ma wartość 3 Sformułowanie owanie neg- dla AlfaBeta Sformułowanie owanie - wymaga przemiennych wywołań rekurencyjnych dwóch graczy (raz dla gracza MAX, dwa dla gracza MIN, itd.) Sformułowanie owanie neg- opiera się tylko na graczu MAX (jedna funkcja rekurencyjna) Przy wyjściu z rekurencji negujemy zwracaną wartość Czy to wystarczy? Nie! Przy zagnieŝdŝeniu eniu rekurencyjnym w wersji neg- negujemy ograniczenia i zamieniamy miejscami 22
23 Algorytm AlfaBeta (zapis neg-) wywołanie: result = AlphaBeta(s, MAXDEPTH, -, ) int AlphaBeta(state s, int depth, int alpha, int beta) { if( is_teral teral_node(s) depth==0 ) return(eval Eval(s, (s,depth)); for(child=1; child<=numofsucc(s); child++) { val = -AlphaBeta(Succ(s,child),depth-1, 1,-beta,-alpha); if( val > alpha ) alpha = val; // alpha=(val,alpha); if( alpha >= beta ) return beta; // cutoff } //endfor return alpha; } Cechy algorytmu AlfaBeta ŚcieŜka krytyczna (ang. principal variation) ścieŝka w grafie przeszukiwania od korzenia do najlepszego liścia Wartości zwracane: w wersji : : ze względu na gracza w korzeniu w wersji neg- : : ze względu na tego czyj jest ruch w liściu Bardzo zawikłany any kod ewentualny błęb łędy pozostają długo ukryte (problemy moŝna zauwaŝyć tylko wtedy, gdy niepoprawne wartości zostaną przepropagowane do korzenia grafu) Efektywność algorytmu zaleŝy y w ogromnym stopniu od kolejności następnik pników w i występowania odcięć 23
24 Analiza algorytmu AlfaBeta Sytuacja idealna jeśli odcięcie cie ma się pojawić,, to powinno wystąpi pić jak najszybciej, czyli najlepiej zaraz po sprawdzeniu pierwszego następnika odcięcie cie α ? zmieniona kolejność (mniej odcięć ęć!) = = = 9 3 = 9 9 = 5 5 3? 5 = 9 = 5 = 9 5 α? zmieniona kolejność 24
25 ZłoŜoność algorytmu AlfaBeta Dla danej głęg łębokości (d)( ) i stałego braching factor (b) Najlepszy przypadek: O(b d/2 ) Najgorszy przypadek: brak odcięć (czyli jak MinMax) Średni przypadek: O(( ((b/log b) b d ) Słabości algorytmu AlfaBeta Efekt horyzontu (ang. horizont effect) Niewidoczny spadek wartości stanu tuŝ za wyznaczoną głębokością przeszukiwania Występuje we wszystkich odmianach algorytmu Wykrywanie stanów w naraŝonych na wystąpienie efektu horyzontu i prowadzenia przeszukiwania za tym stanami - problem otwarty 25
26 Rozszerzenia algorytmu AlfaBeta Doskonalenie funkcji oceny stanu (funkcji heurystycznej) Modyfikacje sposobu przeszukiwania grafu zastosowanie pamięci (np. tablica przejść ść) porządkowanie następnik pników manipulowanie zakresem α-β zmienna głęg łębokość przeszukiwania przeszukiwanie eksploracyjne Rozwiązania zania sprzętowe (np. obliczenia równolegr wnoległe) e) Wariant fail-soft algorytmu AlfaBeta Klasyczna postać algorytmu wartości zwracane zawsze z przedziału u [α,[ β] Wariant fail-soft algorytmu AlfaBeta [Fishburn 1] zwraca dowolne wartości niezaleŝnie od początkowego zakresu [α,[ β] Wariant fail-soft algorytmu AlfaBeta stanowi podstawę do wszelkich jego modyfikacji, wykorzystujących manipulacje zakresem [α, β] 26
27 Algorytm AlfaBeta fail-soft (zapis neg-) wywołanie: result = AlphaBetaFS FS(s, MAXDEPTH, -, ) int AlphaBetaFS FS(state s, int depth, int alpha, int beta) { if( is_teral teral_node(s) depth==0 ) return(eval Eval(s)); best = - ; for(child=1; child<=numofsucc(s); child++) { val = -AlphaBetaFS(Succ(s,child),depth-1, 1,-beta, beta,-alpha); alpha); if( val > best ) best = val; if( best >= beta ) break; // cutoff if( best > alpha) alpha = best; } //endfor return best; } Znaczenie zakresu α-β ZałóŜmy, Ŝe e dla wierzchołka n o faktycznej wartości f procedura AlfaBetaFS(n (n, α, β) zwraca wartość g. MoŜemy wyróŝni nić trzy następuj pujące sytuacje: α < g < β (sukces) g jest równe r faktycznej wartości f g α (failing low) g jest górnym ograniczeniem dla f (oznaczane jako f + ), tzn. f g g β(failing high) - g jest dolnym ograniczeniem dla f (oznaczane jako f ), tzn. f g 27
28 Zakresy α-β: : sytuacja failing low (g α) f + =41 α = -1, β = f + =41 f + =36 f + =41 f + =36 f + =41 f + =12 f + =34 f + = Zakresy α-β: failing low Wywołanie procedury alfa-beta dla wierzchołka n z parametrami AlfaBetaFS(n (n, -1, ) (wszystkie liście mają wartości mniejsze) spowoduje: we wszystkich wierzchołkach MIN wystąpienie odcięć ęćα, bo wartości wszystkich następnik pników w sąs g α= -1 we wszystkich wierzchołkach MAX brak jakichkolwiek cięć ęćβ,, bo wartości wszystkich następnik pników w sąs g < β = Otrzymane drzewo przeszukiwania będzie b zawierać po jednym potomku dla kaŝdego wierzchołka MIN i wszystkie potomne dla kaŝdego wierzchołka MAX. 2
29 Failing low dlaczego górne g ograniczenie? all... one all one Zakresy α-β: : sytuacja failing high (g β ) f - =5 α = -, β = - +1 f - =5 f - =5 f - =0 f - =5 f - =
30 Zakresy α-β: failing high Wywołanie procedury alfa-beta dla wierzchołka n z parametrami AlfaBetaFS(n (n, -, - +1) (wszystkie liście mają wartości większe) spowoduje: we wszystkich wierzchołkach MAX wystąpienie odcięć β,, bo wartości wszystkich następnik pników w sąs g β=- +1 we wszystkich wierzchołkach MIN brak jakichkolwiek cięć ęćα,, bo wartości wszystkich następnik pników w sąs g > α = - Otrzymane drzewo przeszukiwania będzie b zawierać po jednym potomku dla kaŝdego wierzchołka MAX i wszystkie potomne dla kaŝdego wierzchołka MIN. Failing high dlaczego dolne ograniczenie? one all... one all
31 AlfaBeta jako przeszukiwanie w głąg łąb Jak określi lić właściwą głębokość przeszukiwania? Czym moŝna przeszukiwać do wierzchołków teralnych? Najczęś ęściej nie! (Zbyt duŝa a przestrzeń) Przeszukiwanie do ustalonej głęg łębokości: Niewłaściwa kolejność następnik pników w (ruchów) moŝe doprowadzić do ogromnego grafu przeszukiwania Co w sytuacji, gdy głęg łębokość jest za mała? a? Co w sytuacji, gdy głęg łębokość jest za duŝa? Iteracyjne pogłę łębianie int iterative_deepening(state s) { depth = 0; { depth++; value = AlfaBeta(s, depth, -, ); if( rescources_up() ) break; // stop } while( depth < MAXDEPTH ) return(value value); } 31
32 Iteracyjne pogłę łębianie Zalety Osiąganie maksymalnej moŝliwej głęg łębokości przeszukiwania przy aktualnie dostępnych zasobach (obliczenia w systemach czasu rzeczywistego!) Gwarancja znalezienia najlepszego rozwiązania zania do określonej głęg łębokości przeszukiwania Wady Wielokrotne przeszukiwanie tych samych obszarów przestrzeni stanów Iteracyjne pogłę łębianie Potencjalne korzyści z poprzednich iteracji Przed przejściem do przeszukiwania na głęg łębokości d+1 moŝna uporządkowa dkować ruchy na podstawie wyników uzyskanych dla głęg łębokości d W większo kszości gier słuszne s jest załoŝenie, iŝi najlepszy pierwszy ruch w przeszukiwaniu na głęg łębokość d stanowi dobre przybliŝenie najlepszego ruchu w przeszukiwaniu na głęg łębokość d+1 Wzrasta prawdopodobieństwo wybrania właściwego w pierwszego ruchu im bliŝej ostatniej (najkosztowniejszej) iteracji 32
33 Iteracyjne pogłę łębianie: zmiana kolejności A B C B A C głębokość d głębokość d+1 Badania eksperymentalne wykazały, y, iŝi koszty wielokrotnego przeszukiwania przestrzeni stanów w sąs niewspółmiernie niskie w stosunku do zysków wynikających z porządkowania ruchów w w wierzchołkach grafu. Sterowanie zakresem α-β Metody manipulowania zakresem odcięć Aspiration Search [Slate&Atkin 77] Metody z imalnym zakresem * NegaScout (PVS) [Reinefeld 3] * Rodzina algorytmów w MTD [Plaat 96] 33
34 Zakresy α-β: Aspiration Search Tradycyjny zakres przeszukiwania (,( ) Co w sytuacji, gdy jesteśmy w pewnym stopniu przewidzieć rezultat przeszukiwania? Przeszukiwanie z zakresem (v(, v + ), gdzie: v spodziewany rezultat zakładane adane odchylenie od tej wartości ( ( >0) Mniejszy zakres alfa-beta oznacza więcej odcięć i mniejszy graf przeszukiwania Kiedy przewidywania się nie sprawdziły (failing-lowlow lub failing-high high), konieczność powtórzenia przeszukiwania z większym zakresem Zakresy α-β: : Algorytm Aspiration Search int IDAspirationSearch(state s, deviation ) { guess = 0; for(depth=1;!resources_up up(); depth++) { alpha = guess- ; ; beta = guess+ ; score = AlphaBetaFS FS(s, depth, alpha, beta); if( score >= beta ) { // failing high alpha = score; beta = ; score = AlphaBetaFS FS(s, depth, alpha, beta); } else if( score <= alpha ) { // failing low alpha = - ;; beta = score; score = AlphaBetaFS FS(s, depth, alpha, beta); } guess = score; } //endfor return(guess); } 34
35 Zakresy α-β: : WłasnoW asności Aspiration Search Nietrywialny problem wyboru początkowej wartości zakresu alfa-beta (wartości guess oraz ) Iteracyjne pogłę łębianie automatyzuje proces manipulowania zakresem α-β wartość korzenia wyznaczona w poprzedniej iteracji jest najlepszym przybliŝeniem środka przedziału u w następnej iteracji Podwójna kontrola przebiegu przeszukiwania: sterowanie głębokością oraz manipulowanie przedziałem em alfa-beta Jeśli nie Aspiration Search,, to co? AspirationSearch nie moŝe e korzystać ze zbyt małego zakresu α-β,, bo koszty powtórze rzeń przeszukiwania byłyby yby zbyt duŝe! AspirationSearch ogranicza się tylko do manipulacji zakresem w korzeniu grafu, dlaczego nie robić tego w kaŝdym wierzchołku grafu? Bardziej efektywne metody operują na imalnym zakresie α-β, tj. β = α+1 ( algorytmy NegaScout oraz MTD(f) ), ale wymagają dodatkowej pamięci do porządkowania ruchów 35
Heurystyczne przeszukiwanie grafów gier dwuosobowych
 Heurystyczne przeszukiwanie grafów gier dwuosobowych Wykład Informatyka Studia InŜynierskie Teoria gier w dziedzinie SI Liczba graczy jednoosobowe, dwuosobowe oraz wieloosobowe Suma wypłat gry o sumie
Heurystyczne przeszukiwanie grafów gier dwuosobowych Wykład Informatyka Studia InŜynierskie Teoria gier w dziedzinie SI Liczba graczy jednoosobowe, dwuosobowe oraz wieloosobowe Suma wypłat gry o sumie
Heurystyczne przeszukiwanie przestrzeni stanów
 Heurystyczne przeszukiwanie przestrzeni stanów Wykład Studia Inżynierskie Realizacja przeszukiwania heurystycznego Systemy eksperckie Gdy problem nie posiada dokładnego rozwiązania zania ze względu na
Heurystyczne przeszukiwanie przestrzeni stanów Wykład Studia Inżynierskie Realizacja przeszukiwania heurystycznego Systemy eksperckie Gdy problem nie posiada dokładnego rozwiązania zania ze względu na
Heurystyczne przeszukiwanie przestrzeni stanów
 Heurystyczne przeszukiwanie przestrzeni stanów Wykład Informatyka Studia InŜynierskie Podstawowe pojęcia teorii grafów przeszukiwania Korzeń grafu Stan, od którego zaczynamy przeszukiwanie grafu (drzewa)
Heurystyczne przeszukiwanie przestrzeni stanów Wykład Informatyka Studia InŜynierskie Podstawowe pojęcia teorii grafów przeszukiwania Korzeń grafu Stan, od którego zaczynamy przeszukiwanie grafu (drzewa)
Mechanizm wyboru następnego wierzchołka w grafie
 Zaawansowane metody przeszukiwania grafów przestrzeni stanów gier dwuosobowych Informatyka Laboratorium Sztucznej Inteligencji 2012 Elementy składowe heurystycznych metod przeszukiwania Definicja stanu
Zaawansowane metody przeszukiwania grafów przestrzeni stanów gier dwuosobowych Informatyka Laboratorium Sztucznej Inteligencji 2012 Elementy składowe heurystycznych metod przeszukiwania Definicja stanu
Rekurencje. Jeśli algorytm zawiera wywołanie samego siebie, jego czas działania moŝe być określony rekurencją. Przykład: sortowanie przez scalanie:
 Rekurencje Jeśli algorytm zawiera wywołanie samego siebie, jego czas działania moŝe być określony rekurencją. Przykład: sortowanie przez scalanie: T(n) = Θ(1) (dla n = 1) T(n) = 2 T(n/2) + Θ(n) (dla n
Rekurencje Jeśli algorytm zawiera wywołanie samego siebie, jego czas działania moŝe być określony rekurencją. Przykład: sortowanie przez scalanie: T(n) = Θ(1) (dla n = 1) T(n) = 2 T(n/2) + Θ(n) (dla n
Algorytmy dla gier dwuosobowych
 Algorytmy dla gier dwuosobowych Wojciech Dudek Seminarium Nowości Komputerowe 5 czerwca 2008 Plan prezentacji Pojęcia wstępne (gry dwuosobowe, stan gry, drzewo gry) Algorytm MiniMax Funkcje oceniające
Algorytmy dla gier dwuosobowych Wojciech Dudek Seminarium Nowości Komputerowe 5 czerwca 2008 Plan prezentacji Pojęcia wstępne (gry dwuosobowe, stan gry, drzewo gry) Algorytm MiniMax Funkcje oceniające
Wyznaczanie strategii w grach
 Wyznaczanie strategii w grach Dariusz Banasiak Katedra Informatyki Technicznej W4/K9 Politechnika Wrocławska Definicja gry Teoria gier i konstruowane na jej podstawie programy stanowią jeden z głównych
Wyznaczanie strategii w grach Dariusz Banasiak Katedra Informatyki Technicznej W4/K9 Politechnika Wrocławska Definicja gry Teoria gier i konstruowane na jej podstawie programy stanowią jeden z głównych
Wprowadzenie do Sztucznej Inteligencji
 Wprowadzenie do Sztucznej Inteligencji Wykład Studia Inżynierskie Przeszukiwanie przestrzeni stanów Przestrzeń stanów jest to czwórka uporządkowana [N,[, S, GD], gdzie: N jest zbiorem wierzchołków w odpowiadających
Wprowadzenie do Sztucznej Inteligencji Wykład Studia Inżynierskie Przeszukiwanie przestrzeni stanów Przestrzeń stanów jest to czwórka uporządkowana [N,[, S, GD], gdzie: N jest zbiorem wierzchołków w odpowiadających
Wprowadzenie do Sztucznej Inteligencji
 Wprowadzenie do Sztucznej Inteligencji Wykład Informatyka Studia InŜynierskie Przeszukiwanie przestrzeni stanów Przestrzeń stanów jest to czwórka uporządkowana [N,[, S, GD], gdzie: N jest zbiorem wierzchołków
Wprowadzenie do Sztucznej Inteligencji Wykład Informatyka Studia InŜynierskie Przeszukiwanie przestrzeni stanów Przestrzeń stanów jest to czwórka uporządkowana [N,[, S, GD], gdzie: N jest zbiorem wierzchołków
Wprowadzenie do Sztucznej Inteligencji
 Wprowadzenie do Sztucznej Inteligencji Wykład Informatyka Studia InŜynierskie Przeszukiwanie przestrzeni stanów Przestrzeń stanów jest to czwórka uporządkowana [N,, S, GD], gdzie: N jest zbiorem wierzchołków
Wprowadzenie do Sztucznej Inteligencji Wykład Informatyka Studia InŜynierskie Przeszukiwanie przestrzeni stanów Przestrzeń stanów jest to czwórka uporządkowana [N,, S, GD], gdzie: N jest zbiorem wierzchołków
Metody teorii gier. ALP520 - Wykład z Algorytmów Probabilistycznych p.2
 Metody teorii gier ALP520 - Wykład z Algorytmów Probabilistycznych p.2 Metody teorii gier Cel: Wyprowadzenie oszacowania dolnego na oczekiwany czas działania dowolnego algorytmu losowego dla danego problemu.
Metody teorii gier ALP520 - Wykład z Algorytmów Probabilistycznych p.2 Metody teorii gier Cel: Wyprowadzenie oszacowania dolnego na oczekiwany czas działania dowolnego algorytmu losowego dla danego problemu.
Heurystyczne przeszukiwanie przestrzeni stanów
 Heurystyczne przeszukiwanie przestrzeni stanów Wykład Informatyka Studia InŜynierskie Realizacja przeszukiwania heurystycznego Systemy eksperckie Gdy problem nie posiada dokładnego rozwiązania zania ze
Heurystyczne przeszukiwanie przestrzeni stanów Wykład Informatyka Studia InŜynierskie Realizacja przeszukiwania heurystycznego Systemy eksperckie Gdy problem nie posiada dokładnego rozwiązania zania ze
Teoria gier. Teoria gier. Odróżniać losowość od wiedzy graczy o stanie!
 Gry dzielimy ze względu na: liczbę graczy: 1-osobowe, bez przeciwników(np. pasjanse, 15-tka, gra w życie, itp.), 2-osobowe(np. szachy, warcaby, go, itp.), wieloosobowe(np. brydż, giełda, itp.); wygraną/przegraną:
Gry dzielimy ze względu na: liczbę graczy: 1-osobowe, bez przeciwników(np. pasjanse, 15-tka, gra w życie, itp.), 2-osobowe(np. szachy, warcaby, go, itp.), wieloosobowe(np. brydż, giełda, itp.); wygraną/przegraną:
Teoria gier. Wykład7,31III2010,str.1. Gry dzielimy
 Wykład7,31III2010,str.1 Gry dzielimy Wykład7,31III2010,str.1 Gry dzielimy ze względu na: liczbę graczy: 1-osobowe, bez przeciwników(np. pasjanse, 15-tka, gra w życie, itp.), Wykład7,31III2010,str.1 Gry
Wykład7,31III2010,str.1 Gry dzielimy Wykład7,31III2010,str.1 Gry dzielimy ze względu na: liczbę graczy: 1-osobowe, bez przeciwników(np. pasjanse, 15-tka, gra w życie, itp.), Wykład7,31III2010,str.1 Gry
Algorytmy i struktury danych
 POLITECHNIKA KRAKOWSKA - WIEiK KATEDRA AUTOMATYKI i TECHNIK INFORMACYJNYCH Algorytmy i struktury danych www.pk.edu.pl/~zk/aisd_hp.html Wykładowca: dr inż. Zbigniew Kokosiński zk@pk.edu.pl Wykład 5: Algorytmy
POLITECHNIKA KRAKOWSKA - WIEiK KATEDRA AUTOMATYKI i TECHNIK INFORMACYJNYCH Algorytmy i struktury danych www.pk.edu.pl/~zk/aisd_hp.html Wykładowca: dr inż. Zbigniew Kokosiński zk@pk.edu.pl Wykład 5: Algorytmy
Heurystyki. Strategie poszukiwań
 Sztuczna inteligencja Heurystyki. Strategie poszukiwań Jacek Bartman Zakład Elektrotechniki i Informatyki Instytut Techniki Uniwersytet Rzeszowski DLACZEGO METODY PRZESZUKIWANIA? Sztuczna Inteligencja
Sztuczna inteligencja Heurystyki. Strategie poszukiwań Jacek Bartman Zakład Elektrotechniki i Informatyki Instytut Techniki Uniwersytet Rzeszowski DLACZEGO METODY PRZESZUKIWANIA? Sztuczna Inteligencja
funkcje rekurencyjne Wykład 12. Podstawy programowania (język C) Funkcje rekurencyjne (1) Funkcje rekurencyjne (2)
 Podstawy programowania (język C) funkcje rekurencyjne Wykład 12. Tomasz Marks - Wydział MiNI PW -1- Tomasz Marks - Wydział MiNI PW -2- Funkcje rekurencyjne (1) W języku C funkcja moŝe wywoływać samą siebie.
Podstawy programowania (język C) funkcje rekurencyjne Wykład 12. Tomasz Marks - Wydział MiNI PW -1- Tomasz Marks - Wydział MiNI PW -2- Funkcje rekurencyjne (1) W języku C funkcja moŝe wywoływać samą siebie.
Tworzenie gier na urządzenia mobilne
 Katedra Inżynierii Wiedzy Teoria podejmowania decyzji w grze Gry w postaci ekstensywnej Inaczej gry w postaci drzewiastej, gry w postaci rozwiniętej; formalny opis wszystkich możliwych przebiegów gry z
Katedra Inżynierii Wiedzy Teoria podejmowania decyzji w grze Gry w postaci ekstensywnej Inaczej gry w postaci drzewiastej, gry w postaci rozwiniętej; formalny opis wszystkich możliwych przebiegów gry z
Algorytmy mrówkowe. H. Bednarz. Wydział Informatyki Zachodniopomorski Uniwersytet Technologiczny w Szczecinie Inteligentne systemy informatyczne
 Algorytmy mrówkowe H. Bednarz Wydział Informatyki Zachodniopomorski Uniwersytet Technologiczny w Szczecinie Inteligentne systemy informatyczne 13 kwietnia 2015 1 2 3 4 Przestrzeń poszukiwań Ograniczenia
Algorytmy mrówkowe H. Bednarz Wydział Informatyki Zachodniopomorski Uniwersytet Technologiczny w Szczecinie Inteligentne systemy informatyczne 13 kwietnia 2015 1 2 3 4 Przestrzeń poszukiwań Ograniczenia
Praktyczne aspekty programowania gier logicznych. Piotr Beling
 Praca magisterska Praktyczne aspekty programowania gier logicznych Piotr Beling nr. albumu: 110341 Promotor: dr inż. Tadeusz Łyszkowski Łódź, 2006 Spis treści Spis treści i 1 Wstęp 1 1.1 Dlaczegowartopisaćgrylogiczne?...
Praca magisterska Praktyczne aspekty programowania gier logicznych Piotr Beling nr. albumu: 110341 Promotor: dr inż. Tadeusz Łyszkowski Łódź, 2006 Spis treści Spis treści i 1 Wstęp 1 1.1 Dlaczegowartopisaćgrylogiczne?...
Algorytmy i struktury danych
 Algorytmy i struktury danych Zaawansowane algorytmy sortowania Witold Marańda maranda@dmcs.p.lodz.pl 1 Sortowanie za pomocą malejących przyrostów metoda Shella Metoda jest rozwinięciem metody sortowania
Algorytmy i struktury danych Zaawansowane algorytmy sortowania Witold Marańda maranda@dmcs.p.lodz.pl 1 Sortowanie za pomocą malejących przyrostów metoda Shella Metoda jest rozwinięciem metody sortowania
Efektywna metoda sortowania sortowanie przez scalanie
 Efektywna metoda sortowania sortowanie przez scalanie Rekurencja Dla rozwiązania danego problemu, algorytm wywołuje sam siebie przy rozwiązywaniu podobnych podproblemów. Metoda dziel i zwycięŝaj Dzielimy
Efektywna metoda sortowania sortowanie przez scalanie Rekurencja Dla rozwiązania danego problemu, algorytm wywołuje sam siebie przy rozwiązywaniu podobnych podproblemów. Metoda dziel i zwycięŝaj Dzielimy
Sztuczna Inteligencja i Systemy Doradcze
 Sztuczna Inteligencja i Systemy Doradcze Przeszukiwanie przestrzeni stanów algorytmy ślepe Przeszukiwanie przestrzeni stanów algorytmy ślepe 1 Strategie slepe Strategie ślepe korzystają z informacji dostępnej
Sztuczna Inteligencja i Systemy Doradcze Przeszukiwanie przestrzeni stanów algorytmy ślepe Przeszukiwanie przestrzeni stanów algorytmy ślepe 1 Strategie slepe Strategie ślepe korzystają z informacji dostępnej
Wstęp do Sztucznej Inteligencji
 Wstęp do Sztucznej Inteligencji Rozwiązywanie problemów-i Joanna Kołodziej Politechnika Krakowska Wydział Fizyki, Matematyki i Informatyki Rozwiązywanie problemów Podstawowe fazy: Sformułowanie celu -
Wstęp do Sztucznej Inteligencji Rozwiązywanie problemów-i Joanna Kołodziej Politechnika Krakowska Wydział Fizyki, Matematyki i Informatyki Rozwiązywanie problemów Podstawowe fazy: Sformułowanie celu -
Programowanie gier logicznych
 Programowanie gier logicznych Piotr Beling Instytut Informatyki Politechnika Łódzka 25 marca 2007 Rozważane gry logiczne dwuosobowe- konflikt interesów występuje pomiędzy dwoma uczestnikami deterministyczne-
Programowanie gier logicznych Piotr Beling Instytut Informatyki Politechnika Łódzka 25 marca 2007 Rozważane gry logiczne dwuosobowe- konflikt interesów występuje pomiędzy dwoma uczestnikami deterministyczne-
Wykład X. Programowanie. dr inż. Janusz Słupik. Gliwice, Wydział Matematyki Stosowanej Politechniki Śląskiej. c Copyright 2016 Janusz Słupik
 Wykład X Wydział Matematyki Stosowanej Politechniki Śląskiej Gliwice, 2016 c Copyright 2016 Janusz Słupik Drzewa binarne Drzewa binarne Drzewo binarne - to drzewo (graf spójny bez cykli) z korzeniem (wyróżnionym
Wykład X Wydział Matematyki Stosowanej Politechniki Śląskiej Gliwice, 2016 c Copyright 2016 Janusz Słupik Drzewa binarne Drzewa binarne Drzewo binarne - to drzewo (graf spójny bez cykli) z korzeniem (wyróżnionym
Heurystyczne metody przeszukiwania
 Heurystyczne metody przeszukiwania Dariusz Banasiak Katedra Informatyki Technicznej W4/K9 Politechnika Wrocławska Pojęcie heurystyki Metody heurystyczne są jednym z ważniejszych narzędzi sztucznej inteligencji.
Heurystyczne metody przeszukiwania Dariusz Banasiak Katedra Informatyki Technicznej W4/K9 Politechnika Wrocławska Pojęcie heurystyki Metody heurystyczne są jednym z ważniejszych narzędzi sztucznej inteligencji.
Programowanie w VB Proste algorytmy sortowania
 Programowanie w VB Proste algorytmy sortowania Sortowanie bąbelkowe Algorytm sortowania bąbelkowego polega na porównywaniu par elementów leżących obok siebie i, jeśli jest to potrzebne, zmienianiu ich
Programowanie w VB Proste algorytmy sortowania Sortowanie bąbelkowe Algorytm sortowania bąbelkowego polega na porównywaniu par elementów leżących obok siebie i, jeśli jest to potrzebne, zmienianiu ich
Jednostki informacji. Bajt moŝna podzielić na dwie połówki 4-bitowe nazywane tetradami (ang. nibbles).
 Wykład 1 1-1 Informatyka nauka zajmująca się zbieraniem, przechowywaniem i przetwarzaniem informacji. Informacja obiekt abstrakcyjny, który w postaci zakodowanej moŝe być przechowywany, przesyłany, przetwarzany
Wykład 1 1-1 Informatyka nauka zajmująca się zbieraniem, przechowywaniem i przetwarzaniem informacji. Informacja obiekt abstrakcyjny, który w postaci zakodowanej moŝe być przechowywany, przesyłany, przetwarzany
Marcel Stankowski Wrocław, 23 czerwca 2009 INFORMATYKA SYSTEMÓW AUTONOMICZNYCH
 Marcel Stankowski Wrocław, 23 czerwca 2009 INFORMATYKA SYSTEMÓW AUTONOMICZNYCH Przeszukiwanie przestrzeni rozwiązań, szukanie na ślepo, wszerz, w głąb. Spis treści: 1. Wprowadzenie 3. str. 1.1 Krótki Wstęp
Marcel Stankowski Wrocław, 23 czerwca 2009 INFORMATYKA SYSTEMÓW AUTONOMICZNYCH Przeszukiwanie przestrzeni rozwiązań, szukanie na ślepo, wszerz, w głąb. Spis treści: 1. Wprowadzenie 3. str. 1.1 Krótki Wstęp
MODELOWANIE RZECZYWISTOŚCI
 MODELOWANIE RZECZYWISTOŚCI Daniel Wójcik Instytut Biologii Doświadczalnej PAN d.wojcik@nencki.gov.pl tel. 022 5892 424 http://www.neuroinf.pl/members/danek/swps/ Podręcznik Iwo Białynicki-Birula Iwona
MODELOWANIE RZECZYWISTOŚCI Daniel Wójcik Instytut Biologii Doświadczalnej PAN d.wojcik@nencki.gov.pl tel. 022 5892 424 http://www.neuroinf.pl/members/danek/swps/ Podręcznik Iwo Białynicki-Birula Iwona
Partition Search i gry z niezupełną informacją
 MIMUW 21 stycznia 2010 1 Co to jest gra? Proste algorytmy 2 Pomysł Algorytm Przykład użycia 3 Monte Carlo Inne spojrzenie Definicja Co to jest gra? Proste algorytmy Grą o wartościach w przedziale [0, 1]
MIMUW 21 stycznia 2010 1 Co to jest gra? Proste algorytmy 2 Pomysł Algorytm Przykład użycia 3 Monte Carlo Inne spojrzenie Definicja Co to jest gra? Proste algorytmy Grą o wartościach w przedziale [0, 1]
A B. Modelowanie reakcji chemicznych: numeryczne rozwiązywanie równań na szybkość reakcji chemicznych B: 1. da dt. A v. v t
 B: 1 Modelowanie reakcji chemicznych: numeryczne rozwiązywanie równań na szybkość reakcji chemicznych 1. ZałóŜmy, Ŝe zmienna A oznacza stęŝenie substratu, a zmienna B stęŝenie produktu reakcji chemicznej
B: 1 Modelowanie reakcji chemicznych: numeryczne rozwiązywanie równań na szybkość reakcji chemicznych 1. ZałóŜmy, Ŝe zmienna A oznacza stęŝenie substratu, a zmienna B stęŝenie produktu reakcji chemicznej
ALGORYTMY I STRUKTURY DANYCH
 ALGORYTMY I STRUKTURY DANYCH Temat : Drzewa zrównoważone, sortowanie drzewiaste Wykładowca: dr inż. Zbigniew TARAPATA e-mail: Zbigniew.Tarapata@isi.wat.edu.pl http://www.tarapata.strefa.pl/p_algorytmy_i_struktury_danych/
ALGORYTMY I STRUKTURY DANYCH Temat : Drzewa zrównoważone, sortowanie drzewiaste Wykładowca: dr inż. Zbigniew TARAPATA e-mail: Zbigniew.Tarapata@isi.wat.edu.pl http://www.tarapata.strefa.pl/p_algorytmy_i_struktury_danych/
P r a w d o p o d o b i eństwo Lekcja 1 Temat: Lekcja organizacyjna. Program. Kontrakt.
 P r a w d o p o d o b i eństwo Lekcja 1 Temat: Lekcja organizacyjna. Program. Kontrakt. Lekcja 2 Temat: Podstawowe pojęcia związane z prawdopodobieństwem. Str. 10-21 1. Doświadczenie losowe jest to doświadczenie,
P r a w d o p o d o b i eństwo Lekcja 1 Temat: Lekcja organizacyjna. Program. Kontrakt. Lekcja 2 Temat: Podstawowe pojęcia związane z prawdopodobieństwem. Str. 10-21 1. Doświadczenie losowe jest to doświadczenie,
Krzysztof Jakubczyk. Zadanie 2
 Zadanie 2 Krzysztof Jakubczyk Moje rozwiązanie nie znajduje strategii pozycyjnej w znaczeniu zdefiniowanym na wykładzie (niezaleŝnie od pozycji startowej), gdyŝ takowa nie istnieje. Przykład: 1 1 0 Środkowa
Zadanie 2 Krzysztof Jakubczyk Moje rozwiązanie nie znajduje strategii pozycyjnej w znaczeniu zdefiniowanym na wykładzie (niezaleŝnie od pozycji startowej), gdyŝ takowa nie istnieje. Przykład: 1 1 0 Środkowa
Poprawność semantyczna
 Poprawność składniowa Poprawność semantyczna Poprawność algorytmu Wypisywanie zdań z języka poprawnych składniowo Poprawne wartościowanie zdań języka, np. w języku programowania skutki wystąpienia wyróżnionych
Poprawność składniowa Poprawność semantyczna Poprawność algorytmu Wypisywanie zdań z języka poprawnych składniowo Poprawne wartościowanie zdań języka, np. w języku programowania skutki wystąpienia wyróżnionych
Alfa-beta Ulepszenie minimax Liczba wierzchołk ow w drzewie gry. maksymalnie wd. minimalnie wbd/2c + wdd/2e Algorytmy przeszukiwania drzewa gry 5
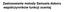 Zastosowanie metody Samuela doboru współczynników funkcji oceniajacej w programie grajacym w anty-warcaby Daniel Osman promotor: dr hab. inż. Jacek Mańdziuk 1 Spis treści Algorytmy przeszukiwania drzewa
Zastosowanie metody Samuela doboru współczynników funkcji oceniajacej w programie grajacym w anty-warcaby Daniel Osman promotor: dr hab. inż. Jacek Mańdziuk 1 Spis treści Algorytmy przeszukiwania drzewa
Przeszukiwanie przestrzeni rozwiązań, szukanie na ślepo, wszerz, wgłąb
 POLITECHNIKA WROCŁAWSKA WYDZIAŁ ELEKTRONIKI INFORMATYKA SYSTEMÓW AUTONOMICZNYCH Przeszukiwanie przestrzeni rozwiązań, szukanie na ślepo, wszerz, wgłąb AUTOR: Krzysztof Górski Indeks: 133247 e-mail: 133247@student.pwr.wroc.pl
POLITECHNIKA WROCŁAWSKA WYDZIAŁ ELEKTRONIKI INFORMATYKA SYSTEMÓW AUTONOMICZNYCH Przeszukiwanie przestrzeni rozwiązań, szukanie na ślepo, wszerz, wgłąb AUTOR: Krzysztof Górski Indeks: 133247 e-mail: 133247@student.pwr.wroc.pl
Algorytmy i. Wykład 5: Drzewa. Dr inż. Paweł Kasprowski
 Algorytmy i struktury danych Wykład 5: Drzewa Dr inż. Paweł Kasprowski pawel@kasprowski.pl Drzewa Struktury przechowywania danych podobne do list ale z innymi zasadami wskazywania następników Szczególny
Algorytmy i struktury danych Wykład 5: Drzewa Dr inż. Paweł Kasprowski pawel@kasprowski.pl Drzewa Struktury przechowywania danych podobne do list ale z innymi zasadami wskazywania następników Szczególny
Modelowanie sytuacji konfliktowych, w których występują dwie antagonistyczne strony.
 GRY (część 1) Zastosowanie: Modelowanie sytuacji konfliktowych, w których występują dwie antagonistyczne strony. Najbardziej znane modele: - wybór strategii marketingowych przez konkurujące ze sobą firmy
GRY (część 1) Zastosowanie: Modelowanie sytuacji konfliktowych, w których występują dwie antagonistyczne strony. Najbardziej znane modele: - wybór strategii marketingowych przez konkurujące ze sobą firmy
Wykład 7 i 8. Przeszukiwanie z adwersarzem. w oparciu o: S. Russel, P. Norvig. Artificial Intelligence. A Modern Approach
 (4g) Wykład 7 i 8 w oparciu o: S. Russel, P. Norvig. Artificial Intelligence. A Modern Approach P. Kobylański Wprowadzenie do Sztucznej Inteligencji 177 / 226 (4g) gry optymalne decyzje w grach algorytm
(4g) Wykład 7 i 8 w oparciu o: S. Russel, P. Norvig. Artificial Intelligence. A Modern Approach P. Kobylański Wprowadzenie do Sztucznej Inteligencji 177 / 226 (4g) gry optymalne decyzje w grach algorytm
MODELOWANIE RZECZYWISTOŚCI
 MODELOWANIE RZECZYWISTOŚCI Daniel Wójcik Instytut Biologii Doświadczalnej PAN Szkoła Wyższa Psychologii Społecznej d.wojcik@nencki.gov.pl dwojcik@swps.edu.pl tel. 022 5892 424 http://www.neuroinf.pl/members/danek/swps/
MODELOWANIE RZECZYWISTOŚCI Daniel Wójcik Instytut Biologii Doświadczalnej PAN Szkoła Wyższa Psychologii Społecznej d.wojcik@nencki.gov.pl dwojcik@swps.edu.pl tel. 022 5892 424 http://www.neuroinf.pl/members/danek/swps/
Algorytmy i struktury danych
 Algorytmy i struktury danych Proste algorytmy sortowania Witold Marańda maranda@dmcs.p.lodz.pl 1 Pojęcie sortowania Sortowaniem nazywa się proces ustawiania zbioru obiektów w określonym porządku Sortowanie
Algorytmy i struktury danych Proste algorytmy sortowania Witold Marańda maranda@dmcs.p.lodz.pl 1 Pojęcie sortowania Sortowaniem nazywa się proces ustawiania zbioru obiektów w określonym porządku Sortowanie
Algorytmy i str ruktury danych. Metody algorytmiczne. Bartman Jacek
 Algorytmy i str ruktury danych Metody algorytmiczne Bartman Jacek jbartman@univ.rzeszow.pl Metody algorytmiczne - wprowadzenia Znamy strukturę algorytmów Trudność tkwi natomiast w podaniu metod służących
Algorytmy i str ruktury danych Metody algorytmiczne Bartman Jacek jbartman@univ.rzeszow.pl Metody algorytmiczne - wprowadzenia Znamy strukturę algorytmów Trudność tkwi natomiast w podaniu metod służących
Wysokość drzewa Głębokość węzła
 Drzewa Drzewa Drzewo (ang. tree) zbiór węzłów powiązanych wskaźnikami, spójny i bez cykli. Drzewo posiada wyróżniony węzeł początkowy nazywany korzeniem (ang. root). Drzewo ukorzenione jest strukturą hierarchiczną.
Drzewa Drzewa Drzewo (ang. tree) zbiór węzłów powiązanych wskaźnikami, spójny i bez cykli. Drzewo posiada wyróżniony węzeł początkowy nazywany korzeniem (ang. root). Drzewo ukorzenione jest strukturą hierarchiczną.
SZTUCZNA INTELIGENCJA
 SZTUCZNA INTELIGENCJA WYKŁAD 12. PRZESZUKIWANIE Częstochowa 2014 Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska ROZWIĄZYWANIE PROBLEMÓW JAKO PRZESZUKIWANIE Istotną rolę podczas
SZTUCZNA INTELIGENCJA WYKŁAD 12. PRZESZUKIWANIE Częstochowa 2014 Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska ROZWIĄZYWANIE PROBLEMÓW JAKO PRZESZUKIWANIE Istotną rolę podczas
Porządek symetryczny: right(x)
 Porządek symetryczny: x lef t(x) right(x) Własność drzewa BST: W drzewach BST mamy porządek symetryczny. Dla każdego węzła x spełniony jest warunek: jeżeli węzeł y leży w lewym poddrzewie x, to key(y)
Porządek symetryczny: x lef t(x) right(x) Własność drzewa BST: W drzewach BST mamy porządek symetryczny. Dla każdego węzła x spełniony jest warunek: jeżeli węzeł y leży w lewym poddrzewie x, to key(y)
Tadeusz Pankowski www.put.poznan.pl/~tadeusz.pankowski
 : idea Indeksowanie: Drzewo decyzyjne, przeszukiwania binarnego: F = {5, 7, 10, 12, 13, 15, 17, 30, 34, 35, 37, 40, 45, 50, 60} 30 12 40 7 15 35 50 Tadeusz Pankowski www.put.poznan.pl/~tadeusz.pankowski
: idea Indeksowanie: Drzewo decyzyjne, przeszukiwania binarnego: F = {5, 7, 10, 12, 13, 15, 17, 30, 34, 35, 37, 40, 45, 50, 60} 30 12 40 7 15 35 50 Tadeusz Pankowski www.put.poznan.pl/~tadeusz.pankowski
Wykład 6. Drzewa poszukiwań binarnych (BST)
 Wykład 6 Drzewa poszukiwań binarnych (BST) 1 O czym będziemy mówić Definicja Operacje na drzewach BST: Search Minimum, Maximum Predecessor, Successor Insert, Delete Struktura losowo budowanych drzew BST
Wykład 6 Drzewa poszukiwań binarnych (BST) 1 O czym będziemy mówić Definicja Operacje na drzewach BST: Search Minimum, Maximum Predecessor, Successor Insert, Delete Struktura losowo budowanych drzew BST
Zaawansowane algorytmy i struktury danych
 Zaawansowane algorytmy i struktury danych u dr Barbary Marszał-Paszek Opracowanie pytań praktycznych z egzaminów. Strona 1 z 12 Pytania praktyczne z kolokwium zaliczeniowego z 19 czerwca 2014 (studia dzienne)
Zaawansowane algorytmy i struktury danych u dr Barbary Marszał-Paszek Opracowanie pytań praktycznych z egzaminów. Strona 1 z 12 Pytania praktyczne z kolokwium zaliczeniowego z 19 czerwca 2014 (studia dzienne)
Sortowanie. Kolejki priorytetowe i algorytm Heapsort Dynamiczny problem sortowania:
 Sortowanie Kolejki priorytetowe i algorytm Heapsort Dynamiczny problem sortowania: podać strukturę danych dla elementów dynamicznego skończonego multi-zbioru S, względem którego są wykonywane następujące
Sortowanie Kolejki priorytetowe i algorytm Heapsort Dynamiczny problem sortowania: podać strukturę danych dla elementów dynamicznego skończonego multi-zbioru S, względem którego są wykonywane następujące
Wnioskowanie jako przeszukiwanie przestrzeni stanów
 Plan wykładu Wnioskowanie jako przeszukiwanie przestrzeni stanów Rozwiązywanie problemów jako poszukiwanie ścieżki rozwiązania Przestrzeń stanów jako graf skierowany Dokładne metody przeszukiwania przestrzeni
Plan wykładu Wnioskowanie jako przeszukiwanie przestrzeni stanów Rozwiązywanie problemów jako poszukiwanie ścieżki rozwiązania Przestrzeń stanów jako graf skierowany Dokładne metody przeszukiwania przestrzeni
Algorytmy i Struktury Danych
 Algorytmy i Struktury Danych Kopce Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 11 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych Wykład 11 1 / 69 Plan wykładu
Algorytmy i Struktury Danych Kopce Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 11 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych Wykład 11 1 / 69 Plan wykładu
Algorytm selekcji Hoare a. Łukasz Miemus
 Algorytm selekcji Hoare a Łukasz Miemus 1 lutego 2006 Rozdział 1 O algorytmie 1.1 Problem Mamy tablicę A[N] różnych elementów i zmienną int K, takie że 1 K N. Oczekiwane rozwiązanie to określenie K-tego
Algorytm selekcji Hoare a Łukasz Miemus 1 lutego 2006 Rozdział 1 O algorytmie 1.1 Problem Mamy tablicę A[N] różnych elementów i zmienną int K, takie że 1 K N. Oczekiwane rozwiązanie to określenie K-tego
Dane są następujące reguły gry losowej: losujemy jedną kartę z pełnej talii (bez jokerów) i sprawdzamy wynik:
 Elementy teorii gier Dane są następujące reguły gry losowej: losujemy jedną kartę z pełnej talii (bez jokerów) i sprawdzamy wynik: wylosowanie karty w kolorze czerwonym (kier lub karo) oznacza wygraną
Elementy teorii gier Dane są następujące reguły gry losowej: losujemy jedną kartę z pełnej talii (bez jokerów) i sprawdzamy wynik: wylosowanie karty w kolorze czerwonym (kier lub karo) oznacza wygraną
TEORIA GIER DEFINICJA (VON NEUMANN, MORGENSTERN) GRA. jednostek (graczy) znajdujących się w sytuacji konfliktowej (konflikt interesów),w
 TEORIA GIER GRA DEFINICJA (VON NEUMANN, MORGENSTERN) Gra składa się z zestawu reguł określających możliwości wyboru postępowania jednostek (graczy) znajdujących się w sytuacji konfliktowej (konflikt interesów),w
TEORIA GIER GRA DEFINICJA (VON NEUMANN, MORGENSTERN) Gra składa się z zestawu reguł określających możliwości wyboru postępowania jednostek (graczy) znajdujących się w sytuacji konfliktowej (konflikt interesów),w
Problem straŝaka w drzewach. Agnieszka Skorupka Matematyka Stosowana FTiMS
 Problem straŝaka w drzewach Agnieszka Skorupka Matematyka Stosowana FTiMS Problem StraŜaka: Co to jest? Problem StraŜaka: Co to jest? Problem StraŜaka: Co to jest? Problem StraŜaka: Co to jest? Problem
Problem straŝaka w drzewach Agnieszka Skorupka Matematyka Stosowana FTiMS Problem StraŜaka: Co to jest? Problem StraŜaka: Co to jest? Problem StraŜaka: Co to jest? Problem StraŜaka: Co to jest? Problem
Metody przeszukiwania
 Metody przeszukiwania Co to jest przeszukiwanie Przeszukiwanie polega na odnajdywaniu rozwiązania w dyskretnej przestrzeni rozwiązao. Zwykle przeszukiwanie polega na znalezieniu określonego rozwiązania
Metody przeszukiwania Co to jest przeszukiwanie Przeszukiwanie polega na odnajdywaniu rozwiązania w dyskretnej przestrzeni rozwiązao. Zwykle przeszukiwanie polega na znalezieniu określonego rozwiązania
Strategie: sposób na opcje
 X-Trade Brokers Dom Maklerski S.A. Strategie: sposób na opcje z wykorzystaniem systemu Option Trader Tomasz Uściński X-Trade Brokers Dom Maklerski S.A. www.xtb.pl 1 Definicja opcji Opcja: Kontrakt finansowy,
X-Trade Brokers Dom Maklerski S.A. Strategie: sposób na opcje z wykorzystaniem systemu Option Trader Tomasz Uściński X-Trade Brokers Dom Maklerski S.A. www.xtb.pl 1 Definicja opcji Opcja: Kontrakt finansowy,
Risk-Aware Project Scheduling. SimpleUCT
 Risk-Aware Project Scheduling SimpleUCT DEFINICJA ZAGADNIENIA Resource-Constrained Project Scheduling (RCPS) Risk-Aware Project Scheduling (RAPS) 1 tryb wykonywania działań Czas trwania zadań jako zmienna
Risk-Aware Project Scheduling SimpleUCT DEFINICJA ZAGADNIENIA Resource-Constrained Project Scheduling (RCPS) Risk-Aware Project Scheduling (RAPS) 1 tryb wykonywania działań Czas trwania zadań jako zmienna
WYKŁAD 9. Algorytmy sortowania elementów zbioru (tablic) Programy: c4_1.c... c4_3.c. Tomasz Zieliński
 WYKŁAD 9 Algorytmy sortowania elementów zbioru (tablic) Programy: c4_1.c... c4_3.c Tomasz Zieliński /* Przyklad 4.1 - SORTOWANIE TABLIC - metoda najprostsza */ #include #define ROZMIAR 11 void
WYKŁAD 9 Algorytmy sortowania elementów zbioru (tablic) Programy: c4_1.c... c4_3.c Tomasz Zieliński /* Przyklad 4.1 - SORTOWANIE TABLIC - metoda najprostsza */ #include #define ROZMIAR 11 void
Algorytmy i struktury danych. Co dziś? Tytułem przypomnienia metoda dziel i zwyciężaj. Wykład VIII Elementarne techniki algorytmiczne
 Algorytmy i struktury danych Wykład VIII Elementarne techniki algorytmiczne Co dziś? Algorytmy zachłanne (greedyalgorithms) 2 Tytułem przypomnienia metoda dziel i zwyciężaj. Problem można podzielić na
Algorytmy i struktury danych Wykład VIII Elementarne techniki algorytmiczne Co dziś? Algorytmy zachłanne (greedyalgorithms) 2 Tytułem przypomnienia metoda dziel i zwyciężaj. Problem można podzielić na
Struktury Danych i Złożoność Obliczeniowa
 Struktury Danych i Złożoność Obliczeniowa Zajęcia 3 Struktury drzewiaste drzewo binarne szczególny przypadek drzewa, które jest szczególnym przypadkiem grafu skierowanego, stopień każdego wierzchołka jest
Struktury Danych i Złożoność Obliczeniowa Zajęcia 3 Struktury drzewiaste drzewo binarne szczególny przypadek drzewa, które jest szczególnym przypadkiem grafu skierowanego, stopień każdego wierzchołka jest
Ćwiczenia: Ukryte procesy Markowa lista 1 kierunek: matematyka, specjalność: analiza danych i modelowanie, studia II
 Ćwiczenia: Ukryte procesy Markowa lista kierunek: matematyka, specjalność: analiza danych i modelowanie, studia II dr Jarosław Kotowicz Zadanie. Dany jest łańcuch Markowa, który może przyjmować wartości,,...,
Ćwiczenia: Ukryte procesy Markowa lista kierunek: matematyka, specjalność: analiza danych i modelowanie, studia II dr Jarosław Kotowicz Zadanie. Dany jest łańcuch Markowa, który może przyjmować wartości,,...,
Rekurencja (rekursja)
 Rekurencja (rekursja) Rekurencja wywołanie funkcji przez nią samą wewnątrz ciała funkcji. Rekurencja może być pośrednia funkcja jest wywoływana przez inną funkcję, wywołaną (pośrednio lub bezpośrednio)
Rekurencja (rekursja) Rekurencja wywołanie funkcji przez nią samą wewnątrz ciała funkcji. Rekurencja może być pośrednia funkcja jest wywoływana przez inną funkcję, wywołaną (pośrednio lub bezpośrednio)
Wstęp do programowania
 Wstęp do programowania Stosy, kolejki, drzewa Paweł Daniluk Wydział Fizyki Jesień 2013 P. Daniluk(Wydział Fizyki) WP w. VII Jesień 2013 1 / 25 Listy Lista jest uporządkowanym zbiorem elementów. W Pythonie
Wstęp do programowania Stosy, kolejki, drzewa Paweł Daniluk Wydział Fizyki Jesień 2013 P. Daniluk(Wydział Fizyki) WP w. VII Jesień 2013 1 / 25 Listy Lista jest uporządkowanym zbiorem elementów. W Pythonie
Wieczorowe Studia Licencjackie Wrocław, Wykład nr 6 (w oparciu o notatki K. Lorysia, z modyfikacjami) Sito Eratostenesa
 Wieczorowe Studia Licencjackie Wrocław, 7.11.2006 Wstęp do programowania Wykład nr 6 (w oparciu o notatki K. Lorysia, z modyfikacjami) Sito Eratostenesa Zaprezentujemy teraz algorytm na wyznaczanie wszystkich
Wieczorowe Studia Licencjackie Wrocław, 7.11.2006 Wstęp do programowania Wykład nr 6 (w oparciu o notatki K. Lorysia, z modyfikacjami) Sito Eratostenesa Zaprezentujemy teraz algorytm na wyznaczanie wszystkich
Wybrane podstawowe rodzaje algorytmów
 Wybrane podstawowe rodzaje algorytmów Tomasz Głowacki tglowacki@cs.put.poznan.pl Zajęcia finansowane z projektu "Rozwój i doskonalenie kształcenia na Politechnice Poznańskiej w zakresie technologii informatycznych
Wybrane podstawowe rodzaje algorytmów Tomasz Głowacki tglowacki@cs.put.poznan.pl Zajęcia finansowane z projektu "Rozwój i doskonalenie kształcenia na Politechnice Poznańskiej w zakresie technologii informatycznych
TEORIA GIER W EKONOMII WYKŁAD 2: GRY DWUOSOBOWE O SUMIE ZEROWEJ. dr Robert Kowalczyk Katedra Analizy Nieliniowej Wydział Matematyki i Informatyki UŁ
 TEORIA GIER W EKONOMII WYKŁAD 2: GRY DWUOSOBOWE O SUMIE ZEROWEJ dr Robert Kowalczyk Katedra Analizy Nieliniowej Wydział Matematyki i Informatyki UŁ Definicja gry o sumie zerowej Powiemy, że jest grą o
TEORIA GIER W EKONOMII WYKŁAD 2: GRY DWUOSOBOWE O SUMIE ZEROWEJ dr Robert Kowalczyk Katedra Analizy Nieliniowej Wydział Matematyki i Informatyki UŁ Definicja gry o sumie zerowej Powiemy, że jest grą o
Wykład 2. Drzewa zbalansowane AVL i 2-3-4
 Wykład Drzewa zbalansowane AVL i -3-4 Drzewa AVL Wprowadzenie Drzewa AVL Definicja drzewa AVL Operacje wstawiania i usuwania Złożoność obliczeniowa Drzewa -3-4 Definicja drzewa -3-4 Operacje wstawiania
Wykład Drzewa zbalansowane AVL i -3-4 Drzewa AVL Wprowadzenie Drzewa AVL Definicja drzewa AVL Operacje wstawiania i usuwania Złożoność obliczeniowa Drzewa -3-4 Definicja drzewa -3-4 Operacje wstawiania
Informatyka I. Wykład 3. Sterowanie wykonaniem programu. Instrukcje warunkowe Instrukcje pętli. Dr inż. Andrzej Czerepicki
 Informatyka I Wykład 3. Sterowanie wykonaniem programu. Instrukcje warunkowe Instrukcje pętli Dr inż. Andrzej Czerepicki Politechnika Warszawska Wydział Transportu 2018 Operacje relacji (porównania) A
Informatyka I Wykład 3. Sterowanie wykonaniem programu. Instrukcje warunkowe Instrukcje pętli Dr inż. Andrzej Czerepicki Politechnika Warszawska Wydział Transportu 2018 Operacje relacji (porównania) A
Co to jest algorytm? przepis prowadzący do rozwiązania zadania, problemu,
 wprowadzenie Co to jest algorytm? przepis prowadzący do rozwiązania zadania, problemu, w przepisie tym podaje się opis czynności, które trzeba wykonać, oraz dane, dla których algorytm będzie określony.
wprowadzenie Co to jest algorytm? przepis prowadzący do rozwiązania zadania, problemu, w przepisie tym podaje się opis czynności, które trzeba wykonać, oraz dane, dla których algorytm będzie określony.
Listy, kolejki, stosy
 Listy, kolejki, stosy abc Lista O Struktura danych składa się z węzłów, gdzie mamy informacje (dane) i wskaźniki do następnych węzłów. Zajmuje tyle miejsca w pamięci ile mamy węzłów O Gdzie można wykorzystać:
Listy, kolejki, stosy abc Lista O Struktura danych składa się z węzłów, gdzie mamy informacje (dane) i wskaźniki do następnych węzłów. Zajmuje tyle miejsca w pamięci ile mamy węzłów O Gdzie można wykorzystać:
Drzewa Decyzyjne, cz.2
 Drzewa Decyzyjne, cz.2 Inteligentne Systemy Decyzyjne Katedra Systemów Multimedialnych WETI, PG Opracowanie: dr inŝ. Piotr Szczuko Podsumowanie poprzedniego wykładu Cel: przewidywanie wyniku (określania
Drzewa Decyzyjne, cz.2 Inteligentne Systemy Decyzyjne Katedra Systemów Multimedialnych WETI, PG Opracowanie: dr inŝ. Piotr Szczuko Podsumowanie poprzedniego wykładu Cel: przewidywanie wyniku (określania
D. Miszczyńska, M.Miszczyński KBO UŁ 1 GRY KONFLIKTOWE GRY 2-OSOBOWE O SUMIE WYPŁAT ZERO
 D. Miszczyńska, M.Miszczyński KBO UŁ GRY KONFLIKTOWE GRY 2-OSOBOWE O SUMIE WYPŁAT ZERO Gra w sensie niżej przedstawionym to zasady którymi kierują się decydenci. Zakładamy, że rezultatem gry jest wypłata,
D. Miszczyńska, M.Miszczyński KBO UŁ GRY KONFLIKTOWE GRY 2-OSOBOWE O SUMIE WYPŁAT ZERO Gra w sensie niżej przedstawionym to zasady którymi kierują się decydenci. Zakładamy, że rezultatem gry jest wypłata,
Wykład 2. Drzewa poszukiwań binarnych (BST)
 Wykład 2 Drzewa poszukiwań binarnych (BST) 1 O czym będziemy mówić Definicja Operacje na drzewach BST: Search Minimum, Maximum Predecessor, Successor Insert, Delete Struktura losowo budowanych drzew BST
Wykład 2 Drzewa poszukiwań binarnych (BST) 1 O czym będziemy mówić Definicja Operacje na drzewach BST: Search Minimum, Maximum Predecessor, Successor Insert, Delete Struktura losowo budowanych drzew BST
Podstawy programowania 2. Temat: Drzewa binarne. Przygotował: mgr inż. Tomasz Michno
 Instrukcja laboratoryjna 5 Podstawy programowania 2 Temat: Drzewa binarne Przygotował: mgr inż. Tomasz Michno 1 Wstęp teoretyczny Drzewa są jedną z częściej wykorzystywanych struktur danych. Reprezentują
Instrukcja laboratoryjna 5 Podstawy programowania 2 Temat: Drzewa binarne Przygotował: mgr inż. Tomasz Michno 1 Wstęp teoretyczny Drzewa są jedną z częściej wykorzystywanych struktur danych. Reprezentują
Kolejka priorytetowa. Często rozważa się kolejki priorytetowe, w których poszukuje się elementu minimalnego zamiast maksymalnego.
 Kolejki Kolejka priorytetowa Kolejka priorytetowa (ang. priority queue) to struktura danych pozwalająca efektywnie realizować następujące operacje na zbiorze dynamicznym, którego elementy pochodzą z określonego
Kolejki Kolejka priorytetowa Kolejka priorytetowa (ang. priority queue) to struktura danych pozwalająca efektywnie realizować następujące operacje na zbiorze dynamicznym, którego elementy pochodzą z określonego
Drzewa binarne. Drzewo binarne to dowolny obiekt powstały zgodnie z regułami: jest drzewem binarnym Jeśli T 0. jest drzewem binarnym Np.
 Drzewa binarne Drzewo binarne to dowolny obiekt powstały zgodnie z regułami: jest drzewem binarnym Jeśli T 0 i T 1 są drzewami binarnymi to T 0 T 1 jest drzewem binarnym Np. ( ) ( ( )) Wielkość drzewa
Drzewa binarne Drzewo binarne to dowolny obiekt powstały zgodnie z regułami: jest drzewem binarnym Jeśli T 0 i T 1 są drzewami binarnymi to T 0 T 1 jest drzewem binarnym Np. ( ) ( ( )) Wielkość drzewa
Statystyka hydrologiczna i prawdopodobieństwo zjawisk hydrologicznych.
 Statystyka hydrologiczna i prawdopodobieństwo zjawisk hydrologicznych. Statystyka zajmuje się prawidłowościami zaistniałych zdarzeń. Teoria prawdopodobieństwa dotyczy przewidywania, jak często mogą zajść
Statystyka hydrologiczna i prawdopodobieństwo zjawisk hydrologicznych. Statystyka zajmuje się prawidłowościami zaistniałych zdarzeń. Teoria prawdopodobieństwa dotyczy przewidywania, jak często mogą zajść
INSTRUKCJE ITERACYJNE
 INSTRUKCJE ITERACYJNE Zadanie nr 1 Przedstaw algorytm za pomocą a i schematów blokowych, który wyświetla na ekranie monitora 10 kolejnych liczb całkowitych począwszy od 1. Zrealizuj problem za pomocą instrukcji
INSTRUKCJE ITERACYJNE Zadanie nr 1 Przedstaw algorytm za pomocą a i schematów blokowych, który wyświetla na ekranie monitora 10 kolejnych liczb całkowitych począwszy od 1. Zrealizuj problem za pomocą instrukcji
Algorytmy i struktury danych. wykład 5
 Plan wykładu: Wskaźniki. : listy, drzewa, kopce. Wskaźniki - wskaźniki Wskaźnik jest to liczba lub symbol który w ogólności wskazuje adres komórki pamięci. W językach wysokiego poziomu wskaźniki mogą również
Plan wykładu: Wskaźniki. : listy, drzewa, kopce. Wskaźniki - wskaźniki Wskaźnik jest to liczba lub symbol który w ogólności wskazuje adres komórki pamięci. W językach wysokiego poziomu wskaźniki mogą również
Modelowanie motywów łańcuchami Markowa wyższego rzędu
 Modelowanie motywów łańcuchami Markowa wyższego rzędu Uniwersytet Warszawski Wydział Matematyki, Informatyki i Mechaniki 23 października 2008 roku Plan prezentacji 1 Źródła 2 Motywy i ich znaczenie Łańcuchy
Modelowanie motywów łańcuchami Markowa wyższego rzędu Uniwersytet Warszawski Wydział Matematyki, Informatyki i Mechaniki 23 października 2008 roku Plan prezentacji 1 Źródła 2 Motywy i ich znaczenie Łańcuchy
Laboratoria nr 1. Sortowanie
 Laboratoria nr 1 Sortowanie 1. Sortowanie bąbelkowe (BbS) 2. Sortowanie przez wstawianie (IS) 3. Sortowanie przez wybieranie (SS) 4. Sortowanie przez zliczanie (CS) 5. Sortowanie kubełkowe (BS) 6. Sortowanie
Laboratoria nr 1 Sortowanie 1. Sortowanie bąbelkowe (BbS) 2. Sortowanie przez wstawianie (IS) 3. Sortowanie przez wybieranie (SS) 4. Sortowanie przez zliczanie (CS) 5. Sortowanie kubełkowe (BS) 6. Sortowanie
Algorytmy i struktury danych. Drzewa: BST, kopce. Letnie Warsztaty Matematyczno-Informatyczne
 Algorytmy i struktury danych Drzewa: BST, kopce Letnie Warsztaty Matematyczno-Informatyczne Drzewa: BST, kopce Definicja drzewa Drzewo (ang. tree) to nieskierowany, acykliczny, spójny graf. Drzewo może
Algorytmy i struktury danych Drzewa: BST, kopce Letnie Warsztaty Matematyczno-Informatyczne Drzewa: BST, kopce Definicja drzewa Drzewo (ang. tree) to nieskierowany, acykliczny, spójny graf. Drzewo może
Sortowanie - wybrane algorytmy
 Sortowanie - wybrane algorytmy Aleksandra Wilkowska Wydział Matematyki - Katedra Matematyki Stosowanej Politechika Wrocławska 2 maja 2018 1 / 39 Plan prezentacji Złożoność obliczeniowa Sortowanie bąbelkowe
Sortowanie - wybrane algorytmy Aleksandra Wilkowska Wydział Matematyki - Katedra Matematyki Stosowanej Politechika Wrocławska 2 maja 2018 1 / 39 Plan prezentacji Złożoność obliczeniowa Sortowanie bąbelkowe
ZASADY PROGRAMOWANIA KOMPUTERÓW ZAP zima 2014/2015. Drzewa BST c.d., równoważenie drzew, kopce.
 POLITECHNIKA WARSZAWSKA Instytut Automatyki i Robotyki ZASADY PROGRAMOWANIA KOMPUTERÓW ZAP zima 204/205 Język programowania: Środowisko programistyczne: C/C++ Qt Wykład 2 : Drzewa BST c.d., równoważenie
POLITECHNIKA WARSZAWSKA Instytut Automatyki i Robotyki ZASADY PROGRAMOWANIA KOMPUTERÓW ZAP zima 204/205 Język programowania: Środowisko programistyczne: C/C++ Qt Wykład 2 : Drzewa BST c.d., równoważenie
Analiza algorytmów zadania podstawowe
 Analiza algorytmów zadania podstawowe Zadanie 1 Zliczanie Zliczaj(n) 1 r 0 2 for i 1 to n 1 3 do for j i + 1 to n 4 do for k 1 to j 5 do r r + 1 6 return r 0 Jaka wartość zostanie zwrócona przez powyższą
Analiza algorytmów zadania podstawowe Zadanie 1 Zliczanie Zliczaj(n) 1 r 0 2 for i 1 to n 1 3 do for j i + 1 to n 4 do for k 1 to j 5 do r r + 1 6 return r 0 Jaka wartość zostanie zwrócona przez powyższą
Uniwersytet Zielonogórski Wydział Elektrotechniki, Informatyki i Telekomunikacji Instytut Sterowania i Systemów Informatycznych
 Uniwersytet Zielonogórski Wydział Elektrotechniki, Informatyki i Telekomunikacji Instytut Sterowania i Systemów Informatycznych ELEMENTY SZTUCZNEJ INTELIGENCJI Laboratorium nr 9 PRZESZUKIWANIE GRAFÓW Z
Uniwersytet Zielonogórski Wydział Elektrotechniki, Informatyki i Telekomunikacji Instytut Sterowania i Systemów Informatycznych ELEMENTY SZTUCZNEJ INTELIGENCJI Laboratorium nr 9 PRZESZUKIWANIE GRAFÓW Z
Algorytmy z powrotami. Algorytm minimax
 Algorytmy z powrotami. Algorytm minimax Algorytmy i struktury danych. Wykład 7. Rok akademicki: 2010/2011 Algorytm z powrotami rozwiązanie problemu budowane jest w kolejnych krokach, po stwierdzeniu (w
Algorytmy z powrotami. Algorytm minimax Algorytmy i struktury danych. Wykład 7. Rok akademicki: 2010/2011 Algorytm z powrotami rozwiązanie problemu budowane jest w kolejnych krokach, po stwierdzeniu (w
prowadzący dr ADRIAN HORZYK /~horzyk e-mail: horzyk@agh tel.: 012-617 Konsultacje paw. D-13/325
 PODSTAWY INFORMATYKI WYKŁAD 8. prowadzący dr ADRIAN HORZYK http://home home.agh.edu.pl/~ /~horzyk e-mail: horzyk@agh agh.edu.pl tel.: 012-617 617-4319 Konsultacje paw. D-13/325 DRZEWA Drzewa to rodzaj
PODSTAWY INFORMATYKI WYKŁAD 8. prowadzący dr ADRIAN HORZYK http://home home.agh.edu.pl/~ /~horzyk e-mail: horzyk@agh agh.edu.pl tel.: 012-617 617-4319 Konsultacje paw. D-13/325 DRZEWA Drzewa to rodzaj
Zadanie 1 Przygotuj algorytm programu - sortowanie przez wstawianie.
 Sortowanie Dane wejściowe: ciąg n-liczb (kluczy) (a 1, a 2, a 3,..., a n 1, a n ) Dane wyjściowe: permutacja ciągu wejściowego (a 1, a 2, a 3,..., a n 1, a n) taka, że a 1 a 2 a 3... a n 1 a n. Będziemy
Sortowanie Dane wejściowe: ciąg n-liczb (kluczy) (a 1, a 2, a 3,..., a n 1, a n ) Dane wyjściowe: permutacja ciągu wejściowego (a 1, a 2, a 3,..., a n 1, a n) taka, że a 1 a 2 a 3... a n 1 a n. Będziemy
Algorytmiczne Aspekty Teorii Gier Rozwiązania zadań
 Algorytmiczne Aspekty Teorii Gier Rozwiązania zadań Bartosz Gęza 19/06/2009 Zadanie 2. (gra symetryczna o sumie zerowej) Profil prawdopodobieństwa jednorodnego nie musi być punktem równowagi Nasha. Przykładem
Algorytmiczne Aspekty Teorii Gier Rozwiązania zadań Bartosz Gęza 19/06/2009 Zadanie 2. (gra symetryczna o sumie zerowej) Profil prawdopodobieństwa jednorodnego nie musi być punktem równowagi Nasha. Przykładem
Struktury danych i złożoność obliczeniowa Wykład 5. Prof. dr hab. inż. Jan Magott
 Struktury danych i złożoność obliczeniowa Wykład. Prof. dr hab. inż. Jan Magott Algorytmy grafowe: podstawowe pojęcia, reprezentacja grafów, metody przeszukiwania, minimalne drzewa rozpinające, problemy
Struktury danych i złożoność obliczeniowa Wykład. Prof. dr hab. inż. Jan Magott Algorytmy grafowe: podstawowe pojęcia, reprezentacja grafów, metody przeszukiwania, minimalne drzewa rozpinające, problemy
Ogólne wiadomości o grafach
 Ogólne wiadomości o grafach Algorytmy i struktury danych Wykład 5. Rok akademicki: / Pojęcie grafu Graf zbiór wierzchołków połączonych za pomocą krawędzi. Podstawowe rodzaje grafów: grafy nieskierowane,
Ogólne wiadomości o grafach Algorytmy i struktury danych Wykład 5. Rok akademicki: / Pojęcie grafu Graf zbiór wierzchołków połączonych za pomocą krawędzi. Podstawowe rodzaje grafów: grafy nieskierowane,
a) 7 b) 19 c) 21 d) 34
 Zadanie 1. Pytania testowe dotyczące podstawowych własności grafów. Zadanie 2. Przy każdym z zadań może się pojawić polecenie krótkiej charakterystyki algorytmu. Zadanie 3. W zadanym grafie sprawdzenie
Zadanie 1. Pytania testowe dotyczące podstawowych własności grafów. Zadanie 2. Przy każdym z zadań może się pojawić polecenie krótkiej charakterystyki algorytmu. Zadanie 3. W zadanym grafie sprawdzenie
Gramatyki atrybutywne
 Gramatyki atrybutywne, część 1 (gramatyki S-atrybutywne Teoria kompilacji Dr inŝ. Janusz Majewski Katedra Informatyki Gramatyki atrybutywne Do przeprowadzenia poprawnego tłumaczenia, oprócz informacji
Gramatyki atrybutywne, część 1 (gramatyki S-atrybutywne Teoria kompilacji Dr inŝ. Janusz Majewski Katedra Informatyki Gramatyki atrybutywne Do przeprowadzenia poprawnego tłumaczenia, oprócz informacji
Iteracyjne rozwiązywanie równań
 Elementy metod numerycznych Plan wykładu 1 Wprowadzenie Plan wykładu 1 Wprowadzenie 2 Plan wykładu 1 Wprowadzenie 2 3 Wprowadzenie Metoda bisekcji Metoda siecznych Metoda stycznych Plan wykładu 1 Wprowadzenie
Elementy metod numerycznych Plan wykładu 1 Wprowadzenie Plan wykładu 1 Wprowadzenie 2 Plan wykładu 1 Wprowadzenie 2 3 Wprowadzenie Metoda bisekcji Metoda siecznych Metoda stycznych Plan wykładu 1 Wprowadzenie
