OPTYKA GEOMETRYCZNA I INSTRUMENTALNA
|
|
|
- Agata Michalik
- 6 lat temu
- Przeglądów:
Transkrypt
1 00-BO5, rok akademicki 08/9 OPTYKA GEOMETRYCZNA I INSTRUMENTALNA dr hab. Rafał Kasztelaic Wykład
2 Światło a materia - dyspersja szybkość propagacji światła w materii zależy od częstotliwości padającej fali współczyik załamaia zależy od długości fali światła (λ) Jest to dyspersja chromatycza, jest oa m.i. odpowiedziale za powstawaie tęczy, czy rozmycie impulsów w światłowodach e.wikipedia.org/wiki/dispersio_(optics) mathsciotes.com
3 Światło a materia - dyspersja Dyspersja powietrza vs. szkła Dyspersja chromatycza jest powszecha Dla fal widzialych przebiega w podoby sposób dla wielu materiałów (współczyik załamaia światła w materiale zmiejsza się wraz ze wzrostem długości fali padającego światła) 3
4 Światło a materia - dyspersja współczyik dyspersji F C liczba Abbego (dyspersja względa) F d C dyspersja cząstkowa λ F = 486, m λ C = 656,3 m λ d = 589,3 m P F F C 4
5 Światło a materia - dyspersja Liczba Abbego - im jest większa, tym dyspersja materiału jest miejsza F d C 5 pl.wikipedia.org/wiki/liczba_abbego
6 Światło a materia - dyspersja Skąd się wzięły λ F, λ C, λ d itp.? Dostępe w dawych latach lampy gazowe emitowały światło o liiach widmowych zależych od cech gazu. λ [m] Symbol liii Źródło światła Zakres widmowy i Hg UV h Hg violet g Hg blue F' Cd blue F H blue e Hg gree d He yellow D Na yellow C' Cd red C H red r He red 768. A' K red 85. s Cs IR t Hg IR 6
7 Światło a materia - metale przewodik prądu współczyik załamaia zespoloy częstość plazmowa odbijaie, pochłaiaie dla częstości większych od częstości plazmowej materiał jest przeźroczysty dla częstości miejszych wykazuje duży współczyik odbicia dla jeszcze miejszych częstości współczyik odbicia maleje, ale trasmisja ie rośie, gdyż rośie absorpcja. występowaie kolejo obszarów o dużej trasmisji, odbiciu i absorpcji, jest charakterystycze dla materiałów przewodzących takich jak metale czy półprzewodiki kopaliawiedzy.pl 7
8 Światło a materia - rozpraszaie zjawisko oddziaływaia światła z materią, w wyiku którego astępuje zmiaa kieruku rozchodzeia się światła, ie (zjawisko) iż odbicie i załamaie światła rozpraszaie światła może być sprężyste - bez zmiay eergii/częstotliwości lub iesprężyste - ze zmiaą eergii/częstotliwości wielkość rozproszeia zależy od długości fali elektromagetyczej, od wielkości cząsteczek atmosfery oraz od długości drogi oddziaływaia fali z atmosferą Przyczyy iejedorodościami układu, w którym zachodzi propagacja fal (cząsteczki substacji, pyły, aerozole, zmiay gęstości itp.). ierówość powierzchi 8
9 Światło a materia - rozpraszaie Wyróżiamy trzy rodzaje rozproszeia: rozpraszaie Rayleigha Zachodzi gdy wielkość cząsteczek, a których zachodzi rozproszeie jest dużo miejsza iż długość fali elektromagetyczej Zachodzi we wszystkich kierukach, bez zmiay długości fali Wyikiem tego rozpraszaia jest iebieski kolor ieba i pochłaiaie UV przez ozo 𝐼~ λ4 kathleehalme.com rozpraszaie Mie Zachodzi gdy wielkość cząsteczek, a których zachodzi rozproszeie jest porówywala z długością fali elektromagetyczej Najsiliejsze jest w kieruku zgodym z falą padającą Nie zależy od długości fali Rozproszeie przede wszystkim a pyłkach, dymie, zaieczyszczeiach i parze wodej 9
10 Światło a materia - rozpraszaie rozpraszaie ieselekcyje Zachodzi gdy wielkość cząsteczek, a których zachodzi rozproszeie jest dużo większa od długości fali elektromagetyczej. Rozproszeie przede wszystkim a kroplach wody i dużych cząsteczkach zaieczyszczeń Rozproszeie ie selektywe jest przyczyą tego, że chmury i mgła są białe. Poieważ wszystkie długości światła widzialego rozpraszae są w podoby sposób rozpraszaie a szorstkiej powierzchi 0
11 Światło a materia - absorpcja Absorpcja (pochłaiaie) fali elektromagetyczej w ośrodku Cząsteczki gazów, zaieczyszczeń i wody w atmosferze wpływają a eergię fali elektromagetyczej. Jeżeli zachodzi osłabieie mocy promieiowaia przy zachowaiu kieruku rozchodzeia fali mówimy o absorpcji. Mechaizm: foto o eergii E = hν może oddziaływać z elektroem walecyjym w atomie lub molekule wewątrz ośrodka materialego. Jeżeli eergia fotou jest rówa różicy eergii pomiędzy dowolym staem wzbudzoym elektrou a staem podstawowym, wówczas foto zostaie pochłoięty. Gdy eergia fotou ie pasuje do żadej różicy eergii staów, wówczas foto albo przechodzi przez ośrodek materialy bez przeszkód albo jest rozpraszay. W wyiku absorpcji fotou atom lub molekuła przechodzi w sta wzbudzoy o wyższej eergii. Wzbudzoe atomy lub molekuły wracają do stau podstawowego emitując jedocześie foto o takiej samej lub miejszej eergii.
12 Światło a materia - pochłaiaie pw.pl
13 Światło a materia - pochłaiaie Przykład: widmo emisyje & widmo absorpcyje 3
14 Światło a materia - pochłaiaie Przykład: absorpcja światła w wodzie 4
15 Propagacja światła 5
16 Propagacja światła Zasada Huygesa Każdy pukt ośrodka, do którego dotarło czoło fali moża uważać za źródło owej fali kulistej. CBSE Class Physics, Wave Optics 6
17 Propagacja światła Zasada Huygesa Każdy pukt ośrodka, do którego dotarło czoło fali moża uważać za źródło owej fali kulistej. CBSE Class Physics, Wave Optics Fale te (fale cząstkowe) iterferują ze sobą, tworząc wypadkową powierzchię falową. 7
18 Propagacja światła Zasada Huygesa 8
19 Propagacja światła Zasada Huygesa 9 hyperphysics.phy-astr.gsu.edu
20 Propagacja światła Zasada Fermata Promień świetly poruszając się między dwoma puktami przebywa ajkrótszą możliwie drogę optyczą, czyli taką, a której przebycie potrzebuje miimalego czasu. 0
21 Propagacja światła Powstawaie cieia puktowe źródło światła brak cieia cień brak cieia
22 Propagacja światła Powstawaie cieia puktowe źródło światła rozciągłe źródło światła brak cieia cień brak cieia brak cieia półcień cień półcień brak cieia
23 Propagacja światła Optyka promiei ray tracig sites.google.com/site/tiffayciglis/fu-stuff/cs-girls-ray-tracig-workshop pl.wikipedia.org 3
24 Propagacja światła Optyka promiei Promień liia wskazująca kieruek rozchodzeia się eergii promieiowaia, prostopadła do powierzchi falowej Wiele zjawisk optyczych ie wymaga aalizy światła jako fali elektromagetyczej i do ich opisu wystarcza operowaie pojęciem promieia świetlego, który jest odbijay lub załamyway a różych powierzchiach W optyce geometryczej zwykle zaiedbujemy zjawiska pochłaiaia fali Zakładamy, że długość fali e-m jest bardzo mała w porówaiu z rozmiarami elemetów tworzących aalizoway układ optyczy Wiązka światła jest obiektem rzeczywistym. Aaliza propagacji wiązki polega a aalizie biegu promiei ją tworzących Pęk promiei wiązka promiei wychodząca (przechodząca) z jedego puktu Droga optycza L = droga geometrycza L = ds rówaie eikoału 4
25 Załamaie i odbicie światła Promień padający i promień odbity/załamay leżą w jedej płaszczyźie 5 L.S. Pedrotti, Fudametals of Photoics
26 Załamaie i odbicie światła Odbicie światła z zasady Huygesa E. R. Huggis, Physics 000, Geometrical Optics i = CAC = AC A = i J. Nowak, M. Zając, Optyka kurs elemetary 6
27 Załamaie i odbicie światła 7 Odbicie światła z zasady Fermata Spośród wielu możliwych dróg, światło biegie po takiej, aby czas poruszaia się po iej był ekstremaly (zwykle ajkrótszy) si si 0 i i x d b x d x a x x d x d b x x a dx dl x d b x a L i i δl = δ ds = 0 B A J. Nowak, M. Zając, Optyka kurs elemetary
28 Załamaie i odbicie światła Odbicie światła 8
29 Załamaie i odbicie światła Odbicie światła góra-dół 9
30 Załamaie i odbicie światła Odbicie światła góra dół lewo prawo przód tył 30
31 Załamaie i odbicie światła Odbicie światła corer reflector e.wikipedia.org/wiki/corer_reflector 3
32 Załamaie i odbicie światła Światło a graicy ośrodków icecube.wisc.edu 3
33 Załamaie i odbicie światła Załamaia światła z zasady Huygesa Prawo Sella λ = AB si θ = λ 0 λ = AB si θ = λ 0 si θ si θ = si θ = si θ 33 E. R. Huggis, Physics 000, Geometrical Optics
34 Załamaie i odbicie światła 34 Załamaie światła z zasady Fermata si ; si 0 0 x s d x s i x h x i x s d x s x h x dx dt c x s d x h t v x s d v x h t si i si i = si i = si i Prawo Sella S = νt t = S ν J. Nowak, M. Zając, Optyka kurs elemetary
35 Załamaie i odbicie światła Załamaie światła metoda Youga Prawo Sella si i si i = AB/AR AB/AR = AR AR = g = g 35
36 Załamaie i odbicie światła Optyka geometrycza - aksjomaty Światło w ośrodku jedorodym propaguje się po liiach prostych promieiach Bezwzględy współczyik załamaia = c, gdzie v prędkość światła w daym ośrodku v Gdy promień przechodzi z ośrodka o bezwzględym współczyiku załamaia do ośrodka o bezwzględym współczyiku załamaia to ulega załamaiu: Promień padający i promień załamay leżą w jedej płaszczyźie Spełioe jest prawo Sella: si α = si β Przy odbiciu obowiązuje prawo odbicia: Promień padający i promień odbity leżą w jedej płaszczyźie Kąt odbicia rówy jest kątowi padaia: α = β 36
37 Załamaie i odbicie światła Optyka geometrycza - aksjomaty Światło w ośrodku jedorodym propaguje się po liiach prostych promieiach Bezwzględy współczyik załamaia = c, gdzie v prędkość światła w daym ośrodku v Gdy promień przechodzi z ośrodka o bezwzględym współczyiku załamaia do ośrodka o bezwzględym współczyiku załamaia to ulega załamaiu: Promień padający i promień załamay leżą w jedej płaszczyźie Spełioe jest prawo Sella: si α = si β Przy odbiciu obowiązuje prawo odbicia: Promień padający i promień odbity leżą w jedej płaszczyźie Kąt odbicia rówy jest kątowi padaia: α = β Optyka geometrycza ograiczeia Brak zależości od długości fali dyspersja Z promieiem ie jest związaa moc światła podział mocy a graicy ośrodków Nie wyjaśia zjawisk dyfrakcji, iterferecji, polaryzacji 37
38 Załamaie i odbicie światła Całkowite wewętrze odbicie (TIR) Przy przechodzeiu światła z ośrodka o większym do ośrodka o miejszym, może astąpić sytuacja, gdy kąt załamaia jest rówy lub większy iż 90 0, co zaczy, że światło ie może przedostać się przez graicę ośrodków. Zjawisko to azywa się całkowitym wewętrzym odbiciem i jest powszeche w przyrodzie oraz szeroko wykorzystywae w techice. TIR (ag. Total Iteral Reflectio) si θ si θ = si θ = si θ > Promień 4 kąt graiczy 38 icecube.wisc.edu
39 Załamaie i odbicie światła Całkowite wewętrze odbicie (TIR) blogs.cisco.com 39 sethsadler.com
40 Załamaie i odbicie światła Całkowite wewętrze odbicie (TIR) E. R. Huggis, Physics 000, Geometrical Optics esfscieceew.wordpress.com
41 Załamaie i odbicie światła Całkowite wewętrze odbicie (TIR) coect.collis.co.uk E. R. Huggis, Physics 000, Geometrical Optics itl.siyavula.com steemit.com 4
42 Propagacja światła w ośrodku iejedorodym GRIN GRadiet INdex optics 4
43 Załamaie i odbicie światła Odbicie światła a graicy ośrodków wzory Fresela Wzory Fresela wskazują, jaka część eergii padającej fali światła jest odbita a graicy ośrodków o różym współczyiku załamaia. Współczyiki odbicia R s i R p zależą od polaryzacji światła. 43
44 Załamaie i odbicie światła Odbicie światła a graicy ośrodków wzory Fresela dla małych kątów Łatwo zauważyć, że dla małych kątów różica współczyika odbicia dla różych polaryzacji staje się mała, czyli obie polaryzacje są odbijae iemal jedakowo. Im większa różica współczyików załamaia, tym większe odbicie. R = + 44
45 Załamaie i odbicie światła Odbicie światła a graicy ośrodków kąt Brewstera Kat pomiędzy promieiem odbitym i załamaym wyosi =π tgθ = 45 commos.wikimedia.org
46 Płytka płasko-rówoległa Płytka płasko-rówoległa: ajprostszy elemet optyczy wprowadza przesuięcie promieia światła Δ, bez zmiay kieruku propagacji Przesuięcie Δ zależy od współczyika załamaia materiału, z którego jest wykoaa płytka Dla światła polichromatyczego astępuje dodatkowo rozszczepieie światła, spowodowae dyspersją d si i cos i si i d cos i si i Dla malych i : d J. Nowak, M. Zając, Optyka kurs elemetary 46 Podiesieie obrazu
47 Płytka płasko-rówoległa z prawa załamaia: i i 47
48 Płytka płasko-rówoległa z prawa załamaia: z jedyki trygoometryczej : i i 48
49 Płytka płasko-rówoległa z prawa załamaia: z jedyki trygoometryczej : z trójkątów: i i 49
50 Płytka płasko-rówoległa z prawa załamaia: z jedyki trygoometryczej : z trójkątów: i i 50
51 Płytka płasko-rówoległa z prawa załamaia: z jedyki trygoometryczej : z trójkątów: i i PRZESUNIĘCIE 5
52 Płytka płasko-rówoległa z prawa załamaia: z jedyki trygoometryczej : z trójkątów: i i PRZESUNIĘCIE PODNIESIENIE 5
53 Płytka płasko-rówoległa 53
54 Pryzmat Pryzmat ośrodek ograiczoy dwiema ierówoległymi płaszczyzami. Krawędź łamiąca prosta powstała z przecięcia obu płaszczyz. Kąt łamiący kąt między płaszczyzami. 54
55 Pryzmat Odchyleie promieia δ jest ajmiejsze, gdy światło biegie przez pryzmat symetryczie mi si si Kli gdy mały kąt łamiący k 55
56 Pryzmat z trójkątów: 56
57 Pryzmat si z trójkątów: z prawa Sella: si arcsi si si si arcsi si 57
58 Pryzmat 58 si arcsi si arcsi si arcsi si arcsi z trójkątów: si arcsi si si si arcsi si si z prawa Sella:
59 Pryzmat 59 si arcsi si arcsi si arcsi si arcsi si arcsi si arcsi z trójkątów: si arcsi si si si arcsi si si z prawa Sella:
60 Pryzmat 60 mi mi mi Przypadek symetryczy:
61 Pryzmat si si si si Przypadek symetryczy: mi mi mi mi si si 6
62 Pryzmat Przypadek symetryczy: mi mi 6 si si Dla klia - φ małe: siθ θ si si mi mi mi mi mi si si
63 Pryzmat mi si si 63
Ćwiczenie: "Ruch harmoniczny i fale"
 Ćwiczenie: "Ruch harmoniczny i fale" Opracowane w ramach projektu: "Wirtualne Laboratoria Fizyczne nowoczesną metodą nauczania realizowanego przez Warszawską Wyższą Szkołę Informatyki. Zakres ćwiczenia:
Ćwiczenie: "Ruch harmoniczny i fale" Opracowane w ramach projektu: "Wirtualne Laboratoria Fizyczne nowoczesną metodą nauczania realizowanego przez Warszawską Wyższą Szkołę Informatyki. Zakres ćwiczenia:
Ćwiczenie 5 Hologram gruby
 Ćwiczenie 5 Hologram gruby 1. Wprowadzenie: Na poprzednim ćwiczeniu zapoznaliśmy się z hologramem Fresnela, który daje nam moŝliwość zapisu obiektu przestrzennego. Wadą jego jednak jest to, iŝ moŝemy go
Ćwiczenie 5 Hologram gruby 1. Wprowadzenie: Na poprzednim ćwiczeniu zapoznaliśmy się z hologramem Fresnela, który daje nam moŝliwość zapisu obiektu przestrzennego. Wadą jego jednak jest to, iŝ moŝemy go
ANALIZA WIDMOWA (dla szkoły średniej) 1. Dane osobowe. 2. Podstawowe informacje BHP. 3. Opis stanowiska pomiarowego. 4. Procedura pomiarowa
 ANALIZA WIDMOWA (dla szkoły średniej) 1. Dane osobowe Data wykonania ćwiczenia: Nazwa szkoły, klasa: Dane uczniów: 1 4 2 5 3 6 2. Podstawowe informacje BHP Możliwość porażenia prądem lampa jest zasilana
ANALIZA WIDMOWA (dla szkoły średniej) 1. Dane osobowe Data wykonania ćwiczenia: Nazwa szkoły, klasa: Dane uczniów: 1 4 2 5 3 6 2. Podstawowe informacje BHP Możliwość porażenia prądem lampa jest zasilana
PRAWA ZACHOWANIA. Podstawowe terminy. Cia a tworz ce uk ad mechaniczny oddzia ywuj mi dzy sob i z cia ami nie nale cymi do uk adu za pomoc
 PRAWA ZACHOWANIA Podstawowe terminy Cia a tworz ce uk ad mechaniczny oddzia ywuj mi dzy sob i z cia ami nie nale cymi do uk adu za pomoc a) si wewn trznych - si dzia aj cych na dane cia o ze strony innych
PRAWA ZACHOWANIA Podstawowe terminy Cia a tworz ce uk ad mechaniczny oddzia ywuj mi dzy sob i z cia ami nie nale cymi do uk adu za pomoc a) si wewn trznych - si dzia aj cych na dane cia o ze strony innych
Od redakcji. Symbolem oznaczono zadania wykraczające poza zakres materiału omówionego w podręczniku Fizyka z plusem cz. 2.
 Od redakcji Niniejszy zbiór zadań powstał z myślą o tych wszystkich, dla których rozwiązanie zadania z fizyki nie polega wyłącznie na mechanicznym przekształceniu wzorów i podstawieniu do nich danych.
Od redakcji Niniejszy zbiór zadań powstał z myślą o tych wszystkich, dla których rozwiązanie zadania z fizyki nie polega wyłącznie na mechanicznym przekształceniu wzorów i podstawieniu do nich danych.
Czas trwania obligacji (duration)
 Czas rwaia obligacji (duraio) Do aalizy ryzyka wyikającego ze zmia sóp proceowych (szczególie ryzyka zmiay cey) wykorzysuje się pojęcie zw. średiego ermiu wykupu obligacji, zwaego rówież czasem rwaia obligacji
Czas rwaia obligacji (duraio) Do aalizy ryzyka wyikającego ze zmia sóp proceowych (szczególie ryzyka zmiay cey) wykorzysuje się pojęcie zw. średiego ermiu wykupu obligacji, zwaego rówież czasem rwaia obligacji
2.Prawo zachowania masy
 2.Prawo zachowania masy Zdefiniujmy najpierw pewne podstawowe pojęcia: Układ - obszar przestrzeni o określonych granicach Ośrodek ciągły - obszar przestrzeni którego rozmiary charakterystyczne są wystarczająco
2.Prawo zachowania masy Zdefiniujmy najpierw pewne podstawowe pojęcia: Układ - obszar przestrzeni o określonych granicach Ośrodek ciągły - obszar przestrzeni którego rozmiary charakterystyczne są wystarczająco
7. REZONANS W OBWODACH ELEKTRYCZNYCH
 OBWODY SYGNAŁY 7. EZONANS W OBWODAH EEKTYZNYH 7.. ZJAWSKO EZONANS Obwody elektryczne, w których występuje zjawisko rezonansu nazywane są obwodami rezonansowymi lub drgającymi. ozpatrując bezźródłowy obwód
OBWODY SYGNAŁY 7. EZONANS W OBWODAH EEKTYZNYH 7.. ZJAWSKO EZONANS Obwody elektryczne, w których występuje zjawisko rezonansu nazywane są obwodami rezonansowymi lub drgającymi. ozpatrując bezźródłowy obwód
SPEKTROSKOPIA LASEROWA
 SPEKTROSKOPIA LASEROWA Spektroskopia laserowa dostarcza wiedzy o naturze zjawisk zachodz cych na poziomie atomów i cz steczek oraz oddzia ywaniu promieniowania z materi i nale y do jednej z najwa niejszych
SPEKTROSKOPIA LASEROWA Spektroskopia laserowa dostarcza wiedzy o naturze zjawisk zachodz cych na poziomie atomów i cz steczek oraz oddzia ywaniu promieniowania z materi i nale y do jednej z najwa niejszych
40. Międzynarodowa Olimpiada Fizyczna Meksyk, 12-19 lipca 2009 r. ZADANIE TEORETYCZNE 2 CHŁODZENIE LASEROWE I MELASA OPTYCZNA
 ZADANIE TEORETYCZNE 2 CHŁODZENIE LASEROWE I MELASA OPTYCZNA Celem tego zadania jest podanie prostej teorii, która tłumaczy tak zwane chłodzenie laserowe i zjawisko melasy optycznej. Chodzi tu o chłodzenia
ZADANIE TEORETYCZNE 2 CHŁODZENIE LASEROWE I MELASA OPTYCZNA Celem tego zadania jest podanie prostej teorii, która tłumaczy tak zwane chłodzenie laserowe i zjawisko melasy optycznej. Chodzi tu o chłodzenia
Wyznaczanie statycznego i kinetycznego współczynnika tarcia przy pomocy równi pochyłej
 Wyznaczanie statycznego i kinetycznego współczynnika tarcia przy pomocy równi pochyłej Równia pochyła jest przykładem maszyny prostej. Jej konstrukcja składa się z płaskiej powierzchni nachylonej pod kątem
Wyznaczanie statycznego i kinetycznego współczynnika tarcia przy pomocy równi pochyłej Równia pochyła jest przykładem maszyny prostej. Jej konstrukcja składa się z płaskiej powierzchni nachylonej pod kątem
KURS GEOMETRIA ANALITYCZNA
 KURS GEOMETRIA ANALITYCZNA Lekcja 1 Działania na wektorach bez układu współrzędnych. ZADANIE DOMOWE www.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowiedź (tylko jedna jest prawdziwa). Pytanie
KURS GEOMETRIA ANALITYCZNA Lekcja 1 Działania na wektorach bez układu współrzędnych. ZADANIE DOMOWE www.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowiedź (tylko jedna jest prawdziwa). Pytanie
Wykorzystywane zjawiska Rodzaje laserów Kontrolowane cechy
 ZASTOSOWANIE LASERÓW W OCHRONIE RODOWISKA W tym przypadku lasery pozwalaj na prowadzenie kontroli stanu sanitarnego - powietrza, - zbiorników wodnych, - powierzchni i pokrycia terenu. Stosowane rodzaje
ZASTOSOWANIE LASERÓW W OCHRONIE RODOWISKA W tym przypadku lasery pozwalaj na prowadzenie kontroli stanu sanitarnego - powietrza, - zbiorników wodnych, - powierzchni i pokrycia terenu. Stosowane rodzaje
Optyka geometryczna i falowa
 Pojęcie podstawowe: promień świetlny. Optyka geometryczna i alowa Podstawowa obserwacja: jeżeli promień świetlny pada na granicę dwóch ośrodków to: ulega odbiciu na powierzchni granicznej za!amaniu przy
Pojęcie podstawowe: promień świetlny. Optyka geometryczna i alowa Podstawowa obserwacja: jeżeli promień świetlny pada na granicę dwóch ośrodków to: ulega odbiciu na powierzchni granicznej za!amaniu przy
Proste struktury krystaliczne
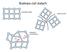 Budowa ciał stałych Proste struktury krystaliczne sc (simple cubic) bcc (body centered cubic) fcc (face centered cubic) np. Piryt FeSe 2 np. Żelazo, Wolfram np. Miedź, Aluminium Struktury krystaliczne
Budowa ciał stałych Proste struktury krystaliczne sc (simple cubic) bcc (body centered cubic) fcc (face centered cubic) np. Piryt FeSe 2 np. Żelazo, Wolfram np. Miedź, Aluminium Struktury krystaliczne
Wymagania edukacyjne z fizyki do gimnazjum Gimnazjum Sióstr Salezjanek w Ostrowie Wielkopolskim
 Wymagania edukacyjne z fizyki do gimnazjum Gimnazjum Sióstr Salezjanek w Ostrowie Wielkopolskim Uczeń uzyskuje z poszczególnych działów fizyki oceny cząstkowe jeżeli sprostał wymaganiom ogólnym, doświadczalnym,
Wymagania edukacyjne z fizyki do gimnazjum Gimnazjum Sióstr Salezjanek w Ostrowie Wielkopolskim Uczeń uzyskuje z poszczególnych działów fizyki oceny cząstkowe jeżeli sprostał wymaganiom ogólnym, doświadczalnym,
wiat o mo e by rozumiane jako strumie fotonów albo jako fala elektromagnetyczna. Najprostszym przypadkiem fali elektromagnetycznej jest fala p aska
 G ÓWNE CECHY WIAT A LASEROWEGO wiat o mo e by rozumiane jako strumie fotonów albo jako fala elektromagnetyczna. Najprostszym przypadkiem fali elektromagnetycznej jest fala p aska - cz sto ko owa, - cz
G ÓWNE CECHY WIAT A LASEROWEGO wiat o mo e by rozumiane jako strumie fotonów albo jako fala elektromagnetyczna. Najprostszym przypadkiem fali elektromagnetycznej jest fala p aska - cz sto ko owa, - cz
Statystyczna analiza danych w programie STATISTICA. Dariusz Gozdowski. Katedra Doświadczalnictwa i Bioinformatyki Wydział Rolnictwa i Biologii SGGW
 Statystyczna analiza danych w programie STATISTICA ( 4 (wykład Dariusz Gozdowski Katedra Doświadczalnictwa i Bioinformatyki Wydział Rolnictwa i Biologii SGGW Regresja prosta liniowa Regresja prosta jest
Statystyczna analiza danych w programie STATISTICA ( 4 (wykład Dariusz Gozdowski Katedra Doświadczalnictwa i Bioinformatyki Wydział Rolnictwa i Biologii SGGW Regresja prosta liniowa Regresja prosta jest
Projekt Inżynier mechanik zawód z przyszłością współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego
 Zajęcia wyrówawcze z fizyki -Zestaw 5 -Teoria Optyka geometrycza i optyka falowa. Prawo odbicia i prawo załamaia światła, Bieg promiei świetlych w pryzmacie, soczewki i zwierciadła. Zjawisko dyfrakcji
Zajęcia wyrówawcze z fizyki -Zestaw 5 -Teoria Optyka geometrycza i optyka falowa. Prawo odbicia i prawo załamaia światła, Bieg promiei świetlych w pryzmacie, soczewki i zwierciadła. Zjawisko dyfrakcji
Kod pracy. Po udzieleniu odpowiedzi do zadań 1 20, wypełnij tabelkę
 ŁÓDZKIE CENTRUM DOSKONALENIA NAUCZYCIELI I KSZTAŁCENIA PRAKTYCZNEGO Kod pracy Wypełnia Przewodniczący Wojewódzkiej Koisji Wojewódzkiego Konkursu Przediotowego z Fizyki Iię i nazwisko ucznia... Szkoła...
ŁÓDZKIE CENTRUM DOSKONALENIA NAUCZYCIELI I KSZTAŁCENIA PRAKTYCZNEGO Kod pracy Wypełnia Przewodniczący Wojewódzkiej Koisji Wojewódzkiego Konkursu Przediotowego z Fizyki Iię i nazwisko ucznia... Szkoła...
Błędy fotografii akwarystycznej
 Błędy fotografii akwarystycznej Błędy metody nr.2 Źle ustawiona lampa błyskowa na stopce - promień odbity zamiast biec pomiędzy lampą błyskową a aparatem trafił w obiektyw. Przy okazji widać ślady po związkach
Błędy fotografii akwarystycznej Błędy metody nr.2 Źle ustawiona lampa błyskowa na stopce - promień odbity zamiast biec pomiędzy lampą błyskową a aparatem trafił w obiektyw. Przy okazji widać ślady po związkach
14P2 POWTÓRKA FIKCYJNY EGZAMIN MATURALNYZ FIZYKI I ASTRONOMII - II POZIOM PODSTAWOWY
 14P2 POWTÓRKA FIKCYJNY EGZAMIN MATURALNYZ FIZYKI I ASTRONOMII - II POZIOM PODSTAWOWY Ruch jednostajny po okręgu Pole grawitacyjne Rozwiązania zadań należy zapisać w wyznaczonych miejscach pod treścią zadania
14P2 POWTÓRKA FIKCYJNY EGZAMIN MATURALNYZ FIZYKI I ASTRONOMII - II POZIOM PODSTAWOWY Ruch jednostajny po okręgu Pole grawitacyjne Rozwiązania zadań należy zapisać w wyznaczonych miejscach pod treścią zadania
Statystyczny opis danych - parametry
 Statystyczy opis daych - parametry Ozaczeia żółty owe pojęcie czerwoy, podkreśleie uwaga * materiał adobowiązkowy Zagadieia. Idea opisu parametryczego. Parametry a. położeia b. rozrzutu c. asymetrii Statystyczy
Statystyczy opis daych - parametry Ozaczeia żółty owe pojęcie czerwoy, podkreśleie uwaga * materiał adobowiązkowy Zagadieia. Idea opisu parametryczego. Parametry a. położeia b. rozrzutu c. asymetrii Statystyczy
Materiały pomocnicze 8 do zajęć wyrównawczych z Fizyki dla Inżynierii i Gospodarki Wodnej
 Materiały pomocnicze 8 do zajęć wyrównawczych z Fizyki dla Inżynierii i Gospodarki Wodnej 1. Ruch drgający. Drgania harmoniczne opisuje równanie: ( ω + φ) x = Asin t gdzie: A amplituda ruchu ω prędkość
Materiały pomocnicze 8 do zajęć wyrównawczych z Fizyki dla Inżynierii i Gospodarki Wodnej 1. Ruch drgający. Drgania harmoniczne opisuje równanie: ( ω + φ) x = Asin t gdzie: A amplituda ruchu ω prędkość
DRGANIA MECHANICZNE. materiały uzupełniające do ćwiczeń. Wydział Samochodów i Maszyn Roboczych studia inżynierskie
 DRGANIA MECHANICZNE materiały uzupełniające do ćwiczeń Wydział Samochodów i Maszyn Roboczych studia inżynierskie prowadzący: mgr inż. Sebastian Korczak część modelowanie, drgania swobodne Poniższe materiały
DRGANIA MECHANICZNE materiały uzupełniające do ćwiczeń Wydział Samochodów i Maszyn Roboczych studia inżynierskie prowadzący: mgr inż. Sebastian Korczak część modelowanie, drgania swobodne Poniższe materiały
dyfuzja w płynie nieruchomym (lub w ruchu laminarnym) prowadzi do wzrostu chmury zanieczyszczenia
 6. Dyspersja i adwekcja w przepływie urbulennym podsumowanie własności laminarnej (molekularnej) dyfuzji: ciągły ruch molekuł (molekularne wymuszenie) prowadzi do losowego błądzenia cząsek zanieczyszczeń
6. Dyspersja i adwekcja w przepływie urbulennym podsumowanie własności laminarnej (molekularnej) dyfuzji: ciągły ruch molekuł (molekularne wymuszenie) prowadzi do losowego błądzenia cząsek zanieczyszczeń
Stechiometria równań reakcji chemicznych, objętość gazów w warunkach odmiennych od warunków normalnych (0 o C 273K, 273hPa)
 Karta pracy I/2a Stechiometria równań reakcji chemicznych, objętość gazów w warunkach odmiennych od warunków normalnych (0 o C 273K, 273hPa) I. Stechiometria równań reakcji chemicznych interpretacja równań
Karta pracy I/2a Stechiometria równań reakcji chemicznych, objętość gazów w warunkach odmiennych od warunków normalnych (0 o C 273K, 273hPa) I. Stechiometria równań reakcji chemicznych interpretacja równań
XIII KONKURS MATEMATYCZNY
 XIII KONKURS MTMTYZNY L UZNIÓW SZKÓŁ POSTWOWYH organizowany przez XIII Liceum Ogólnokształcace w Szczecinie FINŁ - 19 lutego 2013 Test poniższy zawiera 25 zadań. Za poprawne rozwiązanie każdego zadania
XIII KONKURS MTMTYZNY L UZNIÓW SZKÓŁ POSTWOWYH organizowany przez XIII Liceum Ogólnokształcace w Szczecinie FINŁ - 19 lutego 2013 Test poniższy zawiera 25 zadań. Za poprawne rozwiązanie każdego zadania
1100-1BO15, rok akademicki 2017/18
 00-BO5, rok akademicki 07/8 Dr hab. Jacek Piewski, Zakład Optyki Iformacyjej E-mail: j.piewski@uw.edu.pl Telefo: (0) 55 3 036 Kosultacje: Warszawa, Pasteura 5 (B), pok. 4.36 po umówieiu via e-mail. Materiały
00-BO5, rok akademicki 07/8 Dr hab. Jacek Piewski, Zakład Optyki Iformacyjej E-mail: j.piewski@uw.edu.pl Telefo: (0) 55 3 036 Kosultacje: Warszawa, Pasteura 5 (B), pok. 4.36 po umówieiu via e-mail. Materiały
Ć W I C Z E N I E N R O-10
 INSTYTUT FIZYKI WYDZIAŁ INŻYNIERII PRODUKCJI I TECHNOLOGII MATERIAŁÓW POLITECHNIKA CZĘSTOCHOWSKA PRACOWNIA OPTYKI Ć W I C Z E N I E N R O-10 POMIAR PRĘDKOŚCI ŚWIATŁA I. Zagadnienia do opracowania 1. Metody
INSTYTUT FIZYKI WYDZIAŁ INŻYNIERII PRODUKCJI I TECHNOLOGII MATERIAŁÓW POLITECHNIKA CZĘSTOCHOWSKA PRACOWNIA OPTYKI Ć W I C Z E N I E N R O-10 POMIAR PRĘDKOŚCI ŚWIATŁA I. Zagadnienia do opracowania 1. Metody
P 0max. P max. = P max = 0; 9 20 = 18 W. U 2 0max. U 0max = q P 0max = p 18 2 = 6 V. D = T = U 0 = D E ; = 6
 XL OLIMPIADA WIEDZY TECHNICZNEJ Zawody II stopnia Rozwi zania zada dla grupy elektryczno-elektronicznej Rozwi zanie zadania 1 Sprawno przekszta tnika jest r wna P 0ma a Maksymaln moc odbiornika mo na zatem
XL OLIMPIADA WIEDZY TECHNICZNEJ Zawody II stopnia Rozwi zania zada dla grupy elektryczno-elektronicznej Rozwi zanie zadania 1 Sprawno przekszta tnika jest r wna P 0ma a Maksymaln moc odbiornika mo na zatem
Udoskonalona wentylacja komory suszenia
 Udoskonalona wentylacja komory suszenia Komora suszenia Kratka wentylacyjna Zalety: Szybkie usuwanie wilgoci z przestrzeni nad próbką Ograniczenie emisji ciepła z komory suszenia do modułu wagowego W znacznym
Udoskonalona wentylacja komory suszenia Komora suszenia Kratka wentylacyjna Zalety: Szybkie usuwanie wilgoci z przestrzeni nad próbką Ograniczenie emisji ciepła z komory suszenia do modułu wagowego W znacznym
PRÓBNY EGZAMIN MATURALNY Z FIZYKI I ASTRONOMII
 dysleksja PRÓBNY EGZAMIN MATURALNY Z FIZYKI I ASTRONOMII Instrukcja dla zdaj cego (poziom rozszerzony) Czas pracy 120 minut 1. Prosz sprawdzi, czy arkusz egzaminacyjny zawiera 8 stron. Ewentualny brak
dysleksja PRÓBNY EGZAMIN MATURALNY Z FIZYKI I ASTRONOMII Instrukcja dla zdaj cego (poziom rozszerzony) Czas pracy 120 minut 1. Prosz sprawdzi, czy arkusz egzaminacyjny zawiera 8 stron. Ewentualny brak
Ć W I C Z E N I E 5. Częstotliwość graniczna
 36 Ć W I Z E N I E 5 PASYWNE FILTY ZĘSTOTLIWOŚI. WIADOMOŚI OGÓLNE Filtrem częstotliwości nazywamy układ o strukturze czwórnika (czwórnik to układ mający cztery zaciski jedna z par zacisków pełni rolę wejścia,
36 Ć W I Z E N I E 5 PASYWNE FILTY ZĘSTOTLIWOŚI. WIADOMOŚI OGÓLNE Filtrem częstotliwości nazywamy układ o strukturze czwórnika (czwórnik to układ mający cztery zaciski jedna z par zacisków pełni rolę wejścia,
PRÓBNY EGZAMIN MATURALNY Z FIZYKI I ASTRONOMII
 dysleksja PRÓBNY EGZAMIN MATURALNY Z FIZYKI I ASTRONOMII Instrukcja dla zdającego (poziom rozszerzony) Czas pracy 120 minut 1. Proszę sprawdzić, czy arkusz egzaminacyjny zawiera 8 stron. Ewentualny brak
dysleksja PRÓBNY EGZAMIN MATURALNY Z FIZYKI I ASTRONOMII Instrukcja dla zdającego (poziom rozszerzony) Czas pracy 120 minut 1. Proszę sprawdzić, czy arkusz egzaminacyjny zawiera 8 stron. Ewentualny brak
Informacje uzyskiwane dzięki spektrometrii mas
 Slajd 1 Spektrometria mas i sektroskopia w podczerwieni Slajd 2 Informacje uzyskiwane dzięki spektrometrii mas Masa cząsteczkowa Wzór związku Niektóre informacje dotyczące wzoru strukturalnego związku
Slajd 1 Spektrometria mas i sektroskopia w podczerwieni Slajd 2 Informacje uzyskiwane dzięki spektrometrii mas Masa cząsteczkowa Wzór związku Niektóre informacje dotyczące wzoru strukturalnego związku
Lekcja 15. Temat: Prąd elektryczny w róŝnych środowiskach.
 Lekcja 15 Temat: Prąd elektryczny w róŝnych środowiskach. Pod wpływem pola elektrycznego (przyłoŝonego napięcia) w materiałach, w których istnieją ruchliwe nośniki ładunku dochodzi do zjawiska przewodzenia
Lekcja 15 Temat: Prąd elektryczny w róŝnych środowiskach. Pod wpływem pola elektrycznego (przyłoŝonego napięcia) w materiałach, w których istnieją ruchliwe nośniki ładunku dochodzi do zjawiska przewodzenia
Spektroskopia UV-VIS zagadnienia
 Spektroskopia absorbcyjna to dziedzina, która obejmuje metody badania materii przy użyciu promieniowania elektromagnetycznego, które może z tą materią oddziaływać. Spektroskopia UV-VS zagadnienia promieniowanie
Spektroskopia absorbcyjna to dziedzina, która obejmuje metody badania materii przy użyciu promieniowania elektromagnetycznego, które może z tą materią oddziaływać. Spektroskopia UV-VS zagadnienia promieniowanie
Zadanie 21. Stok narciarski
 Numer zadania Zadanie. Stok narciarski KLUCZ DO ZADA ARKUSZA II Je eli zdaj cy rozwi e zadanie inn, merytorycznie poprawn metod otrzymuje maksymaln liczb punktów Numer polecenia i poprawna odpowied. sporz
Numer zadania Zadanie. Stok narciarski KLUCZ DO ZADA ARKUSZA II Je eli zdaj cy rozwi e zadanie inn, merytorycznie poprawn metod otrzymuje maksymaln liczb punktów Numer polecenia i poprawna odpowied. sporz
Repetytorium z Matematyki Elementarnej Wersja Olimpijska
 Repetytorium z Matematyi Elemetarej Wersja Olimpijsa Podae tutaj zadaia rozwiązywae były w jedej z grup ćwiczeiowych Są w więszości ieco trudiejsze od pozostałych zadań przygotowaych w ramach przedmiotu
Repetytorium z Matematyi Elemetarej Wersja Olimpijsa Podae tutaj zadaia rozwiązywae były w jedej z grup ćwiczeiowych Są w więszości ieco trudiejsze od pozostałych zadań przygotowaych w ramach przedmiotu
Techniki korekcyjne wykorzystywane w metodzie kinesiotapingu
 Techniki korekcyjne wykorzystywane w metodzie kinesiotapingu Jak ju wspomniano, kinesiotaping mo e byç stosowany jako osobna metoda terapeutyczna, jak równie mo e stanowiç uzupe nienie innych metod fizjoterapeutycznych.
Techniki korekcyjne wykorzystywane w metodzie kinesiotapingu Jak ju wspomniano, kinesiotaping mo e byç stosowany jako osobna metoda terapeutyczna, jak równie mo e stanowiç uzupe nienie innych metod fizjoterapeutycznych.
1100-1BO15, rok akademicki 2016/17
 00-BO5, rok akademicki 06/7 Dr Jacek Piewski, Zakład Optyki Iformacyjej E-mail: j.piewski@uw.edu.pl Telefo: (0) 55 46 84 Kosultacje: Warszawa, Pasteura 7, pok. 58, wtorki, czwartki po umówieiu via e-mail.
00-BO5, rok akademicki 06/7 Dr Jacek Piewski, Zakład Optyki Iformacyjej E-mail: j.piewski@uw.edu.pl Telefo: (0) 55 46 84 Kosultacje: Warszawa, Pasteura 7, pok. 58, wtorki, czwartki po umówieiu via e-mail.
0. Napisać imię i nazwisko
 0. Napisać imię i nazwisko 1. Wypisać 4 fundamentalne oddziaływania, które są źródłem wszystkich sił. Grawitacyjne, jądrowe słabe, jądrowe silne, elektromagnetyczne. Cząsteczkami przenoszącymi oddziaływania
0. Napisać imię i nazwisko 1. Wypisać 4 fundamentalne oddziaływania, które są źródłem wszystkich sił. Grawitacyjne, jądrowe słabe, jądrowe silne, elektromagnetyczne. Cząsteczkami przenoszącymi oddziaływania
4.9 Badanie stanu polaryzacji światła(o8)
 212 Fale 4.9 Badanie stanu polaryzacji światła(o8) Celem ćwiczenia jest zapoznanie się z różnymi rodzajami polaryzacji światła, sposobami uzyskania danego typu polaryzacji oraz doświadczalnego sprawdzenia
212 Fale 4.9 Badanie stanu polaryzacji światła(o8) Celem ćwiczenia jest zapoznanie się z różnymi rodzajami polaryzacji światła, sposobami uzyskania danego typu polaryzacji oraz doświadczalnego sprawdzenia
Agrofi k zy a Wyk Wy ł k ad V Marek Kasprowicz
 Agrofizyka Wykład V Marek Kasprowicz Spektroskopia p nauka o powstawaniu i interpretacji widm powstających w wyniku oddziaływań wszelkich rodzajów promieniowania na materię ę rozumianą jako zbiorowisko
Agrofizyka Wykład V Marek Kasprowicz Spektroskopia p nauka o powstawaniu i interpretacji widm powstających w wyniku oddziaływań wszelkich rodzajów promieniowania na materię ę rozumianą jako zbiorowisko
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 15, Radosław Chrapkiewicz, Filip Ozimek
 Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 5, 3.04.0 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 4 - przypomnienie interferencja
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 5, 3.04.0 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 4 - przypomnienie interferencja
Fizyka Laserów wykład 10. Czesław Radzewicz
 Fizyka Laserów wykład 10 Czesław Radzewicz Struktura energetyczna półprzewodników Regularna budowa kryształu okresowy potencjał Funkcja falowa elektronu. konsekwencje: E ψ r pasmo przewodnictwa = u r e
Fizyka Laserów wykład 10 Czesław Radzewicz Struktura energetyczna półprzewodników Regularna budowa kryształu okresowy potencjał Funkcja falowa elektronu. konsekwencje: E ψ r pasmo przewodnictwa = u r e
WOJEWÓDZKI KONKURS FIZYCZNY
 KOD UCZNIA Liczba uzyskanych punktów (maks. 40): Młody Fizyku! WOJEWÓDZKI KONKURS FIZYCZNY Etap rejonowy Masz do rozwiązania 20 zadań (w tym 3 otwarte). Całkowity czas na rozwiązanie wynosi 90 minut. W
KOD UCZNIA Liczba uzyskanych punktów (maks. 40): Młody Fizyku! WOJEWÓDZKI KONKURS FIZYCZNY Etap rejonowy Masz do rozwiązania 20 zadań (w tym 3 otwarte). Całkowity czas na rozwiązanie wynosi 90 minut. W
Badanie silnika asynchronicznego jednofazowego
 Badanie silnika asynchronicznego jednofazowego Cel ćwiczenia Celem ćwiczenia jest poznanie budowy i zasady funkcjonowania silnika jednofazowego. W ramach ćwiczenia badane są zmiany wartości prądu rozruchowego
Badanie silnika asynchronicznego jednofazowego Cel ćwiczenia Celem ćwiczenia jest poznanie budowy i zasady funkcjonowania silnika jednofazowego. W ramach ćwiczenia badane są zmiany wartości prądu rozruchowego
MATEMATYKA 9. INSTYTUT MEDICUS Kurs przygotowawczy do matury i rekrutacji na studia medyczne Rok 2017/2018 FUNKCJE WYKŁADNICZE, LOGARYTMY
 INSTYTUT MEDICUS Kurs przygotowawczy do matury i rekrutacji na studia medyczne Rok 017/018 www.medicus.edu.pl tel. 501 38 39 55 MATEMATYKA 9 FUNKCJE WYKŁADNICZE, LOGARYTMY Dla dowolnej liczby a > 0, liczby
INSTYTUT MEDICUS Kurs przygotowawczy do matury i rekrutacji na studia medyczne Rok 017/018 www.medicus.edu.pl tel. 501 38 39 55 MATEMATYKA 9 FUNKCJE WYKŁADNICZE, LOGARYTMY Dla dowolnej liczby a > 0, liczby
Korekta jako formacja cenowa
 Korekta jako formacja cenowa Agenda Co to jest korekta i jej cechy Korekta a klasyczne formacje cenowe Korekta w teorii fal Geometria Czas - jako narzędzie Przykłady Korekta To ruch ceny na danym instrumencie
Korekta jako formacja cenowa Agenda Co to jest korekta i jej cechy Korekta a klasyczne formacje cenowe Korekta w teorii fal Geometria Czas - jako narzędzie Przykłady Korekta To ruch ceny na danym instrumencie
Promocja i identyfikacja wizualna projektów współfinansowanych ze środków Europejskiego Funduszu Społecznego
 Promocja i identyfikacja wizualna projektów współfinansowanych ze środków Europejskiego Funduszu Społecznego Białystok, 19 grudzień 2012 r. Seminarium współfinansowane ze środków Unii Europejskiej w ramach
Promocja i identyfikacja wizualna projektów współfinansowanych ze środków Europejskiego Funduszu Społecznego Białystok, 19 grudzień 2012 r. Seminarium współfinansowane ze środków Unii Europejskiej w ramach
KONKURS PRZEDMIOTOWY Z FIZYKI dla uczniów gimnazjów województwa lubuskiego 23 marca 2012 r. zawody III stopnia (finałowe)
 Pieczęć KONKURS PRZEDMIOTOWY Z FIZYKI dla uczniów gimnazjów województwa lubuskiego 23 marca 2012 r. zawody III stopnia (finałowe) Witamy Cię na trzecim etapie Konkursu Przedmiotowego z Fizyki i życzymy
Pieczęć KONKURS PRZEDMIOTOWY Z FIZYKI dla uczniów gimnazjów województwa lubuskiego 23 marca 2012 r. zawody III stopnia (finałowe) Witamy Cię na trzecim etapie Konkursu Przedmiotowego z Fizyki i życzymy
TEST DIAGNOZUJACY Z FIZYKI DLA UCZNIÓW KLAS I GIMNAZJUM
 Henryk Rej nauczyciel fizyki Gimnazjum Nr 1 43-100 Tychy ul. Brzozowa 24 PROPOZYCJA ZAJĘĆ Z FIZYKI: TEST DIAGNOZUJACY Z FIZYKI DLA UCZNIÓW KLAS I GIMNAZJUM CELE OGÓLNY: popularyzacja nauk przyrodniczych
Henryk Rej nauczyciel fizyki Gimnazjum Nr 1 43-100 Tychy ul. Brzozowa 24 PROPOZYCJA ZAJĘĆ Z FIZYKI: TEST DIAGNOZUJACY Z FIZYKI DLA UCZNIÓW KLAS I GIMNAZJUM CELE OGÓLNY: popularyzacja nauk przyrodniczych
Zakłócenia. Podstawy projektowania A.Korcala
 Zakłócenia Podstawy projektowania A.Korcala Pojęciem zakłóceń moŝna określać wszelkie niepoŝądane przebiegi pochodzenia zewnętrznego, wywołane zarówno przez działalność człowieka, jak i zakłócenia naturalne
Zakłócenia Podstawy projektowania A.Korcala Pojęciem zakłóceń moŝna określać wszelkie niepoŝądane przebiegi pochodzenia zewnętrznego, wywołane zarówno przez działalność człowieka, jak i zakłócenia naturalne
'()(*+,-./01(23/*4*567/8/23/*98:)2(!."/+)012+3$%-4#"4"$5012#-4#"4-6017%*,4.!"#$!"#%&"!!!"#$%&"#'()%*+,-+
 '()(*+,-./01(23/*4*567/8/23/*98:)2(!."/+)012+3$%-4#"4"$5012#-4#"4-6017%*,4.!"#$!"#%&"!!!"#$%&"#'()%*+,-+ Ucze interpretuje i tworzy teksty o charakterze matematycznym, u ywa j zyka matematycznego do opisu
'()(*+,-./01(23/*4*567/8/23/*98:)2(!."/+)012+3$%-4#"4"$5012#-4#"4-6017%*,4.!"#$!"#%&"!!!"#$%&"#'()%*+,-+ Ucze interpretuje i tworzy teksty o charakterze matematycznym, u ywa j zyka matematycznego do opisu
EKONOMETRIA. Temat wykładu: Co to jest model ekonometryczny? Dobór zmiennych objaśniających w modelu ekonometrycznym CZYM ZAJMUJE SIĘ EKONOMETRIA?
 EKONOMETRIA Temat wykładu: Co to jest model ekoometryczy? Dobór zmieych objaśiających w modelu ekoometryczym Prowadzący: dr iż. Zbigiew TARAPATA e-mail: Zbigiew.Tarapata Tarapata@isi.wat..wat.edu.pl http://
EKONOMETRIA Temat wykładu: Co to jest model ekoometryczy? Dobór zmieych objaśiających w modelu ekoometryczym Prowadzący: dr iż. Zbigiew TARAPATA e-mail: Zbigiew.Tarapata Tarapata@isi.wat..wat.edu.pl http://
Wiedza niepewna i wnioskowanie (c.d.)
 Wiedza niepewna i wnioskowanie (c.d.) Dariusz Banasiak Katedra Informatyki Technicznej Wydział Elektroniki Wnioskowanie przybliżone Wnioskowanie w logice tradycyjnej (dwuwartościowej) polega na stwierdzeniu
Wiedza niepewna i wnioskowanie (c.d.) Dariusz Banasiak Katedra Informatyki Technicznej Wydział Elektroniki Wnioskowanie przybliżone Wnioskowanie w logice tradycyjnej (dwuwartościowej) polega na stwierdzeniu
Kalendarz Maturzysty 2010/11 Fizyka
 Kalendarz Maturzysty 2010/11 Fizyka Kalendarz Maturzysty 2010/11 Fizyka Patryk Kamiński Drogi Maturzysto, Oddajemy Ci do rąk profesjonalny Kalendarz Maturzysty z fizyki stworzony przez naszego eksperta.
Kalendarz Maturzysty 2010/11 Fizyka Kalendarz Maturzysty 2010/11 Fizyka Patryk Kamiński Drogi Maturzysto, Oddajemy Ci do rąk profesjonalny Kalendarz Maturzysty z fizyki stworzony przez naszego eksperta.
INSTRUKCJA BHP PRZY RECZNYCH PRACACH TRANSPORTOWYCH DLA PRACOWNIKÓW KUCHENKI ODDZIAŁOWEJ.
 INSTRUKCJA BHP PRZY RECZNYCH PRACACH TRANSPORTOWYCH DLA PRACOWNIKÓW KUCHENKI ODDZIAŁOWEJ. I. UWAGI OGÓLNE. 1. Dostarczanie posiłków, ich przechowywanie i dystrybucja musza odbywać się w warunkach zapewniających
INSTRUKCJA BHP PRZY RECZNYCH PRACACH TRANSPORTOWYCH DLA PRACOWNIKÓW KUCHENKI ODDZIAŁOWEJ. I. UWAGI OGÓLNE. 1. Dostarczanie posiłków, ich przechowywanie i dystrybucja musza odbywać się w warunkach zapewniających
Zagospodarowanie magazynu
 Zagospodarowanie magazynu Wymagania wobec projektu magazynu - 1 jak najlepsze wykorzystanie pojemności związane z szybkością rotacji i konieczną szybkością dostępu do towaru; im większa wymagana szybkość
Zagospodarowanie magazynu Wymagania wobec projektu magazynu - 1 jak najlepsze wykorzystanie pojemności związane z szybkością rotacji i konieczną szybkością dostępu do towaru; im większa wymagana szybkość
Wyznaczanie współczynnika sprężystości sprężyn i ich układów
 Ćwiczenie 63 Wyznaczanie współczynnika sprężystości sprężyn i ich układów 63.1. Zasada ćwiczenia W ćwiczeniu określa się współczynnik sprężystości pojedynczych sprężyn i ich układów, mierząc wydłużenie
Ćwiczenie 63 Wyznaczanie współczynnika sprężystości sprężyn i ich układów 63.1. Zasada ćwiczenia W ćwiczeniu określa się współczynnik sprężystości pojedynczych sprężyn i ich układów, mierząc wydłużenie
Kurs z matematyki - zadania
 Kurs z matematyki - zadania Miara łukowa kąta Zadanie Miary kątów wyrażone w stopniach zapisać w radianach: a) 0, b) 80, c) 90, d), e) 0, f) 0, g) 0, h), i) 0, j) 70, k), l) 80, m) 080, n), o) 0 Zadanie
Kurs z matematyki - zadania Miara łukowa kąta Zadanie Miary kątów wyrażone w stopniach zapisać w radianach: a) 0, b) 80, c) 90, d), e) 0, f) 0, g) 0, h), i) 0, j) 70, k), l) 80, m) 080, n), o) 0 Zadanie
TEST WIADOMOŚCI: Równania i układy równań
 Poziom nauczania: Gimnazjum, klasa II Przedmiot: Matematyka Dział: Równania i układy równań Czas trwania: 45 minut Wykonała: Joanna Klimeczko TEST WIADOMOŚCI: Równania i układy równań Liczba punktów za
Poziom nauczania: Gimnazjum, klasa II Przedmiot: Matematyka Dział: Równania i układy równań Czas trwania: 45 minut Wykonała: Joanna Klimeczko TEST WIADOMOŚCI: Równania i układy równań Liczba punktów za
Nawiewniki wyporowe do wentylacji kuchni
 Nawiewniki wyporowe do wentylacji kuchni 15 Nawiewniki JHP OPIS Nawiewniki JHP przeznaczone są do wyporowej dystrybucji powietrza. Przystosowane zostały do wentylacji pomieszczeń kuchennych, gdzie występują
Nawiewniki wyporowe do wentylacji kuchni 15 Nawiewniki JHP OPIS Nawiewniki JHP przeznaczone są do wyporowej dystrybucji powietrza. Przystosowane zostały do wentylacji pomieszczeń kuchennych, gdzie występują
ZASTOSOWANIE LASERÓW W METROLOGII. - miernictwo, nauka o pomiarach. Obejmuje wszystkie teoretyczne i praktyczne problemy zwi zane z pomiarami.
 ZASTOSOWANIE LASERÓW W METROLOGII Metrologia - miernictwo, nauka o pomiarach. Obejmuje wszystkie teoretyczne i praktyczne problemy zwi zane z pomiarami. Cechy wi zki wiat a laserowego wykorzystywane w
ZASTOSOWANIE LASERÓW W METROLOGII Metrologia - miernictwo, nauka o pomiarach. Obejmuje wszystkie teoretyczne i praktyczne problemy zwi zane z pomiarami. Cechy wi zki wiat a laserowego wykorzystywane w
Świat fizyki. Podręcznik dla uczniów gimnazjum. Część 3. Pod redakcją Barbary Sagnowskiej
 Świat fizyki Podręcznik dla uczniów gimnazjum Część 3 Pod redakcją Barbary Sagnowskiej Kraków 2010 R ZamKor Autorzy Barbara Sagnowska, Maria Rozenbajgier, Ryszard Rozenbajgier, Danuta Szot-Gawlik, Małgorzata
Świat fizyki Podręcznik dla uczniów gimnazjum Część 3 Pod redakcją Barbary Sagnowskiej Kraków 2010 R ZamKor Autorzy Barbara Sagnowska, Maria Rozenbajgier, Ryszard Rozenbajgier, Danuta Szot-Gawlik, Małgorzata
Warszawska Giełda Towarowa S.A.
 KONTRAKT FUTURES Poprzez kontrakt futures rozumiemy umowę zawartą pomiędzy dwoma stronami transakcji. Jedna z nich zobowiązuje się do kupna, a przeciwna do sprzedaży, w ściśle określonym terminie w przyszłości
KONTRAKT FUTURES Poprzez kontrakt futures rozumiemy umowę zawartą pomiędzy dwoma stronami transakcji. Jedna z nich zobowiązuje się do kupna, a przeciwna do sprzedaży, w ściśle określonym terminie w przyszłości
MATEMATYKA 4 INSTYTUT MEDICUS FUNKCJA KWADRATOWA. Kurs przygotowawczy na studia medyczne. Rok szkolny 2010/2011. tel. 0501 38 39 55 www.medicus.edu.
 INSTYTUT MEDICUS Kurs przygotowawczy na studia medyczne Rok szkolny 00/0 tel. 050 38 39 55 www.medicus.edu.pl MATEMATYKA 4 FUNKCJA KWADRATOWA Funkcją kwadratową lub trójmianem kwadratowym nazywamy funkcję
INSTYTUT MEDICUS Kurs przygotowawczy na studia medyczne Rok szkolny 00/0 tel. 050 38 39 55 www.medicus.edu.pl MATEMATYKA 4 FUNKCJA KWADRATOWA Funkcją kwadratową lub trójmianem kwadratowym nazywamy funkcję
tel/fax 018 443 82 13 lub 018 443 74 19 NIP 7343246017 Regon 120493751
 Zespół Placówek Kształcenia Zawodowego 33-300 Nowy Sącz ul. Zamenhoffa 1 tel/fax 018 443 82 13 lub 018 443 74 19 http://zpkz.nowysacz.pl e-mail biuro@ckp-ns.edu.pl NIP 7343246017 Regon 120493751 Wskazówki
Zespół Placówek Kształcenia Zawodowego 33-300 Nowy Sącz ul. Zamenhoffa 1 tel/fax 018 443 82 13 lub 018 443 74 19 http://zpkz.nowysacz.pl e-mail biuro@ckp-ns.edu.pl NIP 7343246017 Regon 120493751 Wskazówki
spektroskopia UV Vis (cz. 2)
 spektroskopia UV Vis (cz. 2) spektroskopia UV-Vis dlaczego? wiele związków organicznych posiada chromofory, które absorbują w zakresie UV duża czułość: zastosowanie w badaniach kinetyki reakcji spektroskop
spektroskopia UV Vis (cz. 2) spektroskopia UV-Vis dlaczego? wiele związków organicznych posiada chromofory, które absorbują w zakresie UV duża czułość: zastosowanie w badaniach kinetyki reakcji spektroskop
Czy można zbudować płaską soczewkę?
 FOTON 124, Wiosna 2014 13 Czy można zbudować płaską soczewkę? Stanisław Urban Instytut Fizyki UJ Każdy z nas zna zasadę działania soczewek optycznych. Zbudowane są one z przezroczystego materiału i mają
FOTON 124, Wiosna 2014 13 Czy można zbudować płaską soczewkę? Stanisław Urban Instytut Fizyki UJ Każdy z nas zna zasadę działania soczewek optycznych. Zbudowane są one z przezroczystego materiału i mają
ZESTAW PRÓB SPRAWNOŚCI FIZYCZNEJ DLA KANDYDATÓW DO KLASY PIERWSZEJ GIMNAZJUM O PROFILU POŁKA NOŻNA CHŁOPCÓW
 ZESTAW PRÓB SPRAWNOŚCI FIZYCZNEJ DLA KANDYDATÓW DO KLASY PIERWSZEJ GIMNAZJUM O PROFILU POŁKA NOŻNA CHŁOPCÓW (wybrane zagadnienia z ogólnego zestawu testu ustalonego przez PZPN) wersja luty 2016 max liczba
ZESTAW PRÓB SPRAWNOŚCI FIZYCZNEJ DLA KANDYDATÓW DO KLASY PIERWSZEJ GIMNAZJUM O PROFILU POŁKA NOŻNA CHŁOPCÓW (wybrane zagadnienia z ogólnego zestawu testu ustalonego przez PZPN) wersja luty 2016 max liczba
WZORU UŻYTKOWEGO PL 65109 Y1 B60Q 1/26 (2006.01) F21W 101/00 (2006.01) Frieske Tomasz, Bydgoszcz, PL 26.10.2009 BUP 22/09
 RZECZPOSPOLITA POLSKA Urząd Patentowy Rzeczypospolitej Polskiej (12) OPIS OCHRONNY WZORU UŻYTKOWEGO (21) Numer zgłoszenia: 117442 (22) Data zgłoszenia: 25.04.2008 (19) PL (11) 65109 (13) Y1 (51) Int.Cl.
RZECZPOSPOLITA POLSKA Urząd Patentowy Rzeczypospolitej Polskiej (12) OPIS OCHRONNY WZORU UŻYTKOWEGO (21) Numer zgłoszenia: 117442 (22) Data zgłoszenia: 25.04.2008 (19) PL (11) 65109 (13) Y1 (51) Int.Cl.
PRÓG RENTOWNOŚCI i PRÓG
 PRÓG RENTOWNOŚCI i PRÓG WYPŁACALNOŚCI (MB) Próg rentowności (BP) i margines bezpieczeństwa Przychody Przychody Koszty Koszty całkowite Koszty stałe Koszty zmienne BP Q MB Produkcja gdzie: BP próg rentowności
PRÓG RENTOWNOŚCI i PRÓG WYPŁACALNOŚCI (MB) Próg rentowności (BP) i margines bezpieczeństwa Przychody Przychody Koszty Koszty całkowite Koszty stałe Koszty zmienne BP Q MB Produkcja gdzie: BP próg rentowności
ZASTOSOWANIE LASERÓW W HOLOGRAFII
 ZASTOSOWANIE LASERÓW W HOLOGRAFII Holografia - dzia optyki zajmuj cy si technikami uzyskiwania obrazów przestrzennych metod rekonstrukcji fali (g ównie wiat a, ale te np. fal akustycznych). Przez rekonstrukcj
ZASTOSOWANIE LASERÓW W HOLOGRAFII Holografia - dzia optyki zajmuj cy si technikami uzyskiwania obrazów przestrzennych metod rekonstrukcji fali (g ównie wiat a, ale te np. fal akustycznych). Przez rekonstrukcj
SPRAWDZIANY Z MATEMATYKI
 SPRAWDZIANY Z MATEMATYKI dla klasy III gimnazjum dostosowane do programu Matematyka z Plusem opracowała mgr Marzena Mazur LICZBY I WYRAŻENIA ALGEBRAICZNE Grupa I Zad.1. Zapisz w jak najprostszej postaci
SPRAWDZIANY Z MATEMATYKI dla klasy III gimnazjum dostosowane do programu Matematyka z Plusem opracowała mgr Marzena Mazur LICZBY I WYRAŻENIA ALGEBRAICZNE Grupa I Zad.1. Zapisz w jak najprostszej postaci
Dobór nastaw PID regulatorów LB-760A i LB-762
 1 z 5 Dobór nastaw PID regulatorów LB-760A i LB-762 Strojenie regulatorów LB-760A i LB-762 Nastawy regulatora PID Regulatory PID (rolnicze np.: LB-760A - poczynając od wersji 7.1 programu ładowalnego,
1 z 5 Dobór nastaw PID regulatorów LB-760A i LB-762 Strojenie regulatorów LB-760A i LB-762 Nastawy regulatora PID Regulatory PID (rolnicze np.: LB-760A - poczynając od wersji 7.1 programu ładowalnego,
Lekcja 173, 174. Temat: Silniki indukcyjne i pierścieniowe.
 Lekcja 173, 174 Temat: Silniki indukcyjne i pierścieniowe. Silnik elektryczny asynchroniczny jest maszyną elektryczną zmieniającą energię elektryczną w energię mechaniczną, w której wirnik obraca się z
Lekcja 173, 174 Temat: Silniki indukcyjne i pierścieniowe. Silnik elektryczny asynchroniczny jest maszyną elektryczną zmieniającą energię elektryczną w energię mechaniczną, w której wirnik obraca się z
ANALIZA OBWODÓW RZĘDU ZEROWEGO PROSTE I SIECIOWE METODY ANALIZY OBWODÓW
 ANALIZA OBWODÓW RZĘDU ZEROWEGO PROSTE I SIECIOWE METODY ANALIZY OBWODÓW Rezystancja zastępcza dwójnika bezźródłowego (m.b. i=0 i u=0) Równoważność dotyczy zewnętrznego zachowania się układów, lecz nie
ANALIZA OBWODÓW RZĘDU ZEROWEGO PROSTE I SIECIOWE METODY ANALIZY OBWODÓW Rezystancja zastępcza dwójnika bezźródłowego (m.b. i=0 i u=0) Równoważność dotyczy zewnętrznego zachowania się układów, lecz nie
Analiza CVP koszty wolumen - zysk
 Analiza CVP koszty wolumen - zysk Na podstawie: W.F. Samuelson, S.G. Marks, Ekonomia Menedżerska, PWE, Warszawa 2009 1 Próg rentowności model w ujęciu księgowym 2 Analiza koszty wolumen zysk- CVP Cost
Analiza CVP koszty wolumen - zysk Na podstawie: W.F. Samuelson, S.G. Marks, Ekonomia Menedżerska, PWE, Warszawa 2009 1 Próg rentowności model w ujęciu księgowym 2 Analiza koszty wolumen zysk- CVP Cost
Właściwości materii - powtórzenie
 Przygotowano za pomocą programu Ciekawa fizyka. Bank zadań Copyright by Wydawnictwa Szkolne i Pedagogiczne sp. z o.o., Warszawa 2011 strona 1 Imię i nazwisko ucznia Data...... Klasa... Zadanie 1. Czy zjawisko
Przygotowano za pomocą programu Ciekawa fizyka. Bank zadań Copyright by Wydawnictwa Szkolne i Pedagogiczne sp. z o.o., Warszawa 2011 strona 1 Imię i nazwisko ucznia Data...... Klasa... Zadanie 1. Czy zjawisko
SERI A 93 S E RI A 93 O FLUSH GRID WITHOUT EDGE TAB
 SERIA E93 CONIC FRINCTION CONIC 2 SERIA 93 SERIA 93 O FLUSH GRID WITHOUT EDGE TAB Podziałka Powierzchnia 30 mm Flush Grid Prześwit 47% Grubość Minimalny promień skrętu taśmy Układ napędowy Szerokość taśmy
SERIA E93 CONIC FRINCTION CONIC 2 SERIA 93 SERIA 93 O FLUSH GRID WITHOUT EDGE TAB Podziałka Powierzchnia 30 mm Flush Grid Prześwit 47% Grubość Minimalny promień skrętu taśmy Układ napędowy Szerokość taśmy
Opinie Polaków na temat zniesienie granic wewnętrznych w UE w rok po wejściu Polski do strefy Schengen
 Opinie Polaków na temat zniesienie granic wewnętrznych w UE w rok po wejściu Polski do strefy Schengen TNS OBOP dla Reprezentacji Komisji Europejskiej w Polsce grudzień 2008 Ośrodek Badania Opinii Publicznej
Opinie Polaków na temat zniesienie granic wewnętrznych w UE w rok po wejściu Polski do strefy Schengen TNS OBOP dla Reprezentacji Komisji Europejskiej w Polsce grudzień 2008 Ośrodek Badania Opinii Publicznej
Wypalanie laserowe. Technologia. wersja polska. Wersja: 1. marzec 2004 r.
 Wypalanie laserowe Technologia Wersja: 1 wersja polska marzec 2004 r. Spis treści Rozdział 1 Zasada działania lasera Znaczenie słowa "LASER"... 3 Zasada działania lasera..... 4 Wypalanie laserowe... 5
Wypalanie laserowe Technologia Wersja: 1 wersja polska marzec 2004 r. Spis treści Rozdział 1 Zasada działania lasera Znaczenie słowa "LASER"... 3 Zasada działania lasera..... 4 Wypalanie laserowe... 5
Dr inż. Andrzej Tatarek. Siłownie cieplne
 Dr inż. Andrzej Tatarek Siłownie cieplne 1 Wykład 3 Sposoby podwyższania sprawności elektrowni 2 Zwiększenie sprawności Metody zwiększenia sprawności elektrowni: 1. podnoszenie temperatury i ciśnienia
Dr inż. Andrzej Tatarek Siłownie cieplne 1 Wykład 3 Sposoby podwyższania sprawności elektrowni 2 Zwiększenie sprawności Metody zwiększenia sprawności elektrowni: 1. podnoszenie temperatury i ciśnienia
Specyfikacja techniczna banerów Flash
 Specyfikacja techniczna banerów Flash Po stworzeniu własnego banera reklamowego należy dodać kilka elementów umożliwiających integrację z systemem wyświetlającym i śledzącym reklamy na stronie www. Specyfikacje
Specyfikacja techniczna banerów Flash Po stworzeniu własnego banera reklamowego należy dodać kilka elementów umożliwiających integrację z systemem wyświetlającym i śledzącym reklamy na stronie www. Specyfikacje
Technologie Informacyjne
 Technologie Informacyjne Szkoła Główna Służby Pożarniczej Zakład Informatyki i Łączności April 11, 2016 Technologie Informacyjne Wprowadzenie : wizualizacja obrazów poprzez wykorzystywanie technik komputerowych.
Technologie Informacyjne Szkoła Główna Służby Pożarniczej Zakład Informatyki i Łączności April 11, 2016 Technologie Informacyjne Wprowadzenie : wizualizacja obrazów poprzez wykorzystywanie technik komputerowych.
Badanie bezszczotkowego silnika prądu stałego z magnesami trwałymi (BLDCM)
 Badanie bezszczotkowego silnika prądu stałego z magnesami trwałymi (BLDCM) Celem ćwiczenia jest zapoznanie się z budową, zasadą działania oraz sterowaniem bezszczotkowego silnika prądu stałego z magnesami
Badanie bezszczotkowego silnika prądu stałego z magnesami trwałymi (BLDCM) Celem ćwiczenia jest zapoznanie się z budową, zasadą działania oraz sterowaniem bezszczotkowego silnika prądu stałego z magnesami
PODSTAWOWE ELEMENTY ELEKTRONICZNE
 PODSTAWOWE ELEMENTY ELEKTRONCZNE Publikacja współfinansowana ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego 1. Diody półprzewodnikowe Złącze PN - podstawa budowy i działania diody,
PODSTAWOWE ELEMENTY ELEKTRONCZNE Publikacja współfinansowana ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego 1. Diody półprzewodnikowe Złącze PN - podstawa budowy i działania diody,
ARKUSZ WICZENIOWY Z MATEMATYKI MARZEC 2012 POZIOM PODSTAWOWY. Czas pracy: 170 minut. Liczba punktów do uzyskania: 50
 pobrano z www.sqlmedia.pl Centralna Komisja Egzaminacyjna ARKUSZ WICZENIOWY Z MATEMATYKI MARZEC 01 POZIOM PODSTAWOWY 1. Sprawd, czy arkusz wiczeniowy zawiera strony (zadania 1 ).. Rozwi zania zada i odpowiedzi
pobrano z www.sqlmedia.pl Centralna Komisja Egzaminacyjna ARKUSZ WICZENIOWY Z MATEMATYKI MARZEC 01 POZIOM PODSTAWOWY 1. Sprawd, czy arkusz wiczeniowy zawiera strony (zadania 1 ).. Rozwi zania zada i odpowiedzi
ELEMENTY OPTYKI GEOMETRYCZNEJ
 ELEMENTY OPTYKI GEOMETRYCZNEJ Optyka to dział fizyki, zajmujący się badaiem atury światła, początkowo tylko widzialego, a obecie rówież promieiowaia z zakresów podczerwiei i adfioletu. Optyka - geometrycza
ELEMENTY OPTYKI GEOMETRYCZNEJ Optyka to dział fizyki, zajmujący się badaiem atury światła, początkowo tylko widzialego, a obecie rówież promieiowaia z zakresów podczerwiei i adfioletu. Optyka - geometrycza
Karta pracy: Ćwiczenie 5.
 Imię i nazwisko: Grupa: Karta pracy: Ćwiczenie 5. Tytuł ćwiczenia: Optymalizacja geometrii prostych cząsteczek organicznych. Analiza populacyjna i rzędy wiązań. Zagadnienia do przygotowania: Przypomnij
Imię i nazwisko: Grupa: Karta pracy: Ćwiczenie 5. Tytuł ćwiczenia: Optymalizacja geometrii prostych cząsteczek organicznych. Analiza populacyjna i rzędy wiązań. Zagadnienia do przygotowania: Przypomnij
Spis treści Wykład 3. Modelowanie fal. Równanie sine-gordona
 Spis treści Wykład 3. Modelowanie fal. Równanie sine-gordona.............. 3 3.1. Równanie sine-gordona.......................... 3 3.1.1. Rozwiązania dla fali biegnącej................... 7 3.2. Równanie
Spis treści Wykład 3. Modelowanie fal. Równanie sine-gordona.............. 3 3.1. Równanie sine-gordona.......................... 3 3.1.1. Rozwiązania dla fali biegnącej................... 7 3.2. Równanie
ZESTAW PRÓB SPRAWNOŚCI FIZYCZNEJ DO KLAS O PROFILU PIŁKARSKIM (szkoła podstawowa, gimnazjum, liceum) wersja luty 2016
 ZESTAW PRÓB SPRAWNOŚCI FIZYCZNEJ DO KLAS O PROFILU PIŁKARSKIM (szkoła podstawowa, gimnazjum, liceum) wersja luty 2016 STOSUJEMY TAKIE SAME TESTY DLA CHŁOPCÓW I DZIEWCZYNEK (RÓŻNE NORMY), MIEJSCE: Boisko
ZESTAW PRÓB SPRAWNOŚCI FIZYCZNEJ DO KLAS O PROFILU PIŁKARSKIM (szkoła podstawowa, gimnazjum, liceum) wersja luty 2016 STOSUJEMY TAKIE SAME TESTY DLA CHŁOPCÓW I DZIEWCZYNEK (RÓŻNE NORMY), MIEJSCE: Boisko
Ć W I C Z E N I E N R O-9
 INSTYTUT FIZYKI WYDZIAŁ INŻYNIERII PRODUKCJI I TECHNOLOGII MATERIAŁÓW POLITECHNIKA CZĘSTOCHOWSKA PRACOWNIA OPTYKI Ć W I C Z E N I E N R O-9 WYZNACZANIE STĘŻENIA CUKRU ZA POMOCĄ POLARYMETRU Plr - 1 1 I.
INSTYTUT FIZYKI WYDZIAŁ INŻYNIERII PRODUKCJI I TECHNOLOGII MATERIAŁÓW POLITECHNIKA CZĘSTOCHOWSKA PRACOWNIA OPTYKI Ć W I C Z E N I E N R O-9 WYZNACZANIE STĘŻENIA CUKRU ZA POMOCĄ POLARYMETRU Plr - 1 1 I.
DOPALACZE. - nowa kategoria substancji psychoaktywnych
 DOPALACZE - nowa kategoria substancji psychoaktywnych CZYM SĄ DOPALACZE? Dopalacze stosowana w Polsce, potoczna nazwa różnego rodzaju produktów zawierających substancje psychoaktywne, które nie znajdują
DOPALACZE - nowa kategoria substancji psychoaktywnych CZYM SĄ DOPALACZE? Dopalacze stosowana w Polsce, potoczna nazwa różnego rodzaju produktów zawierających substancje psychoaktywne, które nie znajdują
Regulamin lodowiska BIAŁY ORLIK przy Zespole Szkół nr 1 w Nowym Dworze Mazowieckim
 Regulamin lodowiska BIAŁY ORLIK przy Zespole Szkół nr 1 w Nowym Dworze Mazowieckim I. Część ogólna 1. Lodowisko jest obiektem sportowym ogólnodostępnym, którego właścicielem jest Miasto Nowy Dwór Mazowiecki,
Regulamin lodowiska BIAŁY ORLIK przy Zespole Szkół nr 1 w Nowym Dworze Mazowieckim I. Część ogólna 1. Lodowisko jest obiektem sportowym ogólnodostępnym, którego właścicielem jest Miasto Nowy Dwór Mazowiecki,
Podstawowe pojęcia: Populacja. Populacja skończona zawiera skończoną liczbę jednostek statystycznych
 Podstawowe pojęcia: Badanie statystyczne - zespół czynności zmierzających do uzyskania za pomocą metod statystycznych informacji charakteryzujących interesującą nas zbiorowość (populację generalną) Populacja
Podstawowe pojęcia: Badanie statystyczne - zespół czynności zmierzających do uzyskania za pomocą metod statystycznych informacji charakteryzujących interesującą nas zbiorowość (populację generalną) Populacja
LVI OLIMPIADA FIZYCZNA 2006/2007 Zawody II stopnia
 LVI OLIMPIADA FIZYCZNA 2006/2007 Zawody II stopnia Zadanie doświadczalne Energia elektronów w półprzewodniku może przybierać wartości należące do dwóch przedziałów: dolnego (tzw. pasmo walencyjne) i górnego
LVI OLIMPIADA FIZYCZNA 2006/2007 Zawody II stopnia Zadanie doświadczalne Energia elektronów w półprzewodniku może przybierać wartości należące do dwóch przedziałów: dolnego (tzw. pasmo walencyjne) i górnego
