SYSTEMY (ALGORYTMY) MRÓWKOWE
|
|
|
- Maciej Sowa
- 9 lat temu
- Przeglądów:
Transkrypt
1 OLIZNI WOLUYJN ITNSS. STRT OMPUTTION ITNSS. OMPUTTION INITIL SUGenration SNING HROM. TO OMPUTRS chromosome VOLUTIONRY OPRTORS N RIVING ITNSS. wykład 7 VLU fitness f. value MIGRTION PHS ITNSS. communication OMPUTTION with other SLTION sugenrations YS TRMINTION ONITION NO SYSTMY (LGORYTMY) MRÓWKOW N 2 Mrówki sąs praktycznie ślepe, lecz potrafią znaleźć najkrótsz tszą drogę do pożywienia i z powrotem. Ich oserwacja yła a inspiracją do powstania (origo,, 996) nowego typu algorytmów zwanych mrówkowymi (ant ant algorithms, ant systems) Zastosowania - zad. optymalizacji kominatorycznej: prolem komiwojażera; harmonogramowanie wyznaczanie tras w sieciach telekomunikacyjnych; wyznaczanie optymalnych tras w ruchu miejskim. 3 food source N - nest 4 Systemy azujące na inteligencji masowej populacja mrówek (podonie jak w ). Każda mrówka w populacji poszukuje rozwiązania zania (najkrótszej drogi). Pozostawianie feromonu na trasie. Wyór r trasy na podstawie ilości feromonu Wielokrotne powtarzanie: trasa optymalna. 5 zas (t) jest dyskretny; W każdej jednostce czasu każda mrówka przemieszcza się o d = pozostawiając jednostkę feromonu. W chwili t = 0 rak feromonu na wszystkich krawędziach. Znaleźć najkrótszą drogę między i...
2 6 z do t = 0 t = t = 2 t = z do Proste podąż ążanie ścieżką z największ kszą ilości cią fero-monu szykie utknięcie w optimum lokalnym. iridia.ul.ac.e/~ /~mdorigo/o/o.htmlo.html Potrzena jest eksploracja ścieżek ek mrówki wyierają ścieżki z prawdopodoieństwem proporcjonalnym do intensywności śladu feromonowego na niej. To, że e mrówka wyierze daną ścieżkę zależy y zarówno od intensywności feromonu jak równier wnież np. odległości od następnego miasta (TSP). W celu zapewnienia raku nieograniczonego wzrostu ilości feromonu parowanie feromonu. 9 0 NTURLNY SYSTM IMMUNOLOGIZNY: LGORYTMY IMMUNO- LOGIZN Jego zadaniem jest ochrona żywego organizmu przed działaniem aniem ocych struktur mających charakter chorootwórcze rcze (patogeny( patogeny), jak wirusy, akterie, grzyy czy niewłaściwie funkcjonujące ce komórki. Wszystkie te struktury, które wywołuj ują reakcję immunologiczną,, nazywane sąs antygenami. ardzo ogólnie: rozpoznawanie antygenów w na zasadzie swój-ocy i eliminowanie tych drugich. 2
3 Może yć przedstawiony w postaci warstwowej: Limfocyty komórki, ędące głównymi g składowymi adaptacyjnego systemu immunologicznego.. Skóra podstawowa ariera ochronna. 2. Warstwa fizjologiczna (temperatura, ph) stwarza warunki niekorzystne dla rozwoju ocych organizmów. 3. Odporność wrodzona (nieswoista) 4. Odporność adaptacyjna (swoista) rozpoznawanie i eliminacja antygenów w przez odpowiednie komórki 3 Limfocyty (głównie typów T i ) ) w wielkich ilościach krążą w płynach p ustrojowych system immunologiczny jest systemem zdecentralizowanym a wszystkie jego komórki mogą się dowolnie przemieszczać. Limfocyty rozpoznają napotykane antygeny i pomagają je eliminować,, przy czym mogą ze soą lokalnie współpracowa pracować. 4 Limfocyty typu - produkcja przeciwciał rozpoznających antygen. Limfocyty typu T - rozpoznawanie swój-ocy. uże zróżnicowanie limfocytów: - pozwala na rozpoznawanie wielu różnych r antygenów; - pierwotnie zyt mała a licza komórek rozpoznających antygen y go zwalczyć. 5 6 SZTUZNY SYSTM IMMUNOLOGIZNY (rtificial Immune System, IS) Ziór metod oliczeniowych inspirowanych zasadami działania ania układ adów odpornościowych kręgowc gowców. w. Tylko niektóre elementy naturalnych układ adów w sąs rane pod uwagę,, typowo: mutacja limfocytów w, proliferacja cja, komórki pamięci, rozpoznawanie antygenów w z użyciem u limfocytów i T. Niektóre zastosowania: - optymalizacja (patogen reprezentuje optimum gloalne, szukane jest najlepiej dopasowane przeciwciało); - zagadnienia zw. z ezpieczeństwem sieciowym (np. NIS - network intrusion detection system) - uczenie maszynowe; - systemy agentowe. 7 IS - POJĘI: Komórka macierzysta wzorzec akceptowany w systemie; Przeciwciało oiekt rozpoznający oiekty nie ędące komórkami macierzystym (wzorce niepożą żądane). ntygen oiekt rozpoznawany i uaktywniający przeciwciała. Komórka pamięciowa przechowuje informacje o rozpoznanym antygenie; przy kolejnym ataku antygenu zostaje on dużo o szyciej rozpoznany. Proliferacja namnażanie anie się komórek. Hipermutacje mutacje, których częstotliwo stotliwość jest przynajmniej o jeden rząd d wielkości większa, niż innych mutacji w organizmie (zwykle jeszcze częś ęściej).
4 POSTWOW MHNIZMY: POSTWOW MHNIZMY: Selekcja klonalna (limfocyty ) Selekcja negatywna (limfocyty T) el namnożenie odpowiednich przeciwciał,, iorących udział w zwalczaniu danego antygenu. Uaktywnione limfocyty dzielą się produkując c wiele klonów, które następnie przechodzą hipermutację y wytworzyć lepiej dopasowane przeciwciała. a. la powstałej populacji zmutowanych klonów oceniany stopień dopasowania każdego z nich do antygenu. Słao S dopasowane sąs usuwane, dorze dopasowane pozostają. el utworzenie zioru przeciwciał - detektorów, które nie sąs uaktywniane przez komórki macierzyste. W procesie selekcji negatywnej limfocytom T pokazywane sąs komórki własne. w Jeśli dany limfocyt rozpozna którąś z nich, jest on usuwany. Nie podlegają mutacji /~stw/ais/ks/natural.html Przykład: IS autorstwa prof.. Wacława awa Kusia. Losowe wygenerowanie komórek pamięciowych. 2. Komórki pamięciowe proliferują i mutują tworząc c limfocyty (licza klonów w zależy y od przystosowania). 3. Oliczenie wartości przystosowania dla limfocytów w. 4. Selekcja na podstawie odległości między każdą komórk rką pamięciow ciową a limfocytami. 5. Mechanizm zatłoczenia usuwa podone komórki pamięci. 6. Procedura jest powtarzana do spełnienia warunku zakończenia (np. licza iteracji). 22 LGORYTMY IMMUNOGNTYZN Są połą łączeniem mechanizmów w genetycznych (ewolucyjnych) i immunologicznych; IS i mają wiele cech wspólnych, np. działanie anie na populacji osoników, stosowanie mechanizmów w selekcji. W algorytmach immunogenetycznych stosowane sąs operatory krzyżowania, mutacji i selekcji (jak ) przy zachowaniu populacji antygenów w i przeciwciał (jak IS). zęsto: do generowania populacji przeciwciał,, y poddać je immunologicznej selekcji negatywnej. unkcja przystosowania zwykle miary azujące na stopniu dopasowania przeciwciała a do antygenu (jak w IS). PRZYKŁY ZSTOSOWŃ 23 24
5 UKŁNI PLNU LKJI Jest prolemem należą żącym do klasy NP-trudnych trudnych. Wiele nietrywialnych ograniczeń. Zadanie opisuje się poprzez: listę nauczycieli n; listę grup g; listę terminów t; listę sal s. Zadanie polega na wygenerowaniu pewnej czteroargumentowej relacji określonej na ziorze nauczycieli, grup, sal i godzin zajęciowych ciowych,, do której należą wszystkie takie i tylko takie czwórki n,g,s,t, że nauczyciel n prowadzi zajęcia z grupą g w sali s i w terminie t. Ograniczenia:. Twarde: Zadana jest licza godzin dla każdego nauczyciela i każdej klasy; W każdej sali i terminie jest tylko jeden nauczyciel; Nauczyciel nie może e uczyć dwu grup naraz; W każdej sali z zaplanowanymi zajęciami znajduje się nauczyciel Ograniczenia: Programy wspomagające układanie planu, np: 2. Miękkie: ele dydaktyczne (rozłożenie przedmiotów w w tygodniu); ele personalne (pozostawienie wolnych niektórych terminów dla niektórych nauczycieli); ele organizacyjne (dodatkowy nauczyciel na każdy termin na zastępstwo). Zadanie układania planu lekcji rozwiązane zane z użyciem u zostało o pomyślnie przetestowane np. dla danych z dużej szkoły y w Mediolanie (99) PROGRMOWNI ROGI W ŚROO- WISKU RUHOMGO ROOT el: Znalezienie się roota w punkcie docelowym ez zaguienia się i kolizji z jakimkolwiek oiektem. Nawigator ewolucyjny (Michalewicz) - połą łączenie planowań: zawczasu i ieżą żącego drogi roota: Początkowo: (planowanie( zawczasu) ) poszukiwanie najlepszej drogi (rozwiązanie zanie optymalne): Rozwiązania: zania: roga planowana jest na wstępie (skuteczne skuteczne jedynie przy założeniu, że środowisko poruszania się roota jest dokładnie znane i nie zmienia się). Wiedza o otoczeniu jest czerpana na ieżą żąco poprzez adanie otoczenia lokalnego ( (pozwala pozwala to na ominięcie nieznanych jak i ruchomych przeszkód). 29 a 30
6 Planowanie ieżą żące rozwiązuje zuje prolemy związane zane z nowymi oiektami na wcześniej zaplanowanej trasie. a d a d a d e UNIKNI KOLIZJI N MORZU Oiekt ruchomy (np. statek) może e yć nieezpieczny dla oiektu własnegow jeśli: Wszedł w zakres oserwacji (5- mil morskich przed dzioem i mile za rufą); Może e przeciąć kurs zadany w nieezpiecznej odległości (jej wartość zależy y od pogody, rejonu pływania i prędko dkości statku); f e unkcja przystosowania uwzględni dnić powinna zarówno warunki ezpieczeństwa żeglugi jak i warunki ekonomiczne Stała a prędko dkość statku własnego: w v =.6w. Stała a prędko dkość statku własnego: w v = 5.6w Zmienna prędko dkość (mutacja prędko dkości) v = {3.6;.6; 3.6}w W GRH (OTHLLO) Gra: Rywalizacja prowadzona przez uczestników w zgodnie z ustalonymi regułami, y osiągn gnąć założony ony cel. Podział: Losowe ( (ruletka); Takie, w których element losowy wpływa na rozgrywkę (rydż); eterministyczne ( (szachy)
7 Gra: Gracze wykonują kolejne ruchy (podejmują decyzje) ze zioru ruchów dopuszczalnych aż do osiągni gnięcia stanu końcowego cowego. Rozgrywka jest poszukiwaniem takich ruchów gracza, które zapewnią mu zwycięstwo stwo. Liście takiego drzewa oznaczają stany końcowe gry: wygrane, remisowe lu przegrane dla gracza. 37 rzewo reprezentuje wszystkie możliwe rozwią-zania zania, np.: warcay: 0 40 węzłów; w; szachy: 0 20 węzłów. w. el gry: znalezienie strategii wygrywającej (niezależnie od posunięć przeciwnika). W ogólnym przypadku wymaga to zudowania i przeszukania całego drzewa zwykle niemożliwe liwe. W efekcie: zwykle ada się tylko część drzewa (możliwie jak najgłę łęiej). 3 Othello (reversi): rozgrywka jest skomplikowana; rak dorego programu grającego; 3 znane strategie gry:. Maksymalnej liczy punktów prowadzi zwykle do lokady ruchów w gracza. 2. Pól l ważonych (cel: przejęcie pól p strategicznych ). 3. Mnimalnej liczy pionków (minimalizacja liczy włas-nych pionów, y zwiększy kszyć możliwo liwości ruchu stosowana ślepo prowadzi do przegranej ). 40 Zast.. do tworzenia programów w grających:. jako narzędzie wspomagające proces szukania dorej strategii gry. Program grający nie wykorzystuje podczas gry, lecz ma wudowaną strategię (znalezioną wcześniej za pomocą ). 2. Zastosowanie jako wudowanego grającego. modułu Proces poszukiwań można opisać za pomocą drzewa rozwiąza zań (korzeń stan początkowy, węzły w kolej- ne stany, jakie ędą możliwe po wykonaniu danego ruchu). na każdym etapie gry odpowiada za znalezienie opty- malnego posunięcia przez program grający. 4
ALGORYTMY IMMUNO- LOGICZNE
 OBLICZENIA EWOLUCYJNE FITNESS F. START COMPUTATION FITNESS F. COMPUTATION INITIAL SUBGenration SENDING CHROM. TO COMPUTERS chromosome wykład AND RECEIVING FITNESS F. EVOLUTIONARY OPERATORS 7 VALUE fitness
OBLICZENIA EWOLUCYJNE FITNESS F. START COMPUTATION FITNESS F. COMPUTATION INITIAL SUBGenration SENDING CHROM. TO COMPUTERS chromosome wykład AND RECEIVING FITNESS F. EVOLUTIONARY OPERATORS 7 VALUE fitness
OBLICZENIA EWOLUCYJNE
 1 OBLICZENIA EWOLUCYJNE FITNESS F. START COMPUTATION FITNESS F. COMPUTATION INITIAL SUBGenration SENDING CHROM. TO COMPUTERS chromosome AND RECEIVING FITNESS F. VALUE fitness f. value wykład 7 FITNESS
1 OBLICZENIA EWOLUCYJNE FITNESS F. START COMPUTATION FITNESS F. COMPUTATION INITIAL SUBGenration SENDING CHROM. TO COMPUTERS chromosome AND RECEIVING FITNESS F. VALUE fitness f. value wykład 7 FITNESS
METODY HEURYSTYCZNE wykład 7
 METODY HEURYSTYCZNE wykład 7 PROJEKTOWANIE BAZ REGUŁ 2 Informacja niezbędna do zaprojektowania sterownika: numeryczna (ilościowa) z czujników pomiarowych; lingwistyczna (jakościowa) od eksperta. Stworzenie
METODY HEURYSTYCZNE wykład 7 PROJEKTOWANIE BAZ REGUŁ 2 Informacja niezbędna do zaprojektowania sterownika: numeryczna (ilościowa) z czujników pomiarowych; lingwistyczna (jakościowa) od eksperta. Stworzenie
Zastosowanie sztucznych systemów immunologicznych w zagadnieniach optymalizacji
 Zastosowanie sztucznych systemów immunologicznych w zagadnieniach optymalizacji 26 października 2011 Agenda Wprowadzenie 1 Wprowadzenie 2 Struktura układu odpornościowego Adaptacja i dywersyfikacja systemu
Zastosowanie sztucznych systemów immunologicznych w zagadnieniach optymalizacji 26 października 2011 Agenda Wprowadzenie 1 Wprowadzenie 2 Struktura układu odpornościowego Adaptacja i dywersyfikacja systemu
OBLICZENIA EWOLUCYJNE
 OBLICZENIA EWOLUCYJNE FITNESS F. START COMPUTATION FITNESS F. COMPUTATION INITIAL SUBPOPULATION SENDING CHROM. TO COMPUTERS chromosome AND RECEIVING FITNESS F. wykład VALUE 5fitness f. value EVOLUTIONARY
OBLICZENIA EWOLUCYJNE FITNESS F. START COMPUTATION FITNESS F. COMPUTATION INITIAL SUBPOPULATION SENDING CHROM. TO COMPUTERS chromosome AND RECEIVING FITNESS F. wykład VALUE 5fitness f. value EVOLUTIONARY
METODY HEURYSTYCZNE 7
 METODY HEURYSTYCZNE wykład 7 PROJEKTOWANIE BAZ REGUŁ 2 Informacja niezbędna do zaprojektowania sterownika: numeryczna (ilościowa) z czujników pomiarowych; lingwistyczna (jakościowa) od eksperta. Stworzenie
METODY HEURYSTYCZNE wykład 7 PROJEKTOWANIE BAZ REGUŁ 2 Informacja niezbędna do zaprojektowania sterownika: numeryczna (ilościowa) z czujników pomiarowych; lingwistyczna (jakościowa) od eksperta. Stworzenie
Plan. Sztuczne systemy immunologiczne. Podstawowy słownik. Odporność swoista. Architektura systemu naturalnego. Naturalny system immunologiczny
 Sztuczne systemy immunologiczne Plan Naturalny system immunologiczny Systemy oparte na selekcji klonalnej Systemy oparte na modelu sieci idiotypowej 2 Podstawowy słownik Naturalny system immunologiczny
Sztuczne systemy immunologiczne Plan Naturalny system immunologiczny Systemy oparte na selekcji klonalnej Systemy oparte na modelu sieci idiotypowej 2 Podstawowy słownik Naturalny system immunologiczny
Algorytmy genetyczne. Materiały do laboratorium PSI. Studia niestacjonarne
 Algorytmy genetyczne Materiały do laboratorium PSI Studia niestacjonarne Podstawowy algorytm genetyczny (PAG) Schemat blokowy algorytmu genetycznego Znaczenia, pochodzących z biologii i genetyki, pojęć
Algorytmy genetyczne Materiały do laboratorium PSI Studia niestacjonarne Podstawowy algorytm genetyczny (PAG) Schemat blokowy algorytmu genetycznego Znaczenia, pochodzących z biologii i genetyki, pojęć
Algorytmy mrówkowe (optymalizacja kolonii mrówek, Ant Colony optimisation)
 Algorytmy mrówkowe (optymalizacja kolonii mrówek, Ant Colony optimisation) Jest to technika probabilistyczna rozwiązywania problemów obliczeniowych, które mogą zostać sprowadzone do problemu znalezienie
Algorytmy mrówkowe (optymalizacja kolonii mrówek, Ant Colony optimisation) Jest to technika probabilistyczna rozwiązywania problemów obliczeniowych, które mogą zostać sprowadzone do problemu znalezienie
Algorytmy genetyczne. Materiały do laboratorium PSI. Studia stacjonarne i niestacjonarne
 Algorytmy genetyczne Materiały do laboratorium PSI Studia stacjonarne i niestacjonarne Podstawowy algorytm genetyczny (PAG) Schemat blokowy algorytmu genetycznego Znaczenia, pochodzących z biologii i genetyki,
Algorytmy genetyczne Materiały do laboratorium PSI Studia stacjonarne i niestacjonarne Podstawowy algorytm genetyczny (PAG) Schemat blokowy algorytmu genetycznego Znaczenia, pochodzących z biologii i genetyki,
Problem Komiwojażera - algorytmy metaheurystyczne
 Problem Komiwojażera - algorytmy metaheurystyczne algorytm mrówkowy algorytm genetyczny by Bartosz Tomeczko. All rights reserved. 2010. TSP dlaczego metaheurystyki i heurystyki? TSP Travelling Salesman
Problem Komiwojażera - algorytmy metaheurystyczne algorytm mrówkowy algorytm genetyczny by Bartosz Tomeczko. All rights reserved. 2010. TSP dlaczego metaheurystyki i heurystyki? TSP Travelling Salesman
PROJEKTOWANIE BAZ REGUŁ
 METODY HEURYSTYCZNE wkład 7 PROJEKTOWANIE AZ REGUŁ Stworzenie baz wiedz dla układu rozmtego zadanie nietrwialne... Siatka Indwidualne funkcje Informacja niezbędna do zaprojektowania sterownika: numerczna
METODY HEURYSTYCZNE wkład 7 PROJEKTOWANIE AZ REGUŁ Stworzenie baz wiedz dla układu rozmtego zadanie nietrwialne... Siatka Indwidualne funkcje Informacja niezbędna do zaprojektowania sterownika: numerczna
Algorytmy mrówkowe. P. Oleksyk. Wydział Informatyki Zachodniopomorski Uniwersytet Technologiczny w Szczecinie Inteligentne systemy informatyczne
 y mrówkowe P. Oleksyk Wydział Informatyki Zachodniopomorski Uniwersytet Technologiczny w Szczecinie Inteligentne systemy informatyczne 14 kwietnia 2015 1 Geneza algorytmu - biologia 2 3 4 5 6 7 8 Geneza
y mrówkowe P. Oleksyk Wydział Informatyki Zachodniopomorski Uniwersytet Technologiczny w Szczecinie Inteligentne systemy informatyczne 14 kwietnia 2015 1 Geneza algorytmu - biologia 2 3 4 5 6 7 8 Geneza
Algorytm genetyczny (genetic algorithm)-
 Optymalizacja W praktyce inżynierskiej często zachodzi potrzeba znalezienia parametrów, dla których system/urządzenie będzie działać w sposób optymalny. Klasyczne podejście do optymalizacji: sformułowanie
Optymalizacja W praktyce inżynierskiej często zachodzi potrzeba znalezienia parametrów, dla których system/urządzenie będzie działać w sposób optymalny. Klasyczne podejście do optymalizacji: sformułowanie
Sztuczne sieci neuronowe i sztuczna immunologia jako klasyfikatory danych. Dariusz Badura Letnia Szkoła Instytutu Matematyki 2010
 Sztuczne sieci neuronowe i sztuczna immunologia jako klasyfikatory danych Dariusz Badura Letnia Szkoła Instytutu Matematyki 2010 Sieci neuronowe jednokierunkowa wielowarstwowa sieć neuronowa sieci Kohonena
Sztuczne sieci neuronowe i sztuczna immunologia jako klasyfikatory danych Dariusz Badura Letnia Szkoła Instytutu Matematyki 2010 Sieci neuronowe jednokierunkowa wielowarstwowa sieć neuronowa sieci Kohonena
Metody przeszukiwania
 Metody przeszukiwania Co to jest przeszukiwanie Przeszukiwanie polega na odnajdywaniu rozwiązania w dyskretnej przestrzeni rozwiązao. Zwykle przeszukiwanie polega na znalezieniu określonego rozwiązania
Metody przeszukiwania Co to jest przeszukiwanie Przeszukiwanie polega na odnajdywaniu rozwiązania w dyskretnej przestrzeni rozwiązao. Zwykle przeszukiwanie polega na znalezieniu określonego rozwiązania
Techniki optymalizacji
 Techniki optymalizacji Algorytm kolonii mrówek Idea Smuga feromonowa 1 Sztuczne mrówki w TSP Sztuczna mrówka agent, który porusza się z miasta do miasta Mrówki preferują miasta połączone łukami z dużą
Techniki optymalizacji Algorytm kolonii mrówek Idea Smuga feromonowa 1 Sztuczne mrówki w TSP Sztuczna mrówka agent, który porusza się z miasta do miasta Mrówki preferują miasta połączone łukami z dużą
OBLICZENIA EWOLUCYJNE
 1 OBLICZENIA EWOLUCYJNE FITNESS F. START COMPUTATION FITNESS F. COMPUTATION INITIAL SUBGenration SENDING CHROM. TO COMPUTERS chromosome AND RECEIVING FITNESS F. VALUE fitness f. value wykład 6 FITNESS
1 OBLICZENIA EWOLUCYJNE FITNESS F. START COMPUTATION FITNESS F. COMPUTATION INITIAL SUBGenration SENDING CHROM. TO COMPUTERS chromosome AND RECEIVING FITNESS F. VALUE fitness f. value wykład 6 FITNESS
Algorytm Genetyczny. zastosowanie do procesów rozmieszczenia stacji raportujących w sieciach komórkowych
 Algorytm Genetyczny zastosowanie do procesów rozmieszczenia stacji raportujących w sieciach komórkowych Dlaczego Algorytmy Inspirowane Naturą? Rozwój nowych technologii: złożone problemy obliczeniowe w
Algorytm Genetyczny zastosowanie do procesów rozmieszczenia stacji raportujących w sieciach komórkowych Dlaczego Algorytmy Inspirowane Naturą? Rozwój nowych technologii: złożone problemy obliczeniowe w
Tworzenie gier na urządzenia mobilne
 Katedra Inżynierii Wiedzy Wykład 11 O czym dzisiaj? labirynty, dużo labiryntów; automaty komórkowe; algorytmy do budowy labiryntów; algorytmy do szukania wyjścia z labiryntów; Blueprints i drzewa zachowań
Katedra Inżynierii Wiedzy Wykład 11 O czym dzisiaj? labirynty, dużo labiryntów; automaty komórkowe; algorytmy do budowy labiryntów; algorytmy do szukania wyjścia z labiryntów; Blueprints i drzewa zachowań
Algorytmy mrówkowe. H. Bednarz. Wydział Informatyki Zachodniopomorski Uniwersytet Technologiczny w Szczecinie Inteligentne systemy informatyczne
 Algorytmy mrówkowe H. Bednarz Wydział Informatyki Zachodniopomorski Uniwersytet Technologiczny w Szczecinie Inteligentne systemy informatyczne 13 kwietnia 2015 1 2 3 4 Przestrzeń poszukiwań Ograniczenia
Algorytmy mrówkowe H. Bednarz Wydział Informatyki Zachodniopomorski Uniwersytet Technologiczny w Szczecinie Inteligentne systemy informatyczne 13 kwietnia 2015 1 2 3 4 Przestrzeń poszukiwań Ograniczenia
Systemy mrówkowe. Opracowali: Dawid Strucker, Konrad Baranowski
 Systemy mrówkowe Opracowali: Dawid Strucker, Konrad Baranowski Wprowadzenie Algorytmy mrówkowe oparte są o zasadę inteligencji roju (ang. swarm intelligence). Służą głównie do znajdowania najkrótszej drogi
Systemy mrówkowe Opracowali: Dawid Strucker, Konrad Baranowski Wprowadzenie Algorytmy mrówkowe oparte są o zasadę inteligencji roju (ang. swarm intelligence). Służą głównie do znajdowania najkrótszej drogi
Algorytmy metaheurystyczne Wykład 6. Piotr Syga
 Algorytmy metaheurystyczne Wykład 6 Piotr Syga 10.04.2017 Wprowadzenie Inspiracje Wprowadzenie ACS idea 1 Zaczynamy z pustym rozwiązaniem początkowym 2 Dzielimy problem na komponenty (przedmiot do zabrania,
Algorytmy metaheurystyczne Wykład 6 Piotr Syga 10.04.2017 Wprowadzenie Inspiracje Wprowadzenie ACS idea 1 Zaczynamy z pustym rozwiązaniem początkowym 2 Dzielimy problem na komponenty (przedmiot do zabrania,
Wybrane podstawowe rodzaje algorytmów
 Wybrane podstawowe rodzaje algorytmów Tomasz Głowacki tglowacki@cs.put.poznan.pl Zajęcia finansowane z projektu "Rozwój i doskonalenie kształcenia na Politechnice Poznańskiej w zakresie technologii informatycznych
Wybrane podstawowe rodzaje algorytmów Tomasz Głowacki tglowacki@cs.put.poznan.pl Zajęcia finansowane z projektu "Rozwój i doskonalenie kształcenia na Politechnice Poznańskiej w zakresie technologii informatycznych
Algorytmy genetyczne. Paweł Cieśla. 8 stycznia 2009
 Algorytmy genetyczne Paweł Cieśla 8 stycznia 2009 Genetyka - nauka o dziedziczeniu cech pomiędzy pokoleniami. Geny są czynnikami, które decydują o wyglądzie, zachowaniu, rozmnażaniu każdego żywego organizmu.
Algorytmy genetyczne Paweł Cieśla 8 stycznia 2009 Genetyka - nauka o dziedziczeniu cech pomiędzy pokoleniami. Geny są czynnikami, które decydują o wyglądzie, zachowaniu, rozmnażaniu każdego żywego organizmu.
Generowanie i optymalizacja harmonogramu za pomoca
 Generowanie i optymalizacja harmonogramu za pomoca na przykładzie generatora planu zajęć Matematyka Stosowana i Informatyka Stosowana Wydział Fizyki Technicznej i Matematyki Stosowanej Politechnika Gdańska
Generowanie i optymalizacja harmonogramu za pomoca na przykładzie generatora planu zajęć Matematyka Stosowana i Informatyka Stosowana Wydział Fizyki Technicznej i Matematyki Stosowanej Politechnika Gdańska
ALGORYTMY EWOLUCYJNE W OPTYMALIZACJI JEDNOKRYTERIALNEJ
 ALGORYTMY EWOLUCYJNE W OPTYMALIZACJI JEDNOKRYTERIALNEJ Zalety: nie wprowadzają żadnych ograniczeń na sformułowanie problemu optymalizacyjnego. Funkcja celu może być wielowartościowa i nieciągła, obszar
ALGORYTMY EWOLUCYJNE W OPTYMALIZACJI JEDNOKRYTERIALNEJ Zalety: nie wprowadzają żadnych ograniczeń na sformułowanie problemu optymalizacyjnego. Funkcja celu może być wielowartościowa i nieciągła, obszar
Techniki optymalizacji
 Techniki optymalizacji Metaheurystyki oparte na algorytmach lokalnego przeszukiwania Maciej Hapke maciej.hapke at put.poznan.pl GRASP Greedy Randomized Adaptive Search Procedure T.A. Feo, M.G.C. Resende,
Techniki optymalizacji Metaheurystyki oparte na algorytmach lokalnego przeszukiwania Maciej Hapke maciej.hapke at put.poznan.pl GRASP Greedy Randomized Adaptive Search Procedure T.A. Feo, M.G.C. Resende,
SCHEMAT ROZWIĄZANIA ZADANIA OPTYMALIZACJI PRZY POMOCY ALGORYTMU GENETYCZNEGO
 SCHEMAT ROZWIĄZANIA ZADANIA OPTYMALIZACJI PRZY POMOCY ALGORYTMU GENETYCZNEGO. Rzeczywistość (istniejąca lub projektowana).. Model fizyczny. 3. Model matematyczny (optymalizacyjny): a. Zmienne projektowania
SCHEMAT ROZWIĄZANIA ZADANIA OPTYMALIZACJI PRZY POMOCY ALGORYTMU GENETYCZNEGO. Rzeczywistość (istniejąca lub projektowana).. Model fizyczny. 3. Model matematyczny (optymalizacyjny): a. Zmienne projektowania
Algorytmy genetyczne w interpolacji wielomianowej
 Algorytmy genetyczne w interpolacji wielomianowej (seminarium robocze) Seminarium Metod Inteligencji Obliczeniowej Warszawa 22 II 2006 mgr inż. Marcin Borkowski Plan: Przypomnienie algorytmu niszowego
Algorytmy genetyczne w interpolacji wielomianowej (seminarium robocze) Seminarium Metod Inteligencji Obliczeniowej Warszawa 22 II 2006 mgr inż. Marcin Borkowski Plan: Przypomnienie algorytmu niszowego
Algorytmy ewolucyjne 1
 Algorytmy ewolucyjne 1 2 Zasady zaliczenia przedmiotu Prowadzący (wykład i pracownie specjalistyczną): Wojciech Kwedlo, pokój 205. Konsultacje dla studentów studiów dziennych: poniedziałek,środa, godz
Algorytmy ewolucyjne 1 2 Zasady zaliczenia przedmiotu Prowadzący (wykład i pracownie specjalistyczną): Wojciech Kwedlo, pokój 205. Konsultacje dla studentów studiów dziennych: poniedziałek,środa, godz
Wyznaczanie strategii w grach
 Wyznaczanie strategii w grach Dariusz Banasiak Katedra Informatyki Technicznej W4/K9 Politechnika Wrocławska Definicja gry Teoria gier i konstruowane na jej podstawie programy stanowią jeden z głównych
Wyznaczanie strategii w grach Dariusz Banasiak Katedra Informatyki Technicznej W4/K9 Politechnika Wrocławska Definicja gry Teoria gier i konstruowane na jej podstawie programy stanowią jeden z głównych
Algorytmy genetyczne
 9 listopada 2010 y ewolucyjne - zbiór metod optymalizacji inspirowanych analogiami biologicznymi (ewolucja naturalna). Pojęcia odwzorowujące naturalne zjawiska: Osobnik Populacja Genotyp Fenotyp Gen Chromosom
9 listopada 2010 y ewolucyjne - zbiór metod optymalizacji inspirowanych analogiami biologicznymi (ewolucja naturalna). Pojęcia odwzorowujące naturalne zjawiska: Osobnik Populacja Genotyp Fenotyp Gen Chromosom
Marcel Stankowski Wrocław, 23 czerwca 2009 INFORMATYKA SYSTEMÓW AUTONOMICZNYCH
 Marcel Stankowski Wrocław, 23 czerwca 2009 INFORMATYKA SYSTEMÓW AUTONOMICZNYCH Przeszukiwanie przestrzeni rozwiązań, szukanie na ślepo, wszerz, w głąb. Spis treści: 1. Wprowadzenie 3. str. 1.1 Krótki Wstęp
Marcel Stankowski Wrocław, 23 czerwca 2009 INFORMATYKA SYSTEMÓW AUTONOMICZNYCH Przeszukiwanie przestrzeni rozwiązań, szukanie na ślepo, wszerz, w głąb. Spis treści: 1. Wprowadzenie 3. str. 1.1 Krótki Wstęp
ALGORYTMY GENETYCZNE ćwiczenia
 ćwiczenia Wykorzystaj algorytmy genetyczne do wyznaczenia minimum globalnego funkcji testowej: 1. Wylosuj dwuwymiarową tablicę 100x2 liczb 8-bitowych z zakresu [-100; +100] reprezentujących inicjalną populację
ćwiczenia Wykorzystaj algorytmy genetyczne do wyznaczenia minimum globalnego funkcji testowej: 1. Wylosuj dwuwymiarową tablicę 100x2 liczb 8-bitowych z zakresu [-100; +100] reprezentujących inicjalną populację
Heurystyki. Strategie poszukiwań
 Sztuczna inteligencja Heurystyki. Strategie poszukiwań Jacek Bartman Zakład Elektrotechniki i Informatyki Instytut Techniki Uniwersytet Rzeszowski DLACZEGO METODY PRZESZUKIWANIA? Sztuczna Inteligencja
Sztuczna inteligencja Heurystyki. Strategie poszukiwań Jacek Bartman Zakład Elektrotechniki i Informatyki Instytut Techniki Uniwersytet Rzeszowski DLACZEGO METODY PRZESZUKIWANIA? Sztuczna Inteligencja
oporność odporność oporność odporność odporność oporność
 oporność odporność odporność nieswoista bierna - niskie ph na powierzchni skóry (mydła!) - enzymy - lizozym, pepsyna, kwas solny żołądka, peptydy o działaniu antybakteryjnym - laktoferyna- przeciwciała
oporność odporność odporność nieswoista bierna - niskie ph na powierzchni skóry (mydła!) - enzymy - lizozym, pepsyna, kwas solny żołądka, peptydy o działaniu antybakteryjnym - laktoferyna- przeciwciała
Optymalizacja. Wybrane algorytmy
 dr hab. inż. Instytut Informatyki Politechnika Poznańska www.cs.put.poznan.pl/mkomosinski, Andrzej Jaszkiewicz Problem optymalizacji kombinatorycznej Problem optymalizacji kombinatorycznej jest problemem
dr hab. inż. Instytut Informatyki Politechnika Poznańska www.cs.put.poznan.pl/mkomosinski, Andrzej Jaszkiewicz Problem optymalizacji kombinatorycznej Problem optymalizacji kombinatorycznej jest problemem
Algorytmy genetyczne
 Algorytmy genetyczne Motto: Zamiast pracowicie poszukiwać najlepszego rozwiązania problemu informatycznego lepiej pozwolić, żeby komputer sam sobie to rozwiązanie wyhodował! Algorytmy genetyczne służą
Algorytmy genetyczne Motto: Zamiast pracowicie poszukiwać najlepszego rozwiązania problemu informatycznego lepiej pozwolić, żeby komputer sam sobie to rozwiązanie wyhodował! Algorytmy genetyczne służą
Planowanie drogi robota, algorytm A*
 Planowanie drogi robota, algorytm A* Karol Sydor 13 maja 2008 Założenia Uproszczenie przestrzeni Założenia Problem planowania trasy jest bardzo złożony i trudny. W celu uproszczenia problemu przyjmujemy
Planowanie drogi robota, algorytm A* Karol Sydor 13 maja 2008 Założenia Uproszczenie przestrzeni Założenia Problem planowania trasy jest bardzo złożony i trudny. W celu uproszczenia problemu przyjmujemy
Zadania laboratoryjne i projektowe - wersja β
 Zadania laboratoryjne i projektowe - wersja β 1 Laboratorium Dwa problemy do wyboru (jeden do realizacji). 1. Water Jug Problem, 2. Wieże Hanoi. Water Jug Problem Ograniczenia dla każdej z wersji: pojemniki
Zadania laboratoryjne i projektowe - wersja β 1 Laboratorium Dwa problemy do wyboru (jeden do realizacji). 1. Water Jug Problem, 2. Wieże Hanoi. Water Jug Problem Ograniczenia dla każdej z wersji: pojemniki
Obliczenia inspirowane Naturą
 Obliczenia inspirowane Naturą Wykład 10 - Mrówki w labiryntach Jarosław Miszczak IITiS PAN Gliwice 05/05/2016 1 / 48 Na poprzednim wykładzie 1... 2... 3... 2 / 48 1 Motywacja biologiczna Podstawowe mechanizmy
Obliczenia inspirowane Naturą Wykład 10 - Mrówki w labiryntach Jarosław Miszczak IITiS PAN Gliwice 05/05/2016 1 / 48 Na poprzednim wykładzie 1... 2... 3... 2 / 48 1 Motywacja biologiczna Podstawowe mechanizmy
KARTA MODUŁU KSZTAŁCENIA
 KARTA MODUŁU KSZTAŁCENIA I. Informacje ogólne 1 Nazwa modułu kształcenia Sztuczna inteligencja 2 Nazwa jednostki prowadzącej moduł Instytut Informatyki, Zakład Informatyki Stosowanej 3 Kod modułu (wypełnia
KARTA MODUŁU KSZTAŁCENIA I. Informacje ogólne 1 Nazwa modułu kształcenia Sztuczna inteligencja 2 Nazwa jednostki prowadzącej moduł Instytut Informatyki, Zakład Informatyki Stosowanej 3 Kod modułu (wypełnia
Propozycje tematów zadań
 Propozycje tematów zadań 1. WARCABY Opracować program do gry w warcaby dla dwu graczy. Program ma umożliwiać przesuwanie kursora na zmianę po polach białych lub czarnych, wskazywanie początku końca ruchu.
Propozycje tematów zadań 1. WARCABY Opracować program do gry w warcaby dla dwu graczy. Program ma umożliwiać przesuwanie kursora na zmianę po polach białych lub czarnych, wskazywanie początku końca ruchu.
Algorytmy mrówkowe. Plan. » Algorytm mrówkowy» Warianty» CVRP» Demo» Środowisko dynamiczne» Pomysł modyfikacji» Testowanie
 Algorytmy mrówkowe w środowiskach dynamicznych Dariusz Maksim, promotor: prof. nzw. dr hab. Jacek Mańdziuk 1/51 Plan» Algorytm mrówkowy» Warianty» CVRP» Demo» Środowisko dynamiczne» Pomysł modyfikacji»
Algorytmy mrówkowe w środowiskach dynamicznych Dariusz Maksim, promotor: prof. nzw. dr hab. Jacek Mańdziuk 1/51 Plan» Algorytm mrówkowy» Warianty» CVRP» Demo» Środowisko dynamiczne» Pomysł modyfikacji»
Archipelag Sztucznej Inteligencji
 Archipelag Sztucznej Inteligencji Istniejące metody sztucznej inteligencji mają ze sobą zwykle niewiele wspólnego, więc można je sobie wyobrażać jako archipelag wysp, a nie jako fragment stałego lądu.
Archipelag Sztucznej Inteligencji Istniejące metody sztucznej inteligencji mają ze sobą zwykle niewiele wspólnego, więc można je sobie wyobrażać jako archipelag wysp, a nie jako fragment stałego lądu.
PLAN WYKŁADU OPTYMALIZACJA GLOBALNA OPERATOR KRZYŻOWANIA ETAPY KRZYŻOWANIA
 PLAN WYKŁADU Operator krzyżowania Operator mutacji Operator inwersji Sukcesja Przykłady symulacji AG Kodowanie - rodzaje OPTYMALIZACJA GLOBALNA Wykład 3 dr inż. Agnieszka Bołtuć OPERATOR KRZYŻOWANIA Wymiana
PLAN WYKŁADU Operator krzyżowania Operator mutacji Operator inwersji Sukcesja Przykłady symulacji AG Kodowanie - rodzaje OPTYMALIZACJA GLOBALNA Wykład 3 dr inż. Agnieszka Bołtuć OPERATOR KRZYŻOWANIA Wymiana
6. Klasyczny algorytm genetyczny. 1
 6. Klasyczny algorytm genetyczny. 1 Idea algorytmu genetycznego została zaczerpnięta z nauk przyrodniczych opisujących zjawiska doboru naturalnego i dziedziczenia. Mechanizmy te polegają na przetrwaniu
6. Klasyczny algorytm genetyczny. 1 Idea algorytmu genetycznego została zaczerpnięta z nauk przyrodniczych opisujących zjawiska doboru naturalnego i dziedziczenia. Mechanizmy te polegają na przetrwaniu
Dobór parametrów algorytmu ewolucyjnego
 Dobór parametrów algorytmu ewolucyjnego 1 2 Wstęp Algorytm ewolucyjny posiada wiele parametrów. Przykładowo dla algorytmu genetycznego są to: prawdopodobieństwa stosowania operatorów mutacji i krzyżowania.
Dobór parametrów algorytmu ewolucyjnego 1 2 Wstęp Algorytm ewolucyjny posiada wiele parametrów. Przykładowo dla algorytmu genetycznego są to: prawdopodobieństwa stosowania operatorów mutacji i krzyżowania.
Algorytmy ewolucyjne. Łukasz Przybyłek Studenckie Koło Naukowe BRAINS
 Algorytmy ewolucyjne Łukasz Przybyłek Studenckie Koło Naukowe BRAINS 1 Wprowadzenie Algorytmy ewolucyjne ogólne algorytmy optymalizacji operujące na populacji rozwiązań, inspirowane biologicznymi zjawiskami,
Algorytmy ewolucyjne Łukasz Przybyłek Studenckie Koło Naukowe BRAINS 1 Wprowadzenie Algorytmy ewolucyjne ogólne algorytmy optymalizacji operujące na populacji rozwiązań, inspirowane biologicznymi zjawiskami,
Strefa pokrycia radiowego wokół stacji bazowych. Zasięg stacji bazowych Zazębianie się komórek
 Problem zapożyczania kanałów z wykorzystaniem narzędzi optymalizacji Wprowadzenie Rozwiązanie problemu przydziału częstotliwości prowadzi do stanu, w którym każdej stacji bazowej przydzielono żądaną liczbę
Problem zapożyczania kanałów z wykorzystaniem narzędzi optymalizacji Wprowadzenie Rozwiązanie problemu przydziału częstotliwości prowadzi do stanu, w którym każdej stacji bazowej przydzielono żądaną liczbę
ZASTOSOWANIE ALGORYTMU GENETYCZNEGO DO KONSTRUKCJI
 ZASTOSOWANIE ALGORYTMU GENETYCZNEGO DO KONSTRUKCJI FUNKCJI OCENIAJĄCEJ W GRZE OTHELLO Tomasz Dąbrowski, Halina Kwaśnicka, Maciej Piasecki Wydziałowy Zakład Informatyki, Politechnika Wrocławska, ul. Wybrzeże
ZASTOSOWANIE ALGORYTMU GENETYCZNEGO DO KONSTRUKCJI FUNKCJI OCENIAJĄCEJ W GRZE OTHELLO Tomasz Dąbrowski, Halina Kwaśnicka, Maciej Piasecki Wydziałowy Zakład Informatyki, Politechnika Wrocławska, ul. Wybrzeże
Uniwersytet Zielonogórski Wydział Elektrotechniki, Informatyki i Telekomunikacji Instytut Sterowania i Systemów Informatycznych
 Uniwersytet Zielonogórski Wydział Elektrotechniki, Informatyki i Telekomunikacji Instytut Sterowania i Systemów Informatycznych ELEMENTY SZTUCZNEJ INTELIGENCJI Laboratorium nr 9 PRZESZUKIWANIE GRAFÓW Z
Uniwersytet Zielonogórski Wydział Elektrotechniki, Informatyki i Telekomunikacji Instytut Sterowania i Systemów Informatycznych ELEMENTY SZTUCZNEJ INTELIGENCJI Laboratorium nr 9 PRZESZUKIWANIE GRAFÓW Z
3. MINIMAX. Rysunek 1: Drzewo obrazujące przebieg gry.
 3. MINIMAX. Bardzo wygodną strukturą danych pozwalającą reprezentować stan i przebieg gry (szczególnie gier dwuosobowych) jest drzewo. Węzły drzewa reprezentują stan gry po wykonaniu ruchu przez jednego
3. MINIMAX. Bardzo wygodną strukturą danych pozwalającą reprezentować stan i przebieg gry (szczególnie gier dwuosobowych) jest drzewo. Węzły drzewa reprezentują stan gry po wykonaniu ruchu przez jednego
Algorytmy ewolucyjne - algorytmy genetyczne. I. Karcz-Dulęba
 Algorytmy ewolucyjne - algorytmy genetyczne I. Karcz-Dulęba Algorytmy klasyczne a algorytmy ewolucyjne Przeszukiwanie przestrzeni przez jeden punkt bazowy Przeszukiwanie przestrzeni przez zbiór punktów
Algorytmy ewolucyjne - algorytmy genetyczne I. Karcz-Dulęba Algorytmy klasyczne a algorytmy ewolucyjne Przeszukiwanie przestrzeni przez jeden punkt bazowy Przeszukiwanie przestrzeni przez zbiór punktów
Algorytmy metaheurystyczne podsumowanie
 dr hab. inż. Instytut Informatyki Politechnika Poznańska www.cs.put.poznan.pl/mkomosinski, Andrzej Jaszkiewicz Problem optymalizacji kombinatorycznej Problem optymalizacji kombinatorycznej jest problemem
dr hab. inż. Instytut Informatyki Politechnika Poznańska www.cs.put.poznan.pl/mkomosinski, Andrzej Jaszkiewicz Problem optymalizacji kombinatorycznej Problem optymalizacji kombinatorycznej jest problemem
LABORATORIUM 4: Algorytmy ewolucyjne cz. 2 wpływ operatorów krzyżowania i mutacji na skuteczność poszukiwań AE
 Instytut Mechaniki i Inżynierii Obliczeniowej Wydział Mechaniczny Technologiczny, Politechnika Śląska www.imio.polsl.pl METODY HEURYSTYCZNE LABORATORIUM 4: Algorytmy ewolucyjne cz. 2 wpływ operatorów krzyżowania
Instytut Mechaniki i Inżynierii Obliczeniowej Wydział Mechaniczny Technologiczny, Politechnika Śląska www.imio.polsl.pl METODY HEURYSTYCZNE LABORATORIUM 4: Algorytmy ewolucyjne cz. 2 wpływ operatorów krzyżowania
Metody Rozmyte i Algorytmy Ewolucyjne
 mgr inż. Wydział Matematyczno-Przyrodniczy Szkoła Nauk Ścisłych Uniwersytet Kardynała Stefana Wyszyńskiego Podstawowe operatory genetyczne Plan wykładu Przypomnienie 1 Przypomnienie Metody generacji liczb
mgr inż. Wydział Matematyczno-Przyrodniczy Szkoła Nauk Ścisłych Uniwersytet Kardynała Stefana Wyszyńskiego Podstawowe operatory genetyczne Plan wykładu Przypomnienie 1 Przypomnienie Metody generacji liczb
10. Wstęp do Teorii Gier
 10. Wstęp do Teorii Gier Definicja Gry Matematycznej Gra matematyczna spełnia następujące warunki: a) Jest co najmniej dwóch racjonalnych graczy. b) Zbiór możliwych dezycji każdego gracza zawiera co najmniej
10. Wstęp do Teorii Gier Definicja Gry Matematycznej Gra matematyczna spełnia następujące warunki: a) Jest co najmniej dwóch racjonalnych graczy. b) Zbiór możliwych dezycji każdego gracza zawiera co najmniej
Zadanie transportowe i problem komiwojażera. Tadeusz Trzaskalik
 Zadanie transportowe i problem komiwojażera Tadeusz Trzaskalik 3.. Wprowadzenie Słowa kluczowe Zbilansowane zadanie transportowe Rozwiązanie początkowe Metoda minimalnego elementu macierzy kosztów Metoda
Zadanie transportowe i problem komiwojażera Tadeusz Trzaskalik 3.. Wprowadzenie Słowa kluczowe Zbilansowane zadanie transportowe Rozwiązanie początkowe Metoda minimalnego elementu macierzy kosztów Metoda
Algorytmy Mrówkowe. Daniel Błaszkiewicz. 11 maja 2011. Instytut Informatyki Uniwersytetu Wrocławskiego
 Algorytmy Mrówkowe Instytut Informatyki Uniwersytetu Wrocławskiego 11 maja 2011 Opis Mrówki w naturze Algorytmy to stosunkowo nowy gatunek algorytmów optymalizacyjnych stworzony przez Marco Dorigo w 1992
Algorytmy Mrówkowe Instytut Informatyki Uniwersytetu Wrocławskiego 11 maja 2011 Opis Mrówki w naturze Algorytmy to stosunkowo nowy gatunek algorytmów optymalizacyjnych stworzony przez Marco Dorigo w 1992
Rozwiązywanie problemów metodą przeszukiwania
 Rozwiązywanie problemów metodą przeszukiwania Dariusz Banasiak Katedra Informatyki Technicznej W4/K9 Politechnika Wrocławska Reprezentacja problemu w przestrzeni stanów Jedną z ważniejszych metod sztucznej
Rozwiązywanie problemów metodą przeszukiwania Dariusz Banasiak Katedra Informatyki Technicznej W4/K9 Politechnika Wrocławska Reprezentacja problemu w przestrzeni stanów Jedną z ważniejszych metod sztucznej
Lp. tydzień wykłady seminaria ćwiczenia
 Lp. tydzień wykłady seminaria ćwiczenia 21.02. Wprowadzeniedozag adnieńzwiązanychzi mmunologią, krótka historiaimmunologii, rozwójukładuimmun ologicznego. 19.02. 20.02. Wprowadzenie do zagadnień z immunologii.
Lp. tydzień wykłady seminaria ćwiczenia 21.02. Wprowadzeniedozag adnieńzwiązanychzi mmunologią, krótka historiaimmunologii, rozwójukładuimmun ologicznego. 19.02. 20.02. Wprowadzenie do zagadnień z immunologii.
Adam Meissner. SZTUCZNA INTELIGENCJA Gry dwuosobowe
 Instytut Automatyki i Inżynierii Informatycznej Politechniki Poznańskiej Adam Meissner Adam.Meissner@put.poznan.pl http://www.man.poznan.pl/~ameis SZTUCZNA INTELIGENCJA Gry dwuosobowe Literatura [1] Sterling
Instytut Automatyki i Inżynierii Informatycznej Politechniki Poznańskiej Adam Meissner Adam.Meissner@put.poznan.pl http://www.man.poznan.pl/~ameis SZTUCZNA INTELIGENCJA Gry dwuosobowe Literatura [1] Sterling
PODSTAWY IMMUNOLOGII Komórki i cząsteczki biorące udział w odporności nabytej (cz.i): wprowadzenie (komórki, receptory, rozwój odporności nabytej)
 PODSTAWY IMMUNOLOGII Komórki i cząsteczki biorące udział w odporności nabytej (cz.i): wprowadzenie (komórki, receptory, rozwój odporności nabytej) Nadzieja Drela ndrela@biol.uw.edu.pl Konspekt do wykładu
PODSTAWY IMMUNOLOGII Komórki i cząsteczki biorące udział w odporności nabytej (cz.i): wprowadzenie (komórki, receptory, rozwój odporności nabytej) Nadzieja Drela ndrela@biol.uw.edu.pl Konspekt do wykładu
WYKORZYSTANIE ALGORYTMÓW GENETYCZNYCH I MRÓWKOWYCH W PROBLEMACH TRANSPORTOWYCH
 Inżynieria Rolnicza 7(105)/2008 WYKORZYSTANIE ALGORYTMÓW GENETYCZNYCH I MRÓWKOWYCH W PROBLEMACH TRANSPORTOWYCH Justyna Zduńczuk, Wojciech Przystupa Katedra Zastosowań Matematyki, Uniwersytet Przyrodniczy
Inżynieria Rolnicza 7(105)/2008 WYKORZYSTANIE ALGORYTMÓW GENETYCZNYCH I MRÓWKOWYCH W PROBLEMACH TRANSPORTOWYCH Justyna Zduńczuk, Wojciech Przystupa Katedra Zastosowań Matematyki, Uniwersytet Przyrodniczy
Algorytmy genetyczne w optymalizacji
 Algorytmy genetyczne w optymalizacji Literatura 1. David E. Goldberg, Algorytmy genetyczne i ich zastosowania, WNT, Warszawa 1998; 2. Zbigniew Michalewicz, Algorytmy genetyczne + struktury danych = programy
Algorytmy genetyczne w optymalizacji Literatura 1. David E. Goldberg, Algorytmy genetyczne i ich zastosowania, WNT, Warszawa 1998; 2. Zbigniew Michalewicz, Algorytmy genetyczne + struktury danych = programy
Model Marczuka przebiegu infekcji.
 Model Marczuka przebiegu infekcji. Karolina Szymaniuk 27 maja 2013 Karolina Szymaniuk () Model Marczuka przebiegu infekcji. 27 maja 2013 1 / 17 Substrat Związek chemiczny, który ulega przemianie w wyniku
Model Marczuka przebiegu infekcji. Karolina Szymaniuk 27 maja 2013 Karolina Szymaniuk () Model Marczuka przebiegu infekcji. 27 maja 2013 1 / 17 Substrat Związek chemiczny, który ulega przemianie w wyniku
Aproksymacja funkcji a regresja symboliczna
 Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(x), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(x), zwaną funkcją aproksymującą
Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(x), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(x), zwaną funkcją aproksymującą
Obrona rozprawy doktorskiej Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
 IBS PAN, Warszawa 9 kwietnia 2008 Obrona rozprawy doktorskiej Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego mgr inż. Marcin Jaruszewicz promotor: dr hab. inż. Jacek Mańdziuk,
IBS PAN, Warszawa 9 kwietnia 2008 Obrona rozprawy doktorskiej Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego mgr inż. Marcin Jaruszewicz promotor: dr hab. inż. Jacek Mańdziuk,
Mrówka Pachycondyla apicalis
 Mrówka Pachycondyla apicalis Mrówki Pachycondyla apicalis wystepują w lasach południowego Meksyku, północnej Argentyny i Kostaryki. Wystepuja zarówno w lasach wilgotnych jak i suchych. Mrówki te polują
Mrówka Pachycondyla apicalis Mrówki Pachycondyla apicalis wystepują w lasach południowego Meksyku, północnej Argentyny i Kostaryki. Wystepuja zarówno w lasach wilgotnych jak i suchych. Mrówki te polują
Algorytmy ewolucyjne (3)
 Algorytmy ewolucyjne (3) http://zajecia.jakubw.pl/nai KODOWANIE PERMUTACJI W pewnych zastosowaniach kodowanie binarne jest mniej naturalne, niż inne sposoby kodowania. Na przykład, w problemie komiwojażera
Algorytmy ewolucyjne (3) http://zajecia.jakubw.pl/nai KODOWANIE PERMUTACJI W pewnych zastosowaniach kodowanie binarne jest mniej naturalne, niż inne sposoby kodowania. Na przykład, w problemie komiwojażera
Wykorzystanie algorytmów mrówkowych w dynamicznym problem
 Wykorzystanie algorytmów mrówkowych w dynamicznym problemie marszrutyzacji Promotor: dr inż. Aneta Poniszewska-Marańda Współpromotor: mgr inż. Łukasz Chomątek 14 czerwca 2013 Przedmiot i cele pracy dyplomowej
Wykorzystanie algorytmów mrówkowych w dynamicznym problemie marszrutyzacji Promotor: dr inż. Aneta Poniszewska-Marańda Współpromotor: mgr inż. Łukasz Chomątek 14 czerwca 2013 Przedmiot i cele pracy dyplomowej
Algorytm hybrydowy dla alokacji portfela inwestycyjnego przy ograniczonych zasobach
 Adam Stawowy Algorytm hybrydowy dla alokacji portfela inwestycyjnego przy ograniczonych zasobach Summary: We present a meta-heuristic to combine Monte Carlo simulation with genetic algorithm for Capital
Adam Stawowy Algorytm hybrydowy dla alokacji portfela inwestycyjnego przy ograniczonych zasobach Summary: We present a meta-heuristic to combine Monte Carlo simulation with genetic algorithm for Capital
6. Projektowanie składu chemicznego stali szybkotn cych o wymaganej twardo ci i odporno ci na p kanie
 6. Projektowanie składu chemicznego stali szybkotn cych o wymaganej twardo ci i odporno ci na p kanie Do projektowania składu chemicznego stali szybkotn cych, które jest zadaniem optymalizacyjnym, wykorzystano
6. Projektowanie składu chemicznego stali szybkotn cych o wymaganej twardo ci i odporno ci na p kanie Do projektowania składu chemicznego stali szybkotn cych, które jest zadaniem optymalizacyjnym, wykorzystano
Tworzenie gier na urządzenia mobilne
 Katedra Inżynierii Wiedzy Teoria podejmowania decyzji w grze Gry w postaci ekstensywnej Inaczej gry w postaci drzewiastej, gry w postaci rozwiniętej; formalny opis wszystkich możliwych przebiegów gry z
Katedra Inżynierii Wiedzy Teoria podejmowania decyzji w grze Gry w postaci ekstensywnej Inaczej gry w postaci drzewiastej, gry w postaci rozwiniętej; formalny opis wszystkich możliwych przebiegów gry z
Algorytmy mrówkowe (ang. Ant Colony Optimization)
 Algorytmy mrówkowe (ang. Ant Colony Optimization) 1. Wprowadzenie do ACO a) mrówki naturalne b) mrówki sztuczne c) literatura (kilka pozycji) 2. ACO i TSP 1. Wprowadzenie do ACO a) mrówki naturalne ślepe,
Algorytmy mrówkowe (ang. Ant Colony Optimization) 1. Wprowadzenie do ACO a) mrówki naturalne b) mrówki sztuczne c) literatura (kilka pozycji) 2. ACO i TSP 1. Wprowadzenie do ACO a) mrówki naturalne ślepe,
Problemy z ograniczeniami
 Problemy z ograniczeniami 1 2 Dlaczego zadania z ograniczeniami Wiele praktycznych problemów to problemy z ograniczeniami. Problemy trudne obliczeniowo (np-trudne) to prawie zawsze problemy z ograniczeniami.
Problemy z ograniczeniami 1 2 Dlaczego zadania z ograniczeniami Wiele praktycznych problemów to problemy z ograniczeniami. Problemy trudne obliczeniowo (np-trudne) to prawie zawsze problemy z ograniczeniami.
Wykorzystanie algorytmów mrówkowych w dynamicznym problem
 Wykorzystanie algorytmów mrówkowych w dynamicznym problemie marszrutyzacji Promotor: dr inż. Aneta Poniszewska-Marańda Współpromotor: mgr inż. Łukasz Chomątek 18 stycznia 2013 Przedmiot i cele pracy dyplomowej
Wykorzystanie algorytmów mrówkowych w dynamicznym problemie marszrutyzacji Promotor: dr inż. Aneta Poniszewska-Marańda Współpromotor: mgr inż. Łukasz Chomątek 18 stycznia 2013 Przedmiot i cele pracy dyplomowej
Wykład 4. Droga i cykl Eulera i Hamiltona
 Wykład 4. i Hamiltona Wykład 4. i Hamiltona 1 / 35 Grafy Eulera Niech G będzie grafem spójnym. Definicja Jeżeli w grafie G istnieje zamknięta droga prosta zawierająca wszystkie krawędzie grafu, to taką
Wykład 4. i Hamiltona Wykład 4. i Hamiltona 1 / 35 Grafy Eulera Niech G będzie grafem spójnym. Definicja Jeżeli w grafie G istnieje zamknięta droga prosta zawierająca wszystkie krawędzie grafu, to taką
PLAN WYKŁADU OPTYMALIZACJA GLOBALNA ALGORYTM MRÓWKOWY (ANT SYSTEM) ALGORYTM MRÓWKOWY. Algorytm mrówkowy
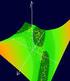
 PLAN WYKŁADU Algorytm mrówowy OPTYMALIZACJA GLOBALNA Wyład 8 dr inż. Agniesza Bołtuć (ANT SYSTEM) Inspiracja: Zachowanie mrówe podczas poszuiwania żywności, Zachowanie to polega na tym, że jeśli do żywności
PLAN WYKŁADU Algorytm mrówowy OPTYMALIZACJA GLOBALNA Wyład 8 dr inż. Agniesza Bołtuć (ANT SYSTEM) Inspiracja: Zachowanie mrówe podczas poszuiwania żywności, Zachowanie to polega na tym, że jeśli do żywności
GRY I ZABAWY UMYSŁOWO- LOGICZNE JAKO FORMA UPOWSZECHNIANIA KULTURY. Donata Fraś
 GRY I ZABAWY UMYSŁOWO- LOGICZNE JAKO FORMA UPOWSZECHNIANIA KULTURY Donata Fraś Gry umysłowe To gry towarzyskie, których rezultat zależy wyłącznie od świadomych decyzji podejmowanych przez partnera Wymagają:
GRY I ZABAWY UMYSŁOWO- LOGICZNE JAKO FORMA UPOWSZECHNIANIA KULTURY Donata Fraś Gry umysłowe To gry towarzyskie, których rezultat zależy wyłącznie od świadomych decyzji podejmowanych przez partnera Wymagają:
RYNEK CIEPŁA REC 2013 OPTYMALIZACJA ROZDZIAŁU OBCIĄŻEŃ POMIĘDZY PRACUJĄCE RÓWNOLEGLE BLOKI CIEPŁOWNICZE
 RYEK CIEPŁA REC 2013 OPTYMALIZACJA ROZDZIAŁU OBCIĄŻEŃ POMIĘDZY PRACUJĄCE RÓWOLEGLE BLOKI CIEPŁOWICZE Prof. dr ha. inż. Henryk Rusinowski Dr ha. inż. Marcin Szega Prof. nzw. w Pol. Śl. Mgr inż. Marcin Plis
RYEK CIEPŁA REC 2013 OPTYMALIZACJA ROZDZIAŁU OBCIĄŻEŃ POMIĘDZY PRACUJĄCE RÓWOLEGLE BLOKI CIEPŁOWICZE Prof. dr ha. inż. Henryk Rusinowski Dr ha. inż. Marcin Szega Prof. nzw. w Pol. Śl. Mgr inż. Marcin Plis
Automatyczny dobór parametrów algorytmu genetycznego
 Automatyczny dobór parametrów algorytmu genetycznego Remigiusz Modrzejewski 22 grudnia 2008 Plan prezentacji Wstęp Atrakcyjność Pułapki Klasyfikacja Wstęp Atrakcyjność Pułapki Klasyfikacja Konstrukcja
Automatyczny dobór parametrów algorytmu genetycznego Remigiusz Modrzejewski 22 grudnia 2008 Plan prezentacji Wstęp Atrakcyjność Pułapki Klasyfikacja Wstęp Atrakcyjność Pułapki Klasyfikacja Konstrukcja
Problem komiwojażera ACO. Zagadnienie optymalizacyjne, polegające na znalezieniu minimalnego cyklu Hamiltona w pełnym grafie ważonym.
 Problem komiwojażera ACO Zagadnienie optymalizacyjne, polegające na znalezieniu minimalnego cyklu Hamiltona w pełnym grafie ważonym. -Wikipedia Problem do rozwiązania zazwyczaj jest przedstawiany jako
Problem komiwojażera ACO Zagadnienie optymalizacyjne, polegające na znalezieniu minimalnego cyklu Hamiltona w pełnym grafie ważonym. -Wikipedia Problem do rozwiązania zazwyczaj jest przedstawiany jako
Programowanie genetyczne, gra SNAKE
 STUDENCKA PRACOWNIA ALGORYTMÓW EWOLUCYJNYCH Tomasz Kupczyk, Tomasz Urbański Programowanie genetyczne, gra SNAKE II UWr Wrocław 2009 Spis treści 1. Wstęp 3 1.1. Ogólny opis.....................................
STUDENCKA PRACOWNIA ALGORYTMÓW EWOLUCYJNYCH Tomasz Kupczyk, Tomasz Urbański Programowanie genetyczne, gra SNAKE II UWr Wrocław 2009 Spis treści 1. Wstęp 3 1.1. Ogólny opis.....................................
Obliczenia Naturalne - Algorytmy immunologiczne
 Literatura Podstawowe pojęcia Obliczenia Naturalne - immunologiczne Paweł Paduch Politechnika Świętokrzyska 10 kwietnia 2014 Paweł Paduch Obliczenia Naturalne - immunologiczne 1 z 44 Plan wykładu Literatura
Literatura Podstawowe pojęcia Obliczenia Naturalne - immunologiczne Paweł Paduch Politechnika Świętokrzyska 10 kwietnia 2014 Paweł Paduch Obliczenia Naturalne - immunologiczne 1 z 44 Plan wykładu Literatura
Elementy kognitywistyki II: Sztuczna inteligencja. WYKŁAD V: Agent wciąż szuka rozwiązania (choć już nie na ślepo)
 Elementy kognitywistyki II: Sztuczna inteligencja WYKŁAD V: Agent wciąż szuka rozwiązania (choć już nie na ślepo) Poprzednio: węzeł reprezentowany jest jako piątka: stan odpowiadający węzłowi rodzic węzła
Elementy kognitywistyki II: Sztuczna inteligencja WYKŁAD V: Agent wciąż szuka rozwiązania (choć już nie na ślepo) Poprzednio: węzeł reprezentowany jest jako piątka: stan odpowiadający węzłowi rodzic węzła
METODY SZTUCZNEJ INTELIGENCJI algorytmy ewolucyjne
 METODY SZTUCZNEJ INTELIGENCJI algorytmy ewolucyjne dr hab. inż. Andrzej Obuchowicz, prof. UZ Instytut Sterowania i Systemów Informatycznych Uniwersytet Zielonogórski A. Obuchowicz: MSI - algorytmy ewolucyjne
METODY SZTUCZNEJ INTELIGENCJI algorytmy ewolucyjne dr hab. inż. Andrzej Obuchowicz, prof. UZ Instytut Sterowania i Systemów Informatycznych Uniwersytet Zielonogórski A. Obuchowicz: MSI - algorytmy ewolucyjne
Algorytmy genetyczne jako metoda wyszukiwania wzorców. Seminarium Metod Inteligencji Obliczeniowej Warszawa 26 X 2005 mgr inż.
 Algorytmy genetyczne jako metoda wyszukiwania wzorców Seminarium Metod Inteligencji Obliczeniowej Warszawa 26 X 2005 mgr inż. Marcin Borkowski Krótko i na temat: Cel pracy Opis modyfikacji AG Zastosowania
Algorytmy genetyczne jako metoda wyszukiwania wzorców Seminarium Metod Inteligencji Obliczeniowej Warszawa 26 X 2005 mgr inż. Marcin Borkowski Krótko i na temat: Cel pracy Opis modyfikacji AG Zastosowania
Podejście memetyczne do problemu DCVRP - wstępne wyniki. Adam Żychowski
 Podejście memetyczne do problemu DCVRP - wstępne wyniki Adam Żychowski Na podstawie prac X. S. Chen, L. Feng, Y. S. Ong A Self-Adaptive Memeplexes Robust Search Scheme for solving Stochastic Demands Vehicle
Podejście memetyczne do problemu DCVRP - wstępne wyniki Adam Żychowski Na podstawie prac X. S. Chen, L. Feng, Y. S. Ong A Self-Adaptive Memeplexes Robust Search Scheme for solving Stochastic Demands Vehicle
Tomasz M. Gwizdałła 2012/13
 METODY METODY OPTYMALIZACJI OPTYMALIZACJI Tomasz M. Gwizdałła 2012/13 Informacje wstępne Tomasz Gwizdałła Katedra Fizyki Ciała Stałego UŁ Pomorska 149/153, p.523b tel. 6355709 tomgwizd@uni.lodz.pl http://www.wfis.uni.lodz.pl/staff/tgwizdalla
METODY METODY OPTYMALIZACJI OPTYMALIZACJI Tomasz M. Gwizdałła 2012/13 Informacje wstępne Tomasz Gwizdałła Katedra Fizyki Ciała Stałego UŁ Pomorska 149/153, p.523b tel. 6355709 tomgwizd@uni.lodz.pl http://www.wfis.uni.lodz.pl/staff/tgwizdalla
Algorytmy memetyczne (hybrydowe algorytmy ewolucyjne)
 Algorytmy memetyczne (hybrydowe algorytmy ewolucyjne) 1 2 Wstęp Termin zaproponowany przez Pablo Moscato (1989). Kombinacja algorytmu ewolucyjnego z algorytmem poszukiwań lokalnych, tak że algorytm poszukiwań
Algorytmy memetyczne (hybrydowe algorytmy ewolucyjne) 1 2 Wstęp Termin zaproponowany przez Pablo Moscato (1989). Kombinacja algorytmu ewolucyjnego z algorytmem poszukiwań lokalnych, tak że algorytm poszukiwań
Drzewa spinające MST dla grafów ważonych Maksymalne drzewo spinające Drzewo Steinera. Wykład 6. Drzewa cz. II
 Wykład 6. Drzewa cz. II 1 / 65 drzewa spinające Drzewa spinające Zliczanie drzew spinających Drzewo T nazywamy drzewem rozpinającym (spinającym) (lub dendrytem) spójnego grafu G, jeżeli jest podgrafem
Wykład 6. Drzewa cz. II 1 / 65 drzewa spinające Drzewa spinające Zliczanie drzew spinających Drzewo T nazywamy drzewem rozpinającym (spinającym) (lub dendrytem) spójnego grafu G, jeżeli jest podgrafem
Algorytmy stochastyczne, wykład 01 Podstawowy algorytm genetyczny
 Algorytmy stochastyczne, wykład 01 J. Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2014-02-21 In memoriam prof. dr hab. Tomasz Schreiber (1975-2010) 1 2 3 Różne Orientacyjny
Algorytmy stochastyczne, wykład 01 J. Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2014-02-21 In memoriam prof. dr hab. Tomasz Schreiber (1975-2010) 1 2 3 Różne Orientacyjny
MODELOWANIE RZECZYWISTOŚCI
 MODELOWANIE RZECZYWISTOŚCI Daniel Wójcik Instytut Biologii Doświadczalnej PAN Szkoła Wyższa Psychologii Społecznej d.wojcik@nencki.gov.pl dwojcik@swps.edu.pl tel. 022 5892 424 http://www.neuroinf.pl/members/danek/swps/
MODELOWANIE RZECZYWISTOŚCI Daniel Wójcik Instytut Biologii Doświadczalnej PAN Szkoła Wyższa Psychologii Społecznej d.wojcik@nencki.gov.pl dwojcik@swps.edu.pl tel. 022 5892 424 http://www.neuroinf.pl/members/danek/swps/
w analizie wyników badań eksperymentalnych, w problemach modelowania zjawisk fizycznych, w analizie obserwacji statystycznych.
 Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(), zwaną funkcją aproksymującą
Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(), zwaną funkcją aproksymującą
Teoria i metody optymalizacji
 II. Optymalizacja globalna Idea: generuj i testuj Do tej grupy naleŝą stochastyczne iteracyjne algorytmy przeszukiwania przestrzeni rozwiązań : metody przeszukiwania lokalnego metody przeszukiwania populacyjnego.
II. Optymalizacja globalna Idea: generuj i testuj Do tej grupy naleŝą stochastyczne iteracyjne algorytmy przeszukiwania przestrzeni rozwiązań : metody przeszukiwania lokalnego metody przeszukiwania populacyjnego.
Badania operacyjne: Wykład Zastosowanie kolorowania grafów w planowaniu produkcji typu no-idle
 Badania operacyjne: Wykład Zastosowanie kolorowania grafów w planowaniu produkcji typu no-idle Paweł Szołtysek 12 czerwca 2008 Streszczenie Planowanie produkcji jest jednym z problemów optymalizacji dyskretnej,
Badania operacyjne: Wykład Zastosowanie kolorowania grafów w planowaniu produkcji typu no-idle Paweł Szołtysek 12 czerwca 2008 Streszczenie Planowanie produkcji jest jednym z problemów optymalizacji dyskretnej,
Obliczenia ewolucyjne - plan wykładu
 Obliczenia ewolucyjne - plan wykładu Wprowadzenie Algorytmy genetyczne Programowanie genetyczne Programowanie ewolucyjne Strategie ewolucyjne Inne modele obliczeń ewolucyjnych Podsumowanie Ewolucja Ewolucja
Obliczenia ewolucyjne - plan wykładu Wprowadzenie Algorytmy genetyczne Programowanie genetyczne Programowanie ewolucyjne Strategie ewolucyjne Inne modele obliczeń ewolucyjnych Podsumowanie Ewolucja Ewolucja
