ZASTOSOWANIE ALGORYTMU GENETYCZNEGO DO KONSTRUKCJI
|
|
|
- Stefan Turek
- 8 lat temu
- Przeglądów:
Transkrypt
1 ZASTOSOWANIE ALGORYTMU GENETYCZNEGO DO KONSTRUKCJI FUNKCJI OCENIAJĄCEJ W GRZE OTHELLO Tomasz Dąbrowski, Halina Kwaśnicka, Maciej Piasecki Wydziałowy Zakład Informatyki, Politechnika Wrocławska, ul. Wybrzeże Wyspiańskiego 27, Wrocław {kwasnicka,piasecki}@ci.pwr.wroc.pl Typowym (choć nie jedynym) podejściem do projektowania gier logicznych jest tworzenie drzewa gry i szukanie optymalnego ruchu na podstawie oceny poszczególnych węzłów w drzewie. Do oceny węzłów (aktualnego stanu gry) stosuje się tzw. funckje oceniające. Dobór tych funkcji ma duże znaczenie dla programu grającego, dlatego też do optymalizacji tej funkcji stosuje się algorytm genetyczny. W pracy przedstawiono sposób tworzenia programu grającego w grę Othello, gdzie algorytm genetyczny dobiera zestaw wag w funkcji oceniającej. Omówiono uzyskane wyniki. 1 Algorytmy ewolucyjne w grach komputerowych Klasycznym wyzwaniem sztucznej inteligencji pozostaje od samego jej początku konstrukcja programów grających w gry logiczne. Mimo osiągniętych spektakularnych sukcesów (np. Deep Blue) zagadnienie ciągle jest na tyle trudne i ogólne, że może stanowić punkt odniesienia dla wypracowywanych rozwiązań. W niniejszej pracy przedstawiona została próba połączenia klasycznego algorytmu gier logicznych α-β obcinania z metodami ewolucyjnymi. Celem było sprawdzenie możliwości automatycznej konstrukcji funkcji oceniającej jedynego czysto heurystycznego elementu algorytmu α-β, całkowicie zależnego od rozpatrywanej gry. Gra jest to rywalizacja, prowadzona przez uczestników gry zgodnie z ustalonymi regułami, mająca na celu osiągnięcie wyznaczonego celu (lub celów). Są gry całkowicie losowe (np. ruletka), gry, w których jakiś element losowy wpływa na rozgrywkę (np. brydż) oraz gry całkowicie deterministyczne, jak np. warcaby czy szachy. Możliwe podejścia Gra rozpoczyna się od przyjęcia stanu początkowego, następnie gracze kolejno wykonują swoje posunięcia (podejmują decyzje), aż do osiągnięcia stanu końcowego. W każdym kroku rozgrywki gracze wykonują wybrane przez nich posunięcia spośród zbioru możliwych ruchów. Rozgrywkę można postrzegać jako poszukiwanie takich ruchów gracza, które zapewniają mu zwycięstwo. Taki proces poszukiwania można opisać za pomocą drzewa rozwiązań, którego korzeń jest stanem początkowym gry, a kolejne węzły są stanami, jakie będą aktualne po wykonaniu każdego ruchu spośród możliwych na danym etapie gry (Bolc, Cytowski, 1989). Potomkowie każdego z tych węzłów będą reprezentować stany gry po możliwych ruchach przeciwników. Liście takiego drzewa oznaczają stany końcowe gry: wygrane, remisowe lub przegrane dla gracza. Już dla dwóch graczy i stosunkowo prostej gry, drzewo takie jest bardzo duże: jest to reprezentacja wszystkich możliwych rozgrywek z danego stanu początkowego (dla warcabów jest to około węzłów, dla szachów ).
2 Strategia gry jest to określenie sekwencji posunięć gracza; strategia wygrywająca, to strategia doprowadzająca gracza do zwycięstwa, niezależnie od posunięć przeciwników. Znalezienie strategii wygrywającej wymagałoby zbudowania i przeszukania całego drzewa, co nie jest możliwe, z wyjątkiem bardzo prostych gier. Dlatego też stosuje się różne heurystyki do oceny aktualnego stanu gry i wyboru kolejnych posunięć, bez konieczności budowy całego drzewa. Jakość poszczególnych węzłów (stanów gry) szacuje się na podstawie wybranych cech charakteryzujących pozycje gry. Definiuje się funkcję wartościującą (oceniającą) poszczególne węzły. Do oszacowania węzłów trzeba wygenerować pewne poddrzewo gry, w którym za pomocą funkcji oceniającej szacujemy węzły na najgłębszym poziomie wygenerowanego drzewa. Pozostaje pytanie, jak głęboko w dół należy przeglądać drzewo. Z jednej strony, im głębiej program przegląda drzewo, tym większe szanse, że lepiej zostaną oszacowane węzły. Z drugiej strony, wydłuża to czas obliczeń, a gra powinna toczyć się w czasie rzeczywistym: komputer nie powinien myśleć zbyt długo. Człowiek grający np. w szachy czy warcaby ocenia przyszły układ na planszy (stan gry) decydując się na kolejny ruch. W jaki sposób dokonuje tej oceny? Na ile korzysta tu z intuicji i doświadczenia, bo przecież nie sprawdza drzewa rozwiązań ani nie przeprowadza obliczeń funkcji oceniającej, nawet jej nie definiuje. Dla komputera potrzebne jest jednoznaczne kryterium, według którego może on ocenić poszczególne układy na planszy. W tym celu buduje się właśnie funkcje oceniające. Budując taką funkcję należy brać pod uwagę specyfikę gry, wybrać cechy ważne dla strategii gry, (w warcabach może to być liczba pionków gracza i przeciwnika, w grze w kółko i krzyżyk może to być liczba rzędów, w których można ustawić trójkę, itp.). Z reguły funkcje oceniające dany stan gry mają postać ważonej sumy wartości wybranych cech, uznanych za istotne dla danej gry: gdzie: E = w1 C1 + w2 C w n C n, (1) E funkcja oceniająca konfigurację na planszy, C i i-ta cecha istotna dla strategii, w i waga oznaczająca wpływ i-tej cechy na ostateczną ocenę pozycji. Wyznaczając strategię gry dla programu zakłada się, że przeciwnik wykona najlepszy dla niego ruch. Aby nie przeglądać całego drzewa stosuje się różne algorytmy heurystyczne, np. algorytm cięć α-β (Bolc, 1989). Ostatnio, wraz ze wzrostem popularności algorytmów ewolucyjnych (EA) coraz częściej podejmowane są próby ich wykorzystania do tworzenia programów grających. Wyróżnić tu można dwa główne podejścia: Zastosowanie EA jako narzędzia wspomagającego proces szukania dobrej strategii gry (Goldberg, 1898). Program grający nie wykorzystuje algorytmu ewolucyjnego, ma wbudowaną znalezioną z pomocą EA strategię, która jest strategią programu. Przystosowanie osobników powinno odzwierciedlać wyniki, jakie uzyskuje dana strategia, bądź jakie uzyskuje się z zastosowaniem danego zestawu wag w prowadzonych rozgrywkach. Osobniki z populacji mogą prowadzić rozgrywki między sobą, można wykorzystać zewnętrznych trenerów, którymi może być dobrany odpowiednio zestaw programów grających lub/i ludzie.
3 Nasuwającym się wykorzystaniem EA jest konstrukcja odpowiedniej funkcji oceniającej ustawienie na planszy (stan gry). Można tu optymalizować wagi dla wybranego zestawu cech istotnych w danej grze. Do tego zadania nadaje się klasyczny algorytm genetyczny, zdefiniowanie problemu w terminach AG też nie powinno stwarzać problemów: chromosomem może być wektor wag, przystosowaniem zaś wyniki w rozgrywkach uzyskiwanych z zastosowaniem danego wektora wag. Inna możliwość, to zastosowanie programowania genetycznego do konstrukcji postaci funkcji oceniającej układ na planszy. W obu podejściach, pierwotny zestaw istotnych dla danej gry cech (C i ) musi być podany. Program grający wykorzystuje jedną z metod przeszukiwania drzewa rozwiązań, na przykład algorytm cięć α-β, a do oceny sytuacji na planszy (węzłów w drzewie) stosuje znalezioną przez EA funkcję oceniającą. Inne podejście, to zdefiniowanie chromosomu osobników jako potencjalnej strategii gry (Kozieja, 1997). Rozwiązanie dawane przez EA jest wprost strategią gry, która może być zaimplementowana w programie grającym. Taki program nie wymaga budowy drzewa rozwiązań ani żadnych heurystyk do oceny sytuacji na planszy. Podejście to wydaje się naturalne, aczkolwiek jest trudniejsze, ponieważ sama reprezentacja osobników może stwarzać trudności. Zastosowanie EA jako wbudowanego modułu do programu grającego, który na każdym etapie gry odpowiada za podjęcie optymalnej decyzji przez program grający (Nowicki 1992, Kot 1997). Zarówno w pierwszym podejściu, jak i w drugim, program może reprezentować kilku graczy, grających różnymi strategiami. 2 Gra OTHELLO Gra Othello w swojej koncepcji jest pochodną gier planszowych typu Go. Wybór Othello do eksperymentu był podyktowany jej dość skomplikowaną rozgrywką i brakiem dobrego algorytmu grającego. Głębokość całkowitego drzewa gry jest olbrzymia co powoduje, że jakość funkcji oceniającej staje się czynnikiem decydującym a b c d e f g h C A B B A C C A B B A C X X X C A B B A C Rysunek 1. Plansza do gry w Othello: start gry i charakterystyczne pola X C A B B A C Głównym celem gry jest zdobycie, jak największej liczby pionków. Gra jest rozgrywana na planszy 8 8 (Rysunek 1) za pomocą zbioru dwukolorowych pionków. Każdy z pionków jest czarny po jednej stronie i biały po drugiej. Gra rozpoczyna się w pozycji inicjującej przedstawionej na Rysunku 1. Grę rozpoczynają pionki czarne i jest ona kontynuowana tak długo, aż któryś z graczy nie może wykonać legalnego ruchu. Zwycięzcą jest gracz z większa liczbą pionków. Ruch jest wykonywany przez postawienie na planszy pionka kolorem gracza do góry. Ruch jest legalny gdy pole przed postawieniem jest puste oraz postawienie pionka umożliwia przejęcie jakiś pionków przeciwnika. Przejęcie pionków
4 następuje przez wzięcie ich w nawias w liniach prostych lub po przekątnych. Wzięcie w nawias może być zastosowane jedynie wobec ciągłej sekwencji (przynajmniej jeden) pionków przeciwnika. Przejmowane pionki zmieniają kolor stają się pionkami gracza wykonującego ruch. Dzięki tym zasadom gra charakteryzuje się dużą dynamika i niestabilnością sytuacji prawie do ostatniej chwili większość pionków może zmienić kolor co daje gwałtowną zmianę rezultatu rozgrywki. Specjalnego charakteru nabierają punkty brzegowe, które zajęte przez jednego z graczy dają mu oparcie np. nie do odebrania są punkty narożne. Z pobieżnej analizy gry wyłaniają się trzy podstawowe strategie. 1. Strategia maksymalnej liczby punktów prowadzi zwykle do blokady ruchów gracza. 2. Strategia ważonych pól uwzględniająca tzw. stabilność pola (związaną z jego położeniem na planszy pola A, B, C na Rysunku 1) oraz negatywny lub neutralny wpływ zajętości pól na rozgrywkę (pola X). 3. Strategia minimalnej liczby pionków gracz stosujący tą strategię dąży do minimalizacji ilości własnych pionków po to aby zwiększyć możliwości własnego ruchu strategia ślepo stosowana prowadzi do przegranej. Autorzy programów grających w Othello, uwzględniając zaprezentowane powyżej strategie podstawowe, rozszerzyli zbiór czynników mogących mieć wpływ na funkcję oceniającą. Lista zidentyfikowanych w literaturze czynników (np. Kai-Fu, 1990, Rosenbloom, 1982) jest długa jednak wykorzystanie niektórych z nich pociąga za sobą duży wzrost złożoności obliczeniowej. Ponadto niektóre czynniki w swoim działaniu się pokrywają. Do rozwiązania prezentowanego tutaj zostały wybrane następujące czynniki: C 1 liczba pionków obu graczy, C 2 liczba legalnych posunięć dla obu graczy, C 3 liczba pionków przeciwnika przyległych do pionków gracza, C 4 liczba pionków każdego z graczy przyległych do pola pustego (potencjalna ruchliwość), C 5 liczba pustych pól przyległych do pionków każdego z graczy. C 6 suma liczby pustych pól przyległych do pionków każdego z graczy (te same pola są liczone wielokrotnie dla poszczególnych pionków), C 7 liczba zajętych rogów przez pionki gracza, C 8 stabilność brzegowa (miara liczbowa wyliczona na podstawie zmodyfikowanych algorytmów (Kai-Fu, 1990, Rosenbloom, 1982). Cechy C 1 C 7 dają po dwie wartości po jednej dla gracza. Pojedyncza wartość wynikowa jest tworzona w nieliniowy sposób według wzoru: ( p q) gdzie p jest wartością dla pierwszego gracza a q dla drugiego. 100 C i =, (2) p + q Zastosowane metody i rozwiązania Rezygnując w pierwszym podejściu z szukania całej strategii rozgrywki za pomocą algorytmu genetycznego, skoncentrowano się na zastosowaniu algorytmu genetycznego jedynie do
5 znalezienia, jak najlepszej postaci funkcji oceniającej. Przyjmując powyższe osiem cech, funkcja oceniająca E wyraża się wzorem: gdzie: 8 E = w i C i, (3) i= 1 C i to miary liczbowe dla cech zidentyfikowanych, jako istotne dla rozgrywki, w i wagi określające udział każdej z cech w wynikowej wartości. Przyjmując to założenie, problem znalezienia jak najlepszej funkcji oceniającej sprowadza się do znalezienia wyznaczającego ją wektora wag w i. Wektor ten w prosty sposób można przekształcić w chromosom: każda waga została zakodowana w kodzie binarnym na 8 bitach, przyjmuje wartości z przedziału [ 127, 128], chromosom powstał przez konkatenację binarnych ciągów, porządek wag w chromosomie jest zgodny z wprowadzoną wcześniej numeracją cech. W implementacji algorytmu genetycznego funkcja przystosowania została wyliczona w oparciu o wyniki osiągane poprzez poszczególne osobniki w rozgrywce z programami trenującymi, gdzie pojedynczym osobnikiem jest implementacja algorytmu α-β wykorzystująca funkcję oceniającą zdefiniowaną poprzez genotyp. Wybór schematu uczenia z nauczycielem został podyktowany dużą złożonością obliczeniową alternatywnego podejścia bazującego na rozgrywce pomiędzy wszystkimi osobnikami w populacji. W wybranym podejściu jakość osiąganych rezultatów zależy od liczby i jakości programów trenujących (mniejsza liczba trenerów prowadzi do uczenia się przez osobniki ich słabych stron). Nie koliduje to jednak z głównym celem eksperymentu, jakim było sprawdzenie możliwości zastosowania analizowanej metody uczenia. Programy trenujące powinny zostać wybrane spośród najlepszych (co jednak nie warunkuje wyniku końcowego), zadecydowała niestety dostępności kodu poszczególnych programów. Tylko to umożliwiało automatyczne prowadzenie rozgrywek (których liczba sięgała setek dla każdej z populacji). Na wartość funkcji przystosowania składają się dwa elementy: rezultat rozgrywki: zwycięstwo, porażka, remis wyrażony poprzez premię punktową (w przypadku zwycięstwa i remisu), różnica w końcowej liczbie pionków. Konieczne było ustalenie wartości premii za wygraną na odpowiednio dużym poziomie w stosunku do maksymalnej możliwej różnicy pionków: np. przyjmując wartość premii za zwycięstwo 500, osobnik A na 10 rozgrywek ma 9 zwycięstw z wynikiem punktowym 64 : 0 i jedną porażką 31 : 33, co daje mu 5714 punktów; natomiast osobnik B ma 10 zwycięstw przewagą 2 punktową, daje mu to Wyraźnie widać, że premia 500 jest za niska aby zawsze premiować osobniki zwyciężające wszystkie swoje partie. Ostatecznie przyjęto wartość Każdy osobnik z populacji rozgrywał po dwa mecze z każdym z nauczycieli (zaczynając raz białymi a raz czarnymi pionkami). Następnie, po obliczeniu funkcji przystosowania, osobniki do reprodukcji były wybierane zgodnie z metodą wyboru wg reszt bez powtórzeń. Klasyczna metoda ruletki została odrzucona jako dająca zbyt dużą wariancję. Prawdopodobieństwo mutacji miało różną wartość dla różnych eksperymentów (patrz
6 następny rozdział). Poza mutacją i krzyżowaniem, z prawdopodobieństwem 0,6 dla wszystkich eksperymentów, nie zastosowane żadnego dalszego operatora. Ze względu na małą wielkość populacji (z powodu dużej złożoności obliczeniowej) zastosowano mechanizm regulacji liczby kopii poprzez użycie skalowania liniowego (Goldberg, 1989): f ' = a f + b, (4) gdzie f przystosowanie pierwotne, a f przystosowanie po przeskalowaniu. Współczynniki a i b zostały dobrane w taki sposób aby średnie przystosowanie nie uległo zmianie w wyniku skalowania oraz średnia liczba potomków o maksymalnym przystosowaniu była wielokrotnością średniego przystosowania pierwotnego f maks = C zw *f śr, gdzie wartość C zw została ustalona na 2. Wartość czynników składowych C i funkcji oceniającej jest bardzo zróżnicowana: waha się od ( 67, 67) dla C 7 do [ 3440, 3440] dla C 8. Aby zapewnić równomierny wpływ poszczególnych wag w i na funkcję oceniającą konieczna poddano normalizacji wartości czynników przed wyliczeniem wartości funkcji oceniającej. Dodatkowo, w końcowej fazie rozgrywki, w momencie osiągnięcia liścia drzewa gry jedyną miarą staje się różnica w ilości pionków [ 64, 64] relatywnie mała w stosunku do rozpiętości przedziału wartości funkcji oceniającej. Niezbędne było zastosowanie odpowiedniego rzutowania. Głębokość przeszukiwania drzewa gry zmieniała się w zależności od liczby pustych pól na planszy: od 3 do 5. Ponieważ nie są to wartości zbyt duże, jakość testowanych programów (osobników) zależała w dużej mierze od jakości funkcji oceniającej. 4 Eksperymenty Przeprowadzono 8 kolejnych eksperymentów z czego dwa ostanie dotyczyły uczenia na bazie rywalizacji wewnątrz populacji. Pierwszy zakończył się niepowodzeniem (brak zbieżności) z powodu oceny osobników tylko na podstawie końcowej różnicy liczby pionków oraz braku rzutowania wartości funkcji oceniającej dla liści. Eksperyment drugi: Liczba osobników = 100 Liczba pokoleń = 23 Liczba nauczycieli = 2 Prawdopodobieństwo mutacji = 0,01 Maksymalna możliwa ocena = 2512 Po poprawieniu błędów uzyskano postęp w uczeniu się widoczny na wykresie (Rysunek 2). Jednocześnie zaobserwowane zostało silne zróżnicowanie pomiędzy najlepszymi osobnikami: wśród zwycięskich osobników trudno było wyznaczyć jakieś typy wag. Prawdopodobnie, ze względu na niewielką liczbę nauczycieli i ich niską jakość, poszczególne osobniki nauczyły się wykorzystywać różne słabe strony nauczycieli. Zaobserwowane wahania w liczbie osobników wygrywających ze wszystkimi nauczycielami były spowodowane przyjętym w eksperymencie drugim zbyt dużym prawdopodobieństwem mutacji. W trzecim eksperymencie, startując z populacją osobników jak w eksperymencie drugim, zwiększono liczbę nauczycieli do 4 osiągając podobne rezultaty. W eksperymencie 4 została zastosowano inną metodę tworzenia nowego pokolenia: metodę ścisku De Jonga (Goldberg, 1989). Procent populacji podlegający reprodukcji został ustalony na 0,2, natomiast współczynnikowi ścisku nadano wartość 3. W rezultacie nastąpił szybki wzrost liczby osobników wygrywających wszystkie partie (10 osobników w 2 pokoleniu). Dalszy wzrost
7 tego wskaźnika był nieregularny i wolny, ale znacznie stabilniejszy w późniejszych pokoleniach (nie wykazujący takich wahnięć jak w eksperymentach 2 i 3). Wartość maksymalna funkcji przystosowania osiągnęła swoje maksimum (8949 co przy czterech nauczycielach oznaczało wysokie wygrane z każdym w każdej partii) w 11 pokoleniu, a następnie utrzymywała się prawie na stałym poziomie (wartość średnia wykazywała stałą tendencję wzrostową). maksymalne średnie Przystosowanie Pokolenie Rysunek 2. Wykres funkcji przystosowania (eksperyment 2) 60 Liczba osobników wygrywających Pokolenie Rysunek 3. Liczba osobników, które wygrały wszystkie rozgrywki z nauczycielami (eksperyment 2) W eksperymencie piątym radykalnie zmniejszono prawdopodobieństwo mutacji, do 0,0001 (w celu skrócenia czasu obliczeń ustalono rozmiar populacji na 30) co doprowadziło do szybkiej zbieżności oraz upodobnienia się osobników zwycięskich (po 36 pokoleniach populacja zawierała prawie identyczne wektory wag). Mimo to najlepszy osobnik z 30 pokolenia wygrywając ze wszystkimi nauczycielami stracił jedynie średnio po 10,5 pionka w grze. Ponowne zwiększenie mutacji w eksperymencie szóstym (do 0,001) doprowadziło znowu do większego zróżnicowania zwycięskich osobników. W eksperymentach siódmym i ósmym podjęto próbę zrealizowania schematu uczenia bez nauczyciela: osobniki rywalizowały wewnątrz populacji każdy z każdym po dwie gry. Przykładowe parametry symulacji to:
8 Liczba osobników = 30 Liczba pokoleń = 11 Prawdopodobieństwo mutacji = 0,0033 Maksymalna możliwa ocena = Niestety nie zaobserwowano tutaj postępu ani w wartości średniej, ani w maksymalnej. Przyczyn może być wiele, np. zbyt mała liczba pokoleń ze względu na długi czas obliczeń lub nieprzydatność stosowanej funkcji przystosowania do porównywania wyników osiąganych w kolejnych pokoleniach w zmieniającym się środowisku. 5 Podsumowanie Przeprowadzone eksperymenty wskazują na skuteczność algorytmów genetycznych w projektowaniu gier logicznych. Powyższe wyniki należy jednak uznać za etap wstępny, uzasadniający celowość kontynuacji prac. Zwłaszcza dotyczy to dwóch ostatnich eksperymentów. Wydaje się, że ewolucja populacji osobników konkurujących w rozgrywkach między sobą powinna produkować lepsze rozwiązania. Z całą pewnością liczba pokoleń jest tu zbyt mała, trudniej jest znaleźć strategię wygrywającą z dwudziestoma dziewięcioma innymi, na dodatek zmieniającymi się w czasie strategiami niż ze stałymi czterema zewnętrznymi trenerami. Korzystny stabilizujący efekt powinno tu dać założenie, że w każdym pokoleniu zmianie ulega jedynie część populacji. Interesujące byłoby porównanie wyników uzyskanych przy zastosowaniu programowania genetycznego zamiast współczynników liniowych produkowane byłyby dowolne funkcje wybranych cech. Podejście to dawałoby możliwość uwzględnienia większego zestawu cech i ewentualnej ich redukcji w trakcie ewolucji. Algorytmy ewolucyjne mogą być również stosowane do szukania całej strategii gry (Goldberg, 1989, Kozieja, 1997, Kwaśnicka, 1999). Stosunkowo trudnym etapem w tym podejściu jest zakodowanie strategii w postaci chromosomu. W szukaniu strategii dla gry menedżerskiej dobre efekty uzyskano gdy część chromosomu stanowił wektor wskaźników liczb rzeczywistych, a część drzewa definiujące funkcyjne zależności pomiędzy różnymi wielkościami. Tak zdefiniowane chromosomy wymagają zdefiniowania odpowiednich operatorów genetycznych. LITERATURA Rosenbloom P.S. (1982), A World-Championship-Level Othello Programm. Artificial Intelligence vol. 19. Kai-Fu Lee, Mahajan Sanjoy (1990), The Development of a World Class Othello Program. Artificial Intelligence vol. 43. Bolc L., Cytowski J. (1989), Metody przeszukiwania heurystycznego (tom I i II), PWN, Warszawa. Goldberg D.E., (1989), Genetic Algorithms in Search, Optimization, and Machine Learning, Addison-Wesley Publishing Company, Inc. Kozieja R. (1997), Zastosowanie algorytmów genetycznych w modelowaniu ekonomicznym: poszukiwanie optymalnej strategii gry kierowniczej, Praca magisterska, Wydziałowy Zakład Informatyki, PWr, Wrocław. Kot W. (1997), Konkurencja firm na rynku gra symulacyjna, Praca magisterska, Wydziałowy Zakład Informatyki, PWr, Wrocław. Kwaśnicka H. (1999), Obliczenia ewolucyjne w sztucznej inteligencji, praca niepublikowana, zgłoszona do wydania Oficynie Wydawniczej Politechniki Wrocławskiej. Nowicki A. (1992), Analiza możliwości wykorzystania ewolucyjnego modelu rozwoju przemysłu do modelowania postępu technicznego w symulacyjnej grze menedżerskiej, praca magisterska, Wydziałowy Zakład Informatyki, PWr, Wrocław.
Algorytm genetyczny (genetic algorithm)-
 Optymalizacja W praktyce inżynierskiej często zachodzi potrzeba znalezienia parametrów, dla których system/urządzenie będzie działać w sposób optymalny. Klasyczne podejście do optymalizacji: sformułowanie
Optymalizacja W praktyce inżynierskiej często zachodzi potrzeba znalezienia parametrów, dla których system/urządzenie będzie działać w sposób optymalny. Klasyczne podejście do optymalizacji: sformułowanie
Wyznaczanie strategii w grach
 Wyznaczanie strategii w grach Dariusz Banasiak Katedra Informatyki Technicznej W4/K9 Politechnika Wrocławska Definicja gry Teoria gier i konstruowane na jej podstawie programy stanowią jeden z głównych
Wyznaczanie strategii w grach Dariusz Banasiak Katedra Informatyki Technicznej W4/K9 Politechnika Wrocławska Definicja gry Teoria gier i konstruowane na jej podstawie programy stanowią jeden z głównych
Programowanie genetyczne, gra SNAKE
 STUDENCKA PRACOWNIA ALGORYTMÓW EWOLUCYJNYCH Tomasz Kupczyk, Tomasz Urbański Programowanie genetyczne, gra SNAKE II UWr Wrocław 2009 Spis treści 1. Wstęp 3 1.1. Ogólny opis.....................................
STUDENCKA PRACOWNIA ALGORYTMÓW EWOLUCYJNYCH Tomasz Kupczyk, Tomasz Urbański Programowanie genetyczne, gra SNAKE II UWr Wrocław 2009 Spis treści 1. Wstęp 3 1.1. Ogólny opis.....................................
Algorytmy genetyczne
 9 listopada 2010 y ewolucyjne - zbiór metod optymalizacji inspirowanych analogiami biologicznymi (ewolucja naturalna). Pojęcia odwzorowujące naturalne zjawiska: Osobnik Populacja Genotyp Fenotyp Gen Chromosom
9 listopada 2010 y ewolucyjne - zbiór metod optymalizacji inspirowanych analogiami biologicznymi (ewolucja naturalna). Pojęcia odwzorowujące naturalne zjawiska: Osobnik Populacja Genotyp Fenotyp Gen Chromosom
Tworzenie gier na urządzenia mobilne
 Katedra Inżynierii Wiedzy Teoria podejmowania decyzji w grze Gry w postaci ekstensywnej Inaczej gry w postaci drzewiastej, gry w postaci rozwiniętej; formalny opis wszystkich możliwych przebiegów gry z
Katedra Inżynierii Wiedzy Teoria podejmowania decyzji w grze Gry w postaci ekstensywnej Inaczej gry w postaci drzewiastej, gry w postaci rozwiniętej; formalny opis wszystkich możliwych przebiegów gry z
Algorytmy ewolucyjne NAZEWNICTWO
 Algorytmy ewolucyjne http://zajecia.jakubw.pl/nai NAZEWNICTWO Algorytmy ewolucyjne nazwa ogólna, obejmująca metody szczegółowe, jak np.: algorytmy genetyczne programowanie genetyczne strategie ewolucyjne
Algorytmy ewolucyjne http://zajecia.jakubw.pl/nai NAZEWNICTWO Algorytmy ewolucyjne nazwa ogólna, obejmująca metody szczegółowe, jak np.: algorytmy genetyczne programowanie genetyczne strategie ewolucyjne
Programowanie genetyczne - gra SNAKE
 PRACOWNIA Z ALGORYTMÓW EWOLUCYJNYCH Tomasz Kupczyk, Tomasz Urbański Programowanie genetyczne - gra SNAKE II UWr Wrocław 2009 Spis treści 1. Wstęp 3 1.1. Ogólny opis.....................................
PRACOWNIA Z ALGORYTMÓW EWOLUCYJNYCH Tomasz Kupczyk, Tomasz Urbański Programowanie genetyczne - gra SNAKE II UWr Wrocław 2009 Spis treści 1. Wstęp 3 1.1. Ogólny opis.....................................
SCHEMAT ROZWIĄZANIA ZADANIA OPTYMALIZACJI PRZY POMOCY ALGORYTMU GENETYCZNEGO
 SCHEMAT ROZWIĄZANIA ZADANIA OPTYMALIZACJI PRZY POMOCY ALGORYTMU GENETYCZNEGO. Rzeczywistość (istniejąca lub projektowana).. Model fizyczny. 3. Model matematyczny (optymalizacyjny): a. Zmienne projektowania
SCHEMAT ROZWIĄZANIA ZADANIA OPTYMALIZACJI PRZY POMOCY ALGORYTMU GENETYCZNEGO. Rzeczywistość (istniejąca lub projektowana).. Model fizyczny. 3. Model matematyczny (optymalizacyjny): a. Zmienne projektowania
Zadanie 5 - Algorytmy genetyczne (optymalizacja)
 Zadanie 5 - Algorytmy genetyczne (optymalizacja) Marcin Pietrzykowski mpietrzykowski@wi.zut.edu.pl wersja 1.0 1 Cel Celem zadania jest zapoznanie się z Algorytmami Genetycznymi w celu rozwiązywanie zadania
Zadanie 5 - Algorytmy genetyczne (optymalizacja) Marcin Pietrzykowski mpietrzykowski@wi.zut.edu.pl wersja 1.0 1 Cel Celem zadania jest zapoznanie się z Algorytmami Genetycznymi w celu rozwiązywanie zadania
Algorytm indukcji klasyfikatora za pomocą EA z automatycznym przełączaniem ukierunkowań
 Algorytm indukcji klasyfikatora za pomocą EA z automatycznym przełączaniem ukierunkowań Anna Manerowska, Michal Kozakiewicz 2.12.2009 1 Wstęp Jako projekt na przedmiot MEUM (Metody Ewolucyjne Uczenia Maszyn)
Algorytm indukcji klasyfikatora za pomocą EA z automatycznym przełączaniem ukierunkowań Anna Manerowska, Michal Kozakiewicz 2.12.2009 1 Wstęp Jako projekt na przedmiot MEUM (Metody Ewolucyjne Uczenia Maszyn)
Aproksymacja funkcji a regresja symboliczna
 Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(x), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(x), zwaną funkcją aproksymującą
Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(x), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(x), zwaną funkcją aproksymującą
Automatyczny dobór parametrów algorytmu genetycznego
 Automatyczny dobór parametrów algorytmu genetycznego Remigiusz Modrzejewski 22 grudnia 2008 Plan prezentacji Wstęp Atrakcyjność Pułapki Klasyfikacja Wstęp Atrakcyjność Pułapki Klasyfikacja Konstrukcja
Automatyczny dobór parametrów algorytmu genetycznego Remigiusz Modrzejewski 22 grudnia 2008 Plan prezentacji Wstęp Atrakcyjność Pułapki Klasyfikacja Wstęp Atrakcyjność Pułapki Klasyfikacja Konstrukcja
Algorytmy genetyczne
 Algorytmy genetyczne Motto: Zamiast pracowicie poszukiwać najlepszego rozwiązania problemu informatycznego lepiej pozwolić, żeby komputer sam sobie to rozwiązanie wyhodował! Algorytmy genetyczne służą
Algorytmy genetyczne Motto: Zamiast pracowicie poszukiwać najlepszego rozwiązania problemu informatycznego lepiej pozwolić, żeby komputer sam sobie to rozwiązanie wyhodował! Algorytmy genetyczne służą
Algorytmy genetyczne. Dariusz Banasiak. Katedra Informatyki Technicznej Wydział Elektroniki
 Dariusz Banasiak Katedra Informatyki Technicznej Wydział Elektroniki Obliczenia ewolucyjne (EC evolutionary computing) lub algorytmy ewolucyjne (EA evolutionary algorithms) to ogólne określenia używane
Dariusz Banasiak Katedra Informatyki Technicznej Wydział Elektroniki Obliczenia ewolucyjne (EC evolutionary computing) lub algorytmy ewolucyjne (EA evolutionary algorithms) to ogólne określenia używane
Obrona rozprawy doktorskiej Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
 IBS PAN, Warszawa 9 kwietnia 2008 Obrona rozprawy doktorskiej Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego mgr inż. Marcin Jaruszewicz promotor: dr hab. inż. Jacek Mańdziuk,
IBS PAN, Warszawa 9 kwietnia 2008 Obrona rozprawy doktorskiej Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego mgr inż. Marcin Jaruszewicz promotor: dr hab. inż. Jacek Mańdziuk,
Marcel Stankowski Wrocław, 23 czerwca 2009 INFORMATYKA SYSTEMÓW AUTONOMICZNYCH
 Marcel Stankowski Wrocław, 23 czerwca 2009 INFORMATYKA SYSTEMÓW AUTONOMICZNYCH Przeszukiwanie przestrzeni rozwiązań, szukanie na ślepo, wszerz, w głąb. Spis treści: 1. Wprowadzenie 3. str. 1.1 Krótki Wstęp
Marcel Stankowski Wrocław, 23 czerwca 2009 INFORMATYKA SYSTEMÓW AUTONOMICZNYCH Przeszukiwanie przestrzeni rozwiązań, szukanie na ślepo, wszerz, w głąb. Spis treści: 1. Wprowadzenie 3. str. 1.1 Krótki Wstęp
Algorytmy genetyczne
 Politechnika Łódzka Katedra Informatyki Stosowanej Algorytmy genetyczne Wykład 2 Przygotował i prowadzi: Dr inż. Piotr Urbanek Powtórzenie Pytania: Jaki mechanizm jest stosowany w naturze do takiego modyfikowania
Politechnika Łódzka Katedra Informatyki Stosowanej Algorytmy genetyczne Wykład 2 Przygotował i prowadzi: Dr inż. Piotr Urbanek Powtórzenie Pytania: Jaki mechanizm jest stosowany w naturze do takiego modyfikowania
Odkrywanie algorytmów kwantowych za pomocą programowania genetycznego
 Odkrywanie algorytmów kwantowych za pomocą programowania genetycznego Piotr Rybak Koło naukowe fizyków Migacz, Uniwersytet Wrocławski Piotr Rybak (Migacz UWr) Odkrywanie algorytmów kwantowych 1 / 17 Spis
Odkrywanie algorytmów kwantowych za pomocą programowania genetycznego Piotr Rybak Koło naukowe fizyków Migacz, Uniwersytet Wrocławski Piotr Rybak (Migacz UWr) Odkrywanie algorytmów kwantowych 1 / 17 Spis
Algorytmy ewolucyjne - algorytmy genetyczne. I. Karcz-Dulęba
 Algorytmy ewolucyjne - algorytmy genetyczne I. Karcz-Dulęba Algorytmy klasyczne a algorytmy ewolucyjne Przeszukiwanie przestrzeni przez jeden punkt bazowy Przeszukiwanie przestrzeni przez zbiór punktów
Algorytmy ewolucyjne - algorytmy genetyczne I. Karcz-Dulęba Algorytmy klasyczne a algorytmy ewolucyjne Przeszukiwanie przestrzeni przez jeden punkt bazowy Przeszukiwanie przestrzeni przez zbiór punktów
Zadania laboratoryjne i projektowe - wersja β
 Zadania laboratoryjne i projektowe - wersja β 1 Laboratorium Dwa problemy do wyboru (jeden do realizacji). 1. Water Jug Problem, 2. Wieże Hanoi. Water Jug Problem Ograniczenia dla każdej z wersji: pojemniki
Zadania laboratoryjne i projektowe - wersja β 1 Laboratorium Dwa problemy do wyboru (jeden do realizacji). 1. Water Jug Problem, 2. Wieże Hanoi. Water Jug Problem Ograniczenia dla każdej z wersji: pojemniki
Dobór parametrów algorytmu ewolucyjnego
 Dobór parametrów algorytmu ewolucyjnego 1 2 Wstęp Algorytm ewolucyjny posiada wiele parametrów. Przykładowo dla algorytmu genetycznego są to: prawdopodobieństwa stosowania operatorów mutacji i krzyżowania.
Dobór parametrów algorytmu ewolucyjnego 1 2 Wstęp Algorytm ewolucyjny posiada wiele parametrów. Przykładowo dla algorytmu genetycznego są to: prawdopodobieństwa stosowania operatorów mutacji i krzyżowania.
6. Klasyczny algorytm genetyczny. 1
 6. Klasyczny algorytm genetyczny. 1 Idea algorytmu genetycznego została zaczerpnięta z nauk przyrodniczych opisujących zjawiska doboru naturalnego i dziedziczenia. Mechanizmy te polegają na przetrwaniu
6. Klasyczny algorytm genetyczny. 1 Idea algorytmu genetycznego została zaczerpnięta z nauk przyrodniczych opisujących zjawiska doboru naturalnego i dziedziczenia. Mechanizmy te polegają na przetrwaniu
SYSTEMY UCZĄCE SIĘ WYKŁAD 10. PRZEKSZTAŁCANIE ATRYBUTÓW. Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska.
 SYSTEMY UCZĄCE SIĘ WYKŁAD 10. PRZEKSZTAŁCANIE ATRYBUTÓW Częstochowa 2014 Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska INFORMACJE WSTĘPNE Hipotezy do uczenia się lub tworzenia
SYSTEMY UCZĄCE SIĘ WYKŁAD 10. PRZEKSZTAŁCANIE ATRYBUTÓW Częstochowa 2014 Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska INFORMACJE WSTĘPNE Hipotezy do uczenia się lub tworzenia
Obliczenia ewolucyjne - plan wykładu
 Obliczenia ewolucyjne - plan wykładu Wprowadzenie Algorytmy genetyczne Programowanie genetyczne Programowanie ewolucyjne Strategie ewolucyjne Inne modele obliczeń ewolucyjnych Podsumowanie Ewolucja Ewolucja
Obliczenia ewolucyjne - plan wykładu Wprowadzenie Algorytmy genetyczne Programowanie genetyczne Programowanie ewolucyjne Strategie ewolucyjne Inne modele obliczeń ewolucyjnych Podsumowanie Ewolucja Ewolucja
Algorytmy ewolucyjne 1
 Algorytmy ewolucyjne 1 2 Zasady zaliczenia przedmiotu Prowadzący (wykład i pracownie specjalistyczną): Wojciech Kwedlo, pokój 205. Konsultacje dla studentów studiów dziennych: poniedziałek,środa, godz
Algorytmy ewolucyjne 1 2 Zasady zaliczenia przedmiotu Prowadzący (wykład i pracownie specjalistyczną): Wojciech Kwedlo, pokój 205. Konsultacje dla studentów studiów dziennych: poniedziałek,środa, godz
Algorytm Genetyczny. zastosowanie do procesów rozmieszczenia stacji raportujących w sieciach komórkowych
 Algorytm Genetyczny zastosowanie do procesów rozmieszczenia stacji raportujących w sieciach komórkowych Dlaczego Algorytmy Inspirowane Naturą? Rozwój nowych technologii: złożone problemy obliczeniowe w
Algorytm Genetyczny zastosowanie do procesów rozmieszczenia stacji raportujących w sieciach komórkowych Dlaczego Algorytmy Inspirowane Naturą? Rozwój nowych technologii: złożone problemy obliczeniowe w
Program "FLiNN-GA" wersja 2.10.β
 POLSKIE TOWARZYSTWO SIECI NEURONOWYCH POLITECHNIKA CZĘSTOCHOWSKA Zakład Elektroniki, Informatyki i Automatyki Maciej Piliński Robert Nowicki - GA Program "FLiNN-GA" wersja 2.10.β Podręcznik użytkownika
POLSKIE TOWARZYSTWO SIECI NEURONOWYCH POLITECHNIKA CZĘSTOCHOWSKA Zakład Elektroniki, Informatyki i Automatyki Maciej Piliński Robert Nowicki - GA Program "FLiNN-GA" wersja 2.10.β Podręcznik użytkownika
LABORATORIUM 4: Algorytmy ewolucyjne cz. 2 wpływ operatorów krzyżowania i mutacji na skuteczność poszukiwań AE
 Instytut Mechaniki i Inżynierii Obliczeniowej Wydział Mechaniczny Technologiczny, Politechnika Śląska www.imio.polsl.pl METODY HEURYSTYCZNE LABORATORIUM 4: Algorytmy ewolucyjne cz. 2 wpływ operatorów krzyżowania
Instytut Mechaniki i Inżynierii Obliczeniowej Wydział Mechaniczny Technologiczny, Politechnika Śląska www.imio.polsl.pl METODY HEURYSTYCZNE LABORATORIUM 4: Algorytmy ewolucyjne cz. 2 wpływ operatorów krzyżowania
ALGORYTMY GENETYCZNE (wykład + ćwiczenia)
 ALGORYTMY GENETYCZNE (wykład + ćwiczenia) Prof. dr hab. Krzysztof Dems Treści programowe: 1. Metody rozwiązywania problemów matematycznych i informatycznych.. Elementarny algorytm genetyczny: definicja
ALGORYTMY GENETYCZNE (wykład + ćwiczenia) Prof. dr hab. Krzysztof Dems Treści programowe: 1. Metody rozwiązywania problemów matematycznych i informatycznych.. Elementarny algorytm genetyczny: definicja
w analizie wyników badań eksperymentalnych, w problemach modelowania zjawisk fizycznych, w analizie obserwacji statystycznych.
 Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(), zwaną funkcją aproksymującą
Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(), zwaną funkcją aproksymującą
Algorytmy genetyczne. Materiały do laboratorium PSI. Studia niestacjonarne
 Algorytmy genetyczne Materiały do laboratorium PSI Studia niestacjonarne Podstawowy algorytm genetyczny (PAG) Schemat blokowy algorytmu genetycznego Znaczenia, pochodzących z biologii i genetyki, pojęć
Algorytmy genetyczne Materiały do laboratorium PSI Studia niestacjonarne Podstawowy algorytm genetyczny (PAG) Schemat blokowy algorytmu genetycznego Znaczenia, pochodzących z biologii i genetyki, pojęć
3. MINIMAX. Rysunek 1: Drzewo obrazujące przebieg gry.
 3. MINIMAX. Bardzo wygodną strukturą danych pozwalającą reprezentować stan i przebieg gry (szczególnie gier dwuosobowych) jest drzewo. Węzły drzewa reprezentują stan gry po wykonaniu ruchu przez jednego
3. MINIMAX. Bardzo wygodną strukturą danych pozwalającą reprezentować stan i przebieg gry (szczególnie gier dwuosobowych) jest drzewo. Węzły drzewa reprezentują stan gry po wykonaniu ruchu przez jednego
SYSTEMY UCZĄCE SIĘ WYKŁAD 4. DRZEWA REGRESYJNE, INDUKCJA REGUŁ. Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska
 SYSTEMY UCZĄCE SIĘ WYKŁAD 4. DRZEWA REGRESYJNE, INDUKCJA REGUŁ Częstochowa 2014 Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska DRZEWO REGRESYJNE Sposób konstrukcji i przycinania
SYSTEMY UCZĄCE SIĘ WYKŁAD 4. DRZEWA REGRESYJNE, INDUKCJA REGUŁ Częstochowa 2014 Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska DRZEWO REGRESYJNE Sposób konstrukcji i przycinania
Algorytmy decyzyjne będące alternatywą dla sieci neuronowych
 Algorytmy decyzyjne będące alternatywą dla sieci neuronowych Piotr Dalka Przykładowe algorytmy decyzyjne Sztuczne sieci neuronowe Algorytm k najbliższych sąsiadów Kaskada klasyfikatorów AdaBoost Naiwny
Algorytmy decyzyjne będące alternatywą dla sieci neuronowych Piotr Dalka Przykładowe algorytmy decyzyjne Sztuczne sieci neuronowe Algorytm k najbliższych sąsiadów Kaskada klasyfikatorów AdaBoost Naiwny
Algorytmy dla gier dwuosobowych
 Algorytmy dla gier dwuosobowych Wojciech Dudek Seminarium Nowości Komputerowe 5 czerwca 2008 Plan prezentacji Pojęcia wstępne (gry dwuosobowe, stan gry, drzewo gry) Algorytm MiniMax Funkcje oceniające
Algorytmy dla gier dwuosobowych Wojciech Dudek Seminarium Nowości Komputerowe 5 czerwca 2008 Plan prezentacji Pojęcia wstępne (gry dwuosobowe, stan gry, drzewo gry) Algorytm MiniMax Funkcje oceniające
Propozycje tematów zadań
 Propozycje tematów zadań 1. WARCABY Opracować program do gry w warcaby dla dwu graczy. Program ma umożliwiać przesuwanie kursora na zmianę po polach białych lub czarnych, wskazywanie początku końca ruchu.
Propozycje tematów zadań 1. WARCABY Opracować program do gry w warcaby dla dwu graczy. Program ma umożliwiać przesuwanie kursora na zmianę po polach białych lub czarnych, wskazywanie początku końca ruchu.
METODY SZTUCZNEJ INTELIGENCJI 2 Opis projektu
 Kamil Figura Krzysztof Kaliński Bartek Kutera METODY SZTUCZNEJ INTELIGENCJI 2 Opis projektu Porównanie metod uczenia z rodziny TD z algorytmem Layered Learning na przykładzie gry w warcaby i gry w anty-warcaby
Kamil Figura Krzysztof Kaliński Bartek Kutera METODY SZTUCZNEJ INTELIGENCJI 2 Opis projektu Porównanie metod uczenia z rodziny TD z algorytmem Layered Learning na przykładzie gry w warcaby i gry w anty-warcaby
Metody przeszukiwania
 Metody przeszukiwania Co to jest przeszukiwanie Przeszukiwanie polega na odnajdywaniu rozwiązania w dyskretnej przestrzeni rozwiązao. Zwykle przeszukiwanie polega na znalezieniu określonego rozwiązania
Metody przeszukiwania Co to jest przeszukiwanie Przeszukiwanie polega na odnajdywaniu rozwiązania w dyskretnej przestrzeni rozwiązao. Zwykle przeszukiwanie polega na znalezieniu określonego rozwiązania
Optymalizacja ciągła
 Optymalizacja ciągła 5. Metoda stochastycznego spadku wzdłuż gradientu Wojciech Kotłowski Instytut Informatyki PP http://www.cs.put.poznan.pl/wkotlowski/ 04.04.2019 1 / 20 Wprowadzenie Minimalizacja różniczkowalnej
Optymalizacja ciągła 5. Metoda stochastycznego spadku wzdłuż gradientu Wojciech Kotłowski Instytut Informatyki PP http://www.cs.put.poznan.pl/wkotlowski/ 04.04.2019 1 / 20 Wprowadzenie Minimalizacja różniczkowalnej
Uniwersytet Zielonogórski Wydział Elektrotechniki, Informatyki i Telekomunikacji Instytut Sterowania i Systemów Informatycznych
 Uniwersytet Zielonogórski Wydział Elektrotechniki, Informatyki i Telekomunikacji Instytut Sterowania i Systemów Informatycznych ELEMENTY SZTUCZNEJ INTELIGENCJI Laboratorium nr 9 PRZESZUKIWANIE GRAFÓW Z
Uniwersytet Zielonogórski Wydział Elektrotechniki, Informatyki i Telekomunikacji Instytut Sterowania i Systemów Informatycznych ELEMENTY SZTUCZNEJ INTELIGENCJI Laboratorium nr 9 PRZESZUKIWANIE GRAFÓW Z
Algorytmy genetyczne. Paweł Cieśla. 8 stycznia 2009
 Algorytmy genetyczne Paweł Cieśla 8 stycznia 2009 Genetyka - nauka o dziedziczeniu cech pomiędzy pokoleniami. Geny są czynnikami, które decydują o wyglądzie, zachowaniu, rozmnażaniu każdego żywego organizmu.
Algorytmy genetyczne Paweł Cieśla 8 stycznia 2009 Genetyka - nauka o dziedziczeniu cech pomiędzy pokoleniami. Geny są czynnikami, które decydują o wyglądzie, zachowaniu, rozmnażaniu każdego żywego organizmu.
Standardowy algorytm genetyczny
 Standardowy algorytm genetyczny 1 Szybki przegląd 2 Opracowany w USA w latach 70. Wcześni badacze: John H. Holland. Autor monografii Adaptation in Natural and Artificial Systems, wydanej w 1975 r., (teoria
Standardowy algorytm genetyczny 1 Szybki przegląd 2 Opracowany w USA w latach 70. Wcześni badacze: John H. Holland. Autor monografii Adaptation in Natural and Artificial Systems, wydanej w 1975 r., (teoria
Algorytmy genetyczne. Materiały do laboratorium PSI. Studia stacjonarne i niestacjonarne
 Algorytmy genetyczne Materiały do laboratorium PSI Studia stacjonarne i niestacjonarne Podstawowy algorytm genetyczny (PAG) Schemat blokowy algorytmu genetycznego Znaczenia, pochodzących z biologii i genetyki,
Algorytmy genetyczne Materiały do laboratorium PSI Studia stacjonarne i niestacjonarne Podstawowy algorytm genetyczny (PAG) Schemat blokowy algorytmu genetycznego Znaczenia, pochodzących z biologii i genetyki,
Adam Meissner. SZTUCZNA INTELIGENCJA Gry dwuosobowe
 Instytut Automatyki i Inżynierii Informatycznej Politechniki Poznańskiej Adam Meissner Adam.Meissner@put.poznan.pl http://www.man.poznan.pl/~ameis SZTUCZNA INTELIGENCJA Gry dwuosobowe Literatura [1] Sterling
Instytut Automatyki i Inżynierii Informatycznej Politechniki Poznańskiej Adam Meissner Adam.Meissner@put.poznan.pl http://www.man.poznan.pl/~ameis SZTUCZNA INTELIGENCJA Gry dwuosobowe Literatura [1] Sterling
operacje porównania, a jeśli jest to konieczne ze względu na złe uporządkowanie porównywanych liczb zmieniamy ich kolejność, czyli przestawiamy je.
 Problem porządkowania zwanego również sortowaniem jest jednym z najważniejszych i najpopularniejszych zagadnień informatycznych. Dane: Liczba naturalna n i ciąg n liczb x 1, x 2,, x n. Wynik: Uporządkowanie
Problem porządkowania zwanego również sortowaniem jest jednym z najważniejszych i najpopularniejszych zagadnień informatycznych. Dane: Liczba naturalna n i ciąg n liczb x 1, x 2,, x n. Wynik: Uporządkowanie
ALGORYTMY GENETYCZNE ćwiczenia
 ćwiczenia Wykorzystaj algorytmy genetyczne do wyznaczenia minimum globalnego funkcji testowej: 1. Wylosuj dwuwymiarową tablicę 100x2 liczb 8-bitowych z zakresu [-100; +100] reprezentujących inicjalną populację
ćwiczenia Wykorzystaj algorytmy genetyczne do wyznaczenia minimum globalnego funkcji testowej: 1. Wylosuj dwuwymiarową tablicę 100x2 liczb 8-bitowych z zakresu [-100; +100] reprezentujących inicjalną populację
Algorytmy stochastyczne, wykład 01 Podstawowy algorytm genetyczny
 Algorytmy stochastyczne, wykład 01 J. Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2014-02-21 In memoriam prof. dr hab. Tomasz Schreiber (1975-2010) 1 2 3 Różne Orientacyjny
Algorytmy stochastyczne, wykład 01 J. Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2014-02-21 In memoriam prof. dr hab. Tomasz Schreiber (1975-2010) 1 2 3 Różne Orientacyjny
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: Kierunek: Informatyka Rodzaj przedmiotu: obowiązkowy w ramach treści kierunkowych, moduł kierunkowy oólny Rodzaj zajęć: wykład, laboratorium I KARTA PRZEDMIOTU CEL PRZEDMIOTU PRZEWODNIK
Nazwa przedmiotu: Kierunek: Informatyka Rodzaj przedmiotu: obowiązkowy w ramach treści kierunkowych, moduł kierunkowy oólny Rodzaj zajęć: wykład, laboratorium I KARTA PRZEDMIOTU CEL PRZEDMIOTU PRZEWODNIK
Wstęp do Sztucznej Inteligencji
 Wstęp do Sztucznej Inteligencji Algorytmy Genetyczne Joanna Kołodziej Politechnika Krakowska Wydział Fizyki, Matematyki i Informatyki Metody heurystyczne Algorytm efektywny: koszt zastosowania (mierzony
Wstęp do Sztucznej Inteligencji Algorytmy Genetyczne Joanna Kołodziej Politechnika Krakowska Wydział Fizyki, Matematyki i Informatyki Metody heurystyczne Algorytm efektywny: koszt zastosowania (mierzony
Algorytmy genetyczne w optymalizacji
 Algorytmy genetyczne w optymalizacji Literatura 1. David E. Goldberg, Algorytmy genetyczne i ich zastosowania, WNT, Warszawa 1998; 2. Zbigniew Michalewicz, Algorytmy genetyczne + struktury danych = programy
Algorytmy genetyczne w optymalizacji Literatura 1. David E. Goldberg, Algorytmy genetyczne i ich zastosowania, WNT, Warszawa 1998; 2. Zbigniew Michalewicz, Algorytmy genetyczne + struktury danych = programy
Algorytmy ewolucyjne (3)
 Algorytmy ewolucyjne (3) http://zajecia.jakubw.pl/nai KODOWANIE PERMUTACJI W pewnych zastosowaniach kodowanie binarne jest mniej naturalne, niż inne sposoby kodowania. Na przykład, w problemie komiwojażera
Algorytmy ewolucyjne (3) http://zajecia.jakubw.pl/nai KODOWANIE PERMUTACJI W pewnych zastosowaniach kodowanie binarne jest mniej naturalne, niż inne sposoby kodowania. Na przykład, w problemie komiwojażera
Algorytmy genetyczne w interpolacji wielomianowej
 Algorytmy genetyczne w interpolacji wielomianowej (seminarium robocze) Seminarium Metod Inteligencji Obliczeniowej Warszawa 22 II 2006 mgr inż. Marcin Borkowski Plan: Przypomnienie algorytmu niszowego
Algorytmy genetyczne w interpolacji wielomianowej (seminarium robocze) Seminarium Metod Inteligencji Obliczeniowej Warszawa 22 II 2006 mgr inż. Marcin Borkowski Plan: Przypomnienie algorytmu niszowego
PLAN WYKŁADU OPTYMALIZACJA GLOBALNA OPERATOR KRZYŻOWANIA ETAPY KRZYŻOWANIA
 PLAN WYKŁADU Operator krzyżowania Operator mutacji Operator inwersji Sukcesja Przykłady symulacji AG Kodowanie - rodzaje OPTYMALIZACJA GLOBALNA Wykład 3 dr inż. Agnieszka Bołtuć OPERATOR KRZYŻOWANIA Wymiana
PLAN WYKŁADU Operator krzyżowania Operator mutacji Operator inwersji Sukcesja Przykłady symulacji AG Kodowanie - rodzaje OPTYMALIZACJA GLOBALNA Wykład 3 dr inż. Agnieszka Bołtuć OPERATOR KRZYŻOWANIA Wymiana
Równoważność algorytmów optymalizacji
 Równoważność algorytmów optymalizacji Reguła nie ma nic za darmo (ang. no free lunch theory): efektywność różnych typowych algorytmów szukania uśredniona po wszystkich możliwych problemach optymalizacyjnych
Równoważność algorytmów optymalizacji Reguła nie ma nic za darmo (ang. no free lunch theory): efektywność różnych typowych algorytmów szukania uśredniona po wszystkich możliwych problemach optymalizacyjnych
Generowanie i optymalizacja harmonogramu za pomoca
 Generowanie i optymalizacja harmonogramu za pomoca na przykładzie generatora planu zajęć Matematyka Stosowana i Informatyka Stosowana Wydział Fizyki Technicznej i Matematyki Stosowanej Politechnika Gdańska
Generowanie i optymalizacja harmonogramu za pomoca na przykładzie generatora planu zajęć Matematyka Stosowana i Informatyka Stosowana Wydział Fizyki Technicznej i Matematyki Stosowanej Politechnika Gdańska
Partition Search i gry z niezupełną informacją
 MIMUW 21 stycznia 2010 1 Co to jest gra? Proste algorytmy 2 Pomysł Algorytm Przykład użycia 3 Monte Carlo Inne spojrzenie Definicja Co to jest gra? Proste algorytmy Grą o wartościach w przedziale [0, 1]
MIMUW 21 stycznia 2010 1 Co to jest gra? Proste algorytmy 2 Pomysł Algorytm Przykład użycia 3 Monte Carlo Inne spojrzenie Definicja Co to jest gra? Proste algorytmy Grą o wartościach w przedziale [0, 1]
Katedra Informatyki Stosowanej. Algorytmy ewolucyjne. Inteligencja obliczeniowa
 Wydział Zarządzania AGH Katedra Informatyki Stosowanej Algorytmy ewolucyjne Treść wykładu Wprowadzenie Zasada działania Podział EA Cechy EA Algorytm genetyczny 2 EA - wprowadzenie Algorytmy ewolucyjne
Wydział Zarządzania AGH Katedra Informatyki Stosowanej Algorytmy ewolucyjne Treść wykładu Wprowadzenie Zasada działania Podział EA Cechy EA Algorytm genetyczny 2 EA - wprowadzenie Algorytmy ewolucyjne
Alfa-beta Ulepszenie minimax Liczba wierzchołk ow w drzewie gry. maksymalnie wd. minimalnie wbd/2c + wdd/2e Algorytmy przeszukiwania drzewa gry 5
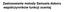 Zastosowanie metody Samuela doboru współczynników funkcji oceniajacej w programie grajacym w anty-warcaby Daniel Osman promotor: dr hab. inż. Jacek Mańdziuk 1 Spis treści Algorytmy przeszukiwania drzewa
Zastosowanie metody Samuela doboru współczynników funkcji oceniajacej w programie grajacym w anty-warcaby Daniel Osman promotor: dr hab. inż. Jacek Mańdziuk 1 Spis treści Algorytmy przeszukiwania drzewa
Instrukcja obsługi programu
 Instrukcja obsługi programu 1. Wstęp Korzystając z aplikacji Reversi.NET moŝesz grać w grę Reversi (alt. Othello). Program pozwala na grę pomiędzy dwiema osobami uŝywającymi tego samego komputera, poprzez
Instrukcja obsługi programu 1. Wstęp Korzystając z aplikacji Reversi.NET moŝesz grać w grę Reversi (alt. Othello). Program pozwala na grę pomiędzy dwiema osobami uŝywającymi tego samego komputera, poprzez
Optymalizacja. Wybrane algorytmy
 dr hab. inż. Instytut Informatyki Politechnika Poznańska www.cs.put.poznan.pl/mkomosinski, Andrzej Jaszkiewicz Problem optymalizacji kombinatorycznej Problem optymalizacji kombinatorycznej jest problemem
dr hab. inż. Instytut Informatyki Politechnika Poznańska www.cs.put.poznan.pl/mkomosinski, Andrzej Jaszkiewicz Problem optymalizacji kombinatorycznej Problem optymalizacji kombinatorycznej jest problemem
Wybrane podstawowe rodzaje algorytmów
 Wybrane podstawowe rodzaje algorytmów Tomasz Głowacki tglowacki@cs.put.poznan.pl Zajęcia finansowane z projektu "Rozwój i doskonalenie kształcenia na Politechnice Poznańskiej w zakresie technologii informatycznych
Wybrane podstawowe rodzaje algorytmów Tomasz Głowacki tglowacki@cs.put.poznan.pl Zajęcia finansowane z projektu "Rozwój i doskonalenie kształcenia na Politechnice Poznańskiej w zakresie technologii informatycznych
Strategie ewolucyjne (ang. evolu4on strategies)
 Strategie ewolucyjne (ang. evolu4on strategies) Strategia ewolucyjna (1+1) W Strategii Ewolucyjnej(1 + 1), populacja złożona z jednego osobnika generuje jednego potomka. Kolejne (jednoelementowe) populacje
Strategie ewolucyjne (ang. evolu4on strategies) Strategia ewolucyjna (1+1) W Strategii Ewolucyjnej(1 + 1), populacja złożona z jednego osobnika generuje jednego potomka. Kolejne (jednoelementowe) populacje
Programowanie celowe #1
 Programowanie celowe #1 Problem programowania celowego (PC) jest przykładem problemu programowania matematycznego nieliniowego, który można skutecznie zlinearyzować, tzn. zapisać (i rozwiązać) jako problem
Programowanie celowe #1 Problem programowania celowego (PC) jest przykładem problemu programowania matematycznego nieliniowego, który można skutecznie zlinearyzować, tzn. zapisać (i rozwiązać) jako problem
Algorytmy ewolucyjne `
 Algorytmy ewolucyjne ` Wstęp Czym są algorytmy ewolucyjne? Rodzaje algorytmów ewolucyjnych Algorytmy genetyczne Strategie ewolucyjne Programowanie genetyczne Zarys historyczny Alan Turing, 1950 Nils Aall
Algorytmy ewolucyjne ` Wstęp Czym są algorytmy ewolucyjne? Rodzaje algorytmów ewolucyjnych Algorytmy genetyczne Strategie ewolucyjne Programowanie genetyczne Zarys historyczny Alan Turing, 1950 Nils Aall
Maciej Piotr Jankowski
 Reduced Adder Graph Implementacja algorytmu RAG Maciej Piotr Jankowski 2005.12.22 Maciej Piotr Jankowski 1 Plan prezentacji 1. Wstęp 2. Implementacja 3. Usprawnienia optymalizacyjne 3.1. Tablica ekspansji
Reduced Adder Graph Implementacja algorytmu RAG Maciej Piotr Jankowski 2005.12.22 Maciej Piotr Jankowski 1 Plan prezentacji 1. Wstęp 2. Implementacja 3. Usprawnienia optymalizacyjne 3.1. Tablica ekspansji
Algorytmy genetyczne jako metoda wyszukiwania wzorców. Seminarium Metod Inteligencji Obliczeniowej Warszawa 26 X 2005 mgr inż.
 Algorytmy genetyczne jako metoda wyszukiwania wzorców Seminarium Metod Inteligencji Obliczeniowej Warszawa 26 X 2005 mgr inż. Marcin Borkowski Krótko i na temat: Cel pracy Opis modyfikacji AG Zastosowania
Algorytmy genetyczne jako metoda wyszukiwania wzorców Seminarium Metod Inteligencji Obliczeniowej Warszawa 26 X 2005 mgr inż. Marcin Borkowski Krótko i na temat: Cel pracy Opis modyfikacji AG Zastosowania
Instrukcje dla zawodników
 Instrukcje dla zawodników Nie otwieraj arkusza z zadaniami dopóki nie zostaniesz o to poproszony. Instrukcje poniżej zostaną ci odczytane i wyjaśnione. 1. Arkusz składa się z 3 zadań. 2. Każde zadanie
Instrukcje dla zawodników Nie otwieraj arkusza z zadaniami dopóki nie zostaniesz o to poproszony. Instrukcje poniżej zostaną ci odczytane i wyjaśnione. 1. Arkusz składa się z 3 zadań. 2. Każde zadanie
KARTA MODUŁU KSZTAŁCENIA
 KARTA MODUŁU KSZTAŁCENIA I. Informacje ogólne 1 Nazwa modułu kształcenia Sztuczna inteligencja 2 Nazwa jednostki prowadzącej moduł Instytut Informatyki, Zakład Informatyki Stosowanej 3 Kod modułu (wypełnia
KARTA MODUŁU KSZTAŁCENIA I. Informacje ogólne 1 Nazwa modułu kształcenia Sztuczna inteligencja 2 Nazwa jednostki prowadzącej moduł Instytut Informatyki, Zakład Informatyki Stosowanej 3 Kod modułu (wypełnia
Algorytmy memetyczne (hybrydowe algorytmy ewolucyjne)
 Algorytmy memetyczne (hybrydowe algorytmy ewolucyjne) 1 2 Wstęp Termin zaproponowany przez Pablo Moscato (1989). Kombinacja algorytmu ewolucyjnego z algorytmem poszukiwań lokalnych, tak że algorytm poszukiwań
Algorytmy memetyczne (hybrydowe algorytmy ewolucyjne) 1 2 Wstęp Termin zaproponowany przez Pablo Moscato (1989). Kombinacja algorytmu ewolucyjnego z algorytmem poszukiwań lokalnych, tak że algorytm poszukiwań
Metody teorii gier. ALP520 - Wykład z Algorytmów Probabilistycznych p.2
 Metody teorii gier ALP520 - Wykład z Algorytmów Probabilistycznych p.2 Metody teorii gier Cel: Wyprowadzenie oszacowania dolnego na oczekiwany czas działania dowolnego algorytmu losowego dla danego problemu.
Metody teorii gier ALP520 - Wykład z Algorytmów Probabilistycznych p.2 Metody teorii gier Cel: Wyprowadzenie oszacowania dolnego na oczekiwany czas działania dowolnego algorytmu losowego dla danego problemu.
Algorytmy stochastyczne, wykład 02 Algorytmy genetyczne
 Algorytmy stochastyczne, wykład 02 Algorytmy genetyczne J. Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2014-02-27 1 Mutacje algorytmu genetycznego 2 Dziedzina niewypukła abstrakcyjna
Algorytmy stochastyczne, wykład 02 Algorytmy genetyczne J. Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2014-02-27 1 Mutacje algorytmu genetycznego 2 Dziedzina niewypukła abstrakcyjna
Modelowanie jako sposób opisu rzeczywistości. Katedra Mikroelektroniki i Technik Informatycznych Politechnika Łódzka
 Modelowanie jako sposób opisu rzeczywistości Katedra Mikroelektroniki i Technik Informatycznych Politechnika Łódzka 2015 Wprowadzenie: Modelowanie i symulacja PROBLEM: Podstawowy problem z opisem otaczającej
Modelowanie jako sposób opisu rzeczywistości Katedra Mikroelektroniki i Technik Informatycznych Politechnika Łódzka 2015 Wprowadzenie: Modelowanie i symulacja PROBLEM: Podstawowy problem z opisem otaczającej
ATOLL. Wykonali: Aleksandra Kuchta, Łukasz Wójcik, Sztuczna Inteligencja, Semestr trzeci, Kierunek Informatyka, Wydział Informatyki i Zarządzania,
 Sztuczna Inteligencja, Semestr trzeci, Kierunek Informatyka, Wydział Informatyki i Zarządzania, Politechnika Poznańska ATOLL Wykonali: Aleksandra Kuchta, WFT, PP, nr 76690, rok IV Łukasz Wójcik, WIiZ,
Sztuczna Inteligencja, Semestr trzeci, Kierunek Informatyka, Wydział Informatyki i Zarządzania, Politechnika Poznańska ATOLL Wykonali: Aleksandra Kuchta, WFT, PP, nr 76690, rok IV Łukasz Wójcik, WIiZ,
Systemy uczące się Lab 4
 Systemy uczące się Lab 4 dr Przemysław Juszczuk Katedra Inżynierii Wiedzy, Uniwersytet Ekonomiczny 26 X 2018 Projekt zaliczeniowy Podstawą zaliczenia ćwiczeń jest indywidualne wykonanie projektu uwzględniającego
Systemy uczące się Lab 4 dr Przemysław Juszczuk Katedra Inżynierii Wiedzy, Uniwersytet Ekonomiczny 26 X 2018 Projekt zaliczeniowy Podstawą zaliczenia ćwiczeń jest indywidualne wykonanie projektu uwzględniającego
Algorytmy sztucznej inteligencji
 www.math.uni.lodz.pl/ radmat Przeszukiwanie z ograniczeniami Zagadnienie przeszukiwania z ograniczeniami stanowi grupę problemów przeszukiwania w przestrzeni stanów, które składa się ze: 1 skończonego
www.math.uni.lodz.pl/ radmat Przeszukiwanie z ograniczeniami Zagadnienie przeszukiwania z ograniczeniami stanowi grupę problemów przeszukiwania w przestrzeni stanów, które składa się ze: 1 skończonego
Wyszukiwanie binarne
 Wyszukiwanie binarne Wyszukiwanie binarne to technika pozwalająca na przeszukanie jakiegoś posortowanego zbioru danych w czasie logarytmicznie zależnym od jego wielkości (co to dokładnie znaczy dowiecie
Wyszukiwanie binarne Wyszukiwanie binarne to technika pozwalająca na przeszukanie jakiegoś posortowanego zbioru danych w czasie logarytmicznie zależnym od jego wielkości (co to dokładnie znaczy dowiecie
OBLICZENIA EWOLUCYJNE
 1 OBLICZENIA EWOLUCYJNE FITNESS F. START COMPUTATION FITNESS F. COMPUTATION INITIAL SUBGenration SENDING CHROM. TO COMPUTERS chromosome AND RECEIVING FITNESS F. VALUE fitness f. value wykład 7 FITNESS
1 OBLICZENIA EWOLUCYJNE FITNESS F. START COMPUTATION FITNESS F. COMPUTATION INITIAL SUBGenration SENDING CHROM. TO COMPUTERS chromosome AND RECEIVING FITNESS F. VALUE fitness f. value wykład 7 FITNESS
Kto jeszcze gra w domino?
 Mirosław Dąbrowski Kto jeszcze gra w domino? Domino, choć wciąż jeszcze można jego zestawy kupić w sklepach z zabawkami, nie należy już chyba do bardzo popularnych dziecięcych rozrywek. Szkoda, bo gra
Mirosław Dąbrowski Kto jeszcze gra w domino? Domino, choć wciąż jeszcze można jego zestawy kupić w sklepach z zabawkami, nie należy już chyba do bardzo popularnych dziecięcych rozrywek. Szkoda, bo gra
Algorytmy genetyczne
 Politechnika Łódzka Katedra Informatyki Stosowanej Algorytmy genetyczne Wykład 2 Przygotował i prowadzi: Dr inż. Piotr Urbanek Powtórzenie Pytania: Jaki mechanizm jest stosowany w naturze do takiego modyfikowania
Politechnika Łódzka Katedra Informatyki Stosowanej Algorytmy genetyczne Wykład 2 Przygotował i prowadzi: Dr inż. Piotr Urbanek Powtórzenie Pytania: Jaki mechanizm jest stosowany w naturze do takiego modyfikowania
Algorytmy ewolucyjne. wprowadzenie
 Algorytmy ewolucyjne wprowadzenie Gracjan Wilczewski, www.mat.uni.torun.pl/~gracjan Toruń, 2005 Historia Podstawowy algorytm genetyczny został wprowadzony przez Johna Hollanda (Uniwersytet Michigan) i
Algorytmy ewolucyjne wprowadzenie Gracjan Wilczewski, www.mat.uni.torun.pl/~gracjan Toruń, 2005 Historia Podstawowy algorytm genetyczny został wprowadzony przez Johna Hollanda (Uniwersytet Michigan) i
Metoda ewolucyjnego doboru współczynników funkcji oceniającej w antywarcabach
 Metoda ewolucyjnego doboru współczynników funkcji oceniającej w antywarcabach Promotor: dr hab. Jacek Mańdziuk Autor: Jarosław Budzianowski Metoda ewolucyjnego doboru współczynników funkcji oceniajacej
Metoda ewolucyjnego doboru współczynników funkcji oceniającej w antywarcabach Promotor: dr hab. Jacek Mańdziuk Autor: Jarosław Budzianowski Metoda ewolucyjnego doboru współczynników funkcji oceniajacej
Spis treści. Przedmowa... XI. Rozdział 1. Pomiar: jednostki miar... 1. Rozdział 2. Pomiar: liczby i obliczenia liczbowe... 16
 Spis treści Przedmowa.......................... XI Rozdział 1. Pomiar: jednostki miar................. 1 1.1. Wielkości fizyczne i pozafizyczne.................. 1 1.2. Spójne układy miar. Układ SI i jego
Spis treści Przedmowa.......................... XI Rozdział 1. Pomiar: jednostki miar................. 1 1.1. Wielkości fizyczne i pozafizyczne.................. 1 1.2. Spójne układy miar. Układ SI i jego
Algorytmy klasyfikacji
 Algorytmy klasyfikacji Konrad Miziński Instytut Informatyki Politechnika Warszawska 6 maja 2015 1 Wnioskowanie 2 Klasyfikacja Zastosowania 3 Drzewa decyzyjne Budowa Ocena jakości Przycinanie 4 Lasy losowe
Algorytmy klasyfikacji Konrad Miziński Instytut Informatyki Politechnika Warszawska 6 maja 2015 1 Wnioskowanie 2 Klasyfikacja Zastosowania 3 Drzewa decyzyjne Budowa Ocena jakości Przycinanie 4 Lasy losowe
Algorytm wstecznej propagacji błędów dla sieci RBF Michał Bereta
 Algorytm wstecznej propagacji błędów dla sieci RBF Michał Bereta www.michalbereta.pl Sieci radialne zawsze posiadają jedną warstwę ukrytą, która składa się z neuronów radialnych. Warstwa wyjściowa składa
Algorytm wstecznej propagacji błędów dla sieci RBF Michał Bereta www.michalbereta.pl Sieci radialne zawsze posiadają jedną warstwę ukrytą, która składa się z neuronów radialnych. Warstwa wyjściowa składa
Algorytmy równoległe: ocena efektywności prostych algorytmów dla systemów wielokomputerowych
 Algorytmy równoległe: ocena efektywności prostych algorytmów dla systemów wielokomputerowych Rafał Walkowiak Politechnika Poznańska Studia inżynierskie Informatyka 2014/15 Znajdowanie maksimum w zbiorze
Algorytmy równoległe: ocena efektywności prostych algorytmów dla systemów wielokomputerowych Rafał Walkowiak Politechnika Poznańska Studia inżynierskie Informatyka 2014/15 Znajdowanie maksimum w zbiorze
Politechnika Wrocławska Wydział Elektroniki INFORMATYKA SYSTEMÓW AUTONOMICZNYCH. Heurystyka, co to jest, potencjalne zastosowania
 Politechnika Wrocławska Wydział Elektroniki INFORMATYKA SYSTEMÓW AUTONOMICZNYCH Autor: Łukasz Patyra indeks: 133325 Prowadzący zajęcia: dr inż. Marek Piasecki Ocena pracy: Wrocław 2007 Spis treści 1 Wstęp
Politechnika Wrocławska Wydział Elektroniki INFORMATYKA SYSTEMÓW AUTONOMICZNYCH Autor: Łukasz Patyra indeks: 133325 Prowadzący zajęcia: dr inż. Marek Piasecki Ocena pracy: Wrocław 2007 Spis treści 1 Wstęp
Instytut Politechniczny Państwowa Wyższa Szkoła Zawodowa. Diagnostyka i niezawodność robotów
 Instytut Politechniczny Państwowa Wyższa Szkoła Zawodowa Diagnostyka i niezawodność robotów Laboratorium nr 6 Model matematyczny elementu naprawialnego Prowadzący: mgr inż. Marcel Luzar Cele ćwiczenia:
Instytut Politechniczny Państwowa Wyższa Szkoła Zawodowa Diagnostyka i niezawodność robotów Laboratorium nr 6 Model matematyczny elementu naprawialnego Prowadzący: mgr inż. Marcel Luzar Cele ćwiczenia:
Opis wykonanych badań naukowych oraz uzyskanych wyników
 Opis wykonanych badań naukowych oraz uzyskanych wyników 1. Analiza danych (krok 2 = uwzględnienie epistazy w modelu): detekcja QTL przy wykorzystaniu modeli dwuwymiarowych z uwzględnieniem różnych modeli
Opis wykonanych badań naukowych oraz uzyskanych wyników 1. Analiza danych (krok 2 = uwzględnienie epistazy w modelu): detekcja QTL przy wykorzystaniu modeli dwuwymiarowych z uwzględnieniem różnych modeli
Algorytmy i schematy blokowe
 Algorytmy i schematy blokowe Algorytm dokładny przepis podający sposób rozwiązania określonego zadania w skończonej liczbie kroków; zbiór poleceń odnoszących się do pewnych obiektów, ze wskazaniem porządku,
Algorytmy i schematy blokowe Algorytm dokładny przepis podający sposób rozwiązania określonego zadania w skończonej liczbie kroków; zbiór poleceń odnoszących się do pewnych obiektów, ze wskazaniem porządku,
Kompresja danych Streszczenie Studia Dzienne Wykład 10,
 1 Kwantyzacja wektorowa Kompresja danych Streszczenie Studia Dzienne Wykład 10, 28.04.2006 Kwantyzacja wektorowa: dane dzielone na bloki (wektory), każdy blok kwantyzowany jako jeden element danych. Ogólny
1 Kwantyzacja wektorowa Kompresja danych Streszczenie Studia Dzienne Wykład 10, 28.04.2006 Kwantyzacja wektorowa: dane dzielone na bloki (wektory), każdy blok kwantyzowany jako jeden element danych. Ogólny
ALGORYTMICZNA I STATYSTYCZNA ANALIZA DANYCH
 1 ALGORYTMICZNA I STATYSTYCZNA ANALIZA DANYCH WFAiS UJ, Informatyka Stosowana II stopień studiów 2 Wnioskowanie statystyczne dla zmiennych numerycznych Porównywanie dwóch średnich Boot-strapping Analiza
1 ALGORYTMICZNA I STATYSTYCZNA ANALIZA DANYCH WFAiS UJ, Informatyka Stosowana II stopień studiów 2 Wnioskowanie statystyczne dla zmiennych numerycznych Porównywanie dwóch średnich Boot-strapping Analiza
Rozdział 2: Metoda największej wiarygodności i nieliniowa metoda najmniejszych kwadratów
 Rozdział : Metoda największej wiarygodności i nieliniowa metoda najmniejszych kwadratów W tym rozdziale omówione zostaną dwie najpopularniejsze metody estymacji parametrów w ekonometrycznych modelach nieliniowych,
Rozdział : Metoda największej wiarygodności i nieliniowa metoda najmniejszych kwadratów W tym rozdziale omówione zostaną dwie najpopularniejsze metody estymacji parametrów w ekonometrycznych modelach nieliniowych,
Techniki Optymalizacji: Stochastyczny spadek wzdłuż gradientu I
 Techniki Optymalizacji: Stochastyczny spadek wzdłuż gradientu I Wojciech Kotłowski Instytut Informatyki Politechniki Poznańskiej email: imię.nazwisko@cs.put.poznan.pl pok. 2 (CW) tel. (61)665-2936 konsultacje:
Techniki Optymalizacji: Stochastyczny spadek wzdłuż gradientu I Wojciech Kotłowski Instytut Informatyki Politechniki Poznańskiej email: imię.nazwisko@cs.put.poznan.pl pok. 2 (CW) tel. (61)665-2936 konsultacje:
WPROWADZENIE DO SZTUCZNEJ INTELIGENCJI
 POLITECHNIKA WARSZAWSKA WYDZIAŁ MECHANICZNY ENERGETYKI I LOTNICTWA MEL WPROWADZENIE DO SZTUCZNEJ INTELIGENCJI NS 586 Dr inż. Franciszek Dul 6. GRY POSZUKIWANIA W OBECNOŚCI PRZECIWNIKA Gry Pokażemy, w jaki
POLITECHNIKA WARSZAWSKA WYDZIAŁ MECHANICZNY ENERGETYKI I LOTNICTWA MEL WPROWADZENIE DO SZTUCZNEJ INTELIGENCJI NS 586 Dr inż. Franciszek Dul 6. GRY POSZUKIWANIA W OBECNOŚCI PRZECIWNIKA Gry Pokażemy, w jaki
Statystyka. Wykład 4. Magdalena Alama-Bućko. 19 marca Magdalena Alama-Bućko Statystyka 19 marca / 33
 Statystyka Wykład 4 Magdalena Alama-Bućko 19 marca 2018 Magdalena Alama-Bućko Statystyka 19 marca 2018 1 / 33 Analiza struktury zbiorowości miary położenia ( miary średnie) miary zmienności (rozproszenia,
Statystyka Wykład 4 Magdalena Alama-Bućko 19 marca 2018 Magdalena Alama-Bućko Statystyka 19 marca 2018 1 / 33 Analiza struktury zbiorowości miary położenia ( miary średnie) miary zmienności (rozproszenia,
Teraz bajty. Informatyka dla szkoły podstawowej. Klasa VI
 1 Teraz bajty. Informatyka dla szkoły podstawowej. Klasa VI 1. Obliczenia w arkuszu kalkulacyjnym Rozwiązywanie problemów z wykorzystaniem aplikacji komputerowych obliczenia w arkuszu kalkulacyjnym wykonuje
1 Teraz bajty. Informatyka dla szkoły podstawowej. Klasa VI 1. Obliczenia w arkuszu kalkulacyjnym Rozwiązywanie problemów z wykorzystaniem aplikacji komputerowych obliczenia w arkuszu kalkulacyjnym wykonuje
Testy De Jonga. Problemy. 1 Optymalizacja dyskretna i ciągła
 Problemy 1 Optymalizacja dyskretna i ciągła Problemy 1 Optymalizacja dyskretna i ciągła 2 Środowisko pomiarowe De Jonga Problemy 1 Optymalizacja dyskretna i ciągła 2 Środowisko pomiarowe De Jonga 3 Ocena
Problemy 1 Optymalizacja dyskretna i ciągła Problemy 1 Optymalizacja dyskretna i ciągła 2 Środowisko pomiarowe De Jonga Problemy 1 Optymalizacja dyskretna i ciągła 2 Środowisko pomiarowe De Jonga 3 Ocena
OPTYMALIZACJA HARMONOGRAMOWANIA MONTAŻU SAMOCHODÓW Z ZASTOSOWANIEM PROGRAMOWANIA W LOGICE Z OGRANICZENIAMI
 Autoreferat do rozprawy doktorskiej OPTYMALIZACJA HARMONOGRAMOWANIA MONTAŻU SAMOCHODÓW Z ZASTOSOWANIEM PROGRAMOWANIA W LOGICE Z OGRANICZENIAMI Michał Mazur Gliwice 2016 1 2 Montaż samochodów na linii w
Autoreferat do rozprawy doktorskiej OPTYMALIZACJA HARMONOGRAMOWANIA MONTAŻU SAMOCHODÓW Z ZASTOSOWANIEM PROGRAMOWANIA W LOGICE Z OGRANICZENIAMI Michał Mazur Gliwice 2016 1 2 Montaż samochodów na linii w
METODY SZTUCZNEJ INTELIGENCJI algorytmy ewolucyjne
 METODY SZTUCZNEJ INTELIGENCJI algorytmy ewolucyjne dr hab. inż. Andrzej Obuchowicz, prof. UZ Instytut Sterowania i Systemów Informatycznych Uniwersytet Zielonogórski A. Obuchowicz: MSI - algorytmy ewolucyjne
METODY SZTUCZNEJ INTELIGENCJI algorytmy ewolucyjne dr hab. inż. Andrzej Obuchowicz, prof. UZ Instytut Sterowania i Systemów Informatycznych Uniwersytet Zielonogórski A. Obuchowicz: MSI - algorytmy ewolucyjne
