Fizyka Statystyczna 1
|
|
|
- Juliusz Wiśniewski
- 8 lat temu
- Przeglądów:
Transkrypt
1 Uniwersytet Wrocławski Instytut Fizyki Teoretycznej Katarzyna Weron Fizyka Statystyczna 1 Skrypt dla studentów Wrocław, maj 2010
2 2
3 Spis treści 1 Elementy termodynamiki Wielkości termodynamiczne Aksjomaty termodynamiki Równanie Fudamentalne i Potencjały Termodynamiczne Parametry intensywne i ekstensywne Równanie Fundamentalne Potencjały termodynamiczne Funkcje odpowiedzi Równania stanu Warunki równowagi Formalna definicja temperatury i intuicja Uwaga o pochodnej cząstkowej Od zachowania mikro do makro - czyli wstęp do fizyki statystycznej Fluktuacje w stanie równowagi Zespół statystyczny Przykład nr 1: Kostki do Gry Przykład 2: Spiny Podstawowe postulaty fizyki statystycznej Entropia Przykład - fermiony Zespoły fizyki Statystycznej Wstęp Zespół Mikrokanoniczny Jeszcze raz o entropii Zespół Kanoniczny Rozkład prawdopodobieństwa Gibbsa Średnia energia Związek pomiędzy fizyką statystyczną i termodynamiką w zespole kanonicznym Zespół Wielki Kanoniczny Związek pomiędzy fizyką statystyczną i termodynamiką w wielkim zespole kanonicznym
4 4 Gazy doskonałe Klasyczny Gaz idealny Paradoks Gibbsa Twierdzenie o ekwipartycji energii Kwantowe gazy doskonałe Fermiony Bozony Granica klasyczna Układ fotonów w równowadze - promieniowanie Ciała Doskonale Czarnego Równania stanu kwantowych gazów idealnych Gdy atomy zachowuja sie jak fale : kondensacja Bosego Einsteina 43 5 Modele fizyki Statystycznej Model Isinga Jednowymiarowy model Isinga bez pola Jednowymiarowy model Isinga z polem Metoda Monte Carlo dla Modelu Isinga Model Perkolacji Metoda MFA dla modelu Perkolacji Grupa Renormalizacyjna w modelu perkolacji bond - decymacja Fizyka statystyczna w mechanice kwantowej Macierz gęstości Ciepło właściwe ciał stałych Model Einsteina Model Debye a
5 5
6 Rozdział 1 Elementy termodynamiki Celem fizyki statycznej jest zrozumienie własności układów makroskopowych, tzn. takich które składają się z dużej 1 liczby cząstek, elektronów, atomów czy innych elementów 2. Typowymi przykładami układów makroskopowych są powietrze w pokoju czy szklanka wody, a przykładowymi pytaniami dotyczącymi układów makroskopowych są: 1. W jaki sposób ciśnienie gazu zależy od temperatury i objętości, którą zajmuje gaz? 2. Ile trzeba dostarczyć energii żeby szklankę wody zamienić w parę? 3. Dlaczego woda ma inne własności niż para mimo, że składa się z takich samych cząstek? 4. Dlaczego żelazo powyżej pewnej temperatury traci własności magnetyczne? 5. Jaka będzie jutro pogoda? Dwa pierwsze pytania dotyczą własności makroskopowych układu, takich jak ciśnienie, objętość czy temperatura i są związane z ciepłem oraz pracą. Tego typu pytania leżą w obszarze termodynamiki czyli metody fenomenologicznej 3 Termodynamika zajmuje się głównie problemami zamiany energii (pracy i ciepła) oraz własnościami równowagowymi. Równowaga jest zjawiskiem makroskopowym i odnosi się do skali czasu znacznie większej niż skala charakteryzująca ruch mikroskopowy. Z punktu widzenia mikroskopowego równowaga jest takim szczególnym stanem ruchu, w którym, w czasie obserwacji, nie zmienia się stan makroskopowy obserwowanego ciała. Podstawą termodynamiki jest założenie, że przy określonych warunkach zewnętrznych dany układ ma jednoznacznie zdefiniowane własności równowagowe. Te zewnętrzne warunki są określone przez zewnętrzne parametry takie jak: temperatura, ciśnienie, pole magnetyczne itd. Oczywiście przy różnych warunkach zewnętrznych układ ma różne własności równowagowe. Przy czym przez własności równowagowe rozumiemy własności strukturalne, termiczne, elektryczne, magnetyczne, elastyczne itd. 1 1 mol substancji zawiera przecież cząstek - to dość dużo! 2 W ostatnich latach fizyka statystyczna wtargnęła również na obce terytoria, takie jak socjologia czy biologia. W takim przypadku elementami układu będą na przykład ludzie, zwierzęta itd. 3 Fenomenologia w fizyce: Widzimy jak przebiega dane zjawisko, znajdujemy jakieś regularności, potrafimy przewidzieć, że takie regularności powinny wystąpić gdzie indziej, ale nie potrafimy tego zjawiska wyjaśnić. 1
7 1.1 Wielkości termodynamiczne Jak już wspomnieliśmy jednym z głównych zagadnień opisywanych przez termodynamikę jest problemem zmiany energii. Energia obiektu może być zmieniona przez zewnętrzne siły, które wykonują pracę na tym obiekcie. Opierając się na analogii mechanicznej możemy powiedzieć, że praca równa się sile razy przesunięcie. I tak na przykład: Praca dw wykonana przez napięcie f ciągnące metalowy pręt na dystansie dx jest równa: dw = fdx. (1.1) Zewnętrzne pole magnetyczne h wykonuje pracę, przy której wzrost energii obiektu związany jest ze wzrostem namagnesowania: dw = hdm. (1.2) Ciśnienie p jest siłą, która powoduje zmianę objętości V, a odpowiadająca temu praca dw = pdv (1.3) Brak znaku minus oznacza, że wzrost ciśnienia powoduje zmniejszanie się objętości. Siłą jest również potencjał chemiczny, który powoduje zmianę liczby cząstek N: dw = µdn (1.4) Dystans X, namagnesowanie M, objętość V, czy liczba cząstek N są uogólnionymi współrzędnymi określającymi stan układu, natomiast napięcie f, pole magnetyczne h, ciśnienie p, oraz potencjał chemiczny µ są uogólnionymi siłami zewnętrznymi, które mogą zmienić odpowiednie współrzędne. Te uogólnione współrzędne są współrzędnymi makroskopowymi (termodynamicznymi). Obok takich współrzędnych istnieją również współrzędne mikroskopowe. Czy istnieje potrzeba uwzględnienia tych ostatnich w termodynamice? Otóż zmiana energii - wypływ z układu lub wpłynięcie do układu - może się odbywać bez jakiejkolwiek zmiany zdefiniowanych powyżej współrzędnych makroskopowych. Takim przepływem energii jest ciepło i jest to wynik zmian w ruchu mikroskopowym układu. Na szczęście do opisu tych zmian nie trzeba brać pod uwagę współrzędnych wszystkich cząstek budujących dane ciało. Wystarczy wprowadzić jedną zmienną uogólnioną, dzięki której można wyrazić ruch mikroskopowy w sposób kolektywny. Tą nową współrzędną jest entropia S, a siłą odpowiedzialną za jej wzrost jest temperatura T. Związany z tym wzrostem przyrost energii dany jest przez: dq = T ds (1.5) Całkowita energia jest podzielona w termodynamice na pracę wykonaną przez zewnętrzne siły nad ciałem, zmieniającą współrzędne makroskopowe oraz ciepło przepływające dzięki zmianom w ruchu molekularnym. Jeżeli dq = 0, wtedy w danym procesie zmiany energii nie ma żadnego przepływu ciepła i taki proces nazywa się procesem adiabatycznym. 2
8 1.2 Aksjomaty termodynamiki Termodynamika jest trudno przyswajalna przez mnogość jej równoważnych sformułowań i związaną z tym praktycznie nierozróżnialność postulatów i wypływających z nich wniosków. 1. Postulat istnienia równowagi termodynamicznej. Każdy układ przy niezmiennych warunkach zewnętrznych znajduje się w stanie równowagi termodynamicznej, a jeżeli przy takich warunkach nie jest w stanie równowagi to w końcu do stanu równowagi termodynamicznej przechodzi. 2. Postulat addytywności. Energia układu jest sumą enegii jego części makroskopowych. 3. Postulat istnienia temperatury - zerowa zasada termodynamiki. Temperatura jest parametrem określającym równowagę termodynamiczną, albo; jeżeli ciało A jest w równowadze z ciałem B i ciało B jest w równowadze z ciałem C to ciało C jest w równowadze z ciałem A. 4. Pierwsza zasada termodynamiki - zasada zachowania energii. du = dq dw (1.6) gdzie du oznacza zmianę energii wewnętrznej układu, dq ilość ciepła dodaną układowi, a dw pracę wykonaną przez układ. 5. Druga zasada termodynamiki. Nie istnieje taki proces termodynamiczny, którego jedynym wynikiem jest pobranie ciepła z danego zbiornika i całkowita zamiana tego ciepła na pracę (Kelvin). Nie istnieje taki proces termodynamiczny, którego jedynym wynikiem jest pobranie ciepła ze zbiornika chłodniejszego i przekazanie go do zbiornika cieplejszego (Clausius). Zasada ta jest zasadą empiryczną, która jak dotąd nigdy nie została złamana, ale z drugiej strony nigdy nie została jednoznacznie udowodniona. Z drugiej zasady termodynamiki wynika, że entropia układu izolowanego cieplnie nie maleje, a więc w konsekwencji stan równowagi układu izolowanego cieplnie jest stanem o maksymalnej entropii. 6. Trzecia zasada termodynamiki - postulat Nernsta. Entropia układu w zerze bezwzględnym jest równa zeru. 1.3 Równanie Fudamentalne i Potencjały Termodynamiczne Aby opisać układ można podawać za każdym razem zbiór wszystkich wielkości termodynamicznych, charakteryzujących stan równowagi termodynamicznej, ale żeby opis ten był bardziej przejrzysty i wygodniejszy w użyciu lepiej ograniczyć się do wyboru zmiennych niezależnych. Oczywiście taki wybór nie jest jednoznaczny - możemy traktować na przykład S, V, N jako zmienne niezależne, a wtedy T, p, µ będą mogły być wyrażone przez te zmienne - pamiętacie siły i współrzędne uogólnione są związane ze sobą przez energię. 3
9 Oczywiście można też wybrać jako trójkę zmiennych niezależnych np. T, V, N lub dokonać jeszcze innego wyboru. Musimy też znaleźć sposób wyrażenie tych zmiennych za pomocą pozostałych wielkości termodynamicznych. Układy w stanie równowagi opisujemy za pomocą pewnych funkcji termodynamicznych - tzw. równania fundamentalnego lub potencjałów termodynamicznych, tzn. transformacji Legendre a równania fundamentalnego. Wszystkie te funkcje mają tę własność, że dzięki nim możemy określić wszystkie wielkości charakteryzujące dany układ. W przypadku równania fundamentalnego zmiennymi niezależnymi są wyłącznie tzw. parametry ekstensywne (patrz dalej), w przeciwieństwie do znacznie ogólniejszego przypadku potencjałów termodynamicznych Parametry intensywne i ekstensywne Wszystkie termodynamiczne parametry układu można podzielić na dwie kategorie 1. Addytywne (ekstensywne), tzn. mające taką własność, że wartość tego parametru dla całego układu równa się sumie wartości tego paratemru identycznych podukładów tworzących dany układ. Przykładami takich parametrów są energia, entropia, objętość, liczba cząstek: U(λS, λv, λn 1,..., λn r ) = λu(s, V, N 1,..., N r ) 2. Nieaddytywne (intensywne), wartość tego parametru dla całego układu równa się wartości tego parametru dla każdego z identycznych podukładów tworzących dany układ, np. temperatura czy ciśnienie: T (λs, λv, λn 1,..., λn r ) = T (S, V, N 1,..., N r ) Równanie Fundamentalne W stanie równowagi układ może być określony jednoznacznie poprzez podanie tzw. równania fundamentalnego, tzn. związku pomiędzy energią wewnętrzną (albo entropią) a pozostałymi parametrami ekstensywnymi. Równanie fundamentalne może więc przybierać następujące postaci: S = S(U, V, N 1,..., N r ) (1.7) U = U(S, V, N 1,..., N r ). (1.8) Parametry intensywne można wprowadzić formalnie obliczając różniczkę zupełną: ( ) ( ) ( ) U U r U du = ds + dv + dn j (1.9) S V,N 1,...,N r V S,N 1,...,N r j=1 N j S,V,...N k Jeżeli przypomnicie sobie I zasadę termodynamiki to intuicyjne będzie...??? (dopisać) Wprowadźmy następujące oznaczenia: ( ) U T temperatura (1.10) S V,N 1,...,N ( ) r U P ciśnienie (1.11) V S,N 1,...,N ( ) r U µ j potencjał chemiczny (1.12) N j S,V,...N k 4
10 Można pokazać, że parametry zdefiniowane wzorem (1.12) są parametrami intensywnymi. Rozważmy w tym celu λ identycznych podukładów tworzących układ zamknięty. Oznaczmy entropię, energię wewnętrzną, objętość, liczbę cząstek i temperaturę każdego z podukładów odpowiednio przez S, U, V, N, T, a te same parametry dla całego układu złożonego z λ identycznych podukładów odpowiednio jako S λ, U λ, V λ, N λ, T λ. Oczywiście dla parametrów ekstensywnych zachodzą równości: Czyli S λ = λs (1.13) U λ = λu (1.14) V λ = λv (1.15) N λ = λn (1.16) du λ = dλu = λdu, (1.17) gdzie z równania fundamentalnego dla układu jedno składnikowego: ( ) ( ) ( ) U U U du = ds + dv + dn. (1.18) S V N Czyli: V,N du λ = λdu ( ) = λ U S V,N ds + S,N S,V ( ) ( ) U U dv + V N S,N S,V dn (1.19) Z drugiej jednak strony: ( ) ( ) ( ) U du λ λ U = ds λ λ U + dv λ λ + dn λ S λ V V λ,n λ N λ S λ,n λ λ S λ,v ( ) ( ) ( ) λ U λ U λ U λ = λ ds + λ dv + λ dn S λ V V λ,n λ N λ S λ,n λ λ S λ,v λ ( ) ( ) ( ) = λ U λ U λ U λ ds + dv + dn. (1.20) S λ V V λ,n λ N λ S λ,n λ λ S λ,v λ Porównując równania otrzymamy: ( ) U λ S λ ( ) U λ V λ ( ) U λ N λ V λ,n λ = S λ,n λ = S λ,v λ = ( ) U S ( ) U V ( ) U N Korzystając z wprowadzonych definicji parametrów intensywnych otrzymujemy więc: V,N S,N S,V (1.21) T λ = T (1.22) p λ = p (1.23) µ λ = µ (1.24) 5
11 Jak widać parametry intensywne pojawiają się jako odpowiednie pochodne cząstkowe parametrów ekstensywnych, a równanie 1.9 przyjmuje postać: r du = T ds P dv + µ j dn j, (1.25) j=1 które jest tożsame z postacią pierwszej zasady termodynamiki Potencjały termodynamiczne Dotychczas termodynamiczną informację o układzie otrzymywaliśmy z równania fundamentalnego, które mogło być zapisane w języku energii albo entropii. W obu tych reprezentacjach parametry ekstensywne odgrywały rolę zmiennych niezależnych a parametry intensywne pojawiały się jako odpowiednie pochodne. Jednakże z punktu widzenia eksperymentu znacznie wygodniej operować parametrami intensywnymi. To właśnie parametry intensywne są łatwo kontrolowane i mierzone. Wygodniej zatem byłoby móc operować nimi jako zmiennymi niezależnymi. Poznaliście już na mechanice klasycznej formalizm, który to umożliwia - transformata Legendre a. Potencjałami termodynamicznymi będziemy nazywali właśnie różne transformaty Legendre a równania fundamentalnego. W różnych podręcznikach nazywają się one różnie, ale nie nazwy są dla nas istotne, ale to jak wygląda potencjał w zależności od tego z jakimi parametrami chcemy mieć do czynienia. W ogólności mamy związek: i chcemy aby zmiennymi niezależnymi zamiast X k były: Umożliwia nam to transformata Legendre a: Y = Y (X 0, X 1,..., X r ) (1.26) P k Y X k. (1.27) Ψ = Y k P k X k. (1.28) Jednym z najważniejszych potencjałów, ze względu na zastosowanie w fizyce statystycznej jest tzw. energia swobodna F, w której rolę parametrów niezależnych grają T, V, N. Zastępujemy więc w równaniu fundamentalnym entropię przez temperaturę. Transformacja Legendre a ma wtedy postać U = U(S, V, N 1, N 2,...) S T T = U S F = U T S (1.29) F = F (T, V, N 1, N 2,...) (1.30) Możemy również wyliczyć różniczkę zupełną (dla prostoty zapisu zrobimy to dla układu jednoskładnikowego). Z jednej strony: df = df (T, V, N) ( ) F df = dt + T V,N ( ) ( ) F F dv + dn. (1.31) V N T,N T,V 6
12 Z drugiej strony, korzystając z transformaty Legendre a: df = d(u T S) = du T ds SdT = T ds P dv + µdn T ds SdT = SdT P dv + µdn (1.32) Wobec tego w formalizmie energii swobodnej zachodzą następujące związki: ( ) F S = T ( ) F P = V ( ) F µ = N V,N T,N T,V. (1.33) Innym szczególnie ważnym z punktu widzenia zastosowań w fizyce statystycznej będzie tak zwany wielki potencjał termodynamiczny Ξ = Ξ(T, V, µ). Przechodząc ze zmiennych niezależnych S, V, N to T, V, µ przy pomocy transformaty Legendre a: Ξ = Ξ(T, V, µ) U = U(S, V, N) Ξ = U T S µn dξ = du T ds SdT µdn Ndµ du = T ds pdv + µdn dξ = SdT pdv Ndµ (1.34) Z drugiej strony możemy policzyć bezpośrednio różniczkę zupełną: Ξ = Ξ(T, V, µ) ( ) Ξ dξ = T dt + V,µ ( ) Ξ dv + V T,µ Porównując oba wyrażenia na różniczkę zupełną Ξ otrzymujemy, że: ( ) Ξ dµ (1.35) µ T,V ( ) Ξ T ( ) Ξ V ( ) Ξ µ V,µ T,µ T,V = S = p = N. (1.36) 7
13 Podobnie można otrzymać inne potencjały termodynamiczne, np. entalpię H: U = U(S, V, N 1, N 2,...) V P P = U V H = U + V P (1.37) H = H(S, P, N 1, N 2 ) (1.38) (1.39) 1.4 Funkcje odpowiedzi Niezwykle ważne z punktu widzenia zrozumienia przejść fazowych, są funkcje, które określają nam jak układ reaguje na zmianę pewnych parametrów zewnętrznych. Przykładami takich funkcji są: α κ T c P c V ( ) 1 V V T P ( ) 1 V V P T ( ) T S = ( ) 1 dq N T P N dt P ( ) T S = ( ) 1 dq N T V N dt V 1.5 Równania stanu współczynnik rozszerzalności cieplnej (1.40) ściśliwość izotermiczna (1.41) ciepło właściwe w stałym ciśnieniu (1.42) ciepło właściwe w stałej objętości (1.43) Ponieważ temperatura, ciśnienie i potencjał chemiczny są pochodnymi cząstkowymi S, V, N 1,..., N r są również funkcjami tych parametrów, tzn. T = T (S, V, N 1,..., N r ) (1.44) P = P (S, V, N 1,..., N r ) (1.45) µ j = µ j (S, V, N 1,..., N r ) (1.46) (1.47) Takie związki pomiędzy parametrami intensywnymi a ekstensywnymi nazywamy równaniami stanu. Znajomość pojedynczego równania stanu nie daje nam pełnej informacji termodynamicznej o układzie. Dopiero znajomość wszystkich równań stanu jest równoważna znajomości równania fundamentalnego. 1.6 Warunki równowagi Rozważmy teraz izolowany układ, tzn. U = const złożony z dwóch podukładów przedzielonych ścianą, która nie przepuszcza cząstek ale przepuszcza ciepło. Energie podukładów oznaczymy przez U 1 i U 2. Z addytywności energii w otrzymujemy natychmiast: U 1 + U 2 = U = const. (1.48) 8
14 Chcemy teraz znaleźć warunek na równowagę takiego układu. Z drugiej zasady termodynamiki w stanie równowagi: ds = 0. (1.49) Ponieważ entropia jest ekstensywna: S = S 1 (U 1, V 1, N 1 ) + S 2 (U 2, V 2, N 2 ). (1.50) Możemy teraz obliczyć: ( ) ( ) S1 S2 ds = du 1 + du 2. (1.51) U 1 V 1,N 1 U 2 V 2,N 2 Pozostałe wyrazy nie występują ponieważ w rozważanym przykładzie dv 1, dv 2, dn 1, dn 2 = 0. Zgodnie z naszą definicją: Ponieważ U 1 + U 2 = const, więc: Czyli: ds = 1 T 1 du T 2 du 2 (1.52) du 1 + du 2 = 0 du 1 = du 2. (1.53) ds = ( 1 T2 1 T1 ) du 2 (1.54) Ponieważ w stanie równowagi ds = 0 dla dowolnej wartości du 2,tzn. dowolny skończony przepływ energii z podukładu 1 do 2 nie zmienia entropii całego układu, czyli 1 T 1 = 1 T 2 (1.55) Oczywiście dotychczas określiliśmy jedynie warunki równowagi w przypadku gdy podukłady nie zmieniają objętości ani nie wymieniają cząstek. Jakie byłyby warunki równowagi w przypadku gdy możliwa byłaby zmiana objętości i liczby cząstek podukładów (ćwiczenia)? Kolejnym problemem jest zbadanie stabilności takiej równowagi, tzn. znalezienie warunku, dla którego ds 2 < 0 lub du 2 > 0. Warunek ds = 0 określa nam bowiem jedynie ekstremum entropii ale nie mówi o tym czy jest to minimum czy maksimum. Pokażcie (ćwiczenia), że warunek stabilności równowagi ma postać: c v, κ T 0 (1.56) 1.7 Formalna definicja temperatury i intuicja Jak wspomniałam można pokazać (ćwiczenia), że temperatura zdefiniowana jako: ( ) U T S jest zgodna z intuicyjną koncepcją temperatury, tzn. V,N 1,...,N r (1.57) 1. Jest parametrem intensywnym, tzn. T (λs, λv, λn 1,..., λn r ) = T (S, V, N 1,..., N r ) 2. W stanie równowagi temperatury podukładów tworzących izolowany układ są sobie równe (to już pokazaliśmy). 3. W przypadku gdy podukład 1 ma wyższą temperaturę niż 2 T 1 > T 2 następuje przepływ energii z podukładu 1 do 2, tzn. du 1 < 0 9
15 1.8 Uwaga o pochodnej cząstkowej Pochodne cząstkowe sprawiają czasami studentom kłopot, którego zwykle powodem jest traktowanie tych pochodnych tak jak zwyczajnych. Wyraźną różnicę pomiędzy tymi dwiema typami pochodnych można zilustrować następującym przykładem, zaczerpniętym z podręcznika G.M. Fichtenholza Rachunek różniczkowy i całkowy. Rozważmy wzór Clapeyrona pv = RT R = const, (1.58) wyrażający związek pomiędzy objętością V, ciśnieniem p i temperaturą absolutną T jednej gramocząsteczki gazu idealnego. Wybierzmy na początek jako zmienne niezależne p, V, wówczas: T p = V R, Jeżeli wybierzemy jako zmienne niezależne p, T, to wówczas: V p = RT p 2, Możemy również wybrać jako zmienne niezależne T, V otrzymując: Obliczmy teraz: p V = RT V 2, p V V T T p T = pv R T V = p R. (1.59) V = RT p V T = R p. (1.60) p = RT V p T = R V. (1.61) =? (1.62) Gdybyśmy mieli do czynienia z pochodnymi zwyczajnymi, które można traktować jak ułamki (skracać), wówczas oczywiście otrzymalibyśmy wynik równy 1. Jak będzie w tym przypadku? p V V T T p = RT R V 2 p V R = RT pv = 1. (1.63) Widać więc na tym przykładzie wyraźną różnicę pomiędzy pochodną zwyczajną a cząstkową. To, że pochodnych cząstkowych nie można traktować jak ułamków staje się jasne gdy zapiszemy powyższe mnożenie w pełnej formie (zaznaczając, która wielkość pozostaje stała): ( ) ( ) ( ) p V T. (1.64) V T p T p V Jak widać w przypadku każdej z trzech pochodnych inna wielkość pozostaje stała, wobec tego każda pochodna jest wykonywana jakby w innym układzie. 10
16 Rozdział 2 Od zachowania mikro do makro - czyli wstęp do fizyki statystycznej Dotychczas zajmowaliśmy się jedynie zachowaniem makroskopowym układów wielocząstkowych, tzn. takim jakie można obserwować eksperymentalnie. Do opisu makroskopowych układów wielocząstkowych służyła nam termodynamika, o której można powiedzieć, że jest działem fizyki zajmującym się zagadnieniem reguł rządzących wymianą energii między ciałami. Dowiedzieliśmy się, że układ w równowadze termodynamicznej może być całkowicie opisany przez podanie niewielkiej liczby zmiennych niezależnych, których wybór zależy od naszej wygody. Możemy więc, w zależności od tego wyboru, opisać układ równaniem fundamentalnym (czyli przy pomocy zmiennych ekstensywnych) w reprezentacji energii bądź entropii lub odpowiednim potencjałem termodynamicznym (czyli transformatą Legendre a równania fundamentalnego polegającą na zastąpieniu wybranych zmiennych ekstensywnych przez intensywne). Teraz chcemy zobaczyć co byłoby gdybyśmy z poziomu makro przeszli na mikro, tzn. zajrzeli wgłąb układu, przyjrzeli się pojedynczym cząstkom, strukturze układu i oddziaływaniom jakie zachodzą między cząstkami. Postęp nauki osiągnięty w pierwszej połowie XX wieku doprowadził do gruntownej znajomości struktury materii w skali mikroskopowej, tzn. rzędu rozmiarów atomów (10 8 cm). Obecnie znamy prawa mechaniki kwantowej opisujące dynamiczne zachowanie cząstek o rozmiarach atomowych. W zasadzie moglibyśmy wykorzystać tę wiedzę przy omawianiu układów makroskopowych. Niestety typowy układ makroskopowy składa się z około atomów wzajemnie ze sobą oddziałujących. Liczba stopni swobody jest więc astronomiczna i nie ma takich komputerów, które dały by sobie radę z tak olbrzymim układem. Poza tym więcej zwykle oznacza również inaczej. W tym tkwi cała istota układów złożonych. Sumaryczne zachowanie takiego układu nie jest po prostu sumą zachowania pojedynczych cząstek. Musimy zatem sformułować nowe pojęcia dostosowane do złożoności układów. 2.1 Fluktuacje w stanie równowagi Prostym przykładem układu wielocząstkowego jest gaz złożony z identycznych cząstek, np. azotu (N 2 ). Jeżeli gaz ten jest rozrzedzony, to średnie odstępy między cząstkami są duże, a oddziaływania między cząsteczkami słabe. Graniczny przypadek gazu rozrzedzonego, w którym oddziaływania między cząsteczkami są zaniedbywalne, nazywamy gazem 11
17 Rysunek 2.1: Cztery różne sposoby, na które można rozmieścić dwie rozróżnialne cząstki w dwóch połówkach naczynia. doskonałym. Jeżeli gaz jest wystarczająco rozrzedzony, a temperatura nie jest zbyt niska to wówczas długość fali de Broglie a cząsteczek jest mniejsza niż odległości między cząsteczkami. W takim wypadku można zaniedbać również zjawiska kwantowe i traktować cząstki jak rozróżnialne kuleczki poruszające się po klasycznych torach. Rozważmy taki klasyczny gaz doskonały złożony z N cząstek zamkniętych w pudle. Przypuśćmy, że nasz układ jest całkowicie izolowany i wyobraźmy sobie, że nasze pudło jest przedzielone na dwie równe części, tak jak na rysunku 3.1. Naprawdę to pudło wcale nie jest przedzielone i cząstki mogą się poruszać swobodnie w całej przestrzeni. Podział jest tylko wirtualny i służy nam do określenia położenia cząstki. Oznaczmy liczbę cząstek po lewej stronie pudła przez n L, a po prawej przez n P. Naturalnie n L + n P = N. Jeżeli N jest liczbą dużą to zwykle będziemy obserwować n L n P. Tak naprawdę jednak to liczby cząstek w każdej połowie naczynia będą fluktuować. Wyobraźmy sobie, że N = 2. Mamy wówczas 4 możliwe konfiguracje (tzn. sposoby rozmieszczenia), przedstawione na rysunku 2.1. Prawdopodobieństwo każdej z tych konfiguracji jest równe i wynosi 1/4. Jak widać prawdopodobieństwo tego, że obie cząstki będą po jednej stronie pudła jest w tym przypadku równe 1/2. Czyli z prawdopodobieństwem 1/2 będziemy mieć sytuację n L n P - czyli fluktuacje ze stanu równowagi. Oczywiście im większa liczba cząstek N tym mniejsze fluktuacje. Jeżeli N = 10 to jakie jest prawdopodobieństwo, że wszystkie cząstki będą po lewej stronie pudła? Wszystkich możliwych konfiguracji jest 2 10 = 1024, czyli prawdopodobieństwo wynosi 1/1024. Dla N = 20 mamy już możliwych konfiguracji, a dla N = 100 mamy około konfiguracji czyli, zgodnie z uwagą jednego z moich studentów pana Macieja Tabiszewskiego, jest rzędu kwintyliona (może komuś to coś ułatwi :)). A przecież układ 1000 cząstek to ciągle nie jest układ nawet w przybliżeniu makroskopowy. Możemy jednak przygotować w ten sposób układ, że umieścimy sztucznie wszystkie cząstki w lewej części pudła. Będzie to stan zdecydowanie bardziej uporządkowany niż gdyby cząstki były rozmieszczone w całym pudle. Ale Natura nie lubi porządku. Można sformułować stwierdzenie: Jeżeli układ izolowany znajduje się w sytuacji znacznie różniącej się od stanu uporządkowania, to (pomijając fluktuacje) będzie on tak się zmieniał w czasie, by w końcu osiągnąć stan jak najbardziej nieuporządkowany - stan 12
18 makrostan mikrostany 2 (1,1) 3 (1,2),(2,1) 4 (1,3),(2,2),(3,1) 5 (1,4),(2,3),(3,2),(4,1) 6 (1,5),(2,4),(3,3),(4,2),(5,1) 7 (1,6),(2,5),(3,4),(4,3),(5,2),(6,1) 8 (2,6),(3,5),(4,4),(5,3),(6,2) 9 (3,6),(4,5),(5,4),(6,3) 10 (4,6),(5,5),(6,4) 11 (5,6),(6,5) 12 (6,6) Tabela 2.1: Makro i mikrostany dla układu dwóch kostek do gry. Makrostan zdefiniowany jako sumaryczna liczba wyrzuconych oczek równowagi. Jak widać naukowcy żyją w zgodzie z naturą - wystarczy zajrzeć do mojego gabinetu. Jeżeli układ początkowo jest w stanie dalekim od równowagi (np. wszystkie cząstki pojednej stronie pudła) to będzie ewoluował w kierunku równowagi, tzn. relaksował. Ten fakt ma daleko idące konsekwencje - istnienie procesów nieodwracalnych. 2.2 Zespół statystyczny Gdybyśmy znali dokładnie stan mikroskopowy, w którym znajduje się układ cząstek w jakiejś dowolnej chwili to potrafilibyśmy w zasadzie, korzystając z praw mechaniki, obliczyć wszystkie własności tego układu w dowolnej innej chwili w sposób szczegółowy. Nie jesteśmy jednak tego w stanie zrobić i dlatego korzystamy z pojęć probabilistycznych. Wobec tego zamiast rozważać jeden układ makroskopowy rozważamy zbiór wielu kopii naszego układu, tzn. zbiór układów o tych samych własnościach makroskopowych, ale różnych mikrostanach. Taki zbiór kopii nazywamy zespołem statycznym Przykład nr 1: Kostki do Gry Wyobraźmy sobie, że mamy do dyspozycji dwie kostki do gry. Makrostan jest zdefiniowany jako sumaryczna liczba wyrzuconych oczek, wówczas mamy następujące makrostany i odpowiadające im mikrostany (patrz Tabela nr 1). Jak widać z tabeli makrostanowi 7 odpowiada maksymalna liczba mikrostanów, dokładnie 6 mikrostanów Przykład 2: Spiny Przypuśćmy, że nasz układ składa się z czterech cząstek o spinie 1/2, z których kazda ma moment magnetyczny µ 0, umieszczonych w polu magnetycznym. Powiedzmy, że nasz układ jest izolowany i jego energia wynosi 0. W jakich mikrostanach będzie się mógł znaleźć nasz układ? 13
19 r σ 1 σ 2 σ 3 σ 4 M E = MB µ 0 4µ 0 B µ 0 2µ 0 B µ 0 2µ 0 B µ 0 2µ 0 B µ 0 2µ 0 B µ 0 2µ 0 B µ 0 2µ 0 B µ 0 2µ 0 B µ 0 2µ 0 B µ 0 4µ 0 B Tabela 2.2: Możliwe mikrostany i energie układu czterech cząstek o spinie 1/2 i momencie magnetycznym µ 0 w polu zewnętrznym. Jeżeli interesuje nas makrostan o energii 0 to odpowiada mu 6 mikrostanów przedstawionych w tabeli nr Podstawowe postulaty fizyki statystycznej Aby otrzymać przewidywania teoretyczne odnośnie prawdopodobieństw i wartości średnich musimy wprowadzić kilka postulatów Entropia W termodynamice entropia została wprowadzona jako miara ruchu molekularnego, uogólniona zmienna, która wyrażała ruch mikroskopowy w sposób kolektywny. Uogólnioną siłą powodującą wzrost tej zmiennej była temperatura. W fizyce statystycznej formułę na entropię można przyjąć jako podstawowe założenie. Przyjmijmy, że badany układ składa się z N cząstek. W danej chwili każda z tych cząstek opisana jest przez 3 zmienne określające jej położenie oraz 3 zmienne opisujące jej pęd. Oznacza to, że w każdej chwili pozycja i pęd wszystkich cząstek reprezentowana jest przez jeden punkt (q 1, q 2,...q 3N, p 1, p 2,...p 3N ) w 6N wymiarowej przestrzeni. Taki punkt nazywany jest stanem układu, a przestrzeń - przestrzenią fazową. Stan układu zmienia się oczywiście w czasie, wykreślając trajektorię w przestrzeni fazowej. Zakłada się, że zmienne opisujące stan układu w przestrzeni fazowej 14
20 spełniają dynamikę Hamiltona: p i = H (2.1) q i q i = H (2.2) p i dla j = 1...3N. W dostatecznie długim czasie obserwacji trajektoria tworzy w przestrzeni fazowej bardzo długą, wielokrotnie przecinającą się linię w pewnym obszarze tej przestrzeni - obszarze ruchu stanów. Jeżeli Ω oznacza objętość tego obszaru to podstawowe założenie mechaniki statystycznej mówi, że entropia jest logarytmem z Ω: S = k B ln Ω (2.3) Ta relacja nie może być wyprowadzona z żadnej znanej zasady, co najwyżej może być zastąpiona innym równorzędnym postulatem. W przypadku układu o dyskretnych stanach Ω nie jest objętością przestrzeni fazowej, ale po prostu liczbą stanów. Pamiętacie przykład z kostkami do gry? Jeżeli układ składał się z jednej kostki to liczba możliwych stanów Ω = 6. Jeżeli układ składał się z dwóch kostek to wówczas Ω = 6 6. Pamiętacie, że entropia ma być wielkością ekstensywną. W przypadku dwóch podukładów o liczbach stanów Ω 1 i Ω 2 (w naszym przykładzie Ω 1 = Ω 2 = 6): S 1 = k B ln Ω 1 S 2 = k B ln Ω 2 S 1 + S 2 = k B (ln Ω 1 + ln Ω 2 ) = k B ln Ω 1 Ω 2. (2.4) Z drugiej jednak strony, jak zobaczyliśmy na przykładzie kostek do gry, liczba stanów całego układu Ω = Ω 1 Ω 2, czyli: Czyli rzeczywiście S = k B ln Ω = k B ln Ω 1 Ω 2. (2.5) S = S 1 + S 2. (2.6) Wybór logarytmu jest więc niejako narzucony przez założenie o ekstensywności entropii. 2.4 Przykład - fermiony Załóżmy, że mamy N fermionów, które mogą obsadzić K stanów o tej samej energii ɛ. Jaka jest entropia takiego układu? Pierwszym krokiem jest znalezienie Ω tzn. całkowitej liczby stanów. Ω jest całkowitą liczbą możliwości rozłożenia N cząstek na K stanów, przy czym w każdym stanie może się znajdować tylko jedna cząsteczka (Zakaz Pauliego dla fermionów). Takie zadanie rozwiązywaliście już przy okazji pierwszej listy zadań na rozgrzewkę. Wiemy, że N poziomów musi być obsadzonych, czyli musimy wylosować K N poziomów, które nie zostaną obsadzone, z kombinatoryki: Ω f = ( K K N ) = K! (K N)!(K K + N)! = K! N!(K N)! = 15 ( K N ) (2.7)
21 Zgodnie z podstawowym założeniem S = k B ln Ω. Czyli: S = K! k B ln N!(K N)! (2.8) = k B [ln K! ln(n!(k N)!)] = k B [ln K! ln N! ln(k N)!] (2.9) Co to jest lnn!?. Pod warunkiem, że N : N! = N (2.10) ln N! = ln 1 + ln 2 + ln ln N (2.11) N 1 ln xdx = [x ln x x] N 1 (2.12) = N ln N N + 1 N ln N N. (2.13) To jest ważny wynik, który często będzie przez nas wykorzystywany znany jako prosta forma reguły Stirlinga (dobrze jest go sobie zapamiętać!): ln N! N ln N N. (2.14) Lepsze przybliżenie N! znajdziemy korzystając z następującej reprezentacji całkowej: N! = Wówczas uzyskamy silniejszą formę reguły Stirlinga: 0 dxx N e x N. (2.15) ln N! N ln N N + 1 ln(2πn). (2.16) 2 Skorzystamy na razie z prostej formy reguły Stirlinga i wówczas: S = K! k B ln N!(K N)! = k B [K ln K K N ln N + N (K N) ln(k N) + (K N)] = k B [K ln K N ln N K ln(k N) + N ln(k N)] (2.17) Zgodnie z pierwszą zasadą termodynamiki 1 : dodatkowo: de = dq dw = T ds + µdn, (2.18) ds = 1 T de µ dn, (2.19) T ale ponieważ energia każdego stanu jest taka sama ɛ, więc całkowita energia E = Nɛ de = ɛdn i wówczas: ds = 1 T ɛdn µ T dn = ɛ µ dn (2.20) T 1 Jeden ze studentów kursu w roku akademickim 2009/2010 zadał pytanie dlaczego w równaniu (2.18) nie pojawił się czynnik pdv. Czy potrafisz odpowiedzieć na to pytanie? 16
22 k B T=0 k B T=0.1 k B T=0.5 k B T=1 f ε µ Rysunek 2.2: Średnie obsadzenie N fermionów na K poziomach energetycznych f = N/K, każdy o energii ɛ. Całkowita energia układu E = Nɛ. Wobec tego obliczmy ze wzoru (2.17): wówczas otrzymamy: Czyli: ds = ds = k B ln K N dn, (2.21) N (ɛ µ) T Oznacza to, że średnie obsadzenie stanów: dn = k B ln K N dn. (2.22) N ln K N (ɛ µ) = N k B T ( ) K (ɛ µ) N 1 = exp k B T (2.23) f = N K = 1 exp (β(ɛ µ)) + 1, (2.24) gdzie β = 1/k B T. Jest to tak zwany rozkład Fermiego-Diraca (patrz rysunek) Oczywiście podobny rachunek można wykonać dla bozonów (na jednym poziomie może znajdować się dowolna liczba cząstek). Jak pokazaliśmy na ćwiczeniach w takim przypadku: (N + K 1)! Ω = (2.25) N!(K 1)! Wykonując analogiczny rachunek jak w przypadku fermionów (ćwiczenie) otrzymamy średnie obsadzenie stanów: f = N K = 1 exp (β(ɛ µ)) 1 17 (2.26)
23 Jest to tak zwany rozkład Bosego-Einsteina. Jak widać w przypadku bozonów musi zachodzić ɛ µ > 0, ponieważ f musi być wielkością dodatnią. Jak widzicie otrzymaliśmy średnie obsadzenia poziomów energetycznych dla bozonów i fermionów rozwiązując proste zadanie kombinatoryczne i korzystając z podstawowego postulatu fizyki statystycznej S = k B ln Ω. Mając entropie moglibyśmy właściwie obliczyć inne wielkości termodynamiczne. 18
24 Rozdział 3 Zespoły fizyki Statystycznej 3.1 Wstęp W poprzednim rozdziale poznaliśmy sposób wyliczenia entropii z objętości przestrzeni stanów dla przypadku układu z zachowaną energią H( x) = E, gdzie x określał stan układu w 6N-wymiarowej przestrzeni fazowej. Oczywiście nie we wszystkich układach energia jest zachowana, czasami nawet liczba cząstek nie jest w układzie stała. Fizyka statystyczna potrafi sobie radzić również z takimi przypadkami - my zaczęliśmy po prostu od tego co najprostsze - układów izolowanych. Zespoły statystyczne takich układów nazywać będziemy odtąd zespołami mikrokanonicznymi. Jak już się przekonaliśmy entropia gra podstawową rolę w przypadku zespołu mikrokanonicznego. Wystarczy określić liczbę dozwolonych stanów odpowiadającą określonemu makrostanowi i następnie ją zlogarytmować. Mając daną entropię możemy już wyliczyć dowolną wielkość termodynamiczną. Jak już się jednak przekonaliśmy wielkości termodynamiczne można wyznaczyć nie tylko z entropii, ale z każdego innego potencjału termodynamicznego, na przykład z energii swobodnej. Przekonamy się, że w przypadku kiedy energia lub liczba cząstek nie jest w układzie zachowana wygodniej będzie nam jako punkt wyjścia obrać energię swobodną. Zespoły statystyczne układów ze zmienną energią nazywać będziemy odtąd zespołami kanonicznymi, a te dla których zmienna jest zarówno energia jak i liczba cząstek zespołami wielkimi kanonicznymi. Oczywiście w gruncie rzeczy, bez względu na to z jakim zespołem mamy do czynienia, to co wyliczamy w fizyce statystycznej czy mierzymy w eksperymencie to pewne średnie (po czasie lub zespole) wielkości termodynamicznych. Jak wyliczyć te średnie? Tak jak zwykle liczy się średnie tzn. A < A >= i A i P (A i ). (3.1) W ogólności więc, aby wyliczyć średnie, które w założeniu pokrywają się z wielkościami termodynamicznymi tzn. mierzonymi musimy znaleźć rozkład prawdopodobieństwa P (A i ). Oczywiście w zależności od tego z jakim układem będziemy mieli do czynienia zależeć będzie postać tego rozkładu. Postulat równego apriori prawdopodobieństwa mówi, że każdy mikrostan jest równie prawdopodobny. Wobec tego prawdopodobieństwo danego makrostanu będzie po prostu równe stosunkowi liczby mikrostanów danego makrostanu do liczby wszystkich mikrostanów: P (A i ) = Ω(A i) Ω. (3.2) 19
25 Rysunek 3.1: Mikrostany układu, w którym makrostan określony jest przez sumę oczek na dwóch kościach. Zaznaczone elipsami zostały makrostany o parzystej sumie oczek. Na poprzednim wykładzie liczyliśmy miedzy innymi rozkład prawdopodobieństwa w przypadku gdy makrostanem była suma oczek na dwóch kościach. obliczmy najpierw średnią liczbę wyrzuconych oczek: A = i A i P (A i ) = = = 7 (3.3) Jak widać w naszym przykładzie wartość oczekiwana pokrywa się z wynikiem o największej liczbie realizacji (najbardziej prawdopodobnym). Prawdopodobieństwo tego średniego stanu wynosi zaś: P (7) = Ω(7) Ω = 6 36 = 1 6. (3.4) Analogicznie, jeżeli w układzie jest zmienna energia to możemy się spodziewać, że prawdopodobieństwo każdego z makrostanów o danej energii będzie zależało od tej energii. Jeżeli zaś zmienna będzie również liczba cząstek to prawdopodobieństwo makrostanu o zadanej energii i liczbie cząstek też będzie od obu tych wielkości zależne. Obliczając rozkład prawdopodobieństwa należy więc przede wszystkim ustalić definicję makrostanu (pamiętacie poprzedni wykład i paradoks Bertranda? dopisać!!!). 3.2 Zespół Mikrokanoniczny Jak już się przekonaliśmy entropia gra podstawową rolę w przypadku zespołu mikrokanonicznego. Wystarczy określić liczbę dozwolonych stanów odpowiadającą określonemu makrostanowi i następnie ją zlogarytmować. Ważnym założeniem, które przy okazji poczyniliśmy było założenie, że średnie po czasie są równe średnim po zespole. O ile średnia z pewnej wielkości φ jest mierzona w eksperymencie po czasie: < φ >= 1 τ t0 +τ t 0 φ( x(t)), (3.5) 20
26 o tyle idea zespołu statystycznego sprowadza liczenie średnich z pewnych wielkości jako tzw. średnie po zespole: < φ >= d (6N) xρ( x)φ( x). (3.6) W naszym przypadku klasycznego układu o stałej energii E mamy: ρ( x) = Cδ(H( x) E), (3.7) gdzie C jest stałą normującą Jeszcze raz o entropii Zamiast pracować z układem o stałej energii dopuścimy teraz niewielkie jej zmiany, tzn. warunek zamiast H( x) = E (3.8) będzie teraz następujący: E < H( x) < E + δe, (3.9) przy czym wszystkie stany x są równoprawdopodobne. Analogiczne założenie o równości prawdopodobieństw robiliśmy w poprzednim rozdziale. Rozważmy teraz układ N rozróżnialnych cząstek. Objętość przestrzeni stanów będzie w tym wypadku następująca: Ω(E) = E<H( x)<e+δe d 6N x, (3.10) a entropia: S(E) = k B ln Ω(E), (3.11) gdzie k B jest stałą Boltzmanna mającą wymiar energii, natomiast Ω(E) jest teraz bezwymiarowe. Można wykazać, że tak zdefiniowana entropia ma wszystkie własności termodynamiczne entropii, tzn. 1. S jest wielkością ekstensywną 2. S spełnia wymagania nakładane na entropię przez II zasadę termodynamiki. 3.3 Zespół Kanoniczny Wyobraźmy sobie teraz dwa układy makroskopowe A 1 i A 2, których energie wynoszą odpowiednio E 1 i E 2. Układy mogą wymieniać między sobą energię, ale są izolowane od reszty świata, tzn.: E 1 + E 2 = E = const. (3.12) Rozważmy przypadek kiedy oba układy są ze sobą w równowadze. Interesuje nas pytanie: Ile wynosi prawdopodobieństwo P (E 1 ) tego, że energia układu A 1 jest równa E 1? Zacznijmy od bardzo prostego przykładu. Rozważmy układy A 1 i A 2, dla których liczba stanów Ω 1, Ω 2 zależy od energii E w sposób przedstawiony w tabeli: 21
27 E Ω 1 Ω Oba układy, będące w kontakcie termicznym, tworzą zamknięty układ A, którego energia E = 13. Ile jest stanów układu A, dla których energia układu A 1 wynosi: (a) E 1 = 4, (b) E 2 = 5, (c) E 3 = 6? Układ A jest zamknięty, tzn. E = E 1 + E 2 = const. Każdemu stanowi układu A 1 o energii E 1 odpowiada Ω 2 (E 2 ) stanów układu A 2 (pamiętacie przykład z dwiema kościami do gry?). Stanów układu A 1 o energii E 1 jest Ω 1 (E 1 ), czyli: Otrzymujemy: Ω(E 1 ) = Ω 1 (E 1 ) Ω 2 (E 2 ) = Ω 1 (E 1 ) Ω 2 (E E 1 ). (3.13) E 1 E 2 = E E 1 Ω 1 (E 1 ) Ω 2 (E 2 ) Ω(E 1 ) = Ω 1 (E 1 ) Ω 2 (E 2 ) Moglibyśmy teraz zadać inne pytanie - jakie jest prawdopodobieństwo tego, że układ A 1 będzie miał energię E 1? Oznaczmy przez Ω liczbę wszystkich mikrostanów układu A. W powyższym przykładzie, żeby otrzymać tę liczbę należałoby zsumować ostatnią kolumnę powyższej tabeli, czyli Ω = = 581. Prawdopodobieństwo tego, że układ A 1 będzie miał energię E 1 jest oczywiście równe wobec tego liczbie stanów układu A takich, że układ A 1 znajdzie się w stanie o energii E 1 podzielonej przez liczbę wszystkich możliwych stanów układu A: P (E 1 ) = Ω(E 1) Ω = CΩ(E 1) = CΩ 1 (E 1 )Ω 2 (E E 1 ), (3.14) gdzie C jest stałą oznaczającą odwrotność liczby wszystkich możliwych mikrostanów (C = 1/Ω) w praktyce wyznacza się ją z warunku normalizacji prawdopodobieństwa. Można zadać pytanie o to, który ze stanów układu A jest najbardziej prawdopodobny. W przytoczonym powyżej przykładzie, będzie to stan, dla którego układ A 1 przyjmie energię E 1 = 5 (proszę spojrzeć do tabelki) i prawdopodobieństwo tego stanu wyniesie 160/581. Pytanie o stan najbardziej prawdopodobny jest oczywiście pytaniem o maksimum P (E 1 ). Maksimum wyznaczamy jak zwykle z warunku: ln P (E 1 ) E 1 = 0. (3.15) 22
28 W naszym przypadku, ze względu na postać P (E 1 ) wygodniej będzie się posługiwać ln P (E 1 ) i szukać maksimum tej funkcji zamiast P (E 1 ). Ponieważ funkcja logarytmiczna jest funkcją monotoniczną to maksimum ln P (E 1 ) pojawi się dla tej samej wartości E 1, co w przypadku funkcji P (E 1 ). Funkcja logarytmiczna ma tę przyjemną własność, że iloczyn (występujący w P (E 1 )) zamienia na sumę, która jest znacznie łatwiejsza do różniczkowania. Rozważymy wobec tego funkcję: ln P (E 1 ) = ln C + ln Ω 1 (E 1 ) + ln Ω 2 (E 2 ) (3.16) Wyznaczamy maksimum tej funkcji z warunku: Wobec tego: ln P E 1 = 0. (3.17) Oczywiście ln P E 1 = ln Ω 1(E 1 ) E 1 + ln Ω 2(E 2 ) E 1 (3.18) = ln Ω 1(E 1 ) + ln Ω 2(E 2 ) E 2 = 0. (3.19) E 1 E 2 E 1 E 2 E 1 = 1, (3.20) ponieważ: E 1 + E 2 = const E 1 E 1 + E 2 E 1 = E 2 E 1 = 0 E 2 E 1 = 1. (3.21) Otrzymujemy więc: Ale: ln Ω 1 (E 1 ) E 1 ln Ω 2(E 2 ) E 2 = 0. (3.22) ln Ω(E) E = 1 k B T co wynika z podstawowego postulatu fizyki statystycznej: Czyli: β, (3.23) S = k B ln Ω. (3.24) Ostatecznie otrzymujemy,że: ln Ω(E) E = S k B E = 1 k B T. (3.25) ln Ω 1 (E 1 ) E 1 ln Ω 2(E 2 ) E 2 = 1 k B T 1 1 k B T 2 = 0. (3.26) 23
29 Czyli w stanie najbardziej prawdopodobnym: 1 T 1 = 1 T 2. (3.27) Jak może pamiętacie, jest to również warunek na stan równowagi termodynamicznej dla układów będących w kontakcie termicznym. W ramach termodynamiki warunek ten wyprowadzaliśmy maksymalizując entropię. Jak widać równowadze termodynamicznej, która jak już mówiliśmy jest pojęciem makroskopowym odpowiada, w ramach fizyki statystycznej, stan najbardziej prawdopodobny. Przypomnijmy sobie tu jeszcze szybko, jak można dojść do warunku na równowagę w ramach termodynamiki. Wychodzimy z postulatu, że w stanie równowagi entropia jest maksymalna i założenia, że entropia jest wielkością ekstensywną: oraz S(E) = S 1 (E 1 ) + S 2 (E 2 ) = S 1 (E 1 ) + S 2 (E E 1 ) (3.28) Jak już pokazaliśmy powyżej: S E 1 = S 1 E 1 + S 2 E 1 = S 1 E 1 + S 2 E 2 E 2 E 1 = 0 (3.29) jeżeli energia układu jako całości jest zachowana. Wobec tego: Rozkład prawdopodobieństwa Gibbsa E 2 E 1 = 1, (3.30) S 1 S 2 = 0 E 1 E 2 (3.31) 1 = 1 T 1 T 2 (3.32) Dotychczas nie interesowaliśmy się tym jak duże są podukłady A 1 i A 2, ani też jakie są ich energie E 1 i E 2. Teraz rozważymy przypadek, w którym E 1 << E (3.33) Będziemy chcieli znowu znaleźć prawdopodobieństwo tego, że układ A 1 znajdzie się w stanie o pewnej energii E 1 = E r. Korzystając z poprzednich rozważań wiemy już, że: P (E 1 = E r ) P (E r ) P r = C 1 Ω 1 (E r )Ω 2 (E E r ). (3.34) Korzystając teraz z warunku E r << E obliczymy Ω 2 (E E r ). Z podstawowego postulatu fizyki statystycznej: ( ) S S = k B ln Ω Ω = exp. (3.35) kb 24
30 Wobec tego: ( ) S2 (E E r ) Ω 2 (E E r ) = exp. (3.36) Teraz skorzystamy z założenia, że E r << E. W takim przypadku możemy entropię rozwinąć w szereg potęgowy Taylora i zaniedbać wyższe potęgi rozwinięcia: S 2 (E) S 2 (E E r ) = S 2 (E) E r E +... = S 2(E) E r T. (3.37) Tutaj pytanie do was - dlaczego nie używam T 1, T 2 czy T r tylko T? Czyli otrzymujemy: ( ) ( S2 (E E r ) S2 Ω 2 (E E r ) = exp = exp E ) r. (3.38) k B k B T Ostatecznie: k B k B Ω 2 (E E r ) = C 2 exp ( βe r ). (3.39) Wobec tego prawdopodobieństwo tego, że układ A 1 znajdzie się w stanie o pewnej energii E 1 = E r wynosi: P r = C 1 C 2 Ω 1 (E r ) exp ( βe r ). (3.40) Jest to tak zwany rozkład Gibbsa. Jeżeli interesowałby nas jeden konkretny stan o energii E r tzn. podstawiamy Ω(E r ) = 1 wówczas: P r = C exp ( βe r ), (3.41) gdzie C możemy wyznaczyć z warunku normowania: 1 P i = 1 C = i exp ( βe i ). (3.42) i Mianownik stałej normującej nazywa się sumą statystyczną Z, ponieważ jest sumą po wszystkich stanach. W rozważanym przypadku mamy do czynienia z tzw. kanoniczną sumą statystyczną: Z = i exp ( βe i ). (3.43) Średnia energia Jak już powiedzieliśmy średnia wartość dowolnej wielkości A wyraża się znanym ze statystyki wzorem: < A >= p r A r. (3.44) r W przypadku rozkładu kanonicznego, szczególnie zwartą postać ma wzór na średnią wartość energii: < E >= r E r e βer p r E r =. (3.45) r Z Zauważmy jednak, że Wobec tego: E r e βer = r r β (e βer ) = β < E >= 1 Z Z β 25 e βer r = Z β. (3.46) = ln Z β. (3.47)
31 3.3.3 Związek pomiędzy fizyką statystyczną i termodynamiką w zespole kanonicznym Jak już się dowiedzieliśmy, dla układu izolowanego, tzn. takiego w którym energia E r i liczba cząstek N r jest stała (E r = E, N r = N), mikrostany są albo osiągalne albo nieosiągalne i entropia dana jest jako logarytm z liczby dostępnych mikrostanów (ew. objętości przestrzeni fazowej w przypadku ciągłym): S r = k B ln Ω(E r, N r ) (3.48) Jeżeli układ jest w kontakcie z termostatem lub rezerwuarem cząstek, wówczas różne mikrostany pojawiają się z różnymi prawdopodobieństwami i potrzebna jest ogólniejsza definicja entropii. W układzie izolowanym, którego energia jest E r = E prawdopodobieństwa różnych mikrostanów mogą być zapisane jako: p r = Entropia zaś wyrażona jest wzorem { 1 Ω(E r) dla E r = E 0 dla E r E (3.49) S = k B ln Ω(E r ) = k ln p r. (3.50) Wszystkie mikrostany mogą być podzielone na dwie klasy - dostępne i niedostępne. W przypadku układu w kontakcie z termostatem mamy zaś do czynienia z bardziej i mniej prawdopodobnymi mikrostanami zgodnie z rozkładem Gibbsa. Oczywiście nadal każdy mikrostan daje wkład do entropii, ale teraz te wkłady są różne. Możemy teraz pomyśleć o uogólnionej definicji entropii jako średniej po wszystkich możliwych mikrostanach: S =< k ln p r >= k p r ln p r. (3.51) r Taka postać entropii nazywa się entropią Gibbsa i jest prawidłowa dla dowolnego rozkładu prawdopodobieństwa mikrostanów. Łatwo zobaczyć, że w przypadku rozkładu mikrokanonicznego natychmiast redukuje się do znanej już wcześniej formuły. Dla zespołu kanonicznego, w którym mamy rozkład Gibbsa otrzymujemy: e βer S = k B p r ln p r = k e βer ln r r Z Z e βer ( = k B ln e βe r ln Z ) = k B Z r r e βer Z (βe r + ln Z) = k B β E r e βer e βer + k B r Z r Z ln Z = k Bβ E r e βer + k B ln Z p r r Z r = k B β < E > +k B ln Z = < E > + k B ln Z. (3.52) T Z tego wynika, że: k B T ln Z =< E > T S. (3.53) Porównując to wyrażenie ze wzorem na energię swobodną w klasycznej termodynamice F = U T S otrzymujemy: F = k B T ln Z (3.54) Pod warunkiem, że założymy U =< E >. Jest to kolejny związek między fizyką statystyczną a termodynamiką - tym razem w przypadku rozkładu kanonicznego. 26
32 3.4 Zespół Wielki Kanoniczny Wyobraźmy sobie raz jeszcze dwa układy makroskopowe A 1 i A 2, których energie wynoszą odpowiednio E 1 i E 2. Układy mogą wymieniać między sobą tym razem zarówno energię, jak i cząstki, ale nadal są izolowane od reszty świata, tzn.: E 1 + E 2 = E = const N 1 + N 2 = N = const (3.55) Rozważmy przypadek kiedy oba układy są ze sobą w równowadze. Interesuje nas pytanie: Ile wynosi prawdopodobieństwo P (E 1, N 1 ) tego, że energia układu A 1 jest równa E 1, a liczba cząstek N 1? Prawdopodobieństwo to jest oczywiście równe liczbie stanów układu A takich, że układ A 1 znajdzie się w stanie (E 1, N 1 ) podzielonej przez liczbę wszystkich możliwych stanów układu A: P (E 1, n 1 ) = Ω(E 1, N 1 ) Ω = CΩ(E 1, N 1 ) = CΩ 1 (E 1, N 1 )Ω 2 (E E 1, N N 1 ),(3.56) gdzie C jest stałą oznaczającą odwrotność liczby wszystkich możliwych mikrostanów (C = 1/Ω) w praktyce wyznacza się ją z warunku normalizacji prawdopodobieństwa. Można zadać pytanie o to, który ze stanów układu A jest najbardziej prawdopodobny. Pytanie o stan najbardziej prawdopodobny jest oczywiście pytaniem o maksimum P (E 1, N 1 ). Maksimum wyznaczamy jak zwykle z warunku: ( ) ( ) P P dp = de 1 + dn 1 = 0 (3.57) E 1 N 1 N 1 E 1 Czyli muszą zajść dwie równości: ( ) P = 0 E 1 N ( ) 1 P N 1 E 1 = 0. (3.58) W tym wypadku wygodniej będzie nam wyznaczać maksimum ln P (E 1, N 1 ) zamiast P (E 1, N 1 ), ponieważ podobnie jak w przypadku zespołu kanonicznego będziemy korzystali ze związku S = k B ln Ω. Oczywiście, ponieważ logarytm jest funkcją monotoniczną to wolno nam to zrobić (argumentacja taka sama jak poprzednio). Pokazaliśmy już, że z warunku otrzymujemy T 1 = T 2. Teraz liczymy: ln P E 1 = 0 (3.59) ln P = ln Ω 1(N 1 ) + ln Ω 2(N 2 ) N 1 N 1 N 1 = ln Ω 1(N 1 ) + ln Ω 2(N 2 ) N 2 N 1 N 2 N 1 = ln Ω 1(N 1 ) ln Ω 2(N 2 ) = 0 (3.60) N 1 N 2 27
Elementy termodynamiki
 Elementy termodynamiki Katarzyna Sznajd-Weron Katedra Fizyki Teoretycznej Politechnika Wrocławska 5 stycznia 2019 Katarzyna Sznajd-Weron (K4) Wstęp do Fizyki Statystycznej 5 stycznia 2019 1 / 27 Wielkości
Elementy termodynamiki Katarzyna Sznajd-Weron Katedra Fizyki Teoretycznej Politechnika Wrocławska 5 stycznia 2019 Katarzyna Sznajd-Weron (K4) Wstęp do Fizyki Statystycznej 5 stycznia 2019 1 / 27 Wielkości
Elementy termodynamiki i wprowadzenie do zespołów statystycznych. Katarzyna Sznajd-Weron
 Elementy termodynamiki i wprowadzenie do zespołów statystycznych Katarzyna Sznajd-Weron Wielkości makroskopowe - termodynamika Termodynamika - metoda fenomenologiczna Fenomenologia w fizyce: widzimy jak
Elementy termodynamiki i wprowadzenie do zespołów statystycznych Katarzyna Sznajd-Weron Wielkości makroskopowe - termodynamika Termodynamika - metoda fenomenologiczna Fenomenologia w fizyce: widzimy jak
Politechnika Wrocławska Katedra Fizyki Teoretycznej. Katarzyna Sznajd-Weron. Fizyka Statystyczna
 Politechnika Wrocławska Katedra Fizyki Teoretycznej Katarzyna Sznajd-Weron Fizyka Statystyczna Skrypt dla studentów Wrocław 2016 2 Spis treści 1 Elementy termodynamiki 1 1.1 Wielkości termodynamiczne..........................
Politechnika Wrocławska Katedra Fizyki Teoretycznej Katarzyna Sznajd-Weron Fizyka Statystyczna Skrypt dla studentów Wrocław 2016 2 Spis treści 1 Elementy termodynamiki 1 1.1 Wielkości termodynamiczne..........................
Równowaga w układach termodynamicznych. Katarzyna Sznajd-Weron
 Równowaga w układach termodynamicznych. Katarzyna Sznajd-Weron Zagadka na początek wykładu Diagram fazowy wody w powiększeniu, problem metastabilności aktualny (Nature, 2011) Niższa temperatura topnienia
Równowaga w układach termodynamicznych. Katarzyna Sznajd-Weron Zagadka na początek wykładu Diagram fazowy wody w powiększeniu, problem metastabilności aktualny (Nature, 2011) Niższa temperatura topnienia
Elementy termodynamiki
 Elementy termodynamiki Katarzyna Sznajd-Weron Katedra Fizyki Teoretycznej Politechnika Wrocławska 11 marca 2019 Katarzyna Sznajd-Weron (K4) Wstęp do Fizyki Statystycznej 11 marca 2019 1 / 37 Dwa poziomy
Elementy termodynamiki Katarzyna Sznajd-Weron Katedra Fizyki Teoretycznej Politechnika Wrocławska 11 marca 2019 Katarzyna Sznajd-Weron (K4) Wstęp do Fizyki Statystycznej 11 marca 2019 1 / 37 Dwa poziomy
Wykład 3. Entropia i potencjały termodynamiczne
 Wykład 3 Entropia i potencjały termodynamiczne dr hab. Agata Fronczak, prof. PW Wydział Fizyki, Politechnika Warszawska 1 stycznia 2017 dr hab. A. Fronczak (Wydział Fizyki PW) Wykład: Elementy fizyki statystycznej
Wykład 3 Entropia i potencjały termodynamiczne dr hab. Agata Fronczak, prof. PW Wydział Fizyki, Politechnika Warszawska 1 stycznia 2017 dr hab. A. Fronczak (Wydział Fizyki PW) Wykład: Elementy fizyki statystycznej
TERMODYNAMIKA FENOMENOLOGICZNA
 TERMODYNAMIKA FENOMENOLOGICZNA Przedmiotem badań są własności układów makroskopowych w zaleŝności od temperatury. Układ makroskopowy Np. 1 mol substancji - tyle składników ile w 12 gramach węgla C 12 N
TERMODYNAMIKA FENOMENOLOGICZNA Przedmiotem badań są własności układów makroskopowych w zaleŝności od temperatury. Układ makroskopowy Np. 1 mol substancji - tyle składników ile w 12 gramach węgla C 12 N
Przegląd termodynamiki II
 Wykład II Mechanika statystyczna 1 Przegląd termodynamiki II W poprzednim wykładzie po wprowadzeniu podstawowych pojęć i wielkości, omówione zostały pierwsza i druga zasada termodynamiki. Tutaj wykorzystamy
Wykład II Mechanika statystyczna 1 Przegląd termodynamiki II W poprzednim wykładzie po wprowadzeniu podstawowych pojęć i wielkości, omówione zostały pierwsza i druga zasada termodynamiki. Tutaj wykorzystamy
Wykład 12. Rozkład wielki kanoniczny i statystyki kwantowe
 Wykład 12 Rozkład wielki kanoniczny i statystyki kwantowe dr hab. Agata Fronczak, prof. PW Wydział Fizyki, Politechnika Warszawska 1 stycznia 2017 dr hab. A. Fronczak (Wydział Fizyki PW) Wykład: Elementy
Wykład 12 Rozkład wielki kanoniczny i statystyki kwantowe dr hab. Agata Fronczak, prof. PW Wydział Fizyki, Politechnika Warszawska 1 stycznia 2017 dr hab. A. Fronczak (Wydział Fizyki PW) Wykład: Elementy
Wykład 1 i 2. Termodynamika klasyczna, gaz doskonały
 Wykład 1 i 2 Termodynamika klasyczna, gaz doskonały dr hab. Agata Fronczak, prof. PW Wydział Fizyki, Politechnika Warszawska 1 stycznia 2017 dr hab. A. Fronczak (Wydział Fizyki PW) Wykład: Elementy fizyki
Wykład 1 i 2 Termodynamika klasyczna, gaz doskonały dr hab. Agata Fronczak, prof. PW Wydział Fizyki, Politechnika Warszawska 1 stycznia 2017 dr hab. A. Fronczak (Wydział Fizyki PW) Wykład: Elementy fizyki
Wstęp do fizyki statystycznej: krytyczność i przejścia fazowe. Katarzyna Sznajd-Weron
 Wstęp do fizyki statystycznej: krytyczność i przejścia fazowe Katarzyna Sznajd-Weron Co to jest fizyka statystyczna? Termodynamika poziom makroskopowy Fizyka statystyczna poziom mikroskopowy Marcin Weron
Wstęp do fizyki statystycznej: krytyczność i przejścia fazowe Katarzyna Sznajd-Weron Co to jest fizyka statystyczna? Termodynamika poziom makroskopowy Fizyka statystyczna poziom mikroskopowy Marcin Weron
Termodynamika Część 6 Związki i tożsamości termodynamiczne Potencjały termodynamiczne Warunki równowagi termodynamicznej Potencjał chemiczny
 Termodynamika Część 6 Związki i tożsamości termodynamiczne Potencjały termodynamiczne Warunki równowagi termodynamicznej Potencjał chemiczny Janusz Brzychczyk, Instytut Fizyki UJ Związek pomiędzy równaniem
Termodynamika Część 6 Związki i tożsamości termodynamiczne Potencjały termodynamiczne Warunki równowagi termodynamicznej Potencjał chemiczny Janusz Brzychczyk, Instytut Fizyki UJ Związek pomiędzy równaniem
Układy statystyczne. Jacek Jurkowski, Fizyka Statystyczna. Instytut Fizyki
 Instytut Fizyki 2015 Stany mikroskopowe i makroskopowe w układzie wielopoziomowym Stany mikroskopowe i makroskopowe w układzie wielopoziomowym N rozróżnialnych cząstek, z których każda może mieć energię
Instytut Fizyki 2015 Stany mikroskopowe i makroskopowe w układzie wielopoziomowym Stany mikroskopowe i makroskopowe w układzie wielopoziomowym N rozróżnialnych cząstek, z których każda może mieć energię
FIZYKA STATYSTYCZNA. d dp. jest sumaryczną zmianą pędu cząsteczek zachodzącą na powierzchni S w
 FIZYKA STATYSTYCZNA W ramach fizyki statystycznej przyjmuje się, że każde ciało składa się z dużej liczby bardzo małych cząstek, nazywanych cząsteczkami. Cząsteczki te znajdują się w ciągłym chaotycznym
FIZYKA STATYSTYCZNA W ramach fizyki statystycznej przyjmuje się, że każde ciało składa się z dużej liczby bardzo małych cząstek, nazywanych cząsteczkami. Cząsteczki te znajdują się w ciągłym chaotycznym
= = Budowa materii. Stany skupienia materii. Ilość materii (substancji) n - ilość moli, N liczba molekuł (atomów, cząstek), N A
 Budowa materii Stany skupienia materii Ciało stałe Ciecz Ciała lotne (gazy i pary) Ilość materii (substancji) n N = = N A m M N A = 6,023 10 mol 23 1 n - ilość moli, N liczba molekuł (atomów, cząstek),
Budowa materii Stany skupienia materii Ciało stałe Ciecz Ciała lotne (gazy i pary) Ilość materii (substancji) n N = = N A m M N A = 6,023 10 mol 23 1 n - ilość moli, N liczba molekuł (atomów, cząstek),
S ścianki naczynia w jednostce czasu przekazywany
 FIZYKA STATYSTYCZNA W ramach fizyki statystycznej przyjmuje się, że każde ciało składa się z dużej liczby bardzo małych cząstek, nazywanych cząsteczkami. Cząsteczki te znajdują się w ciągłym chaotycznym
FIZYKA STATYSTYCZNA W ramach fizyki statystycznej przyjmuje się, że każde ciało składa się z dużej liczby bardzo małych cząstek, nazywanych cząsteczkami. Cząsteczki te znajdują się w ciągłym chaotycznym
Krótki przegląd termodynamiki
 Wykład I Przejścia fazowe 1 Krótki przegląd termodynamiki Termodynamika fenomenologiczna oferuje makroskopowy opis układów statystycznych w stanie równowagi termodynamicznej bądź w stanach jemu bliskich.
Wykład I Przejścia fazowe 1 Krótki przegląd termodynamiki Termodynamika fenomenologiczna oferuje makroskopowy opis układów statystycznych w stanie równowagi termodynamicznej bądź w stanach jemu bliskich.
Wykład 8 i 9. Hipoteza ergodyczna, rozkład mikrokanoniczny, wzór Boltzmanna
 Wykład 8 i 9 Hipoteza ergodyczna, rozkład mikrokanoniczny, wzór Boltzmanna dr hab. Agata Fronczak, prof. PW Wydział Fizyki, Politechnika Warszawska 1 stycznia 2017 dr hab. A. Fronczak (Wydział Fizyki PW)
Wykład 8 i 9 Hipoteza ergodyczna, rozkład mikrokanoniczny, wzór Boltzmanna dr hab. Agata Fronczak, prof. PW Wydział Fizyki, Politechnika Warszawska 1 stycznia 2017 dr hab. A. Fronczak (Wydział Fizyki PW)
Termodynamiczny opis przejść fazowych pierwszego rodzaju
 Wykład II Przejścia fazowe 1 Termodynamiczny opis przejść fazowych pierwszego rodzaju Woda występuje w trzech stanach skupienia jako ciecz, jako gaz, czyli para wodna, oraz jako ciało stałe, a więc lód.
Wykład II Przejścia fazowe 1 Termodynamiczny opis przejść fazowych pierwszego rodzaju Woda występuje w trzech stanach skupienia jako ciecz, jako gaz, czyli para wodna, oraz jako ciało stałe, a więc lód.
Termodynamiczny opis układu
 ELEMENTY FIZYKI STATYSTYCZNEJ Przedmiot badań fizyki statystycznej układy składające się z olbrzymiej ilości cząstek (ujawniają się specyficzne prawa statystyczne). Termodynamiczny opis układu Opis termodynamiczny
ELEMENTY FIZYKI STATYSTYCZNEJ Przedmiot badań fizyki statystycznej układy składające się z olbrzymiej ilości cząstek (ujawniają się specyficzne prawa statystyczne). Termodynamiczny opis układu Opis termodynamiczny
Zespół kanoniczny N,V, T. acc o n =min {1, exp [ U n U o ] }
![Zespół kanoniczny N,V, T. acc o n =min {1, exp [ U n U o ] } Zespół kanoniczny N,V, T. acc o n =min {1, exp [ U n U o ] }](/thumbs/64/51033976.jpg) Zespół kanoniczny Zespół kanoniczny N,V, T acc o n =min {1, exp [ U n U o ] } Zespół izobaryczno-izotermiczny Zespół izobaryczno-izotermiczny N P T acc o n =min {1, exp [ U n U o ] } acc o n =min {1, exp[
Zespół kanoniczny Zespół kanoniczny N,V, T acc o n =min {1, exp [ U n U o ] } Zespół izobaryczno-izotermiczny Zespół izobaryczno-izotermiczny N P T acc o n =min {1, exp [ U n U o ] } acc o n =min {1, exp[
Termodynamika. Część 4. Procesy izoparametryczne Entropia Druga zasada termodynamiki. Janusz Brzychczyk, Instytut Fizyki UJ
 Termodynamika Część 4 Procesy izoparametryczne Entropia Druga zasada termodynamiki Janusz Brzychczyk, Instytut Fizyki UJ Pierwsza zasada termodynamiki procesy kwazistatyczne Zgodnie z pierwszą zasadą termodynamiki,
Termodynamika Część 4 Procesy izoparametryczne Entropia Druga zasada termodynamiki Janusz Brzychczyk, Instytut Fizyki UJ Pierwsza zasada termodynamiki procesy kwazistatyczne Zgodnie z pierwszą zasadą termodynamiki,
Termodynamika Część 7 Trzecia zasada termodynamiki Metody otrzymywania niskich temperatur Zjawisko Joule'a Thomsona Chłodzenie magnetyczne
 Termodynamika Część 7 Trzecia zasada termodynamiki Metody otrzymywania niskich temperatur Zjawisko Joule'a Thomsona Chłodzenie magnetyczne Janusz Brzychczyk, Instytut Fizyki UJ Postulat Nernsta (1906):
Termodynamika Część 7 Trzecia zasada termodynamiki Metody otrzymywania niskich temperatur Zjawisko Joule'a Thomsona Chłodzenie magnetyczne Janusz Brzychczyk, Instytut Fizyki UJ Postulat Nernsta (1906):
Termodynamika. Część 11. Układ wielki kanoniczny Statystyki kwantowe Gaz fotonowy Ruchy Browna. Janusz Brzychczyk, Instytut Fizyki UJ
 Termodynamika Część 11 Układ wielki kanoniczny Statystyki kwantowe Gaz fotonowy Ruchy Browna Janusz Brzychczyk, Instytut Fizyki UJ Układ otwarty rozkład wielki kanoniczny Rozważamy układ w równowadze termicznej
Termodynamika Część 11 Układ wielki kanoniczny Statystyki kwantowe Gaz fotonowy Ruchy Browna Janusz Brzychczyk, Instytut Fizyki UJ Układ otwarty rozkład wielki kanoniczny Rozważamy układ w równowadze termicznej
WYKŁAD 15. Gęstość stanów Zastosowanie: oscylatory kwantowe (ª bosony bezmasowe) Formalizm dla nieoddziaływujących cząstek Bosego lub Fermiego
 WYKŁAD 15 Gęstość stanów Zastosowanie: oscylatory kwantowe (ª bosony bezmasowe) Formalizm dla nieoddziaływujących cząstek Bosego lub Fermiego 1 Statystyka nieoddziaływujących gazów Bosego i Fermiego Bosony
WYKŁAD 15 Gęstość stanów Zastosowanie: oscylatory kwantowe (ª bosony bezmasowe) Formalizm dla nieoddziaływujących cząstek Bosego lub Fermiego 1 Statystyka nieoddziaływujących gazów Bosego i Fermiego Bosony
Wykład 4. II Zasada Termodynamiki
 Wykład 4 II Zasada Termodynamiki Ogólne sformułowanie: istnienie strzałki czasu Pojęcie entropii i temperatury absolutnej Ćwiczenia: Formy różniczkowe Pfaffa 1 I sza Zasada Termodynamiki: I-sza zasada
Wykład 4 II Zasada Termodynamiki Ogólne sformułowanie: istnienie strzałki czasu Pojęcie entropii i temperatury absolutnej Ćwiczenia: Formy różniczkowe Pfaffa 1 I sza Zasada Termodynamiki: I-sza zasada
Wykład FIZYKA I. 14. Termodynamika fenomenologiczna cz.ii. Dr hab. inż. Władysław Artur Woźniak
 Wykład FIZYKA I 14. Termodynamika fenomenologiczna cz.ii Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej http://www.if.pwr.wroc.pl/~wozniak/fizyka1.html GAZY DOSKONAŁE Przez
Wykład FIZYKA I 14. Termodynamika fenomenologiczna cz.ii Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej http://www.if.pwr.wroc.pl/~wozniak/fizyka1.html GAZY DOSKONAŁE Przez
II Zasada Termodynamiki c.d.
 Wykład 5 II Zasada Termodynamiki c.d. Pojęcie entropii i temperatury absolutnej II zasada termodynamiki dla procesów nierównowagowych Równania Gibbsa dla procesów quasistatycznych Równania Eulera Relacje
Wykład 5 II Zasada Termodynamiki c.d. Pojęcie entropii i temperatury absolutnej II zasada termodynamiki dla procesów nierównowagowych Równania Gibbsa dla procesów quasistatycznych Równania Eulera Relacje
Statystyka nieoddziaływujących gazów Bosego i Fermiego
 Statystyka nieoddziaływujących gazów Bosego i Fermiego Bozony: fotony (kwanty pola elektromagnetycznego, których liczba nie jest zachowana mogą być pojedynczo pochłaniane lub tworzone. W konsekwencji,
Statystyka nieoddziaływujących gazów Bosego i Fermiego Bozony: fotony (kwanty pola elektromagnetycznego, których liczba nie jest zachowana mogą być pojedynczo pochłaniane lub tworzone. W konsekwencji,
4 Przekształcenia pochodnych termodynamicznych
 4 Przekształcenia pochodnych termodynamicznych 4.1 Relacje Maxwella Pierwsza zasada termodynamiki może być zapisana w postaci niezależnej od reprezentacji jako warunek znikania formy Pfaffa: Stąd musi
4 Przekształcenia pochodnych termodynamicznych 4.1 Relacje Maxwella Pierwsza zasada termodynamiki może być zapisana w postaci niezależnej od reprezentacji jako warunek znikania formy Pfaffa: Stąd musi
IX. MECHANIKA (FIZYKA) KWANTOWA
 IX. MECHANIKA (FIZYKA) KWANTOWA IX.1. OPERACJE OBSERWACJI. a) klasycznie nie ważna kolejność, w jakiej wykonujemy pomiary. AB = BA A pomiar wielkości A B pomiar wielkości B b) kwantowo wartość obserwacji
IX. MECHANIKA (FIZYKA) KWANTOWA IX.1. OPERACJE OBSERWACJI. a) klasycznie nie ważna kolejność, w jakiej wykonujemy pomiary. AB = BA A pomiar wielkości A B pomiar wielkości B b) kwantowo wartość obserwacji
Wstęp do Fizyki Statystycznej
 Wstęp do Fizyki Statystycznej Katarzyna Sznajd-Weron Katedra Fizyki Teoretycznej Politechnika Wrocławska 11 października 2016 Katarzyna Sznajd-Weron (K4) Wstęp do Fizyki Statystycznej 11 października 2016
Wstęp do Fizyki Statystycznej Katarzyna Sznajd-Weron Katedra Fizyki Teoretycznej Politechnika Wrocławska 11 października 2016 Katarzyna Sznajd-Weron (K4) Wstęp do Fizyki Statystycznej 11 października 2016
Podstawowe pojęcia Masa atomowa (cząsteczkowa) - to stosunek masy atomu danego pierwiastka chemicznego (cząsteczki związku chemicznego) do masy 1/12
 Podstawowe pojęcia Masa atomowa (cząsteczkowa) - to stosunek masy atomu danego pierwiastka chemicznego (cząsteczki związku chemicznego) do masy 1/12 atomu węgla 12 C. Mol - jest taką ilością danej substancji,
Podstawowe pojęcia Masa atomowa (cząsteczkowa) - to stosunek masy atomu danego pierwiastka chemicznego (cząsteczki związku chemicznego) do masy 1/12 atomu węgla 12 C. Mol - jest taką ilością danej substancji,
Projekt Inżynier mechanik zawód z przyszłością współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego
 Zajęcia wyrównawcze z fizyki -Zestaw 4 -eoria ermodynamika Równanie stanu gazu doskonałego Izoprzemiany gazowe Energia wewnętrzna gazu doskonałego Praca i ciepło w przemianach gazowych Silniki cieplne
Zajęcia wyrównawcze z fizyki -Zestaw 4 -eoria ermodynamika Równanie stanu gazu doskonałego Izoprzemiany gazowe Energia wewnętrzna gazu doskonałego Praca i ciepło w przemianach gazowych Silniki cieplne
Termodynamika Część 3
 Termodynamika Część 3 Formy różniczkowe w termodynamice Praca i ciepło Pierwsza zasada termodynamiki Pojemność cieplna i ciepło właściwe Ciepło właściwe gazów doskonałych Ciepło właściwe ciała stałego
Termodynamika Część 3 Formy różniczkowe w termodynamice Praca i ciepło Pierwsza zasada termodynamiki Pojemność cieplna i ciepło właściwe Ciepło właściwe gazów doskonałych Ciepło właściwe ciała stałego
Wykład 14. Termodynamika gazu fotnonowego
 Wykład 14 Termodynamika gazu fotnonowego dr hab. Agata Fronczak, prof. PW Wydział Fizyki, Politechnika Warszawska 16 stycznia 217 dr hab. A. Fronczak (Wydział Fizyki PW) Wykład: Elementy fizyki statystycznej
Wykład 14 Termodynamika gazu fotnonowego dr hab. Agata Fronczak, prof. PW Wydział Fizyki, Politechnika Warszawska 16 stycznia 217 dr hab. A. Fronczak (Wydział Fizyki PW) Wykład: Elementy fizyki statystycznej
Co to jest model Isinga?
 Co to jest model Isinga? Fakty eksperymentalne W pewnych metalach (np. Fe, Ni) następuje spontaniczne ustawianie się spinów wzdłuż pewnego kierunku, powodując powstanie makroskopowego pola magnetycznego.
Co to jest model Isinga? Fakty eksperymentalne W pewnych metalach (np. Fe, Ni) następuje spontaniczne ustawianie się spinów wzdłuż pewnego kierunku, powodując powstanie makroskopowego pola magnetycznego.
ELEMENTY FIZYKI STATYSTYCZNEJ
 ELEMENTY FIZYKI STATYSTYCZNEJ Przedmiot badań fizyki statystycznej układy składające się z olbrzymiej ilości cząstek (ujawniają się specyficzne prawa statystyczne). 15.1. Termodynamiczny opis układu Opis
ELEMENTY FIZYKI STATYSTYCZNEJ Przedmiot badań fizyki statystycznej układy składające się z olbrzymiej ilości cząstek (ujawniają się specyficzne prawa statystyczne). 15.1. Termodynamiczny opis układu Opis
Elementy fizyki statystycznej
 5-- lementy fizyki statystycznej ermodynamika Gęstości stanów Funkcje rozkładu Gaz elektronów ermodynamika [K] 9 wszechświat tuż po powstaniu ermodynamika to dział fizyki zajmujący się energią termiczną
5-- lementy fizyki statystycznej ermodynamika Gęstości stanów Funkcje rozkładu Gaz elektronów ermodynamika [K] 9 wszechświat tuż po powstaniu ermodynamika to dział fizyki zajmujący się energią termiczną
Rozkłady: Kanoniczny, Wielki Kanoniczny, Izobaryczno-Izotermiczny
 Rozkłady: Kanoniczny, Wielki Kanoniczny, Izobaryczno-Izotermiczny 1 Rozkład Mikrokanoniczny (przypomnienie) S= k B ln( (E,V,{x i },{N j }) ) Z fenomenologii: Niestety, rachunki przy użyciu rozkładu mikrokanonicznego
Rozkłady: Kanoniczny, Wielki Kanoniczny, Izobaryczno-Izotermiczny 1 Rozkład Mikrokanoniczny (przypomnienie) S= k B ln( (E,V,{x i },{N j }) ) Z fenomenologii: Niestety, rachunki przy użyciu rozkładu mikrokanonicznego
Termodynamika. Cel. Opis układu niezależny od jego struktury mikroskopowej Uniwersalne prawa. William Thomson 1. Baron Kelvin
 Cel Termodynamika Opis układu niezależny od jego struktury mikroskopowej Uniwersalne prawa Nicolas Léonard Sadi Carnot 1796 1832 Rudolf Clausius 1822 1888 William Thomson 1. Baron Kelvin 1824 1907 i inni...
Cel Termodynamika Opis układu niezależny od jego struktury mikroskopowej Uniwersalne prawa Nicolas Léonard Sadi Carnot 1796 1832 Rudolf Clausius 1822 1888 William Thomson 1. Baron Kelvin 1824 1907 i inni...
Podstawy termodynamiki
 Podstawy termodynamiki Organizm żywy z punktu widzenia termodynamiki Parametry stanu Funkcje stanu: U, H, F, G, S I zasada termodynamiki i prawo Hessa II zasada termodynamiki Kierunek przemian w warunkach
Podstawy termodynamiki Organizm żywy z punktu widzenia termodynamiki Parametry stanu Funkcje stanu: U, H, F, G, S I zasada termodynamiki i prawo Hessa II zasada termodynamiki Kierunek przemian w warunkach
Agata Fronczak Elementy fizyki statystycznej
 Agata Fronczak Elementy fizyki statystycznej Skrypt do wykładu i ćwiczeń rachunkowych dla kierunku Fotonika (rok III, semestr 5) na Wydziale Fizyki PW Warszawa 2016 Spis treści 1. Termodynamika klasyczna,
Agata Fronczak Elementy fizyki statystycznej Skrypt do wykładu i ćwiczeń rachunkowych dla kierunku Fotonika (rok III, semestr 5) na Wydziale Fizyki PW Warszawa 2016 Spis treści 1. Termodynamika klasyczna,
Wielki rozkład kanoniczny
 , granica termodynamiczna i przejścia fazowe Instytut Fizyki 2015 Podukład otwarty Podukład otwarty S opisywany układ + rezerwuar R Podukład otwarty S opisywany układ + rezerwuar R układ S + R jest izolowany
, granica termodynamiczna i przejścia fazowe Instytut Fizyki 2015 Podukład otwarty Podukład otwarty S opisywany układ + rezerwuar R Podukład otwarty S opisywany układ + rezerwuar R układ S + R jest izolowany
Klasyczna mechanika statystyczna Gibbsa I
 Wykład III Mechanika statystyczna Klasyczna mechanika statystyczna Gibbsa I Wstępne uwagi Materia nas otaczająca, w szczególności gazy będące centralnym obiektem naszego zainteresowania, zbudowane są z
Wykład III Mechanika statystyczna Klasyczna mechanika statystyczna Gibbsa I Wstępne uwagi Materia nas otaczająca, w szczególności gazy będące centralnym obiektem naszego zainteresowania, zbudowane są z
Statystyki kwantowe. P. F. Góra
 Statystyki kwantowe P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2016 Statystyki kwantowe Rozpatrujemy gaz doskonały o Hamiltonianie H = N i=1 p i 2 2m. (1) Zamykamy czastki w bardzo dużym pudle o idealnie
Statystyki kwantowe P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2016 Statystyki kwantowe Rozpatrujemy gaz doskonały o Hamiltonianie H = N i=1 p i 2 2m. (1) Zamykamy czastki w bardzo dużym pudle o idealnie
Wykład Praca (1.1) c Całka liniowa definiuje pracę wykonaną w kierunku działania siły. Reinhard Kulessa 1
 1.6 Praca Wykład 2 Praca zdefiniowana jest jako ilość energii dostarczanej przez siłę działającą na pewnej drodze i matematycznie jest zapisana jako: W = c r F r ds (1.1) ds F θ c Całka liniowa definiuje
1.6 Praca Wykład 2 Praca zdefiniowana jest jako ilość energii dostarczanej przez siłę działającą na pewnej drodze i matematycznie jest zapisana jako: W = c r F r ds (1.1) ds F θ c Całka liniowa definiuje
Szkła specjalne Przejście szkliste i jego termodynamika Wykład 5. Ryszard J. Barczyński, 2017 Materiały edukacyjne do użytku wewnętrznego
 Szkła specjalne Przejście szkliste i jego termodynamika Wykład 5 Ryszard J. Barczyński, 2017 Materiały edukacyjne do użytku wewnętrznego Czy przejście szkliste jest termodynamicznym przejściem fazowym?
Szkła specjalne Przejście szkliste i jego termodynamika Wykład 5 Ryszard J. Barczyński, 2017 Materiały edukacyjne do użytku wewnętrznego Czy przejście szkliste jest termodynamicznym przejściem fazowym?
Chemia Fizyczna Technologia Chemiczna II rok Wykład 1. Kierownik przedmiotu: Dr hab. inż. Wojciech Chrzanowski
 Chemia Fizyczna Technologia Chemiczna II rok Wykład 1 Kierownik przedmiotu: Dr hab. inż. Wojciech Chrzanowski Kontakt,informacja i konsultacje Chemia A ; pokój 307 Telefon: 347-2769 E-mail: wojtek@chem.pg.gda.pl
Chemia Fizyczna Technologia Chemiczna II rok Wykład 1 Kierownik przedmiotu: Dr hab. inż. Wojciech Chrzanowski Kontakt,informacja i konsultacje Chemia A ; pokój 307 Telefon: 347-2769 E-mail: wojtek@chem.pg.gda.pl
Fizyka statystyczna. This Book Is Generated By Wb2PDF. using
 http://pl.wikibooks.org/wiki/fizyka_statystyczna This Book Is Generated By Wb2PDF using RenderX XEP, XML to PDF XSL-FO Formatter 18-05-2014 Table of Contents 1. Fizyka statystyczna...4 Spis treści..........................................................................?
http://pl.wikibooks.org/wiki/fizyka_statystyczna This Book Is Generated By Wb2PDF using RenderX XEP, XML to PDF XSL-FO Formatter 18-05-2014 Table of Contents 1. Fizyka statystyczna...4 Spis treści..........................................................................?
Definicje i przykłady
 Rozdział 1 Definicje i przykłady 1.1 Definicja równania różniczkowego 1.1 DEFINICJA. Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie F (t, x, ẋ, ẍ,..., x (n) ) = 0. (1.1) W równaniu tym t jest
Rozdział 1 Definicje i przykłady 1.1 Definicja równania różniczkowego 1.1 DEFINICJA. Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie F (t, x, ẋ, ẍ,..., x (n) ) = 0. (1.1) W równaniu tym t jest
Fizyka statystyczna Potencjały termodynamiczne i warunki równowagi Geometria Drugiej Zasady Termodynamiki
 Fizyka statystyczna Potencjały termodynamiczne i warunki równowagi Geometria Drugiej Zasady Termodynamiki P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2016 Energia wewnętrzna jako funkcja jednorodna
Fizyka statystyczna Potencjały termodynamiczne i warunki równowagi Geometria Drugiej Zasady Termodynamiki P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2016 Energia wewnętrzna jako funkcja jednorodna
Wykład FIZYKA I. 15. Termodynamika statystyczna. Dr hab. inż. Władysław Artur Woźniak
 Wykład FIZYKA I 15. Termodynamika statystyczna Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej http://www.if.pwr.wroc.pl/~wozniak/fizyka1.html TERMODYNAMIKA KLASYCZNA I TEORIA
Wykład FIZYKA I 15. Termodynamika statystyczna Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej http://www.if.pwr.wroc.pl/~wozniak/fizyka1.html TERMODYNAMIKA KLASYCZNA I TEORIA
Wykład Temperatura termodynamiczna 6.4 Nierówno
 ykład 8 6.3 emperatura termodynamiczna 6.4 Nierówność Clausiusa 6.5 Makroskopowa definicja entropii oraz zasada wzrostu entropii 6.6 Entropia dla czystej substancji 6.8 Cykl Carnota 6.7 Entropia dla gazu
ykład 8 6.3 emperatura termodynamiczna 6.4 Nierówność Clausiusa 6.5 Makroskopowa definicja entropii oraz zasada wzrostu entropii 6.6 Entropia dla czystej substancji 6.8 Cykl Carnota 6.7 Entropia dla gazu
1 Rachunek prawdopodobieństwa
 1 Rachunek prawdopodobieństwa 1. Obliczyć średnią i wariancję rozkładu Bernouliego 2. Wykonać przejście graniczne p 0, N w rozkładzie Bernouliego przy zachowaniu stałej wartości średniej: λ = N p = const
1 Rachunek prawdopodobieństwa 1. Obliczyć średnią i wariancję rozkładu Bernouliego 2. Wykonać przejście graniczne p 0, N w rozkładzie Bernouliego przy zachowaniu stałej wartości średniej: λ = N p = const
Temperatura jest wspólną własnością dwóch ciał, które pozostają ze sobą w równowadze termicznej.
 1 Ciepło jest sposobem przekazywania energii z jednego ciała do drugiego. Ciepło przepływa pod wpływem różnicy temperatur. Jeżeli ciepło nie przepływa mówimy o stanie równowagi termicznej. Zerowa zasada
1 Ciepło jest sposobem przekazywania energii z jednego ciała do drugiego. Ciepło przepływa pod wpływem różnicy temperatur. Jeżeli ciepło nie przepływa mówimy o stanie równowagi termicznej. Zerowa zasada
Fizyka statystyczna Zerowa Zasada Termodynamiki. P. F. Góra
 Fizyka statystyczna Zerowa Zasada Termodynamiki P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2015 Stan układu Fizyka statystyczna (i termodynamika) zajmuje się przede wszystkim układami dużymi, liczacymi
Fizyka statystyczna Zerowa Zasada Termodynamiki P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2015 Stan układu Fizyka statystyczna (i termodynamika) zajmuje się przede wszystkim układami dużymi, liczacymi
Rzadkie gazy bozonów
 Rzadkie gazy bozonów Tomasz Sowiński Proseminarium Fizyki Teoretycznej 15 listopada 2004 Rzadkie gazy bozonów p.1/25 Bardzo medialne zdjęcie Rok 1995. Pierwsza kondensacja. Zaobserwowana w przestrzeni
Rzadkie gazy bozonów Tomasz Sowiński Proseminarium Fizyki Teoretycznej 15 listopada 2004 Rzadkie gazy bozonów p.1/25 Bardzo medialne zdjęcie Rok 1995. Pierwsza kondensacja. Zaobserwowana w przestrzeni
Fizyka statystyczna Zwyrodniały gaz Fermiego. P. F. Góra
 Fizyka statystyczna Zwyrodniały gaz Fermiego P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2016 Fermiony w niskich temperaturach Wychodzimy ze znanego już wtrażenia na wielka sumę statystyczna: Ξ = i=0
Fizyka statystyczna Zwyrodniały gaz Fermiego P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2016 Fermiony w niskich temperaturach Wychodzimy ze znanego już wtrażenia na wielka sumę statystyczna: Ξ = i=0
Wykład 1. Anna Ptaszek. 5 października Katedra Inżynierii i Aparatury Przemysłu Spożywczego. Chemia fizyczna - wykład 1. Anna Ptaszek 1 / 36
 Wykład 1 Katedra Inżynierii i Aparatury Przemysłu Spożywczego 5 października 2015 1 / 36 Podstawowe pojęcia Układ termodynamiczny To zbiór niezależnych elementów, które oddziałują ze sobą tworząc integralną
Wykład 1 Katedra Inżynierii i Aparatury Przemysłu Spożywczego 5 października 2015 1 / 36 Podstawowe pojęcia Układ termodynamiczny To zbiór niezależnych elementów, które oddziałują ze sobą tworząc integralną
Wykład FIZYKA I. 5. Energia, praca, moc. http://www.if.pwr.wroc.pl/~wozniak/fizyka1.html. Dr hab. inż. Władysław Artur Woźniak
 Wykład FIZYKA I 5. Energia, praca, moc Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej http://www.if.pwr.wroc.pl/~wozniak/fizyka1.html ENERGIA, PRACA, MOC Siła to wielkość
Wykład FIZYKA I 5. Energia, praca, moc Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej http://www.if.pwr.wroc.pl/~wozniak/fizyka1.html ENERGIA, PRACA, MOC Siła to wielkość
II. Równania autonomiczne. 1. Podstawowe pojęcia.
 II. Równania autonomiczne. 1. Podstawowe pojęcia. Definicja 1.1. Niech Q R n, n 1, będzie danym zbiorem i niech f : Q R n będzie daną funkcją określoną na Q. Równanie różniczkowe postaci (1.1) x = f(x),
II. Równania autonomiczne. 1. Podstawowe pojęcia. Definicja 1.1. Niech Q R n, n 1, będzie danym zbiorem i niech f : Q R n będzie daną funkcją określoną na Q. Równanie różniczkowe postaci (1.1) x = f(x),
3 Potencjały termodynamiczne i transformacja Legendre a
 3 Potencjały termodynamiczne i transformacja Legendre a literatura: Ingarden, Jamiołkowski i Mrugała, Fizyka Statystyczna i ermodynamika, 9 W.I Arnold, Metody matematyczne mechaniki klasycznej, 14 3.1
3 Potencjały termodynamiczne i transformacja Legendre a literatura: Ingarden, Jamiołkowski i Mrugała, Fizyka Statystyczna i ermodynamika, 9 W.I Arnold, Metody matematyczne mechaniki klasycznej, 14 3.1
Rozważmy nieustalony, adiabatyczny, jednowymiarowy ruch gazu nielepkiego i nieprzewodzącego ciepła. Mamy następujące równania rządzące tym ruchem:
 WYKŁAD 13 DYNAMIKA MAŁYCH (AKUSTYCZNYCH) ZABURZEŃ W GAZIE Rozważmy nieustalony, adiabatyczny, jednowymiarowy ruch gazu nielepkiego i nieprzewodzącego ciepła. Mamy następujące równania rządzące tym ruchem:
WYKŁAD 13 DYNAMIKA MAŁYCH (AKUSTYCZNYCH) ZABURZEŃ W GAZIE Rozważmy nieustalony, adiabatyczny, jednowymiarowy ruch gazu nielepkiego i nieprzewodzącego ciepła. Mamy następujące równania rządzące tym ruchem:
Informacja o przestrzeniach Sobolewa
 Wykład 11 Informacja o przestrzeniach Sobolewa 11.1 Definicja przestrzeni Sobolewa Niech R n będzie zbiorem mierzalnym. Rozważmy przestrzeń Hilberta X = L 2 () z iloczynem skalarnym zdefiniowanym równością
Wykład 11 Informacja o przestrzeniach Sobolewa 11.1 Definicja przestrzeni Sobolewa Niech R n będzie zbiorem mierzalnym. Rozważmy przestrzeń Hilberta X = L 2 () z iloczynem skalarnym zdefiniowanym równością
Termodynamika. Energia wewnętrzna ciał
 ermodynamika Energia wewnętrzna ciał Cząsteczki ciał stałych, cieczy i gazów znajdują się w nieustannym ruchu oddziałując ze sobą. Sumę energii kinetycznej oraz potencjalnej oddziałujących cząsteczek nazywamy
ermodynamika Energia wewnętrzna ciał Cząsteczki ciał stałych, cieczy i gazów znajdują się w nieustannym ruchu oddziałując ze sobą. Sumę energii kinetycznej oraz potencjalnej oddziałujących cząsteczek nazywamy
Wykład 3. Zerowa i pierwsza zasada termodynamiki:
 Wykład 3 Zerowa i pierwsza zasada termodynamiki: Termodynamiczne funkcje stanu. Parametry extensywne i intensywne. Pojęcie równowagi termodynamicznej. Tranzytywność stanu równowagi i pojęcie temperatury
Wykład 3 Zerowa i pierwsza zasada termodynamiki: Termodynamiczne funkcje stanu. Parametry extensywne i intensywne. Pojęcie równowagi termodynamicznej. Tranzytywność stanu równowagi i pojęcie temperatury
16 Jednowymiarowy model Isinga
 16 Jednowymiarowy model Isinga Jest to liniowy łańcuch N spinów mogących przyjmować wartości ± 1. Mikrostanem układu jest zbiór zmiennych σ i = ±1, gdzie i = 1,,..., N (16.1) Określają one czy i-ty spin
16 Jednowymiarowy model Isinga Jest to liniowy łańcuch N spinów mogących przyjmować wartości ± 1. Mikrostanem układu jest zbiór zmiennych σ i = ±1, gdzie i = 1,,..., N (16.1) Określają one czy i-ty spin
Termodynamika. Część 12. Procesy transportu. Janusz Brzychczyk, Instytut Fizyki UJ
 Termodynamika Część 12 Procesy transportu Janusz Brzychczyk, Instytut Fizyki UJ Zjawiska transportu Zjawiska transportu są typowymi procesami nieodwracalnymi zachodzącymi w przyrodzie. Zjawiska te polegają
Termodynamika Część 12 Procesy transportu Janusz Brzychczyk, Instytut Fizyki UJ Zjawiska transportu Zjawiska transportu są typowymi procesami nieodwracalnymi zachodzącymi w przyrodzie. Zjawiska te polegają
Fizykochemiczne podstawy inżynierii procesowej
 Fizykochemiczne podstawy inżynierii procesowej Wykład II Podstawowe definicje cd. Podstawowe idealizacje termodynamiczne I i II Zasada termodynamiki Proste przemiany termodynamiczne PRZYPOMNIENIE Z OSTATNIEGO
Fizykochemiczne podstawy inżynierii procesowej Wykład II Podstawowe definicje cd. Podstawowe idealizacje termodynamiczne I i II Zasada termodynamiki Proste przemiany termodynamiczne PRZYPOMNIENIE Z OSTATNIEGO
Podstawy termodynamiki
 Podstawy termodynamiki Temperatura i ciepło Praca jaką wykonuje gaz I zasada termodynamiki Przemiany gazowe izotermiczna izobaryczna izochoryczna adiabatyczna Co to jest temperatura? 40 39 38 Temperatura
Podstawy termodynamiki Temperatura i ciepło Praca jaką wykonuje gaz I zasada termodynamiki Przemiany gazowe izotermiczna izobaryczna izochoryczna adiabatyczna Co to jest temperatura? 40 39 38 Temperatura
Termodynamika (1) Bogdan Walkowiak. Zakład Biofizyki Instytut Inżynierii Materiałowej Politechnika Łódzka. poniedziałek, 23 października 2017
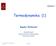 Wykład 1 Termodynamika (1) Bogdan Walkowiak Zakład Biofizyki Instytut Inżynierii Materiałowej Politechnika Łódzka Biofizyka 1 Zaliczenie Aby zaliczyć przedmiot należy: uzyskać pozytywną ocenę z laboratorium
Wykład 1 Termodynamika (1) Bogdan Walkowiak Zakład Biofizyki Instytut Inżynierii Materiałowej Politechnika Łódzka Biofizyka 1 Zaliczenie Aby zaliczyć przedmiot należy: uzyskać pozytywną ocenę z laboratorium
Następnie przypominamy (dla części studentów wprowadzamy) podstawowe pojęcia opisujące funkcje na poziomie rysunków i objaśnień.
 Zadanie Należy zacząć od sprawdzenia, co studenci pamiętają ze szkoły średniej na temat funkcji jednej zmiennej. Na początek można narysować kilka krzywych na tle układu współrzędnych (funkcja gładka,
Zadanie Należy zacząć od sprawdzenia, co studenci pamiętają ze szkoły średniej na temat funkcji jednej zmiennej. Na początek można narysować kilka krzywych na tle układu współrzędnych (funkcja gładka,
Układ termodynamiczny Parametry układu termodynamicznego Proces termodynamiczny Układ izolowany Układ zamknięty Stan równowagi termodynamicznej
 termodynamika - podstawowe pojęcia Układ termodynamiczny - wyodrębniona część otaczającego nas świata. Parametry układu termodynamicznego - wielkości fizyczne, za pomocą których opisujemy stan układu termodynamicznego,
termodynamika - podstawowe pojęcia Układ termodynamiczny - wyodrębniona część otaczającego nas świata. Parametry układu termodynamicznego - wielkości fizyczne, za pomocą których opisujemy stan układu termodynamicznego,
Wykład 4 Przebieg zmienności funkcji. Badanie dziedziny oraz wyznaczanie granic funkcji poznaliśmy na poprzednich wykładach.
 Wykład Przebieg zmienności funkcji. Celem badania przebiegu zmienności funkcji y = f() jest poznanie ważnych własności tej funkcji na podstawie jej wzoru. Efekty badania pozwalają naszkicować wykres badanej
Wykład Przebieg zmienności funkcji. Celem badania przebiegu zmienności funkcji y = f() jest poznanie ważnych własności tej funkcji na podstawie jej wzoru. Efekty badania pozwalają naszkicować wykres badanej
TERMODYNAMIKA I TERMOCHEMIA
 TERMODYNAMIKA I TERMOCHEMIA Termodynamika - opisuje zmiany energii towarzyszące przemianom chemicznym; dział fizyki zajmujący się zjawiskami cieplnymi. Termochemia - dział chemii zajmujący się efektami
TERMODYNAMIKA I TERMOCHEMIA Termodynamika - opisuje zmiany energii towarzyszące przemianom chemicznym; dział fizyki zajmujący się zjawiskami cieplnymi. Termochemia - dział chemii zajmujący się efektami
Fizyka statystyczna i termodynamika Wykład 1: Wstęp. Katarzyna Sznajd-Weron Katedra Fizyki Teoretycznej
 Fizyka statystyczna i termodynamika Wykład 1: Wstęp Katarzyna Sznajd-Weron Katedra Fizyki Teoretycznej http://www.if.pwr.wroc.pl/~katarzynaweron/ Mój plan zajęć Strona kursu Kim jestem? Prof. dr hab. Katarzyna
Fizyka statystyczna i termodynamika Wykład 1: Wstęp Katarzyna Sznajd-Weron Katedra Fizyki Teoretycznej http://www.if.pwr.wroc.pl/~katarzynaweron/ Mój plan zajęć Strona kursu Kim jestem? Prof. dr hab. Katarzyna
Wykład 2. Przykład zastosowania teorii prawdopodobieństwa: procesy stochastyczne (Markova)
 Wykład 2 Przykład zastosowania teorii prawdopodobieństwa: procesy stochastyczne (Markova) 1. Procesy Markova: definicja 2. Równanie Chapmana-Kołmogorowa-Smoluchowskiego 3. Przykład dyfuzji w kapilarze
Wykład 2 Przykład zastosowania teorii prawdopodobieństwa: procesy stochastyczne (Markova) 1. Procesy Markova: definicja 2. Równanie Chapmana-Kołmogorowa-Smoluchowskiego 3. Przykład dyfuzji w kapilarze
Występują fluktuacje w stanie równowagi Proces przejścia do stanu równowagi jest nieodwracalny proces powrotny jest bardzo mało prawdopodobny.
 Wykład 14: Fizyka statystyczna Zajmuje sie układami makroskopowymi (typowy układ makroskopowy składa się z ok. 10 25 atomów), czyli ok 10 25 równań Newtona? Musimy dopasować inne pojęcia do opisu takich
Wykład 14: Fizyka statystyczna Zajmuje sie układami makroskopowymi (typowy układ makroskopowy składa się z ok. 10 25 atomów), czyli ok 10 25 równań Newtona? Musimy dopasować inne pojęcia do opisu takich
Przemiany termodynamiczne
 Przemiany termodynamiczne.:: Przemiana adiabatyczna ::. Przemiana adiabatyczna (Proces adiabatyczny) - proces termodynamiczny, podczas którego wyizolowany układ nie nawiązuje wymiany ciepła, lecz całość
Przemiany termodynamiczne.:: Przemiana adiabatyczna ::. Przemiana adiabatyczna (Proces adiabatyczny) - proces termodynamiczny, podczas którego wyizolowany układ nie nawiązuje wymiany ciepła, lecz całość
Statystyka nieoddziaływujących gazów Bosego: kondensacja Bosego- Einsteina
 Statystyka nieoddziaływujących gazów Bosego: kondensacja Bosego- Einsteina Silnie zwyrodniały gaz bozonów o niezerowej masie spoczynkowej Gdy liczba cząstek nie jest zachowywana, termodynamika nieoddziaływujących
Statystyka nieoddziaływujących gazów Bosego: kondensacja Bosego- Einsteina Silnie zwyrodniały gaz bozonów o niezerowej masie spoczynkowej Gdy liczba cząstek nie jest zachowywana, termodynamika nieoddziaływujących
Janusz Adamowski METODY OBLICZENIOWE FIZYKI Kwantowa wariacyjna metoda Monte Carlo. Problem własny dla stanu podstawowego układu N cząstek
 Janusz Adamowski METODY OBLICZENIOWE FIZYKI 1 Rozdział 20 KWANTOWE METODY MONTE CARLO 20.1 Kwantowa wariacyjna metoda Monte Carlo Problem własny dla stanu podstawowego układu N cząstek (H E 0 )ψ 0 (r)
Janusz Adamowski METODY OBLICZENIOWE FIZYKI 1 Rozdział 20 KWANTOWE METODY MONTE CARLO 20.1 Kwantowa wariacyjna metoda Monte Carlo Problem własny dla stanu podstawowego układu N cząstek (H E 0 )ψ 0 (r)
Funkcje wymierne. Funkcja homograficzna. Równania i nierówności wymierne.
 Funkcje wymierne. Funkcja homograficzna. Równania i nierówności wymierne. Funkcja homograficzna. Definicja. Funkcja homograficzna jest to funkcja określona wzorem f() = a + b c + d, () gdzie współczynniki
Funkcje wymierne. Funkcja homograficzna. Równania i nierówności wymierne. Funkcja homograficzna. Definicja. Funkcja homograficzna jest to funkcja określona wzorem f() = a + b c + d, () gdzie współczynniki
Fizyka statystyczna Fenomenologia przejść fazowych. P. F. Góra
 Fizyka statystyczna Fenomenologia przejść fazowych P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2015 Przejście fazowe transformacja układu termodynamicznego z jednej fazy (stanu materii) do innej, dokonywane
Fizyka statystyczna Fenomenologia przejść fazowych P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2015 Przejście fazowe transformacja układu termodynamicznego z jednej fazy (stanu materii) do innej, dokonywane
WYKŁAD 2 TERMODYNAMIKA. Termodynamika opiera się na czterech obserwacjach fenomenologicznych zwanych zasadami
 WYKŁAD 2 TERMODYNAMIKA Termodynamika opiera się na czterech obserwacjach fenomenologicznych zwanych zasadami Zasada zerowa Kiedy obiekt gorący znajduje się w kontakcie cieplnym z obiektem zimnym następuje
WYKŁAD 2 TERMODYNAMIKA Termodynamika opiera się na czterech obserwacjach fenomenologicznych zwanych zasadami Zasada zerowa Kiedy obiekt gorący znajduje się w kontakcie cieplnym z obiektem zimnym następuje
Miejsce biofizyki we współczesnej nauce. Obszary zainteresowania biofizyki. - Powrót do współczesności. - obiekty mikroświata.
 Zakład Biofizyki Miejsce biofizyki we współczesnej nauce - trochę historii - Powrót do współczesności Obszary zainteresowania biofizyki - ekosystemy - obiekty makroświata - obiekty mikroświata - język
Zakład Biofizyki Miejsce biofizyki we współczesnej nauce - trochę historii - Powrót do współczesności Obszary zainteresowania biofizyki - ekosystemy - obiekty makroświata - obiekty mikroświata - język
RÓWNANIE SCHRÖDINGERA NIEZALEŻNE OD CZASU
 X. RÓWNANIE SCHRÖDINGERA NIEZALEŻNE OD CZASU Równanie Schrődingera niezależne od czasu to równanie postaci: ħ 2 2m d 2 x dx 2 V xx = E x (X.1) Warunki regularności na x i a) skończone b) ciągłe c) jednoznaczne
X. RÓWNANIE SCHRÖDINGERA NIEZALEŻNE OD CZASU Równanie Schrődingera niezależne od czasu to równanie postaci: ħ 2 2m d 2 x dx 2 V xx = E x (X.1) Warunki regularności na x i a) skończone b) ciągłe c) jednoznaczne
Wykład 3 Zjawiska transportu Dyfuzja w gazie, przewodnictwo cieplne, lepkość gazu, przewodnictwo elektryczne
 Wykład 3 Zjawiska transportu Dyfuzja w gazie, przewodnictwo cieplne, lepkość gazu, przewodnictwo elektryczne W3. Zjawiska transportu Zjawiska transportu zachodzą gdy układ dąży do stanu równowagi. W zjawiskach
Wykład 3 Zjawiska transportu Dyfuzja w gazie, przewodnictwo cieplne, lepkość gazu, przewodnictwo elektryczne W3. Zjawiska transportu Zjawiska transportu zachodzą gdy układ dąży do stanu równowagi. W zjawiskach
- prędkość masy wynikająca z innych procesów, np. adwekcji, naprężeń itd.
 4. Równania dyfuzji 4.1. Prawo zachowania masy cd. Równanie dyfuzji jest prostą konsekwencją prawa zachowania masy, a właściwie to jest to prawo zachowania masy zapisane dla procesu dyfuzji i uwzględniające
4. Równania dyfuzji 4.1. Prawo zachowania masy cd. Równanie dyfuzji jest prostą konsekwencją prawa zachowania masy, a właściwie to jest to prawo zachowania masy zapisane dla procesu dyfuzji i uwzględniające
n p 2 i = R 2 (8.1) i=1
 8.9 Rozkład Maxwella Jest to rozkład prędkości cząstek w gazie doskonałym. Wielkość f (p) jest gęstością prawdopodobieństwa znalezienia cząstki o pędzie p. Różnica pomiędzy rozkładem Maxwella i rozkładem
8.9 Rozkład Maxwella Jest to rozkład prędkości cząstek w gazie doskonałym. Wielkość f (p) jest gęstością prawdopodobieństwa znalezienia cząstki o pędzie p. Różnica pomiędzy rozkładem Maxwella i rozkładem
Zasady termodynamiki
 Zasady termodynamiki Energia wewnętrzna (U) Opis mikroskopowy: Jest to suma średnich energii kinetycznych oraz energii oddziaływań międzycząsteczkowych i wewnątrzcząsteczkowych. Opis makroskopowy: Jest
Zasady termodynamiki Energia wewnętrzna (U) Opis mikroskopowy: Jest to suma średnich energii kinetycznych oraz energii oddziaływań międzycząsteczkowych i wewnątrzcząsteczkowych. Opis makroskopowy: Jest
Fizyka statystyczna Zasady Termodynamiki. P. F. Góra
 Fizyka statystyczna Zasady Termodynamiki P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2016 Stan układu Fizyka statystyczna (i termodynamika) zajmuje się przede wszystkim układami dużymi, liczacymi sobie
Fizyka statystyczna Zasady Termodynamiki P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2016 Stan układu Fizyka statystyczna (i termodynamika) zajmuje się przede wszystkim układami dużymi, liczacymi sobie
Podstawowe prawa opisujące właściwości gazów zostały wyprowadzone dla gazu modelowego, nazywanego gazem doskonałym (idealnym).
 Spis treści 1 Stan gazowy 2 Gaz doskonały 21 Definicja mikroskopowa 22 Definicja makroskopowa (termodynamiczna) 3 Prawa gazowe 31 Prawo Boyle a-mariotte a 32 Prawo Gay-Lussaca 33 Prawo Charlesa 34 Prawo
Spis treści 1 Stan gazowy 2 Gaz doskonały 21 Definicja mikroskopowa 22 Definicja makroskopowa (termodynamiczna) 3 Prawa gazowe 31 Prawo Boyle a-mariotte a 32 Prawo Gay-Lussaca 33 Prawo Charlesa 34 Prawo
Maszyny cieplne substancja robocza
 Maszyny cieplne cel: zamiana ciepła na pracę (i odwrotnie) pracują cyklicznie pracę wykonuje substancja robocza (np.gaz, mieszanka paliwa i powietrza) która: pochłania ciepło dostarczane ze źródła ciepła
Maszyny cieplne cel: zamiana ciepła na pracę (i odwrotnie) pracują cyklicznie pracę wykonuje substancja robocza (np.gaz, mieszanka paliwa i powietrza) która: pochłania ciepło dostarczane ze źródła ciepła
Temperatura, ciepło, oraz elementy kinetycznej teorii gazów
 Temperatura, ciepło, oraz elementy kinetycznej teorii gazów opis makroskopowy równowaga termodynamiczna temperatura opis mikroskopowy średnia energia kinetyczna molekuł Równowaga termodynamiczna A B A
Temperatura, ciepło, oraz elementy kinetycznej teorii gazów opis makroskopowy równowaga termodynamiczna temperatura opis mikroskopowy średnia energia kinetyczna molekuł Równowaga termodynamiczna A B A
Fizyka statystyczna Zespół kanoniczny i wielki zespół kanoniczny Statystyki kwantowe. P. F. Góra
 Fizyka statystyczna Zespół kanoniczny i wielki zespół kanoniczny Statystyki kwantowe P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2015 Zespół kanoniczny Zespół mikrokanoniczny jest (przynajmniej w warstwie
Fizyka statystyczna Zespół kanoniczny i wielki zespół kanoniczny Statystyki kwantowe P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2015 Zespół kanoniczny Zespół mikrokanoniczny jest (przynajmniej w warstwie
WYKŁAD 12 ENTROPIA I NIERÓWNOŚĆ THERMODYNAMICZNA 1/10
 WYKŁAD 12 ENROPIA I NIERÓWNOŚĆ HERMODYNAMICZNA 1/10 ENROPIA PŁYNU IDEALNEGO W PRZEPŁYWIE BEZ NIECIĄGŁOŚCI Załóżmy, że przepływ płynu idealnego jest gładki, tj. wszystkie pola wielkości kinematycznych i
WYKŁAD 12 ENROPIA I NIERÓWNOŚĆ HERMODYNAMICZNA 1/10 ENROPIA PŁYNU IDEALNEGO W PRZEPŁYWIE BEZ NIECIĄGŁOŚCI Załóżmy, że przepływ płynu idealnego jest gładki, tj. wszystkie pola wielkości kinematycznych i
Podstawy fizyki sezon 1 X. Elementy termodynamiki
 Podstawy fizyki sezon 1 X. Elementy termodynamiki Agnieszka Obłąkowska-Mucha AGH, WFIiS, Katedra Oddziaływań i Detekcji Cząstek, D11, pok. 111 amucha@agh.edu.pl http://home.agh.edu.pl/~amucha Temodynamika
Podstawy fizyki sezon 1 X. Elementy termodynamiki Agnieszka Obłąkowska-Mucha AGH, WFIiS, Katedra Oddziaływań i Detekcji Cząstek, D11, pok. 111 amucha@agh.edu.pl http://home.agh.edu.pl/~amucha Temodynamika
wymiana energii ciepła
 wymiana energii ciepła Karolina Kurtz-Orecka dr inż., arch. Wydział Budownictwa i Architektury Katedra Dróg, Mostów i Materiałów Budowlanych 1 rodzaje energii magnetyczna kinetyczna cieplna światło dźwięk
wymiana energii ciepła Karolina Kurtz-Orecka dr inż., arch. Wydział Budownictwa i Architektury Katedra Dróg, Mostów i Materiałów Budowlanych 1 rodzaje energii magnetyczna kinetyczna cieplna światło dźwięk
3a. Wstęp: Elementarne równania i nierówności
 3a. Wstęp: Elementarne równania i nierówności Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie zima 2017/2018 Grzegorz Kosiorowski (Uniwersytet Ekonomiczny 3a. Wstęp: w Krakowie) Elementarne równania
3a. Wstęp: Elementarne równania i nierówności Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie zima 2017/2018 Grzegorz Kosiorowski (Uniwersytet Ekonomiczny 3a. Wstęp: w Krakowie) Elementarne równania
