Model błony neuronowej
|
|
|
- Stefan Teodor Kosiński
- 8 lat temu
- Przeglądów:
Transkrypt
1 Model błony neuronowej 1 Modelowanie pewnych aspektów czynności mózgu Neuron McCullocha i Pits a. Pierwsze próby matematycznego opisu czynności neuronów i próby zrozumienia w oparciu o te modele czynności układów neuronalnych miały miejsce we wczesnych latach 40-tych kiedy to McCulloch i Pits opublikowali pierwszy uproszczony model neuronu znany obecnie pod nazwą perceptron. Perceptron posiada pewną ilość wejść, które mnożone są przez wagi i sumowane. W ten sposób obliczane jest pobudzenie neuronu. Jeśli pobudzenie to przekracza wartość progową to neuron generuje niezerowe wyjście, w przeciwnym wypadku na wyjściu neuronu jest zero. Sieci budowane z tego typu jednostek (na ogół z ciągłą i różniczkowalną funkcją odpowiedzi) są w stanie dokonywać w zasadzie dowolnych przekształceń danych wejściowych. Powstanie Computational Neuroscience. Dalsze prace nad sieciami neuronowymi doprowadziły do powstania dwóch dziedzin nauki: sieci neuronowe (neuropodobne) głównie z zastosowaniami inżynierskimi; oraz computational neuroscience. Ta ostania cechuje się realizmem biologicznym. Jako realizm biologiczny rozumiem tu taką konstrukcję modelu, że wszystkie jego elementy, a także wejście i wyjście ma konkretną interpretację w anatomii i fizjologii. Potrzeba konstruowania takich modeli bierze się z przekonania, że nawet bardzo szczegółowa znajomość anatomii i fizjologii nie da nam pełnego zrozumienia działania układu nerwowego. 1.1 Sprzężenie pomiędzy modelowaniem a eksperymentem interpretacja i konsolidacja danych doświadczalnych intuicja co do zmiany zachowania układu przy zmianie parametrów 1
2 bezpośrednie uwidocznienie efektów założeń poczynionych przy konstrukcji modelu 1.2 Złożoność mózgu Oto kilka charakterystycznych liczb: Ludzki mózg składa się z około neuronów, każdy z nich wytwarza około 10 4 synaptycznych kontaktów z innymi neuronami. Gęstość połączeń jest niezwykle duża dowolny neuron korowy znajduje się nie dalej niż dwa lub trzy połączenia synaptyczne od dowolnego innego neuronu korowego. Co więcej przetwarzanie informacji w mózgu zachodzi w kilku skalach przestrzennych Przestrzenne skale organizacji mózgu 2
3 Struktura Fragment błony neuronu Neuron Średnica (mm) 10 3 Ilość Neuronów Opis Obwód i.e. Pętle sprzężeń zwrotnych Minikolumna Przestrzenny zasięg połączeń hamujących Kolumna korowa skala wejścia dla długozasięgowych połączeń specyficznych Makrokolumna Zasięg rozgałęzień aksonu pojedynczej komórki piramidalnej skala przestrzenna dla wyjść pobudzających Skala regionalna Średnia długość włókien korowo-korowych; skala długozasięgowych połączeń pobudzających; typowa skala dla pól Broadmana; Czynność elektryczna musi być skorelowana na obszarze co najmniej tej wielkości aby dawać mierzalny wkład do czynności EEG rejestrowanej na czaszce bez uśredniania. Skala płatów mamy dziesięć płatów zdefiniowanych przez największe bruzdy. Skala typowa dla stan- dardowych pomiarów EEG Półkule Najdłuższe włókna korowo-korowe 2 Typy modeli używanych w neuronauce modele kompartmentowe modele punktowe modele populacyjne modele globalne 3
4 3 Pobudliwa błona komórkowa Biofizyczne modele czynności elektrycznej neuronów opisują głównie własności elektryczne błony neuronów. Neuron otoczony jest cieniutką błoną ( nm) dwuwarstwą lipidową oddzielającą wnętrze od zewnętrza. Pozwala ona na utrzymywanie różnicy stężeń różnych jonów i różnicy potencjału elektrycznego. Różnice stężeń jonów są dodatkowo utrzymywane przez aktywne procesy metaboliczne takie jak pompa sodowo-potasowa. Aktywne własności błony neuronowej są zdeterminowane przez zestaw kanałów jonowych w które dana błona jest wyposażona. 4
5 4 Aktywne kanały jonowe Makroskopowe przewodnictwo błony jest efektem przepływu jonów przez mikroskopijne kanały jonowe przenikające przez błonę. Każdy kanał składa się z kilku prostszych podjednostek bramek które regulują przepływ jonów przez kanał. Każda z bramek może być w jednym z dwóch stanów sprzyjającym albo niesprzyjającym. Kiedy wszystkie bramki są w stanie sprzyjającym kanał jest otwarty i jony mogą przez niego przepływać. Jeżeli choć jedna bramka jest w stanie niesprzyjającym kanał jest zamknięty, przepływ jonów przez niego jest niemożliwy. 5 Teoria Hodgkina-Huxleya Bramki podlegają pierwszorzędowej kinetyce: niesprzyjajcy α(v ) β(v ) sprzyjajcy gdzie α(v ) i β(v ) są prędkościami reakcji zależnymi od napięcia. Prawdopodobieństwo, że bramka jest w stanie sprzyjającym jest zatem: ṗ = α(v )(1 p) β(v )p 5
6 Równanie to można zapisać w innej formie uwidaczniającej proces dochodzenia do wartości asymptotycznych: gdzie ṗ = p (V ) p τ(v ) p (V ) = τ(v ) = α(v ) α(v ) + β(v ) 1 α(v ) + β(v ) (1) (2) Zakładamy, że bramki są niezależne. Względne stężenie kanałów otwartych jest zatem (jeśli mamy M bramek typu m i H bramek typu h) : o k = m M h H Prądy jonowe podlegają prawu Ohma, przy czym przewodnictwo jest proporcjonalne do względnego stężenia kanałów otwartych: I k = ḡ k m M h H (V E k ) g k jest maksymalnym przewodnictwem, kiedy wszystkie kanały są otwarte; E k jest potencjałem równowagowym (tzn że nawet jeśli kanał jest otwarty to i tak prąd przez niego nie płynie) dla danego typu jonów. 6 Model jednego kompartmentu Teoria Hodgkina-Huxleya może być bezpośrednio zastosowana do zamodelowania pojedynczego izopotencjalnego i jednorodnego fragmentu neuronu. Fragment jest reprezentowany przez obwód elektryczny: 6
7 Outside C m g k Inside E k Prawo zachowania ładunku w tym obwodzie daje nam: C m V = gdzie C m pojemność elektryczna błony. k ḡ k m M k k h k(v E k ) (3) 7 Generacja potencjału czynnościowego W stanie spoczynkowym bramki aktywujące Na + (m) są w stanie niesprzyjającym zaś bramki inaktywujące h są w stanie sprzyjającym, Kanały K + mają tylko bramki aktywujące (n) i są one w stanie niesprzyjającym. Kiedy potencjał przekracza wartość progową bramki m zmieniają konformację na sprzyjającą; kanał Na + otwiera się, jony Na + napływają do wnętrza komórki i depolaryzują ją jeszcze bardziej. Przy zwiększonej depolaryzacji otwierają się kanały K+. Jony K + wypływają z komórki i potencjał jej obniża się. Jednocześnie bramki inaktywujące Na + przechodzą w stan niesprzyjający i zamykają kanał Na +. Dalszy wypływ jonów K + powoduje hiperpolaryzację komórki W stanie hiperpolaryzacji bramki aktywujące Na + przechodzą w stan niesprzyjający oraz zamyka się kanał K +. 7
8 8 Kompartmentowe modele neuronów Izopotencjalny kompartmnet jest punktem wyjścia dla bardziej realistycznych modeli neuronów uwzgledniających ich skomplikowana geometrię i niejednorodność własności błony w różnych miejscach neuronu. Model komórki Purkinje go opracowany przez De Schutter a and Bower a. 8
9 9 Łączenie neuronów w sieci Aby zbudować sieć musimy połączyć neurony przy pomocy synaps. Jak już wspominaliśmy typowy neuron w korze ssaków ma 10 4 synaps. Procesy zachodzące w synapsie: przybycie potencjału czynnościowego do kolbki synaptycznej uwolnienie neurotransmitera bezpośrednie lub pośrednie otwarcie chemicznie bramkowanych kanałów w błonie postsynaptycznej zmiana przewodnictwa błony postsynaptycznej Dla wielu typów synaps udaje się na szczęście opisać ten skomplikowany proces jako zmianę przewodnictwa błony postsynaptycznej zależną jedynie od czasu. zgodnie z prawem Ohma prąd synaptyczny dany jest równaniem: I syn = g syn (t) (V m E syn ) Całkiem niezłe przybliżenie zmian przewodnictwa błony postsynaptycznej daje tzw. funkcja alfa : g syn (t) = g max t t p e (t tp) gdzie t p jest czasem, po którym funkcja osiąga maksimum g max lub bardziej ogólna funkcja dwueksponencjalna: g syn (t) = g max τ 1 τ 2 ( e t τ 1 e t τ 2 ), for τ 1 > τ 2 9
10 10 Model Hodgkina-Huxleya nerwu kałamarnicy Równania Hodgkina-Huxleya dla nerwu kałamarnicy: dv dn dm dh gdzie: = [ I inj ḡ Na m 3 h(v V Na ) ḡ K n 4 (V V K ) g L (V V L ) ] /C(4) = α n (V )(1 n) β n (V )n (5) = α m (V )(1 m) β m (V )m (6) = α h (V )(1 h) β h (V )h (7) α n (V ) = 0.01(V + 55) 1 exp[ (V + 55)/10] (8) β n (V ) = 0.125exp[ (V + 65)/80] (9) α m (V ) = 0.1(V + 40) 1 exp[ (V + 40)/10] (10) β m (V ) = 4exp[ (V + 65)/18] (11) α h (V ) = 0.07exp[ (V + 65)/20] (12) β n (V ) = exp[ (V + 35)/10] (13) Stałe w tym modelu to: C = 1; g Na = 120; V Na = 50; g K = 36; V K = 77; g L = 0.3; V L = 54; W powyższych równaniach napięcia dane są w mv, gęstości prądów w µa/cm 2, pojemność elektryczna w µf/cm 2 zaś czas w ms Zadania Korzystając z kodów symulacji zamieszczonych na stronie wykładowej proszę: 1. Zbadać występowanie potencjałów czynnościowych dla I = 0 i I = Poszukać wartości prądu, dla której występuje pojedynczy potencjał. Czy można wywołać pojedynczy potencjał o połowkowej wysokości? 10
11 Na ile ostra jest granica prądu wstrzykniętego wywołującego potencjał czynnościowy? 3. Czy jest graniczna wartość prądu powodująca wywołanie ciągu potencjałów? 4. Co dzieje się z potencjałami wraz ze wzrostem I? Czy dla dowolnie dużych prądów można obserwować oscylacje? 5. Co się stanie jeśli neuron gwałtownie wyjdzie ze stanu hiperpolaryzacji? 11 Model FitzHugh-Nagumo Skala czasowa dla zmiennej m w tym modelu jest dużo krótsza niż pozostałe stałe czasowe. Proszę się o tym przekonać wykreślając ich przebiegi czasowe. Pierwsze przybliżenie polega więc na tym aby przyjąć, że czyli: dm = 0 m(v ) = m (V ) = α m (V ) α m (V ) + β m (V ) Następnie przyjmujemy, że n + h = 0.8. To nam daje: dv dn = [ I ḡ Na m 3 (0.8 n)(v V Na ) ḡ K n 4 (V V K ) g L (V V L ) ] (14) /C = α n (V )(1 n) β n (V )n (15) W fizjologicznym zakresie parametrów można przybliżyć te równania tak po przejściu do jednostek bezwymiarowych można otrzymać układ opisywany przez dwie zmienne: dv = f(v) w + I (16) dw = bv γw (17) f(v) = v(a v)(v 1) (18) gdzie 0 < a < 1 b, γ > 0 v nadal odpowiada napięciu zaś w zmiennym m, n, h. Zadanie: Narysować portret fazowy w zależności od parametrów a, b, γ. 11
12 Zadanie: Numerycznie zbadać model dv dw = v 1 3 v3 w + I (19) = 0.08(v w) (20) i pokazać, że ma on jakościowe zachowania analogiczne jak model HH. Na podstawie analizy obrazu fazowego wyjaśnić mechanizmy: występowania progu na generowanie potencjałów występowania ciągów potencjałów czynnościowych wygaszenia potencjałów dla dużej wartości I występowania odbicia po hiperpolaryzacji 12
Modelowanie pewnych aspektów czynności mózgu
 Tutorial: Modelowanie czynności neuronów i pewnych aspektów czynności mózgu 1 Modelowanie pewnych aspektów czynności mózgu Neuron McCullocha i Pits a. Pierwsze próby matematycznego opisu czynności neuronów
Tutorial: Modelowanie czynności neuronów i pewnych aspektów czynności mózgu 1 Modelowanie pewnych aspektów czynności mózgu Neuron McCullocha i Pits a. Pierwsze próby matematycznego opisu czynności neuronów
Potencjał spoczynkowy i czynnościowy
 Potencjał spoczynkowy i czynnościowy Marcin Koculak Biologiczne mechanizmy zachowania https://backyardbrains.com/ Powtórka budowy komórki 2 Istota prądu Prąd jest uporządkowanym ruchem cząstek posiadających
Potencjał spoczynkowy i czynnościowy Marcin Koculak Biologiczne mechanizmy zachowania https://backyardbrains.com/ Powtórka budowy komórki 2 Istota prądu Prąd jest uporządkowanym ruchem cząstek posiadających
Wstęp do sieci neuronowych, wykład 15, Neuron Hodgkina-Huxleya
 Wstęp do sieci neuronowych, wykład 15, Neuron Hodgkina-Huxleya Maja Czoków, Jarosław Piersa, Andrzej Rutkowski Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2019-01-21 Projekt pn. Wzmocnienie
Wstęp do sieci neuronowych, wykład 15, Neuron Hodgkina-Huxleya Maja Czoków, Jarosław Piersa, Andrzej Rutkowski Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2019-01-21 Projekt pn. Wzmocnienie
Budowa i zróżnicowanie neuronów - elektrofizjologia neuronu
 Budowa i zróżnicowanie neuronów - elektrofizjologia neuronu Neuron jest podstawową jednostką przetwarzania informacji w mózgu. Sygnał biegnie w nim w kierunku od dendrytów, poprzez akson, do synaps. Neuron
Budowa i zróżnicowanie neuronów - elektrofizjologia neuronu Neuron jest podstawową jednostką przetwarzania informacji w mózgu. Sygnał biegnie w nim w kierunku od dendrytów, poprzez akson, do synaps. Neuron
Elektrofizjologia neuronu
 Spis treści Co to jest neuron? 2008-11-13 Spis treści Co to jest neuron? Wstęp Rola jonów w działaniu neronu Potencjał membranowy Stan równowagi Bramki jonowe Dynamika bramek jonowych Model Hodgkina-Huxley
Spis treści Co to jest neuron? 2008-11-13 Spis treści Co to jest neuron? Wstęp Rola jonów w działaniu neronu Potencjał membranowy Stan równowagi Bramki jonowe Dynamika bramek jonowych Model Hodgkina-Huxley
Cel modelowania neuronów realistycznych biologicznie:
 Sieci neuropodobne XI, modelowanie neuronów biologicznie realistycznych 1 Cel modelowania neuronów realistycznych biologicznie: testowanie hipotez biologicznych i fizjologicznych eksperymenty na modelach
Sieci neuropodobne XI, modelowanie neuronów biologicznie realistycznych 1 Cel modelowania neuronów realistycznych biologicznie: testowanie hipotez biologicznych i fizjologicznych eksperymenty na modelach
Błona komórkowa grubość od 50 do 100 A. Istnieje pewna różnica potencjałów, po obu stronach błony, czyli na błonie panuje pewne
 Błona komórkowa grubość od 50 do 100 A Istnieje pewna różnica potencjałów, po obu stronach błony, czyli na błonie panuje pewne napięcie elektryczne, zwane napięciem na błonie. Różnica potencjałów to ok.
Błona komórkowa grubość od 50 do 100 A Istnieje pewna różnica potencjałów, po obu stronach błony, czyli na błonie panuje pewne napięcie elektryczne, zwane napięciem na błonie. Różnica potencjałów to ok.
Droga impulsu nerwowego w organizmie człowieka
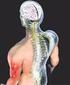 Droga impulsu nerwowego w organizmie człowieka Impuls nerwowy Impuls nerwowy jest zjawiskiem elektrycznym zachodzącym na powierzchni komórki nerwowej i pełni podstawową rolę w przekazywaniu informacji
Droga impulsu nerwowego w organizmie człowieka Impuls nerwowy Impuls nerwowy jest zjawiskiem elektrycznym zachodzącym na powierzchni komórki nerwowej i pełni podstawową rolę w przekazywaniu informacji
Błona komórkowa grubość od 50 do 100 A. Istnieje pewna różnica potencjałów, po obu stronach błony, czyli na błonie panuje pewne
 Błona komórkowa grubość od 50 do 100 A Istnieje pewna różnica potencjałów, po obu stronach błony, czyli na błonie panuje pewne napięcie elektryczne, zwane napięciem na błonie. Różnica potencjałów to ok.
Błona komórkowa grubość od 50 do 100 A Istnieje pewna różnica potencjałów, po obu stronach błony, czyli na błonie panuje pewne napięcie elektryczne, zwane napięciem na błonie. Różnica potencjałów to ok.
Wprowadzenie do pulsujących sieci neuronowych
 Zakład Algebry i Kombinatoryki Wydział Matematyki i Nauk Informacyjnych 31 maja 2017 Wstęp Plan prezentacji Biologiczna inspiracja modeli neuronów. Modelowe neuronów naturalnych. Neurony trzeciej generacji
Zakład Algebry i Kombinatoryki Wydział Matematyki i Nauk Informacyjnych 31 maja 2017 Wstęp Plan prezentacji Biologiczna inspiracja modeli neuronów. Modelowe neuronów naturalnych. Neurony trzeciej generacji
Praktyczne aspekty modelowania układu nerwowego
 Praktyczne aspekty modelowania układu nerwowego Ćwiczenia 2 Model Hodgkina-Huxleya dr Daniel Wójcik na podstawie The Book of GENESIS Wprowadzenie do interfejsu graficznego GENESIS Przećwiczymy obsługę
Praktyczne aspekty modelowania układu nerwowego Ćwiczenia 2 Model Hodgkina-Huxleya dr Daniel Wójcik na podstawie The Book of GENESIS Wprowadzenie do interfejsu graficznego GENESIS Przećwiczymy obsługę
Fizjologia człowieka
 Akademia Wychowania Fizycznego i Sportu w Gdańsku Katedra: Promocji Zdrowia Zakład: Biomedycznych Podstaw Zdrowia Fizjologia człowieka Osoby prowadzące przedmiot: Prof. nadzw. dr hab. Zbigniew Jastrzębski
Akademia Wychowania Fizycznego i Sportu w Gdańsku Katedra: Promocji Zdrowia Zakład: Biomedycznych Podstaw Zdrowia Fizjologia człowieka Osoby prowadzące przedmiot: Prof. nadzw. dr hab. Zbigniew Jastrzębski
Z47 BADANIA WŁAŚCIWOŚCI ELEKTROFIZJOLOGICZNYCH BŁON KOMÓRKOWYCH
 Z47 BADANIA WŁAŚCIWOŚCI ELEKTROFIZJOLOGICZNYCH BŁON KOMÓRKOWYCH I. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z podstawową wiedzą na temat pomiarów elektrofizjologicznych żywych komórek metodą Patch
Z47 BADANIA WŁAŚCIWOŚCI ELEKTROFIZJOLOGICZNYCH BŁON KOMÓRKOWYCH I. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z podstawową wiedzą na temat pomiarów elektrofizjologicznych żywych komórek metodą Patch
Co to są wzorce rytmów?
 Sieci neuropodobne XII, Centralne generatory wzorców 1 Co to są wzorce rytmów? Centralne generatory rytmów są układami neuronowymi powodujących cykliczną aktywację odpowiednich mięśni, mogą działać w pewnym
Sieci neuropodobne XII, Centralne generatory wzorców 1 Co to są wzorce rytmów? Centralne generatory rytmów są układami neuronowymi powodujących cykliczną aktywację odpowiednich mięśni, mogą działać w pewnym
Biologiczne mechanizmy zachowania
 Biologiczne mechanizmy zachowania Przekaźnictwo chemiczne w mózgu mgr Monika Mazurek IPs UJ Odkrycie synaps Ramon y Cajal (koniec XIX wieku) neurony nie łączą się między sobą, między nimi jest drobna szczelina.
Biologiczne mechanizmy zachowania Przekaźnictwo chemiczne w mózgu mgr Monika Mazurek IPs UJ Odkrycie synaps Ramon y Cajal (koniec XIX wieku) neurony nie łączą się między sobą, między nimi jest drobna szczelina.
Transport przez błony
 Transport przez błony Transport bierny Nie wymaga nakładu energii Transport aktywny Wymaga nakładu energii Dyfuzja prosta Dyfuzja ułatwiona Przenośniki Kanały jonowe Transport przez pory w błonie jądrowej
Transport przez błony Transport bierny Nie wymaga nakładu energii Transport aktywny Wymaga nakładu energii Dyfuzja prosta Dyfuzja ułatwiona Przenośniki Kanały jonowe Transport przez pory w błonie jądrowej
Elementy kognitywistyki II: Sztuczna inteligencja. WYKŁAD X: Sztuczny neuron
 Elementy kognitywistyki II: Sztuczna inteligencja WYKŁAD X: Sztuczny neuron Koneksjonizm: wprowadzenie 1943: Warren McCulloch, Walter Pitts: ogólna teoria przetwarzania informacji oparta na sieciach binarnych
Elementy kognitywistyki II: Sztuczna inteligencja WYKŁAD X: Sztuczny neuron Koneksjonizm: wprowadzenie 1943: Warren McCulloch, Walter Pitts: ogólna teoria przetwarzania informacji oparta na sieciach binarnych
Praktyczne aspekty modelowania układu nerwowego
 Praktyczne aspekty modelowania układu nerwowego Ćwiczenia 1 Modelowanie układu nerwowego w GENESIS dr Daniel Wójcik d.wojcik [malpa] nencki.gov.pl na podstawie The Book of GENESIS Modelowanie 1)Tworzymy
Praktyczne aspekty modelowania układu nerwowego Ćwiczenia 1 Modelowanie układu nerwowego w GENESIS dr Daniel Wójcik d.wojcik [malpa] nencki.gov.pl na podstawie The Book of GENESIS Modelowanie 1)Tworzymy
SIECI NEURONOWE Liniowe i nieliniowe sieci neuronowe
 SIECI NEURONOWE Liniowe i nieliniowe sieci neuronowe JOANNA GRABSKA-CHRZĄSTOWSKA Wykłady w dużej mierze przygotowane w oparciu o materiały i pomysły PROF. RYSZARDA TADEUSIEWICZA BUDOWA RZECZYWISTEGO NEURONU
SIECI NEURONOWE Liniowe i nieliniowe sieci neuronowe JOANNA GRABSKA-CHRZĄSTOWSKA Wykłady w dużej mierze przygotowane w oparciu o materiały i pomysły PROF. RYSZARDA TADEUSIEWICZA BUDOWA RZECZYWISTEGO NEURONU
Od neuronu do sieci: modelowanie układu nerwowego
 Od neuronu do sieci: modelowanie układu nerwowego Drzewa dendrytyczne teoria kabla i modele przedziałowe dr Daniel Wójcik na podstawie The Book of GENESIS Dendryty Największy składnik mózgu co do wielkości
Od neuronu do sieci: modelowanie układu nerwowego Drzewa dendrytyczne teoria kabla i modele przedziałowe dr Daniel Wójcik na podstawie The Book of GENESIS Dendryty Największy składnik mózgu co do wielkości
Sztuczne sieci neuronowe
 www.math.uni.lodz.pl/ radmat Cel wykładu Celem wykładu jest prezentacja różnych rodzajów sztucznych sieci neuronowych. Biologiczny model neuronu Mózg człowieka składa się z około 10 11 komórek nerwowych,
www.math.uni.lodz.pl/ radmat Cel wykładu Celem wykładu jest prezentacja różnych rodzajów sztucznych sieci neuronowych. Biologiczny model neuronu Mózg człowieka składa się z około 10 11 komórek nerwowych,
Właściwości błony komórkowej
 Właściwości błony komórkowej płynność asymetria selektywna przepuszczalność Transport przez błony Współczynnik przepuszczalności [cm/s] RóŜnice składu jonowego między wnętrzem komórki ssaka a otoczeniem
Właściwości błony komórkowej płynność asymetria selektywna przepuszczalność Transport przez błony Współczynnik przepuszczalności [cm/s] RóŜnice składu jonowego między wnętrzem komórki ssaka a otoczeniem
Tkanka nerwowa. Komórki: komórki nerwowe (neurony) sygnalizacja komórki neurogleju (glejowe) ochrona, wspomaganie
 Komórki: komórki nerwowe (neurony) sygnalizacja komórki neurogleju (glejowe) ochrona, wspomaganie Tkanka nerwowa Substancja międzykomórkowa: prawie nieobecna (blaszki podstawne) pobudliwość przewodnictwo
Komórki: komórki nerwowe (neurony) sygnalizacja komórki neurogleju (glejowe) ochrona, wspomaganie Tkanka nerwowa Substancja międzykomórkowa: prawie nieobecna (blaszki podstawne) pobudliwość przewodnictwo
Ćwiczenie 1: Model Hodgkina Huxleya
 Ćwiczenie 1: Model Hodgkina Huxleya 1 Wstęp Równania Hodgkina-Huxleya we współczesnej notacji wyglądają tak: dv dn dm dh gdzie: = [ I inj ḡ Na m 3 h(v V Na ) ḡ K n 4 (V V K ) g L (V V L ) ] /C(1) = α n
Ćwiczenie 1: Model Hodgkina Huxleya 1 Wstęp Równania Hodgkina-Huxleya we współczesnej notacji wyglądają tak: dv dn dm dh gdzie: = [ I inj ḡ Na m 3 h(v V Na ) ḡ K n 4 (V V K ) g L (V V L ) ] /C(1) = α n
Właściwości błony komórkowej
 Właściwości błony komórkowej płynność asymetria selektywna przepuszczalność Transport przez błony Cząsteczki < 150Da Błony - selektywnie przepuszczalne RóŜnice składu jonowego między wnętrzem komórki ssaka
Właściwości błony komórkowej płynność asymetria selektywna przepuszczalność Transport przez błony Cząsteczki < 150Da Błony - selektywnie przepuszczalne RóŜnice składu jonowego między wnętrzem komórki ssaka
Wstęp do sztucznych sieci neuronowych
 Wstęp do sztucznych sieci neuronowych Michał Garbowski Zachodniopomorski Uniwersytet Technologiczny w Szczecinie Wydział Informatyki 15 grudnia 2011 Plan wykładu I 1 Wprowadzenie Inspiracja biologiczna
Wstęp do sztucznych sieci neuronowych Michał Garbowski Zachodniopomorski Uniwersytet Technologiczny w Szczecinie Wydział Informatyki 15 grudnia 2011 Plan wykładu I 1 Wprowadzenie Inspiracja biologiczna
Transportowane cząsteczki CO O, 2, NO, H O, etanol, mocznik... Zgodnie z gradientem: stężenia elektrochemicznym gradient stężeń
 Transportowane cząsteczki Transport przez błony Transport bierny szybkość transportu gradien t stężeń kanał nośnik Transport z udziałem nośnika: dyfuzja prosta dyfuzja prosta CO 2, O 2, NO,, H 2 O, etanol,
Transportowane cząsteczki Transport przez błony Transport bierny szybkość transportu gradien t stężeń kanał nośnik Transport z udziałem nośnika: dyfuzja prosta dyfuzja prosta CO 2, O 2, NO,, H 2 O, etanol,
biologiczne mechanizmy zachowania seminarium + laboratorium M.Eng. Michal Adam Michalowski
 biologiczne mechanizmy zachowania seminarium + laboratorium M.Eng. Michal Adam Michalowski michal.michalowski@uwr.edu.pl michaladamichalowski@gmail.com michal.michalowski@uwr.edu.pl https://mmichalowskiuwr.wordpress.com/
biologiczne mechanizmy zachowania seminarium + laboratorium M.Eng. Michal Adam Michalowski michal.michalowski@uwr.edu.pl michaladamichalowski@gmail.com michal.michalowski@uwr.edu.pl https://mmichalowskiuwr.wordpress.com/
Q t lub precyzyjniej w postaci różniczkowej. dq dt Jednostką natężenia prądu jest amper oznaczany przez A.
 Prąd elektryczny Dotychczas zajmowaliśmy się zjawiskami związanymi z ładunkami spoczywającymi. Obecnie zajmiemy się zjawiskami zachodzącymi podczas uporządkowanego ruchu ładunków, który często nazywamy
Prąd elektryczny Dotychczas zajmowaliśmy się zjawiskami związanymi z ładunkami spoczywającymi. Obecnie zajmiemy się zjawiskami zachodzącymi podczas uporządkowanego ruchu ładunków, który często nazywamy
Laboratorium Fizjologii
 Laboratorium Fizjologii Wstęp do neurofizjologii - potencjał czynnościowy i połączenia synaptyczne 1 Wstęp Potencjał równowagi Jeśli po dwu stronach przegrody przepuszczalnej dla jonów wytworzyć różnicę
Laboratorium Fizjologii Wstęp do neurofizjologii - potencjał czynnościowy i połączenia synaptyczne 1 Wstęp Potencjał równowagi Jeśli po dwu stronach przegrody przepuszczalnej dla jonów wytworzyć różnicę
Modelowanie wektora magnetycznego serca na podstawie jonowych prądów komórkowych
 Modelowanie wektora magnetycznego serca na podstawie jonowych prądów komórkowych Wstęp Podstawy modelu komórkowego Proces pobudzenia serca Wektor magnetyczny serca MoŜliwości diagnostyczne Wstęp Przepływający
Modelowanie wektora magnetycznego serca na podstawie jonowych prądów komórkowych Wstęp Podstawy modelu komórkowego Proces pobudzenia serca Wektor magnetyczny serca MoŜliwości diagnostyczne Wstęp Przepływający
MODELOWANIE RZECZYWISTOŚCI
 MODELOWANIE RZECZYWISTOŚCI Daniel Wójcik Instytut Biologii Doświadczalnej PAN d.wojcik@nencki.gov.pl tel. 022 5892 424 http://www.neuroinf.pl/members/danek/swps/ Podręcznik Iwo Białynicki-Birula Iwona
MODELOWANIE RZECZYWISTOŚCI Daniel Wójcik Instytut Biologii Doświadczalnej PAN d.wojcik@nencki.gov.pl tel. 022 5892 424 http://www.neuroinf.pl/members/danek/swps/ Podręcznik Iwo Białynicki-Birula Iwona
Dr inż. Marta Kamińska
 Nowe techniki i technologie dla medycyny Dr inż. Marta Kamińska Układ nerwowy Układ nerwowy zapewnia łączność organizmu ze światem zewnętrznym, zezpala układy w jedną całość, zprawując jednocześnie nad
Nowe techniki i technologie dla medycyny Dr inż. Marta Kamińska Układ nerwowy Układ nerwowy zapewnia łączność organizmu ze światem zewnętrznym, zezpala układy w jedną całość, zprawując jednocześnie nad
Tkanka nerwowa. neurony (pobudliwe) odbieranie i przekazywanie sygnałów komórki glejowe (wspomagające)
 Tkanka nerwowa neurony (pobudliwe) odbieranie i przekazywanie sygnałów komórki glejowe (wspomagające) Sygnalizacja w komórkach nerwowych 100 tys. wejść informacyjnych przyjmowanie sygnału przewodzenie
Tkanka nerwowa neurony (pobudliwe) odbieranie i przekazywanie sygnałów komórki glejowe (wspomagające) Sygnalizacja w komórkach nerwowych 100 tys. wejść informacyjnych przyjmowanie sygnału przewodzenie
Krwiobieg duży. Krwiobieg mały
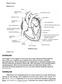 Mięsień sercowy Budowa serca Krązenie krwi Krwiobieg duży Krew (bogata w tlen) wypływa z lewej komory serca przez zastawkę aortalną do głównej tętnicy ciała, aorty, rozgałęzia się na mniejsze tętnice,
Mięsień sercowy Budowa serca Krązenie krwi Krwiobieg duży Krew (bogata w tlen) wypływa z lewej komory serca przez zastawkę aortalną do głównej tętnicy ciała, aorty, rozgałęzia się na mniejsze tętnice,
Właściwości błony komórkowej
 Właściwości błony komórkowej płynność asymetria selektywna przepuszczalność Glikokaliks glikokaliks cytoplazma jądro błona komórkowa Mikrografia elektronowa powierzchni limfocytu ludzkiego (wybarwienie
Właściwości błony komórkowej płynność asymetria selektywna przepuszczalność Glikokaliks glikokaliks cytoplazma jądro błona komórkowa Mikrografia elektronowa powierzchni limfocytu ludzkiego (wybarwienie
Twierdzenie 2: Własności pola wskazujące na istnienie orbit
 Cykle graniczne Dotychczas zajmowaliśmy się głównie znajdowaniem i badaniem stabilności punktów stacjonarnych. Wiele ciekawych procesów ma naturę cykliczną. Umiemy już sobie poradzić z cyklicznością występującą
Cykle graniczne Dotychczas zajmowaliśmy się głównie znajdowaniem i badaniem stabilności punktów stacjonarnych. Wiele ciekawych procesów ma naturę cykliczną. Umiemy już sobie poradzić z cyklicznością występującą
Transport przez błonę komórkową cd. Modelowanie
 Transport przez błonę komórkową cd. Modelowanie Kanały jonowe posiadają zdolność do kontrolowanego przepuszczania jonów. występowanie w nich tzw. pora wodna hydrofilowa przestrzeń wewnątrz białka, przez
Transport przez błonę komórkową cd. Modelowanie Kanały jonowe posiadają zdolność do kontrolowanego przepuszczania jonów. występowanie w nich tzw. pora wodna hydrofilowa przestrzeń wewnątrz białka, przez
TEORIA TRANZYSTORÓW MOS. Charakterystyki statyczne
 TEORIA TRANZYSTORÓW MOS Charakterystyki statyczne n Aktywne podłoże, a napięcia polaryzacji złącz tranzystora wzbogacanego nmos Obszar odcięcia > t, = 0 < t Obszar liniowy (omowy) Kanał indukowany napięciem
TEORIA TRANZYSTORÓW MOS Charakterystyki statyczne n Aktywne podłoże, a napięcia polaryzacji złącz tranzystora wzbogacanego nmos Obszar odcięcia > t, = 0 < t Obszar liniowy (omowy) Kanał indukowany napięciem
c stężenie molowe, V średnia prędkość molekuł
 Elektrodyfuzja, prąd jonowy i biopotencjały elektryczne.. Zjawiska elektryczne towarzyszące dyfuzji jonów oraz różnice ich stężeń powodują, że potencjały elektryczne roztworów po obu stronach błony są
Elektrodyfuzja, prąd jonowy i biopotencjały elektryczne.. Zjawiska elektryczne towarzyszące dyfuzji jonów oraz różnice ich stężeń powodują, że potencjały elektryczne roztworów po obu stronach błony są
Pomiar rezystancji metodą techniczną
 Pomiar rezystancji metodą techniczną Cel ćwiczenia. Poznanie metod pomiarów rezystancji liniowych, optymalizowania warunków pomiaru oraz zasad obliczania błędów pomiarowych. Zagadnienia teoretyczne. Definicja
Pomiar rezystancji metodą techniczną Cel ćwiczenia. Poznanie metod pomiarów rezystancji liniowych, optymalizowania warunków pomiaru oraz zasad obliczania błędów pomiarowych. Zagadnienia teoretyczne. Definicja
Kanały jonowe i pompy błonowe
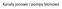 Kanały jonowe i pompy błonowe Jak badad przepływ jonów? Patch-clamp -zassanie powoduje ścisłe połączenie błony komórkowej z kapilarą (opornośd miedzy wnętrzem pipety a otaczającym roztworem = 10^9 omów)
Kanały jonowe i pompy błonowe Jak badad przepływ jonów? Patch-clamp -zassanie powoduje ścisłe połączenie błony komórkowej z kapilarą (opornośd miedzy wnętrzem pipety a otaczającym roztworem = 10^9 omów)
Inteligentne systemy informacyjne
 Inteligentne systemy informacyjne Moduł 10 Mieczysław Muraszkiewicz www.icie.com.pl/lect_pw.htm M. Muraszkiewicz strona 1 Sieci neuronowe szkic Moduł 10 M. Muraszkiewicz strona 2 Dwa nurty M. Muraszkiewicz
Inteligentne systemy informacyjne Moduł 10 Mieczysław Muraszkiewicz www.icie.com.pl/lect_pw.htm M. Muraszkiewicz strona 1 Sieci neuronowe szkic Moduł 10 M. Muraszkiewicz strona 2 Dwa nurty M. Muraszkiewicz
OBLICZENIA ZA POMOCĄ PROTEIN
 OBLICZENIA ZA POMOCĄ PROTEIN KODOWANIE I PRZETWARZANIE INFORMACJI W ORGANIZMACH Informacja genetyczna jest przechowywana w DNA i RNA w postaci liniowych sekwencji nukleotydów W genach jest przemieniana
OBLICZENIA ZA POMOCĄ PROTEIN KODOWANIE I PRZETWARZANIE INFORMACJI W ORGANIZMACH Informacja genetyczna jest przechowywana w DNA i RNA w postaci liniowych sekwencji nukleotydów W genach jest przemieniana
Metody Sztucznej Inteligencji II
 17 marca 2013 Neuron biologiczny Neuron Jest podstawowym budulcem układu nerwowego. Jest komórką, która jest w stanie odbierać i przekazywać sygnały elektryczne. Neuron działanie Jeżeli wartość sygnału
17 marca 2013 Neuron biologiczny Neuron Jest podstawowym budulcem układu nerwowego. Jest komórką, która jest w stanie odbierać i przekazywać sygnały elektryczne. Neuron działanie Jeżeli wartość sygnału
ANALOGOWY MODEL TRANSMISJI SYNAPTYCZNEJ
 Ćwiczenie nr 17 ANALOGOWY MODEL TRANSMISJI SYNAPTYCZNEJ Aparatura Komputer wraz z neurosymulatorem, Cobra3. Przebieg ćwiczenia W ramach ćwiczenia przeprowadzone zostaną następujące badania: A. Wyznaczanie
Ćwiczenie nr 17 ANALOGOWY MODEL TRANSMISJI SYNAPTYCZNEJ Aparatura Komputer wraz z neurosymulatorem, Cobra3. Przebieg ćwiczenia W ramach ćwiczenia przeprowadzone zostaną następujące badania: A. Wyznaczanie
biologiczne mechanizmy zachowania seminarium + laboratorium M.Eng. Michal Adam Michalowski
 biologiczne mechanizmy zachowania seminarium + laboratorium M.Eng. Michal Adam Michalowski michal.michalowski@uwr.edu.pl michaladamichalowski@gmail.com michal.michalowski@uwr.edu.pl https://mmichalowskiuwr.wordpress.com/
biologiczne mechanizmy zachowania seminarium + laboratorium M.Eng. Michal Adam Michalowski michal.michalowski@uwr.edu.pl michaladamichalowski@gmail.com michal.michalowski@uwr.edu.pl https://mmichalowskiuwr.wordpress.com/
Biologiczne mechanizmy zachowania - fizjologia. zajecia 1 :
 Biologiczne mechanizmy zachowania - fizjologia zajecia 1 : 8.10.15 Kontakt: michaladammichalowski@gmail.com https://mmichalowskiuwr.wordpress.com/ II gr 08:00 10:0 III gr 10:15 11:45 IV gr 12:00 13:30
Biologiczne mechanizmy zachowania - fizjologia zajecia 1 : 8.10.15 Kontakt: michaladammichalowski@gmail.com https://mmichalowskiuwr.wordpress.com/ II gr 08:00 10:0 III gr 10:15 11:45 IV gr 12:00 13:30
Czynności komórek nerwowych. Adriana Schetz IF US
 Czynności komórek nerwowych Adriana Schetz IF US Plan wykładu 1. Komunikacja mędzykomórkowa 2. Neurony i komórki glejowe jedność architektoniczna 3. Czynności komórek nerwowych Komunikacja międzykomórkowa
Czynności komórek nerwowych Adriana Schetz IF US Plan wykładu 1. Komunikacja mędzykomórkowa 2. Neurony i komórki glejowe jedność architektoniczna 3. Czynności komórek nerwowych Komunikacja międzykomórkowa
Wzmacniacze operacyjne
 Wzmacniacze operacyjne Cel ćwiczenia Celem ćwiczenia jest badanie podstawowych układów pracy wzmacniaczy operacyjnych. Wymagania Wstęp 1. Zasada działania wzmacniacza operacyjnego. 2. Ujemne sprzężenie
Wzmacniacze operacyjne Cel ćwiczenia Celem ćwiczenia jest badanie podstawowych układów pracy wzmacniaczy operacyjnych. Wymagania Wstęp 1. Zasada działania wzmacniacza operacyjnego. 2. Ujemne sprzężenie
Czym jest prąd elektryczny
 Prąd elektryczny Ruch elektronów w przewodniku Wektor gęstości prądu Przewodność elektryczna Prawo Ohma Klasyczny model przewodnictwa w metalach Zależność przewodności/oporności od temperatury dla metali,
Prąd elektryczny Ruch elektronów w przewodniku Wektor gęstości prądu Przewodność elektryczna Prawo Ohma Klasyczny model przewodnictwa w metalach Zależność przewodności/oporności od temperatury dla metali,
Sztuczna inteligencja
 Sztuczna inteligencja Wykład 6. Sieci biologiczne. Wstęp do sztucznych sieci neuronowych. źródła informacji: G. Fischbach Mind and Brain, Scientific American 1994 S. Silbernagl, A. Despopoulos Atlas fizjologii,
Sztuczna inteligencja Wykład 6. Sieci biologiczne. Wstęp do sztucznych sieci neuronowych. źródła informacji: G. Fischbach Mind and Brain, Scientific American 1994 S. Silbernagl, A. Despopoulos Atlas fizjologii,
1 Kinetyka reakcji chemicznych
 Podstawy obliczeń chemicznych 1 1 Kinetyka reakcji chemicznych Szybkość reakcji chemicznej definiuje się jako ubytek stężenia substratu lub wzrost stężenia produktu w jednostce czasu. ν = c [ ] 2 c 1 mol
Podstawy obliczeń chemicznych 1 1 Kinetyka reakcji chemicznych Szybkość reakcji chemicznej definiuje się jako ubytek stężenia substratu lub wzrost stężenia produktu w jednostce czasu. ν = c [ ] 2 c 1 mol
Opracowanie modelu matryc mikroelektrodowych oraz układu scalonego do elektrycznej stymulacji żywych sieci neuronowych
 Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie Wydział Fizyki i Informatyki Stosowanej Zakład Elektroniki Jądrowej Rozprawa doktorska Opracowanie modelu matryc mikroelektrodowych oraz układu
Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie Wydział Fizyki i Informatyki Stosowanej Zakład Elektroniki Jądrowej Rozprawa doktorska Opracowanie modelu matryc mikroelektrodowych oraz układu
Diagnostyka i protetyka słuchu i wzroku. Układ nerwowy człowieka. Przygotowała: prof. Bożena Kostek
 Diagnostyka i protetyka słuchu i wzroku Układ nerwowy człowieka Przygotowała: prof. Bożena Kostek receptory ośrodkowy układ nerwowy efektory układ autonomiczny ... ośrodkowy układ nerwowy receptory...
Diagnostyka i protetyka słuchu i wzroku Układ nerwowy człowieka Przygotowała: prof. Bożena Kostek receptory ośrodkowy układ nerwowy efektory układ autonomiczny ... ośrodkowy układ nerwowy receptory...
Wykład 1 i 2. Termodynamika klasyczna, gaz doskonały
 Wykład 1 i 2 Termodynamika klasyczna, gaz doskonały dr hab. Agata Fronczak, prof. PW Wydział Fizyki, Politechnika Warszawska 1 stycznia 2017 dr hab. A. Fronczak (Wydział Fizyki PW) Wykład: Elementy fizyki
Wykład 1 i 2 Termodynamika klasyczna, gaz doskonały dr hab. Agata Fronczak, prof. PW Wydział Fizyki, Politechnika Warszawska 1 stycznia 2017 dr hab. A. Fronczak (Wydział Fizyki PW) Wykład: Elementy fizyki
II. Równania autonomiczne. 1. Podstawowe pojęcia.
 II. Równania autonomiczne. 1. Podstawowe pojęcia. Definicja 1.1. Niech Q R n, n 1, będzie danym zbiorem i niech f : Q R n będzie daną funkcją określoną na Q. Równanie różniczkowe postaci (1.1) x = f(x),
II. Równania autonomiczne. 1. Podstawowe pojęcia. Definicja 1.1. Niech Q R n, n 1, będzie danym zbiorem i niech f : Q R n będzie daną funkcją określoną na Q. Równanie różniczkowe postaci (1.1) x = f(x),
Wykład Drgania elektromagnetyczne Wstęp Przypomnienie: masa M na sprężynie, bez oporów. Równanie ruchu
 Wykład 7 7. Drgania elektromagnetyczne Wstęp Przypomnienie: masa M na sprężynie, bez oporów. Równanie ruchu M d x kx Rozwiązania x = Acost v = dx/ =-Asint a = d x/ = A cost przy warunku = (k/m) 1/. Obwód
Wykład 7 7. Drgania elektromagnetyczne Wstęp Przypomnienie: masa M na sprężynie, bez oporów. Równanie ruchu M d x kx Rozwiązania x = Acost v = dx/ =-Asint a = d x/ = A cost przy warunku = (k/m) 1/. Obwód
Biologiczne mechanizmy zachowania - fizjologia. zajecia 6 :
 Biologiczne mechanizmy zachowania - fizjologia zajecia 6 : 12.11.15 Kontakt: michaladammichalowski@gmail.com https://mmichalowskiuwr.wordpress.com/ I gr 08:30 10:00 (s. Cybulskiego; 08.10. 19.11.) II gr
Biologiczne mechanizmy zachowania - fizjologia zajecia 6 : 12.11.15 Kontakt: michaladammichalowski@gmail.com https://mmichalowskiuwr.wordpress.com/ I gr 08:30 10:00 (s. Cybulskiego; 08.10. 19.11.) II gr
Metodę poprawnie mierzonego prądu powinno się stosować do pomiaru dużych rezystancji, tzn. wielokrotnie większych od rezystancji amperomierza: (4)
 OBWODY JEDNOFAZOWE POMIAR PRĄDÓW, NAPIĘĆ. Obwody prądu stałego.. Pomiary w obwodach nierozgałęzionych wyznaczanie rezystancji metodą techniczną. Metoda techniczna pomiaru rezystancji polega na określeniu
OBWODY JEDNOFAZOWE POMIAR PRĄDÓW, NAPIĘĆ. Obwody prądu stałego.. Pomiary w obwodach nierozgałęzionych wyznaczanie rezystancji metodą techniczną. Metoda techniczna pomiaru rezystancji polega na określeniu
Lekcja 5. Temat: Prawo Ohma dla części i całego obwodu
 Lekcja 5. Temat: Prawo Ohma dla części i całego obwodu Prąd płynący w gałęzi obwodu jest wprost proporcjonalny do przyłożonej siły elektromotorycznej E, a odwrotnie proporcjonalne do rezystancji R umieszczonej
Lekcja 5. Temat: Prawo Ohma dla części i całego obwodu Prąd płynący w gałęzi obwodu jest wprost proporcjonalny do przyłożonej siły elektromotorycznej E, a odwrotnie proporcjonalne do rezystancji R umieszczonej
W celu obliczenia charakterystyki częstotliwościowej zastosujemy wzór 1. charakterystyka amplitudowa 0,
 Bierne obwody RC. Filtr dolnoprzepustowy. Filtr dolnoprzepustowy jest układem przenoszącym sygnały o małej częstotliwości bez zmian, a powodującym tłumienie i opóźnienie fazy sygnałów o większych częstotliwościach.
Bierne obwody RC. Filtr dolnoprzepustowy. Filtr dolnoprzepustowy jest układem przenoszącym sygnały o małej częstotliwości bez zmian, a powodującym tłumienie i opóźnienie fazy sygnałów o większych częstotliwościach.
INSTRUKCJA DO ĆWICZENIA NR 7
 KATEDRA MECHANIKI STOSOWANEJ Wydział Mechaniczny POLITECHNIKA LUBELSKA INSTRUKCJA DO ĆWICZENIA NR 7 PRZEDMIOT TEMAT OPRACOWAŁ LABORATORIUM MODELOWANIA Przykładowe analizy danych: przebiegi czasowe, portrety
KATEDRA MECHANIKI STOSOWANEJ Wydział Mechaniczny POLITECHNIKA LUBELSKA INSTRUKCJA DO ĆWICZENIA NR 7 PRZEDMIOT TEMAT OPRACOWAŁ LABORATORIUM MODELOWANIA Przykładowe analizy danych: przebiegi czasowe, portrety
Wymagania edukacyjne: Elektrotechnika i elektronika. Klasa: 1Tc TECHNIK MECHATRONIK. Ilość godzin: 4. Wykonała: Beata Sedivy
 Wymagania edukacyjne: Elektrotechnika i elektronika Klasa: 1Tc TECHNIK MECHATRONIK Ilość godzin: 4 Wykonała: Beata Sedivy Ocena Ocenę niedostateczną uczeń który Ocenę dopuszczającą Wymagania edukacyjne
Wymagania edukacyjne: Elektrotechnika i elektronika Klasa: 1Tc TECHNIK MECHATRONIK Ilość godzin: 4 Wykonała: Beata Sedivy Ocena Ocenę niedostateczną uczeń który Ocenę dopuszczającą Wymagania edukacyjne
Ćwiczenie 2 LABORATORIUM ELEKTRONIKI POLITECHNIKA ŁÓDZKA KATEDRA PRZYRZĄDÓW PÓŁPRZEWODNIKOWYCH I OPTOELEKTRONICZNYCH
 LABORATORIUM LKTRONIKI Ćwiczenie Parametry statyczne tranzystorów bipolarnych el ćwiczenia Podstawowym celem ćwiczenia jest poznanie statycznych charakterystyk tranzystorów bipolarnych oraz metod identyfikacji
LABORATORIUM LKTRONIKI Ćwiczenie Parametry statyczne tranzystorów bipolarnych el ćwiczenia Podstawowym celem ćwiczenia jest poznanie statycznych charakterystyk tranzystorów bipolarnych oraz metod identyfikacji
biologia w gimnazjum OBWODOWY UKŁAD NERWOWY
 biologia w gimnazjum 2 OBWODOWY UKŁAD NERWOWY BUDOWA KOMÓRKI NERWOWEJ KIERUNEK PRZEWODZENIA IMPULSU NEROWEGO DENDRYT ZAKOŃCZENIA AKSONU CIAŁO KOMÓRKI JĄDRO KOMÓRKOWE AKSON OSŁONKA MIELINOWA Komórka nerwowa
biologia w gimnazjum 2 OBWODOWY UKŁAD NERWOWY BUDOWA KOMÓRKI NERWOWEJ KIERUNEK PRZEWODZENIA IMPULSU NEROWEGO DENDRYT ZAKOŃCZENIA AKSONU CIAŁO KOMÓRKI JĄDRO KOMÓRKOWE AKSON OSŁONKA MIELINOWA Komórka nerwowa
Szkła specjalne Przejście szkliste i jego termodynamika Wykład 5. Ryszard J. Barczyński, 2017 Materiały edukacyjne do użytku wewnętrznego
 Szkła specjalne Przejście szkliste i jego termodynamika Wykład 5 Ryszard J. Barczyński, 2017 Materiały edukacyjne do użytku wewnętrznego Czy przejście szkliste jest termodynamicznym przejściem fazowym?
Szkła specjalne Przejście szkliste i jego termodynamika Wykład 5 Ryszard J. Barczyński, 2017 Materiały edukacyjne do użytku wewnętrznego Czy przejście szkliste jest termodynamicznym przejściem fazowym?
Właściwości błony komórkowej
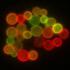 Właściwości błony komórkowej płynność asymetria selektywna przepuszczalność szybka dyfuzja: O 2, CO 2, N 2, benzen Dwuwarstwa lipidowa - przepuszczalność Współczynnik przepuszczalności [cm/s] 1 Transport
Właściwości błony komórkowej płynność asymetria selektywna przepuszczalność szybka dyfuzja: O 2, CO 2, N 2, benzen Dwuwarstwa lipidowa - przepuszczalność Współczynnik przepuszczalności [cm/s] 1 Transport
KRYTERIA OCENIANIA Z MATEMATYKI W OPARCIU O PODSTAWĘ PROGRAMOWĄ I PROGRAM NAUCZANIA MATEMATYKA 2001 DLA KLASY DRUGIEJ
 KRYTERIA OCENIANIA Z MATEMATYKI W OPARCIU O PODSTAWĘ PROGRAMOWĄ I PROGRAM NAUCZANIA MATEMATYKA 2001 DLA KLASY DRUGIEJ TREŚCI KSZTAŁCENIA WYMAGANIA PODSTAWOWE WYMAGANIA PONADPODSTAWOWE Liczby wymierne i
KRYTERIA OCENIANIA Z MATEMATYKI W OPARCIU O PODSTAWĘ PROGRAMOWĄ I PROGRAM NAUCZANIA MATEMATYKA 2001 DLA KLASY DRUGIEJ TREŚCI KSZTAŁCENIA WYMAGANIA PODSTAWOWE WYMAGANIA PONADPODSTAWOWE Liczby wymierne i
Prąd elektryczny - przepływ ładunku
 Prąd elektryczny - przepływ ładunku I Q t Natężenie prądu jest to ilość ładunku Q przepływającego przez dowolny przekrój przewodnika w ciągu jednostki czasu t. Dla prądu stałego natężenie prądu I jest
Prąd elektryczny - przepływ ładunku I Q t Natężenie prądu jest to ilość ładunku Q przepływającego przez dowolny przekrój przewodnika w ciągu jednostki czasu t. Dla prądu stałego natężenie prądu I jest
PRAWO OHMA DLA PRĄDU PRZEMIENNEGO
 ĆWICZENIE 53 PRAWO OHMA DLA PRĄDU PRZEMIENNEGO Cel ćwiczenia: wyznaczenie wartości indukcyjności cewek i pojemności kondensatorów przy wykorzystaniu prawa Ohma dla prądu przemiennego; sprawdzenie prawa
ĆWICZENIE 53 PRAWO OHMA DLA PRĄDU PRZEMIENNEGO Cel ćwiczenia: wyznaczenie wartości indukcyjności cewek i pojemności kondensatorów przy wykorzystaniu prawa Ohma dla prądu przemiennego; sprawdzenie prawa
Ćwiczenie 1b. Silnik prądu stałego jako element wykonawczy Modelowanie i symulacja napędu CZUJNIKI POMIAROWE I ELEMENTY WYKONAWCZE
 Politechnika Łódzka Katedra Mikroelektroniki i Technik Informatycznych 90-924 Łódź, ul. Wólczańska 221/223, bud. B18 tel. 42 631 26 28 faks 42 636 03 27 e-mail secretary@dmcs.p.lodz.pl http://www.dmcs.p.lodz.pl
Politechnika Łódzka Katedra Mikroelektroniki i Technik Informatycznych 90-924 Łódź, ul. Wólczańska 221/223, bud. B18 tel. 42 631 26 28 faks 42 636 03 27 e-mail secretary@dmcs.p.lodz.pl http://www.dmcs.p.lodz.pl
Temat: Sztuczne Sieci Neuronowe. Instrukcja do ćwiczeń przedmiotu INŻYNIERIA WIEDZY I SYSTEMY EKSPERTOWE
 Temat: Sztuczne Sieci Neuronowe Instrukcja do ćwiczeń przedmiotu INŻYNIERIA WIEDZY I SYSTEMY EKSPERTOWE Dr inż. Barbara Mrzygłód KISiM, WIMiIP, AGH mrzyglod@ agh.edu.pl 1 Wprowadzenie Sztuczne sieci neuronowe
Temat: Sztuczne Sieci Neuronowe Instrukcja do ćwiczeń przedmiotu INŻYNIERIA WIEDZY I SYSTEMY EKSPERTOWE Dr inż. Barbara Mrzygłód KISiM, WIMiIP, AGH mrzyglod@ agh.edu.pl 1 Wprowadzenie Sztuczne sieci neuronowe
Zespół kanoniczny N,V, T. acc o n =min {1, exp [ U n U o ] }
![Zespół kanoniczny N,V, T. acc o n =min {1, exp [ U n U o ] } Zespół kanoniczny N,V, T. acc o n =min {1, exp [ U n U o ] }](/thumbs/64/51033976.jpg) Zespół kanoniczny Zespół kanoniczny N,V, T acc o n =min {1, exp [ U n U o ] } Zespół izobaryczno-izotermiczny Zespół izobaryczno-izotermiczny N P T acc o n =min {1, exp [ U n U o ] } acc o n =min {1, exp[
Zespół kanoniczny Zespół kanoniczny N,V, T acc o n =min {1, exp [ U n U o ] } Zespół izobaryczno-izotermiczny Zespół izobaryczno-izotermiczny N P T acc o n =min {1, exp [ U n U o ] } acc o n =min {1, exp[
Recenzja pracy doktorskiej mgr Tomasza Świsłockiego pt. Wpływ oddziaływań dipolowych na własności spinorowego kondensatu rubidowego
 Prof. dr hab. Jan Mostowski Instytut Fizyki PAN Warszawa Warszawa, 15 listopada 2010 r. Recenzja pracy doktorskiej mgr Tomasza Świsłockiego pt. Wpływ oddziaływań dipolowych na własności spinorowego kondensatu
Prof. dr hab. Jan Mostowski Instytut Fizyki PAN Warszawa Warszawa, 15 listopada 2010 r. Recenzja pracy doktorskiej mgr Tomasza Świsłockiego pt. Wpływ oddziaływań dipolowych na własności spinorowego kondensatu
Model Marczuka przebiegu infekcji.
 Model Marczuka przebiegu infekcji. Karolina Szymaniuk 27 maja 2013 Karolina Szymaniuk () Model Marczuka przebiegu infekcji. 27 maja 2013 1 / 17 Substrat Związek chemiczny, który ulega przemianie w wyniku
Model Marczuka przebiegu infekcji. Karolina Szymaniuk 27 maja 2013 Karolina Szymaniuk () Model Marczuka przebiegu infekcji. 27 maja 2013 1 / 17 Substrat Związek chemiczny, który ulega przemianie w wyniku
TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM
 TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM AKADEMIA MORSKA Katedra Telekomunikacji Morskiej ĆWICZENIE 5 BADANIE STABILNOŚCI UKŁADÓW ZE SPRZĘŻENIEM ZWROTNYM 1. Cel ćwiczenia Celem ćwiczenia jest ugruntowanie
TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM AKADEMIA MORSKA Katedra Telekomunikacji Morskiej ĆWICZENIE 5 BADANIE STABILNOŚCI UKŁADÓW ZE SPRZĘŻENIEM ZWROTNYM 1. Cel ćwiczenia Celem ćwiczenia jest ugruntowanie
E dec. Obwód zastępczy. Napięcie rozkładowe
 Obwód zastępczy Obwód zastępczy schematyczny obwód elektryczny, ilustrujący zachowanie się badanego obiektu w polu elektrycznym. Elementy obwodu zastępczego (oporniki, kondensatory, indukcyjności,...)
Obwód zastępczy Obwód zastępczy schematyczny obwód elektryczny, ilustrujący zachowanie się badanego obiektu w polu elektrycznym. Elementy obwodu zastępczego (oporniki, kondensatory, indukcyjności,...)
LABORATORIUM ELEKTRONIKI ĆWICZENIE 4 POLITECHNIKA ŁÓDZKA KATEDRA PRZYRZĄDÓW PÓŁPRZEWODNIKOWYCH I OPTOELEKTRONICZNYCH
 LABORATORIUM ELEKTRONIKI ĆWICZENIE 4 Parametry statyczne tranzystorów polowych złączowych Cel ćwiczenia Podstawowym celem ćwiczenia jest poznanie statycznych charakterystyk tranzystorów polowych złączowych
LABORATORIUM ELEKTRONIKI ĆWICZENIE 4 Parametry statyczne tranzystorów polowych złączowych Cel ćwiczenia Podstawowym celem ćwiczenia jest poznanie statycznych charakterystyk tranzystorów polowych złączowych
TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM
 TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM AKADEMIA MORSKA Katedra Telekomunikacji Morskiej ĆWICZENIE 7 BADANIE ODPOWIEDZI USTALONEJ NA OKRESOWY CIĄG IMPULSÓW 1. Cel ćwiczenia Obserwacja przebiegów wyjściowych
TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM AKADEMIA MORSKA Katedra Telekomunikacji Morskiej ĆWICZENIE 7 BADANIE ODPOWIEDZI USTALONEJ NA OKRESOWY CIĄG IMPULSÓW 1. Cel ćwiczenia Obserwacja przebiegów wyjściowych
Lekcja 9. Pierwsze i drugie prawo Kirchhoffa. 1. I prawo Kirchhoffa
 Lekcja 9. Pierwsze i drugie prawo Kirchhoffa 1. I prawo Kirchhoffa Pierwsze prawo Kirchhoffa mówi, że dla każdego węzła obwodu elektrycznego suma algebraiczna prądów jest równa zeru. i 0 Symbol α odpowiada
Lekcja 9. Pierwsze i drugie prawo Kirchhoffa 1. I prawo Kirchhoffa Pierwsze prawo Kirchhoffa mówi, że dla każdego węzła obwodu elektrycznego suma algebraiczna prądów jest równa zeru. i 0 Symbol α odpowiada
Linia dwuprzewodowa Obliczanie pojemności linii dwuprzewodowej
 Linia dwuprzewodowa Obliczanie pojemności linii dwuprzewodowej 1. Wstęp Pojemność kondensatora można obliczyć w prosty sposób znając wartości zgromadzonego na nim ładunku i napięcia między okładkami: Q
Linia dwuprzewodowa Obliczanie pojemności linii dwuprzewodowej 1. Wstęp Pojemność kondensatora można obliczyć w prosty sposób znając wartości zgromadzonego na nim ładunku i napięcia między okładkami: Q
Zjawiska w niej występujące, jeśli jest ona linią długą: Definicje współczynników odbicia na początku i końcu linii długiej.
 1. Uproszczony schemat bezstratnej (R = 0) linii przesyłowej sygnałów cyfrowych. Zjawiska w niej występujące, jeśli jest ona linią długą: odbicie fali na końcu linii; tłumienie fali; zniekształcenie fali;
1. Uproszczony schemat bezstratnej (R = 0) linii przesyłowej sygnałów cyfrowych. Zjawiska w niej występujące, jeśli jest ona linią długą: odbicie fali na końcu linii; tłumienie fali; zniekształcenie fali;
WZMACNIACZ OPERACYJNY
 1. OPIS WKŁADKI DA 01A WZMACNIACZ OPERACYJNY Wkładka DA01A zawiera wzmacniacz operacyjny A 71 oraz zestaw zacisków, które umożliwiają dołączenie elementów zewnętrznych: rezystorów, kondensatorów i zwór.
1. OPIS WKŁADKI DA 01A WZMACNIACZ OPERACYJNY Wkładka DA01A zawiera wzmacniacz operacyjny A 71 oraz zestaw zacisków, które umożliwiają dołączenie elementów zewnętrznych: rezystorów, kondensatorów i zwór.
Ćwiczenie 4 Badanie ładowania i rozładowania kondensatora
 Karolina Kruk 276656 Ćwiczenie 4 Badanie ładowania i rozładowania kondensatora Wstęp teoretyczny. Kondensator tworzą dwa przewodniki-okładziny lub elektrody, które rozdzielono dielektrykiem. Jeżeli do
Karolina Kruk 276656 Ćwiczenie 4 Badanie ładowania i rozładowania kondensatora Wstęp teoretyczny. Kondensator tworzą dwa przewodniki-okładziny lub elektrody, które rozdzielono dielektrykiem. Jeżeli do
Wyciskamy z cytryny... prąd elektryczny. Wpisany przez Administrator środa, 04 lipca :26 -
 Jak nazwa działu wskazuje będę tu umieszczał różne rozwiązania umożliwiające pozyskiwanie energii elektrycznej z niekonwencjonalnych źródeł. Zaczniemy od eksperymentu, który każdy może wykonać sobie w
Jak nazwa działu wskazuje będę tu umieszczał różne rozwiązania umożliwiające pozyskiwanie energii elektrycznej z niekonwencjonalnych źródeł. Zaczniemy od eksperymentu, który każdy może wykonać sobie w
Spis treści. Własności tkanki nerwowej
 W rozdziale tym poznamy mechanizmy neuronalne odpowiedzialne za powstawanie potencjałów na czaszce, mierzonych jako sygnały EEG. Rozdział ten jest opracowany w oparciu o Nunez (1981, 1995, 2006). Spis
W rozdziale tym poznamy mechanizmy neuronalne odpowiedzialne za powstawanie potencjałów na czaszce, mierzonych jako sygnały EEG. Rozdział ten jest opracowany w oparciu o Nunez (1981, 1995, 2006). Spis
1.2 Funktory z otwartym kolektorem (O.C)
 Wydział EAIiIB Laboratorium Katedra Metrologii i Elektroniki Podstaw Elektroniki Cyfrowej Wykonał zespół w składzie (nazwiska i imiona): Ćw. 4. Funktory TTL cz.2 Data wykonania: Grupa (godz.): Dzień tygodnia:
Wydział EAIiIB Laboratorium Katedra Metrologii i Elektroniki Podstaw Elektroniki Cyfrowej Wykonał zespół w składzie (nazwiska i imiona): Ćw. 4. Funktory TTL cz.2 Data wykonania: Grupa (godz.): Dzień tygodnia:
0 + 0 = 0, = 1, = 1, = 0.
 5 Kody liniowe Jak już wiemy, w celu przesłania zakodowanego tekstu dzielimy go na bloki i do każdego z bloków dodajemy tak zwane bity sprawdzające. Bity te są w ścisłej zależności z bitami informacyjnymi,
5 Kody liniowe Jak już wiemy, w celu przesłania zakodowanego tekstu dzielimy go na bloki i do każdego z bloków dodajemy tak zwane bity sprawdzające. Bity te są w ścisłej zależności z bitami informacyjnymi,
Definicja i własności wartości bezwzględnej.
 Równania i nierówności z wartością bezwzględną. Rozwiązywanie układów dwóch (trzech) równań z dwiema (trzema) niewiadomymi. Układy równań liniowych z parametrem, analiza rozwiązań. Definicja i własności
Równania i nierówności z wartością bezwzględną. Rozwiązywanie układów dwóch (trzech) równań z dwiema (trzema) niewiadomymi. Układy równań liniowych z parametrem, analiza rozwiązań. Definicja i własności
Obliczenia inspirowane Naturą
 Obliczenia inspirowane Naturą Wykład 03 (uzupełnienie Wykładu 02) Jarosław Miszczak IITiS PAN Gliwice 31/03/2016 1 / 17 1 2 / 17 Dynamika populacji Równania Lotki-Voltery opisują model drapieżnik-ofiara.
Obliczenia inspirowane Naturą Wykład 03 (uzupełnienie Wykładu 02) Jarosław Miszczak IITiS PAN Gliwice 31/03/2016 1 / 17 1 2 / 17 Dynamika populacji Równania Lotki-Voltery opisują model drapieżnik-ofiara.
Wykład Pole elektryczne na powierzchniach granicznych 8.10 Gęstość energii pola elektrycznego
 Wykład 7 8.9 Pole elektryczne na powierzchniach granicznych 8.0 Gęstość energii pola elektrycznego 9. Prąd elektryczny 9. Natężenie prądu, wektor gęstości prądu 9. Prawo zachowania ładunku 9.3 Model przewodnictwa
Wykład 7 8.9 Pole elektryczne na powierzchniach granicznych 8.0 Gęstość energii pola elektrycznego 9. Prąd elektryczny 9. Natężenie prądu, wektor gęstości prądu 9. Prawo zachowania ładunku 9.3 Model przewodnictwa
Procesy stochastyczne w kardiologii od elektrofizjologii do zmienności rytmu serca cz. 1. Monika Petelczyc Wydział Fizyki Politechnika Warszawska
 Procesy stochastyczne w kardiologii od elektrofizjologii do zmienności rytmu serca cz. 1 Monika Petelczyc Wydział Fizyki Politechnika Warszawska Od poziomu makro do komórki http://www.myofilament.org/photosandmovies/movies.htm
Procesy stochastyczne w kardiologii od elektrofizjologii do zmienności rytmu serca cz. 1 Monika Petelczyc Wydział Fizyki Politechnika Warszawska Od poziomu makro do komórki http://www.myofilament.org/photosandmovies/movies.htm
Ćwiczenie 1 Metody pomiarowe i opracowywanie danych doświadczalnych.
 Ćwiczenie 1 Metody pomiarowe i opracowywanie danych doświadczalnych. Ćwiczenie ma następujące części: 1 Pomiar rezystancji i sprawdzanie prawa Ohma, metoda najmniejszych kwadratów. 2 Pomiar średnicy pręta.
Ćwiczenie 1 Metody pomiarowe i opracowywanie danych doświadczalnych. Ćwiczenie ma następujące części: 1 Pomiar rezystancji i sprawdzanie prawa Ohma, metoda najmniejszych kwadratów. 2 Pomiar średnicy pręta.
Dywergencja/konwergencja połączeń między neuronami
 OD NEURONU DO SIECI: MODELOWANIE UKŁADU NERWOWEGO Własności sieci, plastyczność synaps Stefan KASICKI SWPS, SPIK wiosna 2007 s.kasicki@nencki.gov.pl Dywergencja/konwergencja połączeń między neuronami 1
OD NEURONU DO SIECI: MODELOWANIE UKŁADU NERWOWEGO Własności sieci, plastyczność synaps Stefan KASICKI SWPS, SPIK wiosna 2007 s.kasicki@nencki.gov.pl Dywergencja/konwergencja połączeń między neuronami 1
EFEKT SOLNY BRÖNSTEDA
 EFEKT SLNY RÖNSTED Pojęcie eektu solnego zostało wprowadzone przez rönsteda w celu wytłumaczenia wpływu obojętnego elektrolitu na szybkość reakcji zachodzących między jonami. Założył on, że reakcja pomiędzy
EFEKT SLNY RÖNSTED Pojęcie eektu solnego zostało wprowadzone przez rönsteda w celu wytłumaczenia wpływu obojętnego elektrolitu na szybkość reakcji zachodzących między jonami. Założył on, że reakcja pomiędzy
Algorytmy sztucznej inteligencji
 Algorytmy sztucznej inteligencji Dynamiczne sieci neuronowe 1 Zapis macierzowy sieci neuronowych Poniżej omówione zostaną części składowe sieci neuronowych i metoda ich zapisu za pomocą macierzy. Obliczenia
Algorytmy sztucznej inteligencji Dynamiczne sieci neuronowe 1 Zapis macierzowy sieci neuronowych Poniżej omówione zostaną części składowe sieci neuronowych i metoda ich zapisu za pomocą macierzy. Obliczenia
Wstęp do teorii sztucznej inteligencji Wykład II. Uczenie sztucznych neuronów.
 Wstęp do teorii sztucznej inteligencji Wykład II Uczenie sztucznych neuronów. 1 - powtórzyć o klasyfikacji: Sieci liniowe I nieliniowe Sieci rekurencyjne Uczenie z nauczycielem lub bez Jednowarstwowe I
Wstęp do teorii sztucznej inteligencji Wykład II Uczenie sztucznych neuronów. 1 - powtórzyć o klasyfikacji: Sieci liniowe I nieliniowe Sieci rekurencyjne Uczenie z nauczycielem lub bez Jednowarstwowe I
Zintegrowana teoria autyzmu Obliczenia płynowe w modelo
 Zintegrowana teoria autyzmu Instytut Informatyki Uniwersytet Marii Curie-Skłodowskiej w Lublinie gmwojcik@gmail.com, Google: gmwojcik INCF 2011 Warszawa, 16 grudnia 2011 1 Spektrum autyzmu - zintegrowana
Zintegrowana teoria autyzmu Instytut Informatyki Uniwersytet Marii Curie-Skłodowskiej w Lublinie gmwojcik@gmail.com, Google: gmwojcik INCF 2011 Warszawa, 16 grudnia 2011 1 Spektrum autyzmu - zintegrowana
