PODSTAWY STATYSTYCZNEJ ANALIZY DANYCH
|
|
|
- Paulina Urbaniak
- 10 lat temu
- Przeglądów:
Transkrypt
1 Wykład 1 Prosta regresja liniowa - model i estymacja parametrów. Regresja z wieloma zmiennymi - analiza, diagnostyka i interpretacja wyników.
2 Literatura pomocnicza J. Koronacki i J. Ćwik Statystyczne systemy uczące się. Wydawnictwo Naukowo- Techniczne, J. Koronacki i J. Mielniczuk Statystyka dla studentów kierunków technicznych i przyrodniczych. Wydawnictwo Naukowo-Techniczne, P. Biecek Przewodnik po pakiecie R.
3 Prosta regresja liniowa Pytanie : Mając próbę zawierającą wartości zmiennych dla badanych obiektów, na przykład X i oraz Y i, pytamy czy istnieje związek pomiędzy tymi wartościami? Szukamy związku liniowego gdzie β 0 i β 1 są współczynnikami. Na przykład pytamy : y = β 0 + β 1 x Czy istnieje związek pomiędzy liczbą wypalanych papierosów a zachorowalnością na raka płuc? Co możemy powiedzieć o związkach pomiędzy wiekiem drzewa a jego wysokością? Czy śmiertelność noworodków wzrasta wraz ze spadkiem wysokości dochodów na osobę? Czy możemy stwierdzić że im więcej lat edukacji tym dłuższa oczekiwana długość życia?
4 Przykład 1.1 Dane DANE1.txt 1 data1 <- read. table (" DANE1. txt ", header = TRUE ) 2 hist ( data1 $X) Histogram of data1$x Frequency data1$x Rysunek: Histogram - DANE1
5 Przykład 1.1(cd) 1 plot ( data1 $X, data1 $Y) Rysunek: DANE1
6 Prosty model regresji liniowej Dla i = 1, 2..., n Y i zmienna objaśniana X i zmienna objaśniająca Model Y i = β 0 + β 1 X i + ε i Y i wartość zmiennej objaśnianej dla i-tego osobnika β 0 - wyraz wolny β 1 - współczynnik nachylenia X i - wartość zmiennej objaśniającej dla i-tego osobnika ε i - błąd losowy o rozkładzie normalnym, ze średnią 0 i wariancją σ 2.
7 Własności prostego modelu regresji liniowej Y i = β 0 + β 1 X i + ε i E(Y i X i ) = β 0 + β 1 X i Var(Y i X i ) = σ 2. Interpretacja prostego modelu regresji liniowej W zależności od znaku i wartości współczynnika β 1, możemy interpretować model na trzy sposoby Gdy X rośnie, wartości Y rosną, maleją lub pozostają bez zmiany
8 Estymacja współczynników modelu Dopasowane równanie regresji Ŷ i = b 0 + b 1 X i Reszty modelu e i = Y i Ŷ i e i = Y i (b 0 + b 1 X i ) Metoda najmniejszych kwadratów (MNK): Wyznaczenie b 0 i b 1 minimalizujących (Y i (b 0 + b 1 X i )) 2 = i i e 2 i
9 Współczynniki modelu wyznaczone metodą MNK Minimalizacja wyrażenia i (Y i (b 0 + b 1 X i )) 2 prowadzi do : b 1 = i (X i X )(Y i Y ) i (X i X ) 2 b 0 = Y b 1 X Są to też estymatory największej wiarogodności
10 Przykład Dopasowanie modelu liniowego 1 X <- data1 $X 2 Y <- data1 $Y 3 lm(y ~ X) 4 5 lm. linear <- lm(y ~ X) 6 lm. linear Wynik Call: lm(formula = Y ~ X) Coefficients: (Intercept) X
11 Przykład 1.1- Podsumowanie wyników modelu 1 summary (lm. linear ) Call: lm(formula = Y ~ X) Residuals: Min 1Q Median 3Q Max Powierzchowna informacja o rozkładzie reszt. Średnia reszt jest z definicji równa zero, a więc mediana powinna być bliska zeru Minimum i maximum powinny być z grubsza równe co do wartości bezwzględnej
12 Przykład 1.1- Podsumowanie wyników modelu Coefficients: Estimate Std. Error t value Pr(> t ) (Intercept) * X e-08 *** Współczynniki regresji Błędy standardowe Wartości statystyki t i p-wartości Signif.codes:0 *** ** 0.01 * *** oznacza 0 < p < ** oznacza < p < 0.01 * oznacza 0.01 < p < 0.05 itd.
13 Przykład 1.1- Podsumowanie wyników modelu Residual standard error: on 38 degrees of freedom Błąd standardowy reszt - opisuje wahania obserwacji wokół prostej regresji przy wyestymowanych współczynnikach modelu. Multiple R-squared: , Adjusted R-squared: Pierwsza wartość to współczynnik korelacji Pearsona Druga wartość to skorygowana wartość R 2 - jeśli przemnożymy ją przez 100%, może być interpretowana jako % redukcji wariancji
14 Przykład Podsumowanie wyników modelu F-statistic: on 1 and 38 DF, p-value: 8.811e-08 Wartość statystyki F dla testowania hipotezy o tym, że współczynnik regresji β 1 jest równy 0. Daje ten sam wynik, co test t dla hipotezy β 1 = 0 - test F jest równy kwadratowi testu t: = (6.592) 2. Jest tak dla każdego modelu z jednym stopniem swobody.
15 Przykład Rysunek prostej regresji 1 plot ( data1 $X, data1 $Y) 2 abline (lm. linear )
16 Przykład Histogram reszt modelu 1 residuals ( lm. linear ) 2 lm. linear. resids <- residuals ( lm. linear ) 3 hist (lm. linear. resids )
17 Przykład Wartości dopasowane 1 fitted (lm. linear ) Funkcja fitted zwraca jako wynik wartości dopasowane przez model - wartości Y które uzyskalibyśmy przy najlepiej dopasowanej prostej regresji, przy danych obserwacjach X w naszym przykładzie : X
18 Przykład Wartości dopasowane 1 plot (X,Y) 2 lines (X, fitted ( lm. linear ))
19 Przykład Wartości dopasowane a reszty 1 plot (X,Y) 2 lines (X, fitted ( lm. linear )) 3 segments (X, fitted (lm. linear ),X,Y)
20 Przykład Wartości dopasowane a reszty 1 plot ( fitted (lm. linear ),resid (lm. linear ))
21 Przykład Wykres kwantyl-kwantyl 1 qqnorm ( resid (lm. linear )) Układ punktów na przekątnej sugeruje, że reszty pochodzą z rozkładu normalnego.
22 Przedziały ufności i przedziały predykcyjne Przedziały ufności Wyrażają niepewność co do wyznaczonej prostej regresji; dokładność z jaką ta prosta jest znana Wąskie przedziały ufności oznaczają dobrze dopasowaną prostą regresji Zazwyczaj są wyznaczone przez łukowate krzywe - prosta regresji jest lepiej wyznaczona w obszarze zagęszczenia obserwacji Przedziały predykcyjne Szersze niż przedziały ufności Wyrażają niepewność na temat przyszłych obserwacji Pomiędzy ich liniami znajduje się znaczna większość obserwacji Wykorzystują założenie o normalności rozkładu błędów
23 Przedziały ufności i przedziały predykcyjne 1 pred. frame <- data. frame (X =4:100) 2 pp <- predict ( lm. linear, int="p", newdata =pred. frame ) 3 pc <- predict ( lm. linear, int="c", newdata =pred. frame ) 4 plot (X,Y, ylim=range (Y, pp, na. rm=t)) 5 pred.x <- pred. frame $X 6 matlines ( pred.x, pc, lty=c (1,2,2), col=" red ") 7 matlines ( pred.x, pp, lty=c (1,3,3), col=" blue ") Tworzymy nowy zakres danych X dla których chcemy wyznaczyć przedziały predykcyjne pp i pc - przedziały predykcyjne i ufności dla nowo wybranych danych Zapewniamy obszar potrzebny na przedziały: ylim=range(y, pp, na.rm=t) Dodajemy linie używając wybranych wartości X
24 Przedziały ufności i przedziały predykcyjne
25 Wartości dopasowane wraz z przedziałami 1 predict ( lm. linear, int="c") 2 predict ( lm. linear, int="p") fit lwr upr fit - wartości oczekiwane (równe wartościom dopasowanym) lwr i upr oznaczają dolne i górne ograniczenia przedziału dla wartości oczekiwanych
26 Korelacja Współczynnik korelacji Symetryczna i niezależna od skali miara związku pomiędzy dwoma zmiennymi losowymi Przyjmuje wartości od 1 do +1, gdzie + 1 oznacza idealną korelację, 0 oznacza brak korelacji. Znak ujemny gdy duże wartości jednej zmiennej są związane z małymi wartościami drugiej zmiennej. Znak dodatni gdy obie zmienne rozsną lub maleją jednocześnie.
27 Korelacja Współczynnik korelacji Pearsona r = i (X i X )(Y i Y ) i (X i X ) 2 i (Y i Y ) 2 r jest mniejsza od 1, chyba że istnieje idealna liniowa zależność pomiędzy X i a Y i. Nazywany współczynnikiem korelacji liniowej 1 cor (X,Y, use=" complete. obs ") 2 cor ( data1, use =" complete. obs ") X Y X Y
28 Testowanie istotności wpółczynnika korelacji Pearsona Testowanie hipotezy o tym, czy współczynnik korelacji jest istotnie różny od zera 1 cor. test (X,Y) Pearson s product-moment correlation data: X and Y t = 6.592, df = 38, p-value = 8.811e-08 alternative hypothesis: true correlation is not equal to 0 95 percent confidence interval: sample estimates: cor Otrzymujemy również 95% przedział ufności dla prawdziwej wartości korelacji
29 Rangowy współczynnik korelacji Spearmana Zastąpienie obserwacji ich rangami (indeksem w porządku rosnącym) Nie wymaga założenia o rozkładzie normalnym. 1 cor. test (X,Y, method =" spearman ") Spearman s rank correlation rho data: X and Y S = , p-value = 1.249e-08 alternative hypothesis: true rho is not equal to 0 sample estimates: rho Warning message: In cor.test.default(x, Y, method = "spearman") : Cannot compute exact p-values with ties
30 Współczynnik korelacji τ Kendala Bazuje na zliczaniu liczby uporządkowanych par obserwacji pary (X1, Y 1) i (X 2, Y 2) są uporządkowane jeśli X 1 X 2 > 0 i Y 1 Y 2 > 0 lub X 1 X 2 < 0 i Y 1 Y 2 < 0 Przy hipotezie zerowej o niezależności powinno być tyle samo par uporządkowanych co nieuporządkowanych
31 Współczynnik korelacji τ Kendala 1 cor. test (X,Y, method =" kendall ") Kendall s rank correlation tau data: X and Y z = , p-value = 1.992e-07 alternative hypothesis: true tau is not equal to 0 sample estimates: tau
32 Regresja z wieloma zmiennymi
33 Regresja z wieloma zmiennymi Większa liczba zmiennych objaśniających Podstawowy model Y i = β 0 + β 1 X i,1 + + β k X i,k + ε i, gdzie X 1, X 2,..., X k są zmiennymi objaśniającymi, X i,j - i-ta obserwacja j-tej zmiennej objaśniającej Parametry β 0, β 1,..., β k estymowane metodą MNK
34 Przykład 1.2 Dane przykładowe: pakiet ISwR, dane cystfibr Dane dotyczą funckjonowania płuc u osób chorych na mukowiscydozę Jak uzyskać dane? Instalacja pakietu ISwR (Packages -> Install Packages) Packages ->Load Package -> ISwR data(cystfibr) Edycja danych: Edit -> Data editor -> cystfibr Przydatne komendy dla zbiorów danych w R 1 data () # lista wszystkich dostępnych zbiorów danych 2 try ( data ( package = " ISwR ") )# lista zbiorów danych w pakiecie ISwR 3 data ( cystfibr ) # załaduj zbiór danych 4 help ( cystfibr ) # informacje o zbiorze danych cystfibr
35 Przykład 1.2 Dane przykładowe: pakiet ISwR, dane cystfibr Dane dotyczą funckjonowania płuc u osób chorych na mukowiscydozę age Wiek w latach sex Płeć 0: mężczyzna, 1:kobieta. height Wzrost (cm). weight Waga (kg). bmp Indeks masy ciała. fev1 Wymuszona objętość oddechowa. rv Pozostała objętość. frc Funkcjonalna pojemność. tlc Całkowita pojemność płuc. pemax Maksymalne ciśnienie oddechowe.
36 Przykład Wykresy zależności parami 1 par ( mex =0.5) 2 pairs ( cystfibr, gap=0, cex. labels =0.9) Argumenty gap i cex.labels usuwają przestrzeń pomiędzy rysunkami i zmniejszają czcionkę. mex zmniejsza odległość między liniami w marginesach Rysunek daje (pobieżny) obraz zależności między zmiennymi
37 Przykład Wykresy zależności parami
38 Przykład Specyfikacja modelu 1 attach ( cystfibr ) 2 lm( pemax~age+sex+ height + weight +bmp+fev1+rv+frc+tlc ) 3 summary ( lm( pemax~age+sex+ height + weight +bmp+fev1+rv+frc+tlc )) Call: lm(formula = pemax ~ age + sex + height + weight + bmp + fev1 + rv + frc + tlc) Residuals: Min 1Q Median 3Q Max
39 Przykład Specyfikacja modelu Coefficients: Estimate Std. Error t value Pr(> t ) (Intercept) age sex height weight bmp fev rv frc tlc Residual standard error: on 15 degrees of freedom Multiple R-squared: , Adjusted R-squared: F-statistic: on 9 and 15 DF, p-value:
40 Przykład Krokowy wybór modelu Chcemy uzyskać model zawierający tylko istotne zmienne (p- wartość poniżej poziomu istotności 0.05) Przeprowadzamy ręczną krokową eliminację zmiennych, na przykład Rozważamy najpierw cechy związane z funkcją płuc (bmp, fev1,rv, frc,tlc) spośród nich wyrzucamy cechę o największej p-wartości powtarzamy do momentu aż wszystkie pozostałe w modelu zmienne związane z funkcją płuc będą miały p-wartość<0.05 może się zdarzyć, że wyeliminujemy wszystkie Następnie rozważamy cechy uwzględniające stan pacjenta, jego wygląd fizyczny ( age, sex, weight, height) postępujemy analogicznie jak wyżej.
41 Przykład Krokowy wybór modelu 1 summary ( lm( pemax~age+sex+ height + weight +bmp+fev1+rv+frc+tlc )) Coefficients: Estimate Std. Error t value Pr(> t ) (Intercept) age sex height weight bmp fev rv frc tlc wyrzucamy zmienną tlc
42 Przykład Krokowy wybór modelu 1 summary ( lm( pemax~age+sex+ height + weight +bmp+fev1+rv+frc )) Coefficients: Estimate Std. Error t value Pr(> t ) (Intercept) age sex height weight bmp fev rv frc wyrzucamy zmienną frc
43 Przykład Krokowy wybór modelu 1 summary ( lm( pemax~age+sex+ height + weight +bmp+fev1+rv)) Coefficients: Estimate Std. Error t value Pr(> t ) (Intercept) age sex height weight bmp fev rv wyrzucamy zmienną rv
44 Przykład Krokowy wybór modelu 1 summary ( lm( pemax~age+sex+ height + weight +bmp+fev1 )) Coefficients: Estimate Std. Error t value Pr(> t ) (Intercept) * age sex height weight * bmp * fev wyrzucamy zmienną fev1
45 Przykład Krokowy wybór modelu 1 summary ( lm( pemax~age+sex+ height + weight +bmp )) Coefficients: Estimate Std. Error t value Pr(> t ) (Intercept) * age sex height weight * bmp * pozostałe w modelu zmienne związane z funkcją płuc (bmp) mają p-wartość<0.05 przechodzimmy do analizy cech uwzględniających stan pacjenta, jego wygląd fizyczny (age, sex, weight, height) wyrzucamy zmienną age
46 Przykład Krokowy wybór modelu 1 summary ( lm( pemax~sex+ height + weight +bmp )) Coefficients: Estimate Std. Error t value Pr(> t ) (Intercept) * sex height weight * bmp wyrzucamy zmienną height
47 Przykład Krokowy wybór modelu 1 summary ( lm( pemax~sex+ weight +bmp )) Coefficients: Estimate Std. Error t value Pr(> t ) (Intercept) ** sex weight *** bmp wyrzucamy zmienną sex
48 Przykład Krokowy wybór modelu 1 summary ( lm( pemax~ weight +bmp )) Coefficients: Estimate Std. Error t value Pr(> t ) (Intercept) ** weight *** bmp wyrzucamy zmienną bmp
49 Przykład Krokowy wybór modelu 1 summary ( lm( pemax~ weight )) Coefficients: Estimate Std. Error t value Pr(> t ) (Intercept) e-05 *** weight *** Zmienna pozostała w modelu jest istotna Ostateczny model pemax = weight
50 Przykład Krokowy wybór modelu Startujemy z modelu uwzględniającego tylko zmienne age, height, weight, które są silnie skorelowane 1 summary ( lm( pemax~age+ height + weight )) Coefficients: Estimate Std. Error t value Pr(> t ) (Intercept) age height weight Wyrzucamy zmienną weight (sami o tym decydując, bez względu na p-wartości)
51 Przykład Krokowy wybór modelu 1 summary ( lm( pemax~age+ height )) Coefficients: Estimate Std. Error t value Pr(> t ) (Intercept) age height Wyrzucamy zmienną height
52 Przykład Krokowy wybór modelu 1 summary ( lm( pemax~age )) Coefficients: Estimate Std. Error t value Pr(> t ) (Intercept) ** age ** Zmienna pozostała w modelu jest istotna Ostateczny model pemax = age
53 Przykład Krokowy wybór modelu 1 summary ( lm( pemax~ height )) Coefficients: Estimate Std. Error t value Pr(> t ) (Intercept) height ** Zmienna pozostała w modelu jest istotna Ostateczny model pemax = height
54 Przykład Krokowy wybór modelu Wnioski Końcowy model silnie zależny od procedury eliminacji Prawdopodobnie istnieje związek pomiędzy cechami fizycznymi pacjentów, który może być opisany za pomocą zmiennych age, height lub weight. Wybór zależny od badacza Decyzja nie może być oparta o dane, a raczej o rozważania teoretyczne oparte na wcześniejszych badaniach
Regresja liniowa wprowadzenie
 Regresja liniowa wprowadzenie a) Model regresji liniowej ma postać: gdzie jest zmienną objaśnianą (zależną); są zmiennymi objaśniającymi (niezależnymi); natomiast są parametrami modelu. jest składnikiem
Regresja liniowa wprowadzenie a) Model regresji liniowej ma postać: gdzie jest zmienną objaśnianą (zależną); są zmiennymi objaśniającymi (niezależnymi); natomiast są parametrami modelu. jest składnikiem
Analiza zależności cech ilościowych regresja liniowa (Wykład 13)
 Analiza zależności cech ilościowych regresja liniowa (Wykład 13) dr Mariusz Grządziel semestr letni 2012 Przykład wprowadzajacy W zbiorze danych homedata (z pakietu R-owskiego UsingR) można znaleźć ceny
Analiza zależności cech ilościowych regresja liniowa (Wykład 13) dr Mariusz Grządziel semestr letni 2012 Przykład wprowadzajacy W zbiorze danych homedata (z pakietu R-owskiego UsingR) można znaleźć ceny
Wykład 12 Testowanie hipotez dla współczynnika korelacji
 Wykład 12 Testowanie hipotez dla współczynnika korelacji Wrocław, 24 maja 2017 Współczynnik korelacji Niech będą dane dwie próby danych X = (X 1, X 2,..., X n ) oraz Y = (Y 1, Y 2,..., Y n ). Współczynnikiem
Wykład 12 Testowanie hipotez dla współczynnika korelacji Wrocław, 24 maja 2017 Współczynnik korelacji Niech będą dane dwie próby danych X = (X 1, X 2,..., X n ) oraz Y = (Y 1, Y 2,..., Y n ). Współczynnikiem
Wykład 12 Testowanie hipotez dla współczynnika korelacji
 Wykład 12 Testowanie hipotez dla współczynnika korelacji Wrocław, 23 maja 2018 Współczynnik korelacji Niech będą dane dwie próby danych X = (X 1, X 2,..., X n ) oraz Y = (Y 1, Y 2,..., Y n ). Współczynnikiem
Wykład 12 Testowanie hipotez dla współczynnika korelacji Wrocław, 23 maja 2018 Współczynnik korelacji Niech będą dane dwie próby danych X = (X 1, X 2,..., X n ) oraz Y = (Y 1, Y 2,..., Y n ). Współczynnikiem
S t a t y s t y k a, część 3. Michał Żmihorski
 S t a t y s t y k a, część 3 Michał Żmihorski Porównanie średnich -test T Założenia: Zmienne ciągłe (masa, temperatura) Dwie grupy (populacje) Rozkład normalny* Równe wariancje (homoscedasticity) w grupach
S t a t y s t y k a, część 3 Michał Żmihorski Porównanie średnich -test T Założenia: Zmienne ciągłe (masa, temperatura) Dwie grupy (populacje) Rozkład normalny* Równe wariancje (homoscedasticity) w grupach
Model regresji wielokrotnej Wykład 14 ( ) Przykład ceny domów w Chicago
 Model regresji wielokrotnej Wykład 14 (4.06.2007) Przykład ceny domów w Chicago Poniżej są przedstawione dane dotyczące cen domów w Chicago (źródło: Sen, A., Srivastava, M., Regression Analysis, Springer,
Model regresji wielokrotnej Wykład 14 (4.06.2007) Przykład ceny domów w Chicago Poniżej są przedstawione dane dotyczące cen domów w Chicago (źródło: Sen, A., Srivastava, M., Regression Analysis, Springer,
Wykład 10 (12.05.08). Testowanie hipotez w rodzinie rozkładów normalnych przypadek nieznanego odchylenia standardowego
 Wykład 10 (12.05.08). Testowanie hipotez w rodzinie rozkładów normalnych przypadek nieznanego odchylenia standardowego Przykład Cena metra kwadratowego (w tys. zł) z dla 14 losowo wybranych mieszkań w
Wykład 10 (12.05.08). Testowanie hipotez w rodzinie rozkładów normalnych przypadek nieznanego odchylenia standardowego Przykład Cena metra kwadratowego (w tys. zł) z dla 14 losowo wybranych mieszkań w
KORELACJA 1. Wykres rozrzutu ocena związku między zmiennymi X i Y. 2. Współczynnik korelacji Pearsona
 KORELACJA 1. Wykres rozrzutu ocena związku między zmiennymi X i Y 2. Współczynnik korelacji Pearsona 3. Siła i kierunek związku między zmiennymi 4. Korelacja ma sens, tylko wtedy, gdy związek między zmiennymi
KORELACJA 1. Wykres rozrzutu ocena związku między zmiennymi X i Y 2. Współczynnik korelacji Pearsona 3. Siła i kierunek związku między zmiennymi 4. Korelacja ma sens, tylko wtedy, gdy związek między zmiennymi
Statystyka w pracy badawczej nauczyciela Wykład 4: Analiza współzależności. dr inż. Walery Susłow walery.suslow@ie.tu.koszalin.pl
 Statystyka w pracy badawczej nauczyciela Wykład 4: Analiza współzależności dr inż. Walery Susłow walery.suslow@ie.tu.koszalin.pl Statystyczna teoria korelacji i regresji (1) Jest to dział statystyki zajmujący
Statystyka w pracy badawczej nauczyciela Wykład 4: Analiza współzależności dr inż. Walery Susłow walery.suslow@ie.tu.koszalin.pl Statystyczna teoria korelacji i regresji (1) Jest to dział statystyki zajmujący
Projekt Nowa oferta edukacyjna Uniwersytetu Wrocławskiego odpowiedzią na współczesne potrzeby rynku pracy i gospodarki opartej na wiedzy
 Projekt Nowa oferta edukacyjna Uniwersytetu Wrocławskiego odpowiedzią na współczesne potrzeby rynku pracy i gospodarki opartej na wiedzy Dane: Eksploracja (mining) Problemy: Jedna zmienna 2000 najwi ększych
Projekt Nowa oferta edukacyjna Uniwersytetu Wrocławskiego odpowiedzią na współczesne potrzeby rynku pracy i gospodarki opartej na wiedzy Dane: Eksploracja (mining) Problemy: Jedna zmienna 2000 najwi ększych
Regresja wieloraka Ogólny problem obliczeniowy: dopasowanie linii prostej do zbioru punktów. Najprostszy przypadek - jedna zmienna zależna i jedna
 Regresja wieloraka Regresja wieloraka Ogólny problem obliczeniowy: dopasowanie linii prostej do zbioru punktów. Najprostszy przypadek - jedna zmienna zależna i jedna zmienna niezależna (można zobrazować
Regresja wieloraka Regresja wieloraka Ogólny problem obliczeniowy: dopasowanie linii prostej do zbioru punktów. Najprostszy przypadek - jedna zmienna zależna i jedna zmienna niezależna (można zobrazować
X Y 4,0 3,3 8,0 6,8 12,0 11,0 16,0 15,2 20,0 18,9
 Zadanie W celu sprawdzenia, czy pipeta jest obarczona błędem systematycznym stałym lub zmiennym wykonano szereg pomiarów przy różnych ustawieniach pipety. Wyznacz równanie regresji liniowej, które pozwoli
Zadanie W celu sprawdzenia, czy pipeta jest obarczona błędem systematycznym stałym lub zmiennym wykonano szereg pomiarów przy różnych ustawieniach pipety. Wyznacz równanie regresji liniowej, które pozwoli
WSTĘP DO REGRESJI LOGISTYCZNEJ. Dr Wioleta Drobik-Czwarno
 WSTĘP DO REGRESJI LOGISTYCZNEJ Dr Wioleta Drobik-Czwarno REGRESJA LOGISTYCZNA Zmienna zależna jest zmienną dychotomiczną (dwustanową) przyjmuje dwie wartości, najczęściej 0 i 1 Zmienną zależną może być:
WSTĘP DO REGRESJI LOGISTYCZNEJ Dr Wioleta Drobik-Czwarno REGRESJA LOGISTYCZNA Zmienna zależna jest zmienną dychotomiczną (dwustanową) przyjmuje dwie wartości, najczęściej 0 i 1 Zmienną zależną może być:
STATYSTYKA MATEMATYCZNA
 STATYSTYKA MATEMATYCZNA 1. Wykład wstępny 2. Zmienne losowe i teoria prawdopodobieństwa 3. Populacje i próby danych 4. Testowanie hipotez i estymacja parametrów 5. Najczęściej wykorzystywane testy statystyczne
STATYSTYKA MATEMATYCZNA 1. Wykład wstępny 2. Zmienne losowe i teoria prawdopodobieństwa 3. Populacje i próby danych 4. Testowanie hipotez i estymacja parametrów 5. Najczęściej wykorzystywane testy statystyczne
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 7
 STATYSTYKA I DOŚWIADCZALNICTWO Wykład 7 Analiza korelacji - współczynnik korelacji Pearsona Cel: ocena współzależności między dwiema zmiennymi ilościowymi Ocenia jedynie zależność liniową. r = cov(x,y
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 7 Analiza korelacji - współczynnik korelacji Pearsona Cel: ocena współzależności między dwiema zmiennymi ilościowymi Ocenia jedynie zależność liniową. r = cov(x,y
Wprowadzenie do analizy korelacji i regresji
 Statystyka dla jakości produktów i usług Six sigma i inne strategie Wprowadzenie do analizy korelacji i regresji StatSoft Polska Wybrane zagadnienia analizy korelacji Przy analizie zjawisk i procesów stanowiących
Statystyka dla jakości produktów i usług Six sigma i inne strategie Wprowadzenie do analizy korelacji i regresji StatSoft Polska Wybrane zagadnienia analizy korelacji Przy analizie zjawisk i procesów stanowiących
MODELE LINIOWE. Dr Wioleta Drobik
 MODELE LINIOWE Dr Wioleta Drobik MODELE LINIOWE Jedna z najstarszych i najpopularniejszych metod modelowania Zależność między zbiorem zmiennych objaśniających, a zmienną ilościową nazywaną zmienną objaśnianą
MODELE LINIOWE Dr Wioleta Drobik MODELE LINIOWE Jedna z najstarszych i najpopularniejszych metod modelowania Zależność między zbiorem zmiennych objaśniających, a zmienną ilościową nazywaną zmienną objaśnianą
Tablica Wzorów Rachunek Prawdopodobieństwa i Statystyki
 Tablica Wzorów Rachunek Prawdopodobieństwa i Statystyki Spis treści I. Wzory ogólne... 2 1. Średnia arytmetyczna:... 2 2. Rozstęp:... 2 3. Kwantyle:... 2 4. Wariancja:... 2 5. Odchylenie standardowe:...
Tablica Wzorów Rachunek Prawdopodobieństwa i Statystyki Spis treści I. Wzory ogólne... 2 1. Średnia arytmetyczna:... 2 2. Rozstęp:... 2 3. Kwantyle:... 2 4. Wariancja:... 2 5. Odchylenie standardowe:...
Modele i wnioskowanie statystyczne (MWS), sprawozdanie z laboratorium 4
 Modele i wnioskowanie statystyczne (MWS), sprawozdanie z laboratorium 4 Konrad Miziński, nr albumu 233703 31 maja 2015 Zadanie 1 Wartości oczekiwane µ 1 i µ 2 oszacowano wg wzorów: { µ1 = 0.43925 µ = X
Modele i wnioskowanie statystyczne (MWS), sprawozdanie z laboratorium 4 Konrad Miziński, nr albumu 233703 31 maja 2015 Zadanie 1 Wartości oczekiwane µ 1 i µ 2 oszacowano wg wzorów: { µ1 = 0.43925 µ = X
ALGORYTMICZNA I STATYSTYCZNA ANALIZA DANYCH
 1 ALGORYTMICZNA I STATYSTYCZNA ANALIZA DANYCH WFAiS UJ, Informatyka Stosowana II stopień studiów 2 Regresja liniowa Korelacja Modelowanie Analiza modelu Wnioskowanie Korelacja 3 Korelacja R: charakteryzuje
1 ALGORYTMICZNA I STATYSTYCZNA ANALIZA DANYCH WFAiS UJ, Informatyka Stosowana II stopień studiów 2 Regresja liniowa Korelacja Modelowanie Analiza modelu Wnioskowanie Korelacja 3 Korelacja R: charakteryzuje
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 5
 STATYSTYKA I DOŚWIADCZALNICTWO Wykład 5 Analiza korelacji - współczynnik korelacji Pearsona Cel: ocena współzależności między dwiema zmiennymi ilościowymi Ocenia jedynie zależność liniową. r = cov(x,y
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 5 Analiza korelacji - współczynnik korelacji Pearsona Cel: ocena współzależności między dwiema zmiennymi ilościowymi Ocenia jedynie zależność liniową. r = cov(x,y
PDF created with FinePrint pdffactory Pro trial version http://www.fineprint.com
 Analiza korelacji i regresji KORELACJA zależność liniowa Obserwujemy parę cech ilościowych (X,Y). Doświadczenie jest tak pomyślane, aby obserwowane pary cech X i Y (tzn i ta para x i i y i dla różnych
Analiza korelacji i regresji KORELACJA zależność liniowa Obserwujemy parę cech ilościowych (X,Y). Doświadczenie jest tak pomyślane, aby obserwowane pary cech X i Y (tzn i ta para x i i y i dla różnych
PAKIETY STATYSTYCZNE
 . Wykład wstępny PAKIETY STATYSTYCZNE 2. SAS, wprowadzenie - środowisko Windows, Linux 3. SAS, elementy analizy danych edycja danych 4. SAS, elementy analizy danych regresja liniowa, regresja nieliniowa
. Wykład wstępny PAKIETY STATYSTYCZNE 2. SAS, wprowadzenie - środowisko Windows, Linux 3. SAS, elementy analizy danych edycja danych 4. SAS, elementy analizy danych regresja liniowa, regresja nieliniowa
Środowisko R Założenie normalności metody nieparametryczne Wykład R4; 4.06.07 Weryfikacja założenia o normalności rozkładu populacji
 Środowisko R Założenie normalności metody nieparametryczne Wykład R4; 4.06.07 Weryfikacja założenia o normalności rozkładu populacji Dane są obserwacje x 1, x 2,..., x n. Czy można założyć, że x 1, x 2,...,
Środowisko R Założenie normalności metody nieparametryczne Wykład R4; 4.06.07 Weryfikacja założenia o normalności rozkładu populacji Dane są obserwacje x 1, x 2,..., x n. Czy można założyć, że x 1, x 2,...,
Korelacja oznacza współwystępowanie, nie oznacza związku przyczynowo-skutkowego
 Korelacja oznacza współwystępowanie, nie oznacza związku przyczynowo-skutkowego Współczynnik korelacji opisuje siłę i kierunek związku. Jest miarą symetryczną. Im wyższa korelacja tym lepiej potrafimy
Korelacja oznacza współwystępowanie, nie oznacza związku przyczynowo-skutkowego Współczynnik korelacji opisuje siłę i kierunek związku. Jest miarą symetryczną. Im wyższa korelacja tym lepiej potrafimy
Wykład 12 ( ): Testy dla dwóch prób w rodzinie rozkładów normalnych
 Wykład 12 (21.05.07): Testy dla dwóch prób w rodzinie rozkładów normalnych Przykład Rozważamy dane wygenerowane losowo; ( podobne do danych z przykładu 7.2 z książki A. Łomnickiego) n 1 = 9 poletek w dąbrowie,
Wykład 12 (21.05.07): Testy dla dwóch prób w rodzinie rozkładów normalnych Przykład Rozważamy dane wygenerowane losowo; ( podobne do danych z przykładu 7.2 z książki A. Łomnickiego) n 1 = 9 poletek w dąbrowie,
STATYSTYKA MATEMATYCZNA
 STATYSTYKA MATEMATYCZNA 1. Wykład wstępny. Teoria prawdopodobieństwa i elementy kombinatoryki 2. Zmienne losowe i ich rozkłady 3. Populacje i próby danych, estymacja parametrów 4. Testowanie hipotez 5.
STATYSTYKA MATEMATYCZNA 1. Wykład wstępny. Teoria prawdopodobieństwa i elementy kombinatoryki 2. Zmienne losowe i ich rozkłady 3. Populacje i próby danych, estymacja parametrów 4. Testowanie hipotez 5.
Spis treści. Przedmowa... XI. Rozdział 1. Pomiar: jednostki miar... 1. Rozdział 2. Pomiar: liczby i obliczenia liczbowe... 16
 Spis treści Przedmowa.......................... XI Rozdział 1. Pomiar: jednostki miar................. 1 1.1. Wielkości fizyczne i pozafizyczne.................. 1 1.2. Spójne układy miar. Układ SI i jego
Spis treści Przedmowa.......................... XI Rozdział 1. Pomiar: jednostki miar................. 1 1.1. Wielkości fizyczne i pozafizyczne.................. 1 1.2. Spójne układy miar. Układ SI i jego
STATYSTYKA - PRZYKŁADOWE ZADANIA EGZAMINACYJNE
 STATYSTYKA - PRZYKŁADOWE ZADANIA EGZAMINACYJNE 1 W trakcie badania obliczono wartości średniej (15,4), mediany (13,6) oraz dominanty (10,0). Określ typ asymetrii rozkładu. 2 Wymień 3 cechy rozkładu Gauss
STATYSTYKA - PRZYKŁADOWE ZADANIA EGZAMINACYJNE 1 W trakcie badania obliczono wartości średniej (15,4), mediany (13,6) oraz dominanty (10,0). Określ typ asymetrii rozkładu. 2 Wymień 3 cechy rozkładu Gauss
Statystyka w analizie i planowaniu eksperymentu
 23 kwietnia 2014 Korelacja - wspó lczynnik korelacji 1 Gdy badamy różnego rodzaju rodzaju zjawiska (np. przyrodnicze) możemy stwierdzić, że na każde z nich ma wp lyw dzia lanie innych czynników; Korelacja
23 kwietnia 2014 Korelacja - wspó lczynnik korelacji 1 Gdy badamy różnego rodzaju rodzaju zjawiska (np. przyrodnicze) możemy stwierdzić, że na każde z nich ma wp lyw dzia lanie innych czynników; Korelacja
Testowanie hipotez statystycznych.
 Bioinformatyka Wykład 4 Wrocław, 17 października 2011 Temat. Weryfikacja hipotez statystycznych dotyczących wartości oczekiwanej w dwóch populacjach o rozkładach normalnych. Model 3. Porównanie średnich
Bioinformatyka Wykład 4 Wrocław, 17 października 2011 Temat. Weryfikacja hipotez statystycznych dotyczących wartości oczekiwanej w dwóch populacjach o rozkładach normalnych. Model 3. Porównanie średnich
Testy dla dwóch prób w rodzinie rozkładów normalnych
 Testy dla dwóch prób w rodzinie rozkładów normalnych dr Mariusz Grządziel Wykład 12; 18 maja 2009 Przykład Rozważamy dane wygenerowane losowo; ( podobne do danych z przykładu 7.2 z książki A. Łomnickiego)
Testy dla dwóch prób w rodzinie rozkładów normalnych dr Mariusz Grządziel Wykład 12; 18 maja 2009 Przykład Rozważamy dane wygenerowane losowo; ( podobne do danych z przykładu 7.2 z książki A. Łomnickiego)
Problem dwóch prób: porównywanie średnich i wariancji z populacji o rozkładach normalnych. Wrocław, 23 marca 2015
 Problem dwóch prób: porównywanie średnich i wariancji z populacji o rozkładach normalnych. Wrocław, 23 marca 2015 Problem dwóch prób X = (X 1, X 2,..., X n ) - próba z rozkładu normalnego N (µ, σ 2 X ),
Problem dwóch prób: porównywanie średnich i wariancji z populacji o rozkładach normalnych. Wrocław, 23 marca 2015 Problem dwóch prób X = (X 1, X 2,..., X n ) - próba z rozkładu normalnego N (µ, σ 2 X ),
Testowanie hipotez dla dwóch zmiennych zależnych. Moc testu. Minimalna liczność próby; Regresja prosta; Korelacja Pearsona;
 LABORATORIUM 4 Testowanie hipotez dla dwóch zmiennych zależnych. Moc testu. Minimalna liczność próby; Regresja prosta; Korelacja Pearsona; dwie zmienne zależne mierzalne małe próby duże próby rozkład normalny
LABORATORIUM 4 Testowanie hipotez dla dwóch zmiennych zależnych. Moc testu. Minimalna liczność próby; Regresja prosta; Korelacja Pearsona; dwie zmienne zależne mierzalne małe próby duże próby rozkład normalny
Współczynnik korelacji. Współczynnik korelacji jest miernikiem zależności między dwiema cechami Oznaczenie: ϱ
 Współczynnik korelacji Współczynnik korelacji jest miernikiem zależności między dwiema cechami Oznaczenie: ϱ Własności współczynnika korelacji 1. Współczynnik korelacji jest liczbą niemianowaną 2. ϱ 1,
Współczynnik korelacji Współczynnik korelacji jest miernikiem zależności między dwiema cechami Oznaczenie: ϱ Własności współczynnika korelacji 1. Współczynnik korelacji jest liczbą niemianowaną 2. ϱ 1,
WIELKA SGH-OWA POWTÓRKA ZE STATYSTYKI REGRESJA LINIOWA
 WIELKA SGH-OWA POWTÓRKA ZE STATYSTYKI REGRESJA LINIOWA Powtórka Powtórki Kowiariancja cov xy lub c xy - kierunek zależności Współczynnik korelacji liniowej Pearsona r siła liniowej zależności Istotność
WIELKA SGH-OWA POWTÓRKA ZE STATYSTYKI REGRESJA LINIOWA Powtórka Powtórki Kowiariancja cov xy lub c xy - kierunek zależności Współczynnik korelacji liniowej Pearsona r siła liniowej zależności Istotność
Testowanie hipotez statystycznych.
 Statystyka Wykład 10 Wrocław, 22 grudnia 2011 Testowanie hipotez statystycznych Definicja. Hipotezą statystyczną nazywamy stwierdzenie dotyczące parametrów populacji. Definicja. Dwie komplementarne w problemie
Statystyka Wykład 10 Wrocław, 22 grudnia 2011 Testowanie hipotez statystycznych Definicja. Hipotezą statystyczną nazywamy stwierdzenie dotyczące parametrów populacji. Definicja. Dwie komplementarne w problemie
Temat zajęć: ANALIZA DANYCH ZBIORU EKSPORT. Część I: analiza regresji
 Temat zajęć: ANALIZA DANYCH ZBIORU EKSPORT Część I: analiza regresji Krok 1. Pod adresem http://zsi.tech.us.edu.pl/~nowak/adb/eksport.txt znajdziesz zbiór danych do analizy. Zapisz plik na dysku w dowolnej
Temat zajęć: ANALIZA DANYCH ZBIORU EKSPORT Część I: analiza regresji Krok 1. Pod adresem http://zsi.tech.us.edu.pl/~nowak/adb/eksport.txt znajdziesz zbiór danych do analizy. Zapisz plik na dysku w dowolnej
ZJAZD 4. gdzie E(x) jest wartością oczekiwaną x
 ZJAZD 4 KORELACJA, BADANIE NIEZALEŻNOŚCI, ANALIZA REGRESJI Analiza korelacji i regresji jest działem statystyki zajmującym się badaniem zależności i związków pomiędzy rozkładami dwu lub więcej badanych
ZJAZD 4 KORELACJA, BADANIE NIEZALEŻNOŚCI, ANALIZA REGRESJI Analiza korelacji i regresji jest działem statystyki zajmującym się badaniem zależności i związków pomiędzy rozkładami dwu lub więcej badanych
Stanisław Cichocki. Natalia Nehrebecka. Wykład 9
 Stanisław Cichocki Natalia Nehrebecka Wykład 9 1 1. Dodatkowe założenie KMRL 2. Testowanie hipotez prostych Rozkład estymatora b Testowanie hipotez prostych przy użyciu statystyki t 3. Przedziały ufności
Stanisław Cichocki Natalia Nehrebecka Wykład 9 1 1. Dodatkowe założenie KMRL 2. Testowanie hipotez prostych Rozkład estymatora b Testowanie hipotez prostych przy użyciu statystyki t 3. Przedziały ufności
Wykład 4 Wybór najlepszej procedury. Estymacja parametrów re
 Wykład 4 Wybór najlepszej procedury. Estymacja parametrów regresji z wykorzystaniem metody bootstrap. Wrocław, 22.03.2017r Wybór najlepszej procedury - podsumowanie Co nas interesuje przed przeprowadzeniem
Wykład 4 Wybór najlepszej procedury. Estymacja parametrów regresji z wykorzystaniem metody bootstrap. Wrocław, 22.03.2017r Wybór najlepszej procedury - podsumowanie Co nas interesuje przed przeprowadzeniem
Permutacyjna metoda oceny istotności regresji
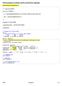 Permutacyjna metoda oceny istotności regresji (bez założenia normalności) f
Permutacyjna metoda oceny istotności regresji (bez założenia normalności) f
Projekt zaliczeniowy z przedmiotu Statystyka i eksploracja danych (nr 3) Kamil Krzysztof Derkowski
 Projekt zaliczeniowy z przedmiotu Statystyka i eksploracja danych (nr 3) Kamil Krzysztof Derkowski Zadanie 1 Eksploracja (EXAMINE) Informacja o analizowanych danych Obserwacje Uwzględnione Wykluczone Ogółem
Projekt zaliczeniowy z przedmiotu Statystyka i eksploracja danych (nr 3) Kamil Krzysztof Derkowski Zadanie 1 Eksploracja (EXAMINE) Informacja o analizowanych danych Obserwacje Uwzględnione Wykluczone Ogółem
Regresja wielokrotna. PDF created with FinePrint pdffactory Pro trial version http://www.fineprint.com
 Regresja wielokrotna Model dla zależności liniowej: Y=a+b 1 X 1 +b 2 X 2 +...+b n X n Cząstkowe współczynniki regresji wielokrotnej: b 1,..., b n Zmienne niezależne (przyczynowe): X 1,..., X n Zmienna
Regresja wielokrotna Model dla zależności liniowej: Y=a+b 1 X 1 +b 2 X 2 +...+b n X n Cząstkowe współczynniki regresji wielokrotnej: b 1,..., b n Zmienne niezależne (przyczynowe): X 1,..., X n Zmienna
BADANIE ZALEśNOŚCI CECHY Y OD CECHY X - ANALIZA REGRESJI PROSTEJ
 WYKŁAD 3 BADANIE ZALEśNOŚCI CECHY Y OD CECHY X - ANALIZA REGRESJI PROSTEJ Było: Przykład. Z dziesięciu poletek doświadczalnych zerano plony ulw ziemniaczanych (cecha X) i oznaczono w nich procentową zawartość
WYKŁAD 3 BADANIE ZALEśNOŚCI CECHY Y OD CECHY X - ANALIZA REGRESJI PROSTEJ Było: Przykład. Z dziesięciu poletek doświadczalnych zerano plony ulw ziemniaczanych (cecha X) i oznaczono w nich procentową zawartość
Wykład 5 Problem dwóch prób - testowanie hipotez dla równości średnich
 Wykład 5 Problem dwóch prób - testowanie hipotez dla równości średnich Magdalena Frąszczak Wrocław, 22.03.2017r Problem Behrensa Fishera Niech X = (X 1, X 2,..., X n ) oznacza próbę z rozkładu normalnego
Wykład 5 Problem dwóch prób - testowanie hipotez dla równości średnich Magdalena Frąszczak Wrocław, 22.03.2017r Problem Behrensa Fishera Niech X = (X 1, X 2,..., X n ) oznacza próbę z rozkładu normalnego
KORELACJE I REGRESJA LINIOWA
 KORELACJE I REGRESJA LINIOWA Korelacje i regresja liniowa Analiza korelacji: Badanie, czy pomiędzy dwoma zmiennymi istnieje zależność Obie analizy się wzajemnie przeplatają Analiza regresji: Opisanie modelem
KORELACJE I REGRESJA LINIOWA Korelacje i regresja liniowa Analiza korelacji: Badanie, czy pomiędzy dwoma zmiennymi istnieje zależność Obie analizy się wzajemnie przeplatają Analiza regresji: Opisanie modelem
Stosowana Analiza Regresji
 prostej Stosowana Wykład I 5 Października 2011 1 / 29 prostej Przykład Dane trees - wyniki pomiarów objętości (Volume), średnicy (Girth) i wysokości (Height) pni drzew. Interesuje nas zależność (o ile
prostej Stosowana Wykład I 5 Października 2011 1 / 29 prostej Przykład Dane trees - wyniki pomiarów objętości (Volume), średnicy (Girth) i wysokości (Height) pni drzew. Interesuje nas zależność (o ile
Wykład 9 Testy rangowe w problemie dwóch prób
 Wykład 9 Testy rangowe w problemie dwóch prób Wrocław, 18 kwietnia 2018 Test rangowy Testem rangowym nazywamy test, w którym statystyka testowa jest konstruowana w oparciu o rangi współrzędnych wektora
Wykład 9 Testy rangowe w problemie dwóch prób Wrocław, 18 kwietnia 2018 Test rangowy Testem rangowym nazywamy test, w którym statystyka testowa jest konstruowana w oparciu o rangi współrzędnych wektora
REGRESJA I KORELACJA MODEL REGRESJI LINIOWEJ MODEL REGRESJI WIELORAKIEJ. Analiza regresji i korelacji
 Statystyka i opracowanie danych Ćwiczenia 5 Izabela Olejarczyk - Wożeńska AGH, WIMiIP, KISIM REGRESJA I KORELACJA MODEL REGRESJI LINIOWEJ MODEL REGRESJI WIELORAKIEJ MODEL REGRESJI LINIOWEJ Analiza regresji
Statystyka i opracowanie danych Ćwiczenia 5 Izabela Olejarczyk - Wożeńska AGH, WIMiIP, KISIM REGRESJA I KORELACJA MODEL REGRESJI LINIOWEJ MODEL REGRESJI WIELORAKIEJ MODEL REGRESJI LINIOWEJ Analiza regresji
Stanisław Cichocki. Natalia Nehrebecka
 Stanisław Cichocki Natalia Nehrebecka 1 1. Wstęp a) Binarne zmienne zależne b) Interpretacja ekonomiczna c) Interpretacja współczynników 2. Liniowy model prawdopodobieństwa a) Interpretacja współczynników
Stanisław Cichocki Natalia Nehrebecka 1 1. Wstęp a) Binarne zmienne zależne b) Interpretacja ekonomiczna c) Interpretacja współczynników 2. Liniowy model prawdopodobieństwa a) Interpretacja współczynników
Statystyka. Wykład 8. Magdalena Alama-Bućko. 10 kwietnia Magdalena Alama-Bućko Statystyka 10 kwietnia / 31
 Statystyka Wykład 8 Magdalena Alama-Bućko 10 kwietnia 2017 Magdalena Alama-Bućko Statystyka 10 kwietnia 2017 1 / 31 Tematyka zajęć: Wprowadzenie do statystyki. Analiza struktury zbiorowości miary położenia
Statystyka Wykład 8 Magdalena Alama-Bućko 10 kwietnia 2017 Magdalena Alama-Bućko Statystyka 10 kwietnia 2017 1 / 31 Tematyka zajęć: Wprowadzenie do statystyki. Analiza struktury zbiorowości miary położenia
Statystyka od podstaw Janina Jóźwiak, Jarosław Podgórski
 Statystyka od podstaw Janina Jóźwiak, Jarosław Podgórski Książka jest nowoczesnym podręcznikiem przeznaczonym dla studentów uczelni i wydziałów ekonomicznych. Wykład podzielono na cztery części. W pierwszej
Statystyka od podstaw Janina Jóźwiak, Jarosław Podgórski Książka jest nowoczesnym podręcznikiem przeznaczonym dla studentów uczelni i wydziałów ekonomicznych. Wykład podzielono na cztery części. W pierwszej
Analiza współzależności zjawisk
 Analiza współzależności zjawisk Informacje ogólne Jednostki tworzące zbiorowość statystyczną charakteryzowane są zazwyczaj za pomocą wielu cech zmiennych, które nierzadko pozostają ze sobą w pewnym związku.
Analiza współzależności zjawisk Informacje ogólne Jednostki tworzące zbiorowość statystyczną charakteryzowane są zazwyczaj za pomocą wielu cech zmiennych, które nierzadko pozostają ze sobą w pewnym związku.
PODSTAWY STATYSTYCZNEJ ANALIZY DANYCH. Wykład 2 Obserwacje nietypowe i wpływowe Regresja nieliniowa
 Wykład 2 Obserwacje nietypowe i wpływowe Regresja nieliniowa Obserwacje nietypowe i wpływowe Obserwacje nietypowe i wpływowe Obserwacje nietypowe w analizie regresji: nietypowe wartości zmiennej Y - prowadzące
Wykład 2 Obserwacje nietypowe i wpływowe Regresja nieliniowa Obserwacje nietypowe i wpływowe Obserwacje nietypowe i wpływowe Obserwacje nietypowe w analizie regresji: nietypowe wartości zmiennej Y - prowadzące
Ekonometria dla IiE i MSEMat Z7
 Ekonometria dla IiE i MSEMat Z7 Rafał Woźniak Faculty of Economic Sciences, University of Warsaw Warszawa, 21-11-2016 Na podstawie zbioru danych cps_small.dat z książki Principles of Econometrics oszacowany
Ekonometria dla IiE i MSEMat Z7 Rafał Woźniak Faculty of Economic Sciences, University of Warsaw Warszawa, 21-11-2016 Na podstawie zbioru danych cps_small.dat z książki Principles of Econometrics oszacowany
7. Estymacja parametrów w modelu normalnym(14.04.2008) Pojęcie losowej próby prostej
 7. Estymacja parametrów w modelu normalnym(14.04.2008) Pojęcie losowej próby prostej Definicja 1 n-elementowa losowa próba prosta nazywamy ciag n niezależnych zmiennych losowych o jednakowych rozkładach
7. Estymacja parametrów w modelu normalnym(14.04.2008) Pojęcie losowej próby prostej Definicja 1 n-elementowa losowa próba prosta nazywamy ciag n niezależnych zmiennych losowych o jednakowych rozkładach
STATYSTYKA MATEMATYCZNA
 STATYSTYKA MATEMATYCZNA 1. Wykład wstępny 2. Teoria prawdopodobieństwa i elementy kombinatoryki 3. Zmienne losowe 4. Populacje i próby danych 5. Testowanie hipotez i estymacja parametrów 6. Test t 7. Test
STATYSTYKA MATEMATYCZNA 1. Wykład wstępny 2. Teoria prawdopodobieństwa i elementy kombinatoryki 3. Zmienne losowe 4. Populacje i próby danych 5. Testowanie hipotez i estymacja parametrów 6. Test t 7. Test
Regresja liniowa w R Piotr J. Sobczyk
 Regresja liniowa w R Piotr J. Sobczyk Uwaga Poniższe notatki mają charakter roboczy. Mogą zawierać błędy. Za przesłanie mi informacji zwrotnej o zauważonych usterkach serdecznie dziękuję. Weźmy dane dotyczące
Regresja liniowa w R Piotr J. Sobczyk Uwaga Poniższe notatki mają charakter roboczy. Mogą zawierać błędy. Za przesłanie mi informacji zwrotnej o zauważonych usterkach serdecznie dziękuję. Weźmy dane dotyczące
weryfikacja hipotez dotyczących parametrów populacji (średnia, wariancja)
 PODSTAWY STATYSTYKI. Teoria prawdopodobieństwa i elementy kombinatoryki. Zmienne losowe i ich rozkłady 3. Populacje i próby danych, estymacja parametrów 4. Testowanie hipotez 5. Testy parametryczne (na
PODSTAWY STATYSTYKI. Teoria prawdopodobieństwa i elementy kombinatoryki. Zmienne losowe i ich rozkłady 3. Populacje i próby danych, estymacja parametrów 4. Testowanie hipotez 5. Testy parametryczne (na
4. Średnia i autoregresja zmiennej prognozowanej
 4. Średnia i autoregresja zmiennej prognozowanej 1. Średnia w próbie uczącej Własności: y = y = 1 N y = y t = 1, 2, T s = s = 1 N 1 y y R = 0 v = s 1 +, 2. Przykład. Miesięczna sprzedaż żelazek (szt.)
4. Średnia i autoregresja zmiennej prognozowanej 1. Średnia w próbie uczącej Własności: y = y = 1 N y = y t = 1, 2, T s = s = 1 N 1 y y R = 0 v = s 1 +, 2. Przykład. Miesięczna sprzedaż żelazek (szt.)
Analiza Danych Sprawozdanie regresja Marek Lewandowski Inf 59817
 Analiza Danych Sprawozdanie regresja Marek Lewandowski Inf 59817 Zadanie 1: wiek 7 8 9 1 11 11,5 12 13 14 14 15 16 17 18 18,5 19 wzrost 12 122 125 131 135 14 142 145 15 1 154 159 162 164 168 17 Wykres
Analiza Danych Sprawozdanie regresja Marek Lewandowski Inf 59817 Zadanie 1: wiek 7 8 9 1 11 11,5 12 13 14 14 15 16 17 18 18,5 19 wzrost 12 122 125 131 135 14 142 145 15 1 154 159 162 164 168 17 Wykres
Zmienne zależne i niezależne
 Analiza kanoniczna Motywacja (1) 2 Często w badaniach spotykamy problemy badawcze, w których szukamy zakresu i kierunku zależności pomiędzy zbiorami zmiennych: { X i Jak oceniać takie 1, X 2,..., X p }
Analiza kanoniczna Motywacja (1) 2 Często w badaniach spotykamy problemy badawcze, w których szukamy zakresu i kierunku zależności pomiędzy zbiorami zmiennych: { X i Jak oceniać takie 1, X 2,..., X p }
Regresja liniowa oraz regresja wielokrotna w zastosowaniu zadania predykcji danych. Agnieszka Nowak Brzezińska Wykład III-VI
 Regresja liniowa oraz regresja wielokrotna w zastosowaniu zadania predykcji danych. Agnieszka Nowak Brzezińska Wykład III-VI Analiza regresji Analiza regresji jest bardzo popularną i chętnie stosowaną
Regresja liniowa oraz regresja wielokrotna w zastosowaniu zadania predykcji danych. Agnieszka Nowak Brzezińska Wykład III-VI Analiza regresji Analiza regresji jest bardzo popularną i chętnie stosowaną
Wykład Centralne twierdzenie graniczne. Statystyka matematyczna: Estymacja parametrów rozkładu
 Wykład 11-12 Centralne twierdzenie graniczne Statystyka matematyczna: Estymacja parametrów rozkładu Centralne twierdzenie graniczne (CTG) (Central Limit Theorem - CLT) Centralne twierdzenie graniczne (Lindenberga-Levy'ego)
Wykład 11-12 Centralne twierdzenie graniczne Statystyka matematyczna: Estymacja parametrów rozkładu Centralne twierdzenie graniczne (CTG) (Central Limit Theorem - CLT) Centralne twierdzenie graniczne (Lindenberga-Levy'ego)
Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć)
 Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć) 1. Populacja generalna a losowa próba, parametr rozkładu cechy a jego ocena z losowej próby, miary opisu statystycznego
Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć) 1. Populacja generalna a losowa próba, parametr rozkładu cechy a jego ocena z losowej próby, miary opisu statystycznego
Statystyka opisowa. Wykład V. Regresja liniowa wieloraka
 Statystyka opisowa. Wykład V. e-mail:e.kozlovski@pollub.pl Spis treści 1 Prosta regresji cechy Y względem cech X 1,..., X k. 2 3 Wyznaczamy zależność cechy Y od cech X 1, X 2,..., X k postaci Y = α 0 +
Statystyka opisowa. Wykład V. e-mail:e.kozlovski@pollub.pl Spis treści 1 Prosta regresji cechy Y względem cech X 1,..., X k. 2 3 Wyznaczamy zależność cechy Y od cech X 1, X 2,..., X k postaci Y = α 0 +
Estymacja parametrów w modelu normalnym
 Estymacja parametrów w modelu normalnym dr Mariusz Grządziel 6 kwietnia 2009 Model normalny Przez model normalny będziemy rozumieć rodzine rozkładów normalnych N(µ, σ), µ R, σ > 0. Z Centralnego Twierdzenia
Estymacja parametrów w modelu normalnym dr Mariusz Grządziel 6 kwietnia 2009 Model normalny Przez model normalny będziemy rozumieć rodzine rozkładów normalnych N(µ, σ), µ R, σ > 0. Z Centralnego Twierdzenia
ANALIZA REGRESJI SPSS
 NLIZ REGRESJI SPSS Metody badań geografii społeczno-ekonomicznej KORELCJ REGRESJ O ile celem korelacji jest zmierzenie siły związku liniowego między (najczęściej dwoma) zmiennymi, o tyle w regresji związek
NLIZ REGRESJI SPSS Metody badań geografii społeczno-ekonomicznej KORELCJ REGRESJ O ile celem korelacji jest zmierzenie siły związku liniowego między (najczęściej dwoma) zmiennymi, o tyle w regresji związek
Stanisław Cichocki Natalia Nehrebecka. Zajęcia 11-12
 Stanisław Cichocki Natalia Nehrebecka Zajęcia 11-12 1. Zmienne pominięte 2. Zmienne nieistotne 3. Obserwacje nietypowe i błędne 4. Współliniowość - Mamy 2 modele: y X u 1 1 (1) y X X 1 1 2 2 (2) - Potencjalnie
Stanisław Cichocki Natalia Nehrebecka Zajęcia 11-12 1. Zmienne pominięte 2. Zmienne nieistotne 3. Obserwacje nietypowe i błędne 4. Współliniowość - Mamy 2 modele: y X u 1 1 (1) y X X 1 1 2 2 (2) - Potencjalnie
Stanisław Cichocki. Natalia Nehrebecka. Wykład 12
 Stanisław Cichocki Natalia Nehrebecka Wykład 12 1 1.Problemy z danymi Zmienne pominięte Zmienne nieistotne 2. Autokorelacja o Testowanie autokorelacji 1.Problemy z danymi Zmienne pominięte Zmienne nieistotne
Stanisław Cichocki Natalia Nehrebecka Wykład 12 1 1.Problemy z danymi Zmienne pominięte Zmienne nieistotne 2. Autokorelacja o Testowanie autokorelacji 1.Problemy z danymi Zmienne pominięte Zmienne nieistotne
Elementy Modelowania Matematycznego Wykład 4 Regresja i dyskryminacja liniowa
 Spis treści Elementy Modelowania Matematycznego Wykład 4 Regresja i dyskryminacja liniowa Romuald Kotowski Katedra Informatyki Stosowanej PJWSTK 2009 Spis treści Spis treści 1 Wstęp Bardzo często interesujący
Spis treści Elementy Modelowania Matematycznego Wykład 4 Regresja i dyskryminacja liniowa Romuald Kotowski Katedra Informatyki Stosowanej PJWSTK 2009 Spis treści Spis treści 1 Wstęp Bardzo często interesujący
Egzamin z ekonometrii wersja IiE, MSEMAT
 Egzamin z ekonometrii wersja IiE, MSEMAT 04-02-2016 Pytania teoretyczne 1. Za pomocą jakiego testu weryfikowana jest normalność składnika losowego? Jakiemu założeniu KMRL odpowiada w tym teście? Jakie
Egzamin z ekonometrii wersja IiE, MSEMAT 04-02-2016 Pytania teoretyczne 1. Za pomocą jakiego testu weryfikowana jest normalność składnika losowego? Jakiemu założeniu KMRL odpowiada w tym teście? Jakie
Modele i wnioskowanie statystyczne (MWS), sprawozdanie z laboratorium 3
 Modele i wnioskowanie statystyczne (MWS), sprawozdanie z laboratorium 3 Konrad Miziński, nr albumu 233703 26 maja 2015 Zadanie 1 Wartość krytyczna c, niezbędna wyliczenia mocy testu (1 β) wyznaczono za
Modele i wnioskowanie statystyczne (MWS), sprawozdanie z laboratorium 3 Konrad Miziński, nr albumu 233703 26 maja 2015 Zadanie 1 Wartość krytyczna c, niezbędna wyliczenia mocy testu (1 β) wyznaczono za
Rozdział 8. Regresja. Definiowanie modelu
 Rozdział 8 Regresja Definiowanie modelu Analizę korelacji można traktować jako wstęp do analizy regresji. Jeżeli wykresy rozrzutu oraz wartości współczynników korelacji wskazują na istniejąca współzmienność
Rozdział 8 Regresja Definiowanie modelu Analizę korelacji można traktować jako wstęp do analizy regresji. Jeżeli wykresy rozrzutu oraz wartości współczynników korelacji wskazują na istniejąca współzmienność
Regresja wielokrotna jest metodą statystyczną, w której oceniamy wpływ wielu zmiennych niezależnych (X1, X2, X3,...) na zmienną zależną (Y).
 Statystyka i opracowanie danych Ćwiczenia 12 Izabela Olejarczyk - Wożeńska AGH, WIMiIP, KISIM REGRESJA WIELORAKA Regresja wielokrotna jest metodą statystyczną, w której oceniamy wpływ wielu zmiennych niezależnych
Statystyka i opracowanie danych Ćwiczenia 12 Izabela Olejarczyk - Wożeńska AGH, WIMiIP, KISIM REGRESJA WIELORAKA Regresja wielokrotna jest metodą statystyczną, w której oceniamy wpływ wielu zmiennych niezależnych
Mikroekonometria 13. Mikołaj Czajkowski Wiktor Budziński
 Mikroekonometria 13 Mikołaj Czajkowski Wiktor Budziński Endogeniczność regresja liniowa W regresji liniowej estymujemy następujące równanie: i i i Metoda Najmniejszych Kwadratów zakłada, że wszystkie zmienne
Mikroekonometria 13 Mikołaj Czajkowski Wiktor Budziński Endogeniczność regresja liniowa W regresji liniowej estymujemy następujące równanie: i i i Metoda Najmniejszych Kwadratów zakłada, że wszystkie zmienne
Wykład 3 Testowanie hipotez statystycznych o wartości średniej. średniej i wariancji z populacji o rozkładzie normalnym
 Wykład 3 Testowanie hipotez statystycznych o wartości średniej i wariancji z populacji o rozkładzie normalnym Wrocław, 08.03.2017r Model 1 Testowanie hipotez dla średniej w rozkładzie normalnym ze znaną
Wykład 3 Testowanie hipotez statystycznych o wartości średniej i wariancji z populacji o rozkładzie normalnym Wrocław, 08.03.2017r Model 1 Testowanie hipotez dla średniej w rozkładzie normalnym ze znaną
STATYSTYKA MATEMATYCZNA
 STATYSTYKA MATEMATYCZNA 1. Wykład wstępny. Teoria prawdopodobieństwa i elementy kombinatoryki. Zmienne losowe i ich rozkłady 3. Populacje i próby danych, estymacja parametrów 4. Testowanie hipotez statystycznych
STATYSTYKA MATEMATYCZNA 1. Wykład wstępny. Teoria prawdopodobieństwa i elementy kombinatoryki. Zmienne losowe i ich rozkłady 3. Populacje i próby danych, estymacja parametrów 4. Testowanie hipotez statystycznych
STATYSTYKA I DOŚWIADCZALNICTWO. Wykład 2
 STATYSTYKA I DOŚWIADCZALNICTWO Wykład Parametry przedziałowe rozkładów ciągłych określane na podstawie próby (przedziały ufności) Przedział ufności dla średniej s X t( α;n 1),X + t( α;n 1) n s n t (α;
STATYSTYKA I DOŚWIADCZALNICTWO Wykład Parametry przedziałowe rozkładów ciągłych określane na podstawie próby (przedziały ufności) Przedział ufności dla średniej s X t( α;n 1),X + t( α;n 1) n s n t (α;
Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć)
 Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć) 1. Populacja generalna a losowa próba, parametr rozkładu cechy a jego ocena z losowej próby, miary opisu statystycznego
Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć) 1. Populacja generalna a losowa próba, parametr rozkładu cechy a jego ocena z losowej próby, miary opisu statystycznego
Własności statystyczne regresji liniowej. Wykład 4
 Własności statystyczne regresji liniowej Wykład 4 Plan Własności zmiennych losowych Normalna regresja liniowa Własności regresji liniowej Literatura B. Hansen (2017+) Econometrics, Rozdział 5 Własności
Własności statystyczne regresji liniowej Wykład 4 Plan Własności zmiennych losowych Normalna regresja liniowa Własności regresji liniowej Literatura B. Hansen (2017+) Econometrics, Rozdział 5 Własności
R-PEARSONA Zależność liniowa
 R-PEARSONA Zależność liniowa Interpretacja wyników: wraz ze wzrostem wartości jednej zmiennej (np. zarobków) liniowo rosną wartości drugiej zmiennej (np. kwoty przeznaczanej na wakacje) czyli np. im wyższe
R-PEARSONA Zależność liniowa Interpretacja wyników: wraz ze wzrostem wartości jednej zmiennej (np. zarobków) liniowo rosną wartości drugiej zmiennej (np. kwoty przeznaczanej na wakacje) czyli np. im wyższe
WERYFIKACJA MODELI MODELE LINIOWE. Biomatematyka wykład 8 Dr Wioleta Drobik-Czwarno
 WERYFIKACJA MODELI MODELE LINIOWE Biomatematyka wykład 8 Dr Wioleta Drobik-Czwarno ANALIZA KORELACJI LINIOWEJ to NIE JEST badanie związku przyczynowo-skutkowego, Badanie współwystępowania cech (czy istnieje
WERYFIKACJA MODELI MODELE LINIOWE Biomatematyka wykład 8 Dr Wioleta Drobik-Czwarno ANALIZA KORELACJI LINIOWEJ to NIE JEST badanie związku przyczynowo-skutkowego, Badanie współwystępowania cech (czy istnieje
Statystyki: miary opisujące rozkład! np. : średnia, frakcja (procent), odchylenie standardowe, wariancja, mediana itd.
 Wnioskowanie statystyczne obejmujące metody pozwalające na uogólnianie wyników z próby na nieznane wartości parametrów oraz szacowanie błędów tego uogólnienia. Przewidujemy nieznaną wartości parametru
Wnioskowanie statystyczne obejmujące metody pozwalające na uogólnianie wyników z próby na nieznane wartości parametrów oraz szacowanie błędów tego uogólnienia. Przewidujemy nieznaną wartości parametru
OBLICZENIE PRZEPŁYWÓW MAKSYMALNYCH ROCZNYCH O OKREŚLONYM PRAWDOPODOBIEŃSTWIE PRZEWYŻSZENIA. z wykorzystaniem programu obliczeniowego Q maxp
 tel.: +48 662 635 712 Liczba stron: 15 Data: 20.07.2010r OBLICZENIE PRZEPŁYWÓW MAKSYMALNYCH ROCZNYCH O OKREŚLONYM PRAWDOPODOBIEŃSTWIE PRZEWYŻSZENIA z wykorzystaniem programu obliczeniowego Q maxp DŁUGIE
tel.: +48 662 635 712 Liczba stron: 15 Data: 20.07.2010r OBLICZENIE PRZEPŁYWÓW MAKSYMALNYCH ROCZNYCH O OKREŚLONYM PRAWDOPODOBIEŃSTWIE PRZEWYŻSZENIA z wykorzystaniem programu obliczeniowego Q maxp DŁUGIE
Stanisław Cichocki. Natalia Nehrebecka. Wykład 10
 Stanisław Cichocki Natalia Nehrebecka Wykład 10 1 1. Testy diagnostyczne Testowanie prawidłowości formy funkcyjnej: test RESET Testowanie normalności składników losowych: test Jarque-Berra Testowanie stabilności
Stanisław Cichocki Natalia Nehrebecka Wykład 10 1 1. Testy diagnostyczne Testowanie prawidłowości formy funkcyjnej: test RESET Testowanie normalności składników losowych: test Jarque-Berra Testowanie stabilności
Przykład 2. Stopa bezrobocia
 Przykład 2 Stopa bezrobocia Stopa bezrobocia. Komentarz: model ekonometryczny stopy bezrobocia w Polsce jest modelem nieliniowym autoregresyjnym. Podobnie jak model podaŝy pieniądza zbudowany został w
Przykład 2 Stopa bezrobocia Stopa bezrobocia. Komentarz: model ekonometryczny stopy bezrobocia w Polsce jest modelem nieliniowym autoregresyjnym. Podobnie jak model podaŝy pieniądza zbudowany został w
( x) Równanie regresji liniowej ma postać. By obliczyć współczynniki a i b należy posłużyć się następującymi wzorami 1 : Gdzie:
 ma postać y = ax + b Równanie regresji liniowej By obliczyć współczynniki a i b należy posłużyć się następującymi wzorami 1 : xy b = a = b lub x Gdzie: xy = też a = x = ( b ) i to dane empiryczne, a ilość
ma postać y = ax + b Równanie regresji liniowej By obliczyć współczynniki a i b należy posłużyć się następującymi wzorami 1 : xy b = a = b lub x Gdzie: xy = też a = x = ( b ) i to dane empiryczne, a ilość
Testy nieparametryczne
 Testy nieparametryczne Testy nieparametryczne możemy stosować, gdy nie są spełnione założenia wymagane dla testów parametrycznych. Stosujemy je również, gdy dane można uporządkować według określonych kryteriów
Testy nieparametryczne Testy nieparametryczne możemy stosować, gdy nie są spełnione założenia wymagane dla testów parametrycznych. Stosujemy je również, gdy dane można uporządkować według określonych kryteriów
Zadanie 1. a) Przeprowadzono test RESET. Czy model ma poprawną formę funkcyjną? 1
 Zadanie 1 a) Przeprowadzono test RESET. Czy model ma poprawną formę funkcyjną? 1 b) W naszym przypadku populacja są inżynierowie w Tajlandii. Czy można jednak przypuszczać, że na zarobki kobiet-inżynierów
Zadanie 1 a) Przeprowadzono test RESET. Czy model ma poprawną formę funkcyjną? 1 b) W naszym przypadku populacja są inżynierowie w Tajlandii. Czy można jednak przypuszczać, że na zarobki kobiet-inżynierów
Ćwiczenie: Wybrane zagadnienia z korelacji i regresji.
 Ćwiczenie: Wybrane zagadnienia z korelacji i regresji. W statystyce stopień zależności między cechami można wyrazić wg następującej skali: Skala Guillforda Przedział Zależność Współczynnik [0,00±0,20)
Ćwiczenie: Wybrane zagadnienia z korelacji i regresji. W statystyce stopień zależności między cechami można wyrazić wg następującej skali: Skala Guillforda Przedział Zależność Współczynnik [0,00±0,20)
Statystyczna analiza danych w programie STATISTICA 7.1 PL (wykład 3) Dariusz Gozdowski
 Statystyczna analiza danych w programie STATISTICA 7.1 PL (wykład 3) Dariusz Gozdowski Katedra Doświadczalnictwa i Bioinformatyki Wydział Rolnictwa i Biologii SGGW Dwuczynnikowa analiza wariancji (2-way
Statystyczna analiza danych w programie STATISTICA 7.1 PL (wykład 3) Dariusz Gozdowski Katedra Doświadczalnictwa i Bioinformatyki Wydział Rolnictwa i Biologii SGGW Dwuczynnikowa analiza wariancji (2-way
Diagnostyka w Pakiecie Stata
 Karol Kuhl Zgodnie z twierdzeniem Gaussa-Markowa, estymator MNK w KMRL jest liniowym estymatorem efektywnym i nieobciążonym, co po angielsku opisuje się za pomocą wyrażenia BLUE Best Linear Unbiased Estimator.
Karol Kuhl Zgodnie z twierdzeniem Gaussa-Markowa, estymator MNK w KMRL jest liniowym estymatorem efektywnym i nieobciążonym, co po angielsku opisuje się za pomocą wyrażenia BLUE Best Linear Unbiased Estimator.
Idea. θ = θ 0, Hipoteza statystyczna Obszary krytyczne Błąd pierwszego i drugiego rodzaju p-wartość
 Idea Niech θ oznacza parametr modelu statystycznego. Dotychczasowe rozważania dotyczyły metod estymacji tego parametru. Teraz zamiast szacować nieznaną wartość parametru będziemy weryfikowali hipotezę
Idea Niech θ oznacza parametr modelu statystycznego. Dotychczasowe rozważania dotyczyły metod estymacji tego parametru. Teraz zamiast szacować nieznaną wartość parametru będziemy weryfikowali hipotezę
W statystyce stopień zależności między cechami można wyrazić wg następującej skali: n 1
 Temat: Wybrane zagadnienia z korelacji i regresji W statystyce stopień zależności między cechami można wyrazić wg następującej skali: Skala Guillforda Przedział Zależność Współczynnik [0,00 0,20) Słaba
Temat: Wybrane zagadnienia z korelacji i regresji W statystyce stopień zależności między cechami można wyrazić wg następującej skali: Skala Guillforda Przedział Zależność Współczynnik [0,00 0,20) Słaba
ANALIZA KORELACJI Korelacja między zmiennymi X i Y jest miarą siły liniowego związku między tymi zmiennymi.
 ANALIZA KORELACJI Większość zjawisk w otaczającym nas świecie występuje nie samotnie a w różnorodnych związkach. Odnosi się to również do zjawisk biologiczno-medycznych. O powiązaniach między nimi mówią
ANALIZA KORELACJI Większość zjawisk w otaczającym nas świecie występuje nie samotnie a w różnorodnych związkach. Odnosi się to również do zjawisk biologiczno-medycznych. O powiązaniach między nimi mówią
Wykład 9 Wnioskowanie o średnich
 Wykład 9 Wnioskowanie o średnich Rozkład t (Studenta) Wnioskowanie dla jednej populacji: Test i przedziały ufności dla jednej próby Test i przedziały ufności dla par Porównanie dwóch populacji: Test i
Wykład 9 Wnioskowanie o średnich Rozkład t (Studenta) Wnioskowanie dla jednej populacji: Test i przedziały ufności dla jednej próby Test i przedziały ufności dla par Porównanie dwóch populacji: Test i
parametrów strukturalnych modelu = Y zmienna objaśniana, X 1,X 2,,X k zmienne objaśniające, k zmiennych objaśniających,
 诲 瞴瞶 瞶 ƭ0 ƭ 瞰 parametrów strukturalnych modelu Y zmienna objaśniana, = + + + + + X 1,X 2,,X k zmienne objaśniające, k zmiennych objaśniających, α 0, α 1, α 2,,α k parametry strukturalne modelu, k+1 parametrów
诲 瞴瞶 瞶 ƭ0 ƭ 瞰 parametrów strukturalnych modelu Y zmienna objaśniana, = + + + + + X 1,X 2,,X k zmienne objaśniające, k zmiennych objaśniających, α 0, α 1, α 2,,α k parametry strukturalne modelu, k+1 parametrów
Regresja logistyczna. Regresja logistyczna. Przykłady DV. Wymagania
 Regresja logistyczna analiza relacji między zbiorem zmiennych niezależnych (ilościowych i dychotomicznych) a dychotomiczną zmienną zależną wyniki wyrażone są w prawdopodobieństwie przynależności do danej
Regresja logistyczna analiza relacji między zbiorem zmiennych niezależnych (ilościowych i dychotomicznych) a dychotomiczną zmienną zależną wyniki wyrażone są w prawdopodobieństwie przynależności do danej
