Sz. Grabowski, W. Bieniecki Usuwanie szumu impulsowego w obrazach kolorowych przy użyciu zmodyfikowanego...

Transkrypt

1 SZYMON GRABOWSKI WOJCIECH BIENIECKI Katedra Informatyki Stosowanej Politechniki Łódzkiej {SGrabow, USUWANIE SZUMU IMPULSOWEGO W OBRAZACH KOLOROWYCH PRZY UŻYCIU ZMODYFIKOWANEGO FILTRU MEDIANOWEGO Recenzent Streszczenie W pracy przedstawiamy filtr medianowy do usuwania szumu impulsowego działający na obrazach kolorowych w modelu RGB. W przeciwieństwie do klasycznej mediany wektorowej (VMF), nowy filtr unika rozmywania krawędzi. Nasz algorytm jest modyfikacją niedawno przedstawionego filtra FMVMF, osiągającą korzystniejsze wartości standardowych miar błędu przy wyższych poziomach zaszumienia impulsowego. Szybkość prezentowanego filtra jest wyższa niż VMF, ale niższa od szybkości FMVMF.. Wprowadzenie Standardową techniką usuwania szumu impulsowego jest filtr medianowy. Dla obrazów szarych (ang. greyscale) polega on na zastąpieniu każdego piksla medianą jego otoczenia, którym jest zwykle nieduża maska kwadratowa (np. 3 x 3 lub 5 x 5) z danym pikslem w jej centrum. Element będący medianą zbioru W (czyli maski, okna (ang. window)) można równoważnie wskazać wzorem: med = arg min f f. () f W i Maska otoczenia zazwyczaj zawiera nieparzystą liczbę punktów fakt ten gwarantuje, iż mediana będzie wartością pewnego punktu z maski. Jest to niewątpliwa zaleta filtru. Kolejnymi zaletami są łatwość implementacji i duża szybkość działania, o ile rozmiar maski nie jest zbyt duży (np. nie przekracza 5 piksli). j i j

2 X Konferencja Sieci i Systemy Informatyczne Łódź, październik 00 W przypadku obrazów kolorowych (np. w modelu RGB) definicja filtru medianowego wymaga istotnej zmiany, gdyż nie jest możliwe liniowe uporządkowanie wektorów wartości piksli. W pracy [] zaproponowano tzw. medianę wektorową (Vector Median lter, VMF) dla obrazów barwnych, wykorzystującą odległości między wektorami np. w metryce euklidesowej. Trahanias zaprezentował inne podejście, polegające na zastąpieniu metryki miejskiej bądź euklidesowej innymi miarami odległości uzględniającymi kąt pomiędzy wektorami kolorów piksli, celem wyeliminowania wektorów położonych nietypowo w przestrzeni barw. Idea zaowocowała kilkoma konkretnymi algorytmami: Basic Vector Directional lter (BVDF) [7], Generalized Vector Directional lter (GVDF) [7] i Directional-Distance lter (DDF) [3]. Vardavulia i in. [8] zaproponowali medianę wektorową w modelu barw HSV, ale jej przewaga w testach nad VMF działającym w przestrzeni RGB jest niewielka. Inną prostą ideą było wprowadzenie stałych [9] oraz adaptacyjnych [] wag do wektorowych filtrów medianowych. Ponieważ szybkość w niektórych aplikacjach jest sprawą pierwszoplanową (np. przy filtracji sekwencji wideo w czasie rzeczywistym), rozważano także odwzorowanie trójwymiarowych wektorów w jeden wymiar przy użyciu krzywych wypełniających przestrzeń [5]. Niestety, filtr RVMF (Reduced Vector Median lter) przedstawiony w wymienionej pracy osiągał nieco gorszy stosunek sygnału do szumu niż oryginalny VMF. Inny ciekawy filtr, zwany Vector Median-Rational Hybrid lter (VMRHF), pokazano w [4]. Wyjście filtra jest ilorazem dwóch wielomianów, czyli funkcją rzeczywistą. ltr ten jest konkurencyjny wobec VMF i DDF przy różnych typach szumu (gaussowskim, impulsowym i mieszanym). Zaskakująco dobre wyniki osiąga Fast Modified Vector Median lter (FMVMF) [6] będący de facto niewielką modyfikacją oryginalnej mediany wektorowej. ltr ten jest punktem wyjścia dla naszego algorytmu.. Mediana wektorowa Rozszerzenie pojęcia mediany (skalarnej) na przestrzeń wektorową nie jest łatwe z powodu braku naturalnego porządku wektorów. Zwróćmy uwagę, iż nie ma sensu filtr zastępujący oryginalną wartość piksla kolorowego wektorem złożonym z median osobnych składowych barwnych piksli sąsiedztwa. Przykładem niech będą wektory maski: v = [50, 00, 30] T, v = [0, 40, 00] T i v 3 = [00, 30, 70] T. Wektor złożony z median składowych miałby wartość [00, 00, 00] T, a zatem byłby pewnym szarym punktem nie występującym (lokalnie) w oryginalnym obrazie. Co więcej, taka wersja

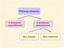
3 mediany kolorowej może spowodować różne przesunięcia lokalnych maksimów na poszczególnych składowych barwnych [0]. Niemniej jednak, pojęcie mediany wektorowej można wprowadzić w sposób logiczny, tj. nawiązujący do definicji mediany skalarnej. Korzystamy ze wzoru (), zastępując różnicę między skalarami odległością między wektorami w sensie zadanej metryki. W praktyce zazwyczaj wykorzystuje się tu metrykę miejską lub euklidesową. Formalnie: N R = min d F, F, () W j = 0 ( ) gdzie R jest medianą (wyjściem filtra), N liczbą punktów w masce W, zaś F i, i = 0K N, pikslami z maski W. Przyjmijmy dodatkowo, że F 0 oznacza piksel, który aktualnie analizujemy (zazwyczaj w centrum maski). Smolka i in. (00) zauważyli, że zaszumiona wartość punktu F 0 może źle wpłynąć na wybór sąsiada, który zastąpi F 0. Zaproponowany przez nich filtr FMVMF pomija w formule sumy liczenie odległości do F 0. Maskę używaną w tej pracy przedstawia Rys.. i j F F 4 F 0 F F 3 Rys.. Maska dla filtru FMVMF. F 0 aktualny piksel. Pikslem, który zastąpi F 0 w filtrze FMVMF jest wektor F k, gdzie N N ( ) ( ) 0, if β + d F0 min d W \ F0 k = N N iopt : = arg min d, if min d < β + W \ F0 W \ F0 N ( ) ( ) d( F0 ), (3) gdzie β jest zadanym stałym parametrem. Nietrudno zauważyć, że filtr ten jest szybszy niż VMF, gdyż dla punktów maski z Rys., z wyjątkiem F 0, liczy się odległości tylko do 3 (a nie 4) wektorów. Wartość parametru β, przy założeniu normalizacji składowych barwnych do przedziału [0, ], została w [6] ustalona eksperymentalnie na 0.75, choć autorzy twierdzą, że generalnie dobre wyniki są uzyskiwane przy wartości β w przedziale [0., ].

4 X Konferencja Sieci i Systemy Informatyczne Łódź, październik Algorytm proponowany Wprowadziliśmy dwie modyfikacje do filtru FMVMF. Po pierwsze, można zauważyć, że nie tylko zaszumiony piksel F 0 utrudnia podjęcie prawidłowej decyzji, ale problem dotyczy całego sąsiedztwa. Dlatego też postanowiliśmy przy predykcji uzwględniać już przetworzone (odszumione) wartości piksli sąsiedztwa, o ile to jest możliwe (przy tradycyjnym porządku skanowania liniami poziomymi od lewej do prawej). Oznacza to, że przy oznaczeniach jak na Rys. przy rozważaniu piksla F 0 bierzemy pod uwagę nowe (odszumione) wartości piksli F i F 4. Od tej zasady jest uczyniony jeden wyjątek: przy liczeniu odległości od F do F 4 w sumie skojarzonej z F uwzględniamy nową wartość tylko piksla F 4, natomiast przy odległości od F 4 do F w sumie skojarzonej z F 4 odwrotnie, tj. bierzemy nową wartość jedynie F. Czynimy tak, aby nie faworyzować punktów F i F 4. Po drugie, nie zmieniamy wartości F 0, jeśli suma odległości skojarzona z co N najwyżej jednym z jego sąsiadów jest mniejsza od β d( F ) + 0, F j. W filtrze FMVMF jeden taki sąsiad wystarczył, aby wymusić zmianę F 0. Ta cecha prezentowanego filtru umożliwia też osiągnięcie wyższej prędkości działania niż jego poprzednik. ltr nazwaliśmy Primum Non Nocere Vector Median lter (PNN-VMF); łacińska sentencja po pierwsze: nie szkodzić podkreśla różnicę pomiędzy naszym filtrem a VMF, który modyfikuje wartości większości piksli w obrazie, czego wizualnym efektem jest rozmywanie krawędzi. W przypadku obrazu Lena z naniesionym 0- procentowym szumem impulsowym, VMF zmodyfikował aż 65.% piksli obrazu, zaś FMVMF i PNN-VMF tylko po 9.6%. 4. Wyniki testów Przeprowadziliśmy testy na obrazach Airplane, Lena i Peppers 5 x 5 w modelu barwnym RGB. Obrazy zostały zakłócone 4-, 0- i 30-procentowym szumem impulsowym. Do oceny jakości filtów użyto następujących miar: znormalizowany średni błąd kwadratowy (NMSE), pierwiastek kwadratowy ze średniego błędu kwadratowego (RMSE) oraz stosunek sygnału do szumu (SNR) (formuły (4) (6)). Oznaczenia w formułach (4) (6): X, Y wymiary obrazu, f ( ) obraz oryginalny; f x, y fe x, y to odległość f () obraz zrekonstruowany. Różnica ( ) ( ) e euklidesowa między odpowiednimi pikslami obu obrazów. f ( x, y) to suma

5 kwadratów składowych barwnych danego piksla obrazu f ( ) (analogiczna definicja f ( x, y) e ). NMSE RMSE SNR X Y ( f ( x, y) f ( )) x= y= e x, y Y f ( x, y) = X X Y x = y = = x= y= ( f ( x, y) f ( x, y) ) X Y X Y f ( ) x = y = e x, y Y ( f ( x, y) fe( x, y) ) = X x = y = e (4) (5) (6) W eksperymentach używaliśmy zawsze metryki miejskiej. Nie zmienialiśmy wartości parametru β zaproponowanej w [6]; wartość ta jest używana w filtrach FMVMF oraz naszym. Tabele -3 przedstawiają wyniki dla poszczególnych obrazów oraz filtrów: VMF, FMVMF i zaproponowanego w niniejszej pracy PPN-VMF. Policzono także wartości miar dla obrazów z naniesionym szumem przed filtracją. Tabela 4 przedstawia czasy filtracji obrazu Lena (z pominięciem we/wy). Testy przeprowadzono na komputerze Celeron 466 z 56 MB pamięci pod systemem Win98 SE PL. Implementacje wszystkich algorytmów wykonano w Delphi 3.0. Jak widać, szybkość filtrów VMF i FMVMF praktycznie nie zależy od stopnia zaszumienia obrazu, natomiast szybkość ta pogarsza się dla filtru PNN-VMF wraz ze wzrostem ilości szumu. Przyczyną takiego zachowania PNN-VMF jest mniejsza przy dużym zaszumieniu liczba sytuacji, w których można przed czasem ocenić, że dany piksel nie będzie zmieniony i wyjść z pętli. FMVMF jest o ponad 30% szybszy od VMF, zaś jego przewaga szybkościowa nad PNN-VMF wynosi od ok. 0% do 5%. Niestety, idea korzystania z nowych (odszumionych) wartości piksli w PNN-VMF oznacza słabszą możliwość cache owania odległości, czego wynikiem jest spadek prędkości w Ściślej biorąc, używamy bardzo zbliżonej wartości β. Ze względów szybkościowych lepiej jest wykonywać obliczenia na liczbach całkowitych (kolory o wartościach 0..55), a w takim przypadku przybliżonym odpowiednikiem β=0.75 dla wartości znormalizowanych jest 9; w praktyce różnice są mikroskopijne.

6 X Konferencja Sieci i Systemy Informatyczne Łódź, październik 00 stosunku do FMVMF. Tym niemniej, PNN-VMF jest szybszy od oryginalnej mediany wektorowej. Tabela Wyniki działania filtrów medianowych na obrazie RGB Lena z dodanym szumem impulsowym % szumu LENA 5 x 5 filtr NMSE [0-3 ] RMSE [0-3 ] SNR % VMF FMVMF PNN-VMF % VMF FMVMF PNN-VMF % VMF FMVMF PNN-VMF Tabela Wyniki działania filtrów medianowych na obrazie RGB Peppers z dodanym szumem impulsowym % szumu PEPPERS 5 x 5 filtr NMSE [0-3 ] RMSE [0-3 ] SNR % VMF FMVMF PNN-VMF % VMF FMVMF PNN-VMF % VMF FMVMF PNN-VMF

7 Tabela 3 Wyniki działania filtrów medianowych na obrazie RGB Airplane z dodanym szumem impulsowym % szumu AIRPLANE 5 x 5 filtr NMSE [0-3 ] RMSE [0-3 ] SNR % VMF FMVMF PNN-VMF % VMF FMVMF PNN-VMF % VMF FMVMF PNN-VMF Czas filtracji obrazu Lena color 5 x 5 % szumu filtr czas (s) VMF FMVMF 0.6 PNN-VMF 0.9 VMF FMVMF 0.6 PNN-VMF 0.30 VMF FMVMF 0.6 PNN-VMF 0.33 Tabela 4 Wyniki te oznaczają, iż prędkość filtru PNN-VMF w opisanej konfiguracji sprzętowej wynosi.3.6 MB/s. 5. Wnioski W pracy przedstawiliśmy nowy filtr medianowy służący do usuwania szumu impulsowego z obrazów kolorowych. ltr ten osiągał zdecydowanie korzystniejsze wartości standardowych miar błędu niż klasyczna mediana wektorowa (VMF) przy

8 X Konferencja Sieci i Systemy Informatyczne Łódź, październik 00 różnych stopniach zaszumienia. Nie można tego powiedzieć o jego poprzedniku, filtrze FMVMF, który obrazy z nałożonym szumem 30-procentowym przetwarzał ze skutecznością nieco gorszą od VMF. Ceną modyfikacji był pewien spadek szybkości działania w stosunku do FMVMF, jednak i nasz filtr jest szybszy od VMF. Wydaje się rzeczą interesującą sprawdzenie zależności między jakością filtru a użytą metryką (czy szerzej: funkcją odległości). Może się okazać, że dla różnego stopnia zaszumienia korzystne są różne funkcje odległości między wektorami, a w takiej sytuacji pożądane byłoby stworzenie filtru dynamicznie dobierającego sobie metrykę, np. w klasie metryk Minkowskiego. Literatura [] Alparone L., Barni M., Bartolini F., Cappellini V., Adaptively weighted vectormedian filters for motion-fields smoothing, Proceedings of the International Conference on Acoustic Speech and Signal Processing ICASSP'96, Atlanta, Georgia, USA, pp , May 7-0, 996. [] Astola J., Haavisto P., Neuvo Y., Vector median filters, Proc. IEEE, vol. 78 no. 4, pp , April 990. [3] Karakos D. G., Trahanias P. E., Combining vector median and vector directional filters: The directional-distance filters, Proceedings of the IEEE Conference on Image Processing, ICIP-95, pp. 7 74, October 995. [4] Khriji L., Gabbouj M., Vector Median-Rational Hybrid lters for Multichannel Image Processing, IEEE Signal Processing Letters, vol. 6, no. 7, pp , July 999. [5] Regazzoni C.S., Teschioni A., A New Approach to Vector Median ltering Based on Space lling Curves, IEEE Transactions on Image Processing 6, pp , 997. [6] Smolka B., Szczepański M., Plataniotis K. N., Venetsanopoulos A. N., New technique of impulse noise suppression in color images, II Konferencja Komputerowe Systemy Rozpoznawania KOSYR00, Miłków k/karpacza, str. 5 3, maj 00. [7] Trahanias P., Venetsanapoulos A., Vector directional filters: A new class of multichannel image processing filters, IEEE Transactions on Image Processing, pp , April 993. [8] Vardavoulia M. I., Andreadis I., Tsalides Ph., A New Vector Median lter for Colour Image Processing, Pattern Recognition Letters (00)

9 [9] Viero T., Öistamö K., Neuvo Y., Three-dimensional median-related filters for color image sequence filtering, IEEE Transactions on Circuits and Systems for Video Technology, vol. 4, no., pp. 9 4, April 994. [0] Zheng J., Valavanis K. P., Gauch J. M., Noise Removal from Color Images, J. Intelligent and Robotic Systems 7 (993),