Algorytmy graficzne. Nieliniowa filtracja obrazów monochromatycznych
|
|
|
- Grażyna Piasecka
- 8 lat temu
- Przeglądów:
Transkrypt
1 Algorytmy graficzne Nieliniowa filtracja orazów monochromatycznych
2 Metody oceny efektywności filtracji Analizując filtry redukujące zakłócenia w orazie cyfrowym konieczne jest określenie ścisłych miar skuteczności algorytmów filtracji. Lista najczęściej wykorzystywanych miar podana jest poniżej. We wszystkich przypadkach f oraz f oznaczają odpowiednio oraz oryginalny (ez zakłócenia) oraz wynik filtracji orazu zakłóconego, natomiast n oraz m oznaczają liczę wierszy i kolumn orazu. Błąd średniokwadratowy Znormalizowany łąd średniokwadratowy Stosunek sygnału szczytowego do szumu (peak signal to noise ratio) PSNR: Stosunek sygnału do szumu (signal to noise ratio) SNR:
3 Filtry minimalny i maksymalny Przykładem filtrów realizujących selektywną filtrację zakłóceń typu sól lu pieprz są filtry minimalny oraz maksymalny. W takim przypadku wartość ieżącego piksela (centrum okna) zastępowana jest odpowiednio przez wartością minimalną lu maksymalną wyznaczoną w sąsiedztwie piksela. Filtr minimalny posiada zdolność redukcji zakłóceń typu sól, natomiast filtr maksymalny zakłóceń typu pieprz. Filtry tego rodzaju zmieniają gloalny poziom jasności w orazie: filtr minimalny zmniejsza jasność, filtr maksymalny zwiększa. Efektem jest też zmniejszanie powierzchni oiektów odpowiednio jasnych lu ciemnych (patrz orazy (c) i (e)). MSE= a c MSE=188.8 MSE= MSE=175.7 MSE= d e f Rys.1. Filtracja orazów zakłóconych przy użyciu filtrów minimalnego i maksymalnego. (a) oraz oryginalny ez zakłócenia; () oraz z 30% zakłóceniem typu sól, (c) wynik filtracji orazu () filtrem minimalnym; (d) oraz (a) po zakłóceniu 30% szumem typu pieprz; (e) wynik filtracji orazu (d) filtrem maksymalnym. Oraz (f) przedstawia wynik zastosowania niewłaściwego filtru: oraz (d) filtrowany przy użyciu filtru minimalnego. Zastosowane filtry realizowane są z maską 3x3 piksele.
4 Idea filtru medianowego Filtracja medianowa polega na przeglądaniu orazu cyfrowego piksel po pikselu z oknem ustalonego rozmiaru, najczęściej oknem nieparzystym lu oknem w kształcie krzyża. Wartość piksela centralnego zastępowana jest medianą ze zioru pikseli w jego sąsiedztwie wyznaczonym przez okno przetwarzania. Mediana jest wartością środkową w uporządkowanym ciągu próek (licz, wartości). Podstawową operacją wykonywaną przez filtr medianowy jest sortowanie zioru wartości pikseli i wyór wartości środkowej tak uporządkowanego ciągu. Przykład. Niech dany jest ciąg (3,100,2). Ciąg po uporządkowaniu ma postać: (2,3,100). Wartością środkową w ciągu jest wartość 3 ędąca medianą. Dla odróżnienia wartość średnia wynosi w tym przypadku 35. Podstawową zaletą filtru medianowego jest odporność na zakłócenia impulsowe, tzn. na oecność w ziorze pikseli o wartości skrajnych, silnie odstających od pozostałych. W takim przypadku wartości odstające w drodze sortowania przyjmują skrajne pozycje w uporządkowanym ciągu pikseli i nie mogą yć wyrane jako mediana. Zdolność filtru medianowego do usuwania zakłóceń tego typu zależy jednak od rozmiaru zakłócenia, tzn. liczy zakłóconych pikseli: licza pikseli zakłóconych musi yć nie większa niż połowa liczy pikseli w loku. Wadą filtracji medianowej jest większa niż w przypadku filtrów uśredniających złożoność oliczeniowa: wymóg sortowania zioru wartości pikseli każdego loku. Zaletą ardzo skuteczne usuwanie zakłóceń impulsowych typu salt and pepper. W przypadku szumu gaussowskiego filtracja medianowa daje znacznie gorsze rezultaty niż w przypadku zakłóceń impulsowych. a i y c i y i y a j z j z j k { k { z k { Rys.1. Porównanie działania filtrów uśredniającego a) i medianowego - ) dla jednowymiarowego ciągu próek. Rys.2.Porównanie działania filtru medianowego i uśredniającego (oa realizowane jako przekształcenie z oknem 3x3). (a) przykładowy lok orazu; () wynik filtracji medianowej; (c) wynik filtracji uśredniającej. Przykład pokazuje, że w przypadku filtracji medianowej zakłócenie silnie odstające od otoczenia zostaje rzeczywiście fizycznie wyeliminowane z orazu. W przypadku filtru uśredniającego zakłócenie jest rozmazywane.
5 Zakłócenia wprowadzane przez filtr medianowy Popularność filtru medianowego wynika ze znakomitej zdolności do redukcji szumu impulsowego oraz rozmywania orazu w mniejszym stopniu niż filtry uśredniające takiego samego rozmiaru. Pomimo swoich zalet filtr medianowy powoduje zniekształcenia orazu. Zniekształcenia te mogą się pogłęiać wraz ze wzrostem liczy iteracji filtracji jak również ze wzrostem rozmiaru okna. Przykłady przedstawione są na rysunkach poniżej. a c d Rys. 1. Przykład zakłócenia generowanego przez filtr medianowy o różnej wielkości okna. (a) oraz oryginalny; (), (c) i (d) przedstawiają wynik filtracji orazu (a) filtrem medianowym z oknem rozmiaru odpowiednio 3x3, 5x5 oraz 9x9. Z czego wynika tego typu zakłócenie? a d d e Rys. 2. Przykład wprowadzania zakłóceń przez filtr medianiowy w orazie naturalnym. Mechanizm degradacji jakości orazu jest podony jak w przypadku rysunku 1. (a) oraz oryginalny; orazy () (e) przedstawiają wynik filtracji z oknem równym odpowiednio 3x3, 5x5, 7x7 oraz 9x9.
6 Filtr medianowy - ilustracja a c d Rys. 1. Przykład filtracji medianowej. (a) oraz oryginalny; () oraz zakłócony 5% szumem sól i pieprz; oraz (c) przedstawia wynik filtracji medianowej z oknem 3x3 piksele. Strzałka wskazuje zakłócenie w orazie po filtracji. Na rysunku (d) przedstawiony został dla porównania wynik filtracji orazu () przez filtr gaussowski 3x3.
7 Filtr medianowy - ilustracja a Rys. 1. Przykład filtracji medianowej. (a) oraz oryginalny; () oraz zakłócony 15% szumem sól i pieprz; orazy (c) i (d) przedstawiają wynik filtracji medianowej z oknem odpowiednio 3x3 oraz 5x5. c d
8 Filtr medianowy - ilustracja a Rys. 1. Przykład filtracji medianowej.; (a) oraz zakłócony 50% szumem sól i pieprz; orazy (), (c) i (d) przedstawiają wynik filtracji medianowej z oknem odpowiednio 3x3, 5x5 oraz 7x7. Widoczne jest postrzępienie i rozmycie krawędzi w orazu po filtracji. c d
9 Filtr medianowy - ilustracja a MSE=590.4 c MSE=150.7 Rys. 1. (a) oraz z nałożonym regularnym zakłóceniem liniowym; () wynik filtracji medianowej z oknem 3x3; (c) wynik filtracji medianowej z oknem 5x5. Zakłócenie tego typu można wyeliminować za pomocą adaptacyjnego filtru medianowego 3x3. Gruość linii siatki na rysunku (a) wynosi 1 piksel.
10 Rodzaje filtrów medianowych - 1 Rekurencyjna filtracja medianowa (recursive median filter, RMF) Jest przypadkiem filtracji medianowej wykonywanej in situ (w miejscu). W takim przypadku wartość piksela centralnego jest modyfikowana w orazie oryginalnym, przed przesunięciem okna do następnego piksela. Posiada lepszą zdolność tłumienia zakłóceń oraz wprowadza mniejsze zniekształcenia sygnału niż zwykła filtracja medianowa (?). Złożoność oliczeniowa ou rodzajów filtracji medianowej jest identyczna. Ważona filtracja medianowa (weighted median filter, WMF) Stanowi uogólnienie prostej filtracji medianowej poprzez wprowadzenie współczynników reprezentujących wagi pikseli sąsiedztwa. Ważenie elementów realizowane jest przez ich powielenie zadaną liczę razy przed wyznaczeniem mediany. Dla przykładu: niech X=(15,10,3,2,5) jest jednowymiarowym ciągiem elementów, natomiast W=(1,2,3,2,1) określa wagi mediany. Wówczas mediana ważona realizowana jest jako mediana z następującego ciągu: (15,10,10,3,3,3,2,2,5). Mediana ważona w tym przypadku jest równa 3 (zwykład mediana: 5). Najczęściej suma wag jest liczą nieparzystą. Taki sposó realizacji filtru medianowego zmniejsza poziom zniekształceń wprowadzanych do orazu. Filtracja medianowa z ważonym elementem centralnym (center weighted median filter, CWMF) Filtr tego typu jest przypadkiem szczególnym filtru realizującego ważoną medianę, w którym ważeniu podlega jedynie element centralny, tzn. jedynie element centralny może yć zwielokrotniony podczas wyznaczania mediany. W przypadku gdy waga w elementu centralnego jest równa w=1 filtr redukuje się do prostego filtru medianowego. Dla w>=n, gdzie n jest liczą elementów w sąsiedztwie elementu centralnego, filtr realizuje przekształcenie identycznościowe: na wyjściu generowany jest element centralny.
11 Rodzaje filtrów medianowych - ilustracja a c d Rys. 1. Przykład filtracji medianowej.; (a) oraz oryginalny; Wiersze (), (c) i (d) przedstawiają wyniki odpowiednio zwykłej filtracji medianowej, rekurencyjnej oraz ważonej dla masek odpowiednio: 3x3, 5x5 oraz 7x7.
12 Rodzaje filtrów medianowych - ilustracja a c MSE=261.3 d MSE=474.1 e MSE=427.6 Rys.1. Porównanie zwykłej filtracji medianowej oraz filtracji ważonej. Oraz (a) oraz oryginalny; () oraz zakłócony 15% szumem impulsowym sól i pieprz; orazy (c) i (d) przedstawiają wynik filtracji medianowej z oknem odpowiednio 3x3 oraz 5x5, natomiast na orazie (e) przedstawiony jest wynik filtracji medianowej ważonej z maską 5x5. Rozkład wag w tym przypadku stanowi dyskretną aproksymację dwuwymiarowej funkcji Gaussa. Jak widać na przykładzie (e), filtracja ważona wprowadza mniejsze zniekształcenia krawędzi w orazie. Jest to szczególnie widoczne w oszarze ust (orazy (d) i (e)).
13 Rodzaje filtrów medianowych - 2 α-trimmed mean filter. Filtr realizujący średnią uciętą (trimmed mean) Filtracja w takim przypadku polega na przypisaniu ieżącemu pikselowi średniej arytmetycznej ze zioru pikseli zawierającego α pikseli najliższych medianie: gdzie f(x,y) i f (x,y) są odpowiednio pikselem przed i po filtracji natomiast W r jest zredukowanym ziorem pikseli z sąsiedztwa ieżącego piksela f(x,y) (aktualnie przetwarzanego). Redukcja zioru polega na zachowaniu α pikseli o wartościach najliższych medianie ze zioru, dzięki czemu średnia tego typu jest mało wrażliwa na wartości odstające. Operacja uśredniania zapewnia redukcję szumu gaussowskiego (lu innego o podonej charakterystyce) natomiast operacja ocięcia pozwala wyeliminować piksele o skrajnych (odstających) wartościach - piksele takie traktuje się tu jak szum impulsowy. Dla α=1 filtr redukuje się do zwykłego filtru medianowego, natomiast dla α=n realizuje prostą filtrację uśredniającą. W tym sensie ocięty filtr uśredniający jest uogólnieniem dwóch wspomnianych filtrów. MSE=596.3 MSE=655.1 MSE=546.2 a c d Rys.1. Porównanie filtru αtmf oraz zwykłego filtru medianowego oraz uśredniajacego dla orazu zakłóconego szumem gaussowskim o zerowej średniej i wariancji wynoszącej 1600 oraz 10% szumem impulsowym. (a) oraz zakłócony; rysunki ()-(d).przedstawiają wynik filtracji odpowiednio medianowej, średniej arytmetycznej oraz średniej uciętej. Wszystkie filtry realizowane z maską 3x3 piksele.błąd MSE dla orazów po filtracji wynosi odpowiednio 597, 652 oraz 549.
14 Adaptacyjny filtr medianowy Cechy zwykłej filtracji medianowej Zaleta: Daje dore rezultaty w usuwaniu zakłóceń impulsowych w przypadku gdy licza pikseli zakłóconych jest mniejsza niż n/2, gdzie n jest liczą pikseli w oknie. Wada: Piksel centralny zastępowany jest medianą ze zioru pikseli w oknie niezależnie od lokalnej statystyki pikseli. Prowadzi to do zędnego wygładzania orazu w oszarze pozawionym zakłóceń impulsowych. Wersja adaptacyjna filtru medianowego polega na przeglądaniu orazu piksel po pikselu z kwadratowym oknem, którego centrum jest piksel ieżący (aktualnie przetwarzany) oraz wykonaniu kroków podanych poniżej: 1. Dla każdego ieżącego piksela f(x,y) orazu f wyznacz listę najliższych sąsiadów określonych przez okno W o rozmiarze NxN wycentrowane na pikselu f(x,y), a następnie wyznacz wartość minimalną, maksymalną oraz środkową (mediana) w oknie: fmin, fmax oraz fmed. Wykonaj test: If fmin < fmed < fmax True False 2.1. Wykonaj test: If fmin < f(x,y) < fmax 2.2. Zwiększ rozmiar okna wyznaczającego sąsiedztwo ieżącego piksela: Nnew=Nold+2 If Nnew < Nmax True True False 3.1. f(x,y)=f(x,y) 3.2. f(x,y)=fmed False Rys.1.Etapy pracy algorytmu adaptacyjnej filtracji medianowej. Przedstawione etapy wykonywane są dla każdego piksela orazu.
15 Adaptacyjny filtr medianowy - ilustracja a c MSE=827.4 Rys.1.Ilustracja działania algorytmu adaptacyjnej filtracji medianowej. (a) oraz zakłócony 30% szumem sól i pieprz oraz siatką w której piksele przyjmują wartość maksymalną równą 255. Na rysunku () przedstawiony jest wynik filtracji przy użyciu filtru adaptacyjnego 3x3. Rysunki (c) i (d) przedstawiają wynik filtracji zwykłym filtrem medianowym odpowiednio 3x3 oraz 7x7. Największym oknem z jakim w tym przypadku działa filtr adaptacyjny (rys. ) jest okno 15x15 pikseli. d MSE=85.4 MSE=230.9 Idea filtru adaptacyjnego sprowadza się do zastąpienia pikseli zaszumionych medianą. Piksele wolne od zakłócenia pozostawiane są ez zmian. Filtr jest przykładem szerokiej klasy filtrów przełączanych (switching filters) inteligentnych. Wartości odstające w ziorze pikseli są interpretowane jako szum niezależnie od ich rzeczywistego charakteru (na wyjściu filtru nigdy nie pojawia się wartość minimalna lu maksymalna). Filtr wykorzystuje okno o zmieniającym się rozmiarze dzięki czemu jest w stanie usuwać zakłócenia zajmujące stosunkowo duży oszar orazu. Redukuje (nawet ekstremalny) szum impulsowy znacznie silniej niż zwykły filtr medianowy o takim samym rozmiarze (patrz ilustracja ook) wygładzając jednocześnie oraz w mniejszym stopniu niż zwykły filtr medianowy.
16 Adaptacyjny filtr medianowy - ilustracja aa MSE= c MSE= d MSE= Rys.1.Przykład filtracji orazu ekstremalnie zaszumionego: 80% zakłócenie sól i pieprz oraz regularna siatka pikseli o wartościach 255. (a) oraz zaszumiony; () wynik filtracji adaptacyjnej z oknem początkowym 3x3; (c) i (d) wynik filtracji zwykłym filtrem medianowym z maską odpowiednio 3x3 oraz 23x23. W tym przypadku największym oknem z jakim pracował filtr adaptacyjny (rozmiar ustalony automatycznie przez algorytm) jest okno 23x23 piksele.
17 Adaptacyjny filtr medianowy - ilustracja 250 a c Rys.1.Porównanie zwykłego filtru medianowego oraz filtru adaptacyjnego. Na rysunku (a) krzywa czarna reprezentuje sygnał oryginalny zakłócony w zaznaczonych oszarach szumem impulsowym (oszary szerokości odpowiednio 5 oraz 8 próek; sygnał składa się z 134 próek). Krzywa zielona i czerwona reprezentują odpowiednio sygnał odszumiony przy użyciu zwykłego filtru medianowego oraz filtru adaptacyjnego; w ou przypadkach filtracja z jednowymiarowym oknem długości 3 (filtr adaptacyjny może regulować rozmiar okna). W oszarze zakłócenia impulsowego krzywa czarna i zielona pokrywają się ze soą (zaznaczone strzałkami). Na rysunkach () i (c) przedstawiony jest wynik filtracji przy użyciu zwykłego filtru medianowego z oknem o długości odpowiednio 11 oraz 17. Filtr o długości 11 jest najmniejszym filtrem (zwykła mediana) który eliminuje pierwsze zakłócenie impulsowe; filtr o długości 17 eliminuje również drugi oszar zakłócenia. Przykład wyraźnie wskazuje, że zakłócenie silnie oddziałuje na oszary sąsiednie: największy z oszarów zakłócenia ma rozmiar 8 sąsiednich próek, ale jest eliminowany dopiero przez filtr analizujący 17 sąsiednich próek. Z czego to wynika?
18 Filtry średniej geometrycznej i harmonicznej Filtracja przy użyciu filtru średniej geometrycznej sprowadza się do zastąpienia wartości piksela ieżącego średnią geometryczną wartości pikseli w oknie NxN: Rys.1. Krzywa czarna sygnał oryginalny; krzywa czerwona i zielona, odpowiednio, wynik filtracji przy użyciu filtru średniej geometrycznej i arytmetycznej. Filtr średniej geometrycznej charakteryzuje podony stopień wygładzania jak filtr uśredniający (średnia arytmetyczna). Różnica polega na odmiennym traktowaniu pikseli o wartości zerowej. Filtr tego typu jest silnie wrażliwy na zakłócenia typu pieprz. a Rys.1. Filtracja orazu z zakłóceniem typu pieprz (20%). (a) oraz zakłócony, () oraz po filtracji.
19 Uśrednianie czasowe orazu a c d e f Skuteczną metodą usuwania szumu z orazów statycznych zakłóconych szumem o zerowej średniej jest uśrednianie czasowe. W praktyce zwykle nie jest możliwe dysponowanie kilkunastoma niezależnymi orazami wygenerowanymi przez to samo źródło. Zmniejsza to możliwość praktycznego wykorzystania tego rodzaju filtru. Rys. Uśrednianie czasowe. a) oraz oryginalny, ) oraz zaszumiony (m=0, s=200); c)-f) uśrednienie, odpowiednio 25, 50, 100, 500 orazów.
Politechnika Świętokrzyska. Laboratorium. Cyfrowe przetwarzanie sygnałów. Ćwiczenie 8. Filtracja uśredniająca i statystyczna.
 Politechnika Świętokrzyska Laboratorium Cyfrowe przetwarzanie sygnałów Ćwiczenie 8 Filtracja uśredniająca i statystyczna. Cel ćwiczenia Celem ćwiczenia jest zdobycie umiejętności tworzenia i wykorzystywania
Politechnika Świętokrzyska Laboratorium Cyfrowe przetwarzanie sygnałów Ćwiczenie 8 Filtracja uśredniająca i statystyczna. Cel ćwiczenia Celem ćwiczenia jest zdobycie umiejętności tworzenia i wykorzystywania
Rekonstrukcja obrazu (Image restoration)
 Rekonstrukcja obrazu (Image restoration) Celem rekonstrukcji obrazu cyfrowego jest odtworzenie obrazu oryginalnego na podstawie obrazu zdegradowanego. Obejmuje ona identyfikację procesu degradacji i próbę
Rekonstrukcja obrazu (Image restoration) Celem rekonstrukcji obrazu cyfrowego jest odtworzenie obrazu oryginalnego na podstawie obrazu zdegradowanego. Obejmuje ona identyfikację procesu degradacji i próbę
Diagnostyka obrazowa
 Diagnostyka obrazowa 1. Cel ćwiczenia Ćwiczenie piąte Filtrowanie obrazu Ćwiczenie ma na celu zapoznanie uczestników kursu Diagnostyka obrazowa z pojęciami szumu na obrazie oraz metodami redukcji szumów
Diagnostyka obrazowa 1. Cel ćwiczenia Ćwiczenie piąte Filtrowanie obrazu Ćwiczenie ma na celu zapoznanie uczestników kursu Diagnostyka obrazowa z pojęciami szumu na obrazie oraz metodami redukcji szumów
Spośród licznych filtrów nieliniowych najlepszymi właściwościami odznacza się filtr medianowy prosty i skuteczny.
 Filtracja nieliniowa może być bardzo skuteczną metodą polepszania jakości obrazów Filtry nieliniowe Filtr medianowy Spośród licznych filtrów nieliniowych najlepszymi właściwościami odznacza się filtr medianowy
Filtracja nieliniowa może być bardzo skuteczną metodą polepszania jakości obrazów Filtry nieliniowe Filtr medianowy Spośród licznych filtrów nieliniowych najlepszymi właściwościami odznacza się filtr medianowy
Filtracja obrazów. w dziedzinie częstotliwości. w dziedzinie przestrzennej
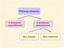 Filtracja obrazów w dziedzinie częstotliwości w dziedzinie przestrzennej filtry liniowe filtry nieliniowe Filtracja w dziedzinie częstotliwości Obraz oryginalny FFT2 IFFT2 Obraz po filtracji f(x,y) H(u,v)
Filtracja obrazów w dziedzinie częstotliwości w dziedzinie przestrzennej filtry liniowe filtry nieliniowe Filtracja w dziedzinie częstotliwości Obraz oryginalny FFT2 IFFT2 Obraz po filtracji f(x,y) H(u,v)
Analiza obrazów - sprawozdanie nr 2
 Analiza obrazów - sprawozdanie nr 2 Filtracja obrazów Filtracja obrazu polega na obliczeniu wartości każdego z punktów obrazu na podstawie punktów z jego otoczenia. Każdy sąsiedni piksel ma wagę, która
Analiza obrazów - sprawozdanie nr 2 Filtracja obrazów Filtracja obrazu polega na obliczeniu wartości każdego z punktów obrazu na podstawie punktów z jego otoczenia. Każdy sąsiedni piksel ma wagę, która
Przetwarzanie obrazów wykład 4
 Przetwarzanie obrazów wykład 4 Adam Wojciechowski Wykład opracowany na podstawie Komputerowa analiza i przetwarzanie obrazów R. Tadeusiewicz, P. Korohoda Filtry nieliniowe Filtry nieliniowe (kombinowane)
Przetwarzanie obrazów wykład 4 Adam Wojciechowski Wykład opracowany na podstawie Komputerowa analiza i przetwarzanie obrazów R. Tadeusiewicz, P. Korohoda Filtry nieliniowe Filtry nieliniowe (kombinowane)
Filtracja obrazu operacje kontekstowe
 Filtracja obrazu operacje kontekstowe Podział metod filtracji obrazu Metody przestrzenne i częstotliwościowe Metody liniowe i nieliniowe Główne zadania filtracji Usunięcie niepożądanego szumu z obrazu
Filtracja obrazu operacje kontekstowe Podział metod filtracji obrazu Metody przestrzenne i częstotliwościowe Metody liniowe i nieliniowe Główne zadania filtracji Usunięcie niepożądanego szumu z obrazu
Diagnostyka obrazowa
 Diagnostyka obrazowa Ćwiczenie piate Filtrowanie obrazu Cel ćwiczenia Ćwiczenie ma na celu zapoznanie uczestników kursu Diagnostyka obrazowa z pojęciami szumu na obrazie oraz metodami redukcji szumów przez
Diagnostyka obrazowa Ćwiczenie piate Filtrowanie obrazu Cel ćwiczenia Ćwiczenie ma na celu zapoznanie uczestników kursu Diagnostyka obrazowa z pojęciami szumu na obrazie oraz metodami redukcji szumów przez
Filtracja obrazu operacje kontekstowe
 Filtracja obrazu operacje kontekstowe Główne zadania filtracji Usunięcie niepożądanego szumu z obrazu Poprawa ostrości Usunięcie określonych wad obrazu Poprawa obrazu o złej jakości technicznej Rekonstrukcja
Filtracja obrazu operacje kontekstowe Główne zadania filtracji Usunięcie niepożądanego szumu z obrazu Poprawa ostrości Usunięcie określonych wad obrazu Poprawa obrazu o złej jakości technicznej Rekonstrukcja
Ćwiczenia z grafiki komputerowej 5 FILTRY. Miłosz Michalski. Institute of Physics Nicolaus Copernicus University. Październik 2015
 Ćwiczenia z grafiki komputerowej 5 FILTRY Miłosz Michalski Institute of Physics Nicolaus Copernicus University Październik 2015 1 / 12 Wykorzystanie warstw Opis zadania Obrazy do ćwiczeń Zadanie ilustruje
Ćwiczenia z grafiki komputerowej 5 FILTRY Miłosz Michalski Institute of Physics Nicolaus Copernicus University Październik 2015 1 / 12 Wykorzystanie warstw Opis zadania Obrazy do ćwiczeń Zadanie ilustruje
Przetwarzanie obrazu
 Przetwarzanie obrazu Przekształcenia kontekstowe Liniowe Nieliniowe - filtry Przekształcenia kontekstowe dokonują transformacji poziomów jasności pikseli analizując za każdym razem nie tylko jasność danego
Przetwarzanie obrazu Przekształcenia kontekstowe Liniowe Nieliniowe - filtry Przekształcenia kontekstowe dokonują transformacji poziomów jasności pikseli analizując za każdym razem nie tylko jasność danego
Przekształcenia kontekstowe. Filtry nieliniowe Typowy przykład usuwania zakłóceń z obrazu
 Definicja Przekształcenia kontekstowe są to przekształcenia które dla wyznaczenia wartości jednego punktu obrazu wynikowego trzeba dokonać określonych obliczeń na wielu punktach obrazu źródłowego. Przekształcenia
Definicja Przekształcenia kontekstowe są to przekształcenia które dla wyznaczenia wartości jednego punktu obrazu wynikowego trzeba dokonać określonych obliczeń na wielu punktach obrazu źródłowego. Przekształcenia
Parametryzacja obrazu na potrzeby algorytmów decyzyjnych
 Parametryzacja obrazu na potrzeby algorytmów decyzyjnych Piotr Dalka Wprowadzenie Z reguły nie stosuje się podawania na wejście algorytmów decyzyjnych bezpośrednio wartości pikseli obrazu Obraz jest przekształcany
Parametryzacja obrazu na potrzeby algorytmów decyzyjnych Piotr Dalka Wprowadzenie Z reguły nie stosuje się podawania na wejście algorytmów decyzyjnych bezpośrednio wartości pikseli obrazu Obraz jest przekształcany
Cyfrowe przetwarzanie obrazów i sygnałów Wykład 7 AiR III
 1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
Filtracja liniowa (metody konwolucyjne, tzn. uwzględniające pewne otoczenie przetwarzanego piksla):
 WYKŁAD 3 Operacje sąsiedztwa Są to operacje, w których na wartość zadanego piksla obrazu wynikowego q o współrz. (i,j) mają wpływ wartości piksli pewnego otoczenia piksla obrazu pierwotnego p o współrzędnych
WYKŁAD 3 Operacje sąsiedztwa Są to operacje, w których na wartość zadanego piksla obrazu wynikowego q o współrz. (i,j) mają wpływ wartości piksli pewnego otoczenia piksla obrazu pierwotnego p o współrzędnych
Przetwarzanie obrazów. Grupy metod przetwarzania obrazu. Przetwarzanie jednopunktowe. Przetwarzanie jednopunktowe. Przetwarzanie jednopunktowe
 Przetwarzanie obrazów Ogólna definicja Algorytm przetwarzający obraz to algorytm który, otrzymując na wejściu obraz wejściowy f, na wyjściu zwraca takŝe obraz (g). Grupy metod przetwarzania obrazu Przekształcenia
Przetwarzanie obrazów Ogólna definicja Algorytm przetwarzający obraz to algorytm który, otrzymując na wejściu obraz wejściowy f, na wyjściu zwraca takŝe obraz (g). Grupy metod przetwarzania obrazu Przekształcenia
Analiza obrazu. wykład 4. Marek Jan Kasprowicz Uniwersytet Rolniczy 2009
 Analiza obrazu komputerowego wykład 4 Marek Jan Kasprowicz Uniwersytet Rolniczy 2009 Filtry górnoprzepustowe - gradienty Gradient - definicje Intuicyjnie, gradient jest wektorem, którego zwrot wskazuje
Analiza obrazu komputerowego wykład 4 Marek Jan Kasprowicz Uniwersytet Rolniczy 2009 Filtry górnoprzepustowe - gradienty Gradient - definicje Intuicyjnie, gradient jest wektorem, którego zwrot wskazuje
Cyfrowe przetwarzanie obrazów i sygnałów Wykład 8 AiR III
 1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
WYKŁAD 3. Przykłady zmian w obrazie po zastosowaniu Uniwersalnego Operatora Punktowego
 WYKŁAD 3 Przykłady zmian w obrazie po zastosowaniu Uniwersalnego Operatora Punktowego 1 Przykłady zmian w obrazie po zastosowaniu Uniwersalnego Operatora Punktowego (c.d.) 2 Zestawienie zbiorcze - Regulacje
WYKŁAD 3 Przykłady zmian w obrazie po zastosowaniu Uniwersalnego Operatora Punktowego 1 Przykłady zmian w obrazie po zastosowaniu Uniwersalnego Operatora Punktowego (c.d.) 2 Zestawienie zbiorcze - Regulacje
Wyższa Szkoła Informatyki Stosowanej i Zarządzania
 Wyższa Szkoła Informatyki Stosowanej i Zarządzania Grupa ID308, Zespół 11 PRZETWARZANIE OBRAZÓW Sprawozdanie z ćwiczeń Ćwiczenie 6 Temat: Operacje sąsiedztwa wyostrzanie obrazu Wykonali: 1. Mikołaj Janeczek
Wyższa Szkoła Informatyki Stosowanej i Zarządzania Grupa ID308, Zespół 11 PRZETWARZANIE OBRAZÓW Sprawozdanie z ćwiczeń Ćwiczenie 6 Temat: Operacje sąsiedztwa wyostrzanie obrazu Wykonali: 1. Mikołaj Janeczek
Cyfrowe Przetwarzanie Obrazów i Sygnałów
 Cyfrowe Przetwarzanie Obrazów i Sygnałów Laboratorium EX Lokalne transformacje obrazów Joanna Ratajczak, Wrocław, 28 Cel i zakres ćwiczenia Celem ćwiczenia jest zapoznanie się z własnościami lokalnych
Cyfrowe Przetwarzanie Obrazów i Sygnałów Laboratorium EX Lokalne transformacje obrazów Joanna Ratajczak, Wrocław, 28 Cel i zakres ćwiczenia Celem ćwiczenia jest zapoznanie się z własnościami lokalnych
Przetwarzanie obrazów rastrowych macierzą konwolucji
 Przetwarzanie obrazów rastrowych macierzą konwolucji 1 Wstęp Obrazy rastrowe są na ogół reprezentowane w dwuwymiarowych tablicach złożonych z pikseli, reprezentowanych przez liczby określające ich jasność
Przetwarzanie obrazów rastrowych macierzą konwolucji 1 Wstęp Obrazy rastrowe są na ogół reprezentowane w dwuwymiarowych tablicach złożonych z pikseli, reprezentowanych przez liczby określające ich jasność
Implementacja filtru Canny ego
 ANALIZA I PRZETWARZANIE OBRAZÓW Implementacja filtru Canny ego Autor: Katarzyna Piotrowicz Kraków,2015-06-11 Spis treści 1. Wstęp... 1 2. Implementacja... 2 3. Przykłady... 3 Porównanie wykrytych krawędzi
ANALIZA I PRZETWARZANIE OBRAZÓW Implementacja filtru Canny ego Autor: Katarzyna Piotrowicz Kraków,2015-06-11 Spis treści 1. Wstęp... 1 2. Implementacja... 2 3. Przykłady... 3 Porównanie wykrytych krawędzi
Cyfrowe przetwarzanie obrazów i sygnałów Wykład 3 AiR III
 1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
Filtracja splotowa obrazu
 Informatyka, S1 sem. letni, 2012/2013, wykład#3 Filtracja splotowa obrazu dr inż. Paweł Forczmański Katedra Systemów Multimedialnych, Wydział Informatyki ZUT 1 / 53 Proces przetwarzania obrazów Obraz f(x,y)
Informatyka, S1 sem. letni, 2012/2013, wykład#3 Filtracja splotowa obrazu dr inż. Paweł Forczmański Katedra Systemów Multimedialnych, Wydział Informatyki ZUT 1 / 53 Proces przetwarzania obrazów Obraz f(x,y)
Zbigniew Sołtys - Komputerowa Analiza Obrazu Mikroskopowego 2016 część 5
 5. FILTRY LINIOWE I STATYSTYCZNE. WYRÓWNYWANIE TŁA. Znacznie większe znaczenie w przetwarzaniu obrazu niż operacje punktowe mają takie przekształcenia w których zmiana poziomu szarości piksela zależy nie
5. FILTRY LINIOWE I STATYSTYCZNE. WYRÓWNYWANIE TŁA. Znacznie większe znaczenie w przetwarzaniu obrazu niż operacje punktowe mają takie przekształcenia w których zmiana poziomu szarości piksela zależy nie
Cyfrowe przetwarzanie obrazów i sygnałów Wykład 10 AiR III
 1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
Podstawy Przetwarzania Sygnałów
 Adam Szulc 188250 grupa: pon TN 17:05 Podstawy Przetwarzania Sygnałów Sprawozdanie 6: Filtracja sygnałów. Filtry FIT o skończonej odpowiedzi impulsowej. 1. Cel ćwiczenia. 1) Przeprowadzenie filtracji trzech
Adam Szulc 188250 grupa: pon TN 17:05 Podstawy Przetwarzania Sygnałów Sprawozdanie 6: Filtracja sygnałów. Filtry FIT o skończonej odpowiedzi impulsowej. 1. Cel ćwiczenia. 1) Przeprowadzenie filtracji trzech
POB Odpowiedzi na pytania
 POB Odpowiedzi na pytania 1.) Na czym polega próbkowanie a na czym kwantyzacja w procesie akwizycji obrazu, jakiemu rodzajowi rozdzielczości odpowiada próbkowanie a jakiemu kwantyzacja Próbkowanie inaczej
POB Odpowiedzi na pytania 1.) Na czym polega próbkowanie a na czym kwantyzacja w procesie akwizycji obrazu, jakiemu rodzajowi rozdzielczości odpowiada próbkowanie a jakiemu kwantyzacja Próbkowanie inaczej
Projekt 2: Filtracja w domenie przestrzeni
 Projekt 2: Filtracja w domenie przestrzeni 1. 2. Wstęp teoretyczny a. Filtracja w domenie przestrzeni b. Krótko o szumie c. Filtracja d. Usuwanie szumu typu Salt and Pepper filtrem medianowym e. Wnioski
Projekt 2: Filtracja w domenie przestrzeni 1. 2. Wstęp teoretyczny a. Filtracja w domenie przestrzeni b. Krótko o szumie c. Filtracja d. Usuwanie szumu typu Salt and Pepper filtrem medianowym e. Wnioski
Reprezentacja i analiza obszarów
 Cechy kształtu Topologiczne Geometryczne spójność liczba otworów liczba Eulera szkielet obwód pole powierzchni środek cięŝkości ułoŝenie przestrzenne momenty wyŝszych rzędów promienie max-min centryczność
Cechy kształtu Topologiczne Geometryczne spójność liczba otworów liczba Eulera szkielet obwód pole powierzchni środek cięŝkości ułoŝenie przestrzenne momenty wyŝszych rzędów promienie max-min centryczność
Algorytmy decyzyjne będące alternatywą dla sieci neuronowych
 Algorytmy decyzyjne będące alternatywą dla sieci neuronowych Piotr Dalka Przykładowe algorytmy decyzyjne Sztuczne sieci neuronowe Algorytm k najbliższych sąsiadów Kaskada klasyfikatorów AdaBoost Naiwny
Algorytmy decyzyjne będące alternatywą dla sieci neuronowych Piotr Dalka Przykładowe algorytmy decyzyjne Sztuczne sieci neuronowe Algorytm k najbliższych sąsiadów Kaskada klasyfikatorów AdaBoost Naiwny
Grafika komputerowa. Dr inż. Michał Kruk
 Grafika komputerowa Dr inż. Michał Kruk Operacje kontekstowe Z reguły filtry używane do analizy obrazów zakładają, że wykonywane na obrazie operacje będą kontekstowe Polega to na wyznaczeniu wartości funkcji,
Grafika komputerowa Dr inż. Michał Kruk Operacje kontekstowe Z reguły filtry używane do analizy obrazów zakładają, że wykonywane na obrazie operacje będą kontekstowe Polega to na wyznaczeniu wartości funkcji,
BIBLIOTEKA PROGRAMU R - BIOPS. Narzędzia Informatyczne w Badaniach Naukowych Katarzyna Bernat
 BIBLIOTEKA PROGRAMU R - BIOPS Narzędzia Informatyczne w Badaniach Naukowych Katarzyna Bernat Biblioteka biops zawiera funkcje do analizy i przetwarzania obrazów. Operacje geometryczne (obrót, przesunięcie,
BIBLIOTEKA PROGRAMU R - BIOPS Narzędzia Informatyczne w Badaniach Naukowych Katarzyna Bernat Biblioteka biops zawiera funkcje do analizy i przetwarzania obrazów. Operacje geometryczne (obrót, przesunięcie,
Sposoby opisu i modelowania zakłóceń kanałowych
 INSTYTUT TELEKOMUNIKACJI ZAKŁAD RADIOKOMUNIKACJI Instrukcja laboratoryjna z przedmiotu Podstawy Telekomunikacji Sposoby opisu i modelowania zakłóceń kanałowych Warszawa 2010r. 1. Cel ćwiczeń: Celem ćwiczeń
INSTYTUT TELEKOMUNIKACJI ZAKŁAD RADIOKOMUNIKACJI Instrukcja laboratoryjna z przedmiotu Podstawy Telekomunikacji Sposoby opisu i modelowania zakłóceń kanałowych Warszawa 2010r. 1. Cel ćwiczeń: Celem ćwiczeń
Reprezentacja i analiza obszarów
 Cechy kształtu Topologiczne Geometryczne spójność liczba otworów liczba Eulera szkielet obwód pole powierzchni środek ciężkości ułożenie przestrzenne momenty wyższych rzędów promienie max-min centryczność
Cechy kształtu Topologiczne Geometryczne spójność liczba otworów liczba Eulera szkielet obwód pole powierzchni środek ciężkości ułożenie przestrzenne momenty wyższych rzędów promienie max-min centryczność
Wyższa Szkoła Informatyki Stosowanej i Zarządzania WIT
 3-1 Wyższa Szkoła Informatyki Stosowanej i Zarządzania WIT Grupa BD2,TC1, Zespół 2 PRZETWARZANIE OBRAZÓW Sprawozdanie z ćwiczeń laboratoryjnych Ćwiczenie nr3 Temat: Operacje sąsiedztwa wygładzanie i wyostrzanie
3-1 Wyższa Szkoła Informatyki Stosowanej i Zarządzania WIT Grupa BD2,TC1, Zespół 2 PRZETWARZANIE OBRAZÓW Sprawozdanie z ćwiczeń laboratoryjnych Ćwiczenie nr3 Temat: Operacje sąsiedztwa wygładzanie i wyostrzanie
Detekcja twarzy w obrazie
 Detekcja twarzy w obrazie Metoda na kanałach RGB 1. Należy utworzyć nowy obrazek o wymiarach analizowanego obrazka. 2. Dla każdego piksela oryginalnego obrazka pobiera się informację o wartości kanałów
Detekcja twarzy w obrazie Metoda na kanałach RGB 1. Należy utworzyć nowy obrazek o wymiarach analizowanego obrazka. 2. Dla każdego piksela oryginalnego obrazka pobiera się informację o wartości kanałów
AKWIZYCJA I PRZETWARZANIE WSTĘPNE
 WYKŁAD 2 AKWIZYCJA I PRZETWARZANIE WSTĘPNE Akwizycja (pozyskiwanie) obrazu Akwizycja obrazu - przetworzenie obrazu obiektu fizycznego (f(x,y)) do postaci zbioru danych dyskretnych (obraz cyfrowy) nadających
WYKŁAD 2 AKWIZYCJA I PRZETWARZANIE WSTĘPNE Akwizycja (pozyskiwanie) obrazu Akwizycja obrazu - przetworzenie obrazu obiektu fizycznego (f(x,y)) do postaci zbioru danych dyskretnych (obraz cyfrowy) nadających
PRZETWARZANIE SYGNAŁÓW
 PRZETWARZANIE SYGNAŁÓW SEMESTR V Wykład VIII Podstawy przetwarzania obrazów Filtracja Przetwarzanie obrazu w dziedzinie próbek Przetwarzanie obrazu w dziedzinie częstotliwości (transformacje częstotliwościowe)
PRZETWARZANIE SYGNAŁÓW SEMESTR V Wykład VIII Podstawy przetwarzania obrazów Filtracja Przetwarzanie obrazu w dziedzinie próbek Przetwarzanie obrazu w dziedzinie częstotliwości (transformacje częstotliwościowe)
Kodowanie transformacyjne. Plan 1. Zasada 2. Rodzaje transformacji 3. Standard JPEG
 Kodowanie transformacyjne Plan 1. Zasada 2. Rodzaje transformacji 3. Standard JPEG Zasada Zasada podstawowa: na danych wykonujemy transformacje która: Likwiduje korelacje Skupia energię w kilku komponentach
Kodowanie transformacyjne Plan 1. Zasada 2. Rodzaje transformacji 3. Standard JPEG Zasada Zasada podstawowa: na danych wykonujemy transformacje która: Likwiduje korelacje Skupia energię w kilku komponentach
W kolejnym kroku należy ustalić liczbę przedziałów k. W tym celu należy wykorzystać jeden ze wzorów:
 Na dzisiejszym wykładzie omówimy najważniejsze charakterystyki liczbowe występujące w statystyce opisowej. Poszczególne wzory będziemy podawać w miarę potrzeby w trzech postaciach: dla szeregu szczegółowego,
Na dzisiejszym wykładzie omówimy najważniejsze charakterystyki liczbowe występujące w statystyce opisowej. Poszczególne wzory będziemy podawać w miarę potrzeby w trzech postaciach: dla szeregu szczegółowego,
STATYSTYKA OPISOWA. LICZBOWE CHARAKTERYSTYKI(MIARY)
 STATYSTYKA OPISOWA. LICZBOWE CHARAKTERYSTYKI(MIARY) Dla opisania rozkładu badanej zmiennej, korzystamy z pewnych charakterystyk liczbowych. Dzielimy je na cztery grupy.. Określenie przeciętnej wartości
STATYSTYKA OPISOWA. LICZBOWE CHARAKTERYSTYKI(MIARY) Dla opisania rozkładu badanej zmiennej, korzystamy z pewnych charakterystyk liczbowych. Dzielimy je na cztery grupy.. Określenie przeciętnej wartości
Podstawy OpenCL część 2
 Podstawy OpenCL część 2 1. Napisz program dokonujący mnożenia dwóch macierzy w wersji sekwencyjnej oraz OpenCL. Porównaj czasy działania obu wersji dla różnych wielkości macierzy, np. 16 16, 128 128, 1024
Podstawy OpenCL część 2 1. Napisz program dokonujący mnożenia dwóch macierzy w wersji sekwencyjnej oraz OpenCL. Porównaj czasy działania obu wersji dla różnych wielkości macierzy, np. 16 16, 128 128, 1024
Filtracja w domenie przestrzeni
 1 Filtracja Filtracja w domenie przestrzeni Filtracja liniowa jest procesem splotu (konwolucji) obrazu z maską (filtrem). Dla dwuwymiarowej i dyskretnej funkcji filtracja dana jest wzorem: L2(m, n) = (w
1 Filtracja Filtracja w domenie przestrzeni Filtracja liniowa jest procesem splotu (konwolucji) obrazu z maską (filtrem). Dla dwuwymiarowej i dyskretnej funkcji filtracja dana jest wzorem: L2(m, n) = (w
Obliczenia inteligentne Zadanie 4
 Sieci SOM Poniedziałek, 10:15 2007/2008 Krzysztof Szcześniak Cel Celem zadania jest zaimplementowanie neuronowej samoorganizującej się mapy wraz z metodą jej nauczania algorytmem gazu neuronowego. Część
Sieci SOM Poniedziałek, 10:15 2007/2008 Krzysztof Szcześniak Cel Celem zadania jest zaimplementowanie neuronowej samoorganizującej się mapy wraz z metodą jej nauczania algorytmem gazu neuronowego. Część
Informatyka, studia dzienne, mgr II st. Przetwarzanie obrazu i dźwięku 2011/2012 Prowadzący: dr inż. Bartłomiej Stasiak czwartek, 8:30
 Informatyka, studia dzienne, mgr II st. semestr I Przetwarzanie obrazu i dźwięku 2011/2012 Prowadzący: dr inż. Bartłomiej Stasiak czwartek, 8:30 Data oddania: Ocena: Grzegorz Graczyk 178717 Andrzej Stasiak
Informatyka, studia dzienne, mgr II st. semestr I Przetwarzanie obrazu i dźwięku 2011/2012 Prowadzący: dr inż. Bartłomiej Stasiak czwartek, 8:30 Data oddania: Ocena: Grzegorz Graczyk 178717 Andrzej Stasiak
Złożoność obliczeniowa zadania, zestaw 2
 Złożoność obliczeniowa zadania, zestaw 2 Określanie złożoności obliczeniowej algorytmów, obliczanie pesymistycznej i oczekiwanej złożoności obliczeniowej 1. Dana jest tablica jednowymiarowa A o rozmiarze
Złożoność obliczeniowa zadania, zestaw 2 Określanie złożoności obliczeniowej algorytmów, obliczanie pesymistycznej i oczekiwanej złożoności obliczeniowej 1. Dana jest tablica jednowymiarowa A o rozmiarze
9. OBRAZY i FILTRY BINARNE 9.1 Erozja, dylatacja, zamykanie, otwieranie
 9. OBRAZY i FILTRY BINARNE 9.1 Erozja, dylatacja, zamykanie, otwieranie Obrazy binarne to takie, które mają tylko dwa poziomy szarości: 0 i 1 lub 0 i 255. ImageJ wykorzystuje to drugie rozwiązanie - obrazy
9. OBRAZY i FILTRY BINARNE 9.1 Erozja, dylatacja, zamykanie, otwieranie Obrazy binarne to takie, które mają tylko dwa poziomy szarości: 0 i 1 lub 0 i 255. ImageJ wykorzystuje to drugie rozwiązanie - obrazy
Wydział Inżynierii Produkcji. I Logistyki. Statystyka opisowa. Wykład 3. Dr inż. Adam Deptuła
 12.03.2017 Wydział Inżynierii Produkcji I Logistyki Statystyka opisowa Wykład 3 Dr inż. Adam Deptuła METODY OPISU DANYCH ILOŚCIOWYCH SKALARNYCH Wykresy: diagramy, histogramy, łamane częstości, wykresy
12.03.2017 Wydział Inżynierii Produkcji I Logistyki Statystyka opisowa Wykład 3 Dr inż. Adam Deptuła METODY OPISU DANYCH ILOŚCIOWYCH SKALARNYCH Wykresy: diagramy, histogramy, łamane częstości, wykresy
Detekcja punktów zainteresowania
 Informatyka, S2 sem. Letni, 2013/2014, wykład#8 Detekcja punktów zainteresowania dr inż. Paweł Forczmański Katedra Systemów Multimedialnych, Wydział Informatyki ZUT 1 / 61 Proces przetwarzania obrazów
Informatyka, S2 sem. Letni, 2013/2014, wykład#8 Detekcja punktów zainteresowania dr inż. Paweł Forczmański Katedra Systemów Multimedialnych, Wydział Informatyki ZUT 1 / 61 Proces przetwarzania obrazów
Rozpoznawanie Twarzy i Systemy Biometryczne
 Filtry Plan wykładu Przegląd dostępnych filtrów Zastosowanie filtrów na różnych etapach pracy systemu Dalsze badania Kontrast i ostrość Kontrast różnica w kolorze i świetle między częściami ś i obrazu
Filtry Plan wykładu Przegląd dostępnych filtrów Zastosowanie filtrów na różnych etapach pracy systemu Dalsze badania Kontrast i ostrość Kontrast różnica w kolorze i świetle między częściami ś i obrazu
Kompresja danych Streszczenie Studia Dzienne Wykład 10,
 1 Kwantyzacja wektorowa Kompresja danych Streszczenie Studia Dzienne Wykład 10, 28.04.2006 Kwantyzacja wektorowa: dane dzielone na bloki (wektory), każdy blok kwantyzowany jako jeden element danych. Ogólny
1 Kwantyzacja wektorowa Kompresja danych Streszczenie Studia Dzienne Wykład 10, 28.04.2006 Kwantyzacja wektorowa: dane dzielone na bloki (wektory), każdy blok kwantyzowany jako jeden element danych. Ogólny
Filtrowanie tekstur. Kinga Laurowska
 Filtrowanie tekstur Kinga Laurowska Wprowadzenie Filtrowanie tekstur (inaczej wygładzanie) technika polegająca na 'rozmywaniu' sąsiadujących ze sobą tekseli (pikseli tekstury). Istnieje wiele metod filtrowania,
Filtrowanie tekstur Kinga Laurowska Wprowadzenie Filtrowanie tekstur (inaczej wygładzanie) technika polegająca na 'rozmywaniu' sąsiadujących ze sobą tekseli (pikseli tekstury). Istnieje wiele metod filtrowania,
Proste metody przetwarzania obrazu
 Operacje na pikselach obrazu (operacje punktowe, bezkontekstowe) Operacje arytmetyczne Dodanie (odjęcie) do obrazu stałej 1 Mnożenie (dzielenie) obrazu przez stałą Operacje dodawania i mnożenia są operacjami
Operacje na pikselach obrazu (operacje punktowe, bezkontekstowe) Operacje arytmetyczne Dodanie (odjęcie) do obrazu stałej 1 Mnożenie (dzielenie) obrazu przez stałą Operacje dodawania i mnożenia są operacjami
Charakterystyki liczbowe (estymatory i parametry), które pozwalają opisać właściwości rozkładu badanej cechy (zmiennej)
 Charakterystyki liczbowe (estymatory i parametry), które pozwalają opisać właściwości rozkładu badanej cechy (zmiennej) 1 Podział ze względu na zakres danych użytych do wyznaczenia miary Miary opisujące
Charakterystyki liczbowe (estymatory i parametry), które pozwalają opisać właściwości rozkładu badanej cechy (zmiennej) 1 Podział ze względu na zakres danych użytych do wyznaczenia miary Miary opisujące
Ćwiczenie 6. Transformacje skali szarości obrazów
 Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 6. Transformacje skali szarości obrazów 1. Obraz cyfrowy Obraz w postaci cyfrowej
Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 6. Transformacje skali szarości obrazów 1. Obraz cyfrowy Obraz w postaci cyfrowej
Kompresja danych DKDA (7)
 Kompresja danych DKDA (7) Marcin Gogolewski marcing@wmi.amu.edu.pl Uniwersytet im. Adama Mickiewicza w Poznaniu Poznań, 22 listopada 2016 1 Kwantyzacja skalarna Wprowadzenie Analiza jakości Typy kwantyzatorów
Kompresja danych DKDA (7) Marcin Gogolewski marcing@wmi.amu.edu.pl Uniwersytet im. Adama Mickiewicza w Poznaniu Poznań, 22 listopada 2016 1 Kwantyzacja skalarna Wprowadzenie Analiza jakości Typy kwantyzatorów
Akademia Górniczo - Hutnicza im. Stanisława Staszica w Krakowie. Projekt. z przedmiotu Analiza i Przetwarzanie Obrazów
 30 czerwca 2015 Akademia Górniczo - Hutnicza im. Stanisława Staszica w Krakowie Projekt z przedmiotu Analiza i Przetwarzanie Obrazów Wykrywanie tablic rejestracyjnych Jagieła Michał IS (GKiPO) Michał Jagieła
30 czerwca 2015 Akademia Górniczo - Hutnicza im. Stanisława Staszica w Krakowie Projekt z przedmiotu Analiza i Przetwarzanie Obrazów Wykrywanie tablic rejestracyjnych Jagieła Michał IS (GKiPO) Michał Jagieła
Przetwarzanie obrazów wykład 7. Adam Wojciechowski
 Przetwarzanie obrazów wykład 7 Adam Wojciechowski Przekształcenia morfologiczne Przekształcenia podobne do filtrów, z tym że element obrazu nie jest modyfikowany zawsze lecz tylko jeśli spełniony jest
Przetwarzanie obrazów wykład 7 Adam Wojciechowski Przekształcenia morfologiczne Przekształcenia podobne do filtrów, z tym że element obrazu nie jest modyfikowany zawsze lecz tylko jeśli spełniony jest
Filtracja nieliniowa obrazu
 Informatyka, S1 sem. letni, 2014/2015, wykład#4 Filtracja nieliniowa obrazu dr inż. Paweł Forczmański Katedra Systemów Multimedialnych, Wydział Informatyki ZUT 1 / 61 Proces przetwarzania obrazów Obraz
Informatyka, S1 sem. letni, 2014/2015, wykład#4 Filtracja nieliniowa obrazu dr inż. Paweł Forczmański Katedra Systemów Multimedialnych, Wydział Informatyki ZUT 1 / 61 Proces przetwarzania obrazów Obraz
Zbigniew Sołtys - Komputerowa Analiza Obrazu Mikroskopowego 2016 część 7
 7. NORMALIZACJA I BINARYZACJA ADAPTATYWNA 7.1. Normalizacja lokalna Zwykłe konwolucje działają w jednakowy sposób na całym obrazie. Plugin Local Normalization przeprowadza filtrowanie Gaussa w zależności
7. NORMALIZACJA I BINARYZACJA ADAPTATYWNA 7.1. Normalizacja lokalna Zwykłe konwolucje działają w jednakowy sposób na całym obrazie. Plugin Local Normalization przeprowadza filtrowanie Gaussa w zależności
FILTRACJE W DZIEDZINIE CZĘSTOTLIWOŚCI
 FILTRACJE W DZIEDZINIE CZĘSTOTLIWOŚCI ( frequency domain filters) Każdy człon F(u,v) zawiera wszystkie wartości f(x,y) modyfikowane przez wartości członów wykładniczych Za wyjątkiem trywialnych przypadków
FILTRACJE W DZIEDZINIE CZĘSTOTLIWOŚCI ( frequency domain filters) Każdy człon F(u,v) zawiera wszystkie wartości f(x,y) modyfikowane przez wartości członów wykładniczych Za wyjątkiem trywialnych przypadków
Luty 2001 Algorytmy (4) 2000/2001
 Mając dany zbiór elementów, chcemy znaleźć w nim element największy (maksimum), bądź najmniejszy (minimum). We wszystkich naturalnych metodach znajdywania najmniejszego i największego elementu obecne jest
Mając dany zbiór elementów, chcemy znaleźć w nim element największy (maksimum), bądź najmniejszy (minimum). We wszystkich naturalnych metodach znajdywania najmniejszego i największego elementu obecne jest
Przetwarzanie obrazu
 Przetwarzanie obrazu Przekształcenia geometryczne Obroty Przesunięcia Odbicia Rozciągnięcia itp Przekształcenia geometryczne Obroty Wielokrotność 90 stopni Inne Przekształcenia geometryczne Obroty Wielokrotność
Przetwarzanie obrazu Przekształcenia geometryczne Obroty Przesunięcia Odbicia Rozciągnięcia itp Przekształcenia geometryczne Obroty Wielokrotność 90 stopni Inne Przekształcenia geometryczne Obroty Wielokrotność
WOJSKOWA AKADEMIA TECHNICZNA
 WOJSKOWA AKADEMIA TECHNICZNA LABORATORIUM CYFROWE PRZETWARZANIE SYGNAŁÓW Stopień, imię i nazwisko prowadzącego Imię oraz nazwisko słuchacza Grupa szkoleniowa Data wykonania ćwiczenia dr inż. Andrzej Wiśniewski
WOJSKOWA AKADEMIA TECHNICZNA LABORATORIUM CYFROWE PRZETWARZANIE SYGNAŁÓW Stopień, imię i nazwisko prowadzącego Imię oraz nazwisko słuchacza Grupa szkoleniowa Data wykonania ćwiczenia dr inż. Andrzej Wiśniewski
Grafika Komputerowa Wykład 2. Przetwarzanie obrazów. mgr inż. Michał Chwesiuk 1/38
 Wykład 2 Przetwarzanie obrazów mgr inż. 1/38 Przetwarzanie obrazów rastrowych Jedna z dziedzin cyfrowego obrazów rastrowych. Celem przetworzenia obrazów rastrowych jest użycie edytujących piksele w celu
Wykład 2 Przetwarzanie obrazów mgr inż. 1/38 Przetwarzanie obrazów rastrowych Jedna z dziedzin cyfrowego obrazów rastrowych. Celem przetworzenia obrazów rastrowych jest użycie edytujących piksele w celu
Przekształcenia sygnałów losowych w układach
 INSTYTUT TELEKOMUNIKACJI ZAKŁAD RADIOKOMUNIKACJI Instrukcja laboratoryjna z przedmiotu Sygnały i kodowanie Przekształcenia sygnałów losowych w układach Warszawa 010r. 1. Cel ćwiczenia: Ocena wpływu charakterystyk
INSTYTUT TELEKOMUNIKACJI ZAKŁAD RADIOKOMUNIKACJI Instrukcja laboratoryjna z przedmiotu Sygnały i kodowanie Przekształcenia sygnałów losowych w układach Warszawa 010r. 1. Cel ćwiczenia: Ocena wpływu charakterystyk
AKWIZYCJA I PRZETWARZANIE WSTĘPNE OBRAZU
 AKWIZYCJA I PRZETWARZANIE WSTĘPNE OBRAZU WYKŁAD 2 Marek Doros Przetwarzanie obrazów Wykład 2 2 Akwizycja (pozyskiwanie) obrazu Akwizycja obrazu - przetworzenie obrazu obiektu fizycznego (f(x, y)) do postaci
AKWIZYCJA I PRZETWARZANIE WSTĘPNE OBRAZU WYKŁAD 2 Marek Doros Przetwarzanie obrazów Wykład 2 2 Akwizycja (pozyskiwanie) obrazu Akwizycja obrazu - przetworzenie obrazu obiektu fizycznego (f(x, y)) do postaci
Zadanie 1 Przygotuj algorytm programu - sortowanie przez wstawianie.
 Sortowanie Dane wejściowe: ciąg n-liczb (kluczy) (a 1, a 2, a 3,..., a n 1, a n ) Dane wyjściowe: permutacja ciągu wejściowego (a 1, a 2, a 3,..., a n 1, a n) taka, że a 1 a 2 a 3... a n 1 a n. Będziemy
Sortowanie Dane wejściowe: ciąg n-liczb (kluczy) (a 1, a 2, a 3,..., a n 1, a n ) Dane wyjściowe: permutacja ciągu wejściowego (a 1, a 2, a 3,..., a n 1, a n) taka, że a 1 a 2 a 3... a n 1 a n. Będziemy
LABORATORIUM PODSTAW TELEKOMUNIKACJI
 WOJSKOWA AKADEMIA TECHNICZNA im. Jarosława Dąbrowskiego w Warszawie Wydział Elektroniki LABORATORIUM PODSTAW TELEKOMUNIKACJI Grupa Podgrupa Data wykonania ćwiczenia Ćwiczenie prowadził... Skład podgrupy:
WOJSKOWA AKADEMIA TECHNICZNA im. Jarosława Dąbrowskiego w Warszawie Wydział Elektroniki LABORATORIUM PODSTAW TELEKOMUNIKACJI Grupa Podgrupa Data wykonania ćwiczenia Ćwiczenie prowadził... Skład podgrupy:
Laboratorium. Cyfrowe przetwarzanie sygnałów. Ćwiczenie 11. Filtracja sygnałów wizyjnych
 Laboratorium Cyfrowe przetwarzanie sygnałów Ćwiczenie 11 Filtracja sygnałów wizyjnych Operacje kontekstowe (filtry) Operacje polegające na modyfikacji poszczególnych elementów obrazu w zależności od stanu
Laboratorium Cyfrowe przetwarzanie sygnałów Ćwiczenie 11 Filtracja sygnałów wizyjnych Operacje kontekstowe (filtry) Operacje polegające na modyfikacji poszczególnych elementów obrazu w zależności od stanu
Diagnostyka obrazowa
 Diagnostyka obrazowa 1. Cel ćwiczenia Ćwiczenie czwarte Przekształcenia morfologiczne obrazu Ćwiczenie ma na celu zapoznanie uczestników kursu Diagnostyka obrazowa z definicjami operacji morfologicznych
Diagnostyka obrazowa 1. Cel ćwiczenia Ćwiczenie czwarte Przekształcenia morfologiczne obrazu Ćwiczenie ma na celu zapoznanie uczestników kursu Diagnostyka obrazowa z definicjami operacji morfologicznych
Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Elektroniki
 Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Elektroniki Przetwarzanie Sygnałów Studia Podyplomowe, Automatyka i Robotyka. Wstęp teoretyczny Zmienne losowe Zmienne losowe
Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Elektroniki Przetwarzanie Sygnałów Studia Podyplomowe, Automatyka i Robotyka. Wstęp teoretyczny Zmienne losowe Zmienne losowe
Katedra Fizyki Ciała Stałego Uniwersytetu Łódzkiego. Ćwiczenie 2 Badanie funkcji korelacji w przebiegach elektrycznych.
 Katedra Fizyki Ciała Stałego Uniwersytetu Łódzkiego Ćwiczenie Badanie unkcji korelacji w przebiegach elektrycznych. Cel ćwiczenia: Celem ćwiczenia jest zbadanie unkcji korelacji w okresowych sygnałach
Katedra Fizyki Ciała Stałego Uniwersytetu Łódzkiego Ćwiczenie Badanie unkcji korelacji w przebiegach elektrycznych. Cel ćwiczenia: Celem ćwiczenia jest zbadanie unkcji korelacji w okresowych sygnałach
Transformata Fouriera i analiza spektralna
 Transformata Fouriera i analiza spektralna Z czego składają się sygnały? Sygnały jednowymiarowe, częstotliwość Liczby zespolone Transformata Fouriera Szybka Transformata Fouriera (FFT) FFT w 2D Przykłady
Transformata Fouriera i analiza spektralna Z czego składają się sygnały? Sygnały jednowymiarowe, częstotliwość Liczby zespolone Transformata Fouriera Szybka Transformata Fouriera (FFT) FFT w 2D Przykłady
Przekształcenia widmowe Transformata Fouriera. Adam Wojciechowski
 Przekształcenia widmowe Transformata Fouriera Adam Wojciechowski Przekształcenia widmowe Odmiana przekształceń kontekstowych, w których kontekstem jest w zasadzie cały obraz. Za pomocą transformaty Fouriera
Przekształcenia widmowe Transformata Fouriera Adam Wojciechowski Przekształcenia widmowe Odmiana przekształceń kontekstowych, w których kontekstem jest w zasadzie cały obraz. Za pomocą transformaty Fouriera
ANALIZA SEMANTYCZNA OBRAZU I DŹWIĘKU
 ANALIZA SEMANTYCZNA OBRAZU I DŹWIĘKU obraz dr inż. Jacek Naruniec Analiza Składowych Niezależnych (ICA) Independent Component Analysis Dąży do wyznaczenia zmiennych niezależnych z obserwacji Problem opiera
ANALIZA SEMANTYCZNA OBRAZU I DŹWIĘKU obraz dr inż. Jacek Naruniec Analiza Składowych Niezależnych (ICA) Independent Component Analysis Dąży do wyznaczenia zmiennych niezależnych z obserwacji Problem opiera
Przetwarzanie obrazów
 Przetwarzanie obrazów Zajęcia 11 Filtracje przestrzenne obrazów rastrowych (2). Zasady wykonania ćwiczenia Obrazy wynikowe do zadań zapisujemy w pliku nazwiskonr.rvc (bieżące nr 1) a komentarze do wyników
Przetwarzanie obrazów Zajęcia 11 Filtracje przestrzenne obrazów rastrowych (2). Zasady wykonania ćwiczenia Obrazy wynikowe do zadań zapisujemy w pliku nazwiskonr.rvc (bieżące nr 1) a komentarze do wyników
Statystyka. Wykład 2. Magdalena Alama-Bućko. 5 marca Magdalena Alama-Bućko Statystyka 5 marca / 34
 Statystyka Wykład 2 Magdalena Alama-Bućko 5 marca 2018 Magdalena Alama-Bućko Statystyka 5 marca 2018 1 / 34 Banki danych: Bank danych lokalnych : Główny urzad statystyczny: Baza Demografia : https://bdl.stat.gov.pl/
Statystyka Wykład 2 Magdalena Alama-Bućko 5 marca 2018 Magdalena Alama-Bućko Statystyka 5 marca 2018 1 / 34 Banki danych: Bank danych lokalnych : Główny urzad statystyczny: Baza Demografia : https://bdl.stat.gov.pl/
Transformata Fouriera
 Transformata Fouriera Program wykładu 1. Wprowadzenie teoretyczne 2. Algorytm FFT 3. Zastosowanie analizy Fouriera 4. Przykłady programów Wprowadzenie teoretyczne Zespolona transformata Fouriera Jeżeli
Transformata Fouriera Program wykładu 1. Wprowadzenie teoretyczne 2. Algorytm FFT 3. Zastosowanie analizy Fouriera 4. Przykłady programów Wprowadzenie teoretyczne Zespolona transformata Fouriera Jeżeli
Metody sztucznej inteligencji Zadanie 1: Perceptron Rosenblatt a w wersji nieliniowej
 Metody sztucznej inteligencji Zadanie : Perceptron Rosenblatt a w wersji nieliniowej dr inż. Przemysław Klęsk Zbiór danych dla zadania do wykonania w domu Zgodnie z tym, co zostało podane na laboratoriach,
Metody sztucznej inteligencji Zadanie : Perceptron Rosenblatt a w wersji nieliniowej dr inż. Przemysław Klęsk Zbiór danych dla zadania do wykonania w domu Zgodnie z tym, co zostało podane na laboratoriach,
Diagnostyka obrazowa
 Diagnostyka obrazowa Ćwiczenie szóste Transformacje obrazu w dziedzinie częstotliwości 1 Cel ćwiczenia Ćwiczenie ma na celu zapoznanie uczestników kursu Diagnostyka obrazowa z podstawowymi przekształceniami
Diagnostyka obrazowa Ćwiczenie szóste Transformacje obrazu w dziedzinie częstotliwości 1 Cel ćwiczenia Ćwiczenie ma na celu zapoznanie uczestników kursu Diagnostyka obrazowa z podstawowymi przekształceniami
zniekształcenia przyjmują różne formy, w zależności od miejsca, w którym powstają
 Opracowali: dr inż. Piotr Suchomski dr inż. Piotr Odya nie ma urządzeń doskonałych każde urządzenie wprowadza do sygnału (fonicznego bądź wizyjnego) zniekształcenia zniekształcenia przyjmują różne formy,
Opracowali: dr inż. Piotr Suchomski dr inż. Piotr Odya nie ma urządzeń doskonałych każde urządzenie wprowadza do sygnału (fonicznego bądź wizyjnego) zniekształcenia zniekształcenia przyjmują różne formy,
Zmienne zależne i niezależne
 Analiza kanoniczna Motywacja (1) 2 Często w badaniach spotykamy problemy badawcze, w których szukamy zakresu i kierunku zależności pomiędzy zbiorami zmiennych: { X i Jak oceniać takie 1, X 2,..., X p }
Analiza kanoniczna Motywacja (1) 2 Często w badaniach spotykamy problemy badawcze, w których szukamy zakresu i kierunku zależności pomiędzy zbiorami zmiennych: { X i Jak oceniać takie 1, X 2,..., X p }
Aproksymacja funkcji a regresja symboliczna
 Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(x), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(x), zwaną funkcją aproksymującą
Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(x), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(x), zwaną funkcją aproksymującą
Kolejny krok iteracji polega na tym, że przechodzimy do następnego wierzchołka, znajdującego się na jednej krawędzi z odnalezionym już punktem, w
 Metoda Simpleks Jak wiadomo, problem PL z dowolną liczbą zmiennych można rozwiązać wyznaczając wszystkie wierzchołkowe punkty wielościanu wypukłego, a następnie porównując wartości funkcji celu w tych
Metoda Simpleks Jak wiadomo, problem PL z dowolną liczbą zmiennych można rozwiązać wyznaczając wszystkie wierzchołkowe punkty wielościanu wypukłego, a następnie porównując wartości funkcji celu w tych
Metody numeryczne Technika obliczeniowa i symulacyjna Sem. 2, EiT, 2014/2015
 Metody numeryczne Technika obliczeniowa i symulacyjna Sem. 2, EiT, 2014/2015 1 Metody numeryczne Dział matematyki Metody rozwiązywania problemów matematycznych za pomocą operacji na liczbach. Otrzymywane
Metody numeryczne Technika obliczeniowa i symulacyjna Sem. 2, EiT, 2014/2015 1 Metody numeryczne Dział matematyki Metody rozwiązywania problemów matematycznych za pomocą operacji na liczbach. Otrzymywane
SYSTEMY UCZĄCE SIĘ WYKŁAD 4. DRZEWA REGRESYJNE, INDUKCJA REGUŁ. Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska
 SYSTEMY UCZĄCE SIĘ WYKŁAD 4. DRZEWA REGRESYJNE, INDUKCJA REGUŁ Częstochowa 2014 Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska DRZEWO REGRESYJNE Sposób konstrukcji i przycinania
SYSTEMY UCZĄCE SIĘ WYKŁAD 4. DRZEWA REGRESYJNE, INDUKCJA REGUŁ Częstochowa 2014 Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska DRZEWO REGRESYJNE Sposób konstrukcji i przycinania
Adam Korzeniewski - p. 732 dr inż. Grzegorz Szwoch - p. 732 dr inż.
 Adam Korzeniewski - adamkorz@sound.eti.pg.gda.pl, p. 732 dr inż. Grzegorz Szwoch - greg@sound.eti.pg.gda.pl, p. 732 dr inż. Piotr Odya - piotrod@sound.eti.pg.gda.pl, p. 730 Plan przedmiotu ZPS Cele nauczania
Adam Korzeniewski - adamkorz@sound.eti.pg.gda.pl, p. 732 dr inż. Grzegorz Szwoch - greg@sound.eti.pg.gda.pl, p. 732 dr inż. Piotr Odya - piotrod@sound.eti.pg.gda.pl, p. 730 Plan przedmiotu ZPS Cele nauczania
-> Średnia arytmetyczna (5) (4) ->Kwartyl dolny, mediana, kwartyl górny, moda - analogicznie jak
 Wzory dla szeregu szczegółowego: Wzory dla szeregu rozdzielczego punktowego: ->Średnia arytmetyczna ważona -> Średnia arytmetyczna (5) ->Średnia harmoniczna (1) ->Średnia harmoniczna (6) (2) ->Średnia
Wzory dla szeregu szczegółowego: Wzory dla szeregu rozdzielczego punktowego: ->Średnia arytmetyczna ważona -> Średnia arytmetyczna (5) ->Średnia harmoniczna (1) ->Średnia harmoniczna (6) (2) ->Średnia
Próba własności i parametry
 Próba własności i parametry Podstawowe pojęcia Zbiorowość statystyczna zbiór jednostek (obserwacji) nie identycznych, ale stanowiących logiczną całość Zbiorowość (populacja) generalna skończony lub nieskończony
Próba własności i parametry Podstawowe pojęcia Zbiorowość statystyczna zbiór jednostek (obserwacji) nie identycznych, ale stanowiących logiczną całość Zbiorowość (populacja) generalna skończony lub nieskończony
Analiza obrazów - sprawozdanie nr 3
 Analiza obrazów - sprawozdanie nr 3 Przekształcenia morfologiczne Przekształcenia morfologiczne wywodzą się z morfologii matematycznej, czyli dziedziny, która opiera się na teorii zbiorów, topologii i
Analiza obrazów - sprawozdanie nr 3 Przekształcenia morfologiczne Przekształcenia morfologiczne wywodzą się z morfologii matematycznej, czyli dziedziny, która opiera się na teorii zbiorów, topologii i
SYSTEMY UCZĄCE SIĘ WYKŁAD 10. PRZEKSZTAŁCANIE ATRYBUTÓW. Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska.
 SYSTEMY UCZĄCE SIĘ WYKŁAD 10. PRZEKSZTAŁCANIE ATRYBUTÓW Częstochowa 2014 Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska INFORMACJE WSTĘPNE Hipotezy do uczenia się lub tworzenia
SYSTEMY UCZĄCE SIĘ WYKŁAD 10. PRZEKSZTAŁCANIE ATRYBUTÓW Częstochowa 2014 Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska INFORMACJE WSTĘPNE Hipotezy do uczenia się lub tworzenia
1 Podstawy rachunku prawdopodobieństwa
 1 Podstawy rachunku prawdopodobieństwa Dystrybuantą zmiennej losowej X nazywamy prawdopodobieństwo przyjęcia przez zmienną losową X wartości mniejszej od x, tzn. F (x) = P [X < x]. 1. dla zmiennej losowej
1 Podstawy rachunku prawdopodobieństwa Dystrybuantą zmiennej losowej X nazywamy prawdopodobieństwo przyjęcia przez zmienną losową X wartości mniejszej od x, tzn. F (x) = P [X < x]. 1. dla zmiennej losowej
Uniwersytet Warszawski, Wydział Fizyki
 TELEDETEKCJA A źródło B oddziaływanie z atmosferą C obiekt, oddziaływanie z obiektem D detektor E zbieranie danych F analiza G zastosowania A C B D E F G Obraz wejściowy Analiza Algorytmy przetwarzania
TELEDETEKCJA A źródło B oddziaływanie z atmosferą C obiekt, oddziaływanie z obiektem D detektor E zbieranie danych F analiza G zastosowania A C B D E F G Obraz wejściowy Analiza Algorytmy przetwarzania
PRZETWARZANIE SYGNAŁÓW LABORATORIUM
 2018 AK 1 / 5 PRZETWARZANIE SYGNAŁÓW LABORATORIUM Ćw. 0 Wykonujący: Grupa dziekańska: MATLAB jako narzędzie w przetwarzaniu sygnałów Grupa laboratoryjna: (IMIĘ NAZWISKO, nr albumu) Punkty / Ocena Numer
2018 AK 1 / 5 PRZETWARZANIE SYGNAŁÓW LABORATORIUM Ćw. 0 Wykonujący: Grupa dziekańska: MATLAB jako narzędzie w przetwarzaniu sygnałów Grupa laboratoryjna: (IMIĘ NAZWISKO, nr albumu) Punkty / Ocena Numer
Cyfrowe przetwarzanie obrazów i sygnałów Wykład 2 AiR III
 1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
