TESTY I KORELACJE cz.2
|
|
|
- Stanisława Kasprzak
- 8 lat temu
- Przeglądów:
Transkrypt
1 TESTY I KORELACJE cz.2 1. JEDNOCZYNNIKOWA ANALIZA WARIANCJI ANOVA W SCHEMACIE MIĘDZYGRUPOWYM Analizę wariancji można podzielić na dwa typy: a) Ze względu na liczbę czynników: Jednoczynnikowa gdy po stronie zmiennych niezależnych jest jedna zmienna; Wieloczynnikowa gdy po stronie zmiennych niezależnych jest ich więcej niż jedna; b) Ze względu na relacje pomiędzy porównywanymi grupami: Schemat międzygrupowy porównywane grupy są względem siebie niezależne (badane jednostki przynależą tylko do jednej z tych grup); Schemat wewnątrzgrupowy porównywane grupy są od siebie zależne, co oznacza w praktyce, że mamy tę samą grupę badanych jednostek, a dane pochodzą z kolejnych pomiarów (np. jak w klasycznym eksperymencie: pretest bodziec posttest). Mamy więc w sumie cztery możliwości: Analiza wariancji jednoczynnikowa w schemacie międzygrupowym; Analiza wariancji jednoczynnikowa w schemacie wewnątrzgrupowym; Analiza wariancji wieloczynnikowa w schemacie międzygrupowym; Analiza wariancji wieloczynnikowa w schemacie wewnątrzgrupowym. My zajmiemy się tylko pierwszą możliwością: analizą wariancji jednoczynnikową w schemacie międzygrupowym, dalej zwaną skrótowo ANOVA. Czyli po stronie zmiennych niezależnych będzie jedna zmienna (jeden czynnik), a dane porównywanych grup nie będą ze sobą powiązane. ANOVA to: Test parametryczny; Porównywanym parametrem jest średnia; ANOVA porównuje średnie z więcej niż dwóch grup. Przypominam, że testem parametrycznym porównującym średnie z dokładnie dwóch grup jest test t-studenta. W przypadku ANOVY grup ma być więc więcej niż 2. Wyznaczać można je podobnie jak w przypadku testu t-studenta: albo zmienna niezależna jest oryginalnie wielowartościowa i w tym stanie ją pozostawiamy; albo zmienna niezależna jest oryginalnie wielowartościowa i dla celów analitycznych rekodujemy ją tak, by zmniejszyć liczbę wartości (i co za tym idzie: porównywanych grup), ale wciąż będzie to więcej niż 2 grupy. 1
2 Układ hipotez: Hipoteza zerowa: nie różnic pomiędzy średnimi w porównywanych grupach; zmienna niezależna nie różnicuje średnich; nie ma związku pomiędzy zmiennymi H 0 : μ 1 = μ 2 = = μ k Hipoteza alternatywna: jest różnica pomiędzy średnimi w porównywanych grupach; zmienna niezależna różnicuje średnie; jest związek pomiędzy zmiennymi; H 1 : ~ H 0 => średnie różnią się, tzn. przynajmniej jedna średnia różni się od pozostałych Logika działania testu Porównanie dwóch typów wariancji Wariancji wewnątrzgrupowych (tzw. wariancje błędu) czyli wewnątrz każdej z porównywanych grup -> tu nie powinno być różnic, grupy w środku mają być jak najbardziej homogeniczne; Wariancji międzygrupowych czyli pomiędzy porównywanymi grupami -> tu, jeśli mamy mówić o zależności pomiędzy zmiennymi, to różnice powinny być, czyli grupy między sobą mają być heterogeniczne. Z ww. logiki działania testu wynikają wymagania, których spełnienia domaga się ANOVA: a) Rozkład zmiennej zależnej w każdej z porównywanych grup ma być normalny: Dla sprawdzenia rozkładu należy wykonać test Kołmogorowa-Smirnowa/test Shapiro-Wilka; Jeśli warunek jest niespełniony, to można rozważać zastąpienie ANOVY jej nieparametrycznym odpowiednikiem: testem Kruskala-Wallisa; W praktyce ten warunek się pomija, bo przyjęto, że ANOVA jest całkiem nieźle odporna na jego niespełnienie. b) Porównywane grupy mają być równoliczne Równość rozkładu sprawdza test chi-kwadrat dla jednej zmiennej; Jeśli warunek jest niespełniony, to można: o rozważać zastąpienie ANOVY jej nieparametrycznym odpowiednikiem: testem Kruskala- Wallisa; o zdekodować zmienną niezależną tak, by grupy były równoliczne może pomóc; W praktyce często równoliczność grup ocenia się na oko i dopuszcza różnice od kilku do kilkudziesięciu jednostek. Należy po prostu pilnować, by dysproporcje w liczebności grup nie były zbyt duże (np. 30 : 200). c) Porównywane grupy mają mieć homogeniczne wariancje Warunek najważniejszy; Homogeniczność wariancji sprawdza test Levene a (jeśli jego istotność jest mniejsza niż 0,05 to wariancje nie są homogeniczne); 2
3 W przypadku niespełnienia warunku homogeniczności wariancji: o Najlepiej zastąpić ANOVĘ jej nieparametrycznym odpowiednikiem: testem Kruskala- Wallisa; o Ewentualnie policzyć ANOVĘ z poprawką, czyli testy Welcha (bardziej konserwatywny) Brown-Forsythe a (bardziej liberalny) Przykład Filtr: rok badania 2010; Zmienna niezależna: wiek w przedziałach -> jej wartości będą stanowiły porównywane grupy; Zmienna zależna: re6 Mężczyzna zarabiać, kobieta w domu Przedstawię wzorcowy sposób przeprowadzania ANOVY. W praktyce najczęściej od razu wykonuje się test analizy wariancji z testem Levene a i ew. potem sprawdza równoliczność grup i rozkład normalny zmiennej zależnej w grupach. Krok 1: Sprawdzamy, czy zmienna zależna w porównywanych grupach ma rozkład normalny. Test Kołmogorowa-Smirnowa Interpretacja wyniku testu: Testy normalności rozkładu Wiek respondenta (Podzielone) Kołmogorow-Smirnow a Statystyka df Istotność <= 25, , , ,000 Mężczyz zarabiać, kobieta w domu 36-45, , , ,000 a. Z poprawką istotności Lillieforsa 56-65, , , ,000 W każdej z grup istotność testu jest mniejsza niż 0,05, co oznacza, że wszędzie rozkład zmiennej zależnej nie jest normalny. 3
4 Aby ocenić jak bardzo rozkłady odstają od rozkładu normalnego należy: przyjrzeć się wygenerowanym histogramom albo dla każdej z grup dokonać następujących obliczeń: o wartość kurtozy przez jej błąd standardowy o wartość skośności przez jej błąd standardowy jeśli wynik mieści się między -2 a 2 to rozkład jest w miarę blisko rozkładu normalnego. Z tabelki Statystyki opisowe można więc wyciągnąć następujące dane (ostatnia kolumna została dodana przeze mnie w Excelu) Statystyki opisowe (DESCRIPTIVES) statystyka Wiek respondenta (Podzielone) Statystyka Błąd standardowy przez błąd stand. Mężczyz <= 25 Skośność -,270,177-1,52 zarabiać, Kurtoza kobieta w -,820,353-2,32 domu Skośność -,276,154-1,80 Kurtoza -,982,306-3, Skośność -,298,168-1,77 Kurtoza -,908,335-2, Skośność,152,167 0,91 Kurtoza -1,060,332-3, Skośność,194,170 1,14 Kurtoza -1,099,339-3, Skośność,659,188 3,51 Kurtoza -,262,374-0,70 Jak widać w przypadku wszystkich grup poza ostatnią wartość większą niż -2 przyjmuje iloraz kurtozy przez jej błąd standardowy. Rozkład zmiennej w tych grupach jest więc nadmiernie spłaszczony w stosunku do rozkładu normalnego. Z kolei w grupie ostatniej rozkład jest zbyt mocno asymetryczny (przesunięty w prawo). Przeprowadzona powyżej analiza rozkładów powinna nas odwieść od wykonywania ANOVY. Jednakże, jak już wcześniej wspomniałam, ANOVA jest dość odporna na niespełnienie warunku normalności rozkładu. Możemy więc przyjąć, że był to jednak bardzo słaby argument przeciw i nadal rozważamy wykonanie analizy wariancji. 4
5 Krok 2 Sprawdzamy, czy porównywane grupy są równoliczne. Najłatwiej ocenić to na oko, czyli po prostu wygenerować rozkład analizowanej zmiennej Wiek respondenta (Podzielone) Częstość Procent Procent ważnych Procent skumulowany <= ,5 15,5 15, ,4 20,4 35, ,8 16,8 52,7 Ważne ,3 17,3 70, ,5 16,5 86, ,6 13,6 100,0 Ogółem ,0 100,0 Wyróżnione przez nas grupy nie są idealnie równoliczne. Najmniejsza z nich to przedział 66 lat i wyżej (171 osób), a największa to przedział lat (257 osób). Różnica między tymi dwiema grupami to 86 osób. Czy to dużo czy mało? Trudno jednoznacznie orzec. Dlatego, gdy nie jesteśmy pewni, czy stwierdzone różnice w liczebności grup są istotne, warto posłużyć się odpowiednim testem. Test chi-kwadrat dla jednej zmiennej Statystyki testu Wiek respondenta (Podzielone) Chi-kwadrat 15,573 a df 5 Istotność asymptotyczna,008 a. 0 komórek (0,0%) ma liczebność oczekiwaną mniejszą od 5. Minimalna liczebność oczekiwana w komórce wynosi 220,0. Interpretacja testu: Istotność testu jest mniejsza niż 0,05 co daje nam podstawy do odrzucenia hipotezy zerowej o losowości rozkładu. W naszym przypadku rozkład zmiennej nie jest losowy i stwierdzone różnice w liczebności grup są istotne (ważne). 5
6 Warunek równoliczności grup także nie został spełniony. Mamy więc już dwa argumenty za rezygnacją z ANOVY. Tyle, że: Przy braku rozkładu normalnego wiemy, że analiza wariancji jest na to odporna. Dysproporcja w liczebności grup nie jest rażąca. Przyjrzyjmy się więc ostatniemu i najważniejszemu warunkowi: homogeniczności wariancji. Jeśli i on nie zostanie spełniony na pewno będziemy musieli zrezygnować z ANOVY na rzecz testu Kruskala-Wallisa. Jeśli wariancje będą homogeniczne, to możemy zostać przy ANOVIE jedynie traktując jej wynik z lekką dozą nieufności. Krok 3: Sprawdzamy homogeniczność wariancji. Test Levene a sprawdzający homogeniczność wariancji wykonamy równocześnie z testem ANOVY. ANALIZA -> PORÓWNYWANIE ŚREDNICH -> JEDNOCZYNNIKOWA ANOVA Zmienna zależna: re6 Mężczyzna zarabiać, kobieta w domu Czynnik (zmienna niezależna): wiek w przedziałach Opcje: o Statystyki opisowe o Test jednorodności wariancji o Brown-Forsythe (na wszelki wypadek, gdyby wyszła niehomogeniczność wariancji) o Welch (na wszelki wypadek, gdyby wyszła niehomogeniczność wariancji) Syntax ONEWAY re6 BY q9age_rek /STATISTICS DESCRIPTIVES HOMOGENEITY BROWNFORSYTHE WELCH /MISSING ANALYSIS. W linii kodu jest ONEWAY [zmienna zależna] BY [zmienna niezależna] Po wykonaniu polecenia najpierw zaglądamy do tabeli testu jednorodności wariancji: Test jednorodności wariancji Mężczyz zarabiać, kobieta w domu Test Levene'a df1 df2 Istotność 1, ,204 6
7 Przypominam, że test ten sprawdza homogeniczność wariancji (jego H o zakłada równość wariancji): Gdy istotność testu Levene a jest mniejsza niż 0,05 -> test jest istotny, a wariancje nie są homogeniczne; Gdy istotność testu Levene a jest większa niż 0,05 -> test jest nieistotny, a wariancje są homogeniczne; W naszym przypadku istotność testu Levene a jest większa niż 0,05, co oznacza, że wariancje są homogeniczne. Tym samym ostatni i najważniejszy warunek ANOVY został spełniony. Nie musimy więc ani rezygnować z ANOVY na rzecz testu Kruskala-Wallisa, ani zamiast ANOVY interpretować wyników testów Welcha i Brown-Forsythe a. Skoro już wiemy, że ANOVA będzie (w miarę) wiarygodnym testem, to jaki jest jej wynik? Istotność testu analizy wariancji jest mniejsza niż 0,05 co oznacza, że jest zależność pomiędzy zmiennymi. Mężczyz zarabiać, kobieta w domu Jednoczynnikowa ANOVA Suma kwadratów df Średni kwadrat F Istotność Między grupami 96, ,362 14,180,000 Wewnątrz grup 1671, ,365 Ogółem 1768, F(df 1, df 2 ) = [wartość]; [istotność] < 0,05 F(5, 1224) = 14,180; p<0,05 [gdyby nie było zależności opis wyglądałby tak: F(5, 1224) = 14,180; p>0,05 ] Interpretacja: Aby sprawdzić, czy odpowiedzi respondentów na pytanie Mężczyzna powinien zarabiać, a kobieta powinna siedzieć w domu są zróżnicowane ze względu na wiek, wykonano jednoczynnikową analizę wariancji ANOVA. Test F(5, 1224) = 14,180; p<0,05 wykazał, że wiek różnicuje opinie. W tym miejscu trzeba pamiętać, że ANOVA mówi nam tylko o tym, czy są różnice w średnich pomiędzy porównywanymi grupami. Nie wskazuje natomiast, w jaki sposób porównywane grupy różnią się od siebie np. u nas która kategoria wiekowo mocniej optuje za tradycyjnym podziałem ról w rodzinie. 7
8 Przybliżoną odpowiedź daje analiza średnich w poszczególnych grupach, którą mamy w tabelce Statystyki opisowe : Mężczyz zarabiać, kobieta w domu Statystyki opisowe N Średnia Odchylenie standardowe Błąd standardowy 95% przedział ufności dla średniej Minimum Maksimum Dolna granica Górna granica <= ,12 1,158,085 2,96 3, ,19 1,202,076 3,04 3, ,08 1,144,079 2,93 3, ,78 1,156,079 2,62 2, ,65 1,207,085 2,48 2, ,39 1,126,087 2,22 2, Ogółem ,89 1,199,034 2,83 2, Widać w niej, że im wyższa kategoria wiekowe, tym średnia ocen niższa (czyli wzrasta akceptacja dla badanego twierdzenia, bo kafeteria ułożona jest odwrotnie: 1 to zdecydowanie się zgadza, a 5 zdecydowanie się nie zgadza ). Czy jednak różnice w średnich pomiędzy poszczególnymi grupami są istotne statystycznie? ANOVA powiedziała tylko tyle, że tam gdzieś są takie ważne statystycznie różnice, nie wskazała zaś gdzie dokładnie. Do szczegółowej analizy służą w tym miejscu testy post hoc. Wariancje homogeniczne Wariancje niehomogeniczne Test Uwagi Test Uwagi S-N-K Bardzo liberalny Games-Howell Nierówne grupy Bonferroni Konserwatywny Mała liczba grup Tukey Konserwatywny Duża liczba grup C Dunnett T2 Konserwatywny Scheffe Bardzo konserwatywny Gabriel Dość liberalny Nierówne grupy Mamy homogeniczne wariancje, więc wybór zawęża się do testów S-N-K, Bonferroniego, Tukey a, Scheffe go i Gabriela. Odrzucimy S-N-K jako bardzo liberalny i Scheffe go jako bardzo konserwatywny. Bardzo liberalny test mógłby nam pokazać, że istnieją różnice tam, gdzie ich nie ma; z kolei bardzo 8
9 konserwatywny może wykazać, że nie ma różnic tam, gdzie faktycznie są. Odrzucimy też Bonferroniego, ponieważ mamy dużo porównywanych grup (dokładnie to 6). Zostaje nam więc konserwatywny Tukey i dość liberalny Gabriel. I te dwa testy post hoc wykonamy, licząc, że ich wynik nie będzie się za bardzo różnił. Jeszcze raz wywołujemy ANOVĘ, tym razem w zakładce Post hoc zaznaczamy Tukey i Gabriel. Przy okazji w zakładce Opcje możemy wszystko poodhaczać. Syntax ONEWAY re6 BY q9age_rek /MISSING ANALYSIS /POSTHOC=TUKEY GABRIEL ALPHA(0.05). Przy korzystaniu z innych testów post hoc w linii kodu /POSTHOC= można wpisać zaraz za znakiem równości, bez przecinków pomiędzy ale ze spacjami, ich nazwy SNK -> dla testu S-N-K TUKEY -> dla testu Tukey a SCHEFFE -> dla testu Scheffe go BONFERRONI -> dla testu Bonferroniego GABRIEL -> dla testu Gabriela T2 -> dla testu T2 GH -> dla testu Games-Howella C -> dla testu C Dunnetta Po nazwach wybranych testów musi pozostać w tej samej linii wpisane ALPHA(0.05). 9
10 Po wykonaniu polecenia dostajemy dwie tabele. Najpierw bardzo dużą opisaną jako Post hoc Porównania wielokrotne Zmienna zależna: Mężczyz zarabiać, kobieta w domu (I) Wiek respondenta (Podzielone) <= Test Tukey'a HSD <= 25 Test Gabriela (J) Wiek respondenta Różnica Błąd Istotność (Podzielone) średnich standardowy (I-J) 95% przedział ufności Dolna Górna granica granica ,065,113,993 -,39, ,043,118,999 -,29, ,347 *,117,036,01, ,476 *,118,001,14,81 66+,735 *,124,000,38 1,09 <= 25,065,113,993 -,26, ,108,109,923 -,20, ,412 *,109,002,10, ,541 *,110,000,23,86 66+,800 *,117,000,47 1,13 <= 25 -,043,118,999 -,38, ,108,109,923 -,42, ,305,114,081 -,02, ,433 *,115,002,10,76 66+,692 *,121,000,35 1,04 <= 25 -,347 *,117,036 -,68 -, ,412 *,109,002 -,72 -, ,305,114,081 -,63, ,129,115,872 -,20,46 66+,387 *,121,017,04,73 <= 25 -,476 *,118,001 -,81 -, ,541 *,110,000 -,86 -, ,433 *,115,002 -,76 -, ,129,115,872 -,46,20 66+,259,122,278 -,09,61 <= 25 -,735 *,124,000-1,09 -, ,800 *,117,000-1,13 -, ,692 *,121,000-1,04 -, ,387 *,121,017 -,73 -, ,259,122,278 -,61, ,065,113 1,000 -,39, ,043,118 1,000 -,30, ,347 *,117,045,00, ,476 *,118,001,13,82 66+,735 *,124,000,37 1,10 <= 25,065,113 1,000 -,26, ,108,109,997 -,21,43 10
11 46-55,412 *,109,002,09, ,541 *,110,000,22,86 66+,800 *,117,000,46 1,14 <= 25 -,043,118 1,000 -,39, ,108,109,997 -,43, ,305,114,108 -,03, ,433 *,115,003,10,77 66+,692 *,121,000,34 1,05 <= 25 -,347 *,117,045 -,69, ,412 *,109,002 -,73 -, ,305,114,108 -,64, ,129,115,989 -,21,46 66+,387 *,121,020,03,74 <= 25 -,476 *,118,001 -,82 -, ,541 *,110,000 -,86 -, ,433 *,115,003 -,77 -, ,129,115,989 -,46,21 66+,259,122,404 -,10,62 <= 25 -,735 *,124,000-1,10 -, ,800 *,117,000-1,14 -, ,692 *,121,000-1,05 -, ,387 *,121,020 -,74 -, ,259,122,404 -,62,10 *. Różnica średnich jest istotna na poziomie Testy post hoc to w gruncie rzeczy nic innego niż seria testów t dla dwóch grup. Jak można się zorientować po budowie tabeli każda grupa jest konfrontowana z każdą. Jeśli różnica średnich dwóch grup jest istotna (w kolumnie Istotność mamy mniej 0,05), to SPSS dodatkowo sygnalizuje to * w kolumnie Różnica średnich. Dla ułatwienia oznaczyłam kolorami istotne różnice pomiędzy grupami. Widać, że po pierwsze oba testy i konserwatywny, i liberalny dały taki sam obraz. Po drugie, że: a) Różnice pomiędzy najmłodszymi grupami respondentów ( do 25 lat, lat oraz lat ) są nieznaczne i nieistotne statystycznie. b) Zdecydowanie odróżnia się grupa najstarszych respondentów: 66 lat i wyżej. 11
12 Te same informacje niesie druga z tabel wygenerowanych przez testy post hoc: Grupy jednorodne. Mężczyz zarabiać, kobieta w domu Wiek respondenta N Podzbiór dla alfa = 0.05 (Podzielone) , ,65 2, ,78 2,78 Test Tukey'a HSD a,b ,08 3,08 <= , ,19 Istotność,227,879,093, , ,65 2, ,78 2,78 Test Gabriela a,b ,08 3,08 <= , ,19 Istotność,329,991,126,999 Wyświetlane są średnie dla grup jednorodnych. a. Użyto średniej harmonicznej wielkości próby = 201,917. b. Liczebności grup nie są równe. Została użyta średnia harmoniczna liczebności grup. Poziomy błędów pierwszego rodzaju nie są zagwarantowane. Tabela pokazuje istotne podobieństwa pomiędzy porównywanymi grupami (czyli między kim a kim brak jest różnic). Ponownie wyniki obu testów (Tukey a i Gabriela) nie różnią się. Z tabeli zaś można wywnioskować, że można by wyłonić 4 podzbiory podobnych grup. Byłyby to jednak podzbiory nierozłączne są takie grupy, które należą do dwóch podzbiorów ( lat, lat, lat ). Ta płynność granic pomiędzy podzbiorami oznacza, że opinie wraz z wiekiem nie zmieniają się radykalnie, ale ewoluują. Wyjątek stanowią tu najstarsi i najmłodsi respondenci te kategorie należą tylko do max jednego podzbioru. Są więc w swoich opiniach najbardziej zdecydowani. 12
13 2. WSPÓŁCZYNNIK KORELACJI RANG RHO SPEARMANA Współczynnik stosowany, gdy obie zmienne są na poziomie porządkowym lub ilościowym. Przykład dla zmiennych: Filtr: rok 2010 re6 - Mężczyzna zarabiać, kobieta w domu (zmienna zależna) re31 Resp osobą religijną/niereligijną (zmienna niezależna) Zanim sprawdzimy czy i jak silna jest korelacja między zmiennymi re6 i re31, trzeba sprawdzić dwie rzeczy: a) braki danych w obu przypadkach odpowiedź z kodem 8 czyli trudno powiedzieć powinna trafić do braków danych; b) kierunek zmiennych kody dla zmiennej re6 ułożone są tak, że im wyższy kod, tym mniejsza akceptacja stwierdzenia (5 zdecydowanie się nie zgadzam ) kody dla zmiennej re31 ułożone są tak, że im wyższy kod, tym mniejsza deklarowana religijność (7 osoba wyjątkowo niereligijna ) Kierunek zmiennych jest ważny, by później bez błędu orzec o kierunku samej zależności. ANALIZA -> KORELACJE -> PARAMI w okienku po prawej stronie umieścić obie analizowane zmienne (w dowolnej kolejności) w opcjach na dole okna zaznaczyć Spearman, a odznaczyć domyślnego Pearsona test istotności zostawić jako dwustronna Syntax NONPAR CORR /VARIABLES=re6 re31 /PRINT=SPEARMAN TWOTAIL NOSIG /MISSING=PAIRWISE. 13
14 Po wywołaniu polecenia otrzymujemy następującą tabelę: Korelacje Mężczyz Resp osobą zarabiać, religijną/niereligij kobieta w domu ną Współczynnik korelacji 1,000,158 ** Mężczyz zarabiać, kobieta w Istotność (dwustronna).,000 domu N rho Spearmana Współczynnik korelacji,158 ** 1,000 Resp osobą Istotność (dwustronna),000. religijną/niereligijną N **. Korelacja jest istotna na poziomie 0.01 (dwustronnie). Korelacja została policzona w obie strony, tzn. każda zmienna została potraktowana raz jako zależna, a raz jako niezależna. Można było wcześniej poprosić o test istotności jednostronny, ale wówczas ważna by była kolejność zmiennych na liście. Tak jak zrobiliśmy jest prościej. Dla nas zmienną niezależną jest religijność respondenta, więc czytamy drugi wiersz tabeli: istotność jest mniejsza niż 0,05 (a nawet mniejsza niż 0,01), co oznacza, że korelacja jest istotna statystycznie; wartość współczynnika korelacji r s = 0,158 co oznacza, że jest to korelacja słaba; znak współczynnika (+) wskazuje, że jest to korelacja wprost proporcjonalna: wzrastającym wartościom (a raczej: kodom odpowiedzi) jednej zmiennej towarzyszą rosnące wartości (kody odpowiedzi) drugiej zmiennej. Interpretacja: Na podstawie wartości współczynnika korelacji rang Spearmana stwierdzono, że istnieje słaba zależność pomiędzy deklaratywną religijnością respondenta a jego opinią nt. podziału ról w rodzinie (r s = 0,158). Korelacja jest wprost proporcjonalna, im mniej religijny respondent, tym częściej odrzucał twierdzenie, że kobieta powinna zajmować się domem, a mężczyzna na dom zarabiać. 14
15 3. WSPOŁCZYNNIK KORELACJI LINIOWEJ R-PEARSONA Współczynnik stosowany, gdy obie zmienne są na poziomie ilościowym. Przykład dla zmiennych: Filtr: rok 2010 re6 - Mężczyzna zarabiać, kobieta w domu (zmienna zależna) q9age Wiek (zmienna niezależna) Zanim sprawdzimy czy i jak silna jest korelacja między zmiennymi re6 i q9age, trzeba sprawdzić dwie rzeczy: c) braki danych w przypadku zmiennej re6 odpowiedź z kodem 8 czyli trudno powiedzieć powinna trafić do braków danych; w przypadku wieku nie ma braków danych; d) kierunek zmiennych kody dla zmiennej re6 ułożone są tak, że im wyższy kod, tym mniejsza akceptacja stwierdzenia (5 zdecydowanie się nie zgadzam ) w przypadku wieku kod jest jednocześnie liczbą lat respondenta. Kierunek zmiennych jest ważny, by później bez błędu orzec o kierunku samej zależności. ANALIZA -> KORELACJE -> PARAMI w okienku po prawej stronie umieścić obie analizowane zmienne (w dowolnej kolejności) w opcjach na dole okna pozostawić domyślnego Pearsona test istotności zostawić jako dwustronna Syntax CORRELATIONS /VARIABLES=re6 q9age /PRINT=TWOTAIL NOSIG /MISSING=PAIRWISE. 15
16 Po wywołaniu polecenia otrzymujemy następującą tabelę: Korelacje Mężczyz zarabiać, Wiek respondenta kobieta w domu Korelacja Pearsona 1 -,228 ** Mężczyz zarabiać, kobieta w domu Istotność (dwustronna),000 N Korelacja Pearsona -,228 ** 1 Wiek respondenta Istotność (dwustronna),000 N **. Korelacja jest istotna na poziomie 0.01 (dwustronnie). Korelacja została policzona w obie strony, tzn. każda zmienna została potraktowana raz jako zależna, a raz jako niezależna. Można było wcześniej poprosić o test istotności jednostronny, ale wówczas ważna by była kolejność zmiennych na liście. Tak jak zrobiliśmy jest prościej. Dla nas zmienną niezależną jest wiek respondenta, więc czytamy drugi wiersz tabeli: istotność jest mniejsza niż 0,05 (a nawet mniejsza niż 0,01), co oznacza, że korelacja jest istotna statystycznie; wartość współczynnika korelacji r xy = -0,228 co oznacza, że jest to korelacja słaba; znak współczynnika (-) wskazuje, że jest to korelacja odwrotnie proporcjonalna: wzrastającym wartościom (a raczej: kodom odpowiedzi) jednej zmiennej towarzyszą malejące wartości (kody odpowiedzi) drugiej zmiennej. Interpretacja: Na podstawie wartości współczynnika korelacji liniowej r-pearsona stwierdzono, że istnieje umiarkowana zależność pomiędzy wiekiem respondenta a jego opinią nt. podziału ról w rodzinie (r xy = -0,228). Korelacja jest odwrotnie proporcjonalna, im starszy respondent, tym częściej akceptował twierdzenie, że kobieta powinna zajmować się domem, a mężczyzna na dom zarabiać. 16
17 Przy współczynniki korelacji liniowej r-pearsona trzeba pamiętać o jeszcze jednej rzeczy. To współczynnik, który świetnie radzi sobie z wykrywaniem zależności prostoliniowych: a) wprost proporcjonalnych b) odwrotnie proporcjonalnych Natomiast ten współczynnik nie radzi sobie z korelacjami krzywoliniowymi. Widzi wówczas nakładające się na siebie dwie linie korelacji liniowej: jedną wprost i jedną odwrotnie proporcjonalną: I w efekcie może wskazać na brak lub bardzo słabą korelację. Dlatego warto przy słabej korelacji liniowej policzyć jeszcze współczynnik eta ( ). Mając wartości współczynników r-pearsona i eta można obliczyć miernik stopnia krzywoliniowości: m = 2 2 r xy Jeśli wynik: m 0,2 to mamy korelacje prostoliniową i interpretację opieramy na r-pearsona m > 0,2 to mamy korelację krzywoliniową i interpretację opieramy na eta. W naszym przypadku: r xy = -0,228 xy = 0,306 m = 2 r 2 xy = (0,306) 2 (-0,228) 2 = 0,094 0,052 = 0,042 miernik krzywoliniowości jest mniejszy niż 0,2, co oznacza, że naszą korelację możemy traktować jako prostoliniową i orzekać o niej na podstawie wartości współczynnika r-pearsona 17
Jednoczynnikowa analiza wariancji
 Jednoczynnikowa analiza wariancji Zmienna zależna ilościowa, numeryczna Zmienna niezależna grupująca (dzieli próbę na więcej niż dwie grupy), nominalna zmienną wyrażoną tekstem należy w SPSS przerekodować
Jednoczynnikowa analiza wariancji Zmienna zależna ilościowa, numeryczna Zmienna niezależna grupująca (dzieli próbę na więcej niż dwie grupy), nominalna zmienną wyrażoną tekstem należy w SPSS przerekodować
ANALIZY WIELOZMIENNOWE
 ANALIZY WIELOZMIENNOWE ANALIZA REGRESJI Charakterystyka: Rozszerzenie analizy korelacji o badanie zależności pomiędzy wieloma zmiennymi jednocześnie; Podstawowe zastosowanie (ale przez nas w tym momencie
ANALIZY WIELOZMIENNOWE ANALIZA REGRESJI Charakterystyka: Rozszerzenie analizy korelacji o badanie zależności pomiędzy wieloma zmiennymi jednocześnie; Podstawowe zastosowanie (ale przez nas w tym momencie
TESTY I KORELACJE cz.1
 TESTY I KORELACJE cz.1 TESTY I KORELACJE - WPROWADZENIE Podstawowe narzędzia statystyki indukcyjnej to testy statystyczne i współczynniki korelacji. Różnice między nimi prezentuje poniższa tabela: TEST
TESTY I KORELACJE cz.1 TESTY I KORELACJE - WPROWADZENIE Podstawowe narzędzia statystyki indukcyjnej to testy statystyczne i współczynniki korelacji. Różnice między nimi prezentuje poniższa tabela: TEST
Testy nieparametryczne
 Testy nieparametryczne Testy nieparametryczne możemy stosować, gdy nie są spełnione założenia wymagane dla testów parametrycznych. Stosujemy je również, gdy dane można uporządkować według określonych kryteriów
Testy nieparametryczne Testy nieparametryczne możemy stosować, gdy nie są spełnione założenia wymagane dla testów parametrycznych. Stosujemy je również, gdy dane można uporządkować według określonych kryteriów
Jak sprawdzić normalność rozkładu w teście dla prób zależnych?
 Jak sprawdzić normalność rozkładu w teście dla prób zależnych? W pliku zalezne_10.sta znajdują się dwie zmienne: czasu biegu przed rozpoczęciem cyklu treningowego (zmienna 1) oraz czasu biegu po zakończeniu
Jak sprawdzić normalność rozkładu w teście dla prób zależnych? W pliku zalezne_10.sta znajdują się dwie zmienne: czasu biegu przed rozpoczęciem cyklu treningowego (zmienna 1) oraz czasu biegu po zakończeniu
Testy t-studenta są testami różnic pomiędzy średnimi czyli służą do porównania ze sobą dwóch średnich
 Testy t-studenta są testami różnic pomiędzy średnimi czyli służą do porównania ze sobą dwóch średnich Zmienne muszą być zmiennymi ilościowym (liczymy i porównujemy średnie!) Są to testy parametryczne Nazwa
Testy t-studenta są testami różnic pomiędzy średnimi czyli służą do porównania ze sobą dwóch średnich Zmienne muszą być zmiennymi ilościowym (liczymy i porównujemy średnie!) Są to testy parametryczne Nazwa
JEDNOCZYNNIKOWA ANOVA
 Analizę ANOVA wykorzystujemy do wykrycia różnic pomiędzy średnimi w więcej niż dwóch grupach/więcej niż w dwóch pomiarach JEDNOCZYNNIKOWA ANOVA porównania jednej zmiennej pomiędzy więcej niż dwoma grupami
Analizę ANOVA wykorzystujemy do wykrycia różnic pomiędzy średnimi w więcej niż dwóch grupach/więcej niż w dwóch pomiarach JEDNOCZYNNIKOWA ANOVA porównania jednej zmiennej pomiędzy więcej niż dwoma grupami
Przykład 2. Na podstawie książki J. Kowal: Metody statystyczne w badaniach sondażowych rynku
 Przykład 2 Na podstawie książki J. Kowal: Metody statystyczne w badaniach sondażowych rynku Sondaż sieciowy analiza wyników badania sondażowego dotyczącego motywacji w drodze do sukcesu Cel badania: uzyskanie
Przykład 2 Na podstawie książki J. Kowal: Metody statystyczne w badaniach sondażowych rynku Sondaż sieciowy analiza wyników badania sondażowego dotyczącego motywacji w drodze do sukcesu Cel badania: uzyskanie
dr hab. Dariusz Piwczyński, prof. nadzw. UTP
 dr hab. Dariusz Piwczyński, prof. nadzw. UTP Porównanie większej niż 2 liczby grup (k>2) Zmienna zależna skala przedziałowa Zmienna niezależna skala nominalna lub porządkowa 2 Istota teorii analizy wariancji
dr hab. Dariusz Piwczyński, prof. nadzw. UTP Porównanie większej niż 2 liczby grup (k>2) Zmienna zależna skala przedziałowa Zmienna niezależna skala nominalna lub porządkowa 2 Istota teorii analizy wariancji
Korelacja oznacza współwystępowanie, nie oznacza związku przyczynowo-skutkowego
 Korelacja oznacza współwystępowanie, nie oznacza związku przyczynowo-skutkowego Współczynnik korelacji opisuje siłę i kierunek związku. Jest miarą symetryczną. Im wyższa korelacja tym lepiej potrafimy
Korelacja oznacza współwystępowanie, nie oznacza związku przyczynowo-skutkowego Współczynnik korelacji opisuje siłę i kierunek związku. Jest miarą symetryczną. Im wyższa korelacja tym lepiej potrafimy
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 6
 STATYSTYKA I DOŚWIADCZALNICTWO Wykład 6 Metody sprawdzania założeń w analizie wariancji: -Sprawdzanie równości (jednorodności) wariancji testy: - Cochrana - Hartleya - Bartletta -Sprawdzanie zgodności
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 6 Metody sprawdzania założeń w analizie wariancji: -Sprawdzanie równości (jednorodności) wariancji testy: - Cochrana - Hartleya - Bartletta -Sprawdzanie zgodności
Efekt główny Efekt interakcyjny efekt jednego czynnika zależy od poziomu drugiego czynnika Efekt prosty
 ANOVA DWUCZYNNIKOWA testuje różnice między średnimi w grupach wyznaczonych przez dwa czynniki i ich kombinacje. Analiza pozwala ustalić wpływ dwóch czynników na wartości zmiennej zależnej (ilościowej!)
ANOVA DWUCZYNNIKOWA testuje różnice między średnimi w grupach wyznaczonych przez dwa czynniki i ich kombinacje. Analiza pozwala ustalić wpływ dwóch czynników na wartości zmiennej zależnej (ilościowej!)
Analiza wariancji - ANOVA
 Analiza wariancji - ANOVA Analizę wariancji, często określaną skrótem ANOVA (Analysis of Variance), zawdzięczamy angielskiemu biologowi Ronaldowi A. Fisherowi, który opracował ją w 1925 roku dla rozwiązywania
Analiza wariancji - ANOVA Analizę wariancji, często określaną skrótem ANOVA (Analysis of Variance), zawdzięczamy angielskiemu biologowi Ronaldowi A. Fisherowi, który opracował ją w 1925 roku dla rozwiązywania
Badanie zależności skala nominalna
 Badanie zależności skala nominalna I. Jak kształtuje się zależność miedzy płcią a wykształceniem? II. Jak kształtuje się zależność między płcią a otyłością (opis BMI)? III. Jak kształtuje się zależność
Badanie zależności skala nominalna I. Jak kształtuje się zależność miedzy płcią a wykształceniem? II. Jak kształtuje się zależność między płcią a otyłością (opis BMI)? III. Jak kształtuje się zależność
Analizy wariancji ANOVA (analysis of variance)
 ANOVA Analizy wariancji ANOVA (analysis of variance) jest to metoda równoczesnego badania istotności różnic między wieloma średnimi z prób pochodzących z wielu populacji (grup). Model jednoczynnikowy analiza
ANOVA Analizy wariancji ANOVA (analysis of variance) jest to metoda równoczesnego badania istotności różnic między wieloma średnimi z prób pochodzących z wielu populacji (grup). Model jednoczynnikowy analiza
Test niezależności chi-kwadrat stosuje się (między innymi) w celu sprawdzenia związku pomiędzy dwiema zmiennymi nominalnymi (lub porządkowymi)
 Test niezależności chi-kwadrat stosuje się (między innymi) w celu sprawdzenia związku pomiędzy dwiema zmiennymi nominalnymi (lub porządkowymi) Czy miejsce zamieszkania różnicuje uprawianie sportu? Mieszkańcy
Test niezależności chi-kwadrat stosuje się (między innymi) w celu sprawdzenia związku pomiędzy dwiema zmiennymi nominalnymi (lub porządkowymi) Czy miejsce zamieszkania różnicuje uprawianie sportu? Mieszkańcy
Dwuczynnikowa ANOVA dla prób niezależnych w schemacie 2x2
 Dwuczynnikowa ANOVA dla prób niezależnych w schemacie 2x2 Poniżej prezentujemy przykładowe pytania z rozwiązaniami dotyczącymi dwuczynnikowej analizy wariancji w schemacie 2x2. Wszystkie rozwiązania są
Dwuczynnikowa ANOVA dla prób niezależnych w schemacie 2x2 Poniżej prezentujemy przykładowe pytania z rozwiązaniami dotyczącymi dwuczynnikowej analizy wariancji w schemacie 2x2. Wszystkie rozwiązania są
P: Czy studiujący i niestudiujący preferują inne sklepy internetowe?
 2 Test niezależności chi-kwadrat stosuje się (między innymi) w celu sprawdzenia czy pomiędzy zmiennymi istnieje związek/zależność. Stosujemy go w sytuacji, kiedy zmienna zależna mierzona jest na skali
2 Test niezależności chi-kwadrat stosuje się (między innymi) w celu sprawdzenia czy pomiędzy zmiennymi istnieje związek/zależność. Stosujemy go w sytuacji, kiedy zmienna zależna mierzona jest na skali
Testowanie hipotez statystycznych. Wnioskowanie statystyczne
 Testowanie hipotez statystycznych Wnioskowanie statystyczne Hipoteza statystyczna to dowolne przypuszczenie co do rozkładu populacji generalnej (jego postaci funkcyjnej lub wartości parametrów). Hipotezy
Testowanie hipotez statystycznych Wnioskowanie statystyczne Hipoteza statystyczna to dowolne przypuszczenie co do rozkładu populacji generalnej (jego postaci funkcyjnej lub wartości parametrów). Hipotezy
Satysfakcja z życia rodziców dzieci niepełnosprawnych intelektualnie
 Satysfakcja z życia rodziców dzieci niepełnosprawnych intelektualnie Zadanie Zbadano satysfakcję z życia w skali 1 do 10 w dwóch grupach rodziców: a) Rodzice dzieci zdrowych oraz b) Rodzice dzieci z niepełnosprawnością
Satysfakcja z życia rodziców dzieci niepełnosprawnych intelektualnie Zadanie Zbadano satysfakcję z życia w skali 1 do 10 w dwóch grupach rodziców: a) Rodzice dzieci zdrowych oraz b) Rodzice dzieci z niepełnosprawnością
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 4
 STATYSTYKA I DOŚWIADCZALNICTWO Wykład 4 Inne układy doświadczalne 1) Układ losowanych bloków Stosujemy, gdy podejrzewamy, że może występować systematyczna zmienność między powtórzeniami np. - zmienność
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 4 Inne układy doświadczalne 1) Układ losowanych bloków Stosujemy, gdy podejrzewamy, że może występować systematyczna zmienność między powtórzeniami np. - zmienność
Test U Manna-Whitneya : Test H Kruskala-Wallisa Test Wilcoxona
 Nieparametryczne odpowiedniki testów T-Studenta stosujemy gdy zmienne mierzone są na skalach porządkowych (nie można liczyć średniej) lub kiedy mierzone są na skalach ilościowych, a nie są spełnione wymagania
Nieparametryczne odpowiedniki testów T-Studenta stosujemy gdy zmienne mierzone są na skalach porządkowych (nie można liczyć średniej) lub kiedy mierzone są na skalach ilościowych, a nie są spełnione wymagania
TESTY NIEPARAMETRYCZNE. 1. Testy równości średnich bez założenia normalności rozkładu zmiennych: Manna-Whitney a i Kruskala-Wallisa.
 TESTY NIEPARAMETRYCZNE 1. Testy równości średnich bez założenia normalności rozkładu zmiennych: Manna-Whitney a i Kruskala-Wallisa. Standardowe testy równości średnich wymagają aby badane zmienne losowe
TESTY NIEPARAMETRYCZNE 1. Testy równości średnich bez założenia normalności rozkładu zmiennych: Manna-Whitney a i Kruskala-Wallisa. Standardowe testy równości średnich wymagają aby badane zmienne losowe
Statystyczna analiza danych w programie STATISTICA (wykład 2) Dariusz Gozdowski
 Statystyczna analiza danych w programie STATISTICA (wykład ) Dariusz Gozdowski Katedra Doświadczalnictwa i Bioinformatyki Wydział Rolnictwa i Biologii SGGW Weryfikacja (testowanie) hipotez statystycznych
Statystyczna analiza danych w programie STATISTICA (wykład ) Dariusz Gozdowski Katedra Doświadczalnictwa i Bioinformatyki Wydział Rolnictwa i Biologii SGGW Weryfikacja (testowanie) hipotez statystycznych
Statystyczna analiza danych w programie STATISTICA 7.1 PL (wykład 3) Dariusz Gozdowski
 Statystyczna analiza danych w programie STATISTICA 7.1 PL (wykład 3) Dariusz Gozdowski Katedra Doświadczalnictwa i Bioinformatyki Wydział Rolnictwa i Biologii SGGW Dwuczynnikowa analiza wariancji (2-way
Statystyczna analiza danych w programie STATISTICA 7.1 PL (wykład 3) Dariusz Gozdowski Katedra Doświadczalnictwa i Bioinformatyki Wydział Rolnictwa i Biologii SGGW Dwuczynnikowa analiza wariancji (2-way
Projekt zaliczeniowy z przedmiotu Statystyka i eksploracja danych (nr 3) Kamil Krzysztof Derkowski
 Projekt zaliczeniowy z przedmiotu Statystyka i eksploracja danych (nr 3) Kamil Krzysztof Derkowski Zadanie 1 Eksploracja (EXAMINE) Informacja o analizowanych danych Obserwacje Uwzględnione Wykluczone Ogółem
Projekt zaliczeniowy z przedmiotu Statystyka i eksploracja danych (nr 3) Kamil Krzysztof Derkowski Zadanie 1 Eksploracja (EXAMINE) Informacja o analizowanych danych Obserwacje Uwzględnione Wykluczone Ogółem
Metodologia badań psychologicznych. Wykład 12. Korelacje
 Metodologia badań psychologicznych Lucyna Golińska SPOŁECZNA AKADEMIA NAUK Wykład 12. Korelacje Korelacja Korelacja występuje wtedy gdy dwie różne miary dotyczące tych samych osób, zdarzeń lub obiektów
Metodologia badań psychologicznych Lucyna Golińska SPOŁECZNA AKADEMIA NAUK Wykład 12. Korelacje Korelacja Korelacja występuje wtedy gdy dwie różne miary dotyczące tych samych osób, zdarzeń lub obiektów
Przedmowa Wykaz symboli Litery alfabetu greckiego wykorzystywane w podręczniku Symbole wykorzystywane w zagadnieniach teorii
 SPIS TREŚCI Przedmowa... 11 Wykaz symboli... 15 Litery alfabetu greckiego wykorzystywane w podręczniku... 15 Symbole wykorzystywane w zagadnieniach teorii mnogości (rachunku zbiorów)... 16 Symbole stosowane
SPIS TREŚCI Przedmowa... 11 Wykaz symboli... 15 Litery alfabetu greckiego wykorzystywane w podręczniku... 15 Symbole wykorzystywane w zagadnieniach teorii mnogości (rachunku zbiorów)... 16 Symbole stosowane
Analiza wariancji jednej zmiennej (UNIANOVA)
 UNIANOVA ocena BY pĺ eä szkoĺ a doĺ wiadczenie /METHOD=SSTYPE(3) /INTERCEPT=INCLUDE /POSTHOC=szkoĹ a(snk) /PLOT=PROFILE(szkoĹ a*doĺ wiadczenie*pĺ eä doĺ wiadczenie*szkoĺ a*pĺ eä szkoĺ a*pĺ eä *doĺ wiadczenie
UNIANOVA ocena BY pĺ eä szkoĺ a doĺ wiadczenie /METHOD=SSTYPE(3) /INTERCEPT=INCLUDE /POSTHOC=szkoĹ a(snk) /PLOT=PROFILE(szkoĹ a*doĺ wiadczenie*pĺ eä doĺ wiadczenie*szkoĺ a*pĺ eä szkoĺ a*pĺ eä *doĺ wiadczenie
ANALIZA WARIANCJI - KLASYFIKACJA JEDNOCZYNNIKOWA
 ANALIZA WARIANCJI - KLASYFIKACJA JEDNOCZYNNIKOWA Na poprzednich zajęciach omawialiśmy testy dla weryfikacji hipotez, że dwie populacje o rozkładach normalnych mają jednakowe wartości średnie. Co jednak
ANALIZA WARIANCJI - KLASYFIKACJA JEDNOCZYNNIKOWA Na poprzednich zajęciach omawialiśmy testy dla weryfikacji hipotez, że dwie populacje o rozkładach normalnych mają jednakowe wartości średnie. Co jednak
KORELACJE I REGRESJA LINIOWA
 KORELACJE I REGRESJA LINIOWA Korelacje i regresja liniowa Analiza korelacji: Badanie, czy pomiędzy dwoma zmiennymi istnieje zależność Obie analizy się wzajemnie przeplatają Analiza regresji: Opisanie modelem
KORELACJE I REGRESJA LINIOWA Korelacje i regresja liniowa Analiza korelacji: Badanie, czy pomiędzy dwoma zmiennymi istnieje zależność Obie analizy się wzajemnie przeplatają Analiza regresji: Opisanie modelem
Zadania ze statystyki cz. 8 I rok socjologii. Zadanie 1.
 Zadania ze statystyki cz. 8 I rok socjologii Zadanie 1. W potocznej opinii pokutuje przekonanie, że lepsi z matematyki są chłopcy niż dziewczęta. Chcąc zweryfikować tę opinię, przeprowadzono badanie w
Zadania ze statystyki cz. 8 I rok socjologii Zadanie 1. W potocznej opinii pokutuje przekonanie, że lepsi z matematyki są chłopcy niż dziewczęta. Chcąc zweryfikować tę opinię, przeprowadzono badanie w
Przykład 1. (A. Łomnicki)
 Plan wykładu: 1. Wariancje wewnątrz grup i między grupami do czego prowadzi ich ocena 2. Rozkład F 3. Analiza wariancji jako metoda badań założenia, etapy postępowania 4. Dwie klasyfikacje a dwa modele
Plan wykładu: 1. Wariancje wewnątrz grup i między grupami do czego prowadzi ich ocena 2. Rozkład F 3. Analiza wariancji jako metoda badań założenia, etapy postępowania 4. Dwie klasyfikacje a dwa modele
RÓWNOWAŻNOŚĆ METOD BADAWCZYCH
 RÓWNOWAŻNOŚĆ METOD BADAWCZYCH Piotr Konieczka Katedra Chemii Analitycznej Wydział Chemiczny Politechnika Gdańska Równoważność metod??? 2 Zgodność wyników analitycznych otrzymanych z wykorzystaniem porównywanych
RÓWNOWAŻNOŚĆ METOD BADAWCZYCH Piotr Konieczka Katedra Chemii Analitycznej Wydział Chemiczny Politechnika Gdańska Równoważność metod??? 2 Zgodność wyników analitycznych otrzymanych z wykorzystaniem porównywanych
Wykład 5: Statystyki opisowe (część 2)
 Wykład 5: Statystyki opisowe (część 2) Wprowadzenie Na poprzednim wykładzie wprowadzone zostały statystyki opisowe nazywane miarami położenia (średnia, mediana, kwartyle, minimum i maksimum, modalna oraz
Wykład 5: Statystyki opisowe (część 2) Wprowadzenie Na poprzednim wykładzie wprowadzone zostały statystyki opisowe nazywane miarami położenia (średnia, mediana, kwartyle, minimum i maksimum, modalna oraz
Analiza wariancji i kowariancji
 Analiza wariancji i kowariancji Historia Analiza wariancji jest metodą zaproponowaną przez Ronalda A. Fishera. Po zakończeniu pierwszej wojny światowej był on pracownikiem laboratorium statystycznego w
Analiza wariancji i kowariancji Historia Analiza wariancji jest metodą zaproponowaną przez Ronalda A. Fishera. Po zakończeniu pierwszej wojny światowej był on pracownikiem laboratorium statystycznego w
PDF created with FinePrint pdffactory Pro trial version http://www.fineprint.com
 Analiza korelacji i regresji KORELACJA zależność liniowa Obserwujemy parę cech ilościowych (X,Y). Doświadczenie jest tak pomyślane, aby obserwowane pary cech X i Y (tzn i ta para x i i y i dla różnych
Analiza korelacji i regresji KORELACJA zależność liniowa Obserwujemy parę cech ilościowych (X,Y). Doświadczenie jest tak pomyślane, aby obserwowane pary cech X i Y (tzn i ta para x i i y i dla różnych
ALGORYTMICZNA I STATYSTYCZNA ANALIZA DANYCH
 1 ALGORYTMICZNA I STATYSTYCZNA ANALIZA DANYCH WFAiS UJ, Informatyka Stosowana II stopień studiów 2 Wnioskowanie statystyczne dla zmiennych numerycznych Porównywanie dwóch średnich Boot-strapping Analiza
1 ALGORYTMICZNA I STATYSTYCZNA ANALIZA DANYCH WFAiS UJ, Informatyka Stosowana II stopień studiów 2 Wnioskowanie statystyczne dla zmiennych numerycznych Porównywanie dwóch średnich Boot-strapping Analiza
Porównanie wyników grupy w odniesieniu do norm Test t dla jednej próby
 Porównanie wyników grupy w odniesieniu do norm Test t dla jednej próby 1. Wstęp teoretyczny Prezentowane badanie dotyczy analizy wyników uzyskanych podczas badania grupy rodziców pod kątem wpływu ich przekonań
Porównanie wyników grupy w odniesieniu do norm Test t dla jednej próby 1. Wstęp teoretyczny Prezentowane badanie dotyczy analizy wyników uzyskanych podczas badania grupy rodziców pod kątem wpływu ich przekonań
Analiza wariancji. dr Janusz Górczyński
 Analiza wariancji dr Janusz Górczyński Wprowadzenie Powiedzmy, że badamy pewną populację π, w której cecha Y ma rozkład N o średniej m i odchyleniu standardowym σ. Powiedzmy dalej, że istnieje pewien czynnik
Analiza wariancji dr Janusz Górczyński Wprowadzenie Powiedzmy, że badamy pewną populację π, w której cecha Y ma rozkład N o średniej m i odchyleniu standardowym σ. Powiedzmy dalej, że istnieje pewien czynnik
Zadanie 1. Analiza Analiza rozkładu
 Zadanie 1 data lab.zad 1; input czas; datalines; 85 3060 631 819 805 835 955 595 690 73 815 914 ; run; Analiza Analiza rozkładu Ponieważ jesteśmy zainteresowani wyznaczeniem przedziału ufności oraz weryfikacja
Zadanie 1 data lab.zad 1; input czas; datalines; 85 3060 631 819 805 835 955 595 690 73 815 914 ; run; Analiza Analiza rozkładu Ponieważ jesteśmy zainteresowani wyznaczeniem przedziału ufności oraz weryfikacja
Zadania ze statystyki cz.8. Zadanie 1.
 Zadania ze statystyki cz.8. Zadanie 1. Wykonano pewien eksperyment skuteczności działania pewnej reklamy na zmianę postawy. Wylosowano 10 osobową próbę studentów, których poproszono o ocenę pewnego produktu,
Zadania ze statystyki cz.8. Zadanie 1. Wykonano pewien eksperyment skuteczności działania pewnej reklamy na zmianę postawy. Wylosowano 10 osobową próbę studentów, których poproszono o ocenę pewnego produktu,
Założenia do analizy wariancji. dr Anna Rajfura Kat. Doświadczalnictwa i Bioinformatyki SGGW
 Założenia do analizy wariancji dr Anna Rajfura Kat. Doświadczalnictwa i Bioinformatyki SGGW anna_rajfura@sggw.pl Zagadnienia 1. Normalność rozkładu cechy Testy: chi-kwadrat zgodności, Shapiro-Wilka, Kołmogorowa-Smirnowa
Założenia do analizy wariancji dr Anna Rajfura Kat. Doświadczalnictwa i Bioinformatyki SGGW anna_rajfura@sggw.pl Zagadnienia 1. Normalność rozkładu cechy Testy: chi-kwadrat zgodności, Shapiro-Wilka, Kołmogorowa-Smirnowa
Charakterystyki liczbowe (estymatory i parametry), które pozwalają opisać właściwości rozkładu badanej cechy (zmiennej)
 Charakterystyki liczbowe (estymatory i parametry), które pozwalają opisać właściwości rozkładu badanej cechy (zmiennej) 1 Podział ze względu na zakres danych użytych do wyznaczenia miary Miary opisujące
Charakterystyki liczbowe (estymatory i parametry), które pozwalają opisać właściwości rozkładu badanej cechy (zmiennej) 1 Podział ze względu na zakres danych użytych do wyznaczenia miary Miary opisujące
( x) Równanie regresji liniowej ma postać. By obliczyć współczynniki a i b należy posłużyć się następującymi wzorami 1 : Gdzie:
 ma postać y = ax + b Równanie regresji liniowej By obliczyć współczynniki a i b należy posłużyć się następującymi wzorami 1 : xy b = a = b lub x Gdzie: xy = też a = x = ( b ) i to dane empiryczne, a ilość
ma postać y = ax + b Równanie regresji liniowej By obliczyć współczynniki a i b należy posłużyć się następującymi wzorami 1 : xy b = a = b lub x Gdzie: xy = też a = x = ( b ) i to dane empiryczne, a ilość
STATYSTYKA - PRZYKŁADOWE ZADANIA EGZAMINACYJNE
 STATYSTYKA - PRZYKŁADOWE ZADANIA EGZAMINACYJNE 1 W trakcie badania obliczono wartości średniej (15,4), mediany (13,6) oraz dominanty (10,0). Określ typ asymetrii rozkładu. 2 Wymień 3 cechy rozkładu Gauss
STATYSTYKA - PRZYKŁADOWE ZADANIA EGZAMINACYJNE 1 W trakcie badania obliczono wartości średniej (15,4), mediany (13,6) oraz dominanty (10,0). Określ typ asymetrii rozkładu. 2 Wymień 3 cechy rozkładu Gauss
Gimnastyka artystyczna
 Gimnastyka artystyczna Zbadano losową próbę N=40 dziewcząt i chłopców z klas o profilu ogólnym i sportowym pod kątem ich ogólnej sprawności fizycznej ocenianej na skali Hirscha (od 0 do 20 pkt.), gdzie
Gimnastyka artystyczna Zbadano losową próbę N=40 dziewcząt i chłopców z klas o profilu ogólnym i sportowym pod kątem ich ogólnej sprawności fizycznej ocenianej na skali Hirscha (od 0 do 20 pkt.), gdzie
Testowanie hipotez. Marcin Zajenkowski. Marcin Zajenkowski () Testowanie hipotez 1 / 25
 Testowanie hipotez Marcin Zajenkowski Marcin Zajenkowski () Testowanie hipotez 1 / 25 Testowanie hipotez Aby porównać ze sobą dwie statystyki z próby stosuje się testy istotności. Mówią one o tym czy uzyskane
Testowanie hipotez Marcin Zajenkowski Marcin Zajenkowski () Testowanie hipotez 1 / 25 Testowanie hipotez Aby porównać ze sobą dwie statystyki z próby stosuje się testy istotności. Mówią one o tym czy uzyskane
GRUPY NIEZALEŻNE Chi kwadrat Pearsona GRUPY ZALEŻNE (zmienne dwuwartościowe) McNemara Q Cochrana
 GRUPY NIEZALEŻNE Chi kwadrat Pearsona Testy stosujemy w sytuacji, kiedy zmienna zależna mierzona jest na skali nominalnej Liczba porównywanych grup (czyli liczba kategorii zmiennej niezależnej) nie ma
GRUPY NIEZALEŻNE Chi kwadrat Pearsona Testy stosujemy w sytuacji, kiedy zmienna zależna mierzona jest na skali nominalnej Liczba porównywanych grup (czyli liczba kategorii zmiennej niezależnej) nie ma
Temat: Badanie niezależności dwóch cech jakościowych test chi-kwadrat
 Temat: Badanie niezależności dwóch cech jakościowych test chi-kwadrat Anna Rajfura 1 Przykład W celu porównania skuteczności wybranych herbicydów: A, B, C sprawdzano, czy masa chwastów na poletku zależy
Temat: Badanie niezależności dwóch cech jakościowych test chi-kwadrat Anna Rajfura 1 Przykład W celu porównania skuteczności wybranych herbicydów: A, B, C sprawdzano, czy masa chwastów na poletku zależy
Żródło:
 Testy t-studenta są testami różnic pomiędzy średnimi czyli służą do porównania ze sobą dwóch średnich Zmienne muszą być zmiennymi ilościowym (liczymy i porównujemy średnie!) Są to testy parametryczne Test
Testy t-studenta są testami różnic pomiędzy średnimi czyli służą do porównania ze sobą dwóch średnich Zmienne muszą być zmiennymi ilościowym (liczymy i porównujemy średnie!) Są to testy parametryczne Test
ISSN 1425-7351 PL9701513 INSTYTUT CHEMII I TECHNIKI JĄDROWEJ INSTITUTE OF NUCLEAR CHEMISTRY AND TECHNOLOGY WARSZAWA 7BM 1
 ISSN 1425-7351 PL9701513 INSTYTUT CHEMII I TECHNIKI JĄDROWEJ INSTITUTE OF NUCLEAR CHEMISTRY AND TECHNOLOGY WARSZAWA 7BM 1 RAPORTY IChTJ. SERIA B nr 2/96 TEST KOMETKOWY. 2. ANALIZA STATYSTYCZNA WYNIKÓW
ISSN 1425-7351 PL9701513 INSTYTUT CHEMII I TECHNIKI JĄDROWEJ INSTITUTE OF NUCLEAR CHEMISTRY AND TECHNOLOGY WARSZAWA 7BM 1 RAPORTY IChTJ. SERIA B nr 2/96 TEST KOMETKOWY. 2. ANALIZA STATYSTYCZNA WYNIKÓW
LABORATORIUM 3. Jeśli p α, to hipotezę zerową odrzucamy Jeśli p > α, to nie mamy podstaw do odrzucenia hipotezy zerowej
 LABORATORIUM 3 Przygotowanie pliku (nazwy zmiennych, export plików.xlsx, selekcja przypadków); Graficzna prezentacja danych: Histogramy (skategoryzowane) i 3-wymiarowe; Wykresy ramka wąsy; Wykresy powierzchniowe;
LABORATORIUM 3 Przygotowanie pliku (nazwy zmiennych, export plików.xlsx, selekcja przypadków); Graficzna prezentacja danych: Histogramy (skategoryzowane) i 3-wymiarowe; Wykresy ramka wąsy; Wykresy powierzchniowe;
WNIOSKOWANIE STATYSTYCZNE
 STATYSTYKA WNIOSKOWANIE STATYSTYCZNE ESTYMACJA oszacowanie z pewną dokładnością wartości opisującej rozkład badanej cechy statystycznej. WERYFIKACJA HIPOTEZ sprawdzanie słuszności przypuszczeń dotyczących
STATYSTYKA WNIOSKOWANIE STATYSTYCZNE ESTYMACJA oszacowanie z pewną dokładnością wartości opisującej rozkład badanej cechy statystycznej. WERYFIKACJA HIPOTEZ sprawdzanie słuszności przypuszczeń dotyczących
Tablica Wzorów Rachunek Prawdopodobieństwa i Statystyki
 Tablica Wzorów Rachunek Prawdopodobieństwa i Statystyki Spis treści I. Wzory ogólne... 2 1. Średnia arytmetyczna:... 2 2. Rozstęp:... 2 3. Kwantyle:... 2 4. Wariancja:... 2 5. Odchylenie standardowe:...
Tablica Wzorów Rachunek Prawdopodobieństwa i Statystyki Spis treści I. Wzory ogólne... 2 1. Średnia arytmetyczna:... 2 2. Rozstęp:... 2 3. Kwantyle:... 2 4. Wariancja:... 2 5. Odchylenie standardowe:...
Weryfikacja hipotez statystycznych
 Weryfikacja hipotez statystycznych Hipoteza Test statystyczny Poziom istotności Testy jednostronne i dwustronne Testowanie równości wariancji test F-Fishera Testowanie równości wartości średnich test t-studenta
Weryfikacja hipotez statystycznych Hipoteza Test statystyczny Poziom istotności Testy jednostronne i dwustronne Testowanie równości wariancji test F-Fishera Testowanie równości wartości średnich test t-studenta
STATYSTYKA I DOŚWIADCZALNICTWO. Wykład 2
 STATYSTYKA I DOŚWIADCZALNICTWO Wykład Parametry przedziałowe rozkładów ciągłych określane na podstawie próby (przedziały ufności) Przedział ufności dla średniej s X t( α;n 1),X + t( α;n 1) n s n t (α;
STATYSTYKA I DOŚWIADCZALNICTWO Wykład Parametry przedziałowe rozkładów ciągłych określane na podstawie próby (przedziały ufności) Przedział ufności dla średniej s X t( α;n 1),X + t( α;n 1) n s n t (α;
Importowanie danych do SPSS Eksportowanie rezultatów do formatu MS Word... 22
 Spis treści Przedmowa do wydania pierwszego.... 11 Przedmowa do wydania drugiego.... 15 Wykaz symboli.... 17 Litery alfabetu greckiego wykorzystywane w podręczniku.... 17 Symbole wykorzystywane w zagadnieniach
Spis treści Przedmowa do wydania pierwszego.... 11 Przedmowa do wydania drugiego.... 15 Wykaz symboli.... 17 Litery alfabetu greckiego wykorzystywane w podręczniku.... 17 Symbole wykorzystywane w zagadnieniach
Statystyka i Analiza Danych
 Warsztaty Statystyka i Analiza Danych Gdańsk, 20-22 lutego 2014 Zastosowania analizy wariancji w opracowywaniu wyników badań empirycznych Janusz Wątroba StatSoft Polska Centrum Zastosowań Matematyki -
Warsztaty Statystyka i Analiza Danych Gdańsk, 20-22 lutego 2014 Zastosowania analizy wariancji w opracowywaniu wyników badań empirycznych Janusz Wątroba StatSoft Polska Centrum Zastosowań Matematyki -
Statystyka. Rozkład prawdopodobieństwa Testowanie hipotez. Wykład III ( )
 Statystyka Rozkład prawdopodobieństwa Testowanie hipotez Wykład III (04.01.2016) Rozkład t-studenta Rozkład T jest rozkładem pomocniczym we wnioskowaniu statystycznym; stosuje się go wyznaczenia przedziału
Statystyka Rozkład prawdopodobieństwa Testowanie hipotez Wykład III (04.01.2016) Rozkład t-studenta Rozkład T jest rozkładem pomocniczym we wnioskowaniu statystycznym; stosuje się go wyznaczenia przedziału
Statystyka i opracowanie danych- W 8 Wnioskowanie statystyczne. Testy statystyczne. Weryfikacja hipotez statystycznych.
 Statystyka i opracowanie danych- W 8 Wnioskowanie statystyczne. Testy statystyczne. Weryfikacja hipotez statystycznych. Dr Anna ADRIAN Paw B5, pok407 adan@agh.edu.pl Hipotezy i Testy statystyczne Każde
Statystyka i opracowanie danych- W 8 Wnioskowanie statystyczne. Testy statystyczne. Weryfikacja hipotez statystycznych. Dr Anna ADRIAN Paw B5, pok407 adan@agh.edu.pl Hipotezy i Testy statystyczne Każde
Spis treści. Laboratorium III: Testy statystyczne. Inżynieria biomedyczna, I rok, semestr letni 2013/2014 Analiza danych pomiarowych
 1 Laboratorium III: Testy statystyczne Spis treści Laboratorium III: Testy statystyczne... 1 Wiadomości ogólne... 2 1. Krótkie przypomnienie wiadomości na temat testów statystycznych... 2 1.1. Weryfikacja
1 Laboratorium III: Testy statystyczne Spis treści Laboratorium III: Testy statystyczne... 1 Wiadomości ogólne... 2 1. Krótkie przypomnienie wiadomości na temat testów statystycznych... 2 1.1. Weryfikacja
LABORATORIUM 8 WERYFIKACJA HIPOTEZ STATYSTYCZNYCH PARAMETRYCZNE TESTY ISTOTNOŚCI
 LABORATORIUM 8 WERYFIKACJA HIPOTEZ STATYSTYCZNYCH PARAMETRYCZNE TESTY ISTOTNOŚCI WERYFIKACJA HIPOTEZ Hipoteza statystyczna jakiekolwiek przypuszczenie dotyczące populacji generalnej- jej poszczególnych
LABORATORIUM 8 WERYFIKACJA HIPOTEZ STATYSTYCZNYCH PARAMETRYCZNE TESTY ISTOTNOŚCI WERYFIKACJA HIPOTEZ Hipoteza statystyczna jakiekolwiek przypuszczenie dotyczące populacji generalnej- jej poszczególnych
Statystyka Opisowa z Demografią oraz Biostatystyka. Aleksander Denisiuk. denisjuk@euh-e.edu.pl
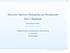 Statystyka Opisowa z Demografią oraz Biostatystyka TesttStudenta Aleksander Denisiuk denisjuk@euh-e.edu.pl Elblaska Uczelnia Humanistyczno-Ekonomiczna ul. Lotnicza 2 82-300 Elblag oraz Biostatystyka p.
Statystyka Opisowa z Demografią oraz Biostatystyka TesttStudenta Aleksander Denisiuk denisjuk@euh-e.edu.pl Elblaska Uczelnia Humanistyczno-Ekonomiczna ul. Lotnicza 2 82-300 Elblag oraz Biostatystyka p.
Analiza wariancji - ANOVA
 Analiza wariancji - ANOVA Analiza wariancji jest metodą pozwalającą na podział zmienności zaobserwowanej wśród wyników eksperymentalnych na oddzielne części. Każdą z tych części możemy przypisać oddzielnemu
Analiza wariancji - ANOVA Analiza wariancji jest metodą pozwalającą na podział zmienności zaobserwowanej wśród wyników eksperymentalnych na oddzielne części. Każdą z tych części możemy przypisać oddzielnemu
Weryfikacja hipotez statystycznych, parametryczne testy istotności w populacji
 Weryfikacja hipotez statystycznych, parametryczne testy istotności w populacji Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych Wydział Informatyki Politechniki
Weryfikacja hipotez statystycznych, parametryczne testy istotności w populacji Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych Wydział Informatyki Politechniki
Liczba godzin Punkty ECTS Sposób zaliczenia. ćwiczenia 30 zaliczenie z oceną. laboratoria 30 zaliczenie z oceną
 Wydział: Psychologia Nazwa kierunku kształcenia: Psychologia Rodzaj przedmiotu: podstawowy Opiekun: dr Andrzej Tarłowski Poziom studiów (I lub II stopnia): Jednolite magisterskie Tryb studiów: Stacjonarne
Wydział: Psychologia Nazwa kierunku kształcenia: Psychologia Rodzaj przedmiotu: podstawowy Opiekun: dr Andrzej Tarłowski Poziom studiów (I lub II stopnia): Jednolite magisterskie Tryb studiów: Stacjonarne
OBLICZENIE PRZEPŁYWÓW MAKSYMALNYCH ROCZNYCH O OKREŚLONYM PRAWDOPODOBIEŃSTWIE PRZEWYŻSZENIA. z wykorzystaniem programu obliczeniowego Q maxp
 tel.: +48 662 635 712 Liczba stron: 15 Data: 20.07.2010r OBLICZENIE PRZEPŁYWÓW MAKSYMALNYCH ROCZNYCH O OKREŚLONYM PRAWDOPODOBIEŃSTWIE PRZEWYŻSZENIA z wykorzystaniem programu obliczeniowego Q maxp DŁUGIE
tel.: +48 662 635 712 Liczba stron: 15 Data: 20.07.2010r OBLICZENIE PRZEPŁYWÓW MAKSYMALNYCH ROCZNYCH O OKREŚLONYM PRAWDOPODOBIEŃSTWIE PRZEWYŻSZENIA z wykorzystaniem programu obliczeniowego Q maxp DŁUGIE
Elementy statystyki STA - Wykład 5
 STA - Wykład 5 Wydział Matematyki i Informatyki Uniwersytet im. Adama Mickiewicza 1 ANOVA 2 Model jednoczynnikowej analizy wariancji Na model jednoczynnikowej analizy wariancji możemy traktować jako uogólnienie
STA - Wykład 5 Wydział Matematyki i Informatyki Uniwersytet im. Adama Mickiewicza 1 ANOVA 2 Model jednoczynnikowej analizy wariancji Na model jednoczynnikowej analizy wariancji możemy traktować jako uogólnienie
VI WYKŁAD STATYSTYKA. 9/04/2014 B8 sala 0.10B Godz. 15:15
 VI WYKŁAD STATYSTYKA 9/04/2014 B8 sala 0.10B Godz. 15:15 WYKŁAD 6 WERYFIKACJA HIPOTEZ STATYSTYCZNYCH PARAMETRYCZNE TESTY ISTOTNOŚCI Weryfikacja hipotez ( błędy I i II rodzaju, poziom istotności, zasady
VI WYKŁAD STATYSTYKA 9/04/2014 B8 sala 0.10B Godz. 15:15 WYKŁAD 6 WERYFIKACJA HIPOTEZ STATYSTYCZNYCH PARAMETRYCZNE TESTY ISTOTNOŚCI Weryfikacja hipotez ( błędy I i II rodzaju, poziom istotności, zasady
Zad. 4 Należy określić rodzaj testu (jedno czy dwustronny) oraz wartości krytyczne z lub t dla określonych hipotez i ich poziomów istotności:
 Zadania ze statystyki cz. 7. Zad.1 Z populacji wyłoniono próbę wielkości 64 jednostek. Średnia arytmetyczna wartość cechy wyniosła 110, zaś odchylenie standardowe 16. Należy wyznaczyć przedział ufności
Zadania ze statystyki cz. 7. Zad.1 Z populacji wyłoniono próbę wielkości 64 jednostek. Średnia arytmetyczna wartość cechy wyniosła 110, zaś odchylenie standardowe 16. Należy wyznaczyć przedział ufności
Spis treści. Księgarnia PWN: Bruce M. King, Edward W. Minium - Statystyka dla psychologów i pedagogów. Wstęp Wprowadzenie...
 Księgarnia PWN: Bruce M. King, Edward W. Minium - Statystyka dla psychologów i pedagogów Wstęp... 13 1. Wprowadzenie... 19 1.1. Statystyka opisowa.................................. 21 1.2. Wnioskowanie
Księgarnia PWN: Bruce M. King, Edward W. Minium - Statystyka dla psychologów i pedagogów Wstęp... 13 1. Wprowadzenie... 19 1.1. Statystyka opisowa.................................. 21 1.2. Wnioskowanie
Metody Statystyczne. Metody Statystyczne
 #7 1 Czy straszenie jest bardziej skuteczne niż zachęcanie? Przykład 5.2. s.197 Grupa straszona: 8,5,8,7 M 1 =7 Grupa zachęcana: 1, 1, 2,4 M 2 =2 Średnia ogólna M=(M1+M2)/2= 4,5 Wnioskowanie statystyczne
#7 1 Czy straszenie jest bardziej skuteczne niż zachęcanie? Przykład 5.2. s.197 Grupa straszona: 8,5,8,7 M 1 =7 Grupa zachęcana: 1, 1, 2,4 M 2 =2 Średnia ogólna M=(M1+M2)/2= 4,5 Wnioskowanie statystyczne
Statystyka matematyczna dla leśników
 Statystyka matematyczna dla leśników Wydział Leśny Kierunek leśnictwo Studia Stacjonarne I Stopnia Rok akademicki 03/04 Wykład 5 Testy statystyczne Ogólne zasady testowania hipotez statystycznych, rodzaje
Statystyka matematyczna dla leśników Wydział Leśny Kierunek leśnictwo Studia Stacjonarne I Stopnia Rok akademicki 03/04 Wykład 5 Testy statystyczne Ogólne zasady testowania hipotez statystycznych, rodzaje
Badania eksperymentalne
 Badania eksperymentalne Pomiar na skali porządkowej mgr Agnieszka Zięba Zakład Badań Marketingowych Instytut Statystyki i Demografii Szkoła Główna Handlowa Najpopularniejsze sposoby oceny wyników eksperymentu
Badania eksperymentalne Pomiar na skali porządkowej mgr Agnieszka Zięba Zakład Badań Marketingowych Instytut Statystyki i Demografii Szkoła Główna Handlowa Najpopularniejsze sposoby oceny wyników eksperymentu
Księgarnia PWN: George A. Ferguson, Yoshio Takane - Analiza statystyczna w psychologii i pedagogice
 Księgarnia PWN: George A. Ferguson, Yoshio Takane - Analiza statystyczna w psychologii i pedagogice Przedmowa do wydania polskiego Przedmowa CZĘŚĆ I. PODSTAWY STATYSTYKI Rozdział 1 Podstawowe pojęcia statystyki
Księgarnia PWN: George A. Ferguson, Yoshio Takane - Analiza statystyczna w psychologii i pedagogice Przedmowa do wydania polskiego Przedmowa CZĘŚĆ I. PODSTAWY STATYSTYKI Rozdział 1 Podstawowe pojęcia statystyki
Populacja generalna (zbiorowość generalna) zbiór obejmujący wszystkie elementy będące przedmiotem badań Próba (podzbiór zbiorowości generalnej) część
 Populacja generalna (zbiorowość generalna) zbiór obejmujący wszystkie elementy będące przedmiotem badań Próba (podzbiór zbiorowości generalnej) część populacji, którą podaje się badaniu statystycznemu
Populacja generalna (zbiorowość generalna) zbiór obejmujący wszystkie elementy będące przedmiotem badań Próba (podzbiór zbiorowości generalnej) część populacji, którą podaje się badaniu statystycznemu
ĆWICZENIE 11 NIEPARAMETRYCZNE TESTY ISTOTNOŚCI
 ĆWICZENIE 11 NIEPARAMETRYCZNE TESTY ISTOTNOŚCI ANALIZA KORELACJI Korelacja 1. Współczynnik korelacji 2. Współczynnik korelacji liniowej definicja 3. Estymacja współczynnika korelacji 4. Testy istotności
ĆWICZENIE 11 NIEPARAMETRYCZNE TESTY ISTOTNOŚCI ANALIZA KORELACJI Korelacja 1. Współczynnik korelacji 2. Współczynnik korelacji liniowej definicja 3. Estymacja współczynnika korelacji 4. Testy istotności
ANALIZA WARIANCJI - KLASYFIKACJA WIELOCZYNNIKOWA
 ANALIZA WARIANCJI - KLASYFIKACJA WIELOCZYNNIKOWA Na poprzednich zajęciach omawialiśmy testy dla weryfikacji hipotez, że kilka średnich dla analizowanej zmiennej grupującej mają jednakowe wartości średnie.
ANALIZA WARIANCJI - KLASYFIKACJA WIELOCZYNNIKOWA Na poprzednich zajęciach omawialiśmy testy dla weryfikacji hipotez, że kilka średnich dla analizowanej zmiennej grupującej mają jednakowe wartości średnie.
Opracowywanie wyników doświadczeń
 Podstawy statystyki medycznej Laboratorium Zajęcia 6 Statistica Opracowywanie wyników doświadczeń Niniejsza instrukcja zawiera przykłady opracowywania doświadczeń jednoczynnikowy i wieloczynnikowych w
Podstawy statystyki medycznej Laboratorium Zajęcia 6 Statistica Opracowywanie wyników doświadczeń Niniejsza instrukcja zawiera przykłady opracowywania doświadczeń jednoczynnikowy i wieloczynnikowych w
Statystyka od podstaw Janina Jóźwiak, Jarosław Podgórski
 Statystyka od podstaw Janina Jóźwiak, Jarosław Podgórski Książka jest nowoczesnym podręcznikiem przeznaczonym dla studentów uczelni i wydziałów ekonomicznych. Wykład podzielono na cztery części. W pierwszej
Statystyka od podstaw Janina Jóźwiak, Jarosław Podgórski Książka jest nowoczesnym podręcznikiem przeznaczonym dla studentów uczelni i wydziałów ekonomicznych. Wykład podzielono na cztery części. W pierwszej
Analiza korelacji
 Analiza korelacji Zakres szkolenia Wstęp Podstawowe pojęcia korelacji Współczynnik korelacji liniowej Pearsona Współczynnik korelacji rang Spearmana Test istotności Zadania 2 Wstęp Do czego służy korelacja:
Analiza korelacji Zakres szkolenia Wstęp Podstawowe pojęcia korelacji Współczynnik korelacji liniowej Pearsona Współczynnik korelacji rang Spearmana Test istotności Zadania 2 Wstęp Do czego służy korelacja:
Testowanie hipotez statystycznych
 Testowanie hipotez statystycznych Hipotezą statystyczną jest dowolne przypuszczenie co do rozkładu populacji generalnej (jego postaci funkcyjnej lub wartości parametrów). Prawdziwość tego przypuszczenia
Testowanie hipotez statystycznych Hipotezą statystyczną jest dowolne przypuszczenie co do rozkładu populacji generalnej (jego postaci funkcyjnej lub wartości parametrów). Prawdziwość tego przypuszczenia
R-PEARSONA Zależność liniowa
 R-PEARSONA Zależność liniowa Interpretacja wyników: wraz ze wzrostem wartości jednej zmiennej (np. zarobków) liniowo rosną wartości drugiej zmiennej (np. kwoty przeznaczanej na wakacje) czyli np. im wyższe
R-PEARSONA Zależność liniowa Interpretacja wyników: wraz ze wzrostem wartości jednej zmiennej (np. zarobków) liniowo rosną wartości drugiej zmiennej (np. kwoty przeznaczanej na wakacje) czyli np. im wyższe
Statystyka. Wykład 7. Magdalena Alama-Bućko. 16 kwietnia Magdalena Alama-Bućko Statystyka 16 kwietnia / 35
 Statystyka Wykład 7 Magdalena Alama-Bućko 16 kwietnia 2017 Magdalena Alama-Bućko Statystyka 16 kwietnia 2017 1 / 35 Tematyka zajęć: Wprowadzenie do statystyki. Analiza struktury zbiorowości miary położenia
Statystyka Wykład 7 Magdalena Alama-Bućko 16 kwietnia 2017 Magdalena Alama-Bućko Statystyka 16 kwietnia 2017 1 / 35 Tematyka zajęć: Wprowadzenie do statystyki. Analiza struktury zbiorowości miary położenia
Błędy przy testowaniu hipotez statystycznych. Decyzja H 0 jest prawdziwa H 0 jest faszywa
 Weryfikacja hipotez statystycznych Hipotezą statystyczną nazywamy każde przypuszczenie dotyczące nieznanego rozkładu badanej cechy populacji, o prawdziwości lub fałszywości którego wnioskuje się na podstawie
Weryfikacja hipotez statystycznych Hipotezą statystyczną nazywamy każde przypuszczenie dotyczące nieznanego rozkładu badanej cechy populacji, o prawdziwości lub fałszywości którego wnioskuje się na podstawie
Dane dotyczące wartości zmiennej (cechy) wprowadzamy w jednej kolumnie. W przypadku większej liczby zmiennych wprowadzamy każdą w oddzielnej kolumnie.
 STATISTICA INSTRUKCJA - 1 I. Wprowadzanie danych Podstawowe / Nowy / Arkusz Dane dotyczące wartości zmiennej (cechy) wprowadzamy w jednej kolumnie. W przypadku większej liczby zmiennych wprowadzamy każdą
STATISTICA INSTRUKCJA - 1 I. Wprowadzanie danych Podstawowe / Nowy / Arkusz Dane dotyczące wartości zmiennej (cechy) wprowadzamy w jednej kolumnie. W przypadku większej liczby zmiennych wprowadzamy każdą
Testowanie hipotez. Hipoteza prosta zawiera jeden element, np. H 0 : θ = 2, hipoteza złożona zawiera więcej niż jeden element, np. H 0 : θ > 4.
 Testowanie hipotez Niech X = (X 1... X n ) będzie próbą losową na przestrzeni X zaś P = {P θ θ Θ} rodziną rozkładów prawdopodobieństwa określonych na przestrzeni próby X. Definicja 1. Hipotezą zerową Θ
Testowanie hipotez Niech X = (X 1... X n ) będzie próbą losową na przestrzeni X zaś P = {P θ θ Θ} rodziną rozkładów prawdopodobieństwa określonych na przestrzeni próby X. Definicja 1. Hipotezą zerową Θ
Zadania ze statystyki, cz.7 - hipotezy statystyczne, błąd standardowy, testowanie hipotez statystycznych
 Zadania ze statystyki, cz.7 - hipotezy statystyczne, błąd standardowy, testowanie hipotez statystycznych Zad. 1 Średnia ocen z semestru letniego w populacji studentów socjologii w roku akademickim 2011/2012
Zadania ze statystyki, cz.7 - hipotezy statystyczne, błąd standardowy, testowanie hipotez statystycznych Zad. 1 Średnia ocen z semestru letniego w populacji studentów socjologii w roku akademickim 2011/2012
Pomiary urodzeń według płci noworodka i województwa.podział na miasto i wieś.
 Pomiary urodzeń według płci noworodka i województwa.podział na miasto i wieś. Województwo Urodzenia według płci noworodka i województwa. ; Rok 2008; POLSKA Ogółem Miasta Wieś Pozamałżeńskie- Miasta Pozamałżeńskie-
Pomiary urodzeń według płci noworodka i województwa.podział na miasto i wieś. Województwo Urodzenia według płci noworodka i województwa. ; Rok 2008; POLSKA Ogółem Miasta Wieś Pozamałżeńskie- Miasta Pozamałżeńskie-
Testy post-hoc. Wrocław, 6 czerwca 2016
 Testy post-hoc Wrocław, 6 czerwca 2016 Testy post-hoc 1 metoda LSD 2 metoda Duncana 3 metoda Dunneta 4 metoda kontrastów 5 matoda Newman-Keuls 6 metoda Tukeya Metoda LSD Metoda Least Significant Difference
Testy post-hoc Wrocław, 6 czerwca 2016 Testy post-hoc 1 metoda LSD 2 metoda Duncana 3 metoda Dunneta 4 metoda kontrastów 5 matoda Newman-Keuls 6 metoda Tukeya Metoda LSD Metoda Least Significant Difference
Wykład 4: Wnioskowanie statystyczne. Podstawowe informacje oraz implementacja przykładowego testu w programie STATISTICA
 Wykład 4: Wnioskowanie statystyczne Podstawowe informacje oraz implementacja przykładowego testu w programie STATISTICA Idea wnioskowania statystycznego Celem analizy statystycznej nie jest zwykle tylko
Wykład 4: Wnioskowanie statystyczne Podstawowe informacje oraz implementacja przykładowego testu w programie STATISTICA Idea wnioskowania statystycznego Celem analizy statystycznej nie jest zwykle tylko
Eksploracja Danych. Testowanie Hipotez. (c) Marcin Sydow
 Testowanie Hipotez Wprowadzenie Testy statystyczne: pocz. XVII wieku (prace J.Arbuthnotta, liczba urodzeń noworodków obu płci w Londynie) Testowanie hipotez: Karl Pearson (pocz. XX w., testowanie zgodności,
Testowanie Hipotez Wprowadzenie Testy statystyczne: pocz. XVII wieku (prace J.Arbuthnotta, liczba urodzeń noworodków obu płci w Londynie) Testowanie hipotez: Karl Pearson (pocz. XX w., testowanie zgodności,
Podstawy statystyki dla psychologów. Podręcznik akademicki. Wydanie drugie poprawione. Wiesław Szymczak
 Podstawy statystyki dla psychologów. Podręcznik akademicki. Wydanie drugie poprawione. Wiesław Szymczak Autor prezentuje spójny obraz najczęściej stosowanych metod statystycznych, dodatkowo omawiając takie
Podstawy statystyki dla psychologów. Podręcznik akademicki. Wydanie drugie poprawione. Wiesław Szymczak Autor prezentuje spójny obraz najczęściej stosowanych metod statystycznych, dodatkowo omawiając takie
ĆWICZENIE 11 ANALIZA KORELACJI I REGRESJI
 ĆWICZENIE 11 ANALIZA KORELACJI I REGRESJI Korelacja 1. Współczynnik korelacji 2. Współczynnik korelacji liniowej definicja 3. Estymacja współczynnika korelacji 4. Testy istotności współczynnika korelacji
ĆWICZENIE 11 ANALIZA KORELACJI I REGRESJI Korelacja 1. Współczynnik korelacji 2. Współczynnik korelacji liniowej definicja 3. Estymacja współczynnika korelacji 4. Testy istotności współczynnika korelacji
Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć)
 Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć) 1. Populacja generalna a losowa próba, parametr rozkładu cechy a jego ocena z losowej próby, miary opisu statystycznego
Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć) 1. Populacja generalna a losowa próba, parametr rozkładu cechy a jego ocena z losowej próby, miary opisu statystycznego
Weryfikacja hipotez statystycznych za pomocą testów statystycznych
 Weryfikacja hipotez statystycznych za pomocą testów statystycznych Weryfikacja hipotez statystycznych za pomocą testów stat. Hipoteza statystyczna Dowolne przypuszczenie co do rozkładu populacji generalnej
Weryfikacja hipotez statystycznych za pomocą testów statystycznych Weryfikacja hipotez statystycznych za pomocą testów stat. Hipoteza statystyczna Dowolne przypuszczenie co do rozkładu populacji generalnej
Jedzenie w kawiarni KLASYCZNE PRZEBOJE
 Jedzenie w kawiarni W pewnej kawiarni puszczano trojakiego rodzaju podkład muzyczny do posiłku ballady rockowe, klasyczne przeboje lub muzykę taneczną. Badano czas przeznaczony przez losowo wybranych gości
Jedzenie w kawiarni W pewnej kawiarni puszczano trojakiego rodzaju podkład muzyczny do posiłku ballady rockowe, klasyczne przeboje lub muzykę taneczną. Badano czas przeznaczony przez losowo wybranych gości
Testowanie hipotez dla dwóch zmiennych zależnych. Moc testu. Minimalna liczność próby; Regresja prosta; Korelacja Pearsona;
 LABORATORIUM 4 Testowanie hipotez dla dwóch zmiennych zależnych. Moc testu. Minimalna liczność próby; Regresja prosta; Korelacja Pearsona; dwie zmienne zależne mierzalne małe próby duże próby rozkład normalny
LABORATORIUM 4 Testowanie hipotez dla dwóch zmiennych zależnych. Moc testu. Minimalna liczność próby; Regresja prosta; Korelacja Pearsona; dwie zmienne zależne mierzalne małe próby duże próby rozkład normalny
Statystyka w zarzadzaniu / Amir D. Aczel, Jayavel Sounderpandian. Wydanie 2. Warszawa, Spis treści
 Statystyka w zarzadzaniu / Amir D. Aczel, Jayavel Sounderpandian. Wydanie 2. Warszawa, 2018 Spis treści Przedmowa 13 O Autorach 15 Przedmowa od Tłumacza 17 1. Wprowadzenie i statystyka opisowa 19 1.1.
Statystyka w zarzadzaniu / Amir D. Aczel, Jayavel Sounderpandian. Wydanie 2. Warszawa, 2018 Spis treści Przedmowa 13 O Autorach 15 Przedmowa od Tłumacza 17 1. Wprowadzenie i statystyka opisowa 19 1.1.
