Metody poprawy jakości obrazu (image enchancement)
|
|
|
- Dominika Górecka
- 8 lat temu
- Przeglądów:
Transkrypt
1 Metody poprawy jakości obrazu imae echacemet) Są to metody wstępeo przetwarzaia obrazu. Celem tych metod jest oóla poprawa jakości obrazu poprzez modyikację jeo jasości, kotrastu lub historamu.
2 Metody poprawy jakości obrazu Metody poprawy jakości obrazu oparte są o kryteria subiektywe wrażeia wzrokowe człowieka). W tych metodach ie są wykorzystywae obiektywe kryteria matematycze.
3 METODY POPRAWY JAKOŚCI OBRAZU OPERACJE PUNKTOWE MODELOWANIE HISTOGRAMU OPERACJE PRZESTRZENNE NADAWANIE KOLORÓW POPRAWA KONTRASTU ELIMINACJA ZNIEKSZTAŁCEŃ POPRAWA KONTRASTU POPRZEZ MODELOWANIE HISTOGRAMU FILTRACJA LINIOWA FILTRACJA NIELINIOWA DETEKCJA KRAWĘDZI PSEUDOKOLORY NADAWANIE KOLORÓW FAŁSZYWYCH WYRÓWNYWANIE JASNOŚCI TŁA ZOOMING
4 Metody poprawy jakości obrazu Jasość J MN M N i j i, j) Kotrast C MN M N i j [ i, j) J ] M, N - wymiary obrazu, i,j) - poziom jasości w pukcie i,j)
5 Wpływ jasości i kotrastu a wyląd obrazu J94, C9 J9, C38 J, C47
6 Historam obrazu Imae : array[..m,..n]o byte; Hist : array[..l-]o loit;... Hist:; or i: to M do or j: to N do Ic Hist[ Imae[i, j] ] );...
7 8 oryialy Wpływ jasości i kotrastu a historam obrazu ciemy jasy
8 Liiowe odwzorowaie poziomów jasości L- m i,j) m i,j) + d d L- m ~ kotrast d ~ jasość OBRAZ WYNIKOWY OPERACJA PUNKTOWA OBRAZ ŹRÓDŁOWY
9 MATLB Demo zmiaa kotrastu i jasość
10 Rozciąaie historamu obrazu To jest rówież odwzorowaie liiowe???) M I N M A X L- i,j) i,j)< MIN L- MAX - i,j)- MIN ), MIN i,j) MAX MIN L- i,j)> MAX
11 Rozciąaie historamu obrazu - przykład MIN, MAX
12 Iwersja poziomów jasości obrazu L- L- Jak zaimplemetować iwersję???
13 Nieliiowe odwzorowaie poziomów jasości L- lx) i,j) T i,j)) sqrtx) x expx) Korekcja γ L- OBRAZ WYNIKOWY OBRAZ ŹRÓDŁOWY Normalizacja! OPERACJA PUNKTOWA
14 Nieliiowe odwzorowaie poziomów jasości - przykłady Obraz oryialy
15 Nieliiowe odwzorowaie poziomów jasości - przykłady Tx 5 5 Tsqrtx) 8 6 4
16 Nieliiowe odwzorowaie poziomów jasości - przykłady Te x 5 5 Tlox) 5 5
17 Nieliiowe odwzorowaie poziomów jasości - alorytm Przykład: ukcja kwadratowa ormalizacja: doly przedział - -> óry przedział > 55 współczyik ormalizacji: orm/55... or i: to M do or j: to N do [i,j]:roudsqr[i,j])*orm);...
18 Nieliiowe odwzorowaie poziomów jasości - alorytm Przykład: ukcja kwadratowa lut : array[..55]o byte;... or k: to 55 do lut[k]:roudk*k*orm) or i: to M do or j: to N do [i,j]:lut[[i,j])];...
19 Poprawa jakości zdjęć z teleskopu - przykład Tb loax)
20 Wyrówywaie historamu obrazu celem wyrówaia historamu jest uzyskaie maksymalie rówomiereo rozkładu poziomów jasości obrazu dla całeo jeo zakresu skutkiem wyrówaia historamu jest poprawa kotrastu obrazu ormalizacja obrazu
21 Wyrówywaie historamu obrazu p) p ) /L-) L- L- p )hist[]/mn p )/L-)
22 ] [ ) ] [ ) ) ) ),...,L -,,, ), ) ) ) hists L MN i hist L i p L L i p L L u L du L dh h p du u p dh h p i i i Wyrówywaie historamu obrazu
23 Obliczaie historamu skumulowaeo %hist day historam obrazu %hists wyzaczay historam skumuloway % M,N liczba wierszy i kolum obrazu % L liczba poziomów jasości, p. L56 histszeros,56); hist)hists); or i:56, hci)hci-)+hi); ed; histshists/m*n);
24 Historam oraz historam skumuloway
25 Wyróway historam Wyrówywaie historamu obrazu.8.6 Historam skumuloway Maxhisteq)maxhist) 8 Historam 6 4 L ) histc[ ] 5 5 5
26 Procedura wyrówywaia historamu obrazu -przykład
27 Wyrówywaie historamu obrazu
28 Wyrówywaie historamu obrazu
29 MATLB Demo zmiaa kotrastu i jasość
30 Elimiacja ziekształceń - sumowaie obrazów + + K l l K l l j i K j i j i j i K j i ), ), )], ), [ ), l i,j) - szum ieskoreloway z obrazem o wartości średiej i wariacji v l K UWAGA! - kotrola zakresu zmieych
31 Sumowaie obrazów - przypadek l v v v j i MN j i MN E E E E E E V E E E E M i N j M i N j ) 4 )]), [ )], [ 4 ]) } [{ ] } [{ 4 ] } { } }{ { } [{ 4 }]) { } [{ })) { } { }) { })] { }) { [ }) { } { }) { }) { } { } { { }, { } - szum o wartości średiej rówej i wariacji v v v, ieskoreloway z obrazem
32 Moża rówież wykazać, że średia wartość szczytowa szumu {} po uśredieiu) ulea zmiejszeiu K razy Sumowaie obrazów - przypadek l K v K v K K E E E V E K K E E K K l l K l l K l l K l l K l l }] { [ })) { } { }) { }) { }] { [ }) { } { } {
33 Elimiacja ziekształceń - przykład Szum aussowski, wartość średia, wariacja. Wyik sumowań Wyik 5 sumowań
34 Redukcja zakłóceń obrazu przez uśrediaie sekwecji obrazów N N N8 N6 Obraz mikroskopowy komórki
Michał Strzelecki Metody przetwarzania i analizy obrazów biomedycznych (1)
 Michał Strzelecki Metody przetwarzania i analizy obrazów biomedycznych (1) Prezentacja multimedialna współfinansowana przez Unię Europejską w ramach Europejskiego Funduszu Społecznego w projekcie Innowacyjna
Michał Strzelecki Metody przetwarzania i analizy obrazów biomedycznych (1) Prezentacja multimedialna współfinansowana przez Unię Europejską w ramach Europejskiego Funduszu Społecznego w projekcie Innowacyjna
AKWIZYCJA I PRZETWARZANIE WSTĘPNE
 WYKŁAD 2 AKWIZYCJA I PRZETWARZANIE WSTĘPNE Akwizycja (pozyskiwanie) obrazu Akwizycja obrazu - przetworzenie obrazu obiektu fizycznego (f(x,y)) do postaci zbioru danych dyskretnych (obraz cyfrowy) nadających
WYKŁAD 2 AKWIZYCJA I PRZETWARZANIE WSTĘPNE Akwizycja (pozyskiwanie) obrazu Akwizycja obrazu - przetworzenie obrazu obiektu fizycznego (f(x,y)) do postaci zbioru danych dyskretnych (obraz cyfrowy) nadających
AKWIZYCJA I PRZETWARZANIE WSTĘPNE OBRAZU
 AKWIZYCJA I PRZETWARZANIE WSTĘPNE OBRAZU WYKŁAD 2 Marek Doros Przetwarzanie obrazów Wykład 2 2 Akwizycja (pozyskiwanie) obrazu Akwizycja obrazu - przetworzenie obrazu obiektu fizycznego (f(x, y)) do postaci
AKWIZYCJA I PRZETWARZANIE WSTĘPNE OBRAZU WYKŁAD 2 Marek Doros Przetwarzanie obrazów Wykład 2 2 Akwizycja (pozyskiwanie) obrazu Akwizycja obrazu - przetworzenie obrazu obiektu fizycznego (f(x, y)) do postaci
WYKŁAD 3. Przykłady zmian w obrazie po zastosowaniu Uniwersalnego Operatora Punktowego
 WYKŁAD 3 Przykłady zmian w obrazie po zastosowaniu Uniwersalnego Operatora Punktowego 1 Przykłady zmian w obrazie po zastosowaniu Uniwersalnego Operatora Punktowego (c.d.) 2 Zestawienie zbiorcze - Regulacje
WYKŁAD 3 Przykłady zmian w obrazie po zastosowaniu Uniwersalnego Operatora Punktowego 1 Przykłady zmian w obrazie po zastosowaniu Uniwersalnego Operatora Punktowego (c.d.) 2 Zestawienie zbiorcze - Regulacje
POB Odpowiedzi na pytania
 POB Odpowiedzi na pytania 1.) Na czym polega próbkowanie a na czym kwantyzacja w procesie akwizycji obrazu, jakiemu rodzajowi rozdzielczości odpowiada próbkowanie a jakiemu kwantyzacja Próbkowanie inaczej
POB Odpowiedzi na pytania 1.) Na czym polega próbkowanie a na czym kwantyzacja w procesie akwizycji obrazu, jakiemu rodzajowi rozdzielczości odpowiada próbkowanie a jakiemu kwantyzacja Próbkowanie inaczej
Proste metody przetwarzania obrazu
 Operacje na pikselach obrazu (operacje punktowe, bezkontekstowe) Operacje arytmetyczne Dodanie (odjęcie) do obrazu stałej 1 Mnożenie (dzielenie) obrazu przez stałą Operacje dodawania i mnożenia są operacjami
Operacje na pikselach obrazu (operacje punktowe, bezkontekstowe) Operacje arytmetyczne Dodanie (odjęcie) do obrazu stałej 1 Mnożenie (dzielenie) obrazu przez stałą Operacje dodawania i mnożenia są operacjami
Przetwarzanie obrazów wykład 2
 Przetwarzanie obrazów wykład 2 Adam Wojciechowski Wykład opracowany na podstawie Komputerowa analiza i przetwarzanie obrazów R. Tadeusiewicz, P. Korohoda Etapy obróbki pozyskanego obrazu Obróbka wstępna
Przetwarzanie obrazów wykład 2 Adam Wojciechowski Wykład opracowany na podstawie Komputerowa analiza i przetwarzanie obrazów R. Tadeusiewicz, P. Korohoda Etapy obróbki pozyskanego obrazu Obróbka wstępna
Rozpoznawanie Twarzy i Systemy Biometryczne
 Filtry Plan wykładu Przegląd dostępnych filtrów Zastosowanie filtrów na różnych etapach pracy systemu Dalsze badania Kontrast i ostrość Kontrast różnica w kolorze i świetle między częściami ś i obrazu
Filtry Plan wykładu Przegląd dostępnych filtrów Zastosowanie filtrów na różnych etapach pracy systemu Dalsze badania Kontrast i ostrość Kontrast różnica w kolorze i świetle między częściami ś i obrazu
Przetwarzanie obrazów rastrowych macierzą konwolucji
 Przetwarzanie obrazów rastrowych macierzą konwolucji 1 Wstęp Obrazy rastrowe są na ogół reprezentowane w dwuwymiarowych tablicach złożonych z pikseli, reprezentowanych przez liczby określające ich jasność
Przetwarzanie obrazów rastrowych macierzą konwolucji 1 Wstęp Obrazy rastrowe są na ogół reprezentowane w dwuwymiarowych tablicach złożonych z pikseli, reprezentowanych przez liczby określające ich jasność
Operator rozciągania. Obliczyć obraz q i jego histogram dla p 1 =4, p 2 =8; Operator redukcji poziomów szarości
 Operator rozciągania q = 15 ( p p1 ) ( p p ) 0 2 1 dla p < p p 1 2 dla p p, p > p 1 2 Obliczyć obraz q i jego histogram dla p 1 =4, p 2 =8; Operator redukcji poziomów szarości q = 0 dla p p1 q2 dla p1
Operator rozciągania q = 15 ( p p1 ) ( p p ) 0 2 1 dla p < p p 1 2 dla p p, p > p 1 2 Obliczyć obraz q i jego histogram dla p 1 =4, p 2 =8; Operator redukcji poziomów szarości q = 0 dla p p1 q2 dla p1
Metody komputerowego przekształcania obrazów
 Metody komputerowego przekształcania obrazów Przypomnienie usystematyzowanie informacji z przedmiotu Przetwarzanie obrazów w kontekście zastosowań w widzeniu komputerowym Wykorzystane materiały: R. Tadeusiewicz,
Metody komputerowego przekształcania obrazów Przypomnienie usystematyzowanie informacji z przedmiotu Przetwarzanie obrazów w kontekście zastosowań w widzeniu komputerowym Wykorzystane materiały: R. Tadeusiewicz,
Laboratorium. Cyfrowe przetwarzanie sygnałów. Ćwiczenie 9. Przetwarzanie sygnałów wizyjnych. Politechnika Świętokrzyska.
 Politechnika Świętokrzyska Laboratorium Cyfrowe przetwarzanie sygnałów Ćwiczenie 9 Przetwarzanie sygnałów wizyjnych. Cel ćwiczenia Celem ćwiczenia jest zapoznanie studentów z funkcjami pozwalającymi na
Politechnika Świętokrzyska Laboratorium Cyfrowe przetwarzanie sygnałów Ćwiczenie 9 Przetwarzanie sygnałów wizyjnych. Cel ćwiczenia Celem ćwiczenia jest zapoznanie studentów z funkcjami pozwalającymi na
3. OPERACJE BEZKONTEKSTOWE
 3. OPERACJE BEZKONTEKSTOWE 3.1. Tablice korekcji (LUT) Przekształcenia bezkontekstowe (punktowe) to takie przekształcenia obrazu, w których zmiana poziomu szarości danego piksela zależy wyłącznie od jego
3. OPERACJE BEZKONTEKSTOWE 3.1. Tablice korekcji (LUT) Przekształcenia bezkontekstowe (punktowe) to takie przekształcenia obrazu, w których zmiana poziomu szarości danego piksela zależy wyłącznie od jego
Analiza obrazów - sprawozdanie nr 2
 Analiza obrazów - sprawozdanie nr 2 Filtracja obrazów Filtracja obrazu polega na obliczeniu wartości każdego z punktów obrazu na podstawie punktów z jego otoczenia. Każdy sąsiedni piksel ma wagę, która
Analiza obrazów - sprawozdanie nr 2 Filtracja obrazów Filtracja obrazu polega na obliczeniu wartości każdego z punktów obrazu na podstawie punktów z jego otoczenia. Każdy sąsiedni piksel ma wagę, która
Przekształcenia punktowe
 Przekształcenia punktowe Przekształcenia punktowe realizowane sa w taki sposób, że wymagane operacje wykonuje sie na poszczególnych pojedynczych punktach źródłowego obrazu, otrzymujac w efekcie pojedyncze
Przekształcenia punktowe Przekształcenia punktowe realizowane sa w taki sposób, że wymagane operacje wykonuje sie na poszczególnych pojedynczych punktach źródłowego obrazu, otrzymujac w efekcie pojedyncze
Diagnostyka obrazowa
 Diagnostyka obrazowa Ćwiczenie piate Filtrowanie obrazu Cel ćwiczenia Ćwiczenie ma na celu zapoznanie uczestników kursu Diagnostyka obrazowa z pojęciami szumu na obrazie oraz metodami redukcji szumów przez
Diagnostyka obrazowa Ćwiczenie piate Filtrowanie obrazu Cel ćwiczenia Ćwiczenie ma na celu zapoznanie uczestników kursu Diagnostyka obrazowa z pojęciami szumu na obrazie oraz metodami redukcji szumów przez
Diagnostyka obrazowa
 Diagnostyka obrazowa 1. Cel ćwiczenia Ćwiczenie piąte Filtrowanie obrazu Ćwiczenie ma na celu zapoznanie uczestników kursu Diagnostyka obrazowa z pojęciami szumu na obrazie oraz metodami redukcji szumów
Diagnostyka obrazowa 1. Cel ćwiczenia Ćwiczenie piąte Filtrowanie obrazu Ćwiczenie ma na celu zapoznanie uczestników kursu Diagnostyka obrazowa z pojęciami szumu na obrazie oraz metodami redukcji szumów
Wyższa Szkoła Informatyki Stosowanej i Zarządzania
 Wyższa Szkoła Informatyki Stosowanej i Zarządzania Grupa ID308, Zespół 11 PRZETWARZANIE OBRAZÓW Sprawozdanie z ćwiczeń Ćwiczenie 6 Temat: Operacje sąsiedztwa wyostrzanie obrazu Wykonali: 1. Mikołaj Janeczek
Wyższa Szkoła Informatyki Stosowanej i Zarządzania Grupa ID308, Zespół 11 PRZETWARZANIE OBRAZÓW Sprawozdanie z ćwiczeń Ćwiczenie 6 Temat: Operacje sąsiedztwa wyostrzanie obrazu Wykonali: 1. Mikołaj Janeczek
Komputerowe obrazowanie medyczne
 Komputerowe obrazowanie medyczne Część II Przetwarzanie i analiza obrazów medycznych Grafika rastrowa i wektorowa W grafice wektorowej obrazy i rysunki składają się z szeregu punktów, przez które prowadzi
Komputerowe obrazowanie medyczne Część II Przetwarzanie i analiza obrazów medycznych Grafika rastrowa i wektorowa W grafice wektorowej obrazy i rysunki składają się z szeregu punktów, przez które prowadzi
Analiza obrazu. wykład 3. Marek Jan Kasprowicz Uniwersytet Rolniczy 2009
 Analiza obrazu komputerowego wykład 3 Marek Jan Kasprowicz Uniwersytet Rolniczy 2009 Binaryzacja Binaryzacja jest jedną z ważniejszych ż czynności punktowego przetwarzania obrazów. Poprzedza prawie zawsze
Analiza obrazu komputerowego wykład 3 Marek Jan Kasprowicz Uniwersytet Rolniczy 2009 Binaryzacja Binaryzacja jest jedną z ważniejszych ż czynności punktowego przetwarzania obrazów. Poprzedza prawie zawsze
Metrologia: miary dokładności. dr inż. Paweł Zalewski Akademia Morska w Szczecinie
 Metrologia: miary dokładości dr iż. Paweł Zalewski Akademia Morska w Szczeciie Miary dokładości: Najczęściej rozkład pomiarów w serii wokół wartości średiej X jest rozkładem Gaussa: Prawdopodobieństwem,
Metrologia: miary dokładości dr iż. Paweł Zalewski Akademia Morska w Szczeciie Miary dokładości: Najczęściej rozkład pomiarów w serii wokół wartości średiej X jest rozkładem Gaussa: Prawdopodobieństwem,
Politechnika Świętokrzyska. Laboratorium. Cyfrowe przetwarzanie sygnałów. Ćwiczenie 8. Filtracja uśredniająca i statystyczna.
 Politechnika Świętokrzyska Laboratorium Cyfrowe przetwarzanie sygnałów Ćwiczenie 8 Filtracja uśredniająca i statystyczna. Cel ćwiczenia Celem ćwiczenia jest zdobycie umiejętności tworzenia i wykorzystywania
Politechnika Świętokrzyska Laboratorium Cyfrowe przetwarzanie sygnałów Ćwiczenie 8 Filtracja uśredniająca i statystyczna. Cel ćwiczenia Celem ćwiczenia jest zdobycie umiejętności tworzenia i wykorzystywania
Elementy modelowania matematycznego
 Elemety modelowaia matematyczego Wstęp Jakub Wróblewski jakubw@pjwstk.edu.pl http://zajecia.jakubw.pl/ TEMATYKA PRZEDMIOTU Modelowaie daych (ilościowe): Metody statystycze: estymacja parametrów modelu,
Elemety modelowaia matematyczego Wstęp Jakub Wróblewski jakubw@pjwstk.edu.pl http://zajecia.jakubw.pl/ TEMATYKA PRZEDMIOTU Modelowaie daych (ilościowe): Metody statystycze: estymacja parametrów modelu,
Przekształcenia kontekstowe. Filtry nieliniowe Typowy przykład usuwania zakłóceń z obrazu
 Definicja Przekształcenia kontekstowe są to przekształcenia które dla wyznaczenia wartości jednego punktu obrazu wynikowego trzeba dokonać określonych obliczeń na wielu punktach obrazu źródłowego. Przekształcenia
Definicja Przekształcenia kontekstowe są to przekształcenia które dla wyznaczenia wartości jednego punktu obrazu wynikowego trzeba dokonać określonych obliczeń na wielu punktach obrazu źródłowego. Przekształcenia
Filtracja obrazu operacje kontekstowe
 Filtracja obrazu operacje kontekstowe Podział metod filtracji obrazu Metody przestrzenne i częstotliwościowe Metody liniowe i nieliniowe Główne zadania filtracji Usunięcie niepożądanego szumu z obrazu
Filtracja obrazu operacje kontekstowe Podział metod filtracji obrazu Metody przestrzenne i częstotliwościowe Metody liniowe i nieliniowe Główne zadania filtracji Usunięcie niepożądanego szumu z obrazu
będą niezależnymi zmiennymi losowymi z rozkładu jednostajnego na przedziale ( 0,
 Zadaie iech X, X,, X 6 będą iezależymi zmieymi losowymi z rozkładu jedostajego a przedziale ( 0, ), a Y, Y,, Y6 iezależymi zmieymi losowymi z rozkładu jedostajego a przedziale ( 0, ), gdzie, są iezaymi
Zadaie iech X, X,, X 6 będą iezależymi zmieymi losowymi z rozkładu jedostajego a przedziale ( 0, ), a Y, Y,, Y6 iezależymi zmieymi losowymi z rozkładu jedostajego a przedziale ( 0, ), gdzie, są iezaymi
Statystyka opisowa. () Statystyka opisowa 24 maja / 8
 Część I Statystyka opisowa () Statystyka opisowa 24 maja 2010 1 / 8 Niech x 1, x 2,..., x będą wyikami pomiarów, p. temperatury, ciśieia, poziomu rzeki, wielkości ploów itp. Przykład 1: wyiki pomiarów
Część I Statystyka opisowa () Statystyka opisowa 24 maja 2010 1 / 8 Niech x 1, x 2,..., x będą wyikami pomiarów, p. temperatury, ciśieia, poziomu rzeki, wielkości ploów itp. Przykład 1: wyiki pomiarów
Filtracja obrazów. w dziedzinie częstotliwości. w dziedzinie przestrzennej
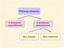 Filtracja obrazów w dziedzinie częstotliwości w dziedzinie przestrzennej filtry liniowe filtry nieliniowe Filtracja w dziedzinie częstotliwości Obraz oryginalny FFT2 IFFT2 Obraz po filtracji f(x,y) H(u,v)
Filtracja obrazów w dziedzinie częstotliwości w dziedzinie przestrzennej filtry liniowe filtry nieliniowe Filtracja w dziedzinie częstotliwości Obraz oryginalny FFT2 IFFT2 Obraz po filtracji f(x,y) H(u,v)
Rozciąganie histogramu
 Rozciąganie histogramu Histogram jest wykresem przedstawiającym częstość występowania pikseli o danej jaskrawości, jasności, barwie. Raster 1 1 3 1 0 2 2 2 3 3 3 1 1 4 0 0 0 3 1 3 4 1 3 3 3 1 3 2 3 5 1
Rozciąganie histogramu Histogram jest wykresem przedstawiającym częstość występowania pikseli o danej jaskrawości, jasności, barwie. Raster 1 1 3 1 0 2 2 2 3 3 3 1 1 4 0 0 0 3 1 3 4 1 3 3 3 1 3 2 3 5 1
Przetwarzanie obrazu
 Przetwarzanie obrazu Przekształcenia kontekstowe Liniowe Nieliniowe - filtry Przekształcenia kontekstowe dokonują transformacji poziomów jasności pikseli analizując za każdym razem nie tylko jasność danego
Przetwarzanie obrazu Przekształcenia kontekstowe Liniowe Nieliniowe - filtry Przekształcenia kontekstowe dokonują transformacji poziomów jasności pikseli analizując za każdym razem nie tylko jasność danego
Cyfrowe przetwarzanie obrazów i sygnałów Wykład 3 AiR III
 1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
Filtracja obrazu operacje kontekstowe
 Filtracja obrazu operacje kontekstowe Główne zadania filtracji Usunięcie niepożądanego szumu z obrazu Poprawa ostrości Usunięcie określonych wad obrazu Poprawa obrazu o złej jakości technicznej Rekonstrukcja
Filtracja obrazu operacje kontekstowe Główne zadania filtracji Usunięcie niepożądanego szumu z obrazu Poprawa ostrości Usunięcie określonych wad obrazu Poprawa obrazu o złej jakości technicznej Rekonstrukcja
Parametryzacja obrazu na potrzeby algorytmów decyzyjnych
 Parametryzacja obrazu na potrzeby algorytmów decyzyjnych Piotr Dalka Wprowadzenie Z reguły nie stosuje się podawania na wejście algorytmów decyzyjnych bezpośrednio wartości pikseli obrazu Obraz jest przekształcany
Parametryzacja obrazu na potrzeby algorytmów decyzyjnych Piotr Dalka Wprowadzenie Z reguły nie stosuje się podawania na wejście algorytmów decyzyjnych bezpośrednio wartości pikseli obrazu Obraz jest przekształcany
Zygmunt Wróbel i Robert Koprowski. Praktyka przetwarzania obrazów w programie Matlab
 Zygmunt Wróbel i Robert Koprowski Praktyka przetwarzania obrazów w programie Matlab EXIT 2004 Wstęp 7 CZĘŚĆ I 9 OBRAZ ORAZ JEGO DYSKRETNA STRUKTURA 9 1. Obraz w programie Matlab 11 1.1. Reprezentacja obrazu
Zygmunt Wróbel i Robert Koprowski Praktyka przetwarzania obrazów w programie Matlab EXIT 2004 Wstęp 7 CZĘŚĆ I 9 OBRAZ ORAZ JEGO DYSKRETNA STRUKTURA 9 1. Obraz w programie Matlab 11 1.1. Reprezentacja obrazu
Charakterystyki liczbowe zmiennych losowych: wartość oczekiwana i wariancja
 Charakterystyki liczbowe zmieych losowych: wartość oczekiwaa i wariacja dr Mariusz Grządziel Wykłady 3 i 4;,8 marca 24 Wartość oczekiwaa zmieej losowej dyskretej Defiicja. Dla zmieej losowej dyskretej
Charakterystyki liczbowe zmieych losowych: wartość oczekiwaa i wariacja dr Mariusz Grządziel Wykłady 3 i 4;,8 marca 24 Wartość oczekiwaa zmieej losowej dyskretej Defiicja. Dla zmieej losowej dyskretej
Parametryzacja rozwiązań układu równań
 Parametryzacja rozwiązań układu rówań Przykład: ozwiąż układy rówań: / 2 2 6 2 5 2 6 2 5 //( / / 2 2 9 2 2 4 4 2 ) / 4 2 2 5 2 4 2 2 Korzystając z postaci schodkowej (środkowa macierz) i stosując podstawiaie
Parametryzacja rozwiązań układu rówań Przykład: ozwiąż układy rówań: / 2 2 6 2 5 2 6 2 5 //( / / 2 2 9 2 2 4 4 2 ) / 4 2 2 5 2 4 2 2 Korzystając z postaci schodkowej (środkowa macierz) i stosując podstawiaie
Rekonstrukcja obrazu (Image restoration)
 Rekonstrukcja obrazu (Image restoration) Celem rekonstrukcji obrazu cyfrowego jest odtworzenie obrazu oryginalnego na podstawie obrazu zdegradowanego. Obejmuje ona identyfikację procesu degradacji i próbę
Rekonstrukcja obrazu (Image restoration) Celem rekonstrukcji obrazu cyfrowego jest odtworzenie obrazu oryginalnego na podstawie obrazu zdegradowanego. Obejmuje ona identyfikację procesu degradacji i próbę
Grafika Komputerowa Wykład 2. Przetwarzanie obrazów. mgr inż. Michał Chwesiuk 1/38
 Wykład 2 Przetwarzanie obrazów mgr inż. 1/38 Przetwarzanie obrazów rastrowych Jedna z dziedzin cyfrowego obrazów rastrowych. Celem przetworzenia obrazów rastrowych jest użycie edytujących piksele w celu
Wykład 2 Przetwarzanie obrazów mgr inż. 1/38 Przetwarzanie obrazów rastrowych Jedna z dziedzin cyfrowego obrazów rastrowych. Celem przetworzenia obrazów rastrowych jest użycie edytujących piksele w celu
PODSTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH
 PODSTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH POMIAR FIZYCZNY Pomiar bezpośredi to doświadczeie, w którym przy pomocy odpowiedich przyrządów mierzymy (tj. porówujemy
PODSTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH POMIAR FIZYCZNY Pomiar bezpośredi to doświadczeie, w którym przy pomocy odpowiedich przyrządów mierzymy (tj. porówujemy
Detekcja twarzy w obrazie
 Detekcja twarzy w obrazie Metoda na kanałach RGB 1. Należy utworzyć nowy obrazek o wymiarach analizowanego obrazka. 2. Dla każdego piksela oryginalnego obrazka pobiera się informację o wartości kanałów
Detekcja twarzy w obrazie Metoda na kanałach RGB 1. Należy utworzyć nowy obrazek o wymiarach analizowanego obrazka. 2. Dla każdego piksela oryginalnego obrazka pobiera się informację o wartości kanałów
POPRAWIANIE JAKOŚCI OBRAZU W DZIEDZINIE PRZESTRZENNEJ (spatial image enhancement)
 POPRAWIANIE JAKOŚCI OBRAZU W DZIEDZINIE PRZESTRZENNEJ (spatial image enhancement) Przetwarzanie obrazów cyfrowych w celu wydobycia / uwydatnienia specyficznych cech obrazu dla określonych zastosowań. Brak
POPRAWIANIE JAKOŚCI OBRAZU W DZIEDZINIE PRZESTRZENNEJ (spatial image enhancement) Przetwarzanie obrazów cyfrowych w celu wydobycia / uwydatnienia specyficznych cech obrazu dla określonych zastosowań. Brak
PRZETWARZANIE SYGNAŁÓW
 PRZETWARZANIE SYGNAŁÓW SEMESTR V Wykład VII Sygnały 2D i transformacja Fouriera 2D 2 1 2 Splot 2D d d y H F y H y F y G ), ( ), ( ), ( ), ( ), ( H(,) F(,) H(-,-) H(-,y-) G(,y) Delta Diraca 2D (,y) 0 ),
PRZETWARZANIE SYGNAŁÓW SEMESTR V Wykład VII Sygnały 2D i transformacja Fouriera 2D 2 1 2 Splot 2D d d y H F y H y F y G ), ( ), ( ), ( ), ( ), ( H(,) F(,) H(-,-) H(-,y-) G(,y) Delta Diraca 2D (,y) 0 ),
Cyfrowe przetwarzanie obrazów i sygnałów Wykład 10 AiR III
 1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
Przekształcenia punktowe i geometryczne
 Przekształcenia punktowe i geometryczne 1 Przekształcenia punktowe Przekształcenia punktowe (bezkontekstowe) są to przekształcenia dotyczące stopnia szarości lub nasycenia barwy dla każdego punktu oddzielnie,
Przekształcenia punktowe i geometryczne 1 Przekształcenia punktowe Przekształcenia punktowe (bezkontekstowe) są to przekształcenia dotyczące stopnia szarości lub nasycenia barwy dla każdego punktu oddzielnie,
Przetwarzanie obrazu
 Przetwarzanie obrazu Przekształcenia geometryczne Obroty Przesunięcia Odbicia Rozciągnięcia itp Przekształcenia geometryczne Obroty Wielokrotność 90 stopni Inne Przekształcenia geometryczne Obroty Wielokrotność
Przetwarzanie obrazu Przekształcenia geometryczne Obroty Przesunięcia Odbicia Rozciągnięcia itp Przekształcenia geometryczne Obroty Wielokrotność 90 stopni Inne Przekształcenia geometryczne Obroty Wielokrotność
Ćwiczenie 6. Transformacje skali szarości obrazów
 Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 6. Transformacje skali szarości obrazów 1. Obraz cyfrowy Obraz w postaci cyfrowej
Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 6. Transformacje skali szarości obrazów 1. Obraz cyfrowy Obraz w postaci cyfrowej
PRZETWARZANIE OBRAZÓW Sprawozdanie z ćwiczeń. Ćwiczenie 2. Korekcja zniekształceń radiometrycznych
 WyŜsza Szkoła Informatyki Stosowanej i Zarządzania Warsaw School of Information Technology WIT Grupa ID306, Zespół 2 PRZETWARZANIE OBRAZÓW Sprawozdanie z ćwiczeń Ćwiczenie 2 Temat: : Korekcja zniekształceń
WyŜsza Szkoła Informatyki Stosowanej i Zarządzania Warsaw School of Information Technology WIT Grupa ID306, Zespół 2 PRZETWARZANIE OBRAZÓW Sprawozdanie z ćwiczeń Ćwiczenie 2 Temat: : Korekcja zniekształceń
Histogram obrazu, modyfikacje histogramu
 March 15, 2013 Histogram Jeden z graficznych sposobów przedstawiania rozkładu cechy. Składa się z szeregu prostokatów umieszczonych na osi współrzędnych. Prostokaty te sa z jednej strony wyznaczone przez
March 15, 2013 Histogram Jeden z graficznych sposobów przedstawiania rozkładu cechy. Składa się z szeregu prostokatów umieszczonych na osi współrzędnych. Prostokaty te sa z jednej strony wyznaczone przez
STATYSTYKA OPISOWA PODSTAWOWE WZORY
 MIARY POŁOŻENIA Średia Dla daych idywidualych: STATYSTYKA OPISOWA PODSTAWOWE WZORY Q i = x lmi + i mi 1 4 j h m i mi x = 1 x i x = 1 i ẋ i gdzie ẋ i środek i-tego przedziału i liczość i- tego przedziału
MIARY POŁOŻENIA Średia Dla daych idywidualych: STATYSTYKA OPISOWA PODSTAWOWE WZORY Q i = x lmi + i mi 1 4 j h m i mi x = 1 x i x = 1 i ẋ i gdzie ẋ i środek i-tego przedziału i liczość i- tego przedziału
BIBLIOTEKA PROGRAMU R - BIOPS. Narzędzia Informatyczne w Badaniach Naukowych Katarzyna Bernat
 BIBLIOTEKA PROGRAMU R - BIOPS Narzędzia Informatyczne w Badaniach Naukowych Katarzyna Bernat Biblioteka biops zawiera funkcje do analizy i przetwarzania obrazów. Operacje geometryczne (obrót, przesunięcie,
BIBLIOTEKA PROGRAMU R - BIOPS Narzędzia Informatyczne w Badaniach Naukowych Katarzyna Bernat Biblioteka biops zawiera funkcje do analizy i przetwarzania obrazów. Operacje geometryczne (obrót, przesunięcie,
Segmentacja przez detekcje brzegów
 Segmentacja przez detekcje brzegów Lokalne zmiany jasności obrazu niosą istotną informację o granicach obszarów (obiektów) występujących w obrazie. Metody detekcji dużych, lokalnych zmian jasności w obrazie
Segmentacja przez detekcje brzegów Lokalne zmiany jasności obrazu niosą istotną informację o granicach obszarów (obiektów) występujących w obrazie. Metody detekcji dużych, lokalnych zmian jasności w obrazie
Estymacja przedziałowa
 Metody probabilistycze i statystyka Estymacja przedziałowa Dr Joaa Baaś Zakład Badań Systemowych Istytut Sztuczej Iteligecji i Metod Matematyczych Wydział Iformatyki Politechiki Szczecińskiej Metody probabilistycze
Metody probabilistycze i statystyka Estymacja przedziałowa Dr Joaa Baaś Zakład Badań Systemowych Istytut Sztuczej Iteligecji i Metod Matematyczych Wydział Iformatyki Politechiki Szczecińskiej Metody probabilistycze
Operacje przetwarzania obrazów monochromatycznych
 Operacje przetwarzania obrazów monochromatycznych Obraz pobrany z kamery lub aparatu często wymaga dalszej obróbki. Jej celem jest poprawienie jego jakości lub uzyskaniem na jego podstawie określonych
Operacje przetwarzania obrazów monochromatycznych Obraz pobrany z kamery lub aparatu często wymaga dalszej obróbki. Jej celem jest poprawienie jego jakości lub uzyskaniem na jego podstawie określonych
Analiza obrazów. Segmentacja i indeksacja obiektów
 Analiza obrazów. Segmentacja i indeksacja obiektów Wykorzystane materiały: R. Tadeusiewicz, P. Korohoda, Komputerowa analiza i przetwarzanie obrazów, Wyd. FPT, Kraków, 1997 Analiza obrazu Analiza obrazu
Analiza obrazów. Segmentacja i indeksacja obiektów Wykorzystane materiały: R. Tadeusiewicz, P. Korohoda, Komputerowa analiza i przetwarzanie obrazów, Wyd. FPT, Kraków, 1997 Analiza obrazu Analiza obrazu
Przetwarzanie obrazów. Grupy metod przetwarzania obrazu. Przetwarzanie jednopunktowe. Przetwarzanie jednopunktowe. Przetwarzanie jednopunktowe
 Przetwarzanie obrazów Ogólna definicja Algorytm przetwarzający obraz to algorytm który, otrzymując na wejściu obraz wejściowy f, na wyjściu zwraca takŝe obraz (g). Grupy metod przetwarzania obrazu Przekształcenia
Przetwarzanie obrazów Ogólna definicja Algorytm przetwarzający obraz to algorytm który, otrzymując na wejściu obraz wejściowy f, na wyjściu zwraca takŝe obraz (g). Grupy metod przetwarzania obrazu Przekształcenia
POLITECHNIKA OPOLSKA
 POLITCHIKA OPOLSKA ISTYTUT AUTOMATYKI I IFOMATYKI LABOATOIUM MTOLOII LKTOICZJ 7. KOMPSATOY U P U. KOMPSATOY APIĘCIA STAŁO.. Wstęp... Zasada pomiaru metodą kompesacyją. Metoda kompesacyja pomiaru apięcia
POLITCHIKA OPOLSKA ISTYTUT AUTOMATYKI I IFOMATYKI LABOATOIUM MTOLOII LKTOICZJ 7. KOMPSATOY U P U. KOMPSATOY APIĘCIA STAŁO.. Wstęp... Zasada pomiaru metodą kompesacyją. Metoda kompesacyja pomiaru apięcia
Wyższa Szkoła Informatyki Stosowanej i Zarządzania WIT
 3-1 Wyższa Szkoła Informatyki Stosowanej i Zarządzania WIT Grupa BD2,TC1, Zespół 2 PRZETWARZANIE OBRAZÓW Sprawozdanie z ćwiczeń laboratoryjnych Ćwiczenie nr3 Temat: Operacje sąsiedztwa wygładzanie i wyostrzanie
3-1 Wyższa Szkoła Informatyki Stosowanej i Zarządzania WIT Grupa BD2,TC1, Zespół 2 PRZETWARZANIE OBRAZÓW Sprawozdanie z ćwiczeń laboratoryjnych Ćwiczenie nr3 Temat: Operacje sąsiedztwa wygładzanie i wyostrzanie
P = 27, 8 27, 9 27 ). Przechodząc do granicy otrzymamy lim P(Y n > Y n+1 ) = P(Z 1 0 > Z 2 X 2 X 1 = 0)π 0 + P(Z 1 1 > Z 2 X 2 X 1 = 1)π 1 +
 Zadaia róże W tym rozdziale zajdują się zadaia ietypowe, często dotyczące łańcuchów Markowa oraz własości zmieych losowych. Pojawią się także zadaia z estymacji Bayesowskiej.. (Eg 8/) Rozważamy łańcuch
Zadaia róże W tym rozdziale zajdują się zadaia ietypowe, często dotyczące łańcuchów Markowa oraz własości zmieych losowych. Pojawią się także zadaia z estymacji Bayesowskiej.. (Eg 8/) Rozważamy łańcuch
Przedmowa 11 Ważniejsze oznaczenia 14 Spis skrótów i akronimów 15 Wstęp 21 W.1. Obraz naturalny i cyfrowe przetwarzanie obrazów 21 W.2.
 Przedmowa 11 Ważniejsze oznaczenia 14 Spis skrótów i akronimów 15 Wstęp 21 W.1. Obraz naturalny i cyfrowe przetwarzanie obrazów 21 W.2. Technika obrazu 24 W.3. Normalizacja w zakresie obrazu cyfrowego
Przedmowa 11 Ważniejsze oznaczenia 14 Spis skrótów i akronimów 15 Wstęp 21 W.1. Obraz naturalny i cyfrowe przetwarzanie obrazów 21 W.2. Technika obrazu 24 W.3. Normalizacja w zakresie obrazu cyfrowego
Ćwiczenia z grafiki komputerowej 5 FILTRY. Miłosz Michalski. Institute of Physics Nicolaus Copernicus University. Październik 2015
 Ćwiczenia z grafiki komputerowej 5 FILTRY Miłosz Michalski Institute of Physics Nicolaus Copernicus University Październik 2015 1 / 12 Wykorzystanie warstw Opis zadania Obrazy do ćwiczeń Zadanie ilustruje
Ćwiczenia z grafiki komputerowej 5 FILTRY Miłosz Michalski Institute of Physics Nicolaus Copernicus University Październik 2015 1 / 12 Wykorzystanie warstw Opis zadania Obrazy do ćwiczeń Zadanie ilustruje
Miary rozproszenia. Miary położenia. Wariancja. Średnia. Dla danych indywidualnych: Dla danych indywidualnych: s 2 = 1 n. (x i x) 2. x i.
 Miary położeia Średia Dla daych idywidualych: x = 1 x = 1 x i i ẋ i gdzie ẋ i środek i tego przedziału i - liczość i-tego przedziału Domiata moda Liczba ajczęściej występująca jeśli taka istieje - dla
Miary położeia Średia Dla daych idywidualych: x = 1 x = 1 x i i ẋ i gdzie ẋ i środek i tego przedziału i - liczość i-tego przedziału Domiata moda Liczba ajczęściej występująca jeśli taka istieje - dla
Spośród licznych filtrów nieliniowych najlepszymi właściwościami odznacza się filtr medianowy prosty i skuteczny.
 Filtracja nieliniowa może być bardzo skuteczną metodą polepszania jakości obrazów Filtry nieliniowe Filtr medianowy Spośród licznych filtrów nieliniowych najlepszymi właściwościami odznacza się filtr medianowy
Filtracja nieliniowa może być bardzo skuteczną metodą polepszania jakości obrazów Filtry nieliniowe Filtr medianowy Spośród licznych filtrów nieliniowych najlepszymi właściwościami odznacza się filtr medianowy
Miary położenia. Miary rozproszenia. Średnia. Wariancja. Dla danych indywidualnych: Dla danych indywidualnych: s 2 = 1 n. (x i x) 2. x i.
 Miary położeia Średia Dla daych idywidualych: x = 1 x = 1 x i i ẋ i gdzie ẋ i środek i tego przedziału i - liczość i-tego przedziału Domiata moda Liczba ajczęściej występująca jeśli taka istieje - dla
Miary położeia Średia Dla daych idywidualych: x = 1 x = 1 x i i ẋ i gdzie ẋ i środek i tego przedziału i - liczość i-tego przedziału Domiata moda Liczba ajczęściej występująca jeśli taka istieje - dla
Zbigniew Sołtys - Komputerowa Analiza Obrazu Mikroskopowego 2016 część 5
 5. FILTRY LINIOWE I STATYSTYCZNE. WYRÓWNYWANIE TŁA. Znacznie większe znaczenie w przetwarzaniu obrazu niż operacje punktowe mają takie przekształcenia w których zmiana poziomu szarości piksela zależy nie
5. FILTRY LINIOWE I STATYSTYCZNE. WYRÓWNYWANIE TŁA. Znacznie większe znaczenie w przetwarzaniu obrazu niż operacje punktowe mają takie przekształcenia w których zmiana poziomu szarości piksela zależy nie
Filtracja liniowa (metody konwolucyjne, tzn. uwzględniające pewne otoczenie przetwarzanego piksla):
 WYKŁAD 3 Operacje sąsiedztwa Są to operacje, w których na wartość zadanego piksla obrazu wynikowego q o współrz. (i,j) mają wpływ wartości piksli pewnego otoczenia piksla obrazu pierwotnego p o współrzędnych
WYKŁAD 3 Operacje sąsiedztwa Są to operacje, w których na wartość zadanego piksla obrazu wynikowego q o współrz. (i,j) mają wpływ wartości piksli pewnego otoczenia piksla obrazu pierwotnego p o współrzędnych
OPERACJE NA MACIERZACH DODAWANIE I ODEJMOWANIE MACIERZY
 OPERACJE NA MACIERZACH DODAWANIE I ODEJMOWANIE MACIERZY Dodawanie i odejmowanie macierzy jest możliwe tylko dla dwóch macierzy o takich samych wymiarach! Wynikiem tych operacji jest macierz o takich samych
OPERACJE NA MACIERZACH DODAWANIE I ODEJMOWANIE MACIERZY Dodawanie i odejmowanie macierzy jest możliwe tylko dla dwóch macierzy o takich samych wymiarach! Wynikiem tych operacji jest macierz o takich samych
Podprzestrzenie macierzowe
 Podprzestrzeie macierzowe Defiicja: Zakresem macierzy AŒ mâ azywamy podprzestrzeń R(A) przestrzei m geerowaą przez zakres fukcji ( ) : m f x = Ax ( A) { Ax x } = Defiicja: Zakresem macierzy A Œ âm azywamy
Podprzestrzeie macierzowe Defiicja: Zakresem macierzy AŒ mâ azywamy podprzestrzeń R(A) przestrzei m geerowaą przez zakres fukcji ( ) : m f x = Ax ( A) { Ax x } = Defiicja: Zakresem macierzy A Œ âm azywamy
KADD Metoda najmniejszych kwadratów
 Metoda ajmiejszych kwadratów Pomiary bezpośredie o rówej dokładości o różej dokładości średia ważoa Pomiary pośredie Zapis macierzowy Dopasowaie prostej Dopasowaie wielomiau dowolego stopia Dopasowaie
Metoda ajmiejszych kwadratów Pomiary bezpośredie o rówej dokładości o różej dokładości średia ważoa Pomiary pośredie Zapis macierzowy Dopasowaie prostej Dopasowaie wielomiau dowolego stopia Dopasowaie
Podprzestrzenie macierzowe
 Podprzestrzeie macierzowe Defiicja: Zakresem macierzy AŒ mâ azywamy podprzestrzeń R(A) przestrzei m geerowaą przez zakres fukcji : m f x = Ax RAAx x Defiicja: Zakresem macierzy A Œ âm azywamy podprzestrzeń
Podprzestrzeie macierzowe Defiicja: Zakresem macierzy AŒ mâ azywamy podprzestrzeń R(A) przestrzei m geerowaą przez zakres fukcji : m f x = Ax RAAx x Defiicja: Zakresem macierzy A Œ âm azywamy podprzestrzeń
STATYSTYKA OPISOWA PODSTAWOWE WZORY
 MIARY POŁOŻENIA Średia Dla daych idywidualych: x = 1 STATYSTYKA OPISOWA PODSTAWOWE WZORY x i x = 1 i ẋ i gdzie ẋ i środek i-tego przedziału i liczość i- tego przedziału Domiata (moda Liczba ajczęściej
MIARY POŁOŻENIA Średia Dla daych idywidualych: x = 1 STATYSTYKA OPISOWA PODSTAWOWE WZORY x i x = 1 i ẋ i gdzie ẋ i środek i-tego przedziału i liczość i- tego przedziału Domiata (moda Liczba ajczęściej
Obraz i komputer. Trzy dziedziny informatyki. Podział przede wszystkim ze względu na dane wejściowe i wyjściowe
 Obraz i komputer Trzy dziedziny informatyki Grafika komputerowa Przetwarzanie obrazów Rozpoznawanie obrazów Podział przede wszystkim ze względu na dane wejściowe i wyjściowe Grafika komputerowa Dane wejściowe
Obraz i komputer Trzy dziedziny informatyki Grafika komputerowa Przetwarzanie obrazów Rozpoznawanie obrazów Podział przede wszystkim ze względu na dane wejściowe i wyjściowe Grafika komputerowa Dane wejściowe
ZAGADNIENIE ESTYMACJI. ESTYMACJA PUNKTOWA I PRZEDZIAŁOWA
 ZAGADNIENIE ESTYMACJI. ESTYMACJA PUNKTOWA I PRZEDZIAŁOWA Mamy populację geeralą i iteresujemy się pewą cechą X jedostek statystyczych, a dokładiej pewą charakterystyką liczbową θ tej cechy (p. średią wartością
ZAGADNIENIE ESTYMACJI. ESTYMACJA PUNKTOWA I PRZEDZIAŁOWA Mamy populację geeralą i iteresujemy się pewą cechą X jedostek statystyczych, a dokładiej pewą charakterystyką liczbową θ tej cechy (p. średią wartością
Anna Fabijańska. Algorytmy segmentacji w systemach analizy ilościowej obrazów
 POLITECHNIKA ŁÓDZKA Wydział Elektrotechniki Elektroniki Informatyki i Automatyki Katedra Informatyki Stosowanej Anna Fabijańska Nr albumu: 109647 Streszczenie pracy magisterskiej nt.: Algorytmy segmentacji
POLITECHNIKA ŁÓDZKA Wydział Elektrotechniki Elektroniki Informatyki i Automatyki Katedra Informatyki Stosowanej Anna Fabijańska Nr albumu: 109647 Streszczenie pracy magisterskiej nt.: Algorytmy segmentacji
ALGORYTMY PRZETWARZANIA OBRAZÓW Projekt. Aplikacja przetwarzająca obrazy z możliwością eksportu i importu do programu MS Excel.
 Grupa IZ07IO1 Wyższa Szkoła Informatyki Stosowanej i Zarządzania WIT ALGORYTMY PRZETWARZANIA OBRAZÓW Projekt Aplikacja przetwarzająca obrazy z możliwością eksportu i importu do programu MS Excel. Wykonali:
Grupa IZ07IO1 Wyższa Szkoła Informatyki Stosowanej i Zarządzania WIT ALGORYTMY PRZETWARZANIA OBRAZÓW Projekt Aplikacja przetwarzająca obrazy z możliwością eksportu i importu do programu MS Excel. Wykonali:
KAM-TECH sklep internetowy Utworzono : 09 listopad 2014
 Model : - AWB, AGC, BLC, DZ OSD Effio-P Double Scan, 0,1Lux (kolor), Producent : CNB Kamera KAM-BFF-41F 700TVL TDN DSS 3D-DNR WDR Eclipsa AWB, AGC, BLC, DZ OSD Effio-P Double Scan, 0,1Lux (kolor), Kamera
Model : - AWB, AGC, BLC, DZ OSD Effio-P Double Scan, 0,1Lux (kolor), Producent : CNB Kamera KAM-BFF-41F 700TVL TDN DSS 3D-DNR WDR Eclipsa AWB, AGC, BLC, DZ OSD Effio-P Double Scan, 0,1Lux (kolor), Kamera
Parametryczne Testy Istotności
 Parametrycze Testy Istotości Wzory Parametrycze testy istotości schemat postępowaia pukt po pukcie Formułujemy hipotezę główą H odośie jakiegoś parametru w populacji geeralej Hipoteza H ma ajczęściej postać
Parametrycze Testy Istotości Wzory Parametrycze testy istotości schemat postępowaia pukt po pukcie Formułujemy hipotezę główą H odośie jakiegoś parametru w populacji geeralej Hipoteza H ma ajczęściej postać
Wektory Funkcje rzeczywiste wielu. Matematyka Studium doktoranckie KAE SGH Semestr letni 2008/2009 R. Łochowski
 Wektory Fukcje rzeczywiste wielu zmieych rzeczywistych Matematyka Studium doktorackie KAE SGH Semestr leti 2008/2009 R. Łochowski Wektory pukty w przestrzei R Przestrzeń R to zbiór uporządkowaych -ek liczb
Wektory Fukcje rzeczywiste wielu zmieych rzeczywistych Matematyka Studium doktorackie KAE SGH Semestr leti 2008/2009 R. Łochowski Wektory pukty w przestrzei R Przestrzeń R to zbiór uporządkowaych -ek liczb
d wymiarowy wektor losowy Niech (Ω, S, P) przestrzeń probabilistyczna Definicja Odwzorowanie X: Ω R nazywamy 1-wymiarowym wektorem
 d wymiarowy wektor losowy Niech (Ω, S, P) przestrzeń probabilistycza Defiicja Odwzorowaie X: Ω R d azywamy d-wymiarowym wektorem losowym jeśli dla każdego (x 1, x 2,,x d ) є R d zbiór Uwaga {ω є Ω: X(ω)
d wymiarowy wektor losowy Niech (Ω, S, P) przestrzeń probabilistycza Defiicja Odwzorowaie X: Ω R d azywamy d-wymiarowym wektorem losowym jeśli dla każdego (x 1, x 2,,x d ) є R d zbiór Uwaga {ω є Ω: X(ω)
Adam Korzeniewski p Katedra Systemów Multimedialnych
 Adam Korzeniewski adamkorz@sound.eti.pg.gda.pl p. 732 - Katedra Systemów Multimedialnych camera obscura to pierwowzór aparatu fotograficznego Aparaty cyfrowe to urządzenia optoelektroniczne, które służą
Adam Korzeniewski adamkorz@sound.eti.pg.gda.pl p. 732 - Katedra Systemów Multimedialnych camera obscura to pierwowzór aparatu fotograficznego Aparaty cyfrowe to urządzenia optoelektroniczne, które służą
Ćwiczenie nr 14. Porównanie doświadczalnego rozkładu liczby zliczeń w zadanym przedziale czasu z rozkładem Poissona
 Ćwiczeie r 4 Porówaie doświadczalego rozkładu liczby zliczeń w zadaym przedziale czasu z rozkładem Poissoa Studeta obowiązuje zajomość: Podstawowych zagadień z rachuku prawdopodobieństwa, Zajomość rozkładów
Ćwiczeie r 4 Porówaie doświadczalego rozkładu liczby zliczeń w zadaym przedziale czasu z rozkładem Poissoa Studeta obowiązuje zajomość: Podstawowych zagadień z rachuku prawdopodobieństwa, Zajomość rozkładów
z przedziału 0,1. Rozważmy trzy zmienne losowe:..., gdzie X
 Matematyka ubezpieczeń majątkowych.0.0 r. Zadaie. Mamy day ciąg liczb q, q,..., q z przedziału 0,. Rozważmy trzy zmiee losowe: o X X X... X, gdzie X i ma rozkład dwumiaowy o parametrach,q i, i wszystkie
Matematyka ubezpieczeń majątkowych.0.0 r. Zadaie. Mamy day ciąg liczb q, q,..., q z przedziału 0,. Rozważmy trzy zmiee losowe: o X X X... X, gdzie X i ma rozkład dwumiaowy o parametrach,q i, i wszystkie
Trzeba pokazać, że dla każdego c 0 c Mc 0. ) = oraz det( ) det( ) det( ) jest macierzą idempotentną? Proszę odpowiedzieć w
 Zad Dae są astępujące macierze: A =, B, C, D, E 0. 0 = = = = 0 Wykoaj astępujące działaia: a) AB, BA, C+E, DE b) tr(a), tr(ed), tr(b) c) det(a), det(c), det(e) d) A -, C Jeśli działaia są iewykoale, to
Zad Dae są astępujące macierze: A =, B, C, D, E 0. 0 = = = = 0 Wykoaj astępujące działaia: a) AB, BA, C+E, DE b) tr(a), tr(ed), tr(b) c) det(a), det(c), det(e) d) A -, C Jeśli działaia są iewykoale, to
Wartość netto (zł) (kolumna 3x5)
 Postępowanie WB.2420.9.2012.NG ZAŁĄCZNIK NR 6 Zadanie nr 2 L.p. Nazwa asortymentu parametry techniczne Ilość Nazwa wyrobu, nazwa producenta, określenie marki, modelu, znaku towarowego Cena jednostkowa
Postępowanie WB.2420.9.2012.NG ZAŁĄCZNIK NR 6 Zadanie nr 2 L.p. Nazwa asortymentu parametry techniczne Ilość Nazwa wyrobu, nazwa producenta, określenie marki, modelu, znaku towarowego Cena jednostkowa
maska 1 maska 2 maska 3 ogólnie
 WYKŁAD 4 Detekcja krawędzi, operacje morfologiczne Detekcja (wykrywanie) krawędzi (edge detection) jest to technika segmentacji obrazu, polegająca na znajdowaniu piksli krawędziowych przez sprawdzanie
WYKŁAD 4 Detekcja krawędzi, operacje morfologiczne Detekcja (wykrywanie) krawędzi (edge detection) jest to technika segmentacji obrazu, polegająca na znajdowaniu piksli krawędziowych przez sprawdzanie
Diagnostyka obrazowa
 Diagnostyka obrazowa Ćwiczenie drugie Podstawowe przekształcenia obrazu 1 Cel ćwiczenia Ćwiczenie ma na celu zapoznanie uczestników kursu Diagnostyka obrazowa z podstawowymi przekształceniami obrazu wykonywanymi
Diagnostyka obrazowa Ćwiczenie drugie Podstawowe przekształcenia obrazu 1 Cel ćwiczenia Ćwiczenie ma na celu zapoznanie uczestników kursu Diagnostyka obrazowa z podstawowymi przekształceniami obrazu wykonywanymi
Techniki wizualizacji. Ćwiczenie 4. Podstawowe algorytmy przetwarzania obrazów
 Doc. dr inż. Jacek Jarnicki Instytut Informatyki, Automatyki i Robotyki Politechniki Wrocławskiej jacek.jarnicki@pwr.wroc.pl Techniki wizualizacji Ćwiczenie 4 Podstawowe algorytmy przetwarzania obrazów
Doc. dr inż. Jacek Jarnicki Instytut Informatyki, Automatyki i Robotyki Politechniki Wrocławskiej jacek.jarnicki@pwr.wroc.pl Techniki wizualizacji Ćwiczenie 4 Podstawowe algorytmy przetwarzania obrazów
KARTA PRZEDMIOTU. W5/1;W16/1 W5 Zna podstawowe metody przetwarzania wstępnego EP WM K_W9/3; obrazów barwnych.
 (pieczęć wydziału) KARTA PRZEDMIOTU 1. Nazwa przedmiotu: PRZETWARZANIE OBRAZÓW CYFROWYCH 3. Karta przedmiotu ważna od roku akademickiego: 2012/2013 4. Forma kształcenia: studia pierwszego stopnia 5. Forma
(pieczęć wydziału) KARTA PRZEDMIOTU 1. Nazwa przedmiotu: PRZETWARZANIE OBRAZÓW CYFROWYCH 3. Karta przedmiotu ważna od roku akademickiego: 2012/2013 4. Forma kształcenia: studia pierwszego stopnia 5. Forma
STATYSTYKA MATEMATYCZNA
 STATYSTYKA MATEMATYCZA 1. Wykład wstępny. Zmienne losowe i teoria prawdopodobieństwa 3. Populacje i próby danych 4. Testowanie hipotez i estymacja parametrów 5. ajczęściej wykorzystywane testy statystyczne
STATYSTYKA MATEMATYCZA 1. Wykład wstępny. Zmienne losowe i teoria prawdopodobieństwa 3. Populacje i próby danych 4. Testowanie hipotez i estymacja parametrów 5. ajczęściej wykorzystywane testy statystyczne
Histogram: Dystrybuanta:
 Zadaie. Szereg rozdzielczy (przyjmujemy przedziały klasowe o długości 0): x0 xi i środek i*środek i_sk częstości częstości skumulowae 5 5 8 0 60 8 0,6 0,6 5 5 9 0 70 7 0,8 0, 5 5 5 0 600 0, 0,6 5 55 8
Zadaie. Szereg rozdzielczy (przyjmujemy przedziały klasowe o długości 0): x0 xi i środek i*środek i_sk częstości częstości skumulowae 5 5 8 0 60 8 0,6 0,6 5 5 9 0 70 7 0,8 0, 5 5 5 0 600 0, 0,6 5 55 8
Automatyczne rozpoznawanie mowy - wybrane zagadnienia / Ryszard Makowski. Wrocław, Spis treści
 Automatyczne rozpoznawanie mowy - wybrane zagadnienia / Ryszard Makowski. Wrocław, 2011 Spis treści Przedmowa 11 Rozdział 1. WPROWADZENIE 13 1.1. Czym jest automatyczne rozpoznawanie mowy 13 1.2. Poziomy
Automatyczne rozpoznawanie mowy - wybrane zagadnienia / Ryszard Makowski. Wrocław, 2011 Spis treści Przedmowa 11 Rozdział 1. WPROWADZENIE 13 1.1. Czym jest automatyczne rozpoznawanie mowy 13 1.2. Poziomy
EGZAMIN MATURALNY Z INFORMATYKI MAJ 2011 POZIOM ROZSZERZONY WYBRANE: CZĘŚĆ I. Czas pracy: 90 minut. Liczba punktów do uzyskania: 20 WPISUJE ZDAJĄCY
 Cetrala Komisja Egzamiacyja Arkusz zawiera iformacje prawie chroioe do mometu rozpoczęcia egzamiu. Układ graficzy CKE 2010 KOD WISUJE ZDAJĄCY ESEL Miejsce a aklejkę z kodem EGZAMIN MATURALNY Z INORMATYKI
Cetrala Komisja Egzamiacyja Arkusz zawiera iformacje prawie chroioe do mometu rozpoczęcia egzamiu. Układ graficzy CKE 2010 KOD WISUJE ZDAJĄCY ESEL Miejsce a aklejkę z kodem EGZAMIN MATURALNY Z INORMATYKI
Wykład III. Granice funkcji. f : R A R, A przedział. f określona w x. K M x. lim. lim. Granice niewłaściwe:
 : R A R, A przedział A, Wykład III Graice ukcji określoa w, S \ Deiicja 3. (deiicja Caucy eo raicy ukcji) : D U,, ( ) : ot Iaczej: Uot D U K M U ot U ot K M Graice iewłaściwe: k K R D M K K R M R D De.
: R A R, A przedział A, Wykład III Graice ukcji określoa w, S \ Deiicja 3. (deiicja Caucy eo raicy ukcji) : D U,, ( ) : ot Iaczej: Uot D U K M U ot U ot K M Graice iewłaściwe: k K R D M K K R M R D De.
KOREKTA ROZKŁADU JASNOŚCI (obrazy monochromatyczne i barwne)
 Ćwiczenia z grafiki komputerowej 1 KOREKTA ROZKŁADU JASNOŚCI (obrazy monochromatyczne i barwne) Miłosz Michalski Institute of Physics Nicolaus Copernicus University Październik 2015 1 / 19 Korekta rozkładu
Ćwiczenia z grafiki komputerowej 1 KOREKTA ROZKŁADU JASNOŚCI (obrazy monochromatyczne i barwne) Miłosz Michalski Institute of Physics Nicolaus Copernicus University Październik 2015 1 / 19 Korekta rozkładu
X i. X = 1 n. i=1. wartość tej statystyki nazywana jest wartością średnią empiryczną i oznaczamy ją symbolem x, przy czym x = 1. (X i X) 2.
 Zagadieia estymacji Puktem wyjścia badaia statystyczego jest wylosowaie z całej populacji pewej skończoej liczby elemetów i zbadaie ich ze względu a zmieą losową cechę X Uzyskae w te sposób wartości x,
Zagadieia estymacji Puktem wyjścia badaia statystyczego jest wylosowaie z całej populacji pewej skończoej liczby elemetów i zbadaie ich ze względu a zmieą losową cechę X Uzyskae w te sposób wartości x,
Cyfrowe Przetwarzanie Obrazów. Karol Czapnik
 Cyfrowe Przetwarzanie Obrazów Karol Czapnik Podstawowe zastosowania (1) automatyka laboratoria badawcze medycyna kryminalistyka metrologia geodezja i kartografia 2/21 Podstawowe zastosowania (2) komunikacja
Cyfrowe Przetwarzanie Obrazów Karol Czapnik Podstawowe zastosowania (1) automatyka laboratoria badawcze medycyna kryminalistyka metrologia geodezja i kartografia 2/21 Podstawowe zastosowania (2) komunikacja
Egzamin maturalny z informatyki Poziom rozszerzony część I
 Zadaie 1. Długość apisów biarych (7 pkt) Opisaa poiżej fukcja rekurecyja wyzacza, dla liczby aturalej 0, długość apisu uzyskaego przez sklejeie biarych reprezetacji liczb aturalych od 1 do 1. ukcja krok
Zadaie 1. Długość apisów biarych (7 pkt) Opisaa poiżej fukcja rekurecyja wyzacza, dla liczby aturalej 0, długość apisu uzyskaego przez sklejeie biarych reprezetacji liczb aturalych od 1 do 1. ukcja krok
Wykład 11 ( ). Przedziały ufności dla średniej
 Wykład 11 (14.05.07). Przedziały ufości dla średiej Przykład Cea metra kwadratowego (w tys. zł) z dla 14 losowo wybraych mieszkań w mieście A: 3,75; 3,89; 5,09; 3,77; 3,53; 2,82; 3,16; 2,79; 4,34; 3,61;
Wykład 11 (14.05.07). Przedziały ufości dla średiej Przykład Cea metra kwadratowego (w tys. zł) z dla 14 losowo wybraych mieszkań w mieście A: 3,75; 3,89; 5,09; 3,77; 3,53; 2,82; 3,16; 2,79; 4,34; 3,61;
Kongruencje Wykład 4. Kongruencje kwadratowe symbole Legendre a i Jac
 Kogruecje kwadratowe symbole Legedre a i Jacobiego Kogruecje Wykład 4 Defiicja 1 Kogruecję w ostaci x a (mod m), gdzie a m, azywamy kogruecją kwadratową; jej bardziej ogóla ostać ax + bx + c może zostać
Kogruecje kwadratowe symbole Legedre a i Jacobiego Kogruecje Wykład 4 Defiicja 1 Kogruecję w ostaci x a (mod m), gdzie a m, azywamy kogruecją kwadratową; jej bardziej ogóla ostać ax + bx + c może zostać
