Modele dla zmiennej binarnej w pakiecie STATA materiały na ćwiczenia z ekonometrii r. Piotr Wójcik, KTRG WNE UW
|
|
|
- Kazimierz Mikołaj Piotrowski
- 8 lat temu
- Przeglądów:
Transkrypt
1 Modele dla zmiennej binarnej w pakiecie STATA materiały na ćwiczenia z ekonometrii r. Piotr Wójcik, KTRG WNE UW Dane Dane wykorzystane w przykładzie pochodzą z pracy McCall, B.P., 1995, The Impact of Unemployment Insurance Benefit Levels on Recipiency, Journal of Business and Economic Statistics, vol. 13, pp Rozpatrujemy próbę 4877 pracowników fizycznych, którzy stracili pracę w USA między rokiem 1982 i Nie wszyscy bezrobotni, którym przysługuje świadczenie z tytułu ubezpieczenia od utraty pracy ubiegają się o nie, być może z powodu związanych z tym kosztów psychologicznych. Procent uprawnionych do takiego świadczenia bezrobotnych, którzy się o nie ubiegają nazwijmy stopą objęcia świadczeniami dla analizowanej próby wyniosła ona zaledwie 68%. Spróbujmy więc przeanalizować co powoduje, że ludzie bezrobotni decydują się zrezygnować z przysługującego im świadczenia. Wysokość świadczenia zależy od stanu zamieszkania, roku utracenia pracy i poprzednich zarobków. Stopa zastąpienia (stosunek wysokości świadczenia do poprzednich dochodów) waha się od 33% do 54% ze średnią dla badanej próby na poziomie 44% i jest potencjalnie istotnym czynnikiem wpływającym na decyzję bezrobotnego o ubieganiu się o świadczenie ubezpieczeniowe. Wpływ na tę decyzję mogą również mieć charakterystyki osobiste (wykształcenie, wiek, płeć, rasa) jak i sytuacja rodzinna i względy budżetowe. Ostatnim typem potencjalnie istotnych zmiennych jest powód zwolnienia: niesatysfakcjonujące wyniki w pracy, likwidacja stanowiska pracy, zakończenie pracy sezonowej. Lista i opis zmiennych: stateur: stanowa stopa bezrobocia (w %); statemb: najniższy stanowy zasiłek dla bezrobotnych; state: kod stanu; age: wiek w latach; tenure: długość okresu zatrudnienia w ostatnim miejscu pracy; slack: zmienna 0-1, 1 jeśli zwolnienie z powodu niesatysfakcjonujących wyników w pracy; abol: zmienna 0-1, 1 jeśli zwolnienie z powodu likwidacji stanowiska pracy; seasonal: zmienna 0-1, 1 jeśli zwolnienie z powodu końca pracy sezonowej; nwhite: zmienna 0-1, 1 jeśli pracownik rasy innej niż biała; school12: zmienna 0-1, 1 jeśli pracownik ukończył więcej niż 12 lat szkoły; male: zmienna 0-1, 1 jeśli mężczyzna; smsa: zmienna 0-1, 1 jeśli mieszka w Standard Metropolitan Statistical Area, czyli w obszarze miejskim; married: zmienna 0-1, 1 jeśli żonaty/zamężna; dkids: zmienna 0-1, 1 jeśli posiada dzieci; dykids: zmienna 0-1, 1 jeśli posiada małe dzieci (0-5 lat); yrdispl: rok utraty pracy (1982=1,..., 1991=10); rr: stopa zastąpienia (stosunek wysokości zasiłku do poprzednich dochodów); rr2: rr do kwadratu; head: zmienna 0-1, 1 jeśli pracownik jest głową rodziny; y: zmienna 0-1, 1 jeśli ubiegał się (i otrzymał) zasiłek; Estymacji dokonamy dla trzech różnych modeli: liniowego modelu prawdopodobieństwa, modelu logit i probit. 1
2 Estymacja liniowego modelu prawdopodobieństwa Zaletą stosowania liniowego modelu prawdopodobieństwa do modelowania dychotomicznej zmiennej objaśnianej jest prostota jego estymacji. Ze względu na dwumianowy rozkład zmiennej objaśnianej nie jest jednak spełniony warunek homoskedastyczności reszt z modelu. Wadą podejścia tego typu jest również fakt, iż nie można zagwarantować, że wartości dopasowane znajdą się w przedziale [0,1]. Estymacji dokonujemy za pomocą polecenia reg: reg y rr rr2 age tenure slack abol seasonal head married dkids dykids smsa nwhite yrdispl school12 male statemb stateur Source SS df MS Number of obs = F( 18, 4858) = Model Prob > F = Residual R-squared = Adj R-squared = Total Root MSE = y Coef. Std. Err. t P> t [95% Conf. Interval] rr rr age tenure slack abol seasonal head married dkids dykids smsa nwhite yrdispl school male statemb stateur _cons Test Breuscha-Pagana na heteroskedastyczność: hettest, rhs Breusch-Pagan / Cook-Weisberg test for heteroskedasticity Ho: Constant variance Variables: rr rr2 age tenure slack abol seasonal head married dkids dykids smsa nwhite yrdispl school12 male statemb stateur chi2(18) = Czyli odrzucamy hipotezę zerową o braku heteroskedastyczności w modelu, co jest zgodne z oczekiwaniami. Heteroskedastyczność nie wpływa na obciążenie estymatora parametrów, powoduje jednak niewłaściwe oszacowanie błędów standardowych dla poszczególnych parametrów, co może wpływać na wnioski dotyczące (nie-)istotności zmiennych. Rozwiązaniem tego problemu jest estymacja z wykorzystaniem błędów standardowych odpornych na heteroskedastyczność (macierz wariancji-kowariancji White a). W naszym przypadku nie zmienia to jednak wniosków dotyczących (nie-)istotności poszczególnych zmiennych. 2
3 reg y rr rr2 age tenure slack abol seasonal head married dkids dykids smsa nwhite yrdispl school12 male statemb stateur, robust Regression with robust standard errors Number of obs = 4877 F( 18, 4858) = Prob > F = R-squared = Root MSE = Robust y Coef. Std. Err. t P> t [95% Conf. Interval] rr rr age tenure slack abol seasonal head married dkids dykids smsa nwhite yrdispl school male statemb stateur _cons Testujemy łączną nieistotność zmiennych nieistotnych indywidualnie na poziomie 5% z wykorzystaniem standardowego testu F: test rr abol seasonal dkids dykids nwhite school12 ( 1) rr = 0 ( 2) abol = 0 ( 3) seasonal = 0 ( 4) dkids = 0 ( 5) dykids = 0 ( 6) nwhite = 0 ( 7) school12 = 0 F( 7, 4858) = 1.50 Prob > F = P-value statystyki testowej F ponad 16% oznacza, że na poziomie 5% nie możemy odrzucić hipotezy zerowej o łącznej nieistotności siedmiu testowanych powyżej zmiennych. Estymujemy więc model bez tych zmiennych. reg y robust rr2 age tenure slack head married smsa yrdispl male statemb stateur, Source SS df MS Number of obs = F( 11, 4865) = Model Prob > F = Residual R-squared = Adj R-squared = Total Root MSE =
4 y Coef. Std. Err. t P> t [95% Conf. Interval] rr age tenure slack head married smsa yrdispl male statemb stateur _cons Test Breuscha-Pagana na heteroskedastyczność: hettest, rhs Breusch-Pagan / Cook-Weisberg test for heteroskedasticity Ho: Constant variance Variables: rr2 age tenure slack head married smsa yrdispl male statemb stateur chi2(11) = Heteroskedastyczność nadal występuje, ale wynika to z charakteru zmiennej objaśnianej i nie wpływa na oszacowania parametrów. Współczynniki oszacowane w liniowym modelu prawdopodobieństwa mają swoją interpretację. W powyższym przykładzie np. każdy kolejny rok stażu w ostatnim miejscu pracy (zmienna tenure) zwiększa prawdopodobieństwa ubiegania się o świadczenie z tytułu utraty pracy o 0,55 pp. Co jest zaskakujące, bycie głową rodziny (zmienna head) zmniejsza to prawdopodobieństwo o 3,77 pp, itd. Modele dla zmiennych binarnych Zmienną objaśnianą jest prawdopodobieństwo wystąpienia określonego zdarzenia uzależnione od wektora zmiennych egzogenicznych: P(Y j = 1 X 1 j,...,x kj ' ) = F( x β ) i przy czym w modelu probit wykorzystujemy dystrybuantę rozkładu normalnego: F( w ) w = Φ ( w ) = exp( t )dt, 2Π 2 natomiast w modelu logit wykorzystywana jest standardowa funkcja logistyczna: F( w ) w e 1 = =, w w 1 + e 1 + e 4
5 Estymacja modelu Logit Estymacji modelu logit dokonujemy za pomocą polecenia logit: logit y rr rr2 age tenure slack abol seasonal head married dkids dykids smsa nwhite yrdispl school12 male statemb stateur Iteration 0: log likelihood = Iteration 1: log likelihood = Iteration 2: log likelihood = Iteration 3: log likelihood = Logit estimates Number of obs = 4877 LR chi2(19) = Log likelihood = Pseudo R2 = y Coef. Std. Err. z P> z [95% Conf. Interval] rr rr age age tenure slack abol seasonal head married dkids dykids smsa nwhite yrdispl school male statemb stateur _cons Zapamiętujemy wyniki estymacji pod nazwą logit1: est store logit1 Testowanie warunków ograniczających przy pomocy testu ilorazu wiarogodności (LR) Nie możemy stosować testu F, bo estymacja nie jest dokonywana MNK, więc nie ma RSS. Ekwiwalentem jest w tym przypadku między innymi test ilorazu wiarogodności. Intuicyjnie rzecz biorąc sprawdzamy, czy narzucone ograniczenia w istotny sposób wpływają na logarytm wiarogodności. Hipoteza zerowa: narzucone warunki ograniczające są prawdziwe. Jeśli H0 jest prawdziwa, statystyka testowa LR=-2[lnL R -lnr U ] ma w przybliżeniu rozkład chi-kwadrat z liczbą stopni swobody równą liczbie narzuconych ograniczeń. Zanim przetestujemy łączną nieistotność zmiennych nieistotnych indywidualnie dokonujemy oszacowania modelu z warunkami ograniczającymi (czyli bez zmiennych nieistotnych): logit y rr2 age tenure slack head married smsa yrdispl male statemb stateur 5
6 Iteration 0: log likelihood = Iteration 1: log likelihood = Iteration 2: log likelihood = Iteration 3: log likelihood = Logit estimates Number of obs = 4877 LR chi2(11) = Log likelihood = Pseudo R2 = y Coef. Std. Err. z P> z [95% Conf. Interval] rr age tenure slack head married smsa yrdispl male statemb stateur _cons Zapamiętujemy wyniki estymacji pod nazwą logit2: est store logit2 Korzystając z zapamiętanych wcześniej wyników dla modelu bez ograniczeń (logit1) i modelu z ograniczeniami (logit2) przeprowadzamy test LR wyświetlając jednocześnie statystyki opisowe. lrtest logit1 logit2, stats likelihood-ratio test LR chi2(7) = (Assumption: logit2 nested in logit1) Prob > chi2 = Model nobs ll(null) ll(model) df AIC BIC logit logit Nie możemy więc odrzucić H0, że narzucone ograniczenia są poprawne. Widać również, że kryteria informacyjne wskazują, że model logit2 jest lepszy niż logit1. Testowanie liniowych warunków ograniczających przy pomocy statystyki Walda: Alternatywną formą testowania hipotez dotyczących oszacowanych parametrów jest statystyka Walda, wywoływana komendą test: test rr abol seasonal dkids dykids nwhite school12 ( 1) rr = 0 ( 2) abol = 0 ( 3) seasonal = 0 ( 4) dkids = 0 ( 5) dykids = 0 ( 6) nwhite = 0 ( 7) school12 = 0 chi2( 7) = Prob > chi2 =
7 Testowanie nieliniowych warunków ograniczających przy pomocy statystyki Walda: Dzięki statystyce Walda można również testować nieliniowe warunki ograniczające narzucane na parametry. Służy do tego polecenie testnl. Jego składnia różni się nieco od składni komendy test zamiast podać nazwy zmiennych, przy których parametry testujemy, musimy użyć zapisu _b[nazwa_zmiennej]. Przetestujmy hipotezę zerową mówiącą, że kwadrat oszacowania parametru przy zmiennej age jest równy 1 stosując dwa równoważne zapisy tej hipotezy: H 0 : β age * β age 1 = 0 testnl _b[age]*_b[age]-1=0 (1) _b[age]*_b[age]-1 = 0 chi2(1) = 4.86e+07 1 H 0 : β age = 0 β age testnl _b[age]-1/_b[age]=0 (1) _b[age]-1/_b[age] = 0 chi2(1) = Mimo że alternatywne sformułowania H0 są równoważne, oszacowana wartość statystyki Walda jest w obu przypadkach różna, co wskazuje, że statystyka Walda nie jest niezmiennicza względem zdefiniowania hipotezy zerowej. Za pomocą polecenia testnl można oczywiście testować również liniowe warunki ograniczające oraz łącznie liniowe i nieliniowe ograniczenia narzucane na parametry, jednak w przypadku testowania wyłącznie hipotez liniowych polecenie test działa szybciej. Interpretacja współczynników i ilorazy szans Interpretacją współczynników z modelu logitowego jest procentowy wpływ jednostkowej zmiany wartości zmiennej objaśniającej na iloraz szans liczony jako stosunek prawdopodobieństwa sukcesu do prawdopodobieństwa porażki. Aby zamiast oszacowań parametrów wygenerować ilorazy szans dla poszczególnych zmiennych należy użyć polecenia logit z opcją or (odds-ratio) lub użyć polecenia logistic. lub logit y rr2 age tenure slack head married smsa yrdispl male statemb stateur, or logistic y rr2 age tenure slack head married smsa yrdispl male statemb stateur Logistic regression Number of obs = 4877 LR chi2(11) = Log likelihood = Pseudo R2 = y Odds Ratio Std. Err. z P> z [95% Conf. Interval] rr age tenure slack head married smsa yrdispl male statemb stateur
8 Obliczanie efektów krańcowych (cząstkowych) Ponieważ wartości parametrów oszacowane w modelach dla zmiennych binarnych są trudne w bezpośredniej interpretacji (interpretowalne są jedynie ich znaki) i jednocześnie nieporównywalne z innymi modelami (np. oszacowania liniowego modelu prawdopodobieństwa, modelu logit i probit dla tej samej zmiennej objaśnianej i analogicznego zbioru zmiennych objaśniających), oblicza się tzw. efekty krańcowe, które można bezpośrednio porównywać między modelami. E( y i x ) = x f ( xβ )β Służy do tego polecenie mfx compute: mfx compute Marginal effects after logit y = Pr(y) (predict) = variable dy/dx Std. Err. z P> z [ 95% C.I. ] X rr age tenure slack* head* married* smsa* yrdispl male* statemb stateur (*) dy/dx is for discrete change of dummy variable from 0 to 1 Efekty krańcowe są porównywalne dla różnych modeli i mogą być interpretowane jest jako wpływ zmiany zmiennej niezależnej o jednostkę na prawdopodobieństwo sukcesu (czyli przyjęcia przez zmienną objaśnianą wartości 1). Np. z powyższego zestawienia wynika, że bycie mężczyzną zmniejsza prawdopodobieństwo ubiegania się o świadczenie z tytułu utraty pracy o 3,88 pp. (fałszywie pojęta męska duma?), natomiast wzrost stanowej stopy bezrobocia o 1 pp. powoduje, że prawdopodobieństwo ubiegania się o świadczenie rośnie o 2 pp. Efekty krańcowe zależą od wartości zmiennych objaśniających. Standardowo liczone są dla przeciętnych wartości zmiennych egzogenicznych. Można je również policzyć dla zadanych wartości wybranych (lub wszystkich) regresorów. Na przykład efekty krańcowe dla żonatego mężczyzny w wieku lat pięćdziesięciu policzymy stosując komendę: mfx compute, at(age=50, married=1, male=1) Marginal effects after logistic y = Pr(y) (predict) = variable dy/dx Std. Err. z P> z [ 95% C.I. ] X rr age tenure slack* head* married* smsa* yrdispl male* statemb stateur
9 Miary dopasowania modelu Standardowo liczone jest pseudo-r 2 raportowane wraz z wynikami estymacji. Aby uzyskać inne miary można ściągnąć pakiet FITSTAT (należy będąc w pakiecie STATA nacisnąć clrl+3, następnie s jak search i zaznaczywszy Search net resources wpisać w okienku wyszukiwania fitstat ; po znalezieniu zainstalować wykonując tę operację na WNE należy utworzyć na dysku L:\ katalog STATA8 inaczej nie zadziała), a następnie po estymacji modelu użyć komendy fitstat: fitstat Measures of Fit for logit of y Log-Lik Intercept Only: Log-Lik Full Model: D(4858): LR(18): Prob > LR: McFadden's R2: McFadden's Adj R2: Maximum Likelihood R2: Cragg & Uhler's R2: McKelvey and Zavoina's R2: Efron's R2: Variance of y*: Variance of error: Count R2: Adj Count R2: AIC: AIC*n: BIC: BIC': Tablica trafności dopasowań Tablica trafności dopasowań może być innym sposobem mierzenia jakości dopasowania modelu do danych. Dla ostatnio przeprowadzonej estymacji uzyskamy ją stosując komendę lstat. lstat Logistic model for y True Classified D ~D Total Total Classified + if predicted Pr(D) >=.5 True D defined as y!= 0 Sensitivity Pr( + D) 95.44% Specificity Pr( - ~D) 14.59% Positive predictive value Pr( D +) 70.73% Negative predictive value Pr(~D -) 59.68% False + rate for true ~D Pr( + ~D) 85.41% False - rate for true D Pr( - D) 4.56% False + rate for classified + Pr(~D +) 29.27% False - rate for classified - Pr( D -) 40.32% Correctly classified 69.88% Standardowo przyjmowane jest, że model przewiduje y i =1 jeżeli oszacowane prawdopodobieństwo jest większe niż 0,5. Jeżeli chcemy zastosować inny punkt odcięcia, np. 0,25, należy użyć następującej komendy: lstat, cutoff(0.25) 9
10 Wartości dopasowane Wygenerujmy wartości dopasowane z oszacowanego modelu logitowego oraz oszacowane prawdopodobieństwo sukcesu (ubiegania się o przysługujące świadczenie): predict xb, xb predict p, p Między wartościami dopasowanymi z modelu a oszacowanym prawdopodobieństwem zachodzi zależność zgodna z przyjętą funkcją gęstości : p = P(Y j = 1 X 1 j,...,x kj ' ) = F( x β ) i czyli dla modelu logitowego p=1/[1+exp(-xb)], natomiast dla modelu probitowego p jest wartością dystrybuanty standardowego rozkładu normalnego w punkcie xb (p=φ(xb)). Narysujmy wykres zależności przewidywanego prawdopodobieństwa sukcesu od długości zatrudnienia w ostatnim miejscu pracy. scatter p tenure Z powyższego wykresu widać, że wraz ze wzrostem stażu w ostatnim miejscu zatrudnienia prawdopodobieństwo ubiegania się o świadczenie przysługujące z tytułu ubezpieczenia od utraty pracy wyraźnie wzrasta. Dla osób, które zanim straciły pracę przepracowały w danej firmie ponad 35 lat prawdopodobieństwo ubiegania się o świadczenie z tytułu utraty pracy wynosi ponad 80%. 10
11 Estymacja modelu Probit Estymacji modelu probit dokonujemy za pomocą polecenia probit: probit y rr rr2 age tenure slack abol seasonal head married dkids dykids smsa nwhite yrdispl school 12 male statemb stateur Iteration 0: log likelihood = Iteration 1: log likelihood = Iteration 2: log likelihood = Iteration 3: log likelihood = Probit estimates Number of obs = 4877 LR chi2(18) = Log likelihood = Pseudo R2 = y Coef. Std. Err. z P> z [95% Conf. Interval] rr rr age tenure slack abol seasonal head married dkids dykids smsa nwhite yrdispl school male statemb stateur _cons Zapamiętujemy wyniki estymacji pod nazwą probit1: est store probit1 Łączną nieistotność parametrów w modelach logit i probit możemy również testować za pomocą statystyki Walda, wywoływanego komendą test. Testujemy ponownie zmienne indywidualnie nieistotne na poziomie 5% (są to te same zmienne, które były indywidualnie nieistotne w obu poprzednich regresjach): test rr abol seasonal dkids dykids nwhite school12 ( 1) rr = 0 ( 2) abol = 0 ( 3) seasonal = 0 ( 4) dkids = 0 ( 5) dykids = 0 ( 6) nwhite = 0 ( 7) school12 = 0 chi2( 7) = Prob > chi2 = Nie możemy odrzucić hipotezy zerowej o łącznej nieistotności tych zmiennych, więc redukujemy model: 11
12 probit y rr2 age tenure slack head married smsa yrdispl male statemb stateur Iteration 0: log likelihood = Iteration 1: log likelihood = Iteration 2: log likelihood = Iteration 3: log likelihood = Probit estimates Number of obs = 4877 LR chi2(11) = Log likelihood = Pseudo R2 = y Coef. Std. Err. z P> z [95% Conf. Interval] rr age tenure slack head married smsa yrdispl male statemb stateur _cons Zapamiętujemy wyniki estymacji pod nazwą probit2: est store probit2 Prawidłowość narzuconych warunków ograniczających możemy potwierdzić również testem LR: lrtest probit1 probit2, stats likelihood-ratio test LR chi2(7) = (Assumption: probit2 nested in probit1) Prob > chi2 = Model nobs ll(null) ll(model) df AIC BIC probit probit Miary dopasowania modelu fitstat Measures of Fit for probit of y Log-Lik Intercept Only: Log-Lik Full Model: D(4865): LR(11): Prob > LR: McFadden's R2: McFadden's Adj R2: Maximum Likelihood R2: Cragg & Uhler's R2: McKelvey and Zavoina's R2: Efron's R2: Variance of y*: Variance of error: Count R2: Adj Count R2: AIC: AIC*n: BIC: BIC':
13 Obliczanie efektów krańcowych W przypadku modelu probit oszacowane parametry nie mają żadnej bezpośredniej interpretacji. Jedynie ich znak może być odczytywany jako pozytywny lub negatywny wpływ analizowanej zmiennej na prawdopodobieństwo sukcesu. Interpretować (i porównywać z innymi modelami) można dopiero efekty krańcowe. mfx compute Marginal effects after probit y = Pr(y) (predict) = variable dy/dx Std. Err. z P> z [ 95% C.I. ] X rr age tenure slack* head* married* smsa* yrdispl male* statemb stateur (*) dy/dx is for discrete change of dummy variable from 0 to 1 Tablica trafności dopasowań lstat Probit model for y True Classified D ~D Total Total Classified + if predicted Pr(D) >=.5 True D defined as y!= 0 Sensitivity Pr( + D) 95.86% Specificity Pr( - ~D) 13.75% Positive predictive value Pr( D +) 70.62% Negative predictive value Pr(~D -) 60.57% False + rate for true ~D Pr( + ~D) 86.25% False - rate for true D Pr( - D) 4.14% False + rate for classified + Pr(~D +) 29.38% False - rate for classified - Pr( D -) 39.43% Correctly classified 69.90% Literatura: McCall, B.P., 1995,The Impact of Unemployment Insurance Benefit Levels on Recipiency, Journal of Business and Economic Statistics, vol. 13, pp Verbeek, M., 2004, A guide to Modern Econometrics, John Wiley & Sons Ltd., wydanie 2. 13
Stanisław Cichocki. Natalia Nehrebecka
 Stanisław Cichocki Natalia Nehrebecka 1 1. Wstęp a) Binarne zmienne zależne b) Interpretacja ekonomiczna c) Interpretacja współczynników 2. Liniowy model prawdopodobieństwa a) Interpretacja współczynników
Stanisław Cichocki Natalia Nehrebecka 1 1. Wstęp a) Binarne zmienne zależne b) Interpretacja ekonomiczna c) Interpretacja współczynników 2. Liniowy model prawdopodobieństwa a) Interpretacja współczynników
Stanisław Cichocki. Natalia Nehrebecka
 Stanisław Cichocki Natalia Nehrebecka 1 1. Wstęp a) Binarne zmienne zależne b) Interpretacja ekonomiczna c) Interpretacja współczynników 2. Liniowy model prawdopodobieństwa a) Interpretacja współczynników
Stanisław Cichocki Natalia Nehrebecka 1 1. Wstęp a) Binarne zmienne zależne b) Interpretacja ekonomiczna c) Interpretacja współczynników 2. Liniowy model prawdopodobieństwa a) Interpretacja współczynników
Stanisław Cichocki. Natalia Nehrebecka
 Stanisław Cichocki Natalia Nehrebecka 1 1. Wstęp a) Binarne zmienne zależne b) Interpretacja ekonomiczna c) Interpretacja współczynników 2. Liniowy model prawdopodobieństwa a) Interpretacja współczynników
Stanisław Cichocki Natalia Nehrebecka 1 1. Wstęp a) Binarne zmienne zależne b) Interpretacja ekonomiczna c) Interpretacja współczynników 2. Liniowy model prawdopodobieństwa a) Interpretacja współczynników
Stanisław Cichocki. Natalia Nehrebecka
 Stanisław Cichocki Natalia Nehrebecka 1 1. Wstęp a) Binarne zmienne zależne b) Interpretacja ekonomiczna c) Interpretacja współczynników 2. Liniowy model prawdopodobieństwa a) Interpretacja współczynników
Stanisław Cichocki Natalia Nehrebecka 1 1. Wstęp a) Binarne zmienne zależne b) Interpretacja ekonomiczna c) Interpretacja współczynników 2. Liniowy model prawdopodobieństwa a) Interpretacja współczynników
Model 1: Estymacja KMNK z wykorzystaniem 4877 obserwacji Zmienna zależna: y
 Zadanie 1 Rozpatrujemy próbę 4877 pracowników fizycznych, którzy stracili prace w USA miedzy rokiem 1982 i 1991. Nie wszyscy bezrobotni, którym przysługuje świadczenie z tytułu ubezpieczenia od utraty
Zadanie 1 Rozpatrujemy próbę 4877 pracowników fizycznych, którzy stracili prace w USA miedzy rokiem 1982 i 1991. Nie wszyscy bezrobotni, którym przysługuje świadczenie z tytułu ubezpieczenia od utraty
1. Pokaż, że estymator MNW parametru β ma postać β = nieobciążony. Znajdź estymator parametru σ 2.
 Zadanie 1 Niech y t ma rozkład logarytmiczno normalny o funkcji gęstości postaci [ ] 1 f (y t ) = y exp (ln y t β ln x t ) 2 t 2πσ 2 2σ 2 Zakładamy, że x t jest nielosowe a y t są nieskorelowane w czasie.
Zadanie 1 Niech y t ma rozkład logarytmiczno normalny o funkcji gęstości postaci [ ] 1 f (y t ) = y exp (ln y t β ln x t ) 2 t 2πσ 2 2σ 2 Zakładamy, że x t jest nielosowe a y t są nieskorelowane w czasie.
Diagnostyka w Pakiecie Stata
 Karol Kuhl Zgodnie z twierdzeniem Gaussa-Markowa, estymator MNK w KMRL jest liniowym estymatorem efektywnym i nieobciążonym, co po angielsku opisuje się za pomocą wyrażenia BLUE Best Linear Unbiased Estimator.
Karol Kuhl Zgodnie z twierdzeniem Gaussa-Markowa, estymator MNK w KMRL jest liniowym estymatorem efektywnym i nieobciążonym, co po angielsku opisuje się za pomocą wyrażenia BLUE Best Linear Unbiased Estimator.
Stanisław Cichocki. Natalia Nehrebecka. Wykład 9
 Stanisław Cichocki Natalia Nehrebecka Wykład 9 1 1. Dodatkowe założenie KMRL 2. Testowanie hipotez prostych Rozkład estymatora b Testowanie hipotez prostych przy użyciu statystyki t 3. Przedziały ufności
Stanisław Cichocki Natalia Nehrebecka Wykład 9 1 1. Dodatkowe założenie KMRL 2. Testowanie hipotez prostych Rozkład estymatora b Testowanie hipotez prostych przy użyciu statystyki t 3. Przedziały ufności
Diagnostyka w Pakiecie Stata
 Karol Kuhl Zgodnie z twierdzeniem Gaussa-Markowa, estymator MNK w KMRL jest liniowym estymatorem efektywnym i nieobciążonym, co po angielsku opisuje się za pomocą wyrażenia BLUE Best Linear Unbiased Estimator.
Karol Kuhl Zgodnie z twierdzeniem Gaussa-Markowa, estymator MNK w KMRL jest liniowym estymatorem efektywnym i nieobciążonym, co po angielsku opisuje się za pomocą wyrażenia BLUE Best Linear Unbiased Estimator.
Egzamin z ekonometrii wersja IiE, MSEMAT
 Pytania teoretyczne Egzamin z ekonometrii wersja IiE, MSEMAT 08-02-2017 1. W jaki sposób przeprowadzamy test Chowa? 2. Pokazać, że jest nieobciążonym estymatorem. 3. Udowodnić, że w modelu ze stałą TSSESS+RSS.
Pytania teoretyczne Egzamin z ekonometrii wersja IiE, MSEMAT 08-02-2017 1. W jaki sposób przeprowadzamy test Chowa? 2. Pokazać, że jest nieobciążonym estymatorem. 3. Udowodnić, że w modelu ze stałą TSSESS+RSS.
Egzamin z ekonometrii wersja ogólna Pytania teoretyczne
 Egzamin z ekonometrii wersja ogólna 08-02-2017 Pytania teoretyczne 1. Za pomocą którego testu testujemy stabilność parametrów? Jakiemu założeniu KMRL odpowiada H0 w tym teście? Jaka jest hipoteza alternatywna
Egzamin z ekonometrii wersja ogólna 08-02-2017 Pytania teoretyczne 1. Za pomocą którego testu testujemy stabilność parametrów? Jakiemu założeniu KMRL odpowiada H0 w tym teście? Jaka jest hipoteza alternatywna
Ekonometria Ćwiczenia 19/01/05
 Oszacowano regresję stopy bezrobocia (unemp) na wzroście realnego PKB (pkb) i stopie inflacji (cpi) oraz na zmiennych zero-jedynkowych związanymi z kwartałami (season). Regresję przeprowadzono na danych
Oszacowano regresję stopy bezrobocia (unemp) na wzroście realnego PKB (pkb) i stopie inflacji (cpi) oraz na zmiennych zero-jedynkowych związanymi z kwartałami (season). Regresję przeprowadzono na danych
Wprowadzenie Testy własności składnika losowego. Diagnostyka modelu. Część 1. Diagnostyka modelu
 Część 1 Testy i ich rodzaje Statystyka NR 2 Cel testowania Testy i ich rodzaje Statystyka NR 2 Cel testowania Testy małej próby Testy i ich rodzaje Statystyka NR 2 Cel testowania Testy małej próby Testy
Część 1 Testy i ich rodzaje Statystyka NR 2 Cel testowania Testy i ich rodzaje Statystyka NR 2 Cel testowania Testy małej próby Testy i ich rodzaje Statystyka NR 2 Cel testowania Testy małej próby Testy
Ekonometria dla IiE i MSEMat Z12
 Ekonometria dla IiE i MSEMat Z12 Rafał Woźniak Faculty of Economic Sciences, University of Warsaw Warszawa, 09-01-2017 Test RESET Ramsey a W pierwszym etapie estymujemy współczynniki regresji w modelu:
Ekonometria dla IiE i MSEMat Z12 Rafał Woźniak Faculty of Economic Sciences, University of Warsaw Warszawa, 09-01-2017 Test RESET Ramsey a W pierwszym etapie estymujemy współczynniki regresji w modelu:
Egzamin z ekonometrii wersja IiE, MSEMAT
 Egzamin z ekonometrii wersja IiE, MSEMAT 04-02-2016 Pytania teoretyczne 1. Za pomocą jakiego testu weryfikowana jest normalność składnika losowego? Jakiemu założeniu KMRL odpowiada w tym teście? Jakie
Egzamin z ekonometrii wersja IiE, MSEMAT 04-02-2016 Pytania teoretyczne 1. Za pomocą jakiego testu weryfikowana jest normalność składnika losowego? Jakiemu założeniu KMRL odpowiada w tym teście? Jakie
Natalia Nehrebecka Stanisław Cichocki. Wykład 10
 Natalia Nehrebecka Stanisław Cichocki Wykład 10 1 1. Testy diagnostyczne 2. Testowanie prawidłowości formy funkcyjnej modelu 3. Testowanie normalności składników losowych 4. Testowanie stabilności parametrów
Natalia Nehrebecka Stanisław Cichocki Wykład 10 1 1. Testy diagnostyczne 2. Testowanie prawidłowości formy funkcyjnej modelu 3. Testowanie normalności składników losowych 4. Testowanie stabilności parametrów
Stanisław Cichocki. Natalia Nehrebecka. Wykład 12
 Stanisław Cichocki Natalia Nehrebecka Wykład 1 1 1. Testy diagnostyczne Testowanie stabilności parametrów modelu: test Chowa. Heteroskedastyczność Konsekwencje Testowanie heteroskedastyczności 1. Testy
Stanisław Cichocki Natalia Nehrebecka Wykład 1 1 1. Testy diagnostyczne Testowanie stabilności parametrów modelu: test Chowa. Heteroskedastyczność Konsekwencje Testowanie heteroskedastyczności 1. Testy
Stanisław Cichocki. Natalia Nehrebecka. Wykład 10
 Stanisław Cichocki Natalia Nehrebecka Wykład 10 1 1. Testy diagnostyczne Testowanie prawidłowości formy funkcyjnej: test RESET Testowanie normalności składników losowych: test Jarque-Berra Testowanie stabilności
Stanisław Cichocki Natalia Nehrebecka Wykład 10 1 1. Testy diagnostyczne Testowanie prawidłowości formy funkcyjnej: test RESET Testowanie normalności składników losowych: test Jarque-Berra Testowanie stabilności
Egzamin z ekonometrii wersja IiE, MSEMat Pytania teoretyczne
 Egzamin z ekonometrii wersja IiE, MSEMat 31-01-2014 Pytania teoretyczne 1. Podać postać przekształcenia Boxa-Coxa i wyjaśnić, do czego jest stosowane w ekonometrii. 2. Wyjaśnić, jakie korzyści i niebezpieczeństwa
Egzamin z ekonometrii wersja IiE, MSEMat 31-01-2014 Pytania teoretyczne 1. Podać postać przekształcenia Boxa-Coxa i wyjaśnić, do czego jest stosowane w ekonometrii. 2. Wyjaśnić, jakie korzyści i niebezpieczeństwa
Binarne zmienne zależne
 Binarne zmienne zależne Zmienna zależna nie jest ciagła ale przyjmuje zero lub jeden Przykład: szukanie determinant bezrobocia (próba przekrojowa) zmienna objaśniana: zerojedynkowa (pracujacy, bezrobotny)
Binarne zmienne zależne Zmienna zależna nie jest ciagła ale przyjmuje zero lub jeden Przykład: szukanie determinant bezrobocia (próba przekrojowa) zmienna objaśniana: zerojedynkowa (pracujacy, bezrobotny)
Egzamin z ekonometrii wersja ogolna
 Egzamin z ekonometrii wersja ogolna 04-02-2016 Pytania teoretyczne 1. Wymienić założenia Klasycznego Modelu Regresji Liniowej (KMRL). 2. Wyprowadzić estymator MNK dla modelu z wieloma zmiennymi objaśniającymi.
Egzamin z ekonometrii wersja ogolna 04-02-2016 Pytania teoretyczne 1. Wymienić założenia Klasycznego Modelu Regresji Liniowej (KMRL). 2. Wyprowadzić estymator MNK dla modelu z wieloma zmiennymi objaśniającymi.
Egzamin z ekonometrii wersja IiE, MSEMAT
 Egzamin z ekonometrii wersja IiE, MSEMAT 02022015 Pytania teoretyczne 1. Podać treść twierdzenia GaussaMarkowa i wyjaśnić jego znaczenie. 2. Za pomocą jakich testów testuje się autokorelację? Jakiemu założeniu
Egzamin z ekonometrii wersja IiE, MSEMAT 02022015 Pytania teoretyczne 1. Podać treść twierdzenia GaussaMarkowa i wyjaśnić jego znaczenie. 2. Za pomocą jakich testów testuje się autokorelację? Jakiemu założeniu
Materiaªy do zaawans. ekon. Z10
 Faculty of Economic Sciences, University of Warsaw Warsaw, 23-04-2012 Probit wiczenie 1. Moshe Ben-Akiva and Steven Lerman, Discrete Choice Analysis, Theory and Application to Travel Demand, MIT Press,
Faculty of Economic Sciences, University of Warsaw Warsaw, 23-04-2012 Probit wiczenie 1. Moshe Ben-Akiva and Steven Lerman, Discrete Choice Analysis, Theory and Application to Travel Demand, MIT Press,
Szacowanie modeli wielowartościowych w pakiecie STATA
 Szacowanie modeli wielowartościowych w pakiecie STATA Uniwersytet Warszawski Wydział Nauk Ekonomicznych 25 kwietnia 2007 W badaniach ekonomicznych i społecznych często odpowiedzi na pytania są kodowane
Szacowanie modeli wielowartościowych w pakiecie STATA Uniwersytet Warszawski Wydział Nauk Ekonomicznych 25 kwietnia 2007 W badaniach ekonomicznych i społecznych często odpowiedzi na pytania są kodowane
Stanisław Cichocki. Natalia Nehrebecka. Wykład 12
 Stanisław Cichocki Natalia Nehrebecka Wykład 12 1 1.Problemy z danymi Zmienne pominięte Zmienne nieistotne 2. Autokorelacja o Testowanie autokorelacji 1.Problemy z danymi Zmienne pominięte Zmienne nieistotne
Stanisław Cichocki Natalia Nehrebecka Wykład 12 1 1.Problemy z danymi Zmienne pominięte Zmienne nieistotne 2. Autokorelacja o Testowanie autokorelacji 1.Problemy z danymi Zmienne pominięte Zmienne nieistotne
Testowanie hipotez statystycznych
 Część 2 Hipoteza złożona Testowanie hipotez łącznych Zapis matematyczny Rozkład statystyki testowej Hipoteza łączna H 0 : Rβ = q Hipoteza złożona Testowanie hipotez łącznych Zapis matematyczny Rozkład
Część 2 Hipoteza złożona Testowanie hipotez łącznych Zapis matematyczny Rozkład statystyki testowej Hipoteza łączna H 0 : Rβ = q Hipoteza złożona Testowanie hipotez łącznych Zapis matematyczny Rozkład
Stanisław Cichocki. Natalia Nehrebecka. Wykład 13
 Stanisław Cichocki Natalia Nehrebecka Wykład 13 1 1. Autokorelacja Konsekwencje Testowanie autokorelacji 2. Metody radzenia sobie z heteroskedastycznością i autokorelacją Uogólniona Metoda Najmniejszych
Stanisław Cichocki Natalia Nehrebecka Wykład 13 1 1. Autokorelacja Konsekwencje Testowanie autokorelacji 2. Metody radzenia sobie z heteroskedastycznością i autokorelacją Uogólniona Metoda Najmniejszych
Stanisław Cichocki. Natalia Nehrebecka. Wykład 10
 Stanisław Cichoci Natalia Nehrebeca Wyład 10 1 1. Testowanie hipotez prostych Rozład estymatora b Testowanie hipotez prostych przy użyciu statystyi t Przedziały ufności Badamy czy hipotezy teoretyczne
Stanisław Cichoci Natalia Nehrebeca Wyład 10 1 1. Testowanie hipotez prostych Rozład estymatora b Testowanie hipotez prostych przy użyciu statystyi t Przedziały ufności Badamy czy hipotezy teoretyczne
Analiza Szeregów Czasowych. Egzamin
 Analiza Szeregów Czasowych Egzamin 12-06-2018 Zadanie 1: Zadanie 2: Zadanie 3: Zadanie 4: / 12 pkt. / 12 pkt. / 12 pkt. / 14 pkt. Projekt zaliczeniowy: Razem: / 100 pkt. / 50 pkt. Regulamin egzaminu 1.
Analiza Szeregów Czasowych Egzamin 12-06-2018 Zadanie 1: Zadanie 2: Zadanie 3: Zadanie 4: / 12 pkt. / 12 pkt. / 12 pkt. / 14 pkt. Projekt zaliczeniowy: Razem: / 100 pkt. / 50 pkt. Regulamin egzaminu 1.
Egzamin z ekonometrii wersja ogólna Pytania teoretyczne
 Egzamin z ekonometrii wersja ogólna 31-01-2014 Pytania teoretyczne 1. Podać postać przekształcenia Boxa-Coxa i wyjaśnić, do czego jest stosowane w ekonometrii. 2. Porównaj zastosowania znanych ci kontrastów
Egzamin z ekonometrii wersja ogólna 31-01-2014 Pytania teoretyczne 1. Podać postać przekształcenia Boxa-Coxa i wyjaśnić, do czego jest stosowane w ekonometrii. 2. Porównaj zastosowania znanych ci kontrastów
Ekonometria egzamin 02/02/ W trakcie egzaminu wolno używać jedynie długopisu o innym kolorze atramentu niż czerwony oraz kalkulatora.
 imię, nazwisko, nr indeksu: Ekonometria egzamin 0/0/0. Egzamin trwa 90 minut.. Rozwiązywanie zadań należy rozpocząć po ogłoszeniu początku egzaminu a skończyć wraz z ogłoszeniem końca egzaminu. Złamanie
imię, nazwisko, nr indeksu: Ekonometria egzamin 0/0/0. Egzamin trwa 90 minut.. Rozwiązywanie zadań należy rozpocząć po ogłoszeniu początku egzaminu a skończyć wraz z ogłoszeniem końca egzaminu. Złamanie
Testy własności składnika losowego Testy formy funkcyjnej. Diagnostyka modelu. Część 2. Diagnostyka modelu
 Część 2 Test Durbina-Watsona Test Durbina-Watsona Weryfikowana hipoteza H 0 : cov(ε t, ε t 1 ) = 0 H 1 : cov(ε t, ε t 1 ) 0 Test Durbina-Watsona Weryfikowana hipoteza H 0 : cov(ε t, ε t 1 ) = 0 H 1 : cov(ε
Część 2 Test Durbina-Watsona Test Durbina-Watsona Weryfikowana hipoteza H 0 : cov(ε t, ε t 1 ) = 0 H 1 : cov(ε t, ε t 1 ) 0 Test Durbina-Watsona Weryfikowana hipoteza H 0 : cov(ε t, ε t 1 ) = 0 H 1 : cov(ε
Egzamin z ekonometrii - wersja ogólna
 Egzamin z ekonometrii - wersja ogólna 06-02-2019 Regulamin egzaminu 1. Egzamin trwa 90 min. 2. Rozwiązywanie zadań należy rozpocząć po ogłoszeniu początku egzaminu a skończyć wraz z ogłoszeniem końca egzaminu.
Egzamin z ekonometrii - wersja ogólna 06-02-2019 Regulamin egzaminu 1. Egzamin trwa 90 min. 2. Rozwiązywanie zadań należy rozpocząć po ogłoszeniu początku egzaminu a skończyć wraz z ogłoszeniem końca egzaminu.
Budowa modelu i testowanie hipotez
 Problemy metodologiczne Gdzie jest problem? Obciążenie Lovella Dysponujemy oszacowaniami parametrów następującego modelu y t = β 0 + β 1 x 1 +... + β k x k + ε t Gdzie jest problem? Obciążenie Lovella
Problemy metodologiczne Gdzie jest problem? Obciążenie Lovella Dysponujemy oszacowaniami parametrów następującego modelu y t = β 0 + β 1 x 1 +... + β k x k + ε t Gdzie jest problem? Obciążenie Lovella
2.3 Modele nieliniowe
 2.3 Modele nieliniowe Do tej pory zajmowaliśmy się modelami liniowymi lub o liniowej formie funkcyjnej i musieliśmy akceptować ich ograniczenia. Metoda Największej Wiarogodności pozwala również na efektywną
2.3 Modele nieliniowe Do tej pory zajmowaliśmy się modelami liniowymi lub o liniowej formie funkcyjnej i musieliśmy akceptować ich ograniczenia. Metoda Największej Wiarogodności pozwala również na efektywną
Heteroskedastyczość w szeregach czasowyh
 Heteroskedastyczość w szeregach czasowyh Czesto zakłada się, że szeregi czasowe wykazuja autokorelację ae sa homoskedastyczne W rzeczywistości jednak często wariancja zmienia się w czasie Dobrym przykładem
Heteroskedastyczość w szeregach czasowyh Czesto zakłada się, że szeregi czasowe wykazuja autokorelację ae sa homoskedastyczne W rzeczywistości jednak często wariancja zmienia się w czasie Dobrym przykładem
Ekonometria. Metodologia budowy modelu. Jerzy Mycielski. Luty, 2011 WNE, UW. Jerzy Mycielski (WNE, UW) Ekonometria Luty, / 18
 Ekonometria Metodologia budowy modelu Jerzy Mycielski WNE, UW Luty, 2011 Jerzy Mycielski (WNE, UW) Ekonometria Luty, 2011 1 / 18 Sprawy organizacyjne Dyżur: środa godz. 14-15 w sali 302. Strona internetowa
Ekonometria Metodologia budowy modelu Jerzy Mycielski WNE, UW Luty, 2011 Jerzy Mycielski (WNE, UW) Ekonometria Luty, 2011 1 / 18 Sprawy organizacyjne Dyżur: środa godz. 14-15 w sali 302. Strona internetowa
Analiza czynników wpływających na poziom wykształcenia.
 Analiza czynników wpływających na poziom wykształcenia. Celem tej pracy jest potwierdzenie lub odrzucenie opinii, którą większość społeczeństwa uznaje za oczywistą, o tym ė w Polsce lepiej wykształceni
Analiza czynników wpływających na poziom wykształcenia. Celem tej pracy jest potwierdzenie lub odrzucenie opinii, którą większość społeczeństwa uznaje za oczywistą, o tym ė w Polsce lepiej wykształceni
Ekonometria egzamin 02/02/ W trakcie egzaminu wolno używać jedynie długopisu o innym kolorze atramentu niż czerwony oraz kalkulatora.
 imię, nazwisko, nr indeksu: Ekonometria egzamin 02/02/2011 1. Egzamin trwa 90 minut. 2. Rozwiązywanie zadań należy rozpocząć po ogłoszeniu początku egzaminu a skończyć wraz z ogłoszeniem końca egzaminu.
imię, nazwisko, nr indeksu: Ekonometria egzamin 02/02/2011 1. Egzamin trwa 90 minut. 2. Rozwiązywanie zadań należy rozpocząć po ogłoszeniu początku egzaminu a skończyć wraz z ogłoszeniem końca egzaminu.
Problem równoczesności w MNK
 Problem równoczesności w MNK O problemie równoczesności mówimy, gdy występuje korelacja między wartościa oczekiwana ε i i równoczesnym x i Model liniowy y = Xβ + ε, E (u) = 0 Powiedzmy, że występuje w
Problem równoczesności w MNK O problemie równoczesności mówimy, gdy występuje korelacja między wartościa oczekiwana ε i i równoczesnym x i Model liniowy y = Xβ + ε, E (u) = 0 Powiedzmy, że występuje w
1 Modele ADL - interpretacja współczynników
 1 Modele ADL - interpretacja współczynników ZADANIE 1.1 Dany jest proces DL następującej postaci: y t = µ + β 0 x t + β 1 x t 1 + ε t. 1. Wyjaśnić, jaka jest intepretacja współczynników β 0 i β 1. 2. Pokazać
1 Modele ADL - interpretacja współczynników ZADANIE 1.1 Dany jest proces DL następującej postaci: y t = µ + β 0 x t + β 1 x t 1 + ε t. 1. Wyjaśnić, jaka jest intepretacja współczynników β 0 i β 1. 2. Pokazać
Metoda najmniejszych kwadratów
 Własności algebraiczne Model liniowy Zapis modelu zarobki = β 0 + β 1 plec + β 2 wiek + ε Oszacowania wartości współczynników zarobki = b 0 + b 1 plec + b 2 wiek + e Model liniowy Tabela: Oszacowania współczynników
Własności algebraiczne Model liniowy Zapis modelu zarobki = β 0 + β 1 plec + β 2 wiek + ε Oszacowania wartości współczynników zarobki = b 0 + b 1 plec + b 2 wiek + e Model liniowy Tabela: Oszacowania współczynników
1 Metoda Największej Wiarogodności
 1 Metoda Największej Wiarogodności 1.0.1 Wprowadzenie Dotychczas omawiane modele szacowane były za pomocą metody najmniejszych kwadratów. Jednak takie modele nie wyczerpują wszystkich możliwości. Istnieje
1 Metoda Największej Wiarogodności 1.0.1 Wprowadzenie Dotychczas omawiane modele szacowane były za pomocą metody najmniejszych kwadratów. Jednak takie modele nie wyczerpują wszystkich możliwości. Istnieje
Regresja liniowa wprowadzenie
 Regresja liniowa wprowadzenie a) Model regresji liniowej ma postać: gdzie jest zmienną objaśnianą (zależną); są zmiennymi objaśniającymi (niezależnymi); natomiast są parametrami modelu. jest składnikiem
Regresja liniowa wprowadzenie a) Model regresji liniowej ma postać: gdzie jest zmienną objaśnianą (zależną); są zmiennymi objaśniającymi (niezależnymi); natomiast są parametrami modelu. jest składnikiem
Ekonometria. Modelowanie zmiennej jakościowej. Jakub Mućk. Katedra Ekonomii Ilościowej
 Ekonometria Modelowanie zmiennej jakościowej Jakub Mućk Katedra Ekonomii Ilościowej Jakub Mućk Ekonometria Ćwiczenia 8 Zmienna jakościowa 1 / 25 Zmienna jakościowa Zmienna ilościowa może zostać zmierzona
Ekonometria Modelowanie zmiennej jakościowej Jakub Mućk Katedra Ekonomii Ilościowej Jakub Mućk Ekonometria Ćwiczenia 8 Zmienna jakościowa 1 / 25 Zmienna jakościowa Zmienna ilościowa może zostać zmierzona
Przyczynowość Kointegracja. Kointegracja. Kointegracja
 korelacja a związek o charakterze przyczynowo-skutkowym korelacja a związek o charakterze przyczynowo-skutkowym Przyczynowość w sensie Grangera Zmienna x jest przyczyną w sensie Grangera zmiennej y jeżeli
korelacja a związek o charakterze przyczynowo-skutkowym korelacja a związek o charakterze przyczynowo-skutkowym Przyczynowość w sensie Grangera Zmienna x jest przyczyną w sensie Grangera zmiennej y jeżeli
WSTĘP DO REGRESJI LOGISTYCZNEJ. Dr Wioleta Drobik-Czwarno
 WSTĘP DO REGRESJI LOGISTYCZNEJ Dr Wioleta Drobik-Czwarno REGRESJA LOGISTYCZNA Zmienna zależna jest zmienną dychotomiczną (dwustanową) przyjmuje dwie wartości, najczęściej 0 i 1 Zmienną zależną może być:
WSTĘP DO REGRESJI LOGISTYCZNEJ Dr Wioleta Drobik-Czwarno REGRESJA LOGISTYCZNA Zmienna zależna jest zmienną dychotomiczną (dwustanową) przyjmuje dwie wartości, najczęściej 0 i 1 Zmienną zależną może być:
NIE STRASZNY NAM KRYZYS, CZYLI JAK NIE DAĆ SIĘ DEPRESJI Determinanty depresji w Polsce
 Model ekonometryczny NIE STRASZNY NAM KRYZYS, CZYLI JAK NIE DAĆ SIĘ DEPRESJI Determinanty depresji w Polsce Michał Danilewski Paweł Klimaszewski UNIWERSYTET WARSZAWSKI WYDZIAŁ NAUK EKONOMICZNYCH WARSZAWA
Model ekonometryczny NIE STRASZNY NAM KRYZYS, CZYLI JAK NIE DAĆ SIĘ DEPRESJI Determinanty depresji w Polsce Michał Danilewski Paweł Klimaszewski UNIWERSYTET WARSZAWSKI WYDZIAŁ NAUK EKONOMICZNYCH WARSZAWA
Stanisław Cichocki Natalia Nehrebecka. Wykład 1
 Stanisław Cichocki Natalia Nehrebecka Wykład 1 1 1. Sprawy organizacyjne Zasady zaliczenia Ćwiczenia Literatura 2. Obciążenie Lovella 3. Metoda od ogólnego do szczególnego 4. Kryteria informacyjne 2 1.
Stanisław Cichocki Natalia Nehrebecka Wykład 1 1 1. Sprawy organizacyjne Zasady zaliczenia Ćwiczenia Literatura 2. Obciążenie Lovella 3. Metoda od ogólnego do szczególnego 4. Kryteria informacyjne 2 1.
Stanisław Cichocki. Natalia Neherebecka. Zajęcia 15-17
 Stanisław Cichocki Natalia Neherebecka Zajęcia 15-17 1 1. Binarne zmienne zależne 2. Liniowy model prawdopodobieństwa a) Interpretacja współczynników 3. Probit a) Interpretacja współczynników b) Miary
Stanisław Cichocki Natalia Neherebecka Zajęcia 15-17 1 1. Binarne zmienne zależne 2. Liniowy model prawdopodobieństwa a) Interpretacja współczynników 3. Probit a) Interpretacja współczynników b) Miary
Stanisław Cichocki. Natalia Nehrebecka. Wykład 13
 Stanisław Cichocki Natalia Nehrebecka Wykład 13 1 1. Testowanie autokorelacji 2. Heteroskedastyczność i autokorelacja Konsekwencje heteroskedastyczności i autokorelacji 3.Problemy z danymi Zmienne pominięte
Stanisław Cichocki Natalia Nehrebecka Wykład 13 1 1. Testowanie autokorelacji 2. Heteroskedastyczność i autokorelacja Konsekwencje heteroskedastyczności i autokorelacji 3.Problemy z danymi Zmienne pominięte
Natalia Nehrebecka Stanisław Cichocki. Wykład 10
 Natalia Nehrebecka Stanisław Cichocki Wykład 10 1 1. Testy diagnostyczne 2. Testowanie prawidłowości formy funkcyjnej modelu 3. Testowanie normalności składników losowych 4. Testowanie stabilności parametrów
Natalia Nehrebecka Stanisław Cichocki Wykład 10 1 1. Testy diagnostyczne 2. Testowanie prawidłowości formy funkcyjnej modelu 3. Testowanie normalności składników losowych 4. Testowanie stabilności parametrów
Stanisław Cichocki. Natalia Nehrebecka
 Stanisław Cichocki Natalia Nehrebecka 1 1. Binarne zmienne zależne 2. Liniowy model prawdopodobieństwa a) Interpretacja współczynników 3. Probit a) Interpretacja współczynników b) Miary dopasowania 4.
Stanisław Cichocki Natalia Nehrebecka 1 1. Binarne zmienne zależne 2. Liniowy model prawdopodobieństwa a) Interpretacja współczynników 3. Probit a) Interpretacja współczynników b) Miary dopasowania 4.
Stanisław Cichocki. Natalia Nehrebecka. Wykład 14
 Stanisław Cichocki Natalia Nehrebecka Wykład 14 1 1.Problemy z danymi Współliniowość 2. Heteroskedastyczność i autokorelacja Konsekwencje heteroskedastyczności i autokorelacji Metody radzenia sobie z heteroskedastycznością
Stanisław Cichocki Natalia Nehrebecka Wykład 14 1 1.Problemy z danymi Współliniowość 2. Heteroskedastyczność i autokorelacja Konsekwencje heteroskedastyczności i autokorelacji Metody radzenia sobie z heteroskedastycznością
Ekonometria egzamin semestr drugi 14/06/09
 imię, nazwisko, nr indeksu: Ekonometria egzamin semestr drugi 14/06/09 1. Przed przystąpieniem do pisania egzaminu należy podpisać wszystkie kartki arkusza egzaminacyjnego (na dole w przewidzianym miejscu).
imię, nazwisko, nr indeksu: Ekonometria egzamin semestr drugi 14/06/09 1. Przed przystąpieniem do pisania egzaminu należy podpisać wszystkie kartki arkusza egzaminacyjnego (na dole w przewidzianym miejscu).
Zadanie 1. a) Przeprowadzono test RESET. Czy model ma poprawną formę funkcyjną? 1
 Zadanie 1 a) Przeprowadzono test RESET. Czy model ma poprawną formę funkcyjną? 1 b) W naszym przypadku populacja są inżynierowie w Tajlandii. Czy można jednak przypuszczać, że na zarobki kobiet-inżynierów
Zadanie 1 a) Przeprowadzono test RESET. Czy model ma poprawną formę funkcyjną? 1 b) W naszym przypadku populacja są inżynierowie w Tajlandii. Czy można jednak przypuszczać, że na zarobki kobiet-inżynierów
, a reszta dla pominiętej obserwacji wynosi 0, RSS jest stałe, T SS rośnie, więc zarówno R 2 jak i R2 rosną. R 2 = 1 n 1 n. rosnie. n 2 (1 R2 ) = 1 59
 Zadanie 1. Ekonometryk szacując funkcję konsumpcji przeprowadził estymację osobno dla tzw. Polski A oraz Polski B. Dla Polski A posiadał n 1 = 40 obserwacji i uzyskał współczynnik dopasowania RA 2 = 0.4,
Zadanie 1. Ekonometryk szacując funkcję konsumpcji przeprowadził estymację osobno dla tzw. Polski A oraz Polski B. Dla Polski A posiadał n 1 = 40 obserwacji i uzyskał współczynnik dopasowania RA 2 = 0.4,
Czasowy wymiar danych
 Problem autokorelacji Model regresji dla szeregów czasowych Model regresji dla szeregów czasowych y t = X t β + ε t Zasadnicze różnice 1 Budowa prognoz 2 Problem stabilności parametrów 3 Problem autokorelacji
Problem autokorelacji Model regresji dla szeregów czasowych Model regresji dla szeregów czasowych y t = X t β + ε t Zasadnicze różnice 1 Budowa prognoz 2 Problem stabilności parametrów 3 Problem autokorelacji
Ekonometria dla IiE i MSEMat Z7
 Ekonometria dla IiE i MSEMat Z7 Rafał Woźniak Faculty of Economic Sciences, University of Warsaw Warszawa, 21-11-2016 Na podstawie zbioru danych cps_small.dat z książki Principles of Econometrics oszacowany
Ekonometria dla IiE i MSEMat Z7 Rafał Woźniak Faculty of Economic Sciences, University of Warsaw Warszawa, 21-11-2016 Na podstawie zbioru danych cps_small.dat z książki Principles of Econometrics oszacowany
Własności statystyczne regresji liniowej. Wykład 4
 Własności statystyczne regresji liniowej Wykład 4 Plan Własności zmiennych losowych Normalna regresja liniowa Własności regresji liniowej Literatura B. Hansen (2017+) Econometrics, Rozdział 5 Własności
Własności statystyczne regresji liniowej Wykład 4 Plan Własności zmiennych losowych Normalna regresja liniowa Własności regresji liniowej Literatura B. Hansen (2017+) Econometrics, Rozdział 5 Własności
Egzamin z Ekonometrii
 Pytania teoretyczne Egzamin z Ekonometrii 18.06.2015 1. Opisać procedurę od ogólnego do szczegółowego na przykładzie doboru liczby opóźnień w modelu. 2. Na czym polega najważniejsza różnica między testowaniem
Pytania teoretyczne Egzamin z Ekonometrii 18.06.2015 1. Opisać procedurę od ogólnego do szczegółowego na przykładzie doboru liczby opóźnień w modelu. 2. Na czym polega najważniejsza różnica między testowaniem
1.9 Czasowy wymiar danych
 1.9 Czasowy wymiar danych Do tej pory rozpatrywaliśmy jedynie modele tworzone na podstawie danych empirycznych pochodzących z prób przekrojowych. Teraz zajmiemy się zagadnieniem budowy modeli regresji,
1.9 Czasowy wymiar danych Do tej pory rozpatrywaliśmy jedynie modele tworzone na podstawie danych empirycznych pochodzących z prób przekrojowych. Teraz zajmiemy się zagadnieniem budowy modeli regresji,
1.7 Ograniczenia nakładane na równanie regresji
 1.7 Ograniczenia nakładane na równanie regresji Często teoria ekonomiczna wskazuje dobór zmiennych do modelu. Jednak nie w każdym przypadku oceny wartości parametrów są statystycznie istotne. Zastanowimy
1.7 Ograniczenia nakładane na równanie regresji Często teoria ekonomiczna wskazuje dobór zmiennych do modelu. Jednak nie w każdym przypadku oceny wartości parametrów są statystycznie istotne. Zastanowimy
Ekonometria egzamin 07/03/2018
 imię, nazwisko, nr indeksu: Ekonometria egzamin 07/03/2018 1. Egzamin trwa 90 minut. 2. Rozwiązywanie zadań należy rozpocząć po ogłoszeniu początku egzaminu a skończyć wraz z ogłoszeniem końca egzaminu.
imię, nazwisko, nr indeksu: Ekonometria egzamin 07/03/2018 1. Egzamin trwa 90 minut. 2. Rozwiązywanie zadań należy rozpocząć po ogłoszeniu początku egzaminu a skończyć wraz z ogłoszeniem końca egzaminu.
2 Logit i logit wielomianowy
 2 Logit i logit wielomianowy 2.1 Logit i miary dopasowania Miary dopasowania modelu do danych empirycznych opisane w niniejszym rozdziale mają szersze zastosowanie, do szerszej klasy modeli z dyskretnymi
2 Logit i logit wielomianowy 2.1 Logit i miary dopasowania Miary dopasowania modelu do danych empirycznych opisane w niniejszym rozdziale mają szersze zastosowanie, do szerszej klasy modeli z dyskretnymi
Systemy pomiarowo-diagnostyczne. Metody uczenia maszynowego wykład II 2017/2018
 Systemy pomiarowo-diagnostyczne Metody uczenia maszynowego wykład II bogumil.konopka@pwr.edu.pl 2017/2018 Określenie rzeczywistej dokładności modelu Zbiór treningowym vs zbiór testowy Zbiór treningowy
Systemy pomiarowo-diagnostyczne Metody uczenia maszynowego wykład II bogumil.konopka@pwr.edu.pl 2017/2018 Określenie rzeczywistej dokładności modelu Zbiór treningowym vs zbiór testowy Zbiór treningowy
Stanisław Cichocki. Natalia Nehrebecka. Wykład 14
 Stanisław Cichocki Natalia Nehrebecka Wykład 14 1 1.Problemy z danymi Zmienne pominięte Zmienne nieistotne Obserwacje nietypowe i błędne Współliniowość - Mamy 2 modele: y X u 1 1 (1) y X X 1 1 2 2 (2)
Stanisław Cichocki Natalia Nehrebecka Wykład 14 1 1.Problemy z danymi Zmienne pominięte Zmienne nieistotne Obserwacje nietypowe i błędne Współliniowość - Mamy 2 modele: y X u 1 1 (1) y X X 1 1 2 2 (2)
Ekonometria egzamin wersja Informatyka i Ekonometria 26/06/08
 imię, nazwisko, nr indeksu: Ekonometria egzamin wersja Informatyka i Ekonometria 26/06/08 1. Egzamin trwa 90 minut. 2. Rozwiązywanie zadań należy rozpocząć po ogłoszeniu początku egzaminu a skończyć wraz
imię, nazwisko, nr indeksu: Ekonometria egzamin wersja Informatyka i Ekonometria 26/06/08 1. Egzamin trwa 90 minut. 2. Rozwiązywanie zadań należy rozpocząć po ogłoszeniu początku egzaminu a skończyć wraz
Zmienne Binarne w Pakiecie Stata
 Karol Kuhl Zbiór (hipotetyczny) dummy.dta zawiera dane, na podstawie których prowadzono analizy opisane poniżej. Nazwy zmiennych oznaczają: doch dochód w jednostkach pieniężnych; plec płeć: kobieta (0),
Karol Kuhl Zbiór (hipotetyczny) dummy.dta zawiera dane, na podstawie których prowadzono analizy opisane poniżej. Nazwy zmiennych oznaczają: doch dochód w jednostkach pieniężnych; plec płeć: kobieta (0),
Mikroekonometria 5. Mikołaj Czajkowski Wiktor Budziński
 Mikroekonometria 5 Mikołaj Czajkowski Wiktor Budziński Zadanie 1. Wykorzystując dane me.hedonic.dta przygotuj model oszacowujący wartość kosztów zewnętrznych rolnictwa 1. Przeprowadź regresję objaśniającą
Mikroekonometria 5 Mikołaj Czajkowski Wiktor Budziński Zadanie 1. Wykorzystując dane me.hedonic.dta przygotuj model oszacowujący wartość kosztów zewnętrznych rolnictwa 1. Przeprowadź regresję objaśniającą
Mikroekonometria 13. Mikołaj Czajkowski Wiktor Budziński
 Mikroekonometria 13 Mikołaj Czajkowski Wiktor Budziński Endogeniczność regresja liniowa W regresji liniowej estymujemy następujące równanie: i i i Metoda Najmniejszych Kwadratów zakłada, że wszystkie zmienne
Mikroekonometria 13 Mikołaj Czajkowski Wiktor Budziński Endogeniczność regresja liniowa W regresji liniowej estymujemy następujące równanie: i i i Metoda Najmniejszych Kwadratów zakłada, że wszystkie zmienne
Modele wielorównaniowe (forma strukturalna)
 Modele wielorównaniowe (forma strukturalna) Formę strukturalna modelu o G równaniach AY t = BX t + u t, gdzie Y t = [y 1t,..., y Gt ] X t = [x 1t,..., x Kt ] u t = [u 1t,..., u Gt ] E (u t ) = 0 Var (u
Modele wielorównaniowe (forma strukturalna) Formę strukturalna modelu o G równaniach AY t = BX t + u t, gdzie Y t = [y 1t,..., y Gt ] X t = [x 1t,..., x Kt ] u t = [u 1t,..., u Gt ] E (u t ) = 0 Var (u
Zadanie 1 Zakładając liniową relację między wydatkami na obuwie a dochodem oszacować MNK parametry modelu: y t. X 1 t. Tabela 1.
 tel. 44 683 1 55 tel. kom. 64 566 811 e-mail: biuro@wszechwiedza.pl Zadanie 1 Zakładając liniową relację między wydatkami na obuwie a dochodem oszacować MNK parametry modelu: gdzie: y t X t y t = 1 X 1
tel. 44 683 1 55 tel. kom. 64 566 811 e-mail: biuro@wszechwiedza.pl Zadanie 1 Zakładając liniową relację między wydatkami na obuwie a dochodem oszacować MNK parametry modelu: gdzie: y t X t y t = 1 X 1
Modele warunkowej heteroscedastyczności
 Teoria Przykład - zwroty z WIG Niskie koszty transakcyjne Teoria Przykład - zwroty z WIG Niskie koszty transakcyjne Racjonalne oczekiwania inwestorów P t = E(P t+1 I t ) 1 + R (1) Teoria Przykład - zwroty
Teoria Przykład - zwroty z WIG Niskie koszty transakcyjne Teoria Przykład - zwroty z WIG Niskie koszty transakcyjne Racjonalne oczekiwania inwestorów P t = E(P t+1 I t ) 1 + R (1) Teoria Przykład - zwroty
1.8 Diagnostyka modelu
 1.8 Diagnostyka modelu Dotychczas zajmowaliśmy się własnościami estymatorów przy spełnionych założeniach KMRL. W praktyce nie zawsze spełnione są wszystkie założenia modelu. Jeżeli któreś z nich nie jest
1.8 Diagnostyka modelu Dotychczas zajmowaliśmy się własnościami estymatorów przy spełnionych założeniach KMRL. W praktyce nie zawsze spełnione są wszystkie założenia modelu. Jeżeli któreś z nich nie jest
Regresja logistyczna (LOGISTIC)
 Zmienna zależna: Wybór opcji zachodniej w polityce zagranicznej (kodowana jako tak, 0 nie) Zmienne niezależne: wiedza o Unii Europejskiej (WIEDZA), zamieszkiwanie w regionie zachodnim (ZACH) lub wschodnim
Zmienna zależna: Wybór opcji zachodniej w polityce zagranicznej (kodowana jako tak, 0 nie) Zmienne niezależne: wiedza o Unii Europejskiej (WIEDZA), zamieszkiwanie w regionie zachodnim (ZACH) lub wschodnim
(LMP-Liniowy model prawdopodobieństwa)
 OGÓLNY MODEL REGRESJI BINARNEJ (LMP-Liniowy model prawdopodobieństwa) Dla k3 y α α α α + x + x + x 2 2 3 3 + α x x α x x + α x x + α x x + ε + x 4 2 5 3 6 2 3 7 2 3 Zał.: Wszystkie zmienne interakcyjne
OGÓLNY MODEL REGRESJI BINARNEJ (LMP-Liniowy model prawdopodobieństwa) Dla k3 y α α α α + x + x + x 2 2 3 3 + α x x α x x + α x x + α x x + ε + x 4 2 5 3 6 2 3 7 2 3 Zał.: Wszystkie zmienne interakcyjne
Szacowanie modeli dla nielosowej selekcji w pakiecie STATA
 Szacowanie modeli dla nielosowej selekcji w pakiecie STATA Paweł Strawiński Uniwersytet Warszawski Wydział Nauk Ekonomicznych 17 kwietnia 2005 1 Dane Przedmiotem badania jest oszacowanie funkcji płacy
Szacowanie modeli dla nielosowej selekcji w pakiecie STATA Paweł Strawiński Uniwersytet Warszawski Wydział Nauk Ekonomicznych 17 kwietnia 2005 1 Dane Przedmiotem badania jest oszacowanie funkcji płacy
Ekonometria egzamin 06/03/ W trakcie egzaminu wolno używać jedynie długopisu o innym kolorze atramentu niż czerwony oraz kalkulatora.
 imię, nazwisko, nr indeksu: Ekonometria egzamin 06/03/2019 1. Egzamin trwa 90 minut. 2. Rozwiązywanie zadań należy rozpocząć po ogłoszeniu początku egzaminu a skończyć wraz z ogłoszeniem końca egzaminu.
imię, nazwisko, nr indeksu: Ekonometria egzamin 06/03/2019 1. Egzamin trwa 90 minut. 2. Rozwiązywanie zadań należy rozpocząć po ogłoszeniu początku egzaminu a skończyć wraz z ogłoszeniem końca egzaminu.
Wprowadzenie Modele o opóźnieniach rozłożonych Modele autoregresyjne o opóźnieniach rozłożonych. Modele dynamiczne.
 opisują kształtowanie się zjawiska w czasie opisują kształtowanie się zjawiska w czasie Najważniejszymi zastosowaniami modeli dynamicznych są opisują kształtowanie się zjawiska w czasie Najważniejszymi
opisują kształtowanie się zjawiska w czasie opisują kształtowanie się zjawiska w czasie Najważniejszymi zastosowaniami modeli dynamicznych są opisują kształtowanie się zjawiska w czasie Najważniejszymi
1 Metoda Najmniejszych Kwadratów (MNK) 2 Interpretacja parametrów modelu. 3 Klasyczny Model Regresji Liniowej (KMRL)
 1 Metoda Najmniejszych Kwadratów (MNK) 1. Co to jest zmienna endogeniczna, a co to zmienne egzogeniczna? 2. Podaj postać macierzy obserwacji dla modelu y t = a + bt + ε t 3. Co to jest wartość dopasowana,
1 Metoda Najmniejszych Kwadratów (MNK) 1. Co to jest zmienna endogeniczna, a co to zmienne egzogeniczna? 2. Podaj postać macierzy obserwacji dla modelu y t = a + bt + ε t 3. Co to jest wartość dopasowana,
Stanisław Cichocki. Natalia Nehrebecka
 Stanisław Cichocki Natalia Nehrebecka 1 1. Wprowadzenie do danych panelowych a) Charakterystyka danych panelowych b) Zalety i ograniczenia 2. Modele ekonometryczne danych panelowych a) Model efektów nieobserwowalnych
Stanisław Cichocki Natalia Nehrebecka 1 1. Wprowadzenie do danych panelowych a) Charakterystyka danych panelowych b) Zalety i ograniczenia 2. Modele ekonometryczne danych panelowych a) Model efektów nieobserwowalnych
Ekonometria ćwiczenia Kolokwium 2 semestr 22/05/05. / 4 pkt. / 4 pkt. / 3 pkt. / 4 pkt. /22 pkt. Regulamin i informacje dodatkowe
 imię, nazwisko, nr indeksu: Ekonometria ćwiczenia Kolokwium 2 semestr 22/05/05 Zadanie 1 Zadanie 2 Zadanie 3 / 4 pkt / 4 pkt / 3 pkt Zadanie 4 / 7 pkt [1/1/1/2/2] Zadanie 5 Razem / 4 pkt /22 pkt Skala
imię, nazwisko, nr indeksu: Ekonometria ćwiczenia Kolokwium 2 semestr 22/05/05 Zadanie 1 Zadanie 2 Zadanie 3 / 4 pkt / 4 pkt / 3 pkt Zadanie 4 / 7 pkt [1/1/1/2/2] Zadanie 5 Razem / 4 pkt /22 pkt Skala
Natalia Nehrebecka Stanisław Cichocki. Wykład 6
 Natalia Nehrebecka Stanisław Cichocki Wykład 6 1 1. Zmienne dyskretne Zmienne zero-jedynkowe 2. Modele z interakcjami 2 Zmienne dyskretne Zmienne nominalne Zmienne uporządkowane 3 4 1 podstawowe i 0 podstawowe
Natalia Nehrebecka Stanisław Cichocki Wykład 6 1 1. Zmienne dyskretne Zmienne zero-jedynkowe 2. Modele z interakcjami 2 Zmienne dyskretne Zmienne nominalne Zmienne uporządkowane 3 4 1 podstawowe i 0 podstawowe
Natalia Nehrebecka. 18 maja 2010
 Natalia Nehrebecka 18 maja 2010 1. Testy diagnostyczne 2. Testowanie prawidłowości formy funkcyjnej modelu 3. Testowanie normalności składników losowych 4. Testowanie stabilności parametrów 5. Testowanie
Natalia Nehrebecka 18 maja 2010 1. Testy diagnostyczne 2. Testowanie prawidłowości formy funkcyjnej modelu 3. Testowanie normalności składników losowych 4. Testowanie stabilności parametrów 5. Testowanie
Stanisław Cichocki Natalia Nehrebecka. Wykład 7
 Stanisław Cichocki Natalia Nehrebecka Wykład 7 1 1. Metoda Największej Wiarygodności MNW 2. Założenia MNW 3. Własności estymatorów MNW 4. Testowanie hipotez w MNW 2 1. Metoda Największej Wiarygodności
Stanisław Cichocki Natalia Nehrebecka Wykład 7 1 1. Metoda Największej Wiarygodności MNW 2. Założenia MNW 3. Własności estymatorów MNW 4. Testowanie hipotez w MNW 2 1. Metoda Największej Wiarygodności
Autokorelacja i heteroskedastyczność
 Autokorelacja i heteroskedastyczność Założenie o braku autokorelacji Cov (ε i, ε j ) = E (ε i ε j ) = 0 dla i j Oczekiwana wielkość elementu losowego nie zależy od wielkości elementu losowego dla innych
Autokorelacja i heteroskedastyczność Założenie o braku autokorelacji Cov (ε i, ε j ) = E (ε i ε j ) = 0 dla i j Oczekiwana wielkość elementu losowego nie zależy od wielkości elementu losowego dla innych
Binarne zmienne zależne
 Binarne zmienne zależne Zmienna zależna nie jest ciagła ale przyjmuje zero lub jeden Przykład: szukanie determinant bezrobocia (próba przekrojowa) zmienna objaśniana: zerojedynkowa (pracujacy, bezrobotny)
Binarne zmienne zależne Zmienna zależna nie jest ciagła ale przyjmuje zero lub jeden Przykład: szukanie determinant bezrobocia (próba przekrojowa) zmienna objaśniana: zerojedynkowa (pracujacy, bezrobotny)
Jednowskaźnikowy model Sharpe`a
 Uniwersytet Warszawski Wydział Nauk Ekonomicznych Milena Jamroziak i Paweł Androszczuk Model ekonometryczny Jednowskaźnikowy model Sharpe`a dla akcji Amici Praca zaliczeniowa napisana pod kierunkiem mgr
Uniwersytet Warszawski Wydział Nauk Ekonomicznych Milena Jamroziak i Paweł Androszczuk Model ekonometryczny Jednowskaźnikowy model Sharpe`a dla akcji Amici Praca zaliczeniowa napisana pod kierunkiem mgr
Ekonometria egzamin wersja ogólna 17/06/08
 imię, nazwisko, nr indeksu: Ekonometria egzamin wersja ogólna 17/06/08 1. Egzamin trwa 90 minut. 2. Rozwiązywanie zadań należy rozpocząć po ogłoszeniu początku egzaminu a skończyć wraz z ogłoszeniem końca
imię, nazwisko, nr indeksu: Ekonometria egzamin wersja ogólna 17/06/08 1. Egzamin trwa 90 minut. 2. Rozwiązywanie zadań należy rozpocząć po ogłoszeniu początku egzaminu a skończyć wraz z ogłoszeniem końca
Egzamin z ekonometrii
 Pytania teoretyczne Egzamin z ekonometrii 22.06.2012 1. Podaj ogólną postać modeli DL i ADL 2. Wyjaśnij jak należy rozumieć przyczynowość w sensie Grangera i jak jest testowana. 3. Jakie są wady liniowego
Pytania teoretyczne Egzamin z ekonometrii 22.06.2012 1. Podaj ogólną postać modeli DL i ADL 2. Wyjaśnij jak należy rozumieć przyczynowość w sensie Grangera i jak jest testowana. 3. Jakie są wady liniowego
Heteroscedastyczność. Zjawisko heteroscedastyczności Uogólniona Metoda Najmniejszych Kwadratów Stosowalna Metoda Najmniejszych Kwadratów
 Formy heteroscedastyczności Własności estymatorów MNK wydatki konsumpcyjne 0 10000 20000 30000 40000 14.4 31786.08 dochód rozporz¹dzalny Zródlo: Obliczenia wlasne, dane BBGD 2004 Formy heteroscedastyczności
Formy heteroscedastyczności Własności estymatorów MNK wydatki konsumpcyjne 0 10000 20000 30000 40000 14.4 31786.08 dochód rozporz¹dzalny Zródlo: Obliczenia wlasne, dane BBGD 2004 Formy heteroscedastyczności
Ekonometria egzamin 31/01/ W trakcie egzaminu wolno używać jedynie długopisu o innym kolorze atramentu niż czerwony oraz kalkulatora.
 imię, nazwisko, nr indeksu: Ekonometria egzamin 31/01/2018 1. Egzamin trwa 90 minut. 2. Rozwiązywanie zadań należy rozpocząć po ogłoszeniu początku egzaminu a skończyć wraz z ogłoszeniem końca egzaminu.
imię, nazwisko, nr indeksu: Ekonometria egzamin 31/01/2018 1. Egzamin trwa 90 minut. 2. Rozwiązywanie zadań należy rozpocząć po ogłoszeniu początku egzaminu a skończyć wraz z ogłoszeniem końca egzaminu.
1.5 Problemy ze zbiorem danych
 1.5 Problemy ze zbiorem danych W praktyce ekonometrycznej bardzo rzadko spełnione są wszystkie założenia klasycznego modelu regresji liniowej. Częstym przypadkiem jest, że zbiór danych którymi dysponujemy
1.5 Problemy ze zbiorem danych W praktyce ekonometrycznej bardzo rzadko spełnione są wszystkie założenia klasycznego modelu regresji liniowej. Częstym przypadkiem jest, że zbiór danych którymi dysponujemy
Weryfikacja hipotez statystycznych
 Weryfikacja hipotez statystycznych Hipoteza Test statystyczny Poziom istotności Testy jednostronne i dwustronne Testowanie równości wariancji test F-Fishera Testowanie równości wartości średnich test t-studenta
Weryfikacja hipotez statystycznych Hipoteza Test statystyczny Poziom istotności Testy jednostronne i dwustronne Testowanie równości wariancji test F-Fishera Testowanie równości wartości średnich test t-studenta
WYKORZYSTANIE MODELU LOGITOWEGO DO ANALIZY BEZROBOCIA WŚRÓD OSÓB NIEPEŁNOSPRAWNYCH W POLSCE W 2010 ROKU
 STUDIA I PRACE WYDZIAŁU NAUK EKONOMICZNYCH I ZARZĄDZANIA NR 31 Beata Bieszk-Stolorz Uniwersytet Szczeciński WYKORZYSTANIE MODELU LOGITOWEGO DO ANALIZY BEZROBOCIA WŚRÓD OSÓB NIEPEŁNOSPRAWNYCH W POLSCE W
STUDIA I PRACE WYDZIAŁU NAUK EKONOMICZNYCH I ZARZĄDZANIA NR 31 Beata Bieszk-Stolorz Uniwersytet Szczeciński WYKORZYSTANIE MODELU LOGITOWEGO DO ANALIZY BEZROBOCIA WŚRÓD OSÓB NIEPEŁNOSPRAWNYCH W POLSCE W
Egzamin z ekonometrii IiE
 Pytania teoretyczne Egzamin z ekonometrii IiE 22.06.2012 1. Kiedy selekcja próby jest problemem i jaki model można stosować w przypadku samoselekcji próby? 2. Jakie są konieczne założenia, by estymator
Pytania teoretyczne Egzamin z ekonometrii IiE 22.06.2012 1. Kiedy selekcja próby jest problemem i jaki model można stosować w przypadku samoselekcji próby? 2. Jakie są konieczne założenia, by estymator
Uogólniony model liniowy
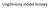 Uogólniony model liniowy Ogólny model liniowy y = Xb + e Każda obserwacja ma rozkład normalny Każda obserwacja ma tą samą wariancję Dane nienormalne Rozkład binomialny np. liczba chorych krów w stadzie
Uogólniony model liniowy Ogólny model liniowy y = Xb + e Każda obserwacja ma rozkład normalny Każda obserwacja ma tą samą wariancję Dane nienormalne Rozkład binomialny np. liczba chorych krów w stadzie
Wprowadzenie Model ARMA Sezonowość Prognozowanie Model regresji z błędami ARMA. Modele ARMA
 Ważną klasę modeli dynamicznych stanowią modele ARMA(p, q) Ważną klasę modeli dynamicznych stanowią modele ARMA(p, q) Modele tej klasy są modelami ateoretycznymi Ważną klasę modeli dynamicznych stanowią
Ważną klasę modeli dynamicznych stanowią modele ARMA(p, q) Ważną klasę modeli dynamicznych stanowią modele ARMA(p, q) Modele tej klasy są modelami ateoretycznymi Ważną klasę modeli dynamicznych stanowią
Stanisław Cichocki. Natalia Nehrebecka. Wykład 4
 Stanisław Cichocki Natalia Nehrebecka Wykład 4 1 1. Własności hiperpłaszczyzny regresji 2. Dobroć dopasowania równania regresji. Współczynnik determinacji R 2 Dekompozycja wariancji zmiennej zależnej Współczynnik
Stanisław Cichocki Natalia Nehrebecka Wykład 4 1 1. Własności hiperpłaszczyzny regresji 2. Dobroć dopasowania równania regresji. Współczynnik determinacji R 2 Dekompozycja wariancji zmiennej zależnej Współczynnik
