GRAFIKA CZASU RZECZYWISTEGO Wprowadzenie do OpenGL
|
|
|
- Roman Seweryn Kołodziejczyk
- 9 lat temu
- Przeglądów:
Transkrypt
1 GRAFIKA CZASU RZECZYWISTEGO Wprowadzenie do OpenGL Grafika komputerowa i wizualizacja, Bioinformatyka S1, II Rok
2 OpenGL Open Graphics Library Jest to API pozwalające na renderowanie grafiki w czasie rzeczywistym, zorientowane na wykorzystanie akceleracji sprzętowej OpenGL nie jest biblioteką Jest to specyfikacja interfejsu programowania (API) Bibliotekami są implementacje OpenGL na konkretne platformy, dostarczane przez producentów sprzętu, systemów operacyjnych itp. Jednym z głównych celów OpenGL jest wieloplatformowość Konkurencją jest Microsoft Direct3D z DirectX 2
3 OpenGL OpenGL opisuje zbiór funkcji i numerycznych stałych, pozwalających na renderowanie grafiki Nie obejmuje procedur obsługi wejścia, czy integracji z systemem operacyjnym w celu utworzenia kontekstu Istnieją multiplatformowe biblioteki dedykowane dla OpenGL, które rozwiązują te problemy: np. GLUT (freeglut), GLFW Założeniem jest, że implementacja OpenGL opiera się głównie na procedurach sprzętowych Operacje wykonywane bezpośrednio przez kartę graficzną, a nie software'owe rozwiązania oparte o CPU Wiele z oferowanych możliwości, jeśli nie są zaimplementowane w procedurach sprzętowych, może być emulowanych na CPU 3
4 OpenGL Historia 1992 OpenGL 1.0 wydany przez Sillicon Graphics (SGI) rozszerzenia OpenGL 1.x 2004 OpenGL 2.0, zorientowany na programowalny potok renderowania (shadery, GLSL) 2006 OpenGL rozwijany jest przez non-profitową organizację Khronos Group 2008 OpenGL 3.0, znaczne ograniczenie API, usunięcie archaicznych podejść 2010 OpenGL 4.0, odpowiednik DirectX 11 (np. teselacja) 2012 OpenGL 4.3, aktualna wersja OpenGL ES Podzbiór standardu OpenGL, przeznaczony do implementacji na urządzeniach mobilnych OpenGL ES 3.0 wersja najbardziej aktualna (2012), kopmpatybilna z OpenGL 4.3 4
5 OpenGL Uproszczony schemat wykorzystania OpenGL w programowaniu grafiki czasu rzeczywistego Program Nasz program OpenGL Implementacja OpenGL dla danej platformy Sterownik, OS Sprzęt System operacyjny Karta graficzna 5
6 OpenGL Architektura wykorzystania OpenGL jako warstwy pośredniej pomiędzy aplikacją, a kartą graficzną opiera się o model klient-serwer Specyfikacja OpenGL wcale nie wymaga, aby obie strony znajdowały się w jednej, fizycznej maszynie! Serwer Klient (implementacja OpenGL) (program) Zlecenia renderowania Opis sceny Używa pamięci głównej Logika programu Użycie wynikowego obrazu Konteksty Renderowanie Komunikacja ze sterownikiem Dostęp do GPU i pamięci graficznej 6
7 OpenGL Działanie OpenGL należy rozumieć jako maszynę stanu Stanem nazywamy aktualne, chwilowe wartości wszystkich parametrów systemu Jeśli zmienimy wartość jakiegoś parametru, pozostaje ona zmieniona do czasu kolejnej zmiany Przykład: Jeśli zaczniemy w jednej klatce rysować czerwony prostokąt, wszystkie następne obiekty będą czerwone jeśli nie dokonamy zmiany koloru. Nawet w następnej klatce! 7
8 OpenGL Układ współrzędnych w OpenGL Trzeba zapamiętać albo mieć pod ręką! +y +x +z Jednostki są zupełnie arbitralne, można przyjąć np. że jedna jednostka to 1 metr (albo 13 cm, albo 2 ft, albo...) 8
9 GLUT GL Utility Toolkit Freeglut jest open-source'owym klonem, z którego będziemy korzystać (w pełni kompatybilny z GLUT) Dostarcza m.in.: Biblioteka narzędziowa do OpenGL Międzyplatformową obsługę urządzeń wejścia (mysz, klawiatura) Łatwe tworzenie okien z kontekstem OpenGL Procedury rysowania prostych brył (sześcian, kula itd.) Implementację pętli głównej (mainloop/gameloop) Wykorzystuje ideę callbacków, czyli funkcji obsługujących zdarzenia W ten sposób programista ma możliwość reakcji na zdarzenia Przypisanie callbacka odbywa się poprzez wywołanie specjalnej funkcji ustawiającej, z wskaźnikiem do funkcji obsługującej zdarzenie jako parametr 9
10 Przykładowy program int main(int argc, char * argv[]) { glutinit(&argc, argv); glutinitwindowsize(640, 360); glutinitdisplaymode(glut_rgba GLUT_DOUBLE GLUT_DEPTH); glutcreatewindow("opengl/glut Example"); glutdisplayfunc(onrender); glutmainloop(); return 0; } void OnRender() { glclear(gl_color_buffer_bit GL_DEPTH_BUFFER_BIT); glulookat(0.0f, 0.0f, -6.0f, 0.0f, 0.0f, 0.0f, 0.0f, 1.0f, 0.0f); glcolor3f(1.0f, 0.0f, 0.0f); glutsolidcube(1.0f); glutswapbuffers(); glflush(); glutpostredisplay(); } 10
11 Programowanie z użyciem OpenGL Nazwy funkcji OpenGL: glnazwafunkcjiparam(...) param jeśli dana funkcja może przyjmować różne rodzaje parametrów, w ten sposób określany jest rodzaj tych parametrów oraz ich liczba, np.: f float, d double, i int, b bool itd. v vector (tablica) glnazwafunkcjiext(...), glnazwafunkcjiarb(...) Funkcjonalności pochodzące z rozszerzeń niebędących częścią standardu. Niektóre z nich w późniejszych wersjach OpenGL przestają posiadać sufiksy EXT i ARB. glvertex3f(float x, float y, float z) glvertex3fv(float *xyz) glvertex2f(float x, float y) glvertex3d(double x, double y, double z) glvertex2i(int x, int y)... Do obsługi rozszerzeń warto użyć biblioteki GLEW Nazwy funkcji GLU oraz GLUT: glunazwafunkcji(...), glutnazwafunkcji(...) 11
12 Częścią stanu OpenGL są dwie podstawowe macierze transformacji: Macierz Modelu-Widoku (GL_MODELVIEW) Łączy w sobie przekształcenia związane zarówno z przejściem ze współrzędnych modelu do współrzędnych świata, jak i ze współrzędnych świata do współrzędnych kamery Macierz Projekcji (GL_PROJECTION) Czyli uwzględnia zarówno przekształcenie konkretnego obiektu na scenie, jak i położenie i obrót kamery Uwzględnia rodzaj projekcji (perspektywiczna/prostokątna), kąt widzenia, płaszczyzny przycinania, proporcje. Tylko jedna z tych macierzy jest w danym momencie edytowalna Wyboru aktualnie edytowanej macierzy dokonuje się za pomocą funkcji glmatrixmode(matrix) matrix GL_MODELVIEW lub GL_PROJECTION 12
13 Umiejscowienie macierzy transformacji w potoku przetwarzania geometrii Współrzędne modelu Macierz modelu Współrzędne świata GL_MODELVIEW Macierz widoku Współrzędne kamery Macierz projekcji Współrzędne projekcji Kanoniczna bryła widzenia Normalizacja, przycinanie itp. GL_PROJECTION Zazwyczaj poza bezpośrednią kontrolą Mapowanie na ekran Współrzędne ekranu 13
14 Aktualnie wybraną do edycji macierz transformacji modyfikujemy za pomocą funkcji: glloadidentity() glloadmatrixf(float *v) Mnoży zawartość macierzy przez macierz odpowiadającą translacji o wektor [x; y; z] glrotatef(float angle, float x, float y, float z) Mnoży zawartość macierzy przez macierz odpowiadającą rotacji o angle stopni wokół wektora [x; y; z] Warto stosować z wersorami, np. [0; 1; 0] glscalef(float xs, float ys, float zs) Mnoży zawartość macierzy przez macierz v gltranslatef(float x, float y, float z) Zastępuje zawartość wartościami 16-elementowej tablicy glmultmatrixf(float *v) Zastępuje zawartość macierzą jednostkową Mnoży zawartość macierzy przez macierz odpowiadającą skalowaniu ze skalami [xs; ys; zs] 14
15 Przykłady Zakładamy, że hipotetyczna funkcja DrawBlackSquare() rysuje czarny kwadrat będący częścią płaszczyzny XY i rozciągający się w zakresie -1..1: +y 1 1 +x +z Na razie nie wnikamy, jak tego dokonuje Scenę obserwujemy z punktu [0; 0; 5], patrząc w kierunku [0; 0; -1], wektor pionu [0; 1; 0] Projekcja perspektywiczna 15
16 Przykłady DrawBlackSquare(); 16
17 Przykłady gltranslatef(2.0f, 0.0f, 0.0f); DrawBlackSquare(); 17
18 Przykłady gltranslatef(2.0f, 0.0f, 0.0f); gltranslatef(0.0f, 1.0f, 0.0f); DrawBlackSquare(); 18
19 Przykłady glrotatef(45.0f, 0.0f, 0.0f, 1.0f); DrawBlackSquare(); 19
20 Przykłady gltranslatef(2.0f, 0.0f, 0.0f); glrotatef(45.0f, 0.0f, 0.0f, 1.0f); DrawBlackSquare(); 20
21 Przykłady glrotatef(45.0f, 0.0f, 0.0f, 1.0f); gltranslatef(2.0f, 0.0f, 0.0f); DrawBlackSquare(); 21
22 Przykłady glrotatef(45.0f, 0.0f, 1.0f, 0.0f); DrawBlackSquare(); 22
23 Przykłady glscalef(1.0f, 2.0f, 1.0f); DrawBlackSquare(); 23
24 Przykłady glscalef(1.0f, 2.0f, 1.0f); DrawBlackSquare(); DrawRedSquare(); Stan macierzy pozostaje zmieniony! 24
25 Przykłady glscalef(1.0f, 2.0f, 1.0f); DrawBlackSquare(); DrawRedSquare(); 25
26 Zapamiętywanie stanu macierzy na stosie glpushmatrix() powoduje, że aktualny stan macierzy zostaje zapamiętany na stosie glpopmatrix() zdejmuje ze stosu ostatnio zapamiętany stan i przywraca go Możliwe jest wielokrotne zagnieżdżanie Podgląd rezultatu: Przy czym należy pamiętać, że zawsze przywracamy ostatni stan DrawGreenSquare(); gltranslatef(2.0f, 0.0f, -1.0f); glrotatef(45.0f, 0.0f, 0.0f, 1.0f); gltranslatef(0.0f, 1.0f, 0.0f); glscalef(1.5f, 1.5f, 1.0f); DrawBlackSquare(); DrawRedSquare(); DrawBlueSquare(); aktualna macierz: M stos 26
27 Zapamiętywanie stanu macierzy na stosie glpushmatrix() powoduje, że aktualny stan macierzy zostaje zapamiętany na stosie glpopmatrix() zdejmuje ze stosu ostatnio zapamiętany stan i przywraca go Możliwe jest wielokrotne zagnieżdżanie Podgląd rezultatu: Przy czym należy pamiętać, że zawsze przywracamy ostatni stan DrawGreenSquare(); gltranslatef(2.0f, 0.0f, -1.0f); glrotatef(45.0f, 0.0f, 0.0f, 1.0f); gltranslatef(0.0f, 1.0f, 0.0f); glscalef(1.5f, 1.5f, 1.0f); DrawBlackSquare(); DrawRedSquare(); DrawBlueSquare(); aktualna macierz: M stos 27
28 Zapamiętywanie stanu macierzy na stosie glpushmatrix() powoduje, że aktualny stan macierzy zostaje zapamiętany na stosie glpopmatrix() zdejmuje ze stosu ostatnio zapamiętany stan i przywraca go Możliwe jest wielokrotne zagnieżdżanie Podgląd rezultatu: Przy czym należy pamiętać, że zawsze przywracamy ostatni stan DrawGreenSquare(); gltranslatef(2.0f, 0.0f, -1.0f); glrotatef(45.0f, 0.0f, 0.0f, 1.0f); gltranslatef(0.0f, 1.0f, 0.0f); glscalef(1.5f, 1.5f, 1.0f); DrawBlackSquare(); DrawRedSquare(); DrawBlueSquare(); aktualna macierz: M stos 28
29 Zapamiętywanie stanu macierzy na stosie glpushmatrix() powoduje, że aktualny stan macierzy zostaje zapamiętany na stosie glpopmatrix() zdejmuje ze stosu ostatnio zapamiętany stan i przywraca go Możliwe jest wielokrotne zagnieżdżanie Podgląd rezultatu: Przy czym należy pamiętać, że zawsze przywracamy ostatni stan DrawGreenSquare(); gltranslatef(2.0f, 0.0f, -1.0f); glrotatef(45.0f, 0.0f, 0.0f, 1.0f); gltranslatef(0.0f, 1.0f, 0.0f); glscalef(1.5f, 1.5f, 1.0f); DrawBlackSquare(); DrawRedSquare(); DrawBlueSquare(); aktualna macierz: M stos 29
30 Zapamiętywanie stanu macierzy na stosie glpushmatrix() powoduje, że aktualny stan macierzy zostaje zapamiętany na stosie glpopmatrix() zdejmuje ze stosu ostatnio zapamiętany stan i przywraca go Możliwe jest wielokrotne zagnieżdżanie Podgląd rezultatu: Przy czym należy pamiętać, że zawsze przywracamy ostatni stan DrawGreenSquare(); gltranslatef(2.0f, 0.0f, -1.0f); glrotatef(45.0f, 0.0f, 0.0f, 1.0f); gltranslatef(0.0f, 1.0f, 0.0f); glscalef(1.5f, 1.5f, 1.0f); DrawBlackSquare(); DrawRedSquare(); DrawBlueSquare(); aktualna macierz: M M0 stos 30
31 Zapamiętywanie stanu macierzy na stosie glpushmatrix() powoduje, że aktualny stan macierzy zostaje zapamiętany na stosie glpopmatrix() zdejmuje ze stosu ostatnio zapamiętany stan i przywraca go Możliwe jest wielokrotne zagnieżdżanie Podgląd rezultatu: Przy czym należy pamiętać, że zawsze przywracamy ostatni stan DrawGreenSquare(); gltranslatef(2.0f, 0.0f, -1.0f); glrotatef(45.0f, 0.0f, 0.0f, 1.0f); gltranslatef(0.0f, 1.0f, 0.0f); glscalef(1.5f, 1.5f, 1.0f); DrawBlackSquare(); DrawRedSquare(); DrawBlueSquare(); aktualna macierz: M M0 stos 31
32 Zapamiętywanie stanu macierzy na stosie glpushmatrix() powoduje, że aktualny stan macierzy zostaje zapamiętany na stosie glpopmatrix() zdejmuje ze stosu ostatnio zapamiętany stan i przywraca go Możliwe jest wielokrotne zagnieżdżanie Podgląd rezultatu: Przy czym należy pamiętać, że zawsze przywracamy ostatni stan DrawGreenSquare(); gltranslatef(2.0f, 0.0f, -1.0f); glrotatef(45.0f, 0.0f, 0.0f, 1.0f); gltranslatef(0.0f, 1.0f, 0.0f); glscalef(1.5f, 1.5f, 1.0f); DrawBlackSquare(); DrawRedSquare(); DrawBlueSquare(); aktualna macierz: M M1 M0 stos 32
33 Zapamiętywanie stanu macierzy na stosie glpushmatrix() powoduje, że aktualny stan macierzy zostaje zapamiętany na stosie glpopmatrix() zdejmuje ze stosu ostatnio zapamiętany stan i przywraca go Możliwe jest wielokrotne zagnieżdżanie Podgląd rezultatu: Przy czym należy pamiętać, że zawsze przywracamy ostatni stan DrawGreenSquare(); gltranslatef(2.0f, 0.0f, -1.0f); glrotatef(45.0f, 0.0f, 0.0f, 1.0f); gltranslatef(0.0f, 1.0f, 0.0f); glscalef(1.5f, 1.5f, 1.0f); DrawBlackSquare(); DrawRedSquare(); DrawBlueSquare(); aktualna macierz: M M1 M0 stos 33
34 Zapamiętywanie stanu macierzy na stosie glpushmatrix() powoduje, że aktualny stan macierzy zostaje zapamiętany na stosie glpopmatrix() zdejmuje ze stosu ostatnio zapamiętany stan i przywraca go Możliwe jest wielokrotne zagnieżdżanie Podgląd rezultatu: Przy czym należy pamiętać, że zawsze przywracamy ostatni stan DrawGreenSquare(); gltranslatef(2.0f, 0.0f, -1.0f); glrotatef(45.0f, 0.0f, 0.0f, 1.0f); gltranslatef(0.0f, 1.0f, 0.0f); glscalef(1.5f, 1.5f, 1.0f); DrawBlackSquare(); DrawRedSquare(); DrawBlueSquare(); aktualna macierz: M M1 M0 stos 34
35 Zapamiętywanie stanu macierzy na stosie glpushmatrix() powoduje, że aktualny stan macierzy zostaje zapamiętany na stosie glpopmatrix() zdejmuje ze stosu ostatnio zapamiętany stan i przywraca go Możliwe jest wielokrotne zagnieżdżanie Podgląd rezultatu: Przy czym należy pamiętać, że zawsze przywracamy ostatni stan DrawGreenSquare(); gltranslatef(2.0f, 0.0f, -1.0f); glrotatef(45.0f, 0.0f, 0.0f, 1.0f); gltranslatef(0.0f, 1.0f, 0.0f); glscalef(1.5f, 1.5f, 1.0f); DrawBlackSquare(); DrawRedSquare(); DrawBlueSquare(); aktualna macierz: M M1 M0 stos 35
36 Zapamiętywanie stanu macierzy na stosie glpushmatrix() powoduje, że aktualny stan macierzy zostaje zapamiętany na stosie glpopmatrix() zdejmuje ze stosu ostatnio zapamiętany stan i przywraca go Możliwe jest wielokrotne zagnieżdżanie Podgląd rezultatu: Przy czym należy pamiętać, że zawsze przywracamy ostatni stan DrawGreenSquare(); gltranslatef(2.0f, 0.0f, -1.0f); glrotatef(45.0f, 0.0f, 0.0f, 1.0f); gltranslatef(0.0f, 1.0f, 0.0f); glscalef(1.5f, 1.5f, 1.0f); DrawBlackSquare(); DrawRedSquare(); DrawBlueSquare(); aktualna macierz: M M0 stos 36
37 Zapamiętywanie stanu macierzy na stosie glpushmatrix() powoduje, że aktualny stan macierzy zostaje zapamiętany na stosie glpopmatrix() zdejmuje ze stosu ostatnio zapamiętany stan i przywraca go Możliwe jest wielokrotne zagnieżdżanie Podgląd rezultatu: Przy czym należy pamiętać, że zawsze przywracamy ostatni stan DrawGreenSquare(); gltranslatef(2.0f, 0.0f, -1.0f); glrotatef(45.0f, 0.0f, 0.0f, 1.0f); gltranslatef(0.0f, 1.0f, 0.0f); glscalef(1.5f, 1.5f, 1.0f); DrawBlackSquare(); DrawRedSquare(); DrawBlueSquare(); aktualna macierz: M M0 stos 37
38 Zapamiętywanie stanu macierzy na stosie glpushmatrix() powoduje, że aktualny stan macierzy zostaje zapamiętany na stosie glpopmatrix() zdejmuje ze stosu ostatnio zapamiętany stan i przywraca go Możliwe jest wielokrotne zagnieżdżanie Podgląd rezultatu: Przy czym należy pamiętać, że zawsze przywracamy ostatni stan DrawGreenSquare(); gltranslatef(2.0f, 0.0f, -1.0f); glrotatef(45.0f, 0.0f, 0.0f, 1.0f); gltranslatef(0.0f, 1.0f, 0.0f); glscalef(1.5f, 1.5f, 1.0f); DrawBlackSquare(); DrawRedSquare(); DrawBlueSquare(); aktualna macierz: M stos 38
39 Definicja geometrii Najprostszą metodą definicji i renderowania geometrii jest tzw. immediate mode Definicja własności wszystkich wierzchołków w każdej klatce Podejście którego współcześnie się już nie stosuje Jest nieefektywne W każdej klatce duża ilość danych przekazywana do karty graficznej Współcześnie używa się buforów w pamięci karty graficznej Jest najłatwiejsze w zrozumieniu Prymityw glbegin(gl_quads); glvertex3f(-1.0f, -1.0f, 0.0f); glvertex3f(1.0f, -1.0f, 0.0f); glvertex3f(1.0f, 1.0f, 0.0f); glvertex3f(-1.0f, 1.0f, 0.0f); glend(); 39
40 Definicja geometrii Prymitywy oferowane przez OpenGL: Źródło obrazu: 40
41 Kolor w OpenGL Częścią stanu OpenGL jest także kolor wierzchołków Kolory określa się za pomocą komponentów RGB(A) Wartości są znormalizowane ( ) Czwarty kanał A może określać przezroczystość Przykłady: (1.0, 0.0, 0.0) (0.0, 1.0, 0.0) (0.0, 0.0, 1.0) (0.0, 0.0, 0.0) (1.0, 1.0, 1.0) (0.5, 0.5, 0.5) (1.0, 0.5, 0.5) (0.0, 0.6, 1.0) Używa się do tego celu funkcji: glcolor3f(float r, float g, float b) lub analogicznych (4f, 3fv, 4fv,...) 41
42 Kolor w OpenGL Przykłady: glcolor3f(1.0f, 0.0f, 0.0f); glbegin(gl_quads); glvertex3f(-1.0f, -1.0f, 0.0f); glvertex3f(1.0f, -1.0f, 0.0f); glvertex3f(1.0f, 1.0f, 0.0f); glvertex3f(-1.0f, 1.0f, 0.0f); glend(); glbegin(gl_quads); glcolor3f(0.0f, 0.0f, 0.0f); glvertex3f(-1.0f, -1.0f, 0.0f); glcolor3f(1.0f, 0.0f, 0.0f); glvertex3f(1.0f, -1.0f, 0.0f); glcolor3f(0.0f, 1.0f, 0.0f); glvertex3f(1.0f, 1.0f, 0.0f); glcolor3f(0.0f, 0.0f, 1.0f); glvertex3f(-1.0f, 1.0f, 0.0f); glend(); 42
43 Kolor w OpenGL Bardziej zaawansowane kolorowanie geometrii może wykorzystywać techniki takie, jak: Oświetlenie (tzw. cieniowanie, ang. shading) Teksturowanie (ang. texture mapping) Źródła obrazów:
44 Proste bryły w GLUT Sześcian glutsolidcube(size), glutwirecube(size) size długość krawędzi Aby uzyskać nieforemny prostopadłościan, należy poddać sześcian skalowaniu, np.: glutwirecube(1.0f); glscalef(4.0f, 2.0f, 0.5f); glutwirecube(1.0f); Należy pamiętać, że w ten sposób zmieniamy stan macierzy transformacji! Następne bryły też będą przeskalowane. 44
45 Proste bryły w GLUT Kula glutsolidsphere(size, slices, stacks), glutwiresphere(size, slices, stacks) size długość promienia slices, stacks liczby podziałów glutwiresphere(1.0f, 10, 10); glutwiresphere(1.0f, 30, 10); glutwiresphere(1.0f, 30, 30); glutwiresphere(1.0f, 10, 30); glutwiresphere(1.0f, 6, 6); 45
46 Proste bryły w GLUT Stożek glutsolidcone(base, height, slices, stacks), glutwirecone(base, height, slices, stacks) base długość promienia podstawy height - wysokość slices, stacks liczby podziałów, analogicznie do kuli glutwirecone(1.0f, 2.0f, 16, 16); 46
47 GRAFIKA CZASU RZECZYWISTEGO Wprowadzenie do OpenGL Grafika komputerowa i wizualizacja, Bioinformatyka S1, II Rok
GRAFIKA CZASU RZECZYWISTEGO Wstęp do programowania grafiki czasu rzeczywistego.
GRAFIKA CZASU RZECZYWISTEGO Wstęp do programowania grafiki czasu rzeczywistego. http://bazyluk.net/zpsb Grafika Komputerowa, Informatyka, I Rok PROGRAMOWANIE GRAFIKI KOMPUTEROWEJ CZASU RZECZYWISTEGO Grafika
Grafika Komputerowa, Informatyka, I Rok
SYNTEZA GRAFIKI 3D Grafika realistyczna i czasu rzeczywistego. Wstęp do programowania grafiki 3D z użyciem OpenGL. Transformacje geometryczne. Grafika Komputerowa, Informatyka, I Rok Synteza grafiki 3D
Bartosz Bazyluk Wprowadzenie Organizacja i tematyka zajęć, warunki zaliczenia.
Wprowadzenie Organizacja i tematyka zajęć, warunki zaliczenia http://bazyluk.net/dydaktyka Grafika Komputerowa i Wizualizacja, Informatyka S1, II Rok O MNIE mgr inż. Pokój 322/WI2 lub 316/WI2 bbazyluk@wi.zut.edu.pl
Bartosz Bazyluk Wprowadzenie Organizacja i tematyka zajęć, warunki zaliczenia.
Wprowadzenie Organizacja i tematyka zajęć, warunki zaliczenia http://bazyluk.net/dydaktyka Gry komputerowe, Informatyka N1, III Rok, 2018 r. O MNIE dr inż. bbazyluk@wi.zut.edu.pl http://bazyluk.net/dydaktyka
Bartosz Bazyluk Wprowadzenie Organizacja i tematyka zajęć, warunki zaliczenia.
Wprowadzenie Organizacja i tematyka zajęć, warunki zaliczenia http://bazyluk.net/dydaktyka Gry komputerowe, Informatyka S1, II Rok, 2018 r. O MNIE dr inż. bbazyluk@wi.zut.edu.pl http://bazyluk.net/dydaktyka
Temat: Transformacje 3D
Instrukcja laboratoryjna 11 Grafika komputerowa 3D Temat: Transformacje 3D Przygotował: dr inż. Grzegorz Łukawski, mgr inż. Maciej Lasota, mgr inż. Tomasz Michno 1 Wstęp teoretyczny Bardzo często programując
Temat: Wprowadzenie do OpenGL i GLUT
Instrukcja laboratoryjna 8 Grafika komputerowa 3D Temat: Wprowadzenie do OpenGL i GLUT Przygotował: dr inż. Grzegorz Łukawski, mgr inż. Maciej Lasota, mgr inż. Tomasz Michno 1 Wstęp teoretyczny OpenGL
Wprowadzenie do QT OpenGL
Wprowadzenie do QT mgr inż. Michał Chwesiuk mgr inż. Tomasz Sergej inż. Patryk Piotrowski 1/21 - Open Graphics Library Open Graphics Library API pozwalające na wykorzystanie akceleracji sprzętowej do renderowania
Przekształcenia geometryczne. Dorota Smorawa
Przekształcenia geometryczne Dorota Smorawa Przekształcenia geometryczne Na poprzednich laboratoriach już dowiedzieliśmy się, na czym polegają podstawowe przekształcenia geometryczne. Trzy podstawowe przekształcenia
Grafika 3D OpenGL część II
#include #include #include float kat=0.0f; void renderujscene(void) { glclearcolor(1.0f,1.0f,1.0f,1.0f); glclear(gl_color_buffer_bit); glpushmatrix(); glrotatef(kat,0,0,1);
Grafika Komputerowa Wykład 4. Synteza grafiki 3D. mgr inż. Michał Chwesiuk 1/30
Wykład 4 mgr inż. 1/30 Synteza grafiki polega na stworzeniu obrazu w oparciu o jego opis. Synteza obrazu w grafice komputerowej polega na wykorzystaniu algorytmów komputerowych do uzyskania obrazu cyfrowego
2 Przygotował: mgr inż. Maciej Lasota
Laboratorium nr 2 1/6 Grafika Komputerowa 3D Instrukcja laboratoryjna Temat: Manipulowanie przestrzenią 2 Przygotował: mgr inż. Maciej Lasota 1) Manipulowanie przestrzenią Istnieją dwa typy układów współrzędnych:
Wprowadzenie. Artur Staszczyk Bartłomiej Filipek
Wprowadzenie Artur Staszczyk www.astaszczyk.com Bartłomiej Filipek www.bartlomiejfilipek.pl Bartlomiej.filipek@gmail.com Podstawy grafiki 3D GPU Co to jest OpenGL Potok Graficzny Inicjalizacja Rendering
Grafika komputerowa INSTRUKCJA DO LABORATORIUM 2: operacje przestrzenne oraz obsługa klawiatury i myszki
Grafika komputerowa INSTRUKCJA DO LABORATORIUM 2: operacje przestrzenne oraz obsługa klawiatury i myszki Strona 1 z 9 C E L Ć W I C Z E N I A Celem ćwiczenia jest zapoznanie się z podstawowymi operacjami
Gry Komputerowe - laboratorium 0
Gry Komputerowe - laboratorium 0 Michał Chwesiuk Zachodniopomorski Uniwersytet Technologiczny w ie Wydział Informatyki 28 Luty 2018 Michał Chwesiuk Laboratorium 0 28 Luty 2018 1/ 18 O mnie mgr inż. Michał
GRAFIKA CZASU RZECZYWISTEGO Podstawy syntezy grafiki 3D i transformacji geometrycznych
GRAFIKA CZASU RZECZYWISTEGO Podstawy syntezy grafiki 3D i transformacji geometrycznych Grafika komputerowa i wizualizacja, Bioinformatyka S1, II Rok Synteza grafiki 3D Pod pojęciem syntezy grafiki rozumiemy
GLKit. Wykład 10. Programowanie aplikacji mobilnych na urządzenia Apple (IOS i ObjectiveC) #import "Fraction.h" #import <stdio.h>
#import "Fraction.h" #import @implementation Fraction -(Fraction*) initwithnumerator: (int) n denominator: (int) d { self = [super init]; } if ( self ) { [self setnumerator: n anddenominator:
Co to jest OpenGL? Oprogramowanie i wykorzystanie stacji roboczych. Wykład 5. OpenGL - Achitektura. OpenGL - zalety. olas@icis.pcz.
Co to jest OpenGL? Oprogramowanie i wykorzystanie stacji roboczych Wykład 5 Dr inż. Tomasz Olas olas@icis.pcz.pl OpenGL (Open Graphics Library) jest niskopoziomowa biblioteka graficzna (API - programowy
Janusz Ganczarski. OpenGL Pierwszy program
Janusz Ganczarski OpenGL Pierwszy program Spis treści Spis treści..................................... 1 1. Pierwszy program.............................. 1 1.1. Rysowanie sceny 3D...........................
Wykład 4. Rendering (1) Informacje podstawowe
Wykład 4. Rendering (1) Informacje podstawowe Z punktu widzenia dzisiejszego programowania gier: Direct3D jest najczęściej wykorzystywanym przez profesjonalnych deweloperów gier API graficznym na platformie
Programowanie Równoległe wykład, 21.01.2013. CUDA, przykłady praktyczne 1. Maciej Matyka Instytut Fizyki Teoretycznej
Programowanie Równoległe wykład, 21.01.2013 CUDA, przykłady praktyczne 1 Maciej Matyka Instytut Fizyki Teoretycznej Motywacja l CPU vs GPU (anims) Plan CUDA w praktyce Wykład 1: CUDA w praktyce l aplikacja
Laboratorium 1. Część I. Podstawy biblioteki graficznej OpenGL.
Laboratorium 1 Część I Podstawy biblioteki graficznej OpenGL. I. Konfiguracja środowiska 1. Ściągamy bibliotekę freeglut i rozpakujemy do głównego folderu dysku systemowego np. C:\freeglut 2. Uruchamiamy
Biblioteka OpenGL: Wprowadzenie
Biblioteka OpenGL: Wprowadzenie Radosław Mantiuk Wydział Informatyki Zachodniopomorski Uniwersytet Technologiczny w Szczecinie OpenGL - Koncepcja i architektura Aplikacja odwołuje się poprzez funkcje API
Gry Komputerowe Laboratorium 1. Zajęcia organizacyjne Animacja z uwzględnieniem czasu. mgr inż. Michał Chwesiuk 1/22. Szczecin,
Gry Komputerowe Laboratorium 1 Zajęcia organizacyjne mgr inż. Michał Chwesiuk 1/22 projektowych Zajęcia projektowe składają się zajęć (plus jedno zajęcie godzinne). Zajęcia polegają na programowania grafiki
OpenGL - Open Graphics Library. Programowanie grafiki komputerowej. OpenGL 3.0. OpenGL - Architektura (1)
OpenGL - Open Graphics Library Programowanie grafiki komputerowej Rados$aw Mantiuk Wydzia$ Informatyki Zachodniopomorski Uniwersytet Technologiczny! OpenGL: architektura systemu do programowania grafiki
1 Temat: Vertex Shader
Instrukcja Architektura procesorów graficznych 1 Temat: Vertex Shader Przygotował: mgr inż. Tomasz Michno 1 Wstęp 1.1 Czym jest shader Shader jest programem (zazwyczaj krótkim), wykonywanym przez kartę
Plan wykładu. Akcelerator 3D Potok graficzny
Plan wykładu Akcelerator 3D Potok graficzny Akcelerator 3D W 1996 r. opracowana została specjalna karta rozszerzeń o nazwie marketingowej Voodoo, którą z racji wspomagania procesu generowania grafiki 3D
Zaawansowane systemy programowania grafiki. Wprowadzenie. Podstawy OpenGL
Zaawansowane systemy programowania grafiki. Wprowadzenie. Podstawy OpenGL Aleksander Denisiuk Uniwersytet Warmińsko-Mazurski Olsztyn, ul. Słoneczna 54 denisjuk@matman.uwm.edu.pl 7 października 2014 1 /
Wprowadzenie do programowania z wykorzystaniem biblioteki OpenGL. Dorota Smorawa
Wprowadzenie do programowania z wykorzystaniem biblioteki OpenGL Dorota Smorawa Pierwszy program Pierwszy program będzie składał się z trzech etapów: Funkcji rysującej scenę 3D, Inicjacji okna renderingu,
Oprogramowanie i wykorzystanie stacji roboczych. Wykład 5
Wykład 5 p. 1/? Oprogramowanie i wykorzystanie stacji roboczych Wykład 5 Dr inż. Tomasz Olas olas@icis.pcz.pl Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska Wykład 5 p. 2/? Co
Bartosz Bazyluk OpenGL Współczesne podejście do programowania grafiki Część II: Programy cieniujące (shadery)
OpenGL Współczesne podejście do programowania grafiki Część II: Programy cieniujące (shadery) Programowanie Gier Komputerowych, Informatyka S, III Rok PLAN WYKŁADU Transformacje geometryczne Pożegnanie
1. Prymitywy graficzne
1. Prymitywy graficzne Prymitywy graficzne są elementarnymi obiektami jakie potrafi bezpośrednio rysować, określony system graficzny (DirectX, OpenGL itp.) są to: punkty, listy linii, serie linii, listy
Wykład 12. Wprowadzenie do malarstwa, str. 1 OpenGL Open Graphics Library. OpenGL składa się z
Wykład 12. Wprowadzenie do malarstwa, str. 1 OpenGL Open Graphics Library OpenGL składa się z teoretycznego modelu grafiki 3D, zestawu typów i funkcji obsługujących różne cechy tego modelu. WjęzykuC: pliki
1 Wstęp teoretyczny. Temat: Manipulowanie przestrzenią. Grafika komputerowa 3D. Instrukcja laboratoryjna Układ współrzędnych
Instrukcja laboratoryjna 9 Grafika komputerowa 3D Temat: Manipulowanie przestrzenią Przygotował: dr inż. Grzegorz Łukawski, mgr inż. Maciej Lasota, mgr inż. Tomasz Michno 1 Wstęp teoretyczny 1.1 Układ
Bartosz Bazyluk SYNTEZA GRAFIKI 3D Grafika realistyczna i czasu rzeczywistego. Pojęcie sceny i kamery. Grafika Komputerowa, Informatyka, I Rok
SYNTEZA GRAFIKI 3D Grafika realistyczna i czasu rzeczywistego. Pojęcie sceny i kamery. Grafika Komputerowa, Informatyka, I Rok Synteza grafiki 3D Pod pojęciem syntezy grafiki rozumiemy stworzenie grafiki
Grafika trójwymiarowa
Strona 1 Grafika 3D w systemie Android Wprowadzenie do OpenGL ES Podstawy rysowania Rzutowanie i kamera Klasa GLSurfaceView Algorytm rysowania Tekstury Strona 2 Grafika 3D w systemie Android W komputerach,
Architektura Procesorów Graficznych
Architektura Procesorów Graficznych Referat: Rendering 3D: potok 3D, możliwości wsparcia sprzętowego, możliwości przyspieszenia obliczeń. Grupa wyrównawcza Cezary Sosnowski 1. Renderowanie Renderowanie
Wprowadzenie do grafiki maszynowej. Wprowadzenie do historii OpenGL
Wprowadzenie do grafiki maszynowej. Wprowadzenie do historii OpenGL Aleksander Denisiuk Uniwersytet Warmińsko-Mazurski Olsztyn, ul. Słoneczna 54 denisjuk@matman.uwm.edu.pl 1 / 29 Wprowadzenie do historii
OPENGL PRZEKSZTAŁCENIA GEOMETRYCZNE
OPENGL PRZEKSZTAŁCENIA GEOMETRYCZNE SPIS TREŚCI 1. Przekształcenia geometryczne... 3 1.1. Obrót... 3 1.2. Skalowanie... 3 1.3. Przesunięcie... 3 1.4. Mnożenie macierzy... 4 1.5. Ładowanie macierzy... 4
Systemy graficzne. dr inż. Mariusz Szwoch
Systemy graficzne dr inż. Mariusz Szwoch Systemy Graficzne Sem. 2 studiów magisterskich Przedmiot specjalności ISI i uzupełniający Wymiar: wykład 15 h (7 2h + 1h zaliczenie) laboratorium 15 h (5 3h) Prowadzący
Zatem standardowe rysowanie prymitywów wygląda następująco:
Instrukcja laboratoryjna 10 Grafika komputerowa 3D Temat: Prymitywy Przygotował: dr inż. Grzegorz Łukawski, mgr inż. Maciej Lasota, mgr inż. Tomasz Michno 1 Wstęp teoretyczny Prymitywy proste figury geometryczne,
Systemy wirtualnej rzeczywistości. Podstawy grafiki 3D
Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Systemy wirtualnej rzeczywistości Laboratorium Podstawy grafiki 3D Wstęp: W drugiej części przedstawione zostaną podstawowe mechanizmy
Ćwiczenia nr 4. TEMATYKA: Rzutowanie
TEMATYKA: Rzutowanie Ćwiczenia nr 4 DEFINICJE: Rzut na prostą: rzutem na prostą l (zwaną rzutnią) w kierunku rzutowania k (k l) nazywamy przekształcenie płaszczyzny przyporządkowujące: a) Punktom prostej
Wykład 12. Wprowadzenie do malarstwa, str. 1 OpenGL Open Graphics Library. OpenGL składa się z
Wykład 12. Wprowadzenie do malarstwa, str. 1 OpenGL Open Graphics Library OpenGL składa się z teoretycznego modelu grafiki 3D, zestawu typów i funkcji obsługujących różne cechy tego modelu. Funkcje OpenGL
Karta przedmiotu. Podstawy programowania procesorów graficznych. realizowanego w ramach projektu PO WER
Karta przedmiotu Podstawy programowania procesorów graficznych realizowanego w ramach projektu PO WER 2017-2019 Wydział Inżynierii Elektrycznej i Komputerowej Kierunek studiów: Informatyka Profil: Ogólnoakademicki
3 Przygotował: mgr inż. Maciej Lasota
Laboratorium nr 3 1/5 Grafika Komputerowa 3D Instrukcja laboratoryjna Temat: Rysowanie prymitywów 3 Przygotował: mgr inż. Maciej Lasota 1) Rysowanie prymitywów Podstawową rodziną funkcji wykorzystywanych
Transformacje. dr Radosław Matusik. radmat
www.math.uni.lodz.pl/ radmat Cel wykładu Celem wykładu jest prezentacja m.in. przestrzeni modelu, świata, kamery oraz projekcji, a także omówienie sposobów oświetlania i cieniowania obiektów. Pierwsze
Dowiedz się, jak tworzyć zapierające dech w piersiach gry 3D i efektowne, trójwymiarowe wizualizacje!
Dowiedz się, jak tworzyć zapierające dech w piersiach gry 3D i efektowne, trójwymiarowe wizualizacje! Jak sprawnie tworzyć podstawowe obiekty, oświetlać je i cieniować? Jak napisać własne programy, korzystając
Elementarne obiekty geometryczne, bufory. Dorota Smorawa
Elementarne obiekty geometryczne, bufory Dorota Smorawa Elementarne obiekty Tworząc scenę 3D, od najprostszej, po najbardziej skomplikowaną, używamy obiektów złożonych, przede wszystkim podstawowych, elementarnych
Grafika Komputerowa Wykład 6. Teksturowanie. mgr inż. Michał Chwesiuk 1/23
Wykład 6 mgr inż. 1/23 jest to technika w grafice komputerowej, której celem jest zwiększenie szczegółowości renderowanych powierzchni za pomocą tekstur. jest to pewna funkcja (najczęściej w formie bitmapy)
Grafika komputerowa Wstęp do OpenGL
Instytut Informatyki Politechniki Warszawskiej Grafika komputerowa Wstęp do OpenGL Zbigniew Szymański z.szymanski@ii.pw.edu.pl listopad 2008 - v1 Prowadzący zajęcia: Sprawy organizacyjne /1/ Zbigniew Szymański
Karty graficzne możemy podzielić na:
KARTY GRAFICZNE Karta graficzna karta rozszerzeo odpowiedzialna generowanie sygnału graficznego dla ekranu monitora. Podstawowym zadaniem karty graficznej jest odbiór i przetwarzanie otrzymywanych od komputera
Programowanie Procesorów Graficznych
Programowanie Procesorów Graficznych Wykład 1 9.10.2012 Prehistoria Zadaniem karty graficznej było sterowanie sygnałem do monitora tak aby wyświetlić obraz zgodnie z zawartościa pamięci. Programiści pracowali
Grafika Komputerowa Wykład 5. Potok Renderowania Oświetlenie. mgr inż. Michał Chwesiuk 1/38
Wykład 5 Potok Renderowania Oświetlenie mgr inż. 1/38 Podejście śledzenia promieni (ang. ray tracing) stosuje się w grafice realistycznej. Śledzone są promienie przechodzące przez piksele obrazu wynikowego
GRAFIKA KOMPUTEROWA. Rozwiązania sprzętowe i programowe. Przyspieszanie sprzętowe. Synteza i obróbka obrazu
Synteza i obróbka obrazu GRAFIKA KOMPUTEROWA Rozwiązania sprzętowe i programowe Przyspieszanie sprzętowe Generowanie obrazu 3D wymaga złożonych obliczeń, szczególnie jeżeli chodzi o generowanie płynnej
Transformacje obiektów 3D
Synteza i obróbka obrazu Transformacje obiektów 3D Opracowanie: dr inż. Grzegorz Szwoch Politechnika Gdańska Katedra Systemów Multimedialnych Lokalny układ współrzędnych Tworząc model obiektu, zapisujemy
Grafika komputerowa Wstęp do OpenGL
Instytut Informatyki Politechniki Warszawskiej Grafika komputerowa Wstęp do OpenGL Zbigniew Szymański z.szymanski@ii.pw.edu.pl listopad 2008 - v1 listopad 2010 - v1d kwiecień 2013 v1e Prowadzący zajęcia:
Janusz Ganczarski. OpenGL Definiowanie sceny 3D
Janusz Ganczarski OpenGL Definiowanie sceny 3D Spis treści Spis treści..................................... 1 1. Definiowanie sceny 3D........................... 1 1.1. Obszar renderingu............................
Grafika komputerowa i wizualizacja. dr Wojciech Pałubicki
Grafika komputerowa i wizualizacja dr Wojciech Pałubicki Grafika komputerowa Obrazy wygenerowane za pomocy komputera Na tych zajęciach skupiamy się na obrazach wygenerowanych ze scen 3D do interaktywnych
Zaawansowany kurs języka Python
PyGame 18 grudnia 2015 Plan wykładu 1 Wprowadzenie Parametry wyświetlania Powierzchnie 2 Klawiatura Mysz Dżojstik 3 Odtwarzanie plików dźwiękowych Odtwarzanie muzyki Samodzielne tworzenie dźwięków 4 3D:
KARTA KURSU. Grafika komputerowa
KARTA KURSU Nazwa Nazwa w j. ang. Grafika komputerowa Computer graphics Kod Punktacja ECTS* 3 Koordynator dr inż. Krzysztof Wójcik Zespół dydaktyczny: dr inż. Krzysztof Wójcik dr inż. Mateusz Muchacki
Przyspieszanie sprzętowe
Synteza dźwięku i obrazu GRAFIKA KOMPUTEROWA Rozwiązania sprzętowe i programowe Przyspieszanie sprzętowe Generowanie obrazu 3D wymaga złoŝonych obliczeń, szczególnie jeŝeli chodzi o generowanie płynnej
GRAFIKA KOMPUTEROWA. Rozwiązania sprzętowe i programowe. Przyspieszanie sprzętowe. Synteza dźwięku i obrazu
Synteza dźwięku i obrazu GRAFIKA KOMPUTEROWA Rozwiązania sprzętowe i programowe Przyspieszanie sprzętowe Generowanie obrazu 3D wymaga złożonych obliczeń, szczególnie jeżeli chodzi o generowanie płynnej
Julia 4D - raytracing
i przykładowa implementacja w asemblerze Politechnika Śląska Instytut Informatyki 27 sierpnia 2009 A teraz... 1 Fraktale Julia Przykłady Wstęp teoretyczny Rendering za pomocą śledzenia promieni 2 Implementacja
Mobilne aplikacje multimedialne. OpenGL
Mobilne aplikacje multimedialne OpenGL Marek Kulawiak Katedra Systemów Geoinformatycznych Wydział Elektroniki, Telekomunikacji i Informatyki Politechniki Gdańskiej Open Graphics Library API do tworzenia
Zadanie 1. Ściana. 1. Potrzebne zmienne w dołączonym do zadania kodzie źródłowym
Zadanie 1. Ściana Zadanie W pliku walls.cpp znajduje się funkcja void draw_back_wall(). Należy uzupełnić ją, ustawiając odpowiednio parametry teksturowania tak, aby na ścianę, która w pierwotnej wersji
Laboratorium grafiki komputerowej i animacji. Ćwiczenie V - Biblioteka OpenGL - oświetlenie sceny
Laboratorium grafiki komputerowej i animacji Ćwiczenie V - Biblioteka OpenGL - oświetlenie sceny Przygotowanie do ćwiczenia: 1. Zapoznać się ze zdefiniowanymi w OpenGL modelami światła i właściwości materiałów.
Grafika komputerowa. Grafika komputerowa. Grafika komputerowa
OpenGL - Koncepcja i architektura Aplikacja odwo!uje si" poprzez funkcje API OpenGL bezpo#rednio do karty graficznej (z pomini"ciem systemu operacyjnego). Programowanie grafiki komputerowej Rados!aw Mantiuk
Efekt lustra 3D w OpenGL z wykorzystaniem bufora szablonowego (stencil buffer)
Efekt lustra 3D w OpenGL z wykorzystaniem bufora szablonowego (stencil buffer) Autor: Radosław Płoszajczak Spis treści I. Wstęp...2 II. Metoda rysująca przeźroczystą szybę...2 III. Bufor szablonowy (stencil
GRAFIKA KOMPUTEROWA 7: Kolory i cieniowanie
GRAFIKA KOMPUTEROWA 7: Kolory i cieniowanie http://galaxy.agh.edu.pl/~mhojny Prowadzący: dr inż. Hojny Marcin Akademia Górniczo-Hutnicza Mickiewicza 30 30-059 Krakow pawilon B5/p.406 tel. (+48)12 617 46
Mobilne Aplikacje Multimedialne
Mobilne Aplikacje Multimedialne Rozszerzona rzeczywistość (AR, Augmented Reality) w Systemie Android Cz.1 Krzysztof Bruniecki Podstawy Algebra liniowa, operacje na wektorach, macierzach, iloczyn skalarny
Rysowanie punktów na powierzchni graficznej
Rysowanie punktów na powierzchni graficznej Tworzenie biblioteki rozpoczniemy od podstawowej funkcji graficznej gfxplot() - rysowania pojedynczego punktu na zadanych współrzędnych i o zadanym kolorze RGB.
Prosty program- cpp. #include <GL/glut.h>
Wizualizacje 3D Prosty program- cpp #include #include #include int main(int argc, char** argv) { glutinit(&argc, argv); glutinitdisplaymode( GLUT_DOUBLE GLUT_RGBA ); glutinitwindowsize(400,
Opis efektów kształcenia dla modułu zajęć
Nazwa modułu: Grafika komputerowa Rok akademicki: 2015/2016 Kod: ITE-1-514-s Punkty ECTS: 5 Wydział: Informatyki, Elektroniki i Telekomunikacji Kierunek: Teleinformatyka Specjalność: - Poziom studiów:
glwindowpos2d void DrawString (GLint x, GLint y, char *string) { glwindowpos2i (x,y); int len = strlen (string); for (int i = 0; i < len; i++)
Wizualizacja 3D glwindowpos2d Funkcja wprowadzona w wersji 1.4 biblioteki OpenGL Funkcja pozwala na ustawienie rastra względem okna, a nie względem macierzy modelu Stosowana podczas pisania tekstów, np.:
RENDERING W CZASIE RZECZYWISTYM. Michał Radziszewski
RENDERING W CZASIE RZECZYWISTYM Michał Radziszewski Plan wykładu Programy geometrii wprowadzenie Miejsce w potoku graficznym Wejścia i wyjścia programów geometrii Wierzchołki, prymitywy, ich nowe rodzaje
Obraz jako funkcja Przekształcenia geometryczne
Cyfrowe przetwarzanie obrazów I Obraz jako funkcja Przekształcenia geometryczne dr. inż Robert Kazała Definicja obrazu Obraz dwuwymiarowa funkcja intensywności światła f(x,y); wartość f w przestrzennych
0. OpenGL ma układ współrzędnych taki, że oś y jest skierowana (względem monitora) a) w dół b) w górę c) w lewo d) w prawo e) w kierunku do
0. OpenGL ma układ współrzędnych taki, że oś y jest skierowana (względem monitora) a) w dół b) w górę c) w lewo d) w prawo e) w kierunku do obserwatora f) w kierunku od obserwatora 1. Obrót dookoła osi
Systemy wirtualnej rzeczywistości. Komponenty i serwisy
Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Systemy wirtualnej rzeczywistości Laboratorium Komponenty i serwisy Wstęp: W trzeciej części przedstawione zostaną podstawowe techniki
Modelowanie i wstęp do druku 3D Wykład 1. Robert Banasiak
Modelowanie i wstęp do druku 3D Wykład 1 Robert Banasiak Od modelu 3D do wydruku 3D Typowa droga...czasem wyboista... Pomysł!! Modeler 3D Przygotowanie modelu do druku Konfiguracja Programu do drukowania
Grafika komputerowa i wizualizacja
Grafika komputerowa i wizualizacja Radosław Mantiuk ( rmantiuk@wi.zut.edu.pl, p. 315 WI2) http://rmantiuk.zut.edu.pl Katedra Systemów Multimedialnych Wydział Informatyki, Zachodniopomorski Uniwersytet
OpenGL model oświetlenia
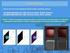Składowe światła OpenGL Światło otaczające (ambient) OpenGL model oświetlenia Nie pochodzi z żadnego określonego kierunku. Powoduje równomierne oświetlenie obiektów na wszystkich powierzchniach i wszystkich
Moc płynąca z kart graficznych
Moc płynąca z kart graficznych Cuda za darmo! Czyli programowanie generalnego przeznaczenia na kartach graficznych (GPGPU) 22 października 2013 Paweł Napieracz /20 Poruszane aspekty Przetwarzanie równoległe
Podstawy programowania, Poniedziałek , 8-10 Projekt, część 1
Podstawy programowania, Poniedziałek 30.05.2016, 8-10 Projekt, część 1 1. Zadanie Projekt polega na stworzeniu logicznej gry komputerowej działającej w trybie tekstowym o nazwie Minefield. 2. Cele Celem
OpenGL i wprowadzenie do programowania gier
OpenGL i wprowadzenie do programowania gier Wojciech Sterna Bartosz Chodorowski OpenGL i wprowadzenie do programowania gier Autorstwo rozdziałów: 1, 2, 3, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 Wojciech Sterna
6 Przygotował: mgr inż. Maciej Lasota
Laboratorium nr 6 1/7 Grafika Komputerowa 3D Instrukcja laboratoryjna Temat: Materiały i oświetlenie 6 Przygotował: mgr inż. Maciej Lasota 1) Wprowadzenie Specyfikacja biblioteki OpenGL rozróżnia trzy
Animowana grafika 3D. Opracowanie: J. Kęsik.
Animowana grafika 3D Opracowanie: J. Kęsik kesik@cs.pollub.pl Rzutowanie Równoległe Perspektywiczne Rzutowanie równoległe Rzutowanie równoległe jest powszechnie używane w rysunku technicznym - umożliwienie
Bartosz Bazyluk GAME LOOP Podstawowy element silnika gry komputerowej. Programowanie Gier Komputerowych, Informatyka S1, III Rok
Bartosz Bazyluk GAME LOOP Podstawowy element silnika gry komputerowej Programowanie Gier Komputerowych, Informatyka S1, III Rok INFORMACJE ORGANIZACYJNE: Prezentacje z wykładów, materiały, informacje można
Trójwymiarowa grafika komputerowa rzutowanie
Trójwymiarowa grafika komputerowa rzutowanie Mirosław Głowacki Wydział Inżynierii Metali i Informatyki Przemysłowej Rzutowanie w przestrzeni 3D etapy procesu rzutowania określenie rodzaju rzutu określenie
Programowanie, część III
9 kwietnia 2010 Biblioteki i podsystemy graficzne Biblioteki graficzne (ang. graphics library) Są potrzebne, aby można było programować grafikę w C++, ponieważ (niestety) we współczesnych systemach komputerowych
Wykład 5. Rendering (2) Geometria
Wykład 5. Rendering (2) Geometria 1. Z ogólnego, niezależnego od implementacji punktu widzenia, dane stanowiące opis geometrii modelu zorganizowane są w skończoną sekwencję (lub grupę sekwencji), którego
OpenGL przezroczystość
OpenGL przezroczystość W standardzie OpenGL efekty przezroczystości uzyskuje się poprzez zezwolenie na łączenie kolorów: Kolor piksela tworzy się na podstawie kolorów obiektu przesłanianego i przesłaniającego
Gry Komputerowe Interaktywna kamera FPP
Gry Komputerowe Interaktywna kamera FPP Michał Chwesiuk Zachodniopomorski Uniwersytet Technologiczny w Szczecinie Wydział Informatyki 28 Marzec 2018 Michał Chwesiuk Laboratorium 2 28 Marzec 2018 1/ 11
Wybrane aspekty teorii grafiki komputerowej - dążenie do wizualnego realizmu. Mirosław Głowacki
Wybrane aspekty teorii grafiki komputerowej - dążenie do wizualnego realizmu Mirosław Głowacki Obraz realistyczny Pojęcie obrazu realistycznego jest rozumiane w różny sposób Nie zawsze obraz realistyczny
Rzutowanie DOROTA SMORAWA
Rzutowanie DOROTA SMORAWA Rzutowanie Rzutowanie jest operacja polegająca na tym, aby odpowiednie piksele na płaskim ekranie były wyświetlane w taki sposób, by sprawiać wrażenie trójwymiarowej głębi (przestrzeni
Wizualizacja 3D. dr inż. Marcin Gabryel
Wizualizacja 3D dr inż. Marcin Gabryel Modele braw CMYK (Cyan, Magenta, Yellow, black) RGB (Red, Green, Blue) HSV (Hue, Saturation, Value) RGB Model polega na sumowaniu sygnałów w poszczególnych kanałach.
OpenGL oświetlenie. Bogdan Kreczmer. Katedra Cybernetyki i Robotyki Wydziału Elektroniki Politechnika Wrocławska
OpenGL oświetlenie Bogdan Kreczmer bogdan.kreczmer@pwr.wroc.pl Katedra Cybernetyki i Robotyki Wydziału Elektroniki Politechnika Wrocławska Kurs: Copyright c 2017 Bogdan Kreczmer Niniejszy dokument zawiera
WIZUALIZACJA INFORMACJI TEKSTOWEJ WSTĘP DO HTML 5 CANVAS
WIZUALIZACJA INFORMACJI TEKSTOWEJ WSTĘP DO HTML 5 CANVAS Autor prezentacji: Michał Kołkowski Promotor: prof dr. hb. Włodzisław Duch SPIS TREŚCI 1. Ogólnie o Canvasie 2. Utworzenie szablonu do pracy z Canvas
Bufor koloru cd. Czyszczenie bufora koloru glclearcolor( )
Wizualizacje 3D Bufor koloru Bufor koloru służy do przechowywania obrazu renderowanej sceny 3D. Typowo OpenGL stosuje dwa bufory koloru: przedni i tylny. Bieżąca scena znajduje się w przednim buforze i
Karta graficzna karta rozszerzeo odpowiedzialna generowanie sygnału graficznego dla ekranu monitora. Podstawowym zadaniem karty graficznej jest
KARTA GRAFICZNA Karta graficzna karta rozszerzeo odpowiedzialna generowanie sygnału graficznego dla ekranu monitora. Podstawowym zadaniem karty graficznej jest odbiór i przetwarzanie otrzymywanych od komputera