POLITECHNIKA WARSZAWSKA. Wydział Elektroniki i Technik Informacyjnych
|
|
|
- Dawid Kania
- 8 lat temu
- Przeglądów:
Transkrypt
1 POLITECHNIKA WARSZAWSKA Wydział Elektroniki i Technik Informacyjnych Rozprawa Doktorska mgra inż. Mateusza Orzechowskiego p.t.: Badania nad ilościową oceną perfuzji tkanki mózgowej z wykorzystaniem dynamicznych badań tomograficznych Promotor: Prof. nzw. dr hab. inż. Krzysztof Zaremba Warszawa, rok wydania 28
2 Streszczenie Badania przedstawione w pracy dotyczą zagadnienia wczesnej diagnostyki stanów patologicznych mózgu, a w szczególności udarów niedokrwiennych. Do nowoczesnych i obiecujących metod w tym obszarze należą badania perfuzyjne, wykonywane metodą czynnościowego obrazowania mózgu zarówno techniką tomografii komputerowej, jak i tomografii rezonansu magnetycznego. Istniejące techniki diagnostyczne umożliwiają jakościową ocenę ukrwienia, natomiast brak jest uznanych metod obiektywnej ilościowej oceny perfuzji, a liczba doniesień literaturowych podnoszących ten problem nie jest duża, mimo ogromnego, stale rosnącego zainteresowania technikami obrazowania funkcjonalnego. Praca stanowi próbę poprawy wiarygodności istniejących metod pomiaru parametrów perfuzji tkanek poprzez zastosowanie oryginalnej metody przetwarzania danych pomiarowych. Ważnym założeniem proponowanej metody jest możliwość jej stosowania dla różnych modalności (tomografii CT i MRI). Głównym celem rozprawy było opracowanie procedur i algorytmów przetwarzania danych w badaniach perfuzyjnych mózgu. Szczególny nacisk został położony na poprawę dokładności ilościowej oceny średniego czasu przejścia MTT, będącego istotnym parametrem predykcyjnym w ocenie obszarów zagrożonych udarem niedokrwiennym. W rozprawie wykazano, że zastosowanie metod korelacyjnych do korekcji opóźnienia funkcji wejściowej pozwala na poprawę oceny średniego czasu przejścia (MTT), a przez to i pozostałych parametrów perfuzji (CBV i CBF). Pokazano również, że proponowane metoda jest uniwersalna pod względem wykorzystywanej techniki obrazowania, zastosowanych środków kontrastowych oraz różnic w sposobie przeprowadzania badania w ramach ustalonego protokołu.
3 Summary The research presented in the paper covers the topic of the early diagnosis of the brain s pathological condition, in particular, the cases of ischemic strokes. The newest and promising methods applied in case of the illness are the perfusion examinations, done by the method of the functional brain imaging with the use of the computer tomography technique as well as the magnetic resonance tomography. The existing diagnosis techniques allow for the qualitative estimation of the blood supply, but there are no acknowledged methods of the objective quantitative estimation of perfusion, and the literature on this subject is insufficient, despite the great and constantly rising interest in the functional imaging techniques. The paper constitutes an attempt to improve the credibility of the existing methods of the parameters measurement of cells perfusion, by using the genuine method of measurement data processing. The important assumption in the proposed method is the ability of its use for various modalities (CT and MRI modality). The main aim of the paper was the development of the procedures and algorithms of data processing in the brain perfusion examinations. Particular emphasis has been put on the improvement of the precision of the quantity estimation of the mean transfer time (MTT), which is a significant predictive parameter in the estimation of the areas at the risk of ischemic stroke. The paper has proved that using the correlation methods in the correction of the entrance function delay allows for the improvement of the mean transfer time and, as a result, of the remaining perfusion parameters (CBV and CBF). It has also been shown that the proposed method is universal in terms of the applied imaging technique, contrast means used as well as the differences in the ways of the research conduct, within the framework of the established protocol.
4
5 Spis treści 1. Wprowadzenie...vii 1.1 Teza pracy...xii 1.2 Układ pracy...xii 2. Tomograficzne techniki obrazowania funkcjonalnego Tomografia komputerowa Tomografia rezonansu magnetycznego Perfuzja System naczyniowy mózgu Pojęcie perfuzji CBF przepływ krwi w mózgu CBV objętość naczyń krwionośnych w mózgu Prędkość przepływu Średni czas przejścia MTT Tomograficzne badanie dynamiczne z wykorzystaniem środka cieniującego Idea obrazów parametrycznych Środki kontrastowe Jodowe środki cieniujące Paramagnetyczne środki cieniujące Teoria rozcieńczania znacznika Iniekcja impulsowa - bolus Iniekcja ciągła skok jednostkowy Model a rzeczywistość Budowa układu krwionośnego Czas iniekcji Stacjonarność układu Recyrkulacja Właściwości znacznika Charakterystyka podstawowych wielkości stosowanych do oceny perfuzji Tętnicza funkcja wejściowa Funkcja przejścia (transportu) Rozplot - dekonwolucja Recyrkulacja Podsumowanie Korekcja opóźnienia funkcji wejściowej Metody korekcji czasu dojścia kontrastu Metoda czasu opóźnienia maksimum koncentracji Metoda progowa Metoda geometryczna Metoda korelacyjna Funkcja kowariancji wzajemnej Symulacje Symulacje z zastosowaniem korelacyjnej metody korekcji opóźnienia bolusa Zastosowanie metody korelacyjnej do analizy rzeczywistych danych tomograficznych Protokół badania Analiza i wyniki Przykładowe wyniki badania klinicznego Podsumowanie...84 i
6 7.1 Wnioski końcowe Kierunki dalszych badań Dodatek Opis przykładowego badania Oprogramowanie do analizy danych perfuzyjnych...89 Bibliografia...98 ii
7 Indeks rysunków Rysunek 3.1. System naczyniowy mózgu...7 Rysunek 3.2. Ilustracja wielkości opisujących perfuzję...8 Rysunek 3.3. Zależności pomiędzy parametrami opisującymi przepływy naczyniowe...11 Rysunek 3.4. Schemat drogi środka cieniującego w badaniu perfuzyjnym...13 Rysunek 3.5. Zmiana kształtu krzywej koncentracji c(t) na drodze od miejsca iniekcji do badanej tkanki...15 Rysunek 3.6. Przykład wyniku typowego badania perfuzyjnego MR...15 Rysunek 3.7. Kolejne fazy krzywej dynamicznej, jakie można wyróżnić w prawidłowo wykonanym badaniu perfuzyjnym...16 Rysunek 3.8. Schemat przetwarzania dynamicznej serii obrazów w mapę parametryczną...18 Rysunek 3.9. Krzywe dynamiczne jasności obrazu w badaniu CT...21 Rysunek 3.1. Krzywe dynamiczne jasności obrazu w badaniu MR...21 Rysunek 4.1. Model systemu kapilar zastosowany w torii rozcieńczania znacznika...23 Rysunek 4.2. Krzywe koncentracji znacznika na wyjściu układu w funkcji czasu...24 Rysunek 4.3. Graficzna reprezentacja równania Rysunek 4.4. Ilustracja różnych sposobów przeprowadzania eksperymentu...31 Rysunek 5.1. Typowy przekrój poprzeczny głowy w badaniu perfuzyjnym...38 Rysunek 5.2. Kształt funkcji przejścia modelu przepływu naczyniowego R(t)...42 Rysunek 5.3. Rozmycie krzywej koncentracji na drodze od miejsca iniekcji...45 Rysunek 5.4. Efekt recyrkulacji znacznika w układzie zamkniętym...47 Rysunek 6.1. Schemat algorytmu przetwarzania tomograficznych danych dynamicznych...5 Rysunek 6.2. Metoda czasu opóźnienia maksimum koncentracji...51 Rysunek 6.3. Metoda progowa wyznaczania czasu opóźnienia krzywej koncentracji względem funkcji wejściowej AIF...52 Rysunek 6.4. Metoda geometryczna wyznaczania opóźnienia krzywej koncentracji względem funkcji wejściowej AIF...55 Rysunek 6.5. Metoda korelacyjna wyznaczania opóźnienia krzywej koncentracji względem funkcji wejściowej AIF...56 Rysunek 6.6. Kształt funkcji residuum R(t) dla różnych czasów dojścia kontrastu...58 Rysunek 6.7. Przykładowe krzywe koncentracji otrzymane w symulacjach dla różnych wartości SNR (linia ciągła)...59 Rysunek 6.8. Wyniki obliczeń funkcji R(t) dla zaszumionych krzywych koncentracji...61 Rysunek 6.9. Metoda uśredniania przestrzennego krzywych koncentracji...62 Rysunek 6.1. Funkcje kowariancji wzajemnej funkcji wejściowej AIF (koncentracji bolusa) i krzywej koncentracji dla tkanek otrzymanych w symulacjach dla różnych SNR...64 Rysunek Wyniki obliczeń czasu opóźnienia funkcji wejściowej względem obserwowanej funkcji AIF różnymi metodami...74 Rysunek Wyniki obliczeń czasu MTT na podstawie danych syntetycznych dla różnych czasów opóźnienia oraz czasu MTT=2 s...75 Rysunek Wyniki obliczeń czasu MTT na podstawie danych syntetycznych dla różnych czasów opóźnienia oraz czasu MTT=4 s...76 Rysunek Wyniki obliczeń czasu MTT na podstawie danych syntetycznych dla różnych czasów opóźnienia oraz czasu MTT=6 s...77 Rysunek Obraz dyfuzyjny...85 Rysunek Mapa parametryczna CBV...85 Rysunek Mapa opóźnienia bolusa względem funkcji wejściowej AIF wyznaczona metodą geometryczną...86 iii
8 Rysunek Mapa opóźnienia bolusa względem funkji weściowej AIF, wyznaczona metodą korelacyjną, proponowaną przez autora...86 Rysunek Mapa CBF wyznaczona bez korekcji opóźnienia bolusa...87 Rysunek 6.2. Mapa CBF wyznaczona z wykorzystaniem metody geometrycznej do korekcji opóźnienia bolusa...87 Rysunek Mapa CBF wyznaczona z wykorzystaniem metody korelacyjnej proponowanej przez autora...88 Rysunek Mapa MTT wyznaczona metodą bez zastosowania korekcji opóźnienia bolusa...88 Rysunek Mapa MTT wyznaczona z zastosowaniem korekcji opóźnienia bolusa metodą geometryczną...89 Rysunek Mapa MTT wyznaczona z zastosowaniem korekcji opóźnienia bolusa metodą korelacyjną proponowaną przez autora...89 Rysunek 8.1. Wygląd okna programu...98 Rysunek 8.2. Menu z funkcjami przetwarzania danych obrazowych...1 Rysunek 8.3. Okno ustawień parametrów obliczeniowych programu...1 Rysunek 8.4. Widok programu podczas wyznaczania funkcji wejściowej AIF...11 Rysunek 8.5. Przykładowy obraz parametryczny (CBF)...12 Rysunek 8.6. Widok z zaznaczonymi przykładowymi regionami zainteresowania...13 Rysunek 8.7. Wykresy średnich krzywych dla regionów zainteresowania...14 iv
9 Spis symboli użytych w pracy ACA Tętnica przednia mózgu AIF Tętnicza funkcja wejściowa (ang. Arterial Input Function) B Indukcja magnetyczna BAT Czas dojścia bolusa do obszaru zainteresowania (ang. Bolus Arrival Time) BD Opóźnienie bolusa (ang. Bolus Delay) C(t) Koncetracja znacznika w funkcji czasu Ca(t) Koncentracja znacznika w tętnicy w funkcji czasu CBF Przepływ krwi (ang. Cerebral Blood Flow) CBV Objętość naczyń krwionośnych (ang. Cerebral Blood Volume) Cmax Maksymalna wartość koncentracji znacznika CT Tomografia komputerowa (ang. Computed Tomography) CV(t) Koncentracja znacznika na wyjściu układu CVOI(t) Koncentracja znacznika w objętości w funkcji czasu t Przyrost czasu DWI Obrazowanie dyfuzji (ang. Diffusion Weighted Imaging) F Przepływ FT Transformata Fouriera FT-1 Odwrotna transformata Fouriera γ Współczynnik żyromagnetyczny GM Materia szara (ang. Gray Matter) WM Materia biała (ang. White Matter) H(t) Dystrybuanta czasów przejścia h(t) Funkcja odpowiedzi impulsowej Ht Hematokryt HU Jednostki Hounsfielda (ang. Hounsfield Units) M Wektor magnetyzacji MCA Tętnica środkowa mózgu µ Liniowy współczynnik pochłaniania promieniowania MRI Tomografia rezonansu magnetycznego (ang. Magnetic Resonance Imaging) MTT Średni czas przejścia (ang. Mean Transit Time) MTTeff Efektywny średni czas przejścia ω Prędkość kątowa ω Rezonansowa prędkość kątowa PET Tomografia pozytonowa (ang. Positron Emission Tomography) v
10 PWI Obrazowanie perfuzji (ang. Perfusion Weighted Imaging) Q Ilość znacznika R(t) Funkcja residuum ρ Gęstość protonowa ROI Region zainteresowania (ang. Region of Interest) S(t) Wartość sygnału w funkcji czasu S Średnia wartość sygnału w fazie przed napłynięciem znacznika SNR Stosunek sygnału do szumu (ang. Signal to Noise Ratio) SPECT Tomografia fotonowa (ang. Single Photon Emission Tomography) Splot funkcji SVD Dekompozycja na wektory szczególne (ang. Singular Value Decomposition) T1 Czas relaksacji podłużnej T2 Czas relaksacji poprzecznej TE Czas echa TR Czas repetycji TTP Czas osiągniecia maksimum koncentracji znacznika (ang. Time To Peak) V Objętość VOI Objętość zaiteresowania (ang. Volume of Interest) vi
11 1. Wprowadzenie Postęp we współczesnej medycynie jest nierozerwalnie związany z postępem w innych dziedzinach nauki, zarówno podstawowych, takich jak fizyka, chemia, biologia, czy genetyka, jak i nauk technicznych takich jak mechanika, inżynieria materiałowa, elektronika czy informatyka. Szczególnie ścisły jest jednak związek z rozwojem elektroniki współczesna diagnostyka i terapia jest nią nasycona w stopniu trudnym do ogarnięcia. Elektronicznie mierzy się ciśnienie tętnicze, pojemność płuc, czynność serca i mózgu, elektroniczne systemy analizują skład krwi i moczu, oceniają stan siatkówki, sterują naświetlaniami w radioterapii. Elektronika i informatyka są podstawami cyfrowych technik obrazowych, bez których trudno sobie wyobrazić współczesną diagnostykę. Jeśli sięgnąć do klasycznej definicji elektroniki, jako dziedziny techniki i nauki zajmującej się wytwarzaniem i przetwarzaniem sygnałów w postaci prądów i napięć elektrycznych lub pól elektromagnetycznych, to spektakularnym przykładem jej związku z medycyną może być obrazowanie techniką jądrowego rezonansu magnetycznego, leżącego w głównym nurcie zainteresowań autora niniejszej rozprawy. Umieszczenie pacjenta w silnym, stałym polu magnetycznym i pobudzenie odpowiednio dobraną sekwencją impulsów tzw. pól gradientowych powoduje, że jądra atomów wodoru stają się źródłami impulsów elektromagnetycznych, niosących informację o parametrach fizyko-chemicznych tkanek, a także o położeniu emitujących impulsy atomów. Skomplikowany system elektroniczny, uzupełniony odpowiednim oprogramowaniem, przetwarza odbierane w cewkach odbiorczych sygnały w trójwymiarową reprezentację wybranych parametrów tkanek. Zainteresowania autora są szczególnie związane z obrazowaniem technikami tomograficznymi. Dziedzina ta, będąca obecnie w fazie wielkiego rozkwitu, pozwala na uzyskanie nie tylko informacji anatomicznej, o budowie i rozmieszczeniu narządów, ale także funkcjonalnej o ich czynności, np. o aktywności neuronalnej mózgu czy jakości filtracji osocza krwi w nerkach. Obrazowanie funkcjonalne znajduje szczególnie szerokie zastosowanie w ocenie ukrwienia tkanek, które stanowi zasadniczy wątek niniejszej pracy. Krążenie krwi jest jednym z podstawowych procesów zapewniających utrzymanie organizmu przy życiu. Jego zadaniem jest zaopatrywanie tkanek w tlen i substancje odżywcze oraz odprowadzanie produktów metabolizmu. Synchroniczna praca serca powoduje stałe przemieszczanie krwi z niskociśnieniowego zbiornika żylnego do wysokociśnieniowego układu tętniczego. Cała objętość krwi jest wtłaczana do mikrokrążenia, gdzie zachodzą procesy wymiany tkankowej tlenu. Wymiana ta zachodzi poprzez błonę podstawną vii
12 i śródbłonek naczyń włosowatych na zasadzie dyfuzji powodowanej różnicą stężeń po obu stronach błony półprzepuszczalnej. Opisane procesy zachodzą w każdym narządzie i są niezbędne dla jego prawidłowego funkcjonowania. Zaburzenia mikrokrążenia mogą spowodować utratę funkcji organu, całego układu, a nawet, w skrajnych przypadkach, śmierć organizmu. Choroby układu naczyniowego mózgu są jedną z najczęstszych przyczyn zgonów i przypadków inwalidztwa. Po nowotworach i chorobach serca stanowią trzecią pod względem częstości przyczynę śmierci. Co dziesiąta osoba w Europie po 5 roku życia umiera z powodu udaru. Śmiertelność w przypadku udaru niedokrwiennego mózgu rośnie wraz z wiekiem. Statystyki polskie są bardziej od europejskich niepokojące. Pod względem zachorowalności na choroby układu naczyniowego mózgu Polacy znajdują się na jednym z pierwszych miejsc w Europie [KOBA5]. Wynik leczenia w udarze mózgu zależy od czasu rozpoczęcia interwencji, rozległości ogniska niedokrwiennego i jego lokalizacji. W celu uzyskania informacji o stanie struktur nerwowych stosuje się trzy zasadnicze grupy metod badania: kliniczne, aparaturowe i laboratoryjne. Po pierwszych ustaleniach dokonanych na podstawie metod klinicznych, badanie struktur nerwowych i ich metabolizmu uzupełnia się metodami dodatkowymi, np. jedną z technik obrazowania. Wybór metody dodatkowej powinien wynikać z takich przesłanek jak: czułość i swoistość danego badania, jego efektywność, bezpieczeństwo i koszt. W badaniach obrazowych mózgu wykorzystuje się techniki radiograficzne, tomografię komputerową (CT), magnetyczny rezonans jądrowy (MRI), ultrasonografię (USG) oraz badania izotopowe: tomografię emisyjną pojedynczego fotonu (SPECT) i pozytonową emisyjną tomografię komputerową (PET). Badanie za pomocą magnetycznego rezonansu jądrowego (MRI) stanowi cenne badanie uzupełniające dla tomografii komputerowej. Ze względu na brak kontaktu z promieniowaniem jonizującym (w odróżnieniu od techniki CT) uważane jest ono za badanie bezpieczne dla pacjenta, a ewentualnie stosowany kontrast gadolinowy, w przeciwieństwie do jodowych środków kontrastowych stosowanych w metodach rentgenowskich, rzadko wywołuje reakcje alergiczne. Technika ta pozwala różnicować skupiska istoty szarej i białej (co jest niezbędne np. w wykrywaniu ognisk demielinizacji czy zmian zwyrodnieniowych istoty białej). Za pomocą MRI można także oceniać stan obszarów słabo widocznych w przypadku zastosowania innych technik obrazowania (np. okolica spoidła wielkiego, przysadki mózgowej czy pnia mózgu). Klasyczne badanie tomografii komputerowej pozwala wykryć niedokrwienie tkanki viii
13 mózgowej stosunkowo późno, dopiero po około 6 godzinach od wystąpienia objawów neurologicznych. W przypadku ostrych stanów niedokrwiennych brak interwencji w takim czasie prowadzi do nieodwracalnych zmiany martwiczych. Spadek ukrwienia mózgu poniżej poziomu krytycznego powoduje deficyt energetyczny komórek nerwowych. W ognisku niedokrwienia dochodzi do tzw. perfuzji luksusowej naczynia rozszerzają się, poprawiając chwilowo przepływ. Jednakże w miarę upływu czasu możliwości autoregulacji krążenia słabną, prowadząc do porażenia naczyń. Wokół ogniska niedokrwienia dochodzi do spadku ciśnienia i przepływu krwi w kierunku obwodu, a następnie do skurczu naczyń otaczających tzw. podkradanie śródczaszkowe i zespół Robin-Hooda. Obszar sąsiadujący z ogniskiem niedokrwienia (penumbra, inaczej nazywana strefą półcienia) jest strefą, którą potencjalnie można uratować podejmując szybką decyzję o kwalifikacji pacjenta do leczenia trombolitycznego (rozpuszczającego skrzeplinę). O tym jak istotnym elementem terapii w udarze niedokrwiennym jest czas świadczą wytyczne [ALBE4] dotyczące postępowania w takich przypadkach. Przyjmuje się, że okno terapeutyczne, tzn. czas, w którym należy podjąć leczenie trombolityczne po wystąpieniu objawów, wynosi 3 godziny. Niestety, tylko niewielki procent pacjentów (1-3%) dociera w tym czasie do wysokospecjalizowanego ośrodka mogącego podjąć terapię [OWE6, AZZI97]. Wynika to z szeregu czynników mogących wpływać na czas dotarcia do szpitala, jak miejsce zamieszkania, poziom opieki zdrowotnej w danym regionie oraz stopień rozwoju edukacji zdrowotnej w społeczeństwie. U prawie wszystkich pacjentów, u których podjęto terapię w czasie okna terapeutycznego, po trzech miesiącach od udaru nie występowały żadne deficyty neurologiczne, tylko w pojedynczych przypadkach pozostał paraliż co najmniej jednej kończyny [PALA6]. Przytoczone dane pokazują jak istotnym elementem terapii w nagłych udarach mózgu są narzędzia diagnostyczne pozwalające na natychmiastową ocenę sytuacji. Do niedawna podstawowym badaniem u chorych z objawami udaru była klasyczna tomografia komputerowa, która, jak wspomniano wcześniej, stanowczo zbyt późno dostarcza lekarzom ważnych informacji na temat zaistniałego udaru. Po czasie 6 godzin, po którym obszar niedokrwienny staje się widoczny w tej technice, dochodzi już zwykle do martwicy neuronów i zastępowania ich tkanką glejową. Można zatem powiedzieć, że klasyczne metody obrazowania są niewystarczające w intrwencyjnej diagnostyce udarów niedokrwiennych. Dopiero możliwość zobrazowania jakości perfuzji daje możliwość podjęcia natychmiastowej decyzji co do sposobu dalszego postępowania. Pojęcie perfuzji rozumiane jest jako proces dostarczania do tkanek składników niezbędnych do ich prawidłowego funkcjonowania. Wiąże się ono bezpośrednio z jakością ix
14 przepływu krwi w tętnicach oraz naczyniach włosowatych (kapilarach). W dalszej części pracy pojęcie perfuzji zostanie powiązane z parametrami przepływu, które będą wyznaczane na podstawie analizy obrazów tomograficznych. Obecnie największe znaczenie we wczesnym wykrywaniu zmian niedokrwiennych mają zatem nowoczesne metody tomograficznych badań perfuzyjnych, wykonywanych zarówno metodą tomografii komputerowej, jak i rezonansu magnetycznego, umożliwiające wykrycie ostrych stanów niedokrwienia praktycznie natychmiast po wystąpieniu objawów neurologicznych. Mimo zalety badań perfuzyjnych, jaką jest możliwość wczesnego wykrycia zmian patologicznych, ich wadą jest fakt, że do tej pory ich wykorzystanie ogranicza się jedynie do jakościowej oceny ukrwienia, sprowadzającej się do porównania obszarów tkanki zdrowej i patologicznej. Takie podejście może być wystarczające w postępowaniu interwencyjnym, w sytuacji gdy pacjent trafia do szpitala z objawami ostrego stanu niedokrwienia i niezbędna jest szybka lokalizacja jego ogniska, pozwalająca na podjęcie prawidłowego leczenia. Jeśli jednak celem jest długoterminowe monitorowanie rozwoju choroby w celu podjęcia leczenia eliminującego stany nagłe, czy też długoterminowe śledzenie skutków leczenia lub przeprowadzonej interwencji chirurgicznej, to ocena jakościowa staje się niewystarczająca. Dlatego niezwykle ważnym, czy wręcz koniecznym, wydaje się poszukiwanie takich metod badawczych, które umożliwiłyby ilościową ocenę parametrów perfuzji niezależnie od techniki badania czy zastosowanych środków kontrastowych i takie właśnie badania stanowią główny wątek niniejszej pracy i zainteresowań autora. Proponowane przez autora metody doskonale sprawdzają się w diagnostyce interwencyjnej, pozwalając na dodatkowe prognozowanie skutków leczenia na podstawie oceny obszaru penumbry (tzw. półcienia). Jak wspomniano, jest to obszar tkanki, w którym nastąpił deficyt ukrwienia związany z udarem, potencjalnie możliwy do uratowania. Informacja ta może być kluczowa w procesie diagnostycznym, ułatwiając ocenę czasu jaki upłynął od wystąpienia udaru oraz szans powodzenia podejmowanego leczenia, co jest szczególnie istotne z punktu widzenia komfortu pacjenta. Złożoność procesu perfuzji tkankowej bezpośrednio przekłada się na trudności związane z przetwarzaniem danych perfuzyjnych oraz z próbami obiektywnej parametryzacji tego procesu. Zdaniem autora, podstawowym problemem związanym z zagadnieniem obiektywnej parametryzacji matematycznego zjawiska, procesu perfuzji w szczególności jest brak w przypadkach odpowiedniego patalogicznych. modelu O ile w przypadkach prawidłowego funkcjonowania układu krążenia model taki może być x
15 tworzony w oparciu o liczne badania na zdrowych ochotnikach, to opracowanie modelu dla stanów chorobowych jest bardzo trudne. Wynika to z faktu bardzo indywidualnego przebiegu choroby. W związku z tym w niniejszej pracy skupiono się na metodach, w których przyjmowanie jakiegokolwiek modelu nie jest konieczne. Kolejną trudnością jest złożoność budowy układu krwionośnego głowy, prowadząca do wielu niejednoznaczności w sposobie dostarczania krwi do wybranego obszaru tkanki (co zostanie szczegółowo opisane w rozdziale 3.1). Mechanizmy autoregulacyjne w stanach patologicznych mogą na tyle zmieniać sposób dystrybucji krwi, że przyjmowanie założeń a priori na podstawie wiedzy o prawidłowej funkcji krążenia może prowadzić do błędnej oceny stanu faktycznego. Dlatego też autor nie podejmował w pracy zagadnienia całkowitej automatyzacji procesu przetwarzania danych, w szczególności doboru funkcji wejściowej AIF, której znaczenie opisane zostało w rozdziale 5.1. Początkowo zamiarem autora było stworzenie metody obiektywnego wyznaczania wszystkich parametrów perfuzji stosowanych w praktyce klinicznej zostaną one szczegółowo opisane w kolejnych rozdziałach pracy. Jednak po konsultacjach w ośrodkach medycznych skupiono się na próbie obiektywizacji parametrów czasowych perfuzji, w szczególności średniego czasu przejścia MTT (ang. Mean Transit Time), które zdaniem lekarzy radiologów niosą najistotniejszą informację diagnostyczną oraz najlepiej pozwalają przewidywać skuteczność podejmowanego leczenia. Potwierdzeniem opisanych trudności jest dzisiejszy stan wiedzy prezentowany w piśmiennictwie światowym. Choć tematyka pomiaru parametrów perfuzji była podejmowana już wiele lat temu [ZIER65], to nadal można znaleźć tylko nieliczne artykuły dotyczące prób stworzenia metod ich obiektywnej, ilościowej oceny [HERZ96, HUNS2, KOSH99, LEEN9, McHE78, MELT, NARI79, NIGH97, PANT84, SCHR98, WIRE, VONK99, OSTE96a]. Analiza wyników tych prac, a w szczególności znaczące różnice i niejednoznaczność prezentowanych wartości parametrów perfuzji, skłaniają jednak do wniosku, że niezbędne jest podjęcie prób stworzenia takich metod, które zapewniłyby odpowiednią powtarzalność wyników, a także ich niezależność od zastosowanej techniki pomiarowej. Tylko w takim bowiem przypadku możliwe będzie porównanie wyników badań przeprowadzanych w różnych ośrodkach medycznych, w różnym czasie i przy pomocy różnych technik obrazowania. Próba poprawy i rozwinięcia istniejących metod stała się motywacją do podjęcia badań stanowiących podstawę niniejszej pracy. xi
16 1.1 Teza pracy Przeprowadzone przez autora pracy badania symulacyjne oraz analiza danych z ośrodków klinicznych pozwalają na postawienie następującej tezy: Istnieje możliwość poprawy dokładności pomiaru parametrów opisujących perfuzję tkankową (a w szczególności średniego czasu przejścia MTT) oraz obniżenia wrażliwości pomiaru na zakłócenia poprzez zastosowanie metody korelacyjnej określania czasu transportu środka kontrastującego do badanego obszaru. 1.2 Układ pracy Praca podzielona została na dwie zasadnicze części. Pierwsza z nich poświęcona jest analizie zjawiska perfuzji oraz omówieniu technik obrazowych i sposobów ich wykorzystania do oceny stanu ukrwienia tkanki. Obejmuje ona rozdziały 2-5. W rozdziale 2 krótko omówiono techniki obrazowania wykorzystywane do badań będących źródłem danych dla analiz przeprowadzonych w pracy. Rozdział 3 omawia zjawisko perfuzji. Opisano w nim procesy związane z krążeniem oraz parametry stosowane w ocenie stanu ukrwienia tkanki. Główny nacisk położono na uzasadnienie konieczności jednoczesnej oceny kilku parametrów. Zwrócono też uwagę na niejednoznaczności ich oceny, wynikające z różnic w stosowanych technikach obrazowania. W rozdziale 4 przedstawiono podstawy teoretyczne techniki obrazowania perfuzyjnego oraz zaproponowano model zjawiska perfuzji stosowany w dalszej analizie. Rozdział 5 zawiera przegląd obecnie stosowanych metod oceny perfuzji tkankowej. Przedstawiono w nim zarówno metody analizy jakościowej, jak i ilościowej. Podjęto też próbę krytycznej oceny tych metod pod kątem stosowania ich w badaniach długoterminowych, czy też wieloośrodkowych. Część druga pracy, zawierająca rozdziały 6-8, stanowi prezentację badań wykonanych przez autora oraz wynikających z nich wniosków. W rozdziale 6 została omówiona metoda korelacyjna pomiaru czasu transportu znacznika do badanego obszaru tkanki oraz jej zastosowanie do przetwarzania danych pomiarowych w metodach pomiaru perfuzji. Efektywność metody oceniono na podstawie analizy danych pochodzących z symulacji komputerowych. Rozdział 7 przedstawia wyniki zastosowania metody proponowanej przez autora xii
17 do analizy danych klinicznych. Wnioski końcowe, potwierdzające tezę postawioną w pracy, zostały sformułowane w rozdziale 8. xiii
18
19 2. Tomograficzne techniki obrazowania funkcjonalnego Wszystkie rozważania przedstawione w niniejszej rozprawie związane są z tomograficznymi technikami obrazowania oraz z przetwarzaniem i analizą uzyskiwanych w nich danych pomiarowych. W ciągu kilkunastu ostatnich lat, dzięki rozwojowi technik komputerowych, są to jedne z najprężniej rozwijających się metod diagnostycznych. Ich główną cechą jest możliwość uzyskiwania obrazów ukazujących przekroje badanego obiektu (łac. tomos - warstwa, podział). Techniki te są szeroko stosowane we wszystkich dziedzinach medycyny, a także w technice (tomografia procesowa). Ze względu na wykorzystywane medium, techniki tomograficzne można podzielić na: tomografię rentgenowską, wykorzystującą promieniowanie X, tomografię komputerową (CT, ang. Computed Tomography), będącą odmianą tomografii rentgenowskiej, tomografię rezonansu magnetycznego (MRI, ang. Magnetic Resonance Imaging), wykorzystującą zjawisko jądrowego rezonansu magnetycznego, tomografie emisyjne: SPECT (ang. Single Photon Emission Computed Tomography) i PET (ang. Positron Emission Tomography). Z punktu widzenia zastosowań będących tematem niniejszej pracy, na szczególną uwagę zasługują dwie z wyżej wymienionych technik: CT i MRI. Obydwie pozwalają na obrazowanie szczegółów o rozmiarach pojedynczych milimetrów oraz uzyskiwanie obrazu badanej warstwy lub objętości w czasie poniżej 1 sekundy, co jest istotne zwłaszcza w badaniach funkcjonalnych. Różnią się jednak zasadniczo sposobem uzyskiwania informacji morfologicznej. 2.1 Tomografia komputerowa Podstawy tomografii komputerowej stworzył w 1917 austriacki matematyk Johann Radon [RADO17]. Udowodnił on, że na podstawie nieskończonej liczby rzutów dwu- lub trójwymiarowego obiektu, wykonanych pod różnymi kątami, można odtworzyć jego pełny obraz. Rekonstrukcji można także dokonać, z ograniczoną dokładnością, na podstawie skończonej liczby rzutów. Głównym ograniczeniem praktycznego zastosowania teorii Radona przez wiele lat były możliwości obliczeniowe ówczesnych komputerów, niewystarczające dla złożonych numerycznie obliczeń związanych z rekonstrukcją obrazów. Dopiero w latach 7. szybki rozwój techniki obliczeniowej stworzył odpowiednie możliwości. W 1972 roku 1
20 Godfrey Hounsfield i Allan Cormack skonstruowali i uruchomili w szpitalu Atkinson Morley Hospital, (Wimbledon, Wielka Brytania) pierwszy tomograf komputerowy, za co w 1979 roku otrzymali Nagrodę Nobla w dziedzinie medycyny i fizjologii. Istotą tomografii komputerowej jest odtworzenie przestrzennego rozkładu liniowego współczynnika pochłaniania promieniowania X, który zależy od liczby atomowej pierwiastków, z których zbudowana jest tkanka oraz od jej gęstości. Dla potrzeb diagnostycznych powstała skala wyrażana w jednostkach Hounsfielda (HU, ang. Hounsfield Units), która różnicuje tkanki w zależności od ich współczynnika promieniowania X. odniesionych Skala do wartości Hounsfielda liniowego wyrażana jest współczynnika pochłaniania w jednostkach pochłaniania względnych, promieniowania monoenergetycznego o energii 73 kev dla wody ( woda,73kev ). Zależność jednostek skali Hounsfielda od współczynnika pochłaniania wyraża się zależnością: [ HU ]= woda,73 kev. woda,73kev (2.1) W praktyce radiologicznej skala ta służy opisowi jasności pikseli otrzymanego obrazu. W tabeli 2.1 zebrano wartości HU odpowiadające typowym tkankom i substancjom. Substancja/tkanka Wartość piksela [HU] powietrze -1 woda wynaczyniona krew płuca tłuszcz istota szara istota biała tkanka kostna Tabela 2.1. Jednostki Hounsfielda dla wybranych substancji i tkanek. Zastosowanie dla obrazów CT znormalizowanej skali pozwala na jednoznaczne rozpoznanie rodzaju tkanki oraz umożliwia porównywanie wyników w badaniach długoterminowych oraz międzyośrodkowych, co jest ogromną zaletą tomografii CT. Niestety, możliwości różnicowania tkanek miękkich (szczególnie w mózgu) bez zastosowania środków kontrastowych jest stosunkowo słaba. Mimo to technika CT jest obecnie szeroko stosowana w diagnostyce obrazowej. Jej niewątpliwą zaletą jest fakt, że współcześnie produkowane tomografy mogą wykonywać obrazy warstwy lub objętości w czasie krótszym od jednej 2
21 sekundy, co w połączeniu z zastosowaniem środków kontrastowych pozwala wykonywać badania dynamiczne, a więc obrazowanie funkcji, a nie tylko morfologii narządów i tkanek. Badania tego typu stosowane są głównie w chorobach układu krążenia, w szczególności w przypadku zespołów niedokrwienia mięśnia sercowego i mózgu. Należy wspomnieć, że opisywana technika, ze względu na wykorzystanie promieniowania jonizującego, nie jest całkowicie obojętna dla pacjenta. Jednorazowe badanie CT odpowiada, pod względem otrzymywanej przez badanego dawki promieniowania, kilku, lub nawet kilkunastu typowym zdjęciom rentgenowskim. Badanie jest bezbolesne i nie wymaga wcześniejszego przygotowania. 2.2 Tomografia rezonansu magnetycznego W przeciwieństwie do CT, tomografia MR nie wykorzystuje promieniowania jonizującego. Istotą obrazowania jest pobudzanie falą radiową atomów wodoru umieszczonych w stałym polu magnetycznym, a następnie odbiór sygnału radiowego generowanego przez wzbudzone atomy podczas ich powrotu do stanu równowagi. Proces obrazowania polega na przestrzennym odwzorowaniu gęstości atomów wodoru w komórkach tkanki oraz ich parametrów: gęstości protonowej oraz czasów relaksacji - podłużnej T1 i poprzecznej T2. Na obraz wynikowy mają więc wpływ trzy różne parametry, a także, dodatkowo, sposób prowadzenia badania (rodzaj sekwencji pobudzającej). Dzięki temu technika ta daje nieporównywalne z innymi możliwości różnicowania tkanek, w szczególności miękkich - o dużej zawartości wodoru (związanego w wodzie lub tłuszczach). Tomografia rezonansu magnetycznego, podobnie jak tomografia komputerowa, musiała czekać wiele lat od momentu odkrycia zjawisk będących jej podstawą do czasu kiedy zaczęto wykorzystywać ją w codziennej praktyce klinicznej. Zjawisko jądrowego rezonansu magnetycznego zostało po raz pierwszy, w 1946 roku, niezależnie opisane przez Felixa Blocha i Edwarda Millsa Purcella, za co w 1952 roku obaj podzielili się nagrodą Nobla. Początkowo zjawisko to było wykorzystywane jedynie w chemii, do badania metodami spektroskopowymi struktur cząsteczek. Dopiero w 197 roku Paul Lauterbur i Sir Peter Mansfield stworzyli podstawy obrazowania z wykorzystaniem zjawiska rezonansu i skonstruowali pierwszy skaner pozwalający otrzymać obrazy tkanek. W 23 roku zostali za to uhonorowani Nagrodą Nobla w dziedzinie medycyny i fizjologii. W klasycznym opisie zjawiska za pomocą równań Blocha wprowadza się wektor, będący sumą wektora magnetyzacji podłużnej M Z i poprzecznej M XY : magnetyzacji M 3
22 dm x ' M = M y ' x', dt T2 dm y ' M y' = M x' 2 B1 M z, dt T2 M Z M Z dm Z = 2 B 1 M y ' dt T1 (2.2) gdzie M wektor magnetyzacji, ω prędkość kątowa zmiennego pola elektromagnetycznego, ω rezonansowa prędkość kątowa, B1 indukcja magnetyczna pobudzenia, γ stała żyromagnetyczna, T1 i T2 czasy relaksacji podłużnej i poprzecznej. Zjawisko rezonansu magnetycznego związane jest z własnym momentem pędu cząstek elementarnych i zbudowanych z nich struktur, takich jak jądra atomowe i atomy. Własny moment pędu tych cząstek nazywany jest spinem. Z niezerowym spinem sprzężony jest moment magnetyczny cząstki. Dopiero po umieszczeniu badanego obiektu (pacjenta) B, momenty magnetyczne ustawiają się w stałym polu magnetycznym o natężeniu w kierunkach uporządkowanych względem linii pola, zgodnie lub przeciwnie do zwrotu wektora B. Ponieważ liczba atomów ustawionych zgodnie i przeciwnie jest różna, wypadkowy makroskopowy wektor magnetyzacji jest różny od zera i w stanie równowagi = M Z. Makroskopowy wektor magnetyzacji zgodny z osią pola B. Oznacza się go jako M poprzecznej w tym stanie jest M XY =. Spowodowane jest to faktem, że atomy w polu B co prawda wirują z tą samą częstotliwością (nazywaną częstotliwością Larmora), ale ich faza jest rozłożona chaotycznie. W chwili gdy badany obiekt zostanie pobudzony zmiennym polem elektromagnetycznym o częstotliwości, prostopadłym do pola B, występuje zjawisko rezonansu magnetycznego. Atomy zaczynają wirować synchronicznie, przez co pojawia się makroskopowy wektor magnetyzacji poprzecznej M XY, oraz poczynają zmieniać swoje ustawienie względem pola głównego, czego wynikiem jest zanik magnetyzacji podłużnej M Z. Wirujący wektor magnetyzacji poprzecznej M XY jest źródłem sygnału, na podstawie którego rekonstruowane są obrazy tomograficzne. Po wyłączeniu pobudzenia układ powraca do stanu równowagi - na skutek oddziaływań spin-sieć odbudowuje się wektor magnetyzacji podłużnej M Z, a na skutek oddziaływań spin-spin pola magnetycznego zanika wektor magnetyzacji poprzecznej M XY, co powoduje zanik sygnału generowanego przez obiekt. Stałe czasowe tych procesów nazywane są czasami relaksacji podłużnej T1 i relaksacji poprzecznej T2. Należy pamiętać, że amplituda sygnału zależy od gęstości protonowej oraz jest wprost proporcjonalna do wartości wektora magnetyzacji 4
23 poprzecznej M Z. Jeśli zatem kolejne pobudzenia zmiennym polem elektromagnetycznym będą powtarzane sekwencyjnie w równych odstępach czasowych TR (ang. repetition time), takich że wektor magnetyzacji podłużnej nie zdąży się pomiędzy nimi całkowicie odbudować, można regulując czasem TR wpływać na amplitudę sygnału. Ze względu na niejednorodności pola magnetycznego rzeczywisty zanik sygnału następuje szybciej niż w warunkach idealnych i zachodzi ze stałą czasową oznaczaną T2*. Istnieje możliwość wyeliminowania wpływu niejednorodności pola poprzez dodatkowe pobudzenie impulsem radiowym powodującym ponowną synchronizację spinów i ponowne pojawienie się sygnału, tzw. echa, po czasie TE (ang. echo time). Amplituda tego sygnału będzie zależna od czasu TE oraz czasu relaksacji T2 badanej tkanki. Czas echa wynika z odstępu czasowego pomiędzy pobudzeniem a impulsem synchronizującym TI (ang. inversion time) i wynosi TE = 2TI. W ogólności wartość sygnału dla opisanej sekwencji zdarzeń (nazywanej sekwencją pobudzającą) opisuje zależność: S=k 1 e 1 e, TR T1 TE T2 gdzie: S poziom sygnału wyrażany w jednostkach arbitralnych, k (2.3) stała zależna od warunków pomiaru, gęstość protonowa, TR czas repetycji, TE czas echa, T1 i T2 czasy relaksacji podłużnej i poprzecznej. Wynikowy obraz tomograficzny jest więc przestrzennym rozkładem amplitud sygnału odebranego z badanego obiektu. Jasność piksela odpowiada wartości amplitudy. Jak widać, zależność ta jest dość złożona (wzór (2.3)). Występują w niej aż trzy zmienne wynikające z właściwości tkanki oraz dwie zależne od sposobu prowadzenia badania. Daje to praktycznie nieograniczone możliwości różnicowania tkanek pod kątem gęstości protonów PD (ang. proton density) i czasów relaksacji T1 i T2. Dlatego technika MR stała się, mimo bardzo wysokich kosztów aparatury, niezastąpiona w obrazowaniu układu centralnego układu nerwowego. Niezaprzeczalną wadą takiej elastyczności opisywanej metody badań jest brak jednoznacznego związku między wartością odbieranego sygnału a jasnością obrazu. Porównywanie wyników badań pochodzących z różnych aparatów staje się praktycznie niemożliwe. Jeżeli podejmowane są próby badań miedzyośrodkowych, to bardzo istotnym elementem tych działań jest kontrola procedur badawczych oraz stosowanie różnego rodzaju fantomów i procedur kalibracyjnych. Podobnie jak w technice CT, rozdzielczość czasowa badań MR umożliwia obrazowanie dynamiczne. W połączeniu ze stosowaniem środków cieniujących lub specjalnych sekwencji pobudzających, innych od stosowanych w rutynowych badaniach, możliwe jest uzyskiwanie 5
24 nie tylko wysokorozdzielczych obrazów morfologicznych, ale i funkcjonalnych. Do tej pory nie wykazano żadnych szkodliwych skutków badania techniką MRI. Badanie jest bezbolesne i nie wymaga wcześniejszego przygotowania pacjenta. Przeciwwskazaniem są wszelkiego rodzaju obiekty metalowe na stałe umieszczone w ciele pacjenta, takie jak implanty, plomby czy rozrusznik serca. Nie muszą one mieć wpływu na bezpieczeństwo badanego, ale zawsze powodują istotne artefakty, które mogą zmniejszyć wartość diagnostyczną otrzymanych obrazów. 6
25 3. Perfuzja Odpowiedni przepływ krwi w mózgu (CBF, ang Cerebral Blood Flow) zapewnia dostarczanie odpowiedniej ilości glukozy i tlenu, niezbędnych do prawidłowego funkcjonowania komórek nerwowych. Wiadomo, że zmiany CBF są dobrym wyznacznikiem zarówno aktywności mózgu, jak i wszelkich zmian patologicznych. Współczesne techniki pomiarowe, w tym tomograficzne techniki obrazowania, dostarczają coraz pełniejszej wiedzy na ten temat. Pomimo tego ciągle jesteśmy dalecy od pełnego zrozumienia tych procesów, a zainteresowanie tematyką perfuzji tkankowej w ostatnich latach rośnie. 3.1 System naczyniowy mózgu Rysunek 3.1. System naczyniowy mózgu. Po lewej stronie obraz angiograficzny wykonany techniką rezonansu magnetycznego; widoczne są główne naczynia krwionośne o średnicach rzędu pojedynczych milimetrów. Po prawej zdjęcie mikroskopowe kapilar; charakterystyczny jest brak wyróżnionego kierunku [DUVE81]. Układ naczyniowy mózgu zbudowany jest z naczyń krwionośnych, których rozmiary zawierają się w przedziale od kilku milimetrów, dla głównych tętnic i żył mózgowych, do pojedynczych mikrometrów, dla kapilar, w których zachodzi bezpośrednia wymiana składników niezbędnych do życia komórek nerwowych. Poziom złożoności układu mózgowego zilustrowany został na rys Przedstawiono na nim wynik badania metodą angiograficznego rezonansu magnetycznego (MRA, ang Magnetic Resonance Angiography), która pozwala obrazować naczynia krwionośne o średnicy rzędu pojedynczych milimetrów oraz mikroskopowy obraz systemu kapilar, tętniczek i wenul. 7
26 3.2 Pojęcie perfuzji Rysunek 3.2. Ilustracja wielkości opisujących perfuzję. Rysunek przedstawia schematycznie układ naczyń w wybranej objętości tkanki. Można wyróżnić kapilary, wenule, tętniczki oraz tętnice i żyły. Przyjmuje się, że CBF jest miarą ilości krwi tętniczej dostarczanej do kapilar (F1+F2) w jednostce czasu w określonej objętości tkanki [BUXT2]. W wielu współczesnych technikach obrazowych do oceny perfuzji wykorzystuje się parametr przepływu naczyniowego. Pojęcie perfuzji odnosi się do procesu zasilania tkanki w składniki niezbędne do jej prawidłowego funkcjonowania. Złożoność tego procesu wymaga wprowadzenia kilku podstawowych pojęć z nim związanych CBF przepływ krwi w mózgu Przepływ krwi (CBF) jest parametrem najczęściej bezpośrednio wiązanym z oceną perfuzji. Jest on miarą ilości krwi tętniczej dostarczanej do określonej objętości tkanki w określonym czasie. Jako jednostkę miary CBF przyjęto ml/1g/min. Typową wartością dla istoty szarej jest 6 ml/1g/min. Ponieważ w technikach znakowania łatwiej posługiwać się jednostkami objętości, a nie masy, często używaną jednostką jest cm3/1cm3/s (czyli,1 s-1). Można wtedy CBF interpretować jako współczynnik proporcjonalny do prędkości przepływu. W tabeli 3.1 przedstawiono przykładowe wartości CBF dla istoty szarej i białej mózgu podawane w literaturze. 8
27 Źródło Płeć M/K Wiek Technika badania GM WM GM:WM [HERZ96] 2/ PET 83±2 16±3 5,2±b.d. [HUNS2] 7/ DSC MRI b.d. b.d. 2,4±,4 [KOSH99] 8/ DSC MRI 37,3±8,4 22±b.d. 1,7±b.d. [LEEN9] 18/ PET 52,1±11 2,3±3,7 2,6±b.d. [McHE78] 15/ 2-36 Xe 77,6±1,4 18,2±2,7 4,3±b.d. [MELT] 5/ PET 62±1 b.d. b.d. [NARI79] 26/ Xe 89,1±7,3 b.d. b.d. [NIGH97] 8/ DSC MRI b.d. b.d. 2,4±b.d. [PANT84] 19/ PET 5,7±1,3 24,5±4,1 2,1±b.d. [SCHR98] 13/ DSC MRI 67,1±16,3 23,7±4,9 2,8±b.d. [WIRE] 25/ DSC MRI 68±28 36±13 1,9±b.d. [VONK99] 41/ 4-86 DSC MRI 66±2 34±11 1,9±b.d. [YAMA86] 17/ PET 42,4±7,8 b.d. b.d. [OSTE96a] 6/ DSC MRI 58,9±b.d. 22±b.d. 2,7±b.d. Tabela 3.1. Podawane w literaturze wartości przepływu CBF (ml/1g/min) w istocie szarej (GM ang. Grey Matter) i białej (WM ang. White Matter) mózgów osób zdrowych (b.d. - brak danych). Pomiary wykonywane technikami: PET Positron Emission Tomography, DSC MRI Dynamic Suscebility Contrast MRI, Xe xenon-enhanced CT CBV objętość naczyń krwionośnych w mózgu Drugim parametrem wiążącym się z perfuzją jest względna objętość krwi CBV (ang. Celebral Blood Volume). Wyraża ona stosunek objętości krwi do całkowitej objętości tkanki (stosunek ten jest w istocie równy stosunkowi objętości naczyń krwionośnych do całkowitej objętości tkanki). Jest to wielkość bezwymiarowa, a np. typową wartością CBV dla istoty szarej jest,4 (lub 4%). Należy zaznaczyć, że wielkość ta odnosi się do wszystkich rodzajów naczyń zawartych w badanym fragmencie tkanki, bez rozróżnienia tętniczek, kapilar i wenul (rys.3.2) [PAWL81]. Zmiany CBV mogą być powodowane wieloma czynnikami, np.: rozszerzaniem tętniczek, otwieraniem się kapilar bądź zwiększaniem objętości wenul na skutek wzrostu ciśnienia będącego następstwem zwiększenia przepływu. Każdy z tych czynników może mieć różny udział w wypadkowej wartości CBV [BERE93], [FRAN92], [GOBE89], [GOBE9], [SHOC88], [VETT9], [WEIS88]. Typowe wartości CBV prezentowane w literaturze przedstawia tabela
28 Źródło Płeć M/K Wiek Technika badania GM WM GM:WM [HUNS2] 7/ MRI b.d. b.d. 2,±,3 [KOSH99] 8/ MRI 4,1±,8 2,9±,4 1,4±b.d. [LEEN9] 18/ PET 4,6±1, 2,6±,4 1,8±b.d. [NIGH97] 8/ MRI b.d. b.d. 2,4±b.d. [PETR98] 3/ MRI b.d. b.d. 1,9±b.d. [SCHR98] 13/ MRI 5,3±,9 2,5±,4 2,1±b.d. [VONK99] 41/ 4-86 MRI 6,5±1, 3,6±,9 1,8±b.d. [YAMA86] 17/ PET 4,1±,5 b.d. b.d. Tabela 3.2. Średnie wartości CBV (ml/1ml) i odchylenia standardowe dla istoty szarej (GM) i białej (WM) mózgu. W niektórych pracach podawany był jedynie stosunek wartości GM:WM. Badania wykonane były na osobach zdrowych techniką rezonansu magnetycznego MRI lub tomografii PET Prędkość przepływu Bezwzględna wartość prędkości krwi w kapilarach ma także oczywisty związek z jakością perfuzji. Mieści się ona w granicach od kilkudziesięciu centymetrów na sekundę w dużych tętnicach do około 1mm/s w kapilarach. W tętnicach przepływ ma charakter silnie pulsacyjny, związany z akcją serca. W kapilarach efekt ten jest mało zauważalny, jednak nadal prędkość przepływu jest zmienna [VILL94], co najprawdopodobniej związane jest z elastycznością czerwonych ciałek oraz ich rozmiarami, które są porównywalne ze średnicą kapilar. Parametry CBF, CBV i prędkość przepływu są istotnymi składnikami oceny perfuzji tkankowej, lecz żaden z nich nie może traktowany jako miara perfuzji bez uwzględniania wartości pozostałych. Na przykład wzrost wartości CBF może być spowodowany poprzez dwa niezależne czynniki: przez zwiększenie prędkości przepływu bez zmian objętości naczyń, bądź też zwiększenie CBV przy zachowaniu stałej prędkości przepływu. Potwierdza to, że ani ocena prędkości ani ocena CBV nie daje jednoznacznej oceny perfuzji. Ilustracją tej sytuacji jest rysunek 3.3. Pokazano na nim schematycznie dwa układy kapilar (1 i 2) o tej samej objętości CBV i takiej samej prędkości przepływu krwi V. Pomimo jednakowej wartości parametrów CBV i V dla obu układów, wartość CBF jest w obu przypadkach różna: CBF1 = 2CBF2, co wynika z różnego przepływu krwi w tętnicach zasilających oba układy: F1 = 2F2. Pokazuje to bardzo dobitnie konieczność równoczesnej oceny kilku parametrów perfuzji. 1
29 Rysunek 3.3. Ilustracja zależności pomiędzy parametrami opisującymi przepływy naczyniowe. Z rysunku wynika, że pomiar CBV i prędkości przepływu nie jest wystarczający do określenia CBF. Wartości CBV i prędkości przepływu w układach 1 i 2 są identyczne, pomimo tego wartości CBF są różne [BUXT2] Średni czas przejścia MTT Z powodów opisanych powyżej w badaniach perfuzyjnych definiuje się jeszcze jeden parametr, nazywany średnim czasem przejścia (MTT, ang. Mean Transit Time), który zastępuje prędkość przepływu i jest bezpośrednio powiązany z wartościami CBV i CBF zależnością: MTT = CBV CBF (3.1) wynikającą z teorii rozcieńczania znacznika [STEW94], która została szczegółowo omówiona w osobnym rozdziale rozprawy (rozdz.4). Korzystając z tej zależności i podstawiając do niej na przykład podane wcześniej wartości CBV i CBF typowe dla istoty szarej (CBV = 4% i CBF = 6ml/min/1ml) otrzymamy MTT = 4 s. Wartości parametru MTT dla istoty białej i szarej zaczerpnięte z literatury przedstawia tabela
30 Źródło Płeć M/K Wiek Technika badania GM WM GM:WM [HUNS2] 7/ DSC MRI b.d. b.d.,9±,1 [KOSH99] 8/ DSC MRI 6,8±1,3 7,8±1,1,8±b.d. [NIGH97] 8/ DSC MRI b.d. b.d. 1,1±b.d. [SCHR98] 13/ DSC MRI 4,7±,8 5,4±1,1,9±b.d. [VONK99] 41/ 4-86 DSC MRI 6,4±1,8 6,9±2,3,9±b.d. [OSTE96a] 6/ DSC MRI 2,62±,6 3,19±,93,8±b.d. Tabela 3.3. Średnie czasy przejścia MTT (s) dla istoty szarej (GM) i białej (WM) podawane w literaturze. Wszystkie pomiary zostały wykonane techniką MR. Z przedstawionego rozumowania wynika, że definicja perfuzji zawiera w sobie wiele subtelności. Najściślej z jakością perfuzji wiąże się wartość CBF, jednak pozostałe parametry również powinny być uwzględniane w ocenie. Nawiązując ponownie do rysunku 3.2 można zauważyć, że w objętości V tkanki mogą się znajdować takie tętnice bądź żyły, które jedynie przez nią przechodzą, nie biorąc udziału w jej zasilaniu. Nasuwa to wniosek, że obserwacja samego przepływu krwi w tkance nie pozwala na ocenę CBF. Pomimo to istnieją techniki opierające się na pomiarze ruchliwości krwinek na przykład Laser Doppler [DOER97], wykorzystujący przesunięcie częstotliwości światła odbitego od poruszających się czerwonych ciałek [DIRN89, STER75]. W technice tej stosunek ilości światła odbitego o widmie przesuniętym do światła o widmie nie przesuniętym jest miarą ilości komórek poruszających się, a przesunięcie widma miarą ich średniej prędkości. Jednak, jak wspomniano, tylko część krwi przepływającej przez badaną objętość składa się na wartość CBF. Wyłania się zatem podstawowe zagadnienie związane z oceną perfuzji. To nie ruchliwość, czy prędkość przepływu krwi w badanej objętości określa CBF, ale dopływ krwi tętniczej do kapilar. Dlatego do oceny objętości krwi tętniczej zaopatrującej dany fragment tkanki wykorzystuje się technikę znaczników, która została opisana w następnym rozdziale. 3.3 Tomograficzne badanie dynamiczne z wykorzystaniem środka cieniującego Tomograficzne badanie dynamiczne polega na wykonaniu, w krótkich odstępach czasowych, serii obrazów tomograficznych tego samego fragmentu ciała. W badaniach perfuzyjnych w czasie akwizycji danych podawany jest do krwioobiegu środek kontrastowy. Czas trwania wstrzyknięcia powinien być możliwe krótki (ang. Bolus injection). Otrzymane w ten sposób obrazy zawierają w sobie informację o zmianach koncentracji środka cieniującego w czasie. 12
31 Rysunek 3.4. Schemat drogi środka cieniującego w badaniu perfuzyjnym: a) żyła w przedramieniu, RV) prawa komora serca, P) płuca, LV) lewa komora serca, b) tętnica zasilająca badany organ, b') tętniczka zasilająca kapilary w wybranym fragmencie badanego organu, c) fragment tkanki odpowiadający pikselowi obrazu. Współczesny sprzęt obrazujący spełnia wymagania stawiane badaniom dynamicznym ośrodkowego układu nerwowego, pozwalając na wykonanie obrazów wielu warstw w ciągu jednej sekundy. Zwykle w pojedynczym badaniu wykonywanych jest kilkadziesiąt obrazów. Typowe badanie perfuzyjne głowy trwa 4 6 sekund. Środek kontrastujący wstrzykiwany jest do żyły w przedramieniu w ciągu kilku sekund. Kontrast miesza się z krwią i pokonuje drogę przez prawą komorę serca, płuca i lewą komorę serca, skąd przez tętnice rozpływa się wraz z krwią do wszystkich organów, co schematycznie pokazano na rysunku 3.4. Niestety, w czasie pokonywania tej drogi środek kontrastowy ciągle miesza się z krwią, a prędkość narastania jego stężenia w kolejnych odcinkach krwiobiegu traci początkowy impulsowy Rysunek 3.5. Przykład wyniku typowego badania perfuzyjnego MR. Na górze widoczny jest oryginalny obraz w chwili przejścia maksymalnej koncentracji środka kontrastującego. Poniżej pokazano zmiany jasności dla pojedynczego piksela. Dla badania MR charakterystyczne jest odwrócenie krzywej, co zostanie szczegółowo omówione w rozdziale dotyczącym środków kontrastowych. 13
32 Rysunek 3.6. Zmiana kształtu krzywej koncentracji c(t) na drodze od miejsca iniekcji do badanej tkanki. Oznaczenia rysunków (a,b,c) odpowiadają opisowi do rysunku 3.4. Na rysunku uwzględniono skalę czasową, co pozwala uwidocznić czas dojścia kontrastu do poszczególnych miejsc. Czas jest momentem rozpoczęcia iniekcji środka cieniującego do żyły, przez t oznaczono moment pojawienia się bolusa w tętnicy zasilającej badany organ, t jest czasem dojścia bolusa od tętnicy zasilającej do badanej tkanki. charakter (rysunek 3.6). Przy dobrze wykonanym badaniu na obrazach analizowanego obszaru powinny być widoczne trzy fazy: 1) stan poprzedzający dotarcie kontrastu, 2) okres przepływu kontrastu, kiedy obserwowane jest napływanie znacznika, a następnie jego wypłukiwanie, 3) powrót do stanu odpowiadającego fazie pierwszej (rys 3.7). Zanik kontrastu po pierwszym przejściu bolusa przeważnie nie jest całkowity. Związane to jest z recyrkulacją oraz ewentualną kumulacją środka cieniującego w tkance. W różnych technikach obrazowych zmiany stężenia znacznika uwidaczniane są w różny sposób w CT wzrost stężenia znacznika powoduje wzrost jasności obrazu, w technice MR, w zależności od techniki wykonywania badania, może powodować albo wzrost albo spadek jasności. Dlatego pierwszym etapem analizy perfuzji jest wyznaczenie zmian koncentracji znacznika (lub wielkości proporcjonalnej do tej koncentracji) na podstawie zmian w jasności obrazu. Sposób przeliczania, zależny od techniki pomiarowej, będzie opisany w dalszej części 14
33 pracy. Otrzymana w ten sposób znormalizowana seria obrazów jest punktem wyjścia do dalszych analiz. Dla każdego piksela należącego do tkanki mózgowej tworzymy w ten sposób krzywą dynamiczną koncentracji środka cieniującego, czyli przebieg koncentracji w funkcji czasu. Rysunek 3.7. Kolejne fazy krzywej dynamicznej, jakie można wyróżnić w prawidłowo wykonanym badaniu perfuzyjnym: 1) faza przed napłynięciem kontrastu, tzw. linia bazowa, 2) faza pierwszego przejścia i wymywania środka cieniującego, 3) powrót do linii bazowej. Linią przerywaną zaznaczono efekt recyrkulacji środka cieniującego Rysunek 3.7 przedstawia wyidealizowany przebieg zmian koncentracji znacznika w funkcji czasu. Nie uwzględniono na nim zaszumienia danych pomiarowych. Źródłem szumów w krzywych dynamicznych jest zarówno sama technika obrazowania, jak też sposób prowadzenia tego typu badania. Dla techniki CT szumy w obrazie związane są ze statystycznym charakterem promieniowania X, jakością detektorów i toru przetwarzającego oraz z jakością generatora wysokiego napięcia. W technice MR szumy w obrazie związane są głównie z drganiami termicznymi spinów oraz jakością toru odbiorczego. Wspomniane źródła szumów wynikają wyłącznie z techniki obrazowania i nie zależą od rodzaju przeprowadzanego badania. W badaniach dynamicznych pojawiają się dodatkowe źródła zakłóceń krzywych kontrastu w funkcji czasu, związane z przebiegiem badania. Należy pamiętać, że obrazowanie w tego typu badaniach trwa kilkadziesiąt sekund, należy się więc liczyć z ruchami pacjenta. Powodują one, że krzywa dynamiczna dla pojedynczego piksela obrazu może zawierać w sobie informację o różnych fragmentach tkanki. O ile ruchy pacjenta można eliminować stosując różnego rodzaju zabezpieczenia (paski i uchwyty unieruchamiające), to eliminacja ruchów związanych z fizjologicznymi czynnościami organizmu jest niemożliwa składają się na nie tętnienia związane z krążeniem krwi, ruchy oddechowe, ruchy jelit w przypadku dynamicznego obrazowania części brzusznej. Kolejnym elementem wprowadzającym zakłócenia do krzywych dynamicznych 15
34 jest sposób podawania kontrastu. Wspomniano wcześniej, że podanie powinno być możliwie krótkie. Oczywiście ograniczeniem jest wytrzymałość naczyń krwionośnych. Typowo podanie kontrastu trwa kilka sekund. Oczekuje się, że prędkość podawania będzie w tym czasie równomierna. Warunek ten jest spełniony gdy stosowane są automatyczne strzykawki. Często jednak zdarza się, że środek kontrastowy podawany jest przez personel medyczny z ręki, trudno wtedy mówić o jednorodnej prędkości podawania. Koncentracja środka cieniującego będzie się zmieniać w zależności od prędkości podawania, wprowadzając dodatkowe zakłócenia w krzywych dynamicznych. Wszystkie opisane powyżej czynniki mają wpływ na jakość otrzymywanych obrazów parametrycznych generowanych na podstawie krzywych dynamicznych. Dokładniej sposób tworzenia obrazu parametrycznego opisany jest w następnym rozdziale. Należy dodać, że oryginalne dane mogą być wstępnie poddawane dodatkowym etapom przetwarzania, takim jak segmentacja, kompensacja ruchów pacjenta czy automatyczna detekcja naczyń krwionośnych. Nie jest to jednak przedmiotem niniejszej pracy, w której skupiono się na przetwarzaniu danych związanych wyłącznie z krzywą dynamiczną kontrastu. 3.4 Idea obrazów parametrycznych Ze względu na bardzo dużą liczbę obrazów otrzymywanych w badaniu perfuzyjnym, ich interpretacja bez odpowiedniego wstępnego przetworzenia jest praktycznie niemożliwa. Dla typowego 4-sekundowego badania perfuzyjnego, w którym obrazowane jest 9 warstw z rozdzielczością czasową równą jednej sekundzie, otrzymuje się 36 obrazów. Taką serię Rysunek 3.8. Schemat przetwarzania dynamicznej serii obrazów w mapę parametryczną. 16
35 obrazów można zaprezentować w formie animacji, wyświetlając w szybkim tempie kolejne obrazy (tzw. cine mode ), ale pozwala to jedynie na bardzo uogólnioną i subiektywną ocenę diagnostyczną, nie dając podstaw do oceny ilościowej procesów perfuzji. Alternatywnym rozwiązaniem jest prezentacja wyniku badania w formie zespołu obrazów parametrycznych, zwanych również mapami parametrycznymi. Rysunek 3.8 przedstawia ideę tworzenia takiego obrazu. Każdemu pikselowi obrazu możemy przyporządkować tzw. krzywą dynamiczną (o długości równej liczbie obrazów w serii), która odwzorowuje zmiany jasności tego piksela w kolejnych obrazach (rys.3.8). Jeśli każdą z takich krzywych opiszemy pojedynczym parametrem, którym może być np., jak pokazano na rys.3.8, czas osiągnięcia maksimum stężenia środka cieniującego mierzony od chwili rozpoczęcia akwizycji - TTP (ang. Time to Peak), to wartość tego parametru możemy przypisać odpowiedniemu elementowi nowego obrazu, o rozmiarach obrazu oryginalnego, tworząc w ten sposób tzw. mapę parametryczną. Mapa taka może, oczywiście, obrazować dowolny parametr krzywych dynamicznych. Metody analizy i przetwarzania krzywych dynamicznych zostały opisane w osobnym rozdziale rozprawy, dotyczącym teorii rozcieńczania znacznika (rozdz.4). Otrzymana w ten sposób mapa jest podstawą do dalszej oceny. Podejście takie daje znaczącą redukcję liczby obrazów diagnostycznych (dla podanego wcześniej przykładu otrzymamy 9 map parametrycznych po jednej dla każdej warstwy w miejsce 36 obrazów oryginalnych). 3.5 Środki kontrastowe Zarówno w tomografii komputerowej, jak i w tomografii MR w celu oceny przepływu krwi stosuje się znaczniki kontrastujące. Ze względu na różne fizyczne mechanizmy tworzenia obrazu, różne są używane kontrasty w tomografii komputerowej są to związki jodowe, natomiast w rezonansie magnetycznym substancje paramagnetyczne Jodowe środki cieniujące W badaniach perfuzyjnych wykonywanych techniką komputerowej tomografii rentgenowskiej stosuje się tzw. pozytywne środki cieniujące [GOLE] rozpuszczalne w wodzie. Do grupy tej należą środki jodowe. Charakteryzują się one znacznie większym od tkanek współczynnikiem pochłaniania promieniowania (od 5 do 1 razy). Z punktu widzenia badań ilościowych ogromną zaletą środków jodowych jest liniowa zależność współczynnika pochłaniania (a - co za tym idzie zmian jasności w obrazie) od koncentracji znacznika. Rysunek 3.9 przedstawia krzywe dynamiczne otrzymane w perfuzyjnym 17
36 Rysunek 3.9. Krzywe dynamiczne jasności obrazu (po lewej) i koncentracji znacznika (po prawej) w badaniu CT. Koncentracja znacznika wyrażona w jednostkach arbitralnych (Arbitrary Units). badaniu CT. Sposób przeliczania jednostek jasności pikseli na wartości proporcjonalne do koncentracji środka cieniującego polega na odjęciu od wszystkich punktów krzywej wartości odpowiadającej linii bazowej S przebiegu: C t =S t S ; S = N baseline 1 N baseline S t. (3.2) t = gdzie Nbaseline oznacza liczbę próbek sygnału należących do linii bazowej, przed napłynięciem kontrastu do badanego obszaru. Jodowe środki kontrastowe mogą, niestety, powodować u pacjentów reakcje uczuleniowe. Wyniki badań epidemiologicznych mówią o występowaniu lekkich powikłań u około 1% badanych. Przypadki ciężkie, wymagające leczenia ale nie zagrażające życiu, pojawiają się u 1-2% populacji osób badanych. Zejścia śmiertelne są niezwykle rzadkie, od 1:5 do 1:1 przypadków [GOLE]. Rysunek 3.1. Krzywe dynamiczne jasności obrazu (po lewej) i koncentracji (po prawej) w badaniu MR. Przeliczenie z jednostek jasności na koncentrację wykonuje się korzystając z zależności (3.3). Wartość linii bazowej S obliczana jest w taki sam sposób jak dla badań CT (wzór (3.2)). Koncentracja znacznika wyrażona w jednostkach arbitralnych (Arbitrary Units). 18
37 3.5.2 Paramagnetyczne środki cieniujące Działanie środków kontrastowych stosowanych w badaniach rezonansu magnetycznego polega na zmianie parametrów magnetycznych tkanek nasyconych takim środkiem [LAUF96]. Środkami najczęściej obecnie stosowanymi w badaniach perfuzyjnych są związki gadolinu, posiadającego 7 wolnych elektronów, które generują lokalne silne niejednorodności pola magnetycznego, powodujące przyspieszenie procesów relaksacyjnych. W badaniach nie wykorzystujących szybkich technik obrazowania podanie związków gadolinu do krwi powoduje wzmocnienie obrazu, rozumiane jako wzrost jasności. Wraz z zastosowaniem szybkich technik, takich jak EPI (ang. Echo Planar Imaging) odkryto nowe właściwości środków gadolinowych. W czasie przejścia kontrastu przez badany organ zaobserwowano spadek jasności w obrazach [VILL88]. Efekt ten jest wynikiem lokalnych zaburzeń pola magnetycznego powodowanych przez znaczny moment magnetyczny gadolinu. W mózgu środek kontrastowy nie przedostaje się do przestrzeni międzykomórkowej, wynikiem czego jest powstawanie silnych mikroskopowych gradientów pola magnetycznego na granicy naczyń krwionośnych [FISE91, ROSE9]. Aby efekt taki mógł być zaobserwowany, konieczne jest podanie środka o dużej koncentracji w krótkim czasie. Badania dynamiczne MR (DSC-MRI, ang. Dynamic Susceptibility Contrast) są aktualnie podstawową techniką badań perfuzyjnych MR [EDEL9, ROSE91]. Krzywe dynamiczne dla badania perfuzyjnego MR pokazano na rysunku 3.1. Zaletą gadolinowych środków kontrastowych jest to, że działania niepożądane występują u zaledwie 1-2% osób badanych, a liczba ciężkich powikłań, wymagających leczenia, dotyczy tylko,1% pacjentów [GOLE]. Zostało udowodnione teoretycznie i potwierdzone eksperymentalnie, że zmiana częstotliwości relaksacji w danym wolumenie (VOI) jest proporcjonalna do koncentracji znacznika [BUXT2]. Koncentrację znacznika można obliczyć przy pomocy relacji: C t S t 1 ln, TE S (3.3) gdzie S(t) jest sygnałem w danym VOI, S jest średnią wartością sygnału w VOI przed wstrzyknięciem znacznika, a TE jest czasem echa. Wadą środków paramagnetycznych istotną z punktu widzenia badań ilościowych jest nieliniowa zależność zmian jasności obrazu od koncentracji znacznika [BUXT2]. 19
38 4. Teoria rozcieńczania znacznika W rozdziale tym opisana zostanie teoria rozcieńczania znacznika, będąca podstawą dalszych rozważań. Znacznikiem nazywać będziemy substancję, która wprowadzona do krwiobiegu może być zidentyfikowana na obrazach tomograficznych. Założeniem teorii rozcieńczania jest to, że środek cieniujący nie może wydostawać się poza objętość naczyń krwionośnych. W przypadku mózgu warunek ten jest zapewniony przez istnienie bariery krew mózg (BBB ang. blood brain barrier). Przyjmijmy model systemu kapilar w tkance. Zakładamy, że system ten w wybranym fragmencie tkanki ma jedno wejście i jedno wyjście (rysunek 4.1) i znajduje się w nim objętość cieczy V, która wpływa i wypływa ze stałym przepływem F. W ogólności system kapilar jest strukturą rozgałęzionych i poprzeplatanych ze sobą naczyń krwionośnych. Następstwem tego jest fakt, że cząsteczki cieczy wpływające do systemu w tym samym momencie czasowym potrzebują różnego czasu na dotarcie do wyjścia. Czas ten zależny jest od drogi, którą przemieszczać się będzie określona cząsteczka. Z tego powodu nie można mówić o pojedynczej wartości określającej czas przejścia, a o rozkładzie prawdopodobieństwa czasów przejścia. Rozkład ten jest obserwowany podczas eksperymentu. Rysunek 4.1. Model systemu kapilar zastosowany w torii rozcieńczania znacznika. W teorii rozcieńczania znacznika w celu określenia objętości V i przepływu F przyjmuje się jeszcze dodatkowe założenia: 1) rozkład czasów przejścia cząsteczek jest niezmienny w trakcie trwania eksperymentu, czyli przepływ jest stacjonarny; 2) właściwości przepływu środka cieniującego i cieczy wypełniającej system są takie same, czyli rozkłady czasów przejścia dla cieczy i dla znacznika są jednakowe; 3) system jest drożny i szczelny, czyli kapilary nie są zatkane oraz ciecz nie ma możliwości opuszczenia systemu inną drogą niż przez wyjście (założenie to jest konieczne tylko do obliczenia objętości V, a nie ma wpływu na obliczenia przepływu F); 4) wykluczona jest recyrkulacja znacznika, czyli 2
39 cząsteczki znacznika w czasie eksperymentu przepływają przez system tylko raz. Aby móc zastosować powyższe założenia, konieczne jest wprowadzenie znacznika przed wejściem do systemu i pomiar jego koncentracji w funkcji czasu na jego wyjściu lub w samej objętości (rysunek 4.1). Znacznik może być wprowadzany na dwa sposoby: w sposób ciągły (zbliżony do skoku jednostkowego) lub w postaci bolusa, czyli krótkotrwałego wstrzyknięcia. W obu przypadkach należy zachować stałą szybkość wprowadzania znacznika. Krzywe koncentracji znacznika na wyjściu układu dla obu przypadków pokazuje rysunek 4.2. Hamilton wykazał, że krzywa dla iniekcji ciągłej jest całką krzywej dla iniekcji w postaci bolusa [HAMI49]. 4.1 Iniekcja impulsowa - bolus Rozpatrzmy w pierwszej kolejności przypadek pobudzenia impulsowego. Przez pobudzenie impulsowe rozumiane jest krótkotrwałe wstrzyknięcie kontrastu w czasie wielokrotnie krótszym od czasu trwania pomiaru. W takich warunkach można zastosować analogię do pobudzenia impulsowego znanego z dziedziny przetwarzania sygnałów. Pobudzenie nieskończenie krótkim impulsem jest w przypadku badań perfuzyjnych, z oczywistych względów, niewykonalne. Biorąc pod uwagę przyjęte w poprzednim podrozdziale założenia, znacznik po wprowadzeniu do systemu po pewnym czasie musi opuścić go w całości przez wyjście. Wynikiem pomiaru koncentracji w funkcji czasu na wyjściu układu jest krzywa o kształcie pokazanym na rysunku 4.2.A. Im większy jest przepływ krwi w badanym obszarze, tym mniejsza będzie koncentracja znacznika, ponieważ wymiesza się on z większą ilością napływającej cieczy. Zależność taka jest podstawą do ilościowej oceny przepływu. Przyjmijmy więc, że q jednostek objętości znacznika zostało Rysunek 4.2. Krzywe koncentracji znacznika na wyjściu układu w funkcji czasu dla iniekcji A) impulsowej (bolus) i B) ciągłej. Linią przerywaną na rysunku A pokazano możliwy do zaobserwowania efekt ponownego napływania znacznika, tzw. recyrkulacji, co zostało opisane w dalszej części pracy. 21
40 wprowadzone na wejściu systemu i oznaczmy koncentrację na wyjściu jako c(t). Ilość znacznika, która opuszcza system w wąskim przedziale czasowym od t do t+dt jest koncentracją znacznika na wyjściu pomnożoną przez objętość cieczy wypływającej przez wyjście w tym samym czasie. Całkowita ilość znacznika może więc być obliczona z zależności: q= c t F dt=f c t dt. (4.1) Wynika stąd, że powierzchnia pod krzywą koncentracji znacznika w funkcji czasu (całka) jest równa q/f. Przepływ F można wyznaczyć jako: q F= c t dt. (4.2) Jak wynika z powyższych rozważań, Fc(t) jest wielkością opisującą szybkość z jaką znacznik opuszcza system w chwili t. Dla dalszych rozważań wygodnie będzie wprowadzić funkcję h t = Fc t, q (4.3) która jest frakcją wprowadzonego znacznika opuszczającą system w jednostce czasu, a przy założeniu, że rozkład czasów przejścia cieczy i znacznika jest taki sam także częścią cząsteczek cieczy, które wpłynęły do systemu w chwili t= i wypłynęły z układu do chwili t. Ponieważ wszystkie cząsteczki wprowadzone w chwili t= muszą w końcu opuścić system, to: h t dt=1. (4.4) Funkcja h(t) jest zatem rozkładem czasów przejścia, lub inaczej funkcją przejścia układu. Podstawowa w tej teorii zależność, że objętość V jest równa iloczynowi przepływu F i średniemu czasowi przejścia cząstek cieczy przez układ może być wyjaśniona w następujący sposób: przyjmujemy, że kapilary w chwili t= są wypełnione cieczą. Czas przejścia cząsteczek cieczy od wejścia do wyjścia układu jest różny, w zależności od drogi. Przyjmijmy, że rozróżniamy cząsteczki na podstawie ich czasu przejścia. Aby określić objętość V systemu konieczne jest określenie objętości tylko tych cząsteczek, których czas przejścia jest zbliżony do t (mieści się w przedziale od t do t+dt) i zsumowania tych objętości dv dla wszystkich kolejnych przedziałów czasowych. Przyjęto, że cząsteczki napływają do 22
41 systemu z szybkością F, a ich część, która opuści system w przedziale czasowym pomiędzy t a t+dt równa jest h(t)dt. Zatem szybkość z jaką napływają i wypływają tego typu cząsteczki wynosi Fh(t)dt. Również cząsteczki tego typu, które znajdowały się w systemie w chwili t= opuszczać go będą z szybkością Fh(t)dt do czasu t, kiedy to wszystkie opuszczą układ. Objętość tych cząsteczek równa będzie iloczynowi czasu potrzebnego na wypłukanie ich z systemu i szybkości wypłukiwania: dv=t Fh(t)dt. Sumując to wyrażenie po czasie otrzymamy: V = tfh t dt=f th t dt. (4.5) Ponieważ h(t) jest rozkładem czasów przejścia, to średni czas przejścia t określony jest jako: t= th t dt, (4.6) V =F t, (4.7) co daje czyli podstawową zależność teorii. Korzystając z zależności (4.2) i (4.3), z uwzględnieniem mierzonej eksperymentalnie krzywej koncentracji znacznika c(t), otrzymamy: tc t dt t=. (4.8) c t dt 4.2 Iniekcja ciągła skok jednostkowy Alternatywnym sposobem podawania znacznika jest wprowadzanie ciągłe, co w warunkach eksperymentu sprowadza się do wstrzykiwania w czasie wielokrotnie dłuższym od czasu pomiaru. Pomiar taki można przybliżyć pobudzeniem systemu skokiem jednostkowym. W tym przypadku koncentracja znacznika na wyjściu będzie wzrastała do chwili, w której ciecz nie wymieszana ze znacznikiem całkowicie nie opuści układu (rysunek 4.2.B). Ponieważ znacznik jest wprowadzany na wejściu do systemu ze stałą szybkością I, to jego koncentracja w cieczy wpływającej do układu będzie równa ilorazowi I / F. Wartość ta jest maksymalną koncentracją jaką można zaobserwować na wyjściu. Oznaczymy ją jako Cmax: 23
42 C max = I. F (4.9) Zależność ta została udowodniona przez Stephensona [STEP48] w następujący sposób: jeśli na wejściu wprowadzamy znacznik z szybkością i(t), niekoniecznie stałą, to koncentracja znacznika na wyjściu C(t) określona będzie przez prędkość wprowadzania znacznika do chwili t i przez funkcję rozkładu czasów przejścia h(t). Rozpatrzmy jaki jest udział w koncentracji wyjściowej w chwili t znacznika wprowadzonego do układu o s jednostek czasowych wcześniej, a dokładnie w przedziale od s do s+dt wcześniej. Ilość znacznika wprowadzona w tym czasie wynosi i(t-s)dt, a fragment tej objętości znacznika opuszczająca układ w chwili t, czyli s jednostek później, wynosi h(s). Zatem ilość znacznika opuszczającego układ w chwili t, a wprowadzonego w czasie od s do s+dt przed chwilą t wynosi h(s) i(t-s)ds. Sumując tą wielkość dla wszystkich chwil czasowych poprzedzających t, szybkość z jaką znacznik wypływa z układu w chwili t możemy zapisać jako i t s h s ds. Ponieważ z drugiej strony szybkość ta jest też równa iloczynowi C(t)F, otrzymujemy C t = 1 i t s h s ds. F (4.1) Przyjmijmy, że znacznik jest wprowadzany jako skok jednostkowy o stałej szybkości wprowadzania I: { i t = dla t. I dla t (4.11) Wówczas równanie (4.1) możemy zapisać w postaci: t I C t = h s ds. F (4.12) Ponieważ h(s) jest funkcją rozkładu czasów przejścia, to wyrażenie t H t = h s ds (4.13) jest dystrybuantą tego rozkładu. Ponieważ h s ds=1 to lim H t =1 i równanie (4.12) można zapisać jako t C t = I H t. F (4.14) Dla odpowiednio długiego czasu t wartość funkcji H(t) dąży do jedności, a C(t) do wartości Cmax, co prowadzi do równania (4.9). 24
43 Objętość systemu jest łatwa do określenia, ponieważ w każdej chwili czasowej t ilość Q(t) znacznika w systemie jest równa różnicy ilości znacznika wpływającego i wypływającego z systemu: t t Q t =Qin t Qout t = It FC t dt = [ I FC t ]dt, (4.15) t Q t = I [1 H t ] dt, gdzie: Qin ilość znacznika na wejściu układu, Qout ilość znacznika na wyjściu układu, co wynika z wzoru (4.14). Dla odpowiednio długich czasów t średnia koncentracja znacznika, która wynosi Q(t)/V, osiąga wartość Cmax: lim t Q t I I = [1 H t ]dt=c max=. V V F (4.16) Stąd: V =F [1 H t ]dt. (4.17) Podstawiając wartości koncentracji otrzymane w eksperymencie, możemy zapisać równanie (4.16) jako V= F [C max C t ]dt. C max (4.18) Słuszność przeprowadzonych rozważań można potwierdzić wykazując, że obie metody (z impulsowym i skokowym podawaniem znacznika) prowadzą do tych samych wyników, co porównując równania (4.8) i (4.16) może nie wydawać się oczywiste. Należy zatem wykazać, że [1 H t ]dt w równaniu (4.16) jest średnim czasem przejścia t, który występuje w równaniu (4.8). Można to wykazać całkując t t [1 H s ]ds=t [1 H t ] sh s ds, (4.19) t [1 H t ] sh s ds. [1 H s ]ds=lim t Z rysunku 4.3 wynika, że wartości obu całek muszą być równocześnie skończone lub nieskończone oraz lim t[1 H t ]=. Ponieważ objętość systemu musi być skończona, t to 1 H s ds= sh s ds= t, 25 (4.2)
44 co wykazuje równoważność równań (4.8) i (4.16). Potwierdza to prawidłowość podstawowej zależności V=F t. Rysunek 4.3. Graficzna reprezentacja równania (4.19). 4.3 Model a rzeczywistość Model jest oczywiście tylko pewnym przybliżeniem stanu faktycznego, a obliczenia, choć poprawne z formalnego punku widzenia, będą na tyle dobre na ile model odpowiada rzeczywistości. Omówimy tutaj pewne niedoskonałości opisanego modelu. Wynikają one przede wszystkim z wprowadzonych uproszczeń Budowa układu krwionośnego Podstawową słabością, którą można zarzucić opisanemu modelowi jest dość restrykcyjne założenie, że badany fragment tkanki posiada tylko jedno wejście i jedno wyjście. Spróbujmy więc odnieść się do tego zarzutu. Można przyjąć, że punkty, w których dokonujemy pomiaru koncentracji nie znajdują się na głównym doprowadzeniu i odprowadzeniu krwi, ale odpowiednio za i przed tymi punktami (rysunek 4.1), tak że tętnica zasilająca jest już podzielona na mniejsze tętniczki, a żyły odprowadzające jeszcze nie są połączone w pojedyncze naczynie. Możemy teraz rozpatrzeć kilka przypadków, jakie mogą wystąpić podczas eksperymentu. Jeżeli wstrzykujemy kontrast do jednej z tętniczek w punkcie A' (rys.4.4), a pomiaru koncentracji wyjściowej dokonujemy, tak jak zakładano w modelu, w punkcie B, czyli mamy do czynienia w wieloma wejściami i jednym wyjściem, to pomiar przepływu będzie 26
45 Rysunek 4.4: Ilustracja różnych sposobów przeprowadzania eksperymentu wskazane różne punkty podawania kontrastu i miejsca obserwacji. prawidłowy, natomiast przy pomiarze objętości popełnimy błąd. Zmierzona objętość obejmować będzie tylko tę część systemu, przez którą przepłynął kontrast i dla której średni czas przejścia będzie taki sam jak dla miejsca wprowadzania kontrastu, co wynika z równania (4.5). Inny przypadek wystąpi gdy wstrzyknięcia dokonamy, tak jak zakładano w modelu, do wejścia głównego (punkt A), ale pomiar koncentracji wyjściowej nastąpi w jednej z żył przed ich połączeniem, czyli na przykład w punkcie oznaczonym B' (rys.4.4). Mamy zatem sytuację, w której układ ma pojedyncze wejście i wiele wyjść. I tym razem pomiar przepływu będzie prawidłowy, natomiast zmierzona objętość będzie zawierać tylko ten fragment układu, dla którego średni czas przejścia jest taki sam jak dla miejsca, w którym dokonywany jest pomiar. Wynika to, tak jak w poprzednim przypadku, z równania (4.5). Gdy wstrzyknięcie następuje w punkcie A', a pomiar koncentracji wyjściowej w punkcie B', sytuacja wymaga przyjęcia kolejnych uproszczeń. Pierwsze z nich polega na przyjęciu, że we wszystkich wyjściach krzywa koncentracji wygląda tak samo, wtedy sytuacja jest taka sama jak dla przypadku z wieloma wejściami i jednym wyjściem. Drugie założenie jest jeszcze bardziej restrykcyjne. Przyjmuje się bowiem, że dla danego wyjścia składowe przepływu pochodzące od różnych wejść są proporcjonalne do przepływu w tych wejściach. Można wtedy przyjąć, że maksymalna koncentracja będzie proporcjonalna do przepływu, a obliczona objętość obejmuje te fragmenty układu, dla których średni czas przejścia ważony przez przepływ w punktach wejściowych jest taki sam jak dla miejsca pomiaru Czas iniekcji Drugą widoczną rozbieżnością pomiędzy założeniami teoretycznymi modelu a rzeczywistymi warunkami pomiaru jest czas wprowadzania znacznika do krwiobiegu. W modelu założono, że całą ilość q znacznika wprowadza się w chwili t=, tak aby 27
46 odpowiadało to pobudzeniu układu deltą Diraca. Jest to oczywiście niemożliwe, chociażby ze względu na wytrzymałość żyły, do której wstrzykiwany jest środek cieniujący. Typowo czas iniekcji wynosi kilka sekund, a szybkość wstrzykiwania nie przekracza 5 ml/s. W dalszej części pracy wykazane jednak zostanie, że kształt krzywej koncentracji w funkcji czasu na wejściu układu może być uwzględniony w obliczeniach i nie ma to wpływu na ich jakość Stacjonarność układu Kolejną niedoskonałością modelu jest przyjęcie założenia o stacjonarności całego układu. O ile w warunkach czysto doświadczalnych spełnienie tego warunku jest łatwe, to przy pomiarach in-vivo zupełnie nie odpowiada to rzeczywistości. Główną przyczyną jest pulsacyjny charakter przepływu krwi w organizmie człowieka. Dodatkowo wpływ mogą mieć zmiany objętości łożyska naczyniowego, choć są to procesy relatywnie wolne w stosunku do czasu trwania pomiaru. Ponieważ są to czynniki czysto fizjologiczne, usunięcie ich jest niemożliwe. Z tego punktu widzenia technika z iniekcją ciągłą jest mniej wrażliwa na opisane zjawiska. Ze względu na długi czas badania, zmiany przepływu wynikające z rytmu serca są w trakcie pomiaru uśredniane. Im więcej uderzeń serca w trakcie badania, tym wyniki pomiaru są bliższe wynikom dla układu stacjonarnego. W czasie eksperymentu z wstrzyknięciem impulsowym również następuje uśrednianie, lecz tylko w zakresie od kilku do kilkunastu uderzeń Recyrkulacja Powtórne napływanie kontrastu do obszaru, w którym prowadzony jest pomiar jest nieuniknione w przypadku zamkniętego obiegu cieczy. A zatem eliminacja wpływu recyrkulacji na wyniki pomiaru w badaniach klinicznych może nastąpić jedynie na etapie przetwarzania danych eksperymentalnych. Metody te zostaną omówione w dalszych rozdziałach pracy. Również przy wprowadzaniu znacznika w sposób ciągły możemy próbować wyeliminować wpływ recyrkulacji, ale w tym przypadku fala recyrkulacji może pojawić się przed zakończeniem podawania środka cieniującego, co może prowadzić do znacznych błędów interpretacji danych. Sposoby minimalizacji wpływu recyrkulacji na obliczenia zostaną omówione w osobnym podrozdziale Właściwości znacznika Jednym z założeń proponowanego modelu przepływu znacznika było przyjęcie, że ciecz i znacznik zachowują się w układzie dokładnie tak samo. Przez perfuzję rozumiemy średni przepływ całej krwi, która składa się jednak z wielu rodzajów komórek. Wiadomo też, że erytrocyty poruszają się szybciej niż pozostałe cząsteczki krwi [ZIER65]. Wynika z tego, 28
47 że parametry przepływu obliczone na podstawie krzywych koncentracji środka cieniującego będą odpowiadały przepływowi i objętości tylko plazmy, w której rozcieńczony jest środek cieniujący, a nie całej krwi. Aby zatem uzyskać prawidłowe wyniki, należy w obliczeniach uwzględnić stosunek objętości krwi do objętości erytrocytów. Parametr ten nazywany jest hematokrytem i oznaczać go będziemy przez Ht. Należy jednak zwrócić uwagę, że hematokryt określany jest na podstawie próbki pobranej z żyły, w której występuje przepływ. W czasie pobierania przez żyłę w jednostce czasu przepływa objętość FE erytrocytów i objętość FP plazmy, czyli całkowita objętość krwi jaka przepływa w jednostce czasu wynosi FE+FP. Zatem obliczona wartość hematokrytu wyniesie [ Ht = ] FE F 1= E 1 F E F P FB i 1 Ht= FP 1, FB (4.21) gdzie FB=FE+FP. A zatem hematokryt zmierzony na podstawie pobranej próbki będzie faktycznie stosunkiem prędkości przepływu erytrocytów do prędkości całej krwi, a nie objętości erytrocytów do objętości całej krwi. Obliczając przepływ krwi na podstawie pomiaru koncentracji znacznika należy więc uwzględnić w obliczeniach współczynnik Ht. W równaniu (4.21) można pominąć operację mnożenia przez 1, wtedy wartość Ht wyrażana jest jako ułamek, a nie w procentach. Obliczenia objętości krwi są jednak bardziej skomplikowane. Z różnicy prędkości przepływu erytrocytów i plazmy wynika różnica w rozkładach czasu przejścia tych substancji. Zatem zastosowanie zależności V=F t spowoduje, że obliczona w ten sposób objętość układu będzie zawyżona, ponieważ średni czas przejścia kontrastu będzie większy niż średni czas przejścia wszystkich składników krwi. Jeśli zapiszemy: F E = zależność F = F P Ht i uwzględnimy 1 Ht V to: t V E VP Ht = t E t P 1 Ht V E =V P i t E t P Ht, 1 Ht (4.22) czyli całkowita objętość krwi VB=VE+VP wynosi V B=V P [ t E t P ] Ht 1. 1 Ht (4.23) Pokazuje to, że aby prawidłowo obliczyć objętość krwi, poza znajomością wartości hematokrytu należałoby ocenić średni czas przejścia elementów morfotycznych. Zostało 29
48 wykazane [ZIER65], że hematokryt wyliczony na podstawie niezależnego pomiaru VP i VE jest mniejszy od zmierzonego przez pobranie krwi z żyły, a współczynnik proporcjonalności, oznaczony jako K, wynosi,91. Jeśli K= (4.24) t E 1. t E Ht t P 1 Ht (4.25) VE F E t E 1 1 = V E V P Ht F E t E F P t P Ht i za FP podstawimy F P =F E 1 Ht, Ht to otrzymamy K= Wykazano eksperymentalnie [FREI49], że średni czas przejścia t P dla osocza waha się w granicach od 1,1 t E do 1,2 t E. Podstawiając średnią wartość z tego zakresu i przyjmując wartość hematokrytu równą 4 otrzymujemy K=,92. Opisane właściwości są uwzględniane dalej przy przejściu z jednostek jasności obrazu na wartości proporcjonalne do koncentracji znacznika. Podsumowując opis teoretycznego modelu stosowanego do ilościowych badań perfuzyjnych mózgu należy powiedzieć, że zarówno w technikach CT, jak i MR wskazane jest stosowanie dożylnego wstrzyknięcia bolusowego. Na wybór ten składa się kilka przyczyn: 1) zjawisko recyrkulacji, które przy wstrzyknięciu tego typu może być łatwo pominięte w czasie przetwarzania danych, 2) obciążenie pacjenta, w szczególności gdy stosowane są jodowe środki kontrastowe oraz 3) ograniczenie ilości używanych środków cieniujących, a co za tym idzie, kosztów badań. Wcześniej wspomniano, że wstrzyknięcie ciągłe (skok jednostkowy) jest korzystniejsze z punktu widzenia uśredniania zjawisk związanych z pulsacyjnym charakterem przepływu krwi, jednak w badaniach perfuzyjnych ze względu na ograniczenie prędkości podawania środka kontrastowego, czas wstrzyknięcia bolusa wynosi kilka sekund, czyli pokrywa kilka uderzeń serca, eliminując w pewnym stopniu wpływ pulsacyjnego charakteru przepływu. Przy badaniach głowy nie stosuje się też, z oczywistych względów, wprowadzania znacznika bezpośrednio na wejściu. Znacznik wprowadzany jest do żyły na przedramieniu. Konsekwencją tego jest mieszanie się znacznika z krwią na drodze od miejsca iniekcji do mózgu i rozmywanie impulsowego charakteru bolusa. Powoduje to, że kształt krzywej koncentracji znacznika na wejściu układu w funkcji czasu (AIF, ang. Arterial Input Function) nie może być przyjmowany a priori i konieczne jest rejestrowanie zarówno krzywej koncentracji wewnątrz układu, jak i na jego wejściu. W technikach tomograficznych jest to łatwo osiągalne, ponieważ protokół badania zapewnia 3
49 takie obrazowanie aby na jednej warstwie (lub jednej z wielu warstw) uwidocznione zostały zarówno fragmenty tkanki, dla której chcemy dokonać oceny perfuzji, jak i tętnice zaopatrujące je w krew. W dalszej części pracy omówione zostaną aktualnie stosowane metody oceny perfuzji oraz zostanie zaproponowana ich modyfikacja, mająca na celu zmniejszenie błędów wynikających ze specyfiki badania. 31
50 5. Charakterystyka podstawowych wielkości stosowanych do oceny perfuzji. Opisana teoria rozcieńczania znacznika jest od wielu lat szeroko stosowana w praktyce klinicznej. Jak wspomniano w poprzednim rozdziale, model, który posłużył do wyprowadzenia teoretycznych zależności odbiega nieco od rzeczywistego zachowania układu krwionośnego. Aby uniknąć błędów w ocenie ukrwienia, możliwe są dwa sposoby działania: przeprowadzenie eksperymentu w taki sposób, aby warunki pomiaru były jak najbardziej zbliżone do zakładanych w modelu i zastosowanie teorii bez dodatkowych uproszczeń; modyfikacja metody przetwarzania danych w taki sposób, by zminimalizować błędy wynikające z rozbieżności pomiędzy modelem a układem rzeczywistym. Pierwsze rozwiązanie jest w praktyce klinicznej trudne do zaakceptowania. Wystarczy wziąć pod uwagę założenie, że środek kontrastowy powinien być wprowadzany na wejściu układu w postaci zbliżonej do pobudzenia impulsowego, co odpowiadałoby wprowadzeniu go z bardzo dużą szybkością do tętnicy szyjnej. Taki protokół badania jest wykluczony ze względu na zagrożenie stwarzane dla pacjenta. Dlatego też oczywistym sposobem postępowania stało się zastosowanie różnych sposobów przetwarzania danych. Szczególnie dynamiczny postęp w tej dziedzinie nastąpił w ostatniej dekadzie. Stało się to możliwe dzięki pojawieniu się szybkich technik tomograficznych, które pozwalają w sposób dynamiczny obrazować przejście kontrastu przez wybrany organ. Aktualnie w dziedzinie badań perfuzyjnych, zarówno w tomografii CT, jak i MR, główny nurt prac związany jest z ilościową oceną parametrów ukrwienia. Celem tych prac jest poszukiwanie takich protokołów badań i algorytmów przetwarzania danych, których rezultatem będą wyniki wyrażone w wartościach bezwzględnych. Tzw. złotym standardem, do którego odnosi się otrzymywane wyniki, jest tomografia PET [OSTE98a, OSTE98b]. Ze względu na ograniczoną dostępność i bardzo wysokie koszty tej techniki zaczęto poszukiwać innych metod obrazowania pozwalających na ocenę perfuzji. Aktualnie większość badań perfuzyjnych wykonuje się techniką CT lub MR. Mówiąc o ocenie ilościowej należy zdać sobie sprawę, że obserwowana w badaniu dla każdego woksela krzywa kontrastu C VOI t zależy od trzech funkcji: koncentracji środka cieniującego na wejściu badanej objętości C a t, funkcji transportu h t będącej rozkładem prawdopodobieństwa czasów przejścia kontrastu przez badaną objętość (woksel), 32
51 bezpośrednio z nią związanej funkcji residuum R t, opisującej jaka część kontrastu wprowadzonego do objętości w chwili t= pozostaje w niej w pozostałych chwilach t. Znajomość wymienionych funkcji jest niezbędna do prawidłowego obliczenia bezwzględnych parametrów perfuzji. 5.1 Tętnicza funkcja wejściowa Jako pierwszy rozpatrzony zostanie problem kształtu przebiegu czasowego koncentracji znacznika na wejściu układu. Jak już wspomniano, ze względów bezpieczeństwa kontrast jest podawany dożylnie w okolicach przedramienia, przez kilka sekund, z szybkością około 3 do 5 ml/s. O ile w miejscu podania można mówić o impulsowym charakterze kształtu krzywej koncentracji (w rozumieniu modelu opisanego w rozdz.4), to w obszarze pomiaru kształt ten będzie zmieniony - rozmyty. Dlatego też wprowadza się pojęcie tętniczej funkcji wejściowej AIF (ang. Arterial Input Function). Konieczność znajomości kształtu funkcji AIF narzuca taki sposób obrazowania, aby tętnica lub tętnice zasilające w krew region zainteresowania były widoczne na obrazach. Nie stanowi to zasadniczego problemu, bowiem w badaniach perfuzyjnych przeważnie wykonuje sie przekroje poprzeczne głowy, na których są widoczne główne tętnice mózgowe (rysunek 5.1). Dla poprawności obliczeń funkcji wejściowej istotny jest prawidłowy wybór pikseli w całości zawierających się w świetle tętnicy. Problem ten nazywany jest w literaturze PVE (ang. partial volume effect) [OSCH1], [SCHA6]. Przypadek gdy wybrany piksel tylko częściowo obejmuje światło tętnicy, a częściowo otaczające je tkanki, prowadzi do błędów w obliczeniach wartości CBV w tkankach. Wynika to z zależności opisujących parametr CBV: C VOI t dt CBV = C a t dt, (5.1) gdzie: CVOI krzywa koncentracji obserwowana w tkance miękkiej, Ca krzywa koncentracji obserwowana w tętnicy. Zaniżenie wartości całki funkcji wejściowej, np. poprzez opisany powyżej efekt, w prosty sposób prowadzi do zawyżenia wartości CBV. Osobnym problemem, który zostanie opisany w osobnym podrozdziale, jest recyrkulacja znacznika. Najprostszą, ale wymagającą dużego doświadczenia od osoby wykonującej analizy metodą określenia obszaru obrazu odpowiadającemu światłu tętnicy jest wybór manualny. Istnieją techniki automatycznej selekcji, oparte głównie na analizie parametrów kształtu 33
52 krzywej koncentracji kontrastu [MURA1], [ASHT5], które wykorzystują fakt, że środek cieniujący pojawia się w tętnicach najwcześniej, koncentracja w nich osiąga największą w całej badanej objętości wartość oraz stosunek maksymalnej wartości krzywej koncentracji do jej szerokości w połowie wysokości (FWHM, ang Full Width at Half Maximum) jest największy. Można zatem stworzyć obraz parametryczny i dokonać jego segmentacji pod kątem wyselekcjonowania klas pikseli odpowiadających tętnicom, tkance miękkiej oraz pozostałym regionom, takim jak kości czy powietrze. Ponieważ nie należy to do głównego nurtu rozprawy, do dalszych rozważań wykorzystywać będziemy technikę doboru manualnego. W typowym badaniu wybiera się od kilku do kilkunastu pikseli. Innym istotnym problemem związanym w funkcją wejściową jest fakt, że mózg zasilany jest w krew przez kilka tętnic (rozdz ). W większości pozycji literaturowych [np.: SMITa, ROSE4, OSTE96a] opisywana jest metoda polegająca na zaznaczaniu pojedynczej tętnicy i przyjęciu założenia, że w pozostałych kształt krzywej koncentracji jest taki sam. Rozwinięciem tej metody jest oznaczanie lewych i prawych arterii [CALA], co wymaga zaznaczenia pikseli należących do lewej i prawej półkuli mózgowej i wykonanie dla nich osobnych obliczeń. Obie metody nie budzą zastrzeżeń w przypadkach braku patologii, jeśli bowiem wszystkie naczynia są drożne, można przyjąć, że przepływ w nich jest zbliżony. W przypadku niedrożności takie założenie zawodzi. a) b) Rysunek 5.1. Typowy przekrój poprzeczny głowy w badaniu perfuzyjnym. Strzałkami oznaczono tętnicę przednią mózgu: a)[xing3], b) prace własne autora. Idealnym zatem byłoby zaznaczenie wszystkich głównych tętnic mózgowia i wykonanie osobnych obliczeń dla każdej z nich. Niestety, takie podejście wymagałoby również zaznaczenia regionów zasilanych w krew przez odpowiadające im tętnice. Być może możliwe byłoby także stworzenie uśrednionego modelu ukrwienia mózgowia i zastosowania go w praktyce klinicznej, lecz wymaga to wykonania dużej liczby badań na zdrowych 34
53 ochotnikach. Możliwe byłoby wtedy stworzenie pewnego wzorca, który mógłby wspomagać automatyczną detekcję tętnic oraz segmentację danych na regiony przez nie zasilane. 5.2 Funkcja przejścia (transportu) Z dotychczasowego opisu problemu wyłania się analogia do poszukiwania funkcji przejścia układu, co jest zagadnieniem znanym w teorii sygnałów. Zakładamy, że jest to system liniowy, stacjonarny i przyczynowy. Określenie funkcji przejścia pozwala na jednoznaczne opisanie parametrów takiego systemu. Z teorii sygnałów wiemy, że sygnał wyjściowy jest splotem sygnału pobudzającego z funkcją przejścia systemu, co będziemy symbolicznie zapisywać jako: t C V t =CBF [ C a t h t ] CBF C a h t d. (5.2) Poszukiwanie funkcji przejścia sprowadza się więc do zagadnienia dekonwolucji (rozplotu) funkcji. W idealnych warunkach pomiarowych, gdy możliwe byłoby pobudzenie impulsowe, otrzymane krzywe koncentracji kontrastu byłyby poszukiwaną przez nas funkcją przejścia. Jednak, jak już wspomniano wcześniej, taki pomiar nie jest możliwy. Funkcja h t jest odpowiedzią impulsową badanej tkanki lub, mówiąc bardziej opisowo, jest rozkładem czasów przejścia cząsteczek kontrastu przez wybrany woksel. Można zatem na tej podstawie obliczyć średni czas przejścia MTT: MTT = t h t dt. (5.3) Występująca we wzorze (5.2) wartość C V t jest koncentracją znacznika na wyjściu układu, czyli w żyle odprowadzającej krew z badanego fragmentu. W praktyce w badaniu tomograficznym obserwujemy natomiast krzywą kontrastu wewnątrz układu C VOI t, a nie na jego wyjściu. Jest to po prostu krzywa dynamiczna dla każdego piksela, którego jasność jest związana z ilością środka kontrastującego jaka znajduje się w danej chwili w naczyniach krwionośnych w objętości tkanki ograniczonej rozmiarem piksela. Dlatego też wzór (5.2) należy zmodyfikować do postaci: t C VOI t =CBF [ C a t R t ] CBF C a R t d, (5.4) gdzie R t jest tzw. funkcją residuum, opisującą jaka część znacznika wprowadzonego w chwili t= nadal pozostaje w badanej objętości (wokselu) w chwili t. Zatem R t =1 H t, (5.5) gdzie H t, jak już wspomniano wcześniej, opisuje jaka część środka cieniującego wprowadzonego w chwili t= opuściła układ do chwili t. Odnosząc to do funkcji transportu 35
54 h t można zapisać: t H t = h d. (5.6) Korzystając z tych zależności można wyrazić średni czas przejścia w zależności od R t, ponieważ t R t =1 h d, (5.7) dr= h t dt, co, podstawiając do zależności (5.3), daje: MTT = t dr, (5.8) [ ] MTT = Rt R t dt = R t dt.. (5.9) Otrzymano w ten sposób zależność MTT od funkcji R t, którą możemy otrzymać rozwiązując równanie (5.4). 5.3 Rozplot - dekonwolucja Do zagadnienia dekonwolucji można podejść w dwojaki sposób. Zależy to od poziomu wiedzy jaką posiadamy na temat działania badanego systemu. Jeśli dysponujemy modelem, stosujemy podejście parametryczne. Obliczenie rozplotu sprowadza się wtedy do optymalizacji parametrów modelu. W odniesieniu do badań perfuzyjnych mózgu funkcję przejścia najczęściej przybliża się funkcją [LASS84], [BASS84]: R t =e t MTT. (5.1) Podejście takie daje dobre rezultaty tylko w przypadku poprawnego działania układu, czyli, w naszym przypadku, braku istotnych patologii przepływu [OSTE99]. Zaletą takiego podejścia jest prostota modelu. Niestety, nie jest on na tyle elastyczny, by można go było Rysunek 5.2. Kształt funkcji przejścia modelu przepływu naczyniowego R(t) przebieg czasowy ilości kontrastu pozostającego w układzie naczyń krwionośnych przy pobudzeniu nieskończenie krótkim impulsem w chwili t=. 36
55 dopasować do sytuacji patologicznych. Wyniki obliczeń są wtedy obarczone dużym błędem. Drugie podejście w identyfikacji parametrów układu jest bardziej uniwersalne. Nie wymaga ono bowiem żadnej wiedzy o badanym układzie. Dysponując danymi pomiarowymi sygnału wejściowego i wyjściowego w przypadku badania dynamicznego z kontrastem są to odpowiednio krzywe koncentracji kontrastu w tętnicach zasilających i w wokselach tkanki obliczamy funkcję przejścia stosując numeryczne metody obliczania rozplotu [OSTE96a, CALA, SMITa, IBAR5]. Z właściwości liniowego splotu wiemy, że splot w dziedzinie czasu jest równoważny mnożeniu w dziedzinie częstotliwości. Korzystając z tej właściwości możemy zapisać splot jako: FT C VOI t = F t FT [C a t R t ]=F t FT [ C a t ] FT [ R t ] ; (5.11) gdzie FT oznacza transformatę Fouriera. Wtedy operację dekonwolucji definiować będziemy jako: R t = { } FT [C VOI t ] 1 FT 1, Ft FT [C a t ] (5.12) gdzie FT-1 oznacza odwrotną transformatę Fouriera. Postępowanie takie wymaga obliczenia transformat Fouriera obu sygnałów, obliczenia ich ilorazu i obliczenia transformaty odwrotnej otrzymanego wyniku. Innym sposobem obliczania dekonwolucji jest metoda macierzowa. Splot zapisujemy wtedy jako: tj i= j C VOI t j = C a R t d t C a t j R t j t i, i= [ C a t 1 C a t 1 t C a t 2 C a t N C a t N 1 ][ ] [ ] R t 1 C VOI t 1 R t 2 = C VOI t 2 C a t 1 R t N C VOI t N (5.13) i rozwiązujemy ten układ równań. Należy pamiętać, że zgromadzone dane są zaszumione, co zostało opisane wcześniej (w rozdziale 3.3). Jakość estymacji funkcji przejścia zależy od stosunku sygnału do szumu (SNR, ang. Signal to Noise Ratio). Z tego powodu obliczenie powyższych równań bez modyfikacji nie prowadzi zazwyczaj do prawidłowego wyniku. Układ równań możemy zmodyfikować wprowadzając wektor błędu i rozwiązać go metodą najmniejszych kwadratów, minimalizując błąd. Inną metodą jest użycie rozkładu macierzy na wartości szczególne (SVD, ang. Singular Value Decomposition) i zastosowanie regularyzacji, co zostanie omówione szczegółowo w kolejnych podrozdziałach. Stosowane są również techniki wstępnej filtracji 37
56 dolnoprzepustowej [OSTE96a, OSTE96b]. Ze względu na szerokie zastosowanie metody SVD do obliczania rozplotu w aktualnie stosowanych rozwiązaniach, zostanie ona omówiona nieco szczegółowiej. Równanie (5.13) można zapisać w postaci macierzowej A b=c, (5.14) gdzie b zawiera elementy wektora R(t) dla i=1... N, c jest macierzą próbek krzywej koncentracji w tkance C VOI t. Szukanym w równaniu (5.14) wektorem jest b, zatem konieczne jest obliczenie macierzy odwrotnej A-1, wtedy b= A 1 c. (5.15) Korzystając z rozkładu macierzy A na wartości szczególne można zapisać ją w postaci A=u w v T, (5.16) gdzie w jest macierzą diagonalną wartości własnych macierzy A: [ w1 w2 w= w N 1 ], wn (5.17) przy czym w 1 w 2 w N 1 w N, natomiast macierze u i v zachowują zależność ut u=v T v= I, (5.18) v vt =I, (5.19) gdzie I oznacza macierz jednostkową. Korzystając z powyższych zależności można napisać: A = u w v 1 T 1 = v T T w u =v w u, (5.2) a ponieważ macierz w jest diagonalna, to [ ] 1 w1 1 w2 w 1= 1 w N 1. (5.21) 1 wn Podstawiając do równania (5.15) otrzymuje się zależność na poszukiwany wektor b: 38
57 1 T (5.22) b=v w u c. Ze względu na charakter danych perfuzyjnych, macierz A może być źle uwarunkowana numerycznie. Wynika to z silnego zaszumienia danych pomiarowych oraz dużej liczby elementów o wartości bliskiej zeru. Efektem tego jest występowanie w macierzy w elementów o wartości bliskiej, a to prowadzi do pojawienia się silnych oscylacji w wynikowym wektorze b. Wynik ten nie ma uzasadnienia w odniesieniu do kształtu funkcji residuum (rys.5.1) i jego fizjologicznego znaczenia. Dlatego też wprowadza się regularyzację macierzy w poprzez odcięcie jej elementów o wartości poniżej ustalonego progu i podstawienie zmodyfikowanej macierzy w': [ w1 ' w'= w2' ], wn ' w N 1 ' (5.23) gdzie { 1 w i ' = wi dla wi, (5.24) dla wi gdzie jest progiem odcięcia. Wtedy równanie (5.22) przyjmuje postać b=v w ' u T c. (5.25) Metoda ta nazywana jest w skrócie TSVD (ang. Truncated Singular Value Decompositon). Osobnym zagadnieniem jest odpowiedni dobór wartości progu. Związane jest to z zagadnieniem regularyzacji, co w pracy tej nie będzie szczegółowo omawiane. Dla rozwiązań z dziedziny badań perfuzyjnych próg ten jest ustalany na poziomie 2% wartości maksymalnej elementów macierzy w [OSTE96a, OSTE96b]. Zaprezentowane podejście odpowiada rozwiązaniu równania (5.15) metodą najmniejszych kwadratów minimalizując normę macierzy A b c. (5.26) Istnieje jeszcze wiele innych metod podejścia do problemu dekonwolucji i kilka z nich było testowanych w ramach prowadzonych badań, lecz ze względu na efektywność oraz dość szerokie zastosowanie w analizie klinicznych badań perfuzyjnych w dalszej części skupiono się na metodzie TSVD oraz jej modyfikacji. Zaszumienie danych pomiarowych nie jest jedynym problemem. Równie istotnym zjawiskiem, mającym wpływ na jakość uzyskiwanego wyniku, jest opóźnienie funkcji 39
58 wejściowej i jej zniekształcenie (rozmycie) (rysunek 3.6), zależne od miejsca obserwacji. O ile krzywe kontrastu dla tkanki mierzone są dokładnie w regionie zainteresowania, to pomiar krzywej wejściowej odbywa się w pewnej odległości od badanej tkanki, przeważnie od kilku do kilkunastu centymetrów. Zatem od miejsca pomiaru do wejścia badanego fragmentu środek cieniujący, którego koncentrację obserwujemy, pokonuje bliżej nie określoną drogę. Tętnica rozdziela się na mniejsze naczynia, rozprowadzające krew po całej objętości tkanki. Należy zatem założyć, że czas dojścia pobudzenia jest różny dla różnych fragmentów mózgu. Zmienia się także kształt krzywej koncentracji znacznika w obszarze zainteresowania, ale w niewielkim stopniu, należy więc skupić się głównie na opóźnieniu bolusa. Ponieważ perfuzja jest proporcjonalna do wartości funkcji residuum dla t=, oznaczonej R() [CALA6], to uwzględnienie opóźnienia funkcji pobudzającej ma niebagatelny wpływ na wyniki, co zostało wykazane w badaniach symulacyjnych. W niektórych publikacjach proponowany jest wybór do obliczeń maksymalnej wartości funkcji residuum w miejsce wartości R(), co do pewnego stopnia ogranicza wpływ opóźnienia [OSTE96a, OSTE96b]. Próby eliminacji wpływu opóźnienia są prezentowane w literaturze. Najprostsza z nich polega na detekcji chwili czasowej, w której krzywa koncentracji przekracza próg 1% wartości maksymalnej [RUMI5]. Ze względu na niskie wartości stosunku sygnału do szumu (SNR) w badaniach tomograficznych, metoda ta jest zawodna szczególnie przy obliczaniu map parametrycznych, gdzie brane są pod uwagę krzywe dla pojedynczych wokseli. Konieczne jest filtrowanie krzywych bądź przestrzenne uśrednianie danych. Stosowane jest więc obliczanie opóźnienia na podstawie uśrednionych krzywych koncentracji obliczanych dla pewnych regionów i wprowadzanie korekcji globalnie dla całego obrazu [WILL6]. Takie podejście sprawdza się w przypadku braku silnych zaburzeń przepływu w mózgowiu. Jeszcze inną metodą jest modyfikacja samego algorytmu SVD prezentowana w [WU3b]. Proponowana jest też metoda geometrycznej analizy krzywych koncentracji [ROSE4]. Metody te zostaną dokładniej omówione w rozdziale poświęconym korekcji opóźnienia krzywej koncentracji tkankowej względem funkcji wejściowej AIF. Należy też pamiętać, że już samo zastosowanie regularyzacji wiąże się ze zmianą kształtu otrzymywanego rozwiązania rozplotu. W wyniku wyzerowywania elementów macierzy w otrzymana funkcja przejścia będzie wygładzona. Opisane powyżej problemy związane z zagadnieniem rozplotu spowodowały, że w niniejszej pracy podjęto próbę takiej modyfikacji istniejących metod, która pozwoli skutecznie korygować wpływ opóźnienia funkcji pobudzającej dla każdego woksela oraz 4
59 eliminować wpływ rozmycia funkcji przejścia wynikającego ze sposobu obliczania rozplotu. Jednym z kryteriów postawionych przez autora była odporność proponowanych metod na szumy, co jest szczególnie istotne przy badaniach wykonanych techniką MR. Technika zastosowana przez autora uwzględnia również fizjologiczną interpretację kształtu funkcji przejścia tkanki. Zostanie to szczegółowo opisane w rozdziale Recyrkulacja Ostatnim istotnym rozważanym w pracy elementem związanym z pomiarem perfuzji metodami tomograficznymi jest recyrkulacja środka cieniującego. W opisywanym modelu przyjmuje się założenie, że wszelkie obliczenia dotyczą krzywych koncentracji związanych z pierwszym przejściem kontrastu przez badany obszar. W warunkach eksperymentu przeprowadzanego na fantomie, w którym obieg cieczy jest otwarty, założenie jest całkowicie słuszne, bowiem wstrzyknięty kontrast nie ma możliwości powtórnego przejścia przez badany obszar. W warunkach badania klinicznego mamy do czynienia z obiegiem zamkniętym, zatem kontrast wraca do prawej komory serca i po przejściu przez płuca trafia do lewej komory, skąd powtórnie wyrzucany jest do krwioobiegu. Efektem tego jest jego ponowne pojawienie się w badanym obszarze po czasie od kilkunastu do kilkudziesięciu sekund. Na krzywej dynamicznej jest to widoczne w postaci powtórnego wzrostu koncentracji (rysunek 5.3). Rysunek 5.3. Efekt recyrkulacji znacznika w układzie zamkniętym. Linią przerywaną zaznaczony jest ponowny wzrost koncentracji znacznika. Najprostszą metodą minimalizacji wpływu recyrkulacji na wyniki pomiarów wydaje się odcięcie fragmentu krzywej, w którym zaczyna być widoczny ponowny wzrost koncentracji znacznika. Wadą tej metody jest ryzyko odrzucenia znaczącej części danych związanych z pierwszym przejściem kontrastu. Prowadzi to do wprowadzenia istotnego błędu w obliczeniach. Dlatego metoda ta może być zastosowana tylko wtedy gdy ponowny wzrost koncentracji środka cieniującego związany z recyrkulacją nie pokrywa się z pierwszym 41
60 przejściem kontrastu (rysunek 5.3). Druga metoda polega na dopasowaniu ( fitowaniu ) krzywej, wynikającej z przyjętego modelu, do oryginalnych danych i prowadzenie dalszych obliczeń na krzywych dopasowanych. Zakłada ona, że przyjęty model odpowiada zjawisku przejścia kontrastu przez tkankę, nie ma zatem problemu odrzucenia danych związanych z pierwszym przejściem. Aktualnie najczęściej stosowane jest przybliżanie kształtu krzywej koncentracji funkcją gamma [THOM64], [DAVE83] lub przyjęcie modelu Sheparda [SHEP52], [SHEP54] uwzględniającego ewentualną kumulację środka kontrastowego w tkance. Niestety, posługiwanie się z góry narzuconym modelem może prowadzić do istotnych błędów, w szczególności w sytuacjach gdy mamy do czynienia z przypadkami patologii. Dodatkowo należy pamiętać, że charakter przepływu w danym miejscu i czasie może się istotnie zmieniać w zależności od stanu pacjenta. Nigdy nie mamy pewności, że przyjęty model odpowiada warunkom przepływu tkankowego panującym w czasie badania. 5.5 Podsumowanie Pomimo opisanych problemów prace nad udoskonalaniem modelu przepływu mózgowego są prowadzone i opisywanie w literaturze ([CIES1], [PIEC1], [CZOS97]). Jednak w dalszej części pracy podjęta została próba zastosowania metody niezależnej od narzuconego z góry modelu oraz od różnic międzyosobniczych. Główny nacisk został położony na eliminację wpływu czasu dojścia kontrastu od tętnicy do obszaru zainteresowania. 42
61 6. Korekcja opóźnienia funkcji wejściowej W rozdziale tym zostanie szczegółowo rozpatrzony problem opóźnienia pomiędzy funkcją wejściową obserwowaną w tętnicy zasilającej a krzywymi koncentracji mierzonymi w badanym obszarze tkanki. Wpływ tego opóźnienia na obliczane parametry perfuzji zostanie zbadany na podstawie danych syntetycznych, wygenerowanych przy pomocy symulacji komputerowych. Następnie zostanie zaproponowana metoda minimalizacji wpływu opóźnienia na wyniki badań. Efekt jej zastosowania zostanie oceniony na przykładzie danych syntetycznych, a ostatecznie metoda zostanie zastosowana do analizy danych rzeczywistych, otrzymanych z badań tomograficznych. Dla danych rzeczywistych porównane będą wyniki otrzymane z zastosowaniem różnych metod korekcji, w tym proponowanej przez autora, i bez zastosowania korekcji. Jak już wspomniano wcześniej, opóźnienie funkcji wejściowej wynika z budowy układu tętnic. Konieczność zaznaczenia na obrazach pikseli mieszczących się w świetle tętnicy zasilającej wymaga zobrazowania stosunkowo dużych tętnic, o średnicy rzędu kilku milimetrów. Jest to niezbędne ze względu na sposób obliczania CBV na podstawie zależności (5.1). W przypadku badań głowy, będących tematyką tej pracy, tętnice takie znajdują się tuż za kołem Willisa. Droga jaką pokonuje krew od tego miejsca do naczyń włosowatych w tkance miękkiej waha się od kilku do kilkunastu centymetrów. Na tej drodze tętnice rozdzielają się wielokrotnie, co powoduje, że czasy dojścia mogą być różne dla różnych regionów zainteresowania. 43
62 Wolumen wejściowy CT lub MR Korekcja ruchu Przeliczenie jasności pikseli na koncentrację znacznika Wyznaczenie funkcji AIF Wyznaczenie maski Korekcja czasu dojścia kontrastu Obliczenie obrazów parametrycznych Prezentacja wyników Rysunek 6.1 Schemat algorytmu przetwarzania tomograficznych danych dynamicznych. Na rysunku zaznaczono etap omawiany w tym rozdziale. Na rysunku 6.1 pokazano schemat algorytmu przetwarzania danych otrzymanych w tomograficznym badaniu dynamicznym. Poszczególne etapy były omówione we wcześniejszych rozdziałach. Nie wszystkie etapy przetwarzania są zawsze realizowane. Na przykład w przypadku braku znaczących artefaktów ruchowych korekcja ruchu może być pominięta, co znacząco skraca czas przetwarzania, a niewiele wpływa na jakość otrzymanych wyników. Podobnie często pomijana jest korekcja czasu dojścia środka kontrastowego. Autor wykazuje jednak, że pominiecie tego etapu może znacząco wpłynąć na wyniki obliczeń, co zostało wykazane w symulacjach i na przykładzie badań klinicznych. 6.1 Metody korekcji czasu dojścia kontrastu W literaturze opisane są różne próby eliminacji wpływu efektu opóźnienia krzywej wejściowej. Czas dojścia środka kontrastowego do badanego obszaru poza tym, że może poprawić jakość obliczeń pozostałych parametrów perfuzji, w szczególności, MTT a zatem pośrednio CBF, sam w sobie jest często używany w praktyce klinicznej. Dokładne wyznaczenie czasu dojścia kontrastu jest o tyle istotne, że rozdzielczości czasowe stosowane w badaniach perfuzyjnych przeważnie wynoszą 1-2 sekundy. Zatem błąd wynoszący jedną 44
63 Rysunek 6.2. Metoda czasu opóźnienia maksimum koncentracji. Na rysunku pokazano również sposób wyznaczania parametru TTP. próbkę w krzywych koncentracji oznacza błąd pomiaru rzędu 1-2 sekundy co przy średnich wartościach parametrów czasowych perfuzji rzędu 4-6 sekund jest wartością istotną. Proponowana przez autora metoda korelacyjna została porównana z trzema innymi metodami, również nie wymagającymi zastosowania modelu. Ideę wspomnianych metod opisano w poniższych podrozdziałach Metoda czasu opóźnienia maksimum koncentracji Pierwsza z analizowanych metod polega na obliczeniu różnicy czasowej pomiędzy punktami, dla których krzywe koncentracji funkcji wejściowej i krzywej koncentracji obserwowanej w wokselu osiągają maksimum (rys.6.2 ). Niewątpliwą zaletą tej metody jest prostota i mała złożoność obliczeniowa. Jednakże metoda ta jest czuła na stosunek sygnału do szumu oraz na zmianę kształtu krzywej tkankowej względem krzywej wejściowej. Im dłuższy czas MTT badanego obszaru tkanki, tym większe rozmycie, a co za tym idzie, większe opóźnienia maksimum krzywej tkankowej nie wynikające z opóźnienia funkcji wejściowej. Dodatkową zaletą zastosowania tej metody jest otrzymanie w procesie przetwarzania dodatkowego parametru czasowego krzywych koncentracji jakim jest TTP (ang. Time to Peak). Parametr ten jest często wykorzystywany w praktyce klinicznej. Przeważnie jednak jest on liczony od momentu rozpoczęcia sekwencji obrazującej, co uniemożliwia porównywanie badań różnych pacjentów. Wynika to faktu że zasadniczy wpływ na wyznaczenie TTP ma moment rozpoczęcia podawania kontrastu. Na rysunku 6.2 przedstawiono ideę opisanej metody korekcji opóźnienia oraz wyznaczania parametru TTP Metoda progowa Druga porównywana metoda polega na poszukiwaniu chwili czasowej, w której krzywe koncentracji przekraczają pewien ustalony arbitralnie próg. Przeważnie jest on ustalony na 45
64 poziomie 1% maksymalnej wartości krzywej koncentracji [RUMI5], co wynika z typowego kształtu tych krzywych koncentracji. Ponieważ narastanie koncentracji w fazie pierwszego przejścia kontrastu jest szybkie, to przy tak określonym progu można przyjąć, że chwila jego przekroczenia pokrywa się z chwilą dojścia kontrastu do obserwowanego woksela. Podobnie jak poprzednia, metoda ta charakteryzuje się niską odpornością na szum oraz rozmycie Rysunek 6.3. Metoda progowa wyznaczania czasu opóźnienia krzywej koncentracji względem funkcji wejściowej AIF. Na rysunku pokazano również sposób wyznaczania parametru BAT określającego czas dojścia kontrastu do miejsca zainteresowania. krzywej tkankowej, w której narastanie koncentracji może być wolniejsze, w szczególności dla dużych czasów MTT. Przy niskim stosunku sygnału do szumu wartości opóźnienia otrzymywane tą metodą są nieakceptowalne, co zostanie pokazane w symulacjach. Efektem zastosowania tej metody jest otrzymanie wartości BAT (ang. Bolus arrival time), który również jest szeroko stosowany w praktyce klinicznej. Na rysunku 6.3 pokazano graficznie sposób zastosowania tej metody do wyznaczania czasu opóźnienia krzywej koncentracji względem funkcji wejściowej AIF oraz wyznaczania parametru BAT. Podobnie jak w przypadku wyznaczania wartości TTP, parametr BAT wyznaczany tą metodą zasadniczo zależy od chwili podania kontrastu Metoda geometryczna Metoda trzecia opiera się na geometrycznej analizie kształtu krzywej koncentracji (rys.6.4 ) [ROSE4]. Polega na wyznaczeniu dla każdego piksela prostej przechodzącej przez dwa punkty należące do krzywej koncentracji: punkt t() oraz punkt, w którym koncentracja osiąga maksimum, a następnie wyznaczeniu punktu krzywej koncentracji leżącego pomiędzy wspomnianymi punktami, którego odległość od powstałej prostej jest największa. Punkt ten przyjmowany jest jako chwila rozpoczęcia napływania kontrastu. W metodzie tej obliczane są równocześnie wspomniane przy wspomnianych wcześniej metodach dwa parametry czasowe krzywych koncentracji, TTP oraz BAT. 46
65 Rysunek 6.4. Metoda geometryczna wyznaczania opóźnienia krzywej koncentracji względem funkcji wejściowej AIF. Zaznaczono również jak wyznaczane są parametry BAT i TTP Metoda korelacyjna Rysunek 6.5. Metoda korelacyjna wyznaczania opóźnienia krzywej koncentracji względem funkcji wejściowej AIF. Rysunek przedstawia funkcję kowariancji wzajemnej krzywej AIF i krzywej koncentracji w obszarze zainteresowania. W niniejszej pracy autor proponuje zastosowanie do korekcji czasu dojścia kontrastu metody korelacyjnej. W metodzie tej dla każdego piksela obliczana jest funkcja kowariancji wzajemnej funkcji wejściowej AIF oraz krzywej koncentracji dla danego piksela. Szczegółowy opis obliczania tej funkcji został przedstawiony w rozdziale Czas opóźnienia krzywej koncentracji dla piksela względem funkcji wejściowej AIF wyznaczany jest jako chwila czasowa, w której funkcja kowariancji wzajemnej osiąga swoje maksimum (rys. 6.5). Próbę zastosowania metody korelacyjnej podjęto ze względu na jej odporność na niski stosunek sygnału do szumu (SNR), co zostało potwierdzone symulacjami przedstawionymi w dalszej części pracy. Ze względu na zmianę kształtu krzywej koncentracji w obszarach zainteresowania względem funkcji wejściowej, można zarzucić tej metodzie, że pomiar opóźnienia dwóch krzywych będzie nieprecyzyjny, ponieważ funkcja kowariancji wzajemnej jest miarą podobieństwa funkcji. Jednak celem obliczeń jest poprawne wyznaczenie średniego czasu przejścia MTT. Jak zostało wykazane w symulacjach, faktycznie metoda korelacyjna proponowana w pracy nie jest najlepszą z opisywanych metod 47
66 do wyznaczenia czasu dojścia kontrastu BAT czy wyznaczania czasu osiągnięcia maksimum TTP, jednak czasy MTT obliczone z wykorzystaniem krzywych koncentracji skorygowanych tą metodą okazały się obarczone najmniejszym błędem. Wszystkie opisane metody zostały uwzględnione w symulacjach i porównane z metodą proponowaną przez autora Funkcja kowariancji wzajemnej Dla dwóch ciągłych i stacjonarnych funkcji czasu: X(t) i Y(t), o wartościach średnich danych równaniami: T 1 m x =lim X t dt, t T (6.1) T 1 m y =lim Y t dt t T (6.2) funkcja kowariancji wzajemnej dana jest następującym wyrażeniem: 1 [ X t m x][y t m y] dt. T T R xy =lim (6.3) Funkcja kowariancji jest miarą podobieństwa sygnałów X(t) i Y(t) dla określonego przesunięcia czasowego τ pomiędzy nimi. Jeżeli między sygnałami X(t) i Y(t) zachodzi jakiś związek przyczynowo-skutkowy, to funkcja ta ma wyraźne maksimum. Argument, dla którego maksimum to występuje określa przesuniecie czasowe między sygnałami. Właściwość ta została wykorzystana do estymacji czasu opóźnienia funkcji wejściowej w metodzie zaproponowanej przez autora. Przytoczone wcześniej wyrażenia na wartości średnie i funkcję kowariancji wzajemnej dotyczą ciągłych funkcji czasu. W rzeczywistym eksperymencie mamy natomiast dostępne dwa szeregi czasowe o skończonej liczbie punktów: x[n], y[n] dla m N. W takim przypadku konieczne jest zastosowanie metody przybliżania (estymacji) zarówno wartości średnich szeregów, jak i funkcji ich kowariancji wzajemnej. Do najczęściej stosowanych estymatorów należą tzw. estymatory największej wiarygodności. Przy wyznaczaniu estymatora największej wiarygodności rozważa się łączne prawdopodobieństwo zaobserwowania próbki N - elementowej, traktowane jako funkcja estymowanego parametru. Jako wartość estymatora największej wiarygodności przyjmuje się tę wartość parametru, dla której rozważane prawdopodobieństwo jest największe. Dla gaussowskiego procesu stochastycznego estymator największej wiarygodności wartości przeciętnej mx definiowany jest następująco: 48
67 m x = 1 N N xi. (6.4) i= Wariancja tego estymatora jest równa: var [ m x ]= E [ x n mn ] = x. N N (6.5) Wraz ze wzrostem liczby obserwacji wariancja wartości średniej maleje, a zatem średnia w próbce jest estymatorem zgodnym wartości przeciętnej. Nieco bardziej skomplikowany jest problem estymatora kowariancji wzajemnej szeregów czasowych. Dla uproszczenia przyjmuje się, że wartości przeciętne obu szeregów są równe zero, tj.: mx = E [ x ]=, m y =E [ y ]=. (6.6) W takim przypadku pojęcia ciągu kowariancji wzajemnych i ciągu korelacji wzajemnych są sobie równoważne. Uwzględniając powyższe założenie przyjmujemy, że funkcja kowariancji wzajemnej dwóch szeregów czasowych, odpowiadająca funkcji R xy= dla ciągłych funkcji czasu, dana jest następującym równaniem: r xy m = E [ x n y n m ], (6.7) czyli, że jest to wartość przeciętna szeregu czasowego, którego poszczególne wyrazy są iloczynami ciągów x i y. W rezultacie estymację kowariancji wzajemnej procesów o zerowych wartościach przeciętnych można traktować jako estymację wartości przeciętnej ciągu xnyn+m. Przy danych N kolejnych wartościach ciągów x(n) i y(n) otrzymuje się (N-m) kolejnych próbek ciągu iloczynów do estymacji rxy(m). Stosując definicję estymatora wartości przeciętnej (6.1) o największej wiarygodności otrzymuje się: { N m 1 1 r xy ' m = x n y n m N m n= dla m N. N m 1 1 r xy ' m = x n m y n N m n= (6.8) Wariancja tego estymatora podana przez Jenkinsa i Wattsa [JENK68] ma następującą postać: r= N var [ r m ] r 2 r r xy r m r xy r m ]. 2 [ xy [ N m] r = ' xy (6.9) Powyższe wyrażenie obowiązuje dla wartości N znacznie większych od m, jednakże ogólnie można przyjąć, że wariancja tego estymatora jest proporcjonalna do 1/N, podobnie jak (6.1). Ponadto, jest to estymator nieobciążony, ponieważ lim {var [ r 'xy m ]}=. N 49 (6.1)
68 Dla wartości m dążącej do N wariancja estymatora r 'xy m staje się wyjątkowo duża. Wynika to z niewielkiej liczby punktów stanowiących podstawę do obliczenia średniej w próbce xnyn+m dla wartości m bliskiej N. W rezultacie estymator r 'xy m nie jest zbyt przydatny w praktyce. Istnieje odmienna postać estymatora ciągu korelacji wzajemnych, dana wzorem: { N m 1 1 r xy m = N 1 r xy m = N x n y n m n= N m 1 dla m N. (6.11) x n m y n n= Estymator r xy m różni się od estymatora r 'xy m postacią czynnika występującego przed znakiem sumy. Porównując wyrażenia (6.3) i (6.2) otrzymujemy: r xy m = Ponieważ wartość przeciętna N m ' r xy m. N estymatora r 'xy m (6.12) jest równa r xy m, czyli E [ r 'xy m ]=r xy m, wartość przeciętna estymatora r xy m dana jest przez: E [ r 'xy m ]= N m r xy m. N Jest to więc estymator obciążony ciągu korelacji o obciążeniu B= (6.13) m r m. Wariancja tego N xy estymatora dana jest wyrażeniem: 1 var [ r xy m ] N r = [ r 2xy r r xy r m r xy r m ]. (6.14) r = Dla dużych wartości przesunięcia m wariancja tego estymatora nie jest tak duża jak estymatora r 'xy m. Jednakże gdy m dąży do N, obciążenie dąży do rxy ( m ), czyli wartość całego estymatora dąży do zera. Jenkins i Watts sugerują, że w wielu przypadkach błąd średniokwadratowy estymatora obciążonego jest mniejszy od błędu średniokwadratowego estymatora nieobciążonego. Często w zastosowaniach praktycznych wygodnie jest się posługiwać znormalizowaną funkcją kowariancji wzajemnej. Normalizacja ta polega na podzieleniu wyrazów sekwencji kowariancji przez iloczyn autokowariancji dla zerowego przesunięcia, tj.: r Nxy m = r xy m. r xx r yy (6.15) Funkcja ta przyjmuje wartości z zakresu od -1 (przy braku korelacji) do 1 (przy dobrej korelacji). 5
69 6.2 Symulacje Z powodu obiektywnej trudności weryfikacji wpływu opóźnienia sygnału wejściowego na jakość pomiaru na podstawie rzeczywistych danych, odpowiednią drogą postępowania wydaje się być wykorzystanie danych syntetycznych, otrzymanych na drodze symulacji komputerowych. Daje nam to pewność kontrolowania warunków pomiarów oraz możliwość skonfrontowania otrzymanych wyników z założonymi parametrami modelu. Przeprowadzone symulacje miały pokazać wpływ opóźnienia na zmiany kształtu krzywych koncentracji znacznika, dlatego w pierwszej fazie wykonano je dla sygnałów nie zaszumionych. Zależność koncentracji środka cieniującego od czasu przyjęto jako opisaną funkcją: C t = { A t t B e D t t t t, t (6.16) gdzie współczynniki A,B i D dobrano tak, aby odpowiadały typowej krzywej wejściowej AIF i wynosiły one A=15, B=2 i D=,2. Model tkanki przyjęty w symulacjach został opisany równaniem (5.1). Na podstawie równania (6.16) wygenerowano krzywe wejściowe AIF dla różnych czasów opóźnienia t, a następnie, korzystając z równania (5.13), obliczono krzywe koncentracji dla tkanki, podstawiając za funkcje AIF wygenerowane krzywe. Po obliczeniu splotu funkcja C VOI t była przeskalowywana w taki sposób, aby odpowiadała wartości parametru CBV=5% i spełniała równanie (5.1). Wartość parametru CBV została przyjęta na podstawie danych literaturowych opisywanych we wcześniejszych rozdziałach. Symulacje wykonano dla pięciu różnych opóźnień oraz trzech rodzajów tkanki, charakteryzujących się różnymi średnimi czasami przejścia MTT. Dla tak otrzymanych krzywych przeprowadzono następnie obliczenia metodą TSVD, opisaną we wcześniejszych rozdziałach. Wyniki symulacji przedstawione są na rysunku 6.6. Następnie, korzystając z zależności (5.9), dla każdej krzywej R t obliczono średni czas przejścia MTT eff, a wyniki zestawiono w tabeli 6.1. Analiza wyników symulacji pokazuje istotne zawyżanie wartości średniego czasu przejścia MTT dla opóźnionej funkcji AIF. Dodatkowym elementem mogącym wpływać na taki wynik jest złe uwarunkowanie numeryczne macierzy A, wprowadzające do obliczanej funkcji R(t) oscylacje. Zostało to omówione w podrozdziale 5.3, dotyczącym metody TSVD obliczania macierzy odwrotnej. Zastosowanie regularyzacji powoduje odfiltrowanie składowych wysokoczęstotliwościowych. W tych warunkach niemożliwe staje się wierne 51
70 odtworzenie ostro narastającego zbocza funkcji residuum R t. Efekt ten został zilustrowany na rysunku 6.6, na którym linią punktowaną przedstawiono krzywą odpowiadającą funkcji residuum przyjętej w symulacji. Oscylacje funkcji R t powodują, że obliczone wartości czasów MTT eff nie zależą liniowo od opóźnienia. 1.2 A) t= s MTT=2 s MTT eff =2.69 s c za s [s ] G) t= s MTT=6 s MTT eff =6.71 s.6 H) t=1 s MTT=6 s MTT eff =7.92 s c z a s [s ] c za s [s ] 3 I) t=6 s MTT=6 s MTT eff =7.95 s R (t).8 1 c z a s [s ] c za s [s ] F) t=6 s MTT=4 s MTT eff =6.5 s 1 R (t) E) t=1 s MTT=4 s MTT eff =6.21 s 1 R (t).8 1 c z a s [s ] 1.2 D) t= s MTT=4 s MTT eff =4.71 s 1 c za s [s ] 1.2 R (t).6.2 c za s [s ] R (t) C) t=6 s MTT=2 s MTT eff =4.13 s 1 R (t) R (t).8 B) t=1 s MTT=2 s MTT eff =4.42 s 1 R (t) R (t) c z a s [s ] Rysunek 6.6. Kształt funkcji residuum R(t) dla różnych czasów dojścia kontrastu ( t ) i różnych czasów MTT tkanek. Na każdym w wykresów cienką linią kropkowaną pokazano model funkcji R(t) użyty w danej symulacji. Obliczone funkcje R(t), oznaczone linią ciągłą, zostały znormalizowane do jednostkowej wartości maksymalnej. Podane zostały też wartości czasu MTT obliczonego dla krzywych R(t), oznaczone jako MTT eff. Linią przerywaną pokazano funkcję nie opóźnioną R(t). Przyjęcie na podstawie szacunkowych obliczeń zawyżonych wartości czasu MTT eff ma niebagatelny wpływ na dalsze obliczenia. Z zależności (3.1) wynika, że wartość CBF zostanie zaniżona. Ma to znaczenie w interpretacji parametrycznych obrazów perfuzyjnych, co jest szczególnie istotne przy ocenie obszaru niedokrwienia i podejmowaniu decyzji o dalszym postępowaniu klinicznym. 52
71 Opóźnienie bolusa Średni czas przejścia przyjęty w symulacji MTT t s 1s 6s 2s 2,69 s 4,42 s 4,13 s 4s 4,71 s 6,21 s 6,5 s 6s 6,71 s 7,92 s 7,95 s Tabela 6.1. Efektywne średnie czasy przejścia MTT eff obliczone na podstawie symulacji dla różnych opóźnień bolusa t i różnych średnich czasów przejścia MTT przyjętych do modelu Aby przybliżyć się do warunków rzeczywistego pomiaru, w kolejnym kroku wykonano symulacje dla sygnałów zaszumionych (źródła szumów zostały omówione wcześniej w rozdziale 3.3). Wygenerowane zostały krzywe dynamiczne (również korzystając z zależności (6.16)), do których dodano szum o rozkładzie normalnym N,, gdzie parametr został tak dobrany, aby zapewnić narzucone poziomy sygnału użytecznego w stosunku do szumu: 5 db, 15 db oraz 25 db. Tym razem symulacje wykonano tylko dla jednej wartości średniego czasu przejścia MTT =4 s. Dla każdego poziomu szumu wykonano natomiast 512 symulacji, co pozwoliło na przebadanie wartości średniej czasu MTT eff oraz określenie odchylenia standardowego otrzymanych wyników. Przykładowe krzywe dla różnych czasów opóźnienia oraz różnego stosunku sygnału do szumu przedstawione są na rysunku 6.7. Na rysunku 6.8 pokazano przykładowe funkcje R t odpowiadające otrzymanym krzywym koncentracji. W tabeli 6.2 zestawiono otrzymane wyniki. 15 A) TR=1s MTT=4 s SNR=25dB 1 C (t) C (t) 1 15 B) TR=1s MTT=4 s SNR=15dB c z a s [s ] c z a s [s ] 4 C) TR=1s MTT=4 s SNR=5dB C (t) c z a s [s ] Rysunek 6.7. Przykładowe krzywe koncentracji otrzymane w symulacjach dla różnych wartości SNR (linia ciągła). Dodatkowo linią przerywaną pokazano funkcję wejściową AIF. Na każdym rysunku widoczne są trzy krzywe koncentracji dla tkanki dla różnych czasów dojścia bolusa t równych s, 2 s i 6 s. 53
72 SNR = 5dB SNR = 15 db SNR = 25 db t s 1s 6s MTT eff 4,39 5,12 5,29 std MTT 1,64 1,71 1,8 MTT eff 4,57 6,25 6,4 std MTT,62,75,68 MTT eff 4,58 6,29 6,3 std MTT,21,24,22 eff eff eff Tabela 6.2. Zestawienie uśrednionych wyników z symulacji dla różnych SNR i różnych czasów opóźnienia bolusa t. Średni czas przejścia kontrastu przyjęty dla modelu wynosił MTT=4 s, liczba uśrednionych wyników n=512. Analiza otrzymanych wyników i porównanie ich z wynikami dla krzywych niezaszumionych (tabela 6.1 dla MTT =2 s ) pokazuje, że wartości średnie otrzymanych czasów MTT eff niewiele odbiegają od wartości otrzymanych w symulacjach bez szumu. Dopiero spojrzenie na wartości odchyleń standardowych daje pojęcie o jakości otrzymanych wyników. Pokrywa się to z oczekiwaniami - pogorszenie stosunku sygnał szum nie wpływa na wartość średnią, a jedynie obciąża wyniki większym błędem. Można zatem wnioskować, że: wszelkie próby filtrowania szumu nie będą miały znaczącego wpływu na minimalizację efektu zawyżania wartości MTT eff spowodowanej opóźnieniem bolusa; przyjęta metoda korekcji opóźnienia musi być odporna na wpływ szumu. Dla potwierdzenia pierwszego z tych wniosków przeprowadzono dodatkowe symulacje, dla takich samych wartości parametrów jak w poprzednich obliczeniach, ale z jedną dodatkową modyfikacją - do wyliczania parametrów brano pod uwagę 9 krzywych i uśredniano je, co odpowiada przestrzennemu uśrednianiu danych. Wyniki dla tak przeprowadzonych symulacji przedstawia tabela
73 .6.8 R (t) c za s [s ] c za s [s ] c za s [s ] I) t=6 s MTT=4 s MTT eff =6.11 s c z a s [s ] H) t=1 s MTT=4 s MTT eff =9.18 s 1 R (t).8 4 c za s [s ] G) t= s MTT=4 s MTT eff =5.69 s F) t=6 s MTT=4 s MTT eff =6.1 s c z a s [s ] E) t=1 s MTT=4 s MTT eff =6.72 s c za s [s ] R (t).8 2 R (t) 2 D) t= s MTT=4 s MTT eff =5.2 s 1 R (t).6.2 c za s [s ] R (t).8.2 C) t=6 s MTT=4 s MTT eff =6.23 s 1 R (t) R (t).8 B) t=1 s MTT=4 s MTT eff =6.9 s 1 R (t) A) t= s MTT=4 s MTT eff =4.37 s c z a s [s ] Rysunek 6.8. Wyniki obliczeń funkcji R(t) dla zaszumionych krzywych koncentracji. Przyjęte wartości SNR wynosiły odpowiednio, 25 db rysunki A), B), C), 15 db rysunki D), E), F) i 5 db rysunki G), H), I). Linią ciągłą oznaczono krzywe pomiarowe, linią przerywaną oznaczono funkcję R(t) bez opóźnienia, a cienką linią przerywaną funkcję R(t) uwzględniającą opóźnienie funkcji AIF. 55
74 Rysunek 6.9. Metoda uśredniania przestrzennego krzywych koncentracji. Liniami cienkimi wykreślone zostały krzywe koncentracji dla pojedynczych pikseli, linia gruba pokazuje krzywą uzyskaną dla średnich wartości koncentracji obliczonych dla 9-ciu sąsiadujących pikseli. Ma to szczególne znaczenie przy stosowaniu metod punktowych korekcji opóźnienia jakie zostały opisane. Wadą uśredniania przestrzennego jest utrata rozdzielczości otrzymywanych obrazów parametrycznych. Na podstawie otrzymanych wyników można postawić wniosek, że uśrednianie nie zmienia efektu wpływu opóźnienia bolusa, co potwierdza porównanie wartości średnich MTT eff z wynikami z tabeli 6.2. Wyniki te nie są zaskoczeniem i wydają się być oczywiste, natomiast potwierdzają słuszność wniosku o konieczności zastosowania takiej metody korekcji opóźnienia, która będzie odporna na zaszumienie sygnału. Uśrednianie przestrzenne będzie stosowane także w analizie rzeczywistych danych tomograficznych. SNR = 5dB SNR = 15 db SNR = 25 db t s 1s 6s MTT eff 4,61 6,23 6,6 std MTT,67,79,72 MTT eff 4,59 6,31 6,2 std MTT,22,24,22 MTT eff 4,6 6,31 6,1 std MTT,8,9,7 eff eff eff Tabela 6.3. Zestawienie uśrednionych wyników z symulacji dla różnych SNR i różnych czasów opóźnienia bolusa t z uśrednianiem przestrzennym krzywych dla 9 pikseli. Średni czas przejścia kontrastu przyjęty dla modelu wynosił MTT=4 s, liczba uśrednionych wyników n=
75 6.3 Symulacje z zastosowaniem korelacyjnej metody korekcji opóźnienia bolusa Analiza wyników oraz charakter krzywych otrzymanych w symulacjach skłoniła autora do zastosowania innej niż wspomniane metody korekcji opóźnienia krzywej tkankowej względem funkcji wejściowej AIF. Opisane w rozdziale 6 metody estymacji czasu opóźnienia są metodami punktowymi, bazującymi na wybranych w sposób charakterystyczny dla danej metody punktami krzywych koncentracji. Stosowanie tego typu metod w warunkach istotnego (względem amplitudy użytecznego sygnału) poziomu zakłóceń prowadzi do błędów, co zostało wykazane w symulacjach. Biorąc pod uwagę charakter zakłóceń, które można charakteryzować jako niezależne gaussowskie (wynika to faktu, że są sumą niezależnych czynników, co zostało opisane w rozdziale 3.3) autor zaproponował wykorzystanie korelacyjnej metody estymacji czasu opóźnienia krzywych koncentracji tkankowej względem funkcji wejściowej AIF. Pozwala to zmniejszyć błędy statystyczne wynikające z zakłóceń. Proponowana w pracy metoda korekcji opóźnienia pomiędzy funkcją wejściową obserwowaną w tętnicy zasilającej a krzywymi koncentracji mierzonymi w badanym obszarze tkanki opiera się na badaniu funkcji kowariancji wzajemnej obu tych przebiegów. Funkcja kowariancji wzajemnej jest w teorii sygnałów miarą podobieństwa dwóch sygnałów. Stosowana jest często do poszukiwania w nieznanym sygnale określonego, znanego wzorca. Jest ona funkcją przesunięcia czasowego między badanym sygnałem wejściowym a szukanym wzorcem. Jeżeli pomiędzy dwoma badanymi sygnałami zachodzi jakaś zależność, tak jak w przypadku krzywych koncentracji środka cieniującego, funkcja kowariancji wzajemnej posiada wyraźne maksimum. Argument, dla którego zostaje osiągnięte maksimum jest równy przesunięciu czasowemu pomiędzy dwoma sygnałami. Dzięki tej właściwości oraz odporności na szum, co zostanie wykazane w symulacjach, funkcja ta wydaje się być bardzo dobrym narzędziem do korekcji opóźnienia bolusa, co jest metodą proponowaną przez autora pracy. W dalszej części pracy funkcja ta będzie traktowana narzędziowo, a więcej szczegółów dotyczących funkcji kowariancji znajduje się w dodatku. Przed zastosowaniem metody do rzeczywistych danych tomograficznych przeprowadzono szereg symulacji, mających na celu zbadanie trafności idei wykorzystania funkcji kowariancji wzajemnej oraz wykazanie jej odporności na szum. Rysunek 6.1 przedstawia funkcje kowariancji wzajemnej dla różnych czasów opóźnienia bolusa i różnych wartości SNR dla ustalonego czasu MTT=4 s. 57
76 D) t= s max=.88 tmax=1 s G) t= s max=.56 tmax=1 s c z a s [s ] c z a s [s ] H) t=1 s max=.75 tmax=2 s F) t=6 s max=.86 tmax=7 s c z a s [s ] c z a s [s ] C ro s s C o v (t) C ro s s C o v (t) E) t=1 s max=.85 tmax=2 s c z a s [s ] c z a s [s ] C ro s s C o v (t) C ro s s C o v (t).6.6 C) t=6 s max=.89 tmax=7 s c z a s [s ].8.8 C ro s s C o v (t) B) t=1 s max=.91 tmax=2 s C r o s s C o v (t).8 C ro s s C o v (t).6 A) t= s max=.91 tmax=1 s C r o s s C o v (t) C r o s s C o v (t).8.6 I) t=6 s max=.69 tmax=7 s c z a s [s ] c z a s [s ] Rysunek 6.1. Funkcje kowariancji wzajemnej funkcji wejściowej AIF (koncentracji bolusa) i krzywej koncentracji dla tkanek otrzymanych w symulacjach dla różnych SNR równych odpowiednio: 25 db rysunki A), B), C), 15 db rysunki D), E), F) i 5 db rysunki G), H), I) i różnych czasów opóźnienia bolusa t. W prezentowanych symulacjach przyjęto MTT=4 s. t max oznacza przesunięcie czasowe funkcji wzorca względem funkcji badanej, dla którego funkcja kowariancji wzajemnej osiąga maksimum. Przedstawione wykresy funkcji kowariancji wzajemnej jednoznacznie pokazują, że niezależnie od poziomu stosunku sygnału do szumu (w badanym zakresie) funkcja ta posiada wyraźne maksimum. Pozwala to na stwierdzenie, że może być ona zastosowana do próby obliczenia czasu opóźnienia krzywej tkankowej względem krzywej tętniczej AIF. Otrzymane tą metodą wyniki zostały porównane z wynikami otrzymanymi pozostałymi metodami, opisanymi wcześniej. Rysunek 6.11 przedstawia średnie czasy opóźnienia obliczone z zastosowaniem wszystkich czterech metod. Dla każdego punktu wynikowego pokazano też odchylenie standardowe wartości średniej. Szczegółowe wyniki zebrane są w tabeli
77 Metoda SNR[dB] kowariacyjna 5 t eff std t std t t eff std t std t t eff std t std t eff eff 15 eff eff 25 eff eff geometryczna 5 t eff std t std t t eff std t std t t eff std t std t eff eff 15 eff eff 25 eff opóżnienie maksimum eff 5 t eff std t std t t eff std t std t t eff std t std t eff eff 15 eff eff 25 eff progowa (z progiem 1%) eff 5 t eff std t std t t eff std t std t t eff std t std t eff eff 15 eff eff 25 eff eff 2s 2,67,59,7 2,94,24,3 3,,, 1,81 1,17,15 1,83,83,1 2,2,22,3 4,56 1,27,16 4,17,61,8 4,17,38,5,11,76,9 1,56 1,39,17 2,59,5,6 Opóźnienie t 4s 4,7,66,8 4,98,13,2 5,,, 3,25 1,78,22 3,83,86,11 4,2,22,3 6,27 1,31,16 6,36,74,9 6,13,33,4,14,73,9 1,94 2,16,27 4,59,5,6 przyjęte w modelu 6s 8s 6,78 8,89,6,65,8,8 6,95 8,97,21,18,3,2 7, 9,,,,, 5,8 6,75 1,83 2,5,23,31 5,77 7,64,9 1,3,11,13 5,97 8,2,25,33,3,4 8,42 1,48 1,22 1,54,15,19 8,25 1,36,71,6,9,8 8,22 1,13,42,33,5,4,2,16 1,63,62,2,8 3,3 4,28 3,11 4,13,39,52 6,64 8,59,48,5,6,6 1 s 1,91,64,8 1,92,27,3 11,,, 8,77 2,35,29 9,47 1,1,14 9,94,24,3 12,55 1,14,14 12,44,64,8 12,17,38,5,16 1,13,14 4,47 4,94,62 1,47,5,6 Tabela 6.4. Wyniki obliczeń opóźnienia funkcji wejściowej dla danych otrzymanych na drodze symulacji, otrzymane z zastosowaniem różnych metod. Średni czas przejścia MTT przyjęty w symulacjach wynosił 4s, Graficzna prezentacja wyników pokazana jest na rysunku Wszystkie wartości w tabeli wyrażone są w sekundach. 59
78 Pierwszym istotnym wnioskiem, jaki nasuwa się po analizie wyników jest wpływ stosunku sygnału do szumu na otrzymane wartości czasu opóźnienia krzywej tkankowej względem krzywej tętniczej AIF. Metoda progowa dla sygnałów silnie zaszumionych jest praktycznie bezużyteczna. Dopiero dla SNR=25 db można powiedzieć, że wyniki otrzymane z jej zastosowaniem są satysfakcjonujące i nieodbiegające od innych testowanych metod. Pozostałe trzy metody wykazują podobną odporność na zaszumienie krzywych dynamicznych. Warto jednak podkreślić, że wartości odchylenia standardowego średniego czasu opóźnienia dla metody korelacyjnej są o rząd wielkości mniejsze od odchyleń dla pozostałych metod. Można na tej podstawie wnioskować, że metoda korelacyjna ma najlepsze właściwości w warunkach niskiej wartości SNR. Analizując wartości średnie otrzymanych czasów opóźnienia można zaobserwować nieprzypadkową rozbieżność otrzymanych wyników. Dla sygnałów o SNR 5 i 15 db metoda progowa zawsze daje wyniki zaniżone względem wartości przyjętych w modelu. Wynika to z faktu, że otrzymana wartość nie jest rzeczywistym czasem opóźnienia krzywej, a czasem pierwszej zaszumionej próbki przypadkowo przekraczającej ustalony w algorytmie próg. Metoda korelacyjna i metoda odległości maksimum krzywych oraz metoda progowa (ale tylko dla sygnałów o SNR=25 db) dają wyniki zawyżone względem przyjętego w symulacjach modelu. Przyczyną tego jest rozmycie krzywej tkankowej wynikające z ustalonego czasu MTT. Ilustracją tego efektu jest rysunek 6.5. Wraz ze wzrostem czasu MTT rozmycie to będzie się powiększać, co wynika z właściwości splotu opisanej zależnością (6.17): Długość F 1 =N 1, Długość F 2 =N 2, Długość F 1 F 2 =N 1 N 2 1, (6.17) gdzie N 1 i N 2 oznaczają liczby próbek splatanych funkcji. Oczywiste zatem staje się, że zarówno metoda progowa, jak i metoda opóźnienia maksimum dadzą wyniki zawyżone. Podobnie można wytłumaczyć zawyżone wyniki otrzymane metodą kowariancyjną. Jak wspomniano wcześniej, funkcja kowariancji wzajemnej jest miarą podobieństwa dwóch sygnałów, stąd przy rozmyciu jednego z nich wprowadzony zostaje błąd przy ocenie ich wzajemnego opóźnienia. Uwzględniając zatem jakość otrzymanych wyników tylko pod kątem czasu opóźnienia, w przeprowadzonych symulacjach metodą dającą wyniki obarczone najmniejszym błędem względem parametrów przyjętych do modelu jest bezwzględnie metoda geometryczna. Wydaje się być ona najlepszą przy ocenie czasu dojścia bolusa (BAT, ang. Bolus Arrival Time) do wybranego regionu zainteresowania. Pozostałe metody dają wyniki, 6
79 które również są pewną miarą czasu dojścia, lecz nie można ich interpretować w sposób bezwzględny, pamiętając, że uwzględniają one również rozmycie krzywej tkankowej wynikającej z czasu MTT. Należy tutaj wspomnieć, że niewątpliwą zaletą metody progowej i wzajemnego opóźnienia maksimum krzywych jest ich prostota. Czas dojścia bolusa (BAT) jest jednym z parametrów mogących pomóc w ocenie stanu układu krążenia, w szczególności może on być związany z wszelkiego rodzaju przewężeniami tętnic. W pracy tej główny nacisk położony jest jednak na estymację średniego czasu przejścia MTT, który jest bezpośrednio związany z oceną perfuzji tkankowej. W związku z tym wykonano dalsze obliczenia na podstawie danych syntetycznych, mające na celu obliczenie MTT i porównanie go z wartościami przyjętymi w modelu do symulacji. Obliczenia wykonano dla różnych wartości parametrów SNR, t i MTT przyjętych w symulacjach. Czas MTT obliczany był na podstawie zależności (5.9) po wprowadzeniu modyfikacji wynikającej z właściwości splotu dotyczącej przesunięcia czasowego oraz fizycznej interpretacji funkcji R t. Właściwości splotu uwzględniające przesunięcia czasowe splatanych funkcji można zapisać jako: a AIF t R t =C VOI t, b AIF t t R t =C VOI t t, c AIF t R t t =C VOI t t. (6.18) W powyższym wzorze równanie a) opisuje idealną sytuację pomiarową, w której możliwa jest obserwacja krzywej koncentracji na samym wejściu do układu naczyń włosowatych, co sprawiłoby, że nie jest wtedy konieczna korekcja opóźnienia i można na podstawie krzywych AIF t i C VOI t obliczać funkcję R t. Niestety, jak już wcześniej wspominano, warunki pomiarowe nie zapewniają takiej możliwości. Obserwowanymi krzywymi są AIF t i C VOI t t, przy czym t jest wartością nieznaną. Zatem równaniem, które można zastosować do obliczeń jest równanie c) z wzoru (6.18), wtedy po obliczeniu rozplotu otrzymamy funkcję R t t. Do prawidłowego obliczenia czasu MTT konieczna jest znajomość parametru t, którego sposób obliczania został zaprezentowany wcześniej z uwzględnieniem kilku metod. Proponowana w pracy metoda korekcji opóźnienia opiera się na jeszcze jednym założeniu, wynikającym z właściwości funkcji R t : a R t = dla t, b R t t = dla t t, (6.19) co wynika z fizycznej interpretacji funkcji residuum, opisującej jaka część środka cieniującego wprowadzonego do układu w chwili t= pozostaje w nim po pewnym czasie t>. 61
80 Przyjmuje się zatem, że dla czasów t< w układzie nie ma znacznika, czyli R(t<)=. Jeśli znacznik zostanie wprowadzony do układu z opóźnieniem t, prawdziwym staje się równanie b) z wzoru (6.18). Powracając do wzoru (5.9), opisującego średni czas przejścia MTT, i uwzględniając właściwości funkcji R(t) podane we wzorze (6.19) można zmodyfikować wzór (5.9) ograniczając dolny zakres całkowania: MTT = R t dt. (6.2) t Korzystając z powyższego wzoru obliczono średnie czasy przejścia dla krzywych R t obliczonych na podstawie symulacji. Ich przykładowe realizacje pokazane są na rysunku 6.8. Dla różnych opóźnień SNR [db] t = s t = 1 s t = 6 s MTT eff 2,54 4,37 4,13 std,12,16,15 MTT eff 2,52 4,3 4,19 std,36,5,51 MTT eff 2,83 3,61 3,99 std 1,24 1,33 1,48 MTT eff 4,58 6,3 6,2 std,19,26,21 MTT eff 4,6 6,2 6,7 std,6,76,68 MTT eff 4,29 5,2 5,42 std 1,59 1,74 2, MTT eff 6,65 7,98 7,98 std,26,31,28 MTT eff 6,56 8,4 7,95 std,81 1,,89 MTT eff 5,54 6,21 6,45 std 2,2 2,5 1,99 MTT [s] Tabela 6.5. Zestawienie wyników obliczeń średniego czasu przejścia MTT eff bez korekcji opóźnienia. 62
81 Dla różnych opóźnień SNR [db] t = s t = 1 s t = 6 s MTT eff 2,54 3,48 3,19 std,11,15,13 MTT eff 2,56 3,48 3,26 std,38,5,46 MTT eff 2,61 2,98 3,14 std 1,21 1,45 1,46 MTT eff 3,61 4,67 4,33 std,19,22,2 MTT eff 3,71 4,77 4,44 std,59,72,64 MTT eff 3,44 3,84 3,94 std 1,55 1,8 1,63 MTT eff 5,66 6,51 6,37 std,26,29,25 MTT eff 5,4 6,37 6,17 std,76,92,83 MTT eff 4,52 4,8 4,87 std 1,95 1,96 1,89 MTT [s] Tabela 6.6. Wyniki obliczeń średniego czasu przejścia MTT eff z wykorzystaniem metody korelacyjnej. W symulacjach przyjęto różne wartości parametrów t, SNR i MTT przyjętego w modelu. W tabelach 6.5 i 6.6 zestawiono wyniki obliczeń czasu MTT eff, zarówno dla metody korelacyjnej (tabela 6.6), jak i bez jej zastosowania (tabela 6.5). Dla każdej kombinacji czasu opóźnienia t, stosunku sygnału do szumu SNR i czasu MTT przyjętych w modelu wykonano 64 symulacje. W tabelach pokazano wartości średnie oraz odchylenia standardowe średniej obliczonego czasu MTTeff. Otrzymane wyniki przedstawione są na rysunku Analiza odchylenia standardowego średnich wartości czasów MTT pokazuje, że wpływ stosunku sygnału do szumu na jakość otrzymanych wyników jest bardzo podobny jak w przypadku obliczeń czasu opóźnienia t krzywej tkankowej względem funkcji wejściowej AIF, co zostało opisane wcześniej. Wartości średnie otrzymanych czasów MTT wskazują, że najmniejszym błędem obarczone są wyniki otrzymane metodą kowariancyjną. Interesujący jest fakt, że pomimo tak dobrych wyników osiągniętych przy obliczaniu czasu 63
82 opóźnienia, metoda geometryczna nie daje najlepszych przybliżeń czasu MTT. Uzasadnieniem tego efektu jest rozmycie funkcji R t wynikające ze sposobu obliczania rozplotu. Jest to wyraźnie widoczne na rysunku 6.8. W części pracy poświęconej technice TSVD obliczania rozplotu opisano zastosowaną w niej metodę regularyzacji polegającą na wyzerowywaniu współczynników macierzy wartości szczególnych mniejszych od ustalonego progu (zostało to szczegółowo opisane w rozdziale 5.3) Jak wspomniano, działanie takie ma na celu wyeliminowanie oscylacji z rozwiązania zagadnienia rozplotu. Równocześnie funkcja wynikowa jest rozmywana, co odpowiada efektowi filtracji dolnoprzepustowej. Niemożliwe zatem staje się odtworzenie gwałtownych zmian wartości funkcji R t. Z jej fizycznej interpretacji wynika, że w chwili t= następuje skok wartości od do 1. Moment ten jest silnie rozmywany w procesie obliczania rozplotu. Można zatem przypuszczać, że część powierzchni pod krzywą poprzedzająca chwilę t= można pominąć przy obliczaniu czasu MTT, ponieważ jest ona wyłącznie efektem zastosowanej techniki obliczeniowej, bez odniesienia do fizycznej interpretacji funkcji przejścia. Wyniki przeprowadzonych symulacji upoważniają do wniosku, że metoda kowariancyjna jest efektywnym narzędziem do korekcji opóźnienia krzywych koncentracji względem funkcji wejściowej AIF w celu zmniejszenia błędu oszacowania średniego czasu przejścia MTT. Wartość t-statystyki SNR [db] t = s t = 1 s t = 6 s 25, 91,82 17, ,75 26,24 3,64 5 2,87 7,25 9, ,68 18,29 131, ,93 3,91 39,5 5 8,66 1,67 12, ,92 78,36 97, ,63 27,81 33,1 5 8,22 11,25 13, ,61 14,28 131, ,96 3,5 37,1 5 9,6 11,76 12,89 MTT [s] Tabela 6.7. Wyniki testów T-studenta przeprowadzonych dla otrzymanych wyników. Licza stopni swobody
83 W celu wykazania, że otrzymane różnice są istotne statystycznie, a nie wynikają jedynie z przypadkowych rozbieżności w poszczególnych realizacjach symulacji, wykonano dodatkowo test T-studenta. Wyniki przedstawiono w tabeli 6.7. Poza przypadkiem dla t= s i MTT=2 s można stwierdzić, że wartości średnie obliczonych czasów MTT eff różnią się od siebie w sposób istotny statystycznie na poziomie ufności p <,5. Świadczy to o tym, że zastosowana metoda w istotny sposób zmienia wartości poszukiwanego parametru. Aby jednak jednoznacznie stwierdzić czy metoda poprawia jakość otrzymywanych wyników (a nie tylko je zmienia), niezbędne jest porównanie wartości średnich z czasem MTT przyjętym do modelu zastosowanego w symulacjach. t = s MTT [s] SNR [db] t =1s t =6s Bez korekcji Z korekcją Bez korekcji Z korekcją Bez korekcji Z korekcją 25 27, % 27, % 118,5 % 74, % 16,5 % 59,5 % 15 26, % 28, % 115, % 74, % 19,5 % 63, % 5 41,5 % 3,5 % 8,5 % 49, % 99,5 % 57, % 25 14,5 % -9,8 % 57,5 % 16,8 % 5,5 % 8,3 % 15 15, % -7,3 % 55, % 19,3 % 51,8 % 11, % 5 7,3 % -14, % 25,5 % -4, % 35,5 % -1,5 % 25 1,8 % -5,7 % 33, % 8,5 % 33, % 6,2 % 15 9,3 % -1, % 34, % 6,2 % 32,5 % 2,8 % 5-7,7 % -24,7 % 3,5 % -2, % 7,5 % -18,8 % Tabela 6.8. Procentowe błędy obliczeń średniego czasu przejścia MTT eff w stosunku do przyjętego w symulacjach czasu MTT dla różnych t, MTT i SNR. Pozycje wyróżnione kolorem szarym oznaczają te przypadki, w których zastosowanie metody korelacyjnej pozwoliło zmniejszyć błąd obliczeń. W tabeli 6.8 zestawione są procentowe błędy uzyskanych wyników względem średniego czasu przejścia MTT przyjętego w symulacjach. Przypadki, dla których uzyskano poprawę wyniku oznaczono kolorem szarym. Przez poprawę wyniku rozumie się mniejszą wartość bezwzględną błędu procentowego. Dla pokazania czy otrzymana wartość MTT eff jest zawyżona czy zaniżona, wynik prezentowany jest ze znakiem. Charakterystyczne jest, że dla opóźnienia t= s, poza przypadkiem dla MTT =2 s, można powiedzieć o pogorszeniu otrzymywanych wyników. Przyczyną tego faktu jest sposób obliczania opóźnienia. Jak wspomniano wcześniej, funkcja kowariancji używana w proponowanej metodzie jest miarą podobieństwa dwóch sygnałów. Pamiętać należy, że porównywane sygnały (krzywe) 65
84 nie są identyczne. Dlatego też dla czasu MTT=2 s, najkrótszego z rozpatrywanych, dla którego krzywa w tkance jest stosunkowo mało rozmyta w porównaniu z funkcją wejściową AIF, różnica błędów obliczeń jest najmniejsza. Potwierdzają to też wartości T-statystyki dla tego przypadku, z których wynika, że otrzymane wartości średnie dla symulacji nie różnią się w sposób istotny statystycznie (dla przyjętego poziomu ufności p<,5). Przy t= dla czasów MTT>2 s, dla których występuje większe rozmycie, metoda korelacyjna może wprowadzać dodatkowy błąd. Wynika to z właściwości funkcji korelacji wzajemnej. Należy bowiem pamiętać, że tylko dla identycznych przebiegów czasowych maksimum funkcji korelacji pokryje się z opóźnieniem pomiędzy tymi przebiegami, a wartość funkcji korelacji w tym punkcie osiągnie wartość 1. Jeżeli przebiegi nie są identyczne, maksimum funkcji korelacji pokazuje tylko dla jakiego przesunięcia czasowego podobieństwo obu przebiegów jest maksymalne. W szczególności, gdy jeden z sygnałów jest rozmyty względem drugiego, tak jak w przypadku krzywych koncentracji, może nastąpić błąd w oszacowaniu opóźnienia pomiędzy danymi sygnałami. Dla pozostałych wartości opóźnień t, metoda korelacyjna w sposób istotny poprawia jakość otrzymanego wyniku MTT eff. Najgorzej prezentują się wyniki dla czasu MTT=2 s, jest to prawdopodobnie związane z tym, że funkcja R t posiada wtedy najostrzejsze zbocza, które jak już wspomniano wcześniej są trudne do odtworzenia podczas obliczania rozplotu. Pomimo tego dla czasu MTT=2 s nastąpiło zmniejszenie błędu procentowego średnio o około 4%. Najlepsze wyniki zostały uzyskane dla czasów MTT>2 s. Dla 11 z 27 przypadków osiągnięto wartość błędu procentowego poniżej 1%, co według autora jest wynikiem bardzo dobrym. Interesujące są wyniki dla sygnałów mocno zaszumionych, przy SNR=5 db, dla których nastąpiło pogorszenie jakości otrzymanego wyniku. Przyczyny tego faktu są trudne do interpretacji, można jednak powiedzieć, że jest to efekt marginalny, ponieważ wartości SNR odpowiadające krzywym otrzymywanym w czasie rzeczywistych badań tomograficznych, zarówno metodą MR jak i CT, przekraczają 2 db. Podsumowując wyniki symulacji można powiedzieć, że proponowana korelacyjna metoda korekcji opóźnienia krzywej koncentracji: dla czasów t w sposób istotny poprawia otrzymywane wyniki obliczeń, w szczególności dla czasów MTT>2 s, które są czasami typowymi dla tkanki mózgowej; dla wartości SNR osiąganych w typowych badaniach wykonywanych w praktyce klinicznej obliczone wartości 66 tomograficznych MTT eff obarczone
85 są błędem mniejszym niż 1%; powyższe dwa wnioski pozwalają na podjęcie próby zastosowania proponowanej metody do rzeczywistych danych tomograficznych, co zostanie zaprezentowane w następnym rozdziale. 67
86 MTT=2s SNR=5dB 1 MTTef [s] t [s] t [s] t [s] 8 1 MTT=2s SNR=15dB 1 MTTef [s] MTT=2s SNR=25dB 1 MTTef [s] Rysunek Wyniki obliczeń czasu opóźnienia funkcji wejściowej względem obserwowanej funkcji AIF różnymi metodami. Czas MTT przyjęty w modelu wynosił 4s. Kolorami oznaczono wyniki dla poszczególnych metod: czerwony metoda korelacyjna, zielony metoda geometryczna, niebieski metoda opóźnienia maksimum, czarny metoda progowa (przyjęty próg 1%). Szczegółowe wyniki przedstawione są w tabeli
87 MTT=2s SNR=5dB MTTef [s] t [s] t [s] t [s] 8 1 MTT=2s SNR=15dB MTTef [s] MTT=2s SNR=25dB MTTef [s] Rysunek Wyniki obliczeń czasu MTT na podstawie danych syntetycznych dla różnych czasów opóźnienia t oraz czasu MTT=2 s przyjętego w modelu, wykonanych z użyciem różnych metod korekcji opóźnienia opisanych w rozdziale. Znaczenie kolorów takie jak na rysunku
88 MTT=4s SNR=5dB MTTef [s] t [s] t [s] t [s] 8 1 MTT=4s SNR=15dB MTTef [s] MTT=4s SNR=25dB MTTef [s] Rysunek Wyniki obliczeń czasu MTT na podstawie danych syntetycznych dla różnych czasów opóźnienia t oraz czasu MTT=4 s przyjętego w modelu, wykonanych z użyciem różnych metod korekcji opóźnienia opisanych w rozdziale. Znaczenie kolorów takie jak na rysunku
89 MTT=6s SNR=5dB MTTef [s] t [s] t [s] t [s] 8 1 MTT=6s SNR=15dB MTTef [s] MTT=6s SNR=25dB MTTef [s] Rysunek Wyniki obliczeń czasu MTT na podstawie danych syntetycznych dla różnych czasów opóźnienia t oraz czasu MTT=6 s przyjętego w modelu, wykonanych z użyciem różnych metod korekcji opóźnienia opisanych w rozdziale. Znaczenie kolorów takie jak na rysunku
90 6.4 Zastosowanie metody korelacyjnej do analizy rzeczywistych danych tomograficznych. Wnioski sformułowane na podstawie analizy wyników otrzymanych na drodze symulacji komputerowych pozwalają na zastosowanie proponowanej metody do badań klinicznych. Analizowane w pracy badania CT zostały wykonane w Centralnym Szpitalu MSWiA, natomiast badania MR w Centralnym Szpitalu Klinicznym w Warszawie. Pacjenci nie byli dobierani w żaden szczególny sposób, przedstawione dane stanowią zatem przypadkową próbkę, a jedynym co łączyło analizowaną grupę jest fakt, że zaistniały wskazania do badania tomograficznego głowy. Pozwala to zatem sprawdzić uniwersalność metody Protokół badania Fakt, że badania wykonane w każdej z modalności przeprowadzono w jednym ośrodku zapewnił stosowanie we wszystkich przypadkach takiego samego protokołu postępowania. W przypadku badań CT wykonywano dynamiczną serię 45 obrazów pojedynczej warstwy, o rozdzielczości 512x512 pikseli, w odstępach czasowych 1 s. Obrazowana warstwa była tak dobrana, aby widoczne były na niej tętnice przednie mózgu (ACA). Zastosowanym środkiem kontrastowym była UROPOLINA 75%. W przypadku badań MR wykonywano dynamiczną serię 6 obrazów od 7 do 9 warstw o rozdzielczości 128x128 pikseli przy TR=1 s i TE=6 ms. Zastosowanym środkiem kontrastowym był MAGNEVIST. Obrazowanie wielu warstw zapewniło możliwość uwidocznienia zarówno tętnic środkowych mózgu (MCA), jak i tętnic przednich (ACA). Aby móc porównywać wyniki otrzymane z obu modalności, jako krzywą wejściową AIF zaznaczano ręcznie tętnicę przednią mózgu, która była widoczna na wszystkich badaniach Analiza i wyniki Dane zebrane w opisany powyżej sposób posłużyły do przeprowadzenia szeregu analiz. Obliczono mapy parametryczne opóźnienia krzywej koncentracji w tkance względem krzywej wejściowej oraz mapy średniego czasu przejścia kontrastu bez korekcji uwzględniającej opóźnienia oraz z korekcją. Na otrzymanych w ten sposób mapach zaznaczano 8 regionów zainteresowania (ROI, ang. Region of Interest), dobranych w ten sposób, aby każdy z nich był zasilany w krew przez inną tętnicę mózgu: ROI_1 i ROI_2 przez tętnice przednie (odpowiednio prawą i lewą), ROI_3 i ROI_4 przez tętnice tylne (odpowiednio prawą i lewą), ROI_5 i ROI_6 przez tętnice środkowe (odpowiednio prawą i lewą), 72
91 ROI_7 i ROI_8 przez tętnice środkowe (odpowiednio prawą i lewą). Dodatkowo podział ten uwzględniał również rodzaj tkanki, którą obejmował region: ROI_1... ROI_6 materia szara, ROI_7... ROI_8 materia biała. Dla każdego ROI obliczono średnią wartość opóźnienia t oraz średniego czasu przejścia MTT eff. Tak otrzymane wyniki zestawiono w tabelach 6.9, 6.1 i 6.11 dla badań CT oraz 6.12, 6.13 i 6.14 dla MR. Wszystkie obliczenia wykonano przy pomocy oprogramowania napisanego w ramach pracy przez autora. Zostało ono szerzej opisane w dodatku 8.2. ROI 1 ROI 2 ROI 3 ROI 4 ROI 5 ROI 6 ROI 7 ROI 8 t [s] t [s] t [s] t [s] t [s] t [s] t [s] t [s] CT_BILE 1,98 2,21 3,13 3,11 1,51 1,78 3,41 3,16 CT_GEHA 2,86 2,37 3,47 3,7 3,34 2,61 4,9 5,32 CT_GWED 2,71 2,67 3,81 3,34 3,4 3,62 4,2 4, CT_KORO 1,98 1,48 3,64 2,77 1,96 1,89 2,7 1,41 CT_LALI 2,38 2,41 2,25 2,63 2,1 2,13 2,21 2,85 CT_PYWL 2,56 2, 3,46 3,71 2,43 2,5 4,25 4,72 CT_WAKA 2,81 3,29 4,48 4,4 2,89 3,41 4,23 4,2 CT_WNWA 1,75 1,66 3,3 2,76 2,4 2,3 3,65 3,61 CT_ZIWA 1,76 1,89 2,72 2,85 2,52 1,97 2,34 2,77 CT_ZUWA 2,1 2,4 3,8 3,21 1,78 1,86 3,1 3,21 identyfikator pacjenta Tabela 6.9. Średnie czasy opóźnienia t krzywej kontrastu względem krzywej wejściowej AIF w regionach zainteresowania obliczone metodą korelacyjną. Dane dotyczą badań przeprowadzonych techniką CT. 73
92 ROI 1 ROI 2 ROI 3 ROI 4 ROI 5 ROI 6 ROI 7 ROI 8 MTT eff [s] MTT eff [s] MTT eff [s] MTT eff [s] MTT eff [s] MTT eff [s] MTT eff [s] MTT eff [s] CT_BILE 3,33 3,85 4,83 4,97 3,69 3,45 5,5 4,3 CT_GEHA 4,79 4,6 5,74 6,6 5,78 4,13 8,45 9,12 CT_GWED 4,81 4,67 5,52 5,66 4,84 6,6 4,97 5,69 CT_KORO 5,2 4,88 5,62 5,36 4,46 4,75 5,13 5,1 CT_LALI 4,28 3,97 3,93 4,29 3,72 3,87 3,92 4,56 CT_PYWL 5,7 4,24 5,59 5,67 4,65 4,33 6,4 7,8 CT_WAKA 6,22 5,91 6,21 5,22 5,86 5,97 7,29 6,3 CT_WNWA 3,59 3,42 4,66 4,33 3,83 3,73 5,32 5,35 CT_ZIWA 3,71 3,49 4,64 4,74 4,21 3,8 4,28 4,38 CT_ZUWA 5,14 5,16 4,51 4,61 3,22 2,69 4,77 4,84 identyfikator pacjenta Tabela 6.1. Średnie czasy przejścia kontrastu dla różnych regionów zainteresowania obliczone bez uwzględnienia opóźnienia krzywej koncentracji względem krzywej wejściowej AIF, Badania wykonane techniką CT. ROI 1 ROI 2 ROI 3 ROI 4 ROI 5 ROI 6 ROI 7 ROI 8 MTT eff [s] MTT eff [s] MTT eff [s] MTT eff [s] MTT eff [s] MTT eff [s] MTT eff [s] MTT eff [s] CT_BILE 2,55 2,93 2,79 3,4 3,18 2,86 3,1 2,91 CT_GEHA 2,14 2,8 1,78 2,16 1,84 2,26 1,89 2,25 CT_GWED 3,17 3,1 3,28 3,23 3,11 3,28 2,8 3,21 CT_KORO 4,47 4,57 4,16 4,43 4,2 4,25 4,1 4,67 CT_LALI 3,24 2,94 2,86 2,96 2,96 2,93 2,81 3,14 CT_PYWL 3,77 3,65 3,25 3,86 3,54 3,75 3,77 3,88 CT_WAKA 5,4 4,28 3,65 3,2 4,75 4,48 4,88 4,29 CT_WNWA 3,6 2,94 3,16 3,8 2,91 3,8 3,19 3,16 CT_ZIWA 3,31 3,22 3,67 3,83 3,48 3,15 3,7 3,8 CT_ZUWA 4,71 4,63 2,64 2,55 2,77 2,19 3,4 3,36 identyfikator pacjenta Tabela Średnie czasy przejścia kontrastu dla różnych regionów zainteresowania obliczone z uwzględnieniem opóźnienia krzywej koncentracji względem krzywej wejściowej AIF. Badania wykonane techniką CT. 74
93 identyfikator pacjenta ROI 1 ROI 2 ROI 3 ROI 4 ROI 5 ROI 6 ROI 7 ROI 8 t [s] t [s] t [s] t [s] t [s] t [s] t [s] t [s] MR_MIMA 2,58 5,97 2,14 3,15 2,68 3,21 2,39 3,52 MR_DUKR 2,28 2,1 2,17 2,15 2, 1,74 2,88 1,2 MR_KRAL 1,16 1,33 1,92 1,77 1,39 1,3 2,48 1,93 MR_LUKO 2,4 2,61 2,6 2,68 1,92 2,71 3,9 3,57 Tabela Średnie czasy opóźnienia t krzywej kontrastu względem krzywej wejściowej AIF w regionach zainteresowania obliczone metodą korelacyjną. Dane dotyczą badań przeprowadzonych techniką MR ROI 1 ROI 2 ROI 3 ROI 4 ROI 5 ROI 6 ROI 7 ROI 8 MTT eff [s] MTT eff [s] MTT eff [s] MTT eff [s] MTT eff [s] MTT eff [s] MTT eff [s] MTT eff [s] MR_MIMA 8,3 16,78 8,29 7,86 1,33 11,45 16,86 9,22 MR_DUKR 7,9 6,81 7,26 7,56 7,2 5,66 11,36 6,6 MR_KRAL 3,59 3,67 4,42 4,29 3,42 3,8 5,68 6,12 MR_LUKO 6,24 6,87 6,77 7,47 5,28 7,57 1,65 11,35 identyfikator pacjenta Tabela Średnie czasy przejścia kontrastu dla różnych regionów zainteresowania obliczone bez uwzględnienia opóźnienia krzywej koncentracji względem krzywej wejściowej AIF. Badania wykonane techniką MR. ROI 1 ROI 2 ROI 3 ROI 4 ROI 5 ROI 6 ROI 7 ROI 8 MTT eff [s] MTT eff [s] MTT eff [s] MTT eff [s] MTT eff [s] MTT eff [s] MTT eff [s] MTT eff [s] MR_MIMA 2,85 5,47 4,51 3,9 3,64 3,5 12,84 9,12 MR_DUKR 3,69 3,41 3,3 3,83 3,78 3,32 4,52 4,73 MR_KRAL 2,84 2,11 2,47 2,69 2,5 2,71 1,51 3,14 MR_LUKO 3,5 2,51 2,6 2,78 2,84 3,17 3,32 3,13 identyfikator pacjenta Tabela Średnie czasy przejścia kontrastu dla różnych regionów zainteresowania obliczone z uwzględnieniem opóźnienia krzywej koncentracji względem krzywej wejściowej AIF. Badania wykonane techniką MR. Na podstawie danych z regionów obliczone zostały wartości średnie w badanych grupach dla każdego regionu. Wyniki zebrano w tabelach 6.15 i
94 ROI 1 ROI 2 ROI 3 ROI 4 ROI 5 ROI 6 ROI 7 ROI 8 t [s] 2,28 2,24 3,31 3,21 2,39 2,34 3,47 3,53 STD t [s],43,52,62,48,58,66,9 1,11 MTT NOCORR [s] 4,6 4,37 5,13 5,15 4,43 4,28 5,6 5,67 STD MTT [s],88,79,71,71,88 1,6 1,4 1,5 MTT CORR [s] 3,55 3,43 3,12 3,22 3,26 3,22 3,31 3,4 STD MTT [s],94,83,66,66,78,76,82,7 Tabela Średnie wartości czasu opóźnienia t i MTT w poszczególnych regionach dla badań wykonanych techniką CT. ROI 1 ROI 2 ROI 3 ROI 4 ROI 5 ROI 6 ROI 7 ROI 8 t [s] 1,83 2,72 1,97 2,15 1,8 3,9 2,37 2,41 STD t [s],67 1,88,59,83,64 2,4,81 1,7 MTT NOCORR [s] 5,16 6,79 5,9 5,4 5,31 7,13 8,36 6,48 STD MTT [s] 2,6 5,78 2,69 2,78 3,33 3,93 5,72 1,69 MTT CORR [s] 2,87 3,1 2,82 2,84 3, 3,4 4,9 4,45 STD MTT [s],63 1,43 1,1 1,17,68,79 4,58 2,77 Tabela Średnie wartości czasu opóźnienia t i MTT w poszczególnych regionach dla badań wykonanych techniką MR. Analizując wartości średniego opóźnienia krzywej kontrastu względem AIF można dostrzec różnice pomiędzy regionami zasilanymi przez różne tętnice mózgu oraz obejmującymi różne tkanki. Regiony ROI_3 i ROI_4, należące do terytorium tętnic tylnych i obejmujących materię szarą, wykazują czas opóźnienia około 1 sekundy względem pozostałych regionów obejmujących również materię szarą. Może to wynikać z faktu, że pozostałe regiony zasilane są przez tętnice środkowe i przednie, które są odgałęzieniami tętnicy szyjnej środkowej, zatem mają wspólny początek. Tętnice tylne natomiast zasilane są bezpośrednio z tętnicy podstawnej, która jest połączeniem tętnic kręgowych. Droga jaką przebywa krew do regionów ROI_3 i ROI_4 jest różna od pozostałych i stąd może wynikać opóźnienie. Opóźnienie w materii białej, która zasilana jest w krew przez tętnice środkowe może natomiast wynikać 1) z różnicy odległości jaką musi pokonać krew i 2) z mniejszego zapotrzebowania na składniki odżywcze, a co za tym idzie, mniejszego przepływu. Wskazane różnice są istotne statystycznie na poziomie ufności p<,1 co zostało 76
95 sprawdzone testem T-studenta. Różnica w średnich czasach opóźnienia t pokrywa się różnicami w średnich czasach przejścia MTT dla odpowiadających sobie regionów. O ile różnice w czasie dojścia znacznika można tłumaczyć budową układu krwionośnego, o tyle średni czas jego przejścia powinien być taki sam dla poszczególnych typów tkanek. Można zatem przypuszczać, że różnice te wynikają z błędu obliczeniowego jaki wprowadza opóźnienie krzywej kontrastu w tkance. Różnice te również zostały sprawdzone testem T-studenta pod kątem istotności statystycznej na poziomie ufności p<,1. Obliczony został też stosunek czasów przejścia MTT dla istoty szarej i białej, który wyniósł dla techniki CT MTT WM =1,21 MTT GM (6.21) MTT WM =1,33. MTT GM (6.22) oraz dla badań MR Inaczej przedstawiają się wyniki dla poszczególnych regionów po zastosowaniu korekcji opóźnienia. Średnie czasy przejścia dla wszystkich regionów osiągają mniejsze wartości ale, co istotniejsze, również nie wykazują różnic istotnych statystycznie, co potwierdzone zostało testem T-studenta. Zmienia się też stosunek czasu średniego przejścia dla materii szarej i białej, dając wyniki zgodne z podawanymi w literaturze [HUNS2, KOSH99, NIGH97, OSTE96b]. Po zastosowaniu korekcji opóźnienia wyniósł on dla badań CT MTT WM =1,2 MTT GM (6.23) MTT WM =1,11. MTT GM (6.24) i dla MR Przedstawione w tym rozdziale wyniki pokazują, że korekcja opóźnienia krzywej koncentracji względem funkcji wejściowej AIF jest istotnym elementem w procesie przetwarzania danych perfuzyjnych. Dodanie tego etapu analizy wprowadza istotną zmianę otrzymywanych wyników, która zgodnie z wspomnianymi w pracy danymi literaturowymi zbliża wyniki do stanu faktycznego Przykładowe wyniki badania klinicznego W ramach prac wyniki otrzymywane różnymi metodami były konsultowane z lekarzem 77
96 radiologiem. Na poniższych rysunkach przedstawione są obrazy parametryczne wykonane przy użyciu oprogramowania opracowanego przez autora pracy. Obrazy te przedstawiają przypadek udaru niedokrwiennego w obrębie zakrętu zaśrodkowego prawej półkuli mózgu. Na obrazie dyfuzyjnym wyraźnie widoczny jest obszar o zwiększonej jasności, wynikający z ograniczonej dyfuzji wody w przestrzeni międzykomórkowej. Świadczy to o nieodwracalnych zmianach w tym obszarze. Obejmuje on głównie korę mózgową, a w mniejszym stopniu istotę białą. Istotna z punktu widzenia podjęcia leczenia jest analiza obrazów parametrycznych perfuzji. Daje ona dodatkową wiedzę na temat obszaru niedokrwienia, w którym nie doszło jeszcze do nieodwracalnych zmian (tzw. strefa półcienia lub penumbry) i szybkie udrożnienie przepływu może uratować zagrożony obszar. Zastosowane metody różnią się pod tym względem, pokazując obszary penumbry o różnej wielkości. Obszar o największej powierzchni jest widoczny przy zastosowaniu metody bez korekcji czasu opóźnienia, szczególnie dobrze widoczny na mapach średniego czasu przejścia MTT. Metoda ta daje największą rozbieżność z obszarem o zmniejszonej dyfuzji i może prowadzić do przeszacowania obszaru penumbry. Zastosowanie metody geometrycznej do korekcji czasu opóźnienia dojścia bolusa daje w obrazach parametrycznych obszar penumbry praktycznie pokrywający się lub nieznacznie większy od obszaru udaru widocznego na obrazach dyfuzyjnych. Sytuacja taka może spowodować dyskwalifikację podjęcia próby udrożnienia przepływu. Może to spowodować powiększenie zawału. Trzecia metoda, proponowana przez autora, daje wynik pośredni w porównaniu ze wspomnianymi metodami. W ocenie lekarza radiologa jest to wynik prawdopodobnie najlepiej oddający stan rzeczywisty. Analizując otrzymane obrazy można powiedzieć, że obszar zaburzonego przepływu krwi najlepiej widoczny jest na obrazach pokazujących parametry czasowe krzywych dynamicznych średni czas przejścia MTT i czas dojścia bolusa od tętnicy zasilającej do obszaru zainteresowania. Na pozostałych mapach parametrycznych (CBV i CBF) obszar ten jest słabiej widoczny. Na rysunkach 6.15 do 6.24 pokazane są wynikowe obrazy parametryczne omawianego przypadku. Dokładny tekst przykładowej opinii lekarza radiologa znajduje się w dodatku
97 Rysunek Obraz dyfuzyjny. Obszary o podwyższonej jasności w prawej półkuli pokazują obszar nieodwracalnych zmian spowodowanych niedokrwieniem. Rysunek Mapa parametryczna CBV. W prawej półkuli można znaleźć słabo widoczny obszar niedokrwienia. Wartości obrazu wyrażone są w jednostkach umownych. 79
98 Rysunek Mapa opóźnienia bolusa względem funkcji wejściowej AIF wyznaczona metodą geometryczną. Rysunek Mapa opóźnienia bolusa względem funkcji wejściowej AIF, wyznaczona metodą korelacyjną, proponowaną przez autora. 8
99 Rysunek Mapa CBF wyznaczona bez korekcji opóźnienia bolusa. W prawej półkuli wyraźnie widoczny jest obszar niedokrwienia o powierzchni znacznie przekraczającej obszar podwyższonej jasności w obrazie dyfuzyjnym. Wartości pikseli wyrażone są w jednostkach umownych. Rysunek 6.2. Mapa CBF wyznaczona z wykorzystaniem metody geometrycznej do korekcji opóźnienia bolusa. W prawej półkuli wyraźnie widoczny jest obszar niedokrwienia o powierzchni przekraczającej obszar podwyższonej jasności w obrazie dyfuzyjnym, szczególne różnice występują w obrębie istoty białej. Wartości pikseli wyrażone są w jednostkach umownych. 81
100 Rysunek Mapa CBF wyznaczona z wykorzystaniem metody korelacyjnej proponowanej przez autora. Widoczny jest obszar niedokrwienia w korze mózgowej pokrywający się z obszarem widocznym na obrazie dyfuzyjnym oraz obszar obniżonej perfuzji w obrębie istoty białej, będący strefą penumbry. Wartości pikseli wyrażone są w jednostkach umownych. Rysunek Mapa MTT wyznaczona metodą bez zastosowania korekcji opóźnienia bolusa. Bardzo wyraźnie widoczny jest obszar nieprawidłowego ukrwienia znacznie przekraczający obszar widoczny na obrazie dyfuzyjnym. Wartości pikseli wyrażone są w sekundach. 82
101 Rysunek Mapa MTT wyznaczona z zastosowaniem korekcji opóźnienia bolusa metodą geometryczną. Widoczne zaburzenia ukrwienia zajmują obszar nieznacznie większy od widocznych na obrazie dyfuzyjnym. Wartości pikseli wyrażone są w sekundach. Rysunek Mapa MTT wyznaczona z zastosowaniem korekcji opóźnienia bolusa metodą korelacyjną proponowaną przez autora. Obszar zaburzonego przepływu w obrębie kory mózgowej dokładnie pokrywa się z obszarem widocznym na obrazie dyfuzyjnym. Jednocześnie w obrębie istoty białej widoczny jest obszar penumbry. Obraz ten został oceniany przez radiologa jako najbardziej prawdopodobne odzwierciedlenie stanu faktycznego. Wartości pikseli wyrażone są w sekundach. 83
102 7. Podsumowanie 7.1 Wnioski końcowe Głównym celem niniejszej rozprawy było opracowanie procedur i algorytmów przetwarzania danych w badaniach perfuzyjnych głowy. Szczególny nacisk został położony na poprawę dokładności oceny średniego czasu przejścia MTT, będącego istotnym parametrem predykcyjnym w ocenie obszarów zagrożonych udarem niedokrwiennym. W pracy zaprezentowano: zarys technik stosowanych w badaniach perfuzyjnych wykorzystywanych w ocenie ukrwienia tkanek, powszechnie stosowane metody jakościowe oceny parametrów perfuzji i ich krytyczną analizę, dotyczącą szczególnie ich wad uniemożliwiających porównywanie wyników w badaniach długoterminowych i wieloośrodkowych, istniejące metody ilościowe, wykorzystujące technikę TSVD w zagadnieniu rozwiązywania rozplotu funkcji, propozycję modyfikacji istniejących metod wykorzystującą techniki korelacyjne do korekcji opóźnienia funkcji wejściowej, symulacje komputerowe potwierdzające poprawność proponowanej metody, zastosowanie obydwu metod do badań klinicznych i porównanie otrzymanych wyników, analizę uniwersalności proponowanej metody pod względem użytej w badaniach techniki obrazowania (CT i MR). Do najistotniejszych zaprezentowanych osiągnięć można zaliczyć: zastosowanie metod korelacyjnych w procesie przetwarzania danych obrazowych, w celu poprawy oceny średniego czasu przejścia MTT, wykazanie poprawności proponowanej metody oraz jej odporności na szum, co jest istotne w szczególności w przypadku badań wykonywanych techniką MR, wykazanie uniwersalności proponowanej metody pod względem stosowanych technik obrazowana, opracowanie oprogramowania do przetwarzania tomograficznych badań perfuzyjnych. Otrzymane wyniki pozwalają na potwierdzenie postawionej w pracy tezy. Wykazano bowiem, że zastosowanie metod korelacyjnych do korekcji opóźnienia funkcji wejściowej pozwala na poprawę oceny średniego czasu przejścia (MTT), a przez to i pozostałych 84
103 parametrów perfuzji (CBV i CBF). Pokazano również, że proponowana metoda jest uniwersalna pod względem wykorzystywanej techniki obrazowania, zastosowanych środków kontrastowych oraz różnic w sposobie przeprowadzania badania w ramach ustalonego protokołu. Zdaniem autora otrzymane wyniki mogą mieć znaczenie nie tylko naukowe. W ocenie lekarzy radiologów metoda proponowana w rozprawie daje lepszą informację diagnostyczną niż metody aktualnie stosowane. Wskazuje to na potrzebę wdrożenia jej do praktyki klinicznej. Prace w tym kierunku zostały podjęte, co zostało nieco szerzej opisane w dodatku dotyczącym oprogramowania. Ze względu na fakt, że prezentowana metoda znajduje zastosowanie przede wszystkim w schorzeniach związanych z zaburzeniami krążenia, a w szczególności udarów mózgu, które są trzecią przyczyną zgonów w krajach wysoko rozwiniętych, wprowadzenie jej do praktyki klinicznej może mieć skutki ekonomiczne i społeczne. Ocena stanu chorego, która pozwala stwierdzić czy podjęcie drogiego leczenia trombolitycznego ma szanse na pozytywny skutek, może pozwolić na znaczne oszczędności w ośrodku podejmującym się opieki nad chorym. Jednocześnie podjęcie takiego leczenia w czasie okna terapeutycznego daje szanse na szybką rehabilitację pacjenta. Poza oczywistym aspektem ekonomicznym skrócenia czasu rehabilitacji bardzo istotną rolę odgrywają tu skutki społeczne. Pacjent może powrócić do swojej roli w rodzinie i najbliższym otoczeniu. Uwzględniając liczbę przypadków udarów niedokrwiennych mózgu, zarówno społeczne, jak i ekonomiczne, korzyści mogą być niebagatelne. 7.2 Kierunki dalszych badań Badania funkcjonalne są stale, a w ostatnich latach bardzo dynamicznie rozwijającą się gałęzią badań obrazowych. Dają one ogromne możliwości diagnostyczne oraz są bardzo cennym narzędziem w monitorowaniu rozwoju choroby, przebiegu leczenia bądź oceny przeprowadzonych zabiegów chirurgicznych. Autor przewiduje dalsze prace w tej dziedzinie. Szczególne zainteresowanie autora budzi technika pomiaru parametrów ukrwienia bez użycia środków kontrastowych, oparta na magnetycznym znakowaniu krwi tętniczej (ASL, ang. Arterial Spin Labeling). Jej zaletą jest brak obciążenia pacjenta dożylnym podaniem środków kontrastowych, co całkowicie eliminuje ryzyko powikłań związanych z ewentualną reakcją uczuleniową. Metoda ta może być stosowana nie tylko do oceny patologicznych zmian w ukrwieniu związanych z jednostkami chorobowymi, ale również w ocenie zmian parametrów przepływu mózgowego powodowanych aktywnością wybranych obszarów mózgu podczas stymulacji różnego 85
104 rodzaju bodźcami (sensorycznymi, ruchowymi, słuchowymi, wzrokowymi, emocjonalnymi, etc.). Wykorzystanie tej metody w badaniach funkcjonalnego rezonansu magnetycznego (fmri) może być cennym uzupełnieniem lub alternatywą dla istniejących technik badawczych takich jak BOLD (ang. Blood Oxygenation Level Dependent), które coraz częściej stają się pomocne w zastosowaniach klinicznych, w szczególności w dziedzinie neurologii i neurochirurgii. Wyniki tych badań niosą bardzo cenną informację, pozwalającą na minimalizację ryzyka powikłań po zabiegach neurochirurgicznych już na etapie ich planowania. Mogą też być wykorzystywane w monitorowaniu procesu rehabilitacji i oceny jej przebiegu. 86
105 8. Dodatek 8.1 Opis przykładowego badania Poniższy opis został sporządzony przez doktor Edytę Maj, z II Kliniki Radiologii Centralnego Szpitala Klinicznego w Warszawie. W algorytmie diagnostycznym wczesnego udaru (faza nadostra; 3-6 godzin od wystąpienia pierwszych objawów) coraz częściej i na szerszą skalę wykorzystywane są obrazy dyfuzyjne (DWI) oraz techniki badania perfuzji tkanki mózgowej (PWI). Informacje uzyskane dzięki tym badaniom są niezbędne do podjęcia decyzji i planowania leczenia metodą trombolizy. DWI (diffusion-weighted imaging) jest metodą, która pozwala na wizualizację obszaru udaru już w 3 min od wystąpienia objawów, a więc znacznie wcześniej niż inne badania obrazowe. W rejonie dotkniętym niedokrwieniem dochodzi do zaburzeń procesów energetycznych w komórkach (synteza ATP), a co za tym idzie, do upośledzenia działania pompy sodowo-potasowej. W wyniku tych przemian następuje zatrzymanie wody w przestrzeni wewnątrzkomórkowej i obrzęk cytotoksyczny komórek. Ograniczenie dyfuzji wody do przestrzeni zewnątrzkomórkowej powoduje wzrost intensywności sygnału w badaniu DWI i obniżenie współczynnika dyfuzji (ADC). Taki obraz w ostrym udarze oznacza zazwyczaj nieodwracalne uszkodzenie tkanki mózgowej, a więc brak wskazań do leczenia trombolitycznego. Wykonanie u tych chorych badania perfuzji tkanki mózgowej pozwala na wizualizację rzeczywistego obszaru obniżonego przepływu krwi. Różnica pomiędzy większym obszarem zaburzeń perfuzji, a mniejszym obszarem nieprawidłowej dyfuzji wyznacza strefę zmian odwracalnych, potencjalnie możliwą do uratowania, określaną mianem penumbry. Stosuje się wiele metod do wyznaczania strefy penumbry. Jednym z istotnych parametrów umożliwiających obrazowanie obszaru hypoperfuzji jest MTT. W przedstawionym poniżej przykładzie w badaniu DWI widoczna jest restrykcja dyfuzji wody w postaci podwyższonej intensywności sygnału w obrębie zakrętu zaśrodkowego prawej półkuli mózgu. Zmiany sygnału dotyczą głównie kory mózgu, a w niewielkim tylko stopniu istoty białej. Obraz przemawia za niedokrwieniem w zakresie unaczynienia gałęzi terminalnych prawej tętnicy środkowej mózgu. Analiza map MTT u tego pacjenta wykazała, że najrozleglejszy obszar hypoperfuzji, 87
106 obejmujący znaczną część płata ciemieniowego prawej półkuli mózgu, uzyskano metodą obliczania tego parametru bez zastosowania modyfikacji. Taki algorytm obliczania MTT daje największą rozbieżność z obszarem zawału obserwowanym w DWI, a tym samym daje największą strefę penumbry. Taki obraz może prowadzić do przeszacowania wielkości obszaru, który można uratować dzięki zastosowaniu trombolizy. Na mapach MTT obliczanych metodą geometryczną obszar hypoperfuzji jest znacznie mniejszy i na części skanów pokrywa się z obszarem zaburzeń dyfuzji obserwowanych w badaniu DWI. Powoduje to praktycznie brak lub niewielką tylko strefę penumbry, co w wielu przypadkach może być podstawą do dyskwalifikacji chorego od leczenia metodą fibrynolizy, w konsekwencji przyczyniając się do powiększenia się ogniska zawałowego. W nowej metodzie obliczania czasu MTT, która jest przedmiotem tego opracowania, hypoperfuzja obejmuje obszar o wymiarach pośrednich w porównaniu z omawianymi powyżej sposobami. Należy sądzić, że jest to obszar najbliższy rzeczywistości i najtrafniej oddający realny zakres upośledzonego przepływu krwi. Wydaje się, że parametr MTT obliczany nową metodą warto wdrożyć do szerszego użytku klinicznego w celu dokładniejszej oceny jego przydatności w określaniu strefy penumbry. 88
107 8.2 Oprogramowanie do analizy danych perfuzyjnych Istotnym etapem prac nad niniejszą rozprawą była implementacja opisywanych metod przetwarzania obrazów perfuzynych. W efekcie tego powstało autorskie oprogramowanie do obliczania i prezentacji parametrycznych obrazów perfuzyjnych. W niniejszym dodatku zostały opisane możliwości oprogramowania oraz interfejs użytkownika. Ze względu na wykorzystywane w rozprawie algorytmy przetwarzania, oprogramowanie zostało napisane w środowisku Matlab 7, które dostarcza wielu gotowych procedur, co pozwoliło skupić się na odpowiednim połączeniu ich w gotowy algorytm otrzymywania perfuzyjnych obrazów parametrycznych. Pozwoliło to uniknąć prac związanych z implementacją podstawowych procedur przetwarzania, takich jak SVD czy funkcja korelacji. W ocenie autora oprogramowanie wykonane w ten sposób całkowicie spełniło oczekiwania pod kątem Rysunek 8.1. Wygląd okna programu. Po lewej obraz oryginalny. Po prawej obraz oryginalny po segmentacji. W dolnej części krzywa dynamiczna. 89
108 efektywności testowania proponowanych metod. Jednocześnie autor zdaje sobie sprawę, że wprowadzenie tego typu oprogramowania do praktyki klinicznej jest niemożliwe. Dlatego też w końcowej fazie prac nad rozprawą podjęto wysiłki w kierunku przeniesienia całości na platformę C++, która umożliwia stworzenie pakietu oprogramowania mogącego spełnić oczekiwania klinicystów, zarówno pod kątem łatwości obsługi, jak też szybkości działania. Prace te znajdują się na etapie testów i poprawiania stabilności pracy. Opis działania programu zostanie zaprezentowany na przykładzie przetwarzania dynamicznego badania perfuzyjnego wykonanego techniką rezonansu magnetycznego. Na rysunku 8.1 pokazano obraz interfejsu po wczytaniu danych obrazowych. Po lewej stronie zawsze, niezależnie od etapu opracowywania badania, widoczne są obrazy oryginalne. Ułatwia to zorientowanie otrzymywanych wyników w przestrzeni badania. Po prawej stronie uwidaczniane są wynikowe obrazy parametryczne lub dodatkowe informacje ułatwiające przeprowadzenie prawidłowych obliczeń. Pod obrazem oryginalnym prezentowana jest na bieżąco krzywa dynamiczna dla piksela znajdującego się pod kursorem myszy (na obrazie oryginalnym lub parametrycznym). Funkcjonalność ta, wraz z możliwością przeglądania całego badania (wszystkich warstw w czasie trwania badania), regulacją kontrastu i jasności obrazu (suwaki po prawej stronie obrazu oryginalnego) oraz możliwością powiększania widoku (przyciski IN i OUT na pasku po lewej stronie), dają możliwość oceny jakości wykonania badania. Przed przystąpieniem do obliczeń należy zwrócić szczególną uwagę na ruchy pacjenta, wielkość zmian w obrazie spowodowaną przejściem środka kontrastującego oraz to czy badanie obejmuje wszystkie fazy przejścia kontrastu, tzn. czas dojścia do badanego regionu, pierwsze przejście i fazę wypłukiwania. Jeśli wymienione warunki są Rysunek 8.2. Menu z funkcjami przetwarzania danych obrazowych. Czerwonym prostokątem oznaczono funkcje przeliczania jasności obrazu na jednostki proporcjonalne do koncentracji środka cieniującego. 9
109 zadowalające, można przejść do obliczeń. Rysunek 8.3: Okno ustawień programu Pierwszym etapem jest segmentacja obrazu. W prezentowanym programie proces segmentacji realizowany jest przez progowanie wartości obrazu. Wyselekcjonowanie z całego obrazu obszarów tkanki pozwala na istotne ograniczenie czasu obliczeń. Suwak po prawej stronie obrazu parametrycznego, przy wciśniętym przycisku MASK, pozwala na dynamiczny dobór wartości progowej. Na bieżąco prezentowany jest obraz, na którym wszystkie piksele odrzucone z procesu dalszego przetwarzania wyświetlane są w kolorze czarnym (rys 8.1). Następnym krokiem jest przeliczenie wartości jasności obrazu na jednostki proporcjonalne do koncentracji środka cieniującego. Sposób przeliczania jest różny dla badań MR i CT, dlatego też należy wybrać odpowiedni element z menu CALCULATION, znajdującego się w górnej części okna (rys. 8.2). Domyślnie do obliczenia wartości linii bazowej w pierwszej fazie badania uśrednianych jest 5 pierwszych punktów czasowych krzywej dynamicznej. Liczba uśrednianych wartości krzywej koncentracji została ustalona doświadczalnie na podstawie poprawnie wykonanych badań. Ponieważ czasami sposób przeprowadzania badania może nieco odbiegać od narzuconego protokołu, program posiada możliwość dopasowania sposobu obliczeń. Parametry te można zmienić otwierając okno ustawień z menu SETTINGS, 91
110 CALCULATION. W oknie dialogowym ustawień (rys.8.3) można zmienić liczbę uśrednianych punktów krzywej (pole FIRST IMG) oraz ograniczyć przetwarzany zakres krzywej czasowej (pole LAST IMG), co może mieć wpływ na czas obliczeń. W grupie pól RATIO VALUES można ustawić przyjmowane do obliczeń ilościowych wartości gęstości tkanki (BRAIN DENS.) oraz hematokrytu dla dużych i małych naczyń krwionośnych (odpowiednio HCT lv i HCT sv). Dodatkowo można wybrać sposób obliczania rozplotu (SVD lub FFT, przy czym w rozprawie nie uwzględniano metody FFT) oraz określić model krzywej, jaki jest przyjmowany w procesie wpasowywania (fitowania) krzywych. Ostatnie ustawienie jest pozostałością początkowych prac nad rozprawą i zostało odrzucone ze względu na nieakceptowalnie długi czas obliczeń. Rysunek 8.4. Widok programu podczas wyznaczania funkcji wejściowej AIF. Po ewentualnym dobraniu wartości parametrów mających wpływ na obliczenia można wykonać przeliczenie wartości jasności obrazu na jednostki proporcjonalne do koncentracji środka cieniującego. Po zakończeniu obliczeń dostępna jest możliwość wyświetlania 92
111 krzywych dynamicznych dla pikseli na dwa sposoby: używając wartości jasności obrazu (pole wyboru RAW pod wykresem) lub w jednostkach odpowiadających koncentracji (pole wyboru CONCENTRATION). Rysunek 8.5. Przykładowy obraz parametryczny (CBF). Kolejnym krokiem jest wybór pikseli odpowiadających tętnicy zasilającej badany region, czyli wyznaczenie funkcji wejściowej AIF. W rozprawie przyjęto manualną metodę doboru, na podstawie wiedzy anatomicznej oraz kształtu krzywej koncentracji. W celu wyznaczenia funkcji wejściowej należy wybrać narzędzie AIF na pasku z lewej strony okna i najeżdżając wskaźnikiem na obrazie zaznaczać odpowiednie piksele przez naciśnięcie lewego przycisku myszy. Wybrane piksele są zaznaczane kolorem czerwonym. Przed przystąpieniem do tej czynności dobrze jest powiększyć wybrany fragment obrazu oraz wyświetlić powstającą funkcję wejściową na obrazie po prawej stronie okna. Można to zrobić wciskając przycisk AIF pod obrazem. W oknie na bieżąco będzie się pojawiać średnia krzywa z zaznaczonych punktów, wraz z pionowymi liniami odchylenia standardowego dla każdego 93
112 punktu krzywej. W przypadku błędnego wyboru piksela należy go odznaczyć, ponownie najeżdżając na niego wskaźnikiem i przyciskając lewy przycisk myszy. Widok programu w trakcie wyznaczania funkcji wejściowej pokazano na rysunku 8.5. Kolejnym etapem przetwarzania danych w programie są obliczenia map parametrycznych. Aby wykonać obliczenia należy wybrać odpowiedni element z menu CALCULATION (rys.8.2). Postęp obliczeń wskazywany jest na pasku poniżej obrazu parametrycznego. Po zakończeniu obrazy parametryczne wyświetlane są w prawej części okna programu. Przyciski poniżej obrazu pozwalają na wybór prezentowanego parametru perfuzji. Na obrazach po lewej i prawej stronie okna programu zawsze wyświetlana jest ta sama warstwa anatomiczna, którą można zmieniać przyciskami pod obrazem oryginalnym. Suwak po prawej stronie obrazu parametrycznego pozwala na zmianę skali kolorów, co może ułatwiać interpretację wyników. Na rysunku 8.4 pokazano wygląd okna programu z przykładowym wynikiem obliczeń. Rysunek 8.6. Widok z zaznaczonymi przykładowymi regionami zainteresowania. 94
113 Istotną cechą programu jest możliwość zaznaczania obszarów zainteresowania (ROI, ang. Region of Interest). Program pozwala na wybór dziesięciu regionów o dowolnym kształcie. W tym celu należy wybrać narzędzie ROI z paska po lewej stronie. Numer rysowanego regionu wybiera się sekwencyjnie naciskając kolorowy przycisk po lewej stronie. Rysowanie regionu wykonuje się naciskając lewy przycisk myszy w kolejnych punktach należących do obrysu obszaru zainteresowania. Aby zakończyć rysowanie należy dwa razy nacisnąć lewy przycisk. Na rysunku 8.6 pokazano wygląd programu z naniesionymi przykładowymi regionami zainteresowania. Po zaznaczeniu regionów zainteresowania można wyświetlić ich średnie parametry perfuzji lub średnie krzywe koncentracji, co pokazano na rysunku 8.7. Regiony zainteresowania są bardzo użytecznym narzędziem wspomagającym interpretację otrzymanych wyników. Szczególnie dobrze sprawdzają się przy porównywaniu regionów podejrzanych o zaburzenia przepływu z regionami referencyjnymi, o przepływie prawidłowym. Aby wyświetlić średnie krzywe dla regionów zainteresowania należy nacisnąć przycisk PLOT po lewej stronie okna. W celu wyświetlenia średnich parametrów przepływu w regionach należy z menu ROIs wybrać element INFO. Rysunek 8.7. Wykresy średnich krzywych dla regionów zainteresowania (po lewej) i okno średnich parametrów perfuzji dla regionów zainteresowania (po prawej). Tak jak wspomniano na początku tego rozdziału, oprogramowanie w opisanej powyżej wersji nie nadaje jeszcze się do zastosowania w codziennej praktyce klinicznej. Dlatego trwają prace nad stworzeniem wersji, która spełni oczekiwania lekarzy radiologów, szczególnie pod kątem łatwości użytkowania, czasu obliczeń, stabilności oraz możliwości pracy programu w istniejących szpitalnych systemach informatycznych. 95
NMR (MAGNETYCZNY REZONANS JĄDROWY) dr Marcin Lipowczan
 NMR (MAGNETYCZNY REZONANS JĄDROWY) dr Marcin Lipowczan Spis zagadnień Fizyczne podstawy zjawiska NMR Parametry widma NMR Procesy relaksacji jądrowej Metody obrazowania Fizyczne podstawy NMR Proton, neutron,
NMR (MAGNETYCZNY REZONANS JĄDROWY) dr Marcin Lipowczan Spis zagadnień Fizyczne podstawy zjawiska NMR Parametry widma NMR Procesy relaksacji jądrowej Metody obrazowania Fizyczne podstawy NMR Proton, neutron,
BADANIA LABORATORYJNE WYKONYWANE W PRZYPADKU NIEDOKRWIENNEGO UDARU MÓZGU
 442 Część II. Neurologia kliniczna BADANIA LABORATORYJNE WYKONYWANE W PRZYPADKU NIEDOKRWIENNEGO UDARU MÓZGU Badania neuroobrazowe Badanie tomografii komputerowej głowy Zasadniczym rozróżnieniem wydaje
442 Część II. Neurologia kliniczna BADANIA LABORATORYJNE WYKONYWANE W PRZYPADKU NIEDOKRWIENNEGO UDARU MÓZGU Badania neuroobrazowe Badanie tomografii komputerowej głowy Zasadniczym rozróżnieniem wydaje
ABC tomografii komputerowej
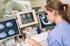 ABC tomografii komputerowej Tomografia (od gr.: tome cięcie i grafein pisanie) metoda pozwalająca na uzyskiwanie obrazów przekrojów badanej okolicy ciała. Określenie o szerokim znaczeniu, najczęściej kojarzone
ABC tomografii komputerowej Tomografia (od gr.: tome cięcie i grafein pisanie) metoda pozwalająca na uzyskiwanie obrazów przekrojów badanej okolicy ciała. Określenie o szerokim znaczeniu, najczęściej kojarzone
Obrazowanie MRI Skopia rtg Scyntygrafia PET
 Wyzwania wynikające z rozwoju metod obrazowania Technika i technologia Konferencja w ramach projektu Wykorzystywanie nowych metod i narzędzi w kształceniu studentów UMB w zakresie ochrony radiologicznej
Wyzwania wynikające z rozwoju metod obrazowania Technika i technologia Konferencja w ramach projektu Wykorzystywanie nowych metod i narzędzi w kształceniu studentów UMB w zakresie ochrony radiologicznej
Wykorzystanie zjawiska rezonansu magnetycznego w medycynie. Mariusz Grocki
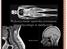 Wykorzystanie zjawiska rezonansu magnetycznego w medycynie. Mariusz Grocki [1] WYŚCIG DO TYTUŁU ODKRYWCY. JĄDRO ATOMU W ZEWNĘTRZNYM POLU MAGNETYCZNYM. Porównanie do pola grawitacyjnego. CZYM JEST ZJAWISKO
Wykorzystanie zjawiska rezonansu magnetycznego w medycynie. Mariusz Grocki [1] WYŚCIG DO TYTUŁU ODKRYWCY. JĄDRO ATOMU W ZEWNĘTRZNYM POLU MAGNETYCZNYM. Porównanie do pola grawitacyjnego. CZYM JEST ZJAWISKO
Zestaw ćwiczeń laboratoryjnych z Biofizyki dla kierunku Elektroradiologia w roku akademickim 2016/2017.
 Zestaw ćwiczeń laboratoryjnych z Biofizyki dla kierunku Elektroradiologia w roku akademickim 2016/2017. w1. Platforma elearningowa stosowana na kursie. w2. Metodyka eksperymentu fizycznego - rachunek błędów.
Zestaw ćwiczeń laboratoryjnych z Biofizyki dla kierunku Elektroradiologia w roku akademickim 2016/2017. w1. Platforma elearningowa stosowana na kursie. w2. Metodyka eksperymentu fizycznego - rachunek błędów.
Zestaw ćwiczeń laboratoryjnych z Biofizyki dla kierunku elektroradiologia w roku akademickim 2017/2018.
 Zestaw ćwiczeń laboratoryjnych z Biofizyki dla kierunku elektroradiologia w roku akademickim 2017/2018. w1. Platforma elearningowa stosowana na kursie. w2. Metodyka eksperymentu fizycznego - rachunek błędów.
Zestaw ćwiczeń laboratoryjnych z Biofizyki dla kierunku elektroradiologia w roku akademickim 2017/2018. w1. Platforma elearningowa stosowana na kursie. w2. Metodyka eksperymentu fizycznego - rachunek błędów.
Techniki Jądrowe w Diagnostyce i Terapii Medycznej
 Techniki Jądrowe w Diagnostyce i Terapii Medycznej Wykład 5, 4 kwietnia 2017 Zygmunt Szefliński Środowiskowe Laboratorium Ciężkich Jonów szef@fuw.edu.pl http://www.fuw.edu.pl/~szef/ Wykład 5 NMR, MRI,
Techniki Jądrowe w Diagnostyce i Terapii Medycznej Wykład 5, 4 kwietnia 2017 Zygmunt Szefliński Środowiskowe Laboratorium Ciężkich Jonów szef@fuw.edu.pl http://www.fuw.edu.pl/~szef/ Wykład 5 NMR, MRI,
dr n.med. Bartosz Żabicki Zakład Radiologii Klinicznej Szpital Kliniczny Przemienienia Pańskiego UM w Poznaniu
 dr n.med. Bartosz Żabicki Zakład Radiologii Klinicznej Szpital Kliniczny Przemienienia Pańskiego UM w Poznaniu Aorta piersiowa i brzuszna Tętnice kończyn dolnych Tętnice kończyn górnych Tętnice dogłowowe
dr n.med. Bartosz Żabicki Zakład Radiologii Klinicznej Szpital Kliniczny Przemienienia Pańskiego UM w Poznaniu Aorta piersiowa i brzuszna Tętnice kończyn dolnych Tętnice kończyn górnych Tętnice dogłowowe
lek. wet. Joanna Głodek Katedra Chirurgii i Rentgenologii z Kliniką Wydział Medycyny Weterynaryjnej Uniwersytet Warmińsko Mazurski w Olsztynie
 lek. wet. Joanna Głodek Katedra Chirurgii i Rentgenologii z Kliniką Wydział Medycyny Weterynaryjnej Uniwersytet Warmińsko Mazurski w Olsztynie W medycynie ludzkiej rezonans magnetyczny (RM) jest jedną
lek. wet. Joanna Głodek Katedra Chirurgii i Rentgenologii z Kliniką Wydział Medycyny Weterynaryjnej Uniwersytet Warmińsko Mazurski w Olsztynie W medycynie ludzkiej rezonans magnetyczny (RM) jest jedną
Metody rezonansowe. Magnetyczny rezonans jądrowy Magnetometr protonowy
 Metody rezonansowe Magnetyczny rezonans jądrowy Magnetometr protonowy Co należy wiedzieć Efekt Zeemana, precesja Larmora Wektor magnetyzacji w podstawowym eksperymencie NMR Transformacja Fouriera Procesy
Metody rezonansowe Magnetyczny rezonans jądrowy Magnetometr protonowy Co należy wiedzieć Efekt Zeemana, precesja Larmora Wektor magnetyzacji w podstawowym eksperymencie NMR Transformacja Fouriera Procesy
Magnetyczny rezonans jądrowy
 Magnetyczny rezonans jądrowy Mateusz Raczyński Jakub Cebulski Katolickie Liceum Ogólnokształcące w Szczecinie im. św. Maksymiliana Marii Kolbego Opiekun naukowy: mgr Magdalena Biskup Cel pracy Przedstawienie
Magnetyczny rezonans jądrowy Mateusz Raczyński Jakub Cebulski Katolickie Liceum Ogólnokształcące w Szczecinie im. św. Maksymiliana Marii Kolbego Opiekun naukowy: mgr Magdalena Biskup Cel pracy Przedstawienie
WSTĘP. Skaner PET-CT GE Discovery IQ uruchomiony we Wrocławiu w 2015 roku.
 WSTĘP Technika PET, obok MRI, jest jedną z najbardziej dynamicznie rozwijających się metod obrazowych w medycynie. Przełomowymi wydarzeniami w rozwoju PET było wprowadzenie wielorzędowych gamma kamer,
WSTĘP Technika PET, obok MRI, jest jedną z najbardziej dynamicznie rozwijających się metod obrazowych w medycynie. Przełomowymi wydarzeniami w rozwoju PET było wprowadzenie wielorzędowych gamma kamer,
Aneks III. Zmiany do odpowiednich punktów druków informacyjnych
 Aneks III Zmiany do odpowiednich punktów druków informacyjnych Uwaga: Zmiany do odpowiednich punktów druków informacyjnych są rezultatem postępowania arbitrażowego. Druki informacyjne mogą zostać zaktualizowane
Aneks III Zmiany do odpowiednich punktów druków informacyjnych Uwaga: Zmiany do odpowiednich punktów druków informacyjnych są rezultatem postępowania arbitrażowego. Druki informacyjne mogą zostać zaktualizowane
I. PROMIENIOWANIE CIEPLNE
 I. PROMIENIOWANIE CIEPLNE - lata '90 XIX wieku WSTĘP Widmo promieniowania elektromagnetycznego zakres "pokrycia" różnymi rodzajami fal elektromagnetycznych promieniowania zawartego w danej wiązce. rys.i.1.
I. PROMIENIOWANIE CIEPLNE - lata '90 XIX wieku WSTĘP Widmo promieniowania elektromagnetycznego zakres "pokrycia" różnymi rodzajami fal elektromagnetycznych promieniowania zawartego w danej wiązce. rys.i.1.
Wyznaczanie profilu wiązki promieniowania używanego do cechowania tomografu PET
 18 Wyznaczanie profilu wiązki promieniowania używanego do cechowania tomografu PET Ines Moskal Studentka, Instytut Fizyki UJ Na Uniwersytecie Jagiellońskim prowadzone są badania dotyczące usprawnienia
18 Wyznaczanie profilu wiązki promieniowania używanego do cechowania tomografu PET Ines Moskal Studentka, Instytut Fizyki UJ Na Uniwersytecie Jagiellońskim prowadzone są badania dotyczące usprawnienia
MOMENT MAGNETYCZNY W POLU MAGNETYCZNYM
 Ćwiczenie nr 16 MOMENT MAGNETYCZNY W POLU MAGNETYCZNYM Aparatura Zasilacze regulowane, cewki Helmholtza, multimetry cyfrowe, dynamometr torsyjny oraz pętle próbne z przewodnika. X Y 1 2 Rys. 1 Układ pomiarowy
Ćwiczenie nr 16 MOMENT MAGNETYCZNY W POLU MAGNETYCZNYM Aparatura Zasilacze regulowane, cewki Helmholtza, multimetry cyfrowe, dynamometr torsyjny oraz pętle próbne z przewodnika. X Y 1 2 Rys. 1 Układ pomiarowy
Magnetyczny Rezonans Jądrowy (NMR)
 Magnetyczny Rezonans Jądrowy (NMR) obserwacja zachowania (precesji) jąder atomowych obdarzonych spinem w polu magnetycznym Magnetic Resonance Imaging (MRI) ( obrazowanie rezonansem magnetycznym potocznie
Magnetyczny Rezonans Jądrowy (NMR) obserwacja zachowania (precesji) jąder atomowych obdarzonych spinem w polu magnetycznym Magnetic Resonance Imaging (MRI) ( obrazowanie rezonansem magnetycznym potocznie
Spektroskopia magnetycznego rezonansu jądrowego - wprowadzenie
 Spektroskopia magnetycznego rezonansu jądrowego - wprowadzenie Streszczenie Spektroskopia magnetycznego rezonansu jądrowego jest jedną z technik spektroskopii absorpcyjnej mającej zastosowanie w chemii,
Spektroskopia magnetycznego rezonansu jądrowego - wprowadzenie Streszczenie Spektroskopia magnetycznego rezonansu jądrowego jest jedną z technik spektroskopii absorpcyjnej mającej zastosowanie w chemii,
Wykład 4. metody badania mózgu II. dr Marek Binder Zakład Psychofizjologii
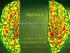 Wykład 4 metody badania mózgu II dr Marek Binder Zakład Psychofizjologii Terminologia SAGITTAL SLICE Number of Slices e.g., 10 Slice Thickness e.g., 6 mm In-plane resolution e.g., 192 mm / 64 = 3 mm IN-PLANE
Wykład 4 metody badania mózgu II dr Marek Binder Zakład Psychofizjologii Terminologia SAGITTAL SLICE Number of Slices e.g., 10 Slice Thickness e.g., 6 mm In-plane resolution e.g., 192 mm / 64 = 3 mm IN-PLANE
Recenzja pracy doktorskiej mgr Tomasza Świsłockiego pt. Wpływ oddziaływań dipolowych na własności spinorowego kondensatu rubidowego
 Prof. dr hab. Jan Mostowski Instytut Fizyki PAN Warszawa Warszawa, 15 listopada 2010 r. Recenzja pracy doktorskiej mgr Tomasza Świsłockiego pt. Wpływ oddziaływań dipolowych na własności spinorowego kondensatu
Prof. dr hab. Jan Mostowski Instytut Fizyki PAN Warszawa Warszawa, 15 listopada 2010 r. Recenzja pracy doktorskiej mgr Tomasza Świsłockiego pt. Wpływ oddziaływań dipolowych na własności spinorowego kondensatu
MAGNETYCZNY REZONANS JĄDROWY - podstawy
 1 MAGNETYCZNY REZONANS JĄDROWY - podstawy 1. Wprowadzenie. Wstęp teoretyczny..1 Ruch magnetyzacji jądrowej, relaksacja. Liniowa i kołowa polaryzacja pola zmiennego (RF)..3 Metoda echa spinowego 1. Wprowadzenie
1 MAGNETYCZNY REZONANS JĄDROWY - podstawy 1. Wprowadzenie. Wstęp teoretyczny..1 Ruch magnetyzacji jądrowej, relaksacja. Liniowa i kołowa polaryzacja pola zmiennego (RF)..3 Metoda echa spinowego 1. Wprowadzenie
Czym jest badanie czynnościowe rezonansu magnetycznego? Oraz jaki ma związek z neuronawigacją?
 Czym jest badanie czynnościowe rezonansu magnetycznego? Oraz jaki ma związek z neuronawigacją? Dolnośląski Szpital Specjalistyczny im. T. Marciniaka Centrum Medycyny Ratunkowej stale podnosi jakość prowadzonego
Czym jest badanie czynnościowe rezonansu magnetycznego? Oraz jaki ma związek z neuronawigacją? Dolnośląski Szpital Specjalistyczny im. T. Marciniaka Centrum Medycyny Ratunkowej stale podnosi jakość prowadzonego
SPEKTROSKOPIA NMR. No. 0
 No. 0 Spektroskopia magnetycznego rezonansu jądrowego, spektroskopia MRJ, spektroskopia NMR jedna z najczęściej stosowanych obecnie technik spektroskopowych w chemii i medycynie. Spektroskopia ta polega
No. 0 Spektroskopia magnetycznego rezonansu jądrowego, spektroskopia MRJ, spektroskopia NMR jedna z najczęściej stosowanych obecnie technik spektroskopowych w chemii i medycynie. Spektroskopia ta polega
Obliczenia polowe silnika przełączalnego reluktancyjnego (SRM) w celu jego optymalizacji
 Akademia Górniczo Hutnicza im. Stanisława Staszica w Krakowie Wydział Elektrotechniki, Automatyki, Informatyki i Elektroniki Studenckie Koło Naukowe Maszyn Elektrycznych Magnesik Obliczenia polowe silnika
Akademia Górniczo Hutnicza im. Stanisława Staszica w Krakowie Wydział Elektrotechniki, Automatyki, Informatyki i Elektroniki Studenckie Koło Naukowe Maszyn Elektrycznych Magnesik Obliczenia polowe silnika
ĆWICZENIE 15 BADANIE WZMACNIACZY MOCY MAŁEJ CZĘSTOTLIWOŚCI
 1 ĆWICZENIE 15 BADANIE WZMACNIACZY MOCY MAŁEJ CZĘSTOTLIWOŚCI 15.1. CEL ĆWICZENIA Celem ćwiczenia jest poznanie podstawowych właściwości wzmacniaczy mocy małej częstotliwości oraz przyswojenie umiejętności
1 ĆWICZENIE 15 BADANIE WZMACNIACZY MOCY MAŁEJ CZĘSTOTLIWOŚCI 15.1. CEL ĆWICZENIA Celem ćwiczenia jest poznanie podstawowych właściwości wzmacniaczy mocy małej częstotliwości oraz przyswojenie umiejętności
Co to jest termografia?
 Co to jest termografia? Słowo Termografia Pochodzi od dwóch słów "termo" czyli ciepło i "grafia" rysować, opisywać więc termografia to opisywanie przy pomocy temperatury zmian zachodzących w naszym organiźmie
Co to jest termografia? Słowo Termografia Pochodzi od dwóch słów "termo" czyli ciepło i "grafia" rysować, opisywać więc termografia to opisywanie przy pomocy temperatury zmian zachodzących w naszym organiźmie
tel. (+4861) fax. (+4861)
 dr hab. inż. Michał Nowak prof. PP Politechnika Poznańska, Instytut Silników Spalinowych i Transportu Zakład Inżynierii Wirtualnej ul. Piotrowo 3 60-965 Poznań tel. (+4861) 665-2041 fax. (+4861) 665-2618
dr hab. inż. Michał Nowak prof. PP Politechnika Poznańska, Instytut Silników Spalinowych i Transportu Zakład Inżynierii Wirtualnej ul. Piotrowo 3 60-965 Poznań tel. (+4861) 665-2041 fax. (+4861) 665-2618
Laboratorium Elektronicznej Aparatury Medycznej I
 Laboratorium Elektronicznej Aparatury Medycznej I Politechnika Wrocławska Wydział Podstawowych Problemów Techniki Katedra Inżynierii Biomedycznej Dr inż. Elżbieta Szul-Pietrzak ĆWICZENIE NR 4 APARATURA
Laboratorium Elektronicznej Aparatury Medycznej I Politechnika Wrocławska Wydział Podstawowych Problemów Techniki Katedra Inżynierii Biomedycznej Dr inż. Elżbieta Szul-Pietrzak ĆWICZENIE NR 4 APARATURA
Wektory, układ współrzędnych
 Wektory, układ współrzędnych Wielkości występujące w przyrodzie możemy podzielić na: Skalarne, to jest takie wielkości, które potrafimy opisać przy pomocy jednej liczby (skalara), np. masa, czy temperatura.
Wektory, układ współrzędnych Wielkości występujące w przyrodzie możemy podzielić na: Skalarne, to jest takie wielkości, które potrafimy opisać przy pomocy jednej liczby (skalara), np. masa, czy temperatura.
Zagadnienia: 1. Partnerzy projektu 2. Badania obrazowe serca 3. Cele 4. Techniki obrazowe serca stosowane w Projekcie 5. Rezultaty
 Zagadnienia: 1. Partnerzy projektu 2. Badania obrazowe serca 3. Cele 4. Techniki obrazowe serca stosowane w Projekcie 5. Rezultaty 1. Partnerzy projektu Krakowski Szpital Specjalistyczny im. Jana Pawła
Zagadnienia: 1. Partnerzy projektu 2. Badania obrazowe serca 3. Cele 4. Techniki obrazowe serca stosowane w Projekcie 5. Rezultaty 1. Partnerzy projektu Krakowski Szpital Specjalistyczny im. Jana Pawła
Zestaw ćwiczeń laboratoryjnych z Biofizyki dla kierunku Fizjoterapia
 Zestaw ćwiczeń laboratoryjnych z Biofizyki dla kierunku Fizjoterapia 1. Ćwiczenie wprowadzające: Wielkości fizyczne i błędy pomiarowe. Pomiar wielkości fizjologicznych 2. Prąd elektryczny: Pomiar oporu
Zestaw ćwiczeń laboratoryjnych z Biofizyki dla kierunku Fizjoterapia 1. Ćwiczenie wprowadzające: Wielkości fizyczne i błędy pomiarowe. Pomiar wielkości fizjologicznych 2. Prąd elektryczny: Pomiar oporu
Elektrofizjologiczne podstawy lokalizacji ogniska padaczkowego. Piotr Walerjan
 Elektrofizjologiczne podstawy lokalizacji ogniska padaczkowego Piotr Walerjan Elektrofizjologia w padaczce Dlaczego stosujemy metody elektrofizjologiczne w diagnostyce padaczki? Ognisko padaczkowe Lokalizacja
Elektrofizjologiczne podstawy lokalizacji ogniska padaczkowego Piotr Walerjan Elektrofizjologia w padaczce Dlaczego stosujemy metody elektrofizjologiczne w diagnostyce padaczki? Ognisko padaczkowe Lokalizacja
Materiały pomocnicze do laboratorium z przedmiotu Metody i Narzędzia Symulacji Komputerowej
 Materiały pomocnicze do laboratorium z przedmiotu Metody i Narzędzia Symulacji Komputerowej w Systemach Technicznych Symulacja prosta dyszy pomiarowej Bendemanna Opracował: dr inż. Andrzej J. Zmysłowski
Materiały pomocnicze do laboratorium z przedmiotu Metody i Narzędzia Symulacji Komputerowej w Systemach Technicznych Symulacja prosta dyszy pomiarowej Bendemanna Opracował: dr inż. Andrzej J. Zmysłowski
MATEMATYCZNY MODEL PĘTLI HISTEREZY MAGNETYCZNEJ
 ELEKTRYKA 014 Zeszyt 1 (9) Rok LX Krzysztof SZTYMELSKI, Marian PASKO Politechnika Śląska w Gliwicach MATEMATYCZNY MODEL PĘTLI ISTEREZY MAGNETYCZNEJ Streszczenie. W artykule został zaprezentowany matematyczny
ELEKTRYKA 014 Zeszyt 1 (9) Rok LX Krzysztof SZTYMELSKI, Marian PASKO Politechnika Śląska w Gliwicach MATEMATYCZNY MODEL PĘTLI ISTEREZY MAGNETYCZNEJ Streszczenie. W artykule został zaprezentowany matematyczny
Październik 2013 Grupa Voxel
 Październik 2013 Grupa Voxel GRUPA VOXEL Usługi medyczne Produkcja Usługi komplementarne ie mózgowia - traktografia DTI RTG TK (CT) od 1 do 60 obrazów/badanie do1500 obrazów/badanie TELE PACS Stacje diagnostyczne
Październik 2013 Grupa Voxel GRUPA VOXEL Usługi medyczne Produkcja Usługi komplementarne ie mózgowia - traktografia DTI RTG TK (CT) od 1 do 60 obrazów/badanie do1500 obrazów/badanie TELE PACS Stacje diagnostyczne
Analiza korespondencji
 Analiza korespondencji Kiedy stosujemy? 2 W wielu badaniach mamy do czynienia ze zmiennymi jakościowymi (nominalne i porządkowe) typu np.: płeć, wykształcenie, status palenia. Punktem wyjścia do analizy
Analiza korespondencji Kiedy stosujemy? 2 W wielu badaniach mamy do czynienia ze zmiennymi jakościowymi (nominalne i porządkowe) typu np.: płeć, wykształcenie, status palenia. Punktem wyjścia do analizy
Tak określił mechanikę kwantową laureat nagrody Nobla Ryszard Feynman ( ) mechanika kwantowa opisuje naturę w sposób prawdziwy, jako absurd.
 Tak określił mechanikę kwantową laureat nagrody Nobla Ryszard Feynman (1918-1988) mechanika kwantowa opisuje naturę w sposób prawdziwy, jako absurd. Równocześnie Feynman podkreślił, że obliczenia mechaniki
Tak określił mechanikę kwantową laureat nagrody Nobla Ryszard Feynman (1918-1988) mechanika kwantowa opisuje naturę w sposób prawdziwy, jako absurd. Równocześnie Feynman podkreślił, że obliczenia mechaniki
rezonans magnetyczny informacje dla pacjentów
 rezonans magnetyczny informacje dla pacjentów MR 1 najważniejsze jest zdrowie Dla wygody naszych pacjentów stworzyliśmy portal Wyniki Online, gdzie, bez wychodzenia z domu, można odebrać wyniki badania
rezonans magnetyczny informacje dla pacjentów MR 1 najważniejsze jest zdrowie Dla wygody naszych pacjentów stworzyliśmy portal Wyniki Online, gdzie, bez wychodzenia z domu, można odebrać wyniki badania
Rozważania rozpoczniemy od fal elektromagnetycznych w próżni. Dla próżni równania Maxwella w tzw. postaci różniczkowej są następujące:
 Rozważania rozpoczniemy od fal elektromagnetycznych w próżni Dla próżni równania Maxwella w tzw postaci różniczkowej są następujące:, gdzie E oznacza pole elektryczne, B indukcję pola magnetycznego a i
Rozważania rozpoczniemy od fal elektromagnetycznych w próżni Dla próżni równania Maxwella w tzw postaci różniczkowej są następujące:, gdzie E oznacza pole elektryczne, B indukcję pola magnetycznego a i
W celu obliczenia charakterystyki częstotliwościowej zastosujemy wzór 1. charakterystyka amplitudowa 0,
 Bierne obwody RC. Filtr dolnoprzepustowy. Filtr dolnoprzepustowy jest układem przenoszącym sygnały o małej częstotliwości bez zmian, a powodującym tłumienie i opóźnienie fazy sygnałów o większych częstotliwościach.
Bierne obwody RC. Filtr dolnoprzepustowy. Filtr dolnoprzepustowy jest układem przenoszącym sygnały o małej częstotliwości bez zmian, a powodującym tłumienie i opóźnienie fazy sygnałów o większych częstotliwościach.
Narodowe Centrum Badań Jądrowych Dział Edukacji i Szkoleń ul. Andrzeja Sołtana 7, Otwock-Świerk
 Narodowe Centrum Badań Jądrowych Dział Edukacji i Szkoleń ul. Andrzeja Sołtana 7, 05-400 Otwock-Świerk ĆWICZENIE L A B O R A T O R I U M F I Z Y K I A T O M O W E J I J Ą D R O W E J Zastosowanie pojęć
Narodowe Centrum Badań Jądrowych Dział Edukacji i Szkoleń ul. Andrzeja Sołtana 7, 05-400 Otwock-Świerk ĆWICZENIE L A B O R A T O R I U M F I Z Y K I A T O M O W E J I J Ą D R O W E J Zastosowanie pojęć
DOSY (Diffusion ordered NMR spectroscopy)
 Wykład 8 DOSY (Diffusion ordered NMR spectroscopy) Dyfuzja migracja cząsteczek pod wpływem gradientu stężenia Pierwsze Prawo Ficka: przepływ cząsteczek jest proporcjonalny do gradientu stężenia: J przepływ
Wykład 8 DOSY (Diffusion ordered NMR spectroscopy) Dyfuzja migracja cząsteczek pod wpływem gradientu stężenia Pierwsze Prawo Ficka: przepływ cząsteczek jest proporcjonalny do gradientu stężenia: J przepływ
Wyznaczanie bezwzględnej aktywności źródła 60 Co. Tomasz Winiarski
 Wyznaczanie bezwzględnej aktywności źródła 60 Co metoda koincydencyjna. Tomasz Winiarski 24 kwietnia 2001 WSTEP TEORETYCZNY Rozpad promieniotwórczy i czas połowicznego zaniku. Rozpad promieniotwórczy polega
Wyznaczanie bezwzględnej aktywności źródła 60 Co metoda koincydencyjna. Tomasz Winiarski 24 kwietnia 2001 WSTEP TEORETYCZNY Rozpad promieniotwórczy i czas połowicznego zaniku. Rozpad promieniotwórczy polega
γ6 Liniowy Model Pozytonowego Tomografu Emisyjnego
 γ6 Liniowy Model Pozytonowego Tomografu Emisyjnego Cel ćwiczenia Celem ćwiczenia jest zaprezentowanie zasady działania pozytonowego tomografu emisyjnego. W doświadczeniu użyjemy detektory scyntylacyjne
γ6 Liniowy Model Pozytonowego Tomografu Emisyjnego Cel ćwiczenia Celem ćwiczenia jest zaprezentowanie zasady działania pozytonowego tomografu emisyjnego. W doświadczeniu użyjemy detektory scyntylacyjne
Wg W. Duch Jak działa mózg. UMK Toruń notatki z wprowadzenia do kognitywistyki. Dostępne na str. www.fizyka.umk.pl/~duch/wyklady/
 Analiza urazów powypadkowych. JuŜ Egipski papirus sprzed 3500 lat wymienia 28 uszkodzeń, dokonywano wtedy trepanacji czaszki by wyciąć guzy. Arystoteles uznał serce za siedlisko uczuć i rozumu. W -3 w.
Analiza urazów powypadkowych. JuŜ Egipski papirus sprzed 3500 lat wymienia 28 uszkodzeń, dokonywano wtedy trepanacji czaszki by wyciąć guzy. Arystoteles uznał serce za siedlisko uczuć i rozumu. W -3 w.
LABORATORIUM Z FIZYKI
 LABORATORIUM Z FIZYKI LABORATORIUM Z FIZYKI I PRACOWNIA FIZYCZNA C w Gliwicach Gliwice, ul. Konarskiego 22, pokoje 52-54 Regulamin pracowni i organizacja zajęć Sprawozdanie (strona tytułowa, karta pomiarowa)
LABORATORIUM Z FIZYKI LABORATORIUM Z FIZYKI I PRACOWNIA FIZYCZNA C w Gliwicach Gliwice, ul. Konarskiego 22, pokoje 52-54 Regulamin pracowni i organizacja zajęć Sprawozdanie (strona tytułowa, karta pomiarowa)
Ćwiczenie M-2 Pomiar przyśpieszenia ziemskiego za pomocą wahadła rewersyjnego Cel ćwiczenia: II. Przyrządy: III. Literatura: IV. Wstęp. l Rys.
 Ćwiczenie M- Pomiar przyśpieszenia ziemskiego za pomocą wahadła rewersyjnego. Cel ćwiczenia: pomiar przyśpieszenia ziemskiego przy pomocy wahadła fizycznego.. Przyrządy: wahadło rewersyjne, elektroniczny
Ćwiczenie M- Pomiar przyśpieszenia ziemskiego za pomocą wahadła rewersyjnego. Cel ćwiczenia: pomiar przyśpieszenia ziemskiego przy pomocy wahadła fizycznego.. Przyrządy: wahadło rewersyjne, elektroniczny
DOZYMETRIA I BADANIE WPŁYWU PROMIENIOWANIA X NA MEDIA BIOLOGICZNE
 X3 DOZYMETRIA I BADANIE WPŁYWU PROMIENIOWANIA X NA MEDIA BIOLOGICZNE Tematyka ćwiczenia Promieniowanie X wykazuje właściwości jonizujące. W związku z tym powietrze naświetlane promieniowaniem X jest elektrycznie
X3 DOZYMETRIA I BADANIE WPŁYWU PROMIENIOWANIA X NA MEDIA BIOLOGICZNE Tematyka ćwiczenia Promieniowanie X wykazuje właściwości jonizujące. W związku z tym powietrze naświetlane promieniowaniem X jest elektrycznie
RADIOMETR MIKROFALOWY. RADIOMETR MIKROFALOWY (wybrane zagadnienia) Opracowanie : dr inż. Waldemar Susek dr inż. Adam Konrad Rutkowski
 RADIOMETR MIKROFALOWY RADIOMETR MIKROFALOWY (wybrane zagadnienia) Opracowanie : dr inż. Waldemar Susek dr inż. Adam Konrad Rutkowski 1 RADIOMETR MIKROFALOWY Wprowadzenie Wszystkie ciała o temperaturze
RADIOMETR MIKROFALOWY RADIOMETR MIKROFALOWY (wybrane zagadnienia) Opracowanie : dr inż. Waldemar Susek dr inż. Adam Konrad Rutkowski 1 RADIOMETR MIKROFALOWY Wprowadzenie Wszystkie ciała o temperaturze
Relacja: III Seminarium Naukowe Tomografia procesowa aplikacje, systemy pomiarowe i algorytmy numeryczne
 Relacja: III Seminarium Naukowe Tomografia procesowa aplikacje, systemy pomiarowe i algorytmy numeryczne W dniu 10.04.2015 odbyło się III Seminarium Naukowe Tomografia procesowa aplikacje, systemy pomiarowe
Relacja: III Seminarium Naukowe Tomografia procesowa aplikacje, systemy pomiarowe i algorytmy numeryczne W dniu 10.04.2015 odbyło się III Seminarium Naukowe Tomografia procesowa aplikacje, systemy pomiarowe
MATERIAŁY POMOCNICZE DO WYKŁADU Z BIO-
 1 MATERIAŁY POMOCNICZE DO WYKŁADU Z BIO- i HYDROAKUSTYKI 11. Metody zobrazowań w diagnostyce medycznej S. Typy ultrasonograficznych prezentacji obrazu W zależności od sposobu rejestracji ech rozróżniamy
1 MATERIAŁY POMOCNICZE DO WYKŁADU Z BIO- i HYDROAKUSTYKI 11. Metody zobrazowań w diagnostyce medycznej S. Typy ultrasonograficznych prezentacji obrazu W zależności od sposobu rejestracji ech rozróżniamy
Modelowanie i symulacja zagadnień biomedycznych PROJEKT BARTŁOMIEJ GRZEBYTA, JAKUB OTWOROWSKI
 Modelowanie i symulacja zagadnień biomedycznych PROJEKT BARTŁOMIEJ GRZEBYTA, JAKUB OTWOROWSKI Spis treści Wstęp... 2 Opis problemu... 3 Metoda... 3 Opis modelu... 4 Warunki brzegowe... 5 Wyniki symulacji...
Modelowanie i symulacja zagadnień biomedycznych PROJEKT BARTŁOMIEJ GRZEBYTA, JAKUB OTWOROWSKI Spis treści Wstęp... 2 Opis problemu... 3 Metoda... 3 Opis modelu... 4 Warunki brzegowe... 5 Wyniki symulacji...
Elektrofizjologiczne podstawy lokalizacji ogniska padaczkowego. Piotr Walerjan PWSIM MEDISOFT
 Elektrofizjologiczne podstawy lokalizacji ogniska padaczkowego Piotr Walerjan PWSIM MEDISOFT Elektrofizjologia w padaczce Dlaczego stosujemy metody elektrofizjologiczne w diagnostyce padaczki? Ognisko
Elektrofizjologiczne podstawy lokalizacji ogniska padaczkowego Piotr Walerjan PWSIM MEDISOFT Elektrofizjologia w padaczce Dlaczego stosujemy metody elektrofizjologiczne w diagnostyce padaczki? Ognisko
Obrazowanie MR u pacjentów po zatruciu tlenkiem węgla.
 Obrazowanie MR u pacjentów po zatruciu tlenkiem węgla. Anna Drelich-Zbroja, Grzegorz Drelich, Maciej Siczek, Jarosław Szponar, Hanna Lewandowska-Stanek (Lublin) Definicja: Zatrucie tlenkiem węgla, podobnie
Obrazowanie MR u pacjentów po zatruciu tlenkiem węgla. Anna Drelich-Zbroja, Grzegorz Drelich, Maciej Siczek, Jarosław Szponar, Hanna Lewandowska-Stanek (Lublin) Definicja: Zatrucie tlenkiem węgla, podobnie
FIZYKA KLASA 7 Rozkład materiału dla klasy 7 szkoły podstawowej (2 godz. w cyklu nauczania)
 FIZYKA KLASA 7 Rozkład materiału dla klasy 7 szkoły podstawowej (2 godz. w cyklu nauczania) Temat Proponowana liczba godzin POMIARY I RUCH 12 Wymagania szczegółowe, przekrojowe i doświadczalne z podstawy
FIZYKA KLASA 7 Rozkład materiału dla klasy 7 szkoły podstawowej (2 godz. w cyklu nauczania) Temat Proponowana liczba godzin POMIARY I RUCH 12 Wymagania szczegółowe, przekrojowe i doświadczalne z podstawy
Szkoła z przyszłością. Zastosowanie pojęć analizy statystycznej do opracowania pomiarów promieniowania jonizującego
 Szkoła z przyszłością szkolenie współfinansowane przez Unię Europejską w ramach Europejskiego Funduszu Społecznego Narodowe Centrum Badań Jądrowych, ul. Andrzeja Sołtana 7, 05-400 Otwock-Świerk ĆWICZENIE
Szkoła z przyszłością szkolenie współfinansowane przez Unię Europejską w ramach Europejskiego Funduszu Społecznego Narodowe Centrum Badań Jądrowych, ul. Andrzeja Sołtana 7, 05-400 Otwock-Świerk ĆWICZENIE
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: Kierunek: Inżynieria Biomedyczna Rodzaj przedmiotu: obowiązkowy moduł kierunkowy ogólny Rodzaj zajęć: wykład, laboratorium TECHNIKI OBRAZOWANIA MEDYCZNEGO Medical Imaging Techniques Forma
Nazwa przedmiotu: Kierunek: Inżynieria Biomedyczna Rodzaj przedmiotu: obowiązkowy moduł kierunkowy ogólny Rodzaj zajęć: wykład, laboratorium TECHNIKI OBRAZOWANIA MEDYCZNEGO Medical Imaging Techniques Forma
Front-end do czujnika Halla
 Front-end do czujnika Halla Czujnik Halla ze względu na możliwość dużej integracji niezbędnych w nim komponentów jest jednym z podstawowych sensorów pola magnetycznego używanych na szeroką skalę. Marcin
Front-end do czujnika Halla Czujnik Halla ze względu na możliwość dużej integracji niezbędnych w nim komponentów jest jednym z podstawowych sensorów pola magnetycznego używanych na szeroką skalę. Marcin
WYMAGANIA EDUKACYJNE FIZYKA ROK SZKOLNY 2017/ ) wyodrębnia z tekstów, tabel, diagramów lub wykresów, rysunków schematycznych
 WYMAGANIA EDUKACYJNE FIZYKA ROK SZKOLNY 2017/2018 I. Wymagania przekrojowe. Uczeń: 1) wyodrębnia z tekstów, tabel, diagramów lub wykresów, rysunków schematycznych lub blokowych informacje kluczowe dla
WYMAGANIA EDUKACYJNE FIZYKA ROK SZKOLNY 2017/2018 I. Wymagania przekrojowe. Uczeń: 1) wyodrębnia z tekstów, tabel, diagramów lub wykresów, rysunków schematycznych lub blokowych informacje kluczowe dla
OPTYMALIZACJA HARMONOGRAMOWANIA MONTAŻU SAMOCHODÓW Z ZASTOSOWANIEM PROGRAMOWANIA W LOGICE Z OGRANICZENIAMI
 Autoreferat do rozprawy doktorskiej OPTYMALIZACJA HARMONOGRAMOWANIA MONTAŻU SAMOCHODÓW Z ZASTOSOWANIEM PROGRAMOWANIA W LOGICE Z OGRANICZENIAMI Michał Mazur Gliwice 2016 1 2 Montaż samochodów na linii w
Autoreferat do rozprawy doktorskiej OPTYMALIZACJA HARMONOGRAMOWANIA MONTAŻU SAMOCHODÓW Z ZASTOSOWANIEM PROGRAMOWANIA W LOGICE Z OGRANICZENIAMI Michał Mazur Gliwice 2016 1 2 Montaż samochodów na linii w
Spośród licznych filtrów nieliniowych najlepszymi właściwościami odznacza się filtr medianowy prosty i skuteczny.
 Filtracja nieliniowa może być bardzo skuteczną metodą polepszania jakości obrazów Filtry nieliniowe Filtr medianowy Spośród licznych filtrów nieliniowych najlepszymi właściwościami odznacza się filtr medianowy
Filtracja nieliniowa może być bardzo skuteczną metodą polepszania jakości obrazów Filtry nieliniowe Filtr medianowy Spośród licznych filtrów nieliniowych najlepszymi właściwościami odznacza się filtr medianowy
Porównanie zdjęć rentgenowskich wewnątrzustnych wykonanych za pomocą RVG.
 Porównanie zdjęć rentgenowskich wewnątrzustnych wykonanych za pomocą RVG. Spis treści: 1. Wstęp... 3 2. Porównanie zdjęć wykonanych na fantomie.... 4 2.1. Test osiowości.... 4 2.2. Test rozdzielczości....
Porównanie zdjęć rentgenowskich wewnątrzustnych wykonanych za pomocą RVG. Spis treści: 1. Wstęp... 3 2. Porównanie zdjęć wykonanych na fantomie.... 4 2.1. Test osiowości.... 4 2.2. Test rozdzielczości....
Ćwiczenie nr 5 : Badanie licznika proporcjonalnego neutronów termicznych
 Ćwiczenie nr 5 : Badanie licznika proporcjonalnego neutronów termicznych Oskar Gawlik, Jacek Grela 16 lutego 29 1 Teoria 1.1 Licznik proporcjonalny Jest to jeden z liczników gazowych jonizacyjnych, występujący
Ćwiczenie nr 5 : Badanie licznika proporcjonalnego neutronów termicznych Oskar Gawlik, Jacek Grela 16 lutego 29 1 Teoria 1.1 Licznik proporcjonalny Jest to jeden z liczników gazowych jonizacyjnych, występujący
Instrukcja do ćwiczenia jednopłaszczyznowe wyważanie wirników
 Instrukcja do ćwiczenia jednopłaszczyznowe wyważanie wirników 1. Podstawowe pojęcia związane z niewyważeniem Stan niewyważenia stan wirnika określony takim rozkładem masy, który w czasie wirowania wywołuje
Instrukcja do ćwiczenia jednopłaszczyznowe wyważanie wirników 1. Podstawowe pojęcia związane z niewyważeniem Stan niewyważenia stan wirnika określony takim rozkładem masy, który w czasie wirowania wywołuje
TERAPIA PROTONOWA. Proseminarium magisterskie 18 X 2005 1/36. Marta Giżyńska
 TERAPIA PROTONOWA Proseminarium magisterskie 18 X 2005 1/36 W skrócie... Cele terapii Słownictwo Własności wiązki protonowej Cele strategiczne Technika wielopolowa Technika rozpraszania Porównanie z techniką
TERAPIA PROTONOWA Proseminarium magisterskie 18 X 2005 1/36 W skrócie... Cele terapii Słownictwo Własności wiązki protonowej Cele strategiczne Technika wielopolowa Technika rozpraszania Porównanie z techniką
PLAN STUDIÓW. efekty kształcenia
 WYDZIAŁ: KIERUNEK: poziom kształcenia: profil: forma studiów: Lp. O/F Semestr 1 kod modułu/ przedmiotu* 1 O PG_00008512 CHEMIA 2 O PG_00019346 PODSTAWY MATEMATYKI 3 O PG_00008606 PODSTAWY PROGRAMOWANIA
WYDZIAŁ: KIERUNEK: poziom kształcenia: profil: forma studiów: Lp. O/F Semestr 1 kod modułu/ przedmiotu* 1 O PG_00008512 CHEMIA 2 O PG_00019346 PODSTAWY MATEMATYKI 3 O PG_00008606 PODSTAWY PROGRAMOWANIA
Wydział Fizyki Uniwersytet w Białymstoku. ul. Lipowa 41, Białystok. tel. (+48 85) fax ( ) EFEKTY KSZTAŁCENIA
 Wydział Fizyki Uniwersytet w Białymstoku ul. Lipowa 41, 15-424 Białystok tel. (+48 85) 745 72 22 fax (+ 48 85) 745 72 23 EFEKTY KSZTAŁCENIA dla kierunku poziom kształcenia profil Fizyka studia 2 stopnia
Wydział Fizyki Uniwersytet w Białymstoku ul. Lipowa 41, 15-424 Białystok tel. (+48 85) 745 72 22 fax (+ 48 85) 745 72 23 EFEKTY KSZTAŁCENIA dla kierunku poziom kształcenia profil Fizyka studia 2 stopnia
Układ moczowy metody diagnostyczne
 Układ moczowy metody diagnostyczne Ultrasonografia (USG) Tomografia komputerowa Zdjęcie przeglądowe jamy brzusznej Urografia Angiografia Cystografia mikcyjna Pielografia wstępujaca Tomografia rezonansu
Układ moczowy metody diagnostyczne Ultrasonografia (USG) Tomografia komputerowa Zdjęcie przeglądowe jamy brzusznej Urografia Angiografia Cystografia mikcyjna Pielografia wstępujaca Tomografia rezonansu
PRAWO OHMA DLA PRĄDU PRZEMIENNEGO
 ĆWICZENIE 53 PRAWO OHMA DLA PRĄDU PRZEMIENNEGO Cel ćwiczenia: wyznaczenie wartości indukcyjności cewek i pojemności kondensatorów przy wykorzystaniu prawa Ohma dla prądu przemiennego; sprawdzenie prawa
ĆWICZENIE 53 PRAWO OHMA DLA PRĄDU PRZEMIENNEGO Cel ćwiczenia: wyznaczenie wartości indukcyjności cewek i pojemności kondensatorów przy wykorzystaniu prawa Ohma dla prądu przemiennego; sprawdzenie prawa
Ć W I C Z E N I E N R J-1
 INSTYTUT FIZYKI WYDZIAŁ INŻYNIERII PRODUKCJI I TECHNOLOGII MATERIAŁÓW POLITECHNIKA CZĘSTOCHOWSKA PRACOWNIA DETEKCJI PROMIENIOWANIA JĄDROWEGO Ć W I C Z E N I E N R J-1 BADANIE CHARAKTERYSTYKI LICZNIKA SCYNTYLACYJNEGO
INSTYTUT FIZYKI WYDZIAŁ INŻYNIERII PRODUKCJI I TECHNOLOGII MATERIAŁÓW POLITECHNIKA CZĘSTOCHOWSKA PRACOWNIA DETEKCJI PROMIENIOWANIA JĄDROWEGO Ć W I C Z E N I E N R J-1 BADANIE CHARAKTERYSTYKI LICZNIKA SCYNTYLACYJNEGO
Politechnika Krakowska im. Tadeusza Kościuszki. Karta przedmiotu. obowiązuje studentów rozpoczynających studia w roku akademickim 2013/2014
 Politechnika Krakowska im. Tadeusza Kościuszki Karta przedmiotu Wydział Mechaniczny obowiązuje studentów rozpoczynających studia w roku akademickim 201/2014 Kierunek studiów: Inżynieria Biomedyczna Forma
Politechnika Krakowska im. Tadeusza Kościuszki Karta przedmiotu Wydział Mechaniczny obowiązuje studentów rozpoczynających studia w roku akademickim 201/2014 Kierunek studiów: Inżynieria Biomedyczna Forma
Inteligentna analiza danych
 Numer indeksu 150946 Michał Moroz Imię i nazwisko Numer indeksu 150875 Grzegorz Graczyk Imię i nazwisko kierunek: Informatyka rok akademicki: 2010/2011 Inteligentna analiza danych Ćwiczenie I Wskaźniki
Numer indeksu 150946 Michał Moroz Imię i nazwisko Numer indeksu 150875 Grzegorz Graczyk Imię i nazwisko kierunek: Informatyka rok akademicki: 2010/2011 Inteligentna analiza danych Ćwiczenie I Wskaźniki
Badanie transformatora
 Ćwiczenie 14 Badanie transformatora 14.1. Zasada ćwiczenia Transformator składa się z dwóch uzwojeń, umieszczonych na wspólnym metalowym rdzeniu. Do jednego uzwojenia (pierwotnego) przykłada się zmienne
Ćwiczenie 14 Badanie transformatora 14.1. Zasada ćwiczenia Transformator składa się z dwóch uzwojeń, umieszczonych na wspólnym metalowym rdzeniu. Do jednego uzwojenia (pierwotnego) przykłada się zmienne
Sposoby opisu i modelowania zakłóceń kanałowych
 INSTYTUT TELEKOMUNIKACJI ZAKŁAD RADIOKOMUNIKACJI Instrukcja laboratoryjna z przedmiotu Podstawy Telekomunikacji Sposoby opisu i modelowania zakłóceń kanałowych Warszawa 2010r. 1. Cel ćwiczeń: Celem ćwiczeń
INSTYTUT TELEKOMUNIKACJI ZAKŁAD RADIOKOMUNIKACJI Instrukcja laboratoryjna z przedmiotu Podstawy Telekomunikacji Sposoby opisu i modelowania zakłóceń kanałowych Warszawa 2010r. 1. Cel ćwiczeń: Celem ćwiczeń
Rys. 1 Schemat układu obrazującego 2f-2f
 Ćwiczenie 15 Obrazowanie. Celem ćwiczenia jest zbudowanie układów obrazujących w świetle monochromatycznym oraz zaobserwowanie różnic w przypadku obrazowania za pomocą różnych elementów optycznych, zwracając
Ćwiczenie 15 Obrazowanie. Celem ćwiczenia jest zbudowanie układów obrazujących w świetle monochromatycznym oraz zaobserwowanie różnic w przypadku obrazowania za pomocą różnych elementów optycznych, zwracając
Spis treści. Przedmowa... XI. Rozdział 1. Pomiar: jednostki miar... 1. Rozdział 2. Pomiar: liczby i obliczenia liczbowe... 16
 Spis treści Przedmowa.......................... XI Rozdział 1. Pomiar: jednostki miar................. 1 1.1. Wielkości fizyczne i pozafizyczne.................. 1 1.2. Spójne układy miar. Układ SI i jego
Spis treści Przedmowa.......................... XI Rozdział 1. Pomiar: jednostki miar................. 1 1.1. Wielkości fizyczne i pozafizyczne.................. 1 1.2. Spójne układy miar. Układ SI i jego
Badanie własności hallotronu, wyznaczenie stałej Halla (E2)
 Badanie własności hallotronu, wyznaczenie stałej Halla (E2) 1. Wymagane zagadnienia - ruch ładunku w polu magnetycznym, siła Lorentza, pole elektryczne - omówić zjawisko Halla, wyprowadzić wzór na napięcie
Badanie własności hallotronu, wyznaczenie stałej Halla (E2) 1. Wymagane zagadnienia - ruch ładunku w polu magnetycznym, siła Lorentza, pole elektryczne - omówić zjawisko Halla, wyprowadzić wzór na napięcie
Widmo fal elektromagnetycznych
 Czym są fale elektromagnetyczne? Widmo fal elektromagnetycznych dr inż. Romuald Kędzierski Podstawowe pojęcia związane z falami - przypomnienie pole falowe część przestrzeni objęta w danej chwili falą
Czym są fale elektromagnetyczne? Widmo fal elektromagnetycznych dr inż. Romuald Kędzierski Podstawowe pojęcia związane z falami - przypomnienie pole falowe część przestrzeni objęta w danej chwili falą
Oddziaływanie cząstek z materią
 Oddziaływanie cząstek z materią Trzy główne typy mechanizmów reprezentowane przez Ciężkie cząstki naładowane (cięższe od elektronów) Elektrony Kwanty gamma Ciężkie cząstki naładowane (miony, p, cząstki
Oddziaływanie cząstek z materią Trzy główne typy mechanizmów reprezentowane przez Ciężkie cząstki naładowane (cięższe od elektronów) Elektrony Kwanty gamma Ciężkie cząstki naładowane (miony, p, cząstki
E107. Bezpromieniste sprzężenie obwodów RLC
 E7. Bezpromieniste sprzężenie obwodów RLC Cel doświadczenia: Pomiar amplitudy sygnału w rezonatorze w zależności od wzajemnej odległości d cewek generatora i rezonatora. Badanie wpływu oporu na tłumienie
E7. Bezpromieniste sprzężenie obwodów RLC Cel doświadczenia: Pomiar amplitudy sygnału w rezonatorze w zależności od wzajemnej odległości d cewek generatora i rezonatora. Badanie wpływu oporu na tłumienie
Termodynamika. Część 12. Procesy transportu. Janusz Brzychczyk, Instytut Fizyki UJ
 Termodynamika Część 12 Procesy transportu Janusz Brzychczyk, Instytut Fizyki UJ Zjawiska transportu Zjawiska transportu są typowymi procesami nieodwracalnymi zachodzącymi w przyrodzie. Zjawiska te polegają
Termodynamika Część 12 Procesy transportu Janusz Brzychczyk, Instytut Fizyki UJ Zjawiska transportu Zjawiska transportu są typowymi procesami nieodwracalnymi zachodzącymi w przyrodzie. Zjawiska te polegają
MAGNETYCZNY REZONANS JĄDROWY (MRJ) NUCLEAR MAGNETIC RESONANCE (NMR)
 MAGNETYCZNY REZONANS JĄDROWY (MRJ) 1 H MRJ, 13 C MRJ... NUCLEAR MAGNETIC RESONANCE (NMR) 1 H NMR, 13 C NMR... Program: 1. Podstawy ogólne (zjawisko fizyczne, wykonanie pomiaru, aparatura) 2. Spektroskopia
MAGNETYCZNY REZONANS JĄDROWY (MRJ) 1 H MRJ, 13 C MRJ... NUCLEAR MAGNETIC RESONANCE (NMR) 1 H NMR, 13 C NMR... Program: 1. Podstawy ogólne (zjawisko fizyczne, wykonanie pomiaru, aparatura) 2. Spektroskopia
Numeryczna symulacja rozpływu płynu w węźle
 231 Prace Instytutu Mechaniki Górotworu PAN Tom 7, nr 3-4, (2005), s. 231-236 Instytut Mechaniki Górotworu PAN Numeryczna symulacja rozpływu płynu w węźle JERZY CYGAN Instytut Mechaniki Górotworu PAN,
231 Prace Instytutu Mechaniki Górotworu PAN Tom 7, nr 3-4, (2005), s. 231-236 Instytut Mechaniki Górotworu PAN Numeryczna symulacja rozpływu płynu w węźle JERZY CYGAN Instytut Mechaniki Górotworu PAN,
SYMULACJA GAMMA KAMERY MATERIAŁ DLA STUDENTÓW. Szacowanie pochłoniętej energii promieniowania jonizującego
 SYMULACJA GAMMA KAMERY MATERIAŁ DLA STUDENTÓW Szacowanie pochłoniętej energii promieniowania jonizującego W celu analizy narażenia na promieniowanie osoby, której podano radiofarmaceutyk, posłużymy się
SYMULACJA GAMMA KAMERY MATERIAŁ DLA STUDENTÓW Szacowanie pochłoniętej energii promieniowania jonizującego W celu analizy narażenia na promieniowanie osoby, której podano radiofarmaceutyk, posłużymy się
Analiza sygnałów biologicznych
 Analiza sygnałów biologicznych Paweł Strumiłło Zakład Elektroniki Medycznej Instytut Elektroniki PŁ Co to jest sygnał? Funkcja czasu x(t) przenosząca informację o stanie lub działaniu układu (systemu),
Analiza sygnałów biologicznych Paweł Strumiłło Zakład Elektroniki Medycznej Instytut Elektroniki PŁ Co to jest sygnał? Funkcja czasu x(t) przenosząca informację o stanie lub działaniu układu (systemu),
Biostatystyka, # 3 /Weterynaria I/
 Biostatystyka, # 3 /Weterynaria I/ dr n. mat. Zdzisław Otachel Uniwersytet Przyrodniczy w Lublinie Katedra Zastosowań Matematyki i Informatyki ul. Głęboka 28, p. 221 bud. CIW, e-mail: zdzislaw.otachel@up.lublin.pl
Biostatystyka, # 3 /Weterynaria I/ dr n. mat. Zdzisław Otachel Uniwersytet Przyrodniczy w Lublinie Katedra Zastosowań Matematyki i Informatyki ul. Głęboka 28, p. 221 bud. CIW, e-mail: zdzislaw.otachel@up.lublin.pl
7. Identyfikacja defektów badanego obiektu
 7. Identyfikacja defektów badanego obiektu Pierwszym krokiem na drodze do identyfikacji defektów było przygotowanie tzw. odcisku palca poszczególnych defektów. W tym celu został napisany program Gaussian
7. Identyfikacja defektów badanego obiektu Pierwszym krokiem na drodze do identyfikacji defektów było przygotowanie tzw. odcisku palca poszczególnych defektów. W tym celu został napisany program Gaussian
Anatomia radiologiczna. Kończyny
 Anatomia radiologiczna. Kończyny Zakład Radiologii i Diagnostyki Obrazowej Uniwersytet Medyczny w Łodzi Kierownik: prof. dr hab. n. med. Ludomir Stefańczyk 1 Jak to się zaczęło 8 listopada 1895, w trakcie
Anatomia radiologiczna. Kończyny Zakład Radiologii i Diagnostyki Obrazowej Uniwersytet Medyczny w Łodzi Kierownik: prof. dr hab. n. med. Ludomir Stefańczyk 1 Jak to się zaczęło 8 listopada 1895, w trakcie
Automatyczne tworzenie trójwymiarowego planu pomieszczenia z zastosowaniem metod stereowizyjnych
 Automatyczne tworzenie trójwymiarowego planu pomieszczenia z zastosowaniem metod stereowizyjnych autor: Robert Drab opiekun naukowy: dr inż. Paweł Rotter 1. Wstęp Zagadnienie generowania trójwymiarowego
Automatyczne tworzenie trójwymiarowego planu pomieszczenia z zastosowaniem metod stereowizyjnych autor: Robert Drab opiekun naukowy: dr inż. Paweł Rotter 1. Wstęp Zagadnienie generowania trójwymiarowego
SCENARIUSZ LEKCJI. TEMAT LEKCJI: Zastosowanie średnich w statystyce i matematyce. Podstawowe pojęcia statystyczne. Streszczenie.
 SCENARIUSZ LEKCJI OPRACOWANY W RAMACH PROJEKTU: INFORMATYKA MÓJ SPOSÓB NA POZNANIE I OPISANIE ŚWIATA. PROGRAM NAUCZANIA INFORMATYKI Z ELEMENTAMI PRZEDMIOTÓW MATEMATYCZNO-PRZYRODNICZYCH Autorzy scenariusza:
SCENARIUSZ LEKCJI OPRACOWANY W RAMACH PROJEKTU: INFORMATYKA MÓJ SPOSÓB NA POZNANIE I OPISANIE ŚWIATA. PROGRAM NAUCZANIA INFORMATYKI Z ELEMENTAMI PRZEDMIOTÓW MATEMATYCZNO-PRZYRODNICZYCH Autorzy scenariusza:
Biofizyczne podstawy diagnostyki medycznej
 Biofizyczne podstawy diagnostyki medycznej 1. Metryczka Nazwa Wydziału: Program kształcenia Wydział Farmaceutyczny z Oddziałem Medycyny Laboratoryjnej Analityka Medyczna, jednolite studia magisterskie,
Biofizyczne podstawy diagnostyki medycznej 1. Metryczka Nazwa Wydziału: Program kształcenia Wydział Farmaceutyczny z Oddziałem Medycyny Laboratoryjnej Analityka Medyczna, jednolite studia magisterskie,
Modelowanie biomechaniczne. Dr inż. Sylwia Sobieszczyk Politechnika Gdańska Wydział Mechaniczny KMiWM 2005/2006
 Modelowanie biomechaniczne Dr inż. Sylwia Sobieszczyk Politechnika Gdańska Wydział Mechaniczny KMiWM 2005/2006 Zakres: Definicja modelowania Modele kinematyczne ruch postępowy, obrotowy, przemieszczenie,
Modelowanie biomechaniczne Dr inż. Sylwia Sobieszczyk Politechnika Gdańska Wydział Mechaniczny KMiWM 2005/2006 Zakres: Definicja modelowania Modele kinematyczne ruch postępowy, obrotowy, przemieszczenie,
Ćwiczenie 2a. Pomiar napięcia z izolacją galwaniczną Doświadczalne badania charakterystyk układów pomiarowych CZUJNIKI POMIAROWE I ELEMENTY WYKONAWCZE
 Politechnika Łódzka Katedra Mikroelektroniki i Technik Informatycznych 90-924 Łódź, ul. Wólczańska 221/223, bud. B18 tel. 42 631 26 28 faks 42 636 03 27 e-mail secretary@dmcs.p.lodz.pl http://www.dmcs.p.lodz.pl
Politechnika Łódzka Katedra Mikroelektroniki i Technik Informatycznych 90-924 Łódź, ul. Wólczańska 221/223, bud. B18 tel. 42 631 26 28 faks 42 636 03 27 e-mail secretary@dmcs.p.lodz.pl http://www.dmcs.p.lodz.pl
Fizyczne podstawy magnetycznego rezonansu jądrowego (NMR) - obrazowania za pomocą rezonansu jądrowego (MRI)
 Postępy Psychiatrii i Neurologii. 1996. 5. 1-8 Fizyczne podstawy magnetycznego rezonansu jądrowego (NMR) - obrazowania za pomocą rezonansu jądrowego (MRI) Physicalfoundations ofnuclear magnetic resonance
Postępy Psychiatrii i Neurologii. 1996. 5. 1-8 Fizyczne podstawy magnetycznego rezonansu jądrowego (NMR) - obrazowania za pomocą rezonansu jądrowego (MRI) Physicalfoundations ofnuclear magnetic resonance
Klasyfikacja przypadków w ND280
 Klasyfikacja przypadków w ND280 Arkadiusz Trawiński Warszawa, 20 maja 2008 pod opieką: prof Danuta Kiełczewska prof Ewa Rondio 1 Abstrakt Celem analizy symulacji jest bliższe zapoznanie się z możliwymi
Klasyfikacja przypadków w ND280 Arkadiusz Trawiński Warszawa, 20 maja 2008 pod opieką: prof Danuta Kiełczewska prof Ewa Rondio 1 Abstrakt Celem analizy symulacji jest bliższe zapoznanie się z możliwymi
Definicje i przykłady
 Rozdział 1 Definicje i przykłady 1.1 Definicja równania różniczkowego 1.1 DEFINICJA. Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie F (t, x, ẋ, ẍ,..., x (n) ) = 0. (1.1) W równaniu tym t jest
Rozdział 1 Definicje i przykłady 1.1 Definicja równania różniczkowego 1.1 DEFINICJA. Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie F (t, x, ẋ, ẍ,..., x (n) ) = 0. (1.1) W równaniu tym t jest
Statystyka w pracy badawczej nauczyciela Wykład 4: Analiza współzależności. dr inż. Walery Susłow walery.suslow@ie.tu.koszalin.pl
 Statystyka w pracy badawczej nauczyciela Wykład 4: Analiza współzależności dr inż. Walery Susłow walery.suslow@ie.tu.koszalin.pl Statystyczna teoria korelacji i regresji (1) Jest to dział statystyki zajmujący
Statystyka w pracy badawczej nauczyciela Wykład 4: Analiza współzależności dr inż. Walery Susłow walery.suslow@ie.tu.koszalin.pl Statystyczna teoria korelacji i regresji (1) Jest to dział statystyki zajmujący
FIZYKA klasa 1 Liceum Ogólnokształcącego (4 letniego)
 2019-09-01 FIZYKA klasa 1 Liceum Ogólnokształcącego (4 letniego) Treści z podstawy programowej przedmiotu POZIOM ROZSZERZONY (PR) SZKOŁY BENEDYKTA Podstawa programowa FIZYKA KLASA 1 LO (4-letnie po szkole
2019-09-01 FIZYKA klasa 1 Liceum Ogólnokształcącego (4 letniego) Treści z podstawy programowej przedmiotu POZIOM ROZSZERZONY (PR) SZKOŁY BENEDYKTA Podstawa programowa FIZYKA KLASA 1 LO (4-letnie po szkole
