Wprowadzenie do Sieci Neuronowych Laboratorium 04 Algorytmy konstrukcyjne dla sieci skierowanych

Transkrypt

1 Projekt pn. Wzmocnienie potencjału dydaktycznego UMK w Toruniu w dziedzinach matematyczno-przyrodniczych realizowany w ramach Poddziałania Programu Operacyjnego Kapitał Ludzki Wprowadzenie do Sieci Neuronowych Laboratorium 04 Algorytmy konstrukcyjne dla sieci skierowanych Maja Czoków, Jarosław Piersa Powtórzenie 1.1 Algorytm uczenia perceptronu Dane: Perceptron o n wejściach, k przykładów uczących E 1 E k wraz z poprawnymi odpowiedziami T 1 T k, gdzie (T i = ±1). Dodatkowym parametrem uczącym jest wartość progu p. Wynik: Wartości wag wi oraz progu p, które dają poprawną klasyfikację. 1. Przypisujemy wagom i progowi małe losowe wartości wokół 0, przypisujemy takiemu układowi wag zerowy czas życia, 2. Przebiegamy przykłady losując z listy 3. Dla wybranego przykładu E j sprawdzamy, czy E j jest dobrze klasyfikowany, Jeśli tak, to zwiększamy mu czas życia o jeden. Jeżeli jest to wynik lepszy niż u dotychczasowego rekordzisty, to zapominamy go (dotychczasowego rekordzistę) i zapisujemy bieżący układ wag jako nowego rekordzistę. Wracamy do 2. Jeżeli nie, to wi := wi + T j Eij p := p T j Nowo powstałemu układowi wag przypisujemy zerowy czas życia. Wracamy do Algorytm kończymy po przebiegnięciu odpowiedniej liczby iteracji. Zwracamy najbardziej żywotny zestaw wag. 1.2 Sieci skierowane Sieci skierowane (ang. feed-forward) są to grafy, w których wierzchołkami są perceptrony. Warstwą wejściową jest zbiór perceptronów, których wejściami są dane. Warstwa wyjściowa zwraca wyniki, które nie są przetwarzane przez inne warstwy. Pozostałe neurony tworzą warstwy ukryte, za wejścia przyjmują sygnały od innych perceptronów, a ich wyjścia są wejściami dla kolejnej warstwy. W grafie nie występują cykle, informacja wyjściowa z neuronu n propagując się po sieci nigdy nie powróci do n. Działanie sieci jest zsynchronizowane: neuron może obliczyć i zwrócić odpowiedź tylko gdy zna wartości wszystkich swoich wejść (niektóre z nich pochodzą od innych neuronów wówczas należy poczekać na nie). 1.3 Algorytm wieżowy / piramidalny Dane: zbiór przykładów uczących E 1 E k wraz z odpowiadającymi poprawnymi odpowiedziami T 1 T k. Wynik: Sieć zwracająca optymalną klasyfikację. 1. Zbuduj sieć składającą się z pojedynczego perceptronu, 2. Wybierz szczytowy neuron i naucz go na przykładach algorytmem kieszonkowym / z zapadką (nie SPLA!), 3. Jeżeli wszystkie przykłady (odpowiednio dużo) są klasyfikowane poprawnie, to zakończ, zwróć aktualną sieć, Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego Wyrażam zgodę na wydruk dokumentu do celów dydaktycznych 1

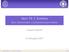
2 (a) Sieć wieżowa. (b) Sieć piramidalna. Rysunek 1: Sieci wieżowa i piramidalna; w tej drugiej dodatkowo dochodzą połączenia od pośrednich neuronów do wszystkich wyższych 4. Jeżeli nie, to dodaj na szczyt sieci dodatkowy perceptron: Jego wejściami są wszystkie wejścia danych: x 1 x n (alg. wieżowy) Dodatkowo jego (n + 1)-szym wejściem jest wyjście poprzedniego szczytowego perceptronu w sieci, (alg. piramidalny) Dodatkowo jego wejściami (n+1 do n+wysokosc) są wyjścia wszystkich niższych perceptronów w sieci, Wartość zwracana przez nową jednostkę jest odpowiedzią całej sieci na danych wejściowych, 5. Wróć do Algorytm kafelkowy Dane: Lista przykładów uczących wraz z poprawnymi klasyfikacjami. Wynik: Sieć klasyfikująca. 1. Rozpocznij od sieci składającej się z warstwy wejściowej L = Dodaj L + 1 kafelek z jednym neuronem nową warstwę. Jego wejściami są wyjścia z kafelka L (dla L = 1: dane wejściowe). Naucz nowy neuron algorytmem kieszonkowym. Jeżeli nauczył się wszystkich przykładów to zakończ zwracając sieć. 3. Jeżeli nie, to (a) do kafelka L + 1 dodaj kolejny neuron, przypisz mu wejścia z kafelka L. (b) naucz nowy neuron algorytmem kieszonkowym z zapadką, ale tylko na najbardziej licznym zbiorze, który daje ten sam zestaw odpowiedzi na wszystkich dotychczasowych neuronach w kafelku L + 1 (tj. z punktu widzenia sieci są jeszcze takie same), ale jednocześnie oczekiwane odpowiedzi ma różne (tj. nie chcemy aby były jednakowe). (c) Jeżeli bieżący kafel wykształcił wierną reprezentację, to wróć do 2 (tj. dodaj nowy kafel do sieci). Jeżeli jeszcze nie, to wróć do 3a (tj. dodaj nowy neuron do bieżącego kafla). 2

3 out Rysunek 2: Sieć warstwowa. Rysunek 3: Architektura upstart 1.5 Architektura Upstart 1. Tworzymy pojedynczą jednostkę U, która widzi wszystkie wejścia. Jej wyjście jest wyjściem całej sieci. 2. Odkładamy U na stos wraz ze wszystkimi przykładami uczącymi. 3. Dopóki stos jest niepusty, powtarzamy: Zdejmujemy ze stosu jednostkę U i i zbiór stowarzyszonych z nią przykładów uczących, Uczymy U i na jej przykładach uczących algorytmem zapadkowym, Jeżeli klasyfikacja U i jest w pełni zgodna, to rozpocznij następną iterację pętli (continue), Jeżeli istnieją źle sklasyfikowane przykłady z oczekiwaną odpowiedzią +1 dla jednostki U i, to tworzymy nową jednostkę U i+, jej wejściami są wszystkie wejścia, jej wyjście wchodzi do U i z dużą wagą dodatnią, odkładamy U i+ na stos z następującym zbiorem uczącym: { E k : U k i = 1, C k U i = +1 } { E k : C k U i = 1 }, to jest przykłady, które są klasyfikowane przez U i jako 1, a powinny +1 oraz przykłady, która powinny być klasyfikowane przez U i jako 1, Zbiór uczący dla U i+ jest 3

4 mniejszy od U i o przykłady dodatnie, które są dobrze klasyfikowane 1, Jeżeli istnieją źle sklasyfikowane przykłady z oczekiwaną odpowiedzią 1 dla U i, to tworzymy nową jednostkę U i, jej wejściami są wszystkie wejścia, jej wyjście wchodzi do U i z dużą wagą dodatnią, odkładamy U i na stos z następującym zbiorem uczącym: { E k : U k i = +1, C k U i = 1 } { E k : C k U i = +1 }, to jest przykłady, które są klasyfikowane przez U i jako +1, a powinny 1 oraz przykłady, która powinny być klasyfikowane przez U i jako +1 2, Zdejmij ze stosu następny neuron (continue), 4. Zwróć uzyskaną sieć. 2 Zadania na zajęcia 2.1 Zadanie 1 Zaimplementuj sieć wieżową dokonującą klasyfikacji punktów na R 2. Zaimplementuj dynamikę sieci wieżowej. Wygodną reprezentacją może być tablica dwuwymiarowa wag w 01 w 11 w n1 W agi tr = w 02 w 12 w n2 w O1,2, w 0k w 1k w nk w Ok 1,k gdzie k = wysokość wieży w 0j = bias do neuronu j-ego (leży jako j-ty na wieży / piramidzie) w ij = waga między wejściem i a neuronem j w Oj 1j = waga między neuronem j-tym, a neuronem j 1-szym (leżącym poniżej) Zauważ, że indeksowanie tablicy jest odwrócone. function out = wieza ( x, wagi ) s = size ( wagi ); n = s (1); k = s (2); % pierwszy neuron x = [1,x]; out = sign ( wagi (1, 1: -1) * x ); % zagadka : dlaczego " -1"? % pozostale neurony for i =2: k x1 = [x, out ]; out = sign ( wagi (1, 1: ) * x1 ); % zagadka : dlaczego tu juz nie ma " -1"? Przygotuj nietrywialne dane uczące wraz z klasyfikacjami, np: M = 100; EX = rand (1, M )*10-5; EY = rand (1, M )*10-5; 1 Gdy będzie mało przykładów dodatnich i dużo ujemnych może się zdarzyć, że nowy neuron wszystko będzie klasyfikował jako minusy. Dla stabilności można wymusić częstsze losowanie przykładów dodatnich. 2 Patrz uwaga powyżej symetryczna sytuacja. 4

5 Q = rand (1, 4)*10-5; % zagadka : co to jest? I1 = find ( (EX -Q (1)).^2 + (EY -Q (2)).^2 < 4); I2 = find ( (EX -Q (3)).^2 + (EY -Q (4)).^2 < 4); INeg = union (I1, I2 ); IPos = setdiff (1:100, INeg ); C = ones (1, M); C( INeg ) = -1; Wyświetl dane Napisz algorytm konstruujący sieć wieżową Algorytm będzie przyjmował dane uczące wymiaru 2 na P współrzędne i 1 na P odpowiedzi, a zwracał tablicę wag wymiaru 4 (wymiar wejścia + bias/próg + waga do poprzedniego neuronu) na K wysokość wieży (ustalana w trakcie algorytmu). Wskazówka! Podczas uczenia przydatna może być funkcja: function out = obliczodpowiedznaprzedostatnimneuronie (x, wagi ) Naucz sieć na danych Wyświetl wynik dla nauczonej sieci 2.2 Zadanie 2 Jeżeli zbiór wag stanowi zestaw parametrów swobodnych sieci, to uczenie jest minimalizacją funkcji błędu: Err(W ) = ilość błędnie sklasyfikowanych przykładów uczących ilość wszystkich przykładów uczących wykres funkcji błędu (ilość błędnie klasyfikowanych przykładów uczących) w zależności od wybranych wag sieci, wyświetl wykres funkcji błędu w zależności od jednej lub dwóch wybranych z tablicy wag (reszta ustalona, zgodnie z wartościami zwróconymi przez algorytm konstrukcyjny), wskazówka przeanalizuj i zmodyfikuj poniższy kod rysujący wykres płaszczyzny w R 3 : wx = -2:.1:+2; wy = -3:.1:+3; err = []; for i =1: length (wx) for j =1: length (wy) err (j,i) = sin (wx(i ).^2 + wy(j ).^2 ); % lub inna funkcja dwoch zmiennych hold off ; mesh (wx, wy, err ); 3 Zadania programistyczne 3.1 Zadanie 1. Klasyfikacja alg. konstrukcyjne Za pomocą algorytmów konstrukcyjnych zbuduj sieć klasyfikującą punkty na płaszczyźnie, przestrzeni, czasoprzestrzeni, (patrz również zadanie 2 z listy 1). Pliki z przykładami uczącemu są dostępne na stronie oraz można (zalecane!) użyć własnych lub poprosić użytkownika aby zaznaczył własne. Program powinien ponadto wyświetlić przykłady uczące z docelową klasyfikacją oraz faktyczną klasyfikacją i statystyki jak dobrze klasyfikuje. Uwagi i wskazówki: Do algorytmów konstrukcyjnych proszę nie używać algorytmu uczenia w wersji SPLA (tj. bez zapadki i kieszeni), 5

6 Można dodać porównanie jakości uczenia sieci (oraz kosztów czasowych i pamięciowych) dla kilku algorytmów oraz pojedynczego perceptronu, Do wyświetlania można wykorzystać gotowe zewnętrzne bibliotek (OpenGL, DirectX, pisany w locie skrypt Matlaba, Octave a, Maple a, R, GnuPlota, generowany plik ps lub pdf, grafikę ASCII), Liczone jako jedno zadanie jeżeli pisany jest samodzielnie lub jako 2 do 3 zadań jeżeli jest połączony z perceptronami, RBF i/lub propagacją wsteczną. 3.2 Zadanie 2. (funkcja błędu) Napisz program, który dla zadanego zbioru przykładów uczących (patrz lista zadań 1) oraz nauczonego perceptronu (lista 1) lub sieci (zadanie powyżej) wyświetli profil funkcji błędu dla dwóch (dla ambitnych: trzech) wybranych wag i przy ustalonych wartościach pozostałych wag. ERROR(w 1,, w n ) = (O w1,..,w k (E k ) T k ) 2 k Choć wykres musi uwzględniać maksymalnie trzy wagi (ze względu na czytelność), można swobodnie wybierać, które z wag mają być zmienne, a które ustalone. Program będzie można również napisać pod sieć nauczoną algorytmem propagacji wstecznej (następne zajęcia) i porównać wyniki oraz koszt czasowy / pamięciowy. 3.3 Referat: Maszyny Wektorów Wspierających (SVM Support Vector Machines) (jeden na grupę zajęciową) Liczone jak pojedyncze zadanie. Teoria: Trevor Hastie, Robert Tibshirani, Jerome Friedman, The Elements of Statistical Learning: data mining, inference, and prediction, Springer, 2009, Rozdział 4.5 ((Optimal) Separating Hyperplanes) i 12 (Support Vector Machines and Kernels) Uwaga: książka jest dostępna elektronicznie z sieci wydziałowej: Corina Cortes, Vladimir Vapnik, Support-vector networks, Machine Learning, Vol 20, Issue 3, 1995 doi: /bf Uczenie: John Platt, Fast Training of Support Vector Machines using Sequential Minimal Optimization, Advances in Kernel Methods - Support Vector Learning, MIT Press 1999,???, Simplified SMO Algorithm, Stanford University, CS229,