synaptycznych wszystko to waży 1.5 kg i zajmuje objętość około 1.5 litra. A zużywa mniej energii niż lampka nocna.

Transkrypt

1 Sieci neuronowe model konekcjonistyczny

2 Plan wykładu Mózg ludzki a komputer Modele konekcjonistycze Perceptron Sieć neuronowa Uczenie sieci Sieci Hopfielda

3 Mózg ludzki a komputer Twój mózg to komórek, kilometrów przewodów i (biliard) połączeń synaptycznych wszystko to waży.5 kg i zajmuje objętość około.5 litra. A zużywa mniej energii niż lampka nocna. Komputer Mózg Jednostki obliczeniowe CPU neuronów Jednostki pamięci 0 9 bitów RAM 0 neuronów 0 0 bitów na dysku 0 4 połączeń Czas operacji 0-8 s 0-3 s Czas transmisji 0 9 bitów/s 0 4 bitów/s Liczba aktywacji/s

4 Mózg ludzki a komputer Szybkość wykonania pojedynczej operacji vs. rozwiązanie skomplikowanego zadania Odporność na pomyłki pojedynczych elementów Zachowanie poprawności działania w p p przypadku informacji niepewnej i niepełnej

5 Cechy modeli konekcjonistycznych k składają się z dużej liczby prostych elementów, zwanych neuronami wagi na połączeniach między tymi elementami "kodują wiedzę sieci sterowanie siecią jest równoległe i rozproszone głównym problemem jest automatyczne uczenie głównym problemem jest automatyczne uczenie sieci

6 Model neuronu

7 Neuron

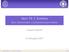
8 Perceptron x w x 2 x 3 w 2 w 3 w 2 Σ w n x n

9 Perceptron wejścia x w x 2 x 3 w 2 w 3 w 2 Σ w n x n

10 Perceptron x w połączeni a wagi x 2 x 3 w 2 w 3 w 2 Σ w n x n

11 Perceptron łączne pobudzenie neuronu u x w x 2 x 3 w 2 w 3 w 2 Σ g w n x n

12 Perceptron charakterystyk a neuronu x w x 2 w 2 w 3 w 2 x 3 Σ ϕ 3 g w n x n

13 Perceptron sygnał wyjściowy x w x 2 w 2 w 3 w 2 x 3 Σ ϕ 3 g o w n x n

14 Perceptron liniowy i x x 2 x 3 w w 2 g( X ) = n i= w i x i g(x) w 2 w 3 Σ ϕ o(x) w n gdy ϕ ( X ) ( ) x o X = n 0 gdy ϕ( X) w 0 < w 0

15 Pó Próg aktywacji jij jako dodatkowa d waga x 0 = w 0 x n g( X ) = x 2 x 3 w w 2 i= 0 g(x) w i x i w 2 w 3 Σ ϕ o(x) w n o( X) x n = ( X ) gdy ϕ X 0 0 gdy ϕ( X) < 0

16 Funkcja aktywacji perceptronu o 0.0 o ( X ) = ( ) gdy gy ϕ X 0 0 gdy ϕ( X) < 0 funkcja progowa o g o ( ) X = + + exp g ( ( ) X sigmoida g

17 Perceptron z wieloma wejściami i x 0 = w ij wyjściami Σ x Σ x 2 x 3 Σ x n Σ

18 y Liniowo separowalny problem klasyfikacji y A (x A, y A ) x A x

19 y Perceptron uczący się klasyfikacji k = 0 k = 00 k = 300 k = 635 x

20 Twierdzenie i Rosenblatta Proces uczenia perceptronu jest zbieżny. Perceptron może się nauczyć dowolnego liniowo separowalnego problemu klasyfikacji.

21 Problem XOR x x x XOR x x 2 x x 2 x XOR x x

22 Wielowarstwowy yp perceptron p rozwiązujący problem XOR x Σ x.0 x 2.0 x 2 Σ

23 Wielowarstwowy yp perceptron p rozwiązujący problem XOR Σ Σ

24 Wielowarstwowy yp perceptron p rozwiązujący problem XOR o(x)= Σ

25 Wielowarstwowy yp perceptron p rozwiązujący problem XOR o (x)= o(x)=0 x 2 x

26 Wielowarstwowy yp perceptron p rozwiązujący problem XOR Σ Σ

27 Wielowarstwowy yp perceptron p rozwiązujący problem XOR o (x)= Σ

28 Wielowarstwowy yp perceptron p rozwiązujący problem XOR o (x)= ,5 o(x)= x 2 x

29 Wielowarstwowy yp perceptron p rozwiązujący problem XOR Σ Σ

30 Wielowarstwowy yp perceptron p rozwiązujący problem XOR o (x)= Σ

31 Wielowarstwowy yp perceptron p rozwiązujący problem XOR o (x)= ,5 o(x)=0 x 2 x

32 Wielowarstwowe sieci i neuronowe x x... 2 x A warstwa wejściowa w ij h h 2... h B warstwa ukryta w2 ij o o 2 o C warstwa wyjściowa...

33 Uczenie sieci neuronowych Dany jest zbiór par (x, y) Losujemy wagi Wybieramy kolejną parę ze zbioru uczącego x... x 2 x A w ij h h 2... h B w2 ij o o 2... o C

34 Uczenie sieci neuronowych Dany jest zbiór par (x, y) Losujemy wagi Wybieramy kolejną parę ze zbioru uczącego Obliczamy wartości w warstwie ukrytej w ij x x... 2 x A h h 2... h B h j = A + e i= 0 w x ij x i j =,..., B w2 ij o o 2... o C

35 Uczenie sieci neuronowych Dany jest zbiór par (x, y) Losujemy wagi Wybieramy kolejną parę ze zbioru uczącego Obliczamy wartości w warstwie ukrytej Obliczamy wartości w warstwie wyjściowej w ij x x... 2 x A h h 2... h B o w2 ij o2 oc o o2... oc h j o j = A + e i= 0 = B + e i= 0 w w 2 x ij x i h ij h i j =,..., B j =,..., C

36 Uczenie sieci neuronowych x x... 2 x A Dany jest zbiór par (x, y) Losujemy wagi Wybieramy kolejną parę ze zbioru uczącego Obliczamy wartości w warstwie ukrytej Obliczamy wartości w warstwie wyjściowej Obliczamy błąd dla elementów w warstwie wyjściowej j w ij h h 2... h B δ2 j = o j ( o j )(o j y j ), j =,..., C w2 ij o o 2... o C

37 Uczenie sieci neuronowych w ij x x... 2 x A Dany jest zbiór par (x, y) Losujemy wagi Wybieramy kolejną parę ze zbioru uczącego Obliczamy wartości w warstwie ukrytej Obliczamy wartości w warstwie wyjściowej Obliczamy błąd dla elementów w warstwie wyjściowej Korygujemy wagi w2 ij h h 2... h B w2 ij := w2 ij + ηδ2 j i = 0,..., B; j =,..., C o o 2... o C

38 Uczenie sieci neuronowych x x... 2 x A Dany jest zbiór par (x, y) Losujemy wagi Wybieramy kolejną parę ze zbioru uczącego Obliczamy wartości w warstwie ukrytej Obliczamy wartości w warstwie wyjściowej Obliczamy błąd dla elementów w warstwie wyjściowej w ij w2 ij h h 2... h B Korygujemy wagi w2 ij Obliczamy błąd dla elementów w warstwie ukrytej δ j = h j ( h j )Σδ2 i w2 ji, j =,..., B o o 2... o C

39 Uczenie sieci neuronowych x x... 2 x A Dany jest zbiór par (x, y) Losujemy wagi Wybieramy kolejną parę ze zbioru uczącego Obliczamy wartości w warstwie ukrytej Obliczamy wartości w warstwie wyjściowej Obliczamy błąd dla elementów w warstwie wyjściowej w ij h h 2... h B Korygujemy wagi w2 ij Obliczamy błąd dla elementów w warstwie ukrytej w2 ij o o 2... o C Korygujemy wagi w ij := w ij + ηδ j x i, i = 0,..., A, j =,..., B

40 Uczenie sieci neuronowych x x... 2 x A Dany jest zbiór par (x, y) Losujemy wagi Wybieramy kolejną parę ze zbioru uczącego Obliczamy wartości w warstwie ukrytej Obliczamy wartości w warstwie wyjściowej Obliczamy błąd dla elementów w warstwie wyjściowej w ij w2 ij h h 2... h B o o 2... o C Korygujemy wagi w2 ij Obliczamy błąd dla elementów w warstwie ukrytej Korygujemy wagi w ij Koniec epoki Backpropagation algorithm

41 Efekt generalizacji w uczeniu sieci neuronowych zbiór uczący zbiór testujący czas treningu

42 Sieci i radialne Neuron sigmoidalny dokonywał podziału przestrzeni na dwie części ę wzdłuż prostej y A y (x A, y A ) x A x Neuron radialny reprezentuje hipersfere, dokonując podziału kołowego wokół punktu centralnego C C

43 Sieci i radialne Φ( ( r ) = r Φ( r ) = sqrt(δ 2 + r 2 ) x r = x c, δ>0 φ w 0 x 2 w φ w 2 y x 3 w3 x 4 φ 3 4 Wektor wejściowy

44 Sieci i radialne x φ w 0 x 2 w φ w 2 y x 3 w3 x 4 φ 3 4 Warstwa k wektorów radialnych

45 Sieci i radialne x φ w 0 x 2 w φ w 2 y x 3 w3 x 4 φ 3 4 Warstwa składająca się z jednego neuronu działającego tak, jak w sieci z liniową funkcją aktywacji

46 Sieci i radialne x φ w 0 x 2 w φ w 2 y x 3 w3 x 4 φ 3 4 Brak wag!

47 Sieci i radialne Przykłady funkcji radialnych x φ w w 0 φ( r ) = r φ( r ) = sqrt(δ 2 + r 2 ) x 2 φ(r) = sqrt(δ 2 + r 2 ) x 3 φ x 4 φ 3 w 3 w 2 φ(r) = exp( r 2 /2δ 2 ) gdzie: c R n punkt centralny neuronu radialnego 4 r = x c odległość wektora wejściowego x R n od Najczęściej centrum c stosowana jest δ>0 parametr norma euklidesowa y

48 Sieci i radialne metody doboru parametrów x x 2 x 3 φ φ w 3 w w 2 w 0 x i d i x i R n d i R i =,, p y x 4 φ 3 F(x i ) = d i, i =,, p 4 F(x) = Σw i φ( x x i )

49 Sieci i radialne metody doboru parametrów x x 2 x 3 φ φ w 3 w w 2 w 0 x i d i x i R n d i R i =,, p y x 4 φ 3 F(x i ) = d i, i =,, p 4 F(x) = Σw i φ( x x i ) Jeżeli ustalimy k = p wówczas zadanie będzie rozwiązywalne Jeżeli ustalimy k = p, wówczas zadanie będzie rozwiązywalne. Jest to jednak za duża liczna neuronów i należy ją ograniczyć.

50 2Sieci i radialne metody doboru parametrów x φ w 0 x 2 φ w w 2 y Funkcja błędu x 3 w 3 wi= 2KE4 x4 φ 3 φ( ) = xd Wartości wag warstwy wyjściowej ustala sie w wyniku procesu uczenia Na Wartości wag warstwy wyjściowej ustala sie w wyniku procesu uczenia. Na początku przypisuje się im wartość losową, a następnie modyfikuje metodą propagacji wstecznej.

51 Sieci i radialne przykład x C x φ w w 0 y x 2 x c < ρ y = n = 2 k = φ( r ) = r w 0 = ρ promień koła w =

52 Sieci i radialne przykład x C x φ w w 0 y x 2 x c > ρ y = 0 n = 2 k = φ( r ) = r w 0 = ρ promień koła w =

53 Uczenie nienadzorowane Odkrywanie regularności w danych Algorytm Hebba Jeżeli aktywne są oba neurony, to waga połączenia ą między ę nimi się ę zwiększa ę x... x i... x A h... h j... h B o o 2... o C w ij w2 ij w ij := w ij + η x i h j h j = n i = Wielkość odpowiedniej zmiany wyznaczana jest na podstawie iloczynu sygnału wejściowego, wchodzącego na dane wejście (to którego wagę zmieniamy) i sygnału wyjściowego produkowanego przez neuron, w którym modyfikujemy wagi. w i x i

54 Uczenie nienadzorowane - wady W porównaniu z procesem uczenia z nauczycielem samouczenie jest zwykle znacznie powolniejsze. Bez nauczyciela nie można z góry określić, który neuron wyspecjalizuje się w rozpoznawania której klasy sygnałów. Powstają trudności przy wykorzystywaniu i interpretacji wyników pracy sieci. Nie można określić, czy sieć uczona w ten sposób nauczy się wszystkich prezentowanych jej wzorców. Sieć przeznaczona do samouczenia musi być większa niż sieć wykonująca to samo zadanie, ale trenowana z udziałem nauczyciela. (Szacunkowo sieć powinna mieć co najmniej j trzykrotnie więcej ę elementów warstwy wyjściowej niż wynosi oczekiwana liczba różnych wzorów, które sieć ma rozpoznawać.)

55 Sieci i Hopfielda

56 Sieci i Hopfielda

57 Sieci i Hopfielda

58 Sieci i Hopfielda

59 Sieci i Hopfielda

60 Stany równowagi

61 Własności ś sieci i Hopfielda rozproszona reprezentacja - informacja jest zapamiętywana jako wzorzec aktywacji rozproszone, asynchroniczne sterowanie - każdy element podejmuje decyzję w oparciu o lokalną wiedzę pamięć ę adresowalna przez zawartość -aby odtworzyć wzorzec zapisany w sieci wystarczy podać fragment informacji tolerancja błędów - jeżeli jakiś element popełni błąd, to cała sieć i tak poda poprawne rozwiązanie

62 Zastosowanie sieci Hopfielda w optymalizacji MASZYNA BOLTZMANA

63 Zastosowanie sieci Hopfielda w optymalizacji MASZYNA BOLTZMANA

64 Problemy rozwiązywane ą za pomocą ą sieci neuronowych Klasyfikacja obiektów na podstawie cech Identyfikacja obiektów Rozpoznawanie obrazów Rozpoznawanie sygnałów (radar, mowa) Diagnostyka urządzeń Sterowanie złożonymi układami Optymalizacja dyskretna

65 Zastosowania sieci i neuronowych Sterowanie w regulatorach lotu (US Air Force) Diagnostyka silników samochodowych (Ford Motor Company) Identyfikacja typów skał napotkanych podczas odwiertów przy poszukiwaniu ropy i gazu (Halliburton) Poszukiwanie bomb na lotnisku JFK w Nowym Jorku (TWA) Prognozy giełdowe

66 Czego nie można wykonać za pomocą sieci neuronowej Operacje na symbolach Edytor tekstu Procesor wyrażeń algebraicznych Obliczenia, w których wymagana jest wysoka dokładność wyniku numerycznego Obsługa kont bankowych Obliczenia inżynierskie (konstrukcyjne) Zadania wymagające rozumowania wieloetapowego Rozstrzyganie o prawdziwości lub fałszywości sekwencji stwierdzeń logicznych (dowodzenie twierdzeń, systemy eksperckie)