Wersja do wydruku - bez części teoretycznej
|
|
|
- Daria Nowacka
- 6 lat temu
- Przeglądów:
Transkrypt
1 Jacek Misiurewicz Krzysztof Kulpa Piotr Samczyński Mateusz Malanowski Piotr Krysik Łukasz Maślikowski Damian Gromek Artur Gromek Marcin K. Bączyk Zakład Teorii Obwodów i Sygnałów Instytut Systemów Elektronicznych Wydział Elektroniki i Technik Informacyjnych Politechnika Warszawska Laboratorium Cyfrowego Przetwarzania Sygnałów Wersja do wydruku - bez części teoretycznej Warszawa 2019
2
3 Ćwiczenie 9 Przetwarzanie obrazów Część teoretyczną w tej wersji opuszczono Zadania do pracy własnej studenta Podobne zadania mogą znaleźć się na wejściówce. Nie dotyczy to zadań oznaczonych tu jako trudne. 1) Przetwarzamy na bieżąco (w czasie rzeczywistym) sygnał dwuwymiarowy z anteny wieloelementowej x(m, n), gdzie indeks m odpowiada numerowi anteny, a indeks n numerowi próbki czasowej. Czy możemy zastosować filtr nieprzyczynowy? (Uwaga, pytanie podchwytliwe!) 1. 2) Oblicz dwuwymiarową DTF obrazu o rozmiarze pikseli: a) całkowicie czarnego (wypełnionego zerami), b) całkowicie białego (wypełnionego jedynkami), c) zawierającego tylko jeden biały piksel w pozycji (0, 0), d) zawierającego osiem pionowych białych pasów i osiem pionowych czarnych pasów, e) to samo, tylko pasy poziome, (zakładamy, że czarny oznaczamy zerem, biały jedynką). Wskazówka: Zauważ, że 2D-DTF można obliczać kolejno najpierw poziomo, potem pionowo (lub odwrotnie). 3) Jakiemu obrazowi będzie odpowiadać widmo o jednej niezerowej próbce w punkcie (0, 0)? Przyjmij wartość próbki taką, aby uzyskać w obrazie tylko czerń lub biel (uwaga na współczynnik skalujący w ODTF). 4) Obraz (sygnał 2D) o rozmiarze pikseli zawierający tylko jeden biały piksel w pozycji (8, 8) przefiltrowano filtrem liniowym o odpowiedzi impulsowej lp2=[ 1 1 1; ; ]; 1 Przyczynowość można badać oddzielnie dla każdego wymiaru!
4 4 Ćwiczenie 9. Przetwarzanie obrazów Zakładając, że jest to filtr nieprzyczynowy (o zerowej fazie): a) zastanów się, która próbka odpowiedzi impulsowej filtru jest próbką h(0, 0), b) oblicz obraz po filtracji (czyli sygnał wyjściowy), c) uzasadnij, że rzeczywiście charakterystyka fazowa jest zerowa. 5) Oblicz ręcznie wynik filtracji obrazu o rozmiarze pikseli filtrem wykrywającym krawędzie: a) obraz czarny z jednym białym pikselem, filtr (nieprzyczynowy), edg1=[0 0 0; ; ]; b) obraz z jedną pionową białą linią, filtr jak wyżej, c)... (wymyśl sobie inne kombinacje). 6) Narysuj linię prostą w obrazie, której odpowiada podany punkt w przeciwdziedzinie transformacji Hougha: a) (0, 0), b) (0, π/2), c) (0, π/4), d) (10, 0), e)... (wymyśl jeszcze kilka). 7) Przefiltruj podany sygnał filtrem medianowym rzędu 5 (dla uproszczenia rozpatrzymy sygnały jednowymiarowe): a) impuls jednostkowy δ(n), b) skok jednostkowy u(n), c) skok jednostkowy z dodanym impulsem: u(n) + δ(n 2), d) skok jednostkowy z dziurką: u(n) δ(n 3) Dostępny sprzęt i oprogramowanie Wczytywanie i przygotowanie obrazów W wielu zadaniach trzeba będzie skądś pozyskać obraz, na którym będziesz ćwiczyć różne algorytmy. Zalecamy tu używać obrazów naturalnych ( fotograficznych ), a nie grafiki przygotowanej przez człowieka lepiej będzie widać większość efektów. Jeśli używasz obrazu zapisanego na dysku (np. z jakiegoś uniwersalnego narzędzia do obsługi kamery), obraz trzeba wczytać. Obrazy wczytujemy poleceniem imread. myimagergb=imread('sciezkadopliku.png'); Można też przeciągnąć plik myszką na okno workspace Matlaba (nazwa zmiennej będzie identyczna z nazwą pliku, bez rozszerzenia). Kamerę podłączoną do komputera można obsłużyć za pomocą drivera vcapg 2. po podłączeniu kamery wystarczy wywołać z poziomu Matlaba poniższy kod. 2 VCAPG nie jest standardowym składnikiem Matlaba, został opracowany w Japonii: http: //
5 9.4. Eksperymenty do wykonania w laboratorium 5 myimagergb=lcps_getsnapshot();% calls VCAPG.MEXW64 loadable function imshow(myimagergb); Może zdarzyć się, że driver się zawiesi wtedy można go zresetować poprzez wywołanie LCPS_getsnapshot(1). Jeśli obraz jest barwny, otrzymasz trójwymiarową tablicę M N 3 z trzema kanałami barw R, G, B; wydobądź jeden z kanałów wczytanego obrazu lub transformuj go do odcieni szarości procedurą rgb2gray, aby uzyskać tablicę M N. myimagegray=rgb2gray(myimagergb); Obrazy typu JPG i PNG wczytywane są w postaci z całkowitoliczbową skalą barwy lub jasności (uint8). Aby uniknąć ograniczeń przy obliczeniach, dokonaj konwersji (rzutowania) na typ liczb zmiennoprzecinkowych. myimage=double(myimagegray); Wskazówka: W ćwiczeniu przy każdym wczytaniu nowego obrazu trzeba będzie powtórzyć powyższe operacje Eksperymenty do wykonania w laboratorium Widmo sygnału dwuwymiarowego Uwaga: w prezentowanym przykładowym kodzie staramy się konsekwentnie pisać nazwy zmiennych małymi literami, jeśli oznaczają one sygnał, a wielkimi jeśli oznaczają widmo Widma prostych obrazów Utwórz obraz o jednolitej jasności o rozmiarze pikseli. img1=ones(32,16); Wyświetl obraz, oblicz i wyświetl jego widmo. imagesc(img1) IMG1=fft2(img1); figure;imagesc(abs(img1)); rozmiar tablicy z transformatą, wartość maksimum widma i lokali- zację maksimum (jako parę indeksów tablicy). Wskazówka: Użyj polecenia colorbar zorientujesz się wtedy jaka jest skala wartości. Łatwiej interpretuje się widmo, gdy jest ono wyświetlone symetrycznie (zero częstotliwości w środku). Użyj polecenia fftshift, które zamienia miejscami dwie połówki wektora lub cztery ćwiartki macierzy. imagesc(fftshift(abs(img1))); Wskazówka: fftshift użyty drugi raz przywróci oryginalny układ ćwiartek widma (będzie to potrzebne, gdy w następnych zadaniach będziesz odtwarzać sygnał z jego widma). na pytanie: Jakie wielkości reprezentowane są na osiach? Jak
6 6 Ćwiczenie 9. Przetwarzanie obrazów powinny być wyskalowane osie (podaj jedną z kilku możliwości)? Rysunek 9.1. Poziome linie o wysokiej częstotliwości Rysunek 9.2. Poziome linie o niskiej częstotliwości Rysunek 9.3. Szachownica o wysokiej częstotliwości Rysunek 9.4. Szachownica o niskiej częstotliwości Wygeneruj obrazy podobne do przedstawionych na rys Dokładne parametry obrazów wybierz zgodnie z numerem stanowiska z tabeli 9.1. W porozumieniu z prowadzącym można obrazy takie wczytać, fotografując za pomocą kamery tablice kartonowe dostępne w laboratorium. Różnice parametrów linii między stanowiskami niech wtedy wynikają z fotografowania z różnej odległości oczywiście nie uda się dokładnie wybrać ich z tabeli. Jest wiele sprytnych sposobów utworzenia takich obrazów jedną z możliwości jest przygotowanie wzorca, który będzie powielony odpowiednią liczbę razy.
7 9.4. Eksperymenty do wykonania w laboratorium 7 Tabela 9.1 Nr stan Liczba wierszy w obrazie M Liczba kolumn w obrazie N Rozmiar szerokiego pasa/kratki [px] Rozmiar wąskiego pasa/kratki [px] wzor=[0 0; 0 0; 1 1; 1 1] Aby uzyskać obraz 8 16, wzorzec 4 2 powielimy 2 razy w pionie i 8 razy w poziomie. IleKopiiPionowo=2; IleKopiiPoziomo=8; Matlab dostarcza specjalne polecenie do powielania macierzy. img2=repmat(wzor, IleKopiiPionowo, IleKopiiPoziomo); Innymi eleganckimi sposobami będzie: przemnożenie dwóch odpowiednio uformowanych wektorów, albo też utworzenie zerowej macierzy i wypełnienie jedynkami sprytnie zaindeksowanych fragmentów. Dla każdego z 4 przypadków oblicz i obejrzyj widmo dwuwymiarowego sygnału wyświetl je w układzie symetrycznym (zero pośrodku czyli po użyciu fftshift). Aby zrozumieć, co oznaczają kolory użyj colorbar. na pytania: Jakie składowe widoczne są na widmie? Opisz je, używając pojęcia częstotliwości przestrzennej (cz. pozioma, cz. pionowa). Czym różni się widmo sygnału pasiastego od widma sygnału kraciastego? Jakiemu sygnałowi (obrazowi) odpowiadają częstotliwości reprezentowane na skraju wykresu? i możesz udzielić słowami, albo poprzez naszkicowanie czterech widm i zaznaczenie na nich istotnych elementów z krótkim podpisem. Obraz szachownicy o małej częstotliwości zachowaj w zmiennej o wybranej nazwie będzie jeszcze potrzebny Widmo obrazu rzeczywistego Przygotowanie obrazu do przetwarzania W zadaniu tym zaleca się pracę na obrazie własnoręcznie uzyskanym z kamery. Tematyka zdjęcia może być dowolna, natomiast zalecane jest, aby studenci na sąsiadujących stanowiskach wybrali różne tematy (twarz, widok sali, scenka na biurku, widok za oknem 3 ) i następnie porównywali między sobą wyniki. 3 Widok za oknem najwygodniej będzie wykorzystać studentowi siedzącemu koło okna. Jeśli okno jest brudne, będzie problem, bo w CS202 okna się nie otwierają, tylko uchylają.
8 8 Ćwiczenie 9. Przetwarzanie obrazów Jeśli nie ma możliwości pozyskania ciekawszego obrazu, można posłużyć się obrazem znajdującym się w katalogu ćwiczenia np. Lenna.png. Wczytaj obraz do zmiennej środowiska Matlab (np. myimage). Przygotuj go do przetwarzania (patrz 9.3.1). Wyświetl obraz w skali szarości (gray zamiast domyślnego mapowania wartości pikseli w skalę fałszywych barw jet). imagesc(myimage);colormap(gray);colorbar; Widmo obrazu Oblicz i obejrzyj widmo rzeczywistego dwuwymiarowego sygnału. Pamiętaj o użyciu fftshift, żeby częstotliwości zerowe były wyświetlane na środku widma. na pytanie: Jakiej częstotliwości odpowiada dominująca próbka widma? Jakiej składowej odpowiada ona w badanym obrazie? Widmo wyświetlone w skali liniowej jest zazwyczaj nieczytelne zawiera jedną dominującą próbkę, przy której pozostałe są niewidoczne. Wyświetl widmo w skali logarytmicznej (wyskaluj je w db). Zawsze przy użyciu miary decybelowej należy zastanowić się, czy mamy do czynienia z amplitudą (lub stosunkiem amplitud) czy też z mocą (lub kwadratem amplitudy albo wariancją, ew. ich stosunkiem); w pierwszym przypadku obliczamy 20 log 10 (x), w drugim 10 log 10 (x). Wskazówka: W Matlabie istnieje funkcja db, zwracająca domyślnie 20*log10(x). na pytanie: Czym różni się widmo badanego obrazu rzeczywistego od widm obrazów z rys ? Filtrowanie sygnałów dwuwymiarowych Przykładowe filtry liniowe Filtry dolnoprzepustowe przepuszczają tylko składowe obrazu o niskiej częstotliwości. Składowe o wyższej częstotliwości są tłumione. Przykłady dwuwymiarowych filtrów dolnoprzepustowych: lp1=[ 1, 1, 1;... 1, 1, 1;... 1, 1, 1]; lp2=[ 1, 1, 1;... 1, 2, 1;... 1, 1, 1]; lp3=[ 1, 2, 1;... 2, 4, 2;... 1, 2, 1]; lp4=[ 1, 1, 2, 1, 1;... 1, 2, 4, 2, 1;... 2, 4, 8, 4, 2;... 1, 2, 4, 2, 1;... 1, 1, 2, 1, 1];
9 9.4. Eksperymenty do wykonania w laboratorium 9 Filtry górnoprzepustowe przepuszczają tylko składowe obrazu o wysokiej częstotliwości. Składowe o niższych częstotliwościach są tłumione. Przykłady dwuwymiarowych filtrów górnoprzepustowych: hp1=[ -1, -1, -1;... -1, 9, -1;... -1, -1, -1]; hp3=[ 1, -2, 1;... -2, 5, -2;... 1, -2, 1]; hp2=[ 0, -1, 0;... -1, 5, -1;... 0, -1, 0]; Piksele obrazu zasadniczo reprezentowane są przez liczby dodatnie. Wskutek odejmowania liczb dodatnich mogą jednak powstać wartości mniejsze od zera. Decyzja, jak postąpić w takiej sytuacji (obciąć wartości ujemne, przesunąć wszystkie wartości w górę, zastąpić wartością bezwzględną,... ) powinna zależeć od interpretacji danych w konkretnym przypadku. Jeśli obraz wyświetlany jest funkcją imagesc, jest on automatycznie przesuwany i skalowany co do wartości tak, aby najmniejszej wartości odpowiadał czarny piksel, a największej biały. Filtry wykrywające krawędzie polegają na odejmowaniu przesuniętych kopii obrazu. Liczba tych kopii i przesunięcie zależy od konkretnego filtru. Matematycznie jest to przybliżone obliczanie wartości pochodnej cząstkowej w danym kierunku. Przykładowe filtry do wykrywania krawędzi: edg1=[0, 0, 0;... -1, 1, 0;... 0, 0, 0]; edg2=[-1, 0, 0;... 0, 1, 0;... 0, 0, 0]; edg3=[-1, 1, 1;... -1, -2, 1;... -1, 1, 1]; edg4=[-1, -1, 1;... -1, -2, 1;... 1, 1, 1]; edg5=[0, -1, 0;... -1, 4, -1;... 0, -1, 0]; edg6=[-1, 0, -1;... 0, 4, 0;... -1, 0, -1]; edg7=[1, 2, 1;... 0, 0, 0;... -1, -2, -1]; Jeżeli zależy nam na wykryciu krawędzi niezależnie od ich kierunku, można zastosować kombinację wyników filtracji w wielu kierunkach np. sumować moduły (albo kwadraty) wyników filtracji.
10 10 Ćwiczenie 9. Przetwarzanie obrazów Filtracja obrazu Tabela 9.2 Nr stan Filtr dolnoprzepustowy Filtr górnoprzepustowy Filtr krawędziowy Dla wczytanego w poprzednim zadaniu obrazu wykonaj filtrację, wykorzystując filtry przedstawione w punkcie , wybrane wg tabeli 9.2 dla Twojego stanowiska. Dla każdego filtru zanotuj jego współczynniki. Dwuwymiarową filtrację wykonuje się, używając polecenia filter2(h,x). Polecenie filter2 w Matlabie realizuje filtrację filtrem nieprzyczynowym zero opóźnienia odpowiada środkowemu elementowi macierzy współczynników filtru. Wyświetl obraz po filtracji, znajdź jego wartość maksymalną i minimalną. Wskazówka: max(max(x)) i min(min(x)) pomogą Ci znaleźć maksimum/minimum w dwuwymiarowej macierzy x. na pytania: (dla każdego z 3 filtrów) Opisz słowami efekt filtracji (możesz, lecz nie musisz naszkicować w protokole wynik filtracji). Jak zmieniła się maksymalna wartość próbek obrazu? Pamiętaj o użyciu colorbar, bo imagesc skaluje obraz. Jak można by zmodyfikować współczynniki filtru, aby uniknąć drastycznej zmiany zakresu wartości próbek? Dla jednego wybranego filtru wykonaj filtrację metodą mnożenia transformaty obrazu i transformaty odpowiedzi impulsowej filtru. Porównaj oba wyniki. Wskazówka: Do mnożenia potrzebujesz obu transformat w tym samym rozmiarze. Gdy odpowiedź impulsowa filtru jest krótsza niż sygnał, musisz ją uzupełnić zerami do rozmiaru M N (zero-padding), wywołując funkcję fft2 z dodatkowymi parametrami: X=fft2(x,M,N); zauważone różnice. Zmierz czasy wykonania filtracji dla tych dwóch sposobów, powtarzając je w pętli (dla poprawy dokładności pomiaru czasu) np. po 10 razy. Pomiar wykonaj dla badanego obrazu rzeczywistego oraz dla zapamiętanej szachownicy z zadania zobaczysz jak czasy wykonania zależą od rozmiaru obrazu. te czasy oraz zapisz wybrany do testu filtr. Wskazówka: Użyj funkcji tic() do uruchomienia stopera i toc() do jego zatrzymania.
11 9.4. Eksperymenty do wykonania w laboratorium 11 na pytanie: Czy wyniki filtracji w obu metodach różnią się, czy też są jednakowe? Czy znajdujesz zastosowania gdzie jedna bądź druga metoda jest lepsza? Wykrywanie krawędzi i detekcja prostych W praktyce automatycznego rozpoznawania elementów obrazów np. w układzie wzroku robota poruszającego się w przestrzeni często konieczne jest rozróżnianie kształtów. Podstawową operacją wykorzystywaną w tym celu jest identyfikacja odcinków prostych, stanowiących krawędzie kształtów. W tym zadaniu użyjemy filtrów potrafiących wykrywać (wzmacniać) krawędzie, poznanych w poprzedniej części ćwiczenia, a następnie zastosujemy transformację Hougha do odnalezienia odcinków prostych w tak wzmocnionym obrazie. Alternatywnie, student może (w porozumieniu z prowadzącym) zamiast wykonać zadanie , gdzie porównuje się obrazy naczyń krwionośnych Wykrywanie krawędzi. Miniprojekt W ramach miniprojektu przygotujemy obraz do wykrywania linii, wzmacniając wyrazistość krawędzi, a następnie zastosujemy gotowe procedury Matlaba implementujące: transformację Hougha (hough()), wizualizację wyniku (plot_hough()), wykrywanie maksimów w przekształconym obrazie (houghpeaks()), odnajdowanie w oryginalnym obrazie odcinków, odpowiadających odnalezionym maksimom (houghlines()), i na koniec narysujemy odnalezione odcinki na oryginalnym obrazie (plot_lines()). Procedura środowiska Matlab hough(), która implementuje transformację Hougha wymaga na wejściu macierzy binarnej (wypełnionej zerami i jedynkami), a więc obrazu dwubarwnego (piksele czarne i białe). W poniższym kodzie założono, że w zmiennej BW jest obraz oryginalny sprogowany do postaci binarnej (0 czarny, 1 biały). Sprawdź, jak wygląda transformacja pojedynczego punktu i prostej: przygotuj obraz binarny z jednym jasnym punktem (a potem z jedną jasną prostą pionową) Oblicz i wyświetl transformatę [H,T,R] = hough(bw,'rhoresolution',0.5,'theta',-90:0.5:89.5); plot_hough(h,t,r); parametry użytej linii (ρ i θ) i lokalizację odpowiadającego im punktu w transformacie.
12 12 Ćwiczenie 9. Przetwarzanie obrazów Wczytaj obraz, który będzie zawierał linie: zrób zdjęcie odpowiedniej sceny, ewentualnie jeśli nie ma możliwości pozyskania indywidualnego zdjęcia skorzystaj ze zdjęcia w katalogu ćwiczenia 'bariera.jpg'. Jeśli zdjęcie jest kolorowe, wybierz jeden z kanałów lub przetwórz je na czarno- -białe (jak w ). Korzystając z wiedzy na temat filtrów detekujących krawędzie przetwórz obraz, i następnie wykonaj operację progowania do wymaganej macierzy binarnej (przykład rys. 9.5). Rysunek 9.5. Przykład obrazu przygotowanego do wywołania na nim funkcji hough() Wskazówka: Konstrukcja Ab=boolean(A>0.5) zwróci macierz binarną z wartościami 1 dla indeksów, dla których wyrażenie logiczne jest prawdziwe. Obejrzyj wynik przetwarzania figure(1) imagesc(bw); colormap(gray); colorbar Spróbuj dobrać sposób filtracji i parametr progowania, aby otrzymać możliwie najlepszy obraz binarny. parametry użytego filtru (oraz ewentualne inne parametry przetwarzania obrazu). Gdy już uzyskasz macierz BW, w której pozostały głównie linie, to wywołaj następujące polecenia w celu detekcji linii i ich wyświetlenia [H,T,R] = hough(bw,'rhoresolution',0.5,'theta',-90:0.5:89.5); P = houghpeaks(h,9,'threshold',ceil(0.3*max(h(:)))); % współczynnik 0.3 w powyższej linii %należy dobrać empirycznie L = houghlines(bw,t,r,p,'fillgap',5,'minlength',7); figure(2)
13 9.4. Eksperymenty do wykonania w laboratorium 13 plot_hough(h,t,r); figure(3) imshow(bw); hold on plot_lines(l); hold off Spróbuj ocenić, jak dobrze udało się wykryć linie: Czy wszystkie linie, które ludzkie oko dostrzega na obrazie zostały wykryte procedurą Hougha? Czy może pojawiły się fałszywe linie? W jakich przypadkach powstały błędy? Spróbuj skomentować skuteczność tej metody wykrywania linii w obrazie Zadanie extra Analiza obrazu naczyń krwionośnych miniprojekt Przebieg naczyń krwionośnych (np. po wierzchniej stronie dłoni lub przedramienia) jest jedną z cech używanych do identyfikacji biometrycznej. Spróbuj wykonać zdjęcie (jedno lub kilka poeksperymentuj z oświetleniem!), a następnie przygotować obraz do wykrywania przebiegu naczyń: wybrać najlepszą warstwę barwną (R, G, B, a może jakaś kombinacja...), usunąć szumy i pozostałości skóry, włosów, zmarszczek... (patrz następne zadania!), wzmocnić linie o sensownej grubości i wybranych kierunkach (zastanów się nad ideą filtru dopasowanego), zastosować transformację Hougha. Jeśli uda Ci się chociaż część z tych zadań, będzie to sukces. Jeśli dobrze wykona się transformacja Hougha, dostaniesz parametry, którymi wystarczy nakarmić jakieś algorytmy sztucznej inteligencji i gotowe! (Oczywiście w naszym laboratorium tą częścią problemu się nie zajmujemy... ). Możesz też spróbować użyć idei filtracji dopasowanej do porównywania obrazów (ale nie jest to łatwe, są problemy np. ze skalowaniem itd. dlatego chętniej przekształca się obraz do postaci parametrycznej i porównuje zestawy parametrów) Usuwanie szumów W tym zadaniu porównamy wyniki filtracji liniowej i nieliniowej (konkretnie medianowej) w zastosowaniu do usuwania szumów różnego typu. Filtrację medianową obrazu w środowisku Matlab można wykonać poleceniem medfilt2. Natomiast filtry oparte na innych statystykach porządkowych (w tym filtr maksymalny i minimalny) mogą być zrealizowane poleceniem ordfilt Usuwanie addytywnego szumu typu sól i pieprz Do wczytanego obrazu image dodaj szum addytywny poleceniem:
14 14 Ćwiczenie 9. Przetwarzanie obrazów NoisyImage=double(imnoise(uint8(image),'salt & pepper',0.2)); Uwaga: Konwersje typów wynikają z założeń poczynionych przez programistów Matlaba, że obrazy będą typu uint8, i naszej potrzeby operowania na wartościach double. Zmierz średniokwadratowy stosunek sygnału do szumu dla otrzymanego obrazu SNR ms = N 1 M 1 i=0 j=0 N 1 M 1 i=0 j=0 [F (i, j)] 2 [F (i, j) F (i, j)] 2 (9.1) gdzie F to obraz oryginalny, a F zaszumiony otrzymaną wartość. Wskazówka: Sumę kwadratów elementów macierzy (występującą we wzorze (9.1)) można oczywiście liczyć w pętli for, ale taka pętla jest nieefektywna z punktu widzenia zarówno programisty, jak i komputera. Znacznie szybciej obliczy się ją poprzez sum(a(:).^2) zwróć uwagę na rozwijanie macierzy do wektora (:) i na podnoszenie do kwadratu element po elemencie. Natomiast zapis A(:)'*A(:) będzie poprawny także dla liczb zespolonych, i na dokładkę bardzo elegancki 4. Spróbuj usunąć zakłócenie, używając zarówno filtrów dolnoprzepustowych, jak i filtru medianowego. Zmierz średniokwadratowy stosunek sygnału do szumu dla otrzymanych obrazów. otrzymane wartości i wykorzystane filtry. na pytanie: Który filtr lepiej usuwa szumy addytywne? Usuwanie szumu multiplikatywnego Szum multiplikatywny polega na tym, że wartości próbek sygnału mnożone są przez wartość próbki szumu. Takie zjawisko może zachodzić, gdy wzmocnienie w torze sygnału zmienia się losowo (np. losowa zmiana czułości pikseli w kamerze). Również efekty nierównomiernego oświetlenia (światło i cień) są zakłóceniami multiplikatywnymi. Do wczytanego obrazu dodaj szum multiplikatywny poleceniem: MulNoisyImage=double(imnoise(uint8(image),'speckle')); Spróbuj usunąć zakłócenie, używając zarówno filtrów dolnoprzepustowych, jak i filtru medianowego. Zmierz średniokwadratowy stosunek sygnału do szumu dla otrzymanych obrazów. otrzymane wartości i wykorzystane filtry. na pytanie: Który filtr lepiej usuwa szumy multiplikatywne? Wskazówka: Szum multiplikatywny można też usuwać po zlogarytmowaniu obrazu wtedy szum multiplikatywny zmienia się w szum addytywny 5. 4 W zagadnieniach matematycznych elegancja jest pojęciem oznaczającym mniej więcej uniwersalność i prostota zapisu. 5 Tę technikę nazywa się w literaturze przetwarzaniem homomorficznym, i stosuje także do usuwania efektów oświetlenia.
15 9.4. Eksperymenty do wykonania w laboratorium 15 Zadanie extra Spróbuj zastosować przetwarzanie homomorficzne, ale nie zapomnij przed wyświetleniem dokonać operacji odwrotnej do logarytmowania! Proste metody kompresji obrazu Kompresja obrazu przez obcinanie widma. Miniprojekt Dla wczytanego obrazu wyznacz widmo. Wybierz współczynnik kompresji k z przedziału 0 do 1. Dla wybranej wartości współczynnika kompresji wytnij ze środka widma koło, tak by stosunek jego pola powierzchni do pola powierzchni całego widma wynosił k (zakładamy nadal, że środek widma odpowiada składowej stałej pamiętaj o użyciu fftshift). Kołową (lub eliptyczną dla M N) maskę zerojedynkową o promieniu r i rozmiarach M, N można uzyskać za pomocą funkcji LCPS_image_mask(r,M,N);, gdzie r (0, 1). Funkcja ta została napisana na potrzeby tego ćwiczenia (rys. 9.6). >> image_mask(0.5,16,16) ans = >> Rysunek 9.6. Wynik działania polecenia image mask Sprawdź, czy rzeczywiście pozostawiłeś w masce k M N jedynek. sum(maska(:))/numel(maska) Odtwórz obraz z uciętego widma. Wyznacz średniokwadratowy stosunek sygnału do szumu SNR ms. Wyraź go w decybelach 6. Powtórz procedurę dla trzech różnych różnych wartości współczynnika kompresji k i zanotuj wyniki. 6 Zastanów się, jakiego wyrażenia użyć: 20 log 10 (x), czy 10 log 10 (x).
16 16 Ćwiczenie 9. Przetwarzanie obrazów Zadanie extra Możliwe jest uruchomienie procedury w pętli, zebranie informacji do wektora i wyświetlenie wyniku w postaci wykresu SNR ms (k). Na wykresie znajdź i zanotuj wartość współczynnika kompresji, dla której stosunek sygnału do szumu wynosi w przybliżeniu K db, gdzie K = = numerstanowiska. na pytanie: Jak można by ocenić błąd kompresji bez odtwarzania obrazu? Wskazówka: Przypomnij sobie twierdzenie Parsevala Zadanie extra Kompresja obrazu z wykorzystaniem transformacji falkowej Przygotuj filtry odpowiadające falce Daubechies stopnia 8 [LoD, HiD, LoR, HiR] = LCPS_daubechies(8); Dokonaj dekompozycji [wv idx] = LCPS_dwt2(img, 1, LoD, HiD); Wyświetl zdekomponowany obraz imagesc(wv); Wskazówka: Obraz zdekomponowany może być wyraźniejszy, jeśli wyświetlimy jego moduł. Zrekonstruuj obraz idealnie oraz po usunięciu składowych szybkozmiennych: img_idrec = LCPS_idwt2(wv, idx, LoR, HiR); wvc=zeros(size(wv)); wvc(1:end/2,1:end/2)=wv(1:end/2,1:end/2); img_crec = LCPS_idwt2(wvc, idx, LoR, HiR); Wyświetl oba obrazy Oblicz i zanotuj średniokwadratowy stosunek sygnału do szumu po rekonstrukcji Zadanie extra Miniprojekt wyznaczenie progu dla zadanego stopnia kompresji Analizując histogram wartości współczynników, dla zadanego stopnia kompresji wyznacz wartość progową lambda, poniżej której współczynniki będą zerowane. Wyzeruj te współczynniki: ch(abs(ch) <= lambda) = 0.0; cv(abs(cv) <= lambda) = 0.0; cd(abs(cd) <= lambda) = 0.0; a następnie odtwórz obraz. Oblicz i zanotuj średniokwadratowy stosunek sygnału do szumu po rekonstrukcji. Przeanalizuj oddzielnie histogramy wartości współczynników w 4 grupach składowych; spróbuj zastosować oddzielne progi dla każdej grupy. Sprawdź, na ile zmniejszyło to błąd rekonstrukcji.
17 9.4. Eksperymenty do wykonania w laboratorium 17 Jeżeli nie uda się uzyskać zadanego stopnia kompresji, użyj dekompozycji w dwóch lub więcej skalach (Kscales=2). [wv idx] = LCPS_dwt2(img, Kscales, LoD, HiD); Zakres dynamiczny obrazów Rozciąganie zakresu dynamicznego poszczególnych kanałów Dla wczytanego kolorowego obrazu wyznacz histogramy dla poszczególnych kanałów. Można do tego wykorzystać gotowe narzędzie w postaci polecenia imhist. Wskazówka: Dobrze jest wykreślić wszystkie histogramy na jednym oknie, wykorzystując polecenie subplot. Rozciągnij zakres dynamiczny poszczególnych kanałów obrazu tak, by wykorzystany był ich cały zakres dynamiczny. Wyświetl poprawiony obraz. Porównaj z obrazem oryginalnym. na pytanie: Opisz swoje wrażenia po rozciągnięciu zakresu dynamicznego obrazu. Czy taki zabieg ma wpływ na wierność odtworzenia kolorów?
Laboratorium Cyfrowego Przetwarzania Sygnałów
 Laboratorium Cyfrowego Przetwarzania Sygnałów Preskrypt do v.204z ćwiczenie nr 9 z 0 (ale w kolejności wykonania siódme!!!) temat: Przetwarzanie obrazów na prawach rękopisu Lista Autorów Zakład Teorii
Laboratorium Cyfrowego Przetwarzania Sygnałów Preskrypt do v.204z ćwiczenie nr 9 z 0 (ale w kolejności wykonania siódme!!!) temat: Przetwarzanie obrazów na prawach rękopisu Lista Autorów Zakład Teorii
Laboratorium Cyfrowego Przetwarzania Sygnałów. Preskrypt do v.2015l ćwiczenie nr 9 z 10 temat: Przetwarzanie obrazów
 Laboratorium Cyfrowego Przetwarzania Sygnałów Preskrypt do v.205l ćwiczenie nr 9 z 0 temat: Przetwarzanie obrazów na prawach rękopisu Lista Autorów Zakład Teorii Obwodów i Sygnałów Instytut Systemów Elektronicznych
Laboratorium Cyfrowego Przetwarzania Sygnałów Preskrypt do v.205l ćwiczenie nr 9 z 0 temat: Przetwarzanie obrazów na prawach rękopisu Lista Autorów Zakład Teorii Obwodów i Sygnałów Instytut Systemów Elektronicznych
Laboratorium Cyfrowego Przetwarzania Obrazów
 Laboratorium Cyfrowego Przetwarzania Obrazów Ćwiczenie 4 Filtracja 2D Opracowali: - dr inż. Krzysztof Mikołajczyk - dr inż. Beata Leśniak-Plewińska - dr inż. Jakub Żmigrodzki Zakład Inżynierii Biomedycznej,
Laboratorium Cyfrowego Przetwarzania Obrazów Ćwiczenie 4 Filtracja 2D Opracowali: - dr inż. Krzysztof Mikołajczyk - dr inż. Beata Leśniak-Plewińska - dr inż. Jakub Żmigrodzki Zakład Inżynierii Biomedycznej,
Analiza obrazów - sprawozdanie nr 2
 Analiza obrazów - sprawozdanie nr 2 Filtracja obrazów Filtracja obrazu polega na obliczeniu wartości każdego z punktów obrazu na podstawie punktów z jego otoczenia. Każdy sąsiedni piksel ma wagę, która
Analiza obrazów - sprawozdanie nr 2 Filtracja obrazów Filtracja obrazu polega na obliczeniu wartości każdego z punktów obrazu na podstawie punktów z jego otoczenia. Każdy sąsiedni piksel ma wagę, która
Ćwiczenie 6. Transformacje skali szarości obrazów
 Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 6. Transformacje skali szarości obrazów 1. Obraz cyfrowy Obraz w postaci cyfrowej
Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 6. Transformacje skali szarości obrazów 1. Obraz cyfrowy Obraz w postaci cyfrowej
Cyfrowe Przetwarzanie Obrazów i Sygnałów
 Cyfrowe Przetwarzanie Obrazów i Sygnałów Laboratorium EX3 Globalne transformacje obrazów Joanna Ratajczak, Wrocław, 2018 1 Cel i zakres ćwiczenia Celem ćwiczenia jest zapoznanie się z własnościami globalnych
Cyfrowe Przetwarzanie Obrazów i Sygnałów Laboratorium EX3 Globalne transformacje obrazów Joanna Ratajczak, Wrocław, 2018 1 Cel i zakres ćwiczenia Celem ćwiczenia jest zapoznanie się z własnościami globalnych
Filtracja obrazu operacje kontekstowe
 Filtracja obrazu operacje kontekstowe Główne zadania filtracji Usunięcie niepożądanego szumu z obrazu Poprawa ostrości Usunięcie określonych wad obrazu Poprawa obrazu o złej jakości technicznej Rekonstrukcja
Filtracja obrazu operacje kontekstowe Główne zadania filtracji Usunięcie niepożądanego szumu z obrazu Poprawa ostrości Usunięcie określonych wad obrazu Poprawa obrazu o złej jakości technicznej Rekonstrukcja
BIBLIOTEKA PROGRAMU R - BIOPS. Narzędzia Informatyczne w Badaniach Naukowych Katarzyna Bernat
 BIBLIOTEKA PROGRAMU R - BIOPS Narzędzia Informatyczne w Badaniach Naukowych Katarzyna Bernat Biblioteka biops zawiera funkcje do analizy i przetwarzania obrazów. Operacje geometryczne (obrót, przesunięcie,
BIBLIOTEKA PROGRAMU R - BIOPS Narzędzia Informatyczne w Badaniach Naukowych Katarzyna Bernat Biblioteka biops zawiera funkcje do analizy i przetwarzania obrazów. Operacje geometryczne (obrót, przesunięcie,
Przekształcenia widmowe Transformata Fouriera. Adam Wojciechowski
 Przekształcenia widmowe Transformata Fouriera Adam Wojciechowski Przekształcenia widmowe Odmiana przekształceń kontekstowych, w których kontekstem jest w zasadzie cały obraz. Za pomocą transformaty Fouriera
Przekształcenia widmowe Transformata Fouriera Adam Wojciechowski Przekształcenia widmowe Odmiana przekształceń kontekstowych, w których kontekstem jest w zasadzie cały obraz. Za pomocą transformaty Fouriera
Diagnostyka obrazowa
 Diagnostyka obrazowa Ćwiczenie szóste Transformacje obrazu w dziedzinie częstotliwości 1 Cel ćwiczenia Ćwiczenie ma na celu zapoznanie uczestników kursu Diagnostyka obrazowa z podstawowymi przekształceniami
Diagnostyka obrazowa Ćwiczenie szóste Transformacje obrazu w dziedzinie częstotliwości 1 Cel ćwiczenia Ćwiczenie ma na celu zapoznanie uczestników kursu Diagnostyka obrazowa z podstawowymi przekształceniami
Podstawy Przetwarzania Sygnałów
 Adam Szulc 188250 grupa: pon TN 17:05 Podstawy Przetwarzania Sygnałów Sprawozdanie 6: Filtracja sygnałów. Filtry FIT o skończonej odpowiedzi impulsowej. 1. Cel ćwiczenia. 1) Przeprowadzenie filtracji trzech
Adam Szulc 188250 grupa: pon TN 17:05 Podstawy Przetwarzania Sygnałów Sprawozdanie 6: Filtracja sygnałów. Filtry FIT o skończonej odpowiedzi impulsowej. 1. Cel ćwiczenia. 1) Przeprowadzenie filtracji trzech
Zygmunt Wróbel i Robert Koprowski. Praktyka przetwarzania obrazów w programie Matlab
 Zygmunt Wróbel i Robert Koprowski Praktyka przetwarzania obrazów w programie Matlab EXIT 2004 Wstęp 7 CZĘŚĆ I 9 OBRAZ ORAZ JEGO DYSKRETNA STRUKTURA 9 1. Obraz w programie Matlab 11 1.1. Reprezentacja obrazu
Zygmunt Wróbel i Robert Koprowski Praktyka przetwarzania obrazów w programie Matlab EXIT 2004 Wstęp 7 CZĘŚĆ I 9 OBRAZ ORAZ JEGO DYSKRETNA STRUKTURA 9 1. Obraz w programie Matlab 11 1.1. Reprezentacja obrazu
Cyfrowe Przetwarzanie Obrazów i Sygnałów
 Cyfrowe Przetwarzanie Obrazów i Sygnałów Laboratorium EX Lokalne transformacje obrazów Joanna Ratajczak, Wrocław, 28 Cel i zakres ćwiczenia Celem ćwiczenia jest zapoznanie się z własnościami lokalnych
Cyfrowe Przetwarzanie Obrazów i Sygnałów Laboratorium EX Lokalne transformacje obrazów Joanna Ratajczak, Wrocław, 28 Cel i zakres ćwiczenia Celem ćwiczenia jest zapoznanie się z własnościami lokalnych
Filtracja obrazu operacje kontekstowe
 Filtracja obrazu operacje kontekstowe Podział metod filtracji obrazu Metody przestrzenne i częstotliwościowe Metody liniowe i nieliniowe Główne zadania filtracji Usunięcie niepożądanego szumu z obrazu
Filtracja obrazu operacje kontekstowe Podział metod filtracji obrazu Metody przestrzenne i częstotliwościowe Metody liniowe i nieliniowe Główne zadania filtracji Usunięcie niepożądanego szumu z obrazu
Spośród licznych filtrów nieliniowych najlepszymi właściwościami odznacza się filtr medianowy prosty i skuteczny.
 Filtracja nieliniowa może być bardzo skuteczną metodą polepszania jakości obrazów Filtry nieliniowe Filtr medianowy Spośród licznych filtrów nieliniowych najlepszymi właściwościami odznacza się filtr medianowy
Filtracja nieliniowa może być bardzo skuteczną metodą polepszania jakości obrazów Filtry nieliniowe Filtr medianowy Spośród licznych filtrów nieliniowych najlepszymi właściwościami odznacza się filtr medianowy
8. Analiza widmowa metodą szybkiej transformaty Fouriera (FFT)
 8. Analiza widmowa metodą szybkiej transformaty Fouriera (FFT) Ćwiczenie polega na wykonaniu analizy widmowej zadanych sygnałów metodą FFT, a następnie określeniu amplitud i częstotliwości głównych składowych
8. Analiza widmowa metodą szybkiej transformaty Fouriera (FFT) Ćwiczenie polega na wykonaniu analizy widmowej zadanych sygnałów metodą FFT, a następnie określeniu amplitud i częstotliwości głównych składowych
Ćwiczenie 4. Filtry o skończonej odpowiedzi impulsowej (SOI)
 Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 4. Filtry o skończonej odpowiedzi impulsowej (SOI) 1. Filtracja cyfrowa podstawowe
Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 4. Filtry o skończonej odpowiedzi impulsowej (SOI) 1. Filtracja cyfrowa podstawowe
Diagnostyka obrazowa
 Diagnostyka obrazowa Ćwiczenie szóste Transformacje obrazu w dziedzinie częstotliwości 1. Cel ćwiczenia Ćwiczenie ma na celu zapoznanie uczestników kursu Diagnostyka obrazowa z podstawowymi przekształceniami
Diagnostyka obrazowa Ćwiczenie szóste Transformacje obrazu w dziedzinie częstotliwości 1. Cel ćwiczenia Ćwiczenie ma na celu zapoznanie uczestników kursu Diagnostyka obrazowa z podstawowymi przekształceniami
Diagnostyka obrazowa
 Diagnostyka obrazowa Ćwiczenie drugie Podstawowe przekształcenia obrazu 1 Cel ćwiczenia Ćwiczenie ma na celu zapoznanie uczestników kursu Diagnostyka obrazowa z podstawowymi przekształceniami obrazu wykonywanymi
Diagnostyka obrazowa Ćwiczenie drugie Podstawowe przekształcenia obrazu 1 Cel ćwiczenia Ćwiczenie ma na celu zapoznanie uczestników kursu Diagnostyka obrazowa z podstawowymi przekształceniami obrazu wykonywanymi
Sposoby opisu i modelowania zakłóceń kanałowych
 INSTYTUT TELEKOMUNIKACJI ZAKŁAD RADIOKOMUNIKACJI Instrukcja laboratoryjna z przedmiotu Podstawy Telekomunikacji Sposoby opisu i modelowania zakłóceń kanałowych Warszawa 2010r. 1. Cel ćwiczeń: Celem ćwiczeń
INSTYTUT TELEKOMUNIKACJI ZAKŁAD RADIOKOMUNIKACJI Instrukcja laboratoryjna z przedmiotu Podstawy Telekomunikacji Sposoby opisu i modelowania zakłóceń kanałowych Warszawa 2010r. 1. Cel ćwiczeń: Celem ćwiczeń
Przetwarzanie obrazów rastrowych macierzą konwolucji
 Przetwarzanie obrazów rastrowych macierzą konwolucji 1 Wstęp Obrazy rastrowe są na ogół reprezentowane w dwuwymiarowych tablicach złożonych z pikseli, reprezentowanych przez liczby określające ich jasność
Przetwarzanie obrazów rastrowych macierzą konwolucji 1 Wstęp Obrazy rastrowe są na ogół reprezentowane w dwuwymiarowych tablicach złożonych z pikseli, reprezentowanych przez liczby określające ich jasność
Grafika Komputerowa Wykład 2. Przetwarzanie obrazów. mgr inż. Michał Chwesiuk 1/38
 Wykład 2 Przetwarzanie obrazów mgr inż. 1/38 Przetwarzanie obrazów rastrowych Jedna z dziedzin cyfrowego obrazów rastrowych. Celem przetworzenia obrazów rastrowych jest użycie edytujących piksele w celu
Wykład 2 Przetwarzanie obrazów mgr inż. 1/38 Przetwarzanie obrazów rastrowych Jedna z dziedzin cyfrowego obrazów rastrowych. Celem przetworzenia obrazów rastrowych jest użycie edytujących piksele w celu
Parametryzacja obrazu na potrzeby algorytmów decyzyjnych
 Parametryzacja obrazu na potrzeby algorytmów decyzyjnych Piotr Dalka Wprowadzenie Z reguły nie stosuje się podawania na wejście algorytmów decyzyjnych bezpośrednio wartości pikseli obrazu Obraz jest przekształcany
Parametryzacja obrazu na potrzeby algorytmów decyzyjnych Piotr Dalka Wprowadzenie Z reguły nie stosuje się podawania na wejście algorytmów decyzyjnych bezpośrednio wartości pikseli obrazu Obraz jest przekształcany
Implementacja filtru Canny ego
 ANALIZA I PRZETWARZANIE OBRAZÓW Implementacja filtru Canny ego Autor: Katarzyna Piotrowicz Kraków,2015-06-11 Spis treści 1. Wstęp... 1 2. Implementacja... 2 3. Przykłady... 3 Porównanie wykrytych krawędzi
ANALIZA I PRZETWARZANIE OBRAZÓW Implementacja filtru Canny ego Autor: Katarzyna Piotrowicz Kraków,2015-06-11 Spis treści 1. Wstęp... 1 2. Implementacja... 2 3. Przykłady... 3 Porównanie wykrytych krawędzi
P R Z E T W A R Z A N I E S Y G N A Ł Ó W B I O M E T R Y C Z N Y C H
 W O J S K O W A A K A D E M I A T E C H N I C Z N A W Y D Z I A Ł E L E K T R O N I K I Drukować dwustronnie P R Z E T W A R Z A N I E S Y G N A Ł Ó W B I O M E T R Y C Z N Y C H Grupa... Data wykonania
W O J S K O W A A K A D E M I A T E C H N I C Z N A W Y D Z I A Ł E L E K T R O N I K I Drukować dwustronnie P R Z E T W A R Z A N I E S Y G N A Ł Ó W B I O M E T R Y C Z N Y C H Grupa... Data wykonania
Według raportu ISO z 1988 roku algorytm JPEG składa się z następujących kroków: 0.5, = V i, j. /Q i, j
 Kompresja transformacyjna. Opis standardu JPEG. Algorytm JPEG powstał w wyniku prac prowadzonych przez grupę ekspertów (ang. Joint Photographic Expert Group). Prace te zakończyły się w 1991 roku, kiedy
Kompresja transformacyjna. Opis standardu JPEG. Algorytm JPEG powstał w wyniku prac prowadzonych przez grupę ekspertów (ang. Joint Photographic Expert Group). Prace te zakończyły się w 1991 roku, kiedy
Laboratorium Przetwarzania Sygnałów
 PTS - laboratorium Laboratorium Przetwarzania Sygnałów Ćwiczenie 4 Transformacja falkowa Opracował: - prof. dr hab. inż. Krzysztof Kałużyński Zakład Inżynierii Biomedycznej Instytut Metrologii i Inżynierii
PTS - laboratorium Laboratorium Przetwarzania Sygnałów Ćwiczenie 4 Transformacja falkowa Opracował: - prof. dr hab. inż. Krzysztof Kałużyński Zakład Inżynierii Biomedycznej Instytut Metrologii i Inżynierii
Przetwarzanie obrazu
 Przetwarzanie obrazu Przekształcenia kontekstowe Liniowe Nieliniowe - filtry Przekształcenia kontekstowe dokonują transformacji poziomów jasności pikseli analizując za każdym razem nie tylko jasność danego
Przetwarzanie obrazu Przekształcenia kontekstowe Liniowe Nieliniowe - filtry Przekształcenia kontekstowe dokonują transformacji poziomów jasności pikseli analizując za każdym razem nie tylko jasność danego
dr inż. Tomasz Krzeszowski
 Metody cyfrowego przetwarzania obrazów dr inż. Tomasz Krzeszowski 2017-05-20 Spis treści 1 Przygotowanie do laboratorium... 3 2 Cel laboratorium... 3 3 Przetwarzanie obrazów z wykorzystaniem oprogramowania
Metody cyfrowego przetwarzania obrazów dr inż. Tomasz Krzeszowski 2017-05-20 Spis treści 1 Przygotowanie do laboratorium... 3 2 Cel laboratorium... 3 3 Przetwarzanie obrazów z wykorzystaniem oprogramowania
DYSKRETNA TRANSFORMACJA FOURIERA
 Laboratorium Teorii Sygnałów - DFT 1 DYSKRETNA TRANSFORMACJA FOURIERA Cel ćwiczenia Celem ćwiczenia jest przeprowadzenie analizy widmowej sygnałów okresowych za pomocą szybkiego przekształcenie Fouriera
Laboratorium Teorii Sygnałów - DFT 1 DYSKRETNA TRANSFORMACJA FOURIERA Cel ćwiczenia Celem ćwiczenia jest przeprowadzenie analizy widmowej sygnałów okresowych za pomocą szybkiego przekształcenie Fouriera
SYMULACJA KOMPUTEROWA SYSTEMÓW
 SYMULACJA KOMPUTEROWA SYSTEMÓW ZASADY ZALICZENIA I TEMATY PROJEKTÓW Rok akademicki 2015 / 2016 Spośród zaproponowanych poniżej tematów projektowych należy wybrać jeden i zrealizować go korzystając albo
SYMULACJA KOMPUTEROWA SYSTEMÓW ZASADY ZALICZENIA I TEMATY PROJEKTÓW Rok akademicki 2015 / 2016 Spośród zaproponowanych poniżej tematów projektowych należy wybrać jeden i zrealizować go korzystając albo
Ćwiczenie 3. Właściwości przekształcenia Fouriera
 Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 3. Właściwości przekształcenia Fouriera 1. Podstawowe właściwości przekształcenia
Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 3. Właściwości przekształcenia Fouriera 1. Podstawowe właściwości przekształcenia
Cyfrowe przetwarzanie obrazów i sygnałów Wykład 7 AiR III
 1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
Przetwarzanie obrazów wykład 6. Adam Wojciechowski
 Przetwarzanie obrazów wykład 6 Adam Wojciechowski Przykłady obrazów cyfrowych i ich F-obrazów Parzysta liczba powtarzalnych wzorców Transformata Fouriera może być przydatna przy wykrywaniu określonych
Przetwarzanie obrazów wykład 6 Adam Wojciechowski Przykłady obrazów cyfrowych i ich F-obrazów Parzysta liczba powtarzalnych wzorców Transformata Fouriera może być przydatna przy wykrywaniu określonych
ANALIZA SEMANTYCZNA OBRAZU I DŹWIĘKU
 ANALIZA SEMANTYCZNA OBRAZU I DŹWIĘKU obraz dr inż. Jacek Naruniec Analiza Składowych Niezależnych (ICA) Independent Component Analysis Dąży do wyznaczenia zmiennych niezależnych z obserwacji Problem opiera
ANALIZA SEMANTYCZNA OBRAZU I DŹWIĘKU obraz dr inż. Jacek Naruniec Analiza Składowych Niezależnych (ICA) Independent Component Analysis Dąży do wyznaczenia zmiennych niezależnych z obserwacji Problem opiera
Grafika komputerowa. Zajęcia IX
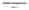 Grafika komputerowa Zajęcia IX Ćwiczenie 1 Usuwanie efektu czerwonych oczu Celem ćwiczenia jest usunięcie efektu czerwonych oczu u osób występujących na zdjęciu tak, aby plik wynikowy wyglądał jak wzor_1.jpg
Grafika komputerowa Zajęcia IX Ćwiczenie 1 Usuwanie efektu czerwonych oczu Celem ćwiczenia jest usunięcie efektu czerwonych oczu u osób występujących na zdjęciu tak, aby plik wynikowy wyglądał jak wzor_1.jpg
P R Z E T W A R Z A N I E S Y G N A Ł Ó W B I O M E T R Y C Z N Y C H
 W O J S K O W A A K A D E M I A T E C H N I C Z N A W Y D Z I A Ł E L E K T R O N I K I Drukować dwustronnie P R Z E T W A R Z A N I E S Y G N A Ł Ó W B I O M E T R Y C Z N Y C H Grupa... Data wykonania
W O J S K O W A A K A D E M I A T E C H N I C Z N A W Y D Z I A Ł E L E K T R O N I K I Drukować dwustronnie P R Z E T W A R Z A N I E S Y G N A Ł Ó W B I O M E T R Y C Z N Y C H Grupa... Data wykonania
LABORATORIUM PODSTAW TELEKOMUNIKACJI
 WOJSKOWA AKADEMIA TECHNICZNA im. Jarosława Dąbrowskiego w Warszawie Wydział Elektroniki LABORATORIUM PODSTAW TELEKOMUNIKACJI Grupa Podgrupa Data wykonania ćwiczenia Ćwiczenie prowadził... Skład podgrupy:
WOJSKOWA AKADEMIA TECHNICZNA im. Jarosława Dąbrowskiego w Warszawie Wydział Elektroniki LABORATORIUM PODSTAW TELEKOMUNIKACJI Grupa Podgrupa Data wykonania ćwiczenia Ćwiczenie prowadził... Skład podgrupy:
Automatyczne tworzenie trójwymiarowego planu pomieszczenia z zastosowaniem metod stereowizyjnych
 Automatyczne tworzenie trójwymiarowego planu pomieszczenia z zastosowaniem metod stereowizyjnych autor: Robert Drab opiekun naukowy: dr inż. Paweł Rotter 1. Wstęp Zagadnienie generowania trójwymiarowego
Automatyczne tworzenie trójwymiarowego planu pomieszczenia z zastosowaniem metod stereowizyjnych autor: Robert Drab opiekun naukowy: dr inż. Paweł Rotter 1. Wstęp Zagadnienie generowania trójwymiarowego
Cyfrowe przetwarzanie obrazów i sygnałów Wykład 8 AiR III
 1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
dr inż. Piotr Odya dr inż. Piotr Suchomski
 dr inż. Piotr Odya dr inż. Piotr Suchomski Podział grafiki wektorowa; matematyczny opis rysunku; małe wymagania pamięciowe (i obliczeniowe); rasteryzacja konwersja do postaci rastrowej; rastrowa; tablica
dr inż. Piotr Odya dr inż. Piotr Suchomski Podział grafiki wektorowa; matematyczny opis rysunku; małe wymagania pamięciowe (i obliczeniowe); rasteryzacja konwersja do postaci rastrowej; rastrowa; tablica
Podstawy MATLABA, cd.
 Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Elektroniki Przetwarzanie Sygnałów Studia Podyplomowe, Automatyka i Robotyka Podstawy MATLABA, cd. 1. Wielomiany 1.1. Definiowanie
Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Elektroniki Przetwarzanie Sygnałów Studia Podyplomowe, Automatyka i Robotyka Podstawy MATLABA, cd. 1. Wielomiany 1.1. Definiowanie
Filtry. Przemysław Barański. 7 października 2012
 Filtry Przemysław Barański 7 października 202 2 Laboratorium Elektronika - dr inż. Przemysław Barański Wymagania. Sprawozdanie powinno zawierać stronę tytułową: nazwa przedmiotu, data, imiona i nazwiska
Filtry Przemysław Barański 7 października 202 2 Laboratorium Elektronika - dr inż. Przemysław Barański Wymagania. Sprawozdanie powinno zawierać stronę tytułową: nazwa przedmiotu, data, imiona i nazwiska
2. Próbkowanie Sygnały okresowe (16). Trygonometryczny szereg Fouriera (17). Częstotliwość Nyquista (20).
 SPIS TREŚCI ROZDZIAŁ I SYGNAŁY CYFROWE 9 1. Pojęcia wstępne Wiadomości, informacje, dane, sygnały (9). Sygnał jako nośnik informacji (11). Sygnał jako funkcja (12). Sygnał analogowy (13). Sygnał cyfrowy
SPIS TREŚCI ROZDZIAŁ I SYGNAŁY CYFROWE 9 1. Pojęcia wstępne Wiadomości, informacje, dane, sygnały (9). Sygnał jako nośnik informacji (11). Sygnał jako funkcja (12). Sygnał analogowy (13). Sygnał cyfrowy
Transformata Fouriera
 Transformata Fouriera Program wykładu 1. Wprowadzenie teoretyczne 2. Algorytm FFT 3. Zastosowanie analizy Fouriera 4. Przykłady programów Wprowadzenie teoretyczne Zespolona transformata Fouriera Jeżeli
Transformata Fouriera Program wykładu 1. Wprowadzenie teoretyczne 2. Algorytm FFT 3. Zastosowanie analizy Fouriera 4. Przykłady programów Wprowadzenie teoretyczne Zespolona transformata Fouriera Jeżeli
Analiza właściwości filtra selektywnego
 Ćwiczenie 2 Analiza właściwości filtra selektywnego Program ćwiczenia. Zapoznanie się z przykładową strukturą filtra selektywnego 2 rzędu i zakresami jego parametrów. 2. Analiza widma sygnału prostokątnego..
Ćwiczenie 2 Analiza właściwości filtra selektywnego Program ćwiczenia. Zapoznanie się z przykładową strukturą filtra selektywnego 2 rzędu i zakresami jego parametrów. 2. Analiza widma sygnału prostokątnego..
Analiza właściwości filtrów dolnoprzepustowych
 Ćwiczenie Analiza właściwości filtrów dolnoprzepustowych Program ćwiczenia. Zapoznanie się z przykładową strukturą filtra dolnoprzepustowego (DP) rzędu i jego parametrami.. Analiza widma sygnału prostokątnego.
Ćwiczenie Analiza właściwości filtrów dolnoprzepustowych Program ćwiczenia. Zapoznanie się z przykładową strukturą filtra dolnoprzepustowego (DP) rzędu i jego parametrami.. Analiza widma sygnału prostokątnego.
PRZETWARZANIE SYGNAŁÓW LABORATORIUM
 2018 AK 1 / 5 PRZETWARZANIE SYGNAŁÓW LABORATORIUM Ćw. 0 Wykonujący: Grupa dziekańska: MATLAB jako narzędzie w przetwarzaniu sygnałów Grupa laboratoryjna: (IMIĘ NAZWISKO, nr albumu) Punkty / Ocena Numer
2018 AK 1 / 5 PRZETWARZANIE SYGNAŁÓW LABORATORIUM Ćw. 0 Wykonujący: Grupa dziekańska: MATLAB jako narzędzie w przetwarzaniu sygnałów Grupa laboratoryjna: (IMIĘ NAZWISKO, nr albumu) Punkty / Ocena Numer
Zadania do wykonania. Rozwiązując poniższe zadania użyj pętlę for.
 Zadania do wykonania Rozwiązując poniższe zadania użyj pętlę for. 1. apisz program, który przesuwa w prawo o dwie pozycje zawartość tablicy 10-cio elementowej liczb całkowitych tzn. element t[i] dla i=2,..,9
Zadania do wykonania Rozwiązując poniższe zadania użyj pętlę for. 1. apisz program, który przesuwa w prawo o dwie pozycje zawartość tablicy 10-cio elementowej liczb całkowitych tzn. element t[i] dla i=2,..,9
Laboratorium Przetwarzania Sygnałów Biomedycznych
 Laboratorium Przetwarzania Sygnałów Biomedycznych Ćwiczenie 3 Analiza sygnału o nieznanej strukturze Opracowali: - prof. nzw. dr hab. inż. Krzysztof Kałużyński - mgr inż. Tomasz Kubik Politechnika Warszawska,
Laboratorium Przetwarzania Sygnałów Biomedycznych Ćwiczenie 3 Analiza sygnału o nieznanej strukturze Opracowali: - prof. nzw. dr hab. inż. Krzysztof Kałużyński - mgr inż. Tomasz Kubik Politechnika Warszawska,
Transformata Fouriera i analiza spektralna
 Transformata Fouriera i analiza spektralna Z czego składają się sygnały? Sygnały jednowymiarowe, częstotliwość Liczby zespolone Transformata Fouriera Szybka Transformata Fouriera (FFT) FFT w 2D Przykłady
Transformata Fouriera i analiza spektralna Z czego składają się sygnały? Sygnały jednowymiarowe, częstotliwość Liczby zespolone Transformata Fouriera Szybka Transformata Fouriera (FFT) FFT w 2D Przykłady
WOJSKOWA AKADEMIA TECHNICZNA
 WOJSKOWA AKADEMIA TECHNICZNA LABORATORIUM CYFROWE PRZETWARZANIE SYGNAŁÓW Stopień, imię i nazwisko prowadzącego Imię oraz nazwisko słuchacza Grupa szkoleniowa Data wykonania ćwiczenia dr inż. Andrzej Wiśniewski
WOJSKOWA AKADEMIA TECHNICZNA LABORATORIUM CYFROWE PRZETWARZANIE SYGNAŁÓW Stopień, imię i nazwisko prowadzącego Imię oraz nazwisko słuchacza Grupa szkoleniowa Data wykonania ćwiczenia dr inż. Andrzej Wiśniewski
Politechnika Świętokrzyska. Laboratorium. Cyfrowe przetwarzanie sygnałów. Ćwiczenie 8. Filtracja uśredniająca i statystyczna.
 Politechnika Świętokrzyska Laboratorium Cyfrowe przetwarzanie sygnałów Ćwiczenie 8 Filtracja uśredniająca i statystyczna. Cel ćwiczenia Celem ćwiczenia jest zdobycie umiejętności tworzenia i wykorzystywania
Politechnika Świętokrzyska Laboratorium Cyfrowe przetwarzanie sygnałów Ćwiczenie 8 Filtracja uśredniająca i statystyczna. Cel ćwiczenia Celem ćwiczenia jest zdobycie umiejętności tworzenia i wykorzystywania
Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Elektroniki
 Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Elektroniki Przetwarzanie Sygnałów Studia Podyplomowe, Automatyka i Robotyka. Wstęp teoretyczny Zmienne losowe Zmienne losowe
Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Elektroniki Przetwarzanie Sygnałów Studia Podyplomowe, Automatyka i Robotyka. Wstęp teoretyczny Zmienne losowe Zmienne losowe
Andrzej Leśnicki Laboratorium CPS Ćwiczenie 7 1/7 ĆWICZENIE 7. Splot liniowy i kołowy sygnałów
 Andrzej Leśnicki Laboratorium CPS Ćwiczenie 7 1/7 ĆWICZEIE 7 Splot liniowy i kołowy sygnałów 1. Cel ćwiczenia Operacja splotu jest jedną z najczęściej wykonywanych operacji na sygnale. Każde przejście
Andrzej Leśnicki Laboratorium CPS Ćwiczenie 7 1/7 ĆWICZEIE 7 Splot liniowy i kołowy sygnałów 1. Cel ćwiczenia Operacja splotu jest jedną z najczęściej wykonywanych operacji na sygnale. Każde przejście
Laboratorium Przetwarzania Sygnałów Biomedycznych
 Laboratorium Przetwarzania Sygnałów Biomedycznych Ćwiczenie 1 Wydobywanie sygnałów z szumu z wykorzystaniem uśredniania Opracowali: - prof. nzw. dr hab. inż. Krzysztof Kałużyński - mgr inż. Tomasz Kubik
Laboratorium Przetwarzania Sygnałów Biomedycznych Ćwiczenie 1 Wydobywanie sygnałów z szumu z wykorzystaniem uśredniania Opracowali: - prof. nzw. dr hab. inż. Krzysztof Kałużyński - mgr inż. Tomasz Kubik
POB Odpowiedzi na pytania
 POB Odpowiedzi na pytania 1.) Na czym polega próbkowanie a na czym kwantyzacja w procesie akwizycji obrazu, jakiemu rodzajowi rozdzielczości odpowiada próbkowanie a jakiemu kwantyzacja Próbkowanie inaczej
POB Odpowiedzi na pytania 1.) Na czym polega próbkowanie a na czym kwantyzacja w procesie akwizycji obrazu, jakiemu rodzajowi rozdzielczości odpowiada próbkowanie a jakiemu kwantyzacja Próbkowanie inaczej
Wydział Elektryczny Katedra Telekomunikacji i Aparatury Elektronicznej
 Politechnika Białostocka Wydział Elektryczny Katedra Telekomunikacji i Aparatury Elektronicznej Instrukcja do zajęć laboratoryjnych z przedmiotu: Przetwarzanie Sygnałów Kod: TS1A400027 Temat ćwiczenia:
Politechnika Białostocka Wydział Elektryczny Katedra Telekomunikacji i Aparatury Elektronicznej Instrukcja do zajęć laboratoryjnych z przedmiotu: Przetwarzanie Sygnałów Kod: TS1A400027 Temat ćwiczenia:
Przekształcenia kontekstowe. Filtry nieliniowe Typowy przykład usuwania zakłóceń z obrazu
 Definicja Przekształcenia kontekstowe są to przekształcenia które dla wyznaczenia wartości jednego punktu obrazu wynikowego trzeba dokonać określonych obliczeń na wielu punktach obrazu źródłowego. Przekształcenia
Definicja Przekształcenia kontekstowe są to przekształcenia które dla wyznaczenia wartości jednego punktu obrazu wynikowego trzeba dokonać określonych obliczeń na wielu punktach obrazu źródłowego. Przekształcenia
TRANSFORMATA FALKOWA 2D. Oprogramowanie Systemów Obrazowania 2016/2017
 TRANSFORMATA FALKOWA 2D Oprogramowanie Systemów Obrazowania 2016/2017 Wielorozdzielczość - dekompozycja sygnału w ciąg sygnałów o coraz mniejszej rozdzielczości na wielu poziomach gdzie: s l+1 - aproksymata
TRANSFORMATA FALKOWA 2D Oprogramowanie Systemów Obrazowania 2016/2017 Wielorozdzielczość - dekompozycja sygnału w ciąg sygnałów o coraz mniejszej rozdzielczości na wielu poziomach gdzie: s l+1 - aproksymata
LABORATORIUM 3 ALGORYTMY OBLICZENIOWE W ELEKTRONICE I TELEKOMUNIKACJI. Wprowadzenie do środowiska Matlab
 LABORATORIUM 3 ALGORYTMY OBLICZENIOWE W ELEKTRONICE I TELEKOMUNIKACJI Wprowadzenie do środowiska Matlab 1. Podstawowe informacje Przedstawione poniżej informacje maja wprowadzić i zapoznać ze środowiskiem
LABORATORIUM 3 ALGORYTMY OBLICZENIOWE W ELEKTRONICE I TELEKOMUNIKACJI Wprowadzenie do środowiska Matlab 1. Podstawowe informacje Przedstawione poniżej informacje maja wprowadzić i zapoznać ze środowiskiem
Wyższa Szkoła Informatyki Stosowanej i Zarządzania
 Wyższa Szkoła Informatyki Stosowanej i Zarządzania Grupa ID308, Zespół 11 PRZETWARZANIE OBRAZÓW Sprawozdanie z ćwiczeń Ćwiczenie 6 Temat: Operacje sąsiedztwa wyostrzanie obrazu Wykonali: 1. Mikołaj Janeczek
Wyższa Szkoła Informatyki Stosowanej i Zarządzania Grupa ID308, Zespół 11 PRZETWARZANIE OBRAZÓW Sprawozdanie z ćwiczeń Ćwiczenie 6 Temat: Operacje sąsiedztwa wyostrzanie obrazu Wykonali: 1. Mikołaj Janeczek
LABORATORIUM AKUSTYKI MUZYCZNEJ. Ćw. nr 12. Analiza falkowa dźwięków instrumentów muzycznych. 1. PODSTAWY TEORETYCZNE ANALIZY FALKOWEJ.
 LABORATORIUM AKUSTYKI MUZYCZNEJ. Ćw. nr 1. Analiza falkowa dźwięków instrumentów muzycznych. 1. PODSTAWY TEORETYCZNE ANALIZY FALKOWEJ. Transformacja falkowa (ang. wavelet falka) przeznaczona jest do analizy
LABORATORIUM AKUSTYKI MUZYCZNEJ. Ćw. nr 1. Analiza falkowa dźwięków instrumentów muzycznych. 1. PODSTAWY TEORETYCZNE ANALIZY FALKOWEJ. Transformacja falkowa (ang. wavelet falka) przeznaczona jest do analizy
Laboratorium. Cyfrowe przetwarzanie sygnałów. Ćwiczenie 9. Przetwarzanie sygnałów wizyjnych. Politechnika Świętokrzyska.
 Politechnika Świętokrzyska Laboratorium Cyfrowe przetwarzanie sygnałów Ćwiczenie 9 Przetwarzanie sygnałów wizyjnych. Cel ćwiczenia Celem ćwiczenia jest zapoznanie studentów z funkcjami pozwalającymi na
Politechnika Świętokrzyska Laboratorium Cyfrowe przetwarzanie sygnałów Ćwiczenie 9 Przetwarzanie sygnałów wizyjnych. Cel ćwiczenia Celem ćwiczenia jest zapoznanie studentów z funkcjami pozwalającymi na
W celu obliczenia charakterystyki częstotliwościowej zastosujemy wzór 1. charakterystyka amplitudowa 0,
 Bierne obwody RC. Filtr dolnoprzepustowy. Filtr dolnoprzepustowy jest układem przenoszącym sygnały o małej częstotliwości bez zmian, a powodującym tłumienie i opóźnienie fazy sygnałów o większych częstotliwościach.
Bierne obwody RC. Filtr dolnoprzepustowy. Filtr dolnoprzepustowy jest układem przenoszącym sygnały o małej częstotliwości bez zmian, a powodującym tłumienie i opóźnienie fazy sygnałów o większych częstotliwościach.
Zad. 3: Układ równań liniowych
 1 Cel ćwiczenia Zad. 3: Układ równań liniowych Wykształcenie umiejętności modelowania kluczowych dla danego problemu pojęć. Definiowanie właściwego interfejsu klasy. Zwrócenie uwagi na dobór odpowiednich
1 Cel ćwiczenia Zad. 3: Układ równań liniowych Wykształcenie umiejętności modelowania kluczowych dla danego problemu pojęć. Definiowanie właściwego interfejsu klasy. Zwrócenie uwagi na dobór odpowiednich
Przetwarzanie obrazów wykład 4
 Przetwarzanie obrazów wykład 4 Adam Wojciechowski Wykład opracowany na podstawie Komputerowa analiza i przetwarzanie obrazów R. Tadeusiewicz, P. Korohoda Filtry nieliniowe Filtry nieliniowe (kombinowane)
Przetwarzanie obrazów wykład 4 Adam Wojciechowski Wykład opracowany na podstawie Komputerowa analiza i przetwarzanie obrazów R. Tadeusiewicz, P. Korohoda Filtry nieliniowe Filtry nieliniowe (kombinowane)
Segmentacja przez detekcje brzegów
 Segmentacja przez detekcje brzegów Lokalne zmiany jasności obrazu niosą istotną informację o granicach obszarów (obiektów) występujących w obrazie. Metody detekcji dużych, lokalnych zmian jasności w obrazie
Segmentacja przez detekcje brzegów Lokalne zmiany jasności obrazu niosą istotną informację o granicach obszarów (obiektów) występujących w obrazie. Metody detekcji dużych, lokalnych zmian jasności w obrazie
FILTRACJE W DZIEDZINIE CZĘSTOTLIWOŚCI
 FILTRACJE W DZIEDZINIE CZĘSTOTLIWOŚCI ( frequency domain filters) Każdy człon F(u,v) zawiera wszystkie wartości f(x,y) modyfikowane przez wartości członów wykładniczych Za wyjątkiem trywialnych przypadków
FILTRACJE W DZIEDZINIE CZĘSTOTLIWOŚCI ( frequency domain filters) Każdy człon F(u,v) zawiera wszystkie wartości f(x,y) modyfikowane przez wartości członów wykładniczych Za wyjątkiem trywialnych przypadków
Instytut Politechniczny Państwowa Wyższa Szkoła Zawodowa. Diagnostyka i niezawodność robotów
 Instytut Politechniczny Państwowa Wyższa Szkoła Zawodowa Diagnostyka i niezawodność robotów Laboratorium nr 6 Model matematyczny elementu naprawialnego Prowadzący: mgr inż. Marcel Luzar Cele ćwiczenia:
Instytut Politechniczny Państwowa Wyższa Szkoła Zawodowa Diagnostyka i niezawodność robotów Laboratorium nr 6 Model matematyczny elementu naprawialnego Prowadzący: mgr inż. Marcel Luzar Cele ćwiczenia:
SPRZĘTOWA REALIZACJA FILTRÓW CYFROWYCH TYPU SOI
 1 ĆWICZENIE VI SPRZĘTOWA REALIZACJA FILTRÓW CYFROWYCH TYPU SOI (00) Celem pracy jest poznanie sposobu fizycznej realizacji filtrów cyfrowych na procesorze sygnałowym firmy Texas Instruments TMS320C6711
1 ĆWICZENIE VI SPRZĘTOWA REALIZACJA FILTRÓW CYFROWYCH TYPU SOI (00) Celem pracy jest poznanie sposobu fizycznej realizacji filtrów cyfrowych na procesorze sygnałowym firmy Texas Instruments TMS320C6711
Ćwiczenie 11. Podstawy akwizycji i cyfrowego przetwarzania sygnałów. Program ćwiczenia:
 Ćwiczenie 11 Podstawy akwizycji i cyfrowego przetwarzania sygnałów Program ćwiczenia: 1. Konfiguracja karty pomiarowej oraz obserwacja sygnału i jego widma 2. Twierdzenie o próbkowaniu obserwacja dwóch
Ćwiczenie 11 Podstawy akwizycji i cyfrowego przetwarzania sygnałów Program ćwiczenia: 1. Konfiguracja karty pomiarowej oraz obserwacja sygnału i jego widma 2. Twierdzenie o próbkowaniu obserwacja dwóch
Tablice mgr Tomasz Xięski, Instytut Informatyki, Uniwersytet Śląski Katowice, 2011
 Tablice mgr Tomasz Xięski, Instytut Informatyki, Uniwersytet Śląski Katowice, 2011 Załóżmy, że uprawiamy jogging i chcemy monitorować swoje postępy. W tym celu napiszemy program, który zlicza, ile czasu
Tablice mgr Tomasz Xięski, Instytut Informatyki, Uniwersytet Śląski Katowice, 2011 Załóżmy, że uprawiamy jogging i chcemy monitorować swoje postępy. W tym celu napiszemy program, który zlicza, ile czasu
1 Podstawy c++ w pigułce.
 1 Podstawy c++ w pigułce. 1.1 Struktura dokumentu. Kod programu c++ jest zwykłym tekstem napisanym w dowolnym edytorze. Plikowi takiemu nadaje się zwykle rozszerzenie.cpp i kompiluje za pomocą kompilatora,
1 Podstawy c++ w pigułce. 1.1 Struktura dokumentu. Kod programu c++ jest zwykłym tekstem napisanym w dowolnym edytorze. Plikowi takiemu nadaje się zwykle rozszerzenie.cpp i kompiluje za pomocą kompilatora,
Ćwiczenie 1. Wprowadzenie do programu Octave
 Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 1. Wprowadzenie do programu Octave Mimo że program Octave został stworzony do
Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 1. Wprowadzenie do programu Octave Mimo że program Octave został stworzony do
Dodatek 4. Zadanie 1: Liczenie plam słonecznych w różnych dniach. Po uruchomieniu programu SalsaJ otworzy się nam okno widoczne na rysunku 4.1.
 Dodatek 4 W niniejszym załączniku przedstawiona została alternatywna metoda realizowania zadań numer 1, 4 i 6 w ćwiczeniu Słońce dla każdego za pomocą programu SalsaJ, który można ściągnąć ze strony internetowej
Dodatek 4 W niniejszym załączniku przedstawiona została alternatywna metoda realizowania zadań numer 1, 4 i 6 w ćwiczeniu Słońce dla każdego za pomocą programu SalsaJ, który można ściągnąć ze strony internetowej
Diary przydatne polecenie. Korzystanie z funkcji wbudowanych i systemu pomocy on-line. Najczęstsze typy plików. diary nazwa_pliku
 Diary przydatne polecenie diary nazwa_pliku Polecenie to powoduje, że od tego momentu sesja MATLAB-a, tj. polecenia i teksty wysyłane na ekran (nie dotyczy grafiki) będą zapisywane w pliku o podanej nazwie.
Diary przydatne polecenie diary nazwa_pliku Polecenie to powoduje, że od tego momentu sesja MATLAB-a, tj. polecenia i teksty wysyłane na ekran (nie dotyczy grafiki) będą zapisywane w pliku o podanej nazwie.
Laboratorium Przetwarzania Sygnałów Biomedycznych
 Laboratorium Przetwarzania Sygnałów Biomedycznych Ćwiczenie 2 Analiza sygnału EKG przy użyciu transformacji falkowej Opracowali: - prof. nzw. dr hab. inż. Krzysztof Kałużyński - inż. Tomasz Kubik Politechnika
Laboratorium Przetwarzania Sygnałów Biomedycznych Ćwiczenie 2 Analiza sygnału EKG przy użyciu transformacji falkowej Opracowali: - prof. nzw. dr hab. inż. Krzysztof Kałużyński - inż. Tomasz Kubik Politechnika
Optymalizacja systemów
 Optymalizacja systemów Laboratorium Sudoku autor: A. Gonczarek Cel zadania Celem zadania jest napisanie programu rozwiązującego Sudoku, formułując problem optymalizacji jako zadanie programowania binarnego.
Optymalizacja systemów Laboratorium Sudoku autor: A. Gonczarek Cel zadania Celem zadania jest napisanie programu rozwiązującego Sudoku, formułując problem optymalizacji jako zadanie programowania binarnego.
Optymalizacja systemów
 Optymalizacja systemów Laboratorium Zadanie nr 3 Sudoku autor: A. Gonczarek Cel zadania Celem zadania jest napisanie programu rozwiązującego Sudoku, formułując problem optymalizacji jako zadanie programowania
Optymalizacja systemów Laboratorium Zadanie nr 3 Sudoku autor: A. Gonczarek Cel zadania Celem zadania jest napisanie programu rozwiązującego Sudoku, formułując problem optymalizacji jako zadanie programowania
Spis treści. strona 1 z 11
 Spis treści 1. Edycja obrazów fotograficznych...2 1.1. Księżyc...2 1.2. Słońce zza chmur...4 1.3. Rzeka lawy...6 1.4. Śnieżyca...7 1.5. Ulewa...8 1.6. Noktowizor...9 strona 1 z 11 1. Edycja obrazów fotograficznych
Spis treści 1. Edycja obrazów fotograficznych...2 1.1. Księżyc...2 1.2. Słońce zza chmur...4 1.3. Rzeka lawy...6 1.4. Śnieżyca...7 1.5. Ulewa...8 1.6. Noktowizor...9 strona 1 z 11 1. Edycja obrazów fotograficznych
Wyższa Szkoła Informatyki Stosowanej i Zarządzania
 Wyższa Szkoła Informatyki Stosowanej i Zarządzania Grupa ID308, Zespół 11 PRZETWARZANIE OBRAZÓW Sprawozdanie z ćwiczeń Ćwiczenie 8 Temat: Operacje sąsiedztwa detekcja krawędzi Wykonali: 1. Mikołaj Janeczek
Wyższa Szkoła Informatyki Stosowanej i Zarządzania Grupa ID308, Zespół 11 PRZETWARZANIE OBRAZÓW Sprawozdanie z ćwiczeń Ćwiczenie 8 Temat: Operacje sąsiedztwa detekcja krawędzi Wykonali: 1. Mikołaj Janeczek
ALGORYTMY PRZETWARZANIA OBRAZÓW Projekt. Aplikacja przetwarzająca obrazy z możliwością eksportu i importu do programu MS Excel.
 Grupa IZ07IO1 Wyższa Szkoła Informatyki Stosowanej i Zarządzania WIT ALGORYTMY PRZETWARZANIA OBRAZÓW Projekt Aplikacja przetwarzająca obrazy z możliwością eksportu i importu do programu MS Excel. Wykonali:
Grupa IZ07IO1 Wyższa Szkoła Informatyki Stosowanej i Zarządzania WIT ALGORYTMY PRZETWARZANIA OBRAZÓW Projekt Aplikacja przetwarzająca obrazy z możliwością eksportu i importu do programu MS Excel. Wykonali:
Operacje przetwarzania obrazów monochromatycznych
 Operacje przetwarzania obrazów monochromatycznych Obraz pobrany z kamery lub aparatu często wymaga dalszej obróbki. Jej celem jest poprawienie jego jakości lub uzyskaniem na jego podstawie określonych
Operacje przetwarzania obrazów monochromatycznych Obraz pobrany z kamery lub aparatu często wymaga dalszej obróbki. Jej celem jest poprawienie jego jakości lub uzyskaniem na jego podstawie określonych
Instrukcja obsługi programu SWWS autorstwa Michała Krzemińskiego
 Instrukcja obsługi programu SWWS autorstwa Michała Krzemińskiego Krótkie informacje o programie można znaleźć zarówno w pliku readme.txt zamieszczonym w podkatalogu DANE jak i w zakładce O programie znajdującej
Instrukcja obsługi programu SWWS autorstwa Michała Krzemińskiego Krótkie informacje o programie można znaleźć zarówno w pliku readme.txt zamieszczonym w podkatalogu DANE jak i w zakładce O programie znajdującej
Zastosowanie Informatyki w Medycynie
 Zastosowanie Informatyki w Medycynie Dokumentacja projektu wykrywanie bicia serca z sygnału EKG. (wykrywanie załamka R) Prowadzący: prof. dr hab. inż. Marek Kurzyoski Grupa: Jakub Snelewski 163802, Jacek
Zastosowanie Informatyki w Medycynie Dokumentacja projektu wykrywanie bicia serca z sygnału EKG. (wykrywanie załamka R) Prowadzący: prof. dr hab. inż. Marek Kurzyoski Grupa: Jakub Snelewski 163802, Jacek
Algorytmy detekcji częstotliwości podstawowej
 Algorytmy detekcji częstotliwości podstawowej Plan Definicja częstotliwości podstawowej Wybór ramki sygnału do analizy Błędy oktawowe i dokładnej estymacji Metody detekcji częstotliwości podstawowej czasowe
Algorytmy detekcji częstotliwości podstawowej Plan Definicja częstotliwości podstawowej Wybór ramki sygnału do analizy Błędy oktawowe i dokładnej estymacji Metody detekcji częstotliwości podstawowej czasowe
Podstawowe funkcje przetwornika C/A
 ELEKTRONIKA CYFROWA PRZETWORNIKI CYFROWO-ANALOGOWE I ANALOGOWO-CYFROWE Literatura: 1. Rudy van de Plassche: Scalone przetworniki analogowo-cyfrowe i cyfrowo-analogowe, WKŁ 1997 2. Marian Łakomy, Jan Zabrodzki:
ELEKTRONIKA CYFROWA PRZETWORNIKI CYFROWO-ANALOGOWE I ANALOGOWO-CYFROWE Literatura: 1. Rudy van de Plassche: Scalone przetworniki analogowo-cyfrowe i cyfrowo-analogowe, WKŁ 1997 2. Marian Łakomy, Jan Zabrodzki:
MATLAB - laboratorium nr 1 wektory i macierze
 MATLAB - laboratorium nr 1 wektory i macierze 1. a. Małe i wielkie litery nie są równoważne (MATLAB rozróżnia wielkość liter). b. Wpisanie nazwy zmiennej spowoduje wyświetlenie jej aktualnej wartości na
MATLAB - laboratorium nr 1 wektory i macierze 1. a. Małe i wielkie litery nie są równoważne (MATLAB rozróżnia wielkość liter). b. Wpisanie nazwy zmiennej spowoduje wyświetlenie jej aktualnej wartości na
Techniki wizualizacji. Ćwiczenie 2. Obraz cyfrowy w komputerze
 Doc. dr inż. Jacek Jarnicki Instytut Informatyki, Automatyki i Robotyki Politechniki Wrocławskiej jacek.jarnicki@pwr.wroc.pl Techniki wizualizacji Ćwiczenie 2 Obraz cyfrowy w komputerze Celem ćwiczenia
Doc. dr inż. Jacek Jarnicki Instytut Informatyki, Automatyki i Robotyki Politechniki Wrocławskiej jacek.jarnicki@pwr.wroc.pl Techniki wizualizacji Ćwiczenie 2 Obraz cyfrowy w komputerze Celem ćwiczenia
0 + 0 = 0, = 1, = 1, = 0.
 5 Kody liniowe Jak już wiemy, w celu przesłania zakodowanego tekstu dzielimy go na bloki i do każdego z bloków dodajemy tak zwane bity sprawdzające. Bity te są w ścisłej zależności z bitami informacyjnymi,
5 Kody liniowe Jak już wiemy, w celu przesłania zakodowanego tekstu dzielimy go na bloki i do każdego z bloków dodajemy tak zwane bity sprawdzające. Bity te są w ścisłej zależności z bitami informacyjnymi,
Wskaźniki a tablice Wskaźniki i tablice są ze sobą w języku C++ ściśle związane. Aby się o tym przekonać wykonajmy cwiczenie.
 Część XXII C++ w Wskaźniki a tablice Wskaźniki i tablice są ze sobą w języku C++ ściśle związane. Aby się o tym przekonać wykonajmy cwiczenie. Ćwiczenie 1 1. Utwórz nowy projekt w Dev C++ i zapisz go na
Część XXII C++ w Wskaźniki a tablice Wskaźniki i tablice są ze sobą w języku C++ ściśle związane. Aby się o tym przekonać wykonajmy cwiczenie. Ćwiczenie 1 1. Utwórz nowy projekt w Dev C++ i zapisz go na
Laboratorium Przetwarzania Sygnałów
 PTS - laboratorium Laboratorium Przetwarzania Sygnałów Ćwiczenie 6 Interpolacja i histogram obrazów Opracowali: dr inż. Krzysztof Mikołajczyk dr inż. Beata Leśniak-Plewińska Zakład Inżynierii Biomedycznej
PTS - laboratorium Laboratorium Przetwarzania Sygnałów Ćwiczenie 6 Interpolacja i histogram obrazów Opracowali: dr inż. Krzysztof Mikołajczyk dr inż. Beata Leśniak-Plewińska Zakład Inżynierii Biomedycznej
Wydział Elektryczny Katedra Telekomunikacji i Aparatury Elektronicznej
 Politechnika Białostocka Wydział Elektryczny Katedra Telekomunikacji i Aparatury Elektronicznej Instrukcja do zajęć laboratoryjnych z przedmiotu: Przetwarzanie Sygnałów Kod: TS1A400027 Temat ćwiczenia:
Politechnika Białostocka Wydział Elektryczny Katedra Telekomunikacji i Aparatury Elektronicznej Instrukcja do zajęć laboratoryjnych z przedmiotu: Przetwarzanie Sygnałów Kod: TS1A400027 Temat ćwiczenia:
Rozpoznawanie obrazów na przykładzie rozpoznawania twarzy
 Rozpoznawanie obrazów na przykładzie rozpoznawania twarzy Wykorzystane materiały: Zadanie W dalszej części prezentacji będzie omawiane zagadnienie rozpoznawania twarzy Problem ten można jednak uogólnić
Rozpoznawanie obrazów na przykładzie rozpoznawania twarzy Wykorzystane materiały: Zadanie W dalszej części prezentacji będzie omawiane zagadnienie rozpoznawania twarzy Problem ten można jednak uogólnić
ĆWICZENIE 6 Transmitancje operatorowe, charakterystyki częstotliwościowe układów aktywnych pierwszego, drugiego i wyższych rzędów
 ĆWICZENIE 6 Transmitancje operatorowe, charakterystyki częstotliwościowe układów aktywnych pierwszego, drugiego i wyższych rzędów. Cel ćwiczenia Badanie układów pierwszego rzędu różniczkującego, całkującego
ĆWICZENIE 6 Transmitancje operatorowe, charakterystyki częstotliwościowe układów aktywnych pierwszego, drugiego i wyższych rzędów. Cel ćwiczenia Badanie układów pierwszego rzędu różniczkującego, całkującego
Ćwiczenia z grafiki komputerowej 5 FILTRY. Miłosz Michalski. Institute of Physics Nicolaus Copernicus University. Październik 2015
 Ćwiczenia z grafiki komputerowej 5 FILTRY Miłosz Michalski Institute of Physics Nicolaus Copernicus University Październik 2015 1 / 12 Wykorzystanie warstw Opis zadania Obrazy do ćwiczeń Zadanie ilustruje
Ćwiczenia z grafiki komputerowej 5 FILTRY Miłosz Michalski Institute of Physics Nicolaus Copernicus University Październik 2015 1 / 12 Wykorzystanie warstw Opis zadania Obrazy do ćwiczeń Zadanie ilustruje
Usługi Informatyczne "SZANSA" - Gabriela Ciszyńska-Matuszek ul. Świerkowa 25, Bielsko-Biała
 Usługi Informatyczne "SZANSA" - Gabriela Ciszyńska-Matuszek ul. Świerkowa 25, 43-305 Bielsko-Biała NIP 937-22-97-52 tel. +48 33 488 89 39 zwcad@zwcad.pl www.zwcad.pl Aplikacja do rysowania wykresów i oznaczania
Usługi Informatyczne "SZANSA" - Gabriela Ciszyńska-Matuszek ul. Świerkowa 25, 43-305 Bielsko-Biała NIP 937-22-97-52 tel. +48 33 488 89 39 zwcad@zwcad.pl www.zwcad.pl Aplikacja do rysowania wykresów i oznaczania
WYDZIAŁ FIZYKI I INFORMATYKI STOSOWANEJ
 WYDZIAŁ FIZYKI I INFORMATYKI STOSOWANEJ Hybrid Images Imię i nazwisko: Anna Konieczna Kierunek studiów: Informatyka Stosowana Rok studiów: 4 Przedmiot: Analiza i Przetwarzanie Obrazów Prowadzący przedmiot:
WYDZIAŁ FIZYKI I INFORMATYKI STOSOWANEJ Hybrid Images Imię i nazwisko: Anna Konieczna Kierunek studiów: Informatyka Stosowana Rok studiów: 4 Przedmiot: Analiza i Przetwarzanie Obrazów Prowadzący przedmiot:
