WIELKOPOWIERZCHNIOWA METODA OKREŚLANIA STOPNIA USZKODZENIA DRZEWOSTANÓW
|
|
|
- Liliana Domańska
- 9 lat temu
- Przeglądów:
Transkrypt
1 PRACE INSTYTUTU BADAWCZEGO LEŚNICTWA, Seria A Elżbieta DMYTERKO 1, Arkadiusz 8RUCHWALD 2 'Instytut Badawczy Leśnictwa Zakład Urządzania i Monitoringu Lasu, Warszawa, ul. Bitwy Warszawskiej 1920, nr 3 E.Dmyterko@ibles.waw.pl 2 Szkola Główna Gospodarstwa Wiejskiego Zakład Dendrometrii i Nauki o Produkcyjności Lasu Warszawa, ul. Rakowiecka 26/30 les_kpl@delta.sggw.waw.pl WIELKOPOWIERZCHNIOWA METODA OKREŚLANIA STOPNIA USZKODZENIA DRZEWOSTANÓW DĘBOWYCH I BUKOWYCH THE METHOD OF ASSESSING THE DEGREE OF DAMAGE OF OAK AND BEECH STANDS APPLICABLE OVER LARGE AREA Abstract. The concept of the met hod of assessing the degree of damage of oak and beech stands applicable over large area has been described in the paper. Three following criteria of damage were used: defoliation, vitality and combined tree damage coe.fficient (e.g. product of defoliation and vitality). The method was tested in oak and beech stands located across the country. The results of the study indicated the number of observation (trees evaluated) per one sample and the sample size (number of stands) to mee! assumed accuracy requirements. Key words: method applicable over large area, defoliation, vżtality, combined tree damage coe.fficient, oak, beech. Prac. Inst. Bad. Leś., A, 2000, 3(901 ):
2 1. WSTĘP Kształtowanie polityki leśnej zarówno na szczeblu krajowym, jak i regionalnym wymaga dysponowania szerokim zakresem informacji o stanie lasu (SZUJECKI 1998). Ważna grupa takich informacji dotyczy jego stanu zdrowotnego. Na zdrowotność lasu może wpływać wiele czynników, które dzieli się na biotyczne, abiotyczne i antropogeniczne. Z tych ostatnich negatywny wpływ na środowisko przyrodnicze wywierają emitowane do atmosfery pyły i gazy z zakładów przemysłowych. Często szkodliwe dla lasu są również zmiany w stosunkach wodnych, które nastąpiły w związku z budową kopalń, regulacją cieków i budową zapór na rzekach. Wiarygodne informacje dotyczące stanu zdrowotnego lasu można szybko uzyskać stosując odpowiednie metody pomiaru, które w leśnictwie noszą nazwę wielkoobszarowych lub wielkopowierzchniowych. Teoria tych metod opiera się na dziale statystyki matematycznej zwanym "metodą reprezentacyjną'' (ZASĘPA 1972, 1991; BRACHA 1996). Na podstawie zebranego i przetworzonego materiału empirycznego uzyskanego w wyniku zastosowania metody reprezentacyjnej możliwe jest właściwe wnioskowanie statystyczne. W Polsce po raz pierwszy zastosowano wielkopowierzchniową metodę inwentaryzacji lasu w 1983 r. (Info1macja o wynikach ; Instrukcja przeprowadzania oceny ). Głównym jej celem było uzyskanie infonnacji o stanie sanitarnym i zdrowotnym lasów w całym kraju (SMYKAŁA 1996; ZAJĄCZKOWSKI 1993). Przyczyną posłużenia się tą metodą był brak dokładnych danych o stanie lasu w związku z klęskową gradacją brudnicy mniszki. Przyjęto, że luyteriami oceny stanu zdrowotnego lasu będą następujące cechy drzew: stanowisko biosocjalne, ubytek aparatu asymilacyjnego, barwa liści i stan strzały. Stwierdzony w 1983 r. zły stan sanitarny i zdrowotny drzewostanów był powodem ponownego użycia w 1985 r. wielkopowierzchniowej metody do oceny stanu lasu. Takjak poprzednio, zastosowano w niej te same cechy drzew jako kryteria oceny stanu zdrowotnego (SMYKAŁA 1996). W 1985 r. w ramach Konwencji o Transgranicznym Przemieszczaniu się Zanieczyszczeń Powietrza na Dalekie Odległości powstał międzynarodowy program badawczy "Ocena i monitoring wpływu zanieczyszczef1 powietrza na lasy" (ICP Forest). Za podstawowe luyterium oceny stanu lasu przyjęto ubytek aparatu asymilacyjnego drzewa (defoliacja). Ocenione drzewa przyporządkowywano odpowiednim klasom, oznaczającym stopień ich uszkodzenia (Draft manual on ). Począwszy od 1989 r. Polska uczestniczy w programie!cp-forest, monitorując lasy według ustalonej w Europie metodyki (W A WRZONIAK i in. 1999). Przeprowadzona w Polsce w 1988 r. kolejna wielkopowierzchniowa inwentaryzacja lasu uwzględniła zalecenia metodyczne stosowane w programie ICP- Forest (SMYKAŁA 1991, 1996; Wyniki wielkopowierzchniowej inwentaryzacji ).
3 Wu!lkopow1erzchmowa metoda określama stopnw uszkodzenia 19 Tym samym możliwe było dokonanie porównań stanu zdrowotnego lasów Polski ze stanem zdrowotnym lasów w innych krajach. Wyniki uzyskane w tej inwentaryzacji pozwa l ały również na oc enę drzewostanów według metody stosowanej w naszym kraju do wyznaczania stref uszkodzenia lasu w nadleśnictwach (TRAMPLER, DMYiERKO 1988). Ostatnią wielkopowierzchniową inwentaryzacj ę stanu zdrowotnego lasu przeprowadzono w 1991 r. s to s ując kryteria oceny poprzedniej tego rodzaju inwentaryzacji (SMYKAŁA 1992, 1996; TRAMPLER 1992; TRAMPLER, DMYTERKO 1992; Wyniki wielkopowierzchniowej inwentaryzacji.1992). Dane uzyskiwane w monitoringu europejskim nie pozwalają na dokonanie dokładnych analiz na szczeblu poszczególnych krajów, a tym bardziej ich regionów. Informacje dla tych poziomów są bowiem obarczone dużym błędem i mogą być traktowane jako sygnalne. Wiarygodne dane można otrzymać stosując odpowiednią metodę inwentaryzacji lasu. Celem pracy jest przedstawienie projektu wielkopowierzchniowej metody określania stopnia uszkodzenia lasu. Weryfikacja metody dotyczyć będzie drzewostanów dębowych i bukowych. W szczególności pos211kiwana będzie minimalna próba spełniająca wanmek założonej dokładności metody. 2. MATERIAŁ BADAWCZY Materiał empiryczny zebrano w 131 drzewostanach dębowych i 150 bukowych. Drzewostany dębowe reprezentujące różne nadleśnictwa pogrupowano w 3 rej ony (ryc. I): - północny N (Bierzwik, Gr~fino, Chojna, Barlinek i Bogdaniec), - centralny C (Łochów, Sokołów Podlaski, Płońsk, Nowa Sól i Krotoszyn), - poh1dniowy S (Wołów, Prndnik i Niepołomice). Drzewostany bukowe położone na terenie 8 nadleśnictw pogrupowano również w analogiczne rejony (ryc. 2): - północny N (Gryfino, Sławno, Wejherowo, Kartuzy), - centralny C (Brzeziny), - południowy S (Stuposiany, Dynów i Sucha Beskidzka). Badania przeprowadzono w drzewostanach litych i mieszanych, jedno- i dwupi ętrowych. W górnej warstwie udział gatunków domieszkowych był niewielki ; w drzewostanach dębowych występowały najczęściej jesion, brzoza, osika Prncę wykonono w mmach dzinlulnośc1 statutowej linnnsowancj przez Komitet Badań Naukowych.
4 20 E. Dmy terko. A. Bruchwa/d Ryc. 1. Lokalizacja d ębowych powierzchni badawczych Fig. 1. Localization of oak research plots Ryc. 2. Lokalizacja bukowych powierzchni badawczych Fig.2. Localization of beech research plots oprac. graficzne map G. Zaj~c.zkowski compurcr grapl1ics by G. Zajączkow s ki
5 Wielkopowierzchniowa metoda określania stopnia uszkodzenia 21 i lipa, a w drzewostanach bukowych dąb i jodła. Dolna warstwa, składająca się głównie z grabu i lipy, występowała w dębinach. Drzewostany były jedno- i wielowiekowe, najmłodsze z nich reprezentowane były przez II klasę wieku, a najstarsze przez IX (buk) i XI (dąb). Bardziej szczegółowy opis tych drzewostanów znajduje się w opublikowanych już pracach (DMYTERKO, BRUCHWALD 1998, 2000). Na drzewach próbnych, średnio po 1 O z każdego drzewostanu, oceniono defoliację i witalność. Do szacowania defoliacji posłużono się atlasem ubytku aparatu asymilacyjnego drzew (MDLLER, STIERLIN 1990), a do witalności - klasyfikację stanu koron wraz z graficznymi schematami (ROLOFF 1986, 1989). Drzewa próbne wybierano z I i II klasy Krafta, a tylko w nielicznych przypadkach z III klasy. Ocenie podlegała górna część koron w okresie pełnego ulistnienia. W niektórych drzewostanach witalność drzew szacowano ponownie w okresie bezlistnym. Defoliacja i witalność były podstawą ustalenia syntetycznego wskaźnika uszkodzenia drzewa (DMYTERKO 1998, 1999). 3. METODA OKREŚLANIA STANU ZDROWOTNEGO LASU Pracę opisującą wielkopowierzchniową metodę określania miąższości obiektu leśnego opartą na losowaniu warstwowym opublikowano w "Sylwanie' 1 (BRUCHWALD 2000). W metodzie tej przyjęto następujące założenia: 1) znane i dostępne są informacje dotyczące każdego drzewostanu mierzonego obiektu leśnego: usytuowanie przestrzenne, wielkość powierzchni, średni wiek i gatunek główny budujący drzewostan; 2) metoda oparta jest na losowaniu warstwowym, a cechami tworzącymi warstwy są wiek i gatunek główny budujący drzewostan; 3) dokładność określania miąższości poszczególnych warstw uzależniona jest od rozkładu wieku i wielkości powierzchni drzewostanów zaliczonych do danej warstwy; warstwy w drzewostanach starszych klas wieku i o większej powierzchni określane są z większą dokładnością. Takie same założenia przyjęto również do opracowania wielkopowierzchniowej metody określania stanu zdrowotnego lasu. Do jego oceny zastosowano następujące kryteria: ubytek aparatu asymilacyjnego drzewa (defoliacja) oraz witalność i syntetyczny wskaźnik uszkodzenia (DMYTERKO 1998). Stąd wielkopowierzchniowa metoda oceny stanu zdrowotnego lasu składa się z trzech wariantów, opartych na różnych kryteriach. Wariant 1. Oparty jest na kryterium defoliacji. Dla obiektu leśnego przeprowadza się warstwowanie, w którym uwzględnia się wiek i gatunek główny drzewa. W poszczególnych warstwach losuje się określoną liczbę miejsc pomiarowych, będących środkami powierzchni w metodzie ustal.ania miąższości. Defo-
6 22 E. Dmyterko, A. Bruchwald liację ocenia się na pewnej liczbie drzew należących do I lub II klasy Krafta, rosnących najbliżej środka powierzchni. Dla drzewostanu (powierzchni) oblicza się średnią wartość defoliacji, a następnie wartość średnią dla warstwy i całego obiektu leśnego. Na podstawie uzyskanych wyników można opracować empiryczny rozkład defoliacji drzewostanów. Buduje się go przyporządkowując wyniki do odpowiednich klas. Rozważyć można dwa warianty budowy rozkładu: 1) szerokości klas stosowane w europejskim programie ICP- Forest: Klasa Defol ia ~ja w % ~IO o > 60 2) jednakowe szerokości klas, równe 25%. W metodzie tej pomijany jest posusz. Wariant 2. Oparty jest na kryterium witalności drzewa. Analogicznie do wariantu 1 przeprowadza się w obiekcie leśnym warstwowanie, uwzględniające wiek i gatunek główny drzewa tworzący drzewostan. Dla utworzonych warstw losuje się miejsca do założenia powierzchni próbnych. Po zlokalizowaniu tych miejsc, na olaeślonej liczbie drzew należących do I lub II klasy Krafta ocenia się witalność. Wartość średnia witalności dla warstw i całego obiektu leśnego jest podstawą wnioskowania o stopniu uszkodzenia lasu. Analizę można pogłębić o empiryczny rozkład witalności. W rozkł a dzie przyjmuje się następujące szerokości klas: Kl as a o 2 3 Wit a lno ś ć <0,50 0,50-1,49 1,50-2,49 ~2, 50 Wariant 3. Za kryterium uszkodzenia przyjmuje się syntetyczny wskaźnik. Po przeprowadzeniu warstwowania, losowania próby i lokalizacji miejsc pomiarowych, na olaeślonej liczbie drzew zaliczonych do grupy górujących lub panujących, rosnących najbliżej środka powierzchni, ocenia się defoliację i witalność. Średnią wartość syntetycznego wskaźnika uszkodzenia dla powierzchni olaeśla się na podstawie wzoru: 0,03IDef + 'LWit Syn= k [1] gdzie: Syn - syntetyczny wskaźnik uszkodzenia, Def- defoliacja drzewa, Wit- wita lność drzewa, k - liczba drzew przyjętych do oceny defoliacji i witalności na powierzchni próbnej.
7 Wielkopowierzchniowa metoda określania stopnia uszkodzenia 23 Analizie podlega średnia wartość syntetycznego wskaźnika dla warstwy i całego obiektu leśnego, a także rozkład tego wskaźnika. Ponieważ cecha ta może przyjmować wartości z przedziału od O do 3, dlatego klasy syntetycznego wskaźnika buduje się podobnie jak klasy witalności. 4. OCENA METODY Aby uściślić metodycznie ocenę dokładności określania badanej cechy, a więc defoliacji, witalności lub syntetycznego wskaźnika uszkodzenia drzew, przyjęto następujące założenia: obiektem oceny są lasy podlegające regionalnej dyrekcji Lasów Państwowych. Ocenę lasów w kraju można uzyskać z informacji zebranych dla poszczególnych regionalnych dyrekcji LP; w lasach zarządzanych przez regionalną dyrekcję LP pomiarowi podlegają tylko drzewostany dębowe lub tylko bukowe. Liczba warstw przy takim założeniu ulega zmniejszeniu do liczby klas wieku reprezentowanych przez drzewostany dębowe lub bukowe w mierzonym obiekcie. Przy pełnej ich rozpiętości będą to następujące klasy wieku: Il, III, IV, V i VI+ starsze drzewostany. Uzyskane wyniki badań uzasadniają potrzebę wyróżnienia jeszcze jednej warstwy: drzewostanów będących w przebudowie, o niskim stopniu zagęszczenia (klasa odnowienia). W klasie tej stwierdzono duże wartości defoliacji drzewostanów, zwłaszcza bukowych (ryc. 3). Na potrzebę wyróżnienia takiej warstwy wskazują także wyniki badań uzyskane w drzewostanach dębowych i sosnowych, wykazujące związek defoliacji ze stopniem zwarcia drzewostanu (BORECKI, WÓJCIK 1996). [ D dąb (oak) ~buk (beech) J -40 ~ --c: ~ 30 ;g IU "C -;;20 "O'.!!;!.g ~ IV V VI klasy wieku (age classes) KO Ryc. 3. Średnie wartości defoliacji dla klas wieku Fig. 3. Mean values of defoliation for age classes
8 24 E. Dmyterlw, A. Bruchwald Średnia wartość badanej cechy dla poszczególnych warstw.x h jest równa: x - =- i Ł-X h nh I i =l,2,...,n1i [2] gdzie: n1i - liczebność próby ustalona dla warstwy, h-indeks poszczególnych warstw liczony od l do!, gdzie l jest liczbą warstw, [2] Nieobciążonym estymatorem średniej wartości badanej cechy X dla populacji jest średnia z próby.x określona na podstawie wzonl I.x = Łwh.xh h = 1, 2.., 1 [3] h=i N w =-h " N ' h=i gdzie: N1i - liczba jednostek statystycznych w warstwie, N - liczba jednostek statystycznych w całej populacji, Błąd standardowy estymatora.x, gdy w warstwie przeprowadza się losowanie bezzwrotne, określa się na podstawie wzoru: [4] gdzie S:, jest wariancją badąnej cechy dla warstwy. Podczas dalszej analizy metody przyjęto następne założenie : liczebności prób w poszczególnych warstwach, w stosunku do liczby jednostek statystycznych w odpowiednich warstwach, są bardzo małe. Założenie to pozwala uprościć wzór [ 4] do postaci: W praktycznym stosowaniu metody zwykle ustala się małą liczbę prób dla poszczególnych warstw. W takim przypadku wariancja dla warstw określona jest z dużym błędem. Upoważnia to do wprowadzenia kolejnego założenia: dla warstw przyjmuje się taką samą wartość wariancji, wyznaczonej ze średniej arytmetycznej odchyleń standardowych dla warstw.
9 Wielkopowierzchniowa metoda określania stopnia uszkodzenia drzewostanów 25 gdzie: h =l, 2,..., l, s 2 =- 1 I n S 2 h h m I m= In". h=i Wzór [5] będzie miał teraz postać: [6] [7] Przeprowadzając analizę metody dla różnych obiektów leśnych uzyska się zwykle zróżnicowany układ wag dla poszczególnych warstw. Dlatego ocena metody dotyczyć powinna konkretnego obiektu leśnego, o określonej, znanej strukturze częstości warstw. Problem ten uproszczono przyjmując następne założenie: rozkład częstości warstw jest jednostajny. Ponieważ suma częstości warstw jest równa jedności, dlatego wzór [7] można sprowadzić do prostej postaci: d(x) = _ rm gdziem jest ustaloną dla całego obiektu leśnego liczebnością próby. Zawarte we wzorze [8] odchylenie standardowe S wynika z dwóch źródeł zmienności: - zmienności cechy drzew drzewostanu (zmienność populacyjna), - zmienności średnich wartości cechy drzewostanu (zmienność międzypopulacyjna w ramach warstw). Wariancję uwzględniającą wymienione źródła zmienności można ująć za pomocą wzo1u: [8] 2 =-+s S 2 si 2 k 2 [9] gdzie: s~ - wariancja charakteryzująca zmienność populacyjną, s~ - wariancja charakteryzująca zmienność międzypopulacyjną w obrębie warstw, k- liczba drzew służących do określenia średniej wartości badanej cechy dla drzewostanu. Wzór [8] przyjmie więc postać: d(x)=- 1 - Fm [l OJ
10 26 E. Dmyterlw, A. Bruchwald Wyrażając ten wzór w procentach otrzymuje się: p(x) d\x) loo [ 11] X W dalszej części rozdziału metoda zostanie przeanalizowana pod kątem badań empirycznych. Dla każdego drzewostanu obliczono wartość średnią i odchylenie standardowe defoliacji, witalności i syntetycznego wskaźnika uszkodzenia drzew. Uwzględniając wszystkie drzewostany obliczono wartości średnie tych miar, a na ich podstawie współczynniki zmienno~ci. Uzyskane wartości miar charakteryzują zmienność populacyjną cech uszkodzenia drzew. Średnie wartości cech uszkodzenia dla drzewostanów stanowiły podstawę obliczenia odchylenia standardowego i współczynnika zmienności, charakteryzujących dyspersję międzypopulacyjną dla warstw. Tworząc warstwy uwzględniono wiek drzewostanów oraz ich położenie geograficzne. Dla kraju wyróżniono 3 rejony (warstwy): północny, centralny i południowy. Podział taki zwiększa efektywność metody losowania warstwowego, średnie bowiem wartości defoliacji i innych cech uszkodzenia są zróżnicowane w poszczególnych rejonach (ryc. 4). Zmienność populacyjna badanych cech mierzona odchyleniem standardowym jest na ogół inniejsza od zmienności międzypopulacyjnej (tab. 1). Stwierdzenie to dotyczy zarówno drzewostanów dębowych, jak i bukowych. Ocenę dokładności wielkopowierzchniowej metody określania uszkodzenia obiektu leśnego przeprowadzono z zastosowaniem wzorów [ 1 OJ i [ 11]. Analiza dotyczyła różnej liczby drzew, uwzględnionej przy określaniu średniej wartości danej cechy drzewostanu i różnej liczebności próby (o dąb (oak) ~buk (beech) J : '2 o ~ 30 ;g QJ "O.._...!!!_20 o.~ ;g ~10 N C S rejony kraju (country regions) Ryc. 4. Średnie wartości defoliacji dla rejonów Polski (N - północny, C - centralny, S - południowy) Fig. 4. Mean values of defoliation for reg1ons of Poland (N - north, C - central, S - south)
11 Wielkopowierzchniowa metoda określania stopnia uszkodzenia drzewostanów 27 Dokładność określania badanej cechy wzrasta wraz ze zwiększaniem liczby drzew służących do ustalania wartości średniej dla drzewostanu, jak i liczby drzewostanów wylosowanych do próby. Analizując spadek wartości błędu dla danej cechy, przy wzroście liczby ocenianych drzew w drzewostanie i takiej samej liczbie drzewostanów pobranych do próby, można dojść do wniosku, że istnieje pewna liczba drzew służąca do określenia średniej wartości badanej cechy dla drzewostanu, powyżej której błąd metody tylko nieznacznie maleje. Dla wariantu 1 metody, w którym kryterium uszkodzenia drzewa jest defoliacja, po przekroczeniu 4 drzew ocenianych w drzewostanie, dokładność metody wzrasta o niewielką wartość. Wzrost dokładności jest tym mniejszy, im większa jest liczba drzewostanów uwzględnionych w metodzie, a więc im większa jest liczba prób. Stwierdzenia te dotyczą defoliacji ocenianej zarówno w drzewostanacą dębowych (ryc. 5), jak i bukowych (ryc. 6). Analogiczny wynik otrzymuje się po przeprowadzeniu analizy wariantu 2 metody, uwzględniającego witalność (ryc. 7), i wariantu 3, uwzględniającego syntetyczny wskaźnik uszkodzenia (ryc. 8). Dokładność poszczególnych wariantów ulega zwiększeniu o niewielkie wartości, gdy liczba drzew służących do olueślenia badanej cechy dla drzewostanu przekracza 4. Aby ustalić dokładność metody przyjęto, że średnia wartość badanej cechy dla drzewostanu (powierzchni próbnej) zostanie olu eślona na 4 drzewach. Położone one będą najbliżej środka powierzchni i będą reprezentowały drzewa I lub II klasy Krafta. Miary cech uszkodzenia dla drzewostanów dębowych i bukowych Measures of damage features for oak and beech stands - Gatunek Liczba Badana cecha' Miary statystyczne drzewa drzewostan ów Feature tested Statistical measurements Tree species Number of stands Ą X s, V, S2 Dąb Dej 38,6 9,72 25,2 8,77 Oak 131 Wit ,309 24,I 0,326 Svn 1, o 0,286 Buk Dej 29,6 9,19 3 1,0 10,18 Bee eh 150 Wit 0,90 0,357 39,7 0,361 Svn o 317 Tabela 1 Table I V2 22,7 25, ,4 40, 'Dej-defoliacja, Wit- witalność, Syn - syntetyczny wskaźnik uszkodzenia drzewa, x- ś1 ednia arytmetyczna, s 1 (Vi) - odchylenie standardowe (współczynnik zmienności) cha.-akteryzujące zmienność populacyjn_ą, s 2 (V 2 ) - odchylenie standardowe (współczynnik zmienności) charakteryzujące zmienność międzypopulacyjną dla warstw Dej - defoliation, Wit. -- vitality, Syn. - combined tree damage coefficients, x - arithmetic mean, s 1 ( V 1 ) - stanpart deviation (variability coefficient) characterizing population variability, s2(v2) - standard deviation (variability coefficient) characterizing variability between populations
12 28 E. Dmyterko. A. Bruchwald 4~--~ , liczba próbek (number of samples) 5 liczba próbek (number of samples) f ao ł drzewa próbne (sample trees) {)00 o -' ' drzewa próbne (sample trees) Ryc. 5. Błąd określania średniej wartości defoliacji dla drzewostanów dębowych Fig. 5. Estimation error of the mean value of defoliation for oak stands Ryc. 6. Błąd określania średniej wartości defoliacji dla drzewostanów bukowych Fig. 6. Estimation error of the rnean value of defoliation for beech stands 4 buk (beech) buk beech) d~b_(o_alq d b oak) drzewa próbne (sample trees) drzewa próbne (sample trees) Ryc. 7. Bląd określania średniej wartości witalności przy 200 próbkach Fig. 7. Estirnation error of the rnean value of vitality (200 stands sample) Ryc. 8. Błąd określania średniej wartości syntetycznego wskaźnika uszkodzenia drzew przy 200 próbkach Fig. 8. Estimation error of the mean value of combined tree damage coefficient (200 stands sample) Błędy charakteryzujące dokładność badanej cechy określono dla zakresu próby od 1 OO do 2000 powierzchni. Gdy próba składa się ze 1 OO drzewostanów, dokładność oceny średniej wartości defoliacji dla obiektu leśnego jest mała (ryc. 9). Dla drzewostanów dębowych otrzymano błąd standardowy około 2,6 /o, a dla drzewostanów bukowych -3,8%. Zwiększenie liczebności próby do 600 powierzchni sprawia, że dla drzewostanów dębowych błąd ten spada do 1,0%, a dla bukowych - do 1,5%. Spadek błędu standardowego do 1 % dla drzewostanów bukowych wymaga oceny około 1400 powierzchni. Analiza dokładności wariantu 2 metody podbudowuje wcześniejsze stwierdzenie: 1 OO powierzchni stanowi za małą próbę do precyzyjnego scharakte-
13 Wielkopowierzchniowa metoda określania stopnia uszkodzenia drzewostanów ~ 0 1~ ir t t-~ ooo liczba próbek (number of samples) ooo liczba próbek (number of samptes) Ryc. 9. Dokładność określania średniej wartości defoliacji dla różnej liczby próbek (pomiar 4 drzew w drzewostanje) Fig. 9. Estirnation error of the mean value of defoliation for a number of sample stands ( assessrnent of 4 trees per stand) Ryc. 10. Dokładność określania średnie.i wartości witalności dla różnej liczby próbek (pomiar 4 drzew w drzewostanie) Fig. I O. Estimation error of the rnean value of vitality for a number of sample stands (assessment of 4 trees per stand) _ ~ o -'-+--+-ll-+--t ł-ł ł--t _µ 1 oo ooo liczba próbek (number of samples) Ryc. 11. Dokładność określania średnie.i wartości syntetycznego wskaźnika uszkodzenia drzew dla różnej liczby próbek (pomiar 4 drzew w drzewostanie) Fig. 11. Estimation error of the mean value of combined tree damage coefficient for a number of sample stands (assessment of 4 trees per stand) ryzowania średniej witalności obiektu leśnego (ryc. 1 O). W wariancie tym rozważyć można propozycję uzyskania błędu nie przeluaczającego 1,5%. Dla drzewostanów dębowych wymaga on zastosowania próby o liczebności około 350 powierzchni, a dla drzewostanów bukowych - około 900 powierzchni. Godny polecenia jest wariant 3 metody, oparty na syntetycznym wskaźniku uszkodzenia drzewa. Próba złożona ze 1 OO drzewostanów daje dość duży błąd w ocenie średniej wartości tego wskaźnika (1yc. 11 ). Wzrost liczebności próby do 700 powierzchni powoduje, że dla drzewostanów dębowych błąd standardowy wynosi około 1,0%, a dla bukowych - około I,4%. Aby uzyskać błąd 1 % w drzewostanach bukowych, należy próbę powięks zyć do około 1500 powierzchni.
14 30 E. Dmyterko, A. Bruchwald 5. PODSUMOWANIE I WNIOSKI Praca przedstawia projekt wielkopowierzchniowej metody określania stopnia uszkodzenia drzewostanów dębowych i bukowych obiektu leśnego. Składa się ona z trzech wariantów, w któ1ych layte1iami uszkodzenia są: defoliacja, witalność i cecha łącząca wymienione kryteria, nazwana syntetycznym wskaźnikiem uszkodzenia drzewa. Metoda opiera się na losowaniu warstwowym. Przy tworzeniu warstw uwzględnione są dwie cechy drzewostanu: wiek i gatunek główny drzewa. W przypadku zastosowania metody na skalę całego kraju warstwowaniem byłyby również objęte regionalne dyrekcje LP. Zakłada się, że wymienione informacje, a także powierzchnie drzewostanów i ich usytuowanie zawarte są w bazie danych Systemu Informatycznego Lasów Państwowych. Baza jest dostępna dla użytkownika metody. W metodzie rozdziela się ogólną liczebność próby na warstwy według opracowanego schematu. Zakłada się w nim, że dokładniej określone będą średnie wartości cechy dla tych warstw, które mają większą powierzchnię i w których znajdują się starsze drzewostany. Projekt skorelowano z wielkopowierzchniową metodą określania miąższości obiektu leśnego (BRUCHWALD 2000). Na podstawie badań sformułowano następujące wnioski: 1. Zmienność badanej cechy dla warstw utworzonych w obiekcie leśnym można podzielić na dwie składowe: populacyjną i międzypopulacyjną. Zarówno dla drzewostanów dębowych, jak i bukowych, populacyjna zmienność defoliacji, witalności i syntetycznego wskaźnika uszkodzenia jest na ogół mniejsza od zmienności międzypopulacyjnej. 2. Błąd wynikający ze zmienności populacyjnej można regulować dobierając określoną liczbę drzew, służących do określania średniej wartości cechy analizowanej dla drzewostanu. Badania wykazały, że do ustalenia średnich wartości cech drzewostanu wystarczy ocenić defoliację, witalność lub syntetyczny wskaźnik na 4 drzewach. Zwiększenie tej liczby drzew powoduje, zarówno w drzewostanach dębowych, jak i bukowych, tylko nieznaczny wzrost dokładności metody. 3. O dokładności metody decyduje głównie zmienność międzypopulacyjna zastosowanych kryteriów. Błąd wynikający z tej zmienności może być regulowany doborem odpowiednio licznej próby (liczby powierzchni próbnych). Oszacowanie wariancji międzypopulacyjnej cech uszkodzenia może okazać się złożonym zagadnieniem. W niektó1ych obiektach drzewostany charakte1yzują się niskim stopniem uszkodzenia - wówczas wariancja będzie mała. W innych obiektach, zwłaszcza powierzchniowo dużych, może wystąpić cały zakres stopni uszkodzenia - wówczas wariancja będzie duża. Z metodycznego punktu widzenia oszacowanie wariancji charakteryzującej zmienność międzypopulacyjną wymaga przeprowadzenia wstępnego badania obiektu metodą reprezentacyjną z zastosowaniem nawet małej próby.
15 Wielkopowierzchniowa metoda określania stopnia uszkodzenia Do oceny dokładności wielkopowierzchniowej metody określania stopnia uszkodzenia drzewostanów dębowych i bukowych zastosowano średnią wartość wariancji międzypopulacyjnej poszczególnych cech, z uwzględnieniem jednak wariancji populacyjnej. Stwierdzono, że gdy liczebność próby wynosi 1 OO drzewostanów, dokładność metody jest mała. Wyraźny wzrost dokładności uzyskuje się przy zwiększeniu liczebności próby do około 500 powierzchni. Zakładając tę samą wielkość próby, większą dokładność metody uzyskano dla drzewostanów dębowych. 5. Godny polecenia jest wariant wielkopowierzchniowej metody oceny stanu zdrowotnego lasu, w którym zastosowano jako layterium syntetyczny wskaźnik uszkodzenia. Błąd standardowy 1,5% określania średniej wartości tego wskaźnika uzyskuje się dla próby wynoszącej około 300 powierzchni w dębinach i około 600 powierzchni w buczynach. Łączna liczba dębów z oszacowaną defoliacją i witalnością wynosiłaby wówczas 1200, a buków Defoliacja i witalność są cechami niemierzalnymi. Szacowanie wartości takich cech powoduje zwykle wystąpienie błędu systematycznego w ocenie ich średnich wartości. Obniżenie prawdopodobieństwa powstawania błędu systematycznego można uzyskać stosując do oceny defoliacji odpowiedni atlas, a do oceny witalności - odpowiedni klucz. Niezbędne jest również przeszkolenie taksatorów przed przystąpieniem do pomiarów i ocen. 7. Zwiększenie dokładności wielkopowierzchniowej metody oceny stanu zdrowotnego lasu można uzyskać ograniczając zmienność międzypopulacyjną badanych cech w obrębie warstw. Celowe jest więc wprowadzenie warstwy drzewostanów zaliczonych do klasy odnowienia. Charakteryzują się one silniejszym uszkodzeniem niż średnio drzewostany w całym obiekcie. W przypadku zastosowania metody wielkopowierzchniowej dla lasów całego kraju uzasadnione jest również wprowadzenie warstw te1ytorialnych, np. utworzonych z lasów podlegających regionalnym dyrekcjom LP. Praca została złożona 30 marca 2000 r. i przyjęta przez Komitet Redakcyjny 15 maja 2000 r. THE METHOD OF ASSESSING THE DEGREE OF DAMAGE OF OAK AND BEECH STANDS APPLICABLE OVER LARGE AREA Surnrnary The concept of the method of assessing the degree of damage of oak and beech stands applicable 0ver large area has been described in the paper. Three following criteria of damage were used: defoliation, vitality and combined tree damage coefficient (e.g. product of
16 32 E. Dmyterko, A. Bruchwald defoliation and vitality). The rnethod is based on stratified drawing. Layers were detem1ined due to stand mean age and dominant tree species. In the case of study conducted over the entire country, stratification should also include the administrative units (Regional Directorate of State Forest). The method was tested in oak and beech stands located across the country. It was also hannonized with the stand volume estimation method (BRUCHWALD 2000). The variability of a given feature in a certain forest area layers might be divided in two constituents: population variability and variability between populations. For both oak and beech stands, population variability of defoliation, vitality and combined tree damage coefficient was usually!ower than variability between populations. Estimation error derived from the population variability might be controlled through the number of observations (trees), the mean value for stand is counted on. Studies have shown that to detennine the stand rnean values of defoliation, vitality or cornbined tree damage coefficient only 4 trees have to be assessed. A grater number of trees caused both in oak and beech stands only slight increase in accuracy. The method accuracy depended mostly on the feature variability between populations. The error derived from this kind of variability might be controlled by the size of sample - the number of stands ( observation plots) included in the study. The evaluation of the varia bili ty of the damage feature between populations might be a complex issue. In some forest complexes damage of stands is low, such is also variability there, while in other forest complexes damage intensity may va1y from stand to stand, causing high variability (as expressed by variance) of a given feature. To overcome such difficulties the initial investigation of the forest complex is required to properly estimate the variance representing variability between population. (transl. P. L.) PIŚMIENNICTWO BORECKI T, WÓJCIK R Ocena stanu uszkodzeń drzewostanów Nadleśnictwa Krotoszyn. Sylwan, 7: BRACHA C Teoretyczne podstawy metody reprezentacyjnej. PWN, Warszawa. BRUCHWALD A Wielkopowierzchniowa metoda określania miąższości obiektu leśnego oparta na losowaniu warstwowym. Sylwan, 3: Draft manual on methodologies and criteria for harmonized sampling, assessrnent, monitoring and ana lysis of the effects of air pollution on forests G!obal environment monitoring system UN-ECE (maszyn. w Zakł. Urządzania Lasu Inst. Bad. Leś. ). DMYTERKO E Metody określania uszkodzenia drzewostanów dębowych. Sylwan, I O: DMYTERKO E Kryteria oceny uszkodzenia drzewostanów bukowych. Sylwan, 9: DMYTERKO E., BRUCJ-IWALD A Weryfikacja metod określania uszkodzenia drzewostanów dębowych. Sylwan, 12: DMYTERKO E., BRUCHWALD A Metody określania stopnia uszkodzenia drzewostanów bukowych i ich weryfikacja. Sylwan, 5: Informacja o wynikach wielkopowierzchniowej inwentaryzacji stanu zdrowotnego i sanitarnego lasu wg stanu na BULiGL, Warszawa, Instrukcja przeprowadzania oceny stanu zdrowotnego i sanitarnego lasu za pomocą statystycznej inwentaryzacji wielkoobszarowej. NZLP, Warszawa, MOLLER E., STIERLIN H., R., Sanasilva Kronenbilder mit Nade!- und Blattverlustprozenten. Eidgenóssische Forschungsanstalt for Wald, Schnee und Landschaft. Birmensdorf.
17 Wielkopowierzchniowa metoda określania stopnia uszkodzenia 33 ROLOFF A Morphologie der Kronenentwicklung von Fagus sy!vatica L. (Rotbuche) unter besonderer Beriicksichtigung mogli cherweise neuartiger Veranderu ngen. O iss. F orstw iss. Fachber. Univ. Gottingen. ROLO FF A Kronenentwickl ung und Vital i tatsbeu rtei Jung ausgewah lter Baumarten der gemar3igtcn Brcitcn. Schriften aus der Forstlichen Fakultat der Universitat Gottingen und der Niedcrsachsischen Forstlichen Versuchsanstalt, Frankfurt am Main. SMYKAŁA J Stan zdrowotny i sanitarny lasu w organizacji gospodarczej Lasy Państwowe w świetle "kryteriów europejskich". Sylwan, 4/6: SMYK.ALA J Stan zdrowotny i sanitarny lasów w Lasach Państwowych w l 991 roku. Sylwan, 7: SMYKAŁA J Wyniki inwentaryzacji wielkopowierzchniowych stanu zdrowotnego i sanitarnego lasów w Polsce. W: Reakc_ie biologiczne drzew na zanieczyszczenia przemysłowe. Tom I. (red.) R. Siwecki. JIJ Kraj. Symp. Kórnik, Wyd. Sorus, Poznań: SZUJECKJ A Zadania urządzania lasu na progu XXI wieku w świetle polityki łe$nej państwa. Sylwan, 5: TRAMPLER T., DMYTERKO E Ocena metodą bioindykacyjną (defoliacji) stanu uszkodzenia lasów w Polsce na podstawie wyników wielkoobszarowej inwentaryzacji 1988 r. Dok. Inst. Bad. Leś Warszawa. TRAMPLER T Opracowanie wyników wielkoobszarowej inwentaryzacji stanu uszkodzenia lasu z I 99 I roki1 w zakresie struktury uszkodzenia drzewostanów. Dok. Inst. Bad. Leś Warszawa. TRAMPLER T., DMYTERKO E Struktura uszkodzenia drzewostanów na podstawie wielkoobszarowej inwentaryzacji stanu uszkodzenia lasu w 199 I roku. Not. Nauk. Inst. Bad. Leśn. 9. W A WRZONIAK J MAŁACHOWSKA J ZAJĄCZKOWSKI S., WYRZYKOWSKI S SOLD N l, FAŁ TY NOWICZ W., SIEROTA Z ZAŁĘSKI A, KOLKA., LECH P., ADAMSKI L Stan uszkodzenia lasów w Polsce w I 998 roku na podstawie badań monitoringowych. Państwowa Inspekcja Ochrony Środowiska. Biblioteka Monitoringu Środowiska, Warszawa. Wyniki wielkopowierzchniowej inwentaryzacji stanu zdrowotnego i sanitarnego lasu w Lasach Państwowych wg stanu na I 985 r. BULiGL, Warszawa, I 986. Wyniki wielkopowierzchniowej inwentaryzacji stanu zdrowotnego i sanitarnego lasu w Lasach Pa1'lstwowych wg stanu na I 988 r. BULiGL, Warszawa, Wyniki wielkopowierzchniowej inwentaryzacji stanu zdrowotnego i sanitarnego lasu w Lasach Pai'tstwowych wg stanu na l 99 I r. BUL i GL, Warszawa, ZAJĄCZKOWSKI S Ocena zdrowotnego i sanitarnego stanu lasu w praktyce urządzeniowej. Pr. Inst. Bad. Leś., Ser. B, 18: ZASĘPA R Metoda reprezentacyjna. PWE, Warszawa. ZASĘPA R Zarys metody reprezentacyjnej. Biblioteka Wiadomości Statystycznych. T.39. GUS i PTS, Warszawa.
ZMIENNOŚĆ SUMY MIĄŻSZOŚCI DRZEW NA POWIERZCHNIACH PRÓBNYCH W RÓŻNOWIEKOWYCH LASACH GÓRSKICH
 SCIENTIARUM POLONORUMACTA Silv. Colendar. Rat. Ind. Lignar. 3(2) 2004, 5-11 ZMIENNOŚĆ SUMY MIĄŻSZOŚCI DRZEW NA POWIERZCHNIACH PRÓBNYCH W RÓŻNOWIEKOWYCH LASACH GÓRSKICH Jan Banaś Akademia Rolnicza w Krakowie
SCIENTIARUM POLONORUMACTA Silv. Colendar. Rat. Ind. Lignar. 3(2) 2004, 5-11 ZMIENNOŚĆ SUMY MIĄŻSZOŚCI DRZEW NA POWIERZCHNIACH PRÓBNYCH W RÓŻNOWIEKOWYCH LASACH GÓRSKICH Jan Banaś Akademia Rolnicza w Krakowie
IDENTYFIKACJA OBSZARÓW O NISKIEJ ZDROWOTNOSCI DRZEWOSTANÓW
 IDENTYFIKACJA OBSZARÓW O NISKIEJ ZDROWOTNOSCI DRZEWOSTANÓW W ŚWIETLE WYNIKÓW MONITORINGU LASÓW Z LAT 2000-2014 Paweł Lech Jadwiga Małachowska Robert Hildebrand Zakład Zarządzania Zasobami Leśnymi Instytut
IDENTYFIKACJA OBSZARÓW O NISKIEJ ZDROWOTNOSCI DRZEWOSTANÓW W ŚWIETLE WYNIKÓW MONITORINGU LASÓW Z LAT 2000-2014 Paweł Lech Jadwiga Małachowska Robert Hildebrand Zakład Zarządzania Zasobami Leśnymi Instytut
Wykład Centralne twierdzenie graniczne. Statystyka matematyczna: Estymacja parametrów rozkładu
 Wykład 11-12 Centralne twierdzenie graniczne Statystyka matematyczna: Estymacja parametrów rozkładu Centralne twierdzenie graniczne (CTG) (Central Limit Theorem - CLT) Centralne twierdzenie graniczne (Lindenberga-Levy'ego)
Wykład 11-12 Centralne twierdzenie graniczne Statystyka matematyczna: Estymacja parametrów rozkładu Centralne twierdzenie graniczne (CTG) (Central Limit Theorem - CLT) Centralne twierdzenie graniczne (Lindenberga-Levy'ego)
Statystyki: miary opisujące rozkład! np. : średnia, frakcja (procent), odchylenie standardowe, wariancja, mediana itd.
 Wnioskowanie statystyczne obejmujące metody pozwalające na uogólnianie wyników z próby na nieznane wartości parametrów oraz szacowanie błędów tego uogólnienia. Przewidujemy nieznaną wartości parametru
Wnioskowanie statystyczne obejmujące metody pozwalające na uogólnianie wyników z próby na nieznane wartości parametrów oraz szacowanie błędów tego uogólnienia. Przewidujemy nieznaną wartości parametru
Estymacja punktowa i przedziałowa
 Temat: Estymacja punktowa i przedziałowa Kody znaków: żółte wyróżnienie nowe pojęcie czerwony uwaga kursywa komentarz 1 Zagadnienia 1. Statystyczny opis próby. Idea estymacji punktowej pojęcie estymatora
Temat: Estymacja punktowa i przedziałowa Kody znaków: żółte wyróżnienie nowe pojęcie czerwony uwaga kursywa komentarz 1 Zagadnienia 1. Statystyczny opis próby. Idea estymacji punktowej pojęcie estymatora
STATYSTYKA MATEMATYCZNA
 STATYSTYKA MATEMATYCZNA 1. Wykład wstępny. Teoria prawdopodobieństwa i elementy kombinatoryki 2. Zmienne losowe i ich rozkłady 3. Populacje i próby danych, estymacja parametrów 4. Testowanie hipotez 5.
STATYSTYKA MATEMATYCZNA 1. Wykład wstępny. Teoria prawdopodobieństwa i elementy kombinatoryki 2. Zmienne losowe i ich rozkłady 3. Populacje i próby danych, estymacja parametrów 4. Testowanie hipotez 5.
Statystyka matematyczna dla leśników
 Statystyka matematyczna dla leśników Wydział Leśny Kierunek leśnictwo Studia Stacjonarne I Stopnia Rok akademicki 03/04 Wykład 5 Testy statystyczne Ogólne zasady testowania hipotez statystycznych, rodzaje
Statystyka matematyczna dla leśników Wydział Leśny Kierunek leśnictwo Studia Stacjonarne I Stopnia Rok akademicki 03/04 Wykład 5 Testy statystyczne Ogólne zasady testowania hipotez statystycznych, rodzaje
Statystyki: miary opisujące rozkład! np. : średnia, frakcja (procent), odchylenie standardowe, wariancja, mediana itd.
 Wnioskowanie statystyczne obejmujące metody pozwalające na uogólnianie wyników z próby na nieznane wartości parametrów oraz szacowanie błędów tego uogólnienia. Przewidujemy nieznaną wartości parametru
Wnioskowanie statystyczne obejmujące metody pozwalające na uogólnianie wyników z próby na nieznane wartości parametrów oraz szacowanie błędów tego uogólnienia. Przewidujemy nieznaną wartości parametru
Pobieranie prób i rozkład z próby
 Pobieranie prób i rozkład z próby Marcin Zajenkowski Marcin Zajenkowski () Pobieranie prób i rozkład z próby 1 / 15 Populacja i próba Populacja dowolnie określony zespół przedmiotów, obserwacji, osób itp.
Pobieranie prób i rozkład z próby Marcin Zajenkowski Marcin Zajenkowski () Pobieranie prób i rozkład z próby 1 / 15 Populacja i próba Populacja dowolnie określony zespół przedmiotów, obserwacji, osób itp.
Zakład Urządzania Lasu. Taksacja inwentaryzacja zapasu
 Zakład Urządzania Lasu Taksacja inwentaryzacja zapasu prace inwentaryzacyjne Wg instrukcji UL 2003 i 2011 Zakład Urządzania Lasu Na najbliższych ćwiczeniach Kolokwium nr 1 PUL, mapy, podział powierzchniowy
Zakład Urządzania Lasu Taksacja inwentaryzacja zapasu prace inwentaryzacyjne Wg instrukcji UL 2003 i 2011 Zakład Urządzania Lasu Na najbliższych ćwiczeniach Kolokwium nr 1 PUL, mapy, podział powierzchniowy
Statystyka i opracowanie danych Podstawy wnioskowania statystycznego. Prawo wielkich liczb. Centralne twierdzenie graniczne. Estymacja i estymatory
 Statystyka i opracowanie danych Podstawy wnioskowania statystycznego. Prawo wielkich liczb. Centralne twierdzenie graniczne. Estymacja i estymatory Dr Anna ADRIAN Paw B5, pok 407 adrian@tempus.metal.agh.edu.pl
Statystyka i opracowanie danych Podstawy wnioskowania statystycznego. Prawo wielkich liczb. Centralne twierdzenie graniczne. Estymacja i estymatory Dr Anna ADRIAN Paw B5, pok 407 adrian@tempus.metal.agh.edu.pl
Inwentaryzacja zasobów drzewnych w IV rewizji urządzania lasu
 Inwentaryzacja zasobów drzewnych w IV rewizji urządzania lasu - ogólnie Obecnie obowiązuje statystyczna metoda reprezentacyjnego pomiaru miąższości w obrębie leśnym. Metoda reprezentacyjna oznacza, iż
Inwentaryzacja zasobów drzewnych w IV rewizji urządzania lasu - ogólnie Obecnie obowiązuje statystyczna metoda reprezentacyjnego pomiaru miąższości w obrębie leśnym. Metoda reprezentacyjna oznacza, iż
Populacja generalna (zbiorowość generalna) zbiór obejmujący wszystkie elementy będące przedmiotem badań Próba (podzbiór zbiorowości generalnej) część
 Populacja generalna (zbiorowość generalna) zbiór obejmujący wszystkie elementy będące przedmiotem badań Próba (podzbiór zbiorowości generalnej) część populacji, którą podaje się badaniu statystycznemu
Populacja generalna (zbiorowość generalna) zbiór obejmujący wszystkie elementy będące przedmiotem badań Próba (podzbiór zbiorowości generalnej) część populacji, którą podaje się badaniu statystycznemu
Warstwowanie drzewostanów w statystycznej metodzie reprezentacyjnej pomiaru miąższości obrębu leśnego praktyczna realizacja założeń
 sylwan 154 (6): 397 404, 2010 Warstwowanie drzewostanów w statystycznej metodzie reprezentacyjnej pomiaru miąższości obrębu leśnego praktyczna realizacja założeń Problems with strata determination in application
sylwan 154 (6): 397 404, 2010 Warstwowanie drzewostanów w statystycznej metodzie reprezentacyjnej pomiaru miąższości obrębu leśnego praktyczna realizacja założeń Problems with strata determination in application
BADANIA ZRÓŻNICOWANIA RYZYKA WYPADKÓW PRZY PRACY NA PRZYKŁADZIE ANALIZY STATYSTYKI WYPADKÓW DLA BRANŻY GÓRNICTWA I POLSKI
 14 BADANIA ZRÓŻNICOWANIA RYZYKA WYPADKÓW PRZY PRACY NA PRZYKŁADZIE ANALIZY STATYSTYKI WYPADKÓW DLA BRANŻY GÓRNICTWA I POLSKI 14.1 WSTĘP Ogólne wymagania prawne dotyczące przy pracy określają m.in. przepisy
14 BADANIA ZRÓŻNICOWANIA RYZYKA WYPADKÓW PRZY PRACY NA PRZYKŁADZIE ANALIZY STATYSTYKI WYPADKÓW DLA BRANŻY GÓRNICTWA I POLSKI 14.1 WSTĘP Ogólne wymagania prawne dotyczące przy pracy określają m.in. przepisy
Weryfikacja hipotez statystycznych, parametryczne testy istotności w populacji
 Weryfikacja hipotez statystycznych, parametryczne testy istotności w populacji Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych Wydział Informatyki Politechniki
Weryfikacja hipotez statystycznych, parametryczne testy istotności w populacji Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych Wydział Informatyki Politechniki
Inwentaryzacja zasobów drzewnych
 Inwentaryzacja zasobów drzewnych Metody inwentaryzacji zapasu. Charakterystyka metody reprezentacyjnej. Przypomnienie Metody inwentaryzacji: - pomiarowa - szacunkowa - pomiarowo-szacunkowa - reprezentacyjna
Inwentaryzacja zasobów drzewnych Metody inwentaryzacji zapasu. Charakterystyka metody reprezentacyjnej. Przypomnienie Metody inwentaryzacji: - pomiarowa - szacunkowa - pomiarowo-szacunkowa - reprezentacyjna
W1. Wprowadzenie. Statystyka opisowa
 W1. Wprowadzenie. Statystyka opisowa dr hab. Jerzy Nakielski Zakład Biofizyki i Morfogenezy Roślin Plan wykładu: 1. O co chodzi w statystyce 2. Etapy badania statystycznego 3. Zmienna losowa, rozkład
W1. Wprowadzenie. Statystyka opisowa dr hab. Jerzy Nakielski Zakład Biofizyki i Morfogenezy Roślin Plan wykładu: 1. O co chodzi w statystyce 2. Etapy badania statystycznego 3. Zmienna losowa, rozkład
Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć)
 Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć) 1. Populacja generalna a losowa próba, parametr rozkładu cechy a jego ocena z losowej próby, miary opisu statystycznego
Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć) 1. Populacja generalna a losowa próba, parametr rozkładu cechy a jego ocena z losowej próby, miary opisu statystycznego
RÓWNOWAŻNOŚĆ METOD BADAWCZYCH
 RÓWNOWAŻNOŚĆ METOD BADAWCZYCH Piotr Konieczka Katedra Chemii Analitycznej Wydział Chemiczny Politechnika Gdańska Równoważność metod??? 2 Zgodność wyników analitycznych otrzymanych z wykorzystaniem porównywanych
RÓWNOWAŻNOŚĆ METOD BADAWCZYCH Piotr Konieczka Katedra Chemii Analitycznej Wydział Chemiczny Politechnika Gdańska Równoważność metod??? 2 Zgodność wyników analitycznych otrzymanych z wykorzystaniem porównywanych
METODY STATYSTYCZNE W BIOLOGII
 METODY STATYSTYCZNE W BIOLOGII 1. Wykład wstępny 2. Populacje i próby danych 3. Testowanie hipotez i estymacja parametrów 4. Planowanie eksperymentów biologicznych 5. Najczęściej wykorzystywane testy statystyczne
METODY STATYSTYCZNE W BIOLOGII 1. Wykład wstępny 2. Populacje i próby danych 3. Testowanie hipotez i estymacja parametrów 4. Planowanie eksperymentów biologicznych 5. Najczęściej wykorzystywane testy statystyczne
Wykład 1. Podstawowe pojęcia Metody opisowe w analizie rozkładu cechy
 Wykład Podstawowe pojęcia Metody opisowe w analizie rozkładu cechy Zbiorowość statystyczna - zbiór elementów lub wyników jakiegoś procesu powiązanych ze sobą logicznie (tzn. posiadających wspólne cechy
Wykład Podstawowe pojęcia Metody opisowe w analizie rozkładu cechy Zbiorowość statystyczna - zbiór elementów lub wyników jakiegoś procesu powiązanych ze sobą logicznie (tzn. posiadających wspólne cechy
Zad. 4 Należy określić rodzaj testu (jedno czy dwustronny) oraz wartości krytyczne z lub t dla określonych hipotez i ich poziomów istotności:
 Zadania ze statystyki cz. 7. Zad.1 Z populacji wyłoniono próbę wielkości 64 jednostek. Średnia arytmetyczna wartość cechy wyniosła 110, zaś odchylenie standardowe 16. Należy wyznaczyć przedział ufności
Zadania ze statystyki cz. 7. Zad.1 Z populacji wyłoniono próbę wielkości 64 jednostek. Średnia arytmetyczna wartość cechy wyniosła 110, zaś odchylenie standardowe 16. Należy wyznaczyć przedział ufności
Po co nam charakterystyki liczbowe? Katarzyna Lubnauer 34
 Po co nam charakterystyki liczbowe? Katarzyna Lubnauer 34 Def. Charakterystyki liczbowe to wielkości wyznaczone na podstawie danych statystycznych, charakteryzujące własności badanej cechy. Klasyfikacja
Po co nam charakterystyki liczbowe? Katarzyna Lubnauer 34 Def. Charakterystyki liczbowe to wielkości wyznaczone na podstawie danych statystycznych, charakteryzujące własności badanej cechy. Klasyfikacja
Badania sondażowe. Schematy losowania. Agnieszka Zięba. Zakład Badań Marketingowych Instytut Statystyki i Demografii Szkoła Główna Handlowa
 Badania sondażowe Schematy losowania Agnieszka Zięba Zakład Badań Marketingowych Instytut Statystyki i Demografii Szkoła Główna Handlowa 1 Próba jako miniatura populacji CELOWA subiektywny dobór jednostek
Badania sondażowe Schematy losowania Agnieszka Zięba Zakład Badań Marketingowych Instytut Statystyki i Demografii Szkoła Główna Handlowa 1 Próba jako miniatura populacji CELOWA subiektywny dobór jednostek
Zróżnicowanie bogactwa gatunkowego w zależności od wielkości próby i przyjętego wariantu inwentaryzacji
 Zróżnicowanie bogactwa gatunkowego w zależności od wielkości próby i przyjętego wariantu inwentaryzacji Edward Stępień, Zbigniew Sierdziński ARTYKUŁY / ARTICLES Abstrakt. W pracy dokonano oceny zasobów
Zróżnicowanie bogactwa gatunkowego w zależności od wielkości próby i przyjętego wariantu inwentaryzacji Edward Stępień, Zbigniew Sierdziński ARTYKUŁY / ARTICLES Abstrakt. W pracy dokonano oceny zasobów
Wnioskowanie statystyczne. Statystyka w 5
 Wnioskowanie statystyczne tatystyka w 5 Rozkłady statystyk z próby Próba losowa pobrana z populacji stanowi realizacje zmiennej losowej jak ciąg zmiennych losowych (X, X,... X ) niezależnych i mających
Wnioskowanie statystyczne tatystyka w 5 Rozkłady statystyk z próby Próba losowa pobrana z populacji stanowi realizacje zmiennej losowej jak ciąg zmiennych losowych (X, X,... X ) niezależnych i mających
Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć)
 Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć) 1. Populacja generalna a losowa próba, parametr rozkładu cechy a jego ocena z losowej próby, miary opisu statystycznego
Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć) 1. Populacja generalna a losowa próba, parametr rozkładu cechy a jego ocena z losowej próby, miary opisu statystycznego
STATYSTYKA MATEMATYCZNA WYKŁAD 3. Populacje i próby danych
 STATYSTYKA MATEMATYCZNA WYKŁAD 3 Populacje i próby danych POPULACJA I PRÓBA DANYCH POPULACJA population Obserwacje dla wszystkich osobników danego gatunku / rasy PRÓBA DANYCH sample Obserwacje dotyczące
STATYSTYKA MATEMATYCZNA WYKŁAD 3 Populacje i próby danych POPULACJA I PRÓBA DANYCH POPULACJA population Obserwacje dla wszystkich osobników danego gatunku / rasy PRÓBA DANYCH sample Obserwacje dotyczące
Zadania ze statystyki, cz.7 - hipotezy statystyczne, błąd standardowy, testowanie hipotez statystycznych
 Zadania ze statystyki, cz.7 - hipotezy statystyczne, błąd standardowy, testowanie hipotez statystycznych Zad. 1 Średnia ocen z semestru letniego w populacji studentów socjologii w roku akademickim 2011/2012
Zadania ze statystyki, cz.7 - hipotezy statystyczne, błąd standardowy, testowanie hipotez statystycznych Zad. 1 Średnia ocen z semestru letniego w populacji studentów socjologii w roku akademickim 2011/2012
ZDROWOTNOŚĆ WYBRANYCH DRZEWOSTANÓW SOSNOWYCH NADLEŚNICTWA SZCZECINEK HEALTH CONDITION OF SELECTED SCOTS PINE STANDS IN SZCZECINEK FOREST DISTRICT
 DOI: 10.5604/20811438.1206153 Kinga Blajer, Cezary Beker Uniwersytet Przyrodniczy w Poznaniu, e-mail: kinga.blajer@gmail.com, bekerc@up.poznan.pl ZDROWOTNOŚĆ WYBRANYCH DRZEWOSTANÓW SOSNOWYCH NADLEŚNICTWA
DOI: 10.5604/20811438.1206153 Kinga Blajer, Cezary Beker Uniwersytet Przyrodniczy w Poznaniu, e-mail: kinga.blajer@gmail.com, bekerc@up.poznan.pl ZDROWOTNOŚĆ WYBRANYCH DRZEWOSTANÓW SOSNOWYCH NADLEŚNICTWA
Statystyka matematyczna. dr Katarzyna Góral-Radziszewska Katedra Genetyki i Ogólnej Hodowli Zwierząt
 Statystyka matematyczna dr Katarzyna Góral-Radziszewska Katedra Genetyki i Ogólnej Hodowli Zwierząt Zasady zaliczenia przedmiotu: część wykładowa Maksymalna liczba punktów do zdobycia 40. Egzamin będzie
Statystyka matematyczna dr Katarzyna Góral-Radziszewska Katedra Genetyki i Ogólnej Hodowli Zwierząt Zasady zaliczenia przedmiotu: część wykładowa Maksymalna liczba punktów do zdobycia 40. Egzamin będzie
Odchudzamy serię danych, czyli jak wykryć i usunąć wyniki obarczone błędami grubymi
 Odchudzamy serię danych, czyli jak wykryć i usunąć wyniki obarczone błędami grubymi Piotr Konieczka Katedra Chemii Analitycznej Wydział Chemiczny Politechnika Gdańska D syst D śr m 1 3 5 2 4 6 śr j D 1
Odchudzamy serię danych, czyli jak wykryć i usunąć wyniki obarczone błędami grubymi Piotr Konieczka Katedra Chemii Analitycznej Wydział Chemiczny Politechnika Gdańska D syst D śr m 1 3 5 2 4 6 śr j D 1
POJĘCIA WSTĘPNE. STATYSTYKA - nauka traktująca o metodach ilościowych badania prawidłowości zjawisk (procesów) masowych.
 [1] POJĘCIA WSTĘPNE STATYSTYKA - nauka traktująca o metodach ilościowych badania prawidłowości zjawisk (procesów) masowych. BADANIE STATYSTYCZNE - ogół prac mających na celu poznanie struktury określonej
[1] POJĘCIA WSTĘPNE STATYSTYKA - nauka traktująca o metodach ilościowych badania prawidłowości zjawisk (procesów) masowych. BADANIE STATYSTYCZNE - ogół prac mających na celu poznanie struktury określonej
Testy nieparametryczne
 Testy nieparametryczne Testy nieparametryczne możemy stosować, gdy nie są spełnione założenia wymagane dla testów parametrycznych. Stosujemy je również, gdy dane można uporządkować według określonych kryteriów
Testy nieparametryczne Testy nieparametryczne możemy stosować, gdy nie są spełnione założenia wymagane dla testów parametrycznych. Stosujemy je również, gdy dane można uporządkować według określonych kryteriów
Testowanie hipotez statystycznych. Wnioskowanie statystyczne
 Testowanie hipotez statystycznych Wnioskowanie statystyczne Hipoteza statystyczna to dowolne przypuszczenie co do rozkładu populacji generalnej (jego postaci funkcyjnej lub wartości parametrów). Hipotezy
Testowanie hipotez statystycznych Wnioskowanie statystyczne Hipoteza statystyczna to dowolne przypuszczenie co do rozkładu populacji generalnej (jego postaci funkcyjnej lub wartości parametrów). Hipotezy
Wydział Matematyki. Testy zgodności. Wykład 03
 Wydział Matematyki Testy zgodności Wykład 03 Testy zgodności W testach zgodności badamy postać rozkładu teoretycznego zmiennej losowej skokowej lub ciągłej. Weryfikują one stawiane przez badaczy hipotezy
Wydział Matematyki Testy zgodności Wykład 03 Testy zgodności W testach zgodności badamy postać rozkładu teoretycznego zmiennej losowej skokowej lub ciągłej. Weryfikują one stawiane przez badaczy hipotezy
IV WYKŁAD STATYSTYKA. 26/03/2014 B8 sala 0.10B Godz. 15:15
 IV WYKŁAD STATYSTYKA 26/03/2014 B8 sala 0.10B Godz. 15:15 WYKŁAD 4 Populacja generalna, próba, losowanie próby, estymatory Statystyka (populacja generalna, populacja próbna, próbka mała, próbka duża, reprezentatywność,
IV WYKŁAD STATYSTYKA 26/03/2014 B8 sala 0.10B Godz. 15:15 WYKŁAD 4 Populacja generalna, próba, losowanie próby, estymatory Statystyka (populacja generalna, populacja próbna, próbka mała, próbka duża, reprezentatywność,
Jeśli powyższy opis nie jest zrozumiały należy powtórzyć zagadnienie standaryzacji zanim przejdzie się dalej!
 CO POWINNIŚMY WIEDZIEĆ (I ROZUMIEĆ) ZABIERAJĄC SIĘ DO CZYTANIA 1. Jeśli mamy wynik (np. z kolokwium) podany w wartościach standaryzowanych (np.: z=0,8) to wiemy, że aby ustalić jaki był wynik przed standaryzacją
CO POWINNIŚMY WIEDZIEĆ (I ROZUMIEĆ) ZABIERAJĄC SIĘ DO CZYTANIA 1. Jeśli mamy wynik (np. z kolokwium) podany w wartościach standaryzowanych (np.: z=0,8) to wiemy, że aby ustalić jaki był wynik przed standaryzacją
LABORATORIUM Populacja Generalna (PG) 2. Próba (P n ) 3. Kryterium 3σ 4. Błąd Średniej Arytmetycznej 5. Estymatory 6. Teoria Estymacji (cz.
 LABORATORIUM 4 1. Populacja Generalna (PG) 2. Próba (P n ) 3. Kryterium 3σ 4. Błąd Średniej Arytmetycznej 5. Estymatory 6. Teoria Estymacji (cz. I) WNIOSKOWANIE STATYSTYCZNE (STATISTICAL INFERENCE) Populacja
LABORATORIUM 4 1. Populacja Generalna (PG) 2. Próba (P n ) 3. Kryterium 3σ 4. Błąd Średniej Arytmetycznej 5. Estymatory 6. Teoria Estymacji (cz. I) WNIOSKOWANIE STATYSTYCZNE (STATISTICAL INFERENCE) Populacja
2. Wyposażenie bazy sprzętu przeciwpożarowego stanowi w szczególności:
 Dziennik Ustaw Nr 73-3950- Poz. 824 10. 1. Zabezpieczeniu przeciwpożarowemu lasów służą pasy przeciwpożarowe w lasach położonych przy obiektach mogących stanowić zagrożenie pożarowe lasu. 2. Wyróżnia się
Dziennik Ustaw Nr 73-3950- Poz. 824 10. 1. Zabezpieczeniu przeciwpożarowemu lasów służą pasy przeciwpożarowe w lasach położonych przy obiektach mogących stanowić zagrożenie pożarowe lasu. 2. Wyróżnia się
Zadania ze statystyki, cz.6
 Zadania ze statystyki, cz.6 Zad.1 Proszę wskazać, jaką część pola pod krzywą normalną wyznaczają wartości Z rozkładu dystrybuanty rozkładu normalnego: - Z > 1,25 - Z > 2,23 - Z < -1,23 - Z > -1,16 - Z
Zadania ze statystyki, cz.6 Zad.1 Proszę wskazać, jaką część pola pod krzywą normalną wyznaczają wartości Z rozkładu dystrybuanty rozkładu normalnego: - Z > 1,25 - Z > 2,23 - Z < -1,23 - Z > -1,16 - Z
Statystyka. Wykład 3. Magdalena Alama-Bućko. 6 marca Magdalena Alama-Bućko Statystyka 6 marca / 28
 Statystyka Wykład 3 Magdalena Alama-Bućko 6 marca 2017 Magdalena Alama-Bućko Statystyka 6 marca 2017 1 / 28 Szeregi rozdzielcze przedziałowe - kwartyle - przypomnienie Po ustaleniu przedziału, w którym
Statystyka Wykład 3 Magdalena Alama-Bućko 6 marca 2017 Magdalena Alama-Bućko Statystyka 6 marca 2017 1 / 28 Szeregi rozdzielcze przedziałowe - kwartyle - przypomnienie Po ustaleniu przedziału, w którym
OPTYMALIZACJA LICZBY WARSTW DLA ALOKACJI NEYMANA
 Tomasz Bąk Uniwersytet Ekonomiczny w Katowicach OPTYMALIZACJA LICZBY WARSTW DLA ALOKACJI NEYMANA Wprowadzenie Losowanie warstwowe jest często wykorzystywaną w praktyce metodą doboru próby w przypadku estymacji
Tomasz Bąk Uniwersytet Ekonomiczny w Katowicach OPTYMALIZACJA LICZBY WARSTW DLA ALOKACJI NEYMANA Wprowadzenie Losowanie warstwowe jest często wykorzystywaną w praktyce metodą doboru próby w przypadku estymacji
Rozkłady statystyk z próby
 Rozkłady statystyk z próby Rozkłady statystyk z próby Przypuśćmy, że wykonujemy serię doświadczeń polegających na 4 krotnym rzucie symetryczną kostką do gry, obserwując liczbę wyrzuconych oczek Nr kolejny
Rozkłady statystyk z próby Rozkłady statystyk z próby Przypuśćmy, że wykonujemy serię doświadczeń polegających na 4 krotnym rzucie symetryczną kostką do gry, obserwując liczbę wyrzuconych oczek Nr kolejny
Oszacowanie i rozkład t
 Oszacowanie i rozkład t Marcin Zajenkowski Marcin Zajenkowski () Oszacowanie i rozkład t 1 / 31 Oszacowanie 1 Na podstawie danych z próby szacuje się wiele wartości w populacji, np.: jakie jest poparcie
Oszacowanie i rozkład t Marcin Zajenkowski Marcin Zajenkowski () Oszacowanie i rozkład t 1 / 31 Oszacowanie 1 Na podstawie danych z próby szacuje się wiele wartości w populacji, np.: jakie jest poparcie
NAPRĘŻENIA ŚCISKAJĄCE PRZY 10% ODKSZTAŁCENIU WZGLĘDNYM PRÓBEK NORMOWYCH POBRANYCH Z PŁYT EPS O RÓŻNEJ GRUBOŚCI
 PRACE INSTYTUTU TECHNIKI BUDOWLANEJ - KWARTALNIK 1 (145) 2008 BUILDING RESEARCH INSTITUTE - QUARTERLY No 1 (145) 2008 Zbigniew Owczarek* NAPRĘŻENIA ŚCISKAJĄCE PRZY 10% ODKSZTAŁCENIU WZGLĘDNYM PRÓBEK NORMOWYCH
PRACE INSTYTUTU TECHNIKI BUDOWLANEJ - KWARTALNIK 1 (145) 2008 BUILDING RESEARCH INSTITUTE - QUARTERLY No 1 (145) 2008 Zbigniew Owczarek* NAPRĘŻENIA ŚCISKAJĄCE PRZY 10% ODKSZTAŁCENIU WZGLĘDNYM PRÓBEK NORMOWYCH
Akademia Morska w Szczecinie. Wydział Mechaniczny
 Akademia Morska w Szczecinie Wydział Mechaniczny ROZPRAWA DOKTORSKA mgr inż. Marcin Kołodziejski Analiza metody obsługiwania zarządzanego niezawodnością pędników azymutalnych platformy pływającej Promotor:
Akademia Morska w Szczecinie Wydział Mechaniczny ROZPRAWA DOKTORSKA mgr inż. Marcin Kołodziejski Analiza metody obsługiwania zarządzanego niezawodnością pędników azymutalnych platformy pływającej Promotor:
Statystyka Matematyczna Anna Janicka
 Statystyka Matematyczna Anna Janicka wykład I, 22.02.2016 STATYSTYKA OPISOWA, cz. I Kwestie techniczne Kontakt: ajanicka@wne.uw.edu.pl Dyżur: strona z materiałami z przedmiotu: wne.uw.edu.pl/azylicz akson.sgh.waw.pl/~aborata
Statystyka Matematyczna Anna Janicka wykład I, 22.02.2016 STATYSTYKA OPISOWA, cz. I Kwestie techniczne Kontakt: ajanicka@wne.uw.edu.pl Dyżur: strona z materiałami z przedmiotu: wne.uw.edu.pl/azylicz akson.sgh.waw.pl/~aborata
Analiza i monitoring środowiska
 Analiza i monitoring środowiska CHC 017003L (opracował W. Zierkiewicz) Ćwiczenie 1: Analiza statystyczna wyników pomiarów. 1. WSTĘP Otrzymany w wyniku przeprowadzonej analizy ilościowej wynik pomiaru zawartości
Analiza i monitoring środowiska CHC 017003L (opracował W. Zierkiewicz) Ćwiczenie 1: Analiza statystyczna wyników pomiarów. 1. WSTĘP Otrzymany w wyniku przeprowadzonej analizy ilościowej wynik pomiaru zawartości
Testowanie hipotez statystycznych cd.
 Temat Testowanie hipotez statystycznych cd. Kody znaków: żółte wyróżnienie nowe pojęcie pomarańczowy uwaga kursywa komentarz 1 Zagadnienia omawiane na zajęciach 1. Przykłady testowania hipotez dotyczących:
Temat Testowanie hipotez statystycznych cd. Kody znaków: żółte wyróżnienie nowe pojęcie pomarańczowy uwaga kursywa komentarz 1 Zagadnienia omawiane na zajęciach 1. Przykłady testowania hipotez dotyczących:
5. WNIOSKOWANIE PSYCHOMETRYCZNE
 5. WNIOSKOWANIE PSYCHOMETRYCZNE Model klasyczny Gulliksena Wynik otrzymany i prawdziwy Błąd pomiaru Rzetelność pomiaru testem Standardowy błąd pomiaru Błąd estymacji wyniku prawdziwego Teoria Odpowiadania
5. WNIOSKOWANIE PSYCHOMETRYCZNE Model klasyczny Gulliksena Wynik otrzymany i prawdziwy Błąd pomiaru Rzetelność pomiaru testem Standardowy błąd pomiaru Błąd estymacji wyniku prawdziwego Teoria Odpowiadania
STATYSTYKA MATEMATYCZNA WYKŁAD 4. WERYFIKACJA HIPOTEZ PARAMETRYCZNYCH X - cecha populacji, θ parametr rozkładu cechy X.
 STATYSTYKA MATEMATYCZNA WYKŁAD 4 WERYFIKACJA HIPOTEZ PARAMETRYCZNYCH X - cecha populacji, θ parametr rozkładu cechy X. Wysuwamy hipotezy: zerową (podstawową H ( θ = θ i alternatywną H, która ma jedną z
STATYSTYKA MATEMATYCZNA WYKŁAD 4 WERYFIKACJA HIPOTEZ PARAMETRYCZNYCH X - cecha populacji, θ parametr rozkładu cechy X. Wysuwamy hipotezy: zerową (podstawową H ( θ = θ i alternatywną H, która ma jedną z
Dokumentacja końcowa
 SZKOŁA GŁÓWNA GOSPODARSTWA WIEJSKIEGO W WARSZAWIE WYDZIAŁ LEŚNY KATEDRA HODOWLI LASU OCENA WZROSTU, JAKOŚCI ORAZ ZAGROŻENIA PRZEZ GRZYBY I OWADY UPRAW NA POWIERZCHNI POHURAGANOWEJ NADLEŚNICTWA PRZEDBÓRZ
SZKOŁA GŁÓWNA GOSPODARSTWA WIEJSKIEGO W WARSZAWIE WYDZIAŁ LEŚNY KATEDRA HODOWLI LASU OCENA WZROSTU, JAKOŚCI ORAZ ZAGROŻENIA PRZEZ GRZYBY I OWADY UPRAW NA POWIERZCHNI POHURAGANOWEJ NADLEŚNICTWA PRZEDBÓRZ
Weryfikacja hipotez statystycznych. KG (CC) Statystyka 26 V / 1
 Weryfikacja hipotez statystycznych KG (CC) Statystyka 26 V 2009 1 / 1 Sformułowanie problemu Weryfikacja hipotez statystycznych jest drugą (po estymacji) metodą uogólniania wyników uzyskanych w próbie
Weryfikacja hipotez statystycznych KG (CC) Statystyka 26 V 2009 1 / 1 Sformułowanie problemu Weryfikacja hipotez statystycznych jest drugą (po estymacji) metodą uogólniania wyników uzyskanych w próbie
WYKŁAD 5 TEORIA ESTYMACJI II
 WYKŁAD 5 TEORIA ESTYMACJI II Teoria estymacji (wyznaczanie przedziałów ufności, błąd badania statystycznego, poziom ufności, minimalna liczba pomiarów). PRÓBA Próba powinna być reprezentacyjna tj. jak
WYKŁAD 5 TEORIA ESTYMACJI II Teoria estymacji (wyznaczanie przedziałów ufności, błąd badania statystycznego, poziom ufności, minimalna liczba pomiarów). PRÓBA Próba powinna być reprezentacyjna tj. jak
Wykład 3 Hipotezy statystyczne
 Wykład 3 Hipotezy statystyczne Hipotezą statystyczną nazywamy każde przypuszczenie dotyczące nieznanego rozkładu obserwowanej zmiennej losowej (cechy populacji generalnej) Hipoteza zerowa (H 0 ) jest hipoteza
Wykład 3 Hipotezy statystyczne Hipotezą statystyczną nazywamy każde przypuszczenie dotyczące nieznanego rozkładu obserwowanej zmiennej losowej (cechy populacji generalnej) Hipoteza zerowa (H 0 ) jest hipoteza
Statystyka matematyczna i ekonometria
 Statystyka matematyczna i ekonometria prof. dr hab. inż. Jacek Mercik B4 pok. 55 jacek.mercik@pwr.wroc.pl (tylko z konta studenckiego z serwera PWr) Konsultacje, kontakt itp. Strona WWW Elementy wykładu.
Statystyka matematyczna i ekonometria prof. dr hab. inż. Jacek Mercik B4 pok. 55 jacek.mercik@pwr.wroc.pl (tylko z konta studenckiego z serwera PWr) Konsultacje, kontakt itp. Strona WWW Elementy wykładu.
Statystyka. #5 Testowanie hipotez statystycznych. Aneta Dzik-Walczak Małgorzata Kalbarczyk-Stęclik. rok akademicki 2016/ / 28
 Statystyka #5 Testowanie hipotez statystycznych Aneta Dzik-Walczak Małgorzata Kalbarczyk-Stęclik rok akademicki 2016/2017 1 / 28 Testowanie hipotez statystycznych 2 / 28 Testowanie hipotez statystycznych
Statystyka #5 Testowanie hipotez statystycznych Aneta Dzik-Walczak Małgorzata Kalbarczyk-Stęclik rok akademicki 2016/2017 1 / 28 Testowanie hipotez statystycznych 2 / 28 Testowanie hipotez statystycznych
Praktyczne aspekty doboru próby. Dariusz Przybysz Warszawa, 2 czerwca 2015
 Praktyczne aspekty doboru próby Dariusz Przybysz Warszawa, 2 czerwca 2015 Określenie populacji Przed przystąpieniem do badania, wybraniem sposobu doboru próby konieczne jest precyzyjne określenie populacji,
Praktyczne aspekty doboru próby Dariusz Przybysz Warszawa, 2 czerwca 2015 Określenie populacji Przed przystąpieniem do badania, wybraniem sposobu doboru próby konieczne jest precyzyjne określenie populacji,
STATYSTYKA - PRZYKŁADOWE ZADANIA EGZAMINACYJNE
 STATYSTYKA - PRZYKŁADOWE ZADANIA EGZAMINACYJNE 1 W trakcie badania obliczono wartości średniej (15,4), mediany (13,6) oraz dominanty (10,0). Określ typ asymetrii rozkładu. 2 Wymień 3 cechy rozkładu Gauss
STATYSTYKA - PRZYKŁADOWE ZADANIA EGZAMINACYJNE 1 W trakcie badania obliczono wartości średniej (15,4), mediany (13,6) oraz dominanty (10,0). Określ typ asymetrii rozkładu. 2 Wymień 3 cechy rozkładu Gauss
ANALIZA DYNAMIKI DOCHODU KRAJOWEGO BRUTTO
 ANALIZA DYNAMIKI DOCHODU KRAJOWEGO BRUTTO Wprowadzenie Zmienność koniunktury gospodarczej jest kształtowana przez wiele różnych czynników ekonomicznych i pozaekonomicznych. Znajomość zmienności poszczególnych
ANALIZA DYNAMIKI DOCHODU KRAJOWEGO BRUTTO Wprowadzenie Zmienność koniunktury gospodarczej jest kształtowana przez wiele różnych czynników ekonomicznych i pozaekonomicznych. Znajomość zmienności poszczególnych
-> Średnia arytmetyczna (5) (4) ->Kwartyl dolny, mediana, kwartyl górny, moda - analogicznie jak
 Wzory dla szeregu szczegółowego: Wzory dla szeregu rozdzielczego punktowego: ->Średnia arytmetyczna ważona -> Średnia arytmetyczna (5) ->Średnia harmoniczna (1) ->Średnia harmoniczna (6) (2) ->Średnia
Wzory dla szeregu szczegółowego: Wzory dla szeregu rozdzielczego punktowego: ->Średnia arytmetyczna ważona -> Średnia arytmetyczna (5) ->Średnia harmoniczna (1) ->Średnia harmoniczna (6) (2) ->Średnia
W kolejnym kroku należy ustalić liczbę przedziałów k. W tym celu należy wykorzystać jeden ze wzorów:
 Na dzisiejszym wykładzie omówimy najważniejsze charakterystyki liczbowe występujące w statystyce opisowej. Poszczególne wzory będziemy podawać w miarę potrzeby w trzech postaciach: dla szeregu szczegółowego,
Na dzisiejszym wykładzie omówimy najważniejsze charakterystyki liczbowe występujące w statystyce opisowej. Poszczególne wzory będziemy podawać w miarę potrzeby w trzech postaciach: dla szeregu szczegółowego,
WNIOSKOWANIE STATYSTYCZNE
 STATYSTYKA WNIOSKOWANIE STATYSTYCZNE ESTYMACJA oszacowanie z pewną dokładnością wartości opisującej rozkład badanej cechy statystycznej. WERYFIKACJA HIPOTEZ sprawdzanie słuszności przypuszczeń dotyczących
STATYSTYKA WNIOSKOWANIE STATYSTYCZNE ESTYMACJA oszacowanie z pewną dokładnością wartości opisującej rozkład badanej cechy statystycznej. WERYFIKACJA HIPOTEZ sprawdzanie słuszności przypuszczeń dotyczących
Statystyka i Analiza Danych
 Warsztaty Statystyka i Analiza Danych Gdańsk, 20-22 lutego 2014 Zastosowania analizy wariancji w opracowywaniu wyników badań empirycznych Janusz Wątroba StatSoft Polska Centrum Zastosowań Matematyki -
Warsztaty Statystyka i Analiza Danych Gdańsk, 20-22 lutego 2014 Zastosowania analizy wariancji w opracowywaniu wyników badań empirycznych Janusz Wątroba StatSoft Polska Centrum Zastosowań Matematyki -
Streszczenie. Słowa kluczowe: towary paczkowane, statystyczna analiza procesu SPC
 Waldemar Samociuk Katedra Podstaw Techniki Akademia Rolnicza w Lublinie MONITOROWANIE PROCESU WAśENIA ZA POMOCĄ KART KONTROLNYCH Streszczenie Przedstawiono przykład analizy procesu pakowania. Ocenę procesu
Waldemar Samociuk Katedra Podstaw Techniki Akademia Rolnicza w Lublinie MONITOROWANIE PROCESU WAśENIA ZA POMOCĄ KART KONTROLNYCH Streszczenie Przedstawiono przykład analizy procesu pakowania. Ocenę procesu
Statystyka w pracy badawczej nauczyciela
 Statystyka w pracy badawczej nauczyciela Wykład 1: Terminologia badań statystycznych dr inż. Walery Susłow walery.suslow@ie.tu.koszalin.pl Statystyka (1) Statystyka to nauka zajmująca się zbieraniem, badaniem
Statystyka w pracy badawczej nauczyciela Wykład 1: Terminologia badań statystycznych dr inż. Walery Susłow walery.suslow@ie.tu.koszalin.pl Statystyka (1) Statystyka to nauka zajmująca się zbieraniem, badaniem
Statystyka. Rozkład prawdopodobieństwa Testowanie hipotez. Wykład III ( )
 Statystyka Rozkład prawdopodobieństwa Testowanie hipotez Wykład III (04.01.2016) Rozkład t-studenta Rozkład T jest rozkładem pomocniczym we wnioskowaniu statystycznym; stosuje się go wyznaczenia przedziału
Statystyka Rozkład prawdopodobieństwa Testowanie hipotez Wykład III (04.01.2016) Rozkład t-studenta Rozkład T jest rozkładem pomocniczym we wnioskowaniu statystycznym; stosuje się go wyznaczenia przedziału
FORECASTING THE DISTRIBUTION OF AMOUNT OF UNEMPLOYED BY THE REGIONS
 FOLIA UNIVERSITATIS AGRICULTURAE STETINENSIS Folia Univ. Agric. Stetin. 007, Oeconomica 54 (47), 73 80 Mateusz GOC PROGNOZOWANIE ROZKŁADÓW LICZBY BEZROBOTNYCH WEDŁUG MIAST I POWIATÓW FORECASTING THE DISTRIBUTION
FOLIA UNIVERSITATIS AGRICULTURAE STETINENSIS Folia Univ. Agric. Stetin. 007, Oeconomica 54 (47), 73 80 Mateusz GOC PROGNOZOWANIE ROZKŁADÓW LICZBY BEZROBOTNYCH WEDŁUG MIAST I POWIATÓW FORECASTING THE DISTRIBUTION
Niepewności pomiarów
 Niepewności pomiarów Międzynarodowa Organizacja Normalizacyjna (ISO) w roku 1995 opublikowała normy dotyczące terminologii i sposobu określania niepewności pomiarów [1]. W roku 1999 normy zostały opublikowane
Niepewności pomiarów Międzynarodowa Organizacja Normalizacyjna (ISO) w roku 1995 opublikowała normy dotyczące terminologii i sposobu określania niepewności pomiarów [1]. W roku 1999 normy zostały opublikowane
Stan zdrowotny drzewostanów sosnowych w Leśnym Zakładzie Doświadczalnym Murowana Goślina w latach
 sylwan 153 (8): 528 533, 2009 Cezary Beker Stan zdrowotny drzewostanów sosnowych w Leśnym Zakładzie Doświadczalnym Murowana Goślina w latach 1992 2006 Health condition of Scots pine stands in Murowana
sylwan 153 (8): 528 533, 2009 Cezary Beker Stan zdrowotny drzewostanów sosnowych w Leśnym Zakładzie Doświadczalnym Murowana Goślina w latach 1992 2006 Health condition of Scots pine stands in Murowana
Weryfikacja hipotez statystycznych
 Weryfikacja hipotez statystycznych Hipoteza Test statystyczny Poziom istotności Testy jednostronne i dwustronne Testowanie równości wariancji test F-Fishera Testowanie równości wartości średnich test t-studenta
Weryfikacja hipotez statystycznych Hipoteza Test statystyczny Poziom istotności Testy jednostronne i dwustronne Testowanie równości wariancji test F-Fishera Testowanie równości wartości średnich test t-studenta
Zadania ze statystyki cz. 8 I rok socjologii. Zadanie 1.
 Zadania ze statystyki cz. 8 I rok socjologii Zadanie 1. W potocznej opinii pokutuje przekonanie, że lepsi z matematyki są chłopcy niż dziewczęta. Chcąc zweryfikować tę opinię, przeprowadzono badanie w
Zadania ze statystyki cz. 8 I rok socjologii Zadanie 1. W potocznej opinii pokutuje przekonanie, że lepsi z matematyki są chłopcy niż dziewczęta. Chcąc zweryfikować tę opinię, przeprowadzono badanie w
Metody doboru próby do badań. Dr Kalina Grzesiuk
 Metody doboru próby do badań Dr Kalina Grzesiuk Proces doboru próby 1. Ustalenie populacji badanej 2. Ustalenie wykazu populacji badanej 3. Ustalenie liczebności próby 4. Wybór metody doboru próby do badań
Metody doboru próby do badań Dr Kalina Grzesiuk Proces doboru próby 1. Ustalenie populacji badanej 2. Ustalenie wykazu populacji badanej 3. Ustalenie liczebności próby 4. Wybór metody doboru próby do badań
Rozkłady statystyk z próby. Statystyka
 Rozkłady statystyk z próby tatystyka Rozkłady statystyk z próby Próba losowa pobrana z populacji stanowi realizacje zmiennej losowej jak ciąg zmiennych losowych (X, X,... X ) niezależnych i mających ten
Rozkłady statystyk z próby tatystyka Rozkłady statystyk z próby Próba losowa pobrana z populacji stanowi realizacje zmiennej losowej jak ciąg zmiennych losowych (X, X,... X ) niezależnych i mających ten
Wykład 2. Statystyka opisowa - Miary rozkładu: Miary położenia
 Wykład 2 Statystyka opisowa - Miary rozkładu: Miary położenia Podział miar Miary położenia (measures of location): 1. Miary tendencji centralnej (measures of central tendency, averages): Średnia arytmetyczna
Wykład 2 Statystyka opisowa - Miary rozkładu: Miary położenia Podział miar Miary położenia (measures of location): 1. Miary tendencji centralnej (measures of central tendency, averages): Średnia arytmetyczna
BADANIE POWTARZALNOŚCI PRZYRZĄDU POMIAROWEGO
 Zakład Metrologii i Systemów Pomiarowych P o l i t e c h n i k a P o z n ańska ul. Jana Pawła II 24 60-965 POZNAŃ (budynek Centrum Mechatroniki, Biomechaniki i Nanoinżynierii) www.zmisp.mt.put.poznan.pl
Zakład Metrologii i Systemów Pomiarowych P o l i t e c h n i k a P o z n ańska ul. Jana Pawła II 24 60-965 POZNAŃ (budynek Centrum Mechatroniki, Biomechaniki i Nanoinżynierii) www.zmisp.mt.put.poznan.pl
Charakterystyki liczbowe (estymatory i parametry), które pozwalają opisać właściwości rozkładu badanej cechy (zmiennej)
 Charakterystyki liczbowe (estymatory i parametry), które pozwalają opisać właściwości rozkładu badanej cechy (zmiennej) 1 Podział ze względu na zakres danych użytych do wyznaczenia miary Miary opisujące
Charakterystyki liczbowe (estymatory i parametry), które pozwalają opisać właściwości rozkładu badanej cechy (zmiennej) 1 Podział ze względu na zakres danych użytych do wyznaczenia miary Miary opisujące
Wykorzystanie teledetekcji satelitarnej przy opracowaniu mapy przestrzennego rozkładu biomasy leśnej Polski
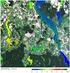 Wykorzystanie teledetekcji satelitarnej przy opracowaniu mapy przestrzennego rozkładu biomasy leśnej Polski Agata Hościło 1, Aneta Lewandowska 1, Dariusz Ziółkowski 1, Krzysztof Stereńczak 2 1 Centrum
Wykorzystanie teledetekcji satelitarnej przy opracowaniu mapy przestrzennego rozkładu biomasy leśnej Polski Agata Hościło 1, Aneta Lewandowska 1, Dariusz Ziółkowski 1, Krzysztof Stereńczak 2 1 Centrum
Statystyka matematyczna Testowanie hipotez i estymacja parametrów. Wrocław, r
 Statystyka matematyczna Testowanie hipotez i estymacja parametrów Wrocław, 18.03.2016r Plan wykładu: 1. Testowanie hipotez 2. Etapy testowania hipotez 3. Błędy 4. Testowanie wielokrotne 5. Estymacja parametrów
Statystyka matematyczna Testowanie hipotez i estymacja parametrów Wrocław, 18.03.2016r Plan wykładu: 1. Testowanie hipotez 2. Etapy testowania hipotez 3. Błędy 4. Testowanie wielokrotne 5. Estymacja parametrów
METODY STATYSTYCZNE W BIOLOGII
 METODY STATYSTYCZNE W BIOLOGII 1. Wykład wstępny 2. Populacje i próby danych 3. Testowanie hipotez i estymacja parametrów 4. Planowanie eksperymentów biologicznych 5. Najczęściej wykorzystywane testy statystyczne
METODY STATYSTYCZNE W BIOLOGII 1. Wykład wstępny 2. Populacje i próby danych 3. Testowanie hipotez i estymacja parametrów 4. Planowanie eksperymentów biologicznych 5. Najczęściej wykorzystywane testy statystyczne
Wykład Ćwiczenia Laboratorium Projekt Seminarium
 Zał. nr 4 do ZW WYDZIAŁ PODSTAWOWYCH PROBLEMÓW TECHNIKI KARTA PRZEDMIOTU Nazwa w języku polskim ELEMENTY STATYSTYKI Nazwa w języku angielskim Elements of Statistics Kierunek studiów (jeśli dotyczy): Matematyka
Zał. nr 4 do ZW WYDZIAŁ PODSTAWOWYCH PROBLEMÓW TECHNIKI KARTA PRZEDMIOTU Nazwa w języku polskim ELEMENTY STATYSTYKI Nazwa w języku angielskim Elements of Statistics Kierunek studiów (jeśli dotyczy): Matematyka
Analiza niepewności pomiarów
 Teoria pomiarów Analiza niepewności pomiarów Zagadnienia statystyki matematycznej Dr hab. inż. Paweł Majda www.pmajda.zut.edu.pl Podstawy statystyki matematycznej Histogram oraz wielobok liczebności zmiennej
Teoria pomiarów Analiza niepewności pomiarów Zagadnienia statystyki matematycznej Dr hab. inż. Paweł Majda www.pmajda.zut.edu.pl Podstawy statystyki matematycznej Histogram oraz wielobok liczebności zmiennej
WIELKA SGH-OWA POWTÓRKA ZE STATYSTYKI. Test zgodności i analiza wariancji Analiza wariancji
 WIELKA SGH-OWA POWTÓRKA ZE STATYSTYKI Test zgodności i analiza wariancji Analiza wariancji Test zgodności Chi-kwadrat Sprawdza się za jego pomocą ZGODNOŚĆ ROZKŁADU EMPIRYCZNEGO Z PRÓBY Z ROZKŁADEM HIPOTETYCZNYM
WIELKA SGH-OWA POWTÓRKA ZE STATYSTYKI Test zgodności i analiza wariancji Analiza wariancji Test zgodności Chi-kwadrat Sprawdza się za jego pomocą ZGODNOŚĆ ROZKŁADU EMPIRYCZNEGO Z PRÓBY Z ROZKŁADEM HIPOTETYCZNYM
Matematyka z el. statystyki, # 6 /Geodezja i kartografia II/
 Matematyka z el. statystyki, # 6 /Geodezja i kartografia II/ Uniwersytet Przyrodniczy w Lublinie Katedra Zastosowań Matematyki i Informatyki ul. Głęboka 28, bud. CIW, p. 221 e-mail: zdzislaw.otachel@up.lublin.pl
Matematyka z el. statystyki, # 6 /Geodezja i kartografia II/ Uniwersytet Przyrodniczy w Lublinie Katedra Zastosowań Matematyki i Informatyki ul. Głęboka 28, bud. CIW, p. 221 e-mail: zdzislaw.otachel@up.lublin.pl
STATYSTYKA MATEMATYCZNA WYKŁAD 4. Testowanie hipotez Estymacja parametrów
 STATYSTYKA MATEMATYCZNA WYKŁAD 4 Testowanie hipotez Estymacja parametrów WSTĘP 1. Testowanie hipotez Błędy związane z testowaniem hipotez Etapy testowana hipotez Testowanie wielokrotne 2. Estymacja parametrów
STATYSTYKA MATEMATYCZNA WYKŁAD 4 Testowanie hipotez Estymacja parametrów WSTĘP 1. Testowanie hipotez Błędy związane z testowaniem hipotez Etapy testowana hipotez Testowanie wielokrotne 2. Estymacja parametrów
METODY STATYSTYCZNE W BIOLOGII
 METODY STATYSTYCZNE W BIOLOGII 1. Wykład wstępny 2. Populacje i próby danych 3. Testowanie hipotez i estymacja parametrów 4. Planowanie eksperymentów biologicznych 5. Najczęściej wykorzystywane testy statystyczne
METODY STATYSTYCZNE W BIOLOGII 1. Wykład wstępny 2. Populacje i próby danych 3. Testowanie hipotez i estymacja parametrów 4. Planowanie eksperymentów biologicznych 5. Najczęściej wykorzystywane testy statystyczne
Biuro Urządzania Lasu i Geodezji Leśnej. Zasoby drewna martwego w lasach na podstawie wyników wielkoobszarowej inwentaryzacji stanu lasu
 Zasoby drewna martwego w lasach na podstawie wyników wielkoobszarowej inwentaryzacji stanu lasu Bożydar Neroj 27 kwietnia 2011r. 1 Zasady wykonywania wielkoobszarowej inwentaryzacji stanu lasu Instrukcja
Zasoby drewna martwego w lasach na podstawie wyników wielkoobszarowej inwentaryzacji stanu lasu Bożydar Neroj 27 kwietnia 2011r. 1 Zasady wykonywania wielkoobszarowej inwentaryzacji stanu lasu Instrukcja
WIELKA SGH-OWA POWTÓRKA ZE STATYSTYKI ROZKŁAD STATYSTYK Z PRÓBY
 WIELKA SGH-OWA POWTÓRKA ZE STATYSTYKI ROZKŁAD STATYSTYK Z PRÓBY Próba losowa prosta To taki dobór elementów z populacji, że każdy element miał takie samo prawdopodobieństwo znalezienia się w próbie Niezależne
WIELKA SGH-OWA POWTÓRKA ZE STATYSTYKI ROZKŁAD STATYSTYK Z PRÓBY Próba losowa prosta To taki dobór elementów z populacji, że każdy element miał takie samo prawdopodobieństwo znalezienia się w próbie Niezależne
Typy rozmieszczenia drzew w drzewostanach sosnowych różnego wieku z odnowienia naturalnego
 Sergii Boiko Typy rozmieszczenia drzew w drzewostanach sosnowych różnego wieku z odnowienia naturalnego Autoreferat rozprawy doktorskiej wykonanej w Zakładzie Hodowli Lasu Instytutu Badawczego Leśnictwa
Sergii Boiko Typy rozmieszczenia drzew w drzewostanach sosnowych różnego wieku z odnowienia naturalnego Autoreferat rozprawy doktorskiej wykonanej w Zakładzie Hodowli Lasu Instytutu Badawczego Leśnictwa
Tablica Wzorów Rachunek Prawdopodobieństwa i Statystyki
 Tablica Wzorów Rachunek Prawdopodobieństwa i Statystyki Spis treści I. Wzory ogólne... 2 1. Średnia arytmetyczna:... 2 2. Rozstęp:... 2 3. Kwantyle:... 2 4. Wariancja:... 2 5. Odchylenie standardowe:...
Tablica Wzorów Rachunek Prawdopodobieństwa i Statystyki Spis treści I. Wzory ogólne... 2 1. Średnia arytmetyczna:... 2 2. Rozstęp:... 2 3. Kwantyle:... 2 4. Wariancja:... 2 5. Odchylenie standardowe:...
Weryfikacja hipotez statystycznych za pomocą testów statystycznych
 Weryfikacja hipotez statystycznych za pomocą testów statystycznych Weryfikacja hipotez statystycznych za pomocą testów stat. Hipoteza statystyczna Dowolne przypuszczenie co do rozkładu populacji generalnej
Weryfikacja hipotez statystycznych za pomocą testów statystycznych Weryfikacja hipotez statystycznych za pomocą testów stat. Hipoteza statystyczna Dowolne przypuszczenie co do rozkładu populacji generalnej
Wykład 4. Plan: 1. Aproksymacja rozkładu dwumianowego rozkładem normalnym. 2. Rozkłady próbkowe. 3. Centralne twierdzenie graniczne
 Wykład 4 Plan: 1. Aproksymacja rozkładu dwumianowego rozkładem normalnym 2. Rozkłady próbkowe 3. Centralne twierdzenie graniczne Przybliżenie rozkładu dwumianowego rozkładem normalnym Niech Y ma rozkład
Wykład 4 Plan: 1. Aproksymacja rozkładu dwumianowego rozkładem normalnym 2. Rozkłady próbkowe 3. Centralne twierdzenie graniczne Przybliżenie rozkładu dwumianowego rozkładem normalnym Niech Y ma rozkład
zbieranie porządkowanie i prezentacja (tabele, wykresy) analiza interpretacja (wnioskowanie statystyczne)
 STATYSTYKA zbieranie porządkowanie i prezentacja (tabele, wykresy) analiza interpretacja (wnioskowanie statystyczne) DANYCH STATYSTYKA MATEMATYCZNA analiza i interpretacja danych przy wykorzystaniu metod
STATYSTYKA zbieranie porządkowanie i prezentacja (tabele, wykresy) analiza interpretacja (wnioskowanie statystyczne) DANYCH STATYSTYKA MATEMATYCZNA analiza i interpretacja danych przy wykorzystaniu metod
Estymacja parametro w 1
 Estymacja parametro w 1 1 Estymacja punktowa: średniej, odchylenia standardowego i frakcji µ - średnia populacji h średnia z próby jest estymatorem średniej populacji = - standardowy błąd estymacji średniej
Estymacja parametro w 1 1 Estymacja punktowa: średniej, odchylenia standardowego i frakcji µ - średnia populacji h średnia z próby jest estymatorem średniej populacji = - standardowy błąd estymacji średniej
METODA PROGNOZOWANIA ZAGROŻENIA
 METODA PROGNOZOWANIA ZAGROŻENIA DRZEWOSTANÓW DĘBOWYCH PRZEZ MIERNIKOWCE Z WYKORZYSTANIEM PUŁAPEK KOŁNIERZOWYCH Tomasz Jaworski, Lidia Sukovata Zakład Ochrony Lasu Instytut Badawczy Leśnictwa Problem badawczy
METODA PROGNOZOWANIA ZAGROŻENIA DRZEWOSTANÓW DĘBOWYCH PRZEZ MIERNIKOWCE Z WYKORZYSTANIEM PUŁAPEK KOŁNIERZOWYCH Tomasz Jaworski, Lidia Sukovata Zakład Ochrony Lasu Instytut Badawczy Leśnictwa Problem badawczy
Struktura wysokości emerytur i rent wypłacanych przez ZUS po waloryzacji w marcu 2018 roku
 Struktura wysokości emerytur i rent wypłacanych przez ZUS po waloryzacji w marcu 2018 roku D DEPARTAMENT STATYSTYKI I PROGNOZ AKTUARIALNYCH Warszawa 2018 Opracowała: Ewa Karczewicz Naczelnik Wydziału Badań
Struktura wysokości emerytur i rent wypłacanych przez ZUS po waloryzacji w marcu 2018 roku D DEPARTAMENT STATYSTYKI I PROGNOZ AKTUARIALNYCH Warszawa 2018 Opracowała: Ewa Karczewicz Naczelnik Wydziału Badań
Procesy przeżywania i ubywania drzew w różnowiekowych lasach zagospodarowanych i chronionych
 Procesy przeżywania i ubywania drzew w różnowiekowych lasach zagospodarowanych i chronionych Jan Banaś, Stanisław Zięba, Robert Zygmunt, Leszek Bujoczek ARTYKUŁY / ARTICLES Abstrakt. W pracy przedstawiono
Procesy przeżywania i ubywania drzew w różnowiekowych lasach zagospodarowanych i chronionych Jan Banaś, Stanisław Zięba, Robert Zygmunt, Leszek Bujoczek ARTYKUŁY / ARTICLES Abstrakt. W pracy przedstawiono
Wykorzystanie testu t dla pojedynczej próby we wnioskowaniu statystycznym
 Wiesława MALSKA Politechnika Rzeszowska, Polska Anna KOZIOROWSKA Uniwersytet Rzeszowski, Polska Wykorzystanie testu t dla pojedynczej próby we wnioskowaniu statystycznym Wstęp Wnioskowanie statystyczne
Wiesława MALSKA Politechnika Rzeszowska, Polska Anna KOZIOROWSKA Uniwersytet Rzeszowski, Polska Wykorzystanie testu t dla pojedynczej próby we wnioskowaniu statystycznym Wstęp Wnioskowanie statystyczne
