Sortowanie. Tomasz Żak zak. styczeń Instytut Matematyki i Informatyki, Politechnika Wrocławska
|
|
|
- Stefan Białek
- 7 lat temu
- Przeglądów:
Transkrypt
1 Tomasz Żak zak Instytut Matematyki i Informatyki, Politechnika Wrocławska styczeń 2014
2 Przypuśćmy, że po sprawdzeniu 30 klasówek układamy je w kolejności alfabetycznej autorów. Jak to zrobić najszybciej? Zastosujmy metodę matematyków uproszczenie zadania i załóżmy, że są TYLKO DWIE klasówki. Wówczas:
3 Przypuśćmy, że po sprawdzeniu 30 klasówek układamy je w kolejności alfabetycznej autorów. Jak to zrobić najszybciej? Zastosujmy metodę matematyków uproszczenie zadania i załóżmy, że są TYLKO DWIE klasówki. Wówczas: albo już są we właściwej kolejności (żeby to sprawdzić musimy odczytać nazwisko na drugiej pracy i porównać z nazwiskiem z pierwszej),
4 Przypuśćmy, że po sprawdzeniu 30 klasówek układamy je w kolejności alfabetycznej autorów. Jak to zrobić najszybciej? Zastosujmy metodę matematyków uproszczenie zadania i załóżmy, że są TYLKO DWIE klasówki. Wówczas: albo już są we właściwej kolejności (żeby to sprawdzić musimy odczytać nazwisko na drugiej pracy i porównać z nazwiskiem z pierwszej), albo przestawić kolejność klasówek (jedna operacja).
5 Przypuśćmy, że po sprawdzeniu 30 klasówek układamy je w kolejności alfabetycznej autorów. Jak to zrobić najszybciej? Zastosujmy metodę matematyków uproszczenie zadania i załóżmy, że są TYLKO DWIE klasówki. Wówczas: albo już są we właściwej kolejności (żeby to sprawdzić musimy odczytać nazwisko na drugiej pracy i porównać z nazwiskiem z pierwszej), albo przestawić kolejność klasówek (jedna operacja). Interesuje nas tylko liczba porównań, odczytywanie nazwisk zajmuje mniej czasu (wystarczy rzut oka).
6 Przypuśćmy, że po sprawdzeniu 30 klasówek układamy je w kolejności alfabetycznej autorów. Jak to zrobić najszybciej? Zastosujmy metodę matematyków uproszczenie zadania i załóżmy, że są TYLKO DWIE klasówki. Wówczas: albo już są we właściwej kolejności (żeby to sprawdzić musimy odczytać nazwisko na drugiej pracy i porównać z nazwiskiem z pierwszej), albo przestawić kolejność klasówek (jedna operacja). Interesuje nas tylko liczba porównań, odczytywanie nazwisk zajmuje mniej czasu (wystarczy rzut oka). Ile operacji trzeba wykonać w przypadku TRZECH klasówek (w najgorszym przypadku)?
7 Przypuśćmy, że po sprawdzeniu 30 klasówek układamy je w kolejności alfabetycznej autorów. Jak to zrobić najszybciej? Zastosujmy metodę matematyków uproszczenie zadania i załóżmy, że są TYLKO DWIE klasówki. Wówczas: albo już są we właściwej kolejności (żeby to sprawdzić musimy odczytać nazwisko na drugiej pracy i porównać z nazwiskiem z pierwszej), albo przestawić kolejność klasówek (jedna operacja). Interesuje nas tylko liczba porównań, odczytywanie nazwisk zajmuje mniej czasu (wystarczy rzut oka). Ile operacji trzeba wykonać w przypadku TRZECH klasówek (w najgorszym przypadku)? Bierzmy drugą i porównujemy z pierwszą (być może je przestawiamy) i mamy je już ustawione.
8 Bierzmy trzecią i porównujemy z pierwszą, jeśli powinna być PRZED pierwszą to koniec, jeśli nie, to porównujemy z drugą i ustawiamy na drugiej lub trzeciej pozycji.
9 Bierzmy trzecią i porównujemy z pierwszą, jeśli powinna być PRZED pierwszą to koniec, jeśli nie, to porównujemy z drugą i ustawiamy na drugiej lub trzeciej pozycji. Dobry sposób, ale już przy 30 kartkówkach i jednej operacji na sekundę mógłby zająć...
10 Bierzmy trzecią i porównujemy z pierwszą, jeśli powinna być PRZED pierwszą to koniec, jeśli nie, to porównujemy z drugą i ustawiamy na drugiej lub trzeciej pozycji. Dobry sposób, ale już przy 30 kartkówkach i jednej operacji na sekundę mógłby zająć nieco ponad 7 minut!
11 Bierzmy trzecią i porównujemy z pierwszą, jeśli powinna być PRZED pierwszą to koniec, jeśli nie, to porównujemy z drugą i ustawiamy na drugiej lub trzeciej pozycji. Dobry sposób, ale już przy 30 kartkówkach i jednej operacji na sekundę mógłby zająć nieco ponad 7 minut! A ja czasem muszę sortować 80 prac! To trwałoby w najgorszym przypadku ponad 50 minut (gdyby każda operacja zabierała jedną sekundę zwykle zabiera dużo więcej).
12 Ponieważ ten wynik zwykle spotyka sie z niedowierzaniem, udowodnijmy go! Ile operacji trzeba wykonać w przypadku CZTERECH klasówek (w najgorszym przypadku)?
13 Ponieważ ten wynik zwykle spotyka sie z niedowierzaniem, udowodnijmy go! Ile operacji trzeba wykonać w przypadku CZTERECH klasówek (w najgorszym przypadku)? Do posortowania trzech potrzebowaliśmy 1+2=3 operacji, więc teraz musimy porównać czwartą klasówkę z PIERWSZĄ, z DRUGĄ i z TRZECIĄ, co daje łącznie = 6 operacji.
14 Ponieważ ten wynik zwykle spotyka sie z niedowierzaniem, udowodnijmy go! Ile operacji trzeba wykonać w przypadku CZTERECH klasówek (w najgorszym przypadku)? Do posortowania trzech potrzebowaliśmy 1+2=3 operacji, więc teraz musimy porównać czwartą klasówkę z PIERWSZĄ, z DRUGĄ i z TRZECIĄ, co daje łącznie = 6 operacji. Piątą klasówkę porównujemy z czterema już posortowanymi, co daje = 10 operacji.
15 Ponieważ ten wynik zwykle spotyka sie z niedowierzaniem, udowodnijmy go! Ile operacji trzeba wykonać w przypadku CZTERECH klasówek (w najgorszym przypadku)? Do posortowania trzech potrzebowaliśmy 1+2=3 operacji, więc teraz musimy porównać czwartą klasówkę z PIERWSZĄ, z DRUGĄ i z TRZECIĄ, co daje łącznie = 6 operacji. Piątą klasówkę porównujemy z czterema już posortowanymi, co daje = 10 operacji. Licząc dalej, otrzymujemy dla 30 kartkówek sumę =?
16 Ponieważ ten wynik zwykle spotyka sie z niedowierzaniem, udowodnijmy go! Ile operacji trzeba wykonać w przypadku CZTERECH klasówek (w najgorszym przypadku)? Do posortowania trzech potrzebowaliśmy 1+2=3 operacji, więc teraz musimy porównać czwartą klasówkę z PIERWSZĄ, z DRUGĄ i z TRZECIĄ, co daje łącznie = 6 operacji. Piątą klasówkę porównujemy z czterema już posortowanymi, co daje = 10 operacji. Licząc dalej, otrzymujemy dla 30 kartkówek sumę =? Podobno kilkuletni Gauss obliczył na lekcji bardzo szybko sumę = 5050.
17 Ponieważ ten wynik zwykle spotyka sie z niedowierzaniem, udowodnijmy go! Ile operacji trzeba wykonać w przypadku CZTERECH klasówek (w najgorszym przypadku)? Do posortowania trzech potrzebowaliśmy 1+2=3 operacji, więc teraz musimy porównać czwartą klasówkę z PIERWSZĄ, z DRUGĄ i z TRZECIĄ, co daje łącznie = 6 operacji. Piątą klasówkę porównujemy z czterema już posortowanymi, co daje = 10 operacji. Licząc dalej, otrzymujemy dla 30 kartkówek sumę =? Podobno kilkuletni Gauss obliczył na lekcji bardzo szybko sumę = = = = = 435.
18 Ponieważ ten wynik zwykle spotyka sie z niedowierzaniem, udowodnijmy go! Ile operacji trzeba wykonać w przypadku CZTERECH klasówek (w najgorszym przypadku)? Do posortowania trzech potrzebowaliśmy 1+2=3 operacji, więc teraz musimy porównać czwartą klasówkę z PIERWSZĄ, z DRUGĄ i z TRZECIĄ, co daje łącznie = 6 operacji. Piątą klasówkę porównujemy z czterema już posortowanymi, co daje = 10 operacji. Licząc dalej, otrzymujemy dla 30 kartkówek sumę =? Podobno kilkuletni Gauss obliczył na lekcji bardzo szybko sumę = = = = = sekund to = 29 4 = minuty
19 Wyobraźmy sobie komputer, który musi posortować milion liczb (jakichś danych). Niech to będzie szybki komputer, wykonujący miliard takich porównań (i przestawień) na sekundę. Opisana powyżej metoda, wymagająca operacji zajęłaby mu...
20 Wyobraźmy sobie komputer, który musi posortować milion liczb (jakichś danych). Niech to będzie szybki komputer, wykonujący miliard takich porównań (i przestawień) na sekundę. Opisana powyżej metoda, wymagająca operacji zajęłaby mu... Obliczmy: = 0,
21 Wyobraźmy sobie komputer, który musi posortować milion liczb (jakichś danych). Niech to będzie szybki komputer, wykonujący miliard takich porównań (i przestawień) na sekundę. Opisana powyżej metoda, wymagająca operacji zajęłaby mu... Obliczmy: = 0, Przy 10 9 operacji na sekundę daje to około 10 3 sekund, czyli ponad 16 minut.
22 Wyobraźmy sobie komputer, który musi posortować milion liczb (jakichś danych). Niech to będzie szybki komputer, wykonujący miliard takich porównań (i przestawień) na sekundę. Opisana powyżej metoda, wymagająca operacji zajęłaby mu... Obliczmy: = 0, Przy 10 9 operacji na sekundę daje to około 10 3 sekund, czyli ponad 16 minut. Gdyby danych było 10 milionów, takie sortowanie zajęłoby /10 9 = 10 5 sekund czyli niemal 28 godzin.
23 Wyobraźmy sobie komputer, który musi posortować milion liczb (jakichś danych). Niech to będzie szybki komputer, wykonujący miliard takich porównań (i przestawień) na sekundę. Opisana powyżej metoda, wymagająca operacji zajęłaby mu... Obliczmy: = 0, Przy 10 9 operacji na sekundę daje to około 10 3 sekund, czyli ponad 16 minut. Gdyby danych było 10 milionów, takie sortowanie zajęłoby /10 9 = 10 5 sekund czyli niemal 28 godzin. UWAGA: detektory LHC produkują około 100 TB danych na sekundę! Tera =
24 Wyobraźmy sobie komputer, który musi posortować milion liczb (jakichś danych). Niech to będzie szybki komputer, wykonujący miliard takich porównań (i przestawień) na sekundę. Opisana powyżej metoda, wymagająca operacji zajęłaby mu... Obliczmy: = 0, Przy 10 9 operacji na sekundę daje to około 10 3 sekund, czyli ponad 16 minut. Gdyby danych było 10 milionów, takie sortowanie zajęłoby /10 9 = 10 5 sekund czyli niemal 28 godzin. UWAGA: detektory LHC produkują około 100 TB danych na sekundę! Tera = liczb naszym sposobem trwałoby około... milion lat. Czyli sposób jest zły! A można to zrobić w 11 dni...
25 Mądre sortowanie klasówek Kluczowa obserwacja: porównań jest tak wiele, bo...
26 Mądre sortowanie klasówek Kluczowa obserwacja: porównań jest tak wiele, bo w gruncie rzeczy porównujemy każdą kartkę z każdą!
27 Mądre sortowanie klasówek Kluczowa obserwacja: porównań jest tak wiele, bo w gruncie rzeczy porównujemy każdą kartkę z każdą! Czy można porównywać za sobą TYLKO NIEKTÓRE kartki?
28 Mądre sortowanie klasówek Kluczowa obserwacja: porównań jest tak wiele, bo w gruncie rzeczy porównujemy każdą kartkę z każdą! Czy można porównywać za sobą TYLKO NIEKTÓRE kartki? Ważna jest liczba porównań im mniej, tym lepiej.
29 Mądre sortowanie klasówek Kluczowa obserwacja: porównań jest tak wiele, bo w gruncie rzeczy porównujemy każdą kartkę z każdą! Czy można porównywać za sobą TYLKO NIEKTÓRE kartki? Ważna jest liczba porównań im mniej, tym lepiej. Rozwiązanie:
30 Mądre sortowanie klasówek Kluczowa obserwacja: porównań jest tak wiele, bo w gruncie rzeczy porównujemy każdą kartkę z każdą! Czy można porównywać za sobą TYLKO NIEKTÓRE kartki? Ważna jest liczba porównań im mniej, tym lepiej. Rozwiązanie: Najpierw dzielimy kartki alfabetycznie na 4 grupy (albo na więcej), potem sortujemy każdą grupę oddzielnie.
31 Mądre sortowanie zbioru liczb z przedziału od 0 do 1000 Nie ma tu naturalnego podziału na grupy alfabetyczne, musimy sami utworzyć grupy. Jeśli wiemy, że danych do sortowania jest dużo, to możemy podzielić je np. na:
32 Mądre sortowanie zbioru liczb z przedziału od 0 do 1000 Nie ma tu naturalnego podziału na grupy alfabetyczne, musimy sami utworzyć grupy. Jeśli wiemy, że danych do sortowania jest dużo, to możemy podzielić je np. na: 10 grup: 0-99, ,...,
33 Mądre sortowanie zbioru liczb z przedziału od 0 do 1000 Nie ma tu naturalnego podziału na grupy alfabetyczne, musimy sami utworzyć grupy. Jeśli wiemy, że danych do sortowania jest dużo, to możemy podzielić je np. na: 10 grup: 0-99, ,..., lub 100 grup: 0-9, 10-19,...,
34 Mądre sortowanie zbioru liczb z przedziału od 0 do 1000 Nie ma tu naturalnego podziału na grupy alfabetyczne, musimy sami utworzyć grupy. Jeśli wiemy, że danych do sortowania jest dużo, to możemy podzielić je np. na: 10 grup: 0-99, ,..., lub 100 grup: 0-9, 10-19,..., Który z tych podziałów daje szybsze sortowanie?
35 Mądre sortowanie zbioru liczb z przedziału od 0 do 1000 Nie ma tu naturalnego podziału na grupy alfabetyczne, musimy sami utworzyć grupy. Jeśli wiemy, że danych do sortowania jest dużo, to możemy podzielić je np. na: 10 grup: 0-99, ,..., lub 100 grup: 0-9, 10-19,..., Który z tych podziałów daje szybsze sortowanie? Uwaga: dzieląc najmądrzej, jak to możliwe (tzn. JAK???) możemy osiągnąć liczbę porównań rzędu stała n log 2 n.
36 Mądre sortowanie zbioru liczb z przedziału od 0 do 1000 Nie ma tu naturalnego podziału na grupy alfabetyczne, musimy sami utworzyć grupy. Jeśli wiemy, że danych do sortowania jest dużo, to możemy podzielić je np. na: 10 grup: 0-99, ,..., lub 100 grup: 0-9, 10-19,..., Który z tych podziałów daje szybsze sortowanie? Uwaga: dzieląc najmądrzej, jak to możliwe (tzn. JAK???) możemy osiągnąć liczbę porównań rzędu stała n log 2 n. Np. dla n = nasze poprzednie sortowanie daje około porównań, a mądre log log 2 (2 20 ) , czyli jest razy szybsze!
37 Mądre sortowanie zbioru liczb z przedziału od 0 do 1000 Nie ma tu naturalnego podziału na grupy alfabetyczne, musimy sami utworzyć grupy. Jeśli wiemy, że danych do sortowania jest dużo, to możemy podzielić je np. na: 10 grup: 0-99, ,..., lub 100 grup: 0-9, 10-19,..., Który z tych podziałów daje szybsze sortowanie? Uwaga: dzieląc najmądrzej, jak to możliwe (tzn. JAK???) możemy osiągnąć liczbę porównań rzędu stała n log 2 n. Np. dla n = nasze poprzednie sortowanie daje około porównań, a mądre log log 2 (2 20 ) , czyli jest razy szybsze! A co zrobić, gdy nie znamy zakresu, z którego pochodzą liczby??? Jak wtedy dzielić na grupy?
38 Algorytmy losowe Gdy trzeba uporządkować ogromny zbiór danych liczbowych (np ) i nie podano zakresu, z jakiego pochodzą te liczby, stosuje się algorytm losowy, polegający na tym, że losuje się jedną z tych liczb i porównuje się pozostałe z wylosowaną liczbą. Takie postępowanie dzieli zbiór liczb na dwie części, a rachunek prawdopodobieństwa wskazuje, że z dużym prawdopodobieństwem oba zbiory mają mniej więcej porównywalną liczbę elementów. Ale to już całkiem inna historia.
39 Small world Eksperyment z listami (Milgram experiment).
40 Small world Eksperyment z listami (Milgram experiment). Eksperyment ze stronami z internecie.
41 Small world Eksperyment z listami (Milgram experiment). Eksperyment ze stronami z internecie. Ile trzeba kroków, aby przejść od jednej strony do dowolnej innej za pomocą linków?
42 Small world Eksperyment z listami (Milgram experiment). Eksperyment ze stronami z internecie. Ile trzeba kroków, aby przejść od jednej strony do dowolnej innej za pomocą linków? Średnio sześć! Niewiarygodne?
43 Small world Eksperyment z listami (Milgram experiment). Eksperyment ze stronami z internecie. Ile trzeba kroków, aby przejść od jednej strony do dowolnej innej za pomocą linków? Średnio sześć! Niewiarygodne? Jakie może być intuicyjne wyjaśnienie tego zjawiska? Uwaga: 40 6 = (4 10) 6 = =???
44 Ty też możesz pracować naukowo! w nauce/
45 Co warto czytać? Książki popularyzujące matematykę, informatykę, fizykę, astronomię itd. Delta miesięcznik popularno-naukowy dla... link: deltami czyli δµ. Autorzy książek: Martin Gardner wszystko, co napisał Hugo Steinhaus Kalejdoskop matematyczny, Sto zadań, Orzeł czy reszka Ian Stewart Jak pokroić tort i inne zagadki matematyczne Np: Zagadka dla piratów. David Wells Cudowne i interesujące łamigłówki matematyczne, na przykład Tajemniczy kwadrat ze strony 158.
46 Tajemniczy kwadrat (w dodatku magiczny!) W 8 kwadracików wpisano symbole według pewnego wzorca. Jaki symbol należy umieścić w prawym dolnym rogu?
47 10 piratów dzieli 100 sztuk złota Stosują nastepującą metodę demokratyczną: Najokrutniejszy proponuje sposób podziału i wszyscy głosują.
48 10 piratów dzieli 100 sztuk złota Stosują nastepującą metodę demokratyczną: Najokrutniejszy proponuje sposób podziału i wszyscy głosują. Jeśli co najmnej połowa (wliczając wnioskodawcę) opowie się za, następuje podział.
49 10 piratów dzieli 100 sztuk złota Stosują nastepującą metodę demokratyczną: Najokrutniejszy proponuje sposób podziału i wszyscy głosują. Jeśli co najmnej połowa (wliczając wnioskodawcę) opowie się za, następuje podział. Jeśli nie, to wnioskodawca ląduje za burtą, a drugi co do okrucieństwa pirat proponuje swój sposób podziału i znów następuje głosowanie i albo sposób jest przyjęty, albo wnioskodawca za burtą itd.
50 10 piratów dzieli 100 sztuk złota Stosują nastepującą metodę demokratyczną: Najokrutniejszy proponuje sposób podziału i wszyscy głosują. Jeśli co najmnej połowa (wliczając wnioskodawcę) opowie się za, następuje podział. Jeśli nie, to wnioskodawca ląduje za burtą, a drugi co do okrucieństwa pirat proponuje swój sposób podziału i znów następuje głosowanie i albo sposób jest przyjęty, albo wnioskodawca za burtą itd. Wszyscy piraci są uporządkowania w zależności od stopnia okrucieństwa, tzn. nie ma dwóch jednakowo okrutnych.
51 10 piratów dzieli 100 sztuk złota Stosują nastepującą metodę demokratyczną: Najokrutniejszy proponuje sposób podziału i wszyscy głosują. Jeśli co najmnej połowa (wliczając wnioskodawcę) opowie się za, następuje podział. Jeśli nie, to wnioskodawca ląduje za burtą, a drugi co do okrucieństwa pirat proponuje swój sposób podziału i znów następuje głosowanie i albo sposób jest przyjęty, albo wnioskodawca za burtą itd. Wszyscy piraci są uporządkowania w zależności od stopnia okrucieństwa, tzn. nie ma dwóch jednakowo okrutnych. Wszyscy kierują sie logiką i wiedzą, że pozostali też działają logicznie.
52 10 piratów dzieli 100 sztuk złota Stosują nastepującą metodę demokratyczną: Najokrutniejszy proponuje sposób podziału i wszyscy głosują. Jeśli co najmnej połowa (wliczając wnioskodawcę) opowie się za, następuje podział. Jeśli nie, to wnioskodawca ląduje za burtą, a drugi co do okrucieństwa pirat proponuje swój sposób podziału i znów następuje głosowanie i albo sposób jest przyjęty, albo wnioskodawca za burtą itd. Wszyscy piraci są uporządkowania w zależności od stopnia okrucieństwa, tzn. nie ma dwóch jednakowo okrutnych. Wszyscy kierują sie logiką i wiedzą, że pozostali też działają logicznie. Wszyscy lubią wyrzucać innych za burtę, ale wolą choćby najmniejszą ilość złota od wyrzucania innych za burtę.
53 10 piratów dzieli 100 sztuk złota Stosują nastepującą metodę demokratyczną: Najokrutniejszy proponuje sposób podziału i wszyscy głosują. Jeśli co najmnej połowa (wliczając wnioskodawcę) opowie się za, następuje podział. Jeśli nie, to wnioskodawca ląduje za burtą, a drugi co do okrucieństwa pirat proponuje swój sposób podziału i znów następuje głosowanie i albo sposób jest przyjęty, albo wnioskodawca za burtą itd. Wszyscy piraci są uporządkowania w zależności od stopnia okrucieństwa, tzn. nie ma dwóch jednakowo okrutnych. Wszyscy kierują sie logiką i wiedzą, że pozostali też działają logicznie. Wszyscy lubią wyrzucać innych za burtę, ale wolą choćby najmniejszą ilość złota od wyrzucania innych za burtę. Nikt nie chce być wyrzucony.
54 10 piratów dzieli 100 sztuk złota Stosują nastepującą metodę demokratyczną: Najokrutniejszy proponuje sposób podziału i wszyscy głosują. Jeśli co najmnej połowa (wliczając wnioskodawcę) opowie się za, następuje podział. Jeśli nie, to wnioskodawca ląduje za burtą, a drugi co do okrucieństwa pirat proponuje swój sposób podziału i znów następuje głosowanie i albo sposób jest przyjęty, albo wnioskodawca za burtą itd. Wszyscy piraci są uporządkowania w zależności od stopnia okrucieństwa, tzn. nie ma dwóch jednakowo okrutnych. Wszyscy kierują sie logiką i wiedzą, że pozostali też działają logicznie. Wszyscy lubią wyrzucać innych za burtę, ale wolą choćby najmniejszą ilość złota od wyrzucania innych za burtę. Nikt nie chce być wyrzucony. Jaki podział przejdzie?
Materiały dla finalistów
Materiały dla finalistów Malachoviacus Informaticus 2016 11 kwietnia 2016 Wprowadzenie Poniższy dokument zawiera opisy zagadnień, które będą niezbędne do rozwiązania zadań w drugim etapie konkursu. Polecamy
operacje porównania, a jeśli jest to konieczne ze względu na złe uporządkowanie porównywanych liczb zmieniamy ich kolejność, czyli przestawiamy je.
Problem porządkowania zwanego również sortowaniem jest jednym z najważniejszych i najpopularniejszych zagadnień informatycznych. Dane: Liczba naturalna n i ciąg n liczb x 1, x 2,, x n. Wynik: Uporządkowanie
Warsztat: Randomizacja w programie Excel
Warsztaty szkoleniowe z zakresu ewaluacji wpływu instrumentów Aktywnych Polityk Rynku Pracy Warsztat: Randomizacja w programie Excel Piotr Ćwiakowski Tomasz Gajderowicz, Kraków, 5 czerwca 2017 r. Przydział
znalezienia elementu w zbiorze, gdy w nim jest; dołączenia nowego elementu w odpowiednie miejsce, aby zbiór pozostał nadal uporządkowany.
Przedstawiamy algorytmy porządkowania dowolnej liczby elementów, którymi mogą być liczby, jak również elementy o bardziej złożonej postaci (takie jak słowa i daty). Porządkowanie, nazywane również często
Algorytmy i struktury danych
Algorytmy i struktury danych ĆWICZENIE 2 - WYBRANE ZŁOŻONE STRUKTURY DANYCH - (12.3.212) Prowadząca: dr hab. inż. Małgorzata Sterna Informatyka i3, poniedziałek godz. 11:45 Adam Matuszewski, nr 1655 Oliver
Algorytmy przeszukiwania
Algorytmy przeszukiwania Przeszukiwanie liniowe Algorytm stosowany do poszukiwania elementu w zbiorze, o którym nic nie wiemy. Aby mieć pewność, że nie pominęliśmy żadnego elementu zbioru przeszukujemy
Jeszcze o algorytmach
Jeszcze o algorytmach Przykłady różnych, podstawowych algorytmów 11.01.2018 M. Rad Plan Powtórka Znajdowanie najmniejszego elementu Segregowanie Poszukiwanie przez połowienie Wstawianie Inne algorytmy
KONSPEKT ZAJĘĆ KOŁA INFORMATYCZNEGO LUB MATEMATYCZNEGO W KLASIE III GIMNAZJUM LUB I LICEUM ( 2 GODZ.)
Joanna Osio asiaosio@poczta.onet.pl Nauczycielka matematyki w Gimnazjum im. Macieja Rataja w Żmigrodzie KONSPEKT ZAJĘĆ KOŁA INFORMATYCZNEGO LUB MATEMATYCZNEGO W KLASIE III GIMNAZJUM LUB I LICEUM ( 2 GODZ.)
Temat 7. Najlżejsze i najcięższe algorytmy sortowania
Temat 7 Najlżejsze i najcięższe algorytmy sortowania Streszczenie Komputery są często używane porządkowania różnych danych, na przykład nazwisk (w porządku alfabetycznym), terminów spotkań lub e-maili
Luty 2001 Algorytmy (4) 2000/2001
Mając dany zbiór elementów, chcemy znaleźć w nim element największy (maksimum), bądź najmniejszy (minimum). We wszystkich naturalnych metodach znajdywania najmniejszego i największego elementu obecne jest
Wstęp do Informatyki zadania ze złożoności obliczeniowej z rozwiązaniami
Wstęp do Informatyki zadania ze złożoności obliczeniowej z rozwiązaniami Przykład 1. Napisz program, który dla podanej liczby n wypisze jej rozkład na czynniki pierwsze. Oblicz asymptotyczną złożoność
Bukiety matematyczne dla gimnazjum
Bukiety matematyczne dla gimnazjum http://www.mat.uni.torun.pl/~kolka/ 1 X 2002 Bukiet I Dany jest prostokąt o bokach wymiernych a, b, którego obwód O i pole P są całkowite. 1. Sprawdź, że zachodzi równość
Prezydent wszystkich kombinacji czyli rzecz o filtrowaniu systemów Lotto
Prezydent wszystkich kombinacji czyli rzecz o filtrowaniu systemów Lotto Czy zastanawiałeś się kiedyś nad tym, że prawdopodobieństwo wylosowania dwóch liczb w lotto o określonej sumie nie jest jednakowe?
Algorytmy sortujące. sortowanie kubełkowe, sortowanie grzebieniowe
Algorytmy sortujące sortowanie kubełkowe, sortowanie grzebieniowe Sortowanie kubełkowe (bucket sort) Jest to jeden z najbardziej popularnych algorytmów sortowania. Został wynaleziony w 1956 r. przez E.J.
Podstawą w systemie dwójkowym jest liczba 2 a w systemie dziesiętnym liczba 10.
ZAMIANA LICZB MIĘDZY SYSTEMAMI DWÓJKOWYM I DZIESIĘTNYM Aby zamienić liczbę z systemu dwójkowego (binarnego) na dziesiętny (decymalny) należy najpierw przypomnieć sobie jak są tworzone liczby w ww systemach
Sortowanie. LABORKA Piotr Ciskowski
Sortowanie LABORKA Piotr Ciskowski main Zaimplementuj metody sortowania przedstawione w następnych zadaniach Dla każdej metody osobna funkcja Nagłówek funkcji wg uznania ale wszystkie razem powinny być
Metody numeryczne w przykładach
Metody numeryczne w przykładach Bartosz Ziemkiewicz Wydział Matematyki i Informatyki UMK, Toruń Regionalne Koło Matematyczne 8 kwietnia 2010 r. Bartosz Ziemkiewicz (WMiI UMK) Metody numeryczne w przykładach
2 Arytmetyka. d r 2 r + d r 1 2 r 1...d d 0 2 0,
2 Arytmetyka Niech b = d r d r 1 d 1 d 0 będzie zapisem liczby w systemie dwójkowym Zamiana zapisu liczby b na system dziesiętny odbywa się poprzez wykonanie dodawania d r 2 r + d r 1 2 r 1 d 1 2 1 + d
Indukcja matematyczna
Indukcja matematyczna 1 Zasada indukcji Rozpatrzmy najpierw następujący przykład. Przykład 1 Oblicz sumę 1 + + 5 +... + (n 1). Dyskusja. Widzimy że dla n = 1 ostatnim składnikiem powyższej sumy jest n
Programowanie w VB Proste algorytmy sortowania
Programowanie w VB Proste algorytmy sortowania Sortowanie bąbelkowe Algorytm sortowania bąbelkowego polega na porównywaniu par elementów leżących obok siebie i, jeśli jest to potrzebne, zmienianiu ich
Algorytmy i Struktury Danych, 2. ćwiczenia
Algorytmy i Struktury Danych, 2. ćwiczenia 2017-10-13 Spis treści 1 Optymalne sortowanie 5 ciu elementów 1 2 Sortowanie metodą Shella 2 3 Przesunięcie cykliczne tablicy 3 4 Scalanie w miejscu dla ciągów
Algorytmy. 1. Sortowanie 2. Statki i okręty. programowanie cz.7. poniedziałek, 2 marca 2009
Algorytmy. Sortowanie 2. Statki i okręty programowanie cz. ALGORYTMY SORTUJĄCE A. Przez zamianę (bąbelkowe) B. Przez wybieranie Najpopularniejsze metody sortowania C. Przez wstawianie Przez zamianę (sortowanie
Programowanie Równoległe i Rozproszone. Algorytm Kung a. Algorytm Kung a. Programowanie Równoległe i Rozproszone Wykład 8. Przygotował: Lucjan Stapp
Programowanie Równoległe i Rozproszone Lucjan Stapp Wydział Matematyki i Nauk Informacyjnych Politechnika Warszawska (l.stapp@mini.pw.edu.pl) 1/34 PRiR Algorytm Kunga Dany jest odcinek [a,b] i ciągła funkcja
L.O. św. Marii Magdaleny w Poznaniu, O POŻYTKACH PŁYN ACYCH Z RZUCANIA MONETA. Tomasz Łuczak
L.O. św. Marii Magdaleny w Poznaniu, 27.11.2015 O POŻYTKACH PŁYN ACYCH Z RZUCANIA MONETA Tomasz Łuczak NA POCZATEK DOBRA WIADOMOŚĆ! Dzięki naszym o hojnym sponsorom: Poznańskiej Fundacji Matematycznej
Wokół Problemu Steinhausa z teorii liczb
Wokół Problemu Steinhausa z teorii liczb Konferencja MathPAD 0 Piotr Jędrzejewicz Wydział Matematyki i Informatyki Uniwersytetu Mikołaja Kopernika w Toruniu Celem referatu jest przedstawienie sposobu wykorzystania
KURS PRAWDOPODOBIEŃSTWO
KURS PRAWDOPODOBIEŃSTWO Lekcja 3 Definicja prawdopodobieństwa Kołmogorowa. Prawdopodobieństwa warunkowe i niezależne. ZADANIE DOMOWE www.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowiedź (tylko
Złożoność obliczeniowa algorytmu ilość zasobów komputera jakiej potrzebuje dany algorytm. Pojęcie to
Złożoność obliczeniowa algorytmu ilość zasobów komputera jakiej potrzebuje dany algorytm. Pojęcie to wprowadzili J. Hartmanis i R. Stearns. Najczęściej przez zasób rozumie się czas oraz pamięć dlatego
Maciej Piotr Jankowski
Reduced Adder Graph Implementacja algorytmu RAG Maciej Piotr Jankowski 2005.12.22 Maciej Piotr Jankowski 1 Plan prezentacji 1. Wstęp 2. Implementacja 3. Usprawnienia optymalizacyjne 3.1. Tablica ekspansji
Prawdopodobieństwo geometryczne
Prawdopodobieństwo geometryczne Krzysztof Jasiński Wydział Matematyki i Informatyki UMK, Toruń V Lieceum Ogólnokształące im. Jana Pawała II w Toruniu 13.03.2014 Krzysztof Jasiński (WMiI UMK) Prawdopodobieństwo
Za pierwszy niebanalny algorytm uważa się algorytm Euklidesa wyszukiwanie NWD dwóch liczb (400 a 300 rok przed narodzeniem Chrystusa).
Algorytmy definicja, cechy, złożoność. Algorytmy napotykamy wszędzie, gdziekolwiek się zwrócimy. Rządzą one wieloma codziennymi czynnościami, jak np. wymiana przedziurawionej dętki, montowanie szafy z
Zastosowanie Excela w matematyce
Zastosowanie Excela w matematyce Komputer w dzisiejszych czasach zajmuje bardzo znamienne miejsce. Trudno sobie wyobrazić jakąkolwiek firmę czy instytucję działającą bez tego urządzenia. W szkołach pierwsze
Luty 2001 Algorytmy (7) 2000/2001 s-rg@siwy.il.pw.edu.pl
System dziesiętny 7 * 10 4 + 3 * 10 3 + 0 * 10 2 + 5 *10 1 + 1 * 10 0 = 73051 Liczba 10 w tym zapisie nazywa się podstawą systemu liczenia. Jeśli liczba 73051 byłaby zapisana w systemie ósemkowym, co powinniśmy
Wstęp do programowania
Wstęp do programowania Algorytmy na tablicach Paweł Daniluk Wydział Fizyki Jesień 2013 P. Daniluk (Wydział Fizyki) WP w. III Jesień 2013 1 / 23 Dwadzieścia pytań Zasady 1 Osoba 1 wymyśla hasło z ustalonej
KWIECIEŃ klasa 2 MATEMATYKA
26. tydzień nauki Jak dzielimy? Jak mnożymy? Temat: Jak dzielimy? Jak mnożymy? Mnożenie i dzielenie liczb w zakresie 50. 7.6 Zagadki matematyczne zapisywanie działań. 7.8 Rozwiązywanie zadań tekstowych
Zabawy matematyczne 2
Dla rodziców Zabawy matematyczne Głównymi celami zabaw matematycznych są rozwijanie zdolności poznawczych i samodzielnego logicznego myślenia dziecka oraz rozumienie określonych podstawowych pojęć matematycznych
Podstawy Informatyki. Sprawność algorytmów
Podstawy Informatyki Sprawność algorytmów Sprawność algorytmów Kryteria oceny oszczędności Miara złożoności rozmiaru pamięci (złożoność pamięciowa): Liczba zmiennych + liczba i rozmiar struktur danych
Scenariusz zajęć do programu kształcenia Myślę- działam- idę w świat
Scenariusz zajęć do programu kształcenia Myślę- działam- idę w świat Aur: Danuta Szymczak Klasa II Edukacja: polonistyczna, muzyczna, społeczna, matematyczna. Cel/cele zajęć: -doskonalenie umiejętności
Algorytmy i Struktury Danych, 2. ćwiczenia
Algorytmy i Struktury Danych, 2. ćwiczenia 2015-10-09 Spis treści 1 Szybkie potęgowanie 1 2 Liczby Fibonacciego 2 3 Dowód, że n 1 porównań jest potrzebne do znajdowania minimum 2 4 Optymalny algorytm do
Prawdopodobieństwo. Prawdopodobieństwo. Jacek Kłopotowski. Katedra Matematyki i Ekonomii Matematycznej SGH. 16 października 2018
Katedra Matematyki i Ekonomii Matematycznej SGH 16 października 2018 Definicja σ-algebry Definicja Niech Ω oznacza zbiór niepusty. Rodzinę M podzbiorów zbioru Ω nazywamy σ-algebrą (lub σ-ciałem) wtedy
Rekurencje. Jeśli algorytm zawiera wywołanie samego siebie, jego czas działania moŝe być określony rekurencją. Przykład: sortowanie przez scalanie:
Rekurencje Jeśli algorytm zawiera wywołanie samego siebie, jego czas działania moŝe być określony rekurencją. Przykład: sortowanie przez scalanie: T(n) = Θ(1) (dla n = 1) T(n) = 2 T(n/2) + Θ(n) (dla n
Algorytmy równoległe: ocena efektywności prostych algorytmów dla systemów wielokomputerowych
Algorytmy równoległe: ocena efektywności prostych algorytmów dla systemów wielokomputerowych Rafał Walkowiak Politechnika Poznańska Studia inżynierskie Informatyka 2014/15 Znajdowanie maksimum w zbiorze
Statystyka matematyczna
Statystyka matematyczna Wykład 1 Magdalena Alama-Bućko 25 lutego 2019 Magdalena Alama-Bućko Statystyka matematyczna 25 lutego 2019 1 / 18 Wykład : 10h (przez 10 tygodni po 45 minut) Ćwiczenia : 15h (45
Porównanie czasów działania algorytmów sortowania przez wstawianie i scalanie
Więcej o sprawności algorytmów Porównanie czasów działania algorytmów sortowania przez wstawianie i scalanie Załóżmy, że możemy wykonać dane zadanie przy użyciu dwóch algorytmów: jednego o złożoności czasowej
Temat 8. Zrobić to szybciej Sieci sortujące
Temat 8 Zrobić to szybciej Sieci sortujące Streszczenie Istnieje granica szybkości z jaką komputer może rozwiązywać konkretny problem. Czasem sposobem na zmianę tego stanu rzeczy jest równoległe użycie
Rekurencja. Przykład. Rozważmy ciąg
Rekurencja Definicje rekurencyjne Definicja: Mówimy, iż ciąg jest zdefiniowany rekurencyjnie, jeżeli: (P) Określony jest pewien skończony zbiór wyrazów tego ciągu, zwykle jest to pierwszy wyraz tego ciągu
Struktury danych i złożoność obliczeniowa Wykład 5. Prof. dr hab. inż. Jan Magott
Struktury danych i złożoność obliczeniowa Wykład 5 Prof. dr hab. inż. Jan Magott DMT rozwiązuje problem decyzyjny π przy kodowaniu e w co najwyżej wielomianowym czasie, jeśli dla wszystkich łańcuchów wejściowych
OLIMPIADA MATEMATYCZNA
OLIMPIADA MATEMATYCZNA Na stronie internetowej wwwomgedupl Olimpiady Matematycznej Gimnazjalistów (OMG) ukazały się ciekawe broszury zawierające interesujące zadania wraz z pomysłowymi rozwiązaniami z
Wybrane wyniki w zakresie umiejętności matematycznych
Wybrane wyniki w zakresie umiejętności matematycznych Struktura badanych umiejętności matematycznych Umiejętności narzędziowe, stosowane w sytuacji typowej stosowane w sytuacji nietypowej Umiejętności
Zmienne losowe i ich rozkłady
Zmienne losowe i ich rozkłady 29 kwietnia 2019 Definicja: Zmienną losową nazywamy mierzalną funkcję X : (Ω, F, P) (R n, B(R n )). Definicja: Niech A będzie zbiorem borelowskim. Rozkładem zmiennej losowej
Rachunek prawdopodobieństwa (Elektronika, studia niestacjonarne) Wykład 1
Rachunek prawdopodobieństwa (Elektronika, studia niestacjonarne) Wykład 1 Przygotowując wykład korzystam głównie z książki Jakubowski, Sztencel Wstęp do teorii prawdopodobieństwa. Jakubowski, Sztencel:
Scenariusz zajęć. Moduł VI. Projekt Gra logiczna zgadywanie liczby
Scenariusz zajęć Moduł VI Projekt Gra logiczna zgadywanie liczby Moduł VI Projekt Gra logiczna zgadywanie liczby Cele ogólne: przypomnienie i utrwalenie poznanych wcześniej poleceń i konstrukcji języka
Scenariusz zajęć nr 8
Autor scenariusza: Małgorzata Marzycka Blok tematyczny: Świat wokół nas Scenariusz zajęć nr 8 Temat dnia: Zabawy matematyką. I. Czas realizacji: 2 jednostki lekcyjne. II. Czynności przed lekcyjne: przygotowanie
Matematyka Dyskretna Zestaw 2
Materiały dydaktyczne Matematyka Dyskretna (Zestaw ) Matematyka Dyskretna Zestaw 1. Wykazać, że nie istnieje liczba naturalna, która przy dzieleniu przez 18 daje resztę 13, a przy dzieleniu przez 1 daje
Instrukcje dla zawodników
Płock, 21 marca 2015 r. Instrukcje dla zawodników Arkusze otwieramy na wyraźne polecenie komisji. Wszystkie poniższe instrukcje zostaną odczytane i wyjaśnione. 1. Arkusz składa się z 3 zadań. 2. Każde
3. Macierze i Układy Równań Liniowych
3. Macierze i Układy Równań Liniowych Rozważamy równanie macierzowe z końcówki ostatniego wykładu ( ) 3 1 X = 4 1 ( ) 2 5 Podstawiając X = ( ) x y i wymnażając, otrzymujemy układ 2 równań liniowych 3x
Maria Romanowska UDOWODNIJ, ŻE... PRZYKŁADOWE ZADANIA MATURALNE Z MATEMATYKI
Maria Romanowska UDOWODNIJ, ŻE... PRZYKŁADOWE ZADANIA MATURALNE Z MATEMATYKI Matematyka dla liceum ogólnokształcącego i technikum w zakresie podstawowym i rozszerzonym Z E S Z Y T M E T O D Y C Z N Y Miejski
ARCHITEKTURA KOMPUTERÓW Systemy liczbowe
ARCHITEKTURA KOMPUTERÓW Systemy liczbowe 20.10.2010 System Zakres znaków Przykład zapisu Dziesiętny ( DEC ) 0,1,2,3, 4,5,6,7,8,9 255 DEC Dwójkowy / Binarny ( BIN ) 0,1 11111 Ósemkowy ( OCT ) 0,1,2,3, 4,5,6,7
Liczby pseudolosowe. #include <stdio.h> #include <stdlib.h> int main() { printf("%d\n", RAND_MAX); return 0; }
Liczby pseudolosowe Standardowa biblioteka języka C w pliku nagłówkowym posiada zadeklarowane dwie funkcje służące do generowania liczb pseudolosowych: rand i srand. Funkcja srand() jako parametr
Statystyka matematyczna
Statystyka matematyczna Wykład 2 Magdalena Alama-Bućko 5 marca 2018 Magdalena Alama-Bućko Statystyka matematyczna 5 marca 2018 1 / 14 Prawdopodobieństwo klasyczne Ω - zbiór wszystkich zdarzeń elementarnych
MODELOWANIE RZECZYWISTOŚCI
MODELOWANIE RZECZYWISTOŚCI Daniel Wójcik Instytut Biologii Doświadczalnej PAN d.wojcik@nencki.gov.pl tel. 022 5892 424 http://www.neuroinf.pl/members/danek/swps/ Podręcznik Iwo Białynicki-Birula Iwona
FINAŁ 17 IGRZYSK MATEMATYCZNYCH SZKÓŁ NIEPUBLICZNYCH. Zadania dla klasy 6
FINAŁ 17 IGRZYSK MATEMATYCZNYCH SZKÓŁ NIEPUBLICZNYCH Zadania dla klasy 6 Na rozwiązanie pięciu zadań masz 90 minut. Kolejność rozwiązywania zadań jest dowolna. Maksymalną liczbę punktów możesz uzyskać
Rachunek prawdopodobieństwa Rozdział 3. Prawdopodobieństwo warunkowe i niezależność zdarzeń.
Rachunek prawdopodobieństwa Rozdział 3. Prawdopodobieństwo warunkowe i niezależność zdarzeń. 3.2. Niezależność zdarzeń Katarzyna Rybarczyk-Krzywdzińska Niezależność dwóch zdarzeń Intuicja Zdarzenia losowe
KURS PRAWDOPODOBIEŃSTWO
KURS PRAWDOPODOBIEŃSTWO Lekcja 2 Klasyczna definicja prawdopodobieństwa ZADANIE DOMOWE www.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowiedź (tylko jedna jest prawdziwa). Pytanie 1 Według klasycznej
Złożoność informacyjna Kołmogorowa. Paweł Parys
Złożoność informacyjna Kołmogorowa Paweł Parys Serock 2012 niektóre liczby łatwiej zapamiętać niż inne... (to zależy nie tylko od wielkości liczby) 100...0 100 100... 100 100 100 25839496603316858921 31415926535897932384
Podstawy Informatyki. Inżynieria Ciepła, I rok. Wykład 9 Rekurencja
Podstawy Informatyki Inżynieria Ciepła, I rok Wykład 9 Rekurencja Rekurencja z łacińskiego oznacza to przybiec z powrotem - osiągniesz rzecz wielką, jeśli zawrócisz po to, by osiągnąć rzeczy małe Przykład:
PRAWDOPODOBIEŃSTWO I KOMBINATORYKA
PRAWDOPODOBIEŃSTWO I KOMBINATORYKA ZADANIE ( PKT) Z urny zawierajacej kule w dwóch kolorach wybieramy losowo dwie. Prawdopodobieństwo wylosowania co najmniej jednej kuli białej jest równe 8, a prawdopodobieństwo
Elementy logiki matematycznej
Elementy logiki matematycznej Przedmiotem logiki matematycznej jest badanie tzw. wyrażeń logicznych oraz metod rozumowania i sposobów dowodzenia używanych w matematyce, a także w innych dziedzinach, w
OD TABLICZKI MNOŻENIA DO LICZB PIERWSZYCH MATEMATYKA ZE SCRATCHEM
Informatyka w Edukacji, XV UMK Toruń, 2018 OD TABLICZKI MNOŻENIA DO LICZB PIERWSZYCH MATEMATYKA ZE SCRATCHEM Ośrodek Edukacji Informatycznej i Zastosowań Komputerów 02-026 Warszawa, ul. Raszyńska 8/10
Typy zadań kombinatorycznych:
Typy zadań kombinatorycznych: I. Ustawianie wszystkich elementów zbioru w pewnej kolejności Przestawieniem nazywamy ustawienie elementów danego zbioru w pewnej kolejności. Liczba przestawień określa na
Rachunek prawdopodobieństwa
Rachunek prawdopodobieństwa Sebastian Rymarczyk srymarczyk@afm.edu.pl Tematyka zajęć 1. Elementy kombinatoryki. 2. Definicje prawdopodobieństwa. 3. Własności prawdopodobieństwa. 4. Zmienne losowe, parametry
Przykładowe zadania na kółko matematyczne dla uczniów gimnazjum
1 Przykładowe zadania na kółko matematyczne dla uczniów gimnazjum Zagadnienia, które uczeń powinien znać przy rozwiązywaniu opisanych zadań: zastosowanie równań w zadaniach tekstowych, funkcje i ich monotoniczność,
Indukcja matematyczna. Zasada minimum. Zastosowania.
Indukcja matematyczna. Zasada minimum. Zastosowania. Arkadiusz Męcel Uwagi początkowe W trakcie zajęć przyjęte zostaną następujące oznaczenia: 1. Zbiory liczb: R - zbiór liczb rzeczywistych; Q - zbiór
Kurs ZDAJ MATURĘ Z MATEMATYKI MODUŁ 2 Teoria liczby rzeczywiste cz.2
1 POTĘGI Definicja potęgi ł ę ę > a 0 = 1 (każda liczba różna od zera, podniesiona do potęgi 0 daje zawsze 1) a 1 = a (każda liczba podniesiona do potęgi 1 dają tą samą liczbę) 1. Jeśli wykładnik jest
KURS WSPOMAGAJĄCY PRZYGOTOWANIA DO MATURY Z MATEMATYKI ZDAJ MATMĘ NA MAKSA. przyjmuje wartości większe od funkcji dokładnie w przedziale
Zestaw nr 1 Poziom Rozszerzony Zad.1. (1p) Liczby oraz, są jednocześnie ujemne wtedy i tylko wtedy, gdy A. B. C. D. Zad.2. (1p) Funkcja przyjmuje wartości większe od funkcji dokładnie w przedziale. Wtedy
WYMAGANIA NA POSZCZEGÓLNE OCENY Z MATEMATYKI W KL. 4
WYMAGANIA NA POSZCZEGÓLNE OCENY Z MATEMATYKI W KL. 4 Na ocenę niedostateczną (1) uczeń nie spełnia wymagań koniecznych. Na ocenę dopuszczającą (2) uczeń spełnia wymagania konieczne, tzn.: 1. posiada i
1. Znajdowanie miejsca zerowego funkcji metodą bisekcji.
1. Znajdowanie miejsca zerowego funkcji metodą bisekcji. Matematyczna funkcja f ma być określona w programie w oddzielnej funkcji języka C (tak, aby moŝna było łatwo ją zmieniać). Przykładowa funkcja to:
Microsoft Small Basic
Microsoft Small Basic Obiekt Math Szacowany czas trwania lekcji: 1 godzina Obiekt Math Podczas tej lekcji dowiesz się, jak: Używać różnych właściwości obiektu Math. Używać różnych operacji obiektu Math.
Moneta 1 Moneta 2 Kostka O, R O,R 1,2,3,4,5, Moneta 1 Moneta 2 Kostka O O ( )
Nowa matura kombinatoryka i rachunek prawdopodobieństwa Zadania zamknięte (0 1 pkt) 1. Doświadczenie losowe polega na rzucie dwiema symetrycznymi monetami i sześcienną kostką do gry. Prawdopodobieństwo
Wykład 4. Określimy teraz pewną ważną klasę pierścieni.
Wykład 4 Określimy teraz pewną ważną klasę pierścieni. Twierdzenie 1 Niech m, n Z. Jeśli n > 0 to istnieje dokładnie jedna para licz q, r, że: m = qn + r, 0 r < n. Liczbę r nazywamy resztą z dzielenia
Statystyka matematyczna
Statystyka matematyczna Wykład 1 Magdalena Alama-Bućko 20 lutego 2017 Magdalena Alama-Bućko Statystyka matematyczna 20 lutego 2017 1 / 21 Wykład : 10h (przez 10 tygodni po 45 minut) Ćwiczenia : 15h (45
EGZAMIN MATURALNY Z INFORMATYKI
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MIN 2016 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę EGZAMIN MATURALNY Z INFORMATYKI POZIOM ROZSZERZONY CZĘŚĆ I DATA: 17
Scenariusz lekcji matematyki: Zastosowanie równań i układów równań do rozwiązywania zadań tekstowych. Scenariusz lekcji
Scenariusz lekcji 1. Informacje wstępne: Klasa: uczniowie klasy I szkoły ponadgimnazjalnej Czas trwania zajęć: 45 minut; Nauczany przedmiot: matematyka. 2. Temat zajęć:. 3. Integracja: międzyprzedmiotowa:
Priorytetyzacja przypadków testowych za pomocą macierzy
Priorytetyzacja przypadków testowych za pomocą macierzy W niniejszym artykule przedstawiony został problem przyporządkowania priorytetów do przypadków testowych przed rozpoczęciem testów oprogramowania.
Matematyka podstawowa X. Rachunek prawdopodobieństwa
Matematyka podstawowa X Rachunek prawdopodobieństwa Zadania wprowadzające: 1. Rzucasz trzy razy monetą a) Napisz zbiór wszystkich wyników tego doświadczenia losowego. Ile ich jest? Wyrzuciłeś większą liczbę
Algorytmy i struktury danych. Wykład 4
Wykład 4 Różne algorytmy - obliczenia 1. Obliczanie wartości wielomianu 2. Szybkie potęgowanie 3. Algorytm Euklidesa, liczby pierwsze, faktoryzacja liczby naturalnej 2017-11-24 Algorytmy i struktury danych
Zadania do samodzielnego rozwiązania
Zadania do samodzielnego rozwiązania I. Podzielność liczb całkowitych 1. Pewna liczba sześciocyfrowa a kończy się cyfrą 5. Jeśli tę cyfrę przestawimy na miejsce pierwsze ze strony lewej, to otrzymamy nową
Opis problemu i przedstawienie sposobu jego rozwiązania w postaci graficznej. Gimnazjum nr 3 im. Jana Pawła II w Hrubieszowie 1
Opis problemu i przedstawienie sposobu jego rozwiązania w postaci graficznej Gimnazjum nr 3 im. Jana Pawła II w Hrubieszowie 1 Etapy rozwiązywania problemu PROBLEM wybór metody rozwiązania ALGORYTM 1.
Zestaw zadań dotyczących liczb całkowitych
V Zestaw zadań dotyczących liczb całkowitych Opracowanie Monika Fabijańczyk ROZDZIAŁ 1 Cechy podzielności Poniższe zadania zostały wybrane z różnych zbiorów zadań, opracowań, konkursów matematycznych.
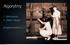
Uwaga: Funkcja zamień(a[j],a[j+s]) zamienia miejscami wartości A[j] oraz A[j+s].
![Uwaga: Funkcja zamień(a[j],a[j+s]) zamienia miejscami wartości A[j] oraz A[j+s].](/thumbs/61/46207972.jpg "Uwaga: Funkcja zamień(a[j],a[j+s]) zamienia miejscami wartości A[j] oraz A[j+s].")
Zadanie 1. Wiązka zadań Od szczegółu do ogółu Rozważmy następujący algorytm: Dane: Algorytm 1: k liczba naturalna, A[1...2 k ] tablica liczb całkowitych. n 1 dla i=1,2,,k wykonuj n 2n s 1 dopóki s
1. A 2. A 3. B 4. B 5. C 6. B 7. B 8. D 9. A 10. D 11. C 12. D 13. B 14. D 15. C 16. C 17. C 18. B 19. D 20. C 21. C 22. D 23. D 24. A 25.
1. A 2. A 3. B 4. B 5. C 6. B 7. B 8. D 9. A 10. D 11. C 12. D 13. B 14. D 15. C 16. C 17. C 18. B 19. D 20. C 21. C 22. D 23. D 24. A 25. A Najłatwiejszym sposobem jest rozpatrzenie wszystkich odpowiedzi
lekcja 8a Gry komputerowe MasterMind
lekcja 8a Gry komputerowe MasterMind Posiadamy już elementarną wiedzę w zakresie programowania. Pora więc zabrać się za rozwiązywanie problemów bardziej złożonych, które wymagają zastosowania typowych
Liczby rzeczywiste. Działania w zbiorze liczb rzeczywistych. Robert Malenkowski 1
Robert Malenkowski 1 Liczby rzeczywiste. 1 Liczby naturalne. N {0, 1,, 3, 4, 5, 6, 7, 8...} Liczby naturalne to liczby używane powszechnie do liczenia i ustalania kolejności. Liczby naturalne można ustawić
MIĘDZYSZKOLNA LIGA PRZEDMIOTOWA MATEMATYKA klasa IV PŁOCK 2014
MIĘDZYSZKOLNA LIGA PRZEDMIOTOWA MATEMATYKA klasa IV PŁOCK 204 KARTA PUNKTACJI ZADAŃ (wypełnia komisja konkursowa): Numer zadania Zad. Zad. 2 Zad. 3 Zad. 4 Zad. 5 Zad. 6 Zad. 7 Zad. 8 SUMA PUNKTÓW Max liczba
W. Guzicki Zadanie 41 z Informatora Maturalnego poziom podstawowy 1
W. Guzicki Zadanie 41 z Informatora Maturalnego poziom podstawowy 1 W tym tekście zobaczymy rozwiązanie zadania 41 z Informatora o egzaminie maturalnym z matematyki od roku szkolnego 014/015 oraz rozwiązania
Dydaktyka matematyki (II etap edukacyjny) II rok matematyki Semestr letni 2018/2019 Ćwiczenia nr 2
Dydaktyka matematyki (II etap edukacyjny) II rok matematyki Semestr letni 2018/2019 Ćwiczenia nr 2 Zadanie domowe Rozwiązanie zadania: o rozumowanie ucznia ( wzroczne, wycięcie i nałożenie, złożenie) o
Programowanie w języku C++ Agnieszka Nowak Brzezińska Laboratorium nr 2
Programowanie w języku C++ Agnieszka Nowak Brzezińska Laboratorium nr 2 1 program Kontynuujemy program który wczytuje dystans i ilości paliwa zużytego na trasie, ale z kontrolą danych. A więc jeśli coś
Ćwiczenia z metodyki nauczania rachunku prawdopodobieństwa
Ćwiczenia z metodyki nauczania rachunku prawdopodobieństwa 25 marca 209 Zadanie. W urnie jest b kul białych i c kul czarnych. Losujemy n kul bez zwracania. Jakie jest prawdopodobieństwo, że pierwsza kula
Matematyka dyskretna. Andrzej Łachwa, UJ, /15
Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl 7/15 Rachunek różnicowy Dobrym narzędziem do obliczania skończonych sum jest rachunek różnicowy. W rachunku tym odpowiednikiem operatora
Analiza algorytmów zadania podstawowe
Analiza algorytmów zadania podstawowe Zadanie 1 Zliczanie Zliczaj(n) 1 r 0 2 for i 1 to n 1 3 do for j i + 1 to n 4 do for k 1 to j 5 do r r + 1 6 return r 0 Jaka wartość zostanie zwrócona przez powyższą