Sprawozdanie. Laboratorium Problemowe, Automatyka i Robotyka, I rok studiów magisterskich. Prowadzący: dr inż. Andrzej Tutaj
|
|
|
- Klaudia Gajda
- 9 lat temu
- Przeglądów:
Transkrypt
1 Sprawozdanie Laboratorium Problemowe, Automatyka i Robotyka, I rok studiów magisterskich Prowadzący: dr inż. Andrzej Tutaj Projekt przygotowali: Dorian Chrzanowski, Paweł Tomasik, Krzysztof Wesołowski Kraków, marca 2 czerwca 20
2 Spis treści Wprowadzenie Opis obiektu sterowania Sposób modelowania obiektu Sterowanie obiektem Opis środowiska pracy Karta pomiarowa Środowisko Matlab/Simulink Modelowanie Metoda strojonego modelu (krótki opis idei) Układ silnik - śmigło Pomiar siły ciągu w funkcji sterowania Pomiar prędkości śmigła w funkcji sterowania Synteza zależności siły ciągu od prędkości Modelowanie dynamiki układu nieliniowego Modelowanie ruchu belki Moment niewyważenia Moment bezwładności oraz tarcia w osi zamocowania Linearyzacja modelu Przygotowanie modelu do linearyzacji Dobór punktu pracy Parametry modelu zlinearyzowanego Synteza regulatora Regulator od stanu obiektu Synteza dyskretnej wersji LQ Wprowadzenie całki uchybu położenia do regulatora Prosty człon całkujący Człon całkujący zintegrowany z obiektem i regulatorem Anti-Windup dla członu całkującego Wykorzystanie obserwatora do odtwarzania stanu Obserwator Kalmana (wersja dyskretna) Odtwarzanie stałego zakłócenia Podsumowanie Wykonane elementy projektu Możliwości rozbudowy/modyfikacji obecnego sterownika Bibliografia Spis ilustracji Rysunki Wykresy Strona 2 z 27
3 Wprowadzenie Przedmiotem sprawozdanie jest przygotowanie sterownika dla jednej osi swobody modelu śmigłowca. W celu przygotowania sterownika wykorzystano nowoczesne metody szybkiego prototypowania (Rapid Prototyping) i projektowania opartego o model (MBD, Model Based Design). Wykorzystano w tym celu środowisko zbudowane w oparciu o oprogramowanie Matlab/Simulink, kartę IO oraz elementy wykonawcze. Pozwoliło to na szybkie (poniżej 30 godzin) przygotowanie modelu obiektu, wybór metody jego sterowania, zaimplementowanie jej i osiągnięcie bardzo dobrych rezultatów. Warto w tym miejscu zaznaczyd, że przygotowano w ten sposób tylko prototyp sterownika, nie nadający się do zastosowania przed zaimplementowaniem go w docelowym układzie sterującym.. Opis obiektu sterowania Obiektem sterowania jest model helikoptera o osi swobody. Jako fizyczny obiekt zastosowano helikopter o 2 osiach swobody (Inteco, 20), z zablokowaną możliwością ruchu w osi Yaw. napędzane śmigło nieużywane śmigło napędzany silnik, tachoprądnica oś obrotu wyposażona w enkoder przeciwwaga Rysunek - Schemat obiektu sterowania Jest to system o jednym wejściu (sterowanie silnikiem napędzającym śmigło) i wielu wyjściach (położenie belki mierzone przez enkoder oraz prędkośd śmigła mierzona przez tachoprądnice). Strona 3 z 27
4 .2 Sposób modelowania obiektu W celu zastosowania MBD zdecydowano o przygotowaniu w pełni nieliniowego modelu badanej części śmigłowca. Wybrano 3 kluczowe dla modelu zmienne stanu położenie belki, prędkośd kątową śmigła, prędkośd kątową belki. O szczegółowej strukturze poszczególnych elementów modelu decydowano dopiero po zebraniu danych eksperymentalnych. Pozwoliło to dopasowad ją do potrzeb tego konkretnego obiektu. Szczegółowy opis struktury modelu znaleźd można w częściach: Układ silnik - śmigło Modelowanie ruchu belki.3 Sterowanie obiektem Celem sterowania była stabilizacja obiektu w wybranym punkcie pracy. Docelowo obiekt miał byd odporny zarówno na zakłócenia o charakterze szumu z zerową wartością średnią jak i stałe zakłócenia. Wybrano regulator liniowo-kwadratowy (LQ), współpracujący z obserwatorem filtrem Kalmana odtwarzającym zmienne stanu. Wprowadzano również modyfikacje zarówno do obserwatora jak i regulatora, mające na celu zwiększenie odporności układu na opisane powyżej zakłócenia. W dalszej części opracowania w ramach prezentacji przebiegów testowych często wykorzystywad będziemy wspominad o filtrze Kalmana czy regulatorze LQ jeszcze przed ich wprowadzeniem (odpowiednio w rozdziałach Błąd! Nie można odnaleźd źródła odwołania. i 5). Spowodowane jest to hęcią uporządkowania opisu tematycznie, podczas gdy faktyczny rozwój aplikacji sterującej był bardziej złożony. 2 Opis środowiska pracy 2. Karta pomiarowa Do komunikacji pomiędzy komputerem sterującym a koocówkami mocy i czujnikami wykorzystano kartę pomiarową PCI. Była to karta RT-DAC4/PCI, zamontowana w komputerze będącym częścią środowiska testowego. RT-DAC4/PCI (Real-Time Data Acquisition Board) jest wielofunkcyjną cyfrową kartą do rejestrowania danych i sterowania w systemach czasu rzeczywistego w środowisku Windows. Zawiera ona układ FPGA firmy Xilinx, z rodziny Spartan II. Komunikuję się z systemem przez układ PLX 9030 i magistralę PCI. Technologia FPGA w połączeniu z wykorzystaniem języków programowania sprzętu umożliwia przeniesienie złożonych operacji cyfrowego przetwarzania danych pomiarowych i kształtowania sygnału sterującego na poziom sprzętu oraz zmianę funkcji karty z poziomu programowego bez konieczności zmian sprzętowych. (Bałys, 2006). 2.2 Środowisko Matlab/Simulink Jako środowisko wykorzystywano pakiet Matlab/Simulink, wyposażony w przyborniki: Real Time Workshop Strona 4 z 27
5 Real Time Windows Target biblioteka do karty RT-DAC4/PCI W pakiecie tym zbudowano modele zgodnie z opisem w rozdziale 3. Wykorzystano go również do implementacji regulatora oraz optymalizacji samego modelu jak i nastaw regulatora. 3 Modelowanie 3. Metoda strojonego modelu (krótki opis idei) Metoda strojonego modelu polega na identyfikacji parametrów modelu, poprzez minimalizację wskaźnika wyliczanego na podstawie zarejestrowanej odpowiedzi obiektu oraz odpowiedzi modelu otrzymanej podczas symulacji. Zmieniając strukturę modelu lub tylko jego współczynniki dopasowuje się jego odpowiedź do otrzymanej na drodze eksperymentu odpowiedzi obiektu. Przyjętym wskaźnikiem jakości była całka z kwadratu różnicy przebiegu zarejestrowanego oraz obliczonego na podstawie modelu. Rysunek 2 - Schemat działania metody strojonego modelu Aby na drodze optymalizacji statycznej dobrad oba współczynniki, zbudowano przybliżony model helikoptera w Simulinku. Następnie przygotowywano funkcję przyjmującą wektor parametrów jako argument, wykonująca symulację i zwracającą obliczony wskaźnik jakości. Ponadto przygotowano skrypt w języku Matlab, korzystający z funkcji fminsearch oraz funkcji optymalizowanej: oo = optimset('display','on','tolx',.000,'tolfun',.000,'maxfunevals',200,'maxiter',200); y = fminsearch('szukaj',x,oo); Strona 5 z 27
6 Warto zwrócid uwagę na problem doboru warunków początkowych. Często są one nieznane lub trudne w zmierzeniu, co utrudniałoby identyfikację (parametry modelu odwzorowywały błędy stanu początkowego zamiast zmian w modelu). Rozwiązaniem tej sytuacji może byd uznanie warunków początkowych za składowe wektora wejściowego funkcji. Pozwala to na ich dopasowanie do odpowiedzi modelu i w efekcie najlepsze dopasowanie odpowiedzi obiektu i modelu. 3.2 Układ silnik - śmigło Układ napędowy śmigłowca to układ składający się kolejno z wyjścia karty IO, wzmacniacza podającego sterowanie PWM na silnik DC, samego silnika oraz zamocowanego na nim śmigła. Jest to układ, którego przybliżone, nieliniowe modelowanie wymaga uwzględnienia wielu elementów związanych z: dynamika silnika elektrycznego, moment bezwładności śmigła, tarcie w silniku i opory aerodynamiczne śmigła, zależnością pomiędzy prędkością obrotową śmigła a siłą ciągu. Dużym ułatwieniem jest tachoprądnica mierząca prędkośd obrotową śmigła Pomiar siły ciągu w funkcji sterowania Pierwszym eksperymentem służącym wyznaczeniu charakterystyki statycznej obiektu było mierzenie siły ciągu w zależności od wartości sterowania podawanego na silnik. W tym celu wykorzystano wagę o dokładności g oraz szalkę z obciążnikami. Podstawę pomiarów ilustruje Rysunek 3. W zależności od kierunku siły ciągów stosowano liczbę ciężarków utrzymującą belkę w pozycji poziomej i mierzono wpływ sterowania na odchylenia wartości mierzonej przez wagę. Umieszczenie wagi pod ogonem helikoptera pozwoliło na wyeliminowanie wpływu strumienia powietrza na pomiary. Strona 6 z 27
7 siła ciągu generowana przez śmigło siłą powstała na skutek działania siły ciągu Rysunek 3 - Idea eksperymentu służącego wyznaczeniu siły ciągu Stosując powyższy schemat zmierzono wartośd odchylenia w gramach, którą z kolei przeliczono na siłę w niutonach. Wykorzystując parametry śmigłowca dokonano zamiany siły przyłożonej do ogona na moment. Wynik obliczeo przedstawia Tabela, ilustruje je również Wykres. W trakcie ich przeprowadzania wykorzystano następujące wartości:, gdzie to stała grawitacji,, gdzie to długośd krótszego ramienia. Tabela - Wyniki zależności momentu i siły ciągu w funkcji sterowania U Δm [g] Siła [N] Moment [Nm] Strona 7 z 27
8 Wykres - Zależnosd momentu generowanego przez śmigło od sterowania Pomiar prędkości śmigła w funkcji sterowania Kolejną ważna do wyznaczenia charakterystyką statyczną była zależnośd prędkości śmigła od sterowania. W trakcie pomiaru należałoby w jak największej ilości punktów pomiarowych (wartościach sterowania) poczekad na ustalenie się prędkości śmigła a następnie odczytad prędkośd w każdym z nich. Aby przyśpieszyd ten żmudny eksperyment zdecydowaliśmy się na pomiar prędkości przy wolnozmiennym sterowaniu. W trakcie dwóch eksperymentów najpierw zarejestrowaliśmy przebieg dla U zmieniającego się od - do, a następnie dla U zmieniającego się od do -. Wynik eksperymentu przedstawia Wykres 2. Niestety prędkośd była kompromisem pomiędzy ilością danych, która udawało się bezproblemowo zebrad w środowisku Matlab/Simulink a chęcią uzyskania jak najmniejszej histerezy. Dalsza obróbka danych polegała na obliczeniu średniej prędkości przy danym sterowaniu (średnia arytmetyczna obu przebiegów), oraz na wygładzeniu otrzymanej różnicy (wartośd oryginalna była zaszumiona ze względu na szumy w sygnale mierzonym na tachoprądnicy). Strona 8 z 27
9 W celu wygładzenia różnicy zastosowano filtrację średnią ruchomą, o ilości próbek równej 200. Ponieważ dane zbierano z częstotliwością próbkowania 0ms, szerokośd okna filtru wynosiła 2s. Wykres 2 - Zmierzona zależnośd prędkości śmigła od sterowania Wykres 3 - Zależnośd prędkości śmigła od sterowania po obróbce Strona 9 z 27
10 Aproksymacje funkcjami pierwszego stopnia wybrano ze względu na chęd użycia bloku Lookup Table do modelowania zmierzonej charakterystyki statycznej. Pozwala na to zastosowanie funkcji oprogramowania Matlab (przyjmującej dane rzeczywiste, liczbę węzłów i dopasowującej funkcje sklejaną minimalizując różnicę kwadratów): app = spap2(kcount-,2,psc_meas_x, psc_meas_y); Synteza zależności siły ciągu od prędkości Oba pomiary pomagały nam odtworzyd zależności siły ciągu i prędkości od sterowania. W rzeczywistym modelu będziemy jednak potrzebowali na podstawie mierzonej prędkości obliczad siłę ciągu. Ponieważ obliczając wartości w Lookup Table wyrażające zależnośd prędkości od sterowania zadbano o wybór punktów -;0.;, synteza tej zależności sprowadza się do sparowania wartości prędkości i siły ciągu. W wyniku takiej operacji otrzymamy kolejną lookup table. Jej kształt ilustruje Wykres 4. Wykres 4 - Zależnośd momentu od prędkości śmigła Odtworzona charakterystyka odpowiada kształtem zależnościom teoretycznym (zależnośd kwadratowa, niesymetryczna budowa śmigła). Użyjemy tej zależności w celu zamodelowania modelu układu śmigło silnik Modelowanie dynamiki układu nieliniowego W celu zamodelowania nieliniowej charakterystyki użyto następującego modelu, który przedstawia Rysunek 4. Istotnym parametrem opisującym działanie układu jest wartośd wzmocnienia opisana, jako pdc_gain (propeller dynamic characteristic gain). W celu wyznaczenie tej zmiennej wykorzystano metodę strojonego modelu (patrz 3.). Strona 0 z 27
11 Control Value to Speed Target Speed Control Value pdc_gain s Integrator 2 Current Speed Speed to Control Value Rysunek 4 - Model dynamiki prędkości śmigła w funkcji sterowania W celu przeprowadzenia identyfikacji skonstruowano schemat porównujący wartośd wyjścia z wartością mierzoną, napisano funkcję obliczającą różnicę oraz przygotowano funkcję, która obliczała wielkośd błędu dla różnych wartości pdc_gain. Pitch pos Propeller CV Pitch ang. v elocity measurements From Workspace Heli model Propeller speed 2 model object Rysunek 5 - Schemat używany do porównywania prędkości śmigła w modelu i obiekcie Ostatecznie obliczona wartośd współczynnika pdc_gain wyniosła. Dla tej wartości zapisano również przebiegi będące efektem optymalizacji (wraz ze sterowaniem dla porównania). Wykres 5 ilustruje te przebiegi, pozwalając również intuicyjnie ocenid jakośd przyjętego modelu jako bardzo dobrą. Strona z 27
12 3.3 Modelowanie ruchu belki Wykres 5 Przebiegi dla optymalnej wartości pdc_gain Przyjęto następujący model fizyczny belki: I Gsin( 0) d F( n) Gdzie: () -przyspieszenie kątowe belki I - moment bezwładności G - moment niewyważenia - kąt odchylenia belki 0 - kąt niewyważenia belki - współczynnik tarcia - prędkośd kątowa belki d - długośd ramienia belki F(n) - siła ciągu w funkcji prędkości obrotowej śmigła Z powyższych parametrów bezpośrednio mierzalne są: długośd ramienia oraz kąt niewyważenia (odchylenie belki od pozycji zerowej w położeniu równowagi przy wyłączonym śmigle) Strona 2 z 27
13 0 = [rad] d = [m] Zależnośd () to równanie różniczkowe nieliniowe, drugiego rzędu. Zakładając, że znana jest charakterystyka F(n), długośd ramienia oraz kąt niewyważenia, na podstawie analizy odpowiedzi układu możliwa jest identyfikacja momentu bezwładności, współczynnika tarcia oraz momentu niewyważenia Moment niewyważenia Identyfikacja momenty niewyważenia wykonano poprzez doświadczalne dobranie takiego sterowania, które utrzymuje belkę w pozycji zerowej. W takiej sytuacji równanie () przyjmuje postad: 0 Gsin(0 0) d F( n) sin( ) G [Nm] d F( n) Moment bezwładności oraz tarcia w osi zamocowania Identyfikację momentu bezwładności oraz współczynnika tarcia wykonano dwiema metodami: metodą strojonego modelu oraz poprzez przybliżenie układu modelem liniowym drugiego rzędu (oscylator harmoniczny tłumiony) Przesuwając układ współrzędnych tak, by kąt wychylenia belki przyjmował wartośd zero w punkcie równowagi przy zatrzymanym śmigle, oraz linearyzując model w tymże punkcie, równanie () przyjmuje postad: x I Gx x Można wykazad, że dla układu opisanego powyższym równaniem różniczkowym: 2 J, 2 2 GT 4 2J (2) T Gdzie T to okres drgao tłumionych, a to dekrement tłumienia opisany zależnością ( amplituda drgao): n log A A in i Zarejestrowano swobodne oscylacje belki. Ai - i-ta Strona 3 z 27
14 Wykres 6 Oscylacje swobodne gasnące Zmierzono czas trwania 0 pełnych okresów (dt) oraz iloraz amplitud pierwszego i dziesiątego cyklu. = -0. T = 2.83s co po podstawieniu do zależności (2) daje następujące wartości szukanych parametrów: J = 0.05 [kg*m 2 ] = 3.6 * 0-3 [Nm*s] W Simulinku zbudowano model odpowiadający obiektowi opisanemu równaniem (). Jako początkowe położenie belki przyjęto wartośd pierwszej próbki z zarejestrowanego przebiegu. Startowa wartośd prędkości wynosiła 0. Odpowiadało to warunkom rzeczywistego eksperymentu, w którym odchylano belkę od położenia równowagi i puszczano rejestrując oscylacje położenia. Horyzont czasowy ustalono na 80 sekund. Jako parametry modelu wstawiono wartości wyznaczone analitycznie w poprzednim kroku. Wykres 7 przedstawia porównanie odpowiedzi modelu do zarejestrowanej trajektorii. Obserwujemy jakościowe podobieostwo pomiędzy przebiegami. Dośd dobrze odwzorowany jest dekrement tłumienia. Wyraźną rozbieżnośd natomiast wykazuje okres drgao. Przyczyną jest fakt, że obiekt w rzeczywistości nie jest liniowy, a co za tym idzie założenie o stałości okresu wniosło obserwowaną niedokładnośd. W rzeczywistości rejestrację rozpoczynano wcześniej niż w momencie zwolnienia belki. Po zapisie danych obcinano początkowe wartości, tak aby początek zarejestrowanego przebiegu odpowiadał maksymalnemu wychyleniu i zerowej prędkości Strona 4 z 27
15 Wykres 7 Metoda analityczna odpowiedź obiektu i modelu Następny krokiem było wykonanie identyfikacji metodą strojonego modelu. Za parametry optymalizacji przyjęto moment bezwładności oraz współczynnik tarcia. Wykorzystano wbudowaną w pakiet Matlab funkcję do bezgradientowego poszukiwania minimum fminsearch. Jako dane startowe do optymalizacji wprowadzono wyniki uzyskane poprzednią metodą. Za wskaźnik jakości przyjęto całkę z kwadratu błędu (różnicy pomiędzy odpowiedzią modelu a zarejestrowaną odpowiedzią obiektu). Wykres 8 przedstawia przebieg zmian wskaźnika jakości w trakcie kolejnych wywołao funkcji. Wykres 9 przedstawia efekt optymalizacj. Niebieski wykres to zarejestrowany przebieg, czerwony zaś to odpowiedź modelu. Wykres 8 - Zmiana wartości wskaźnika jakości w kolejnych iteracjach Strona 5 z 27
16 Wykres 9 Metoda strojonego modelu - Odpowiedź obiektu i modelu W trakcie procedury strojenia otrzymano następujące wyniki: Różnią się one od tych wyznaczonych metodą analityczną o ok 20%. Można je jednak uznad za bardziej wiarygodne, ze względu na zdecydowanie większe podobieostwo przebiegów: teoretycznego i rzeczywistego. Identyfikacja parametrów belki nasuwa kilka spostrzeżeo: Przybliżenie oporów ruchu tarcie wiskotycznym jest najprawdopodobniej głównym źródłem niedokładności modelowania Przy małych amplitudach drgao rzeczywiste tłumienie drgao jest silniejsze niż to wyznaczone teoretycznie. Tarcie w fizyce jest zjawiskiem bardzo trudnym do modelowania i przybliżanie go zależnością liniową musi prowadzid do niedokładności Kolumna helikoptera zablokowana jest w osi pionowej. Dla różnych prędkości śmigła moment generowany przez opór powietrza (kompensowany przez blokadę) jest inny. Fakt ten powoduje zmienną siłę docisku pomiędzy kolumną a blokadą, a w konsekwencji również zmienny współczynnik tarcia 4 Linearyzacja modelu Zadaniem sterowania była stabilizacja obiektu w wybranym punkcie. Pozwoliło to na dobór tego punktu a następnie przybliżenie zachowania obiektu w jego otoczeniu modelem liniowym. Strona 6 z 27
17 4. Przygotowanie modelu do linearyzacji Pakiet Matlab/Simulink wspiera dobór punktu pracy oraz umożliwia linearyzacje modelu w tak dobranym punkcie. Aby było to jednak możliwe konieczne jest przygotowanie modelu o wejściach i wyjściach taki jak w obiekcie. Rysunek 6, Rysunek 7 oraz Rysunek 8 ilustrują cały model wykorzystany w linearyzacji. U Pitch pos Propeller CV Pitch ang. v elocity Propeller speed Heli model pitch Terminator 2 propv Rysunek 6 - Model helikoptera jako osobny plik mdl Propeller CV Target Speed Control Value Current Speed Propeller speed to torque Pitch position External torque Angular velocity Pendulum Pitch pos 2 Pitch ang. velocity 3 Propeller speed Rysunek 7 - Model helikoptera - zawartośd 2 Angular velocity External torque /J s s Pitch position b/j G/J sin(u[] - fi0) Rysunek 8 - Zawartośd modelu wahadła 4.2 Dobór punktu pracy Jako punkt pracy wybrano helikopter w poziomym położeniu. Po dobraniu oczekiwanego położenia pozostało obliczenie wartości sterowania gwarantującego zerowe pochodne zmiennych stanu w punkcie pracy. Znając oczekiwaną wartośd zmiennych stanu można wywoład funkcję: [xr,ur,yr] = trim('hmodel', [0,0,0]', 0.0, 0,, [], []); W wywołaniu powyższym przekazujemy kolejne argumenty: Strona 7 z 27
18 nazwa modelu o strukturze opisanej na początku rozdziału 4, wartości początkowe dla algorytmu poszukiwania punktu równowagi, kolejno: o zmienne stanu X0, o zmienna sterowania U0, o zmienna wyjścia Y0. indeksy wartości: o dla których stan początkowy X0, o dla których stan sterowania U0, o dla których stan wyjścia Y0, ma pozostad niezmieniony w trakcie pracy algorytmu. efektem działania funkcji jest zbiór parametrów charakteryzujących punkt równowagi: xr = ur = yr = Parametry modelu zlinearyzowanego Po dobraniu pełnego stanu równowagi możemy zająd się linearyzacją modelu w punkcie pracy. Zlinearyzowany model będzie dobrze opisywał dynamikę odchyłek od punktu równowagi, pod warunkiem że będą się one odbywały w pobliżu tego punktu. Do linearyzacji używamy kolejnej funkcji oprogramowania Matlab: [A,B,C,D]=linmod('hmodel',xr,ur); Sc=ss(A,B,C,D); Funkcja ta zwraca macierze stanu modelu odchyłkowego z których następnie od razu budujemy system ciągły LTI (Linear Time Invariant): a = x x2 x3 x 0 0 x x b = u x 0 x x3 0 c = x x2 x3 y 0 0 y2 0 0 Strona 8 z 27
19 d = u y 0 y2 0 5 Synteza regulatora Dla liniowego modelu (a takim dysponujemy po linearyzacji) istnieje regulator od stanu, optymalny w sensie minimalizacji całkowego kryterium jakości. Dobierzemy nastawy takiego regulatora, korzystając po raz kolejny z możliwości oprogramowania Matlab. 5. Regulator od stanu obiektu Regulator od stanu (w przeciwieostwie do regulatorów operujących na wyjściu obiektu) pozwala na pełną i optymalną kontrolę obiektu dynamicznego. Jego konstrukcja wymaga znajomości modelu obiektu (który przygotowano w rozdziale 3) oraz bieżącego stanu systemu. W naszym systemie 2 zmienne stanu są bezpośrednio mierzone. 5.2 Synteza dyskretnej wersji LQ Ponieważ nasz system kontrolowany jest przez cyfrowy sterownik (komputer) z stałym okresem próbkowania, zbudujemy sterownik uwzględniający specyfikę dyskretnych systemów. O ile obliczanie wartości wzmocnienia regulatora jest proste zarówno analitycznie (sprowadza się do rozwiązania układu kilku równao liniowo kwadratowych), o tyle wyzwaniem może byd dobór współczynników do kryterium jakości. Po wielu eksperymentach z jakością sterowania doszliśmy do dającej intuicyjnie dobre rezultaty macierzy: lqq = [ 0 0; 0 0 0; ]; lqr = 0.; za syntezę regulatora odpowiada funkcja: K = lqrd(lqa, lqb, lqq, lqr, 0.0); dyskretyzuje ona model ciągły i przy podanych macierzach wskaźnika jakości dobiera optymalne sterowanie. Wynik takie operacji do gotowa do zastosowania w sprzężeniu zwrotnym macierz, taka że optymalne : K = Przykładowy przebieg ilustrujący działanie regulatora przedstawia Wykres 0. Strona 9 z 27
20 Wykres 0 - Położenie belki śmigłowca w odpowiedz na skok 5.3 Wprowadzenie całki uchybu położenia do regulatora Regulator LQ jak każdy regulator proporcjonalny stabilizuje do zera tylko w gdy docelowa wartośd zmiennych stanu i sterowania jest zerowa. W omawianym przypadku statyczny feedforward obliczony przy linearyzacji pozwala na stabilizację w punkcie równowagi. Celem regulatora nie jest działanie przy różnych punktach zadanych, dlatego z tego punktu widzenia można by zakooczyd projektowanie regulatora. W praktyce jednak występują inne czynniki, które mogą powodowad niepożądaną zmianę punktu równowagi wokół którego pracuje regulator: niedokładności modelowania, gdyż na podstawie modelu wyznaczono zarówno punkt pracy jak i nastawy regulatora, zakłócenie zewnętrzne, takie jak na przykład przyłożony stały moment. Chcąc uniknąd takiego odchylenia obiektu od zadanego punktu wprowadzono człon całkujący w dwóch wariantach omówionych kolejno w podrozdziałach 5.3. i Prosty człon całkujący Pierwszym zastosowanym sposobem likwidacji uchybu była całka sumująca błąd i zwiększająca sterowanie. Dała ona satysfakcjonujące efekty (likwidacje uchybu) przy dużych skutkach ubocznych oscylacje). Strona 20 z 27
21 Nie przeanalizowano dokładniej jej działania, chcąc położyd nacisk na lepszą metodę likwidacji uchybu integracje całki i regulatora LQ, gdzie całka staje się dodatkową zmienną stanu Człon całkujący zintegrowany z obiektem i regulatorem Lepszym niż opisany w punkcie 5.3. sposobem na dodanie całki z uchybu jest zintegrowanie całki z regulatorem. Całka dla regulatora staje się elementem obiektu, a nastawy wyliczone są już dla rozszerzonego układu. Daje to szereg korzyści: spójny opis matematyczny (zmienia się tylko rząd obiektu), gwarancja stabilności układu zamkniętego (daje nam to regulator LQ), możliwośd regulacji wrażliwości regulatora na odchyłkę wraz z pozostałymi parametrami w macierzy kosztów (całka jest dodatkową zmienną stanu). Konstrukcję takiego regulatora przedstawia Rysunek 9. Głównym, istotnym z naszego punktu widzenia wejściem tak przygotowanego regulatora jest stan obiektu (3 zmienne, mierzone i odtwarzane, patrz rozdział Błąd! Nie można odnaleźd źródła odwołania.. Wyjściem jest z kolei terowanie, które po dodaniu do wartości feedforward jest podawana na silnik. State in -K* uvec LQ gain Control out s 2 sat_overshoot 0 Rysunek 9 - Regulator LQ z dodanym całkowaniem Efekt działania członu całkującego w sytuacji występowania stałego, nieuwzględnionego w modelu obciążenia przedstawia Wykres. Strona 2 z 27
22 Wykres - Porównanie odpowiedzi zakłóconego obiektu w zależności od zastosowanego regulatora Anti-Windup dla członu całkującego Dodatkowa zmienna stanu jest matematycznym zabiegiem pozwalającym wprowadzid do regulatora całkę z uchybu. Niezależnie od sposobu implementacji całkowanie takie zwiększa rząd układu, a w szczególności powoduje oscylacje. Jest to m.in. spowodowane całkowaniem błędu także w momencie gdy jest to już zabieg nieskuteczny gdy wartośd sygnału wyjściowego jest już i tak maksymalna. Wykres 2 ilustruje wpływ całkowania na odpowiedź układu. Widoczne jest znaczne przeregulowanie wywołane wprowadzeniem części całkującej. W celu zmniejszenia tego efektu stosuje się mechanizmy ograniczający całkowanie przy nasyceniu wyjścia. W projektowanym regulatorze zdecydowano się wykorzystad jedną z prostszych konstrukcyjnie strategii wartośd sterowania przewyższająca poziom nasycenia jest odejmowana od odchyłki stanu wchodzącej na całkę. Powoduje to zaprzestanie narastania lub nawet zmniejszenie wartości dodatkowej zmiennej stanu gdy nasycenie jest osiągane. Pomimo jego zastosowania odpowiedź niezakłóconego obiektu z i bez całki wskazuje, że całka jest rozwiązaniem którego należy używad z odpowiednią ostrożnością. Strona 22 z 27
23 Wykres 2 - Wpływ całkowania na odpowiedź układu regulacji na skok Szczegółowe informacje o zastosowanej i innych konstrukcjach anti-windup można znaleźd w opracowaniu (Instytut Sterowania i Elektroniki Przemysłowej, 20). 6 Wykorzystanie obserwatora do odtwarzania stanu Zasadniczą rolą obserwatora jest odtwarzanie tych zmiennych stanu obiektu, które nie są bezpośrednio mierzalne. W wielu jednak przypadkach wykorzystywana jest też inna jego własnośd, jaką jest filtracja zakłóceo. Gdy pomiar którejś ze zmiennych stanu obarczony jest dużym błędem, lub gdy szumy pomiarowe mają znaczną amplitudę, niekiedy lepsze wyniki daje obserwacja tej zmiennej stanu z wykorzystaniem obserwatora asymptotycznego niż bezpośrednie jej mierzenie. W przypadku omawianego obiektu nie dysponujemy bezpośrednimi odczytami prędkości kątowej belki. Jest ona aproksymowana ilorazem różnicowym wskazao enkodera, jednak jakośd tak wyliczonej wartości pozostawia wiele do życzenia. Problem ujawnia się głównie przy niewielkich prędkościach, gdzie w jednostce czasu enkoder zmienia swoje wskazania o jedną bądź dwie jednostki. Sytuację taką ilustruje Wykres 3. Jeśli sterowanie uzależnione będzie od mierzonej w ten sposób prędkości, to wartośd zadana podawana na element wykonawczy będzie również cechowała się gwałtownymi pikami, co jest pod wieloma względami niekorzystne. Strona 23 z 27
24 Wykres 3 Efekt różniczkowania odczytów z enkodera 6. Obserwator Kalmana (wersja dyskretna) Z powodów opisanych we wstępie zdecydowano się na implementacje obserwatora asymptotycznego, którego zadaniem miało byd odtwarzanie prędkości kątowej belki. Zakładamy, że obiekt po linearyzacji i dyskretyzacji opisany może byd równiami: x( k ) A x( k) B y( k) Cx( k) v( k) d d u( k) Gw( k) Gdzie człony Gw (k) oraz v (k) odpowiadają odpowiednio za zakłócenia działające na obiekt i na jego wyjście. Do wyznaczenia wzmocnienia Kalmana (macierzy K ) należało oszacowad macierze kowariancji szumów (L i N). Zakłócenia, jakie oddziałują na omawiany obiekt i na jego wyjście nie spełniają oczywiście założeo teorii projektowania filtru Kalmana, ale praktyka pokazuje, że mimo to zastosowanie takiego filtru może przynieśd dobre efekty. Arbitralnie przyjęto, że: G Obliczona na tej podstawie macierz K jest równa: K Matematyczny opis dyskretnego obserwatora przedstawia równanie (3) xˆ ( k ) A xˆ( k) B u( k) K( y( k) Cxˆ( k)) (3) d d Macierz wyjścia C została zmodyfikowana tak, by nie uwzględniad prędkości kątowej belki. Wyjściem z obiektu jest tylko położenie belki oraz odczyt z tachoprądnicy. Na ich podstawie wyznaczana jest brakująca zmienna stanu. Wykres 4 przedstawia efekt działania tak zaprojektowanego obserwatora. Strona 24 z 27
25 Wykres 4 Efekt działania filtru Kalmana Obserwujemy zdecydowane zredukowanie zakłóceo będących efektem kwantyzacji odczytów z enkodera. Ponieważ obserwator i obiekt startują z różnych warunków początkowych w początkowych chwilach czasu estymata znacząco różni się od stanu mierzonego. 6.2 Odtwarzanie stałego zakłócenia Dotychczasowe rozważania na temat obserwatora asymptotycznego były prowadzone przy założeniu, że zakłócenia działające na układ mają zerową wartośd średnią. Jest to założenie niepraktyczne, zwłaszcza w przypadku analizy momentów działających na belkę. W poprzednim rozdziale omawiany był problem stałego obciążenia zawieszonego na jednym z jej kooców. Standardowy regulator LQ nie radził sobie z taką sytuacją i konieczne było wprowadzenie całki z uchybu jako dodatkowej zmiennej stanu. Rozwiązanie problemu stałego zakłócenia, jakie przedstawione będzie poniżej w praktyce również sprowadza się do całkowania uchybu i podawania wartości tej całki jako wejście do regulatora. Wykorzystane jednak zostało bardziej formalne podejście do problemu. Założono istnienie dodatkowej zmiennej stanu odpowiedzialnej za moment siły działający na belkę. Zmienna ta wpływa na przyspieszenie kątowe belki (pochodna trzeciej zmiennej stanu). Wzmocnienie jest równe odwrotności momentu bezwładności belki J. Na nią zaś nie oddziałuje ani sterowanie ani żadna inna zmienna stanu. Nie wpływa też na wyjście z systemu. Zakładając, że macierze równao stanu zlinearyzowanego modelu oznaczone były jako A, B, C (macierz bezpośredniego sterowania pominięta), macierze układu rozszerzonego A e, B e, C e przedstawiają się następująco: 0 A J B 0 A e, B e, C e 0 0 C Dla tak wyliczonych macierzy przeliczono ponownie macierz Kalmana K. Wymagało to rozszerzenia macierzy M i N. Wyniki obliczeo przedstawiono poniżej: Strona 25 z 27
26 G, K Efekt działania był podobny do tego, jaki został uzyskany przy regulatorze LQ uwzględniającym całkę z uchybu. Istotną różnicą jest fakt, że istnieje możliwośd pomiaru momentu wymuszającego. Znając ten moment, przyspieszenie ziemskie oraz długośd ramienia belki istnieje możliwośd odtwarzania masy zawieszonej na jej koocu. Przeprowadzono szereg eksperymentów z przedmiotami o znanej masie (wyznaczonej przy pomocy wagi). Okazuje się, że dla obciążenia rzędu kilkunastu gram masa wyznaczona przez obserwator dośd dobrze pokrywa się z rzeczywistą masą obiektu. Dla większych obciążeo silnie dają o sobie znad nieliniowości modelu i błąd tak wykonanego pomiaru rośnie. 7 Podsumowanie 7. Wykonane elementy projektu W trakcie dwiczenia wykonano wszystkie etapy prototypowania regulatora: opis matematyczny modelu obiektu sterowania, identyfikacja parametrów modelu w oparciu o istniejący obiekt rzeczywisty, linearyzacja modelu, przygotowanie kompensatora dynamicznego, opartego o: o filtr Kalmana, o regulator LQ, analizę przebiegów powstałych w trakcie pracy regulatora z obiektem. Przygotowany sterownik, dobrze kontrolował pracę obiektu, stabilizując położenie, minimalizując uchyb regulacji. 7.2 Możliwości rozbudowy/modyfikacji obecnego sterownika Obecnie sterownik działa bardzo dobrze, dostrzegliśmy jednak parę możliwości poprawienia jego pracy. Implementacja nieliniowego obserwatora lub ewentualna zmiana struktury obiektu w obserwatorze, tak żeby jego wejściem stała się siła ciągu (moment ciągu) obliczona dla bieżącej prędkości. Zmiana struktury i strojenie parametrów zabezpieczenia AntiWindup. Wykorzystanie danych z dodatkowych zmiennych obserwatora jako źródło dodatkowego sterowania (identyfikacja błędów modelowania i ich kompensacja poprzez feedforward). Strona 26 z 27
27 8 Bibliografia Bałys, P. (2006, Listopad). Liniowy moduł robotyczny NSK współpracujący w czasie rzeczywistym z manipulatorem. Pobrano z lokalizacji Instytut Sterowania i Elektroniki Przemysłowej. (20). Materiał na temat stosowanych rozwiązao Anti-Windup. Pobrano z lokalizacji Inteco. (20, 06 ). Two Rotor Aerodynamical System. Pobrano z lokalizacji 9 Spis ilustracji 9. Rysunki Rysunek - Schemat obiektu sterowania... 3 Rysunek 2 - Schemat działania metody strojonego modelu... 5 Rysunek 3 - Idea eksperymentu służącego wyznaczeniu siły ciągu... 7 Rysunek 4 - Model dynamiki prędkości śmigła w funkcji sterowania... Rysunek 5 - Schemat używany do porównywania prędkości śmigła w modelu i obiekcie... Rysunek 6 - Model helikoptera jako osobny plik mdl... 7 Rysunek 7 - Model helikoptera - zawartośd... 7 Rysunek 8 - Zawartośd modelu wahadła... 7 Rysunek 9 - Regulator LQ z dodanym całkowaniem Wykresy Wykres - Zależnosd momentu generowanego przez śmigło od sterowania... 8 Wykres 2 - Zmierzona zależnośd prędkości śmigła od sterowania... 9 Wykres 3 - Zależnośd prędkości śmigła od sterowania po obróbce... 9 Wykres 4 - Zależnośd momentu od prędkości śmigła... 0 Wykres 5 Przebiegi dla optymalnej wartości pdc_gain... 2 Wykres 6 Oscylacje swobodne gasnące... 4 Wykres 7 Metoda analityczna odpowiedź obiektu i modelu... 5 Wykres 8 - Zmiana wartości wskaźnika jakości w kolejnych iteracjach... 5 Wykres 9 Metoda strojonego modelu - Odpowiedź obiektu i modelu... 6 Wykres 0 - Położenie belki śmigłowca w odpowiedz na skok Wykres - Porównanie odpowiedzi zakłóconego obiektu w zależności od zastosowanego regulatora Wykres 2 - Wpływ całkowania na odpowiedź układu regulacji na skok Wykres 3 Efekt różniczkowania odczytów z enkodera Wykres 4 Efekt działania filtru Kalmana Strona 27 z 27
O 2 O 1. Temat: Wyznaczenie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego
 msg M 7-1 - Temat: Wyznaczenie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego Zagadnienia: prawa dynamiki Newtona, moment sił, moment bezwładności, dynamiczne równania ruchu wahadła fizycznego,
msg M 7-1 - Temat: Wyznaczenie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego Zagadnienia: prawa dynamiki Newtona, moment sił, moment bezwładności, dynamiczne równania ruchu wahadła fizycznego,
Mechatronika i inteligentne systemy produkcyjne. Modelowanie systemów mechatronicznych Platformy przetwarzania danych
 Mechatronika i inteligentne systemy produkcyjne Modelowanie systemów mechatronicznych Platformy przetwarzania danych 1 Sterowanie procesem oparte na jego modelu u 1 (t) System rzeczywisty x(t) y(t) Tworzenie
Mechatronika i inteligentne systemy produkcyjne Modelowanie systemów mechatronicznych Platformy przetwarzania danych 1 Sterowanie procesem oparte na jego modelu u 1 (t) System rzeczywisty x(t) y(t) Tworzenie
Obiekt. Obiekt sterowania obiekt, który realizuje proces (zaplanowany).
 SWB - Systemy wbudowane w układach sterowania - wykład 13 asz 1 Obiekt sterowania Wejście Obiekt Wyjście Obiekt sterowania obiekt, który realizuje proces (zaplanowany). Fizyczny obiekt (proces, urządzenie)
SWB - Systemy wbudowane w układach sterowania - wykład 13 asz 1 Obiekt sterowania Wejście Obiekt Wyjście Obiekt sterowania obiekt, który realizuje proces (zaplanowany). Fizyczny obiekt (proces, urządzenie)
Regulator PID w sterownikach programowalnych GE Fanuc
 Regulator PID w sterownikach programowalnych GE Fanuc Wykład w ramach przedmiotu: Sterowniki programowalne Opracował na podstawie dokumentacji GE Fanuc dr inż. Jarosław Tarnawski Cel wykładu Przypomnienie
Regulator PID w sterownikach programowalnych GE Fanuc Wykład w ramach przedmiotu: Sterowniki programowalne Opracował na podstawie dokumentacji GE Fanuc dr inż. Jarosław Tarnawski Cel wykładu Przypomnienie
BADANIE DRGAŃ TŁUMIONYCH WAHADŁA FIZYCZNEGO
 ĆWICZENIE 36 BADANIE DRGAŃ TŁUMIONYCH WAHADŁA FIZYCZNEGO Cel ćwiczenia: Wyznaczenie podstawowych parametrów drgań tłumionych: okresu (T), częstotliwości (f), częstotliwości kołowej (ω), współczynnika tłumienia
ĆWICZENIE 36 BADANIE DRGAŃ TŁUMIONYCH WAHADŁA FIZYCZNEGO Cel ćwiczenia: Wyznaczenie podstawowych parametrów drgań tłumionych: okresu (T), częstotliwości (f), częstotliwości kołowej (ω), współczynnika tłumienia
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA
 WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 9. Dobór nastaw
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 9. Dobór nastaw
Podstawy Automatyki. Wykład 7 - obiekty regulacji. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 7 - obiekty regulacji Instytut Automatyki i Robotyki Warszawa, 2018 Obiekty regulacji Obiekt regulacji Obiektem regulacji nazywamy proces technologiczny podlegający oddziaływaniu zakłóceń, zachodzący
Wykład 7 - obiekty regulacji Instytut Automatyki i Robotyki Warszawa, 2018 Obiekty regulacji Obiekt regulacji Obiektem regulacji nazywamy proces technologiczny podlegający oddziaływaniu zakłóceń, zachodzący
Automatyka i pomiary wielkości fizykochemicznych. Instrukcja do ćwiczenia VI Dobór nastaw regulatora typu PID metodą Zieglera-Nicholsa.
 Automatyka i pomiary wielkości fizykochemicznych Instrukcja do ćwiczenia VI Dobór nastaw regulatora typu PID metodą Zieglera-Nicholsa. 1. Wprowadzenie Regulator PID (regulator proporcjonalno-całkująco-różniczkujący,
Automatyka i pomiary wielkości fizykochemicznych Instrukcja do ćwiczenia VI Dobór nastaw regulatora typu PID metodą Zieglera-Nicholsa. 1. Wprowadzenie Regulator PID (regulator proporcjonalno-całkująco-różniczkujący,
Sposoby modelowania układów dynamicznych. Pytania
 Sposoby modelowania układów dynamicznych Co to jest model dynamiczny? PAScz4 Modelowanie, analiza i synteza układów automatyki samochodowej równania różniczkowe, różnicowe, równania równowagi sił, momentów,
Sposoby modelowania układów dynamicznych Co to jest model dynamiczny? PAScz4 Modelowanie, analiza i synteza układów automatyki samochodowej równania różniczkowe, różnicowe, równania równowagi sił, momentów,
Automatyka i Regulacja Automatyczna Laboratorium Zagadnienia Seria II
 Automatyka i Regulacja Automatyczna Laboratorium Zagadnienia Seria II Zagadnienia na ocenę 3.0 1. Podaj transmitancję oraz naszkicuj teoretyczną odpowiedź skokową układu całkującego z inercją 1-go rzędu.
Automatyka i Regulacja Automatyczna Laboratorium Zagadnienia Seria II Zagadnienia na ocenę 3.0 1. Podaj transmitancję oraz naszkicuj teoretyczną odpowiedź skokową układu całkującego z inercją 1-go rzędu.
Podstawy Automatyki. Wykład 9 - Dobór regulatorów. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 9 - Dobór regulatorów. Instytut Automatyki i Robotyki Warszawa, 2017 Dobór regulatorów Podstawową przesłanką przy wyborze rodzaju regulatora są właściwości dynamiczne obiektu regulacji. Rysunek:
Wykład 9 - Dobór regulatorów. Instytut Automatyki i Robotyki Warszawa, 2017 Dobór regulatorów Podstawową przesłanką przy wyborze rodzaju regulatora są właściwości dynamiczne obiektu regulacji. Rysunek:
Metody Optymalizacji Laboratorium nr 4 Metoda najmniejszych kwadratów
 Laboratorium Metod Optymalizacji 216 Metody Optymalizacji Laboratorium nr 4 Metoda najmniejszych kwadratów 1. Za pomocą funkcji lsqcurvefit dobrać parametry a i b funkcji: Posiadając następujące dane pomiarowe:
Laboratorium Metod Optymalizacji 216 Metody Optymalizacji Laboratorium nr 4 Metoda najmniejszych kwadratów 1. Za pomocą funkcji lsqcurvefit dobrać parametry a i b funkcji: Posiadając następujące dane pomiarowe:
Doświadczalne wyznaczanie współczynnika sztywności (sprężystości) sprężyn i współczynnika sztywności zastępczej
 Doświadczalne wyznaczanie (sprężystości) sprężyn i zastępczej Statyczna metoda wyznaczania. Wprowadzenie Wartość użytej można wyznaczyć z dużą dokładnością metodą statyczną. W tym celu należy zawiesić
Doświadczalne wyznaczanie (sprężystości) sprężyn i zastępczej Statyczna metoda wyznaczania. Wprowadzenie Wartość użytej można wyznaczyć z dużą dokładnością metodą statyczną. W tym celu należy zawiesić
Ćw. 18: Pomiary wielkości nieelektrycznych II
 Wydział: EAIiE Kierunek: Imię i nazwisko (e mail): Rok:. (2010/2011) Grupa: Zespół: Data wykonania: Zaliczenie: Podpis prowadzącego: Uwagi: LABORATORIUM METROLOGII Ćw. 18: Pomiary wielkości nieelektrycznych
Wydział: EAIiE Kierunek: Imię i nazwisko (e mail): Rok:. (2010/2011) Grupa: Zespół: Data wykonania: Zaliczenie: Podpis prowadzącego: Uwagi: LABORATORIUM METROLOGII Ćw. 18: Pomiary wielkości nieelektrycznych
Cyfrowe algorytmy sterowania AR S1 semestr 4 Projekt 4
 Cyfrowe algorytmy sterowania AR S1 semestr 4 Projekt 4 MPC Sterowanie predykcyjne Cel: Poznanie podstaw regulacji predykcyjnej i narzędzi do badań symulacyjnych Wykonali: Konrad Słodowicz Patryk Frankowski
Cyfrowe algorytmy sterowania AR S1 semestr 4 Projekt 4 MPC Sterowanie predykcyjne Cel: Poznanie podstaw regulacji predykcyjnej i narzędzi do badań symulacyjnych Wykonali: Konrad Słodowicz Patryk Frankowski
1. Regulatory ciągłe liniowe.
 Laboratorium Podstaw Inżynierii Sterowania Ćwiczenie: Regulacja ciągła PID 1. Regulatory ciągłe liniowe. Zadaniem regulatora w układzie regulacji automatycznej jest wytworzenie sygnału sterującego u(t),
Laboratorium Podstaw Inżynierii Sterowania Ćwiczenie: Regulacja ciągła PID 1. Regulatory ciągłe liniowe. Zadaniem regulatora w układzie regulacji automatycznej jest wytworzenie sygnału sterującego u(t),
Problemy optymalizacji układów napędowych w automatyce i robotyce
 Akademia Górniczo-Hutnicza im. Stanisława Staszica Wydział Elektrotechniki, Automatyki, Informatyki i Elektroniki Katedra Automatyki Autoreferat rozprawy doktorskiej Problemy optymalizacji układów napędowych
Akademia Górniczo-Hutnicza im. Stanisława Staszica Wydział Elektrotechniki, Automatyki, Informatyki i Elektroniki Katedra Automatyki Autoreferat rozprawy doktorskiej Problemy optymalizacji układów napędowych
Dla naszego obiektu ciągłego: przy czasie próbkowania T p =2.
 1. Celem zadania drugiego jest przeprowadzenie badań symulacyjnych układu regulacji obiektu G(s), z którym zapoznaliśmy się w zadaniu pierwszym, i regulatorem cyfrowym PID, którego parametry zostaną wyznaczone
1. Celem zadania drugiego jest przeprowadzenie badań symulacyjnych układu regulacji obiektu G(s), z którym zapoznaliśmy się w zadaniu pierwszym, i regulatorem cyfrowym PID, którego parametry zostaną wyznaczone
Automatyka i sterowania
 Automatyka i sterowania Układy regulacji Regulacja i sterowanie Przykłady regulacji i sterowania Funkcje realizowane przez automatykę: regulacja sterowanie zabezpieczenie optymalizacja Automatyka i sterowanie
Automatyka i sterowania Układy regulacji Regulacja i sterowanie Przykłady regulacji i sterowania Funkcje realizowane przez automatykę: regulacja sterowanie zabezpieczenie optymalizacja Automatyka i sterowanie
Szybkie prototypowanie w projektowaniu mechatronicznym
 Szybkie prototypowanie w projektowaniu mechatronicznym Systemy wbudowane (Embedded Systems) Systemy wbudowane (ang. Embedded Systems) są to dedykowane architektury komputerowe, które są integralną częścią
Szybkie prototypowanie w projektowaniu mechatronicznym Systemy wbudowane (Embedded Systems) Systemy wbudowane (ang. Embedded Systems) są to dedykowane architektury komputerowe, które są integralną częścią
Podstawy Automatyki. Wykład 7 - Jakość układu regulacji. Dobór nastaw regulatorów PID. dr inż. Jakub Możaryn. Instytut Automatyki i Robotyki
 Wykład 7 - Jakość układu regulacji. Dobór nastaw regulatorów PID Instytut Automatyki i Robotyki Warszawa, 2015 Jakość układu regulacji Oprócz wymogu stabilności asymptotycznej, układom regulacji stawiane
Wykład 7 - Jakość układu regulacji. Dobór nastaw regulatorów PID Instytut Automatyki i Robotyki Warszawa, 2015 Jakość układu regulacji Oprócz wymogu stabilności asymptotycznej, układom regulacji stawiane
Politechnika Wrocławska, Wydział Informatyki i Zarządzania. Modelowanie
 Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Procesy wykładniczego wzrostu i spadku (np populacja bakterii, rozpad radioaktywny, wymiana ciepła) można modelować równaniem
Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Procesy wykładniczego wzrostu i spadku (np populacja bakterii, rozpad radioaktywny, wymiana ciepła) można modelować równaniem
Podstawy opracowania wyników pomiarów z elementami analizy niepewności pomiarowych
 Podstawy opracowania wyników pomiarów z elementami analizy niepewności pomiarowych dla studentów Biologii A i B dr hab. Paweł Korecki e-mail: pawel.korecki@uj.edu.pl http://www.if.uj.edu.pl/pl/edukacja/pracownia_i/
Podstawy opracowania wyników pomiarów z elementami analizy niepewności pomiarowych dla studentów Biologii A i B dr hab. Paweł Korecki e-mail: pawel.korecki@uj.edu.pl http://www.if.uj.edu.pl/pl/edukacja/pracownia_i/
Ćwiczenie 6 - Bezpośrednie sterowanie cyfrowe
 Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie KATEDRA AUTOMATYKI LABORATORIUM Aparatura Automatyzacji Ćwiczenie 6. Bezpośrednie sterowanie cyfrowe Wydział EAIiE kierunek AiR rok II Zespół
Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie KATEDRA AUTOMATYKI LABORATORIUM Aparatura Automatyzacji Ćwiczenie 6. Bezpośrednie sterowanie cyfrowe Wydział EAIiE kierunek AiR rok II Zespół
INSTRUKCJA Regulacja PID, badanie stabilności układów automatyki
 Opracowano na podstawie: INSTRUKCJA Regulacja PID, badanie stabilności układów automatyki 1. Kaczorek T.: Teoria sterowania, PWN, Warszawa 1977. 2. Węgrzyn S.: Podstawy automatyki, PWN, Warszawa 1980 3.
Opracowano na podstawie: INSTRUKCJA Regulacja PID, badanie stabilności układów automatyki 1. Kaczorek T.: Teoria sterowania, PWN, Warszawa 1977. 2. Węgrzyn S.: Podstawy automatyki, PWN, Warszawa 1980 3.
Ćwiczenie M-2 Pomiar przyśpieszenia ziemskiego za pomocą wahadła rewersyjnego Cel ćwiczenia: II. Przyrządy: III. Literatura: IV. Wstęp. l Rys.
 Ćwiczenie M- Pomiar przyśpieszenia ziemskiego za pomocą wahadła rewersyjnego. Cel ćwiczenia: pomiar przyśpieszenia ziemskiego przy pomocy wahadła fizycznego.. Przyrządy: wahadło rewersyjne, elektroniczny
Ćwiczenie M- Pomiar przyśpieszenia ziemskiego za pomocą wahadła rewersyjnego. Cel ćwiczenia: pomiar przyśpieszenia ziemskiego przy pomocy wahadła fizycznego.. Przyrządy: wahadło rewersyjne, elektroniczny
DRGANIA SWOBODNE UKŁADU O DWÓCH STOPNIACH SWOBODY. Rys Model układu
 Ćwiczenie 7 DRGANIA SWOBODNE UKŁADU O DWÓCH STOPNIACH SWOBODY. Cel ćwiczenia Doświadczalne wyznaczenie częstości drgań własnych układu o dwóch stopniach swobody, pokazanie postaci drgań odpowiadających
Ćwiczenie 7 DRGANIA SWOBODNE UKŁADU O DWÓCH STOPNIACH SWOBODY. Cel ćwiczenia Doświadczalne wyznaczenie częstości drgań własnych układu o dwóch stopniach swobody, pokazanie postaci drgań odpowiadających
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 206/207
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 206/207
Laboratorium Komputerowe Systemy Pomiarowe
 Jarosław Gliwiński, Łukasz Rogacz Laboratorium Komputerowe Systemy Pomiarowe ćw. Programowanie wielofunkcyjnej karty pomiarowej w VEE Data wykonania: 15.05.08 Data oddania: 29.05.08 Celem ćwiczenia była
Jarosław Gliwiński, Łukasz Rogacz Laboratorium Komputerowe Systemy Pomiarowe ćw. Programowanie wielofunkcyjnej karty pomiarowej w VEE Data wykonania: 15.05.08 Data oddania: 29.05.08 Celem ćwiczenia była
Opis ćwiczenia. Cel ćwiczenia Poznanie budowy i zrozumienie istoty pomiaru przyspieszenia ziemskiego za pomocą wahadła rewersyjnego Henry ego Katera.
 ĆWICZENIE WYZNACZANIE PRZYSPIESZENIA ZIEMSKIEGO ZA POMOCĄ WAHADŁA REWERSYJNEGO Opis ćwiczenia Cel ćwiczenia Poznanie budowy i zrozumienie istoty pomiaru przyspieszenia ziemskiego za pomocą wahadła rewersyjnego
ĆWICZENIE WYZNACZANIE PRZYSPIESZENIA ZIEMSKIEGO ZA POMOCĄ WAHADŁA REWERSYJNEGO Opis ćwiczenia Cel ćwiczenia Poznanie budowy i zrozumienie istoty pomiaru przyspieszenia ziemskiego za pomocą wahadła rewersyjnego
Wyznaczanie przyspieszenia ziemskiego za pomocą wahadła prostego
 Ćwiczenie M6 Wyznaczanie przyspieszenia ziemskiego za pomocą wahadła prostego M6.1. Cel ćwiczenia Celem ćwiczenia jest wyznaczenie przyspieszenia ziemskiego poprzez analizę ruchu wahadła prostego. M6..
Ćwiczenie M6 Wyznaczanie przyspieszenia ziemskiego za pomocą wahadła prostego M6.1. Cel ćwiczenia Celem ćwiczenia jest wyznaczenie przyspieszenia ziemskiego poprzez analizę ruchu wahadła prostego. M6..
Układ regulacji ze sprzężeniem zwrotnym: - układ regulacji kaskadowej - układ regulacji stosunku
 Układ regulacji ze sprzężeniem zwrotnym: - układ regulacji kaskadowej - układ regulacji stosunku Przemysłowe Układy Sterowania PID Opracowanie: dr inż. Tomasz Rutkowski Katedra Inżynierii Systemów Sterowania
Układ regulacji ze sprzężeniem zwrotnym: - układ regulacji kaskadowej - układ regulacji stosunku Przemysłowe Układy Sterowania PID Opracowanie: dr inż. Tomasz Rutkowski Katedra Inżynierii Systemów Sterowania
Ćw. 18: Pomiary wielkości nieelektrycznych II
 Wydział: EAIiE Kierunek: Imię i nazwisko (e mail): Rok:. (../..) Grupa: Zespół: Data wykonania: Zaliczenie: Podpis prowadzącego: Uwagi: LABORATORIUM METROLOGII Ćw. 18: Pomiary wielkości nieelektrycznych
Wydział: EAIiE Kierunek: Imię i nazwisko (e mail): Rok:. (../..) Grupa: Zespół: Data wykonania: Zaliczenie: Podpis prowadzącego: Uwagi: LABORATORIUM METROLOGII Ćw. 18: Pomiary wielkości nieelektrycznych
Instrukcja do ćwiczenia jednopłaszczyznowe wyważanie wirników
 Instrukcja do ćwiczenia jednopłaszczyznowe wyważanie wirników 1. Podstawowe pojęcia związane z niewyważeniem Stan niewyważenia stan wirnika określony takim rozkładem masy, który w czasie wirowania wywołuje
Instrukcja do ćwiczenia jednopłaszczyznowe wyważanie wirników 1. Podstawowe pojęcia związane z niewyważeniem Stan niewyważenia stan wirnika określony takim rozkładem masy, który w czasie wirowania wywołuje
Aproksymacja funkcji a regresja symboliczna
 Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(x), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(x), zwaną funkcją aproksymującą
Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(x), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(x), zwaną funkcją aproksymującą
Regulator PID w sterownikach programowalnych GE Fanuc
 Regulator PID w sterownikach programowalnych GE Fanuc Wykład w ramach przedmiotu: Sterowniki programowalne Opracował na podstawie dokumentacji GE Fanuc dr inż. Jarosław Tarnawski Cel wykładu Przypomnienie
Regulator PID w sterownikach programowalnych GE Fanuc Wykład w ramach przedmiotu: Sterowniki programowalne Opracował na podstawie dokumentacji GE Fanuc dr inż. Jarosław Tarnawski Cel wykładu Przypomnienie
Serwomechanizmy sterowanie
 Serwomechanizmy sterowanie Tryby pracy serwonapędu: - point-to-point, - śledzenie trajektorii (często znanej), - regulacja prędkości. Wymagania: - odpowiedź aperiodyczna, - możliwość ograniczania przyspieszenia
Serwomechanizmy sterowanie Tryby pracy serwonapędu: - point-to-point, - śledzenie trajektorii (często znanej), - regulacja prędkości. Wymagania: - odpowiedź aperiodyczna, - możliwość ograniczania przyspieszenia
Wyznaczanie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego (Katera)
 Politechnika Łódzka FTMS Kierunek: nformatyka rok akademicki: 2008/2009 sem. 2. Termin: 6 V 2009 Nr. ćwiczenia: 112 Temat ćwiczenia: Wyznaczanie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego
Politechnika Łódzka FTMS Kierunek: nformatyka rok akademicki: 2008/2009 sem. 2. Termin: 6 V 2009 Nr. ćwiczenia: 112 Temat ćwiczenia: Wyznaczanie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego
Regulatory o działaniu ciągłym P, I, PI, PD, PID
 Regulatory o działaniu ciągłym P, I, PI, PD, PID Regulatory o działaniu ciągłym (analogowym) zmieniają wartość wielkości sterującej obiektem w sposób ciągły, tzn. wielkość ta może przyjmować wszystkie
Regulatory o działaniu ciągłym P, I, PI, PD, PID Regulatory o działaniu ciągłym (analogowym) zmieniają wartość wielkości sterującej obiektem w sposób ciągły, tzn. wielkość ta może przyjmować wszystkie
Aplikacje Systemów. Nawigacja inercyjna. Gdańsk, 2016
 Aplikacje Systemów Wbudowanych Nawigacja inercyjna Gdańsk, 2016 Klasyfikacja systemów inercyjnych 2 Nawigacja inercyjna Podstawowymi blokami, wchodzącymi w skład systemów nawigacji inercyjnej (INS ang.
Aplikacje Systemów Wbudowanych Nawigacja inercyjna Gdańsk, 2016 Klasyfikacja systemów inercyjnych 2 Nawigacja inercyjna Podstawowymi blokami, wchodzącymi w skład systemów nawigacji inercyjnej (INS ang.
Dobór parametrów regulatora - symulacja komputerowa. Najprostszy układ automatycznej regulacji można przedstawić za pomocą
 Politechnika Świętokrzyska Wydział Mechatroniki i Budowy Maszyn Centrum Laserowych Technologii Metali PŚk i PAN Zakład Informatyki i Robotyki Przedmiot:Podstawy Automatyzacji - laboratorium, rok I, sem.
Politechnika Świętokrzyska Wydział Mechatroniki i Budowy Maszyn Centrum Laserowych Technologii Metali PŚk i PAN Zakład Informatyki i Robotyki Przedmiot:Podstawy Automatyzacji - laboratorium, rok I, sem.
Sterowanie w programie ADAMS regulator PID. Przemysław Sperzyński
 Sterowanie w programie ADAMS regulator PID Przemysław Sperzyński Schemat regulatora K p e t e t = u zad t u akt (t) M = K p e t + K i e t + K d de(t) u zad uakt M K i e t K d de t Uchyb regulacji człony
Sterowanie w programie ADAMS regulator PID Przemysław Sperzyński Schemat regulatora K p e t e t = u zad t u akt (t) M = K p e t + K i e t + K d de(t) u zad uakt M K i e t K d de t Uchyb regulacji człony
Sterowanie napędów maszyn i robotów
 Wykład 7b - Układy wieloobwodowe ze sprzężeniem od zmiennych stanu Instytut Automatyki i Robotyki Warszawa, 2014 Układy wieloobwodowe ze sprzężeniem od zmiennych stanu Zadanie przestawiania Postać modalna
Wykład 7b - Układy wieloobwodowe ze sprzężeniem od zmiennych stanu Instytut Automatyki i Robotyki Warszawa, 2014 Układy wieloobwodowe ze sprzężeniem od zmiennych stanu Zadanie przestawiania Postać modalna
Ćw. nr 31. Wahadło fizyczne o regulowanej płaszczyźnie drgań - w.2
 1 z 6 Zespół Dydaktyki Fizyki ITiE Politechniki Koszalińskiej Ćw. nr 3 Wahadło fizyczne o regulowanej płaszczyźnie drgań - w.2 Cel ćwiczenia Pomiar okresu wahań wahadła z wykorzystaniem bramki optycznej
1 z 6 Zespół Dydaktyki Fizyki ITiE Politechniki Koszalińskiej Ćw. nr 3 Wahadło fizyczne o regulowanej płaszczyźnie drgań - w.2 Cel ćwiczenia Pomiar okresu wahań wahadła z wykorzystaniem bramki optycznej
Doświadczalne wyznaczanie współczynnika sztywności (sprężystości) sprężyny
 Doświadczalne wyznaczanie współczynnika sztywności (sprężystości) Wprowadzenie Wartość współczynnika sztywności użytej można wyznaczyć z dużą dokładnością metodą statyczną. W tym celu należy zawiesić pionowo
Doświadczalne wyznaczanie współczynnika sztywności (sprężystości) Wprowadzenie Wartość współczynnika sztywności użytej można wyznaczyć z dużą dokładnością metodą statyczną. W tym celu należy zawiesić pionowo
Sterowanie układem zawieszenia magnetycznego
 Politechnika Śląska w Gliwicach Wydział: Automatyki, Elektroniki i Informatyki Kierunek: Automatyka i Robotyka Specjalność: Komputerowe systemy sterowania Sterowanie układem zawieszenia magnetycznego Maciej
Politechnika Śląska w Gliwicach Wydział: Automatyki, Elektroniki i Informatyki Kierunek: Automatyka i Robotyka Specjalność: Komputerowe systemy sterowania Sterowanie układem zawieszenia magnetycznego Maciej
Podstawy Automatyki. wykład 1 (26.02.2010) mgr inż. Łukasz Dworzak. Politechnika Wrocławska. Instytut Technologii Maszyn i Automatyzacji (I-24)
 Podstawy Automatyki wykład 1 (26.02.2010) mgr inż. Łukasz Dworzak Politechnika Wrocławska Instytut Technologii Maszyn i Automatyzacji (I-24) Laboratorium Podstaw Automatyzacji (L6) 105/2 B1 Sprawy organizacyjne
Podstawy Automatyki wykład 1 (26.02.2010) mgr inż. Łukasz Dworzak Politechnika Wrocławska Instytut Technologii Maszyn i Automatyzacji (I-24) Laboratorium Podstaw Automatyzacji (L6) 105/2 B1 Sprawy organizacyjne
UWAGA. Wszystkie wyniki zapisywać na dysku Dane E: Program i przebieg ćwiczenia:
 Cel ćwiczenia: Zapoznanie się z. metodami badania i analitycznego wyznaczania parametrów dynamicznych obiektów rzeczywistych na przykładzie mikrotermostatu oraz z metodami symulacyjnymi umożliwiającymi
Cel ćwiczenia: Zapoznanie się z. metodami badania i analitycznego wyznaczania parametrów dynamicznych obiektów rzeczywistych na przykładzie mikrotermostatu oraz z metodami symulacyjnymi umożliwiającymi
4. Właściwości eksploatacyjne układów regulacji Wprowadzenie. Hs () Ys () Ws () Es () Go () s. Vs ()
 4. Właściwości eksploatacyjne układów regulacji 4.1. Wprowadzenie Zu () s Zy ( s ) Ws () Es () Gr () s Us () Go () s Ys () Vs () Hs () Rys. 4.1. Schemat blokowy układu regulacji z funkcjami przejścia 1
4. Właściwości eksploatacyjne układów regulacji 4.1. Wprowadzenie Zu () s Zy ( s ) Ws () Es () Gr () s Us () Go () s Ys () Vs () Hs () Rys. 4.1. Schemat blokowy układu regulacji z funkcjami przejścia 1
1. Podstawowe pojęcia
 1. Podstawowe pojęcia Sterowanie optymalne obiektu polega na znajdowaniu najkorzystniejszej decyzji dotyczącej zamierzonego wpływu na obiekt przy zadanych ograniczeniach. Niech dany jest obiekt opisany
1. Podstawowe pojęcia Sterowanie optymalne obiektu polega na znajdowaniu najkorzystniejszej decyzji dotyczącej zamierzonego wpływu na obiekt przy zadanych ograniczeniach. Niech dany jest obiekt opisany
Badanie kaskadowego układu regulacji na przykładzie serwomechanizmu
 Badanie kaskadowego układu regulacji na przykładzie serwomechanizmu 1. WSTĘP Serwomechanizmy są to przeważnie układy regulacji położenia. Są trzy główne typy zadań serwomechanizmów: - ruch point-to-point,
Badanie kaskadowego układu regulacji na przykładzie serwomechanizmu 1. WSTĘP Serwomechanizmy są to przeważnie układy regulacji położenia. Są trzy główne typy zadań serwomechanizmów: - ruch point-to-point,
PLAN REALIZACJI MATERIAŁU NAUCZANIA FIZYKI W GIMNAZJUM WRAZ Z OKREŚLENIEM WYMAGAŃ EDUKACYJNYCH
 PLAN REALIZACJI MATERIAŁU NAUCZANIA FIZYKI W GIMNAZJUM WRAZ Z OKREŚLENIEM WYMAGAŃ EDUKACYJNYCH Krzysztof Horodecki, Artur Ludwikowski, Fizyka 1. Podręcznik dla gimnazjum, Gdańskie Wydawnictwo Oświatowe
PLAN REALIZACJI MATERIAŁU NAUCZANIA FIZYKI W GIMNAZJUM WRAZ Z OKREŚLENIEM WYMAGAŃ EDUKACYJNYCH Krzysztof Horodecki, Artur Ludwikowski, Fizyka 1. Podręcznik dla gimnazjum, Gdańskie Wydawnictwo Oświatowe
Politechnika Wrocławska, Wydział Informatyki i Zarządzania. Modelowanie
 Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Wyznacz transformaty Laplace a poniższych funkcji, korzystając z tabeli transformat: a) 8 3e 3t b) 4 sin 5t 2e 5t + 5 c) e5t e
Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Wyznacz transformaty Laplace a poniższych funkcji, korzystając z tabeli transformat: a) 8 3e 3t b) 4 sin 5t 2e 5t + 5 c) e5t e
Silnik prądu stałego (NI Elvis 2) Dobieranie nastaw regulatorów P, PI, PID. Filtr przeciwnasyceniowy Anti-windup.
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podstawy Automatyki Silnik prądu stałego (NI Elvis 2) Dobieranie nastaw regulatorów P, PI, PID. Filtr przeciwnasyceniowy
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podstawy Automatyki Silnik prądu stałego (NI Elvis 2) Dobieranie nastaw regulatorów P, PI, PID. Filtr przeciwnasyceniowy
Spis treści. Przedmowa... XI. Rozdział 1. Pomiar: jednostki miar... 1. Rozdział 2. Pomiar: liczby i obliczenia liczbowe... 16
 Spis treści Przedmowa.......................... XI Rozdział 1. Pomiar: jednostki miar................. 1 1.1. Wielkości fizyczne i pozafizyczne.................. 1 1.2. Spójne układy miar. Układ SI i jego
Spis treści Przedmowa.......................... XI Rozdział 1. Pomiar: jednostki miar................. 1 1.1. Wielkości fizyczne i pozafizyczne.................. 1 1.2. Spójne układy miar. Układ SI i jego
Pochodna i różniczka funkcji oraz jej zastosowanie do obliczania niepewności pomiarowych
 Pochodna i różniczka unkcji oraz jej zastosowanie do obliczania niepewności pomiarowych Krzyszto Rębilas DEFINICJA POCHODNEJ Pochodna unkcji () w punkcie określona jest jako granica: lim 0 Oznaczamy ją
Pochodna i różniczka unkcji oraz jej zastosowanie do obliczania niepewności pomiarowych Krzyszto Rębilas DEFINICJA POCHODNEJ Pochodna unkcji () w punkcie określona jest jako granica: lim 0 Oznaczamy ją
Temat /6/: DYNAMIKA UKŁADÓW HYDRAULICZNYCH. WIADOMOŚCI PODSTAWOWE.
 1 Temat /6/: DYNAMIKA UKŁADÓW HYDRAULICZNYCH. WIADOMOŚCI PODSTAWOWE. Celem ćwiczenia jest doświadczalne określenie wskaźników charakteryzujących właściwości dynamiczne hydraulicznych układów sterujących
1 Temat /6/: DYNAMIKA UKŁADÓW HYDRAULICZNYCH. WIADOMOŚCI PODSTAWOWE. Celem ćwiczenia jest doświadczalne określenie wskaźników charakteryzujących właściwości dynamiczne hydraulicznych układów sterujących
Automatyka i robotyka ETP2005L. Laboratorium semestr zimowy
 Automatyka i robotyka ETP2005L Laboratorium semestr zimowy 2017-2018 Liniowe człony automatyki x(t) wymuszenie CZŁON (element) OBIEKT AUTOMATYKI y(t) odpowiedź Modelowanie matematyczne obiektów automatyki
Automatyka i robotyka ETP2005L Laboratorium semestr zimowy 2017-2018 Liniowe człony automatyki x(t) wymuszenie CZŁON (element) OBIEKT AUTOMATYKI y(t) odpowiedź Modelowanie matematyczne obiektów automatyki
INSTRUKCJA DO ĆWICZENIA NR 7
 KATEDRA MECHANIKI STOSOWANEJ Wydział Mechaniczny POLITECHNIKA LUBELSKA INSTRUKCJA DO ĆWICZENIA NR 7 PRZEDMIOT TEMAT OPRACOWAŁ LABORATORIUM MODELOWANIA Przykładowe analizy danych: przebiegi czasowe, portrety
KATEDRA MECHANIKI STOSOWANEJ Wydział Mechaniczny POLITECHNIKA LUBELSKA INSTRUKCJA DO ĆWICZENIA NR 7 PRZEDMIOT TEMAT OPRACOWAŁ LABORATORIUM MODELOWANIA Przykładowe analizy danych: przebiegi czasowe, portrety
Nazwisko i imię: Zespół: Data: Ćwiczenie nr 1: Wahadło fizyczne. opis ruchu drgającego a w szczególności drgań wahadła fizycznego
 Nazwisko i imię: Zespół: Data: Cel ćwiczenia: Ćwiczenie nr 1: Wahadło fizyczne opis ruchu drgającego a w szczególności drgań wahadła fizycznego wyznaczenie momentów bezwładności brył sztywnych Literatura
Nazwisko i imię: Zespół: Data: Cel ćwiczenia: Ćwiczenie nr 1: Wahadło fizyczne opis ruchu drgającego a w szczególności drgań wahadła fizycznego wyznaczenie momentów bezwładności brył sztywnych Literatura
CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE
 CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE Do opisu członów i układów automatyki stosuje się, oprócz transmitancji operatorowej (), tzw. transmitancję widmową. Transmitancję widmową () wyznaczyć można na podstawie
CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE Do opisu członów i układów automatyki stosuje się, oprócz transmitancji operatorowej (), tzw. transmitancję widmową. Transmitancję widmową () wyznaczyć można na podstawie
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
1. POJĘCIA PODSTAWOWE I RODZAJE UKŁADÓW AUTOMATYKI
 Podstawy automatyki / Józef Lisowski. Gdynia, 2015 Spis treści PRZEDMOWA 9 WSTĘP 11 1. POJĘCIA PODSTAWOWE I RODZAJE UKŁADÓW AUTOMATYKI 17 1.1. Automatyka, sterowanie i regulacja 17 1.2. Obiekt regulacji
Podstawy automatyki / Józef Lisowski. Gdynia, 2015 Spis treści PRZEDMOWA 9 WSTĘP 11 1. POJĘCIA PODSTAWOWE I RODZAJE UKŁADÓW AUTOMATYKI 17 1.1. Automatyka, sterowanie i regulacja 17 1.2. Obiekt regulacji
Podstawy opracowania wyników pomiarów z elementami analizy niepewności pomiarowych
 Podstawy opracowania wyników pomiarów z elementami analizy niepewności pomiarowych dla studentów Chemii (2018) Autor prezentacji :dr hab. Paweł Korecki dr Szymon Godlewski e-mail: szymon.godlewski@uj.edu.pl
Podstawy opracowania wyników pomiarów z elementami analizy niepewności pomiarowych dla studentów Chemii (2018) Autor prezentacji :dr hab. Paweł Korecki dr Szymon Godlewski e-mail: szymon.godlewski@uj.edu.pl
Regulacja dwupołożeniowa.
 Politechnika Krakowska Wydział Inżynierii Elektrycznej i Komputerowej Zakład eorii Sterowania Regulacja dwupołożeniowa. Kraków Zakład eorii Sterowania (E ) Regulacja dwupołożeniowa opis ćwiczenia.. Opis
Politechnika Krakowska Wydział Inżynierii Elektrycznej i Komputerowej Zakład eorii Sterowania Regulacja dwupołożeniowa. Kraków Zakład eorii Sterowania (E ) Regulacja dwupołożeniowa opis ćwiczenia.. Opis
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podstawy Automatyki Regulacja temperatury z wykorzystaniem sterownika PLC Zadania do ćwiczeń laboratoryjnych
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podstawy Automatyki Regulacja temperatury z wykorzystaniem sterownika PLC Zadania do ćwiczeń laboratoryjnych
Statyczne badanie wzmacniacza operacyjnego - ćwiczenie 7
 Statyczne badanie wzmacniacza operacyjnego - ćwiczenie 7 1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z podstawowymi zastosowaniami wzmacniacza operacyjnego, poznanie jego charakterystyki przejściowej
Statyczne badanie wzmacniacza operacyjnego - ćwiczenie 7 1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z podstawowymi zastosowaniami wzmacniacza operacyjnego, poznanie jego charakterystyki przejściowej
Pomiar rezystancji metodą techniczną
 Pomiar rezystancji metodą techniczną Cel ćwiczenia. Poznanie metod pomiarów rezystancji liniowych, optymalizowania warunków pomiaru oraz zasad obliczania błędów pomiarowych. Zagadnienia teoretyczne. Definicja
Pomiar rezystancji metodą techniczną Cel ćwiczenia. Poznanie metod pomiarów rezystancji liniowych, optymalizowania warunków pomiaru oraz zasad obliczania błędów pomiarowych. Zagadnienia teoretyczne. Definicja
Instrukcja do ćwiczenia 6 REGULACJA TRÓJPOŁOŻENIOWA
 Instrukcja do ćwiczenia 6 REGULACJA TRÓJPOŁOŻENIOWA Cel ćwiczenia: dobór nastaw regulatora, analiza układu regulacji trójpołożeniowej, określenie jakości regulacji trójpołożeniowej w układzie bez zakłóceń
Instrukcja do ćwiczenia 6 REGULACJA TRÓJPOŁOŻENIOWA Cel ćwiczenia: dobór nastaw regulatora, analiza układu regulacji trójpołożeniowej, określenie jakości regulacji trójpołożeniowej w układzie bez zakłóceń
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podstawy Automatyki Badanie i synteza kaskadowego adaptacyjnego układu regulacji do sterowania obiektu o
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podstawy Automatyki Badanie i synteza kaskadowego adaptacyjnego układu regulacji do sterowania obiektu o
Programowanie celowe #1
 Programowanie celowe #1 Problem programowania celowego (PC) jest przykładem problemu programowania matematycznego nieliniowego, który można skutecznie zlinearyzować, tzn. zapisać (i rozwiązać) jako problem
Programowanie celowe #1 Problem programowania celowego (PC) jest przykładem problemu programowania matematycznego nieliniowego, który można skutecznie zlinearyzować, tzn. zapisać (i rozwiązać) jako problem
Prowadzący(a) Grupa Zespół data ćwiczenia Lp. Nazwisko i imię Ocena LABORATORIUM 4. PODSTAW 5. AUTOMATYKI
 Instytut Automatyki i Robotyki Prowadzący(a) Grupa Zespół data ćwiczenia Lp. Nazwisko i imię Ocena 1. 2. 3. LABORATORIUM 4. PODSTAW 5. AUTOMATYKI Ćwiczenie PA7b 1 Badanie jednoobwodowego układu regulacji
Instytut Automatyki i Robotyki Prowadzący(a) Grupa Zespół data ćwiczenia Lp. Nazwisko i imię Ocena 1. 2. 3. LABORATORIUM 4. PODSTAW 5. AUTOMATYKI Ćwiczenie PA7b 1 Badanie jednoobwodowego układu regulacji
Tematy prac dyplomowych w Katedrze Awioniki i Sterowania. Studia: I stopnia (inżynierskie)
 Tematy prac dyplomowych w Katedrze Awioniki i Sterowania Studia I stopnia (inżynierskie) Temat: Skalowanie czujników prędkości kątowej i orientacji przestrzennej 1. Analiza właściwości czujników i układów
Tematy prac dyplomowych w Katedrze Awioniki i Sterowania Studia I stopnia (inżynierskie) Temat: Skalowanie czujników prędkości kątowej i orientacji przestrzennej 1. Analiza właściwości czujników i układów
w analizie wyników badań eksperymentalnych, w problemach modelowania zjawisk fizycznych, w analizie obserwacji statystycznych.
 Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(), zwaną funkcją aproksymującą
Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(), zwaną funkcją aproksymującą
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA
 WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 2. REPREZENTACJA
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 2. REPREZENTACJA
Imię i nazwisko (e mail) Grupa:
 Wydział: EAIiE Kierunek: Imię i nazwisko (e mail) Rok: Grupa: Zespół: Data wykonania: LABORATORIUM METROLOGII Ćw. 12: Przetworniki analogowo cyfrowe i cyfrowo analogowe budowa i zastosowanie. Ocena: Podpis
Wydział: EAIiE Kierunek: Imię i nazwisko (e mail) Rok: Grupa: Zespół: Data wykonania: LABORATORIUM METROLOGII Ćw. 12: Przetworniki analogowo cyfrowe i cyfrowo analogowe budowa i zastosowanie. Ocena: Podpis
MECHANIKA 2. Drgania punktu materialnego. Wykład Nr 8. Prowadzący: dr Krzysztof Polko
 MECHANIKA 2 Wykład Nr 8 Drgania punktu materialnego Prowadzący: dr Krzysztof Polko Wstęp Drgania Okresowe i nieokresowe Swobodne i wymuszone Tłumione i nietłumione Wstęp Drgania okresowe ruch powtarzający
MECHANIKA 2 Wykład Nr 8 Drgania punktu materialnego Prowadzący: dr Krzysztof Polko Wstęp Drgania Okresowe i nieokresowe Swobodne i wymuszone Tłumione i nietłumione Wstęp Drgania okresowe ruch powtarzający
Kodowanie i kompresja Streszczenie Studia Licencjackie Wykład 11,
 1 Kwantyzacja skalarna Kodowanie i kompresja Streszczenie Studia Licencjackie Wykład 11, 10.05.005 Kwantyzacja polega na reprezentowaniu dużego zbioru wartości (być może nieskończonego) za pomocą wartości
1 Kwantyzacja skalarna Kodowanie i kompresja Streszczenie Studia Licencjackie Wykład 11, 10.05.005 Kwantyzacja polega na reprezentowaniu dużego zbioru wartości (być może nieskończonego) za pomocą wartości
W celu obliczenia charakterystyki częstotliwościowej zastosujemy wzór 1. charakterystyka amplitudowa 0,
 Bierne obwody RC. Filtr dolnoprzepustowy. Filtr dolnoprzepustowy jest układem przenoszącym sygnały o małej częstotliwości bez zmian, a powodującym tłumienie i opóźnienie fazy sygnałów o większych częstotliwościach.
Bierne obwody RC. Filtr dolnoprzepustowy. Filtr dolnoprzepustowy jest układem przenoszącym sygnały o małej częstotliwości bez zmian, a powodującym tłumienie i opóźnienie fazy sygnałów o większych częstotliwościach.
Sterowanie Napędów Maszyn i Robotów
 Wykład 3 - Metodyka projektowania sterowania. Opis bilansowy Instytut Automatyki i Robotyki Warszawa, 2015 Metodyka projektowania sterowania Zrozumienie obiektu, możliwości, ograniczeń zapoznanie się z
Wykład 3 - Metodyka projektowania sterowania. Opis bilansowy Instytut Automatyki i Robotyki Warszawa, 2015 Metodyka projektowania sterowania Zrozumienie obiektu, możliwości, ograniczeń zapoznanie się z
lim Np. lim jest wyrażeniem typu /, a
 Wykład 3 Pochodna funkcji złożonej, pochodne wyższych rzędów, reguła de l Hospitala, różniczka funkcji i jej zastosowanie, pochodna jako prędkość zmian 3. Pochodna funkcji złożonej. Jeżeli funkcja złożona
Wykład 3 Pochodna funkcji złożonej, pochodne wyższych rzędów, reguła de l Hospitala, różniczka funkcji i jej zastosowanie, pochodna jako prędkość zmian 3. Pochodna funkcji złożonej. Jeżeli funkcja złożona
ELEMENTY AUTOMATYKI PRACA W PROGRAMIE SIMULINK 2013
 SIMULINK część pakietu numerycznego MATLAB (firmy MathWorks) służąca do przeprowadzania symulacji komputerowych. Atutem programu jest interfejs graficzny (budowanie układów na bazie logicznie połączonych
SIMULINK część pakietu numerycznego MATLAB (firmy MathWorks) służąca do przeprowadzania symulacji komputerowych. Atutem programu jest interfejs graficzny (budowanie układów na bazie logicznie połączonych
Wahadło odwrocone (NI Elvis 2) Modelowanie i stabilizacja w dolnym położeniu równowagi.
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podstawy Automatyki Wahadło odwrocone (NI Elvis 2) Modelowanie i stabilizacja w dolnym położeniu równowagi.
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podstawy Automatyki Wahadło odwrocone (NI Elvis 2) Modelowanie i stabilizacja w dolnym położeniu równowagi.
PLAN REALIZACJI MATERIAŁU NAUCZANIA FIZYKI W KLASIE PIERWSZEJ GIMNAZJUM WRAZ Z OKREŚLENIEM WYMAGAŃ EDUKACYJNYCH
 PLAN REALIZACJI MATERIAŁU NAUCZANIA FIZYKI W KLASIE PIERWSZEJ GIMNAZJUM WRAZ Z OKREŚLENIEM WYMAGAŃ EDUKACYJNYCH Krzysztof Horodecki, Artur Ludwikowski, Fizyka 1. Podręcznik dla gimnazjum, Gdańskie Wydawnictwo
PLAN REALIZACJI MATERIAŁU NAUCZANIA FIZYKI W KLASIE PIERWSZEJ GIMNAZJUM WRAZ Z OKREŚLENIEM WYMAGAŃ EDUKACYJNYCH Krzysztof Horodecki, Artur Ludwikowski, Fizyka 1. Podręcznik dla gimnazjum, Gdańskie Wydawnictwo
Bierne układy różniczkujące i całkujące typu RC
 Instytut Fizyki ul. Wielkopolska 15 70-451 Szczecin 6 Pracownia Elektroniki. Bierne układy różniczkujące i całkujące typu RC........ (Oprac. dr Radosław Gąsowski) Zakres materiału obowiązujący do ćwiczenia:
Instytut Fizyki ul. Wielkopolska 15 70-451 Szczecin 6 Pracownia Elektroniki. Bierne układy różniczkujące i całkujące typu RC........ (Oprac. dr Radosław Gąsowski) Zakres materiału obowiązujący do ćwiczenia:
Sprawozdanie Ćwiczenie nr 14 Sprężyna
 Sprawozdanie Ćwiczenie nr 14 Sprężyna Karol Kraus Budownictwo I rok Studia niestacjonarne Gr. I A 1.Wstęp teoretyczny Celem wykonanego zadania jest wyznaczenie stałej sprężystości metodą statyczną i dynamiczna,
Sprawozdanie Ćwiczenie nr 14 Sprężyna Karol Kraus Budownictwo I rok Studia niestacjonarne Gr. I A 1.Wstęp teoretyczny Celem wykonanego zadania jest wyznaczenie stałej sprężystości metodą statyczną i dynamiczna,
Ć W I C Z E N I E N R M-2
 INSYU FIZYKI WYDZIAŁ INŻYNIERII PRODUKCJI I ECHNOLOGII MAERIAŁÓW POLIECHNIKA CZĘSOCHOWSKA PRACOWNIA MECHANIKI Ć W I C Z E N I E N R M- ZALEŻNOŚĆ OKRESU DRGAŃ WAHADŁA OD AMPLIUDY Ćwiczenie M-: Zależność
INSYU FIZYKI WYDZIAŁ INŻYNIERII PRODUKCJI I ECHNOLOGII MAERIAŁÓW POLIECHNIKA CZĘSOCHOWSKA PRACOWNIA MECHANIKI Ć W I C Z E N I E N R M- ZALEŻNOŚĆ OKRESU DRGAŃ WAHADŁA OD AMPLIUDY Ćwiczenie M-: Zależność
UKŁAD AUTOMATYCZNEJ REGULACJI SILNIKA SZEREGOWEGO PRĄDU STAŁEGO KONFIGUROWANY GRAFICZNIE
 UKŁAD AUOMAYCZNEJ REGULACJI SILNIKA SZEREGOWEGO PRĄDU SAŁEGO KONFIGUROWANY GRAFICZNIE Konrad Jopek (IV rok) Opiekun naukowy referatu: dr inż. omasz Drabek Streszczenie: W pracy przedstawiono układ regulacji
UKŁAD AUOMAYCZNEJ REGULACJI SILNIKA SZEREGOWEGO PRĄDU SAŁEGO KONFIGUROWANY GRAFICZNIE Konrad Jopek (IV rok) Opiekun naukowy referatu: dr inż. omasz Drabek Streszczenie: W pracy przedstawiono układ regulacji
Autoreferat Rozprawy Doktorskiej
 Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie Wydział Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej Autoreferat Rozprawy Doktorskiej Krzysztof Kogut Real-time control
Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie Wydział Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej Autoreferat Rozprawy Doktorskiej Krzysztof Kogut Real-time control
ĆWICZENIE 15 BADANIE WZMACNIACZY MOCY MAŁEJ CZĘSTOTLIWOŚCI
 1 ĆWICZENIE 15 BADANIE WZMACNIACZY MOCY MAŁEJ CZĘSTOTLIWOŚCI 15.1. CEL ĆWICZENIA Celem ćwiczenia jest poznanie podstawowych właściwości wzmacniaczy mocy małej częstotliwości oraz przyswojenie umiejętności
1 ĆWICZENIE 15 BADANIE WZMACNIACZY MOCY MAŁEJ CZĘSTOTLIWOŚCI 15.1. CEL ĆWICZENIA Celem ćwiczenia jest poznanie podstawowych właściwości wzmacniaczy mocy małej częstotliwości oraz przyswojenie umiejętności
Regulacja dwupołożeniowa (dwustawna)
 Regulacja dwupołożeniowa (dwustawna) I. Wprowadzenie Regulacja dwustawna (dwupołożeniowa) jest często stosowaną metodą regulacji temperatury w urządzeniach grzejnictwa elektrycznego. Polega ona na cyklicznym
Regulacja dwupołożeniowa (dwustawna) I. Wprowadzenie Regulacja dwustawna (dwupołożeniowa) jest często stosowaną metodą regulacji temperatury w urządzeniach grzejnictwa elektrycznego. Polega ona na cyklicznym
Automatyka i sterowanie w gazownictwie. Regulatory w układach regulacji
 Automatyka i sterowanie w gazownictwie Regulatory w układach regulacji Wykładowca : dr inż. Iwona Oprzędkiewicz Nazwa wydziału: WIMiR Nazwa katedry: Katedra Automatyzacji Procesów AGH Ogólne zasady projektowania
Automatyka i sterowanie w gazownictwie Regulatory w układach regulacji Wykładowca : dr inż. Iwona Oprzędkiewicz Nazwa wydziału: WIMiR Nazwa katedry: Katedra Automatyzacji Procesów AGH Ogólne zasady projektowania
Tematy prac dyplomowych w Katedrze Awioniki i Sterowania Studia I stopnia (inżynierskie)
 Tematy prac dyplomowych w Katedrze Awioniki i Sterowania Studia I stopnia (inżynierskie) Temat: Pomiar prędkości kątowych samolotu przy pomocy czujnika ziemskiego pola magnetycznego 1. Analiza właściwości
Tematy prac dyplomowych w Katedrze Awioniki i Sterowania Studia I stopnia (inżynierskie) Temat: Pomiar prędkości kątowych samolotu przy pomocy czujnika ziemskiego pola magnetycznego 1. Analiza właściwości
Drgania wymuszone - wahadło Pohla
 Zagadnienia powiązane Częstość kołowa, częstotliwość charakterystyczna, częstotliwość rezonansowa, wahadło skrętne, drgania skrętne, moment siły, moment powrotny, drgania tłumione/nietłumione, drgania
Zagadnienia powiązane Częstość kołowa, częstotliwość charakterystyczna, częstotliwość rezonansowa, wahadło skrętne, drgania skrętne, moment siły, moment powrotny, drgania tłumione/nietłumione, drgania
Dynamika procesu zmienna stała. programowalne zmiany parametrów r.
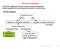 Sterowanie adaptacyjne Sterowanie adaptacyjne polega na dostosowywaniu (adaptacji) nastaw regulatora do zmian parametrów obiektu (w trakcie pracy) Techniki adaptacji Dynamika procesu zmienna stała regulator
Sterowanie adaptacyjne Sterowanie adaptacyjne polega na dostosowywaniu (adaptacji) nastaw regulatora do zmian parametrów obiektu (w trakcie pracy) Techniki adaptacji Dynamika procesu zmienna stała regulator
PODSTAWY AUTOMATYKI I MIERNICTWA PRZEMYSŁOWEGO Laboratorium 3 Regulatory PID i ich strojenie, Regulacja dwupołożeniowa
 Rok akademicki 2015/2016 Semestr letni PODSTAWY AUTOMATYKI I MIERNICTWA PRZEMYSŁOWEGO Laboratorium 3 Regulatory PID i ich strojenie, Regulacja dwupołożeniowa Wstęp teoretyczny: W układzie regulacji określa
Rok akademicki 2015/2016 Semestr letni PODSTAWY AUTOMATYKI I MIERNICTWA PRZEMYSŁOWEGO Laboratorium 3 Regulatory PID i ich strojenie, Regulacja dwupołożeniowa Wstęp teoretyczny: W układzie regulacji określa
Szukanie rozwiązań funkcji uwikłanych (równań nieliniowych)
 Szukanie rozwiązań funkcji uwikłanych (równań nieliniowych) Funkcja uwikłana (równanie nieliniowe) jest to funkcja, która nie jest przedstawiona jawnym przepisem, wzorem wyrażającym zależność wartości
Szukanie rozwiązań funkcji uwikłanych (równań nieliniowych) Funkcja uwikłana (równanie nieliniowe) jest to funkcja, która nie jest przedstawiona jawnym przepisem, wzorem wyrażającym zależność wartości
Wpływ nieliniowości elementów układu pomiarowego na błąd pomiaru impedancji
 Wpływ nieliniowości elementów układu pomiarowego na błąd pomiaru impedancji Wiesław Miczulski* W artykule przedstawiono wyniki badań ilustrujące wpływ nieliniowości elementów układu porównania napięć na
Wpływ nieliniowości elementów układu pomiarowego na błąd pomiaru impedancji Wiesław Miczulski* W artykule przedstawiono wyniki badań ilustrujące wpływ nieliniowości elementów układu porównania napięć na
