Teksturowanie obiektów z wykorzystaniem reprogramowalnych modułów do obliczania cieniowania
|
|
|
- Bogumił Matusiak
- 10 lat temu
- Przeglądów:
Transkrypt
1 Wydział Informatyki Politechnika Szczecińska Praca magisterska Teksturowanie obiektów z wykorzystaniem reprogramowalnych modułów do obliczania cieniowania Daniel Kos promotor: dr inż. Radosław Mantiuk Szczecin 2003
2 2 Spis treści 1. Wstęp Proces teksturowania Miejsce procesu teksturowaniu w potoku przetwarzania grafiki trójwymiarowej Definicja tekstury Proces nakładania tekstury Rodzaje tekstur Tekstury rastrowe Tekstury proceduralne Przykłady tekstur proceduralnych Sprzętowa realizacja procesu teksturowania Architektura współczesnych kart graficznych Pixel i Vertex Shader Zasada działania Vertex Shader a Zasada działania Pixel Shader a Przegląd implementacji programów Pixel i Vertex Shadera Tekstury uzyskiwane metodą bump mappingu Tekstury powstałe w wyniku przekształceń afinicznych Tekstury generowane za pomocą gotowych wzorów Tekstury rysowane ołówkiem Tekstury generowane na podstawie fluktuacji światła Tekstury oparte na funkcji szumu Tekstury fraktalne Tekstury uzyskiwane drogą symulacji reakcji dyfuzji Implementacja wybranych algorytmów teksturowania Generator szumu Perlin a Generator cząsteczek Generator komórek Analiza wydajnościowa procesu teksturowania Środowisko i procedura testowa Wyniki testów Podsumowanie Literatura
3 3 1. Wstęp Coraz więcej wymaga się od graficznych systemów czasu rzeczywistego. Gracze żądają realistycznie wyglądających gier, twórcy efektów specjalnych i różnego rodzaju animacji domagają się wiernego podglądu swojej pracy w czasie rzeczywistym, żeby móc na bieżąco korygować wszelkie błędy czy to związane z ruchem poszczególnych przedmiotów na scenie, czy też mimice tworzonych postaci. Większy realizm w systemach czasu rzeczywistego osiąga się głównie poprzez: użycie obiektów o zwiększonej liczbie wielokątów 1 stosowanie większej ilości tekstur 2 i zwiększania ich dokładności (rozdzielczości). Zwiększanie chociażby jednego z wymienionych czynników wymaga coraz silniejszych procesorów graficznych. Im więcej wielokątów na przetwarzanej scenie 3, tym wydajniejsza musi być jednostka przetwarzania geometrii, im większe tekstury, tym więcej pamięci musi mieć do dyspozycji procesor graficzny. Ponieważ opracowanie i produkcja nowych rozwiązań sprzętowych jest kosztowna, próbuje się wprowadzać różnego rodzaju techniki optymalizacyjne. I tak - dla geometrii sceny opracowano szereg algorytmów próbujących zmniejszyć liczbę wielokątów wchodzących w jej skład przy minimalnym uszczerbku na jakości wyświetlanej grafiki. Dla tekstur opracowano bezstratne algorytmy kompresujące takie jak DXTC czy też FXT1. Jednakże odkąd (rok 1998) pojawiły się karty graficzne wyposażone w tzw. szadery, dzięki którym możliwa jest ingerencja w potok sprzętowego przetwarzania geometrii i rasteryzacji wielokątów, realnym stało się użycie tekstur proceduralnych 4 generowanych w czasie rzeczywistym. O ile użycie klasycznych tekstur rastrowych (powstałych jako skan, ręcznie rysowany obrazek, lub w wyniku działania matematyki 5 ) jest bardzo powszechne, to używanie dynamicznie generowanych tekstur proceduralnych jest sporadyczne. Jak będzie można się przekonać w dalszej części tej pracy, posiadają one wiele cennych zalet, lecz niestety nie pozostają bez wad. Na ile te zalety i wady mają wpływ na realizm generowanej grafiki, a ile na wydajność systemu wizualizacji postaram się odpowiedzieć w dalszej części lektury. Celem niniejszej pracy jest ocena wydajności i przydatności procesu teksturo- 1 podstawowe prymitywy tworzące obiekty trójwymiarowe, najczęściej trójkąt, czworokąt 2 przeważnie dwuwymiarowa mapa bitowa 3 zbiór obiektów 3D tworzących określoną kompozycję 4 patrz rozdział tekstura proceduralna nie generowana w czasie rzeczywistym
4 4 wania proceduralnego przy użyciu aktualnie dostępnych procesorów graficznych przeznaczonych dla masowego odbiorcy 1, w szczególności poznanie opowiedzi na następujące pytania: 1. Jakie nowe możliwości niesie za sobą zastosowanie teksturowania proceduralnego? 2. Jakie zalety w stosunku do tradycyjnych technik teksturowania posiada teksturowanie proceduralne? 3. Na ile obecnie dostępne technologie pozwalają wykorzystać tą technikę? 4. Jaką wydajność oferują dzisiejsze procesory grafiki w zakresie wykorzystania tekstur proceduralnych? 5. Jaka przyszłość rysuje się przed użyciem tekstur proceduralnych? Pracę podzieliłem na następujące rozdziały: Rozdział 2 omawia wszystko co jest związane z teksturowaniem, począwszy od wiadomości ogólnych związanych z grafiką trójwymiarową takich jak etapy potoku graficznego, poprzez definicje tekstur rastrowych i proceduralnych, aż do sposobów nakładania tekstur na wielokąty. Rozdział ten omawia także sprzętową realizację procesu teksturowania oraz jednostki cieniowania pixel i vertex shader. Rozdział 3 zawiera implementację trzech wybranych metod teksturowania przy zastosowaniu technologii Pixel i Vertex Shader a. Rozdział 4 zajmuje się analizą wydajnościową programów z rodziału 3. Rozdział 5 to posumowanie i określenie celów na przyszłość. 1 geforce (3, 4, FX), readeon (8500 i wyżej)
5 5 2. Proces teksturowania 2.1. Miejsce procesu teksturowaniu w potoku przetwarzania grafiki trójwymiarowej Żeby lepiej zrozumieć proces teksturowania warto przyjrzeć się całej ścieżce przetwarzania grafiki 3D. Klasyczny potok przetwarzający składa się z następujących faz (rysunek 1). Rysunek 1. Potok przetwarzania grafiki trójwymiarowej 1. Przekształcenia modelowania - dokonywanie przekształceń w przestrzeni obiektów 6. Na tym etapie każdy obiekt zostaje przeskalowany, przesunięty i obrócony. Naturalnie mogą tu wystąpić inne rodzaje przekształceń np.: odchylenie w lewo, pofalowanie lub inne przekształcenia deformujące. 6 lokalny układ współrzędnych obiektu, którego punkt (0,0) znajduje się przeważnie w środku obiektu
6 2.2 Definicja tekstury 6 2. Obcinanie przez bryłę widzenia. Ponieważ urządzenie wyświetlające ma ograniczone rozmiary dokonuje się obcinania sceny 3D do tzw. bryły widzenia 7 której wymiary określa rzut wirtualnej kamery. Tak przekształcone wierzchołki 3D można teraz bezpiecznie przekształcić na współrzędne 2D. 3. Rzut na płaszczyznę rzutowania - zobrazowanie obiektu 3D na urządzeniu wyświetlającym. Najczęściej dokonywanym rzutowaniem jest rzutowanie perspektywistyczne i równoległe. 4. Rasteryzacja wielokątów. Tutaj następuje rysowanie otrzymanych wielokątów 2D. Albo wypełnieia się je określonym kolorem albo nakłada teksturę. Czasami też rysuje się jedynie same kontury (widać wtedy szkielet sceny). Uwzglęnia się przy tym oświetlenie i stosuje odpowiednie metody cieniowania (cieniowane płaskie, gourauda, cieniowanie per-pixel (phong)). Można też stosować dodatkowe efekty takie jak bump mapping czy emboss. 5. Obraz finalny. Po narysowaniu wszystkich wielokątów można uzyskany obraz wyświetlić na monitorze. Jak wynika z powyższego rysunku proces teksturowania dokonuje się w jednym z końcowych etapów potoku graficznego. Ma on miejsce po dokonaniu wszelkich możliwych transformacji w przestrzeni 3D i wyznaczeniu współrzędnych w układzie 2D. Jest to jeden z najbardziej czasochłonnych etapów potoku 3D Definicja tekstury Nakładanie tekstur (ang. texture mapping) to jeden z podstawowych efektów stosowanych w grafice trójwymiarowej. Dzięki niemu bezbarwne zarysy obiektów stają się realistycznymi przedmiotami. Zamiast modelować skomplikowane obiekty aż do najdrobniejszych szczegółów, co pochłania dużo czasu i miejsca w pamięci, proste, bezbarwne bryły geometryczne pokrywa się dwuwymiarowymi bitmapami nadając im żądany wygląd. Przykład, aby przedstawić na ekranie wieżowiec widziany z zewnątrz, wystarczy zwykły prostopadłościan i po jednej teksturze do zrzutowania na każdą z pięciu ścian budynku (jeśli chcemy by ściany różniły się). Inny przykład obiektu obłożonego teksturą przedstawia rysunek 4. Tekstura jest to n-wymiarowa mapa bitowa powstała w wyniku skanowania obrazów rzeczywistych albo ręcznie rysowanych lub powstała w wyniku działania pewnej funkcji F (x 0, x 1, x n ). Jak wynika z definicji najważniejszym kryterium 7 bryła widzenia - ogranicza tę część świata, która po rzutowaniu znajdzie się wewnątrz okna widzenia
7 2.2 Definicja tekstury 7 podziału tekstur jest ilość posiadanych wymiarów. Najczęściej obecnie spotyka się tekstury dwu i trzywymiarowe (rysunek 2 i 3). Rysunek 2. Przykład obiektu obłożonego teksturą 2D Rysunek 3. Różnica między teksturą 2D a 3D Rysunek 4 przedstawia teksturę w nieznacznym powiększeniu. Poszczególne piksele 8 tekstury nazywamy tekselami (ang. texture element). 8 podstawowy, najmniejszy element obrazu
8 2.3 Proces nakładania tekstury 8 Rysunek 4. Przykład tekstury 2.3. Proces nakładania tekstury Żeby nałożyć teksturę na wielokąt trzeba najpierw wyznaczyć współrzędne tekstury na jego poszczególnych wierzchołkach (rysunek 10). Można to zrobić jedną z podanych niżej metod mapowania 9 : Mapowanie UV. Ta metoda mapuje teksturę dopasowując ją do obiektu tam, gdzie zachodzi potrzeba rozciągając ją lub ściągając. Mapy tekstury zachowują swoją względną pozycję wobec obiektu, nawet kiedy obiekt zostaje skręcony lub pofałdowany. To jedyna metoda nie wykorzystująca mapowania projekcyjnego polegającego na rzutowaniu obrazu na powierzchnię. Jest to najczęściej spotykana metoda mapowania. Większość dostępnych pakietów 3D 10 zawiera specjalne narzędzia wspierające ten typ mapowania. 9 inaczej odwzorowanie 10 Maya, 3D Studio MAX
9 2.3 Proces nakładania tekstury 9 Rysunek 5. Mapowanie UV Mapowanie planarne. Ta metoda przepycha teksturę poprzez obiekt. Tekstura pojawia się na wszystkich ścianach obiektu, nawet wewnątrz i od tyłu. Rysunek 6. Mapowanie planarne Owinięcie względem poszczególnej osi dokonywane jest według następujących wzorów: x) u = S z z cz, v = S y y cy y) u = S x x cx, v = S z z cz z) u = S x x cx, v = S y y cy gdzie S x, S y, S z to współczynniki skalujące teksturę wzdłuż odpowiednich osi. Można je wyznaczyć na zasadzie s=1/(rozmiar bryły w danej osi). Mapowanie sferyczne. Jest to metoda, która owija sferycznie teksturę wokół obiektu, powodując zbieganie się jej na górnym i dolnym biegunie.
10 2.3 Proces nakładania tekstury 10 Rysunek 7. Mapowanie sferyczne Owinięcie sferyczne względem poszczególnej osi dokonywane jest według wzorów: x) u = S ( ) u z arc tg ou, 2 π y y) u = S ( ) u x 2 π arc tg ou, z z) u = S ( ) u x arc tg ou, 2 π y v = S v π v = S v π v = S v π ( ) x arc tg ov x2 + y 2 + z 2 ( ) y arc tg ov x2 + y 2 + z 2 ( ) z arc tg ov x2 + y 2 + z 2 gdzie S u, S v to współczynniki skalujące a ou, ov to współrzędne środka tekstury. Mapowanie cylindryczne. Ta metoda powoduje owinięcie tekstury wokół obiektu w cylindryczny sposób. Tekstura rozmazuje się do środka obiektu na jego szczycie i dnie, jeśli jest dłuższa od obiektu (w górę lub w dół). Rysunek 8. Mapowanie cylindryczne Owinięcie względem poszczególnej osi dokonywane jest według wzorów: x) u = S ( ) u z arc tg ou, v = S v x ov 2 π y y) u = S ) u ou, v = S v y ov ( x 2 π arc tg z ( ) x y z) u = S u arc tg 2 π ou, v = S v z ov
11 2.3 Proces nakładania tekstury 11 gdzie S u, S v to współczynniki skalujące a ou, ov to współrzędne środka tekstury. Mapowanie sześcienne (kubiczne). Jest to metoda nakładania tekstury z sześciu stron, nawet jeśli zaznaczony obiekt nie jest prostopadłościanem. Rysunek 9. Mapowanie kubiczne Rysunek 10. Przyporządkowanie współrzędnych tekstury odpowiednim wierzchołkom Po wyznaczeniu odpowiednich współrzędnych tekstury można przystąpić do jej nakładania na siatkę geometryczną. Na przykładzie trójkąta przedstawię najbardziej rozpowszechniony 11 algorytm teksturowania scan-line 12. Algorytm ten polega na interpolacji współrzędnych tekstury przypisanych do odpowiednich wierzchołków trójkąta wzdłuż jego przeciwległych krawędzi i dla każdej pary takich współrzędnych interpolacji wzdłuż linii łączącej te krawędzie. Dla każdej tak wyznaczonej współrzędnej zostaje pobrany odpowiedni teksel z mapy bitowej, który następnie jest umieszczany na trójkącie. Oto co się dokładnie dzieje: 1. W pierwszym kroku sortuje się współrzędne trójkąta względem osi y, od najwyżej położonego wierzchołka do położonego najniżej, wyznaczając przy okazji najdłuższą krawędź trójkąta. 11 algorytm ten w wersji klasycznej jest też najwolniejszy 12 skanowanie linia po linii
12 2.3 Proces nakładania tekstury Następnie wyznacza się przyrosty na osi x i na osi u dla każdej krawędzi trójkąta dx n = x n+1 x n y n+1 y n du n = u n+1 u n y n+1 y n dv n = v n+1 v n y n+1 y n 3. gdzie n - numer kolejnej krawędzi < > Wypełnianie trójkąta przebiega według poniższego pseudokodu: dxs = dx0 ; / p r z y r o s t y na l e w e j krawędzi t r ó j k ą t a / dus = du0 ; dvs = dv0 ; dxe = dx1 ; / p r z y r o s t y na prawej krawędzi t r ó j k ą t a / due = du1 ; dve = dv1 ; xs = xe = x0 ; / nadanie w a r t o ś c i początkowych / us = ue = u0 ; vs = ve = v0 ; / dla każdej l i n i i z k t ó r e j składa s i ę t r ó j k ą t / f o r ( y = y0 ; y <=y2 ; y++) { du = ( ue us ) / ( xe xs ) ; / p r z y r o s t du na l i n i i ł ą c z ą c e j / / p r z e c i w l e g ł e krawędzie t r ó j k ą t a / dv = ( ve vs ) / ( xe xs ) ; / p r z y r o s t dv na l i n i i ł ą c z ą c e j / / p r z e c i w l e g ł e krawędzie t r ó j k ą t a / u = us ; v = vs ; f o r ( x = xs ; x <= xe ; x++) { / pobranie t e k s e l a z mapy b i t o w e j i wstawienie / / go w odpowiednie m i e j s c e na t r ó j k ą c i e / p u t p i x e l ( x, y, RGB(u, v ) ) ; } u += du ; v += dv ; / sprawdzenie czy n i e n a s t ą p i ł a zmiana krawędzi / / po prawej s t r o n i e / i f ( y == v1. y ) { dxe = dx2 ; due = du2 ;
13 2.3 Proces nakładania tekstury 13 } dve = dv2 ; us += dus ; / o b l i c z e n i e k o l e j n y c h w a r t o ś c i / vs += dvs ; / x, u i v po l e w e j s t r o n i e / xs += dxs ; } xe += dxe ; / o b l i c z e n i e k o l e j n y c h w a r t o ś c i / ue += due ; / x, u i v po prawej s t r o n i e / ve += dve ; Przedstawiony algorytm można dość znacznie przyspieszyć. Pierwszą rzeczą którą warto wiedzieć, jest taka, że delty cząstkowe na obszarze całego trójkąta są stałe, co oznacza, że nie trzeba liczyć przyrostów dla tekstury po prawej stronie trójkąta [3]. Jednak największy wpływ na prędkość wykonywania algorytmu ma pętla wewnętrzna, która wypełnia pojedynczą linię trójkąta. W czasach kiedy cała wizualizacja dokonywała się programowo prześcigano się w pomysłach na jej optymalizację, obecnie nie ma to większego znaczenia, gdyż cały proces teksturowania wykonują procesory graficzne. (rysunek 11) Rysunek 11. Schemat algorytmu nakładania tekstury
14 2.3 Proces nakładania tekstury 14 Przedstawiony algorytm ma jedną zasadniczą wadę. Nie uwzględnia przestrzeni w której leży trójkąt. Interpolacja dokonuje się jedynie w oparciu o zrzutowane wartości 2D. Prowadzi to do dość znaczących błędów w obrazie, objawiającymi się zniekształceniami tekstur tym większymi im bardziej dany wielokąt jest odchylony od rzutni w przestrzeni 3D (zniekształcenia nie występują kiedy wielokąt jest równoległy do płaszczyzny rzutującej). Różnice między algorytmem z i bez korekcji perspektywy przedstawia rysunek 12.Żeby podany powyżej algorytm dokonywał korekcji perspektywy, każdą współrzędną (u, v) trójkąta i każdy przyrost tekstury trzeba dodatkowo podzielić przez wartość współrzędnej z odpowiedniego wierzchołka. Trzeba też interpolować wartości z dla każdej krawędzi. Niestety, uwzględnienie korekcji perspektywy znacząco obniża wydajność algorytmu, ze względu na fakt, że w pętli wypełniającej poszczególne linie trójkąta dla każdego piksela trzeba dokonać dwóch dzieleń odpowiednio dla u i dla v (lub dwóch mnożeń przez odwrotność dzielenia czyli 1 co jest nieznacznie szybsze). z Ponieważ dzielenie jest operacją pochłaniającą stosunkowo dużo czasu procesora, radzono sobie w inny sposób. Dokonywano go tylko co pewną, ustaloną liczbę pikseli (najczęściej 8 lub 16). Wartości pomiędzy dzieleniami były interpolowane. Rezultatem była zadawalająca prędkość i nieznaczne uszczerbki na wyświetlanym obrazie. Mimo różnych zabiegów optymalizacyjnych wydajność softwarowych algorytmów pozostawia wiele do życzenia. O ile ich zadaniem jest tylko nakładanie tekstur to radzą sobie nienajgorzej, to gdy zachodzi potrzeba dodania innych efektów (oświetlenie, nakładanie dwóch tekstur jednocześnie) trzeba zwrócić się ku rozwiązaniom sprzętowym. Rysunek 12. Tekstura z (po lewej) i bez korekcji perspektywy
15 2.4 Rodzaje tekstur Rodzaje tekstur Tekstury rastrowe Tekstura rastrowa to najczęściej prostokątna bitmapa typu RGBA 13. Dzięki temu może przedstawiać dowolny obraz. Mimo prostej organizacji i prostego sposobu tworzenia (np.: poprzez skanowanie) tekstury rastrowe mają kilka istotnych wad: z góry ustalona rozdzielczość - tekstura o wymiarach 128x128 dobrze wygląda na ekranie tylko wtedy, kiedy wielokąt na który jest nałożona po zrzutowaniu w pole widzenia zajmuje nieznacznie większą lub mniejszą powierzchnię niż powierzchnia tekstury. Kiedy powierzchnia wielokąta przewyższa znacznie powierzchnię tekstury (np.: kiedy zbliżamy się do ściany) powstaję niepożądany efekt pikselizacji. Dzieje się tak ponieważ nie ma odwzorowania 1:1 piksela tekstury (teksela) do piksela wielokąta. Innymi słowy, na wiele pikseli wielokąta przypada jeden teksel z mapy bitowej. Z kolei, kiedy zachodzi sytuacja odwrotna, na jeden piksel przypada wiele tekseli, generowany obraz ulega deformacjom (tekstura traci szczegóły, niemożliwe staje się odczytanie niesionej przez nią informacji). Aby zminimalizować ten efekt stosuje kilka różnych technik: metoda najbliższego sąsiada - wybiera teksel leżący najbliżej środka stawianego piksela. Niestety metoda ta powoduje duże zniekształcenia obrazu, ponieważ wybierany jest tylko jeden teksel z wielu mających wpływ na dany piksel. filtrowanie dwuliniowe - wybiera cztery sąsiadujące teksele i uśrednia je. Jest to metoda niewiele lepsza od poprzedniej, dająca w wyniku lekko rozmazany obraz (rysunek 13). Zawodzi, kiedy na jeden piksel ma wpływ więcej niż cztery teksele. 13 każdy jej teksel składa się z czterech składowych koloru: czerwonego, zielonego, niebieskiego i kanału alfa
16 2.4 Rodzaje tekstur 16 Rysunek 13. Filtrowanie dwuliniowe mip-mapping 14 - dla określonej tekstury jest tworzonych kilka mniejszych, z których każda następna stanowi 25% poprzedniej (wysokość i szerokość zmniejsza się o połowę). Ważnym jest, aby przy ich tworzeniu zastosować odpowiednie filtrowanie (najlepiej filtr Gaussa) i korekcję gamma, żeby uzyskać taki sam kontrast jak tekstura wyjściowa. Metoda mip-mappingu polega na wybraniu takiej mimmapy, której powierzchnia jest najbliższa powierzchni renderowanego wielokąta (zachodzi wtedy odwzorowanie powierzchni piksela do teksela w stosunku 1:1 lub przynajmniej (2:1) (reguła Nyquist a 15 )). W tym celu wyznacza się tzw. współczynnik d (rysunek 14). Można go wyznaczyć kilkoma sposobami. Jeden z nich polega na użyciu dłuższej krawędzi czworoboku utworzonego przez odwzorowanie powierzchni piksela na powierzchnię nakładanej tekstury w celu aproksymacji stopnia jego pokrycia. Drugim jest użycie największej bezwzględnej wartości z czterech różniczek: u x, v x, u y, v y Każda różniczka określa o ile współrzędne tekstury zmieniły się w stosunku do osi ekranu. Na przykład u jest miarą zmiany wartości współrzędnej u wzdłuż x osi ekranu x dla jednego piksela. 15 Reguła Nyquist a mówi, że częstotliwość samplowania musi być conajmniej dwukrotnością częstotliowści samplowanej próbki
17 2.4 Rodzaje tekstur 17 Rysunek 14. Mip-mapping Rysunek 15. Efekt działania algorytmu mip-mappingu (po lewej - brak mip-mappingu) filtrowanie trzyliniowe - jest to połączenie mip-mappingu i filtrowania dwuliniowego. Na podstawie współczynnika d wybiera się dwie mipmapy, z których następuje pobranie i uśrednienie czterech sąsiadująych tekseli. Tak powstałe wartości są liniowo interpolowane w zależności od odległości każdej mipmapy do współczynnika d (który w tym przypadku nie jest wartością całkowitą, lecz ułamkową, określającą odległoś pomiędzy odpowiednimi poziomami piramidy mipmap). Rysunek 16. Filtrowanie trzyliniowe rip-mapping - metoda podobna do mip-mappingu, z tą różnicą, że tworzone są także mapy zmieniające tylko wysokość lub tylko szerokość w stosunku
18 2.4 Rodzaje tekstur 18 do mapy wyjściowej (rysunek 17). W celu odczytania odpowiedniego teksela koordynaty tekstury składają się z czterech współrzędnych: (u,v) - do określenia odpowiedniego teksela danej podtekstury i dodatkowych dwóch (s,t) do lokalizacji odpowiedniej podtekstury. Rysunek 17. Rip-mapping tablice sumacyjne - metoda tworząca tablicę o rozmiarze tekstury, ale przeznaczającą większą liczbę bitów na przechowywanie wartości kolorów (np.: 16 bitów na każdą poszczególną składową r,g,b). Następnie dla każdego elementu tej tablicy należy obliczyć i zapamiętać sumę wszystkich tekseli wchodzących w skład prostokąta, którego lewy, dolny róg znajduje się w punkcie (0,0) tablicy, a prawy, górny w punkcie o współrzędnych odpowiadającym współrzędnym tablicy aktualnie przetwarzanego elementu. W trakcie teksturowania określany jest prostokąt ograniczający projekcję obszaru piksela na obszar tekstury. W celu ustalenia wartości koloru piksela uśrednia się wartości odczytane z tablicy dla obszaru tego prostokąta za pomocą formuły: c = s[x ur, y ur ] s[x ur, y ll ] s[x ll, y ur ] + s[x ll, y ll ]) (x ur x ll )(y ur y ll ) gdzie x i y są współrzędnymi teksela wyznaczonym przez prostokąt ograniczający, a s[x,y] wartością z tablicy sumacyjnej dla danego piksela. filtrowanie anizotropowe - inne określenie dla technik rip-mappingu i tablic sumacyjnych. Często łączy się je dla osiągnięcia lepszych rezultatów. Metody filtrowania oparte na tych algorytmach mogą pobierać wartości tekseli, które znajdują się na obszarach nie będącymi kwadratami. Rezultat działania takich algorytmów przedstawia rysunek 18. Choć dają dobre wyniki, nie pozostają bez wad, z których największą wydaje się być zapotrzebowanie na duże ilości pamięci. Tablica sumacyjna dla tekstury o wymiarach 256x256 wymaga co
19 2.4 Rodzaje tekstur 19 najmniej dwukrotnie więcej pamięci niż sama tekstura, a ripmapy trzy razy więcej. Rysunek 18. Filtrowanie anizotropowe duże wymogi odnośnie pamięci - Jeśli założyć, że na scenie znajduje się 20 różnych obiektów, a na każdy obiekt przypadają dwie tekstury o wymiarach 256x256 pikseli, gdzie piksel zajmuje 4 bajty (po 8 bitów na każdą składową koloru r,g,b,a) - to okaże się, że potrzeba 10 megabajtów pamięci na zapamiętanie samych tylko tekstur. To dużo - jeśli brać pod uwagę fakt, że bardzo często w systemach czasu rzeczywistego przechodzi się z jednej sceny do drugiej i przejście to musi być płynne. Jeżeli procesor graficzny nie dysponuje odpowiednią ilością pamięci dla wszystkich scen będzie musiał je doczytać z pamięci masowej, co przeważnie objawia się zacięciami w generowanej animacji. Trzeba dodatkowo zauważyć, że przeważnie stosuje się mip-mapping, co w naszym przykładzie zakładając 3 poziomowy mip-mapping zapotrzebowanie na pamięć zwiększy się do 13 megabajtów. Z apetytem na pamięć próbuje się walczyć wprowadzając liczne rodzaje algorytmów kompresujących. Procesor graficzny trzyma w pamięci skompresowaną postać tekstury i w czasie rasteryzacji dynamicznie ją rozkodowuje i sięga po odpowiedni teksel. Jak pokazuje rzeczywistość pomimo wyposażania procesorów graficznych w mechanizmy kompresji danych, stale rośnie ilość pamięci, którą one dysponują. Jeszcze nie tak dawno standardem było 32 Mb. Obecnie instaluje się już nawet 256 Mb. większe zapotrzebowanie na przepustowość pamięci - rysunek 19 pokazuje jak wiele wymaga się od magistrali pamięci procesora graficznego. Najbardziej wymagające pod tym względem są: Bufor ramki przechowywany w pamięci lokalnej, który składa się z frontowego i tylnego, a w przypadku potrójnego buforowania nawet z trzeciego bufora. Te bufory mają rozmiar dokładnie odpowiadający rozdzielczości ekranu po-
20 2.4 Rodzaje tekstur 20 mnożonej przez głębię koloru. Jednostka renderująca korzysta z bufora ramki kilka razy na każdy piksel. Bufor Z jest również tak samo duży, jak rozdzielczość ekranu razy głębia bufora Z. Bufor Z kładzie wielki nacisk na przepustowość pamięci, ponieważ jest najczęściej używaną częścią pamięci graficznej (odwołanie do bufora Z następuje w zawsze kiedy stawiany jest nowy piksel). Bufor tekstur, który przechowuje skompresowane, bądź nie, tekstury, do których dostęp jest szybszy w pamięci lokalnej, aniżeli gdyby jednostka renderująca musiała ściągać je z pamięci systemowej przez szynę AGP. Znowu, tekstury muszą być odczytane kilka razy na każdy piksel, w zależności od opcji filtrowania i ilości tekstur nakładanych na piksel. Na końcu, ale nie mniej ważny jest RAMDAC, który musi odczytać frontowy bufor ramki, by wyświetlić go na ekranie. Im wyższa rozdzielczość i im wyższa częstotliwość odświeżania, tym częściej RAMDAC musi mieć dostęp do bufora ramki. Jak widać bufor tekstur ma dość istotny wpływ na przepustowość pamięci, co z kolei przekłada się na płynność wyświetlanej animacji. Rysunek 19. Obciążenie pamięci lokalnej procesora graficznego
21 2.4 Rodzaje tekstur Tekstury proceduralne Tekstura proceduralna jest to tekstura, która powstaje wskutek działania funkcji F (). Funkcja ta przeważnie ma następującą postać: kolor = F (x, y, z,...) gdzie x,y,z to współrzędne punktu, dla którego jest generowana tekstura, a kropki oznaczają dodatkowe parametry sterujące funkcją lub wpływające na jej działanie. Ciało funkcji to zbiór dowolnych instrukcji danego języka programowania, które w wyniku swojego działania zwracają kolor dla aktualnie wyświetlanego punktu. Z punktu widzenia momentu użycia funkcji F () można wyróżnić dwa typy tekstur proceduralnych: 1. generowane statycznie - funkcja F () służy do wygenerowania tekstury przed uruchomieniem systemu generującego grafikę 3D (ang. engine). Tak wygenerowana tekstura jest używana jako tekstura rastrowa. 2. generowane dynamicznie - funkcja F () wołana jest w trakcie działania programu generującego obraz 3D każdorazowo w momencie stawiania piksela w buforze ramki na etapie rasteryzacji wielokąta. Podejście pierwsze, choć nie eliminuje wad tekstur rastrowych 16 ma jedną, niezaprzeczalną zaletę. Pozwala znacznie ograniczyć rozmiar programu 17 (zakładając, że większość tekstur jest generowana w taki właśnie sposób). Po drugie, można zawsze, gdy zaistnieje taka potrzeba wygenerować te same tekstury, ale w większej rozdzielczości. Jest to bardzo ważna zaleta, zwłaszcza teraz, kiedy użytkownicy komputerów dysponują kartami graficznymi o zróżnicowanej mocy i możliwościach. Ktoś, kto posiada mocną jednostkę komputerową może sobie zażyczyć tekstur o wysokiej rozdzielczości, ktoś inny wręcz odwrotnie. Do tej pory należało dołączyć do programu dla każdej tekstury kilka jej wersji dla każdej uwzględnionej przez producenta oprogramowania rozdzielczości. Poszerzało to znacznie rozmiary danego programu. Po trzecie może się okazać że wygenerowanie przykładowo stu tekstur o rozmiarach 512x512 jest szybsze niż odczytanie ich z pamięci masowej (zwłaszcza CD-ROM u). Skraca się wtedy czas oczekiwania na załadowanie następnej planszy w grze. Podejście drugie nie dość że uwalnia od wcześniej wymienionych wad i ograniczeń tekstur rastrowych, to łączy zalety wymienione w punkcie poprzednim. Znika 16 patrz rozdział poprzedni - Tekstury rastrowe 17 rozmiar programu - program wykonywalny razem z danymi potrzebnymi do jego działania
22 2.4 Rodzaje tekstur 22 więc zapotrzebowanie na duże ilości pamięci i wysoką jej przepustowość 18, a w stosunku do tekstur proceduralnych generowanych statycznie znika problem skończonej rozdzielczości (inaczej mówiąc dokładności, widocznych detali) tekstury. Teraz nie ma już tekstury o z góry określonych rozmiarach. Rozważmy wcześniej już użyty przykład zbliżania się do ściany. Przy tradycyjnym podejściu, kiedy gracz podchodził bliżej ściany, widział coraz więcej jej detali (zakładając, że ściana składa się z chropowatych cegieł), ale tylko do momentu kiedy powierzchnia tekstury nie przekraczała powierzchni renderowanego wielokąta. Potem widział już tylko coraz większe piksele (rysunek 20). Używając prostej funkcji generującej takie cegiełki problem całkowicie znika, ponieważ rozdzielczość staje się nieskończona (oczywiście jeśli odpowiednio napisze się taką procedurę, np.: można do niej przekazywać odległość obserwatora (gracza) od ściany i w zależności od jej wartości generować odpowiednio cegiełki). Rysunek 20. Powiększanie tekstury proceduralnej i rastrowej Pomimo niezaprzeczalnych zalet tekstur proceduralnych, nie da się nimi zastąpić tekstur rastrowych ze względu na dwie największe ich wady: 1. brak możliwości uzyskania dowolnego obrazu. Nie da się na przykład (lub jest to bardzo skomplikowane) wygenerować ludzkiej twarzy (skórę jak najbardziej, ale nie takie elementy, jak oczy czy nos) 2. czasochłonność. Skomplikowane wzory (lub te nawet pozornie proste) mogą wymagać użycia zaawansowanej matematyki o dużej złożoności obliczeniowej, co uniemożliwia ich użycie w czasie rzeczywistym. 18 tylko odnośnie tekstur
23 2.4 Rodzaje tekstur Przykłady tekstur proceduralnych Tekstury proceduralne idealnie nadają się do odwzorowywania wszelkiego rodzaju wzorów, powierzchni czy materiałów charakteryzujących się pewną regularnością. Inaczej mówiąc takich, których dowolnie wybrane fragmenty są do siebie podobne. Takim materiałem jest np.: szachownica (krata) albo marmur. Poniżej przedstawię kilka przykładów tekstur proceduralnych wraz z programami je generującymi: k o l o r Okręgi ( x, y, p a l e t a ) { a = x 0.5 b = y 0.5 c = s q r t ( a a + b b ) return p a l e t a [ c ] } Okręgi gdzie x, y - współrzędne stawianego piksela < > paleta elementowa tablica kolorów Rysunek 21. Wynik działania funkcji Okręgi Cegły k o l o r Cegła ( x, y, wysokość, szerokość, odstęp ) { p r z e s u n i ę c i e = s z e r o k o ś ć / 2. 0 ; s t a t i c k = 0. 0 ; i f ( k == 0.0) p r z e s u n i ę c i e = 0.0 e l s e
24 2.4 Rodzaje tekstur 24 p r z e s u n i ę c i e = s z e r o k o ś ć / 2. 0 xp = ( x + p r z e s u n i ę c i e ) mod ( s z e r o k o ś ć + odstęp ) yp = y mod ( wysokość + odstęp ) i f ( xp < odstęp yp < odstęp ) return k o l o r b i a ł y e l s e return kolor czerwony } i f ( yp == 0.0 && x == 1.0) k = 1 k Rysunek 22. Wynik działania funkcji Cegła Dużo lepsze efekty można osiągnąć stosując funkcję szumu, która jest bardzo powszechnie stosowana w celu nadania generowanym teksturom pozorów naturalności. Najczęściej stosowanym typem takiej funkcji jest funkcja opracowana w 1985 roku przez Ken a Pelin a [5]. Podstawowym założeniem tej funkcji jest utworzenie ciągu liczb losowych i interpolowanie jego wartości dla elementów pośrednich. Dodatkowo sumuje się szumy o różnej częstotliwości i amplitudzie. Liczbę sumowanych map szumu określa się jako oktawy. W celu uzyskania różnych efektów końcowych stosuje się również przekształcenia uzyskanej wartości szumu, a dla wartości wejściowych funkcji stosuje się skalowanie (co odpowiada przybliżaniu, oddalaniu się od generowanej tekstury). Dla danej tekstury została wygenerowana odpowiednia paleta barw (256 elementowa tablica kolorów RGB, na odpowiedni indeks w tej tablicy wskazuje N(x) 256, gdzie N(x) oznacza wartość końcową funkcji szumu). Dla uzyskanych wyników podaję wartości f reqm od (modulator częstotliwości dla kolejnej mapy) i amplm od (modulator amplitudy dla kolejnej mapy) oraz liczbę oktaw. Przy pomocy programu Noise Generator [8] uzyskałem następujące tekstury.
25 2.4 Rodzaje tekstur 25 Modulator częstotliwości: 2.0 Modulator amplitudy: 0.65 Liczba oktaw: 5 Skala: 200 Wartość końcowa: N(x) = N(x) Rysunek 23. Marmur Modulator częstotliwości: 2.0 Modulator amplitudy: 0.55 Liczba oktaw: 4 Skala: 510 Wartość końcowa: N(x) = N(x) 10 Round(N(x)) Rysunek 24. Drzewo Modulator częstotliwości: 2.0 Modulator amplitudy: 0.65 Liczba oktaw: 5 Skala: 35 Rysunek 25. Korona drzewa
26 2.4 Rodzaje tekstur 26 Modulator częstotliwości: 2.0 Modulator amplitudy: 0.75 Liczba oktaw: 3 Skala: 200 Wartość końcowa: N(x) = N(x) Rysunek 26. Rozbłyski
27 2.5 Sprzętowa realizacja procesu teksturowania Sprzętowa realizacja procesu teksturowania Architektura współczesnych kart graficznych Za proces teksturowania w akcelatorach graficznych odpowiedzialne są jednostki teksturujące (ang. texture units) organizowane w potoki. W zależności od modelu karty różna jest ich ilość i właściwości. Obecnie najczęściej spotykane konfiguracje to 4 potoki zawierające po 2 jednostki teksturujące lub 8 potoków zawierających po 1 jednostce teksturującej. Organizacja potokowa umożliwia rasteryzację kilku pikseli wielokąta na raz. Im więcej potoków tym szybciej resteryzowany jest wielokąt. Jeżeli na dany potok przypada więcej niż jedna jednostka teksturująca procesor graficzny może w 1 cyklu nałożyć n-tekstur na dany piksel (n-ilość jednostek). W pierwszym przypadku mówi się o szybkości wypełniania pikseli (ang. pixel fillrate),w drugim o szybkości wypełniania tekseli (ang. texel fillrate). Mając do wypełnienia określoną scenę, na której każdy obiekt pokryty jest dwiema teksturami, karta o architekturze 8x1 wykona to zadanie w tym samym czasie co karta zbudowana w architekturze 4x2 (zakładają zgodność wszystkich innych parametrów karty tj. częstotliwość układu, przepustowość pamięci itd.). Pierwsza karta wykorzysta dwa potoki (każdy dla jednej tekstury) na dany piksel, karta druga zaś nałoży w każdym potoku dwie tekstury od razu. W każdym przypadku wypełnianie odbywa się dla 4 pikseli naraz. Jeżeli jednak na każdy obiekty tej sceny przypadałaby tylko jedna tekstura, to karta pierwsza wykona to zadanie 2 razy szybciej. Widać więc przewagę organizacji 8x1. Ideałem byłaby organizacja 8x2, wiąże się to jednak z ilością użytych tranzystorów, co ma znaczący wpływ na stopień skomplikowania konstrukcji, ilość wytwarzanego ciepła, a także cenę końcową układu. Zanim nastąpi proces wypełniania wielokąta w pierwszym etapie procesor geometrii przetwarza dane sceny 3D (rotacja, obcinanie, rzutowanie, oświetlenie) i przekazuje je do jednostki rasteryzującej (ang. triangle setup rasterizer), która wyznacza metodą interpolacji współrzędne poszczególnych krawędzi i wszystkie inne wartości przypisane wierzchołkom aktualnie przetwarzanego wielokąta. Wszystkie te dane przekazywane są następnie do jednostki teksturującej, której zadaniem jest wyznaczenie na podstawie odpowiedniego algorytmu (przeważnie scan-line przedstawiony w rozdziale poprzednim) albo koloru, albo odpowiedniej wartości z tekstury dla każdego piksela wchodzącego w skład poszczególnych linii rasteryzowanego wielokąta. Zadaniem jednostki teksturującej jest również dokonywanie korekcji perspektywy i filtrowania (dwu/trój-liniowego, anizotropowego). W obecnie produkowanych układach jednostki teksturujące są elementami programowalnych jednostek rasteryzujących (pixel shader). Przykła-
28 2.5 Sprzętowa realizacja procesu teksturowania 28 dy organizacji wiodących obecnie akcelatorów graficznych przedstawiają rysunki 27 i 28. Rysunek 27. Schemat karty ATI Radeon 9700 Rysunek 28. Schemat karty geforce 5800
29 2.5 Sprzętowa realizacja procesu teksturowania Pixel i Vertex Shader Pierwsze akcelatory grafiki 3D wspomagały jedynie ostatni etap ścieżki przetwarzania - rasteryzację wielokątów (S3 Virge, 3DFX Voodoo). Kolejne generacje tylko usprawniały ten proces (Riva TNT, Voodoo 2 ) dokładając więcej potoków renderujących. Przełomem okazało się wprowadzenie układu firmy nvidia geforce 256, który oferował sprzętową jednostkę przetwarzania oświetlenia i geometrii. Nadal jednak programista był skazany na używanie z góry przewidzianych funkcji graficznych oferowanych przez procesor karty graficznej. O ile mógł dokonać sprzętowej rotacji lub translacji wierzchołków, nałożyć tekstury, ustalić rodzaj światła (kolor, natężenie, rozproszenie), to nie był w stanie zmusić karty do dokonywania innych (przeważnie specjalistycznych) operacji np.: wygięcia obiektu na kształt sinusoidy, zmieniania koloru każdego punktu tekstury w zależności od kąta padania światła itd. Kiedy jednak koncern nvidia wyprodukował pierwsze karty geforce 3 sytuacja zmieniła się diametralnie. Użytkownik nie tylko otrzymał układ realizujący wszystkie podstawowe funkcje grafiki 3D, ale otrzymał także możliwość ingerowania we wnętrze potoku 3D. Stało się to możliwe dzięki zastosowaniu w pełni programowalnych jednostek przetwarzania geometrii i rasteryzacji, które otrzymały nazwy - odpowiednio vertex i pixel shader 19 (rysunek 29) Zasada działania Vertex Shader a W tradycyjnym potoku przetwarzania 20 często dochodziło do podziału pracy między procesorem głównym a procesorem graficznym, a czasem nawet do jej dublowania. Działo się tak dlatego, ponieważ karta graficzna nie wspierała wszystkich przekształceń geometrii, które wymyślił twórca aplikacji. Programowalna jednostka przetwarzania geometrii daje programiście pełną swobodę w wymyślaniu nawet skomplikowanych efektów graficznych, które do tej pory z powodu ograniczeń w funkcjonalności jednostki T&L, bądź zbyt słabej wydajności procesora głównego nie były możliwe do uzyskania. Dzięki jednostce vertex shader możliwe są do uzyskania takie efekty jak np.: geometria proceduralna (symulacja ubrań (naturalne ruchy materiału nałożonego na bryłę sztywną będącą w ruchu), bańki mydlane) zaawansowane przenikanie werteksów używane do morfingu generacja tekstur 19 jednostki cieniowania werteksów i pikseli 20 tu - karty ze sprzętową jednostką T&L
30 2.5 Sprzętowa realizacja procesu teksturowania 30 Rysunek 29. Miejsce jednostek pixel i vertex shader a w potoku graficznym zaawansowana interpolacja klatek kluczowych (złożone ruchy twarzy i wymowa) system cząsteczek modyfikacja widoku perspektywy w czasie rzeczywistym (efekt soczewki, efekt bycia pod wodą) zaawansowane oświetlenie modeli 3D (często używane razem z pixel shader em) Rysunek 30 przedstawia wewnętrzną organizację vertex shader a. Zasada jego działania opiera się na przetwarzaniu na zasadzie kolejki tylko jednego wierzhchołka naraz. Oznacza to, że program vertex shadera wykonuje się dla każdego wierzchołka sceny osobno. W momencie gdy zostaje uruchomiony program vertex shader a odłączona zostaje jednostka T&L. Na wejściu w rejestrach od v0 do v15 vertex shader dostaje wszystkie dane aktualnie przetwarzanego wierzchołka:
31 2.5 Sprzętowa realizacja procesu teksturowania 31 v0 pozycja wierzchołka v1 waga mieszana v2 indeksy mieszania v3 normalna v4 wielkość punktu v5 kolor wierzchołka v6 kolor odbicia v7... v14 współrzędne kolejnych 8 tekstur Rejestry od r0 do rn 21 służą do zapisywania i odczytywania wartości tymczasowych, np.: koloru tekstury. Rejestry od c0 do cn są rejestrami pamięci stałej dla liczb zmiennoprzecinkowych, poprzez które można przekazywać parametry programu, np.: rozwinięcia funkcji sinus. Analogiczne zastosowanie mają rejestry i0... in (dla wartości całkowitych) i b0... bn (dla wartości logicznych). Ostatni rejestr a zwiera ofset (przesunięcie), które wskazuje na aktualnie czytany rejestr pamięci stałej. Na wyjściu zwracane są przetworzone współrzędne wierzchołka, jego kolor, a także wszystkie inne dane skojarzone z określonym wierzchołkiem, a potrzebne w dalszej ścieżce przetwarzania. Każdy rejestr ma długość 128 bitów, co wystarcza do przechowania czterech liczb zmiennoprzecinkowych (np.: współrzędnych x,y,z,w wierzchołka). Program vertex shader a to zbiór instrukcji realizujących takie zadania jak iloczyn skalarny, mnożenie wektora przez macierz, dodawanie itp. W zależności od wersji vertex shadera różna może być liczba instrukcji i różny stopień ich zaawansowania. Przykładowo wersja 1.3 przewiduje liczbę instrukcji do 128, w wersji 2.0 już do 256. Poniższa tabelka przedstawia zasadnicze różnice pomiędzy dostępnymi wersjami vertex shader ów. Wersja Vertex Shader a Liczba dopuszczalnych instrukcji Liczba rejestrów pamięci stałej Liczba rejestrów tymczasowych Liczba rejestrów wejścia Zasada działania Pixel Shader a Zanim procesor graficzny postawi piksel na ekranie wykonuje program pixel shadera (rysunek 31). Dzięki pixel shader owi możliwe są do uzyskania efekty takie jak: 21 liczba dostępnych rejestrów jest zależna od wersji shadera, wersja omawiana w tej pracy ma numer 1.3
32 2.5 Sprzętowa realizacja procesu teksturowania 32 Rysunek 30. Wewnętrzna architektura vertex shader a cienie, oświetlenie liczone dla pojedynczych pikseli, zaawansowane efekty przezroczystości, efekt mgły, wypukłości Na wejściu pixel shader otrzymuje dane z jednostki przetwarzania geometrii T&L albo z vertex shader a. Tymi danymi są współrzędne punktu w przestrzeni na który nakładana jest tekstura, jego kolor, współrzędne nakładanych tekstur, i tak jak poprzednio specjalne parametry przekazywane poprzez rejestry pamięci stałej. Specyficzny jest proces przetwarzania pojedynczego piksela. Jak widać to na rysunku 32 pierwszym krokiem, jaki wykonuje pixel shader jest skopiowanie danych wejściowych, po to aby móc bezpiecznie dokonywać operacji arytmetycznych (operowanie na oryginalnych wartościach może doporwadzić do przekłamanych wyników). W kroku drugim następuje rozdzielenie koloru na dwie części: na składowe r,g,b i kanał przezroczystości alfa. Teraz pixel shader wykonuje swój program dla tych wartości (równolegle) i po zakończeniu uzyskany wynik przekazuje do bufora ramki. Na wynik można nałożyć maskę, np. w celu nieuwzglęniania składowej r przy tworzeniu ostatecznej wartości koloru, który zawsze jest zapisywany w rejestrze r0. Ważną rzeczą w przypadku pixel shadera jest mechanizm
33 2.5 Sprzętowa realizacja procesu teksturowania 33 Rysunek 31. Wewnętrzna architektura pixel shader a adresowania tekstur (samplowanie, rysunek 33), czyli pobieranie odpowiednich tekseli z tekstur. Samplowanie dokonuje się w oparciu o cztery informacje: 1. instrukcji adresowania użytej w pixel shaderze, 2. współrzędnych mapowania, 3. aktualnie ustawionej teksturze na danym poziomie tekstury (ang. stage), 4. różnych atrybutów obróbki tekstury ustawionych dla danego poziomu. Rysunek 33 przedstawia drogę, jaką mogą przebyć współrzędne mapowania w shaderach od wersji od 1.0 do 1.3, zanim zostaną użyte do uzyskania koloru tekstury przypisanej danemu wielokątowi. Jak widać, dróg tych jest kilka a każda z nich charakteryzuje się inną specyfiką: kolor czerwony. W takim przypadku rejestry tekstury są ładowane bezpośrednio współrzędnymi mapowania a pixel shader posługując się nimi pobiera z określonego miejsca na teksturze odpowiedni kolor bez żadnych dodatkowych obliczeń.
34 2.5 Sprzętowa realizacja procesu teksturowania 34 Rysunek 32. Przetwarzanie pojedynczego piksela kolor niebieski. Współrzędne mapowania są przekazywane do tzw. samplera tekstury, który bazując na kilku wspomnianych wyżej typach danych pobierze odpowiedni kolor z tekstury i umieści jego wartości w rejestrach tekstury. Tekstura musi być ustawiona na jakimś konkretnym poziomie, z którego pobierane są dane o samplingu. Numer współrzędnych mapowania (wierzchołek ma ich aż osiem par, podobnie jest z ilością dostępnych poziomów tekstur) zawsze koresponduje z numerem docelowego rejestru zastosowanego w instrukcji shadera. kolor żółty i zielony. Pewne instrukcje adresowe tekstur w konkretnych wersjach pixel shadera przeprowadzają różne transformacje na wejściowych współrzędnych teksturowania w celu utworzenia nowych współrzędne. Następnie mogą one być użyte do samplowania tekstury (kolor zielony) lub być bezpośrednio przekazywane jako dane dla rejestrów tekstury (kolor żółty).
35 2.5 Sprzętowa realizacja procesu teksturowania 35 Rysunek 33. Mechanizm adresowania tekstur Dla wersji pixel shadera 1.4 rejestry tekstur maja trochę inne znaczenie niż w wersjach poprzednich. Zawierają one współrzędne tekstury więc widać niejako podobieństwo do sposobu oznaczonego w poprzednich wersjach kolorem czerwonym. Są to rejestry tylko do odczytu (używane jako rejestry wejściowe dla instrukcji adresowych) i nie można na nich przeprowadzać operacji arytmetycznych. Fakt, że posiadamy współrzędne tekstury w rejestrach oznacza tylko tyle, że teraz zbiór współrzędnych mapowania i numer poziomu tekstury wcale nie musza się zgadzać. Numer poziomu, z którego dokonywane jest samplowanie tekstury określany jest przez docelowy numer rejestru, ale zbiór współrzędnych tekstury jest określany przez nowy rejestr wejściowy tn. Blok z rysunku 33 nazwany zmiana współrzędnych nie jest obecny w shaderze w wersji 1.4, ponieważ modyfikacja współrzędnych tekstury przed samplowaniem tekstury jest osiągana w prosty sposób przez użycie arytmetycznych instrukcji poprzedzonych tzw. zależnym odczytem, co oznacza, że dane tekstury, które dostaniemy w wyniku samplowania będą zależeć od pewnych operacji, które dokonamy wcześniej. Dla wersji shadera odczyt zależny także jest możliwy, ale jest bardzo ograniczony i sprowadza się tylko do zastosowania instrukcji adresowej używającej jako parametru wejściowego rezultatu poprzednio zastosowanej instrukcji adresowej. Dla wersji 1.4 shadera odczyt zależny ma o wiele większe możliwości, ponieważ współrzędne mapowania mogą pochodzić nie tylko z poprzedniej instrukcji adresowej, ale także z prawie dowolnej instrukcji arytmetycznej. Następne wersje pixel shader a ułatwiają programowanie jeszcze bardziej. Porównanie możliwości przedstawia poniższa tabelka.
36 2.5 Sprzętowa realizacja procesu teksturowania 36 Wersja Pixel Shader a Liczba instrukcji Liczba rej. pamięci stałej Liczba rej. tymczasowych Liczba rej. tekstury Liczba rej. koloru
37 37 3. Przegląd implementacji programów Pixel i Vertex Shadera 3.1. Tekstury uzyskiwane metodą bump mappingu Praca [17] używa pixel i vertex shader a do uzyskania złudzenia wypukłości powierzchni (bump-mapping). W przeciwieństwie do klasycznych metod używających tekstury o stałych rozmiarach, zawierającej informację o rozkładzie światła na danym materiale, autorzy generują taką mapę w czasie rzeczywistym. Zapobiega to błędom w generowanej grafice, które miały miejsce przy użyciu innych metod w momencie, kiedy odległość tekstury od obserwatora ulegała zmianie. Wymaga jednak, aby powierzchnia bryły była materiałem określonym fraktalnie, a model oświetlenia bazował na tzw. mikro-odcinkach (ang. microfacets). Rysunek 34. Tekstura uzyskana metodą bump-mappingu 3.2. Tekstury powstałe w wyniku przekształceń afinicznych Praca [19] pokazuje jak używać arytmetyki przekształceń afinicznych do generowania tekstur proceduralnych. Autorzy używają języka shaderów Render- Man a, który można jednak łatwo przkszatłcić na język shaderów obecnych kart graficznych (np.: Cg). Arytmetyka afiniczna (ang. affine aritchmetic) podobnie jak arytmetyka przedziałów (ang. interval aritchmetic) gwarantuje określone zakresy (ang. bounds) dla uzyskiwanych wyników, biorąc pod uwagę reszty i błędy zaokrągleń. Jendak w przeciwieństwie do arytmetyki przedziałów śledzi ścieżkę korelacji pomiędzy wartościami powstałymi a wejściowymi, zapobiegając w ten sposób dużym utratom dokładności w stosowanych obliczeniach.
38 3.3 Tekstury generowane za pomocą gotowych wzorów 38 Rysunek 35. Przykład tekstury uzyskanej za pomocą arytmetyki afinicznej 3.3. Tekstury generowane za pomocą gotowych wzorów Metoda składania tekstury z kawałków innych, mniejszch tekstur o określonych wzorach (grupowanych tematycznie, np.: powierzchna ziemi, każda z tekstur zawiera inną jej część, jedna kępkę trawy, druga fragment gruntu, a trzecia kwiatek). Pozwala ona generować urozmaicone, niepowtarzające się wzory, przydatne w odwzorowywaniu rozległych przestrzeni. W pracy [13] użytkownik komponuje teksturę dla danej powierzchni z pewnych, wcześniej określonych wzorów, ustala rozmiar wirtualnej siatki, określa dopuszczalne kombinacje wzorów i inne zależności rzutujące na wybór określonego wzoru charakterystyczne dla danego przypadku (np.: odległość od punktu, czas). Następnie przestrzeń koordynatów tekstury dla danej sceny jest dzielona na kształt tejże właśnie wirtualnej siatki. Zadaniem pixel shader a jest wybranie właściwej kratki siatki dla pary współrzędnych (u, v), i określenie odpowiedniego wzoru na podstawie analizy parametrów zdefiniowanych przez użytkownika. Rysunek 36.
39 3.4 Tekstury rysowane ołówkiem Tekstury rysowane ołówkiem Metoda tworzenia tekstur sprawiających wrażenie rysowanych ołówkiem opiera się na następującym schemacie. Dla danego obiektu jest generowany trójwymiarowy wzór T, który następnie dla każdego piksela jest porównywany z wartością natężenia światła tego obiektu I. Wynik porówniania decyduje, czy stawiany piksel jest koloru białego, czy czarnego. W celu zmiękczenia przejścia pomiędzy tymi dwoma kolorami wyznaczana jest różnica między T a I, którą mnoży się przez pewien stały współczynnik c większy od 1. Praca [14] modyfikuje tą metodę łącząc kilka wzorów na jednej teksturze, przydzielając każdemu z nich inną wartość odcienia szarości. Rysunek 37. Przykład tekstury rysowanej ołówkiem 3.5. Tekstury generowane na podstawie fluktuacji światła Program [12] używa programów pixel i vertex shader a do utworzenia efektu błyszczącej, oscylującej powierzchni oceanu złożonej z wielu poruszających się w różnych kierunkach fal. Programy vertex i pixel shader a zostały użyte do implementacji odwzorowania kubicznej mapy otoczenia, deformacji siatki symulującej większe fale, a także do implementacji dwóch map wypukłości symulujących fale mniejsze i indeksowanej mapy Fresnela dla uzyskania odpowiedniego koloru tafli wody. Geometrię wejściową stanowi siatka czworokątów z jednym zbiorem koordynatów tekstury, normalnych i stycznych. Mapa otoczenia to prerenderowana tekstura słońca i chmur. Vertex shader jest odpowiedzialny za generowanie kombinacji sinusoidalnych fal zaburzających pozycję wierzchołków siatki i generowanie fal kosinusoidalnych zaburzających przestrzeń wektorów stycznych do tych wierzchołków. Każda sinusoidalna fala posada w pełni sterowalny kierunek, częstotliwość, szybkość i przesunięcie, które są zapamiętywane w rejestrach pamięci stałej vertex shader a.
40 3.6 Tekstury oparte na funkcji szumu 40 Pixel shader jest odpowiedzialny za utworzenie wypukłej, odbijającej otoczenie powierzchni wody. Żeby osiągnąć pożądany efekt najpierw uśrednia wartości z dwóch przesuwających się map wypukłości i na ich podstawie generuje wektor normalny. Następnie przekształca przestrzeń wektorów normalnych do przestrzeni świata i oblicza wektor odbicia dla każdego piksela. Wektor odbicia zostaje użyty to pobrania odpowiedniego teksela z mapy środowiska. Program pixel shadera oblicza także wektor odbicia zwierciadlanego 2 N V i używa go do pobrania odpowiedniego teksela z jednowymiarowej mapy Fresnela. Mapa Fresnela nadaje wodzie bardziej zielonego wyglądu jeśli patrzeć na nią prosto z góry i bardziej niebieskiego jeśli patrzeć na nią stojąc na brzegu. W ostatniej fazie pixel shader składa kolor wody z wartości uzyskanych z mapy Fresnela, z mapy otoczenia i z innych wartości odbić połyskowych również uzyskanych z mapy otoczenia. Wartość pobraną z mapy otoczenia pierwiastkuje się w celu uzyskania bardziej jaskrawych kolorów i zwiększenia kontrastu wody. Żeby uzyskać światła połyskowe na wodzie, składowa połysku jest pobierana z zielonej wartości składowej koloru mapy otoczenia. Ponieważ pożądanym efektem są odbicia w wodzie odpowiadające jasnym punktom na niebie wartość tę podnosi się do ósmej potęgi. Efektem końcowym jest ciemna woda, za wyjątkiem najjaśniejszych obszarów mapy otoczenia, która się w niej odbija. Rysunek 38. Wynik działania programu Ocean Water 3.6. Tekstury oparte na funkcji szumu Szeroko stosowana funkcja opisywana również w tej pracy, używana do realizacji zarówno statycznych jak i animowanych tekstur. Przy jej pomocy można osiągnąć takie efekty jak: chmury [11], marmur czy drewno [16].
41 3.7 Tekstury fraktalne 41 Rysunek 39. Wynik działania programu [18] 3.7. Tekstury fraktalne Program [10] za pomocą pixel shader a oblicza wartości fraktala Manderbolta wykonując dla każdego piksela 64 iteracje, co daje łączną liczbę 500 instrukcji. Każda iteracja ma następującą postać: ABSrt = AB AB; AB = ( ABSrt. x ABSrt. y SC. x, 2 AB. x AB. y + SC. y ) ; i f ( ( ABSrt. x + ABSrt. x ) < K i l l V a l u e ) Color += ColorAdd ; g d z i e : Color = ( 0, 0, 0, 0 ) ; ColorAdd = ( , , , ) ; AB = ( 0, 0 ) ; SC współrzędne p i k s e l a Rysunek 40. Wynik działania programu Manderbolt Fractal 3.8. Tekstury uzyskiwane drogą symulacji reakcji dyfuzji Program [9] używa dyskretnego całkowania pary równań PDE (Partial Differential Equations) znanej jako system reakcji dyfuzji Gray-Scott a. System ten reprezentuje wzajemnie koncentrujące się reakcje chemiczne. Poprzez wyświetlanie koncentracji w dwóch kanałach koloru można uzyskać zaskakujące wzory.
42 3.8 Tekstury uzyskiwane drogą symulacji reakcji dyfuzji 42 Użyty tu program dokonuje dyfuzji uśredniając sąsiadów poszczególnych pikseli (skalowanych przez wartość współczynnika dyfuzji) i wyznacza wartość reakcji oraz środkową część wyniku dyfuzji bazując na równaniach PDE, których postać jest następująca: (U)(x, y) = D u lap(u(x, y)) U(x, y) V (x, y) 2 + F (1 U(x, y)) (V )(x, y) = D v lap(v (x, y)) + U(x, y) V (x, y) 2 (F + k) V (x, y) lap(f(x, y)) = f(x + 1, y) + f(x 1, y) + f(x, y + 1) + f(x, y 1) 4 f(x, y) Vertex shader dokonuje wstępnych obliczeń potrzebnych do symulacji i renderingu. Pixel shader wyznacza mapę wypukłości światła rozproszonego (ang. diffuse light) tworząc mapy normalnych wynikających z koncentracji chemicznego U, oraz dokonuje uśrednień wspomnianych wyżej. Rysunek 41. Wynik działania programu Reaction Diffusion
43 4. Implementacja wybranych algorytmów teksturowania 43 Ponieważ pixel shader w wersji ma dość ograniczone możliwości (problemy z adresowaniem, liczba dostępnych instrukcji), które okazują się niewystarczające przy sprzętowej realizacji tekstur proceduralnych, na potrzeby tej pracy zostały użyte karty graficzne dysponujące pixel shader em w wersji 2.0+, w którym oprócz zniesienia większości powyższych ograniczeń dodano wiele nowych cech, takich jak np.: konstrukcje if, then, else, while, zwiększoną precyzję liczenia koloru czy możliwość samplowania tekstury dowolną ilość razy w trakcie działania programu pixel shadera. Dodatkowo wykorzystany został kompilatora języka pixel shader a firmy nvidia C for Graphics (Cg) [15], który wspiera wszystkie dostępne wersje i jest dodatkowo zgodny ze standardem OpenGL ARB 22, który obsługują zarówno karty firmy nvidia jak i ATI Technologies Inc. Użycie języka wyższego poziomu w znacznym stopniu ułatwia pisanie programów shadera i dodatkowo uniezależnia od producenta danego procesora graficznego (mogą występować różnice między shader ami różnych producentów nawet dla tych samych wersji) Generator szumu Perlin a Funkcja szumu perlin a służy do generowania spójnego (koherentnego) szumu w przestrzeni. Pojęcie spójnego szumu oznacza, że dla dwóch dowolnych punktów przestrzeni wartość funkcji szumu zmienia się płynnie w trakcie przesuwania się od jednego punktu do drugiego. Inaczej mówiąc, nie występują nagłe skoki wartości pomiędzy punktami będącymi w bliskim sąsiedztwie (rysunek 42). Funkcja szumu pobiera n współrzędnych z n-wymiarowej przestrzeni i dla tych współrzędnych zwraca wartość z przedziału < >. Przedstawiony poniżej algorytm generowania szumu perlin a odnosi się do przestrzeni dwuwymiarowej, ale w prosty (analogiczny) sposób można go rozszerzyć tak, aby działał w większej liczbie wymiarów (korzyści z tego wynikające przedstawię na końcu tego rozdziału). 22 OpenGL ARB - Architecture Review Board, organizacja normalizująca standard OpenGL (w jej skład wchodzi mn. 3D Labs, nvidia, ATI, Intel)
44 4.1 Generator szumu Perlin a 44 Rysunek 42. Różnica między szumem zwykłym i koherentnym W przestrzeni 2D funkcję szumu można zapisać jako: szum2d(x, y) = z gdzie x, y, z są wartościami rzeczywistymi. Funkcję szumu definiuje się w oparciu o regularną siatkę, której punkty są określone dla liczb całkowitych. Każdy punkt o współrzędnych rzeczywistych leży pomiędzy punktami tej siatki. Szukanie wartości funkcji szumu dla takich współrzędnych przebiega następująco: Najpierw szuka się najbliżej położonych punktów siatki otaczających dany punkt. Dla przestrzeni 2D są to cztery punkty, odpowiednio (x0, y0), (x0, y1), (x1, y1) i (x1, y1) (rysunek 43). Rysunek 43. Cztery punkty siatki otaczające punkt (x, y) Następnym krokiem jest zdefiniowanie funkcji g(x g, y g ) = (g x, g y )
45 4.1 Generator szumu Perlin a 45 gdzie x g, y g to punkty siatki z przypisanymi pseudolosowymi 23, znormalizowanymi gradientami 24 (rysunek 44). Rysunek 44. Pseudolosowe gradienty przypisane punktom siatki Dla każdego punktu siatki generowane są także wektory biegnące od danego punktu siatki do punktu (x, y) (rysunek 45). Rysunek 45. Wektory biegnące od punktów siatki do punktu dla którego generowana jest wartość szumu Mając określone gradienty oraz powyższe wektory, można obliczyć wartość szumu dla punktu (x, y). Dokonuje się tego przez wyznaczenie wpływu gradien- 23 funkcja szumu dla każdego punktu siatki zawsze zwraca tę samą wartość niezależnie od tego, ile razy jest wywoływana (w przeciwieństwie do klasycznej funkcji losowej, która zwraca przy każdym wywołaniu różną wartość dla tego samego argumentu) 24 w tym przypadku gradient oznacza uporządkowaną parę wektorów wskazujących na określony punkt przestrzeni
46 4.1 Generator szumu Perlin a 46 tów na wartość końcową funkcji i wyznaczeniu średniej ważonej tych wpływów. Wpływ gradientów na wartość końcową oblicza się wyznaczając iloczyn skalarny pomiędzy gradientami a odpowiednimi wektorami biegnącymi od punktów siatki do punktu (x, y). Dla przestrzeni 2D powstaną cztery wartości: s = g(x0, y0) ((x, y) (x0, y0)) t = g(x1, y0) ((x, y) (x1, y0)) u = g(x0, y1) ((x, y) (x0, y1)) v = g(x1, y1) ((x, y) (x1, y1)) Rysunek 46 przedstawia graficzną reprezentację obliczonych wartości wpływów. Żeby wyliczyć końcową wartość funkcji można uśrednić s i t dla górnych narożników, u i v dla dolnych i tak powstałe wartości uśrednić raz jeszcze. Niestety tak uzyskany szum nie wygląda zbyt naturalnie. Lepszą metodą jest interpolacja wartości pomiędzy s i t oraz u i v za pomocą funkcji krzywej np.: c(p) = 3p 2 2p 3 (rysunek 47). Rysunek 46. Graficzna reprezentacja wpływu gradientów punktów siatki Rysunek 47. Wykres funkcji c(p) = 3p 2 2p 3
47 4.1 Generator szumu Perlin a 47 Dzięki zastosowaniu takiej krzywej wartości wejściowe nie są uśredniane, ale interpolowane wzdłuż łagodnego łuku dając w efekcie lepszy rezultat końcowy (lepszą jakość szumu). Wartość końcową funkcji generuje się w następujący sposób: Najpierw znajdywana jest wartość krzywej S x (p) w punkcie p = x x0 (rysunek 48), którą odwzorowuje się z przedziału < > na przedział < s... t > (średnia a) i < u... v > (średnia b) używając interpolacji liniowej. Obliczenia mają następującą postać: Rysunek 48. Szukanie średnich a i b S x = 3(x x0) 2 2(x x0) 3 a = s + S x (t s) b = u + S x (v u) Kolejnym krokiem jest znalezienie wartość krzywej S y (p) w punkcie p = y y0, którą interpoluje się tak jak poprzednio za pomocą funkcji liniowej uzyskując wartość z przedziału < a... b > będącej poszukiwaną wartością końcową (średnia c). (rysunek 49). Rysunek 49. Obliczanie wartości końcowej
48 4.1 Generator szumu Perlin a 48 S y = 3(y y0) 2 2(y y0) 3 c = a + S y (b a) Tak uzyskany szum charakteryzuje się mały stopniem zróżnicowania. Dlatego końcowy szum uzyskuje się sumując szumy o różnej częstotliwości i amplitudzie (rysunek 50) według poniższego równania: N(x) = n i=1 szum(f requency i x) Ampitude i Rysunek 50. Poszczególne składowe funkcji szumu [6] gdzie n - liczba oktaw 25 przeważnie z zakresu < >, ampl - maksymalna amplituda szumu, freq - częstotliwość szumu. Program korzysta z lekko 25 oktawa - funkcja szumu uzyskana dla określonej częstotliwości i amplitudy
49 4.1 Generator szumu Perlin a 49 zmodyfikowanego wzoru na składanie szumu: n N(x) = szum(f reqency x) Amplitude i=1 Wartość początkowa f req i ampl wynosi 1. Wartości w kolejnych przejściach są modyfikowane w sposób: F reqency = F reqency F reqmod Amplitude = Amplitude AmplM od Program oblicza wartość szumu Perlin a dla każdego punktu wyświetlanego obiektu. Wartość ta wykorzystywana jest do obliczenia indeksu wskazującego na odpowiedni kolor przechowywany w jednowymiarowej teksturze przechowującej odpowiednio spreparowaną paletę kolorów. Kod programu wygląda następująco: const f l o a t FreqMod = 2. 0 ; / modulator c z ę s t o t l i w o ś c i / const f l o a t AmplMod = ; / modulator amplitudy / const f l o a t TexWidth = 256; / s z e r o k o ś ć t e k s t u r y szumu / const f l o a t TexHeight = ; / wysokość t e k s t u r y szumu / const f l o a t TexDepth = 256; / głębokość t e k s t u r y szumu / const f l o a t TexScale = 1. 0 / ; / współ. skalowania t e k s t u r y / const i n t Octaves = 4 ; / l i c z b a oktaw / f l o a t PerlinNoise3D ( f l o a t x, f l o a t y, f l o a t z, sampler3d NoiseTex ) { i n t i x = ( i n t ) x ; / wyznaczenie współrzędnych pierwszego / i n t i y = ( i n t ) y ; / lewego, górnego punktu s i a t k i szumu / i n t i z = ( i n t ) z ; f l o a t dx = x i x ; / wyznaczenie współrzędnych punktu / f l o a t dy = y i y ; / l e ż ą c e g o pomiędzy punktami s i a t k i / f l o a t dz = z i z ; / szumu / / przeskalowanie współrzędnych t e k s t u r y do / / p r z e d z i a ł u <0..1 > / f l o a t tx0 = ( i x + 0 ) / TexWidth ; f l o a t tx1 = ( i x + 1 ) / TexWidth ; f l o a t yknots [ 2 ], zknots [ 2 ] ; / wyznaczenie w a r t o ś c i szumu dla punktu ( dx, dy, dz ) na / / z a s a d z i e i n t e r p o l a c j i l i n i o w e j w a r t o ś c i szumu sąsiadu / / j ą c y c h z e sobą punktów w każdym kolejnym wymiarze. / f o r ( i n t j = 0 ; j <= 1; j++) { f l o a t tz = ( i z + j ) / TexDepth ; f o r ( i n t i = 0 ; i <= 1; i ++) { f l o a t ty = ( i y + i ) / TexHeight ;
50 4.1 Generator szumu Perlin a 50 / pobranie w a r t o ś c i szumu dla poszczególnych punktów / / s i a t k i szumu / f l o a t a = tex3d ( NoiseTex, f l o a t 3 ( tx0, ty, tz ) ). r ; f l o a t b = tex3d ( NoiseTex, f l o a t 3 ( tx1, ty, tz ) ). r ; } yknots [ j ] = l e r p ( a, b, dx ) ; } zknots [ k ] = l e r p ( yknots [ 0 ], yknots [ 1 ], dy ) ; f l o a t r e s u l t = l e r p ( zknots [ 0 ], zknots [ 1 ], dz ) ; return clamp ( r e s u l t, 1. 0, 1. 0 ) ; } f l o a t 4 main ( in f l o a t 3 TexCoord0 : TEXCOORD0, in f l o a t 2 TexCoord1 : TEXCOORD1, uniform f l o a t Depth, uniform sampler3d Texture0, uniform sampler2d Texture1 ) : COLOR { / przeskalowanie współ. t e k s t u r y a k t u a l n i e rysowanego punktu / / do p r z e d z i a ł u < > / f l o a t tx = TexCoord0. x TexWidth ; f l o a t ty = TexCoord0. y TexHeight ; f l o a t tz = TexCoord0. z TexDepth ; f l o a t Frequency = 1. 0 ; / i n i c j a l i z a c j a w a r t o ś c i początkowych / f l o a t Amplitude = 1. 0 ; f l o a t Total = 0. 0 ; f o r ( i n t i = 0 ; i < Octaves ; i++) { / sumowanie powstałych z a b ur z e ń / Total += PerlinNoise3D ( tx Frequency TexScale, ty Frequency TexScale, Depth, Texture0 ) Amplitude ; } Frequency = FreqMod ; / z w i ę k s z a n i e c z ę s t o t l i w o ś c i szumu / Amplitude = AmplMod ; / z w i ę k s z a n i e amplitudy / Total = Total ; clamp ( Total, 0. 0, 1. 0 ) ; / pobranie odpowiedniego koloru z p a l e t y kolorów / } return tex2d ( Texture1, f l o a t 2 ( Total, 0 ) ) ; Do programu przekazywana jest tekstura 3D odpowiadająca siatce wartości szumu z przedziału < >. Ponieważ szum jest generowany dla przestrze-
51 4.1 Generator szumu Perlin a 51 ni trójwymiarowej, a uzyskiwane wartości odwzorowywane są na powierzchnię dwuwymiarowej tekstury, przekazywany jest dodatkowo parametr Depth zmieniający sie krokowo o nieduże wartości. Ta zmiana powoduje animację tekstury. Po kompilacji program składał się z 316 instrukcji maszynowych. Wyniki działania programu przedstawia rysunek 51. Modyfikując wartość końcową i używając odpowiednich amplidtud i częstotliwości oraz palety kolorów można uzyskać tekstury takie jak w rozdziale Rysunek 51. Rezultat działania programu Perlin Shader
52 4.2 Generator cząsteczek Generator cząsteczek Generowana tekstura to zbiór świecących cząsteczek lub plazma - w zależności od użytej palety kolorów. Można jej użyć np. do uzyskania ciekawej powierzchni planety (Jowisz - podrysunek 3 z rysunku 53), lub jako mapy odbić świateł np. na kasku kosmonauty (wylosowane punkty muszą być wtedy zrzutowanymi na powierzchnię tekstury pozycjami gwiazd w przestrzeni 3D). W pierwszej fazie program losuje współrzędne dziesięciu punktów leżących na teksturze (rysunek 52). Następnie dla każdego punktu generowanej tekstury oblicza odległość pomiędzy tym punktem, a każdym punktem wylosowanym na początku. Suma odwrotności tych odległości zastaje uśredniona i pomnożona przez eksperymentalnie dobrany współczynnik (warunkujący różne efekty wizualne) dając w efekcie indeks w palecie kolorów reprezentowanej przez jednowymiarową teksturę. W każdej iteracji ulegają zmianie wylosowane punkty tekstury w taki sposób, aby poruszały się po elipsach o losowej długości promieni wyznaczonych na początku działania programu. Dzięki zmianie pozycji wylosowanych punktów uzyskuje się animację tekstury. Rysunek 52. Algorytm generowania cząteczek Listing programu pixel shader a: / l i c z b a wyświetlanych c z ą s t e c z e k / const i n t MaxPnt = 1 0; / współczynnik o d l e g ł o ś c i im większy, tym mniejsze / / będą rysowane c z ą s t e c z k i /
53 4.2 Generator cząsteczek 53 const f l o a t Factor = ; f l o a t p a r t i c l e ( f l o a t 2 vpos, f l o a t 2 vpnt [ MaxPnt ] ) { f l o a t d i s t = 0 ; f o r ( i n t i = 0 ; i < MaxPnt ; i++) { / o b l i c z e n i e o d l e g ł o ś c i pomiędzy stawianym pikselem / / a i tą c z ą s t e c z k ą / f l o a t l e n = d i s t a n c e ( vpos, vpnt [ i ] ) ; / sumowanie odwrotności o d l e g ł o ś c i od poszczególnych / / c z ą s t e c z e k / } d i s t += 1.0 / l e n ; / skalowanie o d l e g ł o ś c i / d i s t /= Factor ; / n o r m a l i z a c j a i negacja o d l e g ł o ś c i / d i s t = 1. 0 ( 1. 0 / ddist ) ; } return d i s t ; f l o a t 4 main ( in f l o a t 2 TexCoord0 : TEXCOORD0, uniform f l o a t 2 vpoints [ MaxPnt ], uniform sampler3d Texture0, uniform sampler2d Texture1 ) : COLOR { f l o a t t o t a l = p a r t i c l e ( f l o a t 2 ( TexCoord0. x, TexCoord0. y ), vpoints ) ; / o b c i ę c i e o d l e g ł o ś c i do p r z e d z i a ł u <0...1 > / clamp ( t o t a l, 0. 0, 1. 0 ) ; } / pobranie koloru z t e k s t u r y z a w i e r a j ą c e j mapę kolorów / return tex2d ( Texture1, f l o a t 2 ( t o t a l, 1 ) ) ; Po kompilacji program składał się ze 105 instrukcji maszynowych. Wynik działania programu przedstawia rysunek 53.
54 4.2 Generator cząsteczek 54 Rysunek 53. Rezultat działania programu Particles
55 4.3 Generator komórek Generator komórek Uzyskana tekstura to odzwierciedlenie systemu komórek żywej tkanki (np.: roślinnej). Zdajdzie ona zastosowanie wszędzie tam, gdzie zachodzi potrzeba pokazania przekroju określonej tkanki. Można ją też stosować w futurystycznych sceneriach, jako np.: powłoka wrot umożliwiających przejście do innego wymiaru. Algorytm działania tego programu to wynik modyfikacji algorytmu programu poprzedniego, która polega na szukaniu najmniejszej odległości pomiędzy generowanym punktem tekstury a punktami wylosowanymi. Zmieniając pozycję punktów kluczowych (odpowiadających pozycji jąder) można uzyskać efekt poruszających się komórek, łączących się i rozdzielających. Algorytm można dodatkowo zmienić tak, aby szukał kilku najmniejszych odległości (np.: 3). Sumę tych odległości trzeba wtedy uśrednić i znormalizować. Efektem będzie kilka warstw (liczba wartsw odpowiada liczbie szukanych odległości) komórek poruszających się nad sobą. Rysunek 54. Algorytm generowania komórek Danymi wejściowymi do programu są współrzędne aktualnie stawianego teksela, tekstura zawierająca paletę kolorów oraz tablica współrzędnych wylosowanych wcześniej punktów. Dla każdego stawianego piksela wywoływana jest funkcja cell, która zwraca wartość z przedziału < >, na podstawie której jest odczytywana wartość z tekstury zawierającej paletę kolorów. / l i c z b a wyświetlanych c z ą s t e c z e k / const i n t MaxPnt = 1 0; / maksymalna o d l e g ł o ś ć pomiędzy dwoma punktami /
56 4.3 Generator komórek 56 / na t e k s t u r z e o wymiarach 1 / 1, c z y l i $ s q r t ( 2 ) $ / const f l o a t MaxDist = f l o a t c e l l ( f l o a t 2 vpos, f l o a t 2 vpnt [ MaxPnt ] ) { f l o a t d i s t = 0 ; f l o a t mindist = 0 ; f o r ( i n t i = 0 ; i < MaxPnt ; i++) { / o b l i c z e n i e o d l e g ł o ś c i pomiędzy stawianym pikselem / / a i tą c z ą s t e c z k ą / f l o a t l e n = d i s t a n c e ( vpos, vpnt [ i ] ) ; / szukanie n a j m n i e j s z e j o d l e g ł o ś c i od c z ą s t e c z k i / / dla aktualnego p i k s e l a / } i f ( i == 0) mindist = l e n ; e l s e i f ( l e n < mindist ) mindist = l e n ; / n o r m a l i z a c j a o d l e g ł o ś c i przeskalowanie do / / p r z e d z i a ł u <0...1 > / d i s t = mindist / MaxPnt ; } return d i s t ; f l o a t 4 main ( in f l o a t 2 TexCoord0 : TEXCOORD0, in f l o a t 2 TexCoord1 : TEXCOORD1, uniform sampler2d Texture0, uniform sampler2d Texture1, uniform f l o a t 2 vpoints [ MaxPnt ] ) ) : COLOR { f l o a t t o t a l = c e l l ( f l o a t 2 ( TexCoord0. x, TexCoord0. y ), Points ) ; / pobranie koloru z t e k s t u r y z a w i e r a j ą c e j mapę kolorów / } return tex2d ( Texture1, f l o a t 2 ( t o t a l, 1 ) ) ; Po kompilacji program składał się ze 123 instrukcji maszynowych. Wynik działania programu przedstawia rysunek 55.
57 4.3 Generator komórek 57 Rysunek 55. Rezultat działania programu Cells
58 58 5. Analiza wydajnościowa procesu teksturowania Celem tego rozdziału jest oszacowanie wydajności jednostek cieniujących obecnych akcelelatorów grafiki 3D. W tym przypadku oszacowanie wydajność oznacza znalezienie granicznej ilości wielokątów, przy której liczba wyświetlanych klatek obrazu na sekundę (ang. fps - frame per second) nie spada poniżej wartości zapewniającą płynną animację (25-30 fps). Ocenie była poddawana także jakość generowanego obrazu Środowisko i procedura testowa Testy zostały wykonane na komputerze klasy PC o następujących parametrach: procesor Athlon XP 2600+, pamięć 512 MB RAM, karta graficzna ATI Radeon Każdy test wykonywał się przez 30 sekund, po czym liczona była średnia liczba wyświetlanych klatek w ciągu sekundy (FPS - frame per second). Testy były przeprowadzane w rozdzielczości 1024x768 o 32 bitowej palecie kolorów. Za teksturowany obiekt posłużyła siatka czworokątów o stałej zajętości powierzchni obrazu, ale o zmieniającej się liczbie wielokątów w osi x i y (rysunek 56). Takie podejście pozwoliło określić, czy przy tej samej ilości renderowanych pikseli liczba wierzchołków przypadająca na tą powierzchnię ma wpływ na prędkość generowania obrazu (im więcej wierzchołków, tym więcej pracy wykonuje triangle setup rasterizer). Żeby określić maksymalną liczbę wielokątów przy jakiej zachowana jest płynność animacji, każdy rodzaj użytej siatki powielano n-razy w osi z. Ważnym elementem przy ocenie wydajności układów cyfrowych wyposażonych w programowalne jednostki cieniujące jest stopień skomplikowania wykonywanych programów, na który się składają: liczba użytych instrukcji rodzaje instrukcji (czy są to instrukcje proste, takie jak: przeniesienie, dodawanie, czy złożone: dzielenie, pierwiastkowanie) ilość odwołań do pamięci tekstur (należy tu też zwrócić uwagę na odczyty zależne (sytuacja kiedy koordynaty tekstury wykorzystywane do odczytu danego teksela nie są wartościami bezpośrednio wyliczonymi przez procesor dla danego piksela, ale modyfikacjami tych wartości lub kiedy wartość teksela danej tekstury jest koordynatem dla innej tekstury odczytywanej w danym przebiegu))
59 5.2 Wyniki testów 59 Użyte szadery w pełni wykorzystują zasoby pixel shader a w wersji 2.0 jeśli chodzi o liczbę i rodzaje instrukcji. Program Perlin Noise 3D po kompilacji składał się z 317 instrukcji, z czego 51 dokonywało mnożenia, 87 dodawania, 32 liczyło odwrotności, a 33 dokonywało odczytów tekstury 3D. Szader Cells miał 89 instrukcji (dla 6 komórek), których rozkład wyglądał następująco - 33 przeniesienia, 12 dodawań, 6 odwrotności, 6 pierwiastków kwadratowych, 6 iloczynów skalarnych, 6 porównań (instrukcje warunkowe) i 1 odczyt wartości z tekstury. Szader Particles po kompilacji składał się (dla 6 cząsteczek) z 66 instrukcji, gdzie 6 dokonywało mnożeń, 20 przeniesień, 13 liczyło odwrotności, 6 wykonywało pierwiastkowanie i wyznaczało iloczyny skalarne, a 1 odczytu tekstury. Testy nie zostały przeprowadzone dla szadera Perlin Noise 3D z powodu braku dostępu do karty geforce FX, która dysponuje rozszerzoną w stosunku do standardu jednostką pixel shader w wersji 2.0 ex, dopuszczającą wykonywanie znacznie większej liczby instrukcji i nie ograniczającej ilości możliwych odczytów tekstury (ps odczyty). Programy Particles i Cells wykonywały się tylko dla sześciu cząsteczek. Dla dziesięciu, programy wynikowe przekraczały dopuszczalną liczbę instrukcji programu (ponad 100, dopuszczalne 96) Wyniki testów Testy zostały przeprowadzone dla następujących siatek czworokątków: 1. 5x5xX (5 czworokątów w osi x, 5 w y) 2. 10x10xX (100xN czworokątów (200xN trójkątów)) 3. 30x30xX (900xN czworokątów) 4. 50x50xX (2500xN czworokątów) gdzie parametr N przyjmował wartości 1,5,15,25. Rysunek 56. Przykład siatki 5x5x1 i 50x50x1. Ta sama zajmowana powierzchnia, różna liczba wierzchołków
60 5.2 Wyniki testów 60 Oto wyniki jakie uzyskano: Rysunek 57. Rezultaty dla programu Particles Rysunek 58. Rezultaty dla programu Cells Uzyskane wyniki prowadzą do następujących wniosków: 1. Ilość użytych wielokątów ma niewielki wpływ na samą szybkość wypełniania pikseli. Pomimo znaczącego zagęszczania siatki wielokątów szybkość wypełniania dla tej samej powierzchni pozostawała mniej więcej na tym samym poziomie. Największy spadek wydajności (w przypadku obu testowanych szaderów) - o 10 klatek na sekundę - wystąpił pomiędzy sceną złożoną z 9000 trójkątów (siatka 30x30x5) a sceną złożoną z 1000 trójkątów (siatka 10x10x5). Jest to 20 procentowy spadek wydajności w stosunku do 900 procentowego wzrostu złożoności sceny, a więc stosunkowo nieduży.
Grafika Komputerowa Wykład 6. Teksturowanie. mgr inż. Michał Chwesiuk 1/23
 Wykład 6 mgr inż. 1/23 jest to technika w grafice komputerowej, której celem jest zwiększenie szczegółowości renderowanych powierzchni za pomocą tekstur. jest to pewna funkcja (najczęściej w formie bitmapy)
Wykład 6 mgr inż. 1/23 jest to technika w grafice komputerowej, której celem jest zwiększenie szczegółowości renderowanych powierzchni za pomocą tekstur. jest to pewna funkcja (najczęściej w formie bitmapy)
Synteza i obróbka obrazu. Tekstury. Opracowanie: dr inż. Grzegorz Szwoch Politechnika Gdańska Katedra Systemów Multimedialnych
 Synteza i obróbka obrazu Tekstury Opracowanie: dr inż. Grzegorz Szwoch Politechnika Gdańska Katedra Systemów Multimedialnych Tekstura Tekstura (texture) obraz rastrowy (mapa bitowa, bitmap) nakładany na
Synteza i obróbka obrazu Tekstury Opracowanie: dr inż. Grzegorz Szwoch Politechnika Gdańska Katedra Systemów Multimedialnych Tekstura Tekstura (texture) obraz rastrowy (mapa bitowa, bitmap) nakładany na
Plan wykładu. Akcelerator 3D Potok graficzny
 Plan wykładu Akcelerator 3D Potok graficzny Akcelerator 3D W 1996 r. opracowana została specjalna karta rozszerzeń o nazwie marketingowej Voodoo, którą z racji wspomagania procesu generowania grafiki 3D
Plan wykładu Akcelerator 3D Potok graficzny Akcelerator 3D W 1996 r. opracowana została specjalna karta rozszerzeń o nazwie marketingowej Voodoo, którą z racji wspomagania procesu generowania grafiki 3D
Oświetlenie. Modelowanie oświetlenia sceny 3D. Algorytmy cieniowania.
 Oświetlenie. Modelowanie oświetlenia sceny 3D. Algorytmy cieniowania. Chcąc osiągnąć realizm renderowanego obrazu, należy rozwiązać problem świetlenia. Barwy, faktury i inne właściwości przedmiotów postrzegamy
Oświetlenie. Modelowanie oświetlenia sceny 3D. Algorytmy cieniowania. Chcąc osiągnąć realizm renderowanego obrazu, należy rozwiązać problem świetlenia. Barwy, faktury i inne właściwości przedmiotów postrzegamy
Filtrowanie tekstur. Kinga Laurowska
 Filtrowanie tekstur Kinga Laurowska Wprowadzenie Filtrowanie tekstur (inaczej wygładzanie) technika polegająca na 'rozmywaniu' sąsiadujących ze sobą tekseli (pikseli tekstury). Istnieje wiele metod filtrowania,
Filtrowanie tekstur Kinga Laurowska Wprowadzenie Filtrowanie tekstur (inaczej wygładzanie) technika polegająca na 'rozmywaniu' sąsiadujących ze sobą tekseli (pikseli tekstury). Istnieje wiele metod filtrowania,
0. OpenGL ma układ współrzędnych taki, że oś y jest skierowana (względem monitora) a) w dół b) w górę c) w lewo d) w prawo e) w kierunku do
 0. OpenGL ma układ współrzędnych taki, że oś y jest skierowana (względem monitora) a) w dół b) w górę c) w lewo d) w prawo e) w kierunku do obserwatora f) w kierunku od obserwatora 1. Obrót dookoła osi
0. OpenGL ma układ współrzędnych taki, że oś y jest skierowana (względem monitora) a) w dół b) w górę c) w lewo d) w prawo e) w kierunku do obserwatora f) w kierunku od obserwatora 1. Obrót dookoła osi
Grafika Komputerowa Wykład 5. Potok Renderowania Oświetlenie. mgr inż. Michał Chwesiuk 1/38
 Wykład 5 Potok Renderowania Oświetlenie mgr inż. 1/38 Podejście śledzenia promieni (ang. ray tracing) stosuje się w grafice realistycznej. Śledzone są promienie przechodzące przez piksele obrazu wynikowego
Wykład 5 Potok Renderowania Oświetlenie mgr inż. 1/38 Podejście śledzenia promieni (ang. ray tracing) stosuje się w grafice realistycznej. Śledzone są promienie przechodzące przez piksele obrazu wynikowego
Animowana grafika 3D. Opracowanie: J. Kęsik.
 Animowana grafika 3D Opracowanie: J. Kęsik kesik@cs.pollub.pl Powierzchnia obiektu 3D jest renderowana jako czarna jeżeli nie jest oświetlana żadnym światłem (wyjątkiem są obiekty samoświecące) Oświetlenie
Animowana grafika 3D Opracowanie: J. Kęsik kesik@cs.pollub.pl Powierzchnia obiektu 3D jest renderowana jako czarna jeżeli nie jest oświetlana żadnym światłem (wyjątkiem są obiekty samoświecące) Oświetlenie
Grafika komputerowa Tekstury
 . Tekstury Tekstury są dwuwymiarowymi obrazkami nakładanymi na obiekty lub ich części, w celu poprawienia realizmu rysowanych brył oraz dodatkowego określenia cech ich powierzchni np. przez nałożenie obrazka
. Tekstury Tekstury są dwuwymiarowymi obrazkami nakładanymi na obiekty lub ich części, w celu poprawienia realizmu rysowanych brył oraz dodatkowego określenia cech ich powierzchni np. przez nałożenie obrazka
Programowanie gier komputerowych Tomasz Martyn Wykład 6. Materiały informacje podstawowe
 Programowanie gier komputerowych Tomasz Martyn Wykład 6. Materiały informacje podstawowe Czym są tekstury? Tekstury są tablicowymi strukturami danych o wymiarze od 1 do 3, których elementami są tzw. teksele.
Programowanie gier komputerowych Tomasz Martyn Wykład 6. Materiały informacje podstawowe Czym są tekstury? Tekstury są tablicowymi strukturami danych o wymiarze od 1 do 3, których elementami są tzw. teksele.
Karty graficzne możemy podzielić na:
 KARTY GRAFICZNE Karta graficzna karta rozszerzeo odpowiedzialna generowanie sygnału graficznego dla ekranu monitora. Podstawowym zadaniem karty graficznej jest odbiór i przetwarzanie otrzymywanych od komputera
KARTY GRAFICZNE Karta graficzna karta rozszerzeo odpowiedzialna generowanie sygnału graficznego dla ekranu monitora. Podstawowym zadaniem karty graficznej jest odbiór i przetwarzanie otrzymywanych od komputera
Automatyczne tworzenie trójwymiarowego planu pomieszczenia z zastosowaniem metod stereowizyjnych
 Automatyczne tworzenie trójwymiarowego planu pomieszczenia z zastosowaniem metod stereowizyjnych autor: Robert Drab opiekun naukowy: dr inż. Paweł Rotter 1. Wstęp Zagadnienie generowania trójwymiarowego
Automatyczne tworzenie trójwymiarowego planu pomieszczenia z zastosowaniem metod stereowizyjnych autor: Robert Drab opiekun naukowy: dr inż. Paweł Rotter 1. Wstęp Zagadnienie generowania trójwymiarowego
Techniki animacji komputerowej
 Techniki animacji komputerowej 1 Animacja filmowa Pojęcie animacji pochodzi od ożywiania i ruchu. Animować oznacza dawać czemuś życie. Słowem animacja określa się czasami film animowany jako taki. Animacja
Techniki animacji komputerowej 1 Animacja filmowa Pojęcie animacji pochodzi od ożywiania i ruchu. Animować oznacza dawać czemuś życie. Słowem animacja określa się czasami film animowany jako taki. Animacja
Grafika Komputerowa Wykład 4. Synteza grafiki 3D. mgr inż. Michał Chwesiuk 1/30
 Wykład 4 mgr inż. 1/30 Synteza grafiki polega na stworzeniu obrazu w oparciu o jego opis. Synteza obrazu w grafice komputerowej polega na wykorzystaniu algorytmów komputerowych do uzyskania obrazu cyfrowego
Wykład 4 mgr inż. 1/30 Synteza grafiki polega na stworzeniu obrazu w oparciu o jego opis. Synteza obrazu w grafice komputerowej polega na wykorzystaniu algorytmów komputerowych do uzyskania obrazu cyfrowego
Animowana grafika 3D. Opracowanie: J. Kęsik.
 Animowana grafika 3D Opracowanie: J. Kęsik kesik@cs.pollub.pl Rzutowanie Równoległe Perspektywiczne Rzutowanie równoległe Rzutowanie równoległe jest powszechnie używane w rysunku technicznym - umożliwienie
Animowana grafika 3D Opracowanie: J. Kęsik kesik@cs.pollub.pl Rzutowanie Równoległe Perspektywiczne Rzutowanie równoległe Rzutowanie równoległe jest powszechnie używane w rysunku technicznym - umożliwienie
GRAFIKA RASTROWA. WYKŁAD 1 Wprowadzenie do grafiki rastrowej. Jacek Wiślicki Katedra Informatyki Stosowanej
 GRAFIKA RASTROWA WYKŁAD 1 Wprowadzenie do grafiki rastrowej Jacek Wiślicki Katedra Informatyki Stosowanej Grafika rastrowa i wektorowa W grafice dwuwymiarowej wyróżnia się dwa rodzaje obrazów: rastrowe,
GRAFIKA RASTROWA WYKŁAD 1 Wprowadzenie do grafiki rastrowej Jacek Wiślicki Katedra Informatyki Stosowanej Grafika rastrowa i wektorowa W grafice dwuwymiarowej wyróżnia się dwa rodzaje obrazów: rastrowe,
Autodesk 3D Studio MAX Teksturowanie modeli 3D
 Autodesk 3D Studio MAX Teksturowanie modeli 3D dr inż. Andrzej Czajkowski Instyt Sterowania i Systemów Informatycznych Wydział Informatyki, Elektrotechniki i Automatyki 25 kwietnia 2017 1 / 20 Plan Wykładu
Autodesk 3D Studio MAX Teksturowanie modeli 3D dr inż. Andrzej Czajkowski Instyt Sterowania i Systemów Informatycznych Wydział Informatyki, Elektrotechniki i Automatyki 25 kwietnia 2017 1 / 20 Plan Wykładu
Oświetlenie obiektów 3D
 Synteza i obróbka obrazu Oświetlenie obiektów 3D Opracowanie: dr inż. Grzegorz Szwoch Politechnika Gdańska Katedra Systemów Multimedialnych Rasteryzacja Spłaszczony po rzutowaniu obraz siatek wielokątowych
Synteza i obróbka obrazu Oświetlenie obiektów 3D Opracowanie: dr inż. Grzegorz Szwoch Politechnika Gdańska Katedra Systemów Multimedialnych Rasteryzacja Spłaszczony po rzutowaniu obraz siatek wielokątowych
Julia 4D - raytracing
 i przykładowa implementacja w asemblerze Politechnika Śląska Instytut Informatyki 27 sierpnia 2009 A teraz... 1 Fraktale Julia Przykłady Wstęp teoretyczny Rendering za pomocą śledzenia promieni 2 Implementacja
i przykładowa implementacja w asemblerze Politechnika Śląska Instytut Informatyki 27 sierpnia 2009 A teraz... 1 Fraktale Julia Przykłady Wstęp teoretyczny Rendering za pomocą śledzenia promieni 2 Implementacja
2 Przygotował: mgr inż. Maciej Lasota
 Laboratorium nr 2 1/6 Grafika Komputerowa 3D Instrukcja laboratoryjna Temat: Manipulowanie przestrzenią 2 Przygotował: mgr inż. Maciej Lasota 1) Manipulowanie przestrzenią Istnieją dwa typy układów współrzędnych:
Laboratorium nr 2 1/6 Grafika Komputerowa 3D Instrukcja laboratoryjna Temat: Manipulowanie przestrzenią 2 Przygotował: mgr inż. Maciej Lasota 1) Manipulowanie przestrzenią Istnieją dwa typy układów współrzędnych:
Karta graficzna karta rozszerzeo odpowiedzialna generowanie sygnału graficznego dla ekranu monitora. Podstawowym zadaniem karty graficznej jest
 KARTA GRAFICZNA Karta graficzna karta rozszerzeo odpowiedzialna generowanie sygnału graficznego dla ekranu monitora. Podstawowym zadaniem karty graficznej jest odbiór i przetwarzanie otrzymywanych od komputera
KARTA GRAFICZNA Karta graficzna karta rozszerzeo odpowiedzialna generowanie sygnału graficznego dla ekranu monitora. Podstawowym zadaniem karty graficznej jest odbiór i przetwarzanie otrzymywanych od komputera
Trójwymiarowa grafika komputerowa rzutowanie
 Trójwymiarowa grafika komputerowa rzutowanie Mirosław Głowacki Wydział Inżynierii Metali i Informatyki Przemysłowej Rzutowanie w przestrzeni 3D etapy procesu rzutowania określenie rodzaju rzutu określenie
Trójwymiarowa grafika komputerowa rzutowanie Mirosław Głowacki Wydział Inżynierii Metali i Informatyki Przemysłowej Rzutowanie w przestrzeni 3D etapy procesu rzutowania określenie rodzaju rzutu określenie
INFORMATYKA WSTĘP DO GRAFIKI RASTROWEJ
 INFORMATYKA WSTĘP DO GRAFIKI RASTROWEJ Przygotowała mgr Joanna Guździoł e-mail: jguzdziol@wszop.edu.pl WYŻSZA SZKOŁA ZARZĄDZANIA OCHRONĄ PRACY W KATOWICACH 1. Pojęcie grafiki komputerowej Grafika komputerowa
INFORMATYKA WSTĘP DO GRAFIKI RASTROWEJ Przygotowała mgr Joanna Guździoł e-mail: jguzdziol@wszop.edu.pl WYŻSZA SZKOŁA ZARZĄDZANIA OCHRONĄ PRACY W KATOWICACH 1. Pojęcie grafiki komputerowej Grafika komputerowa
dr inż. Jarosław Forenc
 Informatyka 2 Politechnika Białostocka - Wydział Elektryczny Elektrotechnika, semestr III, studia stacjonarne I stopnia Rok akademicki 2010/2011 Wykład nr 7 (24.01.2011) dr inż. Jarosław Forenc Rok akademicki
Informatyka 2 Politechnika Białostocka - Wydział Elektryczny Elektrotechnika, semestr III, studia stacjonarne I stopnia Rok akademicki 2010/2011 Wykład nr 7 (24.01.2011) dr inż. Jarosław Forenc Rok akademicki
1. Prymitywy graficzne
 1. Prymitywy graficzne Prymitywy graficzne są elementarnymi obiektami jakie potrafi bezpośrednio rysować, określony system graficzny (DirectX, OpenGL itp.) są to: punkty, listy linii, serie linii, listy
1. Prymitywy graficzne Prymitywy graficzne są elementarnymi obiektami jakie potrafi bezpośrednio rysować, określony system graficzny (DirectX, OpenGL itp.) są to: punkty, listy linii, serie linii, listy
Animowana grafika 3D Laboratorium 3
 3DStudio MAX teksturowanie modelu budynku dla potrzeb gry 3D W ćwiczeniu tym zakładamy, że mamy już ukończony model naszego budynku. Składa się on z wielu elementów: ścian, okien, drzwi, dachu itp. W teorii
3DStudio MAX teksturowanie modelu budynku dla potrzeb gry 3D W ćwiczeniu tym zakładamy, że mamy już ukończony model naszego budynku. Składa się on z wielu elementów: ścian, okien, drzwi, dachu itp. W teorii
Grafika rastrowa (bitmapa)-
 Grafika komputerowa Grafika rastrowa Grafika rastrowa (bitmapa)- sposób zapisu obrazów w postaci prostokątnej tablicy wartości, opisujących kolory poszczególnych punktów obrazu (prostokątów składowych).
Grafika komputerowa Grafika rastrowa Grafika rastrowa (bitmapa)- sposób zapisu obrazów w postaci prostokątnej tablicy wartości, opisujących kolory poszczególnych punktów obrazu (prostokątów składowych).
Proste metody przetwarzania obrazu
 Operacje na pikselach obrazu (operacje punktowe, bezkontekstowe) Operacje arytmetyczne Dodanie (odjęcie) do obrazu stałej 1 Mnożenie (dzielenie) obrazu przez stałą Operacje dodawania i mnożenia są operacjami
Operacje na pikselach obrazu (operacje punktowe, bezkontekstowe) Operacje arytmetyczne Dodanie (odjęcie) do obrazu stałej 1 Mnożenie (dzielenie) obrazu przez stałą Operacje dodawania i mnożenia są operacjami
Analiza obrazów - sprawozdanie nr 2
 Analiza obrazów - sprawozdanie nr 2 Filtracja obrazów Filtracja obrazu polega na obliczeniu wartości każdego z punktów obrazu na podstawie punktów z jego otoczenia. Każdy sąsiedni piksel ma wagę, która
Analiza obrazów - sprawozdanie nr 2 Filtracja obrazów Filtracja obrazu polega na obliczeniu wartości każdego z punktów obrazu na podstawie punktów z jego otoczenia. Każdy sąsiedni piksel ma wagę, która
Architektura Procesorów Graficznych
 Architektura Procesorów Graficznych Referat: Rendering 3D: potok 3D, możliwości wsparcia sprzętowego, możliwości przyspieszenia obliczeń. Grupa wyrównawcza Cezary Sosnowski 1. Renderowanie Renderowanie
Architektura Procesorów Graficznych Referat: Rendering 3D: potok 3D, możliwości wsparcia sprzętowego, możliwości przyspieszenia obliczeń. Grupa wyrównawcza Cezary Sosnowski 1. Renderowanie Renderowanie
Baltie 3. Podręcznik do nauki programowania dla klas I III gimnazjum. Tadeusz Sołtys, Bohumír Soukup
 Baltie 3 Podręcznik do nauki programowania dla klas I III gimnazjum Tadeusz Sołtys, Bohumír Soukup Czytanie klawisza lub przycisku myszy Czytaj klawisz lub przycisk myszy - czekaj na naciśnięcie Polecenie
Baltie 3 Podręcznik do nauki programowania dla klas I III gimnazjum Tadeusz Sołtys, Bohumír Soukup Czytanie klawisza lub przycisku myszy Czytaj klawisz lub przycisk myszy - czekaj na naciśnięcie Polecenie
Przetwarzanie obrazów wykład 4
 Przetwarzanie obrazów wykład 4 Adam Wojciechowski Wykład opracowany na podstawie Komputerowa analiza i przetwarzanie obrazów R. Tadeusiewicz, P. Korohoda Filtry nieliniowe Filtry nieliniowe (kombinowane)
Przetwarzanie obrazów wykład 4 Adam Wojciechowski Wykład opracowany na podstawie Komputerowa analiza i przetwarzanie obrazów R. Tadeusiewicz, P. Korohoda Filtry nieliniowe Filtry nieliniowe (kombinowane)
Podstawy Informatyki Wykład V
 Nie wytaczaj armaty by zabić komara Podstawy Informatyki Wykład V Grafika rastrowa Paint Copyright by Arkadiusz Rzucidło 1 Wprowadzenie - grafika rastrowa Grafika komputerowa tworzenie i przetwarzanie
Nie wytaczaj armaty by zabić komara Podstawy Informatyki Wykład V Grafika rastrowa Paint Copyright by Arkadiusz Rzucidło 1 Wprowadzenie - grafika rastrowa Grafika komputerowa tworzenie i przetwarzanie
Zadania domowe. Ćwiczenie 2. Rysowanie obiektów 2-D przy pomocy tworów pierwotnych biblioteki graficznej OpenGL
 Zadania domowe Ćwiczenie 2 Rysowanie obiektów 2-D przy pomocy tworów pierwotnych biblioteki graficznej OpenGL Zadanie 2.1 Fraktal plazmowy (Plasma fractal) Kwadrat należy pokryć prostokątną siatką 2 n
Zadania domowe Ćwiczenie 2 Rysowanie obiektów 2-D przy pomocy tworów pierwotnych biblioteki graficznej OpenGL Zadanie 2.1 Fraktal plazmowy (Plasma fractal) Kwadrat należy pokryć prostokątną siatką 2 n
Grafika komputerowa. Dla DSI II
 Grafika komputerowa Dla DSI II Rodzaje grafiki Tradycyjny podział grafiki oznacza wyróżnienie jej dwóch rodzajów: grafiki rastrowej oraz wektorowej. Różnica pomiędzy nimi polega na innej interpretacji
Grafika komputerowa Dla DSI II Rodzaje grafiki Tradycyjny podział grafiki oznacza wyróżnienie jej dwóch rodzajów: grafiki rastrowej oraz wektorowej. Różnica pomiędzy nimi polega na innej interpretacji
Wybrane aspekty teorii grafiki komputerowej - dążenie do wizualnego realizmu. Mirosław Głowacki
 Wybrane aspekty teorii grafiki komputerowej - dążenie do wizualnego realizmu Mirosław Głowacki Zagadnienia Jak rozumiemy fotorealizm w grafice komputerowej Historyczny rozwój kart graficznych Przekształcenia
Wybrane aspekty teorii grafiki komputerowej - dążenie do wizualnego realizmu Mirosław Głowacki Zagadnienia Jak rozumiemy fotorealizm w grafice komputerowej Historyczny rozwój kart graficznych Przekształcenia
Wybrane aspekty teorii grafiki komputerowej - dążenie do wizualnego realizmu. Mirosław Głowacki
 Wybrane aspekty teorii grafiki komputerowej - dążenie do wizualnego realizmu Mirosław Głowacki Obraz realistyczny Pojęcie obrazu realistycznego jest rozumiane w różny sposób Nie zawsze obraz realistyczny
Wybrane aspekty teorii grafiki komputerowej - dążenie do wizualnego realizmu Mirosław Głowacki Obraz realistyczny Pojęcie obrazu realistycznego jest rozumiane w różny sposób Nie zawsze obraz realistyczny
GRK 5. dr Wojciech Palubicki
 GRK 5 dr Wojciech Palubicki Uproszczony Potok Graficzny (Rendering) Model Matrix View Matrix Projection Matrix Viewport Transform Object Space World Space View Space Clip Space Screen Space Projection
GRK 5 dr Wojciech Palubicki Uproszczony Potok Graficzny (Rendering) Model Matrix View Matrix Projection Matrix Viewport Transform Object Space World Space View Space Clip Space Screen Space Projection
Transformacja współrzędnych geodezyjnych mapy w programie GEOPLAN
 Transformacja współrzędnych geodezyjnych mapy w programie GEOPLAN Program GEOPLAN umożliwia zmianę układu współrzędnych geodezyjnych mapy. Można tego dokonać przy udziale oprogramowania przeliczającego
Transformacja współrzędnych geodezyjnych mapy w programie GEOPLAN Program GEOPLAN umożliwia zmianę układu współrzędnych geodezyjnych mapy. Można tego dokonać przy udziale oprogramowania przeliczającego
Spośród licznych filtrów nieliniowych najlepszymi właściwościami odznacza się filtr medianowy prosty i skuteczny.
 Filtracja nieliniowa może być bardzo skuteczną metodą polepszania jakości obrazów Filtry nieliniowe Filtr medianowy Spośród licznych filtrów nieliniowych najlepszymi właściwościami odznacza się filtr medianowy
Filtracja nieliniowa może być bardzo skuteczną metodą polepszania jakości obrazów Filtry nieliniowe Filtr medianowy Spośród licznych filtrów nieliniowych najlepszymi właściwościami odznacza się filtr medianowy
FORMATY PLIKÓW GRAFICZNYCH
 FORMATY PLIKÓW GRAFICZNYCH Różnice między nimi. Ich wady i zalety. Marta Łukasik Plan prezentacji Formaty plików graficznych Grafika wektorowa Grafika rastrowa GIF PNG JPG SAV FORMATY PLIKÓW GRAFICZNYCH
FORMATY PLIKÓW GRAFICZNYCH Różnice między nimi. Ich wady i zalety. Marta Łukasik Plan prezentacji Formaty plików graficznych Grafika wektorowa Grafika rastrowa GIF PNG JPG SAV FORMATY PLIKÓW GRAFICZNYCH
Wprowadzenie do rysowania w 3D. Praca w środowisku 3D
 Wprowadzenie do rysowania w 3D 13 Praca w środowisku 3D Pierwszym krokiem niezbędnym do rozpoczęcia pracy w środowisku 3D programu AutoCad 2010 jest wybór odpowiedniego obszaru roboczego. Można tego dokonać
Wprowadzenie do rysowania w 3D 13 Praca w środowisku 3D Pierwszym krokiem niezbędnym do rozpoczęcia pracy w środowisku 3D programu AutoCad 2010 jest wybór odpowiedniego obszaru roboczego. Można tego dokonać
Zadanie 1. Ściana. 1. Potrzebne zmienne w dołączonym do zadania kodzie źródłowym
 Zadanie 1. Ściana Zadanie W pliku walls.cpp znajduje się funkcja void draw_back_wall(). Należy uzupełnić ją, ustawiając odpowiednio parametry teksturowania tak, aby na ścianę, która w pierwotnej wersji
Zadanie 1. Ściana Zadanie W pliku walls.cpp znajduje się funkcja void draw_back_wall(). Należy uzupełnić ją, ustawiając odpowiednio parametry teksturowania tak, aby na ścianę, która w pierwotnej wersji
Grafika 2D. Animacja Zmiany Kształtu. opracowanie: Jacek Kęsik
 Grafika 2D Animacja Zmiany Kształtu opracowanie: Jacek Kęsik Wykład przedstawia podstawy animacji zmiany kształtu - morfingu Animacja zmiany kształtu Podstawowe pojęcia Zlewanie (Dissolving / cross-dissolving)
Grafika 2D Animacja Zmiany Kształtu opracowanie: Jacek Kęsik Wykład przedstawia podstawy animacji zmiany kształtu - morfingu Animacja zmiany kształtu Podstawowe pojęcia Zlewanie (Dissolving / cross-dissolving)
Przewodnik po soczewkach
 Przewodnik po soczewkach 1. Wchodzimy w program Corel Draw 11 następnie klikamy Plik /Nowy => Nowy Rysunek. Następnie wchodzi w Okno/Okno dokowane /Teczka podręczna/ Przeglądaj/i wybieramy plik w którym
Przewodnik po soczewkach 1. Wchodzimy w program Corel Draw 11 następnie klikamy Plik /Nowy => Nowy Rysunek. Następnie wchodzi w Okno/Okno dokowane /Teczka podręczna/ Przeglądaj/i wybieramy plik w którym
Plan wykładu. Wykład 3. Rzutowanie prostokątne, widoki, przekroje, kłady. Rzutowanie prostokątne - geneza. Rzutowanie prostokątne - geneza
 Plan wykładu Wykład 3 Rzutowanie prostokątne, widoki, przekroje, kłady 1. Rzutowanie prostokątne - geneza 2. Dwa sposoby wzajemnego położenia rzutni, obiektu i obserwatora, metoda europejska i amerykańska
Plan wykładu Wykład 3 Rzutowanie prostokątne, widoki, przekroje, kłady 1. Rzutowanie prostokątne - geneza 2. Dwa sposoby wzajemnego położenia rzutni, obiektu i obserwatora, metoda europejska i amerykańska
Grafika komputerowa i wizualizacja
 Grafika komputerowa i wizualizacja Radosław Mantiuk ( rmantiuk@wi.zut.edu.pl, p. 315 WI2) http://rmantiuk.zut.edu.pl Katedra Systemów Multimedialnych Wydział Informatyki, Zachodniopomorski Uniwersytet
Grafika komputerowa i wizualizacja Radosław Mantiuk ( rmantiuk@wi.zut.edu.pl, p. 315 WI2) http://rmantiuk.zut.edu.pl Katedra Systemów Multimedialnych Wydział Informatyki, Zachodniopomorski Uniwersytet
Metody numeryczne Technika obliczeniowa i symulacyjna Sem. 2, EiT, 2014/2015
 Metody numeryczne Technika obliczeniowa i symulacyjna Sem. 2, EiT, 2014/2015 1 Metody numeryczne Dział matematyki Metody rozwiązywania problemów matematycznych za pomocą operacji na liczbach. Otrzymywane
Metody numeryczne Technika obliczeniowa i symulacyjna Sem. 2, EiT, 2014/2015 1 Metody numeryczne Dział matematyki Metody rozwiązywania problemów matematycznych za pomocą operacji na liczbach. Otrzymywane
Modelowanie i wstęp do druku 3D Wykład 1. Robert Banasiak
 Modelowanie i wstęp do druku 3D Wykład 1 Robert Banasiak Od modelu 3D do wydruku 3D Typowa droga...czasem wyboista... Pomysł!! Modeler 3D Przygotowanie modelu do druku Konfiguracja Programu do drukowania
Modelowanie i wstęp do druku 3D Wykład 1 Robert Banasiak Od modelu 3D do wydruku 3D Typowa droga...czasem wyboista... Pomysł!! Modeler 3D Przygotowanie modelu do druku Konfiguracja Programu do drukowania
Parametryzacja obrazu na potrzeby algorytmów decyzyjnych
 Parametryzacja obrazu na potrzeby algorytmów decyzyjnych Piotr Dalka Wprowadzenie Z reguły nie stosuje się podawania na wejście algorytmów decyzyjnych bezpośrednio wartości pikseli obrazu Obraz jest przekształcany
Parametryzacja obrazu na potrzeby algorytmów decyzyjnych Piotr Dalka Wprowadzenie Z reguły nie stosuje się podawania na wejście algorytmów decyzyjnych bezpośrednio wartości pikseli obrazu Obraz jest przekształcany
1. Podstawowe algorytmy techniki rastrowe a) dwa przecinające się odcinki mogą nie mieć wspólnego piksela (T) b) odcinek o współrzędnych końcowych
 1. Podstawowe algorytmy techniki rastrowe a) dwa przecinające się odcinki mogą nie mieć wspólnego piksela (T) b) odcinek o współrzędnych końcowych (2,0), (5,6) narysowany przy wykorzystaniu algorytmu Bresenhama
1. Podstawowe algorytmy techniki rastrowe a) dwa przecinające się odcinki mogą nie mieć wspólnego piksela (T) b) odcinek o współrzędnych końcowych (2,0), (5,6) narysowany przy wykorzystaniu algorytmu Bresenhama
TECHNIKI MULTIMEDIALNE LABORATORIUM GIMP: Projektowanie tła
 TECHNIKI MULTIMEDIALNE LABORATORIUM GIMP: Projektowanie tła 1. Cel ćwiczenia Celem ćwiczenia jest nabycie umiejętności tworzenia tła poprzez wykorzystanie funkcji dostępnych w programie GIMP. 2. Wiadomości
TECHNIKI MULTIMEDIALNE LABORATORIUM GIMP: Projektowanie tła 1. Cel ćwiczenia Celem ćwiczenia jest nabycie umiejętności tworzenia tła poprzez wykorzystanie funkcji dostępnych w programie GIMP. 2. Wiadomości
Implementacja sieci neuronowych na karcie graficznej. Waldemar Pawlaszek
 Implementacja sieci neuronowych na karcie graficznej Waldemar Pawlaszek Motywacja Czyli po co to wszystko? Motywacja Procesor graficzny GPU (Graphics Processing Unit) Wydajność Elastyczność i precyzja
Implementacja sieci neuronowych na karcie graficznej Waldemar Pawlaszek Motywacja Czyli po co to wszystko? Motywacja Procesor graficzny GPU (Graphics Processing Unit) Wydajność Elastyczność i precyzja
Ćwiczenia nr 7. TEMATYKA: Krzywe Bézier a
 TEMATYKA: Krzywe Bézier a Ćwiczenia nr 7 DEFINICJE: Interpolacja: przybliżanie funkcji za pomocą innej funkcji, zwykle wielomianu, tak aby były sobie równe w zadanych punktach. Poniżej przykład interpolacji
TEMATYKA: Krzywe Bézier a Ćwiczenia nr 7 DEFINICJE: Interpolacja: przybliżanie funkcji za pomocą innej funkcji, zwykle wielomianu, tak aby były sobie równe w zadanych punktach. Poniżej przykład interpolacji
Podstawy OpenCL część 2
 Podstawy OpenCL część 2 1. Napisz program dokonujący mnożenia dwóch macierzy w wersji sekwencyjnej oraz OpenCL. Porównaj czasy działania obu wersji dla różnych wielkości macierzy, np. 16 16, 128 128, 1024
Podstawy OpenCL część 2 1. Napisz program dokonujący mnożenia dwóch macierzy w wersji sekwencyjnej oraz OpenCL. Porównaj czasy działania obu wersji dla różnych wielkości macierzy, np. 16 16, 128 128, 1024
Wydajność systemów a organizacja pamięci, czyli dlaczego jednak nie jest aż tak źle. Krzysztof Banaś, Obliczenia wysokiej wydajności.
 Wydajność systemów a organizacja pamięci, czyli dlaczego jednak nie jest aż tak źle Krzysztof Banaś, Obliczenia wysokiej wydajności. 1 Organizacja pamięci Organizacja pamięci współczesnych systemów komputerowych
Wydajność systemów a organizacja pamięci, czyli dlaczego jednak nie jest aż tak źle Krzysztof Banaś, Obliczenia wysokiej wydajności. 1 Organizacja pamięci Organizacja pamięci współczesnych systemów komputerowych
Waldemar Izdebski - Wykłady z przedmiotu SIT / Mapa zasadnicza 30
 Waldemar Izdebski - Wykłady z przedmiotu SIT / Mapa zasadnicza 30 2.3. Model rastrowy Rastrowy model danych wykorzystywany jest dla gromadzenia i przetwarzania danych pochodzących ze skanowania istniejących
Waldemar Izdebski - Wykłady z przedmiotu SIT / Mapa zasadnicza 30 2.3. Model rastrowy Rastrowy model danych wykorzystywany jest dla gromadzenia i przetwarzania danych pochodzących ze skanowania istniejących
Obraz jako funkcja Przekształcenia geometryczne
 Cyfrowe przetwarzanie obrazów I Obraz jako funkcja Przekształcenia geometryczne dr. inż Robert Kazała Definicja obrazu Obraz dwuwymiarowa funkcja intensywności światła f(x,y); wartość f w przestrzennych
Cyfrowe przetwarzanie obrazów I Obraz jako funkcja Przekształcenia geometryczne dr. inż Robert Kazała Definicja obrazu Obraz dwuwymiarowa funkcja intensywności światła f(x,y); wartość f w przestrzennych
GRAFIKA KOMPUTEROWA. Plan wykładu. 1. Początki grafiki komputerowej. 2. Grafika komputerowa a dziedziny pokrewne. 3. Omówienie programu przedmiotu
 GRAFIKA KOMPUTEROWA 1. Układ przedmiotu semestr VI - 20000 semestr VII - 00200 Dr inż. Jacek Jarnicki Instytut Cybernetyki Technicznej p. 226 C-C 3, tel. 320-28-2323 jacek@ict.pwr.wroc.pl www.zsk.ict.pwr.wroc.pl
GRAFIKA KOMPUTEROWA 1. Układ przedmiotu semestr VI - 20000 semestr VII - 00200 Dr inż. Jacek Jarnicki Instytut Cybernetyki Technicznej p. 226 C-C 3, tel. 320-28-2323 jacek@ict.pwr.wroc.pl www.zsk.ict.pwr.wroc.pl
Technologie Informacyjne
 Grafika komputerowa Szkoła Główna Służby Pożarniczej Zakład Informatyki i Łączności December 12, 2016 1 Wprowadzenie 2 Optyka 3 Geometria 4 Grafika rastrowa i wektorowa 5 Kompresja danych Wprowadzenie
Grafika komputerowa Szkoła Główna Służby Pożarniczej Zakład Informatyki i Łączności December 12, 2016 1 Wprowadzenie 2 Optyka 3 Geometria 4 Grafika rastrowa i wektorowa 5 Kompresja danych Wprowadzenie
Zamiana reprezentacji wektorowej na rastrową - rasteryzacja
 MODEL RASTROWY Siatka kwadratów lub prostokątów stanowi elementy rastra. Piksel - pojedynczy element jest najmniejszą rozróŝnialną jednostką powierzchniową, której własności są opisane atrybutami. Model
MODEL RASTROWY Siatka kwadratów lub prostokątów stanowi elementy rastra. Piksel - pojedynczy element jest najmniejszą rozróŝnialną jednostką powierzchniową, której własności są opisane atrybutami. Model
GRK 5. dr Wojciech Palubicki
 GRK 5 dr Wojciech Palubicki Projekty (dwu-osobowe) Napisać symulacje lotu kosmicznego w OpenGLu: Korzystając tylko z bibliotek które na ćwiczeniach zostały omówione Interaktywna symulacja Wszystkie wielokąty
GRK 5 dr Wojciech Palubicki Projekty (dwu-osobowe) Napisać symulacje lotu kosmicznego w OpenGLu: Korzystając tylko z bibliotek które na ćwiczeniach zostały omówione Interaktywna symulacja Wszystkie wielokąty
Rozpoznawanie obrazów na przykładzie rozpoznawania twarzy
 Rozpoznawanie obrazów na przykładzie rozpoznawania twarzy Wykorzystane materiały: Zadanie W dalszej części prezentacji będzie omawiane zagadnienie rozpoznawania twarzy Problem ten można jednak uogólnić
Rozpoznawanie obrazów na przykładzie rozpoznawania twarzy Wykorzystane materiały: Zadanie W dalszej części prezentacji będzie omawiane zagadnienie rozpoznawania twarzy Problem ten można jednak uogólnić
Aproksymacja funkcji a regresja symboliczna
 Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(x), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(x), zwaną funkcją aproksymującą
Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(x), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(x), zwaną funkcją aproksymującą
Wybrane aspekty teorii grafiki komputerowej - dążenie do wizualnego realizmu. Mirosław Głowacki
 Wybrane aspekty teorii grafiki komputerowej - dążenie do wizualnego realizmu Mirosław Głowacki Zagadnienia Jak rozumiemy fotorealizm w grafice komputerowej Historyczny rozwój kart graficznych Przekształcenia
Wybrane aspekty teorii grafiki komputerowej - dążenie do wizualnego realizmu Mirosław Głowacki Zagadnienia Jak rozumiemy fotorealizm w grafice komputerowej Historyczny rozwój kart graficznych Przekształcenia
Temat: Zaprojektowanie procesu kontroli jakości wymiarów geometrycznych na przykładzie obudowy.
 Raport z przeprowadzonych pomiarów. Temat: Zaprojektowanie procesu kontroli jakości wymiarów geometrycznych na przykładzie obudowy. Spis treści 1.Cel pomiaru... 3 2. Skanowanie 3D- pozyskanie geometrii
Raport z przeprowadzonych pomiarów. Temat: Zaprojektowanie procesu kontroli jakości wymiarów geometrycznych na przykładzie obudowy. Spis treści 1.Cel pomiaru... 3 2. Skanowanie 3D- pozyskanie geometrii
str 1 WYMAGANIA EDUKACYJNE ( ) - matematyka - poziom podstawowy Dariusz Drabczyk
 str 1 WYMAGANIA EDUKACYJNE (2017-2018) - matematyka - poziom podstawowy Dariusz Drabczyk Klasa 3e: wpisy oznaczone jako: (T) TRYGONOMETRIA, (PII) PLANIMETRIA II, (RP) RACHUNEK PRAWDOPODOBIEŃSTWA, (ST)
str 1 WYMAGANIA EDUKACYJNE (2017-2018) - matematyka - poziom podstawowy Dariusz Drabczyk Klasa 3e: wpisy oznaczone jako: (T) TRYGONOMETRIA, (PII) PLANIMETRIA II, (RP) RACHUNEK PRAWDOPODOBIEŃSTWA, (ST)
Podstawy grafiki komputerowej
 Podstawy grafiki komputerowej Krzysztof Gracki K.Gracki@ii.pw.edu.pl tel. (22) 6605031 Instytut Informatyki Politechniki Warszawskiej 2 Sprawy organizacyjne Krzysztof Gracki k.gracki@ii.pw.edu.pl tel.
Podstawy grafiki komputerowej Krzysztof Gracki K.Gracki@ii.pw.edu.pl tel. (22) 6605031 Instytut Informatyki Politechniki Warszawskiej 2 Sprawy organizacyjne Krzysztof Gracki k.gracki@ii.pw.edu.pl tel.
Maskowanie i selekcja
 Maskowanie i selekcja Maska prostokątna Grafika bitmapowa - Corel PHOTO-PAINT Pozwala definiować prostokątne obszary edytowalne. Kiedy chcemy wykonać operacje nie na całym obrazku, lecz na jego części,
Maskowanie i selekcja Maska prostokątna Grafika bitmapowa - Corel PHOTO-PAINT Pozwala definiować prostokątne obszary edytowalne. Kiedy chcemy wykonać operacje nie na całym obrazku, lecz na jego części,
Chocofur szkolenie średniozaawansowane
 Chocofur szkolenie średniozaawansowane Lech Sokołowski CHOCOFUR.COM Poniższe opracowanie stanowi esencję wiedzy przekazywanej na szkoleniu. Jest to zbiór notatek zawierający najważniejsze punkty omawianych
Chocofur szkolenie średniozaawansowane Lech Sokołowski CHOCOFUR.COM Poniższe opracowanie stanowi esencję wiedzy przekazywanej na szkoleniu. Jest to zbiór notatek zawierający najważniejsze punkty omawianych
Antyaliasing w 1 milisekundę. Krzysztof Kluczek
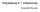 Antyaliasing w 1 milisekundę Krzysztof Kluczek Zasada działania Założenia: Metoda bazująca na Morphological Antialiasing (MLAA) wejście: obraz wyrenderowanej sceny wyjście: zantyaliasowany obraz Krótki
Antyaliasing w 1 milisekundę Krzysztof Kluczek Zasada działania Założenia: Metoda bazująca na Morphological Antialiasing (MLAA) wejście: obraz wyrenderowanej sceny wyjście: zantyaliasowany obraz Krótki
Grafika Komputerowa Wykład 1. Wstęp do grafiki komputerowej Obraz rastrowy i wektorowy. mgr inż. Michał Chwesiuk 1/22
 Wykład 1 Wstęp do grafiki komputerowej rastrowy i wektorowy mgr inż. 1/22 O mnie mgr inż. michalchwesiuk@gmail.com http://mchwesiuk.pl Materiały, wykłady, informacje Doktorant na Wydziale Informatyki Uniwersytetu
Wykład 1 Wstęp do grafiki komputerowej rastrowy i wektorowy mgr inż. 1/22 O mnie mgr inż. michalchwesiuk@gmail.com http://mchwesiuk.pl Materiały, wykłady, informacje Doktorant na Wydziale Informatyki Uniwersytetu
IX. Rachunek różniczkowy funkcji wielu zmiennych. 1. Funkcja dwóch i trzech zmiennych - pojęcia podstawowe. - funkcja dwóch zmiennych,
 IX. Rachunek różniczkowy funkcji wielu zmiennych. 1. Funkcja dwóch i trzech zmiennych - pojęcia podstawowe. Definicja 1.1. Niech D będzie podzbiorem przestrzeni R n, n 2. Odwzorowanie f : D R nazywamy
IX. Rachunek różniczkowy funkcji wielu zmiennych. 1. Funkcja dwóch i trzech zmiennych - pojęcia podstawowe. Definicja 1.1. Niech D będzie podzbiorem przestrzeni R n, n 2. Odwzorowanie f : D R nazywamy
Podstawy grafiki komputerowej. Teoria obrazu.
 WAŻNE POJĘCIA GRAFIKA KOMPUTEROWA - to dział informatyki zajmujący się wykorzystaniem oprogramowania komputerowego do tworzenia, przekształcania i prezentowania obrazów rzeczywistych i wyimaginowanych.
WAŻNE POJĘCIA GRAFIKA KOMPUTEROWA - to dział informatyki zajmujący się wykorzystaniem oprogramowania komputerowego do tworzenia, przekształcania i prezentowania obrazów rzeczywistych i wyimaginowanych.
RENDERING W CZASIE RZECZYWISTYM. Michał Radziszewski
 RENDERING W CZASIE RZECZYWISTYM Michał Radziszewski Plan wykładu Programy geometrii wprowadzenie Miejsce w potoku graficznym Wejścia i wyjścia programów geometrii Wierzchołki, prymitywy, ich nowe rodzaje
RENDERING W CZASIE RZECZYWISTYM Michał Radziszewski Plan wykładu Programy geometrii wprowadzenie Miejsce w potoku graficznym Wejścia i wyjścia programów geometrii Wierzchołki, prymitywy, ich nowe rodzaje
Grafika Komputerowa Wybrane definicje. Katedra Informatyki i Metod Komputerowych Uniwersytet Pedagogiczny im. KEN w Krakowie apw@up.krakow.
 Grafika Komputerowa Wybrane definicje Katedra Informatyki i Metod Komputerowych Uniwersytet Pedagogiczny im. KEN w Krakowie apw@up.krakow.pl Spis pojęć Grafika komputerowa Grafika wektorowa Grafika rastrowa
Grafika Komputerowa Wybrane definicje Katedra Informatyki i Metod Komputerowych Uniwersytet Pedagogiczny im. KEN w Krakowie apw@up.krakow.pl Spis pojęć Grafika komputerowa Grafika wektorowa Grafika rastrowa
Wykład z Technologii Informacyjnych. Piotr Mika
 Wykład z Technologii Informacyjnych Piotr Mika Uniwersalna forma graficznego zapisu algorytmów Schemat blokowy zbiór bloków, powiązanych ze sobą liniami zorientowanymi. Jest to rodzaj grafu, którego węzły
Wykład z Technologii Informacyjnych Piotr Mika Uniwersalna forma graficznego zapisu algorytmów Schemat blokowy zbiór bloków, powiązanych ze sobą liniami zorientowanymi. Jest to rodzaj grafu, którego węzły
GRK 4. dr Wojciech Palubicki
 GRK 4 dr Wojciech Palubicki Uproszczony Potok Graficzny (Rendering) Model Matrix View Matrix Projection Matrix Viewport Transform Object Space World Space View Space Clip Space Screen Space Projection
GRK 4 dr Wojciech Palubicki Uproszczony Potok Graficzny (Rendering) Model Matrix View Matrix Projection Matrix Viewport Transform Object Space World Space View Space Clip Space Screen Space Projection
Przekształcanie wykresów.
 Sławomir Jemielity Przekształcanie wykresów. Pokażemy tu, jak zmiana we wzorze funkcji wpływa na wygląd jej wykresu. A. Mamy wykres funkcji f(). Jak będzie wyglądał wykres f ( ) + a, a stała? ( ) f ( )
Sławomir Jemielity Przekształcanie wykresów. Pokażemy tu, jak zmiana we wzorze funkcji wpływa na wygląd jej wykresu. A. Mamy wykres funkcji f(). Jak będzie wyglądał wykres f ( ) + a, a stała? ( ) f ( )
Ustawienia materiałów i tekstur w programie KD Max. MTPARTNER S.C.
 Ustawienia materiałów i tekstur w programie KD Max. 1. Dwa tryby własności materiału Materiał możemy ustawić w dwóch trybach: czysty kolor tekstura 2 2. Podstawowe parametry materiału 2.1 Większość właściwości
Ustawienia materiałów i tekstur w programie KD Max. 1. Dwa tryby własności materiału Materiał możemy ustawić w dwóch trybach: czysty kolor tekstura 2 2. Podstawowe parametry materiału 2.1 Większość właściwości
1 LEKCJA. Definicja grafiki. Główne działy grafiki komputerowej. Programy graficzne: Grafika rastrowa. Grafika wektorowa. Grafika trójwymiarowa
 1 LEKCJA Definicja grafiki Dział informatyki zajmujący się wykorzystaniem komputerów do generowania i przetwarzania obrazów (statycznych i dynamicznych) oraz wizualizacją danych. Główne działy grafiki
1 LEKCJA Definicja grafiki Dział informatyki zajmujący się wykorzystaniem komputerów do generowania i przetwarzania obrazów (statycznych i dynamicznych) oraz wizualizacją danych. Główne działy grafiki
Diagnostyka obrazowa
 Diagnostyka obrazowa Ćwiczenie drugie Podstawowe przekształcenia obrazu 1 Cel ćwiczenia Ćwiczenie ma na celu zapoznanie uczestników kursu Diagnostyka obrazowa z podstawowymi przekształceniami obrazu wykonywanymi
Diagnostyka obrazowa Ćwiczenie drugie Podstawowe przekształcenia obrazu 1 Cel ćwiczenia Ćwiczenie ma na celu zapoznanie uczestników kursu Diagnostyka obrazowa z podstawowymi przekształceniami obrazu wykonywanymi
Maciej Piotr Jankowski
 Reduced Adder Graph Implementacja algorytmu RAG Maciej Piotr Jankowski 2005.12.22 Maciej Piotr Jankowski 1 Plan prezentacji 1. Wstęp 2. Implementacja 3. Usprawnienia optymalizacyjne 3.1. Tablica ekspansji
Reduced Adder Graph Implementacja algorytmu RAG Maciej Piotr Jankowski 2005.12.22 Maciej Piotr Jankowski 1 Plan prezentacji 1. Wstęp 2. Implementacja 3. Usprawnienia optymalizacyjne 3.1. Tablica ekspansji
Implementacja filtru Canny ego
 ANALIZA I PRZETWARZANIE OBRAZÓW Implementacja filtru Canny ego Autor: Katarzyna Piotrowicz Kraków,2015-06-11 Spis treści 1. Wstęp... 1 2. Implementacja... 2 3. Przykłady... 3 Porównanie wykrytych krawędzi
ANALIZA I PRZETWARZANIE OBRAZÓW Implementacja filtru Canny ego Autor: Katarzyna Piotrowicz Kraków,2015-06-11 Spis treści 1. Wstęp... 1 2. Implementacja... 2 3. Przykłady... 3 Porównanie wykrytych krawędzi
Programowanie Procesorów Graficznych
 Programowanie Procesorów Graficznych Wykład 1 9.10.2012 Prehistoria Zadaniem karty graficznej było sterowanie sygnałem do monitora tak aby wyświetlić obraz zgodnie z zawartościa pamięci. Programiści pracowali
Programowanie Procesorów Graficznych Wykład 1 9.10.2012 Prehistoria Zadaniem karty graficznej było sterowanie sygnałem do monitora tak aby wyświetlić obraz zgodnie z zawartościa pamięci. Programiści pracowali
Gry komputerowe: efekty specjalne cz. 2
 1/43 Gry komputerowe: efekty specjalne cz. 2 Przygotowała: Anna Tomaszewska 2/43 Mapowanie środowiska - definicja aproksymacje odbić na powierzchnie prosto- i krzywoliniowej," oświetlanie sceny." obserwator
1/43 Gry komputerowe: efekty specjalne cz. 2 Przygotowała: Anna Tomaszewska 2/43 Mapowanie środowiska - definicja aproksymacje odbić na powierzchnie prosto- i krzywoliniowej," oświetlanie sceny." obserwator
Transformacje obiektów 3D
 Synteza i obróbka obrazu Transformacje obiektów 3D Opracowanie: dr inż. Grzegorz Szwoch Politechnika Gdańska Katedra Systemów Multimedialnych Lokalny układ współrzędnych Tworząc model obiektu, zapisujemy
Synteza i obróbka obrazu Transformacje obiektów 3D Opracowanie: dr inż. Grzegorz Szwoch Politechnika Gdańska Katedra Systemów Multimedialnych Lokalny układ współrzędnych Tworząc model obiektu, zapisujemy
Algorytmy zrandomizowane
 Algorytmy zrandomizowane http://zajecia.jakubw.pl/nai ALGORYTMY ZRANDOMIZOWANE Algorytmy, których działanie uzależnione jest od czynników losowych. Algorytmy typu Monte Carlo: dają (po pewnym czasie) wynik
Algorytmy zrandomizowane http://zajecia.jakubw.pl/nai ALGORYTMY ZRANDOMIZOWANE Algorytmy, których działanie uzależnione jest od czynników losowych. Algorytmy typu Monte Carlo: dają (po pewnym czasie) wynik
Ćwiczenie 1 Automatyczna animacja ruchu
 Automatyczna animacja ruchu Celem ćwiczenia jest poznanie procesu tworzenia automatycznej animacji ruchu, która jest podstawą większości projektów we Flashu. Ze względu na swoją wszechstronność omawiana
Automatyczna animacja ruchu Celem ćwiczenia jest poznanie procesu tworzenia automatycznej animacji ruchu, która jest podstawą większości projektów we Flashu. Ze względu na swoją wszechstronność omawiana
Ćwiczenie 4 - Podstawy materiałów i tekstur. Renderowanie obrazu i animacji
 Ćwiczenie 4 - Podstawy materiałów i tekstur. Renderowanie obrazu i animacji Materiał jest zbiorem informacji o właściwościach powierzchni. Składa się na niego kolor, sposób odbijania światła i sposób nakładania
Ćwiczenie 4 - Podstawy materiałów i tekstur. Renderowanie obrazu i animacji Materiał jest zbiorem informacji o właściwościach powierzchni. Składa się na niego kolor, sposób odbijania światła i sposób nakładania
Politechnika Świętokrzyska. Laboratorium. Cyfrowe przetwarzanie sygnałów. Ćwiczenie 8. Filtracja uśredniająca i statystyczna.
 Politechnika Świętokrzyska Laboratorium Cyfrowe przetwarzanie sygnałów Ćwiczenie 8 Filtracja uśredniająca i statystyczna. Cel ćwiczenia Celem ćwiczenia jest zdobycie umiejętności tworzenia i wykorzystywania
Politechnika Świętokrzyska Laboratorium Cyfrowe przetwarzanie sygnałów Ćwiczenie 8 Filtracja uśredniająca i statystyczna. Cel ćwiczenia Celem ćwiczenia jest zdobycie umiejętności tworzenia i wykorzystywania
SYSTEMY OPERACYJNE I SIECI KOMPUTEROWE
 SYSTEMY OPERACYJNE I SIECI KOMPUTEROWE WINDOWS 1 SO i SK/WIN 006 Wydajność systemu 2 SO i SK/WIN Najprostszym sposobem na poprawienie wydajności systemu, jeżeli dysponujemy zbyt małą ilością pamięci RAM
SYSTEMY OPERACYJNE I SIECI KOMPUTEROWE WINDOWS 1 SO i SK/WIN 006 Wydajność systemu 2 SO i SK/WIN Najprostszym sposobem na poprawienie wydajności systemu, jeżeli dysponujemy zbyt małą ilością pamięci RAM
Obrót wokół początku układu współrzędnych o kąt φ można wyrazić w postaci macierzowej następująco
 Transformacje na płaszczyźnie Przesunięcie Przesunięcie (translacja) obrazu realizowana jest przez dodanie stałej do każdej współrzędnej, co w postaci macierzowej można przedstawić równaniem y'] = [ x
Transformacje na płaszczyźnie Przesunięcie Przesunięcie (translacja) obrazu realizowana jest przez dodanie stałej do każdej współrzędnej, co w postaci macierzowej można przedstawić równaniem y'] = [ x
V Konkurs Matematyczny Politechniki Białostockiej
 V Konkurs Matematyczny Politechniki iałostockiej Rozwiązania - klasy pierwsze 27 kwietnia 2013 r. 1. ane są cztery liczby dodatnie a b c d. Wykazać że przynajmniej jedna z liczb a + b + c d b + c + d a
V Konkurs Matematyczny Politechniki iałostockiej Rozwiązania - klasy pierwsze 27 kwietnia 2013 r. 1. ane są cztery liczby dodatnie a b c d. Wykazać że przynajmniej jedna z liczb a + b + c d b + c + d a
FRAKTALE I SAMOPODOBIEŃSTWO
 FRAKTALE I SAMOPODOBIEŃSTWO Mariusz Gromada marzec 2003 mariusz.gromada@wp.pl http://multifraktal.net 1 Wstęp Fraktalem nazywamy każdy zbiór, dla którego wymiar Hausdorffa-Besicovitcha (tzw. wymiar fraktalny)
FRAKTALE I SAMOPODOBIEŃSTWO Mariusz Gromada marzec 2003 mariusz.gromada@wp.pl http://multifraktal.net 1 Wstęp Fraktalem nazywamy każdy zbiór, dla którego wymiar Hausdorffa-Besicovitcha (tzw. wymiar fraktalny)
Wykład 4. Rendering (1) Informacje podstawowe
 Wykład 4. Rendering (1) Informacje podstawowe Z punktu widzenia dzisiejszego programowania gier: Direct3D jest najczęściej wykorzystywanym przez profesjonalnych deweloperów gier API graficznym na platformie
Wykład 4. Rendering (1) Informacje podstawowe Z punktu widzenia dzisiejszego programowania gier: Direct3D jest najczęściej wykorzystywanym przez profesjonalnych deweloperów gier API graficznym na platformie
PAMIĘCI. Część 1. Przygotował: Ryszard Kijanka
 PAMIĘCI Część 1 Przygotował: Ryszard Kijanka WSTĘP Pamięci półprzewodnikowe są jednym z kluczowych elementów systemów cyfrowych. Służą do przechowywania informacji w postaci cyfrowej. Liczba informacji,
PAMIĘCI Część 1 Przygotował: Ryszard Kijanka WSTĘP Pamięci półprzewodnikowe są jednym z kluczowych elementów systemów cyfrowych. Służą do przechowywania informacji w postaci cyfrowej. Liczba informacji,
Opis postępowania przy eksportowaniu geometrii z systemu Unigraphics NX do pakietu PANUKL (ver. A)
 1 Opis postępowania przy eksportowaniu geometrii z systemu Unigraphics NX do pakietu PANUKL (ver. A) Przedstawiony poniżej schemat przygotowania geometrii w systemie Unigraphics NX na potrzeby programu
1 Opis postępowania przy eksportowaniu geometrii z systemu Unigraphics NX do pakietu PANUKL (ver. A) Przedstawiony poniżej schemat przygotowania geometrii w systemie Unigraphics NX na potrzeby programu
Jak napisać program obliczający pola powierzchni różnych figur płaskich?
 Część IX C++ Jak napisać program obliczający pola powierzchni różnych figur płaskich? Na początku, przed stworzeniem właściwego kodu programu zaprojektujemy naszą aplikację i stworzymy schemat blokowy
Część IX C++ Jak napisać program obliczający pola powierzchni różnych figur płaskich? Na początku, przed stworzeniem właściwego kodu programu zaprojektujemy naszą aplikację i stworzymy schemat blokowy
